Bài toán vận tải buf - Đê cương - Tài liệu tham khảo | Đại học Hoa Sen
Bài toán vận tải buf - Đê cương - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học.
Môn: giáo dục quốc phòng (hp1234)
Trường: Đại học Hoa Sen
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Tác giả:
Tài liệu liên quan:
Preview text:
MÔ HÌNH VẬN TẢI
(phần học mở rộng) 1 2 3 4
Giới thiệu bài toán vận tải
Bài bài toán vận tải bằng các Bài tập thực hành
Giải bài toán bằng phần mềm phương pháp 413 MỤC TIÊU CHƯƠNG
1. Hiểu được cách tìm lời giải ban đầu trong bài toán vận tải bằng
phương pháp góc tây bắc, chi phí bé nhất và xấp xỉ Vogel
2. Hiểu được cách tìm lời giải tối ưu trong bài toán vận tải bằng
phương pháp Duyệt tuần tự và Phân phối cải tiến
3. Thực hành các bài tập vận tải
4. Dùng phần mềm Excel và QM để giải bài toán vận tải 414
I. GIỚI THIỆU BÀI TOÁN VẬN TẢI 1.1. Giới thiệu chung
• Mô hình vận tải dùng trong bài toán vận tải từ các nguồn đến các đích, chẳng
như vận tải sản phẩm từ các nhà máy đến các nhà kho trong hệ thống phân phối.
• Mô hình vận tải xác định kế hoạch vận chuyển với mục tiêu cực tiểu chi phí
chuyển, đồng thời thỏa mãn các ràng buộc về các giới hạn cung ở các điểm nguồn
các giới hạn cầu ở các điểm đích.
• Mô hình vận tải còn được mở rộng ứng dụng sang các bài toán hoạch định tồn
điều độ nhân lực, phân công công việc… 415
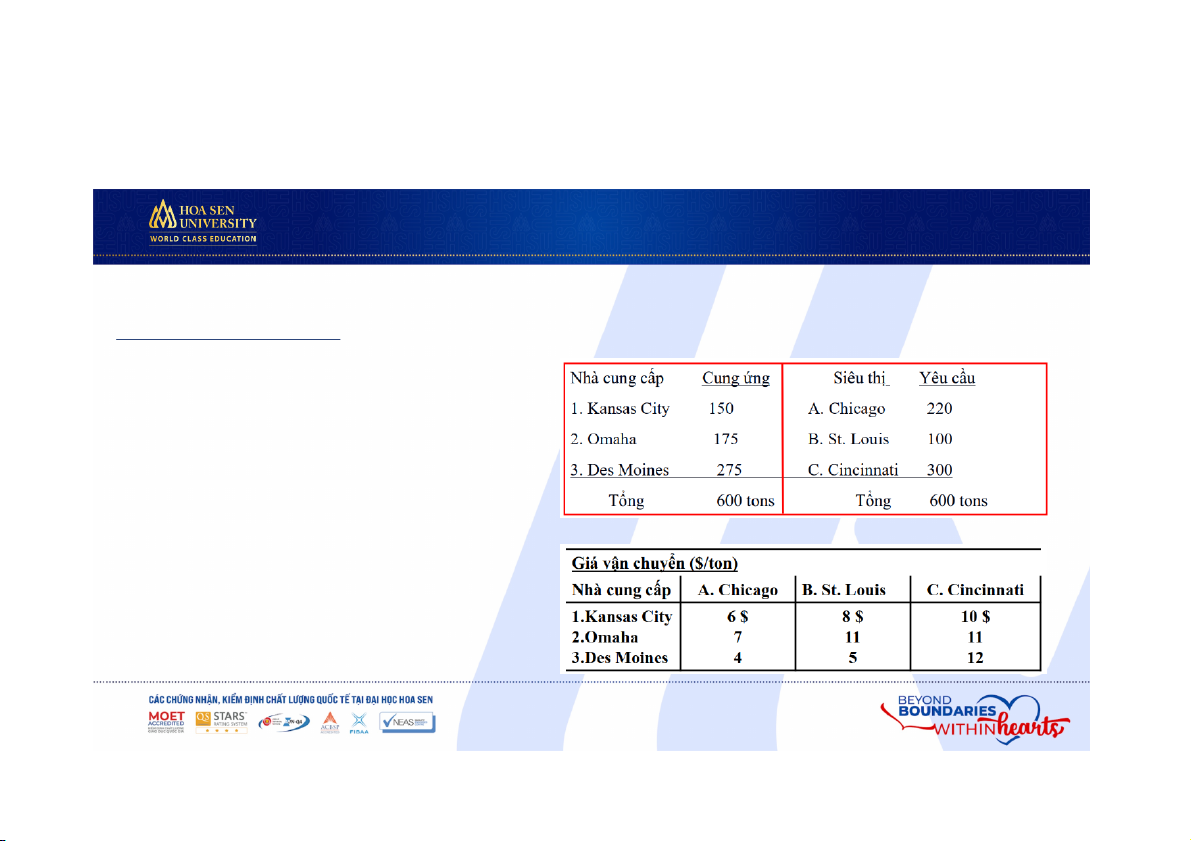
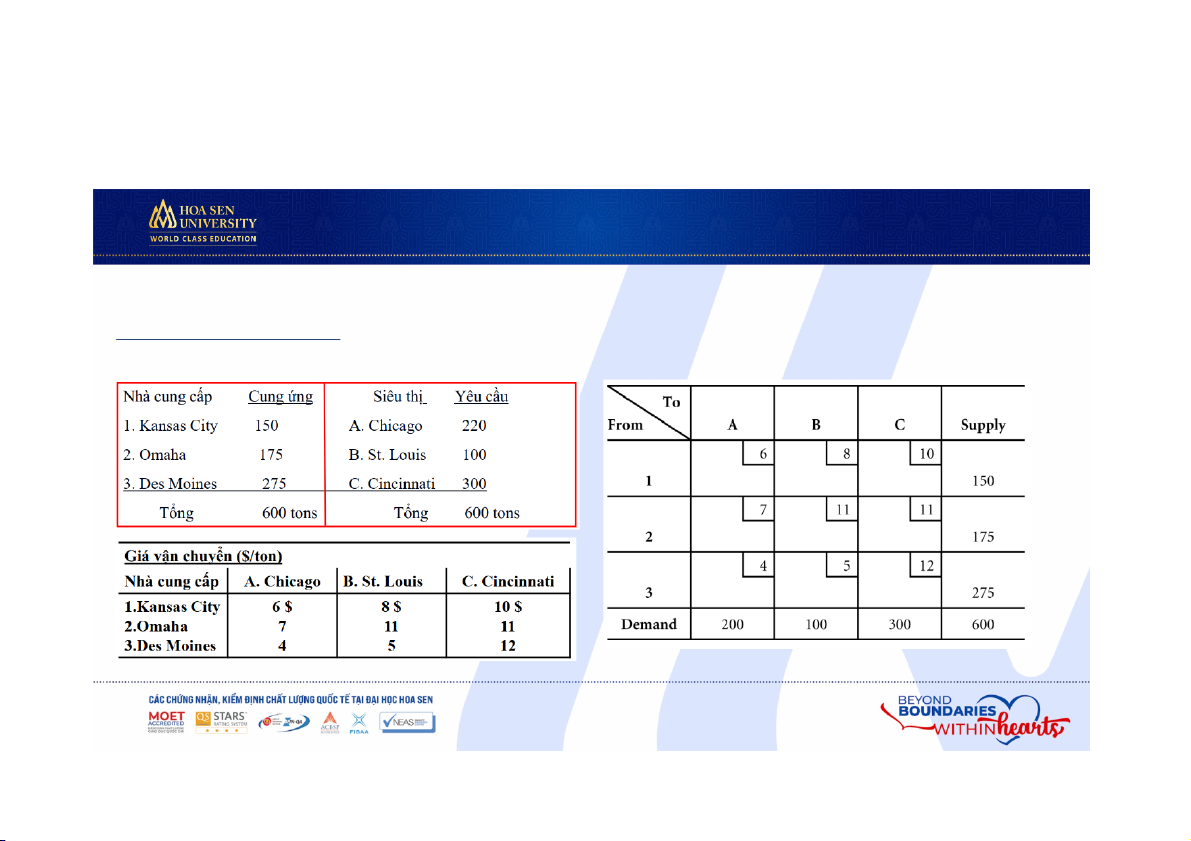
I. GIỚI THIỆU BÀI TOÁN VẬN TẢI 1.2. Bài toán ví dụ
• Với số liệu về cung ứng của nhà
cung cấp, yêu cầu của siêu thị, giá
vận chuyển cho trong bảng bên
• Bao nhiêu tấn hàng chuyển vận từ
nhà cung cấp đến hệ thống siêu
thị hàng tháng với tiêu chí cực tiểu phí vận chuyển? 416
I. GIỚI THIỆU BÀI TOÁN VẬN TẢI 1.2. Bài toán ví dụ
• Mô hình bài toán Minimize Z = 6x 1A + 8x1B + 10x1C + 7x2A + 11x2B + 11x2C + 4x 3A + 5x3B + 12x3C St: • x1A + x1B + x1C = 150 • x2A + x2B + x2C = 175 • x3A + x3B + x3C = 275 • x1A + x2A + x3A = 200 • x1B + x2B + x3B = 100 • x1C + x2C + x3C = 300 • xij ≥ 0
xij = Tấn hàng được chuyển từ nhà cung cấp i, i = 1, 2, 3, đến nhà máy j, j = A,B,C 417
I. GIỚI THIỆU BÀI TOÁN VẬN TẢI 1.2. Bài toán ví dụ 418
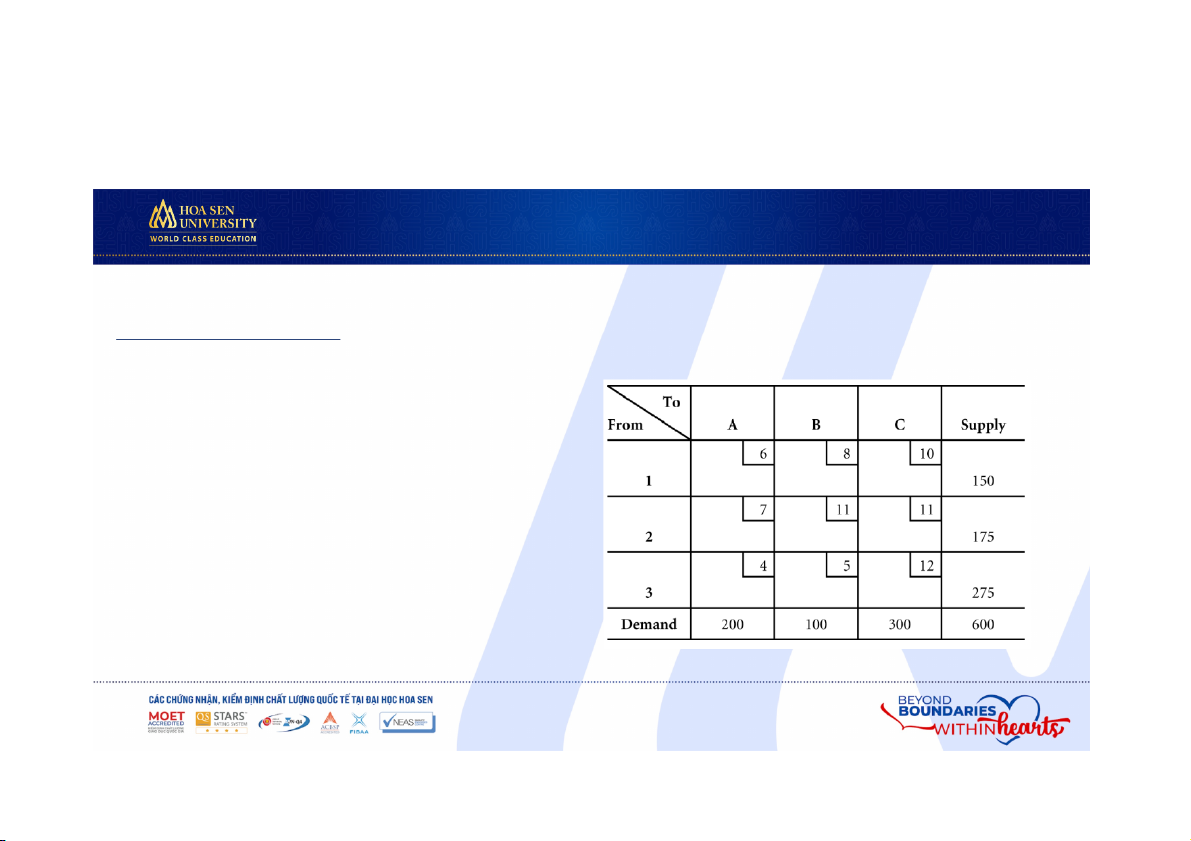
I. GIỚI THIỆU BÀI TOÁN VẬN TẢI 1.2. Bài toán ví dụ
• Mỗi ô của bảng vận tải tương tự như
biến ở bài toán tối ưu để chỉ chi phí
cho việc di chuyển từ nhà cung cấp đến đích.
• Khả năng của nhà cung cấp và yêu
cầu từ đích sẽ được ghi ở cột bên
phải và hàng cuối của bảng vận tả .i Cấu trúc bảng vận tải 419
I. GIỚI THIỆU BÀI TOÁN VẬN TẢI 1.2. Bài toán ví dụ Cấu trúc bảng vận tải 420
II. GIẢI BÀI TOÁN VẬN TẢI
2.1. Các bước giải bài toán
Bước 1: Tìm lời giải ban đầu
Phương pháp để tìm lời giải bài ban đầu
- Phương pháp góc Tây Bắc
- Phương pháp chi phí bé nhất
- Phương pháp xấp xỉ Vogel
Bước 2: Tìm lời giải tối ưu
Phương pháp để tìm lời giải tối ưu - Duyệt tuần tự - Phân phối cải tiến 421