Bảng tóm tắt công thức Toán 12

Bảng tóm tắt công thức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

18 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
BAÛNG TOÙM TAÉT COÂNG THÖÙC TOAÙN 12
COÂNG THÖÙC LUÕY THÖØA
Cho caùc soá döông
,ab
vaø
,mn
. Ta coù:
0
1a
. ...........
n
n thöøa soá
a a a a
vôùi
1
n
n
a
a
( ) ( )
m n mn n m
a a a
.
m n m n
a a a
m
mn
n
a
a
a
()
n n n
a b ab
n
n
n
aa
bb



1
2
1
3
3
n
m
n
m
aa
aa
aa


COÂNG THÖÙC LOGARIT
Cho caùc soá
, 0, 1a b a
. Ta coù:
log
a
b a b
10
lg log logb b b
ln log
e
bb
log 1 0
a
log 1
a
a
log
b
a
ab
1
log log
m
a
a
bb
m
log log
n
aa
b n b
log log
m
n
a
a
n
bb
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
bc
c




log
log log
a
bb
b
ca
ab
ac
log .log log
a b a
b c c
log
log
log
a
b
a
c
c
b
1
log
log
a
b
b
a
HAØM SOÁ LUÕY THÖØA – MUÕ – LOGARIT
HAØM LUÕY THÖØA
HAØM SOÁ MUÕ
HAØM SOÁ LOGARIT
Daïng:
yx
yu
vôùi
u
laø ña
thöùc ñaïi soá.
Taäp xaùc ñònh:
Neáu
.
ÑK
u
Neáu
0.
ÑK
u
Neáu
0.
ÑK
u
Ñaïo haøm:
1
1
.
y x y x
y u y u u





Daïng:
x
u
ya
ya
vôùi
0
.
1
a
a
Taäp xaùc ñònh:
.D
Ñaïo haøm:
ln
ln .
xx
ux
y a y a a
y a y a a u
.
Ñaëc bieät:
()
( ) .
xx
uu
ee
e e u
.
Söï bieán thieân:
x
ya
Neáu
1a
thì haøm ñoàng bieán
treân . Neáu
01a
thì
haøm nghòch bieán treân .
Daïng:
log
log
a
a
yx
yu
vôùi
0
.
1
a
a
Ñaëc bieät:
ln ;a e y x
10 log lga y x x
.
Ñieàu kieän xaùc ñònh:
0u
.
Ñaïo haøm:
1
log
ln
log
ln
a
a
y x y
xa
u
y u y
ua
.
Ñaëc bieät:
1
(ln )
(ln )
x
x
u
u
u
.
Söï bieán thieân:
log
a
yx
Neáu
1a
: haøm ñoàng bieán
treân
(0; )
. Neáu
01a
:
haøm nghòch bieán treân
(0; )
ÑOÀ THÒ HAØM MUÕ VAØ HAØM LOGARIT
ÑOÀ THÒ HAØM SOÁ MUÕ
ÑOÀ THÒ HAØM SOÁ LOGARIT
Ta thaáy:
0 1; 0 1
xx
a a b b
.
Ta thaáy:
1; 1.
xx
c c d d
So saùnh a vôùi b: Ñöùng treân cao, baén muõi teân
töø traùi sang phaûi, truùng
x
a
tröôùc neân
ab
.
So saùnh c vôùi d: Ñöùng treân cao, baén muõi teân
töø traùi sang phaûi, truùng
x
c
tröôùc neân
.cd
Vaäy
0 1 .b a d c
Ta thaáy:
log 0 1; log 0 1
ab
x a x b
.
Ta thaáy:
log 1; log 1.
cd
x c x d
So saùnh a vôùi b: Ñöùng treân cao, baén muõi teân
töø phaûi sang traùi, truùng
log
b
x
tröôùc:
.ba
So saùnh c vôùi d: Ñöùng treân cao, baén muõi teân
töø phaûi sang traùi, truùng
log
d
x
tröôùc:
.dc
Vaäy
01a b c d
.
PHÖÔNG TRÌNH MUÕ VAØ LOGARIT
Phöông trình muõ
Phöông trình Logarit
Daïng cô baûn:
( ) ( )
( ) ( )
f x g x
a a f x g x
Daïng cô baûn:
log ( ) log g( ) ( ) ( ) 0
aa
f x x f x g x
Daïng logarit hoùa:
()
( ) ( )
( ) log
( ) ( ).log
fx
a
f x g x
a
a b f x b
a b f x g x b
Daïng muõ hoùa:
log ( ) ( )
b
a
f x b f x a
(khoâng caàn ñieàu kieän)
BAÁT PHÖÔNG TRÌNH MUÕ VAØ LOGARIT
Baát Phöông trình muõ
Baát Phöông trình Logarit
Daïng cô baûn:
1
( ) ( )
01
( ) ( )
( ) ( )
( ) ( )
a
f x g x
a
f x g x
a a f x g x
a a f x g x

Daïng cô baûn:
1
01
log ( ) log ( ) ( ) ( ) 0
log ( ) log ( ) 0 ( ) ( )
a
aa
a
aa
f x g x f x g x
f x g x f x g x

COÂNG THÖÙC ÑAÏO HAØM
0k
Vôùi
k
laø haèng soá
1
()xx

1
( ) .u u u


1
2
x
x
2
u
u
u

2
11
xx




2
1 u
uu




xx
ee
.
uu
e e u

ln
xx
a a a
.ln .
uu
a a a u

sin cosxx
sin cosu u u

cos sinxx

cos sinu u u

2
2
1
tan 1 tan
cos
xx
x
2
2
tan 1 tan
cos
u
u u u
u

2
2
1
cot 1 cot
sin
xx
x
2
2
cot 1 cot
sin
u
u u u
u

COÂNG THÖÙC NGUYEÂN HAØM
( ) ( ) ( ) ( )f x dx F x C F x f x
. ( ) ( )k f x dx k f x dx

( ) ( ) ( ) ( )f x g x dx f x dx g x dx
kdx kx C
1)
kdx kx C
22dx x C
( 3) 3dx x C
2)
1
1
x
x dx C

1
1 ( )
( ) .
1
MR
ax b
ax b dx C
a

4
3
4
x
x dx C
3
1
2
3
2
2
3/ 2 3
x
xdx x dx C x C

11 11
10
1 (1 ) (1 )
(1 2 ) .
2 11 22
xx
x dx C C


3)
1 1 1
ln ln
MR
dx x C dx ax b C
x ax b a


11
ln 1 3
1 3 3
dx x C
x

4)
22
1 1 1 1 1
.
()
MR
dx C dx C
x x ax b a ax b



2
1 1 1 1
.
(2 3) 2 2 3 4 6
dx C C
x x x
3
2
2
1 1 1
10 ln 10
3
x
x dx x x C
x x x



55
4
11
ln
5
xx
dx x dx x C
xx




5)
1
MR
x x ax b ax b
e dx e C e dx e C
a



1
1
x x x
e dx e C e C

6)
ln
x
x
a
a dx C
a

1
.
ln
bx c
MR
bx c
a
a dx C
ba

5
5
ln5
x
x
dx C
2
9
39
ln9
x
xx
dx dx C

2 5 2 5
25
1 3 3
3.
2 ln3 2ln3
xx
x
dx C C

1 2 1 2 1
1
2 2 2
2
x x x x x x
e e dx e e dx e e C

1
1 1 6
2 .3 2 .3 . 6
3 3 3ln6
x
x x x x x
dx dx dx C
7)
sin cosxdx x C
1
sin( ) cos( )
MR
ax b dx ax b C
a

4;
2
1
sin 4 cos 4
2 4 2
ab
x dx x C

8)
cos sinxdx x C
1
cos( ) sin( )
MR
ax b dx ax b C
a

1;
3
1
cos sin sin
3 1 3 3
ab
x dx x C x C
3sin 2cos 3cos 2sinx x dx x x C
2
1 1 1
sin 1 cos2 sin2
2 2 2
xdx x dx x x C




(haï baäc)
9)
2
2
1
1 tan tan
cos
dx x dx x C
x

2
11
tan
cos
MR
dx ax b C
ax b a

2
22
1 2cos 1
2 tan 2
cos cos
x
dx dx x x C
xx




2
11
tan3
cos 3 3
dx x C
x

2
1
1 tan tan
MR
ax b dx ax b C
a



2
2;
1
1 tan 2 tan 2
2
ab
x dx x C





10)
2
2
1
1 cot cot
sin
dx x dx x C
x

2
11
cot
sin
MR
dx ax b C
ax b a

2
1
1 cot cot
MR
ax b dx ax b C
a



22
22
sin 1 1
cot
sin sin 2
x x x
dx x dx x C
xx




2
11
cot8
sin 8 8
dx x C
x
2
1
1 cot 3 cot3
3
x dx x C


22
2 2 2 2 2 2
1 sin cos 1 1
tan cot
sin cos sin cos cos sin
xx
dx dx dx x x C
x x x x x x



DIEÄN TÍCH VAØ THEÅ TÍCH
Hình phaúng giôùi haïn bôûi caùc ñöôøng
()y f x
,
truïc
Ox
,
,x a x b
thì coù dieän tích:
()
b
a
S f x dx
Hình phaúng giôùi haïn bôûi caùc ñöôøng
()y f x
,
()y g x
,
,x a x b
thì coù dieän tích:
( ) ( )
b
a
S f x g x dx
Khi xoay hình phaúng
()
,
y f x
x a x b

quanh
Ox
,
ta ñöôïc khoái truï troøn coù theå tích
2
()
b
a
V f x dx
Khi xoay hình phaúng
()
()
,
y f x
y g x
x a x b

quanh
Ox
,
ta ñöôïc khoái truï troøn coù theå tích
22
( ) ( )
b
a
V f x g x dx

Xeùt hình khoái ñöôïc giôùi haïn bôûi hai maët phaúng
,x a x b
. Khi caét khoái naøy ta ñöôïc thieát dieän coù
dieän tích
()Sx
(laø haøm lieân tuïc treân [a;b]). Theå tích khoái naøy treân
;ab
laø:
()
b
a
V S x dx
.
COÂNG THÖÙC CHUYEÅN ÑOÄNG
Xeùt haøm quaûng ñöôøng
( ),St
haøm vaän toác
()vt
vaø haøm gia toác
()at
. Ba haøm naøy seõ bieán thieân theo
t
.
( ) ( ) ( ) ( )S t v t dt v t S t
( ) ( ) ( ) ( )v t a t dt a t v t
COÂNG THÖÙC LÖÔÏNG GIAÙC
1. Heä thöùc cô baûn:
22
sin cos 1


sin
tan
cos
cos
cot
sin
tan .cot 1

2
2
1
1 tan
cos

2
2
1
1 cot
sin

sin( 2 ) sin
cos( 2 ) cos
k
k


tan( ) tan
cot( ) cot
k
k


2. Cung lieân keát:
Ñoái:
vaø
Buø:
vaø

Phuï:
vaø
2
Khaùc pi:
;
Khaùc
:;
22
Pi

sin( ) sin

sin( ) sin

sin cos
2





sin( ) sin
sin cos
2





cos( ) cos


cos( ) cos
cos sin
2





cos( ) cos
cos sin
2




tan( ) tan

tan( ) tan
tan cot
2





tan( ) tan

tan cot
2




cot( ) cot

cot( ) cot
cot tan
2





cot( ) cot

cot tan
2




Cos Ñoái
Sin Buø
Phuï Cheùo
Khaùc pi
Tang, Cotang
Khaùc pi chia 2
Sin baïn cos
3. Coâng thöùc coäng:
sin( ) sin .cos sin .cos
sin( ) sin .cos sin .cos
a b a b b a
a b a b b a
cos( ) cos .cos sin .sin
cos( ) cos .cos sin .sin
a b a b a b
a b a b a b
tan tan
tan( )
1 tan .tan
ab
ab
ab

tan tan
tan( )
1 tan .tan
ab
ab
ab

4. Coâng thöùc nhaân ñoâi, nhaân ba:
sin2 2sin .cos
22
22
cos2 cos sin
2cos 1 1 2sin


2
2tan
tan2
1 tan
3
sin3 3sin 4sin

3
cos3 4cos 3cos

3
2
3tan tan
tan3
1 3tan

5. Coâng thöùc haï baäc
2
1 cos2
sin
2
2
1 cos2
cos
2
2
1 cos2
tan
1 cos2
6. Coâng thöùc bieán ñoåi toång thaønh tích:
cos cos 2cos .cos
22
a b a b
ab


cos cos 2sin .sin
22
a b a b
ab

sin sin 2sin .cos
22
a b a b
ab


sin sin 2cos .sin
22
a b a b
ab


sin( )
tan tan
cos .cos
ab
ab
ab

sin( )
tan tan
cos .cos
ab
ab
ab

sin cos 2.sin 2.cos
44

sin cos 2sin 2 cos
44

7. Coâng thöùc bieán ñoåi tích thaønh toång:
1
cos .cos cos( ) cos( )
2
a b a b a b
1
sin .sin cos( ) cos( )
2
a b a b a b
1
sin .cos sin( ) sin( )
2
a b a b a b
Cos.Cos thì Cos coäng coäng Cos tröø
Sin.Sin thì Cos tröø tröø Cos coäng
Sin.Cos thì Sin coäng coäng Sin tröø
PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
2
sin sin ( )
2
u v k
u v k
u v k


2
cos cos
2
u v k
u v k
u v k

Ñaëc bieät:
sin 1 2
2
sin 1 2
2
sin 0
u u k
u u k
u u k
k
Ñaëc bieät:
cos 1 2
cos 1 2
cos 0
2
u u k
u u k
u u k

k
tan tanu v u v k
k
cot cotu v u v k
k
TOÅ HÔÏP – XAÙC SUAÁT
QUY TAÉC COÄNG
QUY TAÉC NHAÂN
Neáu pheùp ñeám ñöôïc chia ra nhieàu tröôøng hôïp,
ta seõ coäng caùc keát quaû laïi.
Neáu pheùp ñeám ñöôïc chia ra laøm nhieàu giai ñoaïn
baét buoäc, ta seõ nhaân caùc keát quaû cuûa moãi giai
ñoaïn aáy.
HOAÙN VÒ
CHÆNH HÔÏP
TOÅ HÔÏP
Saép xeáp (ñoåi choã) cuûa
n
phaàn
töû khaùc nhau, ta coù soá caùch
xeáp laø
!
n
Pn
vôùi
n
.
Caùch tính:
! 1.2..... 1n n n
.
Quy öôùc soác:
0! 1.
Choïn
k
phaàn töû töø
n
phaàn töû
(khoâng saép xeáp thöù töï), ta coù
soá caùch choïn laø
k
n
C
.
Caùch tính:
!
!!
k
n
n
C
n k k
vôùi
,
.
0
nk
kn
Choïn
k
phaàn töû töø
n
phaàn töû
(coù saép xeáp thöù töï), ta ñöôïc soá
caùch choïn laø
k
n
A
.
Caùch tính:
!
!
k
n
n
A
nk
vôùi
,
.
0
nk
kn
XAÙC SUAÁT
Coâng thöùc:
()
()
()
nX
PX
n
Trong ñoù:
( ):nX
soá phaàn töû cuûa
taäp bieán coá
;X
( ):n
soá phaàn töû
khoâng gian maãu .
()PX
laø xaùc suaát
ñeå bieán coá
X
xaûy ra vôùi
X 
.
Tính chaát:
0 ( ) 1PX
.
( ) 0; ( ) 1PP
.
( ) 1 ( )P X P X
vôùi
X
laø bieán coá ñoái cuûa
X
.
KHAI TRIEÅN NHÒ THÖÙC NEWTÔN
Khai trieån daïng lieät keâ:
Trong caùc coâng thöùc beân,
ta luoân coù
, 2.nn
0 1 1 2 2 2 1 1
.........
n
n n n n n n n
n n n n n
a b C a C a b C a b C ab C b
.
Ñaëc bieät:
0 1 2 2 1 1
1 .........
n
n n n n
n n n n n
x C C x C x C x C x

(*).
Heä quaû 1:
0 1 2 1
......... 2
n n n
n n n n n
C C C C C
(töùc laø thay
1x
vaøo (*)).
Heä quaû 2: Vôùi
n
chaün, chæ caàn thay
1x 
vaøo (*), ta coù:
0 1 2 1 0 2 4 1 3 1
......... 0 ...... ......
n n n n
n n n n n n n n n n n n
C C C C C C C C C C C C

Khai trieån toång quaùt:
Trong caùc coâng thöùc beân,
ta luoân coù
, 2.nn
Khai trieån:
0
n
n
k n k k
n
k
a b C a b

. Soá haïng toång quaùt:
1
k n k k
kn
T C a b
Phaân bieät heä soá vaø soá haïng:
( 1) .
k k n k k
n
HEÄ SOÁ
SOÁ HAÏNG
C a b x
.
Nhôù raèng soá haïng khoâng chöùa
x
öùng vôùi
0.
CAÁP SOÁ COÄNG – CAÁP SOÁ NHAÂN
CAÁP SOÁ COÄNG
CAÁP SOÁ NHAÂN
1. Ñònh nghóa:
Daõy soá
n
u
ñöôïc goïi laø caáp soá coäng khi vaø
chæ khi
1nn
u u d

vôùi
*
n
.
Caáp soá coäng nhö treân coù soá haïng ñaàu
1
,u
coâng sai
.d
2. Soá haïng toång quaùt:
1
( 1)
n
u u n d
vôùi
*
.n
3. Tính chaát caùc soá haïng:
11
2
k k k
u u u


vôùi
k
vaø k
2.
4. Toång n soá haïng ñaàu tieân:
1
12
()
... .
2
n
nn
u u n
S u u u
1. Ñònh nghóa:
Daõy soá
n
u
ñöôïc goïi laø caáp soá nhaân khi vaø
chæ khi
1
.
nn
u u q
vôùi
*
n
.
Caáp soá nhaân nhö treân coù soá haïng ñaàu
1
,u
coâng boäi
q
.
2. Soá haïng toång quaùt:
1
1
.
n
n
u u q
vôùi
*
.n
3. Tính chaát caùc soá haïng:
2
11
.
k k k
u u u

vôùi
k
vaø k
2.
4. Toång n soá haïng ñaàu tieân:
1
12
(1 )
...
1
n
nn
uq
S u u u
q
vôùi
1.q
KHAÛO SAÙT HAØM SOÁ & BAØI TOAÙN LIEÂN QUAN
XEÙT TÍNH ÑÔN ÑIEÄU
HAØM BAÄC BA
32
y ax bx cx d
( 0)a
HAØM NHAÁT BIEÁN
( 0)
ax b
y ad bc
cx d
Böôùc 1: Tìm taäp xaùc ñònh
D
.
Böôùc 2: Tính
()y f x

; cho
0y
12
, ...
Tìm nghieäm
xx
Böôùc 3: Laäp baûng bieán thieân.
(Neân choïn giaù trò x ñaïi dieän cho
töøng khoaûng thay vaøo
y
ñeå tìm
daáu cuûa
y
treân khoaûng ñoù).
Böôùc 4: Döïa vaøo baûng bieán
thieân ñeå keát luaän veà söï ñoàng
bieán, nghòch bieán cuûa haøm soá.
Ñaïo haøm
2
32y ax bx c
.
Haøm soá ñoàng bieán treân taäp
xaùc ñònh
0,yx
0
0
a

.
Haøm soá nghòch bieán treân
taäp xaùc ñònh
0,yx
0
0
a

.
Ñaïo haøm
2
()
ad bc
y
cx d
.
Haøm soá ñoàng bieán treân
töøng khoaûng xaùc ñònh
0.ad bc
Haøm soá nghòch bieán
treân töøng khoaûng xaùc
ñònh
0.ad bc
ÑIEÀU KIEÄN CÖÏC TRÒ
CÖÏC TRÒ HAØM BAÄC BA
32
y ax bx cx d
( 0)a
CÖÏC TRÒ HAØM BAÄC BOÁN
42
y ax bx c
( 0)a
Haøm soá coù ñieåm cöïc trò laø
00
( ; )xy
0
00
( ) 0
()
yx
y x y
.
(giaû thieát laø haøm soá lieân tuïc
taïi
0
x
).
Ñaïo haøm
2
32y ax bx c
.
Haøm soá coù hai cöïc trò
0
(*)
0
y
a

.
Ñeå tìm ñieàu kieän cho haøm soá
khoâng coù cöïc trò: Böôùc 1:
laøm theo coâng thöùc (*).
Böôùc 2: phuû ñònh keát quaû.
Phöông trình ñöôøng thaúng ñi
qua hai ñieåm cöïc trò:
( ). ( )
()
18
f x f x
y f x
a
Ñaïo haøm
3
42y ax bx

.
Ñieàu kieän cöïc trò
Ba cöïc trò
0ab
Moät cöïc trò
22
0
0
ab
ab

Coù cöïc trò
22
0ab
Cho
,,A B C
laø ba ñieåm cöïc
trò, ta coù:
3
3
8
cos
8
ba
BAC
ba
5
3
32
ABC
b
S
a
.
Neáu
0
0
( ) 0
( ) 0
fx
fx
thì haøm soá
()fx
ñaït cöïc ñaïi taïi
0
.xx
Neáu
0
0
( ) 0
( ) 0
fx
fx
thì haøm soá
()fx
ñaït cöïc tieåu taïi
0
.xx
TÌM MAX-MIN TREÂN ÑOAÏN
Tìm Max-Min cuûa
()fx
treân ñoaïn
;ab
TÌM MAX-MIN TREN KHOAÛNG
Tìm Max-Min cuûa
()fx
treân khoaûng
( ; )ab
Böôùc 1: Tính
()y f x
.
Tìm caùc nghieäm
( ; )
i
x a b
khi cho
( ) 0fx
.
Böôùc 2: Tính caùc giaù trò
( ), ( )f a f b
vaø
( ),...
i
fx
(neáu coù).
Böôùc 3: So sanh taát caû giaù trò trong böôùc 2 ñeå
keát luaän veà giaù trò lôùn nhaát, nhoû nhaát.
Böôùc 1: Tính
()y f x
.
Tìm caùc nghieäm
( ; )
i
x a b
khi cho
( ) 0fx
.
Böôùc 2: Caàn tính
lim , lim
x a x b
yy
. (Neáu thay
( ; )ab
baèng
( ; )
thì ta tính theâm
lim
x
y

).
Böôùc 3: Laäp baûng bieán thieân vaø suy ra giaù trò
lôùn nhaát, nhoû nhaát treân khoaûng.
ÑAËC
BIEÄT
Neáu haøm
()fx
ñoàng bieán treân
[ ; ]ab
thì
[ ; ]
[ ; ]
max ( ) ( )
min ( ) ( )
x a b
x a b
f x f b
f x f a
Neáu haøm
()fx
nghòch bieán treân
[ ; ]ab
thì
[ ; ]
[ ; ]
max ( ) ( )
min ( ) ( )
x a b
x a b
f x f a
f x f b
TIEÄM CAÄN ÑÖÙNG
TIEÄM CAÄN NGANG
Ñònh nghóa:
0
xx
y
(x höõu haïn, y voâ haïn),
ta coù tieäm caän ñöùng
0
xx
. Löu yù: ñieàu kieän
0
xx
coù theå ñöôïc thay baèng
0
xx
(giôùi
haïn beân traùi) hoaëc
0
xx
(giôùi haïn beân
phaûi).
Caùch tìm TCÑ: Neáu
0
xx
laø moät nghieäm
cuûa maãu soá maø khoâng phaûi laø nghieäm cuûa
töû soá thì
0
xx
chính laø moät TCÑ cuûa ñoà thò.
Ñònh nghóa:
0
x
yy
(x voâ haïn, y höõu haïn),
ta coù tieäm caän ngang
0
yy
.
Caùch tìm TCN: Ñôn giaûn nhaát laø duøng CASIO
Böôùc 1: Nhaäp haøm soá vaøo maùy.
Böôùc 2:
10 ^10
NEXT NEXT
CALC X
10 ^10
NEXT NEXT
CALC X
Böôùc 3: Neáu keát quaû thu ñöôïc laø höõu haïn (töùc
laø
0
y
) thì ta keát luaän TCN:
0
yy
.
Ñoà thò haøm soá
ax b
y
cx d
vôùi
( 0, 0)c ad bc
coù moät TCÑ:
d
x
c
, moät TCN:
.
a
y
c
Neân nhôù, ñoà thò coù theå coù nhieàu tieäm caän ñöùng, nhöng chæ coù toái ña laø 2 tieäm caän ngang.
TÌM TOÏA ÑOÄ GIAO ÑIEÅM HOAËC SOÁ GIAO ÑIEÅM HAI ÑOÀ THÒ
Xeùt hai ñoà thò
1
( ) : ( )C y f x
vaø
2
( ) : ( )C y g x
.
Böôùc 1 : Laäp phöông trình hoaønh ñoä giao ñieåm
cuûa
12
( )&( )CC
:
( ) ( )f x g x
. (*)
Böôùc 2 : Giaûi phöông trình (*) ñeå tìm caùc
nghieäm
12
, ,...xx
(neáu coù), suy ra
12
, ...yy
PHÖÔNG TRÌNH TIEÁP TUYEÁN
DAÏNG 1
Vieát phöông trình tieáp tuyeán
cuûa ñoà thò
( ): ( )C y f x
taïi
ñieåm
00
( ; ) ( )M x y C
DAÏNG 2
Vieát phöông trình tieáp tuyeán cuûa
ñoà thò
( ): ( )C y f x
bieát tieáp
tuyeán coù heä soá goùc k.
DAÏNG 3
Vieát phöông trình tieáp tuyeán cuûa
ñoà thò
( ): ( )C y f x
bieát tieáp
tuyeán ñi qua
( ; )
AA
A x y
.
Böôùc 1: Tính ñaïo haøm
y
, töø
ñoù coù heä soá goùc
0
( ).k y x
Böôùc 2 : Vieát phöông trình
tieáp tuyeán cuûa ñoà thò daïng
00
()y k x x y
.
Böôùc 1: Goïi
00
( ; )M x y
laø tieáp
ñieåm vaø tính ñaïo haøm
y
.
Böôùc 2: Cho
0
()y x k
, töø ñoù
tìm ñöôïc tieáp ñieåm
00
( ; ).xy
Böôùc 3: Vieát phöông trình
tieáp tuyeán :
Böôùc 1: Tieáp tuyeán coù daïng :
0 0 0
( )( )y y x x x y
(*) vôùi
00
( ).y f x
Böôùc 2: Thay toïa ñoä ñieåm
A
vaøo
(*)
ñeå tìm ñöôïc
0
.x
Böôùc 3: Thay
0
x
tìm ñöôïc vaøo
00
()y k x x y
.
(*) ñeå vieát phöông trình tieáp
tuyeán.
SOÁ PHÖÙC VAØ CAÙC YEÁU TOÁ LIEÂN QUAN
Soá phöùc coù daïng:
z a bi
vôùi
2
,
1
ab
i
(i: laø ñôn vò aûo). Kyù hieäu taäp soá phöùc: .
Thaønh phaàn
Hình hoïc
Minh hoïa
Phaàn thöïc: a.
Neáu
0a
thì
z bi
ñöôïc goïi laø
soá thuaàn aûo.
Phaàn aûo: b.
Neáu
0b
thì
za
laø soá thöïc.
Khi
0ab
thì
0z
vöøa laø soá
thuaàn aûo vöøa laø soá thöïc.
Ñieåm
( ; )M a b
bieåu dieãn
cho
z
treân heä truïc
.Oxy
Moâ-ñun:
22
z OM a b
.
Soá phöùc lieân hôïp – Soá phöùc
nghòch ñaûo
Caên baäc hai
Phöông trình baäc hai
Cho
z a bi
. Khi ñoù:
Soá phöùc lieân hôïp cuûa noù
laø
z a bi
.
Soá phöùc nghòch ñaûo laø
1
11
z
z a bi
2 2 2 2
ab
i
a b a b
.
Caên baäc hai cuûa
0a
laø
.a
Caên baäc hai cuûa
0a
laø
ia
.
Caên baäc hai cuûa soá phöùc
z a bi
laø hai soá phöùc daïng
w x yi
vôùi
22
2
x y a
xy b
.
Phöông trình
2
0za
coù
hai nghieäm phöùc
.za
Phöông trình
2
0za
coù
hai nghieäm phöùc
z i a
.
Phöông trình
2
0az bz c
vôùi
0
seõ coù hai nghieäm
phöùc laø:
1,2
2
bi
z
a
.
KHOÁI ÑA DIEÄN VAØ THEÅ TÍCH CUÛA CHUÙNG
I. MOÄT SOÁ HÌNH PHAÚNG CÔ BAÛN:
1. Tam giaùc vuoâng:
▪
2 2 2
Pitago
AB AC BC
▪
2
.AB BH BC
▪
2
.AC CH BC
▪
2
.AH BH CH
▪
2 2 2
1 1 1
AH AB AC
22
.AB AC
AH
AB AC
▪
sin
AC
B
BC
(ñoái/huyeàn) ▪
cos
AB
B
BC
(keà/huyeàn) ▪
tan
AC
B
AB
(ñoái/keà) ▪
cot
AB
B
AC
(keà/ñoái)
2. Tam giaùc ñeàu:
Giaû söû tam giaùc
ABC
ñeàu coù caïnh
;a
troïng taâm
;G
caùc ñöôøng
cao (truøng vôùi trung tuyeán) goàm
AH
,
.BK
▪ Ñöôøng cao:
( ) 3 3
.
22
caïnh a
AH BK
▪
2 2 3 3 1 1 3 3
. ; . .
3 3 2 3 3 3 2 6
a a a a
AG AH GH AH
▪ Dieän tích:
22
( ) 3 3
.
44
ABC
caïnh a
S
3. Tam giaùc thöôøng:
Giaû söû tam giaùc
ABC
coù
,,a BC b AC c AB
; caùc ñöôøng
cao
,,
a b c
h h h
laàn löôït öùng vôùi caïnh
, , .a b c
Kyù hieäu
,Rr
laàn löôït
laø baùn kính ñöôøng troøn ngoaïi tieáp, noäi tieáp ∆.
A
C
B
H
a
a
a
G
K
H
B
C
A
▪ Ñònh lí Sin:
2
sin sin sin
a b c
R
A B C
.
▪ Ñònh lí Coâ-sin:
2 2 2
2 .cosa b c bc A
;
2 2 2 2 2 2
2 .cos ; 2 .cos .b a c ac B c a b ab C
▪ Dieän tích:
1 1 1
. . . ;
2 2 2
ABC a b c
S h a h b h c
1 1 1
.sin .sin .sin
2 2 2
ABC
S ab C ac B bc A
;
4
ABC
abc
S pr
R
;
( )( )( )
2
ABC
Coâng thöùc Heâ Roâng
a b c
S p p a p b p b vôùi p
(nöûa chu vi).
4. Hình vuoâng:
Cho hình vuoâng
ABCD
coù caïnh
;a
hai ñieåm
,MN
laàn löôït laø
trung ñieåm cuûa
,;CD AD
I
laø taâm hình vuoâng.
▪ Ñöôøng cheùo:
( ) 2 2
AC BD
AC BD caïnh a
.
2
2
a
IA IB IC ID
neân
I
laø taâm ñöôøng troøn ñi qua
boán ñænh hình vuoâng.
▪ Dieän tích:
22
()
ABCD
S caïnh a
; chu vi:
4.pa
▪ Vì
ABN ADM
, ta chöùng minh ñöôïc:
.AM BN
5. Hình chöõ nhaät:
Cho hình chöõ nhaät
ABCD
taâm
I
coù
,.AB a AD b
▪ Ñöôøng cheùo:
22
AC BD a b
.
22
1
2
IA IB IC ID a b
neân
I
laø taâm ñöôøng troøn ñi
qua boán ñieåm
, , , .A B C D
▪ Dieän tích:
.
ABCD
S a b
; chu vi:
2( ).p a b
6. Hình thoi:
Cho hình thoi
ABCD
coù taâm
,I
caïnh baèng
.a
▪ Ñöôøng cheùo:
;AC BD
2 2 .sin 2 .sin .AC AI AB ABI a ABI
▪ Dieän tích:
1
.
2
ABCD
S AC BD
;
2 2 2
ABCD ABC ACD ABD
S S S S
.
Ñaëc bieät: Neáu hình thoi coù goùc
0
60BD
(
0
120AC
) thì
ta chia hình thoi ra laøm hai tam giaùc ñeàu:
.ABC ACD
AC a
vaø
2
3
;
4
ABC ACD
a
SS
2
3
2.
2
ABCD ABC
a
SS
II. THEÅ TÍCH KHOÁI CHOÙP:
7. Hình choùp:
1
.
3
ñ
V h S
7.1. Hình choùp tam giaùc ñeàu
▪ Taát caû caïnh beân baèng nhau.
▪ Ñaùy laø tam giaùc ñeàu caïnh
.a
▪
()SH ABC
vôùi
H
laø troïng taâm
∆
.ABC
▪
2
2
3
13
.
4
34
Theå tích
ñ
a
a
S
Vh
SH h
Goùc giöõa caïnh beân vaø maët
Goùc giöõa maët beân vaø maët ñaùy:
S
đ
h
A
B
C
D
S
H
7.2. Töù dieän ñeàu:
▪ Ñaây cuõng laø hình choùp tam
giaùc ñeàu, ñaëc bieät laø caïnh
beân baèng caïnh ñaùy. Theå
tích:
3
2
12
a
V
.
ñaùy:
,( )SA ABC SAH
,( )SC ABC SCH
.
( ), ( )SAB ABC SMH
( ),( )SBC ABC SNH
.
7.3. Hình choùp töù giaùc ñeàu:
▪ Taát caû caïnh beân baèng nhau.
▪ Ñaùy laø hình vuoâng caïnh
.a
▪
()SO ABCD
vôùi
O
laø taâm hình
vuoâng
.ABCD
▪
2
2
1
.
3
Theå tích
ñ
Sa
V h a
SO h
.
Goùc giöõa caïnh beân vaø maët
ñaùy:
,( )SA ABCD SAO
,( )SB ABCD SBO
.
Goùc giöõa maët beân vaø maët ñaùy:
( ), ( )SAB ABCD SMO
( ),( )SBC ABCD SNO
.
7.4. Hình choùp coù caïnh beân
SA vuoâng goùc vôùi maët
phaúng ñaùy.
Ñaùy laø tam giaùc
Ñaùy laø töù giaùc ñaëc bieät
▪
1
.
3
Theå tích
ABC
ñ ABC
h SA
V SA S
SS
.
▪ Goùc giöõa caïnh beân vaø maët ñaùy:
,( )
,( )
SB ABC SBA
SC ABC SCA
.
▪
1
.
3
Theå tích
ABCD
ñ ABCD
h SA
V SA S
SS
.
▪ Goùc giöõa caïnh beân vaø maët ñaùy:
,( )
,( )
SB ABCD SBA
SC ABCD SCA
.
7.5. Hình choùp coù maët beân
(SAB) vuoâng goùc vôùi maët
phaúng ñaùy.
Ñaùy laø tam giaùc
Ñaùy laø töù giaùc ñaëc bieät
▪ Ñöôøng cao
h SH
cuõng laø
ñöôøng cao cuûa ∆SAB.
▪ Goùc giöõa caïnh beân vaø maët ñaùy:
,( )
,( )
SA ABC SAH
SC ABC SCH
.
▪ Ñöôøng cao
h SH
cuõng laø
ñöôøng cao cuûa ∆SAB.
▪ Goùc giöõa caïnh beân vaø maët ñaùy:
,( )
,( )
SA ABCD SAH
SC ABCD SCH
.
III. THEÅ TÍCH KHOÁI LAÊNG TRUÏ:
1. Hình laêng truï thöôøng:
Hai ñaùy laø hai hình gioáng
nhau vaø naèm trong hai maët
phaúng song song.
Caùc caïnh beân song song vaø
baèng nhau. Caùc maët beân laø
caùc hình bình haønh.
Theå tích:
.
ñ
V h S
.
Ñaùy laø tam giaùc
Ñaùy laø töù giaùc
..
ABC A B C
V AH S AH S
..
ABCD A B C D
V AH S AH S
2. Hình laêng truï ñöùng:
Caùc caïnh beân cuøng vuoâng goùc
vôùi hai maët ñaùy neân moãi
caïnh beân cuõng laø ñöôøng cao
cuûa laêng truï.
Laêng truï tam giaùc ñeàu:
Laø laêng truï ñöùng vaø coù hai
ñaùy laø hai tam giaùc ñeàu
baèng nhau.
Ñaùy laø tam giaùc
Ñaùy laø töù giaùc
Theå tích:
.
ñ
V h S
vôùi
h AA BB CC
.
Theå tích:
.
ñ
V h S
vôùi
h AA BB CC DD
.
3. Hình hoäp:
Laø laêng truï coù taát caû caùc maët
laø hình bình haønh.
Theå tích:
.
ñ
V h S
.
3.1 Hình hoäp chöõ nhaät:
3.2. Hình laäp phöông:
Laø laêng truï ñöùng coù ñaùy laø
hình chöõ nhaät.
V abc
vôùi
,,a b c
laø ba kích
thöôùc khaùc nhau cuûa hình hoäp
chöõ nhaät.
Laø hình hoäp chöõ nhaät coù taát caû
caùc caïnh baèng nhau.
3
Va
vôùi
a
laø caïnh cuûa hình
laäp phöông.
MAËT TRUÏ – MAËT NOÙN – MAËT CAÀU
MAËT NOÙN
Caùc yeáu toá maët noùn:
Moät soá coâng thöùc:
Hình thaønh: Quay vuoâng
Ñöôøng cao:
h SO
. (
SO
cuõng ñöôïc goïi laø truïc cuûa hình
noùn).
Baùn kính ñaùy:
.r OA OB OM
Ñöôøng sinh:
.l SA SB SM
Goùc ôû ñænh:
.ASB
Chu vi ñaùy:
2.pr
Dieän tích ñaùy:
đ
2
.Sr
Theå tích:
đ
2
11
. . .
33
V h S h r
(lieân töôûng khoái choùp).
Dieän tích xung quanh:
.
xq
S rl
h
l
l
l
r
O
A
B
S
M
SOM
quanh truïc
SO
, ta ñöôïc
maët noùn nhö hình beân vôùi:
h SO
r OM
.
Thieát dieän qua truïc:
SAB
caân taïi
.S
Goùc giöõa ñöôøng sinh vaø maët
ñaùy:
.SAO SBO SMO
Dieän tích toaøn phaàn:
2
.
tp xq
S S S rl r
đ
MAËT TRUÏ
Caùc yeáu toá maët truï:
Moät soá coâng thöùc:
Hình thaønh: Quay hình chöõ
nhaät
ABCD
quanh ñöôøng
trung bình
OO
, ta coù maët truï
nhö hình beân.
Ñöôøng cao:
.h OO
Ñöôøng sinh:
.l AD BC
Ta coù:
.lh
Baùn kính ñaùy:
.r OA OB O C O D
Truïc (∆) laø ñöôøng thaúng ñi qua
hai ñieåm
,.OO
Thieát dieän qua truïc: Laø hình
chöõ nhaät
.ABCD
Chu vi ñaùy:
2.pr
Dieän tích ñaùy:
đ
2
.Sr
Theå tích khoái truï:
2
..V h S h r
đ
.
Dieän tích xung quanh:
2 . .
xq
S r h
Dieän tích toaøn phaàn:
2
2 2 . 2 .
tp xq
S S S r h r
đ
MAËT CAÀU
Moät soá coâng thöùc:
Maët caàu ngoaïi tieáp ña dieän
Maët caàu noäi tieáp ña dieän
Hình thaønh: Quay ñöôøng
troøn taâm
I
, baùn kính
2
AB
R
quanh truïc
AB
, ta coù
maët caàu nhö hình veõ.
Taâm
,I
baùn kính
R IA IB IM
.
Ñöôøng kính
2AB R
.
Thieát dieän qua taâm maët caàu:
Laø ñöôøng troøn taâm
I
, baùn
kính
R
.
Dieän tích maët caàu:
2
4SR
Theå tích khoái caàu:
3
4
3
R
V
Maët caàu
ngoaïi tieáp ña
dieän laø maët
caàu ñi qua taát
caû ñænh cuûa ña
dieän ñoù.
Maët caàu noäi
tieáp ña dieän laø
maët caàu tieáp
xuùc vôùi taát caû
caùc maët cuûa ña
dieän ñoù.
CAÙCH TÌM BAÙN KÍNH MAËT CAÀU NGOAÏI TIEÁP HÌNH CHOÙP THÖÔØNG GAËP
1. Hình choùp coù caùc ñænh nhìn moät caïnh
döôùi moät goùc vuoâng.
2. Hình choùp ñeàu.
Xeùt hình choùp coù
()SA ABC
vaø
Xeùt hình choùp coù
()SA ABCD
vaø
ABCD
laø hình chöõ
Xeùt hình choùp tam
giaùc ñeàu coù caïnh beân
baèng
b
vaø ñöôøng cao
Xeùt hình choùp töù giaùc
ñeàu coù caïnh beân baèng
b vaø chieàu cao
SO h
0
90ABC
.
Ta coù
0
90SAC SBC
neân maët caàu ngoaïi
tieáp hình choùp coù taâm
I
laø trung ñieåm
SC
,
baùn kính
.
2
SC
R
nhaät hoaëc hình vuoâng.
Ta coù:
SAC SBC
0
90SDC
Suy ra maët caàu ngoaïi
tieáp hình choùp coù taâm
I
laø trung ñieåm
SC
,
baùn kính
.
2
SC
R
SH h
.
Baùn kính maët caàu
ngoaïi tieáp hình choùp
treân laø
2
2
b
R
h
.
Baùn kính maët caàu
ngoaïi tieáp hình choùp
treân laø
2
2
b
R
h
.
3. Hình choùp coù caïnh beân vuoâng goùc vôùi
maët phaúng ñaùy.
4. Hình choùp coù maët beân vuoâng goùc vôùi
maët ñaùy.
Xeùt hình choùp coù
SA
(ñaùy) vaø
SA h
; baùn kính
ñöôøng troøn ngoaïi tieáp
cuûa ñaùy laø
ñ
r
.
Khi ñoù maët caàu ngoaïi
tieáp hình choùp coù baùn
kính
2
2
2
ñ
h
Rr
.
Neáu ñaùy laø tam giaùc
ñeàu caïnh
a
thì
3
3
ñ
a
r
.
Neáu ñaùy laø hình vuoâng
caïnh
a
thì
2
2
ñ
a
r
.
Neáu ñaùy laø hình chöõ
nhaät caïnh
,ab
thì
22
2
ñ
ab
r
.
Xeùt hình choùp coù maët beân
()SAB
(ñaùy), baùn
kính ngoaïi tieáp ñaùy laø
ñ
r
, baùn kính ngoaïi tieáp
SAB
laø
b
r
,
()d AB SAB
(ñaùy).
Khi ñoù baùn kính maët caàu ngoaïi tieáp hình choùp laø
2
22
4
ñb
d
R r r
.
HÌNH HOÏC GIAÛI TÍCH TRONG KHOÂNG GIAN
1. Heä truïc toïa ñoä Oxyz:
Heä truïc goàm ba truïc
,,Ox Oy Oz
ñoâi moät vuoâng goùc nhau.
Truïc
:Ox
truïc hoaønh, coù vectô ñôn vò
(1;0;0)i
.
Truïc
Oy
: truïc tung, coù vectô ñôn vò
(0;1;0)j
.
Truïc
:Oz
truïc cao, coù vectô ñôn vò
(0;0;1).k
Ñieåm
(0; 0;0)O
laø goác toïa ñoä.
2. Toïa ñoä vectô: Vectô
( ; ; )u xi yj zk u x y z
.
Cho
1 2 3 1 2 3
( ; ; ), ( ; ; )a a a a b b b b
. Ta coù:
1 1 2 2 3 3
( ; ; )a b a b a b a b
a
cuøng phöông
b
()a kb k R
11
3
12
2 2 1 2 3
1 2 3
33
, ( , , 0).
a kb
a
aa
a kb b b b
b b b
a kb
1 2 3
( ; ; )ka ka ka ka
11
22
33
ab
a b a b
ab
1 1 2 2 3 3
. . . .a b a b a b a b
222
1 2 2
a a a a
2
2 2 2 2
1 2 3
a a a a a
1 1 2 2 3 3
. 0 0a b a b a b a b a b
1 1 2 2 3 3
2 2 2 2 2 2
1 2 3 1 2 3
.
cos( , )
.
.
a b a b a b
ab
ab
ab
a a a b b b
3. Toïa ñoä ñieåm:
( ; ; ) ( ; ; )M x y z OM x y z
. Cho
( ; ; ) , ( ; ; ) , ( ; ; )
A A A B B B C C C
A x y z B x y z C x y z
, ta coù:
( ; ; )
B A B A B A
AB x x y y z z
2 2 2
( ) ( ) ( )
B A B A B A
AB x x y y z z
Toaï ñoä trung ñieåm M cuûa ñoaïn thaúng AB:
; ; .
2 2 2
A B A B A B
x x y y z z
M
Toaï ñoä troïng taâm G cuûa tam giaùc ABC:
; ; .
3 3 3
A B C A B C A B C
x x x y y y z z z
G
4. Tích coù höôùng cuûa hai vectô:
Ñònh nghóa: Cho
1 2 3
( , , )a a a a
,
1 2 3
( , , )b b b b
, tích coù höôùng cuûa
a
vaø
b
laø:
2 3 3 1
12
2 3 3 2 3 1 1 3 1 2 2 1
2 3 3 1
12
, ; ; ; ;
a a a a
aa
a b a b a b a b a b a b a b
b b b b
bb
.
Tính chaát:
[ , ]a b a
[ , ]a b b
[ , ] . .sin ,a b a b a b
Ñieàu kieän cuøng phöông của hai vectô
&ab
laø
,0ab
vôùi
0 (0;0;0).
Ñieàu kieän ñoàng phaúng cuûa ba vectô
,ab
vaø
c
laø
[ , ]. 0.a b c
Dieän tích hình bình haønh ABCD:
,.
ABCD
S AB AD
Dieän tích tam giaùc ABC:
1
,.
2
ABC
S AB AC
Theå tích khoái hoäp:
. ' ' ' '
[ , ]. '.
ABCD A B C D
V AB AD AA
Theå tích töù dieän:
1
,.
6
ABCD
V AB AC AD
.
5. Phöông trình maët caàu:
Daïng 1:
2 2 2 2
( ) : ( ) ( ) ( )S x a y b z c R
()
2
( ; ; )
Maët caàu S coù
I a b c
RR
Daïng 2:
2 2 2
( ) : 2 2 2 0S x y z ax by cz d
()
2 2 2
( ; ; )
Maët caàu S coù
I a b c
R a b c d
Phöông trình
2 2 2
2 2 2 0x y z ax by cz d
laø phöông trình maët caàu
2 2 2
0a b c d
.
Baøi toaùn 5.1. Vieát phöông trình maët caàu taâm
I vaø ñi qua ñieåm M.
Böôùc 1: Tính baùn kính
R IM
.
Böôùc 2: Vieát phöông trình maët caàu daïng 1.
Baøi toaùn 5.2. Vieát phöông trình maët caàu coù
ñöôøng kính AB.
Böôùc 1: Tìm taâm I laø trung ñieåm AB. Baùn kính
2
AB
R IA IB
.
Böôùc 2: Vieát phöông trình maët caàu daïng 1.
6. Phöông trình maët phaúng:
Löu yù: Vectô phaùp tuyeán (VTPT) cuûa maët
phaúng laø vectô khaùc
0
naèm treân ñöôøng thaúng
vuoâng goùc vôùi maët phaúng ñoù.
Maët phaúng
0 0 0
( ; ; )
()
( ; ; )
qua M x y z
P
VTPT n a b c
thì phöông
trình
0 0 0
( ) : ( ) ( ) ( ) 0P a x x b y y c z z
.
Ngöôïc laïi, moät maët phaúng baát kyø ñeàu coù phöông
trình daïng
0ax by cz d
, maët phaúng
naøy coù
( ; ; )VTPT n a b c
.
Baøi toaùn 6.1. Vieát phöông trình maët phaúng
trung tröïc cuûa ñoaïn thaúng AB.
Baøi toaùn 6.2. Vieát phöông trình maët phaúng
ñi qua ba ñieåm A, B, C.
Böôùc 1: Tìm trung ñieåm I cuûa ñoaïn AB vaø tính
toïa ñoä
AB
.
Böôùc 2: Phöông trình
qua
mp( )
VTPT
I
P
n AB
.
Böôùc 1: Tính toïa ñoä
,AB AC
vaø suy ra
,AB AC


.
Böôùc 2: Phöông trình
qua
mp( )
VTPT ,
A
P
n AB AC


Baøi toaùn 6.3. Vieát phöông trình maët phaúng
qua M vaø chöùa ñöôøng thaúng d vôùi
Md
.
Böôùc 1: Choïn ñieåm
Ad
vaø moät VTCP
.
d
u
Tính
,
d
AM u


.
Böôùc 2: Phöông trình
qua
mp( )
VTPT ,
d
M
P
n AM u


Baøi toaùn 6.4. Vieát phöông trình maët phaúng
caét Ox, Oy, Oz laàn löôït taïi
( ; 0; 0), (0; ; 0),A a B b
(0; 0; )Cc
vôùi
, , 0a b c
.
Phöông trình maët
phaúng ñöôïc vieát
theo ñoaïn chaén
( ) : 1 .
x y z
P
a b c
Khoaûng caùch töø ñieåm ñeán maët phaúng
Khoaûng caùch giöõa hai maët phaúng song song
Cho
0 0 0
( ; ; )
( ): 0
M x y z
mp P ax by cz d
.
Khi ñoù:
0 0 0
2 2 2
,( )
ax by cz d
d M P
abc

.
Cho hai maët phaúng
1
2
( ): 0
( ): 0
P ax by cz d
Q ax by cz d
.
Khi ñoù:
12
2 2 2
( ),( )
dd
d P Q
abc

vôùi
12
dd
.
Goùc giöõa hai maët phaúng
Vò trí töông ñoái giöõa hai maët phaúng
Cho hai maët phaúng (), () coù phöông trình:
1 1 1 1
2 2 2 2
( ): 0
( ): 0
P a x b y c z d
Q a x b y c z d
Goùc giöõa
( )&( )PQ
ñöôïc tính:
1 2 1 2 1 2
2 2 2 2 2 2
1 1 1 2 2 2
.
cos ( ),( )
.
.
PQ
PQ
nn
a a bb c c
PQ
nn
a b c a b c


Chuù yù:
00
0 ( ),( ) 90PQ
.
Cho hai maët phaúng (), () coù phöông trình:
1 1 1 1
2 2 2 2
( ): 0
( ): 0
P a x b y c z d
Q a x b y c z d
. Ta coù:
1 1 1 1
2 2 2 2
( ) ( )
a b c d
PQ
a b c d
.
1 1 1 1
2 2 2 2
( ) ( )
a b c d
PQ
a b c d
.
( )&( )PQ
caét nhau
1 1 1 2 2 2
: : : :a b c a b c
.
1 2 1 2 1 2
( ) ( ) 0P Q a a bb c c
.
Löu yù: Caùc tæ soá treân coù nghóa khi maãu khaùc 0.
Ví trò töông ñoái giöõa maët phaúng vaø maët caàu
Cho maët phaúng
( ): 0P ax by cz d
vaø maët caàu
()S
coù taâm
I
vaø baùn kính R.
Tröôøng hôïp 1:
,( )d I P R
()P
vaø
()S
khoâng coù ñieåm chung.
Tröôøng hôïp 2:
,( )d I P R
()P
vaø
()S
coù
Tröôøng hôïp 3:
,( )d I P R
()P
caét
()S
moät ñieåm chung. Khi ñoù ta noùi
()P
tieáp xuùc
()S
hoaëc
()P
laø tieáp dieän cuûa
( ).S
Ta coù:
()IM P
vôùi
M
laø tieáp ñieåm.
theo giao tuyeán laø moät ñöôøng troøn.
Ñöôøng troøn giao tuyeán coù taâm H (laø trung ñieåm
AB), baùn kính
22
r R IH
vôùi
,( ) .IH d I P
7. Phöông trình ñöôøng thaúng:
Ñöôøng thaúng
1 2 3
qua ( ; ; )
VTCP ( ; ; )
A A A
A x y z
d
u u u u
coù:
Vectô chæ phöông (VTCP) cuûa ñöôøng thaúng d laø
vectô khaùc
0
, coù giaù naèm treân d hoaëc song song vôùi d.
Phöông trình tham soá
1
2
3
:
A
A
A
x x u t
d y y u t
z z u t



vôùi
t laø tham soá.
Phöông trình chính taéc
1 2 3
:
A A A
x x y y z z
d
u u u

vôùi
1 2 3
. . 0u u u
.
Löu yù: Neáu coù caëp vectô khaùc
0
khoâng cuøng phöông sao cho
ad
bd
thì
d
coù VTCP laø:
,
d
u a b


.
7.1. Ví trò töông ñoái giöõa hai ñöôøng thaúng:
Xeùt vò trí töông ñoái cuûa hai ñöôøng thaúng vôùi
1
1
qua
VTCP
M
d
u
,
1
2
qua
VTCP
N
d
u
.
Böôùc I
Böôùc II
Keát luaän
Hai ñöôøng thaúng
song song hoaëc truøng nhau.
(Hai ñöôøng thaúng truøng nhau)
Hai ñöôøng thaúng
caét nhau hoaëc cheùo nhau.
caét
cheùo nhau
7.2. Ví trò töông ñoái giöõa ñöôøng thaúng vaø maët phaúng:
Xeùt vò trí töông ñoái giöõa ñöôøng thaúng vaø maët phaúng .
Böôùc I:
Böôùc II:Giaûi PT (*), ta gaëp
1 trong 3 tröôøng hôïp sau
Keát luaän
Thay phöông trình tham soá vaøo
PT (*) voâ nghieäm
12
,dd
12
,0uu
12
,dd
1
;0u MN
12
dd
1
;0u MN
12
dd
12
,0uu
12
,dd
12
, . 0u u MN
1
d
2
d
12
, . 0u u MN
12
&dd
01
02
03
:
x x u t
d y y u t
z z u t
( ) : 0P ax by cz d
d
()dP
phöông trình , ta ñöôïc PT (*):
PT (*) coù 1 nghieäm
0
0
0
xx
yy
zz
caét taïi ñieåm
coù toïa ñoä
0 0 0
( ; ; )x y z
.
PT (*) coù voâ soá nghieäm
7.3. Khoaûng caùch töø ñieåm ñeán ñöôøng thaúng:
Cho ñieåm
M
vaø ñöôøng thaúng
d
(coù
phöông trình tham soá hoaëc chính taéc).
Böôùc 1: Choïn ñieåm
Ad
vaø moät VTCP
d
u
.
Böôùc 2:
,
,
d
d
u AM
d M d
u


.
7.4. Goùc giöõa hai ñöôøng thaúng:
Cho hai ñöôøng thaúng
12
,dd
laàn löôït coù VTCP laø
12
,uu
.

Ta coù:
12
12
12
.
cos ,
.
uu
dd
uu
.
7.5. Goùc giöõa ñöôøng thaúng vaø maët phaúng:
Cho ñöôøng thaúng d coù VTCP
u
vaø maêt phaúng
()P
coù VTPT
n
.

Ta coù:
.
sin ,( )
.
un
dP
un
.
8. Hình chieáu vaø ñieåm ñoái xöùng:
Baøi toaùn
Phöông phaùp
Tìm hình chieáu
cuûa ñieåm treân
maët phaúng .
Goïi d laø ñöôøng thaúng
qua
()
A
P
Vieát pt tham
soá cuûa d vôùi VTCP cuûa d cuõøng laø VTPT cuûa (P).
Goïi
()H d P
. Thay pt tham soá cuûa d vaøo pt
mp (P) ta tìm ñöôïc toïa ñoä H.
Tìm ñieåm
ñoái xöùng vôùi qua
.
Ta coù H laø trung ñieåm
2
2
2
A H A
A H A
A H A
x x x
AA y y y
z z z


.
Tìm hình chieáu
cuûa ñieåm treân
ñöôøng thaúng d.
Caùch I
Goïi
()H theo t
(döïa vaøo pt tham soá cuûa d).
.0
d
AH d AH u

Tìm ñöôïc

Toïa ñoä H.
Caùch II
Goïi
qua
()
()
A
P
Pd
Vieát pt
mp( )P
.
Goïi
()H d P
. Thay pt tham soá cuûa
d vaøo pt mp (P) ta tìm ñöôïc toïa ñoä H.
Tìm ñieåm
ñoái xöùng vôùi qua
ñöôøng thaúng d.
Ta coù H laø trung ñieåm
2
2
2
A H A
A H A
A H A
x x x
AA y y y
z z z


.
Bieân soaïn: Hoaøng Xuaân Nhaøn
Email goùp yù: thayxuannhan@gmail.com
()P
0 1 0 2 0 3
( ) ( ) ( ) 0a x u t b y u t c z u t d
d
()P
()dP
A
()P
A
A
()P
A
.......t
A
A
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BAÛNG TOÙM TAÉT COÂNG THÖÙC TOAÙN 12
COÂNG THÖÙC LUÕY THÖØA
Cho caùc soá döông a, b vaø , m n  . Ta coù: n a a a a vôùi * n   n 0 a  1  . ...........  1 an thöøa soá n a m a   ( m )n mn   ( n)m a a am . n m n a a a    m na n a 1 n n n 2 aa   a am n n n  ( )n a b ab      m a a n bb  1 3 3  a a COÂNG THÖÙC LOGARIT Cho caùc soá ,
a b  0, a  1. Ta coù:  
log b    a b
 lg b  log b  log b
 ln b  log b a 10 e  log 1  0  log a 1  log b a b a a a 1 n  log b b  log n
b n log b  log n b b m log m loga a m a a a a m  log b b a ab
 log (bc)  log b  log c
 log    log b  log c   a a a a a ac  log c log b b a ac log c 1  log .
b log c  log c a  log c  log b a b a log b b a log a a b
HAØM SOÁ LUÕY THÖØA – MUÕ – LOGARIT HAØM LUÕY THÖØA HAØM SOÁ MUÕ HAØM SOÁ LOGARIT y log x a 0 y x xa vôùi .  y a a 0 Daïng: Daïng: vôùi u laø ña y log u a 1   Daïng: vôùi . y u u y a a 1 a
Ñaëc bieät: a e y lnx ; thöùc ñaïi soá.
Taäp xaùc ñònh: D . a 10 y logx lgx .  u . Ñaïo haøm:
Ñieàu kieän xaùc ñònh: 0
Taäp xaùc ñònh: Ñaïo haøm: x x y a y a lna . 1 y log x y Neáu ÑK u . u x y a y a ln . a u a xlna . u y log u y Neáu ÑK u 0. ( x e ) x e Ñaëc bieät: . a ulna ( u e ) u e . u 1 Neáu ÑK u 0. (ln ) x xÑaëc bieät: . Söï bieán thieân: x y a u (ln ) uÑaïo haøm:
Neáu a 1 thì haøm ñoàng bieán u
Söï bieán thieân: y log x a   1 y x 
y   x  treân . Neáu 0 a 1 thì
Neáu a 1 : haøm ñoàng bieán   1 y u 
y  u  . u haøm nghòch bieán treân . treân (0; ) . Neáu 0 a 1 :
haøm nghòch bieán treân (0; )
ÑOÀ THÒ HAØM MUÕ VAØ HAØM LOGARIT
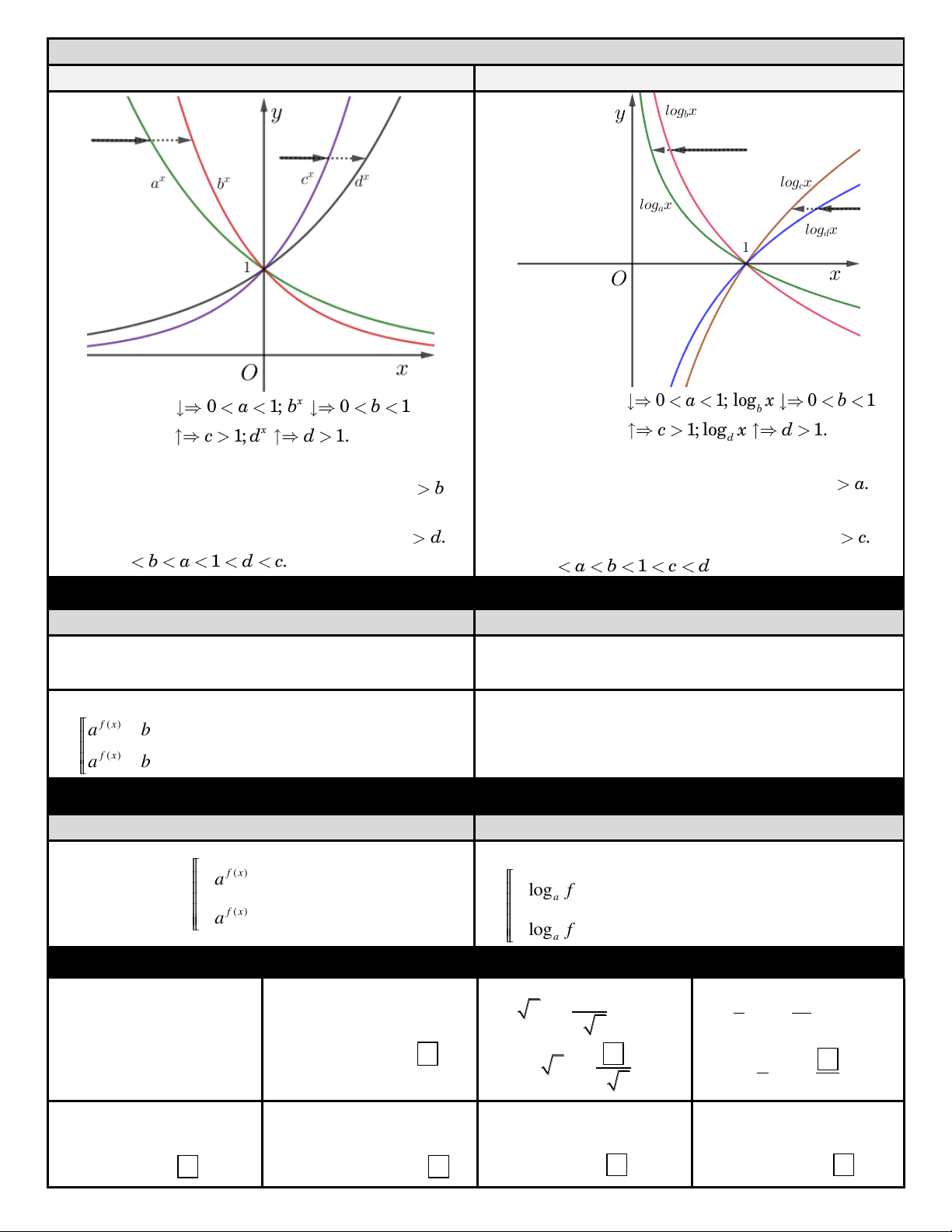
ÑOÀ THÒ HAØM SOÁ MUÕ
ÑOÀ THÒ HAØM SOÁ LOGARIT x x x a x b . Ta thaáy: a 0 a 1; b 0 b 1.  Ta thaáy: log 0 1; log 0 1 a bx x x c x d Ta thaáy: c c 1; d d 1.  Ta thaáy: log 1; log 1. c d
So saùnh a vôùi b: Ñöùng treân cao, baén muõi teân
So saùnh a vôùi b: Ñöùng treân cao, baén muõi teân
töø traùi sang phaûi, truùng x
a tröôùc neân a b.
töø phaûi sang traùi, truùng log x tröôùc: b . a b
So saùnh c vôùi d: Ñöùng treân cao, baén muõi teân
So saùnh c vôùi d: Ñöùng treân cao, baén muõi teân
töø traùi sang phaûi, truùng x
c tröôùc neân c . d
töø phaûi sang traùi, truùng log x tröôùc: d . c d  Vaäy 0 b a 1 d . c  Vaäy 0 a b 1 c d .
PHÖÔNG TRÌNH MUÕ VAØ LOGARIT Phöông trình muõ
Phöông trình Logarit  Daïng cô baûn:
 Daïng cô baûn: f (x) g ( x) aa
f (x)  g(x) log f ( ) x  log g( ) x f ( ) x g( ) x  0 a a  Daïng logarit hoùa: f ( x)     a
b f (x)  log b
Daïng muõ hoùa: log f (x) b f (x) b a a a
(khoâng caàn ñieàu kieän) f ( x) g ( x) ab
f (x)  g(x).log b a
BAÁT PHÖÔNG TRÌNH MUÕ VAØ LOGARIT
Baát Phöông trình muõ
Baát Phöông trình Logarit  Daïng cô baûn: a 1  f ( x) g ( x)  aa
f (x)  g(x) a 1   Daïng cô baûn:
 log f (x)  log g(x)  f (x)  g(x)  0 a a 0a 1  f ( x) g ( x)  aa
f (x)  g(x) 0a 1 
 log f (x)  log g(x)  0  f (x)  g(x) a a
COÂNG THÖÙC ÑAÏO HAØM     1  1        x  1     2 k  0  1
(x )   x 2 xx x
Vôùi k laø haèng soá   1  (
u )  u   . u     u    u  1 u       2 u 2  u u       x x ee   x x aa ln a
 sin x  cos x
 cos x  sin x       u u ee . u   u u aa .ln . a u 
sinu  u cosu 
cosu   u sinu 1 1    tan x 2  1 tan x  cot x     2 1 cot x 2  2 cos x sin x    u  u  tan u   u  2 1 tan u  cot u     u  2 1 cot u 2  2  cos u sin u
COÂNG THÖÙC NGUYEÂN HAØM
f (x)dx F(x)  C F (
x)  f (x) 
k. f (x)dx k f (x)dx  
   f (x)  g(x)dx f (x)dx g(x)dx   
kdx kx C
1) kdx kx C  
2dx  2x C   ( 3  )dx  3  x C   3 1  4 1 2)  x x 2 x dx   C   3 x dx   Cx 2 3    2 xdx x dx   C x C   1 4 3 / 2 3  1   ax b MR 1 ( )  11 11
(ax b) dx  .  C  1 (1 x) (1 x)  10      a  1 (1 2x) dx . C C  2  11 2  2 3) 1 1 1 MR 1 1
dx  ln x C  dx
ln ax b C    dx  ln 1 3x Cx ax b a 1 3x 3    4) 1 1 1 1 1 1 MR 1 1 1 dx    C  dx  .  C    dx  .  C    C  2 2 x x (ax b) a ax b 2 (2x  3) 2 2x  3 4x  6 3  1 1  x 1 5 5 x 1  1  x  2 x   10 dx
 ln x  10x C     4 dx x dx   ln x C     2  x x  3 x xx  5 5) x 1 x x MR axb 1   ax b
e dx e C  e dx eC    x x e dx eC e   Ca 1  x x x 6) a x x 9 x 5 x a dx   C   5 dx   C   2 3 dx  9 dx   C   ln a ln 5 ln 9    1 bxc a 2 x 5 2 x 5 MR bx c  a dx  .  Cx 1 3 3  2 5 3 dx  .  C   Cb ln a 2 ln 3 2 ln 3 x xx xx 1   x xx x 1 1 x 6   1  2    2 1 2  2 x 1   2 x e e dx e e dx e e C  1 2 .3 dx  2 .3 . dx  6 dx   C    2 3 3 3ln 6
7) sin xdx  cos x C     1     sin 4x
dx   cos 4x   C       2  4  2  MR 1
 sin(ax b)dx   cos(ax b)  Caa4; b 2 8)         
cos xdx  sin x C  1  cos  x dx  sin
x C  sin  x C         3  1   3   3  MR 1
 cos(ax b)dx  sin(ax b)  C     a a 1; b 3 1 1  1   2 sin xdx  
 1cos2xdx x sin2x C  
  3sin x 2cos xdx  3
 cos x  2sin x C 2 2  2  (haï baäc) 2 9) 1 1 2 cos x  1  dx     2
1 tan x dx  tan x C       2  dx 2 dx tan x 2x C     cos x 2 2 cos x  cos xMR 1 1  dx
tan ax b C  1 1 2   
cos ax b   a dx tan 3x C  2 cos 3x 3 MR 1 2    1   tan 
ax bdx  tanax bC   1 a  2 1   tan 
  2xdx  tan  2xC   2   a 2;  b    2 2 10) 1 x sin x 1  1  x dx     2
1 cot x dx   cot x C       2  dx x dx cot x C     sin x 2 2 sin x  sin x  2 MR 1 1  dx  
cot ax b C  1 1 2    
sin ax b   a dx cot 8x C  2 sin 8x 8 1 MR 1 2  1   cot 
ax bdx   cotax bC    2 1
  cot 3xdx   cot 3x C    a 3 2 2 1 sin x  cos x  1 1   dx dx  
dx  tan x  cot x C      2 2 2 2 2 2 sin x cos x sin x cos x
 cos x sin x
DIEÄN TÍCH VAØ THEÅ TÍCH
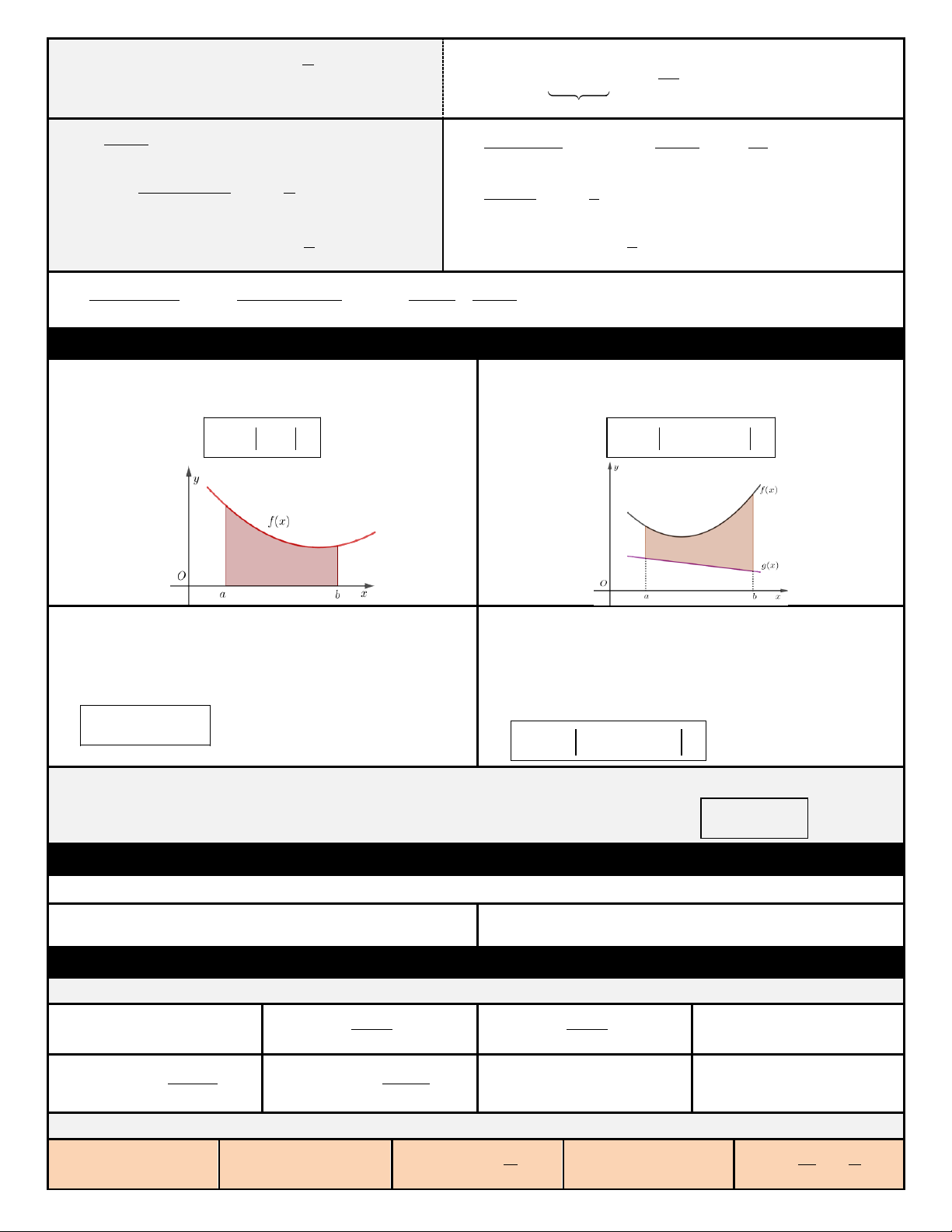
 Hình phaúng giôùi haïn bôûi caùc ñöôøng y f (x) ,
 Hình phaúng giôùi haïn bôûi caùc ñöôøng y f (x) ,
truïc Ox , x  ,
a x b thì coù dieän tích:
y g(x) , x  ,
a x b thì coù dieän tích: b b S f (x) dxS
f (x)  g(x) dxa a
y f (x) y f x   Khi xoay hình phaúng ( )  quanh Ox ,
 Khi xoay hình phaúng  y g(x) quanh Ox ,
x a, x b
x a, x b
ta ñöôïc khoái truï troøn coù theå tích 
ta ñöôïc khoái truï troøn coù theå tích b 2 V   f (x)dxb a 2 2 V  
f (x)  g (x) dxa
 Xeùt hình khoái ñöôïc giôùi haïn bôûi hai maët phaúng x  ,
a x b . Khi caét khoái naøy ta ñöôïc thieát dieän coù dieän tích b
S(x) (laø haøm lieân tuïc treân [a;b]). Theå tích khoái naøy treân  ;
a b laø: V S(x)dx  . a
COÂNG THÖÙC CHUYEÅN ÑOÄNG
Xeùt haøm quaûng ñöôøng S(t), haøm vaän toác v(t) vaø haøm gia toác a(t) . Ba haøm naøy seõ bieán thieân theo t .  S(t) 
v(t)dt v(t)  S (  t)   v(t) 
a(t)dt a(t)  v (  t) 
COÂNG THÖÙC LÖÔÏNG GIAÙC
1. Heä thöùc cô baûn: sin cos  2 2 sin   cos  1  tan   cot   tan.cot  1 cos sin 1 1 s
 in(  k2 )  sin
tan(  k )  tan  2 1 tan   1 cot       2  2 cos  2 sin 
cos(  k2 )  cos 
cot(  k )  cot  2. Cung lieân keát: Pi
Ñoái: vaø  
Buø: vaø  
Phuï: vaø  Khaùc pi: ;   Khaùc : ;  2 2 2             sin( )   sin sin   cos   sin(   )  sin sin( )  sin sin cos  2   2        cos(   )  cos
cos( )   cos cos   sin  
cos( )  cos cos   sin    2   2        tan(   )   tan
tan( )   tan tan   cot   tan( )  tan tan    cot    2   2        cot(   )   cot
cot( )   cot cot   tan   cot( )  cot cot    tan    2   2  Khaùc pi Khaùc pi chia 2 Cos Ñoái Sin Buø Phuï Cheùo Tang, Cotang Sin baïn cos
3. Coâng thöùc coäng:
 sin(a b)  sin .
a cos b  sin . b cos a
 cos(a b)  cos .
a cos b  sin . a sin b
 sin(a b)  sin .
a cos b  sin . b cos a
 cos(a b)  cos .
a cos b  sin . a sin b tan a  tan b a b tan(a b)  tan tan tan(a b)  1 tan . a tan b 1 tan . a tan b
4. Coâng thöùc nhaân ñoâi, nhaân ba: 2 2
cos 2  cos   sin  2 tan sin 2  2sin.cos tan 2  2 2
 2cos  1 1 2sin  2 1 tan  3    3 3 tan tan
sin 3  3sin  4sin  3
cos3  4cos   3cos tan 3  2 1 3 tan 
5. Coâng thöùc haï baäc 1 cos 2 1 cos 2 1 cos 2 2 sin    2 cos    2 tan   2 2 1 cos 2
6. Coâng thöùc bieán ñoåi toång thaønh tích: a b a b a b a b
cos a  cos b  2 cos .cos
cos a  cos b   2sin .sin 2 2 2 2 a b a b a b a b
sin a  sin b  2sin .cos
sin a  sin b  2 cos .sin 2 2 2 2 sin(a b) a b
tan a  tan b  sin( )
tan a  tan b  cos . a cos b cos . a cos b             sin  cos  2.sin    2.cos      
sin  cos  2 sin      2 cos    4   4   4   4 
7. Coâng thöùc bieán ñoåi tích thaønh toång: 1 1 1 cos .
a cos b  cos(a  )
b  cos(a  ) b  sin .
a sin b  cos(a  )
b  cos(a  ) b  sin .
a cos b  sin(a  )
b  sin(a  ) b  2 2 2
Cos.Cos thì Cos coäng coäng Cos tröø
Sin.Sin thì Cos tröø tröø Cos coäng
Sin.Cos thì Sin coäng coäng Sin tröø
PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
u v k2
u v k2
 sin u  sin v  (k  ) 
 cosu  cos v  k   
u    v k2 u v   k2 
sin u  1  u   k2 2
cos u  1  u k 2 
Ñaëc bieät: sin u  1
  u    k2 k  
Ñaëc bieät: cosu  1
  u    k2 k   2 
sin u  0  u k
cos u  0  u   k 2
 tan u  tan v u v k k  
 cot u  cot v u v k k  
TOÅ HÔÏP – XAÙC SUAÁT QUY TAÉC COÄNG QUY TAÉC NHAÂN
Neáu pheùp ñeám ñöôïc chia ra nhieàu tröôøng hôïp,
Neáu pheùp ñeám ñöôïc chia ra laøm nhieàu giai ñoaïn
ta seõ coäng caùc keát quaû laïi.
baét buoäc, ta seõ nhaân caùc keát quaû cuûa moãi giai ñoaïn aáy. HOAÙN VÒ CHÆNH HÔÏP TOÅ HÔÏP
 Choïn k phaàn töû töø n phaàn töû  Choïn k phaàn töû töø n phaàn töû
 Saép xeáp (ñoåi choã) cuûa n phaàn
(khoâng saép xeáp thöù töï), ta coù
(coù saép xeáp thöù töï), ta ñöôïc soá
töû khaùc nhau, ta coù soá caùch
soá caùch choïn laø k C . caùch choïn laø k A . n n
xeáp laø P n! vôùi n . n n n k ! k !     Caùch tính: C  Caùch tính: A Caùch tính: n
n k!k! nn k!
n!  1.2.....n   1 n . , n k , n k
 Quy öôùc soác: 0! 1. vôùi . vôùi . 0 k n 0 k n n XCoâng thöùc: ( ) P( X )   Tính chaát: n()
0  P( X )  1 . Trong ñoù: soá phaàn töû cuûa XAÙC SUAÁT ( n X ) : taäp bieán coá P( )   0; P( )  1 . X ; n( )  :soá phaàn töû
khoâng gian maãu . P(X ) laø xaùc suaát
P( X )  1 P( X ) vôùi X laø bieán coá ñoái cuûa X .
ñeå bieán coá X xaûy ra vôùi X   .
KHAI TRIEÅN NHÒ THÖÙC NEWTÔN n     a b 0 n 1 n 1 2 n 2 2 n 1 n 1
C a C a b C a b ......... n n
C ab C b . n n n n n
Khai trieån daïng lieät keâ: n nnn n       (*). Ñaëc bieät:x 0 1 2 2 1 1 1 C C x C x .........C x C x n n n n n
Trong caùc coâng thöùc beân, Heä quaû 1: 0 1 2 n 1
C C C  ......... n C
C  2n (töùc laø thay x 1 vaøo (*)). n n n n n
ta luoân coù n , n  2. Heä quaû 2: Vôùi n chaün, chæ caàn thay x  1  vaøo (*), ta coù: 0 1 2 n 1  n 0 2 4 n 1 3 n 1 C C C ......... C C 0 C C C ...... C C C ......C               n n n n n n n n n n n n nn  
Khai trieån: a bk n k k
 C a b . Soá haïng toång quaùt: k n k k TC a b
Khai trieån toång quaùt: n k 1  n k 0
 Phaân bieät heä soá vaø soá haïng: k C ( 1)k n k k a b . x .
Trong caùc coâng thöùc beân, n ta luoân coù HEÄ SOÁ
n  , n  2. SOÁ HAÏNG
Nhôù raèng soá haïng khoâng chöùa x öùng vôùi 0.
CAÁP SOÁ COÄNG – CAÁP SOÁ NHAÂN CAÁP SOÁ COÄNG CAÁP SOÁ NHAÂN 1. Ñònh nghóa: 1. Ñònh nghóa:
 Daõy soá u ñöôïc goïi laø caáp soá coäng khi vaø  Daõy soá u ñöôïc goïi laø caáp soá nhaân khi vaø n n  chæ khi u
u d vôùi * n  . chæ khi u
u .q vôùi * n  . n 1  n n 1  n
Caáp soá coäng nhö treân coù soá haïng ñaàu u ,
Caáp soá nhaân nhö treân coù soá haïng ñaàu u , 1 1 coâng sai d.
coâng boäi q .
2. Soá haïng toång quaùt:
2. Soá haïng toång quaùt:
u u  (n 1)d vôùi * n  . n 1  1 u u . n q   vôùi * n  . n 1
3. Tính chaát caùc soá haïng:
3. Tính chaát caùc soá haïng: u
u  2u vôùi k vaø k 2. k 1  k 1  k vôùi  2 u .u u k vaø k 2. k 1  k 1  k
4. Toång n soá haïng ñaàu tieân:
4. Toång n soá haïng ñaàu tieân:
(u u )n  1
S u u  ... nu  . u (1 nq ) n 1 2 n 2  1
S u u  ...  u
vôùi q  1. n 1 2 n 1 q
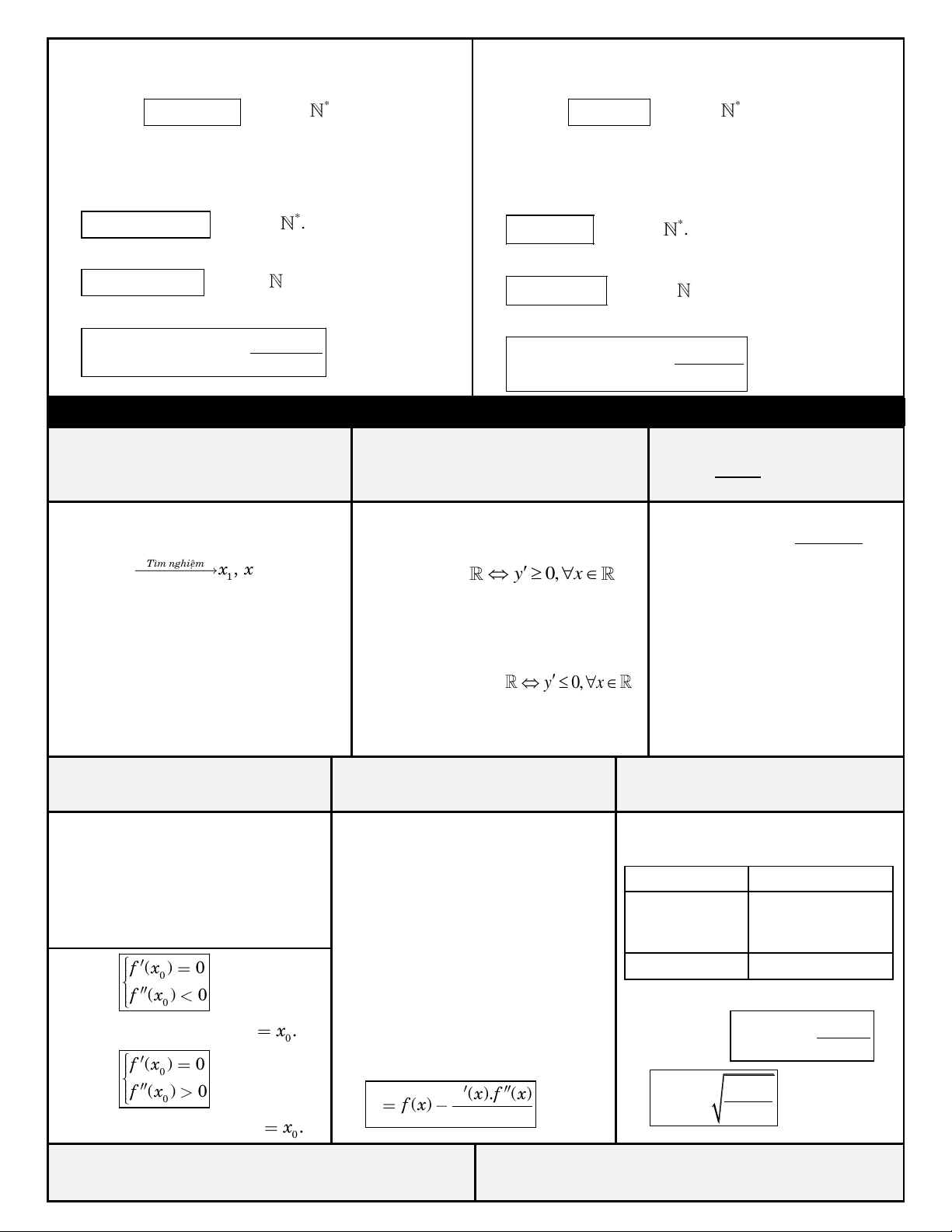
KHAÛO SAÙT HAØM SOÁ & BAØI TOAÙN LIEÂN QUAN HAØM BAÄC BA HAØM NHAÁT BIEÁN
XEÙT TÍNH ÑÔN ÑIEÄU ax b 3 2
y ax bx cx d (a  0) y
(ad bc  0) cx d
Böôùc 1: Tìm taäp xaùc ñònh D .   Ñaïo haøm 2
y  3ax  2bx c .   ad bc
Böôùc 2: Tính y  f (  x) ; cho     .
Haøm soá ñoàng bieán treân taäp Ñaïo haøm y 2 (cx d )
y  0 Tìm nghieäm x , x ... 1 2
xaùc ñònhy  0, x    
Haøm soá ñoàng bieán treân
Böôùc 3: Laäp baûng bieán thieân. a  0
(Neân choïn giaù trò x ñaïi dieän cho   .
töøng khoaûng xaùc ñònh   0
töøng khoaûng thay vaøo y ñeå tìm
ad bc  0.  daáu cuûa
Haøm soá nghòch bieán treân
y treân khoaûng ñoù).taäp xaùc ñònh
Haøm soá nghòch bieán y  0, x  
Böôùc 4: Döïa vaøo baûng bieán
treân töøng khoaûng xaùc
thieân ñeå keát luaän veà söï ñoàng a  0   .
ñònh ad bc  0.
bieán, nghòch bieán cuûa haøm soá.   0
CÖÏC TRÒ HAØM BAÄC BA
CÖÏC TRÒ HAØM BAÄC BOÁN
ÑIEÀU KIEÄN CÖÏC TRÒ 3 2
y ax bx cx d (a  0) 4 2
y ax bx c (a  0)
 Haøm soá coù ñieåm cöïc trò laø        .  Ñaïo haøm 3 y 4ax 2bx .   Ñaïo haøm 2 y 3ax 2bx c y (  x )  0
 Ñieàu kieän cöïc trò (x ; y ) 0   .
 Haøm soá coù hai cöïc trò 0 0
y(x )  yBa cöïc trò ab  0 0 0 a  0
(giaû thieát laø haøm soá lieân tuïc   (*) .   ab  0  0 taïi  Moät cöïc trò x ). y 2 2    0 a b 0
 Ñeå tìm ñieàu kieän cho haøm soá f (x ) 0
khoâng coù cöïc trò: Böôùc 1: Coù cöïc trò 2 2 a b  0  Neáu 0 thì haøm soá f (x ) 0
laøm theo coâng thöùc (*).  Cho , A ,
B C laø ba ñieåm cöïc 0
Böôùc 2: phuû ñònh keát quaû. 3 b  8a f ( )
x ñaït cöïc ñaïi taïi x x . 0  trò, ta coù: 
Phöông trình ñöôøng thaúng ñi cos BAC 3 b  8a f (x ) 0 qua hai ñieåm cöïc trò:  Neáu 0 thì haøm soá f (x ) 0 0 f ( ) x .f ( ) x 5 b y f ( ) x S  . 18a ABC  3 32  a f ( )
x ñaït cöïc tieåu taïi x x . 0
TÌM MAX-MIN TREÂN ÑOAÏN
TÌM MAX-MIN TREN KHOAÛNG
Tìm Max-Min cuûa f (x) treân ñoaïn  ; a b
Tìm Max-Min cuûa f (x) treân khoaûng ( ; a ) b y f x .   Böôùc 1: Tính ( )
Böôùc 1: Tính y f ( ) x . Tìm caùc nghieäm x ( ; a ) b khi cho f ( ) x 0 . Tìm caùc nghieäm x ( ; a ) b khi cho f ( ) x 0 . i i y y. (Neáu thay 
Böôùc 2: Caàn tính lim , lim ( ; a ) b
Böôùc 2: Tính caùc giaù trò f ( ) a , f ( )
b vaø f (x ),... i x a x b (neáu coù). baèng ( ;   )
 thì ta tính theâm lim y ). x
Böôùc 3: So sanh taát caû giaù trò trong böôùc 2 ñeå
Böôùc 3: Laäp baûng bieán thieân vaø suy ra giaù trò
keát luaän veà giaù trò lôùn nhaát, nhoû nhaát.
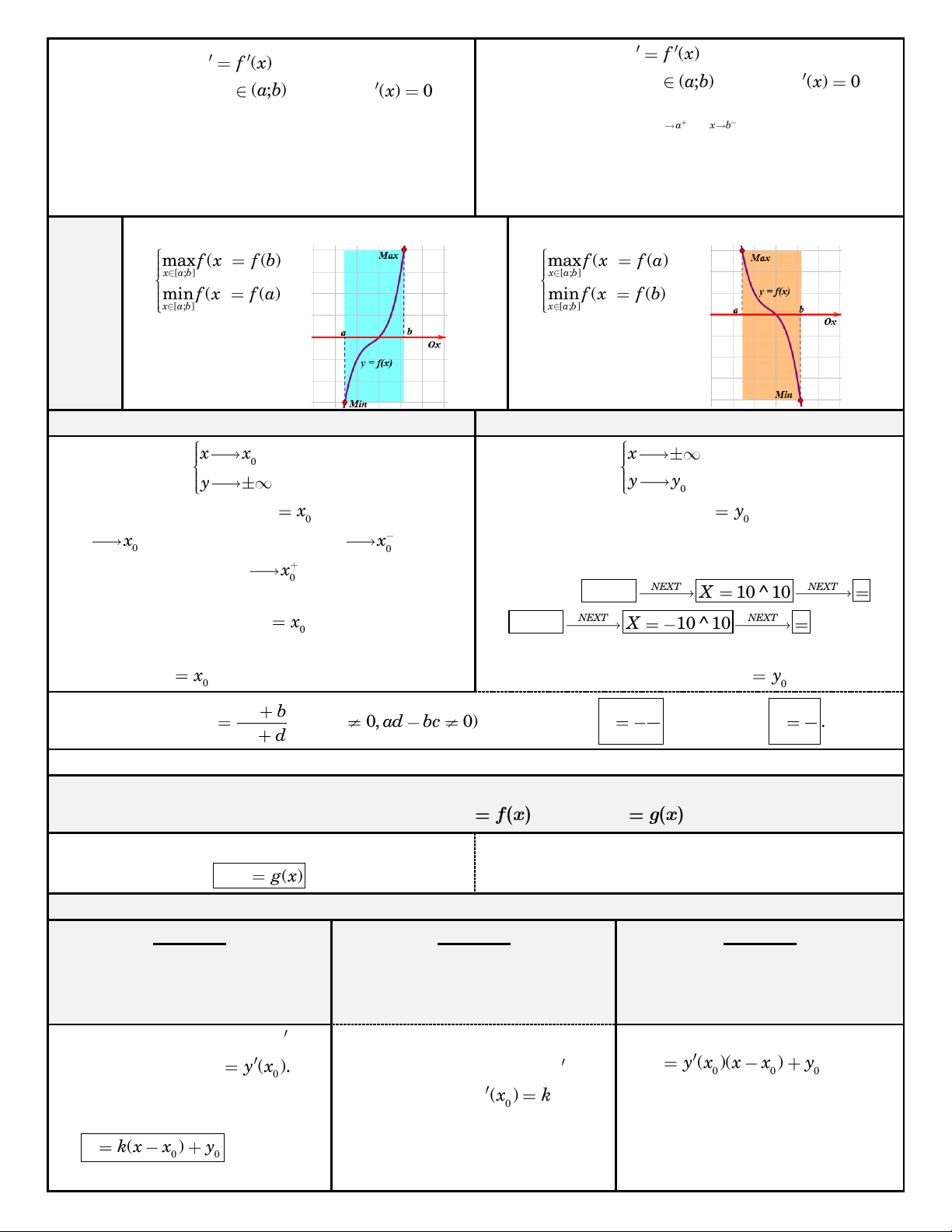
lôùn nhaát, nhoû nhaát treân khoaûng.  Neáu haøm f ( )
x ñoàng bieán treân [ ; a ] b thì  Neáu haøm f ( )
x nghòch bieán treân [ ; a ] b thì maxf ( ) x f ( ) b maxf ( ) x f ( ) a x [a;b] x [a;b] ÑAËC min f ( ) x f ( ) a min f ( ) x f ( ) b x [a;b] x [a;b] BIEÄT TIEÄM CAÄN ÑÖÙNG TIEÄM CAÄN NGANG x x xÑònh nghóa: 0
(x höõu haïn, y voâ haïn),  Ñònh nghóa:
(x voâ haïn, y höõu haïn), y y y0
ta coù tieäm caän ñöùng x
x . Löu yù: ñieàu kieän
ta coù tieäm caän ngang y y . 0 0 x
x coù theå ñöôïc thay baèng x x (giôùi  0 0
Caùch tìm TCN: Ñôn giaûn nhaát laø duøng CASIO
haïn beân traùi) hoaëc x
x (giôùi haïn beân
Böôùc 1: Nhaäp haøm soá vaøo maùy. 0 phaûi). Böôùc 2: NEXT 10 ^10 NEXT CALC X
Caùch tìm TCÑ: Neáu x
x laø moät nghieäm NEXT 10 ^10 NEXT CALC X 0
cuûa maãu soá maø khoâng phaûi laø nghieäm cuûa
Böôùc 3: Neáu keát quaû thu ñöôïc laø höõu haïn (töùc
töû soá thì x
x chính laø moät TCÑ cuûa ñoà thò.
laø y ) thì ta keát luaän TCN: y y . 0 0 0 a  Ñoà thò haøm soá ax b y vôùi (c 0, ad bc 0) coù moät TCÑ: d x , moät TCN: y . cx d c c
Neân nhôù, ñoà thò coù theå coù nhieàu tieäm caän ñöùng, nhöng chæ coù toái ña laø 2 tieäm caän ngang.
TÌM TOÏA ÑOÄ GIAO ÑIEÅM HOAËC SOÁ GIAO ÑIEÅM HAI ÑOÀ THÒ
Xeùt hai ñoà thò(C ) : y
f (x) vaø(C ) : y
g(x). 1 2
Böôùc 1 : Laäp phöông trình hoaønh ñoä giao ñieåm
Böôùc 2 : Giaûi phöông trình (*) ñeå tìm caùc
cuûa (C ) &(C ) : f ( ) x g( ) x . (*)
nghieäm x , x ,... (neáu coù), suy ra y , y ... 1 2 1 2 1 2
PHÖÔNG TRÌNH TIEÁP TUYEÁN DAÏNG 1 DAÏNG 2 DAÏNG 3
Vieát phöông trình tieáp tuyeán
Vieát phöông trình tieáp tuyeán cuûa Vieát phöông trình tieáp tuyeán cuûa
cuûa ñoà thò (C) : y f (x) taïi
ñoà thò (C) : y f (x) bieát tieáp
ñoà thò (C) : y f (x) bieát tieáp
ñieåm M (x ; y )(C)
tuyeán coù heä soá goùc k. tuyeán ñi qua ( A x ; y ) . 0 0 A A
Böôùc 1: Tính ñaïo haøm y , töø
Böôùc 1: Goïi M(x ; y ) laø tieáp  0 0
Böôùc 1: Tieáp tuyeán coù daïng :
ñoù coù heä soá goùc k y (x ).
ñieåm vaø tính ñaïo haøm y . y
y (x )(x x ) y (*) vôùi 0 0 0 0
Böôùc 2 : Vieát phöông trình
Böôùc 2: Cho y (x ) k , töø ñoù
y f (x ). 0 0 0
tieáp tuyeán cuûa ñoà thò daïng
tìm ñöôïc tieáp ñieåm (x ; y ).
Böôùc 2: Thay toïa ñoä ñieåm A 0 0 y ( k x x ) y .
vaøo (*) ñeå tìm ñöôïc x . 0 0
Böôùc 3: Vieát phöông trình 0 tieáp tuyeán :
Böôùc 3: Thay x tìm ñöôïc vaøo 0 y ( k x x ) y .
(*) ñeå vieát phöông trình tieáp 0 0 tuyeán.
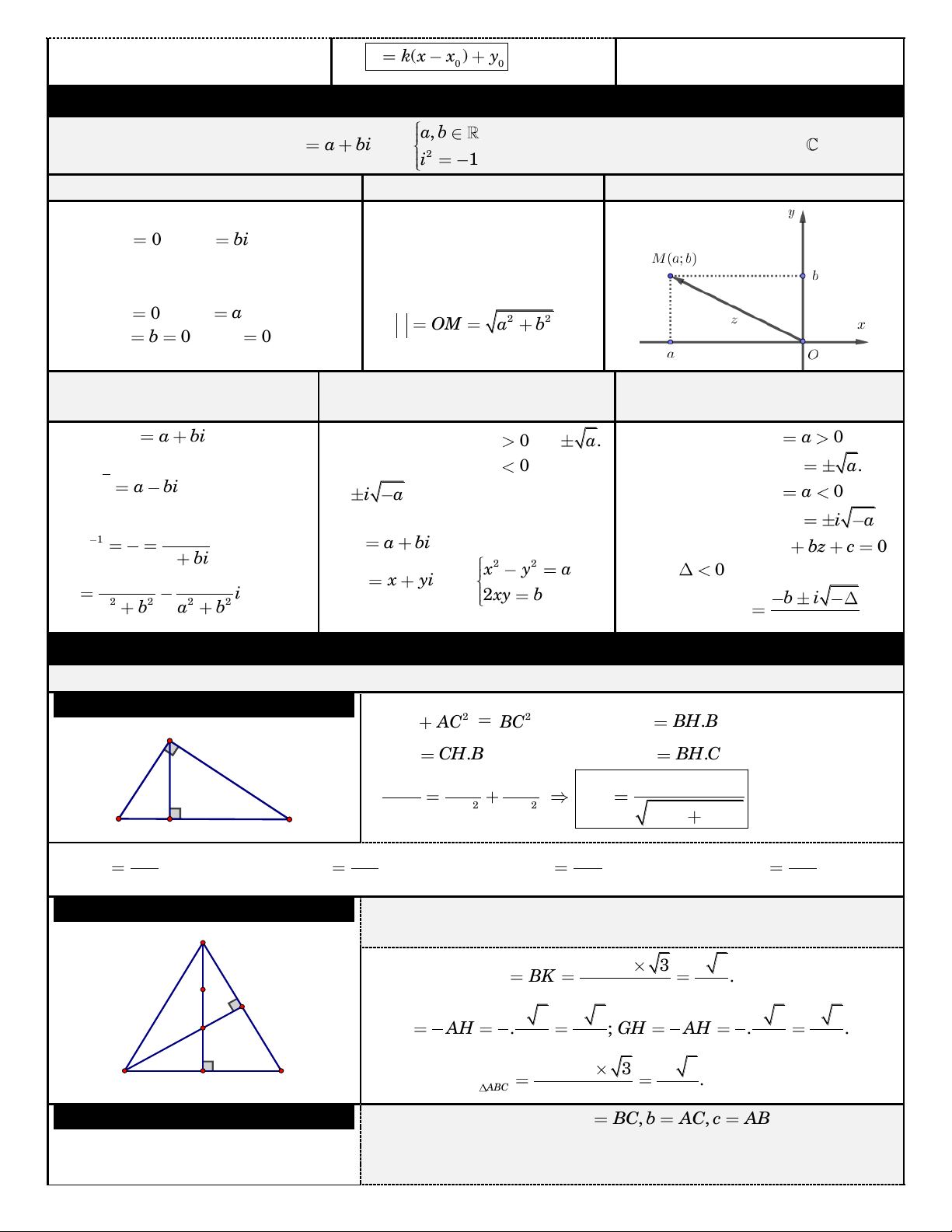
SOÁ PHÖÙC VAØ CAÙC YEÁU TOÁ LIEÂN QUAN , a b
Soá phöùc coù daïng: z a bi vôùi
(i: laø ñôn vò aûo). Kyù hieäu taäp soá phöùc: . 2 i 1 Thaønh phaàn Hình hoïc Minh hoïa
Phaàn thöïc: a. Neáu a 0 thì z
bi ñöôïc goïi laø  Ñieåm M( ; a ) b bieåu dieãn soá thuaàn aûo.
cho z treân heä truïc Ox . y
Phaàn aûo: b.Moâ-ñun: Neáu b 0 thì z
a laø soá thöïc. 2 2 z OM a b .  Khi a b 0 thì z 0 vöøa laø soá
thuaàn aûo vöøa laø soá thöïc.
Soá phöùc lieân hôïp – Soá phöùc Caên baäc hai
Phöông trình baäc hai nghòch ñaûo Cho z a bi . Khi ñoù:
 Caên baäc hai cuûa a 0 laø
a.  Phöông trình 2 z a 0 coù
Soá phöùc lieân hôïp cuûa noù
 Caên baäc hai cuûa a 0 laø hai nghieäm phöùc z a. laø z a bi . i a .  Phöông trình 2 z a 0 coù
Soá phöùc nghòch ñaûo laø
 Caên baäc hai cuûa soá phöùc hai nghieäm phöùc z i a . 1 1 1 z z
a bi laø hai soá phöùc daïng  az bz c z a bi Phöông trình 2 0 2 2 x y a vôùi 0 seõ coù hai nghieäm a b w x yi vôùi . i . 2xy b 2 2 2 2 a b a b b i phöùc laø: z . 1,2 2a
KHOÁI ÑA DIEÄN VAØ THEÅ TÍCH CUÛA CHUÙNG
I. MOÄT SOÁ HÌNH PHAÚNG CÔ BAÛN: 1. Tam giaùc vuoâng: Pitago ▪ 2 2 2 2 AB AC BC ▪ AB B . H BC A ▪ 2 2 AC C . H BC ▪ AH B . H CH 1 1 1 AB.AC ▪ AH 2 2 2 AH AB AC 2 2 AB AC B C H AC AB AC AB ▪ sin B (ñoái/huyeàn) ▪ B (keà/huyeàn) ▪ B (ñoái/keà) ▪ B BC cos BC tan AB cot AC (keà/ñoái) 2. Tam giaùc ñeàu:
Giaû söû tam giaùc ABC ñeàu coù caïnh ; a troïng taâm ; G caùc ñöôøng A
cao (truøng vôùi trung tuyeán) goàm AH , BK. (caïn ) h 3 a 3 a ▪ Ñöôøng cao: AH BK . 2 2 a K 2 2 a 3 a 3 1 1 a 3 a 3 ▪ AG AH . ; GH AH . . G 3 3 2 3 3 3 2 6 2 2 C (caïn ) h 3 a 3 B H a ▪ Dieän tích: S . ABC 4 4
3. Tam giaùc thöôøng:
Giaû söû tam giaùc ABC coù a B , C b A , C c AB ; caùc ñöôøng
cao h , h , h laàn löôït öùng vôùi caïnh , a , b . c Kyù hieäu , R r laàn löôït a b c
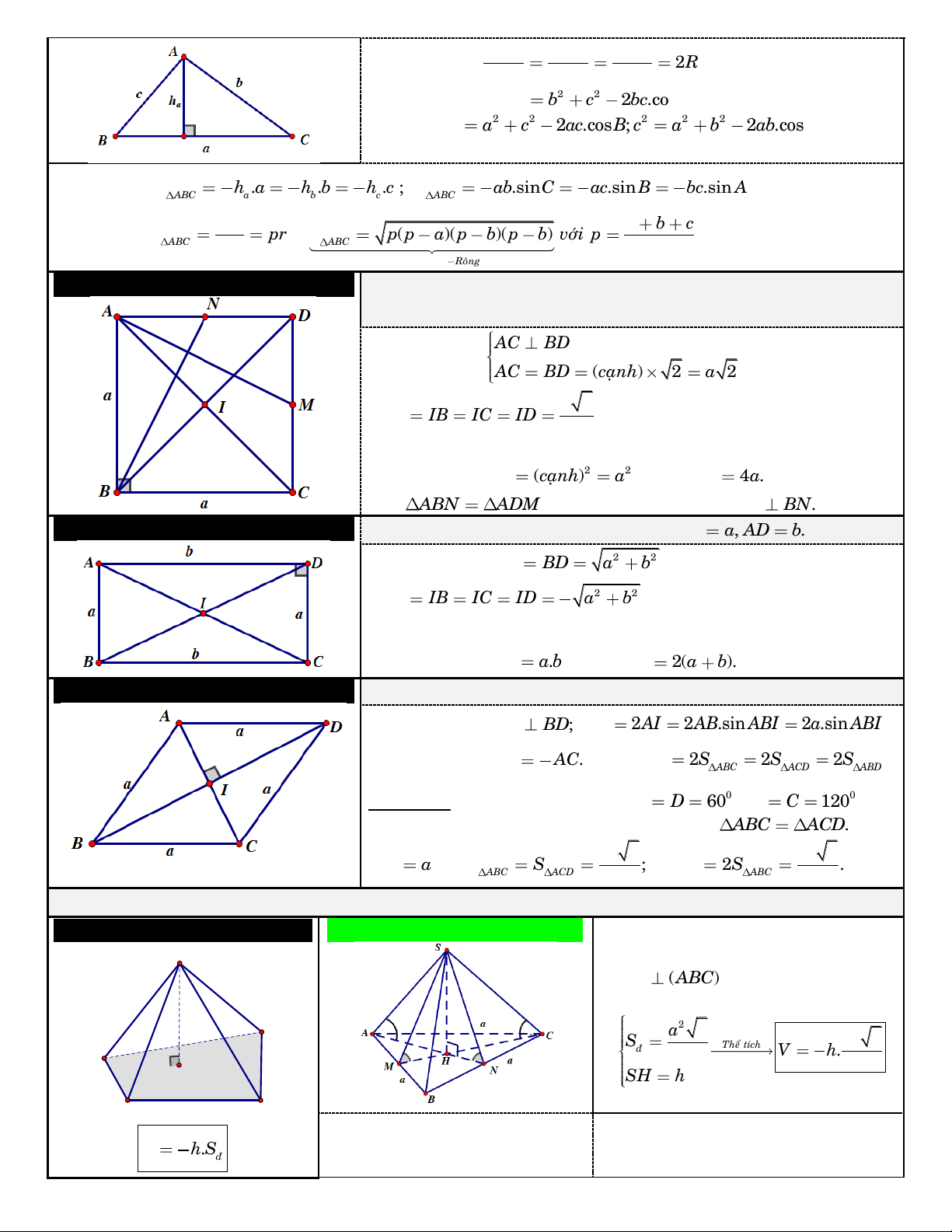
laø baùn kính ñöôøng troøn ngoaïi tieáp, noäi tieáp ∆. a b c ▪ Ñònh lí Sin: 2R. sin A sinB sinC ▪ Ñònh lí Coâ-sin: 2 2 2 a b c 2b . c cos A ; 2 2 2 2 2 2 b a c 2a . c cos ; B c a b 2a . b cos . C ▪ Dieän tích: 1 1 1 S h .a h .b h .c ; 1 1 1 S a . b sinC a . c sinB b . c sin A ; ABC 2 a 2 b 2 c ABC 2 2 2 abc S pr ; a b c S ( p p ) a (p ) b (p ) b vôùi p (nöûa chu vi). ABC 4R ABC 2
Coâng thöùc Heâ Roâng 4. Hình vuoâng:
Cho hình vuoâng ABCD coù caïnh ;
a hai ñieåm M, N laàn löôït laø trung ñieåm cuûa C , D A ;
D I laø taâm hình vuoâng. AC BD ▪ Ñöôøng cheùo: . AC BD (caïn ) h 2 a 2 a 2 IA IB IC ID
neân I laø taâm ñöôøng troøn ñi qua 2 boán ñænh hình vuoâng. ▪ Dieän tích: 2 2 S (caïn ) h a ; chu vi: p 4 . a ABCD ▪ Vì ABN
ADM , ta chöùng minh ñöôïc: AM BN.
5. Hình chöõ nhaät:
Cho hình chöõ nhaät ABCD taâm I coù AB , a AD . b ▪ Ñöôøng cheùo: 2 2 AC BD a b . 1 2 2 IA IB IC ID a
b neân I laø taâm ñöôøng troøn ñi 2 qua boán ñieåm , A , B , C . D ▪ Dieän tích: S .
a b ; chu vi: p 2(a ) b . ABCD 6. Hình thoi:
Cho hình thoi ABCD coù taâm I, caïnh baèng . a
▪ Ñöôøng cheùo: AC B ; D AC 2AI 2A . B sin ABI 2 . a sin ABI. ▪ Dieän tích: 1 S A . C BD ; S 2S 2S 2S . ABCD 2 ABCD ABC ACD ABD
Ñaëc bieät: Neáu hình thoi coù goùc 0 B D 60 ( 0 A C 120 ) thì
ta chia hình thoi ra laøm hai tam giaùc ñeàu: ABC AC . D 2 a 3 2 a 3 AC a vaø S S ; S 2S . ABC ACD 4 ABCD ABC 2
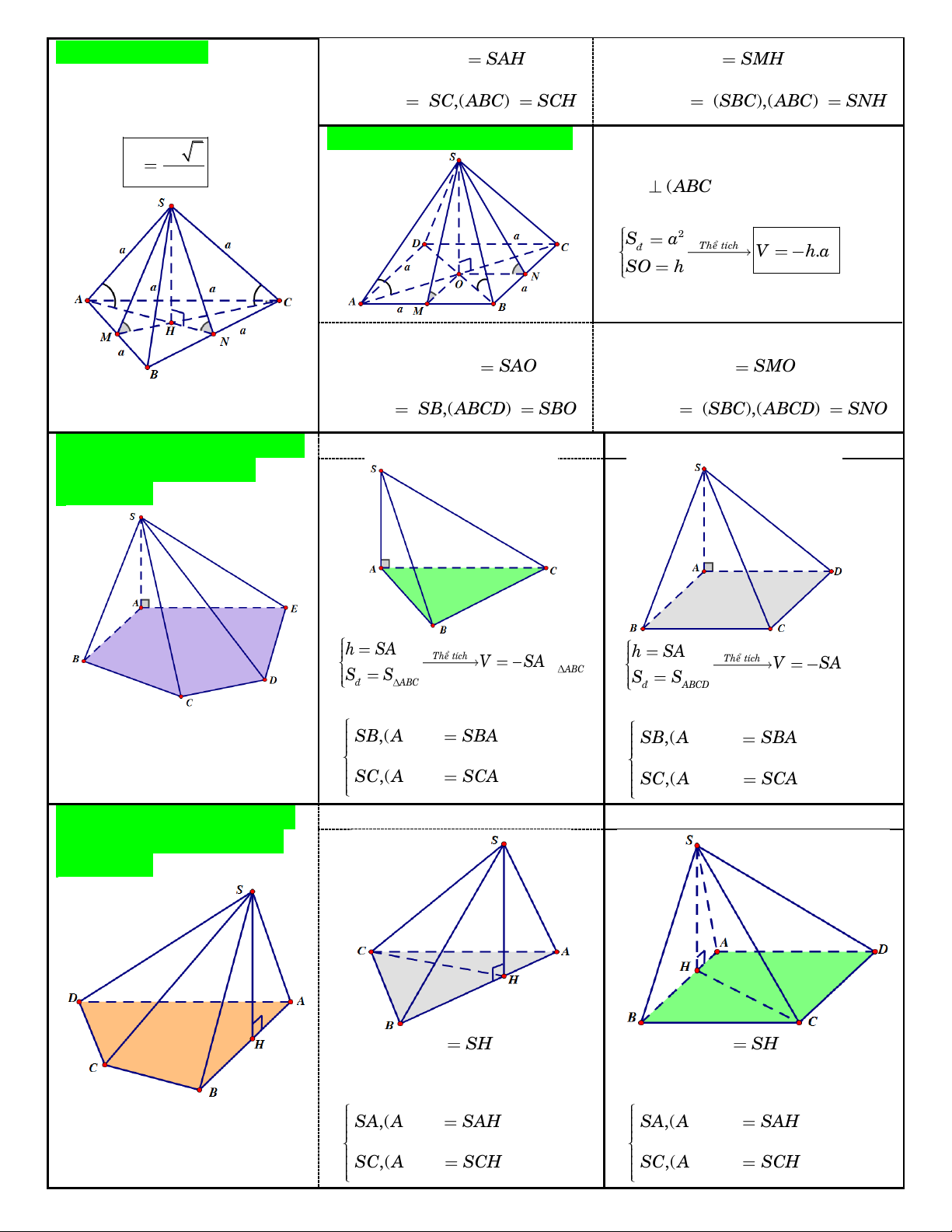
II. THEÅ TÍCH KHOÁI CHOÙP: 7. Hình choùp:
7.1. Hình choùp tam giaùc ñeàu ▪ Taát caû caïnh beân baèng nhau. S
▪ Ñaùy laø tam giaùc ñeàu caïnh . a ▪ SH (AB )
C vôùi H laø troïng taâm ∆ AB . C h 2 D a 3 2 S Theå tích 1 a 3 ▪ ñ V . A 4 h H 3 4 SH h Sđ B C 1
Goùc giöõa caïnh beân vaø maët Goùc giöõa maët beân vaø maët ñaùy: V . h S 3 ñ
7.2. Töù dieän ñeàu: ñaùy: S , A (AB ) C SAH (SA ) B ,(AB ) C SMH
▪ Ñaây cuõng laø hình choùp tam
giaùc ñeàu, ñaëc bieät laø caïnh S , C (AB ) C SCH . (SB ) C ,(AB ) C SNH .
beân baèng caïnh ñaùy. Theå
7.3. Hình choùp töù giaùc ñeàu:
▪ Taát caû caïnh beân baèng nhau. 3 tích: a 2 V .
▪ Ñaùy laø hình vuoâng caïnh . a 12 ▪ SO (ABC )
D vôùi O laø taâm hình vuoâng ABC . D 2 S a ñ Theå tích 1 ▪ 2 V . h a . SO h 3
Goùc giöõa caïnh beân vaø maët Goùc giöõa maët beân vaø maët ñaùy: ñaùy: S , A (ABC ) D SAO (SA ) B ,(ABC ) D SMO S , B (ABC ) D SBO . (SB ) C ,(ABC ) D SNO .
7.4. Hình choùp coù caïnh beân Ñaùy laø tam giaùc
Ñaùy laø töù giaùc ñaëc bieät
SA vuoâng goùc vôùi maët phaúng ñaùy. h SA Theå tích 1 h SA Theå tích 1 ▪ V S . A S . V S . A S . S S 3 ABC ▪ S S 3 ABCD ñ ABC ñ ABCD
▪ Goùc giöõa caïnh beân vaø maët ñaùy:
▪ Goùc giöõa caïnh beân vaø maët ñaùy: , SB (ABC) SBA , SB (ABC ) D SBA . . , SC (ABC) SCA , SC (ABC ) D SCA
7.5. Hình choùp coù maët beân Ñaùy laø tam giaùc
Ñaùy laø töù giaùc ñaëc bieät
(SAB) vuoâng goùc vôùi maët phaúng ñaùy. ▪ Ñöôøng cao h SH cuõng laø ▪ Ñöôøng cao h SH cuõng laø
ñöôøng cao cuûa ∆SAB.
ñöôøng cao cuûa ∆SAB.
▪ Goùc giöõa caïnh beân vaø maët ñaùy: ▪ Goùc giöõa caïnh beân vaø maët ñaùy: , SA (ABC) SAH , SA (ABC ) D SAH . . , SC (ABC) SCH , SC (ABC ) D SCH
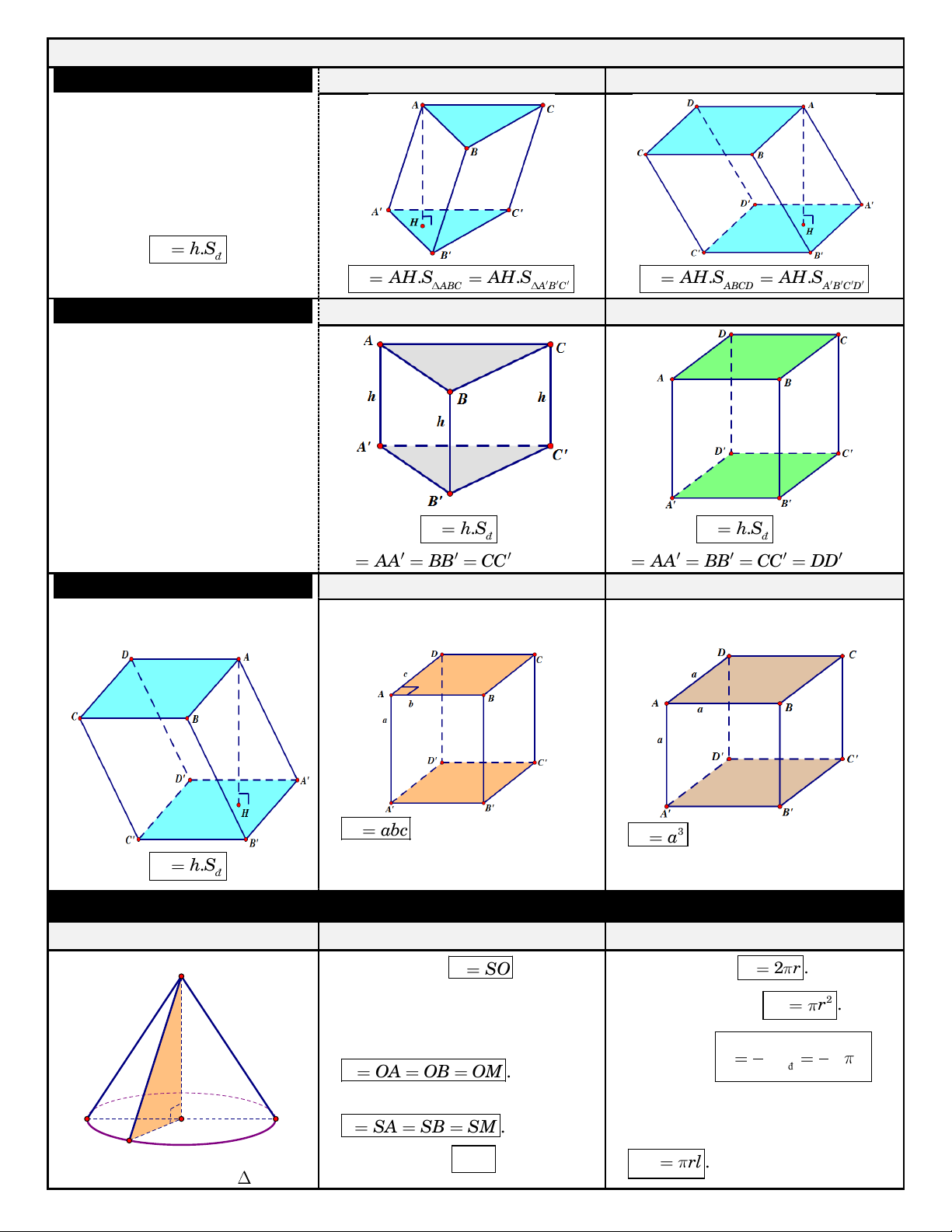
III. THEÅ TÍCH KHOÁI LAÊNG TRUÏ:
1. Hình laêng truï thöôøng: Ñaùy laø tam giaùc
Ñaùy laø töù giaùc
 Hai ñaùy laø hai hình gioáng
nhau vaø naèm trong hai maët phaúng song song.
 Caùc caïnh beân song song vaø
baèng nhau. Caùc maët beân laø caùc hình bình haønh.  Theå tích: V . h S . ñ V AH.S AH.S V AH.S AH.S ABC A B C ABCD A B C D
2. Hình laêng truï ñöùng: Ñaùy laø tam giaùc
Ñaùy laø töù giaùc
 Caùc caïnh beân cuøng vuoâng goùc
vôùi hai maët ñaùy neân moãi
caïnh beân cuõng laø ñöôøng cao cuûa laêng truï.
Laêng truï tam giaùc ñeàu:
Laø laêng truï ñöùng vaø coù hai
ñaùy laø hai tam giaùc ñeàu baèng nhau.  Theå tích: V . h S vôùi Theå tích: V . h S vôùi ñ ñ h AA BB CC . h AA BB CC DD . 3. Hình hoäp:
3.1 Hình hoäp chöõ nhaät:
3.2. Hình laäp phöông:
 Laø laêng truï coù taát caû caùc maët  Laø laêng truï ñöùng coù ñaùy laø
 Laø hình hoäp chöõ nhaät coù taát caû laø hình bình haønh. hình chöõ nhaät. caùc caïnh baèng nhau. a b c laø ba kích  V abc vôùi , ,  3 V
a vôùi a laø caïnh cuûa hình
thöôùc khaùc nhau cuûa hình hoäp  Theå tích: V . h S . laäp phöông. ñ chöõ nhaät.
MAËT TRUÏ – MAËT NOÙN – MAËT CAÀU MAËT NOÙN
Caùc yeáu toá maët noùn:
Moät soá coâng thöùc: S
Ñöôøng cao: h SO . ( SO
Chu vi ñaùy: p 2 r .
cuõng ñöôïc goïi laø truïc cuûa hình  Dieän tích ñaùy: 2 S r . noùn). đ l
Baùn kính ñaùy: 1 1 hTheå tích: 2 l V h.S h. r . l r OA OB OM . đ 3 3  Ñöôøng sinh:
(lieân töôûng khoái choùp). A B r O l SA SB SM .
Dieän tích xung quanh: M
Goùc ôû ñænh: ASB . S rl . Hình thaønh: Quay vuoâng xq
SOM quanh truïc SO , ta ñöôïc  Thieát dieän qua truïc: SAB
Dieän tích toaøn phaàn:
maët noùn nhö hình beân vôùi: caân taïi . S 2 S S S rl r . h SO tp xq đ .
Goùc giöõa ñöôøng sinh vaø maët r OM ñaùy: SAO SBO SMO . MAËT TRUÏ
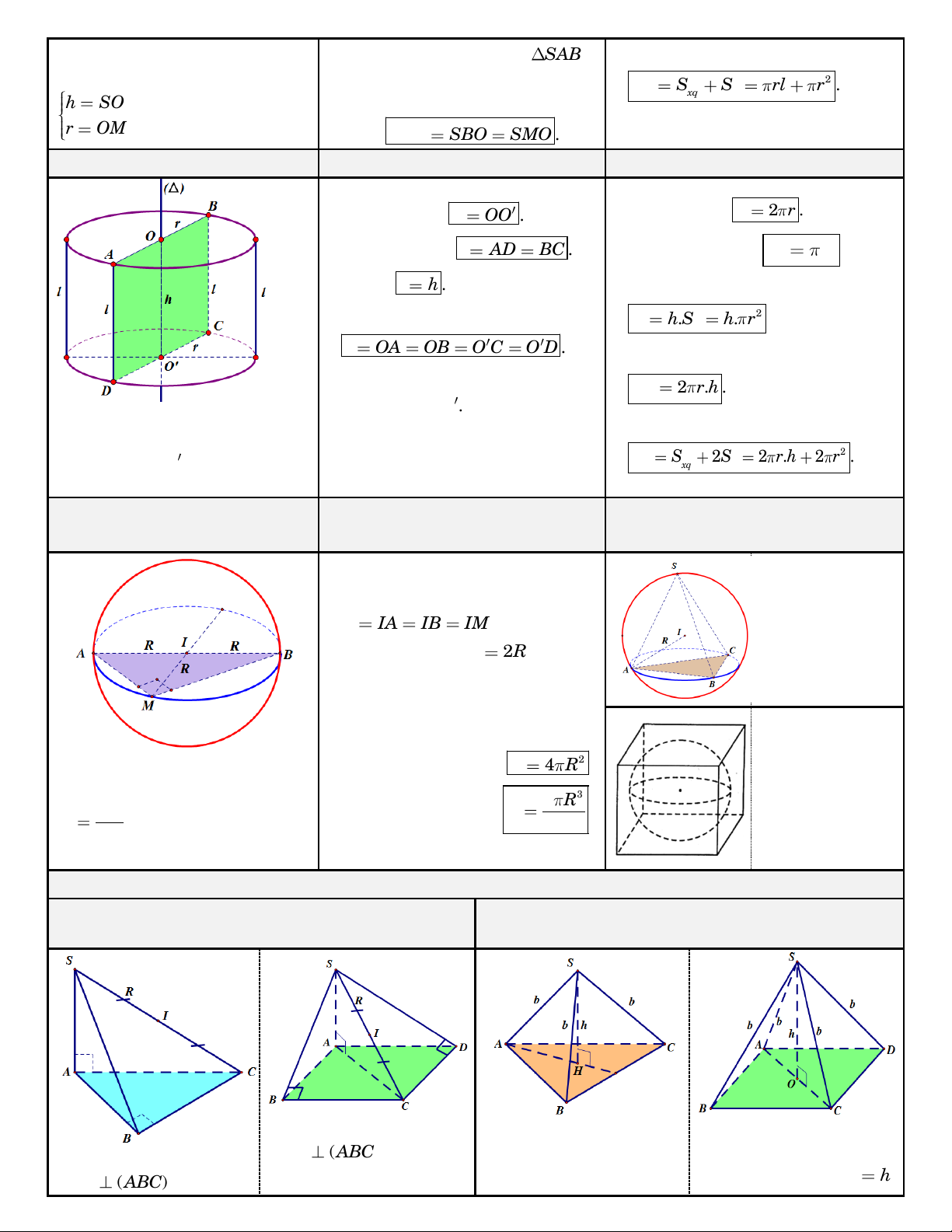
Caùc yeáu toá maët truï:
Moät soá coâng thöùc:
Ñöôøng cao: h OO .
Chu vi ñaùy: p 2 r .
Ñöôøng sinh: l AD BC .
Dieän tích ñaùy: 2 S r . đ Ta coù: l h .
Theå tích khoái truï:
Baùn kính ñaùy: 2 V . h S . h r . đ r OA OB O C O D .
Dieän tích xung quanh:
Truïc (∆) laø ñöôøng thaúng ñi qua S 2 . r h . hai ñieåm , O O . xq
Hình thaønh: Quay hình chöõ 
nhaät ABCD quanh ñöôøng
Dieän tích toaøn phaàn:
Thieát dieän qua truïc: Laø hình
trung bình OO , ta coù maët truï 2 chöõ nhaät ABC . D S S 2S 2 . r h 2 r . tp xq đ nhö hình beân.
Maët caàu ngoaïi tieáp ña dieän MAËT CAÀU
Moät soá coâng thöùc:
Maët caàu noäi tieáp ña dieän Maët caàu
Taâm I, baùn kính ngoaïi tieáp ña R IA IB IM . dieän laø maët  caàu ñi qua taát
Ñöôøng kính AB 2R. caû ñænh cuûa ña
Thieát dieän qua taâm maët caàu: dieän ñoù.
Laø ñöôøng troøn taâm I , baùn kính R .  Maët caàu noäi tieáp ña dieän laø
Hình thaønh: Quay ñöôøng
Dieän tích maët caàu: 2 S 4 R
troøn taâm I , baùn kính maët caàu tieáp 3 4 R AB V xuùc vôùi taát caû R
quanh truïc AB , ta coù  Theå tích khoái caàu: 3 2 caùc maët cuûa ña maët caàu nhö hình veõ. dieän ñoù.
CAÙCH TÌM BAÙN KÍNH MAËT CAÀU NGOAÏI TIEÁP HÌNH CHOÙP THÖÔØNG GAËP
1. Hình choùp coù caùc ñænh nhìn moät caïnh 2.
döôùi moät goùc vuoâng. Hình choùp ñeàu.  Xeùt hình choùp coù  Xeùt hình choùp tam
 Xeùt hình choùp töù giaùc  SA (ABC ) D vaø
giaùc ñeàu coù caïnh beân
ñeàu coù caïnh beân baèng Xeùt hình choùp coù SA (AB ) C vaø
ABCD laø hình chöõ
baèng b vaø ñöôøng cao
b vaø chieàu cao SO h 0 ABC 90 . nhaät hoaëc hình vuoâng. SH h.  Baùn kính maët caàu  ngoaïi tieáp hình choùp Ta coù  Ta coù: SAC SBC  Baùn kính maët caàu 0 2 SAC SBC 90 ngoaïi tieáp hình choùp 0 SDC 90 treân laø b R . 2 neân maët caàu ngoaïi Suy ra maët caàu ngoaïi treân laø b R . 2h
tieáp hình choùp coù taâm tieáp hình choùp coù taâm 2h
I laø trung ñieåm SC ,
I laø trung ñieåm SC , SC SC baùn kính R . baùn kính R . 2 2
3. Hình choùp coù caïnh beân vuoâng goùc vôùi
4. Hình choùp coù maët beân vuoâng goùc vôùi maët phaúng ñaùy. maët ñaùy.
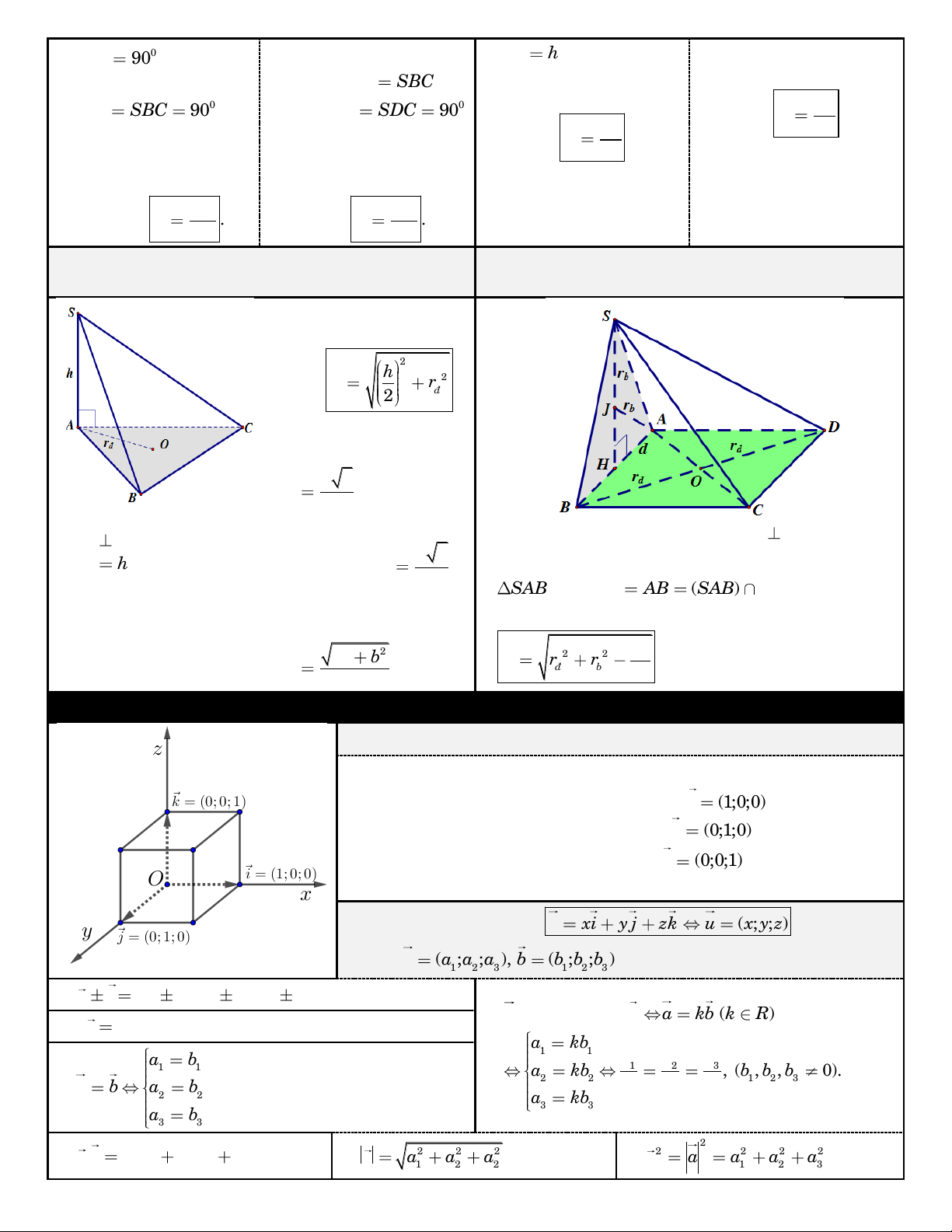
 Khi ñoù maët caàu ngoaïi
tieáp hình choùp coù baùn 2 kính h 2 R r . 2 ñ
 Neáu ñaùy laø tam giaùc ñeàu caïnh a thì a 3 r . ñ 3  Xeùt hình choùp coù  SA (ñaùy) vaø
Neáu ñaùy laø hình vuoâng  Xeùt hình choùp coù maët beân (SA ) B (ñaùy), baùn SA h; baùn kính a 2 caïnh a thì r .
kính ngoaïi tieáp ñaùy laø r , baùn kính ngoaïi tieáp ñ ñ
ñöôøng troøn ngoaïi tieáp 2
SAB laø r , d AB (SA ) B (ñaùy). b cuûa ñaùy laø r .
 Neáu ñaùy laø hình chöõ ñ nhaät caïnh , a b thì
 Khi ñoù baùn kính maët caàu ngoaïi tieáp hình choùp laø 2 2 2 a b 2 2 d r . R r r . ñ b ñ 2 4
HÌNH HOÏC GIAÛI TÍCH TRONG KHOÂNG GIAN
1. Heä truïc toïa ñoä Oxyz:
 Heä truïc goàm ba truïc O , x O ,
y Oz ñoâi moät vuoâng goùc nhau.
 Truïc Ox : truïc hoaønh, coù vectô ñôn vò i (1;0;0) .
 Truïc Oy : truïc tung, coù vectô ñôn vò j (0;1;0) .
 Truïc Oz : truïc cao, coù vectô ñôn vò k (0;0;1).  Ñieåm (
O 0;0;0) laø goác toïa ñoä.
2. Toïa ñoä vectô: Vectô u xi y j zk u ( ; x ; y ) z . Cho a
(a ;a ;a ), b (b ;b ;b ) . Ta coù: 1 2 3 1 2 3  a b (a b ; a b ; a b ) 1 1 2 2 3 3
a cuøng phöông b a kb (k ) R
ka (ka ; ka ; ka ) 1 2 3 a kb 1 1 a b a a a 1 1 1 2 3 a kb
, (b , b , b 0). 2 2 1 2 3 a b a b b b b  1 2 3 2 2 a kb 3 3 a b 3 3 2  . a b a .b a .b a .b a a a a  2 2 2 2 a a a a a 1 1 2 2 3 3 2 2 2 1 2 2 1 2 3 . a b a b a b a b  cos( , a ) b a b . a b 0 a b a b a b 0  1 1 2 2 3 3 1 1 2 2 3 3 2 2 2 2 2 2 a .b a a a . b b b 1 2 3 1 2 3
3. Toïa ñoä ñieåm: M( ; x ; y ) z OM ( ; x ; y ) z . Cho (
A x ; y ; z ) , (
B x ; y ; z ) , (
C x ; y ;z ) , ta coù: A A A B B B C C CAB (x x ; y y ;z z )  AB x x y y z z B A B A B A 2 2 2 ( ) ( ) ( ) B A B A B A
 Toaï ñoä trung ñieåm M cuûa ñoaïn thaúng AB:
 Toaï ñoä troïng taâm G cuûa tam giaùc ABC: x x y y z z x x x y y y z z z A B M ; A B ; A B . A B C G ; A B C ; A B C . 2 2 2 3 3 3
4. Tích coù höôùng cuûa hai vectô:
Ñònh nghóa: Cho a
(a , a , a ) , b (b , b , b ) , tích coù höôùng cuûa a vaø b laø: 1 2 3 1 2 3 a a a a a a 2 3 3 1 1 2 , a b ; ; a b a b ;a b a b ;a b a b . 2 3 3 2 3 1 1 3 1 2 2 1 b b b b b b 2 3 3 1 1 2  Tính chaát: [ , a ] b a [ , a ] b b [ , a ] b a .b .sin , a b
 Ñieàu kieän cuøng phöông của hai vectô a & b laø  Ñieàu kieän ñoàng phaúng cuûa ba vectô , a b vaø c , a b 0 vôùi 0 (0;0;0). laø [ , a ] b .c 0.
Dieän tích hình bình haønh ABCD:
Dieän tích tam giaùc ABC: 1 S A , B AD . S A , B AC . ABCD ABC 2
Theå tích khoái hoäp: V [A , B A ] D .AA'. V AB AC AD .
ABCD.A'B'C' ' D
Theå tích töù dieän: 1 , . ABCD 6
5. Phöông trình maët caàu: Daïng 1: 2 2 2 2 ( ) S : (x ) a (y ) b (z ) c R Daïng 2: 2 2 2 ( ) S : x y z
2ax 2by 2cz d 0 I( ; a ; b ) c I( ; a ; b ) c
Maët caàu (S) coù
Maët caàu (S) coù 2 R R 2 2 2 R a b c d  Phöông trình 2 2 2 x y z
2ax 2by 2cz d
0 laø phöông trình maët caàu 2 2 2
a b c d  0 .
Baøi toaùn 5.1. Vieát phöông trình maët caàu taâm Baøi toaùn 5.2. Vieát phöông trình maët caàu coù
ñöôøng kính AB.
I vaø ñi qua ñieåm M.
Böôùc 1: Tìm taâm I laø trung ñieåm AB. Baùn kính
Böôùc 1: Tính baùn kính R IM . AB R   IA IB . 2
Böôùc 2: Vieát phöông trình maët caàu daïng 1.
Böôùc 2: Vieát phöông trình maët caàu daïng 1.
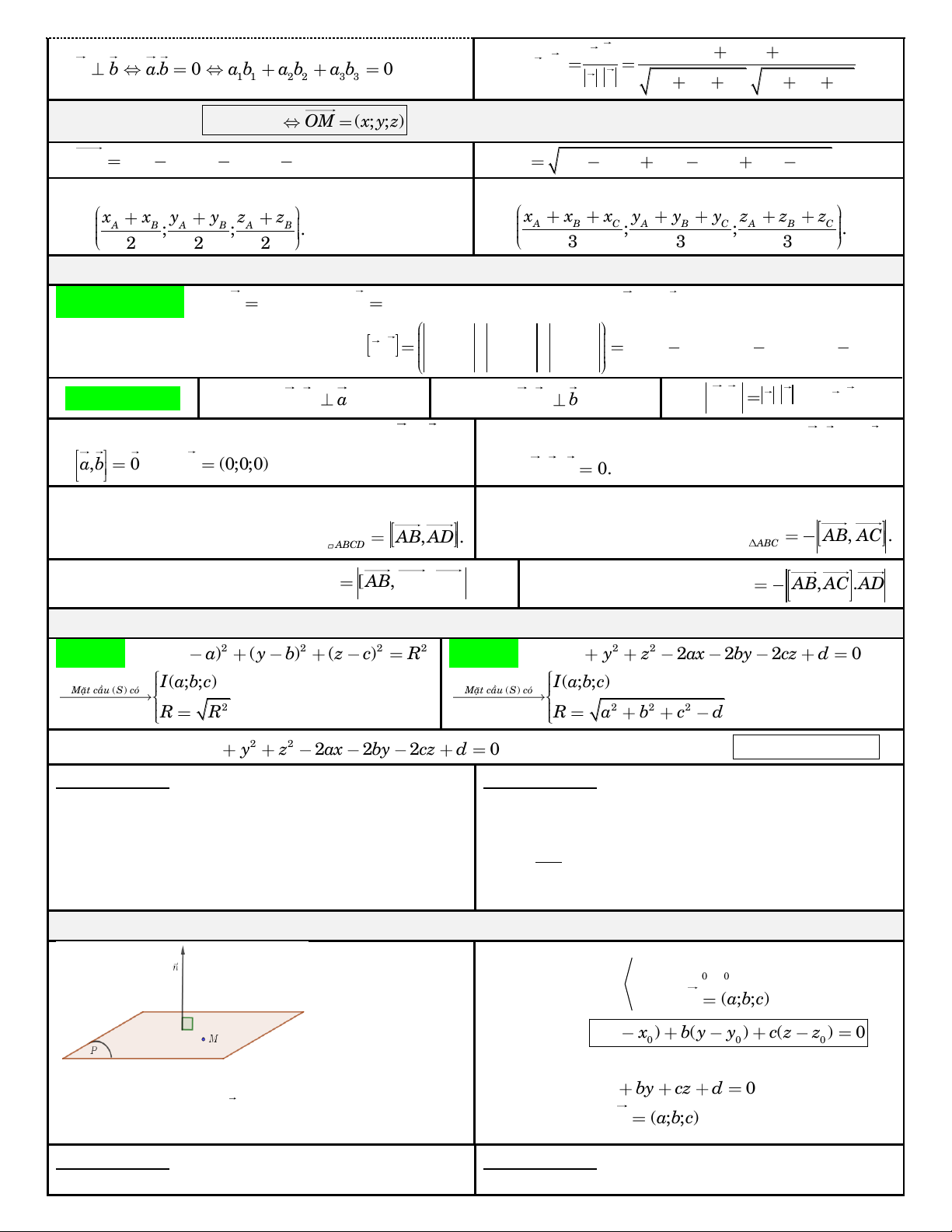
6. Phöông trình maët phaúng:
qua M(x ; y ;z )  Maët phaúng 0 0 0 (P) thì phöông VTPT n ( ; a ; b ) c trình ( ) P : ( a x x ) ( b y y ) ( c z z ) 0 . 0 0 0
 Ngöôïc laïi, moät maët phaúng baát kyø ñeàu coù phöông
Löu yù: Vectô phaùp tuyeán (VTPT) cuûa maët
trình daïng ax by cz d 0 , maët phaúng
phaúng laø vectô khaùc 0 naèm treân ñöôøng thaúng naøy coù VTPT n ( ; a ; b ) c .
vuoâng goùc vôùi maët phaúng ñoù.
Baøi toaùn 6.1. Vieát phöông trình maët phaúng
Baøi toaùn 6.2. Vieát phöông trình maët phaúng
trung tröïc cuûa ñoaïn thaúng AB.
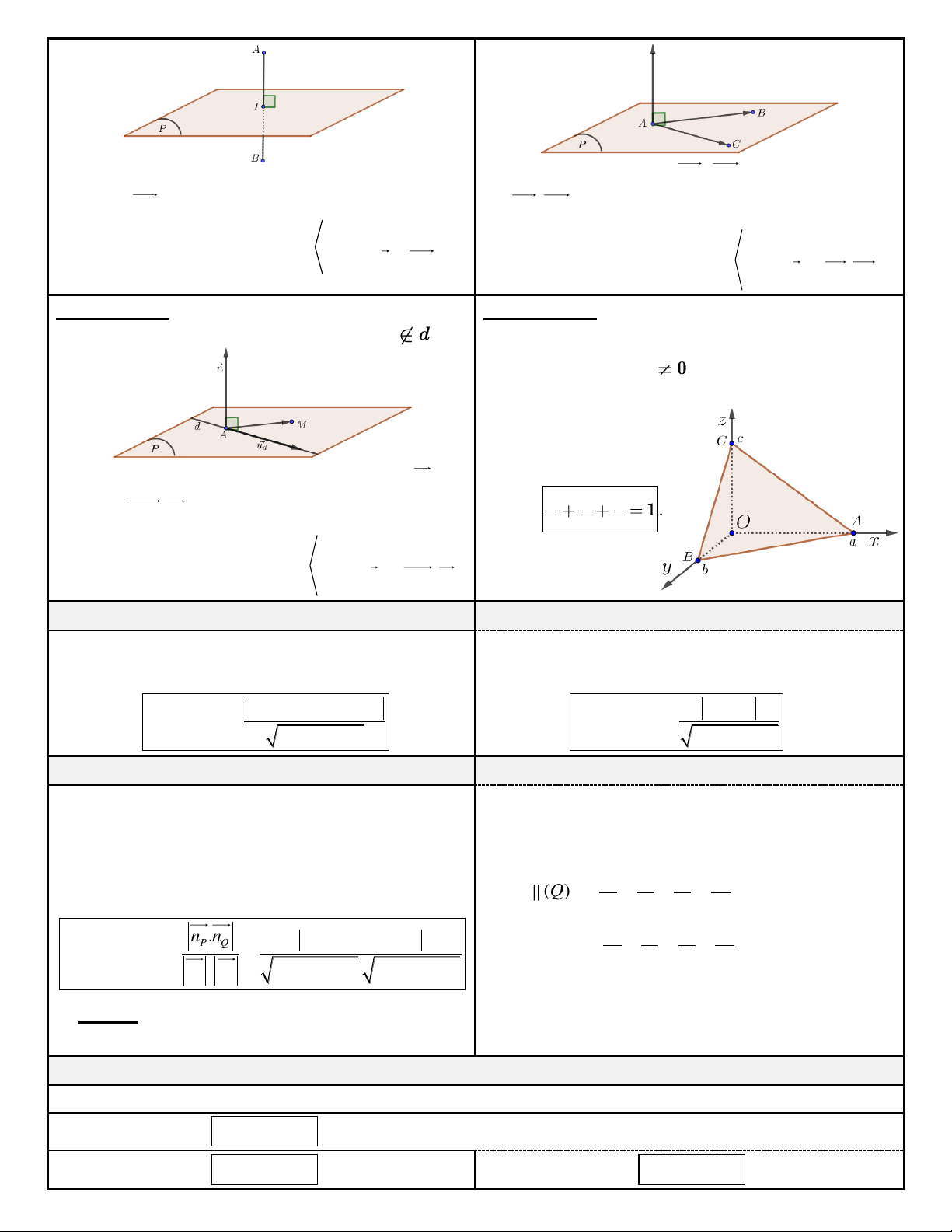
ñi qua ba ñieåm A, B, C.
Böôùc 1: Tìm trung ñieåm I cuûa ñoaïn AB vaø tính  Böôùc 1: Tính toïa ñoä A , B AC vaø suy ra toïa ñoä AB . AB, AC   . qua I
Böôùc 2: Phöông trình mp(P) . qua A VTPT n AB
Böôùc 2: Phöông trình mp(P)
VTPT n   AB, AC  
Baøi toaùn 6.3. Vieát phöông trình maët phaúng
Baøi toaùn 6.4. Vieát phöông trình maët phaúng
qua M vaø chöùa ñöôøng thaúng d vôùi M d .
caét Ox, Oy, Oz laàn löôït taïi ( A ; a 0; 0), ( B 0; ; b 0),
C(0; 0;c) vôùi , a , b c 0 .  Phöông trình maët phaúng ñöôïc vieát  theo ñoaïn chaén
Böôùc 1: Choïn ñieåm Ad vaø moät VTCP u . d x y z
Tính AM ,u  (P) : 1 . d   . a b c qua M
Böôùc 2: Phöông trình mp(P)
VTPT n   AM ,u d  
Khoaûng caùch töø ñieåm ñeán maët phaúng
Khoaûng caùch giöõa hai maët phaúng song song
M (x ; y ; z )
(P) : ax by cz d  0  Cho 0 0 0  .  Cho hai maët phaúng 1  .
mp(P) : ax by cz d  0
(Q) : ax by cz d  0  2
ax by cz d d d
 Khi ñoù: d M ,(P) 0 0 0  .
 Khi ñoù: d (P),(Q) 1 2 
vôùi d d . 1 2 2 2 2
a b c 2 2 2
a b c
Goùc giöõa hai maët phaúng
Vò trí töông ñoái giöõa hai maët phaúng
Cho hai maët phaúng (), () coù phöông trình:
 Cho hai maët phaúng (), () coù phöông trình:
(P) : a x b y c z d  0 1 1 1 1  . Ta coù:
(P) : a x b y c z d  0  1 1 1 1 
(Q) : a x b y c z d  0  2 2 2 2
(Q) : a x b y c z d  0  2 2 2 2 a b c d     .   1 1 1 1 (P) (Q)
Goùc giöõa (P) & ( ) Q ñöôïc tính: a b c d 2 2 2 2 n n   a b c d P Q a a b b c c  1 1 1 1 (P)  (Q)     .
cos (P), (Q) . 1 2 1 2 1 2   a b c d 2 2 2 2 2 2 n . n
a b c . a b c 2 2 2 2 P Q 1 1 1 2 2 2  (P) & ( )
Q caét nhau  a : b : c a : b : c . 1 1 1 2 2 2
Chuù yù: 0   P Q  0 0 ( ), ( )  90 .  (P)  ( )
Q a a b b c c  0 . 1 2 1 2 1 2
Löu yù: Caùc tæ soá treân coù nghóa khi maãu khaùc 0.
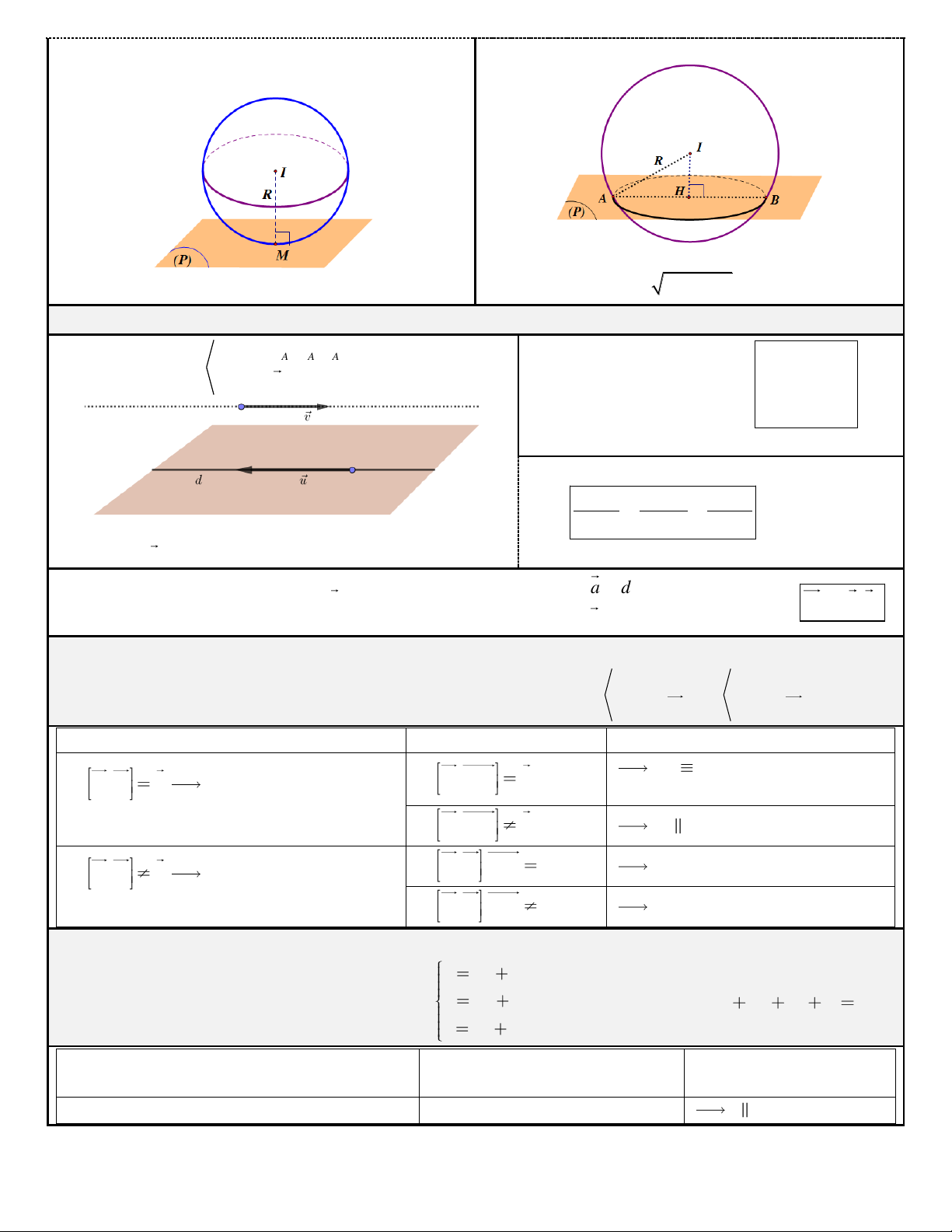
Ví trò töông ñoái giöõa maët phaúng vaø maët caàu Cho maët phaúng ( )
P : ax by cz d  0 vaø maët caàu (S ) coù taâm I vaø baùn kính R.
Tröôøng hôïp 1: d I,(P)  R  (P) vaø (S) khoâng coù ñieåm chung.
Tröôøng hôïp 2: d I,(P)  R  (P) vaø (S) coù  Tröôøng hôïp 3: d I,(P)  R  (P) caét (S)
moät ñieåm chung. Khi ñoù ta noùi (P) tieáp xuùc
theo giao tuyeán laø moät ñöôøng troøn.
(S ) hoaëc (P) laø tieáp dieän cuûa (S).
Ñöôøng troøn giao tuyeán coù taâm H (laø trung ñieåm
Ta coù: IM  (P) vôùi M laø tieáp ñieåm. AB), baùn kính 2 2 r
R IH vôùi IH d I,(P).
7. Phöông trình ñöôøng thaúng: qua (
A x ; y ; z )
x x u t  Ñöôøng thaúng A A A d coù: A 1 
VTCP u  (u ;u ;u )
 Phöông trình tham soá d : y y u t vôùi 1 2 3 A 2
z z u tA 3 t laø tham soá.
 Phöông trình chính taéc x x y y z z d : A A A  
vôùi u .u .u  0 . 1 2 3
Vectô chæ phöông (VTCP) cuûa ñöôøng thaúng d laø u u u 1 2 3
vectô khaùc 0 , coù giaù naèm treân d hoaëc song song vôùi d. a d
Löu yù: Neáu coù caëp vectô khaùc 0 khoâng cuøng phöông sao cho 
thì d coù VTCP laø: u  a,bd   . b   d
7.1. Ví trò töông ñoái giöõa hai ñöôøng thaúng: qua M qua N
Xeùt vò trí töông ñoái cuûa hai ñöôøng thaúng d , d vôùi d , d . 1 2 1 VTCP u 1 VTCP u 1 2 Böôùc I Böôùc II Keát luaän d d u ,u 0 Hai ñöôøng thaúng  u ;MN 0 1 2 1 2 1
(Hai ñöôøng thaúng truøng nhau)
d , d song song hoaëc truøng nhau. 1 2  u ;MN 0 d d 1 1 2 u ,u .MN 0 du ,u 0
Hai ñöôøng thaúng d , d d caét 1 2 1 2 1 2 1 2
caét nhau hoaëc cheùo nhau.
u ,u .MN 0
d & d cheùo nhau 1 2 1 2
7.2. Ví trò töông ñoái giöõa ñöôøng thaúng vaø maët phaúng: x x u t 0 1
Xeùt vò trí töông ñoái giöõa ñöôøng thaúng d : y y
u t vaø maët phaúng ( ) P : ax by cz d 0 . 0 2 z z u t 0 3
Böôùc II:Giaûi PT (*), ta gaëp Böôùc I: Keát luaän
1 trong 3 tröôøng hôïp sau
 Thay phöông trình tham soá d vaøo  PT (*) voâ nghieäm d ( ) P
phöông trình (P) , ta ñöôïc PT (*): x x0 ( a x u ) t ( b y u ) t ( c z u ) t d 0 
d caét (P) taïi ñieåm 0 1 0 2 0 3
 PT (*) coù 1 nghieäm  y y 0 
coù toïa ñoä (x ; y ; z ) . z z  0 0 0 0
 PT (*) coù voâ soá nghieäm d ( ) P
7.3. Khoaûng caùch töø ñieåm ñeán ñöôøng thaúng:
Böôùc 1: Choïn ñieåm Ad vaø moät VTCP u . d
 Cho ñieåm M vaø ñöôøng thaúng d (coù u AM
phöông trình tham soá hoaëc chính taéc). d  
Böôùc 2: d M d  , ,  . ud
7.4. Goùc giöõa hai ñöôøng thaúng: u .u
 Cho hai ñöôøng thaúng d , d laàn löôït coù VTCP laø u , u . 
 Ta coù: cosd ,d  . 1 2  1 2 1 2 1 2 u . u 1 2
7.5. Goùc giöõa ñöôøng thaúng vaø maët phaúng: u n
 Cho ñöôøng thaúng d coù VTCP u vaø maêt phaúng (P) coù VTPT n .   Ta coù: d P  . sin , ( )  . u . n
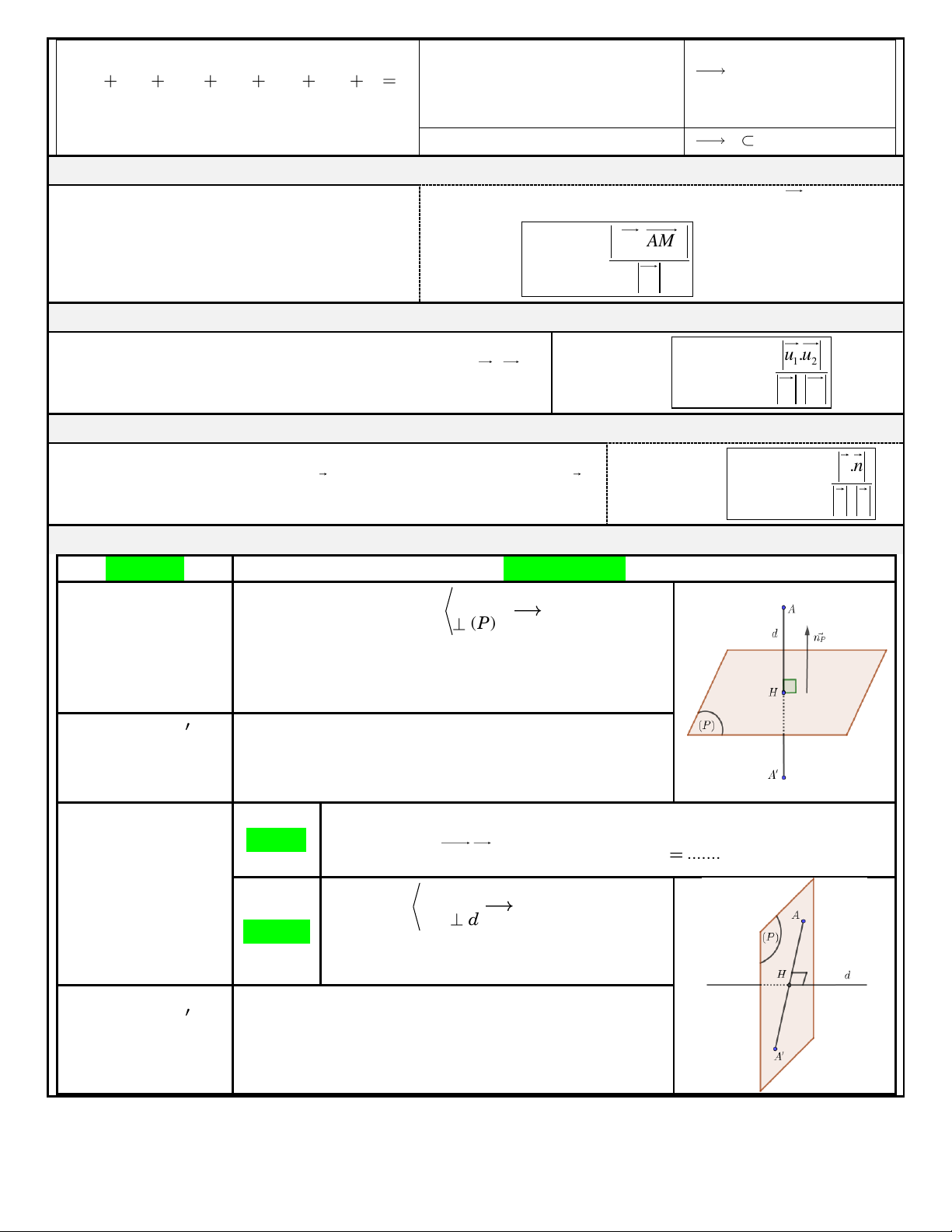
8. Hình chieáu vaø ñieåm ñoái xöùng: Baøi toaùn Phöông phaùp qua A
 Goïi d laø ñöôøng thaúng Vieát pt tham  Tìm hình chieáu (P) cuûa ñieåm A treân
soá cuûa d vôùi VTCP cuûa d cuõøng laø VTPT cuûa (P). maët phaúng (P).
 Goïi H d (P) . Thay pt tham soá cuûa d vaøo pt
mp (P) ta tìm ñöôïc toïa ñoä H.  Tìm ñieåm A x    2x x A H A
ñoái xöùng vôùi A qua 
 Ta coù H laø trung ñieåm AA  y   .  2 y y A H A (P) .  z     2z z A H A
 Goïi H (theo t) (döïa vaøo pt tham soá cuûa d).
Caùch I AH d AH.u  0  Tìm ñöôïc t ....... Toïa ñoä H. d  Tìm hình chieáu cuûa ñieåm A treân qua A  Goïi (P) Vieát pt mp( ) P . ñöôøng thaúng d. (P) d
Caùch II  Goïi H d (P). Thay pt tham soá cuûa
d vaøo pt mp (P) ta tìm ñöôïc toïa ñoä H.     Tìm ñieåm A x  2x x A H A
ñoái xöùng vôùi A qua  Ta coù H laø trung ñieåm AA  y   .  2 y y A H A ñöôøng thaúng d. z     2z z A H A
Bieân soaïn: Hoaøng Xuaân Nhaøn
Email goùp yù: thayxuannhan@gmail.com