Báo cáo Bài Tập Chương 3 Thuật Toán Sắp Xếp và Tìm Kiếm | Môn Phân tích thiết kế hệ thống - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 59078336
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI KHOA CÔNG NGHỆ THÔNG TIN
CHUYÊN NGÀNH KHOA HỌC MÁY TÍNH
Báo cáo bài tập chương 3 – Nhóm 11
Giảng viên: Đào Việt Cường Thành viên: Bùi Mạnh Tiến - 0213868 Mai Trí Toàn - 0214068 Nguyễn Anh Tuấn - 0214768
Ngô Thị Thùy Linh - 0210168 BÀI LÀM
Câu 1: Trình bày thuật toán sắp xếp trộn, so sánh với các thuật toán sắp xếp có độ phức tạp O(n^2).
Merge sort: Merge sort hoạt động trên nguyên tắc chia để trị. Merge sort chia nhỏ nhiều lần một mảng
(array) thành hai mảng con bằng nhau cho đến khi mỗi mảng con (sub-array) bao gồm một phần tử duy
nhất. Cuối cùng, tất cả các mảng con đó được hợp nhất để sắp xếp mảng kết quả.
chia mảng thành hai nửa cho đến khi mỗi phần chỉ còn một phần tử
trộn hai mảng con đã được sắp xếp thành một mảng duy nhất lOMoAR cPSD| 59078336
Thuật toán của merge sort:
Ví dụ cụ thể (code java):
import java.util.Arrays; class Main { private static void
merge(int[] left, int[] right, int[] arr) { int i = 0, j = 0, k = 0;
// duyet qua tung phan tu cua mang ben trai, so sanh voi tung phan tu cua mang
// ben phai while (i < left.length && j < right.length) {
// neu phan tu duoc duyet cua mang ben trai < phan tu duoc duyet cua mang ben lOMoAR cPSD| 59078336
// phai thi them phan tu ben trai vao
if (left[i] < right[j]) { arr[k++] = left[i++];
// neu khong thi them phan tu ben phai vao } else { arr[k++] = right[j++]; } }
// truong hop bi thua phan tu, khong the so sanh duoc -> add thang vao luon
while (i < left.length) { arr[k++] = left[i++]; }
while (j < right.length) { arr[k++] = right[j++]; }
} private static void mergeSort(int[]
arr) { int length = arr.length; if
(length <= 1) return; int mid = length / 2;
// chia doi mang ban dau thanh 2 mang int[]
leftSide = Arrays.copyOfRange(arr, 0, mid); int[]
rightSide = Arrays.copyOfRange(arr, mid, length); // lOMoAR cPSD| 59078336
de quy thuat toan tren 2 mang vua chia doi
mergeSort(leftSide); mergeSort(rightSide);
// ghep nguoc lai 2 mang bi chia doi thanh 1
merge(leftSide, rightSide, arr); }
public static void main(String[] args) {
int[] array = {1, 3, 2, 10, 6, 9, 8};
System.out.println("Mảng ban đầu:");
System.out.println(Arrays.toString(array)); mergeSort(array);
System.out.println("Mảng đã sắp xếp:"); System.out.println(Arrays.toString(array)); }} In ra kết quả là:
Độ phức tạp của thuật toán:
• TH tốt nhất: O(nlogn) khi mảng đã được sắp xếp
• TH trung bình: O(nlogn) khi mảng được sắp xếp ngẫu nhiên TH xấu nhất: O(nlogn) khi
mảng được sắp xếp theo thứ tự ngược lại
Chia mảng: Mỗi lần chia, sẽ chia mảng làm đôi, số lần chia mảng n phần tử là log2n.
Gộp mảng: Gộp mảng lại, cần duyệt qua từng phần tử trong các mảng con nên thời gian để thực hiện là O(n) cho mỗi mảng con.
Tổng thời gian để thực hiện là: T(n) = 2T (n / 2) + O(n) Nghiệm của phương trình này là O(nlogn) nên
thời gian thực hiện thuật toán là O(nlogn). lOMoAR cPSD| 59078336
So sánh với các thuật toán sắp xếp có độ phức tạp O(n^2) là : • Buble sort • Selection sort • Insertion sort
Buble sort, Selection sort, Insertion sort: thích hợp cho mảng nhỏ ít giá trị hoặc đơn giản là cần 1 thuật toán
dễ hiểu và áp dụng. Time complexity trong trường hợp tồi tệ nhất của cả 2 thuật toàn đề là O(n^2), vì vậy
chúng không hiệu quả khi làm việc với các tập dữ liệu lớn.
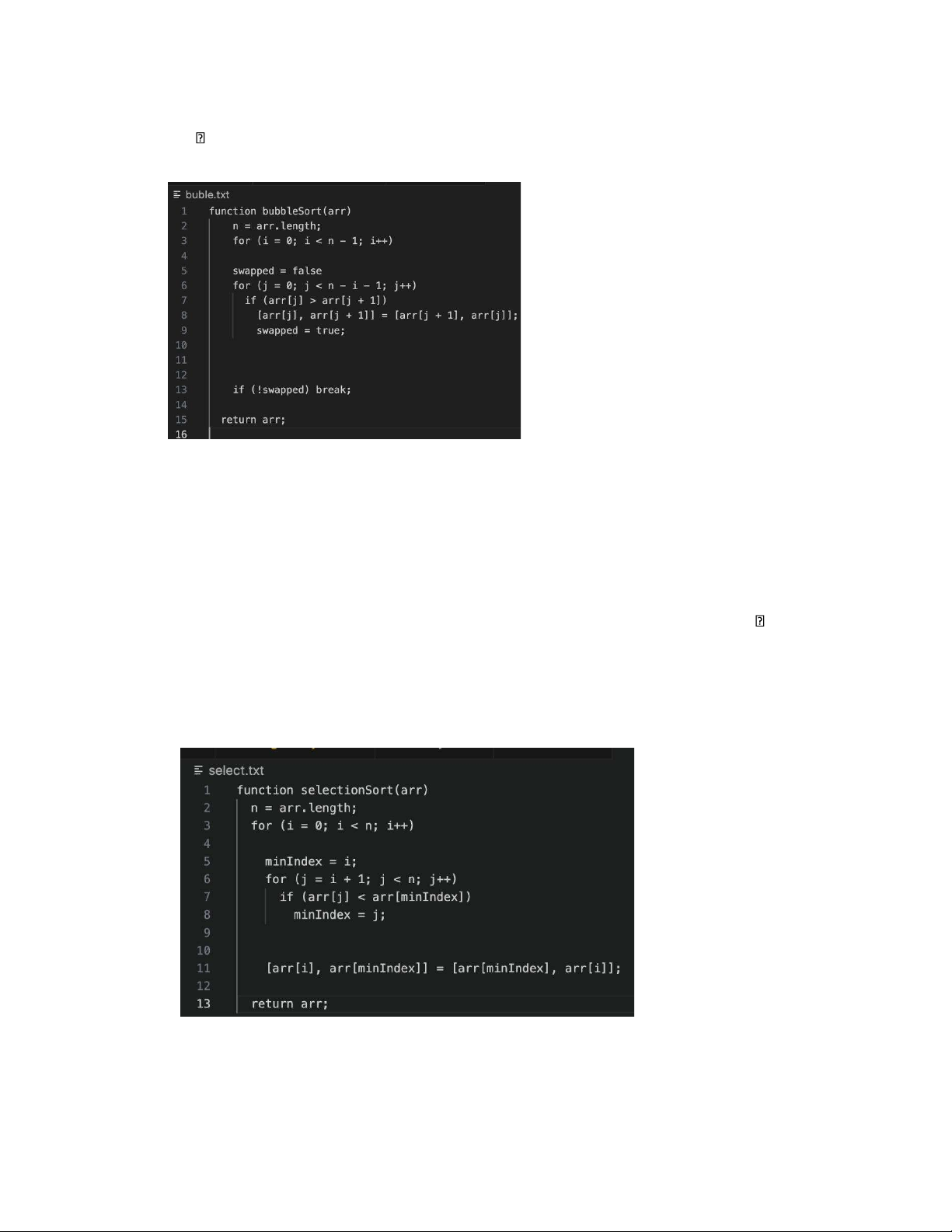
- Buble sort( sắp xếp nổi bọt): ý tưởng chính là duyệt qua danh sách cần sắp xếp liên tục, so sánh
từng cặp phần tử liền kề và hoán đổi chúng nếu sai thứ tự
• bắt đầu từ đầu danh sách, so sánh 2 phần tử đầu tiên
• nếu phần tử thứ nhất lớn hơn phần tử thứ hai, hoán đổi chúng
• tiếp tục với cặp phần tử tiếp theo cho đến cuối danh sách
• lặp lại quá trình trên cho đến khi không có sự hoán đổi nào sảy ra trong một lần duyệt lOMoAR cPSD| 59078336
thuật toán của Buble sort:
- Selection sort( sắp xếp lựa chọn): hoạt động bằng cách liên tục tìm phần tử nhỏ nhất (hoặc lớn
nhất) trong danh sách chưa được sắp xếp và đưa nó về vị trí đúng trong danh sách
• duyệt qua toàn bộ mảng để tìm phần tử nhỏ nhất
• hoán đổi phần tử nhỏ nhất với phần tử đầu tiên của mảng
• tiếp tục với phần còn lại của mảng (bỏ qua phần tử đầu tiên đã được sắp xếp) thuật toán của Selection sort: lOMoAR cPSD| 59078336
- Insertion Sort ( sắp xếp chèn): xây dựn danh sách đã sắp xếp từng phần tử một. Nó lấy mỗi phần
tử và chèn vào vị trí thích hợp trong danh sách đã sắp xếp trước đó
bắt đầu từ phần tử thứ hai trong mảng
• so sánh phần tử hiện tại với các phần tử trước đó
• di chuyển các phần tử nhỏ hơn lên một vị trí để tạo chỗ trông chèn phần tử hiện tại vào
vị trí thích hợp thuật toán của Insertion sort:
- Merge sort( sắp xếp trộn): là thuật toán sắp xếp ổn định và đảm bảo hiệu suất với độ phức tạp 0(n
logn) trong mọi trường hợp. Merge sort thường được lựa chọn khi cần đảm bảo tính ổn định và
hiệu suất tôt cho tập dữ liệu lớn.
Câu 2: Trình bày thuật toán tìm kiếm nhị phân, so sánh với tìm kiếm bằng cách duyệt tuần tự từ
đầu đến cuối mảng.
Tìm kiếm nhị phân(binary search): thực hiện tìm kiếm trên một dãy phần tử có thứ tự bằng cách thu hẹp
phạm vi tìm kiếm còn lại một nửa (nhị phân) so với lượt tìm kiếm trước đó cho đến khi tìm thấy phần tử
thỏa mãn điều kiện hoặc phạm vi tìm kiếm không còn phần tử nào (không tìm thấy).
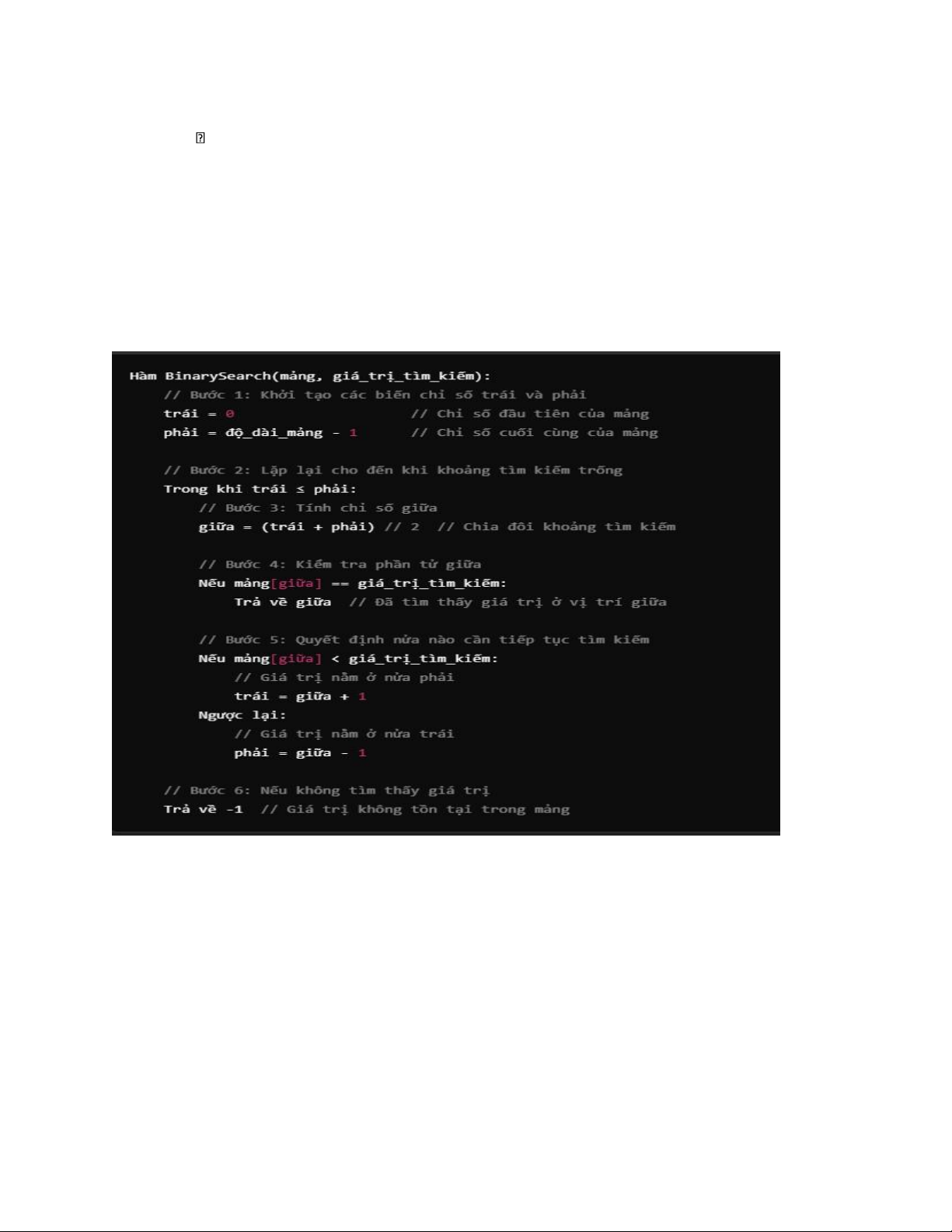
Ý tưởng của thuật toán:
- Ban đầu , phạm vi tìm kiếm từ đầu đến cuối dãy ( đặt left = 0, right = n-1) lOMoAR cPSD| 59078336
- Tính vị trí chính giữa đoạn mid = (left + right) / 2 - So sánh a[mid] với x:
• nếu a[mid] == x : trả về vị trí mid rồi kết thúc
nếu a[mid] > x : right = mid -1 (thu hẹp về nửa bên trái)
• nếu a[mid] < x : left = mid + 1 (thu hẹp về nửa bên phải)
- Nếu left <= right , tiếp tục tìm kiếm trên đoạn [ left , right]. Ngược lại, trả về kết quả -1 (không tìm thấy).
MÃ GIẢ cho Thuật Toán:
So sánh tìm kiếm nhị phân với phép duyệt tuần tự từ đầu đến cuối mảng. 1. Nguyên lý hoạt động
• Tìm kiếm tuyến tính:
• Duyệt qua từng phần tử của mảng từ đầu đến cuối để tìm giá trị cần tìm.
• Nếu tìm thấy, trả về vị trí của phần tử; nếu không, kết thúc sau khi duyệt hết mảng. lOMoAR cPSD| 59078336 • Tìm kiếm nhị phân:
• Yêu cầu mảng phải được sắp xếp trước.
• So sánh phần tử ở giữa mảng với giá trị cần tìm: lOMoAR cPSD| 59078336
• Nếu bằng, trả về vị trí.
• Nếu lớn hơn, tìm trong nửa bên trái.
• Nếu nhỏ hơn, tìm trong nửa bên phải.
• Quá trình lặp lại cho đến khi tìm thấy hoặc mảng con không còn phần tử nào.
2. Độ phức tạp thời gian
- Tìm kiếm tuyến tính:
• Có độ phức tạp là O(n) vì phải duyệt từ đầu mảng đến cuối mảng có n phần tử.
• Trường hợp xấu nhất sẽ phải duyệt đến cuối mảng mới tìm ra kết quả.
- Tìm kiếm nhị phân: n
• Có độ phức tạp là O(log2 n) do n lần nhị phân xuống còn 1 phần tử : k = 1 => k = log2n 2
• Số lần giảm đi đáng kể vì mảng đã được chia đôi ở mỗi bước.
3.Điều kiện sử dụng và tốc độ thực thi - Tìm kiếm tuyến tính:
• Không yêu cầu mảng sắp xếp.
• Dễ sử dụng cho mọi dữ liệu.
• Phù hợp với mảng kích thước nhỏ chưa sắp xếp.
- Tìm kiếm nhị phân:
• Chỉ áp dụng cho mảng đã được sắp xếp
• Đạt hiểu quả cao hơn đối với mảng có kích thước lớn.
Câu 3: Trình bày thuật toán tìm max-min bằng cách chia để trị, so sánh với tìm max-min bằng cách
duyệt từ đầu đến cuối mảng. 1.Mã giả
• Lược đồ thuật toán: MinMax(a,L,R):(int,int) ≡ lOMoAR cPSD| 59078336
//Tìm giá trị min,max dãy a từ vị trí L đến R if (R-L<=1){
return(min(aL,aR),max(aL,aR));} else {
(min1,max1) = MinMax(a,L,(L+R)/2);
(min2,max2) = MinMax(a,(L+R)/2+1,R);
return(min(min1,min2),max(max1,max2)); } End.
• Lời gọi ban đầu với dãy n phần tử: MinMax(a,0,n-1)
2.Giải thích từng bước
• Điều kiện cơ sở:
o Nếu khoảng cách giữa L và R là 1 hoặc nhỏ hơn (tức là R - L <= 1), nghĩa là chỉ có một
hoặc hai phần tử trong khoảng này. Khi đó:
o So sánh hai giá trị a[L] và a[R]. o Trả về giá trị nhỏ nhất và lớn nhất giữa a[L] và a[R].
• Trường hợp tổng quát :
o Nếu khoảng cách giữa L và R lớn hơn 1, nghĩa là có nhiều hơn hai phần tử trong khoảng này:
o Chia dãy a thành hai nửa bằng cách tính điểm giữa (L + R) / 2. o Gọi đệ quy
MinMax(a, L, (L + R) / 2) để tìm min1 và max1 cho nửa đầu. o Gọi đệ quy
MinMax(a, (L + R) / 2 + 1, R) để tìm min2 và max2 cho nửa sau. o Kết hợp kết quả từ
hai nửa: o min là giá trị nhỏ hơn giữa min1 và min2. o max là giá trị lớn hơn giữa max1 và max2.
o Trả về cặp giá trị (min, max). o Sau khi có kết quả từ hai nửa, lấy giá trị nhỏ nhất giữa
min1 và min2, và giá trị lớn nhất giữa max1 và max2 để tạo thành kết quả cuối cùng.
3. chứng mình tính đúng và độ phức tạp của thuật toán
• Tính đúng của thuật toán
Chứng minh quy nạp theo n là số phần tử của dãy o Điều kiện cơ sở: Với
n <=1, thuật toán trả về min(aL,aR),max(aL,aR)
=> Thuật toán đúng o Trường hợp tổng quát: Chứng minh thuật
toán đúng với n = k+1 Theo giả thiết quy nạp: lOMoAR cPSD| 59078336
min1 = min(a[L], ..., a[(L+R)/2])
min2 = min(a[(L+R)/2+1, ..., a[R])
min(min1, min2) = min(a[L], ..., a[R])
Tương tự: max(max1, max2) = max(a[L], ..., a[R]) => Thuật toán đúng
• Độ phức tạp thuật toán: o T(n)=O(1)
khi n<=2 o T(n) =2T(n/2) +O(1) khi n>2
Độ phức tạp : T(n) = O(n) 4. so
sánh 2 phương pháp tìm max min
• Độ phức tạp thời gian: o Cả hai phương pháp đều có độ phức tạp thời gian là O(n).
• Độ phức tạp không gian:
o Phương pháp duyệt tuyến tính có độ phức tạp không gian là O(1), thấp hơn so với
phương pháp chia để trị với độ phức tạp không gian là O(log n) do sử dụng ngăn xếp đệ quy. • Số phép so sánh :
o Thuật toán chia để trị thực hiện ít phép so sánh hơn (khoảng 1.5n - 2) so với thuật toán
duyệt từ đầu đến cuối (2n - 2) khi n lớn.
Câu 4: Trình bày thuật toán tìm dãy con liên tiếp có tổng lớn nhất, so sánh với tìm dãy con liên tiếp
có tổng lớn nhất bằng cách thực hiện hai vòng lặp lồng nhau. Trình bày thuật toán tìm dãy con liên
tiếp có tổng lớn nhất public class chiatri { public static int maxCrossingSum(int[] arr, int left, int mid, int right) { int sum = 0;
int leftSum = Integer.MIN_VALUE; lOMoAR cPSD| 59078336
for (int i = mid; i >= left; i--) { sum += arr[i]; leftSum = Math.max(leftSum, sum); } sum = 0; int rightSum =
Integer.MIN_VALUE; for (int i = mid +
1; i <= right; i++) { sum += arr[i];
rightSum = Math.max(rightSum, sum); } return leftSum + rightSum; }
public static int maxSubArraySumDivideAndConquer(int[] arr, int left, int right) { if (left == right) { return arr[left];
} int mid = (left + right) / 2; int maxLeft =
maxSubArraySumDivideAndConquer(arr, left, mid); int maxRight =
maxSubArraySumDivideAndConquer(arr, mid + 1, right); int maxCross
= maxCrossingSum(arr, left, mid, right); return Math.max(maxLeft,
Math.max(maxRight, maxCross)); }
Tính độ phức tạp thuật toán: lOMoAR cPSD| 59078336
1. Công thức truy hồi o Khi n>1: T(n)=2T(n/2)+O(n) o Khi n=1: T(n)=O(1)
2. Giải công thức truy hồi o Mỗi mức của cây đệ quy:
Tổng chi phí O(n). o Ở mức gốc (mức đầu tiên), kích
thước bài toán là nnn. o Ở mức thứ hai, kích thước
mỗi bài toán con là n/2. o Ở mức thứ ba, kích thước
mỗi bài toán con là n/4, và cứ tiếp tục.
o Tiến trình này dừng khi kích thước bài toán còn 1, tức là: (n/2^k)=1 suy ra k=logn o Kết quả: T(n)=O(nlogn).
Kết luận: Thuật toán chia để trị có độ phức tạp O(nlogn).
Chứng minh tính đúng:
1. Giả thiết quy nạp •
Giả sử thuật toán đúng với mọi dãy có độ dài n<=k, tức là: •
Thuật toán luôn trả về tổng lớn nhất của dãy con liên tiếp trong mọi mảng có n<=k.
2. Chứng minh tổng quát
Chứng minh rằng thuật toán đúng với dãy có độ dài n=k+1. Trường hợp cơ sở :
Nếu mảng chỉ có một phần tử (n=1), thuật toán trả về: return arr[left];
Đây là tổng lớn nhất duy nhất, do mảng chỉ chứa một phần tử.
Kết luận: Thuật toán đúng với n=1
Trường hợp tổng quát : lOMoAR cPSD| 59078336
Xét mảng có n=k+1phần tử, thuật toán chia mảng thành hai nửa:
1. Nửa trái: từ left đến mid.
2. Nửa phải: từ mid + 1 đến right. Bước chia nhỏ
Gọi đệ quy để tìm tổng lớn nhất ở từng nửa: int maxLeft =
maxSubArraySumDivideAndConquer(arr, left, mid); int maxRight =
maxSubArraySumDivideAndConquer(arr, mid + 1, right); •
Theo giả thiết quy nạp, các lời gọi đệ quy này đúng vì kích thước mỗi nửa mảng <=k •
Do đó: o maxLeft là tổng lớn nhất của dãy con liên tiếp trong nửa trái.
o maxRight là tổng lớn nhất của dãy con liên tiếp trong nửa phải. Bước gộp kết quả
Tính tổng lớn nhất của dãy con cắt qua điểm giữa mid bằng hàm maxCrossingSum:
int maxCross = maxCrossingSum(arr, left, mid, right); •
Hàm maxCrossingSum đã được chứng minh đúng (xem phần trước). •
maxCross là tổng lớn nhất của mọi dãy con cắt qua điểm giữa mid. Tìm tổng lớn nhất Kết quả trả về là:
return Math.max(maxLeft, Math.max(maxRight, maxCross)); •
Tổng lớn nhất của dãy con liên tiếp phải thuộc một trong ba trường hợp:
1. Nằm hoàn toàn trong nửa trái (maxLeft).
2. Nằm hoàn toàn trong nửa phải (maxRight).
3. Cắt qua điểm giữa (maxCross). •
Kết quả trả về là tổng lớn nhất trong ba giá trị này, đảm bảo tính đúng. 3. Kết luận lOMoAR cPSD| 59078336
Với mọi n=k+1, thuật toán luôn trả về tổng lớn nhất của dãy con liên tiếp. Do đó, theo nguyên lý quy nạp,
thuật toán đúng với mọi n≥1.
So sánh Chia để trị và Hai vòng lặp lồng nhau trong bài toán tìm dãy con liên tiếp có tổng lớn nhất
1. Thuật toán Chia để trị Ý tưởng chính:
1. Chia mảng thành hai nửa:
o Gọi dãy con liên tiếp có tổng lớn nhất trong nửa trái là maxLeft. o Gọi
dãy con liên tiếp có tổng lớn nhất trong nửa phải là maxRight.
o Gọi dãy con liên tiếp có tổng lớn nhất cắt qua điểm giữa là maxCross.
2. Tổng lớn nhất sẽ là:
maxSum=max(maxLeft,maxRight,maxCross)
3. Lặp lại quá trình này đệ quy trên các nửa nhỏ hơn cho đến khi chỉ còn 1 phần tử. Độ phức tạp: •
Thời gian: O(nlogn) (vì mỗi cấp độ chia đôi cần O(n) để tính maxCross, và có tổng cộng logn cấp độ đệ quy). •
Không gian: O(logn) (do ngăn xếp đệ quy).
2. Hai vòng lặp lồng nhau Ý tưởng chính: 1. Dùng hai vòng lặp:
o Vòng ngoài chọn điểm bắt đầu của dãy con.
o Vòng trong tính tổng của tất cả các dãy con bắt đầu từ điểm đó và so sánh để tìm tổng lớn nhất. Độ phức tạp: •
Thời gian: O(n2) (mỗi phần tử được xem xét nnn lần trong vòng lặp). •
Không gian: O(1) (chỉ dùng biến tạm). lOMoAR cPSD| 59078336 Kết luận: •
Chia để trị tốt hơn về mặt hiệu suất, nhưng phức tạp hơn trong triển khai. •
Hai vòng lặp lồng nhau đơn giản và dễ hiểu, nhưng không hiệu quả khi kích thước mảng lớn.
Câu 5: Trình bày thuật toán tìm cặp điểm gần nhất bằng cách chia để trị, so sánh với tìm cặp điểm
gần nhất bằng cách duyệt từng cặp.
Thuật toán tìm cặp điểm gần nhất theo phương pháp chia để trị (Divide and Conquer) là một giải
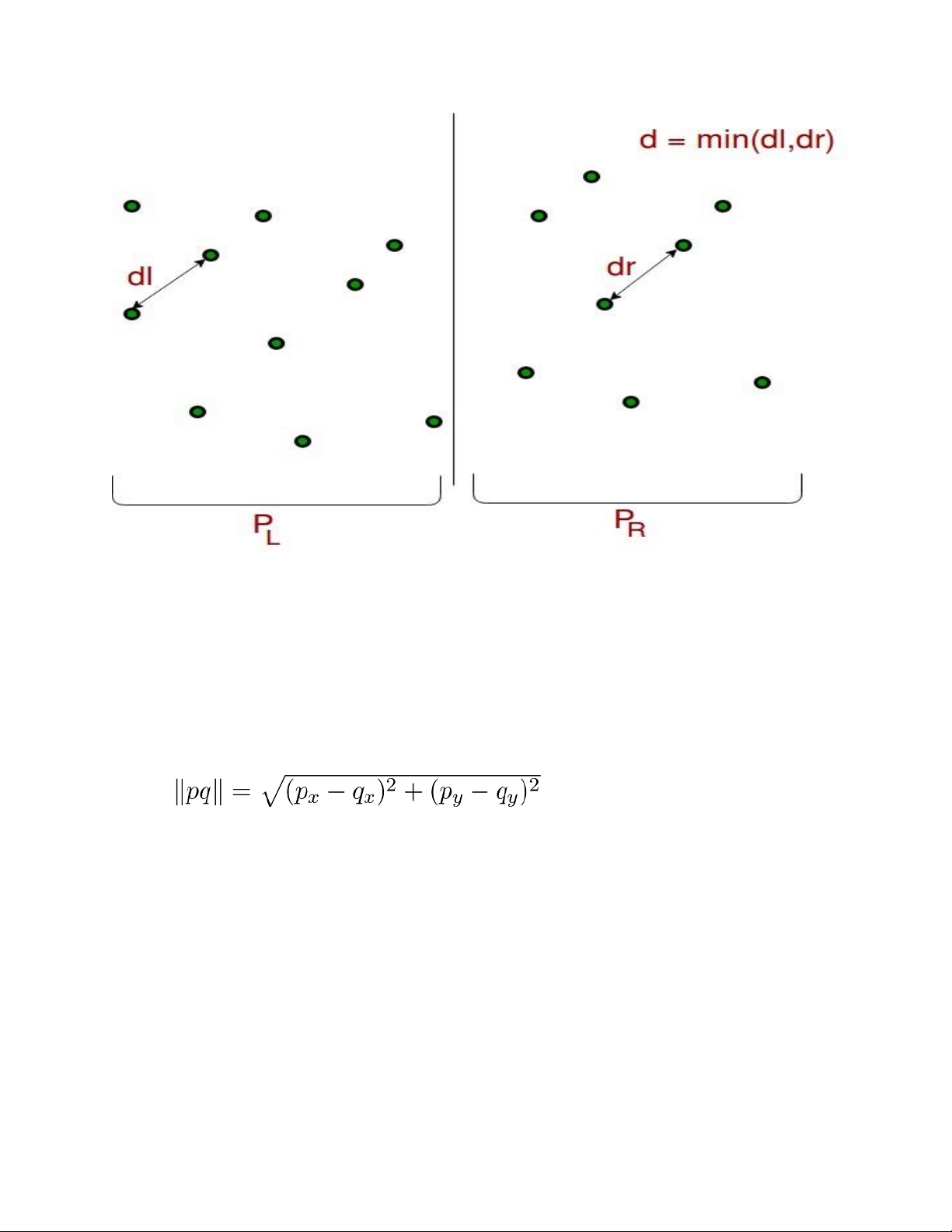
pháp hiệu quả với độ phức tạp O(nlog(n)), so với cách duyệt mọi cặp điểm (O(n^2)). Ý tưởng chính: 1.Chia để trị: •
Chia tập các điểm thành hai nửa bằng nhau dựa trên tọa độ x. •
Tìm cặp điểm gần nhất trong mỗi nửa (gọi là khoảng cách DL và DR). •
Khoảng cách nhỏ nhất giữa hai nửa là d = min(DL,DR). 2.Kết hợp kết quả: •
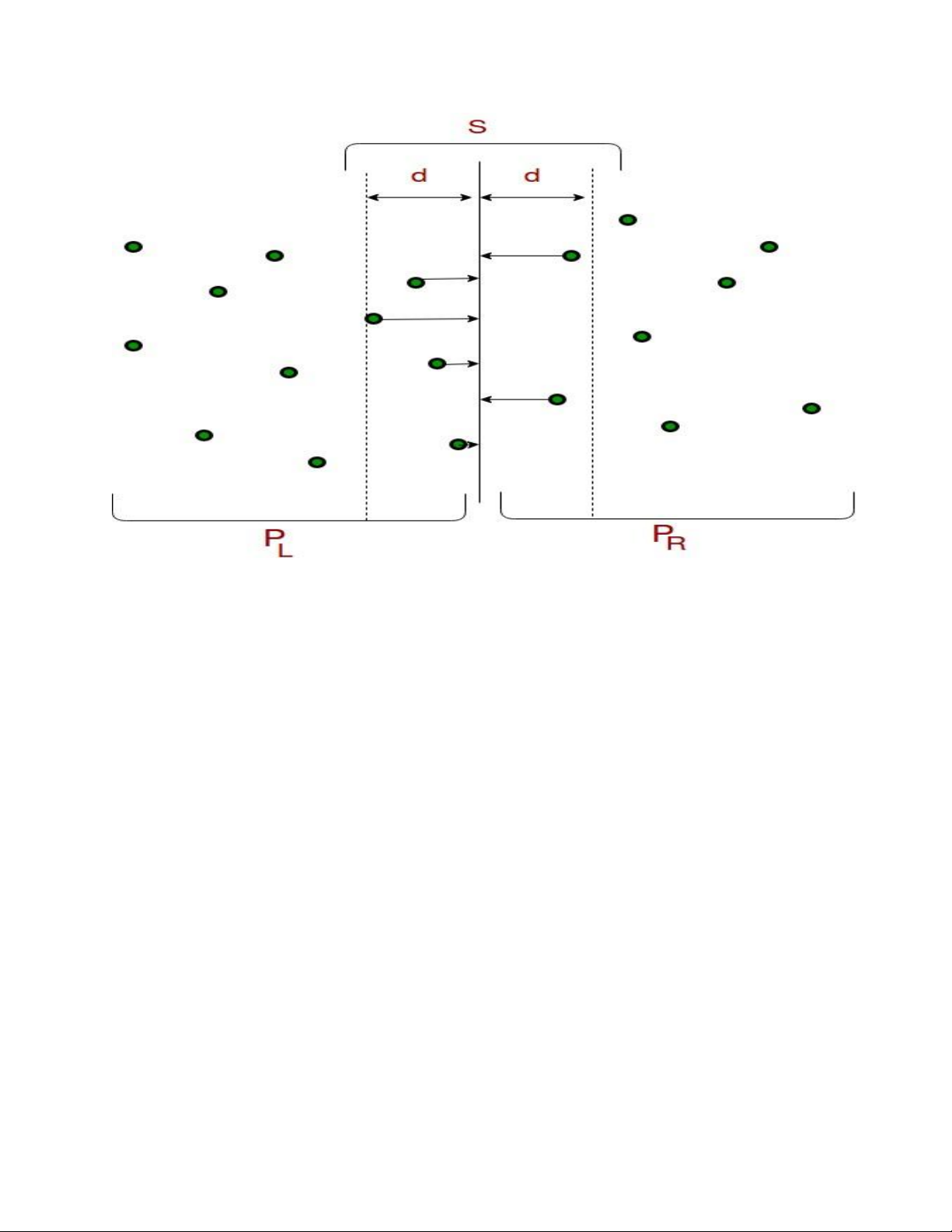
Xem xét các điểm nằm trong dải giữa hai nửa (khoảng cách từ đường chia trung tâm đến mỗi điểm nhỏ hơn d). •
Kiểm tra cặp điểm nằm trong dải để tìm khoảng cách nhỏ nhất.
3.Cải tiến với sắp xếp trước: •
Sắp xếp các điểm theo tọa độ x và y để giảm số lượng cặp điểm cần kiểm tra trong bước dải giữa.
Xử lý thuật toán: lOMoAR cPSD| 59078336
1) Tìm điểm giữa trong việc sắp xếp mảng, chúng tôi có thể lấy P[n/2] làm điểm giữa.
2) Chia mảng đã cho thành hai nửa. Bảng đầu tiên chứa các điểm từ P[0] đến P[n/2]. Bảng thứ haichứa
các điểm từ P[n/2+1] đến P[n-1].
3) Đệ quy tìm khoảng cách nhỏ nhất trong cả hai mảng con. Cho các khoảng cách đó là dl và dr.
Tìm giá trị nhỏ nhất của dl và dr. Cho giá trị nhỏ nhất là d. theo công thức: lOMoAR cPSD| 59078336
4) Từ 3 bước trên, ta có giới hạn trên d của khoảng cách nhỏ nhất. Bây giờ ta cần xét các cặp sao cho
mộtđiểm trong cặp nằm ở nửa bên trái và điểm còn lại nằm ở nửa bên phải. Xét đường thẳng đứng đi
qua P[n/2] và tìm tất cả các điểm có tọa độ x gần hơn d so với đường thẳng đứng ở giữa. Xây dựng
một mảng A[] của tất cả các điểm như vậy.
5) Sắp xếp mảng A[] theo tọa độ y. Tìm khoảng cách nhỏ nhất trong A[].
6) Cuối cùng trả về giá trị nhỏ nhất của d và khoảng cách được tính toán trong bước trên (bước 5)
So sánh tìm cặp theo pp chia để trị và duyệt tuần tự từng cặp:
1. Phương pháp Duyệt từng cặp (Brute Force) Ý tưởng: •
Duyệt qua tất cả các cặp điểm trong tập điểm. •
Tính khoảng cách của từng cặp và tìm cặp có khoảng cách nhỏ nhất. Ưu điểm: lOMoAR cPSD| 59078336 •
Đơn giản: Dễ hiểu và dễ cài đặt. •
Hiệu quả khi số điểm nhỏ: Với n ≤10 phương pháp này chạy nhanh. Nhược điểm: n(n−1) •
Chậm với số điểm lớn: Với n điểm, phải duyệt =
cặp, dẫn đến độ phức tạp 2 O(n2). •
Không phù hợp cho các ứng dụng yêu cầu xử lý dữ liệu lớn hoặc thời gian thực.
2. Phương pháp Chia để trị (Divide and Conquer) Ý tưởng: •
Chia tập điểm thành hai nửa theo tọa độ x. •
Tìm cặp điểm gần nhất trong mỗi nửa bằng cách gọi đệ quy. •
Xử lý thêm dải giữa (giao hai nửa) để đảm bảo không bỏ sót các cặp điểm nằm ở hai phía. Ưu điểm: •
Hiệu quả hơn: Độ phức tạp O(n logn), phù hợp với số lượng điểm lớn. •
Tiết kiệm thời gian: Dựa vào tính chất hình học, chỉ cần kiểm tra một số lượng nhỏ điểm trong dải giữa. Nhược điểm: •
Phức tạp hơn để cài đặt: Đòi hỏi việc sắp xếp trước và xử lý nhiều trường hợp đặc biệt. •
Có thể gây tốn bộ nhớ hơn do việc sao chép và tạo mảng con trong mỗi bước chia.