Báo cáo bài tập lớn môn Xác suất thống kê | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 59031616
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG KHOA CƠ BẢN I
BỘ MÔN XÁC SUẤT THÔNG KÊ
BÁO CÁO BÀI TẬP LỚN GVHD: VŨ VĂN QUÂN
Lớp: Xác suất thống kê Nhóm: 01
Hà Nội – 2024 lOMoAR cPSD| 59031616 THÀNH VIÊN NHÓM STT Họ và tên MSV 1 Nguyễn Trung Đạt B23DCCN142 2 Nguyễn Bình Đức B23DCCN177 3 Đỗ Thị Thu Huế B23DCCN355 4 Cát Hoàng Kiệt B23DCCN471 5 Nguyễn Đức Minh B23DCCN555 6 Trần Đỗ Lan Phương B23DCCN667 7 Đặng Thanh Thuý B23DCCN807 8 Phạm Quang Toản B23DCCN835 9 Tô Quang Trung B23DCCN863 10 Phạm Đức Tuấn B23DCCN889
I) ĐỊNH NGHĨA CỔ ĐIỂN VỀ XÁC SUẤT
Giả sử phép thử thoả mãn hai điều kiện sau:℘ (i)
Không gian mẫu có một số hữu hạn phần tử. (ii)
Các kết quả xảy ra đồng khả năng.
Khi đó ta định nghĩa xác suất của biến cố A là :
P(A) = Số trườnghợpthuậnlợi đối với ASố trườnghợpcó thể
Nếu xem biến cố A như là tập con của không gian mẫu Ω thì : lOMoAR cPSD| 59031616
P(A) = Số phầntử của ASố phầntử củaΩ
BÀI 1: Một phòng LAB gồm 12 máy hỏng và 8 máy mới. Hai bạn học sinh vào
phòng để thi CODE THCS2. Tính xác xuất để người thứ 2 ngồi vào máy mới. Giải
• Số cách 2 học sinh ngồi vào phòng là C120. C119 = 380 (cách)
• Nếu học sinh 1 ngồi vào máy cũ và học sinh 2 ngồi vào máy mới thì có C112. C18 = 96 (cách)
• Nếu học sinh 1 ngồi vào máy mới và học sinh 2 ngồi vào máy mới thì có C18. C17 = 56 (cách)
Suy ra xác suất cần tìm là p = =
BÀI 2: Có 30 tấm thẻ được đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 6 tấm thẻ. Tính xác
suất để trong 6 tấm thẻ được chọn ra có 4 tấm thẻ mang số lẻ, 2 tấm thẻ mang số
chẵn trong đó chỉ có đúng một tấm thẻ mang số chia hết cho 4.
• Số phần tử của không gian mẫu là: n(Ω) = C630 • Trong 30 tấm thẻ
- Có 15 tấm thẻ mang số lẻ
- Có 8 tấm thẻ mang số chẵn và không chia hết cho 4
- Có 7 tấm thẻ mang số chẵn và chia hết cho 4
• Gọi A là biến cố cần tính xác suất. Ta có: n(A) = C415. C18. C17 n( A) 435
• Vậy, xác suất cần tính là: P(A) = = n(Ω) 56
BÀI 3: Một đề thi icpc gồm 5 bài level khó và 10 bài level trung bình. Giáo viên
chọn ngẫu nhiên 3 bài thi. Tính xác suất để 3 bài thi gồm cả level khó và trung bình.
• Ta có: n(Ω) = C315
• Số cách chọn 3 học sinh có cả khó và trung bình là: C25. C110 + C15. C210 Xác suất
để 3 học sinh được chọn có cả nam và nữ là C315 7 2 1 1 2 = 5
C5.C10+C5.C10
BÀI 4: Gieo một con xúc xắc cân đối và đồng chất. Giả sử xúc xắc xuất hiện mặt b chấm. Tính
xác suất để phương trình x2 + b.x + 2 = 0 có 2 nghiệm phân biệt. lOMoAR cPSD| 59031616
• Có 6 khả năng xảy ra khi tung xúc xắc nên số phần tử không gian mẫu: n(Ω) = 6
• Gọi A là biến cố phương trình có 2 nghiệm phân biệt
Khi và chỉ khi: ∆ > 0 b2 – 8 > 0 b {3;4;5;6} n(A) = 4. n( A) 2
• Xác suất cần tìm P(A) = = n(Ω) 3
BÀI 5: Cho đa giác đều 32 cạnh. Gọi S là tập hợp các tứ giáo tọa thành có 4
đỉnh lấy từ các đỉnh của đa giác đều. Chọn ngẫu nhiên một phần tử của S. Tính
xác suất để được một hình chữ nhật.
• Số tứ giác tạo thành với 4 đỉnh lấy từ các đỉnh của đa giác đều là C432
• Suy ra n(S) = n(Ω) = C432
• Gọi A là biến cố được tứ giác là một hình chữ nhật
• Số đường chéo đa giác qua tâm của đa giác đều là: 16
• Số hình chữ nhật tạo thành: n( A) = C216 n ( A ) 899
• Xác suất cần tìm P(A) = = n (Ω) 3
Câu 1: Một lô hàng gồm 1000 sản phẩm trong đó có 50 phế phẩm. Lấy ngẫu nhiên từ lô
hàng 1 sản phẩm. Xác suất để lấy được sản phẩm tốt là?
Gọi A là biến cố: “ lấy được 1 sản phẩm tốt”
Không gian mẫu =1000 n(A) =950
Xác suất cần tìm là P(A)= =0.95
Câu 2: Một hộp có 5 viên bi đỏ và 9 viên bi xanh. Chọn ngẫu nhiên 2 viên bi. Xác suất để
chọn được 2 viên bi khác màu là?
Gọi A là biến cố: “Chọn được 2 viên bi khác màu”
Không gian mẫu = 14C2=91 n(A)= 5C1.9C1=45
Xác suất cần tìm là P(A)=
Câu 3: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn
lần đều xuất hiện mặt sấp là? lOMoAR cPSD| 59031616
Gọi A là biến cố” Cả bốn lần gieo đều xuất hiện mặt sấp”
Không gian mẫu=24=16 n(A)=1.1.1.1=1
Xác suất cần tìm là P(A)=
Câu 4: Gieo ngẫu nhiên hai con xúc xắc cân đối đồng chất. Xác suất để tổng số chấm của
hai con xúc xắc bằng 6 là?
Gọi A là biến cố: “Tổng số chấm 2 con xúc xắc là 6” Không gian mẫu =6.6=36
Ta có 1+5 = 2+4 = 3+3 = 4+2 = 5+1 =6 n(A)=5
Xác suât cần tìm là P(A)=
Câu 5: Có bốn tấm bìa được đánh số từ 1 đến 4. Rút ngẫu nhiên ba tấm. Xác suất của
biến cố “Tổng các số trên ba tấm bìa bằng 8” là?
Gọi A là biến cố: “ tổng số trên tấm bìa bằng 8” Không gian mẫu = 4C3 =4 Ta có 1+3+4=8 => n(A)=1
Xác suất cần tìm là P(A)=
Câu 6: Một người chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày cỡ khác nhau. Xác suất
để hai chiếc chọn được tạo thành một đôi là?
Gọi A là biến cố : “ 2 chiếc được chọn được tạo 1 đôi” Không gian mẫu =8C2=2
Ta có chiếc giày thứ nhất có 8 cách chọn, chiếc thứ hai có 1 cách chọn để cùng đôi với
chiếc thứ nhất => n(A)=8
Xác suât cần tìm là P(A)= =
Câu 7: Một hộp chứa ba quả cầu trắng và hai quả cầu đen. Lấy ngẫu nhiên đồng thời hai
quả. Xác suất để lấy được cả hai quả trắng là? lOMoAR cPSD| 59031616
Gọi A là biến cố “ lấy được cả 2 quả trắng”
Không gian mẫu =5C2=10 n(A)=3C2
Xác suất cần tìm là P(A)=
Câu 8: Một hộp chứa sáu quả cầu trắng và bốn quả cầu đen. Lấy ngẫu nhiên đồng thời
bốn quả. Tính xác suất sao cho có ít nhất một quả màu trắng?
Gọi A là biến cố: “Trong bốn quả chọn được ít nhất một quả trắng” Không gian mẫu = 10C4 =210
Gọi A ngang là là biến cố: “Trong bốn quả không chọn được 1 quả trắng nào” =>n(A ngang) =4C4=1
=> Xác suất cần tìm là P(A) =1- P(A ngang)= 1- =
Câu 9: Một hộp có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Chọn ngẫu nhiên từ hộp 4
viên bi, tính xác suất để 4 viên bi được chọn có số bi đỏ lớn hơn số bi vàng và nhất thiết phải có mặt bi xanh.
Không gian mẫu là số cách chọn ngẫu nhiên 4 viên bi từ hộp chứa 12 viên bi. Suy ra số
phần tử của không gian mẫu là = 12C4 =495
Gọi A là biến cố “4 viên bi chọn được số bi đỏ lớn hơn số bi vàng cà nhất thiết phải có mặt
bi xanh”. Ta có các TH thuận lợi sau:
TH1: chọn 1 bi đỏ và 3 bi xanh có 5C1.4C3 cách
TH2: chọn 2 bi đỏ và 2 bi xanh có 5C2.4C2 cách
TH3: chọn 3 bi đỏ và 1 bi xanh có 5C3.4C1 cách
TH4: chọn 2 bi đỏ, 1 bi vàng và 1 bi xanh nên có 5C2.3C1.4C1 cách P(A)= =
Câu 10: Có 3 bó hoa. Bó thứ nhất có 8 hoa hồng, bó thứ hai có 7 bông hoa ly, bó thứ ba có
6 bông hoa huệ. Chọn ngẫu nhiên 7 hoa từ ba bó hoa trên để cắm vào lọ hoa, tính xác
suất để trong 7 hoa được chọn có số hoa hồng bằng số hoa ly. Không gian mẫu = 21C7=116280
Gọi A là biến cố” 7 hoa được chọn có số hoa hồng băng số hoa ly” nên ta có các trường hợp sau:
TH1: Chọn 1 hoa hồng, 1 hoa ly và 5 hoa huệ nên có 8C1.7C1.6C5 cách
TH2: Chọn 2 hoa hồng, 2 hoa ly và 2 hoa huệ nên có 8C2.7C2.6C3 cách lOMoAR cPSD| 59031616
TH3 : Chọn 3 hoa hồng, 3 hoa ly và 1 hoa huệ nên có 8C3.7C3.6C1 cách n(A)=TH1+TH2 +TH3 =23856
Xác xuát cần tìm là P(A)= =
Câu 11: Có 13 học sinh của một trường THPT đạt danh hiệu học sinh xuất sắc trong đó
khối 12 có 8 học sinh nam và 3 học sinh nữ, khối 11 có 2 học sinh nam. Chọn ngẫu nhiên 3
học sinh bất kỳ để trao thưởng, tính xác suất để 3 học sinh được chọn có cả nam và nữ
đồng thời có cả khối 11 và khối 12. Không gian mẫu =13C3 = 286
Gọi A là biến cố “ 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối
12” nên ta có các TH thuận lợi cho biến cố A là
TH1: Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có 2C1.8C1.3C1 cách
TH2: Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có 2C1.3C2 cách
TH3: Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có 2C2.3C1 cách n(A)=57
Xác suât cần tìm là P(A)=
Câu 12: Một chiếc hộp đựng 7 viên bi màu xanh, 6 viên bi màu đen, 5 viên bi màu đỏ, 4
viên bi màu trắng. Chọn ngẫu nhiên ra 4 viên bi, tính xác suất để lấy được ít nhất 2 viên bi cùng màu?
Không gian mẫu là số cách chọn ngẫu nhiên 4viên bi từ 22 viên bi đã cho. Suy ra số phần
tử của không gian mẫu là =22C4=7315
Gọi A là biến cố '' Lấy được 4 viên bi trong đó có ít nhất hai viên bi cùng màu '' . Để tìm số
phần tử của A , ta đi tìm số phần tử của biến cố A ngang , với biến cố A ngang là lấy được
4 viên bi trong đó không có hai viên bi nào cùng màu.
n(A ngang) =7C1.6C1.5C1.4C1=840 n(A)=7315-840=6475 Xác suât cần tìm P(A) = =
Câu 13: Một hộp đựng 8 quả cầu trắng, 12 quả cầu đen. Lần thứ nhất lấy ngẫu nhiên 1 quả
cầu trong hộp, lần thứ hai lấy ngẫu nhiên 1 quả cầu trong các quả cầu còn lại. Tính xác
suất để kết quả của hai lần lấy được 2 quả cầu cùng màu Không gian mẫu = 20C1.19C1
Gọi A là biến cố '' 2 quả cầu được lấy cùng màu '' . Ta có các trường hợp thuận lợi cho biến cố A như sau: lOMoAR cPSD| 59031616
TH1: Lần thứ nhất lấy quả màu trắng và lần thứ hai cũng màu trắng nên có 8C1.7C1 cách
TH2: Lần thứ nhất lấy quả màu đen và lần thứ hai cũng màu đen nên có 12C1.11C1 cách n(A)=TH1 + TH2
Xác suất cần tìm P(A) =
Câu 14: Một hộp chứa 12 viên bi kích thước như nhau, trong đó có 5 viên bi màu xanh
được đánh số từ 1 đến 5 ; có 4 viên bi màu đỏ được đánh số từ 1 đến 4 và 3 viên bi màu
vàng được đánh số từ 1 đến 3 . Lấy ngẫu nhiên 2 viên bi từ hộp, tính xác suất để 2 viên
bi được lấy vừa khác màu vừa khác số. Không gian mẫu =12C2 = 66
Gọi A là biến cố '' 2 viên bi được lấy vừa khác màu vừa khác số '' nên có có cách TH thuận
lời cho biến cố A như sau:
TH1: Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi đỏ là 4.4 = 16 cách
TH2: Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi vàng là 3.4 = 12 cách.
TH3: Số cách lấy 2 viên bi gồm: 1 bi đỏ và 1 bi vàng là 3.3 = 9 cách
Suy ra số phần tử của biến cố A là n( A)= 16 +12 + 9 = 37 Xác suất cần tim P(A) =
Câu 15: Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6
viên bi từ hộp, tính xác suất để 6 viên bi được lấy ra có đủ cả ba màu Không gian mẫu =14C6=3003
Gọi A là biến cố '' 6 viên bi được lấy ra có đủ cả ba màu '' . Để tìm số phần tử của biến cố A
ta đi tìm số phần tử của biến cố A ngang tức là 6 viên bi lấy ra không có đủ ba màu như sau:
TH1: Chọn 6 viên bi chỉ có một màu nên TH1 có 1 cách
TH2 : Chọn 6 viên bi có đúng 2 màu xanh và đỏ có 8C6 cách
Chọn 6 viên bi có đúng 2 màu đỏ và vàng có 11C6-6C6 cách
Chọn 6 viên bi có đúng 2 màu xanh và vàng có 9C6-6C6 cách =>n(A ngang) =1 +572 =573 => n(A) =3003-573=2430
=> xác suất cần tìm là P(A) = =
II) ĐỊNH NGHĨA XÁC SUẤT THEO HÌNH HỌC lOMoAR cPSD| 59031616
Giả sử không gian mẫu Ω có thể biểu diễn tương ứng với một miền nào đó có
diện tích ( thể tích , độ dài ) hữu hạn và biến cố A tương ứng với một miền con
của Ω thì xác suất của biến cố A được định nghĩa : diệntích A P(A) = diệntíchΩ Ví dụ 1:
Một hình vuông có cạnh là 4 cm, bên trong có một hình tròn nội tiếp. Nếu chọn
ngẫu nhiên một điểm trong hình vuông, xác suất để điểm đó rơi vào trong hình tròn là bao nhiêu? Lời giải:
Diện tích hình vuông: S vuông = 42 = 16cm2
Bán kính của hình tròn nội tiếp là r = = 2cm
Diện tích hình tròn: S tròn = π r2 = π 22 = 4c m2
Xác suất để điểm đó rơi vào hình tròn là: Stròn 4 π π
P = S vuông = 16 = 4 ≈ 0 ,785 Ví dụ 2:
Một hình chữ nhật có chiều dài 12 cm và chiều rộng 8 cm được vẽ bên
trong một hình vuông có cạnh 10 cm. Tính xác suất để một điểm chọn ngẫu
nhiên trong hình vuông rơi vào trong hình chữ nhật. Lời giải:
Diện tích hình vuông: S vuông = 102 = 100c m2
Diện tích hình chữ nhật: S chữ nhật = 6.8 =48cm2 Xác
suất để điểm chọn rơi vào hình chữ nhật là: S chữ nhật 48
P = S vuông = 100 = 0,48 Ví dụ 3:
Giả sử có hai hình tròn đồng tâm: hình tròn nhỏ có bán kính 3 cm và hình tròn
lớn có bán kính 6 cm. Nếu chọn ngẫu nhiên một điểm trong hình tròn lớn, tính lOMoAR cPSD| 59031616
xác suất để điểm đó nằm trong vùng giữa hai hình tròn (vùng nằm ngoài hình
tròn nhỏ nhưng bên trong hình tròn lớn). Lời giải:
Diện tích hình tròn lớn: S lớn = π.62 = 36π c m2
Diện tích hình tròn nhỏ: S nhỏ = π.32 = 9π c m2
Diện tích vùng giữa hai hình tròn (vùng không nằm trong hình tròn nhỏ nhưng
nằm trong hình tròn lớn) là:
S vùng = S lớn - S nhỏ = 36π - 9π = 27π cm2
Xác suất để điểm chọn ngẫu nhiên trong hình tròn lớn rơi vào vùng giữa hai
hình tròn là tỷ lệ diện tích vùng đó so với diện tích của hình tròn lớn: S vùng 27π
P = Slớn = 36π = 0,75 Ví dụ 4:
Hai người hẹn gặp nhau ở công viên trong khoảng thời gian từ 5h10 đến
6h00 để cùng đi tập thể dục. Hai người quy ước ai đến không thấy người
kia sẽ chỉ chờ trong vòng 10 phút. Giả sử rằng thời điểm hai người đến công
viên là ngẫu nhiên trong khoảng từ 5h10 đến 6h00. Tính xác suất để hai người gặp nhau. Lời giải:
Gọi x, y là thời gian người thứ nhất và người thứ hai đến. Ta có tập kết cục
đồng khả năng là lOMoAR cPSD| 59031616
G = {(x, y) ∈ R2 | 0 ≤ x, y ≤ 50}
Gọi H "hai người gặp được nhau". Khi đó tập kết cục thuận lợi là
H = { (x, y) G: |x − y| ≤ 10}∈ 502−402 Suy ra P = = 0,36 2 50 Ví dụ 5:
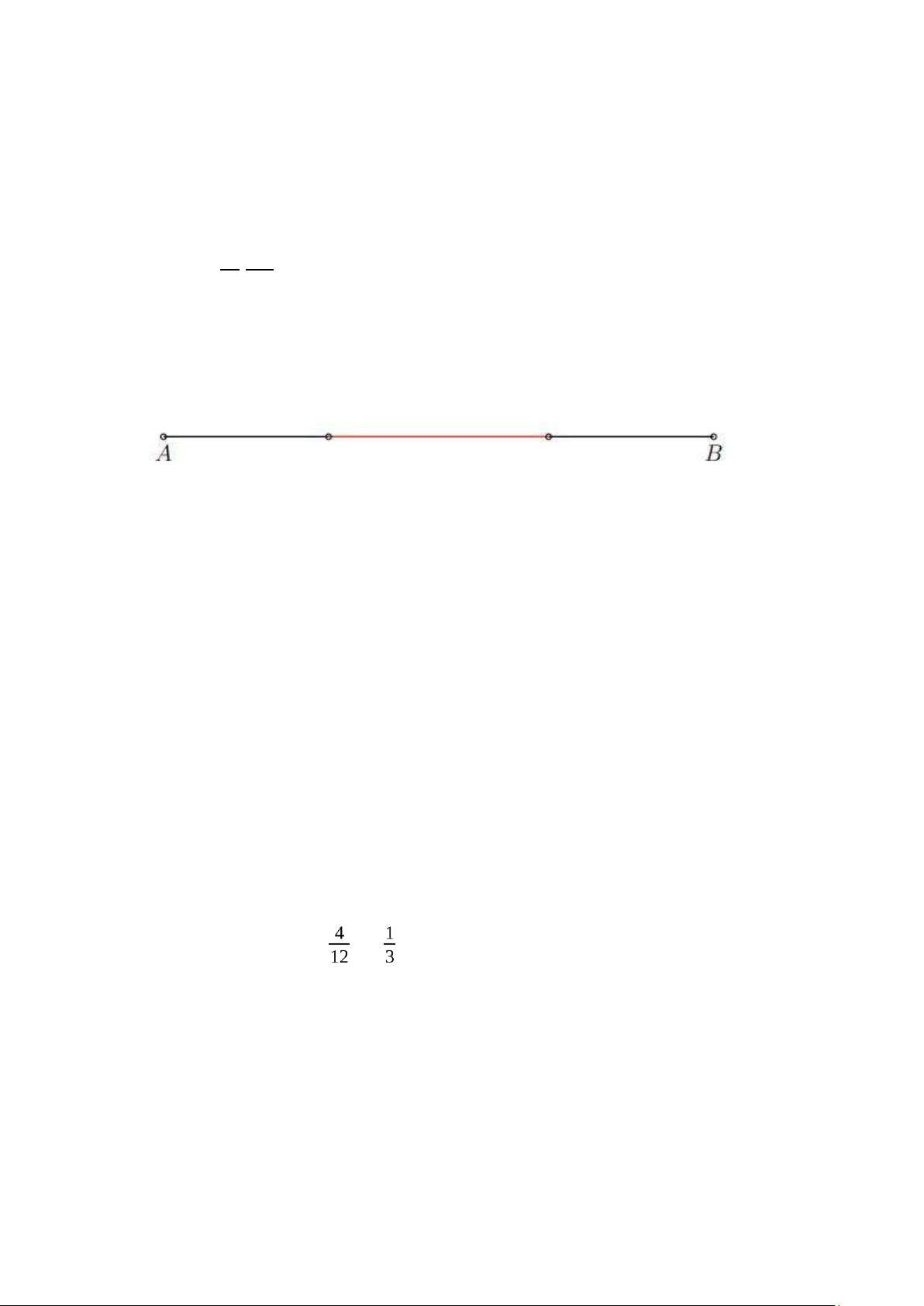
Cho đoạn thẳng AB có độ dài 12 cm. Lấy một điểm C bất kỳ trên đoạn thẳng
đó. Tính xác suất chênh lệch độ dài giữa hai đoạn thẳng AC và CB không vượt quá 4cm Lời giải:
Gọi x là độ dài AC, hiển nhiên CB = 12 − x. Số kết cục đồng khả năng ở đây là
độ dài đoạn thẳng AB, chính là 12 cm.
Gọi A là "chênh lệch độ dài giữa AC và CB không quá 4 cm", khi đó, A biểu thị bởi miền hình học
H = { x [0, 12] mà |x − (12 − x)| ≤ 4 } ∈
Giải bất phương trình |2x – 12| ≤ 4 suy ra 4 ≤ x ≤ 8
Vì H là đoạn thẳng có độ dài 8 − 4 = 4 (cm) nên ta dễ dàng tính P(A) theo định nghĩa hình học: P(A) = = Ví dụ 6:
Cho đoạn thẳng AB độ dài 12 cm. Lấy hai điểm C, D bất kỳ trên đoạn AB (C
nằm giữa A và D). Tính xác suất độ dài AC, CD, DB tạo thành 3 cạnh một tam giác. lOMoAR cPSD| 59031616
Gọi x, y lần lượt là độ dài các đoạn thẳng AC, CD.
Khi đó ta có DB = 12 − x − y, với điều kiện x ≥ 0, y ≥ 0, 12 − x − y ≥ 0.
Miền đồng khả năng là
G = { (x, y) ∈ R2 |x ≥ 0, y ≥ 0, 12 − x − y ≥ 0}
Gọi A là "độ dài AC, CD, DB tạo thành 3 cạnh tam giác" thì miền kết cục thuận lợi cho A là
H ={(x, y) G | x + y > 12 − x − y, x + (12 − x − y) > y, y + (12 − x − y) > x}∈ |H|
12.12÷2−6.6.3÷2
Như vậy, xác suất của sự kiện A là P(A) = |G| = 12.12÷2 = 0,5 Ví dụ 7:
Đường dây điện dài ngầm nối với 1 trạm dài 1km . Tính xác suất để dây bị đứt
cách tổng đài không quá 100 m.
Chiều dài tổng thể của dây là L=1000 m, và ta muốn tính xác suất rằng dây sẽ bị
đứt trong khoảng cách không quá 100 m từ tổng đài, tức là khoảng từ 0 đến 100 m trên đoạn dây.
Xác suất này sẽ được tính bằng công thức: P = = 0,1 Ví dụ 8: lOMoAR cPSD| 59031616
Giả sử có một tờ giấy kẻ các đường thẳng song song cách đều nhau với khoảng
cách d, và ta có một cây kim dài l (với l ≤ d). Ta thả cây kim một cách ngẫu
nhiên lên tờ giấy. Tính xác suất để cây kim cắt một trong các đường thẳng.
Gọi θ là góc giữa cây kim và các đường thẳng song song (góc này sẽ được
chọn ngẫu nhiên từ khoảng 0 đến )
Gọi xxx là khoảng cách từ tâm của cây kim đến đường thẳng gần nhất d
(khoảng cách này là một số ngẫu nhiên từ 0 đến 2 do tính đối xứng).
Cây kim sẽ cắt một đường thẳng nếu khoảng cách từ tâm kim đến đường
thẳng gần nhất nhỏ hơn hoặc bằng sin(θ), tức là:
Để tìm xác suất cây kim cắt đường thẳng, ta cần tính tỷ lệ giữa vùng mà cây
kim cắt đường thẳng so với toàn bộ không gian khả dĩ của các vị trí của cây kim.
Xác suất này sẽ được tính bằng công thức tích phân: π d P = 2 . l
Công thức trên được suy ra từ việc tích phân qua mọi giá trị của θ và tính đến
góc ngẫu nhiên của cây kim khi nó rơi xuống tờ giấy.
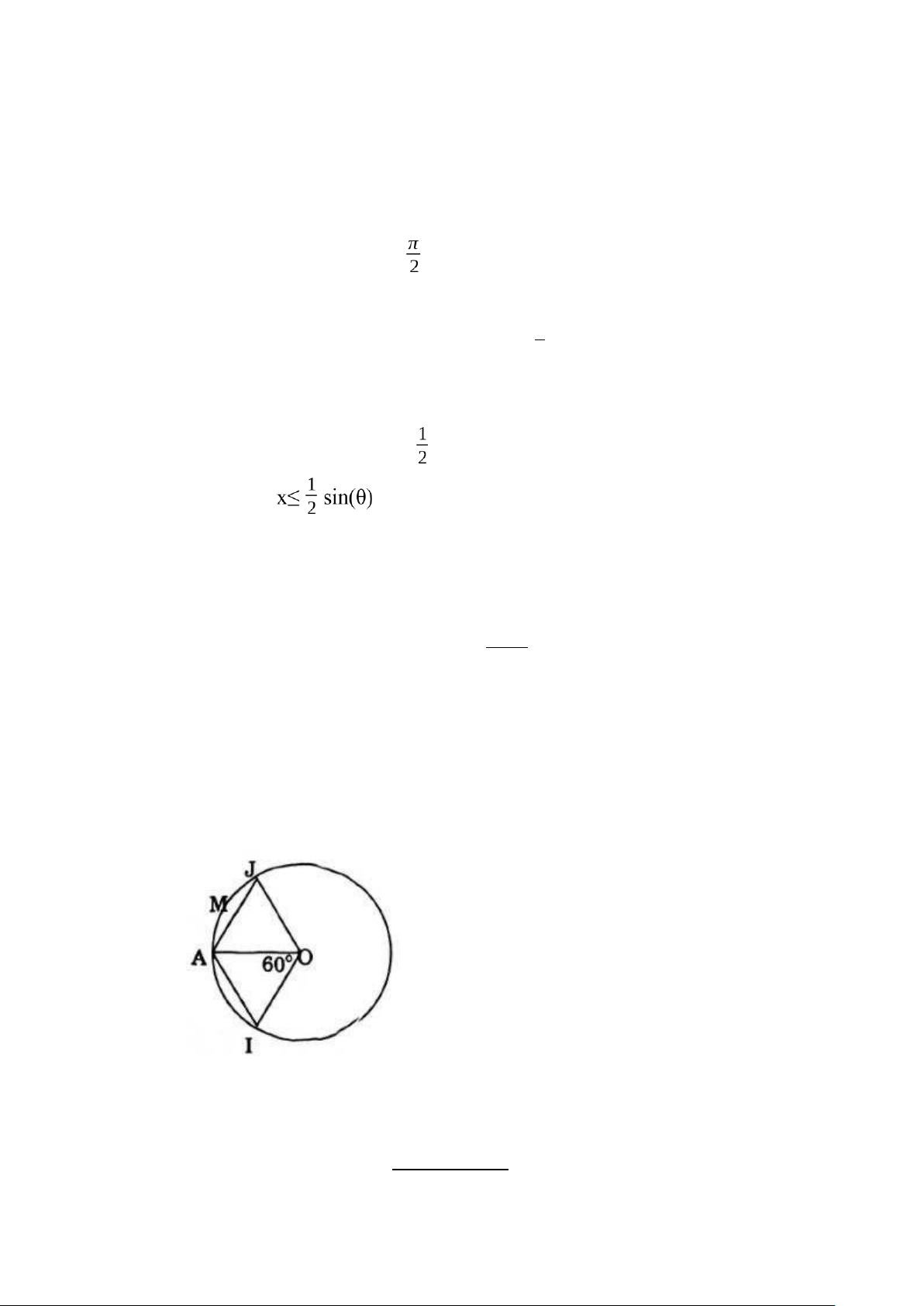
1. Trên một vòng tròn bán kính R có một điểm A cố định. Chọn ngẫu nhiên trên
vòng tròn đó một điểm. Tính xác suất để điểm này cách A không quá R.
Điểm M có thể chọn tùy ý trên vòng tròn nên miền đồng khả năng là cả vòng tròn.
Muốn biến cố: “Điểm M cách A không quá R” xảy ra thì điểm M chỉ được nằm
trên cung IJ (như hình vẽ). độdài cung IJ 1 Vậy P ( A )= độdài(O) =3 lOMoAR cPSD| 59031616
2. Trên đoạn thẳng OA ta chọn ngẫu nhiên hai điểm B và C có độ dài tương
ứnglà OB=x, OC=y (y≥x). Tìm xác suất sao cho độ dài của đoạn BC bé hơn độ dài của đoạn OB.
Giả sử đoạn thẳng OA có chiều dài bằng l.
Với mỗi cách chọn hai điểm B và C có độ dài tương ứng là OB=x, OC=y
(y≥x) sẽ cho ta tương ứng một điểm M(x;y) trên mặt phẳng tọa độ Oxy.
Vì: 0≤x≤l; 0≤y≤l; y≥x suy ra miền biểu diễn điểm M(x;y) là tam giác OMP như hình vẽ bên dưới.
Để độ dài của đoạn BC bé hơn độ dài của đoạn OB thì y−xDo đó: Miền biểu diễn các kết cục thuận lợi là tam giác ONP diệntíchONP 1 Vậy P= = diện tíchOMP 2 2 và y=
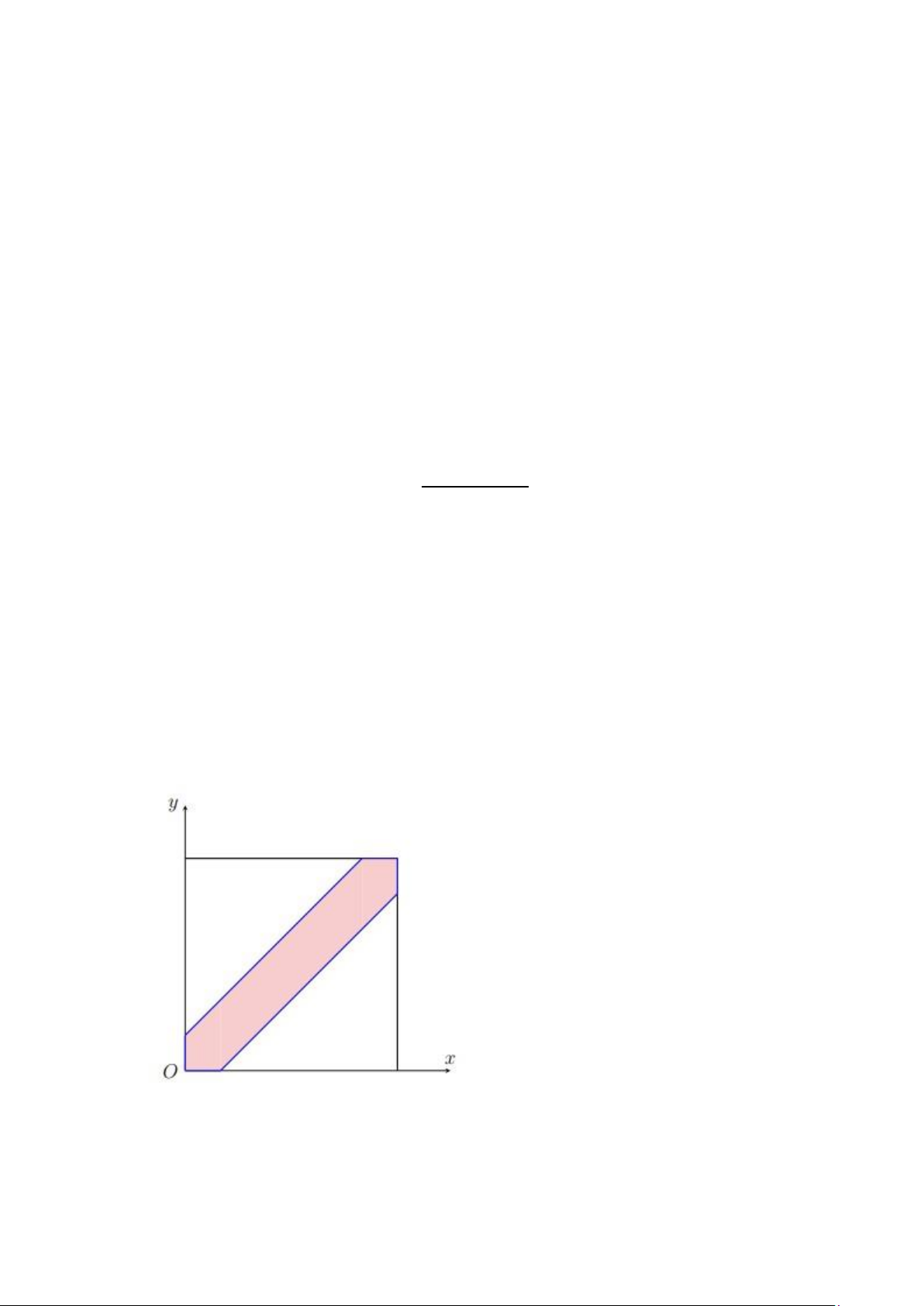
Diện tích hình vuông (H) bằng S=1. 2 Hai đường cong y=x , y=
√ x. cắt nhau tại O(0;0) và A(1;1) là hai đỉnh hình lOMoAR cPSD| 59031616 vuông (H).
Diện tích hình giới hạn bởi hai đường cong là: S' Vậy xác suất cần tìm: S' 1 P= = S 3
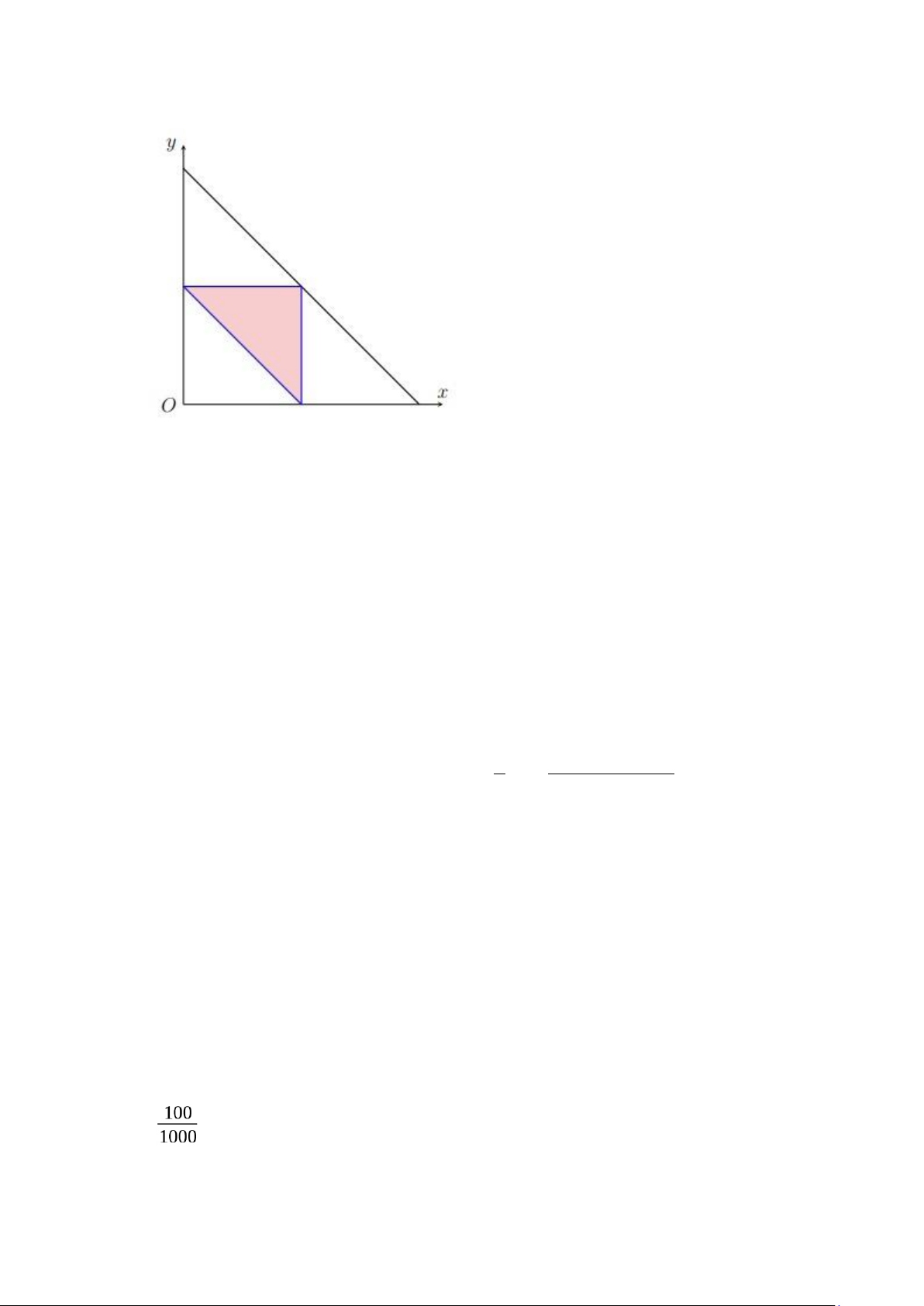
4. Có một đoạn thẳng chiều dài l. Bẻ gẫy ngẫu nhiên thành 3 đoạn. Tính xác suất
để 3 đoạn đó tạo thành được một tam giác.
Nếu ta xem đoạn thẳng như một trục số từ O đến l, ta ký hiệu x là tọa độ
điểm chia thứ nhất và y là tọa độ điểm chia thứ hai (trên trục Ol) thì đoạn
thẳng được chia thành ba đoạn có độ dài tương ứng là: x, y–x và l-y
Mỗi cách chia đoạn thẳng sẽ được biểu thị bằng một điểm M(x;y) trên mặt phẳng tọa độ Oxy. Ta nhận thấy 0
Gọi X là biến cố ba đoạn tạo thành được một tam giác.
Muốn tạo tam giác thì tổng hai cạnh phải lớn hơn cạnh thứ ba, do đó:
Suy ra miền thuận lợi cho X chính là tam giác ΔIJK. SIJK 1 Vậy P(A)= = SOAB 4 lOMoAR cPSD| 59031616
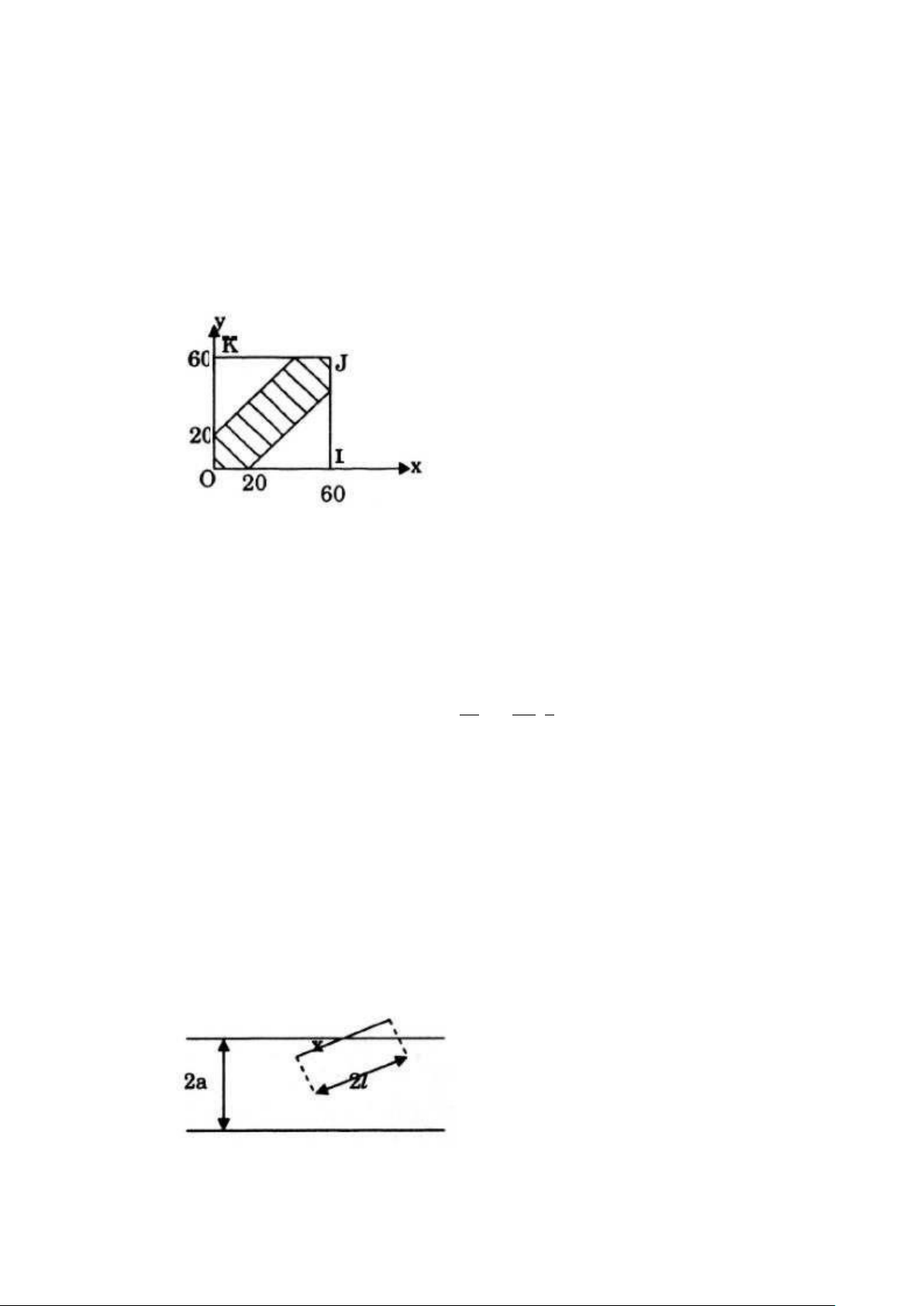
5. Hai người A và B hẹn gặp nhau tại một địa điểm xác định trong vòng từ 0 đến
1 giờ. Người đến trước chờ người kia quá 20 phút thì sẽ bỏ đi. Tính xác suất
để họ gặp được nhau, biết rằng mỗi người có thể đến chỗ hẹn vào thời điểm
bất kỳ trong khoảng thời gian trên.
Gọi x là thời gian đến của A, y là thời gian đến của B (tính bằng phút).
Mọi kết cục đồng khả năng là mọi cặp số (x;y) mà 0≤x≤60, 0≤y≤60.
Tập hợp này được biểu diễn bởi hình vuông OIJK (như hình vẽ).
Các kết cục thích hợp cho hai người gặp nhau là những cặp (x;y) sao
cho: |x–y|≤20 ⇔x−20≤y≤x+20.
Trên hình vẽ, tập hợp này ứng với miền con của hình vuông OIJK, gồm
phần nằm giữa các đường thẳng y=x+20 và y=x–20. Vậy xác suất phải tìm bằng: 2 2
P( A)=6060−240 =59
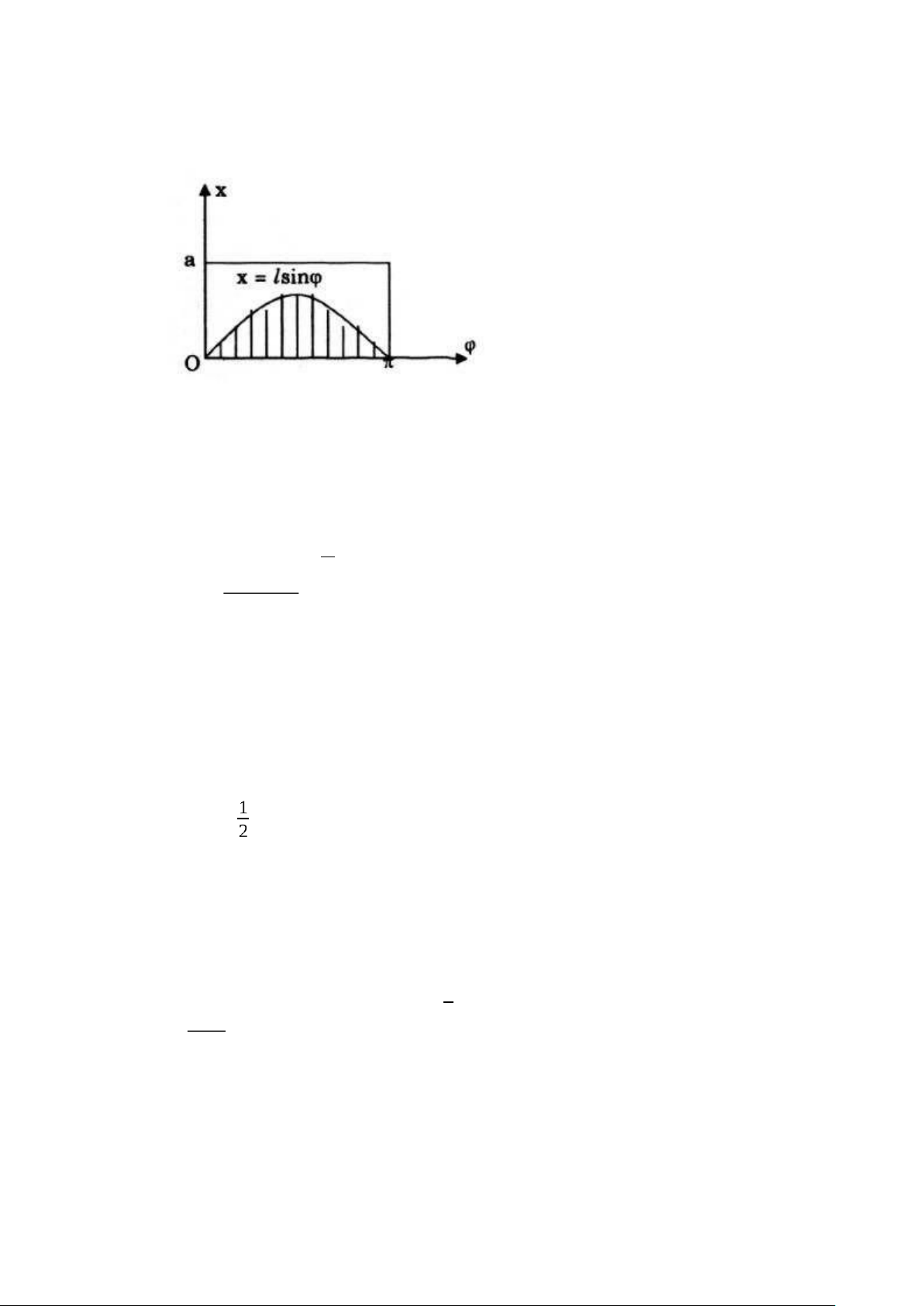
6. Trên mặt phẳng kẻ sẵn các đường thẳng song song cách đều nhau
mộtkhoảng có độ dài 2a, người ta gieo ngẫu nhiên một chiếc kim dài 2l (lđường thẳng đó.
Gọi x là khoảng cách từ trung điểm của kim đến đường thẳng song
song gần nhất và φ là góc mà kim tạo với các đường này. Ta có:
0≤x≤a, 0≤ φ ≤π lOMoAR cPSD| 59031616
Do đó có thể biểu diễn miền đồng khả năng bởi một hình chữ nhật có cạnh là a và π
Ta thấy rằng để kim cắt đường thẳng song song, điều kiện cần và đủ là: 0≤x≤lsinφ.
Từ các giả thiết của bài toán, suy ra xác suất phải tìm bằng tỷ số diện tích
miền gạch chéo và diện tích hình chữ nhật: π
∫0 lsinφdφ 2l P ( H )= = aπ aπ
7. Cho hai biến ngẫu nhiên độc lập X và Y đều phân phối đều trên đoạn [0, 1].
Tính xác suất để X+Y≤1
Sự kiện X+Y≤1 chính là tập hợp các điểm trong mặt phẳng sao cho tổng tọa
độ của chúng nhỏ hơn hoặc bằng 1. Miền này là tam giác nằm dưới đường
thẳng X+Y=1, có đỉnh tại các điểm (0,1), (1,0), và (0,0). Đáp số:
8. Giả sử có một hình vuông với cạnh dài 10 cm. Bên trong hình vuông, ta vẽ
một hình tròn nội tiếp (hình tròn lớn nhất có thể nằm hoàn toàn bên trong
hình vuông). Chọn ngẫu nhiên một điểm trong hình vuông, tính xác suất để
điểm đó nằm trong hình tròn. stròn π P= = svuông 4
9. Cho một hình chữ nhật có chiều dài 8 cm và chiều rộng 6 cm. Bên trong hình
chữ nhật, ta vẽ một hình elip nội tiếp (hình elip lớn nhất có thể nằm hoàn toàn
bên trong hình chữ nhật). Chọn ngẫu nhiên một điểm trong hình chữ nhật, lOMoAR cPSD| 59031616
tính xác suất để điểm đó nằm trong hình elip. Bán kính trục lớn hình elip: a= =4 cm
Bán kính trục nhỏ hình elip: b= =3cm
Diện tích elip: S=πab=12π(cm2) Selip π P= = shcn 4
10.Giả sử có hai hình tròn đồng tâm: hình tròn nhỏ có bán kính 3 cm và hình tròn
lớn có bán kính 6 cm. Nếu chọn ngẫu nhiên một điểm trong hình tròn lớn, tính
xác suất để điểm đó nằm trong vùng giữa hai hình tròn (vùng nằm ngoài hình
tròn nhỏ nhưng bên trong hình tròn lớn).
Tính diện tích vùng giữa 2 hình tròn: S = 36π−9π=27 π Đáp số:
11.Cho một tam giác đều có cạnh dài 12 cm. Bên trong tam giác này, ta vẽ một
hình tròn nội tiếp. Chọn ngẫu nhiên một điểm trong tam giác, tính xác suất
để điểm đó nằm trong hình tròn. Diện tích tam giác: S Bán kính cm
Diện tích hình tròn S=π(2√3)2=12π(cm2) P stam giác 3 √3
12.Giả sử có một mục tiêu hình tròn với bán kính 10 cm. Bên trong hình tròn này,
có một hình vuông với cạnh dài 10 cm, nội tiếp hoàn toàn bên trong hình tròn.
Tính xác suất để viên đạn bắn trúng ngẫu nhiên vào mục tiêu rơi vào vùng bên trong hình vuông. Svuông 1 P= = stròn π
13.Cho một mục tiêu có hình tròn với bán kính 12 cm. Trong mục tiêu này, có
một vùng hồng tâm hình tròn đồng tâm với bán kính 3 cm. Nếu một người lOMoAR cPSD| 59031616
bắn ngẫu nhiên một viên đạn vào mục tiêu, tính xác suất để viên đạn rơi trúng vùng hồng tâm. Shồng tâm 1 P= == stròn 144π 16
14.Một mục tiêu gồm 5 vòng tròn đồng tâm, mỗi vòng có bán kính khác nhau là 1
cm, 2 cm, 3 cm, 4 cm, và 5 cm. Một người bắn viên đạn ngẫu nhiên vào mục
tiêu này. Tính xác suất để viên đạn trúng vòng tròn thứ 3 (vòng có bán kính từ 2 cm đến 3 cm). S 3 vòng trònt 5 π 1 P= = = stổng 25 π 5
15.Một người bắn súng cố gắng bắn trúng một mục tiêu đang di chuyển. Mục
tiêu có thể di chuyển qua lại trên một đoạn thẳng dài 100 m với vận tốc không
đổi là 5 m/s. Người bắn biết rằng viên đạn mất 2 giây để đi đến mục tiêu và
mỗi lần bắn, mục tiêu có thể nằm ở bất kỳ vị trí nào trên đoạn thẳng đó. Giả
sử xác suất để bắn trúng phụ thuộc vào khoảng cách giữa viên đạn và vị trí
thực của mục tiêu. Tính xác suất để bắn trúng mục tiêu nếu mục tiêu di chuyển không ngừng.
Vị trí mục tiêu: Sau 2 giây, mục tiêu đã di chuyển thêm được: Δx=5×2=10 m
Vậy, nếu mục tiêu có thể xuất phát từ bất kỳ vị trí nào trên đoạn thẳng dài 100
m, thì sau khi viên đạn đến, mục tiêu có thể nằm ở bất kỳ vị trí nào trong một đoạn dài 10 m.
Xác suất trúng mục tiêu: Nếu viên đạn nhắm chính xác vào vị trí ban đầu của
mục tiêu, xác suất để mục tiêu vẫn nằm trong khoảng mà viên đạn có thể
trúng được (trong khoảng 10 m) là: P= =0.1
III) XÁC SUẤT CÓ ĐIỀU KIỆN lOMoAR cPSD| 59031616
Định nghĩa và các tính chất của xác suất có điều kiện
Xác suất của biến cố B được tính trong điều kiện biết rằng biến cố A đã xảy ra
được gọi là xác suất của B với điều kiện A, ký hiệu P(B|A). Tính chất
-Nếu P(A) > 0 thì : P(B|A) = P ( AB ) P ( A)
- Khi cố định A với P(A) > 0 thì xác suất có điều kiện P(B|A) có tất cả các tính
chất của xác suất thông thường đối với biến cố B.
Công thức xác suất đầy đủ :
Giả sử , A A A 1 2 , ..., n là một hệ đầy đủ các biến cố, khi đó với mọi biến
cố B của cùng một phép thử, ta có :
Ví dụ 1: Một công ty có 2 loại sản phẩm A và B. Tỉ lệ sản phẩm A bị lỗi là 5%, trong khi tỉ lệ
sản phẩm B bị lỗi là 10%. Nếu một sản phẩm được chọn ngẫu nhiên và nó bị lỗi, xác suất để
sản phẩm đó là loại A là bao nhiêu(trong đó số sản phẩm A chiếm 60% tổng số sản phẩm, số
sản phẩm B chiếm 40% tổng số sản phẩm)? Giải
Gọi C là biến cố “sản phẩm được chọn là loại A”
Gọi D là biến cố “chọn được sản phẩm và bị lỗi”
=> CD là biến cố chọn được sản phẩm A và nó bị lỗi P(CD)=0.6*0.05=0.03
P(D)=P(C)*P(D|C)+P(C¿∗P(D∨C)=¿0.6*0.05+0.4*0.1=0.07
P(C∨D)= P(CD)=0.03=3 P(D) 0.07 7
Vậy xác suất chọn được sản phẩm A và nó bị lỗi là