Báo cáo cuối kỳ Mhhmp: Mô phỏng cánh tay robot 3 bậc tự do. Môn Mô hình hoá và mô phỏng hệ thống điều khiển | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.

lOMoAR cPSD| 58833082
Mô phỏng cánh tay robot 3 bậc tự do sử dụng Matlab
Nguyễn Siêu Phong, Trương Quang Minh
Khoa Điện tử Viễn thông, Trường Đại học Công nghệ - ĐHQGHN
21020733@vnu.edu.vn , 21021616@vnu.edu.vn
Tóm tắt: Báo cáo này trình bày kết quả mô
phỏng về một cánh tay robot 3 bậc tự do sử dụng
nguyên lý động lực học dựa trên quy tắc Denavit -
II. MÔ HÌNH TOÁN HỌC
Hartenberg (DH), quy tắc giúp xác định số bậc tự
do và số khâu liên kết. Kết quả mô phỏng được
Cánh tay robot 3 bậc tự do di chuyển trên một
thực hiện bằng ngôn ngữ lập trình Matlab bằng
mặt phẳng thông qua ba khớp xoay. Mỗi khớp được
việc vẽ các khớp cánh tay trên mặt phẳng Oxy từ
điều chỉnh mở một servo trong thực tế
đầu vào là 2 biến số x, y.
A. Động học thuận tay máy
I. GIỚI THIỆU CHUNG
Tính đến thời điểm hiện tại, Robotics được định
nghĩa như việc nghiên cứu, thiết kế và áp dụng hệ
thống người máy để thực hiện các công việc lặp đi
lặp lại hoặc những công việc nguy hiểm. Công nghệ
Robotics đóng vai trò quan trọng trong ngành công
nghiệp sản xuất cũng như trong các môi trường
thay đổi và phức tạp như các quy trình lắp ráp, gia
công kim loại, hàn, vận chuyển vật liệu hoặc trong
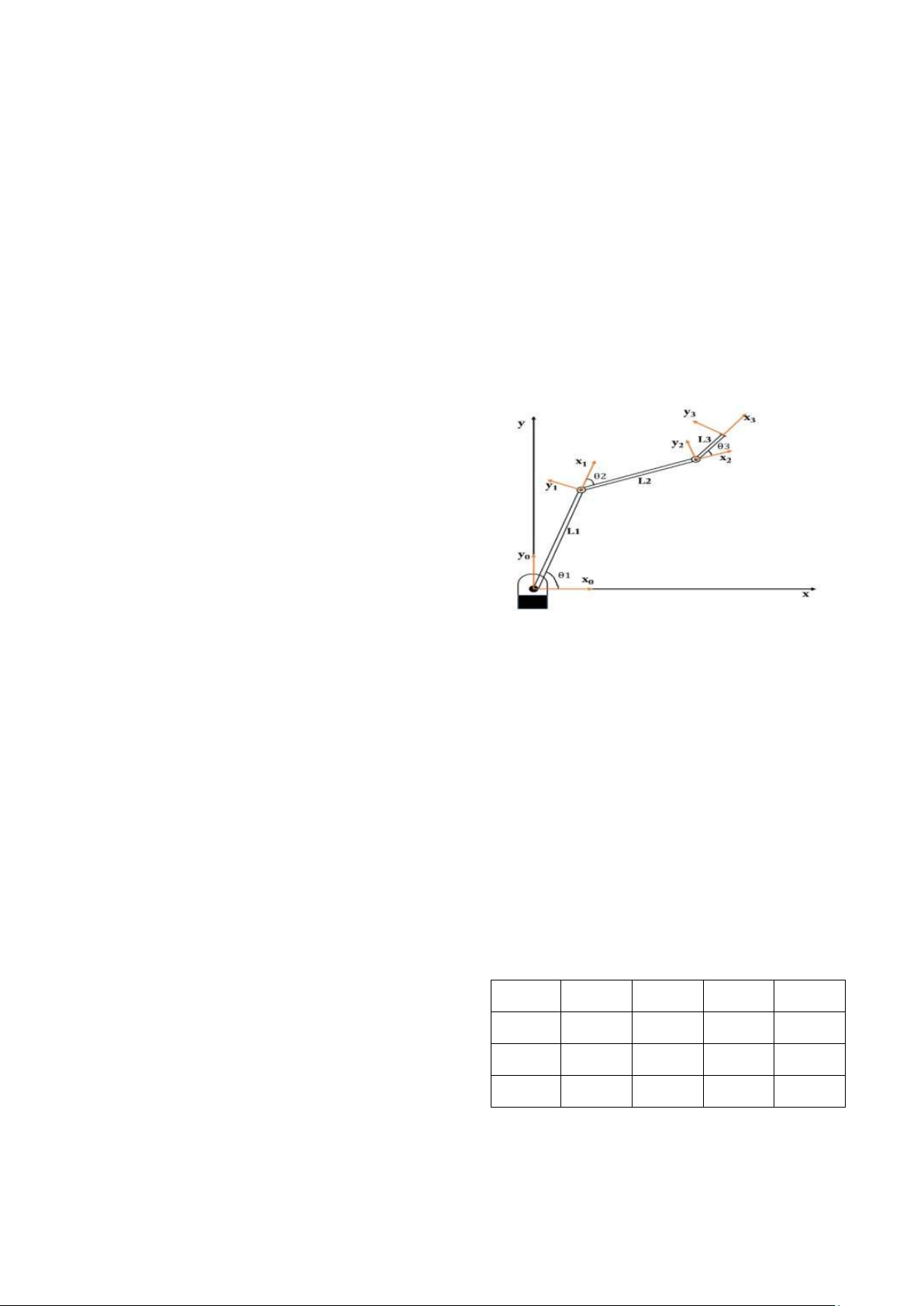
Hình 1. Mô hình cánh tay 3 bậc tự do Mô
các lĩnh vực khác như chăm sóc sức khỏe hoặc
tả động học của cánh tay robot dựa trên quy tắc
nghiên cứu không gian bên ngoài trái đất.
Denavit - Hartenberg (DH). Quy tắc này là một
Cánh tay robot là một ví dụ điển hình, giúp tối
phương pháp quan trọng trong việc mô tả động
ưu hóa việc di chuyển vật liệu và giúp quy trình
học của cánh tay robot, giúp xác định số bậc tự
sản xuất linh hoạt hơn. Thay vì dựa vào lao động
do và các liên kết trong hệ thống. Trong mô hình
con người để thực hiện việc này, sự tự động hóa
cánh tay robot có 3 khớp liên kết, hệ trục tọa độ
thông qua cánh tay robot giảm nguy cơ chấn
được gắn ở mỗi khớp xoay. Thông qua mô hình
thương cho người lao động và tăng hiệu suất làm
gắn trục của cánh tay robot ba bậc tự do, bảng
việc. Điều này không chỉ giảm thiểu sai sót con thông số D-H (Denavit-
người mà còn tiết kiệm thời gian và nguyên liệu
Hartenberg) được tạo ra như trong Bảng 1. Đây
trong quá trình sản xuất.
là một cách tiếp cận cụ thể để mô tả các thông số
Trên cơ sở đó, trong nghiên cứu này, chúng tôi
và liên kết giữa các khớp trong cấu trúc của robot,
sử dụng các tính năng tính toán và vẽ đồ thị của
cung cấp cơ sở quan trọng để hiểu và điều khiển
Matlab để mô phỏng quá trình hoạt động của cánh chuyển động của nó.
tay này. Từ đó giúp các kĩ sư có thể thấy được
Bảng 1. Thông số Denavit-Hartenberg
chuyển động trực quan của nó. 𝑖𝑖 𝑎𝑖 𝛼𝑖 𝑑𝑖 𝜃𝑖
Báo cáo được chia làm 4 phần. Tiếp theo là mô 1 𝐿1 0 0 𝜃1
hình toán học của Denavit – Hartenberg ở phần 3 2 𝐿
và đánh giá kết quả ở phần 4. Cuối cùng kết luận 2 0 0 𝜃2 ở phần 4 3 𝐿3 0 0 𝜃3 lOMoAR cPSD| 58833082
Các ma trận biến đổi như sau:
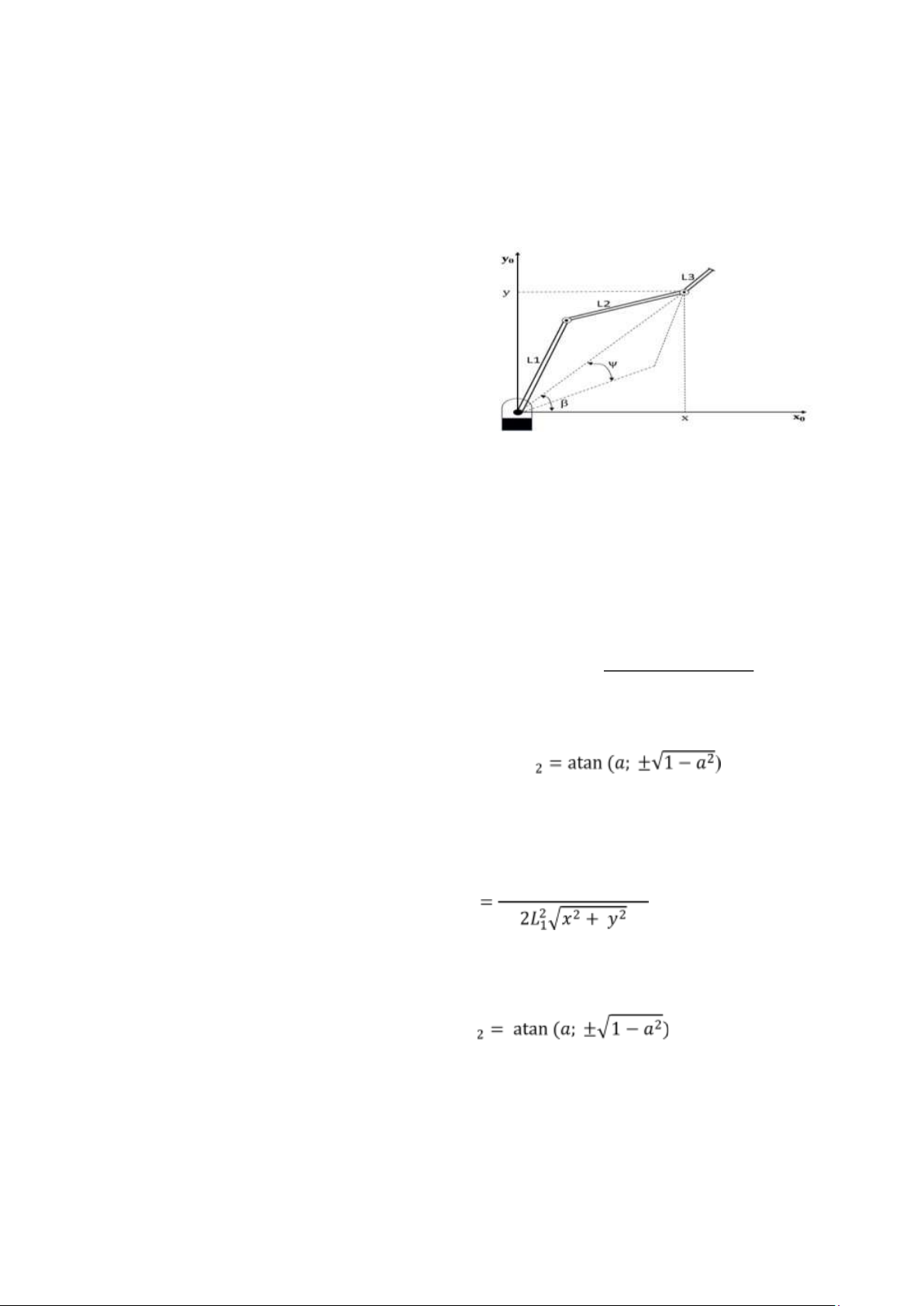
B. Động học nghịch tay máy
cos 𝜃1 − sin 𝜃1 0 𝐿1 cos 𝜃1 cos 𝜃1 0 𝟎𝑻 = [sin 𝜃1 1 𝐿1 sin 𝜃1] 𝟏 0 0 0 0 0 0 1
cos 𝜃2 − sin 𝜃2 0 𝐿2 cos 𝜃2 cos 𝜃2 0 𝟏𝑻 = [sin 𝜃2 1 𝐿2 sin 𝜃2 ] 𝟐 0 0 0 0 0 0 1
Từ phương trình tính động học thuận đặt:
cos 𝜃3 − sin 𝜃3 0 𝐿3 cos 𝜃3
𝑥 = 𝐿1 cos 𝜃1 + 𝐿2 cos(𝜃1 + 𝜃2) cos 𝜃3 0 𝟐𝑻 = [sin 𝜃3 1 𝐿3 sin 𝜃3 ] 𝑦 = 𝐿 𝟑 0
1 sin 𝜃1 + 𝐿2 sin(𝜃1 + 𝜃2) 0 0 0 0
𝑥2 + 𝑦2 = 𝐿21 + 𝐿22 − 2𝐿1𝐿2 cos(180 + 𝜃2) 0 1 Đặt 𝑎 = cos 𝜃2
Từ các ma trận trên, ta có: 𝑐 𝑥 123 −𝑠123 0
2 + 𝑦2 − 𝐿21 − 𝐿22 𝑃𝑥 0 𝑎 = 𝟎𝑻 = [𝑠123 𝑐123 1 𝑃 2𝐿 𝑦] 1𝐿2 𝟑 0 0 0 𝑃𝑧 0 0 1 Trong đó: Suy ra 𝜃
𝑠123 = sin(𝜃1 + 𝜃2 + 𝜃3);
𝛽 = 𝑎𝑡𝑎𝑛2(𝑦, 𝑥)
𝑐123 = cos(𝜃1 + 𝜃2 + 𝜃3); Đặt 𝑏 = cos (𝜓)
𝑃𝑥 = 𝐿1 cos 𝜃1 + 𝐿2 cos(𝜃1 + 𝜃2) + 𝐿3cos(𝜃1
𝑥2 + 𝑦2 + 𝐿21 − 𝐿22 + 𝜃2 + 𝜃3); 𝑃 𝑏
𝑦 = 𝐿1 sin 𝜃1 + 𝐿2 sin(𝜃1 + 𝜃2) + 𝐿
𝜓 = 𝑎𝑟𝑐𝑜𝑠(𝑏) 3sin(𝜃1 + 𝜃2 + 𝜃3);
𝑃𝑧 = 0 Hướng của Robot được xác định thông 𝜃1 = 𝛽 ± 𝜓 qua công thức: 𝜃 𝛾 = 𝜃1 + 𝜃2+ 𝜃3
𝜃3 = 𝛾 − 𝜃1 − 𝜃2
Trong đó γ là hướng của robot
III. MÔ PHỎNG VÀ ĐÁNH GIÁ
Sau khi hoàn thành các mô hình toán học, chúng
tôi sẽ mô phỏng quá trình này bằng ngôn ngữ lập trình Matlab. lOMoAR cPSD| 58833082
A. Thiết lập tham số
hoặc không nên chọn (do các ràng buộc và va •
chạm vật lý xảy ra như va chạm giữa các khâu, 𝐿1 = 5;
giới hạn không gian làm việc, dây dẫn,... hoặc do • 𝐿2 = 3;
bước nhảy đột ngột của biến khớp từ kết quả •
nghiệm của phương trình lượng giác). Kết quả mô 𝐿3 = 2;
phỏng chuyển động ở đây đã dựa trên việc lựa • x = 5, y = 9;
chọn 1 tập nghiệm để phù hợp nhất với khả năng
chuyển động thực tế của robot.
Sử dụng một vòng lặp trong Matlab ta sẽ thấy
được sự thay đổi góc của các khớp tay. Ở đây, tôi
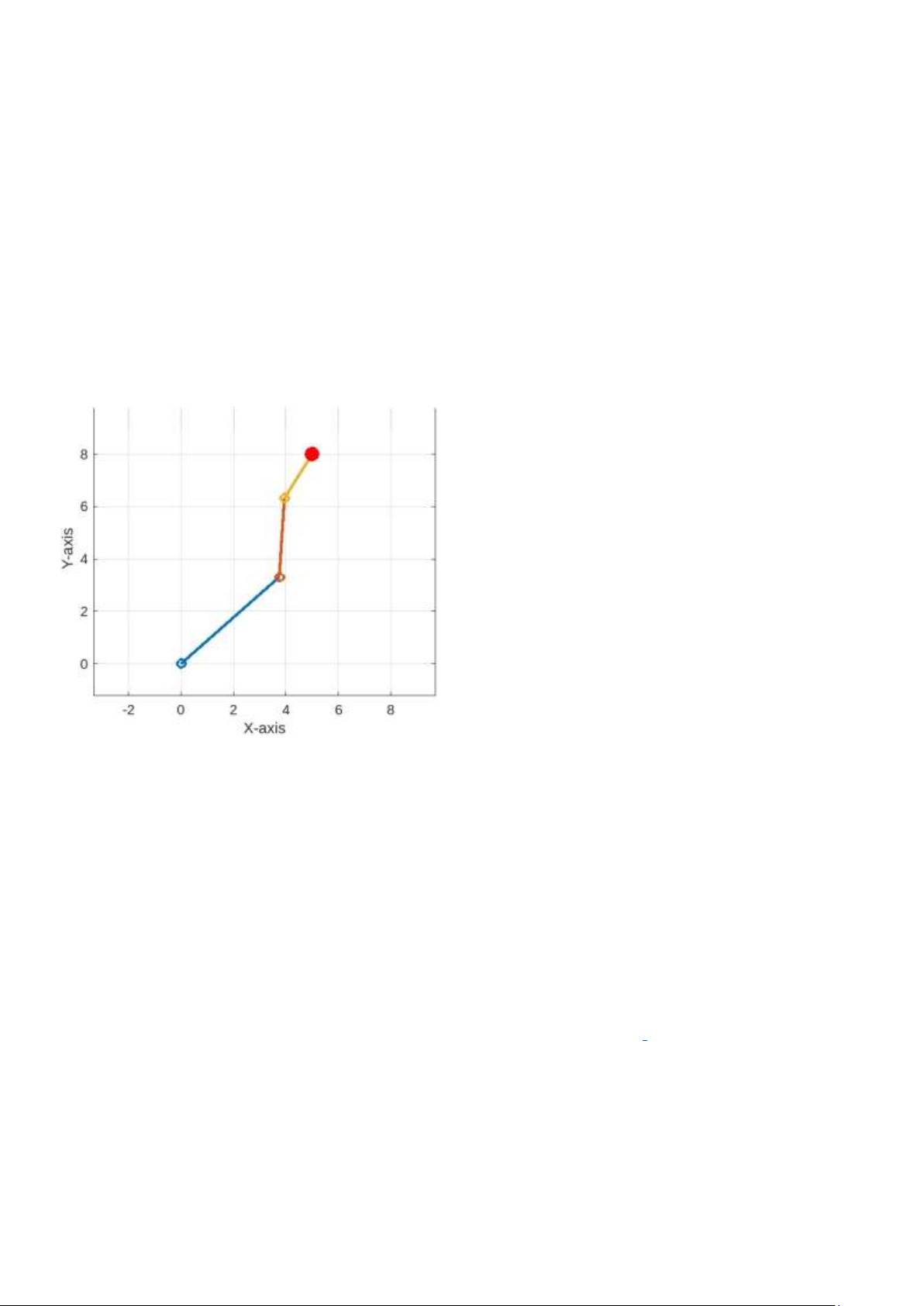
B. Kết quả đầu ra
sử dụng thêm tham số steps và công cụ pause. • 𝜃1 = 41.4556
step = 50; pause(0.05); • 𝜃2 = 44.8624 • 𝜃3 = -28.3234
Sau mỗi 0.05 giây thì sẽ vẽ một đồ thị mới lên trục
tọa Oxy, từ đó sẽ tạo ra dạng chuyển động của cánh tay robot.
IV. KẾT LUẬN
Trong bài báo cáo này, chúng tôi đã trình bày
việc mô phỏng 2D động học nghịch của cánh tay
Robot 3 bậc tự do thông qua Matlab. Kết quả mô
phỏng cho thấy việc thiết lập phương trình động học
và giải nghiệm của bài toán động học ngược đã
được thực hiện đúng và phù hợp với chuyển động thực tế của Robot. REFERENCES
[1] Trần Đình Hòa, Nguyễn Văn Khiêm, Trần Đức
Hình 2. Kết quả mô phỏng
Thiện, Design, simulation, fabrication, and
control of a 3-DOF planar robotic manipulator.
Việc giải bài toán động học ngược dựa trên mô
hình toán học và hệ phương trình sẽ cho nhiều tập
nghiệm, vì các phương trình lượng giác thường trả
[2] Nasr M. Ghaleb and Ayman A. Aly, Modeling
về 2 nghiệm cho mỗi biến khớp. Tuy nhiên, đối
and Control of 2-DOF Robot Arm
với cấu trúc vật lý thực tế của robot, sẽ có nhiều
tập nghiệm từ lý thuyết mà robot không thể đạt tới
[3] Nguyễn Đức Sang, 3D modeling and inverse
kinematics simulation of a 6-DOF arm robot
using a combination of CAD software and multibody tools in MATLAB/Simulink.