Báo cáo khởi nghiệp: Phân công công việc ứng dụng thuật giải Heuristic môn Trí tuệ nhân tạo | Trường Đại học Kinh Doanh và Công Nghệ Hà Nội

lOMoAR cPSD| 58457166
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC KINH DOANH VÀ CÔNG NGHỆ HÀ NỘI -----OOO-----
BÁO CÁO KHỞI NGHIỆP
Đề tài: Trình bài bài toán phân việc - ứng dụng nguyên lý thứ tự
của thuật giải Heuristic, ứng dụng cụ thể, minh họa dữ liệu thực tế. Nhóm 4 Thành viên nhóm :
Nguyễn Tú Tài – MSV: 2621211196
Nguyễn Anh Thư – MSV: 2621211011
Vũ Thị Bích Thủy – MSV: 2621221250
Nguyễn Mạnh Tiến – MSV: 2621210052
Nguyễn Quang Trường – MSV: 2621211067 Lớp: TH26.19
Giáo viên hướng dẫn: Hải Yến Hà Nội - 3/2024 lOMoAR cPSD| 58457166 MỤC LỤC
I. LÝ DO CHỌN ĐỀ TÀI..............................................................................................................3
II. MỤC TIÊU CỦA ĐỀ TÀI.........................................................................................................4
III. GIỚI THIỆU TỔNG QUAN VỀ ĐỀ TÀI............................................................................6
IV. TƯ TƯỞNG CỦA THUẬT HEURISTIC............................................................................7 V.
BÀI TOÁN PHÂN VIỆC – ỨNG DỤNG CỦA NGUYÊN LÝ THỨ TỰ CỦA
THUẬT GIẢI HEURISTIC.............................................................................................................8
VI. CÀI ĐẶT THUẬT TOÁN........................................................................................................11
VII. THU THẬP DỮ LIỆU THỰC TẾ.......................................................................................15 lOMoAR cPSD| 58457166 I.
LÝ DO CHỌN ĐỀ TÀI
Bài toán phân việc được chọn để áp dụng nguyên lý thứ tự của thuật giải Heuristic vì một số lý do sau: 1.
Đơn giản và trực quan: Bài toán phân việc là một bài toán tối ưu hóa phổ biến và
dễ hiểu, giúp người mới học dễ dàng nắm bắt được ý tưởng của thuật giải Heuristic. 2.
Hiệu quả: Nguyên lý thứ tự giúp giảm thiểu thời gian hoàn thành tổng thể bằng
cách ưu tiên các công việc có thời gian thực hiện lớn hơn. Điều này giúp tối ưu hóa sử dụng tài nguyên. 3.
Ứng dụng thực tế: Bài toán phân việc có nhiều ứng dụng trong thực tế, từ lập lịch
sản xuất trong công nghiệp đến quản lý dự án trong phần mềm. Việc hiểu rõ cách giải
quyết bài toán này có thể hữu ích trong nhiều lĩnh vực. 4.
Minh họa cho Heuristic: Bài toán phân việc cung cấp một ví dụ minh họa tốt cho
việc làm thế nào Heuristic có thể cung cấp giải pháp tốt (mặc dù không phải lúc nào cũng
tối ưu) một cách nhanh chóng và hiệu quả. II.
MỤC TIÊU CỦA ĐỀ TÀI
Mục tiêu của bài toán phân việc là tối ưu hóa việc sắp xếp và phân chia các tác vụ hoặc công
việc vào các tài nguyên khả dụng sao cho đạt được một số tiêu chí nhất định, chẳng hạn như
tối thiểu hóa thời gian hoàn thành, tối ưu hóa sử dụng tài nguyên, tối thiểu hóa chi phí, hoặc
cân bằng công việc giữa các tài nguyên.
• Tối ưu hóa Thời gian: Một trong những mục tiêu phổ biến trong bài toán phân việc
là tối thiểu hóa thời gian hoàn thành tổng cộng của các công việc. Điều này có thể
áp dụng trong các lĩnh vực như lập lịch sản xuất, quản lý dự án, hoặc quản lý nguồn nhân lực.
• Tối ưu hóa Sử dụng tài nguyên: Một mục tiêu khác là tối ưu hóa việc sử dụng các
tài nguyên như máy móc, nhân lực, hoặc nguyên liệu. Bằng cách phân chia công việc lOMoAR cPSD| 58457166
một cách hiệu quả, ta có thể giảm thiểu lãng phí tài nguyên và tăng hiệu suất tổng thể của hệ thống.
• Tối ưu hóa Chi phí: Trong một số trường hợp, mục tiêu của bài toán có thể là tối
thiểu hóa chi phí liên quan đến thực hiện các công việc. Điều này bao gồm cả chi phí
lao động, chi phí vận chuyển, và các chi phí khác có thể phát sinh trong quá trình thực hiện công việc.
• Cân bằng Công việc và Tài nguyên: Trong một số trường hợp, mục tiêu không chỉ
là tối ưu hóa một tiêu chí duy nhất mà còn là cân bằng công việc và tài nguyên. Điều
này đảm bảo rằng không có tài nguyên nào bị quá tải trong khi có tài nguyên khác
lại ít được sử dụng.
• Đáp ứng Yêu cầu Cụ thể: Cuối cùng, mục tiêu của bài toán phân việc cũng có thể
là đáp ứng các yêu cầu cụ thể của hệ thống hoặc môi trường. Ví dụ, trong một môi
trường sản xuất, việc phân chia công việc phải đảm bảo tuân thủ các ràng buộc về
quy trình sản xuất, tiêu chuẩn chất lượng, hoặc yêu cầu an toàn.
Tóm lại, sử dụng các thuật giải heuristic có thể giúp tìm ra giải pháp khả thi và gần
tối ưu cho bài toán phân việc một cách hiệu quả trong thực tế, kể cả khi không có khả năng
tìm kiếm toàn bộ không gian giải phápKhi áp dụng thuật giải heuristic trong bài toán phân
việc, mục tiêu là tìm kiếm một giải pháp gần đúng nhưng vẫn chấp nhận được trong một
thời gian hợp lý. Thay vì tìm kiếm giải pháp tối ưu hoàn hảo, thuật giải heuristic tập trung
vào việc tạo ra một lời giải hiệu quả trong thực tế và có thể thực thi được. lOMoAR cPSD| 58457166 III.
GIỚI THIỆU TỔNG QUAN VỀ ĐỀ TÀI
Trong lĩnh vực nghiên cứu giải quyết các vấn đề, chúng ta thường đối mặt với những thách thức như sau:
• Có những bài toán mà cho đến nay, chúng ta vẫn chưa tìm ra một phương pháp giải
dựa trên thuật toán và không chắc chắn liệu có thuật toán tồn tại hay không.
• Một số bài toán đã có thuật toán để giải, nhưng không được chấp nhận vì thời gian
giải quá lớn hoặc các điều kiện cần thiết cho thuật toán khó đáp ứng.
• Có những bài toán được giải theo những phương pháp không tuân thủ hoàn toàn các
nguyên tắc của thuật toán, nhưng vẫn được chấp nhận.
Những nhận định này đã thúc đẩy sự cần thiết phải đổi mới khái niệm về thuật toán. Chúng
ta đã mở rộng hai tiêu chuẩn của thuật toán: tính xác định và tính đúng đắn. Việc mở rộng
tính xác định của thuật toán đã được thể hiện qua các giải thuật đệ quy và ngẫu nhiên. Tính
đúng của thuật toán giờ đây không còn là điều kiện bắt buộc đối với một số phương pháp
giải bài toán, đặc biệt là các phương pháp giải gần đúng. Trong thực tế, chúng ta thường
chấp nhận những phương pháp giải mang lại kết quả tốt (mặc dù không phải lúc nào cũng
tốt) nhưng ít phức tạp và hiệu quả hơn. Ví dụ, nếu việc giải một bài toán bằng thuật toán tối
ưu đòi hỏi máy tính phải hoạt động trong nhiều năm, thì chúng ta có thể sẵn lòng chấp nhận
một giải pháp gần tối ưu mà chỉ cần máy tính chạy trong vài ngày hoặc vài giờ.
Những phương pháp giải được chấp nhận nhưng không hoàn toàn tuân thủ các tiêu chuẩn
của thuật toán thường được gọi là các thuật giải. Khái niệm mở rộng này của thuật toán đã
mở ra cánh cửa mới cho chúng ta trong việc tìm kiếm phương pháp để giải quyết các bài toán được đặt ra.
Một trong những thuật giải thường được áp dụng trong khoa học trí tuệ nhân tạo là các
phương pháp giải theo kiểu Heuristic. Đây là một phương pháp giải quyết bài toán phân
việc dựa trên nguyên lý thứ tự, giúp tối ưu hóa quá trình giải quyết bài toán và đạt được kết
quả tốt trong thời gian ngắn hơn. lOMoAR cPSD| 58457166 IV.
TƯ TƯỞNG CỦA THUẬT HEURISTIC
Heuristic là một phương pháp giải quyết vấn đề mở rộng từ khái niệm thuật toán. Nó mang
đến cách tiếp cận vấn đề với các đặc điểm sau:
• Thường xuyên tìm ra giải pháp tốt (nhưng không nhất thiết là tốt nhất)
• Việc áp dụng Heuristic thường dẫn đến kết quả nhanh chóng và dễ dàng hơn so với
thuật toán tối ưu, do đó giảm chi phí.
• Heuristic thường phản ánh cách suy nghĩ và hành động tự nhiên của con người.
Có nhiều cách để xây dựng một thuật giải Heuristic, thường dựa vào một số nguyên lý cơ bản như sau:
• Nguyên lý vét cạn thông minh: Khi không gian tìm kiếm lớn trong một vấn đề tìm
kiếm, ta thường cố gắng hạn chế không gian tìm kiếm hoặc thực hiện một loại tìm
kiếm đặc biệt dựa trên đặc điểm của vấn đề để nhanh chóng tìm ra mục tiêu.
• Nguyên lý tham lam (Greedy): Sử dụng tiêu chuẩn tối ưu (trên phạm vi toàn cục)
của vấn đề để làm tiêu chuẩn chọn lựa hành động cho phạm vi cục bộ của từng bước
(hoặc từng giai đoạn) trong quá trình tìm kiếm giải pháp.
• Nguyên lý thứ tự: Thực hiện hành động dựa trên một cấu trúc thứ tự hợp lý của
không gian khảo sát để nhanh chóng đạt được một giải pháp tốt.
• Hàm Heuristic: Khi xây dựng các thuật giải Heuristic, người ta thường sử dụng các
hàm Heuristic. Đây là các hàm ước lượng, giá trị của hàm phụ thuộc vào trạng thái
hiện tại của vấn đề tại mỗi bước giải. Nhờ giá trị này, ta có thể chọn cách hành động
tương đối hợp lý trong từng bước của thuật giải.
V. BÀI TOÁN PHÂN VIỆC – ỨNG DỤNG CỦA NGUYÊN LÝ THỨ TỰ
CỦA THUẬT GIẢI HEURISTIC
Một công ty nhận được hợp đồng gia công m chi tiết máy J1, J2, … Jm. Công ty có n máy
gia công lần lượt là P1, P2, … Pn. Mọi chi tiết đều có thể được gia công trên bất kỳ máy nào.
Một khi đã gia công một chi tiết trên một máy, công việ sẽ tiếp tục cho đến lúc hoàn thành,
không thể bị cắt ngang. Để gia công một việc J1 trên một máy bất kỳ ta cần dùng một thời lOMoAR cPSD| 58457166
gian tương ứng là t1. Nhiệm vụ của công ty là phải làm sao gia công xong toàn bộ n chi tiết
trong thời gian sớm nhất.
Chúng ta xét bài toán trong trường hợp có 3 máy P1, P2, P3 và 6 công việc với thời gian là
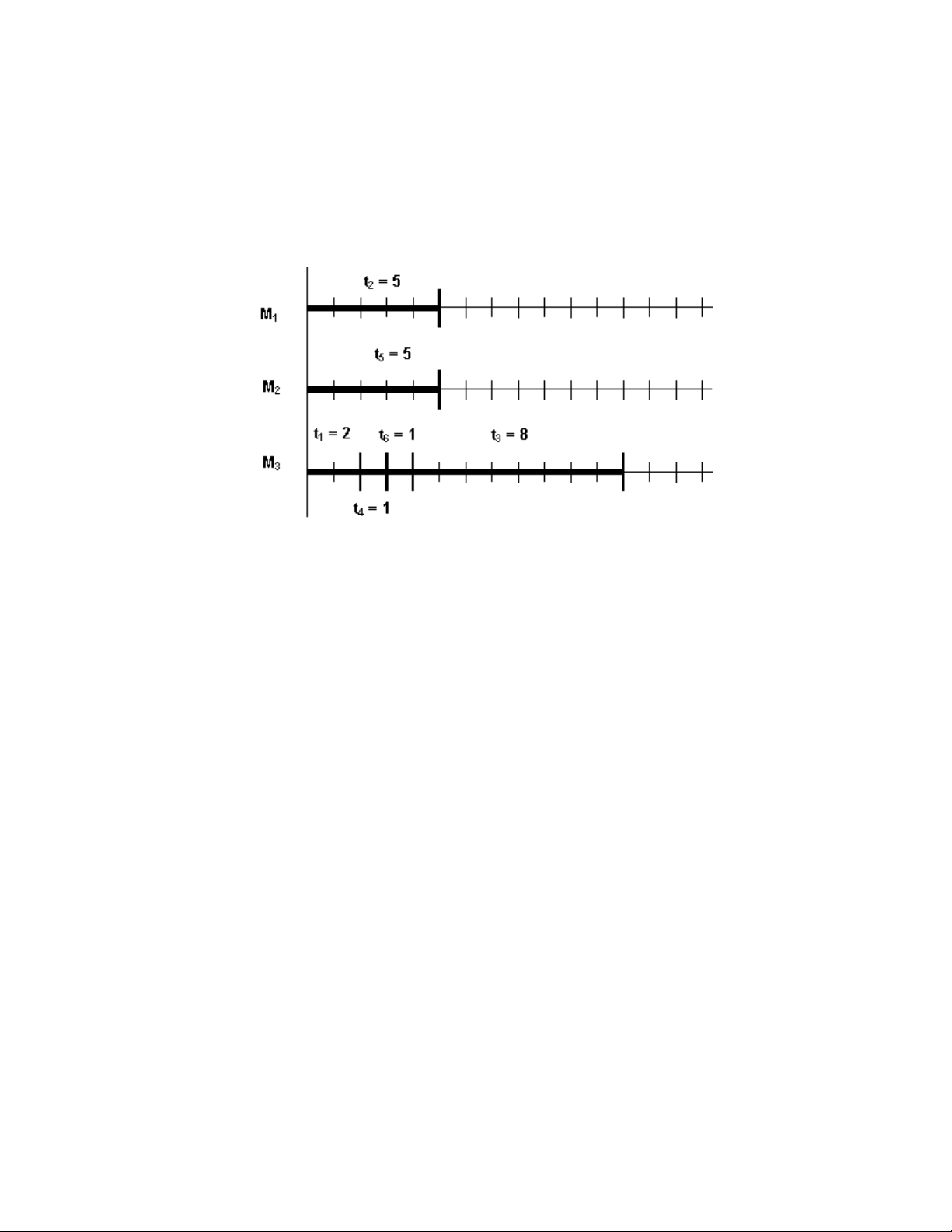
t1=2, t2=5, t3=8, t4=1, t5=5, t6=1. ta có một phương án phân công (L) như hình sau:
Theo hình này, tại thời điểm t=0, ta tiến hành gia công chi tiết J2 trên máy P1, J5 trên P2 và
J1 tại P3. Tại thời điểm t=2, công việc J1 được hoàn thành, trên máy P3 ta gia công tiếp chi
tiết J4. Trong lúc đó, hai máy P1 và P2 vẫn đang thực hiện công việc đầu tiên mình … Sơ đồ
phân việc theo hình ở trên được gọi là lược đồ GANTT. Theo lược đồ này, ta thấy thời gian
để hoàn thành toàn bộ 6 công việc là 12. Nhận xét một cách cảm tính ta thấy rằng phương
án (L) vừa thực hiện là một phương án không tốt. Các máy P1 và P2 có quá nhiều thời gian rãnh.
Thuật toán tìm phương án tối ưu L0 cho bài toán này theo kiểu vét cạn có độ phức tạp cỡ
O(mn) (với m là số máy và n là số công việc). Bây giờ ta xét đến một thuật giải Heuristic
rất đơn giản (độ phức tạp O(n)) để giải bài toán này. •
Sắp xếp các công việc theo thứ tự giảm dần về thời gian gia công. •
Lần lượt sắp xếp các việc theo thứ tự đó vào máy còn dư nhiều thời gian nhất.
Với tư tưởng như vậy, ta sẽ có một phương án L* như sau: lOMoAR cPSD| 58457166
Rõ ràng phương án L* vừa thực hiện cũng chính là phương án tối ưu của trường hợp này vì
thời gian hoàn thành là 8, đúng bằng thời gian của công việc J3. Ta hy vọng rằng một giải
Heuristic đơn giản như vậy sẽ là một thuật giải tối ưu. Nhưng tiếc thay, ta dễ dàng đưa ra
được một trường hợp mà thuật giải Heuristic không đưa ra được kết quả tối ưu.
Nếu gọi T* là thời gian để gia công xong n chi tiết máy do thuật giải Heuristic đưa ra và
T0 là thời gian tối ưu thì người ta đã chứng minh được rằng M là số máy lOMoAR cPSD| 58457166
Với kết quả này, ta có thể xác lập được sai số mà chúng ta phải gánh chịu nếu dùng
Heuristic thay vì tìm một lời giải tối ưu. Chẳng hạn với số máy là 2 (M=2) ta có
và đó chính là sai số cực đại mà trường hợp ở trên đã gánh chịu. Theo công thức này, số
máy càng lớn thì sai số càng lớn.
Trong trường hợp M lớn thì tỷ số 1/M xem như bằng 0 . Như vậy, sai số tối đa mà ta phải
chịu là T* ≤ 4/3 T0, nghĩa là sai số tối đa là 33%. Tuy nhiên, khó tìm ra được những trường
hợp mà sai số đúng bằng giá trị cực đại, dù trong trường hợp xấu nhất. Thuật giải Heuristic
trong trường hợp này rõ ràng đã cho chúng ta những lời giải tương đối tốt. VI.
CÀI ĐẶT THUẬT TOÁN
Cách cài đặt thuật giải Heuristic cho bài toán phân việc sử dụng Python. Đoạn code sẽ sắp
xếp các công việc theo thứ tự giảm dần về thời gian gia công, sau đó lần lượt phân công các
công việc theo thứ tự đó vào máy còn nhiều thời gian nhất. Kết quả trả về là thời gian hoàn
thành công việc trên tất cả các máy. Đây là một cách tiếp cận đơn giản nhưng hiệu quả để
giải quyết bài toán phân việc:
def assign_jobs(jobs, num_machines): # Sắp xếp công việc theo
thứ tự giảm dần về thời gian gia công sorted_jobs = sorted(jobs, reverse=True)
# Khởi tạo danh sách máy với thời gian
rỗi machines = [0]*num_machines
# Lần lượt sắp xếp các công việc theo thứ tự đó vào máy còn nhiều thời gian
nhất for job in sorted_jobs: # Tìm máy còn nhiều thời gian nhất
min_machine = min(range(num_machines), key=lambda index: machines[index])
# Thêm công việc vào máy machines[min_machine] += job
# Trả về thời gian hoàn thành công việc trên tất cả các
máy return max(machines) lOMoAR cPSD| 58457166
# Danh sách thời gian gia công của các công việc
jobs = [2, 5, 8, 1, 5, 1] # Số lượng máy num_machines = 3
print(assign_jobs(jobs, num_machines))
Dưới đây là một ví dụ về thuật giải Heuristic cho bài toán phân việc sử dụng Python:
Yêu cầu: giải quyết bài toán phân công công việc sử dụng thuật giải Heuristic. Cụ thể:
Có 3 máy (P1, P2, P3) và 6 công việc với thời gian là t1=2, t2=5, t3=8, t4=1, t5=5, t6=1.
-> Mục tiêu là phân công các công việc cho các máy sao cho thời gian hoàn thành tất cả
công việc là ngắn nhất.
Để giải quyết bài toán này, chúng ta sử dụng thuật giải Heuristic với các bước như sau:
1. Sắp xếp các công việc theo thứ tự giảm dần về thời gian gia công.
2. Lần lượt sắp xếp các công việc theo thứ tự đó vào máy còn nhiều thời gian nhất.
Đoạn code để giải bài toán:
def assign_jobs(jobs, num_machines): # Sắp xếp công việc theo
thứ tự giảm dần về thời gian gia công sorted_jobs =
sorted(jobs, reverse=True) # Khởi tạo danh sách máy với
thời gian rỗi machines = [0]*num_machines
# Lần lượt sắp xếp các công việc theo thứ tự đó vào máy còn nhiều thời gian
nhất for job in sorted_jobs: # Tìm máy còn nhiều thời gian nhất min_machine =
min(range(num_machines), key=lambda index:
machines[index]) # Thêm công việc vào máy machines[min_machine] lOMoAR cPSD| 58457166
+= job # Trả về thời gian hoàn thành công việc trên tất cả các máy return max(machines)
# Danh sách thời gian gia công của các công việc
jobs = [2, 5, 8, 1, 5, 1] # Số lượng máy num_machines = 3
# Gọi hàm assign_jobs result =
assign_jobs(jobs, num_machines) print(result) lOMoAR cPSD| 58457166
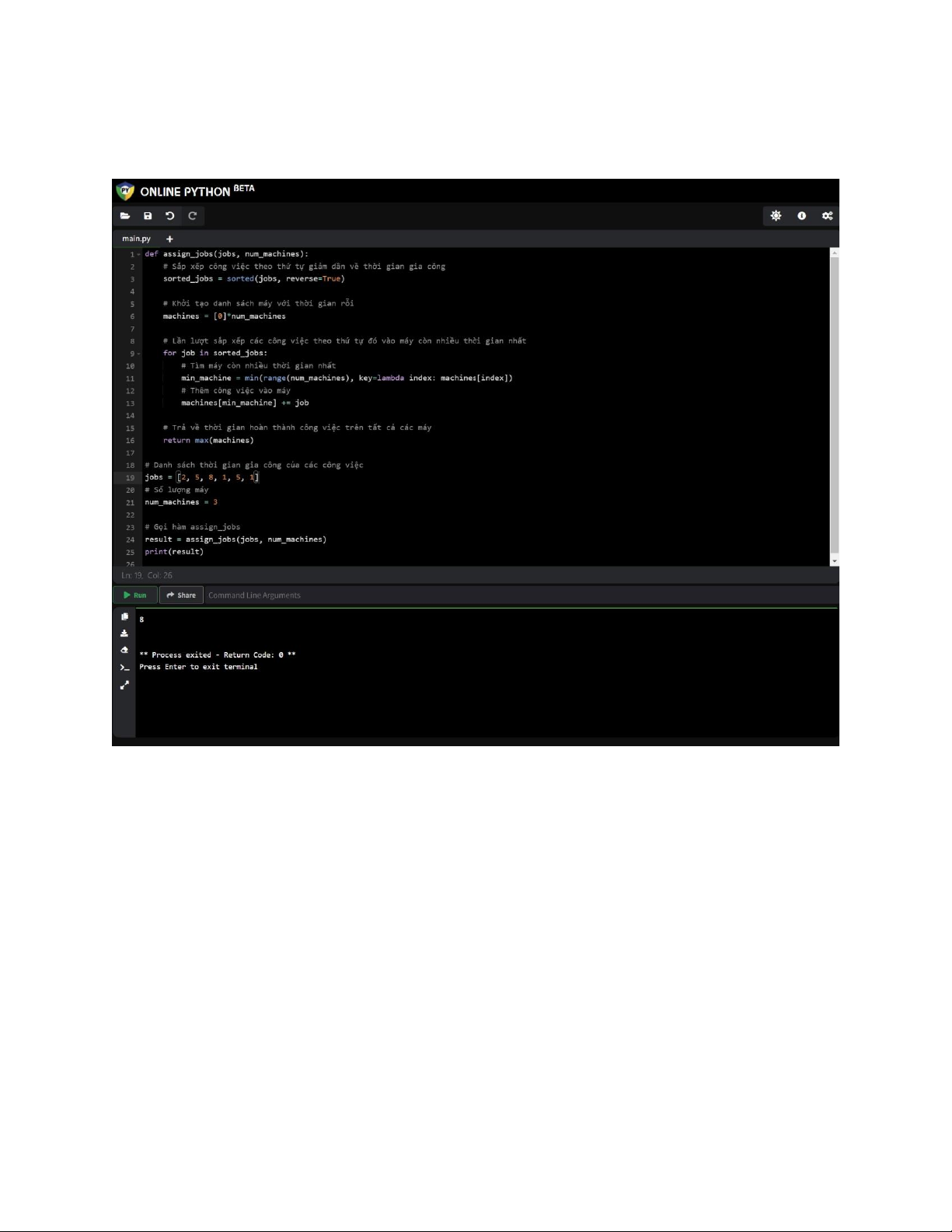
Hình ảnh chạy chương trình và kết quả
Kết quả cuối cùng là thời gian hoàn thành tất cả công việc trên tất cả các máy. Trong ví dụ
này, kết quả là 8 đơn vị thời gian. Điều này có nghĩa là, dù máy nào hoàn thành công việc
cuối cùng, thì thời gian hoàn thành công việc đó là 8 đơn vị thời gian. VII.
THU THẬP DỮ LIỆU THỰC TẾ
Để thu thập dữ liệu thực tế cho bài toán phân việc sử dụng thuật giải Heuristic, có thể tiến hành các bước sau: lOMoAR cPSD| 58457166
1. Xác định công việc: Đầu tiên, cần xác định rõ ràng các công việc cần được phân
công. Điều này có thể bao gồm việc xác định nhiệm vụ cụ thể, thời gian cần thiết để
hoàn thành công việc, và bất kỳ yêu cầu hoặc ràng buộc nào khác liên quan đến công việc.
2. Xác định tài nguyên: Tiếp theo, cần xác định các tài nguyên có sẵn để thực hiện các
công việc. Trong trường hợp của bài toán phân việc, điều này có thể bao gồm số
lượng máy có sẵn và khả năng của chúng.
3. Thu thập dữ liệu: Bây giờ, có thể bắt đầu thu thập dữ liệu. Điều này có thể bao gồm
việc quan sát hoặc thực hiện thí nghiệm để xác định thời gian cần thiết để hoàn thành
mỗi công việc trên mỗi máy, hoặc việc phỏng vấn các nhân viên hoặc chuyên gia để
thu thập thông tin về cách họ phân công công việc.
4. Phân tích và xử lý dữ liệu: Cuối cùng, sau khi thu thập dữ liệu, cần phân tích và xử
lý nó để chuẩn bị cho việc sử dụng thuật giải Heuristic. Điều này có thể bao gồm
việc sắp xếp các công việc theo thứ tự giảm dần về thời gian gia công, hoặc xác định
máy nào còn nhiều thời gian nhất để phân công công việc.