Báo cáo kĩ thuật giảm chiều dữ liệu | Đại học Điện lực

lOMoARcPSD|50662567 java full couse
Cong nghe thong tin (Đại học Điện lực) Scan to open on Studocu
Studocu is not sponsored or endorsed by any college or university
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
KHOA CÔNG NGHỆ THÔNG TIN
BÁO CÁO CHUYÊN ĐỀ HỌC PHẦN KỸ THUẬT
GIẢM CHIỀU DỮ LIỆU Đ Ề T ÀI:
Sinh viên thực hiện : ĐINH VĂN NHƯ ĐẶNG MINH TUẤN
Giảng viên hướng dẫn : Ngành
: CÔNG NGHỆ THÔNG TIN Chuyên ngành : TTNT&TGMT Lớp : D15TTNT&TGMT Khóa : 2020- 2025
Hà Nội, tháng 3 năm 20
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567 PHIẾU CHẤM ĐIỂM ST
Họ và tên sinh viên Nội dung thực Điể Chữ ký T hiện m 1 ĐẶNG MINH TUẤN 20810320100 2 ĐINH VĂN NHƯ 20810320135
Họ và tên giảng viên Chữ ký Ghi chú Giảng viên chấm 1: Giảng viên chấm 2:
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567 Mục lục
Lời mở đầu...........................................................................................................................................5
CHƯƠNG 1: GIỚI THIỆU CHUNG VỀ 2 THUẬT TOÁN PCA VÀ LDA....................................6
1. Tổng quan về thuật tuấn PCA và LDA......................................................................................6
2. Mục đích của bài báo cáo............................................................................................................6
CHƯƠNG 2: THUẬT TOÁN PCA....................................................................................................8
1. PCA...............................................................................................................................................8
1.1. Các khái niệm cơ bản của PCA:.............................................................................................8
1.1.1. Độ lớn phương sai (Variance):.........................................................................................8
1.1.2. Thành phần chính (Principal Component):......................................................................8
1.1.3. Không gian con (Subspace):............................................................................................8
1.1.4. Tỉ lệ phương sai giữ lại (Explained Variance Ratio):.......................................................8
1.1.5. Điểm số (Score):..............................................................................................................8
1.1.6. Ma trận trọng số (Wetght Matrix):...................................................................................8
2. Nguyên lý hoạt động....................................................................................................................8
3. Cách tính PCA.............................................................................................................................9
4. Ưu điểm, nhược điểm và hạn chế...............................................................................................9
5. Ứng dụng của PCA....................................................................................................................10
5.1. Giảm chiều dữ liệu:..............................................................................................................10
5.2. Phân tích đặc trưng:.............................................................................................................10
5.3. Trực quan hóa dữ liệu:.........................................................................................................10
5.4. Nén dữ liệu:..........................................................................................................................10
5.5. Tiền xử lý dữ liệu:.................................................................................................................10
5.6. Tính toán phân cụm:.............................................................................................................10
CHƯƠNG 3: THUẬT TOÁN LDA..................................................................................................11
1. Khái niệm LDA..........................................................................................................................11
2. Nguyên lý hoạt động..................................................................................................................11
3. Các bước tính toán:...................................................................................................................11
4. Ưu điểm, nhược điểm và hạn chế.............................................................................................12
5. Ứng dụng....................................................................................................................................12
CHƯƠNG 4: SO SÁNH GIỮA PCA VÀ LDA................................................................................14
1. So sánh về nguyên tắc hoạt động..............................................................................................14
2. So sánh về cách tính toán:.........................................................................................................14
3. So sánh về ứng dụng..................................................................................................................15
4. Các trường hợp nào nên sử dụng PCA và LDA......................................................................15
CHƯƠNG 5: KẾT LUẬN.................................................................................................................16
1. Tính cần thiết của hai thuật toán..............................................................................................16
2. Hướng phát triển trong tương lai.............................................................................................16
Tài liệu tham khảo.............................................................................................................................17
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567 Lời mở đầu
Trong lĩnh vực xử lý tín hiệu và phân tích dữ liệu, các thuật toán giảm
chiều dữ liệu là rất quan trọng để giảm thiểu kích thước của dữ liệu mà không
làm mất đi thông tin quan trọng. Trong báo cáo này, chúng ta sẽ tìm hiểu hai
thuật toán giảm chiều dữ liệu phổ biến là PCA (Principal Component Analysis)
và LDA (Linear Discriminant Analysis).
PCA là một phương pháp giảm chiều dữ liệu phi tuyến, nó giúp chúng ta
tìm ra các thành phần chính của dữ liệu, từ đó giảm thiểu kích thước của dữ liệu
mà vẫn giữ được thông tin quan trọng. PCA có ứng dụng rất rộng rãi trong các
bài toán nhận diện ảnh, nhận dạng khuôn mặt, và phân tích dữ liệu.
LDA là một phương pháp giảm chiều dữ liệu tuyến tính, nó giúp chúng ta
tìm ra các thành phần chính của dữ liệu có liên quan đến một biến mục tiêu nào
đó. LDA được sử dụng rộng rãi trong các bài toán phân loại dữ liệu, nhận dạng
chữ viết tay, và phân tích hình ảnh.
Trong báo cáo này, chúng ta sẽ tìm hiểu chi tiết về các thuật toán PCA và
LDA, cách chúng hoạt động, cách thực hiện, và ứng dụng của chúng trong thực
tế. Chúng ta hy vọng rằng báo cáo này sẽ giúp bạn có được cái nhìn tổng quan
về hai thuật toán quan trọng này và áp dụng chúng vào các bài toán thực tế.
Lời mở đầu (Nên viết về vấn đề giảm chiều dữ liệu? vì sao phải giảm chiều?)
Chương 1. Phát biểu bài toán 1.1. Bài toán giảm chiều
1.2. Các kĩ thuật dang được sử dụng
1.3. Một số kiến thức nền
Chương 2. Thuật toán giảm chiều PCA và LDA 2.1 PCA 2.1.1 ý tưởng của PCA
2.1.2 Các bước thực hiện của PCA 2.1.3 Nhận xét
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567 2.2 LDA 2.2.1 ý tưởng của PCA
2.2.2 Các bước thực hiện của PCA 2.2.3 Nhận xét 2.3 So sánh PCA và LDA
Chương 3. Thực nghiệm thuật toán
3.1. Dữ liệu và môi trường thực nghiệm
3.2 Thực nghiệm demo thuật toán Kết luận
CHƯƠNG 1: GIỚI THIỆU CHUNG VỀ 2 THUẬT TOÁN PCA VÀ LDA
1. Tổng quan về thuật toán PCA và LDA.
PCA (Principal Component Analysis) và LDA (Linear Discriminant
Analysis) là hai thuật toán quan trọng trong lĩnh vực phân tích dữ liệu và xử lý
tín hiệu. Cả hai đều được sử dụng để giảm chiều dữ liệu, nhưng mỗi thuật toán
lại có mục đích và phương pháp thực hiện khác nhau.
PCA giúp giảm số chiều của các tập dữ liệu bằng cách tìm ra các thành
phần chính đại diện cho phân bố của dữ liệu. Các thành phần này được sắp xếp
theo thứ tự giảm dần của độ lớn của độ phân tán của chúng, và số lượng thành
phần được giảm xuống dựa trên mức độ giảm thiểu tổng số thông tin của dữ liệu.
PCA có thể được sử dụng để nén dữ liệu, trực quan hóa dữ liệu, và giảm
thiểu nhiễu trong dữ liệu.LDA, ngược lại, được sử dụng để tìm ra các đặc trưng
quan trọng nhất giúp phân loại các tập dữ liệu khác nhau. LDA tìm ra các trục
mới trong không gian nhiều chiều sao cho các lớp dữ liệu được phân tách tốt
nhất. Điều này giúp cho việc phân loại dữ liệu trở nên chính xác hơn và giảm
thiểu sự chồng chéo giữa các lớp. LDA thường được sử dụng trong các bài toán
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
phân loại ảnh, phân tích ngôn ngữ tự nhiên, và các bài toán liên quan đến dữ liệu văn bản.
Cả hai thuật toán đều có những ứng dụng quan trọng trong các lĩnh vực
như khoa học dữ liệu, trí tuệ nhân tạo, và các bài toán tương tự. Tuy nhiên, cần
lưu ý rằng mỗi thuật toán có những giới hạn và điểm yếu riêng, và việc sử dụng
chúng cần phải cân nhắc kỹ lưỡng để đảm bảo tính chính xác và hiệu quả của kết quả.
2. Mục đích của bài báo cáo.
Mục đích của bài báo cáo này là giới thiệu về hai thuật toán quan trọng
trong lĩnh vực xử lý dữ liệu và trích xuất đặc trưng, đó là Linear Discriminant
Analysis (LDA) và Principal Component Analysis (PCA). Bài báo cáo sẽ trình
bày các khái niệm cơ bản, nguyên lý hoạt động và cách sử dụng của hai thuật
toán này, từ đó giúp người đọc hiểu rõ hơn về cách thức áp dụng và ứng dụng trong thực tế.
Bài báo cáo cũng giải thích tầm quan trọng của LDA và PCA trong việc
xử lý dữ liệu và trích xuất đặc trưng. LDA và PCA là hai trong số các phương
pháp trích xuất đặc trưng phổ biến và hiệu quả nhất, được sử dụng rộng rãi
trong nhiều lĩnh vực, từ phân loại ảnh, nhận dạng khuôn mặt, phân tích tín hiệu
âm thanh, phân tích tín hiệu vô tuyến, đến nhận dạng từ văn bản. Việc hiểu rõ
về LDA và PCA sẽ giúp các nhà nghiên cứu và chuyên gia trong lĩnh vực xử lý
dữ liệu có thể tận dụng tối đa các tính năng của hai thuật toán này để giải quyết
các bài toán phức tạp và cải thiện chất lượng kết quả.
Vì vậy, bài báo cáo này là cần thiết và hữu ích để giúp người đọc có cái
nhìn tổng quan về hai thuật toán LDA và PCA, từ đó có thể ứng dụng chúng
trong thực tế một cách hiệu quả.
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
CHƯƠNG 2: THUẬT TOÁN PCA 1. PCA
PCA (Principal Component Analysis) là một thuật toán phân tích dữ liệu
được sử dụng để giảm chiều dữ liệu trong đó các biến độc lập được giảm xuống
thành các biến kết hợp tuyến tính (principal components) bằng cách sử dụng
phương pháp giảm thiểu phương sai (variance minimization). PCA có thể giúp
tìm ra các biến quan trọng nhất trong dữ liệu, từ đó giảm chiều dữ liệu mà
không làm mất đi nhiều thông tin.
Trong PCA, các biến được giảm chiều sao cho các thành phần chính
(principal components) giải thích tổng phương sai của dữ liệu một cách tối đa.
Các thành phần chính được tính toán dựa trên các vector riêng (eigenvectors)
của ma trận hiệp phương sai (covariance matrix) của dữ liệu.
PCA được sử dụng rộng rãi trong các lĩnh vực như xử lý ảnh, nhận diện
khuôn mặt, nhận dạng giọng nói, phân tích dữ liệu về tài chính và kinh tế, v.v.
1.1. Các khái niệm cơ bản của PCA:
1.1.1. Độ lớn phương sai (Variance):
Là độ lớn của sự phân chia của dữ liệu. Nó cho biết mức độ phân tnas của dữ liệu trong không gian.
1.1.2. Thành phần chính (Principal Component):
Là một vector đại diện cho hướng chính của sự phân tán của dữ liệu. Các thành
phần chính được sắp xếp theo thứ tự giảm dần của độ lớn phương sai của chúng.
1.1.3. Không gian con (Subspace):
Là không gian con của không gian ban đầu được xác định bằng cách lấy các thành phần chính.
1.1.4. Tỉ lệ phương sai giữ lại (Explained Variance Ratio):
Là tỉ lệ phương sai được giải thích bởi số lượng thành phần chính được chọn. Tỉ
lệ này cho biết phần trăm đóng góp của từng thành phần chính vào sự phân tán của dữ liệu. 1.1.5. Điểm số (Score):
Là một giá trị số đại diện cho mỗi điểm dữ liệu trong không gian con. Các điểm
số này được tính bằng cách nhân ma trận dữ liệu với ma trận trọng số được tạo
ra bởi các thành phần chính.
1.1.6. Ma trận trọng số (Wetght Matrix):
Là ma trận chứa các vector thành phần chính. Ma trận trọng số này được sử
dụng để tính toán các điểm số liệu.
2. Nguyên lý hoạt động
PCA (Principal Component Analysis) là một phương pháp phân tích dữ
liệu thống kê được sử dụng để giảm kích thước của dữ liệu và tìm ra các thành
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
phần chính của dữ liệu. Nguyên tắc hoạt động của PCA là chuyển đổi không
gian các biến đầu vào thành một không gian mới với số chiều thấp hơn sao cho
các điểm dữ liệu vẫn giữ lại được tính chất chính của dữ liệu.
PCA thực hiện bằng cách tìm ra các thành phần chính của dữ liệu, tức là
các hướng trong không gian dữ liệu mà có phương sai lớn nhất. Các thành phần
chính này có thể được sử dụng để xây dựng một mô hình tóm tắt dữ liệu, trong
đó dữ liệu được biểu diễn dưới dạng một số lượng nhỏ các thành phần chính
thay vì số lượng lớn các biến đầu vào ban đầu.
PCA được sử dụng rộng rãi trong lĩnh vực khoa học dữ liệu và machine
learning để giảm kích thước của dữ liệu và tìm ra các tính chất chính của dữ
liệu. PCA cũng có thể được sử dụng để loại bỏ nhiễu và các biến không quan
trọng khỏi dữ liệu, từ đó giúp cải thiện độ chính xác của các mô hình phân tích dữ liệu. 3. Cách tính PCA
Các bước thực hiện:
Bước 1. Chuẩn bị dữ liệu: Chuẩn bị ma trận dữ liệu có kích thước m x n
trong đó m là số lượng quan sát và n là số lượng biến
Bước 2. Chuẩn hóa dữ liệu: Chuẩn hóa ma trận dữ liệu bằng cách trừ đi
trung bình tứng biến và chia cho độ lệch chuẩn
Bước 3. Tính ma trận hiệp phương sai của dữ liệu chuẩn hóa
Bước 4. Tính giá trị riêng và các vector riêng của ma trận hiệp phương
sai: Sử dụng phép tính ma trận để tính toán các giá trị riêng và vector riêng
Bước 5. Chọn các thành phần chính: Sắp xếp các giá trị riêng theo thứ tự
giảm dần và chọn các vector riêng tương ứng. Các vector riêng này được gọi là thành phần chính
Bước 6. Tính toán ma trận chiếu bằng cách lấy các vector riêng tương
ứng với các giá trị riêng được chọn và ghép lại chúng thành ma trận chiếu
Bước 7. Giảm chiều dữ liệu: Áp dụng ma trận chiếu đã tính được để giảm chiều dữ liệu ban đầu
4. Ưu điểm, nhược điểm và hạn chế * Ưu điểm:
- Giảm chiều dữ liệu giúp giảm chiều của dữ liệu mà vẫn giữ được thông
tin quan trọng nhất, giúp cho việc xử lý và trực quan hóa dữ liệu dễ dàng hơn.
- Giảm tác động của nhiễu trong dữ liệu bằng cách tách nó ra khỏi các thành phần chính.
- Không phụ thuộc vào phân phối dữ liệu, PCA hoạt động tốt với các dữ
liệu có phân phối không đồng đều, chẳng hạn như dữ liệu không đạt chuẩn hoặc dữ liệu có nhiễu.
- Giữ lại những thông tin quan trọng nhất giúp người dùng dễ dàng hiểu
được bản chất của dữ liệu.
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567 *Nhược điểm:
- Mất mát thông tin khi giảm chiều dữ liệu vì có thể mất đi dữ liệu quan trọng
- Không phù hợp với dữ liệu phi tuyến, PCA chỉ phù hợp với các dữ liệu tuyến tính
- Không giải quyết được các vấn đề nhiễu lớn, trong trường hợp có nhiều
nhiễu lớn thì PCA không giải quyết được các vấn đề liên quan đến nhiễu. * Hạn chế:
- Không cho phép giải thích một cách rõ ràng những yếu tố đã được giảm chiều
- Sử dụng lương tính toán lớn, đặc biệt khi xử lý các tập dữ liệu lớn, điều
này làm tăng thời gian tính toán và tốn nhiều tài nguyên hơn.
- Có thể mất mát một số thông tin, điều này có thể ảnh hưởng đến khả
năng dự đoán và hiểu được bản chất của dữ liệu
- Phụ thuộc vào độ tương quan, nếu các biến không tương quan thì PCA không hiệu quả
5. Ứng dụng của PCA
5.1. Giảm chiều dữ liệu:
PCA được sử dụng để giảm chiều dữ liệu trong các bài toán có số lượng
đặc trưng (features) lớn giúp giảm thiểu kích thước của dữ liệu và tăng tốc độ xử lý.
5.2. Phân tích đặc trưng:
PCA giúp phân tích đặc trăng của dữ liệu và tìm ra các đặc trưng quan
trọng nhất của dữ liệu. Điều này có thể giúp cho việc đưa ra quyết định xác
định, dự đoán và phân loại dữ liệu
5.3. Trực quan hóa dữ liệu:
PCA có thể sử dụng để trực quan hóa dữ liệu trong một không gian hai
hoặc ba chiều để giúp phân tích và hiểu dữ liệu hơn. 5.4. Nén dữ liệu:
PCA cũng có thể được sử dụng để nén dữ liệu và giảm kích thước của tập
dữ liệu, giúp tiết kiệm không gian lưu trữ.
5.5. Tiền xử lý dữ liệu:
PCA cũng được sử dụng để tiền xử lý dữ liệu trước khi đưa vào các thuật
toán Machine Learning khác như SVM, KNN, Neural Networks.
5.6. Tính toán phân cụm:
PCA cũng có thể được sử dụng để tính toán phân cụm của dữ liệu, giúp
phân tích và tổ chức các nhóm dữ liệu dựa trên đặc tính chung.
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
CHƯƠNG 3: THUẬT TOÁN LDA 1. Khái niệm LDA
LDA (Linear Discriminant Analysis) là một thuật toán trong học máy và
thị giác máy tính, được sử dụng để phân loại các đối tượng vào các lớp khác
nhau. Nó là một phương pháp giảm chiều dữ liệu giống như PCA, tuy nhiên
LDA sử dụng thông tin về lớp của các điểm dữ liệu để tìm các thành phần chính.
LDA được sử dụng để giảm số chiều của tập dữ liệu bằng cách giữ lại các
thành phần chính nhất định của dữ liệu, đồng thời tăng tính phân biệt giữa các
lớp. LDA là một thuật toán được giám sát, có nghĩa là nó sử dụng thông tin về
lớp của các điểm dữ liệu để tối đa hóa khoảng cách giữa các lớp và tối thiểu hóa
khoảng cách giữa các điểm trong cùng một lớp.
Thuật toán LDA sử dụng phương pháp tính toán ma trận phân tích giá trị
riêng và vectơ riêng, tương tự như PCA. Tuy nhiên, PCA sử dụng toàn bộ tập
dữ liệu để tính toán ma trận, trong khi LDA chỉ sử dụng thông tin lớp của các điểm dữ liệu.
Các thành phần chính của LDA được sắp xếp theo thứ tự giảm dần của
giá trị riêng, tương ứng với các vectơ riêng có liên quan. Các thành phần chính
này có thể được sử dụng để giảm số chiều của tập dữ liệu, đồng thời tăng độ
chính xác trong việc phân loại các đối tượng vào các lớp khác nhau.
2. Nguyên lý hoạt động
Thuật toán LDA là một phương pháp học có giám sát, dùng để phân loại
các mẫu dữ liệu vào các lớp đã biết. Nguyên tắc hoạt động của LDA là tìm một
chiều mới sao cho khoảng cách giữa các lớp là lớn nhất và khoảng cách giữa
các điểm trong cùng một lớp là nhỏ nhất.
Để tìm được chiều mới này, thuật toán LDA bắt đầu bằng cách tính ma
trận hiệp phương sai của dữ liệu đầu vào và ma trận hiệp phương sai giữa các
lớp. Sau đó, nó tính toán các vector riêng và giá trị riêng của ma trận hiệp
phương sai giữa các lớp. Vector riêng và giá trị riêng này được sử dụng để xác
định chiều mới tối ưu.
Thuật toán LDA tìm kiếm chiều mới dựa trên giá trị riêng lớn nhất của
ma trận hiệp phương sai giữa các lớp. Vì vậy, thuật toán LDA có thể giúp giảm
số chiều của dữ liệu mà vẫn giữ được tính chất phân loại của dữ liệu ban đầu.
3. Các bước tính toán:
Bước 1. Chuẩn bị dữ liệu: Chuẩn bị dữ liệu bao gồm việc tách các lớp dữ
liệu thành các tập dữ liệu con
Bước 2. Tính toán ma trận trung bình cho từng lớp dữ liệu.
Bước 3: Tính toán ma trận phân tán trong lớp dữ liệu.
Bước 4. Tính toán ma trận phân tán giữa các lớp.
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
Bước 5. Tính toán ma trận tối ưu bằng cách giải phương trình tổng quát LDA
Bước 6. Trích dẫn đặc trưng từ ma trận tối ưu bằng cách sắp xếp các
vector riêng theo thứ tự giảm dần của giá trị riêng
4. Ưu điểm, nhược điểm và hạn chế * Ưu điểm:
- LDA có thể xử lý tập dữ liệu đa chiều với số lượng lớn và tạo ra các đặc
trưng mới đáng tin cậy hơn
- LDA giúp xác định các đặc trưng quan trọng nhất rtong tập dữ liệu và
giảm thiểu sự phụ thuộc giữa các đặc trưng. Điều này giúp tăng tính hiệu quả
của mô hình dự đoán được xây dựng trên các đặc trưng
- LDA có thể giúp giảm thiểu tình trạng overfitting và underfitting trong mô hình học máy * Nhược điểm:
- LDA yêu cầu dữ liệu đầu vào phải tuân thủ theo giả định về phân phối
chuẩn và các lớp dữ liệu cần có độ tách tốt
- Khi số lượng mẫu huấn luyện quá nhỏ so với số lượng đặc trưng, LDA
có thể không hoạt động hiệu quả
- LDA không phù hợp cho các bài toán phân loại phi tuyến tính * Hạn chế
- LDA phải được sử dụng kết hợp với các kỹ thuật tiền xử lý dữ liệu để
đảm bảo tính toàn vẹn của tập dữ liệu ban đầu
- LDA yêu cầu số lượng quan sát lớn hơn số lượng biến có thể tạo ra các
đặc trưng mới đáng tin cậy hơn 5. Ứng dụng
5.1. Phân tích chủ đề: LDA là một công cụ phổ biến để phân tích chủ đề
của các tài liệu văn bản. Nó có thể giúp phát hiện ra những chủ đề chính trong
tài liệu và đưa ra các từ khóa liên quan đến chủ đề đó.
5.2. Tóm tắt văn bản: LDA có thể được sử dụng để tạo ra các tóm tắt văn
bản tự động. Bằng cách phân tích chủ đề của các câu trong tài liệu, LDA có thể
tổng hợp các ý chính trong tài liệu và tạo ra một tài liệu tóm tắt.
5.3. Phân loại văn bản: LDA cũng có thể được sử dụng để phân loại các
tài liệu văn bản vào các nhóm khác nhau dựa trên chủ đề của chúng.
5.4. Gợi ý nội dung: LDA có thể được sử dụng để gợi ý các nội dung liên
quan đến người dùng dựa trên lịch sử tìm kiếm của họ hoặc các tài liệu khác mà họ đã xem trước đó.
5.6. Phân tích đa biến: LDA cũng có thể được sử dụng để phân tích đa
biến, nghĩa là phân tích các tài liệu chứa nhiều biến đầu vào, chẳng hạn như các
tài liệu văn bản chứa các từ khóa liên quan đến nhiều chủ đề khác nhau.
5.7. Tìm kiếm thông tin: LDA có thể giúp tìm kiếm thông tin nhanh chóng
và hiệu quả hơn bằng cách đưa ra các từ khóa liên quan đến chủ đề được tìm
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
kiếm và phân tích các tài liệu văn bản để xác định các tài liệu có liên quan nhất.
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
CHƯƠNG 4: SO SÁNH GIỮA PCA VÀ LDA
1. So sánh về nguyên tắc hoạt động
PCA và LDA là hai thuật toán phân tích dữ liệu phổ biến trong Machine
Learning và các lĩnh vực liên quan đến dữ liệu. Tuy nhiên, hai thuật toán này có
nguyên tắc hoạt động khác nhau.
PCA và LDA đều sử dụng các ma trận để tìm ra các vector mới mà dữ
liệu được chiếu lên. Tuy nhiên, PCA tập trung vào tìm kiếm các vector phân biệt
nhất có thể giữa các điểm dữ liệu, trong khi LDA tập trung vào tìm kiếm các
vector phân biệt giữa các lớp của dữ liệu.
Điều này đồng nghĩa với việc PCA có thể được sử dụng để giảm kích
thước của dữ liệu và khai thác các đặc trưng chính của dữ liệu mà không cần
quan tâm đến lớp hoặc nhãn của các điểm dữ liệu, trong khi LDA được sử dụng
để tìm ra các đặc trưng phân biệt giữa các lớp và phân loại dữ liệu.
Tóm lại, PCA và LDA là hai thuật toán phân tích dữ liệu khác nhau về
nguyên tắc hoạt động và ứng dụng. PCA thường được sử dụng để giảm kích
thước của dữ liệu và khai thác các đặc trưng chính của dữ liệu mà không cần
quan tâm đến lớp hoặc nhãn của các điểm dữ liệu, trong khi LDA được sử dụng
để tìm ra các đặc trưng phân biệt giữa các lớp và phân loại dữ liệu.
2. So sánh về cách tính toán: PCA LDA
Tính toán - Tìm ra các thành phần chính LDA tìm ra các đặc trưng quan
của dữ liệu bằng cách tính
trọng của dữ liệu bằng cách tính
toán những vector riêng của
toán ma trận tương quan giữa các
ma trận hiệp phương sai và
lớp và trong lớp. Sau đó, LDA sử
sắp xếp chúng theo giá trị
dụng ma trận chiến để chiếu dữ riêng tương ứng.
liệu ban đầu vào không gian mới
- Sau đó, PCA sử dụng các có số chiều thấp hơn
vertor riêng này để chiếu dữ
liệu ban đầu vào không gian
mới có số chiều thấp hơn Kết quả
PCA tập trung vào việc giảm LDA tập trung vào việc giảm
thiểu sự phân tán của dữ liệu, thiểu sự khác biệt giữa các lớp
vì vậy các thành phần chính
của dữ liệu, vì vậy các đặc trưng
của PCA không phụ thuộc
của LDA phụ thuộc vào các lớp
vào các lớp của dữ liệu. Kết
của dữ liệu. Kết quả của LDA là
quả của PCA là các thành
các đặc trưng quan trọng để phân
phần chính của dữ liệu, được việt
sắp xếp theo độ quan trọng giảm dần
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
3. So sánh về ứng dụng
PCA và LDA là hai thuật toán khác nhau có các ứng dụng khác nhau.
PCA được sử dụng rộng rãi trong phân tích dữ liệu và trích xuất đặc trưng
của dữ liệu. Nó được sử dụng để giảm chiều dữ liệu, tìm ra một số chiều mới
mà dữ liệu có thể được biểu diễn trong đó các chiều này được sắp xếp theo mức
độ giảm dần của độ phân tán của dữ liệu. Các ứng dụng của PCA bao gồm nhận
dạng khuôn mặt, phân tích âm thanh và phân tích hình ảnh.
LDA được sử dụng phổ biến trong nhận dạng mẫu và phân loại. Nó giúp
tìm ra các trục mới để biểu diễn dữ liệu sao cho khoảng cách giữa các lớp được
tối đa hóa và khoảng cách trong lớp được tối thiểu hóa. Ứng dụng của LDA bao
gồm nhận dạng khuôn mặt, phân loại tài liệu và phân loại hình ảnh y tế.
Tuy nhiên, PCA và LDA cũng có những điểm khác biệt. PCA tập trung
vào việc giảm chiều dữ liệu, trong khi LDA tập trung vào việc phân loại dữ liệu.
PCA không cần biết thông tin về lớp của dữ liệu, trong khi LDA yêu cầu thông
tin này để phân loại dữ liệu. Do đó, nếu mục tiêu của bạn là giảm chiều dữ liệu
thì PCA là lựa chọn tốt, trong khi nếu mục tiêu của bạn là phân loại dữ liệu thì
LDA là sự lựa chọn tốt hơn.
4. Các trường hợp nào nên sử dụng PCA và LDA
* Các trường hợp nên sử dụng PCA:
- Khi muốn giảm chiều dữ liệu mà không cần quan tâm đến các lớp của dữ liệu
- Khi dữ liệu có nhiều chiều và không thể trực quan hóa
- Khi dữ liệu có nhiều biến quan sát và cần giảm chiều để tránh overfitting
- Khi dữ liện có nhiễu lớn hơn cần giảm nhiều
* Các trường hợp nên sử dụng LDA:
- Khi muốn giảm chiều dữ liệu và tập trung vào sự khác biệt giữa các lớp của dữ liệu
- Khi muốn phân loại dữ liệu thành các lớp khác nhau
- Khi muốn xác định các đặc trưng quan trọng của dữ liệu và tìm hiểu cách mà
chúng ảnh hưởng đến việc phân loại dữ liệu
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
CHƯƠNG 5: KẾT LUẬN
1. Tính cần thiết của hai thuật toán
Hai thuật toán LDA và PCA là hai công cụ mạnh mẽ trong phân tích dữ
liệu và trích xuất thông tin. PCA cho phép giảm chiều dữ liệu, giảm nhiễu và
tăng tốc độ tính toán, trong khi LDA có thể giúp tạo ra các hình ảnh phân loại
tốt hơn cho các tập dữ liệu.
Tuy nhiên, việc sử dụng LDA và PCA còn phụ thuộc vào tình huống cụ
thể và tính chất của dữ liệu. Trong một số trường hợp, PCA có thể không phù
hợp với dữ liệu có tính chất phi tuyến tính hoặc dữ liệu phân phối không chuẩn.
LDA thường được sử dụng trong các ứng dụng phân loại, nhưng nó cũng có thể
không hoạt động tốt đối với các tập dữ liệu không cân bằng hoặc có số lượng mẫu thấp.
Vì vậy, việc sử dụng hai thuật toán này nên được xem xét kỹ lưỡng và
đánh giá cẩn thận để đảm bảo tính chính xác và hiệu quả của phân tích dữ liệu.
2. Hướng phát triển trong tương lai
Trong tương lai, việc nghiên cứu và phát triển hai thuật toán LDA và
PCA vẫn rất cần thiết. Một số hướng nghiên cứu có thể bao gồm:
2.1. Áp dụng LDA và PCA vào các bài toán phân loại và nhận dạng dữ
liệu lớn và phức tạp, như phân loại ảnh, nhận dạng khuôn mặt, hoặc phân tích dữ liệu y học.
2.2. Nghiên cứu các biến thể của hai thuật toán này để tối ưu hóa hiệu
suất và độ chính xác. Ví dụ như, Linear Discriminant Analysis (LDA) và
Quadratic Discriminant Analysis (QDA) có thể được kết hợp để tạo ra mô hình tốt hơn.
2.3. Phát triển các phương pháp kết hợp LDA và PCA để giải quyết các
bài toán phân tích dữ liệu đa biến, phân tích đa cấp độ, hoặc phân tích dữ liệu đồng thời.
2.4. Tìm hiểu các ứng dụng của LDA và PCA trong các lĩnh vực khác như
xử lý ngôn ngữ tự nhiên, phân tích tương tác người-máy, và các ứng dụng của
máy học trên dữ liệu đồ thị.
Với sự phát triển của khoa học và công nghệ, việc nghiên cứu và ứng
dụng các thuật toán LDA và PCA sẽ tiếp tục đóng vai trò quan trọng trong các
lĩnh vực như khoa học dữ liệu, trí tuệ nhân tạo, và các ứng dụng máy tính khác.
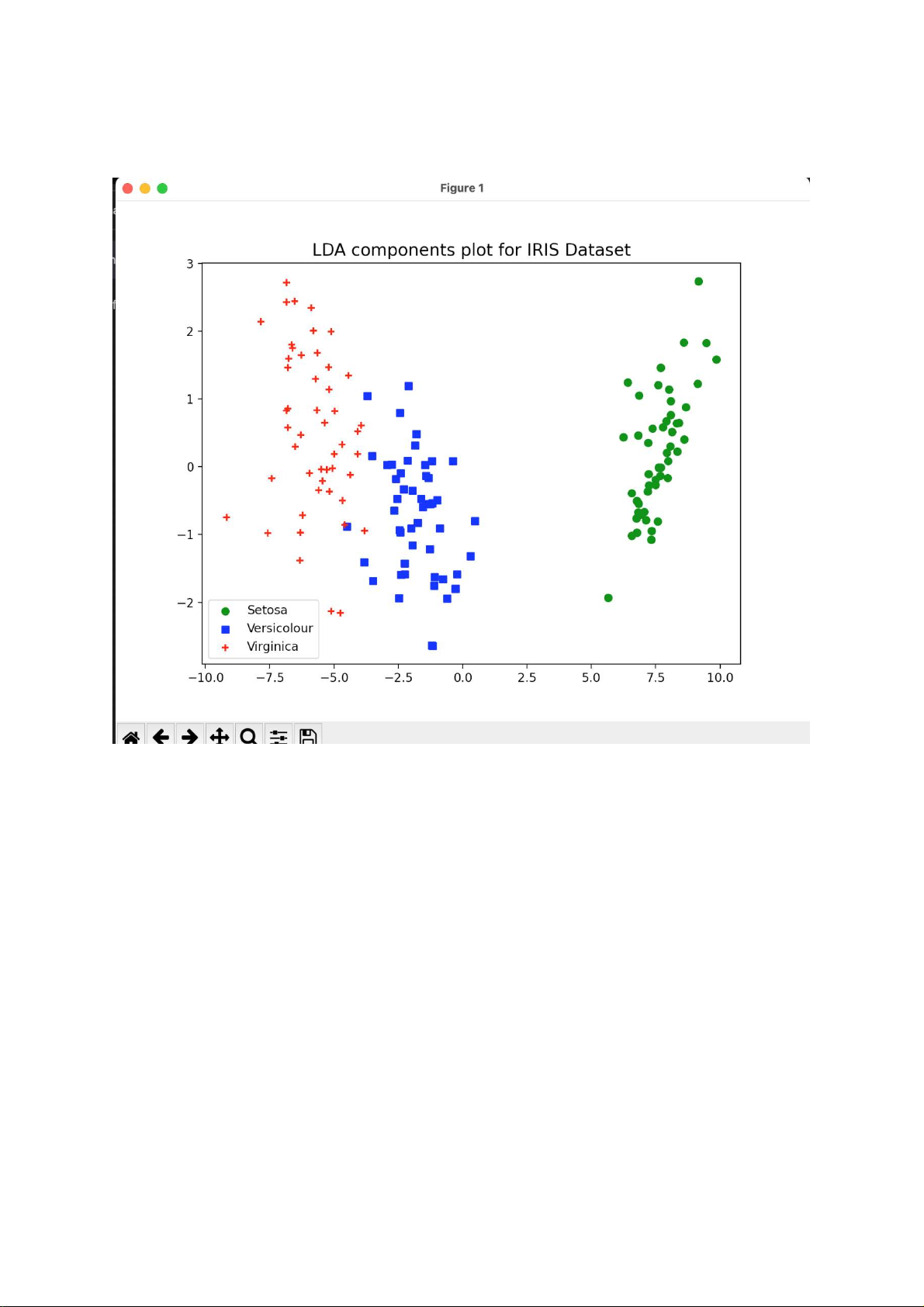
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567 CHƯƠNG 6: DEMO Mô tả LDA
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
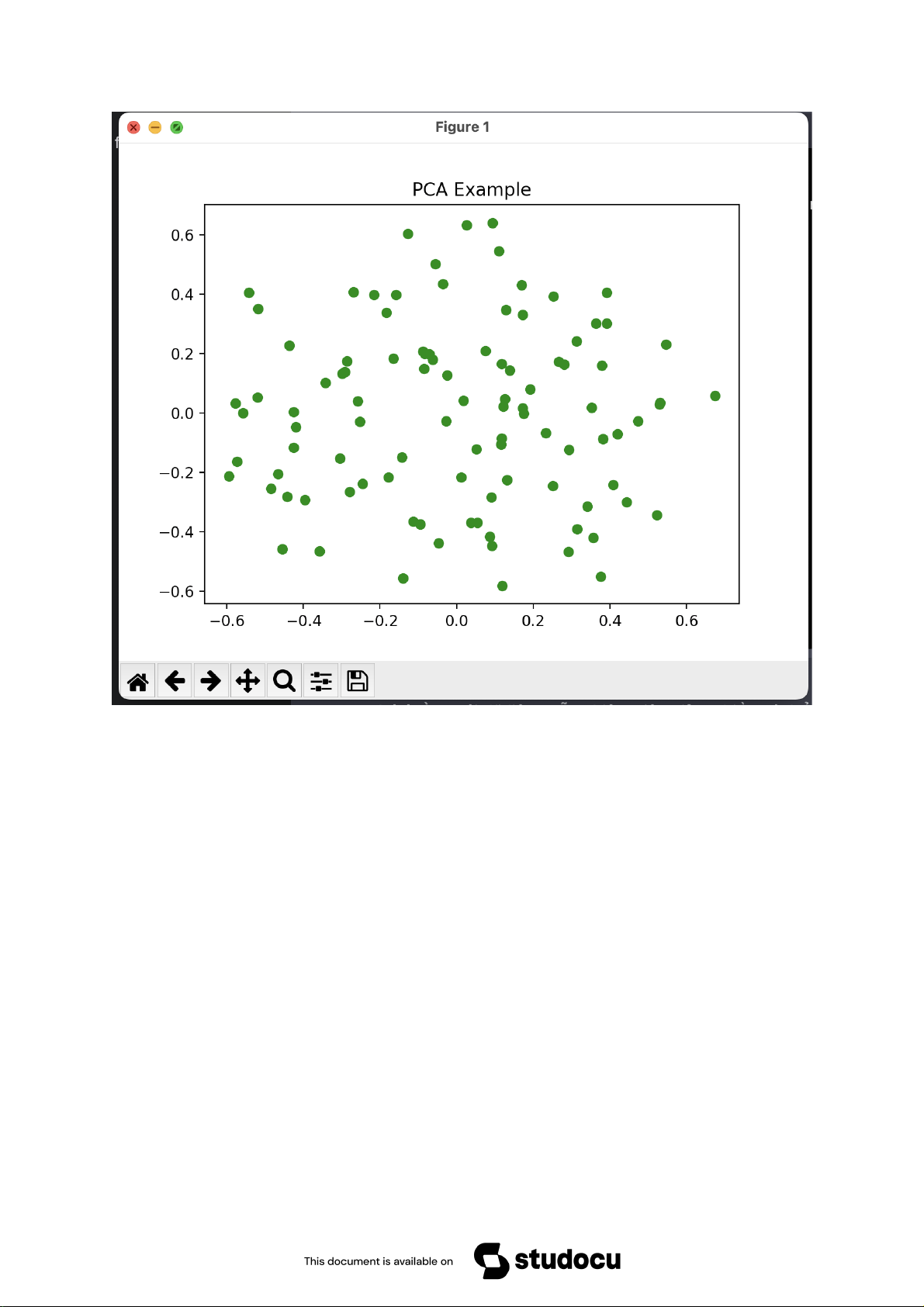
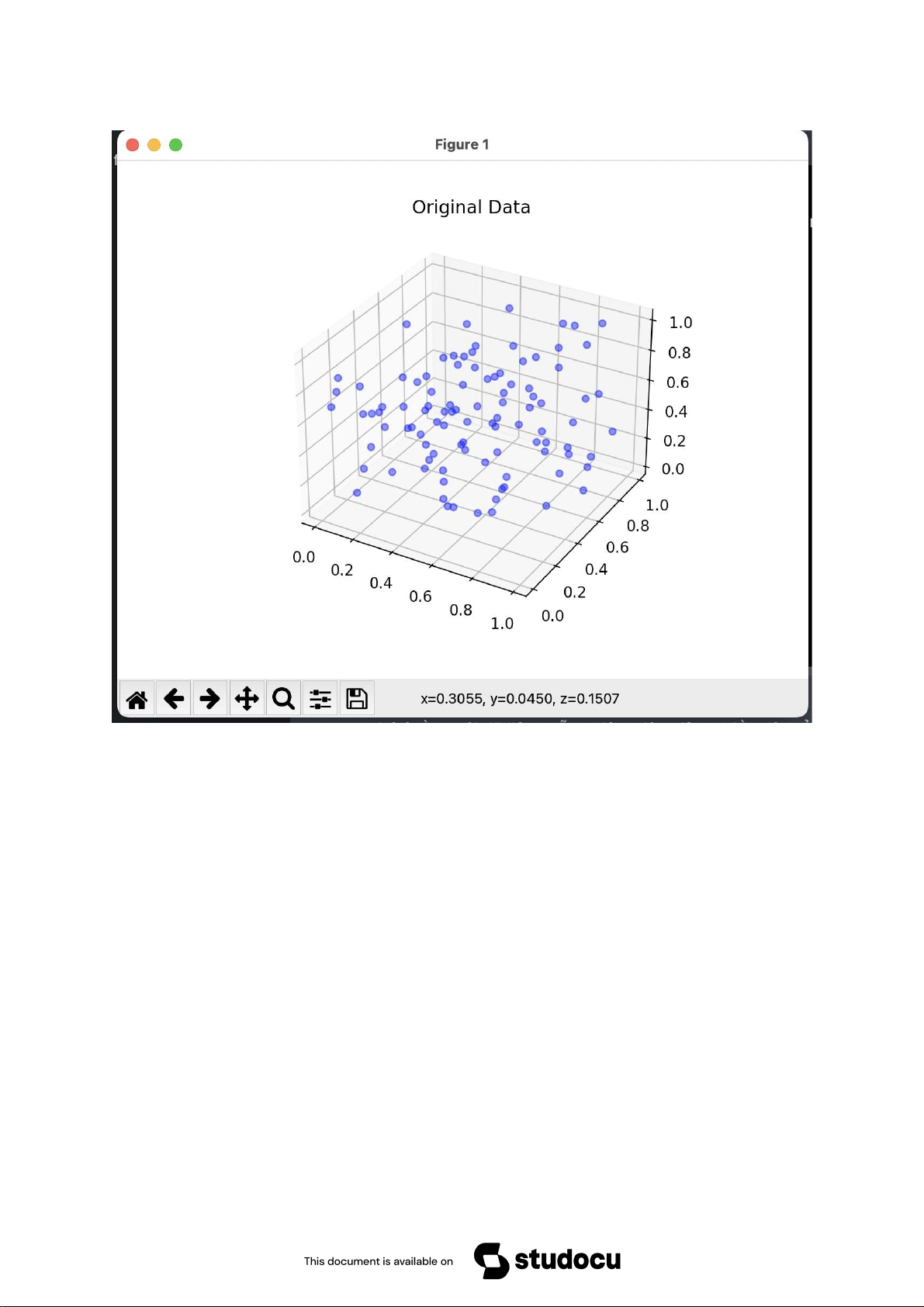
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567 Ví dụ PCA
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com) lOMoARcPSD|50662567
Mã giả tự khởi tạo dữ liệu
Downloaded by B?p Tr??ng Thành (baptruongthanh@gmail.com)