Báo cáo thực hành DSA môn Cấu trúc dữ liệu - Giải thuật | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58457166
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG
KHOA VIỄN THÔNG 1
BỘ MÔN CẤU TRÚC DỮ LIỆU & GIẢI THUẬT
BÁO CÁO THỰC HÀNH Môn: Cấu
trúc dữ liệu và giải thuật
Giảng viên hướng dẫn
: Phạm Hoàng Anh
Họ và tên sinh viên
: Nguyễn Duy Anh Mã sinh viên
: B23DCKD 002 Lớp
: D23CQKD02 - B Nhóm
: 18
Hà Nội
– 2025 lOMoAR cPSD| 58457166 LỜI NÓI ĐẦU
Cấu trúc dữ liệu và Giải thuật (Data Structures and Algorithms – DSA) là một trong những
nền tảng quan trọng bậc nhất trong lĩnh vực Khoa học máy tính. Việc nắm vững kiến thức
và kỹ năng triển khai các cấu trúc dữ liệu cũng như thuật toán không chỉ giúp sinh viên giải
quyết hiệu quả các bài toán lập trình, mà còn là tiền đề để phát triển các ứng dụng phần mềm tối ưu và bền vững.
Thông qua các buổi thực hành của học phần này, em đã có cơ hội tiếp cận sâu hơn với các
cấu trúc dữ liệu cơ bản như mảng, danh sách liên kết, ngăn xếp, hàng đợi, cây, đồ thị,... cùng
với các thuật toán kinh điển như tìm kiếm, sắp xếp, đệ quy, quay lui, quy hoạch động và tìm
đường. Việc trực tiếp triển khai, kiểm thử và tối ưu hóa các giải pháp thuật toán không những
giúp em củng cố kiến thức lý thuyết mà còn nâng cao khả năng tư duy logic, phân tích và giải quyết vấn đề.
Báo cáo này là tổng hợp kết quả thực hành của em trong suốt quá trình học tập, với mong
muốn ghi nhận lại những gì đã học được và làm nền tảng cho các môn học chuyên sâu hơn trong tương lai.
Em xin chân thành cảm ơn thầy Phạm Hoàng Anh đã tận tình giảng dạy và hướng dẫn em
trong suốt quá trình học môn Cấu trúc dữ liệu và Giải thuật. lOMoAR cPSD| 58457166 MỤC LỤC
Bài 1: Phân số đơn vị ....................................................................................................... 4
Code: .............................................................................................................................. 5
Lưu đồ thuật toán: ....................................................................................................... 6
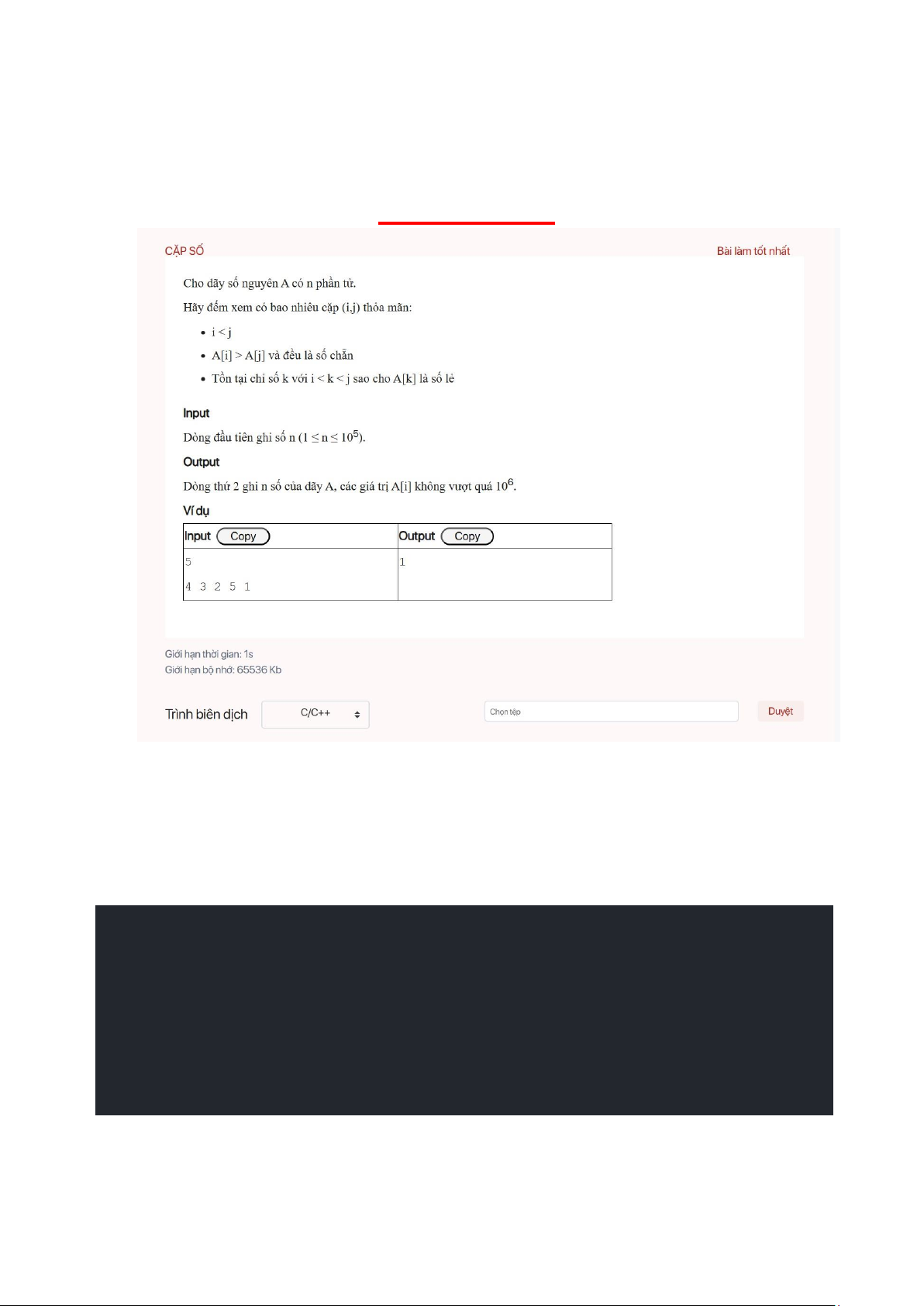
Bài 2: Cặp số ..................................................................................................................... 8
Code: .............................................................................................................................. 8
Lưu đồ thuật toán: ..................................................................................................... 10
Giải thích thuật toán: ................................................................................................. 12
Bài 3: Nhịp chứng khoán ............................................................................................... 15
Code: ............................................................................................................................ 17
Lưu đồ thuật toán: ..................................................................................................... 18
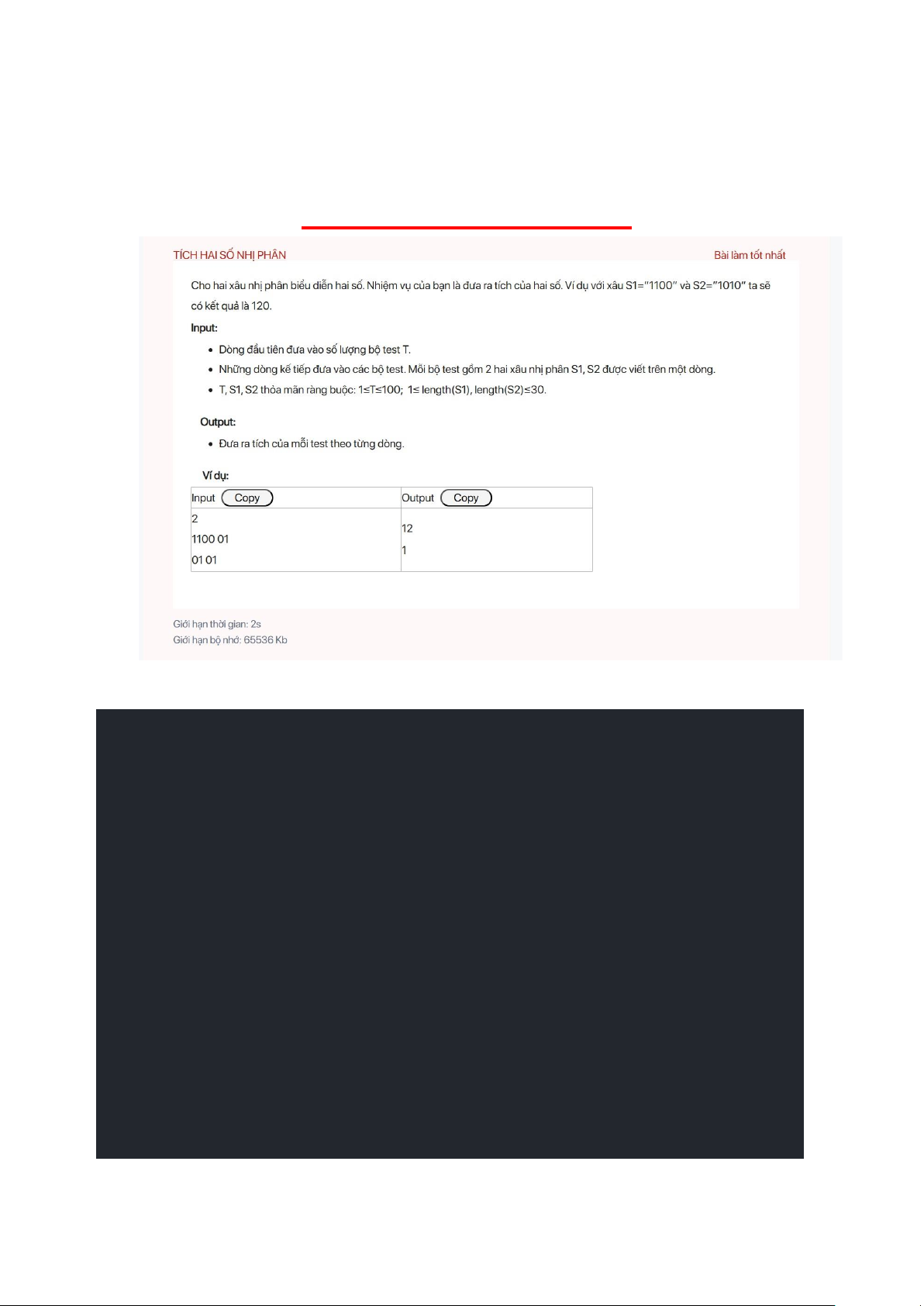
Bài 4: Tích 2 số nhị phân ............................................................................................... 20
Code: ............................................................................................................................ 20
Lưu đồ thuật toán: ..................................................................................................... 21
Bài 5: Đường đi theo BFS trên đồ thị vô hướng .......................................................... 25
Code: ............................................................................................................................ 26
Lưu đồ thuật toán: ..................................................................................................... 28
Bài 6: Kiểm tra chu trình trên đồ thị có hướng .......................................................... 31
Code: ............................................................................................................................ 31
Lưu đồ thuật toán: ..................................................................................................... 34
Bài 7: Dijkstra ................................................................................................................ 36
Code: ............................................................................................................................ 36
Lưu đồ thuật toán: ..................................................................................................... 38
Chú ý: .............................................................................................................................. 41 lOMoAR cPSD| 58457166
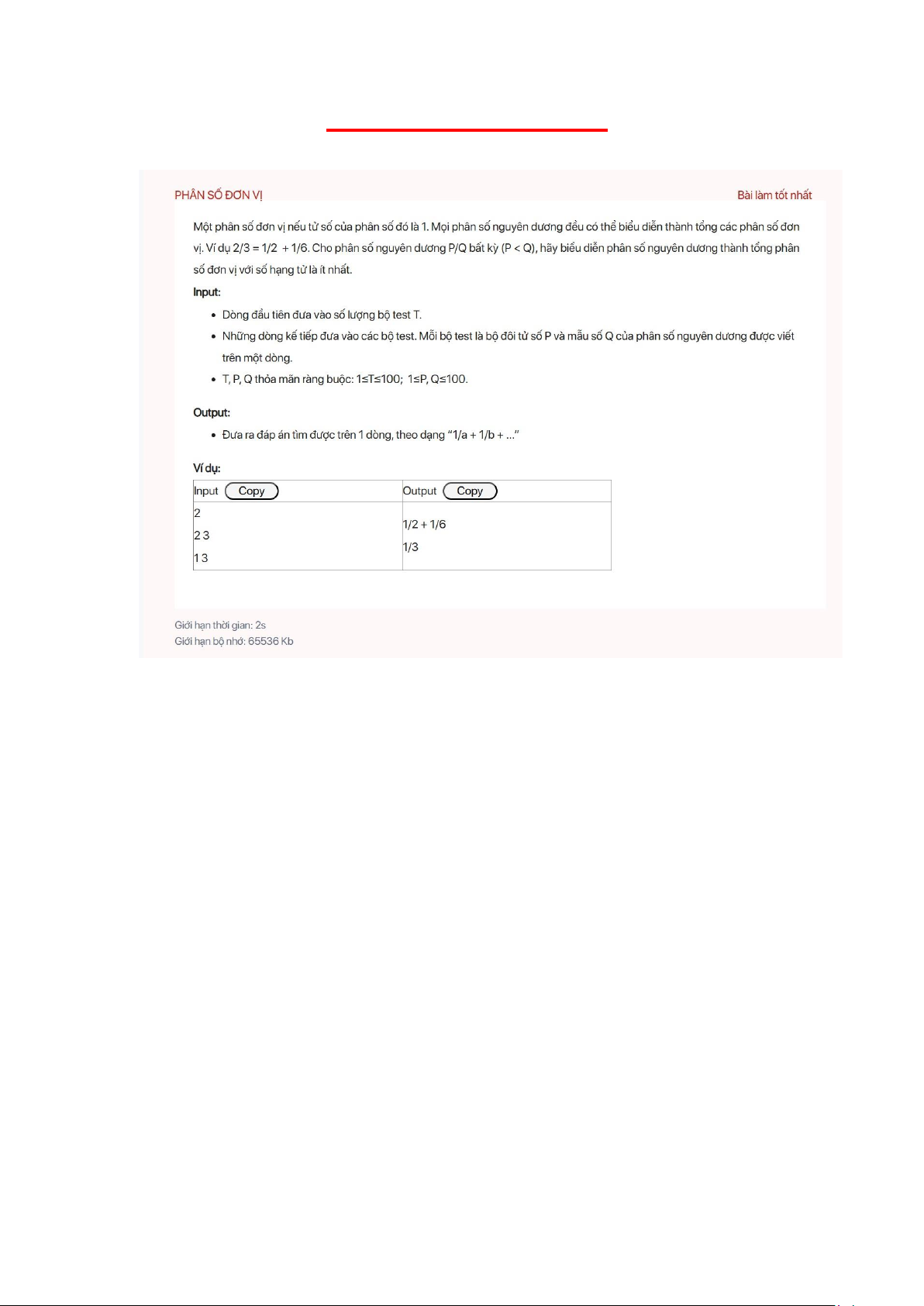
Bài 1: Phân số đơn vị lOMoAR cPSD| 58457166 Code: #include #define ll long long #define pb push_back #define bp pop_back
#define faster ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); using
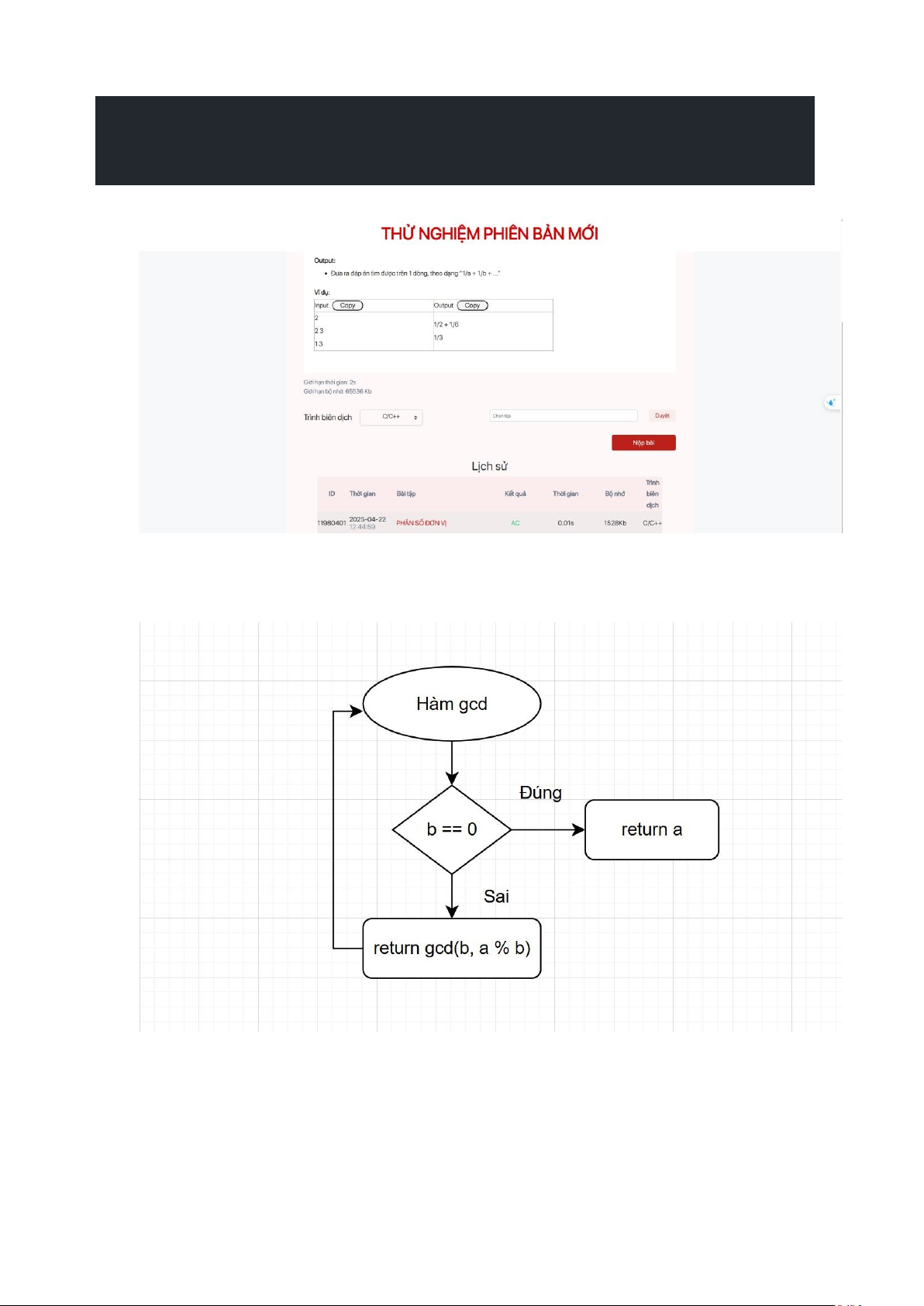
namespace std; ll gcd(ll a, ll b){ if(b
== 0) return a; return gcd(b, a % b); } int main(){ faster;
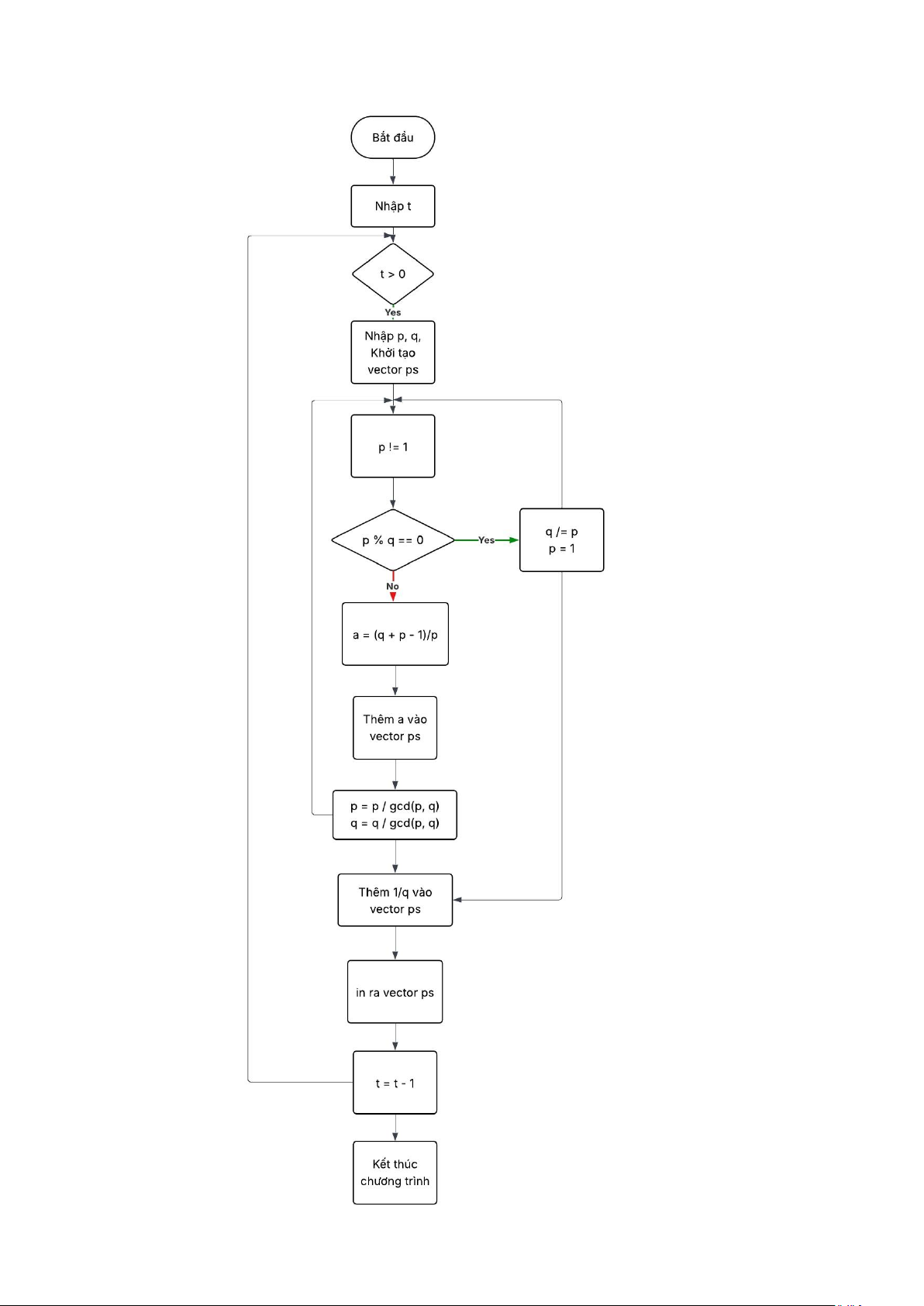
ll t; cin >> t; while(t--){
ll p, q; cin >> p >> q; vector ps; while(p != 1){ if(q % p == 0){ q /= p; p = 1; break; } ll a = (q + p - 1)/p; ps.pb("1/" + to_string(a)); p = p * a - q; q = q * a; ll rutgon = gcd(p, q); p = p/rutgon; q = q/rutgon;
} ps.pb("1/" + to_string(q));
for(int i = 0; i < ps.size(); i++){
cout << ps[i]; if(i != ps.size() - 1) cout << " + "; } lOMoAR cPSD| 58457166 cout << "\n"; } return 0; }
Lưu đồ thuật toán: lOMoAR cPSD| 58457166 lOMoAR cPSD| 58457166 Bài 2: Cặp số Code: #include #define ll long long #define pb push_back #define bp pop_back #define mod 1000000007
#define faster ios::sync_with_stdio(false); cin.tie(NULL);
cout.tie(NULL); using namespace std; lOMoAR cPSD| 58457166 int BIT[1000001]; void update(int i){
for(; i <= 1000000; i += i & -i){ BIT[i]++; } } int get(int i){ int sum = 0; for(; i; i -= i & -i){ sum += BIT[i]; } return sum; } int main(){ faster; stack
st; int n; cin >> n; int a[n + 1];
int ans = 0; for(int i = 1; i <= n; i++)
cin >> a[i]; for(int i = n; i >= 1; i-- ){ if(a[i] % 2 == 0){ ans += get(a[i] - 1); st.push(a[i]); } else{ while(!st.empty()){ update(st.top()); st.pop(); } } } cout << ans; return 0; } lOMoAR cPSD| 58457166
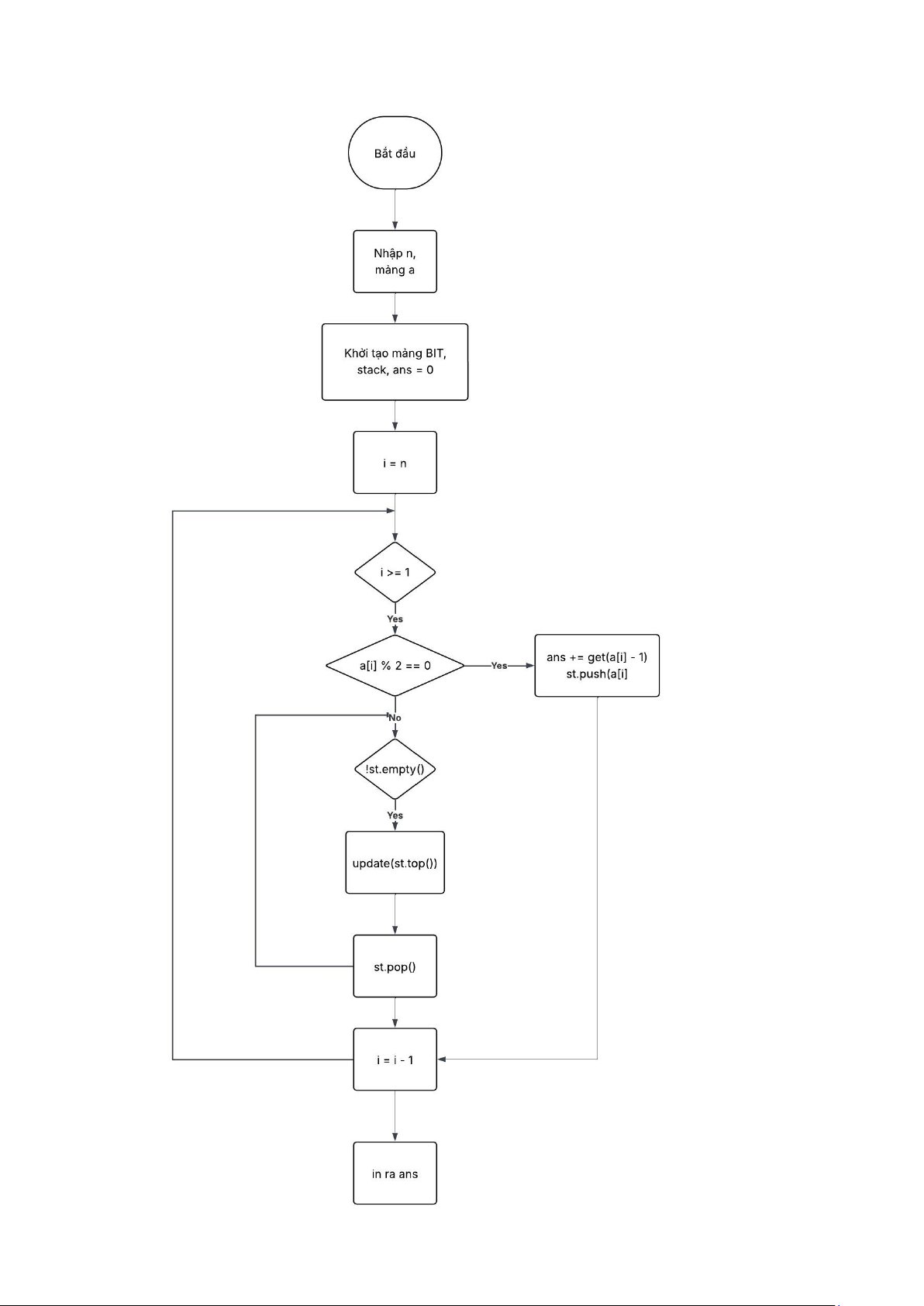
Lưu đồ thuật toán: lOMoAR cPSD| 58457166 lOMoAR cPSD| 58457166
Giải thích thuật toán:
• Giải thích về cây Fenwick (cây BIT): là 1 cấu trúc dữ liệu
được lưu dưới 1 mảng (thông thường là BIT[1000001]) các
giá trị sẽ được cập nhật bằng cách cộng thêm vào những giá
trị mà từ vị trí thứ i cộng với (vị trí i and với -i) sẽ là vị trí
tiếp theo mà giá trị từ bit i sẽ đóng góp giá trị của nó vào vị trí đấy.
• Sử dụng cây Fenwick để lưu trữ các số chẵn đã gặp, nhằm
đếm nhanh các số bé hơn số đang xét. • ví dụ: số 5: 0000 1001 •
biểu diễn số -5: dùng phép bù 2 •
b1: bù 1 của số 5: 1111 0110 • 1111 0110 • + 1 • 1111 0111 - xây dựng cây BIT[] - BIT[i] = a[i]: i lẻ -
BIT[i] = a[1] + a[2] + ... + a[i] nếu i là lũy thừa của 2 - Trường hợp đặc biệt -
ví dụ: bit 12: xét từ phải qua trái gặp bit 1 đầu tiên
để xem lưu bao nhiêu bit tính từ 12 trở về -
12: biểu diễn sang hệ nhị phân: 1100 - 1 1 00 -
2^2 ---> 4 bit: 9, 10, 11, 12 lOMoAR cPSD| 58457166
• Ngược lại thì hàm get sẽ truy ngược lại các vị trí mà tạo nên đến vị trí bằng i Ví dụ
• Áp dụng với bài toán trên ta sẽ tận dụng điều này để cập
nhật các bit tạo nên 1 số chẵn nào đó đã duyệt qua là 1 để
đánh dấu số đó đã xuất hiện để nhận biết số đó có xuất hiện
khi duyệt đến số chẵn tiếp.
1. Duyệt ngược mảng (từ n về 1)
• Việc duyệt từ cuối mảng về đầu là có chủ đích, bởi vì trong
bài toán yêu cầu i < j.
• Khi xét phần tử tại chỉ số i, các phần tử ở phía sau nó (j >
i) đã được duyệt qua → tức là có thể được xét là j trong các cặp (i, j) tiềm năng. 2. Cây Fenwick Tree (BIT)
• Dùng để đếm nhanh số lượng các số chẵn nhỏ hơn a[i] đã
xuất hiện trước đó (tức là nằm sau i trong mảng gốc). • Cụ thể:
o Khi gọi get(a[i] - 1) → sẽ trả về số lượng các số chẵn < a[i]
đã được cập nhật vào BIT. lOMoAR cPSD| 58457166
o Những số chẵn này chỉ được cập nhật khi có một số lẻ xuất
hiện giữa i và j, đảm bảo đúng điều kiện đề bài.
3. Stack lưu các số chẵn chưa được kích hoạt
• Khi gặp số lẻ tại chỉ số k, ta xem như đã tìm được một chỉ số
nằm giữa i và j → điều kiện thứ ba được đảm bảo.
• Lúc này, tất cả các số chẵn đã gặp trước đó (đang lưu trong
stack) mới được phép đưa vào BIT (bằng cách gọi update()).
• Đây là ý tưởng chính: chỉ sau khi có một số lẻ "ngăn cách"
giữa i và j, thì các số chẵn phía sau mới được công nhận là
hợp lệ để tạo cặp (i, j). − Chú ý: • Khi gặp số chẵn:
• Gọi get(a[i]-1) để đếm các số chẵn nhỏ hơn a[i] đã có trong BIT.
• Nếu chưa từng gặp số lẻ trước đó, thì BIT vẫn rỗng, nên
get() sẽ trả về 0 → không tăng ans. − Ví dụ
• Trường hợp chưa có số lẻ: a = [..., 4, ...]
• Duyệt tới số 4 (chẵn), nhưng vì chưa gặp số lẻ → BIT chưa
được cập nhật gì cả → get(3) = 0 → ans += 0 • Khi gặp số lẻ: lOMoAR cPSD| 58457166 a = [..., 4, 3, 2, ...]
Duyệt tới 3 → gọi update() cho 4, cập nhật BIT tại các chỉ số liên quan (4, 8, 16, ...)
Sau đó gặp 2, gọi get(1) → vẫn là 0 → vì 2 nhỏ hơn 4, nhưng chưa được cập nhật
cặp (2, 4) không thỏa mãn điều kiện a[i] > a[j] và có số lẻ nằm giữa
Trường hợp có số lẻ giữa 2 số chẵn hợp lệ: a = [6, 3, 4, ...]
Sau khi 3 (lẻ) xuất hiện, 4 được đưa vào BIT.
Khi duyệt đến 6, gọi get(5) → thấy 4 đã trong BIT → ans += 1
→ tồn tại số lẻ giữa 6 và 4 thỏa mãn điều kiện i < j và a[i] > a[j].
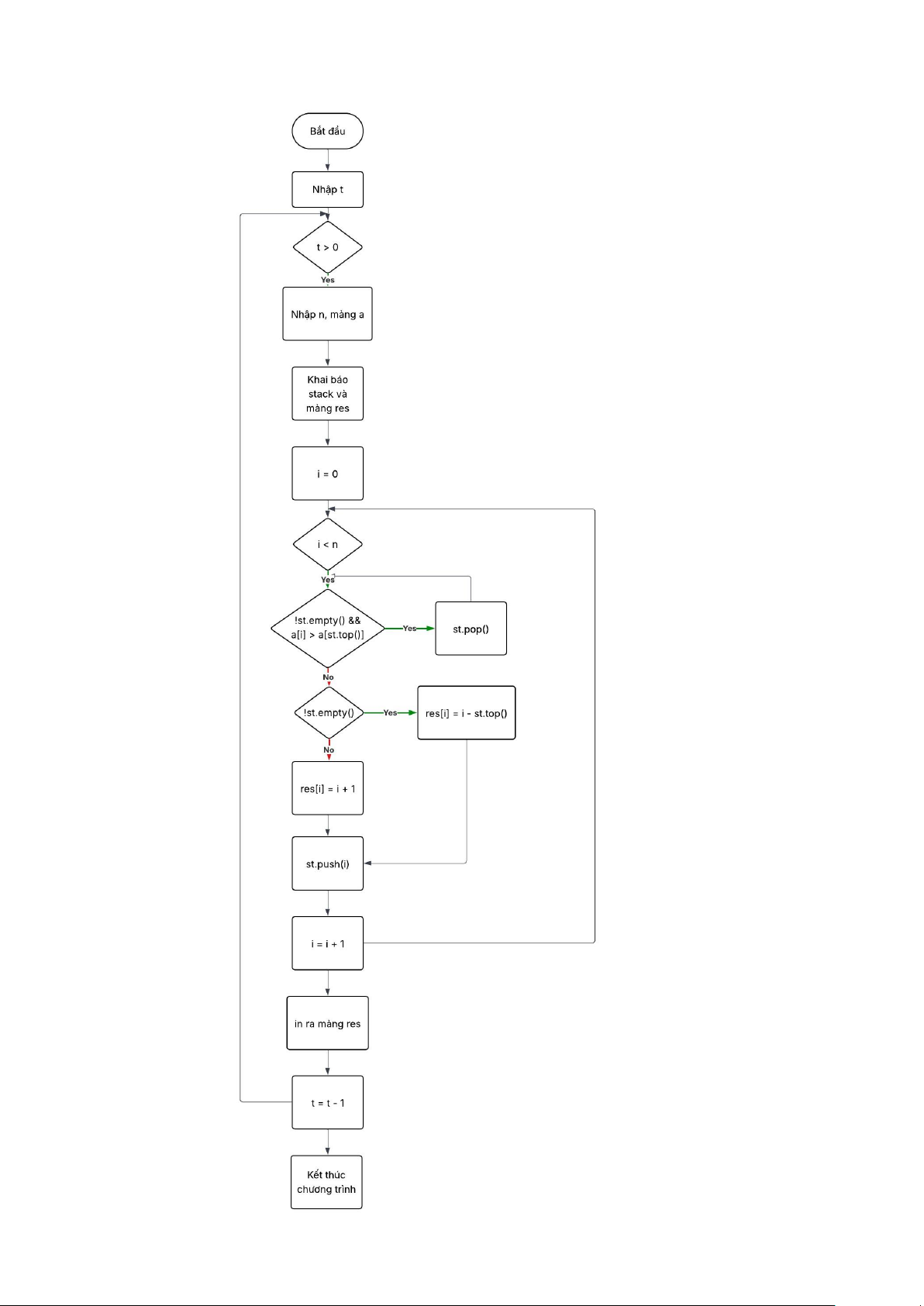
Bài 3: Nhịp chứng khoán lOMoAR cPSD| 58457166 lOMoAR cPSD| 58457166 Code: #include #define ll long long #define pb push_back #define bp pop_back #define mod 1000000007
#define faster ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); using namespace std;
int main(){ faster; int t; cin >> t;
while(t--){ int n; cin >> n; int a[n];
for(int i = 0; i < n; i++) cin >> a[i]; int
res[n]; stack st; for(int i = 0;
i < n; i++){ while(!st.empty() && a[i] >= a[st.top()]){ st.pop(); } if(!st.empty()){ res[i] = i - st.top(); } else res[i] = i + 1; st.push(i);
} for(int i = 0; i < n; i++) cout << res[i] << " "; cout << "\n"; } return 0; } lOMoAR cPSD| 58457166
Lưu đồ thuật toán: lOMoAR cPSD| 58457166 lOMoAR cPSD| 58457166
Bài 4: Tích 2 số nhị phân Code: #include #define pb push_back #define bp pop_back #define ll long long
#define faster ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL); using namespace std; ll binpow(ll a, ll b){ if(b == 0) return 1; ll x = binpow(a, b / 2); if(b % 2 == 0) return x * x; else return x * x * a; }