Tiểu luận Thuật toán Dijkstra môn Cấu trúc dữ liệu - Giải thuật | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58457166 H
Ọ C VI Ệ N CÔNG NGH Ệ BƯU CHÍNH VI Ễ N THÔNG KHOA VI Ễ N THÔNG 1 TI
Ể U LU Ậ N MÔN H Ọ C THU
Ậ T TOÁN DIJIKSTRA
H ọ c ph ầ n: C ấ u trúc d ữ li ệ u và Gi ả i thu ậ t
Nhóm tiểu luận : 13
Giảng viên hướng dẫn
: Lê Hải Châu
Danh sách sinh viên
: Vũ Đức Vinh – B22DCVT586
: Vũ Đức Giang – B22DCVT168
: Trần Trung Nghĩa – B22DCVT391
: Nguyễn Quang Tinh – B22DCVT464
Hà N ộ i – 2025 lOMoAR cPSD| 58457166
DANH SÁCH THÀNH VIÊN CỦA NHÓM Họ và tên Mã sinh viên Nhiệm vụ
Vũ Đức Vinh (Nhóm trưởng) B22DCVT586
Duyệt nội dung tiểu luận, vận
hành và tối ưu code, mô tả các
ứng dụng chính của đề tài vào trong đời sống Vũ Đức Giang B22DCVT168
Làm nội dung, thiết kế các
testcase cho việc kiểm thử code Trần Trung Nghĩa B22DCVT391
Làm nội dung, vận hành và tối ưu code Nguyễn Quang Tinh B22DCVT464
Làm nội dung xây dựng lịch sử
hình thành và các đặc điểm của thuật toán lOMoAR cPSD| 58457166 MỤC LỤC
I. MỞ ĐẦU ..................................................................................................................................... 3
II. NỘI DUNG CHÍNH................................................................................................................... 4
1. Kiến thức cơ sở: ...................................................................................................................... 4
2. Định nghĩa ............................................................................................................................... 4
3. Đặc điểm của thuật toán .......................................................................................................... 5
3.1. Yêu cầu về đồ thị ............................................................................................................. 5
3.2. Tiếp cận tham lam ............................................................................................................ 6
3.3. Sử dụng hàng đợi ưu tiên ................................................................................................. 7
3.4. Độ phức tạp thời gian ....................................................................................................... 8
3.5. Tính chất của đường đi ngắn nhất .................................................................................... 9
4. Mô tả thuật toán .................................................................................................................... 10
5. Triển khai thuật toán Dijkstra bằng ngôn ngữ C++ ...............................................................11
6. Kiểm thử thuật toán qua các testcase .................................................................................... 15
7. Giới hạn của thuật toán ......................................................................................................... 19 7.1
Thuật toán không áp dụng được với đồ thị có trọng số âm :
.......................................... 19 7.2 Không hiệu quả với đồ thị không liên thông:
................................................................. 20 7.3
Không tối ưu cho bài toán đường đi ngắn nhất giữa tất cả các cặp đỉnh (All-Pairs
Shortest Path - APSP) ........................................................................................................... 20 7.4 Không phát hiện chu trình âm
......................................................................................... 20 7.5 Không lưu trữ đường đi cụ thể
........................................................................................ 21 8. Các ứng dụng của thuật toán
................................................................................................. 21
8.1. Tìm đường đi ngắn nhất trong giao thông, logistic ........................................................ 21
8.2. Định tuyến mạng ............................................................................................................ 22
8.3. Quản lý tài nguyên trong hệ thống phân tán .................................................................. 23
8.4. Ứng dụng trong kỹ thuật hàng không vũ trụ .................................................................. 24
III. TÀI LIỆU THAM KHẢO: ..................................................................................................... 25 lOMoAR cPSD| 58457166
I. MỞ ĐẦU
Trong thế giới ngày càng kết nối của chúng ta, việc tìm kiếm con đường tối ưu giữa các điểm không chỉ là
một bài toán lý thuyết hấp dẫn mà còn mang lại giá trị thực tiễn to lớn. Từ việc định tuyến dữ liệu trong
các mạng máy tính phức tạp, đến hỗ trợ người dùng tìm đường đi ngắn nhất trên hệ thống định vị GPS, hay
thậm chí tối ưu hóa lộ trình trong quản lý logistics, nhu cầu giải quyết bài toán đường đi ngắn nhất đã trở
thành một phần không thể thiếu trong cuộc sống hiện đại. Chính trong bối cảnh đó, thuật toán Dijkstra
nổi lên như một công cụ quan trọng, một giải pháp kinh điển và hiệu quả, được ứng dụng rộng rãi trong
khoa học máy tính và lý thuyết đồ thị. Được phát triển bởi nhà khoa học máy tính lỗi lạc người Hà Lan
Edsger W. Dijkstra vào năm 1956 và công bố chính thức vào năm 1959, thuật toán này không chỉ đánh dấu
một cột mốc quan trọng trong lịch sử phát triển của ngành khoa học máy tính mà còn đặt nền móng cho
nhiều ứng dụng công nghệ tiên tiến sau này.
Thuật toán Dijkstra được thiết kế để giải quyết bài toán đường đi ngắn nhất từ một nguồn (singlesource
shortest path), một trong những bài toán cơ bản và phổ biến nhất trong lý thuyết đồ thị. Cụ thể, nó tìm ra
đường đi ngắn nhất từ một đỉnh nguồn cố định đến tất cả các đỉnh khác trong một đồ thị, có thể là đồ thị có
hướng hoặc vô hướng, với điều kiện tiên quyết là các cạnh của đồ thị phải có trọng số không âm. Điều
kiện này không phải là một hạn chế ngẫu nhiên mà là yếu tố cốt lõi đảm bảo tính đúng đắn của thuật toán.
Nếu đồ thị chứa các cạnh có trọng số âm, thuật toán Dijkstra sẽ không thể đảm bảo kết quả chính xác do
cách nó dựa trên nguyên tắc tham lam (greedy principle) để chọn lựa các đỉnh tiếp theo dựa trên khoảng
cách nhỏ nhất đã biết. Sự đơn giản trong ý tưởng, kết hợp với hiệu quả vượt trội khi áp dụng vào các đồ thị
thỏa mãn điều kiện, đã khiến thuật toán này trở thành một công cụ không thể thay thế trong nhiều lĩnh vực.
Về mặt lịch sử, thuật toán Dijkstra ra đời trong một giai đoạn mà khoa học máy tính còn non trẻ, và các bài
toán tối ưu hóa trên đồ thị chưa được nghiên cứu sâu rộng như ngày nay. Edsger W. Dijkstra, người đã phát
minh ra thuật toán này trong một khoảnh khắc ngẫu hứng khi đang ngồi tại một quán cà phê, không ngờ
rằng sáng tạo của mình sẽ trở thành một di sản khoa học vượt thời gian. Ban đầu, ông phát triển thuật toán
để minh họa khả năng tính toán của máy tính cho một nhóm khán giả không chuyên, nhưng kết quả lại
vượt xa kỳ vọng, trở thành một nền tảng lý thuyết quan trọng. Từ đó đến nay, thuật toán đã được cải tiến,
mở rộng và tích hợp vào vô số hệ thống công nghệ hiện đại.
Ứng dụng thực tế của thuật toán Dijkstra là một minh chứng rõ ràng cho giá trị của nó. Trong lĩnh vực
mạng máy tính, thuật toán này được sử dụng trong các giao thức định tuyến như OSPF (Open Shortest
Path First) để tìm đường đi hiệu quả nhất cho dữ liệu, giảm thiểu độ trễ và tối ưu hóa băng thông. Trong
công nghệ GPS, nó giúp người dùng xác định tuyến đường ngắn nhất giữa hai địa điểm, cân nhắc các yếu
tố như khoảng cách hoặc thời gian di chuyển. Ngoài ra, thuật toán còn xuất hiện trong các bài toán tối ưu
hóa khác, chẳng hạn như lập kế hoạch sản xuất, quản lý chuỗi cung ứng, hay thậm chí phân tích mạng xã
hội để tìm kiếm các kết nối quan trọng. Chính sự linh hoạt và hiệu quả của nó đã biến thuật toán Dijkstra
thành một công cụ không chỉ có ý nghĩa học thuật mà còn mang lại lợi ích thực tiễn rõ rệt.
Mặc dù vậy, thuật toán Dijkstra không phải là không có giới hạn. Điều kiện trọng số không âm là một ràng
buộc lớn, khiến nó không thể áp dụng trực tiếp cho các đồ thị có trọng số âm – một vấn đề mà các thuật
toán khác như Bellman-Ford đã được phát triển để giải quyết. Hơn nữa, trong các đồ thị lớn với số lượng
đỉnh và cạnh khổng lồ, hiệu suất của thuật toán có thể bị ảnh hưởng nếu không sử dụng các cấu trúc dữ
liệu tối ưu như hàng đợi ưu tiên (priority queue). Những yếu tố này đặt ra nhu cầu hiểu rõ không chỉ cách
thức hoạt động của thuật toán mà cả bối cảnh và các đặc điểm kỹ thuật của nó.
Với tầm quan trọng và sự phổ biến như vậy, việc tìm hiểu sâu hơn về thuật toán Dijkstra là điều cần thiết
cho bất kỳ ai quan tâm đến khoa học máy tính, lập trình, hoặc các lĩnh vực ứng dụng liên quan. Trong bài lOMoAR cPSD| 58457166
báo này, chúng ta sẽ khám phá chi tiết định nghĩa của thuật toán, cách thức hoạt động từng bước của nó,
cũng như các đặc điểm nổi bật và những giới hạn cần lưu ý khi triển khai. Qua đó, người đọc sẽ có được
một cái nhìn toàn diện, không chỉ về lý thuyết mà còn về cách thuật toán này tiếp tục định hình thế giới công nghệ ngày nay. II. NỘI DUNG CHÍNH
1. Kiến thức cơ sở:
Khái niệm đồ thị, trọng số, đường đi, độ dài đường đi •
Đồ thị: Là một cấu trúc toán học bao gồm tập hợp các đỉnh (nodes) và các cạnh (edges) nối giữa
chúng. Đồ thị được dùng để mô hình hóa các mối quan hệ giữa các đối tượng. •
Trọng số: Là giá trị số được gán cho mỗi cạnh, thường biểu thị chi phí, khoảng cách hoặc thời gian
di chuyển giữa hai đỉnh. •
Đường đi: Là một chuỗi các đỉnh được nối với nhau bởi các cạnh, ví dụ: từ đỉnh A qua B đến C là
một đường đi (A → B → C). •
Độ dài đường đi: Là tổng trọng số của tất cả các cạnh trên đường đi đó.
Đồ thị vô hướng, có hướng, đồ thị liên thông •
Đồ thị vô hướng: Các cạnh không có hướng, nghĩa là nếu có cạnh nối giữa A và B, ta có thể đi từ
A đến B hoặc từ B đến A. •
Đồ thị có hướng: Các cạnh có hướng rõ ràng, ví dụ cạnh từ A đến B chỉ cho phép đi từ A đến B, không ngược lại. •
Đồ thị liên thông:
+ Với đồ thị vô hướng: tồn tại đường đi giữa mọi cặp đỉnh.
+ Với đồ thị có hướng: từ một đỉnh bất kỳ có thể đến được mọi đỉnh khác và ngược lại (nếu xét tính liên thông mạnh).
Bài toán đường đi ngắn nhất (Single Source Shortest Path – SSSP) •
Mục tiêu: Tìm đường đi ngắn nhất từ một đỉnh nguồn (source) đến tất cả các đỉnh khác trong đồ thị có trọng số. •
Ứng dụng: Định tuyến mạng, bản đồ đường đi, tối ưu hóa giao thông. 2. Định nghĩa
Thuật toán Dijkstra là một thuật toán quan trọng trong lĩnh vực khoa học máy tính, được thiết kế để giải
quyết bài toán tìm đường đi ngắn nhất từ một đỉnh nguồn đến tất cả các đỉnh khác trong một đồ thị có
hướng hoặc vô hướng, với điều kiện tất cả các cạnh đều có trọng số không âm. Được đặt theo tên của nhà
khoa học máy tính người Hà Lan Edsger W. Dijkstra, thuật toán này thuộc nhóm các phương pháp giải bài
toán đường đi ngắn nhất từ một nguồn (single-source shortest path). Nó không chỉ tìm ra khoảng cách lOMoAR cPSD| 58457166
ngắn nhất mà còn xác định được đường đi cụ thể từ đỉnh nguồn đến mỗi đỉnh khác, miễn là các đỉnh đó có thể tiếp cận được.
Thuật toán được phát triển vào năm 1956 và được công bố chính thức vào năm 1959 trong một bài báo
khoa học của Dijkstra. Ý tưởng cốt lõi của nó là sử dụng chiến lược tham lam (greedy approach), liên tục
chọn đỉnh có khoảng cách nhỏ nhất từ đỉnh nguồn và cập nhật các khoảng cách đến các đỉnh kề, đảm bảo
rằng mỗi quyết định được đưa ra là tối ưu tại thời điểm đó. Mô tả bài toán: •
Cho một đồ thị < G=(V,E), trong đó:
+ V: tập hợp các đỉnh. + E: tập hợp các cạnh.
+ Hàm trọng số <:E→R+ (trọng số không âm). •
Tìm đường đi ngắn nhất từ đỉnh nguồn s V đến mọi đỉnh khác trong V.
3. Đặc điểm của thuật toán
3.1. Yêu cầu về đồ thị
Thuật toán Dijkstra chỉ hoạt động hiệu quả trên các đồ thị có trọng số không âm, tức là mọi cạnh trong đồ
thị phải có trọng số lớn hơn hoặc bằng 0. Yêu cầu này xuất phát từ chiến lược tham lam của thuật toán: khi
một đỉnh được chọn và đánh dấu là đã xử lý, khoảng cách đến đỉnh đó được coi là ngắn nhất và không thể
cải thiện thêm. Nếu đồ thị chứa cạnh có trọng số âm, giả định này không còn đúng, dẫn đến kết quả sai. Do
đó, trong trường hợp có trọng số âm, các thuật toán khác như Bellman-Ford sẽ phù hợp hơn.
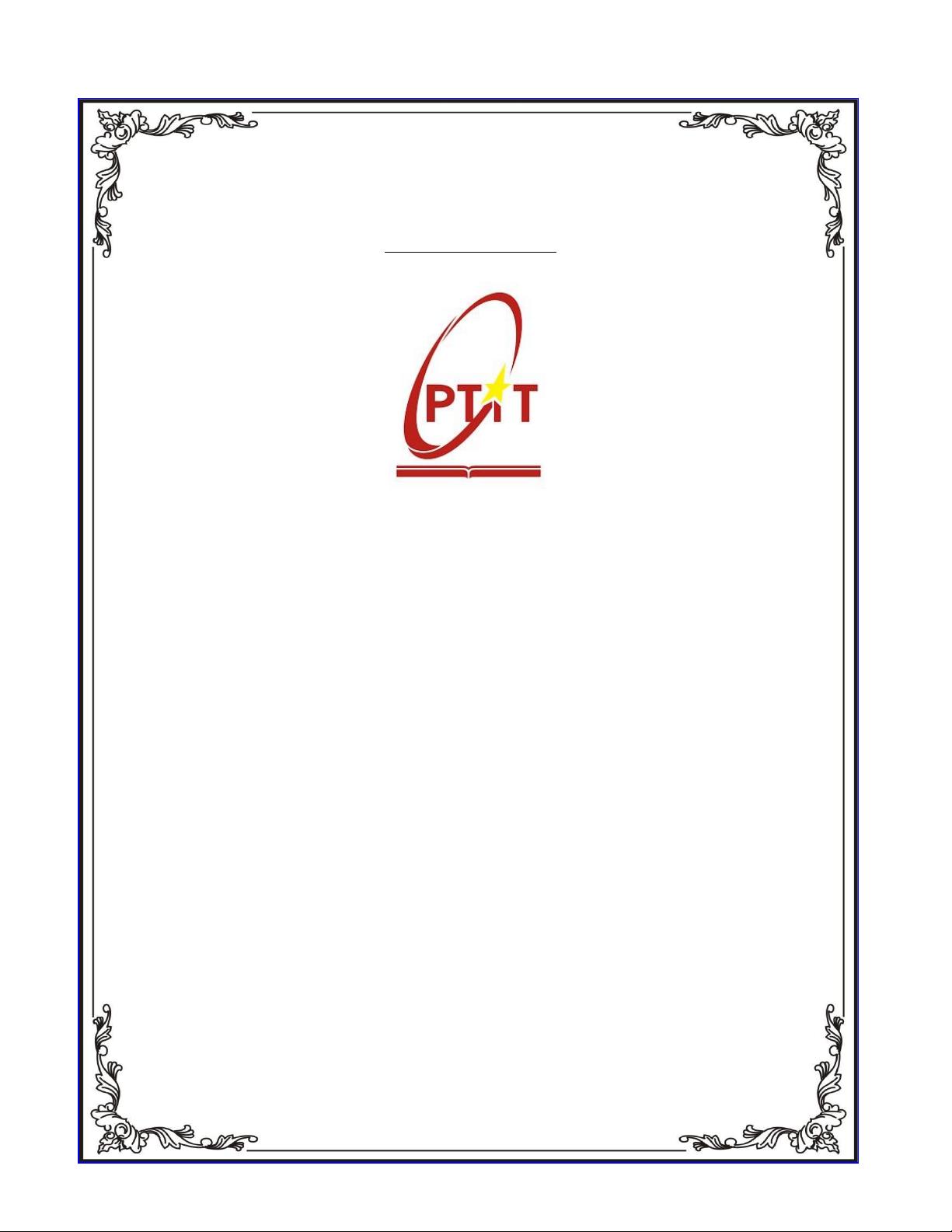
Thuật toán Dijkstra yêu cầu đồ thị phải có trọng số không âm. Khi thêm cạnh vào đồ thị, ta cần kiểm tra để
đảm bảo rằng trọng số của mỗi cạnh đều lớn hơn hoặc bằng 0. lOMoAR cPSD| 58457166
Giải thích: Đoạn mã kiểm tra trọng số khi thêm cạnh. Nếu trọng số âm, thông báo lỗi được in ra và cạnh
không được thêm vào đồ thị.
3.2. Tiếp cận tham lam
Thuật toán Dijkstra sử dụng chiến lược tham lam (greedy approach) để tìm đường đi ngắn nhất. Tại mỗi
bước, nó chọn đỉnh chưa xử lý có khoảng cách nhỏ nhất từ đỉnh nguồn, sau đó cập nhật khoảng cách đến
các đỉnh kề nếu phát hiện đường đi ngắn hơn qua đỉnh vừa chọn. Quá trình này lặp lại cho đến khi tất cả
các đỉnh được xử lý hoặc không còn đỉnh nào có thể tiếp cận. Nhờ tính chất tham lam, thuật toán đảm bảo
rằng mỗi quyết định cục bộ tối ưu sẽ dẫn đến kết quả toàn cục tối ưu khi hoàn tất.
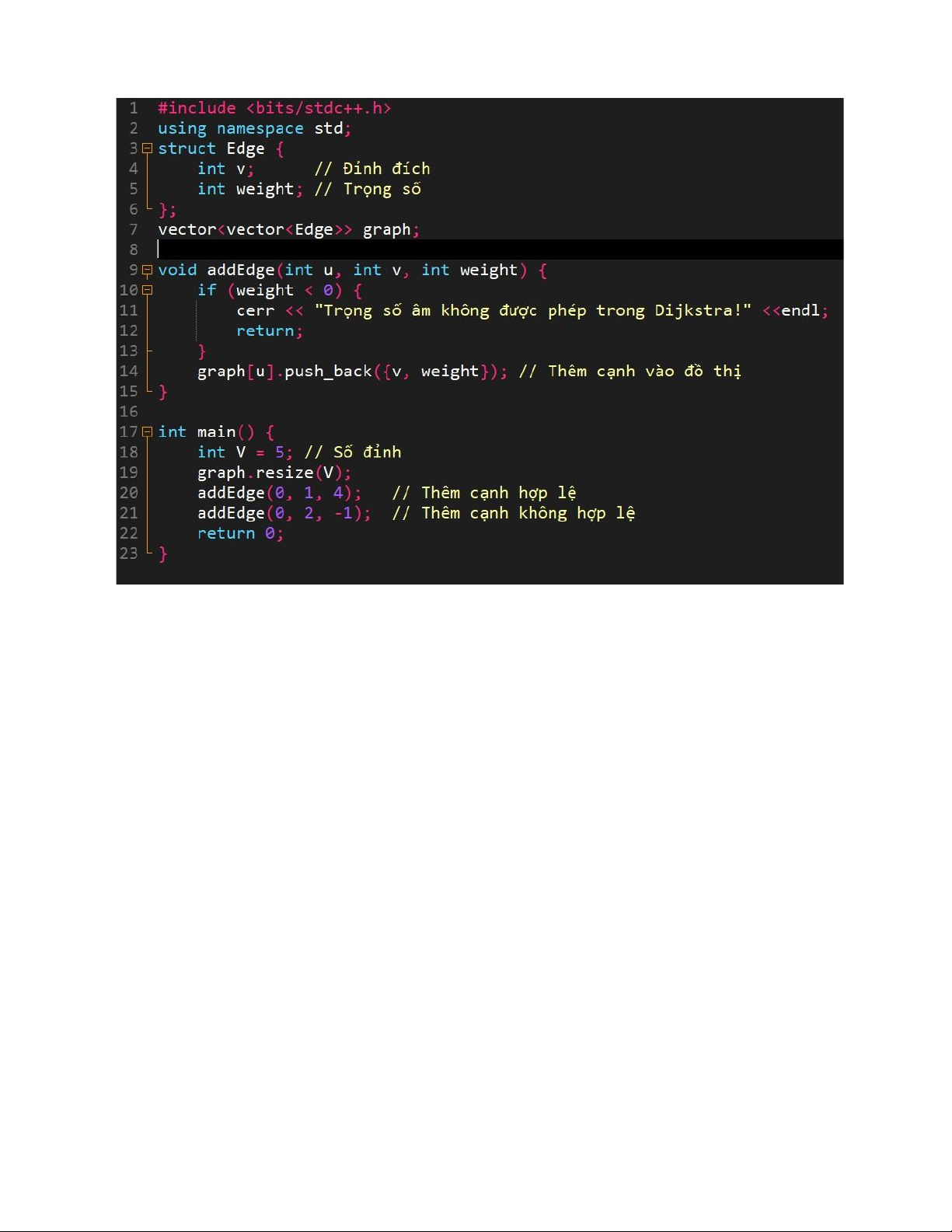
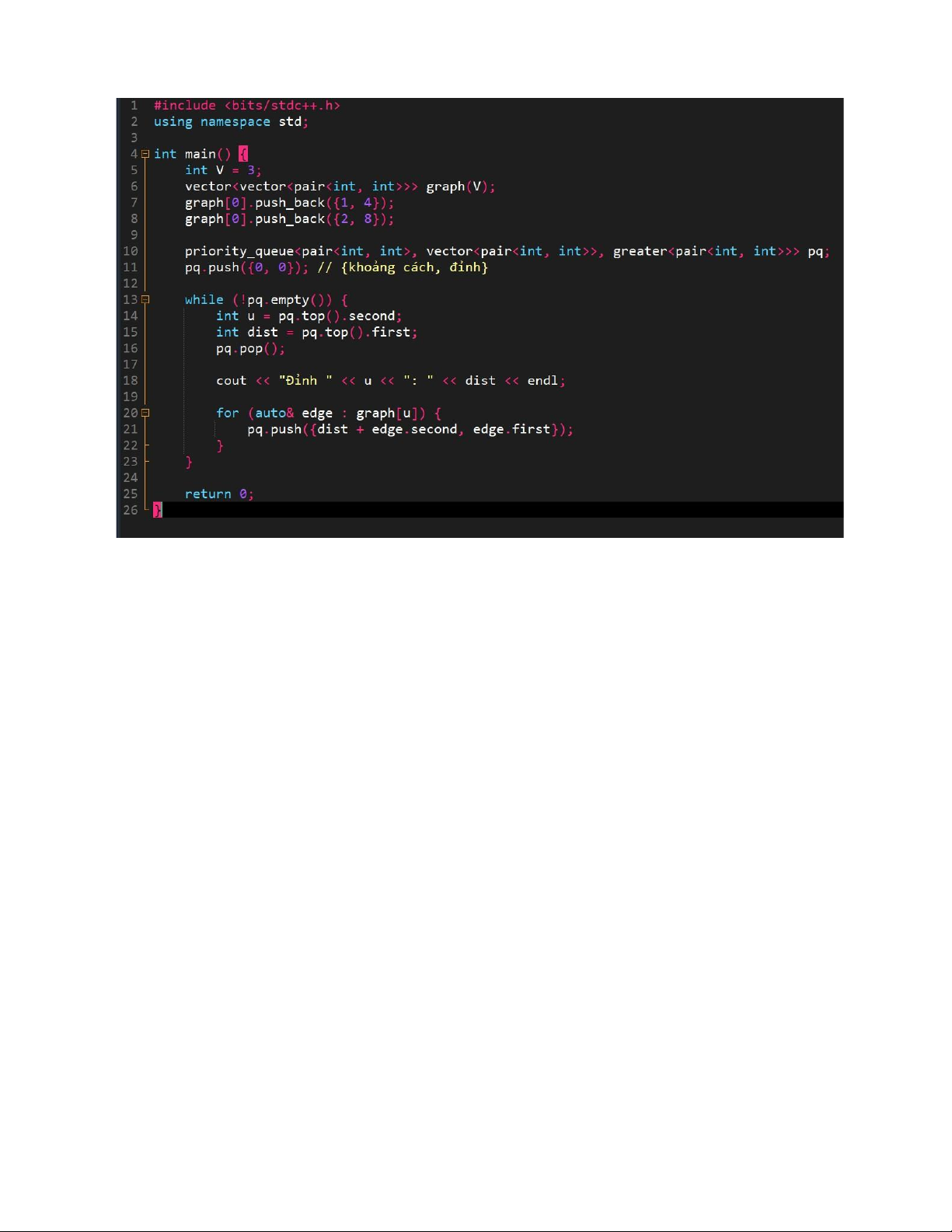
Dijkstra sử dụng chiến lược tham lam, luôn chọn đỉnh có khoảng cách nhỏ nhất từ đỉnh nguồn trong số các
đỉnh chưa xử lý. Điều này được triển khai bằng cách sử dụng hàng đợi ưu tiên. lOMoAR cPSD| 58457166
Giải thích: Hàng đợi ưu tiên pq lưu trữ cặp {khoảng cách, đỉnh}, với đỉnh có khoảng cách nhỏ nhất luôn ở
đầu. Mỗi bước, ta lấy đỉnh này ra để xử lý.
3.3. Sử dụng hàng đợi ưu tiên
Để tăng hiệu quả trong việc chọn đỉnh có khoảng cách nhỏ nhất, thuật toán Dijkstra thường được triển khai
với hàng đợi ưu tiên (priority queue). Cấu trúc dữ liệu này cho phép truy xuất nhanh đỉnh có khoảng cách
nhỏ nhất mà không cần duyệt qua toàn bộ tập hợp các đỉnh chưa xử lý. Trong thực tế: •
Binary heap: Là lựa chọn phổ biến, dễ triển khai và hiệu quả cho nhiều trường hợp. •
Fibonacci heap: Có thể được sử dụng để cải thiện độ phức tạp thời gian, nhưng ít phổ biến hơn do chi phí triển khai cao.
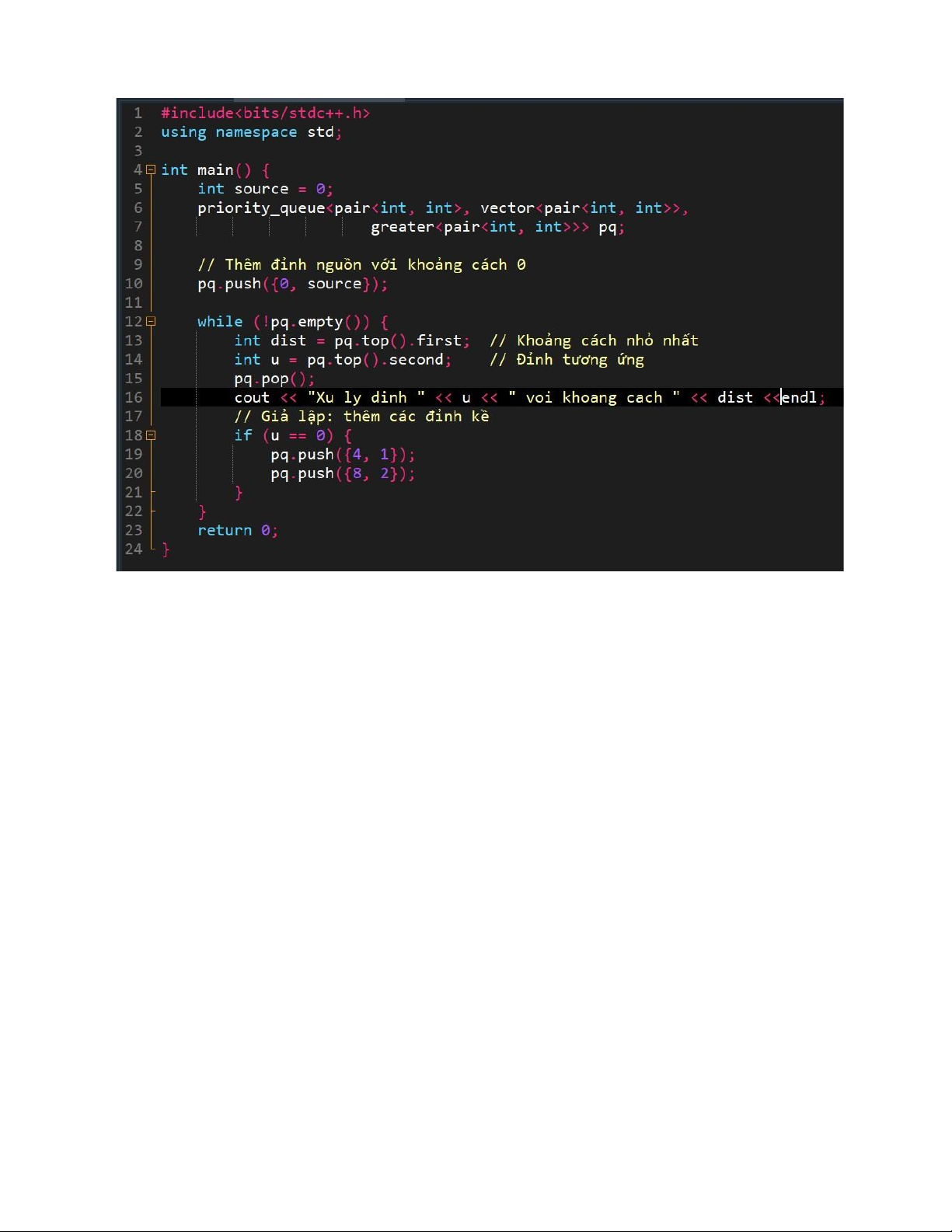
Việc sử dụng hàng đợi ưu tiên giúp giảm đáng kể độ phức tạp thời gian so với cách triển khai đơn giản bằng mảng. lOMoAR cPSD| 58457166
Giải thích: set tự động sắp xếp các đỉnh theo khoảng cách. Khi cần cập nhật, ta có thể xóa phần tử cũ và
thêm phần tử mới với khoảng cách đã cập nhật.
3.4. Độ phức tạp thời gian
Độ phức tạp thời gian của thuật toán Dijkstra phụ thuộc vào cách triển khai hàng đợi ưu tiên: •
Dùng mảng: Nếu lưu trữ khoảng cách trong mảng và duyệt qua tất cả các đỉnh để tìm khoảng cách
nhỏ nhất, độ phức tạp là ( O(V^2) ), với (V) là số đỉnh. Cách này phù hợp với đồ thị dày (dense graph). •
Dùng binary heap: Độ phức tạp giảm xuống O((V + E) log V) , với (E) là số cạnh. Đây là triển
khai phổ biến cho đồ thị thưa (sparse graph). •
Dùng Fibonacci heap: Độ phức tạp có thể đạt O(Vlog V + E), nhưng ít được sử dụng trong thực
tế do phức tạp trong triển khai.
Triển khai với binary heap thường là lựa chọn tối ưu, cân bằng giữa hiệu suất và độ đơn giản.
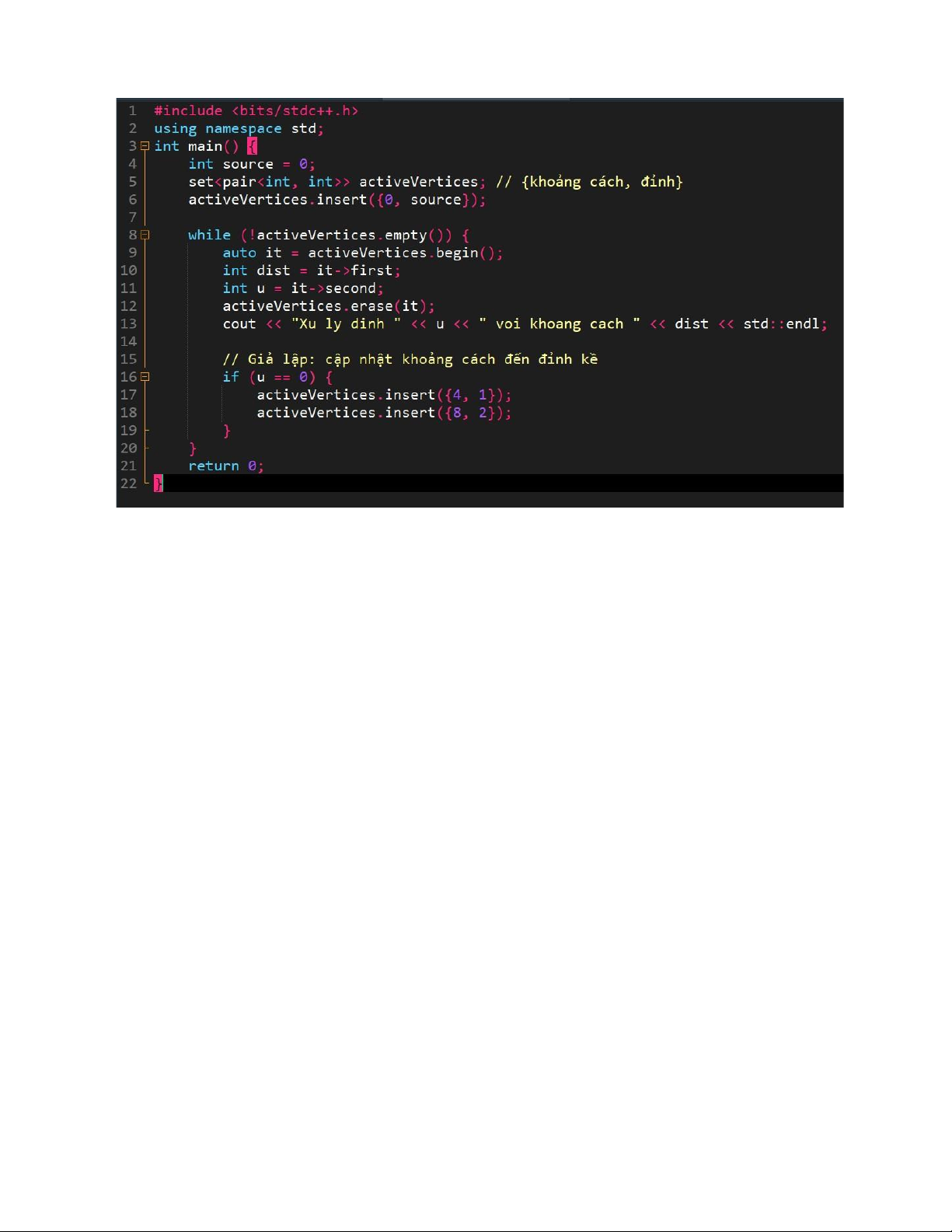
Với priority_queue (binary heap), độ phức tạp thời gian là O((V+E)log V). Dưới đây là một ví dụ đơn
giản minh họa vòng lặp chính. lOMoAR cPSD| 58457166
Giải thích: Vòng lặp chính sử dụng pq để xử lý các đỉnh, với mỗi thao tác thêm/xóa có độ phức tạp
O(logV), dẫn đến tổng độ phức tạp như trên.
3.5. Tính chất của đường đi ngắn nhất
Thuật toán Dijkstra đảm bảo tìm được đường đi ngắn nhất từ đỉnh nguồn đến tất cả các đỉnh khác trong đồ
thị, với điều kiện không có cạnh trọng số âm. Nó duy trì một tập hợp các đỉnh mà đường đi ngắn nhất đến
chúng đã được xác định, và tại mỗi bước, tập hợp này được mở rộng bằng cách thêm đỉnh có khoảng cách
nhỏ nhất từ đỉnh nguồn. Ngoài ra, thuật toán có thể tái tạo đường đi ngắn nhất bằng cách lưu trữ thông tin
về đỉnh trước đó (predecessor) trong quá trình thực thi. lOMoAR cPSD| 58457166
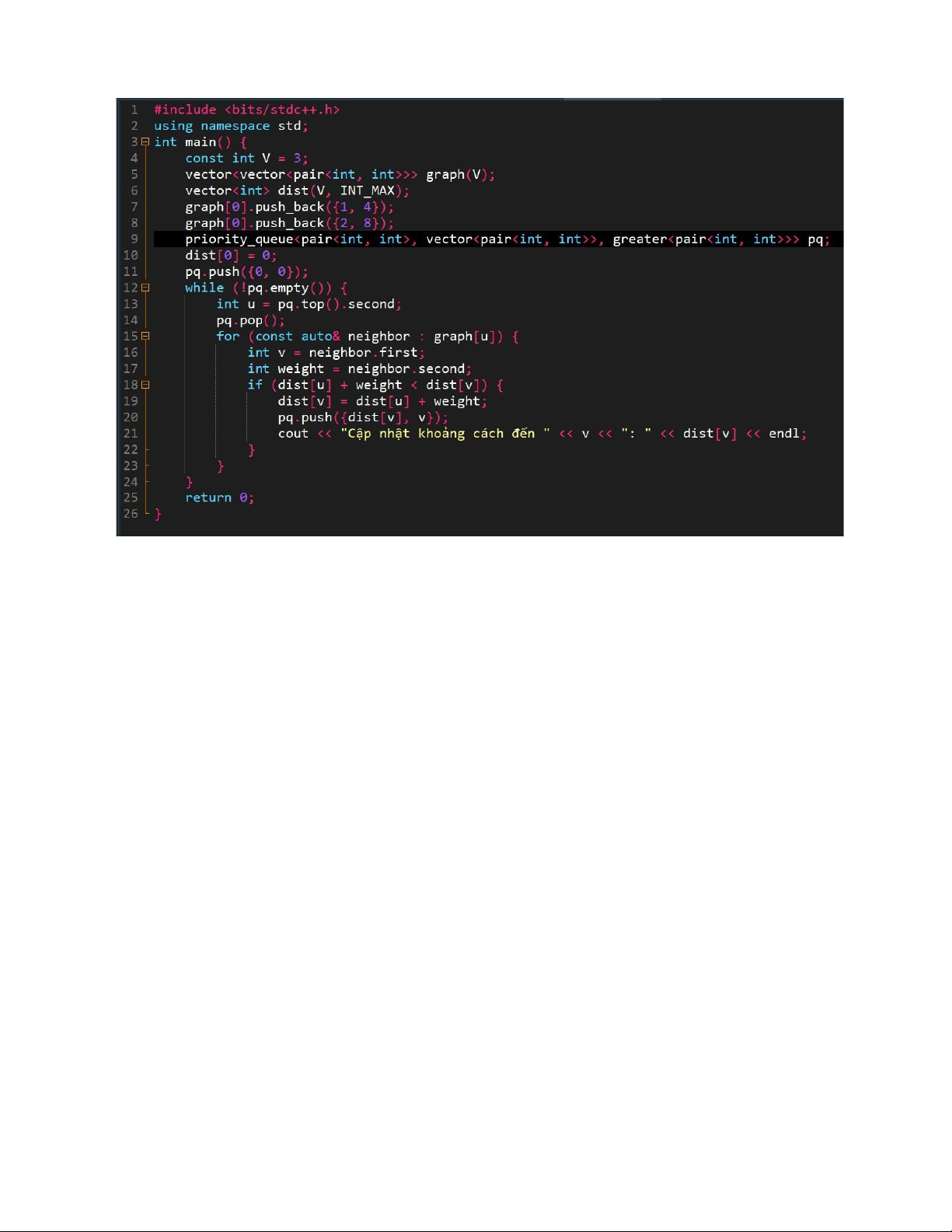
Giải thích: Nếu tìm được đường đi ngắn hơn đến đỉnh v qua u, khoảng cách được cập nhật và v được đưa
vào hàng đợi để xử lý tiếp.
Ví dụ minh họa: Giả sử đồ thị có các đỉnh A, B, C với các cạnh: A->B (trọng số 4), A->C (trọng số 2), C-
>B (trọng số 1). Khi chạy Dijkstra từ đỉnh A:
1. Ban đầu, khoảng cách đến A là 0, đến B và C là vô cực.
2. Chọn A, cập nhật khoảng cách: d(B) = 4, d(C) = 2.
3. Chọn C (khoảng cách nhỏ nhất), cập nhật: d(B) = min(4, 2+1) = 3.
4. Chọn B, không có cập nhật thêm vì không còn đỉnh nào chưa xử lý. Kết quả: Đường đi ngắn nhất
từ A đến B là A->C->B với tổng trọng số là 3.
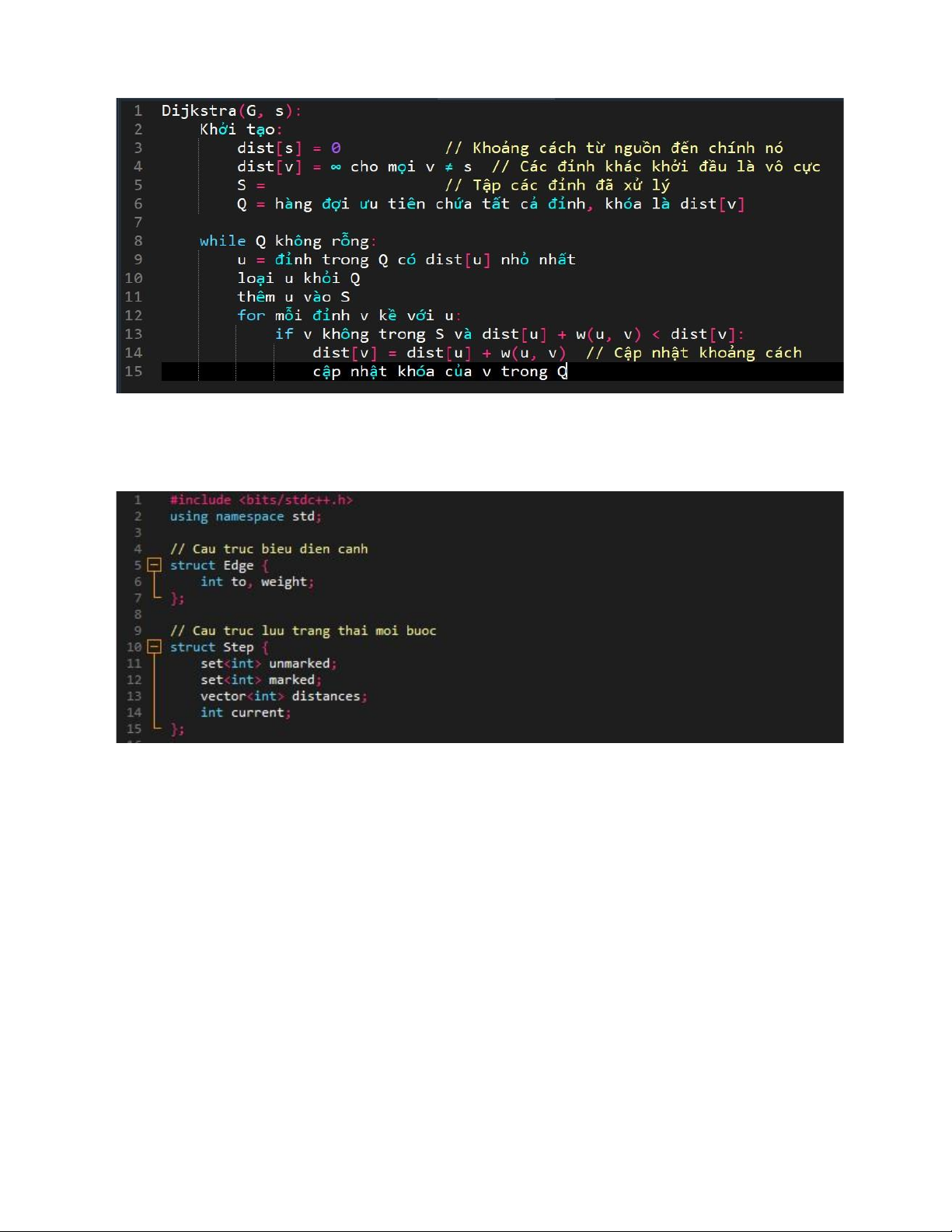
4. Mô tả thuật toán Dạng giả mã (pseudocode) lOMoAR cPSD| 58457166
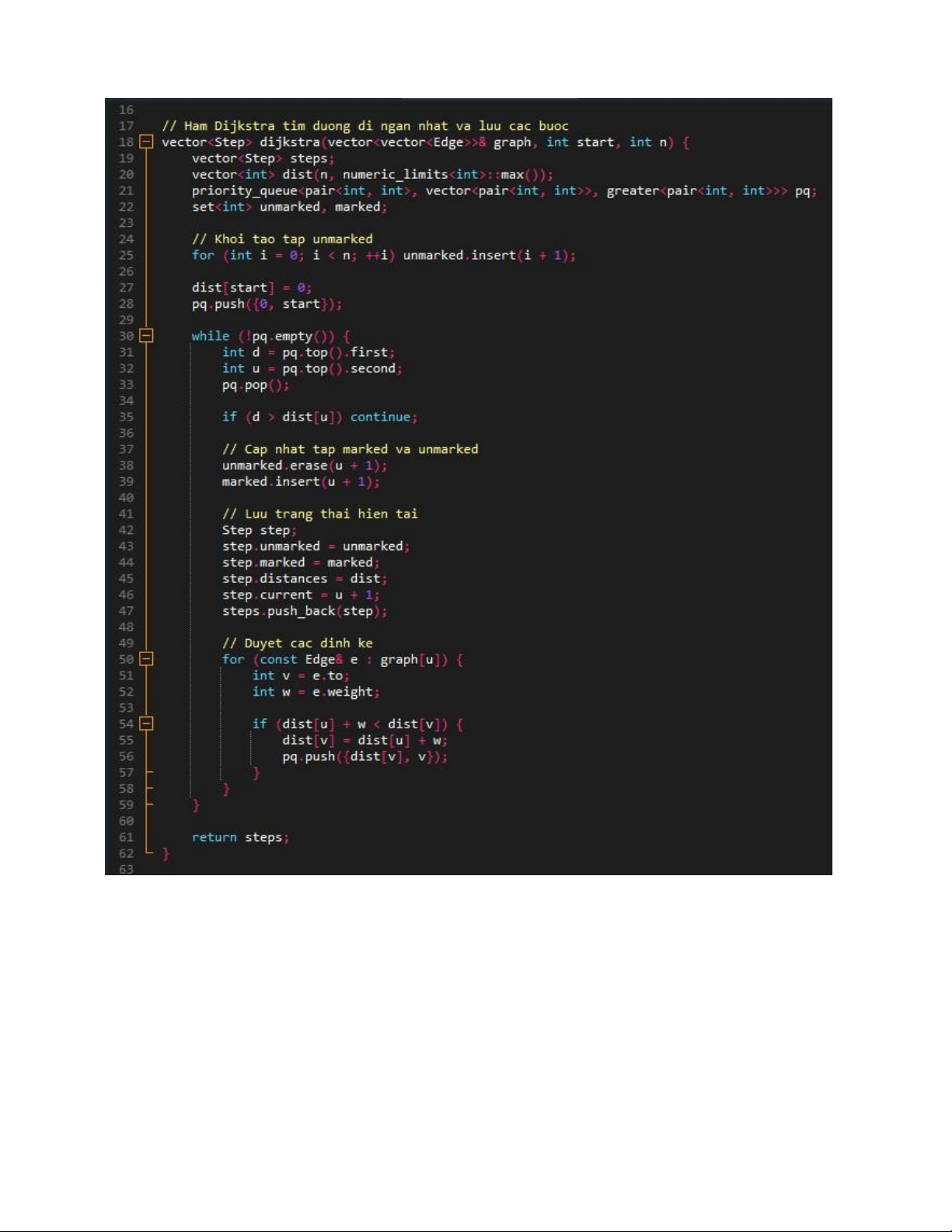
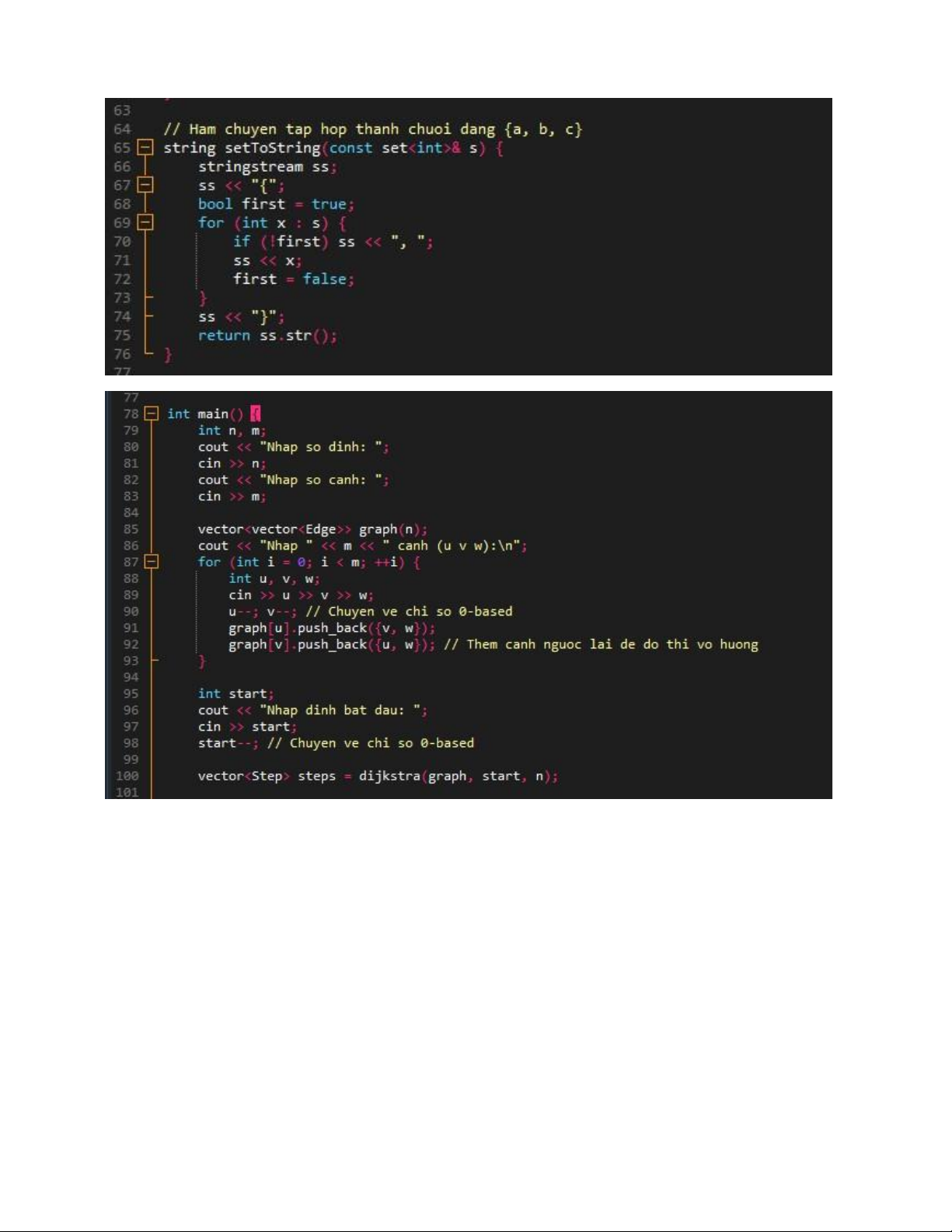
5. Triển khai thuật toán Dijkstra bằng ngôn ngữ C++
Mã chương trình mô phỏng bằng c++ lOMoAR cPSD| 58457166 lOMoAR cPSD| 58457166 lOMoAR cPSD| 58457166
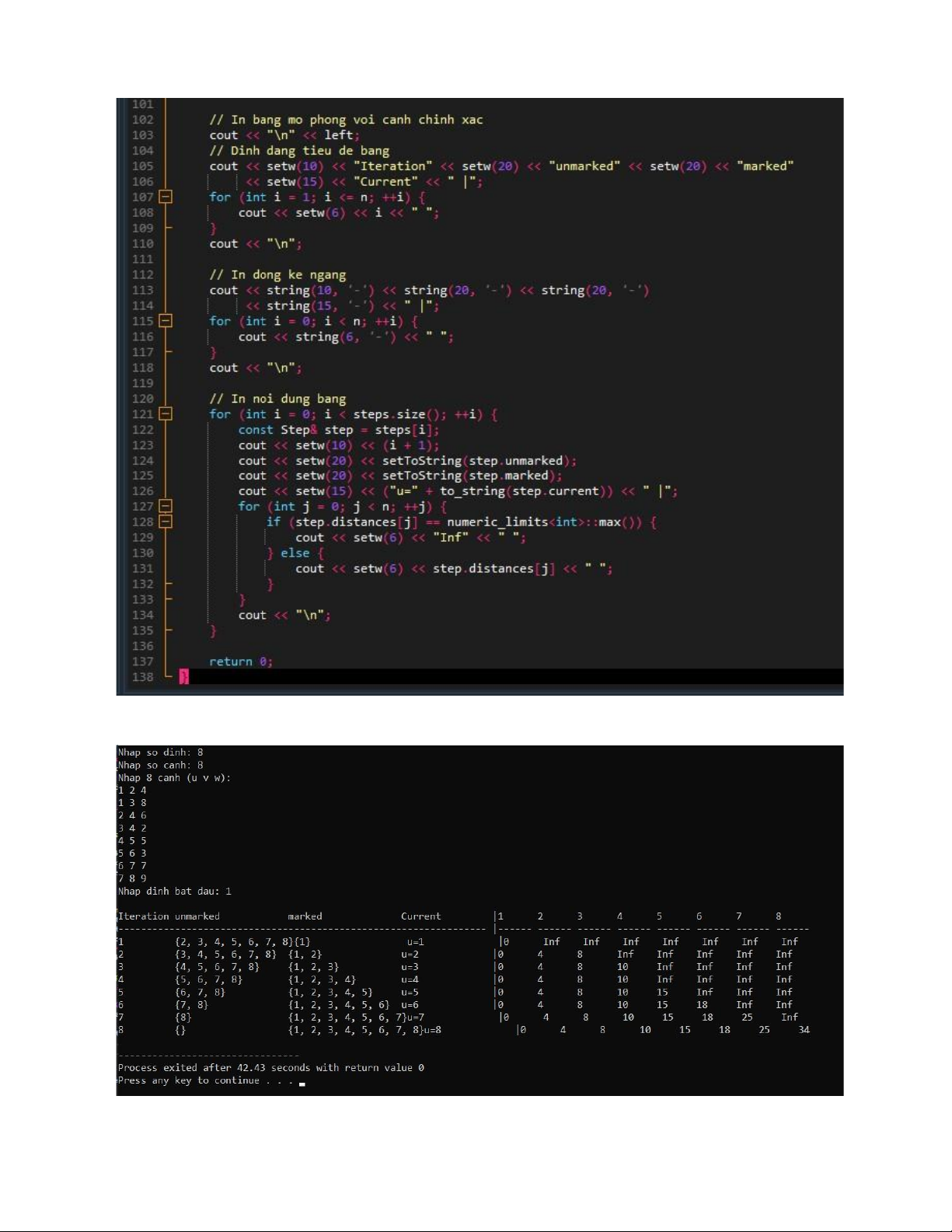
Kết quả mô phỏng:
6. Kiểm thử thuật toán qua các testcase - Testcase 1: lOMoAR cPSD| 58457166
priority_queue phải xử lý rất nhiều cạnh.
Vì mỗi đỉnh có cạnh tới mọi đỉnh khác, tổng số cạnh O(n²).
Với n = 8, vẫn chạy tốt, nhưng nếu tăng n lên 1000 → số cạnh ~500.000 → chương trình chậm và tốn RAM do lưu steps. Hướng tối ưu: •
Không lưu steps nếu chỉ cần đường đi cuối. •
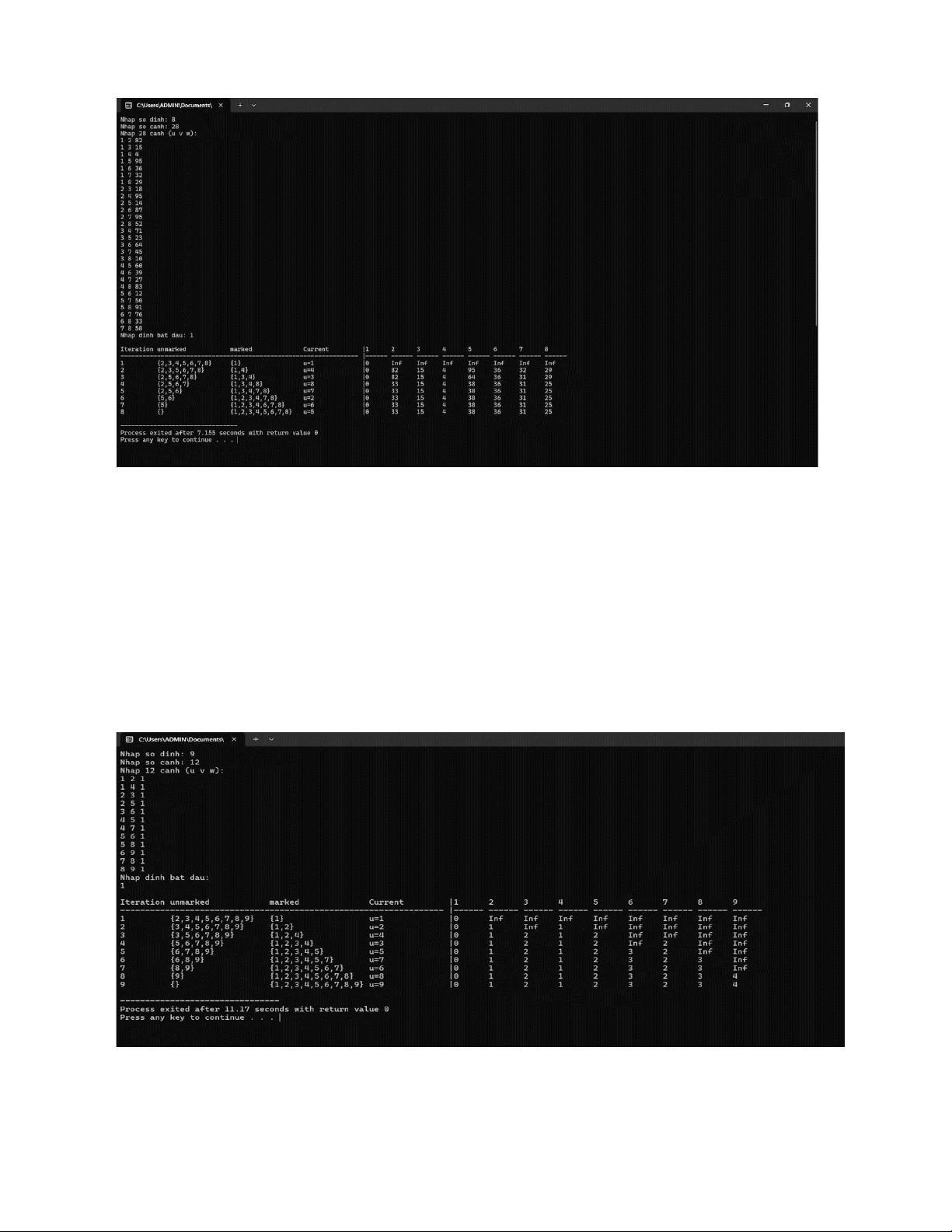
Dùng vector> thay vì struct Edge. - Testcase 2:
Dijkstra chạy ổn vì độ bền tuyến tính (O(E log V)), ít cạnh.
Nhưng nếu mở rộng thành lưới 100x100 → n = 10.000, E ≈ 20.000: •
Dijkstra vẫn chạy được nhưng steps rất tốn RAM. lOMoAR cPSD| 58457166 •
Việc in ra steps sẽ cực kỳ chậm. Hướng tối ưu: •
Cho phép tắt/bật in bước (steps) qua flag hoặc tham số. •
Dùng vector thay set để kiểm tra đánh dấu nhanh hơn. - Testcase 3:
Mỗi đỉnh chỉ có 1 cạnh đến cha/con → Dijkstra chạy tuyến tính.
Tốt nhất cho demo, không cần tối ưu thêm. Tối ưu hóa: •
Dễ dàng chạy BFS thay vì Dijkstra (vì mọi trọng số = 1). - Testcase 4: lOMoAR cPSD| 58457166
Cạnh từ đỉnh 1 đến các đỉnh còn lại có trọng số lớn •
Nhưng có đường đi tốt hơn qua chuỗi liên tiếp (trọng số = 1) •
Dijkstra ban đầu chọn đỉnh kế tiếp theo heap lớn → đưa vào heap những đường đi rất tệ (chi phí lớn). •
Sau đó phát hiện có đường tốt hơn, phải cập nhật heap lại. •
Cấu trúc heap bị "nhiễu loạn" bởi nhiều cập nhật không hiệu quả. Hướng tối ưu: •
Thêm kiểm tra visited[] để không đẩy lại đỉnh đã xử lý. •
Dùng decrease-key nếu dùng heap tối ưu (Fibonacci heap), hoặc dùng thư viện như std::set để xóa
lại phần tử cũ trong pq. - Testcase 5: lOMoAR cPSD| 58457166
Trọng số chạm ngưỡng của kiểu int •
Nếu dùng int, dễ bị tràn số khi cộng dồn trọng số. •
Độ phức tạp không cao, nhưng độ chính xác cần đảm bảo. Hướng tối ưu: •
Dùng long long thay cho int cho biến dist. •
Nếu vẫn cần tốc độ nhanh, chỉ cần unsigned int với kiểm tra tràn. - Testcase 6:
Đồ thị gồm nhiều thành phần liên thông rời rạc.
• Heap bị "nhiễu" bởi các đỉnh không liên thông (giá trị Inf ). lOMoAR cPSD| 58457166
• Các thao tác push và pop trên heap tốn thời gian nhưng không mang lại kết quả hữu ích. - Nguyên nhân: •
Thiếu cơ chế phát hiện sớm các đỉnh không liên thông. •
Không tận dụng được thông tin về cấu trúc đồ thị. Hướng tối ưu •
Phát hiện thành phần liên thông trước o Dùng DFS/BFS để phân loại các đỉnh vào từng thành phần
liên thông. o Chỉ chạy Dijkstra trên thành phần chứa đỉnh nguồn.
o Loại bỏ ngay các đỉnh không liên thông → giảm kích thước heap.
o Tiết kiệm thời gian do không xử lý các đỉnh vô nghĩa. •
Cải tiến cấu trúc heap o Sử dụng set hoặc priority_queue kết hợp với bảng visited để tránh đẩy
lại các đỉnh đã xử lý. o Triển khai decrease-key (nếu dùng Fibonacci heap).
7. Giới hạn của thuật toán
Mặc dù thuật toán Dijkstra là một công cụ mạnh mẽ để giải quyết bài toán đường đi ngắn nhất từ một đỉnh
nguồn (Single Source Shortest Path - SSSP) trong đồ thị, nó vẫn tồn tại một số giới hạn quan trọng. Những
giới hạn này xuất phát từ các giả định và tính chất của thuật toán, đặc biệt liên quan đến trọng số của cạnh,
cấu trúc đồ thị, và cách thức triển khai
7.1 Thuật toán không áp dụng được với đồ thị có trọng số âm : Lý do:
• Thuật toán Dijkstra hoạt động dựa trên nguyên tắc tham lam (greedy), nghĩa là tại mỗi bước, nó
chọn đỉnh chưa được xử lý có khoảng cách nhỏ nhất từ đỉnh nguồn và "cố định nhãn" (coi khoảng
cách đến đỉnh đó là tối ưu, không cập nhật lại). Điều này chỉ đúng nếu tất cả các cạnh có trọng số không âm.
• Khi có trọng số âm, việc cố định nhãn có thể dẫn đến sai sót, vì một đường đi có trọng số âm có
thể làm giảm tổng khoảng cách đến một đỉnh đã được xử lý, điều mà thuật toán không xét đến.
Phương pháp thay thế: Sử dụng thuật toán Bellman-Ford, với độ phức tạp < O(VE), có khả năng xử
lý đồ thị có trọng số âm và phát hiện chu trình âm (negative cycle) nếu có.
7.2 Không hiệu quả với đồ thị không liên thông: Lý do:
• Trong một đồ thị không liên thông, có ít nhất một đỉnh không thể tiếp cận được từ đỉnh nguồn.
Thuật toán Dijkstra vẫn cố gắng xử lý tất cả các đỉnh trong hàng đợi ưu tiên, nhưng các đỉnh không
liên thông sẽ có khoảng cách là vô cực (INF), dẫn đến việc thực hiện các bước không cần thiết.