

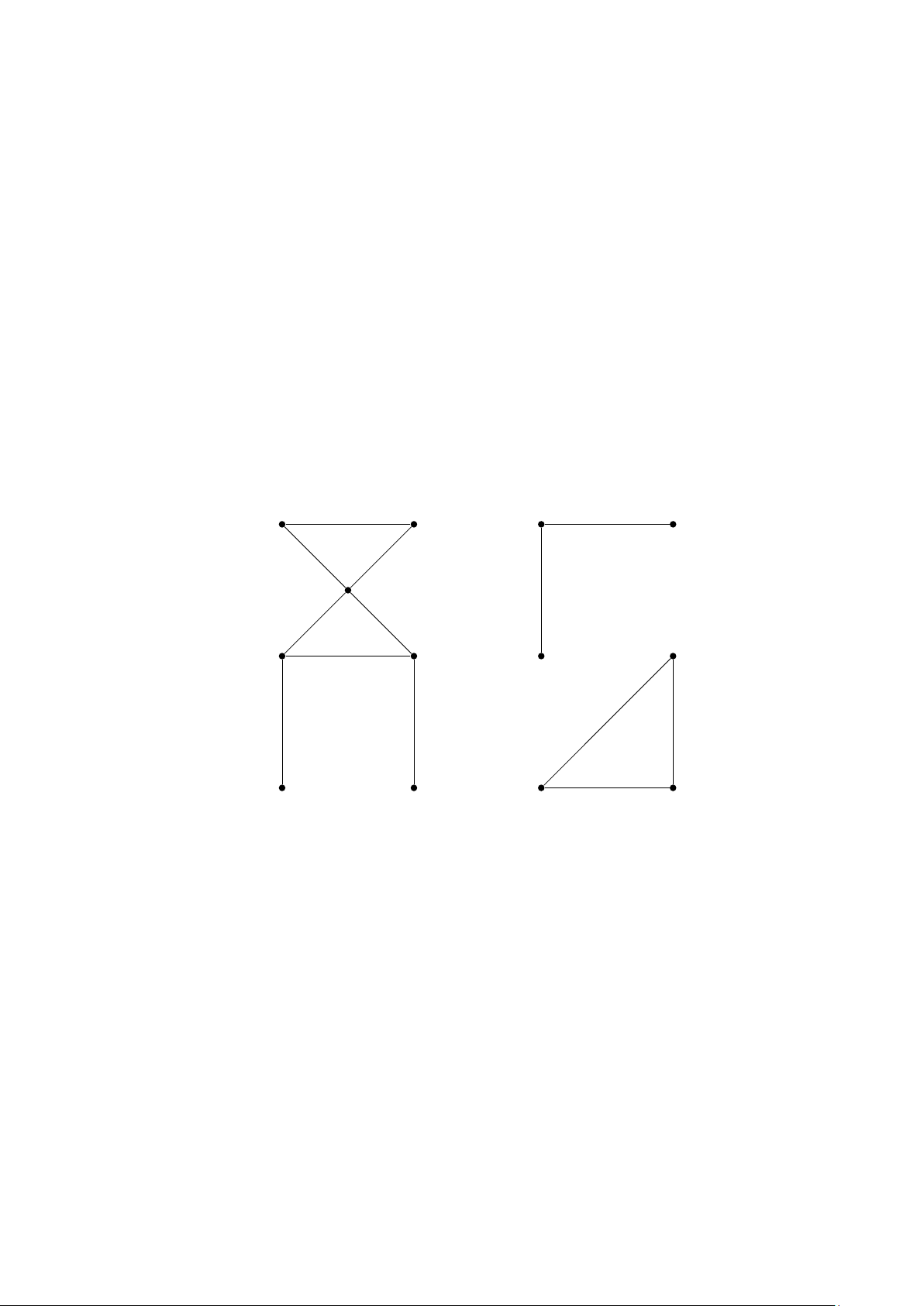
Preview text:
lOMoAR cPSD| 58591236
BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC ĐỒNG THÁP BÁO CÁO TIỂU LUẬN
HỌC PHẦN LÝ THUYẾT ĐỒ THỊ TÍNH LIÊN THÔNG
Người hướng dẫn:NCS. Ngô Tấn Phúc
Người tham gia thực hiện: Nguyễn Tấn Phát Văn Thị Huỳnh Thư Nguyễn Ngọc Ngân Nguyễn Trúc Quỳnh
Nguyễn Lê Huỳnh Du Phạm Bùi Bảo Trân Lê Phan Nhật Trường Đồng Tháp, 11/2024 1 Mở đầu
Nhiều bài toán có thể được mô hình với các đường đi dọc theo các cạnh của đồ thị. Ví dụ, người
ta dùng đồ thị để nghiên cứu bài toán xác định xem có thể gửi một thông báo giữa hai máy tínn
qua đường truyền thông trung gian được hay không. Dùng mô hình có đường đi trong đồ thị
cũng có thể giải được các bài toán tìm đường tối ưu cho xe phát thư, xe đổ rác, cho việc chẩn
đoán trong mạng máy tính. 2 Đường đi
Định nghĩa 1. Đường đi độ dài n từ u tới v, với n là một số nguyên dương, trong một đồ thị vô
hướng là một dãy các cạnh e1,e2,...,en của đồ thị sao cho f(e1) = {x0,x1},f(e2) = {x1,x2},...,f(en) =
{xn−1,xn}, với x0 = u và xn = v. Khi đồ thị là đơn ta kí hiệu đường đi này bằng dãy các đỉnh x0,x1,...,xn
(vì danh sách các đỉnh này xác định duy nhất đường đi). Đường đi được gọi là một chu trình
nếu nó bắt đầu và kết thác tại cùng một đỉnh, tức là u = v. Đường đi hoặc chu trình khi đó gọi
là đi qua các đỉnh x1,x2,...,xn−1. Đường đi hay chu trình gọi là đơn nếu nó không chứa cùng một cạnh quá một lần.
Khi không cần phân biệt các cạnh bội ta sẽ ký hiệu đương đi e1,e2,...,en trong đó f(ei) = {xi−1,xi}
với i = 1,2,...,n bằng dây các đỉnh x0,x1,...,xn. Ký hiệu này xác định đường đi chỉ theo các đỉnh mà
nó đi qua. Có thể có nhiều đường đi qua dãy các đỉnh này.
Ví dụ 1. Trong đồ thị đơn trên Hình 1,a,d,c,f,e là đường đi đơn độ dài 4 vì {a,d},{d,c},{c,f} và
{f,e} đều là các cạnh.
Tuy vậy d,e,c,a không là đường đi vì {e,c} không là cạnh của đồ thi. Còn b,c,f,e,b là một chu
trình độ dài 4 vì {b,c},{c,f},{f,e} và {e,b} là các cạnh và đường đi này bắt đầu và kết thúc tại b.
Đường đi a,b,c,d,a,b độ dài 5 không là đường đi đơn vì nó chứa cạnh {a,b} hai lần. a b c d e f Hình 1: Đồ thị đơn.
Đường đi và chu trình trong đồ thị có hướng cũng đã được đưa vào từ Chương 5. Bây giờ
ta định nghĩa đường đi như thế cho đa đồ thị có hướng.
Định nghĩa 2. Đường đi độ dài n, với n nguyên dương, từ u tới v trong đa đồ
thị có hướng là dãy các cạnh e1,e2,...,en của đồ thị sao cho f(e1) = {x0,x1},f(e2) = {x1,x2},...,f(en) =
{xn−1,xn}, với x0 = u và xn = v. Khi không có cạnh bội trong đồ thị ta kí hiệu đường đi này bằng
dãy các đỉnh x0,x1,...,xn. Đường đi bắt đầu và kết thúc tại cùng một đỉnh được gọi là một chu
trình. Đường đi hay chu trình gọi là đơn nếu nó không chứa cùng một cạnh quá một lần.
Khi không cần phân biệt các cạnh bội ta sẽ ký hiệu đương đi e1,e2,...,en trong đó f(ei = {xi−1,xi})
với i = 1,2,...,n bằng dây các đỉnh x0,x1,...,xn. Ký hiệu này xác định đường đi chỉ theo các đỉnh mà
nó đi qua. Có thể có nhiều đường đi qua dãy các đỉnh này.
3 Tính Liên Thông Trong Đồ Thị Vô Hướng
Định nghĩa 3. Một đồ thị vô hướng được gọi là liên thông nếu có đường đi giữa mọi cặp đỉnh
phân biệt của đồ thị.
Ví dụ 2. Đồ thị G trên Hình 2 là liên thông vì giữa mọi cặp đỉnh phân biệt đều có đường đi.
Tuy vậy, đồ thị H trên Hình 2 là không liên thông. Chẳng hạn, giữa các đỉnh a và d không có đường đi trong H. a b c f d c e g e a b d f G H
Hình 2: Đồ thị G và H.
Định lý 1. Giữa mọi cặp đỉnh phân biệt của một đồ thị vô hướng liên thông luôn có đường đi đơn.
Chứng minh: Giả sử u và v là hai đỉnh phân biệt của một đồ thị vô hướng liên thông G =
(V,E). Vì G là liên thông nên có ít nhất một đường đi giữa u và v. Gọi x0,x1,...,xn với x0 = u và xn =
v, là dãy các đỉnh của đường đi có độ dài ngắn nhất. Đây chính là đường đi đơn cần tìm. Thật
vậy, giả sử nó không là đường đi đơn, khi đó, xi = xj với 0 ≤ i < j. Điều này có nghĩa là giữa các
đỉnh u và v có đường đi ngắn hơn qua các đỉnh x0,x1,...,xi−j,xj,...,xn nhận được bằng cách xóa đi
các cạnh tương ứng với dãy các đỉnh xi,...,xj−1.
Một đồ thị liên thông là hợp của hai hay nhiều đồ thị con liên thông, mỗi cặp các đồ thị con
này không có đỉnh chung. Các đồ thị con liên thông rời nhau như vậy được gọi là các thành
phần liên thông của đồ thị đang xét.
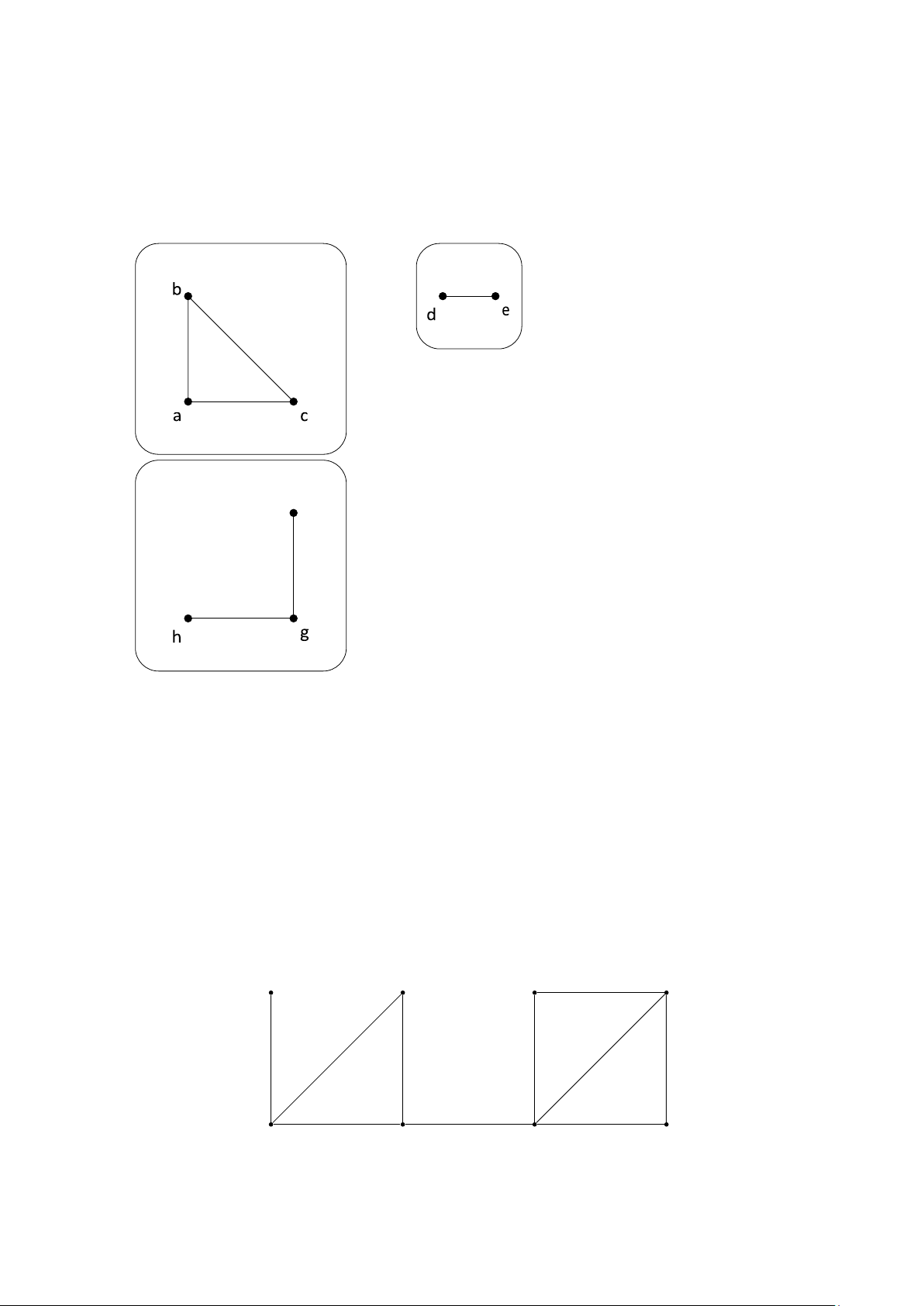
Ví dụ 3. Đồ thị G là hợp của ba đồ thị con liên thông rời nhau G1, G2 và G3 như chỉ ra trên
Hình 3. Ba đồ thị con này là 3 thành phần liên thông của G. G2 f G1 G3
Hình 3: Đồ thị G và các thành phần liên thông G1, G2 và G3 của nó.
Đỉnh cắt (hay điểm khớp) là đỉnh mà nếu xóa đỉnh này và các cạnh liên thuộc với nó khỏi đồ
thị thì số thành phần liên thông của đồ thị sẽ tăng thêm. Việc xóa đỉnh cắt khỏi một đồ thị liên
thông sẽ tạo ra một đồ thị con không liên thông.
Cạnh cắt (hay cạnh cầu) là cạnh mà khi ta bỏ nó đi sẽ tạo ra một đồ thị có nhiều thành phần
liên thông hơn so với đồ thị xuất phát.
Ví dụ 4. Tìm các đỉnh cắt và cạnh cắt của đồ thị G trên Hình 4. a d f g b c e h
Hình 4: Đồ thị G.
Giải: Đỉnh cắt của G là b,c và e. Xóa một trong các đỉnh này (và các cạnh nối với nó) sẽ làm
mất tính liên thông của đồ thị. Các cạnh cắt (cầu) là {a,b} và {c,e} . Xóa một trong các cầu này
sẽ làm đồ thị mất tính liên thông.
4 Tính liên thông trong đồ thị có hướng
Có hai khái niệm về tính liên thông của đồ thị có hướng tùy theo chúng ta có quan tâm tới
hướng của các cạnh hay không.
Định nghĩa 4. Đồ thị có hướng gọi là liên thông mạnh nếu có đường đi từ a tới b và từ b tới
a với mọi đỉnh a và b của đồ thi.
Trong đồ thị có hướng liên thông mạnh luôn tốn tại dãy các cạnh có hướng từ một đỉnh bất
kỳ tới một đỉnh bất kỳ khác của đồ thị. Đồ thị có hướng có thể không là liên thông mạnh nhưng
vẫn còn liên thông theo một nghĩa nào đó. Để chính xác điều này ta có định nghĩa sau
Định nghĩa 5. Đồ thị có hướng gọi là liên thông yếu nếu có đường đi giữa hai đỉnh bất kỳ
của đồ thị vô hướng nền.
Do vậy đồ thị có hướng là liên thông yếu nếu và chỉ nếu luôn tồn tại đường đi giữa hai đỉnh
khi ta không quan tâm tới hướng của các cạnh. Rõ ràng mọi đồ thị có hướng liên thông mạnh
cũng là đồ thị liên thông yếu.
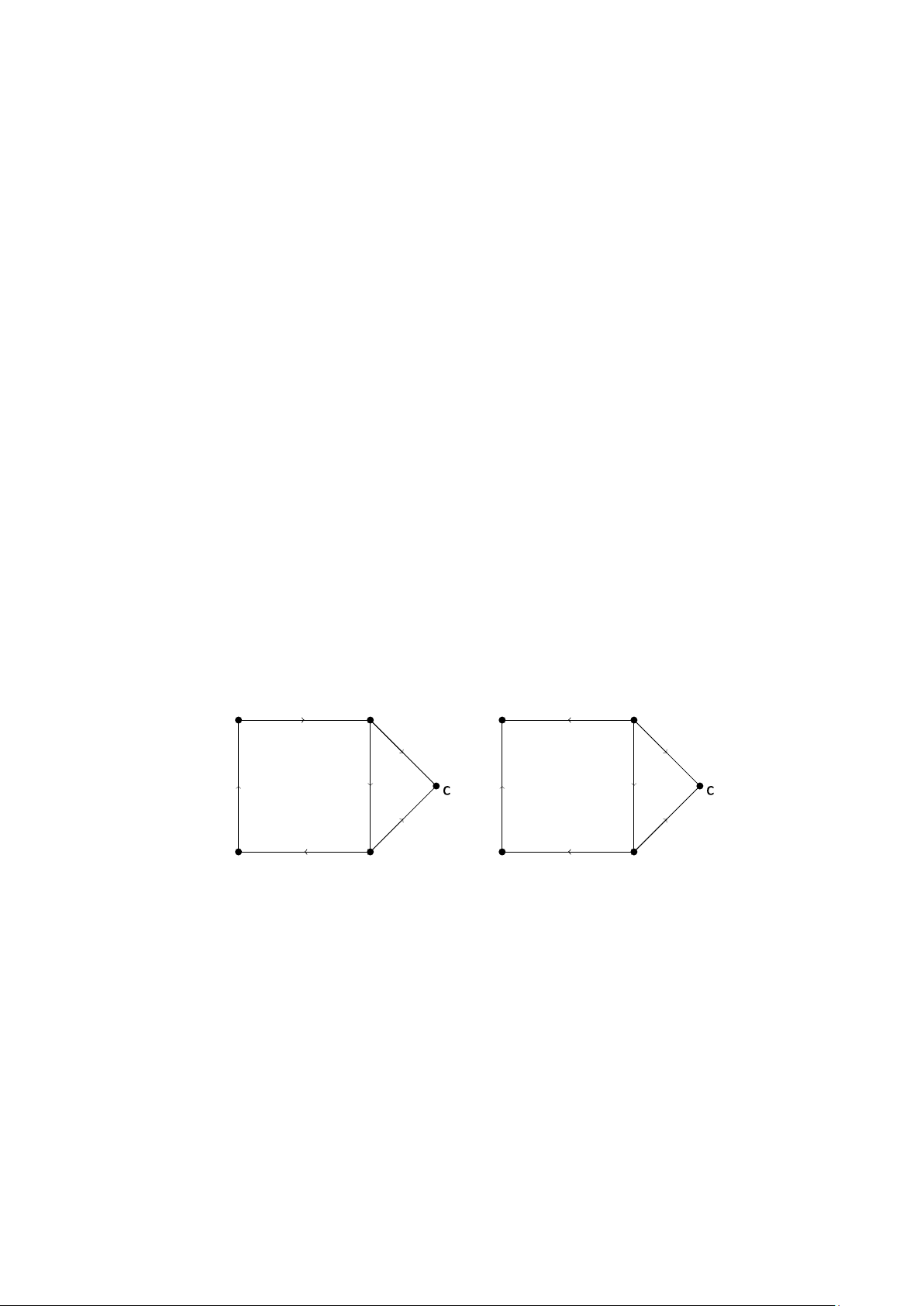
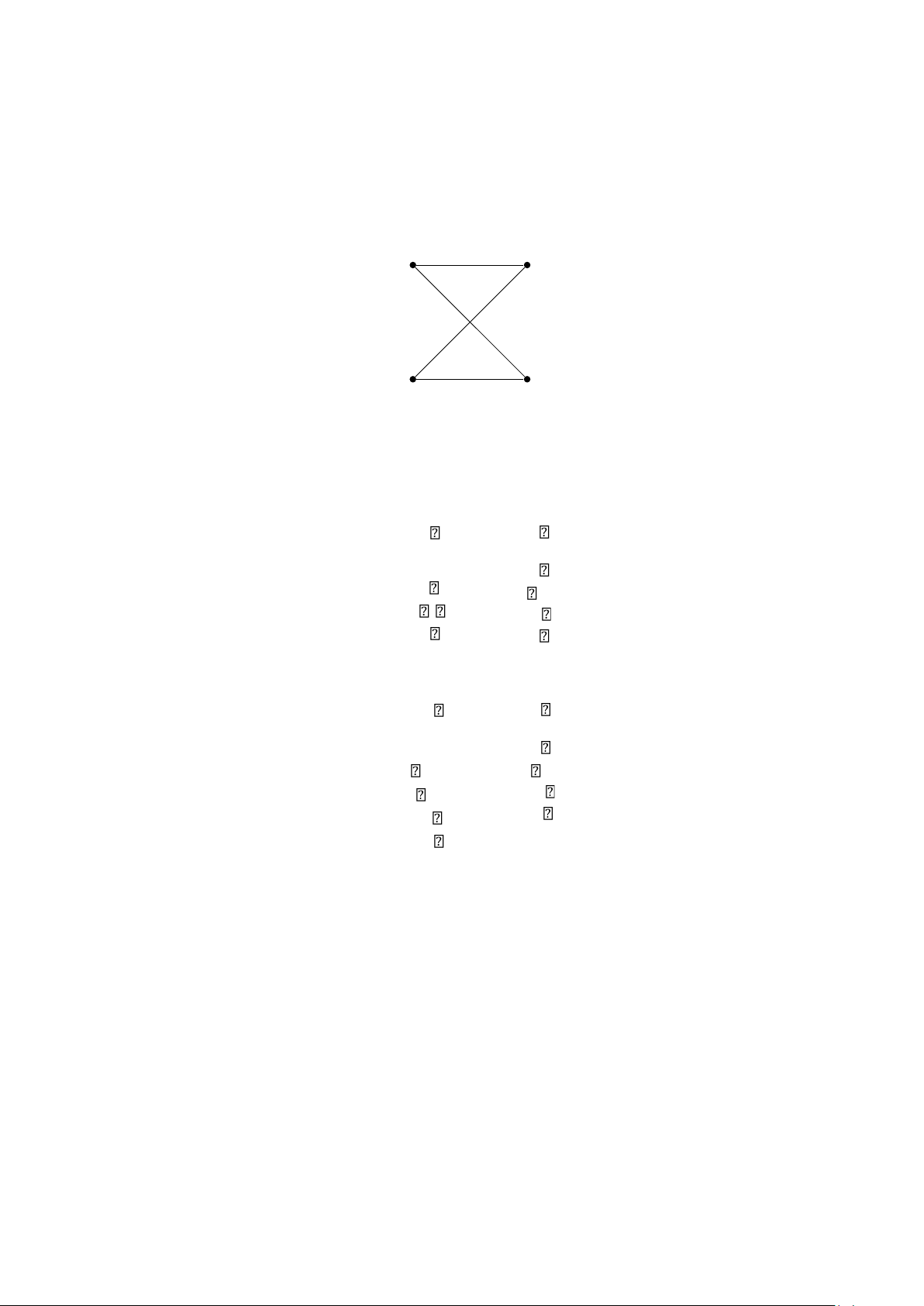
Ví dụ 5. Các đồ thị có hướng trên Hình 5 có là liên thông mạnh không? Có là liên thông yếu không? a b a b e d e d G H
Hình 5: Các đồ thị có hướng G và H.
Giải. G là liên thông mạnh vì có đường đi giữa hai đỉnh bất kỳ của đồ thị có hướng này. Vì
vậy G cũng là liên thông yếu. Còn H không là liên thông mạnh. Không có đường đi có hướng từ
a tới b trong đồ thị này. Tuy vậy H là liên thông yếu vì có đường đi bất kỳ giữa hai đỉnh của đồ
thị vô hướng nền của H.
5 Đường đi và sự đẳng cấu
Có một số cách dùng đường đi và chu trình để xác định xem hai đồ thị có đẳng cấu hay không.
Chẳng hạn sự tồn tại chu trình đơn với độ dài đặc biệt là một bất biến rất có ích để chỉ ra hai
đồ thị là không đẳng cấu. Thêm vào đó, đường đi có thể dùng để xây dựng các ánh xạ có khả
năng là các phép đẳng cấu.
Như vậy, một bất biến đẳng cấu rất có ích đối với các đơn đồ thị là sự tồn tại chu trình đơn
với độ dài k lớn hơn 2. Ví dụ 6 minh họa cách dùng bất biến này để chứng tỏ hai đồ thị là không đẳng cấu.
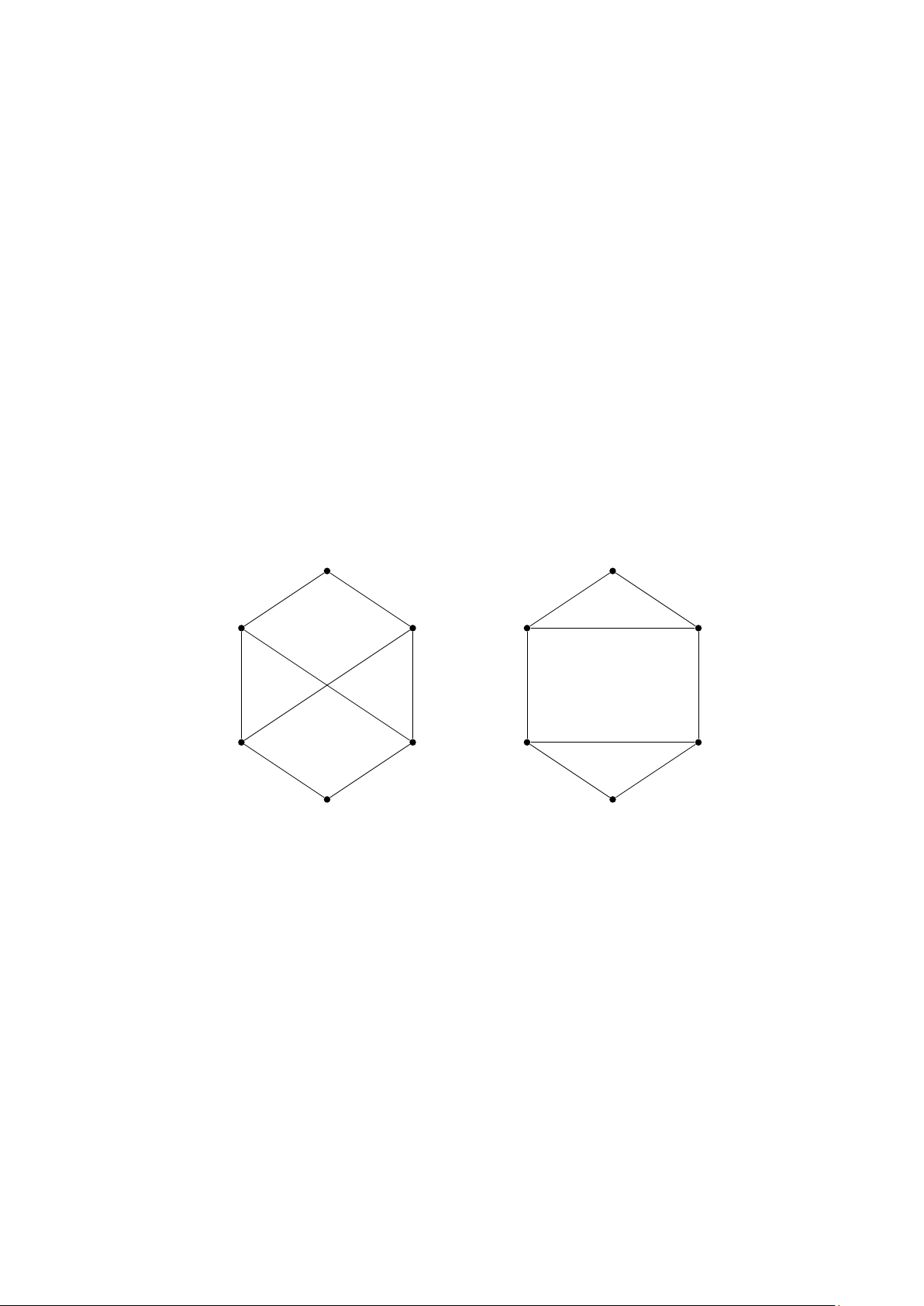
Ví dụ 6. Xác định xem hai đô thị trên Hình 6 có là đẳng cấu với nhau không?
Giải: Cả hai đồ thị G và H đều có 6 đỉnh và 8 cạnh. Mỗi đồ thị có bốn đỉnh bậc 3, hai đỉnh
bậc 2. Vì thế ba bất biến - số đỉnh, số cạnh, bậc của các đỉnh, của hai đồ thị là như u 1 v 1 u 6 u 2 v 6 v 2 u 5 u 3 v 5 v 3 u 4 v 4 G H
Hình 6: Các đồ thị G và H.
nhau. Tuy nhiên H có chu trình đơn độ dài 3, cụ thể v1,v2,v6,v1 trong đó G không có chu trình
đơn độ dài 3 (ta có thể kiểm tra trực tiếp điều khẳng định này và dễ thấy tất các chu trình
đơn của G đều có độ dài 4). Vì sự tồn tại chu trình đơn độ dài 3 là một bất biến đối với phép
đẳng cấu nên các đồ thị G và H là không đẳng cấu.
Chúng ta đã chỉ ra cách dùng sự tồn tại của một loại đường đi, cụ thể là chu trình đơn độ
dài đặc biệt, để chứng minh hai đồ thị là không đẳng cấu. Chúng ta cũng có thể dùng đường đi
để tìm các ánh xạ có khả năng là các đẳng cấu.
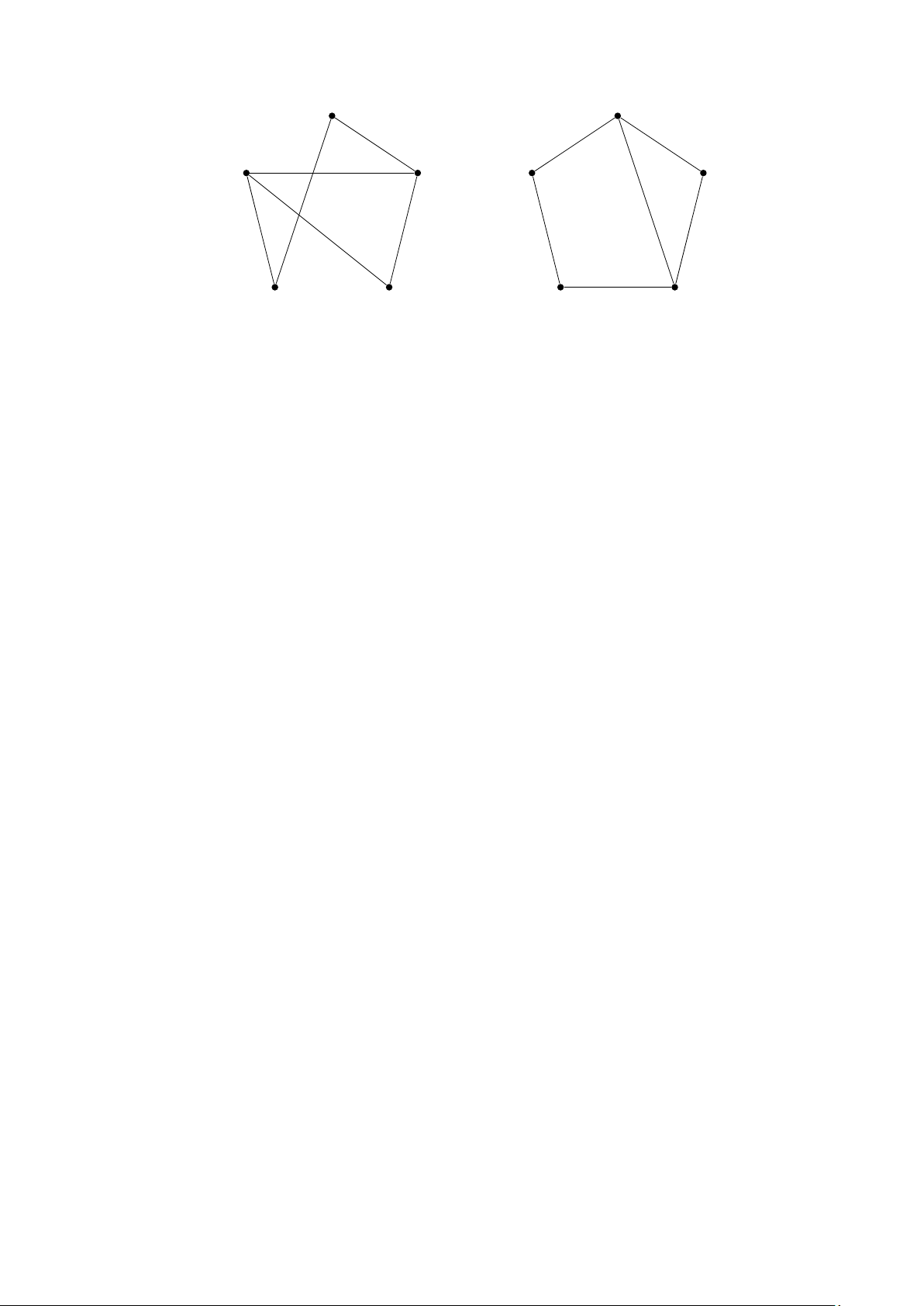
Ví dụ 7. Xác định xem hai đô thị G và H trên Hình 7 có là đẳng cấu với nhau không? u2 v1 u 1 u 3 v 5 v 2 u 5 u 4 v 4 v 3 G H
Hình 7: Các đồ thị G và H.
Giải: Cả hai đồ thị G và H đều có 5 đỉnh và 6 cạnh, cả hai đều có hai đỉnh bậc 3 và ba đỉnh
bậc 2, cả hai đều có một chu trình đơn độ dài 3, một chu trình đơn độ dài 4 và chu trình đơn
độ dài 5. Vì tất cả các bất biến đều phù hợp nên G và H có thể là đẳng cấu. Để tìm phép đẳng
cấu, ta đi theo hướng đi qua tất cả các đỉnh sao cho các đỉnh tương ứng trong hai đồ thị có cùng bậc .
Ví dụ, các đường đi u1, u4, u3, u2, u5 trong G và v3, v2, v1, v5, v4 trong H. Cả hai đều đi qua
mọi đỉnh của đồ thị xuất phát từ đỉnh bậc 3, đi qua các đỉnh bậc 2, 3, 2 và kết thúc ở đỉnh bậc
2 .Theo các đường này, trên đồ thị ta có ánh xạ f sao cho f(u1) = v3, f(u4) = v2, f(u3) = v1, f(u2)
= v5 và f(u5) = v4. Ánh xạ này là một đẳng cấu và như vậy G và H là hai đồ thị đẳng cấu hoặc
bằng cách chỉ ra f bảo tồn các cạnh hoặc chỉ ra với một cách sắp xếp các đỉnh thích hợp hai ma
trận liên kế của các đồ thị G và H là như nhau.
6 Đếm đường đi giữa các đỉnh
Số đường đi giữa hai đỉnh của đồ thị có thể xác định được khi sử dụng ma trận liền kề.
Định lý 2. Cho G là một đồ thị với ma trận liền kề A theo thứ tự các đỉnh v1,v2,...,vn (với các
cạnh vô hướng hoặc có hướng hay là cạnh bội, có thể có khuyên). Số các đường đi khác nhau
độ dài r từ vi tới vj trong đó r là một số nguyên dương, bằng giá trị của phần tử (i,j) của ma trận Ar
Chứng minh. Ta sử dụng quy nạp toán học để chứng minh định lý này. Gọi G là đồ thị với
ma trận liền kề A (giả sử sắp xếp các đỉnh theo thứ tự v1,v2,...,vn ). Giả sử số các đường đi có độ
dài 1 đến vj là phần tử (i,j) của A, vì phần tử này là số cạnh từ vi tới vj.
Giả sử phần tử ( i,j ) của ma trận Ar là số các đường đi khác nhau độ dài r từ vi tới vj. Đây là
giả thiết quy nạp. Vì Ar+1 = ArA, nên phần tử ( i,j ) của Ar+1 bằng bi1a1j + bi2a2j + ... + binanj trong
đó bik là phần tử (i,k) của Ar. Theo giả thiết quy nạp bik là số đường đi độ dài r từ vi tới vk.
Đường đi độ dài r + 1 từ vi tới vj sẽ được tạo nên từ đường đi độ dài r từ vi tới đỉnh trung
gian vk nào đó và một cạnh từ vk tới vj. Theo quy tắc nhân số các đường đi như thế là tích của
số đường đi độ dài r từ vi tới vk, tức là bik, và số các cạnh từ vk tới vj tức là akj. Khi cộng các tích
này lại theo tất cả các đỉnh trung gian vk có thể ta sẽ nhận được kết quả mong muốn.
Ví dụ 8. Bao nhiêu đường đi độ dài 4 từ a tới d trong đồ thị đơn G trên Hình 8? a b d c
Hình 8: Đồ thị G.
Giải: Ma trận liền kề của đồ thị G theo thứ tự a, b, c, d là 1 1 0 0 0 0 1 1 0 0 1 A = 1 1 1 0 0
Vì thế số đường đi độ dài 4 từ a tới d là giá trị của phần tử (i, j) của A4. Vì 0 0 8 8 8 8 0 8 8 4 0 0 0 0 A = 0 8 8
nên có đúng 8 đường đi độ dài 4 từ a tới d. Kiểm tra trực tiếp trên đồ thị ta được 8 đường đi
độ dài 4 từ a tới d là : a,b,a,b,d; a, b,a,c,d;a,b,d,b,d;a,b,d,c,d;a,c,a,b,d;a,c,a,c,d; a,c,d,b,d; và a,c,d,c,d.
Định lý 2 có thể dùng để tìm độ dài của đường đi ngắn nhất giữa hai đỉnh của đồ thị, và
cũng có thể dùng để xác định xem đồ thị có liên thông hay không. Bài tập
Bài 1. Mỗi danh sách các đỉnh sau đây có tạo nên đường đi trong đồ thị đã cho không? Đường
đi nào là đơn? Đường đi nào là chu trình? Độ dài của các đường đi này là bao nhiêu? a b c d e
a) a, e, b, c, b.
b) e, b, a, d, b, e.
c) a, e, a, d, b, c, a.
d) c, b, d, a, e, c.
Bài 2. Mỗi danh sách các đỉnh sau đây có tạo nên đường đi trong đồ thị đã cho không? Đường
đi nào là đơn? Đường đi nào là chu trình? Độ dài của các đường đi này là bao nhiêu? a b c d e
a) a, b, e, c, b
b) a, d, b, e, a
c) a, d, a, d, a
d) a, b, e, c, b, d, a.
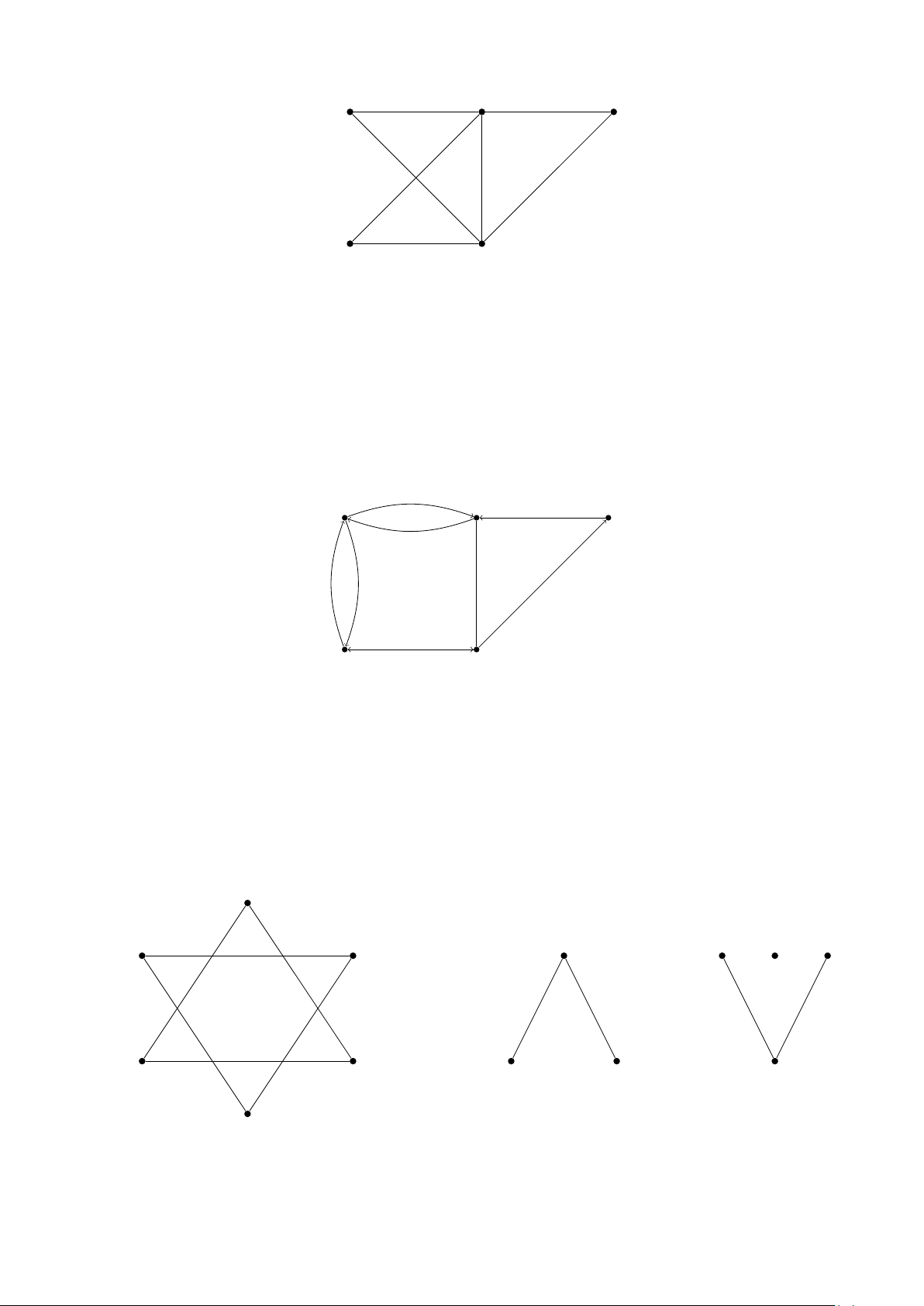
Bài 3. Trong các hình sau hãy xác định xem đồ thị nào có tính liên thông. Mỗi đồ thị có bao
nhiêu thành phần liên thông? Hãy tìm các thành phần liên thông đó.
Bài 4. Hãy tìm số đường đi giữa hai đỉnh c và d trong đồ thị trên Hình 1 có độ dài: a b c d e f a) 2 b) 3 c) 4 d) 5
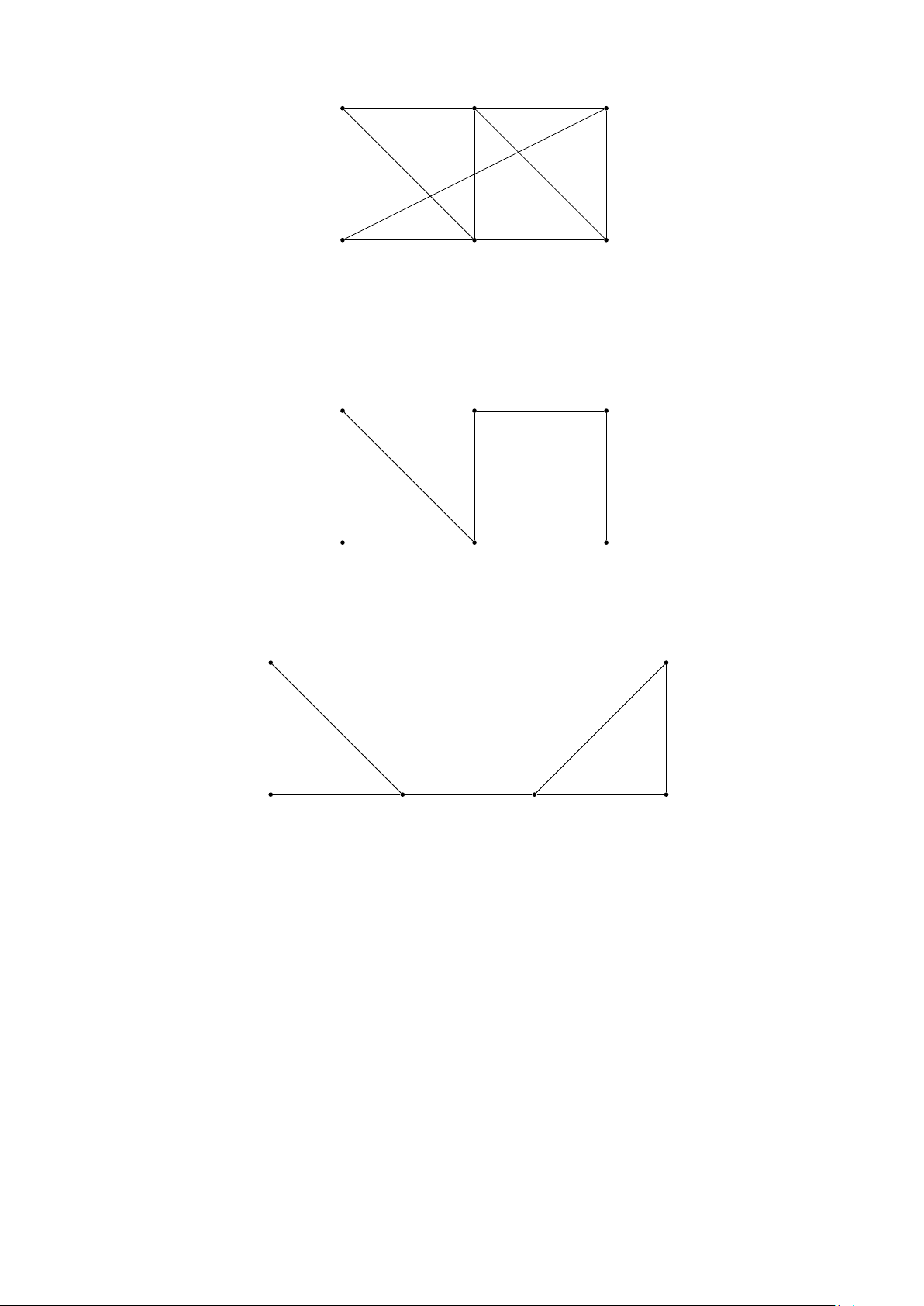
Bài 5. Hãy tìm tất cả các đỉnh cắt, cạnh cắt của đồ thị a) a d e b c f b) a f b c d e


