Báo cáo tiểu luận Ứng dụng của cây môn Lý thuyết đồ thị | Đại học Đồng Tháp

TRƯỜNG: ĐẠI HỌC ĐỒNG THÁP
KHOA: SƯ PHẠM TOÁN – TIN
- - -    - - -
BÁO CÁO TIỂU LUẬN
HỌC PHẦN LÍ THUYẾT ĐỒ THỊ
ỨNG DỤNG CỦA CÂY
Nhóm 5 Lương Thị Kim Thảo
Trần Thị Bịch Hạnh Nguyễn Thị Mỹ An
Nguyễn Phùng Linh Đan Đào Minh Điền Hồ Văn Thảo
Giáo viên hướng dẫn:
Ngô Tấn Phúc 1. Cây
Định nghĩa 1. Cây là một đồ thị vô hướng, liên thông và không có chu trình đơn.
Vì cây không thể có chu trình đơn, nên cây không thể có cạnh bội và khuyên.
Vậy mọi cây đều là đồ thị đơn.
Định nghĩa 2. Cây m- phân là cây có gốc mà tất cả đỉnh trong của nó không có hơn m
con. Cây được gọi là m-phân đầy đủ nếu mọi đỉnh trong có đúng m con. Cây 2 - phân
được gọi là cây nhị phân.
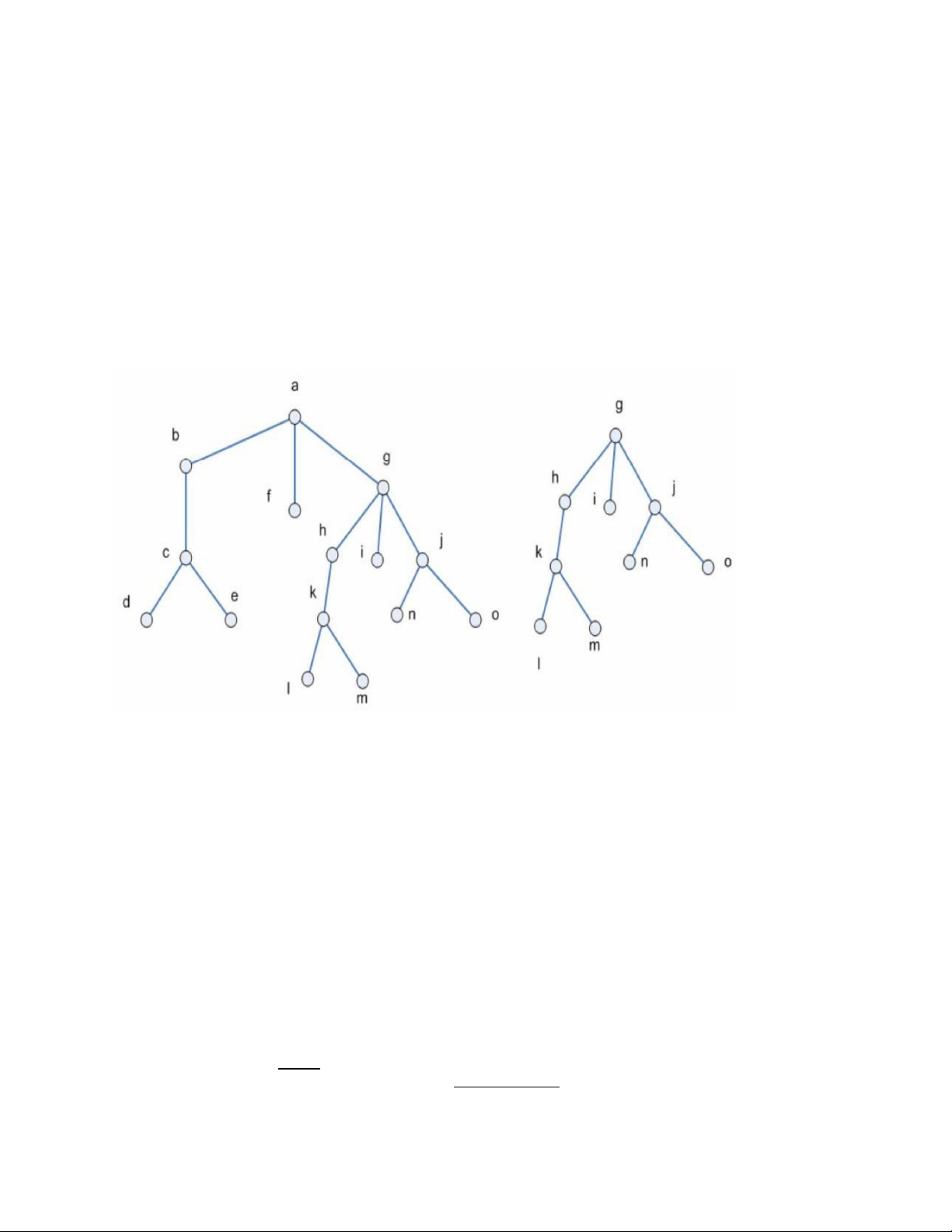
Ví dụ 1. Trong cây như hình, hãy tìm cha của c, con của g, các tổ tiên của e, con cháu của
b, tất cả các đỉnh trong và lá. Đâu là cây con với gốc tại g.
Giải - Cha của c là b. - Con của g là h, i, j.
- Các tổ tiên của e là c,b,a.
- Các con cháu của b là c, d, e - Các đỉnh trong: a, b, c, g, h, k, j.
- Các lá: d, e, f, l, m, n, o,i. - Cây con gốc g.
Định lý 1. Cây với n đỉnh có đúng n −1 cạnh. Cây m- phân với độ cao h được gọi là cân
đối nếu các đỉnh đều ở mức h hoặc h −1.
Định lý 2. Cây m - phân đầy đủ với i đỉnh trong sẽ có tất cả n = mi. +1 đỉnh.
Định lí 3. Cây m - phân đầy đủ với ;
(i) n đỉnh có i = n −1 đỉnh trong và l =
(m −1)n +1 lá; m m
(ii) i đỉnh trong có n = +mi 1 đỉnh và l = (m −1)i +1 lá; (iii) có n = ml −1 đỉnh và i = l
−1 đỉnh trong. m −1 m −1
Hệ quả 1. Nếu cây m - phân cao h có l lá, khi đó h logm l . Nếu cây m - phân đầy đủ và
cân đối, khi đó h = logm l
2. Cây nhị phân tìm kiếm
Cây nhị phân tìm kiếm là một cây nhị phân trong đó mỗi con của một đỉnh gọi là con
trái và phải, không có đỉnh nào có nhiều hơn một con trái và một con phải.
- Bắt đầu là cây có đúng một đỉnh gọi là gốc.
- Mỗi đỉnh được gán bằng một khóa (mỗi giá trị của khóa xác định chỉ một phần tử).
- Bắt đầu từ gốc đi sang trái nếu các phần tử lớn hơn khóa của đỉnh và tương tự nếu
phần tử nhỏ hơn khóa của đỉnh.
Chiều cao của cây bằng h = log (
2 n +1) , với n đỉnh.
Cây tìm kiếm nhị phân dùng để định vị các phần tử dưa trên một loạt các phép so sánh.
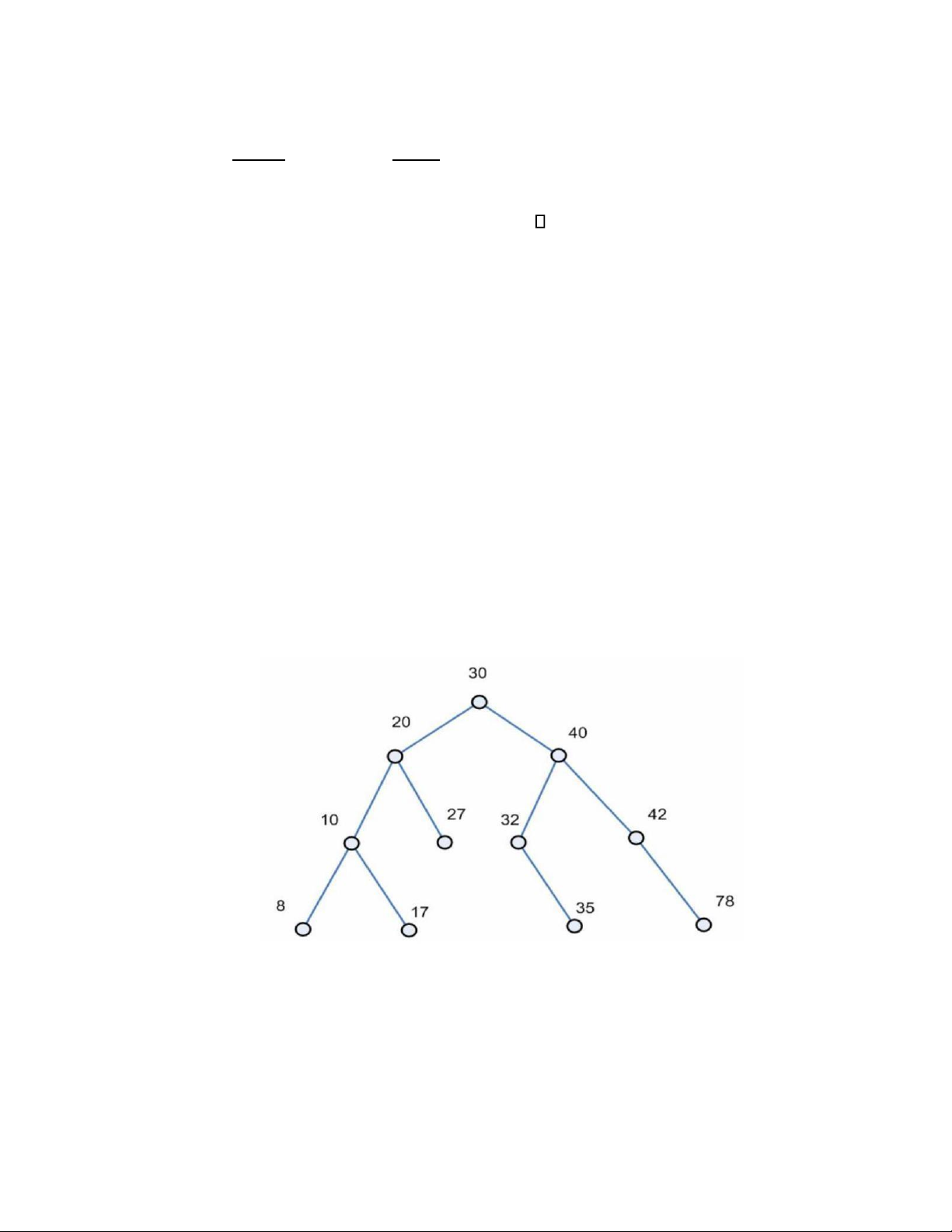
Ví dụ 2. Hãy tạo cây tìm kiếm nhị phân cho các từ sau : 30,20,10,40,32,27,17,8, 42,78,35. Giải
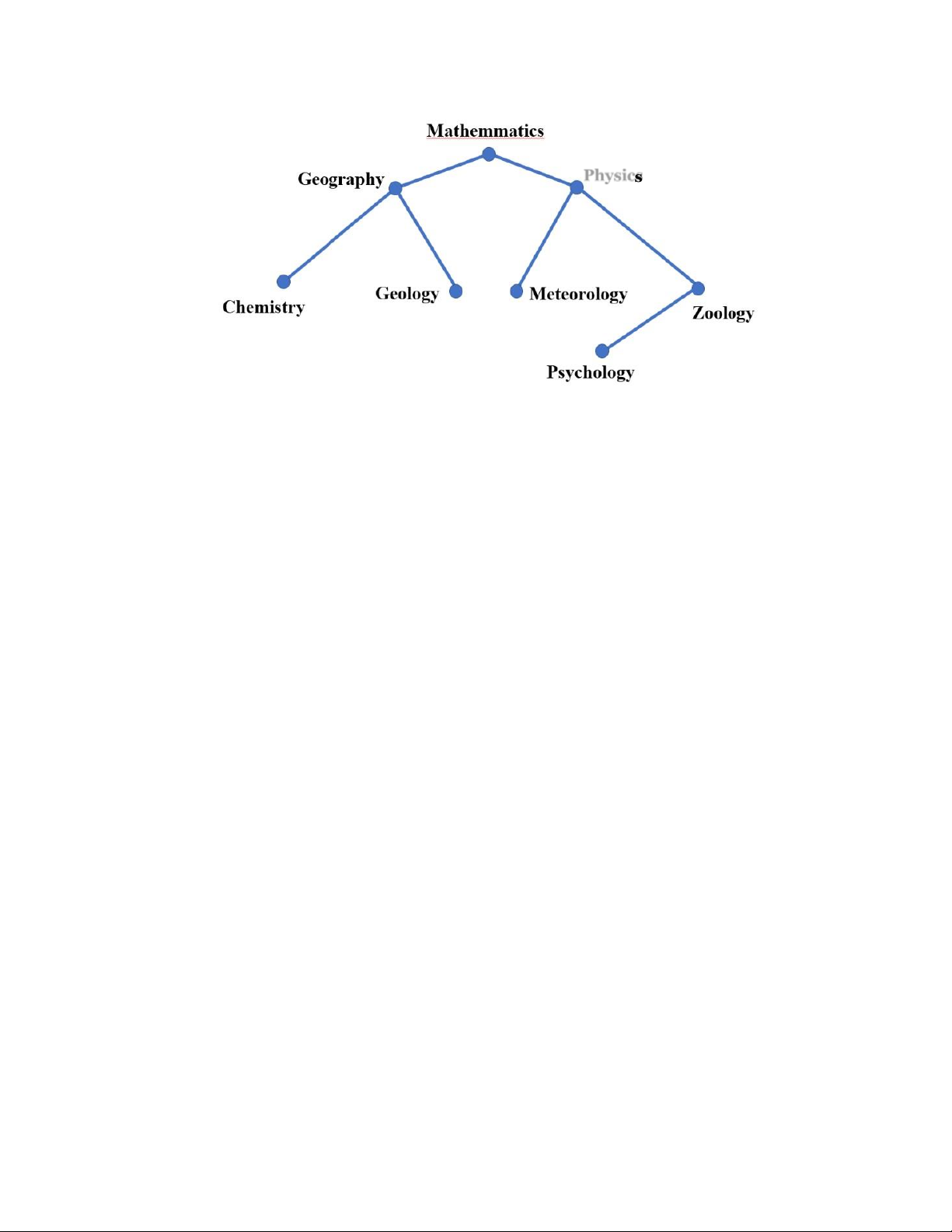
Ví dụ 3. Hãy tạo cây tìm kiếm nhị phân cho các từ sau : mathematics, physics, geography,
zoology, meteology, geology, psychology và chemistry (dùng thứ tự từ điển) Giải Physics
3. Cây quyết định
Các cây có gốc trong đó mỗi đỉnh trong ứng với một quyết định và mỗi cây con tại một
đỉnh ứng với một kết cục có thể tại đỉnh đó.
Lời giải của bài toán được gán là những đường đi đến các lá.
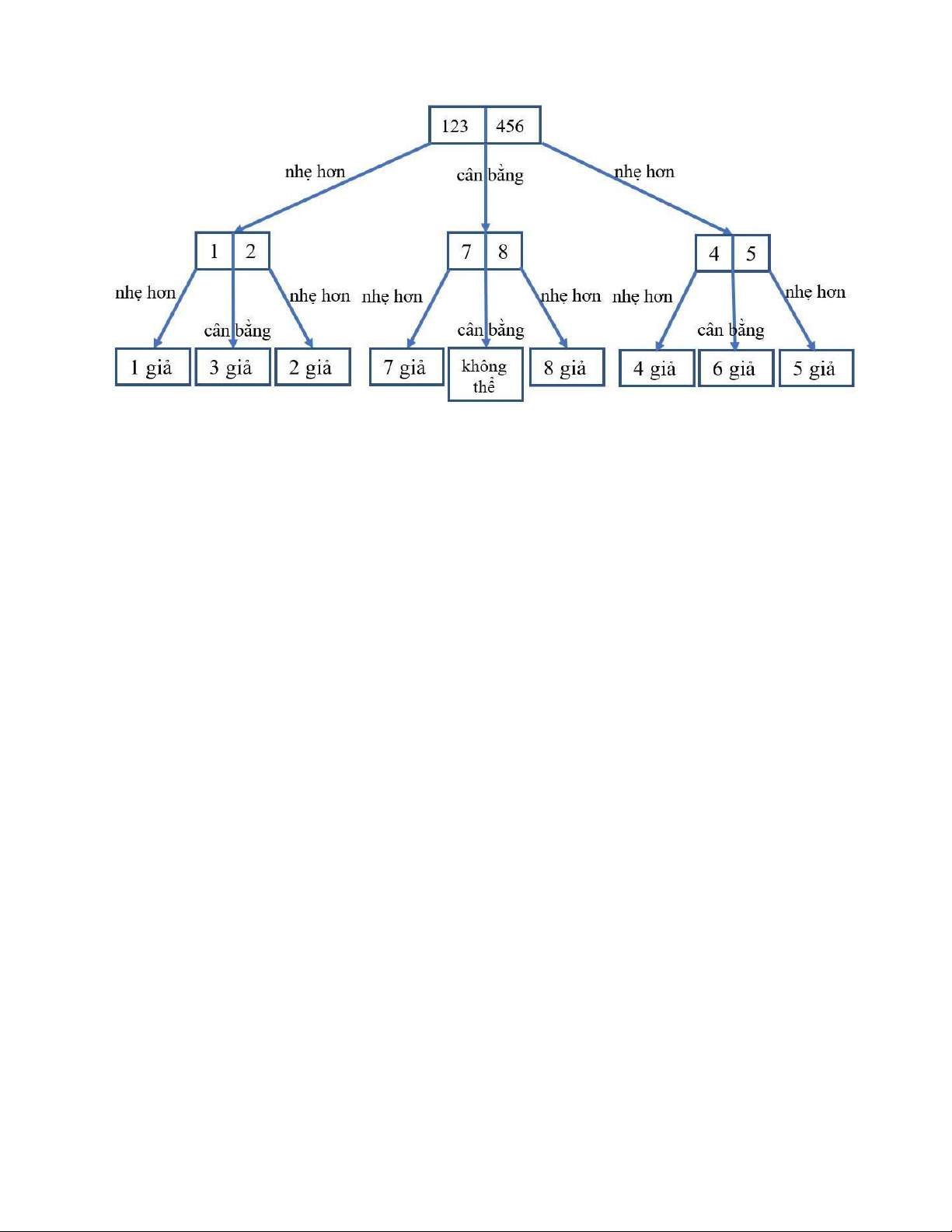
Chiều cao của cây bằng logm n , với m- phân n đỉnh Ví dụ 4. Giả sử rằng có 8 đồng xu,
có cùng trọng lượng và 1 đồng xu giả nhẹ hơn đồng khác. Hỏi cần bao nhiều lần sử dụng
một cân để xác định đồng xu nào trong 8 đồng xu là giả. Đưa ra một thuật toán tìm đồng xu giả ? Giải
Từ hệ quả 1 suy ra chiều cao của cây quyết định log 8 = 3
2 . Vì thế cần ít nhất 2 lần cân để
xác định đồng xu giả.
Gọi các đồng xu được đánh số lần lượt từ 1 đến 8. Khi đó, ta mô tả thuật toán như sau:
4. Các mã tiền tố
Sử dụng xâu bit với độ dài khác nhau để mã hóa các chữ cái.
- Chữ cái xuất hiện với tần suất nhiều sử dụng xâu bit ngắn.
- Chữ cái ít xuất hiện sử dụng xâu bit dài.
Để đảm bảo mỗi xâu bit chỉ tương ứng duy nhất một chữ cái thì các chữ cái được mã hóa
sao cho xâu bit mã hóa cho mỗi chữ cái không bao giờ xuất hiện như là một phần đầu của
xâu bit mã hóa cho chữ cái khác, mã có tính chất như vậy gọi là mã tiềm tố.
Cây nhị phân biểu diễn một mã tiền tố: - Lá gán là các kí tự
- Cạnh được gán nhãn 0 nếu là cạnh con trái, gán nhãn 1 nếu là cạnh con phải
- Xâu bit mã hóa chữ cái là một dãy các nhãn của các cạnh trong đường đi từ gốc tới
lá mà chữ cái đó là nhãn.
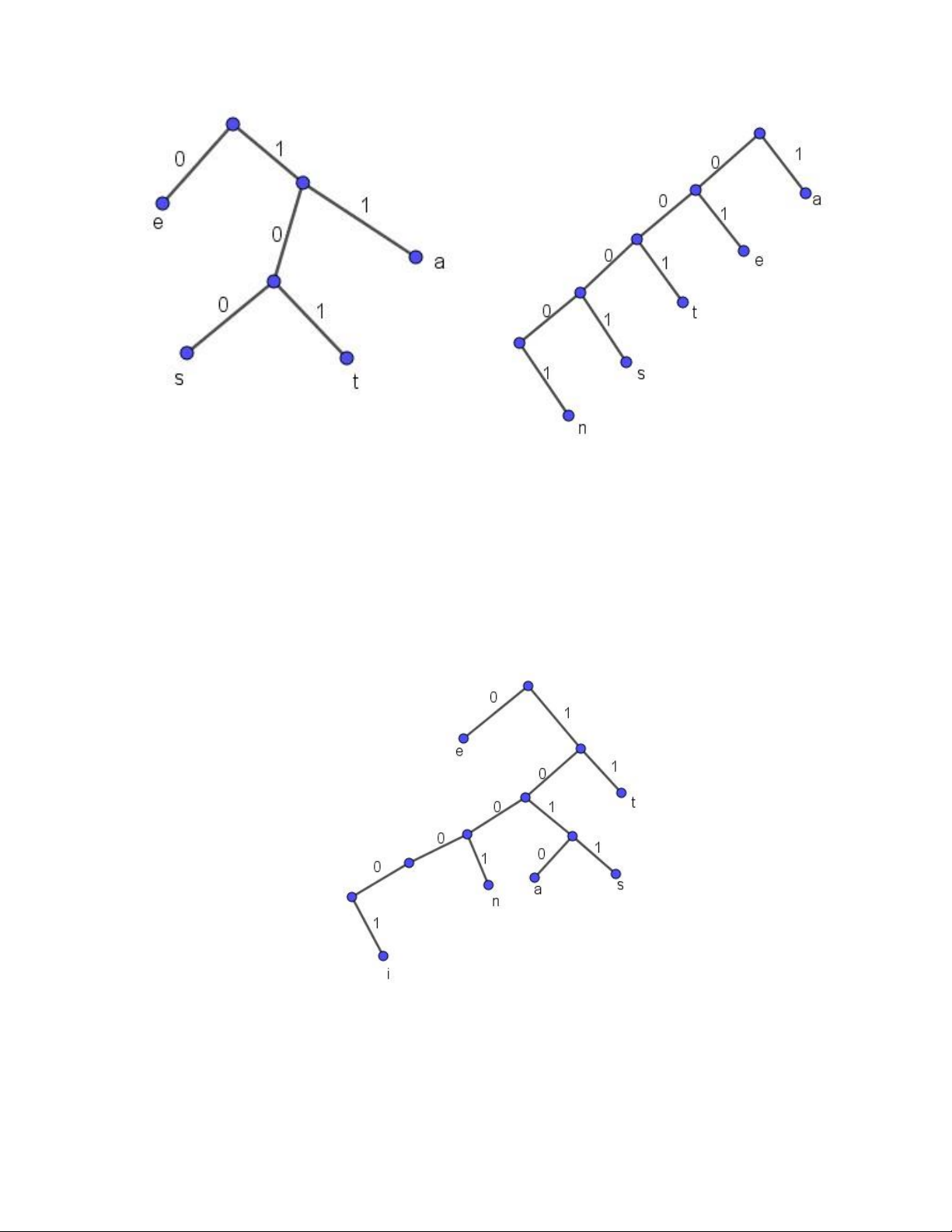
Ví dụ 5. Cho cây trong hình sau biểu diễn việc mã tiền tố cho các chữ cái a, e, n, s, t. Hãy
cho biết các xâu bit ứng với các chữ cái? Giải e là 0 a là 10 t là 110 n là 1110 s là 1111. BÀI TẬP
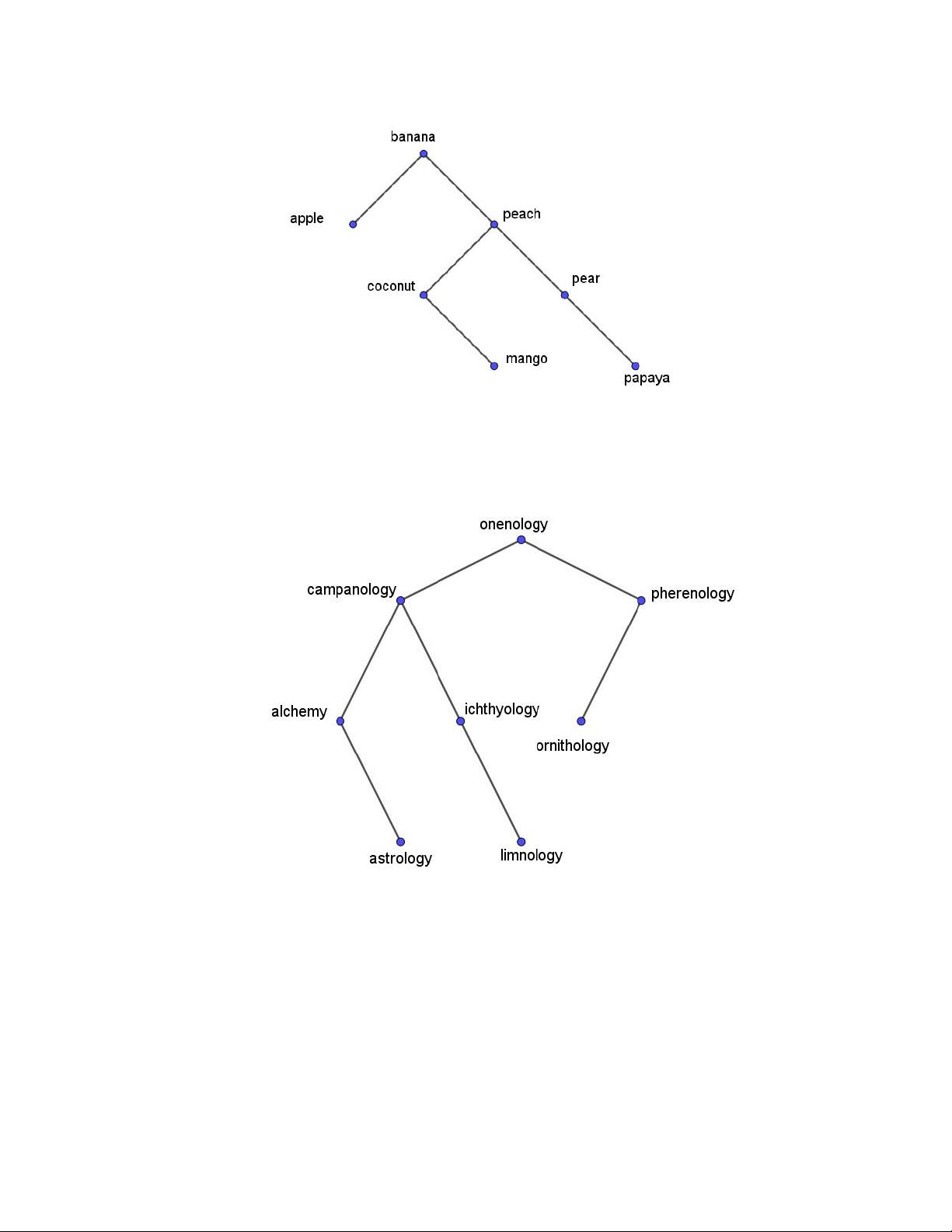
1. Hãy xây dựng cây tìm kiếm nhị phân cho các từ banana, peach, apple, pear, coconut,
mango và papaya theo thứ tự từ điển. Giải
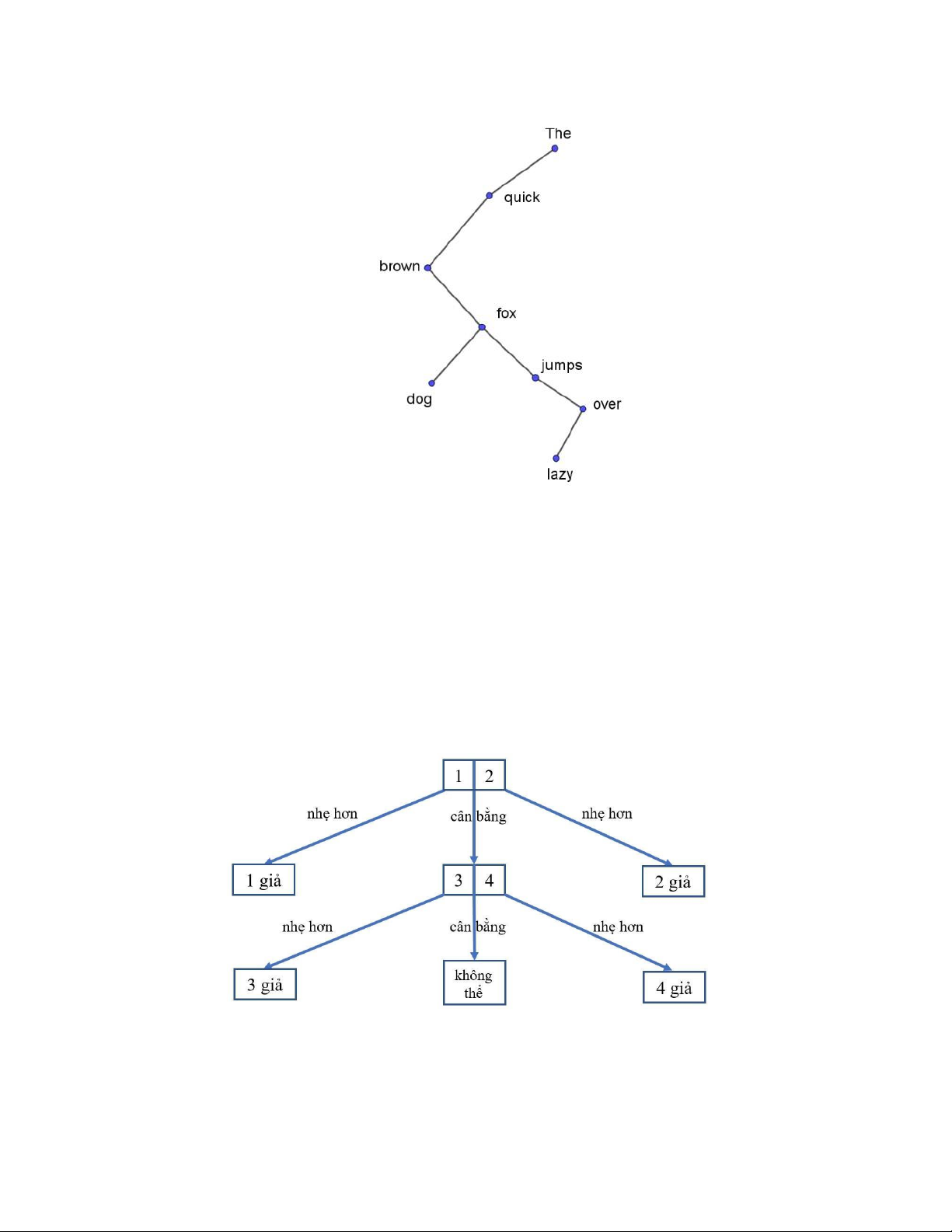
2. Hãy xây dựng cây tim kiếm nhị phân cho các từ oenology, phrenology, campanology,
ornithology, ichthyology, limnology, alchemy và astrology theo thứ tự từ điển. Giải
3. Dùng thứ tự từ điển, hãy xây dưng cây tìm kiếm nhị phân cho câu
"The quick brown fox jumps over the lazy dog” Giải
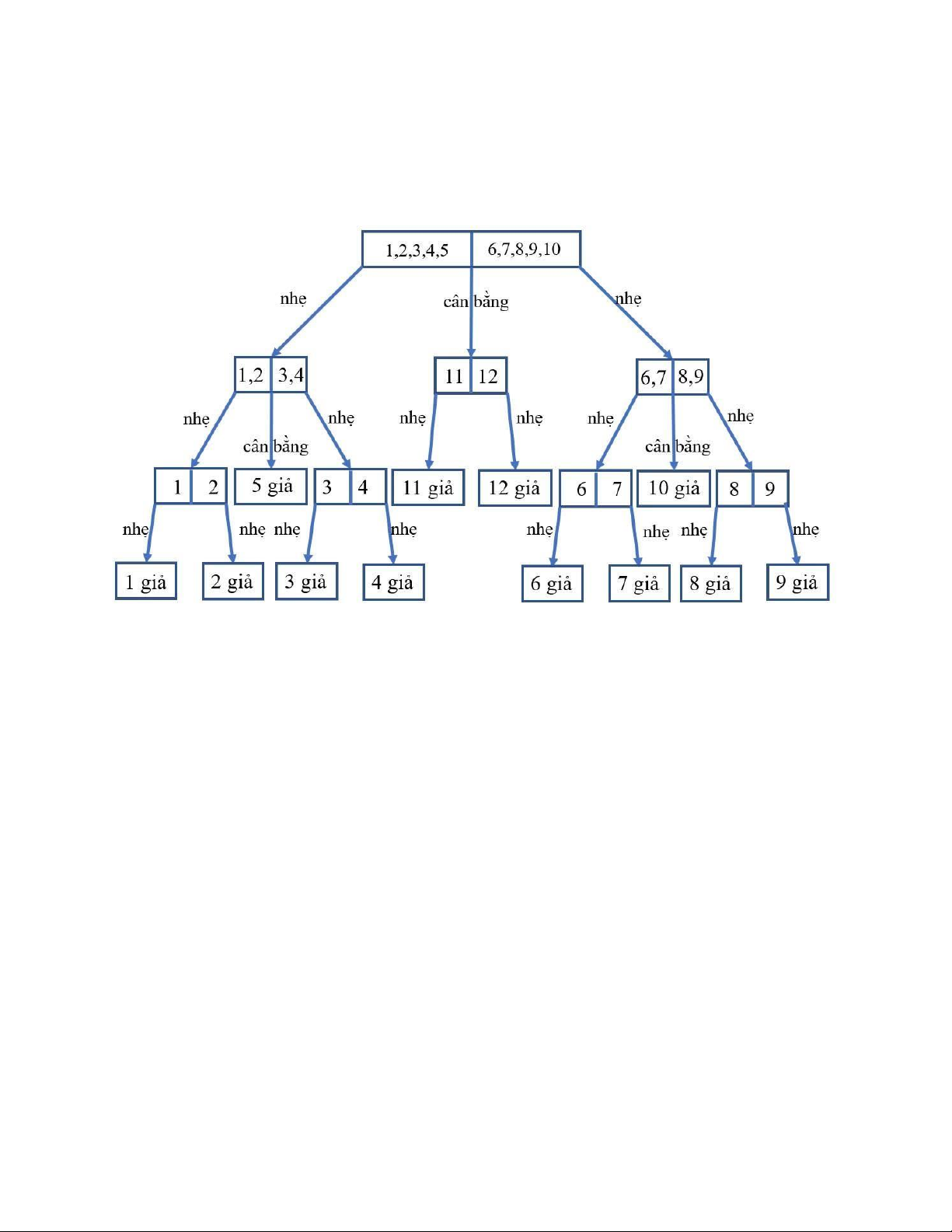
4. Cần phải cân bao nhiêu lần bằng một chiếc cân hai đĩa để tìm một đồng xu giả trong
bốn đồng xu? Biết rằng đồng xu giả có trọng lượng nhẹ hơn các đồng xu thật . Mô tả thuật
toán tìm đồng xu nhẹ với số lần cân tìm được? Giải
Từ hệ quả 1 suy ra được chiều cao của cây quyết định h = log 8 = 3
2. Vì thế cần ít nhất 2 lần cân.
Gọi các đồng xu được đánh số từ 1 đến 4. Khi đó, ta mô tả thuật toán như sau:
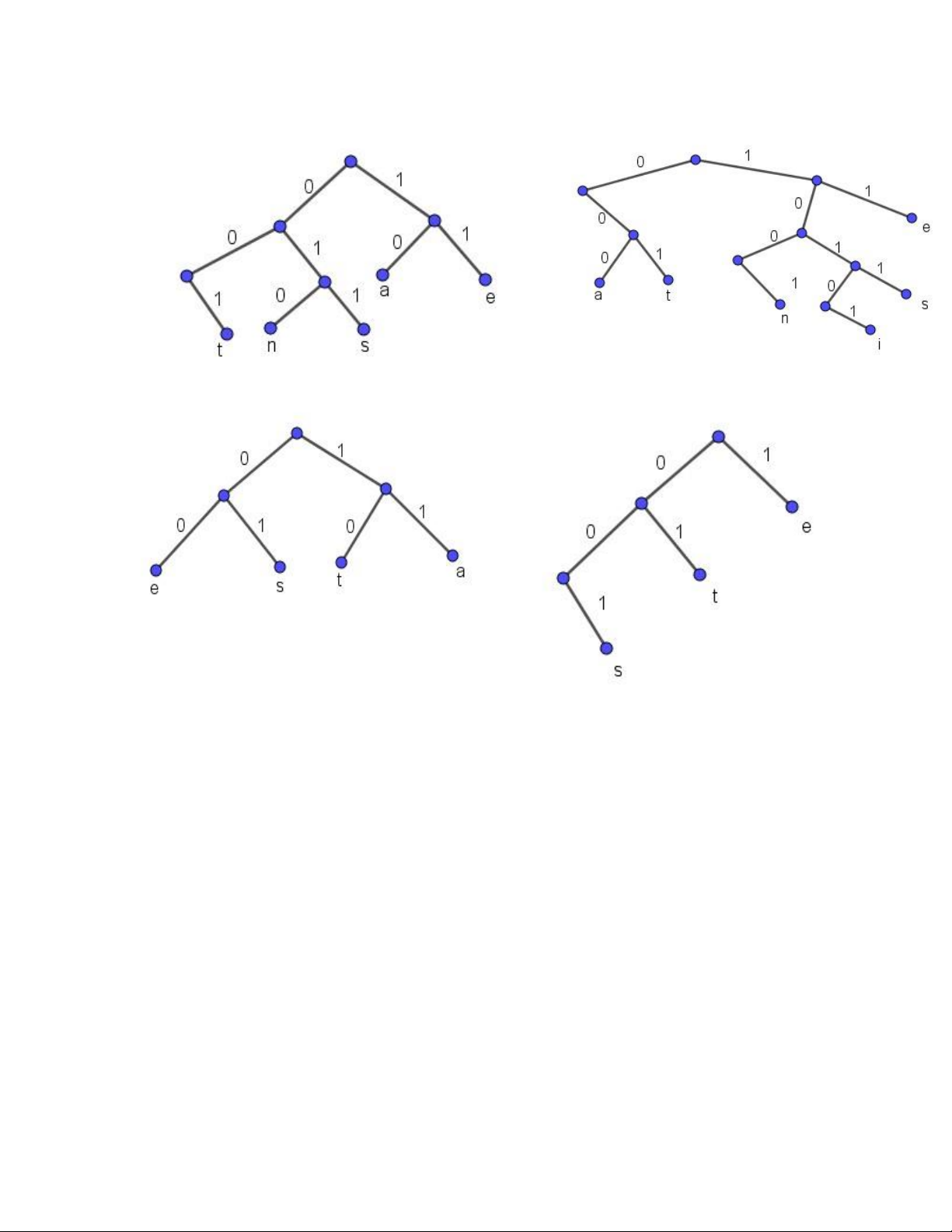
5*. Cần phải cân bao nhiêu lần cân bằng một chiếc cân hai đĩa để tìm đồng xu giả trong
mười hai đồng xu ? Biết rằng đồng xu giả có trọng lượng nhẹ hơn các đồng xu thật. Mô tả
thuật toán tìm đồng xu giả với số lần cân tìm được. Giải
Theo hệ quả 1: ta suy ra được chiều cao của cây quyết định log 12 = 3
3 . Vì thế cần ít nhất 3 lần cân.
Gọi các đồng xu được đánh số từ 1 đến 12
6. Xác định cái nào là mã tiền tố trong các sơ đồ mã sau đây :
a) a :11, :00, :10, e t s :01;
b) a :0, :1, :01, e t s :001;
c) a :101, :11, :001, :011, e t s n :010;
d) a :010, :11, :011, :1011, :1001, e t s n i :10101. Giải a) b) c) d)
7. Dựng cây nhị phân với mã tiền tố biểu diễn các lược đồ mã hoá sau :
a) a : 11 , : 0, :101, : 100e t s ;
b) a : 1, : 01, : 001,e t s = 0001, n = 00001;
c) a : 1010, : 0, :1 1,e t
s :1011, :1001, n i :100001. Giải a) b) c)
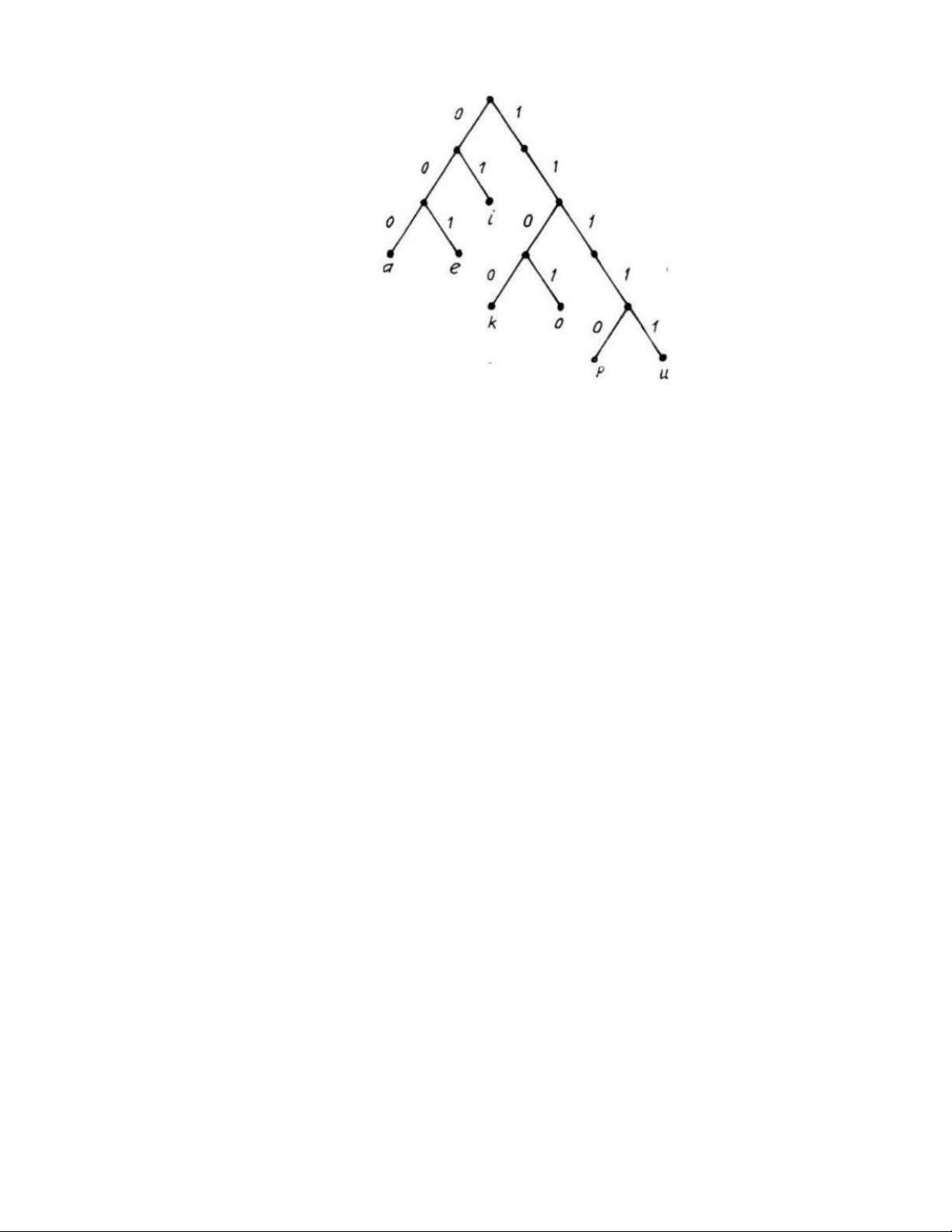
8. Hãy xác định mã của a, , , ,e i k o p u , , nếu sơ đồ mã biểu diễn bằng cây ở hình bên. Giải
a : 000; : 001; : 01; :1100; :1101e i k o
;p :11110;u :11111
9. Cho sơ đồ màa :001, :0001, :1, :0000, :0100, : 011. b e r s t x : 01010 hãy tìm các từ được biểu diễn bởi a) 01110100011; b) 0001110000; c) 01100101010 . Giải a) test b) beer c) tax