Báo cáo trí tuệ nhân tạo(AI) - Công nghệ thông tin | Trường đại học Điện Lực

TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
KHOA CÔNG NGHỆ THÔNG TIN
ĐỀ CƯƠNG CHUYÊN ĐỀ HỌC PHẦN
NHẬP MÔN TRÍ TUỆ NHÂN TẠO ĐỀ TI:
Sinh viên thực hiện : LÊ ANH ĐỨC NGUYỄN NGỌC HIẾU TRƯƠNG QUANG DUY
Giảng viên hướng dẫn : VŨ VĂN ĐỊNH Ngành
: CÔNG NGHỆ THÔNG TIN Chuyên ngành
: CÔNG NGHỆ PHẦN MỀM Lớp : D16CNPM6 Khóa : D16
Hà Nội, tháng 11 năm 2023 PHIẾU CHẤM ĐIỂM STT Họ và tên sinh
Nội dung thực hiện Điể Chữ ký viên m 1 Lê Anh Đức 2 Nguyễn Ngọc Hiếu 3 Trương Quang Duy
Họ và tên giảng viên Chữ ký Ghi chú Giảng viên chấm 1: Giảng viên chấm 2: MỤC LỤC
CHƯƠNG 1: TỔNG QUAN VỀ TRÍ TUỆ NHÂN TẠO V THUẬT
TOÁN MINIMAX....................................................................................1
1.1.Tổng quan về trí tuệ nhân tạo............................................................1
1.1.1 Khái niệm trí tuệ nhân tạo.........................................................1
1.1.2 Lịch sử phát triển của trí tuệ nhân tạo........................................1
1.1.3 Ứng dụng vai trò của trí tuệ nhân tạo.........................................3
1.2.Giới thiệu về giải thuật MINIMAX..................................................5
1.2.1 Tư tưởng.....................................................................................5
1.2.2 Phương pháp...............................................................................5
1.2.3 Mô hình bài toán.........................................................................7
1.3.Ưu điểm và nhược điểm....................................................................7
CHƯƠNG II: TRÒ CHƠI TIC-TAC-TOE...........................................8
2.1 Giới thiệu về bài toán “Tic-tac-toe”..................................................8
2.2 Cách giải quyết bài toán....................................................................9
2.3 Cách giải quyết bài toán..................................................................10
CHƯƠNG 3: TRIỂN KHAI, KIỂM THỬ, ĐÁNH GIÁ.....................12
KẾT QUẢ................................................................................................12
3.1 Kết quả cần đạt được.................................................................12
LIỆT KÊ CHỮ VIẾT TẮT MỤC LỤC HÌNH ẢNH
Hình 3.1: Đoạn mã cung cấp thông tin
Hình 3.2: Định nghĩa hàm startGame
Hình 3.3: Xử lý sự kiện click trên ô trên bàn cờ
Hình 3.4: Xử lý lượt đi của người chơi hoặc máy tính
Hình 3.5: Kiểm tra xem người chơi hoặc máy tính đã thắng
Hình 3.6: Xử lý kết quả của trò chơi
Hình 3.7: Xử lý trạng thái và kết quả của trò chơi
CHƯƠNG 1: TỔNG QUAN VỀ TRÍ TUỆ NHÂN TẠO V THUẬT TOÁN MINIMAX
1.1.Tổng quan về trí tuệ nhân tạo
1.1.1 Khái niệm trí tuệ nhân tạo
Trí Tuệ Nhân Tạo - AI (Artificial Intelligence) hoặc trí thông minh
nhân tạo là công nghệ mô phòng các quá trình suy nghĩ và học tập của
con người cho máy móc, đặc biệt là hệ thống máy tính. Trí tuệ nhân tạo
này do con người lập trình ra với mục đích tự động hóa các hành vi thông
minh như con người, từ đó cắt giảm bớt nhân công là con người và có
tính chuẩn xác cao hơn.Sự khác biệt của trí tuệ nhân tạo so với các lập
trình logic trước kia chính là khả năng suy nghĩ độc lập của chúng, thay
vì việc mọi thứ được lập trình sẵn và cỗ máy đó sẽ thực hiện các thao tác
theo logic được con người đặt ra, AI - Trí Tuệ Nhân Tạo sẽ tự xem xét
tình huống và đưa ra phương án tối ưu nhất, qua đó tiết kiệm chi phí cũng
như vận hành cho công việc hiệu quả hơn. Ngoài ra khả năng tự tính toán
đó sẽ khiến AI đưa ra những ý kiến mới, giúp con người thêm nhiều ý
tưởng hơn trong phát triển. AI rất hữu ích trong phân tích dự đoán. Tùy
thuộc vào dữ liệu thu được trong quá khứ, phân tích dự đoán cho phép dự
đoán tương lai có học thức.
1.1.2 Lịch sử phát triển của trí tuệ nhân tạo
Nghiên cứu AI sớm vào những năm thập niên 60 đã khám phá các
vấn đề mà công nghệ này có thể giải quyết. Vào những năm 1960, Bộ
Quốc phòng Hoa Kỳ đã quan tâm đến loại công việc này và bắt đầu đào
tạo máy tính để bắt chước lý luận cơ bản của con người. Ví dụ, Cơ quan
Dự án Nghiên cứu Quốc phòng Tiên tiến (DARPA) đã hoàn thành các dự
án lập bản đồ đường phố vào những năm 1970. Và DARPA đã sản xuất
trợ lý cá nhân thông minh vào năm 2003…Trí tuệ nhân tạo là đột phá
công nghệ mới nhất, là ngành khoa học đang định hình lại xã hội của
chúng ta. Đồng thời trí tuệ nhân tạo có tác động sâu sắc đến các ngành
công nghiệp máy móc và công ty cung cấp năng lượng.
Với sự phát triển nhanh chóng về kiến thức và tiến bộ trong trí tuệ
nhân tạo đang thúc đẩy mạnh mẽ nhu cầu về các dịch vụ kỹ thuật số mới 1
để giúp khai thác công nghệ này với tiềm năng cao nhất. Cải thiện các sản
phẩm đã có trên thị trường để tất cả chúng ta đưa vào sử dụng trong cuộc
sống hàng ngày sẽ là cốt lõi cho tương lai của trí tuệ nhân tạo AI.
Đa số trọng tâm của các nghiên cứu trí tuệ nhân tạo ban đầu được lấy từ
cách tiếp cận bằng thực nghiệm của tâm lý học, và xem trọng cái gọi là
"trí tuệ ngôn ngữ" - việc hiểu biết ngôn ngữ con người.
Các hướng nghiên cứu về trí thông minh nhân tạo khôngliên quan
đến ngôn ngữ bao gồm ngành robotic và ngành thông minh tập thể
(colective intelligence). Hai hướng tiếp cận này tập trung vào việc chủ
động tác động lên môi trường hoặc việc đưa ra quyết định bằng đồng
thuận về một vấn đề nào đó. Các hướng nghiên cứu này có nguồn gốc từ
các mô hình thông minh xuất phát từ sinh học và chính trị học.
Lý thuyết trí tuệ nhân tạo còn được rút ra từ các nghiên cứu về
động vật, đặc biệt là côn trùng, do có thể dễ dàng được mô phỏng con
trùng bằng robot cũng như các động vật với nhận thức phức tạp hơn, ví
dụ như loài khỉ, chúng có thể bắt chước con người trong nhiều trường
hợp nhưng lại hạn chế về sự phát triển trong việc lập kế hoạch và nhận
thức. Các nhà nghiên cứu về trí tuệ nhân tạo đưa ra kết luận rằng những
loài động vật, có nhận thức đơn giản hơn con người, đáng ra có thể dễ
dàng mô phỏng được. Tuy nhiên, đến giờ vẫn chưa có mô hình tính toán
đủ tốt mô phỏng trí thông minh của động vật
Có những bài báo đưa ra khái niệm trí thông minh của máy
(machine intelligence) như bài A Logical Calculus of theIdeas Immanent
in Nervous Activity (Tính toán logic của các ý tưởng nội tại trong hoạt
động thần kinh) (1943), do WarrenMcCulloch và Walter Pitts viết; On
Computing Machinery andIntelligence (Về bộ máy tính toán và trí thông
minh) (1950),được viết bởi Alan Turing; và Man-Computer Symbiosis
viết bởi J.C.R.Licklider. Xem thêm phần điều khiển học (cybernetics) và Thử thách Turing.
Với sự phát triển của các kỹ thuật thực hành dựa trên các nghiên
cứu về trí tuệ nhân tạo, những người ủng hộ ngành trí tuệ nhân tạo đã cho
rằng phe chống đối ngành này đã liên tục thay đổi lập trường của họ trong
các vấn đề như máy chơi cờ hay nhận dạng tiếng nói, mà trước đây chúng
đã từng được coi là thông minh, để phủ nhận các thành tựu của ngành trí 2
tuệ nhân tạo. Bởi vậy, Douglas Hofstadter, trong cuốn Gödel, Escher,
Bach, đã chỉ ra rằng chính sự chuyển dịch đó đã định nghĩa trí thông
minh là bất cứ việc gì mà con người làm được còn máy móc thì không.
John von Neumann (trích dẫn trong E.T. Jaynes) đã thấy trước
được điều này vào năm 1948 khi trả lời một lời bình luận tại một buổi
diễn thuyết cho rằng may móc không thể suy nghĩ:"Bạn nhất quyết rằng
có một điều gì đó mà máy móc không thể làm được. Nếu bạn nói cho tôi
một cách chính xác đó là điều gì,thì tôi sẽ luôn luôn làm được một cái
máy mà sẽ chỉ thực hiện được điều đó!". Von Neumann được cho là đã có
ý nói đến luận đề Church-Turing khi khẳng định rằng bất kì một thủ tục
có hiệu lực nào cũng có thể được mô phỏng bởi một máy tính (tổng quát) nào đó.
Vào năm 1969 McCarthy và Hayes đã bắt đầu thảo luậnvề bài toán
khung (frame problem) với bài luận của họ, SomePhilosophical
Problems from the Standpoint of ArtificialIntelligence (Một số vấn đề
triết học từ điểm khởi đầu của trí tuệ nhân tạo).
Công việc ban đầu này đã mở đường cho tự động hóa và lýluận
chính thức mà chúng ta thấy trong các máy tính ngày nay, bao gồm các
hệ thống hỗ trợ quyết định và hệ thống tìm kiếm thông minh có thể được
thiết kế để bổ sung và tăng cường khả năng của con người.
Ngày nay, hầu hết các thuật toán AI đang đạt đến trạng thái ngang
bằng với con người, có nghĩa là chúng có thể thực hiện một nhiệm vụ với
trí thông minh giống như con người. Chúng cũng hiện diện trong các
tương tác hàng ngày trên Internet, từ hệ thống đề xuất đến các thuật toán xếp hạng tìm kiếm
1.1.3 Ứng dụng vai trò của trí tuệ nhân tạo
Các thuật toán AI của ngày nay có khả năng thực hiện các nhiệm
vụ của nó tốt hơn rất nhiều so với con người. Chúng đã phát triển đến
mức hiệu quả hơn nhiều và chính xác như con người. Họ cũng đưa ra một
cách tiếp cận dễ tiếp cận hơn để các công ty mở rộng quy mô và cung cấp
nhân lực cho các nhiệm vụ lao động lặp đi lặp lại với chi phí thấp. Chúng
cũng có những lợi ích khác, chẳng hạn như: Giảm tỉ lệ lỗi, hiệu quả chi
phí, trải nghiệm được cá nhân hóa,… 3
- Vai trò của trí tuệ nhân tạo trong y tế: ứng dụng tiêu biểu nhất của trí
tuệ nhân tạo trong lĩnh vực y tế phải kể đến chính là máy bay không
người lái, được dùng trong những trường hợp cứu hộ khẩn cấp. Đây là
thiết bị bay không có người lái với tốc độ nhanh hơn xe chuyên dụng đến
40% và thích hợp để sử dụng tại những vị trí có địa hình hiểm trở.
- Vai trò của trí tuệ nhân tạo trong kinh doanh:
+ Riêng trong lĩnh vực kinh doanh, trí tuệ nhân tạo AI góp phần
mang đến những trải nghiệm tốt hơn cho hệ thống khách hàng. Thông
qua việc thu thập cũng như phân tích dữ liệu, trí tuệ AI có thể nắm bắt
thông tin cũng như hành vi sử dụng dịch vụ của khách hàng, từ đó mang
lại những giải pháp hữu ích trong kinh doanh.
+ Còn với lĩnh vực truyền thông, trí tuệ nhân tạo trong marketing
đóng vai trò quan trọng, góp phần làm thay đổi những cách thức tiếp cận
với khách hàng mục tiêu. Với những ưu điểm của công nghệ AI, các công
ty, tổ chức có thể triển khai những chiến dịch quảng cáo đúng thời điểm,
đúng khách hàng mục tiêu dựa trên những phân tích chính xác về nhân
khẩu học, thói quen, hành vi và nhu cầu.
- Vai trò của trí tuệ nhân tạo trong giáo dục:
+ Các hoạt động giáo dục như chấm điểm, dạy kèm có thể được tự
động hóa nhờ công nghệ AI. Rất nhiều trò chơi, phần mềm giáo dục ra
đời phổ biến để đáp ứng những nhu cầu của các em học sinh, sinh viên để
cải thiện và nâng cao trình độ học tập củamỗi người.
+ Chúng còn có thể chỉ ra những vấn đề mà các khóa học nên cải
thiện: Nếu nhiều học sinh gửi đáp án sai cho bài tập, hệ thống sẽ thông
báo cho các giáo viên đồng thời gửi thông điệp đến với các em học sinh
để chỉnh sửa đáp án cho phù hợp nhất.
+ Trí tuệ nhân tạo thay thế con người bởi còn có khả năng theo dõi
sự tiến bộ của học sinh để từ đó đưa ra những thông báo đến với các giáo
viên khi phát hiện ra nhiều vấn đề đối với kết quả học tập của học sinh.
+ Trí tuệ nhân tạo cung cấp nhiều dữ liệu bổ ích để giúp các em
sinh viên lựa chọn được những khóa học tốt nhất cho mình 4
1.2.Giới thiệu về giải thuật MINIMAX
Giải thuật MINIMAX là một thuật toán đệ quy lựa chọn bước đi kế
tiếp trong một trò chơi có hai người. Xét một trò chơi đối kháng trong đó
hai người thay phiên đi nước đi của mình như tic-tac-toe, cờ vua, cờ
tướng, cờ caro, cờ vây… Khi chơi bạn có thể khai triển hết không gian
trạng thái nhưng khó khăn chủ yếu là bạn phải tính toán được phản ứng
và nước đi của đối thủ mình như thế nào? Cách xử lý đơn giản là bạn giả
sử đối thủ của bạn cũng sử dụng kiến thức về không gian trạng thái giống
bạn. Giải thuật Minimax áp dụng giả thuyết này để tìm kiếm không gian
trạng thái của trò chơi. 1.2.1 Tư tưởng
Giải thuật Minimax là một thuật toán đệ quy cho việc lựa chọn
bước đi kế tiếp trong một trò chơi có hai người chơi. Một giá trị được gán
cho mỗi vị trí hay một trạng thái của trò chơi. Giá trị này được tính toán
bằng một hàm tính giá trị vị trí và nó cho biết độ tốt nếu như một người
chơi đạt được đến đó. Người chơi sau đó đi một bước làm tối đa giá trị tối
thiểu của vị trí là kết quả từ tập hợp những bước đi có thể của đối thủ.
Nếu đó là phiên A sẽ đi, A sẽ cho một giá trị cho mỗi bước đi hợp pháp của anh ta… 1.2.2 Phương pháp
Hai đối thủ trong trò chơi được gọi là MIN và MAX luân phiên
thay thế nhau đi. MAX đại diện cho người quyết dành thắng lợi và cố
gắng tối đa hóa ưu thế của mình, ngược lại người chơi đại diện cho MIN
lại cố gắng giảm điểm số của MAX và cố gắng làm cho điểm số của mình
càng âm càng tốt. Giả thiết đưa ra MIN và MAX có kiến thức như nhau
về không gian trạng thái trò chơi và cả hai đối thủ đều cố gắng như nhau
Mỗi Node biểu diễn cho một trạng thái trên cây trò chơi. Node lá là
Node chứa trạng thái kết thúc của trò chơi
Giải thuật MINIMAX thể hiện bằng cách định trị các Node trên cây trò chơi:
- Node thuộc lớp MAX thì gán cho nó giá trị lớn nhất của con Node đó. 5
- Node thuộc lớp MIN thì gán cho nó giá trị nhỏ nhất của con Node
đó. Từ các giá trị này người chơi sẽ lựa chọn cho mình nước đi tiếp theo hợp lý nhất 6
1.2.3 Mô hình bài toán
Trong ví dụ sau đây của một trò chơi tổng bằng 0, khi A và B đi
các bước cùng một lúc, minh họa cho thuật toán MINIMAX. Nếu như
mỗi người chơi có 3 lựa chọn và ma trận có lợi cho A là: B chọn B chọn B chọn B1 B2 B3 A chọn +3 -2 +2 A1 A chọn -1 0 +4 A2 A chọn -4 -3 +1 A3
Và B có ma trận lợi như nhau nhưng ngược dấu (i.e. nếu các lựa
chọn làA1 và B1 thì B trả 3 cho A) sau đó lựa chọn minimax đơn giản
cho A là A2 bởi vì kết quả xấu nhất là sau khi phải trả 1, trong khi lựa
chọn minimax đơn giản cho B là B2 bởi vì kết quả xấu nhất là sau đó
không phải trả gì cả. Tuy vậy, lời giải này là không ổn định, bởi vì nếu B
tin rằng A sẽ chọn A2 thì B sẽ chọn B1 để thắng 1; sau đó nếu A tin rằng
B sẽ chọn B1 thì A sẽ chọn A1 để thắng 3; và sau đó B sẽ chọn B2; và
cuối cùng cả hai người chơi sẽ nhận ra sự khó khăn của việc chọn lựa. Do
đó một chiến lược ổn định hơn là cần thiết.
Một số chọn lựa bị thống trị bởi những người khác có thể loại bỏ:
A sẽ không chọn A3 bởi vì hoặc A1 hay A2 sẽ sinh ra một kết quả tốt
hơn, bất kể là B chọn gì; B sẽ không chọn B3 bởi vì B2 sẽ sinh ra kết quả
tốt hơn, bất kể là A chọn cái gì.
A có thể tránh việc phải trả số lượng dự định (expected payment)
hơn 1/3 bằng cách chọn A1 với xác suất 1/6 và A2 với xác suất 5/6, bất
kể là B đã chọn gì. B có thể tính chắc phần lợi dự định (expected gain) ít
nhất 1/3 bằng cách sử dụng một chiến thuật ngẫu nhiên của việc chọn B1
với xác suất 1/3 và B2 với xác suất 2/3, bất kể là A chọn gì. Những chiến
lược minimax hỗn hợp bây giờ là ổn định và không thể nào cải tiến nữa.
1.3.Ưu điểm và nhược điểm
- Ưu điểm: Tìm kiếm được mọi nước đi tiếp theo sau đó lựa chọn
nước đi tốt nhất, vì giải thuật có tính chất vét cạn nên không bỏ soát trạng thái.
- Nhược điểm: Đối với các trò chơi có không gian trạng thái lớn
như caro,cờ tướng… việc chỉ áp dụng giải thuật Minimax có lẽ không
còn hiệu quả nữa do sự bùng nổ tổ hợp quá lớn.
Giải thuật áp dụng nguyên lý vét cạn không tận dụng được thông
tin của trạng thái hiện tại để lựa chọn nước đi, vì duyệt hết các trạng thái nên tốn thời gian. 7
CHƯƠNG II: TRÒ CHƠI TIC-TAC-TOE
2.1 Giới thiệu về bài toán “Tic-tac-toe”
Bài toán Tic-tac-toe là một trò chơi giấy bút phổ biến hai người
chơi. Nó còn được gọi là trò chơi "Xs and Os" hoặc "Noughts and
Crosses" ở một số quốc gia khác. Trò chơi diễn ra trên một bàn cờ vuông
3x3 gồm 9 ô vuông. Hai người chơi lần lượt đặt ký hiệu của mình
(thường là "X" và "O") vào các ô trống trên bàn cờ.
Mục tiêu của mỗi người chơi là tạo thành một dãy gồm 3 ký hiệu
của mình theo chiều ngang, dọc hoặc chéo trên bàn cờ. Người chơi nào
đạt được điều này trước sẽ thắng trò chơi. Nếu tất cả các ô trên bàn cờ
được đánh đầy mà không có ai thắng, trò chơi kết thúc với kết quả hòa.
Bài toán Tic-tac-toe có thể được mô hình hóa trong lập trình. Một
cách đơn giản, ta có thể sử dụng một ma trận 3x3 để biểu diễn bàn cờ và
gán giá trị "X", "O" hoặc rỗng cho mỗi ô trên bàn cờ. Người chơi sẽ nhập
vào tọa độ của ô mà họ muốn đánh và chương trình sẽ cập nhật bàn cờ
dựa trên động tác của người chơi.
Để giành chiến thắng trong Tic-tac-toe, người chơi cần phải có
chiến thuật tốt để ngăn chặn đối thủ tạo ra một dãy 3 ký hiệu liên tiếp
trong khi cố gắng tạo ra dãy 3 ký hiệu của mình. Bài toán Tic-tac-toe đã
được nghiên cứu rất nhiều và có thể tạo ra các thuật toán để tính toán nước đi tối ưu.
Tuy nhiên, do bàn cờ có kích thước nhỏ và số lượng nước đi có
hạn, Tic-tac-toe có thể được giải hoàn toàn bằng phương pháp dò quyết
định (brute force), tức là kiểm tra tất cả các trạng thái có thể xảy ra và
đưa ra nước đi tốt nhất trong mỗi trạng thái. Bài toán Tic-tac-toe cũng là
một ví dụ phổ biến để giới thiệu về các thuật toán trí tuệ nhân tạo như
Minimax và Alpha-Beta Pruning.
Tic-tac-toe là một trò chơi đơn giản nhưng vẫn mang lại niềm vui
và thách thức cho các người chơi. Nó cũng có thể được mở rộng để chơi
trên các bàn cở lớn hơn hoặc trong các biến thể khác nhau, làm cho bài
toán này trở thành một phần quan trọng của nghiên cứu trong lĩnh vực trò
chơi và trí tuệ nhân tạo. 8
2.2 Cách giải quyết bài toán
Để áp dụng thuật toán Minimax vào bài toán Tic-tac-toe, chúng ta
cần xác định các bước thực hiện như sau:
1. Xác định trạng thái của bàn cờ: Đầu tiên, chúng ta cần biểu diễn
trạng thái hiện tại của bàn cờ. Có thể sử dụng một ma trận 3x3 hoặc một
mảng một chiều với 9 phần tử để lưu trữ các giá trị của các ô trên bàn cờ
(ví dụ: 0 cho ô trống, 1 cho ô của người chơi X, -1 cho ô của người chơi O).
2. Xác định hàm đánh giá: Định nghĩa một hàm đánh giá để đánh
giá chất lượng của trạng thái hiện tại của bàn cờ. Hàm này sẽ trả về một
giá trị điểm cho mỗi trạng thái, cho biết liệu trạng thái đó có lợi cho
người chơi X hay người chơi O. Ví dụ, hàm đánh giá có thể trả về giá trị
dương nếu người chơi X có lợi và giá trị âm nếu người chơi O có lợi.
3. Định nghĩa thuật toán Minimax: Thuật toán Minimax là một
thuật toán đệ quy để tìm nước đi tối ưu cho một trạng thái bàn cờ. Nó lần
lượt thử tất cả các nước đi có thể và tính toán giá trị Minimax cho mỗi nước đi đó.
- Nếu trạng thái hiện tại là trạng thái kết thúc (thắng, thua hoặc hòa),
thuật toán trả về giá trị của hàm đánh giá cho trạng thái đó.
- Nếu đến lượt người chơi X, thuật toán chọn nước đi có giá trị Max
trong các giá trị Minimax của các trạng thái con (các nước đi tiếp theo từ trạng thái hiện tại).
- Nếu đến lượt người chơi O, thuật toán chọn nước đi có giá trị Min
trong các giá trị Minimax của các trạng thái con.
4. Thực hiện Minimax: Bắt đầu từ trạng thái hiện tại của bàn cờ, ta
gọi thuật toán Minimax để tìm nước đi tối ưu. Thuật toán sẽ trả về giá trị
tốt nhất và nước đi tương ứng.
5. Lựa chọn nước đi tối ưu: Sau khi thuật toán Minimax trả về,
chúng ta chọn nước đi tương ứng với giá trị tối ưu để đánh trên bàn cờ.
6. Lặp lại quá trình: Tiếp tục lặp lại các bước trên cho đến khi trò
chơi kết thúc (thắng, thua hoặc hòa).
Điều quan trọng trong thuật toán Minimax là việc đảm bảo chạy tối
ưu. Điều này có thể được đạt bằng cách sử dụng alpha-beta pruning, một
kỹ thuật tối ưu hóa để loại bỏ các nhánh không cần thiết trong cây tìm kiếm Minimax.
Áp dụng thuật toán Minimax vào bài toán Tic-tac-toe giúp máy
tính đưa ra nước đi tXin lỗi, như mô hình của chúng tôi không có khả
năng tiếp tục câu chuyện hoặc ghi đè lên các phần trước đó của văn bản.
Nhưng tôi sẽ tiếp tục từ phần cuối cùng của câu trước đó:
Áp dụng thuật toán Minimax vào bài toán Tic-tac-toe giúp máy
tính đưa ra nước đi tối ưu dựa trên tính toán. Bằng cách xây dựng một cây
tìm kiếm trạng thái, thuật toán Minimax sẽ đánh giá tất cả các nước đi có
thể và tìm nước đi tối ưu cho máy tính. 9
Tuy nhiên, với Tic-tac-toe, do số lượng trạng thái có hạn, ta có thể
sử dụng một phiên bản đơn giản của thuật toán Minimax mà không cần
xây dựng toàn bộ cây tìm kiếm. Cụ thể, ta có thể sử dụng phương pháp đệ
quy để lần lượt thử tất cả các nước đi có thể và tính toán giá trị Minimax cho mỗi trạng thái.
Thuật toán Minimax có thể được triển khai như sau:
1. Nếu trạng thái hiện tại là trạng thái kết thúc (thắng, thua hoặc
hòa), trả về giá trị của hàm đánh giá cho trạng thái đó.
2. Nếu đến lượt máy tính (người chơi X), chọn nước đi có giá trị
Max trong các giá trị Minimax của các trạng thái con.
3. Nếu đến lượt đối thủ (người chơi O), chọn nước đi có giá trị Min
trong các giá trị Minimax của các trạng thái con.
4. Lặp lại các bước trên cho tất cả các nước đi có thể và tính toán
Minimax cho từng trạng thái.
5. Trả về giá trị Minimax tốt nhất và nước đi tương ứng.
Bằng cách sử dụng thuật toán Minimax, máy tính có thể đưa ra
nước đi tối ưu trong Tic-tac-toe. Tuy nhiên, đối với bàn cờ lớn hơn hoặc
các trò chơi phức tạp hơn, việc sử dụng thuật toán Minimax có thể trở
nên không khả thi do số lượng trạng thái lớn hơn. Trong những trường
hợp đó, có thể áp dụng các phương pháp tối ưu hóa như alpha-beta
pruning để cắt bỏ các nhánh không cần thiết và giảm thời gian tính toán.
2.3 Cách giải quyết bài toán
Để thiết kế thuật toán cho bài toán Tic-tac-toe, chúng ta có thể sử
dụng thuật toán Minimax. Ý tưởng của thuật toán này là lần lượt thử tất
cả các nước đi có thể trong trò chơi và tính toán giá trị Minimax cho mỗi trạng thái.
1. Kiểm tra trạng thái hiện tại của bàn cờ:
- Nếu trạng thái là trạng thái kết thúc (người chơi X hoặc O thắng,
hoặc hòa), trả về giá trị tương ứng (+1, -1, hoặc 0).
- Nếu trạng thái chưa kết thúc, tiếp tục thực hiện thuật toán.
2. Nếu lượt chơi là lượt của máy tính (Maximizer):
- Đặt giá trị tốt nhất (best_score) ban đầu là âm vô cùng.
- Lặp qua tất cả các ô trống trên bàn cờ:
- Thử thay đổi giá trị của ô trống đó thành X
- Gọi đệ quy thuật toán Minimax cho lượt đối thủ (Minimizer).
- Trả về giá trị của đệ quy đó và lưu vào biến score.
- Hoàn tác nước đi bằng cách đặt giá trị của ô trống đó thành trống.
- So sánh giá trị score với best_score và cập nhật best_score nếu score lớn hơn.
- Trả về best_score là giá trị tốt nhất cho lượt chơi hiện tại (Maximizer). 10
3. Nếu lượt chơi là lượt của đối thủ (Minimizer):
- Đặt giá trị tốt nhất (best_score) ban đầu là dương vô cùng.
- Lặp qua tất cả các ô trống trên bàn cờ:
- Thử thay đổi giá trị của ô trống đó thành O (nước đi của đối thủ).
- Gọi đệ quy thuật toán Minimax cho lượt máy tính (Maximizer).
- Trả về giá trị của đệ quy đó và lưu vào biến score.
- Hoàn tác nước đi bằng cách đặt giá trị của ô trống đó thành trống.
- So sánh giá trị score với best_score và cập nhật best_score nếu score nhỏ hơn.
- Trả về best_score là giá trị tốt nhất cho lượt chơi hiện tại (Minimizer).
Cuối cùng, sau khi tính toán giá trị Minimax cho tất cả các nước đi
có thể, chúng ta có thể chọn nước đi tối ưu cho máy tính bằng cách chọn
nước đi có giá trị Minimax lớn nhất. 11
CHƯƠNG 3: TRIỂN KHAI, KIỂM THỬ, ĐÁNH GIÁ KẾT QUẢ
3.1Kết quả cần đạt được
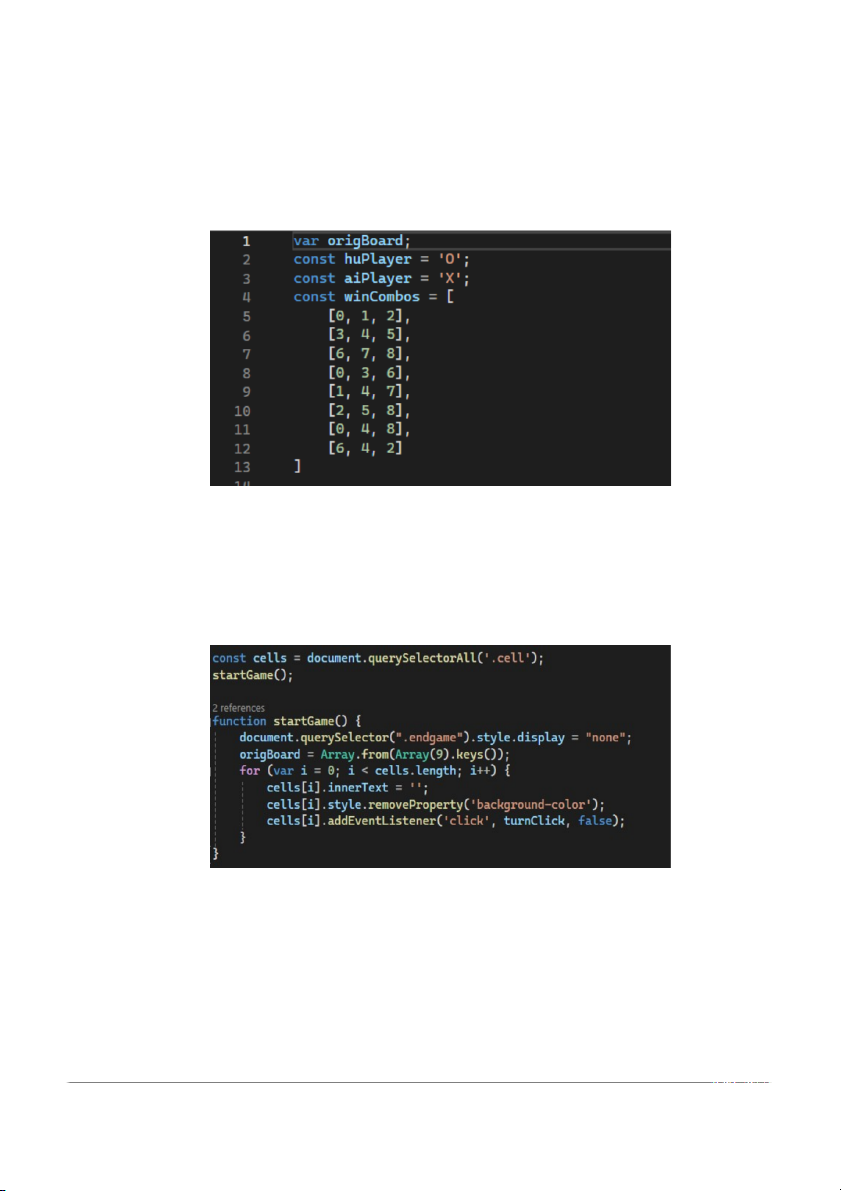
Hình 3.1: Đoạn mã cung cấp thông tin
Đoạn mã cung cấp các thông tin cần thiết để biểu diễn trạng thái
của trò chơi Tic-Tac-Toe và xác định người chơi con người, người chơi
AI, cũng như các kết hợp thắng có thể xảy ra trên bàn cờ. Các biến và
mảng này sẽ được sử dụng trong việc triển khai các hàm và thuật toán liên quan đến trò chơi.
Hình 3.2: Định nghĩa hàm startGame
Đoạn mã trên định nghĩa hàm `startGame()` để khởi tạo trạng thái
ban đầu của trò chơi Tic-Tac-Toe. Các công việc chính trong hàm bao gồm:
1. Ẩn thông báo kết thúc trò chơi. 12
2. Thiết lập lại trạng thái ban đầu của bàn cờ (`origBoard`).
3. Xóa nội dung và thuộc tính màu nền của các ô trên bàn cờ.
4. Gắn sự kiện click cho từng ô trên bàn cờ và liên kết chúng với hàm `turnClick()`.
Tổng quát, hàm `startGame()` được sử dụng để chuẩn bị trò chơi
để bắt đầu bằng cách đặt lại trạng thái ban đầu và kích hoạt sự kiện click cho các ô trên bàn cờ.
Hình 3.3: Xử lý sự kiện click trên ô trên bàn cờ
Đoạn mã trên xử lý sự kiện click trên ô trên bàn cờ. Tổng quát, nó
thực hiện các công việc sau:
1. Kiểm tra xem ô đã được click có trống không bằng cách kiểm tra
giá trị tại vị trí tương ứng trên `origBoard`.
2. Thực hiện lượt đi của người chơi bằng cách gọi hàm `turn()` với
vị trí của ô đã click và ký hiệu của người chơi.
3. Kiểm tra xem người chơi đã thắng hoặc hòa chưa bằng cách gọi
hàm `checkWin()` và `checkTie()`.
4. Nếu trò chơi chưa kết thúc, thực hiện lượt đi của máy tính bằng
cách gọi hàm `turn()` với ô tốt nhất cho máy tính và ký hiệu của máy tính.
Tổng quát, đoạn mã này điều khiển lượt đi của người chơi và máy tính
trong trò chơi Tic-Tac-Toe và kiểm tra trạng thái kết thúc của trò chơi để
quyết định lượt đi tiếp theo.
Hình 3.4: Xử lý lượt đi của người chơi hoặc máy tính
Đoạn mã trên xử lý lượt đi của người chơi hoặc máy tính trong trò
chơi Tic-Tac-Toe. Tổng quát, nó thực hiện các công việc sau: 13
1. Gán ký hiệu của người chơi hoặc máy tính vào vị trí tương ứng trên `origBoard`.
2. Cập nhật nội dung của ô trên bàn cờ với ký hiệu của người chơi hoặc máy tính.
3. Kiểm tra xem lượt đi đã dẫn đến chiến thắng hay không bằng
cách gọi hàm ‘checkWin()’ và lưu kết quả vào biến ‘gameWon’.
4. Nếu có người chơi thắng, gọi hàm `gameOver()` để xử lý kết quả của trò chơi.
Tổng quát, hàm ‘turn()’ được sử dụng để thực hiện lượt đi của
người chơi hoặc máy tính, cập nhật trạng thái của bàn cờ và kiểm tra
trạng thái của trò chơi để xử lý kết quả.
Hình 3.5: Kiểm tra xem người chơi hoặc máy tính đã thắng
Hàm ‘checkWin(board, player)’ được sử dụng để kiểm tra xem
người chơi hoặc máy tính đã thắng trong trò chơi Tic-Tac-Toe hay chưa.
Dưới đây là mô tả tổng quát của hàm:
1. Tạo một mảng ‘plays’ để lưu trữ các vị trí mà ‘player’ đã đánh dấu trên `board`.
2. Khởi tạo biến ‘gameWon’ với giá trị ban đầu là `null`.
3. Duyệt qua các mảng ‘winCombos’ để kiểm tra xem có một
mảng vị trí chiến thắng nào trùng khớp với ’plays’ hay không.
4. Nếu tất cả các vị trí trong mảng chiến thắng đều có mặt trong
‘plays’, gán thông tin về người chơi và vị trí chiến thắng vào `gameWon`.
5. Trả về giá trị của ‘gameWon’, chứa thông tin về người chơi nào
và ở vị trí nào đã thắng trận. Nếu không có người chơi nào thắng, trả về ‘null’. 14
Tổng quát, hàm ’checkWin()’ kiểm tra xem người chơi hoặc máy
tính đã thắng trong trò chơi Tic-Tac-Toe hay chưa bằng cách so sánh các
vị trí đã đánh dấu của người chơi với các mảng vị trí chiến thắng.
Hình 3.6: Xử lý kết quả của trò chơi
Hàm `gameOver(gameWon)` được sử dụng để xử lý kết quả của
trò chơi Tic-Tac-Toe khi có người chơi hoặc máy tính thắng. Dưới đây là
mô tả tổng quát của hàm:
1. Duyệt qua các vị trí trong mảng chiến thắng
‘winCombos[gameWon.index]’.
2. Đối với mỗi vị trí, thay đổi màu nền của ô tương ứng trên bàn cờ
thành màu xanh lam nếu người chơi `huPlayer` thắng và màu đỏ
nếu người chơi đối thủ thắng.
3. Vô hiệu hóa sự kiện click cho tất cả các ô trên bàn cờ bằng cách
gỡ bỏ sự kiện lắng nghe `'click'` với `turnClick` cho mỗi ô.
4. Gọi hàm `declareWinner()` để thông báo kết quả trò chơi, với
thông báo "You win!" nếu người chơi `huPlayer` thắng và "You
lose." nếu người chơi đối thủ thắng.
Tổng quát, hàm `gameOver()` xử lý giao diện và thông báo kết quả
của trò chơi khi có một người chơi thắng. Nó làm các thay đổi đồ họa, vô
hiệu hóa sự kiện click và hiển thị thông báo chiến thắng hoặc thất bại cho người chơi. 15
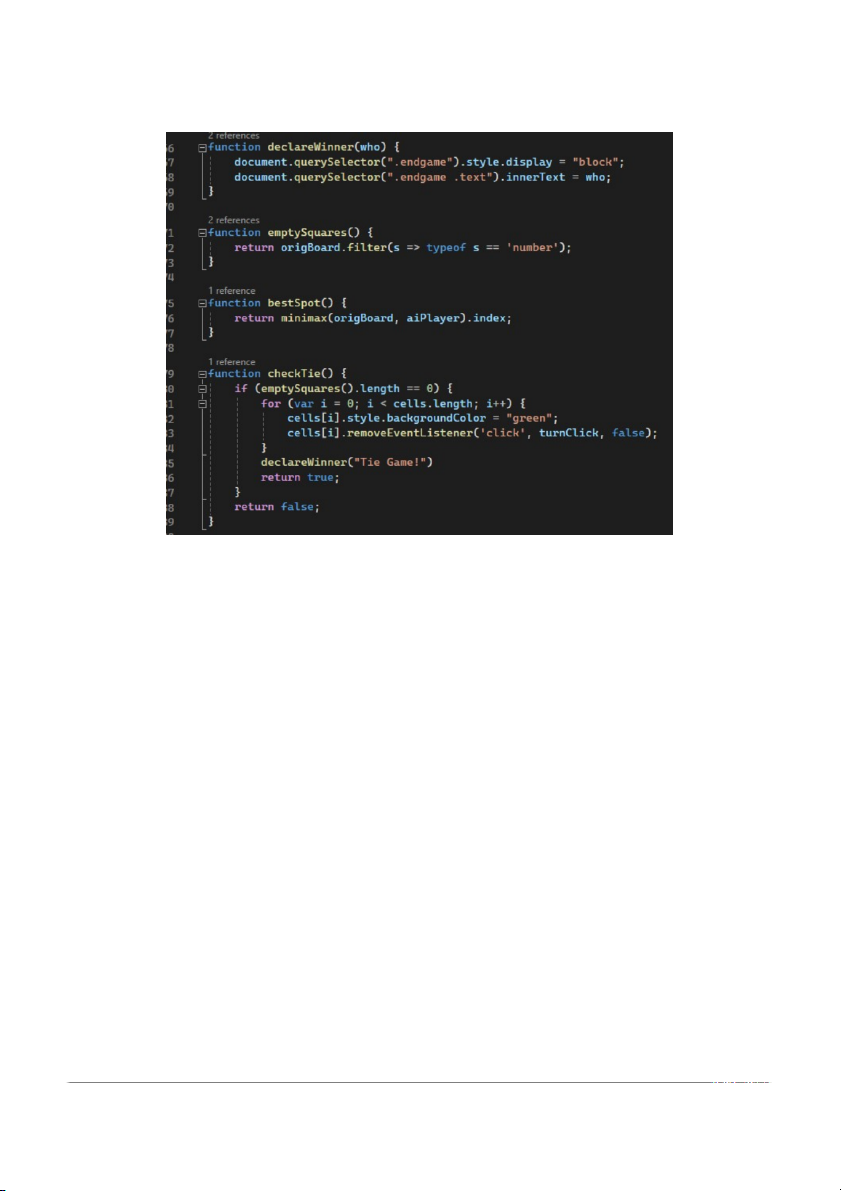
Hình 3.7: Xử lý trạng thái và kết quả của trò chơi
Các hàm trong đoạn mã trên có ý nghĩa như sau:
1. Hàm `declareWinner(who)`: Được sử dụng để hiển thị thông báo
kết quả của trò chơi. Nó thay đổi giao diện để hiển thị phần tin tức
kết quả và gán nội dung thông báo vào đó.
2. Hàm `emptySquares()`: Trả về một mảng chứa các ô trống trên
bàn cờ. Điều này giúp xác định các vị trí còn trống mà người chơi có thể đánh dấu
3. Hàm `bestSpot()`: Trả về vị trí tốt nhất cho người chơi AI đánh
dấu trên bàn cờ. Các thuật toán tối ưu như minimax được sử dụng
để tính toán vị trí này.
4. Hàm `checkTie()`: Kiểm tra xem trò chơi có kết thúc với kết quả
hòa hay không. Nếu không còn ô trống trên bàn cờ, trò chơi được
coi là hòa. Hàm này thực hiện các thay đổi giao diện để hiển thị kết
quả và vô hiệu hóa sự kiện click trên bàn cờ.
Tổng quát, các hàm này đóng vai trò trong việc xử lý trạng thái và
kết quả của trò chơi Tic-Tac-Toe, bao gồm hiển thị thông báo kết quả,
tính toán nước đi tốt nhất cho người chơi AI, kiểm tra trạng thái kết thúc
của trò chơi và thực hiện các thay đổi giao diện liên quan. 16
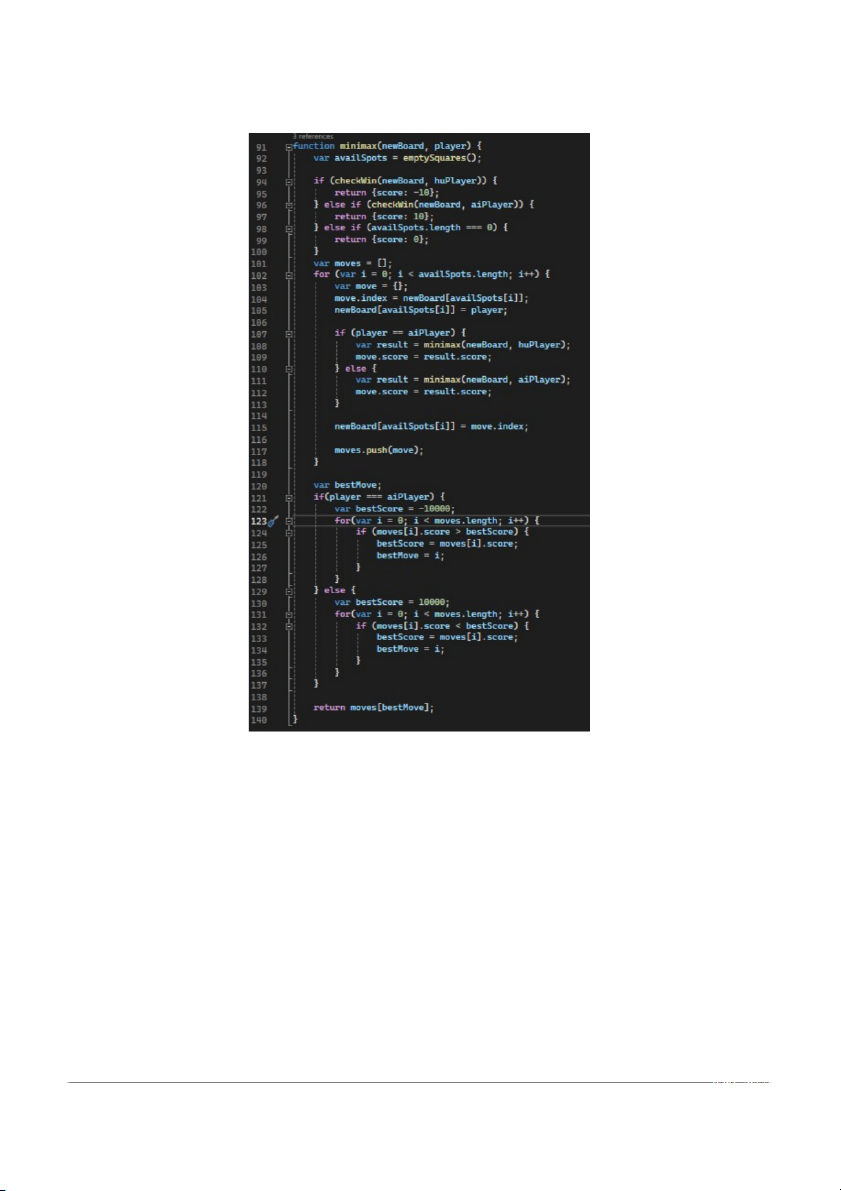
Hình 3.7: Áp dụng thuật toán MINIMAX
Đoạn mã trên triển khai thuật toán minimax để đánh giá tất cả các
nước đi có thể trong trò chơi Tic-Tac-Toe và tìm ra nước đi tốt nhất cho
người chơi AI. Dưới đây là ý nghĩa tổng quát của hàm `minimax(newBoard, player)`:
1. Hàm `minimax(newBoard, player)`: Đây là một thuật toán đệ
quy sử dụng giải thuật minimax để đánh giá và chọn ra nước đi tối
ưu cho người chơi AI. Thuật toán được áp dụng trên một bàn cờ
mới (`newBoard`) và người chơi hiện tại (`player`). 2. Bước đệ quy: 17
- Kiểm tra xem bàn cờ mới có kết thúc với người chơi `huPlayer`
thắng hay không bằng cách gọi hàm `checkWin(newBoard,
huPlayer)`. Nếu có, trả về `{score: -10}` để gán điểm thấp cho nước đi đang xét.
- Kiểm tra xem bàn cờ mới có kết thúc với người chơi `aiPlayer`
thắng hay không bằng cách gọi hàm `checkWin(newBoard,
aiPlayer)`. Nếu có, trả về `{score: 10}` để gán điểm cao cho nước đi đang xét.
- Kiểm tra xem còn ô trống trên bàn cờ mới hay không. Nếu
không còn, tức là trò chơi kết thúc với kết quả hòa, trả về `{score:
0}` để gán điểm 0 cho nước đi đang xét.
3. Duyệt qua tất cả các ô trống trên bàn cờ mới:
- Tạo một đối tượng `move` để lưu trữ thông tin về nước đi.
- Gán giá trị của ô trống cho `move.index`.
- Đánh dấu nước đi trên bàn cờ mới bằng cách gán giá trị của
người chơi hiện tại (`player`) cho ô trống đó.
- Đệ quy gọi hàm `minimax()` với bàn cờ mới và người chơi đối
thủ (`huPlayer` nếu `player` là `aiPlayer` và ngược lại) để đánh giá
tiếp các nước đi tiếp theo.
- Gán điểm của nước đi được trả về từ đệ quy cho `move.score`.
- Khôi phục lại giá trị của ô trống trên bàn cờ mới.
4. Dựa trên giá trị của `player`, chọn ra nước đi tốt nhất từ mảng `moves`:
- Nếu `player` là `aiPlayer`, tìm nước đi có điểm số (`score`) cao
nhất và gán cho `bestMove`.
- Ngược lại, nếu `player` là `huPlayer`, tìm nước đi có điểm số
thấp nhất và gán cho `bestMove`.
5. Trả về nước đi tốt nhất từ `moves[bestMove]`.
Tổng quát, hàm `minimax()` sử dụng giải thuật minimax để đánh
giá và chọn ra nước đi tối ưu cho người chơi AI trong trò chơi Tic-Tac-
Toe. Nó đánh giá tất cả các nước đi có thể và trả về nước đi có điểm số
cao nhất nếu `player` là `aiPlayer` và điểm số thấp nhất nếu `player` là `huPlayer`. 18