Báo cáo Ứng dụng thuật toán BFS trong tìm đường môn Trí tuệ nhân tạo | Trường Đại học Kiến trúc Đà Nẵng

PHÒNG GIÁO DỤC & ĐÀO TẠO
TRƯỜNG ĐẠI HỌC KIẾN TRÚC ĐÀ NẴNG
KHOA: CÔNG NGHỆ THÔNG TIN
BÁO CÁO BÀI TẬP LỚN
MÔN HỌC TRÍ TUỆ NHÂN TẠO
Chủ đề báo cáo: Áp dụng thuật toán Best First Search vào việc tìm đường
đi từ một điểm đến một điểm khác trong bản đồ của một phường
Giảng viên hướng dẫn: Nguyễn Năng Hùng Vân
Sinh viên thực hiện: Lê Văn Nhật MSSV: 2151220116 Lớp: 21CT3 I. Lời mở đầu
Bài báo cáo này trình bày về việc áp dụng thuật toán BFS vào tìm đường đi trong
bản đồ của 1 phường. Thuật toán BFS là một thuật toán tìm kiếm trong đồ thị,
trong đó việc tìm kiếm chỉ bao gồm 2 thao tác: (a) cho trước một đỉnh của đồ thị;
(b) thêm các đỉnh kề với đỉnh vừa cho vào danh sách có thể hướng tới tiếp theo.
Trong đồ thị không có trọng số, thuật toán BFS luôn tìm ra đường đi ngắn nhất
có thể. Thuật toán BFS bắt đầu từ đỉnh gốc và lần lượt nhìn các đỉnh kề với đỉnh
gốc. Sau đó, với mỗi đỉnh trong số đó, thuật toán lại lần lượt nhìn trước các đỉnh
kề với nó mà chưa được quan sát trước đó và lặp lại.
Bài toán tìm đường đi trong bản đồ là một bài toán thường gặp trong cuộc sống.
Bài toán này có thể được mô hình hóa thành bài toán tìm kiếm trong đồ thị. Trong
đó, mỗi đỉnh của đồ thị đại diện cho một điểm trong bản đồ, và mỗi cạnh của đồ
thị đại diện cho một đường đi giữa hai điểm.
Việc áp dụng thuật toán BFS vào tìm đường đi trong bản đồ có nhiều ưu điểm như sau: •
Thuật toán BFS đơn giản và dễ hiểu, dễ triển khai. •
Thuật toán BFS có hiệu quả cao trong trường hợp đường đi không bị tắc nghẽn.
Trong bài báo cáo này, chúng ta sẽ mô hình hóa bản đồ của 1 phường thành một
đồ thị không có trọng số. Sau đó, chúng ta sẽ sử dụng thuật toán BFS để tìm
đường đi giữa hai điểm trong bản đồ.
Mục tiêu của bài báo cáo
Mục tiêu của bài báo cáo này là: •
Mô hình hóa bản đồ của 1 phường thành một đồ thị không có trọng số. •
Tìm hiểu về thuật toán BFS. •
Sử dụng thuật toán BFS để tìm đường đi giữa hai điểm trong bản đồ. II. Giới thiệu
1. Giới thiệu về thuật toán và ý nghĩa của việc áp dụng thuật toán vào việc tìm
kiếm đường đi a. Giới thiệu:
• Thuật toán Best First Search (BFS) là một thuật toán tìm kiếm đường đi theo thứ
tự ưu tiên. Thuật toán này bắt đầu từ một nút gốc và tiếp tục mở rộng các nút có
giá trị ước tính thấp nhất cho đến khi tìm thấy nút đích.
• Giá trị ước tính là một hàm được sử dụng để đánh giá mức độ gần của một nút
đối với nút đích. Thuật toán BFS sẽ mở rộng các nút có giá trị ước tính thấp nhất
trước tiên, vì điều này có nhiều khả năng dẫn đến nút đích hơn. b. Ý nghĩa:
Ý nghĩa của việc áp dụng thuật toán BFS vào tìm kiếm đường đi trong bản đồ là
thuật toán này có thể tìm ra đường đi ngắn nhất từ một điểm khởi đầu đến một điểm đích.
2. Mục tiêu và phạm vi vào việc sử dụng thuật toán trong việc tìm đường đi a. Mục tiêu:
Mục tiêu của việc sử dụng BFS trong tìm đường đi trong bản đồ của một phường
là tìm ra đường đi ngắn nhất từ một điểm khởi đầu đến một điểm đích. Điều này
có thể được sử dụng cho nhiều mục đích khác nhau b. Phạm vi:
• Phạm vi của việc sử dụng BFS trong tìm đường đi trong bản đồ của một phường
phụ thuộc vào kích thước và độ phức tạp của bản đồ. Đối với các bản đồ nhỏ và
đơn giản, BFS có thể được sử dụng hiệu quả. Tuy nhiên, đối với các bản đồ lớn
và phức tạp, BFS có thể không hiệu quả.
• Trong trường hợp bản đồ của một phường, BFS có thể được sử dụng hiệu quả để
tìm đường đi từ một điểm khởi đầu đến một điểm đích trong phạm vi phường. Điều này
là do các phường thường có kích thước nhỏ và cấu trúc đơn giản.
III. Thuật toán Best First Search 1. Mô tả cơ bản
• Thuật toán Best First Search (BFS) là một thuật toán tìm kiếm đường đi theo thứ
tự ưu tiên. Thuật toán này bắt đầu từ một nút gốc và tiếp tục mở rộng các nút có
giá trị ước tính thấp nhất cho đến khi tìm thấy nút đích. • Cách hoạt động:
- Cho đỉnh xuất phát vào Open
- Nếu Open rỗng thì tìm kiếm thất bại, kết thúc việc tìm kiếm
- Lấy đỉnh đầu trong Open ra và gọi dó là Phi, cho Phi vào Closed
- Nếu Phi là đỉnh đích thì tìm kiếm thành công, kết thúc việc tìm kiếm
- Tìm tất cả các đỉnh con của Phi không thuộc Open và Closed cho vào Open theo
thứ tự tang dần về khoảng cách ước lượng đến đích
- Trở lại việc xét Open rỗng
• Cấu trúc dữ kiệu sử dụng
BFS sử dụng hai cấu trúc dữ liệu chính:
• Danh sách mở: Danh sách này chứa tất cả các nút chưa được mở.
• Danh sách đã mở: Danh sách này chứa tất cả các nút đã được mở.
• Nguyên lý làm việc
BFS dựa trên nguyên tắc rằng nút có giá trị ước tính thấp nhất có nhiều khả năng
là nút đích hơn. Do đó, thuật toán sẽ mở rộng các nút có giá trị ước tính thấp nhất trước tiên. Ưu điểm
• Thuật toán BFS luôn tìm thấy đường đi ngắn nhất từ một điểm khởi đầu đến một điểm đích.
• Thuật toán BFS là thuật toán đơn giản và dễ hiểu. Nhược điểm
• Thuật toán BFS có thể không hiệu quả trong các trường hợp đồ thị lớn và phức tạp.
IV. Bản đồ của một phường 1. Mô tả, cấu trúc, dữ liệu:
Bản đồ của một phường là một mô hình thu nhỏ của một khu vực địa lý, thường
là một khu vực đô thị. Bản đồ này thường được sử dụng để tìm đường đi, định vị
các địa điểm và hiểu cấu trúc của khu vực.
Cấu trúc của bản đồ của một phường thường bao gồm các yếu tố sau: •
Các đường giao thông: Đây là yếu tố quan trọng nhất của bản đồ, vì nó cho biết
cách di chuyển giữa các điểm khác nhau trong khu vực. •
Các địa điểm: Đây là các điểm quan tâm trong khu vực, chẳng hạn như tòa nhà,
công viên, trường học, v.v. •
Các đặc điểm địa lý: Đây là các đặc điểm tự nhiên của khu vực, chẳng hạn như sông, núi, v.v.
Dữ liệu có thể sử dụng cho việc tìm đường đi trong bản đồ của một phường bao gồm: •
Tọa độ của các điểm: Đây là dữ liệu cần thiết để xác định vị trí của các điểm trên bản đồ. •
Khoảng cách giữa các điểm: Đây là dữ liệu cần thiết để tính toán độ dài của đường đi. •
Thông tin về các đường giao thông: Đây là dữ liệu cần thiết để xác định các tuyến
đường có thể di chuyển được.
2. Vấn đề, mục tiêu:
Vấn đề cụ thể và mục tiêu cần giải quyết trong việc tìm đường đi từ một điểm
đến điểm khác trên bản đồ của phường là: •
Vấn đề cụ thể: Xác định một tuyến đường ngắn nhất hoặc nhanh nhất từ một điểm
khởi đầu đến một điểm đích trên bản đồ của phường. •
Mục tiêu cần giải quyết: Tìm ra tuyến đường tối ưu đáp ứng các tiêu chí của người
dùng, chẳng hạn như độ dài đường đi, thời gian di chuyển, chi phí di chuyển, v.v. V.
Áp dụng thuật toán 1. Mô tả thuật toán:
Cách thức triển khai thuật toán
Thuật toán BFS có thể được triển khai theo các bước sau:
1. Khởi tạo: Bắt đầu từ nút gốc của đồ thị.
2. Thêm nút gốc vào danh sách mở.
3. Lặp lại các bước sau cho đến khi tìm thấy nút đích hoặc danhsách mở trống: o
Lấy nút có giá trị ước tính thấp nhất từ danh sách mở.
o Nếu nút đó là nút đích, thì kết thúc thuật toán.
o Ngược lại, thêm tất cả các nút kề với nút đó vào danh sách mở. Xử lý dữ liệu
Dữ liệu cần thiết để triển khai thuật toán BFS cho tìm đường đi trong bản đồ của phường bao gồm: •
Tọa độ của các điểm: Đây là dữ liệu cần thiết để xác định vị trí của các điểm trên bản đồ. •
Khoảng cách giữa các điểm: Đây là dữ liệu cần thiết để tính toán độ dài của đường đi. •
Thông tin về các đường giao thông: Đây là dữ liệu cần thiết để xác định các tuyến
đường có thể di chuyển được.
2. Lập trình thuật toán: #hàm tìm kiếm BFS
from queue import PriorityQueue as pq
def tk_BFS(S=Node('A'), G=Node('N')): • #B1 • Open = pq() • Open.put(S) • #B2 • while True: • if Open.empty() == True: •
print("tìm kiếm không thành công") • return • #B3 • Closed = pq() •
O = Open.get() Closed.put(O) #B4: • if O.name == G.name: •
print('Tìm kiếm thành công') • #in đường đi • induongdi(O) • return • #B5 • i = 0 •
while i < len(data[O.name]) - 1: • name = data[O.name][i] • h = data[O.name][-1] •
tam = Node(name = name, h = h) • tam.par = O •
if not kiemtra(tam, Open) and not kiemtra(tam, Closed): • Open.put(tam) • i += 1
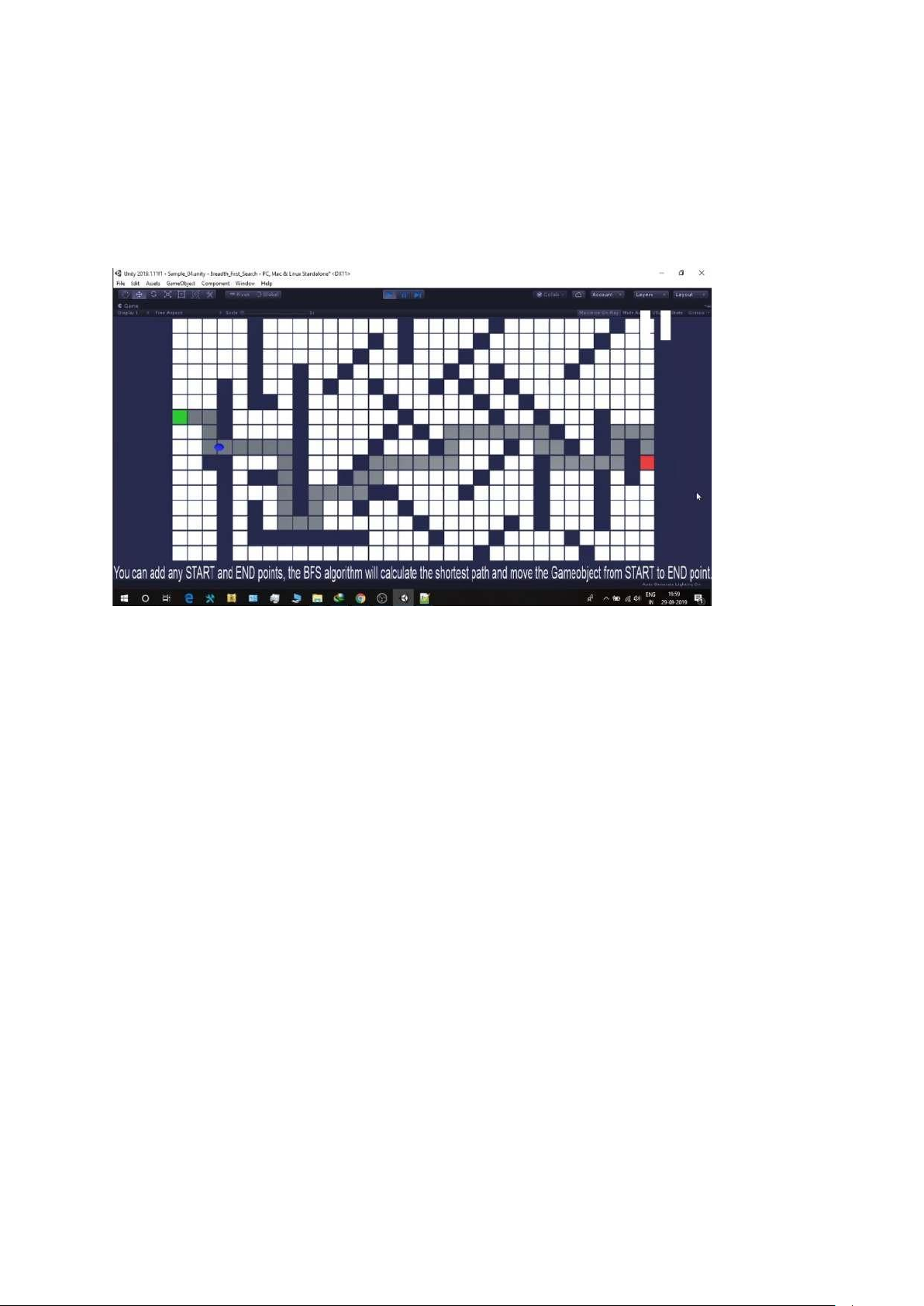
VI. Kết quả, đánh giá 1. Kết quả:
Kết quả thu được từ việc áp dụng thuật toán BFS vào tìm đường đi trên bản đồ
của phường là một tuyến đường ngắn nhất hoặc nhanh nhất từ một điểm khởi đầu
đến một điểm đích. Tuyến đường này luôn tồn tại trong các đồ thị không có vòng lặp. 2. Đánh giá: • Tính hiệu quả •
Thuật toán BFS là một thuật toán tìm đường đi đơn giản và hiệu quả. Nó luôn tìm
thấy đường đi ngắn nhất trong các đồ thị không có vòng lặp. Tuy nhiên, thuật
toán BFS có thể không hiệu quả trong các đồ thị lớn và phức tạp. • Độ chính xác •
Thuật toán BFS luôn tìm thấy đường đi ngắn nhất trong các đồ thị không có vòng
lặp. Do đó, thuật toán này có độ chính xác cao.
VII. Kết luận 1. Ý nghĩa:
Thuật toán BFS có thể được sử dụng để tìm đường đi ngắn nhất hoặc nhanh nhất
từ một điểm khởi đầu đến một điểm đích trên bản đồ của một phường. Việc áp
dụng thuật toán BFS có ý nghĩa quan trọng trong các ứng dụng thực tế, chẳng hạn như: •
Ứng dụng chỉ đường: Các ứng dụng chỉ đường trên điện thoại thông minh sử
dụng thuật toán BFS để giúp người dùng tìm đường đi từ một điểm đến điểm khác. •
Ứng dụng giao thông: Các ứng dụng giao thông sử dụng thuật toán BFS để giúp
người dùng tìm đường đi tránh tắc đường. •
Ứng dụng vận tải: Các ứng dụng vận tải sử dụng thuật toán BFS để lập kế hoạch
tuyến đường cho các phương tiện giao thông. 2. Kết quả:
Kết quả của việc áp dụng thuật toán BFS trong việc tìm đường đi trên bản đồ của
một phường là một tuyến đường ngắn nhất hoặc nhanh nhất từ một điểm khởi
đầu đến một điểm đích. Tuyến đường này luôn tồn tại trong các đồ thị không có vòng lặp.
3. Đánh giá tổng quan:
Thuật toán BFS là một thuật toán tìm đường đi đơn giản và hiệu quả, có thể được
sử dụng để tìm đường đi trong bản đồ của một phường. Trong tình huống cụ thể
của việc tìm đường đi trong các phường nhỏ và đơn giản, thuật toán BFS là một lựa chọn phù hợp.
Việc áp dụng thuật toán BFS vào tìm kiếm đường đi trong bản đồ của 1 phường
có nhiều ưu điểm như sau: •
Thuật toán BFS đơn giản và dễ hiểu, dễ triển khai. •
Thuật toán BFS có hiệu quả cao trong trường hợp đường đi không bị tắc nghẽn. •
Thuật toán BFS có thể tìm ra nhiều đường đi giữa hai điểm, bao gồm cả đường
đi ngắn nhất và đường đi nhanh nhất.
Tuy nhiên, thuật toán BFS cũng có một số nhược điểm như sau: •
Thuật toán BFS có thể không hiệu quả trong trường hợp đường đi bị tắc nghẽn. •
Thuật toán BFS có thể tiêu tốn nhiều bộ nhớ trong trường hợp đồ thị có kích thước lớn.
Nhìn chung, việc áp dụng thuật toán BFS vào tìm kiếm đường đi trong bản đồ
của 1 phường là một giải pháp hiệu quả và có thể được sử dụng trong nhiều ứng dụng thực tế.
Dưới đây là một số ví dụ cụ thể về việc áp dụng thuật toán BFS vào tìm kiếm
đường đi trong bản đồ của 1 phường: •
Ứng dụng trong hệ thống định vị GPS. •
Ứng dụng trong hệ thống giao thông thông minh. •
Ứng dụng trong hệ thống điều hướng đường bộ.
Trong tương lai, việc áp dụng thuật toán BFS vào tìm kiếm đường đi trong bản
đồ của 1 phường sẽ ngày càng trở nên phổ biến và được sử dụng trong nhiều ứng dụng mới. MỤC LỤC I.
Lời mở đầu....................................................................................................2
II. Giới thiệu....................................................................................................3
1. Giới thiệu về thuật toán và ý nghĩa của việc áp dụng thuật toán vào
việc tìm kiếm đường đi....................................................................................3 a.
Giới thiệu:...............................................................................................3
b. Ý nghĩa:...................................................................................................3
2. Mục tiêu và phạm vi vào việc sử dụng thuật toán trong việc tìm
đường đi............................................................................................................3 a.
Mục tiêu:.................................................................................................3
b. Phạm vi:..................................................................................................3
III. Thuật toán Best First Search....................................................................4
1. Mô tả cơ bản..............................................................................................4
IV. Bản đồ của một phường............................................................................5
1. Mô tả, cấu trúc, dữ liệu:...........................................................................5
2. Vấn đề, mục tiêu:.......................................................................................6 V.
Áp dụng thuật toán.......................................................................................6
1. Mô tả thuật toán:.......................................................................................6
2. Lập trình thuật toán:................................................................................7
VI. Kết quả, đánh giá......................................................................................8
1. Kết quả:......................................................................................................8
2. Đánh giá:....................................................................................................8
VII. Kết luận......................................................................................................8
1. Ý nghĩa:......................................................................................................8
2. Kết quả:......................................................................................................9
3. Đánh giá tổng quan:..................................................................................9