Báo cáo Xây dựng ứng dụng đánh caro giữa người và máy môn Trí tuệ nhân tạo | Trường Đại học Kiến trúc Đà Nẵng

TRƯỜNG ĐẠI HỌC KIẾN TRÚC ĐÀ NẴNG
KHOA CÔNG NGHỆ THÔNG TIN
TRƯỜNG ĐẠI HỌC KIẾN TRÚC ĐÀ NẴNG
DANANG ARCHITECTURE UNIVERSITY
BÀI TẬP LỚN TRÍ TUỆ NHÂN TẠO ĐỀ TÀI:
Xây dựng ứng dụng đánh Caro giữa người và máy Giáo Viên : Nguyễn Năng Hùng Vân Sinh Viên : Đoàn Thanh Tùng Trần Thị Yến Nhi MSSV : 2151220256 2151220257
Đà Nẵng, Ngày 02 Tháng 01 Năm 2024 Lời mở đầu
Hiện nay, việc ứng dụng trí tuệ nhân tạo vào việc phát triển game đã trở nên vô
cùng phổ biến, đặc biệt là những game mang tính trí tuệ cao. Và cờ Caro là một
game như vậy. Chính vì lý do đó mà chúng em đã quyết định lựa chọn cờ Caro
làm để tài cho bài tập lớn môn trí tuệ nhân tạo. Đây là tài liệu dùng để miêu tả
một cách cơ bản về việc xây dựng game cờ Caro. Trong game có sử dụng thuật
toán MiniMax với độ sâu là 4 và thuật toán cắt cụt alpha-beta để giảm thời gian
tính toán. Tài liệu này giúp ta có một cái nhìn tổng quát về việc áp dụng thuật
toán MiniMax và cắt cụt alpha-beta vào game cờ Caro. Do thời gian có hạn nên
chúng em chưa thể tối ưu được các thuật toán sử dụng trong game, nhưng chúng
em sẽ cố gắng hoàn thiện trong thời gian sớm nhất.
Nhóm thực hiện đề tài này với mục đích xây dựng game Caro có tính nhân
tạo cao. Tuy nhiên trong quá trình thực hiện không thể tránh khỏi có những sai
sót, chúng em rất mong nhận được những góp ý và đánh giá của cô.
I.Giới thiệu đề tài “Game Caro”
Game gồm có 2 người chơi, một người cầm quân X, một người cầm quân O. Hai
người chơi sẽ lần lượt đưa đánh quân tương ứng của mình trên một bàn cờ MxN ô (thường thì M = N). Luật chơi:
Quân X là quân được đánh trước. Hai người chơi có thể đánh vào bất kỳ ô nào
trên bàn cờ miễn là ô đó chưa được đánh.
Trò chơi kết thúc khi một trong hai người chơi có 5 quân thằng hàng liên tiếp
nhau (ngang, dọc hoặc chéo).
Dưới đây là bàn cờ caro kích thước 15x15
II.Thuât toán MiniMax và thuật toán cắt cụt Alpha-Beta 1. Thuật toán MiniMax a. Nguyên lý: •
Có 2 người chơi là Min và Max. •
Một chiến lược tối ưu là một chuỗi các nước đi giúp đưa đến
trạng thái đích mong muốn. •
Chiến lược của MAX bị ảnh hưởng ( phụ thuộc ) vào các nước
đi của MIN –và ngược lại. •
MAX cần chọn một chiến lược giúp cực đại hóa giá trị của
hàm mục tiêu – với giả sử là MIN đi các nước đi tối ưu. •
Chiến lược này được xác định bằng việc xét các giá trị
MINIMAX đối với mỗi nút trong cây biểu diễn trò chơi. •
MAX chọn các nước đi tương ứng với giá trị MINIMAX cực
đại ( MIN chọn các nước đi ứng với giá trị MINIMAX cực tiểu. b. Áp dụng vào game Caro:
Người chơi cầm quân X đóng vai trò như Max, người chơi cầm quân O
đóng vai trò như Min. Để quyết định nước đi tiếp theo, ta xây dựng một thủ tục
đệ quy gồm 2 hàm max_value() để tìm nước đi tiếp theo cho quân X,
min_value() để tìm nước đi tiếp theo cho quân O. Để giảm thời gian của giải
thuật đệ quy, ta giới hạn độ sâu của giải thuật bằng 4.
int max_value(state s, int dept){ if(terminal_test()
|| dept >= 4) return eval(s); v = -;
for(duyệt tất cả các trạng thái con s’ của
s){ v = max(v, min_value(s’, dept + 1)); } retur n v; }
int min_value(state s, int dept){ if(terminal_test()
|| dept >= 4 ) return eval(s); v = +;
for(duyệt tất cả các trạng thái con s’ của
s){ v = min(v, max_value(s’, dept + 1)); } retur n v; }
Hàm xác định trạng thái kết thúc terminal_test():
Hàm có nhiệm vụ xác định xem trò chơi có kết thúc hay không khi một
quân cờ được đánh thêm vào. Hàm hoạt động như sau:
• Từ vị trí thêm quân cờ, kiểm tra theo các chiều ngang, dọc, chéo(ví
dụ kiểm tra theo chiều ngang: giả sử quân cờ đánh vào là X, duyệt
theo hướng bên trái cho đến khi gặp quân O hoặc tường thì dừng lại,
tiếp tục duyệt theo hướng bên phải tương tự để xác định số quân X liên tiếp nhau).
• Nếu số quân X (hoặc O) liên tiếp là 5 thì trả lại giá trị true, ngược
lại trả về giá trị false.
2.Thuật toán cắt cụt alpha-beta
Trong chiến lược Minimax với độ sâu hạn chế thì số đỉnh của cây trò chơi
phải xét vẫn còn rất lớn với h>=3. Khi đánh giá đỉnh utới độ sâu h, thuật toán
Minimax đòi hỏi phải đánh giá tất cả các đỉnh của cây gốc u với độ sâu h. Tuy
nhiên, phương pháp cắt cụt alpha-beta cho phép cắt bỏ những nhánh không cần
thiết cho việc đánh giá đỉnh u. Phương pháp này làm giảm bớt số đỉnh phải xét
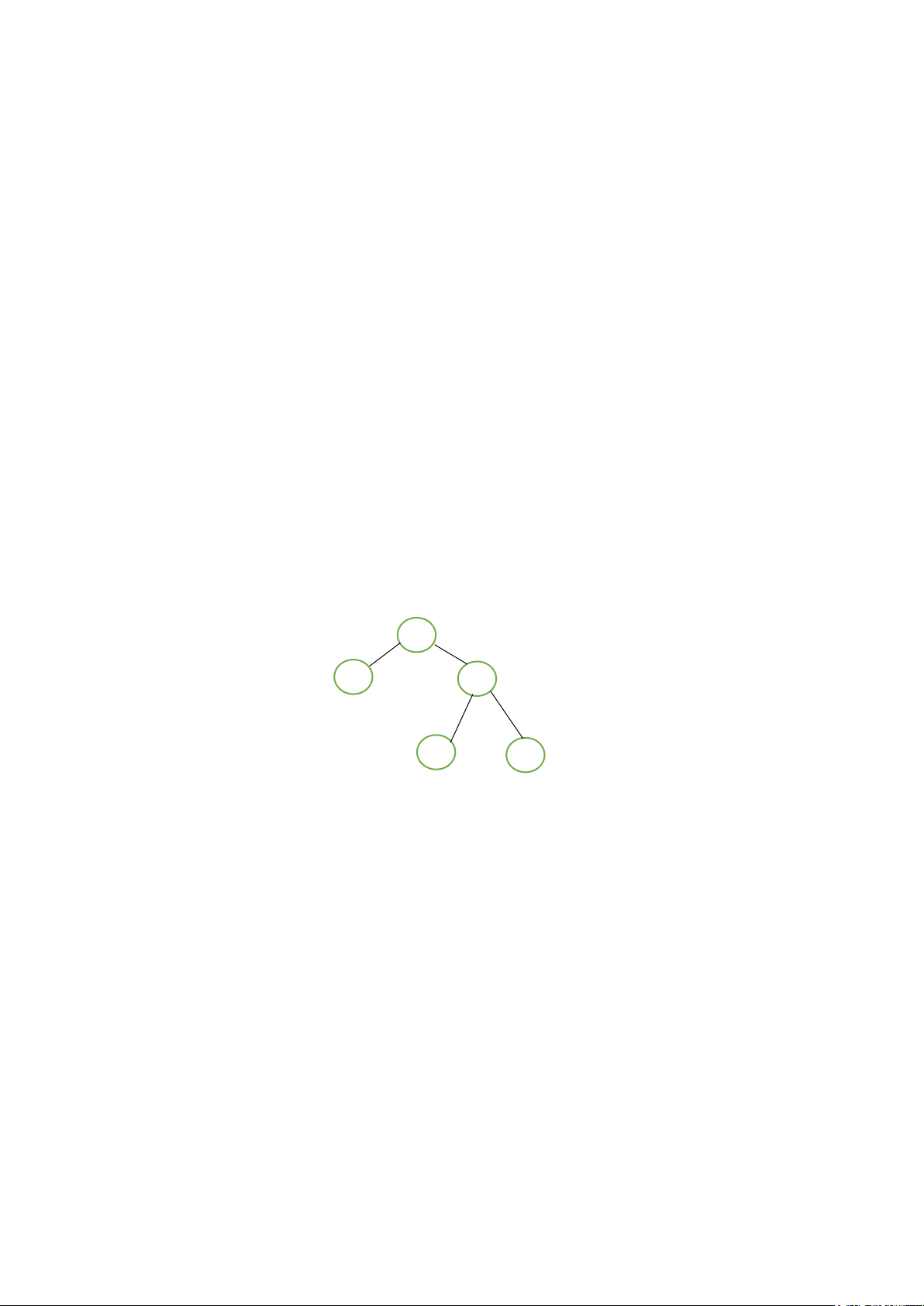
mà không ảnh hưởng đến kết quả đánh giá đỉnh u. Ý tưởng: Giả sử tại thời
điểm hiện tại đang ở đỉnh Trắng a, đỉnh a có anh em là v đã được đánh giá. Giả
sử cha của đỉnh a là b, b có anh em là u đã được đánh giá, và cha của b là c như hình sau: C U B min V A max max
Khi đó ta có giá trị đỉnh Trắng c ít nhất là giá trị của u, giá trị của đỉnh Đen b
nhiều nhất là giá trị của v. Do đó, nếu eval(u) > eval(v) ta không cần đi xuống để
đánh giá đỉnh a nữa mà vẫn không ảnh hưởng đến đánh giá đỉnh c. Hay nói cách
khác, ta có thểcắt bỏ cây con gốc a. Lập luận tương tự cho trường hợp a là đỉnh
Đen, trường hợp này nếu eval(u)đặt kỹ thuật này, đối với các đỉnh nằm trên đường đi từ gốc tới đỉnh hiện thời, ta
sử dụng tham số α để ghi lại giá trị lớn nhất trong các giá trị của các đỉnh con đã
đánh giá của một đỉnh Trắng, tham số β để ghi lại giá trịnhỏ nhất trong các giá
trị của các đỉnh con đã đánh giá của một đỉnh Đen.
int max_value(state s, int dept, int alpha, int beta) {
if(terminal_test() || dept >= 4) return eval(s); v = -;
for(duyệt tất cả các trạng thái con s’ của s){ v =
max(v, min_value(s’, dept + 1, alpha, beta)); } if(v > beta) return v; alpha = max(alpha, v); return v; }
int min_value(state s, int dept, int alpha, int beta) {
if(terminal_test() || dept >= 4 ) return eval(s); v =
+; for(duyệt tất cả các trạng thái con s’ của s){ v =
min(v, max_value(s’, dept + 1, alpha, beta)); }
if(v < alpha) return v; beta= min(beta, v); return v; } 3.Hàm đánh giá
Hàm đánh giá là một hàm quan trọng trong việc xây dựng trò chơi cờ caro. Hàm
này giúp cho điểm trạng thái của bàn cờ để từ đó xây dựng cây trò chơi. Việc
xây dựng hàm lượng giá hợp lý, chính xác sẽ giúp cho hệ thống có đánh giá
chính xác về trạng thái bàn cờ để đưa ra nước đi thông minh hơn.
Trong game caro, để tính điểm cho trạng thái bàn cờ ta đưa ra các tiêu chí
sau: Trong trường hợp chắc chắn thắng, điểm cộng sẽ là
+Int32.MAX_VALUE đối với X và -Int32.MAX_VALUE đối với O.
• Trong trường hợp có nước 3, điểm cộng sẽ là +300 đối với X và -300 đối với O
• Trong trường hợp có nước 4, điểm cộng sẽ là +600 đối với X và -600 đối với O
II.Cài đặt chương trình
Chương trình gồm các lớp như sau: 2. Lớp Board
Là lớp để lưu lại trạng thái của bàn cờ Biến:
• COLUMN, ROW: số cột và hàng của bàn cờ
• PieceState: các trạng thái có thể có của một quân cờ(X, O, chưa đánh hoặc không hợp lệ).
• boardState: là một mảng lưu lại các trạng thái của các quân cờ. byte[] boardState; Hàm:
• GetPieceAt(): Lấy trạng thái của quân cờ tại một tọa độ xác đinh.
• IsOccupied(): Xác định xem tại một vị trí xác định đã có quân cờ nào đươc đánh chưa.
• AddPiece(): Thêm một quân cờ vào bàn cờ.
• IsWinner(): Kiểm tra trạng thái hiện tại của bàn cờ đã kết thúc chưa. 3. Lớp CaroAI Biến:
• MINMAX_DEPTH: độ sâu của giải thuật MiniMax
• numMoves, numComparisons: số nút con duyệt qua và số lượng phép so
sánh cần sử dụng trong giải thuật MiniMax (dùng để đánh giá thuật toán).
• computerPiece, playerPiece: dùng để xác định kiểu quân cờ của người
chơi và máy(X hay O). Hàm:
• MinimaxHelper(): xác định nếu thêm một quân cờ vào trạng thái hiện tại
của bàn cờ có làm trạng thái hiện tại trở thành trạng thái kết thúc hay
không, nếu không thì sử dụng giải thuật MiniMax.
• MiniMax(): cài đặt giải thuật MiniMax.
private Result MiniMax(Node node, int depth, int alpha, int
beta, bool needMax) { if (depth <= 0 ||
node.IsTerminalNode()) { var result = new Result(); var score =
node.GetObjectiveValue(computerPiece);
result.setScore(score); return result; } var best = new Result();
foreach (var child in node.getChildren()) { var result2 =
MiniMax(child, depth-1, alpha, beta, !needMax);
var score = result2.getScore();
numComparisons++; if (needMax) { if
(score > alpha) { alpha = score; best = new Result(); best.add(child);
best.addAll(result2.gameNodes); } if (beta <= alpha) { break; }
} else { if (score < beta) { best = new Result(); best.add(child);
best.addAll(result2.gameNodes); beta = score; } if (beta <= alpha) { break; } } }
var retval = needMax ? alpha :
beta; best.setScore(retval); return best; } 4.Lớp Result Biến: •
score: điểm của trạng thái bàn cờ. •
gameNodes: là một mảng chứa các nút con của nút đang xét Hàm: • GetMove(): •
getScore(): lấy điểm của trạng thái bàn cờ. •
setScrore(): gán điểm của trạng thái bàn cờ. • Add(): II.
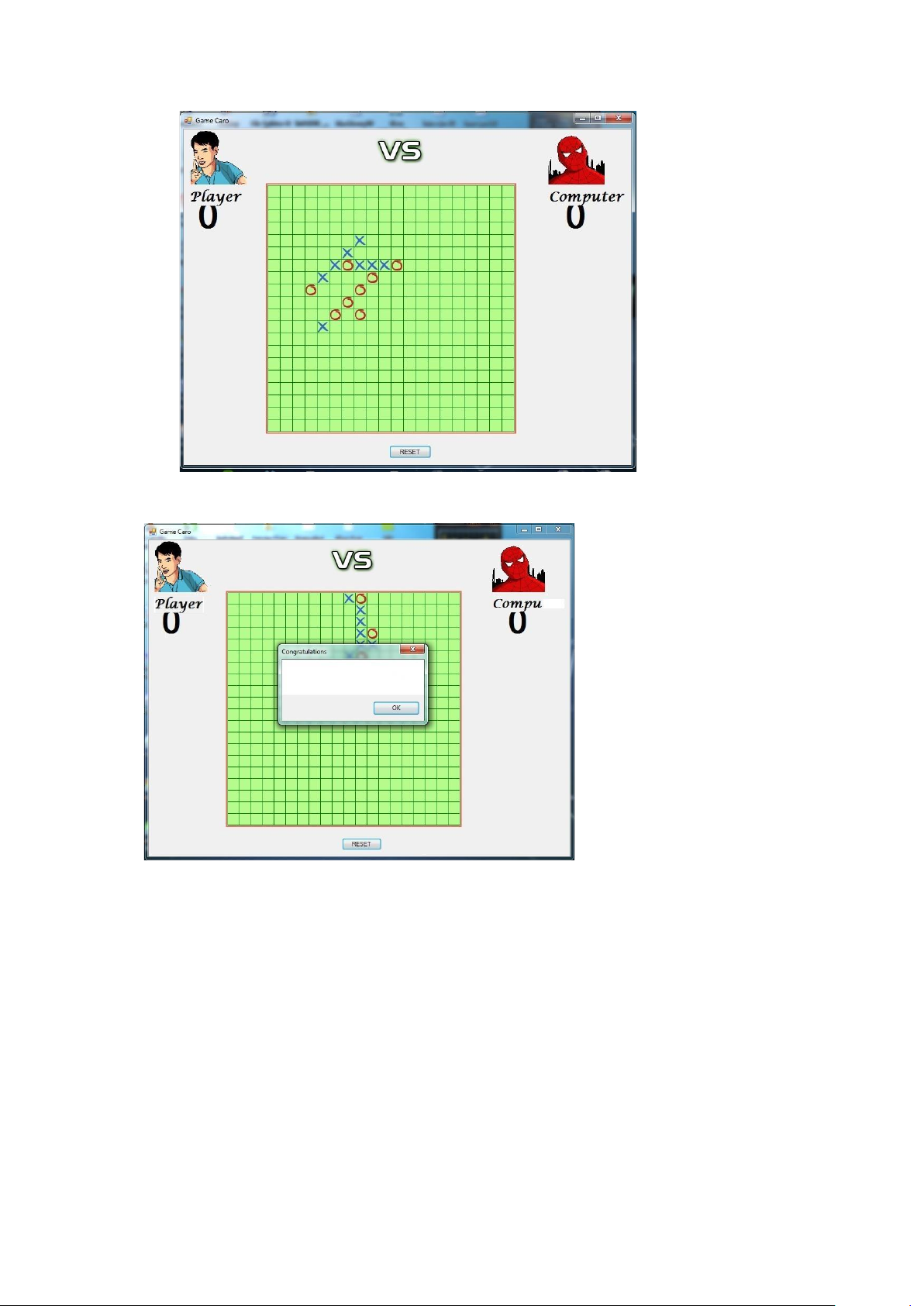
Giao diện chương trình DEMO 1. Giao diện khi vào game 2.Giao diện khi chơi
3.Giao diện khi chiến thắng tes
Xin chúc miJng!Ban Iá ngiJói chién thang!