





Preview text:
ĐỀ 1
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 10
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
x − y + 2 0
Câu 1. Miền nghiệm của hệ bất phương trình
là phần mặt phẳng chứa điểm 2x + y 3 A. (1; ) 1 . B. (1;2) . C. (2; ) 1 − . D. ( 1 − ;2) .
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu a chia hết cho 9 thì a chia hết cho 3 .
B. Nếu em chăm chỉ thì em thành công.
C. Nếu a b thì 2 2 a b .
D. Nếu một tam giác có một góc bằng 0
60 thì tam giác đó đều.
Câu 3. Phát biểu nào sau đây đúng?
A. Hai vectơ không bằng nhau thì độ dài của chúng không bằng nhau.
B. Hai vectơ bằng nhau thì có giá trùng nhau hoặc song song.
C. Hai vectơ không bằng nhau thì chúng không cùng hướng.
D. Hai vectơ có độ dài không bằng nhau thì không cùng hướng.
Câu 4. Trong hệ tọa độ Oxy, cho A(2;− )
3 ; B(4;7) . Tìm tọa độ trung điểm I của đoạn AB . A. I (8; 2 − ) 1
B. I (6;4)
C. I (3;2) D. I (2;10)
Câu 5. Cho hình bình hành ABCD. Mệnh đề nào sau đây sai?
A. AB = DC .
B. AB + AC = AD .
C. BA+ BC = BD.
D. AB + AD = AC .
Câu 6. Cho tam giác ABC biết 0
c = 5cm; b = 8cm, A = 60 . Bán kính đường tròn nội tiếp tam giác ABC bằng 10 3
A. r = 3cm .
B. r = 2 3cm . C. r = cm . D. r =1cm . 31
Câu 7. Cân nặng (kg) của một nhóm học sinh nữ lớp 10A cho bởi số liệu sau: 38 39 44 44 46 47 47 48 52 55
Tìm số trung vị của mẫu số liệu trên. A. 46,5 . B. 44 . C. 46 . D. 47 .
Câu 8. Cho tập hợp A = 1 − ;0;1;
2 . Khẳng định nào sau đây là đúng? A. A = 1 − ; ) 3 *. B. A = ( 1 − ; ) 3 Q . C. A = 1 − ; ) 3 . D. A = 1 − ;3) .
Câu 9. Cho tam giác ABC có trung tuyến AM . Hãy phân tích AM theo hai vectơ AB và AC .
AB + AC
AB − AC
AB + AC
A. AM = AB + BC . B. AM = . C. AM = . D. AM = . 2 2 2 −
Câu 10. Theo dõi thời gian làm một bài toán (tính bằng phút) của 40 học sinh, giáo viên lập được bảng sau:
Phương sai của mẫu số liệu trên gần với số nào nhất? A. 6 .
B. 9 . C. 40 . D. 12 .
Câu 11. Đường kính của một đồng hồ cát là 8,52m với độ chính xác đến 1cm . Dùng giá trị gần đúng của là
3,14 cách viết chuẩn của chu vi (sau khi quy tròn) là
A. Đáp án khác. B. 26,6. C. 26,8. D. 26,7. Trang 1
Câu 12. Cho tập hợp A = 1;2;3;
4 . Số các tập con của tập A là A. 16. B. 8 . C. 12 . D. 10.
Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho các tập hợp A = {x x 2}; B ={x −3 x +1 4}; C ={x − 2023 x −1 2022};
D = {x | 2x 7}. Khi đó: a) C = [ 2021 − ; 2023) . 7 b) D = ; + . 2 c) B = ( 4 − ;3] .
d) A = (2;+) .
Câu 2. Cho ba điểm ( A 1; 2
− ), B(0;4),C(3;2) . Khi đó: a) AB = ( 1 − ;6) .
b) AC = (2;4); BC = (3; 2 − ) . 1
c) Tọa độ trung điểm của đoạn AB là I ;1 . 2
d) Tọa độ điểm N sao cho AN + 2BN − 4CN = 0 là N (11;12) .
Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
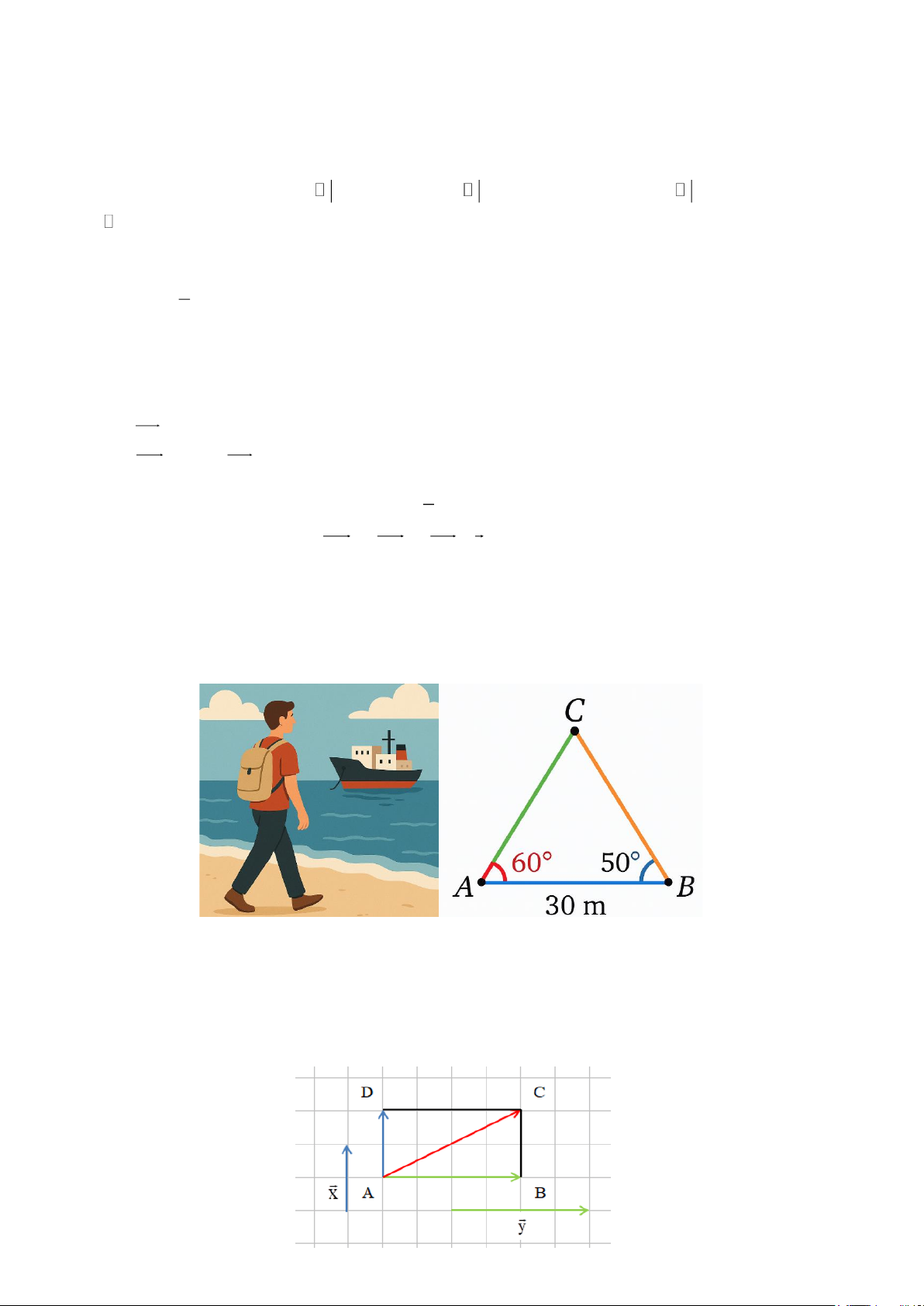
Câu 1. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi.
Người đó tiến hành đo đạc và thu được kết quả: AB 30 ,
m CAB 60 ,CBA 50 = = =
. Tính khoảng cách từ vị trí
A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét). r
Câu 2. Một Ca nô di chuyển từ bờ sông bên này sang bờ sông bên kia, theo phương x (vuông góc với hai bờ ur
sông); dòng sông chảy theo hướng y (song song với 2 bờ như hình dưới). Biết vận tốc của Ca nô là 30 km / h
và của dòng nước là 2 km / h . Hỏi vận tốc của Ca nô so với bờ sông là bao nhiêu (làm tròn kết quả đến hàng phần trăm)? Trang 2
Câu 3. Có 100 học sinh tham dự kỳ thi học sinh giỏi Toán (thang điểm là 20) kết quả được cho bởi bảng sau. Điểm
9 10 11 12 13 14 15 16 17 18 19
Tần số 1 1 3 5 8 13 19 24 14 10 2
Số trung vị của mẫu số liệu trên bằng bao nhiêu?
Câu 4. Bác Hai có một mảnh đất rộng 6 ha. Bác dự tính trồng cà chua và bắp cho mùa vụ sắp tới. Nếu trồng
bắp thì bác Hai cần 10 ngày để trồng một ha. Nếu trồng cà chua thì bác Hai cần 20 ngày để trồng một ha. Biết
rằng mỗi ha bắp sau thu hoạch bán được 30 triệu đồng, mỗi ha cà chua sau thu hoạch bán được 50 triệu đồng
và bác Hai chỉ còn 100 ngày để canh tác cho kịp mùa vụ. Số tiền (triệu đồng) nhiều nhất mà bác Hai có thể thu
được sau mùa vụ này là bao nhiêu?
Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Câu 1. Cho tam giác ABC có góc nhọn tại A . Vẽ bên ngoài tam giác ABC các tam giác vuông cân đỉnh A
là ABD và ACE. Gọi M là trung điểm BC . Chứng minh AM ^ DE.
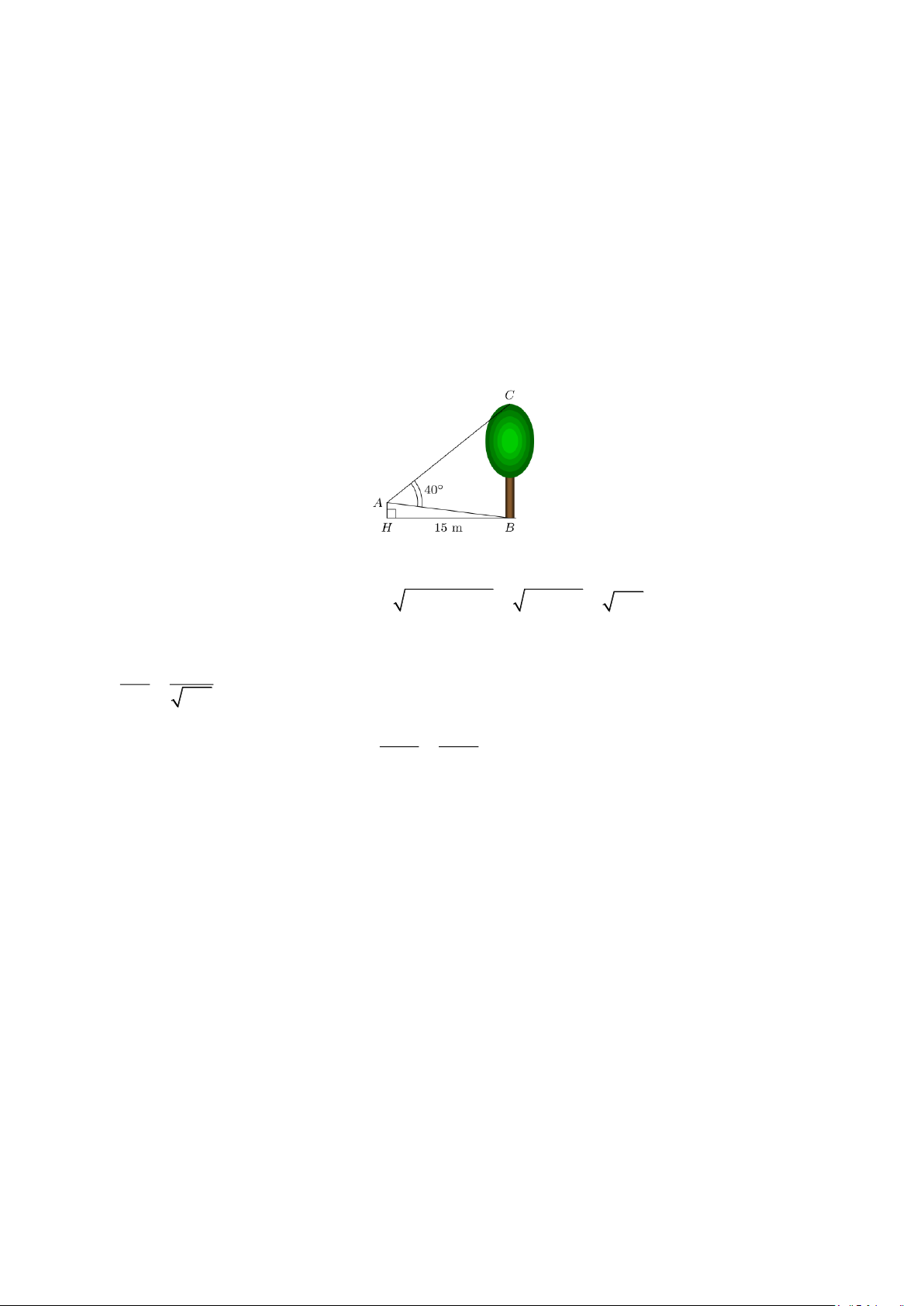
Câu 2. Từ vị trí A người ta quan sát một cây cao. Biết AH = 3 (m), HB =15 (m), BAC 40 = . Khi đó chiều cao của cây là.
Câu 3. Trong lớp 11A có 16 học sinh giỏi Toán, 15 học sinh giỏi môn Lý và 11 học sinh giỏi môn Hóa. Biết
rằng có 9 học sinh vừa giỏi Toán và Lý (có thể giỏi thêm môn Hóa), 6 học sinh vừa giỏi Lý và Hóa (có thể
giỏi thêm môn Toán), 8 học sinh vừa giỏi Hóa và Toán (có thể giỏi thêm môn Lý) và trong đó chỉ có đúng 11
học sinh giỏi đúng hai môn. Hỏi có bao nhiêu học sinh của lớp giỏi cả ba môn Toán, Lý, Hóa.
Câu 4. Người ta dự định dùng 2 nguyên liệu là mía và củ cải đường để chiết xuất ít nhất 140 kg đường kính
(độ tinh khiết cao) và 9 kg đường cát (có lẫn tạp chất màu). Từ mỗi tấn mía giá 4 triệu đồng, có thể chiết xuất
được 20 kg đường kính và 0, 6 kg đường cát. Từ mỗi tấn củ cải đường giá 3 triệu đồng ta chiết xuất được 10
kg đường kính và 1,5 kg đường cát. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên
liệu là ít nhất. Biết cơ sở cung cấp nguyên liệu chỉ cung cấp không quá 10 tấn mía và không quá 9 tấn củ cải đường. LỜI GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. Trang 3
x − y + 2 0
Câu 1. Miền nghiệm của hệ bất phương trình
là phần mặt phẳng chứa điểm 2x + y 3 A. (1; ) 1 . B. (1;2) . C. (2; ) 1 − . D. ( 1 − ;2) . Lời giải Chọn B
Lần lượt thay các bộ số vào hệ bất phương trình ta được một nghiệm của hệ bất phương trình trên là (1;2) .
x − y + 2 0
Vậy miền nghiệm của hệ bất phương trình
là phần mặt phẳng chứa điểm (1;2) . 2x + y 3
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu a chia hết cho 9 thì a chia hết cho 3 .
B. Nếu em chăm chỉ thì em thành công.
C. Nếu a b thì 2 2 a b .
D. Nếu một tam giác có một góc bằng 0
60 thì tam giác đó đều. Lời giải Chọn A
Câu 3. Phát biểu nào sau đây đúng?
A. Hai vectơ không bằng nhau thì độ dài của chúng không bằng nhau.
B. Hai vectơ bằng nhau thì có giá trùng nhau hoặc song song.
C. Hai vectơ không bằng nhau thì chúng không cùng hướng.
D. Hai vectơ có độ dài không bằng nhau thì không cùng hướng. Lời giải Chọn B
Theo định nghĩa hai vectơ bằng nhau thì chúng cùng phương nên có giá trùng nhau hoặc song song.
Câu 4. Trong hệ tọa độ Oxy, cho A(2;− )
3 ; B(4;7) . Tìm tọa độ trung điểm I của đoạn AB . A. I (8; 2 − ) 1
B. I (6;4)
C. I (3;2) D. I (2;10) Lời giải Chọn C 2 + 4 3 − + 7 Ta có I ; = (3;2). 2 2
Câu 5. Cho hình bình hành ABCD. Mệnh đề nào sau đây sai?
A. AB = DC .
B. AB + AC = AD .
C. BA+ BC = BD.
D. AB + AD = AC . Lời giải Chọn B B C A D
Ta có AB + AD = AC ; BA+ BC = BD đúng theo quy tắc hình bình hành
AB = DC đúng theo tính chất hình bình hành và định nghĩa véctơ bằng nhau.
AB + AC = AD sai. Trang 4
Câu 6. Cho tam giác ABC biết 0
c = 5cm; b = 8cm, A = 60 . Bán kính đường tròn nội tiếp tam giác ABC bằng 10 3
A. r = 3cm .
B. r = 2 3cm . C. r = cm . D. r =1cm . 31 Lời giải Chọn A Ta có 2 2 2 2 0
a = b + c − 2bccos A = 8 + 5 − 2.8.5. o c s60 = 7cm . 1 1 a + b + c 7 + 8 + 5 0 2
S = bc sin A = .8.5.sin 60 = 10 3cm ; p = = = 10cm 2 2 2 2 S 10 3 Suy ra r = = = 3cm . p 10
Câu 7. Cân nặng (kg) của một nhóm học sinh nữ lớp 10A cho bởi số liệu sau: 38 39 44 44 46 47 47 48 52 55
Tìm số trung vị của mẫu số liệu trên. A. 46,5 . B. 44 . C. 46 . D. 47 . Lời giải Chọn A
Dãy trên đã sắp xếp không giảm, và có 10số trong mẫu số liệu.
Số liệu thứ 5 là 46 và số liệu thứ 6 là 47. 46 + 47
Vậy số trung vị là M = = 46,5 . e 2
Câu 8. Cho tập hợp A = 1 − ;0;1;
2 . Khẳng định nào sau đây là đúng? A. A = 1 − ; ) 3 *. B. A = ( 1 − ; ) 3 Q . C. A = 1 − ; ) 3 . D. A = 1 − ;3) . Lời giải Chọn D
Câu 9. Cho tam giác ABC có trung tuyến AM . Hãy phân tích AM theo hai vectơ AB và AC .
AB + AC
AB − AC
AB + AC
A. AM = AB + BC . B. AM = . C. AM = . D. AM = . 2 2 2 − Lời giải Chọn B
AB + AC
Ta có AB + AC = AM + MB + AM + MC = 2AM nên AM = . 2
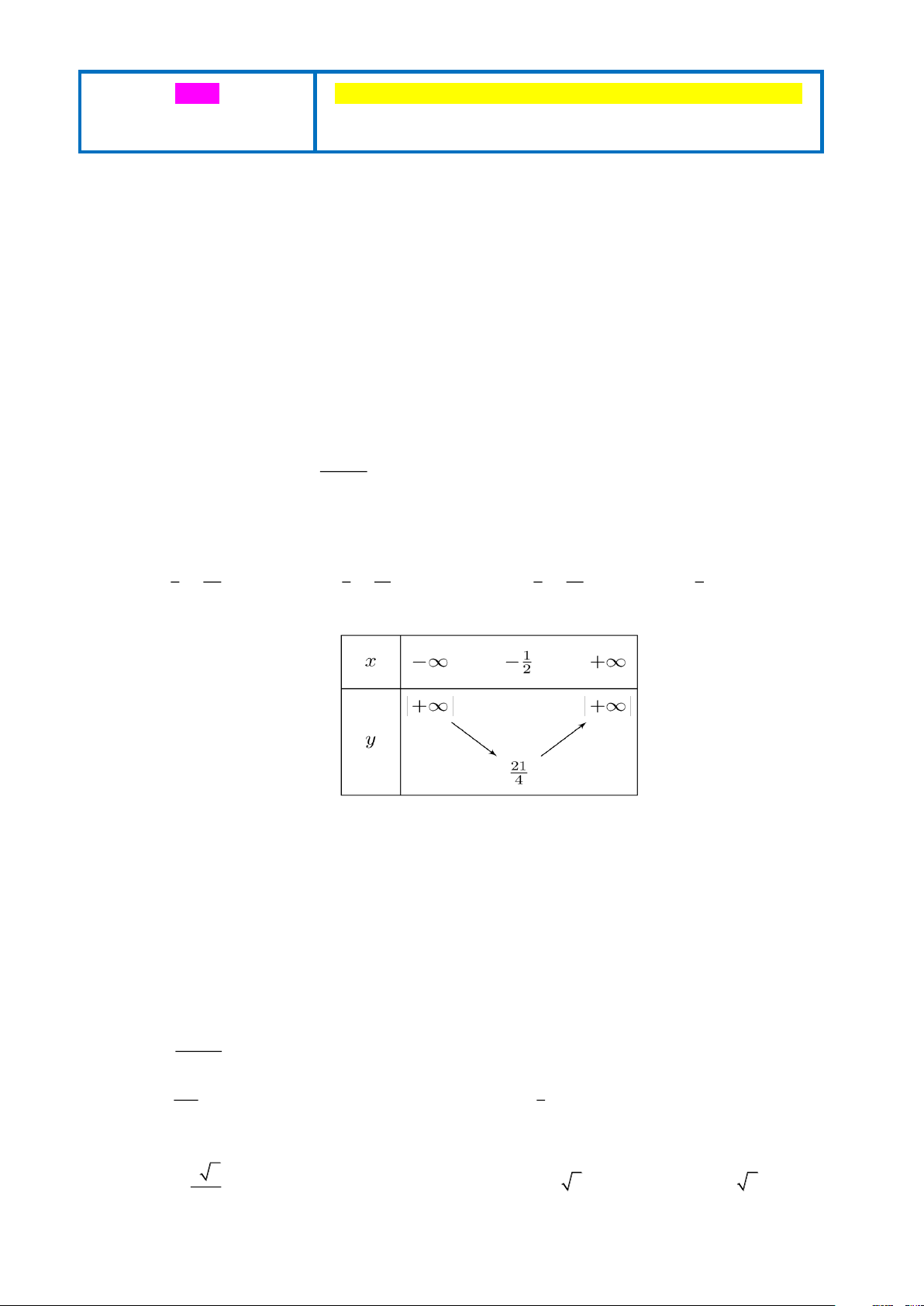
Câu 10. Theo dõi thời gian làm một bài toán (tính bằng phút) của 40 học sinh, giáo viên lập được bảng sau:
Phương sai của mẫu số liệu trên gần với số nào nhất? A. 6 .
B. 9 . C. 40 . D. 12 . Lời giải Chọn A
x .n + x .n + ...+ x .n 317
Ta có giá trị trung bình của mẫu số liệu là 1 1 2 2 k k x = = . N 40 Trang 5
(x − x + x − x +...+ x − x 1 )2 ( 2 2 )2 ( n )2
Phương sai của mẫu số liệu là s = = 6. N
Câu 11. Đường kính của một đồng hồ cát là 8,52m với độ chính xác đến 1cm . Dùng giá trị gần đúng của là
3,14 cách viết chuẩn của chu vi (sau khi quy tròn) là
A. Đáp án khác. B. 26,6. C. 26,8. D. 26,7. Lời giải Chọn D
Gọi d là đường kính thì d = 8,52m 1cm 8,51m d 8,53m .
Khi đó chu vi là C = d và 26,7214 C 26,7842 C = 26,7528 0,0314 . 0,1 Ta có 0,0314 0,05 =
nên cách viết chuẩn của chu vi là 26,7. 2
Câu 12. Cho tập hợp A = 1;2;3;
4 . Số các tập con của tập A là A. 16. B. 8 . C. 12 . D. 10. Lời giải Chọn A
Vì tập A có 4 phần tử nên số tập con của A là 4 2 = 16 .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai.
Câu 1. Cho các tập hợp A = {x x 2}; B ={x −3 x +1 4}; C ={x − 2023 x −1 2022};
D = {x | 2x 7}. Khi đó: a) C = [ 2021 − ; 2023) . 7 b) D = ; + . 2 c) B = ( 4 − ;3] .
d) A = (2;+) . Lời giải a) S b) Đ c) Đ d) S A = [2; +) 3 − x +1 4 4
− x 3; B = (−4;3]. 2
− 023 x −1 2022 2
− 022 x 2023; 7 7 C = [ 20
− 22;2023) . 2x 7 x ; D = ; + . 2 2 (Sai) A = (2;+) . (Vì): A = [2; +) . (Đúng) B = ( 4 − ;3] . (Vì): 3 − x +1 4 4
− x 3; B = (−4;3]. (Sai) C = [ 2021 − ; 2023) . (Vì): 2
− 023 x −1 2022 2
− 022 x 2023; C = [ 20 − 22;2023) . 7 (Đúng) D = ; + . 2 7 7
(Vì): 2x 7 x ; D = ; + . 2 2
Câu 2. Cho ba điểm ( A 1; 2
− ), B(0;4),C(3;2) . Khi đó: Trang 6 a) AB = ( 1 − ;6) .
b) AC = (2;4); BC = (3; 2 − ) . 1
c) Tọa độ trung điểm của đoạn AB là I ;1 . 2
d) Tọa độ điểm N sao cho AN + 2BN − 4CN = 0 là N (11;12) . Lời giải a) Đ b) Đ c) Đ d) S a. AB = ( 1 − ;6) .
b. AC = (2;4); BC = (3; 2 − ) 1+ 0 1 x = = I 1 c. Vì 2 2
I là trung điểm của đoạn AB nên . Vậy I ;1 . −2 + 4 2 y = = 1 I 2
d. Gọi N( ;
x y) . Ta có: AN = (x −1; y + 2); BN = ( ;
x y − 4);CN = (x − 3; y − 2)
x −1+ 2x − 4(x −3) = 0 x =11
Vi AN + 2BN − 4CN = 0 .N(11;2) .
y + 2 + 2(y − 4) − 4(y − 2) = 0 y = 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 4.
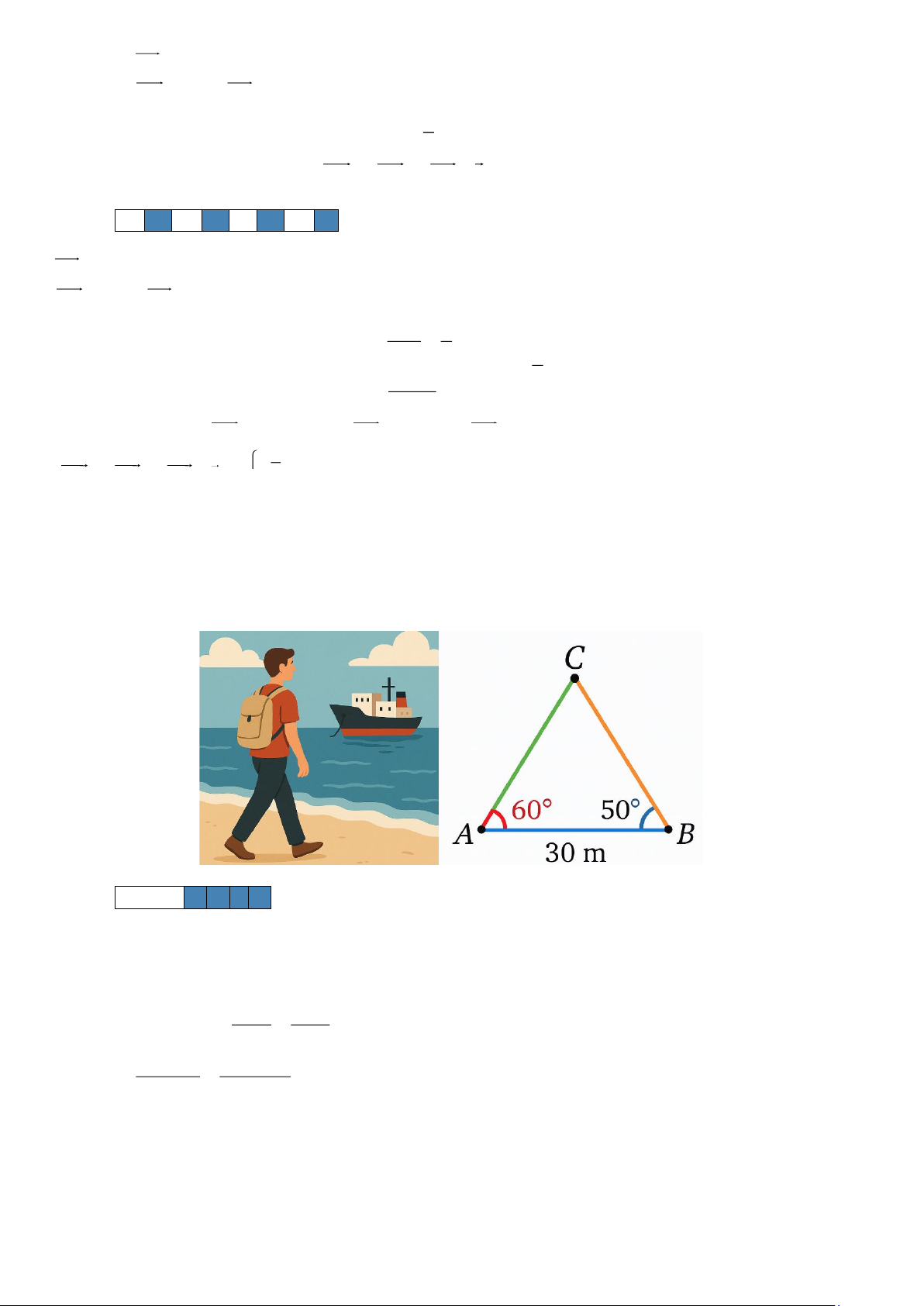
Câu 1. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi.
Người đó tiến hành đo đạc và thu được kết quả: AB 30 ,
m CAB 60 ,CBA 50 = = =
. Tính khoảng cách từ vị trí
A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét). Lời giải Trả lời 2 4 , 5
Xét tam giác ABC . Ta có: ˆ
C 180 60 50 70 = − − = . BA AC
Áp dụng định lí sin ta có: = . sin C sin B BAsin B 30sin 50 Suy ra AC = = 24,5( m) . sin C sin 70
Vậy khoảng cách từ vị trí A đến con tàu C là khoảng 24,5 m . r
Câu 2. Một Ca nô di chuyển từ bờ sông bên này sang bờ sông bên kia, theo phương x (vuông góc với hai bờ ur
sông); dòng sông chảy theo hướng y (song song với 2 bờ như hình dưới). Biết vận tốc của Ca nô là 30 km / h Trang 7
và của dòng nước là 2 km / h . Hỏi vận tốc của Ca nô so với bờ sông là bao nhiêu (làm tròn kết quả đến hàng phần trăm)? Lời giải Trả lời 3 0 , 0
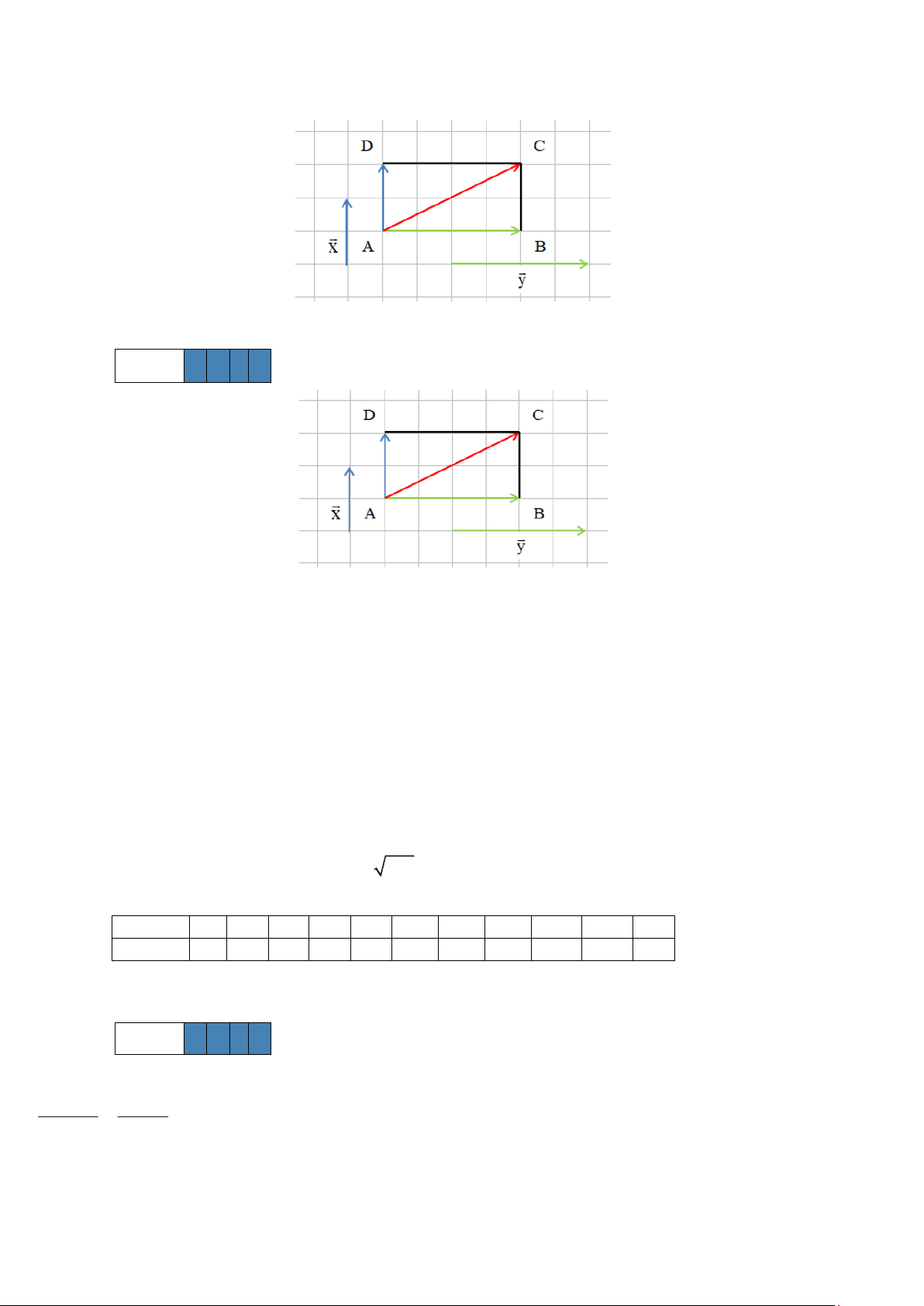
Ca nô di chuyển từ bờ sông bên này sang bờ sông bên kia, đi theo hướng từ A đến D , khi đó vận tốc Ca nô so ur uuur ur
với mặt nước là: v = AD và có độ lớn là | v |= 30km / h 1 1 uur uuur
Dòng sông chảy theo hướng dọc bờ sông, đi theo hướng từ A đến B , khi đó vận tốc là: v = AB và có độ lớn 2 uur
là | v |= 2km / h. 2 r ur uur
Khi đó vận tốc của ca nô so với bờ sông là: v = v + v 1 2 ur uur uuur uuur uuur
Độ lớn là: | v + v | | = AD + AB | | = AC |= AC 1 2
Áp dụng định lý Pitago, ta có: 2 2 2 2 2
AC = AB + AD = 30 + 2 = 904 AC = 904 30,07 ( km / h ).
Câu 3. Có 100 học sinh tham dự kỳ thi học sinh giỏi Toán (thang điểm là 20) kết quả được cho bởi bảng sau. Điểm
9 10 11 12 13 14 15 16 17 18 19
Tần số 1 1 3 5 8 13 19 24 14 10 2
Số trung vị của mẫu số liệu trên bằng bao nhiêu? Lời giải Trả lời 1 5 , 5
Sắp xếp 100 giá trị theo thứ tự không giảm ta được hai giá trị đứng giữa là x =15, x =16 nên số trung vị là 50 51 x + x 15 +16 50 51 = =15,5 2 2
Câu 4. Bác Hai có một mảnh đất rộng 6 ha. Bác dự tính trồng cà chua và bắp cho mùa vụ sắp tới. Nếu trồng
bắp thì bác Hai cần 10 ngày để trồng một ha. Nếu trồng cà chua thì bác Hai cần 20 ngày để trồng một ha. Biết
rằng mỗi ha bắp sau thu hoạch bán được 30 triệu đồng, mỗi ha cà chua sau thu hoạch bán được 50 triệu đồng
và bác Hai chỉ còn 100 ngày để canh tác cho kịp mùa vụ. Số tiền (triệu đồng) nhiều nhất mà bác Hai có thể thu
được sau mùa vụ này là bao nhiêu? Trang 8 Lời giải Trả lời 2 6 0
Gọi diện tích trồng bắp là x ha, x 0 . Số ngày công trồng bắp là 10x ngày
Diện tích trồng cà chua là y ha, y 0 . Số ngày công trồng cà chua là 20 y ngày x 0 x 0 y 0 y 0
Dựa vào dữ kiện của đề bài ta có hệ bất phương trình . x + y 6 x + y 6 10
x + 20y 100 x + 2y 10
Miền nghiệm của hệ là miền tứ giác ABCD (kể cả các cạnh), với A(0;0), B(0;5) , C(2;4) , D(6;0) .
Số tiền bác Hai thu được khi canh tác 6 ha đất trong 100 ngày là F = 30x + 50y (triệu đồng)
Ta thấy F = 30x + 50y đạt giá trị lớn nhất chỉ có thể tại các đỉnh.
Tại A(0; 0) thì F = 0 ; tại B(0;5) thì F = 250 ;
tại C(2;4) thì F = 260 ; tại D(6;0) thì F =180.
Vậy số tiền nhiều nhất mà bác Hai có thể thu được sau mùa vụ này là 260 triệu đồng khi trồng 2 ha bắp và 4 ha cà chua.
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài. Trang 9
Câu 1. Cho tam giác ABC có góc nhọn tại A . Vẽ bên ngoài tam giác ABC các tam giác vuông cân đỉnh A
là ABD và ACE. Gọi M là trung điểm BC . Chứng minh AM ^ DE. Lời giải uuuur uuur
Ta chứng minh AM.DE = 0 .Thật vậy uuuur uuur uuuur uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur
2AM.DE = (AM + AC)(AE- AD)= A .BAE- A .BAD+ AC.AE- AC.AD uuur uuur uuur uuur = .
AB AE- AC.AD = AB AE cos( 0 + ) A - AC AD cos( 0 . . 90 . . 90 + ) A = AC AD cos( 0 + ) A - AC AD cos( 0 . . 90 . . 90 + ) A = 0 . Vậy AM ^ DE.
Câu 2. Từ vị trí A người ta quan sát một cây cao. Biết AH = 3 (m), HB =15 (m), BAC 40 = . Khi đó chiều cao của cây là. Lời giải
Vì tam giác AHB vuông tại H nên ta có 2 2 2 2
AB = AH + HB = 3 +15 = 234 15,3 (m). Ta có BH 15 sin BAH 0,984 BAH 78,6 ABC 78,6 ACB 61, 4 = = . AB 234 BC AB
Áp dụng định lý sin cho tam giác ABC ta có = . sin A sin C
Suy ra BC 12, 7 (m).
Câu 3. Trong lớp 11A có 16 học sinh giỏi Toán, 15 học sinh giỏi môn Lý và 11 học sinh giỏi môn Hóa. Biết
rằng có 9 học sinh vừa giỏi Toán và Lý (có thể giỏi thêm môn Hóa), 6 học sinh vừa giỏi Lý và Hóa (có thể
giỏi thêm môn Toán), 8 học sinh vừa giỏi Hóa và Toán (có thể giỏi thêm môn Lý) và trong đó chỉ có đúng 11
học sinh giỏi đúng hai môn. Hỏi có bao nhiêu học sinh của lớp giỏi cả ba môn Toán, Lý, Hóa. Lời giải
Gọi T , L ,H lần lượt là tập hợp các học sinh giỏi môn Toán, Lý, Hóa; B là tập hợp học sinh giỏi đúng hai môn.
Theo giả thiết ta có n(T)= 16 ,n( ) L = 15 ,n( )
B = 11; n(T Ç )
L = 9 ,n(LÇ H)= 6 và
n(H ÇT)= 8 .
a) Xét tổng n(T Ç )
L + n(LÇ H)+ n(H ÇT) thì mỗi phần tử của tập hợp T ÇLÇH được
tính ba lần do đó ta có: n(T Ç )
L + n(LÇ H)+ n(H ÇT)- 3n(T Ç LÇ H)= n( ) B . Trang 10 1
Hay n(T Ç L Ç H)= n é ê (T ) L
n(L H) n(H T) n( ) B ù Ç + Ç + Ç - = 4 3 ë úû .
Vậy có 4 học sinh giỏi cả ba môn Toán, Lý, Hóa.
Câu 4. Người ta dự định dùng 2 nguyên liệu là mía và củ cải đường để chiết xuất ít nhất 140 kg đường kính
(độ tinh khiết cao) và 9 kg đường cát (có lẫn tạp chất màu). Từ mỗi tấn mía giá 4 triệu đồng, có thể chiết xuất
được 20 kg đường kính và 0, 6 kg đường cát. Từ mỗi tấn củ cải đường giá 3 triệu đồng ta chiết xuất được 10
kg đường kính và 1,5 kg đường cát. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên
liệu là ít nhất. Biết cơ sở cung cấp nguyên liệu chỉ cung cấp không quá 10 tấn mía và không quá 9 tấn củ cải đường. Lời giải
Đặt x và y lần lượt là số tấn mía và củ cải đường cần dùng. 0 x 10 0 y9
Từ giả thiết, ta có hệ bất phương trình: 2x + y 14
2x+5y30.
Ta cần xác định x, y thỏa mãn hệ trên và T = 4x + 3y có giá trị nhỏ nhất.
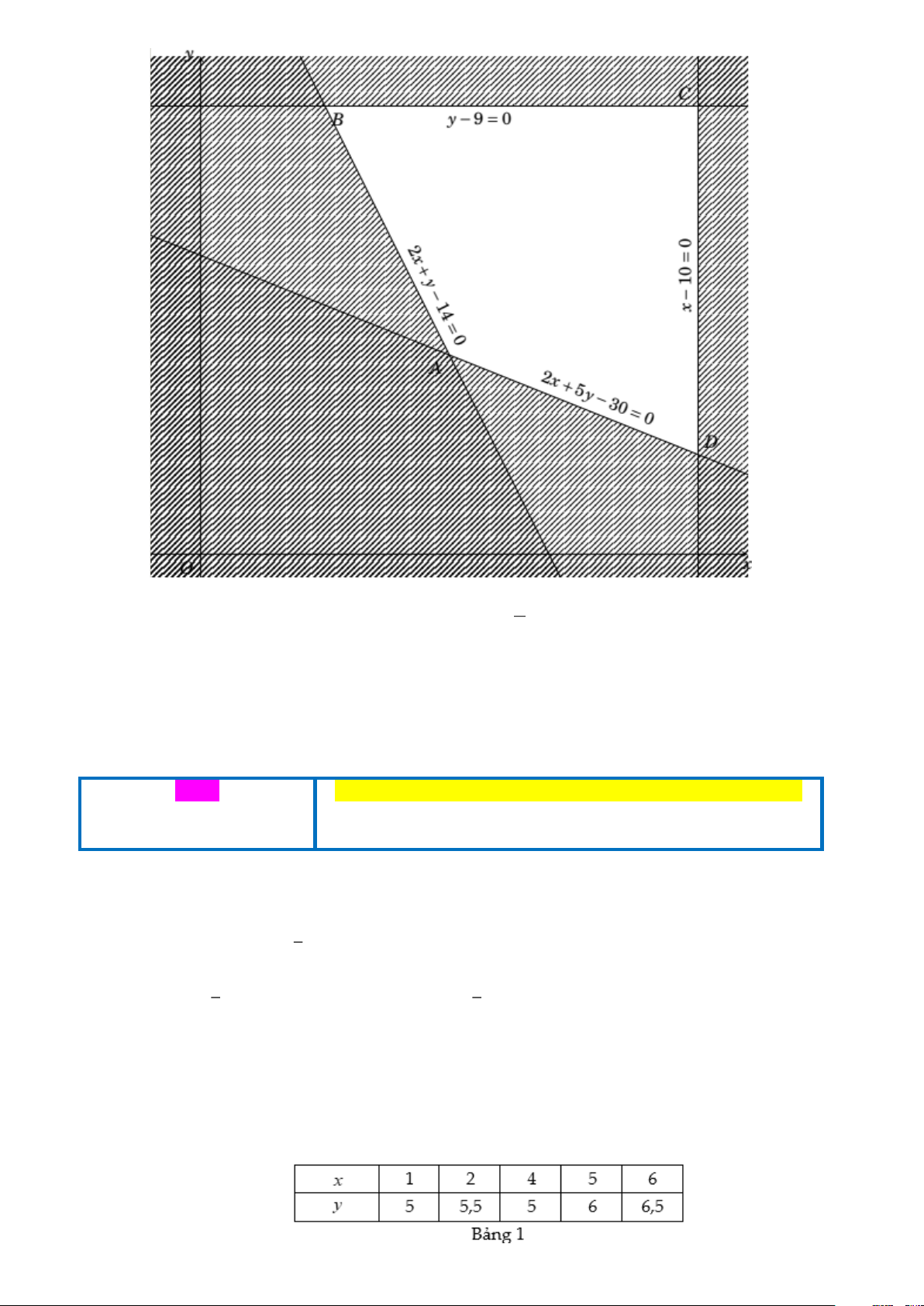
Biểu diễn miền nghiệm của hệ bất phương trình: Trang 11 5
Ta được miền nghiệm của hệ là tứ giác ABCD với (5
A ; 4) , B ;9
, C(10;9) , D(10;2) . 2
Thay tọa độ các điểm trên vào T , ta được chi phí nguyên liệu ít nhất khi x = 5 và y = 4 .
Vậy cần dùng 5 tấn mía và 4 tấn củ cải đường thì thỏa mãn yêu cầu bài toán. -------- HẾT-------- ĐỀ 2
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 10
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án. é 3 ù
Câu 1: Cho các tập hợp A = ê- 3; ú, B = (- 1;+ ¥ ). Khi đó tập hợp A Ç B bằng: ê 2 ú ë û ìï 3 üï ìï 3 üï A. ïí x ¡ | 3 x ï Î - £ £ ý . B. ïí x ¡ | 1 x ï Î - < £ . ï ý 2 ï ïî ïþ ï 2 ï ïî ïþ
C. {x Î ¡ | - 3 < x £ - 1}.
D. {x Î ¡ | x ³ - 1}.
Câu 2: Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn? 2 ìï 5x + y ³ 3 2
ìï 3x - 4y > 2
ìï x - 4xy £ 3y ìï x + 2y ³ 6 A. ïí . B. ïí . C. ïí . D. ïí . 2
ï 2x - 3xy < 5 2 ï ï ï ï î - 2x + 5y > 4 ïî y + 3 > 0 ïî x - 3y < 15 ïî
Câu 3: Cho hai bảng gồm có các đại lượng x ; y như sau. Bảng nào là hàm số Trang 12
A. Chỉ có bảng 1. B. Chỉ có bảng 2.
C. Cả bảng 1 và bảng 2. D. Không có bảng nào.
Câu 4: Cho parabol (P ) 2
: y = 3x - 2x + 1. Điểm nào sau đây là đỉnh của (P )? 1 æ 2 ö æ 1 2 ö 1 æ 2 ö
A. I (0;1). B. I çç ; ÷÷ ç ÷ ç ÷ ç .
C. I ç- ; ÷.
D. I ç ;- ÷. 3 3 ÷ è ø ç 3 3 ÷ è ø ç3 3 ÷ è ø Câu 5: Cho hàm số 2
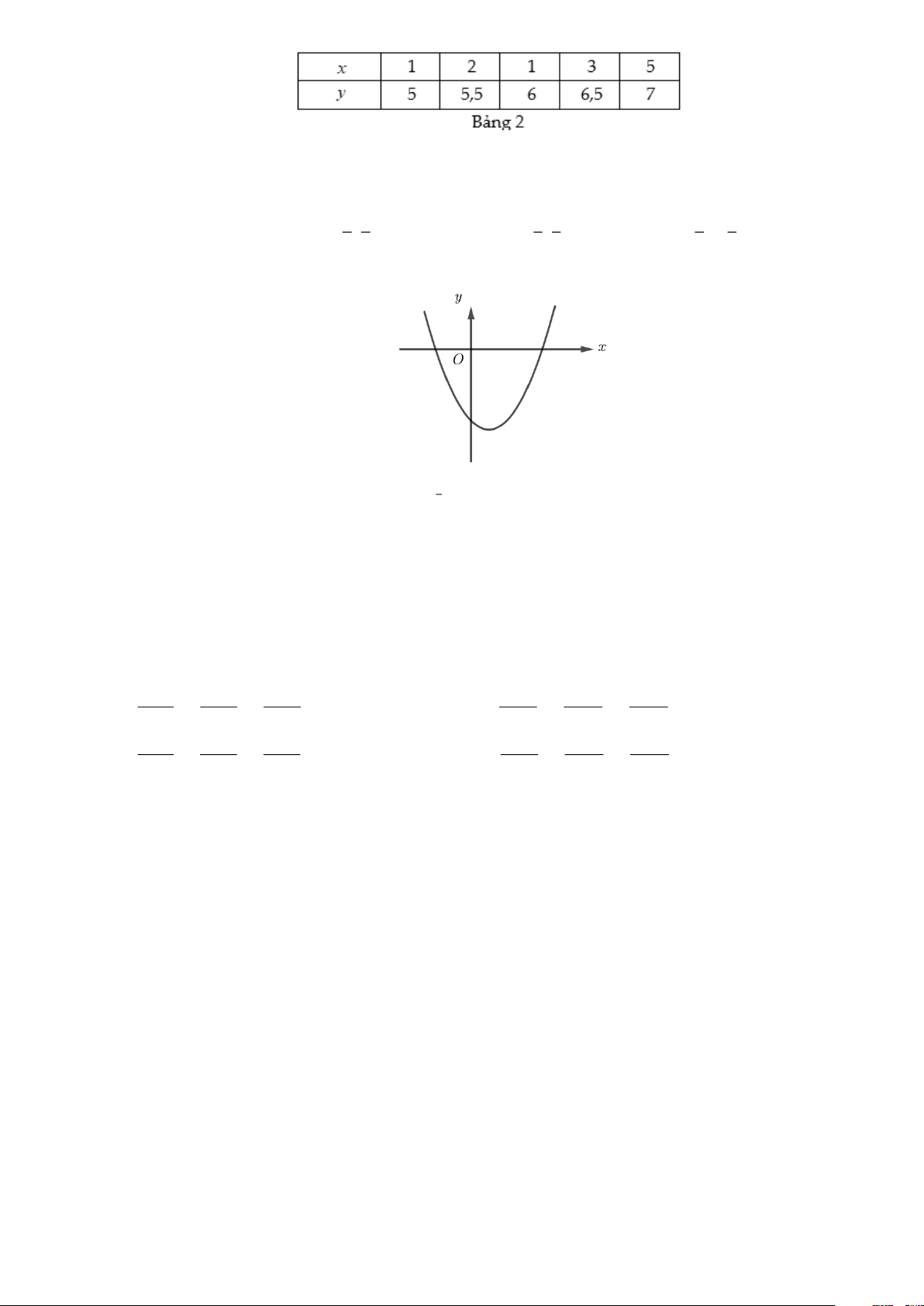
y = ax + bx + c có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
A. a > 0,b < 0,c < 0 . B. a > 0,b < 0,c > 0 . C. a < 0,b < 0,c < 0 . D. a > 0,b > 0,c > 0 .
Câu 6: Tìm số quy tròn của số gần đúng b , biết rằng b = 0,1792 ± 0, 002. A. 0,17 . B. 0,18 . C. 0,19 . D. 0, 2 .
Câu 7: Trong các đẳng thức sau, đẳng thức nào đúng? A. ( 0
sin 180 - a ) = - cos a . B. ( 0
sin 180 - a ) = - sin a . C. ( 0
sin 180 - a ) = cos a . D. ( 0
tan 180 - a ) = - tan a .
Câu 8: Trong tam giác A BC với BC = , a AC = ,
b AB = c và R là bán kính đường tròn ngoại tiếp tam giác
A BC . Hệ thức nào sau đây đúng? a b c a b c A. = = = R . B. = = = R . sin A sin B sinC cos A cos B cosC a b c a b c C. = = = 2R . D. = = = 2R . sin A sin B sinC cos A cos B cosC
Câu 9: Cho tam giác A BC có AB = 5 ;BC = 7 ; AC = 8 . Số đo góc A bằng A. 45° . B. 90° . C. 60° . D. 30° .
Câu 10: Mệnh đề nào sau đây đúng?
A. Có duy nhất một véc tơ cùng phương với mọi véc tơ.
B. Có ít nhất 2 véc tơ cùng phương với mọi véc tơ.
C. Có vô số véc tơ cùng phương với mọi véc tơ.
D. Không có véc tơ nào cùng phương với mọi véc tơ. uuur uuur
Câu 11: Cho O là tâm hình bình hành ABCD . Hỏi véctơ (AO - DO ) bằng véctơ nào? uuur uuur uuur uuur A. A C . B. BA . C. BC . D. DC . uuur uuur
Câu 12: Cho 4 điểm A , B , C , D phân biệt thỏa A B = - 2DC . Chọn khẳng định sai? uuur uuur uuur uuur
A. A B và DC cùng phương.
B. A B và CD cùng hướng.
C. AB = - 2DC .
D. AB = 2CD .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai.
Câu 1: Mẫu số liệu dưới đây thống kê thời gian chờ xe bus (đơn vi: phút) của 10 học sinh ở cùng một bến: 1 4 5 6 6 8 10 11 12 25
a) Không có học sinh nào chờ quá 30 phút.
b) Thời gian chờ xe bus trung bình của 10 học sinh là: 8 phút.
c) Khoảng tứ phân vị của mẫu số liệu là: D = 5 (phút). Q Trang 13
d) Phương sai của mẫu số liệu là: 2 s = 39, 36
Câu 2: Cho DA BC đều. Các điểm ,
D E, F lần lượt là trung điểm của các cạnh A B, A C, BC . Khi đó: uuur uuur
a) Hai vectơ DF, A C ngược hướng. uuur uuur uuur
b) DA + DF = DE . uuur uuur c) 1 DF = - A C . 2 uuur uuur
d) DF.BE = 0 .
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1: Một công ty dịch vụ cho thuê xe ô tô vào dịp tết nguyên đán với giá thuê mỗi chiếc xe ô tôt như sau:
Khách phải thuê tối thiểu phải thuê trọn ba ngày tết (mùng 1, 2, 3 ) với giá 1000000 đồng/ngày; những ngày còn
lại (nếu khách còn thuê) sẽ được tính giá thuê là 700000 đồng/ngày. Giả sử T (x ) là tổng số tiền mà khách phải
trả khi thuê một chiếc xe ô tô của công ty và x là số ngày thuê của khách. Anh Bình định dành ra một khoản
tối đa là 10 triệu đồng cho phí thuê xe đi chơi trong dịp tết nguyên đán, khi đó anh Bình có thể thuê xe của
công ty trên tối đa bao nhiêu ngày?
Câu 2: Mẫu số liệu sau đây cho biết điểm số của 5 bài kiểm tra thường xuyên môn Toán của bạn Dũng và Minh như sau:
Tính tổng độ lệch chuẩn của bài kiểm tra của hai bạn (làm tròn đến hàng đơn vị).
Câu 3: Cho tam giác A BC có · ·
BC = 10, ABC = 60 ,
° BAC = 80° . Tính chu vi tam giác A BC (làm tròn đến hàng đơn vị).
Câu 4: Cho hình chữ nhật ABCD . Kẻ BK ^ AC,K Î AC . Gọi M, N lần lượt là trung điểm của A K và CD . Số đo góc ·
BMN bằng bao nhiêu độ?. PHẦN IV. Tự luận Câu 1: Cho hàm số 2
y = ax + bx + c (a ¹ 0) đạt giá trị nhỏ nhất là 4 tại x = 2 và đồ thị của nó cắt trục
tung tại điểm có tung độ là 6 . Khi đó 2a - b + c bằng bao nhiêu?
Câu 2: Trong một đợt khảo sát về tốc độ viết của học sinh lớp 3, người ta cho hai nhóm học sinh chép một
đoạn văn trong 15 phút. Bảng dưới đây thống kê số chữ mỗi bạn viết được.
a) Sử dụng số trung bình để so sánh tốc độ viết của học sinh hai nhóm.
b) Sử dụng trung vị để so sánh tốc độ viết của học sinh hai nhóm.
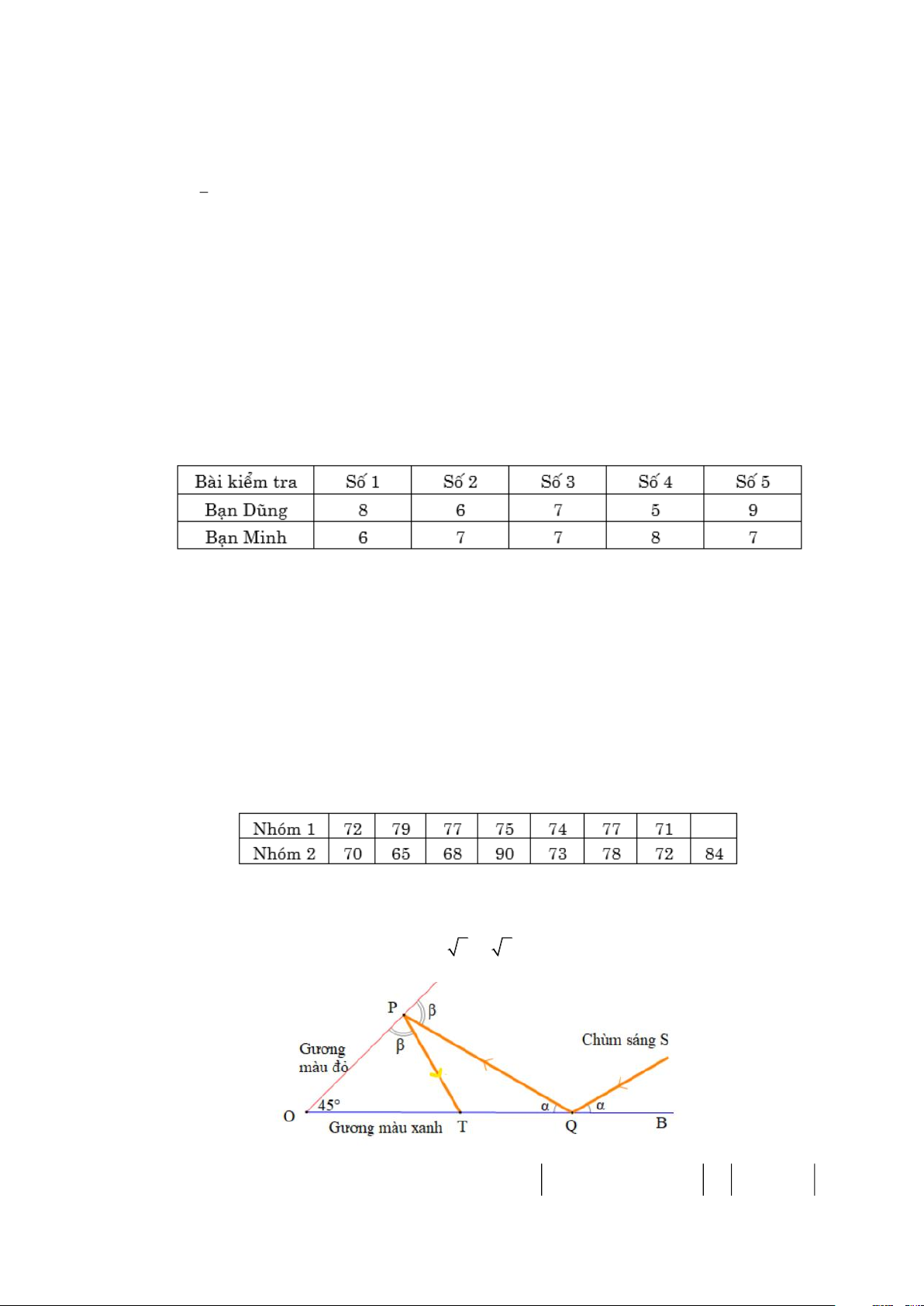
Câu 3: Trong sơ đồ, chùm sáng S hướng vào gương màu xanh, phản xạ vào gương màu đỏ và sau đó phản xạ
vào gương màu xanh như hình vẽ, biết OP = 2, OQ = 2 +
6 , biết góc giữa hai gương bằng 450. Tính PT . uuur uuur uuur uuur uuur
Câu 4: Cho tam giác đều A BC có cạnh a . Điểm M thoả mãn 2MA + 3MB + 4MC = MB - MA thuộc
một đường tròn cố định. Tính bán kính đường tròn đó. --------HẾT-------- Trang 14 ĐỀ 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 10
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1: Cho A = (- ¥ ;- 2ù = é û, B 3;+ ¥ ) ë
, C = (0;4). Khi đó tập (A È B )ÇC là: A. 3 é ;4ù - ¥ - ù ë û. B. ( ; 2 È (3;+ ¥ ) û . C. 3 é ;4) - ¥ - È é ë . D. ( ; 2) 3;+ ¥ ) ë
ìï x - y < 1
Câu 2: Cho hệ bất phương trình sau: ïí
. Cặp số (x ;y ) nào sau đây thỏa mãn hệ bất phương trình đã ï 2x + y ³ 3 ïî cho? A. (0;3). B. (1;0). C. (2;0). D. (- 1;1). x - 3
Câu 3: Tập xác định của hàm số y = là 2x - 2 A. ¡ \ {1}. B. ¡ \ {3}. C. ¡ \ {2}. D. (1;+ ¥ ).
Câu 4: Tìm tọa độ đỉnh I của đồ thị hàm số 2
y = - 3x + 5x - 3 . æ 5 37 ö 5 æ 11 ö æ 5 59 ö 5 æ ö A. I çç- ; ÷ - ÷ ç ÷ ç ÷ ç ÷ ç . B. I ç ;- ÷. C. I ç- ;- ÷. D. I ç ;- 3÷. 6 4 ÷ è ø ç6 12 ÷ è ø ç 3 3 ÷ è ø ç3 ÷ è ø
Câu 5: Bảng biến thiên sau là của hàm số nào? A. 2
y = 3x + 3x + 6 . B. 2
y = - 3x + 3x + 6 . C. 2
y = 3x - 3x + 6 . D. 2
y = - 3x - 3x + 6 .
Câu 6: Cho số gần đúng a = 213516 với độ chính xác d = 2000. Hãy viết số quy tròn của số a . A. 214000 . B. 213516 . C. 210000 . D. 200000 .
Câu 7: Cho 0° < a < 180° và a ¹ 90° . Khẳng định nào sau đây sai?
A. tan(180° - a ) = - tan a .
B. sin(180° - a ) = sin a .
C. cot(180° - a ) = - cot a .
D. cos(180° - a ) = cos a .
Câu 8: Cho DA BC với các cạnh AB = , c A C = ,
b BC = a . Gọi R, r,S lần lượt là bán kính đường tròn ngoại
tiếp, nội tiếp và diện tích của tam giác A BC . Trong các phát biểu sau, phát biểu nào sai? a A. R = . B. 2 2 2
a + b - c = 2ab cosC . 2 sin A abc 1 C. S = . D. S = ab sinC 2R 2
Câu 9: Cho tam giác A BC có µ µ B = 60 ,
° A = 75° và A B = 5 . Tính độ dài cạnh A C . A. 5 6 A C = . B. AC = 10 . C. A C = 5 2 . D. A C = 5 3 . 2
Câu 10: Gọi O là giao điểm hai đường chéo A C và BD của hình bình hành ABCD . Đẳng thức nào sau đây sai? Trang 15 uuur uuur uuur uuur uuur uuur uuur uuur
A. A B = DC .
B. A D = BC .
C. A O = OC .
D. OB = OD .
Câu 11: Cho tam giác A BC , gọi M là trung điểm của A B . Mệnh đề nào sau đây là đúng? uuur uuuur uur uuur uuuur uuur
A. MC + A M = CA .
B. MC + A M = A C . uuur uuuur uuur uuur uuuur uuur
C. MC + A M = BC .
D. MC + A M = A B .
Câu 12: Cho tam giác A BC , gọi M, N là trung điểm của BC, AC . Mệnh đề nào sau đây là đúng? uuuur 1 uuur uuuur 1 uuur uuuur 1 uuur uuuur 1 uuur A. MN = BC . B. MN = A C . C. MN = A B . D. MN = BA . 2 2 2 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai.
Câu 1: Một cơ sở chăn nuôi gia cầm tiến hành nuôi thử nghiệm giống gà đẻ trứng mới. Khi gà đã cho trứng họ
tiến hành khảo sát với 20 quả được cân nặng cho ở bảng sau: Xét các mệnh đề sau:
a) Giá trị nhỏ nhất của mẫu là 29 .
b) Giá trị trung bình của mẫu là x = 40, 7 .
c) Khoảng tứ phân vị DQ = 2 .
d) Độ lệch chuẩn của mẫu là s » 3, 69 . uuur uuur r
Câu 2: Cho tam giác A BC có A B = a;A C = 2a, A = 60° . M là điểm thỏa mãn 2MA + 3MB = 0 .
a) Điểm M nằm giữa hai điểm A và B . uuuur 3 uuur b) A M = A B . 5 uuur 2 uuur 3 uuur c) CM = - A C + A B . 5 5 uur uuur 17 d) 2 CA.CM = a . 5
PHẦN III. Câu trắc nghiệm trả lời ngắn
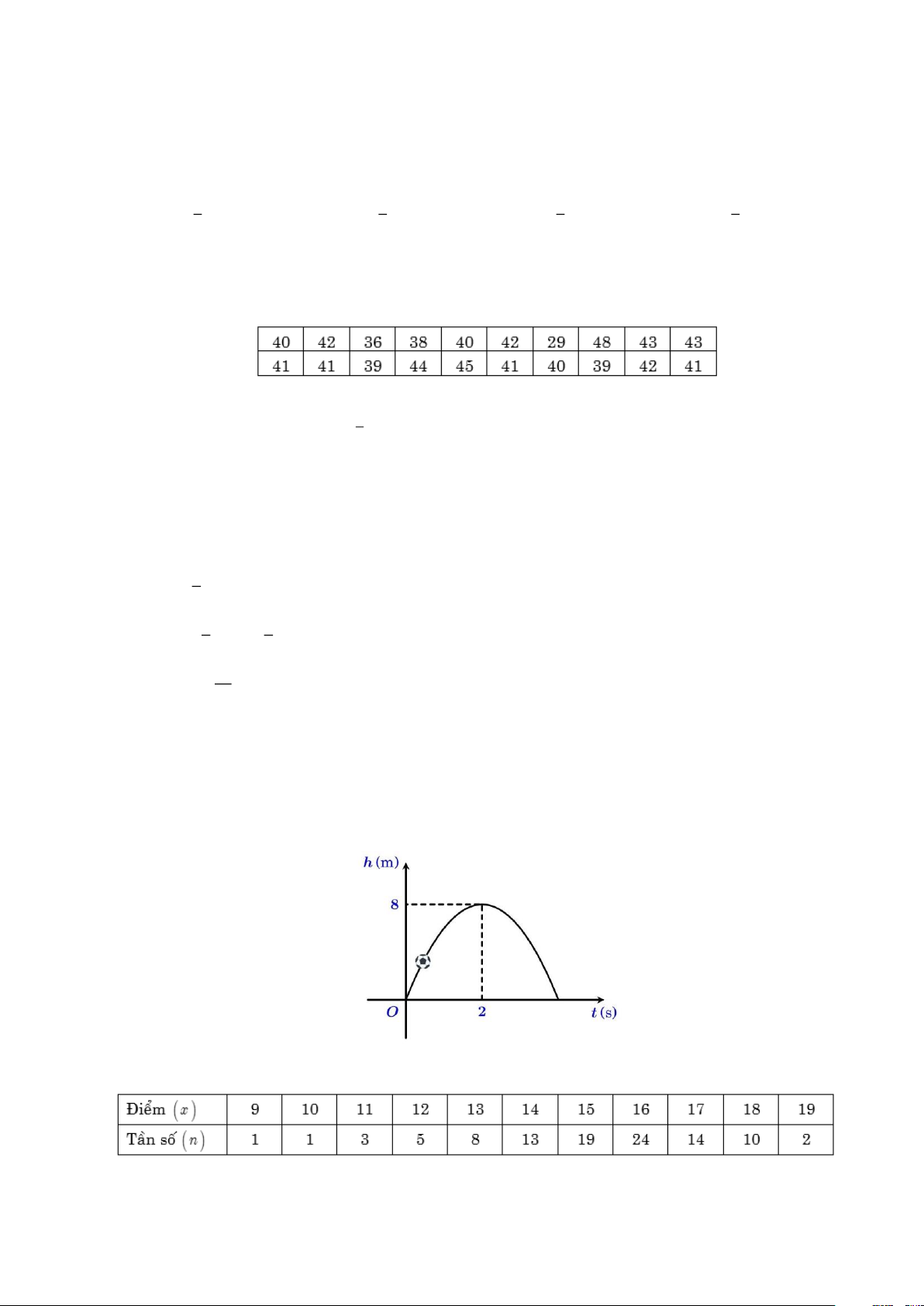
Câu 1: Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Hình vẽ bên dưới minh họa
quỹ đạo của quả bóng là một phần của cung parabol trong mặt phẳng tọa độ Oth , trong đó t là thời gian kể từ
khi quả bóng được đá lên và h là độ cao của quả bóng, trục Ot nằm dưới mặt đất. Giả thiết rằng quả bóng
được đá từ mặt đất. Sau khoảng 2(s), quả bóng đó lên đến vị trí cao nhất là 8(m ). Hỏi sau 3(s) thì quả bóng
cách mặt đất bao nhiêu mét.
Câu 2: Điểm số của 100 học sinh tham dự kỳ thi học sinh giỏi toán ở tỉnh Bắc Ninh được thống kê theo bảng sau:
Tìm trung bình cộng của bảng số liệu trên
Câu 3: Cho tam giác A BC có AB = 3 , BC = 7 và · 0
BAC = 60 . Tính độ dài cạnh A C .
Câu 4: Cho DA BC đều cạnh là 3. Điểm M thỏa mãn: 2 2 2
2MA + MB + MC = 18 , khi đó tập hợp điểm M
thuộc đường tròn có bán kính bằng bao nhiêu? Kết quả làm tròn đến hàng phần mười. Trang 16 PHẦN IV. Tự luận Câu 1: Cho hàm số 2
y = x - 4x + 3 , có đồ thị là (P ) .
a) Vẽ đồ thị (P ) .
b) Dựa vào đồ thị tìm điều kiện của tham số m để đường thẳng y = m cắt đồ thị (P )tại 2 điểm phân biệt.
Câu 2: Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:
a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu: 9 8 15 8 20
b) Giá của một số loại giày : 350 300 650 300 450 500 300 250 .
c) Số kênh được chiếu của một số hãng truyền hình cáp: 36 38 33 34 32 30 34 35 .
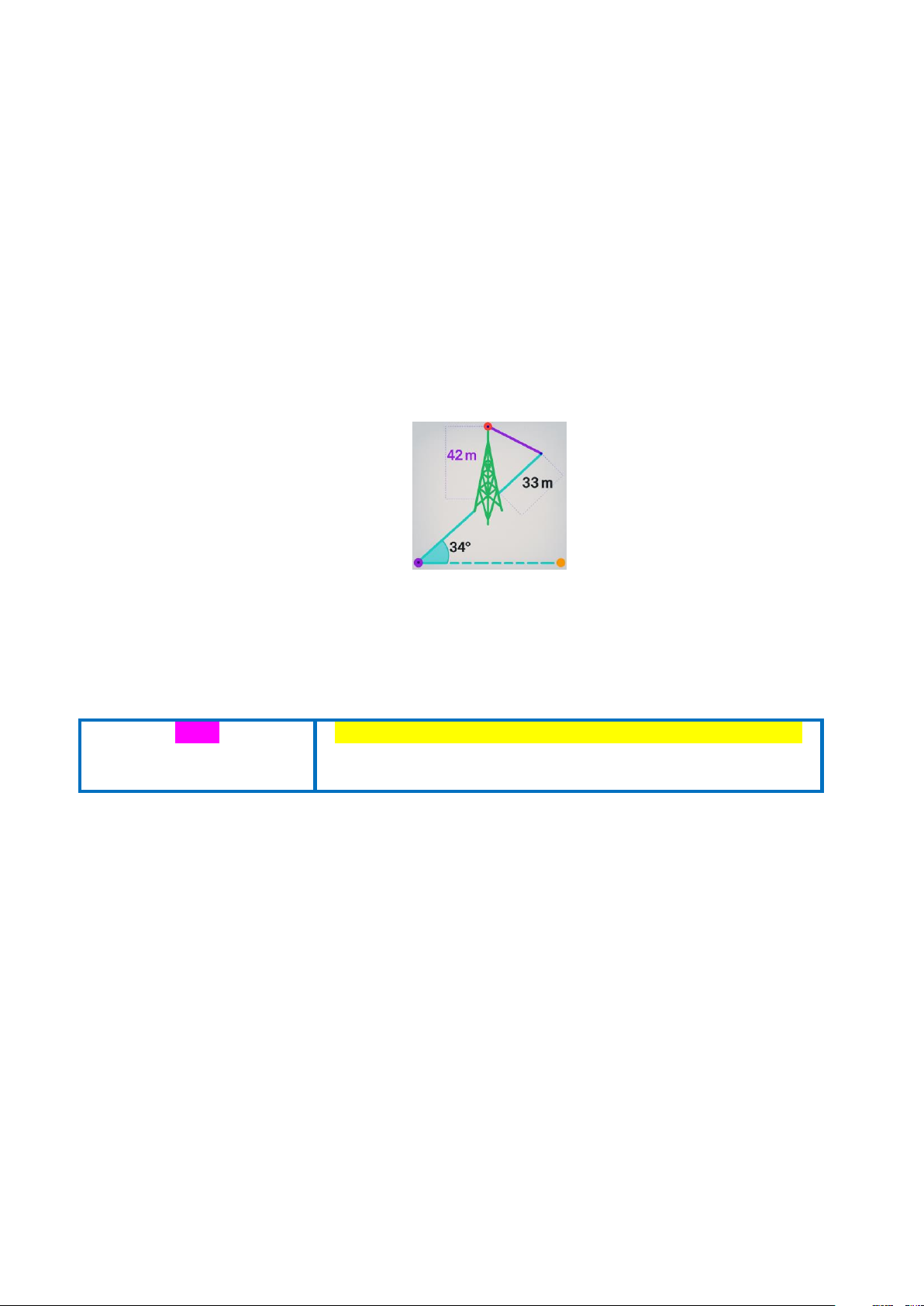
Câu 3: Một tháp viễn thông cao 42 m được dựng thẳng đứng trên một sườn dốc 34° so với phương ngang. Từ
đỉnh tháp người ta neo một sợi cáp xuống một điểm trên sườn dốc cách chân tháp 33 m như Hình. Tính chiều
dài của sợi dây cáp đó.
Câu 4: Cho hình thoi ABCD cạnh a , ·
BCD = 60° . Gọi G là trọng tâm của tam giác BCD , K là trung điểm uur uur r uuur uuur r uuur
của A D . Cho điểm I , J thỏa mãn hệ thức IK + 2IB = 0, 5JG - 3JC = 0 . Biểu diễn véc tơ BG theo các véc uuur uuur
tơ A B, A D . Tính độ dài của đoạn thẳng CI . --------HẾT-------- ĐỀ 4
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 10
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1. Trong các phát biểu sau, phát biểu nào là mệnh đề.
A. 2n + 1 là một số tự nhiên lẻ.
B. Việt Nam có bao nhiêu tỉnh thành?
C. Hà Nội không phải là thủ đô của Việt Nam. D. Con yêu mẹ lắm!
Câu 2. Cho hai tập: A = (1;5) và B = 3 é ;8ù ë
û. Mệnh đề nào đúng trong các mệnh đề sau?
A. A È B = (3;5ù Ç = é = ù = ù û. B. A B 3;5) ë . C. A \ B (5;8û. D. A \ B (1;3û.
Câu 3. Thầy giáo dạy môn giáo dục thể chất cho 45 học sinh lớp 10C đăng kí học ít nhất một trong hai môn thể
thao tự chọn là môn bóng đá và môn cầu lông. Có 30 học sinh đăng kí môn bóng đá, 25 học sinh đăng kí môn
cầu lông. Hỏi có bao nhiêu học sinh đăng kí cả hai môn thể thao? A. 5 . B. 15 . C. 10 . D. 12 .
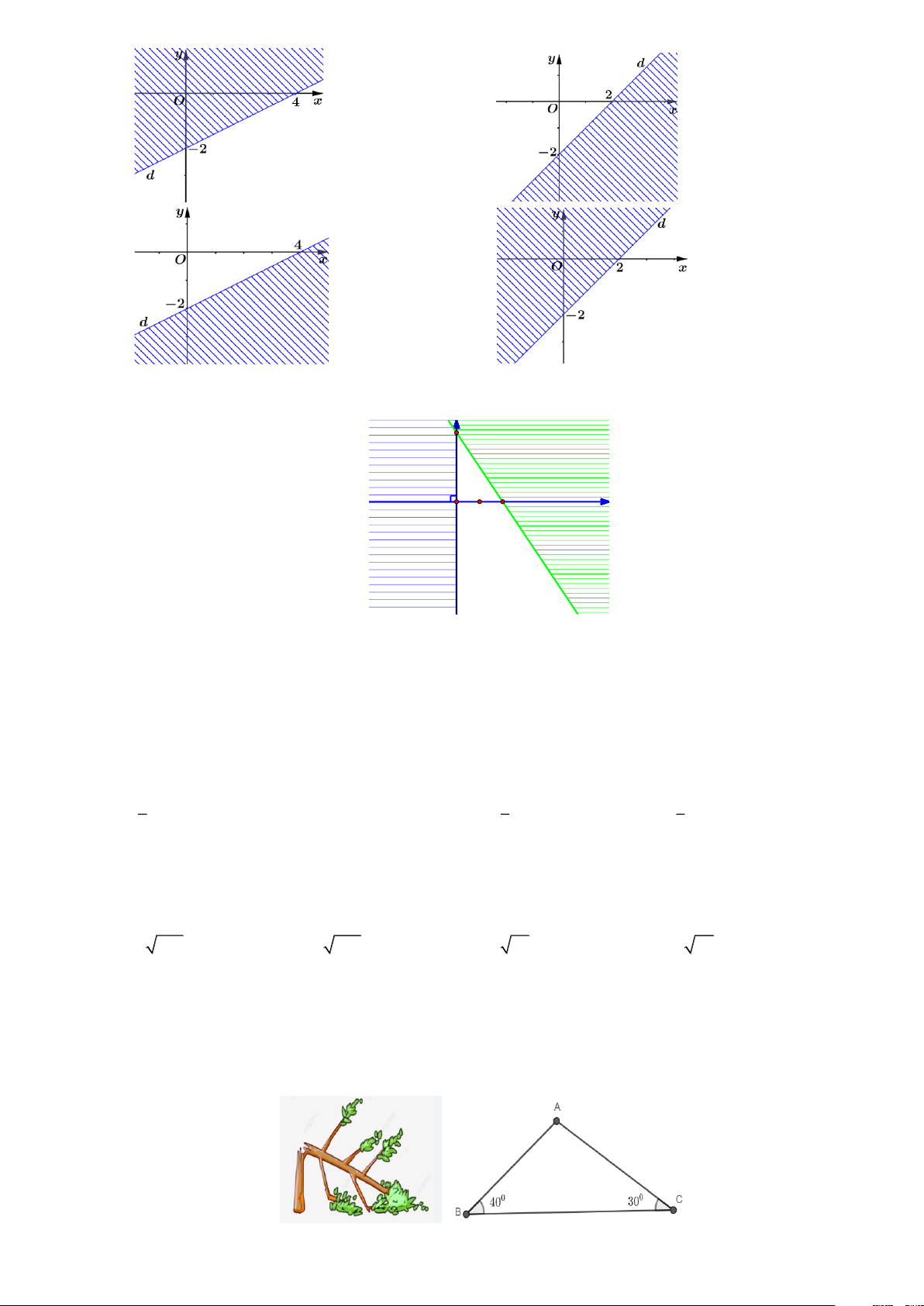
Câu 4. Miền nghiệm của bất phương trình x - 2y ³ 4 là nửa mặt phẳng không bị gạch bỏ nào trong các hình dưới đây? Trang 17 A. . B. . C. . D. .
Câu 5. Miền không bị gạch trong hình vẽ dưới (không kể biên) là miền nghiệm của hệ bất phương trình nào dưới đây? y 3 O 2 x ìï x ³ 0 ìï x > 0 ìï x > 0 ìï y > 0 A. ïí . B. ï . C. ï . D. ï . ï í í í 3x + 2y £ 6 ïî ï 3x + 2y ³ 6 ïî
ï 3x + 2y < 6 ïî
ï 3x + 2y < 6 ïî
Câu 6. Điểm nào sau đây thuộc đồ thị hàm số 2
y = x - 2x - 2025 ?
A. M (2;2025).
B. N (- 1;0).
C. P (2;- 2025).
D. Q (0;2025).
Câu 7. Trong hệ trục tọa độ Oxy , cho đường thẳng d : y = x + 1 cắt parabol (P ) 2
: y = x - 1 tại 2 điểm phân
biệt A, B . Khi đó diện tích tam giác OAB bằng? 3 9 1 A. . B. 1 . C. . D. . 2 2 2
Câu 8. Cho a là góc thỏa o o
90 < a < 180 . Khi đó khẳng định nào sai?
A. sin a > 0 .
B. cos a < 0 .
C. tan a > 0 .
D. cot a < 0 .
Câu 9. Cho tam giác A BC có AC = 6 , AC = 8 và µ
A = 60° . Kết quả nào trong các kết quả sau là độ dài của cạnh BC ? A. 2 148 . B. 148 C. 52 . D. 2 52
Câu 10. Một cái cây dạng thẳng đứng bị gió mạnh làm gãy không hoàn toàn (hai đoạn thân bị gãy vẫn dính
liền nhau tạo thành tam giác như hình vẽ). Một người muốn đo chiều cao của cây trước khi gãy, người ấy đó
được đoạn thẳng nối từ gốc cây đến ngọn cây (sau khi đã gãy) là BC = 5 m , hai góc · · ABC = 40 , ° BCA = 30° .
Chiều dài của cây trước khi bị gãy gần giá trị nào nhất dưới đây? (giả sử sự biến dạng lúc gãy không ảnh hưởng
đến tổng độ dài của cây). A. 6 . B. 8 C. 10 . D. 12
Câu 11. Cho số gần đúng a = 15, 36 . Sai số tuyệt đối của a trong khoảng nào? Trang 18
A. 0, 001 £ D < 0, 01 . B. 0, 0001 £ D < 0, 001 .C. 0, 01 £ D < 0,1 . D. 0,1 £ D < 1 . a a a a
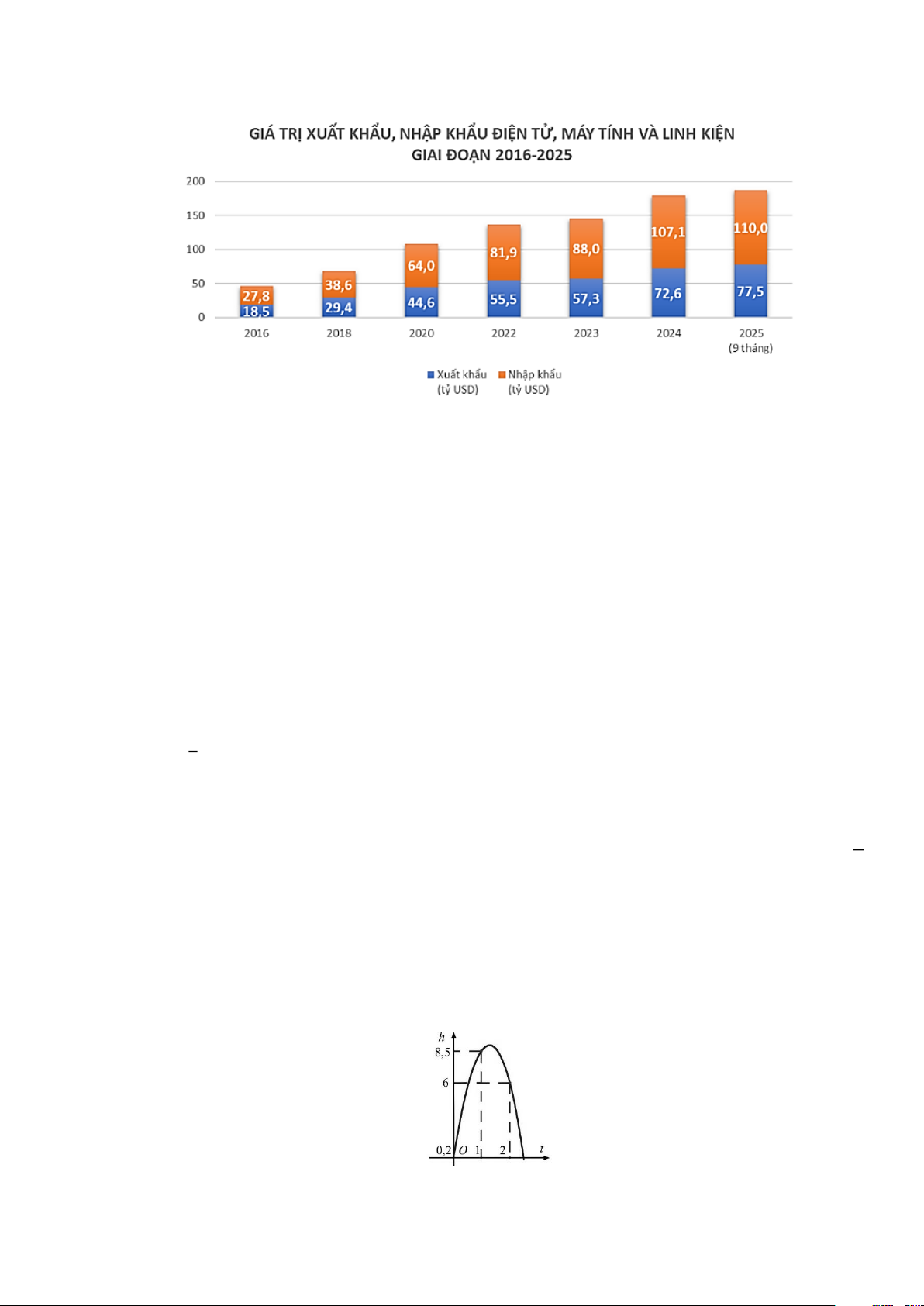
Câu 12. Quan sát biểu đồ sau và cho biết trong giai đoạn 2016 - 2025 năm nào có tổng giá trị xuất khẩu và
nhập khẩu cao nhất? A. Năm 2020 . B. Năm 2022 . C. Năm 2024 .
D. Năm 2025 (9 tháng).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số bậc hai 2
y = - 2x + 8x - 5 có đồ thị (P ).
a) (P ) có bề lõm hướng xuống dưới.
b) Trục đối xứng của (P ) là đường thẳng y = 3 .
c) Đỉnh của (P ) là điểm I (2;- 5).
d) Hàm số đã cho đồng biến trên khoảng (- ¥ ;0).
Câu 2. Cho DA BC có M là trung điểm của BC , G là trọng tâm. uuur uuur
a) MB và BC cùng hướng. uuur uuur
b) MB = - MC . uuur uuur
c) GA = 2GM . uuur 1 uuur uuur d) A G = (AB + AC ). 3
PHẦN III. Câu trắc nghiệm trả lời ngắn ìï x ³ 0 ïïïï y ³ 0 p
Câu 1. Biết rằng miền nghiệm của hệ bất phương trình: ïí
là một miền tứ giác có diện tích S = ï x + y £ 6 ï q
ïïï 3x + y £ 9 ïî
với p và q tối giản. Tính tổng p + q .
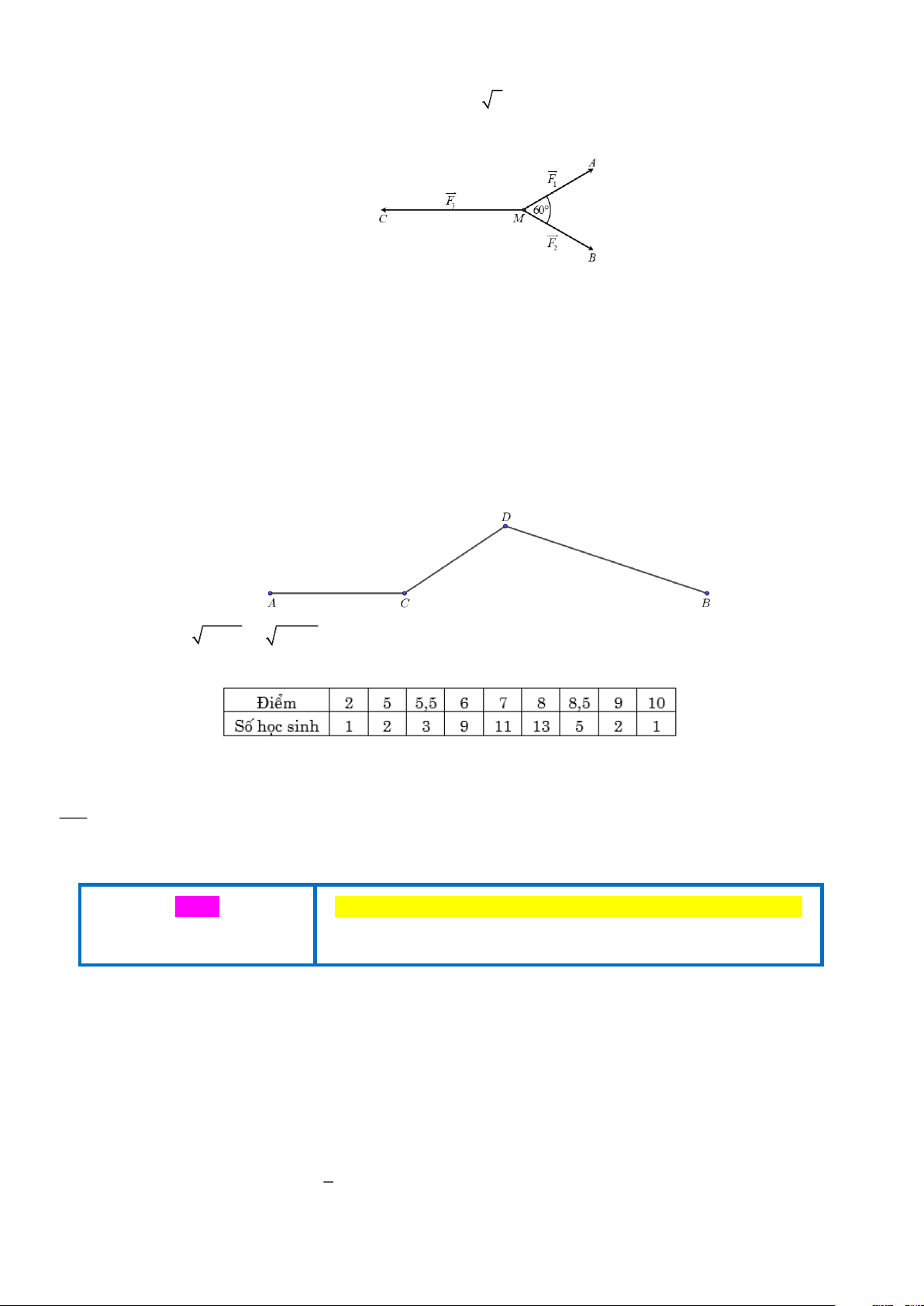
Câu 2. Xét hệ tọa độ Oth trên mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh
biểu thị độ cao h (tính bằng mét) (như hình vẽ bên dưới). Một quả bóng được đá lên từ điểm A (0;0,2) và
chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8, 5m sau 1 giây và đạt độ cao 6m sau 2
giây. Vào thời điểm nào thì quả bóng chạm đất? (làm tròn kết quả đến hàng phần trăm) Trang 19 uur uuur uur uuur uur uuur
Câu 3. Cho ba lực F = MA , F = MB , F = MC cùng tác động vào một vật tại điểm M và vật đứng yên 1 2 3 uur uur
(theo hình vẽ). Cho biết cường độ của F , F đều bằng 20 3(N ) và góc ·
AMB = 60° . Biết cường độ lực của 1 2 uur
F bằng a(N ) . Tính a . 3
Câu 4. Một rạp chiếu phim có sức chứa 800 người. Với giá vé 40 nghìn đồng mỗi người trung bình sẽ có 300
người đến rạp chiếu phim mỗi ngày. Để tăng doanh thu, rạp chiếu phim đã khảo sát thị trường và thấy rằng nếu
giá vé cứ giảm 10 nghìn đồng sẽ có thêm 100 người đến rạp chiếu phim mỗi ngày. Gọi A (nghìn đồng) là giá
vé để doanh thu từ tiền bán vé của rạp chiếu phim là lớn nhất. Giá trị của A là? PHẦN IV. Tự luận
Câu 1: Ở một giải đua ô tô địa hình, một vận động cần hoàn thành chặng đường từ A đến B gồm 3 đoạn:
đường bằng, leo dốc và xuống dốc như hình vẽ bên dưới. Trên đoạn đường bằng A C dài 10km , xe chạy với
vận tốc 100km / h . Xe leo dốc CD với vận tốc là 10km / h và xe xuống dốc DB với vận tốc là 50km / h .
Biết rằng: BC = 20km , · DCB = 45° và ·
DBC = 30° . Hỏi vận động viên mất bao nhiêu giờ để hoàn thành
chặng đường từ A đến B ?.
Câu 2: Hàm số y = 1 - x +
x + 2 có tập xác định là D = a é ;bù ë
û. Tính a + 2b .
Câu 3: Thống kê điểm thi cuối kì 1 môn Toán của lớp 10A1 ta được bảng sau
Hãy cho biết mẫu số liệu trên có bao nhiêu giá trị ngoại lệ?
Câu 4: Cho hình chữ nhật ABCD có AB = 2BC , gọi N là điểm thuộc cạnh CD sao cho AC ^ BN . Tính tỉ DN số . CN --------HẾT-------- ĐỀ 5
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 10
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1: Cho hai tập hợp A = {- 7;1;5;7},B = {- 3;5;7;13}. Tìm tập hợp A Ç B .
A. {- 7;- 3;1;5;7;13}. B. {- 7; } 1 . C. {13}. D. {5;7}.
Câu 2: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? 1
A. 2x - 5y + 3z £ 0.
B. + 2y - 4 > 0 .
C. 2x + 5y = 3 .
D. 2x + 3y < 5 . x
Câu 3: Cho hàm số y = f (x ) có đồ thị như hình vẽ. Khi đó f (0) bằng Trang 20



