














































Preview text:
SỞ GDĐT TỈNH QUẢNG NAM
ĐỀ THI ĐỀ NGHỊ KỲ THI OLYMPIC 24/3
TRƯỜNG THPT NGUYỄN DUY HIỆU Năm học 2016- 2017
Môn: VẬT LÝ – Lớp 10
Thời gian làm bài: 150 phút
(Đề thi có 02 trang, gồm 06 câu) Bài 1 (4 điểm):
Một vật rơi tự do đi được 10m cuối cùng của quãng đường trong khoảng thời gian
0,25s. Cho g = 9,8m/s2. Tính:
a. Vận tốc của vật khi chạm đất và độ cao từ đó vật bắt đầu rơi?
b. Giả sử cũng từ độ cao này người ta ném thẳng đứng một vật thứ hai (cùng một lúc
với khi thả vật thứ nhất rơi tự do). Hỏi phải ném vật thứ hai với vận tốc ban đầu có
hướng và độ lớn như thế nào để vật này chạm mặt đất trước vật rơi tự do 1 giây. Bài 2 (4 điểm):
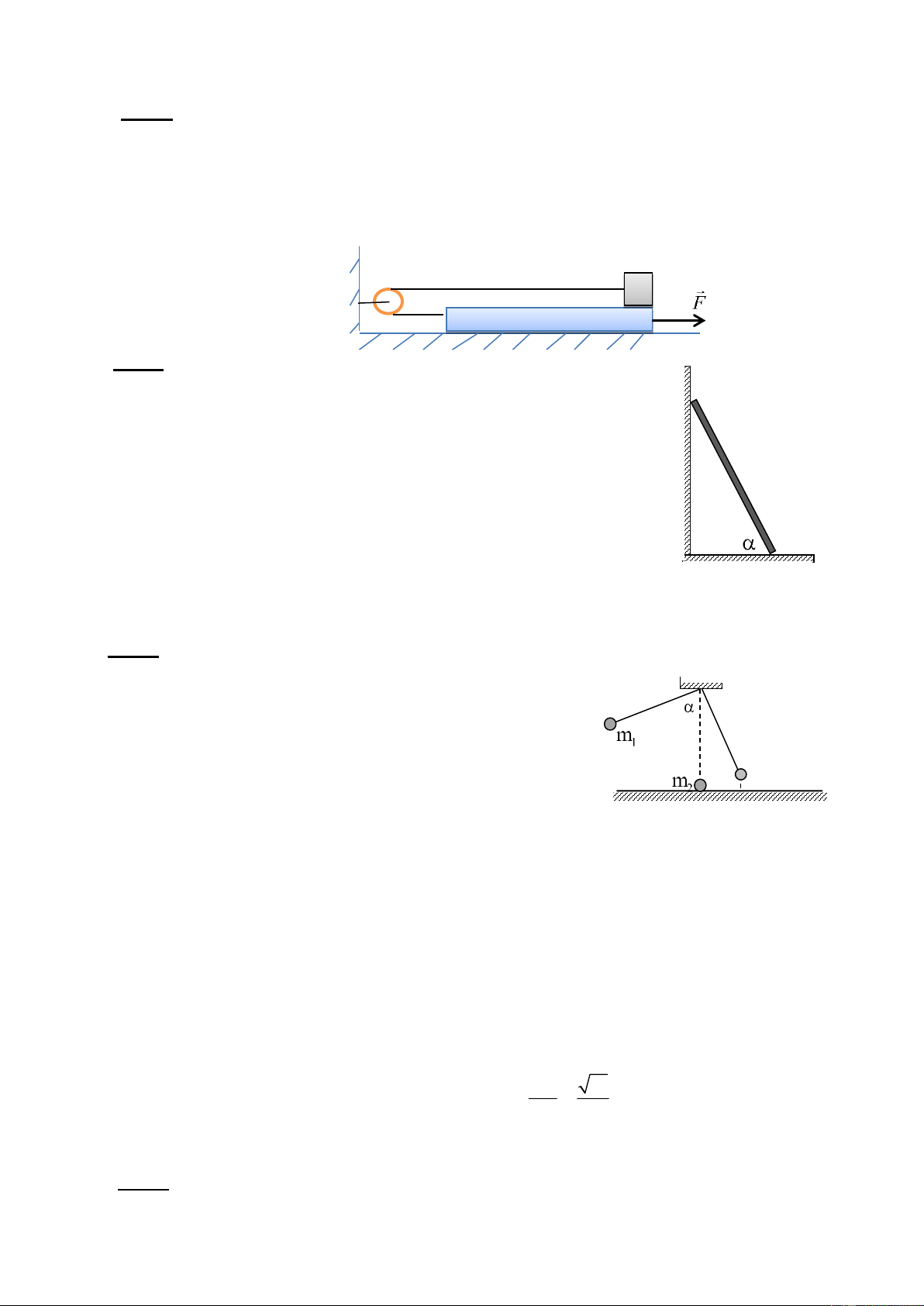
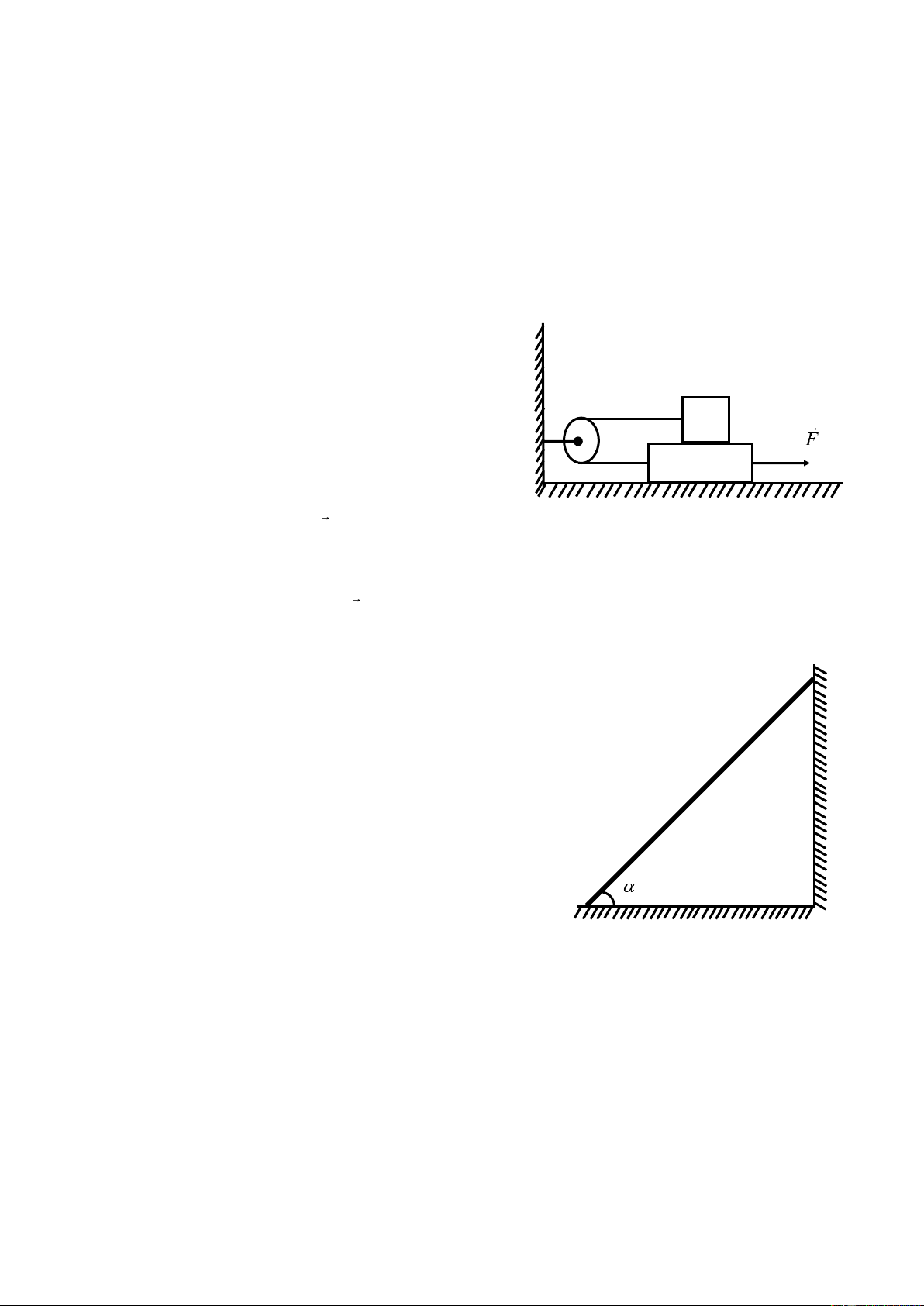
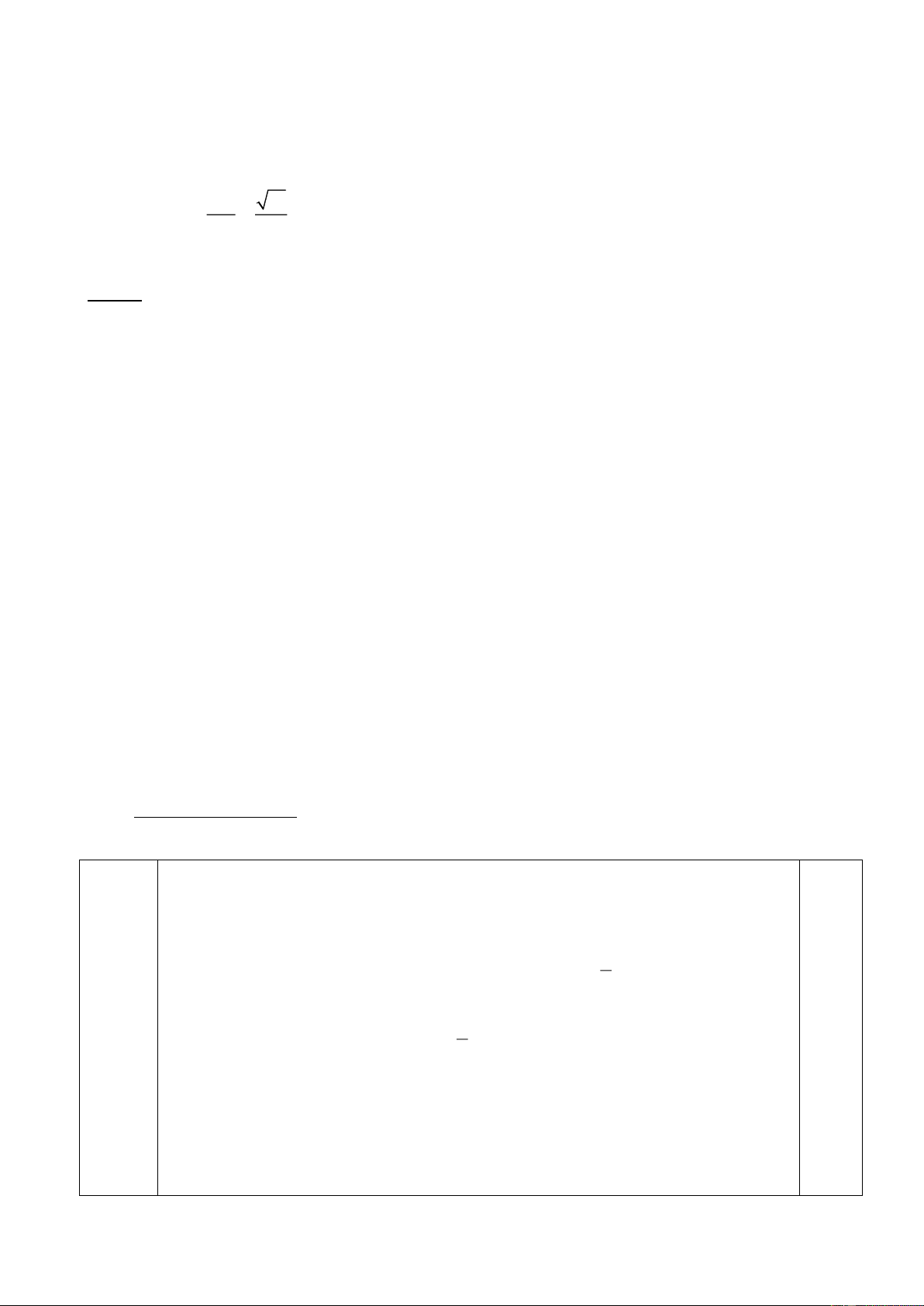
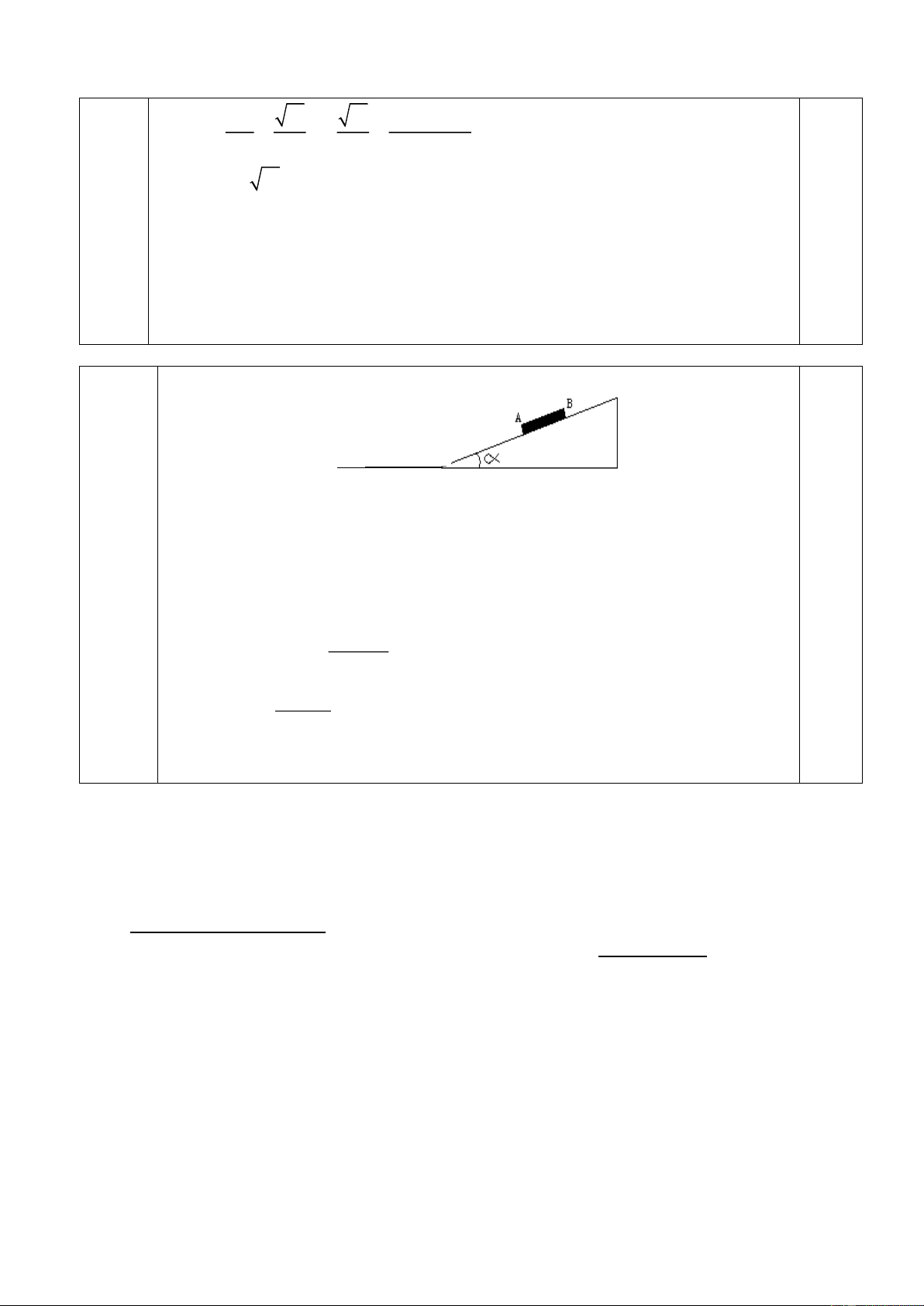
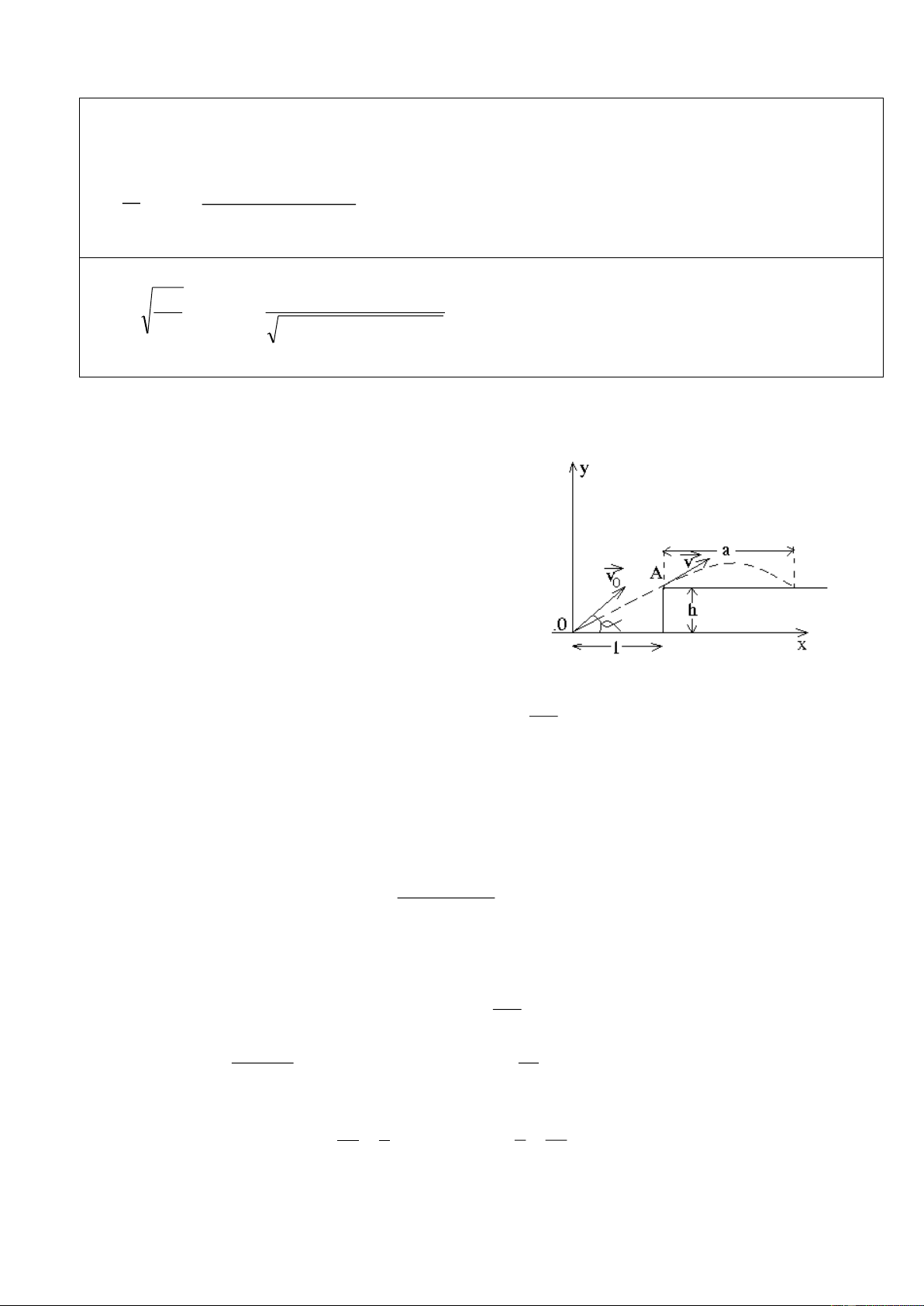
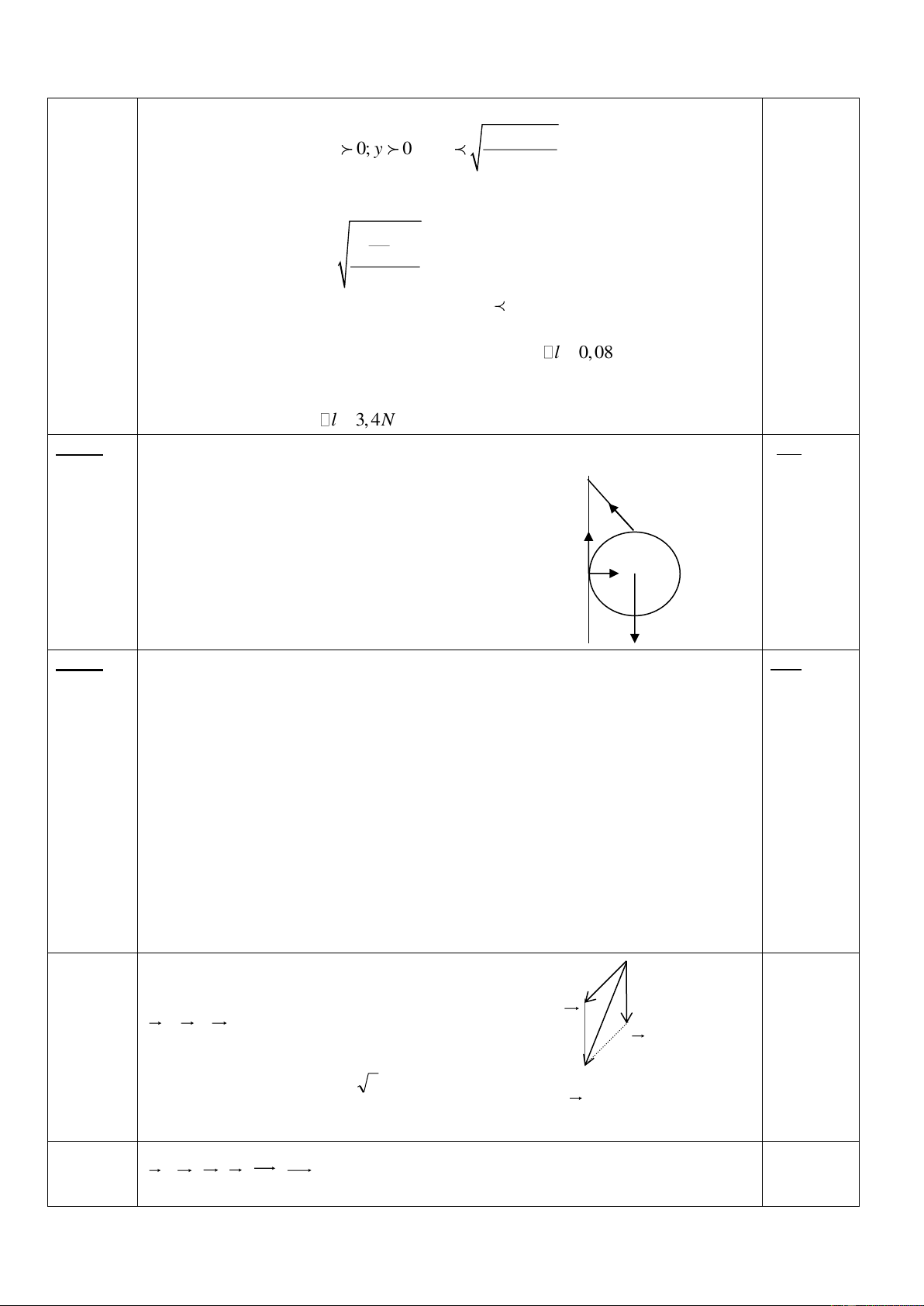
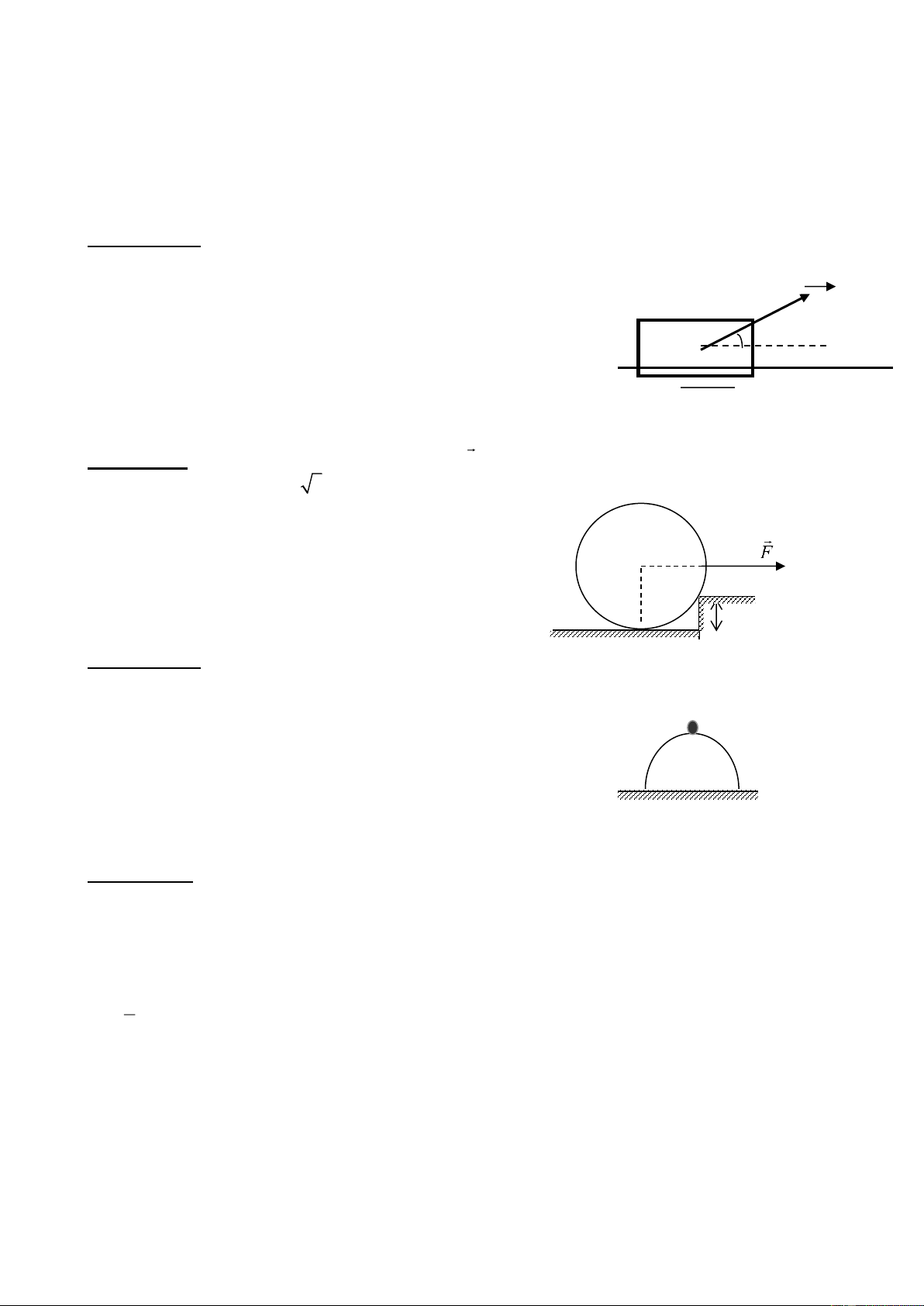
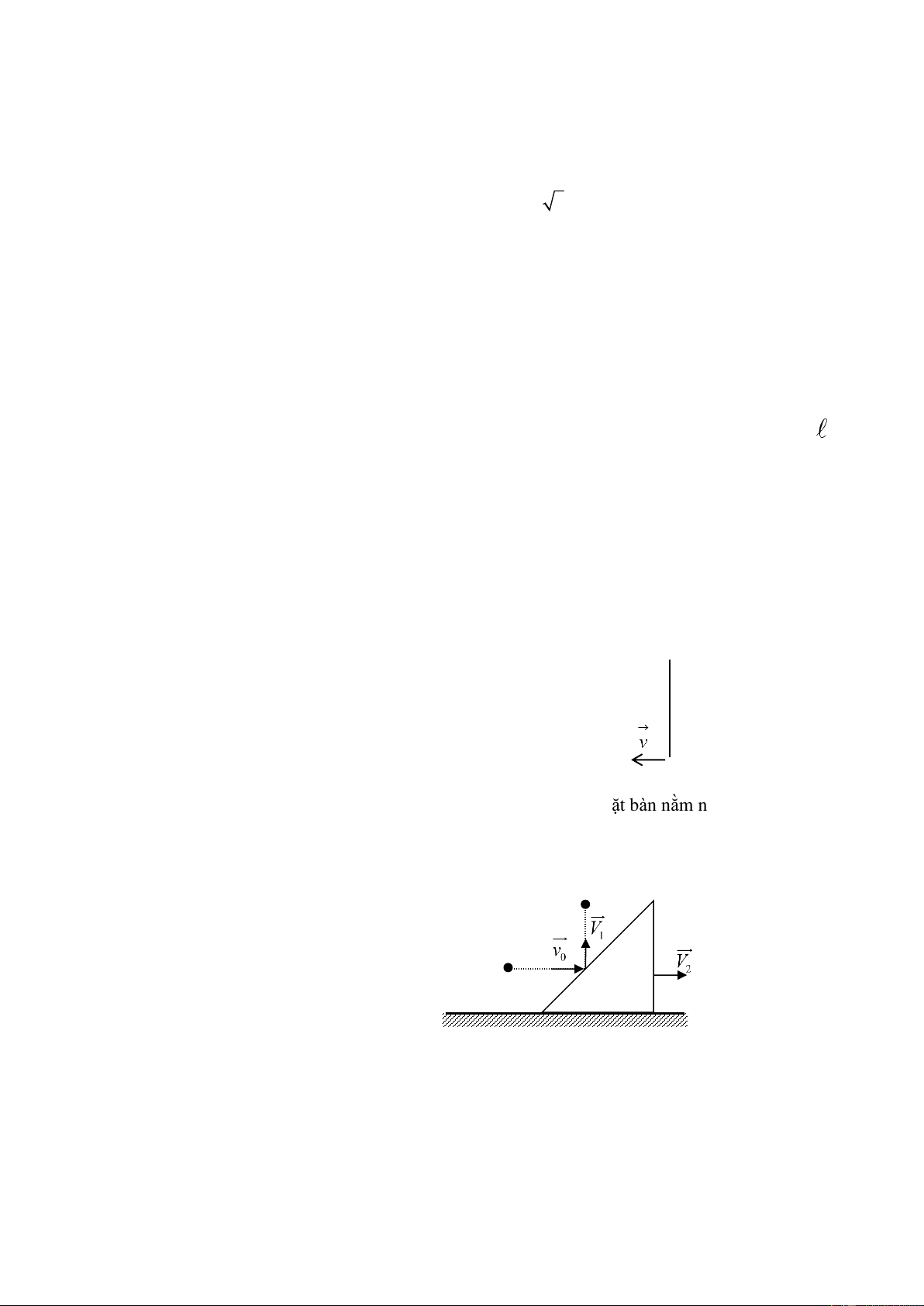
Một vật có trọng lượng P=100N được giữ đứng yên trên mặt phẳng nghiêng góc α
bằng lực F có phương nằm ngang (hình 2).
Biết tanα=0,5 và hệ số ma sát trượt μ=0,2. Lấy g=10m/s2.
a) Tính giá trị lực F lớn nhất.
b) Tính giá trị lực F nhỏ nhất. Hình 2 Bài 3 (3 điểm):
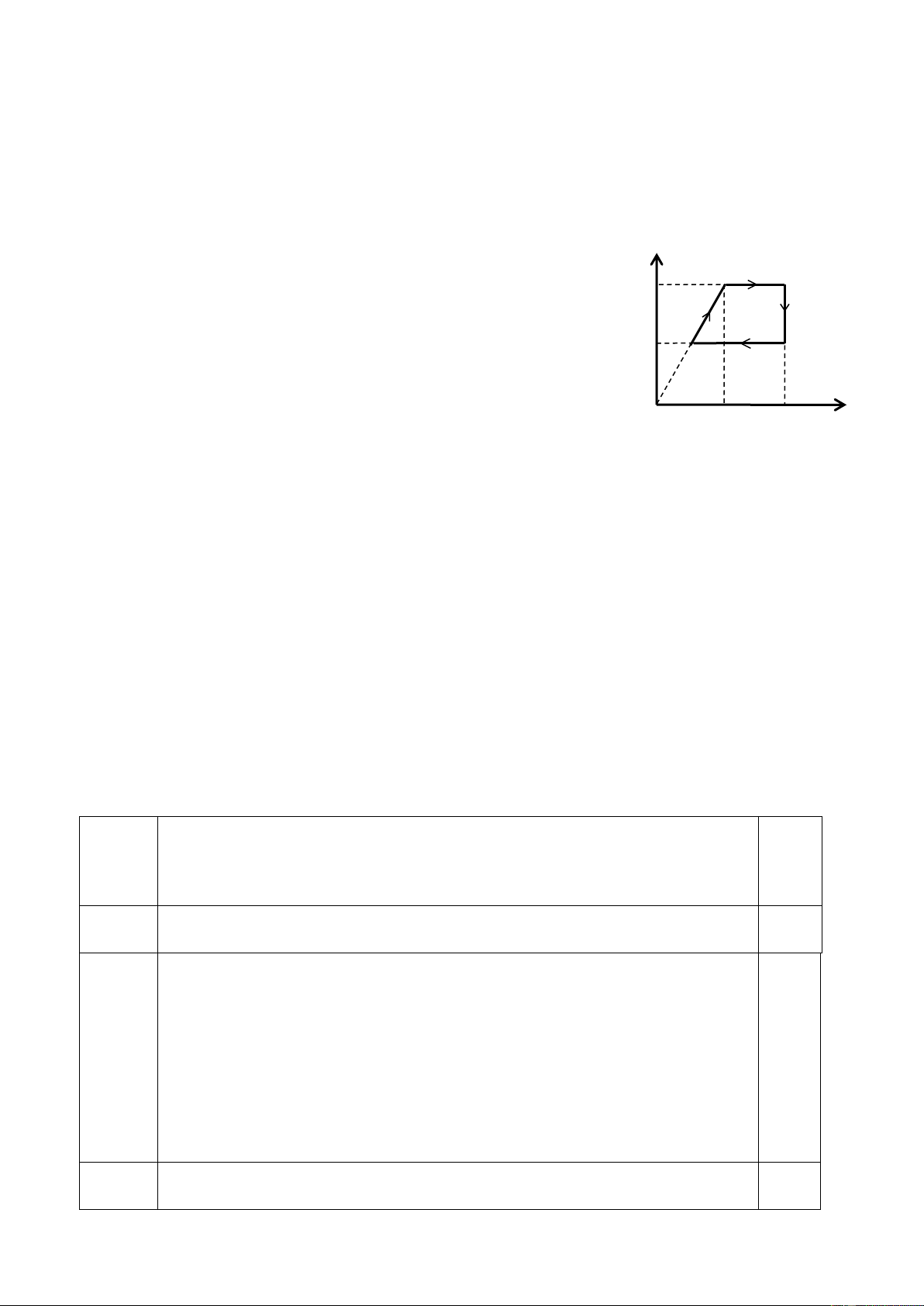
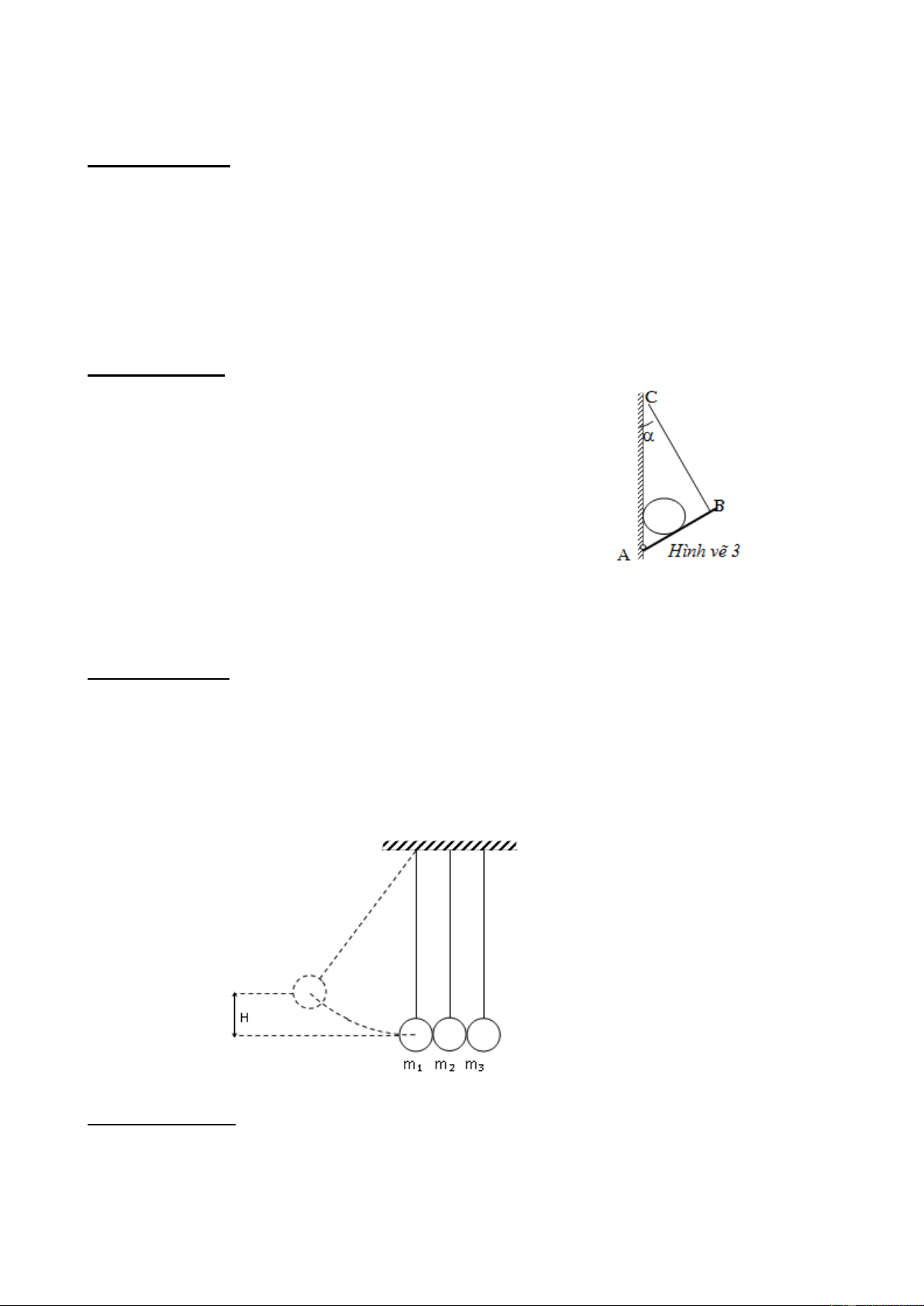
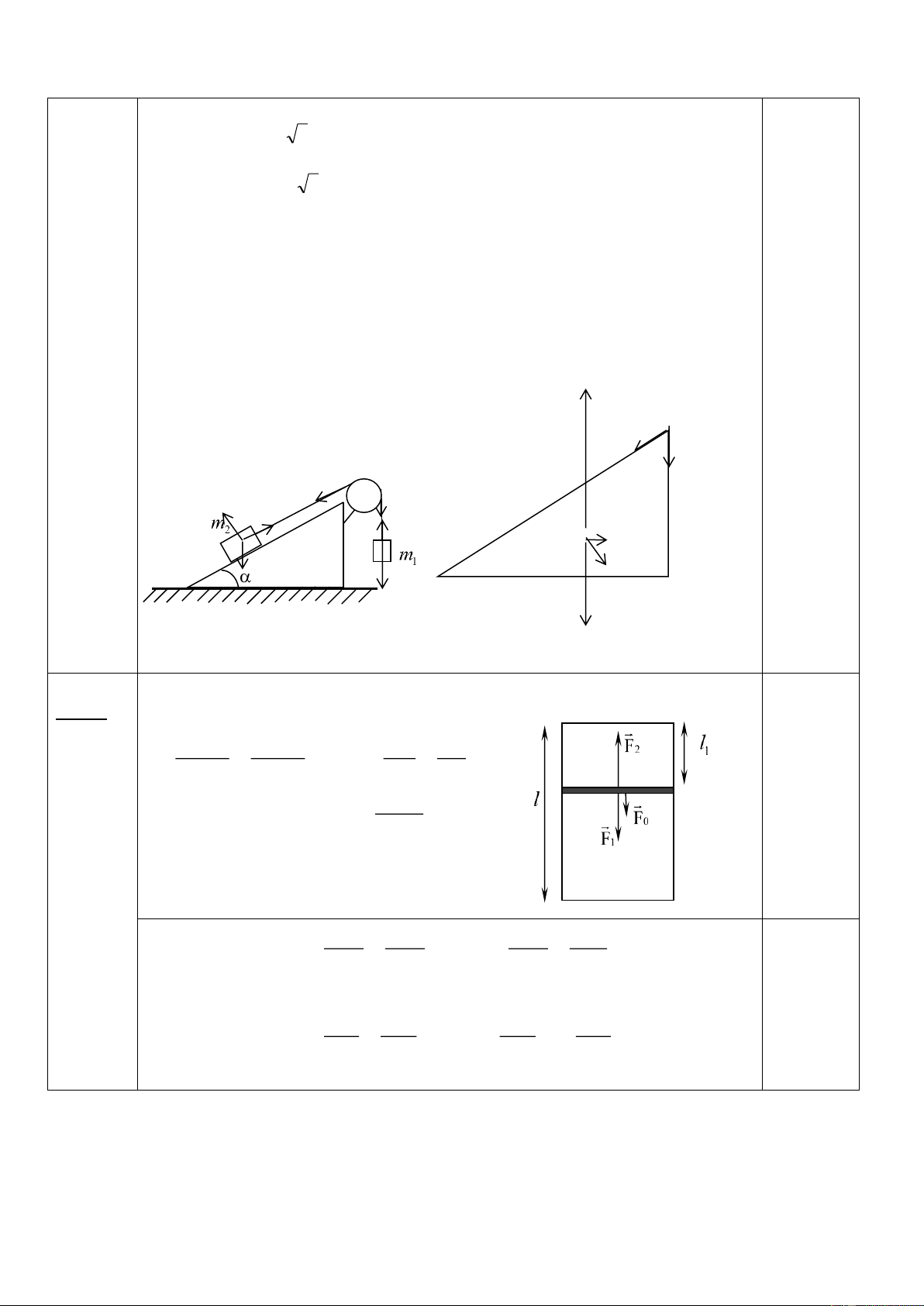
Một thanh AB dài 2m khối lượng m = 2kg được giữ C B
nghiêng một góc trên mặt sàn nằm ngang bằng
một sợi dây nằm ngang BC dài 2m nối đầu B của
thanh với một bức tường thẳng đứng; đầu A của A
thanh tựa lên mặt sàn. Hệ số ma sát giữa thanh và )
mặt sàn bằng 3 (như hình 3). 2 Hình 3
a) Tìm các giá trị của để thanh có thể cân bằng.
b) Tính các lực tác dụng lên thanh và khoảng cách AD từ đầu A của thanh đến
góc tường D khi góc = 450. Lấy g = 10m/s2. Bài 4 (4 điểm):
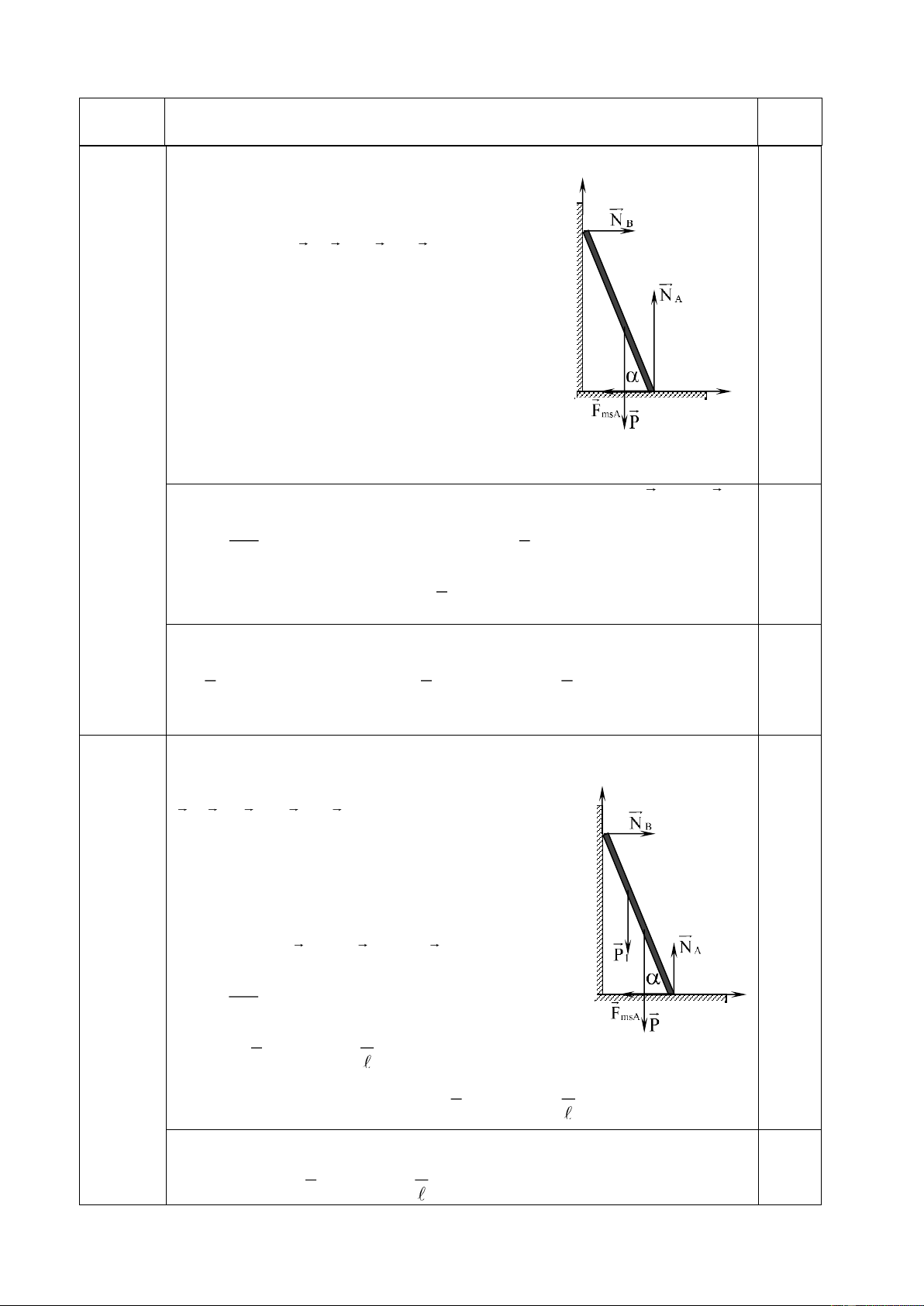
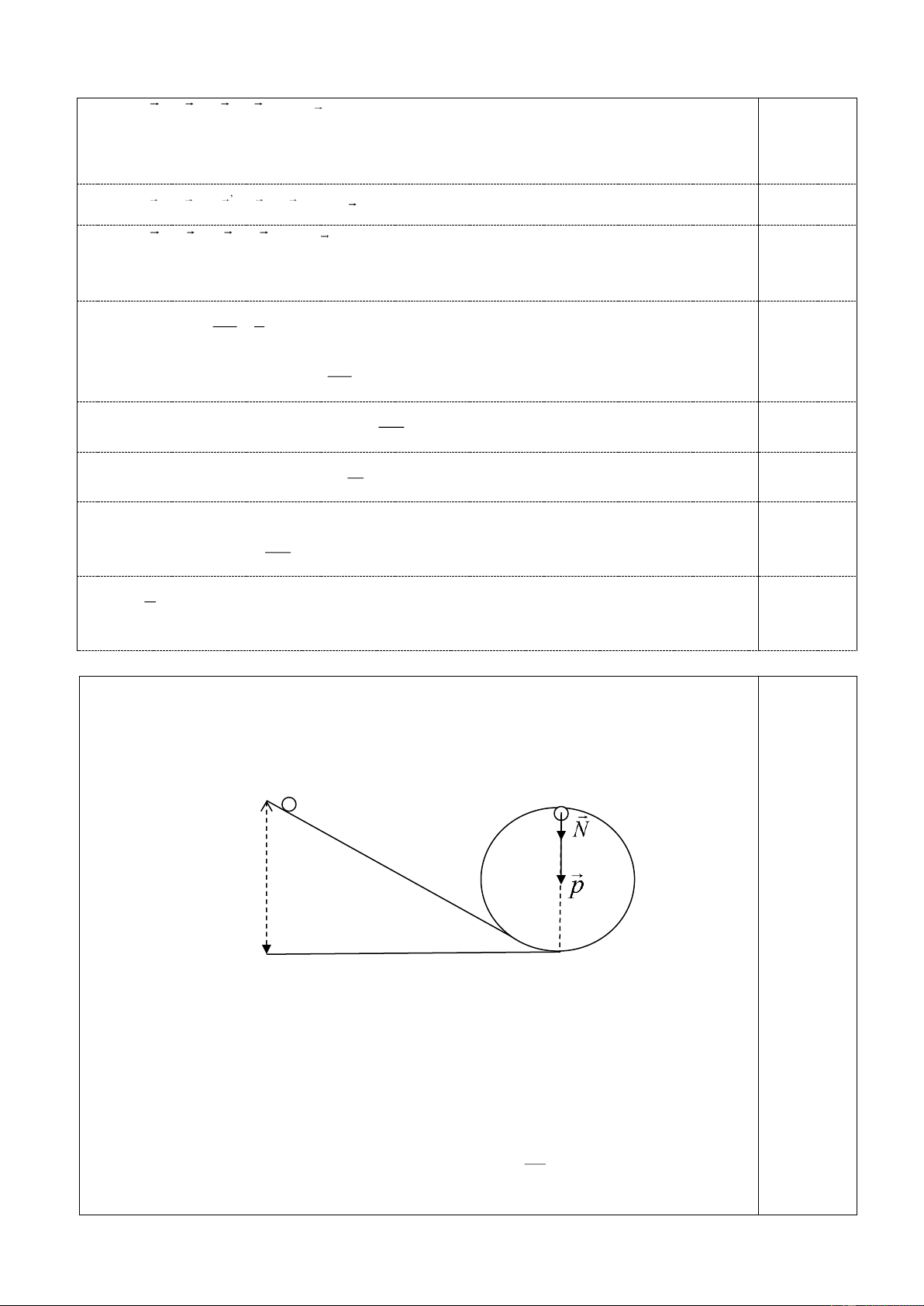
Một quả cầu nặng m=100g được treo ở đầu một sợi dây nhẹ, không co dãn, dài l=1m
(đầu kia của dây cố định). Truyền cho quả cầu ở vị trí cân bằng một vận tốc đầu v0
theo phương ngang. Khi dây treo nghiêng góc α =30o so với phương thẳng đứng thì
gia tốc của quả cầu có phương ngang. Cho g=10m/s2, bỏ qua mọi ma sát. a) Tìm vận tốc v0.
b) Tính lực căng dây và vận tốc của vật tại vị trí có góc lệch = 40o. Bài 5 (3 điểm): P
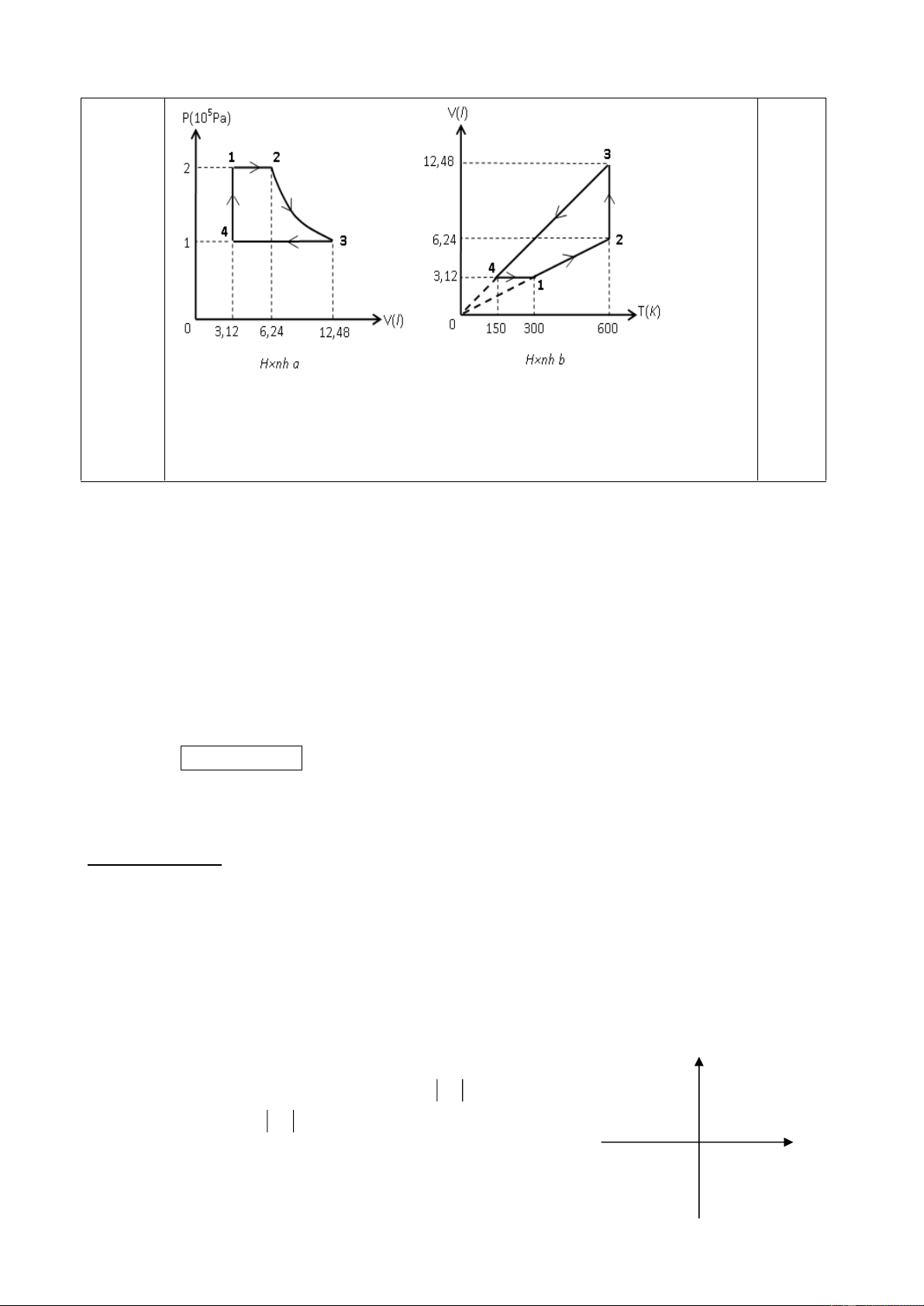
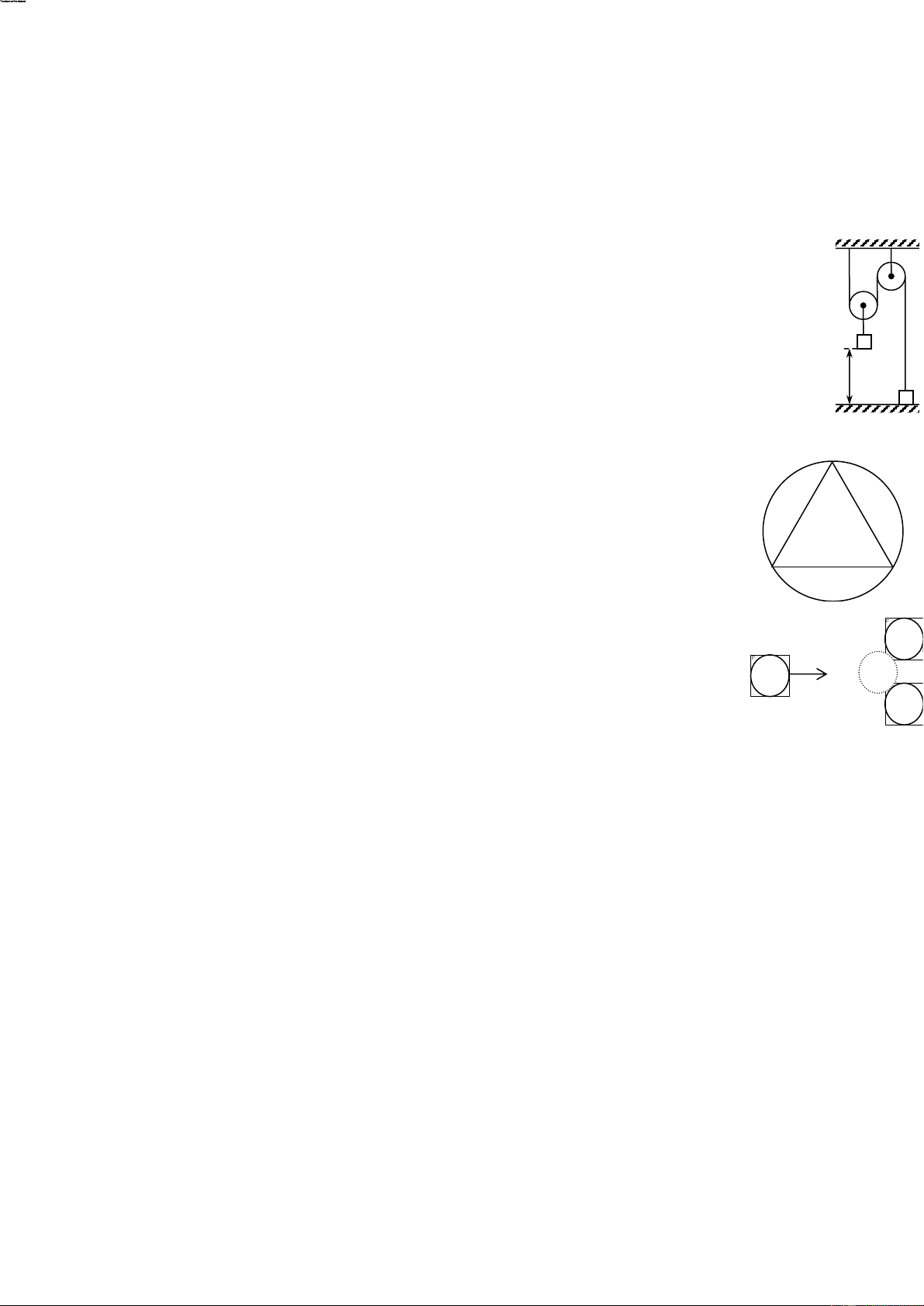
Có 1 g khí Heli (coi là khí lý tưởng đơn nguyên tử) 2P0 1 2
thực hiện một chu trình: 1 – 2 – 3 – 4 – 1 được biểu
diễn trên giản đồ P-T như hình 5. P0 Cho P 4 3 0 = 105Pa; T0 = 300K.
a) Tìm thể tích của khí ở trạng thái 4. T
b) Hãy nói rõ chu trình này gồm các đẳng quá trình 0 T0 2T0
nào. Vẽ lại chu trình này trên giản đồ P-V và trên giản Hình 5
đồ V-T (cần ghi rõ giá trị bằng số và chiều biến đổi của chu trình).
Bài 6 (2 điểm): Thí nghiệm thực hành
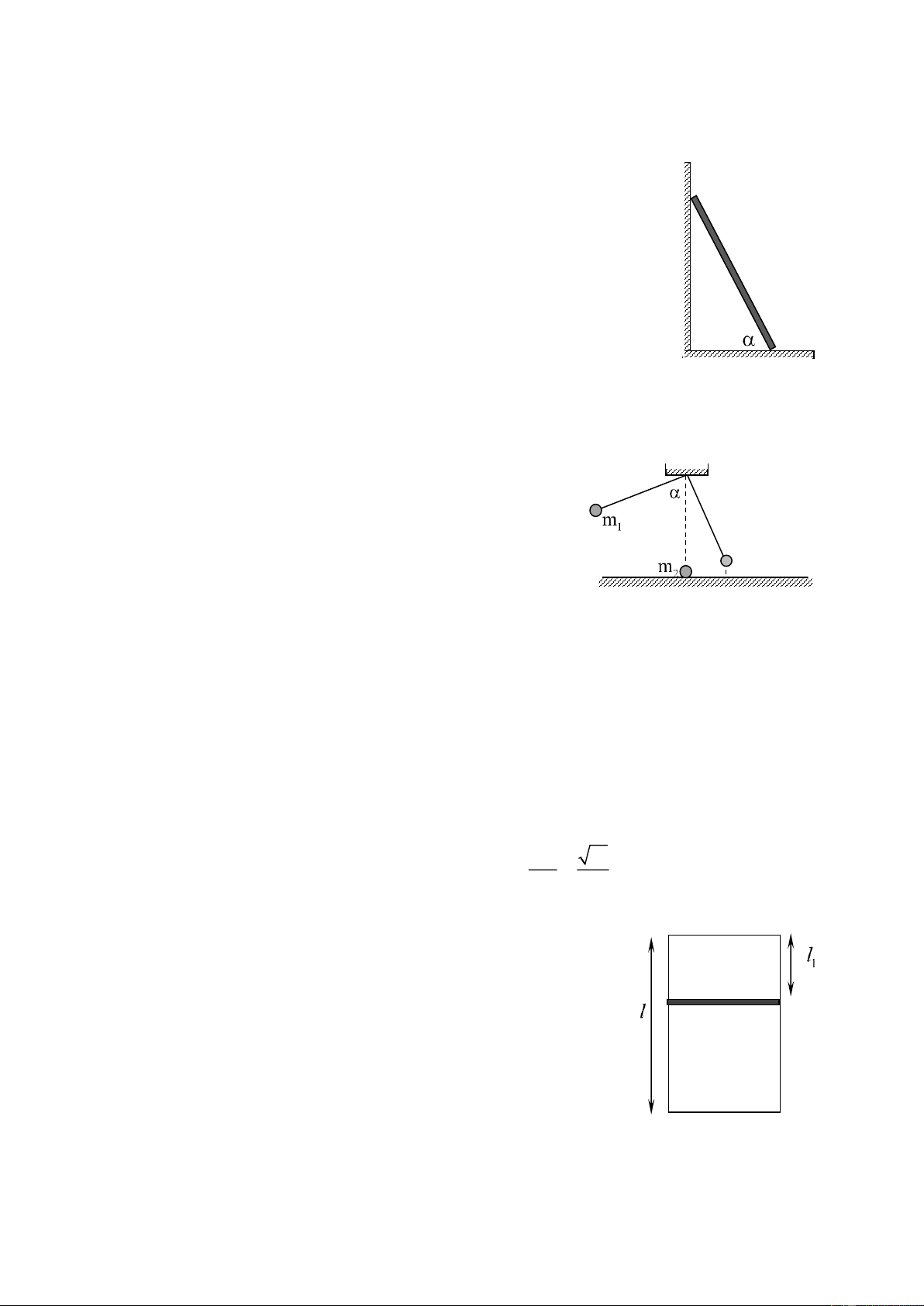
Xác định khối lượng của thanh gỗ. Cho các đồ dùng :
1 thanh gỗ cứng hình hộp chữ nhật, kích thước 800 × 20 × 15 (mm); 1 giá thí nghiệm.
1 thước thẳng có vạch chia mm;
1 hộp quả cân (đủ loại từ nhỏ đến lớn); 1 bút nỉ; 1 dây nhựa nhỏ. Yêu cầu :
+ Nêu phương án thí nghiệm xác định khối lượng của thanh gỗ đó.
+ Nêu cách tính sai số của phép đo.
********** HẾT **********
• Thí sinh không được sử dụng tài liệu.
• Giám thị coi thi không giải thích gì thêm.
ĐÁP ÁN ĐỀ THI ĐỀ NGHỊ KỲ THI OLYMPIC 24/3 TỈNH QUẢNG NAM
MÔN VẬT LÝ 10 - NĂM HỌC 2016-2017
-----------***----------- Bài 1. (4,0 điểm)
a. Chọn gốc tọa độ tại nơi thả vật, chiều dương hướng xuống, 0,5
gốc thời gian lúc thả vật. 2
Tại A (tại mặt đất ): g t 0,5 A y = h = (1) A 2 2 g t
Tại B (cách mặt đất 10m) : y = h −10 B = (2) B 2 0,5
t − t = 0, 25 s → t = t − 0, 25 (3) 0,25 A B B A 2 2 gt gt A B Từ (1) và (2) ta có : = +10 (4) 0,25 2 2
(4 điểm) Thay (3) vào (4) ta có : gt = g (t − )2 2 0, 25
+ 20 → 4,9t = 0,6125 + 20 → t = 4,2066 s A A A A
v = gt = 9,8.4, 2066 = 41, 225m / s A A 0,5 2 g.tA h = = 86,71m 0,5 2 2 gt '
b. y = h = v .t ' A +
(t ' = t −1 = 3, 2066s) v = 11, 33m / s A 0 A A A 0 2 0,5 0,5 và ném xuống. Bài 2. (4,0 điểm)
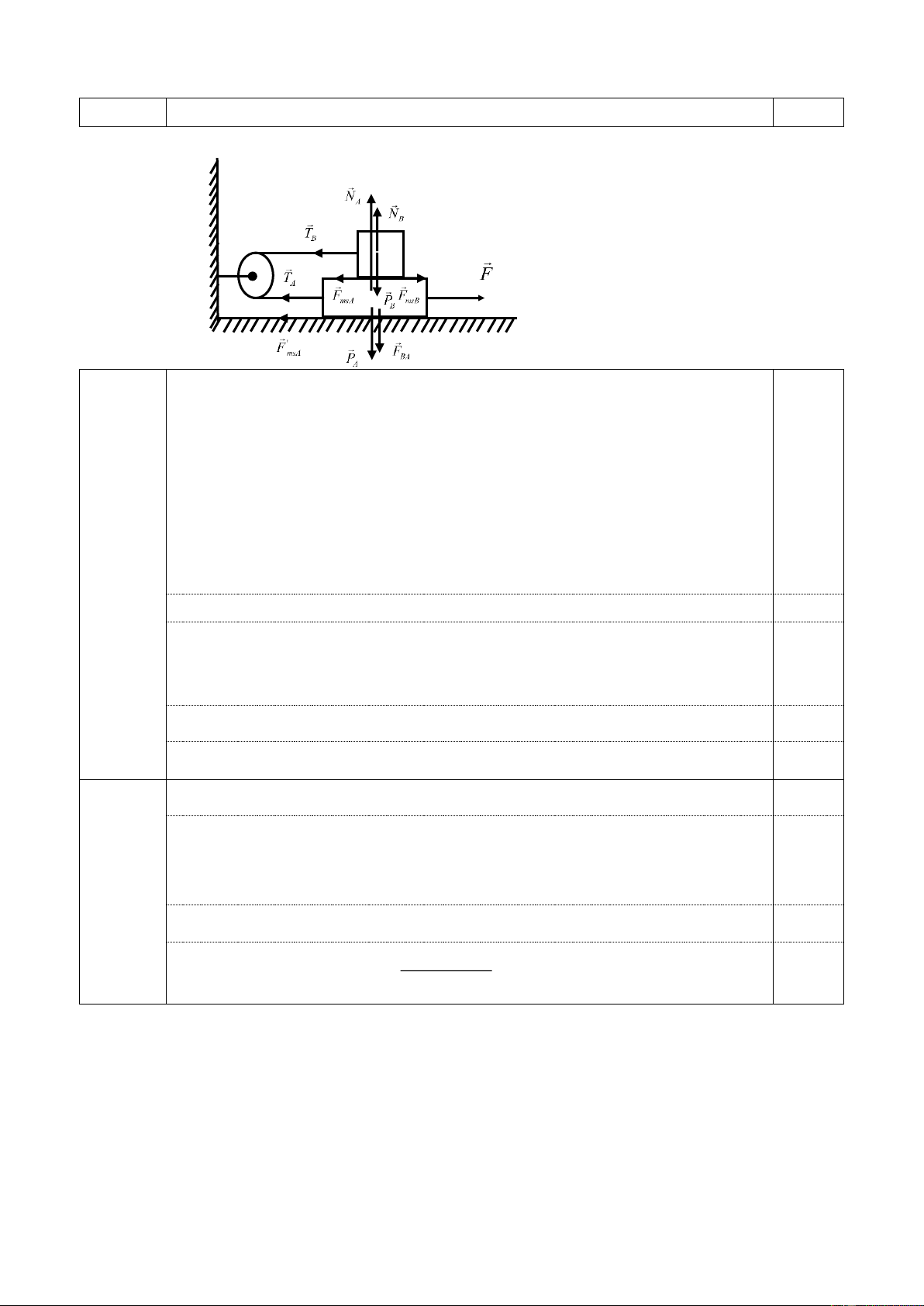
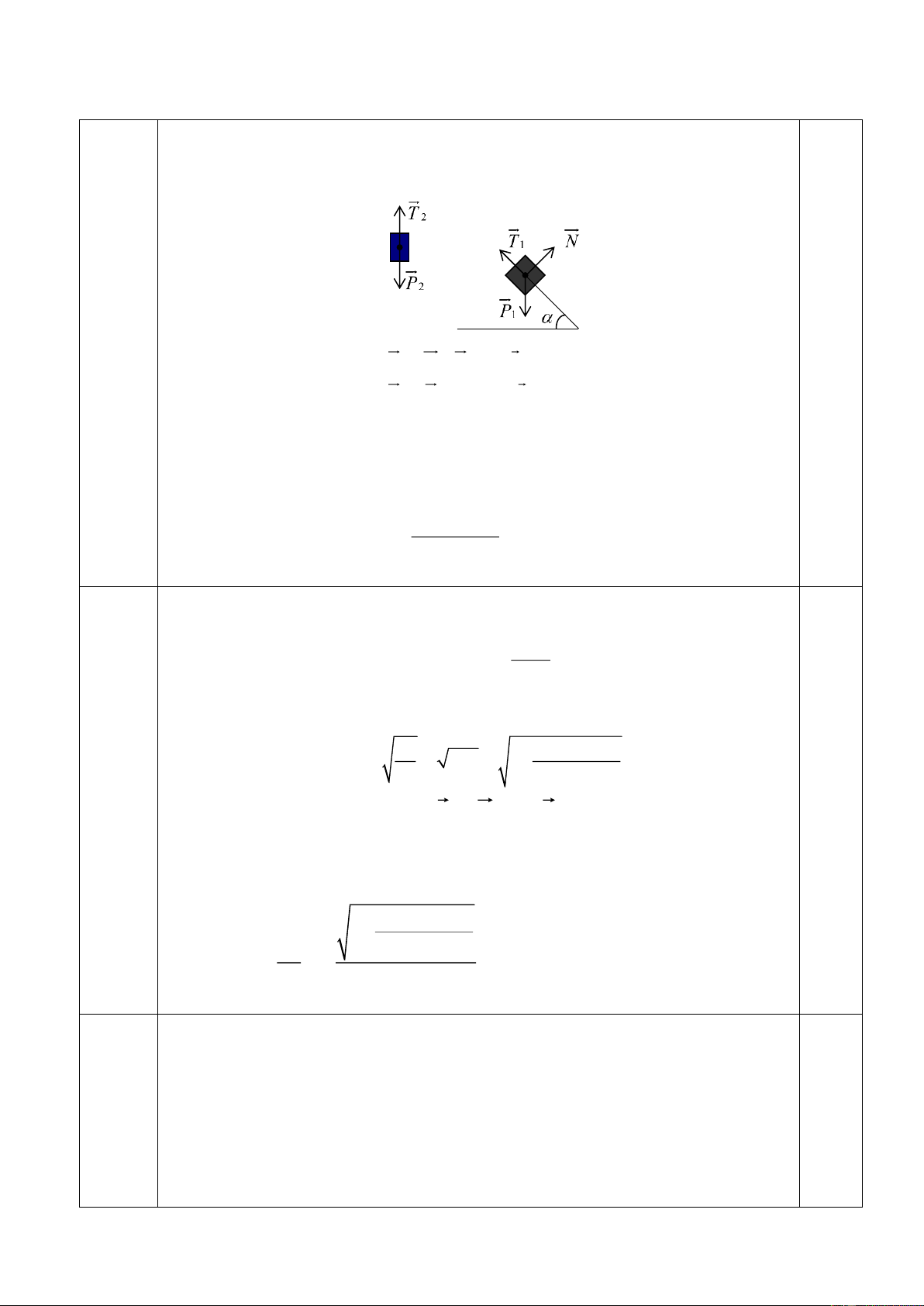
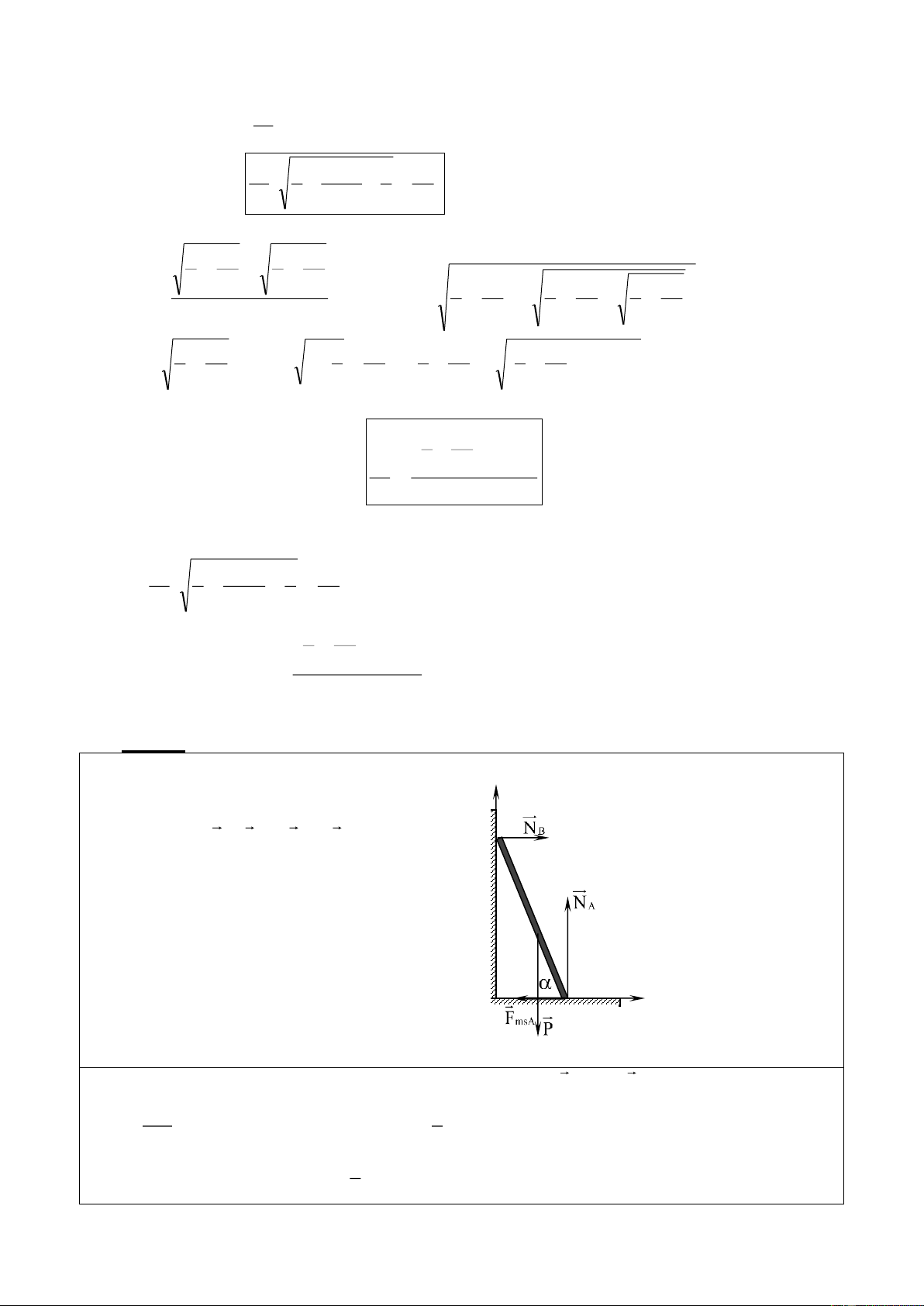
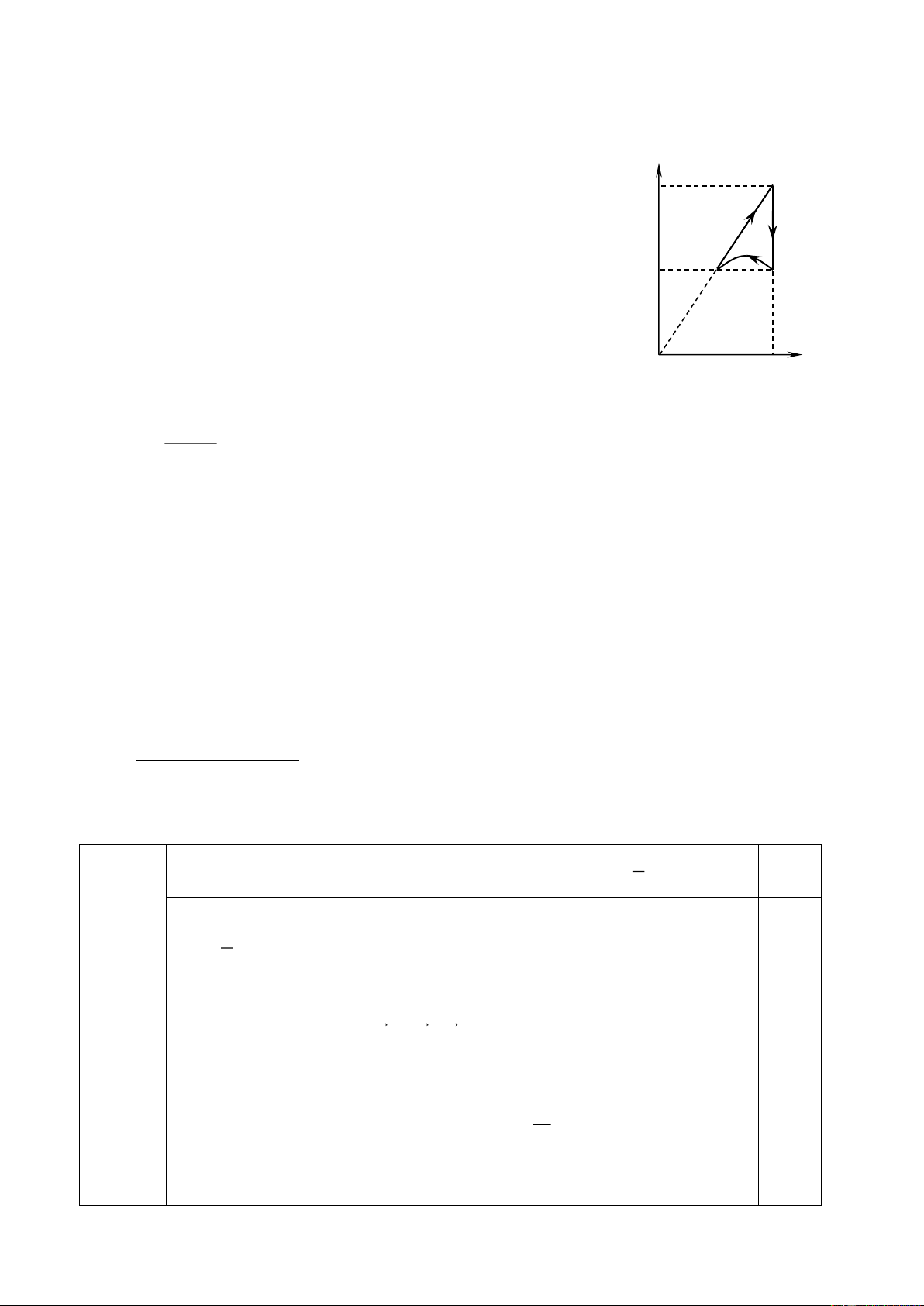
a) Lực F có giá trị lớn nhất khi vật có xu hướng đi lên. Khi đó
các lực tác dụng lên vật như hình vẽ. Do vật cân bằng nên
N + F + F + P = 0 ms 0,5
Chiếu lên phương mặt phẳng nghiêng và phương vuông góc
với mặt phẳng nghiêng ta được: 0,5 = − F Fcos P sin ms = + N Fsin P cos + P(sin cos ) Do : F N F 0,5 ms − cos sin + α P(tan ) = (4 điểm) − 1 tan P(tan + ) F = max 1 − tan
Thay số ta được: F 77 8 , N 0,5 max .
b) Lực F có giá trị nhỏ nhất khi vật có xu hướng đi xuống. 0,5
Khi đó lực ma sát đổi chiều so với hình vẽ. Do vật cân bằng nên
N + F + F + P = 0 . ms
Chiếu lên phương mặt phẳng nghiêng và phương vuông góc
với mặt phẳng nghiêng ta được: F
= −F cos + Psin 0,5 ms
N = F sin + P cos
P(sin − cos ) P(tan − )
Do : F N F = 0,5 ms cos + sin 1+ tan P(tan − ) F = min 1+ tan . 0,5
Thay số ta được: F 27,27N max . Bài 3. (3,0 điểm)
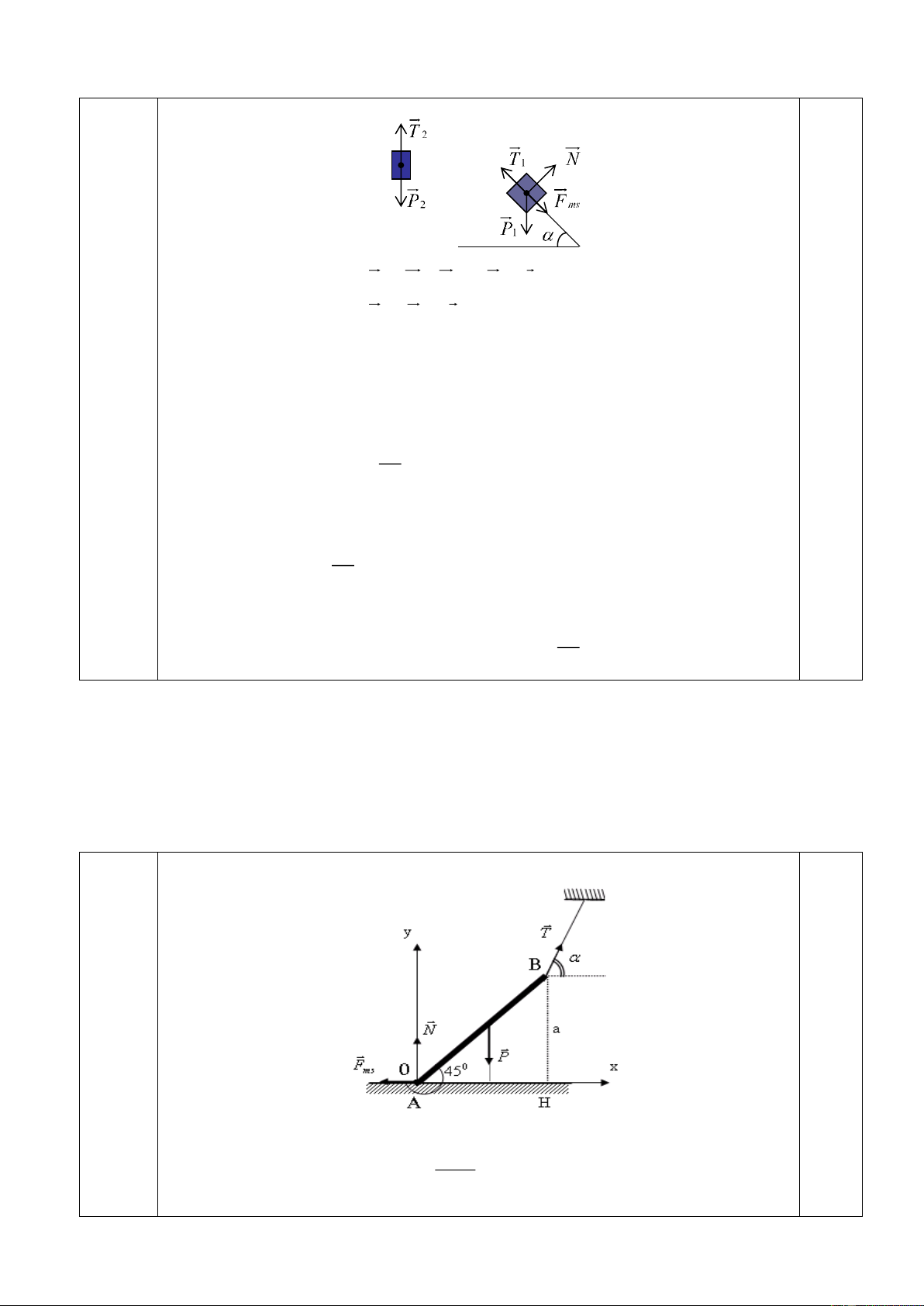
Các lực tác dụng lên thanh AB là trọng lực, lực ma sát, phản
lực của mặt sàn lực căng của dây. Các lực được biểu diễn như hình vẽ. C T B 0,5 N P A ) F ms
Áp dụng điều kiện cân bằng tổng quát của vật rắn cho thanh (3 điểm) AB ta có. 0,25
P + F + N + T = 0 (1) ms
Thanh cân bằng khi momen tác dụng lên thanh đối với trục
quay tạm thời tại A bằng 0 : M bằng 0 vì lưc có giá P = MT (Momen của N và Fms 0,25 đi qua trục quay). Hay T.AB.sin = P. cos (2) 2 0,25 1 T = Pcotg (3) 2
Chiếu (1) lên phương nằm ngang và phương thẳng đứng ta có: Fms – T = 0 (4) 0,25 -P + T = 0 (5) 1
Hay Fms = T = mgcotg (6) và N = P = mg (7) 0,25 2 Lực ma sát F
ms phải là lực ma sát nghỉ, do đó ta có Fms Kn 0,25
Từ (6) và (7) 1 mg.cotg kmg cotg 2k = 3 2 300 0,25
Khi = 450 thay vào (6) và (7) ta được : 0,25 Fms = T = 10N N = P = 20N 0,5
Từ hình vẽ ta có : AD = BC – AB cos = 0,59m.
Bài 4. (4,0 điểm)
a) Khi dây treo nghiêng góc α=300 so với phương thẳng đứng,
vật M chịu tác dụng của các lựcnhư hình vẽ. Do gia tốc có phương ngang nên: = . 30o T cos mg (1) 0,5 O
Mặt khác, xét theo phương hướng tâm MO ta α có: T 2 mv T − m os30o gc =
(2) (Với v là vận tốc của vật m M 0,5 l a tại M). P 0,5 Từ (1) và (2) suy ra: gl 2 v = (3) 2 3
(4 điểm) Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí M và khi vật ở vị trí cân bằng 12 − 5 3 0,5 ta được: v 2
0 =v2+2gl(1 – cos300) = gl → 6 v 0,5 0 ≈ 2,36m/s
b) Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí =40o và
khi vật ở vị trí cân bằng ta được: 2 2 o 2
v = v + 2gl(1− os40 c
) → v = v − 2gl(1− os c
40o ) 0, 94(m / s) o o 0,5
Xét theo phương sợi dây ta có: 2 2 mv 0,5 o o 0,1.0, 94 T = m os gc 40 + = 0,1.10. os c 40 + = 0,86N l 1 Bài 5. (3,0 điểm)
a) Quá trình 1 – 4 có P tỷ lệ thuận với T nên là quá trình
đẳng tích, vậy thể tích ở trạng thái 1 và 4 là bằng nhau: 0,5 V
. Sử dụng phương trình C 1 = V4 -M ở trạng thái 1 ta có: m m RT PV = RT , suy ra: 1 V = 1 1 1 1 P 0,5 1
Thay số: m = 1g; = 4g/mol; R = 8,31 J/(mol.K); T
1 = 300K và P1 = 2.105 Pa ta được: 1 8,31.300 0,5 3 − 3 V = = 3,12.10 m 1 5 4 2.10
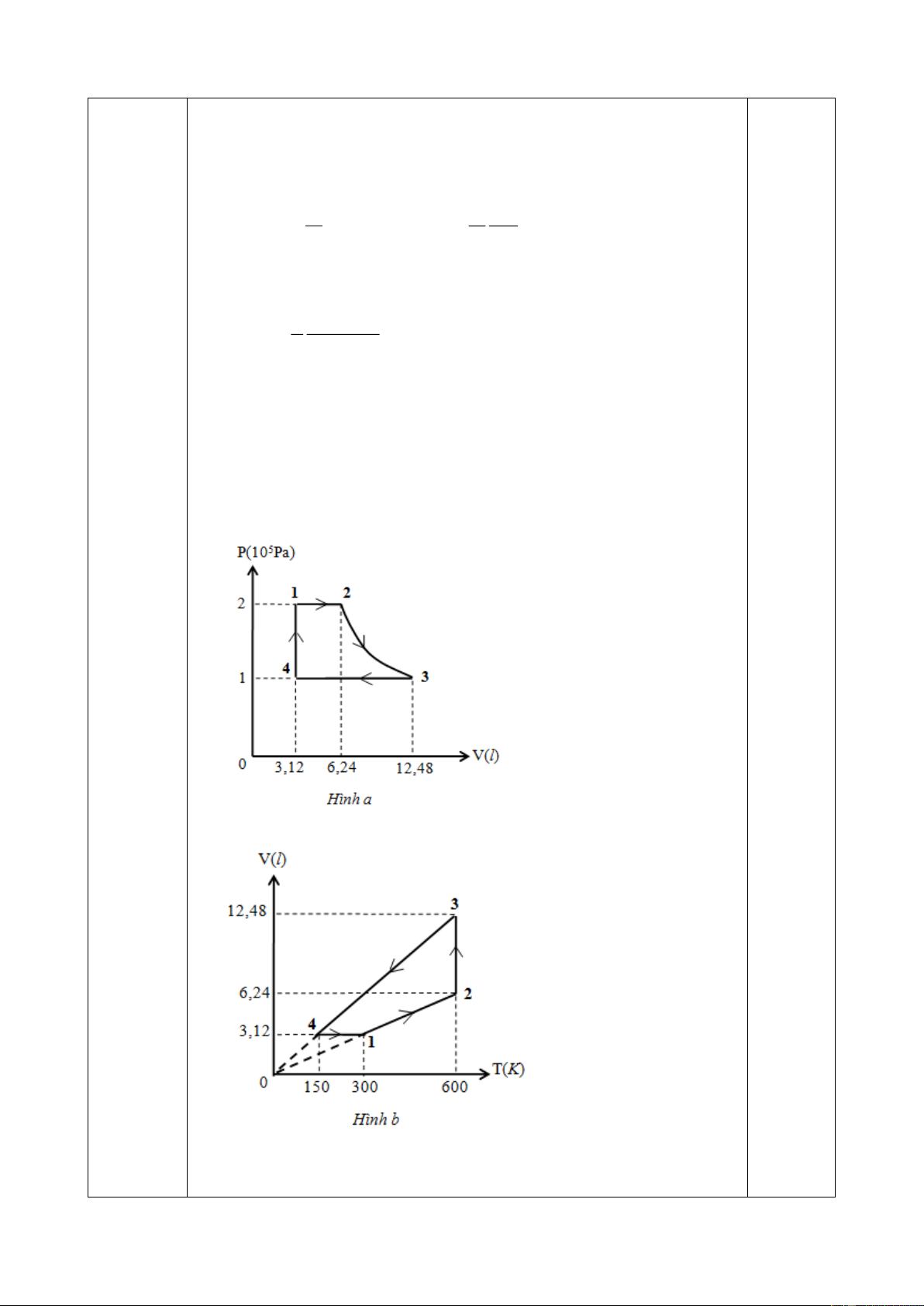
b) Từ hình vẽ ta xác định được chu trình này gồm các đẳng quá trình sau: 1 – 2 là đẳng áp; 2 – 3 là đẳng nhiệt; (3 điểm) 0,5 3 – 4 là đẳng áp; 4 – 1 là đẳng tích.
Vì thế có thể vẽ lại chu trình này trên giản đồ P -V (hình a) và trên giản đồ V -T (hình b) như sau: 0,5 0,5 Bài 6. (2,0 điểm) lắp đặt dụng cụ 0,25
Điều kiện cân bằng của thanh gỗ có dạng : 0,25 m OA . l M.OG=m.OA M= =m OG d trong đó :
gọi M,m lần lượt là khối lượng của thanh gỗ và quả cân; G
là trọng tâm của thanh gỗ; A là điểm treo quả cân
l là khoảng cách từ tâm vị trí đặt quả cân đến O.
2. Tiến trình thí nghiệm (0,75 điểm) 0,5
Bước 1 : buộc dây vào thanh gỗ , treo vào giá thí nghiệm. Di
chuyển điểm treo dây sao cho thanh nằm thăng bằng. Đánh dấu vị trí trọng tâm G
Bước 2 : di chuyển điểm treo dây đến vị trí O khác G, cố định dây treo tại O, đo OG bằng d
Bước 3 : buộc dây vào quả cân có khối lựơng m và treo vào thanh
gỗ (phía đối diện với G qua O). Di chuyển điểm treo quả cân đến
vị trí A sao cho thanh gỗ nằm ngang thăng bằng đo OA bằng l
lặp lại nhiều lần (ví dụ 5 lần) để lập bảng số liệu. 0,25 lần đo d m l M 1 2 3 4 5
3. Xử lí số liệu
- Tính giá trị trung bình: 5 5 5 0,25 M d l i i i M = i 1 = = ; d = i 1 = = ; l = i 1 = = 5 5 5
d l 0,25
-Sai số của phép đo : l ; d
; M = M . + d l
- Viết kết quả:M= M ± M 0,25
Thiếu hoặc sai đơn vị: trừ 0,2 5 điểm cho mỗi lần và 0,5 điểm cho toàn bài.
Học sinh làm theo cách khác đúng vẫn cho điểm tối đa
TRƯỜNG THPT LÊ QUÝ ĐÔN
ĐỀ THAM KHẢO OLYMPIC TỈNH QUẢNG NAM NĂM HỌC 2016-2017 MÔN: VẬT LÝ 10
Thời gian: 150 phút( không kể thời gian giao đề)
Câu 1( 4 điểm). Từ trên cao người ta thả rơi một hòn bi, sau đó t giây người ta thả một
cái thước dài cho rơi thẳng đứng, trong khi rơi thước luôn thẳng đứng. Ban đầu điểm cao
nhất của thước thấp hơn độ cao ban đầu của hòn bi là 3,75m. Khi hòn bi đuổi kịp thước thì
chênh lệch vận tốc giữa hai vật là 5m/s. Sau khi đuổi kịp thước 0,2s thì bi vượt qua được
thước. Tìm khoảng thời gian t, quãng đường mà đã đi được cho đến lúc đuổi kịp thước và
chiều dài của thước. ( lấy g = 10m/s2)
Câu 2( 4 điểm). Một tấm ván khối lượng M = 2kg có thể trượt không ma sát trên mặt
sàn nằm ngang và khối gỗ khối lượng m = 1kg đặt tiếp xúc và nối với nhau bằng một sợi
dây mắc qua một ròng rọc( bỏ qua khối lượng của ròng rọc và sợi dây không dãn). Hệ số
ma sát trượt giữa gỗ và ván là 0,3. Tác dụng vào tấm ván lực F = 9N theo phương song
song với mặt sàn. Hỏi sau thời gian t = 0,5s kể từ lúc tác dụng lực F thì gỗ trượt quãng
đường bao nhiêu so với ván. ( lấy g = 10m/s2) m M Câu 3( 4,0 điểm):
Một chiếc thang đồng chất có chiều dài AB = l = 2,7m,
trọng lượng P. Đầu A của thang tựa vào sàn nhà nằm ngang, đầu B B
của thang tựa vào tường thẳng đứng. Khối tâm G của thang ở cách
đầu A một đoạn 0,9m. Thang cân bằng ở vị trí hợp với sàn nhà một góc 0
= 60 như hình vẽ. Gọi µ là hệ số ma sát giữa thang với sàn,
bỏ qua ma sát giữa thang và tường. G
1. Tìm giá trị nhỏ nhất của µ để thang còn chưa bị trượt.
2. Cho = 0,32 . Một người có trọng lượng P = 3P trèo lên 1
thang. Hỏi người đó trèo được một đoạn tối đa bằng bao nhiêu (so A
với đầu A) để thang còn chưa bị trượt. Câu 4(4,0 điểm):
Một sợi dây nhẹ không giãn, chiều dài l = 1m, một O
đầu cố định, một đầu gắn với vật nặng khối lượng
m = 300g tại nơi có gia tốc trọng trường 2 g = 10(m / s ) . B 1
Ban đầu vật m1 ở vị trí B, dây treo hợp với phương thẳng đứng góc K (với 0 0
0 90 ), thả vật m1 với vận tốc ban
đầu bằng không. Mốc tính thế năng trùng với mặt sàn nằm D C
ngang đi qua điểm A và vuông góc với OA như hình vẽ, A
OA = OB = l . Bỏ qua mọi ma sát và lực cản tác dụng lên vật m1, dây luôn căng trong quá
trình vật m1 chuyển động. 1. Cho 0 = 90 . Xác định:
a. Cơ năng của vật m1 ngay lúc thả.
b. Xác định độ lớn lực căng dây tại vị trí dây treo hợp với phương thẳng đứng góc 0 30 (ở phía bên trái OA).
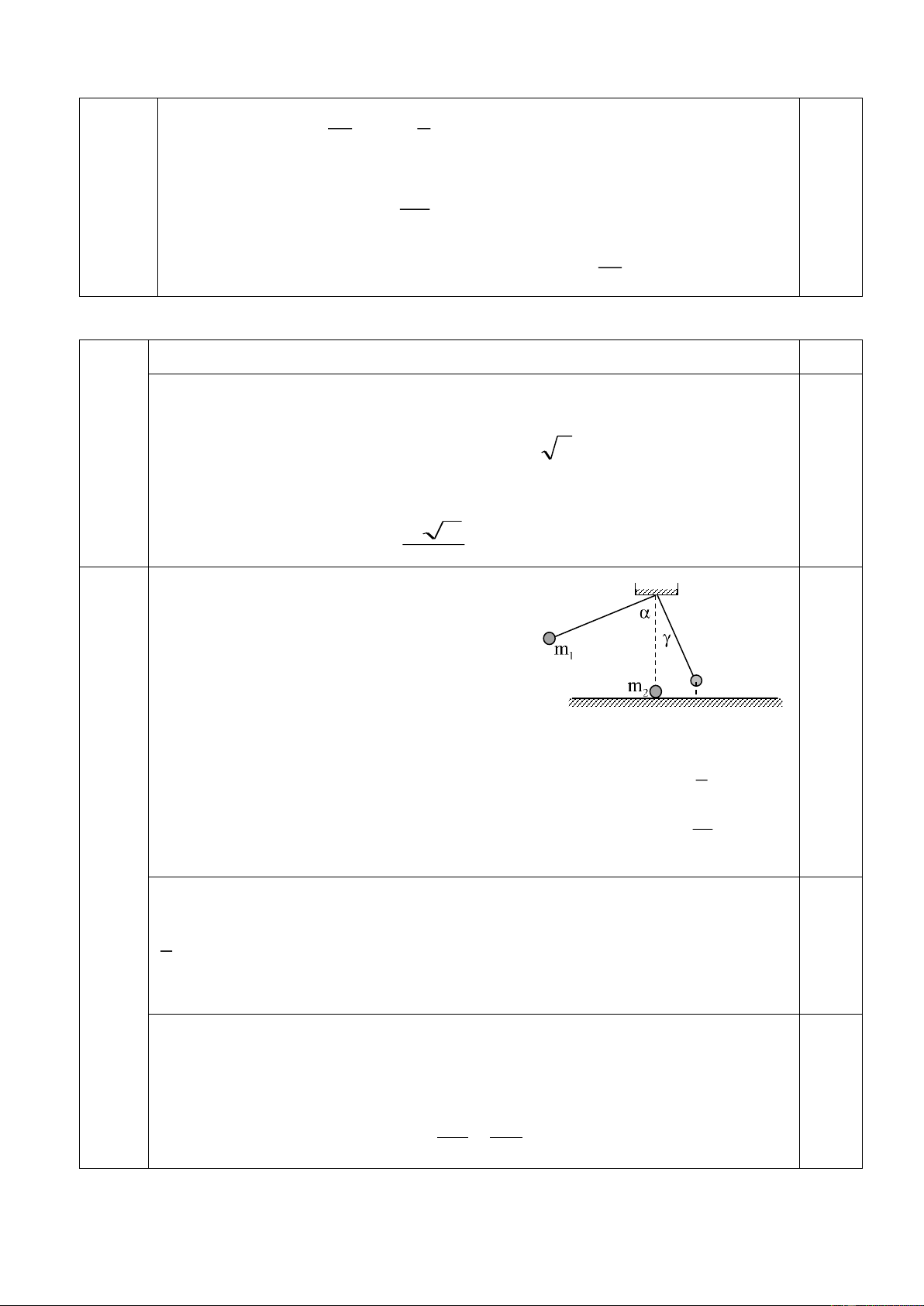
2. Khi vật m1 chuyển động tới vị trí A, nó va chạm hoàn toàn đàn hồi xuyên tâm với
vật m2 = 100g (đang đứng yên tại vị trí A). Sau va chạm vật m1 tiếp tục chuyển động theo
quỹ đạo tròn bán kính l = 1m đến vị trí có độ cao lớn nhất (vị trí K), D là chân đường vuông
góc từ K xuống mặt sàn. Vật m2 chuyển động dọc theo mặt sàn nằm ngang đến vị trí C thì
dừng lại. Hệ số ma sát giữa m2 và mặt sàn là 0,1. Biết AD 15 = . AC 90 Xác định góc . Câu 5( 4 điểm).
Có 1 gam khí Heli (coi là khí lý tưởng, khối lượng mol M=4g/mol) thực hiện một chu
trình 1 - 2 - 3 - 4 - 1 được biểu diễn trên giản đồ P-T như hình vẽ. Cho P0 = 105Pa; T0 = 300K.
1. Tìm thể tích của khí ở trạng thái 4.
2. Hãy nói rõ chu trình này gồm các đẳng quá trình nào. Vẽ lại chu trình này trên giản
đồ P-V và trên giản đồ V-T (yêu cầu ghi rõ giá trị bằng số và chiều biến đổi của chu trình
trên các giản đồ này). P 2P0 1 2 P0 4 3 T 0 T0 2T0
---------------------Hết-------------------- TRƯỜNG THPT LÊ QUÝ ĐÔN
ĐÁP ÁN ĐỀ THAM KHẢO OLYMPIC TỈNH QUẢNG NAM NĂM HỌC 2016-2017 MÔN: VẬT LÝ 10
Thời gian: 150 phút( không kể thời gian giao đề) Câu Nội dung Điểm (điểm) Chi tiết Câu 1 (4,0đ)
Thời gian bi đuổi kịp thước là t1, vận tốc của bi và thước lúc bi đuổi kịp thước là u1 và v1 u = gt 0,25 1 1
v = gt ( t2 là thời gian từ lúc thước bắt đầu rơi cho đến lúc hòn bi đuổi 0,25 1 2 kịp thước)
t = t − t 2 1 0,5
Khi bi đuổi kịp thước u − v = 5 1 1 Suy ra t= 0,5s 0,5
Đoạn đường mà hòn bi và thước đã rơi cho tới lúc đuổi kịp thước: 0,25 1 H = gt 2 = t 5 2 1 2 1 1 0,25 h = t ( 5 − ) 5 , 0 2 1 màH − h = 75 , 3 m 1 1 0,25 → t = s 1 1
Quãng đường hòn bi đi được đến lúc đuổi kịp thước : 1 2 2 0,25 H = gt = 5t =5m 1 1 1 2
Khi bi đuổi kịp thước vận tốc của mỗi vật là
u = 10m / s 0,25 1 v = m 5 / s 0,25 1
Đoạn đường bi cần để vượt qua thước là 1 H = u . 2 t + gt = , 2 2m(t = , 0 2s) 2 1 3 2 3 3 0,25
Đoạn đường thước đi được từ lúc bi đuổi kịp nó đến lúc vượt qua nó: 1 0,25 h = v . 2 t + gt = , 1 2m(t = , 0 2s) 2 1 3 2 3 3
Chiều dài của thước là H2-h2 =1m 0,5 Câu 2 (4 đ) m T fms (+) T M fms (+) Vẽ đúng 2 lực T 0,25 Vẽ đúng 2 lực ma sát 0,25
Chọn chiều dương của mỗi vật 0,25
Vật M: F − T − f = M a . 0,75 ms
Vật m: T − f = m a . 0.75 ms 0,5 F − 2 f
= (m. + M )a ms F − 2 mg 2 0,75 a = = 1m / s m + M
Gia tốc của m so với M là a’= 2a= 2m/s2 0,5 S= ½. a’ t2 = 0,25m 0,5 Câu 3 (4,0đ) 1 (2,5đ)
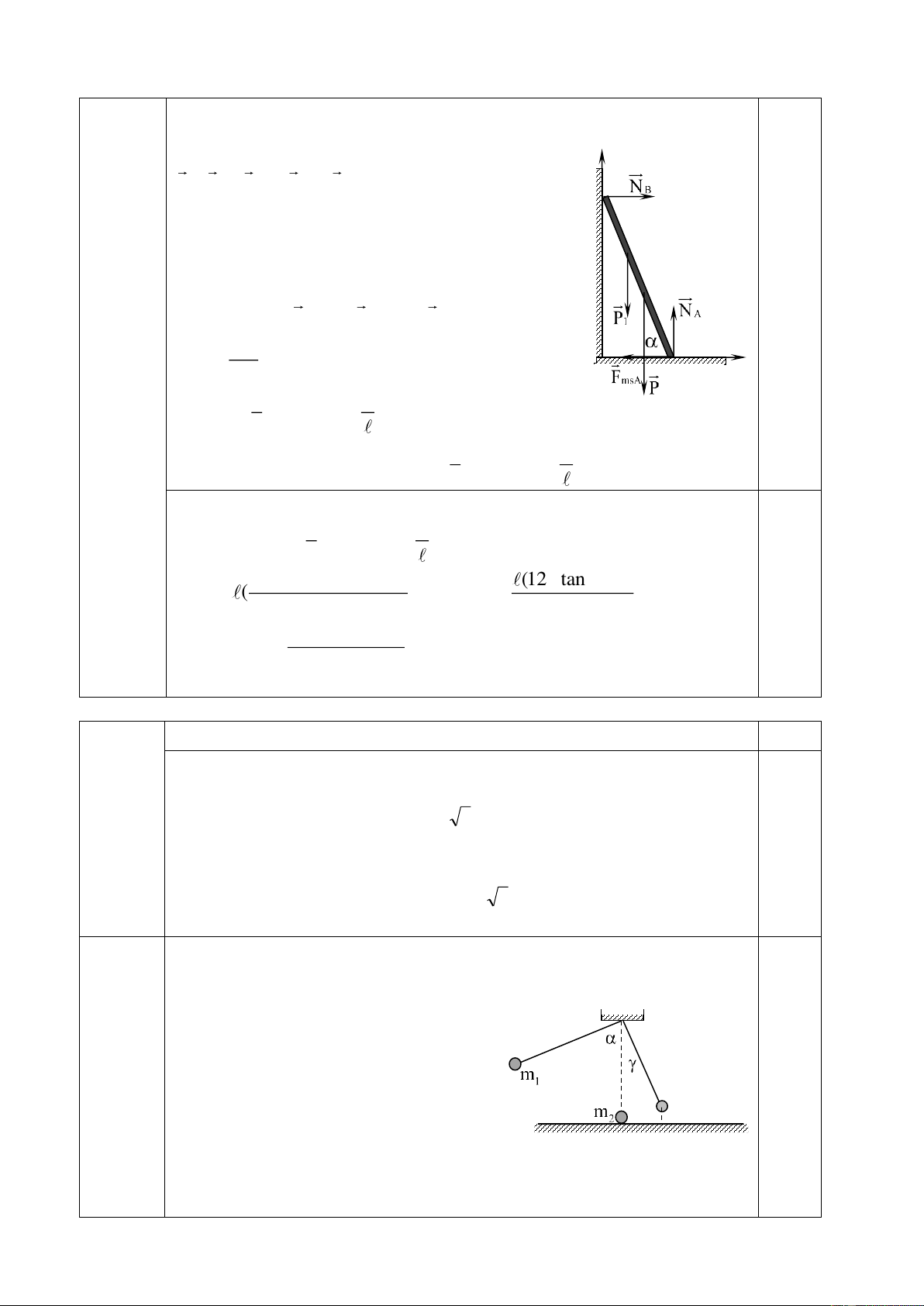
Chọn hệ trục tọa độ x’Oy’ như hình vẽ. y’ - Vẽ đúng các lực 0,5
- Điều kiện cân bằng lực cho thang: B P + N + N + F = 0 B A msA
Chiếu lên trục Oy’, ta có: N 0,25 A = P (1)
Chiếu lên trục Ox’, ta có: N = F (2) 0,25 B msA G 0,25 x’ A
Chọn trục quay tại A, theo quy tắc mô men lực, ta có : M(P) = M(N ) B AB 1 P. .cos = N .AB.sin ; N = P.cot (3) ; B B 3 3 0,5 Từ (2) và (3), ta có: 1 F = N = P.cot msA B 3 0,25
Để thang không bị trượt thì : F .N 0,25 msA A 1 1 1 .P.cot .
P cot = cot 3 3 min 3
Vậy, giá trị nhỏ nhất của hệ số ma sát là: = 0,25 0,192 min
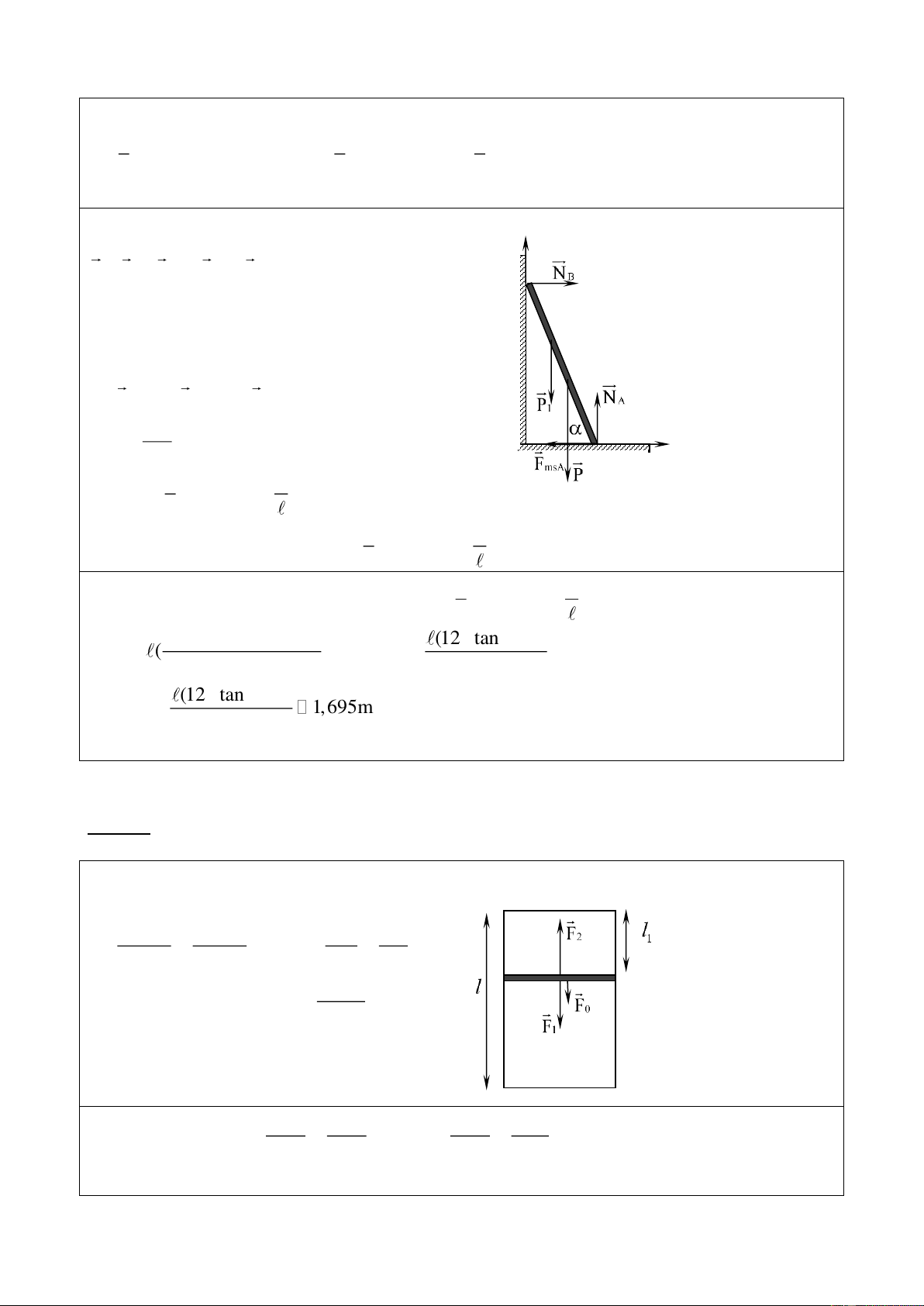
2 (1,5đ) Chọn hệ trục tọa độ xOy như hình vẽ. Gọi khoảng cách từ vị trí người đến A là x. Do thanh nằm cân bằng, ta có: y’ P + P + N + N + F = 0 1 B A msA
Chiếu lên trục Oy’, ta có: N B A = P + P1 (1)
Chiếu lên trục Ox’, ta có: N − F = 0 ; B msA N = F (2’) B msA 0,25
Chọn trục quay tại A, theo quy tắc mô men G lực, ta có : M(P) + M(P ) = M(N ) 1 B AB x’ P.
.cos + P .x.cos = N .AB.sin 1 B 3 A 1 x
N = P.cot + P . .cot (3') B 1 3 0,25
Từ (2’) và (3’), ta có: 1 x F
= N = P.cot + P . .cot msA B 1 3 0,25 Để thang không bị trượt thì : 1 x F .N
P.cot + P . .cot (P + P ) msA A 1 1 3 0,25 3(P + P ).tan − P (12 tan −1) 1 x ( ) x ; 3.P 9 0,25 1 (12 tan −1) x = 1, 695m max 9 0,25
Vậy người đó trèo được tối đa một đoạn 1,695m . Câu 4 (4,0đ)
a. Cơ năng của vật m = = = 1 là W m gl 0,3.10.1 3(J) 0,5 1
1 (1,5đ) b. Áp dụng định luật bảo toàn cơ năng cho vật, tìm tốc độ của vật ở vị trí góc lệch 0 = 30 , ta được: 2 0 0,5
v = 2gl cos = 2.10.1.cos30 = 10 3 v 4,1618m / s
- Áp dụng định luật II Niu - tơn cho vật m = 2 tại vị trí 0 30 , chiếu lên phương bán kính, chiều hướng vào tâm, ta được : 9 3 0,5 0
T = 3m g cos = 3.0, 3.10.cos30 = N 7, 79N 1 2 - Vận tốc của vật m = − 0,5 1 ngay trước va chạm là 2 v 2gl(1 cos ) 2 (2,5đ)
- Gọi v , v tương ứng là vận tốc của 1 2 O
mỗi vật ngay sau va chạm. B K A D C
- Áp dụng định luật bảo toàn động lượng, cơ năng cho hệ hai vật m1 ,
m2 ngay trước và ngay sau va chạm (chiều dương có phương nằm
ngang, hướng từ trái sang phải) v v = = + 1 m v m v m v 2 1 1 1 2 2 0,5 2 2 2 m v = m v + m v 3v 1 1 1 2 2 v = 2 2 - Xét vật m1:
Áp dụng định luật bảo toàn cơ năng cho vật tại vị trí A và vị trí K, ta được : 1 0,5 2 2
m v = m gl(1− cos) v = 8gl(1− cos) cos = 0, 75 + 0, 25 cos 1 1 1 2 AD = lsin - Xét vật m2:
Áp dụng định luật II Niu - tơn cho vật theo phương ngang, chiều dương hướng sang phải. a = g − 2 2 2
Khi vật dừng lại tại C. Suy ra: v 9v 2 AC = = 0,5 2a 8 g 2 Theo đề AD 15 15 4 sin = = AC 90 90 9(1− cos) 2 2 4sin = 15(1− cos )
16(1− cos ) =15(1− cos ) (1) Đặt x = cos 0
x = 0,5 cos = 0,5 = 60 (T / m) 2 (1) 4x − 6x + 2 0
x =1 cos =1 = 0 (L) 0,5 Vậy 0 = 60 Câu 5 (4,0đ)
1(1,5đ) Quá trình 1- 4: đẳng tích nên V1 = V4. 0,5
Sử dụng pt C-M ở TT1 ta có: m m RT PV = RT V = 1 1 1 , suy ra: 1 1 P 0,5 1
Thay số: m = 1g; = 4g/mol; R = 8,31 J/(mol.K); T 1 = 300K vµ P1 = 2.105 Pa ta được: 1 8,31.300 3 − 3 V = = 3,12.10 m 1 5 4 2.10 0,5
2(2,5đ) Từ hình vẽ, xác định được:
1-2: đẳng áp; 2-3: đẳng nhiệt; 3-4: đẳng áp; 4-1: đẳng tích 1,0
Vẽ lại chu trình này trên giản đồ p-V và V-T như hình vẽ: 0,5x2 Đúng kích thước, đầy đủ số liệu (0,5 đ)
Ghi chú: nếu HS thay 1atm = 105Pa, R=0,082 thì V4=3,075 l; V2=6,15 l;V3=12,3 l.
---------------------Hết--------------------
SỞ GD & ĐT QUẢNG NAM
KỲ THI OLYMPIC KHỐI 10 - THPT
TRƯỜNG THPT NÔNG SƠN MÔN THI: VẬT LÍ Thời gian: 150 phút ĐỀ ĐỀ NGHỊ Câu 1: (4 điểm)
Câu 1.1 ( 2 điểm ): Trên sân ga một người đi bộ dọc theo đường sắt bên một đoàn tàu
đang chuyển động. Nếu người đó đi cùng chiều với đoàn tàu thì tàu sẽ vượt qua người trong
khoảng thời gian t1 = 2,5 phút. Nếu người đi ngược chiều với tàu thì thời gian từ lúc gặp đầu
tàu đến lúc gặp đuôi tàu là t2 = 70 giây. Tính thời gian từ lúc gặp đầu tàu đến lúc gặp đuôi
tàu trong hai trường hợp:
a. Người đứng yên nhìn đoàn tàu đi qua.
b. Tàu đứng yên người đi dọc bên đoàn tàu.
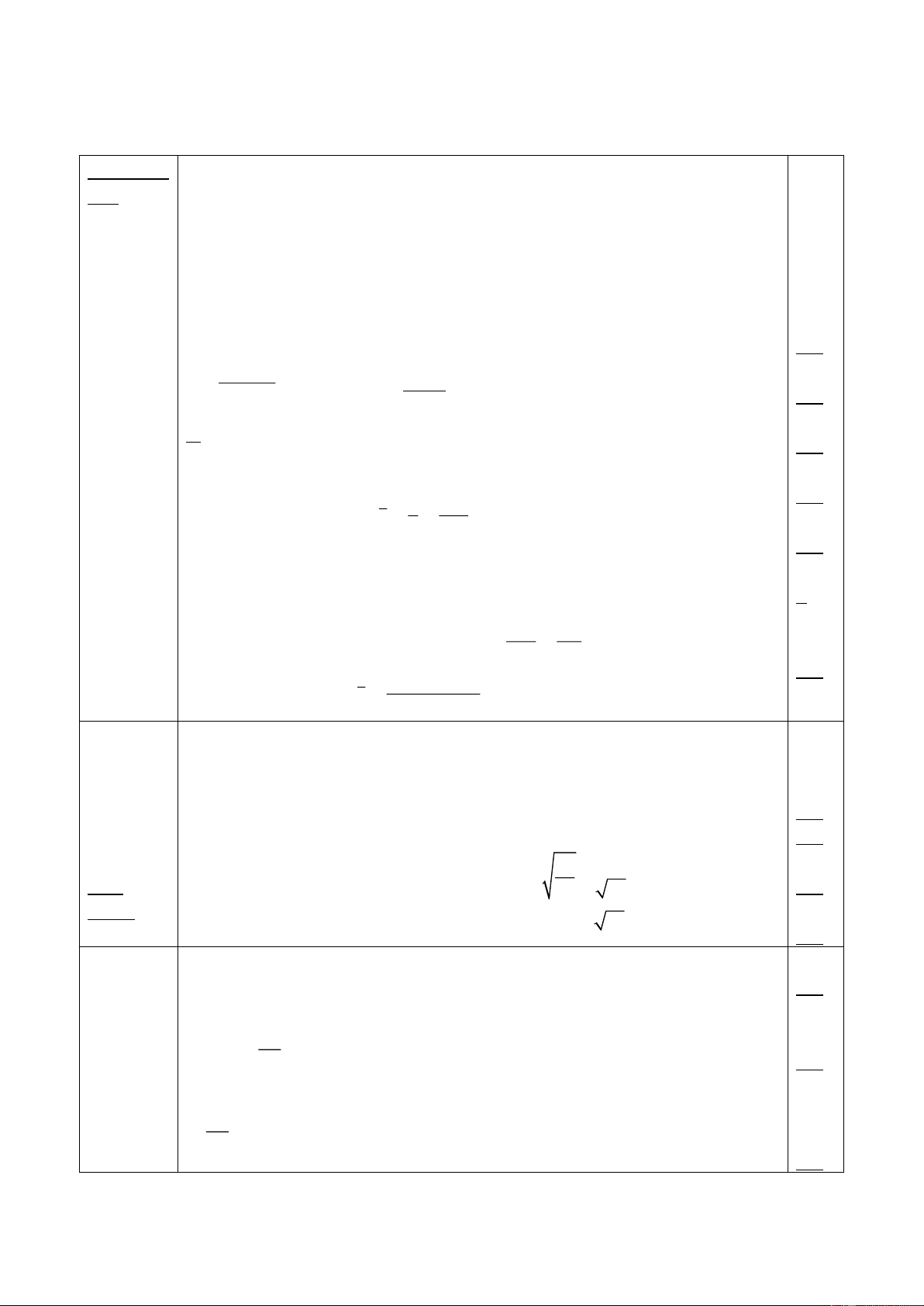
Câu 1.2 ( 2điểm ): Hai xe ô tô bắt đầu chuyển động
thẳng, nhanh dần đều hướng đến một ngã tư như hình vẽ 1. x2
Tại thời điểm ban đầu, xe 1 ở A với OA = x và có gia tốc 01
a1; xe 2 ở B với OB = x và có gia tốc a 02 2. A O Cho a x
1 = 3m/s2, x01 = -15m; a2= 4m/s2, x02 = -30m 1
a. Tìm khoảng cách giữa chúng sau 5s kể từ thời điểm B ban đầu.
b. Sau bao lâu hai chất điểm lại gần nhau nhất? Tính khoảng cách giữa chúng lúc đó. Hình vẽ 1
Câu 2 ( 4 điểm ): Một hộp chứa cát ban đầu đứng yên, được kéo trên sàn ngang bằng một
sợi dây chịu được sức căng cực đại là Tmax. Hệ số ma sát giữa hộp và sàn là µ. Góc hợp bởi
dây và phương ngang là .
a. Tính gia tốc của hộp biết lực kéo tác dụng vào dây là F.
b. Để kéo được lượng cát lớn nhất thì góc phải là bao nhiêu?
Áp dụng bằng số: Tmax= 500N, µ = 0,25.
c. Trọng lượng tổng cộng của hộp cát ứng với góc tính được ở câu b là bao nhiêu?
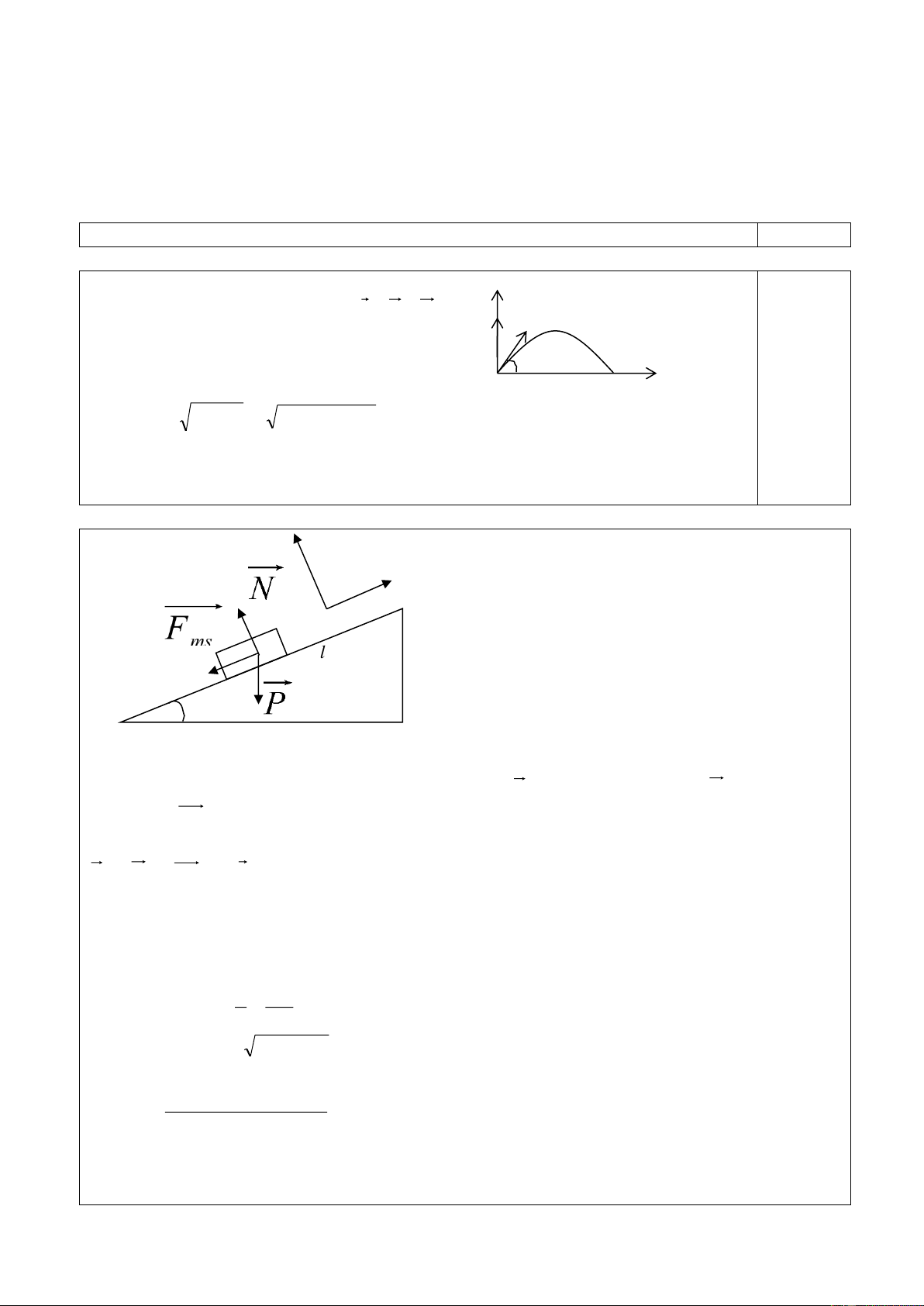
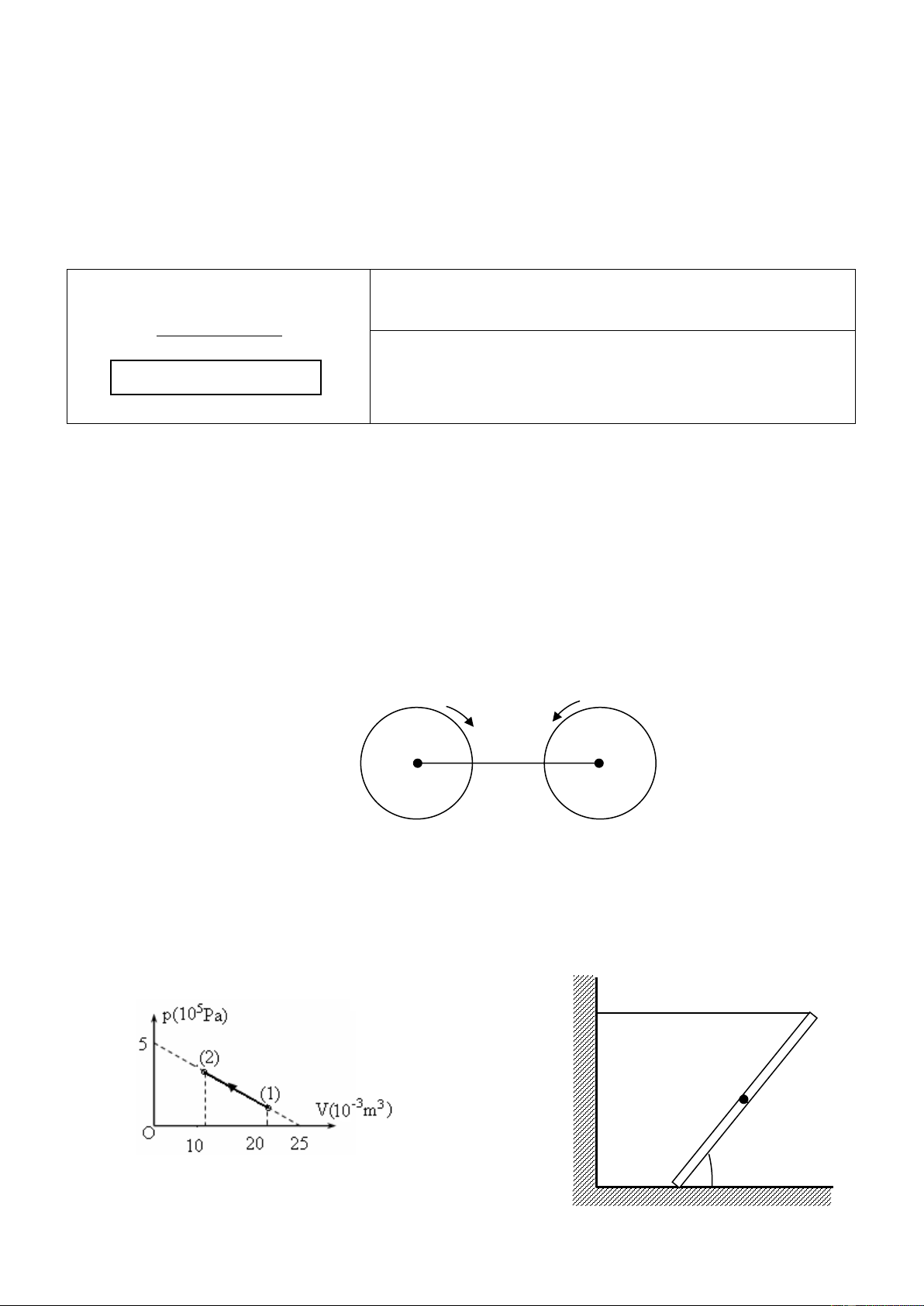
Câu 3 ( 3 điểm ): Cho hệ cân bằng như hình vẽ 3. Thanh
AB tiết diện đều đồng chất, khối lượng m = 2 kg, chiều
dài l = 40 cm có thể quay quanh bản lề A. Sợi dây CB
vuông góc với thanh và tạo với tường thẳng đứng góc
= 300. Đĩa tròn hình trụ bán kính R = 10 cm, khối lượng
M = 8 kg. Tìm độ lớn các lực tác dụng vào đĩa và thanh
AB. Bỏ qua mọi ma sát. Lấy g = 10m/s2.
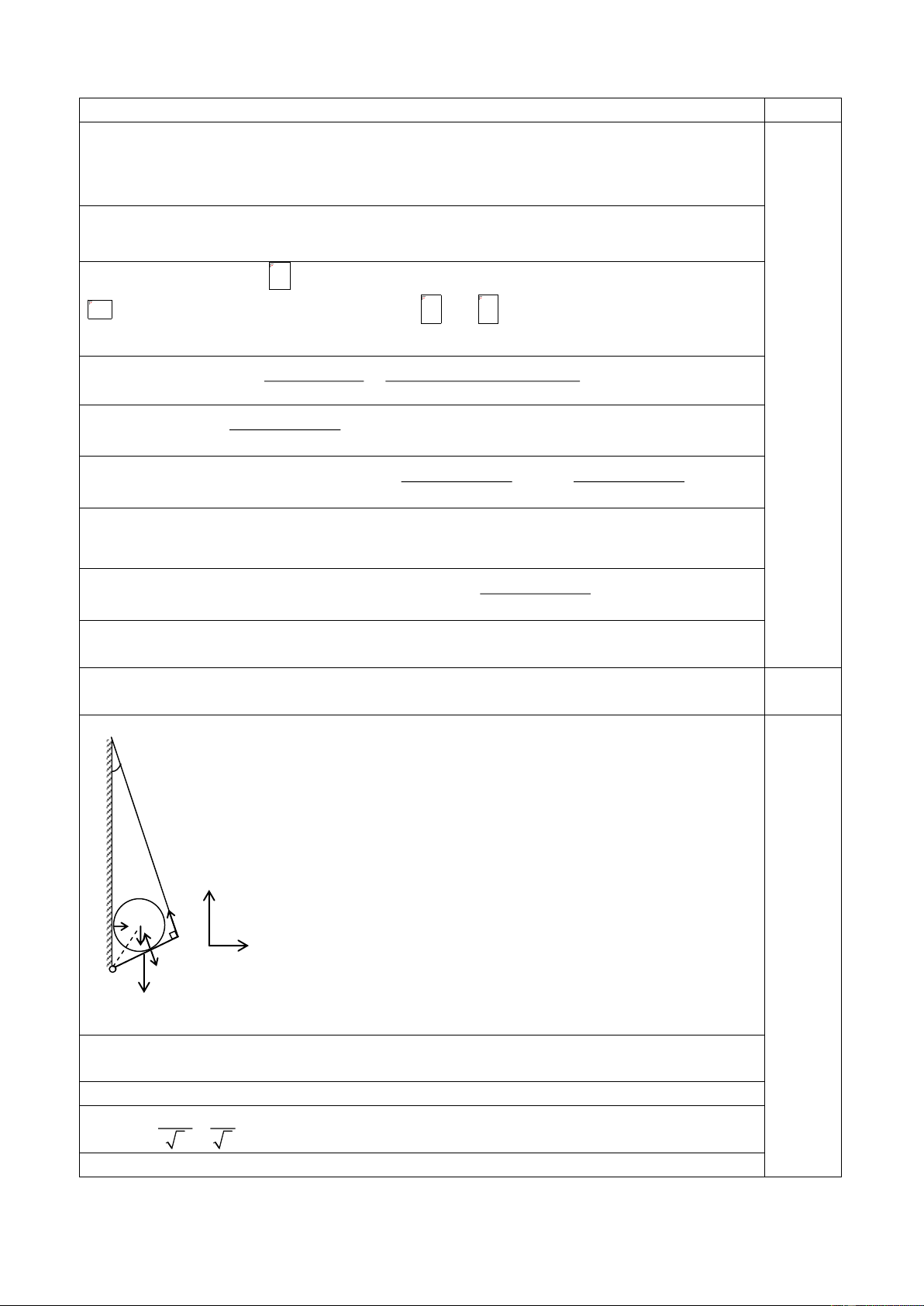
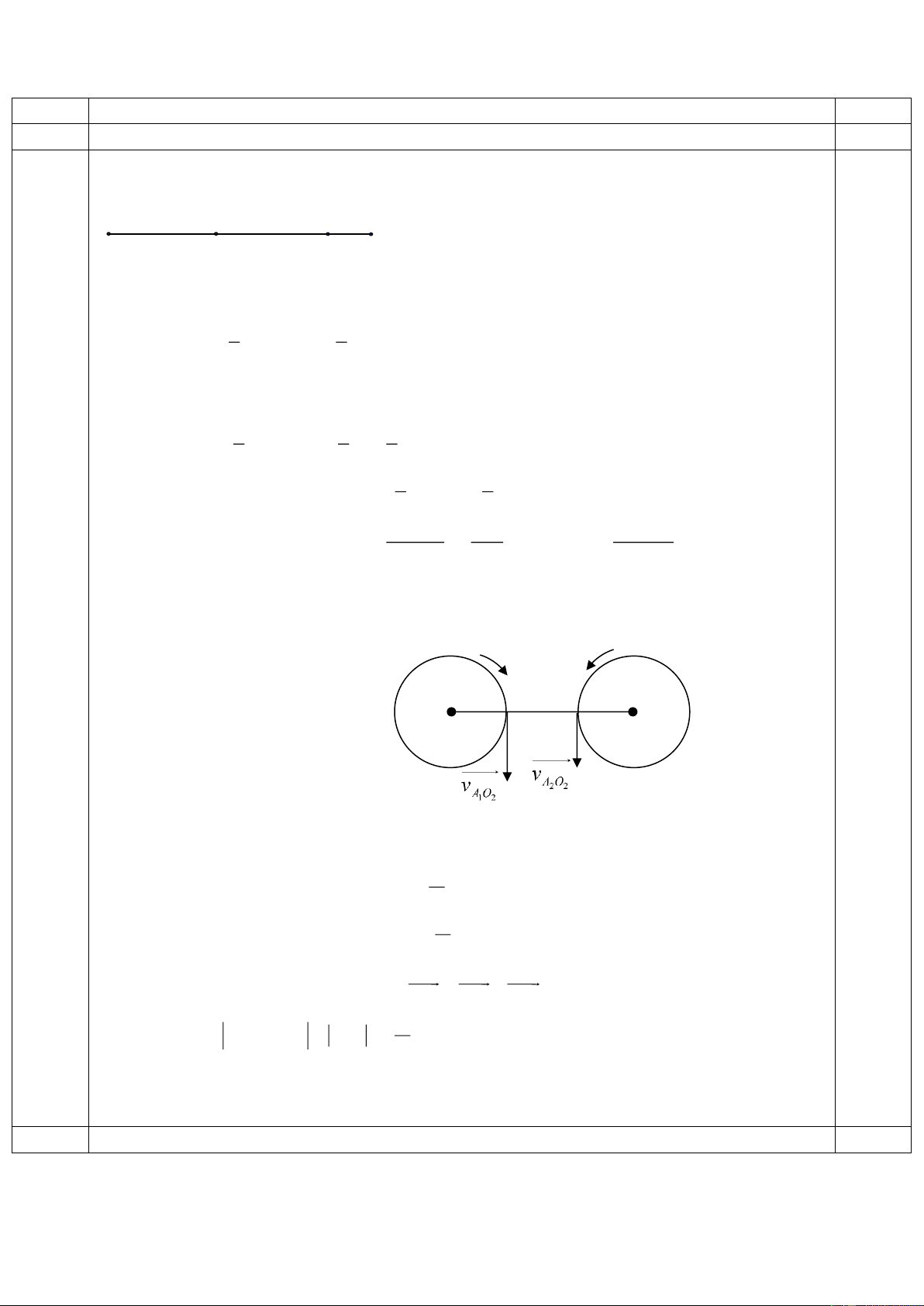
Câu 4 ( 4 điểm ): Ba quả cầu có cùng bán kính, khối lượng khác nhau, được buộc vào các
sợi dây có chiều dài giống nhau và tiếp xúc với nhau (hình 4). Quả cầu m1 được kéo lệch lên
đến độ cao H rồi thả ra. Cho rằng các quả cầu va chạm hoàn toàn đàn hồi xuyên tâm. Sau va
chạm giữa quả cầu thứ nhất với quả cầu thứ hai và giữa quả cầu thứ hai với quả cầu thứ ba
thì cả ba quả cầu có cùng động lượng.
a. Tìm mối liên hệ của m2 và của m3 theo m1.
b. Tìm độ cao cực đại của các quả cầu 1 và 2 theo H. Hình vẽ 4
Câu 5 ( 3 điểm ): Một xilanh đặt nằm ngang, hai đầu kín, có thể tích 2V0 và chứa khí lí
tưởng ở áp suất p0. Khí trong xilanh được chia thành hai phần bằng nhau nhờ một pit-tông
mỏng, cách nhiệt có khối lượng m. Chiều dài của xilanh là 2l. Ban đầu khí trong xilanh có
nhiệt độ là T0, pit-tông có thể chuyển động không ma sát dọc theo xi lanh.
a. Nung nóng chậm một phần khí trong xilanh để nhiệt độ tăng thêm T và làm lạnh
chậm phần còn lại để nhiệt độ giảm đi T. Hỏi pit-tông dịch chuyển một đoạn bằng
bao nhiêu khi có cân bằng?
b. Đưa hệ về trạng thái ban đầu (có áp suất p0, nhiệt độ T0). Cho xilanh chuyển động
nhanh dần đều theo phương ngang dọc theo trục của xi lanh với gia tốc a thì thấy pit-
tông dịch chuyển một đoạn x so với vị trí cân bằng ban đầu. Tìm gia tốc a. Coi nhiệt
độ không đổi khi pit-tông di chuyển và khí phân bố đều
Câu 6: (2 điểm) :Xác định vận tốc của khối gỗ tại chân mặt phẳng nghiêng khi thả khối gỗ
này không vận tốc đầu tại đỉnh của một mặt phẳng nghiêng có chiều dài l = 50(cm), chiều cao h = 25(cm).
Dụng cụ: khối gỗ, giá thí nghiệm, máng nhựa thước dẹp, máy đo thời gian hiện số và 2 cổng quang điện.
----------------------- HẾT -------------------------
ĐÁP ÁN ĐỀ THI OLYMPIC KHỐI 10 THPT
Câu 1: ( 4 điểm ) Điểm Câu 1.1 ( 2 điểm ) l 0,25
a. Khi người đứng yên nhìn đoàn tàu qua: t = a v1
Gọi vận tốc của tàu là v1, của người là v2, chiều dài đoàn tàu là l. Khi
đi cùng chiều vận tốc của tàu so với người là vc= v1- v2. 0,25 Thời gian l l 0,25 t = = (1) 1 v v − v c 1 2 Khi đi ngược l l 0,25
chiều vn= v1 + v2 , thời gian t = = (2) 2 v v + v n 1 2 Từ (1) và (2) => (v 4 0,25
1 - v2).t1 = (v1 + v2).t2 => v2 = v1 hoặc v1 = 2,75v2 11 . 11 l . 11 t 7 0,25 thay v a 2 vào (1) => t = = t = t 5 , 95 giây 1 7v 7 a 11 1 1 l 0,25
b. Khi tàu đứng yên: t = b v2 l t 0,25 thay v b 1 vào (2) => t = = t = 262 5 , giây 2 75 , 3 v 75 , 3 b 2
Câu 1.2 ( 2 điểm )
a. Phương trình chuyển động của xe đi từ A: 1 2 2 0,25 x = x + a t = 1 − 5 +1,5t 1 01 1 2
Phương trình chuyển động của xe đi từ B: 1 2 2 x = x + a t = 3 − 0 + 2t 2 02 2 2 0,25
Khoảng cách giữa hai xe tại thời điểm t 1 2 2 2 2 2 4 2 2 2 0,25
d = x + x =
(a + a )t + (a x + a x )t + x + x (1) 1 2 1 2 1 01 2 02 01 02 4
Sau 5s, khoảng cách giữa chúng: d= 30,1 m 0,25 2 2 2 25 25 0,25 b. 2 2 2
d = x + x = ( 2 1,5t −15) + ( 2 2t − 30) 4 2 =
t −165t + 1125 = ( 2t −13,2 +36 1 2 ) 4 4 2 d 36 d = 6 . min d
= 6 t = 13,2 = 3,63s 0,25 min
c. Để hai xe gặp nhau: x = x = 0 0,25 1 2 a x x = x = 0 1 01 = 1 2 a x 0,25 2 02 Câu 2 ( 4 điểm )
a. Các lực tác dụng lên bao cát: 0,25 - Trọng lực 𝑃 ⃗ - Phản lực - Lực tác dụng:
- Lực ma sát trượt của mặt sàn:
Theo định luật II Niu Tơn Ta có: 𝑃⃗ + 𝑁 ⃗ + 𝐹 + 𝐹 ⃗⃗⃗⃗ 0,25 𝑚𝑠𝑡 = 𝑚𝑎 ( 1) Chiếu (1) lên 0,5
- Trục Ox theo phương chuyển động: Fcos α – Fmst = ma - Trục Oy theo hướng : N – P + Fsinα= 0 0,5
N = P - Fsinα = mg - Fsinα và Fmst = N = ( mg – Fsinα ) F cos − F
F cos − (mg − F sin ) 0,5
Gia tốc của hộp: a ms = = (2) m m m(a + ) 0,25 b. Từ (2) => F = g cos + sin + +
Để dây không đứt: F m(a g) cos sin Tmax => T = m T max max cos + sin a + g 0,5 (cos + sin ) tan = = , 0 25 0 m lớn nhất khi 14 max (a + g ) a = 0 0,5 min cos + sin
c. Trọng lượng hộp cát lúc này: Pmax = mmax.g = T max 0,5 Thay số: Pmax 2061,6 N 0,25 Câu 3 ( 3 điểm ) C N O 0,5 1 . N2 B Pđ H G N3 A Pt Đối với đĩa:
Pđ = Mg = 80 N, Pt = mg = 20 N 0,25 N2cos300 = Mg 0,25 → N Mg 2 = 2 160 = N ≈ 92,4 N 3 3 0,25 N1 = N2sin300 0,25 → 80 N1 = N ≈ 46,19 N 3 0,25
Đối với thanh AB: AH = Rtan600 = R 3 cm. 0,25
Áp dụng quy tắc mô men đối với trục quay ở A 0,25 l mg cos300 + N3.R 3 =T.l. 2 l 0 mg cos30 + N R 3 → 3. T = 2 48,7 N 0,25 l
Phản lực ở trục quay A: Nx + N3sin300 = Tsin300 → Nx - 21,9 N 0,25 Ny + Tcos300 = mg + N3cos300 → Ny 57,9 N 0,25 Phản lực ở trục quay: N = 2 2 N + N = 61,9 N x y 0,25 Câu 4 ( 4 điểm )
a. + Xét va chạm của quả cầu 1 với quả cầu 2: Gọi v là vận tốc của quả cầu m1
trước va chạm. Do sau va chạm giữa quả cầu thứ nhất với quả cầu thứ hai và giữa 0,25
quả cầu thứ hai với quả cầu thứ ba thì cả ba quả cầu có cùng động lượng nên vận tốc quả cầu m v 1 sau va chạm là
. Gọi v2 là vận tốc quả cầu 2 trước va chạm với 3 quả cầu 3.
Áp dụng định luật bảo toàn động lượng: v 0,5 m v = m + m v (1) 1 1 2 2 3
Va chạm hoàn toàn đàn hồi xuyên tâm nên áp dụng định luật bảo toàn cơ năng ta 2 v 0,5 có: 2 2 m v = m + m v (2) 1 1 2 2 9 0,25
Giải hệ (1), (2) ta được: 4 m1 v = ; v m = 2 2 3 2
+ Xét va chạm của quả cầu 2 với quả cầu 3: sau va chạm với quả cầu 3, quả cầu 0,25 2 có vận tốc v
2 ; quả cầu 3 có vận tốc v 3 2 0,5
Áp dụng định luật bảo toàn động lượng: v2 m v = m + m v (3) 2 2 2 3 3 2 0,5 2 v
Áp dụng định luật bảo toàn cơ năng ta có: 2 2 2 m v = m + m v (4) 2 2 2 3 3 4 0,25
Giải hệ (3), (4) ta được: 3 m m 2 1 v = v ; m = = 3 2 3 2 3 6
b. Độ cao cực đại m1 sau va chạm được tìm từ định luật bảo toàn cơ năng: 2 1 v 0,25 m = m gH 1 1 1 2 9 2 0,25 v 2gH H H = = = 1 18g 18g 9 0,25
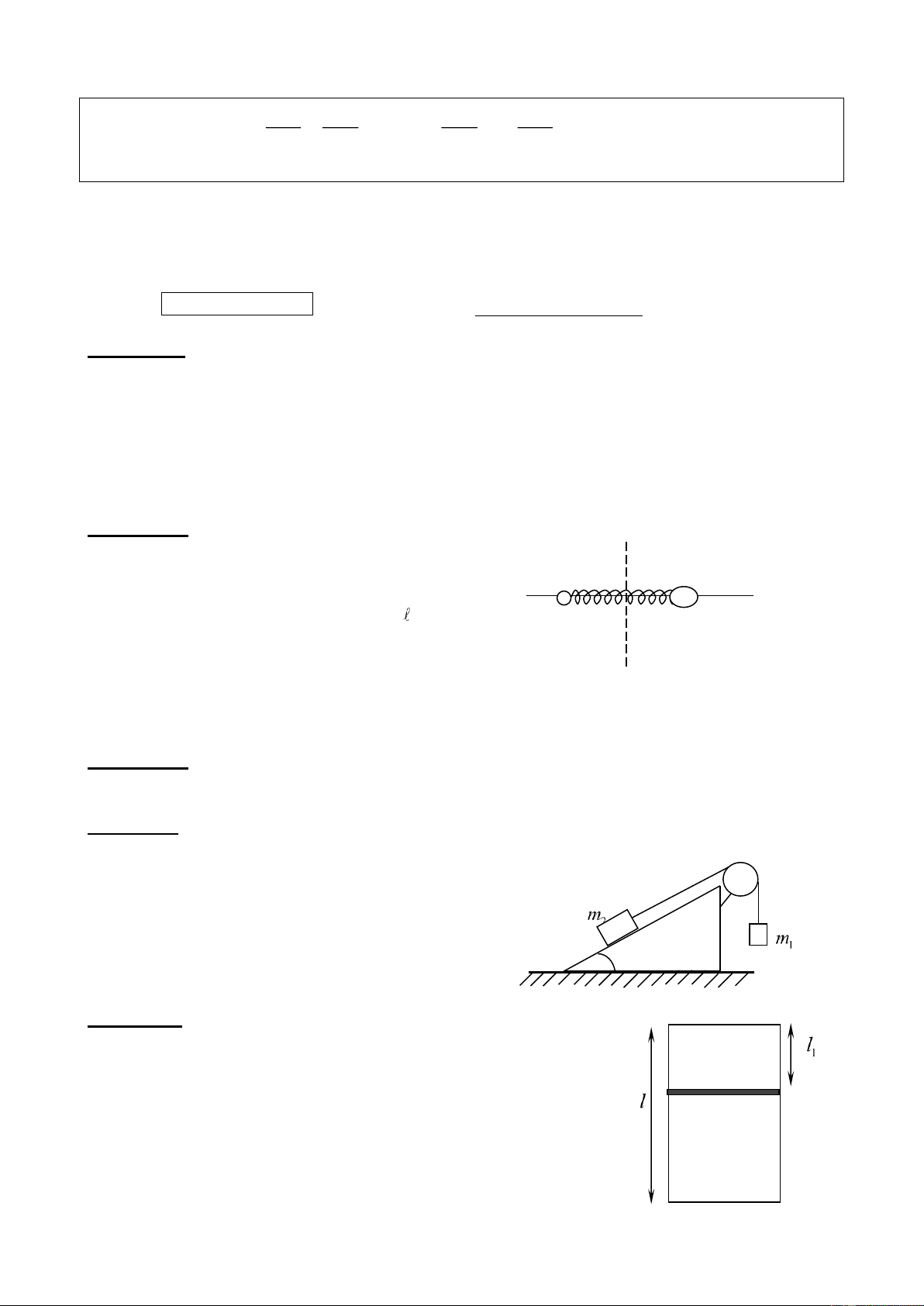
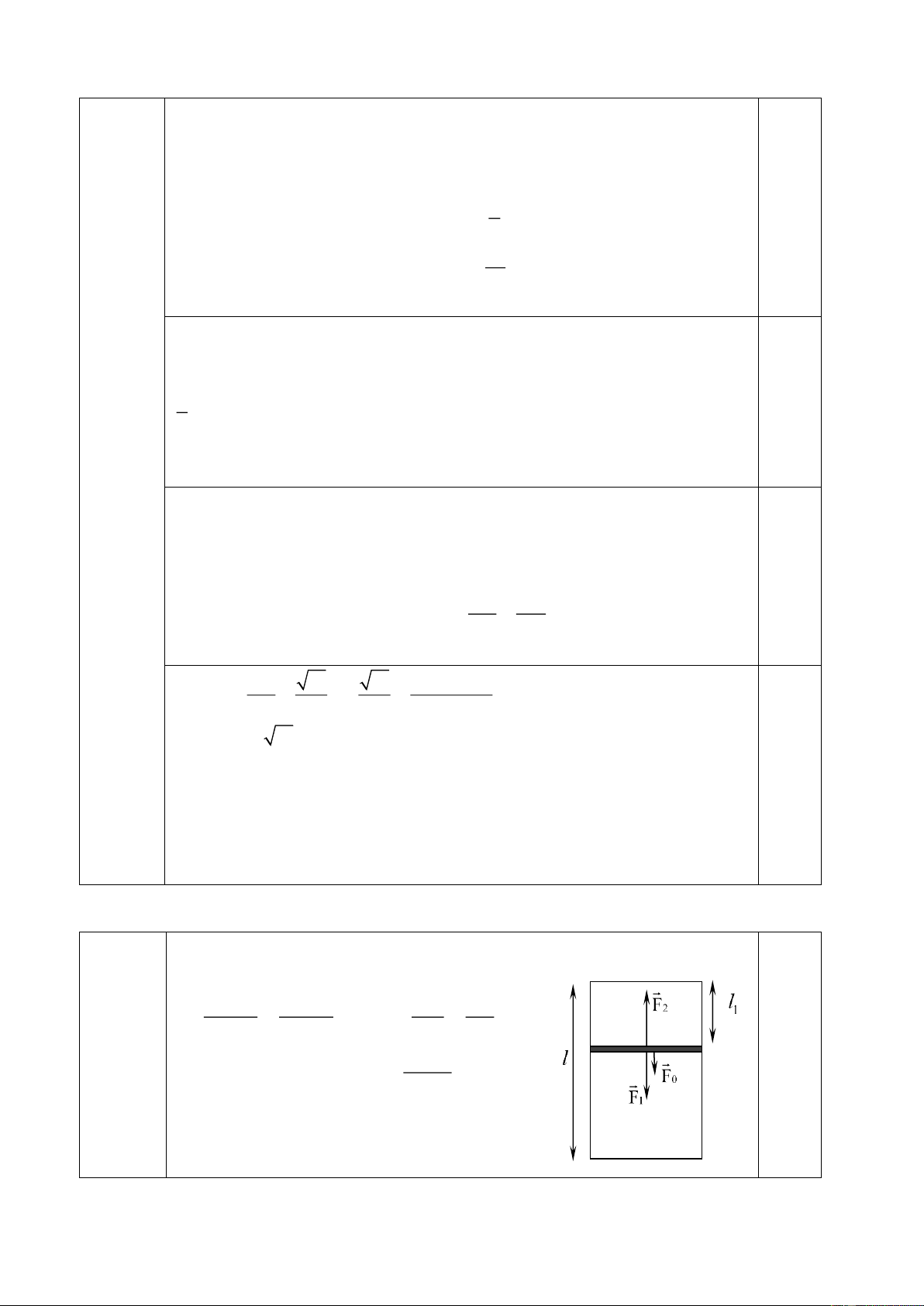
Độ cao cực đại m2 sau va chạm được tìm từ định luật bảo toàn cơ năng: 2 1 v2 m = m gH 2 2 2 2 4 0,25 16 2 2 v v 16.2gH 4H 2 9 H = = = = 2 8g 8g 9.8g 9 Câu 5 ( 3 điểm ) F2 F1
a. Phần xi lanh bi nung nóng: P V PV PV o o 1 1 1 1 = = 0,5 P T T T + T 1, V1 P2, V2 o 1 0 P V P V P V
Phần xi lanh bị làm lạnh: o o 2 2 2 2 = = T T T − T 0,5 o 2 0 + Vì P V T T 1 = P2 → 1 0 = (1) 0,25 V T − T 2 0
Gọi đoạn di chuyển của pit-tông là x, ta có:
V1 = (l + x)S và V2 = (l - x)S (2) 0,25
(l + x)S T + T lT 0 Từ (1) và (2) ta có ( = → x = l − x )S T − T T 0,5 0 0
b. P2V2 = P0V → P2 = P0V0 /(l - x)S (1) 0,25
P1V1 = P0V → P2 = P0V0/(l + x)S (2) 0,25 Từ (1), (2), và (3) ( PV PV 0 - 0 )S = ma → a = 2P0V0x/(l2 – x2)m 0,5
S (l − r) S (l + r)
Câu 6(2 điểm): Phương án thí nghiệm - Dụng cụ:
khối gỗ, giá thí nghiệm, máng nhựa thước dẹp, máy đo thời gian hiện số và 2 cổng 0,5 quang điện. - Tiến hành thí nghiệm:
+ Đặt hai cổng quang điện cách nhau 50 cm.
+ Đặt máy đo thời gian ở chế độ MODE A B với ĐCNN 0,001 s
+ Đặt khối gỗ lên phần đỉnh mp nghiêng, đáy tiếp xúc với mp nghiêng, mặt đứng 0.5
gần sát với cổng quang nhưng chưa che khuất tia hồng ngoại.
+ Ấn nút RESET, thả cho vật trượt.
Ta đo được thời gian t.
Vì vật chuyển động thẳng nhanh dần đều với vận tốc đầu bằng 0. 2 Dựa vào công thức at 2S S = ta suy ra a = 2 2 t 0,5
Sau đó áp dụng công thức tính v = at tính được vận tốc tại chân mặt phẳng nghiêng. 0,5
SỞ GD & ĐT QUẢNG NAM KỲ THI OLYMPIC TRUYỀN THỐNG 24/3
LẦN THỨ HAI TẠI QUẢNG NAM
ĐỀ THI MÔN VẬT LÝ LỚP 10
Thời gian làm bài 150 phút
Câu 1 – Động học chất điểm (4 điểm)
Hai vật được ném đồng thời từ một điểm với vận tốc như nhau cùng bằng v0 = 40m/s.
Một vật được ném lên theo phương thẳng đứng, còn vật kia được ném lên dưới một góc =
600 so với phương ngang. Hãy tìm:
a. Vận tốc tương đối giữa hai vật?
b. Khoảng cách giữa hai vật sau 1s kể từ lúc bắt đầu ném?
Câu 2 – Động lực học chất điểm (4 điểm)
Một vật đang chuyển động trên đường ngang với vận tốc 20m/s thì trượt lên một cái
dốc dài 100m, cao 10m. Tìm gia tốc của vật khi lên dốc. Vật có lên tới được đỉnh dốc
không? Nếu có, hãy tìm vận tốc của vật tại đỉnh dốc và thời gian lên dốc? Cho biết hệ số ma
sát giữa vật và mặt dốc là = 0,1. Lấy g = 10m/s2.
Câu 3 – Tĩnh học vật rắn (3 điểm)
Cột AB là một thanh cứng đồng chất tiết
diện đều dài m, khối lượng M = 10kg được đặt A
nghiêng một góc = 600 so với phương ngang
trên mặt đất nhám, hệ số ma sát k = 0,4. Đầu A
được neo chặt vào đất băng một dây thép khối m
lượng không đáng kể nghiêng góc = 300 so với
phương ngang. Cột và dây thép cùng nằm B
trong một mặt phẳng thẳng đứng.Tại đầu A của cột người ta treo một vật nặng m.
a. Cho m = 0,1kg.Tính lực căng của dây thép?
b. Tìm khối lượng lớn nhất của vật m để đầu B của cột chưa bị trượt.
c. Người ta treo vật vào một điểm C nằm trên thanh AB. Tìm điều kiện của điểm C để
vật nặng có khối lượng lớn đến mấy đầu B cũng không trượt? Lấy g = 10m/s2.
Câu 4 – Các định luật bảo toàn (4 điểm):
a) Một lò xo khối lượng không đáng kể, có độ cứng k=100N/m.
Người ta móc một đầu lò xo vào khối gỗ có khối lượng M=3,99kg, đầu
kia móc cố định vào một bức tường. Hệ được đặt lên mặt phẳng nhẵn M
nằm ngang (hình vẽ). Một viên đạn có khối lượng m=10g bay theo m k
phương ngang với vận tốc v0 song song với lò xo đến đập vào khối gỗ
và dính trong gỗ. Sau va chạm, lò xo bị nén tối đa một đoạn là
xm=30cm. Tính v0.
b) Một cái đĩa có khối lượng M=400g treo dưới một lò xo L có khối
lượng không đáng kể và có độ cứng k=50N/m. Một cái vòng nhỏ khối lượng
m=100g được thả rơi từ độ cao h=10cm xuống đĩa, đĩa và vòng bắt đầu dao L h
động. Coi va chạm giữa đĩa và vòng là va chạm mềm. Tính biên độ của dao động này.
Câu 5 – Chất khí – Sự chuyển thể của các chất (3 điểm): P
Có 1g khí Heli (coi là khí lý tưởng, khối lượng mol 2P0 1 2
M=4g/mol) thực hiện một chu trình 1 - 2 - 3 - 4 - 1 được biểu
diễn trên giản đồ P-T như hình vẽ. Cho P0 = 105Pa; T0 = 300K. P0 4 3 T 0 T0 2T0
1. Tìm thể tích của khí ở trạng thái 4.
2. Hãy nói rõ chu trình này gồm các đẳng quá trình nào. Vẽ lại chu trình này trên giản
đồ P-V và trên giản đồ V-T (cần ghi rõ giá trị bằng số và chiều biến đổi của chu trình).
Câu 6 – Phương án thực hành (2 điểm)
Chỉ sử dụng thước đo chiều dài, hãy nêu phương án xác định hệ số ma sát giữa một
thanh cứng, nhẹ với một tấm tôn.
-----------------HẾT----------------
KỲ THI OLYMPIC TRUYỀN THỐNG 24/3
LẦN THỨ HAI TẠI QUẢNG NAM
ĐÁP ÁN MÔN VẬT LÝ LỚP 10 NỘI DUNG ĐIỂM Câu 1
-Chọn hệ trục xOy như hình vẽ y 0,5
a. Vận tốc tương đối giữa hai vật v = v − v 0,5 1 2 Ta có v x = v1x - v2x= - v0cos
vy = v1y - v2y= (v0 - gt) - (v0sin -gt) 0,5 = v0 (1 - sin) O x 1,0 Suy ra v = 2 2
v + v = 2v 1 ( − sin ) x y 0 0,5
thay số được v = 3,27 (m/s)
b. Khoảng cách giữa hai vật sau 1s 1,0 s = vt = 3,27(m) Câu 2 y x h l 0,25 Hình vẽ
- Các lực tác dụng lên vật khi lên dốc là: Trọng lực P , phản lực vuông góc N và 0,25 lực ma sát F . ms
- Áp dụng định luật II Niu-tơn, ta có: 0,25
P + N + F = m a . (1) ms
- Chiếu phương trình (1) lên trục Ox (dọc theo mặt dốc hướng lên) và trục Oy
(vuông góc với mặt dốc hướng lên): - P cos + N = 0 (2) 0,25 - P sin - Fms = ma (3) 0,25 Trong đó: sin h 10 0,25 = = = 0,1 l 100 cos = 2 1 − cos 0,995 0,25
Từ (2) và (3) suy ra: Fms= N= mg cos 0,25
− Psin − mg cos 0,5 và a =
= −g(sin + cos) m a = -1,995m/s2. 0,5
Gọi s là chiều dài tối đa vật có thể đi lên trên mặt dốc (cho đến lúc vận tốc bằng v = 0) ta có: 2 2 v − v 0,25 0 s = ( )
4 , với v = 0 m/s, v0= 20 m/s 2a
Suy ra s = 100,25m > l = 100m. Như vậy, vật lên tới được đỉnh dốc. 0,25
Khi lên đến đỉnh dốc, vận tốc v 2 2
1 của vật tính theo công thức v − v = as 2 , với 1 0 0,25
s = l = 100m v = 2al + v2 = m 1 / s . 1 0 − 0,25 Thời gian lên dốc: v v t 1 0 = = 52 , 9 s a Câu 3 a. (1điểm) - biểu diễn lực x 0 y
- Áp dụng quy tắc momen lực với trục quay qua B:
T.l/2 = mg.l/2 + Mg.l/4 T = g(m + M/2) 0,5 Thay số T = 51N 0,5
b. (1 điểm)Tìm m cực đại để cột không bị trượt
- Áp dụng điều kiện cân bằng lực ;
theo phương Ox: N = Tsin + mg + Mg=T/2 + 10m + 100 (1) 0,25 theo phương Oy: F ms = Tcos kN = Tcos
Để không bị trượt thì knghỉ = ktrượt= k = 0,4 T 3 0,2T + 4m +40 = (2) 0,25 2
- Áp dụng quy tắc momen lực như ở câu a) 0,25
T = g(m + M/2) = 10m + 50 (3) 0,25 m = 2,52 kg
c. (1 điểm) Tìm vị trí điểm C để với mọi m treo tại đó hệ luôn cân bằng - Đặt BC0 = l0
Áp dụng điều kiện cân bằng lực ta có phương trình (2) 0,25
- Điều kiện cân bằng momen :
T.l/2 = mg.l0 /2 + Mg.l/4 Thay số 0,25 T = 10ml0 + 50 (4) 50 − 25 3 4 +
Thay (4) vào (2) ta có: l m 0 = 5 3 − 2 4 Khi m → thì l 0,25 0 = = 0,6(m) = 60cm 5 3 − 2
KL: Vậy khi C thấp hơn hoặc bằng C0 thì thì hệ cân bằng với mọi m tùy ý 0,25 Câu 4
1) Theo định luật bảo toàn động lượng: m v= v0 (1) m + M 0,5
Theo định luật bảo toàn cơ năng: 1 1 (m+M)v2= kx2m (2) 2 2 0,5 Từ (1) và (2) ta có v xm 0=
k(m + M ) =600m/s m
2) Gọi v là vận tốc của vòng sau khi chạm vào đĩa. Theo định luật bảo toàn cơ 0,5 năng ta có v= 2gh 0,5
Sau va chạm, vòng và đĩa có cùng vận tốc V: mv mv=(M+m)V V = M + m 0,5 Ký hiệu x mg
0 là độ giãn thêm của lò xo khi có thêm vòng m thì x0= k 0,25
Như vậy năng lượng để kích thích hệ dao động bằng W= (M + ) 2 2 2 2 m V kx m g hk 0 2 + = + 1 . (1) 2 2 2k M + m 0,5
Gọi A là biên độ dao động ta có: W= 1 kA2 (2) 2 0,25 Từ (1) và (2) ta có mg 2hk A= 1 + = 02 . 0 m 3 = 2 cm 3 =3,46cm k (M + m)g 0,5 Câu 5
1. Quá trình 1 – 4 có P tỷ lệ thuận với T nên là quá trình đẳng tích, vậy thể 0,5
tích ở trạng thái 1 và 4 là bằng nhau: V1 = V4. Sử dụng phương trình C-M ở trạng thái 1 ta có: m m RT PV = RT , suy ra: 1 V = 0,5 1 1 1 1 P1
Thay số: m = 1g; = 4g/mol; R = 8,31 J/(mol.K); T1 = 300K và P1 = 2.105 Pa ta được: 1 8,31.300 0,5 3 − 3 V = = 3,12.10 m 1 5 4 2.10
Từ hình vẽ ta xác định được chu trình này gồm các đẳng quá trình sau:
1 – 2 là đẳng áp; 2 – 3 là đẳng nhiệt; 0,5
3 – 4 là đẳng áp; 4 – 1 là đẳng tích. …………………
Vì thế có thể vẽ lại chu trình này trên giản đồ P-V (hình a) và trên giản đồ V- T (hình b) như sau:
(Mỗi hình vẽ đúng cho 0,5đ) 0,5 0,5
Ghi chú: nếu HS thay 1atm = 105Pa, R=0,082 thì V4=3,075 l; V2=6,15 l;V3=12,3 l. Câu 6
Đặt tấm tôn nằm cố định trên mặt phẳng ngang. Dựng thanh thẳng đứng trên 0,5
tấm tôn. Tác dụng lực F vào đầu kia của thanh theo phương thẳng đứng
xuống. Thay đổi phương của lực F một chút cho thanh từ từ ngả xuống. Đến
khi góc giữa thanh và phương ngang bằng thì thanh bắt đầu trượt, ta có: F
= F.cos = N F sin 0,5 ms = cot 0,5
Do độ cao của đầu thanh khi đó bằng h, chièu dài thanh bằng l ta được: l 2 − h2 = 0,5 h
SỞ GIÁO DỤC ĐÀO TẠO QUẢNG NAM
TRƯỜNG THPT CHU VĂN AN
ĐỀ THI OLYMPIC VẬT LÝ LỚP 10 (NĂM HỌC 2016-2017) Thời Gian : 150 phút Bài 1 (4 điểm):
Một chất điểm chuyển động từ A đến B (cách A một đoạn s = 315m) . Cứ chuyển động được 3 giây
thì chất điểm lại nghỉ 1 giây. Trong 3 giây đầu chất điểm chuyển động với vận tốc v = 5 m / s . 0
Trong các khoảng 3 giây tiếp theo chất điểm chuyển động với vận tốc 2vo, 3v0, …, nv0. Tìm vận tốc
trung bình của chất điểm trên quãng đường AB?
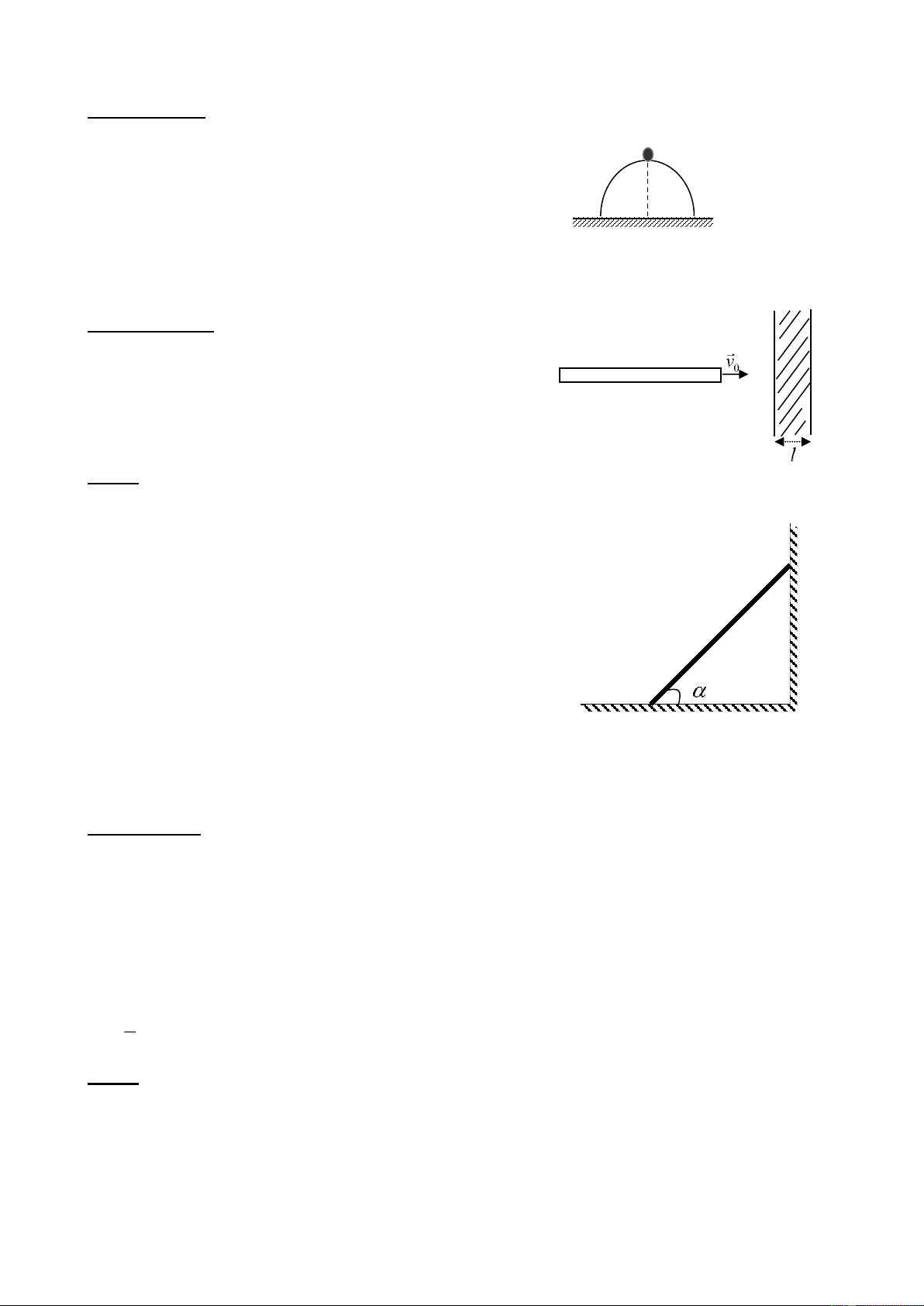
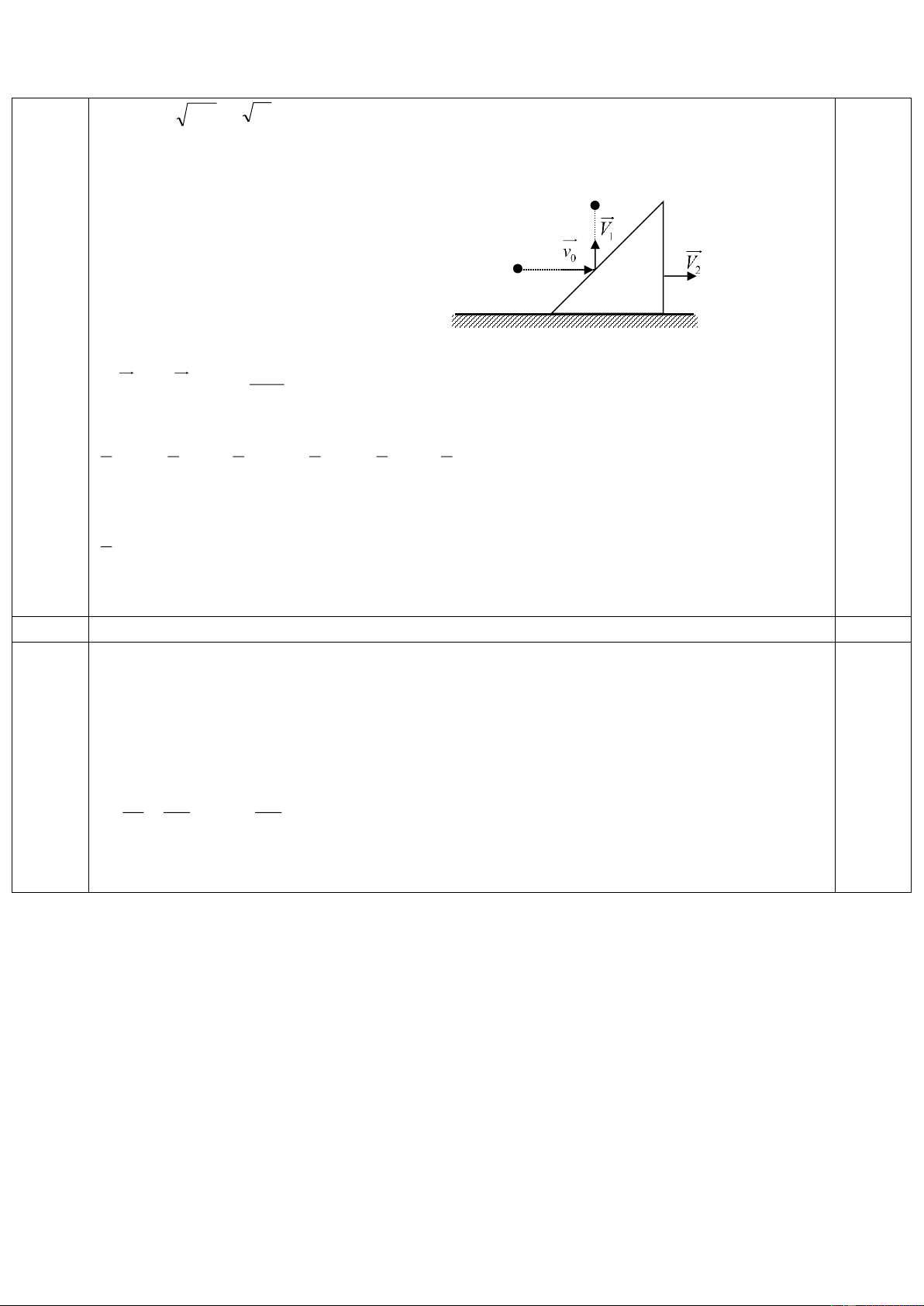
Bài 2(4 điểm): Một vật dạng bán cầu, bán kính R được
đặt trên mặt phẳng nằm ngang. Trên đỉnh bán cầu có đặt
một vật nhỏ khối lượng m (xem hình 1).Vật m bắt đầu m
trượt xuống với vận tốc ban đầu không đáng kể. Bỏ qua
ma sát giữa vật m và bán cầu. Tìm vị trí vật m bắt đầu rời R
khỏi bán cầu trong hai trường hợp:
1) Bán cầu được giữ cố định.
2) Bán cầu có khối lượng M = m và có thể trượt không Hình 1
ma sát trên mặt phẳng nằm ngang.
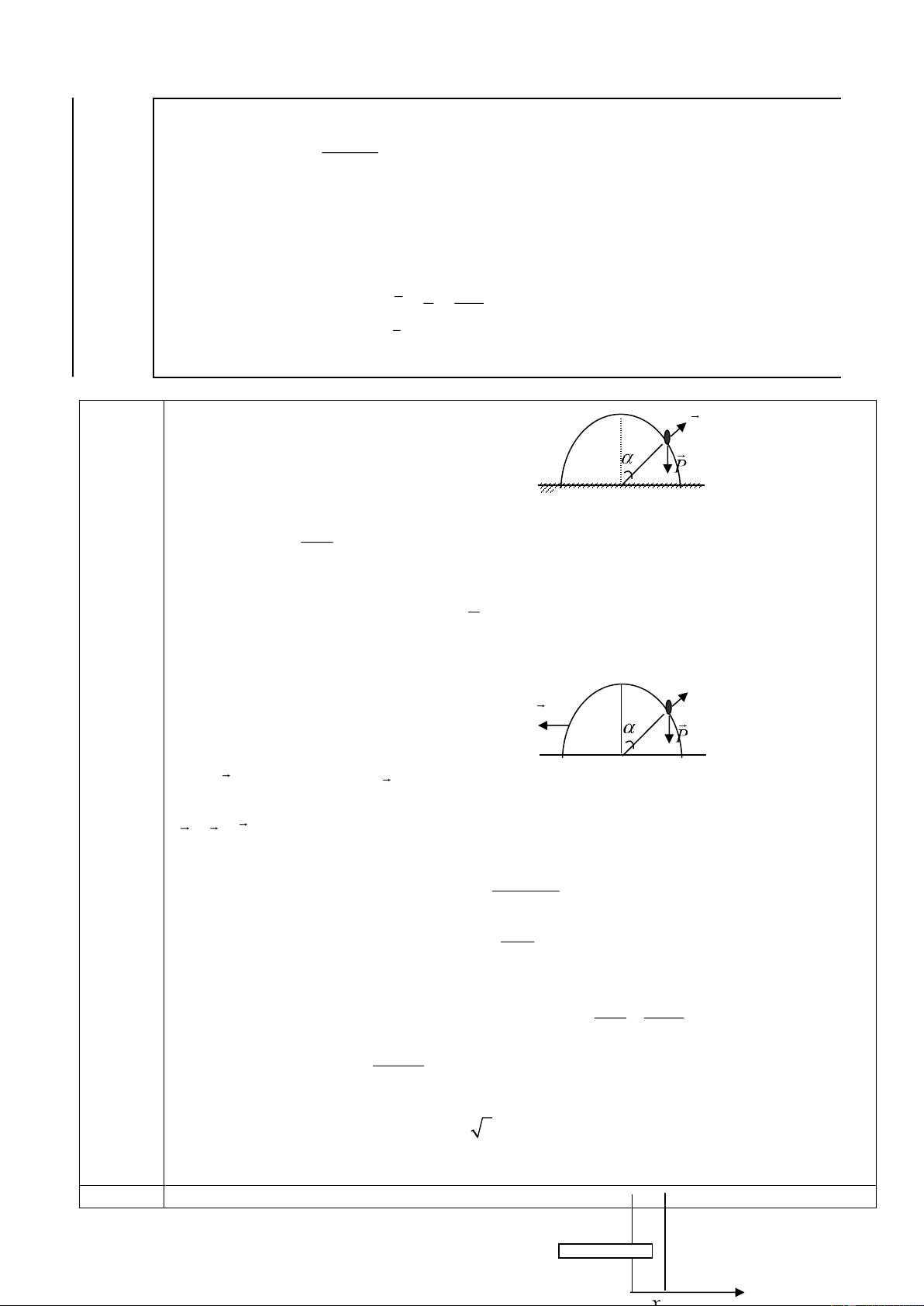
Bài 3 (4 điểm): Một ván trượt dài L = 4m, khối lượng
phân bố đều theo chiều dài, đang chuyển động với vận tốc
v0 = 5m/s trên mặt băng nằm ngang thì gặp một dải đường
nhám có chiều rộng l = 2m vuông góc với phương chuyển
động (xem hình 2). Sau khi vượt qua dải nhám ván có vận
tốc v = 3m/s. Lấy g = 10m/s Hình 2
2. Tính hệ số ma sát trượt giữa
ván trượt với dải đường nhám.
Bài 4: (3 điểm)
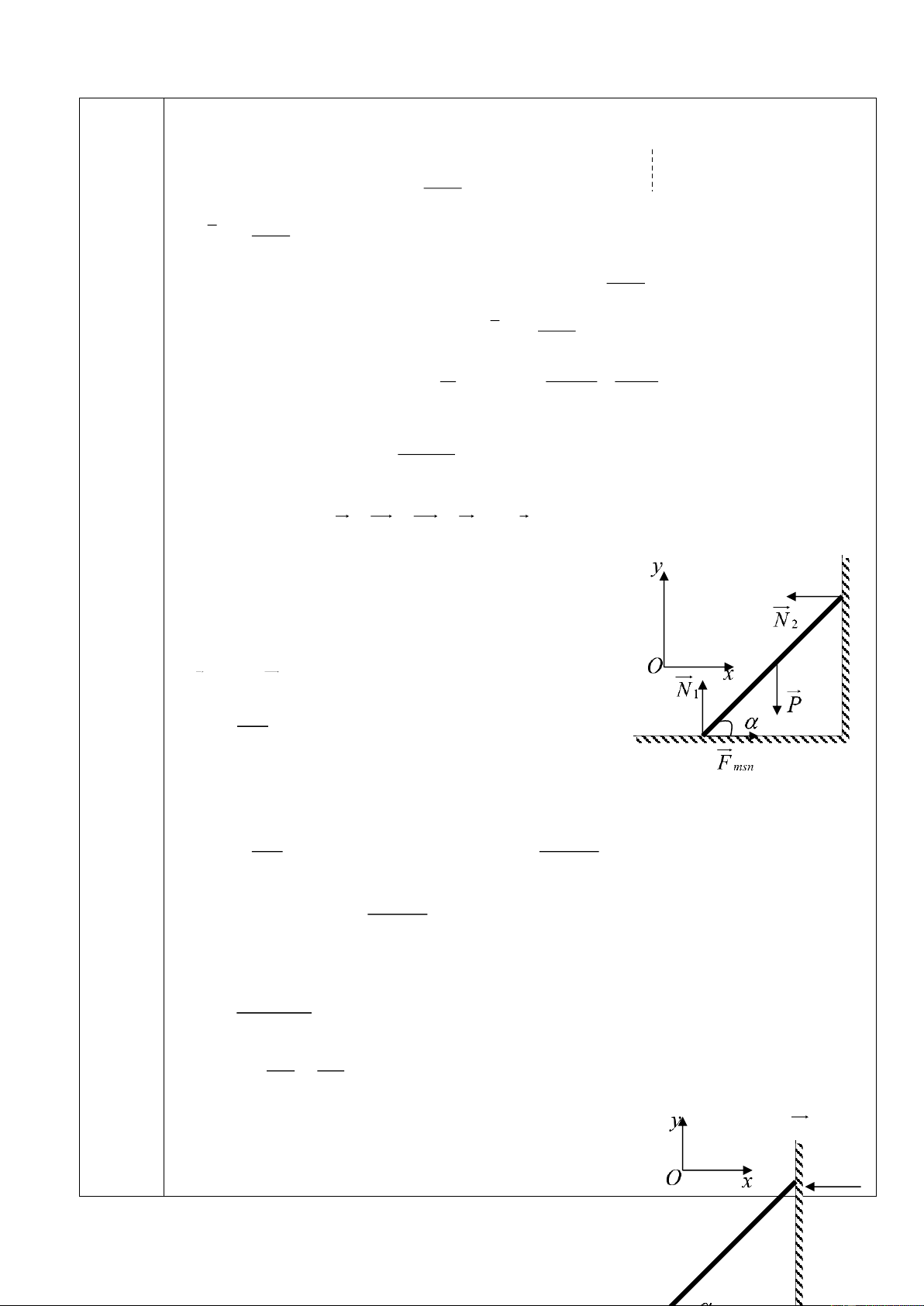
Một thanh AB đồng chất khối lượng m = 20kg dựa
vào tường trơn nhẵn dưới góc nghiêng . Hệ số ma sát B
giữa thang và sàn là = 0,6
a) Thang đứng yên cân bằng, tìm các lực tác dụng lên thanh khi = 45
b) Tìm các giá trị để thang đứng yên không trượt A A trên sàn
c) Một người có khối lượng m = 40kg leo lên thang khi = 45. Hỏi người này lên
tới vị trí M nào trên thang thì thang sẽ bị trượt. Biết rằng thang dài l = 2m. Lấy g = 10m/s2.
Bài 5 (3điểm): Một ống hình trụ thẳng đứng có thể tích V. Ở phía dưới pít tông khối lượng m, diện
tích S, có một lượng khí lý tưởng đơn nguyên tử ở nhiệt độ T0. Pít tông ở vị trí cân bằng chia ống
thành hai nửa bằng nhau. Người ta đun nóng khí từ từ đến khi nhiệt độ khí là 4T0. Ở phía trên có
làm hai vấu để pít tông không bật ra khỏi ống.Hỏi khí trong ống đã nhận được một nhiệt lượng là
bao nhiêu? Bỏ qua bề dày pít tông và ma sát giữa pít tông và thành ống. Cho áp suất khí quyển bên
ngoài là P0 và nội năng của một mol khí lý tưởng đơng nguyên tử được tính theo công thức 3 U = RT 2
Bài 6: (2 điểm). Trình bày phương án thí nghiệm xác định hệ số ma sát giữa một mẩu gỗ với
mặt phẳng nghiêng, biết rằng độ nghiêng của mặt phẳng là không đổi và không đủ lớn để
cho mẩu gỗ tự trượt xuống. Dụng cụ cho: Lực kế, mẩu gỗ, mặt phẳng nghiêng, sợi chỉ đủ dài. ĐÁP ÁN Bài 1 Đặt: t = ( 3 s) 1
4 điểm Gọi quãng đường mà chất điểm đi được sau nt giây là s: 1
s = s + s + ...+ s 1 2 n
Trong đó s1 là quãng đường đi được của chất điểm trong 3 giây đầu tiên. s2,s3,…,sn là các
quãng đường mà chất điểm đi được trong các khoảng 3 giây kế tiếp (1điểm) Suy ra:
s = v t + 2v t + ... + nv t = v t (1+ 2 + ... + n) 0. 1 0 1 0 1 0 1 n(n +1) s =
v t = 7, 5n(n +1) (m) (1 điểm ) 0 1 2 n = 6
Với s = 315 m 7,5n(n+1) = 315
(loại giá trị n=-7) (1 điểm) n = −7
Thời gian chuyển động:
t = nt + n −1 = ( 23 s) 1 s 315
Vận tốc trung bình: v = = t 23
v = 13, 7(m / s) . (1 điểm) N 1) 2.0 điểm
- áp dụng định lý động năng: Vận tốc tại M: 2 v = 2gR(1− os c ) (1)
- Định luật II Niu tơn : Bài 2 2 4 điểm mv mgcos − N = (2) R
- Từ (1) và (2) suy ra : N =mg(3cos -2)
- vật bắt đầu trượt khi N = 0 2 os c = 3 2) 2.0 điểm M m V
- Gọi V là vận tốc bán cầu, u là vận tốc của
M so với bán cầu. Vận tốc của m so với đất là :
v = u +V
- Theo phương ngang động lượng bảo oàn nên : mu cos
mv = MV m(u cos −V ) = MV V = (1) x M + m 2 mu
- Khi m bắt đầu rời khỏi M thì : mg cos = 2
u = gR cos(2) R - Mặt khác ; 2 2 2
v = V + u − 2uV cos (3) 2 2 mv MV
- Ap dụng định luật bảo toàn cơ năng : mgR(1− os c ) = + (4) 2 2 m
- Từ (1),(2),(3),(4) suy ra: 3 o
c s − 3cos + 2 = 0 M + m - Với M=m ,ta có : 3 o
c s − 6 cos + 4 = o
- Giải phương trình này ta được cos = 3 −1 0
- Chọ hệ tọa độ 0x như hình
- Khi đầu tấm ván có tọa độ : 0 x l ,lực ma sát x
tác dụng lên xe có độ lớn: F mg ms1 = x L Bài 3 mg F = l 1 ms 2L 4 mg điểm
- Khi l x L : lực ma sát không đổi và có độ lớn F = l ms 2 L mg
- Khi đuôi của ván có tọa độ : 0 x l : F = l ms3 2L 2 m mgl mgl 2 2 − = + −
- áp dụng định lý đông năng,ta có : (v v ) (L l) 0 2 L L 2 2 v v - 0 − = = 0,4 2gl
a) Thang cân bằng: P + N + N + F = msn 0 (1 điểm) 1 2 Bài 4 F = N 3 điểm
Chiếu lên Ox, Oy (hình vẽ): msn 2 B
N = P = 200N 1 Mặt khác: M = M P / A N / A 2 AB = A mg. .cos N .A . B sin 2 2 ( 0.5 điểm) A
N =100N = F 2 msn
b) Tính để thang không trượt trên sàn: AB P = = Ta có: . P .cos N .A . B sin N 2 2 2 2 tan P Vì N = F F = 2 msn msn 2 tan Mặt khác: F
N = P (0.5 điểm) msn 1 P P2tan 1 1 tan = 2 1, 2 40 N 2 (1 điểm) c) Đặt AM = x B A
Ta có: P + P + N + N + F = msn 0 M 1 1 2 F = N
Chiếu lên Ox, Oy (hình vẽ): msn 2 N = P + P 1 P 1 1 N1 P Mặt khác: M + M = M P / A 1 P / A N2 / A AB mg.
.cos + P x cos = N .A . B sin F msn 1 2 2 P P x 1 N = + = F (1) 2 2 msn AB
Thang bắt đầu trượt khi: F
= N = P + P (2) msn 1 ( 1 ) Từ (1) và (2): x = 1,3m (1 điểm) Bài 5 mg V
- Khi pít tông ở VTCB, Các thông số khí : P1= P0 + ; 0 ; T0 s 2 PV PV Số mol khí 1 1 1 0 n = = mol RT 2RT 1 0
- Trong giai đoạn đầu,pít tông chưa chạm vấu khí biến đổi đẳng áp, khi bắt 1.điểm
đầu chạm vấu khí có nhiệt độ T2 V V V Áp dung: 1 2 = T = T = 2T 2 0 0 T T V 2 1 2 1.điểm
- Nhiệt lượng truyền cho khí trong quá trình này : V 3 PV PV 3 5 1 1 Q = A + U = P
+ n R(T −T ) = + RT = PV 1 1 2 1 0 2 2 2 2RT 2 1 4 0
- Sau khi pít tông chạm vấu, thể tích không đổi,dây là quá trình đẳng tích Khí nhận nhiệt lượng chỉ làm tăng nội năng: 3 PV 3 3 1 Q = n R2T = R2T = PV 2 0 0 1 2 2RT 2 2 0 Tổng nhiệt lượng mà khí đã nhận : 11 11 mg
Q = Q + Q = PV = (P + )V 1 2 1 0 4 4 s 1.điểm Bài 6
- Móc lực kế vào mẩu gỗ và kéo nó trượt đều đi lên mặt phẳng nghiêng, khi đó ta có:
F1 = kPcos + Psin (1), (F1 là số chỉ của lực kế khi đó). (0,5 điểm)
- Tương tự, kéo vật chuyển động đều đi xuống ta có: F2 = kPcos -
Psin (2).(0.5 điểm) F − F
- Trừ vế với vế của (1) cho (2) ta có: F 1 1-F2=2Psin → sin 2 = 2P
(3). (0.5 điểm) F + F
- Cộng vế với vế phương trình (1) và (2) ta có: cos 1 2 = (4). 2P
- Do sin2+cos2 = 1 nên ta có: F − F F + F F + F 1 2 2 1 2 2 1 2 1 = ( ) + ( ) → k = 2 2 2P 2kP
4P − (F − F ) 1 2 (0.5điểm)
- Các lực đều được đo bằng lực kế, nên k hoàn toàn đo được.
TRƯỜNG THPT LÊ HỒNG PHONG
KỲ THI OLYMPIC 24/3 QUẢNG NAM NĂM 2017 ĐỀ THI THỬ
Môn Vật lí - Lớp 10
Thời gian làm bài: 150 phút, không kể thời gian giao đề. Đề thi gồm có 01 trang.
Bài 1:(4điểm) Có 2 xe cùng khởi hành từ A về B. Vận tốc xe 1 trên nửa đoạn đường đầu là
45 km/h, nửa đoạn đường còn lại là 30 km/h .Vận tốc xe 2 trong nửa thời gian đầu là
45 km/h và trong nửa thời gian còn lại 30 km/h .Tính:
a) Vận tốc trung bình mỗi xe ? từ đó cho biết xe nào đến B sớm hơn ?
b) Chiều dài quãng đường AB và thời gian chuyển động mỗi xe? Biết xe này đến sớm hơn xe kia 6 phút .
Bài 2:(4điểm )Cho vật m = 2kg có thể trượt có ma sát( =0,1)
trên mặt phẳng ngang ( g= 10 m/s2)(hình 1)
a) Truyền cho vật vận tốc ban đầu v0 = 1 m/ s F
theo phương ngang .Xác định : Thời gian và quãng
đường vật chuyển động cho đến khi dừng lại ?
b) Tác dụng lực F tạo với phương ngang góc
= 300 làm vật chuyển động đều .Xác định: Lực F? Hình 1
c) Góc phải bằng bao nhiêu để vật trượt đều Với lực F nhỏ nhất ?
Bài 3:(4 điểm ) Chiếc thang có khối lượng m = 20 kg ,chiểu dài L = 4m , dựa vào tường
nhẵn , thang hợp với mặt sàn góc .Biết hệ số ma sát giữa thang và mặt sàn =0,5 .
a) Thang đứng yên cân bằng , Tìm các lực tác dụng lên thang ? ( Cho = 600 )
b) Tìm điều kiện của góc để thang đứng yên không trượt ?
c) Một người có khối lượng M=50 kg leo lên thang ( với = 600 ) .Tìm vị trí cao
nhất của người đó ở trên thang để thang không trượt ? ( g = 10 m/ s2)và hệ số ma sát lúc này chỉ còn là :0,4
Bài 4: (4 điểm) Một cái giỏ nhỏ khối lượng m được treo vào đầu dưới của một lò xo có đầu
trên cố định. Khi giỏ đang đứng yên ở vị trí cân bằng, lò xo dãn một đoạn 2,5 cm thì người
ta bỏ nhẹ vào giỏ một vật nặng có khối lượng m' (m' = m). Sau đó, cả vật và giỏ chuyển động cùng nhau.
a. Xác định vận tốc cực đại của hệ vật và giỏ.
b. Tìm độ dãn cực đại của lò xo.
Lấy g = 9,8 m/s2. Bỏ qua lực cản của không khí.
Bài 5 (4 điểm)
Một xylanh hình trụ nằm ngang chiều dài 2l được chia bởi
một pitông mỏng không dẫn nhiệt thành hai phần bằng nhau. Trong
mỗi phần có chứa một mol khí lí tưởng đơn nguyên tử ban đầu đều ở
nhiệt độ T. Pittông được nối với thành bình bên trái bằng một lò xo có chiều dài tự nhiên l,
độ cứng k. Truyền chậm cho khí bên phải nhiệt lượng .
a) Nếu toàn bộ xylanh cách nhiệt thì nhiệt độ của bình bên trái cũng tăng. Tại sao ?
b) Thật ra khối khí bên trái tiếp xúc nhiệt với bên ngoài nên luôn được giữ ở nhiệt độ
T . Do đó pitông dịch chuyển về bên trái một khoảng x = l / 2. Hãy tính độ biến thiên nhiệt
độ của khối khí bên phải và nhiệt lượng Q’ mà khối khí bên trái đã trao đổi với bên ngoài và
nhiệt lượng đã truyền cho khối khí bên phải
----------------HẾT---------
TRƯỜNG THPT LÊ HỒNG PHONG
KỲ THI OLYMPIC 24/3 QUẢNG NAM NĂM 2017
TRƯỜNG THPT LÊ HỒNG PHONG ĐA THI THỬ
Môn Vật lí - Lớp 10 ĐỀ THI THỬ
Thời gian làm bài: 150 phút, không kể thời gian giao đề. Đề thi gồm có 01 trang. Bài giải Điểm Bài1 2v v 1 a) v =36 km/h 4điểm TB 1 = 1 2 v + v 1 2
---------------------------------------------------------------------------------------- 1 vTB2 = (v1+v2) /2 =37,5 km/h
---------------------------------------------------------------------------------------- 1,0 b) s =90 km/h 1 txe 1=2,5h txe 2 =2,4h Bài 2 a) a= - M g = - 1m /s2 1,0 4điểm
--------------------------------------------------------------------------------------------------------------------------------------- s = 0,5 m 1.0 t = 1s
b)+Viết phương trình định luật 2 N : 0.25
--------------------------------------------------------------------------------------
+Chiếu phương trình lên 2 trục 0x và 0y 0.25
---------------------------------------------------------------------------------------
+Giải hệ phương trình ta được: mg 0,5 F= os
c +sin =2,18 N
-------------------------------------------------------------------------------------- 1.0 mg c)Từ công thức : F= os c +sin
Dựa vào tính chất của bất đẳng thức ta có :
1/cos = µ/sin =>µ = tan =0.1 => =5,70 Bài 3 a)NB =Fms =57,7N 1.0 4điểm
--------------------------------------------------------------------------------- N A =P =200N 1.0
------------------------------------------------------------------------------------
b)Tan 1=> 450 1.0
==============================================================================
c)Viết phương trình cân bằng cho vật o,25
-----------------------------------------------------------------------------------
Chiếu phương trình cân bằng lên 2 trục 0x và 0y 0.25
-------------------------------------------------------------------------------------
Viết phương trình cân bằng mô men cho vật 0.25
-------------------------------------------------------------------------------------
Điều kiện để thang không trượt là :N B Fms max
---------------------------------------------------------------------------------- / ( p + p ) p 0.25 => X= l tan −
l → X 3, 08m / / p 2 p
Vật nặng m, ở vị trí cân bằng lò xo dãn ∆ℓ0 = 2,5 cm => hệ 2 vật (giỏ và vật nặng) có
khối lượng 2m thì khi cân bằng lò xo dãn 2∆ℓ0 = 5 cm 0,5 Bài
Khi đặt vật vào giỏ, hệ mất cân bằng. Trọng lực mạnh hơn lực đàn hồi, vật chạy 4a
nhanh dần về vị trí cân bằng mới (2đ) 0,5
Áp dụng bảo toàn cơ năng: k(∆ℓ0)2/2 = k(2∆ℓ0)2/2 − (2m)g(∆ℓ0) + (2m)v2/2 0,5
Chú ý : k∆ℓ0 = mg => v2 = g∆ℓ0/2 => vmax = 35 cm/s 0,5
Qua vị trí cân bằng, vật tiếp tục chuyển động theo quán tính, đến khi tạm dừng lò xo dãn cực đại ∆ℓmax 0,5
gốc thế năng hấp dẫn chọn ở vị trí mà vật và giỏ bắt đầu chuyển động 4b
Bảo toàn cơ năng ta có: k(∆ℓ (2đ)
0)2/2 = k(∆ℓmax)2/2 − (2m)g(∆ℓmax − ∆ℓ0) 0,5
Thay mg = k∆ℓ0 => (∆ℓ0)2 = (∆ℓmax)2 − 4(∆ℓ0) (∆ℓmax) + 4(∆ℓ0)2 0,5
x2 − 4x + 3 = 0, với x = ∆ℓmax/∆ℓ0 > 1
Lấy nghiệm x = 3 => ∆ℓmax = 3∆ℓ0 = 7,5 cm 0,5
Bài 5 (4 điểm) Câu a Nội dung 1,0 đ
Khi truyền nhiệt lượng cho khối khí bên phải, nhiệt độ của khí trong
phần này tăng lên và dãn nở 0,25 đ
Phần bên trái bị nén nghĩa là phần này đã nhận công 0,25 đ
Do đó nội năng của khí trong phần này tăng 0,25 đ
nên nhiệt độ của khí trong phần này cũng tăng 0,25 đ Câu Nội dung 3,0 đ b Gọi kl 0,25 đ
S là tiết diện của xylanh. Khi pittông cân bằng ta có : P = P + 1 2 2S 2 3 V 3 kl 0,5 đ PV = PV = 3P + 1 1 1 2 2 2 2 2 2 0,25 đ Sử dụng phương 3 kl
trình Clapayrông – Menđêlêep ta có T = 3T + 1 4 R 2 3kl 0,25 đ T = 2T + 4R 2
Công mà khối khí bên phải thực hiện được: 1 l A = A' + k 0,5 đ 2 2
Với A' là độ lớn của công mà khối khí bên trái đã nhận được
Nhiệt lượng mà phần bên trái đã truyền ra bên ngoài: V 0,5 đ ' 2
Q ' = A = RT ln = RT ln(2) V 1
Nhiệt lượng mà khối khí bên phải đã hấp thụ từ bên ngoài 1 3 0,5 đ 2 Q = A + U
= RT ln(2) + kl + R T 8 2 5 0,25 đ
Hay Q = RT 3 + ln(2) 2 + kl 4
SỞ GD & ĐT QUẢNG NAM
KỲ THI OLYMPIC 24_3 . NĂM HỌC 2016-2017
TRƯỜNG THPT NGUYỄN HIỀN
ĐỀ THI MÔN: VẬT LÝ 10
Thời gian làm bài 150 phút không kể thời gian giao đề. -----------------
------------------------ ĐỀ THI ĐỀ XUẤT Câu 1(4đ):
1. (2đ)Trên trục Ox một chất điểm chuyển động biến đổi đều theo chiều dương có hoành độ ở
các thời điểm t ; t ; t tương ứng là: x ; x ; x . Biết rằng: t − t = t − t = t . Hãy tính gia 1 2 3 1 2 3 3 2 2 1
tốc theo x ; x ; x và t, cho biết tính chất chuyển động. 1 2 3
2. (2đ) Trên quãng đường nhất định, một chất điểm chuyển động nhanh dấn đều không vận
tốc đầu với gia tốc a mất thời gian T. Tính thời gian chất điểm chuyển động trên quãng
đường này nếu chuyển động của chất điểm là luôn phiên giữa chuyển động với gia tốc a trong thời gian T T T1 =
và chuyển động đều trong thời gian T2 = . 10 20
Câu 2: (4 điểm) Cho cơ hệ như hình vẽ:
Cho biết: Hệ số ma sát giữa M và sàn là k2, giữa M và m là k m
1.Tác dụng một lực F lên M
theo phương hợp với phương ngang một góc . M Hãy tìm F
min để m thoát khỏi M và tính góc tương ứng
Câu 3 (3 đ): Thang AB đồng nhất khối lượng m=20 kg dựa vào tường trơn nhẵn dưới góc
nghiêng . Hệ số ma sát giữa thang và sàn là = 0, 6 . Lấy g = 10 m/s2.
a) Thang đứng yên cân bằng, tìm các lực tác dụng lên thang khi 0 = 45 .
b) Tìm giá trị của để thang đứng yên không trượt trên sàn.
c) Một người có khối lượng m 0 = 1=40 kg leo lên thang khi
45 . Hỏi người này lên tới vị trí O'
nào trên thang thì thang sẽ bị trượt. Biết thang dài l = 2 m
Câu 4(4đ): Hai khối A và B có khối lượng mA=9kg, mB=40kg đặt trên mặt phẳng nằm ngang. Hệ
số ma sát giữa mặt phẳng ngang và mỗi khối đều là µ=0,1. Hai
khối được nối với nhau bằng một lò xo nhẹ, độ cứng k=150N/m.
Khối B dựa vào tường thẳng đứng. Ban đầu hai khối nằm yên và
lò xo không biến dạng. Một viên đạn có khối lượng m=1kg bay
theo phương ngang với vận tốc v đến cắm vào trong khối A. Cho g=10m/s2. Hình câu 2
a) Cho v=10m/s. Tìm độ co lớn nhất của lò xo.
b) Viên đạn có vận tốc v là bao nhiêu thì khối B có thể dịch chuyển sang trái ?
Câu 5 : (3,0 điểm)
Một nhiệt lượng kế ban đầu không chứa gì, có nhiệt độ t0. Đổ vào nhiệt lượng kế một ca nước
nóng thì thấy nhiệt độ của nhiệt lượng kế tăng thêm 5 0C. Lần thứ hai, đổ thêm một ca nước nóng
như trên vào thì thấy nhiệt độ của nhiệt lượng kế tăng thêm 3 0C nữa. Hỏi nếu lần thứ ba đổ thêm
vào cùng một lúc 5 ca nước nóng nói trên thì nhiệt độ của nhiệt lượng kế tăng thêm bao nhiêu độ nữa ?
Bài 6 : ( 2,0 điểm)
Cho một thanh gỗ thẳng dài có thể quay quanh một trục lắp cố định ở một giá thí nghiệm, một
thước chia tới milimet, một bình hình trụ lớn đựng nước (đã biết khối lượng riêng của nước), một
bình hình trụ lớn đựng dầu hoả, một lọ nhỏ rỗng, một lọ nhỏ chứa đầy cát có nút đậy kín, hai sợi
dây. Hãy trình bày một phương án xác định khối lượng riêng của dầu hoả
……………………………..Hết……………………………… SỞ GD – ĐT QUẢNG NAM
KÌ THI OLYMPIC 24 THÁNG 03
TRƯỜNG THPT NGUYỄN THÁI BÌNH MÔN: VẬT LÍ 10 TỔ VẬT LÍ
Năm học: 2016 - 2017 (Đề thi có 02 trang)
Thời gian làm bài: 150 phút.
Họ và tên học sinh:..................................................................... Trường: ............................................. Câu 1 (4 điểm).
1.1. Lúc 6 giờ sáng một người đi xe đạp chuyển động đều với vận tốc 12 km/h gặp một
người đi bộ đi ngược chiều, chuyển động đều với tốc độ 4 km/h trên cùng một đoạn đường
thẳng. Người đi xe đạp dừng lại lúc 6 giờ 30 phút để nghỉ 30 phút, sau đó anh ta quay lại
đuổi theo người đi bộ với vận tốc như trước. Hãy xác định vị trí người đi xe đạp đuổi kịp người đi bộ.
1.2. Hai xe ô tô chuyển động thẳng đều theo hai con đường vuông góc với nhau, xe A đi về
hướng Tây với tốc độ 50 km/h, xe B đi về hướng Nam với tốc độ 30 km/h. Lúc 8h, xe A và
B còn cách giao điểm của hai đường lần lượt là 4,4 km và 4 km và đi về phía giao điểm.
Xác định thời điểm mà khoảng cách giữa hai xe nhỏ nhất. Câu 2 (4 điểm).
Đặt một vật A có khối lượng mA = 4 kg trên một
mặt bàn nằm ngang. Trên vật A có đặt vật B có
khối lượng mB = 2 kg nối với vật A bằng một sợi
dây vắt qua ròng rọc cố định như hình vẽ 1. Bỏ
qua khối lượng của ròng rọc và của dây. Cho biết B
hệ số ma sát giữa vật A và vật B bằng 0,5 và gia
tốc trọng trường g = 10 m/s2 . A
2.1. Khi ma sát giữa vật A và mặt bàn không đáng
kể. Tính độ lớn của lực F cần kéo vật A theo Hình 1
phương ngang để nó chuyển động với gia tốc có độ lớn bằng 5 m/s2.
2.2. Nếu kéo vật A với một lực F như trên và để vật A chuyển động thẳng đều thì hệ số ma
sát giữa vật A và mặt bàn có giá trị bằng bao nhiêu? Câu 3 (3 điểm). B
Một thang AB dài 2 m, tiết diện đều và đồng chất, khối
lượng 20 kg được dựa vào một bức tường thẳng đứng
trơn nhẵn dưới góc nghiêng . Hệ số ma sát giữa
thang và mặt sàn bằng 0,6 như hình vẽ 2. 3.1. Khi góc nghiêng 0
= 45 thang đứng cân bằng.
Tính độ lớn các lực tác dụng lên thang.
3.2. Để cho thang đứng yên không trượt trên sàn thì
góc phải thỏa mãn điều kiện gì? Cho biết gia tốc A
trọng trường g = 10 m/s2. Hình 2 Câu 4 (4 điểm).
Một quả cầu được xem là chất điểm có khối lượng m, được treo vào điểm cố định O bằng
sợi dây mảnh, nhẹ có chiều dài l. Hệ được đặt trong trọng trường tại nơi có gia tốc g. Truyền
cho quả cầu ở vị trí cân bằng A một vận tốc đầu v0 theo phương nằm ngang. Lúc này vật
chuyển động trên cung AB ứng với góc lệch cực đại . Bỏ qua sức cản của không khí. 0
4.1. Hãy thiết lập công thức tính vận tốc và lực căng dây tác dụng lên vật tại vị trí ứng với
góc bất kỳ theo m, l, g, , ? 0
4.2. Khi dây treo nghiêng một góc = 300 so với phương thẳng đứng, gia tốc quả cầu có
hướng nằm ngang. Xác định góc góc lệch cực đại ? 0 Câu 5 (3 điểm).
Một ống thủy tinh hình trụ hẹp, kín hai đầu, dài 105 cm, đặt nằm ngang. Giữa ống có một
cột thủy ngân dài 21 cm, phần còn lại của ống chứa không khí ở áp suất p0 = 72 cm Hg. Khi
ống được đặt thẳng đứng hãy tính
5.1. độ dịch chuyển của cột thủy ngân trong ống?
5.2. áp suất không khí ở phần dưới của ống? Câu 6 (2 điểm). Cho các dụng cụ sau: - Một mẫu gỗ. - Lực kế.
- Mặt phẳng nghiêng có góc nghiêng không đổi và chưa biết giá trị góc nghiêng. - Dây chỉ.
Trình bày phương án thí nghiệm để xác định hệ số ma sát trượt giữa mặt mẫu gỗ với mặt phẳng
nghiêng. Biết rằng độ nghiêng của mặt phẳng không đủ lớn để cho mẫu gỗ tự trượt xuống.
....................Hết....................
ĐÁP ÁN ĐỀ OLYMPIC Câu 1 Nội dung Điểm
Chọn đúng hệ qui chiếu
+ Gốc tọa độ là địa điểm 2 xe gặp nhau 0,5đ + Mốc thời gian lúc 6 h
+ Chiều dương là chiều chuyển động của người đi bộ 1.1
+ Phương trình chuyển động của người đi bộ x = 4t km 0,25đ (2,0đ) 1
+ Phương trình chuyển động của người đi xe đạp x = −6 +12(t −1) km 2 0,5đ
+ Hai xe gặp nhau x = x và tìm được t = 2,25 h 0,5đ 1 2
+ Kết luận đúng vị trí hai xe gặp có tọa độ 9 km 0,25đ
Chọn đúng hệ qui chiếu (chọn hướng Bắc trùng với chiều dương trục oy,
hướng Đông trùng với chiều dương trục ox) 1.2
+ Gốc tọa độ là giao điểm của hai con đường 0,25đ (2,0đ) + Mốc thời gian lúc 8 h
+ Chiều dương là chiều của trục tọa độ
+ Phương trình chuyển động của xe A x = 5
− 0t + 4,4 km 0,25đ
+ Phương trình chuyển động của xe B y = 3 − 0t + 4 km 0,25đ
+ Khoảng cách giữa hai xe là 2 2 2
d = x + y = 3400t − 680t + 35, 36 0,5đ
+ Khoảng cách nhỏ nhất khi 2
d min và khi đó t = 0,1 h 0,5đ
+ Khoảng cách nhỏ nhất tại thời điểm 8 h 6 phút 0,25đ Câu 2 Nội dung Điểm
+ Vẽ hình đúng hoặc kể tên đúng các lực tác dụng lên vật A và vật B 1,0đ 2.1 (2,5đ)
+ Hai vật chuyển động cùng độ lớn gia tốc a. Lực căng dây có độ lớn T 0,25đ
+ Xét theo phương sợi dây
T−F =m . 0,5đ msB B a −T −F +F =m . msA A a + F = F
= k.m .g msA msB B 0,25đ
+ Rút ra đúng công thức F = (m + m )a + 2k.m .g = 50 N A B B 0,5đ
+ Vật A chịu tác dụng thêm lực ma sát từ mặt bàn là ' F 0,25đ msA
+ Xét theo phương sợi dây 'T−F =0 0,5đ msB 2.2 ' ' −T −F −F +F =0 msA msA (1,5đ)
+ Lực ma sát do mặt bàn tác dụng lên vật A là ' ' F = k m + m g msA ( A B ) 0,25đ
F − 2k.m .g
+ + Rút ra đúng công thức ' B k = ( = m + 0,5đ m g A B ) 0,5 Câu 3 Nội dung Điểm
+ Vẽ đúng các lực tác dụng lên thang B I 0,75đ A 3.1 (2,0đ)
+ Xét mô men lực đối với điểm A + M = M N2 P 0,5đ P N = =100 N 2 2 tan
+ Áp dụng điều kiện cân bằng của thang
+ N + P + N + F = 0 2 1 ms + Xét theo hướng 0,75đ N ta có F = N = 100 N 2 ms 2
+ Xét theo hướng N ta có N = P = 200 N 1 1
+ Để thanh không trượt thì lực ma sát phải là lực ma sát nghỉ F k.N 0,5đ ms 1 3.2 P + kP 0,25đ (1,0đ) 2 tan + Tính đúng 0 40 0,25đ Câu 4 Nội dung Điểm
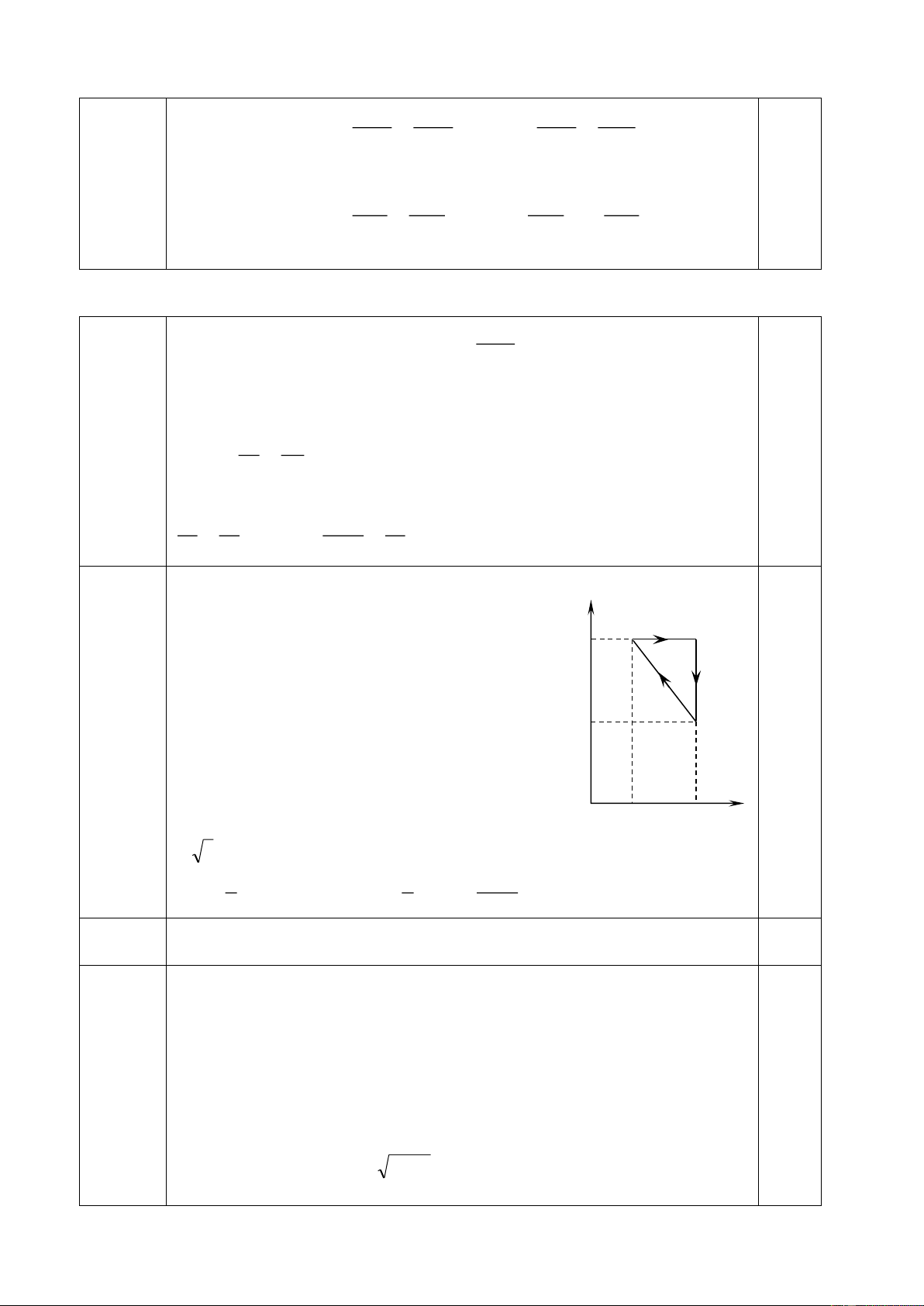
+ Chọn mốc thế năng tại vị trí vị trí cân bằng A.
+ Theo định luật bảo toàn cơ năng: 1 0,5đ
mv2 + mgl( 1 - cos ) = mgl( 1 - cos ) 0 2 4.1
v = 2gl(cos − cos ) (1) 0,5đ (2,0đ) 0
+ Theo định luật II Newton v 2 0,5đ T - mgcos = m (2) l
+ Thay (1) vào (2) T = mg(3cos - 2cos ) 0,5đ 0 2 + Từ v (1) cos = cos - (3) 0,5đ 0 2gl
+ Tại vị trí ứng với góc = 300 gia tốc có phương nằm ngang nên hợp lực F có phương nằm ngang 0,5đ mg T = cos 4.2 (2,0đ) 1 v2 = gl( − cos ) (4) 0,5đ cos 3cos 2 −1
+ Thay (4) vào (3) cos = 0,25đ 0 2 cos + Thay số 5 3 cos = = 43,810 0,25đ 0 0 12 Câu 5 Nội dung Điểm
+ Thể tích mỗi bên: V0 = S.l1 và áp suất p0. Khi ống đặt thẳng đứng. Gọi x là
độ dịch chuyển của cột thủy ngân khi đi xuống.
- Áp dụng định luật Bôi lơ – Mariot cho khí ở hai phần 0,5đ
+ Khí phần trên p0 .V0 = p1 .V1 p0.S.l1 = p1.S.(l1 + x) (1)
+ Khí phần dưới p0 .V0 = p2 .V2 p0.S.l1 = (p1 + h).S.(l1 – x) (2) 0,5đ 5.1 (2,0đ) p l . p l + Từ (1) và (2) p 0 1 . 0 1 − 1 = = h 0,5đ l + x l − x 1 1
+ Thay số: p0 = 72cm, h = 21cm, l1 = 42cm 0,25đ
x2 + 288x – 1764 = 0
x = -294cm < 0 (loại) hoặc x = 6cm 0,25đ
Vậy độ dịch chuyển của cột thủy ngân trong ống là x = 6cm. p l .
+ Áp suất không khí ở phần dưới của ống p 0 1 2 = p1 + h = + h 0,5đ 5.2 l + x 1 (1,0đ) + Thay số: p2 = 84cmHg 0,5đ Câu 6 Nội dung Điểm
+ Móc lực kế vào mẫu gỗ và kéo nó trượt đều đi lên mặt phẳng nghiêng, khi đó 0,5đ
F1 = Pcos + Psin (1), (F1 là số chỉ của lực kế khi đó).
+ Tương tự, kéo vật chuyển động đều đi xuống ta có: 0,5đ
F2 = Pcos - Psin (2). F F (2,0đ) 1 2 sin − = (3). 0,25đ 2P F + F 1 2 cos = (4). 0,25đ 2 P F − F F + F F + F + Từ (3) và (4) 1 2 2 1 2 2 1 2 1 = ( ) + ( ) → = 2 2 2P 2 P
4P − (F − F ) 1 2 0,5đ
- Các lực đều được đo bằng lực kế, từ đó tính được giá trị . GHI CHÚ :
1. Trên đây là biểu điểm tổng quát của từng phần, từng câu.
2. Học sinh làm bài không nhất thiết phải theo trình tự của hướng dẫn chấm. Mọi cách giải
khác có căn cứ cho kết quả đúng cũng cho điểm tối đa tương ứng với từng bài, từng câu, từng phần
của hướng dẫn chấm này.
SỞ GIÁO DỤC & ĐÀO TẠO QUẢNG NAM ĐỀ OLYMPIC LỚP 10
TRƯỜNG THPT NGUYỄN TRÃI MÔN: VẬT LÍ THỜI GIAN: 150 PHÚT Câu 1 ( 4đ )
Một chất điểm chuyển động từ A đến B cách A một đoạn s. Cứ chuyển động được 3
giây thì chất điểm lại nghỉ 1 giây. Trong 3 giây đầu chất điểm chuyển động với vận
tốc không đổi v0 = 5 m/s. Trong các khoảng thời gian 3 giây tiếp theo chất điểm
chuyển động với vận tốc 2v
, … , nv . Tìm tốc độ trung bình của chất điểm trên o, 3v0 0
quãng đường AB trong các trường hợp: a. s = 315 m b. s = 325 m Câu 2 ( 4 đ ):
Một vật bắt đầu trượt từ đỉnh một mặt phẳng
nghiêng dài 10m, cao 6m. Biết hệ số ma sát trượt
giữa vật và mặt phẳng nghiêng là =0,5, lấy g=10m/s2.
a) Tính thời gian vật đi hết mặt phẳng nghiêng và
vận tốc ở chân mặt phẳng nghiêng.
b) Khi đi hết mặt phẳng nghiêng, vật tiếp tục trượt
lên một cung tròn có bán kính R. Tìm bán kính lớn nhất của cung tròn để vật có thể đi hết được
cung tròn đó. Bỏ qua ma sát trên cung tròn. Câu 3( 3đ ): C A
Thanh AB có khối lượng m1 = 2kg gắn vào bức tường thẳng đứng bởi bản lề B,
đầu A treo một vật nặng có khối lượng m
2 = 3kg và được giữ cân bằng nhờ dây m2
AC nằm ngang (đầu C cột chặt vào tường), khi đó góc = 300 (hình). Hãy xác B
định lực căng dây và hướng, độ lớn của phản lực của tường lên đầu B. Lấy g = 10m/s2. Câu 4: ( 4 đ ):
Vật m2 đang đứng yên trên mặt sàn nằm ngang nhẳn cách bờ tường một khoảng d. Vật m ), vật m
1 chuyển động tới va chạm hoàn toàn đàn hồi với vật m2 (m1 > m2 2 lại
va chạm đàn hồi với bờ tường và gặp m1 lần 2.
a/ Va chạm lần 2 xảy ra cách bờ tường một khoảng là bao nhiêu?
b/ Tìm điều kiện để điểm va chạm lần 2 cách điểm va chạm lần 1 một khoảng là d/2 ?
Câu 5: ( 3 đ ): Một mol khí lí tưởng thực hiện quá trình giãn nở từ trạng thái 1 (P P
0, V0) đến trạng thái 2 (P0/2, 2V0) có đồ thị trên hệ toạ độ 1
P-V như hình vẽ. Xác định nhiệt độ của khí ứng với các áp suất Po, Po/2 và nhiệt P0
độ cực đại của khối khí trong quá trình đó? 2 P /2 0 V Câu 6: ( 2 đ ): V 2V 0 0
Nêu phương án thực hành để lập đồ thị phụ thuộc của lực đàn hồi
của một sợi dây cao su vào độ giãn của nó. Biết dụng cụ và vật liệu: dây cao su, vật
nặng(có khối lượng chưa biết), thước kẻ, giá treo.
----------------------------------hết------------------------------------
ĐÁP ÁN VÀ HƯỚNG DẪN CHÂM OLYMPIC VẬT LÝ 10 Câu 1 ( Đặt: t = ( 3 s) 1 4đ )
Gọi quảng đường mà chất điểm đi được sau nt giây là s: 1
s = s + s + ...+ s 1 2 n
Trong đó s1 là quảng đường đi được của chất điểm trong 3 giây đầu tiên. s ,…,s 2,s3
n là các quảng đường mà chất điểm đi được trong các khoảng 3 giây kế tiếp.
Suy ra: S = v t + 2v t + ...+ nv t = v t 1 ( + 2 + ...+ n) . 0 1 0 1 0 1 0 1 0,5 n(n + ) 1 S = v t = 5 , 7 n(n + ) 1 (m) 2 0 1 0,5 n = 6
a.Khi s = 315 m 7,5n(n+1) = 315 (loại giá trị n=-7) n = −7 0,5 Thời gian chuyển động:
t = nt + n −1 = ( 23 s) 1 0,5 Tốc độ trung bình: s 315 v = = = 13,7 m/s t 23 0,5
b. Khi s = 325 m :
Thời gian đi 315 mét đầu là 23 giây 1
Thời gian đi 10 mét cuối là: 10 10 t = = = 0.29(s) v 7 5 . n 1 + 0,5 Tốc độ trung bình: 325 v = = 13,38 m/s 23 + , 0 29 + 1 a)
Chọn chiều dương là chiều chuyển động, mốc thời gian lúc bắt đầu chuyển động.
+Biểu diễn đúng các lực tác dụng lên vật 0,5
+Gia tốc của vật trên mặt phẳng nghiêng: a=g(sin-cos)=2m/s2 0,5 2s = Câu t
+Thời gian đi hết mặt phẳng nghiêng: a 0,5 2(4đ) = 10 (s)
+Vận tốc ở chân mặt phẳng nghiêng: v= at = 2 10 (m/s) 0,5 b)
+Để vật đi hết cung tròn thì phải qua đỉnh của cung tròn ta xét tại 0,5 đỉnh cung: 2 v ' P+N=m R 0,5
Để vật không rời khỏi cung tròn thì N0 2 v '
m R P với v’2=v2-4Rg 1,0 2 v
v2-4RgRg v25Rg R 5g =0,8(m) Câu
3( Chọn trục Oxy như hình vẽ. Vẽ hình phân tích lực : 0,5 3đ ): Ox C A Oy
Quy tắc mô men lực đối với trục quay B: m 2 AB B
MP1 + MP2 = MT P1. 2 .sin + 1 40 3
P2.AB.sin = T.AB cos T = 3 N
ĐKCB: P + P + T + N = 0 1 2 0,5 40 3
Chiếu lên ox: - T + Nx = 0 Nx = T = 3 N 0,5
Chiếu lên oy: Ny – P1 – P2 = 0 Ny = P1 + P2 = 50 N N 0,5 x 0 = = 2 2 sin 24,8 N + N N= x y = 55 N và N (hợp với tường góc 24,80)
Câu 4: ( Gọi v1,v1’lần lượt là vận tốc của vật 1 trước và sau khi va chạm. 4 đ ):
Gọi v2 vàv2’ là vận tốc của vật 2 trước và sau khi va chạm (các vận
tốc v1,v2,v1’,v2’ mang giá trị đại số). v2 = 0
ĐLBT Động lượng: m1v1 = m1v1’ + m2v2’ 0,25 1 1 1 2 2 2 m v = m v ' + m v ' ĐLBT Động Năng: 1 1 1 1 2 2 2 2 2 0,25
m − m v + 2m v m − m ' ( 1 2 ) 0,5 1 2 2 v = 1 2 v 1 m + m 1 m + m Suy ra 1 2 = 1 2
m − m v + 2m v 2m ' ( 2 1 ) 2 1 1 1 v = = v 2 1 0,5 m + m m + m 1 2 1 2 (do v2 = 0)
Nhận thấy v1’,v2’ đều dương, chứng tỏ sau va cham chúng chuyển động cùng chiều ox.
Gọi điểm va chạm lần 2 cách tường một đoạn x, thời gian giữa 2 lần va cham là : d + x d − x t = = 0,5 v ' v ' 2 1
Thế v1’ và v2’ từ trên vào ta suy ra : m + m 1 2 1 d m 3 − m x = 1 2 - d d d 1 x = d − =
Để va chạm lần 2 cách lần 1 một đoạn 2 thì: 2 2 m + m d 1 2 d = − hay 3m m 2 m = 3m 1 2 1 2
Câu 5: ( - Vì đồ thị trên P-V là đoạn thẳng nên ta có: P = αV + β (*); trong đó 0,25 3 đ ):
α và β là các hệ số phải tìm. 0,25
- Khi V = V0 thì P = P0 nên: P = αV + β 0 0 (1)
- Khi V = 2V0 thì P = P0/2 nên: P /2 = 2αV + β 0 0 (2) 0,5 α = - P / 2V β = 3P / 2 - Từ (1) và (2) ta có: 0 0 ; 0 0,25 3P P 0,25 0 0 P = - V 0,25
- Thay vào (*) ta có phương trình đoạn thẳng đó : 2 2V0 (**) 0,5
- Mặt khác, phương trình trạng thái của 1 mol khí : PV = RT 0,5 (***)- 3V 2V 0 0 2 T = P - P 0,5
- Từ (**) và (***) ta có : R RP0 P V 0 0
- Khi P = P0 và P = P0/2 thì T = T1 =T2 = R ; 3V 4V 0 0 T = - P 3P0 (P) P = - Ta có : R RP T = 0 0 (P) 4 ; 3P 9V P 0 P = 0 0 cho nên khi
4 thì nhiệt độ chất khí là T = Tmax = 8R
Câu 6: ( - Treo vật có khối lượng m vào dây cao su rồi đo độ giãn ∆l1 của 0,5 2 đ ):
dây. Độ giãn tương ứng với lực đàn hồi có độ lớn F1 = mg.
- Sau đó chập đôi sợi dây lại và treo vật m vào sợi dây đã chập đôi. 0,5
Độ giãn tương ứng với trường hợp này là ∆l2, còn lực đàn hồi của mỗi sợi dây là F2=mg/2. 0,5
- Tương tự chập 3,4,5,… ta có độ giãn tương ứng là ∆l3, ∆l4,
∆l5….và lực đàn hồi là: F3=mg/3, F4=mg/4, F5=mg/5…. 0,5
- Lập bảng số liệu. Căn cứ số liệu vẽ đồ thị suej phụ thuộc của lực
đàn hồi vào độ giãn của dây cao su.
SỞ GD ĐT QUẢNG NAM
ĐỀ THAM KHẢO OLYMPIC 24 - 3
TRƯỜNG THPT SÀO NAM
Năm học 2016 – 2017
Môn thi: VẬT LÝ – KHỐI 10
Thời gian làm bài: 180 phút
( Đề thi gồm: 06 câu ; 02 trang)
Câu 1: (4,0 điểm) Một xe con đang chuyển động thẳng đều với vận tốc vo , tới điểm A thì người lái
xe nhìn thấy một xe tải tới điểm B phía trước, đang chuyển động cùng chiều, thẳng đều, với vận tốc
v1 < vo. Người lái xe con lập tức hãm phanh: xe con chuyển động thẳng chậm dần đều với gia tốc có
độ lớn là a. Hỏi khoảng cách tối thiểu của hai xe kể từ lúc người lái xe hãm phanh phải là bao nhiêu
để không xảy ra tai nạn?
Câu 2: (4,0 điểm) Cho cơ hệ như hình vẽ. Mặt phẳng nghiêng góc α so với phương ngang, hai vật
khối lượng m1, m2 có kích thước không đáng kể, gia tốc
trọng trường là g. Dây không giãn vắt qua ròng rọc. Bỏ m1
qua: khối lượng của ròng rọc,khối lượng dây nối và ma sát m
giữa dây và ròng rọc. Ban đầu giữ vật m 2 2 cách đất một khoảng h. h
1. Bỏ qua ma sát giữa m1 với mặt phẳng nghiêng. Biết m2 a
> m1sin, buông cho hệ chuyển động tự do.
a. Tính gia tốc mỗi vật?
b. Tìm khoảng thời gian từ lúc m2 bắt đầu chạm đất đến lúc dây bắt đầu căng trở lại? 1 m
2. Cho hệ số ma sát giữa m1 với mặt phẳng nghiêng là . Tìm tỉ số để sau khi buông hệ hai m2
vật m1, m2 đứng yên không chuyển động?
Câu 3: (3,0 điểm) Thanh AB đồng chất . Đầu A tựa vào sàn nhám.
Đầu B giữ cân bằng bởi sợi dây treo vào C. Hệ số ma sát giữa
thanh và sàn là K. Hỏi dây BC nghiêng với phương ngang góc α
bao nhiêu thì thanh trượt.
Câu 4: (3 điểm) Một xi lanh hình trụ chiều cao h tiết diện S = 100
cm2 đặt thẳng đứng. Xi lanh được chia làm hai phần nhờ pit tông cách nhiệt mỏng khối lượng 500g.
Khí trong hai phần là cùng loại ở cùng nhiệt độ 270C và có khối lượng m1 và m2
với m2 = 2m1. Pit tông có thể chuyển động không ma sát trong xi lanh và cân m1
bằng khi cách đáy dưới một đoạn h 3 = 2 = h .Lấy 2 g 10(m / s ) . 5
a. Tính áp suất khí trong hai phần của xi lanh. m2
b. Sau đó người ta rút bớt một lượng khí ở phần 2 ra ngoài có khối lượng m2.
Rồi tăng nhiệt độ ngăn hai lên đến 370C thì thấy pit tông cách đều hai đáy xi lanh. Tính m2 theo m1.
Câu 5: (4 điểm) Một sợi dây nhẹ không giãn, chiều dài l
= 1m, một đầu cố định, một đầu gắn với vật nặng khối O
lượng m = 300g tại nơi có gia tốc trọng trường 1 2 B
g = 10(m / s ) . Ban đầu vật m1 ở vị trí B, dây treo hợp
với phương thẳng đứng góc (với 0 0
0 90 ), thả vật K
m1 với vận tốc ban đầu bằng không. Mốc tính thế năng
trùng với mặt sàn nằm ngang đi qua điểm A và vuông góc D C
với OA như hình vẽ, OA = OB = A
l . Bỏ qua mọi ma sát và
lực cản tác dụng lên vật m1, dây luôn căng trong quá trình vật m1 chuyển động. 1. Cho 0 = 90 . Xác định:
a. Cơ năng của vật m1 ngay lúc thả.
b. Xác định độ lớn lực căng dây tại vị trí dây treo hợp với phương thẳng đứng góc 0 30 (ở phía bên trái OA).
2. Khi vật m1 chuyển động tới vị trí A, nó va chạm hoàn toàn đàn hồi xuyên tâm với vật m2 = 100g
(đang đứng yên tại vị trí A). Sau va chạm vật m1 tiếp tục chuyển động theo quỹ đạo tròn bán kính l
= 1m đến vị trí có độ cao lớn nhất (vị trí K), D là chân đường vuông góc từ K xuống mặt sàn. Vật
m2 chuyển động dọc theo mặt sàn nằm ngang đến vị trí C thì dừng lại. Hệ số ma sát giữa m2 và mặt sàn là 0,1. Biết AD 15 = . Xác định góc . AC 90
Câu 6: (2 điểm) Cho bộ dụng cụ gồm: khối lập phương, mặt phẳng nghiêng nối tiếp với mặt phẳng
ngang và thước chia độ.
Xác định hệ số ma sát trượt giữa khối lập phương và mặt phẳng nghiêng. Biết tính chất bề mặt
trên mặt phẳng nghiêng và mặt phẳng ngang là giống nhau.
……………………..Hết………………….. SỞ GD ĐT QUẢNG NAM
HƯỚNG DẪN CHẤM OLYMPIC TRƯỜNG THPT SÀO NAM MÔN VẬT LÝ- 10
Năm học 2016 – 2017
Câu 1: (4 điểm)
Chọn trục tọa độ x/x gắn với xe tải, chiều dương cùng chiều chuyển động của xe,
gốc tọa độ O trùng với điểm B, gốc thời gian lúc xe con bắt đầu hãm phanh. 0,5
- Phương trình chuyển động của: x2 = v1.t 1 0,5
- Phương trình chuyển động của xe con: x a.t2 1 = -AB + v0.t - 2
- Khi xe con gặp xe tải thì: x 1,0 1 = x2 1 1 (4đ) AB + (v1-v0).t + a.t2 = 0 (1). 1,0 2
- Để xe con chỉ gặp xe tải một lần và dừng lại, hoặc không gặp xe tải tức là không
xảy ra tai nạn thì (1) có 0. 0,5
(v1 –v0)2 – 2aAB 0 AB (v1 –v0)2/2a
- Vậy: ABmin = (v1 –v0)2/2a 0,5 Câu 2: (4 điểm)
a. Tính gia tốc mỗi vật:
+ lực tác dụng lên mỗi vật như hình vẽ 0,25 1.a (1 đ) 0,25 T
+ N + P = m a
+ Phương trình định luật II: 1 1 1 1 T + = 2 P2 m a2 2 0,25
+ Chiếu lên các trục tọa độ ta có: T
− P sin = m a 1 1 T − + P = m a 2 2 0,25 P − P sin 1 2 a = m + m 1 2
b.- Thời gian từ lúc m2 bắt đầu chuyển động đến khi bắt đầu chạm đất : 2h h=0,5at2 t= 0,25 1.b a (1,5 đ)
- Vận tốc của m1 lúc m2 chạm đất: 2h P − P sin 1 2 v = a = 2ha = 2h 01 a m + m 0,5 1 2 - Gia tốc của m P1 + N = m a 1 sau khi dây trùng : ' 1 0,25
Chiếu lên các trục toạ độ được a ' = −g sin
- Thời gian từ lúc m2 chạm đất đến khi dây căng trở lại bằng 2 lần thời gian từ lúc
m2 bắt đầu chạm đất đến khi m1 bắt đầu dừng lại trên mặt phẳng nghiêng rồi đi P − P sin 1 2 2h v m + m 0,5 xuống: 01 1 2 t = 2 − = 2 a ' g sin
* Trường hợp vật m1 có xu hướng trượt lên:
+ lực tác dụng như hình vẽ 0,25 2 0,25 (1,5 đ) 0, 5 T + + + = 1 N F ms 1 P 0
+ Hệ cân bằng nên ta có: T + = 2 P2 0
+ Chiếu lên các trục tọa độ và biến đổi ta thu được: F = P − P sin 0, 25 ms 2 1
+ Hệ đứng yên nên lực ma sát là ma sát nghỉ: F
= P − P sin Pcos ms 2 1 1 m 0, 25 2 sin + o c s m 1
* Trường hợp vật m1 có xu hướng trượt xuống: m2
Tương tự trên ta có: sin − o c s m1 m
Kết hợp cả hai trường hợp ta được: 2 sin − os c sin + os c m1 Câu 3: (3 điểm) 0,5 Điều kiện cân bằng:
P + N + F + T = 0 ms F Trên Ox : F ms 0,5 ms = T cos α => T = (1) 3 co s (3 đ) Trên Oy : N + T sin α = P P − N 0,5 => T = (2) Si n
Kết hợp (1) và (2) ta có : F P − N ms = co s Si n Chọn B làm trục quay thì : MN + MFms = Mp a =>(Fms + N)a = P. 0,5 2 p => N + F ms = 2 p => N = - Fms 2
Thanh AB bắt đầu trượt nếu lực ma sát bằng lực ma sát trượt F ms = μ.N 0,5 P Khi đó N = - μ.N 2 0,5 P => N = 2( + ) 1 N P − N => = co s sin P P 1 ( + 2) => = ( 2 + ) 1 Cos 2( + s ) 1 in 1+ 2 => tan α =
Câu 4: (3 điểm)
a. Phương trình M – C cho khí trong bình ở mỗi ngăn ta có 2h m 1 p S = RT 1 1 0,25 5 4.a 3 2m 0,25 (1 đ) 1 p S h = RT 2 1 5 Ta có 0,25 mg p = p + 2 1 S 0,25
Giải 3 phương trình trên ta được:
p2 = 2000 (N/m2) và p1 = 1500 (N/m2)
Phương trình M – C cho khí trong hai ngăn sau khi đã tăng nhiệt độ ngăn 2. h m 1 p ' S = RT 1 1 0,5 2 h (m − m ) 2 = 4.b p ' S RT 2 2 2 0,25 (2 đ) 0, 5 2h h Ta có p S = p' S 1 1 0,25 5 2 → p’1 = 1200 (N/m2) 0,25 mg p ' = p ' + =1700(Pa) 2 1 S 0,25 39
Thay p’1 và p’2 vào phương trình M – C tính được m = m 1 62
Câu 5: (4 điểm)
a. Cơ năng của vật m W = m gl = 0,3.10.1 = 3(J) 1 là 1 0,5
b. Áp dụng định luật bảo toàn cơ năng cho vật, tìm tốc độ của vật ở vị trí góc lệch 0 = 30 , ta được: 1 2 0 (1,5đ) = = = = 0,5 v 2gl cos c 1 . 10 . 2 os30 10 3 v 1 , 4 61 m 8 / s
- Áp dụng định luật II Niu - tơn cho vật m = 2 tại vị trí 0
30 , chiếu lên phương bán
kính, chiều hướng vào tâm, ta được : 0,5 9 3 T = m 3 g cos = N = 79 , 7 N 1 2
- Vận tốc của vật m1 ngay trước va chạm là O 2 v = 2gl(1− cos) 0,25 B
- Gọi v , v tương ứng là vận tốc của mỗi vật 1 2 ngay sau va chạm. K 2
- Áp dụng định luật bảo toàn động lượng, cơ A D C
(2,5 đ) năng cho hệ hai vật m 1 , m2 ngay trước và ngay
sau va chạm (chiều dương có phương nằm v v = = + 1 m v m v m v
ngang, hướng từ trái sang phải) 2 0,5 1 1 1 2 2 2 2 2 m v = m v + m v 3v 1 1 1 2 2 v = 2 2 - Xét vật m1:
Áp dụng định luật bảo toàn cơ năng cho vật tại vị trí A và vị trí K, ta được : 1 2 2
m v = m gl(1− cos) v = 8gl(1− cos) cos = 0, 75 + 0, 25cos 1 1 1 2 0,5 AD = lsin - Xét vật m2:
Áp dụng định luật II Niu - tơn cho vật theo phương ngang, chiều dương hướng sang phải. 0,25 a = g − 2 2 2 v 9v
Khi vật dừng lại tại C. Suy ra: 2 AC = = 0, 5 2a 8 g 2 AD 15 15 4sin Theo đề = = AC 90 90 9(1− cos ) 2 2 4sin = 15(1−cos )
16(1−cos ) =15(1−cos ) (1) Đặt x = cos 0
x = 0,5 cos = 0,5 = 60 (T / m) 0,5 2 (1) 4x − 6x + 2 0
x =1 cos =1 = 0 (L) Vậy 0 = 60 Câu 6: (2 điểm): M P N H 6
Thả không vận tốc đầu khối lập phương từ đỉnh M của mặt phẳng nghiêng. Vật (2 đ)
trượt đến P thì dừng lại. 1
Ta có : WtA = AFmsMN + AFmsNP
mg.MH = μmgcosα.NM+ μmg.NP MH = μ(MNcosα + NP) 0,5 NH MH = μ(MN. + NP) MN MH 0,5 μ = PH
Dùng thước đo độ dài các đoạn MH và PH, ta tính được μ.
Chú ý : Học sinh làm theo cách khác, nếu đúng vẫn cho điểm tối đa theo ý tương ứng.
……………Hết………………
SỞ GD&ĐT QUẢNG NAM KÌ THI OLYMPIC 24 - 3
Trường THPT Nguyễn Khuyến LẦN THỨ 2 Môn: VẬT LÝ 10 ĐỀ THI ĐỀ XUẤT
Thời gian: 150 phút (không kể thời gian giao đề)
Bài 1: (4 điểm)
a. Trên sân ga một người đi bộ dọc theo đường sắt bên một đoàn tàu đang
chuyển động. Nếu người đó đi cùng chiều với đoàn tàu thì tàu sẽ vượt qua người
trong khoảng thời gian t1 = 2,5 phút. Nếu người đi ngược chiều với tàu thì thời gian
từ lúc gặp đầu tàu đến lúc gặp đuôi tàu là t2 = 70 giây. Tính thời gian từ lúc gặp đầu
tàu đến lúc gặp đuôi tàu trong hai trường hợp:
TH1: Người đứng yên nhìn đoàn tàu đi qua.
TH2: Tàu đứng yên người đi dọc bên đoàn tàu.
b. Xét ba đoạn đường đi được liên tiếp bằng nhau trước khi dừng lại của một vật
chuyển động chậm dần đều, người ta thấy đoạn đường giữa nó đi được trong 1s. Tính
thời gian vật đi hết ba đoạn đường bằng nhau nói trên. Bài 2: (4 điểm)
Ba vật có khối lượng như nhau m = 5kg được nối với nhau bằng các sợi dây không
giãn, khối lượng không đáng kể trên mặt bàn ngang. Biết dây chỉ chịu được lực căng
tối đa là T0=20N. Hệ số ma sát giữa bàn và các m3 m2 m1
vật 1, 2, 3 lần lượt là =0,3; =0,2; = 0,1. 1 2 3
Người ta kéo vật với lực F nằm ngang như hình vẽ. Lấy g=10m/s2.
a) Tính gia tốc mỗi vật và lực căng các dây nối nếu F=31,5N.
b) Tăng dần độ lớn của lực F, hỏi Fmin bằng bao nhiêu để một trong hai dây bị đứt?
Bài 3: (4 điểm)
Mét vËt tr-ît kh«ng ma s¸t vµ kh«ng cã vËn tèc A C
ban ®Çu.Tõ ®é cao h theo mét m¸ng nghiªng
nèi víi mét m¸ng trßn b¸n kÝnh r(H×nh vẽ).
TÝnh ®é cao h tèi thiÓu ®Ó vËt ®i ®Õn o h
®iÓm cao nhÊt cña m¸ng trßn mµ kh«ng t¸ch r ra khái m¸ng. M
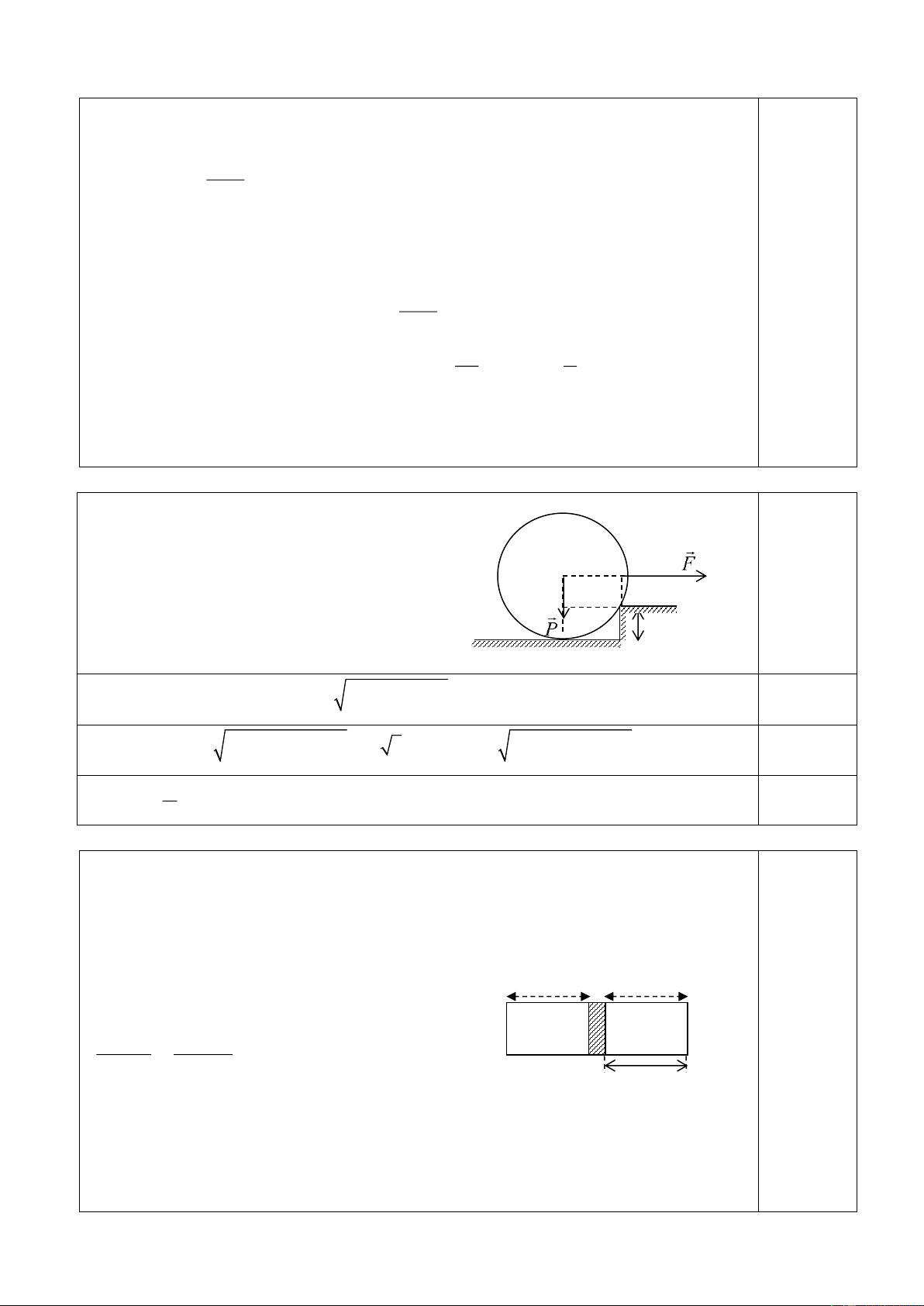
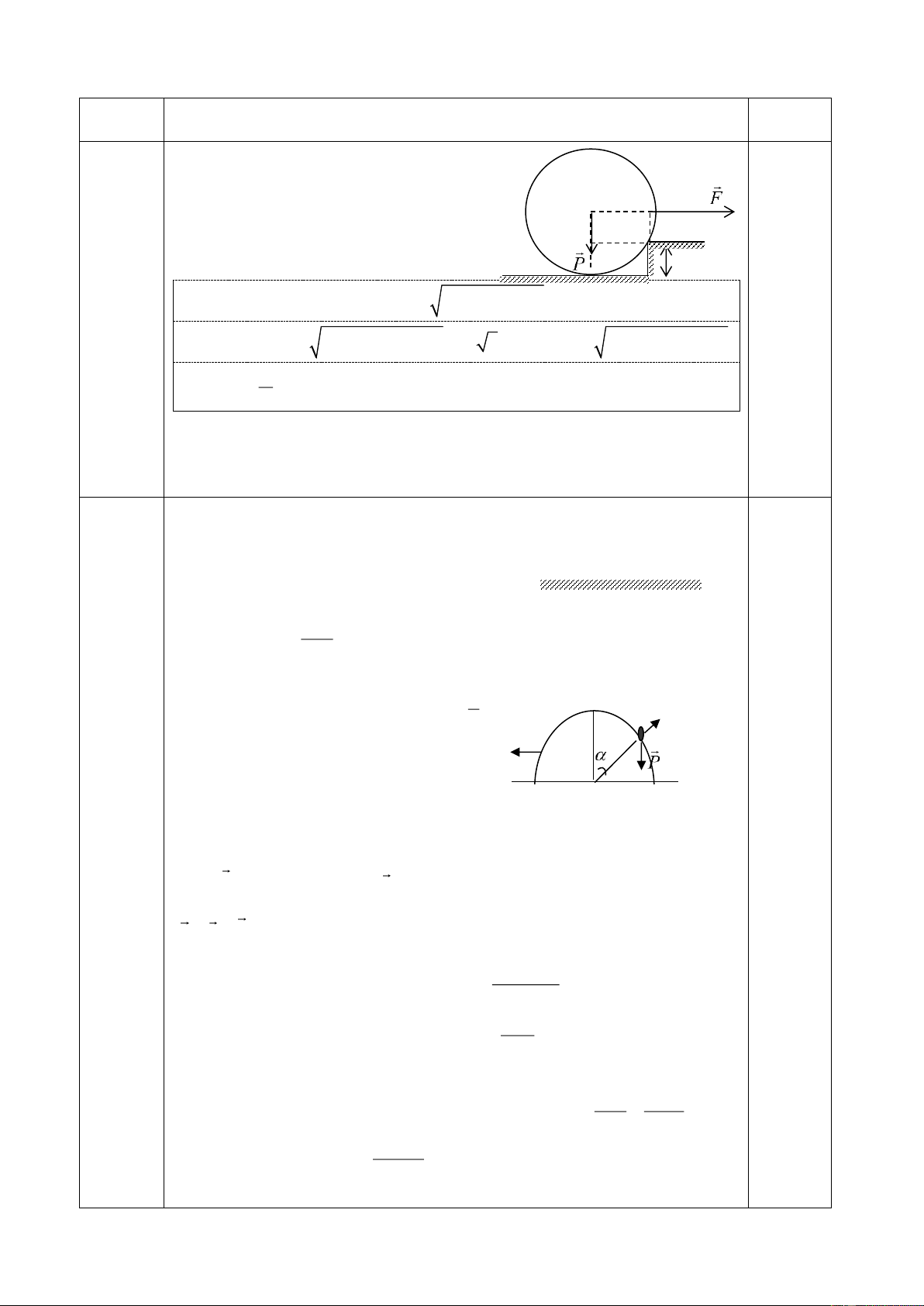
Bài 4: (3 điểm) Bánh xe có bán kính R. Lực kéo F theo
phương nằm ngang, hướng đến trục bánh xe. Lực này có
độ lớn bằng 3 lần trọng lượng của bánh xe. Xác định
độ cao cực đại của bậc thềm để bánh xe vượt qua. R . h
Bài 5: (3 điểm)
Mét xi lanh n»m ngang trong cã pÝt t«ng c¸ch nhiÖt. PÝt t«ng ë lA lB
vÞ trÝ chia xi lanh thµnh hai phÇn b»ng nhau, mçi phÇn chøa
mét khèi l-îng khÝ nh- nhau ë nhiÖt ®é 170C vµ ¸p suÊt 2atm. A B
ChiÒu dµi cña mçi phÇn xi lanh ®Õn pÝt t«ng lµ 30cm. Muèn
pÝt t«ng dÞch chuyÓn 2 cm th× ph¶i ®un nãng khÝ ë mét 30 Cm
phÝa lªn thªm bao nhiªu ®é ? ¸p suÊt cña khÝ khi pÝt t«ng ®· di chuyÓn b»ng bao nhiªu ?
Bài 6: (2 điểm) Cho các dụng cụ sau:
- Một mặt phẳng nghiêng
- Một khối gỗ có khối lượng m đã biết.
- Một thước có độ chia tới mm.
- Một đồng hồ có kim giây.
Trình bày phương án thí nghiệm xác định nhiệt lượng tỏa ra khi khối gỗ trượt
trên mặt phẳng ngiêng ( không có vận tốc ban đầu)
…………. Hết ……………..
Họ và tên thí sinh:............................................Số báo danh...................................
Giám thị 1: ......................................................Giám thị 2...................................... HƯỚNG DẪN CHẤM NỘI DUNG THANG ĐIỂM Bài 1: (4 đ) Điểm
a. TH1: Khi người đứng yên nhìn đoàn tàu qua: l 0,25đ t = a v1
Gọi vận tốc của tàu là v , của người là v , chiều dài đoàn tàu là 1 2 l. Khi
đi cùng chiều vận tốc của tàu so với người là vc= v1- v2. 0,25đ Thời gian l l 0,25đ t = = (1) 1 v v − v c 1 2 Khi đi ngược l l 0,25đ chiều v = =
n= v1 + v2 , thời gian t (2) 2 v v + v n 1 2 Từ (1) và (2) => (v 4 0,25đ
1 - v2).t1 = (v1 + v2).t2 => v2 = v1 hoặc v1 = 2,75v2 11 . 11 l . 11 t 7 0,25đ thay v t = = a t = t 2 vào (1) => 5 , 95 giây 1 7v 7 a 11 1 1 TH2: Khi tàu đứng yên: l 0,25đ t = b v2 l t 0,25đ thay v t = = b t = 1 vào (2) => 262 5 , giây 2 75 , 3 v 75 , 3 b 2 b. Ta có: 2 −v = 2as 3 2 − v = 4as 2 2 − v = 6as 1 v = 2v ; v = 3v 2 3 1 3
…………………………………………………………………….. 0,50đ Suy ra v − v v ( 2 − 3) 2 1 3 t = = 1 a a 0,25đ
………………………………………………………………… v − v − 2v + v 3 2 3 3 0,25đ t = = 2 a a
………………………………………………………………… 0,25đ −v3 t =
……………………………………………………….. 3 a t3
= 2 +1 t = 2 +1(s) …………………………………… 3 t2 0,25đ t 1 = ( 2 + ) 1 ( 3 − 2) t = 2 + 1
3 − 2 (s) ………………… 1 ( )( ) t 0,25đ 2
Thời gian đi hết ba đoạn đường: t = ( 2 + )
1 ( 3 − 2) +1+ 2 +1= 3 + 6 (s) …………………………... 0,25đ Bài 2: (4 điểm)
a) Định luật II Newton cho các vật; 0.25đ
P + N + T + F = ma 1 1 1 1 ms 1
Vật 1: 0x : F −T − F = ma 1 1 ms
0 y : N = mg
→ F − T − mg = ma (1) 1 1 1 , Vật 2: 0.25đ '
P + N + T + T + F = ma
→ T − T − mg = ma (2) 2 2 1 2 ms 2 2 1 2 2 Vật 3: '
P + N + T + F
= ma → T − mg = ma (3) 0.25đ 3 3 2 ms3 3 2 3 Từ 1,2,3 F 1 → a =
− ( + + )g 1 2 3 3m 3 F 0.5đ Do 2
= 3 = 2 → a =
− 2 g = 0,1m / s 1 3; 2 3 3 3m Lực căng dây: 2F 0,5đ
T = F − mg − ma =
− mg =16N 1 1 3 3 F 0.25đ
T = mg + ma =
− mg = 5,5N 2 3 3 3
b) Thấy T1 >T2 nên nếu đứt thì dây nối giữa vật 1 và 2 sẽ đứt trước. Dây sẽ bị đứt khi ta có: 2F 1.0đ T =
− mg T 1 3 0 3 3 → F
(T + mg) = 37,5N 0 3 2 1.0đ
Vậy lực kéo F nhỏ nhất để dây đứt là 37,5N
Bài 3: (4 điểm) A C M h r 0,5®
T¹i vÞ trÝ C cao nhÊt vËt m chÞu t¸c dông : N , P
¸p dông ®Þnh luËt II Niu T¬n cho vËt t¹i vÞ trÝ cao nhÊt :
N + P = m a (1) 0,5® v2
ChiÕu (1) lªn ph-¬ng h-íng t©m N + P = maht = m (2) 0,25® r
§Ó vËt ®i qua ®iÓ cao nhÊt C kh«ng t¸ch ra khái m¸ng víi ®iÒu kiÖn : N 0 0,5®
NghÜa lµ vËt ®¹t vËn tèc tèi thiÓu t¹i C khi N = 0 tøc lµ : v 2 0,25® (2) P = m min v 2 min = gr (3) r
Chän mèc thÕ n¨ng t¹i ch©n m¸ng nghiªng :
Lóc ®ã : ¸p ®Þnh luËt b¶o toµn c¬ n¨ng :
C¬ n¨ng cña vËt t¹i A b»ng c¬ n¨ng tèi thiÓu t¹i C : 1® 2 v W min
A = WminC mghmin = mg2r + m (4) 2 1® gr 5
Tõ (3) thay vµo (4) ta ®-îc: gh min = g2r + hmin= r . 2 2
VËy vËt cÇn ®Æt t¹i vÞ trÝ trªn mÆt ph¼ng nghiªng cã ®é cao tèi thiÓu hmin = 2,5r
Bài 4: (3 điểm)
Bánh xe vượt qua được bậc thềm (A) (A) M M 1® F P d1 A d2 h F.d .
P d F.(R − h) P R − (R − h)2 2 1 2 0,5®
F.( R − h
) = P R − (R − h )2 . 3 R − h
= R − R − h 1® m m ( m ) ( m )2 2 2 ax ax ax ax R 0,5® h = ax m 2
Bài 5: (3 điểm)
Gäi V1A,V2A thÓ tÝch xi lanh phÇn A tr-íc vµ sau khi ®èt nãng.
Gäi V1B, V2B thÓ tÝch xi lanh phÇn B tr-íc vµ sau khi phitt«ng dÞch chuyÓn
PhÇn A: Tr¹ng th¸i 1: p1A, T1A, V1A 0,25® Tr¹ng th¸i 2: p lA l 2A , T2A, V2A B
¸p dông ph-¬ng tr×nh tr¹ng th¸i : A B p V p V 1A 1A 2 A 2 A = (1) T T 0,5® 1 A 2 A 30 Cm
PhÇn B : Tr¹ng th¸i 1: p1B, T1B, V1B 0,25®
Tr¹ng th¸i 2: p2B , T2B, V2B 0,25®
V× phÝt t«ng c¸ch nhiÖt nªn phÇn B nhiÖt ®é kh«ng ®æi khi phÝt t«ng dÞch chuyÓn. 0,5®
Do ®ã qu¸ tr×nh thay ®æi tr¹ng th¸i phÇn B lµ qu¸ tr×nh ®¼ng nhiÖt.
(T1B = T2B= T1A)¸p dông hÖ thøc ®Þnh luËt B«i L¬ - Mariot : p1BV1B = p2BV2B (2) 0,25®
Theo bµi ra : V1A = V1B , p1B = p1A (3) vµ khi phÝt t«ng dÞch chuyÓn 2cm
th× c©n b»ng nªn : p2B = p2A (4)
Tõ (2), (3), (4): p1AV1A = p2AV2B (5) p V p V V V V l 32
Tõ (1) vµ (5): 2A 2B 2 A 2 A = 2B 2 A =
lu«n cã 2A = 2 A = T T T T V l 28 1 A 2 A 1 A 2 A 2 B 2 B T 32 32 Nªn 2A =
T2A = .(17 + 273) = 331,43 (K) 0,5® T 28 28 1 A
NhiÖt ®é cÇn t¨ng thªm : t = 331,43 – 290 = 41,43(0C) p V l 28 30 30 0,5® Tõ (5) 1 A 2 B = = 2B = p2A = p1A. = 2. = 2.14atm P V l 30 28 28 2 A 1 A 1 A
Bài 6: (2 điểm)
Gọi: h là chiều cao của mặt phẳng nghiêng;
l là chiều dài mặt nghiêng.
Nhiệt lượng tỏa ra khi khối gỗ trượt trên mặt phẳng nghiêng không có vận tốc đầu là: 2 mv 2 at 0,5đ Q = mgh − với 2 v = 2al; l = 2 2 2 2l 0,5đ
Suy ra: Q = m gh − 2 t
Thả cho vật trượt từ đỉnh mặt nghiêng đến chân mặt nghiêng. Đo h và l 0,5đ
bằng thước đo t bằng đồng hồ sẽ tính được Q. 0,5đ TRƯỜNG THPT DUY TÂN
KỲ THI OLYMPIC NĂM HỌC: 2016- 2017 TỔ : VẬT LÝ MÔN: Vật Lý 10
Thời gian: 150 phút
Câu 1(4 điểm): Từ trên cao người ta thả hòn bi rơi, sau t giây người ta thả một cái thước dài cho rơi
thẳng đứng; trong khi thước rơi luôn thẳng đứng. Ban đầu điểm cao nhất của thước thấp hơn độ cao
ban đầu của hòn bi 3,75m. Khi hòn bi đuổi kịp thước thì chênh lệch vận tốc giữa hai vật là 5m/s.
Sau khi đuổi kịp thước 0,2s thì hòn bi vượt qua được thước. Tìm khoảng thời gian; chiều dài của
thước; quãng đường mà hòn bi đã đi được cho đến lúc đuổi kịp thước; độ cao ban đầu tối thiểu phải
thả viên bi để nó vượt qua được thước. Lấy g = 10m/s2
Câu 2( 4 điểm):Một người lồng một hòn bi có lỗ xuyên suốt và có khối lượng m vào một que sắt
AB nghiêng góc so với mặt bàn nằm ngang. Lúc đầu bi đứng yên.
1.Cho que tịnh tiến trong mặt phẳng thẳng đứng chứa nó với gia tốc nằm ngang a0 hướng sang
trái hình vẽ. Giả sử không có ma sát giữa bi và que. Tính B
a. Gia tốc a của bi đối với que.
b.Phản lực Q của que lên bi A
c.Tìm điều kiện để bi
- Chuyển động về phái đầu A
- Chuyển động về phái đầu B A - Đứng yên
2. Hỏi như câu 1 nhưng cho biết a0 = 2g( g là gia tốc trọng trường) và có ma sát giữa bi và que, với hệ số ma sát k = 1 3
Câu 3( 3 điểm) : Một chiếc thang có chiều dài AB = l và đầu A tựa vào sàn nhà nằm ngang, đầu B
tựa vào tường thẳng đứng. Khối tâm C của thanh cách dầu A đoạn l . Thang làm với sàn một góc 3
1. Chứng minh rằng thang không thể cân bằng nếu không có ma sát.
2. Gọi k là hệ số ma sát ở sàn và tường. Biết = 600 . Tính giá trị nhỏ nhất của k để thang đứng cân bằng.
3. Cho k = kmin. Thang có trượt không , nếu:
a.Một người có trọng lượng bằng trọng lượng của thang đứng ở điểm C. 2l
b. Người ấy đứng ở điểm D cách đầu A đoạn 3
Câu 4( 4 điểm):Một vật nhỏ khối lượng m trượt từ độ cao h qua vòng xiếc bán kính R. Bỏ qua ma sát.
1. Tính lực nén của vật lên vòng xiếc tại vị trí ( hình vẽ)
2. Tính h để vật có thể qua được vòng xiếc.
3. Khi vật không qua vòng xiếc, định vị trí nơi vật bắt đầu rời khỏi vòng xiếc hoặc trượt trở xuống.
Câu 5( 3 điểm):Một bình chứa 0,3kg heli. Sau một thời gian do bị hở, khí heli thoát ra một phần.
Nhiệt độ tuyệt đối của khí giảm 10%, áp suất giảm 20%. Tính số nguyên tử heli thoát ra khỏi bình.
Câu 6( 2 điểm): Nêu phương án đo độ cứng của một lò xo bằng phương pháp cân bằng. B . D . C O A Hình Câu 3 Hình Câu 4
……..…………HẾT……………………..
TRƯỜNG THPT DUY TÂN
HƯỚNG DẪN CHẤM ĐỀ OLYMPIC, NĂM 2016 - 2017 TỔ : VẬT LÝ MÔN: VẬT LÝ 10 Câu Nội dung Điểm Câu 1
- Chọn gốc thời gian bắt đầu thả vật
- Kí hiệu: thời gian bi đuổi kịp thước t1, vận tốc của bi và của thước 0,5
lúc bi đuổi kịp u1 và v1; t2: thời gian thước bắt đầu rơi cho đến lúc bi đuổi kịp thước
Có: u1 = gt1; v1 = gt2 ( t2 = t1 –t) 1
u1 – v1 = 5 , suy ra: t = 0,5s Ta có: H 1 = 5 2 t và h 1 1 = 5(t1 – 0,5)2 H 0,5
1 – h1 = 3,75, suy ra: t1 = 1s và t2 = 0,5s và u1 = 10m/s và v1 = 5m/s
* Đoạn đường hòn bi càn phải đi vượt qua thướt: 1 0,5 H2 = u1t3 + 2 gt = 2,2m( t 3 3 = 0,2s) 2
* Đoạn đường thước rơi được từ lúc hòn bi đuổi kịp cho đến luc 0,5 vượt qua: 1 h2 = v1t3 + 2 gt = 1,2m 3 0,5 2
* Chiều dài của thước; l = H 2 – h2 = 1m
* Quãng đường hòn bi đi được cho đến lúc đuuỏi kịp: s = H 0,5 1 = 5m
Độ cao tối thiểu: H = H1 + H2 = 7,2m Câu 2
1. Chọn trục xoy gắn que, oy vuông góc với que.
Bi chịu tác dụng: P;Q;F 0,25 qt
Ta có: m a = P + Q + F qt 0,5
Chiếu lên trục ox, oy: a = a 0cos - gsin Q = m(gcos + a 0,5 0sin )
* Về phía A: a< 0 , suy ra: a tg > 0 0,25 g
* Về phía B: a > 0, suy ra: tg a < 0 0,25 g
* Đứng yên: a = 0, suy ra: tg a = 0 0,25 g 2. Bi chịu tác dụng: Q ; P ;
Q F ; F (F = k.Q = ) qt ms ms 3 0,25
- Viết biểu thức: ĐL II Niutơn
- Chiếu lên : Ox, Oy: Q = mg( cos + 2sin ) và mg = -mgsin + 0,5 Q 2mgcos 0,5 3
* Đi xuống: a = g (7cos -sin ) < 0 , suy ra: > 820 0,25 3
* Đi lên: a = 5g (cos -sin ) > 0, suy ra: <450 0,25 3
* Đứng yên: a = 0; 450 820 0,25 Câu 3
1. Nếu không có ma sát thì 3 lực: ;
P N ;N không đồng qui, nên 1 2 thang không cân bằng 0,5
2. Điều kiện cân bằng lên thanh và xét momen trục A k P P cos - Có: 1 = . 1 + k k 3 sin + k cos 1 1 2 2
Thay : k1 = k2 = k và =600 - Suy ra: k = 0,18
3 a. k không phụ thuộc vào trọng lượng, thang vẫn cân bằng 0,5
b. Khi ở D, trọng lượng người bằng thang, nên trọng tâm ở trung
điểm thang và trọng lượng 2P
- Dựa vào phần 2/câu 3: suy ra : k2 +2 3 k- 1 = 0 1
- suy ra: k = 0,267 > 0,18. Vậy thang trượt Câu 4 2
1. Định luật II Niutơn: Q = v m − mg cos (1) R 1
Định luật báo toàn cơ năng: 2
v = 2gh − 2gR 1 ( + cos ) (2) 2h Từ 1 và 2: Q = mg( − 2 − 3cos) R Theo ĐL III Niutơn: N = Q = 2h mg( − 2 − 3cos) R 1 2.Điều kiện : N 0 h 5 , 2 R 1 min 3.Điều kiện: 2h 2 N = 0 cos = − min 3R 3 1 Câu 5 Ban đầu: m1 P V = RT ( 1) 1 1 0,5 m Lúc sau: 2 P V = RT ( 2) 2 2 2 Từ 1 và 2: 8 m = m 2 1 9 Suy ra: m = 3 , 33 33g 0,5 m Suy ra: 23 N = N = , 50 10 . 2 A nguyên tử Câu 6:
1. Tiến trình thí nghiệm: Đo chiều dài ban đầu lò xo chưa bị biến
dạng. Sau đó lấn lượt treo một số quả cân 50g, 25g..vào lò xo, rồi đo 0,5
độ dài tương ứng l1, l2…của lò xo 2. Tính sai số: m g k i = k k + k + k 1 2 3 k = 1,5 3
k − k + k − k + k − k 1 2 3 k = 3
k = k k ĐÊ HSG LÍ 10 CÂU 1
Một vật nhỏ m được treo vào trần một chiếc ôtô bằng một dây l mảnh
nhẹ không đàn hồi. Xe ôtô đang chuyển động nhanh dần đều m xuống h
một dốc nghiêng một góc α = 300 so với phương ngang, xe có gia tốc α
a sao cho dây treo vật vuông góc với sàn của xe (hình vẽ).
1) Xác định gia tốc a của xe? Lấy g = 10m/s2.
2) Vật đang treo cách sàn ôtô h = 2m, đốt nhẹ dây treo.
a) Vật sẽ rơi theo phương nào? Xác định thời gian rơi của
vật và vận tốc của vật đối với xe khi vật chạm sàn xe?
b) Biết điểm treo cách mép cuối của xe một khoảng l = 3m, phía sau xe hở. Hỏi
phải đốt dây khi xe có vận tốc tối thiểu bằng bao nhiêu để vật rơi ra ngoài xe? CÂU 2
Có hai vật m1 và m2 chuyển động thẳng đều với vận tốc v
. Vật m xuất phát từ A, vật m xuất phát 1 và v2 1 2 từ B. (H vẽ).
Tìm biểu thức tính khoảng cách ngắn nhất giữa
chúng trong quá trình chuyển động, và thời gian đạt
được khoảng cách đó? Biết khoảng cách ban đầu của
chúng l và góc giữa hai đường thẳng là .
Áp dụng bắng số: l =350m; v = 1=5m/s; v2=10m/s; 0 60
CÂU 3. Một súng cối được đặt dưới một căn hầm có độ sâu h .Hỏi phải đặt súng
cách vách hầm một khoảng bằng bao nhiêu so với phương ngang để tầm bay xa S của
đạn trên mặt đất là lớn nhất ? Tính tầm bay xa này , biết vận tốc đầu của đạn khi rời nòng súng là v0 CÂU 4 B
Một chiếc thang đồng chất có chiều dài AB = l = 2,7m, trọng lượng P.
Đầu A của thang tựa vào sàn nhà nằm ngang, đầu B của thang tựa vào tường
thẳng đứng. Khối tâm G của thang ở cách đầu A một đoạn 0,9m. Thang cân
bằng ở vị trí hợp với sàn nhà một góc 0
= 60 như hình vẽ. Gọi µ là hệ
số ma sát giữa thang với sàn, bỏ qua ma sát giữa thang và tường. G
1. Tìm giá trị nhỏ nhất của µ để thang còn chưa bị trượt.
2. Cho = 0,32 . Một người có trọng lượng P = 3P trèo 1 A
lên thang. Hỏi người đó trèo được một đoạn tối đa
bằng bao nhiêu (so với đầu A) để thang còn chưa bị trượt. P1 CÂU 5
Một bình kín hình trụ đặt thẳng đứng có chiều dài l được
chia thành hai ngăn nhờ một pittông cách nhiệt (bỏ qua bề dày P2
của pittông). Hai ngăn chứa cùng một chất khí lí tưởng,
ngăn trên chứa một 1mol khí, ngăn dưới chứa 5 mol khí.
Khi chất khí ở hai ngăn có cùng nhiệt độ T1 thì pittông
ở vị trí cân bằng và cách đầu trên của bình một đoạn
l = 0, 25l . Gọi P 1
0 là áp suất của riêng pittông tác
dụng lên chất khí ở ngăn dưới. Biết các thông số
trạng thái P, V, T và n (mol) liên hệ với nhau bằng
công thức: PV = nRT (với R là hằng số). Bỏ qua mọi ma sát.
1. Tính áp suất P1 và P2 của không khí trong hai ngăn theo P0.
2. Chất khí ở ngăn dưới được giữ ở nhiệt độ T1. Hỏi phải thay đổi nhiệt độ chất khí ở ngăn
trên đến giá trị bằng bao nhiêu (theo T1) để pittông cân bằng ở vị trí cách đều hai đầu của bình? ĐÁP ÁN CÂU 1
+ Xét chuyển động của vật trong
hệ quy chiếu phi quán tính gắn với xe.
Vật chịu thêm tác dụng của lực quán tính
F = −ma , hình vẽ. α α
1) Khi cân bằng vật có 3lực tác dụng
Điều kiện m cân bằng đối với xe: P +T + F = 0 => P' = P + F = T −
Từ hình vẽ => sinα = F/P = a/g => a =gsinα = ... = 5m/s2. 2) Khi đốt dây:
a) Vật có 2 lực P và F tác dụng nên nó sẽ rơi theo phương của P' = P + F = T − (
phương vuông góc với sàn xe và mặt phẳng nghiêng) với gia tốc trọng trường biểu kiến:
g’= P’/m = Pcosα/m = gcosα =...= 5 3 m/s2. + Thời gian rơ 2h i t = = ... 0.68s R g '
+ Vận tốc của vật đối với xe khi chạm sàn: v = 2g 'h = ...... 5,89m / s
b) Khi đốt dây xe có vận tốc vx, quãng đường xe đi được trong thời gian vật rơi là s. Điều kiện để vật rơ 1 i ra ngoài xe là: 2 s = v t + at l x R 2 R l at => R v − 2,71m / s x t 2 R CÂU 2
Gi¶ sö sau thêi gian t kho¶ng c¸ch gi÷a hai vËt lµ ng¾n
nhÊt. Kho¶ng c¸ch ®ã sÏ lµ: d = ' 2 A B + BB'2 2 − ' A . B BB'.cos
d = (l − v t)2 + (v t)2 − (
2 l − v t)v t cos 1 2 1 2 = 2 2 2 2 (v
+ 2v v cos + v )t − 2l(v + v cos)t + l 1 1 2 2 1 2
Ta xem biÓu thøc trong c¨n lµ mét tam thøc bËc hai, Èn sè t , víi 2 2 2 = 4
− l v sin , d sÏ ®¹t 2
gi¸ trÞ nhá nhÊt khi tam thøc ®ã nhËn gi¸ trÞ nhá nhÊt, hay d = d min + b l(v v cos ) t − = 1 2 t = 2a → 2 2
v + 2v v cos + v 1 1 2 2
Thay số ta được t = 20s
Vµ kho¶ng c¸ch bÐ nhÊt gi÷a chóng lóc ®ã sÏ lµ: − lv sin d = d = 2 min 4a min 2 2 v
+ 2v v cos + v 1 1 2 2 Thaysố ta được: d = 458,7m min CÂU 3
Ph-¬ng tr×nh vËn tèc cña vËt theo ph-¬ng ox : v = v cos x 0
Ph-¬ng tr×nh vËn tèc cña vËt theo ph-¬ng oy:
v = v sin − gt y 0
Ph-¬ng tr×nh chuyÓn ®éng:
x = v cos t 0 ; 2 gt
y = v sin t − 0 2 Ph-¬ng tr×nh vËn tèc: v = v cos ; x 0
v = v sin − gt y 0
§Ó tÇm xa x lµ lín nhÊt th× t¹i A vËn tèc cña vËt ph¶i hîp víi mÆt ngang mét
gãc 450 cã nghÜa lµ t¹i A: sin − cos
v = v t = v (1) x y 0 g
H¬n n÷a ta ph¶i cã sau thêi gian nµy:
v cos t = x = l ( ) 2 l 0 2 y = gt h
v sin t − = h ) 3 ( 0 2 l 2 v Tõ (2) t = (3) kÕt hîp víi (1) 0 l =
cos.(sin − cos ) (4) v cos g 0
Thay t tõ (1) vµo (3) ta ®-îc: gh 1 gh 2 1 sin = + ; 2 cos = − 2 v 2 2 2 v 0 0 ThÕ vµo (4): 2 v 0 l =
(sin cos − cos2 ) g 2 v 1 2 2 g h 1 gh l = 0 ( − − + ) g 4 4 v 2 2 v 0 0 Tõ (1) :
1 + gh − 1 − gh 2 2 2 v 2 v 0 0 1 gh 1 gh 1 gh t =
v v = v + − + − − 0 y 0 2 g 2 2 2 v 2 v 2 v 0 0 0 1 gh gh gh gh 2 1 1 1 v = − v = v ( − ) + ( − ) = ( − ) ( 2 v + ) 1 y 2 2 A 0 0 v 2 2 v 2 2 v 2 2 v 0 0 0 0 1 gh − (.v2 + 2 2 0 )1 v 2 v S = A 0 = max g g
VËy ph¶i ®Æt sóng c¸ch v¸ch hÇm mét kho¶ng: 2 v 1 2 2 g h 1 gh 0 l = ( − − +
) th× tÇm xa cña ®¹n trªn mÆt ®Êt lµ lín nhÊt vµ g 4 4 v 2 2 v 0 0 1 gh − (.v2 + 0 )1 2 v 2 tÇm xa nµy b»ng 0 . g CÂU 4
Chọn hệ trục tọa độ x’Oy’ như hình vẽ. y’
- Điều kiện cân bằng lực cho thang: P + N + N + F = 0 B B A msA
Chiếu lên trục Oy’, ta có: NA = P (1)
Chiếu lên trục Ox’, ta có: N = F (2) B msA G x’ A
Chọn trục quay tại A, theo quy tắc mô men lực, ta có : M(P) = M(N ) B AB 1 P. .cos = N .AB.sin ; N = P.cot (3) ; B B 3 3 Từ (2) và (3), ta có: 1 F = N = P.cot msA B 3
Để thang không bị trượt thì : F .N msA A 1 1 1 .P.cot .
P cot = cot 3 3 min 3
Vậy, giá trị nhỏ nhất của hệ số ma sát là: = 0,192 min
Chọn hệ trục tọa độ xOy như hình vẽ. Gọi khoảng cách từ vị trí người đến A là x.
Do thanh nằm cân bằng, ta có: y’ P + P + N + N + F = 0 1 B A msA Chiếu lên trục Oy’ B , ta có: NA = P + P1 (1)
Chiếu lên trục Ox’, ta có: N − F = 0 ; N = F B msA B msA (2’)
Chọn trục quay tại A, theo quy tắc mô men lực, G ta có : M(P) + M(P ) = M(N ) 1 B AB P.
.cos + P .x.cos = N .AB.sin x’ 1 B 3 A 1 x
N = P.cot + P . .cot (3') B 1 3
Từ (2’) và (3’), ta có: 1 x F
= N = P.cot + P . .cot msA B 1 3
Để thang không bị trượt thì 1 x : F .N
P.cot + P . .cot (P + P ) msA A 1 1 3 3(P + P ).tan − P (12 tan −1) 1 x ( ) x ; 3.P 9 1 (12 tan −1) x = 1, 695m max 9
Vậy người đó trèo được tối đa một đoạn 1,695m . CÂU 5
Do pittông ở trạng thái cân bằng, ta có: F = F + F 2 1 0 P .S = P .S + P .S 2 1 0 n RT n RT RT 3P 2 1 1 1 1 0 = + P = 0 0,75V 0, 25V V 8 n RT Ta có: 1 1 P V = n RT P = = 1,5P 1 1 1 1 1 0 V1 P = P + P = 2,5P 2 1 0 0 ' '
Xét ngăn dưới, ta có: P V P V P V 15P 2 2 2 2 ' 2 2 0 = ; P = = 2 T T V 4 1 1 2
Do pittông ở trạng thái cân bằng, ta có: P ' = P '+ P = 2,75P 2 1 0 0 ' ' ' '
Xét ngăn dưới, ta có: P V P V P V 11T 1 1 1 1 ' 1 1 1 = ; T = T = ' 1 1 T T P V 3 1 1 1 1 UBND TỈNH QUẢNG NAM KỲ THI OLYMPIC 24/3
SỞ GIÁO DỤC VÀ ĐÀO TẠO
LỚP 10 THPT NĂM HỌC 2016 -2017 Môn thi: Vật lý ĐỀ THAM KHẢO
Thời gian làm bài: 150 phút
Câu 1(4 đ): Vật A được ném thẳng đứng lên trên từ độ cao 300m so với mặt đất với vận tốc ban
đầu 20m / s . Sau đó 1s vật B được ném thẳng đứng lên trên từ độ cao 250m so với măt đất với vận
tốc ban đầu 25m / s . Bỏ qua sức cản không khí, lấy g = 2
10m / s . Chọn gốc toạ độ ở mặt đất, chiều
dương hướng thẳng đứng lên trên, gốc thời gian là lúc ném vật A.
1. Viết phương trình chuyển động của các vật A, B; tính thời gian chuyển động của các vật.
2. Thời điểm nào hai vật có cùng độ cao; xác định vận tốc các vật tại thời điểm đó.
3. Trong thời gian chuyển động khoảng cách lớn nhất giữa hai vật là bao nhiêu và đạt được lúc nào.
Câu 2(4 đ): Thanh CD vuông góc với trục thẳng
đứng OZ và quay quanh trục này với vận tốc góc Z
. Hai hòn bi A và B có khối lượng M và m nối
với nhau bằng một lò xo khối lượng không đáng B A
kể, có độ cứng k và có chiều dài tự nhiên C o D 0 (Hình
vẽ 1). Hai hòn bi có thể trượt không ma sát trên thanh. Hình 1
Tính các khoảng cách OA = ;
x OB = y ứng với trạng thái cân bằng của hai hòn bi; biện luận.
Áp dụng: M = 0,1kg = 2 ;
m l = 0, 2(m); k = 40N / ;
m = 3 vòng/s 0
Tính x, y và lực đàn hồi của lò xo.
Câu 3(4 đ): Một quả cầu nặng đồng chất được treo bằng dây vào một điểm cố định trên tường
thẳng đứng. Xác định hệ số ma sát giữa tường với quả cầu sao cho, khi cân bằng, điểm nối dây với
quả cầu nằm trên đường thẳng đứng đi qua tâm quả cầu.
Câu 4(4 đ):: Cho cơ hệ như (hình vẽ 2). Biết = 300, m1 = 3 kg, m2 = 2 kg, M = 2 kg, ma sát giữa
m2 và M là không đáng kể. Bỏ qua khối lượng dây nối và ròng rọc, dây không dãn, lấy g = 10 m/s2. 1. M đứng yên.
a. Tìm gia tốc của các vật m1 và m2.
b. Tìm áp lực của dây lên ròng rọc.
2. Tìm điều kiện của hệ số ma sát giữa M và mặt
bàn nằm ngang để M không bị trượt trên bàn M Hình 2 Câu 5 (4 đ):
Một bình kín hình trụ đặt thẳng đứng có chiều dài l được chia P1
thành hai ngăn nhờ một pittông cách nhiệt (bỏ
qua bề dày của pittông). Hai ngăn chứa cùng một chất khí lí tưởng,
ngăn trên chứa một 1mol khí, ngăn dưới chứa 5 mol
khí. Khi chất khí ở hai ngăn có cùng nhiệt độ T1 thì pittông
ở vị trí cân bằng và cách đầu trên của bình một đoạn P
l = 0, 25l . Gọi 2 1
P0 là áp suất của riêng pittông tác dụng lên chất khí ở ngăn dưới. Biết
các thông số trạng thái P, V, T và n (mol) liên hệ với nhau bằng công
thức: PV = nRT (với R là hằng số). Bỏ qua mọi ma sát.
1. Tính áp suất P1 và P2 của không khí trong hai ngăn theo P0.
2. Chất khí ở ngăn dưới được giữ ở nhiệt độ T1. Hỏi phải thay đổi nhiệt độ chất khí ở ngăn
trên đến giá trị bằng bao nhiêu (theo T1) để pittông cân bằng ở vị trí cách đều hai đầu của bình? -------Hết-------
Họ và tên thí sinh:………………………………….SBD:……….
HỨỚNG DẪN CHẤM HSG LÝ 10 NĂM HỌC 2016 – 2017 Câu Hướng dẫn giải Điểm Câu 1 1.
Viết phương trình chuyển động của các vật: (4đ)
Chọn trục Ox hướng lên , gốc tại mặt đất, t = 0 khi ném vật A ta có; 2
x = 300 + 20t − 5t 0,5 1
..................................................... 2
x = 250 + 25(t −1) − 5(t −1) ; → t 1 0,5 2
.............................................................. Vật A chạm đất khi 2
x = 0;→ 300 + 20t − 5t = 0 1 0,5
Giải pt ta có: t = 10s;t = 6 − s 0 (loại) 11 12
…………………………………………………………………….. 2
x = 0 → 250 + 25(t −1) − 5(t −1) = 0 Vật B chạm đất khi 2 → 0,5 t = 11 ; s t = 4
− s 0(loai) 21 2
…………………………………………………………………….. 0,5
Thời gian chuyển động của B là: t = t −1 = 10s . 21
………………………………………………………………….. x = x 1 2 2.
Hai vật cùng độ cao khi: 2 2
300 + 20t − 5t = 250 + 25(t −1) − 5(t −1) 0,5 → t = 5,3s
……………………………………………………………………….
Vận tốc của A khi đó: v = 20 − gt = 33 − m / s 0,25 A
…………………………………………………………………… 0,25
Vận tốc của B khi đó: v = 25 −10(t −1) = 18m / . s B
……………………………………………………………………… 0,25 3.
Khoảng cách lớn nhất giữa hai vật.
Khoảng cách giữa hai vật trong thời gian chuyển động: s
= x − x = 80 −15t ; với điều kiện: 1s≤ t ≤ 10s. 0,25 2 1
……………………………………………………………………… s = 80 −15.10 = 70m ( a M x) Câu 2 (4đ)
Khi cân bằng lò xo bị giãn một đoạn l
= x + y − l . 0,5 0
…………………………………………………………………………
Lực đàn hồi của lò xo F = k l
chính là lực hướng tâm của hai hòn bi. 0,5
F = F = F . 1 2 2 2 F = M ; x F = m ;
y F = k(x = y − l ) 1 2 0
………………………………………………………………………. 0,5 Đẳng thức x m F = F cho ta: = . (1) 1 2 y M
……………………………………………………………………… 0,5
Đẳng thức: F = F 2
→ M x = k(x + y −l ) ; (2) 1 0 Từ (1) và (2)) Ta có: mkl Mkl 0 0 0,5 x = ; y = (3) 2 2
k(M + m) − Mm
k(m + m) − Mm
…………………………………………………………………….. 0,5
Biện luận: Với điều kiện (M ) m k x 0; y 0 + →
; ( nghĩa là độ cứng lò Mm
xo đủ lớn để giữ hai hòn bi).
………………………………………………………………………… M k( +1) 0,5 Áp dụng bằng số: m = = 34,6rad / . s ax M M
= 3vong / s =18,84rad / s ax M
…………………………………………………………………..
Thay các giá trị vào (3) ta có: x = 0,095 ; m y = 0,19 ; m l = 0, 085m 0,25
…………………………………………………………………. 0,25
Lực đàn hồi: F = k. l = 3, 4N Câu 3
Khi quả cầu đứng cân bằng các lực tác dụng vào nó: (4đ)
Sức căng T; lực ma sát Fms; phản lực N;trọng lực P. 1
…………………………………………………………………………
Đối với trục quay lqua điểm A, T
vuông góc mặt phẳng hình vẽ : A 1,5 Fms Fms.R – N.R = 0.
……………………………………………………………………….. N 1 hay Fms = N.
………………………………………………………………………… 0,5 Mặt khác F P ms ≤ k.N → k 1. Câu 4
Chọn chiều dương là chiều chuyển động. (4đ)
Đối với m1 có các lực tác dụng: P1; T1.
.............................................................................................................. 0,25
Đối với m1 có các lực tác dụng: P2; T2
......................................................................................................................................................................... P1 – T1 = m1a1
...................................................................................................................................................................... T2 – P2sin = m2a2
...................................................................................................................................................................... 0,25
Do dây không dãn nên: a1 = a2 = a; T1 = T2 = T
............................................................................................................... 0,25 a
1 = a2 = (P1 – P2sin)/(m1 + m2) = 4 m/s2
....................................................................................................................................................................... 0,25 Hình vẽ 1 T = P1 – m1a = 18 N
.........................................................................
Áp lực tác dụng lên trục của ròng rọc: T 2
Q = T + T Hvẽ:0,25 1 2 T 1
.......................................................................... 0,25
Độ lớn: Q = 2T.cos300 = 18 3 N Q
Các lực tác dụng vào vật M:
P , N , T ,T , ' N , F 2 1 2 ms
............................................................................................................. N 0,25 2’ = P2cos = 10 3 N
.......................................................................................................... Fmsn = T2x – N2x = 4 3 N.
............................................................................................................... N = P + T1 + T2y + N2y’ 0,25
................................................................................................................
= P + T1 + T2sin + N2x’cos 0,25
............................................................................................................... = 62 N 0,25
.............................................................................................................
Để M không bị trượt trên bàn thì ma sát giữa M và bàn là ma sát nghỉ: Fmsn N
................................................................................... 0,25 → N Fmsn/N = 0,11
.................................................................................. T2 0,25 T1 T2 N2 T2 T1 H vẽ2: 1 F T1 msn P2 M N P1 2’ Hình 1 Hình 2 P
Do pittông ở trạng thái cân bằng, ta có: F = F + F (4 đ) 2 1 0 Câu 5 P .S = P .S + P .S 0,5 2 1 0 n RT n RT RT 3P 2 1 1 1 1 0 = + P = 0 0,75V 0, 25V V 8 0,5 n RT Ta có: 1 1 P V = n RT P = = 1,5P 1 1 1 1 1 0 V 0,5 1 P = P + P = 2,5P 2 1 0 0 0,5 ' '
Xét ngăn dưới, ta có: P V P V P V 15P 2 2 2 2 ' 2 2 0 = ; P = = 2 T T V 4 0,5 1 1 2
Do pittông ở trạng thái cân bằng, ta có: P ' = P '+ P = 2,75P 2 1 0 0 0,5 ' ' ' '
Xét ngăn dưới, ta có: P V P V P V 11T 1 1 1 1 ' 1 1 1 = ; T = T = ' 1 1 T T P V 3 1 1 1 1 1
ĐỀ THAM KHẢO OLYMPIC LÝ- 10 NĂM 2017- TRẦN CAO VÂN
Bài 1:( 4điểm) Một ô tô con bắt đầu chuyển động thẳng nhanh dần đều với gia tốc 1,5 m/s2
, đúng lúc đó một ôtô tải chuyển động cùng chiều vượt qua nó với tốc độ 36 km/h và gia tốc
0,5 m/s2 . Sau 10 s thì hai xe giảm gia tốc xuống còn 0,2 m/s2 và 0,1 m/s2 . Hỏi khi ô tô con
đuổi kịp ôtô tải thì tốc độ của mỗi xe là bao nhiêu?
Bài 2:(4 điểm). Trong hệ thống trên hình 1, khối lượng vật 1 bằng 6,0 lần khối lượng vật
2. Chiều cao h = 20cm. Khối lượng của ròng rọc và của dây cũng như các lực ma sát được
bỏ qua. Lấy g = 10m/s2. Ban đầu vật 2 được giữ đứng yên trên mặt đất, các sợi dây không
dãn có phương thẳng đứng. Thả vật 2, hệ bắt đầu chuyển động. Xác định:
a. gia tốc của các vật ngay sau khi vật 2 được thả ra; 1
b. độ cao tối đa đối với mặt đất mà vật 2 đạt được. h 2
Bài 3:(3 điểm). Một mặt bàn tròn đồng chất, đặt trên 3 chân thẳng đứng, lắp ở mép bàn
tại các điểm A,B,C sao cho ABC là tam giác đều cạnh a =0,9m. A
Chiều dài các chân bằng nhau, khối lượng mặt bàn là m0 = 6kg.
a . Đặt vật nhỏ m1 lên điểm M1 trên mặt bàn, áp lực đè lên các
chân A,B,C lần lượt là 20N, 30N ,40N. Tìm m1 và vị trí điểm M1.
b. Phải đặt m2 có khối lượng tối thiểu bao nhiêu? ở đâu thì bàn bị lật. Cho g =10m/s2. B C
Bài 4:(4 điểm). Ba vòng đệm nhỏ giống nhau A,B,C nằm yên trên một
mặt phẳng ngang nhẵn.Người ta truyền cho vòng A một vận tốc v B 0 theo A
hướng vuông góc với đường nối tâm O2, O3 của vòng B và C, vòng này C
đến va chạm đồng thời với cả 2 vòng B và C. Khoảng cách giữa 2 tâm
của các vòng B và C trước va chạm bằng n lần đường kính mỗi vòng.
Biết các va chạm là hoàn toàn đàn hồi.
a .Khi n=1và v0=1m/s. Tính vận tốc của ba vòng sau va chạm.
b. Tìm điều kiện của n để cho vòng A bắn ngược lại; dừng lại; tiếp tục tiến lên sau khi va chạm.
Bài 5:(3 điểm). Một bóng thám không chứa đầy hiđrô. Vỏ bóng có thể tích không đổi
V = 75m3 và khối lượng M= 7kg; phía dưới có lỗ nhỏ. Thả cho bóng bay lên, hỏi nó tới độ
cao tối đa nào? Biết rằng áp suất khí quyển giảm ½ mỗi lần độ cao tăng 5km, và nhiệt độ ở
tầng trên của khí quyển là
T = 218K. Áp suất khí quyển ở mặt đất là p0 = 105Pa; µkhông khí = 29g/mol; µhidro = 2g/mol; R = 8,31J/mol.K.
Bài 6 :(2 điểm).Khi một xe lửa xuất phát từ ga, có một thời gian chuyển động của nó là
nhanh dần đều. Hãy xác định gia tốc của xe lửa trong thời gian này bằng cách dùng một sợi
dây, một quả cân 100g và một chiếc thước đo độ dài.
................................................................................HẾT............................................................ .........
ĐÁP ÁN OLYMPIC LÝ 10-2017-TRẦN CAO VÂN Câu Nội dung Điểm Câu 1
Giả thiết 2 xe gặp nhau trước khi giảm gia tốc: (4đ) ta có phương trình: x1 = x2 1 1 .1,5.t2 = 10.t +
.0,5.t2 …………………………………………………………… 0,5 2 2
t = 20s……………………………………………………………………………... 0,25
Ta thấy t > 10 s ( không thỏa mãn)
Vậy 2 xe gặp nhau sau khi giảm tốc……………………………………………….. 0,25
Phương trình xe 1 sau 10 s: x 1
.0,2.(t-10)2 …………………. 1 = 75 + 15(t-10) + 2 0,75
Phương trình xe 2 sau 10 s: x
1 .0,1.(t-10)2 ……………….. 2 = 125 + 15( t-10) + 2 0,75 Lúc gặp nhau: x1 = x2 1 1 75 + 15(t-10) +
.0,2.(t-10)2 = 125 + 15( t-10) + .0,1.(t-10)2 2 2
t = 10+ 10 10 = 41,62 s ……………………………………………………….. 0,5
Khi đó vận tốc ôtô con: v 0,5
1 = 76,79(Km/h) ………………………………………… vận tốc ôtô tải: v 0,5
2 = 65,4 (Km/h) ………………………………………….. Gọi T là lực căng dây
Vẽ hình, biểu diễn lực………………………………………………………………………. 0,25 − Gia tốc vật 2: T P 2 a =
…………………………………………………………………. Câu 2 2 m 0,5 (4đ) 2 − − Gia tốc vật 1: P T 2 P . T 2 1 2 a = =
……………………………………………………... 0,5 1 m m . 1 2
Với ròng rọc động: a = a . 2
………………………………………………………………. 2 1 0,25 − Kết quả: 2 4 a = a . 2 =
g ………………………………………………………………. 2 1 + 4 0,5 Thay số: 2 a = m 8 / s ; 2
a = 4m / s …………………………………………………………. 2 1 0,5
Vật chuyển động nhanh dần đều với gia tốc a
2 từ mặt đất đến độ cao 2h và đạt vận tốc cực
đại ở độ cao này: v2 = a . 2 h 2 .
(1)…………………………………………………… 0,5 max 2
Sau đó, vật chuyển động chậm dần với gia tốc g từ độ cao 2h đến h max: 0,5 v2 = h .( g . 2 − h
2 ) (2)………………………………………………………………….. max max Từ (1) và (2) ta có 0,5 h = 6h , Thay số: h
= 72cm ………………………………. max + max 4 Câu 3a Khi chưa đặt m
1, áp lực đè lên các chân bàn: (1,5đ)
NA=NB=NC = P0/3 = 20N........................................................................................ 0,25
Đặt m1 : N1A = 20N → N’A =0 .
N1B = 30N → N’B =10N .
N1C = 40N → N’C = 20N.
m1 = 3kg ............................................................................................. 0,5 Và M BC 1
............................................................................................... ' ' ' + ' 0,25 N B N C N B N C = = a CM 0,25 1 BM 1
.................................................................. CM 0,25
1 = 0,3(m).........................................................................................
Gọi M2 là vị trí đặt vật m2
Trục quay BC. Bàn lật khi: MP2 MP0 Câu
m2gd2 m0gd0......................................................................................................... 0,25 3b d0=R/2 0,25 (1,5đ) m .R / 2 m 0 2
..................................................................................................... d 0,25 2
m2min d2max=R/2................................................................................................. 0,25
m2min = m0 = 6kg.................................................................................................... 0,25
M2 là trung điểm cung BC...................................................................................... 0,25
Chọn hệ trục Oxy( Ox cùng hướng chuyển động của vòng A, Oy hướng lên)
Vì va chạm là đàn hồi nên lực tương tác giữa chúng vuông góc với các mặt tiếp xúc( Câu
hướng vào tâm các vòng tròn), là góc hợp bởi Ox với vectơ vận tốc vòng B sau va 4a chạm. (2đ) R 1 sin 0 = = = 30 2R 2
..................................................................................... 0,25
Do tính chất đối xứng của va chạm nên:
+ v cùng hướng Ox................................................................................................ 1 0,25
+ v , hợp với Ox góc 300; v2 = v3=v.................................................................. 0,25 2 v3
ĐLBT động lượng theo phương Ox: 0,25
mv0 = 2mvcos + mv1 v = v 3 + (1)............................................................ 0 v1 ĐLBT động năng: 0,25 1 2 1 2 1 2 2 2 2 m v = 2 m + = 2 +
(2)......................................................... 0 v m v1 v0 v v1 2 2 2 0,5
(1) & (2): v1 = - 0,2m/s........................................................................................... 0,25
v2 = v3 = 0,693m/s............................................................................. Từ (1) v − v 0 1 v = ) 3 ( 2 cos
...................................................................................... 0,25
(1)&(2): v = 2vcos2α + 2v1cosα(4).......................................................................... Câu 0,25 4b
(3)&(4): v0-v1=2(v0-v1)cos2α + 4v1cos2α (5).......................................................... (2đ) 0,25
Thay: cos2α = 1- sin2α và sinα = n/2 vào (5): 2 − v (2 ) 0 n v 1= − 2 6 − n 0,5
......................................................................................................
...................................................................................................................................
+ Vòng A bật ngược lại : n < 2
............................................................................. 0,25
+ Vòng A dừng lại n= 2 ...................................................................................... 0,25
+ Vòng A đi tiếp: n> 2 .......................................................................................... 0,25 Câu 5
Gọi mH, m là khối lượng hiđrô và không khí ở cùng điều kiện p, V, T (3đ)
Khi đến độ cao cực đại: FA = Pvỏ + PH …………………………………………………………………….. 0,25
Vdg = Mg + mHg……………………………………………. 0,25
Có m = M + mH…………………………………………………. 0,25 m m
Áp dụng pt trạng thái: pV = RT H =
RT (1)………………………………. 0,25 H m m m − m M 7 H H = = = =
= 259mol ………………. − − 0 , 0 27 0,5 H H H
(1) : Tính được p = 6256Pa……………………………………………………….. 0,5 p 0
16 lần......................................................................... 0,25 p 4 1 1 0,25 =
............................................................................ 2 16
Vậy h= 4x5= 20km......................................................................... 0,5 0 Câu 6 x (2đ) A B 0,25 D Vẽ hình . C
Buộc quả cân vào đầu sợi dây, treo lên trần tàu………………………………...
Tàu lửa chuyển động nhanh dần đều, con lắc lệch cho đến khi hợp lực F của trọng lực
P và sức căng dây R của dây đủ truyền cho quả cân gia tốc của xe 0,25
lửa……………………………………………………………………………………
Từ sự đồng dạng của hai tam giác AOB và ACD , ta có: 0,5 𝑨𝑫 𝑨𝑩 𝒎𝒂 𝒙 𝒙 = hay = hay 𝒂 = 𝒈
................................................................... 𝑨𝑪 𝑶𝑩 𝒎𝒈 √𝒍𝟐−𝒙𝟐 √𝒍𝟐−𝒙𝟐
Dùng thước đo AB = x, đo AO = 𝒍➔ gia tốc a của tàu……………………………. 0,5 0,5
SỞ GD ĐT QUẢNG NAM
KÌ THI OLYMPIC LỚP 10 THPT
Năm học 2016 – 2017 ĐỀ CHÍNH THỨC Môn thi: VẬT LÝ
Thời gian làm bài: 150 phút
( Đề thi gồm: 06 câu ; 02 trang) Câu 1 (4,0 điểm):
Các giọt nước mưa rơi khỏi một đám mây trong thời tiết lặng gió. Giả sử các giọt
nước mưa giống nhau và có dạng hình cầu, rơi với vận tốc ban đầu bằng không, theo
phương thẳng đứng. Biết đám mây ở độ cao đủ lớn, coi trọng trường tại nơi khảo sát là đều và 2 g = 10(m / s ) .
1. Bỏ qua mọi sức cản. Tìm quãng đường một giọt nước mưa rơi được trong 3 giây
đầu và trong giây thứ 5.
2. Xét một giọt nước mưa rơi chịu lực cản của không khí là Fc = -kv (với k là hằng
số, v là vận tốc của giọt nước đối với đất). Tại lúc gia tốc của nó đạt tới giá trị 2 6 (m / s ) thì
vận tốc của nó đạt giá trị 12 (m / s) . Khi xuống tới gần mặt đất, thì giọt nước mưa rơi với
vận tốc không đổi v’ , lúc này giọt nước trượt vào tấm kính thẳng đứng ở cửa bên của một ô
tô đang chuyển động thẳng đều theo phương ngang, giọt mưa để lại trên kính một vết nước
hợp với phương thẳng đứng một góc 300, xem vận tốc giọt nước theo phương thẳng đứng
khi trượt trên kính vẫn là v’ . Tính tốc độ của ô tô và cho biết người lái xe có vi phạm luật
giao thông vì lỗi vượt quá tốc độ quy định không? Biết tốc độ tối đa cho phép của ô tô là 70 (km/h). Câu 2 ( 3,0 điểm):
Một chiếc thang đồng chất có chiều dài AB = l = 2,7m, trọng
lượng P. Đầu A của thang tựa vào sàn nhà nằm ngang, đầu B của B
thang tựa vào tường thẳng đứng. Khối tâm G của thang ở cách đầu A
một đoạn 0,9m. Thang cân bằng ở vị trí hợp với sàn nhà một góc 0
= 60 như hình vẽ. Gọi µ là hệ số ma sát giữa thang với sàn, bỏ
qua ma sát giữa thang và tường. G
1. Tìm giá trị nhỏ nhất của µ để thang còn chưa bị trượt.
2. Cho = 0,32 . Một người có trọng lượng P = 3P trèo lên 1
thang. Hỏi người đó trèo được một đoạn tối đa bằng bao nhiêu (so A
với đầu A) để thang còn chưa bị trượt. Câu 3 (4,0 điểm):
Một sợi dây nhẹ không giãn, chiều dài l = 1m,
một đầu cố định, một đầu gắn với vật nặng khối lượng O
m = 300g tại nơi có gia tốc trọng trường 2 g = 10(m / s ) . 1 B
Ban đầu vật m1 ở vị trí B, dây treo hợp với phương
thẳng đứng góc (với 0 0
0 90 ), thả vật m1 với vận K
tốc ban đầu bằng không. Mốc tính thế năng trùng với
mặt sàn nằm ngang đi qua điểm A và vuông góc với OA A D C
như hình vẽ, OA = OB = l . Bỏ qua mọi ma sát và lực
cản tác dụng lên vật m1, dây luôn căng trong quá trình vật m1 chuyển động. 1. Cho 0 = 90 . Xác định:
a. Cơ năng của vật m1 ngay lúc thả.
b. Xác định độ lớn lực căng dây tại vị trí dây treo hợp với phương thẳng đứng góc 0 30 (ở phía bên trái OA).
2. Khi vật m1 chuyển động tới vị trí A, nó va chạm hoàn toàn đàn hồi xuyên tâm với
vật m2 = 100g (đang đứng yên tại vị trí A). Sau va chạm vật m1 tiếp tục chuyển động theo
quỹ đạo tròn bán kính l = 1m đến vị trí có độ cao lớn nhất (vị trí K), D là chân đường vuông
góc từ K xuống mặt sàn. Vật m2 chuyển động dọc theo mặt sàn nằm ngang đến vị trí C thì
dừng lại. Hệ số ma sát giữa m2 và mặt sàn là 0,1. Biết AD 15 = . AC 90 Xác định góc . Câu 4 (3 điểm):
Một bình kín hình trụ đặt thẳng đứng có chiều dài l được P1
chia thành hai ngăn nhờ một pittông cách nhiệt (bỏ qua bề dày
của pittông). Hai ngăn chứa cùng một chất khí lí tưởng, ngăn
trên chứa một 1mol khí, ngăn dưới chứa 5 mol khí. Khi chất khí
ở hai ngăn có cùng nhiệt độ T1 thì pittông ở vị trí cân bằng và P2
cách đầu trên của bình một đoạn l = 0, 25l . Gọi P 1 0 là áp suất
của riêng pittông tác dụng lên chất khí ở ngăn dưới. Biết các
thông số trạng thái P, V, T và n (mol) liên hệ với nhau bằng
công thức: PV = nRT (với R là hằng số). Bỏ qua mọi ma sát.
1. Tính áp suất P1 và P2 của không khí trong hai ngăn theo P0.
2. Chất khí ở ngăn dưới được giữ ở nhiệt độ T1. Hỏi phải thay đổi nhiệt độ chất khí ở
ngăn trên đến giá trị bằng bao nhiêu (theo T1) để pittông cân bằng ở vị trí cách đều hai đầu của bình? T Câu 5 (4 điểm): 2T 2 1
Cho n = 1mol khí lí tưởng biến đổi qua các trạng thái
được biểu diễn trên đồ thị T-V như hình vẽ.
- Quá trình 1→2 là một đoạn thẳng có đường kéo dài đi qua gốc tọa độ. 1 T1 3
- Quá trình 2→3 là quá trình đẳng tích.
- Quá trình 3→1 là một đoạn cong thuộc đường cong có
phương trình T = T (a − bV)V (trong đó T V 1
1 là nhiệt độ ở trạng
thái 1, a, b là hằng số dương). Biết T = 300K , V O 1 1 = 1 (lít). Các
thông số trạng thái P, V, T và n (mol) liên hệ với nhau bằng công thức PV = nRT, với J R= 8,31 . mol.K
1. Xác định P1, P2 , P3.
2. Tính công của chất khí trong các quá trình 1→2 ; 2→3 ; 3→1.
Câu 6 (2 điểm): Có một cân đĩa. Do sơ suất trong khâu chế tạo nên hai cánh tay đòn không
thật sự bằng nhau. Hãy đề xuất phương án thí nghiệm để xác định đúng khối lượng của vật cần cân.
Dụng cụ : hộp quả cân biết khối lượng, vật có khối lượng chưa biết.
……………………..Hết…………………..
SỞ GD ĐTQUẢNG NAM
HƯỚNG DẪN MÔN VẬT LÝ 10
Năm học 2016 – 2017 Câu 1 (4 điểm): 1(2đ)
Quãng đường giọt nước rơi được trong 3 (s) đầu là 1 1 : 2 S = gt = 45(m) 2
Quãng đường giọt nước rơi được trong giây thứ 5 là : 1 1 2 2 S = 10.(5 − 4 ) = 45(m) 2 2(2đ)
Chọn chiều dương là chiều chuyển động của giọt nước mưa.
- Áp dụng Định luật II Niu-tơn cho giọt nước F = P + F hl C
Chiếu lên chiều dương, ta có: ma = P - F C
Tại thời điểm a = 6 (m/s2), v = 12 (m/s), ta có: m m.6 = m.10 − k.12 ; = 3 (1) 0,5 k
Khi rơi gần mặt đất, do giọt nước chuyển động thẳng đều, ta có: ' P = F mg = kv '; C 0,5
Thay (1) vào, ta có: v’ = 30(m/s).
Gọi giọt nước là vật 1; ô tô là vật 2; mặt đất là vật 3. v = v + v 13 12 23 Biết v 13 = v’ = 30(m/s) và v hợp với v 12 13 góc 300. 0,5 Từ hình vẽ: v 0 23 tan 30 = ; v13 0
v = v tan30 =10 3(m / s) = 62,35(km / h) 70(km / h) 0,5 23 13
Vậy người lái xe không vi phạm giao thông về tốc độ. Câu 2 (4 điểm): 1 (2đ)
Chọn hệ trục tọa độ x’Oy’ như hình vẽ. y’
- Điều kiện cân bằng lực cho thang: P + N + N + F = 0 B B A msA
Chiếu lên trục Oy’, ta có: N A = P (1)
Chiếu lên trục Ox’, ta có: N = F (2) B msA 0,5 G x’ A
Chọn trục quay tại A, theo quy tắc mô men lực, ta có : M(P) = M(N ) B AB 1 P. .cos = N .AB.sin ; N = P.cot (3) ; B B 3 3 0,5 Từ (2) và (3), ta có: 1 F = N = P.cot msA B 3
Để thang không bị trượt thì : F .N 0,5 msA A 1 1 1 .P.cot .
P cot = cot 3 3 min 3
Vậy, giá trị nhỏ nhất của hệ số ma sát là: = 0,5 0,192 min 2 (2đ)
Chọn hệ trục tọa độ xOy như hình vẽ. Gọi khoảng cách từ vị trí người đến A là x.
Do thanh nằm cân bằng, ta có: y’ P + P + N + N + F = 0 1 B A msA Chiếu lên trục Oy’ B , ta có: N A = P + P1 (1)
Chiếu lên trục Ox’, ta có: N − F = 0 ; B msA N = F (2’) B msA 1
Chọn trục quay tại A, theo quy tắc mô men G
lực, ta có : M(P) + M(P ) = M(N ) 1 B AB x’ P.
.cos + P .x.cos = N .AB.sin 1 B 3 A 1 x
N = P.cot + P . .cot (3') B 1 3
Từ (2’) và (3’), ta có: 1 x F
= N = P.cot + P . .cot msA B 1 3
Để thang không bị trượt thì : 1 x F .N
P.cot + P . .cot (P + P ) msA A 1 1 3 3(P + P ).tan − P (12 tan −1) 1 1 x ( ) x ; 3.P 9 1 − 12 ( tan ) 1 xmax = = 695 , 1 m 9
Vậy người đó trèo được tối đa một đoạn 1,695m . Câu 4 (3 điểm):
a. Cơ năng của vật m = = = 1 là W m gl 0, 3.10.1 3(J) 0,5 1 1 (2đ)
b. Áp dụng định luật bảo toàn cơ năng cho vật, tìm tốc độ của vật ở vị trí góc lệch 0 = 30 , ta được:
v2 = 2glcosβ = 2.10.1.cos300 = 10 0,5 3 → v = 4,1618m/s
- Áp dụng định luật II Niu - tơn cho vật m = 2 tại vị trí 0 30 , chiếu lên
phương bán kính, chiều hướng vào tâm, ta được
T = 3m1gcosβ = 3.0,3.10.cos300 = 4,5 3 N = 7,79N 0,5 0,5 - Vận tốc của vật m = − 1 ngay trước va chạm là 2 v 2gl(1 cos ) 2 (2đ)
- Gọi v , v tương ứng là vận tốc của 1 2 O
mỗi vật ngay sau va chạm. B K D C A
- Áp dụng định luật bảo toàn động lượng, cơ năng cho hệ hai vật m1 ,
m2 ngay trước và ngay sau va chạm (chiều dương có phương nằm
ngang, hướng từ trái sang phải) v 0,5 v = = + 1 m v m v m v 1 1 1 2 2 2 2 2 2 m v = m v + m v 3v 1 1 1 2 2 v = 2 2 - Xét vật m1:
Áp dụng định luật bảo toàn cơ năng cho vật tại vị trí A và vị trí K, ta được : 1 2 2
m v = m gl(1− cos) v = 8gl(1− cos) cos = 0, 75 + 0, 25 cos 1 1 1 2 0,5 AD = lsin - Xét vật m2:
Áp dụng định luật II Niu - tơn cho vật theo phương ngang, chiều dương hướng sang phải. a = g − 2 2 2
Khi vật dừng lại tại C. Suy ra: v 9v 2 AC = = 0,5 2a 8 g 2 Theo đề AD 15 15 4 sin = = AC 90 90 9(1− cos) 2 2 4sin = 15(1− cos )
16(1− cos ) =15(1− cos ) (1) Đặt x = cos 0
x = 0,5 cos = 0,5 = 60 (T / m) 2 (1) 4x − 6x + 2 0
x =1 cos =1 = 0 (L) 0,5 Vậy 0 = 60 Câu 4 (4 điểm):
Do pittông ở trạng thái cân bằng, ta có: F = F + F 0,5 2 1 0 1 (2,0 P .S = P .S + P .S đ) 2 1 0 n RT n RT RT 3P 2 1 1 1 1 0 = + P = 0,5 0 0,75V 0, 25V V 8 n RT 0,5 Ta có: 1 1 P V = n RT P = = 1,5P 1 1 1 1 1 0 V 1 P = P + P = 2,5P 0,5 2 1 0 0 ' '
Xét ngăn dưới, ta có: P V P V P V 15P 2 2 2 2 ' 2 2 0 = = = 2 (2,0 ; P 2 T T V 4 0,5 đ) 1 1 2
Do pittông ở trạng thái cân bằng, ta có: P ' = P '+ P = 2, 75P 2 1 0 0 0,5 ' ' ' '
Xét ngăn dưới, ta có: P V P V P V 11T 1 1 1 1 ' 1 1 1 = ; T = T = ' 1 1 T T P V 3 1,0 1 1 1 1 Câu 5 (3 điểm): nRT - Ở trạng thái 1: 5 P V = nRT; P = = 24,93.10 (Pa) 1 (1,5 1 1 1 V 0,5 đ) 1
- Quá trình từ 1 → 2 là quá trình đẳng áp, ta có: 5 P = P = 24,93.10 (Pa) 2 1 V V Ta có : 1 2 = ; V = 2V 0,5 2 1 T T 1 2
- Quá trình từ 2 → 3 là quá trình đẳng tích, ta có: P P T .P P 0,5 3 2 3 2 2 5 = ; P = = = 12,465.10 (Pa) 3 T T T 2 3 2 2
+) Quá trình 1 → 2 là quá trình đẳng áp, chất 2 (1,5 khí thực hiện công: p 0,25 đ)
A = P (V − V ) = −P V = −nRT = 2493 − (J) 0,25 12 1 1 2 1 1 1 p 1 1 2
+) Quá trình 2 → 3 là quá trình đẳng tích, ta có: A 0,5 23 = 0(J).
+) Xét quá trình 3 →1, chất khí nhận công p 3 3
Ta có : T = T a − bV V và PV = nRT 1 ( ) Suy ra : P = nRa − nRbV
Ta thấy P là hàm bậc nhất của V với hệ số V O a < 0. 0,5 Đ
ồ thị của nó được biểu diễn trên trục (P,V) như hình vẽ. 1 3 7479 A = p + p V − V = nRT = (J) 31 ( 1 3)( 2 1) 1 2 4 4 Câu 6(2đ)
m : khối lượng của vật 1
Bước 1 : Đặt vật ở đĩa cân bên trái, quả cân m1 bên phải sao cân thăng bằng.
Bước 2 : Đặt vật ở đĩa cân bên phải, quả cân m1 bên trái sao cân thăng bằng. Phương trình cân bằng : Pl1 = P1l2 hay ml1 = m1l2 (1) 0,5 P2l1 = Pl2 hay m2l1 = ml2 (2)
Từ (1) và (2) suy ra m = m m 0,5 1 2
Chú ý : Học sinh làm theo cách khác, nếu đúng vẫn cho điểm tối đa theo ý tương ứng. MA TRẬN ĐỀ THI Câu Nội dung Điểm 1 Động học chất điểm. 3,00 2
Động lực học chất điểm. 4,00 3 Tĩnh học vật rắn. 3,00 4
Các định luật bảo toàn. 4,00 5
Chất khí – Sự chuyển thể của các chất. 3,00 6 Nhiệt động lực học. 3,00
- Thời gian làm bài: 150 phút.
- Tổng điểm tối đa của bài thi là 20 điểm
.SỞ GD & ĐT QUẢNG NAM ĐỀ THI OLYMPIC LỚP 10 THPT NĂM 2016-2017 Môn: Vật lý
Thời gian làm bài: 150 phút
Bài 1:(3điểm) Có 2 xe cùng khởi hành từ A về B. Vận tốc xe 1 trên nửa đoạn đường đầu là
45 km/h, nửa đoạn đường còn lại là 30 km/h .Vận tốc xe 2 trong nửa thời gian đầu là
45 km/h và trong nửa thời gian còn lại 30 km/h .Tính:
c) Vận tốc trung bình mỗi xe ? từ đó cho biết xe nào đến B sớm hơn ?
d) Chiều dài quãng đường AB và thời gian chuyển động mỗi xe? Biết xe này đến sớm hơn xe kia 6 phút .
Bài 2:(4điểm )Cho vật m = 2kg có thể trượt có ma sát( =0,1)
trên mặt phẳng ngang ( g= 10 m/s2)(hình 2)
d) Truyền cho vật vận tốc ban đầu v0 = 1 m/ s F
theo phương ngang .Xác định : Thời gian và quãng
đường vật chuyển động cho đến khi dừng lại ?
e) Tác dụng lực F tạo với phương ngang góc
= 300 làm vật chuyển động đều .Xác định: Lực F? Hình 1
f) Góc phải bằng bao nhiêu để vật trượt đều Với lực F nhỏ nhất ?
Bài 3(3 điểm) : Bánh xe có bán kính R. Lực kéo F theo phương nằm ngang, hướng đến trục bánh
xe. Lực này có độ lớn bằng 3 lần trọng lượng của bánh xe. Xác định độ cao cực đại của bậc thềm
để bánh xe vượt qua. R h
Bài 4(4 điểm:) Một vật dạng bán cầu, bán kính R được đặt trên mặt phẳng nằm ngang. Trên đỉnh
bán cầu có đặt một vật nhỏ khối lượng m (xem hình 1).Vật m bắt đầu trượt xuống với vận tốc ban
đầu không đáng kể. Bỏ qua ma sát giữa vật m và bán cầu. Tìm vị trí vật m bắt đầu rời khỏi bán cầu trong hai trường hợp: m
1) Bán cầu được giữ cố định.
2) Bán cầu có khối lượng M = m và có thể trượt không ma sát R
trên mặt phẳng nằm ngang. Hình 2
Bài 5:(3 điểm )Một ống hình trụ thẳng đứng có thể tích V. Ở phía dưới pít tông khối lượng m, diện
tích S, có một lượng khí lý tưởng đơn nguyên tử ở nhiệt độ T0. Pít tông ở vị trí cân bằng chia ống
thành hai nửa bằng nhau. Người ta đun nóng khí từ từ đến khi nhiệt độ khí là 4T0. Ở phía trên có
làm hai vấu để pít tông không bật ra khỏi ống.Hỏi khí trong ống đã nhận được một nhiệt lượng là
bao nhiêu? Bỏ qua bề dày pít tông và ma sát giữa pít tông và thành ống. Cho áp suất khí quyển bên
ngoài là P0 và nội năng của một mol khí lý tưởng đơng nguyên tử được tính theo công thức 3 U = RT 2 Bài 6 (3 điểm)
Tính công sinh ra khi 0,5 (mol) khí lý tưởng
thực hiện một chu trình biến đổi 1-2-3-1. Biết T1=T3=350K; T2= 600K.
HƯỚNG DẪN CHẤM MÔN VẬT LÝ LỚP 10 Bài Đáp án Điểm 2v v c) v =36 km/h TB 1 = 1 2 v + v 1 2
---------------------------------------------------------------------------------------- 1,0 vTB2 = (v1+v2) /2 =37,5 km/h
---------------------------------------------------------------------------------------- d) s =90 km/h 1,0 txe 1=2,5h txe 2 =2,4h 1,0 Bài 1 3 điểm N b) a= - M g = - 1m /s
--------------------------------------------------------------------------------------------------------------------------------------- s = 0,5 m t = 1s Bài 2
b)+Viết phương trình định luật 2 N :
4 điểm -------------------------------------------------------------------------------------- 1,0
+Chiếu phương trình lên 2 trục 0x và 0y
--------------------------------------------------------------------------------------- 1.0
+Giải hệ phương trình ta được: Mmg 0.25 F= os c +Msin =2,18 N
-------------------------------------------------------------------------------------- 0.25 Mmg c)Từ công thức : F= os c +Msin 0,5
Dựa vào tính chất của bất đẳng thức ta có :
1/cos = K/sin =>K = tan =0.1 => =5,70 1.0 d1
Bánh xe vượt qua được bậc thềm A (A) (A) d2 M M 1,0 h F P Bài 3 3 điểm F.d .
P d F.(R − h) P R − (R − h)2 2 1 2 0,5
F.( R − h
) = P R − (R − h )2 . 3 R − h
= R − R − h m m ( m ) ( m )2 2 2 ax ax ax ax R 1,0 h = ax m 2 0,5 _ 1)
- áp dụng định lý động năng: Vận tốc tại M: 2 v = 2gR(1− os c ) (1)
- Định luật II Niu tơn : 2 mv mgcos − N = (2) R 1.0
- Từ (1) và (2) suy ra : N =mg(3cos -2) Bài 4
- vật bắt đầu trượt khi N = 0 2 os c = 4 điểm 3 1.0 2) M m V 1.0
- Gọi V là vận tốc bán cầu,
u là vận tốc của
M so với bán cầu. Vận tốc của m so với đất là : 1.0
v = u +V
- Theo phương ngang động lượng bảo oàn nên : mu cos
mv = MV m(u cos −V ) = MV V = (1) x M + m 2 mu
- Khi m bắt đầu rời khỏi M thì : mg cos = 2
u = gR cos(2) R - Mặt khác ; 2 2 2
v = V + u − 2uV cos (3) 2 2 mv MV
- Ap dụng định luật bảo toàn cơ năng : mgR(1− os c ) = + (4) 2 2 m
- Từ (1),(2),(3),(4) suy ra: 3 o
c s − 3cos + 2 = 0 M + m - Với M=m ,ta có : 3 o
c s − 6 cos + 4 = o
- Giải phương trình này ta được cos = 3 −1 Bài 5
Trong giai đoạn đầu,pít tông chưa chạm vấu khí biến đổi đẳng áp, khi bắt 1.0 3 điểm
đầu chạm vấu khí có nhiệt độ T2 V V V Áp dung: 1 2 = T = T = 2T 2 0 0 T T V 2 1 2
- Nhiệt lượng truyền cho khí trong quá trình này : V 3 PV PV 3 5 1 1 Q = A + U = P
+ n R(T −T ) = + RT = PV 1.0 1 1 2 1 0 2 2 2 2RT 2 1 4 0
- Sau khi pít tông chạm vấu, thể tích không đổi,dây là quá trình đẳng tích Khí nhận nhiệt lượng chỉ làm tăng nội năng: 3 PV 3 3 1 Q = n R2T = R2T = PV 2 0 0 1 2 2RT 2 2 0 Tổng nhiệt lượng mà khí đã nhận : 1.0 11 11 mg
Q = Q + Q = PV = (P + )V 1 2 1 0 4 4 s Bài 6 p V = nRT 1,0 1 1 1 3 điểm p V = nRT 3 3 3 2 T T Theo giả thiết ta có: 3 1 p V = nRT p V = p V = nR (1) 1 3 2 3 1 1 1 T T 2 2 T T 3 3 p = p = p 3 2 1 T T 2 2 Theo Công sinh ra là: 1,0 1 1 A =
( p − p )(V −V ) A =
( p V − p V − p V + p V ) (2) 1 3 3 1 1 3 1 1 3 3 3 1 2 2 2 Từ (1) và (2) suy ra: 1 T1 A =
nR(T − T − T + ) = 216, 4(J ) 2 1 3 2 T 1,0 2
SỞ GIÁO DỤC & ĐÀO TẠO
KỲ THI OLYMPIC 24/3 LỚP 10 THPT QUẢNG NAM
NĂM HỌC 2016 – 2017 Môn thi : VẬT LÝ ĐỀ CHÍNH THỨC
Thời gian : 150 phút (không kể thời gian giao đề)
Ngày thi : 25/03/2017
(Đề thi có 2 trang, 6 bài toán) Bài 1 (4đ).
1. Một chất điểm đang chuyển động thẳng đều, khi đi qua điểm A với vận tốc vA thì chuyển
sang chuyển động thẳng chậm dần đều, chất điểm đi thêm được 25,6m (kể từ A) thì dừng lại hẳn.
Thấy quãng đường đi được trong giây đầu tiên (từ lúc bắt đầu chuyển động chậm dần đều) dài gấp
15 lần quãng đường đi được trong giây cuối cùng. Hãy tính gia tốc chuyển động và vận tốc vA của chất điểm.
2. Có hai người quan sát A1 và A2 đứng trên hai hệ quay tròn đều ngược chiều nhau như
hình vẽ. Biết O1, O2 là các tâm quay của hai hệ tròn; O1O2 = 5m; O1A1 = O2A2 = 2m; ω1 = ω2 = 1
rad/s. Tính vận tốc dài của A1 đối với A2 tại thời điểm hai người có vị trí như hình vẽ. ω ω2 1 O1 A1 A2 O2 Bài 2(4đ).
1. Một Xy lanh kín hai đầu đặt thẳng đứng, bên trong có một Píttông cách nhiệt, chia Xy
lanh thành hai phần, mỗi phần chứa cùng một lượng khí ở cùng nhiệt độ T1 = 400K, áp suất P2 của
phần phía dưới Píttông gấp 2 lần áp suất P1của phần nằm trên Píttông. Cần nung nóng phần dưới
Píttông lên thêm nhiệt độ bằng bao nhiêu để thể tích trong hai phần Xy lanh bằng nhau ?
2. Một khối khí lý tưởng biến đổi từ trạng thái (1) sang trạng thái (2) theo quy luật biểu diễn
như hình vẽ. Biết rằng ở trạng thái (1) nhiệt độ T1=300K, V1=20.10-3 m3.
a. Tìm biểu thức liên hệ giữa áp suất p và thể tích V của khối khí.
b. Xác định nhiệt độ cao nhất của quá trình. C B G α O A Bài 3(3đ).
Một thanh sắt đồng chất, tiết diện đều, dài AB = 1,5m, có khối lượng m = 3kg được giữ
nghiêng một góc α trên mặt sàn nằm ngang nhờ một sợi dây BC nằm ngang có chiều dài BC =
1,5m, nối đầu trên B của thanh AB với một bức tường thẳng đứng, đầu dưới A của thanh tựa trên
mặt sàn (hình vẽ). Biết hệ số ma sát giữa thanh và mặt sàn là 3 / 2 .
1. Góc nghiêng α phải có giá trị bao nhiêu để thanh có thể cân bằng ?
2. Tính độ lớn các lực tác dụng lên thanh và khoảng cách OA từ đầu A của thanh đến góc tường khi α = 450. Lấy g = 10m/s2. Bài 4(4đ).
Con ếch khối lượng m1 = 300g ngồi trên đầu một tấm ván khối lượng m2 = 3kg, chiều dài
=1,375 m ; tấm ván nổi trên mặt hồ. Ếch nhảy lên theo phương hợp với phương ngang một góc
=150 dọc theo tấm ván. Tìm vận tốc ban đầu v0 của con ếch để nó nhảy trúng đầu kia của tấm ván.
Bỏ qua mọi ma sát. Lấy g = 10m/s2. Bài 5 (3đ).
1. Một hòn bi nhỏ treo ở đầu một sợi dây mảnh, không co dãn, đầu kia của sợi dây được treo
vào một cái đinh O cố định , chiều dài sợi dây = 30 cm (hình vẽ). Hỏi tại điểm thấp nhất A phải
truyền cho hòn bi một vận tốc theo phương ngang nhỏ nhất bằng bao nhiêu để nó có thể quay tròn
trong mặt phẳng thẳng đứng? Cho g = 10 m/s2 . Bỏ qua các lực cản. O • • A
2. Hình bên: Một nêm có khối lượng m
2 = 2kg được đặt trên mặt b
àn nằm ngang nhẳn. Một
quả cầu khối lượng m1 = 0,5kg đang bay ngang với vận tốc v0 = 10m/s thì va chạm tuyệt đối đàn
hồi vào mặt nêm rồi bậc lên cao theo phương thẳng đứng với vận tốc V1 còn nêm chuyển động theo
phương cũ của m1 với vận tốc V2. Tính độ cao cực đại mà quả cầu lên tới. Lấy g = 10m/s2. Bỏ qua ma sát. m m 1 2 Bài 6(2đ).
Cho một cái lò xo chưa biết hệ số đàn hồi, một giá treo, một quả cân đã biết khối lượng và
một cái thước có độ chia chính xác. Trình bày một phương án xác định khối lượng của một vật ?
…………………………………….…………….HẾT……………………………………………......
Giám thị coi thi không giải thích gì thêm !
HƯỚNG DẪN CHẤM ĐỀ THI OLYMPIC LÝ 10 NĂM 2016-2017 BÀI NỘI DUNG ĐIỂM Bài 1 4,0
Câu 1 - Biểu diễn quãng đường của vật trên hình vẽ. (2đ) 0,25 A B C D v v v A C D
- Xét đoạn đường AB trong giây đầu tiên: 0,25 1 a 2 s = v .1 + a.1 = v + (1) AB A A 2 2
- Xét đoạn đường CD trong giây cuối cùng: v = v + a.1 = 0 v = - a (2) D C C 0,25 1 a a 2 s = v .1 + a.1 = - a + = - (3) CD C 2 2 2 0,25 a a
- Từ (1) và (3) ta được: v + = 15. ( - ) v = - 8a (4) 0,25 A A 2 2 2 2 2 2 v - v - v - (- 8a)
- Xét cả quãng đường AD: D A A s = = 25,6 = (5) 0,25 AD 2a 2a 2a => 2 a = - 0,8 (m/s ) . 0,25
Từ (4) => v = 6,4 (m/s) A 0,25 ω2 ω1 Câu 2 (2đ) O1 A1 A2 O2 0,25
- Xét tại thời điểm A1 và A2 có vị trí như hình vẽ
- Xem A1 và A2 cùng chuyển động tròn đều quanh tâm O2 với các bán kính lần lượt R1 = 3m, R2 0,25 = 2m. m - Vận tốc của A = 1 đối với O2: v R = 3 A O 1 1 1 2 s 0,25 m - Vận tốc của A = 2 đối với O2: v R = 2 A O 2 2 2 2 s 0,25
- Áp dụng công thức cộng vận tốc, ta có: v = v + v A A A O O A 1 2 1 2 2 2 m 0,5 - Độ lớn: v = v − v = 3− 2 =1 A A A O A O 1 2 1 2 2 2 s 0,5 Bài 2 4,0 Câu 1
* Trước khi nung phần dưới Pittong:
(2,5đ) - Ngăn trên: PV = nRT 1 1 1 0,25
- Ngăn dưới: P V = nRT (hai ngăn cùng nhiệt độ) 0,25 2 2 1 - P2 = 2P1 => V1 = 2V2 (1) 0,25
* Sau khi nung phần dưới Pittong: V +V 3 - ' ' 1 2 V = V =
= V (thể tích hai ngăn sau khi nung bằng nhau) (2) 0,25 1 2 1 2 4 4
- Ngăn trên đẳng nhiệt: ' ' '
PV = PV P = P (3) 0,25 1 1 1 1 1 1 3
- Áp suất gây ra bởi Pittong P 0: + Trước khi nung: P 0,25 2 = P1 + P0 + Sau khi nung: P ’ ’ 0,25 2 = P1 + P0 7 = − = − = => ' ' ' P P P P P P P (4) 0 2 1 2 1 2 1 3 0,25 ' ' PV PV 2 2 2 2 = =
- Phương trình trạng thái cho ngăn dưới: T 700K 2 T T 0,25 1 2 - Nung thêm 300K. Câu 2 0,25 (1,5đ)
- Dạng của đường thẳng: p = aV+b 0,25
- Thế V=0, p=5.105Pa; p=0, V=25.10-3m3 ta được : a=-2.107; b=5.105 → p= 0,25 - 7 5 2.10 V + 5.10 . 0,25
- Tại (1) ta có V1=20 .10-3 m3, p1=1.105 Pa. T1=300K. 3 0,25
- Kết hợp P1V1 = nRT1và PV = nRT → 7 2 5 T = ( 2 − .10 V + 5.10 V) 20 0,25
- T cực đại khi V =1 2,5.10-3m3 = 0,25 m T ax 468,75K Bài 3 3,0 Y C B G O α X A
1. – Áp dụng điều kiện cân bằng quay đối với trục đi qua điểm A: 0,5 AB mg cos mg cot g
M = M T.OC = .
P AG cos T.AB sin = mg. cos T = = (1) T P 2 2sin 2 0,25
- Áp dụng điều kiện cân bằng tịnh tiến: P + N + F + T = 0 (2) 0,25 ms
+ Chiếu (2) lên trục OX được: Fms – T = 0 (3) 0,25
+ Chiếu (2) lên trục OY được: N – P = 0 (4) 0,5
- Muốn thanh cân bằng thì lực ma sát phải là lực ma sát nghỉ nên: Fms < μN (5) 0,5 mg cot g
- Từ (1), (3), (4) và (5) suy ra: 0
mg cot g 2 30 2 0,25 2. Khi α = 450 ta có: F 0,25 ms = T = 15N; N = P = 30N; 0,25
OA = BC – ABcosα ≈ 0,44m. Bài 4 4,0 Câu 1 (2đ)
- Bỏ qua mọi ma sát, theo phương ngang động lượng của hệ ếch và ván được bảo toàn. m
1v0cos + m2v2 = 0. ( với v2 là vận tốc của tấm ván.), suy ra độ lớn vận tốc của ván: 0,5 m v2 = 1 v0cos . m 2
- Gọi quãng đường ếch nhảy tới là s1 ; quãng đường tấm ván chuyển động lui là s2.
- Thời gian ếch nhảy quãng đường s1, cũng là thời gian tấm ván di chuyển quãng đường s2
. Thời gian đó là: t = 2v sin 0 g 0,25
Để ếch nhảy trúng ván thì ta có: s1 + s2 = 0,25
Với s1 = v0cos .t và s2 = v2.t 0,25 2v sin m 2v sin v0cos . 0 + 1 v0cos . 0 = g m g 2 0,25 .g v = 0 m 0,25 1 1+ sin 2 m 2 Thay số= > v 0 =5m/s 0,25 Bài 5 3,0
Câu 1 - Gọi B là điểm cao nhất. Muốn hòn bi quay tròn trong mp thẳng đứng thì lực căng dây TB 0 0,25
(1,5đ) - Tại B : TB + mg = mv2/ TB = m(v2/ - g) 0 v2Bmin = g 0,5
- ĐLBTcơ năng (gốc thế năng tại A) : 1/2mv2A = mg.2 + 1/2mv2B v 0,5 Amin= 5 g = 15 (m/s) 0,25 Câu 2 (1,5đ) m m 1 2
- Theo phương ngang, ngoại lực tác dụng lên hệ bằng không nên động lượng bảo toàn. Ta có: m v 1 0
m v = m v v = = 2,5 m / s (1) 1 0 2 2 2 m 2 0,5
- Va chạm đàn hồi nên động năng bảo toàn: 1 1 1 1 1 1 2 2 2 2 2 2 m v = m v + m v m v = m v − m v = 18, 75J (2) 1 0 1 1 2 2 1 1 1 0 2 2 2 2 2 2 2 2
- Chọn gốc thế năng hấp dẫn tại vị trí m 0,5
1 va chạm với m2 và gọi h là độ cao lớn nhất của m1 lên
được sau va chạm (tính từ điểm va chạm). Áp dụng định luật bảo toàn cơ năng cho vật m1: 1 2
m v = m gh h = 3,75m 1 1 1 2 0,5 Bài 6 2,0
* Gọi khối lượng của quả cân là m, khối lượng của vật là M
- Treo quả cân vào lò xo treo thẳng đứng trên giá. Dùng thước đo độ biến dạng của lò xo l1 0,25
- Treo vật vào lò xo treo thẳng đứng trên giá. Dùng thước đo độ biến dạng của lò xo l2 0,25
- Theo định luật Húc ta có: F1 = kl1, F2 = kl2 = = 0,25
- Khi quả cân cân bằng ta có: P F mg k l 1 1 1 0, 25
- Khi vật cân bằng ta có: P = F Mg = k l 2 0, 25 M l l 2 = M 2 = m m l l 1 1 0,5
- Dùng thước đo l1 và l2 suy ra M 0,25 Chú ý:
- Học sinh làm bài theo cách khác đúng vẫn cho điểm tối đa.
- Sai hoặc thiếu đơn vị trừ 0,25điểm/01 lần nhưng không quá 2 lần cho toàn bài.



