Đề thi học sinh giỏi Vật lý 10 tỉnh Hải Dương năm 2019 (có đáp án)

SỞ GIÁO DỤC  ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 10 THPT HẢI DƯƠNG NĂM HỌC 2018-2019 Môn thi: VẬT LÝ
Thời gian làm bài: 180 phút ĐỀ CHÍNH THỨC Ngày thi: 03/04/2019
(Đề thi gồm: 6 câu, 02 trang) Câu 1: (1,0 điểm)
1. Từ một khí cầu đang chuyển động thẳng đứng xuống dưới với tốc độ không đổi
bằng 2m/s, người ta ném một vật nhỏ theo phương thẳng đứng lên phía trên với tốc độ ban
đầu bằng 18m/s so với đất. Biết khí cầu chưa chạm đất trong quá trình vật chuyển động.
Bỏ qua sức cản của không khí lên vật, lấy g = 10 m/s2.
a. Tính khoảng cách giữa khí cầu và vật khi vật lên đến vị trí cao nhất.
b. Sau thời gian bao lâu thì vật rơi trở lại gặp khí cầu?
2. Một người đứng ở sân ga ngang với đầu toa thứ nhất của một đoàn tầu. Khi đoàn
tầu bắt đầu chuyển bánh nhanh dần đều thì toa thứ nhất đi qua người ấy sau thời gian 10s.
Hỏi toa thứ 5 đi qua người ấy trong thời gian bao lâu? Biết các toa có cùng độ dài, bỏ qua khoảng nối các toa. Câu 2: (2,5 điểm)
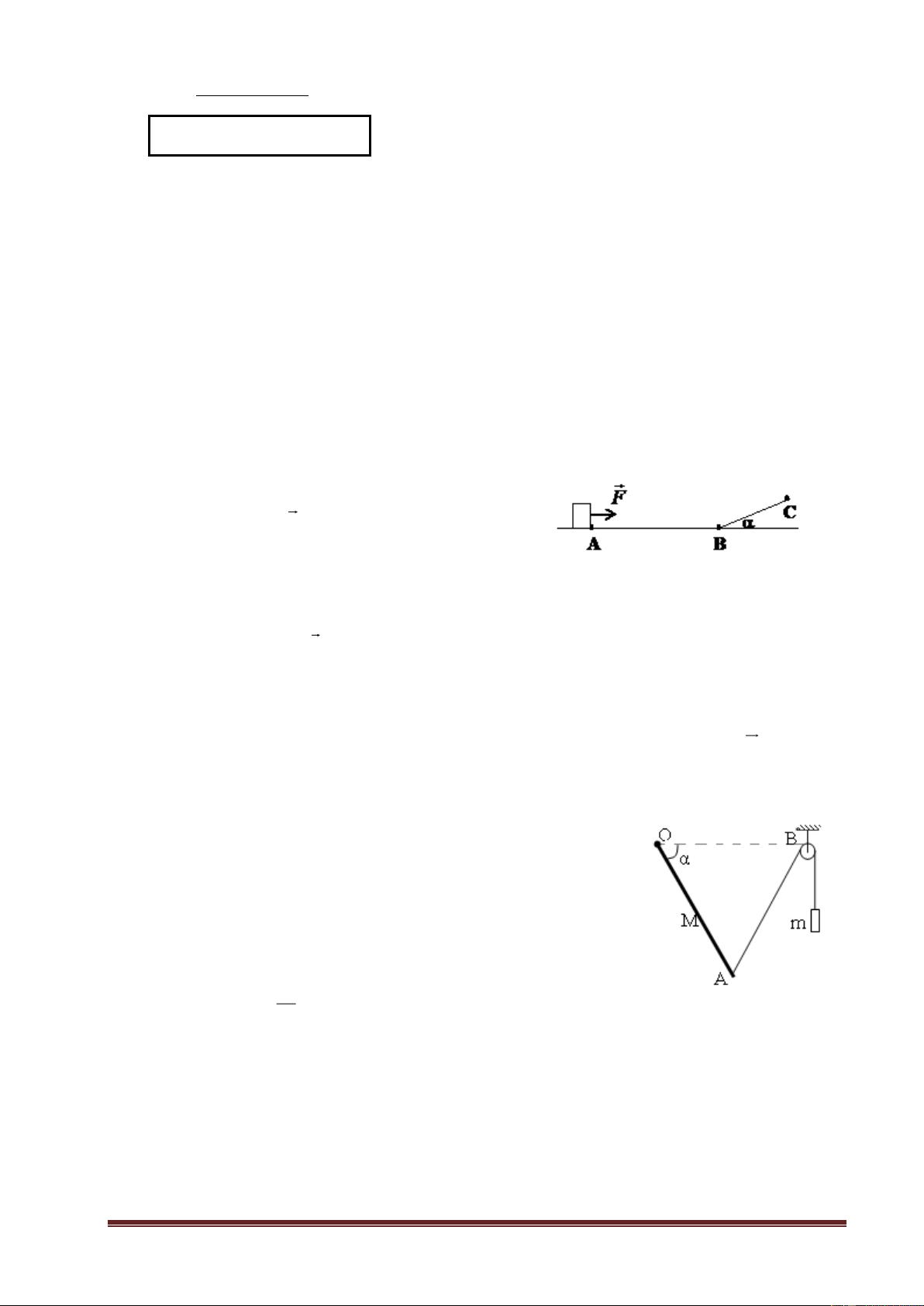
Một vật nhỏ có khối lượng 10 kg đang đứng
yên tại điểm A trên mặt phẳng nằm ngang thì chịu
tác dụng của lực kéo F theo phương ngang. Biết hệ
số ma sát giữa vật và mặt phẳng ngang là  = 0, 4 . 1
Lấy g=10m/s2. Biết AB=18m, độ lớn lực F trên AB bằng 50N.
1. Xác định gia tốc của vật trên đoạn AB và thời gian vật đi đến điểm B.
2. Sau khi tới B vật chuyển động lên mặt phẳng nghiêng BC hợp với mặt phẳng
ngang góc α = 300. Lực F giữ nguyên hướng như khi chuyển động trên mặt phẳng ngang.
Hệ số ma sát giữa vật và mặt phẳng nghiêng là  = 0,5 . 2
a. Độ lớn của lực kéo F = 50 N. Hỏi vật lên đến vị trí cách B một đoạn lớn nhất là bao
nhiêu. Biết mặt phẳng nghiêng BC đủ dài.
b. Độ dài của mặt phẳng nghiêng BC = 6m. Xác định độ lớn nhỏ nhất của lực F để vật
lên được đến đỉnh của mặt phẳng nghiêng. Câu 3: (1,5 điểm)
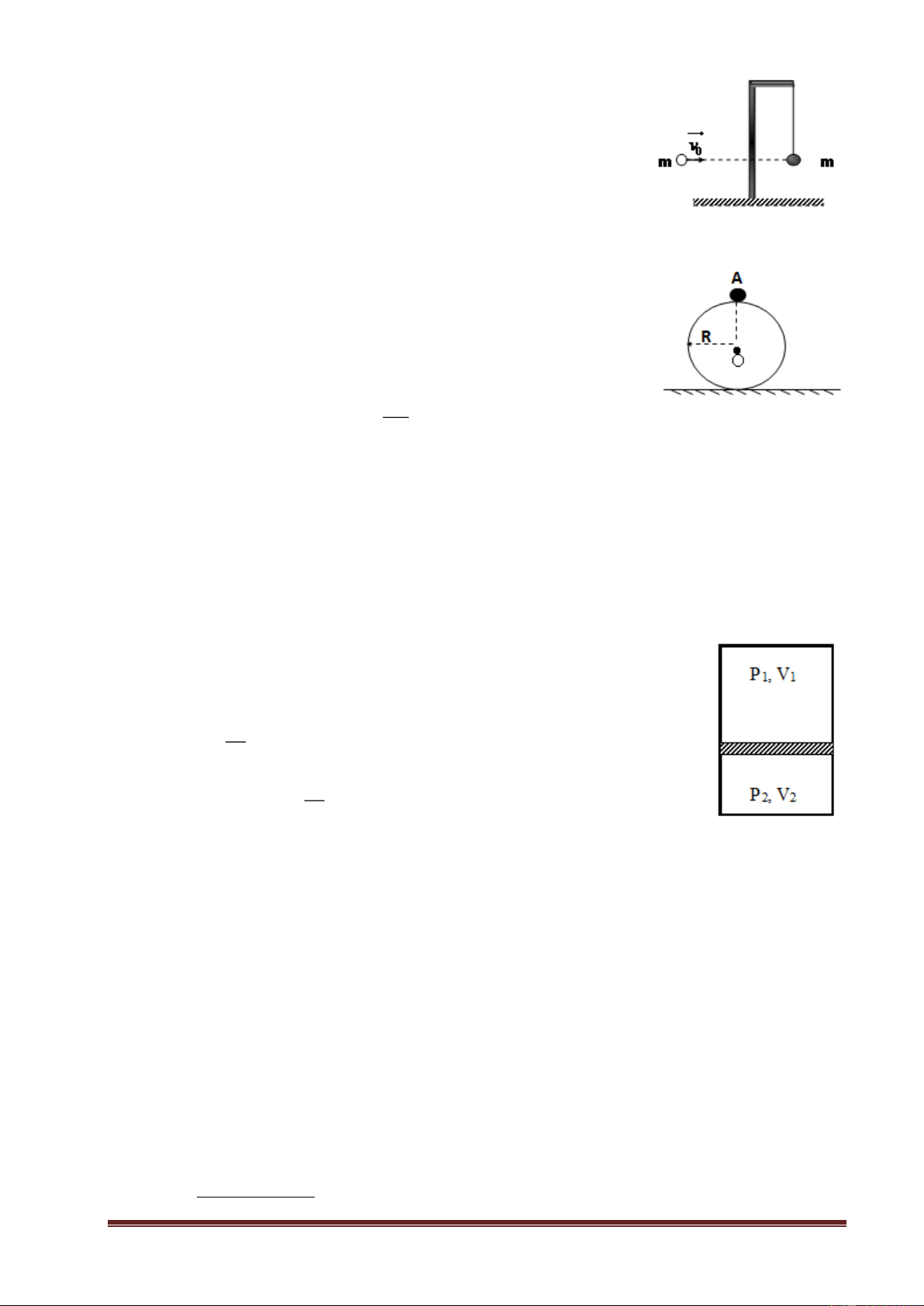
Cho một cơ hệ như hình vẽ, thanh đồng chất OA tiết
diện đều, khối lượng M, có thể quay tự do quanh trục O cố
định. Đầu A của thanh được nối với một vật có khối lượng m
bằng dây nhẹ AB vắt qua ròng rọc cố định B. Biết OB nằm
ngang và OB=OA. Khi hệ ở trạng thái cân bằng góc α=600. Bỏ
qua ma sát, khối lượng và kích thước của ròng rọc. m 1. Tìm tỷ số M
2. Tìm độ lớn của lực do trục quay tác dụng lên thanh ở đầu O.
Câu 4: (2,5 điểm)
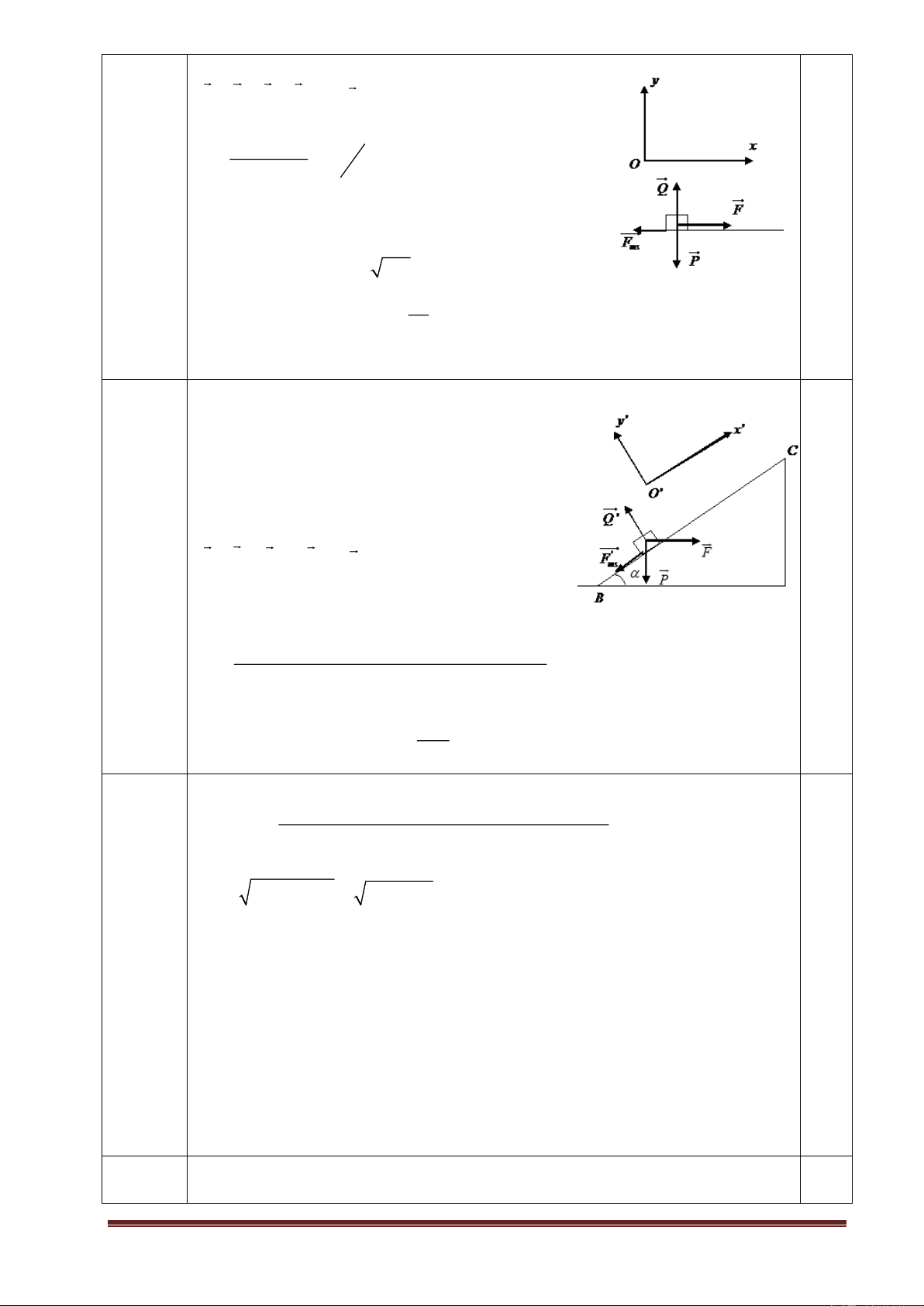
1. Treo một quả cầu nhỏ khối lượng m bằng sợi dây
nhẹ, không dãn, chiều dài l vào một giá như hình vẽ. Một viên
đạn nhỏ cũng có khối lượng m bay ngang với tốc độ v0 găm
vào quả cầu và ở trong đó. Giá trị nhỏ nhất của v0 bằng bao
nhiêu để vật chuyển động tròn quanh điểm treo.
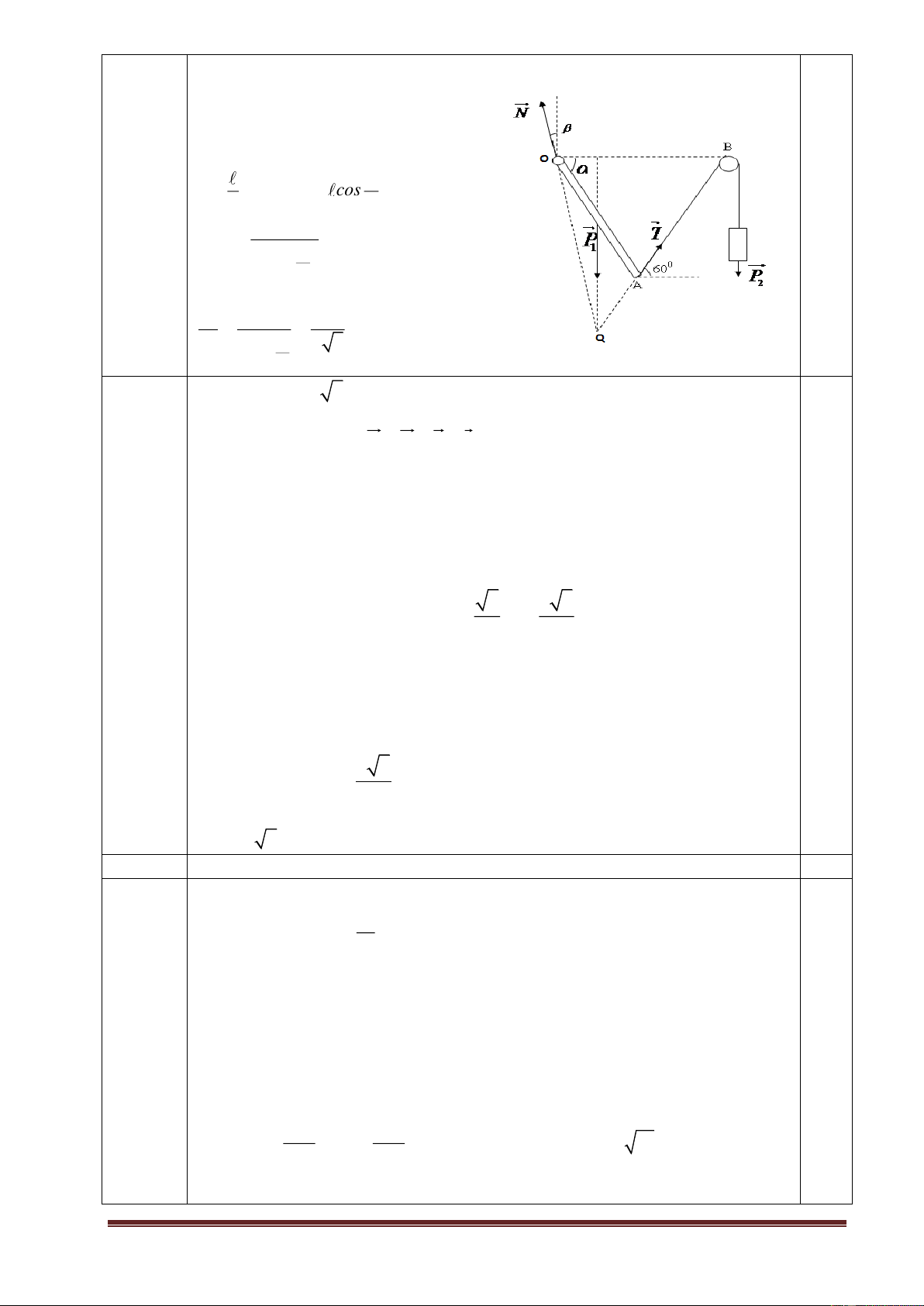
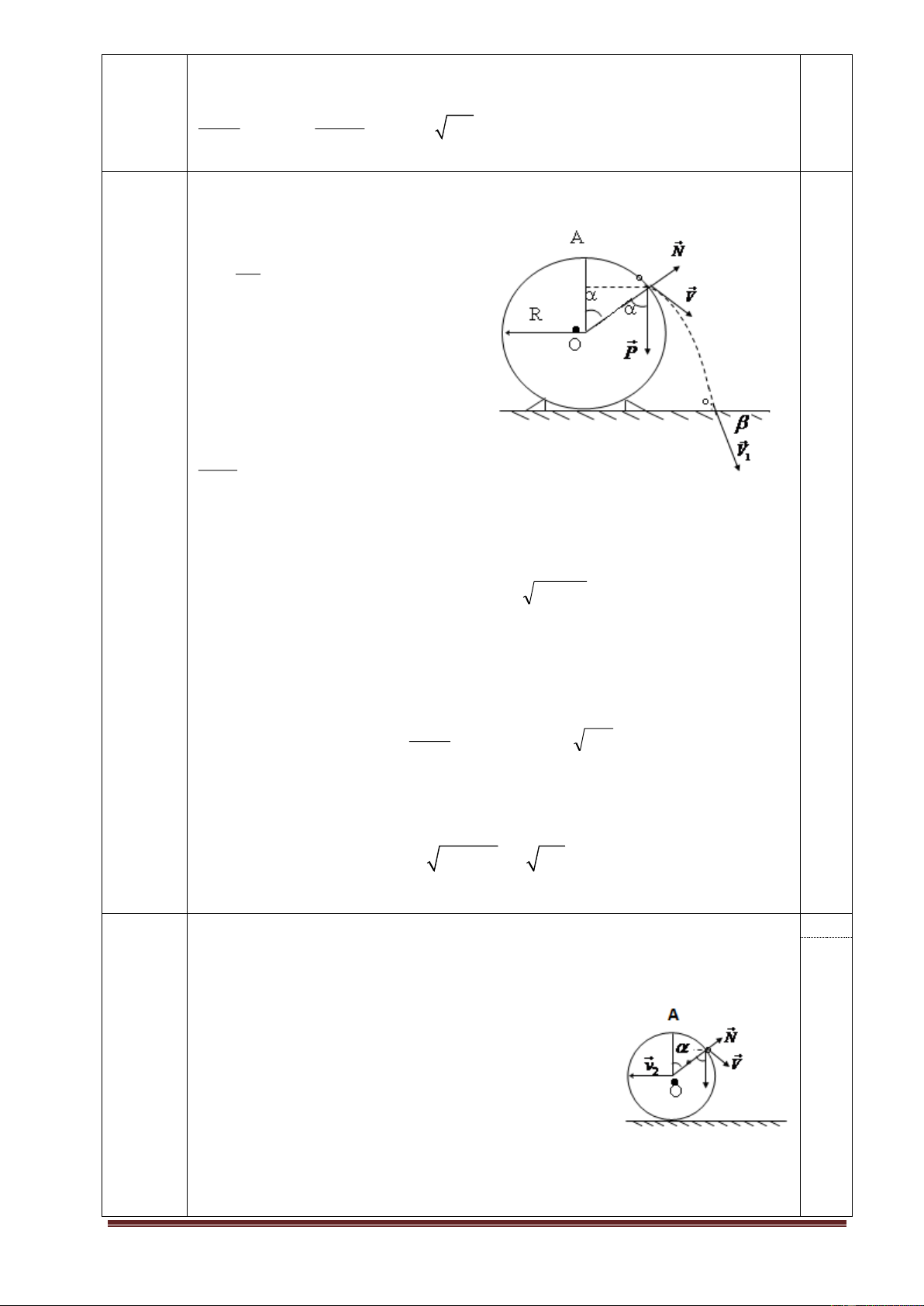
2. Một quả cầu bán kính R, khối lượng M được đặt trên mặt bàn nằm ngang.Từ
đỉnh A của quả cầu, một vật nhỏ khối lượng m trượt không ma
sát với tốc độ ban đầu bằng 0.
a. Quả cầu được giữ cố định trên bàn.Vật sẽ rời mặt cầu ở độ cao
nào so với mặt bàn và xác định góc giữa véc tơ vận tốc của vật
với phương ngang khi chạm mặt bàn.
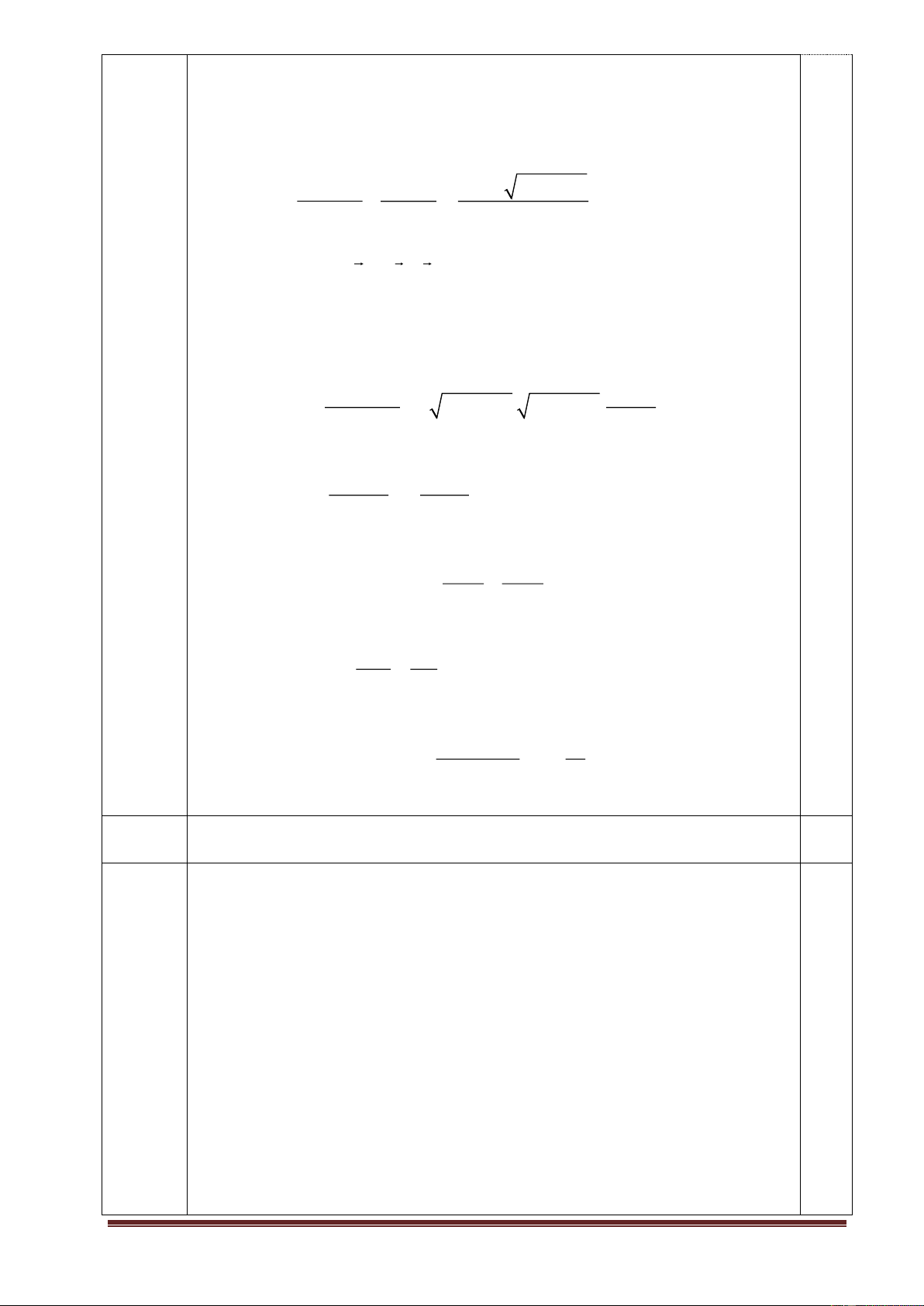
b. Quả cầu nằm tự do trên mặt bàn nhẵn. Xác định tỉ số M/m để 7R
vật nhỏ rời mặt cầu tại tại độ cao so với mặt bàn. 4 Câu 5: (1,5 điểm)
1. Một của hàng bán bóng bay dùng một bình bằng thép dung tích 62 lít chứa khí
(coi khí là lí tưởng) ở áp suất 4,5MPa để bơm bóng bay bằng cách mở van để khí tự tràn
vào bóng, sau khi bơm dung tích mỗi quả bóng là 8,52 lít, áp suất khí trong bóng
1,05.105Pa. Người bán hàng dùng bình này sẽ bơm được bao nhiêu quả bóng bay. Biết nhiệt độ không đổi.
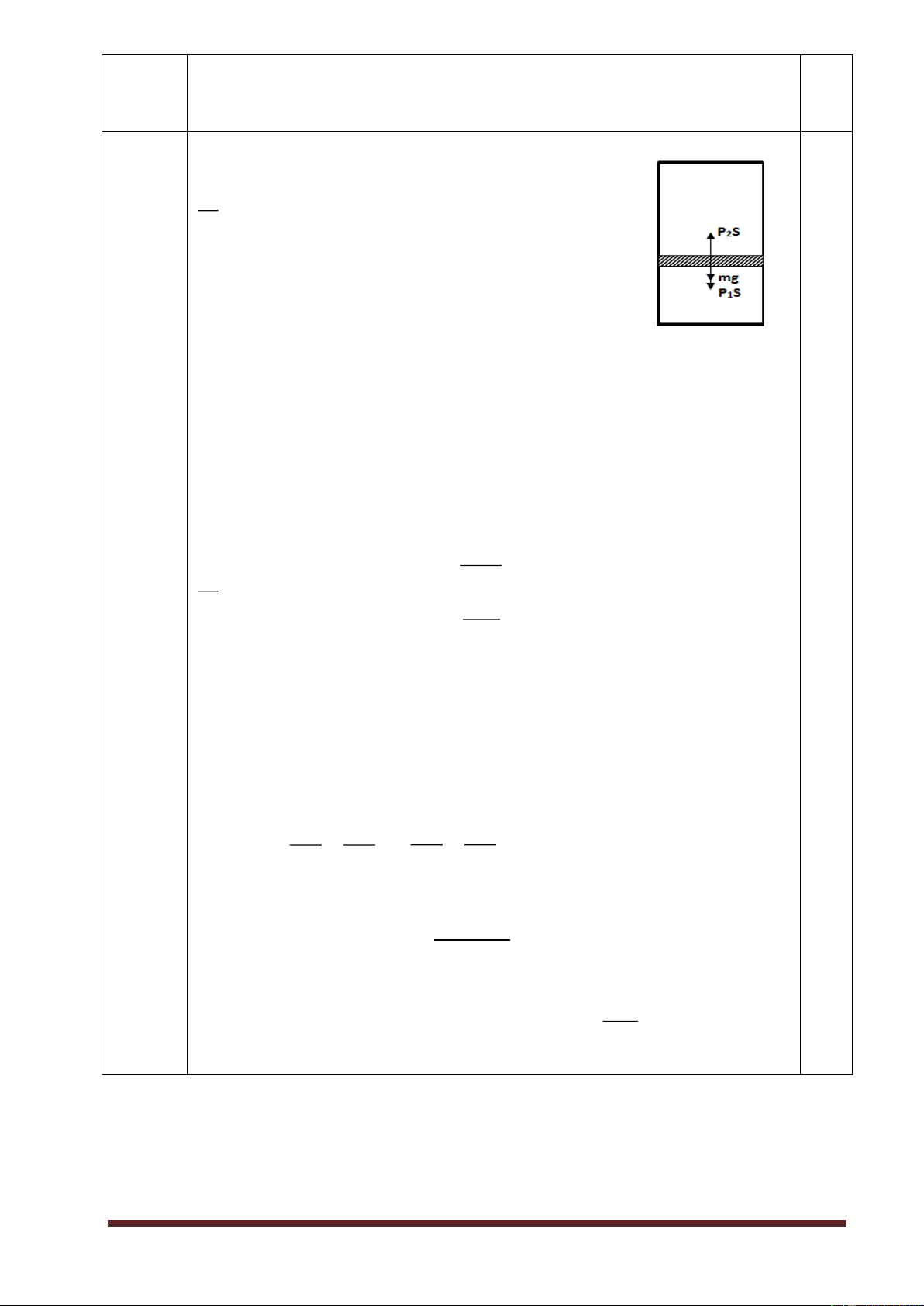
2. Một xilanh kín đặt thẳng đứng, khí trong xilanh được ngăn
cách thành hai phần nhờ một pittông, pittông có thể trượt không ma sát
dọc theo xilanh. Biết khối lượng khí trong hai phần bằng nhau và luôn
cùng nhiệt độ. Ban đầu nhiệt độ khí là 270C thì tỉ số thể tích phần trên V
và phần dưới 1 = 4 . Nếu nhiệt độ tăng lên đến 3270C thì tỉ số thể tích V2 ' V
phần trên và phần dưới 1 là bao nhiêu? ' V2 Câu 6: (1 điểm)
Cho một cái bàn đặt trên mặt phẳng ngang, một số khúc gỗ giống nhau, dây nối,
ròng rọc cố định, thước đo chiều dài. Hãy thiết kế phương án thí nghiệm để xác định hệ số
ma sát trượt giữa khúc gỗ và mặt bàn. Bỏ qua khối lượng của ròng rọc và dây nối.
............................Hết...........................
Họ và tên thí sinh:...........................................Số báo danh:.........................
Chữ kí giám thị 1:.................................... Chữ kí giám thị 2:.......................
SỞ GIÁO DỤC  ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH HẢI DƯƠNG
LỚP 10 THPT - NĂM HỌC 2018 – 2019 Môn thi: VẬT LÝ
HƯỚNG DẪN CHẤM (BẢN DỰ THẢO) Câu 1 (1điểm)
1(0,5 đ) Chọn trục tọa độ Oy theo phương thẳng đứng, chiều dương hướng lên
trên, gốc O tạ vị trí của khí cầu khi vật bắt đầu được ném lên.
phương trình chuyển động của khí cầu: y = −v t (1) 1 01 2 gt
- Phương trình chuyển động của vật: y = v t −
;v = v − gt (2) 2 02 2 02 2 v
- Vật lên đến vị trí cao nhất khi v  = 2 = 0 02 t g 2
khoảng cách giữa hai vật khi đó AB= v v v 02 01 02 + = 19,8(m) 2g g 0,25
Khi vật và khí cầu gặp nhau: y 1 = y2 gt  −v = v −  t = 4(s) 01 02 0,25 2
2(0,5 đ) Toa thứ nhất vượt qua người ấy sau thời gian t1: 2 at 2S 1 0,25 s =  t = 2 1 a
n toa đầu tiên vượt qua người ấy mất thời gian t : n . 2 a t 2nS n ns =  t = ; n 2 a
n −1 toa đầu tiên vượt qua người ấy mất thời gian t : n 1 − 2 at ( 2 n − ) 1 S (n − ) 1 n 1 − s =  t = − 2 n 1 a
Toa thứ n vượt qua người ấy trong thời gian t  : 2S
t = t − t = ( n − − ) 1 n n− n . 1 a
( n − n −1)t t = 1  2,36 (s) 0,25 Câu 2 (2,5 đ) 1.
Vẽ hình, phân tích lực, chọn hệ trục tọa độ. (1,0 đ)
P + Q + F + F = ma 0,25 ms
- Chiếu lên các trục toạ độ xác định được: F −  mg 1 = = 1m a 2 m s 0,25
* Vận tốc và thời gian vật đến B 0,25 =
- Vận tốc tại B : v 2as B = 6 m/s v 0,25 - Thời gian vật đến B: B t = = 6(s) a 2a (0,75 đ)
- Vẽ hình, phân tích lực khi vật đi trên mặt phẳng nghiêng - Ta có: '
P + Q '+ F + F = ma ' 0,25 ms
- Chiếu lên các trục thu được: F ( os
c  −  sin − mg(sin +  cos ) 2 ) 2 2 a ' = = 6 − , 25m / s 0,25 m
- Vị trí D vật lên được cách B lớn nhất, có v D=0 2 − v Khoảng cách DB: B DB = = 2,88m 0,25 2a ' 2b (0,75 đ) F ( os
c  −  sin ) − mg(sin +  os c  ) ta có 2 2 a = 1 m Ta có: v C = 0 2 = + = + v v 2a BC 36 12a C B 1 1 = 0  a1=-3 m/s2 0,5  F = 102,8N 0,25
vậy lực nhỏ nhất bằng 102,8N Câu 3 (1,5 đ) 1 Ta có : T = P2 0,25 (1,0 đ)
Áp dụng quy tắc mômen cho thanh với trục quay O.  Mg cos  = T cos 2 2 Mg.cos → 0,5 T =  2cos 2 m cos 1 = = M  2 3 2cos 0,25 2 2 Theo ý 1: M=2 3 m (0,5 đ)
Thanh cân bằng nên: P + N + T = 0 1
Giá của phản lực N ở chốt O phải đi qua giao điểm Q của trọng lực P 1 và lực căng dây T
Chiếu lên phương thẳng đứng: 0,25 3 3 3 0
 N cos  = P − P sin 60 = mg (1) 1 2 = Mg - mg 2 2 0,25 Chiếu lên phương ngang: 0   = N sin P cos 60 = mg/2 (2) 2 3 3 Giải hệ (1), (2): N2 = (mg )2 + (mg/2)2 2  N = 7. . m g Câu 4 1
Theo định luật bảo toàn động lượng ta suy ra vận tốc hai vật sau va chạm (1,0đ) v 0
mv = 2mv  v = 0 2 0,25
Để vật chuyển động tròn, tại điểm cao nhất lực căng dây phải thỏa mãn điều kiện: 0,25 T  0 Định luật II Newton: 2 2 mv mv 2 T + mg =  T =
− mg  0  v  gl  v = gl min l l 0,25
- Theo định luật bảo toàn cơ năng 2 2 2mv 2mv 0,25 0 min = 4mgl +  v = 2 5gl 0 8 2 2a ĐLIINT, ta có: (0,75đ)
mgcos − N = ma với n 2 V a = n R
+ Vật rời khỏi mặt quả cầu : N=0
=> V2 = gR cos (1). ĐLBTCN:
mV2 = mg(R − Rcos) 2
=> V 2 = 2gR (1 − cos ) (2) 0,25  = Giải hệ (1)((2) => cos 2 / ; 3 V = gR 2 / 3 .
Độ cao khi rời mặt cầu: h = R + Rcosα = 5R/3 0,25 
* khi chạm vào mặt bàn vận tốc V dưới góc β 1 2 mV ĐLBTCN 2mgR 1 = => V = 2 gR. 1 2
+ Theo phương ngang vận tốc không đổi
=> Vcos = V cos => 2/3. 2gR / 3 =2 gR cos  =>  =74,20 1 0,25 2b
2) Quả cầu đặt tự do, đặt M/m=x (0,75đ)
+ m bắt đầu rời M khi N=0 và aM=0, lúc đó M
có vận tốc v2, m có vận tốc v đối với M
+ hình vẽ => cosα = ( 7R/4- R)/R = 3/4
ĐLIINT cho m: mg.cosα = mv2/R => v2 =gRcosα (1) ĐLBTĐL theo phương ngang 0,25 0 = Mv2 + m(v2 – v.cosα) mv cos v cos cos gR cos => v = 2 = = (*) m + M 1+ x 1+ x
Vận tốc của m: v = v + v m 2 => v2 + + − m= 2 2 v v 2vv o c s(180 ) 2 2 3 2 gR os c  os c  = gR cos +
− 2 gRcos . gRcos . 2 (1+ x) 1 + x 0.25 3 3 os c  os c  =gR( cos + − 2 ) (**) 2 (1+ x) 1 + x 0.25 2 2 ĐLBTCN : mgR(1 Mv mv - cosα) = 2 m + 2 2 2 2 xv v 0.25 gR(1- cosα) = 2 m + (***)  2 2 3 o c s  11
(*) và (**) vào (***) => x = −1 = 3cos − 2 16 Câu 5 (1.5đ) 1
Gọi n là số quả bóng bay, thể tích khí chứa trong n quả bóng (0,75đ) V = n.V0 Trạng thái 1: 6 p = 4,5MPa = 4,5.10 Pa 1  V = 62lit  0,25 1 Trạng thái 2: 5 p =1,05.10 Pa 2 
V = V + V = V + nV ;V = 8,52lit  2 1 1 0 0 0,25 Ta có: P V = P V => n=305 (quả) 1 1 2 2 0.25 2
+ Lúc đầu, ta có các phương trình (0,75đ) V 1 = 4 V2 (1) P V = P V => P 1 1 2 2 2=4P1 (2) 0,25 P1S+mg=P2S => mg=3P1S (3) + Lúc sau ta có  5nV2 V  = V   1  + 1 = n 1 n  V  vì V1+V2 =V1'+V2' => V 2  2 V  = 2  n + 1 (4) P V   = PV => P' 0,25 1 1 2 2 2=nP'1 (5) mg=(P'2-P'1)S=(n-1) P'1S (6) PV   PV PV   PV Mặt khác: 1 1 1 1 = => 1 1 1 1 = (7) T ' T 600 300 1 1 8(n + 1)P Thế (1), (4) vào (7) => 1 P = 1 5n 0,25 + Ta có: Từ (3) và (6): 3P n 1S=(n-1) P'1S =>3=(n-1) 8( 1) => n=2,3 5n Câu 6 (1,0đ) + Cơ sở lý thuyết
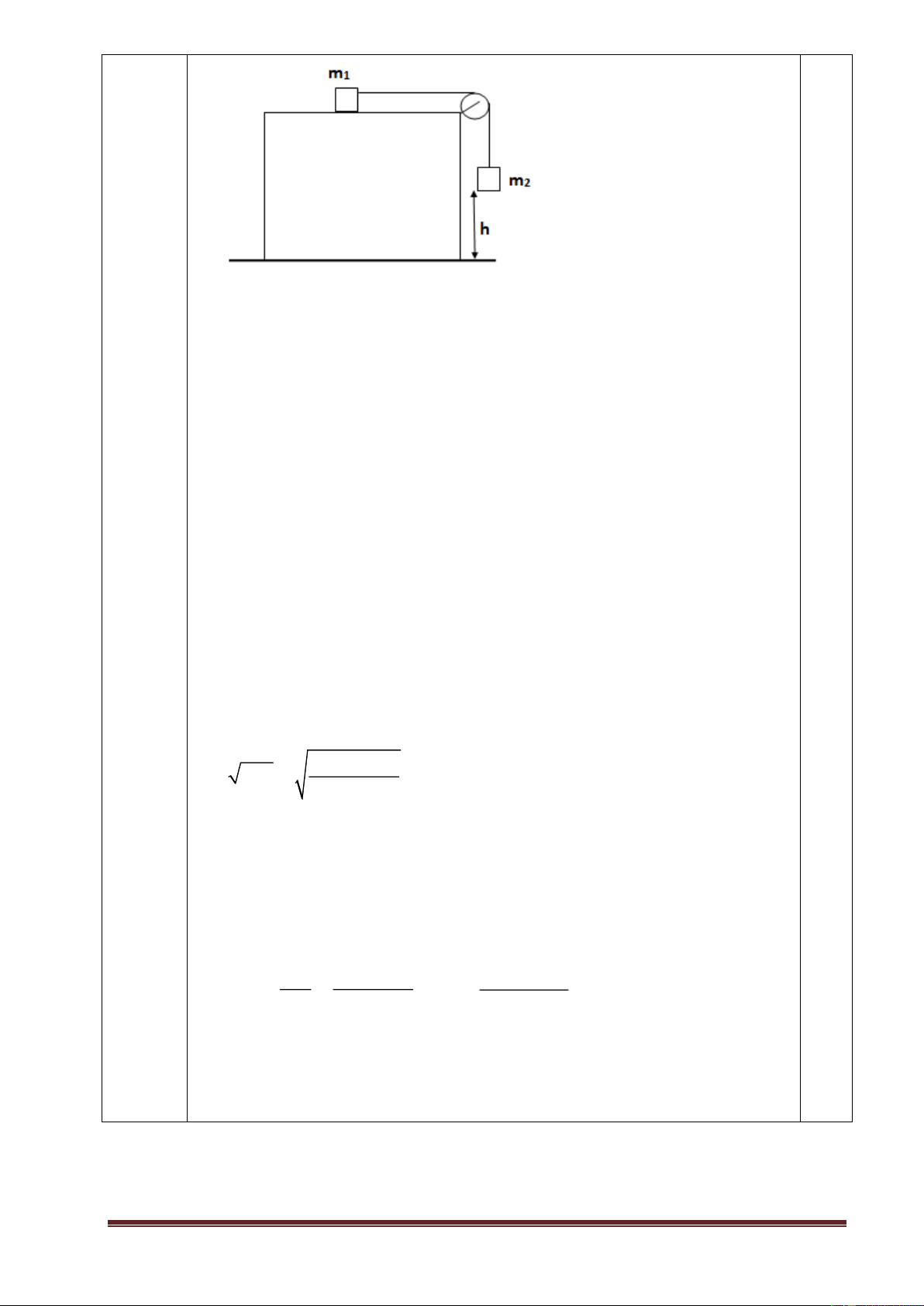
Bố trí các vật như hình, trong đó vật m
1 là 1 khúc gỗ, m2 =nm1 sao cho khi thả
tay thì hệ chuyển động, khi m
2 chạm đất thì m1 tiếp tục trượt và dừng lại trước 0,25 khi chạm vào ròng rọc. Khi m2 chưa chạm đất: gia tốc của hệ
a=(m2g-  m1g)/(m1+m2)=(n-  )g/(n+1)
Tốc độ của 2 vật lúc m 2 chạm đất 2(n − )gh 0,25 v = 2ah = n +1
Khi m2 chạm đất, gọi s là quãng đường m1 tiếp tục đi cho đến khi dừng lại gia tốc của m 1: a1= -  g 2 −v (n − )gh nh Ta có: s = =  = 2a (n + => 1) g s(n +1) + h 1 0,25
+ Dùng thước đo h, s. n biết, suy ra  . 0,25
Học sinh giải theo cách khác nhưng kết quả đúng thì vẫn cho đủ số điểm.