



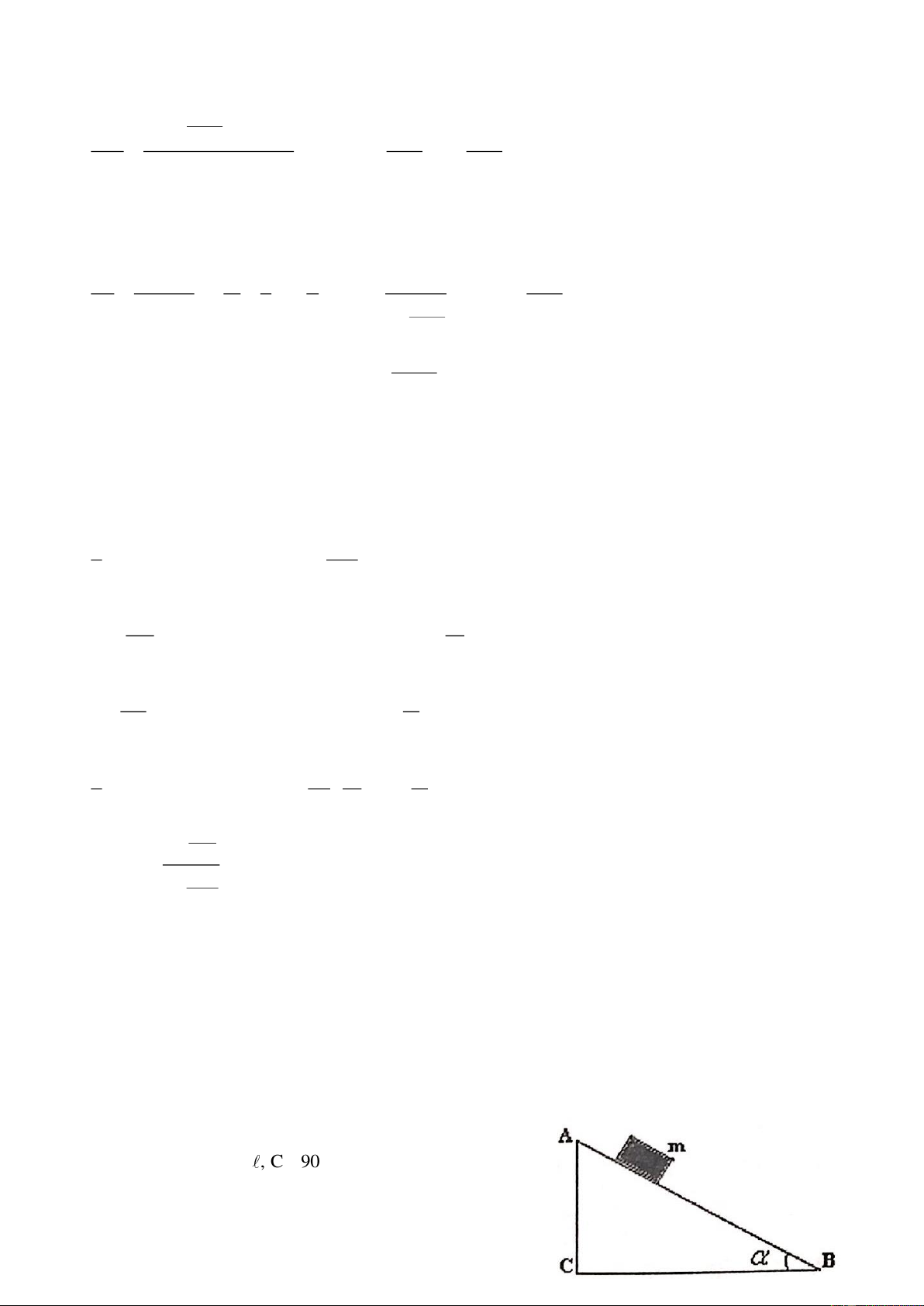











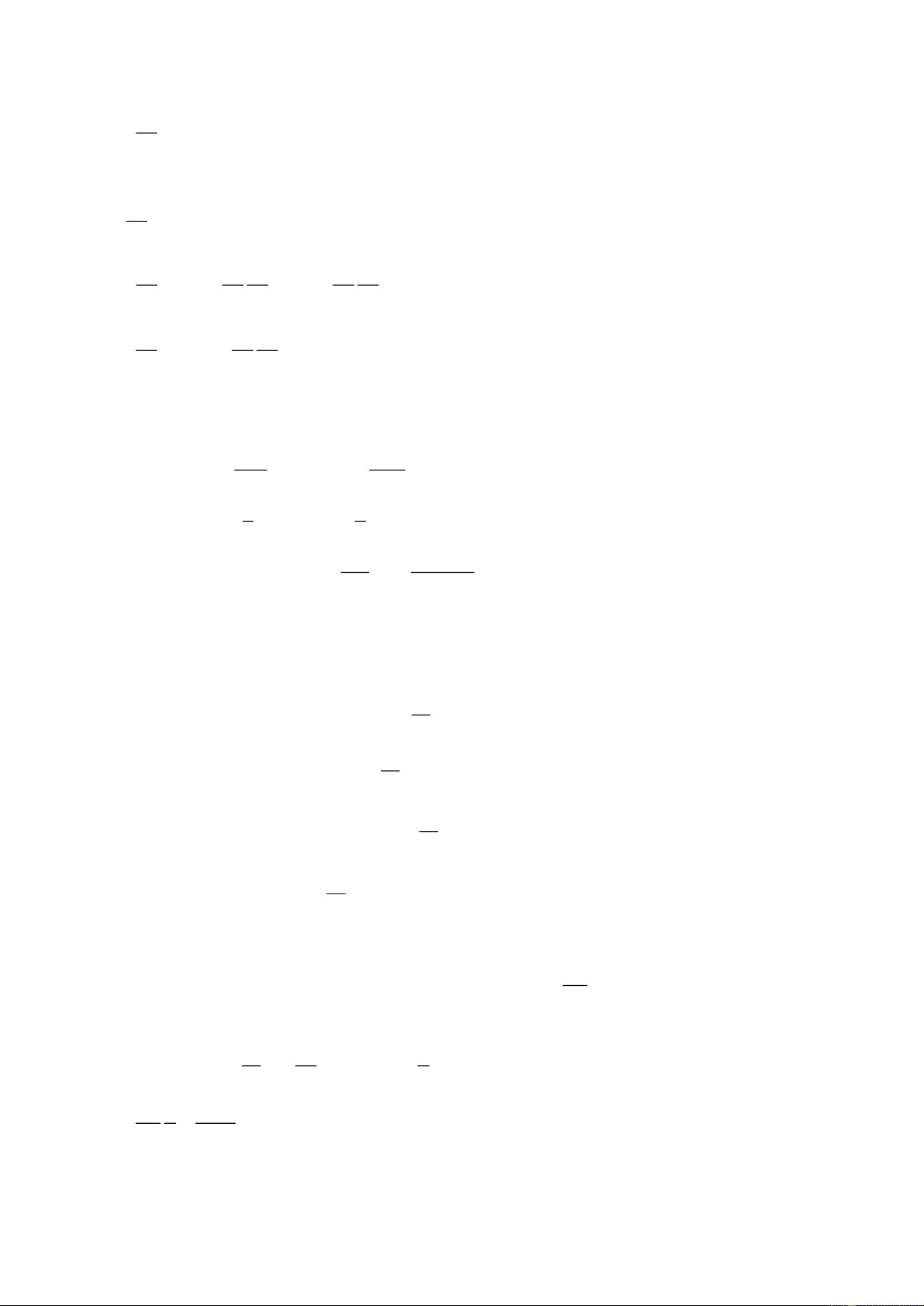
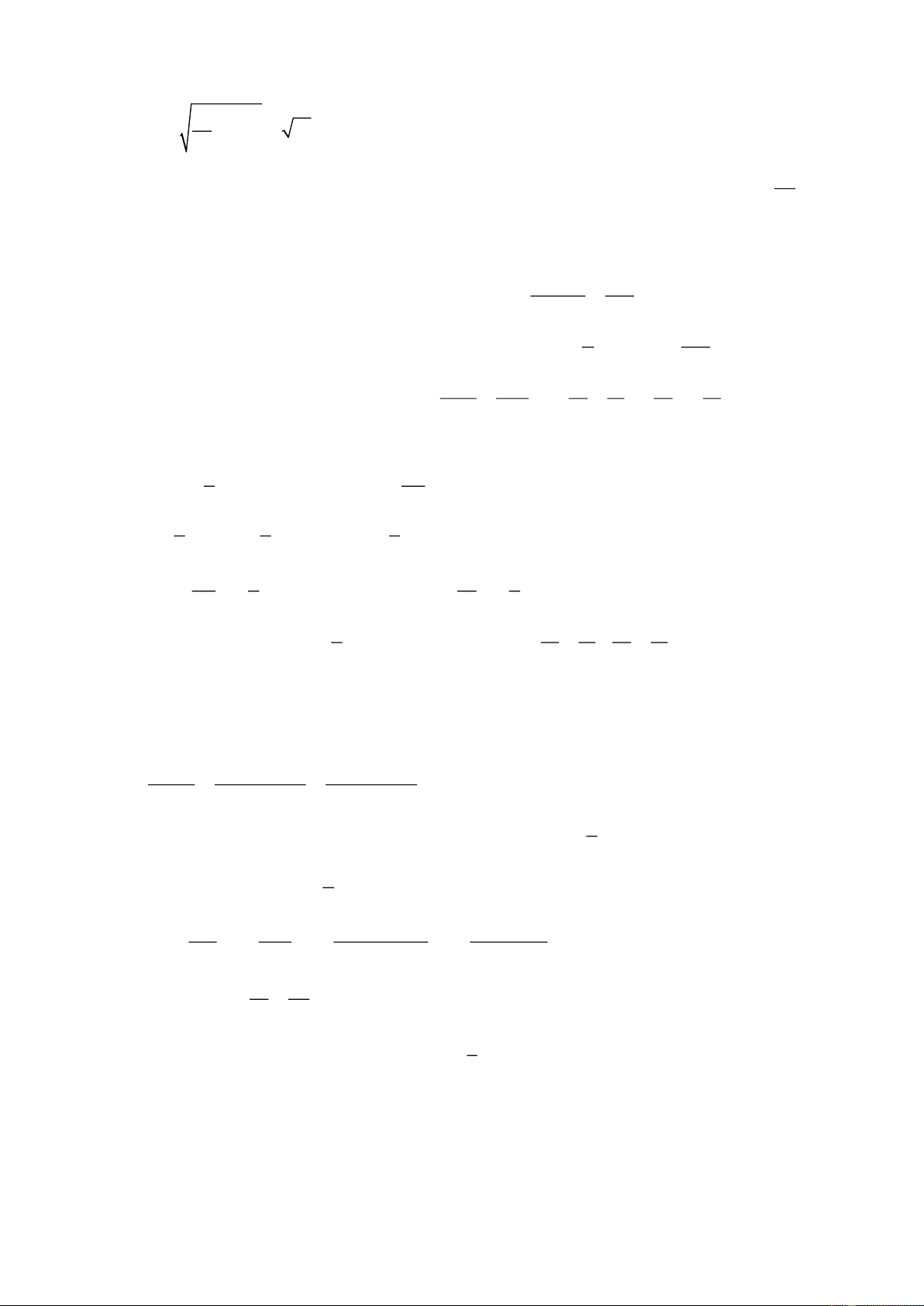

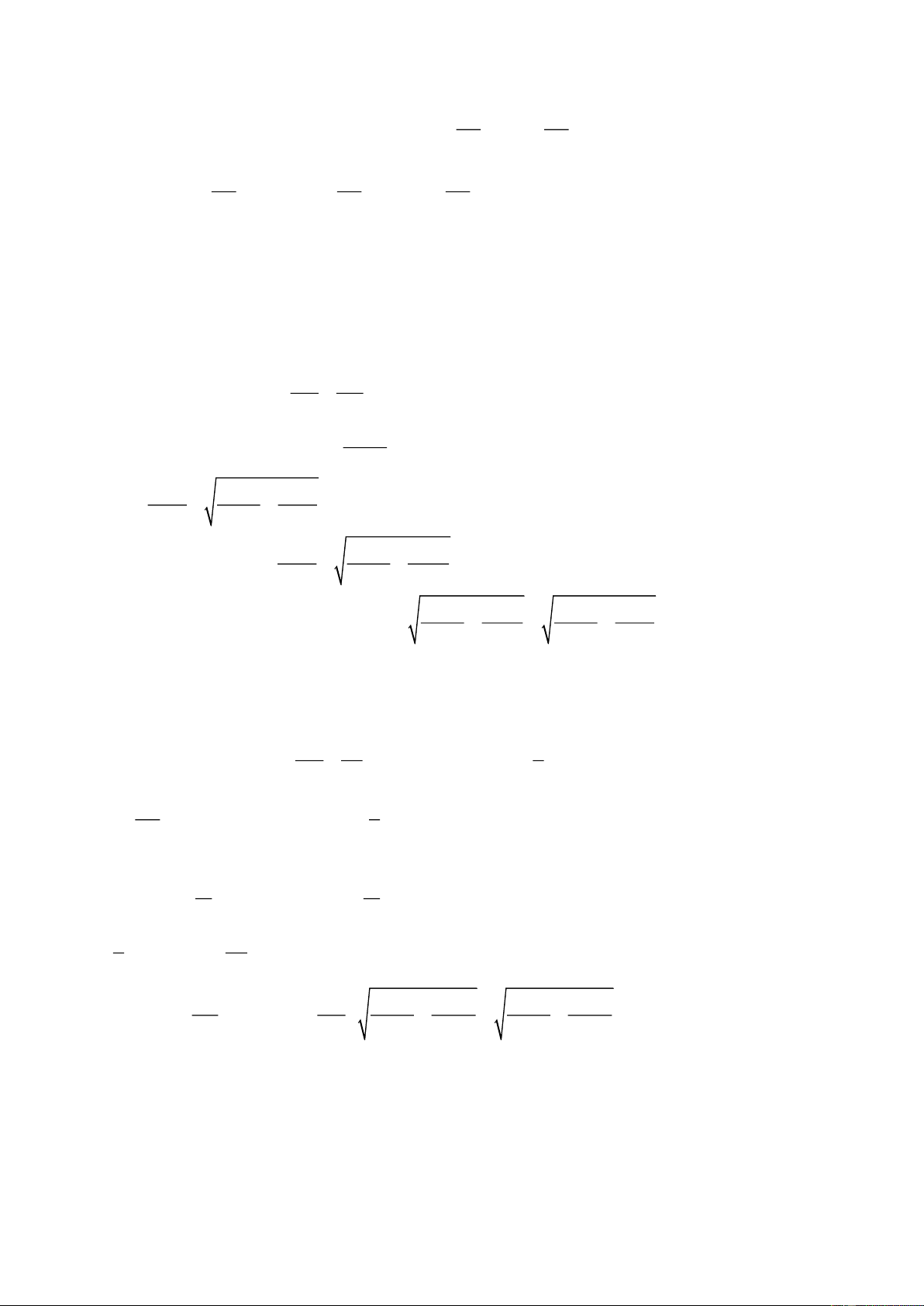


Preview text:
ĐỀ OLYMPIC QUỐC GIA 2016-2017 Câu 1: (5 điểm)
Một chiếc công-ten-nơ đang nằm yên trên mặt đất ngang, phẳng thì được một cần cẩu kéo lên theo
phương thẳng đứng với gia tốc 2
a = 0, 5m / s . Sau khi rời mặt đất 4s, từ mặt trên của công-ten-nơ, một
hòn đá được bắn ra với vận tốc v = 5, 4m / s (đối với công-ten-nơ) theo phương hợp với phương 0 ngang một góc 0
= 30 . Biết công-ten-nơ cao h = 3m, lấy 2
g = 10m / s . Coi hòn đá như một chất điểm. Hãy tính:
a. Tính thời gian từ lúc bắn hòn đá đến lúc nó rơi xuống mặt đất.
b. Tính tầm bay xa của hòn đá. Câu 2: (5 điểm)
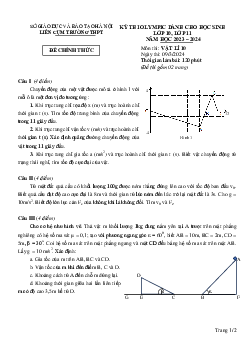
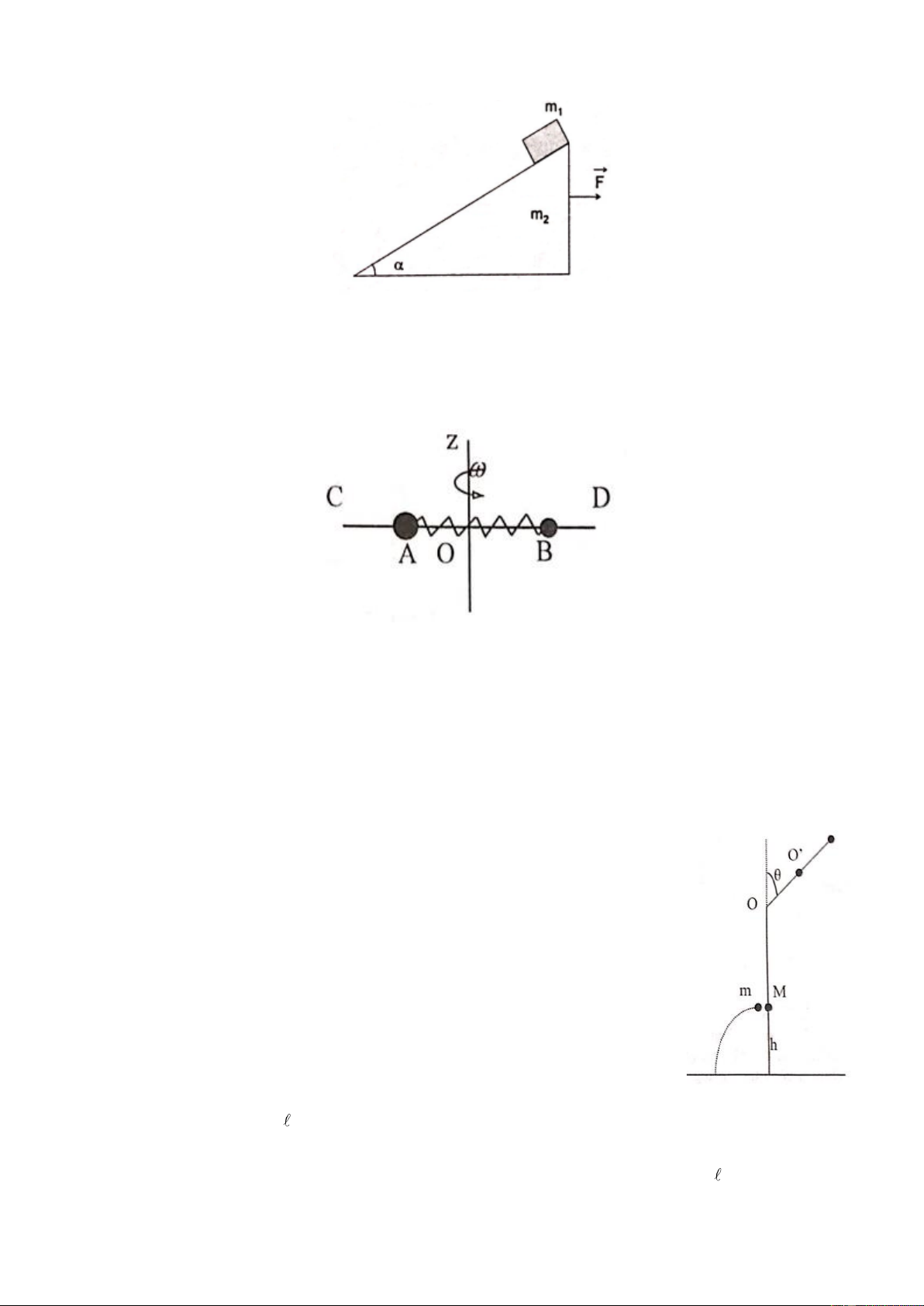
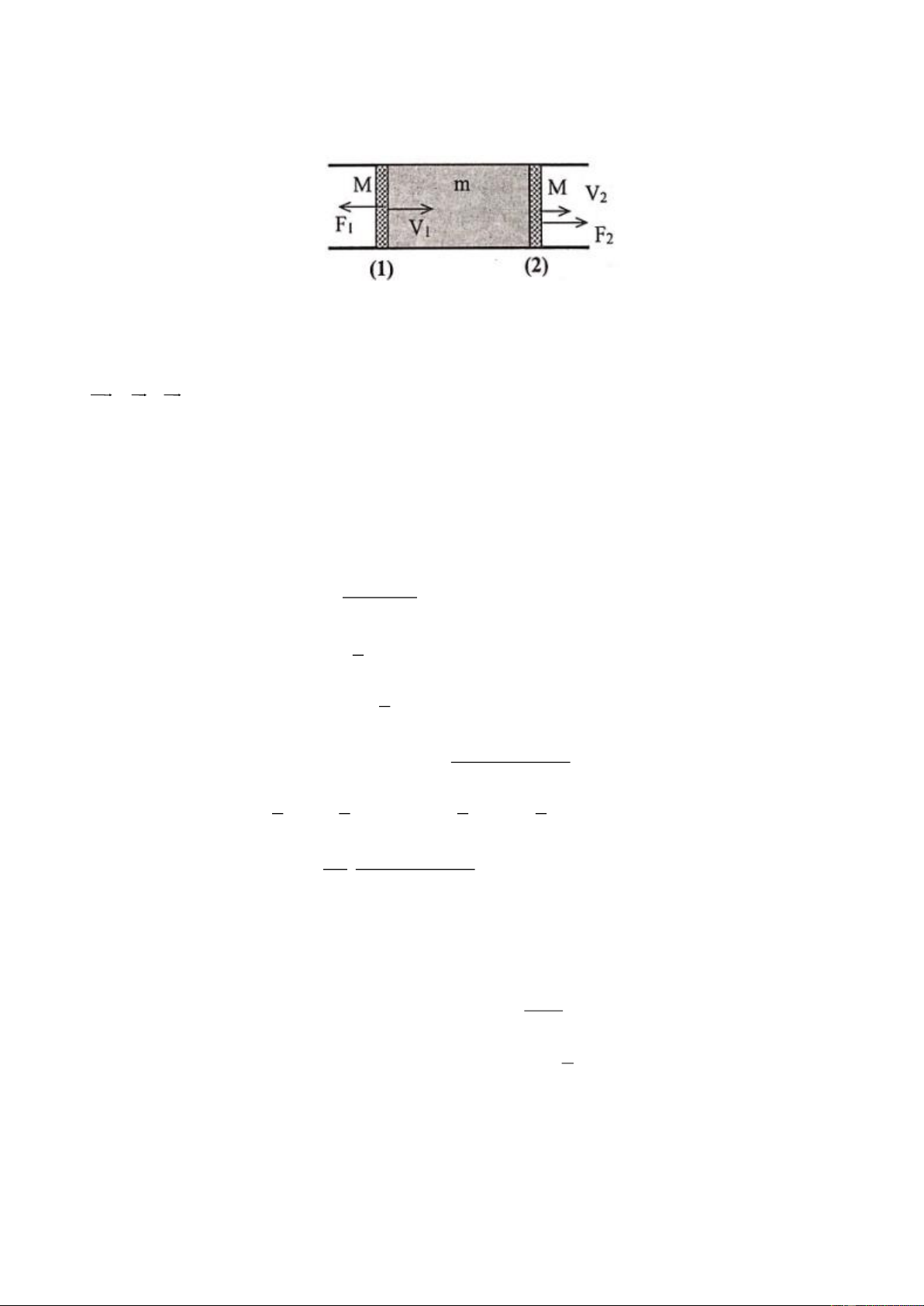
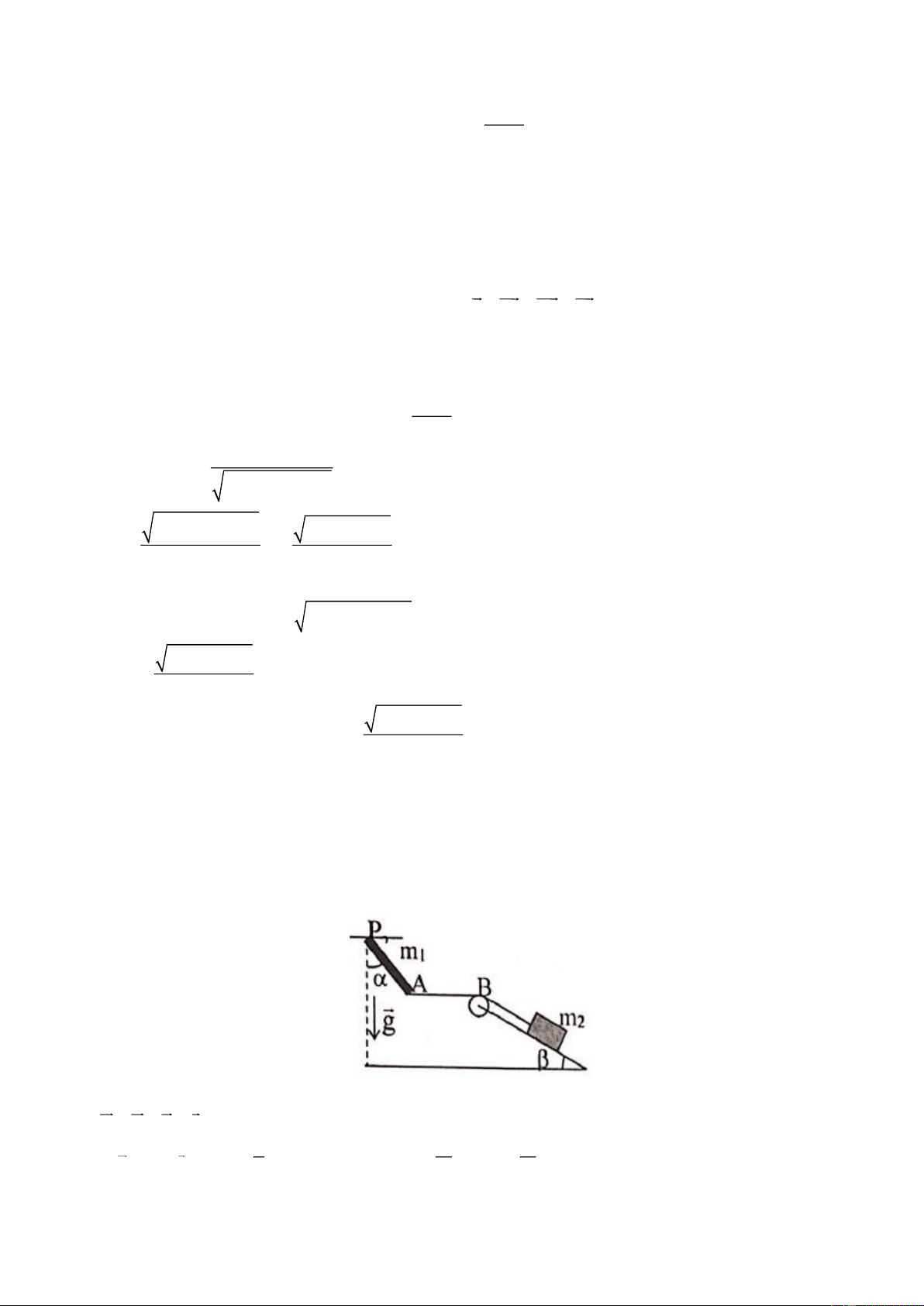
Hai vật có khối lượng m = 100 g và m = 500 g được nối với nhau bằng dây mảnh, nhẹ, không dãn, 1 2
nằm yên trên mặt bàn ngang và phẳng. Dây được vắt qua ròng rọc nhẹ, còn trục ròng rọc được buộc
vào đuôi của một xe đồ chơi khối lượng M = 500g như hình (nhìn từ trên xuống).
Bỏ qua ma sát lăn giữa các bánh xe và mặt bàn, ma sát tại trục quay của ròng rọc. Hệ số ma sát giữa
hai vật và bàn là = 0, 2 . Dây không trượt trên ròng rọc khi cơ hệ chuyển động. Lấy 2 g = 10m / s . Tác
dụng vào xe một lực F theo phương ngang có độ lớn tăng dần. Tìm độ lớn tối thiểu của F để:
a. Xe có thể chuyển động.
b. Cả hai vật cùng chuyển động. Câu 3: (5 điểm)
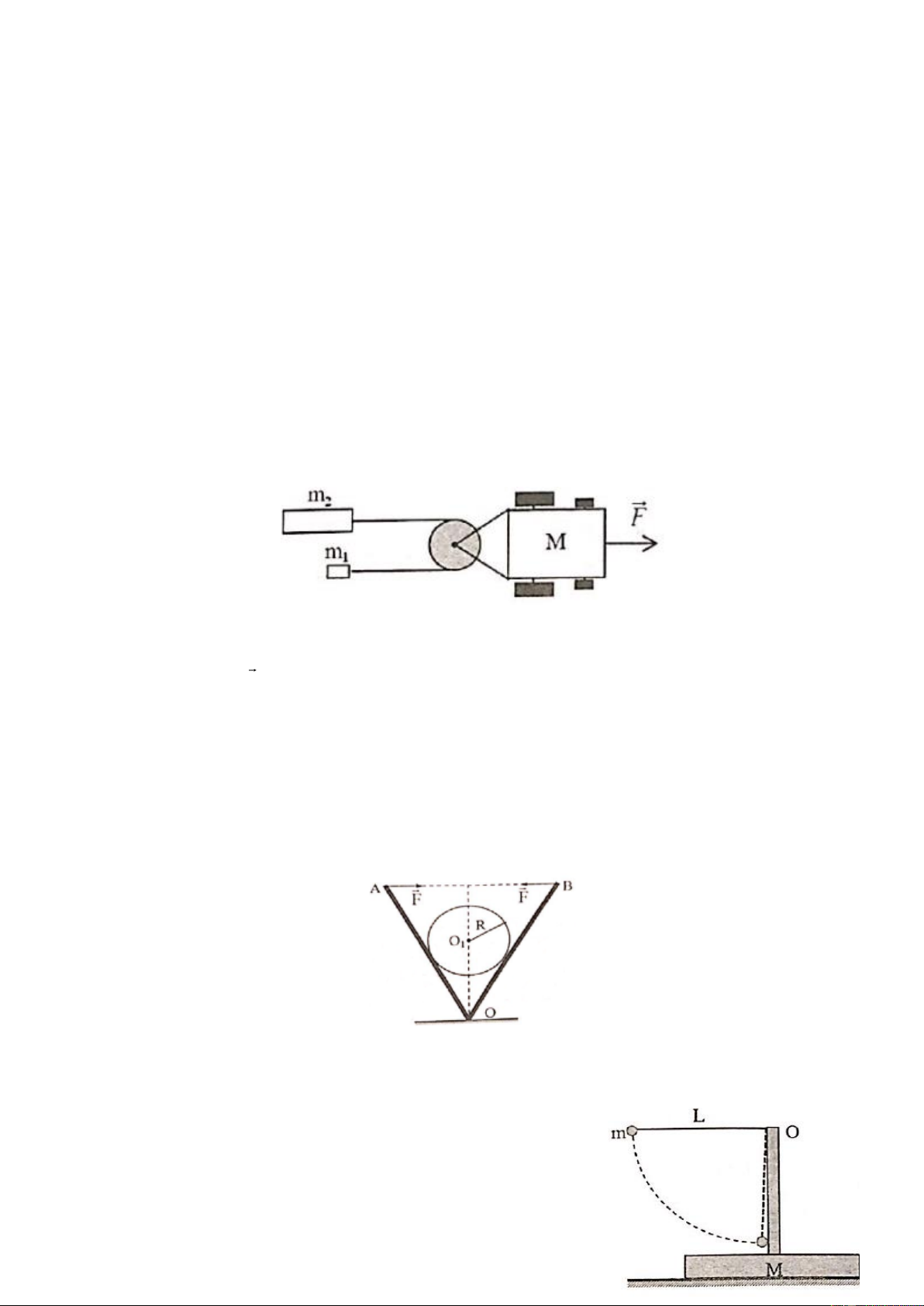
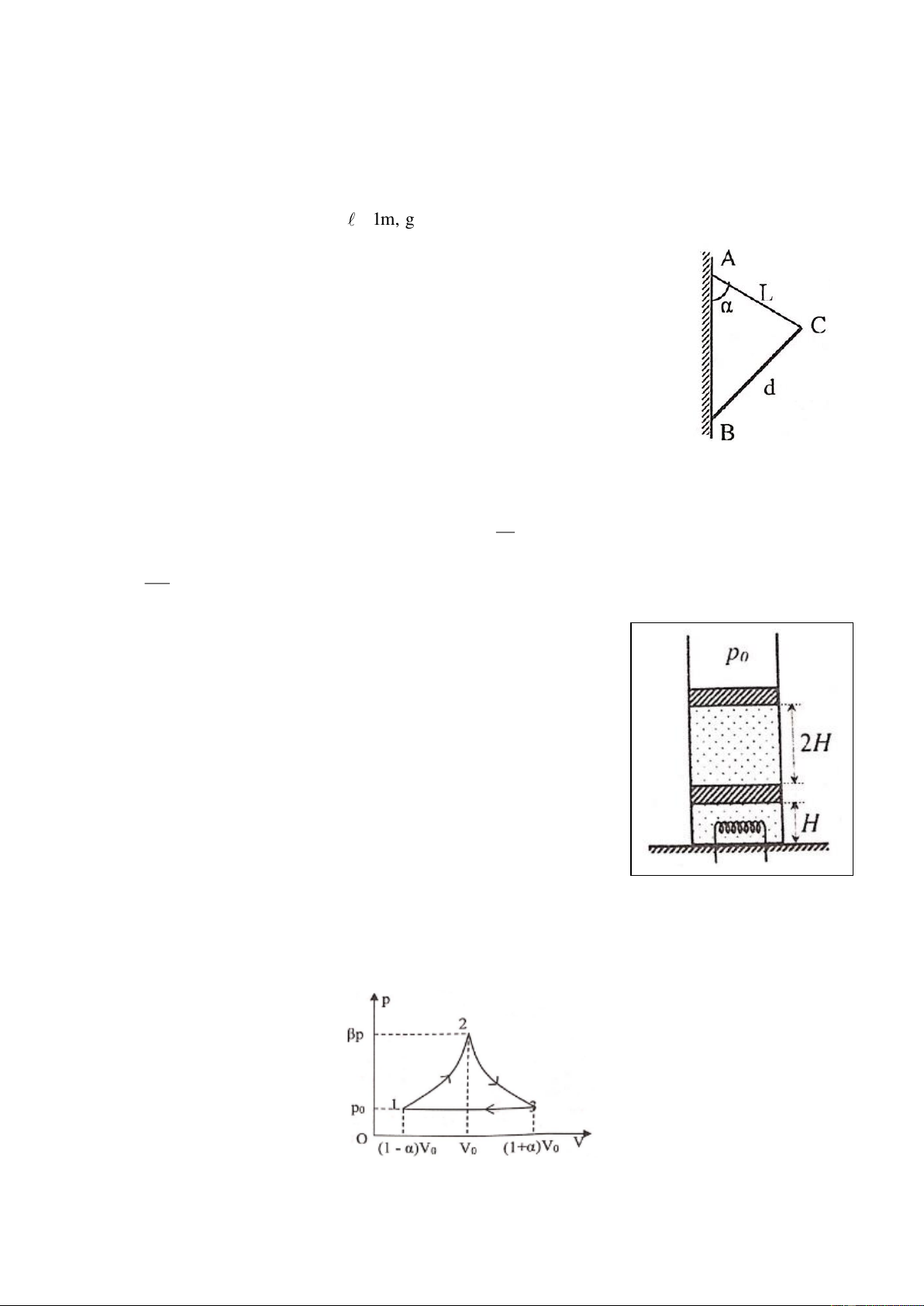
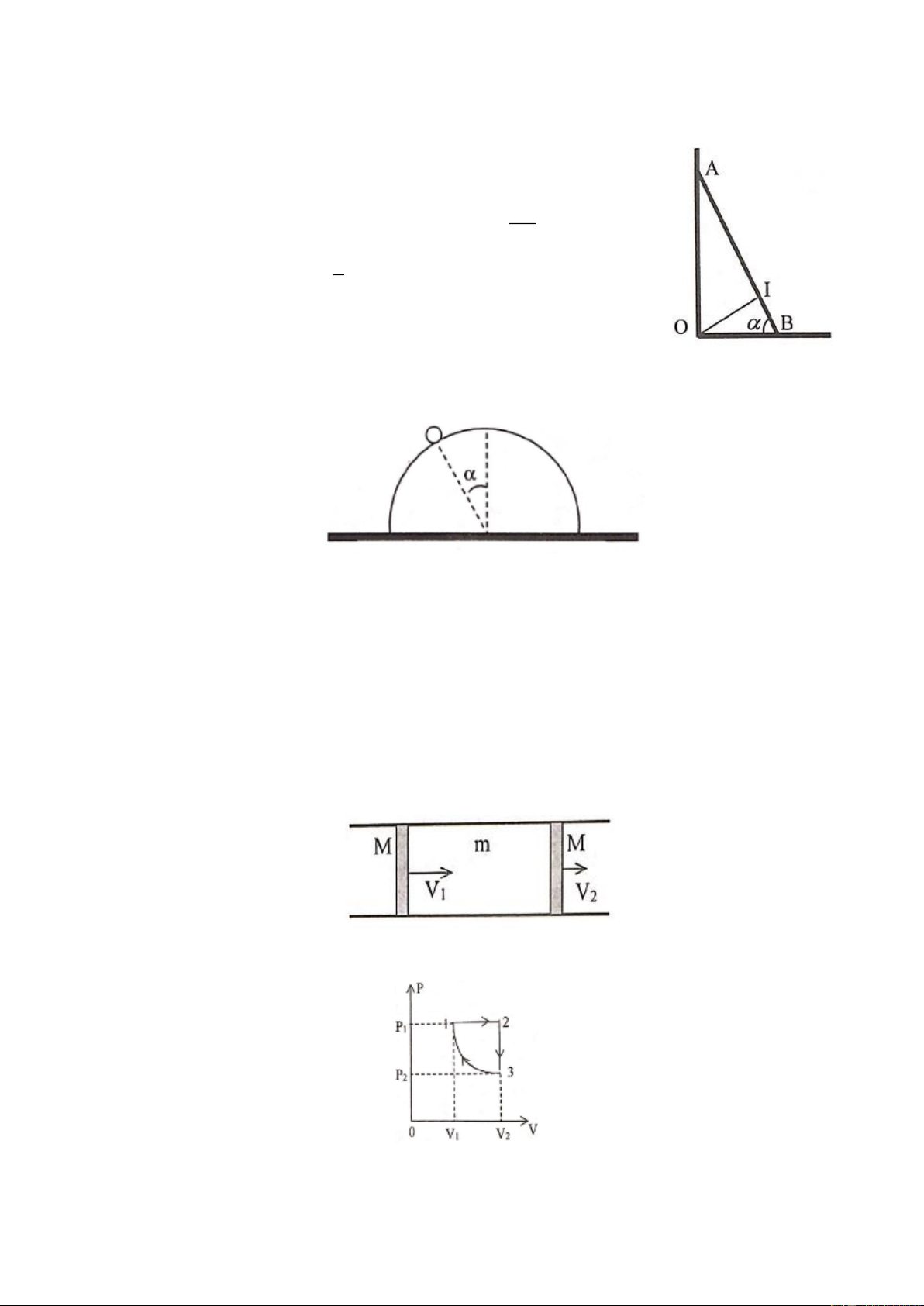
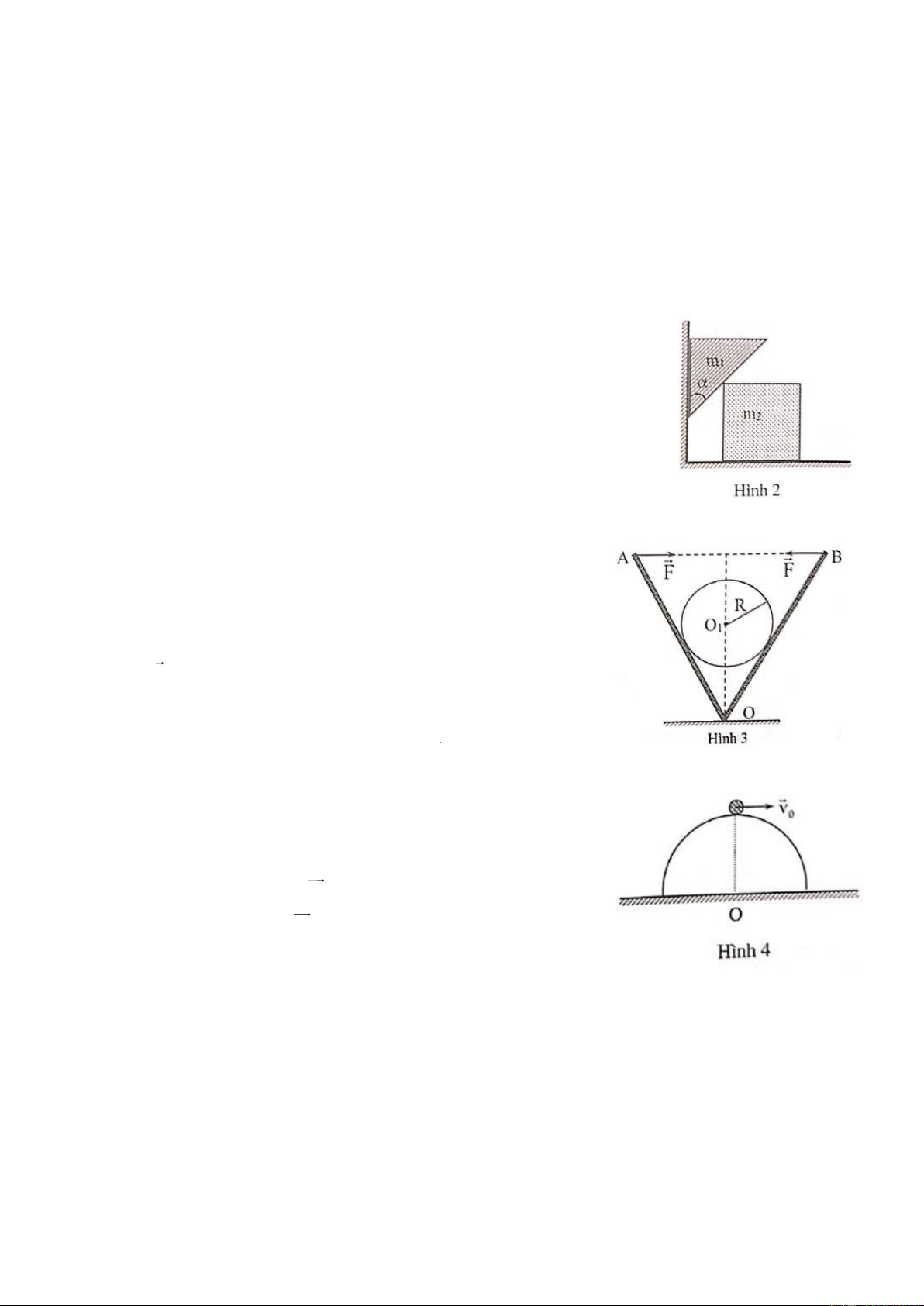
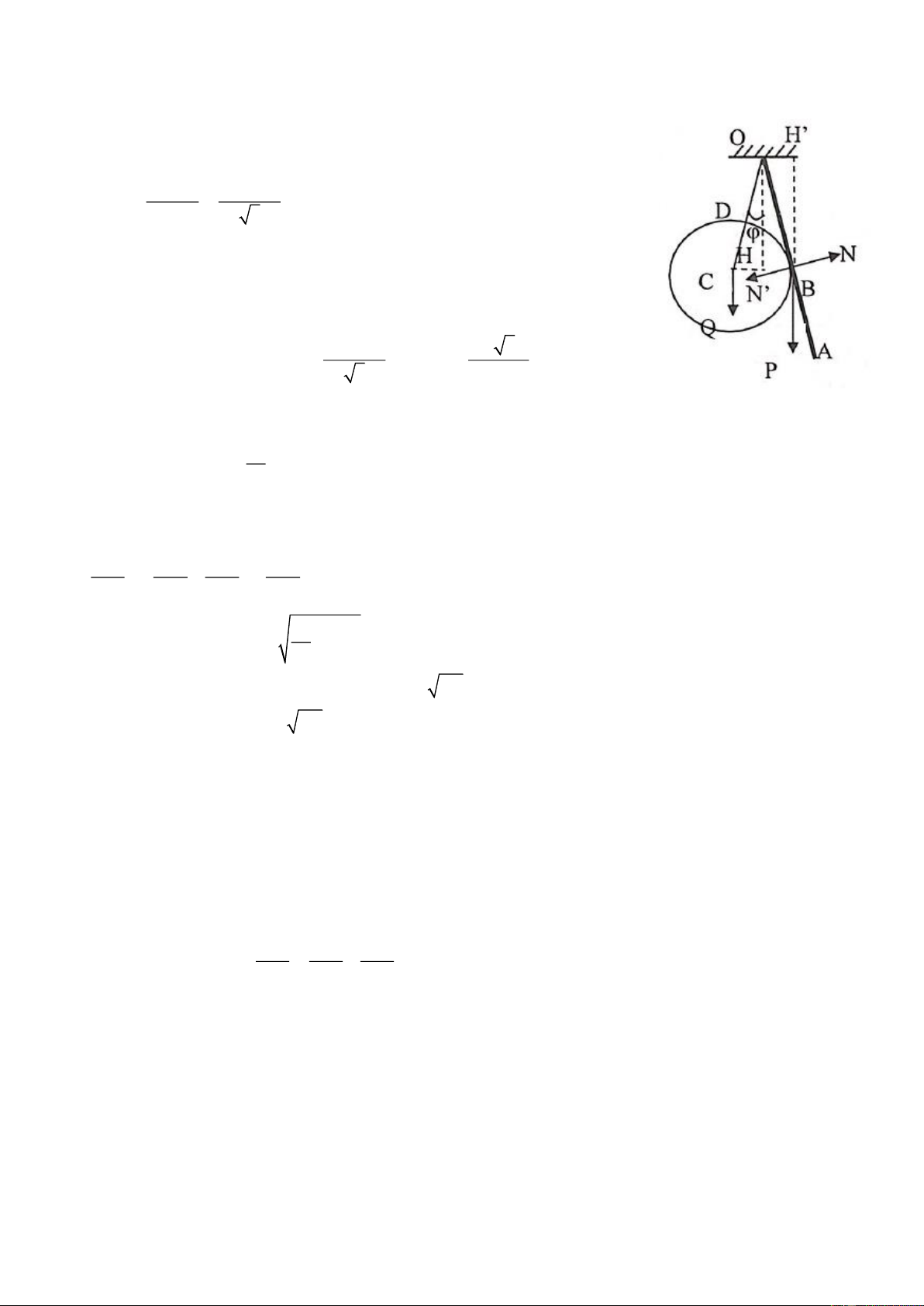
Hai tấm phẳng nhẹ cứng OA và OB được nối với nhau bằng bản lề tại O. Người ta đặt một khối trụ
tròn trọng lượng P, đồng chất, tiết diện đều bán kính R vào giữa hai tấm sao cho trục O của nó song 1
song với trục O của bản lề. Hai trục này nằm ngang và cùng nằm trong mặt phẳng thẳng đứng vuông
góc với mặt phẳng hình vẽ.
Để khối trụ nằm yên cân bằng giữa hai tấm sao cho góc AOB = 2 ,
AB = a người đồng thời tác
dụng vào hai tấm tại A và B hai lực trực đối nằm ngang, cùng độ lớn F hướng vào nhau. Biết rằng hệ
số ma sát nghỉ giữa khối trụ và mỗi tấm phẳng đều là . Bỏ qua
ma sát ở bản lề O. Hãy xác định độ lớn của lực F. Câu 4: (5 điểm)
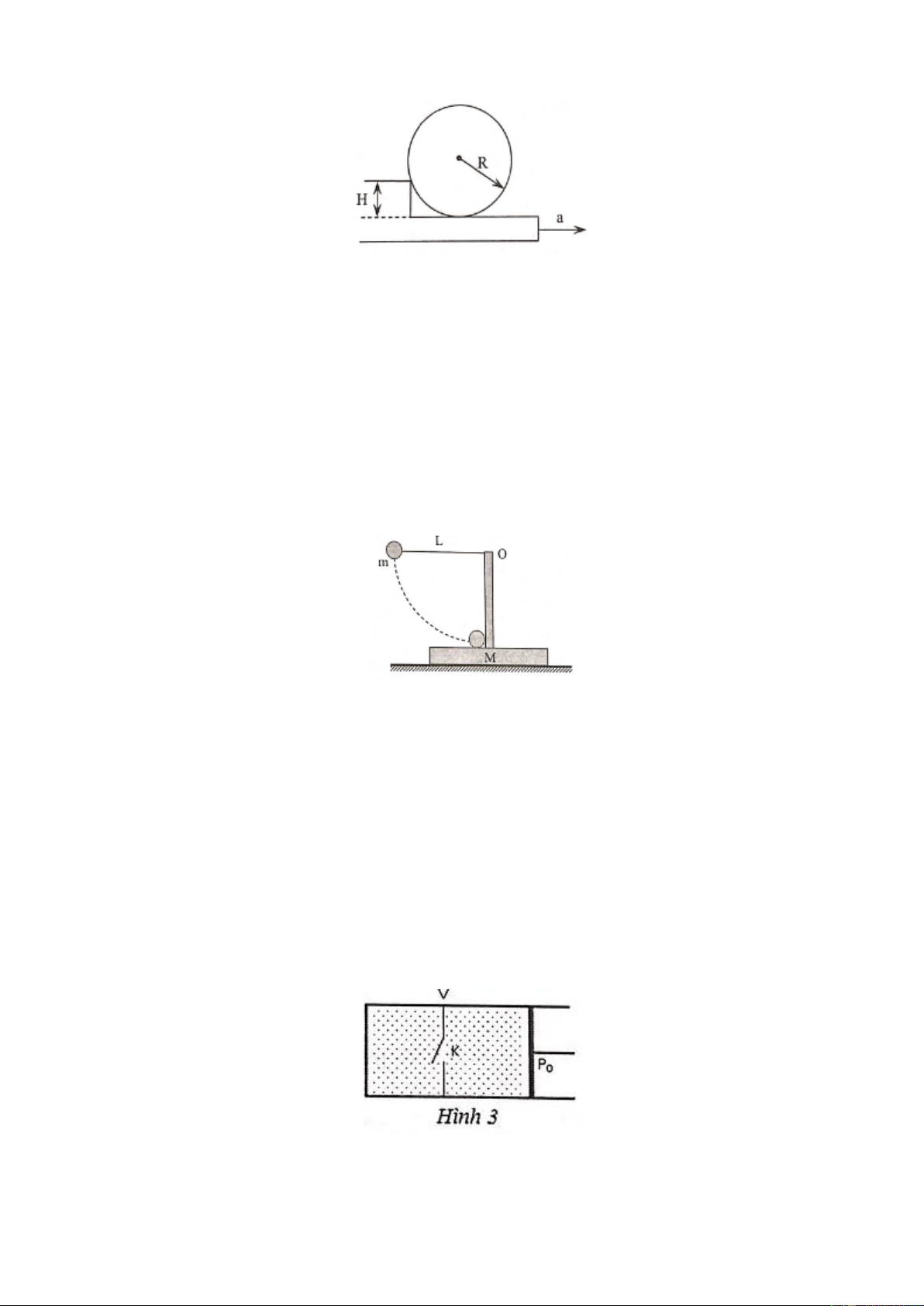
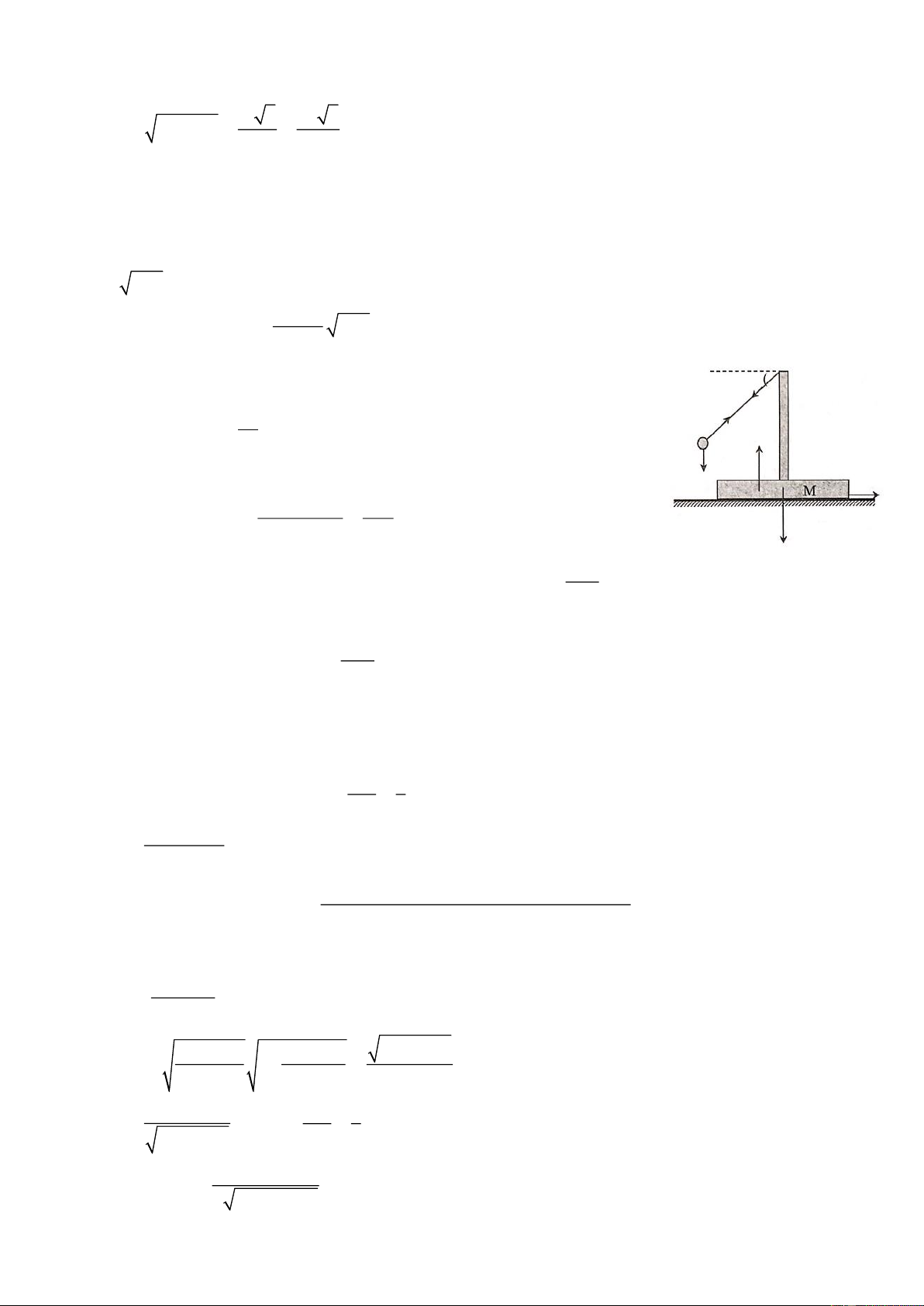
Dùng một sợi dây mảnh, nhẹ, không dãn, chiều dài L để treo quả cầu nhỏ vào đầu trụ gỗ có đế đặt
trên mặt bàn ngang và phẳng như hình vẽ. Khối lượng quả cầu là m, khối lượng của trụ và đế là M =
4m. Đưa quả cầu đến vị trí dây treo nằm ngang và thả nhẹ. Coi va chạm giữa quả cầu và trụ hoàn toàn
không đàn hồi và sự va chạm không gây ra chuyển động quay cho hệ.
a. Tính vận tốc của hệ ngay sau va chạm. Biết rằng đế gỗ không dịch chuyển trong suốt quá trình rơi.
b. Sau va chạm, hệ dịch chuyển được độ dài bao xa thì dừng lại? Biết hệ số ma sát giữa đế và mặt bàn là = = . 1 n
c. Để đế gỗ không dịch chuyển trong suốt quá trình quả cầu rơi xuống thì hệ số ma sát nghỉ giữa
mặt bàn và đế gỗ phải có giá trị nhỏ nhất là bao nhiêu? Câu 5: (5 điểm)
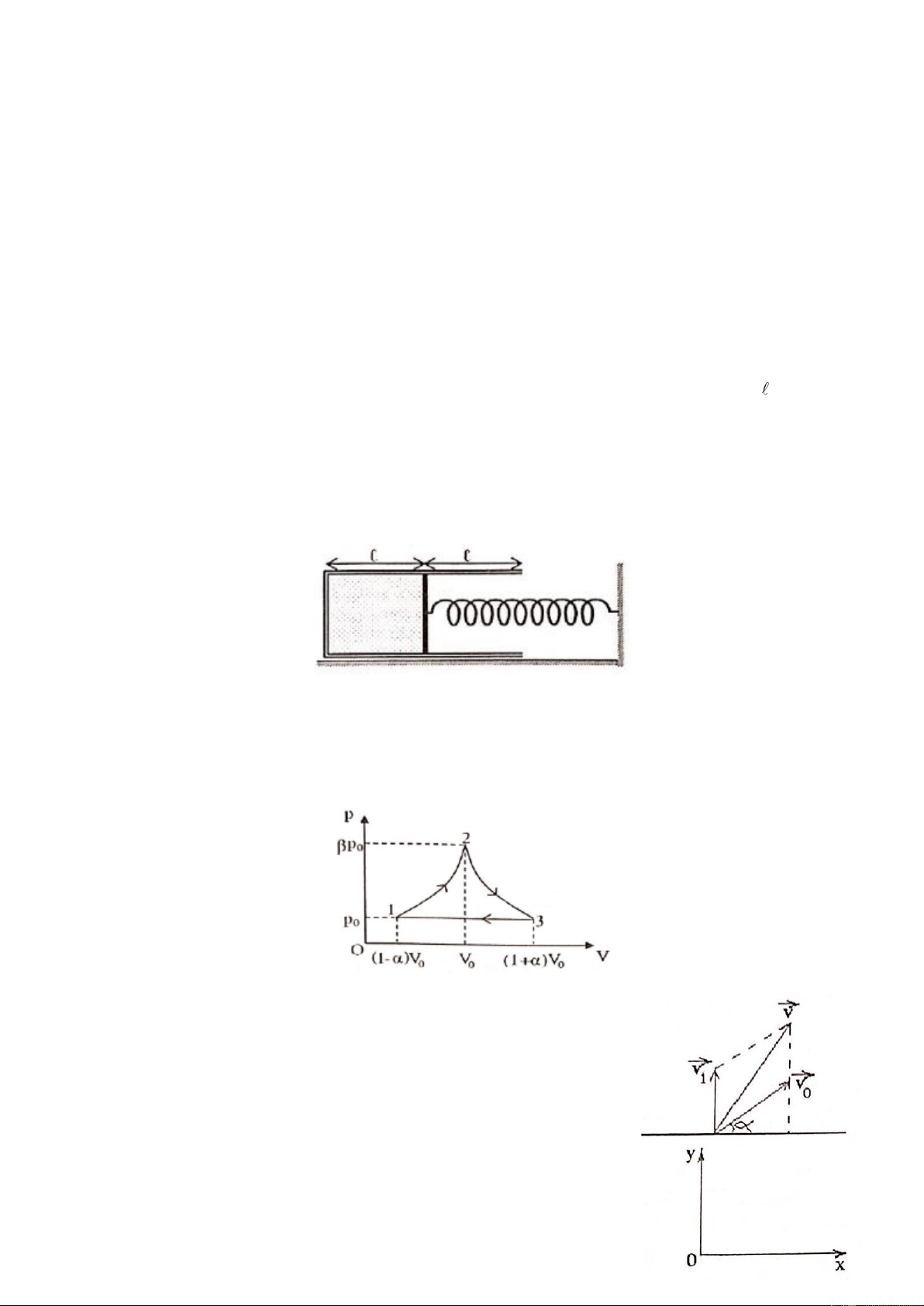
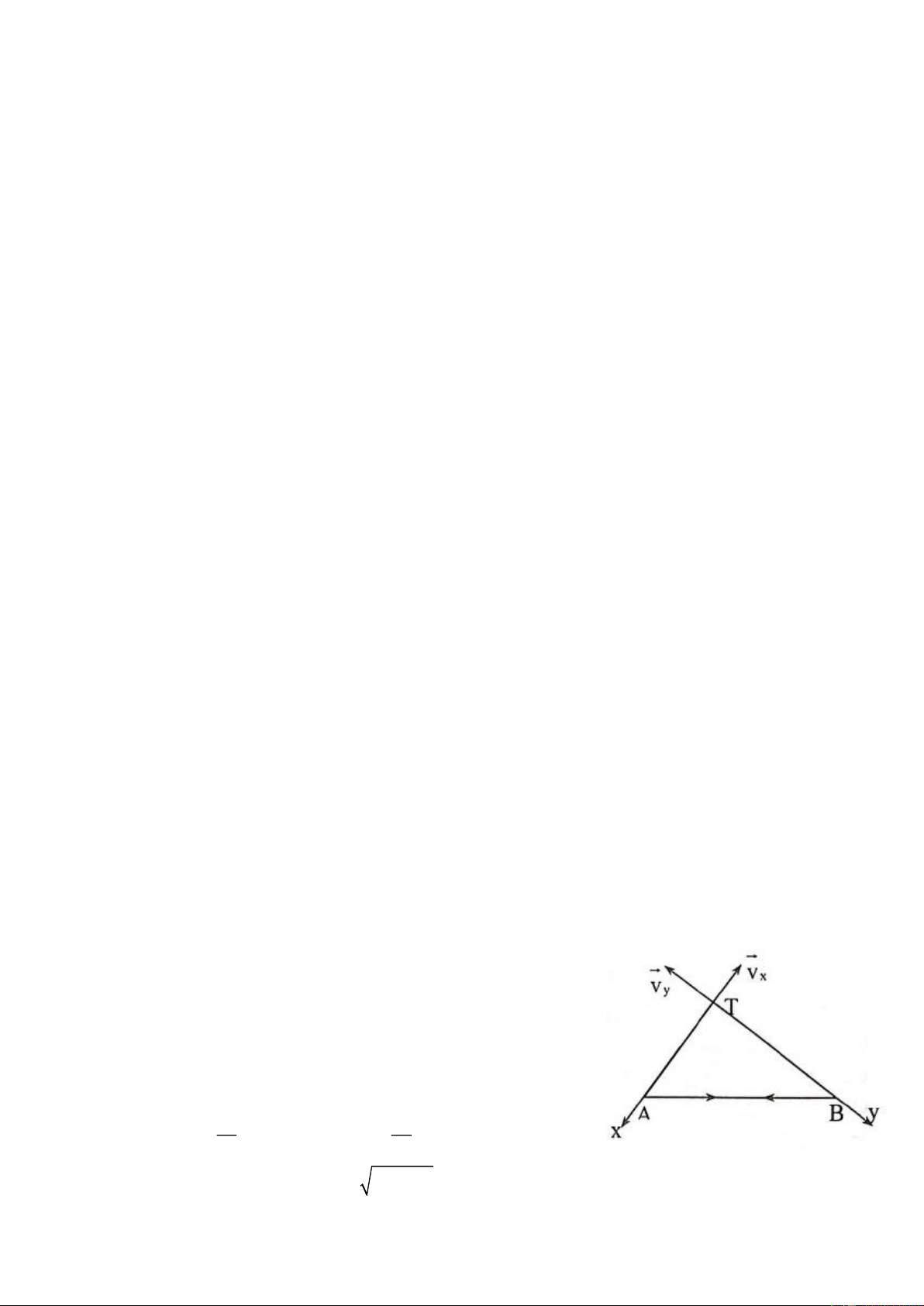
Hệ gồm một xilanh và một pittông có khối lượng tổng cộng là m, xilanh có chiều dài 2 , pittông có
tiết diện là S và được nối với tường cố định bằng một lò xo nhẹ có độ cứng là k. Ban đầu pittông nằm
chính giữa xilanh và trong xilanh có chứa khí lý tưởng ở áp suất p , nhiệt độ T . Cần tăng chậm nhiệt 0 0
độ của khối khí trong xilanh lên một lượng T là bao nhiêu để thể tích của nó tăng lên gấp đôi? Biết
xilanh có thể trượt trên mặt sàn nằm ngang với hệ số ma sát = = . Bỏ qua ma sát giữa xilanh và t n
pittông. Áp suất khí quyển là p . 0 Câu 6: (5 điểm)
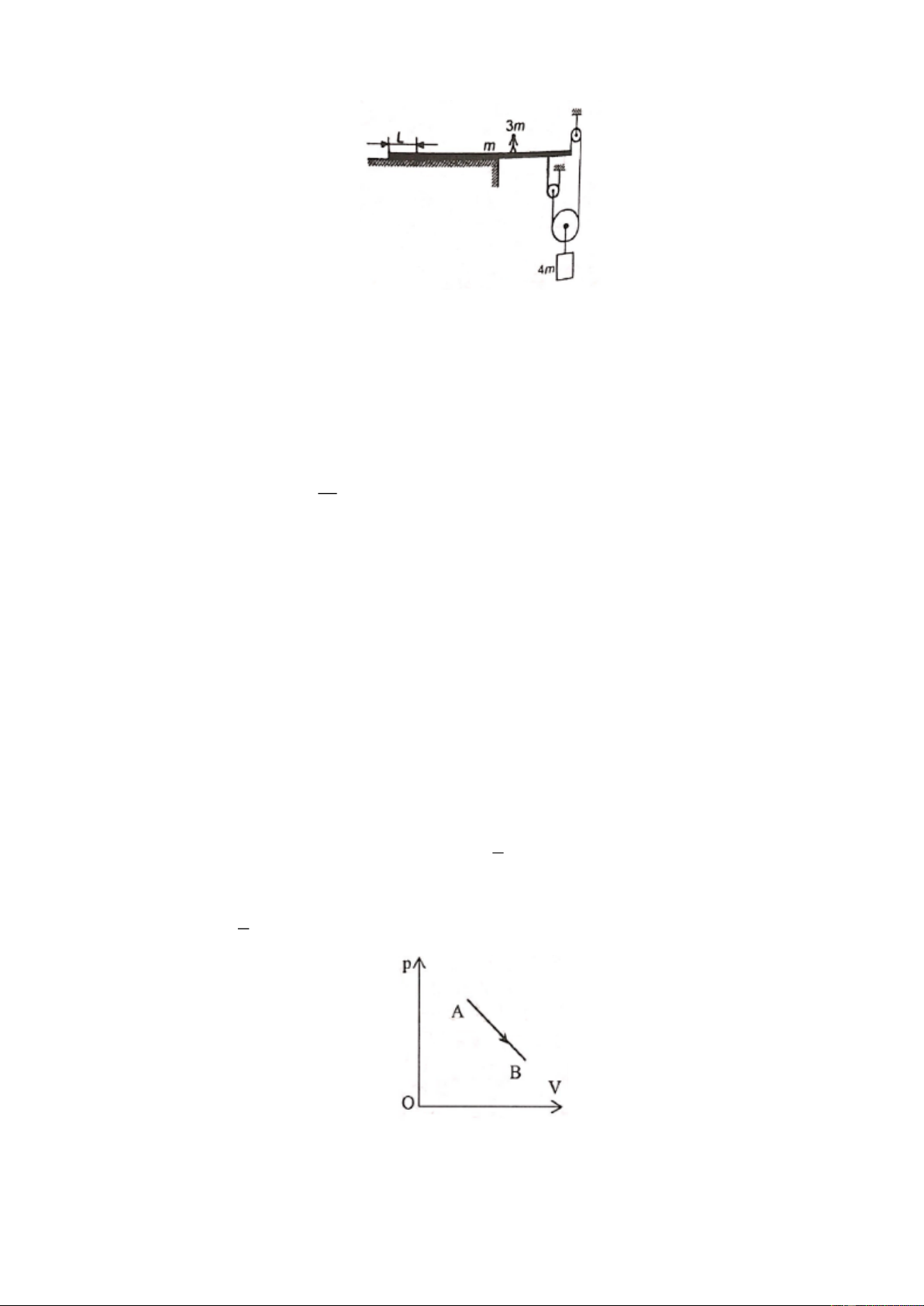
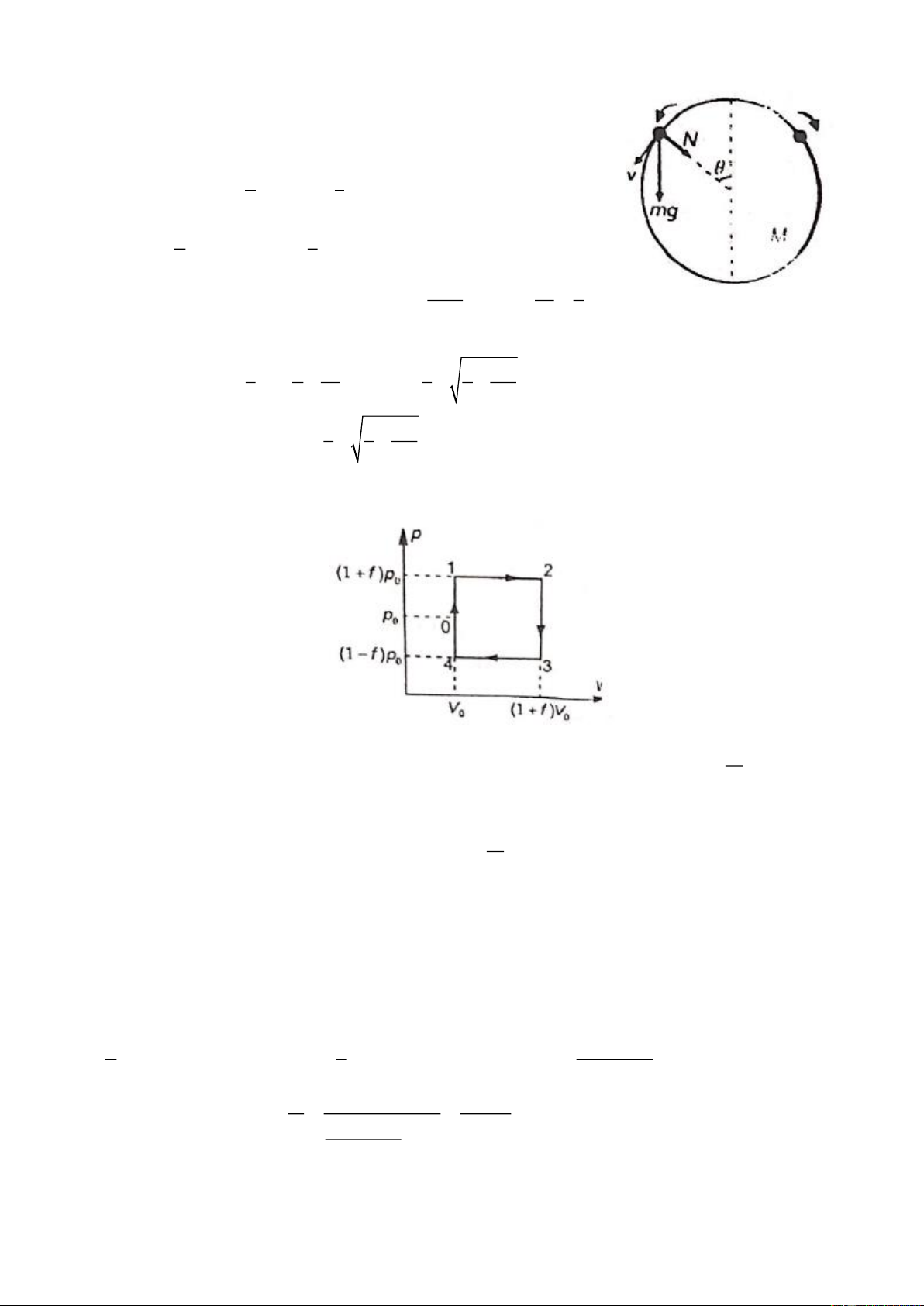
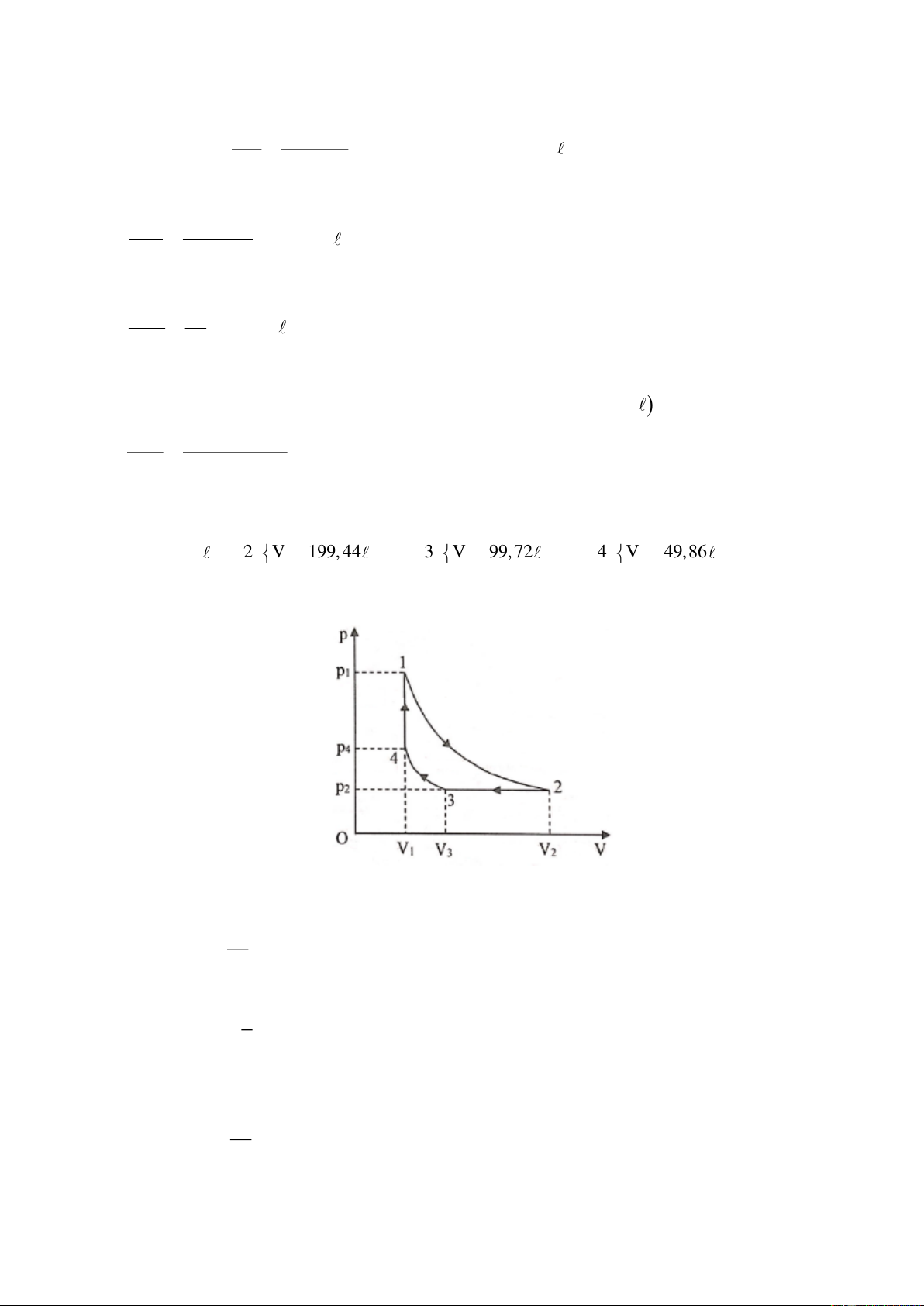
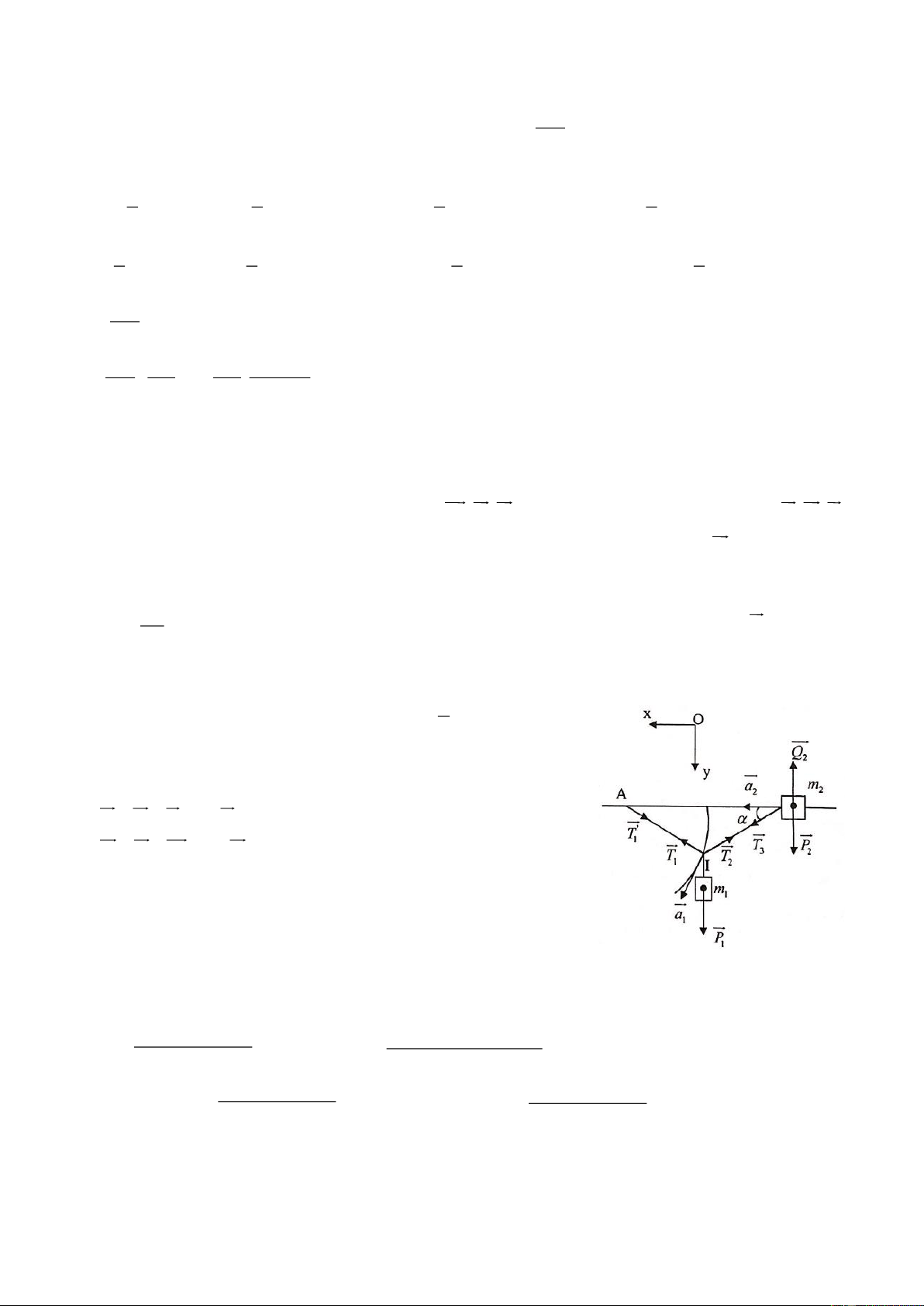
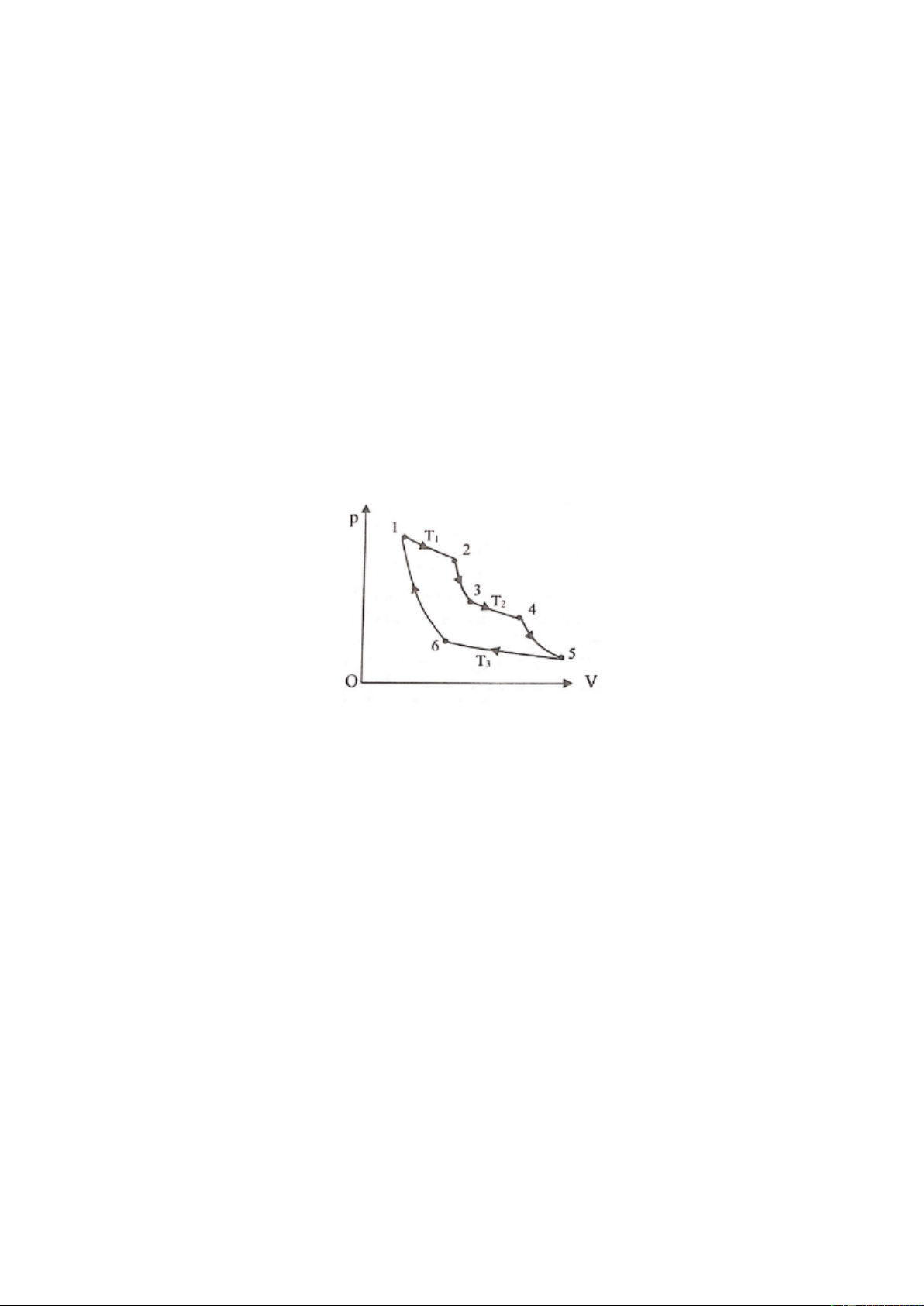
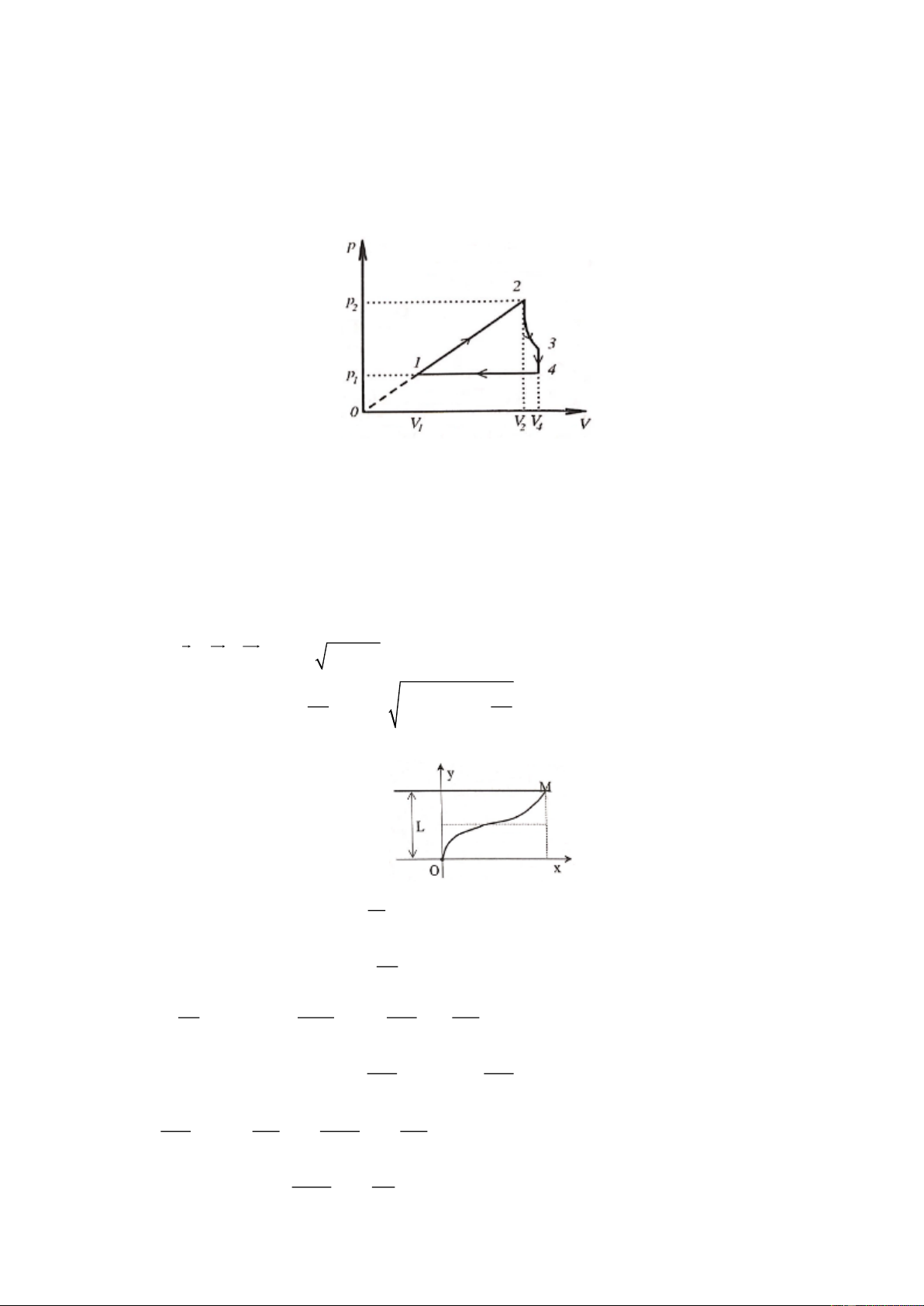
Một mol khí lý tưởng thực hiện một chu trình 1 – 2 – 3 – 1 như hình vẽ: 2 – 3 là quá trình đoạn
nhiệt; quá trình 1 – 2 có đường biểu diễn đối xứng với đường biểu diễn của quá trình 2 – 3 qua đường
thẳng đứng; 3 – 1 là quá trình đẳng áp. Tính hiệu suất của chu trình này theo , ,
với là hệ số đoạn nhiệt HƯỚNG DẪN GIẢI Câu 1:
a. Tính thời gian từ lúc ném đã đến lúc nó rơi xuống mặt đất Sau 4s độ 1 1
cao mặt trên côngteno là: 2 2 h + at = 3 + .0,5.4 = 7 m 2 2
Vận tốc của côngteno lúc đó: v = a.t = 0, 5.4 = 2 m / s 1
Gọi v là vận tốc của viên đá đối với côngteno thì vận tốc viên đá đối với đất: v = v + v 0 0 1 3
Chiếu lên Ox: v = v cos = 5, 4. = 2,7 3 m / s x 0 ( ) 2 5, 4 Oy: v = v + v sin = 2 + = 4,7 m / s y 1 0 ( ) 2
Chọn trục Oxy như hình vẽ gắn vào mặt đất. Phương trình chuyển động của hòn đá theo phương Oy: 2 gt 2 y = 7 + v t − = 7 + 4,7.t − 5t y 2
Lúc đá rơi xuống đất: 2
y = 0 5t − 4, 7t − 7 = 0 t = 1, 74s
b. Tầm bay xa hòn đá: L = v t = 2, 7. 3.1, 74 = 8,14m x Câu 2:
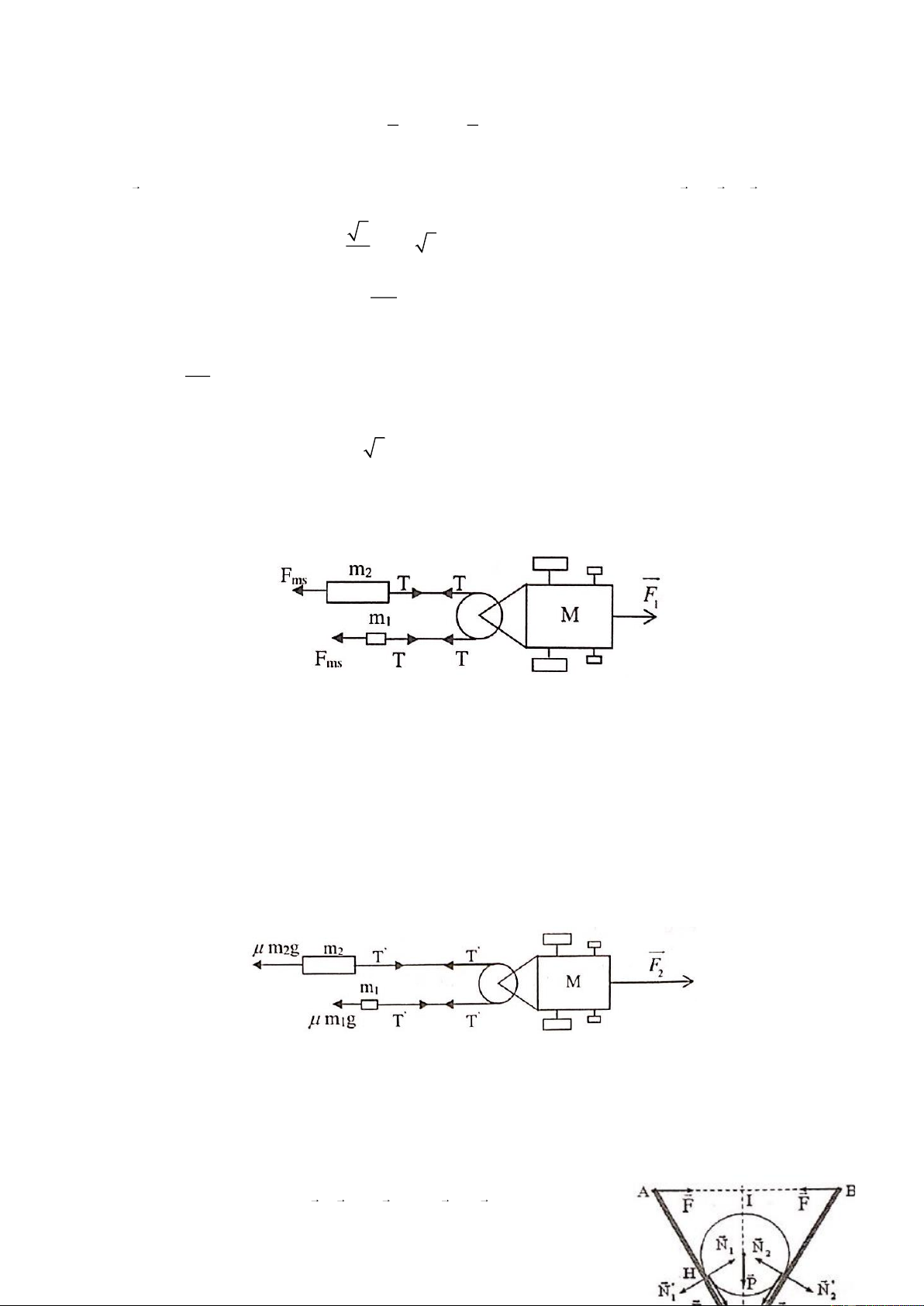
Lực ma sát nghỉ cực đại tác dụng lên m là F = m g 1 ms 1
Lực ma sát nghỉ cực đại tác dụng lên vật là F = m
g → vật m chưa chuyển động. ms 2 2
Điều kiện để xe và vật m bắt đầu chuyển động: 1 F = 2T = 2 m g 1 1 F = 0, 4 N 1 ( )
Khi vật m bắt đầu chuyển động tức xe và vật m đã chuyển động có gia tốc. 2 1
Định luật 2 Newto áp dụng cho: Xe: F − 2T ' = Ma (1) 2 1 Vật m : T '− m g = m a (2) 1 1 1 2 Vật m : T '− m g = 0 (3) 2 2
Do xe di chuyển một đoạn S thì vật m di chuyển một đoạn 2S trong cùng thời gian → a = 2a 1 2 1 (3) → T' = m g 2 (2) → m g − m g = m .2a → a = 2 g 2 1 1 1 1 ( ) 1 → F −10 m g = M.2 g = 2 g m + M = 4 N 2 1 ( 2 ) ( ) Câu 3:
- Phương trình cân bằng lực: P + + + + = m F s1 Fms2 N N 0 1 2
- Chiếu lên trục OI: −P − F cos − F
cos + N sin + N sin = 0 ms1 ms2 1 1
Do đối xứng: N = N = N F = F = F 1 2 ms1 ms2 ms 2N sin − P F = ms 2 cos − − Để 2N sin P
trụ không trượt lên: F N → N ms 2 cos
Xét thanh OA: chọn O là trục quay. Quy tắc momen: OI
N .OH = F.OI N.OH = F.OI N = F 1 OH OI AI a OA I O O H → = = 1 OH O H 2R 1 2N sin − P a PR → . F → F 2 cos 2R a (sin − cos )
Trường hợp 2: Trụ có khuynh hướng trượt xuống tương tự như trên: chú ý các lực ma sát hướng ngược lại. PR
- Điều kiện để trụ không trượt xuống: F a (sin + cos ) PR PR
* Điều kiện để trụ đứng yên: ( + ) F a sin cos a (sin − cos ) Câu 4:
a. Gọi vận tốc quả cầu trước và sau khi va chạm là v và v’: v = 2gL = ( + ) m mv m M v ' v ' = 2gL m + M
b. Sau khi va chạm dưới tác dụng của lực ma sát đế gỗ chuyển động chậm dần đến khi dừng lại.
Quãng đường đế gỗ dịch chuyển được là x: − = − ( + ) '2 v f x 0 m M (1) ms 2 Với f = m + M g (2) ms ( ) 2 m L L Từ (1) và (2) cho: x = = (m + M)2 25 2 mv
c. Gọi góc giữa phương ngang và dây treo là : mgL sin = (3) 2 2 mv T − mg = (4) 2 f − T cos = 0 (5) ms N − T sin − Mg = 0 (6) Từ (3) và (4) suy ra: T = 3mg.sin (7) Từ (5) và (7) suy ra: f = 3mg.sin . cos (8) ms
Để đế gỗ không di chuyển thì: f N (9) ms sin 2 sin 2
Từ (6), (7), (8) và (9), ta có: = 2M 8 2 2 + 2sin + 2sin 3m 3 Đặ sin 2 t y = → = y min max 8 2 + 2sin 3 3 Biến đổi ta được: y = 4 7 tan + tan
Áp dụng bất đẳng thức Côsi: y 0,28, suy ra = 0, 28 max min Câu 5:
Vì ban đầu áp suất bên trong và áp suất bên n đều bằng P nên lò xo không biến dạng. 0
Trường hợp 1: Nếu , khi đó xilanh sẽ đ F F hay kl mg đứng yên h ( msn )max kl P + 0 P Sl S kl
Gọi T là nhiệt độ cuối cùng của khối khí thì: 0 = .2Sl → T = 2T 1+ 0 T T SP 0 0 2kl Từ đó: T = T − T = T 1+ 0 0 SP 0
Trường hợp 2: kl m g mg Do nung chậm nên: kx = m g x = k
Gọi P là áp suất chất khí trong xilanh ở thời điểm cuối: 1 mg P S = P S + kx = P S + m g P = P + 1 0 0 1 0 S
Áp dụng phương trình trạng thái có: mg P + 2lS 0 P Sl S mg 0 = → T = 2T 1+ 1 0 T T P S 0 1 0 2 m g Từ đó tìm được: T = T − T = T 1+ 1 1 0 0 SP 0 Câu 6:
Áp dụng phương trình trạng thái của khí lý tưởng ta có: (1−)p V p V 1+ p V 0 0 0 0 ( ) 0 0 T = , T = , T = 1 2 3 R R R C R Do
p = và C − C = R nên C = C p V V −1 V
Do quá trình 2 → 3 là quá trình đoạn nhiệt ta có: Q = 0 23 U = C (T − T ) p V 0 0 = − +1+ 23 V 3 2 ( ) −1
Công chất khí sinh ra trong quá trình 2 → 3 là: A = − U = C (T − T ) p V 0 0 = −1− 23 23 V 3 2 ( ) −1
Do quá trình 1 → 2 và 2 → 3 đối xứng qua đường thẳng đứng nên công chất khí sinh ra trong hai quá p V trình bằng nhau: 0 0 A = A = −1− 12 23 ( ) −1 U = C (T − T ) p V 0 0 = −1+ 12 V 2 1 ( ) −1
Nhiệt lượng khí nhận được trong quá trình 1 → 2 là: 2p V 0 0 Q = A + U = −1 12 12 23 ( ) −1
Quá trình 3 →1 là đẳng áp: U = C (T − T ) p V 0 0 = 2 − 31 V 1 3 ( ) −1 A = p V − V = p V 2 − 31 0 ( 1 3 ) 0 0 ( ) 2p V
Nhiệt lượng khí truyền ra môi trường: 0 0 Q = A + U = −1 31 31 31 ( ) −1 2p V
Tổng công mà khí thực hiện: 0 0 A ' = A ' + A ' + A ' = −1− 12 23 31 ( ) −1 A '
Hiệu suất của chu trình này là: H = = 1− Q −1 12
THPT CHUYÊN BẾN TRE – BẾN TRE Câu 1: (5 điểm)
Trên quãng đường nhất định, một chất điểm chuyển động nhanh dần đều không vận tốc đầu với gia
tốc a mất thời gian T. Tính thời gian chất điểm chuyển động trên quãng đường này nếu chuyển động T
của chất điểm là luân phiên giữa chuyển động với gia tốc a trong thời gian T = và chuyển động 1 10 đề T u trong thời gian T = . 2 20 Câu 2: (5 điểm)
Trên mặt phẳng nằm ngang có một nêm khối lượng m = 4kg , chiều dài mặt phẳng nghiêng 2 L = 12m và 0
= 30 . Trên nêm đặt khúc gỗ m = 1kg . Biết hệ số ma sát giữa gỗ và nêm = 0,1. Bỏ 1
qua ma sát giữa nêm và mặt phẳng ngang. Tìm lực F đặt vào nêm để khúc gỗ trượt hết chiều dài mặt
phẳng nghiêng trong thời gian t = 2s từ trạng thái đứng yên. Lấy 2 g = 10m / s . Câu 3: (5 điểm)
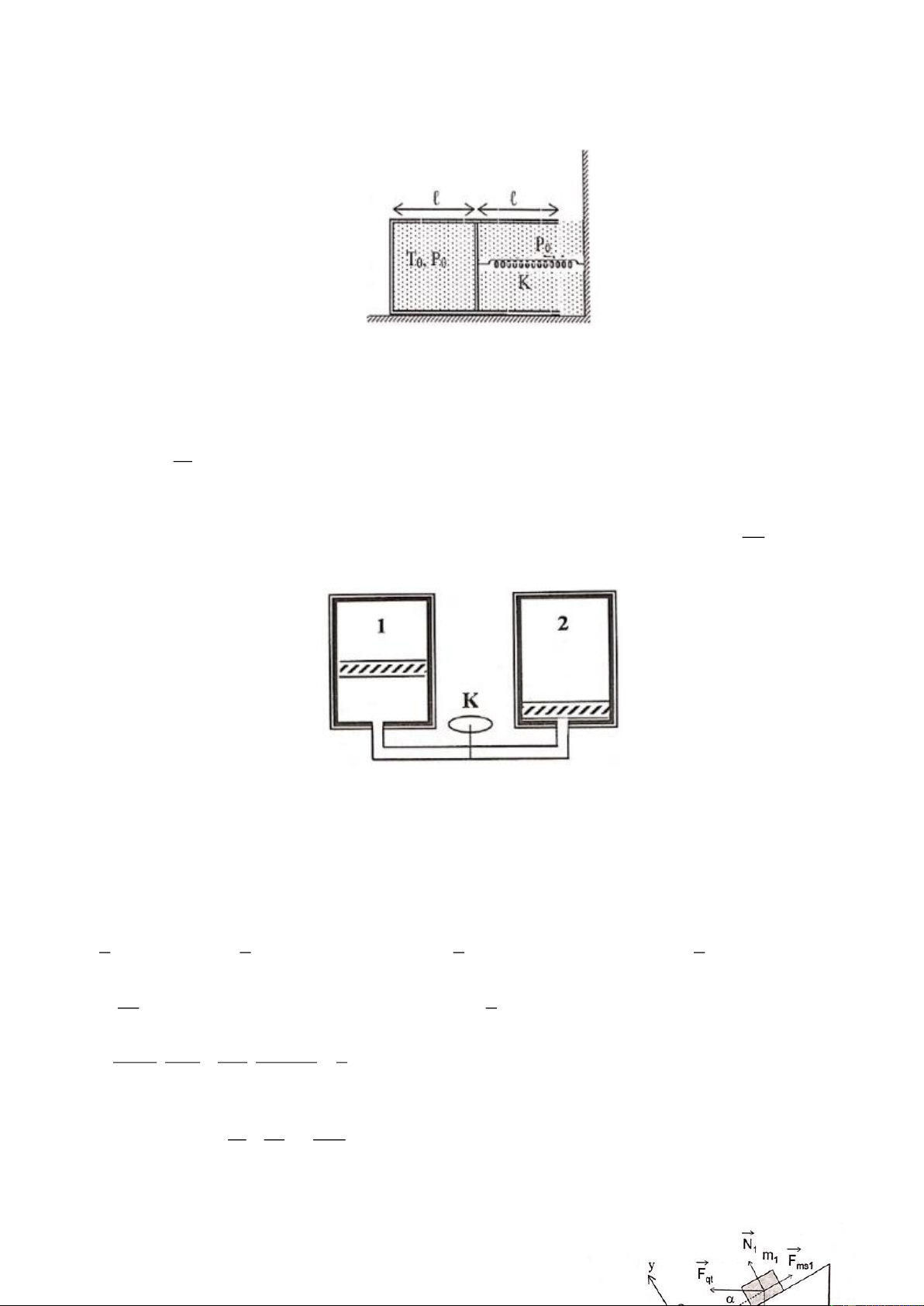
Thanh CD vuông góc với trục thẳng đứng Oz và quay quanh trục này với vận tốc góc . Hai hòn bi
A và B có khối lượng m và m nối với nhau bằng một lò xo có độ cứng k và có chiều dài tự nhiên l A B 0
. Hai hòn bi có thể trượt không ma sát trên thanh CD. Tìm các vị trí cân bằng của hai hòn bi? Cân bằng có bền không? Câu 4: (5 điểm)
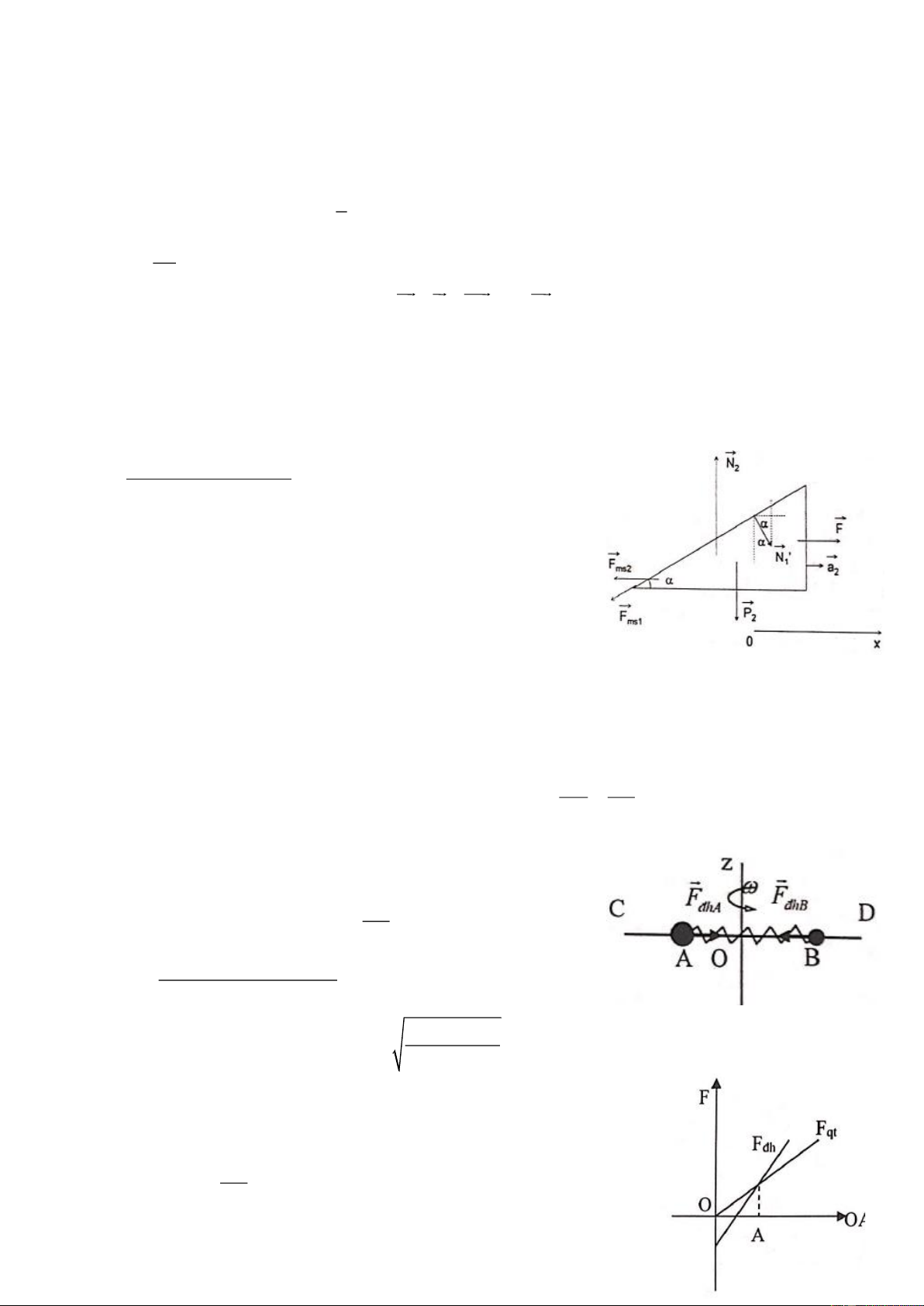
Một quả cầu nhỏ có khối lượng M = 1kg được treo vào điểm O bằng sợi
dây treo mảnh nhẹ, có chiều dài L = 1m. quả cầu M đang nằm cân bằng cách
mặt đất h = 0,5m thì quả cầu (2) có khối lượng m = 1kg chuyển động theo
phương ngang với vận tốc v = 10m / s tới va chạm xuyên tâm với quả cầu M. 0
Sau va chạm, quả cầu m bật ngược lại và rơi xuống đất, đi được quãng đường
theo phương ngang s = 2m, còn quả cầu M chuyển động lên trên. Khi dây treo
họp với phương thẳng đứng một góc 0
= 60 thì dây vướng đinh tại O’ cách
O một đoạn là x. Để quả cầu M chuyển động tròn quanh O’ thì khoảng cách x
tối thiểu là bao nhiêu? Lấy 2 g = 10m / s . Câu 5: (5 điểm)
Một xilanh chiều dài 2 , bên trong có một pittông có tiết diện S. Xilanh có thể trượt có ma sát trên
mặt phẳng ngang với hệ số ma sát (hình vẽ). Bên trong xilanh, phía bên trái có một khối khí ở nhiệt
độ T và áp suất bằng áp suất khí quyển bên ngoài P , pittông cách đáy khoảng . Giữa bức tường 0 0
thẳng đứng và pittông có một là xo nhẹ độ cứng K. Cần phải tăng nhiệt độ của khối khí trong xilanh
lên một lượng T bằng bao nhiêu để thể tích của nó tăng lên gấp đôi, nếu ma sát giữa xilanh và
pittông có thể bỏ qua. Khối lượng tổng cộng của xilanh và pittông bằng m. Câu 6: (5 điểm)
Hai xilanh giống hệt nhau được nối với nhau bằng một ống cách nhiệt có kích thước nhỏ, trên ống
nối có lắp một van K, lúc đầu K đóng. Trong xilanh 1, phía dưới pittông khối lượng M, có chứa một
lượng khí lí tưởng đơn nguyên tử có khối lượng mol , nhiệt độ T . Trong xilanh 2, có pittông khối 0 lượ M ng m =
và không chứa khí. Phần trên của pittông trong hai xilanh là chân không. Sau đó van K 2
được mở để khí từ xilanh 1 tràn qua xilanh 2. Xác định nhiệt độ của khí sau khi khí đã cân bằng nhiệt độ v
ng, biết rằng khi đó phần trên của pittông trong xilanh 2 vẫn còn khoảng trống. Cho = 0,1, với v M
là số mol khí; ma sát giữa pittông và xilanh là rất nhỏ. HƯỚNG DẪN GIẢI Câu 1:
Gọi n là số lần chất điểm chuyển động với thời gian T 2 Ta có: 1 1 1 1 1 2 2 2 2 aT + aT T + aT + aT T + 2aT T + aT + aT T + 3aT T +...+ aT + (n − ) 2 1 aT T + naT T aT 1 1 2 1 1 1 1 2 1 1 1 1 2 1 1 1 1 2 2 2 2 2 2 2 T 1 1 1 + 3 + 5 +...+ (2n − ) 1 + T T 1+ 2 + ... + n aT 1 2 ( ) 2 2 2 1 2n.n 1 (n + ) 1 n 1 2 . + .
3n + n − 200 0 n = 8 2.100 2 200 2 2
Vậy thời gian chất điểm chuyển động: = ( T T 24T t 8 T + T = 8 + = = 1, 2T 1 2 ) 10 20 20 Câu 2:
Gọi a là gia tốc của nêm so với mặt đất 2
a là gia tốc của vật m đối với nêm 12 1 - Xét m : 1
Chọn hệ quy chiếu gắn kiền với nêm như hình vẽ 1
Gia tốc của m đối với 2 m : L = a .t 1 2 12 2 2L 2 a = = 6m / s 12 2 t
Áp dụng đinh luật II Niuton cho vật m : F + P + F = m a 1 qt 1 ms1 1 12 Theo phương Ox: cos .
F + m gsin − F = m a qt 1 ms1 1 12
Theo phương Oy: N = m g cos − m a sin 1 1 1 2 → F = N
= m g cos − m a sin ms 1 ( 1 1 2 )
Ta được: m g sin + m a cos − m g cos + m a sin = m a 1 1 2 1 1 2 1 12 a + g cos − gsin 12 2 a = 2m / s 2 cos + sin - Xét nêm:
Chọn hệ quy chiếu gắn với đất F + N ' sin − F cos = m a 1 ms1 2 2 N = m g cos = m a sin 1 1 1 2
F = m g cos − m a sin ms ( 1 1 2 ) 2
F = m a + m cos − (g + a ) 2 sin .
cos + a sin 4,9N 2 2 1 2 2 Câu 3:
Chọn hệ quy chiếu gắn với O, hai hòn bi A và B chuyển động tròn đều với vận tốc góc , các lực tác
dụng lên A và B như hình vẽ. Ta có: 2 F = m a kl = m OA dhA A nA A OA m 2 2 B m OA = m OB = (1) A B 2 F = m a kl = m OB OB m dhB B nB A B Mặt khác: F
= F = kl = k OA + B− l (2) dhA dhB ( 0 )
Thay (1) vào (2) ta được: m F
= k OA + OB − l = k OA1+
− l = m OA dhA ( 0 ) A 2 0 A m B km l B 0 OA = (3) k (m + m ) 2 − m m A B A B k (m + m A B )
Ta có điều kiện OA 0 nên suy ra: (4) m m A B
Bây giờ ta xét xem hệ cân bằng có bền không, xét sự cân bằng của bi A
chẳng hạn, ta chọn hệ qui chiếu gắn với bi A, khi đó bi A sẽ chịu tác
dụng của lực đàn hồi và lực quán tính ly tâm là: m A F = k OA1+ − l và 2 F = m OA dhA 0 m qt A B m + m Từ (4) ta có 2 A B m k
tức là hệ số góc của F nhỏ hơn hệ số góc của F nên ta mới vẽ A m qt dh B
được đồ thị hai lực bên cạnh.
Điểm A là vị trí cân bằng hiện tại của quả cầu A nếu vì lý do gì đó mà OA tăng lên thì ta thấy ngay F dh
sẽ lớn hơn F nên cũng sẽ kéo bi A trở lại vị trí cũ. Vậy cân bằng của hệ là bền. qt Câu 4:
Gọi v là vận tốc sau va chạm quả cầu M, và v’ là vận tốc sau va chạm quả cầu m. Sau va chạm quả cầu
m là chuyển động ném ngang nên ta được: s 2 v ' = = = 2m / s 2h 2.5 g 10
Áp dụng định luật bảo toàn động lượng cho hệ (m, M) ngay trước và sau va chạm ta có: m (v + v ' 1 10 + 2 0 ) ( ) mv = Mv − mv ' v = = = 6m / s 0 M 2
Khi dây treo chạm vào đinh O’ thì quả cầu M có thể chuyển động tròn quanh O’ thì tại vị trí cao nhất lực căng dây T 0 .
Theo định luật bảo toàn cơ năng: 1 1 1 3 MgR 1 2
Mv = Mg l + (l − R ) 0 2 2 2 cos 60 + R + Mu Mv = Mgl + + Mu 2 2 2 2 2 2
Áp dụng định luật II Niuton cho quả cầu M tại vị trí cao nhất. Ta được: 2 2 Mu v − 3gl T = − Mg 0 R
= 0,3m x l − R = 0,7m R 2g Câu 5:
Trường hợp 1: F kl m
g kl . Khi đó xilanh sẽ đứng yên ms
Gọi T là nhiệt độ cuối cùng của khối khí thì: kl P + .2S l 0 P Sl S kl 0 = T = 2T 1+ 0 T T SP 0 0 kl Từ đó: T = T − T = T 1+ 0 0 SP 0
Trường hợp 2: m g kl
- Giai đoạn xilanh vẫn còn đứng yên: mg
Gọi x là độ nén cực đại của lò xo. Pittông còn đứng yên cho đến khi kx = m g x = k
Gọi T là nhiệt độ của khối khí tại thời điểm lò xo nén cực đại. P là áp suất chất khí trong xilanh ở 1 1 thời điểm này thì: mg P S = P S + kx = P S + m g P = P + 1 0 0 1 0 S
- Áp dụng phương trình trạng thái ta có: mg P + l + x S 0 ( ) P Sl S m g m g 0 = T = 1+ 1+ T 1 0 T T SP kl 0 1 0
- Giai đoạn xilanh dịch chuyển:
Khi T T thì pittông bắt đầu dịch chuyển, bắt đầu từ thời điểm này áp suất chất khí trong xilanh là 1 không đổi. Ta có: T S(l + x) T 1 x 2T m g 12 1 1 = = 1+ T = = 2T 1+ T 0 0 T S.2l T 2 l mg P S + 0 1 kl 2 m g Từ đó ta tìm được: T = T − T = T 1+ 0 0 SP 0 Câu 6:
Khi K mở, toàn bộ lượng khí chuyển qua xilanh 2
Kí hiệu: H là độ cao cột khí trong bình 1 khi K chưa mở 0
H và T lần lượt là độ cao và nhiệt độ cột khí trong xilanh 2 khi K mở và khí đã cân bằng nhiệt động
Áp dụng nguyên lý I nhiệt động lực học ta có: 3 ( v g vR T − T = MgH − mgH + H − H (1) 0 ) 0 ( 0 ) 2 2
Trước khi K mở, ở xilanh 1: Mg v P =
; V = H S → MgH = vRT → gH = RT (2) 0 0 0 0 0 0 0 S M
Sau khi K mở và khí đã cân bằng nhiệt động, ở xilanh 2: mg v P =
; V = HS → mgH = vRT → gH = RT (3) S m
Thế (2) và (3) vào (1) ta được: 3 ( v v v vT T − T = vR T − T + RT − RT 0 ) ( 0 ) 0 2 2 M m v 1+ 5M → T = T = 0,98T 0 0 2v 1+ 5M
THPT CHUYÊN HÙNG MẪN ĐẠT – KIÊN GIANG Câu 1: (5 điểm)
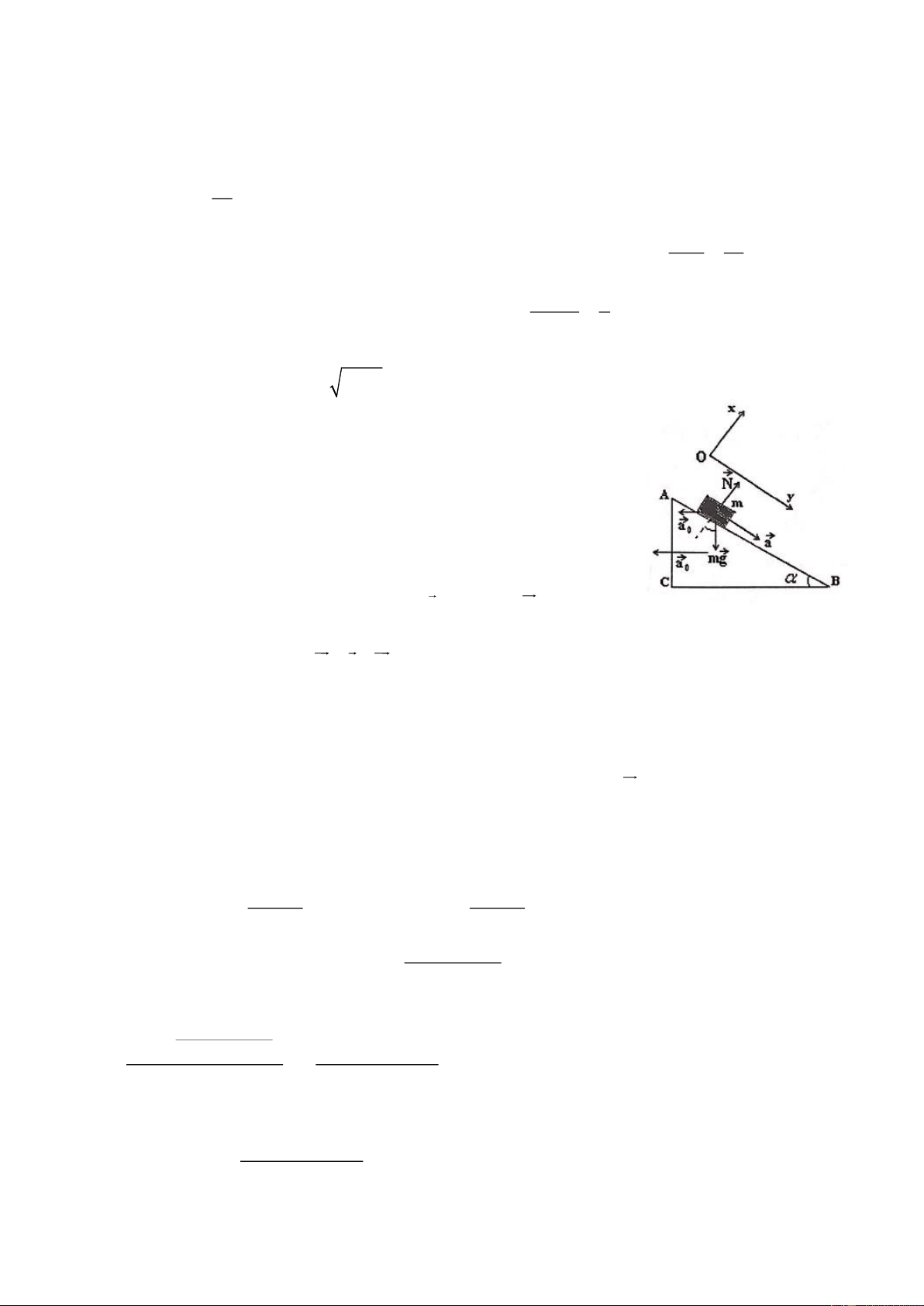
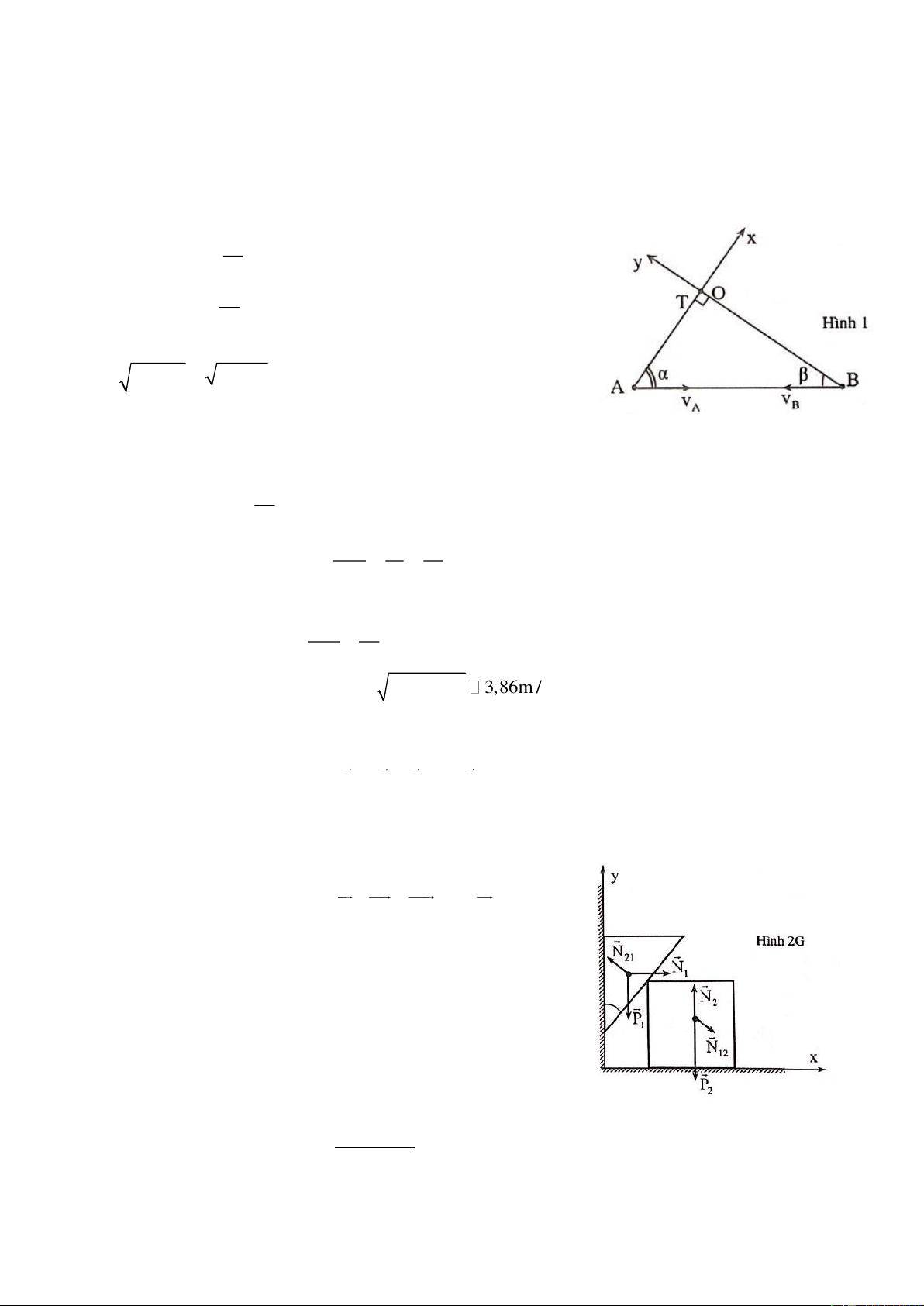
Hai cầu thủ bóng đá A và B chạy trên một đường thẳng đến gặp nhau với cùng tốc độ 5m/s. Để điều
hành tốt trận đầu, trọng tài chạy chỗ sao cho luôn đứng cách cầu thủ hậu vệ A 18m và cách cách cầu
thủ tiền đạo B 24m. Khi khoảng cách giữa A và B bằng 30m thì vận tốc và gia tốc của trọng tài là bao nhiêu? Câu 2: (5 điểm)
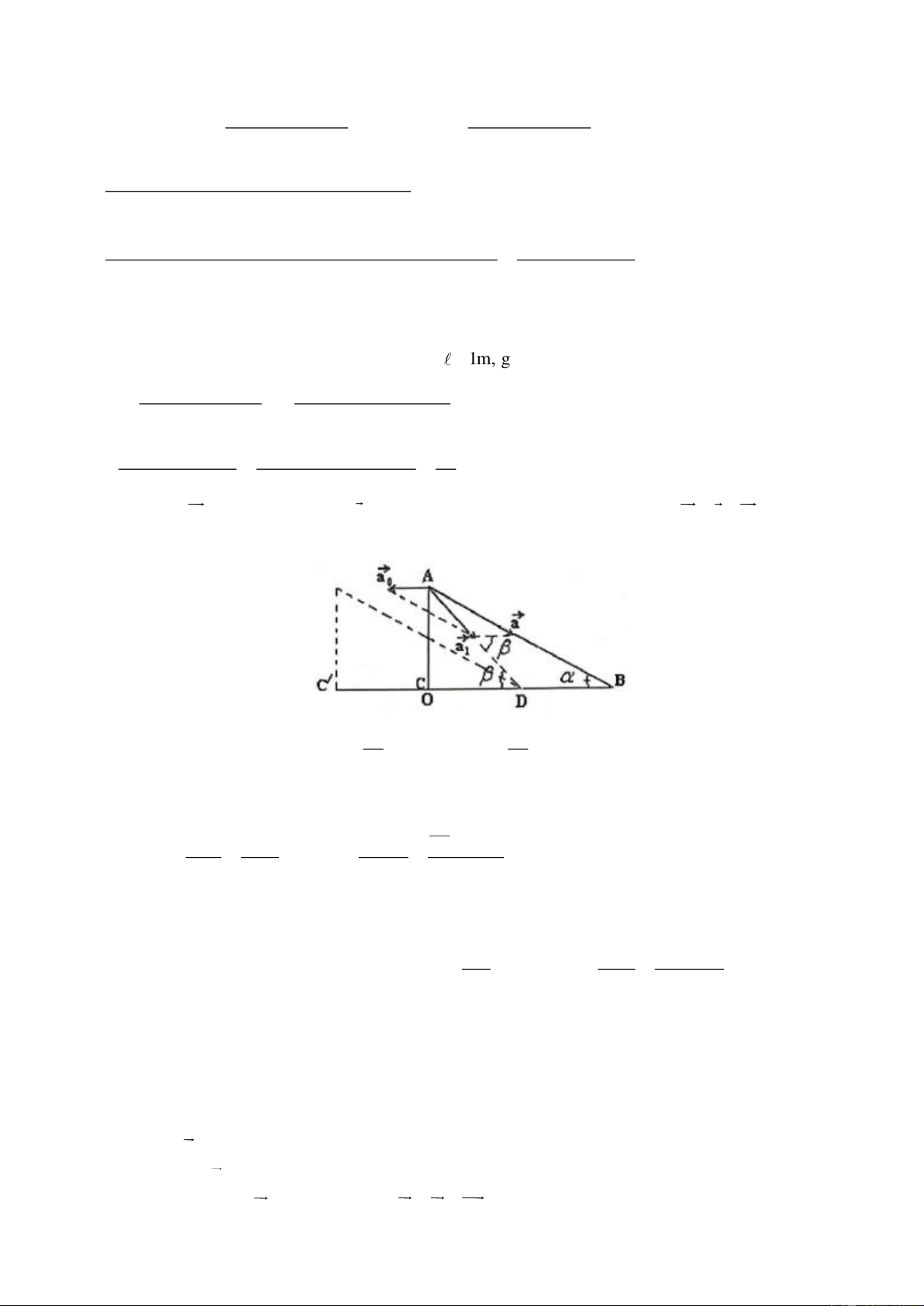
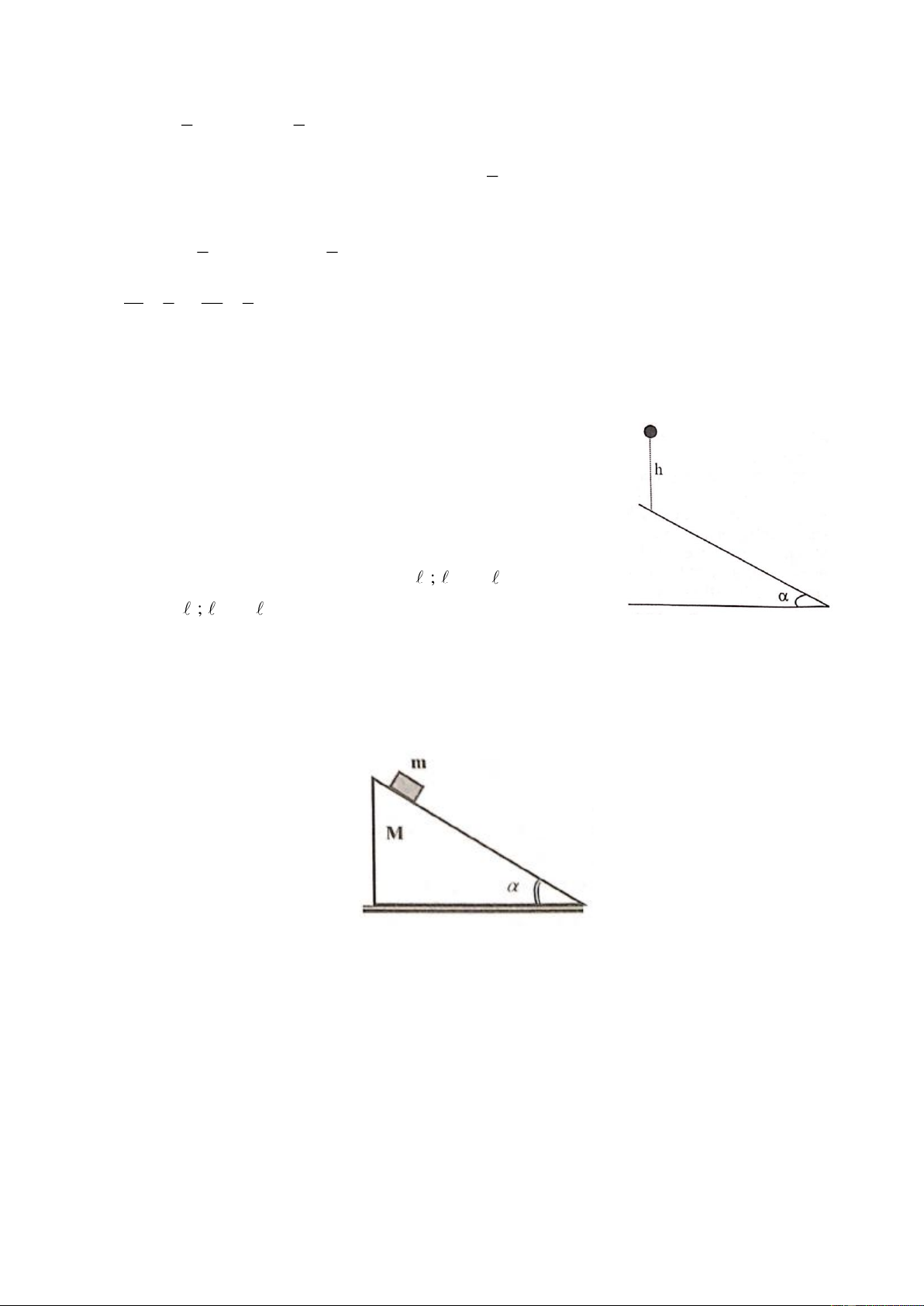
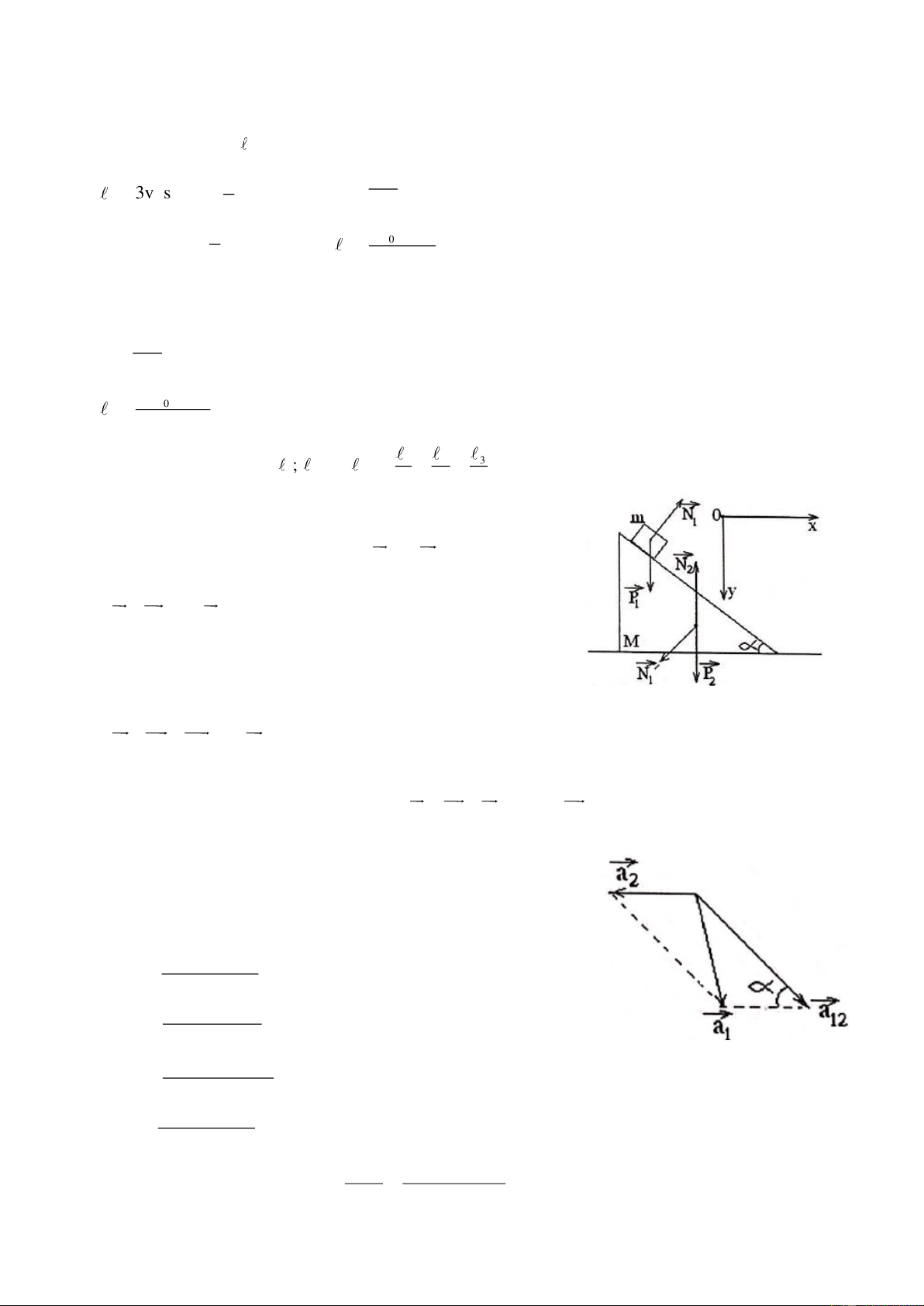
Một vật có khối lượng có thể trượt không ma sát trên một cái nêm ABC; 0
AB = , C = 90 , B = . Nêm ban đầu đứng
yên, khối lượng của nêm là M và có thể trượt không ma sát
trên mặt sàn nằm ngang như hình vẽ. Cho vật m trượt từ đỉnh A của nêm không vận tốc đầu.
a. Thiết lập biểu thức tính gia tốc a của vật đối với nêm và gia tốc a của nêm đối với sàn. 0
b. Lấy hệ tọa độ xOy gắn với sàn, ban đầu trùng với BCA. Tính hoành độ của vật m và của đỉnh C
khi vật trượt tới đỉnh B. Quỹ đạo của vật thường là gì? Cho 0 2 m = 0,1kg, M = 2m, = 30 , =1m, g =10m / s Câu 3: ( 5 điểm)
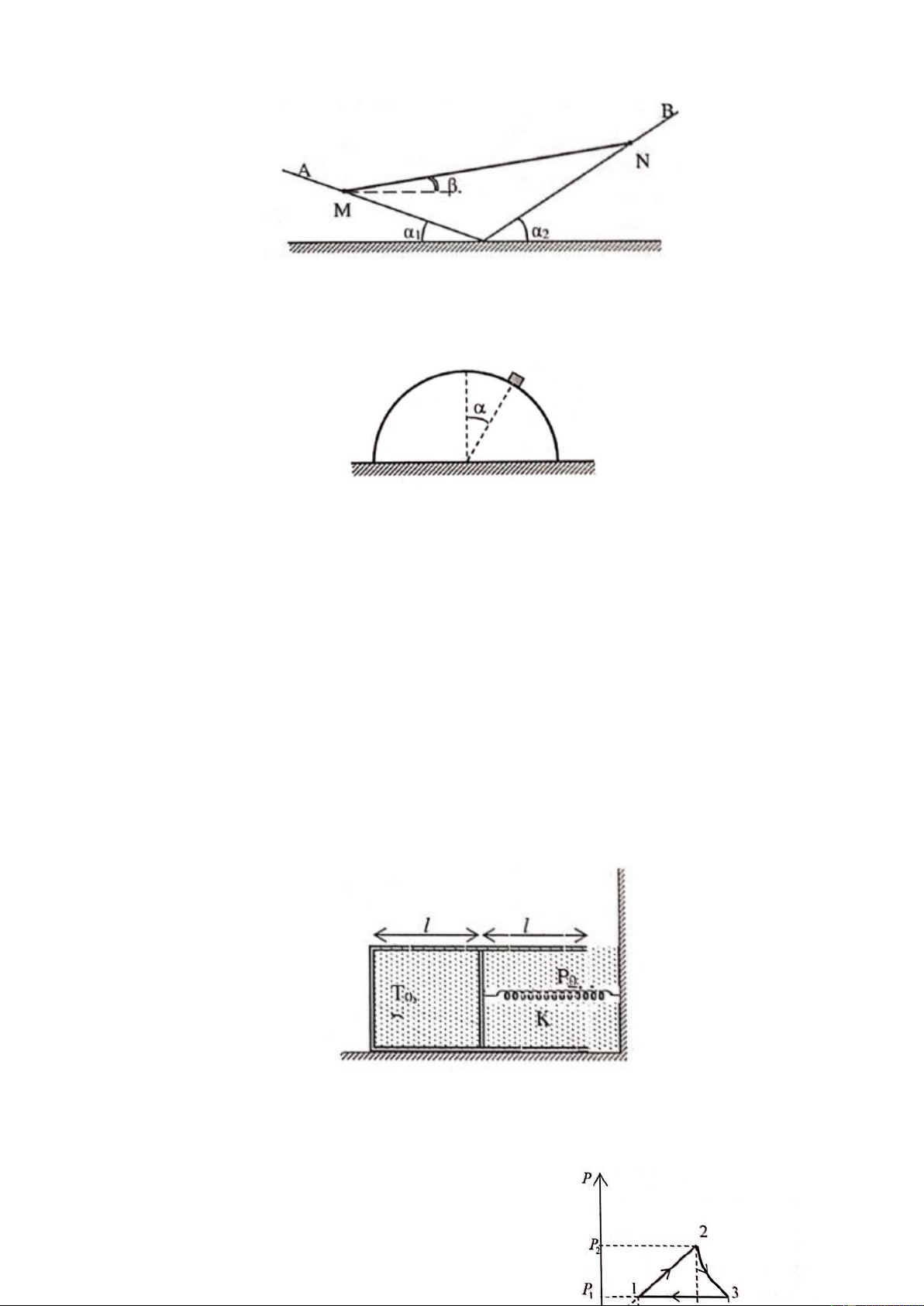
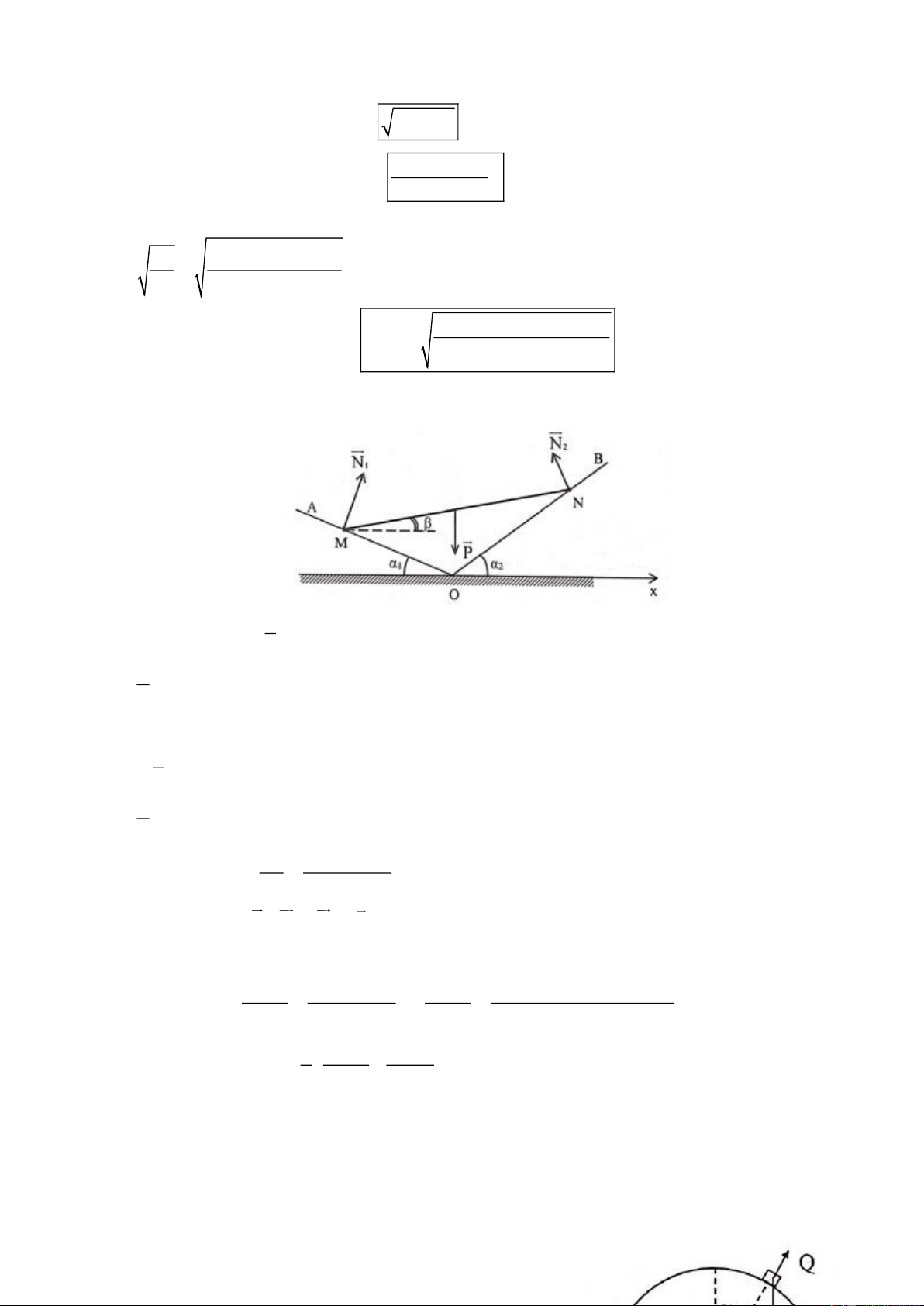
Một thanh đồng chất BC tựa vào tường thẳng đứng tại B nhờ dây AC dài L
hợp với tường một góc như hình. Biết thanh BC có độ dài d. Hỏi hệ số ma
sát giữa thanh và tường phải thỏa điều kiện nào để thanh cân bằng? Câu 4: ( 5 điểm)
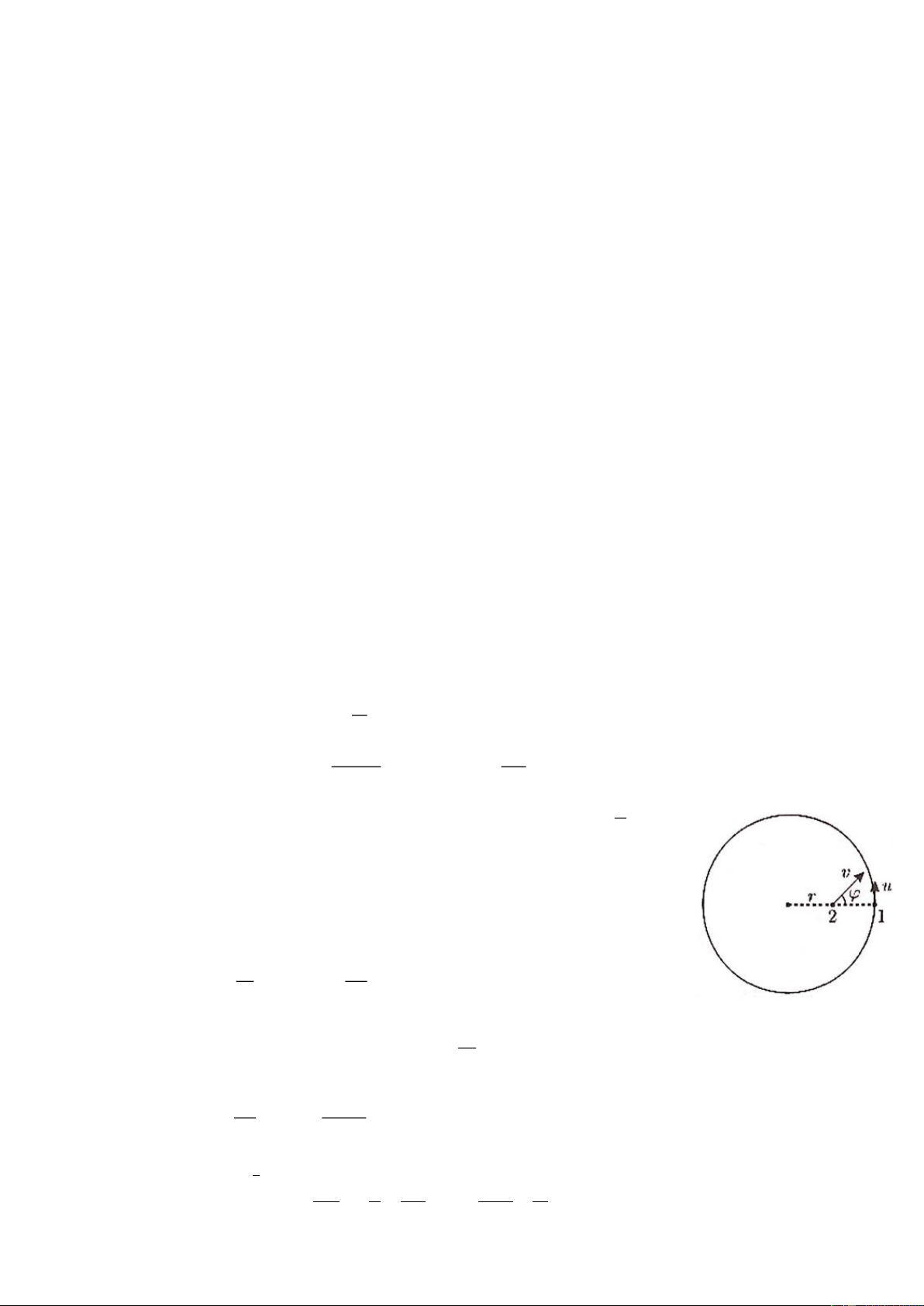
Một quả cầu nhẵn có khối lượng M và bán kính R trên mặt nhẵn nằm ngang. Từ đỉnh quả cầu trượt
tự do một vật nhỏ có khối lượng m như hình vẽ. Tỉ số m bằng bao nhiêu thì vật nhỏ rời mặt quả cầu ở M
độ cao 7R so với mặt bàn ? 4 Câu 5: ( 5 điểm)
Một xilanh tiết diện S đặt thẳng đứng gồm 2 ngăn chứa cùng một
chất khí lý tưởng đơn nguyên tử. Trong xilanh có hai pít-tông, mỗi pít-
tông có khối lượng m. Khoảng cách giữa đáy xilanh và pít-tông phía
dưới là H, khoảng cách giữa hai pit-tông là 2H.
Thành xilanh và pít-tông phía trên không dẫn nhiệt. Pít-tông phía dưới
dưới dẫn nhiệt và có thể bỏ qua nhiệt dung của nó. Mỗi pít-tông sẽ di
chuyển được một khoản bao nhiêu sau khi cấp cho khí một nhiệt
lượng Q ( từ dây đốt nóng như hình vẽ)?
Áp suất bên ngoài không đổi và bằng p . Bỏ qua ma sát. 0 Câu 6: ( 5 điểm)
Một mol khí lí tưởng thực hiện một chu trình 1→ 2 → 3 →1 như hình vẽ.
Quá trình 2 → 3 là quá trình đoạn nhiệt.
Quá trình 1 → 2 đối xứng với quá trình 2 → 3 qua đường thẳng đứng. Các thông số , , đã biết.
Tính hiệu suất của chu trình. HƯỚNG DẪN GIẢI Câu 1:
Vận tốc chuyển động của trọng tài:
- Khi khoảng cách giữa hai cầu thủ là 30m, tam giác ATB vuông tại T
- Vì khoảng cách giữa trọng tài và các cầu thủ là không đổi nên:
+ Vận tốc của trọng tài T và cầu thủ A trên phương Tx bằng nhau.
+ Vận tốc của trọng tài và cầu thủ B trên phương Ty bằng nhau. Với 18 24 V = −v. = 3 − m / s; V = −v. = 4 − m / s x y 30 30
Vậy tốc độ của trọng tài là 2 2 V = V + V = 5m / s T x y
Gia tốc của trọng tài:
- Xét chuyển động của trọng tài trong hệ quy chiếu quán tính gắn với cầu thủ A:
+ Cầu thủ B chuyển động với tốc độ : 5 + 5 = 10m/s
+ Trọng tài chuyển động trên đường kính tròn bán kính AT- theo phương By: 24 V = V ' =10. = 8m / s T/A y 30 2 V 32
- Gia tốc hướng tâm của trọng tài - gia tốc của trọng tài trên phương Tx: T/ A 2 a = = m / s x AT 9 2 VT/B(x) 3
- Tương tự: xét trong hệ quy chiếu gắn với cầu thủ B: 2 a = = m / s y BT 2
Vậy gia tốc của trọng tài là: 2 2 2 a = a + 3,86m / s x y Câu 2:
a. Tính gia tốc a của vật đối với nêm và gia tốc a của nêm đối với 0 sàn.
- Chọn hệ trục tọa độ xOy như hình vẽ.
Động lượng của hệ bằng 0
Vật đi xuống sang phải thi nêm phải sang trái
giá trị đại số gia tốc của nêm là a 0 0
- Vật m chịu tác dụng của 2 lực: Trọng lực mg , phản lực N của nêm vuông góc với AB
+ Gia tốc của vật đối với sàn: a = a + a 1 0
+ Phương trình chuyển động của vật:
Theo phương AB: mg sin = m(a + a cos (1) 0 )
Theo thương vuông góc với AB: N − mg cos = ma sin (2) 0
- Phương trình chuyển động của nêm chịu thành phần nằm ngang của −N
Chọn trục Ox trùng với hướng chuyển động của nêm - N sin = Ma (3) 0 - Từ (2) và (3) ta có: Nsin N sin N − mg cos = m. − sin N + m.sin = mg cos M M N( M.mg cos 2
M + m sin ) = M mg cos N = (4) 2 M + m sin
- Thế vào phương trình (3) ta được: M.mg cos sin 2 M + msin mg.sin 2 a = = − (5) 0 M 2 ( 2 M + m sin )
-Thế vào phương trình (1) ta được: mg sin 2 mg sin = a a + − 2( cos 2 M + m sin ) 2 2 m g sin 2 cos m g sin 2 cos mg sin = ma. = + 2 ( a g sin 2 M + m sin ) 2 ( 2 M + m sin ) 3
2Mg sin + 2mg sin + mg sin 2 . cos = 2 ( 2 M + m sin ) 2Mg sin + 2mg sin ( 2 1− cos ) 2 + 2mgsin . cos (M + m)g.sin = = (6) 2( 2 M + m sin ) 2 M + m sin
b. Lấy hệ tọa độ xOy gắn với sàn, O trùng với đỉnh C. Tính hoành độ của vật m và của đỉnh C khi
vật trượt tới đỉnh B. Quỹ đạo của đường là gì? - Thay các giá trị 0 2 m = 0,1kg, M = 2m, = 30 ,
=1m, g =10m / s vào biểu thức (5) và (6): 0 mg.sin 2 0,1.10.sin 60 a = − = − = − 2 (M + msin ) 2 (0, 2 + 0,1.sin 30 ) 2 1, 92m / s 0 2 2 0 (M + m)g.sin (0,2+0, ) 0 1 .10.sin 30 20 2 a = = = m / s 2 2 0 M + m sin 0, 2 + 0,1.sin 30 3
- Nhận thấy: a có hướng cố định, a có hướng cố định song song với AB nên a = a + a cũng có 0 1 0
hướng cố định hợp với phương ngang một góc . 2 20 2 20 + Ta có: 2 2 2 a = a + a − 2aa cos = + (1,92) − 2 (1,92) 0 cos 30 1 0 0 3 3 2 a = 5,1m / s 1 20 0 sin 30 sin sin a sin + Mặt khác: 3 0 = sin = = = 0,6536 = 40,8 a a a 5,1 1 1
Vậy quỹ đạo vật m là đường thẳng AD nghiêng góc 0 40,8 so với phương ngang. AC AC 0, 5
- Xét tam giác ACD với AC = 0,5m ta có: tan = x = OD = = = 0,58 m 1 0 ( ) OD tan tan 40,8
Vậy hoành độ của vật m là 0,58 (m)
- Trong thời gian vật đi xuống thì nêm trượt sang trái và B trùng với D thì C ở vị trí C’ với hoành độ:
x = − (CB − OD) = − (ABcos − OD) = − ( 0 1.cos 30 − 0, 58 = 0, 29 m 2 ) ( ) Câu 3:
- Các lực tác dụng vào thanh BC + Trọng lực P : P = mg + Lực căng dây T
+ Phản lực của tường Q được phân tích: Q = N + F (1) ms
- Chọn hệ quy chiếu Bxy như hình vẽ
- Khi hệ cân bằng ta có: P + T + N + F = 0 (2) ms Bx: N = T.sin (3) By: f = mg − T.cos (4) ms
- Cân bằng momen của hệ đối với trục quay qua B Đặt AB = h và ABC = d d sin
P. .sin = T.h.sin T = mg. (5) 2 2h.sin
- Áp dụng định lí hàm sin trong tam giác ABC: d L h d.sin ( + ) = = (6) ( +) h = sin sin sin sin Từ (3), (5), (6): mg.d.sin mg.sin .sin T = ( (7) + ) N = 2sin 2sin ( + ) Từ (4): cos .sin f = mg1− (8) ms 2sin ( ) +
- Để có cân bằng phải có ma sát nghỉ và f
kN , với k là hệ số ma sát ms Từ (4): cos .sin mg.sin .cos mg 1− ( ) k. (9) 2sin + 2sin ( + ) 2sin . cos + sin . cos 2 1 Hay: k = + (10) sin . sin tan tan 2 2 2 − Từ (6): L.sin d L .sin sin = cos = (11) d d 2 2 2 2 d − L .sin 1 Từ (10): k + L.sin tan Câu 4:
Khi m bắt đầu rời khỏi M thì m có vận tốc v đối với M và M có vận tốc v đối với đất. 1 2
Bảo toàn động lượng theo phương ngang: Mv + m (v − v sin ) mv sin 1 = 0 → v = (1) 2 2 1 2 m + M m (v + v Mv )2 2 1 2
Bảo toàn cơ năng ta có: mgR (1− sin ) 2 = + 2 2
2mgR (1− sin ) = (m + M) 2 2 v + mv + 2mv v cos + (2) 2 1 1 2 2 Từ (1) và (2) ta có: 2mgR (1−sin ) 2 2 2 2 m sin 2m sin 2 2 2 = v + mv − v 1 1 1 m + M m + M m + M 2 v = 2gR 1− sin (3) 1 ( ) 2 M + m cos
Khi vật m bắt đầu rời khỏi M, gia tốc của vật M bằng 0 và phản lực của M lên m cũng bằng 0
Định luật II Niuton cho vật m trong hệ quy chiếu gắn với M là: 2 v1 2 mg sin = m v = gR sin (4) 1 R m + M
Từ (3) và (4) suy ra: sin = 2(1− sin ) 2 M + m cos m 3sin − 2 3sin − 2 = = 2 3 M
2 − 2sin − sin cos sin − 3sin + 2 7R − R 3 m 16 Vì 4 sin = = nên ta có: = R 4 M 11 Câu 5:
Áp suất ở cả hai ngăn không đổi và tương ứng với ngăn trên và ngăn dưới là: mg 2mg p = p + ; p = p + (1) 1 0 2 0 S S
Vì pit tông ở dưới dẫn nhiệt nên nhiệt độ khí hai ngăn bằng nhau. Từ phươg trình trạng thái rút ra quan
hệ giữa biến thiên thể tích và biến thiên nhiệt độ của khí ở mỗi ngăn: p V = n R T ; p V = n R T (2) 1 1 1 1 2 2 2 2
Trong đó số mol khí n , n được xác định từ điều kiện ban đầu: 1 2 p .2HS p .HS 1 2 n = ; n = (3) 1 2 RT RT 1 1
Từ (2) và (3) ta nhận được: V = 2 V 1 2
Từ đó ta tính được độ dịch chuyển của pit tông dưới và pit tông trên là: V V + V 2 1 2 x = ; x = = 2x 2 1 2 S S Gọi U
, A là biến thiên nội năng và công thực hiện bởi cả hệ 3R = ( 3 3 3 U n T + n T = p V + p V = V 2p + p = 3p S + 4mg x 1 1 2 2 ) ( 1 1 2 2 ) 2 ( 1 2 ) ( 0 ) 2 2 2 2 2 2mg mg 2mg mg A = + p V + + p V = + p V + + p .2 V 0 2 0 1 0 2 0 2 S S S S 4mg = + 3p V = 4mg + 3p S x 0 2 ( 0 ) 2 S Lại có: Q = U + A 3 Q =
(3p S+ 4mg x + 4mg +3p S x = 7,5p S+10mg x 0 ) 2 ( 0 ) 2 ( 0 ) 2 2 ĐS: 6Q 2Q x = ; x = 1 5(3p S + 4mg) 2 5 3p S + 4mg 0 ( 0 ) Câu 6:
Áp dụng phương trình trạng thái của khí lí tưởng ta có: (1−)p V p V 1+ p V 0 0 0 0 ( ) 0 0 T = ; T = ; T = 1 2 3 R R R C R Do
p = và C − C = R nên C = C p V V −1 V
Do quá trình 2 → 3 là quá trình đoạn nhiệt ta có: Q = 0 23 U = C (T − T ) p V 0 0 = − +1+ 23 V 3 2 ( ) −1
Công chất khí sinh ra trong quá trình 2 → 3 là: A = − U = C (T − T ) p V 0 0 = −1− 23 23 V 3 2 ( ) −1
Do quá trình 1 → 2 và 2 → 3 đối xứng qua đường thẳng đứng nên công chất khí sinh ra trong hai quá p V trình bằng nhau: 0 0 A = A = −1− 12 23 ( ) −1 p V U = C (T − T ) 0 0 = −1+ 12 V 2 1 ( ) −1
Nhiệt lượng khí nhận được trong quá trình 1 → 2 là: 2p V 0 0 Q = A + U = −1 12 12 23 ( ) −1
Quá trình 3 →1 là đẳng áp: U = C (T − T ) p V 0 0 = 2 − 31 V 1 3 ( ) −1 A = p V − V = p V 2 − 31 0 ( 1 3 ) 0 0 ( ) 2p V
Nhiệt lượng khí truyền ra môi trường: 0 0 Q = A + U = −1 31 31 31 ( ) −1 2p V
Tổng công mà khí thực hiện: 0 0 A ' = A ' + A ' + A ' = −1− 12 23 31 ( ) −1 A '
Hiệu suất của chu trình là H = = 1− Q −1 12
THPT CHUYÊN HÙNG VƯƠNG – BÌNH DƯƠNG Câu 1: (5 điểm)
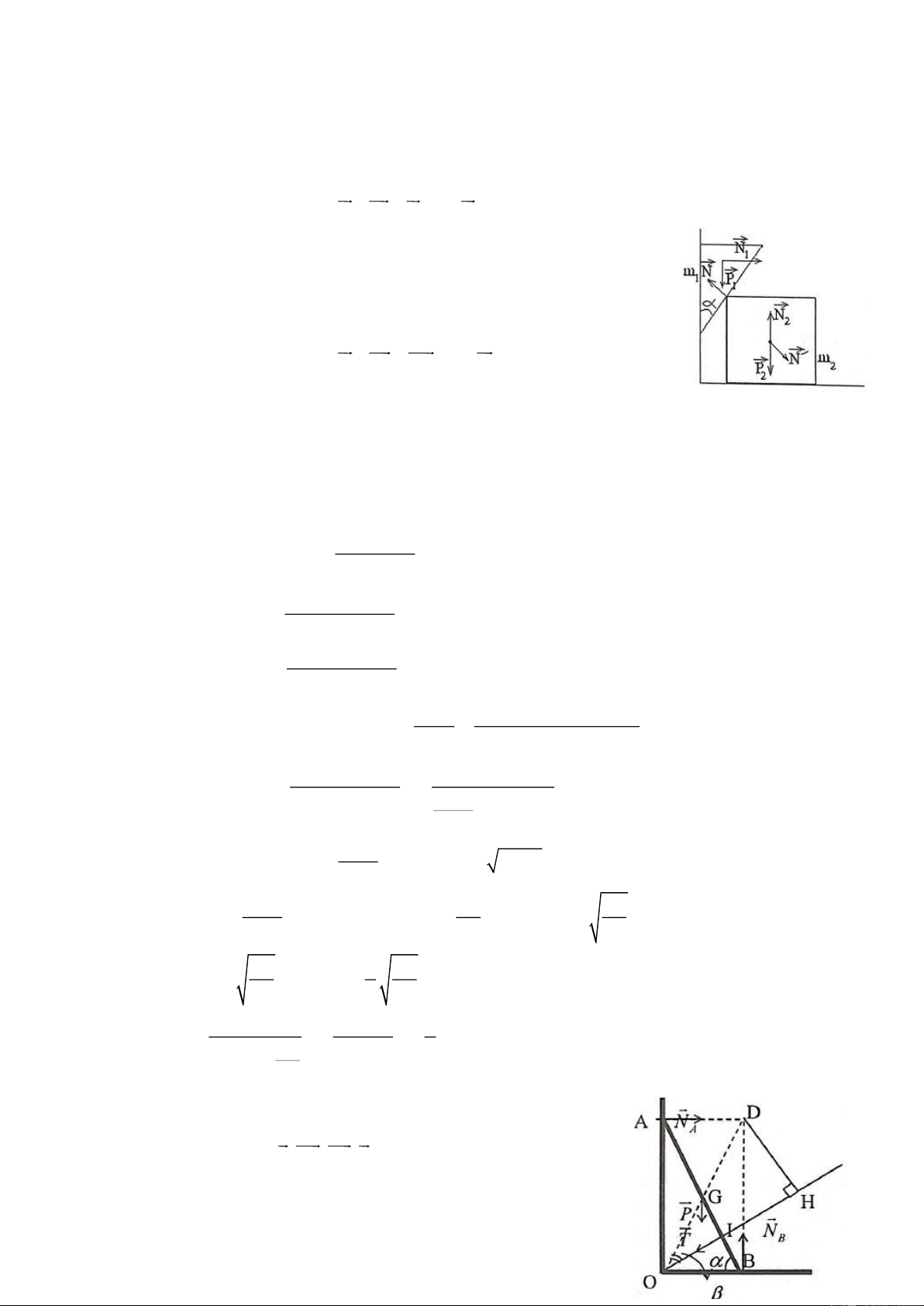
Một học sinh thứ nhất chạy trên đường tròn tâm O bán kính R = 30m với tốc độ không đổi bằng
u = 3,14m / s . Học sinh thứ hai bắt đầu chạy từ tâm O với tốc độ không đổi v = 2u và luôn nằm trên
bán kính nối tâm O với học sinh thứ nhất.
a. Khi học sinh thứ hai đến điểm M (OM = r) thì vecto vận tốc của cậu ta hợp với OM một góc . r Chứng tỏ rằng sin = 2R
b. Sau bao lâu thì học sinh thứ hai đuổi kịp học sinh thứ nhất. Câu 2: (5 điểm)
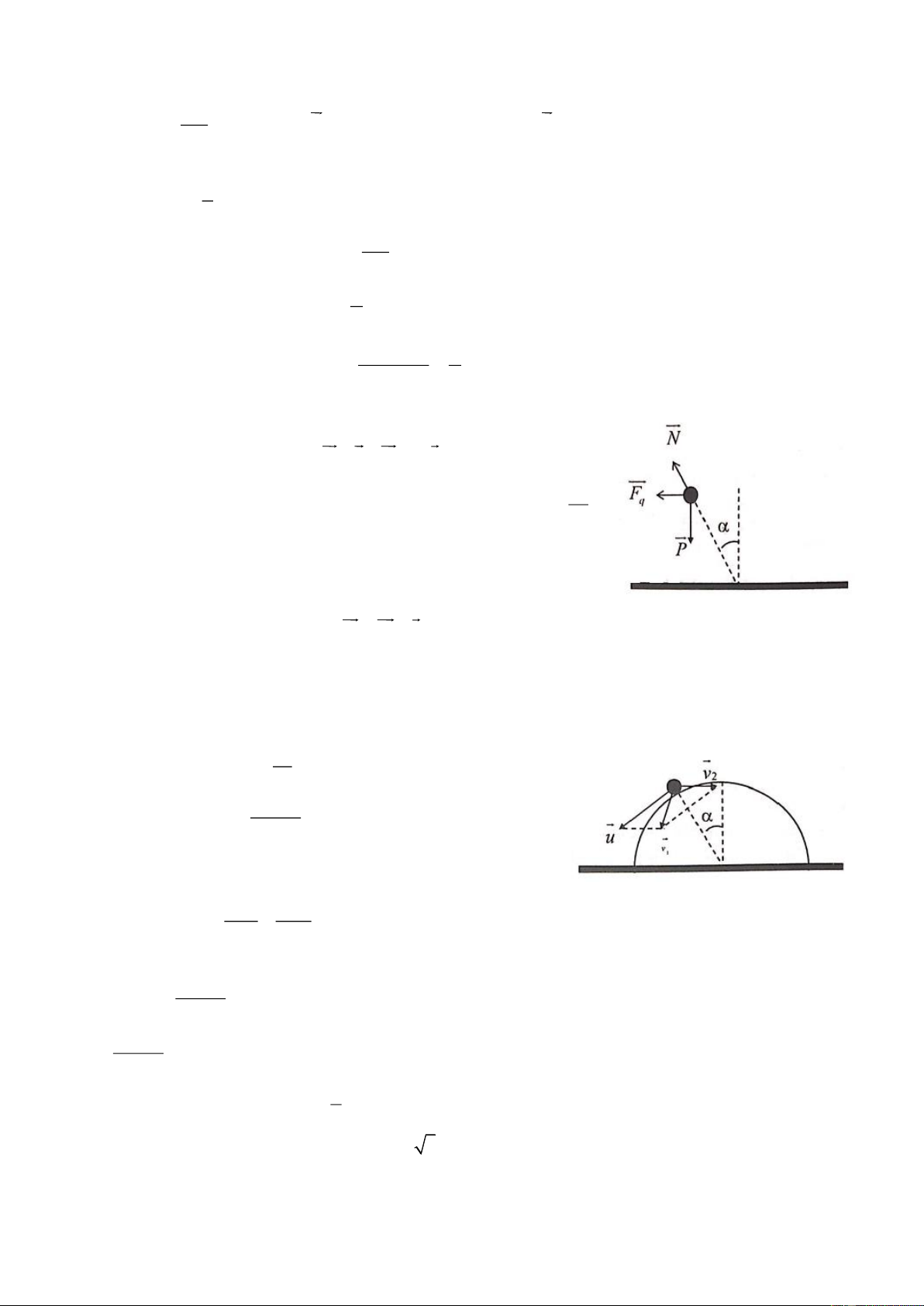
Khối lăng trụ tam giác vuông khối lượng m , với góc như hình 1
vẽ có thể trượt theo đường thẳng đứng và tựa lên khối lập phương khối
lượng m , còn khối lập phương có thể trượt trên mặt phẳng ngang. Bỏ 2 qua mọi ma sát.
a. Tính gia tốc của mỗi khối và áp lực giữa hai khối.
b. Xác định sao cho a là lớn nhất. Tính giá trị gia tốc của mỗi 2
khối trong trường hợp đó Câu 3: (5 điểm)
Thanh AB đồng nhất, trọng lượng P dựa vào tường thẳng đứng và sàn
nằm ngang (hình vẽ). Bỏ qua mọi ma sát. Thanh được giữ nhờ dây OI. AB
1. Chứng tỏ rằng thanh không thể cân bằng nếu AI 2 3
2. Tìm lực căng dây khi AI = AB và 0 = 60 4 Câu 4: (5 điểm)
Một vật có dạng là một bán cầu khối lượng M được đặt trên một mặt phẳng nằm ngang không ma sát (hình vẽ).
Một vật nhỏ có khối lượng m bắt đầu trượt không ma sát từ đỉnh bán cầu. Gọi là góc mà bán kính
nối vật với tâm bán cầu hợp với phương thẳng đứng khi vật bắt đầu tách khỏi bán cầu.
1. Thiết lập mối quan hệ giữa M, m và góc . 2. Tìm khi M = m. Câu 5: (5 điểm)
Trong một xilanh cách nhiệt khá dài nằm ngang có nhốt 1 mol khí lý tưởng đơn nguyên tử có khối
lượng m nhờ hai pittông cách nhiệt có khối lượng bằng nhau và bằng M, hai pittông này có thể chuyển
động không ma sát trong xilanh (hình vẽ). Lúc đầu hai pittông đứng yên, nhiệt độ của khí trong xilanh
là T . Truyền cho hai pittông các vận tốc v , v cùng chiều (v = 3v , v = v . Tìm nhiệt độ cực đại 1 0 2 0 ) 0 1 2
mà khí trong xilanh đạt được, biết bên ngoài là chân không. Câu 6: (5 điểm)
Một mol khí lý tưởng thực hiện chu trình thuận nghịch 1231 được biểu diễn trên hình vẽ.
- Nội năng U của một mol khí lý tưởng có biểu thức U = kRT . Trong đó k là hệ số có giá trị tùy thuộc
vào loại khí lý tưởng (k = 1,5 ứng với khí đơn nguyên tử; k = 2,5 ứng với khí lưỡng nguyên tử); R là
hằng số khí; T là nhiệt độ tuyệt đối.
- Công mà khí thực hiện trong quá trình trong quá trình đẳng áp 1-2 gấp n lần công mà ngoại lực thực
hiện để nén khí trong quá trình đoạn nhiệt 3-1.
a. Tìm hệ thức giữa n, k và hiệu suất H của chu trình.
b. Cho biết khí nói trên là khí lưỡng nguyên tử và hiệu suất h = 25%. Xác định n.
c. Giả sử khối khí lưỡng nguyên tử trên thực hiện một quá trình thuận nghịch nào đó được biểu diễn
trong mặt phẳng pV bằng một đoạn thẳng có đường kéo dài đi qua gốc tọa độ. Tính nhiệt dung của
khối khí trong quá trình đó. HƯỚNG DẪN GIẢI Câu 1: u
a. Vận tốc góc của HS1 là =
. Do cả hai luôn nằm trên một bán kính nên r cũng quay quanh R v sin r
tâm với vận tốc góc , hay = . Do đó sin = r 2R
b. Dễ thấy rằng trong quá trình đuổi bắt, góc thay đổi từ 0 đến (vì r 6 thay đổi từ 0 đến R)
Xét trong khoảng thời gian dt, góc tăng d , r tăng dr ta có: r = 2r.sin
Lấy vi phân hai vế ta được: dr = 2R cos . d dr d Chia hai vế cho dt: = 2R.cos . dt dt dr
Do vận tốc theo phương bán kính là v.cos nên = v.cos do vậy dt d (v.dt) v.cos = 2R.cos . d = dt 2R 6 t vdt v.t 2 R R
Lấy tích phân hai vế: d = = t = = 5s 2R 6 2R 6v 6 0 0
Vậy thời gian học sinh 2 đuổi kịp học sinh 1 là 5s. Câu 2: a. Xét vật m : 1
Áp dụng định luật II Newton có: P + N + N = m a 1 1 1 1
Chiếu lên trục Ox thu được: −N cos + N = 0 −N cos + N = 0 21 1 1
Chiếu lên trục Oy thu được: P − N sin = m a P − N sin = m a 1 21 1 1 1 1 1 (1) - Xét vật m : 2
Áp dụng định luật II Newton có: P + N + N = m a 1 2 12 2 2
Chiếu lên trục Ox thu được:
N cos = m a N cos = m a (2) 12 2 2 2 2
Mặt khác khi m dời sang phải một đoạn x thì m đi xuống một đoạn y, ta có: 2 1
x = y. tan a = a . tan (3) 2 1 Từ (1) và (2) suy ra Nsin = m g − m a m g − a 1 1 1 1 ( 1 ) tan = (4) N cos = m a m a 2 2 2 2 m1 a = g 1 2 m + m tan Từ (3) và (4) suy ra 1 2 m tan 1 a = g 2 2 m + m tan 1 2 m a m m tan Áp lực giữa m và m là: 2 2 1 2 N = N = N = = 1 2 12 21 cos ( 2 m + m tan cos 1 2 ) m tan m b. Gia tốc của 1 1 m : a = g = g 2 2 2 m + m tan m1 1 2 + m tan 2 tan m
Áp dụng bất đẳng thức Cô-si có: 1 + m tan 2 m m 2 1 2 tan m m m Dấu “=” xảy ra khi: 1 2 1 1 = m tan tan = = arc tan 2 tan m m 2 2 m g m Vậy khi 1 = arc tan thì 1 a = m 2 min 2 m 2 2 Lúc đó có: m m g 1 1 a = g = g = 1 m + 1 m m 2 1 1 m + m . 1 2 m2 Câu 3:
1. Gọi G là trung điểm của thanh AB
Thanh chịu tác dụng của P, N , N , T A B AB + Nếu AI
momen của T cùngc hiều với momen của P (đối với trục quay D) nêm thanh không 2 thể cân bằng. 3 2. Khi AI = AB và 0
= 60 : Khi đó OGB đều, I là trung điểm của GB nên 0 G OI = = 30 4 Xét momen đố OB i với điểm D ta có: P. = T.DH 2 OB = AB.cos P với cos = Tsin DH = OD.sin = AB.sin 2 0 P.cos 60 P Thay 0 0
= 60 , = 30 ta được: T = = 0 2.sin 30 2 Câu 4:
1. Xét vật trong hệ quy chiếu gắn với bán cầu
Theo định luật II Niuton ta có: N + P + F = ma q 2 u
Chiếu các lực lên phương bán kính: mg cos − N − F sin = m q R (1)
Lúc m bắt đầu rời bán cầu thì: 2
N = 0, F = 0 u = gR cos q (2)
Áp dụng công thức cộng vận tốc: v = v + u 1 2 2 2 2
v = v + u − 2v u.cos 3 1 2 2 ( ) Suy ra: v = u cos − v 4 1x 2 ( )
+ Theo phương ngang, động lượng của hệ “vật M-m” được bảo toàn M mv − Mv = 0 v = v (5) 1x 2 1x 2 m m Từ (4) và (5) v = u cos (6) 2 m + M
+ Áp dụng định luật bảo toàn cơ năng, chọn mốc thế năng tại
vị trí vật bắt đầu ròi khỏi bán cầu mgR (1− cos ) 2 2 mv Mv 1 2 = + (7) 2 2
Thay (2), (3) vào (6) vào (7) ta được: m 2 2 2gR = 3 − cos u với 2 u = gR cos m + M m 3 cos − 3cos + 2 = 0 (8) m + M 1
2. Khi m = M thì từ (8) ta có 3 cos − 3cos + 2 = 0 2 3
cos − 6cos + 4 = 0 có nghiệm 0 cos 3 −1 43 Câu 5:
- Đối với pit tông (1): lực tác dụng vào pittông theo phương ngang là lực đẩy F ngược chiều v nên 1 1
pittông (1) chuyển động chậm dần đều.
- Đối với pittông (2): tương tự, lực đẩy F cùng chiều với v nên pittông (2) chuyển động nhanh dần 2 2 đều.
- Trong quá trình hai pittông chuyển động, khối khí nhốt trong xilanh chuyển động theo.
- Chọn hệ quy chiếu gắn với pittông (2), vận tốc của pittông (1) đối với pittông (2) là:
v = v − v → pittông (1) chuyển động về phía pit tông (2) chậm dần rồi dừng lại lúc t , sau đó 12 1 2 0
t t thì pit tông (1) chuyển động xa dần với pit tông (2) và khí lại giãn nở. 0
- Gọi G là khối tâm của khối khí trong xilanh lúc t t : khí bị nén, G chuyển động về phía pit tông (2) 0
- Lúc t t : khí bị giãn, G chuyển động ra xa dần pit tông (2). 0
Vậy ở nhiệt độ t thì v = 0 → cả hai pit tông cùng khối khí chuyển động cùng vận tốc v. 0 G
- Định luật bảo toàn động lượng ta có: M3v + Mv = (2M + m) 4Mv0 v → v = 0 0 (2M + m) 1
- Động năng cảu hệ lúc đầu: = + = đ1 W M ( 2 2 v v ) 2 5Mv 1 2 0 2 1
- Động năng của hệ lúc ở t là: = + đ W 2 (2M m) 2 v 0 2 2 Mv 2M + 5m 0 ( )
→ độ biến thiên động năng: W = − = đ W 2 đ W 1 2M + m i 3 3 3 - Nội năng của khí: U = nRT = nRT → U = nR T = nR (T −T max 0 ) 2 2 2 2 2 2 Mv 2M + 5m 0 ( ) - Vì U = W nên T = T + . do n = 1 max 0 ( ) 3R 2M + m Câu 6:
a. Công mà khí thực hiện được trong quá trình đẳng áp 1-2: A = p V − V = R T − T 12 ( 2 1) ( 2 1)
Công trong quá trình đẳng tích 2-3: A = 0 23 − Theo đề A
bài, công trong quá trình đoạn nhiệt 3-1 là: 12 A = 31 n 1
Công thực hiện trong toàn chu trình: A = A + A + A = 1− R T −1 12 23 31 ( 2 1 ) n
Ta lại có Q = 0 (quá trình đoạn nhiệt) 31
Trong quá trình đẳng tích 2-3: Q = A + U = U kR T − T 0 vì T T 23 23 23 23 ( 3 2) 3 2
Như vậy chất khí chỉ nhận nhiệt trong quá trình 1-2: Q = Q = A + U = k +1 k T − T 12 12 12 ( ) ( 2 1) 1 1− A n −1
Hiệu suất của chu trình: n H = = = (1) + ( + ) n −1= nh(k + ) 1 Q k 1 n k 1 b. Thay số: n = 8 c. Phương trình đoạ p
n thẳng đi qua gốc tọa độ có dạng: = const (2) V
Phương trình trạng thái: pV = RT (3) 5
Xét quá trình nguyên tố: dQ = dA + dU = pdV + RdT (4) 2
Từ (2), (3) ta có: pdV − Vdp = 0; pdV + Vdp = RdT 1 pdV = RdT 2 1 5 dQ
dQ = RdT + RdT = 3RdT C = = 3R 2 2 dT
THPT CHUYÊN HÙNG VƯƠNG - GIA LAI Câu 1:
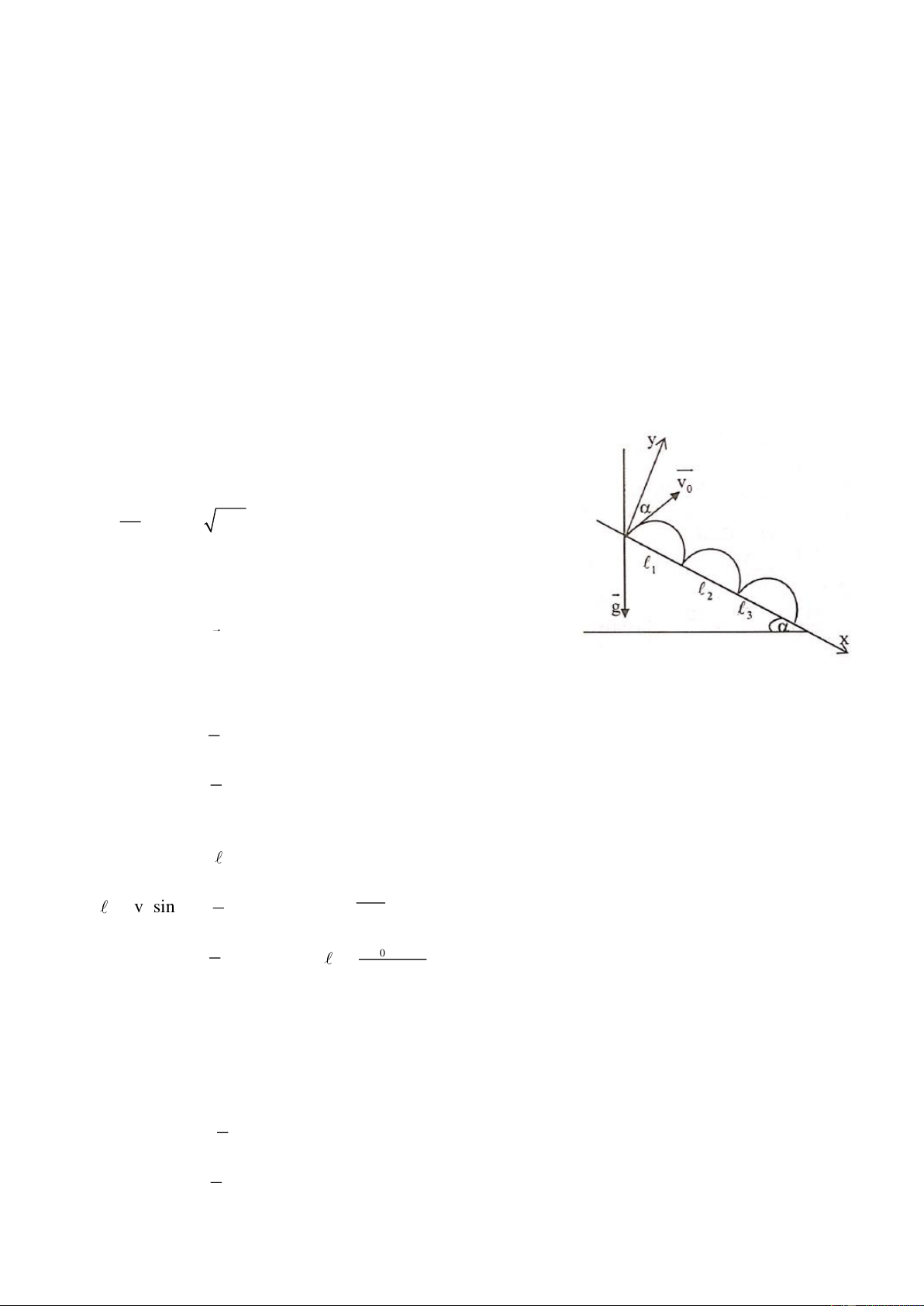
Hai vật nhỏ cùng lúc được ném lên với vận tốc có cùng độ lớn v nhưng các hướng khác nhau. Góc 0
hợp bởi hai vận tốc của hai vật tùy ý. Biết hai vật chạm đất cùng một vị trí và khoảng cách xa nhất trên không của chúng là L =19m . Lấy 2
g = 10m / s . Hãy xác định vận tốc ban đầu v của hai vật. max 0 Câu 2:
Một hình trụ có khối lượng m và bán kính r đang đứng yên và tựa vào một khối hộp như hình vẽ.
Khối hộp được kéo sang trái với vận tốc v không đổi. Lúc đầu khối hộp ở sát cạnh tường, bỏ qua ma
sát giữa hình trụ với tường và khối hộp. Hãy xác định
a. Dạng quỹ đạo chuyển động của tâm hình trụ so với điểm A.
b. Điều kiện của vận tốc v để khối hộp vẫn còn tiếp xúc với trụ khi khoảng cách giữa hai điểm A và
B là r 2 và các lực tác dụng lên thành hình trụ khi khoảng cách giữa A và B là r 2 . Câu 3:
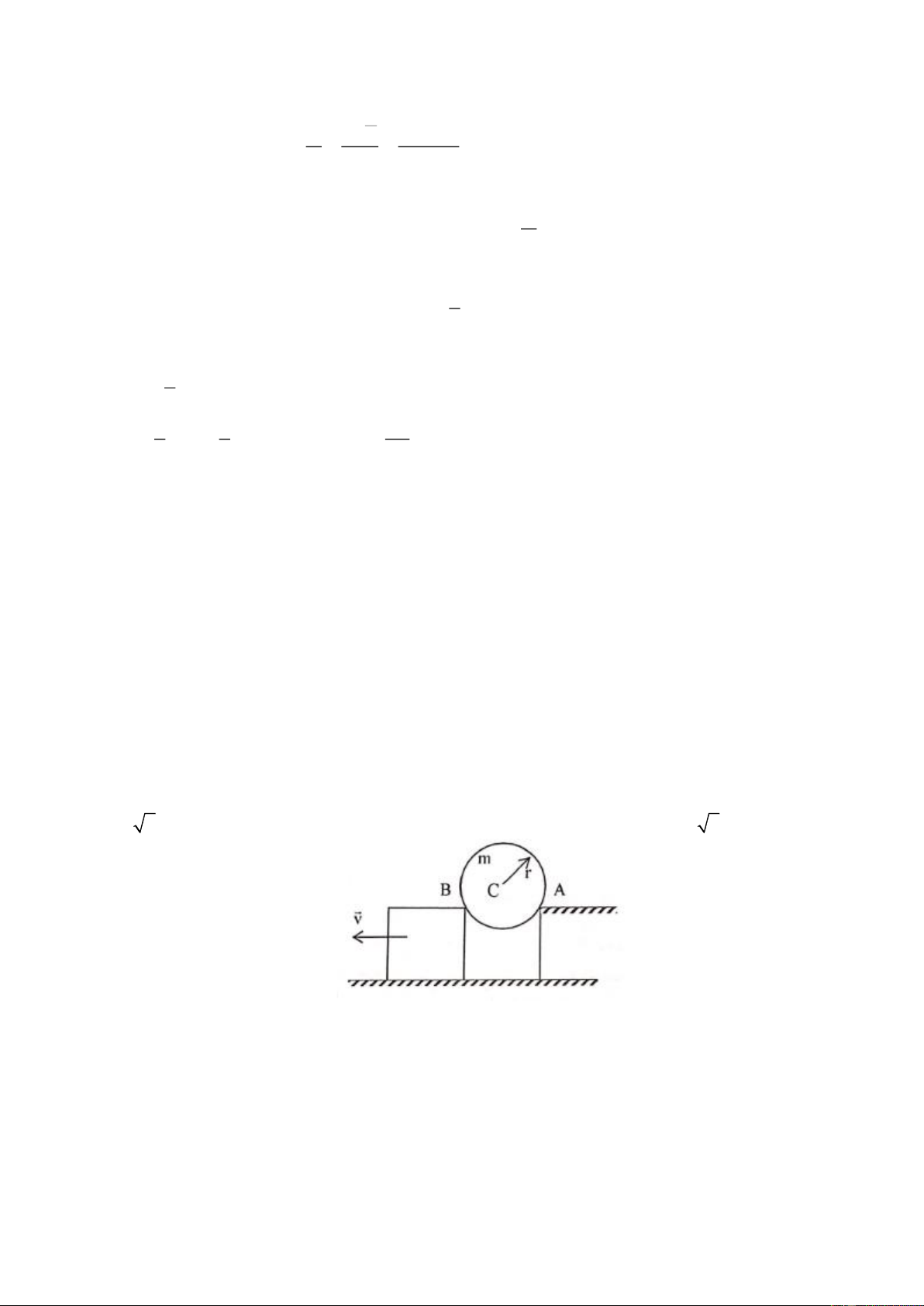
Một tấm gỗ khối lượng m nằm nhô ra khỏi cạnh bàn một đoạn 3/7 chiều dài của nó. Chiều dài của
một phần bảy tấm gỗ là L = 1m. Người ta dùng các ròng rọc và dây nhẹ để treo phần nhô ra, một vật
khối lượng 4m. Một người khối lượng 3m có thể đứng cách mép bàn một đoạn có chiều dài nằm trong
khoảng giá trị nào để tấm gỗ vẫn nằm ngang. Câu 4:
Hai quả cầu nhỏ khối lượng m, mỗi quả được coi như chất điểm được lồng vào một vòng nhẵn khối
lượng M bán kính R. Vòng cứng đứng thẳng đứng trên sàn nhà. Ban đầu hai quả cầu ở điểm cao nhất
của vòng cứng, tác động nhẹ vào hai quả cầu để chúng trượt xuống theo vòng, một quả trượt sang phải,
quả kia trượt sang trái. Để cho vòng tròn nẩy lên khỏi sàn trong quá trình chuyển động của hai quả cầu thì:
a. Lực lớn nhất của hai quả cầu tác dụng lên vòng là bao nhiêu (tính theo m và g). m
b. giá trị nhỏ nhất của tỉ số
là bao nhiêu. Tìm độ lớn góc giữa đường nối vật với tam vòng và M
phương thẳng đứng mà tại đó vòng nẩy lên. Câu 5:
Một hình trụ nằm ngang có một đầu kín và đầu còn lại có một pittông có thể di chuyển có ma sát
bên trong hình trụ. Bên trong hình trụ có chứa khí lý tưởng đơn nguyên tử với thể tích V , áp suất p 0 0
cùng giá trị với áp suất khí quyển bên ngoài.
Pittông được gắn kín, lực ma sát giữa pittông và hình trụ chiếm f phần áp lực mà khí quyển bên
ngoài tác dụng lên pittông. Khí bên trong được làm nóng chậm cho đến khi nó trở về vị trí ban đầu.
Sau đó khí được nung nóng trở lại đến trạng thái đầu. Các thông số p , V , f đã biết. 0 0
a. Biểu diễn quá trình biến đổi trên đồ thị p – V.
b. Tính hiệu suất chu trình. Câu 6:
Giản đồ p – V biểu diễn quá trình biến đổi chậm của một mol khí lí tưởng từ điểm A đến điểm B. 1
Biết tỉ số áp suất của khí ở các trạng thái B và A là
. Để khí nhận nhiệt từ bên ngoài trong cả quá 2
trình thì tỉ số thể tích của khí ở các trạng thái B và A phải thỏa mãn điều kiện gì? (Biết nội năng của 3 khí lý tưởng là U = RT ) 2 HƯỚNG DẪN GIẢI Câu 1: 2 v sin 2
Ta có tầm bay xa của vật khi ném xiên 0 L = g
Vì hai vật có vận tốc ban đầu có độ lớn bằng nhau và rơi cùng một vị trí nên các góc ném , của 1 2
hai vật phải thỏa mãn điều kiện 0
+ = 90 , tức là ban đầu hai vận tốc đối xứng nhau qua phương 1 2 0
45 . Thờin gia vậy ở dưới bay trong không khí ít hơn thời gian vật ở trên, thời gian đó là: 2v sin ( 0 45 − 0 ) t = g
Xét trong hệ quy chiếu gắn với vật ở dưới thì vật ở trên chuyển động thẳng đều với vận tốc là v = 2v sin 0
Khoảng cách giữa hai vật sau thời gian t là: 2 4v sin . sin ( 0 45 − ) 2 0 2v0 d = v .t = = cos 2 − 45 − cos 45 0 ( ( 0 ) 0 ) g g Ta thấy d lớn nhất khi ( 0
2 − 45 ) lớn nhất bằng 1 0 = 22,5 2 2v 1 Vậy 0 d = 1− =19 v =18m / s max 0 g 2 Câu 2:
a. Khi khối hộp vẫn còn tiếp xúc với trụ thì khối trụ cũng tiếp xúc với bậc nên tâm C khối trụ luôn
cách mép bậc một đoạn r tức là tâm khối trụ chuyển động trên cung tròn tâm A, bán kính r.
b. Xét thời điểm khi bán kính AC tạo với phương ngang một góc . Tâm C nằm cách đều khối hộp x v v
và bậc thang do đó ta có B Bx x = x = = C Cx 2 2 2
Vecto vận tốc v phương vuông góc với bán kính quỹ đạo AC. C v V Ta có: v = v .sin = v = Cx C C 2 2.sin 2 2 v v
Gia tốc hướng tâm hướng từ C về A có độ lớn: C a = = r 2 r 4r.sin
Tâm C chuyển động đều theo phương ngang nên các phản lực tại A và B bằng nhau. Theo phương CA
ta có: N cos 2 + mg sin − N = ma B A C 2 2 v m v 2 2 − sin .N = m − gsin N = gsin − B 2 B 2 2 4r.sin 2sin 4r.sin - Khi AB = r 2 thì = 4
Điều kiện để hộp vẫn còn tiếp xúc với khối trụ là 2 3
N 0 v 4gr.sin = gr 2 B
- Với v gr 2 thì khi AB = r 2 , lực do khối hộp và bậc tác dụng lên khối trụ là 2 g v N = N = m − B A 2 2r Câu 3:
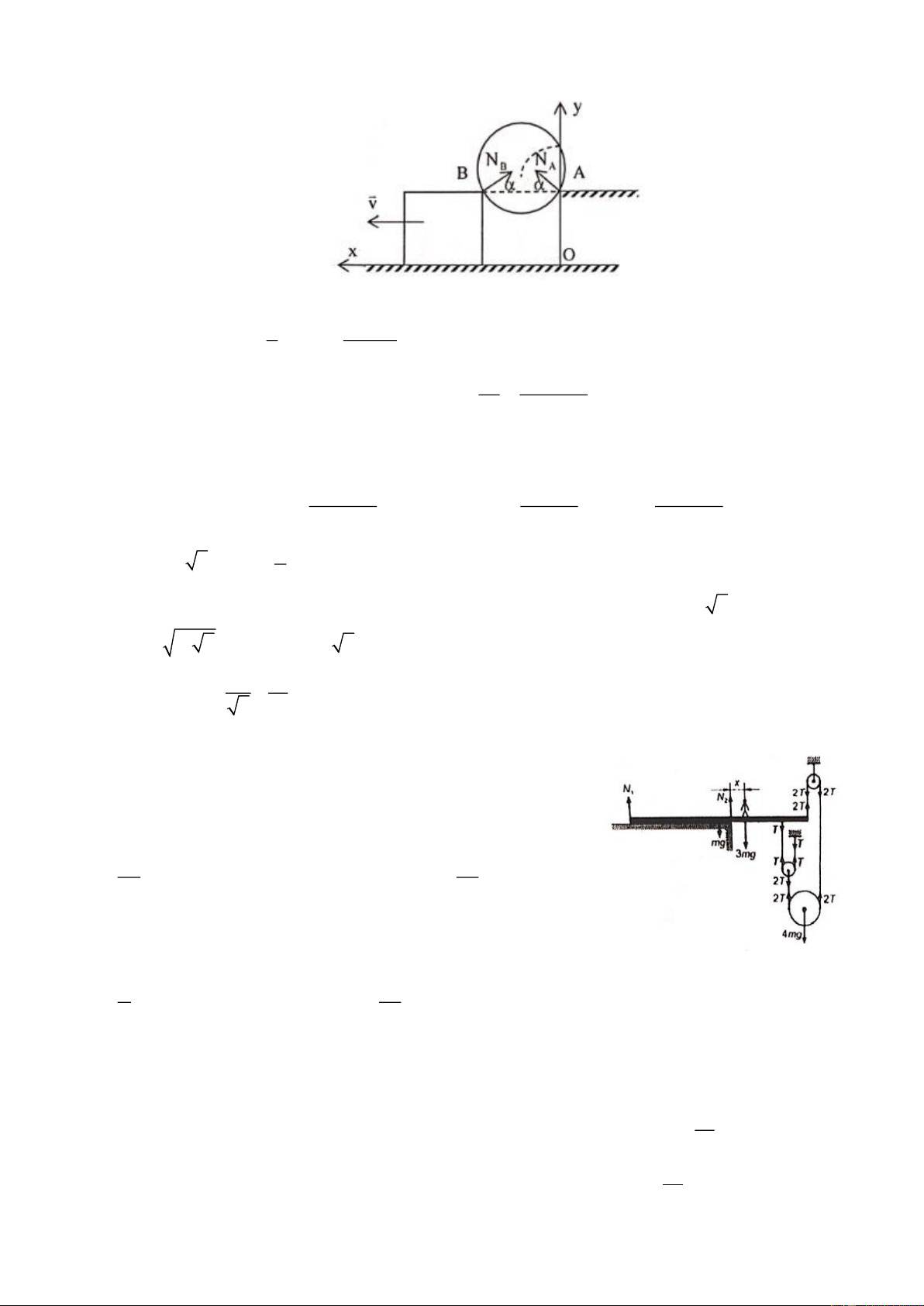
Ta thấy tấm gỗ có thể bị lật xuống mép bàn hoặc bị nâng đầu bên
phải lên. Từ điều kiện cân bằng ta có T = mg
- Xét trường hợp đầu phải của bảng bị nâng lên. Áp dụng điều kiện cân bằng ta có 7L + ( 5L mg
3mg 4L + x + 6.L.T = 2T.7L x = − = 2 − ,5m 1 ) 1 2 2
Tức là người có thể đứng mép 2,5m về bên trái.
- Xét trường hợp bảng bị lật xuống. ÁP dụng điều kiện cân bằng ta có: L 3L mg + 2T.3L = 3mgx + T.2L x = =1,5m 2 2 2 2
Tức là người có thể đứng cách mép bàn 2,5m bên phải. Câu 4:
a. Do tính đối xứng nên trong quá trình hai quả cầu trượt xuống vòng vẫn đứng yên một chỗ. Tại vị 2 v
trí góc , xét vật m, theo gia tốc hướng tâm ta có phương trình mg cos + N = m R 2 v
Theo định luật bảo toàn cơ năng ta có (gốc thế năng ở tâm O) mgR cos + m mgR 2
Từ hai phương trình trên ta rút ra được N = mg (2 − 3cos )
Theo phương thẳng đứng lực do hai quả cầu tác dụng lên quả cầu là 2 1 1
F = 2N cos = 6mg − cos − 9 3 2 1 Vậy F = mg khi cos = max 3 3 b. Để 2mg m 3
vòng nẩy lên được thì F Mg Mg max 3 M 2
- Khi thỏa mãn điều kiện vòng được nẩy lên ta có 2 1 2 m 1 1 M F = Mg 6 cos − = − cos = − 3 3 M 3 9 6m Ở 1 1 M
đây ta lấy nghiệm cos = − 3 9 6m
Vì cos thay đổi từ 1 đến -1 nên nghiệm này xảy ra trước. Câu 5: a. Đầ F
u tiên khí phải tăng nhiệt độ trong quá trình đẳng tích cho đến khi f p = p + = 1+ f p khi 1 0 ( ) 0 S
đó pittông bắt đầu dịch chuyển, quá trình tiếp theo là đẳng áp cho đến thể tích V = 1+ f V 2 ( ) 0 F
Sau đó quá trình làm lạnh đẳng tích áp suất f p = p − = 1− f p 3 0 ( ) 0 S
Tiếp theo là làm lạnh đẳng áp đến thể tích V = V 4 0
Để quay lại trạng thái ban đầu cần nung nóng đẳng tích đến áp suất p . 0
b. Công mà khí thực hiện trong chu trình 2 A = 2f p V 0 0
Khí nhận nhiệt lượng trong 41 và 12 là Q = nC T − T + nC T − T V ( 1 4 ) V ( 2 1 ) 3 = ( + ) − ( − ) 5 + 1 f p V 1 f p V + (1+ f )2 f 11 5f p V − 1+ f p V = p V 0 0 0 0 0 0 ( ) ( ) 0 0 0 0 2 2 2 2 A 2f p V 4f
Hiệu suất chu trình là H = = = Q f ( 0 11+ 5f ) 0 11+ 5f p V 0 0 2 Câu 6:
Theo nguyên lí I nhiệt động lực học ta có Q + A 3 3 Ta có U = R (T − T = p V − p V 2 1 ) ( 2 2 1 1) 2 2 1
Công mà khí nhận được trong quá trình trên là A = − (p + p V − V 2 1 ) ( 2 1 ) 2
Để khí nhận nhiệt từ môi trường thì Q > 0 3 = − = ( 1 Q U A p V − p V + p + p V − V 0 2 2 1 1 ) ( 2 1)( 2 1) 2 2 p 1 V 3 Với 2 2 = p 2 V 2 1 1
THPT CHUYÊN KRÔNG NÔ – ĐẮK NÔNG Câu 1: (4 điểm)
Một quả bóng rơi tự do từ độ cao h xuống một mặt phẳng
nghiêng góc so với mặt phẳng ngang. Sau khi va chạm tuyệt đối
đàn hồi với mặt phẳng nghiêng, bóng lại tiếp tục nảy lên, rồi lại va
chạm vào mặt phẳng nghiêng và tiếp tục nảy lên, và cứ tiếp tục như
thế. Giả sử mặt phẳng nghiêng đủ dài để quá trình va chạm của vật
xảy ra liên tục. Khoảng cách giữa các điểm rơi liên tiếp từ lần thứ
nhất đến lần thứ tư theo thứ tự lần lượt là ; và . Tìm hệ thức 1 2 3 liên hệ giữa ; và 1 2 3 Câu 2: (5 điểm)
Một vật nhỏ có khối lượng m bắt đầu trượt không ma sát từ đỉnh của một chiếc nêm như hình
vẽ bên. Biết nêm có khối lượng M, góc nêm là và có thể trượt không ma sát trên mặt phẳng ngang.
a. Xác định gia tốc của m và M đối với mặt đất?
b. Cho chiều dài mặt nêm là L. Tính vận tốc của M ngay sau khi m trượt xuống chân M? Câu 3: (5 điểm)
Hai máng OA và OB nằm trong một mặt phẳng thẳng đứng và nghiêng góc và so với 1 2
đường nằm ngang. Một thanh đồng chất MN có trọng lượng P tì lên hai máng như hình vẽ. Bỏ qua ma
sát giữa thanh và máng. Ở vị trí cân bằng thanh MN nghiêng góc so với đường nằm ngang. Tìm góc
nghiêng theo và ; áp dụng bằng số: 0 0 = 30 ; = 45 . 1 2 1 2 Câu 4: (5 điểm)
Trên mặt phẳng ngang có một bán cầu khối lượng m. Từ điểm cao nhất của bán cầu có một vật
nhỏ khối lượng m trượt không vận tốc đầu xuống. Ma sát giữa vật nhỏ và bán cầu có thể bỏ qua. Gọi
là góc giữa phương thẳng đứng và bán kính véc tơ nối tâm bán cầu với vật như hình vẽ.
1. Giả sử bán cầu được giữ yên.
a. Dựa vào định luật bảo toàn cơ năng và định luật II Niuton để xác định vận tốc của vật, áp lực
của vật lên mặt bán cầu khi vật chưa rời bán cầu, từ đó tìm góc = khi vật rời bán cầu. m
b. Xét vị trí có . Tìm và các thành phần gia tốc tiếp tuyến và gia tốc pháp tuyến của vật; m
áp lực của bán lên mặt phẳng ngang khi đó.
2. Giả sử giữa bán cầu và mặt phẳng ngang có ma sát với hệ số ma sát là . Tính giá trị của , biết rằng khi 0
= 30 thì bán cầu bắt đầu bị trượt trên mặt phẳng ngang. Câu 5: (5 điểm)
Một xilanh có chiều dài 2l, bên trong có một pittông có tiết diện S. Xilanh có thể trượt ma sát
trên mặt phẳng ngang với hệ số ma sát (hình vẽ). Bên trong xilanh, phía bên trái có một khối khí ở
nhiệt độ T và áp suất bằng áp suất khí quyển bên ngoài P , pittông cách đáy khoảng l. Giữa bức tường 0 0
thẳng đứng và pit tông có một lò xo nhẹ độ cứng K. Cần phải tăng nhiệt độ của khối khí lên một lượng
T bằng bao nhiêu để thể tích của nó tăng lên gấp đôi, nếu ma sát giữa xilanh và pittông có thể bỏ qua.
Khối lượng tổng cộng của xilanh và pittông bằng m. Câu 6: (5 điểm)
Cho một mol khí lý tưởng đơn nguyên tử biến đổi theo một chu trình thuận nghịch được biểu
diễn trên đồ thị như hình 3, trong đó đoạn thẳng 1 – 2 là đường kéo dài đi qua gốc tọa độ O và quá
trình 2 – 3 là quá trình đoạn nhiệt. Biết T = 300K, p = 2p . 1 2 1
a. Tính các nhiệt độ T , T . 2 3
b. Tính hiệu suất của chu trình. HƯỚNG DẪN GIẢI Câu 1:
Chọn hệ trục Oxy như hình vẽ
Vận tốc ban đầu của quả bóng sau va chạm lần 1 với mặt phẳng nghiêng là 2 v0 h = → v = 2gh 0 2g
Do va chạm của bóng và mặt phẳng nghiêng là va chạm đàn
hồi nên tuân theo định luật phản xạ gương và độ lớn vận tốc
được bảo toàn sau mỗi va chạm.
Vec tơ vận tốc v hợp với trục Oy một góc . 0
Phương trình chuyển động của quả bóng sau lần va chạm đầu tiên là 1 2 x = v sin t + g sin t 0 2 1 y = v cost − gcost 0 2
Sau thời gian t quả bóng va chạm với mặt phẳng nghiêng lần thứ hai tại vị trí cách điểm va chạm lần 1
đầu một khoảng . Khi đó ta có 1 2v 1 0 2 t v sin t g sin t = = + 1 1 0 g 2 → 2 1 4v sin 0 0 = v cos t − g cos t = = 8h sin 0 1 2 g
Sau va chạm, vật lại bật lên với vận tốc ban đầu được tính
v = v + a t = v sin + gsin t = 3v sin 1x 0x x 0 1 0
v = v + a t = −v cos + g cos t = v cos 1y 0y y 0 1 0
Phương trình chuyển động của quả bóng sau lần va chạm thứ hai là 1 2 x = 3v sin t + g sin t 0 2 1 y = v cost − gcost 0 2
Sau thời gian t quả bóng va chạm với mặt phẳng nghiêng lần thứ ba tại vị trí cách điểm va chạm lần 2 thứ hai một khoảng . Khi đó ta có 2 2v 1 0 2 t 3v sin t g sin t = = + 2 2 0 2 g 2 → 2 1 2 8v sin 0 0 = v cos t − g cos t = =16h sin 0 2 1 2 g
Sau va chạm, vật lại bật lên và tính tương tự ta được thời gian từ lúc va chạm đến lúc bật lên và
khoảng cách từ vị trí va chạm lần thứ 3 đến vị trí va chạm lần thứ tư lần lượt bằng 2v0 t = 3 g 2 12v sin 0 = = 24h sin 3 g
Vậy hệ thức liên hệ giữa ; và là: 1 2 3 = = 1 2 3 1 2 3 Câu 2:
a. Chọn hệ quy chiếu gắn với mặt đất như hình vẽ.
Gọi gia tốc của m và M lần lượt là a và a 1 2
Phương trình chuyển động của m: P + N = m a 1 1 1 1
Chiếu lên 0x: N sin = ma 1 1 1x ( ) 0y :P − N cos = ma 2 1 1 1y ( )
Phương trình chuyển động của M: P + N + N ' = Ma 2 2 1 2
Chiếu lên 0x: −N sin = −Ma 3 1 2 ( )
Mặt khác theo công thức cộng gia tốc: a = a + a
4 ( a là gia tốc của m đối với M). Chiếu 1 12 2 ( ) 12 (4) lên ox và oy ta có: a
= a cos − a ; a = a sin 1x 12 2 1y 12 Từ đó suy ra: a = a + a tan 5 1y ( 1x 2) ( )
Giải hệ (1), (2), (3) và (5) ta được: mM cos N = g 1 2 M + m sin M sin cos a = g 1x 2 M + m sin ( m + M) (*) 2 sin a = g 1y 2 M + m sin m sin cos a = 2 2 M + m sin a M + m sin 1y ( )
Gia tốc của m đối với M: a = = g 12 2 sin M + m sin
Gia tốc của m đối với mặt đất: 2 2 a = a
+ a (Với a và a được tính ở (*)) 1 1x 1y 1x 1y m sin cos
Gia tốc của M đối với đất sẽ là: a = g 2 2 M + m sin
b. Thời gian cần để m chuyển động trên mặt nêm M là: 2L ( 2 M + m sin 2L ) t = = a M + m g sin 12 ( ) 2gL sin
Vận tốc của M lúc đó: v = a t = m cos 2 2 (M + m)( 2 M + m sin ) Câu 3:
- Thanh cân bằng với trục quay qua M: l M = M
P. .cos = N .l.sin ( 0 90 − − P/M N 2/M 2 ( 2 )) 2 P
.cos = N .cos − 1 2 ( 2 ) ( ) 2
- Thanh cân bằng với trục quay qua N: M = M P/ N N1/ N l
P. .cos = N .l.sin ( 0 90 − − 1 ( 21 )) 2 P
.cos = N .cos − 2 1 ( 1 ) ( ) 2 N cos ( − 1 2 ) Từ (1) và (2) ta có: = 3 N cos + 2 ( 1 ) ( ) - Thanh cân bằng: P + + = 1 N N2 0 (4)
Chiếu (4) lên trục Ox ta được: N sin = N sin 5 1 1 2 2 ( ) sin cos ( − sin
cos cos + sin sin 2 2 ) Từ (3), (5) ta có: 2 2 2 = = sin cos + sin
cos cos + sin sin 1 ( 1 ) 1 1 1 1 1 1
Biến đổi ta được: tan = − (6) 2 tan tan 1 2 Thay 0 0
= 30 ; = 45 vào (6) tìm được 0 = 20 1 2 Câu 4:
1. Khi vật trượt trên mặt cầu vật chịu tác dụng của hai trọng lực P và phản lực Q của mặt cầu có
tổng hợp tạo ra gia tốc với hai thành phần tiếp tuyến và hướng tâm.
Quá trình chuyển động tuân theo sự bảo toàn cơ năng: 1 2 mv = mgR − (1 cos ) 2 2 mv F P.cos Q = − = ht R a. Suy ra: v =
2gR (1− cos ), Q = (3cos − 2).mg
Vật rời bán cầu khi bắt đầu xảy ra Q = 0. Lúc đó: 2 0 cos = cos = → 48,2 m m 3
b. Xét vị trí có : m 2 v
Các thành phần gia tốc: a =
= 2g 1− cos , a = gsin n ( ) t R
Lực mà bán cầu tác dụng lên sàn bao gồm hai thành phần: áp lực N và lực đẩy ngang F : N = P + Q.cos = mg ( 2 1− 2 cos + 3cos ngang cCu )
2. Bán cầu bắt đầu trượt trên sàn khi 0
= 30 , lúc đó vật chưa rời khỏi mặt cầu. Thành phần nằm
ngang của lực do vật đẩy bán cầu là: F
= Qsin = 3cos − 2 mg.sin ngang ( ) Ta có: F = F = . N ms ngang F 3cos− 2 mg.sin 3cos− 2 sin ngang ( ) ( ) = = = N mg ( 2 1− 2 cos + 3cos ) 2 1− 2 cos + 3cos
Thay số: 0,197 0, 2 Câu 5:
Trường hợp 1: F kl m
g kl . Khi đó xilanh sẽ đứng yên. ms
Gọi T là nhiệt độ cuối cùng của khối thì: kl P + .2S l 0 P Sl S kl 0 = T = 2T 1+ 0 T T SP 0 0 2kl Từ đó: T = T − T = T 1+ 0 0 SP 0
Trường hợp 2: m g kl
Gọi x là độ nén cực đại của lò xo.
Pittông còn đứng yên chi đế mg n khi kx = m g x = k
Gọi T là nhiệt độ của khối khí tại thời điểm lò xo nén cực đại. P là áp suất chất khí trong xilanh ở 1 1 mg
thời điểm này thì: P S = P S + kx = P S + m g P = P + 1 0 0 1 0 S
- Áp dụng phương trình trạng thái có: kl P + . l + x S 0 ( ) P Sl S m g m g 0 = T = 1+ 1+ T 1 0 T T SP kl 0 1 0
+) Khi T T thì pit tông bắt đầu dịch chuyển, bắt đầu từ thời điểm này áp suất chất khí trong 1
xilanh là không đổi. Ta có: T S(l + x) T 1 x 2T m g 1 1 1 = = 1+ T = = 2T 1+ T 0 0 T S.2l T 2 l mg P S + 0 1 kl mg Từ đó tìm được: T = T − T = T 1+ 0 0 SP 0 Câu 6: a. Quá trình 1 – 2: p p p 2 1 2 = V = V = 2V 2 1 1 V V p 2 1 1 p .V 2 2 T = T . = 4T = 1200K 2 1 1 p .V 1 1 1 P
Xét quá trình 2 – 3: P V P V = , suy ra 2 V = V = 1,52V 2 2 3 3 3 2 2 P 3 V V V Xét quá trình 3 – 1: 1 3 3 = → T = T = 3, 04T = 912K 3 1 1 T T V 1 3 1 b. Quá trình 1 – 2: U = Cv. T − T = 4,5RT 12 ( 2 1) 1 1 A =
. p + p . V − V = 1,5.p .V = 1,5.R.T 12 ( 2 1) ( 2 1) 1 1 1 2 Q = U + A = 6.R.T 12 12 12 1 Quá trình 2 – 3: A = − U = C − v. T − T =1,44.R.T 23 23 ( 3 2) 1 Q = 0 23 Quá trình 3 – 1 có: U = Cv. T − T = 3 − ,06.R.T 31 ( 1 3) 1 A = p . V − V = 2 − ,04RT 13 1 ( 1 3 ) 1 Q = U + A = 5 − ,1RT 31 31 31 1 A = A + A + A = 0,9RT 12 23 31 1
Nhiệt lượng khí nhận là: Q = Q = 6.R.T 12 1 A 0, 9RT
Hiệu suất của chu trình: 1 H = = tính được H 15% Q 6RT 12 1
THPT CHUYÊN LÊ HOÀNG KHA – TÂY NINH Câu 1: (5 điểm)
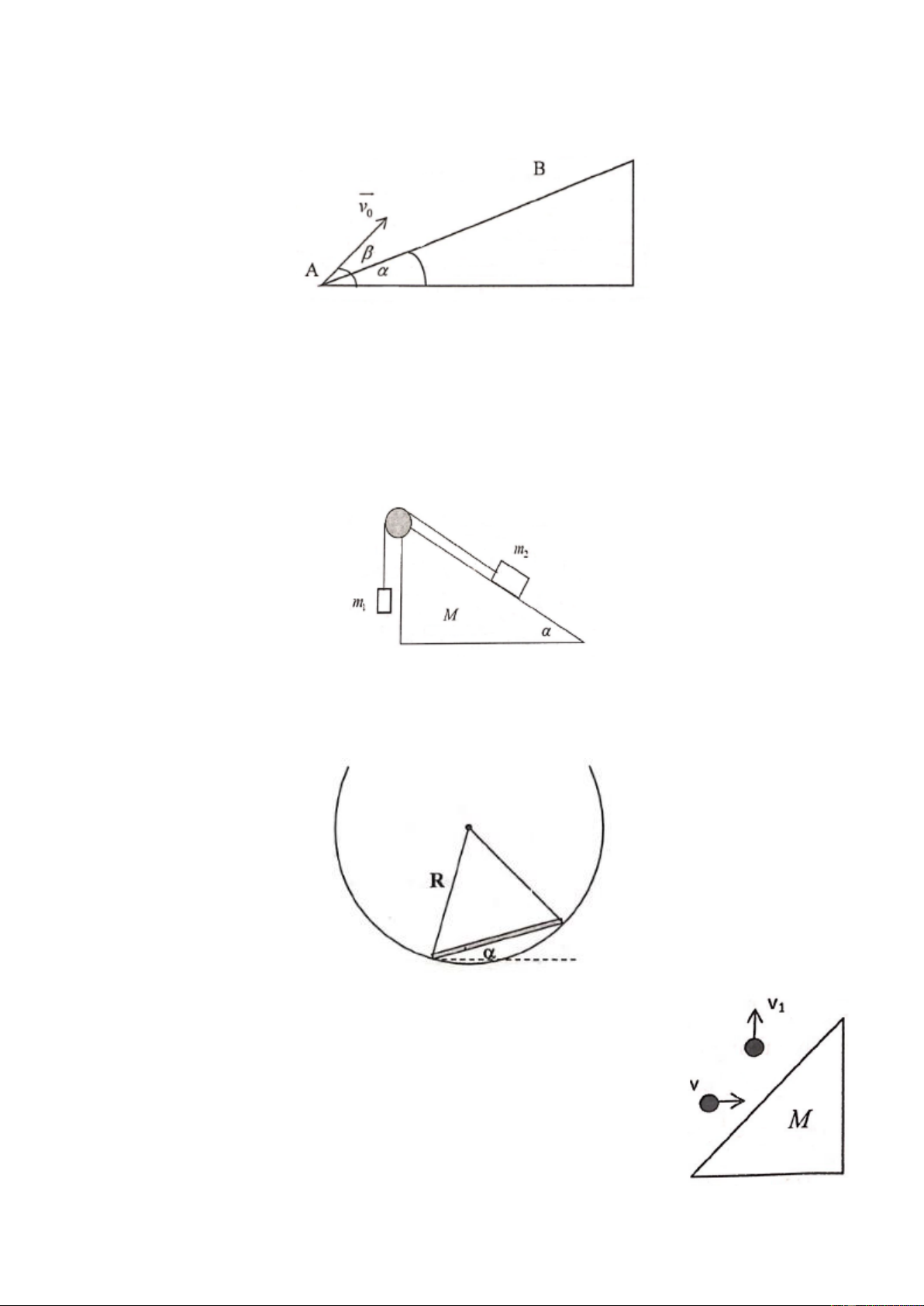
Ném một viên đá từ điểm A trên măth phẳng nghiêng với vận tốc v hợp với mặt phẳng ngang một 0 góc 0 = 60 , biết 0
= 30 . Bỏ qua sức cản của không khí.
a. Tính khoảng cách AB từ điểm ném đến điểm viên đá rơi chạm vào mặt phẳng nghiêng.
b. Tìm góc hợp bởi phương vecto vận tốc và phương ngang ngay sau viên đá chạm mặt phẳng
nghiêng và bán kính quỹ đạo của viên đá tại B. Câu 2: (5 điểm)
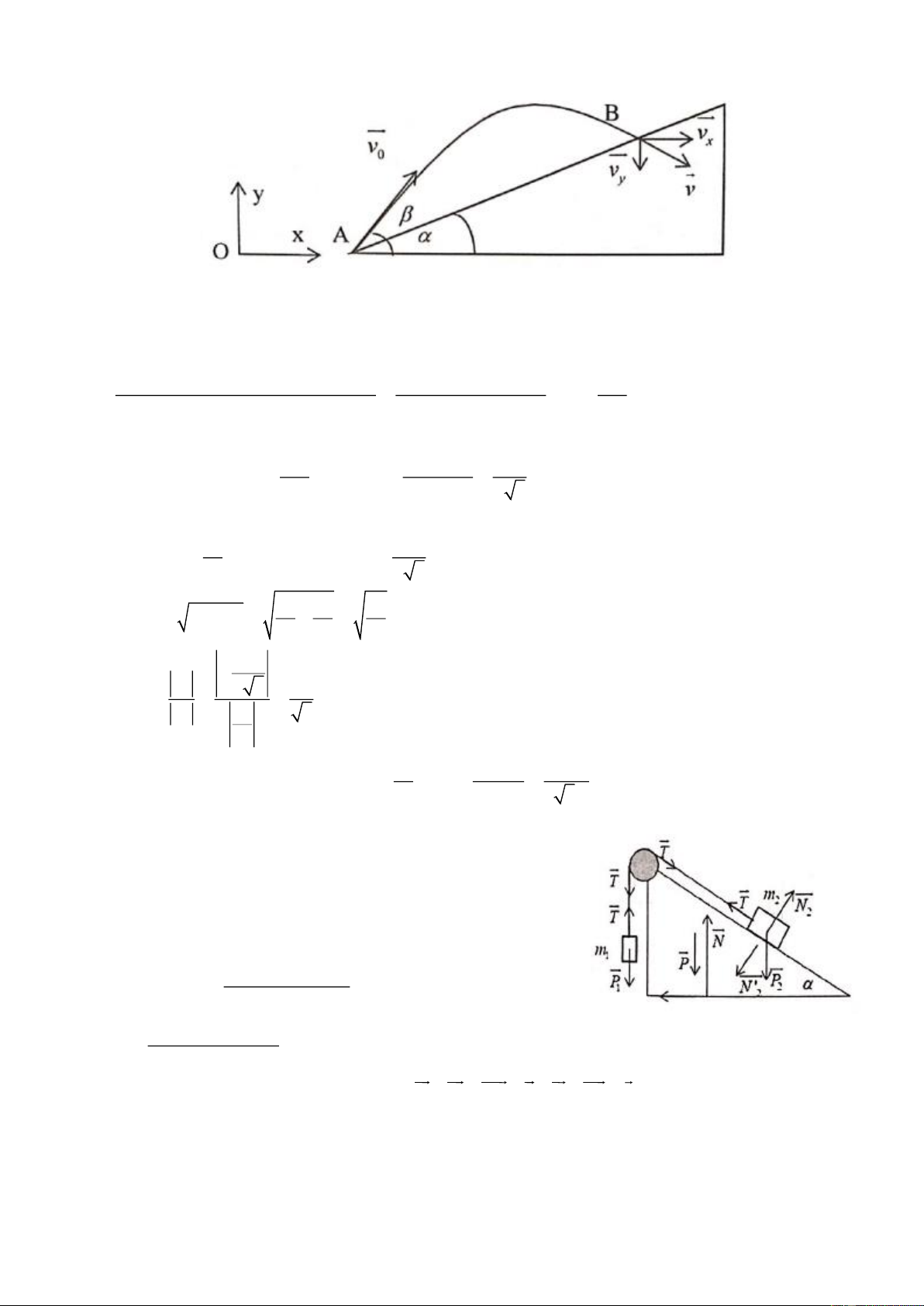
Một mặt phẳng nghiêng khối lượng M nằm trên mặt sàn có hệ số ma sát nghỉ . Một vật khối
lượng m được treo bởi một sợi dây vắt qua một ròng rọc ở đầu phía trên mặt phẳng nghiêng và nối 1
với vật m (hình vẽ). Bỏ qua khối lượng dây và khối lượng ròng rọc. Vật m chuyển động lên trên, 2 2
không ma sát với mặt phẳng nghiêng. Mặt phẳng nghiêng hợp tạo với phương ngang góc .
a. Tìm gia tốc của m , m và lực căng dây khi rất lớn. 1 2
b. Tìm hệ số ma sát nghỉ nhỏ nhất để mặt phẳng nghiêng còn đứng yên. Câu 3: (5 điểm)
Thanh đồng chất, nằm trong một chỏm cầu nhám, hệ số ma sát k, độ dài của thanh bằng bán kính
chỏm cầu. Hỏi thanh có thể tạo với đường nằm ngang góc lớn nhất bằng bao nhiêu mà vẫn cân bằng?
Biết thanh nằm trong mặt phẳng thẳng đứng qua tâm chỏm cầu. Câu 4: (5 điểm)
Một quả cầu khối lượng m bay theo phương ngang với vận tốc v. Sau khi
va chạm tuyệt đối đàn hồi với mặt phẳng nghiêng của nêm nó bật thẳng đứng
lên trên. Biết nêm có khối lượng M. Bỏ qua ma sát giữa nêm và sàn. Tìm độ
cao cực đại mà quả cầu đạt được sau va chạm. Câu 5: (5 điểm)
Một mol khí lý tưởng lưỡng nguyên tử thuẹc hiện một chu trình như sau:
Từ trạng thái 1 có áp suất 5
p = 10 Pa , nhiệt độ T = 600K dãn nở đẳng nhiệt 1 1
sang trạng thái 2 có áp suất 4
p = 2,5.10 Pa ; rồi bị nén đẳng áp đến trạng thái 3 có nhiệt độ T = 300K; 2 3
rồi bị nén đẳng nhiệt đến trạng thái 4; sau đó trở lại trạng thái 1 bằng quá trình đẳng tích.
1. Xác định đầy đủ các thông số tương ứng với các trạng thái 1, 2, 3, 4 của khí. Vẽ đồ thị biểu diễn
cu trình trong hệ tọa độ (pV)
2. Tính công mà khí sinh ra trong cả chu trình và hiệu suất của chu trình. Câu 6: (5 điểm)
Một bình kim loại có thể tích V chứa không khí ở áp suất khí quyển p . Người ta dùng bơm có thể 0
tích làm việc V tiến hành hút khí ra 3 lần. Sau đó, cũng bơm này bắt đầu bơm khí từ khí quyển vào 0
bình và cũng thực hiện bơm khí vào 3 lần, khi đó áp suất trong bình lớn gấp 2 lần áp suất khí quyển.
Các điều kiện bên ngoài là (p ,T không đổi. Các quá trình diễn ra đủ chậm, khí bơm vào và khí trong 0 )
bình có khối lượng mol là (g / mol) .
a. Tìm hệ thức giữa thể tích làm việc của bơm và thể tích bình.
b. Khối lượng khí trong bình sau 3 lần hút giảm bao nhiêu % so với ban đầu? HƯỚNG DẪN GIẢI Câu 1:
a. Trong quá trình chuyển động vật chỉ chịu tác dụng của trọng lực P . Phương trình chuyển động
của vật theo hai trục Ox và Oy: x = v cos . t 1 0 ( ) 1 2 y = v sin . t − gt 2 0 ( ) 2 x = l cos (3)
Vị trí viên đá chạm mặt phẳng nghiêng: y = l sin (4)
Giải hệ phương trình (1), (2), (3), (4) ta tìm được: 2 −v cos . (sin . cos − sin . cos ) 2 −v cos . sin ( −) 2 2v 0 0 0 l = = l = 2 2 g.cos g.cos 3g
b. Khi vật chạm mặt phẳng nghiêng: 2 2v 2v cos 2v 0 0 0
x = l cos v cos . t = cos t = = 0 2 3g g cos g 3
Vận tốc của vật tại B: v v 0 0 v = v cos = ; v = v sin − gt = − x 0 y 0 2 2 3 2 2 2 v v v Suy ra: 2 2 0 0 0 v = v + v = + = x y 4 12 3 v0 − vy 2 3 1 0 tan = = = = 30 v v 3 x 0 2 2 2 2 v v 2v Lực hướng tâm tại B: 0 F = mg cos = m R = = ht R g cos 3 3.g Câu 2:
a. Khi đủ lớn, mặt phẳng nghiêng còn đứng yên.
Phương trình chuyển động của m và m là: 1 2 P − T = m a 1 1 T − P sin = m a 2 2 (m − m sin g 1 2 ) Ta tính được: a = m + m 1 2 m m 1+ sin g 1 2 ( ) Và T = m + m 1 2
b. Xét mặt phẳng nghiêng khi cân bằng: T + T + N ' + P + N + F = 0 1 2 2 ms Suy ra: F = T cos − N sin msn 2
N = N cos + P + T 1+ sin với N = P cos 2 ( ) 2 2
Để mặt phẳng nghiêng đứng yên: F N msn m cos m − m sin 2 ( 1 2 )
M (m + m ) + m m (1+ sin )2 + (m + m ) 2 m cos 1 2 1 2 1 2 2 Câu 3:
Lực tác dụng vào thanh được biểu diễn trên hình vẽ:
Điều kiện cân bằng momen đối với điểm A và B: R 0 0 P
cos − N R sin 60 − kN R cos 60 = 0 (1) 2 2 2 R 0 0 P
cos − N R sin 60 − kN R cos 60 = 0 (2) 1 1 2 N 3 − k 1 ( )
Phương trình (1), (2) suy ra: N = (3) 2 3 + k
Điều kiện cân bằng lực: P + N + N + F + F = 0 (4) 1 2 ms1 ms2
Chiếu (4) lên trục Ox ta có: N sin ( 0 30 − ) + kN cos( 0 30 − ) = N cos( 0 60 − ) − kN sin ( 0 60 − (5) 1 1 2 2 ) 1 3 3 1 Suy ra: N cos − sin + kN cos + sin 1 1 2 2 2 2 1 3 3 1 = N cos + sin − kN cos − sin 2 2 2 2 2 2 N 1+ k 3 cos −
3 − k sin = N 1− k 3 cos + 3 + k sin 1 ( ) ( ) 2 ( ) ( ) (6)
Từ phương trình (3), (6) suy ra:
( 3+k)(1+k 3)−( 3−k)(1−k 3) 4k tg = = 2( 2 3 − k ) 2 3 − k Câu 4:
Xét trường hợp m M : Sau va chạm M đứng yên
Do va chạm tuyệt đối đàn hồi, dựa vào định luật bảo toàn động lượng và định luật bảo toàn cơ năng, ta
suy ra quả cầu chỉ thay đổi phương còn độ lớn vận tốc không đổi. (suy ra mặt nghiêng hợp với phương ngang góc 0 45 ) 2 Khi đó: v v = v h = 1 max 2g
Xét trường hợp m không quá bé so với M: sau va chạm cả hai cùng chuyển động
Gọi V là vận tốc của nêm sau va chạm
Áo dụng định luật bảo toàn động lượng theo phương ngang: m mv = MV V = v (1) M 2 2 2 mv mv MV
Áp dụng định luật bảo toàn cơ năng: 1 = + (2) 2 2 2 2 2 M − m v v M − m 2 2 ( ) Từ (1) và (2): 1 v = v h = = 1 max M 2g 2gM Câu 5:
1. Xác định các thông số trạng thái và vẽ đồ thị:
Áp dụng phương trình trạng thái cho khí ở trạng thái 1: RT 8, 31.600 1 3 p V RT V 49,86.10− = = = = m = 49,86 1 1 1 1 5 ( 3) ( ) p 10 1
Từ trạng thái 1 sang trạng thái 2, khí dãn nở đẳng nhiệt: T = T = 600K 2 1 5 p V 10 .49,86 1 1 V = = =199,44 2 4 ( ) p 2, 5.10 2
Từ trạng thái 2 sang trạng thái 3, khí bị nén đẳng áp: 4 p = p = 2, 4.10 Pa 3 2 T V V 3 2 2 V = = = 99,72 3 ( ) T 2 2
Từ trạng thái 3 sang trạng thái 4, khí bị nén đẳng nhiệt: T = T = 300K 4 3
Từ trạng thái 4 sang trạng thái 1, khí biến đổi đẳng tích: V = V = 49,86 4 1 ( ) 4 p V 2, 4.10 .99, 72 3 3 5 p = = = 0,48.10 Pa 4 ( ) V 49, 68 4
Như vậy ta có các trạng thái của khí: 5 4 4 4 p =10 Pa p = 2.14.10 Pa p = 2,4.10 Pa p = 4,8.10 Pa 1 2 3 4 ( )
1 V = 49,86 2 V = 199, 44 3 V = 99,72 4 V = 49,86 1 ( ) 2 ( ) 3 ( ) 4 T = 600K T = 600K T = 300K T = 300K 1 2 3 4 Đồ thị như hình
2. Tính công và hiệu suất của cả chu trình:
+ Quá trình 1-2 là quá trình dãn đẳng nhiệt có U
= 0 , khí nhận nhiệt lượng: 12 V2 Q = A = RT ln = 8,31.600.1,386 = 6911 J 12 12 1 ( ) V1
+ Quá trình 2-3 là quá trình nén đẳng áp, khí nhận nhiệt lượng: 7 Q
= C T − T = R T − T = 3,5.8,31. 300 − 600 = 8 − 726 J 23 p ( 3 2 ) ( 3 2 ) ( ) ( ) 2
Thực tế trong quá trình này khí tỏa nhiệt Q ' = Q − = 8726 J 23 23 ( )
+ Quá trình 3-4 là quá trình nén đẳng nhiệt, khí nhận nhiệt lượng: V4 Q = A = RT ln = 8,31.300. 0 − ,693 1 − ,728 J 34 34 3 ( ) ( ) V3
Thực tế trong quá trình này khí tỏa nhiệt Q ' = Q − =1728 J 34 34 ( )
+ Quá trình 4-1 là quá trình đẳng tích, khí nhận nhiệt lượng: 5 Q = C T − T
= R T − T = 2,5.8,31. 600 − 300 = 6232 J 41 V ( 1 4 ) ( 1 4) ( ) ( ) 2
+ Công do khí sinh ra trong cả chu trình: U = 0
A = Q = Q + Q + Q + Q = 2689 J 12 23 34 41 ( ) A 2689
+ Hiệu suất của chu trình: H = = 0, 2046 = 20, 46% Q + Q 6911+ 6232 12 41 Câu 6: + Quá trình hút khí:
Lúc đầu khí trong bình có (V, p 0 )
Kéo pittông lần thứ 1, khí trong bình đi vào bơm, khí có (V + V , p 0 1 ) p V
Nhiệt độ của khí không đổi nên ta có: p V = p (V + V ) 0 p = 0 1 0 1 V + V0 2 p V V
Bơm lần 2, khí có áp suất: 1 p = = p 2 0 V + V V + V 0 0 3 p V V
Bơm lần 3, khí có áp suất: 2 p = = p 3 0 V + V V + V 0 0
+ Quá trình bơm khí: trước khi bơm khí trong bình có áp suất p 3 p V
Mỗi lần bơm, áp suất khí trong bình tăng thêm một lượng 0 0 p = V
Sau 3 lần bơm, khí trong bình có áp suất bằng p với 3 3 3p V V 3V 1 3V 0 0 0 0 p = p + = p + = p + 3 0 0 V V + V V V + 0 V 0 1 V V
Theo điều kiện của bài toán: p = 2p , đặt 0 x = 0 V 3 3 1 1 Ta có phương trình: 2 = + 3x 2 − 3x = 1+ x 1+ x V
Giải phương trình ta được x 0,58 nghĩa là 0 0, 58 V
b. Khối lượng của khí trong bình ban đầu là: m = p V 0 0 RT 3 p V V
Khối lượng còn lại của khí sau 3 lần hút: 0 m = p V = 1 3 RT RT V + V 0
Độ giảm khối lượng khí trong bình sau 3 lần hút: 3 3 p V V p V V 0 0 m = m − m = = 1 − 0 1 RT V + V RT V + V 0 0 3 m V =1− = 74,65% m V + V 0 0
THPT CHUYÊN LÊ KHIẾT – QUẢNG NGÃI Câu 1: (5 điểm)
Hai vận động viên A và B chạy trên một đường thẳng từ rất xa đến gặp nhau với cùng tốc độ 5m/s.
Để điều hành tốt cuộc thi, trọng tài chạy chỗ sao cho: luôn đứng cách A 18m và cách B 24m. Khi
khoảng cách giữa A và B bằng 30m thì tốc độ và độ lớn của trọng tài là bao nhiêu? Câu 2: (5 điểm)
Khối lăng trụ tam giác vuông khối lượng m , có góc ở đáy là , tựa trên 1
khối lập phương khối lượng m như hình 2. Khối có thể trượt xuống dọc 2
theo tường thẳng đứng và khối m có thể trượt trên sàn ngang sang phải. 2
Ban đầu hệ đứng yên. Bỏ qua mọi ma sát.
a. Tính gia tốc của mỗi khối và áp lực giữa hai khối.
b. Xác định để gia tốc khối lập phương m có giá trị lớn nhất. Tính gia 2
tốc của mỗi khối trong trường hợp đó. Câu 3: (5 điểm)
Giữa hai tấm phẳng nhẹ, cứng OA và OB được nối với nhau
bằng khớp ở O. Người ta đặt một hình trụ tròn đồng chất, với trục
O song song với trục O. Hai trục này cùng nằm ngang và nằm 1
trong mặt phẳng thẳng đứng như hình 3. Dưới tác dụng của hai lực
trực đối F nằm ngang, đặt tại hai điểm A và B, hai tấm ép trụ lại.
Trụ có trọng lượng P, bán kính R.
Hệ số ma sát giữa trụ và mỗi tấm phẳng là k. Biết = = . Xác định độ AOB 2 ; AB a
lớn của lực F để trụ cân bằng. Câu 4: (5 điểm)
Bán cầu bán kính R = 1m đặt nằm cố định trên sàn ngang. Tại
đỉnh của bán cầu, người ta đặt một quả cầu nhỏ (hình 4). Bỏ qua
ma sát giữa vật với bán cầu và lực cản không khí, lấy 2 g = 10m / s
. Truyền cho vật vận tốc đầu v theo phương ngang. 0
1. Xác định độ lớn của v để vật không rời bán cầu ngay khi 0 truyền vận tốc.
2. Xác định vị trí vật chạm sàn so với tâm O của bán cầu theo phương ngang, nếu: a. v = 5m / s 0 b. v = 1m / s 0 Câu 5: (5 điểm)
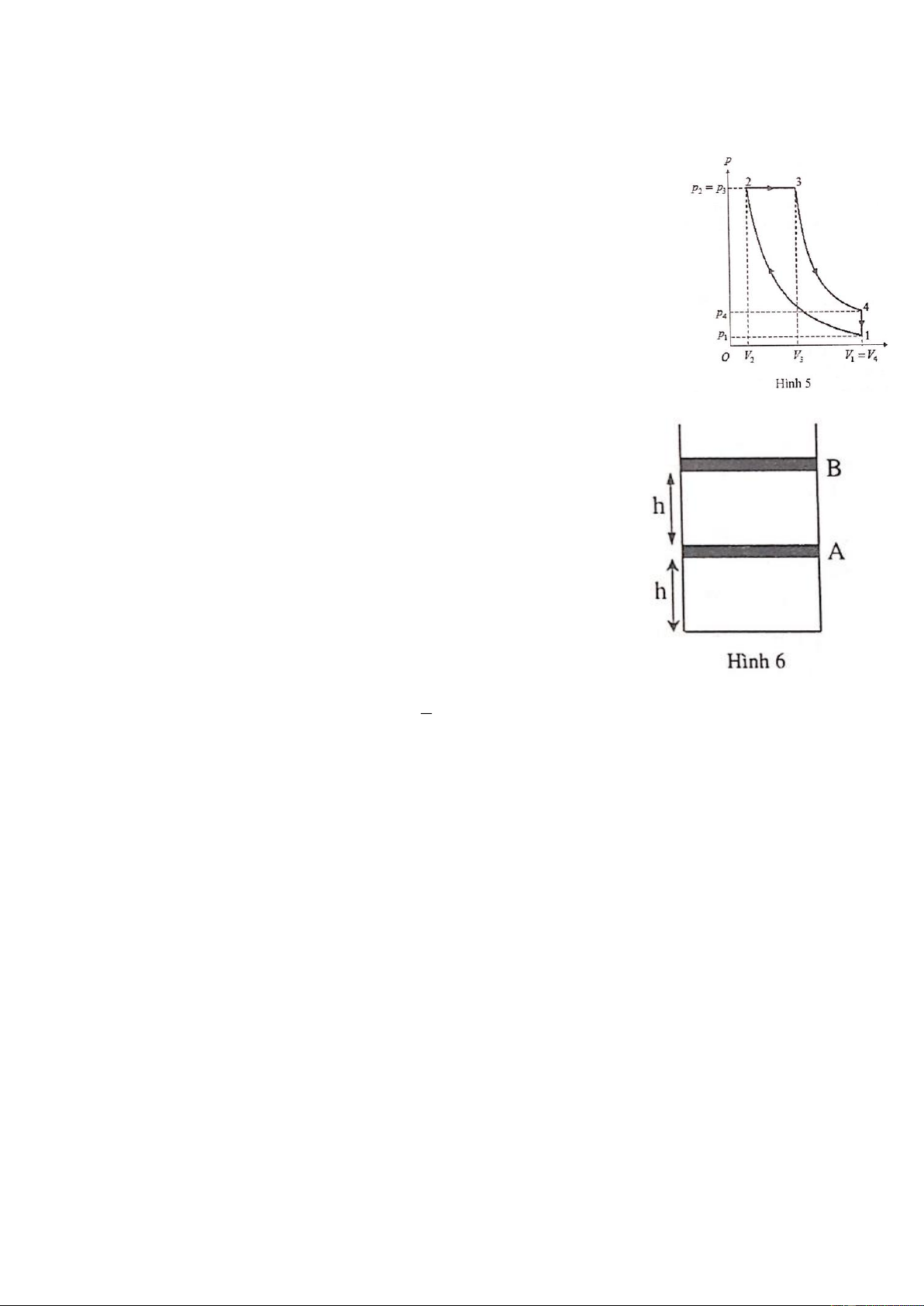
Một mol khí lý tưởng lưỡng nguyên tử biến đổi trạng thái nhiệt theo
nhiệt một chu trình thuận nghịch được biểu diễn trên đồ thị ở hình 5. Trong
đó 1→ 2 và 3 → 4 là các quá trình đoạn nhiệt, 2 → 3 là quá trình đẳng áp,
4 →1 là quá trình đẳng tích.
Biết p = 1atm, T = 320K, V = 12V , V = 2V 1 1 1 2 3 2
a. Tính p , T , p , T , p , T . 2 2 3 3 4 4
b. Nhiệt lượng khí nhận được là Q ở quá trình nào? Nhiệt lượng khí nhả ra 1
là Q ' ở quá trình nào? Tính Q , Q ' và từ đó tính hiệu suất của chu trình. 2 1 2 Câu 6: (5 điểm)
Trong bình hình trụ thẳng đứng, thành xung quanh cách nhiệt, có hai
pittông: pittông A nhẹ (trọng lượng có thể bỏ qua) và dẫn nhiệt, pittông
B có khối lượng đáng kể và cách nhiệt. Hai pittông tại thành hai ngăn
trong bình (hình 6). Mỗi ngăn chứa một mol khí lý tưởng lưỡng nguyên
tử và có chiều cao là h = 0,5m. Ban đầu hệ ở trạng thái cân bằng nhiệt.
Làm cho khí trong bình nóng lên thật chậm bằng cách truyền cho khí
(qua đáy dưới) một nhiệt lượng Q =100(J) .
Pittông A có ma sát với thành bình và không chuyển động, pittông B
chuyển động không ma sát với thành bình. Tính lực ma sát tác dụng lên
pit tông A. Biết nội năng U của một mol khí lưỡng nguyên tử phụ thuộc 5
vào nhiệt độ T của khí theo công thức U =
RT với R là hằng số khí 2 lý tưởng. HƯỚNG DẪN GIẢI Câu 1:
Khi khoảng cách giữa hai vận động viên là 30m thì vị trí của A, B và trọng tài T tạo thành một tam
giác vuông tại T. Lúc đó vận tốc của trọng tài theo Ox và Oy lần lượt là v và v . Vì khoảng cách x y
giữa trọng tài và các vận động viên là không đổi nên 18 v = v cos = 5. = 3m / s x A 30 24 v = v cos = 5. = 4m / s y B 30
Vậy tốc độ của trọng tài là 2 2 2 2 v = v + v = 3 + 4 = 5m / s x y
- Xét hệ quy chiếu gắn với A:
+ Tốc độ của B đối với A là: v =10m / s B,A
+Trọng tài chuyển động trên đường tròn tâm A, bán kính AT với tốc độ 24 v = v .cos =10. = 8m / s T,A B,A 30 2 2 v 8 32
Nên gia tốc hướng tâm là T,A 2 a = = = m / s T,A AT 18 9
- Xét hệ quy chiếu gắn với B: 2 2 v 6
Tương tự ta tìm được: T,B 2 a = = = 1,5m / s T,B BT 24
Vậy độ lớn gia tốc của trọng tài là 2 2 2 a = a + a 3,86m / s T,A T,B Câu 2: a. Xét vật m : 1
Áp dụng định luật II Newton có: P + N + N = m a 1 1 1 1
Chiếu lên trục Ox thu được: −N cos + N = 0 −N cos + N = 0 21 1 1
Chiếu lên trục Oy thu được: P − N sin = m a P − N sin = m a (1) 1 21 1 1 1 1 1 - Xét vật m : 2
Áp dụng định luật II Newton có: P + N + N = m a 1 2 12 2 2
Chiếu lên trục Ox thu được:
N cos = m a N cos = m a (2) 12 2 2 2 2
Mặt khác khi m dời sang phải một đoạn x thì m đi xuống 2 1 một đoạn y, ta có:
x = y. tan a = a . tan 2 1 (3) Từ (1) và (2) suy ra Nsin = m g − m a m g − a 1 1 1 1 ( 1 ) tan = N cos = m a m a 2 2 2 2 (4) m1 a = g 1 2 m + m tan Từ (3) và (4) suy ra 1 2 m tan 1 a = g 2 2 m + m tan 1 2 m a m m tan Áp lực giữa m và m là: 2 2 1 2 N = N = N = = 1 2 12 21 cos ( 2 m + m tan cos 1 2 ) m tan m b. Gia tốc của 1 1 m : a = g = g 2 2 2 m + m tan m1 1 2 + m tan 2 tan m
Áp dụng bất đẳng thức Cô-si có: 1 + m tan 2 m m 2 1 2 tan m m m Dấu “=” xảy ra khi: 1 2 1 1 = m tan tan = = arc tan 2 tan m m 2 2 m g m Vậy khi 1 = arc tan thì 1 a = m 2 min 2 m 2 2 Lúc đó có: m m 1 1 a = g = g = 0, 5g 1 m + 1 m m 1 1 m + m . 1 2 m2 Câu 3:
* Trường hợp 1: Trụ có khuynh hướng trượt lên:
- Các lực tác dụng lên trụ như hình 3G
- Phương trình cân bằng lực: P + F + F + N + N = 0 ms1 ms2 1 2
- Chiếu lên trục OI: −P − F cos − F
cos + N sin + N sin = 0 ms1 ms2 1 1 2N sin − P Có: N = N = N F = F = F F = 1 2 ms1 ms2 ms ms 2 cos − Để 2N sin P
trụ không trượt lên: F kN kN ms 2 cos
Xét thanh OA: chọn O làm trục quay. Quy tắc momen: OI
N ' .OH = F.OI N.OH = F.OI N = F 1 OH OI AI a OAI OO H = = 1 OH O H 2R 1 2N sin − P a PR k F F 2 cos 2R s (sin − k cos )
* Trường hợp 2: Trụ có khuynh hướng trượt xuống, tương tự như trên: chú ý các lực ma sát hướng ngược lại PR
Điều kiện để trụ không trượt xuống: F a (sin + k cos ) PR PR
* Điều kiện để trụ đứng yên: ( − ) F a sin k cos a (sin + k cos ) Câu 4:
1. Áp dụng định luật II Newton cho vật ngay khi truyền vận tốc: P + N = ma 2 v
Chiếu lên chiều của AO thu được: 0 N = m g − R
Để vật không rời bán cầu ngay khi truyền vận tốc thì N 0 v gR v 3,16m / s 0 0
2. a. Khi v = 5m / s thì ngay khi truyền vận tốc, vật rời bán cầu và chuyển động ném ngang. Do 0 2R 2.1
vậy, vị trí vật chạm sàn so với O được xác định L = v = 5 = 2, 24m 0 g 10
b. Khi v = 1m / s thì vật trượt trên bán cầu rồi rời bán cầu tại B được xác định bởi góc = AOB 0 2 2 v
Áp dụng định luật bảo toàn cơ năng và định luật II Newton xác định được: 0 cos = + = 0,7 3 3gR
+ Vận tốc của vật ngay khi rời bán cầu: 2
v = v + 2gR 1− cos = 7 m / s 0 ( )
Sau khi rời bán cầu, vật chuyển động ném xiên xuống:
+ Vận tốc của vật theo phương ngang và theo phương thẳng đứng ngay khi vật rời bán cầu là: v = v.cos = 0, 7 7 m / s x 2
v = v. 1− cos = 1,89 m / s y
+ Áp dụng định luật bảo toàn cơ năng xác định được độ lớn vận tốc của vật ngay trước khi chạm sàn: 2 v = v + 2gR = 21 m / s s 0
+ Vận tốc của vật theo phương thẳng đứng ngay trước khi chạm sàn: 2 2 2
v = v − v = 21− 7.0, 7 = 4,19 m / s sy sy x
+ Thời gian chuyển động của vật từ lúc rời bán cầu đến khi chạm sàn là: v − v − sy s 4,19 1,89 t = = = 0,23s g 10 R
+ Tầm bay xa của vật so với O: L = + v .t =1,133m x 2 Câu 5:
a. Khí lưỡng nguyên tử thì số bậc tự do là i = 5 (i + 2) 7 = = = 1, 4 i 5 V 1 p = p = 32,4atm 2 1 V 2 1 − V 1 T = T = 864,6K 2 1 V 2 p = p = 32, 4 atm 3 2 V3 T = T = 1729, 2 K 3 2 V2 V V V V V 3 3 2 3 2 p = p = p = p = 2,6atm 4 3 3 3 V V V V V 4 2 4 2 1 1 − 1 − V V V 3 3 2 T = T = T = 844,5K 4 3 3 V V V 4 2 1
b. Nhiệt lượng nhận là Q ở quá trình đẳng áp 2-3 1
Nhiệt lượng nhả ra Q ' ở quá trình đẳng tích 4-1 2 i + 2 5 + 2 Q = C T − T = R T − T =
.8,31. 1729, 2 − 864, 6 = 25146,9 J 1 p ( 3 2 ) ( 3 2) ( ) ( ) 2 2 i 5 Q ' = C T − T = R T − T =
.8,31. 844,5 − 320 = 10896,5 J 2 V ( 4 1 ) ( 4 1) ( ) ( ) 2 2 Q ' 10896, 5
Hiệu suất của chu trình là 2 H = 1− = 1− = 0,5667 = 56,67% Q 25146, 9 1 Câu 6:
Gọi nhiệt độ ban đầu của hệ là T , nhiệt độ sau cùng là T 0
Áp suất ban đầu của khí trong hai ngăn bằng nhau: p 0 T
Áp suất cuối cùng trong ngăn dưới là: 1 p = p 1 0 T0 T
Thể tích cuối cùng của ngăn trên: 1 V = V 1 0 T0 Độ T
tăng thể tích ngăn trên: 1 V = V − V = −1V 1 0 0 T 0 T Công sinh ra: 1 A ' = p . V
= p −1V = R T − T 0 0 0 ( 1 0 ) T 0 Độ tăng nội năng: U = 2C T − T = 5R T − T V ( 1 0 ) ( 1 0) Q Theo nguyên lý I: Q = U
+ A ' Q = 6R (T − T T − T = 1 0 ) 1 0 6R
Lực ma sát tác dụng lên A: = ( T V 1 F p − p S = p −1 = R T − T 1 0 ) 1 0 0 ( 1 0 ) T h h 0 Q 1 100 F = R = 33,3N 6R h 6.0, 5
THPT LÊ QUÝ ĐÔN – BÌNH ĐỊNH Câu 1: (5 điểm)
Trên quãng đường S nhất định, một chất điểm chuyển động nhanh dần đều không vận tốc ban đầu
với gia tốc a mất thời gian T. Tính thời gian chất điểm chuyển động trên quãng đường này nếu chuyển
động của chất điểm là luân phiên giữa chuyển động với gia tốc a trong thời gian T = 0,1T và chuyển 1
động đều trong thời gian T = 0, 05T . 2 Câu 2: (5 điểm)
Cho hệ cơ như hình vẽ, sợi dây dài 2L (khối lượng không đáng kể và không đàn hồi). Một đầu buộc
chặt vào A, đầu kia nối với m , m di chuyển không ma sát dọc theo thanh. Tại trung điểm I của dây 2 2
có gắn chặt vật m . Ban đầu giữ m đứng yến, dây hợp với phương ngang một góc . Xác định gia 1 2
tốc của m ngay sau khi thả và xác định lực căng dây. 2 Câu 3: (5 điểm)
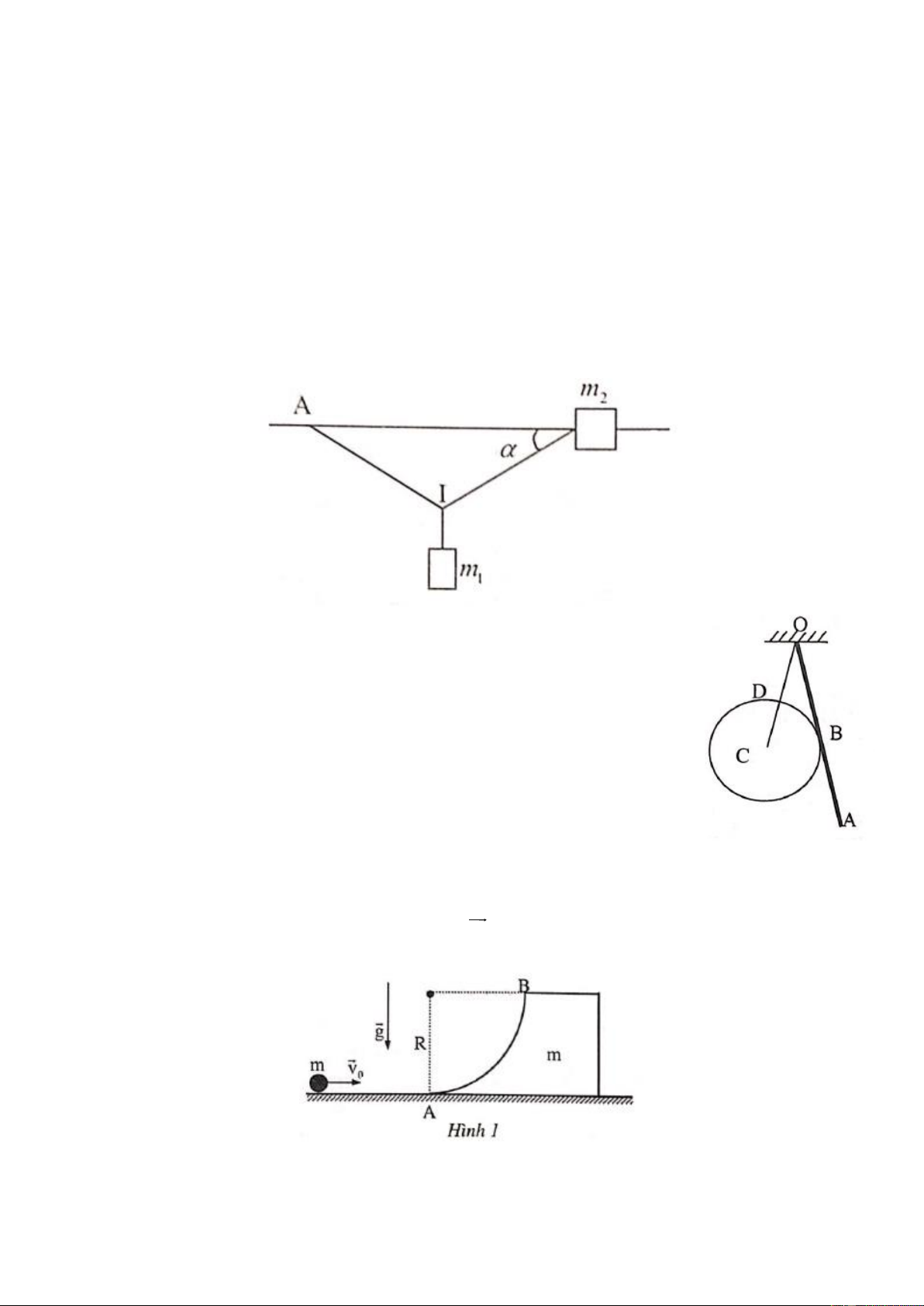
Thanh đồng chất OA có trọng lượng P quay được quanh điểm O và tựa tại
điểm giữa B của nó lên quả cầu đồng chất C có trọng lượng Q, bán kính R được
treo vào trục O, nhờ dây OD dài bằng bán kính R của quả cầu. Cho góc 0
BOC = = 30 . Tính góc nghiêng của dây OD hợp với đường thẳng đứng khi hệ cân bằng. Câu 4: (5 điểm)
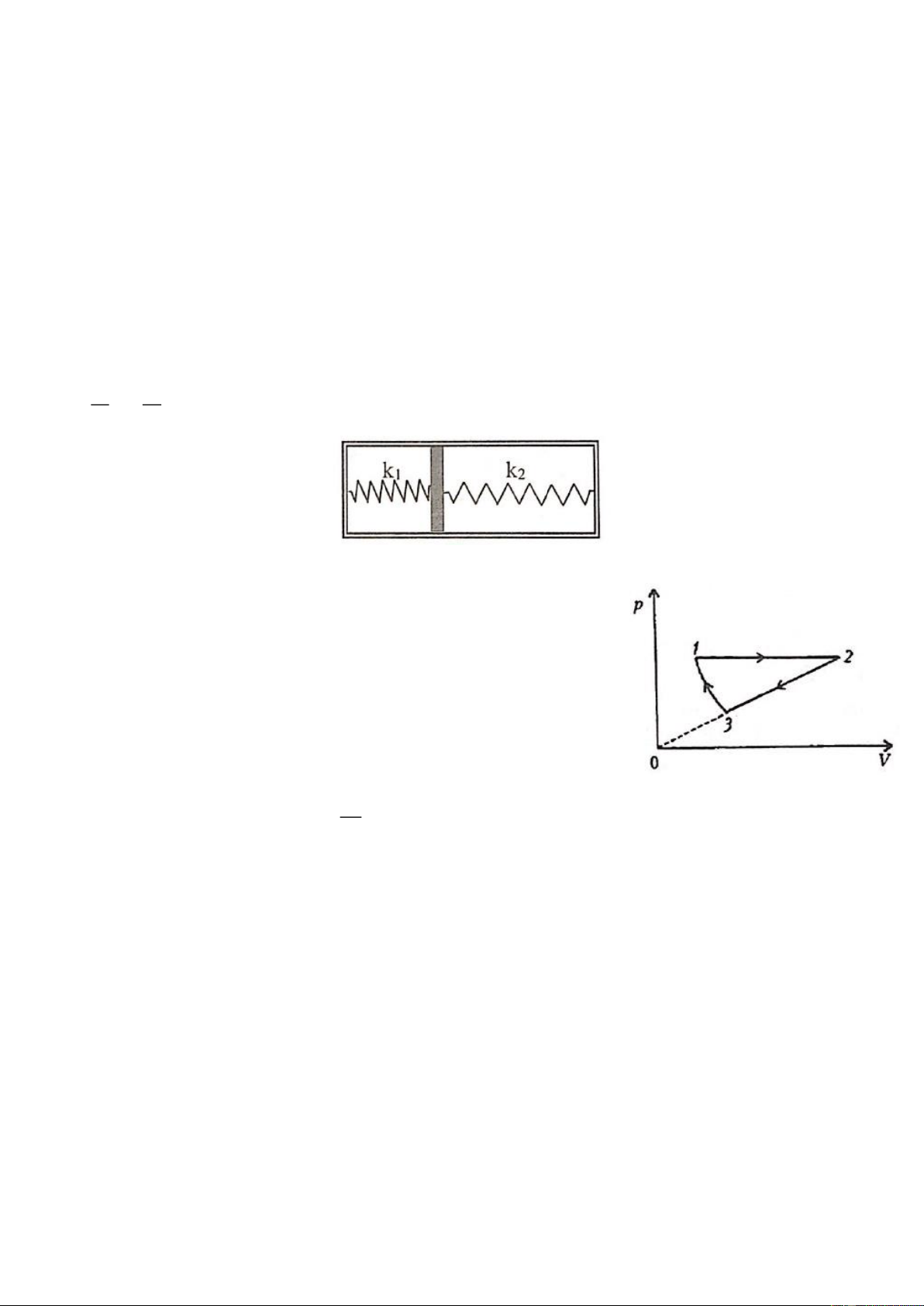
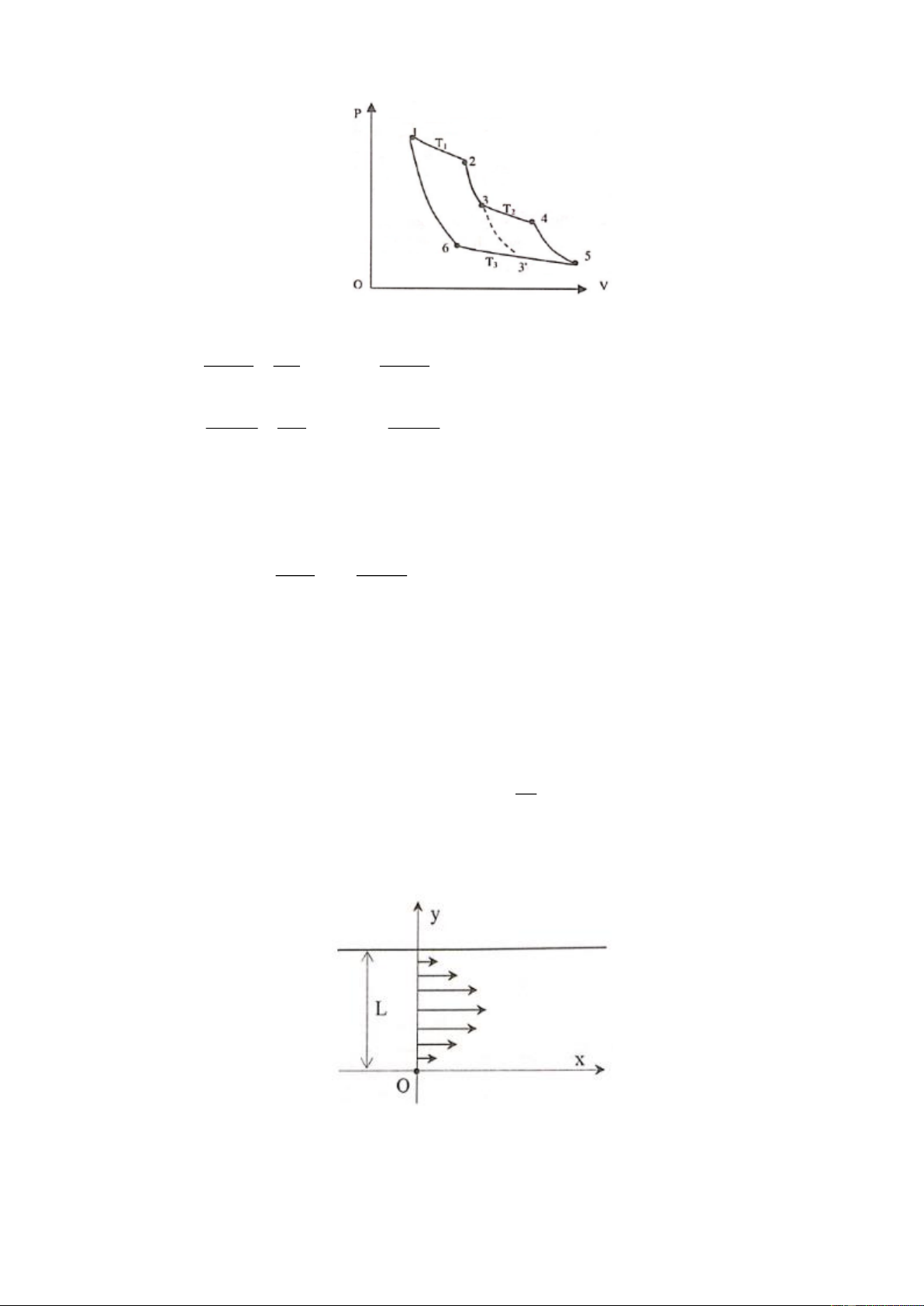
Trên mặt bàn nằm ngang có một miếng gỗ khối lượng m, tiết diện như hình 1 (hình chữ nhật chiều
cao R đã bị khoét bỏ ¼ hình tròn bán kính R). Ban đầu miếng gỗ đứng yên. Một hòn bi sắt có cùng
khối lượng với miếng gỗ chuyển động với vận tốc v đến đẩy miếng gỗ. Bỏ qua ma sát và sức cản của 0
không khí. Gia tốc trọng trường là g.
a. Tính các thành phần nằm ngang v và thẳng đứng v của hòn bi khi nó đi tới điểm B của miếng x y
gỗ. Tìm điều kiện để hòn bi vượt qua B.
b. Giả thiết điều kiện vượt qua B được thỏa mãn. Trong gia đoạn tiếp theo hòn bi và miếng gỗ
chuyển động như thế nào? Tìm các vận tốc cuối cùng của hai vật. c. Áp dụng số: 2
v = 5m / s; R = 0,125m; g = 10m / s . Tính độ cao tối đa mà hòn bi đạt được (tính 0 từ mặt bàn). Câu 5: (5 điểm)
Một xilanh nằm ngang, bên trong có một pittông ngăn xilanh thành hai phần: phần bên trái chứa khí
lý tưởng đơn nguyên tử, phần bên phải là chân không. Hai lò xo có độ cứng k và k gắn vào pittông 1 2
và đáy xilanh như hình vẽ. Lúc đầu pittông được giữ ở vị trí mà cả hai lò xo đều chưa bị biến dạng,
trạng thái khí lúc đó là (P , V ,T . giải phóng pittông thì khi pittông ở vị trí cân bằng trạng thái khí là 1 1 1 )
(P ,V ,T với V = 3V . Bỏ qua các lực ma sát, xilanh, pittông, các lò xo đều cách nhiệt. Tính tỉ số 2 2 2 ) 2 1 P T 2 và 2 . P T 1 1 Câu 6: (5 điểm)
Một khối khí Hêli ở trong một xilanh có pit tông di chuyển được.
Người ta đốt nóng khối khí này trong điều kiện áp suất không đổi,
đưa khí từ trạng thái 1 tới trạng thái 2.
Công mà khí thực hiện trong quá trình này là A . Sau đó, khí bị nén 12
theo quá trình 2-3, trong đó áp suất p tỷ lệ thuận với thể tích V.
Đồng thời khối khí nhận một công là A ' A ' 0 . Cuối cùng khí 23 ( 23 )
được nén đoạn nhiệt về trạng thái ban đầu.
Hãy xác định công A mà khí thực hiện trong quá trình này. Tính 31 V
hiệu suất chu trình này, biết rằng 2 = V1 HƯỚNG DẪN GIẢI Câu 1:
Gọi n: số lần chất điểm chuyển động với thời gian T 2 2 aT
Khi vật chuyển động nhanh dần đều suốt quãng đường: S = (1) 2
Khi vật chuyển động luân phiên nhanh dần đều, thẳng đều thì: a a a a 2 2 2 2 S = T + v T + T + v T + v T + T + v T + v T +...+ T + v T + v T 1 1 2 1 1 1 2 2 1 2 1 3 2 1 n 1 − 1 n 2 2 2 2 2 a a a a 2 2 2 2 = T + aT T + T + aT T + 2aT T + T + 2aT T + 3aT T +...+ T + n −1 aT T + naT T 1 1 2 1 1 1 1 2 1 1 1 1 2 1 ( ) 1 1 1 2 2 2 2 2 2 aT 1 =
(1+3+5+...+(2n − )1)+aTT 1+2+...+n 1 2 ( ) 2 2 aT 1 1 n n +1 2 ( ) = n + . (2) 2 100 100 2 Từ (1) và (2) 2
3n + n − 200 = 0 n = 8
Vậy thời gian chất điểm chuyển động: t = 8(T + T −1, 2T 1 2 ) Câu 2:
Ngay sau khi thả m chịu tác dụng của các lực Q , P , T ; còn m chịu tác dụng của các lực T , T , P 2 2 2 3 1 1 2 1
Khi đó m chuyển động sang trái, chỉ có thành phần gia tốc theo phương ngang là a . Vật m chuyển 2 2 1
động tròn quanh A. Ngay sau khi thả m ra, gia tốc của m theo phương hướng tâm bằng không 2 1 2 V 1 a =
= 0 do V = 0. Vậy m chỉ có thành phần gia tốc theo phương tiếp tuyến là a . 1n 1 R 1 1
Chọn hệ trục Oxy như hình vẽ. Do khối lượng của dây không đáng kể nên T = T 2 3
Trên phương dây treo, ta có: a cos = a cos − 2 2 1 2 a = 2a sin (1) 2 1
Áp dụng định luật II Niuton cho mỗi vật T + T + P = m a 1 2 1 1 1 T + P + Q = m a 3 2 2 2 2
Chiếu lên các trục Ox và Oy, ta được: (
T − T cos = m a = m a sin 1 2 ) 1 1x 1 1
−(T + T sin + P = m a cos (2) 1 2 ) 1 1 1 T cos = T cos = m a 3 2 2 2
Giải hệ (1) và (2), ta được: m g cos m + 2m m g sin 1 ( 1 2 ) 1 a = T = 1 2 1 2 m + 4m sin m + 4m sin 1 2 1 2 m g sin 2 2m m g sin 1 1 2 a = 2a sin = T = T = 2m a tan = 2 1 2 2 3 2 1 2 m + 4m sin m + 4m sin 1 2 1 2 Câu 3:
- Điều kiện cân bằng momen lực của quả cầu đối với tâm quay O
Q.CH = N.OB Q.2R sin = N.2R cos Q sin 2Q sin N = = (1) cos 3
- Điều kiện cân bằng momen lực của thanh OA đối với tâm quay O = = ( 0 N.OB P.OH ' P.OB.sin 30 − ) = ( 0 N P.sin 30 − ) (2) 2Q sin P 3 Từ (1) và (2): P.sin ( 0 30 − ) = tan = 3 4Q + 3P Câu 4:
a. Áp dụng BTĐL và chiếu hệ thức vecto xuống phương ngang: v0 mv = 2mv → v = (1) 0 x x 2
với v là thành phần theo phương ngang của vận tốc hòn bi và vận tốc miếng gỗ sau khi tiếp xúc. x
- Áp dụng BTCN hệ hòn bi + miếng gỗ: 2 2 2 2 mv mv mv y mv 0 x x = + + + mgR (2) 2 2 1 2 2 v Từ (1) và (2) rút ra: 0 v = − 2gR y 2
- Điều kiện để hòn bi vượt qua B: v 0 → 2 gR y
b. Khi điều kiện v 2 gR được thỏa mãn thì sau khi hòn bi tới B, + miếng gỗ vẫn chuyển động 0
đều theo phương ngang với vận tốc v x
+ Còn hòn bi vạch ra một parabol, xét trong hệ quy chiếu đứng yên gắn với mặt đất.
+ Còn xét trong hệ quy chiếu gắn với miếng gỗ thì hòn bi là vật được ném thẳng đứng lên cao với vận
tốc ban đầu v , nên cuối cùng hòn bi lại rơi xuống đến đúng điểm B của miếng gỗ. y
Sau khi rơi xuống tới điểm B của miếng gỗ thì hòn bi sẽ trượt xuống theo cung BA của miếng gỗ và
đẩy miếng gỗ đi nhanh hơn.
- giả sử khi tới A hòn bi có vận tốc v , còn miếng gỗ có vận tốc v thì áp dụng BTĐL và BTCN: 1 2 2 2 2 mv mv mv mv = m v + v và 0 1 2 = + 0 ( 1 2) 2 2 2
Từ đó rút ra phương trình 2 v − v v = 0 1 1 0
- Phương trình này có 2 nghiệm v = 0 và v = v 1 1 0
+ Ta loại nghiệm v = v vì điều đó không thể xảy ra được (do v khác không) 1 0 2
- Như vậy khi trở lại A vận tốc của hòn bi là v = 0 . Hòn bi đứng yên, còn miếng gỗ chuyển động với 1
vận tốc ban đầu của hòn bi: v = v 2 0
(Như vậy hiện tượng xảy ra giống như va chạm đàn hồi của hai vật có cùng khối lượng)
c. Xét trong hệ qui chiếu đứng yên với mặt đất, sau khi hòn bi tới B nó vạch ra một parabol. 2 v Tại B: 0 v = − 2gR = 10m / s y 2 2 v
- Gọi h là chiều cao của đỉnh parabol do hòn bi vạch ra sau khi nó rời khỏi B, ta có y h = = 0,5m 2g
Vậy độ cao tối đa mà hòn bi đạt được là: H = h + R = 0, 635m Câu 5: V − V 2V
Khi pittông cân bằng, độ biến dạng của mỗi lò xo là x: 2 1 1 x = = S S Điề x 2V
u kiện cân bằng của pittông: P S = (k + k ) x P = (k + k ) = (k + k ) 1 (1) 2 1 2 2 1 2 1 2 2 S S Phương trình trạ P V P V P P T P
ng thái cho khối khí bên phải: 2 2 1 1 2 1 2 2 = 3 = = 3 (2) T T T T T P 2 1 2 1 1 1
Hệ không trao đổi nhiệt: Q = U + A = 0 A = − U 1 A = W = (k + k )x = 2(k + k ) 2 V 2 1 t 1 2 1 2 2 2 S Mà 3 = ( ) 3 = ( 3 U PV P V − P V = 3P − P V 2 2 1 1 ) ( 2 1) 1 2 2 2 2(k + k ) 2 V 3 V 3 1 = − 3P − P V 2 k + k = − 3P − P (3) 2 ( ) ( ) 1 1 2 2 1 1 1 2 2 ( 2 1) S 2 S 2 Thay (1) vào (3) ta đượ 3 P 3 T 9 c: P = − (3P − P ) 2 2 11P = 3P = ; = 2 2 1 2 1 2 P 11 T 11 1 1 Câu 6:
Trong quá trình đẳng áp 1-2, công do khối khí thực hiện là: A = vR T − T (1) 12 ( 2 1)
Trong quá trình 2-3, đây là quá trình đa biến với chỉ số đa biến n = 1 − vR T vR (T − T vR T − T 3 2 ) ( 2 3) A ' = = = (2) 2−3 n −1 n −1 2 Trong quá trình đoạ 3
n nhiệt 3-1, công mà khối khí sinh ra là: A = vR T − T (3) 31 ( 3 1) 2 3 Từ (1), (2) và (3) suy ra A = A − 2A ' 3 1 − ( 1−2 23 ) 2 Q ' Q ' 2R T − T 4 T − T 2 23 ( 2 3) ( 2 3) Ta có = 1− =1− = 1− =1− Q Q 2, 5R T T 5 T − T 1 12 ( 2− 1) ( 2 1) T V Mà 1-2: đẳng áp nên 2 2 = = T V 1 1 5 2-3: đa biến với n = 1
− và 3-1: đoạn nhiệt với = nên 3 2 − 2 − 2 − 2 T V = −T V T V = T V− 2 2 3 3 2 2 3 3 1 − 1 − 2/3 2/3 T V = T V T V = T V 1 1 3 3 1 1 3 3 2 V T 3 3 = V T 2 2 T1 1/ 4 = 3 2 2 T 3 T V V V T T 1 3 3 2 2 3 3 = = = = T V V V T T 3 1 2 1 2 1 ( 1/4 4 − )
Hiệu suất của chu trình là: = 1− 5( − ) 1
THPT CHUYÊN LÊ QUÝ ĐÔN – KHÁNH HÒA Câu 1: (5 điểm)
Trong huấn luyện quân sự, người chiến sĩ ở cách tường một
khoảng s bắt đầu nhảy với vận tốc v hướng về phía tường. Khi 0
tới sát tường, anh ta đạp vào mặt tường một lần làm cho toàn
thân bật lên thẳng đứng. Hệ số ma sát giữa tường và đế giày là
. Hỏi để trọng tâm của người đó có thể lên đến độ cao lớn nhất
thì góc nhảy phải bằng bao nhiêu? Câu 2: (5 điểm)
Một chiếc gậy có chiều dai 2L trượt trên hai cạnh của một góc
vuông. Chính giữa gậy có gắn một hạt tròn khối lượng m cố định.
Điểm A chuyển động với vận tốc v không đổi. Tại thời điểm 0 = 45
thì m tác dụng lên gậy một lực bao nhiêu? Câu 3: (5 điểm)
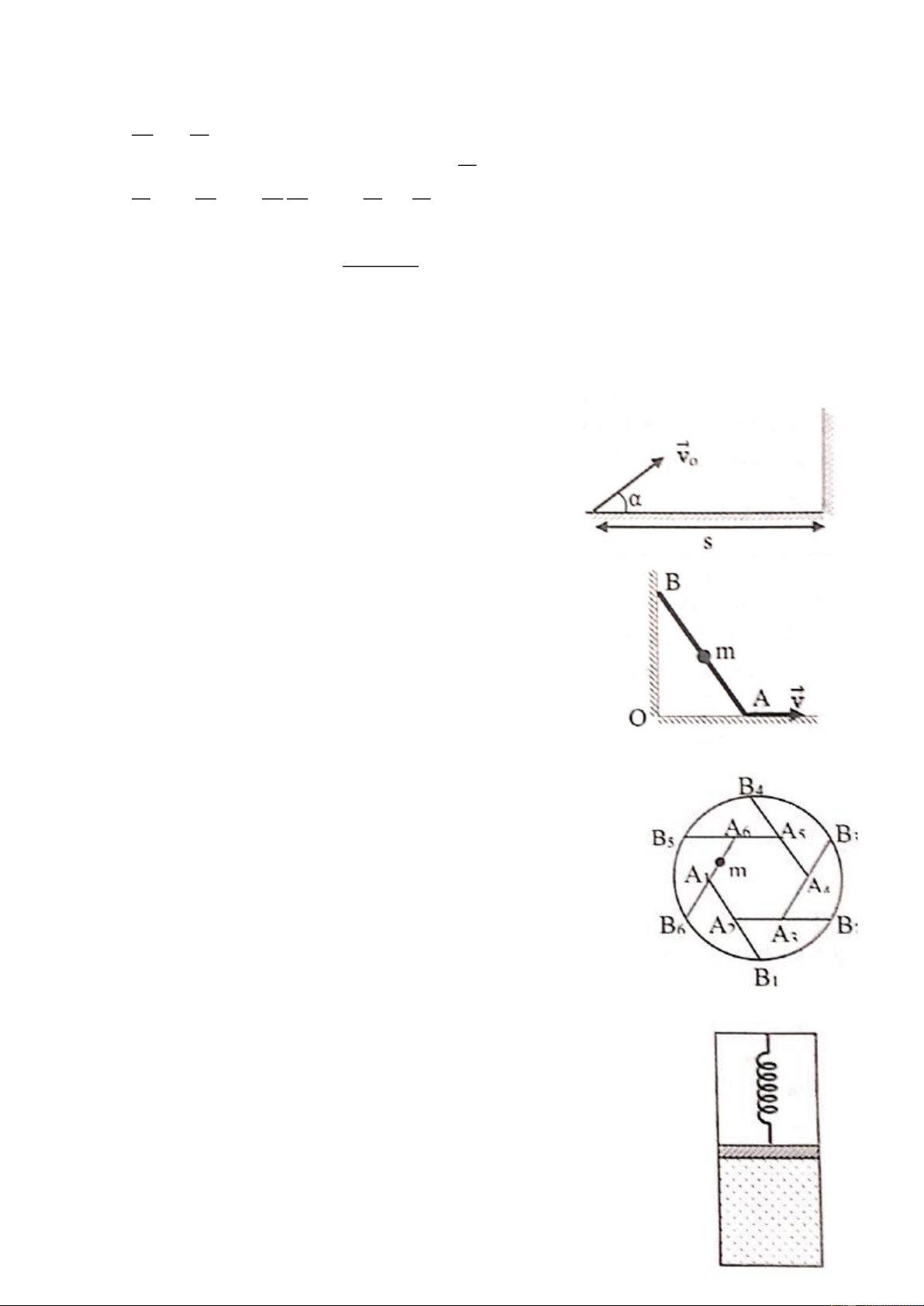
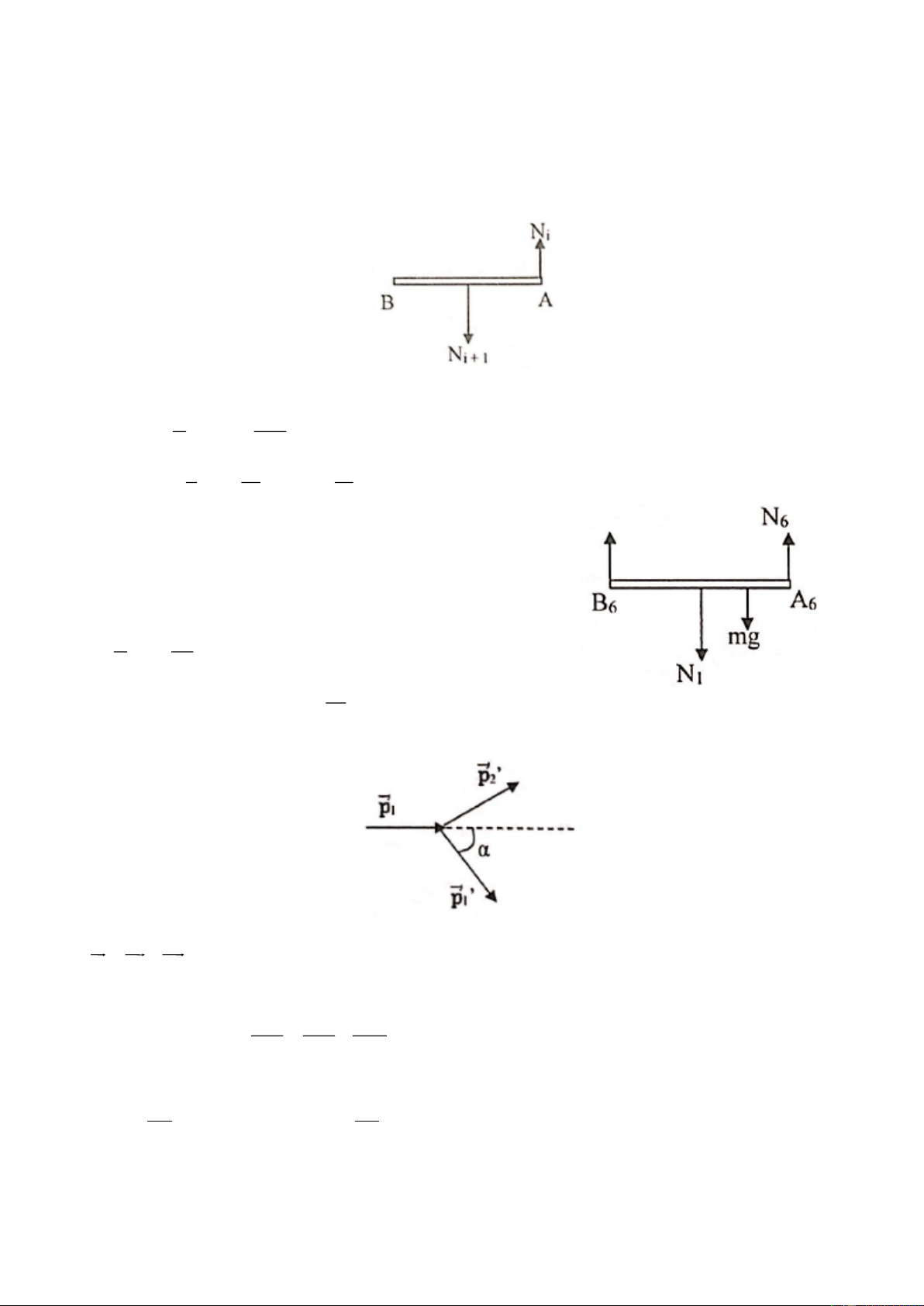
Có 6 thanh mỏng, nhẹ, giống nhau A B i = 1,.., 6 gác tựa vào i i ( )
nhau nằm ngang trên miệng bát như hình vẽ. Một đầu gác trên miệng
bát, đầu kia đặt chính giữa thanh khác. Đặt một chất điểm khối lượng
m trên trung điểm đoạn A A . Tính áp lực của thanh A B lên thanh 1 6 1 1 A B . 6 6 Câu 4: (5 điểm)
Một hạt khối lượng m đến va chạm hoàn toàn đàn hồi với một hạt khác 1
khối lượng m (m m ban đầu đứng yên. Xác định góc lệch hướng 2 1 ) 2
chuyển động lớn nhất của hạt đầu tiên sau va chạm. Câu 5: (5 điểm)
Một bình hình trụ thành mỏng, tiết diện ngang S, đặt thẳng đứng. Trong
bình có một piston, khối lượng M, bề dày không đáng kể, Piston được nối với
mặt trên của bình bằng một lò xo có độ cứng k (hình vẽ). Trong bình và ở phía
dưới piston có một lượng khí lý tưởng đơn nguyên tử, khối lượng m và khối lượng mol là . Lúc đầu
nhiệt độ của khí trong bình là T . Biết rằng chiều dài lò xo khi không biến dạng vừa bằng chiều cao 1
của bình, phía trên piston là chân không. Bỏ qua khối lượng của lò xo và ma sát giữa piston với thành
bình. Bình và piston làm bằng vật liệu cách nhiệt lý tưởng. Lúc đầu hệ đang ở trạng thái cân bằng cơ học.
Sau đó người ta nung nóng khí trong bình đến nhiệt độ T T T sao cho piston dịch chuyển rất 2 ( 2 1 )
chậm đến trạng thái cân bằng mới.
a. Tìm độ dịch chuyển của piston.
b. Tính nhiệt lượng đã truyền cho khí. Câu 6: (5 điểm)
Một mol khí lý tưởng thực hiện một chu trình gồm 3 quá trình đẳng nhiệt ở các nhiệt độ T , T , T 1 2 3
xen kẽ với 3 quá trình đoạn nhiệt. Trong các quá trình giãn đẳng nhiệt ở nhiệt độ T và T thể tích khí 1 2
tăng lên k lần (hình vẽ). Tính
a. Công A’ mà khí sinh ra.
b. Tính hiệu suất của chu trình. HƯỚNG DẪN GIẢI Câu 1:
Người thực hiện chuyển động ném xiên: v = v cos ; v = v sin − gt x 0 y 0 2 1 s
Trọng tâm nâng lên cao một đoạn là: h = s.tan − g 1 2 v cos 0
Khi chân đạp vào tường, nhờ xung lượng của lực ma sát nghỉ cực đại để đưa người nâng lên: mv = N. t x (mv = F . t = N . t = m v y ) ms x Suy ra: v = v' − v = v y y y x 2 v '
Quá trình bật thẳng lên, trọng tâm được nâng lên cao một đoạn: y h = 2 2g 2 v
Vậy tổng độ cao trọng tâm của người là: 0 h = h + h =
cos + sin − s 1 2 ( ) 2g
Để h max thì (cos + sin ) đạt max → với 1
Dấu bằng xảy ra khi: tan = Câu 2: Vì O
AB vuông tại O, hạt m ở trung điểm C nên: CO = CA = CB khi gậy chuyển động thì CO vẫn
không đổi, vậy m chuyển động trên cung tròn tâm O, bán kính R = L. 2 v
Vận tốc v của hạt có hướng tiếp tuyến với vòng tròn này với gia tốc hướng tâm: C a = C n L Ở v v
thời điểm bất kì, vận tốc v của hạt là: v = v + v với A v = = (không đổi) C C x y x 2 2
không có lực theo phương ngang N thẳng đứng Khi 0
= 45 thì v hướng dọc theo AB C v v v = v = v = v 2 = x y C x 2 2 2 v 2 v Gia tốc: a = ; a = 2a = n 2L y n L 2 2 v
Với hạt m: P + N = ma N = mg − ma N = m g − y L 2 Câu 3:
Các thanh A B ,..., A B chịu tác dụng lực hoàn toàn tương tự nhau, và khác với thanh A B 1 1 5 5 6 6
Xét thanh AB thứ i: chịu tác dụng với phản lực của thanh trước N , phản lực ở miệng bát và áp lực của i thanh kế tiếp Ni 1 + (hình vẽ)
Chọn điểm B ở miệng bát làm trục quay, từ điều kiện cân bằng momen ta có: L Ni 1 N L = N N + = i i 1 + i 2 2 Do đó: 1 1 1 N = N = N = ... = N (1) 1 2 2 3 5 6 2 2 2
Xét thanh A B : chịu tác dụng của phản lực N của thanh 6 6 6
A B phản lực tại miệng bát B , áp lực N của thanh A B và 5 5 6 1 1 1 trọng lực của m
Chọn B làm trục quay, từ điều kiện cân bằng momen ta có: 6 L 3L N + mg = N L (2) 1 6 2 4 1
Từ (1) và (2) ta tìm được: N = mg 1 42 Câu 4:
Định luật bảo toàn động lượng: 2 2 2
p = p ' + p ' p ' = p − 2p p ' cos + p ' (1) 1 1 2 2 1 1 1 1
Định luật bảo toàn cơ năng: 2 2 2 p p ' p ' 1 1 2 = + = + đ W 1 W đ'1 W đ'2 (2) 2m 2m 2m 1 1 2 Thay (1) vào (2), ta có: m m 2 2 2 2 p ' 1+
− 2p' p cos + p 1− = 0 1 1 1 1 m m 1 1
→ phương trình bậc 2 theo p ' 1 Đ m m
iều kiện có nghiệm: ' 0 (cos . p ) 2 2 2 2 2 − 1+ p 1− 0 1 1 2 m m 1 1 2 2 m m m 2 2 2 2 2 cos 1− sin sin 2 2 m m m 1 1 1 Câu 5:
a. Gọi h , h là chiều cao của cột khí trong xilanh đồng thời cũng là độ biến dạng của piston khi khí 1 2
ở trạng thái (1) và (2).
Trạng thái 1: p S = Mg + kh (1) 1 1
Trạng thái 2: p S = Mg + kh (2) 2 2 Mg kh Mặt khác 1 p V = vRT + h S = vRT (3) 1 1 1 1 1 S S Mgh 2 2 1
Mgh + kh − vRT = 0 h + − vRT = 0 1 1 1 1 1 k 2 2 −Mg M g vRT1 h = + + 1 2 2k 4k k 2 2 −Mg M g vRT Hoàn toàn tương tự 2 h = + + 2 2 2k 4k k 2 2 2 2 Độ M g vRT M g vRT
dịch chuyển của piston: 2 1 h = h − h = + − + 2 1 2 2 4k k 4k k
b. Áp suất khí lúc này thay đổi liên tục, và nó cũng không thuộc một quá trình biến đổi quen thuộc nào
Áp dụng nguyên lí I: Q = U + A ' 12 12 12 h2 Mg kh = = = + = ( − ) 1 A ' pdV pSdh Sdh Mg h h + k ( 2 2 h − h 12 2 1 2 1 ) S S 2 1 h 3m = ( − )+ ( − ) 1 Q R T T Mg h h + ( 2 2 h − h 12 2 1 2 1 2 1 ) 2 2
Biến đổi rút gọn ta chú ý: m m 2 2 Mgh + kh = RT ; Mgh + kh = RT 1 1 1 2 2 2 1 k ( m 2 2 h − h = R T − T − Mg h − h 2 1 ) ( 2 1) ( 2 1) 2 2 Đáp 2m Mg M g mRT M g mRT số Q = R (T − T ) 2 2 2 2 1 1 + + − + 12 2 1 2 2 2 4k k 4k k Câu 6:
a. Công A’ khí sinh ra trong chu trình:
Chia thành 2 chu trình Cac-no như hình vẽ: A ' = A ' + A ' chu trình 1 2 T − T A ' T − T Mặt khác 1 3 1 1 3 H = = A ' = RT ln k 1 1 1 T Q T 1 1 1 T − T A ' T − T Tương tự 2 3 2 2 3 H = = A ' = RT ln k 2 2 2 T Q T 2 2 2 A '
= RT ln k + RT ln k − 2RT ln k chu trình 1 2 3
b. Nhiệt khí nhận được trong chu trình: Q
= Q + Q = RT ln k + RT ln k = R T + T ln k nhan 1 2 1 2 ( 1 2) A ' 2T Hiệu suất chu trình: 3 H = = 1− Q T + T nhan 1 2
THPT CHUYÊN LÊ QUÝ ĐÔN – NINH THUẬN Câu 1: (5 điểm)
Một con thuyền bơi qua sông theo phương vuông góc với dòng chảy, với vận tốc không đổi là v . 1
Tại mọi nơi dòng chảy luôn song song với hai bờ, nhưng giá trị vận tốc của nó phụ thuộc vào khoảng cách đế y
n bờ, được biểu diễn theo công thức: v = v sin
(L: chiều rộng của con sông), v và L là 2 0 L 0
hằng số (hình 1). Hãy tìm:
a. Giá trị vận tốc con thuyền tính trong hệ quy chiếu gắn với bờ sông.
b. Xác định khoảng cách từ điểm O đến điểm thuyền cập bến ở bờ bên kia theo phương Ox Câu 2: (5 điểm)
Một tấm ván nằm ngang có một bậc thanh độ cao H. Trên tấm có một khối trụ bán kính R > H có
thể chuyển động tựu do trên tấm ván và tựa vào bậc thang (Hình 2). Tấm ván chuyển động theo
phương ngang với gia tốc a. Xác định gia tốc lớn nhất có thể được để hình trụ không nảy lên trên bậc thang. Bỏ qua ma sát. Câu 3: (5 điểm)
Thanh OA dài l = 1m, có khối lượng m = 2kg phân bố đều, một đầu gắn với bản lề O, đầu kia 1 buộc vào s. Câu 4: (5 điểm)
Dùng sợi dây mảnh dài L, khối lượng không đáng kể, để treo quả cầu nhỏ vào đầu trụ gỗ có đế đặt
trên mặt bàn ngang như hình vẽ. Khối lượng quả cầu là m, khối lượng của trụ và đế là M = 4m. Cầm
quả cầu kéo căng sợi dây theo phương ngang và thả nó rơi không vận tốc ban đầu. Coi va chạm giữa
quả cầu và trụ hoàn toàn không đàn hồi.
1. Trong quá trình quả cầu rơi, đế gỗ không dịch chuyển. Hệ số ma sát giữa bàn và đế là .
a. Tính vận tốc của hệ sau va chạm.
b. Sau va chạm đế gỗ dịch chuyển được độ dài bao xa thì dừng lại?
2. Trong quá trình quả cầu rơi xuống để đế gỗ không dịch chuyển thì hệ số ma sát nhỏ nhất là bao
nhiêu? Hệ số ma sát nghỉ cực đại giữa đế và mặt bàn xuất hiện lớn nhất ứng với góc treo sợi dây so với
phương nằm ngang là bao nhiêu? Câu 5: (5 điểm)
Xilanh có tiết diện trong 2
S = 100cm cùng với pittông p và vách ngăn V làm bằng chất cách nhiệt
(hình 3). Nắp K của vách mở khi áp suất bên phải lớn hơn áp suất bên trái.
Ban đầu phần bên trái của xilanh có chiều dài l = 1,12m chứa m = 12g khí Hêli, phần bên phải 1
cũng có chiều dài l = 1,12m chứa m = 2g khí Hêli và nhiệt độ cả hai bên đều bằng T = 273K . Ấn từ 2 0
từ pittông sang trái, ngừng một chút khi nắp mở và đẩy pittông tới sát vách V.
Tìm công đã thực hiện biết áp suất không khí bên ngoài 5 2
P = 10 N / m nhiệt dung riêng đẳng tích 0
và đẳng áp của Hêli bằng 3 C = 3,15.10 J / kg. độ; 3
C = 5, 25.10 J / kg .độ. Bỏ qua mọi ma sát. v p Câu 6: (5 điểm)
Cho một mol khí lý tưởng đơn nguyên tử biến đổi theo một chu trình thuận nghịch được biểu diễn
trên đồ thị như hình vẽ trong đó đoạn thẳng 1-2 có đường kéo dài đi qua gốc tọa độ O và quá trình 2-3
là đoạn nhiệt. Biết T = 300K, p = 3p , V = 4V 1 2 1 4 1
a. Tính các nhiệt độ T , T , T 2 3 4
b. Tính hiệu suất của chu trình. HƯỚNG DẪN GIẢI Câu 1: a. Ta có: 2 2 v = v + v v = v + v 1 2 1 2 y y Với 2 2 2 v = v ; v = v = v .sin V = v + v .sin 1 y 2 x 0 1 0 L L
b. Xác định khoảng cách từ điểm O đến điểm thuyền cập bến ở bờ bên kia theo phương Ox y
+ Theo Oy: y = y + v .t = v .t t = (1) 0 y 1 v1 y
+ Theo Ox: dx = v .dt = v .dt = v .sin .dt x 2 0 L y v y v L v 1 0 1 x = v .sin .dt = v .sin .dt = − .cos .t + C 0 0 L L v L 1 Đ v L v L iều kiện ban đầu: x (0) 0 0 = 0 o = − + C C = v v 1 1 v L v 2v L v Vậy: 0 1 0 2 1 x = 1− cos .t = .sin .t v L v 2L 1 1 2v L y Phương trình quỹ đạo: 0 2 x = .sin v 2L 1 Khi sang đế 2v L
n bờ bên kia (tại M), ta có: 0 y = L x =
là khoảng cách từ điểm xuất phát đến điểm v 1 cập bến theo Ox. Câu 2:
- Chọn hệ quy chiếu gắn với ván đang chuyển động với gia tốc a.
+ Trọng lực P , phản lực N tại mặt ván ngang. 1
+ Phản lực N tại chỗ tiếp xúc với bậc, có phương xuyên tâm trụ, lực quán tính F 2 qt
- Giả sử khối trụ vẫn nằm yên trên tấm ván. Ta có: P + N + N + F = 0 1 2 qt
→ N + N .sin = mg; N cos = ma với là góc nhọn giữa phương N và phương ngang. 1 2 2 2 → N + ma.tan = mg 1 Để g
khối trụ nằm yên ta có: N 0 hay a 1 tan R − H Dễ thấy tan = R − (R − H)2 R − ( − )2 2 R R H H (2R − H) → a g = g (1) R − H R − H
- Xét trục quay qua A chỗ tiếp xúc với bậc. Điều kiện để khối trụ có thể quay quanh A: N 0 và F R − H mg R − R − H qt ( ) ( )2 2 1 H (2R − H) Hay a g (2) R − H H (2R − H)
- Kết hợp (1) và (2) ta suy ra: a = g max R − H Câu 3: Q = T; Q = P x y 1 Q + P + T = 0 1 1 P P 1 1 M = M P sin = T cos → T = Q = 1 P /O T/O 1 1 x 2 2 2 P 5 20 5 2 2 1 Q = Q + Q = = = 22,36N x y 2 2 m 4, 2kg
Muốn hệ không cân bằng thì 2 m 1, 3kg 2 Câu 4:
a. Gọi vận tốc quả cầu trước và sau va chạm là v và v’: v = 2gL = ( + ) m mv m M v ' v ' = 2gL m + M
Sau va chạm dưới tác dụng của lực ma sát đế gỗ chuyển động chậm dần đến
khi dừng lại. Quãng đường đế gỗ dịch chuyển được là x: = − ( + ) 2 2 v f x 0 m M (1) ms 2 Với f = m + M g (2) ms ( ) 2 m L L Từ (1) và (2) cho: x = = (m + M)2 25 2 mv
b. Gọi góc giữa phương ngang và dây treo là : mgL sin = 2 (3) 2 mv
Từ sơ đồ chịu lực: T = mg sin = (4) L f − T cos = 0 (5)
N − T sin − Mg = 0 (6)
Khi đế gỗ không dịch chuyển f N (7) 2M 8 Từ (3) tới (7): = f và A = = min ( ) 3m 3 () sin 2 f = 2 a + 2sin 2 cos 2( 2 A + 2sin ) − sin 2 . 4sin . cos
Tìm cực đại hàm số: f ().f ' = ( = A + 2sin ) 0 2 2 Thay 2 2
cos 2 = 2 cos −1 = 1− 2sin ta có: A 2 sin = 2(A + ) 1 A A A (A + 2) sin 2 = 2 ( + ) 1− = A A 1 2 (A + ) 1 A +1 () 1 2M 8 f = với A = = A (A + 2) 3m 3 3m = f = = 0, 283 min max ( ) 2 2 M + 3mM 8 2 0 sin =
sin = 0,6030 = 37 05' 22 Câu 5: Lúc đầ m RT m RT u áp suất khí bên trái 1 0 P = .
lớn hơn áp suất bên phải vách: 2 0 P = . 1 lS 2 lS
Khối khí bên phải bị nén đoạn nhiệt từ thể tích V = lS xuống V , áp suất của nó tăng lên đến P : 0 1 1 1 1 P m g g 2 2 P V = P V → V = V = V (1) 2 0 1 1 1 0 0 P m 1 1 1− Khi đó nhiệt độ P V m ở bên phải: 1 1 2 T = T = T = 559K (2) 1 0 0 P V m 2 0 1
Sau khi nắp K mở hai khí hòa trộn vào nhau và có cùng nhiệt độ T : 2 1 +
C m (T − T ) = C m (T − T ) m T m T m m 1 0 2 1 1 2 → T = = T 1+ = 314K (3) V 1 2 0 V 2 1 0 2 0 m + m m + m m 1 2 1 2 1
Sau đó lượng khí m = m + m bị nén đoạn nhiệt từ thể tích V = V + V đến V , nhiệt độ tăng từ T 1 2 0 1 0 2 đế −
n T, ta có: T.V − = T (V + V )g 1 g 1 (4) 0 2 0 1
Thay (1) và (3) vào (4) ta được: 1 1 − V + V m .T m 0 1 1 0 2 T = T = 1+ = 382K (5) 2 V m + m m 0 1 2 1
Công do lực tác dụng lên pit tông và áp suất khí quyển P thực hiện làm tăng nội năng của chất khí bị 0
nén đoạn nhiệt: A = A + A = U = C m + m T − T (6). Với A = P Sl 1 2 V ( 1 2 ) ( 0 ) 1 0
Thay (5) vào (6), rồi thay số vào ta được: A = 3678 J 2 ( ) Câu 6: p p p a. 2 1 2 = V = V = 3V 2 1 1 V V p 2 1 1 p V 2 2 T = T . = 9T = 2700K 2 1 1 p V 1 1 5 3 V 3 Quá trình 2-3: 2 V = V = 4V ; p = p = p 0,619.p 3 4 1 3 2 2 2 V 4 3 p 1,857.p 3 1 V Quá trình 4-1: 4 T = T = 4T = 1200K 4 1 1 V1 b. Quá trình 1-2: U = C T − T =12RT 12 V ( 2 1 ) 1 1 A = p + p V − V = 4p V = 4RT 12 ( 2 1)( 2 1) 1 1 1 2 Q = U + A = 16RT 12 12 12 1 Quá trình 2-3: A = − U
= −C T − T = 2,355.RT ; Q = 0 23 23 V ( 3 2 ) 1 23 Quá trình 3-4: U = C T − T = 5 − ,145RT ; A = 0 34 V ( 4 3 ) 1 34 Q = U + A = 5 − ,145RT 34 34 34 1 Quá trình 4-1 có: U = C T − T = 4 − ,5RT 41 V ( 1 4 ) 1 A = p V − V = 3 − RT 41 1 ( 1 4 ) 1 Q = U + A = 7, − 5RT 41 41 41 1 A = A + A + A + A = 3,355RT 12 23 34 41 1
Nhiệt lượng khí nhận là: Q = Q = 16RT 12 1 A 3, 355RT
Hiệu suất của chu trình: 1 H = = = 0, 2097 hay H 21% Q 16RT 12 1