





















Preview text:
ĐỀ SỐ 06
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
Câu 1. Đẳng thức nào sau đây đúng với mọi số dương x ? x A. (log x) = . B. ( ) ln10 log x = . C. ( x) 1 log = .
D. (log x) = x ln10 . ln10 x x ln10
Câu 2. Thể tích hình lập phương cạnh 3 là: A. 3 . B. 3 . C. 6 3 . D. 3 3 .
Câu 3. Trong các hàm số sau,hàm số nào đồng biến trên tập xác định của nó? x 3
A. y = ln x . B. y = log x . C. y = . D. 3 y x− = . 0,99 4
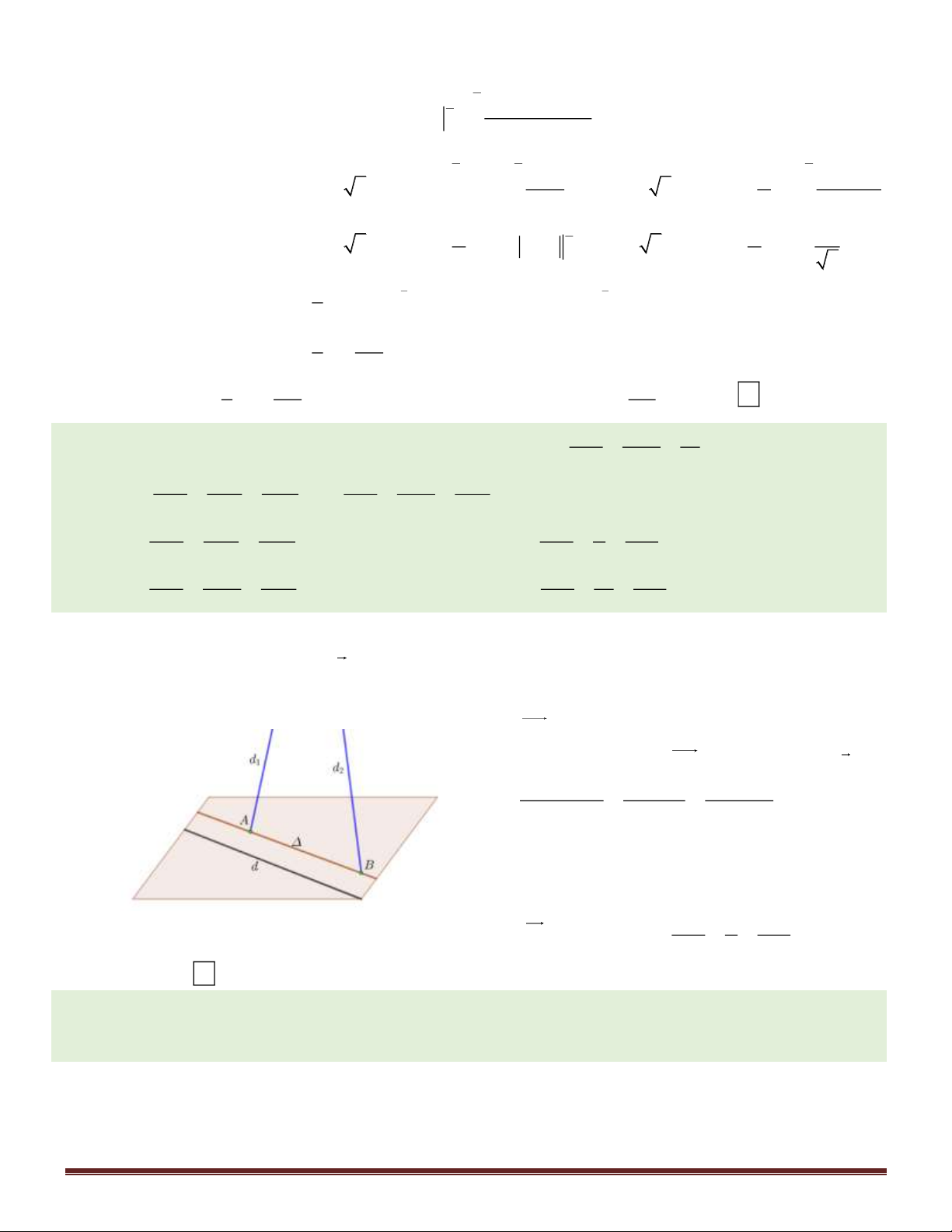
Câu 4. Trong không gian với hệ tọa độ Oxyz , khoảng cách từ A( 2 − ;1; 6
− ) đến mặt phẳng (Oxy) là 7 A. 6 . B. 2 . C. 1. D. . 41
Câu 5. Bất phương trình ( x − )( 2 3
1 x + 3x − 4) 0 có bao nhiêu nghiệm nguyên nhỏ hơn 6? A. 9 . B. 5 . C. 7 . D. Vô số.
Câu 6. Tập xác định D của hàm số y = log (2x− )1 là 2022 1 1
A. D = (0;+ ) . B. D = . C. D = ; + . D. ; + . 2 2
Câu 7. Kí hiệu z là nghiệm phức có phần ảo dương của phương trình 2
4z −16z +17 = 0. Trên mặt phẳng 0
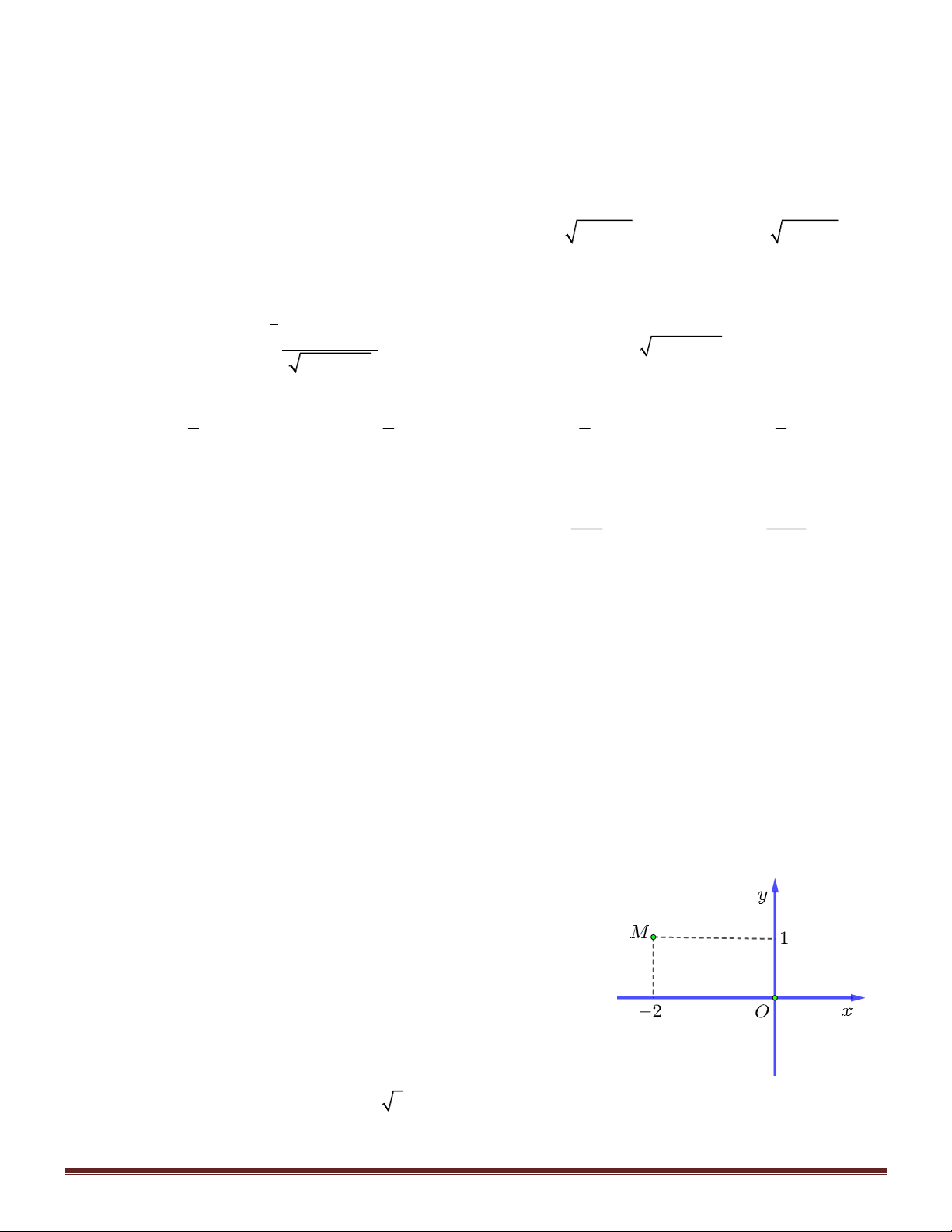
toạ độ, điểm nào dưới dây là điểm biểu diễn của số phức w = iz . 0 1 1 1 1 A. M − ;2 . B. M ;1 . C. M ; 2 . D. M − ;1 . 2 2 4 4 1 2 3 4
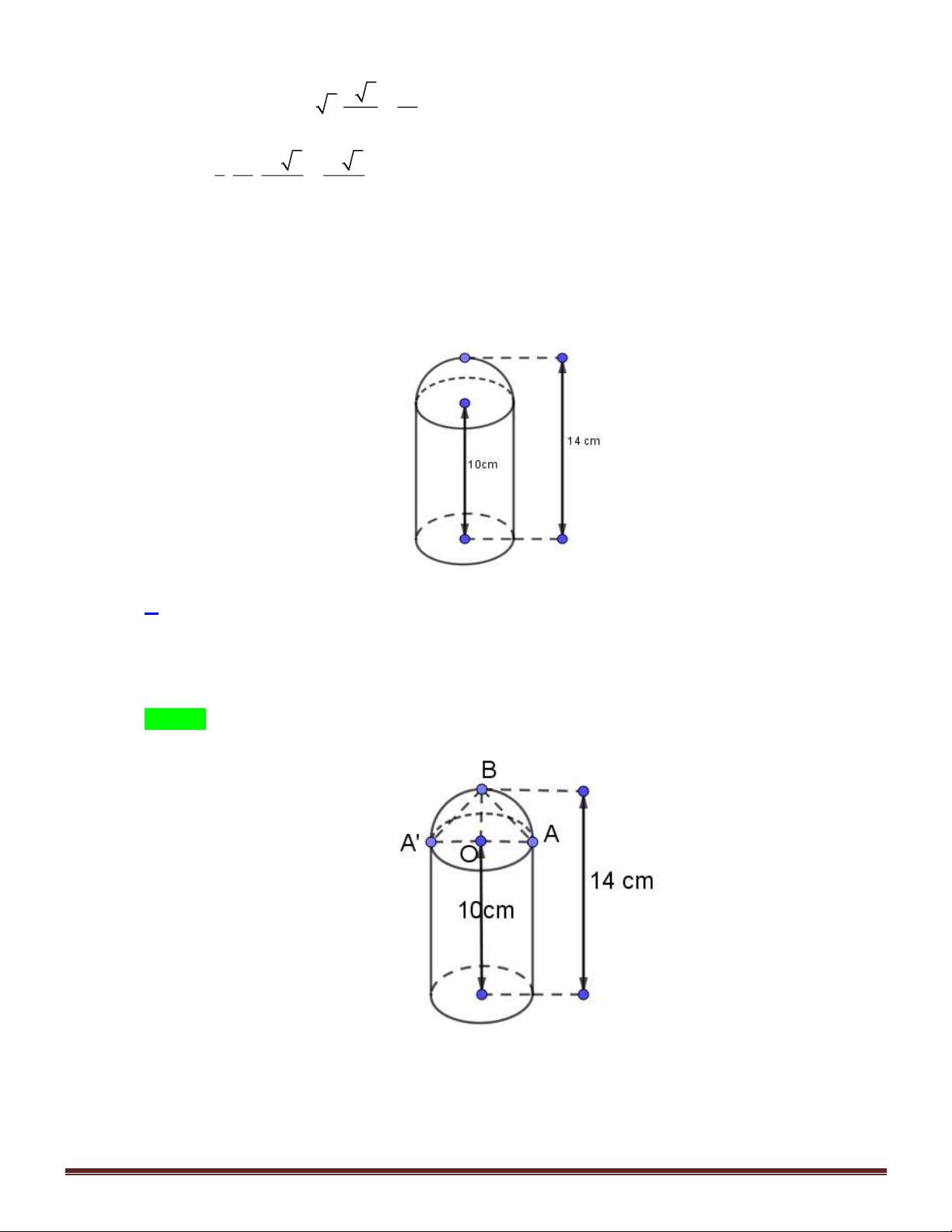
Câu 8. Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông cạnh bằng a . Tính diện tích toàn
phần S của hình trụ. 2 a 2 3 a A. 2 S = 4a . B. 2 S = a . C. S = . D. S = . 2 2 Câu 9. Cho ,
x y là hai số thực thỏa mãn 2 x −1+ yi = 1
− + 2i . Giá trị của 2x + y là A. 5 . B. 4 . C. 2 . D. 2 .
Câu 10. Cho z = 3 + 5i . Tính z . A. 8 . B. 8 . C. 34 . D. 34 .
Câu 11. Tâm đối xứng của đồ thị hàm số nào sau đây cách gốc tọa độ một khoảng lớn nhất ? 2x −1 1− x A. y = . B. y = . C. 3 2
y = 2x − 3x − 2 . D. 3
y = −x + 3x − 2 . x + 3 1+ x
Câu 12. Trong không gian với hệ trục tọa độ Oxyz , xác định tọa độ tâm I của mặt cầu (S) 2 2 2
: x + y + z − 4x + 2y − 8z = 0 . A. I ( 2 − ;1;− 4) . B. I ( 4 − ;2;−8) .
C. I (2;−1;4) .
D. I (4;− 2;8) . Trang 1
Câu 13. Họ nguyên hàm của hàm số 2 x x y e e− = − là 1 A. 2 x −x e − e + C . B. 2 2 x −x e + e +C . 2 1 C. 2 − 2 x −x e − e +C . D. 2 x x e + e + C . 2
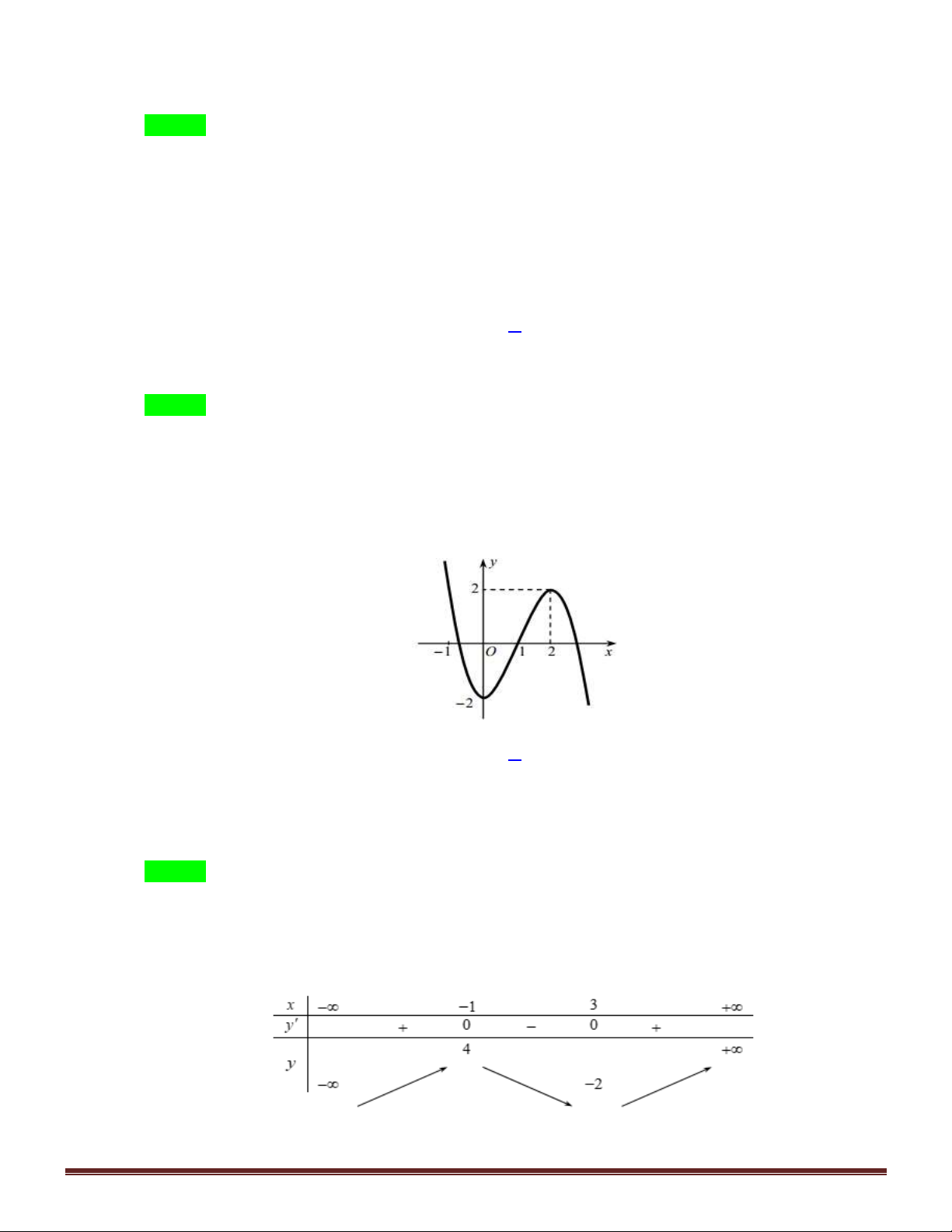
Câu 14. Hàm số nào dưới đây có đồ thị như trong hình bên ? A. 3
y = −x + 3x −1. B. 4 2
y = −x + 2x −1. C. 4 2
y = x − 2x −1. D. 3
y = x − 3x −1.
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2, AD = 4 ; SA vuông góc với mặt
phẳng đáy và SA = 6 . Tính thể tích của khối chóp. A. 8 . B. 16 . C. 24 . D. 48 .
Câu 16. Cho hàm số f ( x) 2
= x + sin x +1. Biết F (x) là một nguyên hàm của f (x) và F (0) =1. Tìm F (x) . x A. F ( x) 3
= x − cos x + x + 2 . B. F ( x) 3 = + cos x + x . 3 x x C. F ( x) 3 =
− cos x + x + 2 . D. F ( x) 3 = − cos x + 2 . 3 3
Câu 17. Cho số phức z = a + bi ( ,
a b ) và xét hai số phức = + ( )2 2 z z và = 2 .
z z + i ( z − z ) . Trong các
khẳng định dưới đây, khẳng định nào đúng?
A. là số thực, là số thực.
B. là số ảo, là số thực.
C. là số thực, là số ảo.
D. là số ảo, là số ảo. x = 1+ 2t
Câu 18. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d : y = 1− t ; t . Đường thẳng d có z = 5+3t
một vec tơ chỉ phương là
A. u = (2;1;3) . B. u = (2; 1 − ;3) .
C. u = (1;1;5) . D. u = ( 2 − ; 1 − ; ) 3 .
Câu 19. Cho a , b , c là các số thực dương thỏa mãn log 5 log 6 log 3 2 a = 4 , 4 b =16, 7 c = 49. Tính giá trị 2 2 2 log 5 log 6 log 3 2 4 7 T = a + b + 3c . A. T = 126 .
B. T = 5 + 2 3 . C. T = 88.
D. T = 3 − 2 3 . 2 4 1 Câu 20. Cho f
(x)dx =1, f
(t)dt = −4. Tính I = f (2y)dy . −2 2 − 2 A. I = 2,5. B. I = 5 − . C. I = 3 − . D. I = 3 .
Câu 21. Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng ( P) : x + 2y − z + 3 = 0 cắt mặt cầu (S) 2 2 2
: x + y + z = 5 theo giao tuyến là một đường tròn có diện tích là: 11 9 15 7 A. . B. . C. . D. . 4 4 4 4
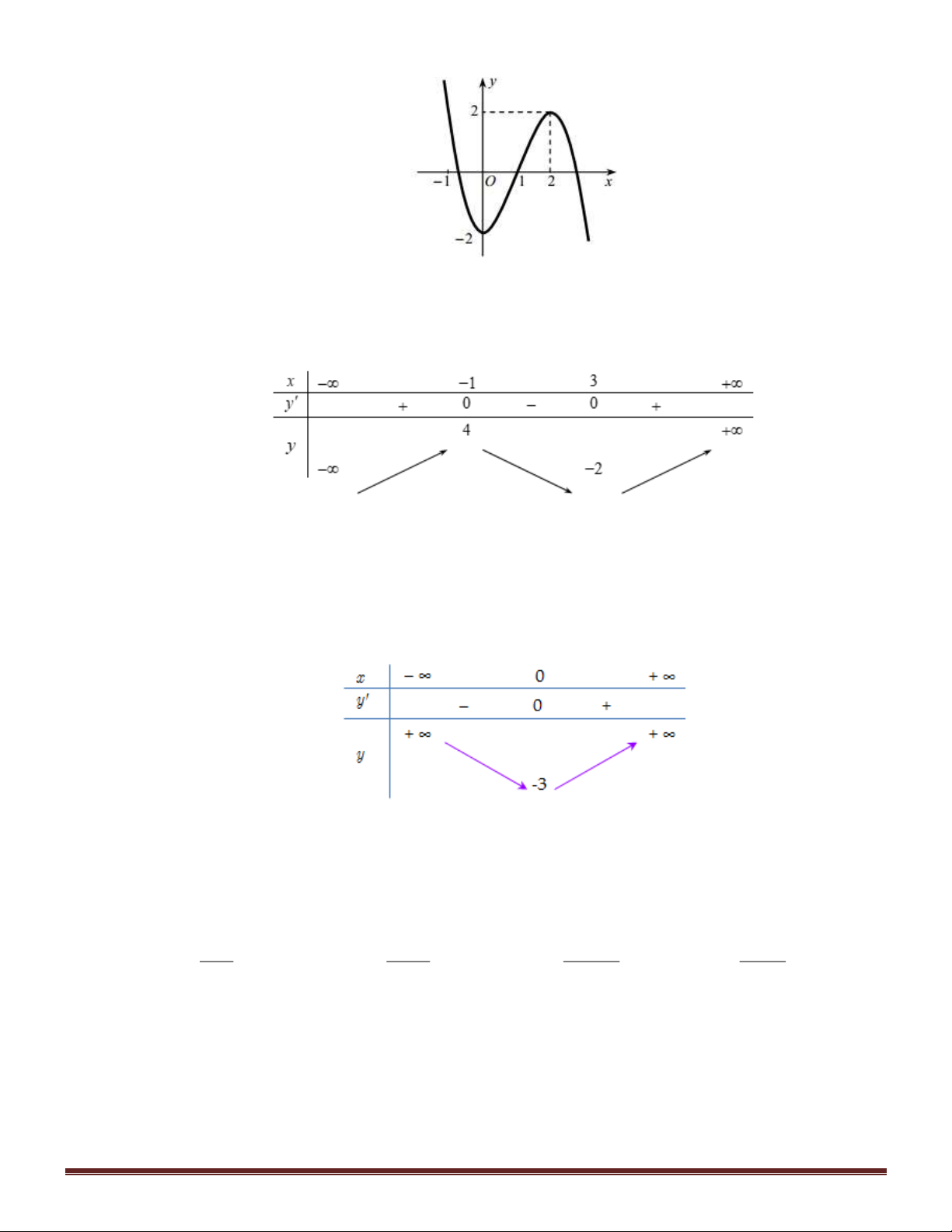
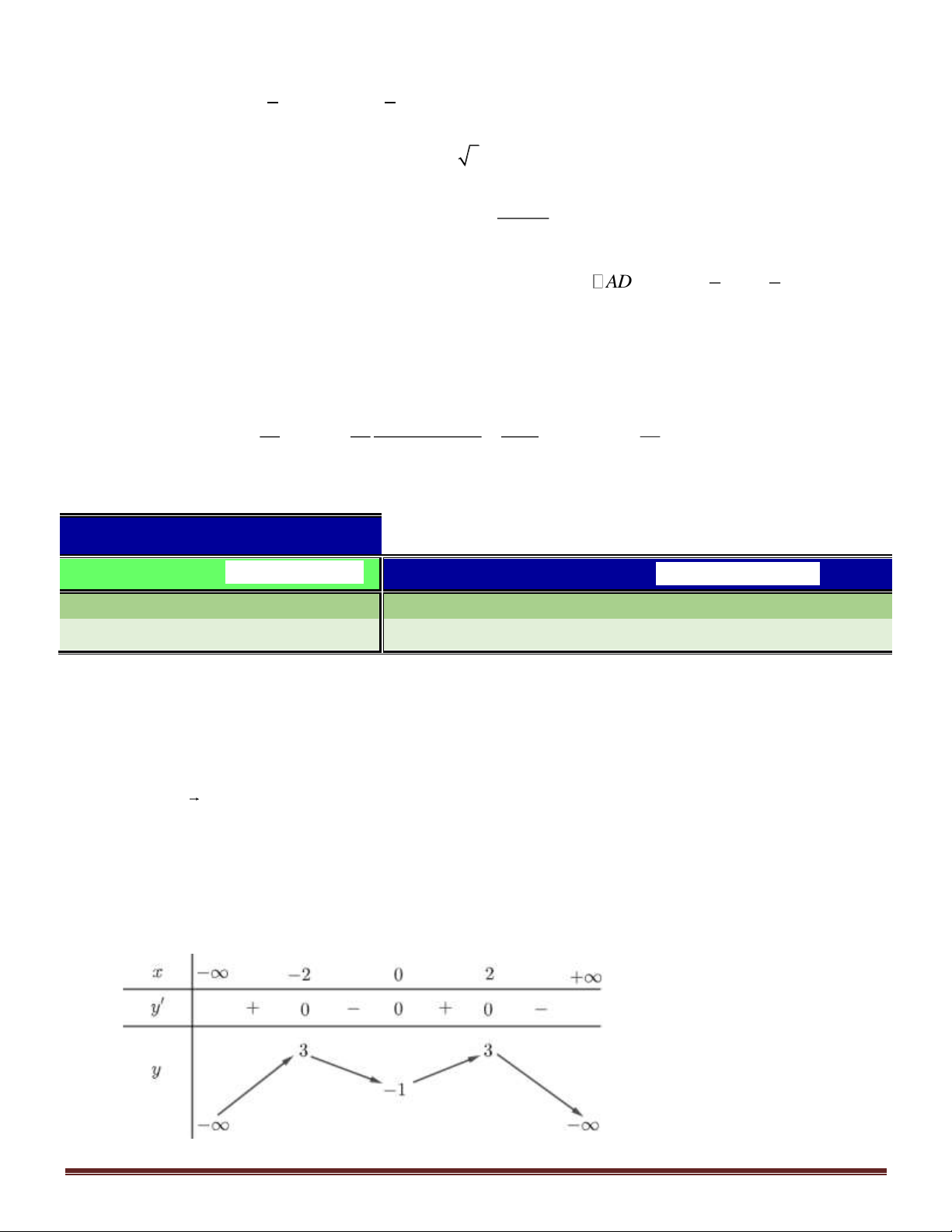
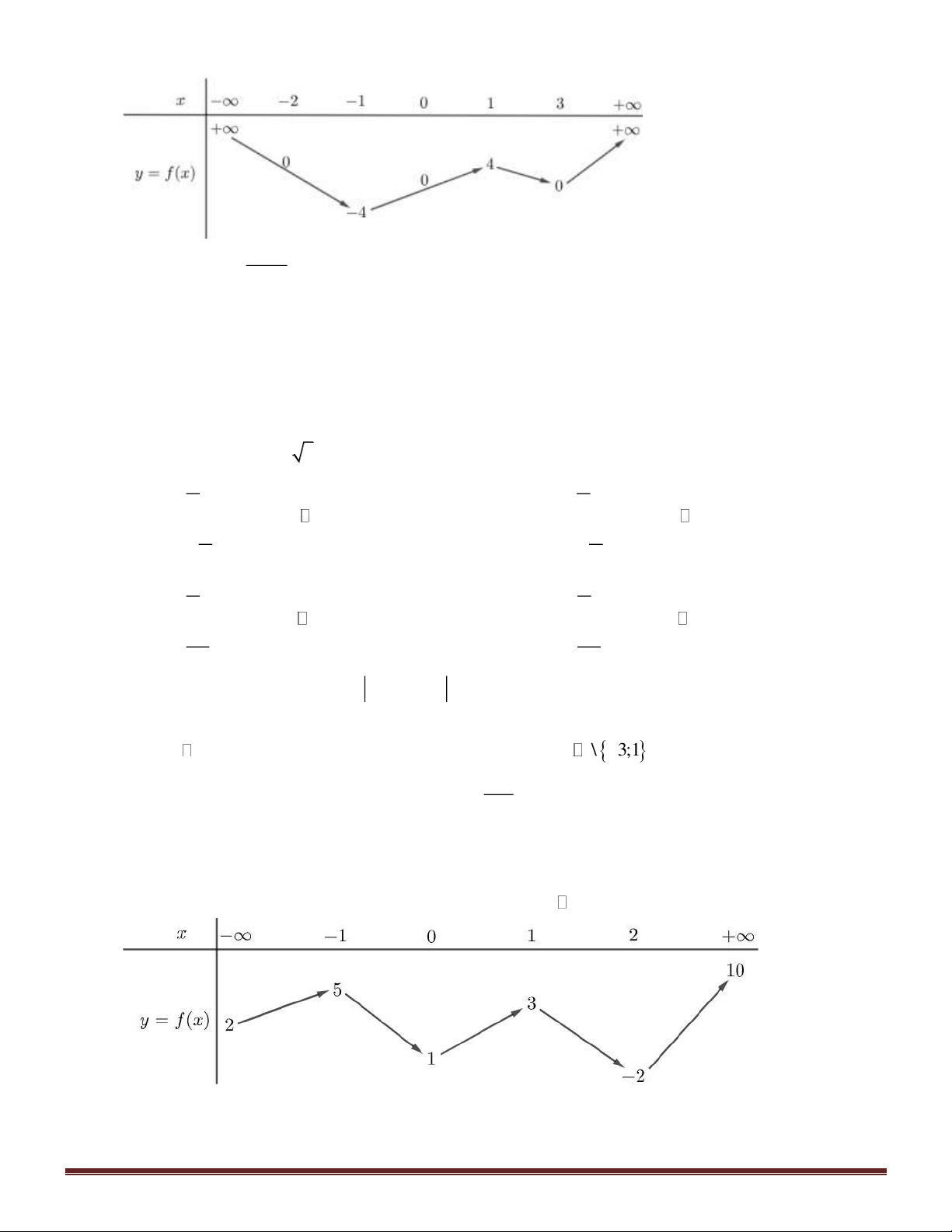
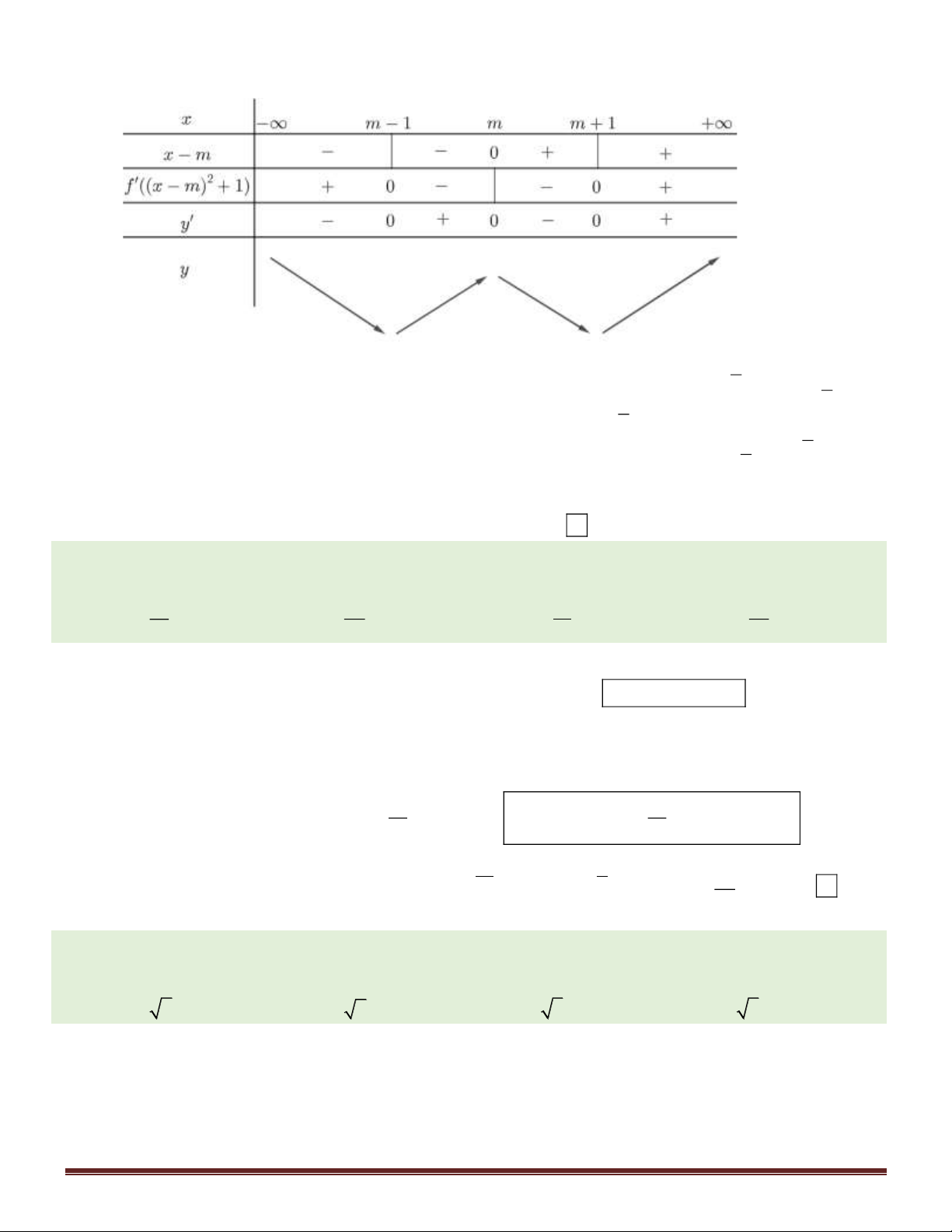
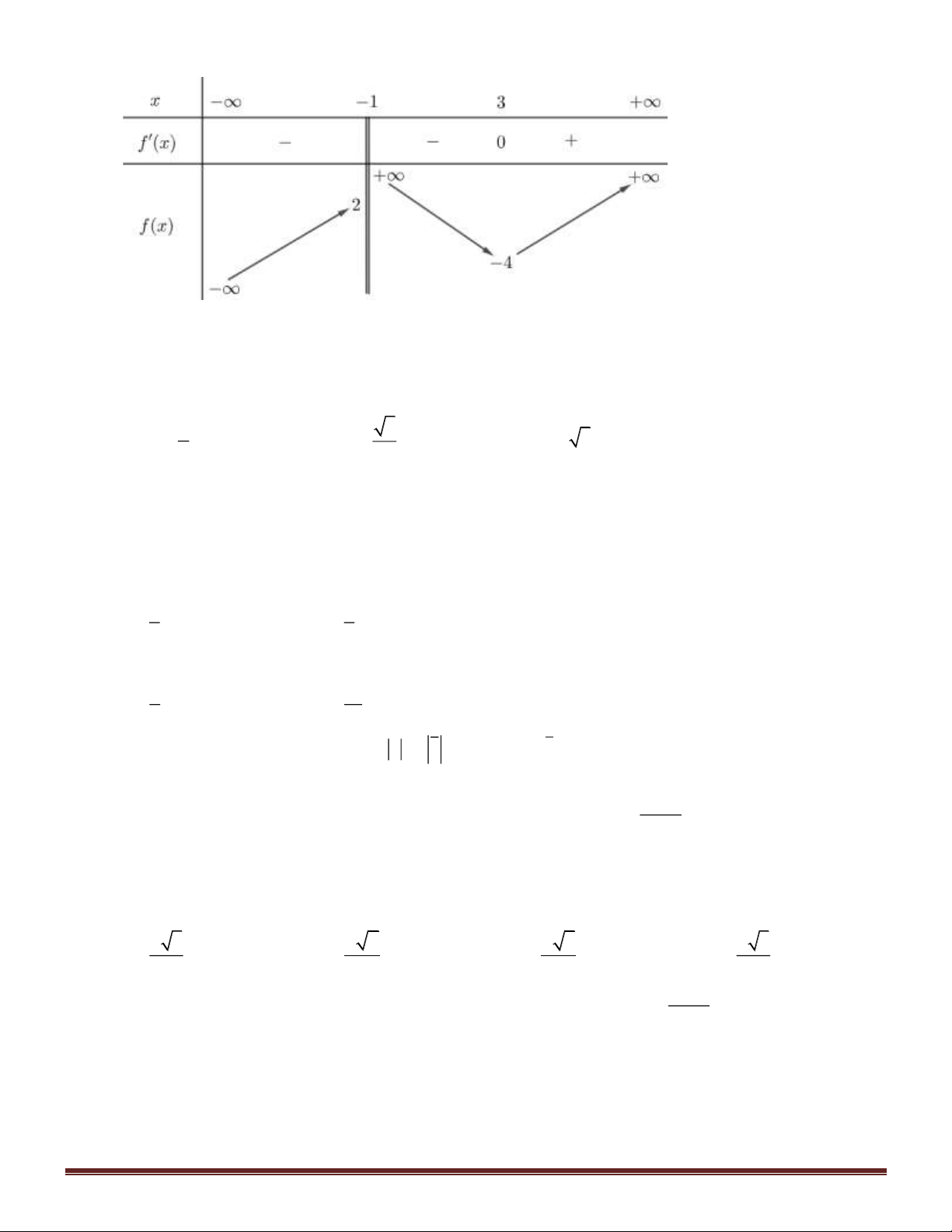
Câu 22. Cho hàm số y = f ( x) xác định trên và có bảng xét dấu của đạo hàm như sau. Trang 2
Khi đó số cực trị của hàm số y = f (x) là A. 3 . B. 2 . C. 4 . D. 1.
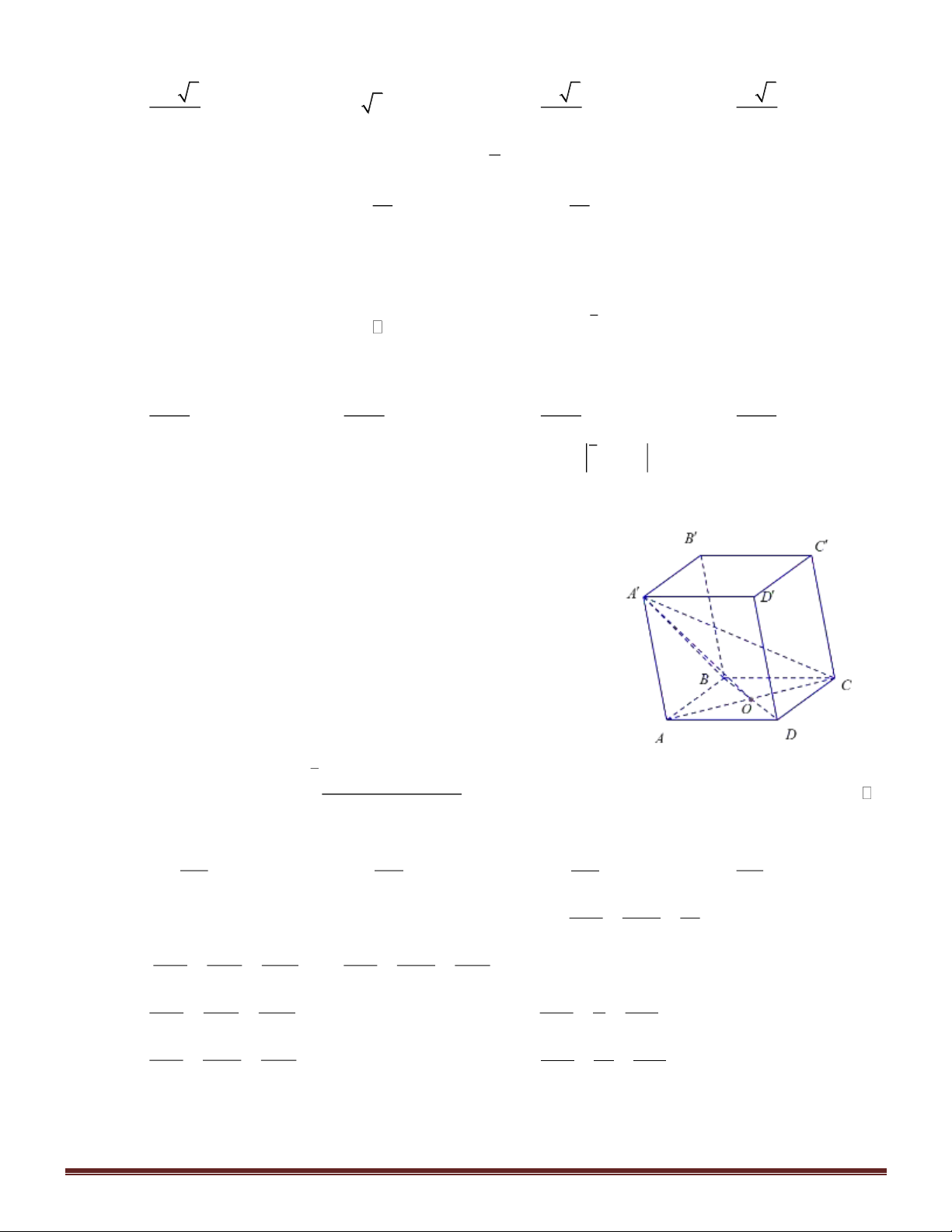
Câu 23. Cho hình lập phương ABC . D A B C D
có cạnh bằng a , gọi là góc giữa đường thẳng A B và mặt phẳng ( BB D D ). Tính sin . 3 3 3 1 A. . B. . C. . D. . 4 2 5 2
Câu 24. Trong không gian với hệ tọa độ Oxyz cho a = 2i + 3 j − k , b = (2;3; 7
− ) . Tìm tọa độ của x = 2a −3b
A. x = (2; −1; 19) . B. x = ( 2 − ; 3; 19) . C. x = ( 2 − ; − 3; 19). D. x = ( 2 − ; −1; 19) . 2x −1
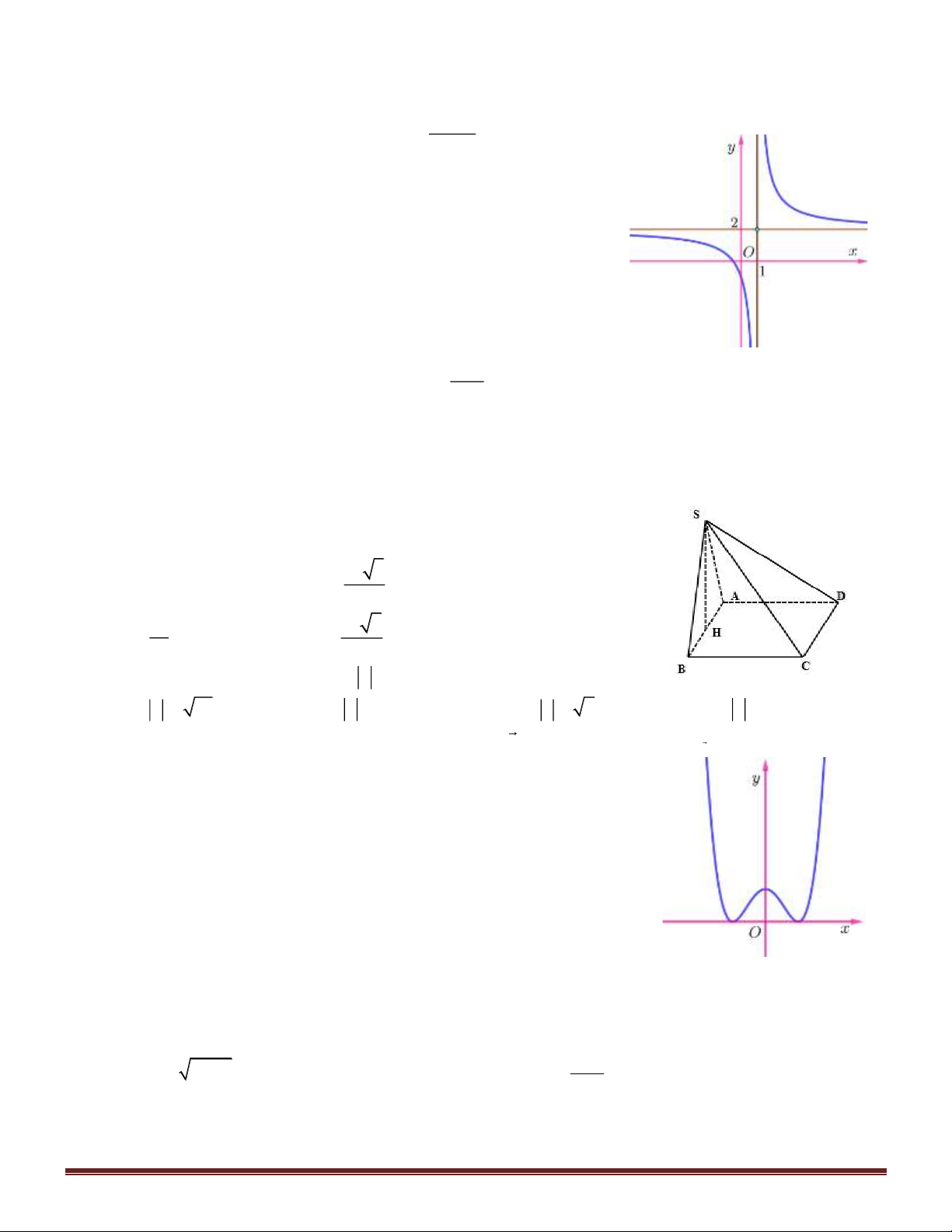
Câu 25. Trên đồ thị hàm số y =
có bao nhiêu điểm có tọa độ nguyên? 3x + 4 A. 1. B. 2. C. 0. D. 4. 2 + 3i Câu 26. Cho z =
. Xác định số phức liên hợp z của z . 4 + 2i 2 8 7 2 1 2 14 2 A. z = + i . B. z = − i . C. z = + i . D. z = + i . 10 20 10 5 10 5 20 5
Câu 27. Cho khối chóp S.ABC có thể tích V , nếu giữ nguyên chiều cao và tăng các cạnh đáy lên 3 lần thì
thể tích khối chóp thu được là A. 3V . B. 6V . C. 9V . D. 12V .
Câu 28. Số phức z = (2 + 3i)(1−i) có phần ảo bằng: A. 0 . B. 1. C. 2 . D. 5 .
Câu 29. Tập tất cả các giá trị của tham số m để hàm số y = (m − ) 3 2
1 x − 6mx − 6x + 5 nghịch biến trên là
đoạn a;b. Khi đó a + b bằng 1 1 A.1. B. − . C. . D. 2 . 2 2
Câu 30. Trong không gian Oxyz , đường thẳng đi qua M ( 1 − ;2; )
1 đồng thời vuông góc với mặt phẳng
(P): x+ y − z +1= 0 có phương trình là x +1 y − 2 z −1 x −1 y + 2 z +1 A. = = . B. = = . 1 1 1 − 1 1 1 − x +1 y +1 z −1 x −1 y −1 z +1 C. = = . D. = = . 1 − 2 1 1 − 2 1
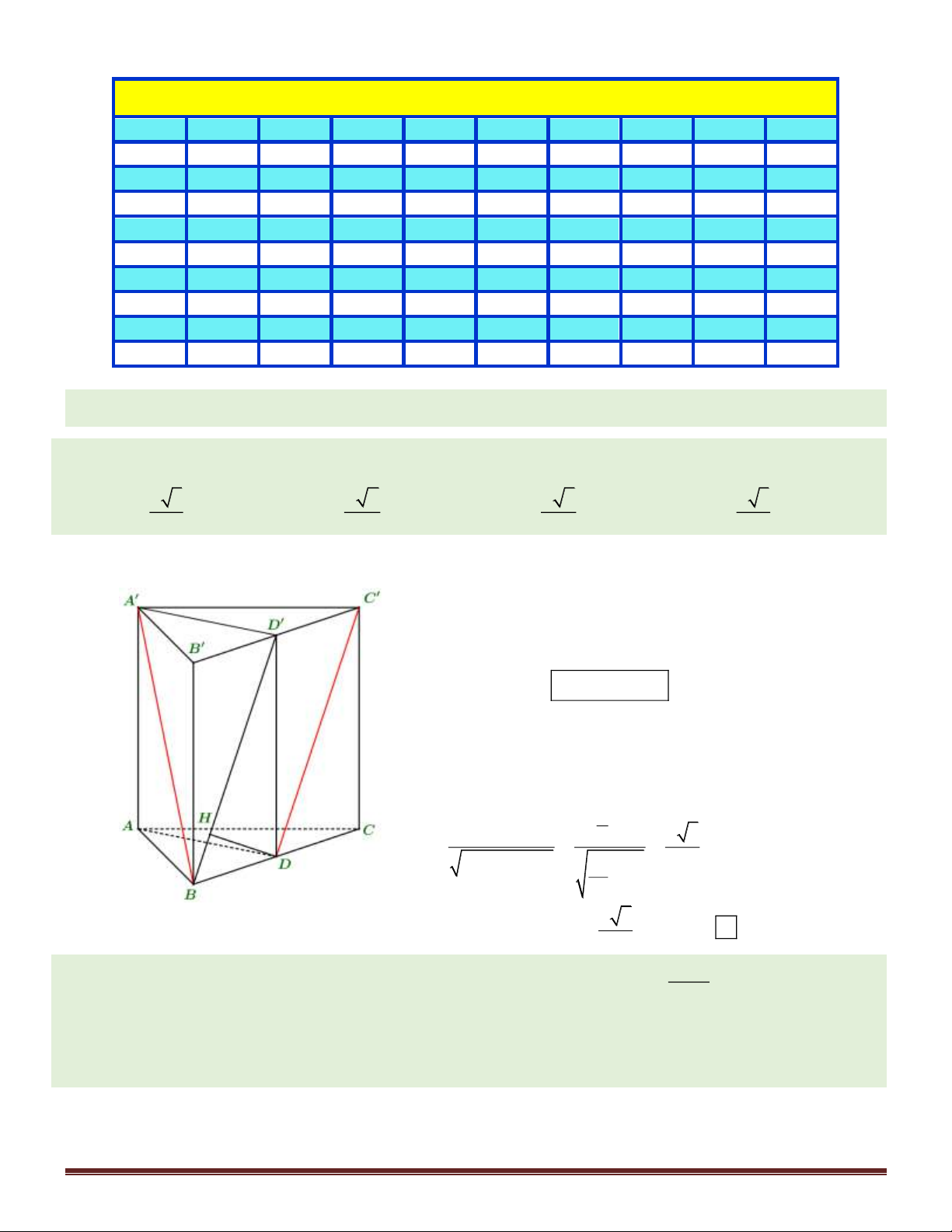
Câu 31. Cho lăng trụ tam giác AB . C A B C
có đáy là tam giác ABC đều cạnh bằng a . Hình chiếu vuông góc
của A trên mặt phẳng ( ABC ) trùng với trung điểm H của cạnh AB . Góc giữa cạnh bên của lăng
trụ và mặt phẳng đáy bằng o
30 . Tính thể tích của khối lăng trụ đã cho theo a . 3 3a 3 a 3 a 3 a A. . B. . C. . D. . 4 4 24 8 5 481 Câu 32. Cho hàm số 3 2 y = x − x − 6x +
. Tìm số các tiếp tuyến của đồ thị hàm số song song với đường 2 27 7
thẳng y = 2x − . 3 Trang 3 A. 3 . B. 2 . C. 1. D. 0 .
Câu 33. Trong không gian Oxyz , cho điểm A(1;2;− )
1 . Mặt phẳng đi qua A và chứa trục Oy là A. y = 2 .
B. x + z = 0 .
C. x − z = 0 .
D. x − 2z = 0 .
Câu 34. Cho ABC . D A B C D
là hình lập phương cạnh 2a . Bán kính mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương bằng a 2 A. 2a 2 . B. . C. a 3 . D. a 2 . 2
Câu 35. Cho một hình nón đỉnh S có chiều cao bằng 8cm , bán kính đáy bằng 6cm . Cắt hình nón đã cho bởi
một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón ( N ) đỉnh S có đường sinh
bằng 4cm . Tính thể tích của khối nón ( N ) . 768 786 2304 2358 A. 3 V = cm . B. 3 V = cm . C. 3 V = cm . D. 3 V = cm . 125 125 125 125
Câu 36. Tập nghiệm của bất phương trình 15.25x 34.15x 15.9x − + 0 là 3 5 3 5 A. (− ; − 1 1;) . B. ; . C. 1 − ; 1 . D. − ; ; . 5 3 5 3 x +1
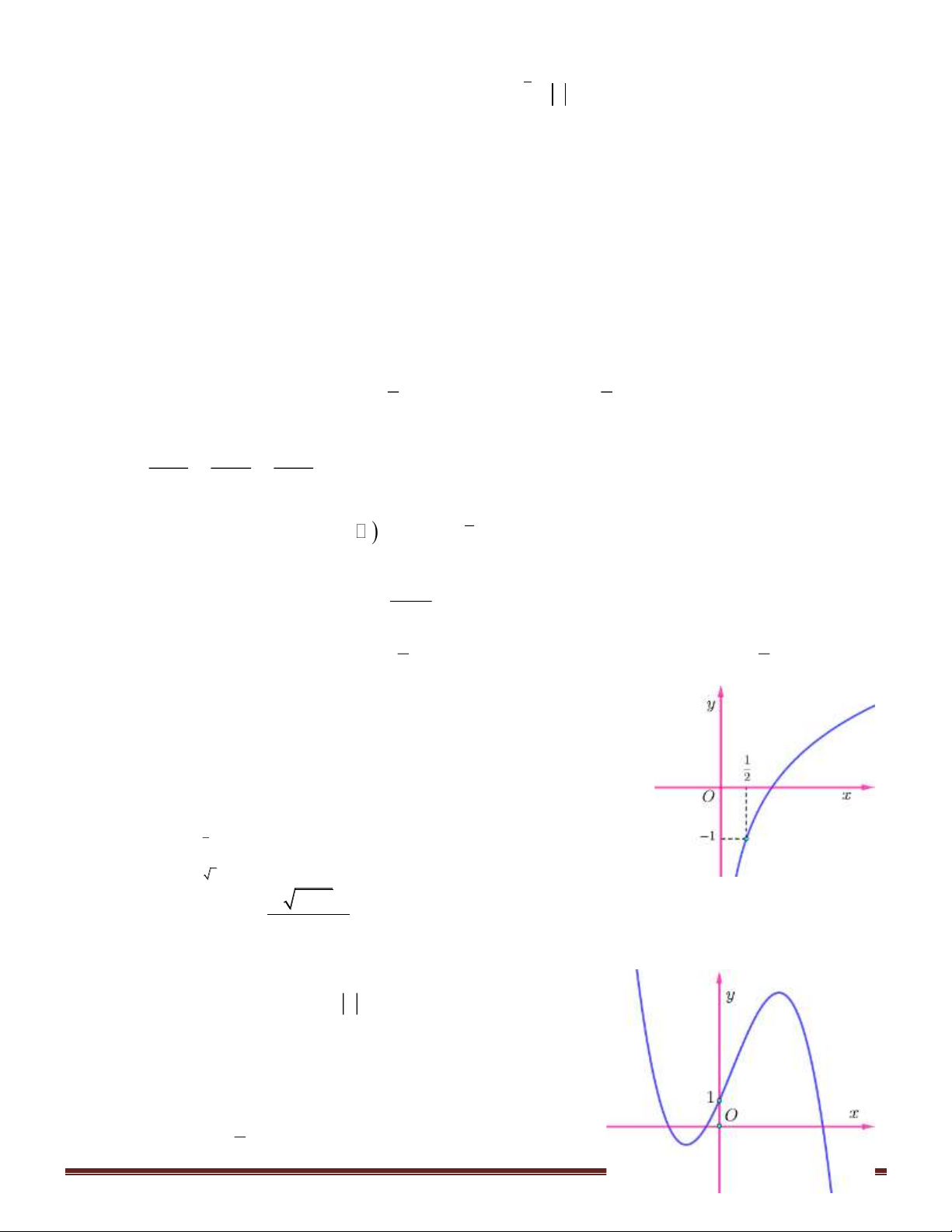
Câu 37. Cho hàm số y =
có đồ thị (C) và đường thẳng d : y = 2
− x + m−1 ( m là tham số thực). Gọi k x + 2 1
, k là hệ số góc của tiếp tuyến tại giao điểm của d và (C) . Khi đó k .k bằng 2 1 2 1 A. 3 . B. 4 . C. . D. 2 . 4
Câu 38. Trong không gian với hệ tọa độ Oxyz , biết mặt phẳng (P) : ax + by + cz + d = 0 với c 0 đi qua hai
điểm A(0;1;0), B(1;0;0) và tạo với mặt phẳng ( yOz) một góc 60. Khi đó giá trị a +b + c thuộc khoảng nào dưới đây? A. (0;3) . B. (3;5) . C. (5;8) . D. (8;1 ) 1 4x +1
Câu 39. Tìm tập nghiệm của bất phương trình log log 1 − 1 2 x −1 2 A. \ 1 . B. (1;+) . 3 C. . D. − ; − (1;+ ) . 2
Câu 40. Trong không gian Oxyz , cho điểm M (1;3;− )
1 và mặt phẳng (P) : x − 2y + 2z =1. Gọi N là hình
chiếu vuông góc của M trên ( P) . Viết phương trình mặt phẳng trung trực của đoạn MN .
A. x − 2y + 2z + 3 = 0 .
B. x − 2y + 2z +1 = 0.
C. x − 2y + 2z − 3 = 0 .
D. x − 2y + 2z + 2 = 0 . (m + )1 x + 2 1
Câu 41. Giả sử giá trị nhỏ nhất của hàm số y = − 1;3 bằng
, mệnh đề nào dưới đây x + trên đoạn m 2 đúng? 1 A. m ( 5 − ; 3 − ). B. m(2;4). C. m( 9 − ; 6 − ) . D. m 1 − ; . 2 0
Câu 42. Cho tích phân a cos 2x cos 4 d
x x = a + b 3
, trong đó a,b là các hằng số hữu tỉ. Tính e + log b . − 2 3 Trang 4 1 A. 2 − . B. −3 . C. . D. 0 . 8
Câu 43. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ( ABC) . Tam giác ABC đều cạnh bằng
a 3 , tam giác SAC cân. Tính khoảng cách h từ A đến (SBC) . 3a a 3 a a 3 A. h = . B. h = . C. . D. h = . 7 4 7 7 Câu 44. Cho hàm số f ( x) liên tục trên tập số thực thỏa mãn 1
f ( x) + ( x − ) f ( 2 x − x) 3 2 5 2 5 4
= 50x − 60x + 23x −1, x
. Hãy tính f (x)dx . 0 A. 2 . B. 1. C. 3 . D. 6 .
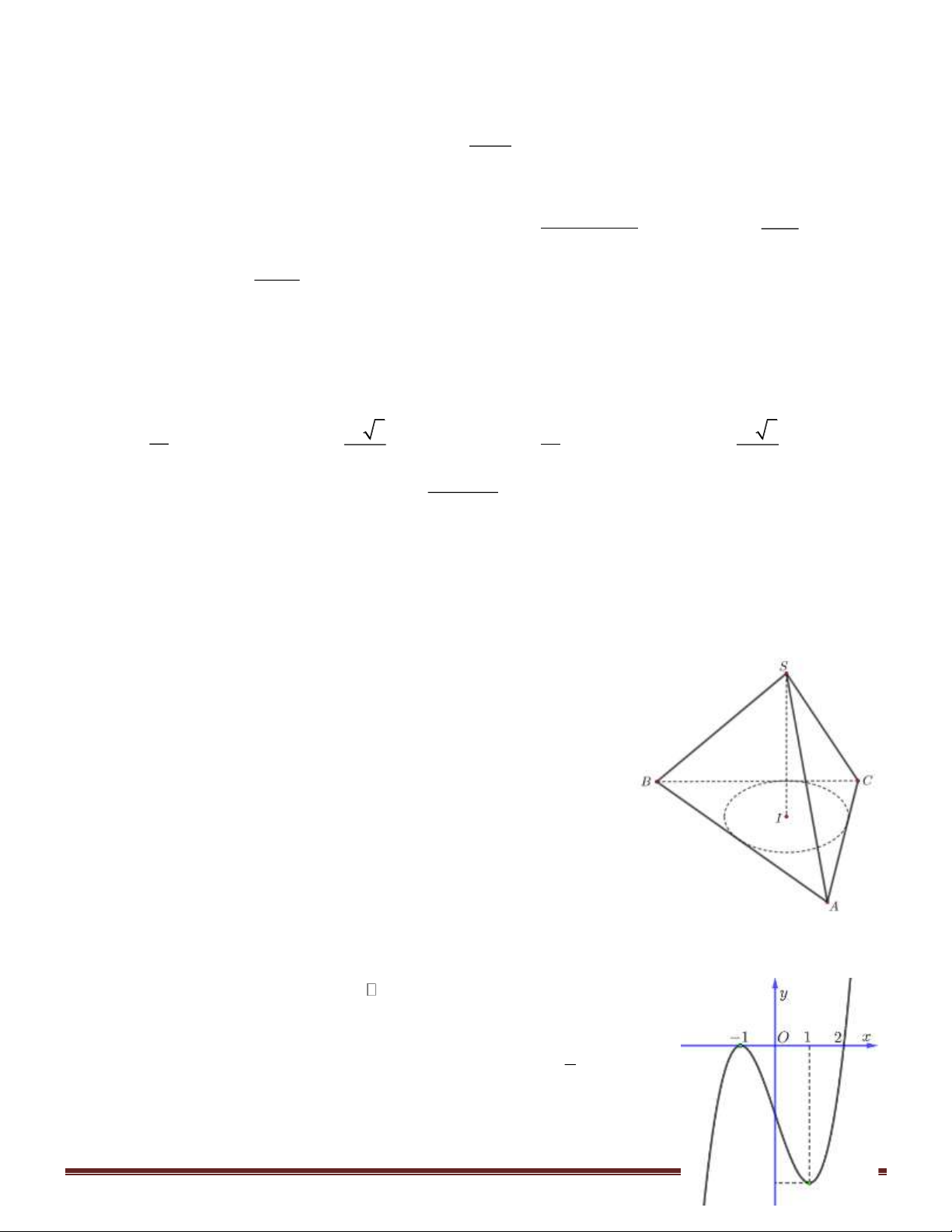
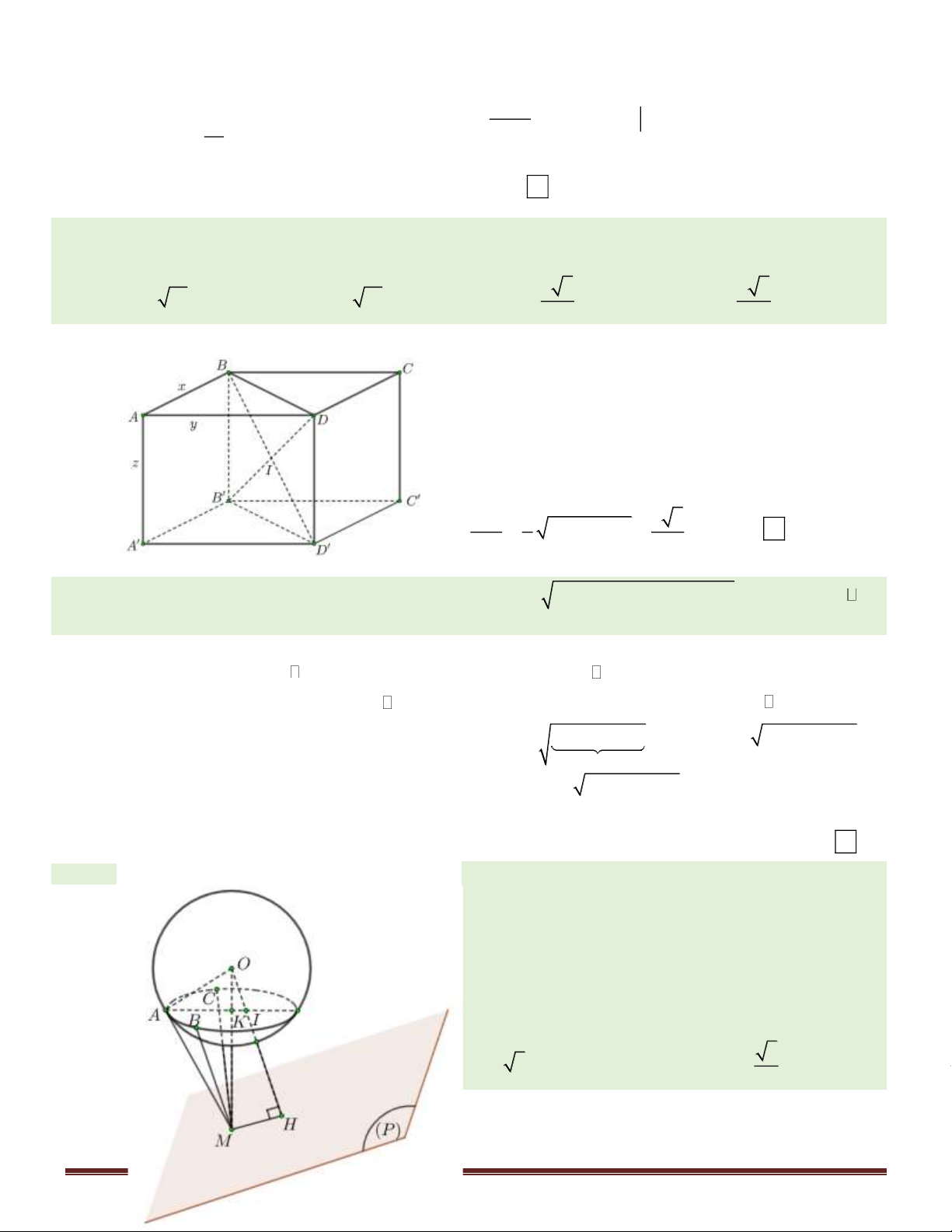
Câu 45. Tính thể tích V của khối chóp tứ giác đều có chiều cao là h và bán kính mặt cầu nội tiếp là r
(h 2r 0) . 2 2 4r h 2 2 4r h 2 2 4r h 2 2 3r h A. V = . B. V = . C. V = . D. V = . 3(h + 2r ) (h+ 2r) 3(h − 2r ) 4(h − 2r )
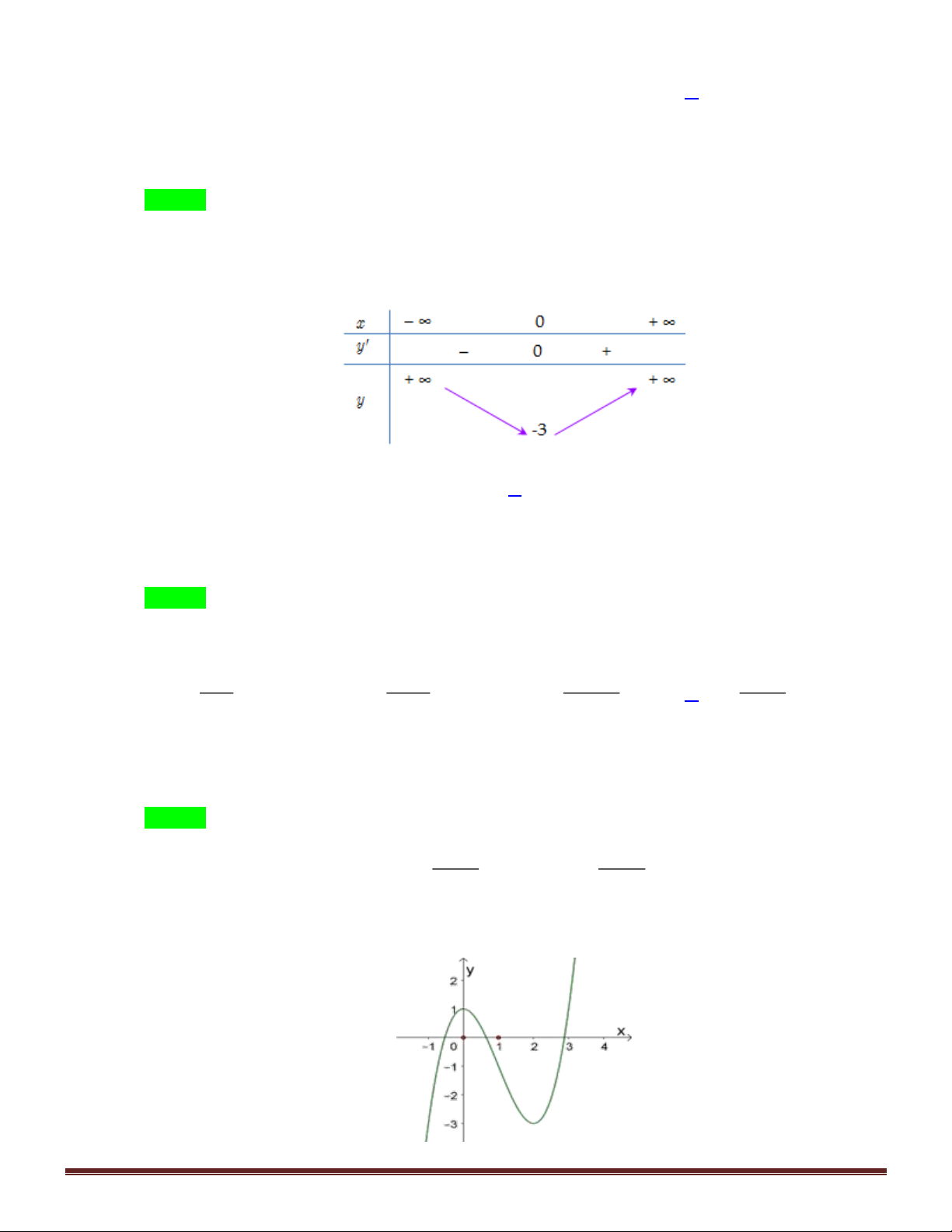
Câu 46. Gọi S là tập tất cả các giá trị thực của tham số m sao cho đường thẳng d : y = mx − m −3 cắt đồ thị (C) 3 2
: y = 2x − 3x − 2 tại ba điểm phân biệt A , B , I (1;− )
3 mà tiếp tuyến của (C) tại A và tại B
vuông góc với nhau. Tính tổng các phần tử của S . A. 1 − . B. 1. C. 2 . D. 5 . 3 1
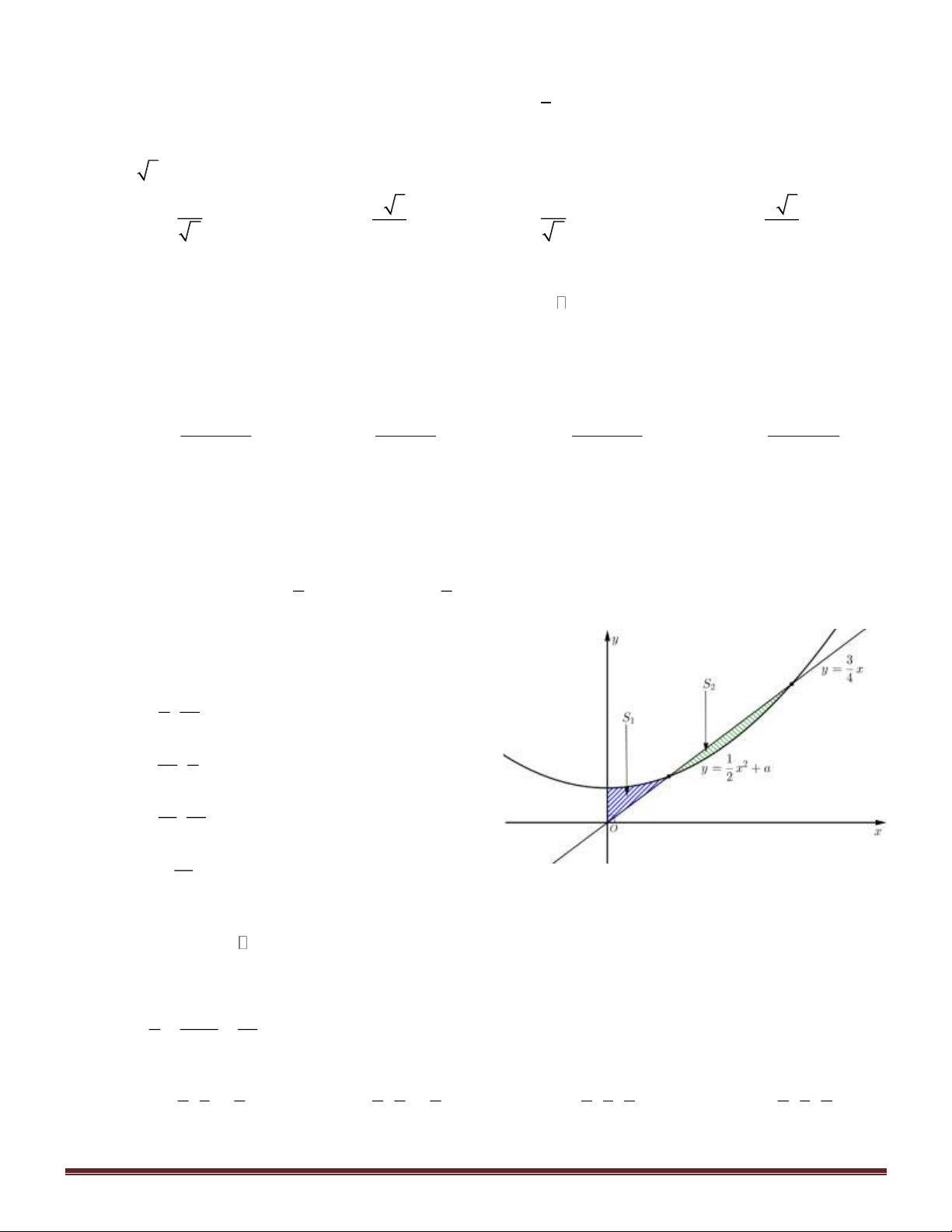
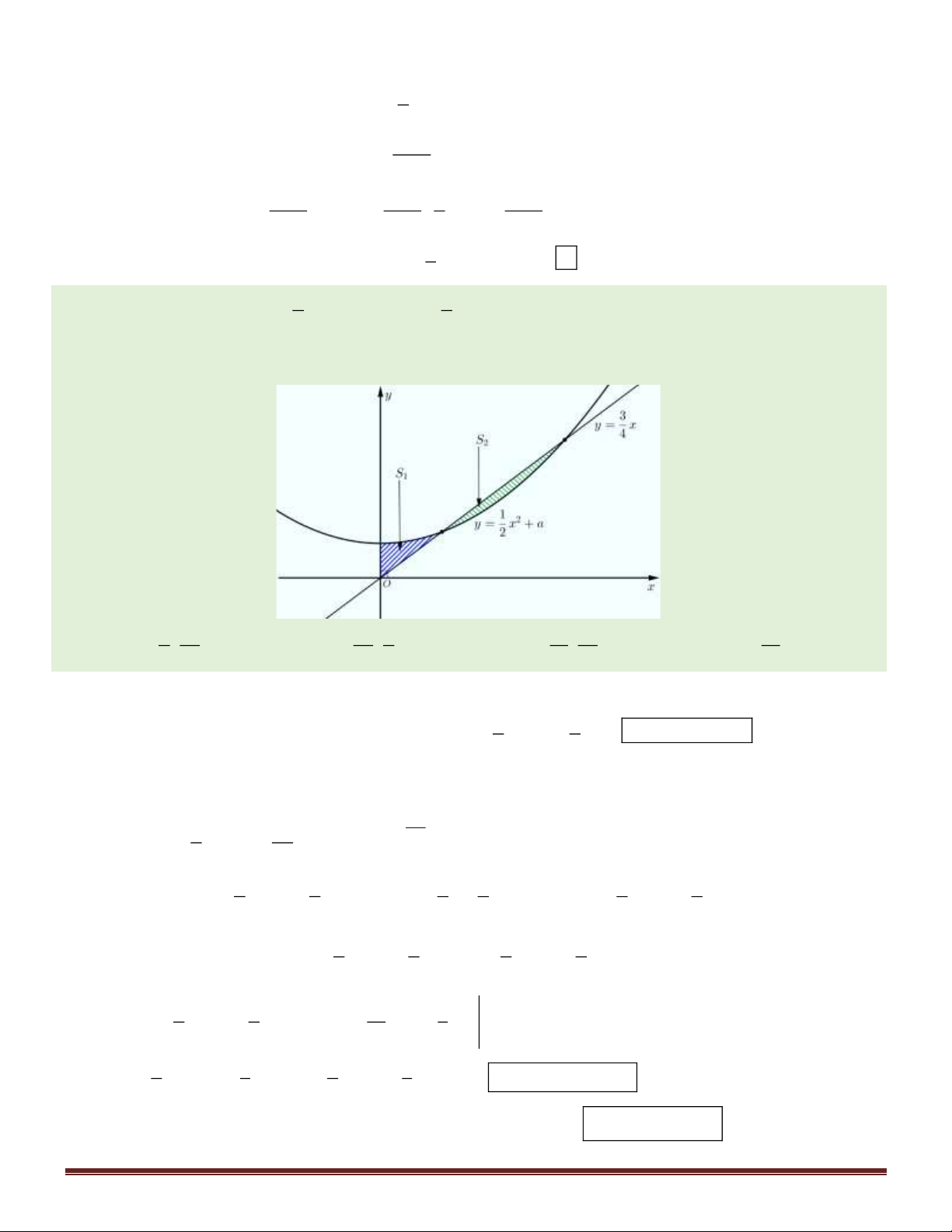
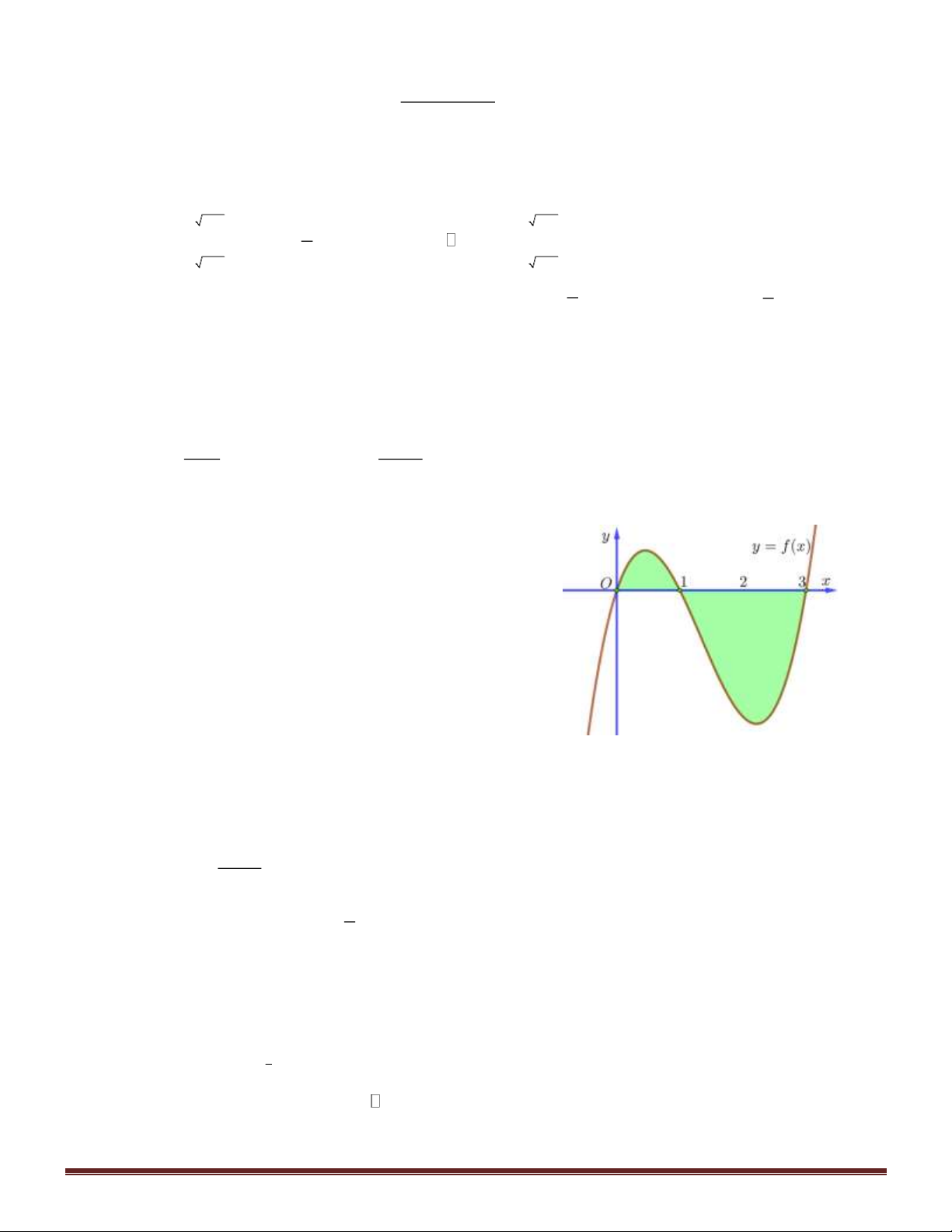
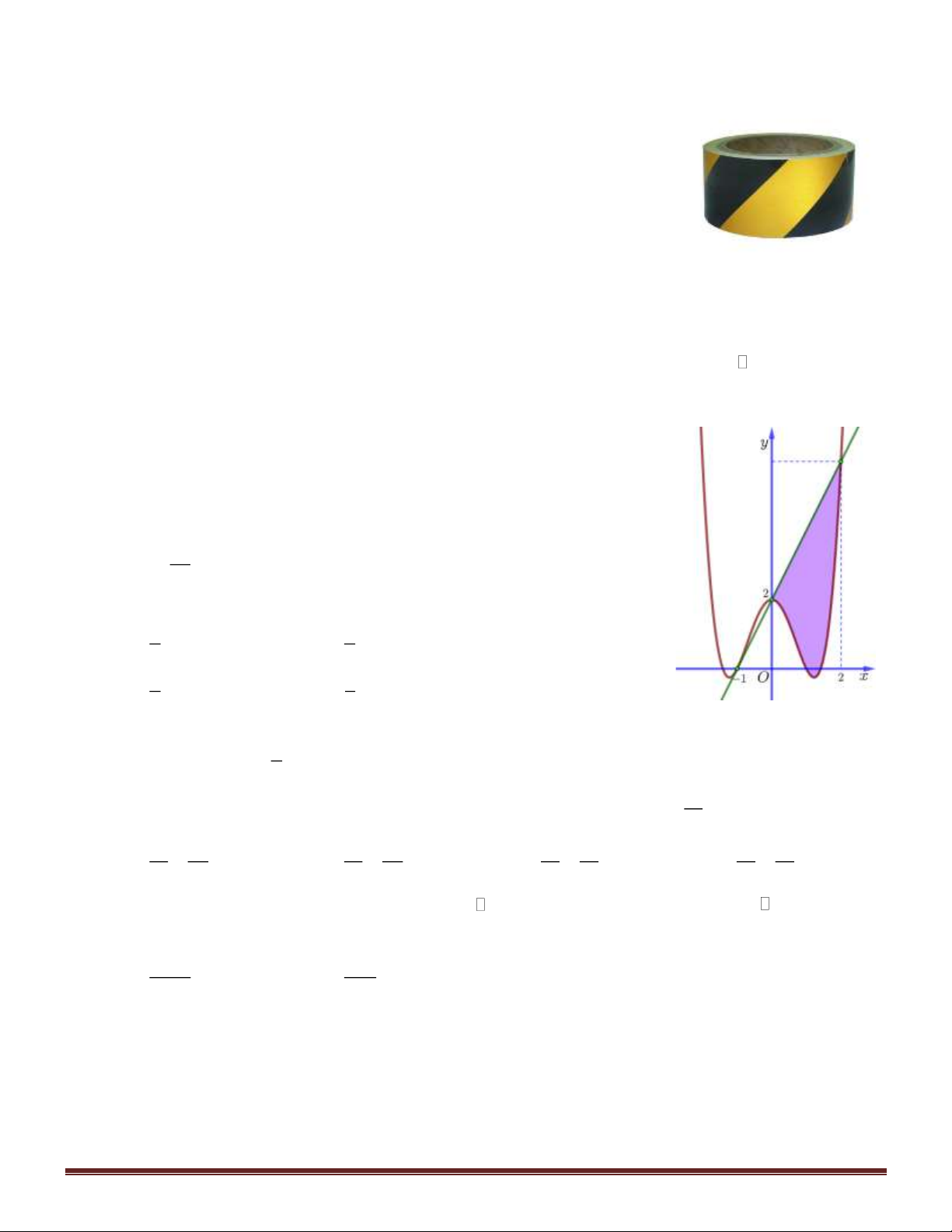
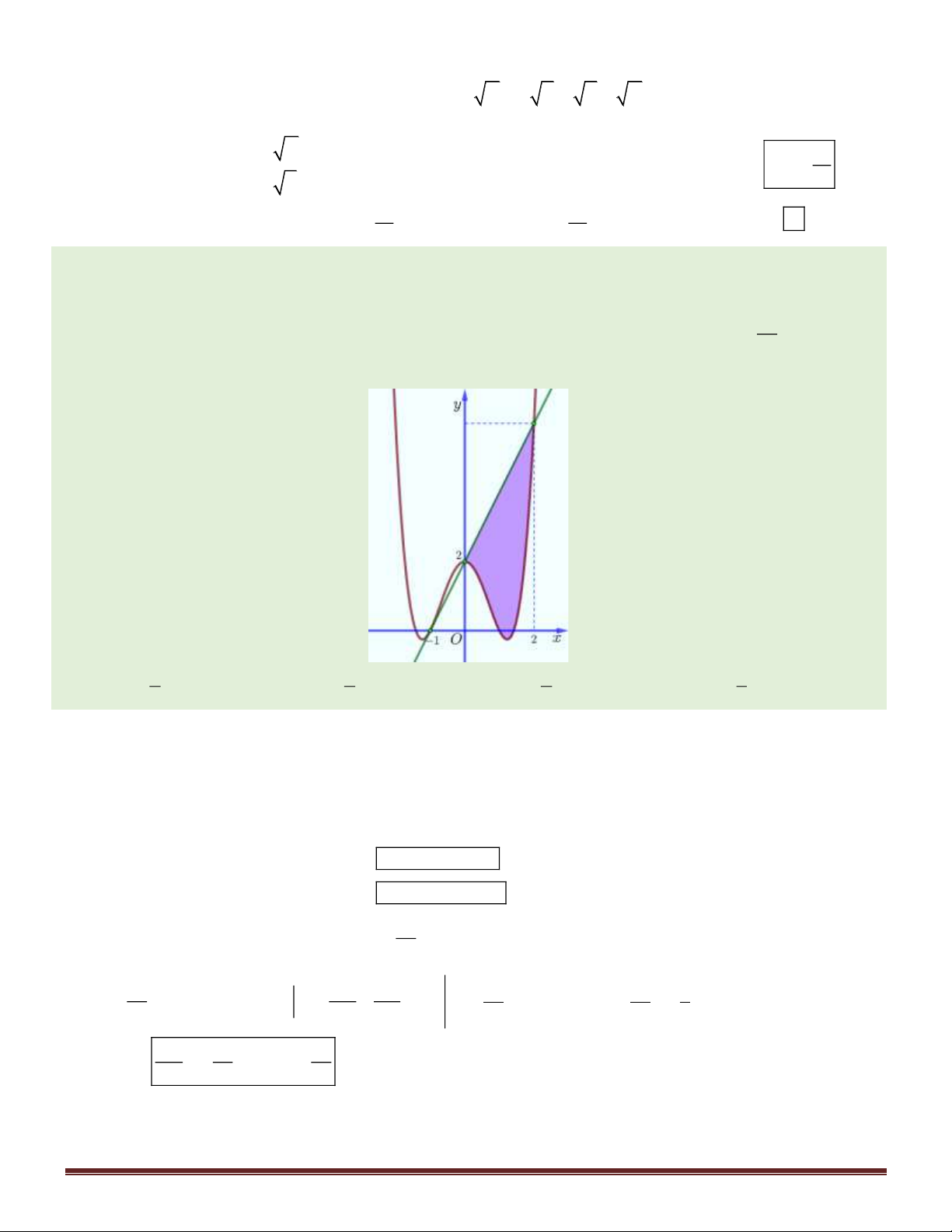
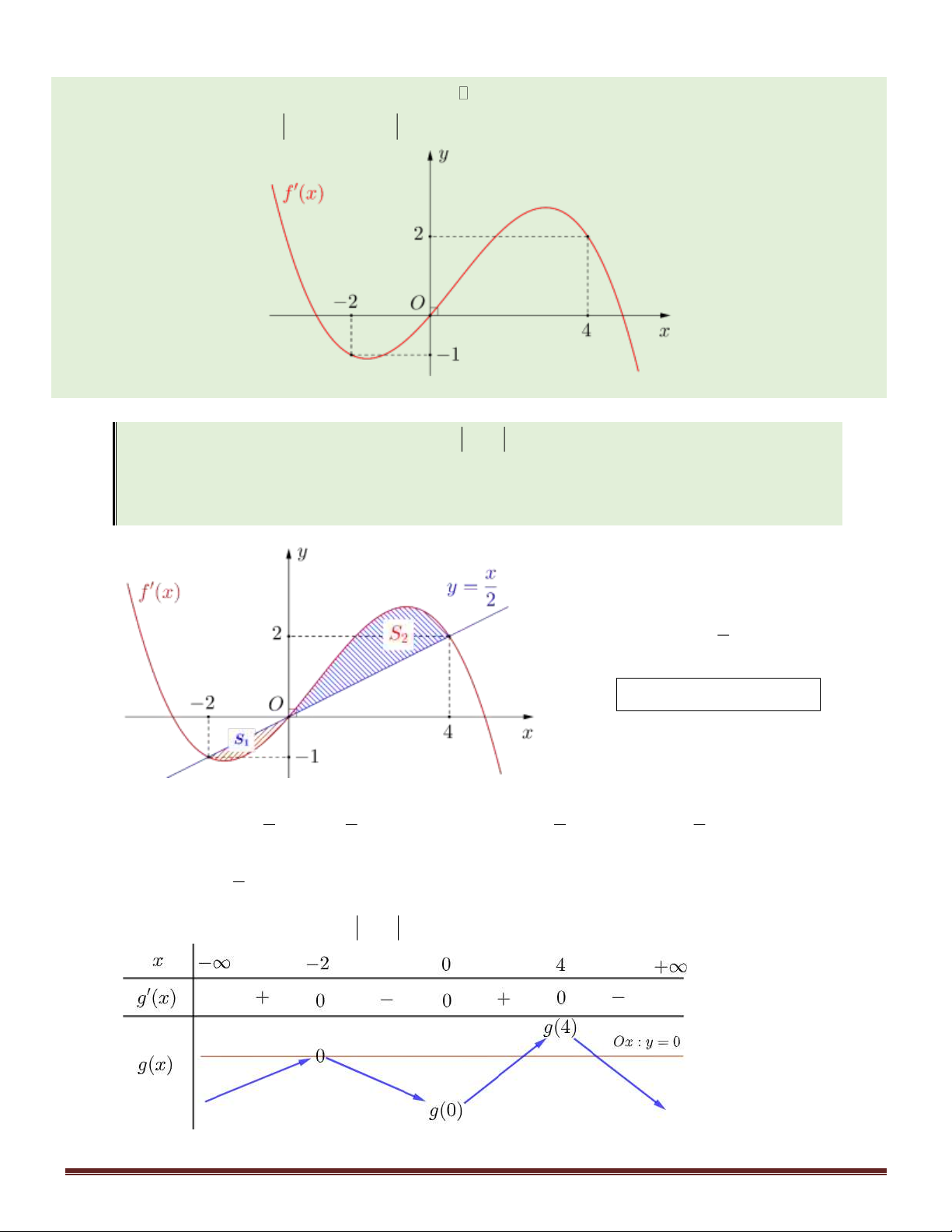
Câu 47. Cho đường thẳng y = x và parabol 2 y =
x + a ( a là tham số thực dương). Gọi S , S lần lượt là 4 2 1 2
diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.
Khi S = S thì a thuộc khoảng nào dưới đây? 1 2 1 9 A. ; . 4 32 7 1 B. ; . 32 4 3 7 C. ; . 16 32 3 D. 0; . 16
Câu 48. Có bao nhiêu giá trị của m để hàm số 9 y = mx + ( 2 m − m + ) 6 x + ( 3 2
m − m − m) 4 2024 2025 3 2 2 x + m − m đồng biến trên . A. Vô số. B. 1. C. 3 . D. 2 .
Câu 49. Trong không gian Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z − 2x + 2z +1 = 0 và đường thẳng x y − 2 z d : = =
. Hai mặt phẳng ( P) , ( P) chứa d và tiếp xúc với (S ) tại T và T . Tìm tọa độ 1 1 1 −
trung điểm H của TT . 5 1 5 5 2 7 5 1 5 7 1 7 A. H ; ; − . B. H ; ; − . C. H − ; ; . D. H − ; ; . 6 3 6 6 3 6 6 3 6 6 3 6 Trang 5 2 x+ x 1 + 2+ x 1 3 3 + − + 2024x − 2024 0
Câu 50. Cho hệ bất phương trình
( m là tham số). Gọi S là tập tất cả 2 x − (m+ 2) 2
x − m + 3 0
các giá trị nguyên của tham số m để hệ bất phương trình đã cho có nghiệm. Tính tổng các phần tử của S . A. 10 . B. 15 . C. 6 . D. 3 .
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 06 1 2 3 4 5 6 7 8 9 10 C D A A C C A D D D 11 12 13 14 15 16 17 18 19 20 A C D C B C A B C A 21 22 23 24 25 26 27 28 29 30 A A D C B B C B B A 31 32 33 34 35 36 37 38 39 40 D C B D A A B A B A 41 42 43 44 45 46 47 48 49 50 C A A A C A C B A D
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 06 Câu 44. Cho hàm số f ( x) liên tục trên tập số thực thỏa mãn 1
f ( x) + ( x − ) f ( 2 x − x) 3 2 5 2 5 4
= 50x − 60x + 23x −1, x
. Hãy tính f (x)dx . 0 A. 2 . B. 1. C. 3 . D. 6 . Hướng dẫn giải:
Theo giả thiết: f ( x) + ( x − ) f ( 2 x − x) 3 2 5 2 5 4
= 50x − 60x + 23x −1, x (*) . 1 1 1
Lấy tích phân hai vế của (*):
f ( x)dx + (5x − 2) f ( 2
5x − 4x)dx = ( 3 2
50x − 60x + 23x − )1dx 0 0 0 1 1 Suy ra f
(x)dx+ (5x−2) f ( 2
5x − 4x)dx = 3 (**). 0 0 I J 1 1
Xét J = (5x − 2) f ( 2
5x − 4x)dx . Đặt 2
t = 5x − 4x dt = (10x − 4)dx dt = (5x − 2)dx . 2 0
x = 0 t = 0 1 1 Đổ 1 1 1 i cận:
. Khi đó: J = f
(t). dt = f
(x)dx = I .
x = 1 t = 1 2 2 2 0 0 1 Thay vào (**), ta đượ 1 Choïn c: I +
I = 3 I = 2. Vậy f ( x)dx . ⎯⎯⎯ → A 2 0 Trang 6
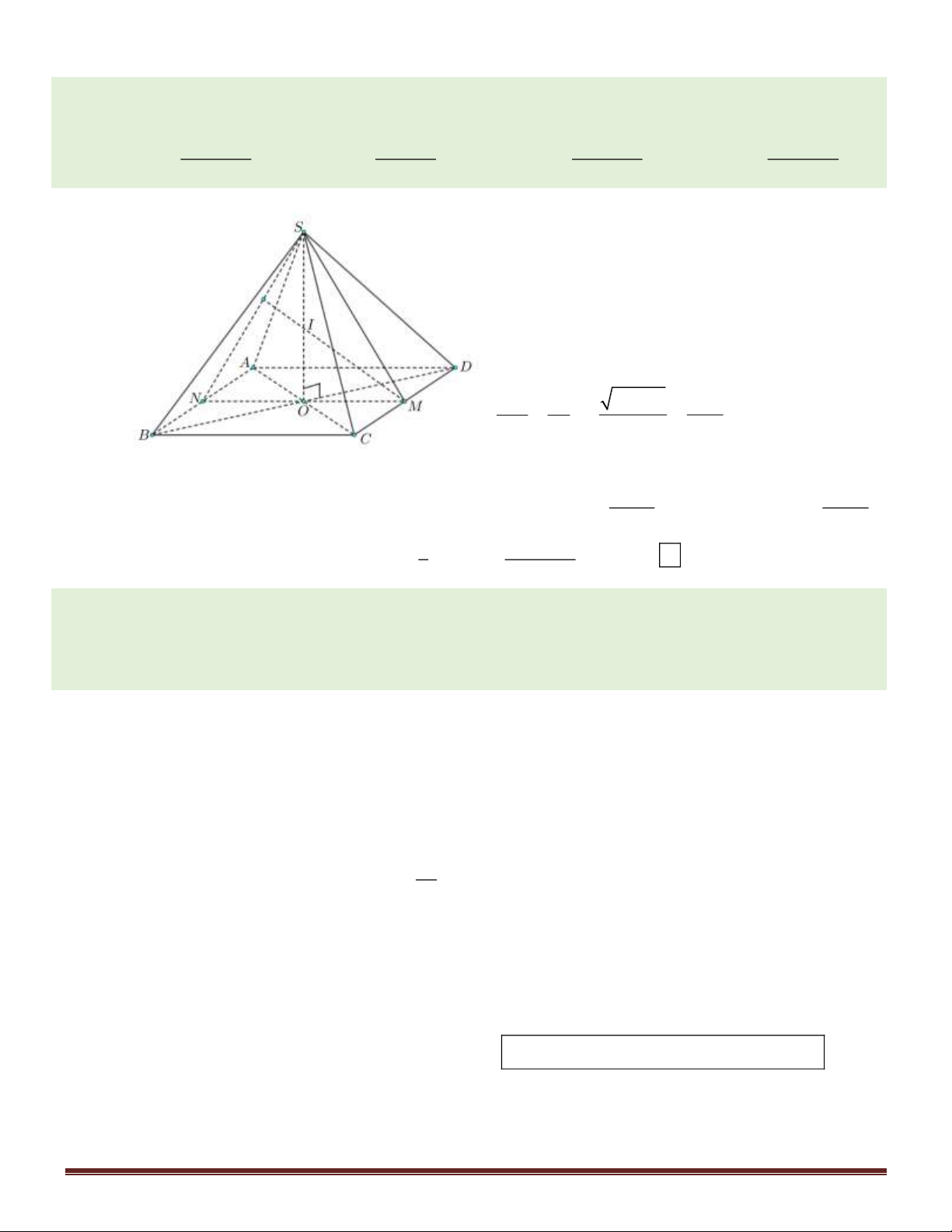
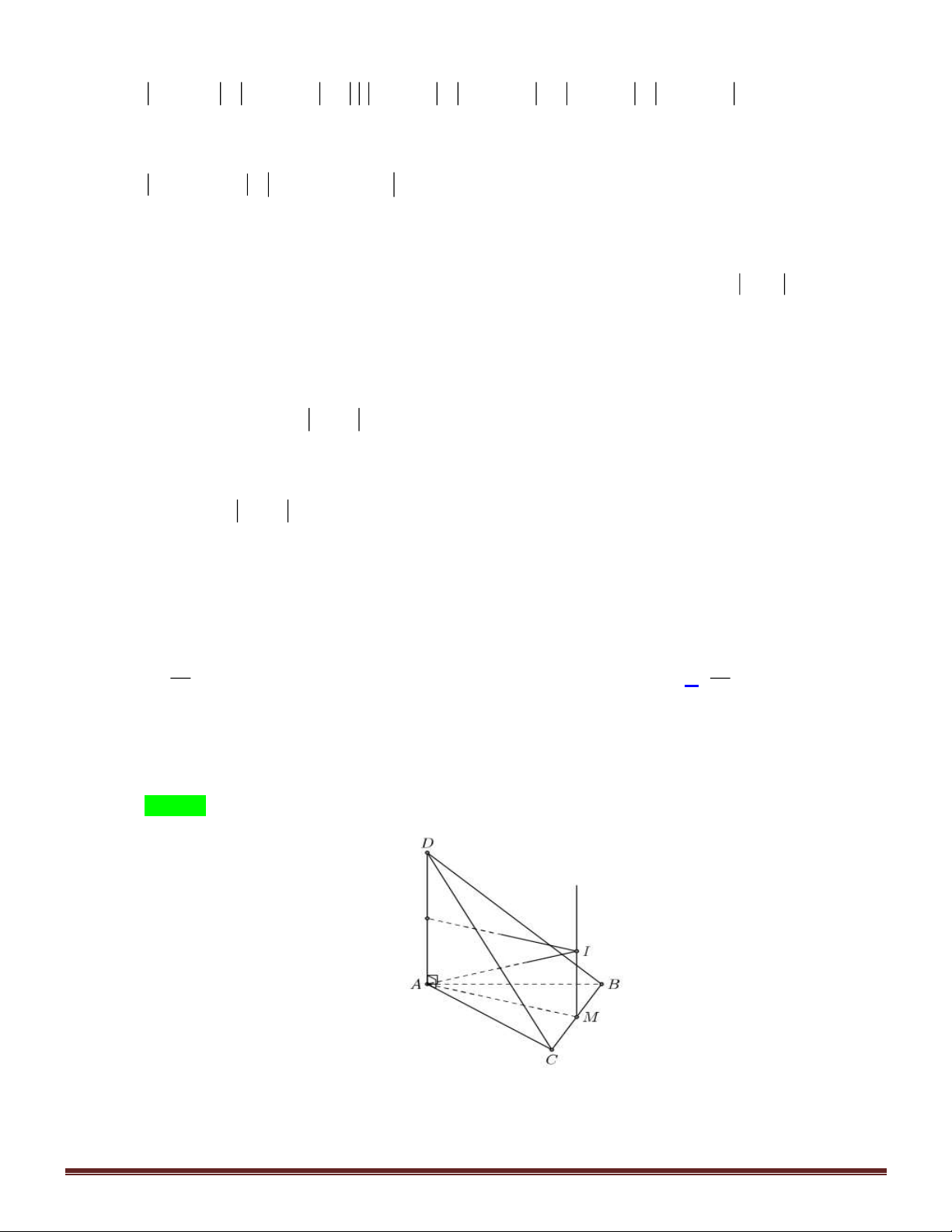
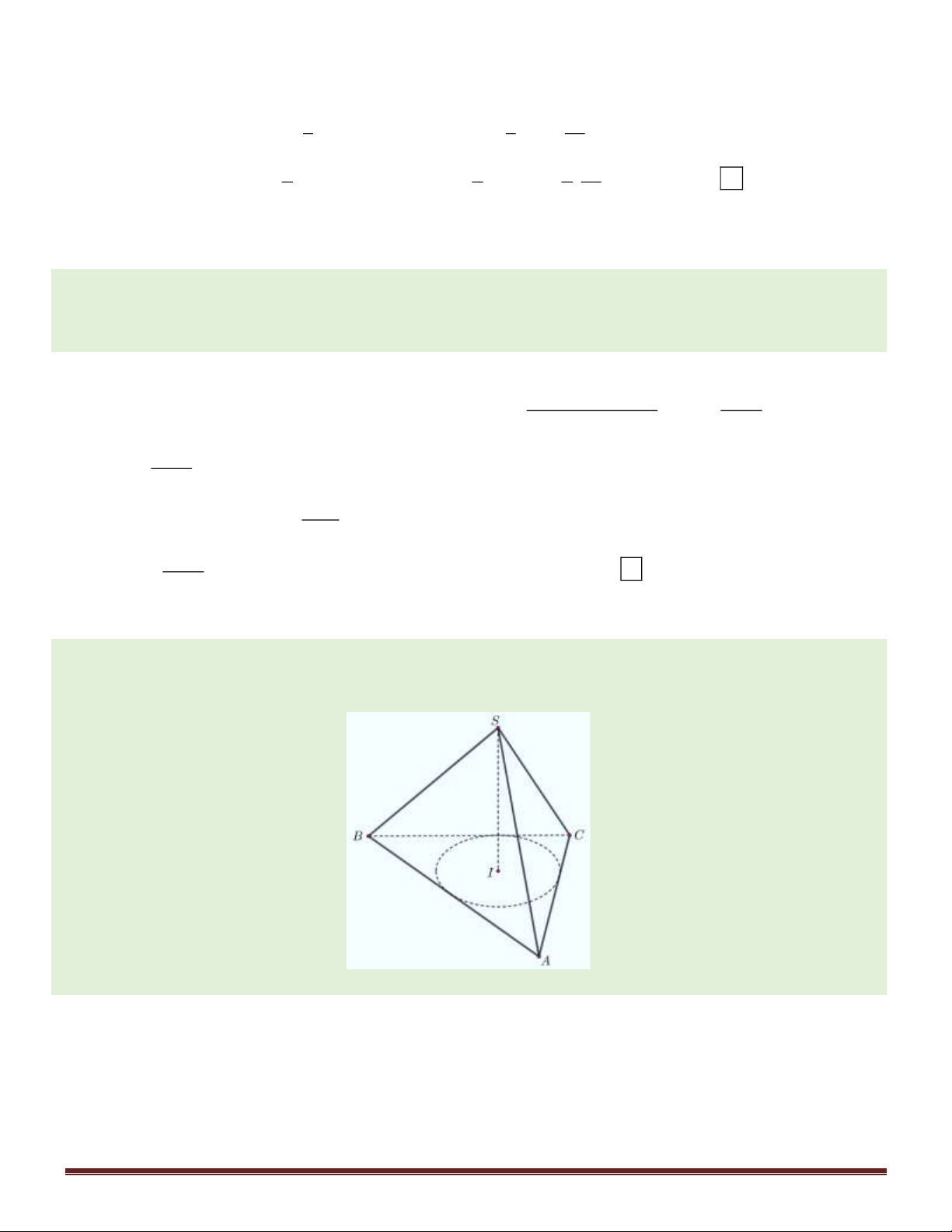
Câu 45. Tính thể tích V của khối chóp tứ giác đều có chiều cao là h và bán kính mặt cầu nội tiếp là r
(h 2r 0) . 2 2 4r h 2 2 4r h 2 2 4r h 2 2 3r h A. V = . B. V = . C. V = . D. V = . 3(h + 2r ) (h+ 2r) 3(h − 2r ) 4(h − 2r) Hướng dẫn giải:
Xét hình chóp tứ giác đều S.ABCD với M, N lần
lượt là trung điểm của CD, AB.
Gọi I là giao điểm ba đường phân giác trong của tam giác S
MN , suy ra I là tâm đường tròn nội tiếp tam giác S
MN . Mặt khác, do S.ABCD là
hình chóp tứ giác đều nên I là tâm mặt cầu nội tiếp
hình chóp này, bán kính mặt cầu là r = IO . Xét S
MO có MI là đường phân giác ta có: SM SI 2 2 + − = h x h r =
(với x = MO ). MO IO x r 2 2 BC =2 x
( + ) = ( − )2 −( − )2 2 2 2 2 2 2 2 2 hr hr r x h x h r x r h r = −r h 2 2 x = S = BC = 4 h − 2r ABCD h − . 2r 2 2 1 4h r Choïn
Vậy thể tích khối chóp S.ABCD là V = . h S = . ⎯⎯⎯ → C 3 ABCD 3(h − 2r)
Câu 46. Gọi S là tập tất cả các giá trị thực của tham số m sao cho đường thẳng d : y = mx − m −3 cắt đồ thị (C) 3 2
: y = 2x − 3x − 2 tại ba điểm phân biệt A , B , I (1;− )
3 mà tiếp tuyến của (C) tại A và tại B
vuông góc với nhau. Tính tổng các phần tử của S . A. 1 − . B. 1. C. 2 . D. 5 . Hướng dẫn giải:
Phương trình hoành độ giao điểm của (C) và (d ) : x = 1 3 2
2x −3x − 2 = mx − m − 3 ( x − ) 1 ( 2
2x − x − m − ) 1 = 0 (*) g ( x) 2
= 2x − x − m −1 = 0
Phương trình (*) có ba nghiệm phân biệt g ( x) = 0 có hai nghiệm phân biệt x 1 = − 1+ 8m + 8 0 9 g m 8 . g ( ) 2
1 = 2.1 −1− m −1 0 m 0
Do hai tiếp tuyến của (C) tại A và B vuông góc nhau nên k .k = 1
− trong đó k , k lần lượt là hệ 1 2 1 2
số góc tiếp tuyến của (C) tại A và B. Ta có : 2
y = 6x − 6x k = ( 2
6x − 6x , k = ( 2 6x − 6x . 2 2 2 ) 1 1 1 ) 2 Do k .k = 1 − nên ( 2 6x − 6x )( 2 6x − 6x = 1 − 36(x x
−36x x x + x + 36x x +1= 0 (*) . 1 2 ) 1 2 ( 1 2 ) 1 1 2 2 ) 1 2 1 2 Trang 7 1 x + x = 1 2 2
Theo định lí Vi-ét, ta có : . m +1 x x = − 1 2 2 2 + + + Do đó ( ) m 1 m 1 1 m 1 * 36 − −36 − + 36 − +1= 0 2
9m +9m+1= 0 . 2 2 2 2 9 Choïn
Tổng các phần tử của S là: m + m = − = 1 − . ⎯⎯⎯ → A 1 2 9 3 1
Câu 47. Cho đường thẳng y = x và parabol 2 y =
x + a ( a là tham số thực dương). Gọi S , S lần lượt là 1 2 4 2
diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.
Khi S = S thì a thuộc khoảng nào dưới đây? 1 2 1 9 7 1 3 7 3 A. ; . B. ; . C. ; . D. 0; . 4 32 32 4 16 32 16 Hướng dẫn giải:
Xét phương trình hoành độ 1 3
giao điểm hai đồ thị: 2 2 x + a =
x 2x − 3x + 4a = 0 ( ) 1 . 2 4
Dựa vào đồ thị, ta thấy rằng phương trình ( )
1 có hai nghiệm dương phân biệt 0 x x 1 2
= 9 − 32a 0 9 3 4a 0 a . S = 0; P = 0 32 2 2 1 x x x 1 3 2 2 3 1 1 3 Ta có: 2 S = x + a − x dx ; 2 2 S = x −
x − a dx = − x + a − x dx . 1 2 4 2 4 2 2 4 0 1 x 1 x 1 x 2 x 1 3 1 3 2 2
S = S S − S = 0 x + a − x dx + x + a − x dx = 0 1 2 1 2 2 4 2 4 0 1 x x 2 x 2 3 1 3 x 3 2 2 x + a − x dx = 0
+ ax − x = 0 2 4 6 8 0 0 1 3 1 3 3 2 2 2
x + ax − x = 0 x + a − x = 0 4x + 24a − 9x = 0 (2) . 2 2 2 2 2 2 2 6 8 6 8
Hơn nữa, x cũng thỏa mãn (1), tức là: 2
2x − 3x + 4a = 0 4a = − ( 2 2x − 3x (3). 2 2 2 2 ) 2 Trang 8 x é = 0 (loaïi) 2 ê Thay (3) vào (2): 2 4x − 6( 2 2x − 3x ) 2 − 9x = 0 8
− x + 9x = 0 ê (do a 0 ). 2 2 2 2 2 2 9 x ê = (nhaän) ê 2 ë 8 9 (3) 27 Choïn Với x = a = 3 7 ; . ⎯⎯⎯ → C 2 8 128 16 32
Câu 48. Có bao nhiêu giá trị của m để hàm số 9 y = mx + ( 2 m − m + ) 6 x + ( 3 2
m − m − m) 4 2024 2025 3 2 2 x + m − m
đồng biến trên . A. Vô số. B. 1. C. 3 . D. 2 . Hướng dẫn giải:
Tập xác định hàm số: D = . Ta có: 8 y = mx + ( 2 m − m + ) 5 x + ( 3 2
m − m − m) 3 9 6 3 2 4 2 x ; 3 5
y = x mx + ( 2 m − m + ) 2 x + ( 3 2 9 6 3 2
4 2m − m − m) = 0 x é = 0 (nghieäm boäi leû) Û ê . 5 2 2 3 2 g
ê (x) = 9mx + 6(m - 3m + 2)x + 4(2m - m - m) = 0 ë
Điều kiện cần: Hàm số đã cho đồng biến trên
x = 0 là nghiệm bội chẵn của phương trình
y = 0 x = 0 là nghiệm bội lẻ của phương trình g ( x) = 0 . m =1 Do đó: g (0) 1 3 2
= 0 2m − m − m = 0 m = − . 2 m = 0
Điều kiện đủ: Thử lại các giá trị m vừa tìm được. Với m = 0, ta có 5
y = 12x (không thỏa mãn y 0, x ). Với m = 1, ta có 8 y = 9x 0, x (thỏa mãn). 1 x = 0 9 45 9 Với m = − , ta có 8 5 5 y = − x + x = − x ( 3 x − 5) = 0 (không thỏa mãn 2 3 2 2 2 x = 5 y 0, x ). Choïn
Vậy có duy nhất 1 giá trị của m thỏa mãn yêu cầu bài toán là m = 1. ⎯⎯⎯ → B
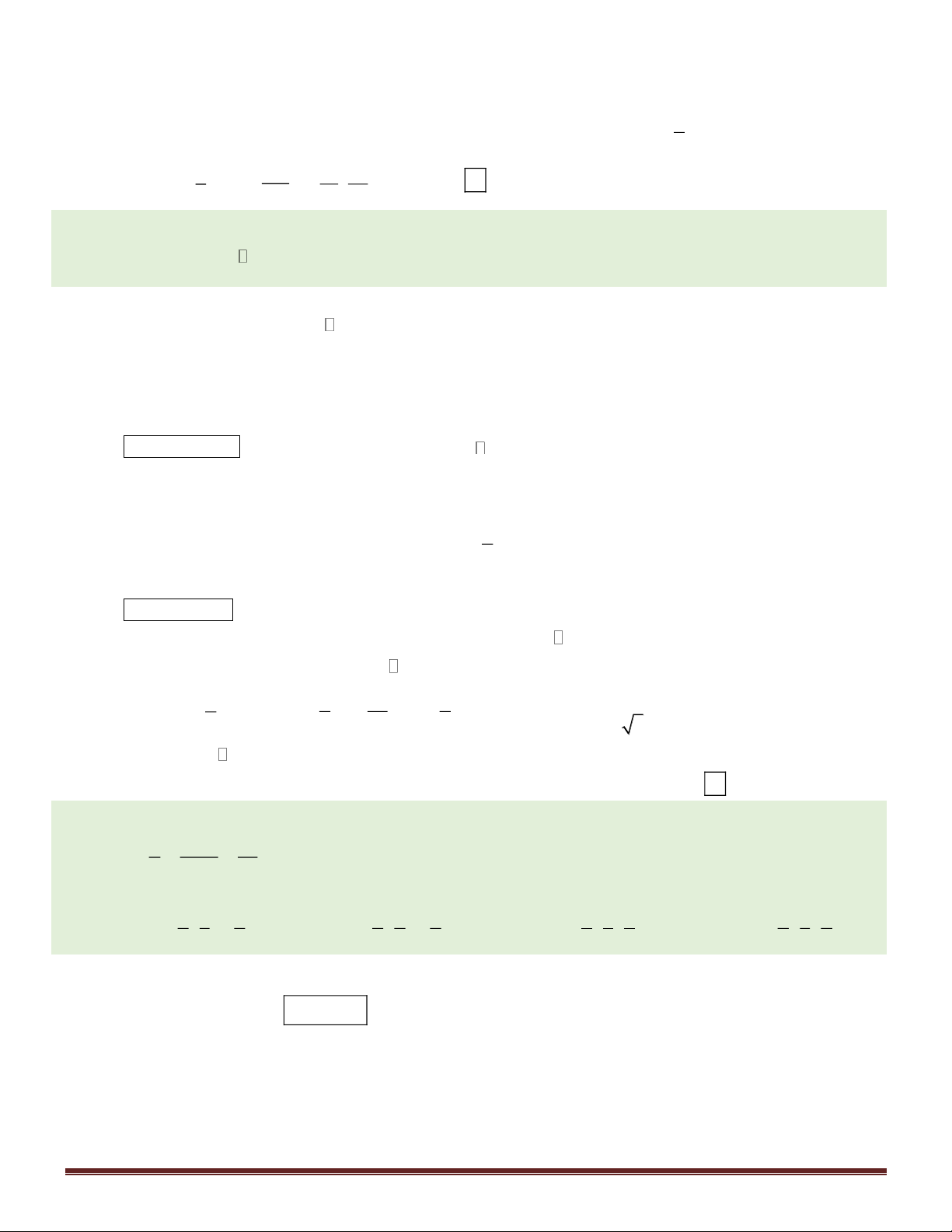
Câu 49. Trong không gian Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z − 2x + 2z +1 = 0 và đường thẳng x y − 2 z d : = =
. Hai mặt phẳng ( P) , ( P) chứa d và tiếp xúc với ( S ) tại T và T . Tìm tọa độ 1 1 1 −
trung điểm H của TT . 5 1 5 5 2 7 5 1 5 7 1 7 A. H ; ; − . B. H ; ; − . C. H − ; ; . D. H − ; ; . 6 3 6 6 3 6 6 3 6 6 3 6 Hướng dẫn giải:
Mặt cầu ( S ) có tâm I (1; 0; − )
1 , bán kính R =1. Gọi K = d (ITT) . Ta có d ⊥ IT
d ⊥ (ITT) nên K là hình chiếu vuông góc của I trên d . d ⊥ IT Trang 9 x = t
Phương trình tham số của d: y = 2 + t với vectơ chỉ z = −t
phương là u = (1;1;− ) 1 . d
Gọi K (t;2 + t; t
− )d , suy ra IK = (t −1;t + 2;1−t) ;
IK ⊥ u IK.u = 0 d d
t −1+ t + 2 −1+ t = 0 t = 0 . Suy ra K (0; 2; 0) và IK = 6 . 2 IH IH.IK 2 2 IT R 1 1 Ta có : = = = = = . 2 IK IK 2 2 IK IK 6 6 1
IH = IK 6IH = IK 6 6(x − = − H )1 1 5 1 5 Choïn 6 y = 2 H ; ; − . ⎯⎯⎯ → A H ( x + = H ) 6 3 6 6 1 1 2 x+ x 1 + 2+ x 1 3 3 + − + 2024x − 2024 0
Câu 50. Cho hệ bất phương trình
( m là tham số). Gọi S là tập tất cả 2 x − (m+ 2) 2
x − m + 3 0
các giá trị nguyên của tham số m để hệ bất phương trình đã cho có nghiệm. Tính tổng các phần tử của S . A. 10 . B. 15 . C. 6 . D. 3 . Hướng dẫn giải: Điều kiện: x 1 − . + + + + + + + + Ta có: 2x x 1 2 x 1 2 x x 1 2 x 1 3 − 3
+ 2024x − 2024 0 3 + 2024x 3 + 2024 ( )1 2x+ x 1 + ( x x ) 2+ x 1 3 1012 2 1 3 + + + + +1012(2+ x+1) (2). Xét hàm số ( ) = 3t f t
+1012t trên ; ( ) = 3t f t ln 3 +1012 0, t
, suy ra f (t) là hàm số đồng biến trên
. Do đó (2) f (2x + x +1) f (2 + x +1) 2x + x +1 2 + x +1 1 − x 1 .
Vậy tập nghiệm của (1) là S = 1 − ;1 . 1
Hệ bất phương trình đã cho có nghiệm khi và chỉ khi 2 x − (m + 2) 2
x − m + 3 0 có tập nghiệm S 2 (3)
thỏa S S tức là (3) có ít nhất một nghiệm thuộc 1 − ; 1 . 2 1 Đặt g ( x m) 2 = x − (m + ) 2 ,
2 x − m + 3 với = (m + )2 2 2 2
+ 4m −12 = 5m + 4m − 8. Trang 10 2 − − 2 11 2 − + 2 11
Trường hợp 1: 0 m . Khi đó g ( , x m) 0, x nên 5 5 1 − ,73 0,93 2 − − 2 11 2 − + 2 11 g ( , x m) 0, x 1 − ; 1 . Vì vậy m
thỏa mãn yêu cầu của bài toán. 5 5 1 − ,73 0,93 2 − + 2 11 m 5 0,93
Trường hợp 2: 0 = . Khi đó g ( ,
x m) 0 có hai nghiệm x x . 1 2 2 − − 2 11 m 5 1 − ,73 Ta cần g ( ,
x m) 0 có nghiệm thuộc đoạn 1 − ;
1 . Tuy nhiên, ta xét trường hợp phủ định với nó là: g (− ) 2 1 0 1
+ m + 2 − m + 3 0 g ( ,
x m) 0 không có nghiệm thuộc đoạn 1 − ; 1 , khi đó: g ( ) 2 1 0 1
− m − 2 − m + 3 0 m 2 − m 3 m −2
(*). Lấy phủ định lại kết quả của (*), ta có: 2 − m 3 . m 2 − m 1 m 3
Hợp kết quả của hai trường hợp trên, ta có m 2 − ;
3 mà m nguyên nên S = 2 − ;−1;0;1;2; 3 . Choïn
Tổng các phần tử của S bằng 3. ⎯⎯⎯ → D ĐỀ SỐ 07
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+ Câu 1.
Từ tập X = 2,3,4,5,
6 có thể lập được bao nhiêu số tự nhiên có ba chữ số mà các chữ số đôi một khác nhau? A. 60 . B. 125 . C. 10 . D. 6 . Câu 2.
Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2
− . Số hạng thứ sáu của (u là: n ) n ) 1 A. u = 160 . B. u = 320 − . C. u = 160 − . D. u = 320 . 6 6 6 6 Câu 3.
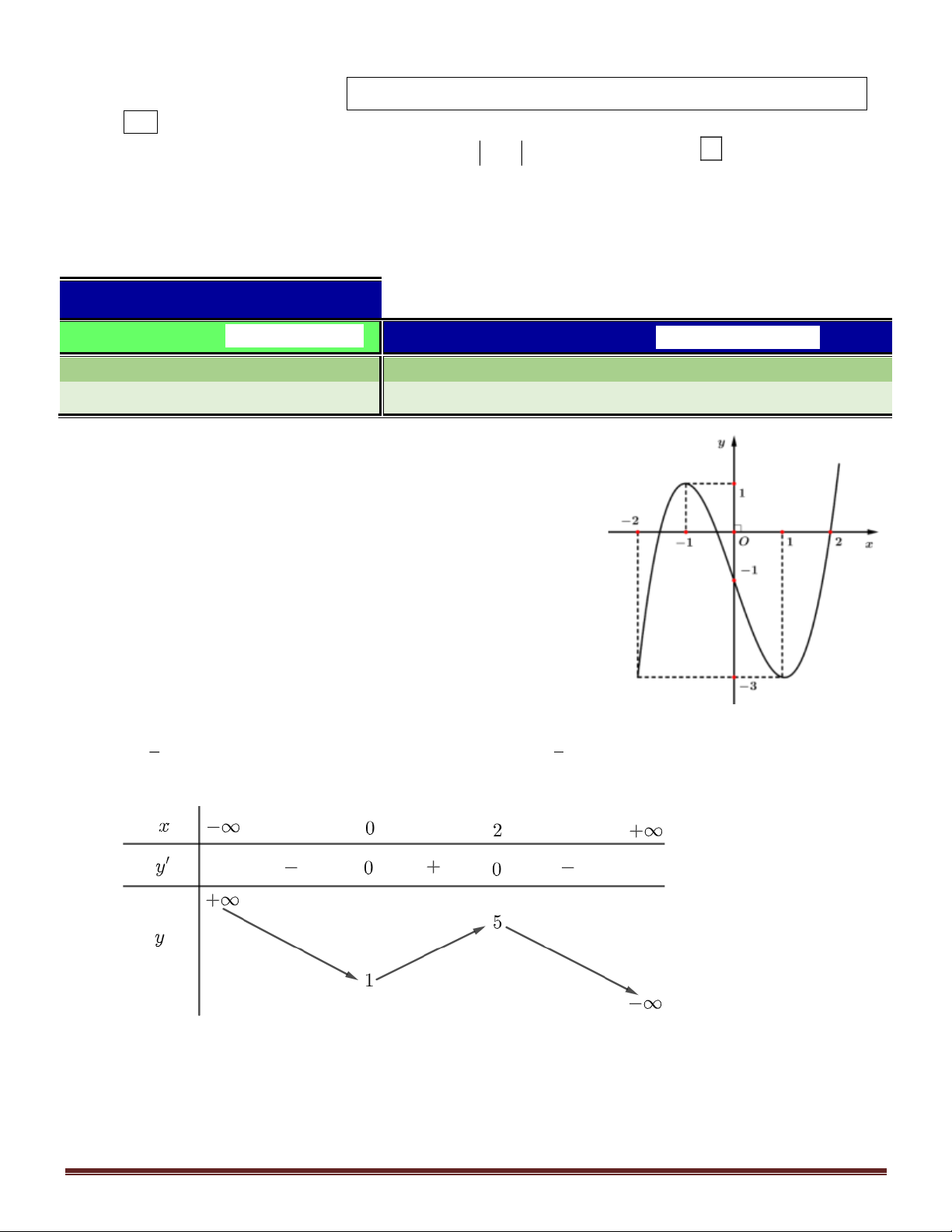
Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ. Hàm số y = f (x) đồng biến trên khoảng nào dưới đây? Trang 11 A. ( 2 − ; 2). B. ( ; − 0). C. (0; 2) . D. (2; + ) . Câu 4.
Cho hàm số y = f (x) có bảng biến thiên như sau
Giá trị cực đại của hàm số y = f ( x) bằng: A. 1 − B. 2 − C. 3 D. 4 Câu 5.
Cho hàm số y = f ( x) có bảng xét dấu như sau:
Hàm số có bao nhiêu điểm cực trị? A. 0 . B. 2 . C. 1. D. 3 . Câu 6.
Đường thẳng y = 2 là tiệm cận ngang của đồ thị nào dưới đây? 2 1+ x 2 − x + 3 2x − 2 A. y = . B. y = . C. y = . D. y = . x +1 1− 2x x − 2 x + 2 Câu 7.
Cho hàm số y = f (x) như hình vẽ dưới đây Trang 12
Hỏi f ( x) là hàm số nào trong các hàm số dưới đây? A. f ( x) 3 2 = x +3x − 4 . B. f ( x) 3 2 = x −3x +1. C. f ( x) 3 = x −3x +1. D. f ( x) 3 2 = −x + 3x +1. Câu 8.
Số giao điểm của đồ thị hàm số 2
y = x − 3x −1 và đồ thị hàm số 3 y = x −1 là A. 3 . B. 0 . C. 2 . D. 1. Câu 9.
Biết log 2 = a , log 5 = b . Tính I = log 5 theo a , b . 6 6 3 b b b b A. I = . B. I = . C. I = . D. I = . 1+ a 1− a a −1 a
Câu 10. Đạo hàm của hàm số 2 3 x y = là: 2 3 x A. 2 3 x y = . B. 2 3 . x y = ln 3. C. y = . D. 2 2.3 . x y = ln 3 . ln 3 ( − )2 1 2 2(1+ 2)
Câu 11. Cho a là một số thực dương. Rút gọn biểu thức P = a .a được kết quả là: A. 1. B. 5 a . C. 3 a . D. 3 a .
Câu 12. Tìm của phương trình x x+4 9 = 3 . A. x = 1 . B. x = 4 . C. x = 3 .
D. x = 2 . Câu 13. Cho , a b 0 và ,
a b 1, biểu thức 3 4 P = log
b .log a có giá trị bằng bao nhiêu? b a A. 18 . B. 24 . C. 12 . D. 6 .
Câu 14. Tìm nguyên hàm của hàm số f ( x) = 2x +1. x A. ( x + ) 2 2 1 dx = + x + C . B. ( x + ) 2 2
1 dx = x + x + C . 2 C. ( x + ) 2 2
1 dx = 2x +1+ C . D. ( x + ) 2 2
1 dx = x + C . Trang 13
Câu 15. Họ nguyên hàm của hàm số f ( x) 2
= 3x + sin x là A. 3
x + cos x + C . B. 3
x + sin x + C . C. 3
x − cos x + C . D. 3
3x − sin x + C . 5 7 7 Câu 16. Nếu f
(x)dx = 3 và f
(x)dx = 9 thì f (x)dx bằng bao nhiêu? 2 5 2 A. 3 . B. 6 . C. 12 . D. −6 . 2
Câu 17. Tích phân I = (2x − )
1 dx có giá trị bằng: 0 A. 1. B. 2. C. 3. D. 0.
Câu 18. Số phức liên hợp của số phức z = 1− 2i là A. 1+ 2i . B. 1 − − 2i . C. 2 − i . D. 1 − + 2i .
Câu 19. Cho hai số phức z = 2 + 3i , z = 4
− − 5i . Số phức z = z + z là 1 2 1 2
A. z = 2 + 2i . B. z = 2 − − 2i .
C. z = 2 − 2i . D. z = 2 − + 2i .
Câu 20. Cho số phức z = 4
− + 5i . Biểu diễn hình học của z là điểm có tọa độ A. ( 4 − ;5). B. ( 4 − ; 5 − ). C. (4; 5 − ) . D. (4;5) .
Câu 21. Một khối chóp tam giác đều có cạnh đáy bằng 2 và chiều cao bằng 3 . Thể tích của khối chóp đó là 2 3 A. V = . B. V = 1 . C. V = 3 . D. V = 2 3 . 3
Câu 22. Một khối lăng trụ có thể tích bằng 18 và diện tích đáy bằng 9 . Chiều cao của khối lăng trụ đó là A. h = 2 . B. h = 9 . C. h = 6 . D. h = 3 .
Câu 23. Công thức tính diện tích xung quanh của hình nón có bán kính đáy r và độ dài đường sinh l 1
A. S = rl .
B. S = 2 rl .
C. S = rl . D. 2
S = rl +r . 3
Câu 24. Một hình trụ có đường kính đáy bằng 6 và chiều cao bằng 4 . Diện tích xung quanh của hình trụ đó là A. S = 48 . B. S = 12 . C. S = 30 . D. S = 24 .
Câu 25. Trong không gian Oxyz , cho hai điểm M (1;3; 2 − ) và N (3; 1 − ; 2
− ). Trung điểm của đoạn thẳng
MN có tọa độ là Trang 14 A. (2; 4 − ;0) . B. (2;1; 2 − ). C. (4;2; 4 − ) . D. (1;2;0) .
Câu 26. Trong không gian Oxyz , mặt cầu (S ) : 2 2 2
x + y + z − 6x + 2 y + 2z + 2 = 0 có bán kính bằng A. 3 . B. 13 . C. 42 . D. 4 .
Câu 27. Trong không gian Oxyz , cho mặt phẳng ( P) : x + y − 2z + 3 = 0 . Điểm nào sau đây không thuộc vào ( P) ? A. M (0;1;2) . B. N (1;0;2) . C. E (1;1; ) 1 . D. F ( 2 − ;1; ) 1 .
Câu 28. Trong không gian Oxyz , véc tơ nào dưới đây là một véc tơ chỉ phương của đường thẳng đi qua
hai điểm A(1;3;2) và B(2;1; ) 1 ? A. u = 3; 2 − ; 1 − . B. u = 1; 2 − ;1 . C. u = 1 − ;2;1 . D. u = 3; 4;3 . 4 ( ) 3 ( ) 2 ( ) 1 ( )
Câu 29. Chọn ngẫu nhiên một số trong 20 số nguyên dương đầu tiên. Xác suất để chọn được số chia hết cho 3 bằng 5 3 1 7 A. . B. . C. . D. . 20 10 2 20
Câu 30. Hàm số nào sau đây nghịch biến trên ? A. 3 2
y = −x + 2x − 4x − 5 . B. 2
y = −x + x +1. 2x +1 C. y = . D. 4 2
y = −x + 2x +1. x −1
Câu 31. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
f (x) = x − 2x − 7x +1 trên
đoạn [-2; 1]. Tồng 3M + 2m bằng A. 5. B. 7. − C. 1. D. 2. − 2 x +4 x 1
Câu 32. Tập nghiệm của bất phương trình 8 là 2 A. − ; − 3 1
− ;+. B. 1; 3 . C. − ;
1 3;+. D. 3 − ;− 1 . 4 4
Câu 33. Nếu 2 −3 f (x)dx = 6 thì 2 f (x)dx bằng 0 0 2 3 4 3 A. . B. . C. . D. . 3 2 3 4 Trang 15
Câu 34. Cho z là số phức có phần ảo dương của phương trình 2
z − 2z + 5 = 0 . Số phức liên hợp của số 0
phức (4 + i) z là 0 A. 2 + 9i . B. 2 − 9i . C. 2 − −9i . D. 2 − + 9i .
Câu 35. Cho hình hộp chữ nhật ABC . D A B C D
¢ ¢ có diện tích các mặt ABCD , BCC B ¢ ¢, CDD C lần lượt là 2 2a , 2 3a , 2
6a . Góc giữa đường thẳng BD và mặt phẳng ( ABCD) bằng B C D A B' C' A' D' 1 3 5 A. tan = . B. tan = . C. tan = . D. tan = 3 . 3 5 3
Câu 36. Cho tứ diện đều D ABC
có độ dài cạnh bằng 3 . Khoảng cách từ điểm B đến mặt phẳng( D AC ) bằng 3 3 A. . B. . C. 2 . D. 2 . 4 2
Câu 37. Trong không gian Oxyz, mặt cầu có tâm I (1; 1
− ;0) và tiếp xúc với mặt phẳng ( )
P : x − 2y + 2z + 6 = 0 có phương trình là: A. 2 2 2
(x −1) + ( y +1) + z = 9 . B. 2 2 2
(x −1) + ( y +1) + z = 3 . C. 2 2 2
(x +1) + ( y −1) + z = 9 . D. 2 2 2
(x +1) + ( y −1) + z = 3 .
Câu 38. Trong không gian Oxyz, đường thẳng đi qua điểm ( A 1
− ;2;3) và song song với đường thẳng x = 3 + t
: y = 4 − 2t có phương trình tham số là z = 5+ 4t x = 1− t x = 1 − + t x = −1+ t x = 1+ t
A. y = −2 + 2t .
B. y = 2 + 2t .
C. y = 2 − 2t .
D. y = 2 − 2t . z = 4 + 3t z = 3 + 4t z = 3 + 4t z = 3 + 4t
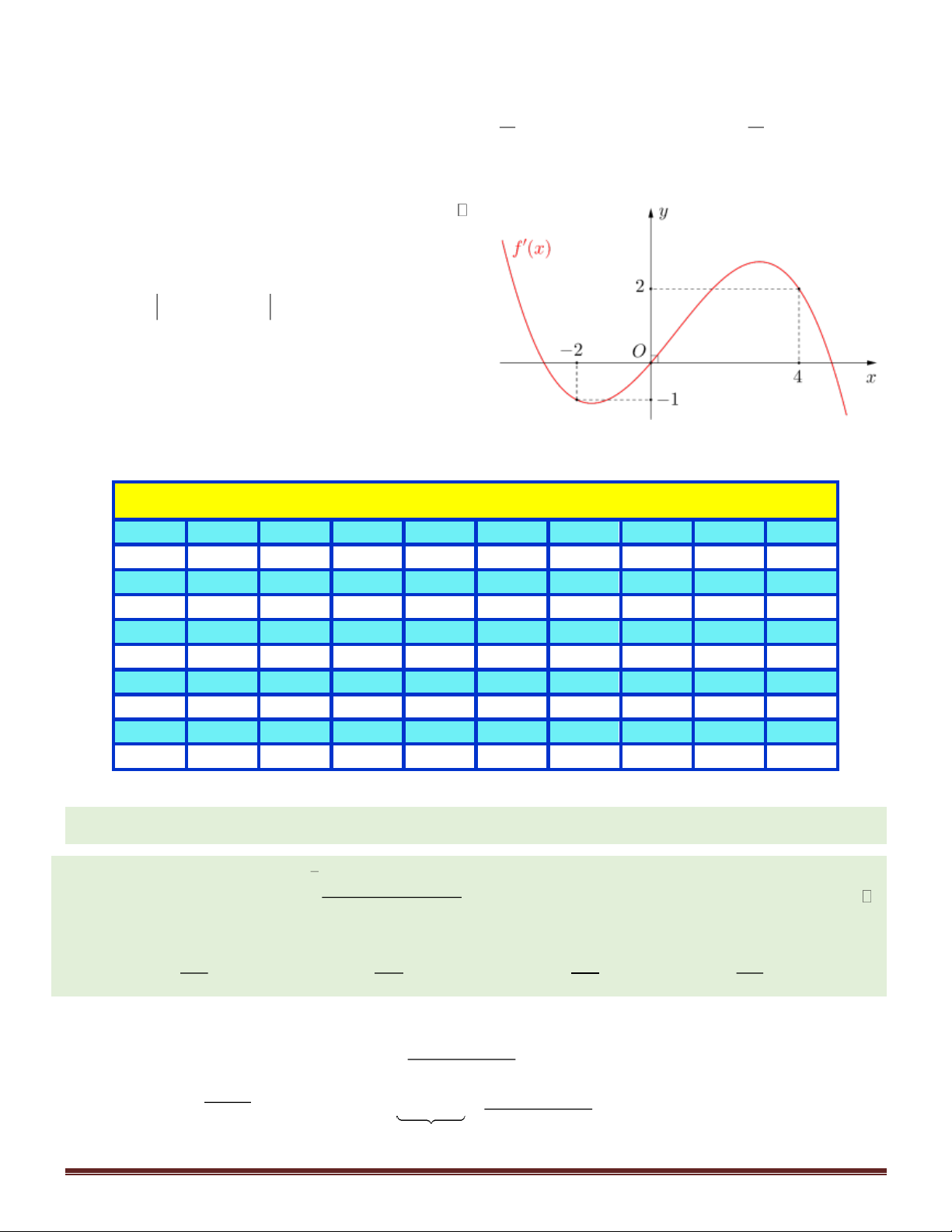
Câu 39. Cho hàm số f (x) , đồ thị hàm số y = f '( )
x là đường cong trong hình dưới. Giá trị lớn nhất của hàm số 2
g(x) = f (2x) − sin x trên đoạn 1 − ; 1 là Trang 16 A. f ( 1 − ). B. f (0) . C. f (2) . D. f (1) .
Câu 40. Số nguyên dương a lớn nhất thỏa mãn điều kiện 3log ( 3
1+ a + a 2log a 3 ) 2 là?
A 2016 . B 2095 . C. 3096 . D. 4095 . x 2 e +1 khi x 0 e f (ln x − ) 1 a
Câu 41. Cho hàm số y = f ( x) = . Tích phân I = dx = + ce biết 2
x − 2x + 2 khi x 0 x b 1/e a , a , b c Z và
tối giản. Tính a + b + c ? b A. 35 . B. 29 . C. 36 . D. 27 . 2
Câu 42. Có bao nhiêu số phức z thỏa mãn (1+ i) z − 2 + 4i = 3 2 và z − i = 1− 2zi ? z A. 0 . B. 1. C. 2 . D. 3 .
Câu 43. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Mặt phẳng (SAB) cân tại S và nằm trong
mặt phẳng vuông góc với đáy, mặt bên (SBC) tạo với đáy một góc 0 60 . Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 a 3 3 a A. . B. . C. . D. . 16 8 8 4
Câu 44. Một công ty mỹ phẩm muốn thay đổi mẫu mã lọ nước tẩy trang gồm phần hình trụ và chỏm cầu
như hình vẽ ở dưới. Lọ nước tẩy trang có bán kính đáy bằng 1cm , phần cổ và nắp lọ được tính
riêng. Chi phí phần thân lọ gần nhất với số tiền nào sau đây biết phần thân hình trụ có giá 1000 đ 2
/1m , phần chỏm cầu có giá 1500 đ 2 /m . Trang 17 A. 1428.7 đ. B. 1475.8 đ. C. 1230.2 đ. D. 1415.1đ. x +1 y z −1 x + 2 y z +1
Câu 45. Trong không gian Oxyz , cho đường thẳng d : = = ; d : = = . 1 1 1 1 − 2 3 1 − 2 x =1
d : y = 1− t t R . Phương trình đường thẳng d cắt 3 đường thẳng d ; d ; d lần lượt tại 3 ( ) 1 2 3 z = t a + b , A ,
B C sao cho B là trung điểm của AC có véc tơ chỉ phương u = ( ; a ;
b c) . Tỉ số T = thuộc c khoảng nào sau đây? A. ( 3 − ;− ) 1 . B. (1; ) 3 . C. (4;6) . D. ( 6 − ; 3 − ) .
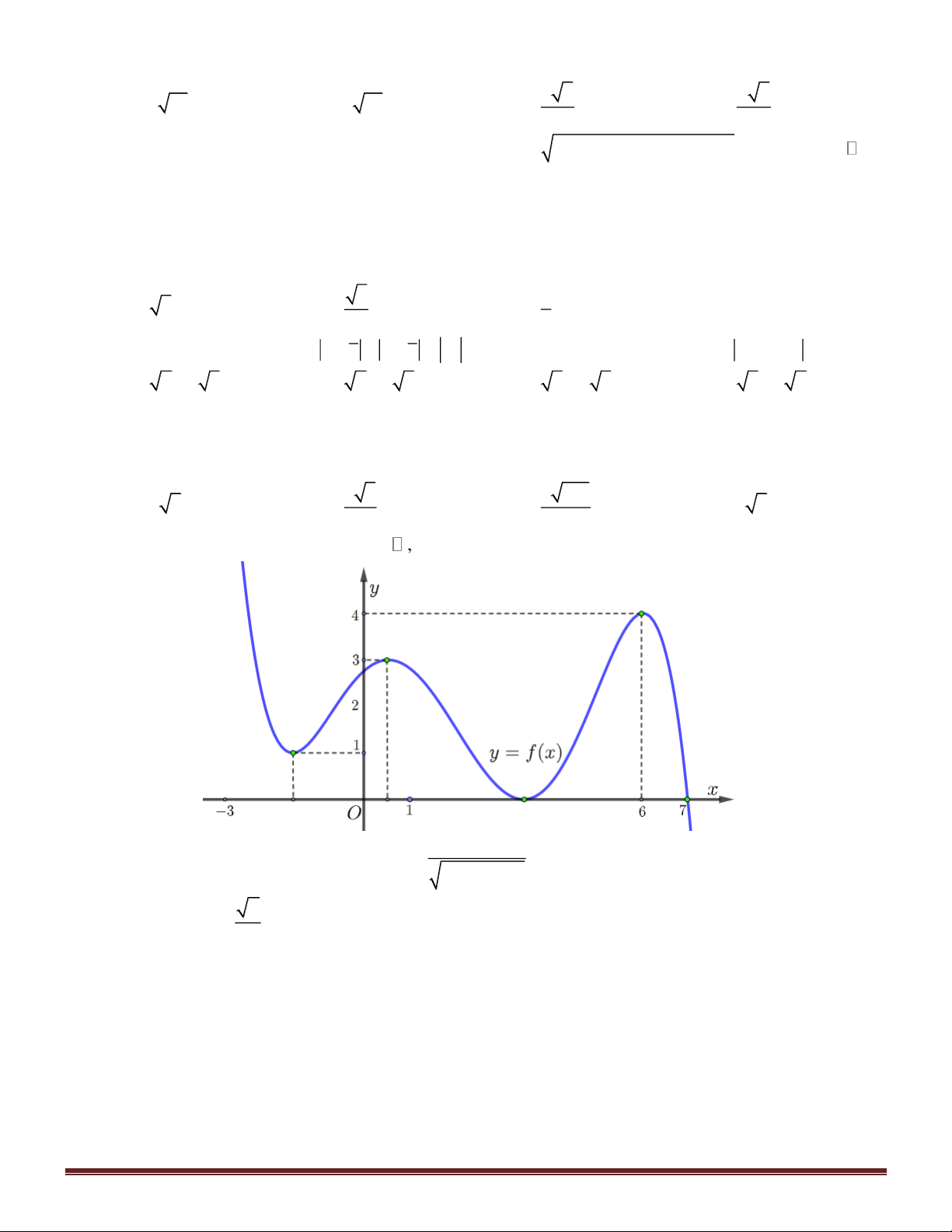
Câu 46. Cho hàm số y = f ( )
x có tập xác định là D =
và có đạo hàm xác định trên , đồ thị hàm số y = f ( )
x như hình vẽ bên dưới. Hỏi hàm số y = f ( 3
x −12x) có bao nhiêu điểm cực trị? A. 11. B. 10. C. 12. D. 9. 1 x+
Câu 47. Biết rằng 2 x = log 1
4− y − 2 y +1
x . Tính giá trị biểu thức 2 ( ) trong đó 0 2 2
P = x + y − xy +1. A. 1. B. 2 . C. 3 . D. 4 .
Câu 48. Một chiếc ly bằng thủy tinh đang chứa nước bên trong được tạo thành khi quay một phần đồ thị hàm số 2x y = xung quanh trục .
Oy Người ta thả vào chiếc ly một viên bi hình cầu có bán kính R Trang 18
thì mực nước dâng lên phủ kín viên bi đồng thời chạm tới miệng ly. Biết điểm tiếp xúc của viên bi
và chiếc ly cách đáy của chiếc ly 3cm (như hình vẽ). Thể tích nước có trong ly gần với giá trị nào
nhất trong các giá trị sau? A. 2 30 cm . B. 2 40 cm . C. 2 50 cm . D. 2 60 cm .
Câu 49. Cho số phức z và z là hai nghiệm của phương trình: 6 − 3i + iz = 2z − 6 − 9i , thỏa mãn: 1 2
z − z = 2. Giá trị của biểu thức: P = z + z tương ứng bằng 1 2 1 2 A. 6 . B. 5 . C. 26 . D. 10 .
Câu 50. Trong không gian Oxyz , cho mặt cầu ( S ) có tâm I ( 1 − ;2; )
1 và đi qua điểm A(1;0;− ) 1 . Xét các điểm ,
B C, D thuộc (S ) sao cho A ,
B AC, AD đôi một vuông góc với nhau. Thể tích của khối tứ
diện ABCD lớn nhất bằng 64 32 A. . B. 32 . C. 64 . D. . 3 3
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT BẢNG ĐÁP ÁN 1.A 2.C 3.C 4.D 5.C 6.D 7.C 8.D 9.B 10.D 11.B 12.B 13.B 14.B 15.C 16.C 17.B 18.A 19.B 20.B 21.B 22.A 23.C 24.D 25.B 26.A 27.C 28.C 29.B 30.A 31.C 32.D 33.C 34.B 35.B 36.D 37.A 38.C 39.B 40.D 41.C 42.C 43.A 44.A 45.A 46.B 47.B 48.A 49.D 50.D
LỜI GIẢI CHI TIẾT Câu 1.
Từ tập X = 2,3,4,5,
6 có thể lập được bao nhiêu số tự nhiên có ba chữ số mà các chữ số đôi một khác nhau? A. 60 . B. 125 . C. 10 . D. 6 . Trang 19 Lời giải Chọn A
Số các số tự nhiên có ba chữ số mà các chữ số đôi một khác nhau được lập từ tập X là số chỉnh
hợp chập 3 của 5 phần tử.
số các số cần lập là 3 A = 60 (số). 5 Câu 2.
Cho cấp số nhân (u có số hạng đầu u = 5 và công bội q = 2
− . Số hạng thứ sáu của (u là: n ) n ) 1 A. u = 160 . B. u = 320 − . C. u = 160 − . D. u = 320 . 6 6 6 6 Lời giải Chọn C
Ta có u = u q = 5.( 2 − )5 5 = 1 − 60 . 6 1 Câu 3.
Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ. Hàm số y = f (x) đồng biến trên khoảng nào dưới đây? A. ( 2 − ; 2). B. ( ; − 0). C. (0; 2) . D. (2; + ) . Lời giải Chọn C
Nhìn vào đồ thị ta thấy hàm số y = f (x) đồng biến trên khoảng (0; 2). Câu 4.
Cho hàm số y = f (x) có bảng biến thiên như sau
Giá trị cực đại của hàm số y = f ( x) bằng: Trang 20 A. 1 − B. 2 − C. 3 D. 4 Lời giải Chọn D
Từ bảng biến thiên suy ra, hàm số đạt cực đại tại x = 1
− và giá trị cực đại của hàm số là y = 4 . Câu 5.
Cho hàm số y = f ( x) có bảng xét dấu như sau:
Hàm số có bao nhiêu điểm cực trị? A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn C Câu 6.
Đường thẳng y = 2 là tiệm cận ngang của đồ thị nào dưới đây? 2 1+ x 2 − x + 3 2x − 2 A. y = . B. y = . C. y = . D. y = . x +1 1− 2x x − 2 x + 2 Lời giải Chọn D − − Trong 4 đáp án trên chỉ x 2x 2 có đáp án 2 2 y = thoả mãn lim = 2 . x + 2 x→ x + 2 Câu 7.
Cho hàm số y = f (x) như hình vẽ dưới đây Trang 21
Hỏi f ( x) là hàm số nào trong các hàm số dưới đây? A. f ( x) 3 2 = x +3x − 4 . B. f ( x) 3 2 = x −3x +1. C. f ( x) 3 = x −3x +1. D. f ( x) 3 2 = −x + 3x +1. Lời giải Chọn C
Dựa vào hình dạng đồ thị hàm số có hai điểm cực trị tại x = 0 và x = 2 , cắt trục tung tại điểm có
tung độ y =1 và có hệ số a 0 .
Như vậy chỉ có hàm số ở phương án C thỏa mãn. Câu 8.
Số giao điểm của đồ thị hàm số 2
y = x − 3x −1 và đồ thị hàm số 3 y = x −1 là A. 3 . B. 0 . C. 2 . D. 1. Lời giải Chọn D
Số giao điểm của 2 đồ thị là số nghiệm của phương trình hoành độ giao điểm. 2 3
x −3x −1 = x −1 3 2
x − x +3x = 0 3 2
x − x +3x = 0 3 2
x − x +3x = 0 x = 0 .
Vậy số giao điểm của hai đồ thị hàm số bằng 1. Câu 9.
Biết log 2 = a , log 5 = b . Tính I = log 5 theo a , b . 6 6 3 b b b b A. I = . B. I = . C. I = . D. I = . 1+ a 1− a a −1 a Lời giải Chọn B log 5 log 5 b Ta có 6 6 log 5 = = = 3 log 3 log 6 − log 2 1− . a 6 6 6
Câu 10. Đạo hàm của hàm số 2 3 x y = là: 2 3 x A. 2 3 x y = . B. 2 3 . x y = ln 3. C. y = . D. 2 2.3 . x y = ln 3 . ln 3 Trang 22 Lời giải Chọn D Ta có: ( 2x ) 2 3 ' 2.3 . x = ln 3 . ( − )2 1 2 2(1+ 2)
Câu 11. Cho a là một số thực dương. Rút gọn biểu thức P = a .a được kết quả là: 5 3 3 A. 1. B. a . C. a . D. a . Lời giải Chọn B ( − )2 ( + ) ( − )2 1 2 2 1 2 1 2 +2(1+ 2) 5 P = a .a = a = a .
Câu 12. Tìm của phương trình x x+4 9 = 3 . A. x = 1 . B. x = 4 . C. x = 3 .
D. x = 2 . Lời giải Chọn B x x+4 Ta có: 9 = 3
2x = x + 4 x = 4. Câu 13. Cho , a b 0 và ,
a b 1, biểu thức 3 4 P = log
b .log a có giá trị bằng bao nhiêu? b a A. 18 . B. 24 . C. 12 . D. 6 . Lời giải Chọn B 3 4 P = log
b .log a = (6log b a = . a ).(4logb ) 24 b a
Câu 14. Tìm nguyên hàm của hàm số f ( x) = 2x +1. x A. ( x + ) 2 2 1 dx = + x + C . B. ( x + ) 2 2
1 dx = x + x + C . 2 C. ( x + ) 2 2
1 dx = 2x +1+ C . D. ( x + ) 2 2
1 dx = x + C . Trang 23 Lời giải Chọn B ( x+ ) 2 2
1 dx = x + x + C .
Câu 15. Họ nguyên hàm của hàm số f ( x) 2
= 3x + sin x là A. 3
x + cos x + C . B. 3
x + sin x + C . C. 3
x − cos x + C . D. 3
3x − sin x + C . Lời giải Chọn C
Họ nguyên hàm của hàm số f ( x) 2
= 3x + sin x là 3
x − cos x + C . 5 7 7 Câu 16. Nếu f
(x)dx = 3 và f
(x)dx = 9 thì f (x)dx bằng bao nhiêu? 2 5 2 A. 3 . B. 6 . C. 12 . D. −6 . Lời giải Chọn C 7 5 7 Ta có: f
(x)dx = f
(x)dx+ f
(x)dx =3+9 =12 . 2 2 5 2
Câu 17. Tích phân I = (2x − )
1 dx có giá trị bằng: 0 A. 1. B. 2. C. 3. D. 0. Lời giải Chọn B 2 I = (2x − ) 1 dx = ( 2 2
x − x) = 2. 0 0
Câu 18. Số phức liên hợp của số phức z = 1− 2i là Trang 24 A. 1+ 2i . B. 1 − − 2i . C. 2 − i . D. 1 − + 2i . Lời giải Chọn A
Số phức liên hợp của số phức z = 1− 2i là z = 1+ 2i .
Câu 19. Cho hai số phức z = 2 + 3i , z = 4
− − 5i . Số phức z = z + z là 1 2 1 2
A. z = 2 + 2i . B. z = 2 − − 2i .
C. z = 2 − 2i . D. z = 2 − + 2i . Lời giải Chọn B
z = z + z = 2 + 3i − 4 − 5i = 2 − − 2i . 1 2
Câu 20. Cho số phức z = 4
− + 5i . Biểu diễn hình học của z là điểm có tọa độ A. ( 4 − ;5). B. ( 4 − ; 5 − ). C. (4; 5 − ) . D. (4;5) . Lời giải Chọn B z = 4
− +5i z = 4
− −5i có phần thực a = 4 − ; phần ảo b = 5
− nên điểm biểu diễn hình học của ( 4 − ; 5 − ) số phức z là .
Câu 21. Một khối chóp tam giác đều có cạnh đáy bằng 2 và chiều cao bằng 3 . Thể tích của khối chóp đó là 2 3 A. V = . B. V = 1 . C. V = 3 . D. V = 2 3 . 3 Lời giải Chọn B 2
Ta có: Đáy là tam giác đều cạnh bằng 2, có diện tích: 2 . 3 S = = 3 . 4 Trang 25 1 1
Thể tích khối chóp: V = Sh = . 3. 3 = 1 . 3 3
Câu 22. Một khối lăng trụ có thể tích bằng 18 và diện tích đáy bằng 9 . Chiều cao của khối lăng trụ đó là A. h = 2 . B. h = 9 . C. h = 6 . D. h = 3 . Lời giải Chọn A
Ta có: Khối lăng trụ có công thức thể tích V 18
V = Bh h = = = 2 B 9
Câu 23. Công thức tính diện tích xung quanh của hình nón có bán kính đáy r và độ dài đường sinh l 1
A. S = rl .
B. S = 2 rl .
C. S = rl . D. 2
S = rl +r . 3 Lời giải Chọn C
Ta có: Công thức tính diện tích xung quanh hình nón S = rl .
Câu 24. Một hình trụ có đường kính đáy bằng 6 và chiều cao bằng 4 . Diện tích xung quanh của hình trụ đó là A. S = 48 . B. S = 12 . C. S = 30 . D. S = 24 . Lời giải Chọn D
Ta có: Đường kính đáy bằng 6 , nên bán kính đáy bằng 3 . l = h = 4
S = 2rl = 2.3.4 = 24 .
Câu 25. Trong không gian Oxyz , cho hai điểm M (1;3; 2 − ) và N (3; 1 − ; 2
− ). Trung điểm của đoạn thẳng
MN có tọa độ là A. (2; 4 − ;0) . B. (2;1; 2 − ). C. (4;2; 4 − ) . D. (1; 2;0) . Lời giải Trang 26 Chọn B
Trung điểm I (x ; y ; z của đoạn thẳng MN có tọa độ là: I I I ) 1+ 3 3 −1 2 − − 2 x = = 2 ; y = =1; z = = 2 − . I 2 I 2 I 2
Câu 26. Trong không gian Oxyz , mặt cầu ( S ) : 2 2 2
x + y + z − 6x + 2 y + 2z + 2 = 0 có bán kính bằng A. 3 . B. 13 . C. 42 . D. 4 . Lời giải Chọn A 2 2
Ta có bán kính mặt cầu ( S ) là 2 3 + (− ) 1 + (− ) 1 − 2 = 3 .
Câu 27. Trong không gian Oxyz , cho mặt phẳng ( P) : x + y − 2z + 3 = 0 . Điểm nào sau đây không thuộc vào ( P) ? A. M (0;1;2) . B. N (1;0;2) . C. E (1;1; ) 1 . D. F ( 2 − ;1; ) 1 . Lời giải Chọn C
Ta thay tọa độ các điểm vào phương trình của mặt phẳng ( P) thì tọa độ điểm E (1;1; ) 1 không thõa mãn.
Câu 28. Trong không gian Oxyz , véc tơ nào dưới đây là một véc tơ chỉ phương của đường thẳng đi qua
hai điểm A(1;3;2) và B(2;1; ) 1 ? A. u = 3; 2 − ; 1 − . B. u = 1; 2 − ;1 . C. u = 1 − ;2;1 . D. u = 3; 4;3 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) Lời giải Chọn C Ta có BA = ( 1 − ;2 )
;1 là một véc tơ chỉ phương của đường thẳng AB .
Câu 29. Chọn ngẫu nhiên một số trong 20 số nguyên dương đầu tiên. Xác suất để chọn được số chia hết cho 3 bằng Trang 27 5 3 1 7 A. . B. . C. . D. . 20 10 2 20 Lời giải Chọn B
Số phần tử của không gian mẫu là ( n ) = 20 .
Gọi biến cố A : “ Chọn được số chia hết 3’’.
Trong 20 số nguyên dương đầu tiên có 6 số chia hết cho 3 là 3; 6; 9; 12; 15; 18 nên ( n ) A = 6 . n( ) A 6 3 Nên P( ) A = = = n( . ) 20 10
Vậy xác suất để chọn được số chia hết cho 3 bằng 3 . 10
Câu 30. Hàm số nào sau đây nghịch biến trên ? A. 3 2
y = −x + 2x − 4x − 5 . B. 2
y = −x + x +1. 2x +1 C. y = . D. 4 2
y = −x + 2x +1. x −1 Lời giải Chọn A Hàm số 3 2
y = −x + 2x − 4x − 5 có 2 2 2 y ' = 3
− x + 4x − 4 = 2
− x − (x − 2) 0, x . Nên hàm số 3 2
y = −x + 2x − 4x − 5 nghịch biến trên .
Câu 31. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
f (x) = x − 2x − 7x +1 trên
đoạn [-2; 1]. Tồng 3M + 2m bằng A. 5. B. 7. − C. 1. D. 2. − Lời giải Chọn C 7 Ta có 2
y = 3x − 4x − 7 , y = 0 x = 1
− (nhận) hoặc x = (loại). 3 y ( 2 − ) = 1 − , y( ) 1 = 7 − , y(− )
1 = 5 . Vậy M = max y = y (− )
1 = 5 ; m = min y = y ( ) 1 = 7 − . x 2 − ; 1 x 2 − ; 1 Trang 28
Tổng 3M + 2m = 3.5 + 2.( 7 − ) =1. 2 x +4 x 1
Câu 32. Tập nghiệm của bất phương trình 8 là 2 A. − ; − 3 1
− ;+. B. 1; 3 . C. − ;
1 3;+. D. 3 − ;− 1 . Lời giải Chọn D 2 2 x +4 x x +4 x 3 − 1 1 1 Ta có 2 2 8 x + 4x 3
− x + 4x + 3 0 3 − x 1 − . 2 2 2 2 x +4 x
Vậy tập nghiệm của bất phương trình 1 8 là 3 − ;− 1 . 2 4 4
Câu 33. Nếu 2 −3 f (x)dx = 6 thì 2 f (x)dx bằng 0 0 2 3 4 3 A. . B. . C. . D. . 3 2 3 4 Lời giải Chọn C 4 − f x 4 4 4 4 4 2 4
2 3 ( ) dx = 2dx − 3 f (x)dx = 8 − 3 f (x)dx 6
= f (x)dx = 2 f (x)dx = . 3 3 0 0 0 0 0 0
Câu 34. Cho z là số phức có phần ảo dương của phương trình 2
z − 2z + 5 = 0 . Số phức liên hợp của số 0
phức (4 + i) z là 0 A. 2 + 9i . B. 2 − 9i . C. 2 − −9i . D. 2 − + 9i . Lời giải Chọn B
z = 1+ 2i (4 + i) z = (4 + i)(1+ 2i) = 2 + 9i 4 + i z = 2 − 9i . 0 ( ) 0 0 Trang 29
Câu 35. Cho hình hộp chữ nhật ABC . D A B C D
¢ ¢ có diện tích các mặt ABCD , BCC B ¢ ¢, CDD C lần lượt là 2 2a , 2 3a , 2
6a . Góc giữa đường thẳng BD và mặt phẳng ( ABCD) bằng B C D A B' C' A' D' 1 3 5 A. tan = . B. tan = . C. tan = . D. tan = 3 . 3 5 3 Lời giải Đặt AB = ; x AD = ; y CC = z . 2 xy = 2a = x 2a Ta có: 2
yz = 3a y = a 2 xz = 6a z = 3a
Góc giữa đường thẳng BD và mặt phẳng ( ABCD) bằng góc BD B = BB z 3a 3 tan = = = = . 2 2 B D x + y a 5 5
Câu 36. Cho tứ diện đều D ABC
có độ dài cạnh bằng 3 . Khoảng cách từ điểm B đến mặt phẳng ( D AC ) bằng 3 3 A. . B. . C. 2 . D. 2 . 4 2 Lời giải Chọn D Trang 30 A B C D
Gọi H là trọng tâm tam giác D
AC thì d (B,( ACD)) = BH . Gọi 3 2
M là trung điểm BC ,ta có: AM = và AH = AM = 1 . , 2 3
Vậy d ( ( ACD)) 2 2 B,
= AB − AH = 2 .
Câu 37. Trong không gian Oxyz, mặt cầu có tâm I (1; 1
− ;0) và tiếp xúc với mặt phẳng ( )
P : x − 2y + 2z + 6 = 0 có phương trình là: A. 2 2 2
(x −1) + ( y +1) + z = 9 . B. 2 2 2
(x −1) + ( y +1) + z = 3 . C. 2 2 2
(x +1) + ( y −1) + z = 9 . D. 2 2 2
(x +1) + ( y −1) + z = 3 . Lời giải Chọn A 1+ 2 + 6
d (I; (P)) = = 3 1+ 4 + 4
Mặt cầu cần tìm có tâm I (1; 1
− ;0) , bán kính R = 3 có phương trình là: 2 2 2
(x −1) + ( y +1) + z = 9
Câu 38. Trong không gian Oxyz, đường thẳng đi qua điểm ( A 1
− ;2;3) và song song với đường thẳng x = 3 + t
: y = 4 − 2t có phương trình tham số là z = 5+ 4t x = 1− t x = 1 − + t x = −1+ t x = 1+ t
A. y = −2 + 2t .
B. y = 2 + 2t .
C. y = 2 − 2t .
D. y = 2 − 2t . z = 4 + 3t z = 3 + 4t z = 3 + 4t z = 3 + 4t Lời giải Trang 31 Chọn C x = 3 + t →
Đường thẳng cần tìm song song với đường thẳng : y = 4 − 2t nên có vtcp u = (1; 2 − ;4) và đi qua z = 5+ 4t x = −1+ t điểm ( A 1
− ;2;3) nên có phương trình là y = 2 − 2t . z = 3+ 4t
Câu 39. Cho hàm số f (x) , đồ thị hàm số y = f '( )
x là đường cong trong hình dưới. Giá trị lớn nhất của hàm số 2
g(x) = f (2x) − sin x trên đoạn 1 − ; 1 là A. f ( 1 − ). B. f (0) . C. f (2) . D. f (1) . Lời giải Chọn B
Đặt t = 2x . Ta có x 1 − ; 1 suy ra t 2 − ;2.
Ta có bảng biến thiên của hàm số f (t) trên đoạ − n 2;2
Từ bảng biến thên ta thấy f (t) f (0) , t 2 − ;2 suy ra f (2 )
x f (0), x 1 − ; 1 . Ta có: 2
g(x) = f (2x) − sin x mà 2
−sin x 0 = sin(0), x 1 − ; 1 Do đó: g( )
x g(0) = f (0) + 0 = f (0).
Dấu bằng xảy ra khi x = 0.
Vậy giá trị lớn nhất của hàm số 2
g(x) = f (2x) − sin x trên đoạn 1 − ; 1 là f (0). Trang 32
Câu 40. Số nguyên dương a lớn nhất thỏa mãn điều kiện 3log ( 3
1+ a + a 2log a 3 ) 2 là? A 2016 . B 2095 . C. 3096 . D. 4095 . Lời giải Chọn D
Giả sử a thỏa mãn: 3log ( 3
1+ a + a 2log a 3 ) 2 . Đặt log a = 3x 64x a =
. Ta được bất phương trình: 3log 1+ 8x + 4x 6x 3 ( ) 2 x x x
3log 1+ 8x + 4x 6x 1 8x 4x 9x + + 1 8 4 + + 1 3 ( ) 9 9 9 x x x
Do hàm số f ( x) 1 8 4 = + +
nghịch biến trên R f (2) và lại có =1 nên 9 9 9
BPT trở thành f ( x) f (2) x 2 . Suy ra 2
a 64 = 4096 nên số nguyên dương lớn nhất thỏa mãn là a = 4095 . x 2 e +1 khi x 0 e f (ln x − ) 1 a
Câu 41. Cho hàm số y = f ( x) = . Tích phân I = dx = + ce biết 2
x − 2x + 2 khi x 0 x b 1/e a , a , b c Z và
tối giản. Tính a + b + c ? b A. 35 . B. 29 . C. 36 . D. 27 . Lời giải Chọn C * Đặ 1
t ln x −1 = t dx = dt . x * Đổi cận:
x = 1/ e t = 2 − 2
x = e t = 1 1 0 1 * Khi đó: I = f
(t)dt = f
(t)dt + f (t)dt 2 − 2 − 0 Trang 33 0 = ( − 2 + 2) 1 2 + ( t I t t dt e + )1dt 2 − 0 32 I = + e 3
Vậy a = 32;b =1;c =1 nên a + b + c = 35. 2
Câu 42. Có bao nhiêu số phức z thỏa mãn (1+ i) z − 2 + 4i = 3 2 và z − i = 1− 2zi ? z A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C
Ta có : (1+ i) z − 2 + 4i = 3 2 z +1+ 3i = 3 .
Vậy tập hợp các điểm biểu diễn z thuộc đường tròn tâm I ( 1 − ;− ) 3 ; R = 3 . 1 2 z −
i = − zi ( + i) 2 z = + i ( + i) 2 1 2 1 2 1 1 2 z = 1+ i z z z 4 2 4 5. z = 1+ 5 z −1− = 0 2 2 z z z =1 = z = − (l) z 1 4 / 5
Vậy tập hợp các điểm biểu diễn z thuộc đường tròn tâm O (0;0); R =1. 2
Vì IO = 10; R + R = 4 nên R − R IO R + R 1 2 1 2 1 2
2 đường tròn cắt nhau tại 2 điểm phân biệt
Câu 43. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Mặt phẳng (SAB) cân tại S và nằm trong
mặt phẳng vuông góc với đáy, mặt bên (SBC) tạo với đáy một góc 0 60 . Thể tích khối chóp S.ABC bằng Trang 34 3 a 3 3 a 3 a 3 3 a A. . B. . C. . D. . 16 8 8 4 Lời giải Chọn A
* Gọi H là trung điểm AB .
Vì tam giác SAB cân tại S nên SH ⊥ AB .
Vì (SAB) ⊥ ( ABC) nên SH ⊥ ( ABC) .
*Gọi M , N lần lượt là trung điểm BC, BM nên HN ⊥ BC . SH ⊥ BC Ta có :
(SHN ) ⊥ BC HN ⊥ BC
Góc giữa 2 mặt phẳng (SBC);( ABC) là góc giữa 2 đường thẳng HN,SN . 1 a 3
* Vì tam giác ABC đều nên HN = AM = . 2 4 Trang 35 a 3 3a 0
SH = tan 60 .HN = 3. = . 4 4 2 3 1 3a a 3 a 3 Vậy V = . . = . 3 4 4 16
Câu 44. Một công ty mỹ phẩm muốn thay đổi mẫu mã lọ nước tẩy trang gồm phần hình trụ và chỏm cầu
như hình vẽ ở dưới. Lọ nước tẩy trang có bán kính đáy bằng 1cm , phần cổ và nắp lọ được tính
riêng. Chi phí phần thân lọ gần nhất với số tiền nào sau đây biết phần thân hình trụ có giá 1000 đ 2
/1m , phần chỏm cầu có giá 1500 đ 2 /m . A. 1428.7 đ. B. 1475.8 đ. C. 1230.2 đ. D. 1415.1đ. Lời giải Chọn A
* Diện tích xung quanh của phần hình trụ là: 2 2
S = 2 .r.l = 2 .1.10 62,8cm = 0.628m 1
* Tính diện tích xung quanh phần chỏm cầu. Trang 36 1 8 Ta có: tan OBA = sin (ABA') = . 4 17
Áp dụng định lí sin trong tam giác ta có: AA ' 17 = 2R R = sin ABA ' 8 17 2 2 S = 2.. . R h = 2..
.4 53.38cm = 0.5338m . 2 8
Vậy chi phí làm vỏ lọ nước tẩy trang là: T = 0.628.1000 + 0.5338.1500 1428.7 đ. x +1 y z −1 x + 2 y z +1
Câu 45. Trong không gian Oxyz , cho đường thẳng d : = = ; d : = = . 1 1 1 1 − 2 3 1 − 2 x =1
d : y = 1− t t R . 3 ( ) z = t
Phương trình đường thẳng d cắt 3 đường thẳng d ; d ; d lần lượt tại , A ,
B C sao cho B là trung 1 2 3 + điể a b
m của AC có véc tơ chỉ phương u = ( ; a ;
b c) . Tỉ số T =
thuộc khoảng nào sau đây? c A. ( 3 − ;− ) 1 . B. (1; ) 3 . C. (4;6) . D. ( 6 − ; 3 − ) . Lời giải Chọn A Gọi các điểm ,
A C lần lượt là A( 1 − + ; s ;
s 1− s);C (1;1−t;t) .
véc tơ chỉ phương của đường thẳng d là u = (2− ;s1−t − ;st + s − ) 1
s s −t +1 1− s + t
Vì B là trung điểm của AC nên B ; ; . 2 2 2 x + 2 y z +1
−x − 3y + 2 = 0 Ta có d : = = 2 3 1 − 2
2x − 3z +1 = 0
Vì B thuôc đường thẳng d nên ta có : 2
−s 3(s − t + ) 1 − + 2 = 0 2 2 3 t − 4s = 1 − t = 1 − / 3 3 (1− s +t) 3 − t + 5s =1 s = 0 s + 4 − − 3 = 0 2 Trang 37 4 4 u = 2; ; − 3 3 a + b 5 Vậy T = = − c 2
Câu 46. Cho hàm số y = f ( )
x có tập xác định là D =
và có đạo hàm xác định trên , đồ thị hàm số y = f ( )
x như hình vẽ bên dưới. Hỏi hàm số y = f ( 3
x −12x) có bao nhiêu điểm cực trị? A. 11. B. 10. C. 12. D. 9. Lời giải Chọn B
Hàm số f (x) đạt cực trị tại các điểm x = 10
− ; x = a(0 ;16); x =16 ; x = b 16
Xét hàm số g ( x) = f (u) = f ( 3 x −12x) với 3
u = x −12x
Công thức đếm nhanh SĐCT của một hàm hợp: u = b u =
SĐCT f (u) = SĐCT 16 u + SNBL u = a u = 10 −
Ta có bảng biến thiên của 3
u = x −12x Trang 38 u = b u =16 Suy ra: SĐCT u = 2 và có: SNBL = 8 u = a u = 10 − u = b u =
Suy ra: SĐCT f (u) = SĐCT 16 u + SNBL = 2 + 8 =10 . u = a u = 10 − 1 x+
Câu 47. Biết rằng 2 x = log 1
4− y − 2 y +1
x . Tính giá trị biểu thức 2 ( ) trong đó 0 2 2
P = x + y − xy +1. A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B 1 1 x+ Ta có + 2 2 x x 4 ( ) 1 . x Ta thấy
−( y − ) y + = −( y + )3 14 2 1 1 + 3 y +1 +14
Xét hàm số f (t) 3 = t
− + 3t +14(t = y +1 0) Bảng biến thiên: Trang 39 Do vậy ta được log 1
4 − y − 2 y +1 4 2 2 ( ) ( ) . x = Từ ( ) ( ) 1 1 và 2 . y = 0 Vậy P = 2 .
Câu 48. Một chiếc ly bằng thủy tinh đang chứa nước bên trong được tạo thành khi quay một phần đồ thị hàm số 2x y = xung quanh trục .
Oy Người ta thả vào chiếc ly một viên bi hình cầu có bán kính R
thì mực nước dâng lên phủ kín viên bi đồng thời chạm tới miệng ly. Biết điểm tiếp xúc của viên bi
và chiếc ly cách đáy của chiếc ly 3cm (như hình vẽ). Thể tích nước có trong ly gần với giá trị nào
nhất trong các giá trị sau? A. 2 30 cm . B. 2 40 cm . C. 2 50 cm . D. 2 60 cm . Lời giải Chọn A Trang 40
Xét mặt phẳng ( ) đi qua trục của chiếc ly. Gọi ( ) là đường tròn lớn của quả cầu. Ta thấy
đường tròn ( ) và đồ thị ( ): 2x C y = tiếp xúc nhau tại .
A Chọn hệ trục Oxy như hình vẽ, ta được A(2;4).
Tiếp tuyến với (C) tại A là(d ) : y = (4ln 2).x −8ln 2 + 4.
Đường thẳng vuông góc với (d ) tại A là () 1 1 : y = − .x + + 4. 4 ln 2 2 ln 2 1+ 8ln 2
Tâm I của đường tròn ( ) là giao điểm của () và Oy, ta được I 0; . 2 ln 2 1 4 Ta có IA = 2; − ,
suy ra thể tích khối cầu 3 3 V =
.IA 40, 26 cm . 2 ln 2 khoi cau 3 yB
Dung tích chiếc ly là V = log y2 3 dy 69,92 cm . 2 1
Thể tích nước chứa trong chiếc ly là 3 V =V −V 29,66cm . nuoc khoi cau
Câu 49. Cho số phức z và z là hai nghiệm của phương trình: 6 − 3i + iz = 2z − 6 − 9i , thỏa mãn: 1 2
z − z = 2. Giá trị của biểu thức: P = z + z tương ứng bằng 1 2 1 2 A. 6 . B. 5 . C. 26 . D. 10 . Lời giải Chọn D
Trước hết ta tìm quỹ tích điểm biểu diễn số phức z thỏa mãn giả thiết: Trang 41
6 − 3i + iz = 2z − 6 − 9i i . z − 3− 6i = 2z − 6 − 9i z − 3− 6i = 2z − 6 − 9i ( ) 1 .
Đặt z = x + iy thay vào (1) ta được:
x + iy − − i =
(x+iy)− − i (x− )2 +(y − )2 = ( x− )2 +( y − )2 3 6 2 6 9 3 6 2 6 2 9 .
(x − )2 + ( y − )2 3 4 =1. Như vậy điể 2 2
m biểu diễn số phức z là đường tròn (C): ( x − 3) + ( y − 4) = 1 z − z = R . 0
Trong đó: z = 3 + 4i và R =1. Điểm I biểu diễn số phức z = 3 + 4i . 0 0
Gọi A là điểm biểu diễn số phức z và B là điểm biểu diễn số phức z khi đó ta có: 1 2
IA = IB = R = 1; AB = z − z = 2 = 2R . Suy ra AB là một đường kính của đường tròn (C). 1 2
Khi đó ta có I là trung điểm của AB tức là: z + z = 2z = 6 + 8i . 1 2 0
Suy ra: P = z + z = 10. 1 2
Câu 50. Trong không gian Oxyz , cho mặt cầu ( S ) có tâm I ( 1 − ;2; )
1 và đi qua điểm A(1;0;− ) 1 . Xét các điểm ,
B C, D thuộc (S ) sao cho A ,
B AC, AD đôi một vuông góc với nhau. Thể tích của khối tứ
diện ABCD lớn nhất bằng 64 32 A. . B. 32 . C. 64 . D. . 3 3 Lời giải Chọn D Đặt AD = , a AB = , b AC = c . Trang 42 Khi đó, 1 1 V = A . B AC.AD = abc . ABCD 6 6
Ta có bán kính mặt cầu (S ) là R = IA = 2 3 . 2 2 b + c
Gọi M là trung điểm của BC . Khi đó, AM = . 2 1 1
Vì tứ diện ABCD nội tiếp trong mặt cầu ( S ) nên ta có IM AD và IM = AD = a . 2 2
Xét tam giác AIM vuông tại M , ta có 2 2 2 2 2 2
AI = AM + IM a + b + c = 48 1 1 a + b + c 1024 32 2 2 2 2 ( )3 2 2 2 Suy ra V = a b c = hay V . ABCD 36 36 27 9 ABCD 3 ĐỀ SỐ 08
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+ Câu 1.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y = x − 3x + 2 trên đoạn 1 − ;
1 .Tính M + m . A. 1. B. 0. C. 2.
D. 3.
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng đi qua điểm M (2;0;− ) 1 và có vectơ chỉ phương a = (4; 6
− ;2). Phương trình tham số của là x = 2 − + 4t x = 2 − + 2t x = 4 + 2t x = 2 + 2t A. y = 6 − t . B. y = 3 − t . C. y = 6 − − 3t .
D. y = −3t . z = 1+ 2t z = 1+ t z = 2 + t z = −1+ t
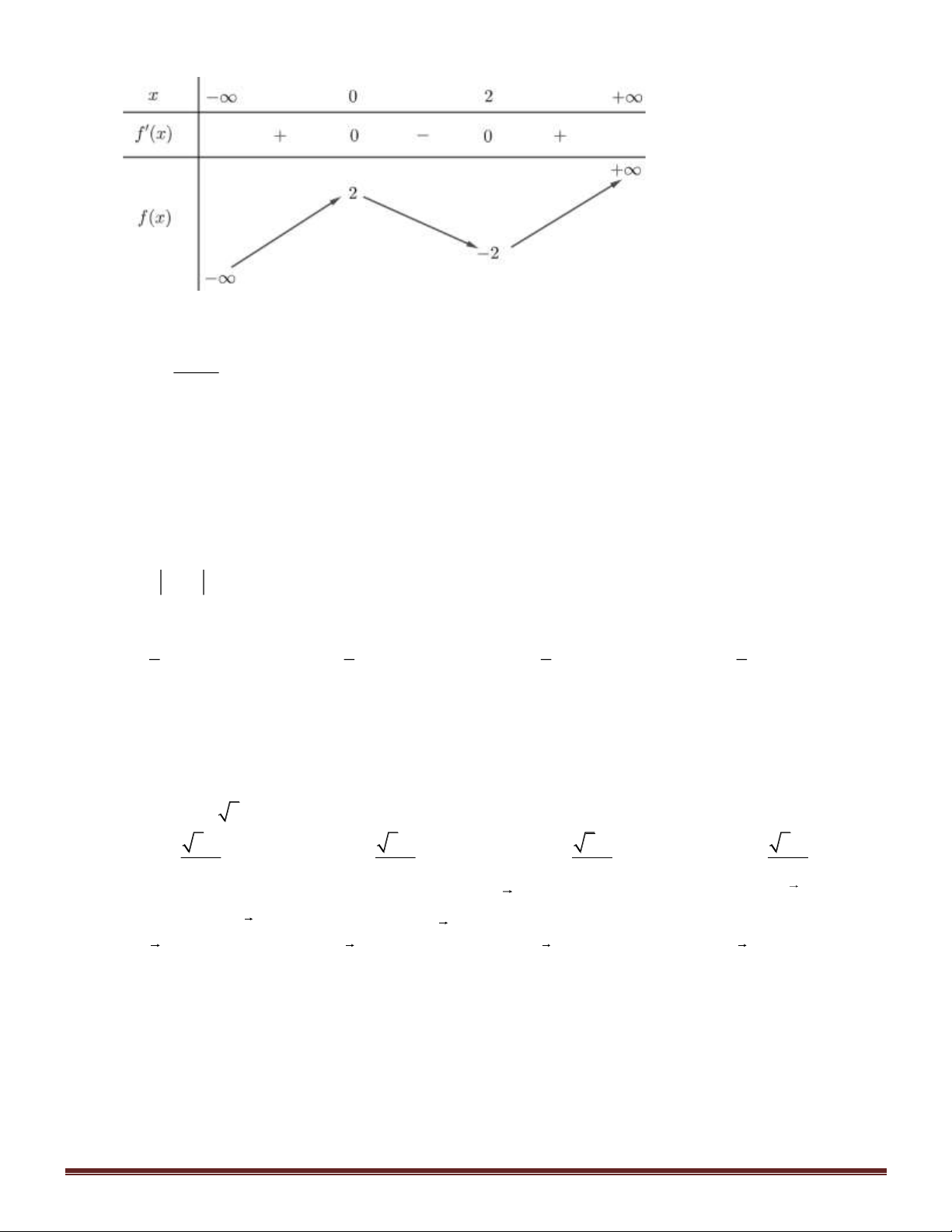
Câu 3. Cho hàm số y = f ( )
x có bảng biến thiên như hình vẽ. Hàm số y = f ( )
x nghịch biến trên khoảng nào dưới đây? Trang 43 A. (0;+) . B. (−; 2 − ). C. (0;2). D. (2;4) . ax + b
Câu 4. Hình vẽ bên là đồ thị của hàm số y = . Đường tiệm cận cx + d
đứng của đồ thị hàm số có phương trình là A. x = 1 . B. x = 2 . C. y =1. D. y = 2 Câu 5. Cho ( ) 5x f x =
thì f ( x + 2) − f ( x) bằng. A. 25 . B. 24 .
C. 25 f ( x) .
D. 24 f ( x).
Câu 6. Biết F ( x) là một nguyên hàm của f ( x) 1 =
và F (0) = 2 thì F ( ) 1 bằng. x +1 A. ln 2 . B. 2 + ln 2. C. 3 . D. 4 .
Câu 7. Tất cả các giá trị của tham số m để hàm số 4 2
y = x − 2x + m cắt trục hoành tại 4 điểm là A. 1 − m 0 .
B. 0 m 1. C. 1 − m 0 .
D. 0 m 1 .
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên
SAB là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với
mặt phẳng ( ABCD) . Tính thể tích khối chóp S.ABCD . 3 a 3 A. 3 a . B. . 6 3 a 3 a 3 C. . D. . 3 2
Câu 9. Cho số phức z = 1
− + 3i . Tính z . A. z = 10 . B. z = 2 . C. z = 2 . D. z = 10 .
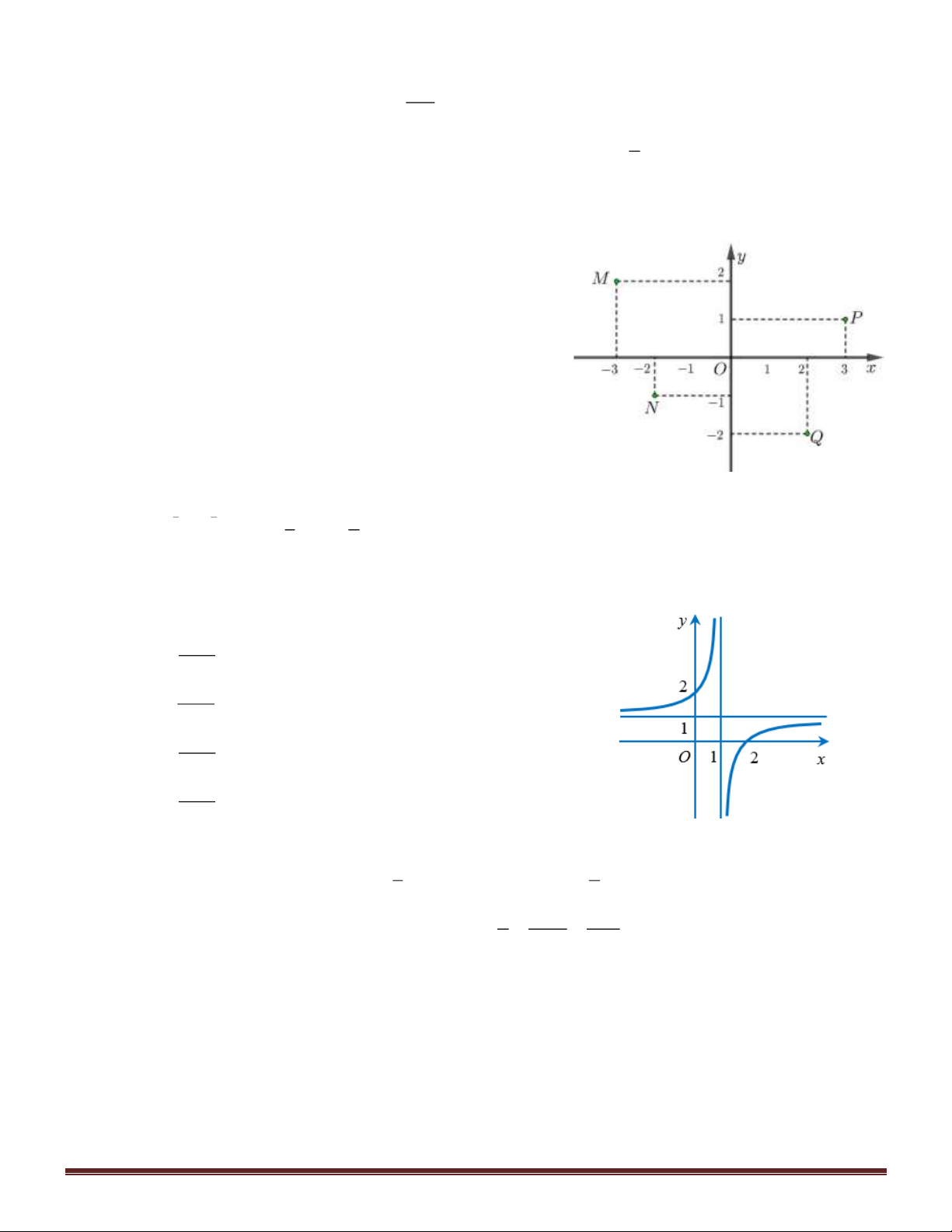
Câu 10. Trong mặt phẳng Oxy , cho điểm A(3; 0) và vectơ v = (1; 2) . Phép tịnh tiến T biến A thành A . Tọa v độ điểm A là
A. A (4; 2) .
B. A (2; −2) .
C. A (−2; 2) .
D. A (2; − ) 1 .
Câu 11. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ? A. 4 2
y = x − 2x +1. B. 4 2
y = x − 2x . C. 4 2
y = −x − 2x −1. D. 3 2
y = x − 2x +1.
Câu 12. Tổng tất cả các nghiệm của phương trình log
x −1 + log x = 1+ log 3x − 5 bằng 2 ( ) 2 2 ( ) A. 7 . B. 6 . C. 5 . D. 4 .
Câu 13. Hàm số nào sau đây đồng biến trên khoảng ( 1 − ; ) 1 ? x +1 A. 2 y = 1− x . B. 2 y = x . C. y = . D. 3
y = −x + 3x . x
Câu 14. Cho khối nón đỉnh S có độ dài đường sinh là a , góc giữa đường sinh và mặt đáy là 60 . Thể tích khối nón là Trang 44 3 3 a 3 a 3 3 a 3 a 3 A. V = . B. V = . C. V = . D. V = . 8 8 8 24 Câu 15. Cho , a ,
b c là các số dương và a 1. Mệnh đề nào sau đây sai? 1 A. log = −log . b
B. log b + c = b c a ( ) log .log . a a b a a b C. log = log b − log . c D. log bc = b + c a ( ) log log . a a a c a a
Câu 16. Cho số phức z = 1− 2i thì số phức liên hợp z có
A. phần thực bằng 1 và phần ảo bằng 2 − .
B. phần thực bằng 2 − và phần ảo bằng 1.
C. phần thực bằng 1 và phần ảo bằng 2 .
D. phần thực bằng 2 và phần ảo bằng 1. 4 2
Câu 17. Cho log 2 = a , log 3 = b . Khi đó giá trị của log là 5 5 5 15 5a − b −1 5a − b +1 5a + b −1 5a + b +1 A. . B. . C. . D. . 2 2 2 2
Câu 18. Cho tứ diện đều ABCD . Gọi là góc giữa đường thẳng
AB và mặt phẳng ( BCD) . Tính cos . A. cos = 0 . 1 B. cos = . 2 3 C. cos = . 3 2 D. cos = . 3 x − 2
Câu 19. Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? 2 x − 4x + 3 A. 1. B. 3 . C. 4 . D. 2 .
Câu 20. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S ) 2 2 2
: x + y + z − 2( x + 2y + 3z) = 0 . Gọi A , B
, C lần lượt là giao điểm (khác gốc tọa độ O ) của mặt cầu (S ) và các trục tọa độ Ox , Oy , Oz .
Phương trình mặt phẳng ( ABC) là:
A. 6x −3y − 2z +12 = 0 .
B. 6x −3y + 2z −12 = 0 .
C. 6x + 3y + 2z −12 = 0 .
D. 6x −3y − 2z −12 = 0 .
Câu 21. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a , SA ⊥ ( ABC) , SA = 3a .
Thể tích của khối chóp S.ABCD là A. 3 V = 6a . B. 3 V = a . C. 3 V = 3a . D. 3 V = 2a .
Câu 22. Cho hàm số f ( x) thỏa mãn f ( x) 2 ' = x (x − ) 1 , x .
R Mệnh đề nào sau đây là mệnh đề đúng?
A. f ( x) đạt cực tiểu tại x =1.
B. f ( x) không có cực trị.
C. f ( x) đạt cực tiểu tại x = 0.
D. f ( x) có hai điểm cực trị.
Câu 23. Cho hàm số y = f ( x) có bảng biến thiên như sau: Trang 45 1
Hàm số g ( x) =
đồng biến trên khoảng nào dưới đây? f ( x) A. ( 2 − ;0) . B. (3;+) . C. (1; 2) . D. (− ; − ) 1 . Câu 24. Hàm số 2 x
y = x e nghịch biến trên khoảng nào? A. ( 2 − ;0). B. (− ; 2 − ). C. ( ; − ) 1 . D. (1;+).
Câu 25. Đường thẳng d : y = x +1 và đường cong (C) 3 2
: y = x − x − x +1 có bao nhiêu điểm chung? A. 2. B. 3. C. 1. D. 0.
Câu 26. Phương trình 2sin x − 3 = 0 có các họ nghiệm là x = + k2 x = + k 3 3 A. , k . B. , k . x = − + k2 x = − + k 3 3 x = + k2 x = + k 3 3 C. , k . D. , k . 2 2 x = + k2 x = + k 3 3
Câu 27. Tập xác định của hàm số 2
y = ln x + 2x − 3 là: A. D = (− ; − 3 1;+) B. D = (− ; − ) 3 (1;+) C. D = D. D = \ 3 − ; 1 . 3 −x
Câu 28. Tất cả các giá trị của tham số m để hàm số 2 y =
+ mx − 2mx +1 có hai điểm cực trị là 3 m 2 A. .
B. 0 m 2.
C. m 2.
D. m 0. m 0
Câu 29. Cho hàm số y = f ( x) liên tục và có bảng biến thiên trên như hình vẽ bên dưới
Tìm giá trị lớn nhất của hàm số y = f (cos x) A. 5. B. 3. C. 10. D. 1. Trang 46
Câu 30. Cho số phức z = 3+ 4 .
i Phần thực của số phức w = z + z là A. 3 . B. 8 . C. 4 . D. 5 .
Câu 31. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm ( A 1;2;4), (
B 3;- 2;2) , mặt cầu đường kính
AB có phương trình là A. (x - )2 2 2
2 + y + (z - 3) = 36. B. (x + )2 2 2
2 + y + (z + 3) = 6. C. (x - )2 2 2 2
+ y + (z - 3) = 6. D. (x - )2 2 2 2
+ y + (z - 3) = 24.
Câu 32. Cho khối chóp S.ABCD có đáy là hình chữ nhật và thể tích bằng 8. Thể tích của khối chóp S.BCD bằng. A. 2 . B. 4 . C. 6 . D. 3 .
Câu 33. Cho hàm số f ( x) 2 = x − 2xln .
x Kí hiệu x là nghiệm của phương trình f ( x) = 0, mệnh đề nào 0 dưới đây đúng? 3 3 A. x 2 − ;0 . B. x ; 2 . C. x 0; .
D. x 2; + . 0 ( ) 0 ( ) 0 2 0 2
Câu 34. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( )
P : 3x + 2y- z + 4 = 0 và đường thẳng x - 2 y - 4 z + 2 d : = =
. Trong các mệnh đề sau, mệnh đề nào đúng? 4 3 1
A. d cắt (P) . B. d Ì ( ) P . C. d ^ ( ) P . D. d //( ) P .
Câu 35. Cho số phức z = a + bi ( , a b ) . Biết 2
z + 2z + i = 5 − i . Giá trị a + b là A. 7 . B. 5 . C. 1. D. 3 . 2 x 1 + 1
Câu 36. Tập nghiệm của bất phương trình 1
(với a là tham số) là 2 1+ a 1 1 A. ( ;0 − ). B. − ; − . C. (0;+ ) . D. − ; + . 2 2
Câu 37. Đường cong trong hình bên là đồ thị của một trong bốn hàm số được
liệt kê ở bốn phương án , A ,
B C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. y = log 2x . 2 ( )
B. y = log x . 2
C. y = log x . 1 2 D. y = log x . 2 x − 2
Câu 38. Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? 2 x − 4x + 3 A. 1. B. 3 . C. 4 . D. 2 .
Câu 39. Cho hàm số bậc ba y = f ( )
x có đồ thị như hình vẽ. Số
nghiệm của phương trình f ( x ) +1 = 0 là A. 4. B. 3. C. 2. D. 1. 4 e 4 1 Câu 40. Biết f
(ln x) dx = 4. Tính tích phân I = f (x)dx . x e 1 Trang 47 A. I = 8 . B. I = 16 . C. I = 2 . D. I = 4 . x
Câu 41. Cho hàm số y = f ( x) có đạo hàm f ( x) = −
. Với a và b là các số dương thỏa mãn a b , giá 2 x +1
trị nhỏ nhất của hàm số f ( x) trên đoạn ; a b bằng:
f (a) + f (b) a + b
A. f (b) .
B. f (a) . C. . D. f . 2 2 3x − 2
Câu 42. Cho hàm số y =
có đồ thị (C) . Có tất cả bao nhiêu đường thẳng cắt (C) tại hai điểm phân x
biệt mà hoành độ và tung độ của hai giao điểm này đều là các số nguyên? A. 10 . B. 4. C. 6. D. 2.
Câu 43. Cho một hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng a. Gọi AB và CD là hai
đường kính tương ứng của hai đáy. Biết góc giữa hai đường thẳng AB và CD bằng 0 30 . Tính thể tích
khối tứ diện ABCD. 3 a 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 12 6 6 12 b + log 5
Câu 44. Cho các số nguyên a, b, c thỏa mãn 2 a +
= log 45. Tổng a + b + c bằng: 6 c + log 3 2 A. 1. B. 4 . C. 2 . D. 0 .
Câu 45. Cho khối lăng trụ tam giác AB . C A B C
mà mặt bên ABB A
có diện tích bằng 4. Khoảng cách giữa
cạnh CC và AB bằng 7. Thể tích khối lăng trụ bằng: A. 10. B. 16. C. 12. D. 14.
Câu 46. Cho hàm số y = f ( x) có đạo hàm liên tục trên 1;2, thỏa mãn f ( x) = x f ( x) 2 .
− x . Biết f ( ) 1 = 3 , tính f (2) . A. 16. B. 2. C. 8. D. 4.
Câu 47. Cho hình nón đỉnh S , đáy là đường tròn nội tiếp tam giác ABC .
Biết rằng AB = BC = 10a , AC = 12a , góc tạo bởi hai mặt phẳng
(SAB) và (ABC) bằng 45. Tính thể tích V của khối nón đã cho. A. 3 V = 3a . B. 3 V = 9a . C. 3 V = 27a . D. 3 V =12 a .
Câu 48. Cho hàm số f ( x) liên tục trên
và có đồ thị hàm số f ( x) như hình
vẽ. Gọi S là tập hợp các giá trị nguyên của tham số m 5 − ; 5 để hàm 1 số y = f ( 2 2
x − 2mx + m + )
1 nghịch biến trên khoảng 0; . Tổng giá 2
trị các phần tử của S bằng A. 10. B. 14. Trang 48 C. 12 − . D. 15. Câu 49. Giả sử ,
a b là các số thực sao cho 3 3 3z 2 + = .10 + .10 z x y a b
đúng với mọi số thực dương , x , y z thỏa
mãn log(x + y) = z và 2 2
log(x + y ) = z +1 . Giá trị của a + b bằng: 31 29 31 25 A. . B. . C. − . D. − . 2 2 2 2
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(3;0;0), B( 3 − ;0;0) và C(0;5; ) 1 . Gọi M
là một điểm nằm trên mặt phẳng tọa độ (Oxy) sao cho MA+ MB =10, giá trị nhỏ nhất của MC là A. 6. B. 2. C. 3. D. 5.
________________HẾT________________
ÑAÙP AÙN ÑEÀ SOÁ 08 1 2 3 4 5 6 7 8 9 10 B D D A D B D B A A 11 12 13 14 15 16 17 18 19 20 A A D D B C A C D C 21 22 23 24 25 26 27 28 29 30 B A C A B C D A A B 31 32 33 34 35 36 37 38 39 40 C B C A D B B D C D 41 42 43 44 45 46 47 48 49 50 A C A A D C B B B B
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 08 3x − 2
Câu 42. Cho hàm số y =
có đồ thị (C) . Có tất cả bao nhiêu đường thẳng cắt (C) tại hai điểm phân x
biệt mà hoành độ và tung độ của hai giao điểm này đều là các số nguyên? A. 10 . B. 4. C. 6. D. 2. Hướng dẫn giải: − Trướ 3x 2
c hết, ta tìm các điểm có tọa độ nguyên thuộc đồ thị hàm số y = (C). x 3x − 2 2 Ta có: y = = 3−
(x 0). Giả sử (x ; y là điểm có tọa độ nguyên thuộc (C), suy ra 0 0 ) x x x 0 x0 2 2 x 1 ; 2 . 0 3− x x 0 0
Do đó, các điểm cần tìm là: A(1; ) 1 , B( 1
− ;5), C(2;2), D( 2 − ;4). Choïn
Số đường thẳng đi qua hai trong bốn điểm A, B, C, D là 2 C = 6 . ⎯⎯⎯ → C 4 Trang 49
Kỹ thuật máy tính bỏ túi:
Trong bài này, khi tìm điểm có tọa độ nguyên của đồ thị hàm số, ta sử dụng máy tính bỏ túi như sau.
Dưới đây là các lệnh của dòng máy VINACAL 680EX PLUS: X − next next MODE ⎯⎯→
⎯⎯→ F ( X ) 3 2 8 next = ⎯⎯→ START : 1 − 0 next ⎯⎯→ END :10 X next ⎯⎯→ STEP :1 next ⎯⎯→ =
Đến đây, các bạn học sinh chỉ cần quan sát xem dòng nào có cặp (X;F(X)) nguyên thì ta chọn làm điểm cần tìm.
Lưu ý rằng: Với dòng máy VINACAL cũ hơn, ta khởi động bằng lệnh next
MODE ⎯⎯→ 7 ; với
mọi dòng máy, khi dùng chức năng Table, màn hình thường có thêm dòng G ( X ) , khi ấy ta nhấn
dấu = để bỏ qua hàm này.
Câu 43. Cho một hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng a. Gọi AB và CD là hai
đường kính tương ứng của hai đáy. Biết góc giữa hai đường thẳng AB và CD bằng 0 30 . Tính thể tích
khối tứ diện ABCD. 3 a 3 a 3 3 a 3 a 3 A. . B. . C. . D. . 12 6 6 12 Hướng dẫn giải:
Xét đường tròn (O) có đường kính AB, đường tròn (O) có đường
kính CD. Ta vẽ thêm các đường kính EF của (O) và GH của (O) sao cho EF/ C / , D GH/ A / B . Khi đó góc ( A , B EF ) = ( A , B CD) 0 = 0 3
, đồng thời ABHG là thiết
diện qua trục của hình trụ nên ABHG là hình vuông cạnh a, suy ra
AB = AG = a .
Thể tích khối lăng trụ AEBF.GDHC là: 1 V = A . G S = A . G A . B EF.sin ( A , B EF ) AEBF .GDHC AEBF 2 3 1 a 3 1 a 0 = Choïn . . a . a . a sin 30 = . Suy ra V = V = . ⎯⎯⎯ → A 2 4 ABCD F . 3 AEB GDHC 12 Trang 50 Lưu ý:
Học sinh có thể dùng công thức nhanh để tìm thể tích tứ diện như sau: 1 V = A . B C . D d AB CD
AB CD . Ta có thể chứng minh công thức này dựa vào ABCD ( , ).sin( , ) 6
hình vẽ bên dưới. Xét trường hợp tổng quát AEBF không chắc là hình bình hành.
Từ tứ diện ABCD, ta dựng hình lăng trụ AEBF.GDHC như hình vẽ. Chứng minh:
Xét tứ giác AEBF với lưu ý: sin (O ,
A OE) = sin (OE,OB) = sin (O ,
B OF ) = sin (O , A OF ) = . Khi đó: S = S + S + S + S AEBF O AE O AF O BF O BE 1 1 1 1 = O . A OE.sin + O . A OF.sin + O . B OE.sin + O . B OF.sin 2 2 2 2 1
= OA(OE + OF ) 1 sin +
OB (OE + OF )sin 2 2 1 1 1 = OA EF + OB EF
= EF (OA + OB) 1 . .sin . .sin sin = . AB EF.sin . 2 2 2 2 1 1 Vậy S = A . B EF.sin = A . B . CD sin AB CD . AEBF ( , ) 2 2 1 1 Ta có: V = V = . . h S ABCD AEBF . 3 GDHC 3 AEBF 1 = d ( AB CD) 1 , . A . B C . D sin ( A , B CD) 3 2 1 V = A . B C . D d AB CD AB CD . ABCD ( , ).sin( , ) 6 b + log 5
Câu 44. Cho các số nguyên a, b, c thỏa mãn 2 a +
= log 45. Tổng a + b + c bằng: 6 c + log 3 2 A. 1. B. 4 . C. 2 . D. 0 . Hướng dẫn giải: b + log 5 b + log 5 log 45 Ta có: 2 2 2 a + = log 45 a + = 6 c + log 3 c + log 3 log 6 2 2 2 + log b ( 23.5 log 5 + + 2 ) b log 5 2 log 3 log 5 2 2 2 2 a + = a + = c + log 3 log 2.3 c + log 3 1+ log 3 2 2 ( ) 2 2 b + log 5 2 + 2 log 3 − 2 + log 5 b + log 5 2 − + log 5 2 2 2 2 2 a + = a + = 2 + c + log 3 1+ log 3 c + log 3 1+ log 3 2 2 2 2
Đồng nhất hệ số hai vế, ta có a = 2, b = 2 − , c =1.
Vậy a + b + c = 2 + ( 2 − ) +1= Choïn 1. ⎯⎯⎯ → A
Câu 45. Cho khối lăng trụ tam giác AB . C A B C
mà mặt bên ABB A
có diện tích bằng 4. Khoảng cách giữa cạnh CC và
bằng 7. Thể tích khối lăng trụ bằng: A. 10. B. 16. C. 12. D. 14. Hướng dẫn giải:
Ta có: CC//AA nên CC// ( ABB A ) AB. Trang 51
Do đó d (CC , AB) = d (CC ,( ABB A
)) = d (C ,(ABB A )) = 7. Khi đó ta có: 1 1 28 V = = = d C , ABB A .S .7.4 . C .ABB A ( ( )) 3 ABB A 3 3 2 3 3 28 Choïn Ta lại có: V = = = = ⎯⎯⎯ → V V V . 14 . D C .ABB A ABC.A B C ABC. A B C C . 3 2 ABB A 2 3
Câu 46. Cho hàm số y = f ( x) có đạo hàm liên tục trên 1;2, thỏa mãn f ( x) = x f ( x) 2 .
− x . Biết f ( ) 1 = 3 , tính f (2) . A. 16. B. 2. C. 8. D. 4. Hướng dẫn giải: .
x f ( x) − x . f ( x) f (x)
Ta có: f ( x) = x f ( x) 2
− x x f (x) − f (x) 2 . . = x = 1 = 1 2 x x f ( x)
= dx = x + C
(với C là hằng số). x f ( ) 1 Mặt khác: f ( ) 1 = 3
= 1+ C 3 = 1+ C C = 2 . 1 f ( x) Choïn Vậy
= x + f (x) 2 2
= x + 2x . Khi đó: f (2) = 8. ⎯⎯⎯ → C x
Câu 47. Cho hình nón đỉnh S , đáy là đường tròn nội tiếp tam giác ABC . Biết rằng AB = BC = 10a ,
AC = 12a , góc tạo bởi hai mặt phẳng (SAB) và ( ABC) bằng 45. Tính thể tích V của khối nón đã cho. A. 3 V = 3a . B. 3 V = 9a . C. 3 V = 27a . D. 3 V =12 a . Hướng dẫn giải: Trang 52
Trong mặt phẳng (ABC), dựng ID ⊥ AB tại D, khi đó góc tạo
bởi hai mặt phẳng (SAB) và ( ABC) chính là SDI = 45 nên
ID = SI = r = h (với r, h lần lượt là bán kính đáy và đường cao của hình nón đã cho). S Ta có: S = . ABC p r r =
(với p là nửa chu vi ABC ). ABC p
Ta có: p =16a , S = p − − − = ( p a)( p a)( p a) 2 10 10 12 48a . ABC 2 48a 1 1 Suy ra r =
= 3a = h . Vậy V = r h = (3a)3 2 3 = 9 a . 16a 3 3 Choïn ⎯⎯⎯ → B
Câu 48. Cho hàm số f ( x) liên tục trên
và có đồ thị hàm số f ( x) như hình vẽ. Gọi S là tập hợp các giá
trị nguyên của tham số m 5 − ;
5 để hàm số y = f ( 2 2
x − 2mx + m + )
1 nghịch biến trên khoảng 1 0;
. Tổng giá trị các phần tử của S bằng 2 A. 10. B. 14. C. 12 − . D. 15. Hướng dẫn giải: x = −
Dựa vào đồ thị của hàm f (x) ta thấy: f ( x) 1 = 0 (1) và x = 2
f ( x) 0 x 2 (2) . 2
Ta có: y = ( x − m) f ( 2 2 2 2
x − 2mx + m + )
1 = 2 ( x − m) f ((x − m) + ) 1 ; x = m x − m = 0 (1) y = 0 − + = − . f ( 2 (x − m)2 + ) (x m) 1 1 (x ) 1 = 0
(x − m)2 +1= 2 − = = + 2 2 x m 1 x m 1
Ta có: ( x − m) +1 = 2 ( x − m) = 1 . x − m = 1 − x = m −1 2 − + 2 2 2 x m 1 x m 1
Xét f (( x − m) + ) ( )
1 0 ( x − m) +1 2 ( x − m) 1 . x − m 1 − x m −1 Trang 53 Bảng biến thiên: 1 m −1 3 2 m Từ đây ta có: Hàm 1 2 y = f ( 2 2
x − 2mx + m + ) 1 nghịch biến trên 0; m 0 . 2 1 1 − m 0 m +1 2 2
Vì m nguyên và m 5 − ;
5 m S = 0;2;3;4; 5 . Choïn
Tổng các phần tử của S là: 0 + 2 + 3 + 4 + 5 = 14 . ⎯⎯⎯ → B Câu 49. Giả sử ,
a b là các số thực sao cho 3 3 3z 2 + = .10 + .10 z x y a b
đúng với mọi số thực dương , x , y z thỏa
mãn log(x + y) = z và 2 2
log(x + y ) = z +1 . Giá trị của a + b bằng: 31 29 31 25 A. . B. . C. − . D. − . 2 2 2 2 Hướng dẫn giải:
log(x + y) = z
x + y =10z Ta có: . Suy ra 2 2
x + y =10(x + y) (*) . 2 2 2 2 z 1
log(x + y ) = z +1
x + y =10 + =10.10z Khi đó: 3 3 3z 2 z 2 2 z 3 z 2 x + y = . a 10 + .
b 10 (x + y)(x − xy + y ) = a(10 ) + ( b 10 ) x0, y 0 2 2 3 2 2 2 2
(x + y)(x − xy + y ) = a(x + y) + b(x + y) x − xy + y = a(x + y) + b(x + y) (*) b b 2 2 2 2 2 2 2 2
x − xy + y = a(x + 2xy + y ) +
(x + y ) x + y − xy = a + ( 2 2
x + y ) + 2axy (**) 10 10 b 1 a + =1 a = − Đồ 29 Choïn
ng nhất hệ số hai vế của (**), ta được: 10
2 . Vậy a + b = . ⎯⎯⎯ → B 2 2a = 1 − b =15
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(3;0;0), B( 3 − ;0;0) và C(0;5; ) 1 . Gọi M
là một điểm nằm trên mặt phẳng tọa độ (Oxy) sao cho MA+ MB =10, giá trị nhỏ nhất của MC là A. 6. B. 2. C. 3. D. 5. Hướng dẫn giải:
Nhận xét: Hai điểm ,
A B cùng thuộc mặt phẳng (Oxy) và MA + MB =10 6 = AB . Do vậy, tập
hợp điểm M là một elip thuộc mặt phẳng (Oxy) với hai tiểu điểm là A và B. Trang 54
Đặt MA+ MB = 2a =10 a = 5,
AB = 2c = 6 c = 3 , 2 2 2 2
b = a − c = 5 − 3 = 4 . Do vậy ( ) 2 2 x y M E : + = 1 hay 2 2 a b ( ) 2 2 x y M E : + = 1. 25 16
Gọi D(0;5;0)là hình chiếu của C trên
mặt phẳng (Oxy) . Khi đó ta có: 2 2 2 CD = 0 + 0 +1 = 1 và 2 2 2
MC = CD + DM = 1+ DM ( )
* . Do vậy MC bé nhất khi và chỉ khi DM bé nhất.
Theo hình vẽ, ta thấy khi M trùng với đỉnh elip (E) thuộc tia Oy thì DM bé nhất, hay M (0;4;0) . Choïn
Suy ra DM =1, khi đó MC = 1+1 = 2 . ⎯⎯⎯ → B ĐỀ SỐ 09
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+ Câu 1.
Cho hàm số y = f ( x) liên tục trên
và có bảng biến thiên sau
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 3.
B. Hàm số đạt cực đại tại x = 2 .
C. Hàm số đạt cực đại tại x = 2 − .
D. Hàm số đạt cực đại tại x = 4 .
Câu 2. Cho hàm số y = f ( x) có bảng biến thiên như sau. Tổng các giá trị nguyên của m để đường thẳng
y = m −1 cắt đồ thị hàm số y = f ( x) tại ba điểm phân biệt bằng Trang 55 A. 6 . B. 1. C. 0 . D. 3 .
Câu 3. Tìm phương trình mặt cầu có tâm là điểm I (1;2;3) và tiếp xúc với trục Oz . 2 2 2 2 2 2 A. ( x − )
1 + ( y − 2) + ( z − 3) = 5 . B. ( x − )
1 + ( y − 2) + ( z − 3) = 13 . 2 2 2 2 2 2 C. ( x − )
1 + ( y − 2) + ( z − 3) = 14 . D. ( x − )
1 + ( y − 2) + ( z − 3) = 10 .
Câu 4. Cho hàm số y = f ( )
x có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2 . B. 3 . C. 4 . D. 1.
Câu 5. Trong không gian Oxyz , gọi là góc giữa hai vectơ a và b , với a và b khác 0 , khi đó cos bằng . a b a . b . a b a.b A. . B. . C. . D. . a . b a.b a + b a . b
Câu 6. Rút gọn biểu thức 3 5 4 P = x
x với x 0. 20 7 20 12 A. 21 P = x . B. 4 P = x . C. 7 P = x . D. 5 P = x .
Câu 7. Hình bên là đồ thị của hàm số nào trong các hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây? A. 3
y = −x + 3x −1. B. 3
y = −x − 3x +1. C. 3
y = x − 3x +1. D. 3
y = x + 3x +1. 2 4 − x
Câu 8. Số tiệm cận của đồ thị hàm số y = x + là 3 A. 0 . B. 1. C. 2 . D. 3 .
Câu 9. Tìm tất cả các giá trị của m để phương trình 2025x = m có nghiệm thực. A. m 1. B. m 0 . C. m 0 . D. m 0 .
Câu 10. Có bao nhiêu cách chọn hai học sinh từ nhóm 41 học sinh? A. 2 41 . B. 2 A . C. 41 2 . D. 2 C . 41 41
Câu 11. Trong không gian Oxyz , cho các điểm (4 A ; 3 − ;2) , ( B 6;1; 7 − ), C(2;8; 1
− ) . Viết phương trình đường
thẳng đi qua gốc tọa độ O và trọng tâm G của tam giác ABC . x y z x y z x y z x y z A. = = . B. = = . C. = = . D. = = . 2 1 − 1 − 2 1 1 − 2 3 1 − 4 1 3 −
Câu 12. Tính thể tích khối chóp tứ giác đều cạnh đáy bằng a , chiều cao bằng 3a . 3 a 3 3 a 3 3 a A. . B. . C. . D. 3 a . 12 4 3 Trang 56 1
Câu 13. Tìm họ nguyên hàm của hàm số y = . 2 2 sin . x cos x
A. 2cot 2x + C .
B. − cot 2x + C .
C. cot 2x + C . D. 2
− cot 2x + C .
Câu 14. Trong không gian Oxyz , điểm nào dưới đây nằm trên mặt phẳng (P) : 2x − y + z − 2 = 0 . A. Q(1; 2 − ;2) . B. N (1; 1 − ;− ) 1 . C. P(2; 1 − ;− ) 1 . D. M (1;1;− ) 1 . 4044 1 4044 Câu 15. Cho biết 2 f
(x) − dx = 2a với a , khi đó f ( x) dx bằng: x 2022 2022 1 1 A. a + ln 2 . B. a − ln 2 . C. a + ln 2 . D. a + ln 2 . 2 4
Câu 16. Cho tập hợp A = 2 3 10
10;10 ;10 ;...10 . Gọi S là tập các số nguyên có dạng log m với m A . Tính 100
tích các phần tử của tập S . A. 60 B. 24 C. 120 D. 720 .
Câu 17. Tính đạo hàm của hàm số y = ln (sin x) . 1 1 − A. y ' = . B. y ' = .
C. y ' = tan x .
D. y ' = cot x . sin x 2 sin x
Câu 18. Cho đồ thị hàm số y = f ( x) . Diện tích S của hình phẳng (phần tô đậm trong hình vẽ) là 1 3
A. S = − f
(x)dx+ f (x)dx. 0 1 1 3 B. S = f
(x)dx− f
(x)dx . 0 1 3 C. S = f (x)dx. 0 1 3 D. S = f
(x)dx+ f (x)dx. 0 1
Câu 19. Cho cấp số cộng (u , biết u = 3 và u = 7 . Giá trị của u bằng n ) 2 4 15 A. 27 . B. 31. C. 35 . D. 29 .
Câu 20. Thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 bằng A. 16 . B. 48 . C. 12 . D. 36 . 2 2 Câu 21. Tích phân dx bằng. 2x +1 0 1 A. 2 ln 5 . B. ln 5 . C. ln 5 . D. 4 ln 5 . 2
Câu 22. Tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x +1 có hệ số góc nhỏ nhất là đường thẳng A. y = 0. B. y = 3 − x − 2.
C. y = x . D. y = 3 − x + 2.
Câu 23. Số giao điểm của đồ thị hàm số 4 2
y = −x + x + 2024 và trục hoành là A. 2. B. 4. C. 3. D. 1.
Câu 24. Hàm số y = ( x + )12 1 xác định khi A. x 1 − . B. x . C. x 1 . D. x 1 − . Trang 57 m
Câu 25. Nếu (2x − )
1 dx = 2 thì m có giá trị bằng 0 m =1 m =1 m = −1 m = −1 A. . B. . C. . D. . m = −2 m = 2 m = 2 m = −2
Câu 26. Cho hình nón có bán kính đáy R , đường cao h . Diện tích xung quanh của hình nón này là
A. Rh .
B. 2 Rh . C. 2 2
R R + h . D. 2 2
2 R R + h .
Câu 27. Tập nghiệm của bất phương trình 2
log x − 3log x + 2 0 là 2 2 A. (2;4) . B. (1; 4) . C. (1; 2) . D. (0;2) . 2 sin 2x + sin x
Câu 28. Cho tích phân I = dx
. Thực hiện phép biến đổi t = 1+ 3cos x , ta có thể đưa I về 1+ 3cos x 0 dạng nào sau đây? 1 2 1 2 2 2 2 2 A. I = ( 2 2t +
)1dt . B. I = ( 2t +2)dt. C. I = ( 2 2t +
)1dt . D. I = ( 2t +2)dt . 9 9 9 9 2 2 1 1
Câu 29. Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông cạnh bằng a . Tính diện tích toàn
phần S của hình trụ. 2 a 2 3 a A. 2 S = 4a . B. 2 S = a . C. S = . D. S = . 2 2
Câu 30. Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
1. Hàm số y = log x có tập xác định là D = (0;+ ) . a
2. Hàm số y = log x đơn điệu trên khoảng (0;+ ) . a
3. Đồ thị hàm số y = log x và đồ thị hàm số x
y = a đối xứng nhau qua đường thẳng y = x . a
4. Đồ thị hàm số y = log x nhận trục Ox là một tiệm cận. a A. 3 . B. 1. C. 4 . D. 2 .
Câu 31. Điều kiện cần và đủ để hàm số 4 2
y = ax + bx + c có hai điểm cực đại và một điểm cực tiểu là
A. a 0, b 0 .
B. a 0 , b 0 .
C. a 0 , b 0 .
D. a 0 , b 0 .
Câu 32. Trong không gian Oxyz , cho mặt phẳng ( ) : 3x − 2y + z + 6 = 0 . Hình chiếu vuông góc của điểm A(2; 1
− ;0) lên mặt phẳng ( ) có tọa độ là A. (1;0; ) 3 . B. (2; 2 − ;3). C. (1;1; )1 − . D. ( 1 − ;1;− ) 1 .
Câu 33. Trong mặt phẳng tọa độ, cho điểm M như hình vẽ bên là điểm
biểu diễn của số phức z . Tính ( + )2 1 z A. ( + z)2 1 = 2 − i . B. ( + z)2 1 = 8 − i . C. ( + z)2 1 = −1+ i . D. ( + z)2 1 = 2 − + 2i .
Câu 34. Cho hình chóp S.ABC có SA = a 3 , SA vuông góc với mặt phẳng (ABC) , tam giác ABC vuông tại ,
B AB = a , tam giác SBC cân. Thể tích khối chóp S.ABC bằng Trang 58 3 2a 3 3 a 3 3 a 3 A. . B. 3 a 3 . C. . D. . 3 3 6 1 Câu 35. Cho , x ,
a b là các số thực dương thỏa mãn log
= 2log a − 6log b . Khi đó giá trị của x là 7 7 49 x 3 b 2 a
A. x = 2a − 3b . B. x = . C. x = . D. 2 3 x = a b . 2 a 3 b
Câu 36. Cho tứ diện ABCD có A ,
B AC, AD đôi một vuông góc với nhau và AB = AC = AD . Góc giữa CD và ( ABC ) bằng A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 .
Câu 37. Cho số phức z = a + bi với , a b
thỏa mãn (1+ i) z + (2 − i) z =13+ 2i . Tính tổng a + b
A. a + b = 1.
B. a + b = 2 − .
C. a + b = 2 .
D. a + b = 0 .
Câu 38. Tính diện tích mặt cầu ngoại tiếp một hình lăng trụ tam giác đều có các cạnh đều bằng a . 2 7 a 2 7 a 2 7 a 2 3 a A. . B. . C. . D. . 3 6 5 7
Câu 39. Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: z + 2 − i = 4 là đường tròn có tâm I và
bán kính R lần lượt là: A. I ( 2 − ;− ) 1 ; R = 4 . B. I ( 2 − ;− ) 1 ; R = 2 . C. I (2;− ) 1 ; R = 4 . D. I (2;− ) 1 ; I (2;− ) 1 .
Câu 40. Cho khối lăng trụ ABC . D A B C D
có thể tích bằng 12, đáy
ABCD là hình vuông tâm O . Thể tích của khối chóp A .BCO bằng A. 1. B. 4 . C. 3 . D. 2 .
4 ln (sin x +15cos x)
Câu 41. Biết rằng tích phân I =
dx = a + b ln 2 + c ln 3 + d ln 5 , trong đó , a , b , c d . 2 cos x 0
Tính T = a + b + c + d . 133 313 135 195 A. T = . B. T = . C. T = . D. . 4 4 4 4 x −1 y + 2 z
Câu 42. Phương trình đường thẳng song song với đường thẳng d : = =
và cắt hai đường thẳng 1 1 1 − x +1 y +1 z − 2 x −1 y − 2 z − 3 d : = = ; d : = = là: 1 2 1 1 − 2 1 − 1 3 x +1 y +1 z − 2 x −1 y z −1 A. = = . B. = = . 1 − 1 − 1 1 1 1 − x −1 y − 2 z − 3 x −1 y z −1 C. = = . D. = = . 1 1 1 − 1 1 − 1 Trang 59
Câu 43. Một tấm đề can hình chữ nhật được cuộn tròn lại theo chiều dài tạo
thành một khối trụ có đường kính 50 (cm) . Người ta trải ra 250 vòng
để cắt chữ và in tranh cổ động, phần còn lại là một khối trụ có đường
kính 45 (cm). Hỏi phần đã trải ra dài bao nhiêu mét (làm tròn đến hàng đơn vị)? A. 373 (m) . B. 187 (m) . C. 384 (m) . D. 192 (m) . Câu 44. Cho hàm số 4 2
y = x + 2mx + m (với m là tham số thực). Tập tất cả các giá trị của tham số m để đồ
thị hàm số đã cho cắt đường thẳng y = 3
− tại bốn điểm phân biệt, trong đó có một điểm có hoành độ
lớn hơn 2 còn ba điểm kia có hoành độ nhỏ hơn 1, là khoảng ( ; a b) (với , a b
; a , b là phân số
tối giản). Khi đó, 15ab nhận giá trị nào sau đây? A. 63 − . B. 63 . C. 95 . D. 95 − . Câu 45. Cho hàm số 4 2
y = ax + bx + c có đồ thị (C) , biết rằng (C) đi qua điểm A( 1
− ;0). Biết tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có
hoành độ lần lượt là 0 và 2 ; đồng thời diện tích hình phẳng giới hạn
bởi đường thẳng d , đồ thị (C) và hai đường thẳng x = 0 , x = 2 có 28 bằng
(phần tô màu trong hình vẽ). Diện tích hình phẳng giới hạn 5
bởi d, (C) và hai đường thẳng x = 1
− , x = 0 bằng 2 1 A. . B. . 5 4 2 1 C. . D. . 9 5
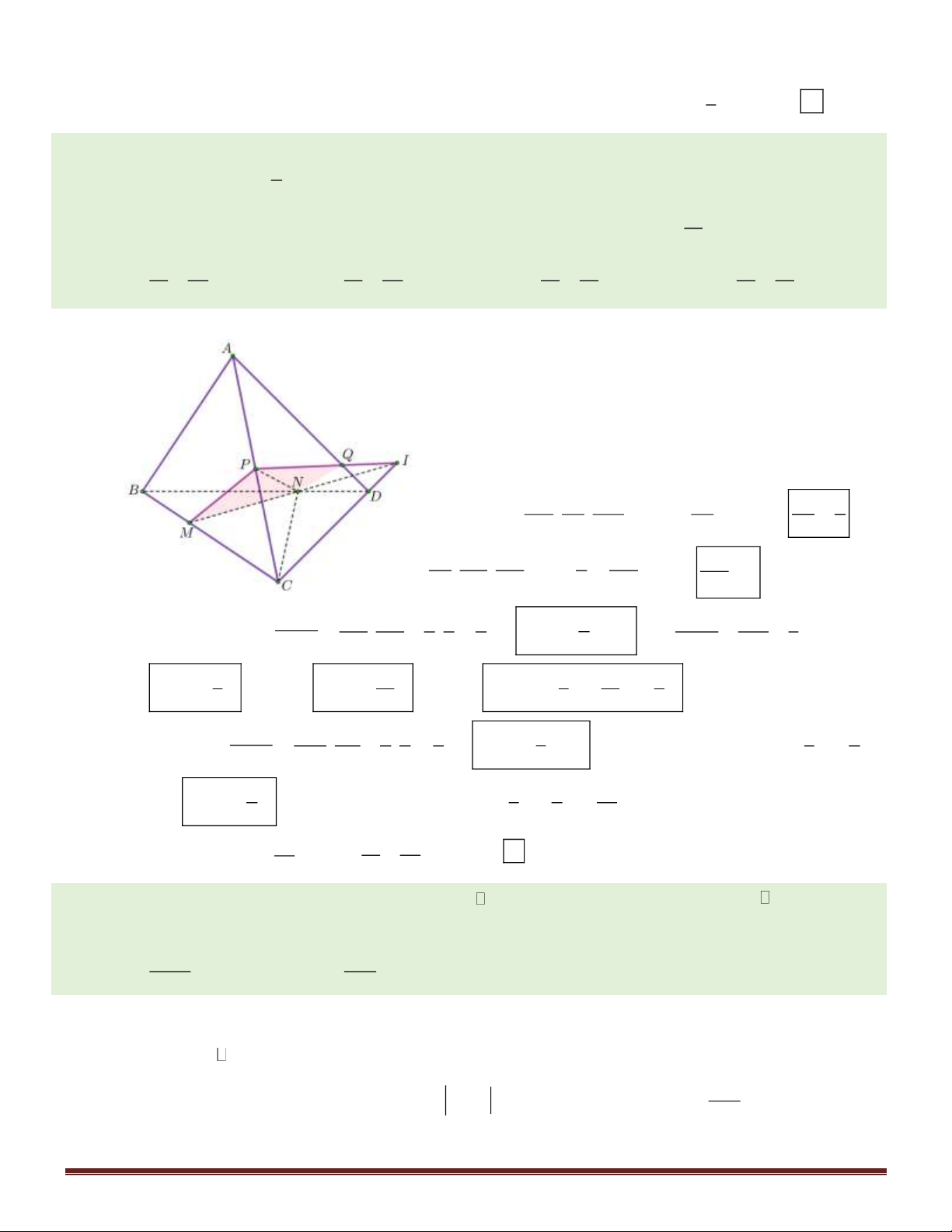
Câu 46. Cho tứ diện ABCD , trên các cạnh BC , BD , AC lần lượt lấy các điểm M , N , P sao cho 3
BC = 3BM , BD =
BN , AC = 2AP . Mặt phẳng (MNP) chia khối tứ diện ABCD thành hai phần 2 V
có thể tích là V , V với V là thể tích khối đa diện chứa đỉnh B. Tính tỉ số 1 . 1 2 1 V2 V 26 V 26 V 3 V 15 A. 1 = . B. 1 = . C. 1 = . D. 1 = . V 13 V 19 V 19 V 19 2 2 2 2
Câu 47. Cho hàm số f ( x) có đạo hàm liên tục trên
thỏa mãn f ( x) + f ( x) 1, x và f (0) = 0.
Tìm giá trị lớn nhất của f ( ) 1 . 2e −1 e −1 A. . B. . C. e −1. D. 2e −1. e e
Câu 48. Trong không gian Oxyz , cho hai điểm A(1;2; )
3 , B(2;3;4) . Một mặt cầu (S ) bán kính R luôn tiếp
xúc với ba mặt phẳng tọa độ và đoạn thẳng AB luôn nằm trong ( S ) (mọi điểm thuộc đoạn thẳng
AB đều nằm trong ( S ) ). Giá trị nguyên lớn nhất của R đạt được là: A. 4. B. 6. C. 5. D. 3. Trang 60
Câu 49. Cho ba số thực dương , a ,
b c thỏa mãn abc = 10 . Biết giá trị lớn nhất của biểu thức m F = 5log . a logb + 2log . b logc + log . c log a bằng với ,
m n nguyên dương và m tối giản. Tổng n n
m + n bằng A. 7 . B. 10 . C. 13 . D. 16 .
Câu 50. Cho hàm số đa thức f ( x) có đạo hàm trên . Biết f ( 2
− ) = 0 và đồ thị của hàm số
y = f ( x) như hình vẽ. Hàm số y = f ( x) 2 4
− x + 4 có bao nhiêu điểm cực trị? A. 3. B. 5. C. 4. D. 2.
__________________HẾT__________________
ÑAÙP AÙN ÑEÀ SOÁ 09 1 2 3 4 5 6 7 8 9 10 B C A C A B C A C D 11 12 13 14 15 16 17 18 19 20 B D D B D C D B D C 21 22 23 24 25 26 27 28 29 30 C D A A C C A C D A 31 32 33 34 35 36 37 38 39 40 A D A C B A A A A A 41 42 43 44 45 46 47 48 49 50 A B A C D B B A A B
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 09
4 ln (sin x +15cos x)
Câu 41. Biết rằng tích phân I =
dx = a + b ln 2 + c ln 3 + d ln 5 , trong đó , a , b , c d . 2 cos x 0
Tính T = a + b + c + d . 133 313 135 195 A. T = . B. T = . C. T = . D. . 4 4 4 4 Hướng dẫn giải: x − x u
= ln (sin x +15cos x) cos 15sin du = dx sin x +15 cos x Đặt 1 . sin x +15 cos d = d x v x 2 v = tan x +15 = cos x cos x C 15 = Trang 61 − Khi đó: = ( x x I
tan x +15) ln (sin x +15cos x) 4 cos 15sin 4 − dx 0 cos x 0 4 4 4 sin x d (cos x)
=16ln 8 2 −15ln15 − dx +15
dx = 16 ln 8 2 −15 ln15 − −15 cos x 4 cos x 0 0 0 1 4
=16ln 8 2 −15ln15 − −15ln cos x = 16ln 8 2 −15ln15 − −15ln 0 4 4 2 7 1 1 − 2 2
= − +16ln 2 −15ln 5 −15ln 3−15ln 2 4 1 127 = − + ln 2 −15 ln 3 −15 ln 5. 4 2 1 127 133 Choïn
Suy ra a = − , b = , c = 1 − 5, d = 1
− 5 . Vậy T = a + b + c + d = . ⎯⎯⎯ → A 4 2 4 x −1 y + 2 z
Câu 42. Phương trình đường thẳng song song với đường thẳng d : = =
và cắt hai đường thẳng 1 1 1 − x +1 y +1 z − 2 x −1 y − 2 z − 3 d : = = ; d : = = là: 1 2 1 1 − 2 1 − 1 3 x +1 y +1 z − 2 x −1 y z −1 A. = = . B. = = . 1 − 1 − 1 1 1 1 − x −1 y − 2 z − 3 x −1 y z −1 C. = = . D. = = . 1 1 1 − 1 1 − 1 Hướng dẫn giải:
Vectơ chỉ phương của d là u = (1;1;− )
1 . Gọi là đường thẳng cần tìm. d Gọi A( 1 − + 2 ; a 1 − + ;
a 2 − a) = d , B 1− ; b 2 + ;
b 3 + 3b = d . 1 ( ) 2 Suy ra: AB = ( b
− − 2a + 2;b − a + 3;3b + a + ) 1 .
Vì song song với d nên AB cùng phương với u , d b
− − 2a + 2 b − a + 3 3b + a +1 suy ra: = = 1 1 1 − b
− − 2a + 2 = b − a + 3 a =1 A (1;0 ) ;1 . b − a + 3 = 3 − b − a −1 b = 1 − B (2;1;0)
Phương trình chính tắc của Δ qua A và có vectơ chỉ − − phương x 1 y z 1 u = − = = (1;1; ) 1 là : . 1 1 1 − Choïn ⎯⎯⎯ → B
Câu 43. Một tấm đề can hình chữ nhật được cuộn tròn lại theo chiều dài tạo thành một khối trụ có đường kính
50 (cm) . Người ta trải ra 250 vòng để cắt chữ và in tranh cổ động, phần còn lại là một khối trụ có
đường kính 45 (cm). Hỏi phần đã trải ra dài bao nhiêu mét (làm tròn đến hàng đơn vị)? Trang 62 A. 373 (m) . B. 187 (m) . C. 384 (m) . D. 192 (m) . Hướng dẫn giải:
☺ Cách giải 1: Gọi a là bề dày của tấm đề can, sau mỗi vòng được quấn thì đường kính của vòng 50 − 45
mới sẽ được tăng lên 2a. Vì vậy: 2a 250 = 50 − 45 a = = 0,01 (cm) . 2 250
Gọi l là chiều dài đã trải ra và h là chiều rộng của tấm đề can (tức chiều cao hình trụ). 2 2 ( 2 2 50 − 45 ) Khi đó ta có: 50 45 Choïn lha = h − h l =
37306 (cm) 373 (m) . ⎯⎯⎯ → A 2 2 4a
☺ Cách giải 2: Gọi a là bề dày của tấm đề can, sau mỗi vòng được quấn thì đường kính của vòng 50 − 45
mới sẽ được tăng lên 2a. Vì vậy: 2a 250 = 50 − 45 a = = 0,01 (cm) . 2 250
Chiều dài của phần trải ra là tổng chu vi của 250 đường tròn có bán kính là một cấp số cộng có số
hạng đầu bằng r = 25 , công sai là d = 0
− ,01 (do khi trải ra thì bán kính các vòng tròn ngày càng 1
giảm với độ giảm bằng bề dày của tấm đề can).
Do đó chiều dài của phần đề can đã trải ra là: (2r + 249d ).250 250 1
l = 2 r + r + ... + r = 2. = 2 (2.25 − 249.0,01) 37314 (cm) 373 (m) . 1 2 250 2 2 S 250 Câu 44. Cho hàm số 4 2
y = x + 2mx + m (với m là tham số thực). Tập tất cả các giá trị của tham số m để đồ
thị hàm số đã cho cắt đường thẳng y = 3
− tại bốn điểm phân biệt, trong đó có một điểm có hoành độ
lớn hơn 2 còn ba điểm kia có hoành độ nhỏ hơn 1, là khoảng ( ; a b) (với , a b
; a , b là phân số
tối giản). Khi đó, 15ab nhận giá trị nào sau đây? A. 63 − . B. 63 . C. 95 . D. 95 − . Hướng dẫn giải:
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số: 4 2
x + 2mx + m = 3 − (1) . Đặt 2
t = x , t 0 . Khi đó phương trình trở thành 2
t + 2mt + m + 3 = 0 (2) . f (t)
Phương trình (1) có bốn nghiệm phân biệt Phương trình (2) có hai nghiệm thỏa mãn 2
= m − m − 3 0 (1) 1− 13
0 t t S = 2 − m 0 3 − m (*). 1 2 (1) 2 P = m+3 0 Trang 63
Khi đó, bốn nghiệm của phương trình (1) là: − t − t t t . 2 1 1 2 1 x 2 x 3 x 4 x t 2 f ( ) 1 0 3 m + 4 0 19 Từ giả thiết, ta có 2
hay t 1 4 t . Suy ra: m − (**) . 1 2 t 1 f (4) 0 9 m +19 0 9 1 19 19 Choïn Từ (*) và (**) suy ra: 3 − m − . Do đó: a = 3 − , b = −
nên 15ab = 95 . ⎯⎯⎯ → C 9 9 Câu 45. Cho hàm số 4 2
y = ax + bx + c có đồ thị (C) , biết rằng (C) đi qua điểm A( 1
− ;0). Biết tiếp tuyến d
tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2 ; đồng thời diện tích hình phẳng 28
giới hạn bởi đường thẳng d , đồ thị (C) và hai đường thẳng x = 0 , x = 2 có bằng (phần tô màu 5
trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, (C) và hai đường thẳng x = 1
− , x = 0 bằng 2 1 2 1 A. . B. . C. . D. . 5 4 9 5 Hướng dẫn giải: Ta có: 3
y = 4ax + 2bx ; tiếp tuyến của (C) tại A là d : y = ( 4
− a − 2b)(x + ) 1 .
Phương trình hoành độ giao điểm của d và (C) là: (− a − b)(x + ) 4 2 4 2
1 = ax + bx + c ( ) 1 .
Theo giả thiết, ta có: Phương trình ( )
1 nhận x = 0 , x = 2 làm nghiệm (ngoài một nghiệm là x = 1 − ) − − = 4
− a − 2b − c = 0 (2) 4a 2b c . 12
− a − 6b = 16a + 4b + c
28a +10b + c = 0 (3) 2 28
Mặt khác, diện tích phần tô màu là: = ( 4
− a − 2b)(x + ) 4 2
1 − ax − bx − c dx 5 0 2 28 ( ax bx = 28 32 8 2
− a − b)(x + ) 5 3 2 2 1 − + + cx = 4( 4
− a − 2b) −
a − b − 2c 0 5 5 3 5 5 3 0 112 32 28 a + b + 2c = −
(4). Từ (2), (3), (4) suy ra a =1, b = 3 − , c = 2 . 5 3 5
Khi đó ta xác định được (C) 4 2
: y = x − 3x + 2 và d : y = 2( x + ) 1 . Trang 64 0 0 1 Choïn Diện tích cần tìm là 4 2 S =
x − 3x + 2 − 2 (x + ) 1 dx = ( 4 2
x − 3x − 2x) dx = . ⎯⎯⎯ → D 5 1 − 1 −
Câu 46. Cho tứ diện ABCD , trên các cạnh BC , BD , AC lần lượt lấy các điểm M , N , P sao cho 3
BC = 3BM , BD =
BN , AC = 2AP . Mặt phẳng (MNP) chia khối tứ diện ABCD thành hai phần 2 V
có thể tích là V , V với V là thể tích khối đa diện chứa đỉnh B. Tính tỉ số 1 . 1 2 1 V2 V 26 V 26 V 3 V 15 A. 1 = . B. 1 = . C. 1 = . D. 1 = . V 13 V 19 V 19 V 19 2 2 2 2 Hướng dẫn giải: Đặt V = V
; trong (BCD), gọi I = MN CD ; trong ABCD
(ACD), gọi Q = IP AD, suy ra Q = AD (MNP) .
Mặt phẳng (MNP) cắt tứ diện ABCD theo thiết diện là tứ giác MNQP .
Áp dụng định lí Menelaus trong các tam giác BCD và NB ID MC ID ID 1 ACD ta có: . . =1 2. .2 = 1 = ; ND IC MB IC IC 4 ID PC QA 1 QA QA . . =1 .1. =1 = 4 . IC PA QD 4 QD QD V AP AQ 1 4 V DN 1
Ta có tỉ số thể tích: ANPQ = . = 2 . = 2 V = V mà ANCD = = V AC AD 2 5 5 ANPQ 5 ANCD V DB 3 ANCD 1 2 1 2 1 V = V ; do vậy V = V . Suy ra V
= V − V = V . ANCD 3 ANPQ 15 N .PQDC 3 15 5 V CM CP 2 1 1 2
Bên cạnh đó: CMNP = . = 1 . = 1 V = V mà V = V −V
= V − V = V . V CB CA 3 2 3 CMNP 3 CBNA CBNA ANCD 3 3 CBNA 2 1 2 19 Vì vậy V
= V . Ta có: V =V +V = V + V = V . CMNP 9 2 N .PQDC CMNP 5 9 45 Do đó V 26 Choïn V = V − 26 V = V . Vậy 1 = . ⎯⎯⎯ → B 1 2 45 V 19 2
Câu 47. Cho hàm số f ( x) có đạo hàm liên tục trên
thỏa mãn f ( x) + f ( x) 1, x và f (0) = 0.
Tìm giá trị lớn nhất của f ( ) 1 . 2e −1 e −1 A. . B. . C. e −1. D. 2e −1. e e Hướng dẫn giải: Ta có: x
, f (x) + f (x) 1 ex ( )+ex ( ) ex f x f x ex ( ) (ex f x ) 1 1 − ex ( ) d x x (ex f x x
) dx e f (x) 1 1 e e. f ( )
1 e −1 f ( ) e 1 1 . 0 0 e 0 0 Trang 65 − Do đó giá trị e 1 Choïn
lớn nhất của f ( ) 1 là . ⎯⎯⎯ → B e
Câu 48. Trong không gian Oxyz , cho hai điểm A(1;2; )
3 , B(2;3;4) . Một mặt cầu (S ) bán kính R luôn tiếp
xúc với ba mặt phẳng tọa độ và đoạn thẳng AB luôn nằm trong (S ) (mọi điểm thuộc đoạn thẳng
AB đều nằm trong ( S ) ). Giá trị nguyên lớn nhất của R đạt được là: A. 4. B. 6. C. 5. D. 3. Hướng dẫn giải:
Do mặt cầu luôn tiếp xúc với ba mặt phẳng tọa độ nên tọa độ tâm mặt cầu là I (a, a, a) , suy ra bán
kính mặt cầu R = a .
Mặt khác, mọi điểm thuộc đoạn thẳng AB đều nằm trong mặt cầu( S ) nên ta có: IA R IA a (1− a
)2 +(2− a)2 +(3− a)2 2 2 2 a 2
2a −12a +14 0 2 2 IB R IB a ( 2 2 − a
)2 +(3− a)2 +(4− a)2 2 a
2a −18a + 29 0 3
− 2 a 3+ 2 9 − 23 a 3+ 2 9 − 23 9 + 23 . 2 a 4,414 2 2 2,102 Choïn
Giá trị nguyên lớn nhất của R là R = 4 . ⎯⎯⎯ → A
Câu 49. Cho ba số thực dương , a ,
b c thỏa mãn abc = 10 . Biết giá trị lớn nhất của biểu thức m F = 5log . a logb + 2log . b logc + log . c log a bằng với ,
m n nguyên dương và m tối giản. Tổng n n
m + n bằng A. 7 . B. 10 . C. 13 . D. 16 . Hướng dẫn giải: Đặt x = log , a y = log ,
b z = log c . Suy ra x + y + z = log (abc) = log10 =1.
Khi đó: F = xy + yz + zx = xy + y ( − x − y) + x( − x − y) 2 2 5 2 5 2 1 1 = 2
− y − x + 2xy + 2y + x x = 2
− y − x + 2xy + 2y + x = 2
− ( y − xy − y) 2 ??? 1 1
− x + x =− 2 y − − − (x − 2)2 5 5 2 2 2 2 + 2 2 2 2 2 3 5
Dấu “=” xảy ra x = 2, y = , z = − . 2 2 Do đó: m 5 Choïn F =
= m = 5,n = 2 m + n = 7 . ⎯⎯⎯ → A max n 2
Lưu ý: Bằng cách nào ta có thể phân tích được các hằng đẳng thức như trên?
▪ Trước hết ta cần dự đoán được điểm rơi trong biểu thức F, mà biểu thức này vốn
là hàm hai biến x, y; vì vậy ta sử dụng cách thức tìm cực trị của hàm hai biến:
F = −2x + 2y +1 = 0 x 3
(*). Giải hệ (*), ta được: x = 2, y = .
F = −4y + 2x + 2 = 0 y 2
▪ Từ đây, ta xây dựng được các hằng đẳng thức phù hợp cho đánh giá của mình. Trang 66
Câu 50. Cho hàm số đa thức f ( x) có đạo hàm trên . Biết f ( 2
− ) = 0 và đồ thị của hàm số y = f (x) như
hình vẽ. Hàm số y = f ( x) 2 4
− x + 4 có bao nhiêu điểm cực trị? A. 3. B. 5. C. 4. D. 2. Hướng dẫn giải:
Ghi nhớ: Số điểm cực trị của hàm số y = f ( x) bằng số cực trị của hàm số y = f (x) cộng
y = f (x)
với số giao điểm (không kể tiếp điểm) hai đồ thị hàm số . y = 0 (Oy)
Đặt g (x) = f (x) 2 4 − x + 4 , suy ra
g( x) = 4 f ( x) − 2x ; x = −2 x
g( x) = 0 f ( x) = x = 0 . 2 x = 4
Do vậy, hàm số g ( x) có ba cực trị (*).
Ta có: g (− ) = f (− ) − (− )2 2 4 2 2 + 4 = 0 .
Từ đồ thị ta so sánh các phần diện tích và
thấy S S . 2 1 4 0 x x 4 0 x x Suy ra: f
(x)− dx − f (x) dx f
(x)− dx+ f
(x)− dx 0 2 2 2 2 0 2 − 0 2 − 4 4 ( ) x f x − dx 0
(4 f (x)− 2x)dx 0 g(4)− g( 2
− ) 0 g (4) g ( 2 − ) = 0. 2 2 − 2 −
Bảng biến thiên hàm g ( x) và g ( x) : Trang 67
Theo bảng biến thiên, ta thấy đồ thị hàm số y = g (x) có hai giao điểm với trục Oy (không tính tiếp xúc) (**). Choïn
Từ (*) và (**) suy ra số cực trị của hàm số y = g ( x) là: 3 + 2 = 5. ⎯⎯⎯ → B ĐỀ SỐ 10
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+ Câu 1.
Hàm số y = f ( x) có đồ thị như hình vẽ bên. Hàm số
y = f ( x) đồng biến trên khoảng nào dưới đây? A. ( 1 − ;2) . B. ( 2 − ; ) 1 . C. ( 2 − ;− ) 1 . D. ( 1 − ; ) 1 .
Câu 2. Số điểm cực trị của đồ thị hàm số 4
y = −x −1 là A. 2 . B. 0 . C. 1. D. 3 .
Câu 3. Nguyên hàm của hàm số f ( x) = sin 3x là: 1 1
A. cos 3x + C .
B. cos 3x + C .
C. − cos 3x + C .
D. − cos3x + C . 3 3
Câu 4. Cho hàm số y = f ( x) có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm. A. x = 0 . B. x = 1 . C. x = 5 . D. x = 2 .
Câu 5. Cho số phức z = 3 + 2i . Tìm phần thực của số phức 2 z A. 9. B. 5. C. 12. D.13.
Câu 6. Trong không gian Oxyz , phương trình mặt cầu (S ) có tâm I (1;0;− )
1 và qua điểm A(2;2;− ) 3 là Trang 68 2 2 2 2 A. ( x − ) 2 1 + y + ( z + ) 1 = 3 . B. ( x + ) 2
1 + y + ( z − ) 1 = 9 . 2 2 2 2 C. ( x + ) 2
1 + y + ( z − ) 1 = 3 . D. ( x − ) 2 1 + y + ( z + ) 1 = 9 .
Câu 7. Trong mặt phẳng tọa độ Oxy , cho vectơ v = (1; 2) . Tìm ảnh của điểm A( 2
− ;3) qua phép tịnh tiến theo vectơ v . A. A(5;− ) 1 . B. A( 1 − ;5). C. A(3;− ) 1 . D. A( 3 − ; ) 1 .
Câu 8. Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20cm . Thể tích khối trụ tương ứng bằng A. 3 800 cm . B. 3 8000 cm . C. 3 400 cm . D. 3 2000 cm .
Câu 9. Số đỉnh của một hình bát diện đều là: A. 6 . B. 8 . C. 12 . D. 4 .
Câu 10. Chọn khẳng định sai.
A. Hàm số y = ln x không có cực trị trên (0;+).
B. Hàm số y = ln x có đồ thị nhận trục tung làm đường tiệm cận đứng.
C. Hàm số y = ln x luôn đồng biến trên (0;+).
D. Hàm số y = ln x có giá trị nhỏ nhất trên (0;+) bằng 0.
Câu 11. Tập xác định của hàm số y = log 4010 − 2005x là 1 ( ) 3 1 A. ; − . B. ( ; − 2. C. (2;+) . D. ( ; − 2) . 2
Câu 12. Cho số phức z = 2 − i . Trên mặt phẳng tọa độ, tìm điểm biểu diễn số phức w = iz . A. P (2 ) ;1 . B. Q (1; 2) . C. N (2;− ) 1 . D. M ( 1 − ;2) . a
Câu 13. Cho log b = 3 ( với a 0, b 0, ab 1). Tính log . ab ab 2 b A. 5 . B. 4 − . C. 10 − . D. 16 − .
Câu 14. Khối nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a có thể tích bằng 3 3 a 3 2 a A. 3 2 a . B. 3 3 a . C. . D. . 3 3
Câu 15. Giá trị lớn nhất của hàm số 4 2
y = 2x − 3x − 5 trên đoạn 1 − ; 1 là A. 0 . B. −5 . C. 1 − . D. 1.
Câu 16. Cho khối lập phương ABC . D A B C D
có thể tích bằng 3
8a . Tính độ dài cạnh của hình lập phương đó. A. a . B. 2a . C. a 2 . D. 2 2a . −
Câu 17. Tập nghiệm của bất phương trình 2x 1 3 27 là: 1 1 A. ; + . B. (3;+) . C. ; + . D. (2;+) . 2 3
Câu 18. Trong không gian Oxyz , cho mặt phẳng (P) : 2x − y +1 = 0 . Véctơ nào dưới đây là một véc-tơ pháp tuyến của ( P) ? A. n = − − − 4 (2; 1 ) ;1 . B. 1 n = (2;0; ) 1 . C. n = 2;1; 1 . D. n = − 3 (2; 1;0) . 2 ( )
Câu 19. Nếu có một khối chóp có thể tích và diện tích đáy lần lượt bằng 3 a và 2
a thì chiều cao của nó bằng a a A. . B. 3a . C. a . D. . 3 6 Trang 69
Câu 20. Tìm nguyên hàm của hàm số ( ) ln x f x = . x 1 A. f (x) 2
dx = ln x + C . B. f (x) 2 dx = ln x + C . 2 C. f
(x)dx = ln x +C. D. ( )d x f x
x = e + C .
Câu 21. Các điểm M, N, ,
P Q trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức z , z , z , z . Khi 1 2 3 4
đó w = 3z + z + z + z bằng 1 2 3 4
A. w = 6 + 4i . B. w = 6 − + 4i .
C. w = 4 − 3i .
D. w = 3 − 4i . Câu 22. Cho hàm số f ( x) có đạo hàm là
f ( x) = x
(x − )2006 (x + )2005 2003 1 2 . Khoảng nghịch biến của hàm số là A. (−;− 2);(0; ) 1 . B. ( 2 − ;0). C. ( 2 − ;0);(1;+) .
D. (−;− 2);(0;+ ) . 1 1 1 1 Câu 23. Nếu 5 3 a a và log log thì b 3 b 2 0 a 1 a 1 0 a 1 a 1 A. . B. . C. . D. . 0 b 1 b 1 b 1 0 b 1
Câu 24. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? x − 2 A. y = . x −1 x + 2 B. y = . x +1 x + 2 C. y = . x −1 x − 2 D. y = . x +1
Câu 25. Biết phương trình 2 log x − 2log
2x −1 = 0 có hai nghiệm x , x . Tính x x . 2 2 ( ) 1 2 1 2 1 1 A. x x = 4 . B. x x = . C. x x = . D. x x = 3 − . 1 2 1 2 8 1 2 2 1 2 x y + 2 z −1
Câu 26. Trong không gian Oxyz , cho đường thẳng : = = đi qua điểm M(2; ; m ) n . Giá trị 1 1 − 3 m + n bằng A. 7 . B. 3 . C. 1 − . D. 1.
Câu 27. Cho hàm số y = f ( x) có bảng biến thiên như sau. Trang 70
Số nghiệm thực của phương trình f ( x) = f (2) là A. 0 . B. 2 . C. 1. D. 3 . 2 2x Câu 28. Cho
dx = a ln 2 + b ln 5 với ,
a b là các số hữu tỉ. Tính S = a + b . 2 x + 4 1 A. S = 2 − . B. S = 1 − . C. S = 3. D. S = 2 .
Câu 29. Cho hình hộp chữ nhật ABC . D A B C D
có AB =1, AD = 2, AA = 3. Thể tích của khối chóp . D A B C D là A. V = 2 . B. V = 1 . C. V = 6 . D. V = 3 .
Câu 30. Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f ( x) , trục Ox và các đường thẳng x = ,
a x = b (a b). b b b b A. f ( x) dx . B. 2 f ( x) dx . C. f ( x) dx . D. f (x)dx. a a a a
Câu 31. Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn cùng màu là: 1 4 1 5 A. . B. . C. . D. . 4 9 9 9
Câu 32. Ông A vay ngân hàng 96 triệu đồng với lãi suất 1% tháng theo hình thức mỗi tháng trả góp số tiền
giống nhau sao cho sau đúng 2 năm thì hết nợ. Hỏi số tiền ông phải trả hàng tháng là bao nhiêu?
(làm tròn đến hai chữ số sau dấu phẩy) A. 4,53 triệu đồng.
B. 4,54 triệu đồng.
C. 4,51 triệu đồng.
D. 4,52 triệu đồng.
Câu 33. Cho hình chóp S.ABC có S , A A ,
B BC đôi một vuông góc với nhau. Tính thể tích khối chóp S.ABC
, biết SA = a 3, AB = BC = a . 3 3a 3 3a 3 3a 3 3a A. V = . B. V = . C. V = . D. V = . 9 2 6 3
Câu 34. Trong không gian với hệ tọa độ Oxyz , cho vectơ a = ( 1
− ;− 2;3) . Tìm tọa độ của véctơ b = (2; ; y z ) ,
biết rằng vectơ b cùng phương với vectơ a .
A. b = (2; 4; − 6) .
B. b = (2;− 4;6) .
C. b = (2; 4;6) .
D. b = (2; − 3;3).
Câu 35. Cho hàm số có bảng biến thiên như sau Trang 71
Tổng các giá trị nguyên của m để đường thẳng y = m cắt đồ thị hàm số tại ba điểm phân biệt bẳng
A. −3 . B. −5 . C. 0 . D. 1 − .
Câu 36. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;1;3) , B( 1 − ;3;2) , C( 1 − ;2; ) 3 . Tính khoảng
cách h từ gốc tọa độ O đến mặt phẳng ( ABC ). 3 3 A. h = . B. h = . C. h = 3 . D. h = 3 . 2 2
Câu 37. Biết rằng a,b là những số thực để phương trình 9x − .3x a
+b = 0 luôn có 2 nghiệm thực phân biệt
x , x . Khi đó tổng x + x bằng 1 2 1 2 A. log b . B. log a . C. b . D. a . 3 3
Câu 38. Cho hình thang cân ABCD , AB // CD , AB = 2 , CD = 4 . Khi quay hình thang quanh trục CD thu
được một khối tròn xoay có thể tích bằng 6 . Diện tích hình thang ABCD bằng: 9 9 A. . B. . C. 6 . D. 3 . 2 4
Câu 39. Giá trị cực tiểu của hàm số x y = e ( 2 x − 3) là: 6 6 A. . B. . C. 3 − e . D. 2 − e . e 3 e 2 2
Câu 40. Có bao nhiêu số phức z thỏa mãn z + z = 50 và z + z = 8 ? A. 4. B.1. C. 2. D. 3. x −1
Câu 41. Tìm tổng tất cả các giá trị của tham số thực m để đồ thị hàm số y =
có hai đường tiệm cận tạo x − m
với hai trục tọa độ một hình chữ nhật có diện tích bằng 5. A. 0. B. 5. C. 4. D. 2.
Câu 42. Cho hình lăng trụ AB . C A B C
có các mặt bên đều là hình vuông cạnh a . Gọi D là trung điểm của
cạnh BC . Tính khoảng cách giữa hai đường thẳng A B và DC. a 3 a 2 a 5 a 3 A. . B. . C. . D. . 6 6 5 4 e f ( x)
Câu 43. Cho hàm số f ( x) có đạo hàm liên tục và có đạo hàm trên 1;e . Biết dx = 1
, f (e) = 2 . Tính x 1 e f (x)ln xdx . 1 A. 2. B. 1. C. 0. D. 3 .
Câu 44. Cho hình hộp chữ nhật ABC . D A B C D
có diện tích các mặt ABC , D ABB A , ADD A lần lượt bằng 2 2 2
30cm , 40cm , 48cm . Bán kính mặt cầu ngoại tiếp hình hộp bằng Trang 72 5 5 2 5 A. 3 10cm. B. 5 10cm. C. cm. D. cm. 2 5
Câu 45. Có bao nhiêu giá trị nguyên của tham số m để hàm y = 5 − msin x − (m + )
1 cos x xác định trên ? A. 6 . B. 8 . C. 7 . D. 5 .
Câu 46. Cho mặt cầu (S ) tâm O , bán kính bằng 2 và mặt phẳng ( P) . Khoảng cách từ O đến ( P) bằng 4 .
Từ điểm M thay đổi trên ( P) kẻ các tiếp tuyến MA, MB , MC tới (S ) với A , B , C là các tiếp
điểm. Biết mặt phẳng ( ABC) luôn đi qua một điểm I cố định. Tính độ dài OI . 3 1 A. 3 . B. . C. . D. 1. 2 2
Câu 47. Cho số phức z thỏa mãn 2
z + z + z − z = z . Giá trị lớn nhất của biểu thức P = z − 5 − 2i bằng: A. 2 + 5 3 . B. 2 + 3 5 . C. 5 + 2 3 . D. 5 + 3 2 .
Câu 48. Trong không gian Oxyz cho mặt phẳng ( ) : x − z − 3 = 0 và điểm M (1;1; )
1 . Gọi A là điểm thuộc tia
Oz , gọi B là hình chiếu của A lên ( ) . Biết rằng tam giác MAB cân tại M . Diện tích của tam giác MAB bằng 3 3 3 123 A. 6 3 . B. . C. . D. 3 3 . 2 2
Câu 49. Cho hàm số y = f ( x) liên tục trên , có đồ thị như hình vẽ. 3 + Giá trị 4m m
của tham số m để phương trình 2
= f (x) + 3 có hai nghiệm phân biệt trên đoạn 2 2 f ( x) + 5 a 3 − ;7) là m = với ,
a b là hai số nguyên tố. Tính T = a + . b b
A. T = 43.
B. T = 35.
C. T = 39.
D. T = 45.
Câu 50. Có tất cả bao nhiêu giá trị nguyên của y sao cho ứng với mỗi y luôn tồn tại không quá 63 số nguyên
x thỏa mãn điều kiện log ( 2 x + y ) + log
( 2y + y +64 log x− y ? 2024 2025 ) 4 ( ) A. 301. B. 302. C. 604. D. 603.
________________HẾT________________ Trang 73
ÑAÙP AÙN ÑEÀ SOÁ 10 1 2 3 4 5 6 7 8 9 10 C C C D B D B D A D 11 12 13 14 15 16 17 18 19 20 D B D C B B D D B B 21 22 23 24 25 26 27 28 29 30 B B C A A B B D A A 31 32 33 34 35 36 37 38 39 40 B D C A B D A A D C 41 42 43 44 45 46 47 48 49 50 A C B C B D B B C C
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 10
Câu 42. Cho hình lăng trụ AB . C A B C
có các mặt bên đều là hình vuông cạnh a . Gọi D là trung điểm của
cạnh BC . Tính khoảng cách giữa hai đường thẳng A B và DC . a 3 a 2 a 5 a 3 A. . B. . C. . D. . 6 6 5 4 Hướng dẫn giải:
Gọi D là trung điểm B C ; trong (BB C C
) , vẽ DH ⊥ BD tại H (1). Ta có:
AD ⊥ B C
AD ⊥ (BB C C ) A D ⊥ DH (2) .
AD ⊥ BB
Từ (1) và (2) suy ra DH ⊥ ( A B D) (3).
Ta có: DC// ( A B D) suy ra:
d ( DC AB) = d ( DC ( A BD
)) = d (D ( A BD ))(3) , , , = DH . Xét B
DD vuông tại D có: a .a B . D DD a 5 2 DH = = = . 2 2 2 + 5 BD DD a 2 + a 4 a Choïn
Vậy d ( DC A B ) 5 , = DH = . ⎯⎯⎯ → C 5 e f ( x)
Câu 43. Cho hàm số f ( x) có đạo hàm liên tục và có đạo hàm trên 1;e . Biết dx = 1
, f (e) = 2 . Tính x 1 e f (x)ln xdx . 1 A. 2. B. 1. C. 0. D. 3 . Hướng dẫn giải: Trang 74 u = f (x) d u = f (x)dx e f ( x) e Đặ e t dx = f
(x)ln x − f (x) dx . Khi đó: ln d x x . d v = v = ln x (x1;e) 1 x 1 1 x e e = Choïn 2 − f (x)ln d x x = 1 f (x)ln d x x = 1 . ⎯⎯⎯ → B 1 1
Câu 44. Cho hình hộp chữ nhật ABC . D A B C D
có diện tích các mặt ABC , D ABB A , ADD A lần lượt bằng 2 2 2
30cm , 40cm , 48cm . Bán kính mặt cầu ngoại tiếp hình hộp bằng 5 5 2 5 A. 3 10cm. B. 5 10cm. C. cm. D. cm. 2 5 Hướng dẫn giải: Đặt AB = , x AD = , y AA = . z Ta có xy = 30 xyz = 240 x = 5 xz = 40 xyz xyz
xyz y = 6. x = , y = , z = yz = 48 yz xz xy z = 8
Tâm mặt cầu ngoại tiếp hình hộp chữ nhật cũng chính là
tâm I của hình hộp. Do đó bán kính mặt cầu cần tìm là BD 1 5 5 2 2 2 R = = 5 + 6 + 8 = Choïn . ⎯⎯⎯ → C 2 2 2
Câu 45. Có bao nhiêu giá trị nguyên của tham số m để hàm y = 5 − msin x − (m + )
1 cos x xác định trên ? A. 6 . B. 8 . C. 7 . D. 5 . Hướng dẫn giải: Hàm số xác định trên
5− msin x −(m+ ) 1 cos x 0, x
msin x + (m+ ) 1 cos x 5, x
. Xét hàm y = msin x + (m+ )
1 cos x (*) với x .
Điều kiện có nghiệm của (*): m + (m + )2 2 2 2 1
y y 2m + 2m +1 hay 2
Maxy = 2m + 2m +1 . +
Vậy yêu cầu bài toán được thỏa mãn khi và chỉ khi 2
Maxy = 2m + 2m +1 5 2
2m + 2m+1 25 4 − m 3 . Choïn
Vì m nguyên nên m 4 − ; 3 − ;...;
3 . Vậy có 8 giá trị nguyên của m thỏa mãn đề bài. ⎯⎯⎯ → B Câu 46.
Cho mặt cầu (S ) tâm O , bán kính bằng 2 và
mặt phẳng ( P) . Khoảng cách từ O đến ( P) bằng 4 .
Từ điểm M thay đổi trên ( P) kẻ các tiếp tuyến MA ,
MB , MC tới (S ) với A , B , C là các tiếp điểm.
Biết mặt phẳng ( ABC ) luôn đi qua một điểm I cố
định. Tính độ dài OI . 3 1 A. 3 . B. . C. . D. . 2 2 Hướng dẫn giải:
Gọi K là giao của mặt phẳng ( ABC ) và OM . Trang 75
Gọi H là hình chiếu của O trên ( P) . Trong mặt phẳng (OMH ) kẻ KI ⊥ OM tại K (I OH ) .
Ta có ( ABC ) là mặt phẳng qua K và vuông góc với OM nên KI ( ABC) . 2 2 OA 2 Ta có 2
OA = OK.OM = OI.OH OI = = = 1. OH 4 Choïn
Mặt khác I thuộc đoạn thẳng OH nên I cố định. Vậy OI =1. ⎯⎯⎯ → D
Câu 47. Cho số phức z thỏa mãn 2
z + z + z − z = z . Giá trị lớn nhất của biểu thức P = z − 5 − 2i bằng: A. 2 + 5 3 . B. 2 + 3 5 . C. 5 + 2 3 . D. 5 + 3 2 . Hướng dẫn giải: Gọi z = x + i
y (với x , y R ) có điểm biểu diễn M. Suy ra z = x − i y và 2 2 2
z = x − y + 2x i y . Theo giả thiết, ta có: 2
z + z + z − z = z x +
y = ( x − y )2 2 2 2 2 2 2 + 4x y 4 4 2 2 2 2 2 x + 2 y =
x + y + 2x y 2 x + 2 y = x + y
x − x + + y − y + = ( x − )2 + ( y − )2 2 2 2 1 2 1 2 1 1 = 2 .
Suy ra tập hợp điểm biểu diễn số phức z là bốn đường tròn tâm I 1 ; 1
và bán kính R = 2 . 1,2,3,4 ( )
Khi đó, P = z − 5 − 2i = MA, với A(5;2) .
Mặt khác, vì A(5;2) thuộc góc phần tư thứ
nhất nên MA lớn nhất M thuộc đường tròn (C có tâm I 1 − ; 1
− và bán kính R = 2 . 3 ( ) 3 ) Do vậy P = I A+ R Max 3 = ( + )2 + ( + )2 5 1 2 1 + 2 = 3 5 + 2 . Choïn ⎯⎯⎯ → B
Câu 48. Trong không gian Oxyz cho mặt phẳng ( ) : x − z − 3 = 0 và điểm M (1;1; )
1 . Gọi A là điểm thuộc tia
Oz , gọi B là hình chiếu của A lên ( ) . Biết rằng tam giác MAB cân tại M . Diện tích của tam giác MAB bằng 3 3 3 123 A. 6 3 . B. . C. . D. 3 3 . 2 2 Hướng dẫn giải: x = t
Gọi A(0;0;a) . Đường thẳng AB qua A và vuông góc với ( ) có phương trình y = 0 ;
z = a −t Trang 76
x = t; y = 0; z = a − t
B là hình chiếu của A lên ( ) nên tọa độ B thỏa mãn hệ x− z −3 = 0 a + 3 a + 3 a − 3 = = = − =
x = t; y = 0; z = a − t x ; y 0; z a + − a 3 a 3 2 2 2 hay B ; 0; . t −
(a − t) − 3 = 0 a + 3 2 2 t = 2 2 2 + − = 2 a 1 a 5 a 3
Tam giác MAB cân tại M nên 2 2
MA = MB 1+1+ (1− a) = +1+ . 2 2 a = 3 − MA = ( 1 − ; 1 − ;2)
A(0;0;3) B(3;0;0) ▪ Nếu a = 3 thì , ; ta có: M , A MB = (3;3;3) . MB = (2; 1 − ;− ) 1 1 3 3 Choïn
Diện tích tam giác MAB : S = M , A MB = ⎯⎯⎯ → B M AB . 2 2 ▪ Nếu a = 3
− thì tọa độ A(0;0; 3 − ) và B(0;0; 3
− ) ; trường hợp này bị loại do A, B trùng nhau.
Câu 49. Cho hàm số y = f ( x) liên tục trên , có đồ thị như hình vẽ. 3 4m + m
Giá trị của tham số m để phương trình 2
= f (x) + 3 có hai nghiệm phân biệt trên đoạn 2 2 f ( x) + 5 a 3 − ;7) là m = với ,
a b là hai số nguyên tố. Tính T = a + . b b
A. T = 43.
B. T = 35.
C. T = 39.
D. T = 45. Hướng dẫn giải: 3 4m + m Ta có: 2 = f (x) 3 2
+ 3 4m + m = f (x) 2
+ 3 2 f (x) + 5 2 2 f ( x) + 5 3 2
m + m = f (x) 2 8 2 2
+ 6 2 f (x) +5
( m)3 + m = ( 2 f ( x) + ) 2 f ( x) 2 2 2 2 5 2
+ 5 + 2 f (x) +5 ( ) * .
Xét hàm số: f (t) 3
= t +t f (t) 2 ; = 3t +1 0, t
f (t) đồng biến trên . Trang 77
Do đó: ( ) f ( m) = f ( 2 f ( x) + ) 2 * 2 2
5 2m = 2 f ( x) + 5 5 m 0 m 2 − f (x) 2 . 4m 5 2 = − f ( x) 2 4m 5 2 = 2
Ta thấy toàn bộ đồ thị hàm số y = f ( x) đều nằm phía trên trục hoành với x 3 − ;7), vì vậy hàm số
y = f ( x) có đồ thị trùng với đồ thị hàm số y = f ( x) với mọi x 3 − ;7). 2 x 3 − ;7) 2 4m − 5 4m − 5 5
Do vậy f ( x) = f (x) = với m (*). 2 2 2 5 m 2 37 a
Dựa vào đồ thị hàm số đã cho, ta thấy (*) tương đương m = = . 2 4m − 5 2 b = 4 2
Vậy a = 37, b = 2 T = a +b = Choïn 39. ⎯⎯⎯ → C
Câu 50. Có tất cả bao nhiêu giá trị nguyên của y sao cho ứng với mỗi y luôn tồn tại không quá 63 số nguyên
x thỏa mãn điều kiện log ( 2 x + y ) + log
( 2y + y +64 log x− y ? 2024 2025 ) 4 ( ) A. 301 B. 302 C. 604 D. 603 Hướng dẫn giải:
Bất phương trình đã cho trở thành: log ( 2 x + y ) + log
( 2y + y +64 −log x− y 0. 2024 2025 ) 4 ( )
Đặt f ( x) = log ( 2 x + y ) + log
( 2y + y +64 −log x− y (ta xem y là tham số). 2024 2025 ) 4 ( ) 2 x + y 0 2 + Điề x y 0
u kiện xác định của f ( x) là: 2 2
y + y + 64 0
x y −y (do , x y nguyên). x − y 0 x − y 0 Với ,
x y nguyên thì ta chỉ xét f ( x) trên nửa khoảng y +1;+). Ta có: f ( x) 1 1 1 = ( − − 0, x y +1 2
x + y )ln 2024 ( x − y)ln 2025 ( x − y)ln 4 1 1 (vì 2
x + y x − y 0, ln 2024 ln 4 ( ). 2
x + y )ln 2024 ( x − y)ln 4
Ta có bảng biển thiên của hàm số f ( x) : Trang 78
Yêu cầu bài toán trở thành: f ( y + 64) 0 log
( 2y + y +64)+log ( 2y + y +64 log 64 2024 2025 ) 4 log 2025.log
( 2y + y +64)+log ( 2y + y +64 log 64 2024 2025 2025 ) 4 log ( 3 2 y + y + 64).(log 2025 + ) 1 3 log ( 2y + y+64 2025 2024 2025 ) log 2025+1 2024 3 2 log + 2024 2025 1
y + y + 64 − 2025 0 3
− 02,2 y 301,2 . Choïn
Vì y nguyên nên y 3 − 02; 3 − 01;...;300;30
1 . Vậy có 604 giá trị của y thỏa mãn. ⎯⎯⎯ → C Trang 79