Trang 1
ĐỀ 31
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Đồ thị hàm số nào sau đây có đường tiệm cận?
A.
42
31y x x= + +
. B.
1
2
x
y
x
−
=
+
. C.
32
23y x x= − +
. D.
1yx=−
.
Câu 2. Điểm cực đại của hàm số
32
33y x x= − −
là
A.
0x =
. B.
2x =
. C.
3x =−
. D.
7x =−
.
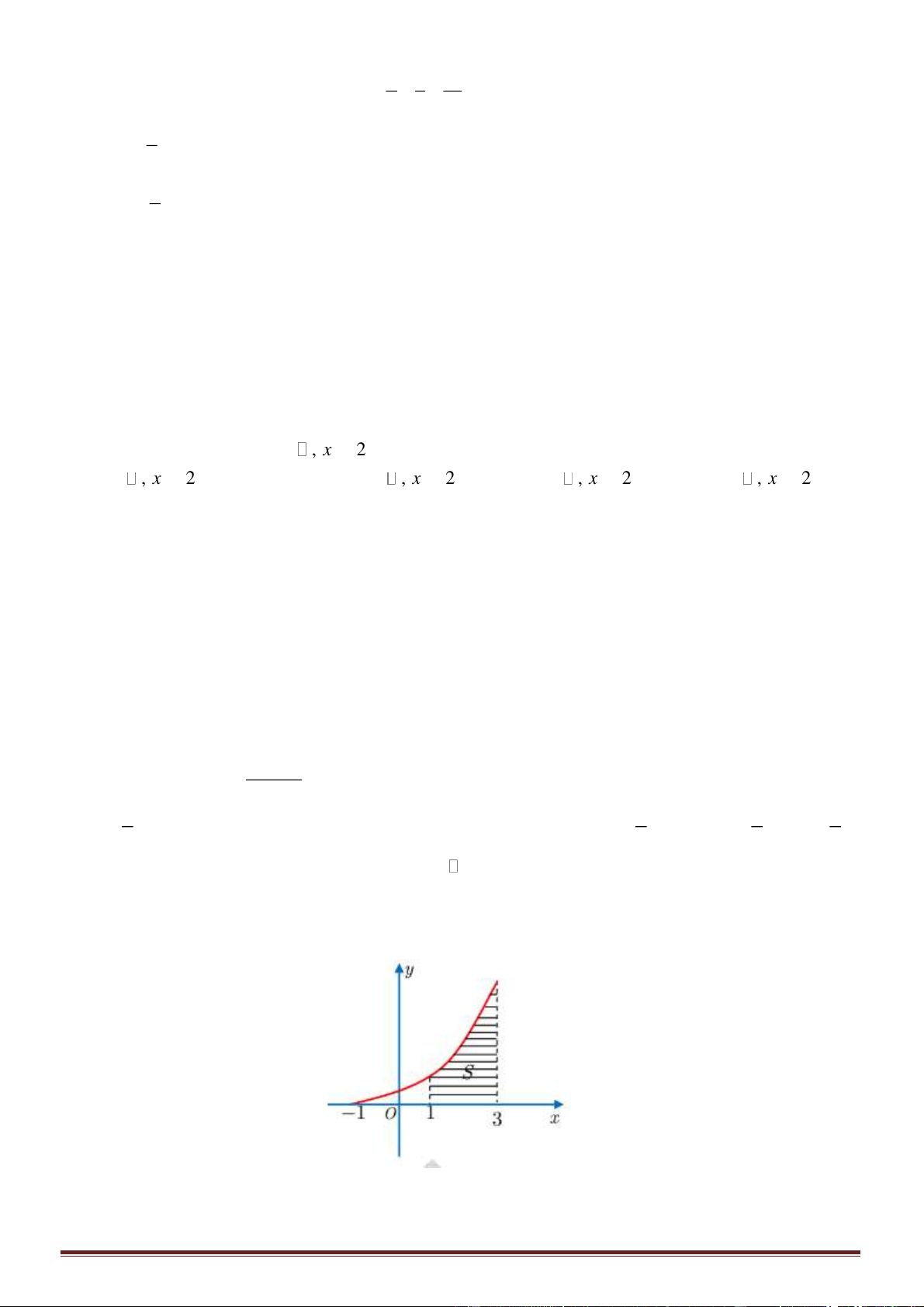
Câu 3. Cho hàm số
( )
y f x=
xác định, liên tục trên
\1
và có bảng biến thiên như hình vẽ dưới
đây:
Hãy chọn khẳng định đúng:
A. Hàm số có
3
cực trị.
B. Hàm số đạt cực đại tại
1x =−
, cực tiểu tại
0x =
.
C. Hàm số đạt cực đại tại
1x =
, cực tiểu tại
0x =
.
D. Hàm số đạt giá trị lớn nhất bằng
1
và giá trị nhỏ nhất bằng
1−
.
Câu 4. Hàm số nào sau đây có đạo hàm là
( )
1
3 ln4
y
x
=
−
.
A.
( )
4
log 3yx=−
. B.
3
4
x
y
−
=
. C.
( )
1
3
ln4
yx=−
. D.
( )
ln 3 .ln4yx=−
Câu 5. Giá trị
2d
b
a
xx
được tính là :
A.
22
ba−
. B.
22
ba+
. C.
ba−
. D.
ba+
.
Câu 6. Cho
z a bi=+
. Mệnh đề nào sau đây đúng.
A. Phần thực là
a
và phần ảo là
bi
. B. Điểm biểu diễn
z
là
( )
;M a b
.
C.
2 2 2
2z a b abi= + +
. D.
22
z a b=+
.
Câu 7. Cho hình chóp tam giác
.S ABC
. Lấy
M
,
N
,
P
lần lượt thuộc cạnh
SA
,
SB
,
SC
thỏa mãn
2SA SM=
,
3SB SN=
,
2SC SP=
. Biết thể tích
.S ABC
là
3
2
a
. Thể tích khối chóp
.S MNP
là
A.
3
4
a
. B.
3
2
7
a
. C.
3
24
a
. D.
3
16
a
.
Câu 8. Đường thẳng nào sau đây vuông góc với
( )
1 2 3
d:
1 2 3
x y z− − −
==
.
A.
1 2 1
1 2 1
x y z+ + −
==
−
. B.
1 1 1
211
x y z+ + +
==
. C.
11
1 2 1
x y z−+
==
−
. D.
1
2 1 1
x y z+
==
−−
.
Câu 9. Mặt phẳng nào sau đây cắt mặt cầu
( )
2 2 2
S : 2 2 4 3 0x y z x y z+ + − − − − =
theo thiết diện là một
đường tròn?
A.
0z y z− + =
. B.
2 2 6 0x y z+ + + =
. C.
2 3 3 0x y z+ + + =
. D. Cả
3
đều sai.
Câu 10. Diện tích xung quanh của hình trụ có chiều cao
,h
đường kính đáy
R
bằng
x
y
y
−
+
1−
0
1
0
+
−
+
−
−
1
1−
+
+
−
Trang 2
A.
2
hR
. B.
2 Rh
. C.
Rh
. D.
4
Rh
.
Câu 11. Trong các dãy số sau, dãy số nào không là cấp số cộng?
A.
1 1 1 1
; ; ; ;...
2 2 2 2
−
−
. B.
0;3;6;9;...
C.
11
1; ;0; ;...
22
−
D.
4;3;2;1;...
Câu 12. Lớp bạn An có
45
học sinh, cô giáo chọn ngẫu nhiên một bạn làm lớp trưởng. Tính xác suất để
bạn An là lớp trưởng.
A.
1
2
. B.
1
45
. C.
2
15
. D.
3
5
.
Câu 13. Hàm số
4 3 2
1 1 1
12
4 3 2
y x x x x= + − − −
đồng biến trên khoảng nào ?
A.
( )
;1− −
. B.
( )
1;0−
. C.
( )
0;1
. D.
( )
1; +
.
Câu 14. Tập tất cả các giá trị
m
để đồ thị hàm số
32
33y x mx x= − + −
có hai điểm cực trị là
A.
( )
1;3−
. B.
( ) ( )
; 3 3;− − +
. C.
( ) ( )
1;2 4; +
. D. Đáp án khác.
Câu 15. Các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
3
1
3
x
yx
x
= − +
+
là
A.
3; 1xy= − =
. B.
1
3;
2
xy= − = −
. C.
1
3;
2
xy= − =
. D.
1
3;
2
xy= = −
.
Câu 16. Ngân hàng đề thi gồm
20
câu hỏi. Mỗi đề gồm
4
câu được chọn ngẫu nhiên từ
20
câu hỏi
trên. Thí sinh
A
đã học thuộc
10
câu trong ngân hàng đề thi. Tính xác suất để thí sinh
A
rút ngẫu nhiên
được
1
đề thi có ít nhất
2
câu đã thuộc
A.
229
323
. B.
227
323
. C.
29
33
. D.
223
322
.
Câu 17. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
2
4.cos .sin .cos
22
xx
f x x=
,
( )
01F =
. Khi đó,
3
F
bằng
A.
19
12
. B.
13
8
. C.
15
8
−
. D.
29
16
−
.
Câu 18. Hàm số
tan 2
3
yx
=−
có chu kì tuần hoàn là
A.
2T
=
. B.
4
T
=
. C.
2
T
=
. D.
T
=
.
Câu 19. Cho số phức
23zi=+
. Mô đun số phức
( )( )
3 2 1w z z i= − + −
là.
A.
3 15
. B.
7 13
. C.
67
. D.
123
.
Câu 20. Quỹ tích điểm
M
biểu diễn số phức
z
thỏa mãn
2z i z i+ − = −
là.
A.
10xy− + =
. B.
2 2 0xy− + =
.
C.
( ) ( )
22
1 2 4xy− + − =
. D.
( ) ( )
22
1 2 4xy+ + + =
.
Câu 21. Một hình thang vuông
ABCD
có đường cao
AD
=
, đáy nhỏ
AB
=
, đáy lớn
2CD
=
. Cho
hình thang đó quay quanh
CD
, ta được vật tròn xoay có thể tích bằng
A.
4
4
3
. B.
4
7
3
. C.
4
10
3
. D.
4
13
3
.
Câu 22. Tập nghiệm của bất phương trình
( )
11
22
log 1 log 3x −
là
A.
( )
4;+
. B.
( )
;1−
. C.
( )
1;4
. D.
( )
1; +
.
Trang 3
Câu 23. Cho hàm số
( )
3x 2
1
yC
x
+
=
−
. Lấy
M
là điểm tùy ý trên
( )
C
. Tích khoảng cách từ điểm
M
đến
hai đường tiệm cận là
A.
4
. B.
5
. C.
2
. D. Không xác định
Câu 24. Cho hàm số
( ) ( )
32
5x 4 ;
m
y x m x m C= − + + −
.Giá trị của
m
để
( )
m
C
tồn tại ít nhất một tiếp
điểm mà tiếp tuyến tại đó vuông góc với đường thẳng
1
3
2
yx=+
là
A.
7
3
m
. B.
5
6
m
. C.
3m
. D.
2m
.
Câu 25. Cho phương trình
( )
2
4 2 1 .2 4 0
xx
mm− + − + =
. Tìm số giá trị nguyên của
m
để phương trình
có hai nghiệm trái dấu
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 26. Cho hình phẳng được giới hạn bởi hai đồ thị hàm số
2
log , 0, 4y x y x= = =
. Đường thẳng
2x =
chia hình phẳng đó thành hai hình có diện tích là
12
SS
. Tỷ lệ thể tích
1
2
2S
S
−
là
A.
2
. B.
7
4
. C.
3
. D. 5.
Câu 27. Cho hàm số
( ) ( )
2
1
d
1
x
t
f x x
tt
=
+
. Tập giá trị của hàm số là
A.
( )
1;+
. B.
( )
0;+
. C.
( )
ln2;1
. D.
( )
0;ln2
.
Câu 28. Thể tích hình hộp chữ nhật đạt giá trị lớn nhất bằng bao nhiêu nếu biết diện tích toàn phần của
hình hộp đã cho là
S
?
A.
3
8
S
. B.
3
27
S
. C.
3
125
S
. D.
3
216
S
.
Câu 29. Cho lục giác đều có cạnh bằng
a
. Quay lục giác quanh đường trung trực của một cạnh ta được
khối tròn xoay có thể tích bằng
A.
3
73
12
a
V
=
. B.
3
73
6
a
V
=
. C.
3
53
12
a
V
=
. D.
3
33
4
a
V
=
.
Câu 30. Cho hình chóp
.S ABCD
.
,MN
là hai điểm trên
,.AB CD
Mặt phẳng
( )
qua
// .MN SA
Điều
kiện của
MN
để thiết diện của hình chóp với
( )
là hình thang là
A.
//MN AD
. B.
//MN BC
.
C.
,MN
là trung điểm
,AB CD
. D.
MN
qua trung điểm
AC
.
Câu 31. Cho
1 2 3
2 , 3 2 , 7 3z i z i z i= + = - = +
. Gọi số phức
z
có mô đun nhỏ nhất thỏa mãn
1 2 3
z z z z- = -
là
0
z
. Tính
0
z
A.
21 5+
. B.
75+
. C.
37 5−
. D.
41 5−
.
Câu 32. Trong không gian
Oxyz
, cho các điểm
( ) ( ) ( )
1;0;0 , 2;0;3 , 0;0;1A B M−
và
( )
0;3;1N
. Mặt
phẳng
( )
P
đi qua các điểm
,MN
sao cho khoảng cách từ điểm
B
đến
( )
P
gấp hai lần khoảng cách từ
điểm
A
đến
( )
P
. Có bao nhiêu mặt phẳng
( )
P
thỏa mãn đề bài?
A. Có hai mặt phẳng
( )
P
. B. Chỉ có một mặt phẳng
( )
P
.
C. Không có mặt phẳng
( )
P
nào. D. Có vô số mặt phẳng
( )
P
.
Câu 33. Có bao nhiêu số nguyên m để hàm số
4 3 2
8 3(2 1) 13= − − − + +y x mx m x
có cực đại mà không có
cực tiểu?
A.
0
. B.
1
. C.
2
. D.
3
.
Trang 4
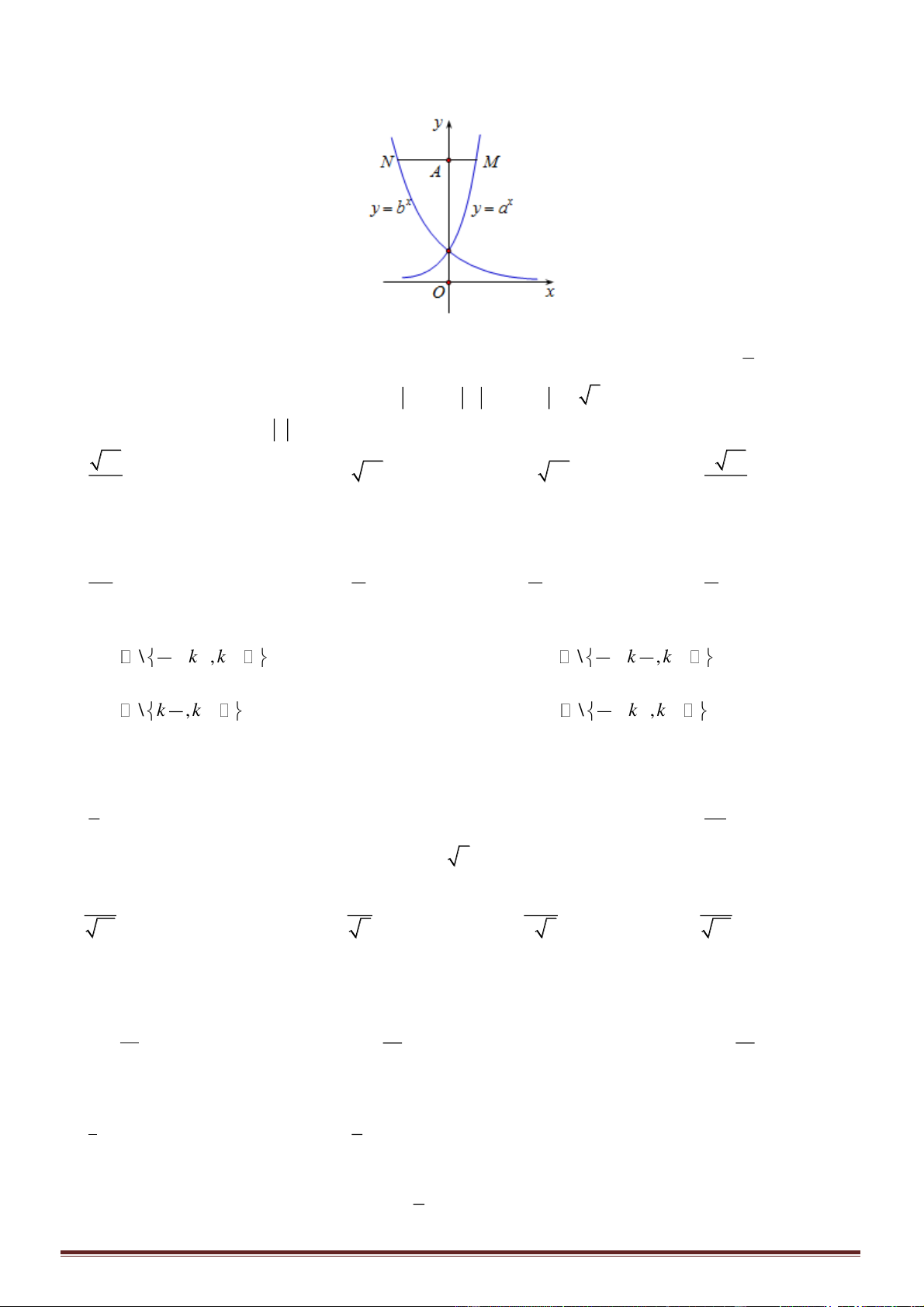
Câu 34. Cho các số thực
a
,
b
khác
1
. Biết rằng bất kỳ đường thẳng nào song song với trục
Ox
mà cắt
các đường
x
ya=
,
x
yb=
, trục tung lần lượt tại
M
,
N
và
A
thì
2AN AM=
(hình vẽ bên).
Mệnh đề nào sau đây đúng?
A.
2
ab=
. B.
2ba=
. C.
2
1ab =
. D.
1
2
ab =
.
Câu 35. Cho số phức
z
thỏa mãn điều kiện
2 2 3 2 5z i z i+ − + − − =
. Gọi
, Mm
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của
z
. Tính giá trị
.Mm
.
A.
65
5
B.
65
C.
2 26
D.
4 65
5
Câu 36. Cho
00
( ) cos ( ) 1f x dx xf x dx
==
. Tính giá trị lớn nhất của
1
2
0
()f x dx
A.
3
2
. B.
2
. C.
3
. D.
4
Câu 37. Tập xác định của hàm số là?
A. . B. .
C. . D. .
Câu 38. Cho mặt phẳng
( )
: 2 1 0x y z
− + − =
và điểm
( ) ( )
0; 1;1 , 1;1; 2AB−−
. Biết
( ) ( )
;;M a b c
sao cho
MA MB+
đạt giá trị nhỏ nhất. Giá trị của
2 2 2
abc++
bằng:
A.
2
9
. B.
26
. C.
78
. D.
14
49
.
Câu 39. Cho tứ diện
ABCD
đều có cạnh bằng
22
. Gọi
G
là trọng tâm của tứ diện
ABCD
và
M
là
trung điểm
AB
. Khoảng cách giữa hai đường thẳng
BG
và
CM
bằng:
A.
2
14
. B.
2
5
. C.
3
25
. D.
2
10
.
Câu 40. Cho hình chóp
.S ABC
có
( )
,SA ABC⊥
ABC
vuông cân tại A,
.SA BC a==
Tính theo a thể
tích V của khối chóp
.S ABC
A.
3
.
12
a
V =
B.
3
.
4
a
V =
C.
3
2.Va=
D.
3
.
2
a
V =
Câu 41. Cho (S) là mặt cầu tâm I(2; 1; -1) và tiếp xúc với mặt phẳng (P) có phương trình: 2x – 2y – z + 3
= 0. Khi đó, bán kính của (S) là:
A.
1
3
B.
4
3
C.
3
D.
2
Câu 42. Cho cấp số nhân có
1
3u =
,
2
3
q =
. Chọn kết quả đúng:
tan2yx=
\,
4
D k k
= +
\,
42
D k k
= +
\,
2
D k k
=
\,
2
D k k
= +
Trang 5
A. Bốn số hạng tiếp theo của cấp số là:
4 8 16
2; ; ; .
3 3 3
B.
1
2
3. .
3
n
n
u
−
=
C.
2
9. 9.
3
n
n
S
=−
D.
( )
n
u
là một dãy số tăng.
Câu 43. Mệnh đề nào sau đây có thể sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường
thẳng thì song song nhau.
Câu 44. Một tổ học sinh có
5
nam và
5
nữ xếp thành một hàng dọc thì số các cách xếp khác nhau là:
A.
25
. B.
10
. C.
10!
. D.
40
.
Câu 45. Cho mệnh đề ‘’
2
, 2 0xx +
’’. Phủ định của mệnh đề trên là:
A.
2
, 2 0xx +
. B.
2
, 2 0xx +
. C.
2
, 2 0xx +
. D.
2
, 2 0xx +
.
Câu 46. Có bao nhiêu tập X thỏa mãn
{1;2} {1;2;3;4;5}X
A.
8.
B.
10.
C.
9.
D.
11.
Câu 47. Phương trình
2
ax 0bx c+ + =
có nghiệm duy nhất khi và chỉ khi:
A.
0a =
. B.
0
0
a
=
hoặc
0
0
a
b
ì
=
ï
ï
í
ï
¹
ï
î
.
C.
0abc= = =
. D.
0
0
a
=
.
Câu 48. Cho phương trình
( )
22
m 3m 2 x m 4m 5 0− + + + + =
. Tìm tất cả các giá trị thực của tham số
m
để phương trình đã cho có nghiệm đúng với mọi
x Î ¡
.
A.
2m =−
. B.
5m =−
. C.
1m =
. D. Không tồn tại.
Câu 49. Phương trình
21
3
1
mx
x
−
=
+
có nghiệm duy nhất khi:
A.
3
.
2
m
B.
0.m
C.
0m
và
3
.
2
m
D.
1
2
m −
và
3
.
2
m
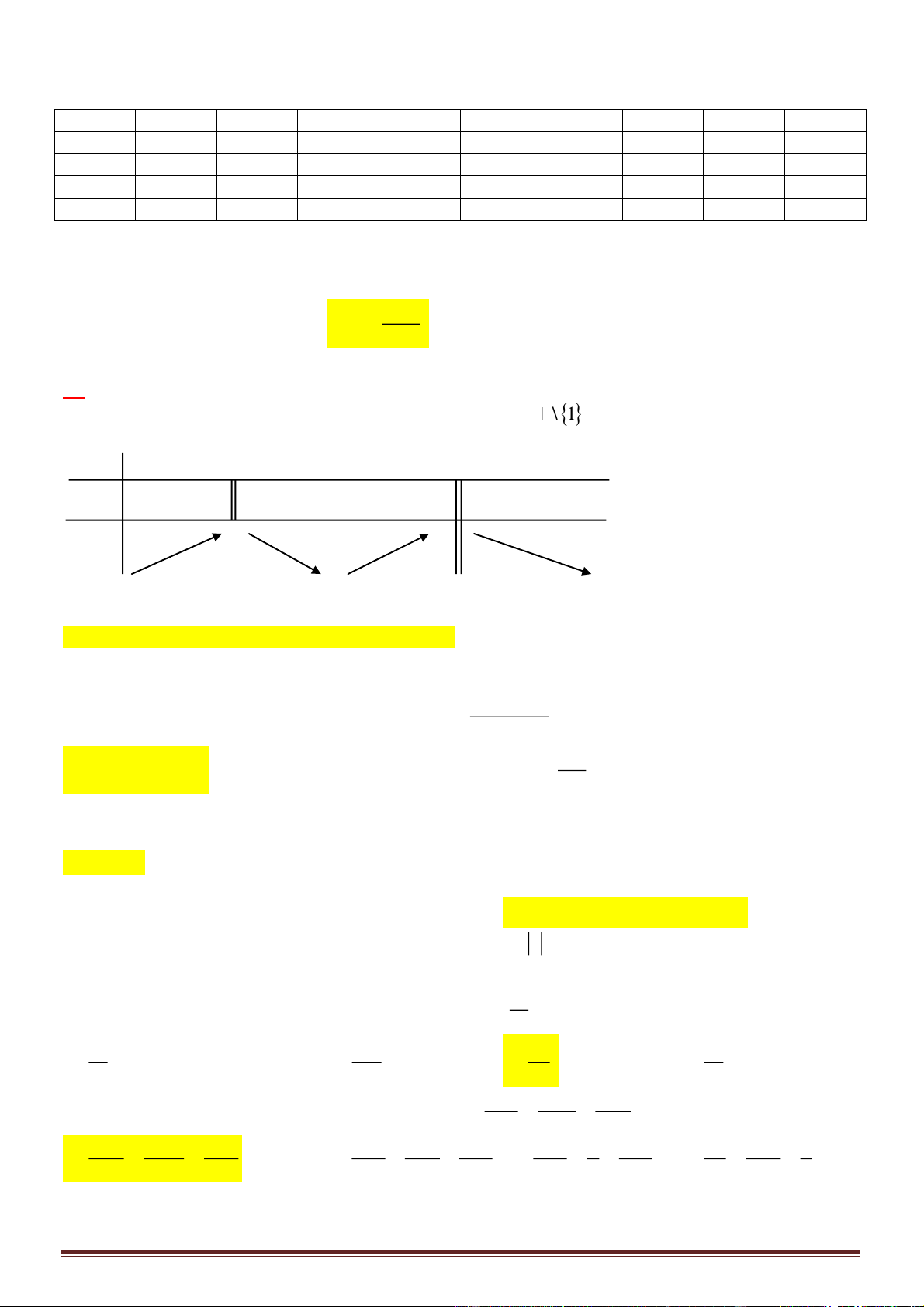
Câu 50. Cho hai hàm số
( )
y f x=
liên tục trên và hàm số
( )
( )
23
y g x x f x==
có đồ thị trên đoạn
1;3−
như hình vẽ. Biết miền hình phẳng được tô sọc có diện tích
6S =
. Tính tích phân
( )
27
1
I f x dx=
.
A.
2I =
. B.
12I =
. C.
24I =
. D.
18I =
.
Trang 6
ĐÁP ÁN
1 B
2 A
3 B
4 A
5 A
6 B
7 C
8 A
9 A
10 B
11 A
12 B
13 D
14 B
15 B
16 A
17 A
18 C
19B
20A
21 A
22 C
23 B
24 A
25 D
26 A
27 D
28 D
29A
30 B
31 D
32 D
33 B
34 C
35 D
36 C
37 B
38 D
39 A
40 A
41 A
42 B
43 C
44 C
45 B
46 A
47 B
48 D
49 D
50 D
GIẢI CHI TIẾT
Câu 1. Đồ thị hàm số nào sau đây có đường tiệm cận?
A.
42
31y x x= + +
. B.
1
2
x
y
x
−
=
+
. C.
32
23y x x= − +
. D.
1yx=−
.
Câu 2. Điểm cực đại của hàm số
32
33y x x= − −
là
A.
0x =
. B.
2x =
. C.
3x =−
. D.
7x =−
.
Câu 3. Cho hàm số
( )
y f x=
xác định, liên tục trên
\1
và có bảng biến thiên như hình vẽ
dưới đây:
Hãy chọn khẳng định đúng:
A. Hàm số có
3
cực trị.
B. Hàm số đạt cực đại tại
1x =−
, cực tiểu tại
0x =
.
C. Hàm số đạt cực đại tại
1x =
, cực tiểu tại
0x =
.
D. Hàm số đạt giá trị lớn nhất bằng
1
và giá trị nhỏ nhất bằng
1−
.
Câu 4. Hàm số nào sau đây có đạo hàm là
( )
1
3 ln4
y
x
=
−
.
A.
( )
4
log 3yx=−
. B.
3
4
x
y
−
=
. C.
( )
1
3
ln4
yx=−
. D. Đáp án khác
Câu 5. Giá trị
2d
b
a
xx
được tính là :
A.
22
ba−
. B.
22
ba+
. C.
ba−
. D.
ba+
.
Câu 6. Cho
z a bi=+
. Mệnh đề nào sau đây đúng.
A. Phần thực là
a
và phần ảo là
bi
. B. Điểm biểu diễn
z
là
( )
;M a b
.
C.
2 2 2
2z a b abi= + +
. D.
22
z a b=+
.
Câu 7. Cho hình chóp tam giác
.S ABC
. Lấy
M
,
N
,
P
lần lượt thuộc cạnh
SA
,
SB
,
SC
thỏa mãn
2SA SM=
,
3SB SN=
,
2SC SP=
. Biết thể tích
.S ABC
là
3
2
a
. Thể tích khối chóp
.S MNP
là
A.
3
4
a
. B.
3
2
7
a
. C.
3
24
a
. D.
3
16
a
.
Câu 8. Đường thẳng nào sau đây vuông góc với
( )
1 2 3
d:
1 2 3
x y z− − −
==
.
A.
1 2 1
1 2 1
x y z+ + −
==
−
. B.
1 1 1
211
x y z+ + +
==
. C.
11
1 2 1
x y z−+
==
−
. D.
1
2 1 1
x y z+
==
−−
.
Câu 9. Mặt phẳng nào sau đây cắt mặt cầu
( )
2 2 2
S : 2 2 4 3 0x y z x y z+ + − − − − =
theo thiết diện là
một đường tròn?
x
y
y
−
+
1−
0
1
0
+
−
+
−
−
1
1−
+
+
−

Trang 7
A.
0z y z− + =
. B.
2 2 6 0x y z+ + + =
. C.
2 3 3 0x y z+ + + =
. D. Cả
3
đều sai.
Câu 10. Diện tích xung quanh của hình trụ có chiều cao
,h
đường kính đáy
R
bằng
A.
2
hR
. B.
2 Rh
. C.
Rh
. D.
4
Rh
.
Câu 11. Trong các dãy số sau, dãy số nào không là cấp số cộng?
A.
1 1 1 1
; ; ; ;...
2 2 2 2
−
−
. B.
0;3;6;9;...
C.
11
1; ;0; ;...
22
−
D.
4;3;2;1;...
Câu 12. Lớp bạn An có
45
học sinh, cô giáo chọn ngẫu nhiên một bạn làm lớp trưởng. Xác suất để bạn
An là lớp trưởng là
A.
1
2
. B.
1
45
. C.
2
15
. D.
3
5
.
Câu 13. Hàm số
4 3 2
1 1 1
12
4 3 2
y x x x x= + − − −
đồng biến trên khoảng nào ?
A.
( )
;1− −
. B.
( )
1;0−
. C.
( )
0;1
. D.
( )
1; +
.
Câu 14. Giá trị
m
để đồ thị hàm số
32
33y x mx x= − + −
có hai điểm cực trị là
A.
( )
1;3−
. B.
( ) ( )
; 3 3;− − +
. C.
( ) ( )
1;2 4; +
. D. Đáp án khác.
Câu 15. Các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
3
1
3
x
yx
x
= − +
+
là
A.
3; 1xy= − =
. B.
1
3;
2
xy= − = −
. C.
1
3;
2
xy= − =
. D.
1
3;
2
xy= = −
.
Câu 16. Ngân hàng đề thi gồm
20
câu hỏi. Mỗi đề gồm
4
câu được chọn ngẫu nhiên từ
20
câu hỏi
trên. Thí sinh
A
đã học thuộc
10
câu trong ngân hàng đề thi. Tính xác suất để thí sinh
A
rút ngẫu nhiên
được
1
đề thi có ít nhất
2
câu đã thuộc
A.
229
323
. B.
227
323
. C.
29
33
. D.
223
322
.
Câu 17. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
2
4.cos .sin .cos
22
xx
f x x=
,
( )
01F =
. Khi đó,
3
F
bằng
A.
19
12
. B.
13
8
. C.
15
8
−
. D.
29
16
−
.
Câu 18. Hàm số
tan 2
3
yx
=−
có chu kì tuần hoàn là
A.
2T
=
. B.
4
T
=
. C.
2
T
=
. D.
T
=
.
Câu 19. Cho số phức
23zi=+
. Mô đun số phức
( )( )
3 2 1w z z i= − + −
là.
A.
3 15
. B.
7 13
. C.
67
. D.
123
.
Câu 20. Quỹ tích điểm
M
biểu diễn số phức
z
thỏa mãn
2z i z i+ − = −
là.
A.
10xy− + =
. B.
2 2 0xy− + =
. C.
( ) ( )
22
1 2 4xy− + − =
. D. Đáp án khác.
Câu 21. Một hình thang vuông
ABCD
có đường cao
AD
=
, đáy nhỏ
AB
=
, đáy lớn
2CD
=
. Cho
hình thang đó quay quanh
CD
, ta được vật tròn xoay có thể tích bằng
A.
4
4
3
. B.
4
7
3
. C.
4
10
3
. D.
4
13
3
.
Câu 22. Tập nghiệm của bất phương trình
( )
11
22
log 1 log 3x −
là
A.
( )
4;+
. B.
( )
;1−
. C.
( )
1;4
. D.
( )
1; +
.

Trang 8
Câu 23. Cho hàm số
( )
3x 2
1
yC
x
+
=
−
. Lấy
M
là điểm tùy ý trên
( )
C
. Tích khoảng cách từ điểm
M
đến
hai đường tiệm cận là:
A.
4
. B.
5
. C.
2
. D. Không xác định
Lời gii
Chn B
Đồ thị
( )
C
có TCĐ là:
1
: 1 0x − =
và TCN là
2
: 3 0y − =
.
Vì
M
là điểm tùy ý trên
( )
C
nên lấy điểm
( ) ( )
0; 2MC−
Gọi
12
;dd
là khoảng cách từ điểm
M
đến hai đường tiệm cận.
Ta có
( )
11
1 0 1
;1
11
x
d d M
−−
= = = =
( )
22
3 2 3
;5
11
y
d d M
− − −
= = = =
Khi đó, Tích khoảng cách từ điểm
M
đến hai đường tiệm cận là
12
.5dd=
.
Câu 24. Cho hàm số
( ) ( )
32
5x 4 ;
m
y x m x m C= − + + −
.Giá trị của
m
để
( )
m
C
tồn tại ít nhất một tiếp
điểm mà tiếp tuyến tại đó vuông góc với đường thẳng
1
3
2
yx=+
là.
A.
7
3
m
. B.
5
6
m
. C.
3m
. D.
2m
.
Lời gii
Chn A
Ta có:
( )
'2
3 10x 4y x m= − + +
Để
( )
m
C
tồn tại ít nhất một tiếp điểm mà tiếp tuyến tại đó vuông góc với đường thẳng
1
3
2
yx= +
( ) ( )
22
3 10x 4 2 3x 10x 6x m m g x− + + = − = − + − =
có ít nhất một nghiệm
Khi và chỉ khi đường thẳng
ym=
cắt đồ thị
( )
2
3x 10x 6gx= − + −
tại ít nhất một điểm.
7
3
m
Câu 25. Cho phương trình
( )
2
4 2 1 .2 4 0
xx
mm− + − + =
. Tìm số giá trị nguyên của
m
để phương trình
có hai nghiệm trái dấu
A.
1
. B.
2
. C.
3
. D.
0
.
Lời gii
Chn D
Đặt
20
x
t =
. Khi đó, phương trình
( ) ( ) ( )
22
1 2 1 4 0g t t m t m = − + − + =
Để phương trình (1) có hai nghiệm trái dấu khi và chỉ khi
( )
0gt=
có hai nghiệm
( ) ( )
( )( )
( ) ( )
22
12
0 1 0 . 1 0 4 2 3 0 3; 2 1;2t t g g m m m m − + − − −
.
Do
.m Z m =
Vậy,không có giá trị nguyên của
m
để phương trình (1) có hai nghiệm trái dấu.
Câu 26. Cho hình phẳng được giới hạn bởi hai đồ thị hàm số
2
log , 0, 4y x y x= = =
. Đường thẳng
2x =
chia hình phẳng đó thành hai hình có diện tích là
12
SS
. Tỷ lệ thể tích
1
2
2S
S
−
là
A.
2
. B.
7
4
. C.
3
. D. 5.
Lời gii
Chn A
Gọi
S
là diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số
2
log , 0, 4y x y x= = =
.
Trang 9
Khi đường thẳng
2x =
chia hình phẳng đó thành hai hình có diện tích là
12
SS
.
Gọi
1
S
là diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số
2
log ,x 2, 4; 0y x x y= = = =
.
Và
2
S
là diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số
2
log , 0, 1; 2y x y x x= = = =
.
Khi đó : Tỷ lệ thể tích
4
2
2
1
2
2
2
1
log dx 2
2
2
log dx
x
S
S
x
−
−
==
.
Câu 27. Cho hàm số
( ) ( )
2
1
d
1
x
t
f x x
tt
=
+
. Tập giá trị của hàm số là:
A.
( )
1;+
. B.
( )
0;+
. C.
( )
ln2;1
. D.
( )
0;ln2
.
Lời gii
Chn D
Ta có
( )
( )
( )
2
1
1 1 1
d d 1 1
d ln ln 1
1
1
x x x
x
tt
f x t t t
tt
t t t t
= = = − = − +
+
++
1
1 2 2
ln ln ln ln ln
1 1 2 1 1
x
t x x x
t x x x
= = − = =
+ + + +
(vì
1x
).
Xét hàm số
( )
2
1
x
gx
x
=
+
với
1x
.
Ta có
( )
( )
2
2
0, 1
1
g x x
x
=
+
suy ra hàm số
( )
gx
đồng biến trên khoảng
( )
1;+
.
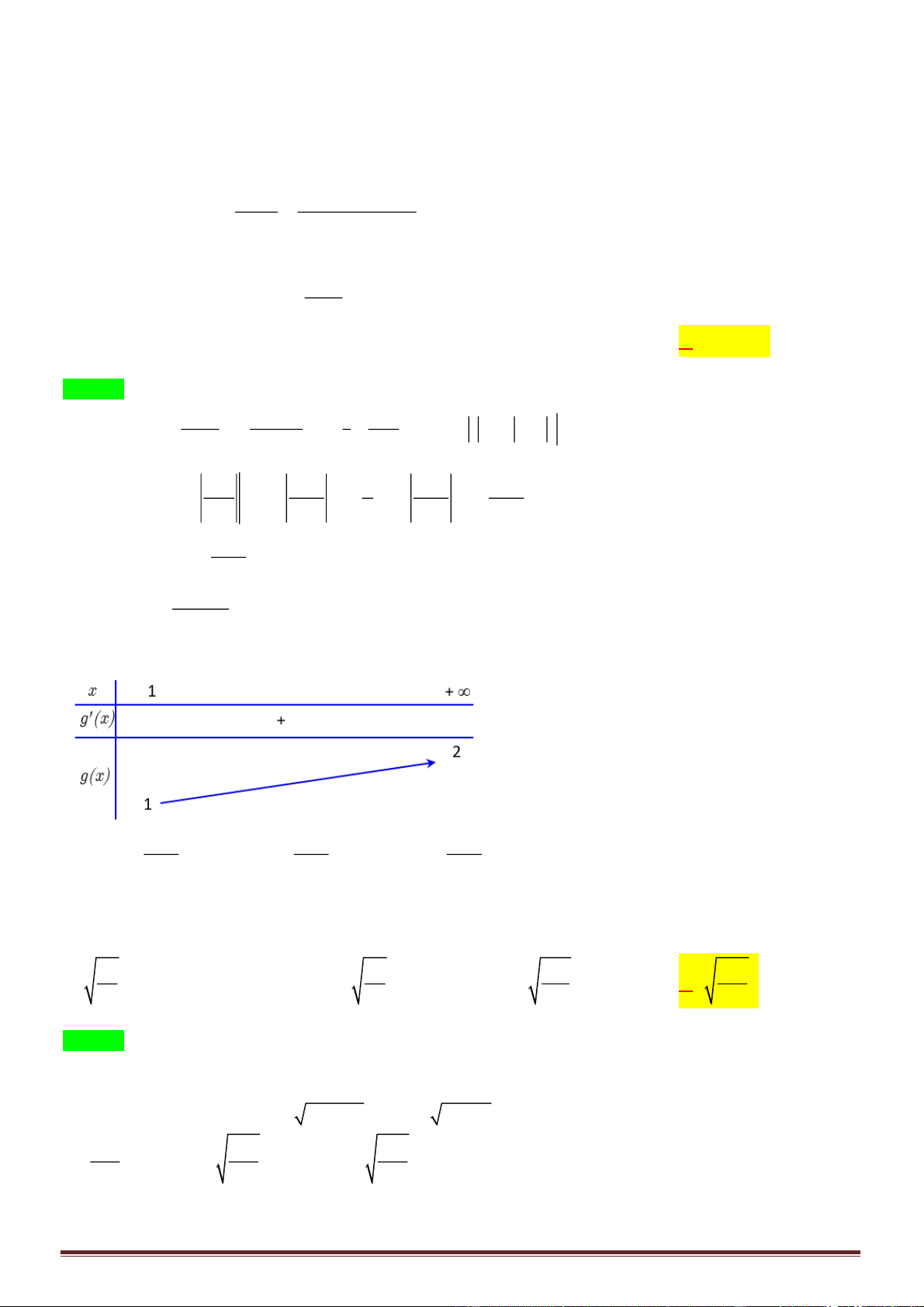
Bảng biến thiên:
Suy ra
( )
1 2 ln1 ln ln2 0 ln ln2 0 ln2
1 1 1
x x x
fx
x x x
+ + +
.
Vậy tập giá trị của hàm số là:
( )
0;ln2
.
Câu 28. Thể tích hình hộp chữ nhật đạt giá trị lớn nhất bằng bao nhiêu nếu biết diện tích toàn phần của
hình hộp đã cho là
S
?
A.
3
8
S
. B.
3
27
S
. C.
3
125
S
. D.
3
216
S
.
Lời gii
Chn D
Gọi
,,abc
lần lượt là ba kích thước của hình hộp chữ nhật, điều kiện
, , 0abc
.
Thể tích hình hộp chữ nhật là
V abc=
.
Ta có:
33
2 2 2 2 2 2
2 2 2 3 8 6= + + S ab ac bc a b c S a b c
3 3 3
2 2 2
216 216 216
S S S
a b c abc V
.

Trang 10
Đẳng thức xảy ra khi và chỉ khi
2
2 2 2
6
6
==
==
= = =
= + +
=
abc
ab bc ca
S
abc
S ab bc ca
Sa
.
Vậy thể tích hình hộp chữ nhật đạt giá trị lớn nhất bằng
3
216
S
khi
6
= = =
S
abc
.
Câu 29. Cho lục giác đều có cạnh bằng
a
. Quay lục giác quanh đường trung trực của một cạnh ta được
khối tròn xoay có thể tích bằng
A.
3
73
12
a
V
=
. B.
3
73
6
a
V
=
. C.
3
53
12
a
V
=
. D.
3
33
4
a
V
=
.
Lời gii
Chn A
Khối tròn xoay tạo thành khi quay lục giác đều quanh đường trung trực của một cạnh là khối hợp bởi 2
khối nón cụt bằng nhau có chiều cao
3
2
a
h =
; bán kính đáy lớn và đáy bé lần lượt là
12
;
2
a
r a r==
.
Thể tích khối tròn xoay cần tìm là:
( )
2
3
2 2 2
1 2 1 2
1 2 3 7 3
22
3 3 2 2 2 12
= = + + = + + =
knc
a a a a
V V h r r rr a a
.
Câu 30. Cho hình chóp
.S ABCD
.
,MN
là hai điểm trên
,.AB CD
Mặt phẳng
( )
qua
// .MN SA
Điều
kiện của
MN
để thiết diện của hình chóp với
( )
là hình thang là
A.
//MN AD
. B.
//MN BC
.
C.
,MN
là trung điểm
,AB CD
. D.
MN
qua trung điểm
AC
.
Câu 31. Cho
1 2 3
2 , 3 2 , 7 3z i z i z i= + = - = +
. Gọi số phức
z
có mô đun nhỏ nhất thỏa mãn
1 2 3
z z z z- = -
là
0
z
. Tính
0
z
A.
21 5+
. B.
75+
. C.
37 5−
. D.
41 5−
.
Câu 32. Trong không gian
Oxyz
, cho các điểm
( ) ( ) ( )
1;0;0 , 2;0;3 , 0;0;1A B M−
và
( )
0;3;1N
. Mặt
phẳng
( )
P
đi qua các điểm
,MN
sao cho khoảng cách từ điểm
B
đến
( )
P
gấp hai lần khoảng cách từ
điểm
A
đến
( )
P
. Có bao nhiêu mặt phẳng
( )
P
thỏa mãn đề bài?
A. Có hai mặt phẳng
( )
P
. B. Chỉ có một mặt phẳng
( )
P
.
C. Không có mặt phẳng
( )
P
nào. D. Có vô số mặt phẳng
( )
P
.
Lời gii
Chn D
Ta có
( ) ( )
3;0;3 , 0;3;0AB MN= − =
.
h
r
1
=a
r
2
=
a
2
O
A
B
H

Trang 11
Vậy
1
: 0 ,
xt
AB y t
zt
=−
=
=
;
0
:,
1
x
MN y t t
z
=
=
=
.
Xét hệ phương trình
( )
1
1
2
2
1
10
1
0 0;0;1
0
1
t
t
t AB MN M
t
t
−=
=
= =
=
=
.
Và
( ) ( )
1;0;1 , 2;0; 2AM BM= − = −
nên
2BM AM=−
.
Khi đó
( )
( )
( )
( )
, 2d ,d B P A P=
với mọi mặt phẳng
( )
P
qua
MN
.
Vậy có vô số mặt phẳng
( )
P
thỏa mãn bài toán.
Câu 33. Có bao nhiêu số nguyên m để hàm số
4 3 2
8 3(2 1) 13= − − − + +y x mx m x
có cực đại mà không có
cực tiểu?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời gii
Chn B.
3 2 2
2
0
4 24 6(2 1) 2 [2 12 3(2 1)] 0
( ) 2 12 3(2 1) (*)
=
= − − − + = − + + + =
= + + +
x
y x mx m x x x mx m
f x x mx m
+) Nếu (*) vô nghiệm thì
'0=y
có nghiệm
10
00
=−
= ⎯⎯⎯→ =
a
CD
xx
(thỏa mãn).
+) Nếu (*) có nghiệm kép
0=
o
xx
thì
=
o
xx
không là cực trị của hàm số
0=
CD
x
, còn nếu (*) có
nghiệm kép
0=x
thì thực chất
3
' 0 0= =yx
, khi đó
0=
CD
x
(thỏa mãn).
+) Nếu (*) có 2 nghiệm phân biệt khác 0 thì số cực trị là 3 (có cực đại và cực tiểu – loại), nếu có 2 nghiệm
phân biệt, có một nghiệm bằng 0 thì để thỏa mãn bài toán điều kiện cần là:
1
(0) 0
2
= = − f m Z
(loại).
Vậy để thỏa mãn bài toán thì (*) hoặc vô nghiệm, hoặc có nghiệm kép
22
1 7 1 7
' 36 6(2 1) 0 6 2 1 0 0
66
−+
= − + − − ⎯⎯⎯→ =
mZ
m m m m m m
Suy ra có 1 số nguyên
0=m
thỏa mãn.
Câu 34. Cho các số thực
a
,
b
khác
1
. Biết rằng bất kỳ đường thẳng nào song song với trục
Ox
mà cắt
các đường
x
ya=
,
x
yb=
, trục tung lần lượt tại
M
,
N
và
A
thì
2AN AM=
(hình vẽ bên).
Mệnh đề nào sau đây đúng?
A.
2
ab=
. B.
2ba=
. C.
2
1ab =
. D.
1
2
ab =
.
Câu 35. Cho số phức
z
thỏa mãn điều kiện
2 2 3 2 5z i z i+ − + − − =
. Gọi
, Mm
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của
z
. Tính giá trị
.Mm
.
A.
65
5
B.
65
C.
2 26
D.
4 65
5

Trang 12
Lời giải
Chọn D
Đặt
( , )z x yi x y= +
. Gọi
( )
; M x y
,
( )
2; 1N −
,
( )
2; 3P
lần lượt là điểm biểu diễn của số phức
z
,
12
2 , 2 3z i z i= − + = +
.
2 2 3 2 5z i z i+ − + − − =
25MN MP + =
, mặt khác
22
4 2 2 5NP = + =
nên điểm
M
thuộc
đoạn thẳng
NP
.
z
đạt giá trị nhỏ nhất
OM
ngắn nhất
1
MM
, với
1
M
là hình chiếu vuông góc của
M
lên đoạn
NP
(quan sát hình hoặc nhận xét góc
NOP
tù do
.0ON OP
nên
1
M
thuộc đoạn
NP
)
z
đạt giá trị lớn nhất
OM OP=
(quan sát hình hoặc so sánh
à ON v OP
).
Phương trình
: 2 4 0NP x y− + =
Vậy
( )
4 4 65
. . , 13. .
5
5
M m OP d O NP= = =
Câu 36. Cho
00
( ) cos ( ) 1f x dx xf x dx
==
. Tính giá trị lớn nhất của
1
2
0
()f x dx
A.
3
2
. B.
2
. C.
3
. D.
4
Lời gii
Chn C
Thêm các số
22
, , 0a b a b +
00
00
cos ( ) cos ( )
( ) ( )
a a xf x dx a xf x dx
b b f x dx bf x dx
==
==
( ) ( ) ( )
2 2 2
22
2
0 0 0
cos ( ) cos ( )a b a x b f x dx a x b dx f x dx
+ = + +
( )
( )
22
2
2 2 2
00
2
cos ( cos 2 cos )
2
ab
a x b dx a x ab x b dx
+
+ = + + =
( )
( )
( )
( )
22
2
22
2
2 2 2 2
22
00
2
2
( ) ( ) , , , 0
2
2
ab
ab
a b f x dx f x dx a b a b
ab
+
+
+ +
+
( )
( )
2
2
2
22
0
2
( ) max
2
ab
f x dx
ab
+
+

Trang 13
( )
( )
2
2
2
22
21
2
13
.,
2
2
a
ab
a
b
P t P
b
ab
a
b
+
+
= = =
+
+
(Xét hàm số)
2
2
0
3
()f x dx
.
Câu 37. Tập xác định của hàm số là?
A. . B. .
C. . D. .
Câu 38. Cho mặt phẳng
( )
: 2 1 0x y z
− + − =
và điểm
( ) ( )
0; 1;1 , 1;1; 2AB−−
. Biết
( ) ( )
;;M a b c
sao cho
MA MB+
đạt giá trị nhỏ nhất. Giá trị của
2 2 2
abc++
bằng:
A.
2
9
. B.
26
. C.
78
. D.
14
49
.
Lời gii
Chn D.
Xét
( )
, 1, 2xf x y yzz = − + −
Với
( ) ( )
0; 1;1 , 1;1; 2−−AB
( ) ( ) ( )
0, 1,1 . 1,1, 2 2. 5 − − = −ff
10 0= −
Suy ra A, B nằm khác phía so với
( )
.
Khi đó
14+ =MA MB AB
( )
min
14 + =MA MB
.
Dấu
""=
xảy ra khi
( )
AB M
=
: 1 2
13
=
= − +
=−
xt
AB y t
zt
( )
; 1 2 ;1 3 − + −M t t t
( )
( ) ( )
1 2 2 1 3 1 0
⎯⎯⎯→ − − + + − − =
M
t t t
2
7
=t
2 3 1
;;
7 7 7
−
M
2 2 2
14
49
+ + =abc
Câu 39. Cho tứ diện
ABCD
đều có cạnh bằng
22
. Gọi
G
là trọng tâm của tứ diện
ABCD
và
M
là
trung điểm
AB
. Khoảng cách giữa hai đường thẳng
BG
và
CM
bằng:
A.
2
14
. B.
2
5
. C.
3
25
. D.
2
10
.
Lời gii.
Chn A.
tan2yx=
\,
4
D k k
= +
\,
42
D k k
= +
\,
2
D k k
=
\,
2
D k k
= +
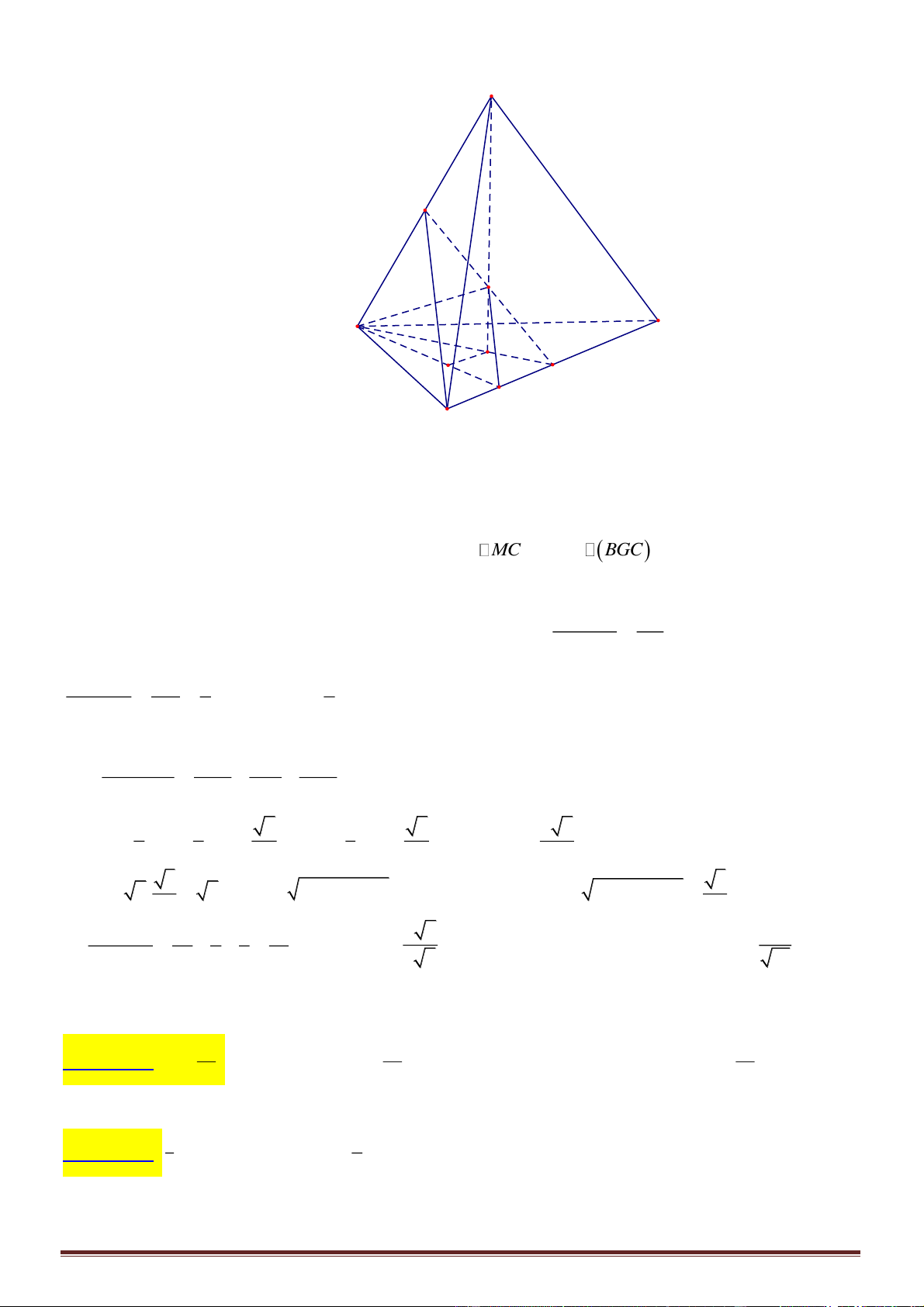
Trang 14
Gọi
N
,
P
lần lượt là trung điểm của
CD
và
CN
,
H
là trọng tâm tam giác
BCD
. Do
G
là trọng tâm
của tứ diện đều
ABCD
nên
G
là trung điểm của
MN
và
( )
GH BCD⊥
Từ
H
kẻ đường thẳng song song với
CD
cắt
BP
tại
I
BN IH⊥
( Do
BN CD⊥
)
Do
G
,
P
lần lượt là trung điểm của
MN
,
NC
nên
GP MC
( )
MC BGC
( )
( )
( )
( )
( )
,
,,
(1)
MC BG
MC BGP C BGP
d d d = =
Do
P
là trung điểm của
CN
,
H
là trọng tâm tam giác
BCD
nên
( )
( )
( )
( )
,
,
1
C BGP
N BGP
d
CP
d NP
==
và
( )
( )
( )
( )
,
,
3
2
N BGP
H BGP
d
BN
d HB
==
( )
( )
( )
( )
,,
3
(2)
2
C BGP H BGP
dd=
Lại có:
GH BN⊥
,
GH IH⊥
,
IH BN⊥
Nên
( )
( )
2 2 2 2
,
1 1 1 1
H BGP
d BH IH HG
= + +
Có
2 1 2
3 6 3
IH PN CD= = =
,
16
33
HN BN==
26
2
3
BH HN==
3
2 2. 6
2
MC ==
,
22
2MN MC NC= − =
1GN=
22
3
3
GH NG HN = − =
( )
( )
2
,
1 9 9 9 63
24 2 3 8
H BGP
d
= + + =
( )
( )
,
22
37
H BGP
d=
, kết hợp với (1) và (2) ta được
( )
,
2
14
CM BG
d =
.
Câu 40. Cho hình chóp
.S ABC
có
( )
,SA ABC⊥
ABC
vuông cân tại A,
.SA BC a==
Tính theo a thể
tích V của khối chóp
.S ABC
A.
3
.
12
a
V =
B.
3
.
4
a
V =
C.
3
2.Va=
D.
3
.
2
a
V =
Câu 41. Cho (S) là mặt cầu tâm I(2; 1; -1) và tiếp xúc với mặt phẳng (P) có phương trình: 2x – 2y – z + 3
= 0. Khi đó, bán kính của (S) là:
A.
1
3
B.
4
3
C.
3
D.
2
G
B
D
C
A
N
H
M
P
I

Trang 15
Câu 42. Cho cấp số nhân có
1
3u =
,
2
3
q =
. Chọn kết quả đúng:
A. Bốn số hạng tiếp theo của cấp số là:
4 8 16
2; ; ; .
3 3 3
B.
1
2
3. .
3
n
n
u
−
=
C.
2
9. 9.
3
n
n
S
=−
D.
( )
n
u
là một dãy số tăng.
Câu 43. Mệnh đề nào sau đây có thể sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường
thẳng thì song song nhau.
Câu 44. Một tổ học sinh có
5
nam và
5
nữ xếp thành một hàng dọc thì số các cách xếp khác nhau là:
A.
25
. B.
10
. C.
10!
. D.
40
.
Câu 45. Cho mệnh đề ‘’
2
, 2 0xx +
’’. Phủ định của mệnh đề trên là:
A.
2
, 2 0xx +
. B.
2
, 2 0xx +
. C.
2
, 2 0xx +
. D.
2
, 2 0xx +
.
Câu 46. Có bao nhiêu tập X thỏa mãn
{1;2} {1;2;3;4;5}X
A.
8.
B.
10.
C.
9.
D.
11.
Câu 47. Phương trình
2
ax 0bx c+ + =
có nghiệm duy nhất khi và chỉ khi:
A.
0a =
. B.
0
0
a
=
hoặc
0
0
a
b
ì
=
ï
ï
í
ï
¹
ï
î
.
C.
0abc= = =
. D.
0
0
a
=
.
Câu 48. Cho phương trình
( )
22
m 3m 2 x m 4m 5 0− + + + + =
. Tìm tất cả các giá trị thực của tham số
m
để phương trình đã cho có nghiệm đúng với mọi
x Î ¡
.
A.
2m =−
. B.
5m =−
. C.
1m =
. D. Không tồn tại.
Câu 49. Phương trình
21
3
1
mx
x
−
=
+
có nghiệm duy nhất khi:
A.
3
.
2
m
B.
0.m
C.
0m
và
3
.
2
m
D.
1
2
m −
và
3
.
2
m
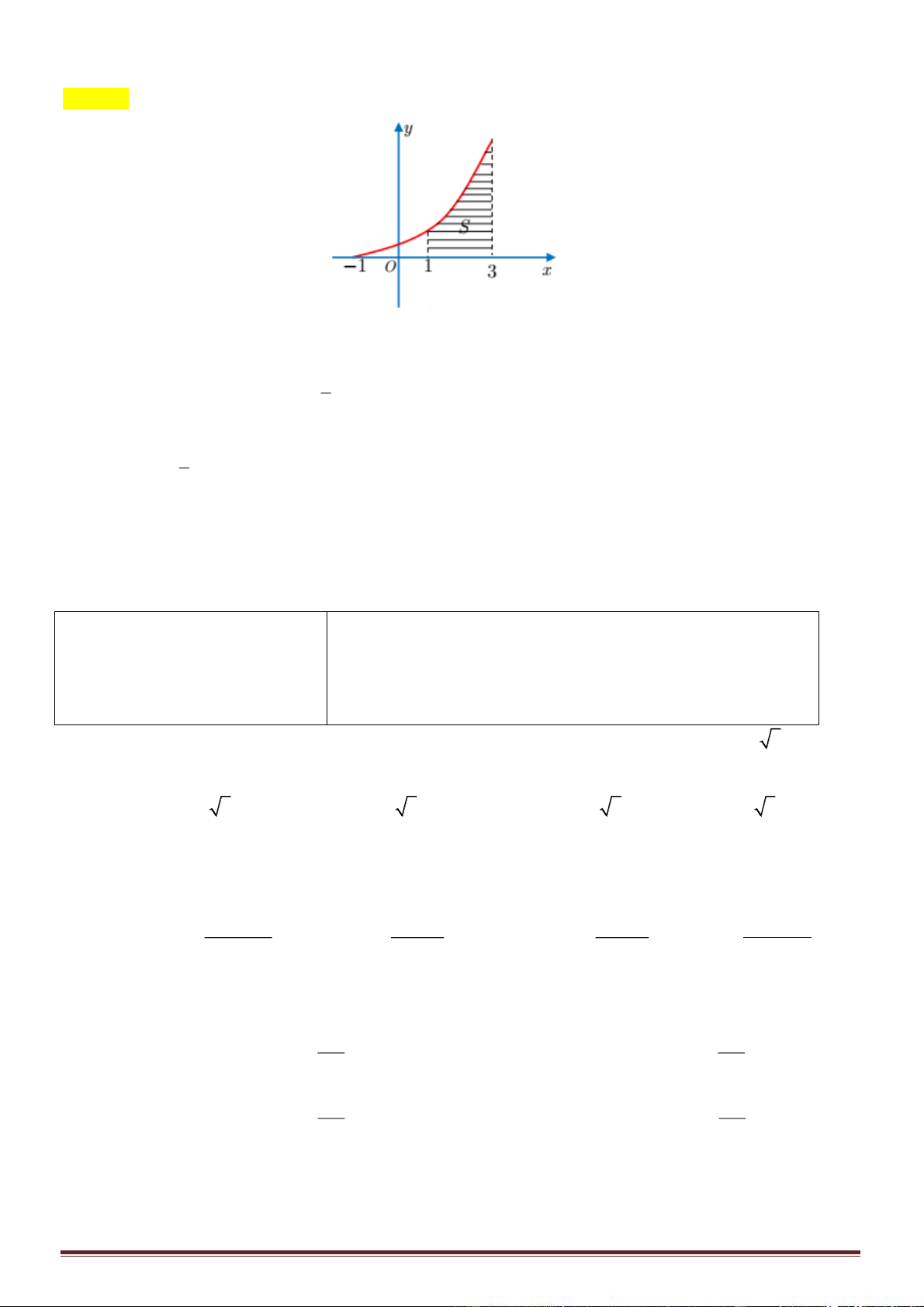
Câu 50. Cho hai hàm số
( )
y f x=
liên tục trên và hàm số
( )
( )
23
y g x x f x==
có đồ thị trên đoạn
1;3−
như hình vẽ. Biết miền hình phẳng được tô sọc có diện tích
6S =
. Tính tích phân
( )
27
1
I f x dx=
.
A.
2I =
. B.
12I =
. C.
24I =
. D.
18I =
.
Trang 16
Lời gii
Chn D.
Ta có:
( )
3
23
1
66S S x f x dx= = =
.
Đặt
3 2 2
1
3
3
t x dt x dx x dx dt= = =
.
Đổi cận:
3 27xt= =
;
11xt= =
.
( )
( )
3 27
23
11
1
3
x f x dx f t dt=
.
( )
( )
27 3
23
11
3. 3.6 18f x dx x f x dx = = =
ĐỀ 32
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và
23SA =
,
2SB =
,
3SC =
. Tính thể tích khối chóp S.ABC.
A.
43V =
. B.
23V =
. C.
63V =
. D.
12 3V =
.
Câu 2. Khẳng định nào sau đây đúng?
A.
( )
!
!!
k
n
k
C
n n k
=
−
. B.
( )
!
!
k
n
k
C
nk
=
−
. C.
( )
!
!
k
n
n
C
nk
=
−
. D.
( )
!
!!
k
n
n
C
k n k
=
−
.
Câu 3. Nguyên hàm của hàm số
( )
3cos 3
x
f x x=−
là:
A.
( )
3
3sin
ln3
x
f x dx x C= − +
. B.
( )
3
3sin
ln3
x
f x dx x C= − + +
.
C.
( )
3
3sin
ln3
x
f x dx x C= + +
. D.
( )
3
3sin
ln3
x
f x dx x C= − − +
.
Câu 4. Nguyên hàm của hàm số
( )
cos3f x x=
là:

Trang 17
A.
3sin3xC−+
. B.
1
sin3
3
xC−+
C.
sin3xC−+
. D.
1
sin3
3
xC+
.
Câu 5. Cho vectơ
( )
1;3;4u =
, tìm vectơ cùng phương với vectơ
u
A.
( )
2; 6; 8 .b = − − −
B.
( )
2; 6;8 .c = − −
C.
( )
2;6;8 .d =−
D.
( )
2; 6; 8 .a = − −
Câu 6. Khối mười hai mặt đều có bao nhiêu đỉnh?
A. 12. B. 16. C. 20. D. 36.
Câu 7. Một khối nón có diện tích xung quanh bằng
2
và bán kính đáy
1
2
. Khi đó độ dài đường
sinh là:
A. 2. B. 3. C. 1. D. 4.
Câu 8. Tìm tiệm cận ngang của đồ thị hàm số
1
2
x
y
x
+
=
−
.
A.
2.y =
B.
1.y =−
. C.
1
.
2
y =
D.
2.x =
Câu 9. Cho hàm số
2
3
x
y
x
−
=
+
. Tìm mệnh đề đúng.
A. Hàm số xác định trên
\3
.
B. Hàm số đồng biến trên
\3−
.
C. Hàm số nghịch biến trên mỗi khoảng xác định.
D. Hàm số đồng biến trên mỗi khoảng xác định.
Câu 10. Cho đồ thị
( )
C
của hàm số
32
3 5 2y x x x= − + − +
. Trong các mệnh đề sau, mệnh đề nào
đúng ?
A.
( )
C
không có điểm cực trị. B.
( )
C
có hai điểm cực tr.
C.
( )
C
có ba điểm cực trị. D.
( )
C
có một điểm cực trị.
Câu 11. Tìm tập xác định
D
của hàm số
( )
3
2
27
p
=-yx
.

Trang 18
A.
{ }
D \ 2= ¡
. B.
D = ¡
. C.
[ )
D 3;= + ¥
. D.
( )
D 3;= + ¥
.
Câu 12. Cho bốn số dương
12
, , a b b
,c và
,1ac¹
, Trong các quy tắc sau, quy tắc nào là đúng?
A.
( )
1 2 1 2
log log .log
a a a
b b b b+=
. B.
log
log
log
c
a
c
b
b
a
=
.
C.
11
1
log log
aa
bb
a
a
=
. D.
11
log log
n
aa
b n b=-
.
Câu 13. Hàm số
32
31y x x= − + +
đồng biến trên khoảng nào dưới đây?
A.
( )
0;+
. B.
( )
0;2
. C.
( )
;2−
D.
( )
;0−
và
( )
2;+
.
Câu 14. Hàm số
42
21y x x= − +
có bao nhiêu điểm cực trị?
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 15. Tìm điểm
M
có hoành độ âm trên đồ thị
( )
3
12
:
33
C y x x= − +
sao cho tiếp tuyến tại
M
vuông góc với đường thẳng
12
33
yx= − +
.
A.
( )
2; 4M −−
. B.
1;
3
M
−
. C.
2;
3
M
. D.
( )
2;0M −
.
Câu 16. Cho hàm số
42
42y x x= − −
có đồ thị
()C
và đồ thị
()P
:
2
1yx=−
. Số giao điểm của
()P
và đồ thị
()C
là
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 17. Cho dãy số
( )
n
u
với
( )
1
21
1
1
1
n
nn
u
uu
+
+
=
= + −
. Số hạng tổng quát
n
u
của dãy số là số hạng nào
dưới đây?
A.
2
n
un=−
. B.
n
u
không xác định . C.
1
n
un=−
. D.
n
un=−
với mọi
n
.
Câu 18. Trong không gian với hệ tọa độ Oxyz cho tam giác ABC với
( ) ( ) ( )
1;4; 1 , 2;4;3 , 2;2; 1A B C−−
. Phương trình tham số của đường thẳng
d
đi qua điểm
A
và song
song với
BC
là
A.
1
4.
12
x
yt
zt
=
=+
= − −
. B.
1
4.
12
x
yt
zt
=
=−
= − +
. C.
1
4.
12
x
yt
zt
=
=+
= − +
. D.
1
4.
12
x
yt
zt
=
=+
=+
.
Câu 19. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) ( ) ( )
1;1;1 , 2;3;4 , 7;7;5M N P
. Tìm tọa độ
điểm
Q
để tứ giác
MNPQ
là hình bình hành.
A.
( )
6; 5;2Q −
. B.
( )
6; 5; 2Q − − −
. C.
( )
6;5;2Q −
. D.
( )
6;5;2Q
.

Trang 19
Câu 20. Trong không gian với hệ toạ độ
Oxyz
, cho ba điểm
( )
3; 2; 2A −−
,
( )
3;2;0B
,
( )
0;2;1C
.
Phương trình mặt phẳng
( )
ABC
là:
A.
2 3 6 0x y z− + =
. B.
4 2 3 0yz+ − =
. C.
3 2 1 0xy+ + =
. D.
2 3 0yz+−=
.
Câu 21. Trong không gian với hệ tọa độ
,Oxyz
phương trình đường thẳng
đi qua điểm
( )
2; 1;3A −
và vuông góc với mặt phẳng
( )
Oxz
là
A.
2
1.
3
x
yt
z
=
=+
=
. B.
2
1.
3
x
yt
z
=
= − +
=
. C.
2
1.
3
xt
y
zt
=+
=−
=+
. D.
2
1.
3
x
yt
z
=
=−
=
.
Câu 22. Nguyên hàm của hàm số
( )
2
cos
()
2 sin
x
fx
x
=
+
là
A.
( )
( )
2
sin
.
2 sin
x
f x dx C
x
=+
+
. B.
( )
1
.
2 sin
f x dx C
x
=+
+
.
C.
1
( ) .
2 sin
f x C
x
= − +
+
. D.
( )
sin
.
2 sin
x
f x dx C
x
=+
+
.
Câu 23.
Tính tích phân
2
4
0
cos sinI x xdx
=
, bằng cách đặt
costx=
, mệnh đề nào đưới đây
đúng
?
A.
1
4
0
I t dt=
. B.
1
4
0
I t dt=−
. C.
2
4
0
I t dt
=
. D.
2
4
0
I t dt
=−
.
Câu 24. Cho hình nón
( )
N
có thiết diện qua trục là tam giác vuông cân, cạnh bên bằng 2a. Tính
thể tích của khối nón
( )
N
theo a.
A.
3
22a
B.
3
22
3
a
C.
3
3
a
. D.
3
a
.
Câu 25.
Cho
a,b,c 1
và
ab
log c 3,log c 10==
. Hỏi biểu thức nào đúng trong các biểu thức sau:
A.
ab
log c 30=
. B.
ab
1
log c
30
=
C.
ab
13
log c
30
=
D.
ab
30
log c
13
=
Câu 26. Tính đạo hàm của hàm số
2x 1
y xe
+
=
A.
( )
2x 1
y' e 2x 1 e
+
=+
. B.
( )
2x
y' e 2x 1 e=+
C.
2x 1
y' 2e
+
=
. D.
2x 1
y' e
+
=
.
Câu 27. Cho số phức
z a bi=+
. Khi
3
z
là một số thực, khẳng định nào sau đây là đúng ?
A.
0b=
và
a
bất kì hoặc
22
3ba=
. B.
3ba=
.
C.
22
5ba=
. D.
0a =
và
b
bất kì hoặc
22
ba=
.

Trang 20
Câu 28. Cho hai số phức
1
12zi=+
và
2
23zi=-
. Xác định phần ảo
a
của số phức
12
32z z z=-
A.
11a =
.
B.
12a =
C.
1a =-
D.
12a =-
.
Câu 29. Cho các số phức
12
, zz
thỏa mãn
12
3, 4zz==
và
12
5.zz-=
Gọi
, AB
lần lượt là điểm
biểu diển các số phức
12
, zz
Tính diện tích
S
của tam giác
OAB
với
O
là gốc tọa độ.
A.
12.S =
. B.
6.S =
. C.
5 2.S =
. D.
25
.
2
S =
.
Câu 30. Một đề trắc nghiệm gồm
20
câu, mỗi câu có
4
đáp án và chỉ có một đáp án đúng. Bạn
Anh làm đúng
12
câu, còn
8
câu bạn Anh đánh hú họa vào đáp án mà Anh cho là đúng. Mỗi câu
đúng được
0,5
điểm. Tính xác suất để Anh được
9
điểm?
A.
63
16384
. B.
9
10
. C.
9
65536
. D.
9
20
.
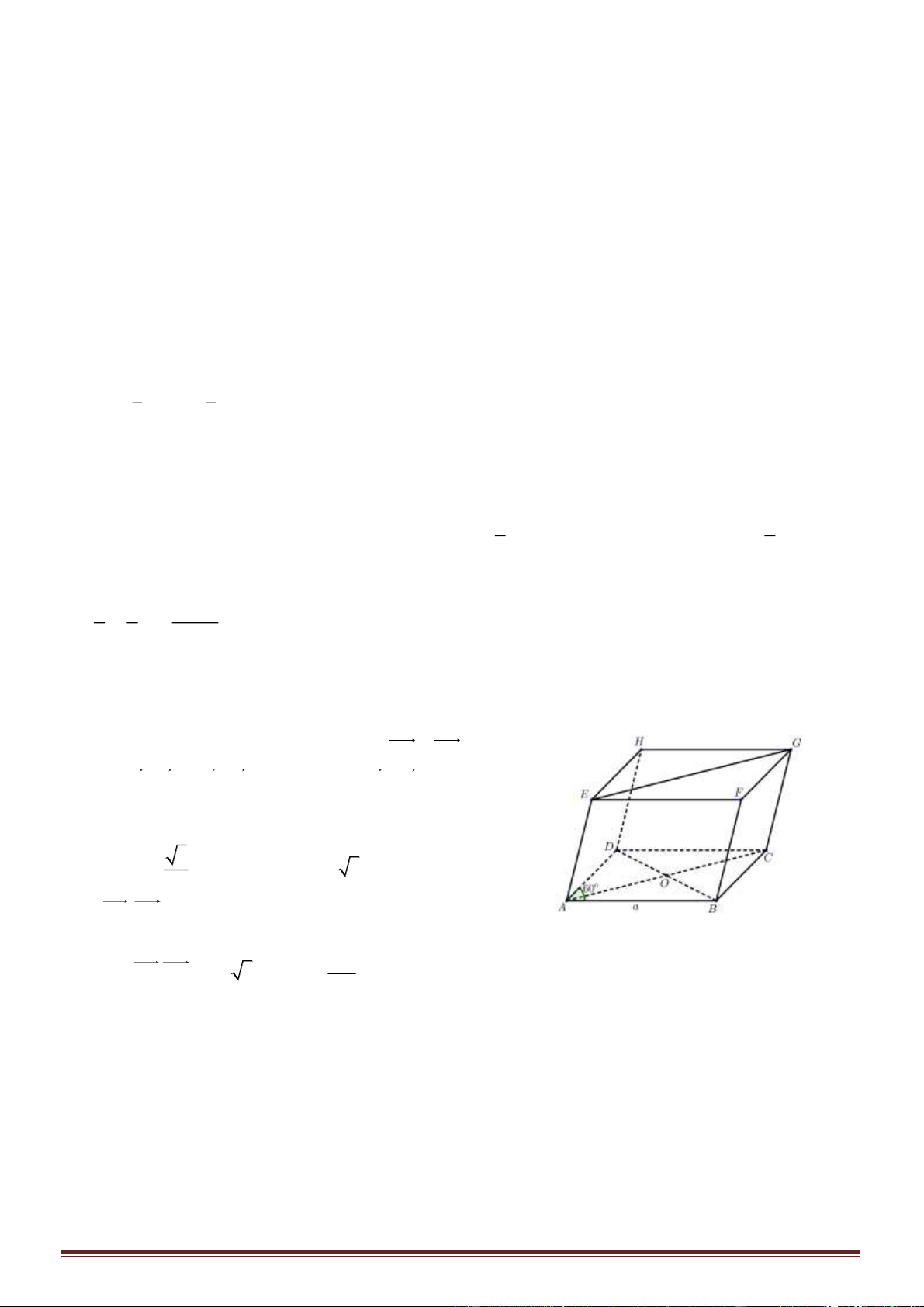
Câu 31 Cho hình hộp
.ABCD EFGH
có đáy là hình thoi cạnh bằng
,a
góc
o
60 .BAD =
Giá trị của
.AB EG
bằng
A.
2
3a
. B.
2
3
2
a
. C.
2
6
2
a
. D.
2
3
2
a
.
Câu 32. Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
, góc
0
60ABC =
,
( )
,SA ABCD⊥
3SA a=
.
Gọi
là góc giữa
SA
và mặt phẳng
( )
SCD
. Tính
tan
.
A.
1
2
B.
1
3
. C.
1
4
. D.
1
5
.
Câu 33. Trong không gian
Oxyz
, cho tứ diện
ABCD
có
(2;1; 1), (3;0;1),C(2; 1;3)AB−−
và
D
thuộc
trục
Oy
. Biết
5
ABCD
V =
và có hai điểm
( ) ( )
1 1 2 2
0; ;0 , 0; ;0D y D y
thỏa mãn yêu cầu bài toán. Khi đó
12
yy+
bằng
A.
1
. B.
2
. C.
3
. D.
0.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
2; 3;7A −
,
( )
0;4; 3B −
và
( )
4;2;5C
.
Biết điểm
( )
0 0 0
;;M x y z
nằm trên
( )
mp Oxy
sao cho
MA MB MC++
có giá trị nhỏ nhất. Khi đó
tổng
0 0 0
P x y z= + +
bằng
A.
0P =
. B.
6P =
. C.
3P =
. D.
3P =−
.
Câu 35. Anh Bách vay ngân hàng 100 triêu đồng, với lãi suất 1,1% / tháng. Anh Bách muốn hoàn
nợ cho ngân hàng theo cách: sau đúng một tháng kể từ ngày vay, anh bắt đầu hoàn nợ, và những
liên tiếp theo cách nhau đúng một tháng. Số tiền hoàn nợ ở mỗi lần là như nhau và trả hết nợ sau
đúng 18 tháng kể từ ngày vay. Hỏi theo cách đó, tổng số tiền lãi mà anh Bách phải trả là bao
nhiêu (làm tròn kết quả hàng nghìn)? Biết rằng, lãi suất ngân hàng không thay đổi trong suốt thời
gian anh Bách vay.
Trang 21
A. 10773700 (đồng). B. 10774000 (đồng).
C. 10773000 (đồng). D. 10773800 (đồng)..
Câu 36. Tính tổng
T
tất cả các nghiệm của phương trình
22
sin cos
5 5 2 5
xx
+=
trên đoạn
[ ]
0;2 .p
A.
.T p=
. B.
3
.
4
T
p
=
. C.
2.T p=
. D.
4.T p=
.
Câu 37. Biết rằng
0
cos
x
e xdx ae b
=+
trong đó
,abQ
. Tính
?P a b=+
A.
1.P =
. B.
0.P =
. C.
1
.
2
P =−
. D.
1.P =−
.
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
3a
, mặt bên
( )
SAB
là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là:
A.
3
93
2
a
. B.
3
2
a
. C.
3
3
2
a
. D.
3
3
3
a
.
Câu 39. Cho hình lăng trụ tam giác đều ABC, A'B'C' có tất cả các cạnh đều bằng a. Tính diện tích
S của mặt cầu ngoại tiếp hình lăng trụ theo a.
A.
2
7
3
a
S
=
. B.
2
5
3
a
S
=
. C.
2
3Sa
=
. D.
2
11
3
a
S
=
.
Câu 40. Có bao nhiêu giá trị nguyên của tham số
2018;2018m−
để hàm số
2
11y x mx= + − −
đồng biến trên
( )
;− +
?
A.
2017
. B.
2019
. . C.
2020
. D.
2018
.
Câu 41. Cho hàm số
( )
y f x=
có đồ thị
( )
y f x
=
như hình vẽ. Đặt
( ) ( )
5g x f x mx= − +
với
m
. Có bao nhiêu giá trị của
m
để hàm số
( )
y g x=
có đúng hai điểm cực trị?
A.
8
. B.
11
. C.
9
.
D.
10
.
Câu 42.
Tìm m để phương trình
22
11
22
1
(m 1)log (x 2) 4(m 5)log 4m 4 0
x2
− − + + + − =
−
có nghiệm trên
5
,4
2
.

Trang 22
A.
7
3m
3
−
. B.
m.
. C.
m.
. D.
7
3m
3
−
.
Câu 43. Nhà hàng có cấu trúc vỏ hình parabol chất liệu tre nứa , nằm trên quần đảo Cát Bà (Hải
Phòng) do công ty kiến trúc Vo Trong Nghia Architects thiết kế.
Nhìn mặt trước mặt sau của mỗi lều là hình parabol, biết rằng mặt sàn
hình chữ nhật chiều rộng 3m, chiều sâu 6m, chiều cao từ mặt sàn lên
đỉnh của parabol là 3m. Tính thể tích V phần không gian bên
trong của mỗi lều.
A.
( )
3
18Vm=
. B.
( )
3
36Vm=
.
C.
( )
3
6Vm=
. D.
( )
3
12Vm=
.
Câu 44. Gọi
S
là tập tất cả các giá trị nguyên của tham số thực
m
sao cho giá trị lớn nhất của
hàm số
42
1
14 48 30
4
y x x x m= − + + −
trên đoạn
0;2
không vượt quá
30
. Tính tổng tất cả các giá trị
của
.S
A.
108
. B.
136
. C.
120
. D.
210
.
Câu 45. Cho hàm số
32
41y x x= − + +
có đồ thị là
( )
C
và điểm
( )
;1Mm
. Gọi
S
là tập hợp tất cả
các giá trị thực của
m
để qua
M
kẻ được đúng
2
tiếp tuyến đến đồ thị
( )
C
. Tổng giá trị tất cả các
phần tử của
S
bằng
A.
5
. B.
40
9
C.
16
9
. D.
20
3
.
Câu 46. Tập tất cả các giá trị của tham số thực
m
để phương trình
( )
2
1 1 3 2 1 5 0m x x x+ + − + + − − =
có đúng hai nghiệm phân biệt là một nửa khoảng
(
;ab
.
Tính
5
7
ba−
.
A.
6 5 2
35
−
. B.
6 5 2
7
−
. C.
12 5 2
35
−
. D.
12 5 2
7
−
.
Câu 47. 47/ Tìm tất cả giá trị của
m
để đồ thị của hàm số
2
2
7
xx
y
+−
=
đi qua điểm
( ;1)Am
A.
1; 2mm==
. B.
1; 2mm= − =
.
C.
1; 2mm= = −
. D.
1; 2mm= − = −
.
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2
2 2 2
: 1 1
4
m
m
S x y z m− + − + − =
(với
0m
là tham số thực) và hai điểm
( )
2;3;5A
,
( )
1;2;4B
. Tìm giá trị nhỏ nhất của
m
để trên
( )
m
S
tồn tại điểm
M
sao cho
22
9MA MB−=
.

Trang 23
A.
1m =
. B.
33m =−
. C.
8 4 3m =−
. D.
43
2
m
−
=
.
Câu 49. Tập hợp các điểm M trong mặt phẳng phức biểu diễn số phức z thoả mãn một trong các
điều kiện sau:
1
2z
z
+=
nằm trên đường tròn. Tìm bán kính đường tròn đó.
A.
2.R =
. B.
1.S =
. C.
2.S =
. D.
5.S =
.
Câu 50. Cho z
1
= 1+i; z
2
= -1-i. Gọi z
3
= a + bi; a,b R sao cho các điểm biểu diễn của z
1
, z
2
, z
3
tạo thành tam giác đều. Tính a
2
+ b
2
.
A. 6. B. 9. C. 0. D. 8.
-----------Hết------------
HƯỚNG DẪN CHẤM
1/ Đáp án : C
Lời gii: Theo giả thiết suy ra diện tích tam giác đáy SAB là : S
đáy
=
1
.2. 3 3
2
=
11
. .3.2 3 2 3
33
SAB
V SC S= = =
2/ Đáp án : D
Lời gii :Ta có:
( )
!
!!
k
n
n
C
k n k
=
−
.
3/Đáp án : A
Lời gii: Dựa vào bảng nguyên hàm suy ra đáp án A đúng.
4/ Đáp án : D
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
C
D
A
D
A
C
D
B
D
A
D
B
B
B
D
C
A
Câu
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
C
D
A
B
C
A
B
D
C
A
B
B
A
D
A
A
C
D
35
3
37
38
39
40
41
42
43
44
45
46
47
48
49
50
TL
C
D
D
C
A
D
C
A
B
B
B
D
C
C
C
A

Trang 24
Lời gii:
11
cos3x cos3x (3 ) sin3
33
dx d x x C= = +
5/ Đáp án : A
Lời gii: Ta có
( )
2; 6; 8 2bu= − − − = −
.
6/ Đáp án : C
Lời gii: Theo định nghĩa khối đa diện đều suy ra khối 12 mặt đều có 20 đỉnh
7/ Đáp án : D
Lời gii: S
xq
= rl
2
4
1
.
2
l
==
8/ Đáp án : B
Lời gii: Ta có
1
lim lim 1
2
xx
x
y
x
→− →−
+
= = −
−
;
1
lim lim 1
2
xx
x
y
x
→+ →+
+
= = −
−
.
Vậy đường thẳng
1y =−
là đường tiệm cận ngang của đồ thị hàm số.
9/ Đáp án : D
Lời gii:
Ta có:
( )
2
5
0
3
y
x
=
+
, với
3x −
. Do đó hàm số đồng biến trên mỗi khoảng xác định.
10/ Đáp án : A
Lời gii: Tập xác định:
D =
. Ta có:
2
3 6 5y x x
= − + −
( )
2
3 1 2 0x= − − −
,
x
.
Suy ra đồ thị hàm số không có điểm cực trị.
11/ Đáp án : D
Lời gii: Áp dụng lý thuyết
''
Lũy thừa với số mũ không nguyên thì cơ số phải dương
''
.
Do đó hàm số
( )
3
2
27
p
=-yx
xác định khi
3
27 0 3- > Û >xx
.
12/ Đáp án : B
Lời gii: Áp dụng lý thuyết, chọn đáp án B
13/ Đáp án : B
Lời gii:
Ta có:
2
36y x x
= − +
.
0y
=
2
3 6 0xx − + =
0
2
x
x
=
=
.
Bảng biến thiên:

Trang 25
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng
( )
0;2
.
14/ / Đáp án : B
Lời gii:
Tập xác định:
D =
.
Đạo hàm:
3
44y x x
=−
.
0y
=
0
1
x
x
=
=
.
Bảng biến thiên:
Do đó hàm số có 3 điểm cực trị.
15/ Đáp án : D
Lời gii:
Gọi
3
0 0 0
12
;
33
M x x x
−+
.
Do tiếp tuyến tại
M
vuông góc với đường thẳng
12
33
yx= − +
nên ta có hệ số góc của tiếp tuyến
tại
M
là
3k =
.
Ta có
2
1yx
=−
. Theo đề bài ta có phương trình
2
13x −=
2
4x=
2x =
.
Theo đề bài điểm
M
có hoành độ âm nên
( )
2;0M −
.
16/ Đáp án : C
Lời gii:
Phương trình hoành độ giao điểm của
( )
P
và
( )
C
:
4 2 2
4 2 1x x x− − = −
( )
42
3 3 0, 1xx − − =
.
Đặt
2
tx=
ta được phương trình trung gian:
( )
2
3 3 0, 2tt− − =
.
Vì
( )
2
có hai nghiệm phân biệt trái dấu nên
( )
1
sẽ có hai nghiệm phân biệt.

Trang 26
Vậy số giao điểm của
()P
và đồ thị
()C
là
2
giao điểm.
17/ Đáp án : A
Lời gii:
Ta có:
2 3 4
0; 1; 2u u u= = − = −
,. Dễ dàng dự đoán được
2
n
un=−
.
18/ Đáp án : C
Lời gii:
Gọi
d
là đường thẳng cẩn tìm.
( ) ( )
0; 2; 4 2 0;1;2BC = − − = −
Vì
d
song song với
BC
nên
d
có vectơ chỉ phương
( )
0;1;2
d
a =
d
qua
( )
1;4; 1A −
và có vectơ chỉ phương
d
a
Vậy phương trình tham số của
d
là
1
4
12
x
yt
zt
=
=+
= − +
19/ Đáp án : D
Lời gii:
Gọi điểm cần tìm
( )
;;Q x y z
( )
1;2;3MN =
,
( )
7 ;7 ;5QP x y z= − − −
MNPQ
là hình bình hành nên
7 1 6
7 2 5
5 3 2
xx
MN QP y y
zz
− = =
= − = =
− = =
Vậy
( )
6;5;2Q
20/ Đáp án : A
Lời gii:
Ta có:
( )
0;4;2AB =
,
( )
3;4;3AC =−
( )
ABC
qua
( )
3; 2; 2A −−
và có vectơ pháp tuyến
( ) ( )
, 4; 6;12 2 2; 3;6AB AC
= − = −
( )
:2 3 6 0ABC x y z − + =
21/ Đáp án : B
Lời gii:
Mặt phẳng
( )
Oxz
có vectơ pháp tuyến
( )
0;1;0j =
Trang 27
Vì
vuông góc với
( )
Oxz
nên
có vectơ chỉ phương
( )
0;1;0aj
==
đi qua điểm
( )
2; 1;3A −
và có vectơ chỉ phương
a
Vậy phương trình tham số của
là
2
1
3
x
yt
z
=
= − +
=
22/ Đáp án : C
Lời gii: Đặt t = 2 + sinx, suy ra: dt = cosxdx
2
11
( ) .
2 sin
dt
f x C C
t t x
= = − + = − +
+
23/ Đáp án : A
Lời gii: đặt
costx=
suy ra dt = -sinxdx
Đổi cận: x = 0 t = 1; x =
2
t = 0
Do đó:
01
2
4 4 4
0 1 0
cos sinI x xdx t dt t dt
= = − =
24/ Đáp án : B
Lời gii: Theo đề suy ra l = 2a. thiết diện qua trục là tam giác vuông cân, cạnh bên bằng 2a nên
cạnh huyền là
22a
tức là đường tròn đáy có đường kính là
22a
suy ra r =
2a
. Suy ra h =
2a
(pitago).
Vậy V =
( )
3
2
2
1 1 2 2
2 . 2
3 3 3
a
r h a a
==
25/ Đáp án : D
Lời gii:
Ta có:
a c b c
11
log c 3 log a ;log c 10 log b
3 10
= = = =
Suy ra
c c c ab
13 30
log a log b log ab log c
30 13
+ = = =
26/ Đáp án : C
Lời gii:
( )
2x 1 2x 1 2x 1 2x 1
y xe y' e 2xe e 2x 1
+ + + +
= = + = +
.
27/ Đáp án : A
Lời gii:
Ta có
( ) ( )
3 3 2 2 3 3 2 2 3
3 3 3 3z a a bi ab b i a ab a b b i= + - - = - + -
Để
3
z
là số thực
( )
2 3 2 2
22
0
3 0 3 0 .
3
b
a b b b a b
ba
é
=
ê
Û - = Û - = Û
ê
=
ë
28/ Đáp án :B
Trang 28
Lời gii: Ta có
( ) ( )
12
3 2 3 1 2 2 2 3z z z i i= - = + - -
( ) ( ) ( ) ( )
3 6 4 6 3 4 6 6 1 12 .i i i i= + + - + = - + + = - +
Vậy
12
32z z z=-
có phần ảo bằng
12a =
.
29/ Đáp án :B
Lời gii:
Từ giả thiết, ta có
3, 4OA OB==
và
5AB =
.
Ta có
2 2 2
OA OB AB OAB+ = ¾ ¾® D
vuông tại
.O
Vậy
11
. .3.4 6
22
S OA OB= = =
.
30/ Đáp án :A
Lời gii:
Trong
8
câu còn lại, xác suất trả lời đúng mỗi câu là
1
4
; xác suất trả lời sai mỗi câu là
3
4
.
Xác suất để Anh được
9
điểm bằng xác suất Anh trả lời đúng
6
câu trong
8
câu còn lại bằng
6 6 2
8
1 3 63
( ) ( )
4 4 16384
C =
.
31/ Đáp án :D
Lời gii:
Ta có
AEGC
là hình bình hành nên
EG AC=
( )
. . . .cos ,AB EG AB AC AB AC AB AC = =
Tam giác
ABD
đều cạnh
a
3
23
2
AO a AC AO a = = =
,
( )
o
, 30AB AC CAB==
Vậy
2
o
3
. . 3 cos30
2
a
AB EG a a==
.
32/ Đáp án :A
Lời gii:

Trang 29
Gọi
M
là trung điểm
CD
.
ABCD
là hình thoi cạnh
a
,
góc
0
60ABC =
nên tam giác
ABC
đều
Do đó tam giác
ACD
cân ở
A
suy ra
AM CD⊥
Mặt khác
SA CD⊥
nên
( )
CD SAD⊥
Do đó góc
giữa
SA
và mặt phẳng
( )
SCD
là
ASM
và
3
1
2
tan
2
3
a
AM
SA
a
= = =
.
33/ Đáp án :A
Lời gii :
(0; ;0)D Oy D y
Ta có:
( ) ( ) ( )
1; 1;2 , 2; 1;1 , 0; 2;4AB AD y AC= − = − − = −
( )
. 0; 4; 2 . . 4 2AB AC AB AC AD y
= − − = − +
1
5 4 2 5 7; 8
6
ABCD
V y y y= − + = = − =
( ) ( )
1 2 1 2
0; 7;0 , 0;8;0 1D D y y − + =
34/ Đáp án :C
Lời gii:
Gọi
G
là điểm sao cho
1S =
( )
2;1;3G
.
Khi đó
MA MB MC+ + =
8 4 8
;;
333
OB
=−
3OA =
.
Nên
MA MB MC++
có giá trị nhỏ nhất khi và chỉ khi
MG
ngắn nhất, khi đó
M
là hình
chiếu vuông góc của
( )
2;1;3G
trên
( )
mp Oxy
. Do đó
( )
2;1;0M =
.
Vậy
0 0 0
2 1 0 3P x y z= + + = + + =
.
35/ Đáp án :C
Lời gii:
Bài toán này người vay trả cuối tháng nên ta có:
Số tiền mà anh Bách phải trả hàng tháng là:
( )
( )
18
6
18
100.0,011. 1,011
m .10
1,011 1
=
−
Tổng số tiền lãi anh Bách phải trả là:
( )
6
m.18 100 10 10774000−=
(đồng).
36/ Đáp án :D

Trang 30
Lời gii: Ta có
2 2 2 2 2
2
sin cos sin 1 sin sin
sin
5
5 5 2 5 5 5 2 5 5 2 5
5
x x x x x
x
-
+ = Û + = Û + =
( ) ( )
2 2 2 2 2
1
22
sin sin sin sin sin
2
5 2 5.5 5 0 5 5 0 5 5 0 5 5
x x x x x
Û - + = Û - = Û - = Û =
2
2
sin
1
2
sin ,
2 4 2
2
sin
2
x
k
x x k
x
pp
é
ê
=
ê
ê
Û = Û Û = + Î
ê
ê
=-
ê
ë
¢
.
Do
[ ]
3 5 7 3 5 7
0;2 ; ; ; 4 .
4 4 4 4 4 4 4 4
x x T
p p p p p p p p
pp
ìü
ïï
ïï
Î ¾ ¾® = ¾ ¾® = + + + =
íý
ïï
ïï
îþ
37/Đáp án : D
Lời gii: Ta có:
0
cos
x
I e xdx ae b
= = +
Đặt:
cos sin
xx
u x du xdx
dv e dx v e
= = −
==
1
0
0
.cos sin
xx
I
I e x e xdx
= +
1
e e I
= − − +
Ta sẽ đi tính
1
0
sin
x
I e xdx
=
.
Đặt:
sin cos
xx
u x du xdx
dv e dx v e
==
==
1
0
0
.sin cos
xx
I
I e x e xdx
= −
I=−
Vậy:
0
cos
x
I e xdx e e I
= = − − −
11
2
22
I e e I e
= − − = − −
.
1ab+ = −
.
38/ Đáp án : C
Lời gii: Hình vuông ABCD có diện tích là
( )
2
2
33aa=
Gọi H là trung điểm AB, tam giác SAB đều nên SH vuông góc AB.
Vì (SAB) vuông góc với đáy và có giao tuyến chung là AB, hơn nữa SH vuông góc AB nên SH
vuông góc với đáy SH là chiều cao của chóp S.ABCD
Tam giác SAB đều có cạnh AB =
3a
nên có chiều cao SH =
33
3.
22
a
a =
Vậy V=
3
2
1 1 3 3
. . .3
3 3 2 2
ABCD
aa
SH S a= = =
39/ Đáp án : A

Trang 31
Lời gii: Gọi G, G
’
lần lượt là trọng tâm tam giác ABC và A
’
B
’
C
’
, I là trung điểm của GG
’
ta có
bán kính mặt cầu ngoại tiếp lăng trụ tam giác đều ABC. A'B'C' là
22
21
6
a
R IG AG= + =
Diện tích mặt cầu là:
22
7
4
3
S R a
==
40/ Đáp án : D
Lời gii:
TXĐ
:
D =
.
2
1
x
ym
x
=−
+
.
Hàm số đồng biến trên
0y
,
x
2
1
x
m
x
+
,
x
( )
1
.
Xét
( )
2
1
x
fx
x
=
+
trên .
( )
lim 1
x
fx
→−
=−
;
( )
lim 1
x
fx
→+
=
.
( )
( )
22
1
11
fx
xx
=
++
0
,
x
nên hàm số đồng biến trên .
Ta có:
2
1
x
m
x
+
,
x
1m −
.
Mặt khác
2018;2018m−
2018; 1m − −
.
Vậy có
2018
số nguyên
m
thoả điều kiện.
41/ / Đáp án : C
Lời gii:
Ta có
( ) ( )
g x f x m
=−
. Suy ra:
( ) ( )
0g x f x m
= =
.
Do đó: Số nghiệm của phương trình
( )
0gx
=
tương đương với số giao điểm của đồ thị hàm số
( )
fx
và đường thẳng
ym=
.
Nhận xét: Hàm số
( )
y g x=
có đúng hai điểm cực trị khi và chỉ khi phương trình
( )
0gx
=
có số
nghiệm lớn hơn bằng
2
, trong đó có đúng
2
nghiệm đơn.
Dựa vào đồ thị và các lập luận trên, suy ra
5
10 13
m
m
,
mà
m
nên
0;1;2;3;4;5;10;11;12m
.

Trang 32
Vậy có
9
giá trị
m
thỏa mãn.
42/ Đáp án : A
Lời gii:
Đặt
1
2
5
t log (x 2).Do x ;4 t 1;1
2
= − −
2
4(m 1)t 4(m 5)t 4m 4 0− + − + − =
2
2
t 5t 1
m m f(t)
t t 1
++
= =
++
với
2
2
t 5t 1
f(t)
t t 1
++
=
++
Xét
2
2
t 5t 1
f(t) , x [ 1;1]
t t 1
++
= −
++
( )
2
2
2
4 4t
f '(t) 0, x [ 1;1]
t t 1
−
= −
++
Hàm số đồng biến trên [-1; 1]
Để phương trình có nghiệm thì đồ thị của 2 hàm số y = m và y = f(t) cắt nhau trên [-1; 1].
7
f( 1) m f(1) 3 m
3
− −
.
43/ Đáp án : B
Lời gii: Giả sử mặt sàn hình chữ nhật là ABCD, trong đó AB=3m, BC= 6m. I là đỉnh parabol.
Gọi O là trung điểm AB. Chọn hệ trục tọa độ Oxy sao cho gốc O, trục Ox trùng AB, Oy trùng OI
Khi đó parabol có phương trình
= − +
2
4
y x 3
3
.Diện tích mặt trước của lều là
= − + =
3
2
2
0
4
S 2 x 3 dx 6
3
2
m
Thể tích cần tìm là
( )
==
2
V 6.S 36 m
44/ Đáp án : B
Lời gii:
Xét hàm số
( )
42
1
14 48 30
4
g x x x x m= − + + −
( )
3
28 48g x x x
= − +
( )
( )
( )
( )
6
04
2
xL
g x x L
x TM
=−
= =
=

Trang 33
( )
0;2
max fx
( ) ( )
0;2
max 0 ; 2gg=
0;2
max 30 ; m 14 30m= − +
30 30
14 30
m
m
−
+
0 16m
Suy ra
16
1
136
x
Sx
=
==
.
45/ Đáp án : B
Lời gii :
Phương trình tiếp tuyến của đồ thị
( )
C
đi qua
( )
;1Mm
và có hệ số góc
k
là:
( )
1y k x m= − +
.
Để qua
M
kẻ được đúng
2
tiếp tuyến đến đồ thị
( )
C
điều kiện là hệ phương trình sau
có đúng hai nghiệm
x
phân biệt
( )
( )
( )
32
32
4 1 1
41
x x k x m
I
x x k
− + + = − +
− + + =
( ) ( )
( )
32
2
4 1 1 1
3 8 2
x x k x m
x x k
− + + = − +
− + =
Thay
( )
2
vào
( )
1
ta được
( )
( )
3 2 2
4 1 3 8 1x x x x x m− + + = − + − +
( )
2
2 3 4 8 0x x m x m
− + + =
( ) ( )
2
0
2 3 4 8 0 3
x
x m x m
=
− + + =
Như vậy, hệ
( )
I
có đúng hai nghiêm khi và chỉ khi phương trình
( )
3
có một nghiệm bằng
0
và
một nghiệm khác
0
; hoặc phương trình
( )
3
có nghiệm duy nhất khác
0
.
Phương trình
( )
3
có nghiệm
0x =
khi và chỉ khi
0m =
. Khi đó, phương trình
( )
3
trở thành
2
0
2 4 0
2
x
xx
x
=
− =
=
;
Do đó
0m =
thỏa mãn.
Phương trình
( )
3
có nghiệm duy nhất khác
0
điều kiện là
( )
2
3 4 4.2.8 0
34
0
4
mm
m
= + − =
+
( )
2
4
3 4 4.2.8 0
4
34
0
9
4
m
mm
m
m
=
= + − =
+
=
.
Như vậy
4
0; ;4
9
S
=
.
Tổng giá trị tất cả các phần tử của
S
là
4 40
04
99
+ + =
.
46/ Đáp án : D
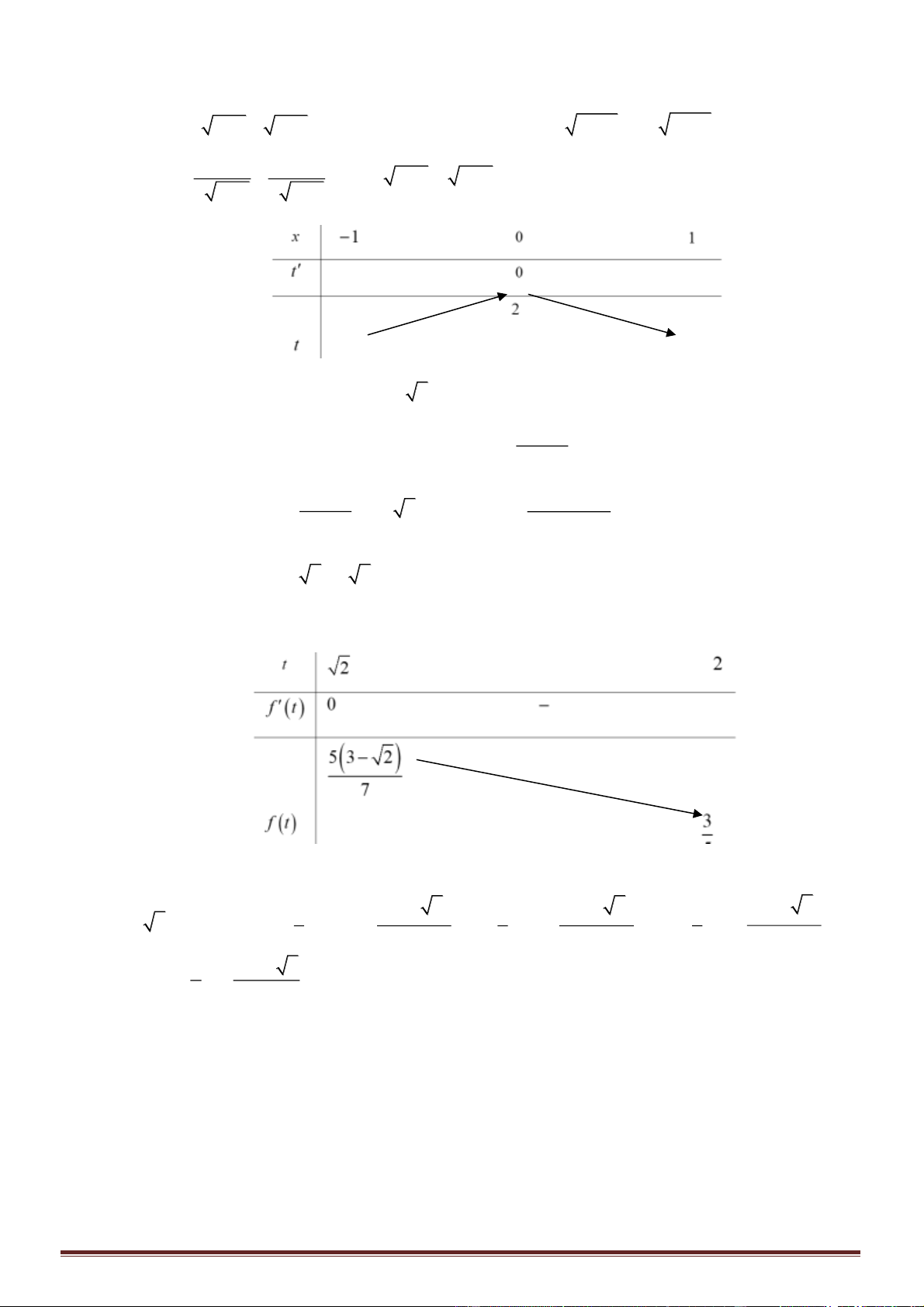
Trang 34
Lời gii :
Đặt
11t x x= + + −
với
11x−
.Khi đó:
22
2 2 1tx= + −
22
2 1 2xt − = −
.
11
0
2 1 2 1
t
xx
= − =
+−
1 1 0x x x − = + =
.
Dựa vào bảng biến thiên ta thấy
22t
.
Ta có phương trình:
( )
2
3 7 0m t t+ + − =
2
7
3
t
m
t
−+
=
+
.
Xét hàm số:
( )
2
7
, 2;2
3
t
f t t
t
−+
=
+
( )
( )
2
2
67
3
tt
ft
t
− − −
=
+
.
( )
0 3 2 2;2f t t
= = −
.
Ta có bảng biến thiên:
Dựa vào bảng biến thiên ta thấy để phương trình có đúng hai nghiệm phân biệt thì
22t
. Khi đó
( )
( )
5 3 2
3
57
ft
−
hay
( )
5 3 2
3
57
m
−
3
5
a=
,
( )
5 3 2
7
b
−
=
5 12 5 2
77
ba
−
− =
.
47/ Đáp án : C
Lời gii :
Ta có :
2
22
1
7 1 2 0
2
mm
m
mm
m
+−
=
= + − =
=−
48/ / Đáp án : C
Lời gii :
+
-

Trang 35
Gọi
( )
;;M x y z
, suy ra
22
9MA MB−=
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
2 3 5 1 2 4 9x y z x y z
− + − + − − − + − + − =
40x y z+ + − =
Suy ra: Tập các điểm
( )
;;M x y z
thỏa mãn
22
9MA MB−=
là mặt phẳng
( )
: 4 0P x y z+ + − =
Trên
( )
m
S
tồn tại điểm
M
sao cho
22
9MA MB−=
khi và chỉ khi
( )
m
S
và
( )
P
có điểm chung
( )
( )
;d I P R
1 1 4
2
111
mm+ + −
++
2 2 3mm −
2
16 16 0mm − +
8 4 3 8 4 3m − +
Vậy giá trị nhỏ nhất của
m
là
8 4 3−
.
49/ Đáp án : C
Lời gii:
Giả sử z = x + yi
2
1
2 1 2z z z
z
+ = + =
(x
2
– y
2
+1)
2
+4x
2
y
2
= 4(x
2
+ y
2
)
(x
2
+ y
2
-1)
2
= 4y
2
22
22
12
12
x y y
x y y
+ − =
+ − = −
Tập hợp các điểm M(x;y) biểu thị số phức z là hợp của hai đường tròn:
x
2
+ y
2
- 2y – 1 = 0 và x
2
+ y
2
+ 2y – 1 = 0 .
1 1 2R = + =
.
50/ Đáp án : A
Lời gii:
Để giải bài toán này ta cần chú ý đến kiến thức sau:
Giả sử M
1
(x
1
;y
1
) biểu diễn số phức z
1
= x
1
+ y
1
i
Giả sử M
2
(x
2
;y
2
) biểu diễn số phức z
2
= x
2
+ y
2
i
Khi đó khoảng cách giữa hai điểm M
1
M
2
bằng môđun của số phức z
1
– z
2
.
Vậy: M
1
M
2
= |z
1
– z
2
| =
( ) ( )
22
1 2 1 2
x x y y− + −
Áp dụng vào bài toán:
Giả sử z
3
= x+yi
Để các điểm biểu diễn của z
1
, z
2
, z
3
tạo thành một tam giác đều thì

Trang 36
1 2 1 3
1 2 2 3
z z z z
z z z z
− = −
−=−
( ) ( )
( ) ( )
( ) ( )
22
22
22
4 4 1 1
1 1 8
0
4 4 1 1
xy
xy
xy
xy
+ = − + −
− + − =
+=
+ = + + +
2y
2
= 6 y =
3
x =
3
Vậy có hai số phức thoả mãn là: z
3
=
3
(1+i) và z
3
= -
3
(1-i).
-----------------
ĐỀ 33
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Tính diện tích xung quanh
xq
S
của hình chóp tứ giác đều có tất cả các cạnh bằng a.
A.
2
33
xq
Sa=
B.
2
23
xq
Sa=
C.
2
43
xq
Sa=
D.
2
3
xq
Sa=
Câu 2: Số điểm cực trị của hàm số
( )
2
2y f x x x= = −
bằng
A. 0 B. 1 C. 2 D. 3
Câu 3: Cho hai điểm
( ) ( )
A 1; 3;6 ;B 5;1; 4− − −
tọa độ trung điểm M của đoạn thẳng AB là:
A.
( )
M 4; 2;2−−
B.
( )
M 2; 1;1−−
C.
( )
M 3; 2;5−
D.
( )
M 6; 4;10−
Câu 4: Quan sát đồ thị ở hình bên và chọn khẳng định sai
A. Hàm số nghịch biến trên khoảng
( )
3; .+
B. Hàm số đồng biến trên khoảng
( )
1;2 .−
C. Hàm số nghịch biến trên khoảng
( )
; 1 .− −
D. Hàm số đồng biến trên khoảng
( )
0;2 .
Câu 5: Cho a, b là các số dương và a khác 1. Mệnh đề nào sau đây đúng?
A.
( )
log ( ) 2 1 log
a
a
ab b=+
B.
( )
1
log ( ) 1 log
2
a
a
ab b=+
C.
log ( ) 2log
a
a
ab b=
D.
1
log ( ) log
2
a
a
ab b=
Câu 6: Cho
( )
1
0
2 ( ) ( ) 5f x g x dx
−=
và
( )
1
0
3 ( ) ( ) 10f x g x dx
+=
. Khi đó
1
0
()f x dx
bằng
A.
5
B.
10
C.
3
D.
15
Câu 7: Khối trụ có bán kính đáy
R
và thiết diện qua trục là hình vuông có thể tích là

Trang 37
A.
3
2 R
B.
3
R
C.
3
1
3
R
D.
2
2 R
Câu 8: Tập nghiệm của bất phương trình
44
log (4 1) log ( 10)xx− = −
A.
B.
3−
C.
3
D.
3;3−
Câu 9: Mặt phẳng chứa 2 điểm và song song với trục Ox có phương trình là
A.
B. C. D.
Câu 10: Họ nguyên hàm của hàm số
( ) 2 sinx
x
fx=+
A.
2
os
ln2
x
cxC−+
B.
2 os
x
cxC−+
C.
2
os
ln2
x
cxC++
D.
2 os
x
cxC++
Câu 11: Cho đường thẳng d:
x 1 y 1 z
1 3 5
+−
==
−
. Một phương trình tham số của đường thẳng trên là
A.
xt
y 1 3t
z 2 5t
=
= − −
= − −
B.
1
xt
3
y 2t
1
z 3t
3
= − +
=
= − +
C.
x 1 t
y 1 3t
z 5t
= − +
=+
=−
D.
xt
y 1 3t
z 2 5t
=
=+
=+
Câu 12Tập nghiệm của bất phương trình:
32
5 21
xx
A A x+
là
A.
3;4S =
. B.
2;4S =
. C.
2;3;4S =
. D.
4S =
.
Câu 13: Cho dãy số
( )
n
u
xác định bởi:
1
1
150
3
−
=
=−
nn
u
uu
với mọi
2n
. Tính tổng S của 100 số hạng đầu
tiên của dãy số đó.
A. S = 150. B. S = 300. C. S = 29850. D. S = 59700
Câu 14: Cho số phức
53zi=+
. Tìm số phức liên hợp của số phức
z
A.
53zi= − +
B.
53zi= − −
C.
35zi= − +
D.
32zi=−
Câu 15: Hàm số nào sau đây có bảng biến thiên như hình bên?
A.
3
2
x
y
x
−
=
−
B.
1
2
x
y
x
+
=
−
C.
21
2
x
y
x
−
=
+
D.
25
2
x
y
x
+
=
+
Câu 16: Xét hàm số
()y f x=
với
1;5x−
có bảng biến thiên như sau:
( )
1;0;1A
( )
1;2;2B −
2 3 0xz+ − =
2 2 0yz− + =
2 1 0yz− + =
0x y z+ − =

Trang 38
x
-1
0
2
5
y
+
0 -
0 +
y
4
+
3
0
Khẳng định nào sau đây là đúng?
A. Hàm số đã cho uôn luôn tồn tại GTLN và GTNN trên đoạn
1;5−
B. Hàm số đã cho đạt GTNN tại
1x =−
và
2x =
trên đoạn
1;5−
C. Hàm số đã cho không tồn taị GTLN trên đoạn
1;5−
D. Hàm số đã cho đạt GTLN bằng 4 tại
5x =
trên đoạn
1;5−
Câu 17: Cho hàm số
42
y ax bx c= + +
trong đó
0; 0ab
.Tìm khẳng định đúng.
A. Hàm số có 2 cực tiểu và 1 cực đại. B. Hàm số có 2 cực đại và 1 cực tiểu.
C. Hàm số có 1 cực đại. D. Hàm số có 1 cực tiểu.
Câu 18: Các số thực x, y thoả mãn :
( )
iyx+y=xi+y+x −−1253
là
A.
( )
7
4
7
1
;=yx;
B.
( )
−
7
4
7
2
;=yx;
C.
( )
−
7
4
7
1
;=yx;
D.
( )
−−
7
4
7
1
;=yx;
Câu 19: Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm
M(3; 2;5),N( 1;6; 3)− − −
. Phương trình
nào sau đây là phương trình của mặt cầu có đường kính là MN
A.
2 2 2
(x 1) (y 2) (z 1) 36+ + + + + =
B.
2 2 2
(x 1) (y 2) (z 1) 6− + − + − =
C.
2 2 2
(x 1) (y 2) (z 1) 6+ + + + + =
D.
2 2 2
(x 1) (y 2) (z 1) 36− + − + − =
Câu 20: Cho
01a
,
log , log
aa
x b y c==
. Tính giá trị của biểu thức
3
log
a
b
P
c
=
theo x và y
A.
11
23
P x y=−
B.
3
P x y=−
C.
23P x y=−
D.
11
32
P x y=−
Câu 21: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
2 2 0zz+ + =
. Giá trị của biểu thức
2016 2016
12
P z z=+
là
A. P = 2
1009
B. P = 0 C. P = 2
2017
D. P = 2
2018
Câu 22: Trong không gian hệ tọa độ Oxyz, cho điểm
( )
A 1;2;1
và mặt phẳng
( )
P :x 2y 2z 1 0+ − − =
. Gọi
B là điểm đối xứng với A qua (P). Độ dài đoạn thẳng AB là
A. 2 B.
4
3
C.
2
3
D. 4
Câu 23: Tập nghiệm của bất phương trình
2
4
1
8
2
xx−
là
A.
( ;1) (3; )− +
B.
(1;3)
C.
( ;3)−
D.
(1; )+
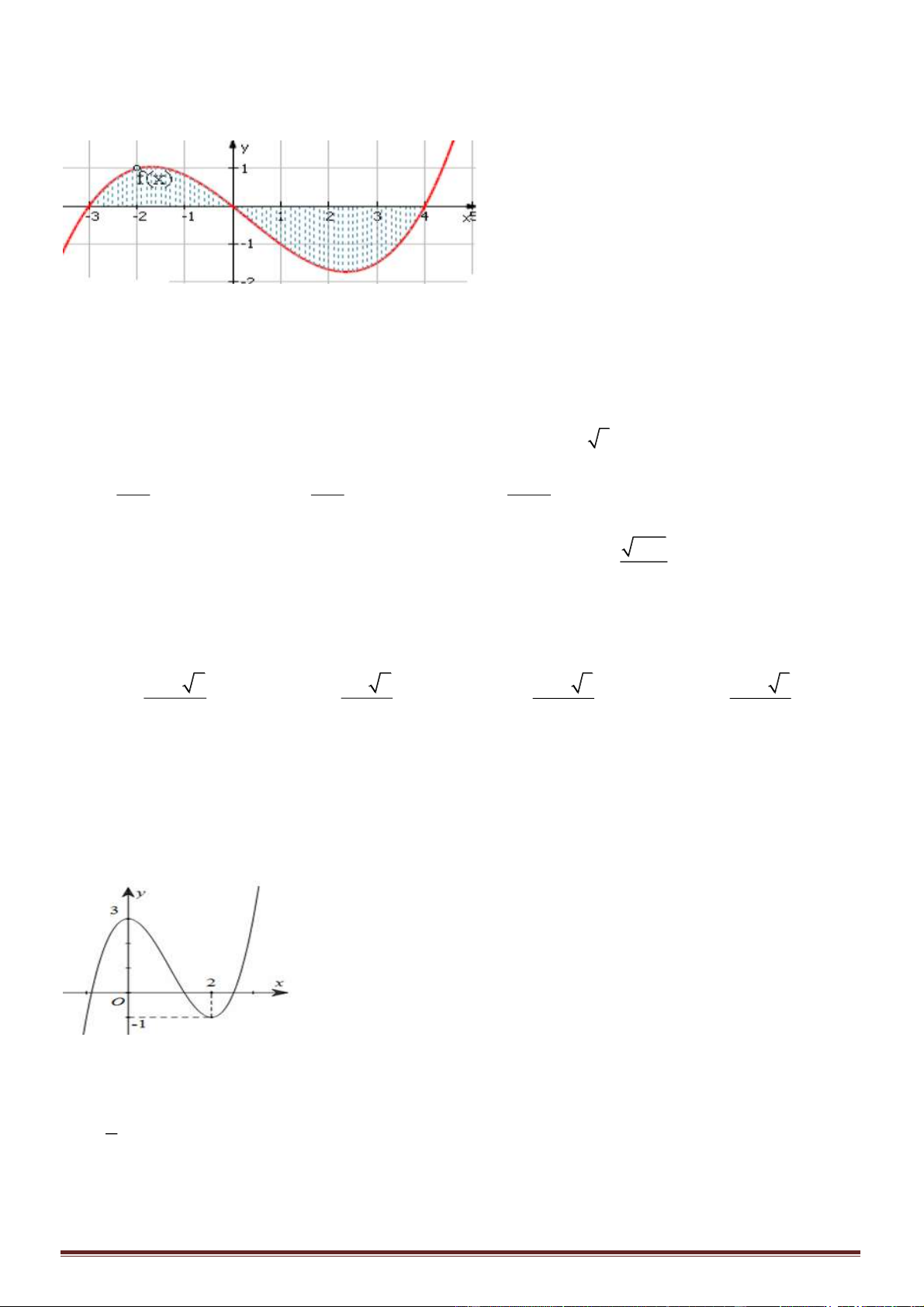
Trang 39
[<A>]/
Câu 24: Cho đồ thị hàm số
()y f x=
. Diện tích hình phẳng (phần gạch trong hình) là:
A.
00
34
( )d ( )df x x f x x
−
+
B.
14
31
( )d ( )df x x f x x
−
+
C.
34
00
( ) ( )f x dx f x dx
−
+
D.
4
3
()f x dx
−
Câu 25: Một khối nón có bán kính đáy
R
và diện tích xung quanh là
2
5 R
. Thể tích khối nón là
A.
3
6
R
B.
3
3
R
C.
3
2
3
R
D.
3
2 R
Câu 26: Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
1
4
x
y
x
−
=
−
là
A. 4 B. 3 C. 2 D. 1
Câu 27: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng 3a.
A.
3
27 2
4
a
V =
B.
3
32
4
a
V =
C.
3
27 3
2
a
V =
D.
3
27 3
4
a
V =
Câu 28: Tính đạo hàm của hàm số
( )
ln sin2yx=
A.
' 2tan2yx=−
B.
' 2cot2yx=
C.
' 2tan2yx=
D.
' 2.cot2yx=−
Câu 29: Cho hàm số
32
33y x x= − +
có đồ thị như hình vẽ. Tìm tập hợp tất cả các giá trị của tham số m
để phương trình
32
30x x m− + =
có ba nghiệm phân biệt
A.
40m−
B.
04m
C.
40m−
C.
04m
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
a
. Cạnh bên
SA
vuông góc với đáy và
2
a
SA =
. Tính góc giữa hai mặt phẳng
(ABC)
và
(SBC)
A.
0
30
B.
0
45
C.
0
60
D.
0
90
Câu 31: Gọi
1
x
và
2
x
là 2 nghiệm của phương trình
12
2 2 3
xx−−
+=
. Tính
22
12
xx+

Trang 40
A. 1 B. 3 C. 5 . D. 9 .
Câu 32: Cho khối nón có bán kính đáy
x
và thiết diện qua trục là một tam giác đều. Bên trong khối nón
chứa hai khối cầu tiếp xúc ngoài với nhau và cùng tiếp xúc với mặt xung quanh của khối nón, khối cầu
lớn tiếp xúc với đáy khối nón. Thể tích của khối cầu nhỏ là
A.
3
3
36
x
B.
3
43
729
x
C.
3
3
91
x
D.
3
4
81
x
Câu 33: Họ nguyên hàm của hàm số
( ) (9 1).sin3f x x x=+
là
A.
1
(9x 1)cos3 sin3
3
x x C− + + +
B.
1
(9x 1)cos3 sin3
3
x x C+ − +
C.
1
(9x 1)cos3 sin3
3
x x C+ + +
D.
(9x 1)cos3 sin3x x C+ + +
Câu 34: Cho hình chóp
.S ABCD
có đáy là hình vuông , cạnh bên
SA
vuông góc với đáy. Biết
= 7SC a
và mặt phẳng
( )
SDC
tạo với mặt phẳng
( )
ABCD
một góc
0
30
. Tính thể tích khối chóp
..S ABCD
A.
3
3a
B.
3
a
C.
3
6a
D.
3
3a
Câu 35: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
x y z 1
d:
1 2 1
+
==
−
và
x 1 y 2 z
d'
2 4 2
−−
= = =
−
. Viết phương trình mặt phẳng (Q) chứa hai đường thẳng d và d’.
A. Không tồn tại
( )
Q
B.
( )
: 2 2 0Q y z− − =
C.
( )
Q : x y 2 0− − =
D.
( )
Q : 2y 4z 1 0− + + =
Câu 36:Tìm m để hàm số
32
3y x x mx m= + + +
nghịch biến trên một khoảng có độ dài nhỏ hơn 1.
A.
1 3m
. B.
3
3
4
m
. C.
3m
. D.
1
3
2
m
.
Câu 37: Xét số phức z thỏa mãn là một số thuần ảo. Biết răng tập hợp tất cả những điểm
biểu diễn của z là một đường tròn, tâm của đường tròn có tọa độ là:
A. (1, 1) B. (1, -1) C. (-1, -1) D. (-1, 1)
Câu 38: Cho
2
2
1
85
ln2 ln3 ln5
6 7 2
x
dx a b c
xx
+
= + +
++
, với a, b, c là các số thực . Giá trị của
32
3a b c++
bằng:
A. 1 B. 2 C. 3 D. 4
Câu 39: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có bảng biến thiên như sau
z 2 3i
u
zi
++
=
−
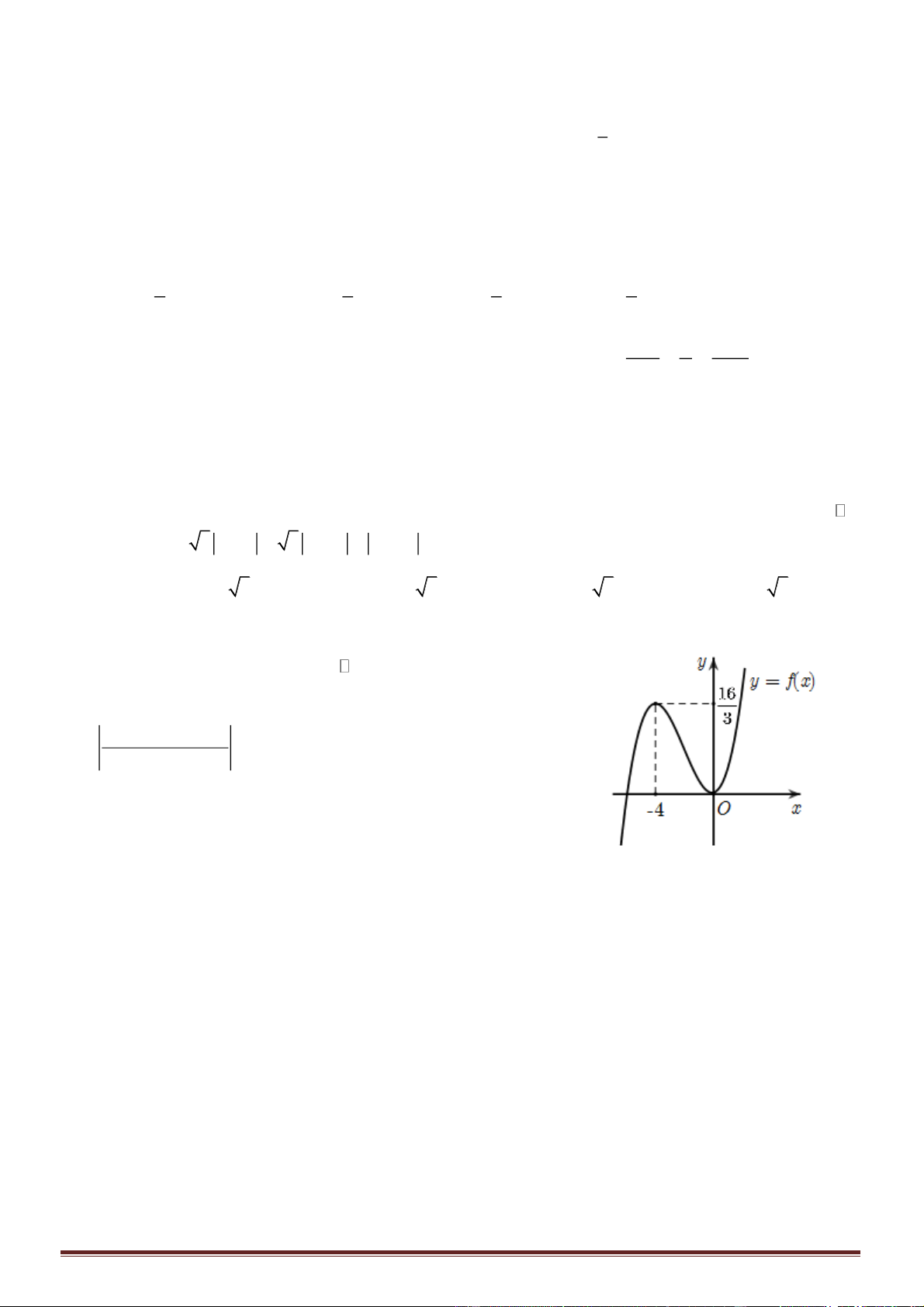
Trang 41
Bất phương trình
( )
2e
x
f x m+
đúng với mọi
( )
1;1x−
khi và chỉ khi
A.
( )
1 2e.mf−
B.
( )
1 2 .m f e − −
C.
( )
1
1.
e
mf − −
D.
( )
1 e.mf−
Câu 40: Gieo một con súc sắc đồng chất và cân đối một lần. Kí hiệu b là số chấm xuất hiện khi gieo. Xác
suất sao cho phương trình sau có nghiệm:
2
10x bx+ + =
là:
A.
5
6
B.
4
6
C.
2
6
D.
3
6
Câu 41: Trong không gian với hệ tọa độ Oxy, cho đường thẳng
12
:
2 1 1
x y z−+
= =
−
và hai điểm
( )
0; 1;3A −
,
( )
1; 2;1B −
. Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho
22
2MA MB+
đạt giá trị nhỏ
nhất.
A.
( )
5;2; 4M −
. B.
( )
1; 1; 1M −−−
. C.
( )
1;0; 2M −
. D.
( )
3;1; 3M −
.
Câu 42: Cho số phức
1zi=+
. Biết rằng tồn tại các số phức
12
5,z a i z b= + =
(trong đó
,ab
,
1b
) thỏa mãn
1 2 1 2
33z z z z z z− = − = −
. Tính
ba−
.
A.
53ba−=
. B.
23ba−=
. C.
43ba−=
. D.
33ba−=
.
Câu 43:
Cho hàm số
( )
y f x=
liên tục trên và có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( )
2
3sin cos 1
44
2cos sin 4
xx
f f m m
xx
− −
= + +
−+
( )
1
có nghiệm?
A.
3
. B.
4
. C.
5
. D. Vô số.
Câu 44: Anh
C
đi làm với mức lương khởi điểm là
x
(triệu đồng)/tháng, và số tiền lương này được
nhận vào ngày đầu tháng. Vì làm việc chăm chỉ và có trách nhiệm nên sau
36
tháng kể từ ngày đi làm,
anh
C
được tăng lương thêm
10%
. Mỗi tháng, anh ta giữ lại
20%
số tiền lương để gửi tiết kiệm vào
ngân hàng với kì hạn
1
tháng và lãi suất là
0,5%
/tháng, theo hình thức lãi kép (tức là tiền lãi của tháng
này được nhập vào vốn để tính lãi cho tháng tiếp theo). Sau
48
tháng kể từ ngày đi làm, anh
C
nhận
được số tiền cả gốc và lãi là
100
triệu đồng. Hỏi mức lương khởi điểm của người đó là bao nhiêu?
A.
8.991.504
đồng. B.
9.891.504
đồng. C.
8.981.504
đồng. D.
9.881.505
đồng.
Câu 45:
Trong không gian với hệ trục tọa độ Oxyz, cho điểm
( )
2;1;1M
và mặt phẳng
( )
: 4 0x y z
+ + − =
và mặt
cầu
( )
2 2 2
: 6 6 8 18 0S x y z x y z+ + − − − + =
. Phương trình đường thẳng d đi qua M và nằm trong mặt
phẳng
( )
cắt mặt cầu
( )
S
theo một đoạn thẳng có độ dài nhỏ nhất là:

Trang 42
A.
2 1 1
:
1 2 1
x y z− − −
= =
−
. B.
2 1 1
:
1 2 1
x y z+ + +
= =
−
.
C.
2 1 1
:
1 2 3
x y z− − −
= =
−
. D.
2 1 1
:
1 2 1
x y z− − −
= =
−−
.
Câu 46: Cho 2 đường tròn
( )
1
;5O
và
( )
2
;3O
cắt nhau tại 2 điểm
A, B sao cho AB là 1 đường kính của đường tròn
( )
2
.O
Gọi (D)
là hình thẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn
lớn, phần được gạch chéo như hình vẽ). Quay (D) quanh trục O
1
,
O
2
ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo
thành.
A.
14
.
3
V
=
B.
68
.
3
V
=
C.
40
.
3
V
=
D.
36 .V
=
Câu 47:
Cho lăng trụ tam giác đều ABC.A’B’C’ , gọi E là trung điểm BC, biết khoảng cách từ C đến (AC’E) bằng
a, và góc giữa C’E và (ACC’A’) là
0
30
. Khi đó thể tích khối trụ ABC.A’B’C’ là
A.
3
9
4
a
B.
3
9
2
a
C.
3
3
2
a
D.
3
3
4
a
Câu 48: Cho hàm số
3 2 3
31
22
y x mx m= − +
có đồ thị (Cm). Tìm tất cả giá trị thực của m để đồ thị (Cm) có
2 điểm cực trị là A và B thỏa mãn AB vuông góc với đường thẳng d:
yx=
A.
1
0
2
m hay m= =
B.
20m hay m= =
C.
1
2
m =
D.
2m =
Câu 49:
Bất phương trình sau có bao nghiệm nguyên?
2
2
24 27 12 24
.
8
24
12 24
x x x x x
xx
x x x
+ + + − +
+−
+ + +
A. 1 B. 2 C. 0 D. 3
Câu 50: Biết rằng đồ thị hàm số bậc 4:
( )
y f x=
được cho như hình vẽ sau:
Tìm số giao điểm của đồ thị hàm số
( ) ( ) ( ) ( )
2
' . ''y g x f x f x f x= = −
và trục Ox.
A.
0
B.
2
C.
4
D.
6

Trang 43
Đáp án
1- D
2-A
3-B
4-B
5-A
6-C
7-A
8-A
9-B
10-A
11-C
12-A
13-A
14-C
15-B
16-C
17-A
18-C
19-D
20-A
21-A
22-B
23-A
24-A
25-C
26-C
27-D
28- B
29-C
30-A
31-C
32-A
33-A
34-B
35-A
36- B
37-C
38-D
39-A
40-A
41-B
42-D
43-A
44-A
45-A
46-C
47-B
48-D
49-A
50- A
LỜI GIẢI CHI TIẾT 17 CÂU VD
Câu 34:Đáp án B
Góc giữa (SDC) và ( ABCD) là góc SDA,
0
3
tan30
3
SA AD AD==
;
SAC
vuông tại A:
2 2 2
2
22
27
3
SA AC SC
AD
AD a
+=
+=
22
7
7
3
3
AD a
AD a
=
=
Suy ra
SA a=
23
11
. ( 3)
33
ABCD
V SAS a a a= = =
Câu 35: Đáp án A
Đường thẳng d qua
(0;0; 1)A −
và có VTCP
(1; 2;1)u =−
Đường thẳng d’ qua
(1;2;0)B
và có VTCP
' ( 2;4;2)u =−
(1;2;1)AB =
, ' ( 8; 4;0)uu
= − −
, ' 8 8 16 0AB u u
= − − = −
Nên d, d’ chéo nhau. Suy ra không tồn tại mp(Q)
Câu 36:Đáp án B
✓ Hàm số đã cho xác định
D=
✓ Ta có:
2
' 3 6y x x m= + +

Trang 44
✓ Hàm số nghịch biến trên một khoảng có độ dài nhỏ hơn 1
'
12
0
1
y
xx
−
2
9 3 0
3
3
3
4 4 1
4
41
m
m
m
m
SP
−
−
−
Câu 37: Đáp án C
Giả sử , khi đó
Tử số bằng
u là số thuần ảo khi và chỉ khi:
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm , bán kính bằng , khuyết 2 điểm
(0;1) và (-2;-3).
Câu 38: Đáp án D
Ta có
22
2
11
8 5 2 1
()
6 7 2 2 1 3 2
x
dx dx
x x x x
+
=+
+ + + +
=
2
1
1
(ln 2 1 ln 3 2)
3
xx+ + +
=
2
ln2 ln3 ln5
3
−+
Do đó a=1; b=-1;
2
3
c =
, nên
32
34a b c+ + =
Câu 39: Đáp án A
( ) 2 ( ) 2
xx
f x e m f x e m + −
,
( 1,1)x −
Đặt
( ) ( ) 2e
x
g x f x=−
''
( ) ( ) 2
x
g x f x e=−
,
( 1,1)x −
thì
'
( ) 0fx
,
20
x
e−
nên
''
( ) ( ) 2 0
x
g x f x e= −
Bảng biến thiên:
x
-1 1
g
’
(x)
-
g(x)
g(-1)
z a ib (a,b R)= +
22
a 2 bi 3i (a 2 (b 3)i)(a (b 1)i)
u
a (b 1)i a (b 1)
+ + + + + + − −
==
+ − + −
22
a b 2a 2b 3 2(2a b 1)i+ + + − + − +
2 2 2 2
a b 2a 2b 3 0 (a 1) (b 1) 5
2a b 1 0 (a;b) (0;1), ( 2; 3)
+ + + − = + + + =
− + − −
I( 1; 1)−−
5

Trang 45
g(1)
Từ bảng biến thiên ta có:
(1) (1) 2m g m f e −
Câu 40: Đáp án A
Ta có
( ) 6n =
Phương trình
2
10x bx+ + =
có nghiệm khi :
22
4 0 4 2 2;3;4;5;6b b b b = −
Vậy xác suất để PT có nghiệm là:
5
6
Câu 41: Đáp án B
Vì M thuộc đường thẳng Δ nên
( )
1 2 ; ; 2M t t t+ − −
.
Ta có
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
2 2 2
2 2 1 1 5 2 2 2 3 18 36 53MA MB t t t t t t t t
+ = + + + + + + + + + + = + +
( )
2
22
2 18 1 35 35,MA MB t t + = + +
.
Vậy
( )
22
min 2 35 1MA MB t+ = = −
hay
( )
1; 1; 1M −−−
.
Câu 42: Đáp án D
Ta có:
1 2 1 2
33z z z z z z− = − = −
.
( ) ( )
( ) ( )
22
2
22
1 4 1 1
25 3 1 16
ab
b a a
− + = − +
− + = − +
( ) ( )
( ) ( )( ) ( ) ( ) ( ) ( )
22
2 2 2 2 2
1 1 15
23
1 2 1 1 1 3 1 1 1
15
ba
b b a a a b a
− − − =
− + − − + − = − + − − −
( ) ( )
( ) ( )( ) ( )
22
22
1 1 15
8 1 30 1 1 7 1 0
ba
b b a a
− − − =
− − − − + − =
( ) ( )
( )
( )
22
1 1 15
23
1
1
3
11
33
4
73
1
7
11
3
2
ba
a
ba
ba
b
ba
− − − =
=−
− = −
− =
=+
− = −
Câu 43: Đáp án A
Đặt
3sin cos 1
2cos sin 4
xx
t
xx
−−
=
−+
( ) ( )
2 1 cos 3 sin 1 4t x t x t + − + = − −
( )
*
.
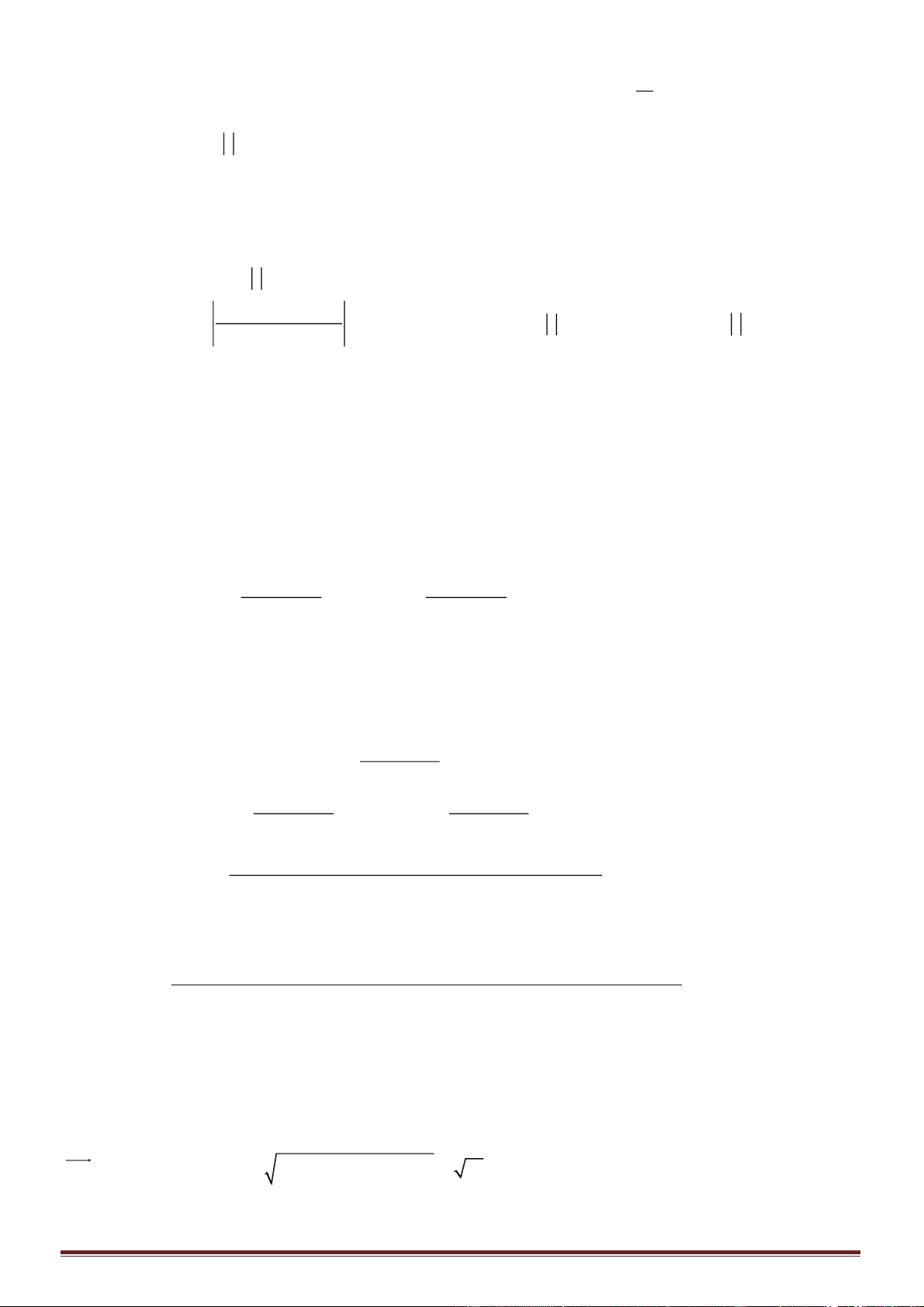
Trang 46
Phương trình
( )
*
có nghiệm
( ) ( ) ( )
2 2 2
2 1 3 4 1t t t+ + + +
9
1
11
t −
.
Suy ra
01t
.
Từ đồ thị
( )
y f x=
ta có
*
( )
y f x=
đồng biến trên
)
0;+
*
( )
)
2
2
4 4 2 0;m m m+ + = + +
.
*
)
0;t +
Nên
( )
2
3sin cos 1
44
2cos sin 4
xx
f f m m
xx
− −
= + +
−+
( )
( )
2
44f t f m m= + +
2
44t m m = + +
Phương trình
( )
1
có nghiệm
2
0 4 4 1mm + +
2
4 4 1mm + +
31m− −
.
Do
3; 2; 1m Z m − − −
.
Câu 44: Đáp án A
+ Lãi suất
0,5% 0,005.r ==
+ Số tiền gốc ban đầu gửi vào mỗi tháng là
0,2 .Ax=
+ Số tiền cả gốc và lãi nhận được sau
36
tháng là
36 36
1
(1 ) 1 (1 ) 1
(1 ). 0,2 (1 ). .
rr
A A r x r
rr
+ − + −
= + = +
+ Bắt đầu từ tháng thứ
37
số tiền gốc người này gửi vào ngân hàng là
( .10%).20% 0,22 .x x x+=
+ Số tiền cả gốc và lãi nhận được sau
48
tháng là:
12
12
1
36 12
13
(1 ) 1
(1 ) 0,22 .(1 ).
(1 ) 1 (1 ) 1
0,2 (1 ) . 0,22 .(1 ). .
r
S A r x r
r
rr
x r x r
rr
+−
= + + +
+ − + −
= + + +
Suy ra:
13 36 12
.
0,2(1 ) (1 ) 1 0,22(1 ) (1 ) 1
rS
x
r r r r
=
+ + − + + + −
Theo giả thiết bài toán ta có:
8
13 36 12
0,005 10
8.991.504
0,2(1 0,005) (1 0,005) 1 0,22(1 0,005) (1 0,005) 1
x
=
+ + − + + + −
đồng.
Vậy mức lương khởi điểm của anh
C
là
8.991.504
đồng.
Câu 45: Đáp án A
Mặt cầu
( )
S
có tâm
( )
3;3;4I
, bán kính
4R =
.
( ) ( ) ( ) ( )
2 2 2
1; 2; 3 1 2 3 14IM IM R= − − − = − + − + − =
.
M
nằm trong mặt cầu
( )
S
nên đường thẳng d luôn cắt mặt cầu tại hai điểm A, B phân biệt.

Trang 47
Gọi H là hình chiếu của
I
lên đường thẳng
d
.
Ta có:
2 2 2
2 2 2 16AB AH R IH IH= = − = −
.
Để
AB
nhỏ nhất khi
IH
lớn nhất.
Mà
IH IM
. Vậy
IH
lớn nhất khi
HM
Hay
IM d⊥
.
Ta có:
( )
( )
( )
( )
( )
( )
1;1;1
, 1; 2;1
1;2;3
d
d
d
un
d
u n MI
d MI
u MI
⊥=
= = −
⊥
⊥=
.
Đường thẳng
d
đi qua
( )
2;1;1M
và có một vecto chỉ phương
( )
1; 2;1
d
u =−
.
Phương trình đường thẳng
d
là:
2 1 1
1 2 1
x y z− − −
==
−
.
Câu 46: Đáp án C
Gọi V
1
là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D
1
được giới hạn bởi các đường
( )
2
9 4 , 0, 4, 7y x y x x= − − = = =
quay trục tung
( )
7
2
1
4
9 4 .V x dx
= − −
Gọi V
2
là thể tích khối tròn xoay sinh ra khi quay hình phẳng D
2
được giới hạn bởi các đường
2
25 , 0, 4, 5y x y x x= − = = =
quay trục tung
( )
5
2
2
4
25 .V x dx
= −
Khi đó thể tích khối tròn xoay cần tính bằng
( )
( )
75
2
2
12
44
9 4 25 .V V V x dx x dx
= − = − − − −
Suy ra
40
.
3
V
=
Câu 47: Đáp án B

Trang 48
:
Kẻ CK
⊥
EC’ (1)
Có
( ') (2)
'
AE EC
AE ECC CK AE
AE C C
⊥
⊥ ⊥
⊥
( ')
d(C,(AC'E)) CK a
CK AEC⊥
= =
Kẻ
( ' ')
'
EH AC
EH ACC A
EH C C
⊥
⊥
⊥
góc giữa C’E và (ACC’A’) là góc EC’H và bằng
0
30
Đặt AB=
x
,,
42
xx
BC AC x HC EC = = = =
Xét
3
' : '
4
x
C EH C H =
2
2 2 2
''
2
x
C C C H HC = − =
2 2 2
1 1 1
6
'
xa
CK C C CE
= + =
Vậy
2
33
, ' 3
2
ABC
a
S C C a==
Thể tích khối lăng trụ ABC.A’B’C’ là
3
9
2
a
Câu 48: Đáp án D
Có
2
' 3 3y x mx=−
1
0
2
'0
0
x y m
y
x m y
= =
=
= =
Để hàm số có 2 điểm cực trị thì
0m
. Gỉa sử
23
11
(0; ), ( ;0) ( ; )
22
A m B m AB m m = −
A'
C'
B'
A
C
B
M
H
K

Trang 49
VTPT của d :
(1; 1) (1;1)nu= − =
. 0 2AB d AB u m⊥ = =
Câu 49: Đáp ánA
Lời giải:Điều kiện:
)
0; .D = +
Ta có
( ) ( )
22
22
24 2 2 24 24 ;24 2 2 24 24x x x x x x x x x x+ − + = + − + + + = + +
Khi đó, bất phương trình trở thành:
( )
( )
2
2
24
24 27
.
8
24
24
xx
xx
xx
xx
+−
++
+−
++
( ) ( )
0
2 24 3 24 5 24 0 1.
25 24
x
x x x x x x x
xx
+ + + − +
+
Câu 50: Đáp án A
Cách giải: Đồ thị hàm số
( )
y f x=
cắt trục hoành tại bốn điểm phân biệt nên
( ) ( )( )( )( )
1 2 3 4
f x a x x x x x x x x= − − − −
( ) ( )( )( ) ( )( )( )
( )( )( ) ( )( )( )
( ) ( ) ( )
2 3 4 1 3 4
1 2 4 1 2 3
1 2 3 4 1 2 3 4
1 2 3 4
'
1 1 1 1
' ; ; ; ' 0 ; ; ;
f x a x x x x x x a x x x x x x
a x x x x x x a x x x x x x
f x f x x x x x x f x x x x x x
x x x x x x x x
= − − − + − − −
+ − − − + − − −
= + + +
− − − −
Đặt
( )
( )
( )
1 2 3 4
1 2 3 4
'
1 1 1 1
; ; ;
fx
h x x x x x x
f x x x x x x x x x
= = + + +
− − − −
Ta có
( )
( ) ( ) ( )
( )
( ) ( ) ( ) ( )
2
1 2 3 4
2 2 2 2
2
1 2 3 4
'' . '
1 1 1 1
' 0 ; ; ;
f x f x f x
h x x x x x x
fx
x x x x x x x x
−
− − − −
= = + + +
− − − −
( ) ( ) ( )
( ) ( ) ( ) ( )
2
1 2 3 4
2
1 2 3 4
'' . ' 0 ; ; ;
' '' . 0 ; ; ;
f x f x f x x x x x x
g x f x f x f x x x x x x
−
= −
Vậy đồ thị hàm số
( ) ( ) ( ) ( )
2
' . ''y g x f x f x f x= = −
không cắt trục Ox.
Trang 50
ĐỀ 34
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Cosin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều có tất cả các cạnh bằng nhau là
A.
1
.
3
B.
1
.
3
C.
3
.
2
D.
1
.
2
Câu 2: Điều kiện xác định của phương trình
6
24
3
x
x
− + =
−
là tập nào sau đây?
A.
\ 3 .
B.
)
2; .+
C.
.
D.
)
2; \ 3 .+
Câu 3: Cho M là trung điểm của đoạn AB. Khẳng định nào sau đây đúng?
A.
IA IB AB+=
với I là điểm bất kì. B.
0.AM BM+=
C.
IA IB IM+=
với I là điểm bất kì. D.
0.AM MB+=
Câu 4: Trong các hàm số sau hàm số nào nghịch biến trên ?
A.
2
3
log .yx=
B.
.
4
x
e
y
=
C.
( )
3
log .yx=
D.
.
4
x
y
−
=
Câu 5: Véc tơ nào trong các véc tơ dưới đây là véc tơ pháp tuyến của đường thẳng
2 1 0?yx+ − =
A. (2;-1). B. (1;2). C. (-2;1). D. (-2;-1).
Câu 6: Cho lăng trụ tam giác
. ' ' 'ABC A B C
, biết thể tích lăng trụ là V. Tính thể tích khối chóp
. ' 'C ABB A
?
A.
2
.
3
V
B.
1
.
3
V
C.
3
.
4
V
D.
1
.
2
V
Câu 7: Tìm số điểm cực trị của đồ thị hàm số
2
1
x
y
x
−
=
+
?
A. 4. B. 1. C. 0. D. 3.
Câu 8: Dãy số nào sau đây là cấp số cộng?
A.
( )
1
:.
nn
uu
n
=
B.
( )
1
: 2, 2.
n n n
u u u n
−
= −
C.
( )
: 2 1.
n
nn
uu=−
D.
( )
1
: 2 , 2.
n n n
u u u n
−
=
Câu 9: Đạo hàm của hàm số
2
ln 1y x x
= + −
là

Trang 51
A.
2
1
.
1x +
B.
2
1
.
1xx+−
C.
2
1
.
1xx++
D.
2
1
.
1x
−
+
Câu 10: Tập hợp tất cả các số thực x thỏa mãn
42
23
32
xx−
là
A.
2
;.
3
−
+
B.
5
;.
2
+
C.
2
;.
5
−
D.
2
;.
3
−
Câu 11: Tập xác định của hàm số
2
log .yx=
A.
( )
0; .+
B.
)
0; .+
C.
\ 0 .
D.
.
Câu 12: Cho hàm số
( )
y f x=
có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên
khoảng nào dưới đây?
x
−
-1 1
+
'y
+ 0 - 0 +
y
+
3
2−
−
A.
( )
1; .− +
B. (-1;1). C.
( )
;1 .−
D.
( )
1; .+
Câu 13: Cho A là tập hợp khác
(
là tập hợp rỗng). Xác định mệnh đề đúng trong các mệnh đề sau.
A.
.A
B.
.AA =
C.
.A
D.
.A =
Câu 14: Khẳng định nào sai trong các khẳng định sau?
A.
cosyx=
tuần hoàn với chu kỳ
.
B.
cosyx=
nghịch biến trên khoảng (0;
.
).
C.
cosyx=
là hàm chẵn. D.
cosyx=
có tập xác định là
.
Câu 15: Số cách chọn ra ba bạn bất kỳ từ một lớp có 30 bạn là
A.
3
30
.C
B.
3
30
.
3
A
C.
3
30
3!. .A
D.
3
30
.A
Câu 16: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
42
21y x x= − + −
trên
đoạn [-2;1]. Tính M + m.
A. 0. B. -9. C. -10. D. -1.
Câu 17: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết
3
.
.
33
SABCD
a
V =
Tính góc giữa SA và mặt phẳng (SCD).
A.
0
60 .
B.
0
45 .
C.
0
30 .
D.
0
90 .
Câu 18: Số nghiệm thuộc đoạn
0;2018
của phương trình
cos2 2sin 3 0xx− + =
là
A. 2017. B. 1009. C. 1010. D. 2018.
Trang 52
Câu 19: Tìm m để hệ phương trình
21
22
mx y
xy
−=
+=
có nghiệm.
A.
4.m
B.
2.m−
C.
2.m
D.
4.m−
Câu 20: Cho a, b, c là các số thực dương và khác 1. Hình vẽ bên là đồ thị của hàm số
log , log , log .
a b c
y x y x y x===
Khẳng định nào sau đây là đúng?
A.
.b c a
B.
.b a c
C.
.a b c
D.
.c a b
Câu 21: Tìm m để hàm số
3
21
khi x 1
1
mx+1 khi x =1
xx
y
x
−−
=
−
liên tục trên
.
A.
4
.
3
−
B.
1
.
3
−
C.
4
.
3
D.
2
.
3
Câu 22: Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số
42
3 2.y x x= − +
Mệnh đề nào dưới đây
đúng?
A. d có hệ số góc âm. B. d song song với đường thẳng x = 3.
C. d có hệ số góc dương. D. d dong dong với đường thẳng y = 3.
Câu 23: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số
2
ln 1y x x
= + +
là hàm số chẵn.
B. Tập giá trị của hàm số
( )
2
ln 1yx=+
là
)
0; .+
C. Hàm số
2
ln 1y x x
= + −
có tập xác định là
.
D.
2
2
1
ln 1 .
1
xx
x
+ + =
+
Câu 24: Giá trị của m để phương trình
32
30x x x m− + − =
có ba nghiệm phân biệt lập thành một cấp số
cộng thuộc khoảng nào trong các khoảng dưới đây?
A. (2;4). B. (-2;0). C. (0;2). D. (-4;2).
Câu 25: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OC = 2a, OA = OB = a. Gọi
M là trung điểm của AB. Tính khoảng cách giữa hai đường thẳng OM và AC.
A.
2
.
3
a
B.
25
.
5
a
C.
2
.
3
a
D.
2
.
2
a

Trang 53
Câu 26: Tìm tập xác định của hàm số
( )
2
2
log .
2
xx
fx
x
+−
=
−
A.
\ 2 .
+
B.
) ( )
0;1 2; . +
C.
( )
2; .+
D.
)
0; \ 2 .+
Câu 27: Một nhóm học sinh gồm 5 bạn nam, và 3 bạn nữ cùng đi xem phim, có bao nhiêu cách xếp 8 bạn
vào 8 ghế hàng ngang sao cho 3 bạn nữ ngồi cạnh nhau?
A. 5!.3!. B. 8! – 5.3!. C. 6!.3!. D.
8!
.
3!
Câu 28: Tính thể tích của khối bát diện đều có tất cả các cạnh bằng 2a.
A.
3
2
.
6
a
B.
3
42
.
3
a
C.
3
82
.
3
a
D.
3
22
.
3
a
Câu 29: Cho hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0.a b c d
B.
0, 0, 0, 0.a b c d
C.
0,b 0,c 0,d 0.a
D.
0, 0, 0, 0.a b c d
Câu 30: Tìm số đường tiệm cận đứng của đồ thị hàm số
2
93
.
x
y
xx
+−
=
+
A. 3. B. 1. C. 0. D. 2.
Câu 31: Cho hình lập phương
. ' ' ' 'ABCD A B C D
có tất cả các cạnh bằng 1. Gọi M là trung điểm của
'.BB
Tính thể tích khối
'.A MCD
A.
1
.
12
B.
2
.
15
C.
4
.
15
D.
1
.
28
Câu 32: Với
25
log 7, log 7.ab==
Tính giá trị của
10
log 7.
A.
.
ab
ab+
B.
1
.
ab+
C.
.ab+
D.
.
ab
ab
+
Trang 54
Câu 33: Một cái phễu có dạng hình nón, chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào
phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm. Nếu bịt kín miệng phễu và lật ngược phễu
lên thì chiều cao của cột nước trong phễu gần bằng nhất với giá trị nào sau đây.
A. 1,07 cm. B. 10 cm. C. 9,35 cm. D. 0,87 cm.
Câu 34: Cho hàm số
( )
y f x=
có bảng biến thiên như hình dưới đây. Tìm tất cả các giá trị của m để
phương trình
( )
2
2
4 logf x x m−=
có 4 nghiệm thực phân biệt.
x
−
0 4
+
'y
- 0 + 0 -
y
+
3
-1
−
A.
( )
0;8 .m
B.
1
;8 .
2
m
C.
( )
1;3 .m−
D.
1
0; .
2
m
Câu 35: Tập tất cả các giá trị của m để phương trình
22
2 1 1 1 0x x m x x m
− − + − + + =
không có
nghiệm thực là tập (a;b). Khi đó
A.
2 2 2.ab− = +
B.
2 2 2.ab− = − −
C.
2.ab−=
D.
2 2.ab− = −
Câu 36: Gọi S là tập nghiệm của phương trình
( ) ( ) ( )
32
22
2
log 1 log 3 2log 1x x x− − − = −
trên
.
Tìm
số phần tử của S.
A. 1. B. 3. C. 4. D. 2.
Câu 37: Tính tổng của tất cả các số có 5 chữ số đôi một khác nhau được lập thành từ tập
1;2;3;4;5 .A=
A. 333.330. B. 7.999.920. C. 1.599.984. D. 3.999.960.
Câu 38: Diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các nghiệm của
phương trình
2
cos 3sin .cos 1.x x x+=
A.
3.
B.
3 10
.
10
C.
3 10
.
5
D.
2.
Câu 39: Tìm tất cả các giá trị của m để hàm số
16mx
y
xm
+
=
+
đồng biến trên
( )
0; +
?
A.
( )
; 4 .m − −
B.
( ) ( )
; 4 4; .m − − +
C.
)
4; .m +
D.
( )
4; .m +
Trang 55
Câu 40: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh AC sao cho AB = 2AM, đường tròn tâm I
đường kính CM cắt BM tại D, đường thẳng CD có phương trình
3 6 0.xy− − =
Biết I(1;-1), điểm
4
;0
3
E
thuộc đường thẳng BC,
.
C
x
Biết điểm B có tọa độ (a;b). Khi đó:
A.
1.ab+=
B.
ab+=
0. C.
ab+=
-1. D.
ab+=
2.
Câu 41: Quay hình chữ nhật ABCD quanh trục AB cố định, đường gấp khúc ADBC cho ta hình trụ (T).
Gọi
MNP
là tam giác đều nội tiếp đường tròn đáy (không chứa điểm A). Tính tỷ số giữa thể tích khối
trụ và thể tích khối chóp A.MNP.
A.
4
.
33
B.
4
.
3
C.
3
.
4
D.
4
.
3
Câu 42: Một người mua một căn hộ với giá 900 triều đồng. Người đó trả trước với số tiền là 500 triệu
đồng. Số tiền còn lại người đó thanh toán theo hình thức trả góp với lãi suất tính trên tổng số tiền còn nợ
là 0,5% mỗi tháng. Kể từ ngày mua, sau đúng mỗi tháng người đó trả số tiền cố định là 4 triệu đồng (cả
gốc lẫn lãi). Tìm thời gian (làm tròn đến hàng đơn vị) để người đó trả hết nợ.
A. 133 tháng. B. 139 tháng. C. 136 tháng. D. 140 tháng.
Câu 43: Cho số phức z thõa
+ − + =(1 ) 1 2 10i z i
; biết biểu diễn hình học của số phức
= + + −w (2 ) 6i z i
là đường tròn tâm I(a, b) bán kính R. Tính a+b+R bằng:
A.
27
. B.
+4 5 5
. C.
12
. D. 10.
Câu 44: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm các
cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC).
Thể tích của khối chóp S.ABC.
A.
3
5
.
8
a
B.
3
5
.
24
a
C.
3
6
.
12
a
D.
3
3
.
24
a
Câu 45: Cho hình chóp đều S.ABC có
0
, 30 .AB a ASB==
Lấy các điểm
', 'BC
lần lượt thuộc các cạnh
SB, SC sao cho chu vi tam giác
''AB C
nhỏ nhất. Tính chu vi đó.
Trang 56
A.
( )
3 1 .a−
B.
3.a
C.
.
13
a
+
D.
( )
1 3 .a+
Câu 46: Cho hàm số
( )
y f x=
có đúng ba điểm cực trị là 0; 1; 2 và có đạo hàm liên tục trên R. Khi đó
hàm số
( )
2
44y f x x=−
có bao nhiêu điểm cực trị?
A. 5. B. 2. C. 3. D. 4.
Câu 47: Cho hình lập phương
. ' ' ' '.ABCD A B C D
Tính góc giữa hai mặt phẳng
( )
''A B C
và
( )
' ' .C D A
A.
0
45 .
B.
0
30 .
C.
0
60 .
D.
0
90 .
Câu 48: Điểm nằm trên đường tròn
( )
22
: 2 4 1 0C x y x y+ − + + =
có khoảng cách ngắn nhất đến đường
thẳng
: 3 0d x y−+=
có tọa độ M(a;b). Khẳng định nào sau đây là đúng?
A.
2.ab=−
B.
.ab=−
C.
2.ab=
D.
.ab=
Câu 49: Cho m, n là các số nguyên dương khác 1. Gọi P là tích các nghiệm của phương trình
( )( )
2018 log log 2017log 2018log 2019.
m n m n
x x x x= + +
P nguyên và đạt giá trị nhỏ nhất khi:
A.
2020
. 2 .mn=
B.
2017
. 2 .mn=
C.
2019
. 2 .mn=
D.
2018
. 2 .mn=
Câu 50: Gọi S là tập tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số
42
1
14 48 30
4
y x x x m= − + + −
trên đoạn [0;2] không vượt quá 30. Tính tổng tất cả các phần tử của S.
A. 108. B. 120. C. 210. D. 136.
ĐÁP ÁN
1-D
2-D
3-B
4-B
5-D
6-A
7-C
8-B
9-D
10-A
11-A
12-D
13-C
14-A
15-A
16-B
17-C
18-B
19-D
20-A
21-A
22-D
23-A
24-B
25-A
26-B
27-C
28-C
29-C
30-B
31-A
32-A
33-D
34-B
35-B
36-A
37-D
38-C
39-D
40-B
41-B
42-B
43-A
44-B
45-D
46-C
57-D
48-C
49-C
50-D
HƯỚNG DẪN GIẢI
Câu 1: Chn D.
Theo giả thiết S.ABCD là hình chóp tứ giác đều có tất cả các cạnh bằng nhau nên đặt
.AB a SB a= =
Gọi O là tâm của hình vuông ABCD thì
( ) ( )
( )
,.SO ABCD SA ABCD SAO⊥ =
Trang 57
Xét tam giác SAO vuông tại O có
2
2
22
1
2
cos .
2
a
a
SO SA AO
SAO
SA SA a
−
−
= = = =
Câu 2: Chn D.
Phương trình xác định khi
2 0 2
.
3 0 3
xx
xx
−
−
Vậy điều kiện xác định của phương trình là
)
2; \ 3 .+
Câu 3: Chn B.
Do M là trung điểm của đoạn AB nên
0.AM BM+=
Câu 4: Chn B.
Hàm số
4
x
e
y
=
có cơ số
01
4
e
a =
nên hàm số nghịch biến trên R.
Câu 5: Chn D.
Véc tơ pháp tuyến của đường thẳng
2 1 0yx+ − =
là
( )
2; 1 .n= − −
Câu 6: Chn A.
Ta có
. ' ' . ' ' '
12
.
33
C ABB A C A B C
V V V V V V= − = − =
Câu 7: Chn C.
Xét hàm số
2
.
1
x
y
x
−
=
+
Tập xác định
\ 1 .D =−
( )
2
3
' 0, 1.
1
yx
x
= −
+
Do đó hàm số không có điểm cực trị.
Câu 8: Chn B.
Xét dãy số
( )
1
: 2, 2.
n n n
u u u n
−
= −
Ta có
1
2, 2.
nn
u u n
−
− =

Trang 58
Do đó (u
n
) là một cấp số cộng.
Câu 9: Chn D.
Ta có
2
2
2
2
2 2 2
22
2
1
1'
11
21
' ln 1 ' .
1 1 1
11
x
xx
xx
x
y x x
x x x x x
x x x
−
+−
− + −
+
= + − = = = =
+ − + − +
+ + −
Câu 10: Chn A.
Ta có
4 2 4 2
2 2 2 2 2
4 2 .
3 3 3 3 3
x x x x
x x x
−−
−
−
Vậy tập hơp tất cả các số thực x thỏa mãn
42
22
33
xx−
là
2
;.
3
−
+
Câu 11: Chn A.
Điều kiện x > 0.
Câu 12: Chn D.
Câu 13: Chn C.
Câu 14: Chn A.
Ta có
( )
cos cosxx+ = −
nên hàm số
cosyx=
không tuần hoàn với chu kyg
.
Câu 15: Chn A.
Câu 16: Chn B.
Ta có:
3
' 4 4 ,y x x= − +
cho
3
0 2;1
' 0 4 4 0 1 2;1 .
1 2;1
x
y x x x
x
= −
= − + = = −
= − −
Ta có:
( ) ( ) ( ) ( )
2 9, 1 0, 0 1, 1 0.y y y y− = − − = = − =
Suy ra
( ) ( )
2;1
max 1 1 0M y f f
−
= = − = =
nên
( )
2;1
min 2 9.n y f
−
= = − = −
Vậy M + m = -9.
Câu 17: Chn C.

Trang 59
Ta có:
( )
.
CD AD
CD SAD
CD SA
⊥
⊥
⊥
Kẻ
,AH SD⊥
suy ra
( )
.
AH SD
AH SCD
AH CD
⊥
⊥
⊥
Từ đây ta có: SH là hình chiếu của SA lên (SCD).
Do đó,
( )
( )
( )
, , .SA SCD SA SH HSA==
Theo giả thiết ta có:
33
2
S.AB
13
..
33
3 3 3 3
CD
a a a
V a SA SA= = =
Xét tam giác SAD vuông tại A, ta có:
0
3
3
3
tan tan 30 .
3
a
SA
HSA DSA HSA
AD a
= = = = =
Vậy
( )
( )
0
, 30 .SA SCD =
Câu 18: Chn B.
Ta có:
2
cos2 2sin 3 0 2sin 2sin 4 0x x x x− + = − − + =
sinx 1
2,
.
2
sinx 2
x k k
ptvn
=
= +
=−
Xét nghiệm nằm trong đoạn
0;2018 .
1 4035
0 2 2018 .
2 4 4
kk
+ −
Do
k
nên
0,1,...,1008 .k
Vậy có 1009 nghiệm của phương trình đã cho thuộc đoạn
0;2018 .
Câu 19: Chn D.
Ta có:
( )
45
2 1 2 1
.
2 2 4 2 4
4 2 4
mx
mx y mx y
x y x y
xy
+=
− = − =
+ = + =
+=
Do đó để hệ phương trình có nghiệm thì
4 0 4.mm+ −
Câu 20: Chn A.

Trang 60
Kẻ đường thẳng y = 1 ta thấy đường thẳng cắt 3 đồ thị
log , log , log
b c a
y x y x y x= = =
lần lượt tại các
điểm
, , .x b x c x a= = =
Dựa vào đồ thị ta thấy b < c < a.
Câu 21: Chn A.
Hàm số liên tục trên các khoảng
( )
;1−
và
( )
1; .+
Hàm số liên tục trên
hàm số liên tục tại điểm
3
1
21
1 lim 1
1
x
xx
xm
x
→
−−
= = +
−
( )
3
3
2
3
11
21
2 1 4
lim 1 1 lim 1 1 1 .
1 3 3
1
xx
x
m m m m
x
xx
→→
−
− = + − = + − = = = −
−
++
Câu 22: Chn D.
Điểm cực đại của đồ thị hàm số là A(0;2).
Phương trình tiếp tuyến tại A(0;2) là y = 2 (d).
Vậy d song song với đường thẳng y =3.
Câu 23: Chn A.
Xét hàm số
( )
2
ln 1y f x x x
= = + +
có tập xác định D = R.
Với
3,x =
ta có:
( ) ( ) ( ) ( )
3 ln 3 2 ln 2 3 3 .ff= + − = −
Suy ra hàm số
( )
2
ln 1y f x x x
= = + +
không là hàm số chẵn.
Câu 24: Chn B.
Xét hàm số
( )
32
3;f x x x x m= − + −
( ) ( )
2
' 3 6 ; '' 6 6.f x x x f x x= − = −
( )
'' 0 1 1 .f x x y m= = = − −
Điểm uốn của đồ thị hàm số là A (1;-1-m).
Phương trình
32
30x x x m− + − =
có ba nghiệm phân biệt lập thành một cấp số cộng.
( )
1; 1 1 0 1.A m Ox m m − − − − = = −
Câu 25: Chn A.
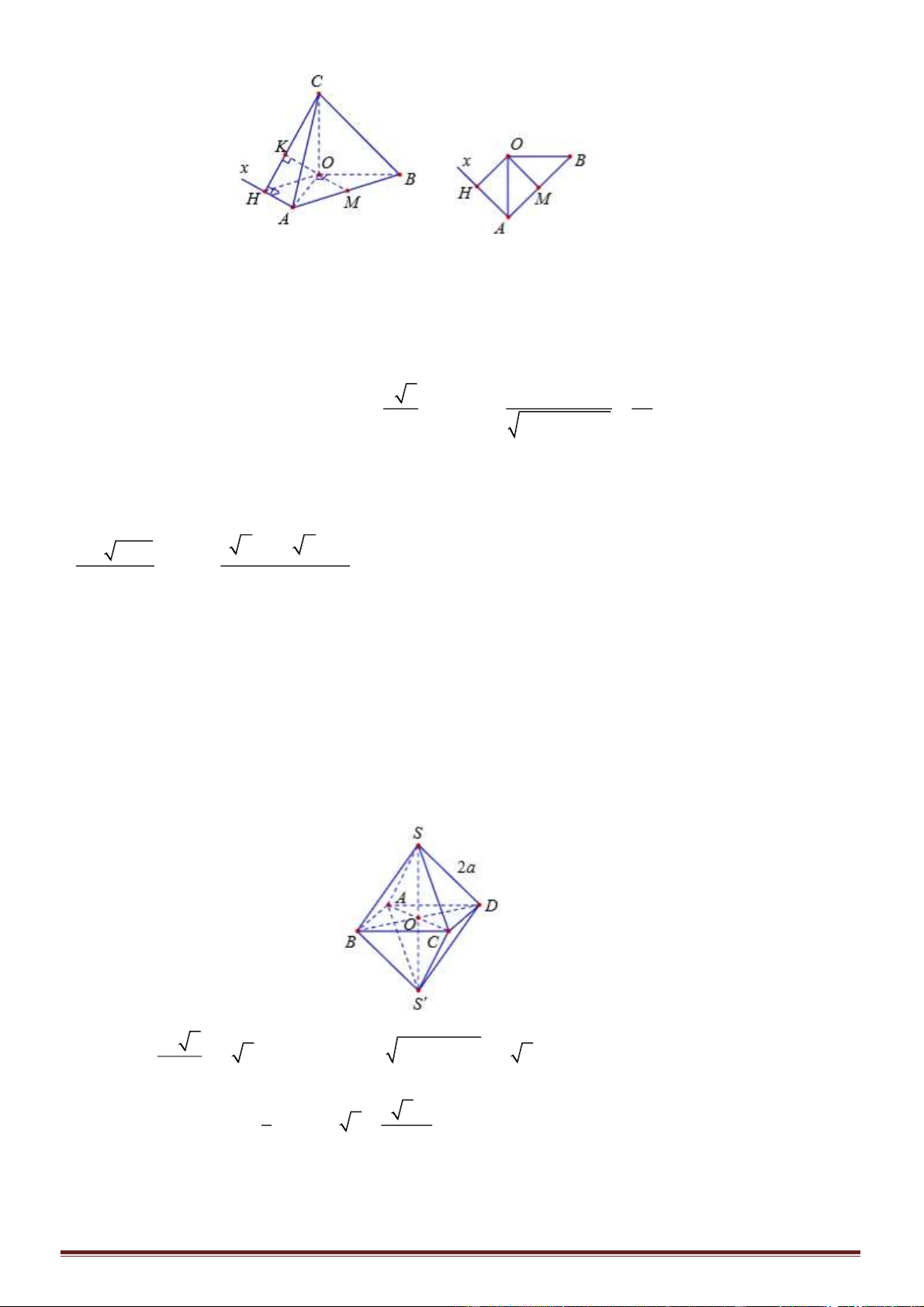
Trang 61
Ta có:
( )
( )
( )
( )
( )
,
;;
.
OM AC
OM CAx O CAx
d d d OK= = =
Với
/ / , , .Ax OM OH Ax OK CH⊥⊥
Vì OHAM là hình vuông nên
2
2
a
OH AM==
nên
22
.2
.
3
OH OC a
OK
OH OC
==
+
Câu 26: Chn B.
Điều kiện xác định của hàm số là
( )( )
) ( )
1
12
2
00
2
22
2 2 2 0;1 2; .
0 0 0
x
xx
xx
x
xx
x x x x
x x x
−+
+−
−−
+
Câu 27: Chn C.
Ta coi 3 bạn nữ là vị trí thì số cách sắp xếp 6 là 6!, sau đó xếp 3 bạn nữ vào vị trí đó là 3! Nên số cách sắp
xếp là 6!.3!.
Câu 28: Chn C.
Ta có
22
22
2, 2 2
2
a
AO a SA a SO SA AO a= = = = − =
Thể tích cần tính là
( )
3
2
1 8 2
2. . 2 . 2 .
33
a
V a a==
Câu 29: Chn C.
Trang 62
2
' 3 2 0y ax bx c= + + =
có 2 nghiệm x
1
, x
2
trái dấu (do hai điểm cực trị của đồ thị hàm số nằm hai phía với
Oy)
3 0 0ac c
loại phương án D.
Dựa vào đồ thị thì ta thấy
12
2
0 0 0
3
b
x x b
a
−
+
nên loại B.
Câu 30: Chn B.
Ta có
( )
( )
( )
( )
2
2
0 0 0
9 3 1 1
lim lim lim
6
1 9 3
93
x x x
xx
xx
xx
x x x
+ + +
→ → →
+−
= = =
+ + +
+
+ + +
Suy ra đường thẳng x = 0 không phải là tiệm cận đứng của đồ thị hàm số.
(tương tự khi
0)x
−
→
2
0
93
lim
x
x
xx
+
→
+−
= −
+
.
Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Câu 31: Chn A.
Cách 1: Dùng HHKG thuần túy:
Ta có
' . ' . ' ' . ' ' . ' '
1 1 1 1
. . .
2 2 2 4
A MCD M A CD M A B CD B A B CD B A B CD
V V V V V= = = =
Gọi I là tâm của hình vuông
' ',BCC B
suy ra
'.BI B C⊥
Mà
BI CD⊥
(do
( )
''CD BCC B⊥
)
Suy ra
( )
''BI BCC B⊥
BI là chiều cao của hình chóp
. ' ' .B A B CD
Thể tích khối chóp
. ' ' .B A B CD
là
. ' ' ' '
1 1 1 1 1 1
. . . . '. ' . ' ' . . 2. 2.1 .
3 3 2 3 2 3
B A B CD A B CD
V BI S BC B C A B= = = =
Vậy
' . ' '
11
.
4 12
A MCD B A B CD
VV==
Cách 2: Dùng hệ tọa độ Oxyz.
Chọn hệ trục tọa độ như hình vẽ.
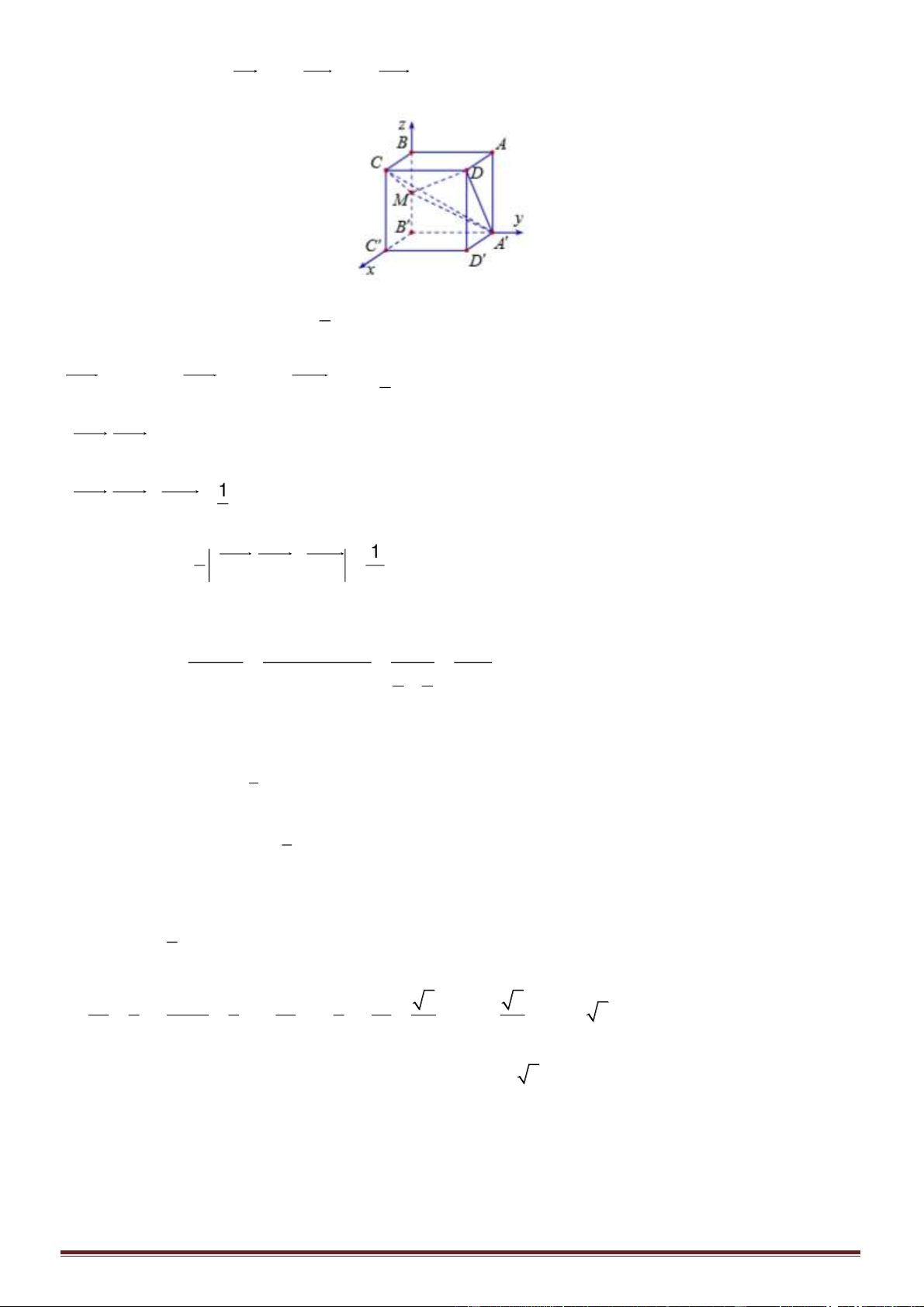
Trang 63
Khi đó
( )
' 0;0;0 , , ' , ' .O B OB Oz OA Oy OC Ox
Suy ra
( ) ( )
1
1;0;1 , 1;1;1 , 0;0; .
2
C D M
( ) ( )
1
' 1; 1;1 , ' 1;0;1 , ' 0; 1; .
2
A C A D A M
= − = −
( )
' , ' 1;0;1 .A C A D
=−
1
' , ' . ' .
2
A C A D A M
=
Ta có
'
11
' , ' . ' .
6 12
A MCD
V A C A D A M
==
Câu 32: Chn A.
Ta có:
10
7 7 7
1 1 1
log 7 .
11
log 10 log 5 log 2
ab
ab
ab
= = = =
++
+
Câu 33: Chn D.
Thể tích cái phễu là
2
1
.
3
V r h=
Thể tích nước đổ vào là
2
1 1 1
1
.
3
V r h=
Sau khi bịt miệng phễu và lật ngược phễu lên thì thể tích phần phễu không chứa nước là
21
7
.
8
V V V V= − =
3
2
33
3
2 2 2 2 2
2
2
11
.
7 7 7 7 7
.20 10 7.
8 8 8 2 2
.
V r h h h
h
V h h
rh
= = = = = =
Suy ra chiều cao cột nước trong phễu là
( )
3
32
20 10 7 0,8706 .h h h cm= − = −
Câu 34: Chn B.
Đặt
( )
2
2
4 4 2 4.t x x x= − = − −
Khi đó, phương trình
( )
2
2
4 logf x x m−=
trở thành:
( )
2
logf t m=

Trang 64
Để phương trình
( )
2
2
4 logf x x m−=
có 4 nghiệm thực phân biệt thì đường thẳng
2
logym=
cắt đồ thị
hàm số
( )
y f t=
tại hai điểm phân biệt thỏa mãn t < 4.
Suy ra
2
1
1 log 3 8.
2
mm−
Vậy
1
;8 .
2
m
Câu 35: Chn B.
Điều kiện
1 1.x−
Xét hàm số
( )
2
1g x x x= + −
trên đoạn [-1;1].
Có:
( ) ( )
2
1
' 1 , ' 0 .
2
1
x
g x g x x
x
= − = =
−
( ) ( )
1
1 1; 1 1; 2.
2
g g g
− = − = =
Suy ra
( )
1 2.gx−
Đặt
2
1 , 1 2.t x x t= + − −
Khi đó, phương trình trở thành:
2
1
0 1 .
1
t mt m t m
t
− + = + + =
−
Xét hàm số
( )
1
1
1
f t t
t
= + +
−
trên tập
1; 2 \ 1 .
−
Có
( )
( )
( )
2
0
1
' 1 . ' 0 .
2
1
t
f t f t
t
t
=
= − =
=
−
x
-1 0 1
2
'y
- 0 + +
y
+
2 2 2+
0
1
2
−
−
Do đó, để phương trình không có nghiệm thực thì giá trị cần tìm của m là
( )
0;2 2 2m+
Suy ra
2 2 2.ab− = − −
Câu 36: Chn A.
Ta có phương trình:
( ) ( ) ( )
32
22
2
log 1 log 3 2log 1x x x− − − = −

Trang 65
Điều kiện xác định: x > 1 và
3.x
Phương trình đã cho
( ) ( )
3
2 2 2
2log 1 log 3 2log 1x x x − = − + −
( ) ( ) ( ) ( )
33
2 2 2 2 2
log 1 log 3 log 1 log 1 log 1 3x x x x x x− = − + − − = − −
( ) ( ) ( )
32
1 1 3 1 3x x x x x − = − − − = −
22
22
2 1 3 3 4 0
1( ).
2 1 3 2 0
2( )
x
x x x x x
xL
x x x x x
xN
− + = − − + =
= −
− + = − − − =
=
Vậy
2.S=
Câu 37: Chn D.
Lấy số tự nhiên có 5 chữ số khác nhau là 5! = 120 số.
Trong 120 số tìm được, ta luôn xếp được 60 cặp số {x;y} sao cho x + y =66666
Vậy tổng của 120 số tìm được là 60x66666=3.999.960.
Câu 38: Chn C.
Ta có phương trình:
22
cos 3sin .cos 1 3sin .cos sin 0x x x x x x+ = − =
( )
sinx 0
sinx 3cosx sinx 0
tanx 3
xk
xk
= =
− =
= = +
với
tan 3=
Gọi A; B là các điểm biểu diễn cho họ nghiệm
( )
x k k=
trên đường tròn lượng giác.
Gọi C; D là các điểm biểu diễn cho họ nghiệm
( )
x k k= +
trên đường tròn lượng giác.
Ta cần tính diện tích hình chữ nhật ABCD.
Xét tam giác vuông AOT có:
22
3
10 sin .
10
AT
OT OA AT
OA
= + = = =
(*)
Xét tam giác ACD có:
sin
2 2 2
AC
ADC
= → =
và
cos .
22
AD
=
Từ (*)
3 3 6 3 10
2sin .cos 2. . . .
2 2 2 2 5
10 10 10
ACBD
AC AD
AC AD S
= = = =
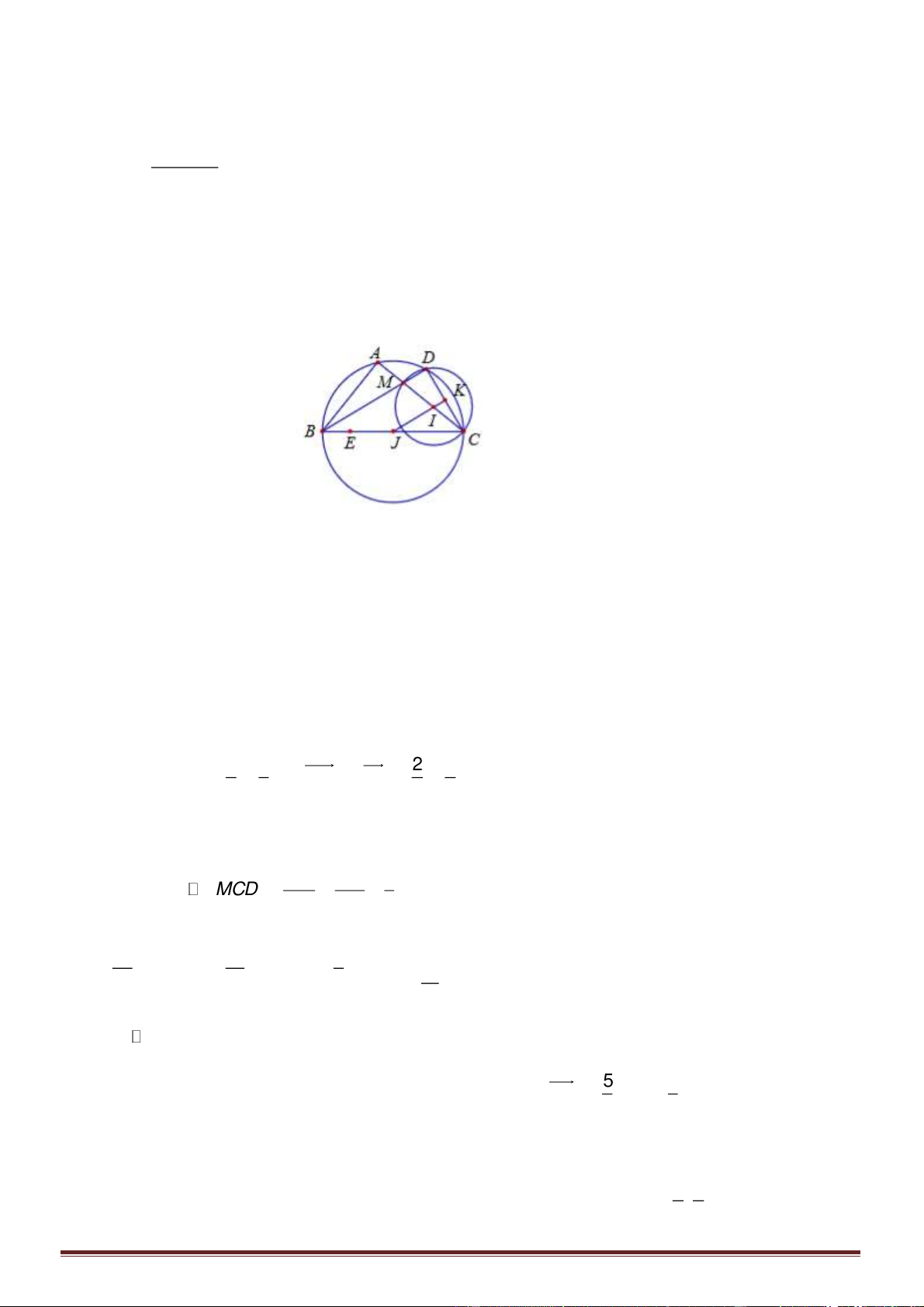
Trang 66
Câu 39: Chn D.
ĐKXĐ:
.xm−
Ta có:
( )
2
2
16
'
m
y
xm
−
=
+
Hàm số đồng biến trên
( )
( )
2
0;
0
0; 4.
44
16 0
m
m
m
mm
m
− +
−
+
−
−
Câu 40: Chn B.
Ta có:
0
90BAC BDC==
nên tứ giác BADC nội tiếp.
Gọi J là trung điểm BC thì J là tâm đường tròn ngaoijt iếp tứ giác BADC.
Suy ra
.JI CD⊥
Đường thẳng JI đi qua I(1;-1) và vuông góc với CD có phương trình là
3 2 0.xy+ − =
Gọi
K IJ CD K=
là trung điểm CD.
Tạo độ điểm K là nghiệm của hệ phương trình
3 6 0
6 8 2 6
; 2 ; .
3 2 0 5 5 5 5
xy
K MD IK
xy
− − =
− = = −
+ − =
( )
: 3 6 0 3 6;C CD x y C c c − − = +
Ta lại có
1
3
3
MD MA
MBA MCD CD MD
CD AB
= = =
22
1
48 16 8
6 2 9. .
11
5 5 5
5
c
cc
c
=−
− − + − − =
=−
Do
C
x
nên nhận
( )
1 3; 1 .cC= − −
Đường thẳng BC đi qua hai điểm C, E nên có véc tơ chỉ phương
( )
51
; 1 5; 3
33
EC
= − = −
phương trình BC:
3 5 4 0.xy+ − =
,J BC IJ=
tọa độ điểm J là nghiệm của hệ phương trình
3 5 4 0
11
;.
3 2 0 2 2
xy
J
xy
+ − =
+ − =

Trang 67
J là trung điểm BC
( )
2;2 .B−
Suy ra
2
0.
2
a
ab
b
=−
+ =
=
Câu 41: Chn B.
Hình trụ (T) có bán kính r = BC và chiều cao h = CD. Thể tích khối trụ là
2
.V r h=
Gọi cạnh của
MNP
là x, khi đó bán kính đường tròn ngoại tiếp
MNP
23
3.
32
x
r x r= =
Khối chóp A.MNP có đáy
MNP
đều và chiều cao AB = DC = h.
Thể tích của khối chóp
( )
2
2
33
1 1 3
' . . . . .
3 3 4 4
MNP
r
rh
V AB S h
= = =
Tỷ số giữa thể tích khối trụ và thể tích khối chóp A.MNP là
2
2
'4
.
3
3
4
V r h
V
rh
==
Câu 42: Chn B.
Gọi A là số tiền người đó vay ngân hàng (đồng), a là số tiền phải trả hàng tháng và r(%) là lãi suất tính
trên tổng số tiền còn nợ mỗi tháng. Ta có:
-Số tiền nợ ngân hàng tháng thứ nhất: R
1
= A(1+r)
-Số tiền nợ ngân hàng tháng thứ hai: R
2
= (A(1+r)-a)(1+r)
( ) ( )
2
11A r a r= + − +
-Số tiền nợ ngân hàng tháng thứ ba:
( ) ( )
(
)
( ) ( ) ( ) ( )
2 3 2
3
1 1 1 1 1 1R A r a r a r A r a r a r= + − + − + = + − + − +
….
-Số tiền nợ ngân hàng tháng thứ n:
( ) ( ) ( )
1
1 1 ... 1
nn
n
R A r a r a r
−
= + − + − − +
Tháng thứ n trả xong nợ:
( )
( )
. . 1
11
n
n
n
Ar r
R a a
r
+
= =
+−
Áp sụng với A = 400 triệu đồng, r = 0,5%, và a = 4 triệu đồng ta có n = 139 tháng.
Câu 43: Chn A.
+ − + = − =(1 ) 1 2 10 2 4 5i z i z i
→ − − = + − → − − = + − =
→ ===
w 4 3 (2 )( 2 ) w 4 3 (2 )( 2 )
3; 20
20
4;
i i z i i i z i
Ra b
Câu 44: Chn B.
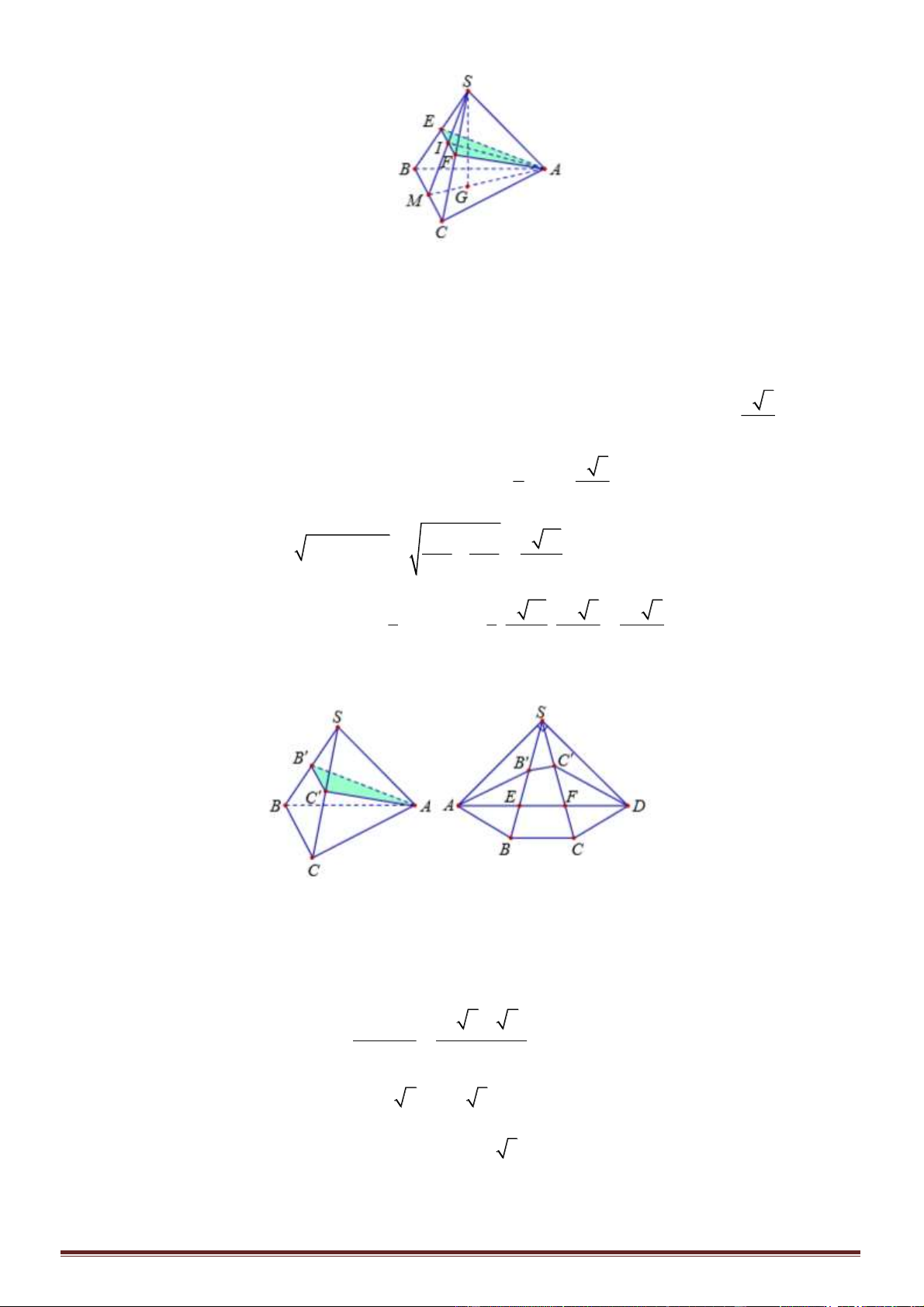
Trang 68
Gọi M là trung điểm BC,
,I EF SM=
suy ra I là trung điểm EF và SM.
Có
( )
ACS ABS c c c AF AE AEF = − − = =
cân tại
.A AI EF⊥
Do
( ) ( )
AEF SBC⊥
nên
( )
.AI SBC AI SM⊥ ⊥
Tam giác ASM có
AI SM⊥
và I là trung điểm SM nên ASM cân tại A, suy ra
3
.
2
a
SA AM==
Gọi G là trọng tâm tam giác
( )
ABC SG ABC⊥
và
23
33
a
AG AM==
Trong tam giác SAG có:
22
22
3 3 15
.
4 9 6
a a a
SG SA AG= − = − =
Vậy thể tích khối chóp S.ABC là
22
.
1 1 15 3 5
. . . .
3 3 6 4 24
SABC ABC
a a a
V SGS= = =
Câu 45: Chn D.
Trải tứ chóp S.ABC ra mặt phẳng (SBC) thì chu vi tam giác
''AB C
bằng
' ' ' ' ' ' ' ' .AB B C C A AB B C C D AD+ + = + +
Dấu “=” xảy ra khi
' , ' .B E C F
Ta có
( )
0
0
62
, 30 .
2
2sin15
a
a
AB a ASB SA SB
+
= = = = =
Lại có
( )
00
30 90 2 1 3 .ASB ASD AD SA a= = = = +
Vậy chu vi tam giác
''AB C
đạt giá trị nhỏ nhất bằng
( )
1 3 .a+
Câu 46: Chn C.
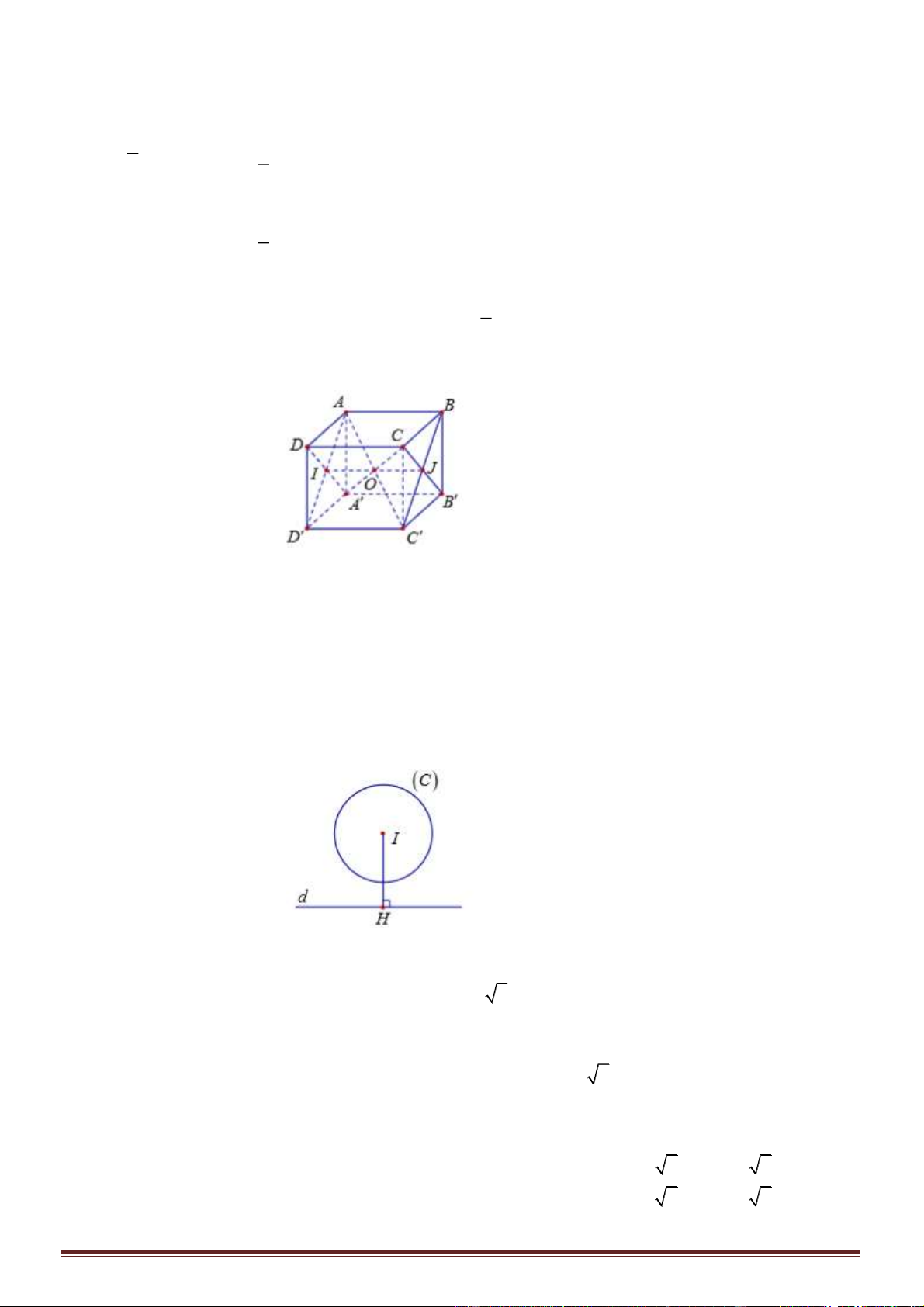
Trang 69
Ta có
( ) ( ) ( )
( )
( )
2 2 2 2
4 4 ' 4 4 '. ' 4 4 4 1 2 . ' 4 4 0f x x x x f x x x f x x
− = − − = − − =
2
2
2
1
1
2
2
4 4 0
0; 1
1
4 4 1
2
4 4 2
x
x
xx
xx
xx
x
xx
=
=
−=
= =
−=
=
−=
Do đó hàm số
( )
2
44y f x x=−
có ba điểm cực trị là
1
0; ;1.
2
Câu 47: Chn D.
Gọi
' ', ' 'I B C BC J A D AD= =
ta có:
( ) ( )
( )
( )
' ' ' '
' ' ' .
' ' '
A B C C D A IJ
IJ B C A B C
IJ BC C D A
=
⊥
⊥
Từ đó suy ra
( ) ( )
( )
( )
0
' ' ; ' ' ' ; ' 90 .A B C C D A B C BC==
Câu 48: Chn C.
Đường tròn (C) có tâm I(1;-2), bán kính R = 2.
Khoảng cách từ tâm I đến đường thẳng d là
( )
;( ) 3 2d I d R=
nên d không cắt (C).
Điểm M(a;b) thỏa mãn yêu cầu bài toán khi và chỉ khi
( )
( )
( )
.
; 3 2 2
MC
d M d
=−
Gọi H là hình chiếu của I lên đường thẳng d, ta có IH:
1 0.xy+ + =
Xét hệ phương trình
2 2 2
1 2; 2 2
2 4 1 0 2 4 2 0
1 0 1
1 2; 2 2
xy
x y x y x x
x y y x
xy
= + = − −
+ − + + = − − =
+ + = = − −
= − = − +

Trang 70
Từ đó suy ra
( )
1 2; 2 2 .M − − +
Do đó
1 2, 2 2ab= − = − +
nên
2.ab=
Câu 49: Chn C.
Điều kiện: x > 0.
Với điều kiện đó phương trình đã cho được biến đỏi tương đương thành phương trình:
( )( )
2018 log log .log 2017log 2018log .log 2019 0(1).
m n m m n m
x m x x m x− − − =
Đặt
log , .
m
t x t=
Khi đó phương trình (1) trở thành phương trình:
( ) ( )
2
2018 log 2017 2018log 2019 0
nn
m t m t− + − =
(2).
Do phương trình (2) c0s
( )
2log . 2019 0
n
m −
nên phương trình (2) có hai nghiệm trái dấu, do đó phương
trình (1) luôn có hai nghiệm dương phân biệt x
1
, x
2
.
Xét
1 2 1 2
2017 2018log
2017
log log log 1.
2018log 2018log
n
m m m
nn
m
x x x x
mm
+
= + = = +
Suy ra:
2017
2017 2017
1.
log 1
2018log
2018 2018
12
..
n
n
n
m
x x m m mn
+
+
= = =
Theo bài m là số nguyên dương khác 1 nên
2,m
do đó
2018
2017
12
2.P x x n=
Mặt khác n là số nguyên dương khác 1 nên
2n
và 2017, 2018 là hai số nguyên tốc cùng nhau nên để P
nguyên và có giá trị nhỏ nhất khi
2018
2.n=
Lúc đó
2018 2019
. 2.2 2 .mn==
Câu 50: Chn D.
Đặt
( )
42
1
14 48 30
4
f x x x x m= − + + −
là hàm số xác định và liên tục trên đoạn [0;2].
Ta có:
( )
3
' 28 48.f x x x= − +
Với mọi
0;2x
ta có
( )
3
' 0 28 48 0 2.f x x x x= − + = =
Mặt khác:
( ) ( )
0 30; 14.f m f x m= − = +
Ta có:
( ) ( ) ( )
[0;2]
max max 0 ; 2 .f x f f=
Theo bài:
( )
( )
( )
[0;2]
00
30 30
30 30 30
max 30 .
30 14 30
14 30
2 30
f
m
m
fx
m
m
f
−
− −
− +
+
0 60
0 16.
44 16
m
m
m
−
Do
0;1;2;3;4;5;...;16 .m m S =
Vậy tổng tất cả 17 giá trị trong tập S là
( )
17 0 16
136.
2
+
=

Trang 71
ĐỀ 35
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Cho hình hình lập phương cạnh
a
. Thể tích khối cầu nội tiếp hình lập phương là
A.
3
2
3
a
. B.
3
6
a
. C.
3
2
a
. D.
3
3
3
a
.
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
hình chữ nhật với
3AB a=
,
2BC a=
, cạnh bên
2SA a=
và
( )
SAB
và
( )
SAD
cùng vuông góc với mặt phẳng đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
4a
. B.
3
a
. C.
3
12a
. D.
3
6a
.
Câu 3: Trong không gian
Oxyz
cho
( ) ( )
2;3; 1 ; 2; 1;3ab− − −
. Sin của góc giữa
a
và
b
bằng
A.
2
7
−
. B.
35
7
. C.
35
7
−
. D.
2
7
.
Câu 4. Với
a
là số thực dương tùy ý,
2
7
log
7
a
bằng
A.
7
2log 1a −
. B.
( )
2
ln 7a
. C.
7
1 2log a+
. D.
7
1
2log a
.
Câu 5: Trong không gian
Oxyz
, cho
( )
1;0;2E −
và
( )
2;1; 5F −
. Phương trình đường thẳng
EF
là
A.
12
3 1 7
x y z−+
==
−
. B.
12
3 1 7
x y z+−
==
−
.
C.
12
1 1 3
x y z−+
==
−
. D.
12
1 1 3
x y z+−
==
.
Câu 6: Cho cấp số nhân
( )
n
u
với
17
1
; 32
2
uu= - = -
. Tìm công bội của cấp số nhân đã cho.
A.
1
2
q =±
B.
2q =±
C.
4q =±
D.
1q =±
Câu 7: Bảng biến thiên ở hình dưới đây là bảng biến thiên của hàm số nào trong các hàm số sau?
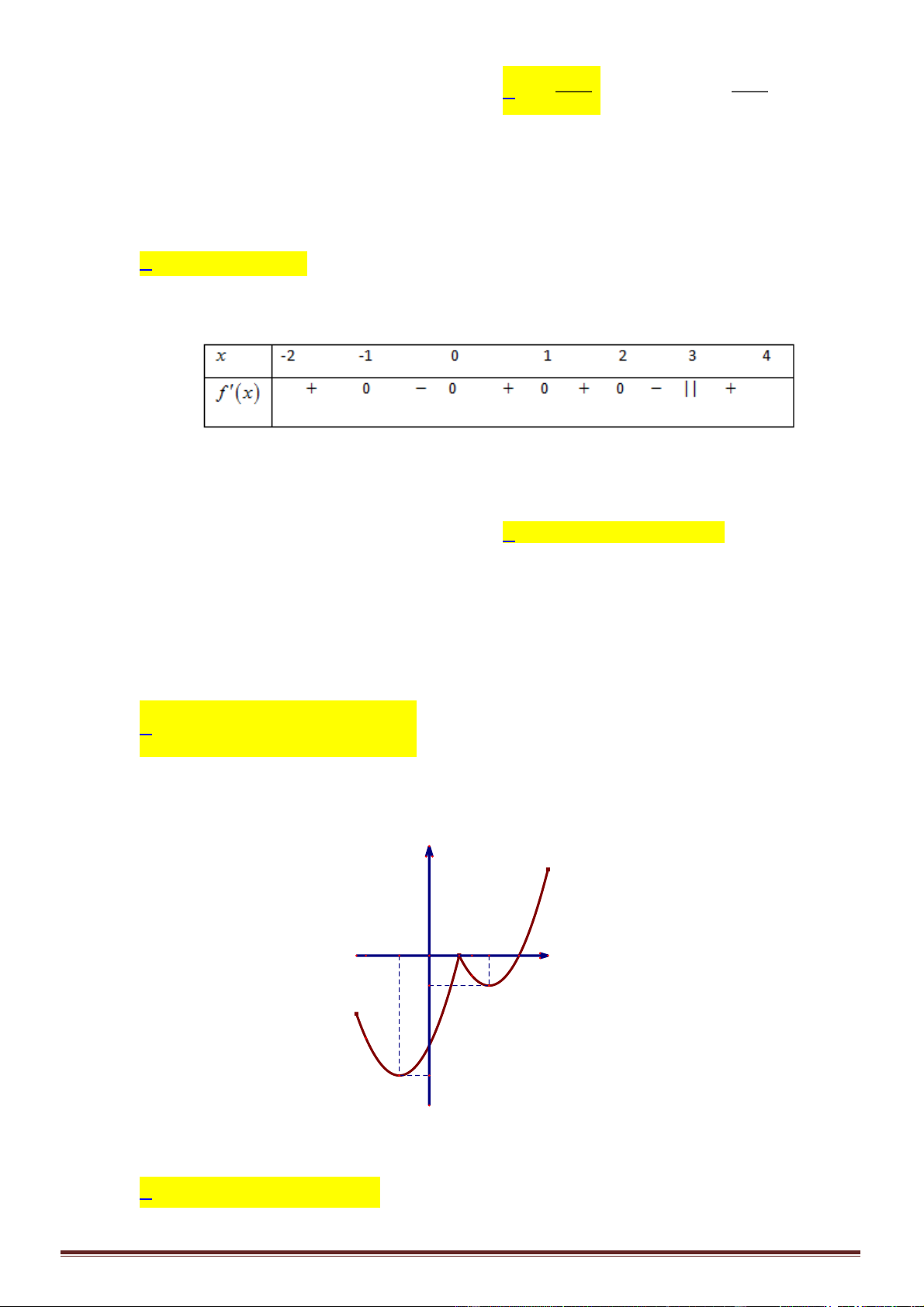
Trang 72
A.
42
21y x x= − + +
. B.
42
21y x x= + +
. C.
3
2
x
y
x
+
=
−
. D.
3
2
x
y
x
−
=
−
.
Câu 8: Trong không gian
Oxyz
, mặt phẳng
( )
P
đi qua điểm
( )
1; 1; 2M −
, đồng thời song song với mặt phẳng
( )
: 2 3 5 0Q x y z+ − + =
có phương trình là
A.
2 3 3 0x y z+ − − =
. B.
2 3 0x y z− + + =
.
C.
2 3 3 0x y z+ − + =
. D.
2 3 0x y z− + − =
.
Câu 9: Cho hàm số
( )
y f x=
liên tục trên
2;4−
và có bảng xét dấu đạo hàm như hình bên.
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại
0x =
. B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực đại tại
2x =
. D. Hàm số đạt cực đại tại
1x =
.
Câu 10: Giả sử
( )
fx
là hàm số bất kỳ liên tục trên khoảng
( )
;
và
( )
, , ;abc
. Mệnh đề nào sau đây
sai?
A.
( ) ( ) ( )
d d d
b b a
a c c
f x x f x x f x x=−
. B.
( ) ( ) ( )
d d d
b c b
a a c
f x x f x x f x x=+
.
C.
( ) ( ) ( )
d d d
b c b
a a c
f x x f x x f x x=−
. D.
( ) ( ) ( )
d d d
b c a
a b c
f x x f x x f x x= − −
.
Câu 11: Cho hàm số
()y f x=
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó
A. Nghịch biến trên khoảng
( )
1;0−
. B. Đồng biến trên khoảng
( )
4; 1−−
.
C. Đồng biến trên khoảng
( )
1;0−
. D. Nghịch biến trên khoảng
( )
1;3
.
3
-1
-4
-1
2
O
1
x
y

Trang 73
Câu 12: Tìm nguyên hàm
( )
Fx
của hàm số
( )
x
f x e x=−
biết
( )
02F =
A.
( )
2
1
2
x
x
F x e= + +
. B.
( )
2
1
2
x
x
F x e= − +
. C.
( )
2
1
2
x
x
F x e= + −
. D.
( )
2
1
2
x
x
F x e= − −
.
Câu 13: Phương trình
( )
log 9 3x +=
có nghiệm là
A.
91
. B.
9991
. C.
1009
. D.
991
.
Câu 14: Tìm công thức tính số các tổ hợp chập
k
của một tập có
n
phần tử.
A.
( )
!
!
k
n
n
C
nk
=
−
. B.
( )
!
!!
k
n
n
C
n k k
=
−
. C.
( )
!
!
k
n
n
A
nk
=
−
. D.
( )
!
!!
k
n
n
A
n k k
=
−
.
Câu 15: Cho các số phức
,z a bi=+
w,x yi=+
với
, , ,a b x y
. Điểm
M
biểu diễn số phức
wz −
có tọa
độ là
A.
( )
;a x b y++
. B.
( )
;a x b y−−
. C.
( )
;a b x y++
. D.
( )
;a b x y−−
.
Câu 16: Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( ): 2 3 2 0P x y z− + − =
,
( ): 3 0Q x y− + =
.Mặt phẳng
( )
vuông góc với cả
()P
và
()Q
đồng thời cắt trục
Ox
tại điểm có
hoành độ bằng 5. Phương trình của mp
( )
là:
A.
3 3 15 0x y z+ + - =
. B.
30x y z+ + + =
. C.
2 6 0xz- + + =
. D.
2 6 0xz- + - =
.
Câu17. Cho số phức
z
thỏa mãn
( )
2019
1
34
1
i
z i i
i
−
=−
+
. Mô đun của
z
bằng
A. 5 B.
1
5
C.
2
5
D.
5
2
Câu 18: Một hình trụ có diện tích xung quanh bằng
8
và có chiều cao bằng đường kính đáy. Thể tích khối trụ
trương ứng bằng
A.
32
. B.
16
. C.
8
. D.
4
.
Câu 19: Biết rằng phương trình
2
log 15log 2 2
x
x −=
có hai nghiệm
1
x
,
2
x
( )
12
xx
. Giá trị của
12
16xx−
bằng
A.
4095
8
−
. B.
30
. C.
34
. D.
4097
8
.
Câu 20: Đạo hàm của hàm số
25
7
( ) 3
x
x
fx
−
+
=
là:
A.
( )
25
'
7
2
19ln3
( ) 3
7
x
x
fx
x
−
+
=
+
. B.
( )
25
'
7
2
19
( ) 3
7
x
x
fx
x
−
+
=
+
C.
( )
25
'
7
2
19
( ) 3
7
x
x
fx
x
−
+
−
=
+
D.
( )
25
'
7
2
19ln3
( ) 3
7
x
x
fx
x
−
+
−
=
+

Trang 74
Câu 21: Cho
( )
42
68f x x x= − +
. Gọi
S
là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
( )
y f x=
và
trục hoành. Mệnh đề nào sau đây sai?
A.
( )
2
2
dS f x x
−
=
. B.
( ) ( )
22
0
2
2 d 2 dS f x x f x x=+
.
C.
( )
2
0
2dS f x x=
. D.
( )
2
0
2dS f x x=
.
Câu 22: Cho hàm số
( )
y f x=
có đạo hàm
( )
=−
32
2f x x x
,
x
. Hàm số
( )
=−2y f x
đồng biến trên
khoảng
A.
( )
+2;
. B.
( )
−;2
. C.
( )
−4;2
. D. .
Câu 23: Cho hàm số
2
3
9
x
y
x
−
=
−
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận ngang là
1y =
.
B. Đồ thị hàm số chỉ có 1 tiệm cận đứng là
3x =−
.
C. Đồ thị hàm số không có tiệm cận đứng.
D. Đồ thị hàm số có hai tiệm cận đứng là
3; 3xx= = −
.
Câu 24: Biết rằng
,
là các số thực thỏa mãn
( ) ( )
2 4 4
3 3 3 81 3 3
−−
+ = +
. Giá trị của
6
+
bằng
A. 1. B. 2. C. 4. D. 3.
Câu 25: Cho hình lăng trụ tam giác đều
.ABC A B C
có
AB a=
. Mặt phẳng
( )
A BC
tạo với mặt phẳng
( )
ABC
một góc
30
. Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3
8
a
. D.
3
3
24
a
.
Câu 26: Cho hàm số
()y f x=
có bảng biến thiên như hình vẽ bên. Hàm số
( 3)y f x= − +
đạt cực đại tại
A.
1x =−
B.
2x =
. C.
0x =
. D.
3x =
.
Câu 27: Cho hình nón tròn xoay có bán kính đáy bằng
2
và diện tích xung quanh bằng
42
. Góc ở đỉnh của
hình nón đã cho bằng
1
-2
1
+
∞
2
0
-1
-
∞
f(x)
x
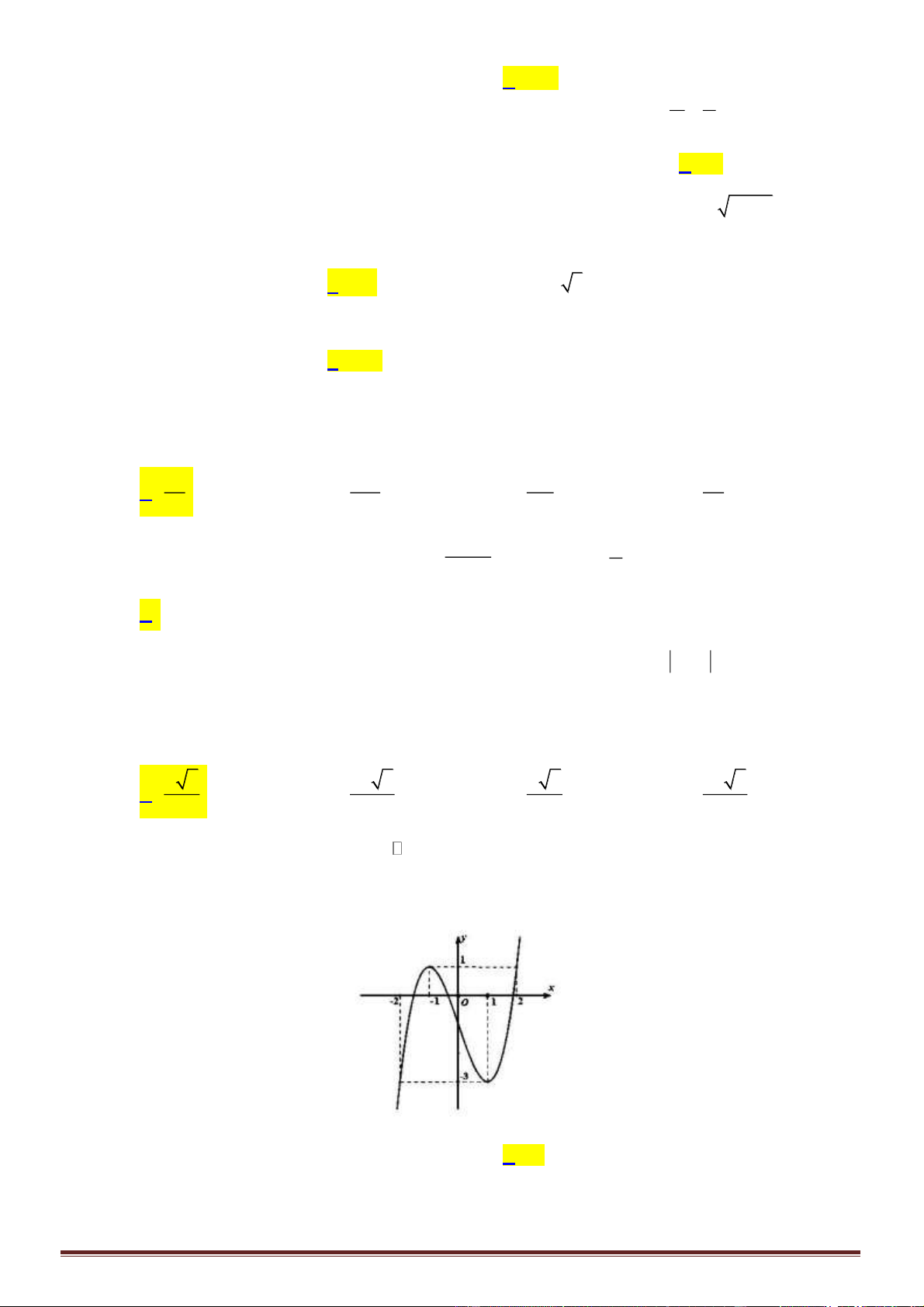
Trang 75
A.
o
60
. B.
o
150
. C.
o
90
. D.
o
120
.
Câu 28: Gọi
12
,zz
là các nghiệm phức của phương trình
2
2 3 0zz+ + =
. Số phức
1 2 1 2
z z z z+
bằng
A.
2
. B.
5
. C.
2−
. D.
5i
.
Câu 29: Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( )
2
25f x x x= + −
. Giá trị của
2
mM+
bằng
A.
5
. B.
25
. C.
5 2 5+
. D.
45
.
Câu 30: Cho hình lập phương
.ABCD A B C D
. Góc giữa hai đường thẳng
AC
và
AB
bằng
A.
45
. B.
60
. C.
30
. D.
120
.
Câu 31: Giải bóng chuyền quốc tế VTV Cup có 12 đội tham gia, trong đó có 3 đội Việt Nam. Ban tổ chức bốc
thăm ngẫu nhiên để chia thành 3 bảng đấu, mỗi bảng 4 đội. Tính xác suất để 3 đội của Việt Nam cùng
nằm ở một bảng đấu.
A.
3
55
. B.
1
330
. C.
1
110
. D.
6
55
.
Câu 32: Tất cả các nguyên hàm của hàm số
( )
2
cos
x
fx
x
=
trên khoảng
0;
2
p
æö
÷
ç
÷
ç
÷
ç
èø
là
A.
( ) ( )
tan ln cos .F x x x x C= + +
B.
( ) ( )
tan ln cos .F x x x x C= - + +
C.
( ) ( )
tan ln cos .F x x x x C= - +
D.
( )
tan ln cos .F x x x x C= - +
Câu 33: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
2a
. Gọi
E
là trung điểm
AB
. Biết góc giữa
CB
và
( )
BCC B
bằng
o
30
. Khoảng cách giữa hai đường thẳng
AB
và
CE
bằng
A.
6
3
a
. B.
26
3
a
. C.
6
6
a
. D.
26
6
a
.
Câu 34: Cho hàm số
( )
y f x=
liên tục trên có đồ thị như hình vẽ bên. Phương trình
( )
( )
10f f x −=
có tất
cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
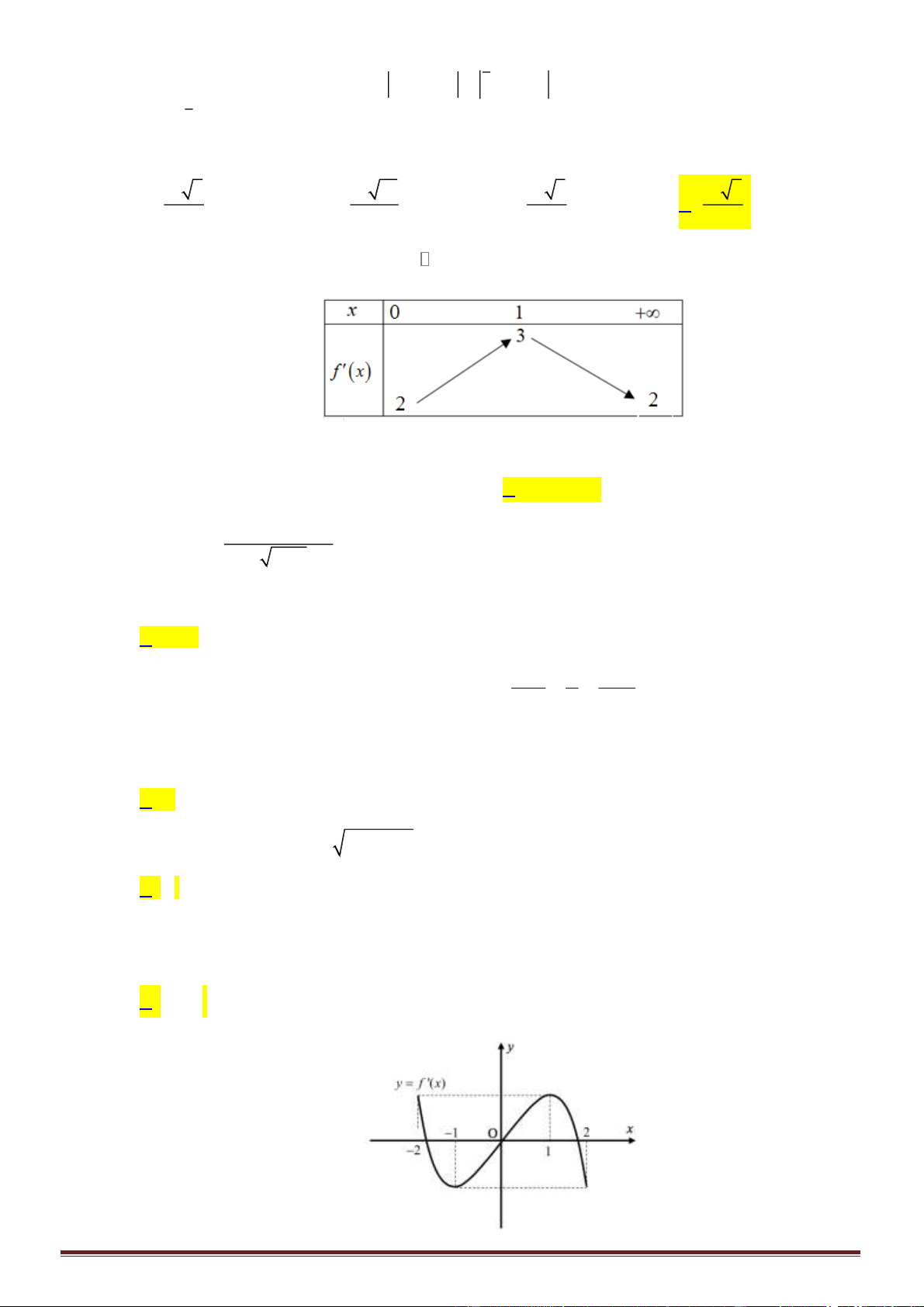
Trang 76
Câu 35: Cho các số phức
z
thỏa mãn
2020
2 1 2z i z i− = − +
. Tập hợp các điểm biểu diễn số phức
2 1 4w z i= − +
trên mặt phẳng tọa độ là một đường thẳng. Khoảng cách từ
( )
2; 3I −
đến đường thẳng
đó bằng
A.
18 5
5
. B.
18 13
13
. C.
10 3
3
. D.
10 5
5
.
Câu 36: Cho hàm số
( )
y f x=
có đạo hàm trên . Bảng biến thiên của hàm số
( )
'y f x=
như hình dưới
Tìm
m
để bất phương trình
( )
2sinm x f x+
nghiệm đúng với mọi
( )
0;x +
.
A.
(0)mf
. B.
(1) 2sin1mf−
. C.
(0)mf
. D.
(1) 2sin1mf−
.
Câu 38: Biết rằng
1
2
d
ln2 ln3 ln5
5 3 9
x
a b c
xx
−
= + +
+ + +
, với
,,abc
là các số hữu tỉ.
Giá trị của
abc++
bằng
A.
10−
. B.
5−
. C.
10
. D.
5
.
Câu 39: Trong không gian
Oxyz
, cho đường thẳng
12
:
2 1 1
x y z
d
+−
==
−
và hai điểm
( 1;3;1)A −
và
( )
0;2; 1B −
. Gọi
( )
;;C m n p
là điểm thuộc đường thẳng
d
sao cho tam giác
ABC
vuông tại
A. Giá trị của tổng
2m n p++
bằng
A.
0
. B.
2
. C.
3
. D.
5−
.
Câu 40: Bất phương trình có bao nhiêu nghiệm nguyên?
A. . B. . C. . D. Vô số.
Câu 41: Cho hàm số có đồ thị hàm như hình vẽ. Hàm số đồng biến trên
khoảng
A. . B. . C. . D. .
( )
( )
2
3 ln 2 0x x x− +
5
4
3
()fx
'( )y f x=
2
(cos )y f x x x= + −
( )
1;2
( )
1;0−
( )
0;1
( )
2; 1−−

Trang 77
Câu 42: Cho hàm số . Gọi là số lớn nhất trong các số nguyên thỏa mãn
. Mệnh đề nào sau đây đúng?
A. . B. . C. . D. .
Câu 43: Cho hàm số thỏa mãn và . Tất cả các nguyên hàm
của là
A. . B. . C. . D. .
Câu 44: Cho hàm số có đồ thị hàm số được cho như hình vẽ bên.
Hàm số có nhiều nhất bao nhiêu cực trị trong khoảng .
A. 6. B. 2. C. 5. D. 3
Câu 45: Cho hình chóp tứ giác đều có , côsin góc hợp bởi hai mặt phẳng và
bằng . Thể tích của khối chóp bằng
A. . B. . C. . D. .
Câu 46: Cây dù ở khu vui chơi “công viên nước” của trẻ em có phần trên là một chỏm cầu, phần than là một khối
nón cụt như hình vẽ. Biết
2ON OD m==
;
40MN cm=
;
40BC cm=
;
20EF cm=
. Tính thể tích
của cây dù
( ) 2 2
xx
fx
−
=−
0
m
m
12
( ) (2 2 ) 0f m f m+ −
)
0
1513;2019m
)
0
1009;1513m
)
0
505;1009m
)
0
1;505m
( )
fx
( ) ( )
2
2 2 ,
x
f x xf x xe x
−
+ =
( )
01f =
( )
2
.e
x
x f x
( )
2
2
1xC++
( )
2
2
2
1
1
2
x
x e C
−
++
( )
2
2
2
1
x
x e C
−
++
( )
2
2
1
1
2
xC++
( )
fx
( )
y f x
=
( ) ( )
2
0y f x x f= + −
( )
3;3−
.S ABCD
21SA a=
( )
SAD
( )
ABCD
1
10
.S ABCD
3
19
3
a
3
2 19
3
a
3
4 19
3
a
3
4 19a
Trang 78
A.
( )
3
336000 cm
( )
3
2750
cm
3
p
. B.
( )
3
896000
3
cm
.
C.
( )
3
112000 cm
( )
3
2050
cm
3
p
. D.
( )
3
896000 cm
( )
3
2250
cm
3
p
.
Câu 47: Giả sử là hai trong các số phức thỏa mãn là một số thuần ảo. Biết rằng
, giá trị nhỏ nhất của bằng
A. . B. . C. . D. .
Câu 48. Cho hàm số có đồ thị như hình vẽ.
Có bao nhiêu số nguyên để phương trình có nghiệm thuộc đoạn ?
A. 11. B. 9. C. 8. D. 10.
A
D
M
F
E
B
O
C
N
12
,zz
( )( )
12z z i+−
12
2zz−=
12
5zz+
13 5−
3 5 13−
3 5 2 13−
5 22−
( )
y f x=
m
1
1
32
x
f x m
+ + =
2;2−

Trang 79
Câu 49: Trong không gian cho hai mặt phẳng và hai
đường thẳng . Đường thẳng song song với hai mặt
phẳng và cắt tương ứng tại . Độ dài đoạn bằng
A. . B. C. D.
Câu 50: Trong không gian
Oxyz
, cho hai điểm
( )
1;2;3A
,
( )
4;4;5B
. Giả sử
M
là điểm thay đổi trong mặt
phẳng
( ):2 2 2019 0.P x y z+ + + =
Tìm giá trị lớn nhất của biểu thức
.P AM BM=−
A.
17
. B.
77
. C.
7 2 3−
. D.
82 5−
.
--Hết—
LỜI GIẢI CHI TIẾT
Câu 1: Cho hình hình lập phương cạnh
a
. Thể tích khối cầu nội tiếp hình lập phương là
A.
3
2
3
a
. B.
3
6
a
. C.
3
2
a
. D.
3
3
3
a
.
Lời gii
Chn B
Khối cầu nội tiếp hình lập phương có bán kính
2
a
R =
.
Vậy thể tích khối cầu nội tiếp hình lập phương là
3
33
4
4
2
3 3 6
a
Ra
V
= = =
.
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
hình chữ nhật với
3AB a=
,
2BC a=
, cạnh bên
2SA a=
và
( )
SAB
và
( )
SAD
cùng vuông góc với mặt phẳng đáy. Thể tích khối chóp
.S ABCD
bằng
A.
3
4a
. B.
3
a
. C.
3
12a
. D.
3
6a
.
Lời gii
Chn A
Oxyz
( )
: 2 1 0,P x y z+ − − =
( )
:2 2 0,P x y z+ − + =
1
11
:,
2 1 2
x y z−+
= =
2
21
:
1 1 2
x y z−−
= =
−
( ) ( )
;PQ
12
,
,HK
HK
8 11
7
5
6.
11
.
7
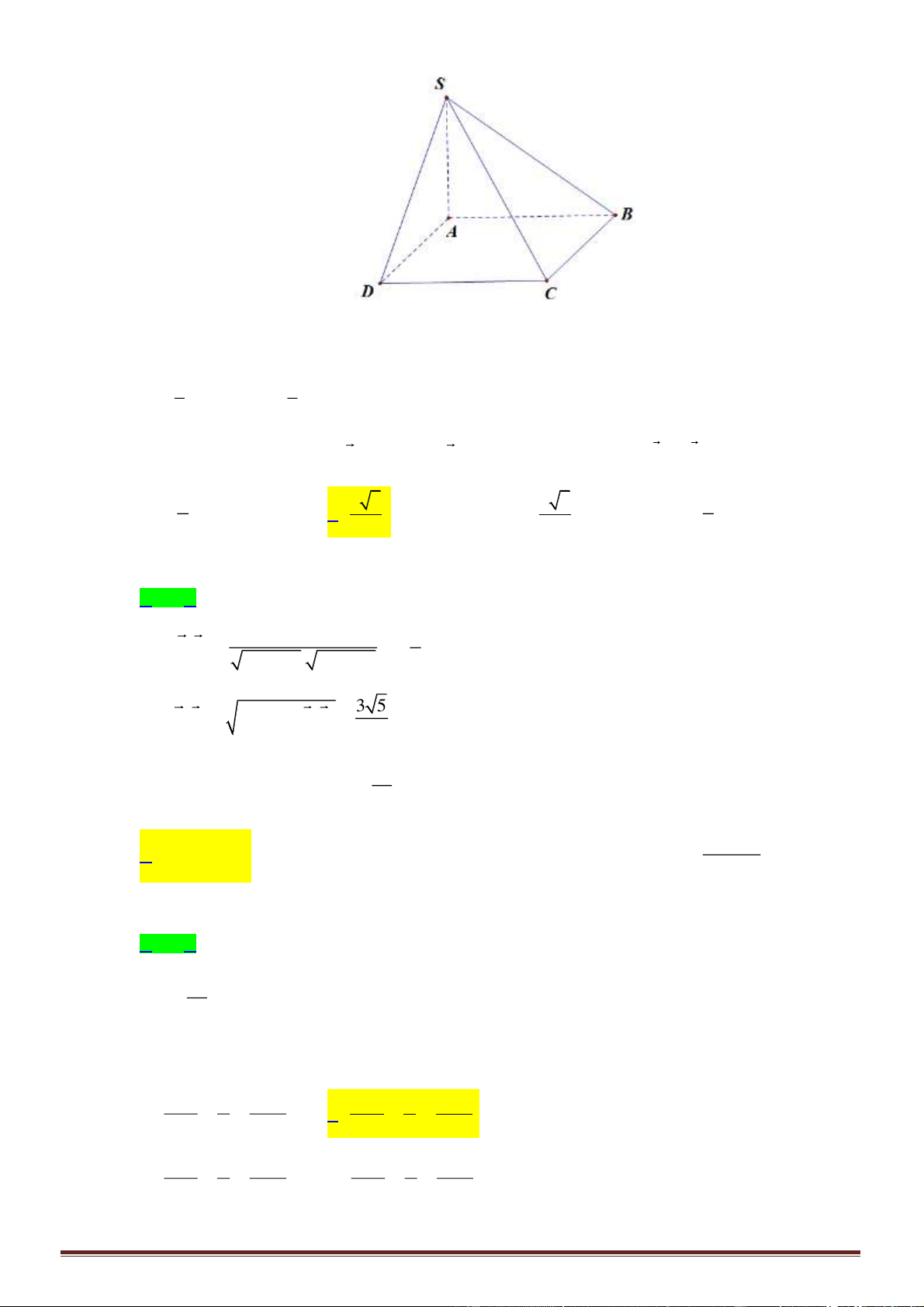
Trang 80
Vì
( )
SAB
và
( )
SAD
cùng vuông góc với mặt phẳng đáy nên
( )
SA ABCD⊥
3
11
. . . .2 .3 .2 4
33
V SA AB BC a a a a= = =
.
Câu 3: Trong không gian
Oxyz
cho
( ) ( )
2;3; 1 ; 2; 1;3ab− − −
. Sin của góc giữa
a
và
b
bằng
A.
2
7
−
. B.
35
7
. C.
35
7
−
. D.
2
7
.
Lời gii
Chn D
( )
42
cos ;
7
4 9 1. 4 1 9
ab
−
= = −
+ + + +
( ) ( )
2
35
sin ; 1 cos ;
7
a b a b= − =
Câu 4. Với
a
là số thực dương tùy ý,
2
7
log
7
a
bằng
A.
7
2log 1a −
. B.
( )
2
ln 7a
. C.
7
1 2log a+
. D.
7
1
2log a
.
Lời gii
Chn A
2
7
log
7
a
2
77
log log 7a=−
7
2log 1a=−
Câu 5: Trong không gian
Oxyz
, cho
( )
1;0;2E −
và
( )
2;1; 5F −
. Phương trình đường thẳng
EF
là
A.
12
3 1 7
x y z−+
==
−
. B.
12
3 1 7
x y z+−
==
−
.
C.
12
1 1 3
x y z−+
==
−
. D.
12
1 1 3
x y z+−
==
.
Lời gii
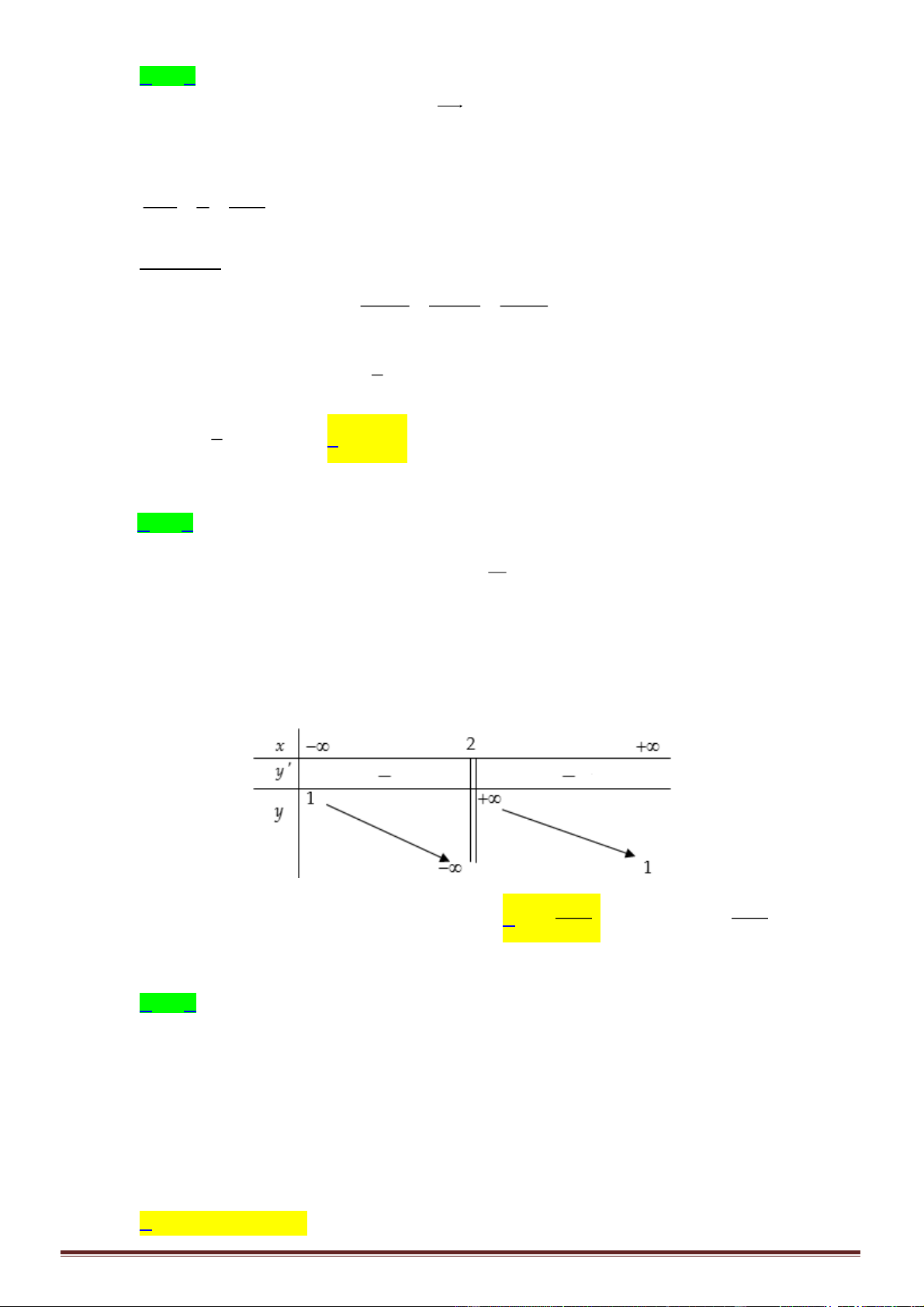
Trang 81
Chn B
Đường thẳng
EF
có véc tơ chỉ phương là
( )
3;1; 7EF =−
.
Đường thẳng
EF
đi qua điểm
( )
1;0;2E −
, có véc tơ chỉ phương
( )
3;1; 7−
nên phương trình
EF
là
12
3 1 7
x y z+−
==
−
.
Tổng quát: Trong không gian
Oxyz
, cho hai điểm
( )
1 1 1
;;A x y z
và
( )
2 2 2
;;B x y z
. Khi đó đường thẳng
AB
có một phương trình dạng
1 1 1
2 1 2 1 2 1
x x y y z z
x x y y z z
− − −
==
− − −
.
Câu 6: Cho cấp số nhân
( )
n
u
với
17
1
; 32
2
uu= - = -
. Tìm công bội của cấp số nhân đã cho.
A.
1
2
q =±
B.
2q =±
C.
4q =±
D.
1q =±
Lời gii
Chn B
( )
n
u
là cấp số nhân nên ta có:
66
7
71
1
. 64
u
u u q q
u
= Þ = =
2.qÞ = ±
Vậy công bội của cấp số nhân đã cho:
2.q =±
Câu 7: Bảng biến thiên ở hình dưới đây là bảng biến thiên của hàm số nào trong các hàm số sau?
A.
42
21y x x= − + +
. B.
42
21y x x= + +
. C.
3
2
x
y
x
+
=
−
. D.
3
2
x
y
x
−
=
−
.
Lời gii
Chn C
Từ bảng biến thiên của hàm số ta thấy: đồ thị hàm số có tiệm cận ngang là đường thẳng
1y =
nên loại
các đáp án A, B, D, vậy chọn C.
Câu 8: Trong không gian
Oxyz
, mặt phẳng
( )
P
đi qua điểm
( )
1; 1; 2M −
, đồng thời song song với mặt phẳng
( )
: 2 3 5 0Q x y z+ − + =
có phương trình là
A.
2 3 3 0x y z+ − − =
. B.
2 3 0x y z− + + =
.
C.
2 3 3 0x y z+ − + =
. D.
2 3 0x y z− + − =
.

Trang 82
Lời gii
Chn C
Do mặt phẳng
( )
P
song song với mặt phẳng
( )
: 2 3 5 0Q x y z+ − + =
nên mặt phẳng
( )
P
nhận vectơ
pháp tuyến
( )
( )
2; 3; 1
Q
n −
làm vectơ pháp tuyến và đi qua điểm
( )
1; 1; 2M −
nên có phương trình:
( ) ( ) ( )
2 1 3 1 2 0 2 3 3 0.x y z x y z− + + − − = + − + =
Câu 9: Cho hàm số
( )
y f x=
liên tục trên
2;4−
và có bảng xét dấu đạo hàm như hình bên.
Mệnh đề nào sau đây sai về hàm số đó?
A. Hàm số đạt cực tiểu tại
0x =
. B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực đại tại
2x =
. D. Hàm số đạt cực đại tại
1x =
.
Lời gii
Chn D
Dựa vào bảng xét dấu của đạo hàm đã cho ta thấy
( )
' 1 0f =
và đạo hàm không đổi dấu khi
x
qua
0
1x =
nên hàm số đã cho không đạt cực đại tại
1x =
.
Câu 10: Giả sử
( )
fx
là hàm số bất kỳ liên tục trên khoảng
( )
;
và
( )
, , ;abc
. Mệnh đề nào sau đây
sai?
A.
( ) ( ) ( )
d d d
b b a
a c c
f x x f x x f x x=−
. B.
( ) ( ) ( )
d d d
b c b
a a c
f x x f x x f x x=+
.
C.
( ) ( ) ( )
d d d
b c b
a a c
f x x f x x f x x=−
. D.
( ) ( ) ( )
d d d
b c a
a b c
f x x f x x f x x= − −
.
Lời gii
Chn C
Đáp án A, B, D đúng vì theo tính chất tích phân.
Đáp án C sai.
Câu 11: Cho hàm số
()y f x=
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng về hàm số đó

Trang 83
A. Nghịch biến trên khoảng
( )
1;0−
. B. Đồng biến trên khoảng
( )
4; 1−−
.
C. Đồng biến trên khoảng
( )
1;0−
. D. Nghịch biến trên khoảng
( )
1;3
.
Lời gii
Chn C
Trên khoảng
( )
1;0−
đồ thị có hướng đi lên nên hàm số đồng biến ứng với khoảng này.
Câu 12: Tìm nguyên hàm
( )
Fx
của hàm số
( )
x
f x e x=−
biết
( )
02F =
A.
( )
2
1
2
x
x
F x e= + +
. B.
( )
2
1
2
x
x
F x e= − +
. C.
( )
2
1
2
x
x
F x e= + −
. D.
( )
2
1
2
x
x
F x e= − −
.
Lời gii
Chn B
Ta có
( )
( )
2
d
2
xx
x
F x e x x e C= − = − +
Theo bài ra
( )
02F =
12C + =
1C=
Vậy
( )
2
1
2
x
x
F x e= − +
.
Câu 13: Phương trình
( )
log 9 3x +=
có nghiệm là
A.
91
. B.
9991
. C.
1009
. D.
991
.
Lời gii
Chn D
Ta có:
( )
log 9 3x +=
3
9 10
90
x
x
+=
+
991
9
x
x
=
−
991x=
.
Câu 14: Tìm công thức tính số các tổ hợp chập
k
của một tập có
n
phần tử.
3
-1
-4
-1
2
O
1
x
y

Trang 84
A.
( )
!
!
k
n
n
C
nk
=
−
. B.
( )
!
!!
k
n
n
C
n k k
=
−
. C.
( )
!
!
k
n
n
A
nk
=
−
. D.
( )
!
!!
k
n
n
A
n k k
=
−
.
Lời gii
Chn B
Số các tổ hợp chập
k
của một tập có
n
phần tử phần tử, kí hiệu là:
( )
!
!!
k
n
n
C
n k k
=
−
.
Câu 15: Cho các số phức
,z a bi=+
w,x yi=+
với
, , ,a b x y
. Điểm
M
biểu diễn số phức
wz −
có tọa
độ là
A.
( )
;a x b y++
. B.
( )
;a x b y−−
. C.
( )
;a b x y++
. D.
( )
;a b x y−−
.
Lời gii
Chn B
+ Theo quy tắc trừ số phức thì
wz −
( ) ( ) ( ) ( )
a bi x yi a x b y i= + − + = − + −
. Suy ra điểm biểu diễn
là điểm có tọa độ
( )
;a x b y−−
.
Câu 16: Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( ): 2 3 2 0P x y z− + − =
,
( ): 3 0Q x y− + =
.Mặt phẳng
( )
vuông góc với cả
()P
và
()Q
đồng thời cắt trục
Ox
tại điểm có
hoành độ bằng 5. Phương trình của mp
( )
là:
A.
3 3 15 0x y z+ + - =
. B.
30x y z+ + + =
. C.
2 6 0xz- + + =
. D.
2 6 0xz- + - =
.
Lời gii
Chn A.
()P
có vectơ pháp tuyến
( )
1; 2;3
P
n =−
,
( )
Q
có vectơ pháp tuyến
( )
1; 1;0
Q
n =−
.
Vì mặt phẳng
( )
vuông góc với cả
( )
P
và
( )
Q
nên
( )
có một vectơ pháp tuyến là
( )
; 3;3;1
PQ
n n n
==
.
Vì mặt phẳng
( )
cắt trục
Ox
tại điểm có hoành độ bằng 3 nên
( )
đi qua điểm
( )
5;0;0M
.
Vậy
( )
đi qua điểm
( )
5;0;0M
và có vectơ pháp tuyến
( )
3;3;1n
=
nên
( )
có phương trình:
3 3 15 0x y z+ + − =
.
Câu17. Cho số phức
z
thỏa mãn
( )
2019
1
34
1
i
z i i
i
−
=−
+
. Mô đun của
z
bằng
A. 5 B.
1
5
C.
2
5
D.
5
2
Lời gii
Chn A

Trang 85
( ) ( )
2019
1
3 4 . 3 4 3 4
1
i
z i i i z i i z i
i
−
= − = − = −
+
. Vậy
5z =
Câu 18: Một hình trụ có diện tích xung quanh bằng
8
và có chiều cao bằng đường kính đáy. Thể tích khối trụ
trương ứng bằng
A.
32
. B.
16
. C.
8
. D.
4
.
Lời gii
Chn C
Theo bài ra ta có
r l h==
2
2 2 8
xq
S rl r
= = =
2r=
Thể tích của khối trụ đã cho là :
23
8V r h r
= = =
.
Câu 19: Biết rằng phương trình
2
log 15log 2 2
x
x −=
có hai nghiệm
1
x
,
2
x
( )
12
xx
. Giá trị của
12
16xx−
bằng
A.
4095
8
−
. B.
30
. C.
34
. D.
4097
8
.
Lời gii
Chn B
Điều kiện
0
1
x
x
2
log 15log 2 2
x
x −=
2
2
15
log 2
log
x
x
− =
2
22
log 2log 15 0xx − − =
2
2
log 5
log 3
x
x
=
=−
32
1
8
x
x
=
=
1
2
32
1
8
x
x
=
=
12
16 30xx − =
.
Câu 20: Đạo hàm của hàm số
25
7
( ) 3
x
x
fx
−
+
=
là:
A.
( )
25
'
7
2
19ln3
( ) 3
7
x
x
fx
x
−
+
=
+
. B.
( )
25
'
7
2
19
( ) 3
7
x
x
fx
x
−
+
=
+
C.
( )
25
'
7
2
19
( ) 3
7
x
x
fx
x
−
+
−
=
+
D.
( )
25
'
7
2
19ln3
( ) 3
7
x
x
fx
x
−
+
−
=
+
Lời gii
Chn A
Áp dụng công thức:

Trang 86
'
'
2 5 2 5 2 5
'
7 7 7
25
( ) 3 ( ) 3 3 ln3.
7
x x x
x x x
x
f x f x
x
− − −
+ + +
−
= = =
+
( )
25
7
2
19ln3
3
7
x
x
x
−
+
=
+
Chú ý áp dụng công thức tính nhanh
( )
,
2
ax+b
cx+d
ad bc
cx d
−
=
+
Câu 21: Cho
( )
42
68f x x x= − +
. Gọi
S
là diện tích của hình phẳng giới hạn bởi đồ thị hàm số
( )
y f x=
và
trục hoành. Mệnh đề nào sau đây sai?
A.
( )
2
2
dS f x x
−
=
. B.
( ) ( )
22
0
2
2 d 2 dS f x x f x x=+
.
C.
( )
2
0
2dS f x x=
. D.
( )
2
0
2dS f x x=
.
Lời gii
Chn D
Phương trình hoành độ giao điểm của đồ thị hàm số
( )
42
68f x x x= − +
và trục hoành:
2
42
2
2
2
6 8 0
2
4
x
x
xx
x
x
=
=
− + =
=
=
Diện tích hình phẳng cần tìm là:
( ) ( )
2
2
d1S f x x
−
=
( ) ( )
2
0
2 d 2f x x=
(do
( )
fx
là hàm số chẵn)
( ) ( )
22
0
2
2 d 2 df x x f x x=+
( ) ( ) ( )
22
0
2
2 d 2 d 3f x x f x x=+
(do trong các khoảng
( ) ( )
0; 2 , 2;2
phương trình
( )
0fx=
vô nghiệm)
Từ
( )
1
,
( )
2
,
( )
3
suy ra các đáp án A, B, C là đúng, đáp án D là sai.
Máy tính: Bấm máy tính kiểm tra, ba kết quả đầu bằng nhau nên đáp án sai là đáp án D.
Câu 22: Cho hàm số
( )
y f x=
có đạo hàm
( )
=−
32
2f x x x
,
x
. Hàm số
( )
=−2y f x
đồng biến trên
khoảng

Trang 87
A.
( )
+2;
. B.
( )
−;2
. C.
( )
−4;2
. D. .
Lời gii
Chn A
+ Ta có
( )
=−
32
2f x x x
suy ra
( ) ( )
( )
= = − = − +
43
32
2
2
43
xx
f x f x dx x x dx C
+ Suy ra
( ) ( )
( ) ( )
−−
= = − = − +
43
2 2 2
2
43
xx
y g x f x C
+ Tính
( ) ( )
=−'2g x f x
=
( ) ( )
−−
−+
43
2 2 2
43
xx
C
=
( ) ( )
32
2 2 2xx− − + −
( )
2
2 xx=−
+ Hàm số đồng biến suy ra
( )
' 0 0.g x x
Chọn A.
Câu 23: Cho hàm số
2
3
9
x
y
x
−
=
−
. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có tiệm cận ngang là
1y =
.
B. Đồ thị hàm số chỉ có 1 tiệm cận đứng là
3x =−
.
C. Đồ thị hàm số không có tiệm cận đứng.
D. Đồ thị hàm số có hai tiệm cận đứng là
3; 3xx= = −
.
Lời gii
Chn B
Điều kiện xác định:
2
3
90
3
x
x
x
−
−
.
A sai vì: Hàm phân thức, có bậc tử (bậc 1) nhỏ hơn bậc mẫu (bậc 2) nên đồ thị có 1 tiệm cận ngang
0y =
.
Giải phương trình:
2
9 0 3xx− = =
.
Kiểm tra giới hạn:
22
33
3 3 1
lim lim
9 9 6
xx
xx
xx
+−
→→
−−
==
−−
(học sinh có thể dùng máy tính kiểm tra), suy ra,
3x =
không là tiệm cận
đứng của đồ thị hàm số.
2
3
3
lim
9
x
x
x
+
→−
−
= −
−
(học sinh có thể dùng máy tính kiểm tra), suy ra
3x =−
là tiệm cận đứng của đồ thị
hàm số.
Câu 24: Biết rằng
,
là các số thực thỏa mãn
( ) ( )
2 4 4
3 3 3 81 3 3
−−
+ = +
. Giá trị của
6
+
bằng
A. 1. B. 2. C. 4. D. 3.
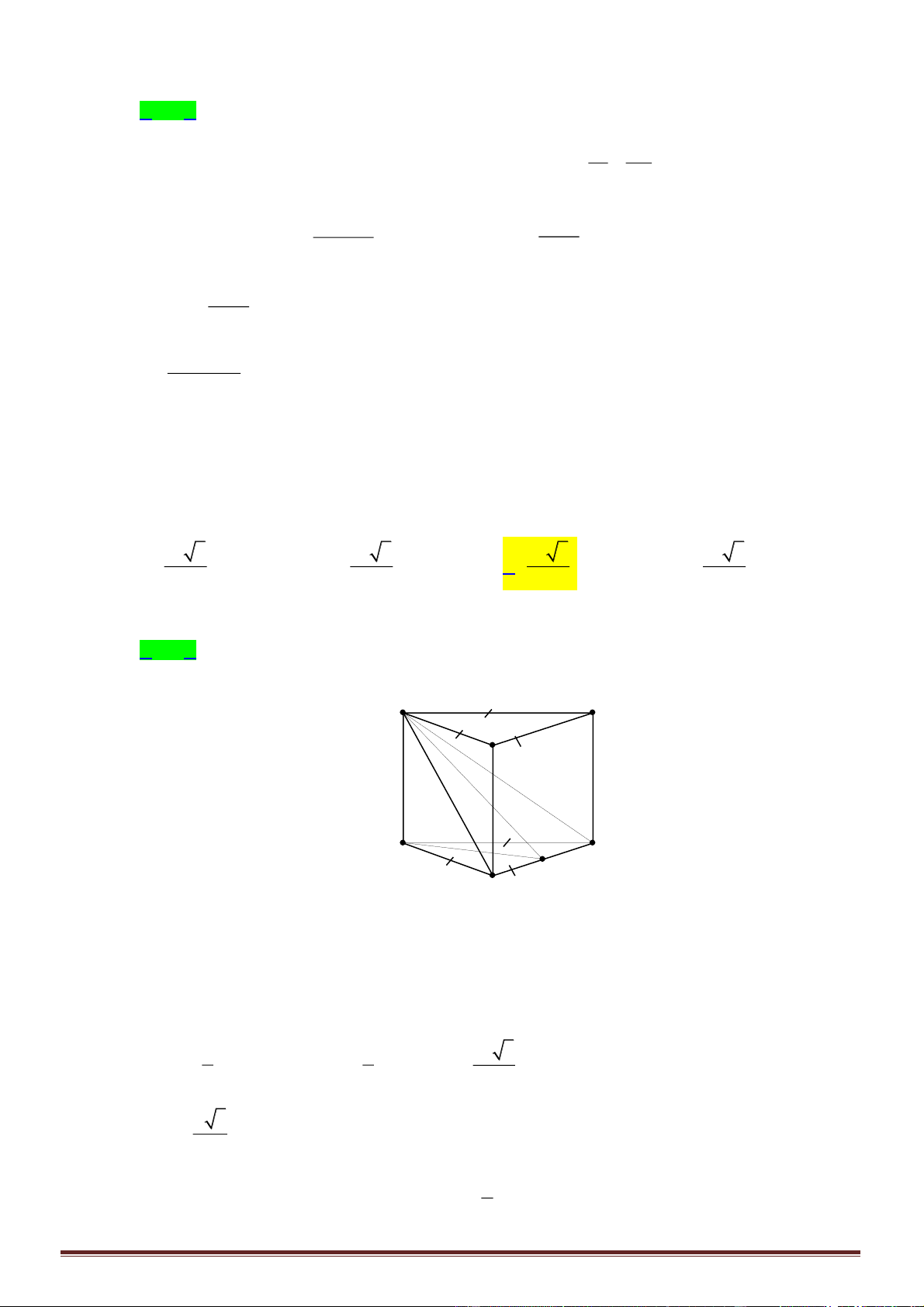
Trang 88
Lời gii
Chn C
Ta có:
( ) ( )
2 4 4
3 3 3 81 3 3
−−
+ = +
( )
24
4
11
3 3 3 81
33
+ = +
.
( )
4
24
4
33
3 3 3 81
3
+
+
+ =
( )
42
4
81
3 3 3 0
3
+
+ − =
.
2
4
81
30
3
+
− =
(do
4
3 3 0
+
).
6
4
3 81
0
3
+
+
−
=
6
3 81 0
+
− =
(do
4
30
+
).
6
3 81
+
=
64
33
+
=
64
+ =
.
Câu 25: Cho hình lăng trụ tam giác đều
.ABC A B C
có
AB a=
. Mặt phẳng
( )
A BC
tạo với mặt phẳng
( )
ABC
một góc
30
. Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3
8
a
. D.
3
3
24
a
.
Lời gii
Chn C
Gọi
M
là trung điểm đoạn
BC
suy ra
AM BC⊥
,
A M BC
⊥
Góc giữa mặt phẳng
( )
A BC
và mặt phẳng
( )
ABC
chính là góc giữa hai đường thẳng
AM
và
AM
suy ra
30A MA
=
1
. .sin
2
ABC
S AB AC BAC
=
1
. .sin60
2
aa
=
2
3
4
a
=
3
2
a
AM =
Tam giác vuông
A AM
có
tan30
2
a
AA AM
==
a
M
B'
C'
A
B
C
A'
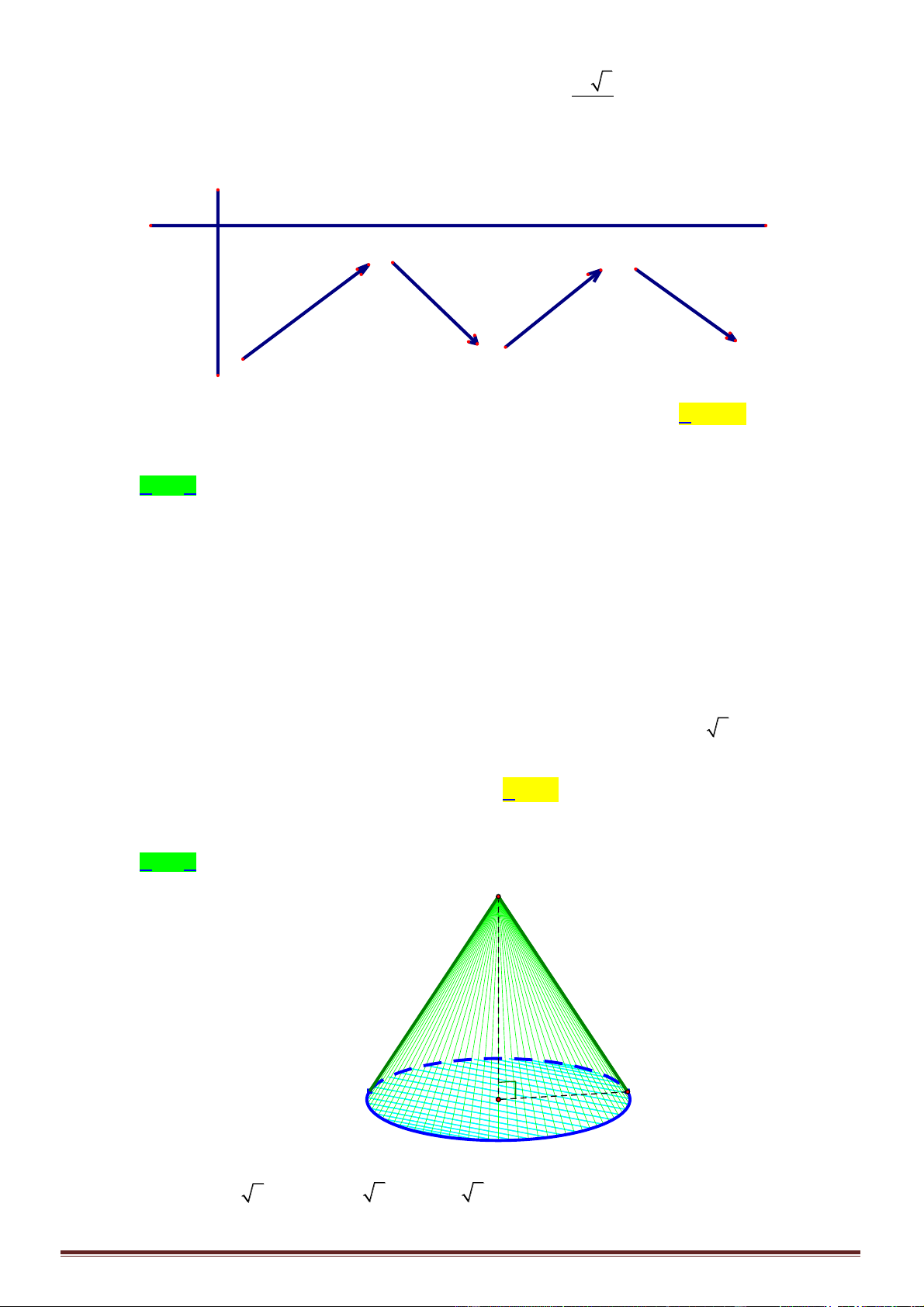
Trang 89
Thể tích khối chóp
.ABC A B C
là:
3
.
3
.'
8
ABC A B C ABC
a
V S AA
==
.
Câu 26: Cho hàm số
()y f x=
có bảng biến thiên như hình vẽ bên. Hàm số
( 3)y f x= − +
đạt cực đại tại
A.
1x =−
B.
2x =
. C.
0x =
. D.
3x =
.
Lời gii
Chn D
Đặt
3xt− + =
.
Ta thấy
( )
3 ( 3) ( )f x f x f t
− + = − − + = −
nên để hàm số
( 3)y f x= − +
đạt cực đại thì hàm số
()y f t=
phải đạt cực tiểu
Theo bảng biến thiên thì hàm số
()y f t=
đạt cực tiểu tại
0t =
Suy ra hàm số
( 3)y f x= − +
đạt cực đại tại
30x− + =
hay
3x =
Câu 27: Cho hình nón tròn xoay có bán kính đáy bằng
2
và diện tích xung quanh bằng
42
. Góc ở đỉnh của
hình nón đã cho bằng
A.
o
60
. B.
o
150
. C.
o
90
. D.
o
120
.
Lời gii
Chn C
Gọi góc ở đỉnh của hình nón bằng
2
.
Ta có:
42
xq
S
=
Rl 4 2
=
l 2 2=
1
-2
1
+
∞
2
0
-1
-
∞
f(x)
x
R
l
h

Trang 90
Nên
R2
sin
l2
==
o
45
=
Vậy góc ở đỉnh của hình nón bằng
o
90
.
Câu 28: Gọi
12
,zz
là các nghiệm phức của phương trình
2
2 3 0zz+ + =
. Số phức
1 2 1 2
z z z z+
bằng
A.
2
. B.
5
. C.
2−
. D.
5i
.
Lời gii
Chn D
2
12
2 3 0
12
zi
zz
zi
= − +
+ + =
= − −
( )( ) ( )( )
1 2 1 2
1 2 1 2 1 2 1 2 2z z z z i i i i+ = − + − + + − − − − = −
.
Vậy
1 2 1 2
2.z z z z+ = −
Cách 2: Phương trình bậc hai
2
2 3 0zz+ + =
có
'
2 = −
là số nguyên âm nên phương trình có hai
nghiệm phức
12
,zz
và
12
zz=
,
21
zz=
.
Áp dụng định lý Viét, ta có:
12
12
2
.3
zz
zz
ì
+ = -
ï
ï
í
ï
=
ï
î
Suy ra:
( )
2
22
1 2 1 2 1 2 1 2 1 2
2 . 4 6 2.z z z z z z z z z z+ = + = + − = − = −
Câu 29: Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( )
2
25f x x x= + −
. Giá trị của
2
mM+
bằng
A.
5
. B.
25
. C.
5 2 5+
. D.
45
.
Lời gii
Chn B
Hàm số xác định và liên tục trên đoạn
5; 5
−
.
Ta có
( )
2
22
25
2
55
x x x
fx
xx
−−
= − =
−−
.
( )
0fx
=
2
2 5 0xx− − =
2
25 xx − =
.
( )
22
0
45
x
xx
−=
2
0
5 20 0
x
x
−=
( )
0
2 5; 5
2
2
x
x
x
x
= −
=
=−
.
Ta có:
( )
5 2 5f − = −
;
( )
25f =
;
( )
5 2 5f =
.
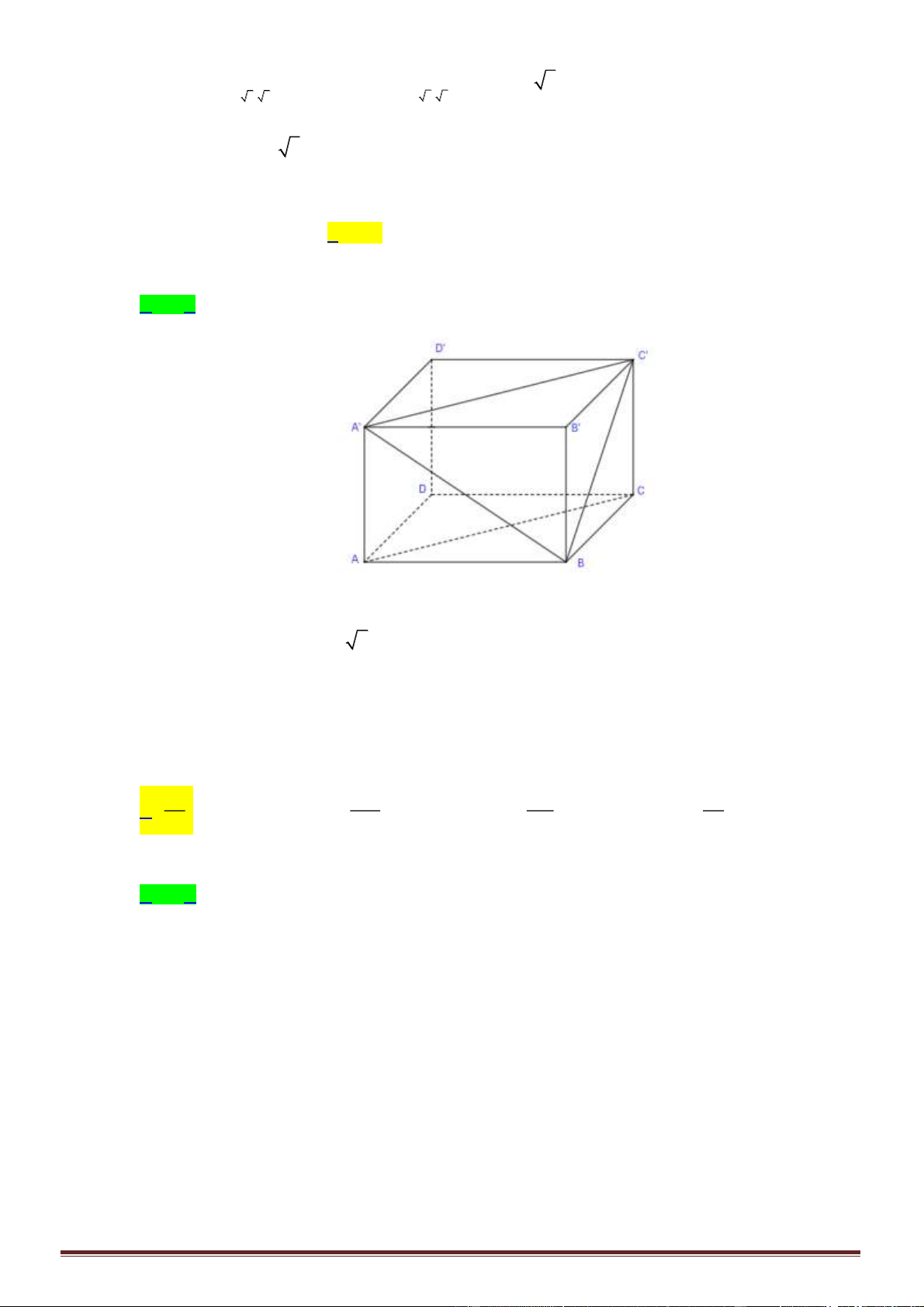
Trang 91
Suy ra
( )
5; 5
max 5M f x
−
==
và
( )
5; 5
min 2 5m f x
−
= = −
.
Vậy
( )
2
2
2 5 5 25mM+ = − + =
.
Câu 30: Cho hình lập phương
.ABCD A B C D
. Góc giữa hai đường thẳng
AC
và
AB
bằng
A.
45
. B.
60
. C.
30
. D.
120
.
Lời gii
Chn B
Do
//AC AC
nên góc giữa hai đường thẳng
AC
và
AB
là góc giữa hai đường thẳng
AC
và
AB
.
Ta có
2A C A B BC a
= = =
( với
a
là độ dài cạnh của hình lập phương )
ABC
đều
0
60BA C
=
góc giữa hai đường thẳng
AC
và
AB
là
60
.
Câu 31: Giải bóng chuyền quốc tế VTV Cup có 12 đội tham gia, trong đó có 3 đội Việt Nam. Ban tổ chức bốc
thăm ngẫu nhiên để chia thành 3 bảng đấu, mỗi bảng 4 đội. Tính xác suất để 3 đội của Việt Nam cùng
nằm ở một bảng đấu.
A.
3
55
. B.
1
330
. C.
1
110
. D.
6
55
.
Lời gii
Chn A
Gọi ba bảng đấu có tên là A, B, C.
Chọn 4 đội cho bảng A có
4
12
C
cách, chọn 4 đội cho bảng B có
4
8
C
cách và 4 đội còn lại vào bảng C có
1 cách.
Theo quy tắc nhân, số cách chia 12 đội thành 3 bảng đấu là:
( )
44
12 8
. .1 34650n C C = =
(cách)
Gọi A là biến cố “3 đội Việt Nam cùng nằm ở một bảng đấu.
Giả sử 3 đội Việt Nam cùng nằm ở bảng A.
Khi đó bảng A sẽ chọn 1 đội trong 9 đội nước ngoài và 3 đội Việt Nam, 8 đội còn lại chia vào bảng B và
C. Trong trường hợp này ta có số cách chọn là
14
98
.1. .1 630CC=
(cách)
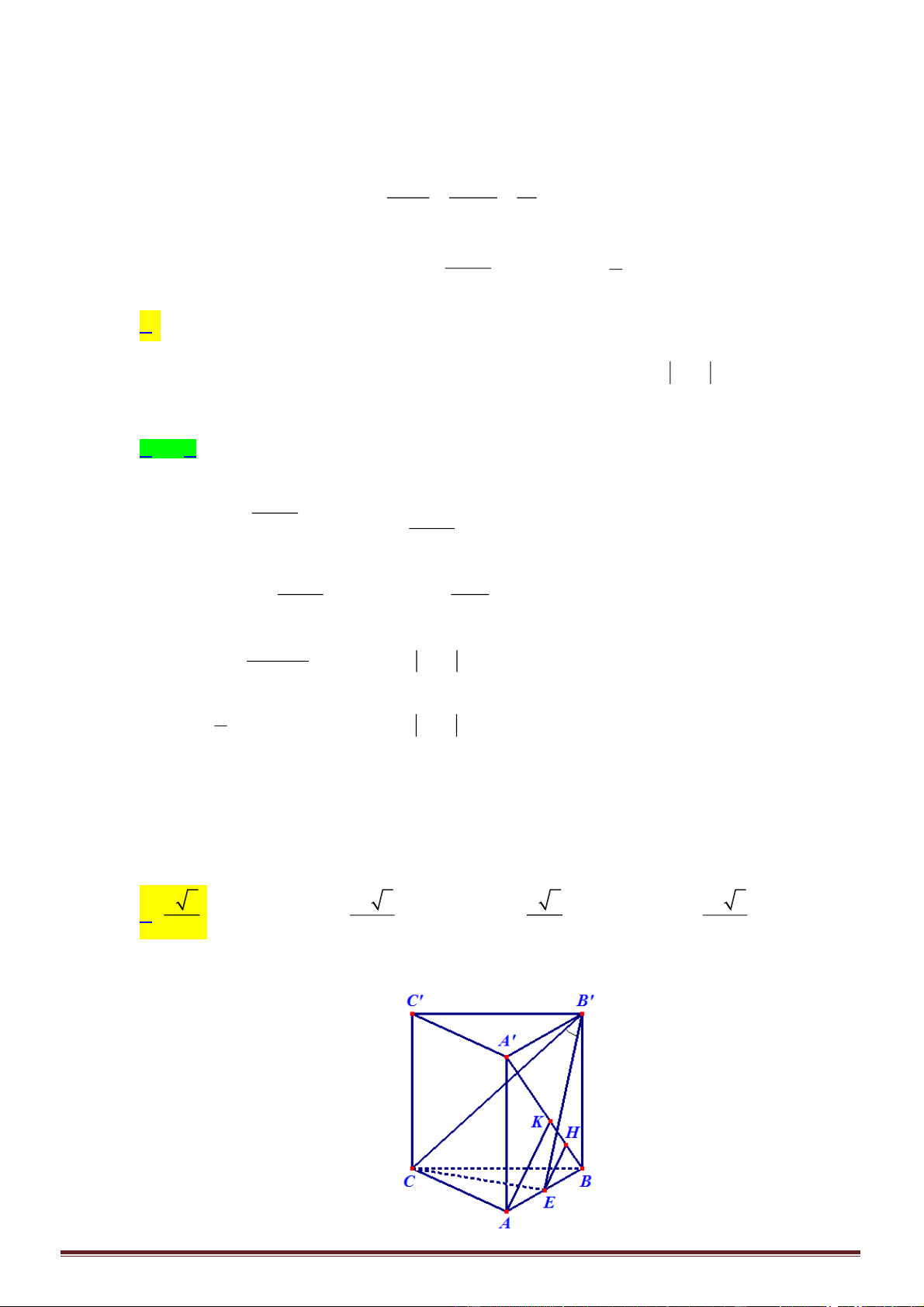
Trang 92
Vì vai trò của các bảng là như nhau nên trường hợp 3 đội Việt Nam ở bảng B hay bảng C đều cho kết
quả như nhau.
Vậy số kết quả thuận lợi cho biến cố A là
( )
14
98
. .3 1890n A C C==
(cách)
Xác suất của biến cố A là:
( )
( )
( )
1890 3
34650 55
nA
PA
n
= = =
.
Câu 32: Tất cả các nguyên hàm của hàm số
( )
2
cos
x
fx
x
=
trên khoảng
0;
2
p
æö
÷
ç
÷
ç
÷
ç
èø
là
A.
( ) ( )
tan ln cos .F x x x x C= + +
B.
( ) ( )
tan ln cos .F x x x x C= - + +
C.
( ) ( )
tan ln cos .F x x x x C= - +
D.
( )
tan ln cos .F x x x x C= - +
Lời gii
Chn A
Gọi
( )
2
d
cos
x
F x x
x
=
ò
. Đặt
2
dd
1
tan
dd
cos
ux
ux
vx
vx
x
ì
=
ï
ï
ì
=
ï
ï
ï
Þ
íí
ïï
=
=
ï
î
ï
ï
î
Khi đó:
( )
2
sin
d tan d
cos cos
xx
F x x x x x
xx
= = -
òò
( )
d cos
tan tan ln cos .
cos
x
x x x x x C
x
= + = + +
ò
Vì
0;
2
x
p
æö
÷
ç
Î
÷
ç
÷
ç
èø
nên
cos 0x >
, suy ra
( )
ln cos ln cosxx=
.
Vậy:
( ) ( )
tan ln cos .F x x x x C= + +
Câu 33: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
2a
. Gọi
E
là trung điểm
AB
. Biết góc giữa
CB
và
( )
BCC B
bằng
o
30
. Khoảng cách giữa hai đường thẳng
AB
và
CE
bằng
A.
6
3
a
. B.
26
3
a
. C.
6
6
a
. D.
26
6
a
.
Lời gii

Trang 93
Thấy
CE AB⊥
,
CE AA
⊥
( )
CE AA B B
⊥
hay
( )
AA B B
chính là mặt phẳng qua
AB
, vuông
góc với
CE
. Gọi
H
là hình chiếu của
E
trên
AB
EH
chính là đoạn vuông góc chung của
AB
và
CE
( )
,d CE A B EH
=
.
Mặt khác
CB
có hình chiếu là
EB
trên
( )
BCC B
là
EB
( )
( )
( )
,,CB BCCB CB EB CB E
= =
o
30CB E
=
2 2. 3CB CE a
= =
2 2 2 2
12 4 2 2CC CB C B a a a
= − = − =
.
Gọi
K
là hình chiếu của
A
trên
AB
.
Ta có
1
2
EH AK=
và
2 2 2 2 2 2
1 1 1 1 1 3
8 4 8AK AA AB a a a
= + = + =
22
3
a
AK=
26
3
3
aa
EH = =
hay
( )
6
,
3
a
d CE A B
=
.
Câu 34: Cho hàm số
( )
y f x=
liên tục trên có đồ thị như hình vẽ bên. Phương trình
( )
( )
10f f x −=
có tất
cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
Lời gii
Chn C
Đặt
( ) ( )
11t f x f x t= − = +
.
Từ đồ thị của hàm số đã cho, phương trình
( )
0ft=
có ba nghiệm phân biệt:
( ) ( ) ( )
1 2 3
2; 1 , 1;0 , 1;2t t t − − −
.
+) Với
( )
11
2; 1 1 1 0tt − − − +
, dựa vào đồ thị đã cho phương trình
( )
1
1f x t=+
có 3 nghiệm
thực
x
phân biệt.
+) Với
( )
22
1;0 0 1 1tt − +
, dựa vào đồ thị đã cho phương trình
( )
2
1f x t=+
có 3 nghiệm
thực
x
phân biệt.
+) Với
( )
33
1;2 2 1 3tt +
, dựa vào đồ thị đã cho phương trình
( )
3
1f x t=+
có 1 nghiệm
x
.

Trang 94
Vậy phương trình đã cho có 7 nghiệm thực phân biệt.
Câu 35: Cho các số phức
z
thỏa mãn
2020
2 1 2z i z i− = − +
. Tập hợp các điểm biểu diễn số phức
2 1 4w z i= − +
trên mặt phẳng tọa độ là một đường thẳng. Khoảng cách từ
( )
2; 3I −
đến đường thẳng
đó bằng
A.
18 5
5
. B.
18 13
13
. C.
10 3
3
. D.
10 5
5
.
Lời gii
Chn D
Giả sử
z a bi=+
( )
;ab
và
w x yi=+
( )
;xy
.
Ta có
2020
2 1 2z i z i− = − +
( )
1010
2
2 1 2a bi i a bi i + − = − − +
( ) ( ) ( )
2 2 2
2
2 1 2a b a b − + = − + −
( )
2 4 1 0 1ab − + =
.
Theo giả thiết:
2 1 4w z i= − +
( )
2 1 4x yi a bi i + = − − +
( )
2 1 4 2x yi a b i + = − + −
.
21
42
xa
yb
=−
=−
1
2
4
2
x
a
y
b
+
=
−
=
( )
2
.
Thay
( )
2
vào
( )
1
ta được:
14
2. 4. 1 0
22
xy+−
− + =
( )
2 6 0xy + − =
.
Vậy:
( )
10 5
,
5
dI=
.
Câu 36: Cho hàm số
( )
y f x=
có đạo hàm trên . Bảng biến thiên của hàm số
( )
'y f x=
như hình dưới
Tìm
m
để bất phương trình
( )
2sinm x f x+
nghiệm đúng với mọi
( )
0;x +
.
A.
(0)mf
. B.
(1) 2sin1mf−
. C.
(0)mf
. D.
(1) 2sin1mf−
.
Lời gii
Chn C.
Ta có
( ) ( )
2sin 2sinm x f x m f x x+ −
.
Đặt
( ) ( )
2sing x f x x=−
.
Ta có
( ) ( )
2cosg x f x x
=−
.
( ) ( )
0 2cosg x f x x
= =
.
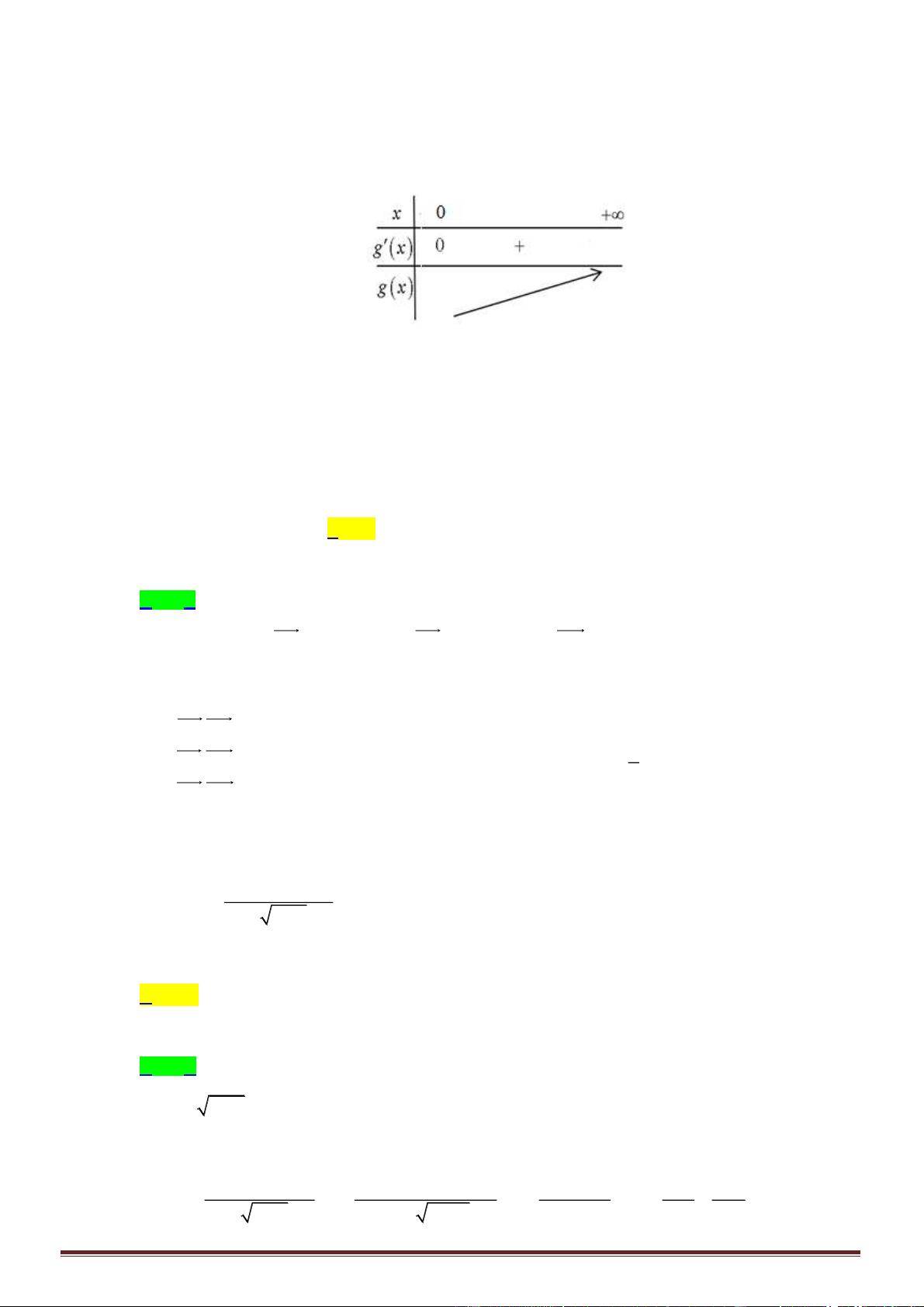
Trang 95
Mà
( ) ( )
2, 0;f x x
+
và
( )
2cosx 2, 0;x +
nên
( ) ( )
0, 0;g x x
+
.
( )
'( ) 2
00
2cos 2
fx
g x x
x
=
= =
=
.
Từ đó ta có bảng biến thiên của
()gx
:
Bất phương trình
( ) ( )( )
2 2 1 3m f x x x + + + +
nghiệm đúng với mọi
( )
3;x − +
( )
0 (0)m g m f
.
Câu 37: Trong không gian
Oxyz
cho
( ) ( ) ( )
2;0;0 ; 0; 2;0 ; 0;0; 2A B C− − −
.
D
là điểm khác
O
sao cho
, , DA DB DC
đôi một vuông góc.
( )
;;I a b c
là tâm mặt cầu ngoại tiếp tứ diện
ABCD
. Tính
S a b c= + +
A.
4−
. B.
1−
. C.
2−
. D.
3−
.
Lờigii
Chn B
Gọi
( )
;;D x y z
( ) ( ) ( )
= 2; ; ; = ; 2; ; = ; ; 2DA x y z DB x y z DC x y z + + +
Vì
, , DA DB DC
đôi một vuông góc nên
( ) ( )
( ) ( )
( ) ( )
2
2
2
.0
2 2 0
4
. 0 2 2 0
3
2 2 0
.0
DA DB
x x y y z
DA DC x x y z z x y z
x y y z z
DB DC
=
+ + + + =
= + + + + = = = = −
+ + + + =
=
( )
;;I a b c
là tâm mặt
Câu 38: Biết rằng
1
2
d
ln2 ln3 ln5
5 3 9
x
a b c
xx
−
= + +
+ + +
, với
,,abc
là các số hữu tỉ.
Giá trị của
abc++
bằng
A.
10−
. B.
5−
. C.
10
. D.
5
.
Lời gii
Chn A
Đặt
3tx=+
2
3tx = +
2 d dt t x=
Đổi cận:
21xt= − =
;
12xt= =
.
Ta có:
1
2
d
5 3 9
x
xx
−
=
+ + +
1
2
d
3 5 3 1 6
x
xx
−
+ + + +
2
2
1
d
2
56
tt
tt
=
++
2
1
32
2d
32
t
tt
=−
++

Trang 96
(
)
22
11
2 3ln 3 2ln 2tt= + − +
( )
2 5ln4 2ln3 3ln5= − + +
=
20ln2 4ln3 6ln5= − + +
Suy ra:
20a =−
,
4b =
,
6c =
. Vậy
10abc+ + = −
Câu 39: Trong không gian
Oxyz
, cho đường thẳng
12
:
2 1 1
x y z
d
+−
==
−
và hai điểm
( 1;3;1)A −
và
( )
0;2; 1B −
. Gọi
( )
;;C m n p
là điểm thuộc đường thẳng
d
sao cho tam giác
ABC
vuông tại
A. Giá trị của tổng
2m n p++
bằng
A.
0
. B.
2
. C.
3
. D.
5−
.
Lời gii
Chn A
Vì
Cd
nên tọa độ của
C
có dạng
( )
1 2 ; ;2C t t t− + −
Ta có
( )
1; 1; 2AB −−
và
( )
2 ; 3;1AC t t t−−
Vì
ABC
vuông tại A nên
1
. 0 2 3 2 2 0 3 1 0
3
AC AB t t t t t
−
= − + − + = + = =
.
5
3
5 1 4 1 5 2 7
; ; 2 0
3 3 3 3 3 3 3
7
3
m
C n m n p
p
−
=
− − − − −
= + + = + + =
=
.
Câu 40: Bất phương trình có bao nhiêu nghiệm nguyên?
A. . B. . C. . D. Vô số.
Lời gii
hn A
Ta có:
.
Vì . Vậy có 5 nghiệm.
Câu 41: Cho hàm số có đồ thị hàm như hình vẽ. Hàm số đồng biến trên
khoảng
A. . B. . C. . D. .
( )
( )
2
3 ln 2 0x x x− +
5
4
3
( )
( )
2
3 ln 2 0x x x− +
( )
( )
2
ln 2 0
30
ln 2 0
x
xx
x
+ =
−
+
21
03
21
x
x
x
+=
+
1
03
1
x
x
x
=−
−
1
03
x
x
=−
1;0;1;2;3xx −
()fx
'( )y f x=
2
(cos )y f x x x= + −
( )
1;2
( )
1;0−
( )
0;1
( )
2; 1−−

Trang 97
Lời gii
Chn A
Phân tích:
Bản chất dạng toán này thường là đặc điểm: Tổng hai hàm dương (hàm đồng biến), tổng hai hàm âm
(hàm nghịch biến)
Tính chất:
Cho hàm số tăng trên khoảng , hàm số tăng trên khoảng . Khi đó ta có
hàm số tăng trên khoảng
+ Quan sát bài toán: , nếu trắc nghiệm thấy ngay đáp án
A.
Hướng dẫn gii:
Ta có:
+ Vì mà
+ Suy ra hay hàm số tăng trên
Câu 42: Cho hàm số . Gọi là số lớn nhất trong các số nguyên thỏa mãn
. Mệnh đề nào sau đây đúng?
A. . B. . C. . D. .
Lời gii
Chn B
Phân tích:
+ Bài toán nếu thế vào:
+ Biểu thức khá phức tạp. Điều này chứng tỏ bài toán cho hàm số chắc chắn có tính
chất đặc biệt.
+ Nhìn yếu tố xuất hiện hàm số . Ta có hàm số lẻ và tăng trên . Đây chính là
chìa khóa ta giải quyết bài toán.
( )
y f x=
1
D
( )
y f x=
2
D
( ) ( )
y f x g x=+
12
D D D=
2
1
' 2 1 0
2
y x x y x x= − = −
( )
' sin . ' cos 2 1y x f x x= − + −
( )
cos 1;1 sin . ' cos 1;1x x f x − − −
2 1 1 1xx−
( )
' sin . ' cos 2 1 0, 1y x f x x x= − + −
[1; )+
( ) 2 2
xx
fx
−
=−
0
m
m
12
( ) (2 2 ) 0f m f m+ −
)
0
1513;2019m
)
0
1009;1513m
)
0
505;1009m
)
0
1;505m
12 12
2 2 2 2
( ) 2 2 2 2 0
m m m m
Pm
− − − +
= − + −
()Pm
()y f x=
( )
22
xx
y f x
−
= = −
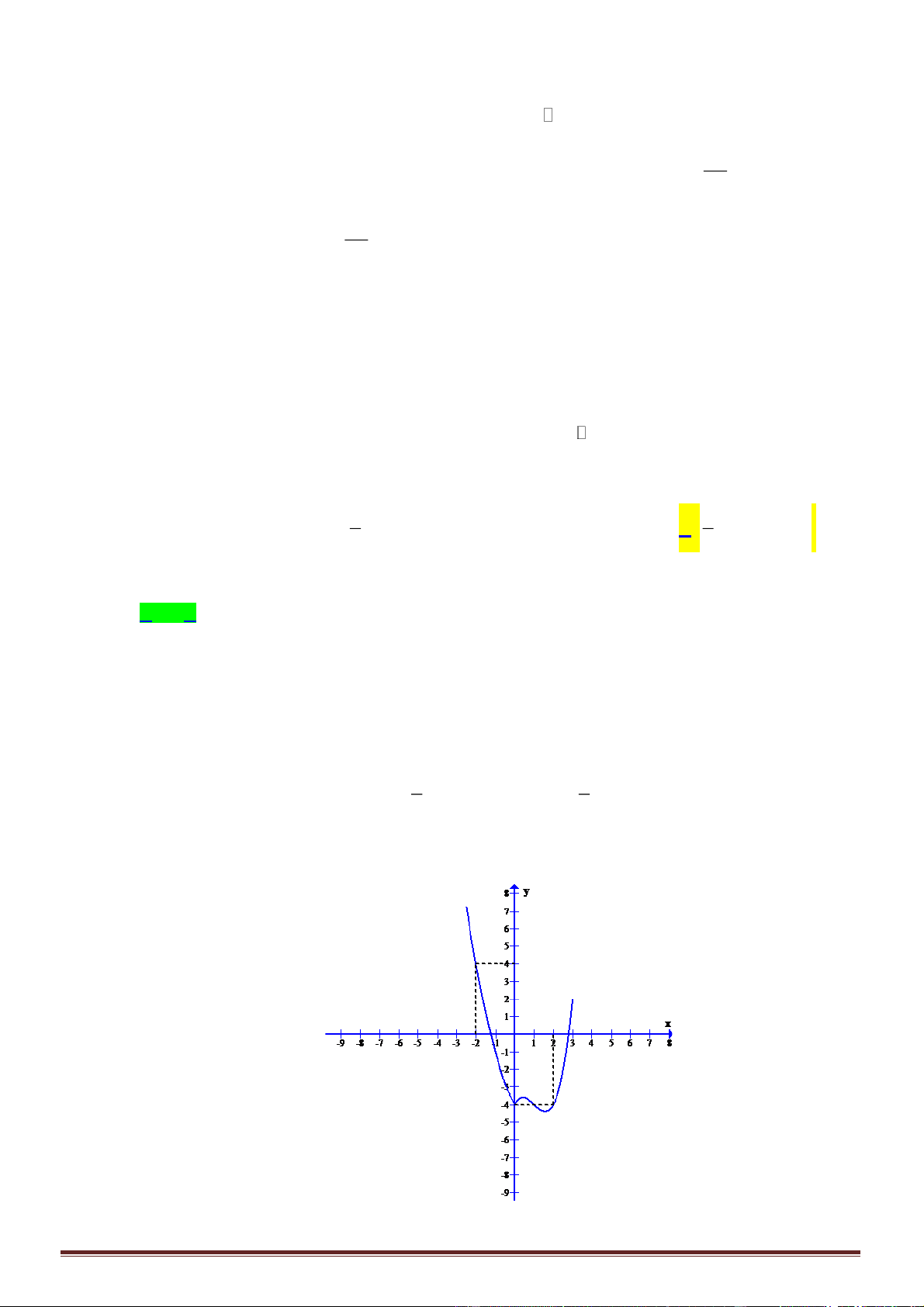
Trang 98
Hướng dẫn gii:
Ta có hàm số hàm số lẻ và tăng trên
Yêu cầu bài toán
nguyên lớn nhất là:
Bài toán tổng quát:
Giải bất phương trình: (*)
Với là hàm số lẻ và tăng (hoặc giảm) trên tập
Câu 43: Cho hàm số thỏa mãn và . Tất cả các nguyên hàm
của là
A. . B. . C. . D. .
Lời gii
Chn D
Ta có
.
Vì .
Vậy .
Câu 44: Cho hàm số có đồ thị hàm số được cho như hình vẽ bên.
( ) 2 2
xx
y f x
−
= = −
( )
( ) ( )
12
12 12
2
2 2 2 2
3
f m f m f m m m m − − = − −
m
12
2
1365
3
m
==
( )
( )
( )
( )
, , 0f u x m f v x m+
()fx
f
D
( )
fx
( ) ( )
2
2 2 ,
x
f x xf x xe x
−
+ =
( )
01f =
( )
2
.e
x
x f x
( )
2
2
1xC++
( )
2
2
2
1
1
2
x
x e C
−
++
( )
2
2
2
1
x
x e C
−
++
( )
2
2
1
1
2
xC++
( ) ( )
2
22
x
f x xf x xe
−
+=
( ) ( )
( )
2 2 2
2 .2
x x x
e f x xf x e xe
−
+ =
( )
( )
2
2
x
e f x x
=
( )
2
2
2d
x
e f x x x x C = = +
(0) 1f =
1C=
( )
( )
2
2
1
x
f x x e
−
= +
( )
2
d
x
xf x e x
( )
2
1dx x x=+
( ) ( )
22
1
1 d 1
2
xx= + +
( )
2
2
1
1
2
xC= + +
( )
fx
( )
y f x
=
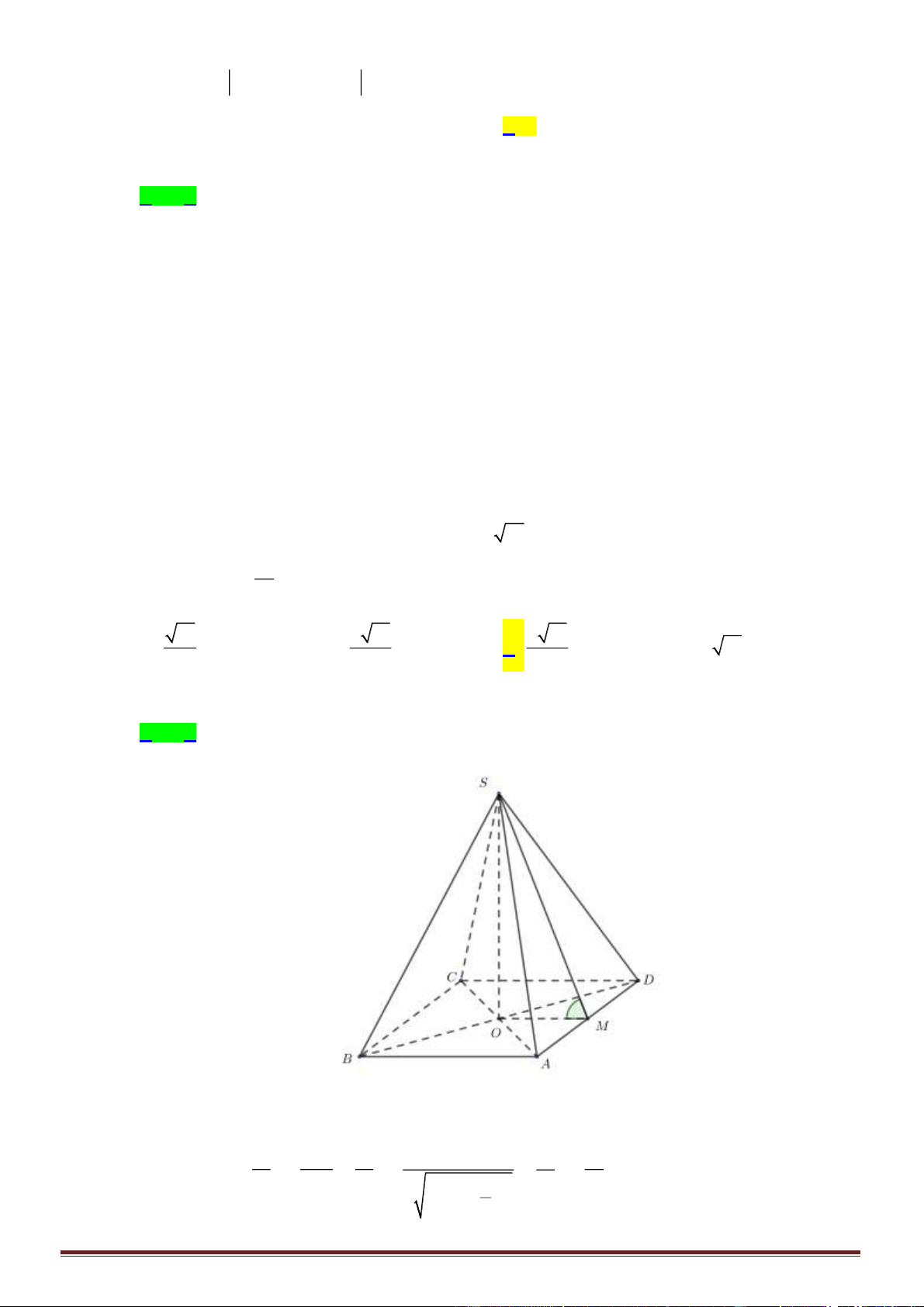
Trang 99
Hàm số có nhiều nhất bao nhiêu cực trị trong khoảng .
A. 6. B. 2. C. 5. D. 3
Lời gii
Chn C
Xét hàm số: .
Ta có ;
Nghiệm phương trình trên là hoành độ giao điểm của hai đồ thị và
Dựa vào đồ thị suy ra phương trình: có hai nghiệm
Trên khoảng , hàm số có hai điểm cực trị là . Do đó đồ thị hàm số
cắt trục hoành tại tối đa 3 điểm.
Câu 45: Cho hình chóp tứ giác đều có , côsin góc hợp bởi hai mặt phẳng và
bằng . Thể tích của khối chóp bằng
A. . B. . C. . D. .
Lời gii
Chn C
Gọi cạnh hình vuông đáy là ,góc hợp bởi hai mặt phẳng và là góc nhọn
.
( ) ( )
2
0y f x x f= + −
( )
3;3−
( ) ( ) ( )
2
0g x f x x f= + −
( ) ( )
//
2g x f x x=+
( ) ( )
//
02g x f x x= = −
2yx=−
( )
/
y f x=
( )
/
2f x x=−
2
2
x
x
=−
=
( )
3;3−
( )
gx
2, 2xx= = −
( )
y g x=
.S ABCD
21SA a=
( )
SAD
( )
ABCD
1
10
.S ABCD
3
19
3
a
3
2 19
3
a
3
4 19
3
a
3
4 19a
x
( )
SAD
( )
ABCD
·
SMO
·
1
cos
10
SMOÞ=
1
10
OM
SM
Û=
22
1
10
1
2 21
4
x
ax
Û=
-
22
21
21
4
xaÛ=
2xaÛ=
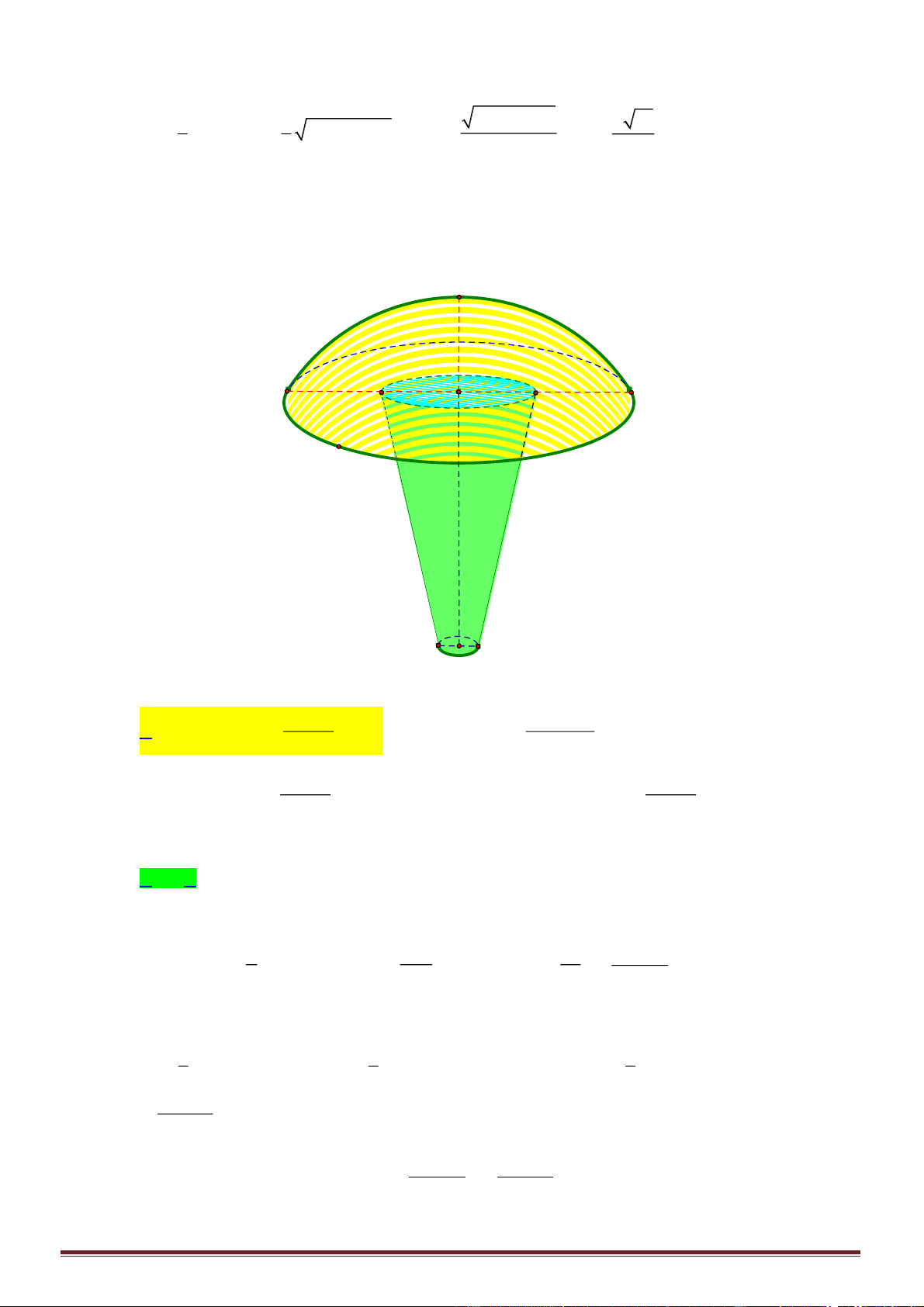
Trang 100
Thể tích của khối chóp bằng
.
Câu 46: Cây dù ở khu vui chơi “công viên nước” của trẻ em có phần trên là một chỏm cầu, phần than là một khối
nón cụt như hình vẽ. Biết
2ON OD m==
;
40MN cm=
;
40BC cm=
;
20EF cm=
. Tính thể tích
của cây dù
A.
( )
3
336000 cm
( )
3
2750
cm
3
p
. B.
( )
3
896000
3
cm
.
C.
( )
3
112000 cm
( )
3
2050
cm
3
p
. D.
( )
3
896000 cm
( )
3
2250
cm
3
p
.
Lời gii
Chn A
Thể tích phần trên của cây dù là thể tích của khối chỏm cầu:
2
1
3
h
V h R
=−
2
..
3
MN
MN ON
=−
2
40
.40 200
3
=−
( )
3
896000
3
cm
=
.
Thể tích phần thân của cây dù là thể tích của khối nón cụt:
( )
22
2 1 2 1 2
1
. . .
3
V h R R R R
= + +
( )
22
1
. . .
3
OM MB OE MB OE
= + +
( )
1
.160. 400 100 200
3
= + +
( )
3
112000
3
cm
=
.
Vậy thể tích của cây dù:
12
V V V=+
896000 112000
33
=+
( )
3
336000 cm
=
.
.S ABCD
1
.
3
ABCD
V SO S=
( )
2
22
1
.4
3
SC OC a=-
22
2
21 2
.4
3
aa
a
-
=
3
4 19
3
a=
A
D
M
F
E
B
O
C
N

Trang 101
Câu 47: Giả sử là hai trong các số phức thỏa mãn là một số thuần ảo. Biết rằng
, giá trị nhỏ nhất của bằng
A. . B. . C. . D. .
Lời gii
Chn B
Đặt
Theo giả thiết là số thuần ảo, suy ra
tập hợp điểm biểu diễn số phức là một đường tròn tâm ,
Giả sử , .Gọi lần lượt là điểm biểu diễn cho các số phức . Suy ra
.
Gọi là điểm thỏa mãn .
Gọi là trung điểm ta có .
Vậy tập hợp điểm là đường tròn tâm , .
Ta có .
Do , là hai đường tròn đồng tâm và
Từ đó suy ra
Câu 48. Cho hàm số có đồ thị như hình vẽ.
12
,zz
( )( )
12z z i+−
12
2zz−=
12
5zz+
13 5−
3 5 13−
3 5 2 13−
5 22−
( ) ( )( ) ( )
22
; 1 2 2 2 2 .z x yi x y z z i x y x y x y i= + + − = + + + − + +
( )( )
12z z i+−
( )
2
2
2 2 2 2
1 5 1 5
2 0 2 1 1 .
4 4 2 4
x y x y x x y y x y
+ + + = + + + + + = + + + =
z
( )
1
C
1
;1
2
I
−−
5
2
R =
z x yi=+
,xy
,AB
12
,zz
12
22z z AB− = =
M
5 0 5 6MA MB OA OB OM+ = + =
H
AB
2
2 2 2
2 2 2
2
1
4
13
36
IH
IH IA HA
IH IM HM
IM
=
=−
=−
=
M
( )
2
C
1
;1
2
I
−−
13
6
r =
12
5 5 6 6z z OA OB OM OM+ = + = =
( )
1
C
( )
2
C
( )
1
OC
12
5 13
5 6 6 6 3 5 13
26
Min
Min
z z OM R r
+ = = − = − = −
( )
y f x=
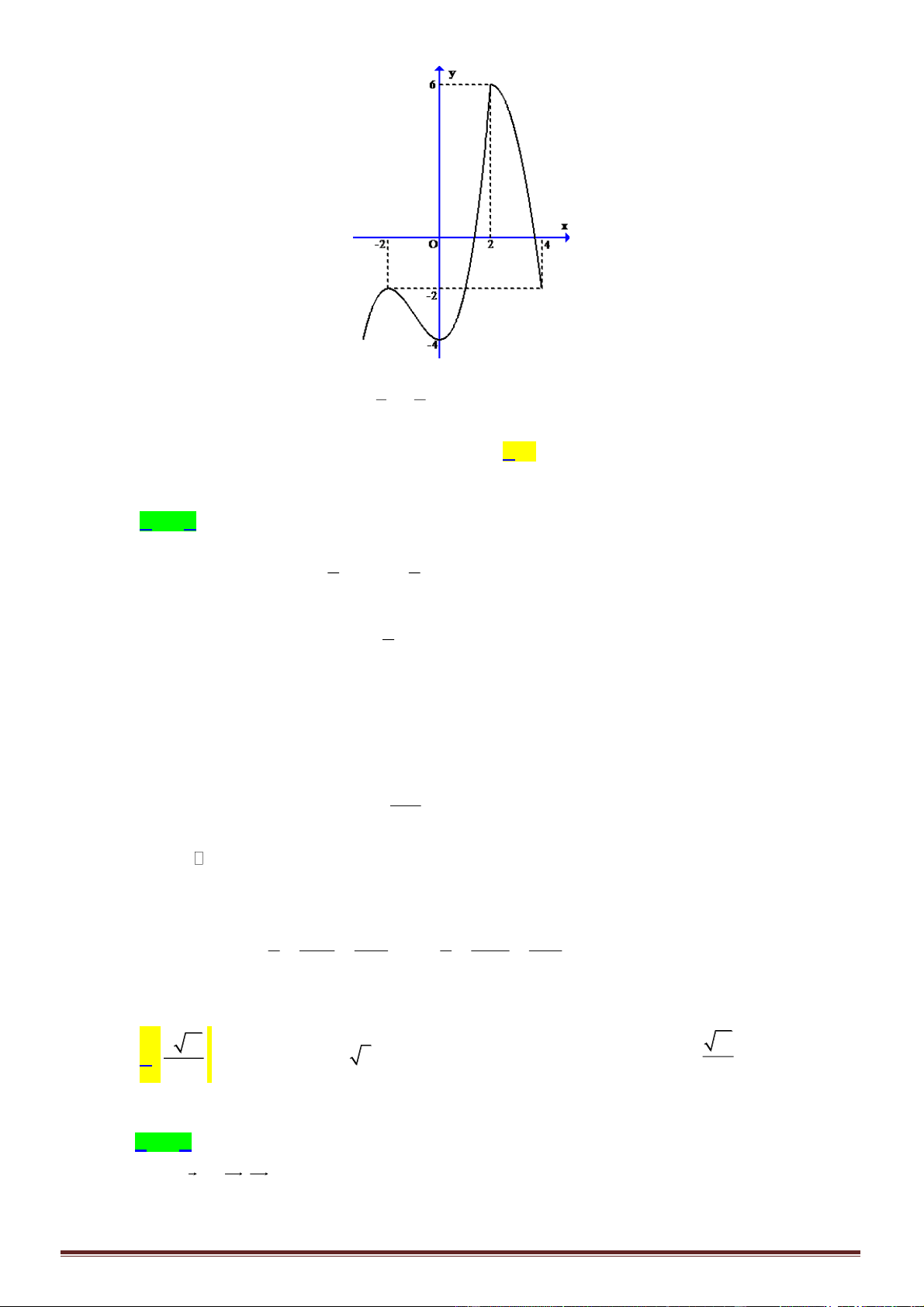
Trang 102
Có bao nhiêu số nguyên để phương trình có nghiệm thuộc đoạn ?
A. 11. B. 9. C. 8. D. 10.
Lời gii
Chn C
Ta có phương trình
1 6 1 3 6
22
xx
fm
+ + + = +
(*)
Xét hàm số
( )
6y f t t=+
với
1
2
x
t =+
. Vì
2;2x−
nên
0;2t
Ta có
( )
' ' 6 0, 0;2y f t t= +
Phương trình (*) có nghiệm
( )
( )
( )
( )
0;2
0;2
min 6 3 6 max 6f t t m f t t + + +
( ) ( )
10
0 3 6 2 12 4
3
f m f m
−
+ +
Vì
m
nên
3; 2; 1;0;1;2;3;4m − − −
Câu 49: Trong không gian cho hai mặt phẳng và hai
đường thẳng . Đường thẳng song song với hai mặt
phẳng và cắt tương ứng tại . Độ dài đoạn bằng
A. . B. C. D.
Lời gii
Chn A
+ Tính
m
1
1
32
x
f x m
+ + =
2;2−
Oxyz
( )
: 2 1 0,P x y z+ − − =
( )
:2 2 0,P x y z+ − + =
1
11
:,
2 1 2
x y z−+
= =
2
21
:
1 1 2
x y z−−
= =
−
( ) ( )
;PQ
12
,
,HK
HK
8 11
7
5
6.
11
.
7
( )
, 1; 1; 3
PQ
u n n
= = − − −
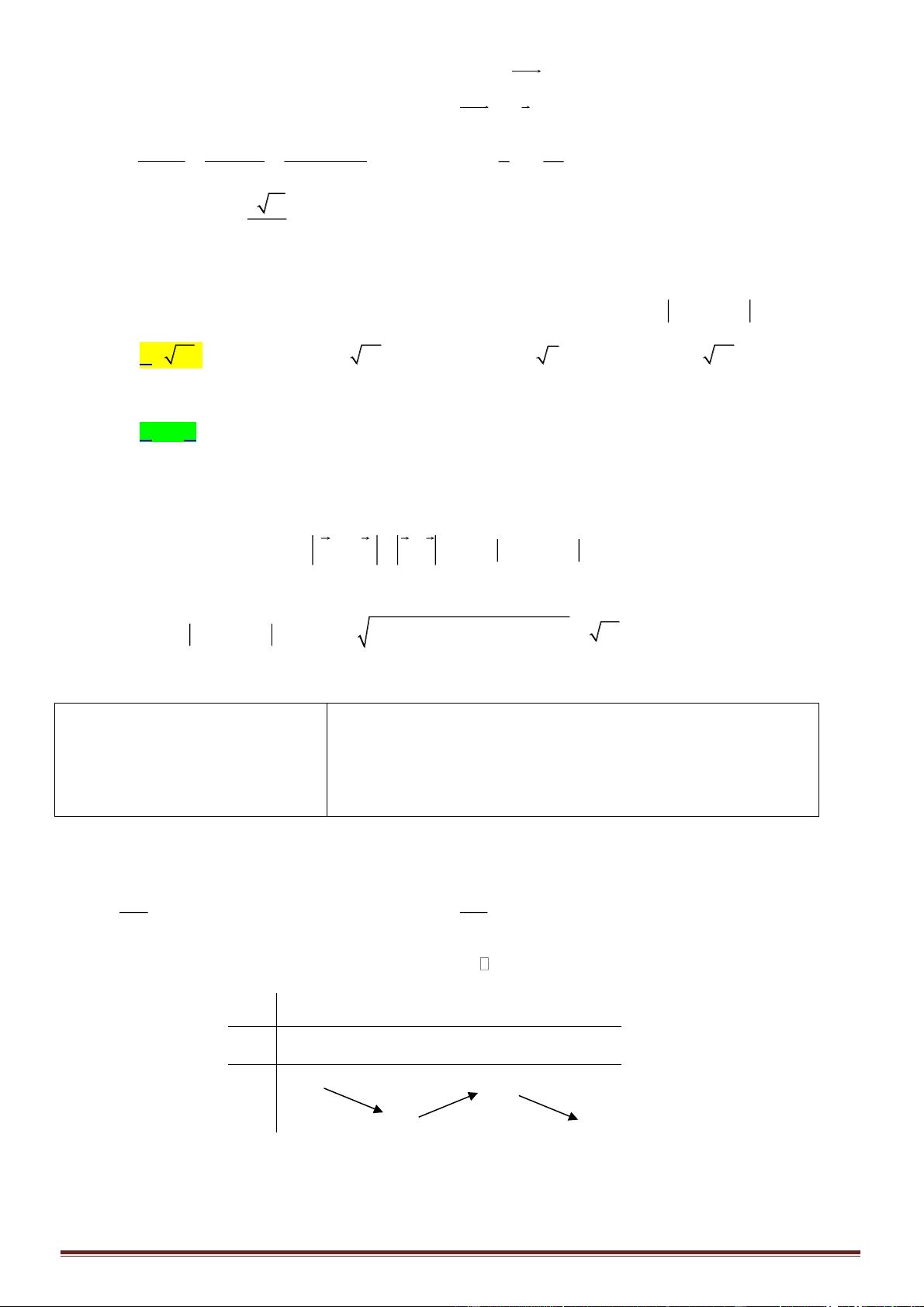
Trang 103
+ Gọi nên
+ Vì song song với 2 mặt phẳng nên suy ra
tính ra được .
+ Suy ra .
Câu 50: Trong không gian
Oxyz
, cho hai điểm
( )
1;2;3A
,
( )
4;4;5B
. Giả sử
M
là điểm thay đổi trong mặt
phẳng
( ):2 2 2019 0.P x y z+ + + =
Tìm giá trị lớn nhất của biểu thức
.P AM BM=−
A.
17
. B.
77
. C.
7 2 3−
. D.
82 5−
.
Lời gii
Chn A
Ta có:
( )( )
2 2 2019 2 2 2019 0
A A A B B B
x y z x y z+ + + + + +
nên các điểm
,AB
đều nằm cùng phía
so với mặt phẳng
()P
và đường thẳng
AB
luôn cắt mặt phẳng
()P
tại một điểm cố định.
Từ bất đẳng thức véc tơ
| | | | .u v u v− −
Ta có
.AM BM AB−
Dấu bằng xảy ra khi
M
là giao
điểm của đường thẳng
AB
với mặt phẳng
()P
.
Do đó
( ) ( ) ( )
2 2 2
4 1 4 2 5 3 17
Max
AM BM AB− = = − + − + − =
, đạt được khi
( )
M AB P=
.
ĐỀ 36
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Thể tích của khối lập phương cạnh bằng 2a là:
A.
3
2
.
3
a
V =
B.
2
4.Va=
C.
3
8
.
3
a
V =
D.
3
8.Va=
Câu 2: Cho hàm số
( )
y f x=
xác định và liên tục trên có bảng biến thiên sau:
x
−
1
3
+
'y
−
0
+
0
−
y
+
1
1−
−
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
( )
1;1−
( ) ( )
2 ;1 ; 1 2 ; ;2 ;1 2H t t t K m m m+ − + − +
( )
2;1 ;2 2 2HK m m t m t= − − − + −
( ) ( )
;PQ
.HK k u=
2 1 2 2 2
1 1 3
m t m t m t− − − + −
==
23
;
77
mt
−
==
8 11
7
HK =

Trang 104
B. Hàm số có đúng một cực trị
C. Hàm số đạt cực đại tại
3x =
và đạt cực tiểu tại
1x =
D. Hàm số có giá trị nhỏ nhất bằng
1−
và giá trị lớn nhất bằng 1
Câu 3. Phương trình trục đối xứng của pa rabol y = x
2
+4 x – 5 là
A. x =2. B.x =-2. C. y =2. D. y = -2.
Câu 4: Hàm số
( )
=y f x
có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có điểm cực đại là
( )
1; 1−
B. Đồ thị hàm số có điểm cực tiểu là
( )
1; 1−
C. Đồ thị hàm số có điểm cực tiểu là
( )
1;3−
D. Đồ thị hàm số có điểm cực tiểu là
( )
1;1
Câu 5: Rút gọn biểu thức
1
6
3
P x . x=
với
x 0.
A.
2
Px=
. B.
Px=
. C.
1
8
Px=
. D.
2
9
Px=
.
Câu 6: Họ nguyên hàm của hàm số
( )
f x 2x sin2x=+
là
A.
2
1
x cos2x C
2
−+
. B.
2
1
x cos2x C
2
++
. C.
2
x 2cos2x C−+
. D.
2
x 2cos2x C++
.
Câu 7. Tọa độ 1 vec tơ pháp tuyến của đường thẳng có phương trình 3x - 2y + 5 = 0 là:
A.
(3;2).n
B.
(2;3).n
C.
( 2;3).n −
D.
(3; 2).n −
Câu 8: Cho cấp số nhân
( )
n
u
, biết:
n n 1
81, 9
+
==uu
. Tính công bội q của cấp số nhân.
A. q =
1
.
9
B. q = 9 . C. q = -72. D. q = 72.
Câu 9: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3;2;1M
. Gọi
12
,MM
lần lượt là hình chiếu
của
M
lên các trục
,Oy Oz
. Tọa độ của vectơ
12
MM
uuuuur
là:
A.
( )
0;2;0
. B.
( )
0; 2;1−
. C.
( )
0;0;1
. D.
( )
0;2;1
.
Câu 10: Từ các chữ số 0,1,2,3,4,5,6,7,8,9. Hỏi có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số phân
biệt?
A. 84 B. 120 C. 720 D. 648
Câu 11 : Có năm cuốn sách Toán khác nhau và năm cuốn sách Hóa khác nhau có bao nhiêu cách sắp xếp
chúng thành một hàng ?
A. 10. B. 5!5! C. 5.5. D. 10!.
Câu 12: Tập nghiệm bất phương trình
( )
2
log x 1 3−
là
A.
( )
;10−
. B.
( )
1;9
. C.
( )
1;10
. D.
( )
;9−
.

Trang 105
Câu 13.Cho
1
cosa
3
=
Tính giá trị của P=
cos2a
A.
7
9
p =
. B.
7
9
P
−
=
. C.
2
3
P =
. D.
11
9
P =
.
Câu 14. Phần thực và phần ảo của số phức z = 2 +i(1+3i) bằng .
A.- 1 và 1. B. 5 và 1. C.2 và 4. D.1 và – 1
Câu 15: Giả sử đồ thị sau là của một trong các hàm được liệt kê ở các đáp án A, B, C, D. Hỏi đó là hàm
số nào?
A.
42
21y x x= − −
. B.
42
2y x x=+
. C.
42
21y x x= − +
. D.
42
2y x x=−
.
Câu 16. Nhị thức f(x)= 2x – 4 nhận giá trị âm khi và chỉ khi
A.
( ;2)x −
. B.
( ; 2)x − −
. C.
(2; )x +
. D.
( 2: )x − +
.
Câu 17.Đường thẳng có phương trình 2x - 4y + 10 = 0 song song với đường thẳng nào có phương trình
dưới đây
A.x -2y + 5= 0. B.x -2y +10 = 0. C.2x+y +5 = 0. D.x +2y +5 = 0.
Câu 18 : Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số f(x) liên tục trên đoạn
a;b
, trục
Ox và hai đường thẳng x = a, x = b quay quanh trục Ox , được tính theo công thức :
A.
( )
b
2
a
V f x dx=
. B.
( )
b
2
a
V f x dx=
. C.
( )
b
a
V f x dx=
. D.
( )
b
a
V f x dx=
.
Câu 19.Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3; 1;2M −
. Điểm
N
đối xứng với
M
qua mặt
phẳng
( )
Oyz
là
A.
( )
0; 1;2N −
. B.
( )
3;1; 2N −
. C.
( )
3; 1;2N −−
. D.
( )
0;1; 2N −
.
Câu 20 .Cho khối chóp tam giác tam giác đều có chiều cao bằng cạnh đáy bằng a .Thể tích của khối
chóp đó là
A.
3
3
.
12
a
V =
B.
3
3
.
6
a
V =
C.
3
3
.
4
a
V =
D.
3
3
.
2
a
V =
Câu 21: Trên tập số phức , cho phương trình
( )
2
az bz c 0 a,b,c ; a 0+ + =
. Khẳng định nào sau
đây sai?
A. Tổng hai nghiệm của phương trình bằng
b
a
−
. B.
2
b 4ac 0 = −
thì phương trình vô nghiệm.
C. Phương trình luôn có nghiệm. D. Tích hai nghiệm của phương trình là
c
a

Trang 106
Câu 22.Trong không gian
Oxyz
, cho điểm
( )
1; 1;3A −
và mặt phẳng
( )
P
có phương trình
2 2 3 0x y z− + + =
. Viết phương trình mặt phẳng
( )
Q
song song với mặt phẳng
( )
P
biết mặt phẳng
( )
Q
cách
A
một đoạn bằng
4
.
A.
2 2 3 0x y z− + + =
hoặc
2 2 21 0x y z− + − =
. B.
2 2 21 0x y z− + − =
.
C.
2 2 6 0x y z− + − − =
. D.
2 2 3 0x y z− + + =
.
Câu 23: Với a, b là các số thực dương. Biểu thức P =
( )
2
a
log a b
bằng
A.
a
2 log b−
. B.
a
2 log b+
. C.
a
1 2log b+
. D.
a
2log b
.
Câu 24: Với cách biến đổi
u 1 3lnx=+
thì tích phân
e
1
ln x
dx
x 1 3ln x+
trở thành :
A.
( )
2
2
1
2
u 1 du
3
−
. B.
( )
2
2
1
2
u 1 du
9
−
. C.
( )
2
2
1
2 u 1 du−
. D.
2
2
1
9 u 1
du
2u
−
.
Câu 25. Cho số phức z thỏa
3 4 6z z i+ − =
.Tìm môdun của số phức z
A.5. B.
5.
C.
10
. D.
10.
Câu 26: Số tiệm cận ngang của đồ thị hàm số
2
x x 1
y
x1
+−
=
+
là A. 2 B. 1 C. 3 D. 0
Câu 27. Một hình nón có đường sinh 2a và thiết diện qua trục là một tam giác vuông .Tính diện tich xung
quanh S của hình nón
A.
2
2 2 a .S
=
B.
2
4 2 a .S
=
C.
2
(2 2 2) a .S
=+
D.
2
(4 2 2) a .V
=+
Câu 28: Có 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Hỏi có bao nhiêu
cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau?
A. 479001600 B. 17280 C. 51840 D. 103680
Câu 29: Phương trình
cos2xm=
có nghiệm khi m là:
A.
2 2.m−
B.
1.m
C.
1 1.m−
D.
2.m
Câu 30: Biết
2
2
2
lim 2
54
an
n
+
=
−
. Giá trị
a
bằng bao nhiêu?
A.
10a =
B.
8a =−
C.
8a =
D.
2a =−
Câu 31. Trong không gian với hệ toạ độ
Oxyz
, cho tam giác
ABC
có
( )
2;2;1A
,
( )
4;4;2B
,
( )
2;4; 3C −−
. Đường phân giác trong
AD
của tam giác
ABC
có một vectơ chỉ phương là:
A.
( )
2;4; 3−−
. B.
( )
6;0;5
. C.
1
0;1;
3
−
. D.
41
; ; 1
33
− − −
.
Câu 32 : Gọi S là tập nghiệm của phương trình
( ) ( )
2
22
2log 2 2 log 3 2xx− + − =
trên R. Tổng các phần tử
của S bằng
A. 8. B.
42+
. C.
82+
. D.
62+
.
Trang 107
Câu 33.Gọi
12
,zz
là 2 nghiệm phức của phương trình
2
2 10 0zz+ + =
.Giá trị của biểu thức
22
12
P z z=+
bằng A.
10.P =
B.
10.P =
C.
20.P =
D.
2 10.P =
Câu 34.Cho hình chóp tam giác đều
.S ABC
có độ dài cạnh đáy bằng
,a
cạnh bên bằng
3.a
Gọi
O
là
tâm của tam giác
,ABC
gọi
1
d
là khoảng cách từ
A
đến mặt phẳng
( )
SBC
và
2
d
là khoảng cách từ
O
đến mặt phẳng
( )
.SAB
Khi đó
12
d d d=+
bằng
A.
2 22
11
a
d =
. B.
2 22
33
a
d =
. C.
8 22
33
a
d =
. D.
8 22
11
a
d =
.
Câu 35: Tìm giá trị thực của tham số m để hàm số
2
2x x 3
khi x > 1
x1
f(x)
m khi x 1
+−
−
=
liên tục tại x = 1.
A.
m 5.=
B.
5
m.
2
=
C.
1
m.
2
=−
D.
m 1.=−
Câu 36: Tập hợp tất cả các giá trị của tham số m để hàm số
( )
32
y x mx m 6 x 1= − − − +
đồng biến trên
khoảng
( )
0;4
: A.
(
;6−
B.
( )
;3−
C.
(
;3−
D.
3;6
Câu 37. Cho số phức z thỏa mãn . Biết tập hợp các điểm biểu diễn số phức
là đường tròn tâm I, bán kính R. Tìm tọa đọ tâm I và bán kính R của đường tròn đó.
A. I(-1;2); B. I(1;2); R=5 C. I(1;2);R=5 D. I(-1;2);R=5
Câu 38.Tính thể tích của một thùng đựng rượu là một hình tròn xoay có hai dáy là hai hình tròn bằng
nhau và chiều cao của bình là 16cm.Đường cong của bình là một cung tròn của đường tròn có bán kính
là 9cm
A.
2864
3
. B,
2846
3
. C.
2864
. D.
2684
3
.
Câu 39: Cho hàm số bậc bốn trùng phương y = f (x) có đồ thị như hình vẽ:
z1=
( )
w 3 4i z 1 2i= − − +
R 5.=

Trang 108
Số nghiệm thực của phương trình
( )
( )
( ) ( )
11
22
2
f f x f x f x+ + = +
A. 2 B. 3 C. 4 D. 5
Câu 40: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Biết
=AB a
, ,
()⊥SA ABCD
và
=SA a
. Tính số đo góc giữa đường thẳng SD và mặt phẳng (SAB) .
A. 45
0
B. 60
0
. C. 30
0
D. 90
0
.
Câu 41: (Biết tổng các hệ số trong khai triển
( )
2
1
n
x+
bằng 1024. Tính số hạng chứa
12
x
.
A.
12
110x
B.
12
120x
C.
12
210x
D.
12
151.200x
Câu 42: Tập hợp tất cả các giá trị của tham số m để phương trình
x x 1
4 m.2 3m 3 0
+
− + − =
có hai nghiệm
trái dấu là
A.
( )
;2−
. B.
( )
1; +
. C.
( )
1;2
. D.
( )
0;2
.
Câu 43. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
( )
2;1;3A
,
( )
6;5;5B
. Gọi
( )
S
là mặt
cầu có đường kính
AB
. Mặt phẳng
( )
P
vuông góc với đoạn
AB
tại
H
sao cho khối nón đỉnh
A
và đáy
là hình tròn tâm
H
(giao của mặt cầu
( )
S
và mặt phẳng
( )
P
) có thể tích lớn nhất, biết rằng
( )
:2 0P x by cz d+ + + =
với
b
,
c
,
d
. Tính
S b c d= + +
.
A.
18S =−
. B.
11S =−
. C.
24S =−
. D.
14S =−
.
Câu 44.Cho hình lập phương
.ABCD A B C D
. Gọi
M
là trung điểm của cạnh
BB
. Mặt phẳng
( )
A MD
chia hình lập phương thành hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện trên
A.
7
17
. B.
8
17
. C.
9
17
. D.
10
17
.
Câu 45: Cho
( )
fx
liên tục trên
1;e
, biết
( )
( )
e
1
fx
dx 1,f e 2.
x
==
Tính
( )
e
1
f ' x ln xdx ?=
A.
1
B.
0
C.
2
D.
3
Câu 46: Cho hàm số
( )
fx
xác định trên
R \ 1
thỏa mãn
( )
2
1
f ' x .
x1
=
−
Biết
( ) ( )
f 3 f 3 0− + =
và
11
f f 2.
22
− + =
Giá trị
( ) ( ) ( )
T f 2 f 0 f 4= − + +
bằng:
A.
19
T ln
25
=
B.
15
T 2 ln
29
=+
C.
19
T 3 ln
25
=+
D.
19
T 1 ln
25
=+
Câu 47.Xét các số phức
z a bi=+
(
,ab
) thoả mãn
3 2 3 6 10z i z i+ + + − − =
. Tính
P a b=+
khi
82zi+−
đạt giá trị nhỏ nhất.
A.
118
25
P =
. B.
9P =
. C.
5P =−
. D.
118
25
P =−
.
Câu 48: Một đoàn tàu có 7 toa. Có 7 hành khách lên tàu. Tính xác suất P để mỗi toa có đúng 1 người lên
tàu .
3AD a=

Trang 109
A.P=
620
117649
B. P=
5040
117649
C. P=
720
117649
D. P=
840
117649
Câu 49.Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 13 0S x y z x y z+ + − − + − =
và đường thẳng
1 2 1
:
1 1 1
x y z
d
+ + −
==
. Tọa độ điểm
M
trên đường thẳng
d
sao cho từ
M
có thể kẻ được
3
tiếp tuyến
,MA
MB
,
MC
đến mặt cầu
( )
S
(
,,A B C
là các tiếp điểm) thỏa mãn
60 , 90 , 120AMB BMC CMA= = =
có dạng
( )
;;M a b c
với
0a
. Tổng
abc++
bằng
A.
1
. B.
10
3
. C.
2
. D.
2−
.
Câu 50: Cho hai hàm số
( )
y f x=
và
( )
y g x=
là hai hàm số liên tục trên có đồ thị hàm số
( )
y f x
=
là đường cong nét đậm, đồ thị hàm số
( )
y g x
=
là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm
A, B, C của
( )
y f x
=
và
( )
y g x
=
trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của
hàm số
( ) ( ) ( )
h x f x g x=−
trên đoạn
;?ac
A.
( ) ( )
;
min 0 .
ac
h x h=
B.
( ) ( )
;
min .
ac
h x h a=
C.
( ) ( )
;
min .
ac
h x h b=
D.
( ) ( )
;
min .
ac
h x h c=
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1. Thể tích của khối lập phương cạnh bằng 2a là:
A.
3
2
.
3
a
V =
B.
2
4.Va=
C.
3
8
.
3
a
V =
D.
3
8.Va=
Câu 2: Cho hàm số
( )
y f x=
xác định và liên tục trên có bảng biến thiên sau:
x
−
1
3
+
'y
−
0
+
0
−
y
+
1
1−
−
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
( )
1;1−
B. Hàm số có đúng một cực trị
C. Hàm số đạt cực đại tại
3x =
và đạt cực tiểu tại
1x =
D. Hàm số có giá trị nhỏ nhất bằng
1−
và giá trị lớn nhất bằng 1
C.
Dựa vào bảng biến thiên:
Hàm số đồng biến trên khoảng
( )
1;3
Loại đáp án A.
Hàm số có hai điểm cực trị
Loại đáp án B.

Trang 110
lim ; lim
xx
yy
→− →+
= + = −
Nên hàm số không có giá trị lớn nhất và nhỏ nhất
Đáp án D sai.
Hàm số đạt cực đại tại
3x =
và đạt cực tiểu tại
1x =
Đáp án C đúng.
Câu 3. Phương trình trục đối xứng của pa rabol y = x
2
+4 x – 5 là
B. x =2. B.x =-2. C. y =2. D. y = -2.
Câu 4: Hàm số
( )
=y f x
có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có điểm cực đại là
( )
1; 1−
B. Đồ thị hàm số có điểm cực tiểu là
( )
1; 1−
C. Đồ thị hàm số có điểm cực tiểu là
( )
1;3−
D. Đồ thị hàm số có điểm cực tiểu là
( )
1;1
: Đáp án B
Câu 5: Rút gọn biểu thức
1
6
3
P x . x=
với
x 0.
A.
2
Px=
. B.
Px=
. C.
1
8
Px=
. D.
2
9
Px=
.
5: Đáp án B.
Ta có:
1 1 1 1
1
3 6 3 6
2
P x .x x x x.
+
= = = =
Câu 6: Họ nguyên hàm của hàm số
( )
f x 2x sin2x=+
là
A.
2
1
x cos2x C
2
−+
. B.
2
1
x cos2x C
2
++
. C.
2
x 2cos2x C−+
. D.
2
x 2cos2x C++
.
6: Đáp án A
( ) ( )
2
1
f x dx 2x sin2x dx x cos2x C
2
= + = − +
Câu 7. Tọa độ 1 vec tơ pháp tuyến của đường thẳng có phương trình 3x - 2y + 5 = 0 là:
A.
(3;2).n
B.
(2;3).n
C.
( 2;3).n −
D.
(3; 2).n −
Câu 8: Cho cấp số nhân
( )
n
u
, biết:
n n 1
81, 9
+
==uu
. Tính công bội q của cấp số nhân.
A. q =
1
.
9
B. q = 9 . C. q = -72. D. q = 72.
Câu 9: Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3;2;1M
. Gọi
12
,MM
lần lượt là hình chiếu
của
M
lên các trục
,Oy Oz
. Tọa độ của vectơ
12
MM
uuuuur
là:
A.
( )
0;2;0
. B.
( )
0; 2;1−
. C.
( )
0;0;1
. D.
( )
0;2;1
.
Lời gii
Chn B.
Ta có:
( ) ( )
12
0;2;0 ; 0;0;1MM
suy ra
( )
12
0; 2;1MM =−
uuuuur
.
Câu 10: Từ các chữ số 0,1,2,3,4,5,6,7,8,9. Hỏi có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số phân
biệt?
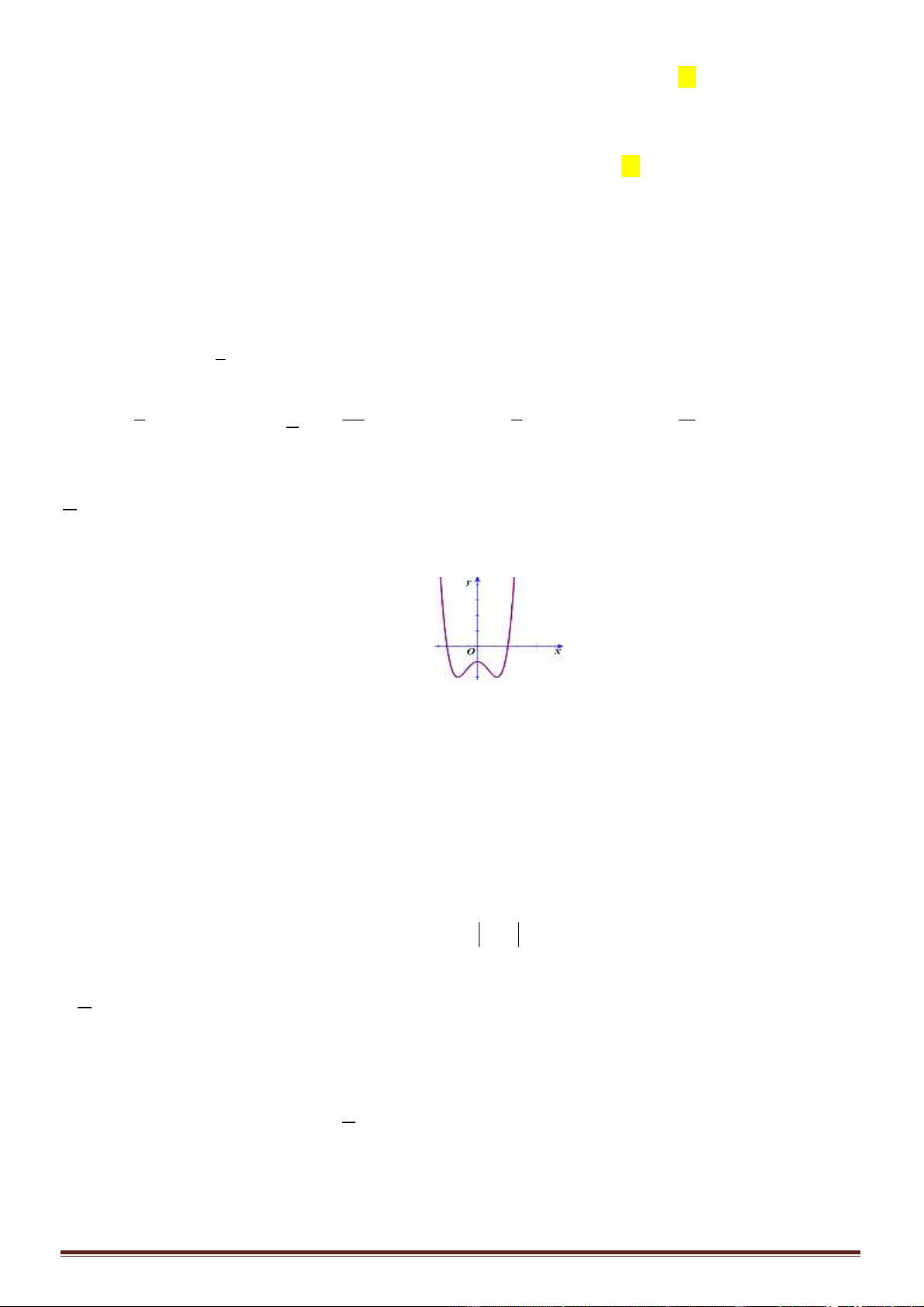
Trang 111
A. 84 B. 120 C. 720 D. 648
Câu 11 : Có năm cuốn sách Toán khác nhau và năm cuốn sách Hóa khác nhau có bao nhiêu cách sắp xếp
chúng thành một hàng ?
A. 10. B. 5!5! C. 5.5. D. 10!.
Câu 12: Tập nghiệm bất phương trình
( )
2
log x 1 3−
là
A.
( )
;10−
. B.
( )
1;9
. C.
( )
1;10
. D.
( )
;9−
.
12: Đáp án B
Bất phương trình đã cho
3
0 x 1 2 1 x 9 −
Câu 13.Cho
1
cosa
3
=
Tính giá trị của P=
cos2a
A.
7
9
p =
. B.
7
9
P
−
=
. C.
2
3
P =
. D.
11
9
P =
.
Câu 14. Phần thực và phần ảo của số phức z = 2 +i(1+3i) bằng .
A.- 1 và 1. B. 5 và 1. C.2 và 4. D.1 và – 1
Câu 15: Giả sử đồ thị sau là của một trong các hàm được liệt kê ở các đáp án A, B, C, D. Hỏi đó là hàm
số nào?
A.
42
21y x x= − −
. B.
42
2y x x=+
. C.
42
21y x x= − +
. D.
42
2y x x=−
.
15: Đáp án A
HS có 3 cực trị nên lọai B
HS cắt Oy tại A(0;-1) nên chọn ACâu 18 : Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số
f(x) liên tục trên đoạn
a;b
, trục Ox và hai đường thẳng x = a, x = b quay quanh trục Ox , được tính theo
công thức :
A.
( )
b
2
a
V f x dx=
. B.
( )
b
2
a
V f x dx=
.
C.
( )
b
a
V f x dx=
. D.
( )
b
a
V f x dx=
.
Câu 16. Nhị thức f(x)= 2x – 4 nhận giá trị âm khi và chỉ khi
A.
( ;2)x −
. B.
( ; 2)x − −
. C.
(2; )x +
. D.
( 2: )x − +
.
Câu 17.Đường thẳng có phương trình 2x - 4y + 10 = 0 song song với đường thẳng nào có phương trình
dưới đây
A.x -2y + 5= 0. B.x -2y +10 = 0. C.2x+y +5 = 0. D.x +2y +5 = 0.
Câu 18 : Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số f(x) liên tục trên đoạn
a;b
, trục
Ox và hai đường thẳng x = a, x = b quay quanh trục Ox , được tính theo công thức :
A.
( )
b
2
a
V f x dx=
. B.
( )
b
2
a
V f x dx=
.

Trang 112
C.
( )
b
a
V f x dx=
. D.
( )
b
a
V f x dx=
.
Chn B.
Câu 19.Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
3; 1;2M −
. Điểm
N
đối xứng với
M
qua mặt
phẳng
( )
Oyz
là
A.
( )
0; 1;2N −
. B.
( )
3;1; 2N −
. C.
( )
3; 1;2N −−
. D.
( )
0;1; 2N −
.
Lời gii
Chn C.
Vì
N
đối xứng với
M
qua mặt phẳng
( )
Oyz
nên
( )
3; 1;2N −−
.
Câu 20 .Cho khối chóp tam giác tam giác đều có chiều cao bằng cạnh đáy bằng a .Thể tích của khối
chóp đó là
A.
3
3
.
12
a
V =
B.
3
3
.
6
a
V =
C.
3
3
.
4
a
V =
D.
3
3
.
2
a
V =
Câu 21: Trên tập số phức , cho phương trình
( )
2
az bz c 0 a,b,c ; a 0+ + =
. Khẳng định nào sau
đây sai?
A. Tổng hai nghiệm của phương trình bằng
b
a
−
. B.
2
b 4ac 0 = −
thì phương trình vô nghiệm.
C. Phương trình luôn có nghiệm. D. Tích hai nghiệm của phương trình là
c
a
Đáp án BTrong tập số phức , khi
2
b 4ac 0 = −
thì phương trình có hai nghiệm phức phân biệt.
Câu 22.Trong không gian
Oxyz
, cho điểm
( )
1; 1;3A −
và mặt phẳng
( )
P
có phương trình
2 2 3 0x y z− + + =
. Viết phương trình mặt phẳng
( )
Q
song song với mặt phẳng
( )
P
biết mặt phẳng
( )
Q
cách
A
một đoạn bằng
4
.
A.
2 2 3 0x y z− + + =
hoặc
2 2 21 0x y z− + − =
. B.
2 2 21 0x y z− + − =
.
C.
2 2 6 0x y z− + − − =
. D.
2 2 3 0x y z− + + =
.
Lời gii
Chn B
( ) ( )
//QP
( )
: 2 2 0Q x y z C − + + =
( )
3C
( )
( )
( )
2
22
1 2 2.3
; 4 4
1 2 2
C
dAQ
+ + +
= =
+ − +
( )
( )
3
9 12
21
CL
C
C TM
=
+ =
=−
Vậy phương trình mặt phẳng
( )
: 2 2 21 0Q x y z− + − =
.
Câu 23: Với a, b là các số thực dương. Biểu thức P =
( )
2
a
log a b
bằng
A.
a
2 log b−
. B.
a
2 log b+
. C.
a
1 2log b+
. D.
a
2log b
.

Trang 113
23: Đáp án B
( )
22
a a a a
log a b log a log b 2 log b= + = +
Câu 24: Với cách biến đổi
u 1 3lnx=+
thì tích phân
e
1
ln x
dx
x 1 3ln x+
trở thành :
A.
( )
2
2
1
2
u 1 du
3
−
. B.
( )
2
2
1
2
u 1 du
9
−
. C.
( )
2
2
1
2 u 1 du−
. D.
2
2
1
9 u 1
du
2u
−
.
24: Đáp án B
Ta có
2
x 1 u 1
3
u 1 3ln x u 1 3ln x 2udu dx,
x e u 2
x
= =
= + = + =
= =
Suy ra
( )
2
e e 2
2
1 1 1
u1
lnx 2 2
3
dx udu u 1 du
u 3 9
x 1 3ln x
−
= = −
+
Câu 25. Cho số phức z thỏa
3 4 6z z i+ − =
.Tìm môdun của số phức z
A.5. B.
5.
C.
10
. D.
10.
Câu 26: Số tiệm cận ngang của đồ thị hàm số
2
x x 1
y
x1
+−
=
+
là A. 2 B. 1 C. 3 D. 0
Đáp án 26B TXD:
)
D 1;= +
2
xx
x x 1
lim y lim 1
x1
→+ →+
+−
= =
+
hàm số có TCN
y1=
Câu 27. Một hình nón có đường sinh 2a và thiết diện qua trục là một tam giác vuông .Tính diện tich xung
quanh S của hình nón
A.
2
2 2 a .S
=
B.
2
4 2 a .S
=
C.
2
(2 2 2) a .S
=+
D.
2
(4 2 2) a .V
=+
Câu 28: Có 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Hỏi có bao nhiêu
cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau?
A. 479001600 B. 17280 C. 51840 D. 103680
Câu 29: Phương trình
cos2xm=
có nghiệm khi m là:
A.
2 2.m−
B.
1.m
C.
1 1.m−
D.
2.m
Câu 30: Biết
2
2
2
lim 2
54
an
n
+
=
−
. Giá trị
a
bằng bao nhiêu?
A.
10a =
B.
8a =−
C.
8a =
D.
2a =−
Câu 31. Trong không gian với hệ toạ độ
Oxyz
, cho tam giác
ABC
có
( )
2;2;1A
,
( )
4;4;2B
,
( )
2;4; 3C −−
. Đường phân giác trong
AD
của tam giác
ABC
có một vectơ chỉ phương là:
A.
( )
2;4; 3−−
. B.
( )
6;0;5
. C.
1
0;1;
3
−
. D.
41
; ; 1
33
− − −
.
Lời gii
Chn C.

Trang 114
Ta có
3, 6AB AC==
. Kí hiệu
( )
;;x y z
là toạ độ điểm
D
.
Vì
AD
là phân giác trong của tam giác
ABC
nên
1
2
DB AB
DC AC
==
.
Do đó, ta có
1
2
DB DC=−
( )
( )
( )
1
42
2
1
44
2
1
23
2
xx
yy
zz
− = − − −
− = − −
− = − − −
2
4
1
3
x
y
z
=
=
=
. Vậy
1
2;4;
3
D
.
2
0;2;
3
AD
=−
2AD u=
, với
1
0;1;
3
u
=−
.
Câu 32 : Gọi S là tập nghiệm của phương trình
( ) ( )
2
22
2log 2 2 log 3 2xx− + − =
trên R. Tổng các phần tử
của S bằng
A. 8. B.
42+
. C.
82+
. D.
62+
.
32: Đáp án B
Điều kiện:
1; 3xx
Ta có:
( ) ( ) ( ) ( )
2 2 2
2 2 2 2
2log 2 2 log 3 2 log 2 2 log 3 2x x x x− + − = − + − =
( ) ( ) ( ) ( )
2 2 2 2
2
log 2 2 . 3 2 2 2 . 3 4x x x x
− − = − − =
( ) ( )
( )( )
( )( )
22
1 3 1
1 3 1
1 3 1
xx
xx
xx
− − =
− − =
− − = −
( )
( )
( )
2
2
22
4 2 0
22
4 4 0
2
x TM
xx
xL
xx
x TM
=+
− + =
= −
− + =
=
Vậy tổng các nghiệm là
2 2 2 4 2+ + = +
Câu 33.Gọi
12
,zz
là 2 nghiệm phức của phương trình
2
2 10 0zz+ + =
.Giá trị của biểu thức
22
12
P z z=+
bằng A.
10.P =
B.
10.P =
C.
20.P =
D.
2 10.P =
Câu 34.Cho hình chóp tam giác đều
.S ABC
có độ dài cạnh đáy bằng
,a
cạnh bên bằng
3.a
Gọi
O
là
tâm của tam giác
,ABC
gọi
1
d
là khoảng cách từ
A
đến mặt phẳng
( )
SBC
và
2
d
là khoảng cách từ
O
đến mặt phẳng
( )
.SAB
Khi đó
12
d d d=+
bằng
A.
2 22
11
a
d =
. B.
2 22
33
a
d =
. C.
8 22
33
a
d =
. D.
8 22
11
a
d =
.
Lời gii
Chn C.
Trang 115
Gọi
M
là trung điểm của
.AB
Kẻ
OH SM⊥
tại
.H
Suy ra
( )
( )
,.d O SAB OH=
( )
( )
,d A SBC
( )
( )
3,d O SBC=
( )
( )
3,d O SAB=
3OH=
.
Ta có
2
2
3 8 3
, 3 , .
3 3 3 6
a a a
OA SO a a OM= = − = =
2 2 2
1 1 1
OH OM SO
=+
2 2 2
12 3 99
88a a a
= + =
2 22
33
a
OH=
( )
( )
4,d d O SAB=
8 22
33
a
=
.
Câu 35: Tìm giá trị thực của tham số m để hàm số
2
2x x 3
khi x > 1
x1
f(x)
m khi x 1
+−
−
=
liên tục tại x = 1.
A.
m 5.=
B.
5
m.
2
=
C.
1
m.
2
=−
D.
m 1.=−
Câu 36: Tập hợp tất cả các giá trị của tham số m để hàm số
( )
32
y x mx m 6 x 1= − − − +
đồng biến trên
khoảng
( )
0;4
: A.
(
;6−
B.
( )
;3−
C.
(
;3−
D.
3;6
36: Đáp án C
Ta có
2
y' 3x 2mx m 6= − − +
Hàm số đồng biến trên
( ) ( )
0;4 y' 0, x 0;4
( ) ( )
2
2
3x 6
3x 2mx m 6 0 m , x 0;4 1
2x 1
+
− − +
+
Xét hàm số
( ) ( ) ( )
( )
( )
( )
2
2
2
6 x x 2
x1
3x 6
f x , x 0;4 f ' x f ' x 0
x2
2x 1
2x 1
+−
=
+
= = =
=
+
+
Ta có bảng biến thiên như sau
x
0
1
4
( )
f ' x
-
0
+
( )
fx
6
6
a
3
a
M
O
A
B
C
S
H
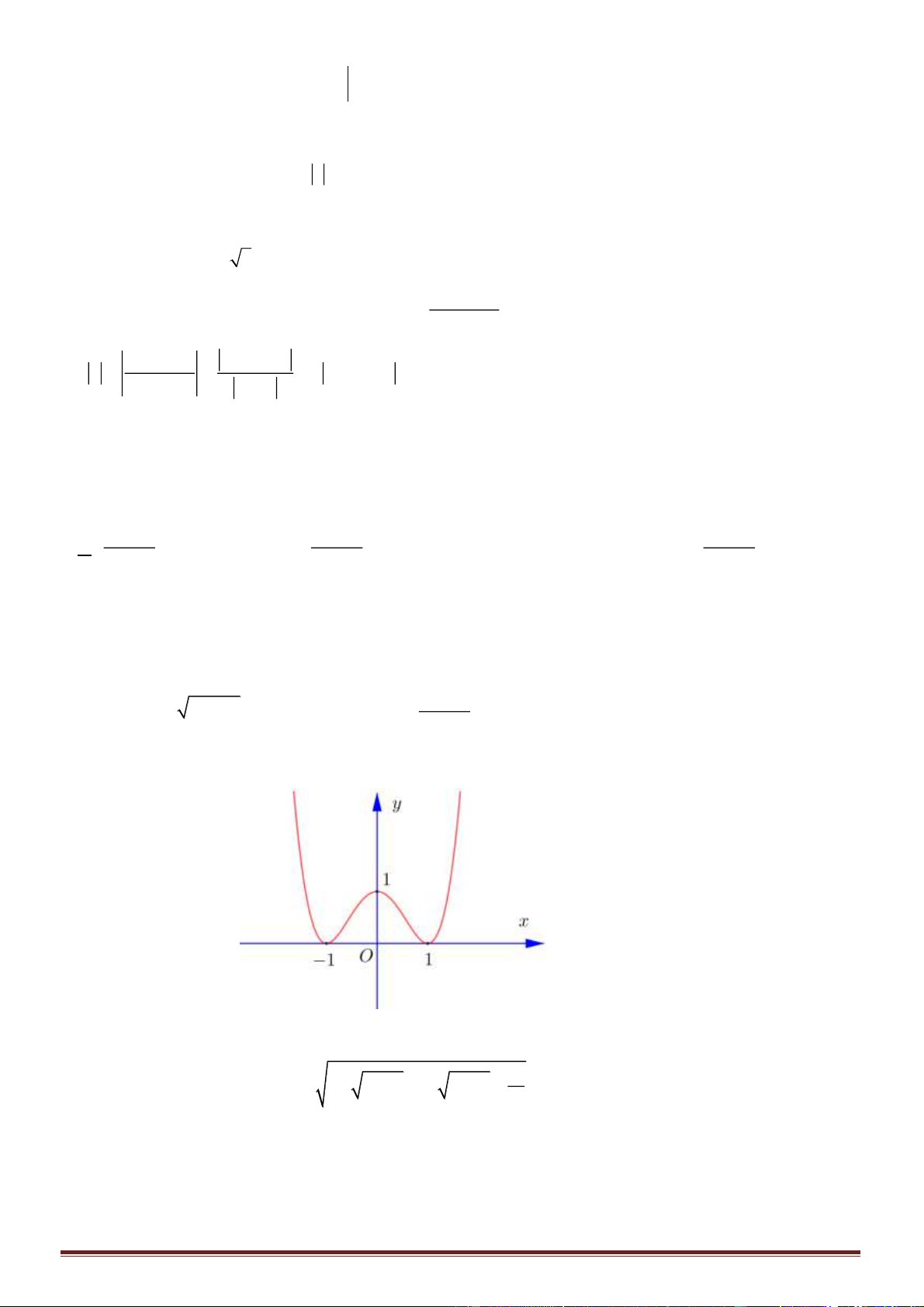
Trang 116
3
Từ bảng biến thiên ta thấy
( )
( )
( ) (
0;4
f x 3 1 m 3 m ;3 −
Câu 37. Cho số phức z thỏa mãn . Biết tập hợp các điểm biểu diễn số phức
là đường tròn tâm I, bán kính R. Tìm tọa đọ tâm I và bán kính R của đường tròn đó.
A. I(-1;2); B. I(1;2); R=5 C. I(1;2);R=5 D. I(-1;2);R=5
37: Đáp án DTa có:
( )
w 1 2i
w 3 4i z 1 2i z
3 4i
+−
= − − + =
−
w 1 2i
w 1 2i
z w 1 2i 5
3 4i 3 4i
+−
+−
= = + − =
−−
Vậy tập hợp điểm biểu diễn w là đường tròn tâm
( )
I 1;2−
, bán kính
R5=
Câu 38.Tính thể tích của một thùng đựng rượu là một hình tròn xoay có hai dáy là hai hình tròn bằng
nhau và chiều cao của bình là 16cm.Đường cong của bình là một cung tròn của đường tròn có bán kính
là 9cm
A.
2864
3
. B,
2846
3
. C.
2864
. D.
2684
3
.
Giải:Câu 38 Ta xem tâm đường tròn là O(gốc tọa độ)đường tròn có phương trình x
2
+ y
2
= 81
Khi đó thể tích của bình là hình tròn xoay giới hạn bởi đường tròn x
2
+ y
2
= 81
và y = 0, x = -8 , x = 8 . thể tích cần tìm là
88
2 2 2
88
2864
( 81 ) (81 )
3
V x dx x dx
−−
= − = − =
Đáp án A
Câu 39: Cho hàm số bậc bốn trùng phương y = f (x) có đồ thị như hình vẽ:
Số nghiệm thực của phương trình
( )
( )
( ) ( )
11
22
2
f f x f x f x+ + = +
A. 2 B. 3 C. 4 D. 5
39: C
Đồ thị hàm số đã cho có dạng
42
21y x x= − +
z1=
( )
w 3 4i z 1 2i= − − +
R 5.=

Trang 117
Đặt
( )
0f x t=
Đặt
( )
( )
( ) ( )
11
22
2
f f x f x f x+ + = +
( ) ( )
( )
2
22
11 1
2 2 2 2
22
f t t t f t t t + + = + + + = +
4 2 4 2 2
5
11 5
6
2 1 2 4 4 6 2 0
1
22
2
t
t t t t t t t
t
=
− + + + = + + − − =
=−
Với
( )
5 25
6 36
t f x= =
phương trình có 4 nghiệm phân biệt
Với
1
2
t =−
phương trình vô nghiệm.
Vậy phương trình đã cho có 4 nghiệm
Câu 40: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Biết
=AB a
, ,
()⊥SA ABCD
và
=SA a
. Tính số đo góc giữa đường thẳng SD và mặt phẳng (SAB) .
A. 45
0
B. 60
0
. C. 30
0
D. 90
0
.
Câu 41: (Biết tổng các hệ số trong khai triển
( )
2
1
n
x+
bằng 1024. Tính số hạng chứa
12
x
.
A.
12
110x
B.
12
120x
C.
12
210x
D.
12
151.200x
Câu 42: Tập hợp tất cả các giá trị của tham số m để phương trình
x x 1
4 m.2 3m 3 0
+
− + − =
có hai nghiệm
trái dấu là
A.
( )
;2−
. B.
( )
1; +
. C.
( )
1;2
. D.
( )
0;2
.
42: Đáp án C
Đặt
x2
t 2 0 t 2m 3 0= − − =
Điều kiện phương trình có 2 nghiệm phân biệt là
2
' m 3m 3 0
S 2m 0 m 1
P 3m 3 0
= − +
=
= −
Khi đó
1
2
x
1
1 2 1 2 2 2
x
2
2t
x log t ;x log t
2t
=
= =
=
Để
( )( )
1 2 1 2 1 2 1 2 1 2
x x 0 0 t 1 t t 1 t 1 0 t t t t 0 − − − −
3m 3 2m 1 m 2 0 m 2 − − + = −
Câu 43. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
( )
2;1;3A
,
( )
6;5;5B
. Gọi
( )
S
là mặt
cầu có đường kính
AB
. Mặt phẳng
( )
P
vuông góc với đoạn
AB
tại
H
sao cho khối nón đỉnh
A
và đáy
là hình tròn tâm
H
(giao của mặt cầu
( )
S
và mặt phẳng
( )
P
) có thể tích lớn nhất, biết rằng
( )
:2 0P x by cz d+ + + =
với
b
,
c
,
d
. Tính
S b c d= + +
.
3AD a=
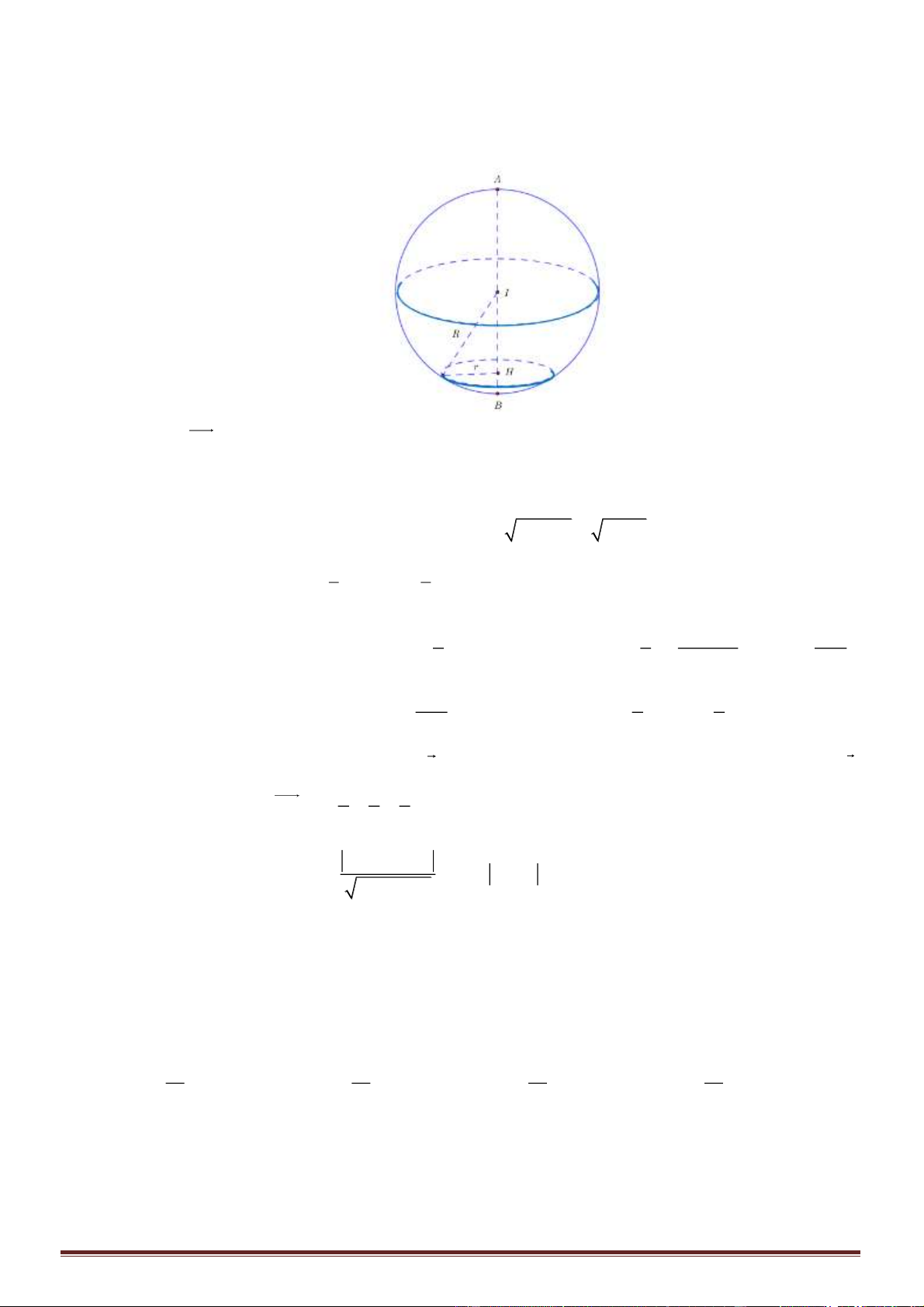
Trang 118
A.
18S =−
. B.
11S =−
. C.
24S =−
. D.
14S =−
.
Lời gii
Chn A.
Ta có
( )
4;4;2AB =
6AB=
suy ra mặt cầu
( )
S
có tâm
( )
4;3;4I
và bán kính
3R =
.
Đặt
( )
03IH x x=
.
Gọi
r
là bán kính đường tròn tâm
H
suy ra
2 2 2
9r R x x= − = −
.
Thể tích khối nón là
( )
( )
2 2 2
11
. . 3 . 3
33
V r AH x x
= = − +
.
Áp dụng bất đẳng thức Cô si ta có
( )( )( )
3
1 1 6 3 3 32
6 2 3 3
6 6 3 3
V x x x V
++
= − + +
.
Vậy thể tích khối nón lớn nhất bằng
32
3
khi
33
63
22
x x x IH− = + = =
.
Mặt phẳng
( )
P
vó vec tơ pháp tuyến
( )
2; ;n b c=
. Vì
( )
P
vuông góc với đoạn
AB
nên ta có
n
cùng phương với
AB
2
2
1
442
b
bc
c
=
==
=
. Vậy
( )
:2 2 0P x y z d+ + + =
.
Mặt khác
( )
( )
22
18 3 15
8 6 4
; 1 1 18 3
18 3 21
2 2 1
dd
d
d I P d
dd
+ = = −
+ + +
= = + =
+ = − = −
++
.
Mặt khác
A
và
I
nằm cùng phía với mặt phẳng
( )
P
nên ta có
( )( )
18
9 18 0
9
d
dd
d
−
+ +
−
. Vậy
21d =−
suy ra
2 1 21 18S b c d= + + = + − = −
.
Câu 44.Cho hình lập phương
.ABCD A B C D
. Gọi
M
là trung điểm của cạnh
BB
. Mặt phẳng
( )
A MD
chia hình lập phương thành hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện trên
A.
7
17
. B.
8
17
. C.
9
17
. D.
10
17
.
Lời gii
Chn A.
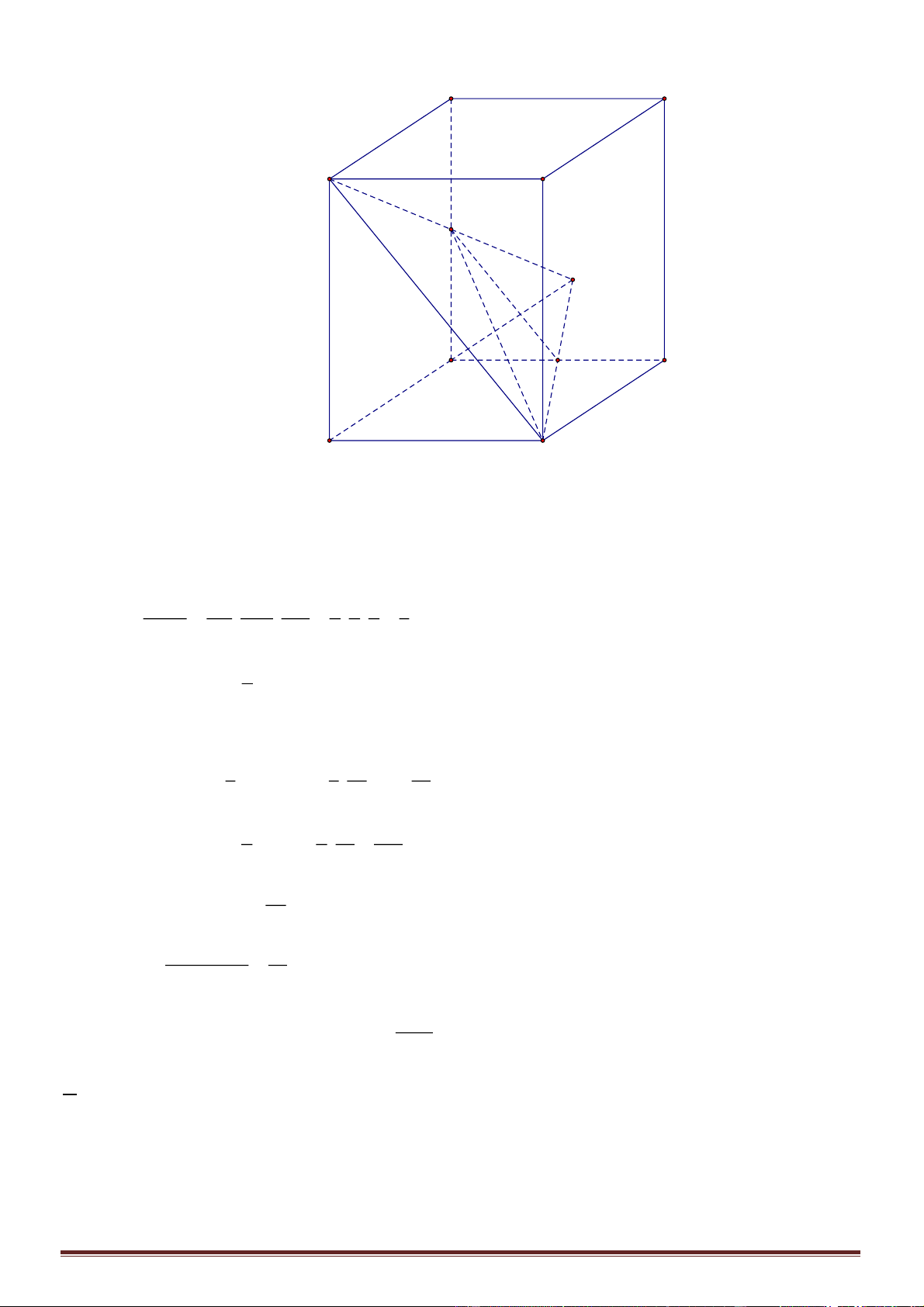
Trang 119
Gọi
,E AM AB N ED BC= =
Mặt phẳng
( )
A MD
chia hình lập phương thành hai khối đa diện:
MNBA DA
và
A DD MNCC B
.
1 1 1 1
. . . .
2 2 2 8
EBMN
EAA D
V
EB EM EN
V EA EA ED
= = =
.
7
8
BMNAA D EAA D
VV
=
Gọi độ dài cạnh hình lập phương là
a
23
11
. . . .2
3 3 2 3
EAA D AA D
aa
V S EA a
= = =
33
7 7 7
.
8 8 3 24
BMNAA D EAA D
aa
VV
= = =
3
17
24
A DD MNCC B
Va
=
7
17
BMNAA D
A DD MNCC B
V
V
=
.
Câu 45: Cho
( )
fx
liên tục trên
1;e
, biết
( )
( )
e
1
fx
dx 1,f e 2.
x
==
Tính
( )
e
1
f ' x ln xdx ?=
A.
1
B.
0
C.
2
D.
3
Câu 45: Đáp án A
Phương pháp: Công thức từng phần:
udv uv vdu=−
Cách giải:
N
M
B
C
D
A
A'
D'
C'
B'
E

Trang 120
( )
( ) ( ) ( )
( ) ( )
( ) ( )
e e e
e
1
1 1 1
e
1
e
1
fx
dx f x dln x f x ln ln xf ' x dx 1
x
f e ln xf ' x dx 1
ln xf ' x dx f e 1 2 1 1
= = − =
− =
= − = − =
Câu 46: Cho hàm số
( )
fx
xác định trên
R \ 1
thỏa mãn
( )
2
1
f ' x .
x1
=
−
Biết
( ) ( )
f 3 f 3 0− + =
và
11
f f 2.
22
− + =
Giá trị
( ) ( ) ( )
T f 2 f 0 f 4= − + +
bằng:
A.
19
T ln
25
=
B.
15
T 2 ln
29
=+
C.
19
T 3 ln
25
=+
D.
19
T 1 ln
25
=+
Cách giải:
( ) ( )
2
1 1 x 1
f x f ' x dx dx ln C
x 1 2 x 1
−
= = = +
−+
( )
( ) ( )
( )
1
2
1 x 1
ln C khi x ; 1 1;
2 x 1
fx
1 1 x
ln C khi x 1;1
2 x 1
−
+ − − +
+
=
−
+ −
+
( ) ( )
1 1 1
1 1 1
f 3 f 3 ln2 C ln C 0 C 0
2 2 2
− + = + + + = =
( )
2 2 2
1 1 1 1
f f 3 ln3 C ln C 2 C 1
2 2 2 3
− + = + + + = =
( )
( ) ( )
( )
1 x 1
ln khi x ; 1 1;
2 x 1
fx
1 1 x
ln khi x 1;1
2 x 1
−
− − +
+
=
−
−
+
( ) ( ) ( )
1 1 1 3 1 9
f 2 f 0 f 4 ln3 ln1 1 ln 1 ln
2 2 2 5 2 5
− + + = + + + = +
Câu 47.Xét các số phức
z a bi=+
(
,ab
) thoả mãn
3 2 3 6 10z i z i+ + + − − =
. Tính
P a b=+
khi
82zi+−
đạt giá trị nhỏ nhất.
A.
118
25
P =
. B.
9P =
. C.
5P =−
. D.
118
25
P =−
.
Lời gii
Chn D.
Đặt
( )
3; 2 ;A −−
( )
3;6B
và điểm
( )
;M a b
biểu diễn số phức
z a bi=+
. Ta có
3 2 3 6 10z i z i+ + + − − =
10MA MB AB + = =
. Suy ra
( )
;M a b
thuộc đoạn
AB
.
Phương trình đường thẳng
AB
là
32
3 3 6 2
xy++
=
++
4
2
3
yx = +
. Do đó
4
2, 3;3
3
b a a= + −

Trang 121
( ) ( )
22
8 2 8 2z i a b+ − = + + −
( )
2
2
4
8 2 2
3
aa
= + + + − =
( )
2
2
4
8
3
aa
++
2
25
16 64
9
aa= + +
2
25 144 5184 1024
9 25 625 25
aa
= + + +
2
25 72 1024 32
, 3;3
9 25 25 5
aa
= + + −
.
82zi+−
đạt giá trị nhỏ nhất bằng
32
5
khi
72 4 118
2
25 3 25
a a b a a= − + = + + = −
.
Câu 48: Một đoàn tàu có 7 toa. Có 7 hành khách lên tàu. Tính xác suất P để mỗi toa có đúng 1 người lên
tàu .
A.P=
620
117649
B. P=
5040
117649
C. P=
720
117649
D. P=
840
117649
.Gii: Đánh số các toa tàu lần lượt là 1,2,3,4,5,6,7 và 7 hành khách lần lượt là A,B,C,D,E,F,G.Mỗi tình
huống là bộ (a
1
;a
2
;…,a
7
) trong đó a
1
,a
2
,….a
7
theo thứ tự là số toa tàu mà hành khách A,B,C,D,E,F,G chọn.
Vậy không gian mẫu có : 7
7
phần tử.
Biến cố mỗi toa tàu có đúng 1 hành khách là 1 hoán vị nên có 7!
Do đó xác suất cần tìm là:
720
117649
Câu 49.Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 2 4 6 13 0S x y z x y z+ + − − + − =
và đường thẳng
1 2 1
:
1 1 1
x y z
d
+ + −
==
. Tọa độ điểm
M
trên đường thẳng
d
sao cho từ
M
có thể kẻ được
3
tiếp tuyến
,MA
MB
,
MC
đến mặt cầu
( )
S
(
,,A B C
là các tiếp điểm) thỏa mãn
60 , 90 , 120AMB BMC CMA= = =
có dạng
( )
;;M a b c
với
0a
. Tổng
abc++
bằng
A.
1
. B.
10
3
. C.
2
. D.
2−
.
Lời gii
Chn D.
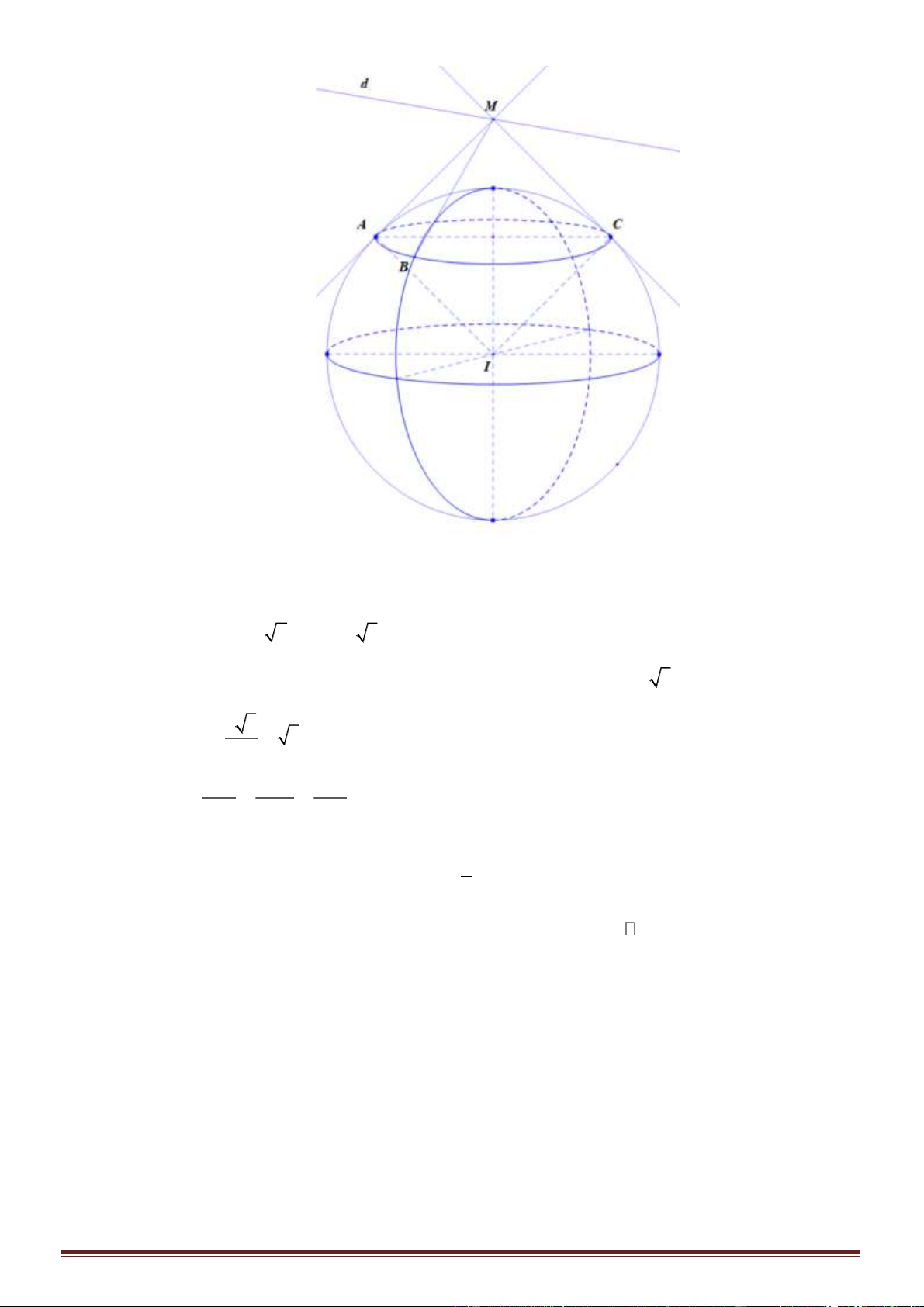
Trang 122
Đặt
0MA x=
.
Ta có
MA MB MC==
nên kết hợp
60 , 90 , 120AMB BMC CMA= = =
ta được
, 2, 3MA x MB x MC x= = =
nên
AC
là đường kính của đường tròn
( )
ABC
.
Xét
( )
2 2 2
: 2 4 6 13 0S x y z x y z+ + − − + − =
có tâm
( )
1;2; 3 , 3 3IR−=
.
33
tan 3AMI
x
==
3x=
6MI=
.
1 2 1
:
1 1 1
x y z
Md
+ + −
= =
( ) ( )
1 ; 2 ;1 , 1M t t t t − + − + +
,
6MI =
( ) ( ) ( )
2 2 2
2 4 4 36ttt − + − + + =
( )
( )
0
1; 2;1
4
3
t
M
tl
=
− −
=
.
Câu 50: Cho hai hàm số
( )
y f x=
và
( )
y g x=
là hai hàm số liên tục trên có đồ thị hàm số
( )
y f x
=
là đường cong nét đậm, đồ thị hàm số
( )
y g x
=
là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm
A, B, C của
( )
y f x
=
và
( )
y g x
=
trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của
hàm số
( ) ( ) ( )
h x f x g x=−
trên đoạn
;?ac
A.
( ) ( )
;
min 0 .
ac
h x h=
B.
( ) ( )
;
min .
ac
h x h a=
C.
( ) ( )
;
min .
ac
h x h b=
D.
( ) ( )
;
min .
ac
h x h c=

Trang 123
50: C Ta có
( ) ( ) ( )
0.
xa
h x f x g x x b
xc
=
= − = =
=
Với
;x a b
thì đồ thị
( )
gx
nằm trên
( )
fx
nên
( ) ( ) ( )
0g x f x h x
hàm số nghịch biến trên
đoạn
;.ab
Tương tự với
;x b c
thì
( )
hx
đồng biến.
Do đó
( ) ( )
;
.
ac
Minh x h b=
ĐỀ 37
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Hỏi hàm số
32
2 3 5y x x= + +
nghịch biến trên khoảng nào?
A.
( )
; 1 .− −
B.
( )
1;0 .−
C.
( )
0; .+
D.
( )
3;1 .−
Câu 2. Cho hàm số
32
32yx x-= +
có đồ thị
( )
C
và điểm
( )
2; 2M -
. Viết phương trình tiếp tuyến
của đồ thị
( )
C
tại điểm
M
.
A.
2y =
. B.
2y =-
. C.
2yx=-
. D.
2yx=
.
Câu 3. Phương trình tiệm cận ngang của đồ thị hàm số y =
2
3
+
+
x
x
là
A. y=-2 B. y=1 C. x=1 D. x=2
Câu 4. Giá trị biểu thức
31
2
22
3
11
8
25 36
A
−−
= + −
bằng:
A.
773
6
B.
123
C. 135 D. -123.
Câu 5. Tập xác định của hàm số
( )
1
3
6yx=−
là
A. R B.
( )
;6−
C.
\6
D.
( )
6;+
.
Câu 6 . Tìm họ nguyên hàm F(x) của hàm số
2
2
11
f(x) x
x3
= − −
.
A.
3
1 x 1
F(x) x C.
x 3 3
= − − − +
B.
3
x 1 x
F(x) C.
3 x 3
= − + − +
C.
42
x x 3
F(x) C.
3x
− + +
=+
D.
42
x x 3
F(x) - C.
3x
++
=+

Trang 124
Câu 7. Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;2],
(0) 5, (2) 2ff==
. Tính
2
0
'( )I f x dx=
.
A.
3I =−
. B.
3I =
. C.
2I =
. D.
7I =
.
Câu 8. Cho Tính .
A. . B. C.
. D. .
Câu 9. Cho hình chóp
.S ABCD
có đáy ABCD là hình vuông tại cạnh a. Cạnh bên
2SA a=
và
vuông góc với mặt phẳng đáy. Tính theo
a
thể tích khối chóp
.S ABCD
.
A.
3
2Va=
. B.
3
3
2
a
V =
. C.
3
3
a
V =
. D.
3
2
3
a
V =
.
Câu 10. Cho hình nón có bán kính đáy bằng 3cm và đường sinh bằng 5cm. Tính diện tích xung
quanh của hình nón đã cho?
A.
2
15 cm
. B.
2
10 cm
. C.
2
5 cm
. D.
2
25 cm
.
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
2 1 0( ):P x y z+ − + =
, vectơ nào
sau đây là một vectơ pháp tuyến
n
của mặt phẳng (P)?
A.
( )
2 1 1;;n =−
B.
( )
2 1 1;;n = − −
C.
( )
2 1 1;;n =−
D.
( )
2 1 1;;n =
Câu 12. Trong không gian với hệ tọa độ Oxyz, hình chiếu của điểm
1 3 2( , , )A
lên mặt phẳng (Oxy)
là điểm N có tọa độ nào sau đây?
A.
2 2 3( , , )N
B.
1 0 0( , , )N
C.
0 3 0( , , )N
D.
1 3 0( , , )N
Câu 13. Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 3 3S x y z+ + − + − =
.
Tìm tọa độ tâm
I
và bán kính
R
của
( )
S
.
A.
( )
1;1;3I −
và
3R =
. B.
( )
1;1;3I −
và
3R =
.
C.
( )
1; 1; 3I −−
và
3R =
. D.
( )
1; 1; 3I −−
và
3R =
.
Câu 14. Một hộp chứa 7 bi xanh khác nhau, 8 bi đỏ khác nhau. Lấy ngẫu nhiên 3 bi từ hộp. Tìm
xác suất để 3 bi lấy ra đều là bi màu xanh.
A.
.
13
1
=P
B.
.
65
8
=P
C.
.
13
6
=P
D.
.
65
48
=P
Câu 15. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ?
= − = + = −
1 2 3
z 1 3i,z 2 i,z 3 4i.
1 2 3
z 2z z+−
2 5i−
2 4i.−
1 4i+
4 6i−
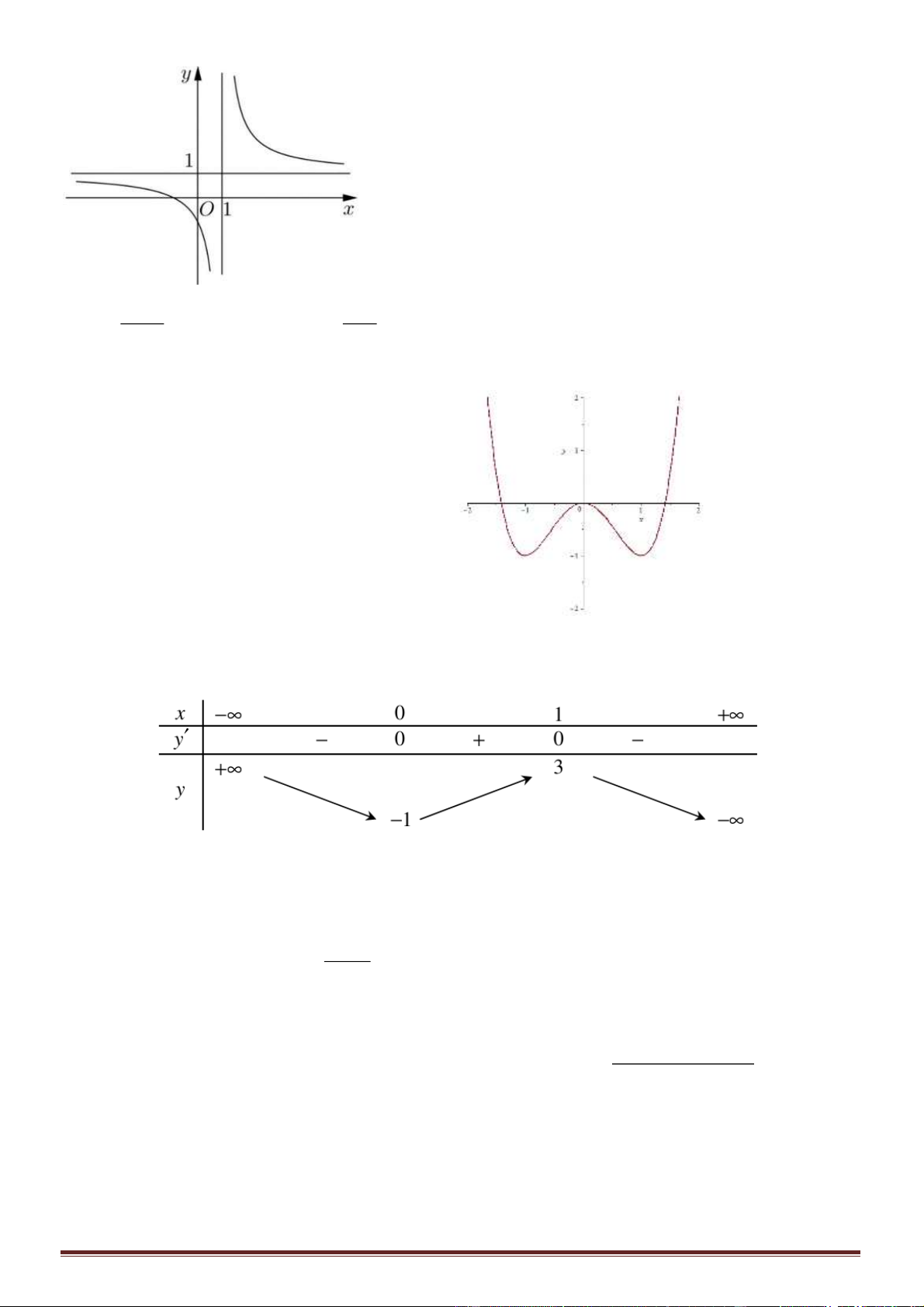
Trang 125
A.
21
1
x
y
x
−
=
−
B.
1
1
x
y
x
+
=
−
C.
42
1y x x= + +
D.
3
31y x x= − −
Câu 16. Cho đồ thị hàm số ở bên phải là đồ thị
của hàm số nào sau đây. Chọn một câu đúng
A.
42
2y x x= − −
B.
42
2y x x=−
C.
42
2y x x=+
D.
3
3y x x= − −
Câu 17. Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
0f x m−=
có ba nghiệm phân biệt.
A.
01m
. B.
0
1
m
m
. C.
13m−
. D.
1
3
m
m
−
.
Câu 18. Đồ thị của hàm số
2
2
4
x
y
x
−
=
−
có số tiệm cận là
A.
0
B.
3
C.
1
. D.
2
Câu 19. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
18 16mx m m
y
xm
− + −
=
+
nghịch biến
trên khoảng
( )
3;− +
?
A.
6
. B.
8
. C. Vô số. D.
5
.
Câu 20. Cho phương trình
2 8 5
3 4.3 27 0
xx++
− + − =
có 2 nghiệm
12
;xx
. Khi đó
12
xx+=
A. 3 B. -5 C. 12 D. -12.
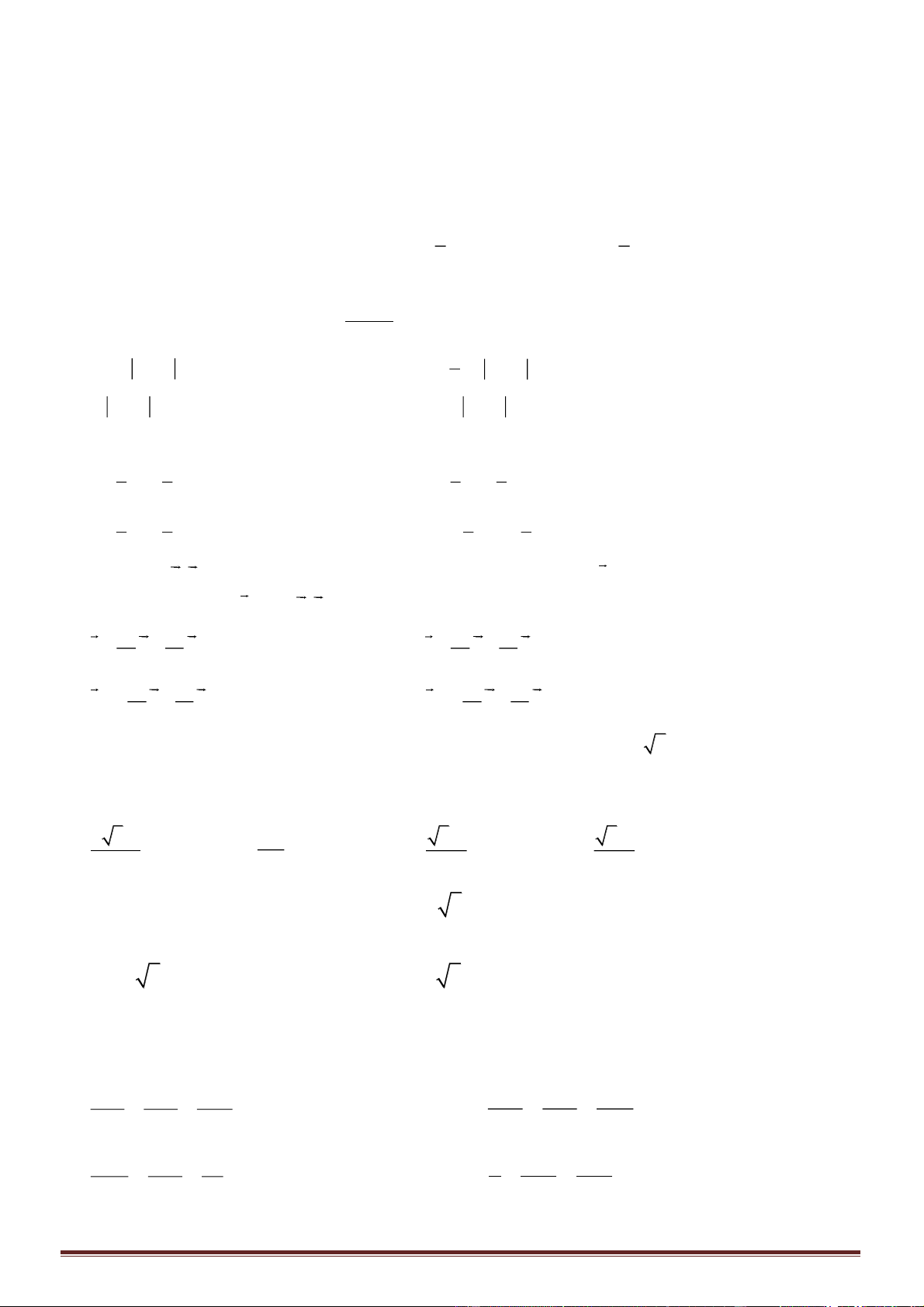
Trang 126
Câu 21. Số nghiệm của phương trình
2
33
log (3 ) log ( 2 3)x x x− = − + +
là:
A. 0 B. 1 C. 2 D. 3.
Câu 22. Tìm tập nghiệm của bất phương trình
2
22
log 2log 8 0xx− −
.
A.
( )
2;4−
B.
( )
4;16
C.
1
;16
4
D.
( )
1
0; 16;
4
+
Câu 23. Tìm nguyên hàm
23
()
21
x
F x dx
x
+
=
+
A.
ln 2 1x x C+ + +
. B.
1
.ln 2 1
2
x x C+ + +
.
C.
ln 2 1xC++
. D.
1 ln 2 1xC+ + +
.
Câu 24. Cặp số thực x, y thỏa mãn là:
A. . B.
.
C. . C. .
Câu25. Cho là biểu diễn của hai số phức và . Gọi là biểu diễn của số phức
. Hãy phân tích theo .
A. . B. .
C. . D. .
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông;
22AC a=
; tam giác SAB là tam
giác đều nằm trong mặt phẳng vuông góc với đáy. M, N, P, Q lần lượt là trung điểm các cạnh SA,
SB, SC, SD. Tính thể tích khối chóp SMNPQ.
A.
3
23
3
a
B.
3
3
8
a
C.
3
3
6
a
D.
3
3
3
a
Câu 27. Cho hình chữ nhật ABCD có AB =
3a
, BC = a. Quay hình chữ nhật đó quanh cạnh
AB, ta được một khối trụ tròn xoay có thể tích bằng bao nhiêu?
A.
3
43a
B.
3
3 a
C.
3
3a
D.
3
12 a
Câu 28. Trong không gian với hệ tọa độ
,Oxyz
lập phương trình đường thẳng AB với A(1; 1; 2) và
B( 2; -1; 0).
A.
.
B.
.
C.
.
D.
.
( ) ( )
2x 1 1 2y i 2 x 3y 2 i+ + − = − + −
13
x ,y
35
==
11
x ,y
55
==
11
x ,y
35
==
13
x ,y
35
= − = −
u,v
+1 3i
−3 2i
x
+6 4i
x
u,v
24 14
x u v
11 11
=+
24 14
x u v
11 11
=−
24 14
x u v
11 11
= − −
24 14
x u v
11 11
= − +
x 1 y 1 z 2
3 2 2
− − −
==
x 1 y 1 z 2
1 2 2
+ + +
==
−
x 2 y 1 z
1 2 2
−+
==
−−
x y 3 z 4
1 2 2
−−
==
−−

Trang 127
Câu 29. Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) qua điểm
4 3 1−( , , )A
và song song
với hai đường thẳng
12
1
1 1 1
3
2 1 2
22
: , :
xt
x y z
d d y t
zt
=+
+ − +
= = =
=+
. Phương trình nào sau đây là
phương trình của mặt phẳng (P)?
A.
4 2 5 5 0x y z+ + + =
B.
4 2 5 5 0x y z+ − + =
C.
4 2 5 5 0x y z− + + + =
D.
4 2 5 5 0x y z− − + + =
Câu 30. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với mặt
phẳng đáy (ABC), SA = AB = a. Tính góc giữa SB và mặt phẳng (ABC).
A. 45
0
. B. 30
0
. C. 60
0
. D. 90
0
.
Câu 31. Cho hàm số
( )
y f x=
có đạo hàm liên tục trên R, hàm số
( )
1y f x
=+
có đồ thị như hình
vẽ bên dưới.
Kết luận nào sau đây sai đối với hàm số
( )
y f x=
A. Hàm số nghịch biến trên
( )
0;1
. B. Hàm số đạt cực đại tại
1x =
.
C. Hàm số có hai điểm cực trị. D. Hàm số nghịch biến trên
( )
2; +
.
Câu 32. Cho hàm số
( ) ( )
32
2 1 1 5y mx m x m x= − + + + +
với
m
là tham số. Gọi
S
là tập hợp tất cả
các giá trị nguyên của
m
để hàm số nghịch biến trên khoảng
( )
;− +
. Tính tổng các phần tử của
S
.
A.
5
.
B.
5−
.
C.
10
.
D.
10−
.
Câu 33. Tìm tất cả các giá trị của m để phương trình
1
25 5 0
xx
m
+
− + =
có nghiệm.
A.
25
4
m −
B.
25
4
m −
C.
25
4
m
D.
25
4
m
Câu 34. Số nghiệm phương trình
3
1
1
21
3
3
11
log ( ) log (2 3 )
33
x
x
−
−
=+
là:
A. 0 B. 1 C. 2 D. 3.
Câu 35. Một nguyên hàm của
f(x) cos3xcos2x=
bằng

Trang 128
A.
11
sinx sin5x.
2 10
+
B.
11
sinx sin5x.
22
+
C.
11
cosx cos5x.
2 10
+
D.
1
sin3xsin2x.
6
Câu 36. Tính diện tích hình phẳng được giới hạn bởi hai đường
2
y x 3x=−
và
y x.=
A.
32
3
B.
16
3
C.
8
3
D. 2.
Câu 37. Giả sử M(z) là điểm trên mặt phẳng tọa độ biểu diễn số phức z. Tập hợp những điểm
M(z) thỏa mãn điều là
A. Đường thẳng . B. Đường thẳng .
C. Đường thẳng . D. Đường thẳng .
Câu 38. Trên mặt cầu tâm O, bán kính R ,lấy một điểm A và gọi (P) là mặt phẳng đi qua A sao
cho góc giữa OA và (P) bằng 30
0
. Đường thẳng d qua A, vuông góc với (P) cắt mặt cầu tại điểm
B. Độ dài đoạn thẳng AB là:
A.
2
R
B.
3
2
R
C. R D.
2R
Câu 39. Trong không gian
Oxyz
, cho hai đường thẳng
1
3 3 2
:
1 2 1
x y z
d
− − +
==
−−
;
2
5 1 2
:
3 2 1
x y z
d
− + −
==
−
và mặt phẳng
( )
: 2 3 5 0P x y z+ + − =
. Đường thẳng d vuông góc với
( )
P
, d
cắt
1
d
và
2
d
. Phương trình nào sau đây là phương trình của đường thẳng d?
A.
11
1 2 3
x y z−+
==
. B.
2 3 1
1 2 3
x y z− − −
==
.
C.
3 3 2
1 2 3
x y z− − +
==
. D.
11
3 2 1
x y z−+
==
.
Câu 40. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông. Gọi H, M lần lượt là trung điểm
của các cạnh AB, CD. Biết SH vuông góc với mặt phẳng (ABCD), khoảng cách từ điểm B đến
mặt phẳng (SHM) bằng
,
2
a
tam giác SAB đều. Tính khoảng cách từ điểm A đến mặt phẳng
(SCD).
A.
21
7
.
a
B.
21
14
.
a
C.
21
21
.
a
D.
21
3
.
a
Câu 41. Phương trình
( )
( )
2
32
11x x x m x+ + = +
có nghiệm thực khi và chỉ khi:
A.
3
6
2
m− −
. B.
13m−
. C.
3m
. D.
13
44
m−
.
Câu 42. Tìm tất cả các giá trị của
m
để đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số
3
32y x mx= − +
cắt đường tròn tâm
( )
1;1 ,I
bán kính bằng
1
tại
2
điểm phân biệt
,AB
sao cho diện tích
tam giác
IAB
đạt giá trị lớn nhất.
2 z i z+ = −
x 9y 3 0+ − =
4x 2y 3 0+ + =
x 2y 3 0+ − =
4x 2 y 3 0− + =

Trang 129
A.
23
2
m
=
. B.
13
2
m
=
. C.
25
2
m
=
. D.
23
3
m
=
.
Câu 43. Tìm tất cả các giá trị thực của để đường thẳng cắt đồ thị hàm số tại
hai điểm phân biệt sao cho .
A. . B. . C. . D. .
Câu 44. Biết F(x) là một nguyên hàm của f(x) thỏa mãn F(2018) =1,
Tính I =
A. I =2017 B. I= 2018 C. I= 2019 D. I=2016
Câu 45. Gọi z là số phức khác 0 sao cho Trong các mệnh đề sau, mệnh đề nào đúng?
A. B. C. D.
Câu 46. Cho hình lăng trụ
.ABC A B C
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc của
A
lên mặt phẳng
( )
ABC
trùng với trọng tâm tam giác
ABC
. Biết khoảng cách giữa hai đường
thẳng
AA
và
BC
bằng
3
4
a
. Tính thể tích
V
của khối lăng trụ
..ABC A B C
A.
3
3
.
24
a
V =
B.
3
3
.
12
a
V =
C.
3
3
.
3
a
V =
D.
3
3
.
6
a
V =
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( ) ( ) ( )
P :x 2y 2z 2018 0, Q :x my m 1 z 2017 0.+ − + = + + − + =
Khi hai mặt phẳng
( ) ( )
P và Q
tạo với
nhau một góc bé nhất thì điểm
M
nào dưới đây nằm trong
( )
Q?
A.
( )
M 2017; 1;1−−
B.
( )
M 2017;1;1−
C.
( )
M 2017;1; 1−−
D.
( )
M 1;1; 2017−
Câu 48. Trong không gian với hệ toạ độ
Oxyz
, gọi
( ): 1
x y z
P
a b c
+ + =
(với
0, 0, 0abc
là mặt
phẳng đi qua điểm
(1;1;2)H
và cắt
,,Ox Oy Oz
lần lượt tại các điểm
,,A B C
sao cho khối tứ diện
OABC
có thể tích nhỏ nhất. Tính
2S a b c= + +
.
A.
15S =
. B.
5S =
. C.
10S =
. D.
4S =
.
Câu 49. Một biển số xe gồm 2 chữ cái đứng trước và 4 chữ số đứng sau. Các chữ cái được lấy từ
26 chữ cái A, B, C,…… Các chữ số được lấy từ 10 chữ số 0, 1, 2….,9. Hỏi có bao nhiêu biển số
xe có 2 chữ cái khác nhau và có đúng 2 chữ số lẻ giống nhau?
A. 487500 B. 91 C. 19500 D. 750
Câu 50. Tìm tất cả các giá trị của tham số
m
để phương trình sau có ba nghiệm phân biệt lập
thành một cấp số nhân:
32
7 ( 6) 0.x x m x m− + + − =
A. m=1, m=8, m= - 27 . B. m=8, m= - 27 .
C. m=1.
D. m=1, m=4, m= 9 .
m
1y x m= + −
21
1
x
y
x
+
=
+
,AB
23AB =
4 10m =
43m =
23m =
2 10m =
2017
1
( 1) 1.F x dx
−
+=
2018
0
. ( ) .x f x dx
3
3
8
z 9.
z
+
2
z 3.
z
+
2
z 3.
z
+
2
z 3.
z
+
2
z 3.
z
+

Trang 130
ĐÁP ÁN
1-B
2-B
3-B
4-A
5-D
6-A
7-A
8-A
9-D
10-A
11-A
12-D
13-B
14-A
15-A
16-B
17-C
18-D
19-D
20-B
21-B
22-C
23-A
24-A
25-A
26-C
27-C
28-C
29-D
30-A
31-A
32-D
33-C
34-B
35-A
36-A
37-A
38-C
39-A
40-A
41-D
42-A
43-A
44-A
45-A
46-B
47-B
48-A
49-A
50-A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 41. Phương trình
( )
( )
2
32
11x x x m x+ + = +
có nghiệm thực khi và chỉ khi:
A.
3
6
2
m− −
. B.
13m−
. C.
3m
. D.
13
44
m−
.
Hướng dẫn gii
Ta có
( )
( )
32
2
32
42
11
21
x x x
x x x m x m
xx
++
+ + = + =
++
(1)
Xét hàm số
32
42
21
x x x
y
xx
++
=
++
xác định trên .
( ) ( ) ( )( )
( )
( )( ) ( )( )
( )
( )
( )( )
( )
3 2 4 2 3 2 4 2
2
42
2 4 2 3 2 3
2
42
6 5 4 2
2
42
42
2
42
2 1 2 1
21
3 2 1 2 1 4 4
21
2 2 1
21
1 2 1
21
x x x x x x x x x x
y
xx
x x x x x x x x x
xx
x x x x x
xx
x x x
xx
+ + + + − + + + +
=
++
+ + + + − + + +
=
++
− − − + + +
=
++
− + + +
=
++
( )( )
42
1
0 1 2 1 0
1
x
y x x x
x
=
= − + + + =
=−
Bảng biến thiên
Trang 131
Phương trình (1) có nghiệm thực khi đường thẳng
ym=
cắt đồ thị hàm số
32
42
21
x x x
y
xx
++
=
++
13
44
m
−
.
Chọn đáp án D.
Câu 42. Tìm tất cả các giá trị của
m
để đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số
3
32y x mx= − +
cắt đường tròn tâm
( )
1;1 ,I
bán kính bằng
1
tại
2
điểm phân biệt
,AB
sao cho diện tích
tam giác
IAB
đạt giá trị lớn nhất.
A.
23
2
m
=
. B.
13
2
m
=
. C.
25
2
m
=
. D.
23
3
m
=
.
Hướng dẫn gii
Ta có
2
33y x m
=−
nên
2
0y x m
= =
.
Đồ thị hàm số
3
32y x mx= − +
có hai điểm cực trị khi và chỉ khi
0m
.
Ta có
( )
32
11
3 2 3 3 2 2 . 2 2
33
y x mx x x m mx x y mx
= − + = − − + = − +
.
Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3
32y x mx= − +
có
phương trình
: 2 2y mx = − +
Ta có:
1 1 1
. . .sin sin
2 2 2
IAB
S IAIB AIB AIB
= =
Diện tích tam giác
IAB
lớn nhất bằng
1
2
khi
sin 1AIB AI BI= ⊥
.
Gọi
H
là trung điểm
AB
ta có:
( )
,
12
22
I
IH AB d
= = =
Mà
( )
,
2
2 1 2
41
I
m
d
m
+−
=
+
Suy ra:
( )
( )
2
,
2
2 1 2
2
4 2 2 4 1
2
41
I
m
d m m
m
+−
= = − = +
+
2
23
8 16 2 0
2
m m m
− + = =
.
Chn A.
Câu 43. Tìm tất cả các giá trị thực của để đường thẳng cắt đồ thị hàm số tại
hai điểm phân biệt sao cho .
m
1y x m= + −
21
1
x
y
x
+
=
+
,AB
23AB =
Δ
H
B
A
I
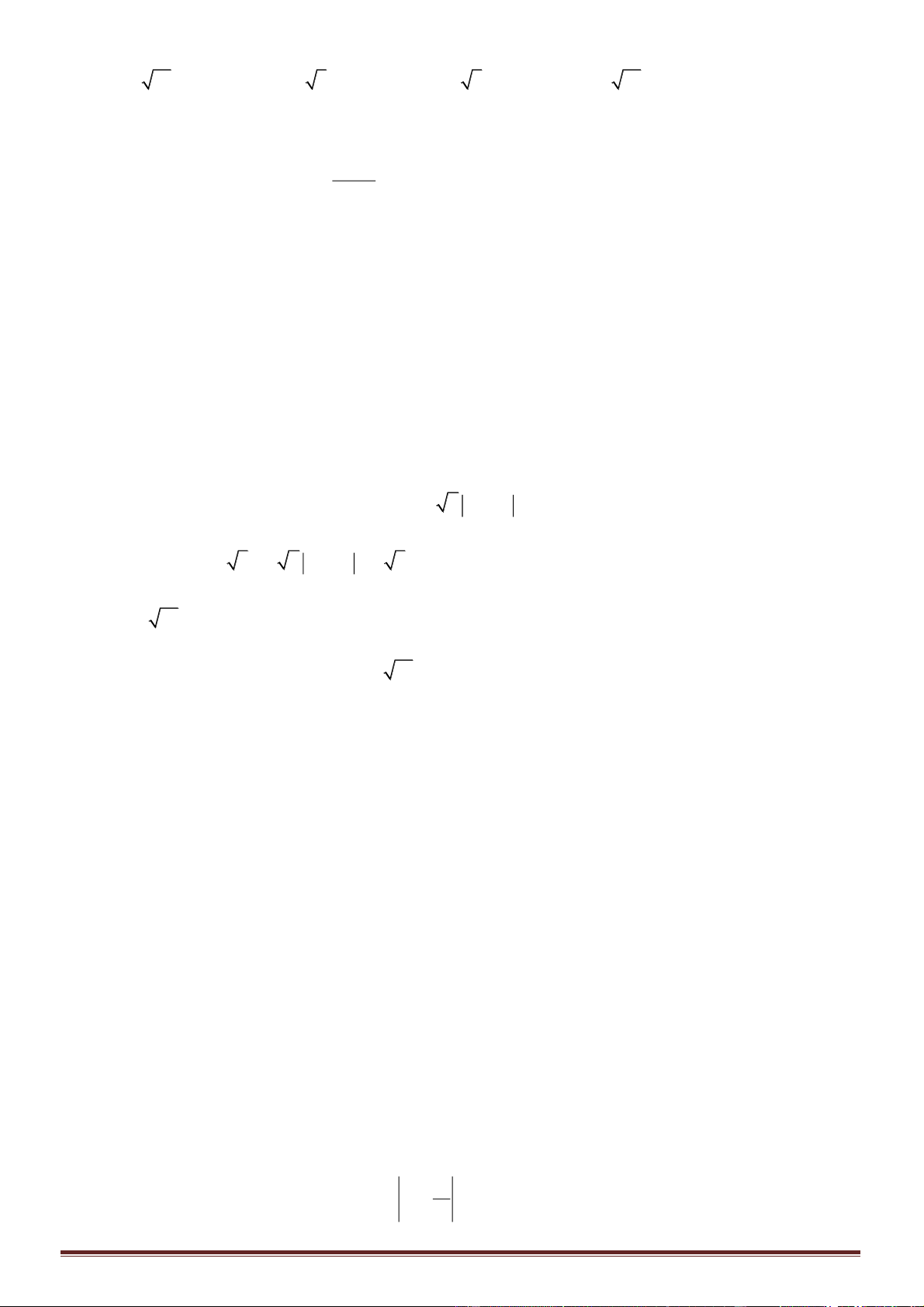
Trang 132
A. . B. . C. . D. .
Hướng dẫn gii
Hoành độ giao điểm là nghiệm PT: .
Đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt khi và chỉ khi phương trình
có hai nghiệm phân biệt khác , hay
.
Khi đó, gọi
12
,xx
là hai nghiệm của phương trình , ta có (Viète).
Giả sử .
Theo giả thiết
Kết hợp với điều kiện ta được .
Chn A
Câu 44. Biết F(x) là một nguyên hàm của f(x) thỏa mãn
F(2018) =1, Tính I =
A. I =2017 B. I= 2018 C. I= 2019 D. I=2016
Hướng dẫn gii
Đặt x=t+1
Câu 45. Gọi z là số phức khác 0 sao cho Trong các mệnh đề sau, mệnh đề nào đúng?
4 10m =
43m =
23m =
2 10m =
( ) ( )
2
2 2 0
21
1
1
1
f x x m x m
x
xm
x
x
= + − + − =
+
= + −
+
−
1y x m= + −
( )
0fx=
1−
( )
( )
2
0
2
8 12 0
*
10
6
10
m
mm
f
m
− +
−
( )
0fx=
12
12
2
2
x x m
x x m
+ = −
=−
( ) ( )
1 1 2 2 2 1
; 1 , ; 1 2A x x m B x x m AB x x+ − + − = −
( )
2
2
2 1 1 2 1 2
2 3 2 2 3 4 6 8 6 0AB x x x x x x m m= − = + − = − + =
4 10m =
( )
*
4 10m =
2017
1
( 1) 1.F x dx
−
+=
2018
0
. ( ) .x f x dx
2018 2018
2018
0
00
. ( ) . ( )| ( )I x f x dx x F x F x dx= = −
2018 2018
00
2018 (2018) ( ) 2018 ( )F F x dx F x dx= − = −
2017
1
2018. ( 1)I F t dt
−
= − +
2017
1
2018. ( 1) 2018 1 2017F x dx
−
= − + = − =
3
3
8
z 9.
z
+

Trang 133
A. B. C. D.
Hướng dẫn gii
Ta có:
, mặt khác ta có:
.
Do đó:
Đặt lúc đó ta được:
Câu 47: Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng
( ) ( ) ( )
P :x 2y 2z 2018 0, Q :x my m 1 z 2017 0.+ − + = + + − + =
Khi hai mặt phẳng
( ) ( )
P và Q
tạo với
nhau một góc bé nhất thì điểm
M
nào dưới đây nằm trong
( )
Q?
A.
( )
M 2017; 1;1−−
B.
( )
M 2017;1;1−
C.
( )
M 2017;1; 1−−
D.
( )
M 1;1; 2017−
Hướng dẫn gii
Vtpt của (P): (1; 2; -2)
Vtpt của (Q): (1; m; m – 1) nên (P) cắt và không vuông góc với (Q)
Gọi
là góc giữa (P) và (Q), 0
0
<
< 90
0
.
cos
=
222
1
2
+− mm
Vì 0
0
<
< 90
0
nên
nhỏ nhất
cos
lớn nhất
222
2
+− mm
nhỏ nhất
m = 1/2
Suy ra mp (Q). chọn B.
Câu 48: Trong không gian với hệ toạ độ
Oxyz
, gọi
( ): 1
x y z
P
a b c
+ + =
(với
0, 0, 0abc
là mặt
phẳng đi qua điểm
(1;1;2)H
và cắt
,,Ox Oy Oz
lần lượt tại các điểm
,,A B C
sao cho khối tứ diện
OABC
có thể tích nhỏ nhất. Tính
2S a b c= + +
.
2
z 3.
z
+
2
z 3.
z
+
2
z 3.
z
+
2
z 3.
z
+
+ = + + + = + + +
3
33
33
2 8 2 2 8 2
z z 3z. z z 6 z
z z z z
zz
+ +
1 2 1 2
z z z z
+ + + +
+ + + + + +
+ − + −
3
3
3
3
3
3
3
2 8 2
z z 6 z
zz
z
2 8 2 2
z z 6 z 9 6 z
z z z
z
22
z 6 z 9 0
zz
=+
1
az
z
( )
( )
− − − + +
32
a 6a 9 0 a 3 a 3a 3 0 a 3.

Trang 134
A.
15S =
. B.
5S =
. C.
10S =
. D.
4S =
.
Hướng dẫn gii
Ta có:
( ;0;0), (0; ;0), (0;0; )A a B b C c
và
1
6
OABC
V abc=
.
Vì
()HP
nên
112
1
a b c
+ + =
(1)
Áp dụng BĐT Cô-si cho 3 số dương
1
a
,
1
b
và
2
c
, ta có:
3
112
112
3
a b c
a b c
++
(2) (dấu “=” xảy ra khi
112
a b c
==
)
Từ (1) và (2), suy ra
2
27
abc
, hay
4
9
V
;
4 1 1 2
9
V
a b c
= = =
, suy ra
3, 6a b c= = =
(do (1)).
2 15S a b c= + + =
Chn A.
Câu 49. Một biển số xe gồm 2 chữ cái đứng trước và 4 chữ số đứng sau. Các chữ cái được lấy từ
26 chữ cái A, B, C,…… Các chữ số được lấy từ 10 chữ số 0, 1, 2….,9. Hỏi có bao nhiêu biển số
xe có 2 chữ cái khác nhau và có đúng 2 chữ số lẻ giống nhau?
A. 487500. B. 91 C. 19500 D. 750
Hướng dẫn gii
- Chữ cái thứ nhất có: 26 cách chọn
Chữ cái thứ nhất có: 25 cách chọn
- Các cặp số lẻ giống nhau có thể là: (1;1); (3;3); (5;5); (7;7); (9;9)
- Chọn cặp số lẻ: có 5 cách
- Xếp 1 cặp số lẻ vào 4 vị trí có:
2
4
C
- Cách sắp xếp cặp số lẻ: 5.
2
4
C
- Chữ số chẵn thứ nhất có: 5 cách
- Chữ số chẵn thứ hai có: 5 cách
Vậy có: 26.25.5.
2
4
C
.5.5 = 487500
Chn A
Câu 50: Tìm tất cả các giá trị của tham số
m
để phương trình sau có ba nghiệm phân biệt lập
thành một cấp số nhân:
32
7 ( 6) 0.x x m x m− + + − =
. 1, 8, 27Am m m= = =−
.
. 8, 27Bm m= = −
.1Cm=
. 1, 4, 9Dm m m= = =
Hướng dẫn gii

Trang 135
Phương trình đã cho tương đương:
1
2
( 1)( 6 ) 0
2
6 0 (1)
x
x x x m
x x m
=
− − + =
− + =
.
Phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi (1) có hai nghiệm phân biệt khác 1,
hay:
' 9 0
9
2
5
1 6.1 0
m
m
m
m
= −
− +
(*).
Khi đó, PT đã cho có ba nghiệm
,
12
xx
và
1
3
x =
, trong đó
,
12
xx
là nghiệm của (1).
Theo định lý Viet ta có
6
12
.
12
xx
x x m
+=
=
(2).
Xét các trường hợp sau:
*) Nếu
22
.
1 3 2 1 2
x x x x x= =
(3). Từ (2) và (3) ta có hệ:
2
60
6
22
12
2; 4; 8
21
2
.
1 2 1 2
3; 9; 27
21
23
1 2 2
xx
xx
x x m
x x m x x
x x m
x x m x
+ − =
+=
= = =
= =
= − = = −
==
.
*) Nếu
2
. . 1
1 2 3 1 2
x x x x x= =
(4). Từ (2) và (4) ta có hệ:
1
6
12
.1
12
m
xx
xx
=
+=
=
.
Vậy, có ba giá trị của m thỏa mãn yêu cầu bài toán là:
1, 8, 27m m m= = = −
.
Chn A
ĐỀ 38
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1 Cho hàm số
( )
y f x=
liên tục trên R và có bảng biến thiên
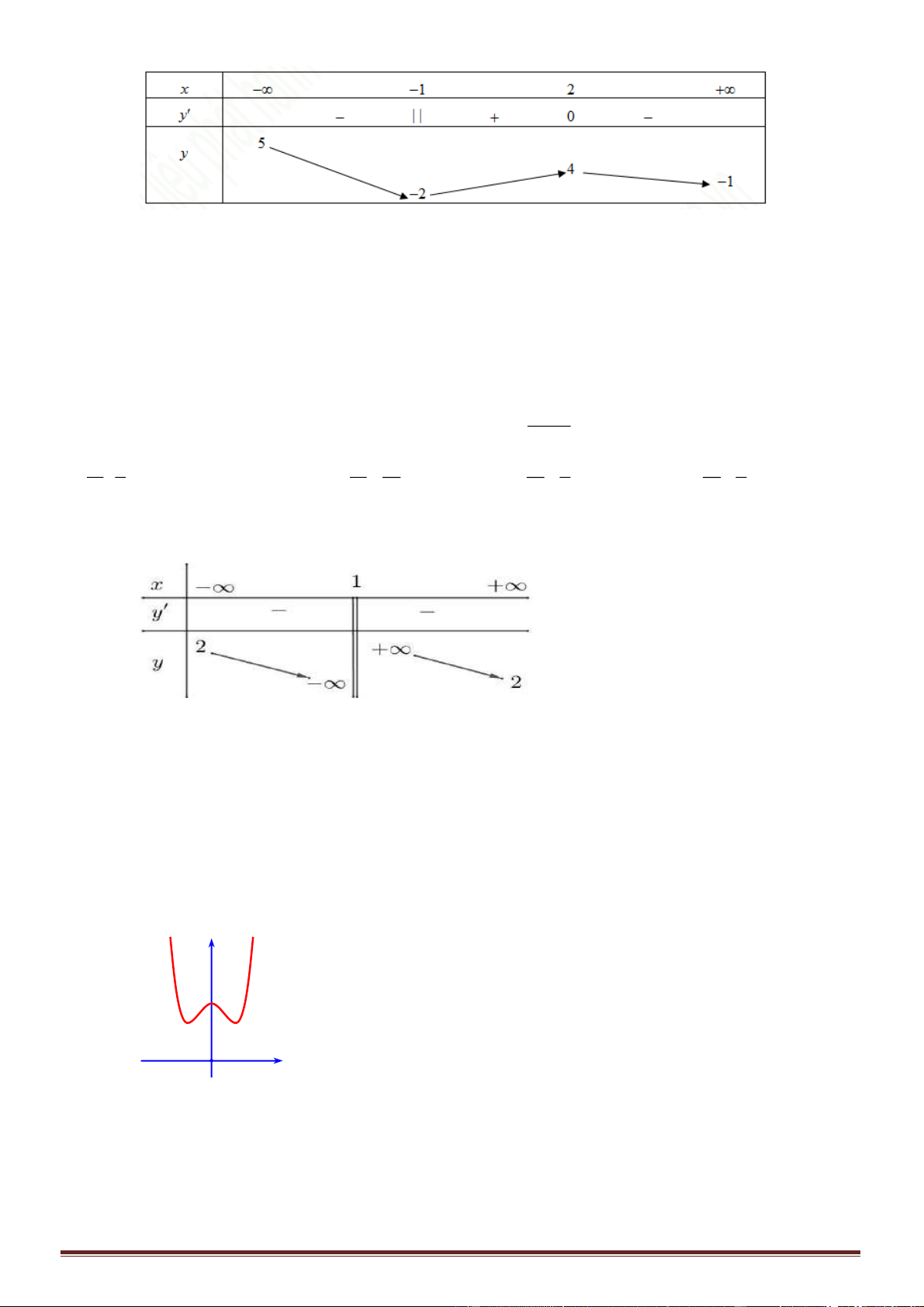
Trang 136
Khẳng định nào sau đây sai?
A. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng
2−
.
B. Hàm số có hai điểm cực trị.
C. Đồ thị hàm số có hai tiệm cận ngang
D. Hàm số có giả trị lớn nhất là 5 và giá trị nhỏ nhất là 2
Câu 2 Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
8
12
f x x
x
=+
+
trên đoạn
1;2
lần lượt là
A .
11
3
;
7
2
B.
11
3
;
18
5
. C.
13
3
;
7
2
. D.
18
5
;
3
2
.
Câu 3 Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A.Đồ thị có tiệm cận đứng là đường thẳng
1x =
và tiệm cận ngan là đường thẳng
2y =
B. Đồ thị hàm số không có đường tiệm cận.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D Đồ thị hàm số có tiệm cận ngang là đường thẳng
1x =
và tiệm cận đứng là đường thẳng
2y =
.
Câu 4 Đường cong hình bên là đồ thị của hàm số nào dưới đây?
A.
42
44y x x= − + +
. B.
42
23y x x= − +
C.
42
32y x x= + +
. D.
32
21y x x= − +
.
Câu 5 Cho hàm số Tiếp tuyến của đồ thị hàm số tại điểm thuộc đồ thị hàm số có
phương trình là :
A. B. C. D.
( )
32
f x x 3x 5.= − +
( )
1;1−
y 3 2x=−
y 9x 10=+
y 1 3x=+
y 3x 4= − +
O
x
y

Trang 137
Câu 6 Số đường tiệm cận của đồ thị hàm số
2
2
1
xx
y
x
+−
=
−
.
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 7 Hình bên là đồ thị của hàm số
( )
y f x=
. Biết rằng tại các điểm
A
,
B
,
C
đồ thị hàm số có tiếp
tuyến được thể hiện trên hình vẽ bên dưới.
Mệnh đề nào dưới đây đúng?
A.
( ) ( ) ( )
C A B
f x f x f x
. B.
( ) ( ) ( )
B A C
f x f x f x
C.
( ) ( ) ( )
A C B
f x f x f x
. D.
( ) ( ) ( )
A B C
f x f x f x
.
Câu 8 Cho hàm số
32
34y x x= + −
có đồ thị
( )
1
C
và hàm số
32
34y x x= − + −
có đồ thị
( )
2
.C
Khẳng
định nào sau đây đúng?
A.
( )
1
C
và
( )
2
C
đối xứng nhau qua gốc tọa độ. B.
( )
1
C
và
( )
2
C
trùng nhau.
C.
( )
1
C
và
( )
2
C
đối xứng nhau qua
.Oy
D.
( )
1
C
và
( )
2
C
đối xứng nhau qua
Ox
.
Câu 9 Cho hàm số bậc ba có đồ thị như hình bên. Tất cả các giá trị của tham số m để hàm số
có 3 điểm cực trị là:
A.m -1 hoặc m 3 B.m -3 hoặc m 1.
C.m=-1 hoặc m=3 D.1 m 3.
Câu 10 Gọi
S
là tập tất cả các giá trị thực của tham số
m
sao cho đường thẳng
:3d y mx m= − −
cắt đồ
thị
( )
32
: 2 3 2C y x x= − −
tại ba điểm phân biệt
A
,
B
,
( )
1; 3I −
mà tiếp tuyến với
( )
C
tại
A
và tại
B
vuông góc với nhau. Tính tổng các phần tử của
S
.
A.-1 B.
1
. C.
2
. D.
5
.
Câu 11 Với các số thực dương a, b bất kì, Mệnh đề nào dưới đây đúng ?
A. B.
C. D.
Câu 12 Tính đạo hàm của hàm số
17
x
y
−
=
A.
17 ln17
x
y
−
=
. B.
1
.17
x
yx
−−
=−
. C.
17
x
y
−
=−
. D.
17 ln17
x
y
−
=−
( )
y f x=
( )
y f x m=+
a 1.
3
aa
2
a1
log 2log b.
b3
=−
3
aa
2
a1
log 3 log b.
b2
=−
3
aa
2
a 1 1
log log b.
b 3 2
=−
3
aa
2
a
log 3 2log b.
b
=−

Trang 138
Câu 13 Số tiền mà My để dành hằng ngày là x (đơn vị nghìn đồng, với x>0,x
R biết x là nghiệm của phương
trình Tính tổng số tiền My để dành được trong một tuần (7 ngày).
A. 35 nghìn đồng. B. 14 nghìn đồng. C. 21 nghìn đồng. D. 28 nghìn đồng.
Câu 14 Nghiệm của bất phương trình là:
A. hoặc x>2. B.
C. –ln2<x<ln2 D. x<-ln2 hoặc x>ln2.
Câu 15 Tìm tất cả giá trị của
m
để phương trình
2
81
xx
m
−
=
có nghiệm.
A.
1
3
m
. B.
0m
. C.
1m
. D.
1
8
m −
.
Câu 16 Một người gửi số tiền
50
triệu đồng vào một ngân hàng với lãi suất
8,4%
/năm. Cứ sau mỗi năm,
số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Người đó sẽ lĩnh được số tiền cả
vốn lẫn lãi là
80
triệu đồng sau
n
năm. Hỏi nếu trong khoảng thời gian này người đó không rút tiền và lãi
suất không thay đổi thì
n
gần nhất với đô nào dưới đây.
A.
4
. B.6 C.
5
. D.
7
.
Câu 17 Cho dãy số
( )
n
u
thỏa mãn
18 18
11
44
e 5 e e e
uu
uu
+ − =
và
1
3
nn
uu
+
=+
với mọi
1n
. Giá trị lớn nhất
của
n
để
3
log ln2018
n
u
bằng
A.
1419
B.
1418
. C.
1420
. D.
1417
.
Câu 18 Biết
( )
;ab
là khoảng chứa tất cả các giá trị của tham số thực
m
để phương trình
( ) ( )
22
2
1
7 3 5 7 3 5 2
xx
x
m
−
− + + =
có đúng bốn nghiệm thực phân biệt. Tính
M a b=+
.
A.
1
8
M =
. B.M=
16
1
C.
7
16
M
−
=
. D.
3
5
M =
.
Câu 19: Hàm số
( )
2
x
F x e=
là nguyên hàm của hàm số nào trong các hàm số sau:
A.
( )
2
2
x
f x xe=
B.
( )
2
2
1
x
f x x e=−
C.
( )
2x
f x e=
D.
( )
2
2
x
e
fx
x
=
Câu 20: Cho hình phẳng giới hạn bởi các đường
tan , 0, 0,
4
y x y x x
= = = =
quay quanh trục Ox. Thể tích của
khối tròn xoay tạo thành bằng:
A. 5 B.
1
4
−
C.
3
2
D.
1
2
+
Câu 21: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx=
và đường thẳng
2yx=
là:
A.
4
3
B.
5
3
C.
3
2
D.
23
15
Câu 22: Cho hàm số
( )
fx
liên tục trên và
( )
6
0
10f x dx =
, thì
( )
3
0
2f x dx
( ) ( )
2
3
3
log x 2 log x 4 0.− + − =
xx
5
ee
2
−
+
1
x
2
1
x2
2

Trang 139
A. 30 B. 20 C. 10 D. 5
Câu 23: Cho hàm số
( )
y f x=
có đạo hàm trên đồng thời thỏa mãn
( ) ( )
0 1 5ff==
. Tính tích phân
( )
( )
1
0
'
fx
I f x e dx=
A. I = 10 B.
5I =−
C. I = 0 D. I = 5
Câu 24: Cho số phức z thỏa mãn phương trình
( ) ( )
2
3 2 2 4i z i i+ + − = +
. Tìm tọa độ điểm M biểu diễn số phức z.
A.
( )
1;1M −
B.
( )
1; 1M −−
C.
( )
1;1M
D.
( )
1; 1M −
Câu 25: Cho số phức
12zi=+
. Tìm tổng phần thực và phần ảo của số phức
2w z z=+
A. 3 B. 5 C. 1 D. 2
Câu 26: Tìm tập hợp điểm biểu diễn số phức z thỏa mãn
( )
1z i i z− = +
.
A. Đường tròn tâm I(0; 1), bán kính
2R =
B. Đường tròn tâm I(1; 0), bán kính
2R =
C. Đường tròn tâm I(-1; 0), bán kính
2R =
D. Đường tròn tâm I(0; -1), bán kính
2R =
Câu 27: Gọi
12
,zz
là các nghiệm của phương trình
2
2 5 0zz− + =
. Tính
22
12
P z z=+
.
A. 10 B. 5 C. 12 D. 4
Câu 28: Cho số phức z có
1z =
. Tìm giá trị lớn nhất của biểu thức
22
1P z z z z= − + + +
.
A.
13
4
B. 3 C.
3
D.
11
4
Câu 29. Gọi
h
và
B
lần lượt là chiều cao và diện tích mặt đáy của hình lăng trụ. Khi đó thể tích
V
của khối lăng
trụ được tính theo công thức nào dưới đây?
A.
1
B.
4
Vh=
B.
B.Vh=
C.
1
B.
6
Vh=
D.
1
B.
3
Vh=
Câu 30. Cho hình chóp
.S ABC
, gọi
M
,
N
lần lượt là trung điểm của
,SA SB
. Tính tỉ số
.
.
S ABC
S MNC
V
V
.
A.
4
. B.
1
2
C.
2
. D.
1
4
Câu 31.Cho khối hộp có đáy là hình chữ nhật với ; . Hai mặt bên
và cùng tạo với đáy góc , cạnh bên của hình hộp bằng .Thể tích khối hộp là:
A.
7
B.
77
C.
5
D.
33
Câu 32. Một mặt cầu có diện tích bằng
2
100 cm
. Khi đó thể tích của khối cầu tương ứng là:
A.
3
1000
3
cm
B.
3
250
3
cm
C.
3
125
3
cm
D.
3
500
3
cm
.ABCD A B C D
3AB =
7AD =
( )
ADD A
( )
ABB A
45
1

Trang 140
Câu 33.Một hình trụ có bán kính đáy
Ra=
và thiết diện qua trục là một hình vuông. Khi đó diện tích
xung quanh của hình trụ là
A.
2
a
B.
2
2 a
C.
2
4 a
D.
2
2
a
Câu 34. Một hình trụ có bán kính
R
, chiều cao
h
và thể tích là
1
V
. Một hình nón có đáy là một đáy của
hình trụ và có đỉnh là tâm của đường tròn đáy còn lại của hình trụ, thể tích của hình nón này là
2
V
. Mối
liên hệ giữa
1
V
và
2
V
là
A.
21
3VV=
B.
12
VV=
C.
21
2VV=
D.
12
3VV=
Câu 35.Trong không gian Oxyz.Cho hai véctơ
)1;0;3(),1;1;2( ba −
.Tính tích vô hướng của hai véctơ
(2;1; 1)a −
và
(3;0;1)b
.
A. 5 B. 6 C.8 D.0
Câu 36. Trong không gian Oxyz cho mặt cầu (S) tâm I(1;-2;3) bán kính r=3. Viết phương trình của mặt cầu (S)
A.
( ) ( ) ( )
2 2 2
1 2 3 3x y z− + + + − =
B.
( ) ( ) ( )
2 2 2
1 2 3 9x y z− + + + − =
C.
( ) ( ) ( )
2 2 2
1 2 3 3x y z− + + + − =
D.
( ) ( ) ( )
2 2 2
1 2 3 9x y z+ + − + + =
Câu 37. Trong không gian Oxyz .Phương trình mặt phẳng (P) qua điểm M(1;0;-2) có một véctơ pháp tuyến
(3;1; 3)n =−
là
A.3x+y-3z+9=0 B.3x+y-3z-9=0 C. 3x+y-3z-7=0 D. -3x+y-3z-9=0
Câu 38. Trong không gian Oxyz .Phương trình đường thẳng (d) đi qua M(2 ; 3 ; -5) và song song với
đường thẳng
22
: 3 4
5
xt
yt
zt
= − +
= −
=−
là
A.
22
3 4 .
55
xt
yt
zt
=+
=−
=−
B.
22
34.
55
xt
yt
zt
=+
=−
= − −
C.
22
3 4 .
55
xt
yt
zt
=−
=−
=−
D.
22
3 4 .
55
xt
yt
zt
= − +
= − +
= − +
Câu 39. Trong không gian Oxyz ,cho mặt cầu (S):
( ) ( )
22
2
1 2 4x y z− + + + =
và (P):x-y+z-1=0.Khẳng định nào
sau đây đúng?
A.(P) tiếp xúc với (S) B.(P) cắt (S)
C.(P) không có điểm chung với (S) D.(S) có tâm I(1;2;0)
Câu 40. Trong không gian với hệ tọa độ Oxyz, cho 3 đường thẳng
1
11
1
2
: 3 ,
23
xt
d y t
zt
= − +
=+
=+
2
22
2
12
: 1 ,
2
xt
d y t
zt
= − +
=+
=+
3
33
3
1
: 4 2 .
3
xt
d y t
zt
=+
=−
=−
Giả sử đường thẳng
d
cắt các đường thẳng
1 2 3
,,d d d
lần lượt tại
,A
,B
C
sao cho
B
là trung
điểm của
AC
. Đường thẳng
d
đi qua điểm nào trong các điểm sau đây?
A.
(4; 1;0).M −
B.
(2;0;2).N
C.
(0;2;4).P
D.
( 1;3;1).Q −

Trang 141
Câu 41. Trong không gian với hệ tọa độ Oxyz,Tìm phương trình mp (P) đi qua M(1; 2; 4) và cắt các tia Ox, Oy, Oz
lần lượt tại A(a; 0; 0), B(0; b; 0), C(0; 0; c) sao cho thể tích của khối tứ diện OABC là nhỏ nhất với a, b, c là số
dương.
A. (P): 3x +6 y + 12z – 1 = 0. B. (P):4 x + 2y + z – 1 = 0.
C. (P): 4x +2y + z – 12 = 0. D. (P): 3x –4y + z +1 = 0.
Câu 42. Cho hai đường thẳng
1
1
( ): 2
1
xt
d y t
z
=+
=−
=
và
2
2 1 1
( ):
1 2 2
x y z
d
− − +
==
−
. Mặt phẳng
()P
thay đổi luôn song
song với cả hai đường thẳng
12
( ),( )dd
. Khi đó giá trị nhỏ nhất của tổng
12
( ,( )) ( ,( ))T d d P d d P=+
là
A.
1
.
3
B.
2
.
3
C.
5
.
3
D.
7
.
3
Câu 43: Số các tổ hợp chập k của một tập hợp gồm n phần tử (1
k
n )
A.
( )
!
k
k
n
n
A
C
nk
=
−
. B.
!
k
k
n
n
A
C
k
=
. C.
( )
!
!
k
n
n
C
nk
=
−
. D.
!( )!
!
k
n
k n k
C
n
−
=
.
Câu 44: Cho cấp số nhân (u
n
) có số hạng đầu u
1
=3 và công bội q = 2. Giá trị của u
4
bằng?
A. 9 B. 24 C. 48 D. 162
Câu 45: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ
?
A. 60
0
B. 90
0
C. 120
0
D. 45
0
Câu 46: Từ các chữ số {1; 2; 3; 4; 5; 6}, lập một số bất kỳ gồm 3 chữ số. Tính xác suất để nhận được số chia hết
cho 6?
Câu 47: Cho hình chóp S.ABC có đáy ABC là tam giác đề cạnh a, SA vuông góc với đáy. Góc giữa SB với mặt
đáy bằng 60
0
. Tính khoảng cách giữa 2 đường thẳng AC và SB theo a?
B. 2a C.
D.
Câu 48: Tìm tất cả các giá trị của tham số m để phương trình
có nghiệm thuộc khoảng
.
Câu 49: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
( ) ( )
1
2
0
34
f 1 , f ' x dx
59
==
và
( )
1
3
0
37
x f x dx .
180
=
Tích phân
( )
1
0
f x 1 dx ?−=
A.
2
30
B.
2
30
−
C.
1
10
−
D.
1
10

Trang 142
Câu 50. Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Gọi S là tập các giá trị
nguyên của m để phương trình
( )
2
2f x x m−=
có đúng bốn nghiệm thực phân
biệt thuộc đoạn
37
;
22
−
. Tổng các phần tử của S bằng
A. -21. B. 12. C. -13. D. 8.
HẾT
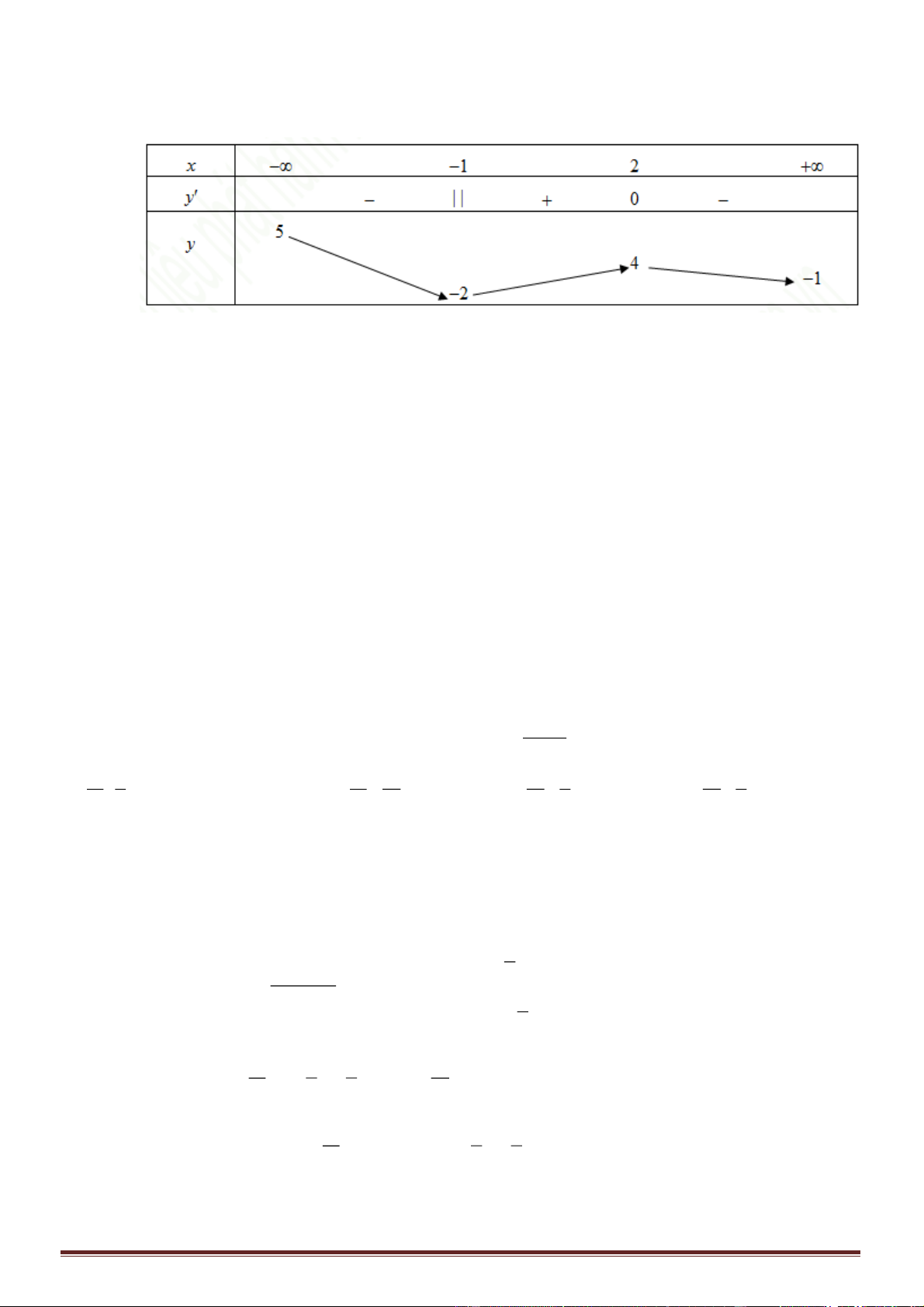
Trang 143
ĐÁP ÁN CHI TIẾT
Câu 1 Cho hàm số
( )
y f x=
liên tục trên R và có bảng biến thiên
Khẳng định nào sau đây sai?
A. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng
2−
.
B. Hàm số có hai điểm cực trị.
C. Đồ thị hàm số có hai tiệm cận ngang
D. Hàm số có giả trị lớn nhất là 5 và giá trị nhỏ nhất là 2
Lời gii
Chọn D
Hàm số không có giá trị lớn nhất do:
( )
lim 5
x
fx
→−
=
và có giá trị nhỏ nhất bằng
2−
tại
1x =−
.
Hàm số có hai điểm cực trị là
1x =−
và
2x =
.
Ta có
( )
lim 5
x
fx
→−
=
và
( )
lim 1
x
fx
→+
=−
nên đồ thị hàm số có hai tiệm cận ngang là
5y =
và
1y =−
.
Câu 2 Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
8
12
f x x
x
=+
+
trên đoạn
1;2
lần lượt là
A .
11
3
;
7
2
B.
11
3
;
18
5
. C.
13
3
;
7
2
. D.
18
5
;
3
2
.
Lời gii
Đáp án A,
Hàm số xác định và liên tục trên đoạn
1;2
Ta có
( )
( )
2
16
1
12
fx
x
=−
+
( )
0fx
=
3
1;2
2
5
1;2
2
x
x
=
= −
.
Khi đó
( )
11
1
3
f =
;
37
22
f
=
;
( )
18
2
5
f =
.
Vậy
( ) ( )
1;2
11
max 1
3
f x f==
;
( )
1;2
37
min
22
f x f
==
.
Câu 3 Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
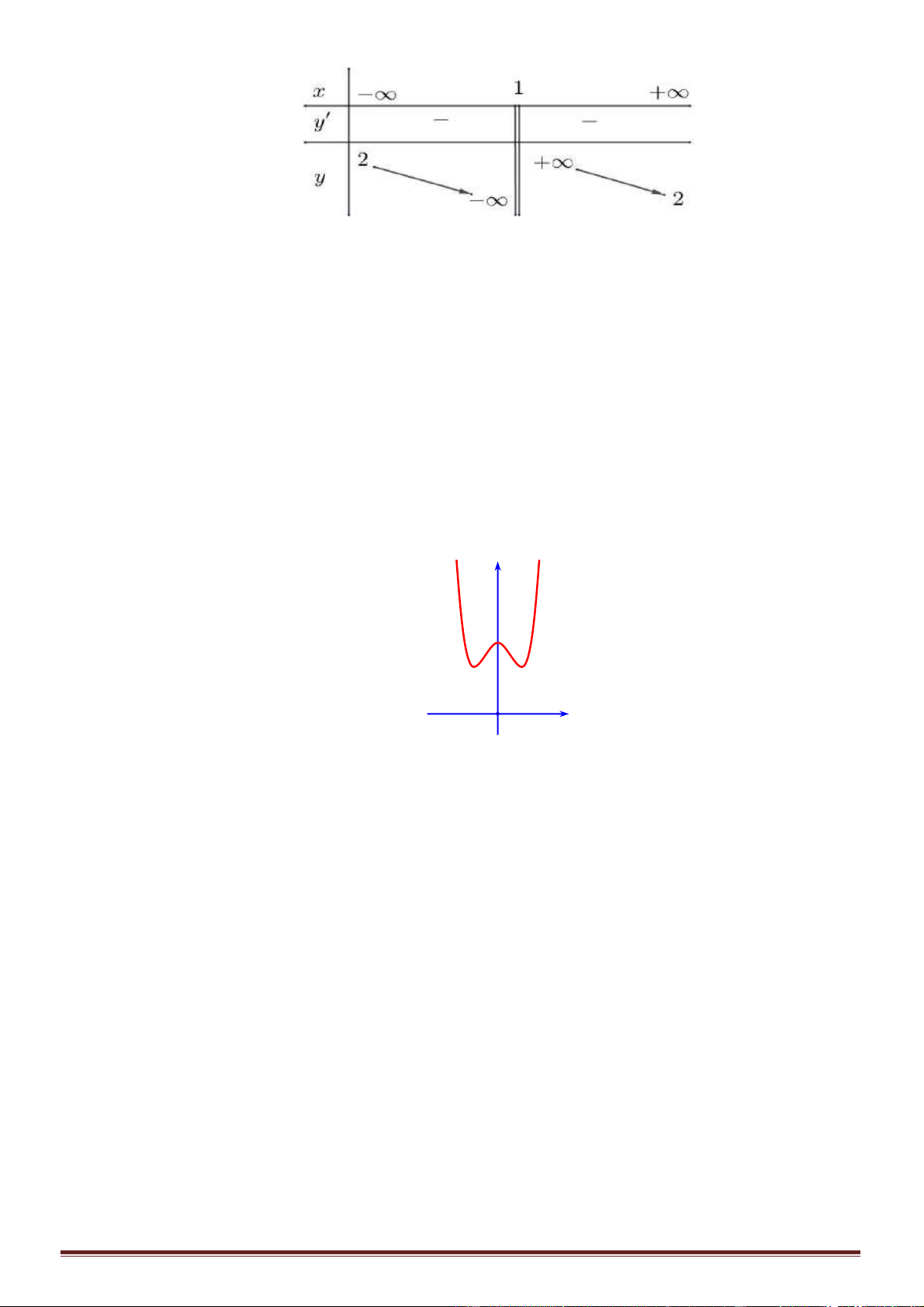
Trang 144
Mệnh đề nào dưới đây đúng?
A.Đồ thị có tiệm cận đứng là đường thẳng
1x =
và tiệm cận ngan là đường thẳng
2y =
B. Đồ thị hàm số không có đường tiệm cận.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D Đồ thị hàm số có tiệm cận ngang là đường thẳng
1x =
và tiệm cận đứng là đường thẳng
2y =
.
Lời gii
Dựa bảng biến thiên ta có đáp án đúng là A.
Câu 4Đường cong hình bên là đồ thị của hàm số nào dưới đây?
A.
42
44y x x= − + +
. B.
42
23y x x= − +
C.
42
32y x x= + +
. D.
32
21y x x= − +
.
Lời gii
Đáp án B.
Đồ thị hàm số đã cho là hàm trùng phương có
0a
và có
3
cực trị.
Câu 5 Cho hàm số Tiếp tuyến của đồ thị hàm số tại điểm thuộc đồ thị hàm số có
phương trình là :
A. B. C. D.
Lời gii
Đáp án B.
Ta có Hệ số góc của tiếp tuyến tại điểm (-1;1) là
Do đó phương trình tiếp tuyến là
( )
32
f x x 3x 5.= − +
( )
1;1−
y 3 2x=−
y 9x 10=+
y 1 3x=+
y 3x 4= − +
3
y' 3x 6x.=−
( )
k y' 1 9= − =
y 9x 10.=+
O
x
y

Trang 145
Câu 6 Số đường tiệm cận của đồ thị hàm số
2
2
1
xx
y
x
+−
=
−
.
A.
1
. B.
4
. C.
3
. D.
2
.
Hướng dẫn gii
Đáp án C.
Tập xác định
(
( )
; 2 1;D = − − +
.
2
2
lim 1
1
x
xx
x
→+
+−
=
−
Đồ thị hàm số có tiệm cận ngang là:
1y =
.
2
2
lim 1
1
x
xx
x
→−
+−
=−
−
Đồ thị hàm số có tiệm cận ngang là:
1y =−
.
2
1
2
lim 1
1
x
xx
x
+
→
+−
=
−
( )( )
1
12
lim
1
x
xx
x
+
→
−+
=
−
1
2
lim
1
x
x
x
+
→
+
=
−
= +
Đồ thị hàm số có tiệm cận đứng
là:
1x =
.
Vậy đồ thị hàm số có
3
đường tiệm cận.
Câu 7 Hình bên là đồ thị của hàm số
( )
y f x=
. Biết rằng tại các điểm
A
,
B
,
C
đồ thị hàm số có tiếp
tuyến được thể hiện trên hình vẽ bên dưới.
Mệnh đề nào dưới đây đúng?
A.
( ) ( ) ( )
C A B
f x f x f x
. B.
( ) ( ) ( )
B A C
f x f x f x
C.
( ) ( ) ( )
A C B
f x f x f x
. D.
( ) ( ) ( )
A B C
f x f x f x
.
Lời gii
Đáp án B
Dựa vào hình vẽ ta có:
( )
0
A
fx
=
,
( )
0
B
fx
,
( )
0
C
fx
.
Vậy
( ) ( ) ( )
B A C
f x f x f x
.
Câu 8 Cho hàm số
32
34y x x= + −
có đồ thị
( )
1
C
và hàm số
32
34y x x= − + −
có đồ thị
( )
2
.C
Khẳng
định nào sau đây đúng?
A.
( )
1
C
và
( )
2
C
đối xứng nhau qua gốc tọa độ. B.
( )
1
C
và
( )
2
C
trùng nhau.
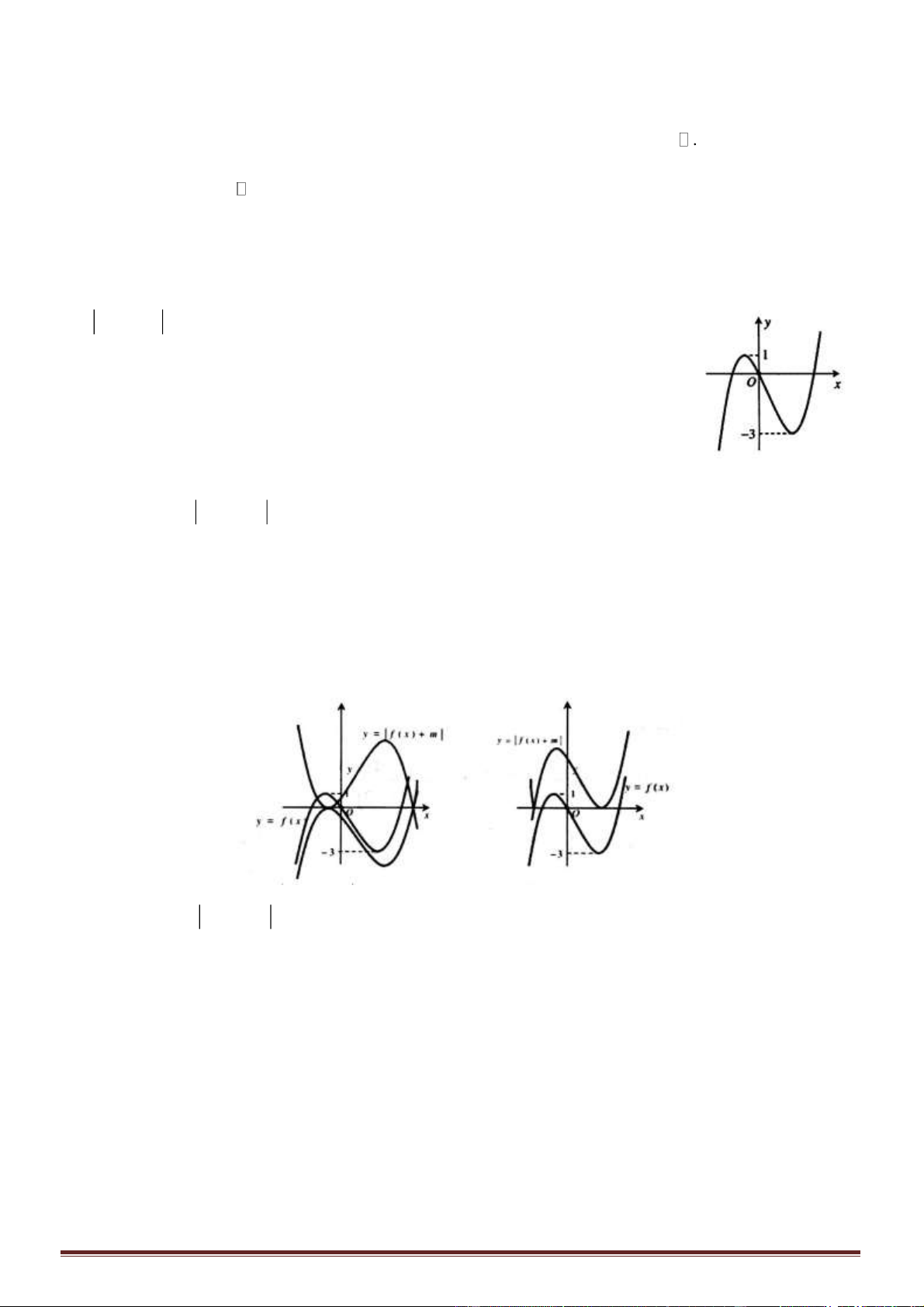
Trang 146
C.
( )
1
C
và
( )
2
C
đối xứng nhau qua
.Oy
D.
( )
1
C
và
( )
2
C
đối xứng nhau qua
Ox
.
Lời gii
Đáp án C.Xét
( )
32
34y f x x x= = + −
và
( )
32
34y g x x x= = − + −
đều xác định trên
.
Với mọi
x
ta luôn có
( ) ( ) ( ) ( )
32
32
3 4 3 4f x x x x x g x− = − + − − = − + − =
Suy ra đồ thị hàm số
( )
y f x=
và
( )
y g x=
đối xứng nhau qua
Oy
, tức
( )
1
C
và
( )
2
C
đối
xứng nhau qua
.Oy
Câu 9 Cho hàm số bậc ba có đồ thị như hình bên. Tất cả các giá trị của tham số m để hàm số
có 3 điểm cực trị là:
A.m -1 hoặc m 3 B.m -3 hoặc m 1.
C.m=-1 hoặc m=3 D.1 m 3.
Lời gii
Đáp án A
Đồ thị hàm số gồm hai phần:
Phần 1 là phần đồ thị hàm số nằm phía trên trục hoành
Phần 2 là phần đối xứng của đồ thị hàm số nằm phía dưới trục hoành qua trục hoành.
Dựa vào đồ thị của hàm số đã cho hình bên ta suy ra dạng đồ thị của hàm số
Khi đó hàm số có ba điểm cực trị khi và chỉ khi đồ thị hàm số và trục hoành tại
nhiều nhất hai điểm chung (nghĩa là có 1 trong 2 điểm cực trị nằm trên trục hoành)
Câu 10 Gọi
S
là tập tất cả các giá trị thực của tham số
m
sao cho đường thẳng
:3d y mx m= − −
cắt đồ
thị
( )
32
: 2 3 2C y x x= − −
tại ba điểm phân biệt
A
,
B
,
( )
1; 3I −
mà tiếp tuyến với
( )
C
tại
A
và tại
B
vuông góc với nhau. Tính tổng các phần tử của
S
.
A.-1 B.
1
. C.
2
. D.
5
.
Lời gii
Đáp án A.Xét phương trình hoành độ giao điểm của
( )
C
và
( )
d
:
32
2 3 2 3x x mx m− − = − −
( )
( )
2
1 2 1 0x x x m − − − − =
(*)
( )
y f x=
( )
y f x m=+
( )
y f x m=+
( )
y f x m=+
( )
y f x m=+
( )
y f x=
( )
y f x m=+
( )
y f x m=+
( )
y f x m=+
1 m 0 m 1
3 m 0 m 3
+ −
− +
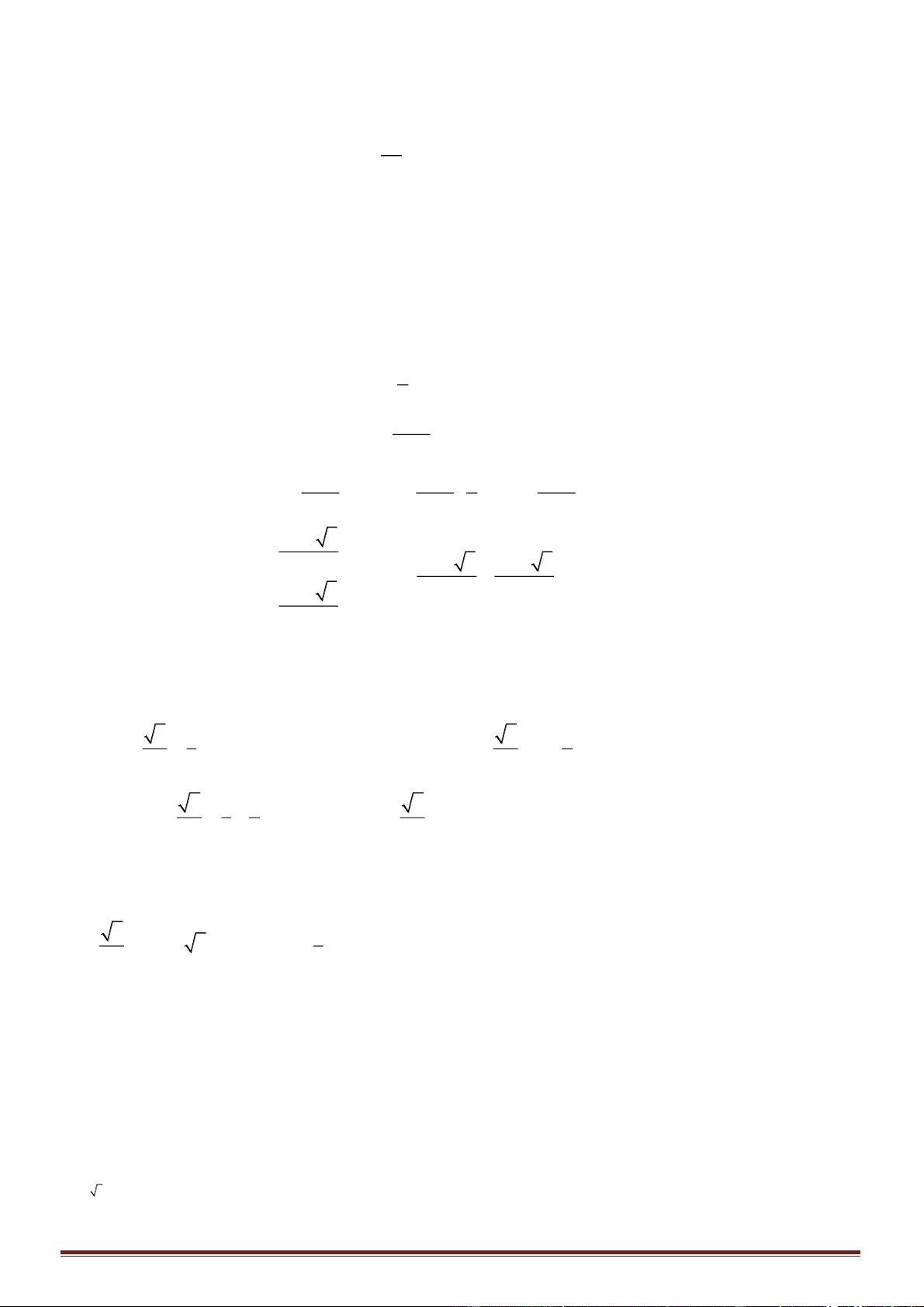
Trang 147
Để đường thẳng
( )
d
cắt đồ thị
( )
C
tại ba điểm phân biệt thì phương trình (*) có ba nghiệm
phân biệt
2
2 1 0x x m − − − =
có hai nghiệm phân biệt
1x
.
2
0
2.1 1 1 0m
− − −
9
8
0
m
m
−
.
Do tiếp tuyến với
( )
C
tại
A
và tại
B
vuông góc với nhau nên
12
.1kk =−
.
Với
1
k
là hệ số góc tiếp tuyến với
( )
C
tại
A
,
2
k
là hệ số góc tiếp tuyến với
( )
C
tại
B
.
Ta có
2
66y x x
=−
( )
2
1 1 1
66k x x = −
;
( )
2
2 2 2
66k x x = −
.
Do
12
.1kk =−
nên
( )( )
22
1 1 2 2
6 6 6 6 1x x x x− − = −
( ) ( )
2
1 2 1 2 1 2 1 2
36 36 36 1 0x x x x x x x x − + + + =
.
Theo định lý vi-et ta có
12
12
1
2
1
2
xx
m
xx
+=
+
=−
khi đó ta có
2
1 1 1 1
36 36 36 1 0
2 2 2 2
m m m+ + +
− − − + − + =
2
35
6
9 9 1 0
35
6
m
mm
m
−+
=
+ + =
−−
=
. Vậy
3 5 3 5
1
66
S
− + − −
= + = −
.
Câu11 Với các số thực dương a, b bất kì, Mệnh đề nào dưới đây đúng ?
A. B.
C. D.
Lời gii
Đáp án A.
Câu12 Tính đạo hàm của hàm số
17
x
y
−
=
A.
17 ln17
x
y
−
=
. B.
1
.17
x
yx
−−
=−
. C.
17
x
y
−
=−
. D.
17 ln17
x
y
−
=−
Lời gii
Đáp án D. Áp dụng công thức:
( )
. ln
uu
a u a a
=
ta có:
( )
17 .ln117 7
x x
y
− −
=−
=
.
Câu13 Số tiền mà My để dành hằng ngày là x (đơn vị nghìn đồng, với x>0,x
R biết x là nghiệm của phương trình
Tính tổng số tiền My để dành được trong một tuần (7 ngày).
A. 35 nghìn đồng. B. 14 nghìn đồng. C. 21 nghìn đồng. D. 28 nghìn đồng.
a 1.
3
aa
2
a1
log 2log b.
b3
=−
3
aa
2
a1
log 3 log b.
b2
=−
3
aa
2
a 1 1
log log b.
b 3 2
=−
3
aa
2
a
log 3 2log b.
b
=−
( )
( )
3
2
3
a a a a
2
a1
log log a log b 2log b.
b3
= − = −
( ) ( )
2
3
3
log x 2 log x 4 0.− + − =
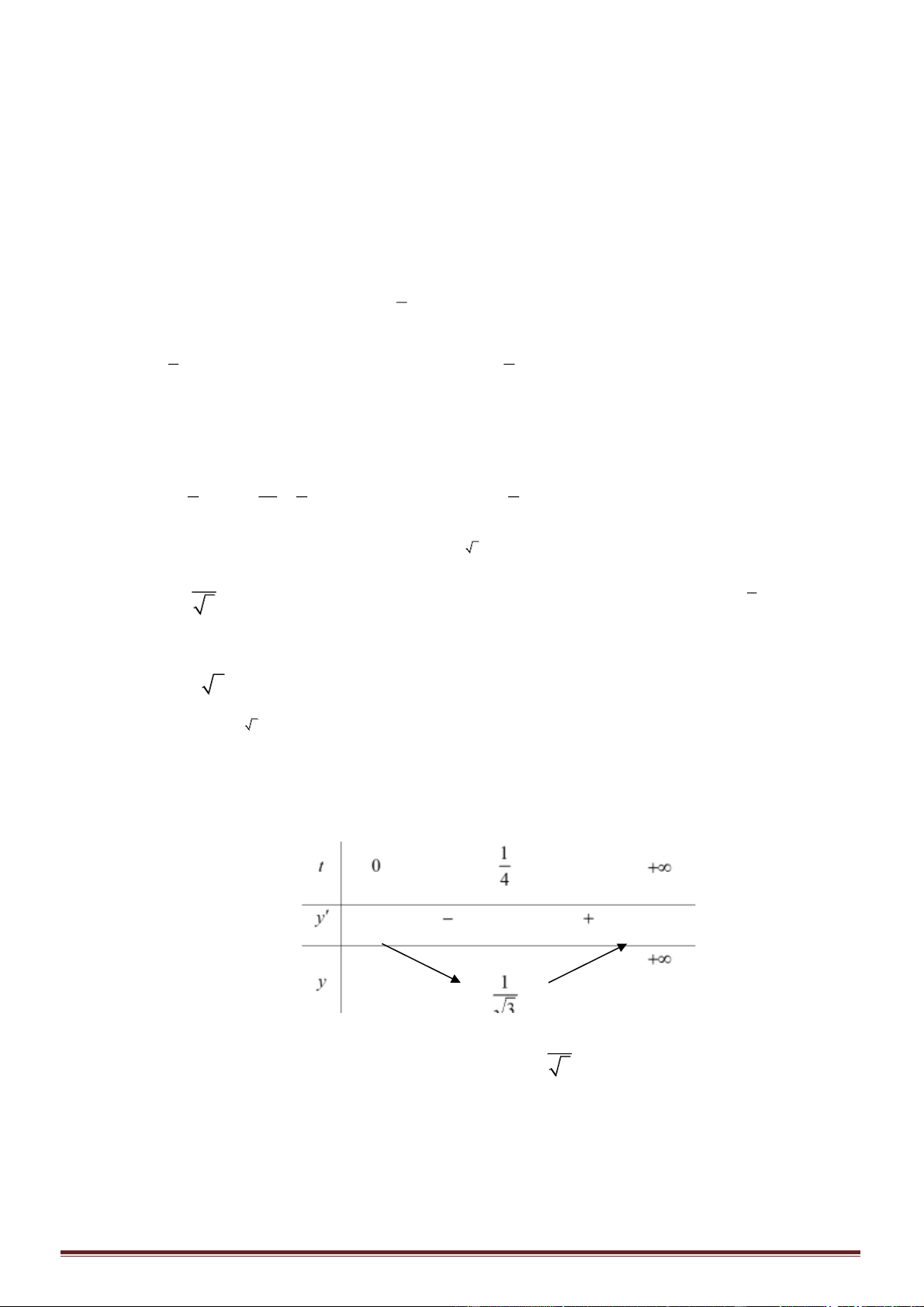
Trang 148
Lời gii
Đáp án C.
Điều kiện Phương trình tương đương
Câu14 Nghiệm của bất phương trình là:
A. hoặc x>2. B.
C. –ln2<x<ln2 D. x<-ln2 hoặc x>ln2.
Đáp án C
Ta có:
Câu15 Tìm tất cả giá trị của
m
để phương trình
2
81
xx
m
−
=
có nghiệm.
A.
1
3
m
. B.
0m
. C.
1m
. D.
1
8
m −
.
Lời gii
Đáp án A* Đặt
tx=
(
0t
)
2
tx=
. PT trở thành
2
2
81
tt
m
−
=
.
Ta có PT
2
81
xx
m
−
=
có nghiệm khi và chỉ khi PT
2
2
81
tt
m
−
=
có nghiệm
0t
.
+ Khảo sát
( )
2
2
81
tt
ft
−
=
(với
0t
) ta có:
( )
( )
2
2
81 . 4 1
tt
f t t
−
=−
.
Lập bảng biến thiên ta được:
* KL: PT
2
2
81
tt
m
−
=
có nghiệm
0t
khi và chỉ khi
1
3
m
.
Câu16 Một người gửi số tiền
50
triệu đồng vào một ngân hàng với lãi suất
8,4%
/năm. Cứ sau mỗi năm,
số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho năm tiếp theo. Người đó sẽ lĩnh được số tiền cả
vốn lẫn lãi là
80
triệu đồng sau
n
năm. Hỏi nếu trong khoảng thời gian này người đó không rút tiền và lãi
suất không thay đổi thì
n
gần nhất với đô nào dưới đây.
A.
4
. B.6 C.
5
. D.
7
.
x 2;x 4.
( ) ( )
22
33
log x 2 log x 4 0− + − =
( ) ( ) ( ) ( )
2 2 2 2
3
log x 2 x 4 0 x 2 x 4 1 x 3.
− − = − − = =
xx
5
ee
2
−
+
1
x
2
1
x2
2
( )
2
x x x x x x
x
5 1 5 1
e e e 2 e 5e 2 0 e 2 ln2 x ln2
2 e 2 2
−
+ + − + −
0
1

Trang 149
Lời gii
Đáp án B
Từ công thức
( )
0
1
n
n
A A r=+
ta có
1
0
log
n
r
A
n
A
+
=
.
Với
80
n
A =
,
0
50A =
,
0,084r =
( )
1 0,084
80
log
50
n
+
=
5,827n
.
Câu 17 Cho dãy số
( )
n
u
thỏa mãn
18 18
11
44
e 5 e e e
uu
uu
+ − =
và
1
3
nn
uu
+
=+
với mọi
1n
. Giá trị lớn nhất
của
n
để
3
log ln2018
n
u
bằng
A.
1419
B.
1418
. C.
1420
. D.
1417
.
Lời gii
Đáp án A
Ta có
1
3
nn
uu
+
=+
với mọi
1n
nên
n
u
là cấp số cộng có công sai
3d =
18 18 18 18
1 1 1 1
4 4 4 4
e 5 e e e 5 e e e e
u u u u
u u u u
+ − = − = −
( )
1
Đặt
18
1
4
ee
u
u
t =−
( )
0t
Phương trình
( )
1
trở thành
2
0
50
25
t
t t t
tt
= − =
=
( )
5 5 0 5 0 0 0t t t t t t t t= − + = + = = =
Với
0t =
ta có :
18
1
4
18 1 1 1 1
e e 4 51 4 17
u
u
u u u u u= = + = =
Vậy
( ) ( )
1
1 17 1 3 3 14
n
u u n d n n= + − = + − = +
Có :
ln2018
ln2018 ln2018
3
3 14
log ln 2018 3 3 14 3 1419,98
3
nn
u u n n
−
+
Vậy giá trị lớn nhất của
n
là
1419
.
Câu18 Biết
( )
;ab
là khoảng chứa tất cả các giá trị của tham số thực
m
để phương trình
( ) ( )
22
2
1
7 3 5 7 3 5 2
xx
x
m
−
− + + =
có đúng bốn nghiệm thực phân biệt. Tính
M a b=+
.
A.
1
8
M =
. B.M=
16
1
C.
7
16
M
−
=
. D.
3
5
M =
.
Lời gii
Đáp án B
Ta có:
( ) ( )
22
2
1
7 3 5 7 3 5 2
xx
x
m
−
− + + =
22
7 3 5 7 3 5 1
2 2 2
xx
m
−+
+ =
.
Vì
22
7 3 5 7 3 5
.1
22
xx
−+
=
nên đặt
2
7 3 5
2
x
t
−
=
,
01t
phương trình trở thành:
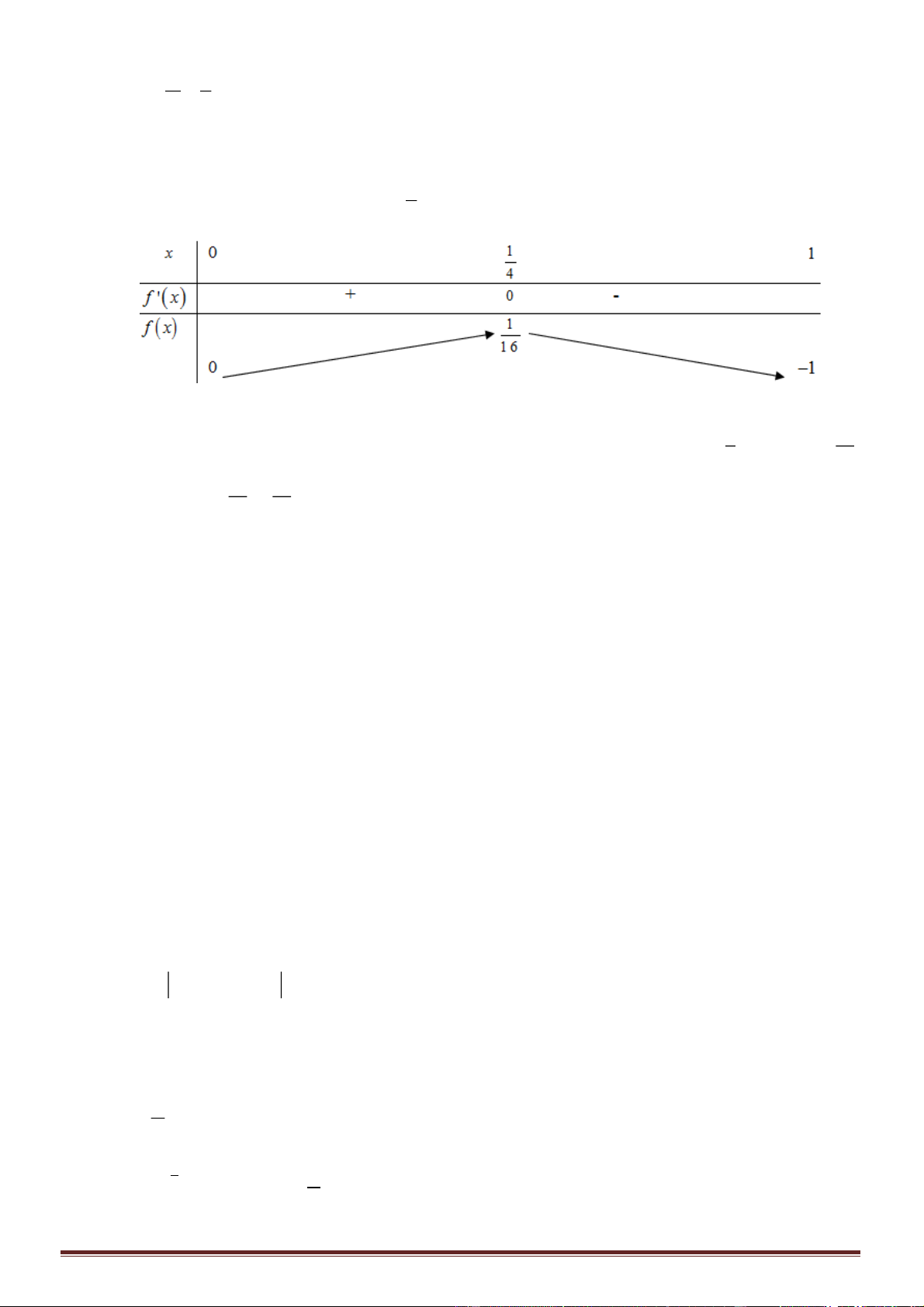
Trang 150
1
2
m
t
t
+=
2
2 2 0t t m − + =
( )
2
2 2 *m t t = − +
.
Xét hàm số
( )
2
2f t t t= − +
,
01t
.
( )
41f t t
= − +
,
( )
1
0
4
f t t
= =
ta có bảng biến thiên:
Để phương trình đã cho có đúng bốn nghiệm thực phân biệt thì phương trình (*) phải có hai nghiệm
phân biệt thỏa mãn
01t
. Dựa vào bảng biến thiên ta thấy
1
02
8
m
1
0
16
m
1
0
16
M = +
1
16
=
.
Câu 19 (NB):
Phương pháp:
Dựa vào định nghĩa nguyên hàm cơ bản: Cho hàm số
( )
y f x=
liên tục trên K (khoảng đoạn hoặc nửa khoảng)
chứa đoạn
;ab
( )
Fx
là một nguyên hàm của
( )
fx
trên K nếu
( ) ( )
',F x f x x K=
Cách gii:
Ta có:
( ) ( )
( )
( )
2 2 2
2
' ' '. 2 .
x x x
f x F x e x e x e= = = =
Chn A
Câu 20 (TH):
Phương pháp:
Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số
( ) ( ) ( )
, , ,y f x y g x x a x b a b= = = =
khi xoay quanh trục
Ox là
( ) ( )
22
b
a
V f x g x dx
=−
.
Cách gii:
Xét phương trình hoành độ giao điểm
tan 0x x k
= =
.
Xét trên
0; 0
4
x
=
.
Khi đó
2
4
0
tan 1
4
V xdx
= = −
.
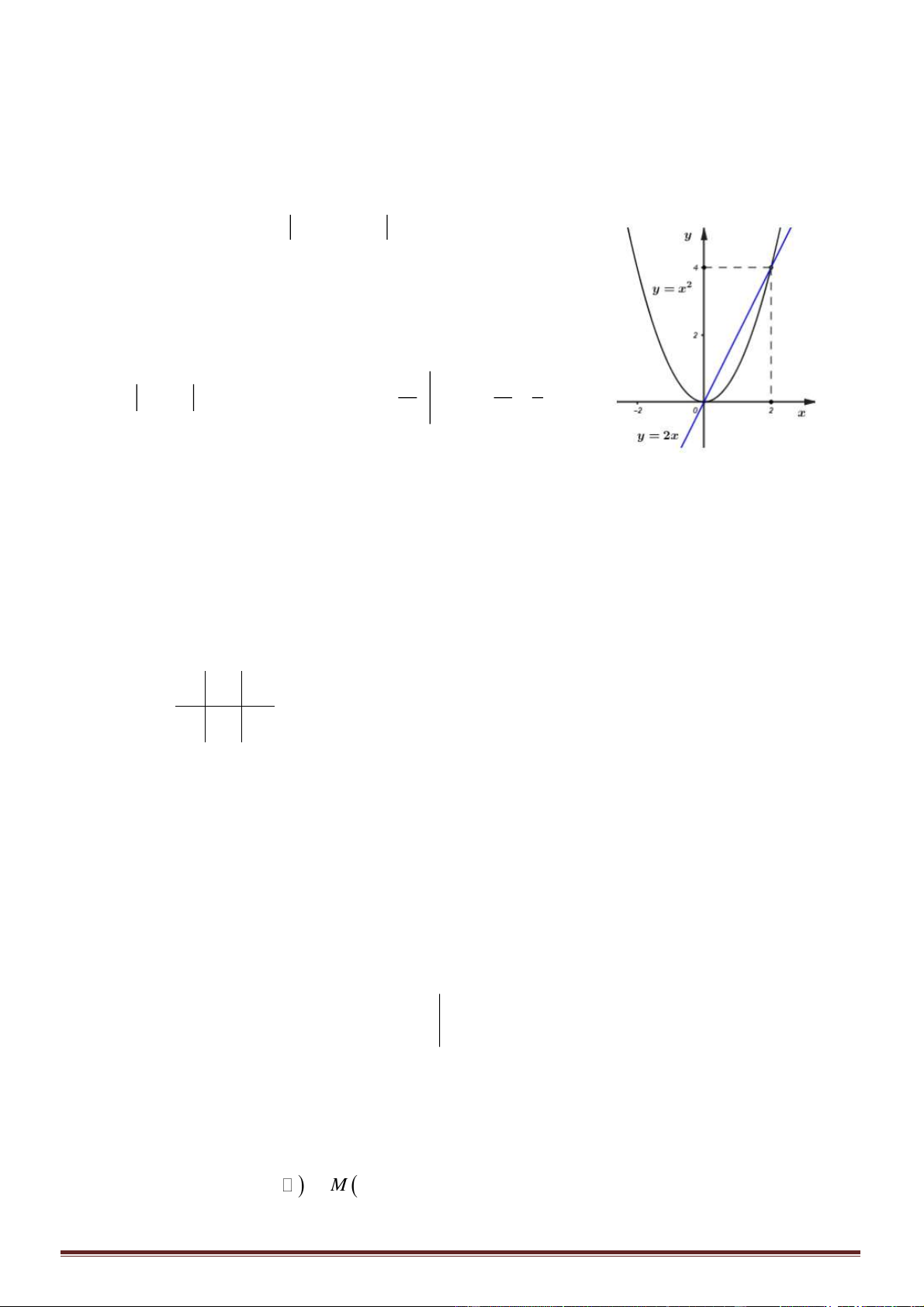
Trang 151
Chn B.
Câu 21 (TH):
Phương pháp
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng
( )
,x a x b a b= =
và các đồ thị hàm số
( ) ( )
,y f x y g x==
là:
( ) ( )
b
a
S f x g x dx=−
.
Cách gii:
Ta có:
22
0
2 2 0
2
x
x x x x
x
=
= − =
=
( )
2
33
22
2 2 2 2
00
0
24
2 2 2
3 3 3
x
S x x dx x x dx x
= − = − = − = − =
Chn A.
Câu 22 (TH):
Phương pháp
Sử dụng phương pháp đổi biến để làm bài.
Cách gii:
22x t dt dx= =
. Đặt
Đổi cận:
Ta có:
( ) ( ) ( )
3 6 6
0 0 0
2 2 2 20f x dx f t dt f x dx= = =
Chn B.
Câu 23 (TH):
Phương pháp
Sử dụng công thức nguyên hàm cơ bản của hàm hợp.
Cách gii:
Ta có:
( )
( ) ( )
( )
( )
( ) ( ) ( )
1
11
10
55
00
0
'0
f x f x f x f f
I f x e dx e d f x e e e e e= = = = − = − =
Chn C.
Câu 24 (TH):
Phương pháp:
Cho số phức
( ) ( )
,;z x yi x y M x y= +
là điểm biểu diễn số phức z.
Cách gii:
x
0
3
t
0
6

Trang 152
Ta có:
( ) ( ) ( ) ( )
( ) ( ) ( )
( )
( )( )
( )
22
22
3 2 2 4 3 2 4 2
3 2 4 4 4 1 3 2 4 4 4 1
1 5 3 2
15
3 2 1 5 1
3 2 3 2
1;1
i z i i i z i i
i z i i i z i i
ii
i
i z i z i
i
M
+ + − = + + = + − −
+ = + − − − + = + − + +
+−
+
+ = + = = = +
++
Chn C.
Câu 25 (NB):
Phương pháp:
Sử dụng các công thức cộng trừ số phức, xác định số phức w .
Cách gii:
Ta có:
1 2 1 2
Re 3
w 2. 2 4 1 2 3 2
Im 2
z i z i
w
z z i i i
w
= + = −
=
= + = + + − = +
=
Tổng phần thực và phần ảo của
2w z z=+
là: 3 + 2 = 5
Chn B.
Câu 26 (VD):
Phương pháp
Cho số phức
( ) ( )
,;z x yi x y M x y= +
là điểm biểu diễn số phức z
Modun của số phức
22
:z x yi z x y= + = +
Cách gii:
Gọi số phức
( )
,z x yi x y= +
( ) ( )( )
( ) ( )
( ) ( ) ( )
2 2 2
2
2 2 2 2 2 2
22
11
1
1
2 1 2 2
2 1 0
z i i z x yi i i x yi
x y i x y y x i
x y x y y x
x y y x xy y y xy x
x y y
− = + + − = + +
+ − = − + +
+ − = − + +
+ − + = − + + + +
+ + − =
Vậy tập hợp biểu diễn số phức z thỏa mãn bài cho là đường tròn có phương trình
22
2 1 0x y y+ + − =
có tâm
( )
0; 1I −
và bán kính
2R =
Chn D.
Câu 27 (TH):

Trang 153
Phương pháp
+) Giải phương trình bậc hai trong tập số phức bằng công thức nghiệm hoặc bấm máy tính sau đó tính giá trị biểu
thức đề bài yêu cầu.
+) Modun của số phức
22
:z x yi z x y= + = +
Cách gii:
( )
2
22
2
2
12
12
2 5 0
12
1 2 1 2 10
zi
zz
zi
P z z
=+
− + =
=−
= + = + + + − =
Chn A.
Câu 28 (VDC):
Phương pháp:
+) Đặt
22
1z a bi a b= + + =
.
+) Biểu diễn
( )
P f a=
, sử dụng MTCT tìm GTLN của P .
Cách gii:
Đặt
z a bi=+
. Ta có
2 2 2 2 2 2
1 1 1 0 1 1z a b a b b a a= + = + = = − −
Theo bài ra ta có:
( )
( )
( )
( )
( )
( ) ( )
( )
( )
22
2
2
22
2
22
2 2 2
2
2
2 2 2 2 2
2
2
22
2
1
11
11
1 2 1
1 1 2
2 1 1 2 1
2 2 2 1 2 1
2 2 4 4 1
2 2 2 1 1 1
P z z z z
P z z z z
P z z z
P a bi a abi b a bi
P a b a b a ab b
P a a b a b a b a
P a a a a a
P a a a
P a a a
= − + + +
= − + + +
= − + + +
= + − + + − + + +
= − + + − + + + +
= − + + + − + + + +
= − + + + − +
= − + + +
= − + + −
Sử dụng MTCT ta tìm được
max
3,25P =
.
Chn A.
Câu 3.(VDC).Cho khối hộp có đáy là hình chữ nhật với ; . Hai mặt bên
và cùng tạo với đáy góc , cạnh bên của hình hộp bằng .Thể tích khối hộp là:
A.
7
B.
77
C.
5
D.
33
Lời gii
.ABCD A B C D
3AB =
7AD =
( )
ADD A
( )
ABB A
45
1
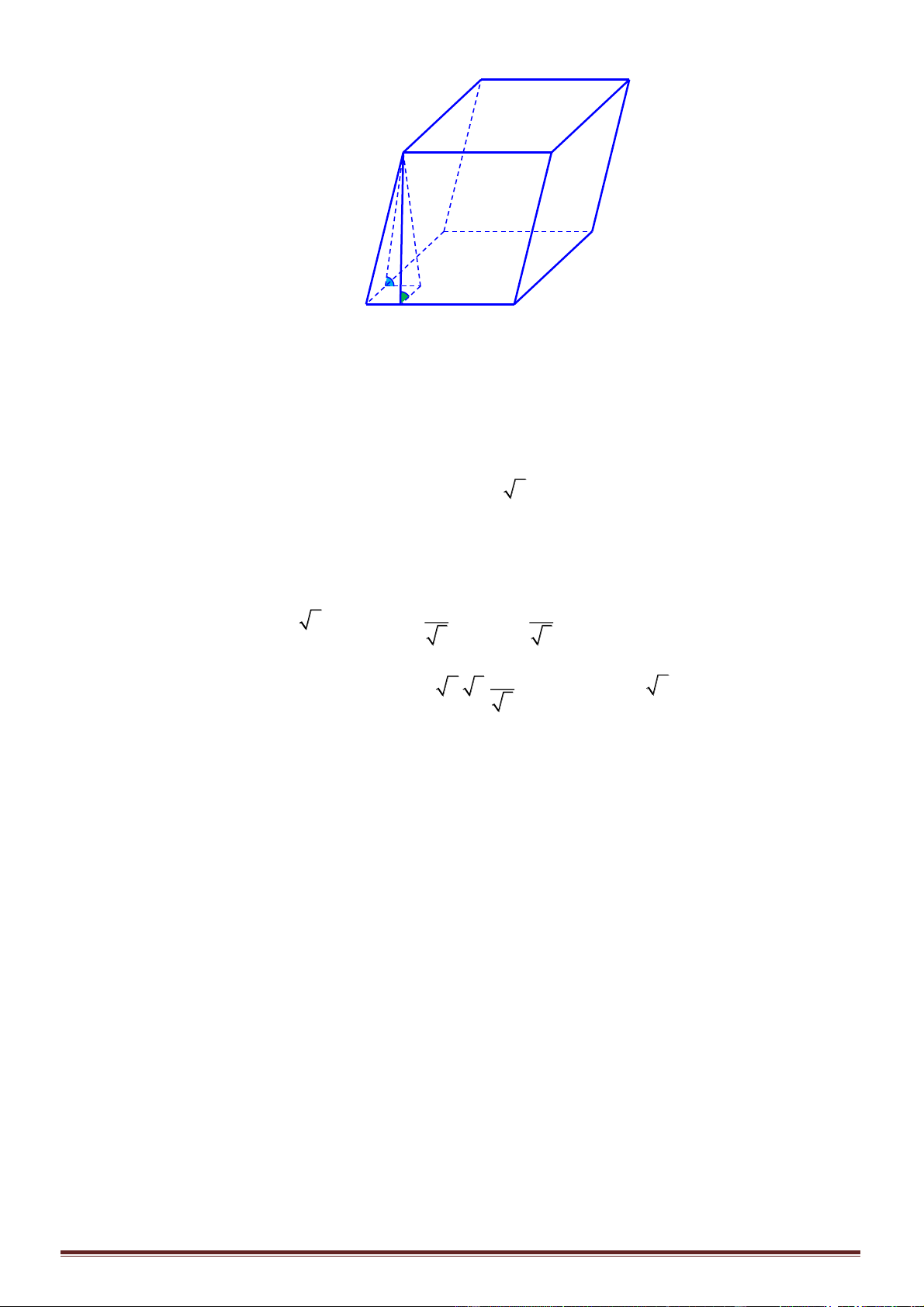
Trang 154
Gọi là hình chiếu vuông góc của lên mặt phẳng ; kẻ , thì
và
Theo giả thiết, ta có
tứ giác là hình vuông cạnh ,
Tam giác vuông cân tại có
Tam giác vuông tại có:
.
Khi đó: .Chọn A
Câu12(VD). Trong không gian với hệ tọa độ Oxyz, cho 3 đường thẳng
1
11
1
2
: 3 ,
23
xt
d y t
zt
= − +
=+
=+
2
22
2
12
: 1 ,
2
xt
d y t
zt
= − +
=+
=+
3
33
3
1
: 4 2 .
3
xt
d y t
zt
=+
=−
=−
Giả sử đường thẳng
d
cắt các đường thẳng
1 2 3
,,d d d
lần lượt tại
,A
,B
C
sao cho
B
là trung điểm của
AC
. Đường thẳng
d
đi qua điểm nào trong các điểm sau đây?
A.
(4; 1;0).M −
B.
(2;0;2).N
C.
(0;2;4).P
D.
( 1;3;1).Q −
Gii
Ta có
1 1 1 2 2 2 3 3 3
( 2 ;3 ;2 3 ), ( 1 2 ;1 ;2 ), (1 ;4 2 ;3 ).A t t t B t t t C t t t− + + + − + + + + − −
Do B là trung điểm của AC nên ta có:
1 3 2 1 2 3 1
1 3 2 1 2 3 2
1 3 2 1 2 3 3
2 1 2 4 4 1 1
3 4 2 2 2 2 2 5 1
2 3 3 4 2 3 2 1 2
t t t t t t t
t t t t t t t
t t t t t t t
− + + + = − + − + = − =
+ + − = + − − = − =
+ + − = + − − = − =
H
A
( )
ABCD
HK AB⊥
HI AD⊥
( ) ( )
(
)
,ABB A ABCD HKA
=
( ) ( )
(
)
,ADD A ABCD HIA
=
45HKA HIA
= =
HKA HIA
=
HI HK=
AIHK
a
( )
0a
2AH a=
AHK
H
HK HA a
==
AHA
H
2 2 2
AA AH A H
=+
( )
2
2
21aa + =
1
3
a=
1
3
AH
=
.
.
ABCD A B C D ABCD
V S A H
=
.
1
7. 3.
3
ABCD A B C D
V
=
.
7
ABCD A B C D
V
=
A
B
C
D
A
B
C
D
I
H
K

Trang 155
Suy ra phương trình đường thẳng d:
1 2 3
1 1 1
x y z− − −
==
−−
suy ra đáp án A
Câu 13. .(VD).Trong không gian với hệ tọa độ Oxyz,Tìm phương trình mp (P) đi qua M(1; 2; 4) và cắt các tia Ox,
Oy, Oz lần lượt tại A(a; 0; 0), B(0; b; 0), C(0; 0; c) sao cho thể tích của khối tứ diện OABC là nhỏ nhất với a, b, c là
số dương.
A. (P): 3x +6 y + 12z – 1 = 0. B. (P):4 x + 2y + z – 1 = 0.
C. (P): 4x +2y + z – 12 = 0. D. (P): 3x –4y + z +1 = 0.
Gii
1
.OB.OC
66
OABC
abc
V OA==
.Phương trình (ABC):
1
x y z
a b c
= = =
.
(ABC) qua M(1;2;4) nên
1
x y z
a b c
= = =
Theo BĐT Coossi :
3
min
1 2 4 8
1 3 36
1 2 4 1
36 3, 6, 12
3
V
a b c abc
V a b c
a b c
= + +
= = = = = = =
Vậy (P): 4x +2y + z – 12 = 0.Chọn C.
Câu 14.(VDC). . Cho hai đường thẳng
1
1
( ): 2
1
xt
d y t
z
=+
=−
=
và
2
2 1 1
( ):
1 2 2
x y z
d
− − +
==
−
. Mặt phẳng
()P
thay đổi
luôn song song với cả hai đường thẳng
12
( ),( )dd
. Khi đó giá trị nhỏ nhất của tổng
12
( ,( )) ( ,( ))T d d P d d P=+
là
A.
1
.
3
B.
2
.
3
C.
5
.
3
D.
7
.
3
Hướng dẫn gii
Ta có đường thẳng
1
()d
qua
1
(1;2;1)M
có véc tơ chỉ phương
1
(1; 1;0)u =−
, đường thẳng
2
()d
qua
2
(2;1; 1)M −
có véc tơ chỉ phương
1
(1; 2;2)u =−
Và
1 2 1 2 1 2 1 2
, ( 2; 2; 1), (1; 1; 2), , . 2 0u u M M u u M M
= − − − = − − =
nên
hai đường
12
( ),( )dd
chéo nhau
+ Nếu
12
( ),( )dd
nằm về hai phía của
()P
thì
1 2 1 2
( ,( )) ( ,( )) ( , )T d d P d d P d d d= + =
+ Nếu
12
( ),( )dd
nằm về một phía của
()P
thì
1 2 1 2
( ,( )) ( ,( )) ( , )T d d P d d P d d d= +
Vậy giá trị nhỏ nhất của tổng T là
1 2 1 2
min 1 2
12
,.
2
( , )
3
,
u u M M
T d d d
uu
= = =
. Chn B.
Câu 49: Đáp án B
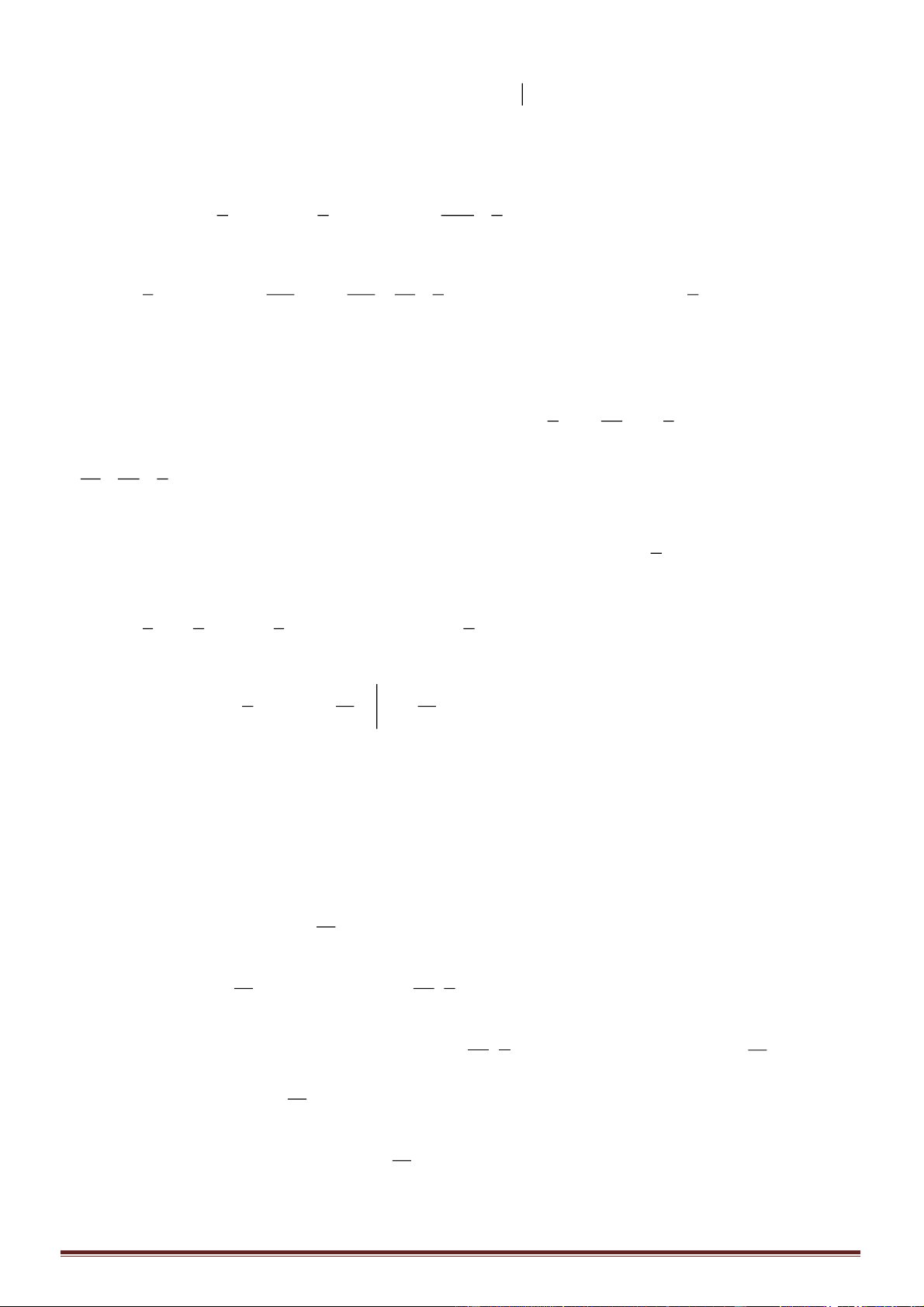
Trang 156
Phương pháp: Sử dụng công thức tích phân từng phần:
bb
b
a
aa
udv uv vdu=−
Cách giải:
Ta có:
( ) ( )
( )
( )
1 1 1
3 4 1 4 4
0
0 0 0
f1
1 1 1
x f x dx x .f(x)| x f ' x dx x f ' x dx
4 4 4 4
= − = −
Mà
( ) ( )
1
3
0
3 37
f 1 , x f x dx
5 180
==
suy ra
( ) ( )
11
44
00
37 3 1 2
x f ' x dx x f ' x dx
180 20 4 9
= − = −
Xét
( ) ( ) ( )
2
1 1 1 1
2
4 4 2 8 2
0 0 0 0
2
4 2 1
f ' x kx dx f ' x dx 2k x f ' x dx k x dx 2k. k .
9 9 9
k 4k 4
0 k 2
9 9 9
−
+ = + + = + +
= − + = =
Khi đó,
( ) ( ) ( ) ( )
1
2
4 4 4 5
0
2
f ' x 2x dx 0 f ' x 2x 0 f ' x 2x f x x C
5
+ = + = = − = − +
Mà
( ) ( )
55
3 2 3 2
f 1 .1 C C 1 f x 1 x
5 5 5 5
= − + = = − = −
( )
1
11
56
00
0
2 1 1
f x 1 dx x dx x
5 15 15
− = − = − = −
Câu 50: Chn B
Cách gii:
Đặt
2
2t x x=−
Ta có:
' 2 2, ' 0 1t x t x= − = = =
Lập bảng biến thiên ta được:
21
[-1; ]
4
t
Ta thấy với mỗi
21
[-1; ]
4
t
sẽ có 2 nghiệm
37
[ ; ]
22
x
−
Do đó: Để
2
( 2 )f x x m−=
có 4 nghiệm thuộc vào đoạn
37
[ ; ]
22
−
thì phương trình f(t)=m,
21
[-1; ]
4
t
phải có 2
nghiệm
21
( ) , [ 1, ]
4
f x m x= = −
có 2 nghiệm
Để đường thẳng y=m cắt đồ thị y=f(x)
21
[ 1, ]
4
x−
tại 2 điểm thì
24m
,m=5
=> m nhận các giá trị 3,4,5

Trang 157
Vậy tổng là 12
ĐỀ 39
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA
⊥
(ABCD), SA = a
2
.
Tính thể tích V của khối chóp S.ABCD?
A. V =
6
2
3
a
. B. V =
4
2
3
a
. C. V =
3
2
3
a
. D. V =
2
3
a
.
Câu 2: Trong các hàm số sau, hàm số nào có đồ thị như hình bên?
A.
3
31= − −y x x
. B.
32
3 3 1= − − −y x x x
.
C.
3
1
31
3
= + −y x x
. D.
32
3 3 1= + − +y x x x
.
Câu 3: Cho hàm số f x( ) xác định và liên tục trên khoảng (− + ; ) , có bảng biến thiên như
hình sau:
Mệnh đề sau đây đúng?
A. Hàm số đồng biến trên khoảng
();3− −
. B. Hàm số nghịch biến trên khoảng
(1;+).
C. Hàm số đồng biến trên khoảng
()1;− +
. D. Hàm số nghịch biến trên khoảng
( 1);−
.
Câu 4: Tính thể tích V của khối lập phương ABCD.A
’
B
’
C
’
D
’
, biết AC
’
=
3a
.
A. V = a
3
. B. V =
4
63
3
a
. C. V = 3
3
3
a
. D. V =
3
3
a
.
Câu 5: Cho khối chóp S.ABC có hai mặt phẳng (SBA) và (SBC) cùng vuông góc với mặt phẳng
(ABC), , đáy ABC là tam giác đều cạnh a, SC =
7a
. Tính độ dài đường cao h của khối chóp?

Trang 158
A. h = a. B. h = 2
2a
. C. h =
6a
. D.
5a
.
Câu 6: Điểm cực đại của đồ thị hàm số
3
35= − +y x x
là điểm:
A. M
(
1;3
)
. B. N
(−
1;7
)
. C. Q
(
3;1
)
.
D. P
(
7;
−
1
)
.
Câu 7: Tìm các số thực m để hàm số
( )
32
2 3 5= + + + −y m x x mx
có cực trị.
A.
2
31
−
−
m
m
. B.
31− m
. C.
3
1
−
m
m
.
D.
21− m
.
Câu 8: Cho hàm số
( )
=y f x
xác định, liên tục trên và có bảng biến thiên như hình sau:
Đồ thị hàm số
( )
=y f x
cắt đường thẳng y
=
2018
2019
tại bao nhiêu điểm?
A. 4 . B. 0 . C. 2 .
D. 1.
Câu 9: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
2
2
1
−
=
−+
x
y
x mx
có đúng 3 đường
tiệm cận.
A.
22− m
. B.
2
2
5
2
−
−
m
m
m
. C.
2
2
−
m
m
.
D.
2
5
2
2
−
m
m
m
.
Câu 10: Tiếp tuyến đồ thị hàm số
32
31= − +y x x
tại điểm A(3;1) là đường thẳng
A.
9 26= − −yx
. B.
93= − −yx
. C.
92= − −yx
.
D.
9 26=−yx
.
Câu 11: Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( )
4
=+f x x
x
trên đoạn 1;3 bằng
A.
65
3
. B. 6 . C. 20 .
D.
52
3
.
Câu 12: Cho hàm số
( )
4 2 2
2 1 1= − − + +y x m x m
. Tìm tất cả các giá trị của tham số m để hàm số có
cực đại, cực tiểu và các điểm cực trị của đồ thị lập thành một tam giác có diện tích lớn nhất.

Trang 159
A.
1
2
=m
. B. m
=
0. C. m
=
1.
D.
1
2
=−m
.
Câu 13: Đường thẳng
2y =
là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây?
A.
21
.
1
x
y
x
+
=
−
B.
34
.
2
x
y
x
−
=
−
C.
1
.
2
x
y
x
+
=
−
D.
1
.
21
x
y
x
−+
=
−+
Câu 14: Rút gọn biểu thức
3
32
4
1
4
.
log
.
=
a
a a a
B
aa
, (Giả sử tất cả các điều kiện đều được thỏa mãn) ta
được kết quả là
A.
60
91
. B.
91
60
−
. C.
3
5
.
D.
5
3
−
.
Câu 15: Số nghiệm của phương trình
1
9 2.3 7 0
+
+ − =
xx
là
A. 0 . B. 2 . C. 4 .
D. 1.
Câu 16: Tập xác định D của hàm số
( )
1
3
1=+yx
là
A.
( )
;1= − −D
. B.
=D
. C.
\1=−D
.
D.
( )
1;− +
.
Câu 17: Giải bất phương trình
( ) ( )
22
log 3 2 log 6 5− −xx
được tập nghiệm là
( )
a; .b
Hãy tính tổng
=+S a b
.
A.
8
3
=S
. B.
28
15
=S
. C.
11
5
=S
.
D.
31
6
=S
.
Câu18: Biết rằng tập các giá trị của tham số
m
để phương trình
( ) ( )
3 9 2 1 3 1 0
xx
m m m− + + − − =
có hai nghiệm phân biệt là một khoảng
( )
;ab
. Tính tích
.ab
.
A.
4
. B.
3−
. C.
2.
. D.
3
.
Câu 19: Giá trị của biểu thức
2 2 2 2
log 2 log 4 log 8 ... log 256M = + + + +
bằng
A.
48
. B.
56
. C.
36
. D.
2
8log 256
.
Câu 20: Tích các nghiệm của phương trình
2
22
log (x 4) log (x 1) 3+ − − =
bằng?
A. 8 B.13 C. 12 D. -12
Câu 21 :Cho số phức z thỏa mãn hệ thức:
( ) ( )
1 2i z 2 3i z 2 2i+ + − = − −
. Tính mô-đun của z?
A.
6
B.
2
C.
3
D.
5
Câu 22 :Cho số phức z thỏa mãn:
z.z 1=
và
z 1 2−=
. Xác định phần thực của z
A. 0 B. -1 C. 1 D. 2
Câu 23 :Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn điều
kiện:
( )
2
log z 3 4i 1− − =
A. Đường thẳng qua gốc tọa độ B. Đường tròn bán kính 1
C. Đường tròn tâm
( )
I 3; 4−
bán kính 2 D. Đường tròn tâm
( )
I 3; 4−
bán kính 3

Trang 160
Câu 24: Công thức nguyên hàm nào sau đây là công thức sai?
A.
d
ln
x
xC
x
=+
.B.
1
d ( 1)
1
x
x x C
+
= + −
+
.C.
d (0 1)
ln
x
x
a
a x C a
a
= +
.D.
2
1
d tan
cos
x x C
x
=+
.
Câu 25:Cho
f
,
g
là hai hàm liên tục trên
1;3
thỏa:
( ) ( )
3
1
3 d 10f x g x x+=
.
( ) ( )
3
1
2 d 6f x g x x−=
. Tính
( ) ( )
3
1
df x g x x+
.
A. 8. B. 9. C.
6
. D. 7.
Câu 26:Giả sử
( ) ( )
2
1
2 1 ln d ln2 , ;x x x a b a b− = +
. Khi đó
ab+
?
A.
5
2
.
B.
2.
C.
1.
D.
3
2
.
Câu 27: Khi đó Biết
4
2
3
d
ln2 ln3 ln5,
x
I a b c
xx
= = + +
+
với
,,abc
là các số nguyên. Tính
.S a b c= + +
A.
6S =
. B.
2S =
. C.
2S =−
. D.
0.S =
Câu 28 :Cho hình phẳng
( )
H
giới hạn bởi các đường
2
; 0; 2.y x y x= = =
Tính thể tích
V
của
khối tròn xoay thu được khi quay
( )
H
quanh trục
Ox
.
A.
8
.
3
V =
B.
32
.
5
V =
C.
8
.
3
V
=
D.
32
5
Câu 29:Ông An có một mảnh vườn hình Elip có độ dài trục lớn bằng
16m
và độ dài trục bé
bằng
10m
. Ông muốn trồng hoa trên một dải đất rộng
8m
và nhận trục bé của elip làm trục đối
xứng (như hình vẽ). Biết kinh phí để trồng hoa là
100.000
đồng/
2
1m
. Hỏi ông An cần bao
nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền được làm tròn đến hàng nghìn.)
A.
7.862.000
đồng. B.
7.653.000
đồng. C.
7.128.000
đồng. D.
7.826.000
đồng.
Câu 30 :Gọi
12
z ,z
là hai nghiệm của phương trình:
2
z 2z 5 0− + =
trên tập số phức. Hãy tính giá trị
của biểu thức:
22
12
A z z=+
A. 11 B. 10 C. 12 D.
x2=
Câu 31 :Trong mặt phẳng Oxy, tìm tọa độ điểm M biểu diễn số phức z thỏa mãn:
( )
z 2i 1 i 2 0− − + =
8m

Trang 161
A.
43
M;
55
B.
43
M;
57
C.
33
M;
55
D.
43
M;
95
Câu 32 :Cho cấp số nhân
()
n
u
có
1
3=−u
và
2=−q
. Tính tổng 10 số hạng đầu tiên của cấp số
nhân.
A.
10
511=−S
. B.
10
1023=S
. C.
10
1025=S
.
D.
10
1025=−S
.
Câu 33 :Từ một hộp có 1000 thẻ được đánh số từ 1 đến 1000 . Chọn ngẫu nhiên ra hai thẻ Tính
xác suất để chọn được hai thẻ sao cho tổng của các số ghi trên hai thẻ nhỏ hơn 700 .
A.
2
1000
243250
C
. B.
2
1000
12181
C
. C.
2
1000
243253
C
.
D.
2
1000
121975
C
.
Câu 34: Một lớp có 15 học sinh nam và 20 học sinh nữ. Có bao nhiêu cách chọn 5 bạn học sinh
sao cho có đúng 3 học sinh nữ.
A.
110790
B.
119700
C.
117900
D.
110970
Câu 35: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
2019; 2019−
để phương trình
( )
2
1 sin sin2 cos2 0m x x x+ − + =
có nghiệm ?
A.
4036
. B.
2021
. C.
4037
. D.
2019
.
Câu 36: Cho lăng trụ đứng ABC. A
’
B
’
C
’
có đáy ABC là tam giác vuông tại B, AB = a, BC =
2a
, mặt phẳng (A
’
BC) tạo với đáy (ABC) một góc 30
0
. Tính thể tích V của khối lăng trụ?
A. V =
6
3
a
. B. V =
12
6
3
a
. C. V =
3
6
3
a
. D. V =
6
6
3
a
.
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = a. Hình chiếu
của S lên mặt phẳng (ABCD) là trung điểm H của cạnh AB, SC tạo với đáy một góc 45
0
. Tính
khoảng cách d từ A đến mặt phẳng (SCD)?
A. d =
4
6a
. B. d =
3
3a
. C. d =
3
6a
. D. d =
6
6a
.\
Câu 38: Cho khối nón (N) có bán kính dáy bằng 3, diện tích xung quanh bằng 15
. Tính thể tích
V của khối nón (N).
A. V = 12
. B. V = 20
. C. V = 36
. D. V = 60
.
Câu 39: Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy
bằng hình tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính của quả bóng bàn. Gọi
S
1
là tổng diện tích của ba quả bóng bàn, S
2
là diện tích xung quanh của hình trụ. Tính tỉ số k =
2
1
S
S
?
A. k = 1. B. k = 2. C. k = 4. D. k =
2
1
.
Câu 40: Cho hình chóp tam giác đều S.ABC. Hình nón (N) có đỉnh S và đường tròn dáy là đường
tròn nội tiếp tam giác ABC. Tỉ số thể tích của hình nón (N) và khối chóp S.ABC bằng bao nhiêu?

Trang 162
A.
4
. B.
3
. C.
33
. D.
32
Câu 41: Trong không gian Oxyz, cho hai điểm A(3; -2; 3), B(-1; 2; 5). Tìm tọa độ trung điểm của
đoạn thẳng AB?
A. (-2; 2; 1). B. (1; 0; 4). C. (2; 0 ;8). D. (2; -2; -1).
Câu 42: Trong không gian Oxyz, cho mặt phẳng (P): 3x + 4y + 2z + 4 = 0 và điểm A(1; -2; 3).
Tính khoảng cách d từ A đến mặt phẳng (P)?
A. d =
9
5
. B. d =
29
5
. C. d =
29
5
. D. d =
3
5
.
Câu 43: Trong không gian Oxyz, cho đường thẳng d:
−=
+=
=
tz
ty
x
5
32
1
(t
R). Vectơ nào sau đây là
vectơ chỉ phương của d?
A.
1
u
= (0; 3; -1). B.
2
u
= (1; 3; -1). C.
3
u
= (1; -3; -1). D.
4
u
= (1; 2; 5).
Câu 44: Trong không gian Oxyz, phương trình nào sau đây là phương trình của mặt cầu có tâm
I(1; 2; -1) và tiếp xúc với mặt phẳng (P): x – 2y – 2z – 8 = 0?
A. (x + 1)
2
+ (y + 2)
2
+ (z – 1)
2
= 3. B. (x – 1)
2
+ (y – 2)
2
+ (z + 1)
2
= 3.
C. (x + 1)
2
+ (y + 2)
2
+ (z – 1)
2
= 9. D. (x – 1)
2
+ (y – 2)
2
+ (z + 1)
2
= 9.
Câu 45: Trong không gian Oxyz, cho ba điểm A(1; 0; 0), B(0; -2; 0), C(0; 0; 3). Phương trình nào
sau đây là phương trình của mặt phẳng (ABC)?
A.
1
123
=+
−
+
zyx
. B.
1
312
=++
−
zyx
. C.
1
321
=+
−
+
zyx
. D.
1
213
=
−
++
zyx
.
Câu 46: Trong không gian Oxyz, cho hai đường thẳng
1
:
1
1
1
2
2
1 −
=
+
=
+ zyx
và
2
:
1
2
1
1
4
2
−
+
=
−
=
−
+ zyx
. Đường vuông góc chung của
1
và
2
đi qua điểm nào trong các điểm sau
đây?
A. M(3; 1; -4). B. N(1; -1; -4). C. P(2; 0; 1). D. Q(0; -2; -5).
Câu 47: Trong không gian Oxyz, cho điểm A(3; 0; -2) và mặt cầu (S): (x – 1)
2
+ (y + 2)
2
+ (z +
3)
2
= 25. Một đường thẳng đi qua A, cắt mặt cầu (S) tại hai điểm M, N. Độ dài ngắn nhất của MN
là bao nhiêu?
A. 8. B. 4. C. 6. D. 10.
Câu 48: Trong không gian Oxyz, cho điểm M(1; 2; 5). Mặt phẳng (P) đi qua điểm M và cắt các
trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm tam giác ABC.
Phương trình nào sau đây là phương trình mặt phẳng (P)?
A.
1
125
=++
zyx
. B. x + 2y +5z – 30 = 0.
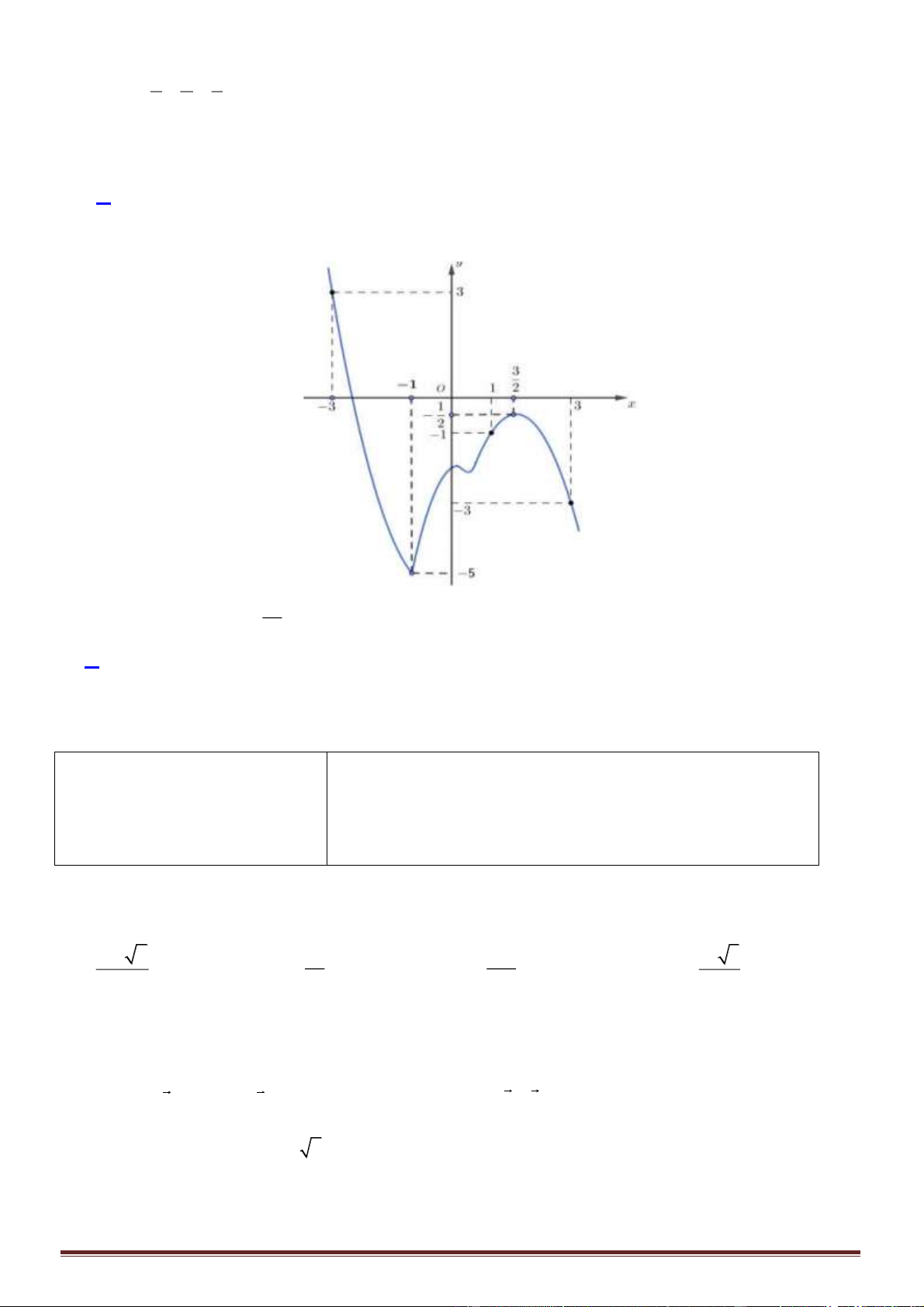
Trang 163
C.
0
125
=++
zyx
. D. x + y + z – 8 = 0.
Câu 49: Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn −2019;2019 để hàm
số
32
61= − + +y x x mx
đồng biến trên khoảng
(1; ).+
A. 2008. B. 2030. C. 2005.
D. 2018.
Câu 50: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
như hình vẽ
Hàm số
( )
2
1
2
x
y f x x= − + −
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
( )
2; 0−
. B.
( )
3; 1−
. C.
( )
3; +
. D.
( )
1; 3
.
……………………………………….HẾT………………………………………
www.thuvienhoclieu.com
ĐỀ 40
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Cho hình lăng trụ tam giác đều có các cạnh đều bằng a . Thể tích khối lăng trụ đều là:
A.
3
22
3
a
B.
3
3
a
C.
3
2
3
a
D.
3
3
4
a
Câu 2: Đồ thi hàm số nào sau đây có 3 điểm cực trị :
A.
42
2 4 1y x x= + +
B.
42
21y x x= + −
C.
42
21y x x= − −
D.
42
21y x x= − − −
Câu 3: Cho
( )
a 3;2;1 ;=
( )
b 2;0;1 .=−
Độ dài của vecto
ab+
bằng:
A. 1 B.
2
C. 3 D. 2
Câu 4: Cho hàm số
( )
y f x=
có bảng biến thiên như sau

Trang 164
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
1;1−
. B.
( )
;1−
. C.
( )
1; +
. D.
( )
1;0−
.
Câu 5. Cho các số thực dương
,ab
. Khẳng định nào sau đây là khẳng định đúng?
A.
( )
log log .logab a b=
. B.
log( ) log loga b a b+ = +
.
C.
log log log
a
ab
b
æö
÷
ç
=-
÷
ç
÷
ç
èø
. D.
log log log( )a b a b- = -
.
Câu 6. Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
12
;
,
( )
11=f
và
( )
2 2018=f
. Tính tích
phân
( )
2
1
=
'.fI x dx
A.
2016= .I
B.
2018= .I
C.
2017= .I
D.
2017=− .I
Câu 7: Cho mặt cầu (S) tâm I bán kính R và có phương trình:
2 2 2
x y z x 2y 1 0+ + − + + =
. Trong
các mệnh đề sau, mệnh đề nào đúng:
A.
1
I ;1;0
2
−
và R=
1
4
B.
1
I ; 1;0
2
−
và R=
1
2
C.
1
I ; 1;0
2
−
và R=
1
2
D.
1
I ;1;0
2
−
và R=
1
2
Câu 8: Phương trình
( )
2
log 3 2 3x-=
có nghiệm là
A.
x =
10
3
B.
x = 2
C.
x =
11
3
D.
x = 3
Câu 9: Trong không gian Oxyz mặt phẳng (P) đi qua điểm M( - 1;2;0) và có VTPT
n (4;0; 5)=−
có phương trình là:
A. 4x - 5y - 4 = 0 B. 4x - 5y + 4 = 0 C. 4x - 5z + 4 = 0 D. 4x - 5z - 4 = 0
Câu 10 . Tìm nguyên hàm
( )
Fx
của hàm số
( )
2= .
x
fx
A.
( )
2
2
=+.
ln
x
F x C
B.
( )
2=+.
x
F x C
C.
( )
22=+ln .
x
F x C
D.
( )
1
2
−
=+..
x
F x x C
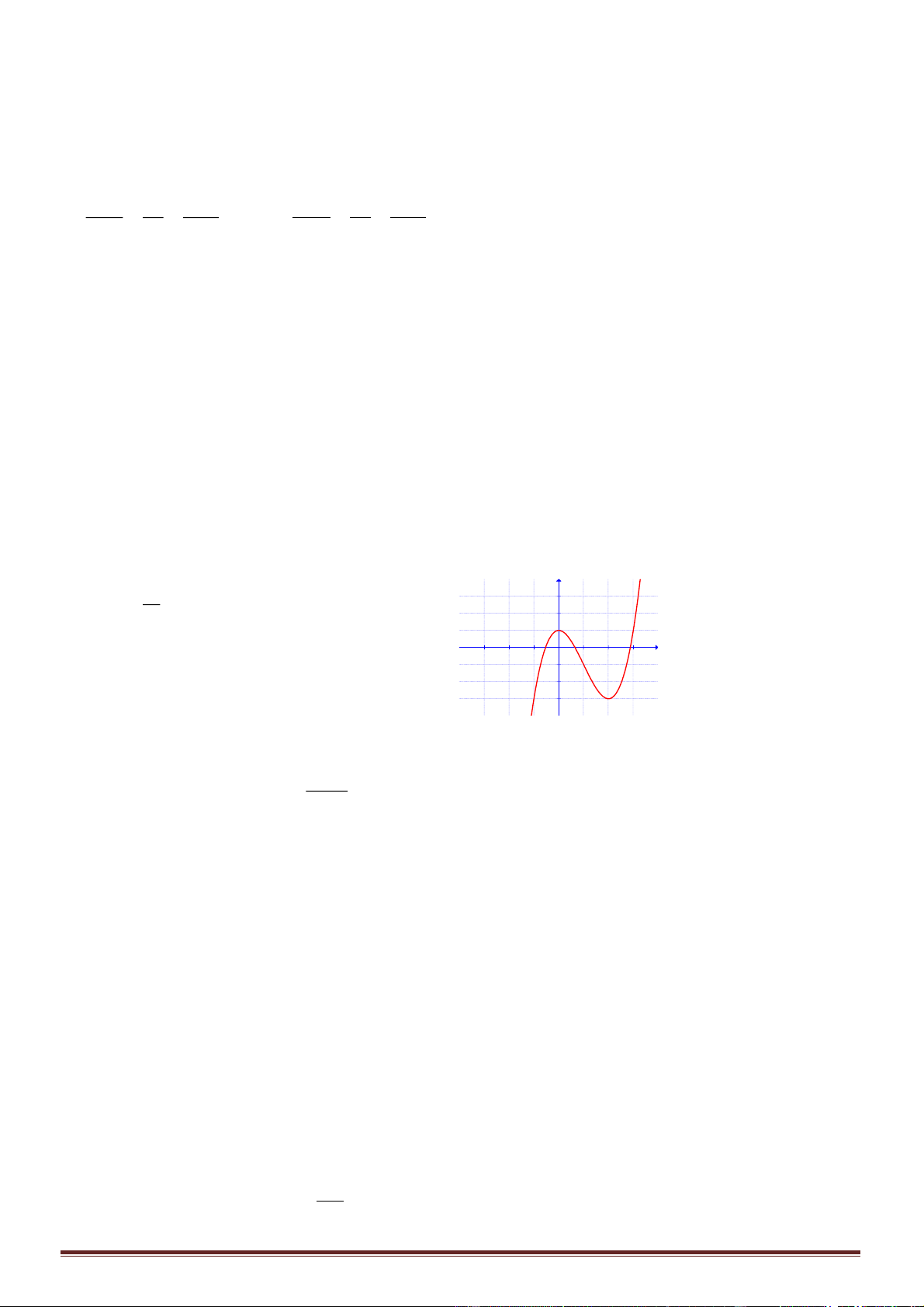
Trang 165
Câu 11:Trong không gian với hệ tọa độ Oxyz cho đường thẳng d:
( )
22
3
35
xt
y t t R
zt
=+
= −
= − +
. Phương
trình nào sau đây là phương trình chính tắc của d ?
A.
23
2 3 5
x y z−+
==
−
B.
23
2 3 5
x y z+−
==
−
C.
23x y z− = = +
D.
23x y z+ = = −
Câu 12: Hệ số của x
7
trong khai triển của (3 – x)
9
là:
A.
7
9
C
B.
7
9
C−
C.
7
9
9C
D.
7
9
9C−
.
Câu 13:Cho cấp số cộng u
1
= -3, u
6
= 27. Công sai của cấp số cộng đó là:
A. 5 B.6 c.7 d.8
Câu 14: Điểm biểu diễn của các số phức z = a + ai với a R, nằm trên đường thẳng có phương
trình là:
A. y = 2x B. y = x C. y = 3x D. y = 4x
Câu 15. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
2
1
3
.
x
yx= - + +
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
B.
32
3 1.y x x= - +
C.
32
3 1.y x x= - + +
D.
32
3 2.y x x= - +
Câu 16: Cho hàm số:
2
1
1
()
1
1
x
neu x
fx
x
a neu x
−
=
−
=
để f(x) liên tục tại điêm x
0
= 1 thì a bằng?
A. 0 B. 1 C. 2 D. -1
Câu 17. Số điểm cực trị của đồ thị hàm số
42
21y x x= + −
là:
A. 0 B. 1 C. 2 D. 3
Câu 18: Thu gọn z = i + (2 – 4i) – (3 – 2i) ta được:
A. z = 1 + 2i B. z = -1 - 2i C. z = 5 + 3i D. z = -1 - i
Câu 19: Phương trình mặt cầu tâm I(-1;-2;3) bán kính R = 2 là:
A.
2 2 2
x y z 2x 4y 6z 10 0+ + + − − + =
B.
2 2 2
x y z 2x 4y 6z 10 0+ + − − + + =
C.
( ) ( ) ( )
2 2 2
2
x 1 y 2 z 3 2− + − + + =
D.
( ) ( ) ( )
2 2 2
2
x 1 y 2 z 3 2+ + + + − =
Câu 20: Cho
log2 b=
.Tính
500
log
4
theo b là:

Trang 166
A.
1 b−
B.
3 b−
C.
3(1 )b−
D.
33b+
.
Câu 21: Trong C, phương trình z
2
+ 4 = 0 có nghiệm là:
A.
=
=−
z 2i
z 2i
B.
=+
=−
z 1 2i
z 1 2i
C.
=+
=−
z 1 i
z 3 2i
D.
=+
=−
z 5 2i
z 3 5i
Câu 22: Trong không gian Oxyz, cho đường thẳng
3 1 3
:
2 1 1
x y z
d
+ + −
==
và mặt phẳng (P) có
phương trình: x+ 2y – z + 5 = 0. Tọa độ giao điểm của d và (P) là
A. (–1;0;4) B. (4;–1;0) C. (–1;4;0) D. (4;0;–1)
Câu 23: Tập nghiệm của bất phương trình
1
4
x1
11
22
−
là:
A.
( )
0; 1
B.
5
1;
4
C.
( )
2;+
D.
( )
;0−
Câu 24: Diện tích hình phẳng (phần bôi đen) trong hình sau được tích theo công thức:
A.
( ) ( )
bc
ab
S f x dx f x dx=+
B.
( ) ( )
cb
ba
S f x dx f x dx=−
C.
( )
c
a
f x dx
D.
( )
c
a
S f x dx=
Câu 25:Cho khối nón có chu vi đường tròn đáy là
6
, chiều cao bằng
7
. Thể tích của khối nón
là
A.
37
B.
97
C.
12
D.
36
Câu 26 . Số đường tiệm cận của đồ thị hàm số
32
21
x
y
x
−
=
+
là:
A. 3 B. 2 C. 0 D. 1
Câu 27: Cho hình chóp đều S.ABCD có cạnh bên và cạnh đáy đều bằng a. Thể tích của khối chóp
S.ABCD là: A.
3
2
6
a
B.
3
2
2
a
C.
3
3
a
D.
3
a
Câu 28. Tìm đạo hàm của hàm số
3
2 logy x x=+
.
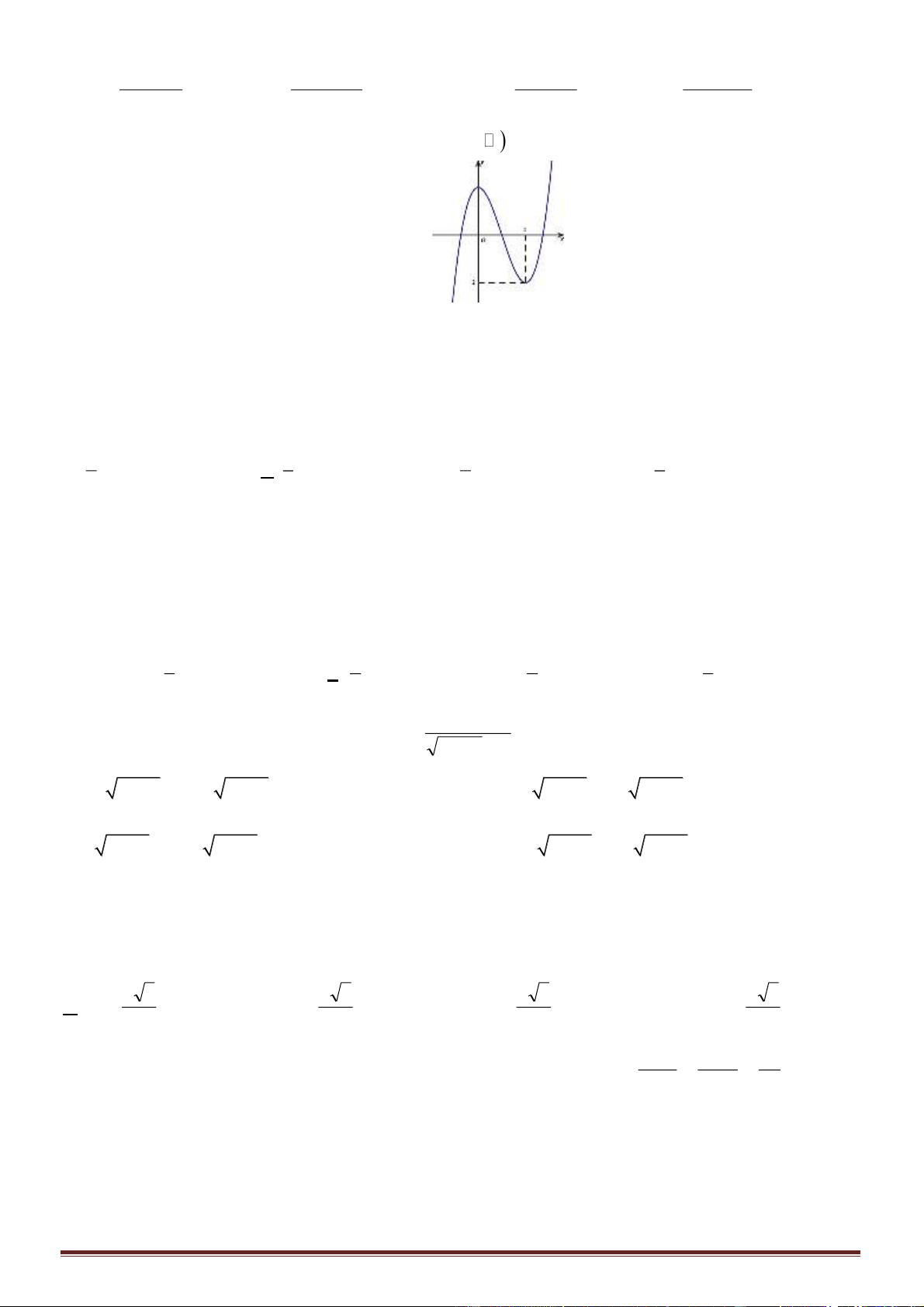
Trang 167
A.
1 .ln9
'.
.ln3
x
y
x
+
=
B.
1 .ln27
'.
.ln3
x
y
x
+
=
C.
1 .ln3
'.
.ln
x
y
x
+
=
D.
1 .ln81
'.
.ln3
x
y
x
+
=
Câu 29:Cho hàm số
32
y ax bx cx d= + + +
( )
, , ,a b c d
. Đồ thị hàm số
( )
y f x=
như hình vẽ bên.
Số nghiệm thực của phương trình
( )
2 4 0fx+=
là
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 30: Cho khối lập phương ABCD.A’B’C’D’. Tỉ số thể tích giữa khối chóp A’.ABCD và khối
lập phương bằng bao nhiêu.
A.
1
2
B.
1
3
C.
1
4
D.
1
5
Câu 31: Biết rằng phương trình
2019)2018(log
2
5
=− xx
có 2 nghiệm
12
,xx
. Tính tổng
12
xx+
.
A.
2018
21
=+ xx
. B.
2019
21
=+ xx
. C.
2018
21
−=+ xx
. D.
2019
21
3=+ xx
.
Câu 32: Mặt phẳng trung trực của đường cao của một khối nón chia nó ra thành hai phần. Tỉ số thể tích của chúng
là:
A.
1
5
. B.
1
7
. C.
1
4
. D.
1
8
.
Câu 33: Họ nguyên hàm của hàm số
412
1
)(
+−
=
x
xf
là
A.
( )
2 1 2 2 1 4− − − + +x ln x C
B.
( )
2 1 2 1 4− − − + +x ln x C
C.
( )
2 1 4 2 1 4− − − + +x ln x C
D.
( )
2 2 1 2 1 4− − − + +x ln x C
Câu 34: Cho hình chóp
ABCDS.
có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S
lên mp (ABCD) trùng với trọng tâm tam giác ABD. Mặt bên SAB tạo với đáy một góc
0
60
. Tính
khoảng cách d từ B đến
).(SADmp
A.
2
3a
d =
. B.
3
3a
d =
. C.
4
3a
d =
. D.
6
3a
d =
.
Câu35 : Trong hệ tọa độ
,Oxyz
cho điểm
)3;2;4( −M
và đường thẳng
12
2
3
2
:
−
=
+
=
+ zyx
d
. Tìm
điểm
/
M
thuộc đường thẳng d sao cho độ dài
/
MM
ngắn nhất.
A.
)1;0;1(
/
M
B.
)2;0;3(
/
M
C.
)0;0;3(
/
M
D.
)1;0;1(
/
−M
Câu 36: Tìm các giá trị của tham số m để hàm số
1)232()1(
223
+++−−+= xmmxmxy
tăng trên
khoảng
);2( +
.

Trang 168
A.
2
2
1
− m
B.
2− m
C.
3m
D.
2
2
3
− m
Câu 37: Trên mp Oxy, tập hợp các điểm biểu diễn số phức
z
thoả mãn điều kiện
− − = + +z 2 3i z 4 i
là
A. Đường tròn
− + − =
22
(C):(x 2) (y 3) 25
B. Đường thẳng:
3 4 13 0xy− − =
C. Đường thẳng:
4 12 7 0xy+ + =
D. Đường thẳng: 3x+y+1=0
Câu 38: Cho
−=
+
e
1
2
1
ln
)ln1(
ln
c
badx
xx
x
. Tìm
cbaS ++=
A. 2 B. 3 C.4 D.
5
Câu 39: Gọi S là tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số y =
3
1
x
3
– mx
2
+ (m
2
– 1)x có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y = 5x –
9. Tính tổng tất cả các phần tử của S.
A. 6. B. 3. C.
5
8
. D. 0.
Câu 40: Cho hình thập giác lồi A
1
A
2
A
3......
A
10
, gọi A là tập hợp các tam giác mà mỗi tam giác có
ba đỉnh là các đỉnh của hình thập giác lồi . Chọn ngẫu nhiển từ A ra một tam giác . Tính xác suất
để chọn được tam giác có các cạnh không là cạnh của hình thập giác.
A.
12
5
B.
12
7
C.
7
5
D.
3
1
Câu 41: Trong không gian
Oxyz
, cho mặt phẳng
( )
P
đi qua điểm
( )
1;2;3M
và cắt các trục
Ox
,
Oy
,
Oz
lần lượt tại các điểm
A
,
B
,
C
(khác
O
). Viết phương trình mặt phẳng
( )
P
sao cho
M
là
trực tâm của tam giác
ABC
.
A.
6 3 2 6 0x y z+ − − =
. B.
2 3 14 0x y z+ + − =
.
C.
2 3 11 0x y z+ + − =
. D.
3
1 2 3
x y z
+ + =
.
Câu 42 : Có bao nhiêu số phức
z
thỏa mãn
ziz =− 2
và
1−=− ziz
A. 1 B. 2 C. 3 D. 4
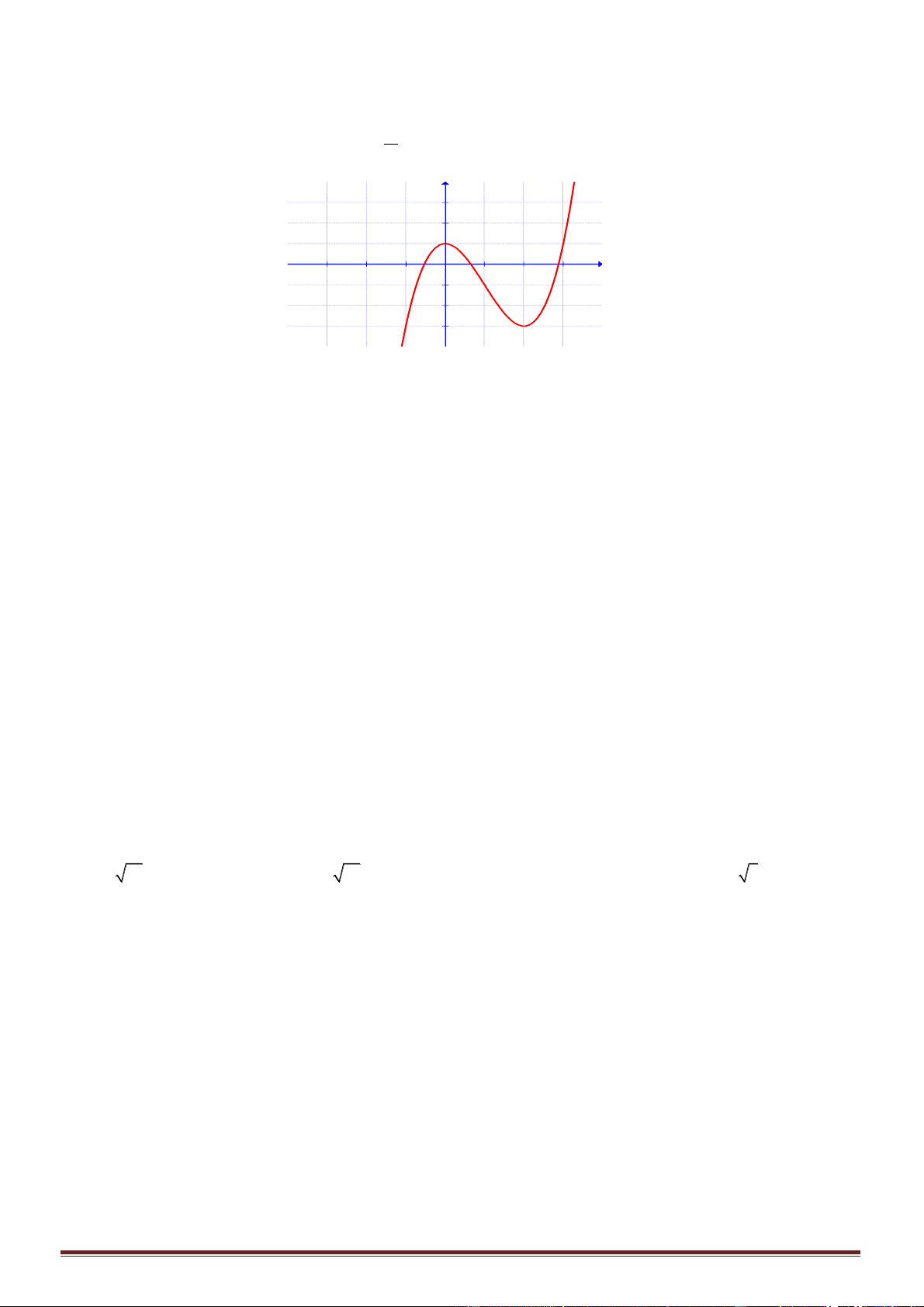
Trang 169
Câu 43: Đường cong trong hình bên là đồ thị của một hàm số
)(xfy =
liên
tục trên
R
. Tìm tất cả các giá trị thực của tham số m để phương trình
mxf =)(cos
có nghiệm thuộc khoảng
);
2
(
là
A.
)1;1(−
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
B.
)1;3(−
C.
)0;3(−
D. (
)0;1−
Câu 44: Ông An gửi 100 triệu vào tiết kiệm trong một thời gian khá lâu mà không rút ra với lãi
suất ổn định trong mấy chục năm qua là 10%/ 1 năm. Tết năm nay do ông kẹt tiền nên rút hết ra
để gia đình đón Tết. Sau khi rút cả vốn lẫn lãi, ông trích ra gần 10 triệu để sắm sửa đồ Tết trong
nhà thì ông còn 250 triệu. Hỏi ông đã gửi tiết kiệm bao nhiêu lâu ?
A. 19 năm B. 17 năm C. 15 năm D. 10 năm
Câu45 : Trong không gian
Oxyz
cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 49S x y z− + + + + =
và
( )
:2 2 10 0x y z
+ − + =
. Tìm bán kính r của đường tròn giao tuyến của
( )
S
và
( )
.
A.
10.r =
B.
2 10.r =
C.
2.r =
D.
2 5.r =
Câu 46: Một tấm tôn hình vuông có cạnh bằng
dm16
, người ta gấp tấm tôn thành 4 phần đều nhau
và dựng lên thành một hình lăng trụ tứ giác đều. Tính thể tích
V
của khối lăng trụ được hình
thành.
A.
3
64dmV =
. B.
3
256dmV =
. C.
3
16dmV =
. D.
3
68dmV =
.
Câu 47: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
, tam giác
SAB
đều, góc giữa
( )
SCD
và
( )
ABCD
bằng
o
60
. Gọi
M
là trung điểm của cạnh
AB
. Biết rằng hình chiếu vuông
góc của đỉnh
S
trên mặt phẳng
( )
ABCD
nằm trong hình vuông
ABCD
. Khoảng cách giữa hai
đường thẳng
SM
và
AC
là

Trang 170
A.
5
5
a
. B.
5
10
a
. C.
35
10
a
. D.
53
3
a
.
Câu 48: Cho hàm số
( )
y f x=
có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của
hàm số
( )
y f x
=
(
( )
y f x
=
liên tục trên R). Xét hàm số
( )
( )
2
3g x f x=−
. Mệnh đề nào dưới đây
sai?
A. Hàm số
( )
gx
đồng biến trên
( )
1;0−
. B. Hàm số
( )
gx
nghịch biến trên
( )
;1− −
.
C. Hàm số
( )
gx
nghịch biến trên
( )
1;2
. D. Hàm số
( )
gx
đồng biến trên
( )
2;+
.
Câu 49: Xét
,xy
là các số thực dương thỏa mãn
2
4
log 2 4 1
xy
xy
xy
+
=−+
+
. Giá trị nhỏ nhất của
( )
4 2 2 2
3
2 2 6x x y x
P
xy
−+
=
+
bằng
A.
25
9
. B.
4
. C.
9
4
. D.
16
9
.
Câu 50: Tìm tất cả các giá trị của tham số m sao cho đường thẳng
:d y x m=+
cắt đồ thị hàm số
21
( ):
1
x
Cy
x
+
=
−
tại hai điểm phân biệt
,MN
sao cho diện tích tam giác
IMN
bằng
4
với
I
là tâm
đối xứng của
()C
A.
3; 1mm= = −
. B.
3; 5mm= = −
. C.
3; 3mm= = −
. D.
3; 1mm= − = −
.
--------- HT ---------
y
O
x
2−
1
2
1−
4
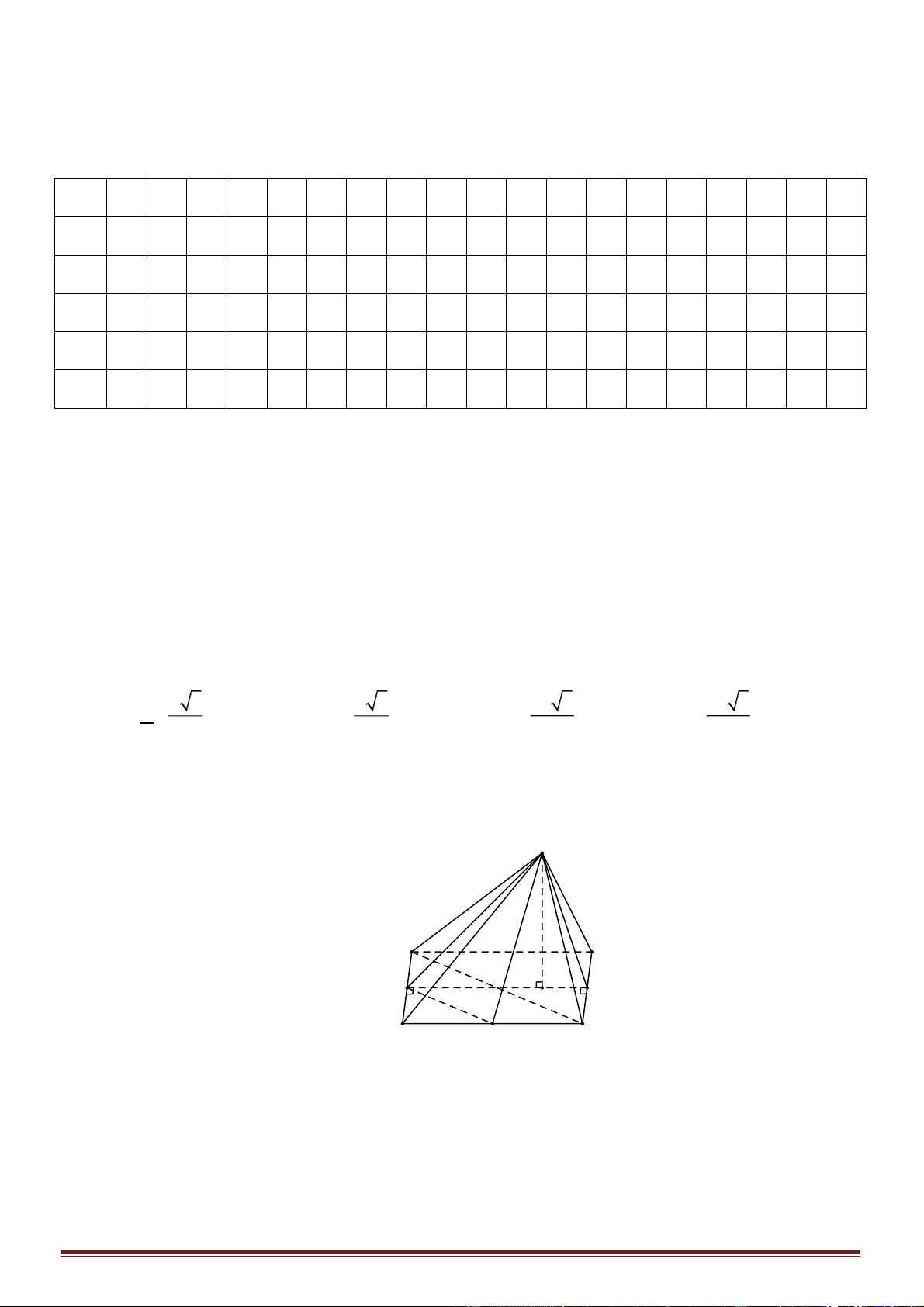
Trang 171
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT 5 CÂU CUỐI
I. Đáp án
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
A
C
C
D
C
C
B
A
C
A
A
D
B
B
B
C
B
D
D
Câu
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
C
A
A
A
A
A
B
A
A
D
B
A
B
C
A
D
D
D
D
Câu
39
40
41
42
43
44
45
46
47
48
49
50
D
A
B
A
B
D
B
B
A
C
D
A
II. GIẢI CHI TIẾT CÂU 46 ĐẾN CÂU 50
Câu 46: Khi gấp tấm tôn theo yêu cầu bài toán thì tạo thành một khối hình hộp có đáy là hình
vuông có cạnh bằng 4dm. Như vậy
3
25616.4.4 dmV ==
.
Câu 47: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
, tam giác
SAB
đều, góc giữa
( )
SCD
và
( )
ABCD
bằng
o
60
. Gọi
M
là trung điểm của cạnh
AB
. Biết rằng hình chiếu
vuông góc của đỉnh
S
trên mặt phẳng
( )
ABCD
nằm trong hình vuông
ABCD
. Khoảng
cách giữa hai đường thẳng
SM
và
AC
là
A.
5
5
a
. B.
5
10
a
. C.
35
10
a
. D.
53
3
a
.
Hướng dẫn gii
Chn A
Gọi
I
là trung điểm cạnh
CD
, khi đó
( )
AB SM
AB SMI
AB MI
⊥
⊥
⊥
.
Do
//CD AB
nên
( )
CD SMI⊥
(( ),( ))SCD ABCD SIM=
.
Vẽ
SH MN⊥
tại
H MN
thì
( )
SH ABCD⊥
.
H
I
N
M
C
B
A
D
S
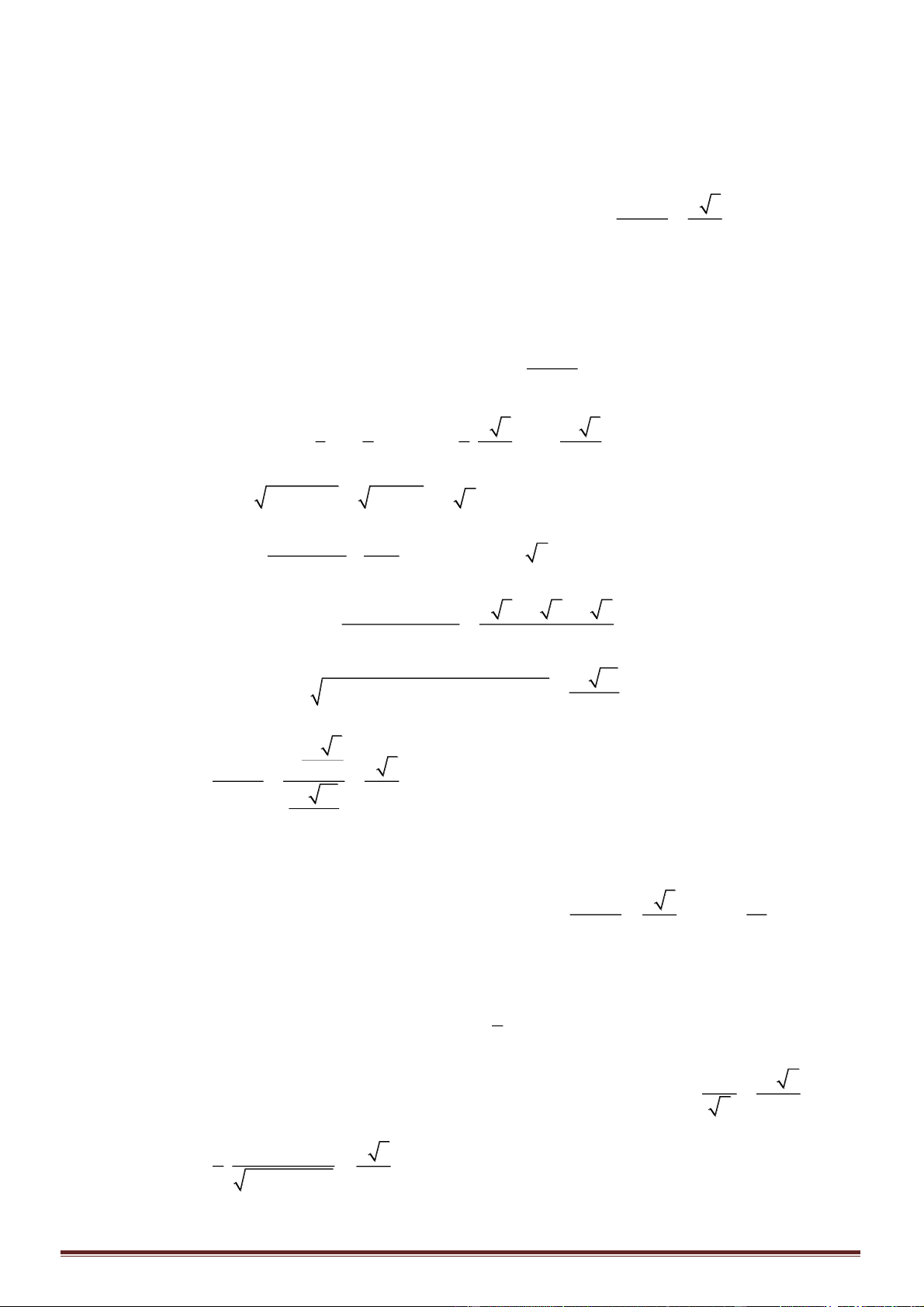
Trang 172
Tam giác
SMI
có
2 2 2
2. . .cosSM MI SI MI SI SIM= + −
2 2 2
3 4 2 .a a SI a SI = + −
22
2 . 0SI a SI a − + =
SI a=
.
Cách 1:
Theo định lý Pythagore đảo thì
SMI
vuông tại
.3
2
SM SI a
S SH
MI
= =
.
Vẽ
SH MN⊥
tại
H MN
thì
( )
SH ABCD⊥
.
Gọi
N
là trung điểm cạnh
BC
ta có
//AC MN
( ) ( )
( )
( )
( )
S
3
, , ,
SMNC
MN
V
d AC SM d AC SMN d C SMN
S
= = =
.
Ta có
3
.
1 1 1 3 3
. . . . . . .
3 2 6 2 12
SMNC S MNB
aa
V V SH BM BN a a= = = =
.
Tam giác
SIC
có
2 2 2 2
2SC SI IC a a a= + = + =
.
Tam giác
SBC
có
2 2 2
22
22
24
SB SC BC
SN a SN a
+
= − = =
.
Tam giác
SMN
có nửa chu vi
3 2 2
22
SM SN MN a a a
p
+ + + +
==
.
Và diện tích
SMN
là
( )( )( )
2
15
4
SMN
a
S p p SM p SN p BC
= − − − =
.
Vậy
( )
3
2
S
3
3
3
5
12
,
5
15
4
SMNC
MN
a
V
a
d AC SM
S
a
= = =
.
Cách 2:
Ta thấy
2 2 2
SM SI MI+=
nên
SMI
vuông tại
S
. Suy ra
.SM SI
SH
MI
=
3
2
a
=
;
3
2
a
HM =
.
Gọi
O AC BD=
;
N
là trung điểm cạnh
BC
ta có
( )
//AC SMN
.
Do đó,
( )
,d AC SM
( )
( )
,d AC SMN=
( )
( )
,d O SMN=
( )
( )
2
,
3
d H SMN=
.
Gọi
K
là hình chiếu của
H
lên
MN
, ta có
HKM
vuông cân tại
K
nên
32
4
2
HM a
HK ==
.
Vậy
( )
22
2.
,.
3
SH HK
d AC SM
SH HK
=
+
5
5
a
=
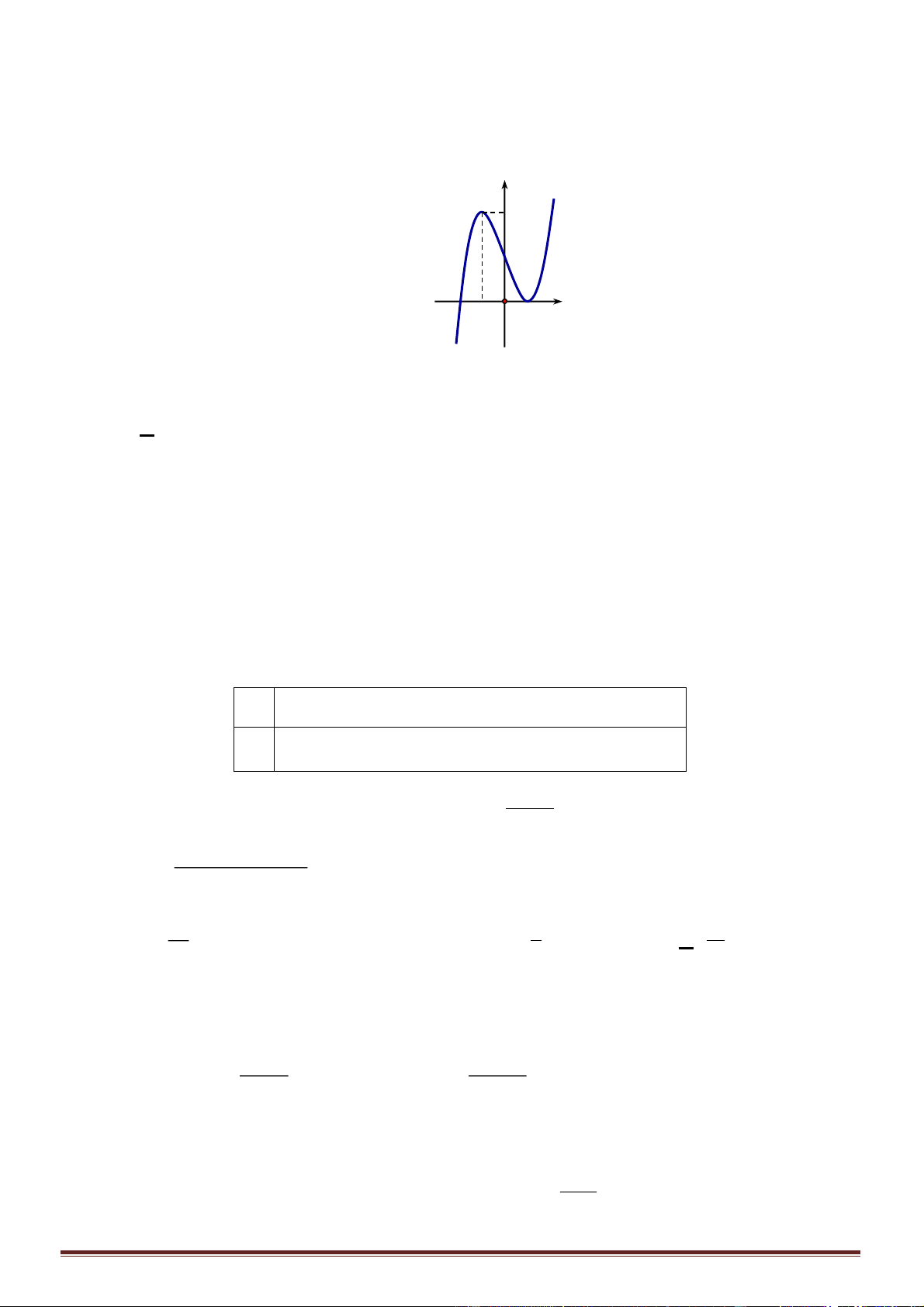
Trang 173
Câu 48: Cho hàm số
( )
y f x=
có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của
hàm số
( )
y f x
=
(
( )
y f x
=
liên tục trên R). Xét hàm số
( )
( )
2
3g x f x=−
. Mệnh đề nào
dưới đây sai?
A. Hàm số
( )
gx
đồng biến trên
( )
1;0−
. B. Hàm số
( )
gx
nghịch biến trên
( )
;1− −
.
C. Hàm số
( )
gx
nghịch biến trên
( )
1;2
. D. Hàm số
( )
gx
đồng biến trên
( )
2;+
.
Lời gii
Chn C
( )
( )
( )
2
3g x f x
=−
( ) ( )
22
33x f x
= − −
( )
2
23xf x
=−
Ta có
( )
0fx
2x −
nên
( )
/3
30fx−
2
32x − −
2
1x
11x −
.
Ta có bảng xét dấu:
x
−
1−
0
1
+
g
−
0
+
0
−
0
+
Câu 49: Xét
,xy
là các số thực dương thỏa mãn
2
4
log 2 4 1
xy
xy
xy
+
=−+
+
. Giá trị nhỏ nhất của
( )
4 2 2 2
3
2 2 6x x y x
P
xy
−+
=
+
bằng
A.
25
9
. B.
4
. C.
9
4
. D.
16
9
.
Lời gii
Chn D
Ta có:
2
4
log 2 4 1
xy
xy
xy
+
=−+
+
2
4
log 2 4
22
xy
xy
xy
+
= −
+
( ) ( ) ( ) ( )
22
log 4 2 4 log 2 2 2 2 2x y x y x y x y + + + = + + +
Xét hàm số
( )
ln 2f t t t=+
trên
( )
0;+
ta có
( ) ( )
1
2 0; 0;
tln2
f t t
= + +
nên ta có:
y
O
x
2−
1
2
1−
4
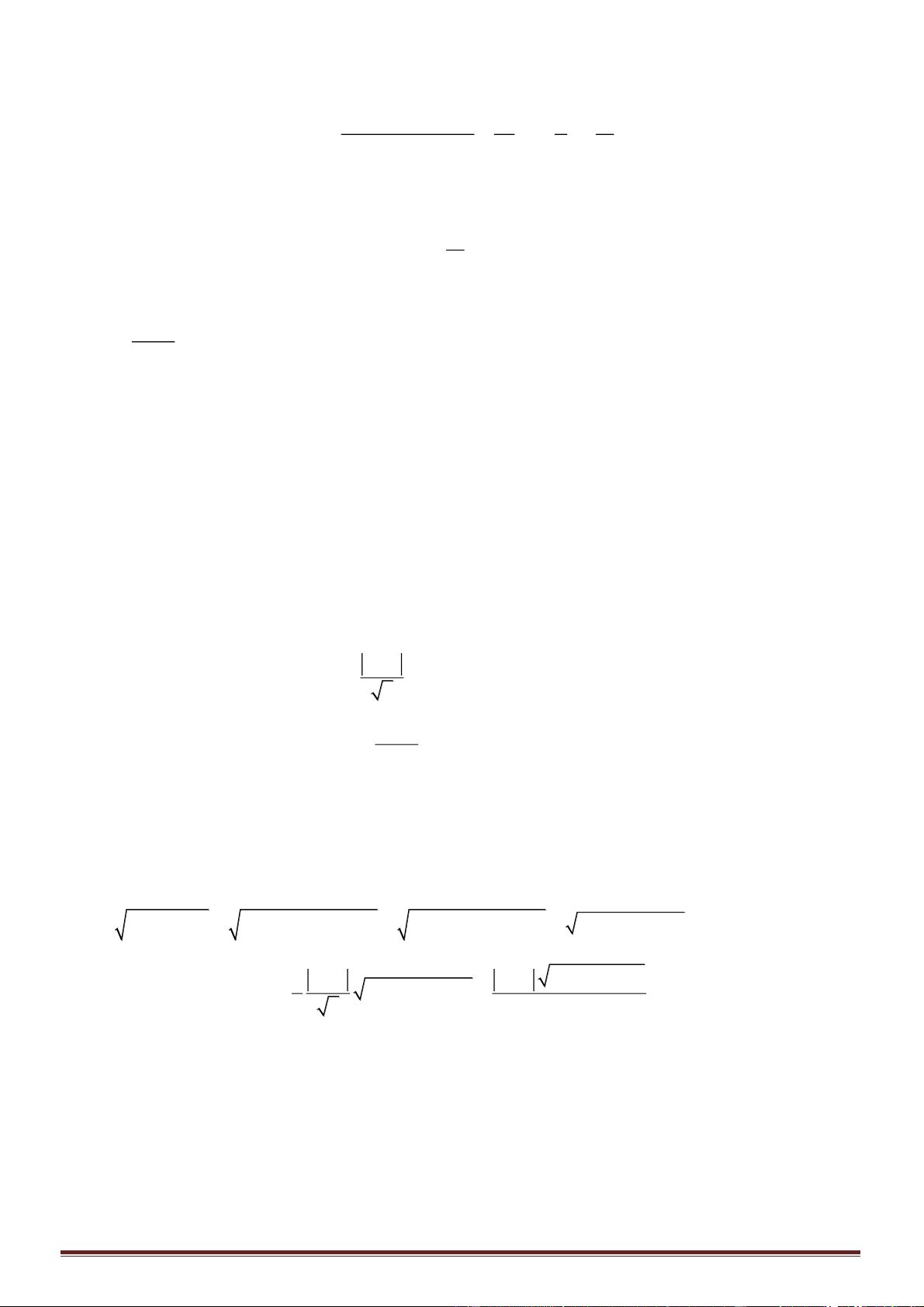
Trang 174
4 2 2 2x y x y x y+ = + =
Thay vào
P
ta được
( )
4 2 2 2
3
2 2 6 24 1 16
27 9
x x y x
Py
y
xy
−+
= = +
+
.
Dấu bằng xảy ra khi
2; 1.xy==
Vậy giá trị nhỏ nhất của
P
là
16
min
9
P =
.
Câu 50:Tìm tất cả các giá trị của tham số m sao cho đường thẳng cắt đồ thị hàm số
tại hai điểm phân biệt sao cho diện tích tam giác bằng với là tâm
đối xứng của
A. . B. . C. . D. .
Hướng dẫn gii:
Chn A.
Đồ thị hàm số có tiện cận đứng .
Đồ thị hàm số có tiện cận ngang
Tâm đối xứng của đồ thị có tọa độ
Xét phương trình hoành độ giao điểm
Gọi là nghiệm phương trình . Theo Viet ta có :
Giả sử
Diện tích tam giác là:
Do
:d y x m=+
21
( ):
1
x
Cy
x
+
=
−
,MN
IMN
4
I
()C
3; 1mm= = −
3; 5mm= = −
3; 3mm= = −
3; 1mm= − = −
1x =
2.y =
( )
1;2I
( )
;
1
:0
2
Id
m
d y x m x y m d
−
= + − + = =
( ) ( )
2
21
3 1 0 1
1
x
x m x m x m
x
+
= + + − − − =
−
12
;xx
( )
1
12
12
3
1
x x m
x x m
+ = −
= − −
( ) ( )
1 1 2 2
; ; ;M x x m N x x m++
( ) ( ) ( )
2 2 2
2
2 1 2 1 1 2
2 2 8 2 3 8 8 2 4 26MN x x x x x x m m m m= − = + − = − + + = − +
IMN
2
2
1 1 2 13
1
2 4 26 4
22
2
m m m m
mm
− − − +
− + = =
( ) ( )
( )
( )
2
22
2
14
1 1 12 64
1 16
m
mm
m
−=
− − + =
− = −
( ) ( )
22
3
1 0 1 4 .
1
m
mm
m
=
− − =
=−

Trang 175
-------- HT ---------
Bấm Tải xuống để xem toàn bộ.