13 trang 33 lượt tải

Bộ Câu Hỏi Trắc Nghiệm Ôn Tập Toán 12 HK2 Năm 2022

66

Bộ câu hỏi trắc nghiệm ôn tập toán HK2 năm 2022 được biên soạn dưới dạng file PDF gồm 13 trang. Tài liệu là kiến thức từ cơ bản đến nâng cao khác nhau, giúp các em nắm bắt rõ cấu trúc câu hỏi để làm cơ sở cho kỳ thi cuối kỳ sắp tới. Mời các em tham khảo thêm nhé!

Chủ đề: Đề HK2 Toán 12 491 tài liệu

Môn: Toán 12 3.9 K tài liệu

Tác giả:

Profile

ha phan

1 năm trước
Danh sách Quiz
/13
Trang1
ĐỀ CƯƠNG ÔN THI MÔN TOÁN 12 HỌC KỲ II
NĂM HỌC: 2021-2022
Câu 1.1:Nguyên hàm của hàm số
42
f x x x
là
A.
53
11
53
x x C
B.
42
x x C
C.
53
x x C
. D.
3
42x x C
Câu 1.2:Họ tất cả nguyên hàm của hàm số
24f x x
là
A.
2
xC
. B.
2
2xC
. C.
2
24x x C
. D.
.
Câu 1.3:Họ tất cả các nguyên hàm của hàm số
26f x x
là
A.
2
xC
. B.
2
6x x C
. C.
2
2xC
. D.
2
26x x C
.
Câu 1.4:Nguyên hàm của hàm số
3
f x x x
là
A.
42
11
42
x x C
B.
2
31xC
C.
3
x x C
D.
42
x x C
Câu 2.1:Chọn khẳng định sai?
A.
1
ln dx x C
x

.B.
1
d lnx x C
x

.C.
2
1
d tan
cos
x x C
x

. D.
sin d cosx x x C
.
Câu 2.2:Chọn khẳng định sai?
A.
1
ln du x C
u

.B.
1
du ln uC
u

. C.
2
1
d cot
sin
x x C
x
. D.
os d sinc x x x C
.
Câu 2.3:Chọn khẳng định sai?
A.
2 ln2.2d
xx
xC
B.
1
2 1 2 1 2 1 .
3
x dx x x C
C.

sin3
cos3
3
x
xdx C
D.
2 1 2
1
2
d
xx
e x e C
e

Câu 2.4:Chọn khẳng định sai?
A.
11
d ln( 5 2) .
5 2 5
x x C
x
= - +
-
ò
B.
7
7 d .
ln 7
x
x
xC=+
ò
C.
2sin d 2cos .x x x C= - +
ò
D.
sin 3
cos3 d .
3
x
x x C=+
ò
Câu 3.1:Tìm một nguyên hàm
()Fx
hàm số
3
( ) 4 4 5f x x x= - +
thỏa mãn
(1) 3.F =
A.
42
( ) 2 5 1.F x x x x= - + -
B.
42
( ) 4 5 1.F x x x x= - + +
C.
42
( ) 2 5 3.F x x x x= - + +
D.
42
1
( ) 2 5
2
F x x x x= - - + ×
Câu 3.2:Tìm một nguyên hàm
()Fx
của hàm số
2
( ) 3 2 5f x x x= + +
thỏa mãn
(1) 4.F =
A.
32
( ) 5 3.F x x x x= - + -
B.
32
( ) 5 3.F x x x x= + + -
C.
32
( ) 5 3.F x x x x= + - +
D.
32
( ) 5 3.F x x x x= + + +
Câu 3.3:Hàm số
42
( ) 5 4 6f x x x= - + -
có
1
nguyên hàm
()Fx
thỏa
(3) 1.F =
Tính
( 3).F -
A.
( 3) 226.F -=
B.
( 3) 225.F - = -
C.
( 3) 451.F -=
D.
( 3) 225.F -=
Câu 3.4:Hàm số
3
( ) 3 2f x x x= + +
có một nguyên hàm
()Fx
thỏa
(2 ) 14.F =
Tính
( 2).F -
A.
( 2) 6.F -=
B.
( 2) 1 4 .F - = -
C.
( 2) 6.F - = -
D.
( 2) 14.F -=
Câu 4.1: Biết
()Fx
là một nguyên hàm của hàm số
1
()
1
fx
x
=
-
và
(2) 1.F =
Giá trị của
(3)F
bằng
Trang2
A.
7
4
×
B.
ln2 1.+
C.
1
2
×
D.
ln 2 1.-
Câu 4.2:Biết
()Fx
là một nguyên hàm của
1
()
21
fx
x
=
+
và
( 1) 5.F -=
Giá trị của
( 4)F -
bằng
A.
1
ln 7 5.
2
-
B.
2ln7 5.+
C.
ln7 5.+
D.
1
ln 7 5.
2
+
Câu 4.3:Biết
()Fx
là một nguyên hàm của hàm
3
()
21
fx
x
=
-
thỏa
(1) 0.F =
Giá trị của
(2 )F
bằng
A.
4ln 2.
B.
3ln 2.
C.
3
ln 3.
2
D.
1.
Câu 4.4:Nguyên hàm
()Fx
của hàm số
1
()
21
fx
x
=
+
biết
e 1 3
22
F
æö
-
÷
ç
÷
=
ç
÷
ç
÷
ç
èø
là
A.
( ) 2ln 2 1 0,5.F x x= + -
B.
( ) 2ln 2 1 1.F x x= + +
C.
1
( ) ln 2 1 1.
2
F x x= + +
D.
( ) 0,5ln 2 1 0,5.F x x= + +
Câu 5.1:Biết
2
1
d2f x x
và
2
1
d6g x x
, khi đó
2
1
df x g x x


bằng
A.
8
. B.
4
. C.
4
. D.
8
.
Câu 5.2:Biết tích phân
1
0
3f x dx
và
1
0
4g x dx 
. Khi đó
1
0
f x g x dx


bằng
A.
7
. B.
7
. C.
1
. D.
1
.
Câu 5.3:Biết tích phân
1
0
3f x dx
và
1
0
4g x dx 
. Khi đó
1
0
2f x g x dx


bằng
A.
5
. B.
7
. C.
1
. D.
1
.
Câu 5.4:Biết
1
0
d2
f x x
và
1
0
d3
g x x
, khi đó
1
0
d


f x g x x
bằng
A.
1
. B.
1
. C.
5
. D.
5
.
Câu 6.1:Cho
1
0
()fx
dx
1
;
3
0
()fx
dx
5
. Tính
3
1
()fx
dx
A.1. B.4. C.6. D.5.
Câu 6.2:Cho
2
1
d3f x x 
và
3
2
d4f x x
. Khi đó
3
1
df x x
bằng
A.12. B.7. C.1. D.
12
.
Câu 6.3:Cho hàm số
fx
liên tục trên
R
và có
24
02
( )d 9; ( )d 4.f x x f x x

Tính
4
0
( )d .I f x x
A.
5I
. B.
36I
. C.
9
4
I
. D.
13I
.
Câu 6.4:Cho
03
10
3 3.f x dx f x dx


Tích phân
3
1
f x dx
bằng
A.
6
B.
4
C.
2
D.
0
Trang3
Câu 7.1:Với
,ab
là các tham số thực. Giá trị tích phân
2
0
3 2 1 d
b
x ax x
bằng
A.
32
b b a b
. B.
32
b b a b
. C.
32
b ba b
. D.
2
3 2 1b ab
Câu 7.2:Cho
2
0
3 2 1 d 6
m
x x x
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
1;2
. B.
;0
. C.
0;4
. D.
3;1
.
Câu 7.3:Giả sử
4
0
2
sin3
2
I xdx a b
,ab
. Khi đó giá trị của
ab
là
A.
1
6
B.
0
C.
3
10
D.
1
5
Câu 7.4:Biết
1
2
0
cos d 1.x x mp =+
ò
Hỏi khẳng định nào sau đây đúng ?
A.
1.mpp=-
B.
1.mpp+=
C.
2.mpp1- =
D.
1 3 .m p-=
Câu 8.1:Tính tích phân
2
2
1
21I x x dx
bằng cách đặt
2
1ux
, mệnh đề nào dưới đây đúng?
A.
3
0
I udu
B.
2
1
1
2
I udu
C.
3
0
2I udu
D.
2
1
I udu
Câu 8.2:Cho tích phân
1
2
0
d
4
x
I
x
nếu đổi biến số
2sin , ;
22
x t t




thì ta được.
A.
3
0
d
π
It
. B.
6
0
d
π
It
. C.
4
0
d
π
I t t
. D.
6
0
d
π
t
I
t
.
Câu 8.3:Cho tích phân
2
0
2 cos .sin dI x x x

. Nếu đặt
2 costx
thì kết quả nào sau đây đúng?
A.
2
3
dI t t
. B.
3
2
dI t t
. C.
. D.
2
0
dI t t
.
Câu 8.4:Cho tích phân
e
1
3ln 1
d
x
Ix
x
. Nếu đặt
lntx
thì
A.
1
0
31
d
e
t
t
It
. B.
e
1
31
d
t
It
t
. C.
e
1
3 1 dI t t
. D.
1
0
3 1 dI t t
.
Câu 9.1:Gọi
S
là diện tích của hình phẳng giới hạn bởi các đường
2
x
y
,
0y
,
0x
,
2x
. Mệnh đề nào
dưới đây đúng?
A.
2
0
2d
x
Sx
B.
2
0
2d
x
Sx
C.
2
2
0
2d
x
Sx
D.
Câu 9.2:Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
e
x
y
,
0y
,
0x
,
2x
. Mệnh đề nào dưới
đây đúng?
A.
2
0
ed
x
Sx
B.
2
0
2 e d
x
Sx
C.
2
0
ed
x
Sx
D.
2
2
0
ed
x
Sx
Trang4
Câu 9.3:Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi
đồ thị hàm số
y f x
, trục
Ox
và hai đường thẳng
,x a x b a b
, xung quanh trục
Ox
.
A.
b
a
V f x dx
B.
2
b
a
V f x dx
C.
2
b
a
V f x dx
D.
b
a
V f x dx
Câu 9.4:Cho hình phẳng
H
giới hạn bởi các đường
2
3yx
,
0y
,
0x
,
2x
. Gọi
V
là thể tích của
khối tròn xoay được tạo thành khi quay
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
2
2
0
3V x dx
B.
2
2
0
3V x dx

C.
2
2
2
0
3V x dx
D.
2
2
2
0
3V x dx

Câu 10.1:Tính diện tích
S
hình phẳng giới hạn bởi các đường
2
1, 1, 2y x x x
và trục hoành.
A.
6S
. B.
16S
. C.
13
6
S
. D.
13S
.
Câu 10.2:Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
2
5yx
,
6yx
,
0x
,
1x
. Tính
S
.
A.
4
3
B.
7
3
C.
8
3
D.
5
3
Câu 10.3:Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
4y x x
và trục
Ox
A.
11
. B.
34
3
. C.
31
3
. D.
32
3
.
Câu 10.4:Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
21yx
, trục hoành và hai đường thẳng
1, 2xx
bằng
A.
2
3
. B.
3
2
. C.
1
3
. D.
7
3
.
Câu 11.1 :Cho hình phẳng
H
giới hạn bởi các đường
2
3, 0, 0, 2y x y x x
. Gọi
V
là thể tích khối
tròn xoay được tạo thành khi quay
H
xung quanh trục
Ox
. Mệnh đề nào sau đây đúng?
A.
2
2
2
0
3dV x x

. B.
2
2
0
3dV x x
. C.
2
2
2
0
3dV x x
. D.
2
2
0
3dV x x

.
Câu 11.2:Gọi
V
là thể tích của khối tròn xoay thu được khi quay hình thang cong, giới hạn bởi đồ thị hàm số
sinyx
, trục Ox, trục Oy và đường thẳng
2
x
, xung quanh trục Ox. Mệnh đề nào dưới đây đúng?
A.
2
2
0
sinV xdx
B.
2
0
sinV xdx
C.
2
2
0
sinV xdx
D.
2
0
sinV xdx
Câu 11.3 :Cho hình phẳng
H
giới hạn bởi các đường
2
2y x x
,
0y
. Quay
H
quanh trục hoành tạo
thành khối tròn xoay có thể tích là
A.
2
2
0
2
x x dx
B.
2
2
2
0
2
x x dx
C.
2
2
2
0
2
x x dx
D.
2
2
0
2
x x dx
Câu 11.4:Cho hình phẳng
H
giới hạn bởi các đường thẳng
2
2, 0, 1, 2y x y x x
. Gọi
V
là thể tích
của khối tròn xoay được tạo thành khi quay
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây đúng?
A.
2
2
1
2dV x x
B.
2
2
2
1
2dV x x

C.
2
2
2
1
2dV x x
D.
2
2
1
2dV x x

Trang5
Câu 12.1:Cho hàm số
y f x
liên tục trên
.
Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
, 0, 1y f x y x
và
5x
(như hình vẽ bên). Mệnh đề nào sau đây đúng?
A.
15
11
( )d ( )dS f x x f x x

. B.
15
11
( )d ( )dS f x x f x x


.
C.
15
11
( )d ( )dS f x x f x x


. D.
15
11
( )d ( )dS f x x f x x

.
Câu 12.2:Cho hàm số
fx
liên tục trên
. Gọi S là diện tích hình phẳng giới hạn bởi các đường
, 0, 1, 2y f x y x x
(như hình vẽ bên). Mệnh đề nào dưới đây đúng?
A.
12
11
dx + dxS f x f x

. B.
12
11
dx dxS f x f x

.
C.
12
11
dx+ dxS f x f x


. D.
12
11
dx dxS f x f x


.
Câu 12.3:Gọi
S
là diện tích hình phẳng
H
giới hạn bởi các đường
y f x
, trục hoành và hai đường thẳng
1x 
,
2x
. Đặt
0
1
da f x x
,
2
0
db f x x
, mệnh đề nào sau đây đúng?
A.
S b a
B.
S b a
C.
S b a
D.
S b a
Câu 12.4:Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A.
2
1
22x dx

B.
2
1
22x dx
C.
2
2
1
2 2 4x x dx
D.
2
2
1
2 2 4x x dx

Trang6
Câu 13.1:Cho hình phẳng
D
giới hạn với đường cong
2
1yx=+
, trục hoành và các đường thẳng
0, 1xx==
. Khối tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
2V
B.
4
3
V
C.
2V
D.
4
3
V
Câu 13.2: Cho hình phẳng
D
giới hạn bởi đường cong
x
ye
, trục hoành và các đường thẳng
0x
,
1x
.
Khối tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.

2
1
2
e
V
B.
2
1
2
e
V
C.
2
3
e
V
D.

2
1
2
e
V
Câu 13.3:Cho hình phẳng
D
giới hạn bởi đường cong
2 cos ,yx
trục hoành và các đường thẳng
0,
2
xx
. Khối tròn xoay tạo thành khi
D
quay quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
( 1)V
B.
1V
C.
1V
D.
( 1)V
Câu 13.4:Cho hình phẳng
D
giới hạn bởi đường cong
2 sinyx
, trục hoành và các đường thẳng
0x
,
x
. Khối tròn xoay tạo thành khi quay
D
quay quanh trục hoành có thể tích
V
bằng bao nhiêu?
A.
21V


B.
2V
C.
21V

D.
2
2V
Câu 14.1:Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A.
13i
B.
13i
C.
13i
D.
13i
Câu 14.2:Số phức
56i
có phần thực bằng
A.
6
. B.
6
. C.
5
. D.
5
Câu 14.3:Số phức có phần thực bằng
3
và phần ảo bằng
4
là
A.
34i
B.
43i
C.
34i
D.
43i
Câu 14.4:Kí hiệu
,ab
lần lượt là phần thực và phần ảo của số phức
3 2 2i
. Tìm
a
,
b
.
A.
3; 2ab
B.
3; 2 2ab
C.
3; 2ab
D.
3; 2 2ab
Câu 15.1:Cho hai số phức
1
2zi
và
2
1zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn của số phức
12
2 zz
có tọa độ là
A.
0; 5
. B.
5; 1
. C.
1; 5
. D.
5; 0
.
Câu 15.2:Cho hai số phức
1
1zi
và
2
2zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
12
2zz
có tọa độ là
A.
(3;5)
. B.
(5;2)
. C.
(5;3)
. D.
(2;5)
.
Câu 15.3:Cho số phức
1
12zi
,
2
3zi
. Tìm điểm biểu diễn của số phức
12
z z z
trên mặt phẳng tọa
độ.
A.
2; 5M
B.
2; 1P 
C.
1;7Q
D.
4; 3N
Câu 15.4:Trong mặt phẳng tọa độ, điểm
M
là điểm biểu diễn của số phức
z
. Điểm nào trong hình vẽ là điểm
biểu diễn của số phức
2z
?
A.Điểm
Q
B.Điểm
E
C.Điểm
P
D.Điểm
N
O
x
y
Q
E
P
N
M
Trang7
Câu 16.1:Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức z’ = -2 + 5i
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
Câu 16.2:Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức z’ = 2 + 3i
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
Câu 16.3:Điểm biểu diễn của các số phức z = 3 + bi với b R, nằm trên đường thẳng có phương trình là:
A. x = 3 B. y = 3 C. y = x D. y = x + 3
Câu 16.4:Điểm biểu diễn của các số phức z = a + ai với a R, nằm trên đường thẳng có phương trình là:
A. y = x B. y = 2x C. y = 3x D. y = 4x
Câu 17.1:Cho số phức z = a - ai với a R, điểm biểu diễn của số phức đối của z nằm trên đường thẳng có
phương trình là:
A. y = 2x B. y = -2x C. y = x D. y = -x
Câu 17.2:Cho số phức z = a + a
2
i với a R. Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên:
A. Đường thẳng y = 2x B. Đường thẳng y = -x + 1
C. Parabol y = x
2
D. Parabol y = -x
2
Câu 17.3:Cho hai số phức z = a + bi; a,b R.
Để điểm biểu diễn của z nằm trong dải (-2; 2) (hình 1) điều kiện của a và b là:
A.
a2
b2
B.
a2
b -2

C.
2 a 2
và b R D. a, b (-2; 2)
Câu 17.4:Cho số phức z = a + bi ; a, R.
Để điểm biểu diễn của z nằm trong dải (-3; 3) (hình 2) điều kiện của a và b là:
A.
a3
b3
B.
a3
b -3

C. a, b (-3; 3) D. a R và -3 < b < 3
Câu 18.1:Cho hai số phức và . Số phức bằng
A. . B. . C. . D. .
Câu 18.2:Cho hai số phức và . Số phức bằng
A. . B. . C. . D. .
Câu 18.3:Cho hai số phức và . Số phức bằng
A. . B. . C. . D. .
Câu 18.4:Cho hai số phức và . Số phức bằng
A. . B. . C. . D. .
Câu 19.1:Cho số phức , số phức bằng
A. . B. C. . D. .
Câu 19.2:Cho hai số phức và . Môđun của số phức bằng

1
32zi

2
2zi
12
zz
5 i
5 i
5 i
5 i
1
12zi
2
4zi
12
zz
33i
33i
33i
33i
1
12zi
2
2zi
12
zz
3 i
3 i
3 i
3 i
1
13zi
2
3zi
12
zz
24i
24i
24i
24i
12zi
23iz
47i
47i
8 i
8 i
12zi
3wi
.z w
x
y
2
O
x
-2
(Hình 1)
-3
3
y
x
O
(Hình 2)
Trang8
A. . B. . C. . D. .
Câu 19.3:Cho số phức , số phức bằng
A. . B. . C. . D. .
Câu 19.4:Cho hai số phức và . Mô đun của số phức bằng
A. . B. . C. . D. .
Câu 20.1:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
= (
z
)
2
là:
A. Trục hoành B. Trục tung
C. Gồm cả trục hoành và trục tung D. Đường thẳng y = x
Câu 20.2:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
là một số ảo là:
A. Trục hoành (trừ gốc toạ độ O) B. Trục tung (trừ gốc toạ độ O)
C. Hai đường thẳng y = ±x D. Đường tròn x
2
+ y
2
= 1
Câu 20.3:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
là một số thực âm
là:
A. Trục hoành và trục tung (trừ gốc toạ độ O) B. Trục tung (trừ gốc toạ độ O)
C. Đường thẳng y = x (trừ gốc toạ độ O) D. Đường thẳng y = -x (trừ gốc toạ độ O)
Câu 20.4:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
là một số thực
dương là:
A. Trục hoành (trừ gốc toạ độ O) B. Trục tung (trừ gốc toạ độ O)
C. Đường thẳng y = x (trừ gốc toạ độ O) D. Đường thẳng y = -x (trừ gốc toạ độ O)
Câu 21.1:Cho số phức z = a + bi. Khi đó số
1
zz
2i
là:
A. Một số thực B. 0 C. Một số thuần ảo D. i
Câu 21.2:Điểm biểu diễn của số phức z =
1
2 3i
là:
A.
2; 3
B.
23
;
13 13



C.
3; 2
D.
4; 1
Câu 21.3:Số phức nghịch đảo của số phức z = 1 -
3i
là:
A.
1
z
=
13
i
22
B.
1
z
=
13
i
44
C.
1
z
= 1 +
3i
D.
1
z
= -1 +
3i
Câu 21.4:Số phức z =
3 4i
4i
bằng:
A.
16 13
i
17 17
B.
16 11
i
15 15
C.
94
i
55
D.
9 23
i
25 25
Câu 22.1:Thu gọn số phức z =
3 2i 1 i
1 i 3 2i


ta được:
A. z =
21 61
i
26 26
B. z =
23 63
i
26 26
C. z =
15 55
i
26 26
D. z =
26
i
13 13
Câu 22.2:Cho số phức z =
13
i
22

. Số phức (
z
)
2
bằng:
A.
13
i
22

B.
13
i
22

C.
1 3i
D.
3i
Câu 22.3:Cho số phức z =
13
i
22

. Số phức 1 + z + z
2
bằng:
52
26
26
50
23 zi
1 iz
5i
15i
15 i
5i
22zi
w2i
wz
40
8
22
2 10
Trang9
A.
13
i
22

. B. 2 -
3i
C. 1 D. 0
Câu 22.4:Cho số phức z 0. Biết rằng số phức nghịch đảo của z bằng số phức liên hợp của nó. Trong các kết
luận nào đúng:
A. z
B. z là một số thuần ảo C.
z1
D.
z2
Câu 23.1:Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức
z
z'
có phần thực là:
A.
22
aa' bb '
ab
B.
22
aa' bb '
a' b '
C.
22
a a '
ab
D.
22
2bb'
a' b'
Câu 23.2:Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức
z
z'
có phần ảo là:
A.
22
aa' bb'
ab
B.
22
a ' b ab'
a ' b '
C.
22
aa' bb '
ab
D.
22
2bb'
a' b'
Câu 23.3:Cho số phức z = x + yi 1. (x, y
). Phần ảo của số
z1
z1
là:
A.
2
2
2x
x 1 y

B.
2
2
2y
x 1 y

C.
2
2
xy
x 1 y
D.
2
2
xy
x 1 y

Câu 23.4:Cho số phức z = x + yi . (x, y
). Tập hợp các điểm biểu diễn của z sao cho
zi
zi
là một số thực
âm là:
A. Các điểm trên trục hoành với -1 < x < 1 B. Các điểm trên trục tung với -1 < y < 1
C. Các điểm trên trục hoành với
x1
x1

D. Các điểm trên trục tung với
y1
y1

Câu 24.1:Cho a R biểu thức a
2
+ 1 phân tích thành thừa số phức là:
A. (a + i)(a - i) B. i(a + i) C. (1 + i)(a
2
- i)
D. Không thể phân tích được thành thừa số phức
Câu 24.2:Cho a R biểu thức 2a
2
+ 3 phân tích thành thừa số phức là:
A. (3 + 2ai)(3 - 2ai) B.
2a 3i 2a 3i
C.
1 i 2a i
D. Không thể phân tích được thành thừa số phức
Câu 24.3:Cho a, b
biểu thức 4a
2
+ 9b
2
phân tích thành thừa số phức là:
A.
4a 9i 4a 9i
B.
4a 9bi 4a 9bi
C.
2a 3bi 2a 3bi
D. Không thể phân tích được thành thừa số phức
Câu 24.4:Cho a, b
biểu thức 3a
2
+ 5b
2
phân tích thành thừa số phức là:
A.
3a 5bi 3a 5bi
B.
3a 5i 3a 5i
C.
3a 5bi 3a 5bi
D. Không thể phân tích được thành thừa số phức
Câu 25.1:Cho phương trình z
2
+ bz + c = 0. Nếu phương trình nhận z = 1 + i làm một nghiệm thì b và c bằng:
A. b = 3, c = 5 B. b = 1, c = 3 C. b = 4, c = 3 D. b = -2, c = 2
Câu 25.2:Cho phương trình
32
z az bz c 0
Nếu z = 1 + i và z = 2 là hai nghiệm của phương trình thì
a, b, c bằng:
A.
a4
b6
c4


B.
a2
b1
c4
C.
a4
b5
c1
D.
a0
b1
c2

Trang10
Câu 25.3:Phương trình bậc hai với các nghiệm:
1
1 5i 5
z
3

,
2
1 5i 5
z
3

là:
A. z
2
- 2z + 9 = 0 B. 3z
2
+ 2z + 42 = 0 C. 2z
2
+ 3z + 4 = 0 D. z
2
+ 2z + 27 = 0
Câu 25.4:Cho P(z) = z
3
+ 2z
2
- 3z + 1. Khi đó P(1 - i) bằng:
A. -4 - 3i B. 2 + i C. 3 - 2i D. 4 + i
Câu 26.1:Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 1 2 3 16 S x y z
. Tâm của
S
có tọa độ
là
A.
1; 2; 3
. B.
1;2;3
. C.
1;2; 3
. D.
1; 2;3
.
Câu 26.2:Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 3 1 1 2S x y z
. Tâm của
S
có tọa độ là
A.
3;1; 1
B.
3; 1;1
C.
3; 1;1
D.
3;1; 1
Câu 26.3:Trong không gian với hệ toạ độ
Oxyz
, cho mặt cầu
22
2
: 2 2 8S x y z
. Tính bán kính
R
của
S
.
A.
8R
B.
4R
C.
22R
D.
64R
Câu 26.4:Trong không gian với hệ toạ độ
Oxyz
, cho mặt cầu
2 2 2
: 5 1 2 9S x y z
. Tính bán
kính
R
của
S
.
A.
3R
B.
18R
C.
9R
D.
6R
Câu 27.1:Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
1;0;3 , 2;3; 4 , 3;1;2A B C
. Tìm tọa độ
điểm
D
sao cho tứ giác
ABCD
là hình bình hành.
A.
6;2; 3D
. B.
2;4; 5D 
. C.
4;2;9D
. D.
4; 2;9D 
.
Câu 27.2:Trong không gian với hệ tọa độ
Oxyz
, cho hình bình hành ABCD biết
(1;1; 2), ( 2; 1;4), (3; 2; 5)A B C
. Tìm tọa độ đỉnh D?
A.
(6;0; 11)D
B.
( 6;1;11)D
C.
(5; 2; 1)D 
D.
( 3;6;1)D
Câu 27.3:Trong không gian với hệ trục tọa độ Oxyz,cho tam giác ABC biết
( 1;3; 4), (2; 1;0)AB
và
G(2;5; 3)
là trọng tâm của tam giác. Tìm tọa độ đỉnh C?
A.
B.
C(4; 9;5)
C.
C(7;12; 5)
D.
Câu 27.4:Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có
(2;2;1), (2;1; 1)AB
và
G( 1;2;3)
là
trọng tâm của tam giác. Tọa độ của điểm C là:
A.(-5;-3;9) B. (-7;-3;9) C. (-7;3;9) D. (-7;3;6)
Câu 28.1:Trong không gian
Oxyz
, cho ba điểm
2;0;0M
,
,
0;0;2P
. Mặt phẳng
MNP
có
phương trình là:A.
0
2 1 2
x y z
. B.
1
2 1 2
x y z
. C.
1
2 1 2
x y z
. D.
1
2 1 2
x y z
Câu 28.2:Trong không gian với hệ tọa độ
Oxyz
, cho
3
điểm
1;0;0A
;
0; 2;0B
;
0;0;3C
. Phương trình
nào dưới dây là phương trình mặt phẳng
ABC
?
A.
1
3 2 1
x y z
. B.
1
2 1 3
x y z
. C.
1
1 2 3
x y z
. D.
1
3 1 2
x y z
.
Câu 28.3:Trong không gian với hệ trục toạ độ
Oxyz
, phương trình nào dưới đây là phương trình của mặt
phẳng
Oyz
?A.
0y
B.
0x
C.
0yz
D.
0z
Câu 28.4:Trong không gian
Oxyz
, mặt phẳng
Oxz
có phương trình là
A.
0xz
. B.
0 x y z
. C.
0y
. D.
0x
.
Trang11
Câu 29.1:Trong không gian
Oxyz
, mặt phẳng đi qua điểm
2; 1;2A
và song song với mặt phẳng
:2 3 2 0P x y z
có phương trình là
A.
2 3 9 0x y z
B.
2 3 11 0x y z
C.
2 3 11 0x y z
D.
2 3 11 0x y z
Câu 29.2:Trong không gian với hệ toạ độ
Oxyz
, cho điểm
3; 1; 2M
và mặt phẳng
: 3 2 4 0x y z
. Phương trình nào dưới đây là phương trình mặt phẳng đi qua
M
và song song với
?A.
3 2 6 0x y z
B.
3 2 6 0x y z
C.
3 2 6 0x y z
D.
3 2 14 0x y z
Câu 29.3:Trong không gian với hệ toạ độ
Oxyz
, phương trình của mặt phẳng
P
đi qua điểm
2;3;1M
và
song song với mặt phẳng
:4 2 3 5 0Q x y z
là
A.
4x-2 3 11 0 yz
B.
4x-2 3 11 0 yz
C.
- 4x+2 3 11 0 yz
D.
4x+2 3 11 0 yz
Câu 29.4:Trong không gian với hệ toạ độ
Oxyz
, phương trình mặt phẳng (P) đi qua điểm
và song
song (Q):
2 7 0x y z
là
A.
2 4 0x y z
B.
2 10 0x y z
C.
2 8 0x y z
D.
2 3 0x y z
Câu 30.1:Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
0;1;1A
) và
1;2;3B
. Viết phương trình của
mặt phẳng
P
đi qua
A
và vuông góc với đường thẳng
AB
.
A.
2 3 0x y z
B.
2 6 0x y z
C.
3 4 7 0x y z
D.
3 4 26 0x y z
Câu 30.2:Trong không gian
Oxyz
, cho hai điểm
2;1;0 , 1; 1;2AB
. Mặt phẳng đi qua
1;1;1M
và vuông
góc với đường thẳng
AB
có phương trình là
A.
2 2 1 0x y z
B.
2 2 1 0x y z
C.
3 2 1 0xz
D.
3 2 1 0xz
Câu 30.3:Trong không gian
,Oxyz
Cho hai điểm
5; 4;2A
và
1;2;4 .B
Mặt phẳng đi qua
A
và vuông góc
với đường thẳng
AB
có phương trình là
A.
2 3 8 0x y z
B.
3 3 13 0x y z
C.
2 3 20 0x y z
D.
3 3 25 0x y z
Câu 30.4:Trong không gian
,Oxyz
cho hai điểm
1;2;1A
và
2;1;0 .B
Mặt phẳng qua
A
và vuông góc với
AB
có phương trình là
A.
3 6 0 x y z
B.
3 6 0 x y z
C.
3 5 0 x y z
D.
3 6 0 x y z
Câu 31.1:Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng cho mă
t phă
ng
P
có phương trình
3 4 2 4 0x y z
và điểm
1; 2;3A
. Tính khoảng cách
d
từ
A
đến
P
A.
5
9
d
B.
5
29
d
C.
5
29
d
D.
5
3
d
Câu 31.2:Tính khoảng cách từ điểm
A( 1;2; 4)
đến mặt phẳng (P):
2 5 0x y z
?
A.
56
3
B.
52
6
C.
26
3
D.
22
3
Câu 31.3:Trong không gian
Oxyz
, khoảng cách giữa hai mặt phẳng
: 2 2 10 0 P x y z
và
: 2 2 3 0 Q x y z
bằng A.
8
3
. B.
7
3
. C.
3
. D.
4
3
.
Câu 31.4:Trong không gian
Oxyz
, khoảng cách giữa hai mặt phẳng
: 2 2 10 0P x y z
và
: 2 2 6 0Q x y z
bằng A.
8
3
. B.
7
3
. C.
3
. D.
4
3
.
Trang12
Câu 32.1:Trong không gian với hệ tọa độ vuông góc Oxyz, cho đường thẳng

xt
d y t t
zt
23
: 5 4 ,
67
. Vectơ nào
sau đây là một vectơ chỉ phương của đường thẳng d?
A.
u (2;5; 6)
B.
u (3; 4;7)
C.
u (2,3,0)
D.
u (5; 4;0)
Câu 32.2:Tìm vectơ chỉ phương của một đường thẳng có phương trình
5 1 4
2 3 7
x y z


A.
(2; 3;7)u 
B.
( 2; 3;7)u
C.
(2;3;7)u
D.
( 2;3;7)u 
Câu 32.3:Trong không gian
Oxyz
, điểm nào dưới đây thuộc đường thẳng
d
:
1
5
23
xt
yt
zt



?
A.
1;2;5P
B.
1;5;2N
C.
1;1;3Q
D.
1;1;3M
Câu 32.4:Trong không gian
Oxyz
, điểm nào dưới đây thuộc đường thẳng
1 2 1
:
1 3 3

x y z
d
?
A.
1;2;1P
. B.
1; 2; 1Q
. C.
1;3;2N
. D.
1;2;1P
.
Câu 33.1:Trong không gian Oxyz, cho đường thẳng đi qua điểm và có vectơ chỉ phương
Phương trình tham số của đường thẳng là
A.
22
3.
1


xt
yt
zt
B.
24
6.
12


xt
yt
zt
C.
22
3.
1


xt
yt
zt
D.
42
6.
2



xt
y
zt
Câu 33.2:Trong không gian với hệ tọa độ
Oxyz
, phương trình nào dưới đây là phương trình của đường thẳng
đi qua
2;3;0A
và vuông góc với mặt phẳng
: 3 5 0?P x y z
A.


1
13
1
xt
yt
zt
B.

1
3
1
xt
yt
zt
C.


13
13
1
xt
yt
zt
D.


13
13
1
xt
yt
zt
Câu 33.3:Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
15
:
1 3 1



x y z
d
và mặt phẳng
:3 3 2 6 0 P x y z
. Mệnh đề nào dưới đây đúng?
A.
d
cắt và không vuông góc với
P
B.
d
vuông góc với
P
C.
d
song song với
P
D.
d
nằm trong
Câu 33.4:Trong không gian tọa độ
Ox ,yz
phương trình nào dưới đây là phương trình chính tắc của đường
thẳng
12
: 3 ?
2
xt
d y t
zt

A.
12
2 3 1
x y z

B.
12
1 3 2
x y z

C.
12
2 3 2
x y z

D.
12
2 3 1
x y z

Câu 34.1:Viết ptđt đi qua hai điểm.Trong không gian với hệ tọa độ
Oxyz
, phương trình tham số của đường
thẳng đi qua hai điểm
1; 1;2A
và
3;2;1B
là
A.
14
13
2
xt
yt
zt


. B.
43
32
1
xt
yt
zt


. C.
12
1
23
xt
yt
zt


. D.
4
3
12
xt
yt
zt


.
2;0; 1M
4; 6;2 .
a
Trang13
Câu 34.2:Trong không gian Oxyz, cho đường thẳng d đi qua hai điểm và . Phương trình
nào sau đây là phương trình chính tắc của đường thẳng d ?
A.
1 2 3
2 3 4
x y z

B.
1 2 3
3 5 7
x y z

. C.
2 3 4
1 2 3
x y z

D.
1 2 3
2 3 4
x y z

Câu 34.3:Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
,
1;0;1B
,
1;1; 2C
. Phương
trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua
A
và song song với đường thẳng
BC
?
A.

2
1
3
xt
yt
zt
. B.

1
3
2 1 1
y
xz
. C.


11
2 1 1
y
xz
. D.
20x y z
.
Câu 34.4:Trong không gian với hệ tọa độ
Oxyz
, phương trình tham số của đường thẳng đi qua
điểm
và song song với đường thẳng
11
2 1 3
x y z

là
A.
2
1
3
xt
yt
z



. B.
22
1
33
xt
yt
zt


. C.
1
1
3
xt
yt
zt


. D.
22
1
33
xt
yt
zt


.
Câu 35.1:Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1; 2; 3A
;
1; 4;1B
và đường thẳng


2
23
:
1 1 2
y
xz
d
. Phương trình nào dưới đây là phương trình của đường thẳng đi qua trung điểm của
đoạn
AB
và song song với
d
?
A.

1
1
1 1 2
y
xz
B.


1
11
1 1 2
y
xz
C.

2
2
1 1 2
y
xz
D.

1
1
1 1 2
y
xz
Câu 35.2:Trong không gian vơ
i hê
to
a đô
Oxyz
, cho đươ
ng thă
ng
có phương trình:
10 2 2
5 1 1
x y z

. Xt mặt phẳng
:10 2 11 0P x y mz
,
m
là tham số thực. Tìm tất cả các
giá trị của
m
để mặt phẳng
P
vuông go
c vơ
i đươ
ng thă
ng
.
A.
2m 
B.
2m
C.
52m
D.
52m
Câu 35.3:Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:2 2 1 0P x y z
và đường thẳng
1 2 1
:
2 1 2
x y z
. Tính khoảng cách
d
giữa
và
P
.
A.
1
3
d
. B.
5
3
d
. C.
2
3
d
. D.
2d
.
Câu 35.4:Trong không gian
Oxyz
, mặt phẳng đi qua điểm
1;2; 2A
và vuông góc với đường thẳng
1 2 3
:
2 1 3
x y z
có phương trình là
A.
3 2 5 0x y z
. B.
2 3 2 0x y z
.
C.
2 3 1 0x y z
. D.
2 3 2 0x y z
.
---------------------------------------- HẾT-----------------------------------------------
1;2;3A
3;5;7B

Tài liệu khác của Toán 12

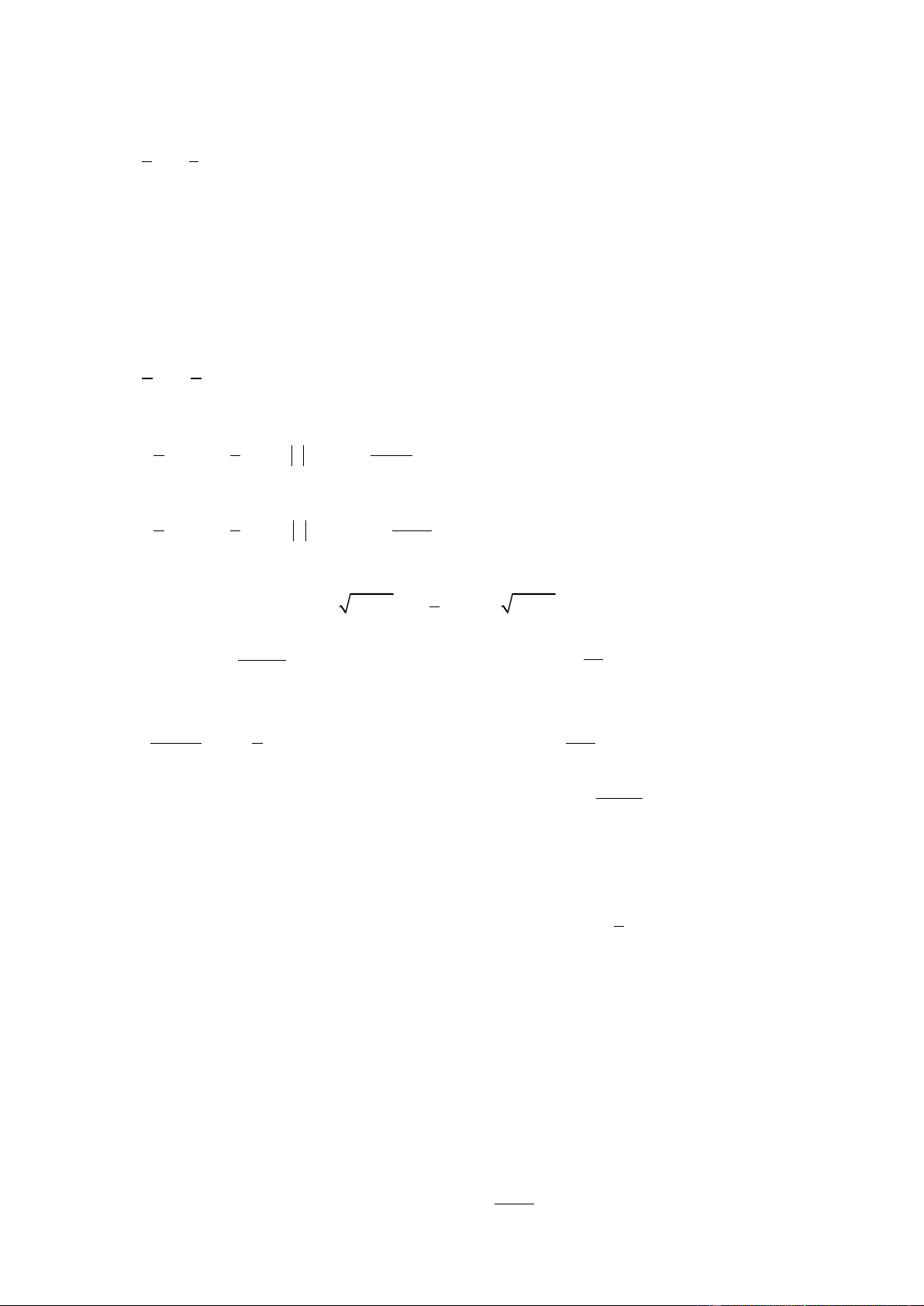
Preview text:

ĐỀ CƯƠNG ÔN THI MÔN TOÁN 12 HỌC KỲ II NĂM HỌC: 2021-2022
Câu 1.1:Nguyên hàm của hàm số   4 2
f x x x là 1 1 A. 5 3 x x C B. 4 2
x x C C. 5 3
x x C . D. 3
4x  2x C 5 3
Câu 1.2:Họ tất cả nguyên hàm của hàm số f x  2x  4 là A. 2
x C . B. 2
2x C . C. 2
2x  4x C . D. 2
x  4x C .
Câu 1.3:Họ tất cả các nguyên hàm của hàm số f x  2x  6 là A. 2
x C . B. 2
x  6x C . C. 2
2x C . D. 2
2x  6x C .
Câu 1.4:Nguyên hàm của hàm số   3
f x x x là 1 1 A. 4 2 x x C B. 2
3x  1 C C. 3
x x C D. 4 2
x x C 4 2
Câu 2.1:Chọn khẳng định sai? 1 1 1 A. ln d x x   C  .B.
dx  ln x C  .C.
dx  tan x C  . D. sin d
x x   cos x C  . x x 2 cos x
Câu 2.2:Chọn khẳng định sai? 1 1 1 A. ln d u x   C  .B.
du  ln u C  . C.
dx  cot x C  . D. os c d
x x  sin x C  . u u 2 sin x
Câu 2.3:Chọn khẳng định sai? 1
A. 2x d  ln 2.2x xC B. 2x 1dx   2x   1
2x 1  C. 3 x x 1 C. xdx    sin 3 cos 3 C D. 2 1 2 d x e x eC  3 2e
Câu 2.4:Chọn khẳng định sai? 1 1 x 7x A. dx = ln(5x - 2) + C . ò B. 7 dx = + C . ò 5x - 2 5 ln 7 sin 3x C.
2 sin x dx = - 2 cos x + C . ò D. cos 3x dx = + C . ò 3
Câu 3.1:Tìm một nguyên hàm F (x ) hàm số 3
f (x) = 4x - 4x + 5 thỏa mãn F (1) = 3. A. 4 2
F(x) = x - 2x + 5x - 1. B. 4 2
F(x) = x - 4x + 5x + 1. 1 C. 4 2
F(x) = x - 2x + 5x + 3. D. 4 2
F (x ) = x - 2x - 5x + × 2
Câu 3.2:Tìm một nguyên hàm F (x ) của hàm số 2
f (x) = 3x + 2x + 5 thỏa mãn F (1) = 4. A. 3 2
F(x) = x - x + 5x - 3. B. 3 2
F(x) = x + x + 5x - 3. C. 3 2
F(x) = x + x - 5x + 3. D. 3 2
F(x) = x + x + 5x + 3. Câu 3.3:Hàm số 4 2
f (x) = - 5x + 4x - 6 có 1 nguyên hàm F (x ) thỏa F (3) = 1. Tính F (- 3).
A. F (- 3) = 226. B. F (- 3) = - 225. C. F (- 3) = 451. D. F (- 3) = 225. Câu 3.4:Hàm số 3
f (x) = x + 3x + 2 có một nguyên hàm F (x ) thỏa F (2) = 14. Tính F (- 2). A. F (- 2) = 6.
B. F (- 2) = - 14.C. F (- 2) = - 6. D. F (- 2) = 14. 1
Câu 4.1: Biết F (x ) là một nguyên hàm của hàm số f (x ) =
và F (2) = 1. Giá trị của F (3) bằng x - 1 Trang1 7 1 A.
×B. ln 2 + 1.C. ×D. ln 2 - 1. 4 2 1
Câu 4.2:Biết F (x ) là một nguyên hàm của f (x) =
và F (- 1) = 5. Giá trị của F (- 4) bằng 2x + 1 1 1 A. ln 7 - 5.
B. 2 ln 7 + 5.C. ln 7 + 5. D. ln 7 + 5. 2 2 3
Câu 4.3:Biết F (x ) là một nguyên hàm của hàm f (x ) =
thỏa F (1) = 0. Giá trị của F (2) bằng 2x - 1 3 A. 4 ln 2. B. 3 ln 2. C. ln 3. D.1. 2 1 e æ 1ö - ç ÷ 3
Câu 4.4:Nguyên hàm F (x ) của hàm số f (x) = biết F ç ÷= ç ÷ là 2x + 1 çè 2 ÷ø 2
A. F(x) = 2 ln 2x + 1 - 0, 5. B. F(x) = 2 ln 2x + 1 + 1. 1
C. F (x ) =
ln 2x + 1 + 1. D. F(x) = 0, 5 ln 2x + 1 + 0, 5. 2 2 2 2 Câu 5.1:Biết f
 xdx  2 và g
 xdx  6, khi đó  f
 x gxdx  bằng 1 1 1 A. 8 . B. 4  . C. 4 . D. 8  . 1 1 1
Câu 5.2:Biết tích phân f
 xdx  3 và gxdx  4   . Khi đó  f
 x gxdx  bằng 0 0 0 A. 7  . B. 7 . C. 1. D.1. 1 1 1
Câu 5.3:Biết tích phân f
 xdx  3 và gxdx  4   . Khi đó  f
 x2gxdx  bằng 0 0 0 A. 5  . B. 7 . C. 1. D.1. 1 1 1 Câu 5.4:Biết  d  2   f x x
và  g xdx  3, khi đó 
f x gx d   x bằng 0 0 0 A. 1. B.1. C. 5  . D. 5 . 1 3 3 Câu 6.1:Cho f (x)  dx  1  ; f (x)  dx  5 . Tính f (x)  dx 0 0 1 A.1. B.4. C.6. D.5. 2 3 3 Câu 6.2:Cho
f xdx  3   và f
 xdx  4. Khi đó f xdx  bằng 1 2 1 A.12. B.7. C.1. D. 12 . 2 4 4
Câu 6.3:Cho hàm số f x liên tục trên R và có f (x)dx  9; f (x)dx  4.   Tính I f (x)d . x  0 2 0 9 A. I  5 . B. I  36 . C. I  . D. I  13 . 4 0 3 3 Câu 6.4:Cho f
 xdx  3 f xdx  3. Tích phân f xdx bằng 1  0 1  A. 6 B. 4 C. 2 D. 0 Trang2 b
Câu 7.1:Với a, b là các tham số thực. Giá trị tích phân  2 3x  2ax   1dx bằng 0 A. 3 2
b b a b . B. 3 2
b b a b . C. 3 2
b ba b . D. 2 3b  2ab 1 m Câu 7.2:Cho  2
3x  2x  
1 dx  6 . Giá trị của tham số m thuộc khoảng nào sau đây? 0 A.  1  ;2 . B.  ;0  . C. 0; 4 . D.  3   ;1 .  4 2
Câu 7.3:Giả sử I  sin 3xdx a b
a,b . Khi đó giá trị của ab là 2 0 1 3 1 A. B. 0 C. D. 6 10 5 1 2 Câu 7.4:Biết
cos px d x = m + 1. ò
Hỏi khẳng định nào sau đây đúng ? 0
A. pm = 1 - p. B.1 + pm = p.C.1 - pm = 2p. D.1 - 3m = p. 2
Câu 8.1:Tính tích phân 2
I  2x x 1dx  bằng cách đặt 2
u x 1, mệnh đề nào dưới đây đúng? 1 3 2 1 3 2 A. I udu B. I udu C. I  2 udu D. I udu  2 0 1 0 1 1 dx    
Câu 8.2:Cho tích phân I  
nếu đổi biến số x  2sin t,t   ;   thì ta được. 2   2 2  0 4 x π π π π 3 6 4 6 dt
A. I  dt  .
B. I  dt  .
C. I tdt  . D. I   . t 0 0 0 0  2
Câu 8.3:Cho tích phân I  2  cos x.sin d x x
. Nếu đặt t  2  cos x thì kết quả nào sau đây đúng? 0  2 3 2 2 A. I tdt  . B. I tdt  . C. I  2 tdt  . D. I tdt  . 3 2 3 0 e 3ln x 1
Câu 8.4:Cho tích phân I  dx
. Nếu đặt t  ln x thì x 1 1 3t 1 e 1 3t 1 e A. I  dt  . B. I  dt  .
C. I  3t    1 dt .
D. I  3t    1 dt . et t 0 1 1 0
Câu 9.1:Gọi S là diện tích của hình phẳng giới hạn bởi các đường 2x y
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A.   2x S dx B.  2x S dx C. 2   2 x S dx D. 2  2 x S dx  0 0 0 0
Câu 9.2:Gọi S là diện tích hình phẳng giới hạn bởi các đường ex y
, y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A.  ex S dx B.  2 ex S dx C.   ex S dx D. 2   e x S dx  0 0 0 0 Trang3
Câu 9.3:Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi
đồ thị hàm số y f x , trục Ox và hai đường thẳng x  ,
a x b a b , xung quanh trục Ox . b b b b A.V f
 xdx B. 2 V   f
 xdx C. 2 V f
 xdx D.V   f  xdx a a a a
Câu 9.4:Cho hình phẳng  H  giới hạn bởi các đường 2
y x  3 , y  0 , x  0 , x  2 . Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2 A.V   2
x  3 dx
B.V    2
x  3 dx C.V   2
x  3 dx
D.V    2 x  3 dx 0 0 0 0
Câu 10.1:Tính diện tích S hình phẳng giới hạn bởi các đường 2
y x 1, x  1
 , x  2 và trục hoành. 13 A. S  6 . B. S  16 . C. S  . D. S 13. 6
Câu 10.2:Gọi S là diện tích hình phẳng giới hạn bởi các đường 2
y x  5 , y  6x , x  0 , x 1. Tính S . 4 7 8 5 A. B. C. D. 3 3 3 3 2
Câu 10.3:Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y  4x x và trục Ox 34 31 32 A.11. B. . C. . D. . 3 3 3
Câu 10.4:Diện tích hình phẳng giới hạn bởi đồ thị hàm số y   x  2 2
1, trục hoành và hai đường thẳng
x  1, x  2 bằng 2 3 1 7 A. . B. . C. . D. . 3 2 3 3
Câu 11.1 :Cho hình phẳng  H  giới hạn bởi các đường 2
y x  3, y  0, x  0, x  2 . Gọi V là thể tích khối
tròn xoay được tạo thành khi quay H  xung quanh trục Ox . Mệnh đề nào sau đây đúng? 2 2 2 2 2 2
A.V    2
x  3 dx . B.V   2 x  3dx . C.V   2
x  3 dx . D.V    2 x  3dx . 0 0 0 0
Câu 11.2:Gọi V là thể tích của khối tròn xoay thu được khi quay hình thang cong, giới hạn bởi đồ thị hàm số 
y  sin x , trục Ox, trục Oy và đường thẳng x
, xung quanh trục Ox. Mệnh đề nào dưới đây đúng? 2     2 2 2 2 A. 2 V  sin xdx
B.V  sin xdxC. 2
V   sin xdx
D.V   sin xdx  0 0 0 0
Câu 11.3 :Cho hình phẳng  H  giới hạn bởi các đường 2
y  2x x , y  0 . Quay  H  quanh trục hoành tạo
thành khối tròn xoay có thể tích là 2 2 2 2 2 2 A.  2 2   x x dx B.   2 2 
x x dx C.  2 2   x x dx D.   2 2   x x dx 0 0 0 0
Câu 11.4:Cho hình phẳng  H  giới hạn bởi các đường thẳng 2
y x  2, y  0, x  1, x  2 . Gọi V là thể tích
của khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2 A.V   2
x  2dx
B.V    2
x  2 dx C.V   2
x  2 dx D.V    2
x  2dx 1 1 1 1 Trang4
Câu 12.1:Cho hàm số y f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 và x  5 (như hình vẽ bên). Mệnh đề nào sau đây đúng? 1 5 1 5
A. S   f (x)dx f (x)dx   . B. S
f (x)dx f (x)dx   . 1  1 1  1 1 5 1 5 C. S
f (x)dx f (x)dx   .
D. S   f (x)dx f (x)dx   . 1  1 1  1
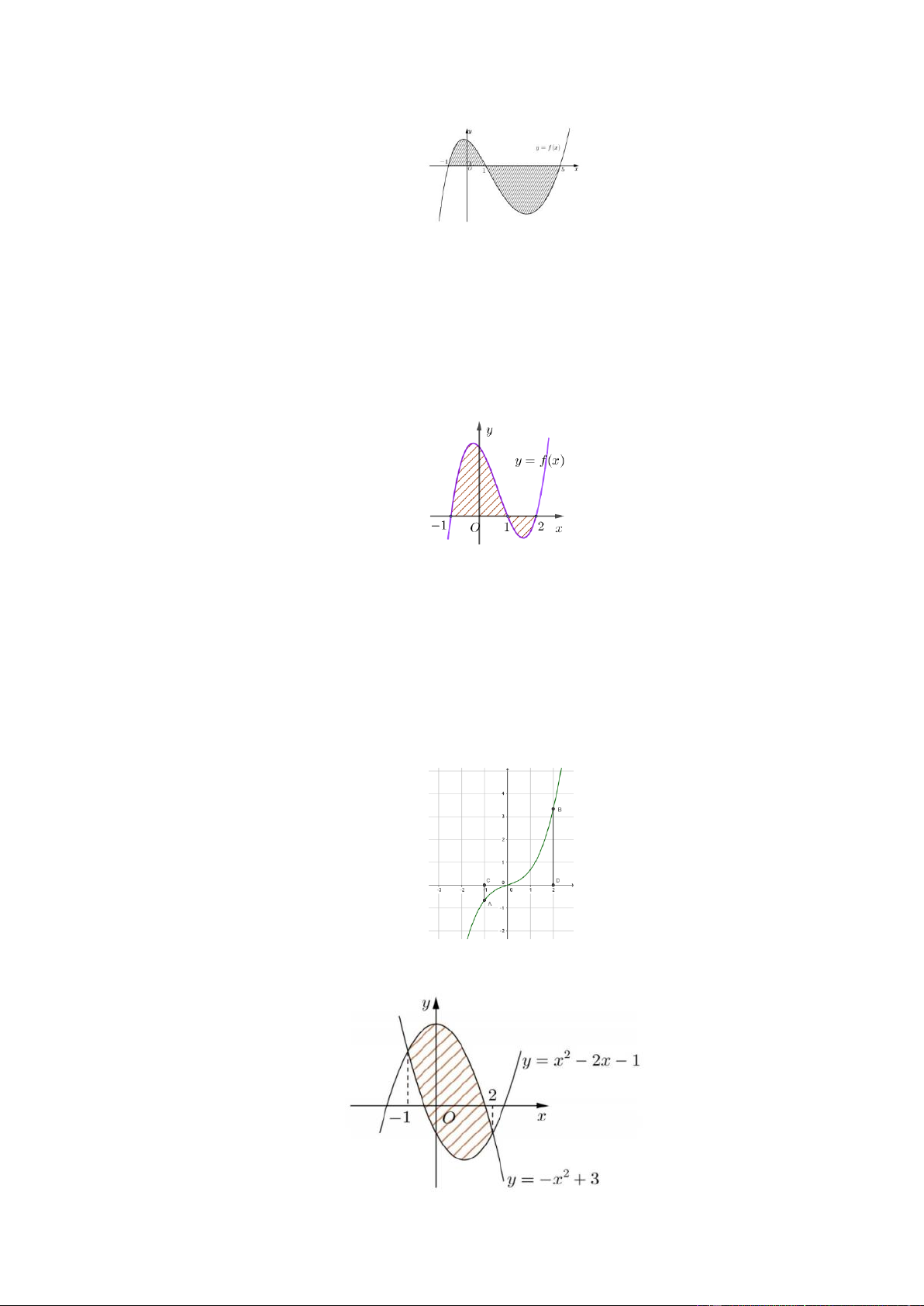
Câu 12.2:Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x, y  0, x  1
 , x  2 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S f
 x dx + f
 x dx .
B. S   f
 x dx f
 x dx . 1  1 1  1 1 2 1 2
C. S   f
 x dx+ f
 x dx . D. S f
 x dx  f
 x dx . 1  1 1  1
Câu 12.3:Gọi S là diện tích hình phẳng  H  giới hạn bởi các đường y f x , trục hoành và hai đường thẳng 0 2 x  1
 , x  2 . Đặt a f
 xdx,b f
 xdx , mệnh đề nào sau đây đúng? 1  0
A. S b a
B. S b a
C. S b   a
D. S b  a
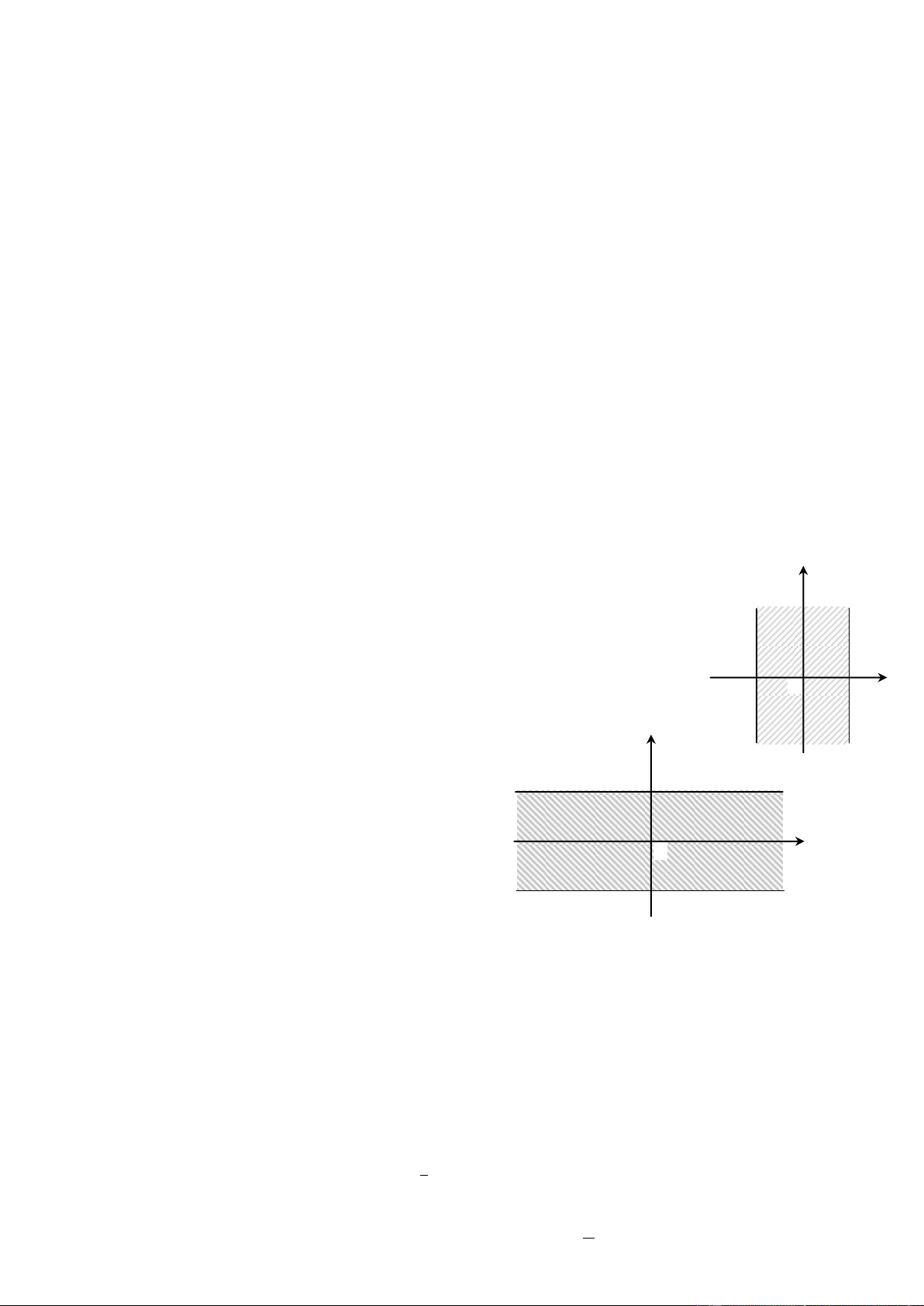
Câu 12.4:Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây? 2 2 2 2 A.   2
x  2dx
B.  2x  2dx C.   2 2
x  2x  4dx D.   2
2x  2x  4dx 1  1  1  1  Trang5
Câu 13.1:Cho hình phẳng D giới hạn với đường cong 2 y =
x + 1 , trục hoành và các đường thẳng
x = 0, x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? 4 4
A.V  2 B.V
C.V  2 D.V 3 3
Câu 13.2: Cho hình phẳng D giới hạn bởi đường cong  x y
e , trục hoành và các đường thẳng x  0 , x  1.
Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?  2e   1 2  2e   e  1  2 e 1 A. V B. V C. V D. V  2 2 3 2
Câu 13.3:Cho hình phẳng D giới hạn bởi đường cong y  2  cos x , trục hoành và các đường thẳng  x  0, x
. Khối tròn xoay tạo thành khi D quay quanh trục hoành có thể tích V bằng bao nhiêu? 2
A. V  (  1)
B. V   1
C. V    1
D. V  (  1)
Câu 13.4:Cho hình phẳng D giới hạn bởi đường cong y  2  sin x , trục hoành và các đường thẳng x  0 ,
x   . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu?
A.V  2    1
B.V  2
C.V  2   1 D. 2 V  2
Câu 14.1:Số phức có phần thực bằng 1 và phần ảo bằng 3 là
A.1 3i B. 1  3i
C.1 3i D. 1  3i
Câu 14.2:Số phức 5  6i có phần thực bằng A. 6  . B. 6 . C. 5  . D. 5
Câu 14.3:Số phức có phần thực bằng 3 và phần ảo bằng 4 là
A. 3  4i
B. 4  3i
C. 3  4i D. 4  3i
Câu 14.4:Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức 3  2 2i . Tìm a , b .
A. a  3;b  2
B. a  3;b  2  2
C. a  3;b  2
D. a  3;b  2 2
Câu 15.1:Cho hai số phức z  2  i và z  1 i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn của số phức 1 2
2z z có tọa độ là 1 2 A. 0; 5 . B. 5;   1 . C.  1  ; 5 . D. 5; 0 .
Câu 15.2:Cho hai số phức z  1 i và z  2  i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 1 2
z  2z có tọa độ là 1 2 A. (3; 5) . B. (5; 2) . C. (5; 3) . D. (2;5) .
Câu 15.3:Cho số phức z  1 2i , z  3
  i . Tìm điểm biểu diễn của số phức z z z trên mặt phẳng tọa 1 2 1 2 độ. A. M 2; 5   B. P  2  ;  1 C. Q  1  ;7 D. N 4; 3  
Câu 15.4:Trong mặt phẳng tọa độ, điểm M là điểm biểu diễn của số phức z . Điểm nào trong hình vẽ là điểm
biểu diễn của số phức 2z ? y Q E M O x N P
A.Điểm Q
B.Điểm E
C.Điểm P D.Điểm N Trang6
Câu 16.1:Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức z’ = -2 + 5i
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
Câu 16.2:Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức z’ = 2 + 3i
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
Câu 16.3:Điểm biểu diễn của các số phức z = 3 + bi với b  R, nằm trên đường thẳng có phương trình là: A. x = 3 B. y = 3 C. y = x D. y = x + 3
Câu 16.4:Điểm biểu diễn của các số phức z = a + ai với a  R, nằm trên đường thẳng có phương trình là: A. y = x B. y = 2x C. y = 3x D. y = 4x
Câu 17.1:Cho số phức z = a - ai với a  R, điểm biểu diễn của số phức đối của z nằm trên đường thẳng có phương trình là: A. y = 2x B. y = -2x C. y = x D. y = -x
Câu 17.2:Cho số phức z = a + a2i với a  R. Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên: A. Đường thẳng y = 2x
B. Đường thẳng y = -x + 1 y C. Parabol y = x2 D. Parabol y = -x2
Câu 17.3:Cho hai số phức z = a + bi; a,b  R.
Để điểm biểu diễn của z nằm trong dải (-2; 2) (hình 1) điều kiện của a và b là: x a  2 a   2  -2 O 2 A.  B.  C. 2
  a  2 và b  R D. a, b  (-2; 2) b  2 b  -2 y x
Câu 17.4:Cho số phức z = a + bi ; a,  R. Để (Hình 1)
điểm biểu diễn của z nằm trong dải (-3; 3) (hình 2) điều kiện của a và b là: 3 a  3 a   3  x A.  B.  b  3 b  -3 O -3 C. a, b  (-3; 3)
D. a  R và -3 < b < 3 (Hình 2)
Câu 18.1:Cho hai số phức z  3  2i z  2  i z z 1 và . Số phức bằng 2 1 2 A. 5  i . B. 5  i . C. 5  i . D. 5  i .
Câu 18.2:Cho hai số phức z  1 2i z  4  i z z 1 và . Số phức bằng 2 1 2 A. 3  3i . B. 3   3i . C. 3   3i . D. 3  3i .
Câu 18.3:Cho hai số phức z  1 2i và z  2  i . Số phức z z bằng 1 2 1 2 A. 3 i . B. 3  i . C. 3 i . D. 3  i . z   i z   i z z
Câu 18.4:Cho hai số phức 1
1 3 và 2 3 . Số phức 1 2 bằng A. 2  4i .
B. 2  4i . C. 2   4i . D. 2  4i .
Câu 19.1:Cho số phức z 1 2i , số phức 2  3iz bằng A. 4  7i . B. 4   7i C. 8  i . D. 8  i .
Câu 19.2:Cho hai số phức z 1 2i và w  3 i . Môđun của số phức . z w bằng Trang7 A. 5 2 . B. 26 . C. 26 . D. 50 .
Câu 19.3:Cho số phức z  2
  3i , số phức 1 iz bằng A. 5  i . B. 1  5i . C.1 5i . D. 5  i .
Câu 19.4:Cho hai số phức z  2  2i và w  2  i . Mô đun của số phức zw bằng A. 40 . B. 8 . C. 2 2 . D. 2 10 .
Câu 20.1:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z2 = ( z )2 là: A. Trục hoành B. Trục tung
C. Gồm cả trục hoành và trục tung D. Đường thẳng y = x
Câu 20.2:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z2 là một số ảo là:
A. Trục hoành (trừ gốc toạ độ O)
B. Trục tung (trừ gốc toạ độ O)
C. Hai đường thẳng y = ±x
D. Đường tròn x2 + y2 = 1
Câu 20.3:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z2 là một số thực âm là:
A. Trục hoành và trục tung (trừ gốc toạ độ O)
B. Trục tung (trừ gốc toạ độ O)
C. Đường thẳng y = x (trừ gốc toạ độ O)
D. Đường thẳng y = -x (trừ gốc toạ độ O)
Câu 20.4:Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z2 là một số thực dương là:
A. Trục hoành (trừ gốc toạ độ O)
B. Trục tung (trừ gốc toạ độ O)
C. Đường thẳng y = x (trừ gốc toạ độ O)
D. Đường thẳng y = -x (trừ gốc toạ độ O) 1
Câu 21.1:Cho số phức z = a + bi. Khi đó số zz là: 2i A. Một số thực B. 0 C. Một số thuần ảo D. i 1
Câu 21.2:Điểm biểu diễn của số phức z = là: 2  3i  2 3  A. 2;  3 B. ; 
 C.3;  2 D.4; 1  13 13 
Câu 21.3:Số phức nghịch đảo của số phức z = 1 - 3i là: 1 3 1 3 A. 1 z =  i B. 1 z =  i C. 1 z = 1 + 3i D. 1 z = -1 + 3i 2 2 4 4 3  4i
Câu 21.4:Số phức z = bằng: 4  i 16 13 16 11 9 4 9 23 A.  i B.  i C.  i D.  i 17 17 15 15 5 5 25 25 3  2i 1  i
Câu 22.1:Thu gọn số phức z =  ta được: 1  i 3  2i 21 61 23 63 15 55 2 6 A. z =  i B. z =  i C. z =  i D. z =  i 26 26 26 26 26 26 13 13 1 3
Câu 22.2:Cho số phức z =  
i . Số phức ( z )2 bằng: 2 2 1 3 1 3 A.   i B.   i C.1  3i D. 3  i 2 2 2 2 1 3
Câu 22.3:Cho số phức z =  
i . Số phức 1 + z + z2 bằng: 2 2 Trang8 1 3 A.   i . B. 2 - 3i C. 1 D. 0 2 2
Câu 22.4:Cho số phức z  0. Biết rằng số phức nghịch đảo của z bằng số phức liên hợp của nó. Trong các kết luận nào đúng: A. z  
B. z là một số thuần ảo C. z  1 D. z  2 z
Câu 23.1:Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức có phần thực là: z ' aa ' bb ' aa ' bb ' a  a ' 2bb ' A. B. C. D. 2 2 a  b 2 2 a '  b ' 2 2 a  b 2 2 a '  b ' z
Câu 23.2:Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức có phần ảo là: z ' aa ' bb ' a ' b  ab ' aa ' bb ' 2bb ' A. B. C. D. 2 2 a  b 2 a '  2 b ' 2 2 a  b 2 2 a '  b ' z  1
Câu 23.3:Cho số phức z = x + yi  1. (x, y   ). Phần ảo của số là: z  1 2x  2y  xy x  y A.  B. C. D. x  12 2  y x 12 2  y x 12 2  y x 12 2  y z  i
Câu 23.4:Cho số phức z = x + yi . (x, y   ). Tập hợp các điểm biểu diễn của z sao cho là một số thực z  i âm là:
A. Các điểm trên trục hoành với -1 < x < 1
B. Các điểm trên trục tung với -1 < y < 1 x  1  y  1 
C. Các điểm trên trục hoành với 
D. Các điểm trên trục tung với  x  1 y  1
Câu 24.1:Cho a  R biểu thức a2 + 1 phân tích thành thừa số phức là: A. (a + i)(a - i) B. i(a + i) C. (1 + i)(a2 - i)
D. Không thể phân tích được thành thừa số phức
Câu 24.2:Cho a  R biểu thức 2a2 + 3 phân tích thành thừa số phức là: A. (3 + 2ai)(3 - 2ai)
B.  2a  3i 2a  3i C.1  i2a  i
D. Không thể phân tích được thành thừa số phức
Câu 24.3:Cho a, b   biểu thức 4a2 + 9b2 phân tích thành thừa số phức là:
A. 4a  9i4a  9i B. 4a  9bi4a  9bi  C. 2a  3bi2a  3bi
D. Không thể phân tích được thành thừa số phức
Câu 24.4:Cho a, b   biểu thức 3a2 + 5b2 phân tích thành thừa số phức là:
A.  3a  5bi 3a  5bi B.  3a  5i 3a  5i C.3a  5bi3a  5bi
D. Không thể phân tích được thành thừa số phức
Câu 25.1:Cho phương trình z2 + bz + c = 0. Nếu phương trình nhận z = 1 + i làm một nghiệm thì b và c bằng: A. b = 3, c = 5 B. b = 1, c = 3 C. b = 4, c = 3 D. b = -2, c = 2
Câu 25.2:Cho phương trình 3  2 z
az  bz  c  0 Nếu z = 1 + i và z = 2 là hai nghiệm của phương trình thì a, b, c bằng: a   4  a  2 a  4 a   0    
A. b  6 B. b  1 C. b  5 D. b  1      c  4   c  4  c  1  c  2  Trang9 1   5i 5 1   5i 5
Câu 25.3:Phương trình bậc hai với các nghiệm: z  , z  là: 1 3 2 3 A. z2 - 2z + 9 = 0 B. 3z2 + 2z + 42 = 0 C. 2z2 + 3z + 4 = 0 D. z2 + 2z + 27 = 0
Câu 25.4:Cho P(z) = z3 + 2z2 - 3z + 1. Khi đó P(1 - i) bằng: A. -4 - 3i B. 2 + i C. 3 - 2i D. 4 + i 2 2 2
Câu 26.1:Trong không gian Oxyz , cho mặt cầu S  : x  
1   y  2   z  3  16 . Tâm của  S  có tọa độ là A.  1  ; 2;3. B. 1; 2;3 . C.  1  ;2;3 . D. 1;  2;3 .
Câu 26.2:Trong không gian 2 2 2
Oxyz , cho mặt cầu S  :  x   3   y   1   z   1
 2 . Tâm của S  có tọa độ là A. 3;1; 1  B. 3; 1   ;1 C.  3  ; 1   ;1 D.  3  ;1;  1 2 2
Câu 26.3:Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S  2
: x   y  2   z  2  8. Tính bán kính
R của  S  .
A. R  8
B. R  4
C. R  2 2
D. R  64 2 2 2
Câu 26.4:Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S : x  5  y  
1  z  2  9 . Tính bán
kính R của S . A. R  3 B. R  18 C. R  9 D. R  6
Câu 27.1:Trong không gian với hệ tọa độ Oxyz , cho các điểm A1;0;3, B2;3; 4  , C  3
 ;1;2 . Tìm tọa độ
điểm D sao cho tứ giác ABCD là hình bình hành. A. D 6; 2; 3  . B. D  2  ;4;5.
C. D 4; 2;9 . D. D  4  ; 2  ;9. Câu 27.2:Trong không gian với hệ tọa
độ Oxyz , cho hình bình hành ABCD biết (
A 1;1;2), B ( 2; 1; 4),C (3; 2; 5). Tìm tọa độ đỉnh D? A. D(6; 0; 1  1)     B. D( 6;1;11)
C. D(5; 2; 1) D. D( 3;6;1)
Câu 27.3:Trong không gian với hệ trục tọa độ Oxyz,cho tam giác ABC biết ( A 1
 ;3;4), B(2;1;0) và G(2;5; 3
 ) là trọng tâm của tam giác. Tìm tọa độ đỉnh C? A. C(5;13; 5)   
B. C(4; 9;5) C. C(7;12; 5) D. C(3;8; 13)
Câu 27.4:Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có (
A 2; 2;1), B(2;1; 1  ) và G(1;2;3) là
trọng tâm của tam giác. Tọa độ của điểm C là:
A.(-5;-3;9) B. (-7;-3;9) C. (-7;3;9) D. (-7;3;6)
Câu 28.1:Trong không gian Oxyz , cho ba điểm M 2;0;0 , N 0; 1;0 , P 0;0; 2 . Mặt phẳng MNP có x y z x y z x y z x y z
phương trình là:A.    0 . B.    1
 . C.    1. D.    1 2 1  2 2 1 2 2 1 2 2 1  2
Câu 28.2:Trong không gian với hệ tọa độ Oxyz , cho 3 điểm A1;0;0 ; B 0; 2
 ;0;C 0;0;3 . Phương trình
nào dưới dây là phương trình mặt phẳng  ABC? x y z x y z x y z x y z A.    1. B.    1. C.    1. D.    1. 3 2  1 2 1 3 1 2  3 3 1 2 
Câu 28.3:Trong không gian với hệ trục toạ độ Oxyz , phương trình nào dưới đây là phương trình của mặt
phẳng Oyz ?A. y  0 B. x  0 C. y z  0 D. z  0
Câu 28.4:Trong không gian Oxyz , mặt phẳng Oxz có phương trình là
A. x z  0.
B. x y z  0 . C. y  0 . D. x  0 . Trang10
Câu 29.1:Trong không gian Oxyz , mặt phẳng đi qua điểm A2; 1
 ;2 và song song với mặt phẳng
P : 2x y  3z  2  0 có phương trình là
A. 2x y  3z  9  0
B. 2x y  3z  11  0 C. 2x y  3z  11  0 D. 2x y  3z 11  0
Câu 29.2:Trong không gian với hệ toạ độ Oxyz , cho điểm M 3;  1;  2 và mặt phẳng
 : 3xy 2z4  0. Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với
 ?A.3xy2z6  0 B.3xy2z6  0 C.3xy2z6  0 D.3xy  2z14  0
Câu 29.3:Trong không gian với hệ toạ độ Oxyz , phương trình của mặt phẳng  P đi qua điểm M  2  ;3  ;1 và
song song với mặt phẳng Q : 4x  2y  3z  5  0 là
A. 4x-2y  3z 11  0 B. 4x-2y  3z 11  0 C. - 4x+2y  3z 11  0 D. 4x+2y  3z 11  0
Câu 29.4:Trong không gian với hệ toạ độ Oxyz , phương trình mặt phẳng (P) đi qua điểm A(1; 3; 1) và song
song (Q): 2x y z  7  0 là
A. 2x y z  4  0             B. 2x y z 10
0 C. 2x y z 8 0 D. 2x y z 3 0
Câu 30.1:Trong không gian với hệ tọa độ Oxyz , cho hai điểm A0;1 
;1 ) và B 1;2;3 . Viết phương trình của
mặt phẳng P đi qua A và vuông góc với đường thẳng AB .
A. x y  2z  3  0
B. x y  2z  6  0 C. x  3y  4z  7  0
D. x  3y  4z  26  0
Câu 30.2:Trong không gian Oxyz , cho hai điểm A2;1;0, B 1; 1
 ;2 . Mặt phẳng đi qua M  1  ;1  ;1 và vuông
góc với đường thẳng AB có phương trình là
A. x  2 y  2z 1  0
B. x  2 y  2z 1  0
C. 3x  2z 1  0
D. 3x  2z 1  0
Câu 30.3:Trong không gian Oxyz, Cho hai điểm A5; 4
 ;2 và B1;2;4. Mặt phẳng đi qua A và vuông góc
với đường thẳng AB có phương trình là
A. 2x  3y z  8  0 B. 3x y  3z 13  0 C. 2x  3y z  20  0 D. 3x y  3z  25  0
Câu 30.4:Trong không gian Oxyz, cho hai điểm A 1  ;2 
;1 và B 2;1;0. Mặt phẳng qua A và vuông góc với
AB có phương trình là
A. 3x y z  6  0
B. 3x y z  6  0 C. x  3y z  5  0
D. x  3y z  6  0
Câu 31.1:Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng cho mă ̣t phẳng  P có phương trình
3x  4 y  2z  4  0 và điểm A1; 2
 ;3 . Tính khoảng cách d từ A đến P 5 5 5 5 A. d B. d C. d D. d  9 29 29 3
Câu 31.2:Tính khoảng cách từ điểm A(1; 2; 4) đến mặt phẳng (P): x y  2z  5  0 ? 5 6 5 2 2 6 2 2 A. B. C. D. 3 6 3 3
Câu 31.3:Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng  P : x  2y  2z 10  0 và  8 7 4
Q : x  2y  2z  3  0 bằng A. . B. . C. 3 . D. . 3 3 3
Câu 31.4:Trong không gian Oxyz , khoảng cách giữa hai mặt phẳng  P : x  2y  2z 10  0 và  8 7 4
Q : x  2y  2z  6  0 bằng A. . B. . C. 3 . D. . 3 3 3 Trang11x  2  t 3
Câu 32.1:Trong không gian với hệ tọa độ vuông góc Oxyz, cho đường thẳng d : y  5 t
4 ,t   . Vectơ nào z 6  t 7
sau đây là một vectơ chỉ phương của đường thẳng d?    
A. u  (2; 5; 6) u (3; 4;7) u (2,3,0) u (5; 4; 0) B.   C. D.   x y z
Câu 32.2:Tìm vectơ chỉ phương của một đường thẳng có phương trình 5 1 4   2 3 7     A. u  (2; 3  ;7) u    u u   B. ( 2; 3;7) C. (2;3;7) D. ( 2;3;7) x 1 t
Câu 32.3:Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d :  y  5  t ? z  23t
A. P 1;2;5
B. N 1;5; 2 C. Q  1  ;1;3
D. M 1;1;3 x 1 y  2 z 1
Câu 32.4:Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d :   ? 1 3 3 A. P  1  ;2  ;1 .
B. Q 1;  2;  1 . C. N  1  ;3;2. D. P 1; 2  ;1 .
Câu 33.1:Trong không gian Oxyz, cho đường thẳng  đi qua điểm M 2;0;  1
 và có vectơ chỉ phương a 4; 6
 ;2. Phương trình tham số của đường thẳng  là x  2   2tx  2   4t
x  2  2t
x  4  2t     A. y  3  t . B. y  6  t . C. y  3  t . D. y  6  .     z  1  t z  1 2  t z  1    t z  2   t
Câu 33.2:Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình của đường thẳng
đi qua A2;3;0 và vuông góc với mặt phẳng P : x  3y z  5  0? x  1 tx  1 tx  1 3tx  1 3t    
A. y  1  3t
B. y  3t
C. y  1  3t
D. y  1  3t     z  1   t z  1   t z  1   t z  1   t x 1 y z  5
Câu 33.3:Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và mặt phẳng 1 3 1
P:3x3y  2z 6  0. Mệnh đề nào dưới đây đúng?
A. d cắt và không vuông góc với  P
B. d vuông góc với  P
C. d song song với  PD.d nằm trong
Câu 33.4:Trong không gian tọa độ Oxyz, phương trình nào dưới đây là phương trình chính tắc của đường x 1 2tx 1 y z  2 x 1 y z  2 x 1 y z  2 x 1 y z  2
thẳng d :  y  3t ? A.   B.        2 3 1 1 3  C. 2 2 3  D. 2 2 3 1 z  2   t
Câu 34.1:Viết ptđt đi qua hai điểm.Trong không gian với hệ tọa độ Oxyz , phương trình tham số của đường
thẳng đi qua hai điểm A1; 1  ;2 và B 3  ;2;  1 là x 1 4t
x  4  3tx 1 2tx  4  t     A. y  1   3t . B. y  3   2t . C. y  1   t . D. y  3   t .     z  2  tz  1 tz  2  3tz  1 2t Trang12
Câu 34.2:Trong không gian Oxyz, cho đường thẳng d đi qua hai điểm A1;2;3 và B 3;5;7 . Phương trình
nào sau đây là phương trình chính tắc của đường thẳng d ? x 1 y  2 z  3 x 1 y  2 z  3 x  2 y  3 z  4 x 1 y  2 z  3 A.   B.   . C.   D.   2 3 4 3 5 7 1 2 3 2 3 4
Câu 34.3:Trong không gian với hệ tọa độ Oxyz cho ba điểm A0; 1; 3 , B1; 0;1 , C 1;1; 2 . Phương
trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua A và song song với đường thẳng BC ? x  2tx y  1 z  3 x  1 y z  1
A. y  1 t . B.   . C.   .
D. x  2y z  0 .  2 1 1 2 1 1 z  3   t
Câu 34.4:Trong không gian với hệ tọa độ Oxyz , phương trình tham số của đường thẳng đi qua   điểm x y z M 2;1; 3
  và song song với đường thẳng 1 1   là 2 1  3 x  2  t
x  2  2tx 1 t
x  2  2t    
A. y  1 t .
B. y  1 t . C. y  1   t . D. y  1   t .     z  3   z  3   3tz  3  tz  3  3t
Câu 35.1:Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2; 3 ; B1; 4;  1 và đường thẳng x  2 y  2 z d   3 :
. Phương trình nào dưới đây là phương trình của đường thẳng đi qua trung điểm của 1 1 2
đoạn AB và song song với d ? x y  1 z  1 x  1 y  1 z  1 x y  2 z  2 x y  1 z  1 A.   B.   C.   D.   1 1 2 1 1 2 1 1 2 1 1 2
Câu 35.2:Trong không gian với hê ̣ to ̣a đô ̣ Oxyz , cho đường thẳng  có phương trình: x 10 y  2 z  2  
. Xét mặt phẳng  P :10x  2y mz 11  0 , m là tham số thực. Tìm tất cả các 5 1 1
giá trị của m để mặt phẳng P vuông góc với đường thẳng  . A. m  2  B. m  2 C. m  52  D. m  52
Câu 35.3:Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng  P : 2x  2y z 1  0 và đường thẳng x 1 y  2 z 1  :  
. Tính khoảng cách d giữa  và  P . 2 1 2 1 5 2 A. d  . B. d  . C. d  . D. d  2 . 3 3 3
Câu 35.4:Trong không gian Oxyz , mặt phẳng đi qua điểm A1; 2; 2
  và vuông góc với đường thẳng x 1 y  2 z  3  :   có phương trình là 2 1 3
A. 3x  2 y z  5  0 .
B. 2x y  3z  2  0 .
C. x  2 y  3z 1  0 .
D. 2x y  3z  2  0 .
---------------------------------------- HẾT----------------------------------------------- Trang13

Tài liệu liên quan: