










Preview text:
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 10 BỘ ĐỀ CHƯƠNG 1 THEO FORM 2025
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Page: CLB GIÁO VIÊN TRẺ TP HUẾ TR¾C NGHIÖM CHUY£N §Ò M«n: To¸n 10 – KNTT MỆNH ĐỀ
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 01_TrNg 2025 Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung tâm Km10- Hương Trà – Huế NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi, thí sinh chỉ chọn một phương án. Câu 1.
Phát biểu nào dưới đây là mệnh đề? A. 2 3 9 .
B. Phong cảnh đẹp quá!
C. 5 x 7 .
D. Bây giờ là mấy giờ? Câu 2.
Các câu sau đây, câu nào không là mệnh đề? A. Phương trình 2
x x 1 0 vô nghiệm.
B. x y 1.
C. 12 không là số nguyên tố.
D. Hai phương trình 2
x 4x 3 0 và 2 2x
x 3 0 có nghiệm chung. Câu 3.
Trong các câu sau, câu nào là mệnh đề đúng?
A. Nếu a b thì 2 2 a b .
B. Nếu a chia hết cho 9 thì a chia hết cho 3 .
C. Nếu bạn tự tin thì bạn thành công.
D. Nếu một tam giác có một góc bằng 60 thì tam giác đó đều. Câu 4.
Trong các mệnh đề, mệnh đề nào sai? A. 2
x , x 3x 2 0. B. 2 x
, x 1 0. C. 2
x , x 0. D. x
, x 1 0. Câu 5.
Cho mệnh đề P x :" 2 x
, x x 1 0". Mệnh đề phủ định của mệnh đề P x là: A. 2 " x
, x x 1 0" . B. 2 " x
, x x 1 0" . C. 2 " x
, x x 1 0" . D. 2
" x , x x 1 0". 1 Câu 6.
Cho mệnh đề P :" x
, x ". Xác định mệnh đề phủ định của mệnh đề P . x 1 1 A. P :" x , x ". B. P :" x , x ". x x 1 1 C. P :" x , x ". D. P :" x , x ".. x x
Câu 7. Xét mệnh đề chứa biến P x 2
: " x , x 2x 0". Tìm một giá trị của biến x để được một mệnh đề đúng. 1 A. x
B. x 3 .
C. x 1 . D. x 0.5 . 4
Câu 8. Mệnh đề nào sau đây sai? 2 2 A. 2 x
,3x 4x 4 0. B. x , x 1 x 1 0. 1 C. x
, x . D. x
, 1 2 3... n 11. x Câu 9.
Cho mệnh đề chứa biến P n : “ 2
n 1 chia hết cho 4 ” với n là số nguyên. Khẳng định nào dưới đây đúng?
A. P 5 đúng và P 2 đúng.
B. P 5 sai và P 2 sai.
C. P 5 đúng và P 2 sai.
D. P 5 sai và P 2 đúng.
Câu 10. Mệnh đề phủ định của mệnh đề P : “ 2 x
: x 2x 5 là số nguyên tố” là A. 2 x
: x 2x 5 không là số nguyên tố. B. 2 x
: x 2x 5 là hợp số. C. 2 x
: x 2x 5 không phải là hợp số. D. 2 x
: x 2x 5 là số thực.
Câu 11. Cho mệnh đề 2 P : “x
: x x” . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề P ? A. 2 “ x
: x x” . B. 2 “ x
: x x” . C. 2 “ x
: x x” . D. 2 “ x
: x x” .
Câu 12. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai (điền dấu X vào ôn chọn)
Câu 1: Các mệnh đề sau đúng hay sai?
a) Nếu IA IB thì I là trung điểm của AB .
b) Nếu a chia hết cho 9 thì a chia hết cho 3 .
c) Nếu x 2 thì x 2 . d) Nếu m, n
là 2 số nguyên dương và 2 2 m
n chia hết cho 3 thì m, n cùng chia hết cho 3.
Câu 2: Các mệnh đề sau đúng hay sai? a) 2 r
, 4r 1 0 . b) * n
,1 2 3 n không chia hết cho 11. c) 2 n
, n n 1 là một số chẵn. 3 2
2x 6x x 3 d) x , 2 2x . 1
Câu 3: Các mệnh đề sau đúng hay sai? 10 a) . 3
b) Phương trình 3x 7 0 có nghiệm thực.
c) Không có số nào cộng với chính nó bằng 0. d) 2022 là hợp số.
Câu 4: Các mệnh đề sau đúng hay sai? 1 a) 3 2 . 3 2 b) 2 2 18 8. c) 2 3 12 là một số hữu tỷ. 2 x 4
d) x 2 là một nghiệm của phương trình 0 . x 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho mệnh đề P : “Phương trình 2
x 3x 8 0 có nghiệm”. Có bao nhiêu giá trị của x để
mệnh đề P đúng? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 2: Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng? (1) P : “ 2 n
, n n ” (2) P : “ 2
x : x 2x 5 là số nguyên tố”
(3) P x : 2 " x
, x x 1 0" Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 3: Tính tổng các giá trị n nguyên sao cho n 5 2n 1 . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 4: Cho mệnh đề 2 P : " x
: x 2mx 4 0", m là tham số thực. Có bao nhiêu giá trị nguyên
của m để mệnh đề P đúng? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 5: Có bao nhiêu số nguyên n để P n : “ 3 2
2n n 7n 1 chia hết cho 2n 1” là mệnh đề đúng? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 6: Tìm tổng các giá trị của x để mệnh đề chứa biến P x : " x là số nguyên thỏa mãn 4 2
x 5x 4 0" đúng. Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
____________________HẾT____________________
Huế, 14h00’ Ngày 09 tháng 6 năm 2024
Page: CLB GIÁO VIÊN TRẺ TP HUẾ TR¾C NGHIÖM CHUY£N §Ò M«n: To¸n 10 – KNTT MỆNH ĐỀ
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 01_TrNg 2025
LỜI GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi, thí sinh chỉ chọn một phương án. Câu 1.
Phát biểu nào dưới đây là mệnh đề? A. 2 3 9 .
B. Phong cảnh đẹp quá!
C. 5 x 7 .
D. Bây giờ là mấy giờ? Lời giải:
Phát biểu A: “ 2 3 9 ” là một phát biểu sai nên là một mệnh đề sai.
Phát biểu B: “Phong cảnh đẹp quá!” Không có tính đúng sai nên không phải là mệnh đề.
Phát biểu C: “ 5 x 7 ” là một mệnh đề chứa biến vì tính đúng sai của khẳng định phụ thuộc vào x .
Phát biểu D: “Bây giờ là mấy giờ?” Không có tính đúng sai nên không phải là mệnh đề. Câu 2.
Các câu sau đây, câu nào không là mệnh đề? A. Phương trình 2
x x 1 0 vô nghiệm.
B. x y 1.
C. 12 không là số nguyên tố.
D. Hai phương trình 2
x 4x 3 0 và 2 2x
x 3 0 có nghiệm chung. Lời giải:
Phát biểu A: Phương trình 2
x x 1 0 vô nghiệm là đúng nên đó là một mệnh đề đúng.
Phát biểu B: x y 1 có thể đúng, có thể sai phụ thuộc vào x, y nên không phải là mệnh đề.
Phát biểu C: 12 không là số nguyên tố, là một khẳng định sai nên là một mệnh đề sai.
Phát biểu D: Hai phương trình đều có 1 nghiệm x 1 nên phát biểu trên là một mệnh đề đúng. Câu 3.
Trong các câu sau, câu nào là mệnh đề đúng?
A. Nếu a b thì 2 2 a b .
B. Nếu a chia hết cho 9 thì a chia hết cho 3 .
C. Nếu bạn tự tin thì bạn thành công.
D. Nếu một tam giác có một góc bằng 60 thì tam giác đó đều. Lời giải:
Phát biểu A: Tính đúng, sai của phát biểu phụ thuộc vào a,b nên khẳng định không phải là một mệnh đề.
Phát biểu B luôn đúng với mọi a nên là một mệnh đề đúng.
Phát biểu C không khẳng định được tính đúng, sai nên không phải là mệnh đề.
Phát biểu D là một mệnh đề sai. Câu 4.
Trong các mệnh đề, mệnh đề nào sai? A. 2
x , x 3x 2 0. B. 2 x
, x 1 0. C. 2
x , x 0. D. x
, x 1 0. Lời giải:
Phát biểu A: đúng vì tồn tại 2 giá trị x 1, x 2 . Phát biểu B: đúng Phát biểu C: sai vì 2
x 0 với x . Phát biểu D: đúng. Câu 5.
Cho mệnh đề P x :" 2 x
, x x 1 0". Mệnh đề phủ định của mệnh đề P x là A. 2 " x
, x x 1 0" . B. 2 " x
, x x 1 0" . C. 2 " x
, x x 1 0" . D. 2
" x , x x 1 0". Lời giải:
Mệnh đề phủ định của mệnh đề P x :" 2 x
, x x 1 0" là 2 " x
, x x 1 0" . 1 Câu 6.
Cho mệnh đề P :" x
, x ". Xác định mệnh đề phủ định của mệnh đề P . x 1 1 A. P :" x , x ". B. P :" x , x ". x x 1 1 C. P :" x , x ". D. P :" x , x ".. x x Lời giải: 1 1
Mệnh đề phủ định của mệnh đề P :" x
, x " là P :" x
, x ". x x
Câu 7. Xét mệnh đề chứa biến P x 2
: " x , x 2x 0". Tìm một giá trị của biến x để được một mệnh đề đúng. 1 A. x
B. x 3 .
C. x 1 . D. x 0.5 . 4 Lời giải:
Vì thay x 3 vào mệnh đề chứa biến P x 2
: " x , x 2x 0", ta có 2
3 2.3 0 là mệnh đề đúng.
Câu 8. Mệnh đề nào sau đây sai? 2 2 A. 2 x
,3x 4x 4 0. B. x , x 1 x 1 0. 1 C. x
, x . D. x
, 1 2 3... n 11. x Lời giải: 2 2 x 1 0 x 1 Vì x 1 x 1 0 x . x 1 0 x 1
Vậy không có giá trị x thỏa mãn. Câu 9.
Cho mệnh đề chứa biến P n : “ 2
n 1 chia hết cho 4 ” với n là số nguyên. Khẳng định nào dưới đây đúng?
A. P 5 đúng và P 2 đúng.
B. P 5 sai và P 2 sai.
C. P 5 đúng và P 2 sai.
D. P 5 sai và P 2 đúng. Lời giải:
Mệnh đề C đúng, vì: P 2
5 5 1 24 chia hết cho 4 còn P 2
2 2 1 3 không chia hết cho 4.
Câu 10. Mệnh đề phủ định của mệnh đề P : “ 2 x
: x 2x 5 là số nguyên tố” là A. 2 x
: x 2x 5 không là số nguyên tố. B. 2 x
: x 2x 5 là hợp số. C. 2 x
: x 2x 5 không phải là hợp số. D. 2 x
: x 2x 5 là số thực.
Câu 11. Cho mệnh đề 2 P : “x
: x x” . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề P ? A. 2 “ x
: x x” . B. 2 “ x
: x x” . C. 2 “ x
: x x” . D. 2 “ x
: x x” .
Khẳng định nào dưới đây đúng? 2 P : “ x
: x x” .
Câu 12. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai (điền dấu X vào ôn chọn)
Câu 1: Các mệnh đề sau đúng hay sai?
a) Nếu IA IB thì I là trung điểm của AB .
b) Nếu a chia hết cho 9 thì a chia hết cho 3 .
c) Nếu x 2 thì x 2 .
d) Nếu m, n
là 2 số nguyên dương và 2 2 m
n chia hết cho 3 thì m, n cùng chia hết cho 3. Lời giải:
a) vì IA IB thì IAB có thể là tam giác cân tại I nên mệnh đề sai.
b) vì phát biểu a chia hết cho 9 thì a chia hết cho 3 luôn đúng với mọi a nên là một mệnh đề đúng.
c) vì x 2 thì x 2 hoặc x 2 nên mệnh đề sai. d) Nhận xét: 2 m ( 2
n ) là các số chính phương nên chia cho 3 có thể dư 0 hoặc 1 ( chứng minh
bằng cách xét m 3k, m 3k 1, m 3k 2 ) Do đó: Nếu 2 2
m , n cùng chia 3 dư 1 thì 2 2
m n chia 3 dư 2 ( trái giả thiết) Nếu 1 trong 2 số 2 2
m , n có 1 số chia hết cho 3 và số còn lại chia hết cho 3 dư 1 thì 2 2 m n chia
3 dư 1 ( trái giả thiết) Suy ra 2 2
m , n cùng chia hết cho 3. Mà 3 là số nguyên tố nên m, n cùng chia hết cho 3 nên mệnh đề đúng.
Câu 2: Các mệnh đề sau đúng hay sai? a) 2 r
, 4r 1 0 . b) * n
,1 2 3 n không chia hết cho 11. c) 2 n
, n n 1 là một số chẵn. 3 2
2x 6x x 3 d) x , 2 2x . 1 Lời giải: 1 a) Vì với 2 r
,4r 1 0 nên mệnh đề đúng. 2
b) Ta chứng tỏ mệnh đề phủ định “ * n
,1 2 3 n chia hết cho 11”. Thật vậy, nếu * n 11
thì 1 2 +3 11 66 chia hết cho 11 nên mệnh đề ban đầu sai.
c) Ta chứng minh mệnh đề phủ định “ 2 n
, n n 1 là một số lẻ” là đúng.
+ Nếu n chẵn thì 2
n n 1 là một số lẻ,
+ Nếu n lẻ, n 2k 1 thì 2 2
n n 1 4k 6k 3 là số lẻ
nên mệnh đề phủ định đúng và mệnh đề ban đầu sai.
x x x 2 3 2 2x 1 x 3 2 6 3 d) vì x ,
x 3 nên mệnh đề đúng. 2 2 2x 1 2x 1
Câu 3: Các mệnh đề sau đúng hay sai? 10 a) . 3
b) Phương trình 3x 7 0 có nghiệm thực.
c) Không có số nào cộng với chính nó bằng 0.
d) 2022 là hợp số. Lời giải: 10
a) Mệnh đề: “ ” là mệnh đề đúng. 3 7
b) Ta có: 3x 7 0 x
nên mệnh đề: “Phương trình 3x 7 0 có nghiệm” là mệnh đề 3 đúng.
c) Vì 0 0 0 nên mệnh đề: “Không có số nào cộng với chính nó bằng 0” là mệnh đề sai.
d) 2022 có các ước số là 1; 2;3;337; 2022 nên mệnh đề: “2022 là hợp số” là mệnh đề đúng.
Câu 4: Các mệnh đề sau đúng hay sai? 1 a) 3 2 . 3 2 b) 2 2 18 8. c) 2 3 12 là một số hữu tỷ. 2 x 4
d) x 2 là một nghiệm của phương trình 0 . x 2 Lời giải: 3 2 3 2 1 1 a) Ta có: 3 2
nên mệnh đề: “ 3 2 ” là 3 2 3 2 3 2 mệnh đề đúng. 2 2 2
b) Ta có: 2 18 2 3 2 2
2 8 nên mệnh đề: “ 2 2 18 8” là mệnh đề sai. 2 2 2
c) Vì 3 12 3 2 3 3 3 27 nên mệnh đề: “ 2 3 12
là một số hữu tỷ” là mệnh đề đúng. 2 x 4 d) Vì phương trình
0 không xác định tại x 2 nên mệnh đề: “ x 2 là một nghiệm x 2 2 x 4 của phương trình
0 ” là mệnh đề sai. x 2
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho mệnh đề P : “Phương trình 2
x 3x 8 0 có nghiệm”. Có bao nhiêu giá trị của x để
mệnh đề P đúng? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: 2
x 3x 8 0 có 23 0 nên phương trình vô nghiệm.
Vậy không có giá trị nào của x để mệnh đề P đúng. Đáp án : 0
Câu 2: Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng? (1) P : “ 2 n
, n n ” (2) P : “ 2
x : x 2x 5 là số nguyên tố”
(3) P x : 2 " x
, x x 1 0" Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
(1) P : “ 2 n
, n n ” sai với n = 1 (2) P : “ 2 x
: x 2x 5 là số nguyên tố” đúng với x = 0
(3) P x : 2 " x
, x x 1 0" đúng Đáp án : 2
Câu 3: Tính tổng các giá trị n nguyên sao cho n 5 2n 1 . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Gọi n là số nguyên thỏa mãn n 5 2n 1 . n 5 2n 1 2
n 5 2n 1 1 Ta có 2n 1 2n 1 2n 1 2n 1 2
2n 5 2n 1 2n 1 11 2n
1 2n 1 là ước của 11. 2n 1 1 n 1 2n 1 1 n 0 . 2n 1 11 n 6 2n 1 11 n 5 Đáp án : 2
Câu 4: Cho mệnh đề 2 P : " x
: x 2mx 4 0", m là tham số thực . Có bao nhiêu giá trị nguyên
của m để mệnh đề P đúng? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Ta có: x mx x m2 2 2 2 4 m 4 .
Vì x m2 0 x nên 2 2
x 2mx 4 0 x
m 4 0 m 2 2 m 2 . Khi đó m 1 ;0; 1 Đáp án : 3
Câu 5: Có bao nhiêu số nguyên n để P n : “ 3 2
2n n 7n 1 chia hết cho 2n 1” là mệnh đề đúng? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: Ta có : 3 2
n n n 2 2 7 1
n n 42n 1 5 2n 1 1 n 1 2n 1 1 n 0 3 2
2n n 7n 1 chia hết cho 2n 1 5 chia hết cho 2n 1 . 2n 1 5 n 3 2n 1 5 n 2
Vậy có 4 giá trị nguyên của n . Đáp án : 4
Câu 6: Tìm tổng các giá trị của x để mệnh đề chứa biến P x : " x là số nguyên thỏa mãn 4 2
x 5x 4 0" đúng. Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: 2 x 1 Ta có: 4 2
x 5x 4 0 x { 2 ; 1 ;1;2}. 2 x 4
Tìm tổng các giá trị của x để mệnh đề chứa biến P x đúng là 2 1 1 2 0 Đáp án : 0.
____________________HẾT____________________
Huế, 14h00’ Ngày 09 tháng 6 năm 2024
Page: CLB GIÁO VIÊN TRẺ TP HUẾ TR¾C NGHIÖM CHUY£N §Ò M«n: To¸n 10 – KNTT TẬP HỢP
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 01_TrNg 2025 Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung tâm Km10- Hương Trà – Huế NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi,
thí sinh chỉ chọn một phương án. Câu 1:
Liệt kê các phần tử của tập hợp X 2 x
| 2x 3x 1 0 . 1 3 A. X 0 . B. X 1 . C. X 1 ; . D. X 1 ; . 2 2
Câu 2: Cho tập hợp A a,b,c, d . Tìm số tập con của tập A . A. 16 . B. 15 . C. 12 . D. 10 . Câu 3:
Tìm x, y để ba tập hợp A 1; 4 , B 4;
x và C x; y ; 4 bằng nhau.
A. x y 1.
B. x y 1 hoặc x 1, y 4 .
C. x 1, y 4 .
D. x 4, y 1 hoặc x y 4 . Câu 4:
Cho S 7; 2;8; 4;9
;12 ; T 1;3;7;
4 . Tìm tập S T . A. 1; 2;3; 4;8;9;7 ;12 . B. 2;8;9 ;12 . C. 4; 7 . D. 1; 3 . Câu 5:
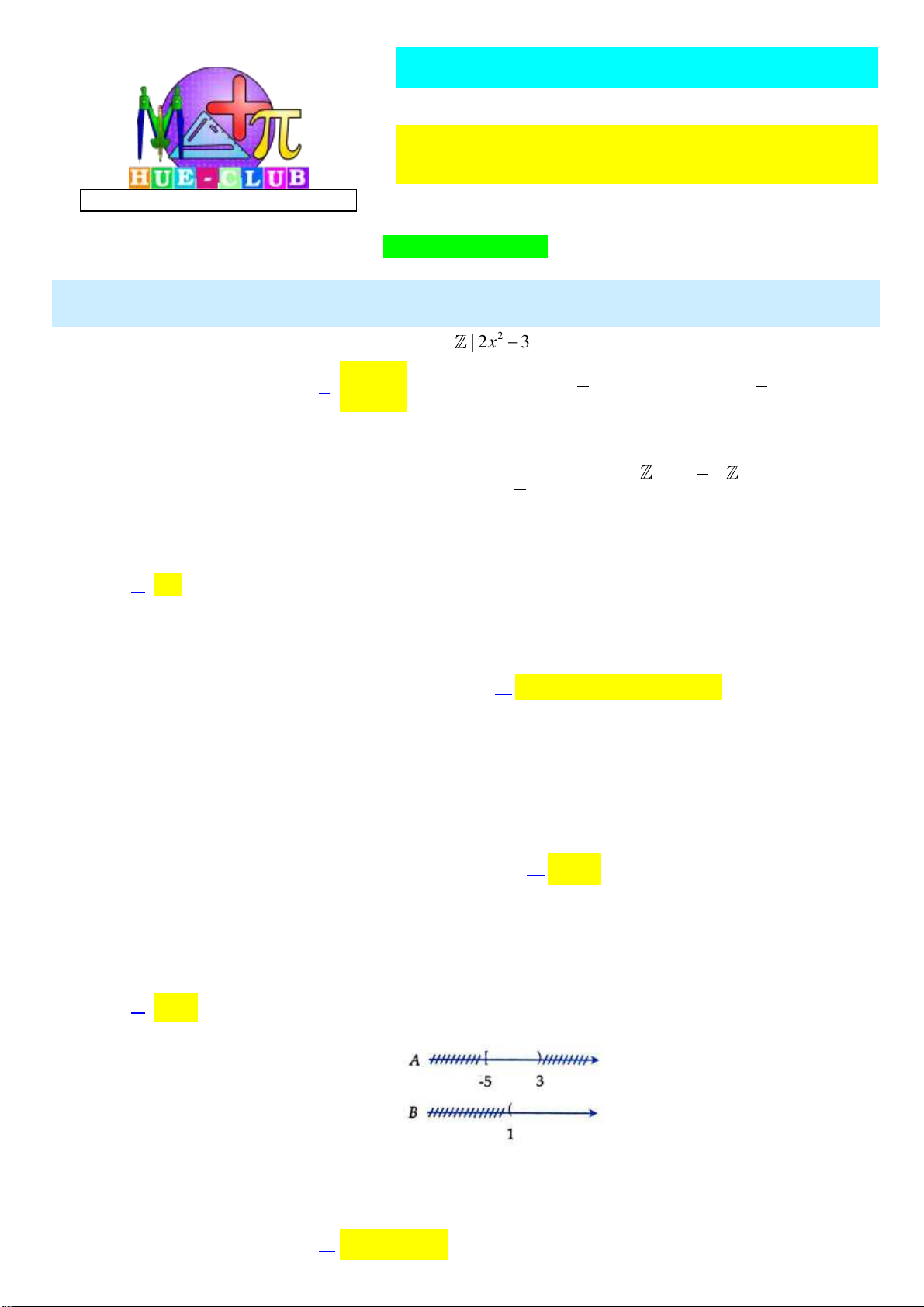
Cho hai tập hợp A 5;3, B 1; . Khi đó A B là tập nào sau đây? A. 1;3. B. 1; 3 . C. 5 ;. D. 5; 1 . Câu 6:
Cho 2 tập hợp: S 1;3;5; 8 ; T 3;5;7;
9 . Tập hợp S T bằng tập hợp nào sau đây? A. 3; 5 . B. 1;3;5;7;8; 9 . C. 1;7; 9 . D. 1;3; 5 . Câu 7:
Cho hai tập hợp A 2
;7, B 1;9. Tìm tập hợp A B . A. 1;7. B. 2;9. C. 2; 1 . D. 7;9. Câu 8:
Cho hai tập hợp A 2, 4, 6,
9 và B 1, 2,3,
4 .Tập hợp A \ B bằng tập nào sau đây?
A. A 1, 2,3, 5 . B. 1;3;6; 9 . C. 6; 9 . D. . Câu 9:
Cho hai tập hợp A 1;5; B 2;7 . Tập hợp A \ B là A. 1; 2. B. 2;5. C. 1;7. D. 1; 2.
Câu 10: Cho tập hợp A 2; . Tìm tập hợp C A . R A. 2; . B. 2; . C. ; 2. D. ; 2 .
Câu 11: Cho hai tập hợp A ( ;
m m 1) và B 1 ;
3 . Tìm tất cả các giá trị của m để A B . m 2 m 2 m 2 A. .
B. 2 m 3 . C. . D. . m 3 m 1 m 3
Câu 12: Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Vật lí, 6 học sinh giỏi Hóa học, 3 học sinh giỏi
cả Toán và Vật lí, 4 học sinh giỏi cả Toán và Hóa học, 2 học sinh giỏi cả Vật lí và Hóa học, 1
học sinh giỏi cả ba môn Toán, Vật lí, Hóa học. Tính số học sinh giỏi ít nhất một môn (Toán,
Vật lí, Hóa học) của lớp 10A . A. 10. B. 20. C. 17. D. 9.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 1: Cho hai tập hợp A 0;1; 2;3;
4 , B 3; 4;5; 6 .
a) A B 0;1;2;3;4;5; 6 .
b) A B 5; 6 .
c) B \ A 0;1; 2 .
d) A B \ A B A \ B B \ A .
Câu 2: Cho các tập hợp A [ 3;1) , B [0;5), C [ ; a a 3].
a) A B [0;1).
b) A B [ 3;5).
c) B \ A [1;5) .
d) A C 6 a 1. 11 m 1
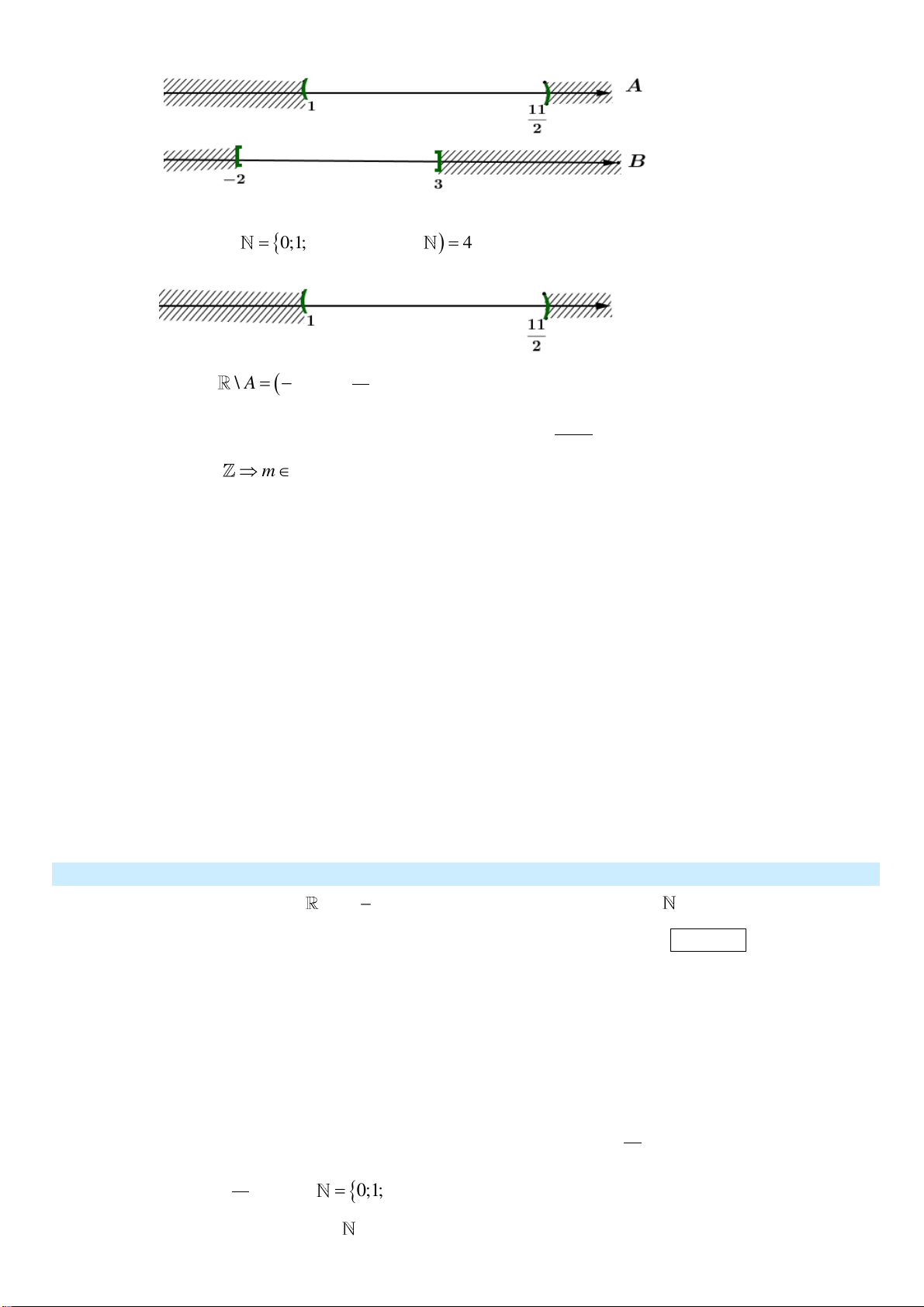
Câu 3: Cho ba tập hợp A 1; ; B 2 ; 3 và C ; . 2 3
a) Giao của hai tập hợp A và B là 1; 3 . b) Tập hợp B gồm 6 phần tử. c) Tập hợp A 11 \ ;1 ; . 2
d) Tổng các giá trị nguyên của m để B C có đúng 3 phần tử là số nguyên bằng 6.
Câu 4: Lớp 10A có 26 học sinh biết chơi đá bóng, 22 học sinh biết chơi cầu lông, 5 học sinh biết
chơi cả hai môn đá bóng và cầu lông, 8 học sinh không biết chơi môn nào.
a) Số học sinh chỉ biết chơi cầu lông mà không biết chơi đá bóng là 17 .
b) Số học sinh chỉ biết chơi đá bóng mà không biết chơi cầu lông là 20 .
c) Số học sinh biết chơi ít nhất một trong hai môn đá bóng hoặc cầu lông là 43 .
d) Sĩ số lớp 10A là 61 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho tập hợp A x x 2 : 2 11 x 3
0 . Số phần tử của A bằng bao nhiêu? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 2: Cho hai tập hợp A 0;5 và B 2;1; 3;
6 . Số phần tử của A B bằng bao nhiêu? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Câu 3: Cho các tập hợp
A x :x 13x 2x 2 0 và
B x x x 2 : 2 3 m 4
0 . Tích các giá trị của tham số m để n A B 3 bằng bao nhiêu? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 4: Một lớp có 45 học sinh, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu
lông. Có 30 em đăng kí môn bóng đá, 25 em đăng kí môn cầu lông. Hỏi có bao nhiêu em
đăng kí cả hai môn thể thao? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 5: Lớp 10A có 45 học sinh trong đó có 25 em học sinh học giỏi môn Toán, 23 em học sinh học
giỏi môn Văn, 20 em học sinh học giỏi môn Tiếng Anh. Đồng thời có 11 em học sinh học giỏi
cả môn Toán và môn Văn, 8 em học sinh học sinh giỏi cả môn Văn và môn Tiếng Anh, 9 em
học sinh học giỏi cả môn Toán và môn Tiếng Anh, biết rằng mỗi học sinh trong lớp học giỏi ít
nhất một trong ba môn Toán, Văn, Tiếng Anh. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba
môn Toán, Văn, Tiếng Anh? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 6: Cho hai tập hợp A x |1 x 2 ; B ; m 2 ;
m . Có bao nhiêu giá trị nguyên của m [ 2023 ;2 ]
024 để A B ? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
____________________HẾT____________________
Huế, 14h00’ Ngày 09 tháng 6 năm 2024
Page: CLB GIÁO VIÊN TRẺ TP HUẾ TR¾C NGHIÖM CHUY£N §Ò M«n: To¸n 10 – KNTT TẬP HỢP
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 01_TrNg 2025
LỜI GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi,
thí sinh chỉ chọn một phương án. Câu 1:
Liệt kê các phần tử của tập hợp X 2 x
| 2x 3x 1 0 . 1 3 A. X 0 . B. X 1 . C. X 1 ; . D. X 1 ; . 2 2 Lời giải: x 1 1 Vì phương trình 2
2x 3x 1 0 có nghiệm 1 nhưng vì x nên . x 2 2 Vậy X 1 .
Câu 2: Cho tập hợp A a,b,c, d . Tìm số tập con của tập A . A. 16 . B. 15 . C. 12 . D. 10 . Lời giải:
Số tập con của tập A là: 4 2 16 . Câu 3:
Tìm x, y để ba tập hợp A 1; 4 , B 4;
x và C x; y ; 4 bằng nhau.
A. x y 1.
B. x y 1 hoặc x 1, y 4 .
C. x 1, y 4 .
D. x 4, y 1 hoặc x y 4 . Lời giải:
Vì A B nên x 1 .
Do B C nên x y 1 hoặc y 4 .
Vậy x y 1 hoặc x 1, y 4 . Câu 4:
Cho S 7; 2;8; 4;9
;12 ; T 1;3;7;
4 . Tìm tập S T . A. 1; 2;3; 4;8;9;7 ;12 . B. 2;8;9 ;12 . C. 4; 7 . D. 1; 3 . Lời giải:
Tập hợp S T gồm các phần tử vừa thuộc X vừa thuộc Y
S T = 4; 7 Câu 5:
Cho hai tập hợp A 5;3, B 1; . Khi đó A B là tập nào sau đây? A. 1; 3 . B. 1; 3 . C. 5 ;. D. 5; 1 . Lời giải:
Ta có thể biểu diễn hai tập hợp A và B, tập A B là phần không bị gạch ở cả A và B nên x 1;3 . Câu 6:
Cho 2 tập hợp: S 1;3;5; 8 ; T 3;5;7;
9 . Tập hợp S T bằng tập hợp nào sau đây? A. 3; 5 . B. 1;3;5;7;8; 9 . C. 1;7; 9 . D. 1;3; 5 . Lời giải:
S T 1;3;5;7;8; 9 . Câu 7:
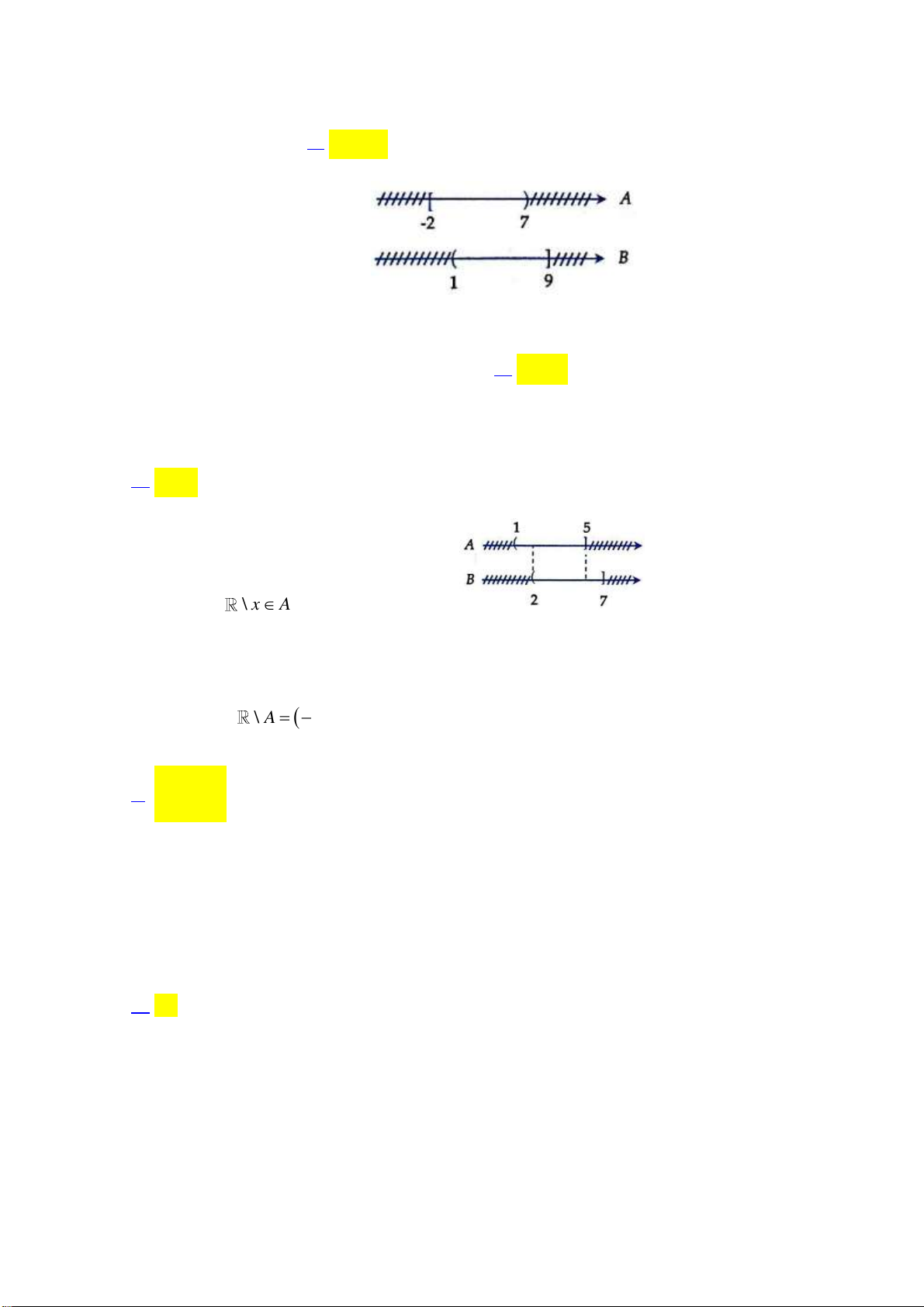
Cho hai tập hợp A 2
;7, B 1;9. Tìm A B . A. 1;7. B. 2;9. C. 2; 1 . D. 7;9. Lời giải: 2
;7 1;9 2 ;9 Câu 8:
Cho hai tập hợp A 2, 4, 6,
9 và B 1, 2,3,
4 .Tập hợp A \ B bằng tập nào sau đây?
A. A 1, 2,3, 5 . B. 1;3;6; 9 . C. 6; 9 . D. . Lời giải: A 2, 4,6,
9 , B 1, 2,3,
4 A \ B 6, 9 . Câu 9:
Cho hai tập hợp A 1;5; B 2;7 . Tập hợp A \ B là A. 1; 2. B. 2;5. C. 1;7. D. 1; 2. Lời giải:
A \ B x
\ x A va x
B x 1; 2 .
Câu 10: Cho tập hợp A 2; . Tìm tập hợp C A . R A. 2; . B. 2; . C. ; 2. D. ; 2 . Lời giải: Ta có: C A \ A ; 2 . R
Câu 11: Cho hai tập hợp A ( ;
m m 1) và B 1 ;
3 . Tìm tất cả các giá trị của m để A B . m 2 m 2 m 2 A. .
B. 2 m 3 . C. . D. . m 3 m 1 m 3 Lời giải: m 1 1 m 2
A B . m 3 m 3
Câu 12: Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Vật lí, 6 học sinh giỏi Hóa học, 3 học sinh giỏi
cả Toán và Vật lí, 4 học sinh giỏi cả Toán và Hóa học, 2 học sinh giỏi cả Vật lí và Hóa học, 1
học sinh giỏi cả ba môn Toán, Vật lí, Hóa học. Tính số học sinh giỏi ít nhất một môn (Toán,
Vật lí, Hóa học) của lớp 10A . A. 10. B. 20. C. 17. D. 9. Lời giải:
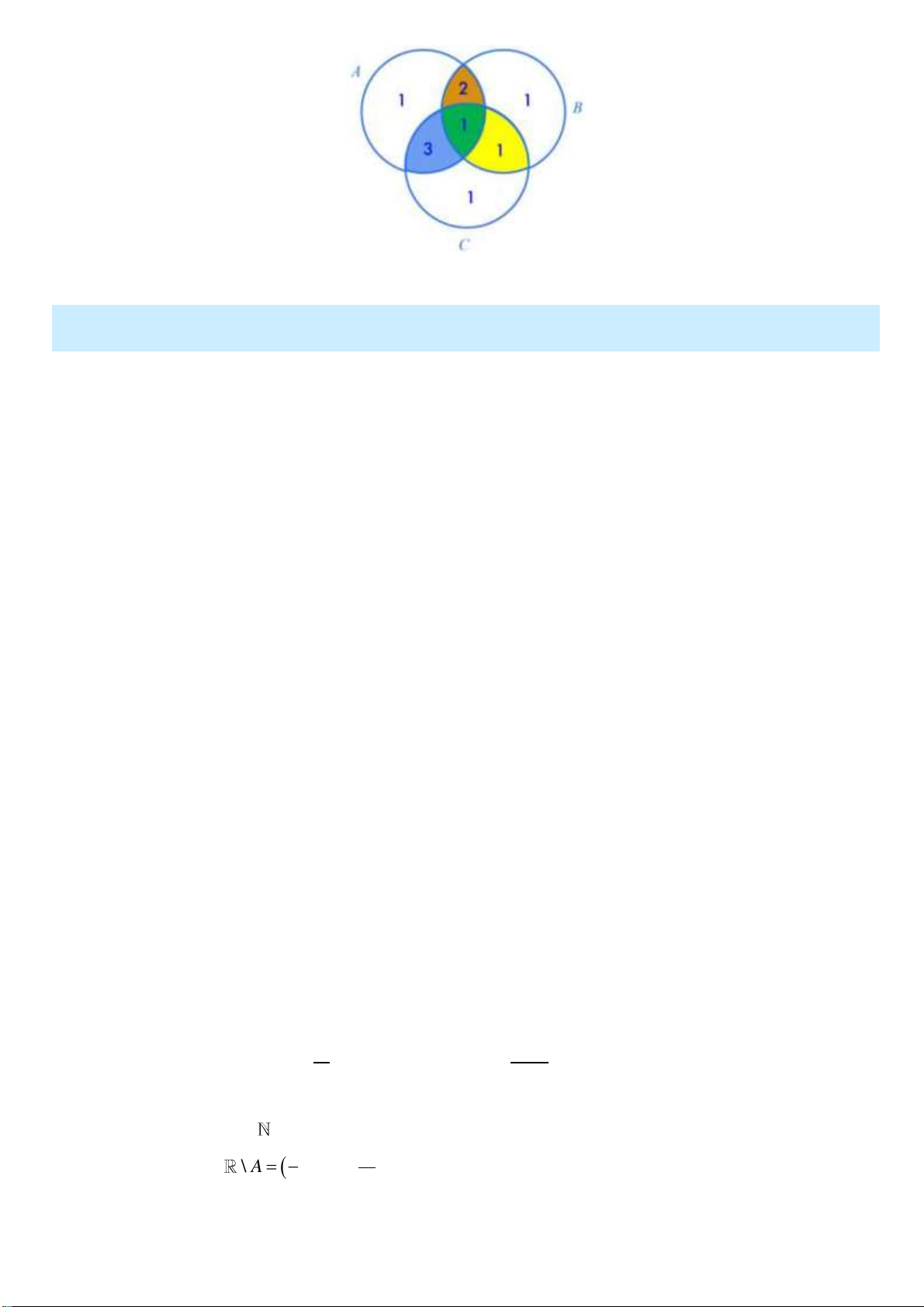
Gọi A , B , C lần lượt là tập hợp các bạn học sinh giỏi Toán, Vật lí, Hóa học.
Ta dùng biểu đồ Ven để giải toán: Dựa vào dữ kiện bài toán, ta biểu diễn các bạn học sinh học
giỏi các môn như hình vẽ dưới.
Chú ý: ta biểu diễn từ số học sinh giỏi cả 3 môn, 2 môn, chỉ một môn.
Nhìn vào biểu đồ, số học sinh giỏi ít nhất 1 trong 3 môn là:
n A B C 1 2 1 3 111 10 (học sinh).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu,
thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 1: Cho hai tập hợp A 0;1; 2;3;
4 , B 3; 4;5; 6 .
a) A B 0;1;2;3;4;5; 6 .
b) A B 5; 6 .
c) B \ A 0;1; 2 .
d) A B \ A B A \ B B \ A . Lời giải:
a) A B 0;1;2;3;4;5; 6 nên mệnh đề đúng.
b) A B 3; 4 nên mệnh đề sai.
c) Ta có B \ A 5; 6 nên mệnh đề sai.
d) A B 0;1;2;3;4;5;
6 , A B 3;
4 nên A B \ A B 0;1;2;5; 6 ;
A \ B 0;1;
2 B \ A 5;
6 nên A \ B B \ A 0;1;2;5;
6 do đó mệnh đề đã cho đúng.
Câu 2: Cho các tập hợp A [ 3;1) , B [0;5), C [ ; a a 3].
a) A B [0;1).
b) A B [ 3;5).
c) B \ A [1;5) .
d) A C 6 a 1. Lời giải:
a) A B [ 3;5) nên mệnh đề đã cho sai.
b) A B [0;1) nên mệnh đề đã cho sai.
c) Ta có B \ A [1;5) nên mệnh đề đã cho đúng.
d) A C khi:
TH 1: a 3 3 hay a 6 (1) TH2: a 1 (2) a 6
Từ (1) và (2) suy ra A C khi
nên mệnh đề đã cho sai. a 1 11 m 1
Câu 3: Cho ba tập hợp A 1; ; B 2 ; 3 và C ; . 2 3
a) Giao của hai tập hợp A và B là 1; 3 . b) Tập hợp B gồm 6 phần tử. c) Tập hợp A 11 \ ;1 ; . 2
d) Tổng các giá trị nguyên của m để B C có đúng 3 phần tử là số nguyên bằng 6 Lời giải:
a) Ta biểu diễn hai tập hợp A và B trên trục số
Suy ra A B 1;
3 nên mệnh đề đúng. b) Ta có B 0;1;2;
3 n B 4 nên mệnh đề sai.
c) Ta có sự biểu diễn tập hợp A Suy ra A 11 \ ;1 ; nên mệnh đề đúng. 2 m 1
d) Để B C có đúng 3 phần tử là số nguyên 0 1 1 m 4 3 Mà m m1;2;
3 Tổng các giá trị nguyên của m là 1 2 3 6 Do đó mệnh đề đúng.
Câu 4: Lớp 10A có 26 học sinh biết chơi đá bóng, 22 học sinh biết chơi cầu lông, 5 học sinh biết
chơi cả hai môn đá bóng và cầu lông, 8 học sinh không biết chơi môn nào.
a) Số học sinh chỉ biết chơi cầu lông mà không biết chơi đá bóng là 17 .
b) Số học sinh chỉ biết chơi đá bóng mà không biết chơi cầu lông là 20 .
c) Số học sinh biết chơi ít nhất một trong hai môn đá bóng hoặc cầu lông là 43 .
d) Sĩ số lớp 10A là 61 . Lời giải:
Dựa vào sơ đồ ven ta suy ra:
a) Số học sinh chỉ biết chơi cầu lông mà không biết chơi đá bóng là 22 5 17 nên mệnh đề đúng.
b) Số học sinh chỉ biết chơi đá bóng mà không biết chơi cầu lông là 26 5 21 . nên mệnh đề sai.
c) Số học sinh biết chơi ít nhất một trong hai môn đá bóng hoặc cầu lông là
22 265 43nên mệnh đề đúng.
d) Sĩ số lớp 10A là 22 26 5 8 51nên mệnh đề sai.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho tập hợp A x x 2 : 2 11 x 3
0 . Số phần tử của A bằng bao nhiêu? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: 2 11
Xét bất phương trình 2x 1
1 x 3 0 2x 11 0 x 2 11 A ; A 0;1;2;3;4; 5 2
Suy ra số phần tử của A bằng 6 . Đáp án : 6
Câu 2: Cho hai tập hợp A 0;5 và B 2;1; 3;
6 . Số phần tử của A B bằng bao nhiêu? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Ta có A B 0;5 2;
6 A B 2;1;2;3;4;5;
6 Số phần tử của A B bằng 7 Đáp án : 7 Câu 3: Cho các tập hợp
A x :x 13x 2x 2 0 và
B x x x 2 : 2 3 m 4
0 . Tích các giá trị của tham số m để n A B 3 bằng bao nhiêu? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: Xét các phương trình: x 1 2 2
x 13x 2x 2 0 x A 1; 3 3 x 2 x 2 2
2 x3x m 4 0 2 m 4 x 3 2 2 m 4 4 m 4 2 m 4 Ta thấy 2 m 0, m , m 2 B ; 2 3 3 3 3 2 m 4 1 m 7 3
Khi đó n A B 3 2 m 4 2 m 6 3 3
Suy ra tích các giá trị của tham số m là 7. 7. 6 . 6 42 . Đáp án : 42
Câu 4: Một lớp có 45 học sinh, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu
lông. Có 30 em đăng kí môn bóng đá, 25 em đăng kí môn cầu lông. Hỏi có bao nhiêu em
đăng kí cả hai môn thể thao? Kết quả: Trình bày:
………………………………………………………………………………….………………………….




