Bộ đề ôn tập môn Toán 12 theo cấu trúc mới – Phạm Lê Duy

Trường THPT Chu Văn An GV: PHẠM LÊ DUY BỘ ĐỀ ÔN TẬP T LỚP 12 Toán T THEO CẤU TRÚC MỚI Năm N Học: H 2024 - 2025
TÀI LIỆU LƯU HÀNH NỘI BỘ
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 GV: PHẠM LÊ DUY / Trang 2/327 MỤC LỤC PHẦN I
Đề kiểm tra theo bài 9 1
Sự đồng biến, nghịch biến của hàm số 11 A Đề 1 11 B Đề 2 15 2
Giá trị lớn nhất và nhỏ nhất của hàm số 20 A Đề 1 20 B Đề 2 24 3 Đường tiệm cận 28 A Đề 1 28 B Đề 2 33 4
Khảo sát sự biến thiên và vẽ đồ thị hàm số 39 A Đề 1 39 B Đề 2 45 5
Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn 51 A Đề 1 51 B Đề 2 58 3
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 6 Ôn tập chương 1 64 A Đề 1 64 B Đề 2 68 7 Véc-tơ trong không gian 73 A Đề 1 73 7
Hệ trục tọa độ trong không gian 77 A Đề 1 77 B Đề 2 81 8
Biểu thức tọa độ của các phép toán véc-tơ 85 A Đề 1 85 B Đề 2 88 9 Ôn tập chương 2 91 A Đề 1 91 B Đề 2 94 10
Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm 98 A Đề 1 98 B Đề 2 106 GV: PHẠM LÊ DUY / Trang 4/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 11
Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm 113 A Đề 1 113 B Đề 2 120 12 Ôn tập chương 3 127 A Đề 1 127 B Đề 2 135 13 Nguyên hàm 142 A Đề 1 142 B Đề 2 146 14 Tích phân 150 A Đề 1 150 B Đề 2 155 15
Ứng dụng hình học của tích phân 159 A Đề 1 159 B Đề 2 166 16 Ôn tập chương 4 172 A Đề 1 172 GV: PHẠM LÊ DUY / Trang 5/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 B Đề 2 177 17
Phương trình mặt phẳng trong không gian 182 A Đề 1 182 B Đề 2 186 18
Phương trình đường thẳng trong không gian 191 A Đề 1 191 B Đề 2 195 19
Công thức tính góc trong không gian 199 A Đề 1 199 B Đề 2 204 20 Phương trình mặt cầu 209 A Đề 1 209 B Đề 2 213 21 Ôn tập chương 5 217 A Đề 1 217 B Đề 2 222 GV: PHẠM LÊ DUY / Trang 6/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 22 Xác suất có điều kiện 226 A Đề 1 226 B Đề 2 231 23
Công thức xác suất toàn phần. Công thức Bayes 235 A Đề 1 235 B Đề 2 240 24 Ôn tập chương 6 245 A Đề 1 245 B Đề 2 250 PHẦN II
Đề ôn thi giữa kì và cuối kì 255 CHƯƠNG 1 Đề ôn thi giữa kì 1 257 1 Ôn tập giữa kỳ 1 257 A Đề 1 257 B Đề 2 263 C Đề 3 269 CHƯƠNG 2 Đề ôn thi cuối kì 1 275 GV: PHẠM LÊ DUY / Trang 7/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 1 Ôn tập học kỳ 1 275 A Đề 1 275 B Đề 2 280 C Đề 3 285 D Đề 4 289 CHƯƠNG 3 Đề ôn thi giữa kì 2 295 1 Ôn tập giữa kì 2 295 A Đề 1 295 B Đề 2 300 C Đề 3 304 CHƯƠNG 4 Đề ôn thi giữa kì 1 309 1 Ôn tập học kỳ 2 309 A Đề 1 309 2
Ôn tập học kỳ 2 - Đề số 2 313 A Đề 3 319 B Đề 4 324 GV: PHẠM LÊ DUY / Trang 8/327 Phần I Đề kiểm tra theo bài 9
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 BÀI 1.
SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ A. ĐỀ 1
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn 8 − 5x Câu 1. Cho hàm số y =
. Khẳng định nào sau đây là sai? −4x − 9 Å 37 ã
A. Hàm số đồng biến trên khoảng −∞; − . 4 Å 9 ã
B. Hàm số đồng biến trên khoảng −∞; − . 4 Å 9 ã
C. Hàm số đồng biến trên khoảng − ; +∞ . 4 Å 37 ã
D. Hàm số nghịch biến trên khoảng −∞; − . 4
Câu 2. Cho hàm số có bảng biến thiên như sau −4 1 x −∞ +∞ 3 2 y0 + 0 − 0 + 218 +∞ + y 27 −17 −∞ 4
Khẳng định nào sau đây là đúng? Å 4 ã
A. Hàm số nghịch biến trên khoảng −∞; − . 3 Å 4 1 ã
B. Hàm số đồng biến trên khoảng − ; . 3 2 Å 7 ã
C. Hàm số nghịch biến trên khoảng ; +∞ . 2 Å 7 ã
D. Hàm số đồng biến trên khoảng −∞; − . 3 Câu 3. GV: PHẠM LÊ DUY / Trang 11/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919
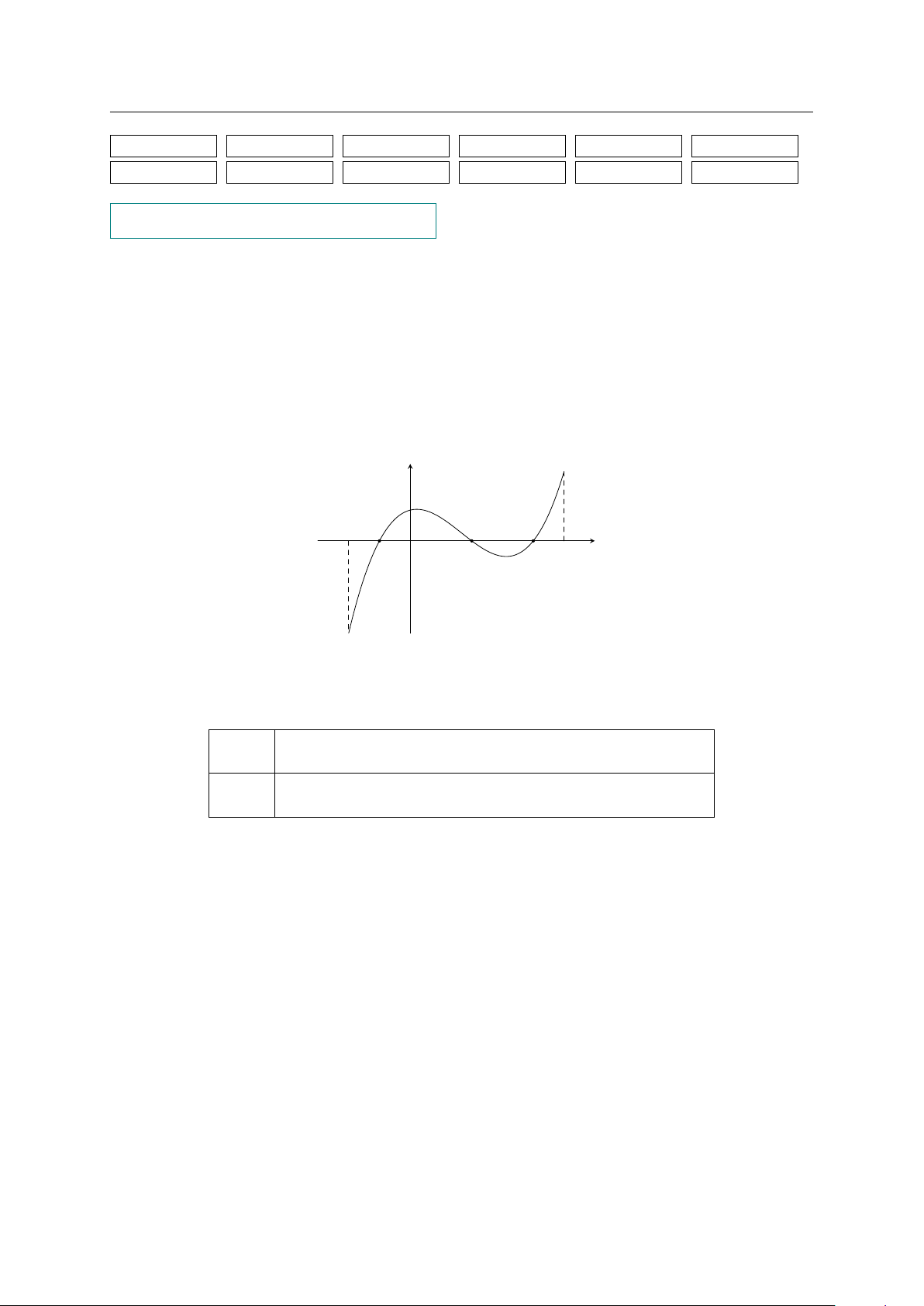
Cho hàm số có đồ thị như hình bên. Khẳng định nào sau đây y là đúng?
A. Hàm số nghịch biến trên khoảng (−∞; 1).
B. Hàm số nghịch biến trên khoảng (−∞; 0). Å 7 ã
C. Hàm số nghịch biến trên khoảng ; +∞ . 3
D. Hàm số đồng biến trên khoảng (−∞; 1). x O 1 7 3 1
Câu 4. Tìm tất cả các giá trị thực của tham số m để hàm số y = − x3 − mx2 + (2m − 3
3)x − m + 2 nghịch biến trên R.
A. m ≤ −3, m ≥ 1. B. −3 < m < 1. C. −3 ≤ m ≤ 1. D. m ≤ 1.
Câu 5. Cho hàm số y = −x3 − mx2 + (4m + 9)x + 5, với m là tham số thực. Có bao
nhiêu giá trị nguyên của m để hàm số nghịch biến trên (−∞; +∞)? A. 5. B. 6. C. 7 . D. 4.
Câu 6. Cho hàm số y = 7x3 + 9x2 − 3x − 4. Khẳng định nào sau đây là sai? 1
A. Giá trị cực đại y = 1.
B. Hàm số đạt cực tiểu tại x = . 7 1 C. Giá trị cực tiểu y = .
D. Hàm số đạt cực đại tại x = −1. 7
Câu 7. Cho hàm số y = f (x) xác định trên R và có bảng biến thiên như hình vẽ sau x −∞ 10 12 +∞ y0 + 0 − 0 + −3 − −∞ y −∞ 3
Hàm số y = f (x) đạt cực đại tại A. x = 10. B. x = 8. C. x = 12. D. x = 17. Câu 8.
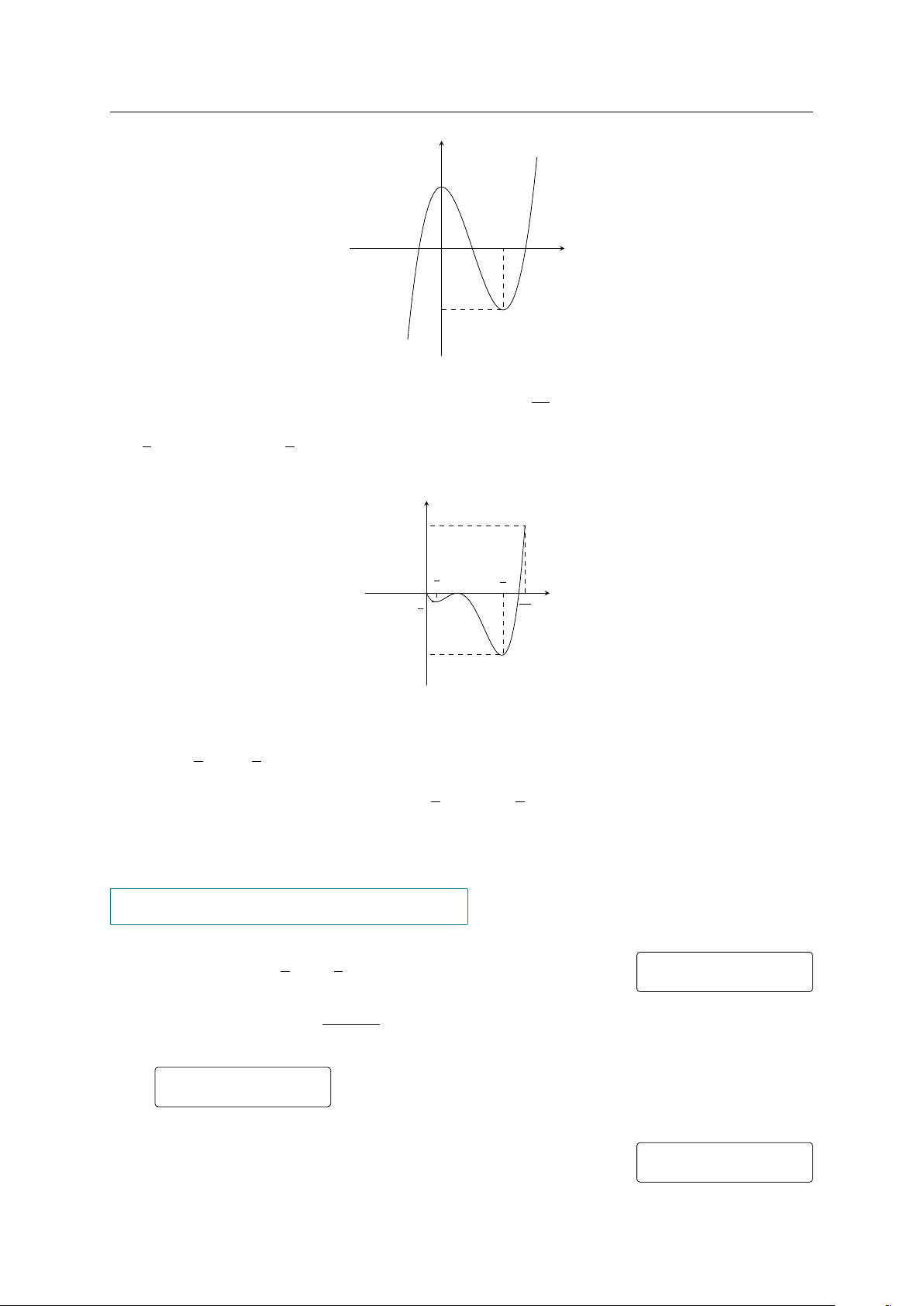
Cho hàm số có đồ thị như hình bên. Khẳng định nào sai? y 3 3 3 −
A. Hàm số có một cực tiểu tại x =
và đạt cực đại tại x = 0. 4 4 4 x O 113 −1
B. Giá trị cực đại y = −1 và giá trị cực tiểu y = − . 32 3
C. Hàm số có một cực tiểu tại x = − . 4 3
D. Hàm số có một cực đại tại x = − . 4 113 − 32 GV: PHẠM LÊ DUY / Trang 12/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919
Câu 9. Cho hàm số y = 8x3 − 6mx2 + 9mx + 6m (m là tham số thực). Giá trị của m để
hàm số đạt cực tiểu tại x = −6 thuộc khoảng nào sau đây? Å 35 ã Å 47 ã Å 23 ã A. −∞; − . B. −∞; − . C. − ; +∞ . D. ∅. 3 3 3
Câu 10. Tìm tất cả các giá trị thực của m để hàm số y = x3 − 3x2 + (m + 1)x + 2 có hai điểm cực trị. A. m < 2. B. m ≤ 2. C. m > 2. D. m < −4. Å 4 ã
Câu 11. Cho hàm số y = x3 − 2mx2 + − m2 − 40m − 144 x − 5 (m là tham số thực). 3
Tìm tất cả các giá trị của m để hàm số có cực trị? A. −11 < m < −6.
B. m < −9 hoặc m > −4. C. −14 < m < −6.
D. m < −9 hoặc m > −6.
Câu 12. Cho hàm số y = (m + 1)x4 − mx2 + 3. Tìm tất cả các giá trị thực của tham số
m để hàm số có ba điểm cực trị.
A. m ∈ (−∞; −1) ∪ [0; +∞). B. m ∈ (−1; 0).
C. m ∈ (−∞; −1] ∪ [0; +∞).
D. m ∈ (−∞; −1) ∪ (0; +∞). 1. D 2. D 3. D 4. C 5. C 6. C 7. A 8. D 9. D 10. A 11. D 12. D
PHẦN 2. Câu trắc nghiệm đúng sai
Câu 1. Cho hàm số y = f (x) = x3 − 3x2 − 1. Các mệnh đề sau đúng hay sai?
a) Hàm số đã cho nghịch biến trên R.
b) Hàm số đã cho đồng biến trên (3; +∞).
c) Hàm số đã cho nghịch biến trên (1; 2).
d) Hàm số g(x) = f (x) + 2 đồng biến trên (−∞; 0). Câu 2.
Cho hàm số y = f (x) có đồ thì như hình vẽ bên. Các mệnh y đề sau đúng hay sai?
a) Hàm số đã cho nghịch biến trên khoảng (−2, 0).
b) Hàm số đã cho đồng biến trên khoảng (−3; 1). O x
c) Hàm số đã cho đồng biến trên khoảng (2; +∞). −3 −2 1 2
d) Hàm số f = |f (x)| nghịch biến trên khoảng (−2, 0). −1
Câu 3. Cho hàm số y = f (x) = x4 − 2x2 − 3. Các mệnh đề sau đúng hay sai?
a) Hàm số đã cho đạt cực đại tại x = 0.
b) Hàm số đã cho đạt cực tiểu tại x = −3. GV: PHẠM LÊ DUY / Trang 13/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919
c) Hàm số đã cho có giá trị cực đại và cực tiểu lần lượt là −4, −3.
d) Đồ thị hàm số g(x) = f (x) + 3 có điểm cực đại là (0; 0) . Câu 4.
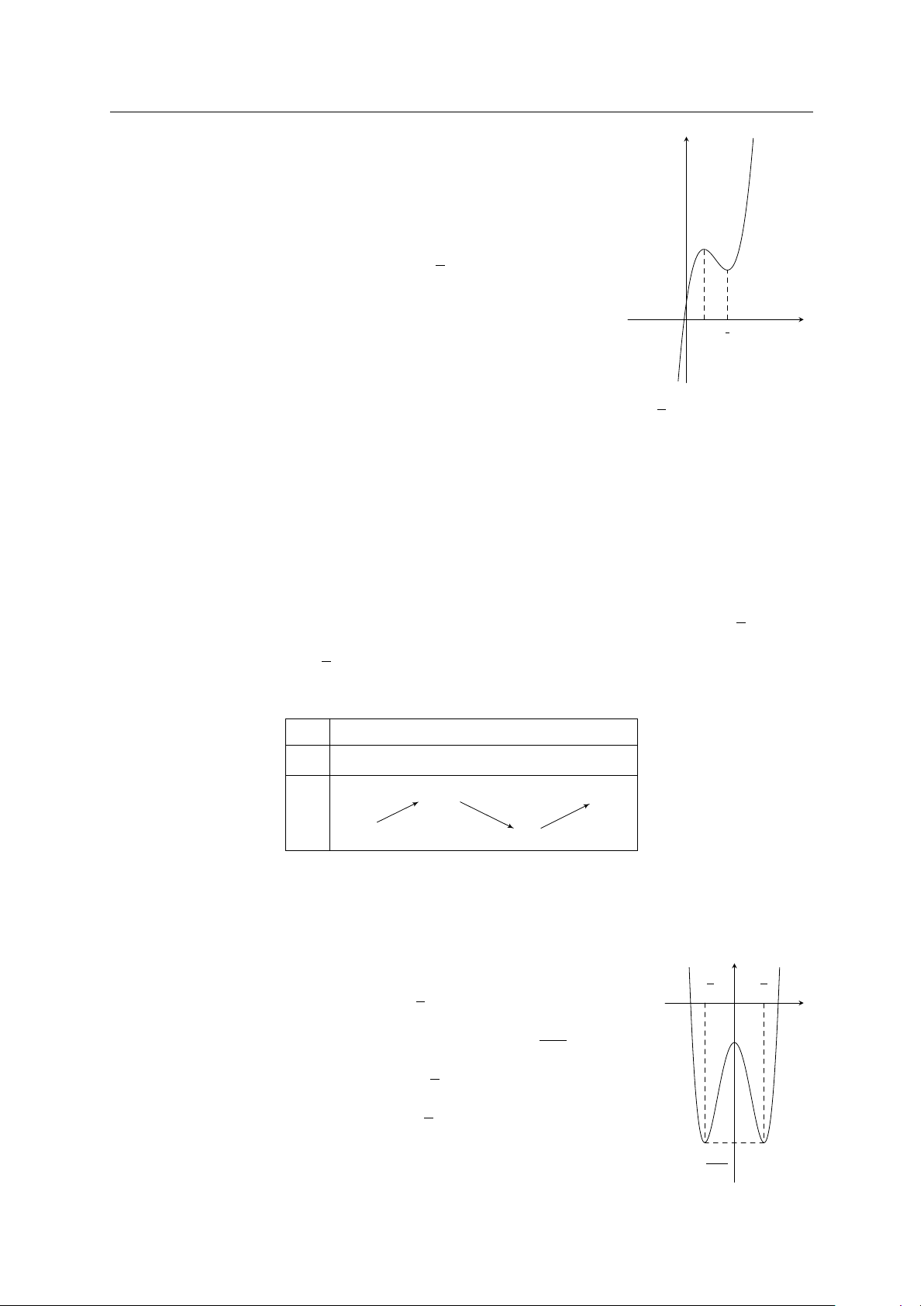
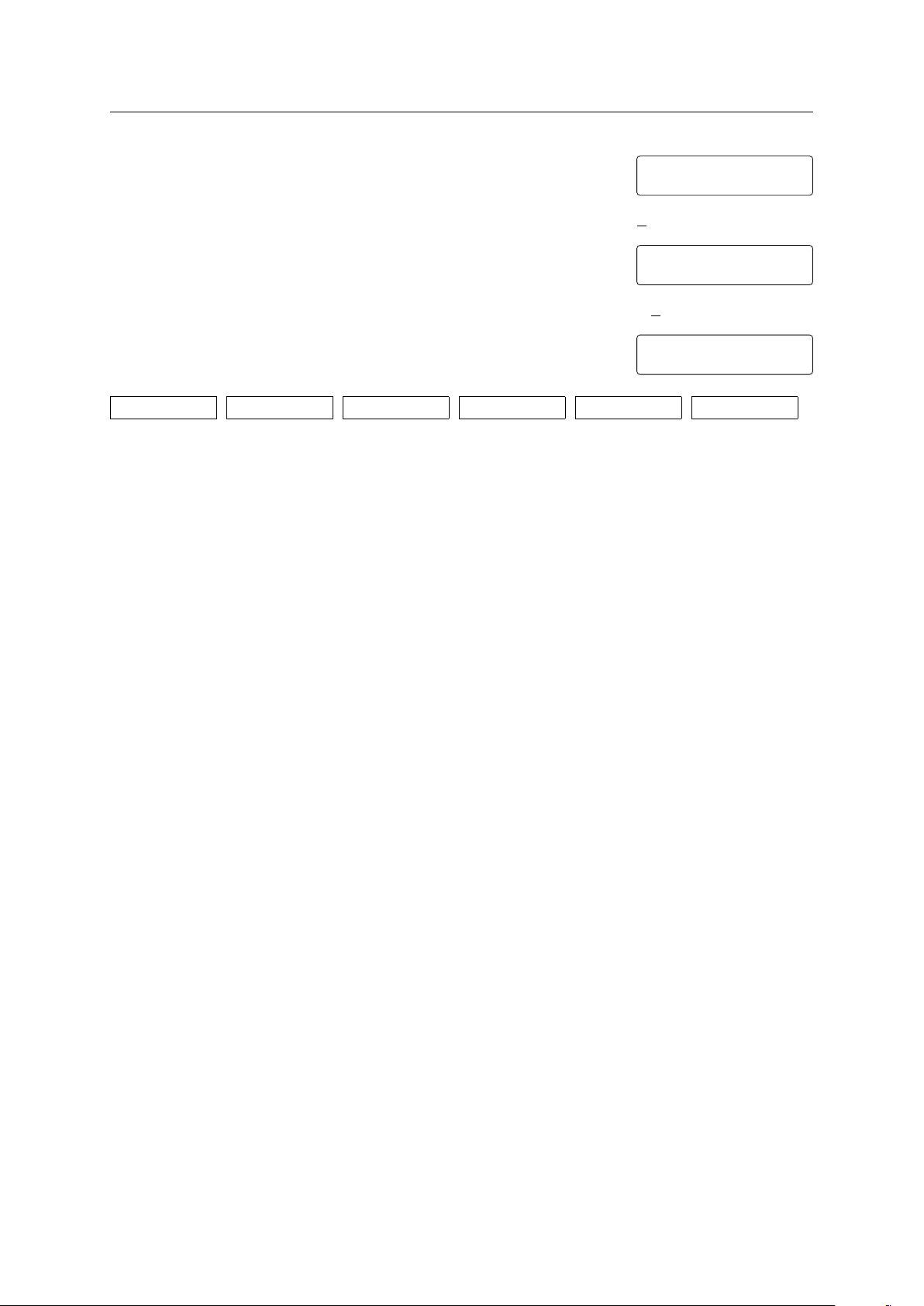
Cho hàm số y = f (x) có đồ thị như hình vẽ bên dưới. y
a) Hàm số đã cho chỉ có 2 cực trị. −1 1 x
b) Hàm số đã cho có giá trị cực tiểu x = −2.
c) Hàm số đã cho có giá trị cực đại y = −1.
d) Đồ thị hàm số y = |f (x)| có điểm cực đại là (0, 2). −2 1. a S b Đ c Đ d Đ 2. a Đ b S c Đ d S 3. a Đ b S c S d S 4. a S b S c Đ d Đ
PHẦN 3. Câu trắc nghiệm trả lời ngắn.
Câu 1. Cho hàm số y = 4x3 + 8x2 − 3x + 3. Giá trị cực đại của hàm số bằng bao nhiêu?
KQ: . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2. Tìm điểm cực tiểu của hàm số y = x3 −5x2 −8x+8? KQ: . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3. Cho hàm số y = −x3 − mx2 + (4m + 9)x + 3 với m là tham số. Có bao nhiêu giá
trị nguyên của m để hàm số nghịch biến trên (−∞; +∞)?
KQ: . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4. Đồ thị hàm số y = x3 − 3x2 + 2ax + b có điểm cực tiểu A(2; −2). Khi đó a + b bằng bao nhiêu?
KQ: . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 − 3(m + 2)x2 +
3(m2 + 4m)x + 1 nghịch biến trên khoảng (0; 1)?
KQ: . . . . . . . . . . . . . . . . . . . . . . . .
Câu 6. Tìm giá trị của tham số m để ba điểm cực trị của đồ thị hàm số y = x4 + (6m −
4)x2 + 1 − m là ba đỉnh của một tam giác vuông? (Kết quả làm tròn đến chữ số hàng phần trăm).
KQ: . . . . . . . . . . . . . . . . . . . . . . . . 1. 12 2. 4 3. 7 4. 2 5. 4 6. 0,33 GV: PHẠM LÊ DUY / Trang 14/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 B. ĐỀ 2
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Các khoảng đồng biến của hàm số y = x4 − 8x2 − 4 là
A. (−∞; −2) và (2; +∞). B. (−2; 0) và (0; +∞). C. (−∞; −2) và (0; 2). D. (−2; 0) và (2; +∞).
Câu 2. Hàm số y = x4 − 2x2 + 1 nghịch biến trên các khoảng nào sau đây? A. (−∞; −1) và (0; 1).
B. (−∞; −1) và (0; +∞). C. (−∞; 0) và (1; +∞). D. (−1; 0) và (1; +∞). x + 1 Câu 3. Cho hàm số y =
. Trong các mệnh đề sau, mệnh đề nào sai? x − 3
A. Hàm số nghịch biến trên từng khoảng xác định của nó.
B. Hàm số nghịch biến trên tập xác định của nó.
C. Hàm số nghịch biến trên khoảng (3; +∞).
D. Hàm số nghịch biến trên khoảng (−∞; 3). 1 1 Câu 4. Cho hàm số y = x3 −
x2 − 12x − 1. Mệnh đề nào sau đây đúng? 3 2
A. Hàm số nghịch biến trên khoảng (−3; +∞).
B. Hàm số đồng biến trên khoảng (−∞; 4).
C. Hàm số đồng biến trên khoảng (−3; 4).
D. Hàm số đồng biến trên khoảng (4; +∞).
Câu 5. Hàm số nào sau đây không đồng biến trên (−∞; +∞) x − 1 A. y = x5 + x3 − 1. B. y = x3 + 2. C. y = . D. y = x + 1. x + 2 √
Câu 6. Cho hàm số y = x − 2 x. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (1; +∞).
B. Hàm số đồng biến trên khoảng (2; +∞).
C. Hàm số đồng biến trên khoảng (0; +∞).
D. Hàm số nghịch biến trên khoảng (−∞; 1).
Câu 7. Cho hàm số y = f (x) xác định liên tục và liên tục trên R và có bảng biến thiên như sau x −∞ 2 +∞ y0 − 0 + +∞ + +∞ + y 0 GV: PHẠM LÊ DUY / Trang 15/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919
Khẳng định nào sau đây đúng?
A. Hàm số có 2 cực trị.
B. Hàm số có giá trị cực đại bằng 2.
C. Hàm số có giá trị cực tiểu bằng 0.
D. Hàm số có giá trị cực đại tại x = 0.
Câu 8. Cho hàm số y = f (x) có bảng biến thiên như sau. Mệnh đề nào dưới đây là sai? x −∞ 0 2 +∞ y0 + 0 − 0 + 3 +∞ + y −∞ 0
A. Hàm số không đạt cực tiểu tại điểm x = 2.
B. Hàm số đạt cực đại tại điểm x = 0.
C. Giá trị cực đại của hàm số là y = 3.
D. Giá trị cực tiểu của hàm số là y = 0.
Câu 9. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ 0 2 +∞ y0 + 0 − 0 + 3 +∞ + y −∞ 0
Tìm giá trị cực đại yCĐ và giá trị cực tiểu yCT của hàm số đã cho. A. yCĐ = 3 và yCT = 2. B. yCĐ = 2 và yCT = 0. C. yCĐ = 3 và yCT = 3. D. yCĐ = 3 và yCT = 0.
Câu 10. Tìm m để hàm số y = x3 + mx2 + (1 − 2m)x + m − 3 đồng biến trên khoảng (−3; 0). √ √ √ √ A. m ≥ 2 3 + 3. B. m ≤ 2 3 − 3. C. m ≥ 6 − 42. D. m ≤ 6 + 42.
Câu 11. Tất cả các giá trị của tham số m sao cho hàm số y = −x3 − 3mx2 + 4m − 1
đồng biến trên khoảng (0; 4) là A. −2 6 m < 0. B. m 6 −4. C. m 6 −2. D. m > 0.
Câu 12. Tìm tất cả các giá trị của tham số m để hàm số y = −x3 + 3x2 + 3mx − 1
nghịch biến trên khoảng (0; +∞). A. m > −1. B. m ≥ −1. C. m ≤ −1. D. m < −1. GV: PHẠM LÊ DUY / Trang 16/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 1. D 2. A 3. B 4. D 5. C 6. B 7. C 8. A 9. D 10. B 11. C 12. C
PHẦN 2. Câu trắc nghiệm đúng sai
Câu 1. Đạo hàm f 0(x) của hàm số y = f (x) có đồ thị như hình bên dưới. Xét tính đúng
sai của các mệnh đề sau
a) Hàm số đạt cực tiểu tại x = −1.
b) Hàm số đồng biến trên (−1; 2) và (4; 5).
c) Hàm số nghịch biến trên (2; 4).
d) Hàm số f (x + 2) đạt cực đại tại x = 0. y y = f 0(x) x −2 −1 O 2 4 5
Câu 2. Cho hàm số y = f (x) xác định trên R và có bảng biến thiên như hình vẽ. x −∞ −1 1 +∞ f 0(x) + 0 − 0 +
Xét tính đúng, sai của các mệnh đề sau.
a) Hàm số có 2 cực trị.
b) Hàm số nghịch biến trên khoảng (−1; 1).
c) Hàm số đồng biến trên khoảng (1; +∞).
d) Hàm số f (1 − x) đồng biến trên khoảng (−1; 1).
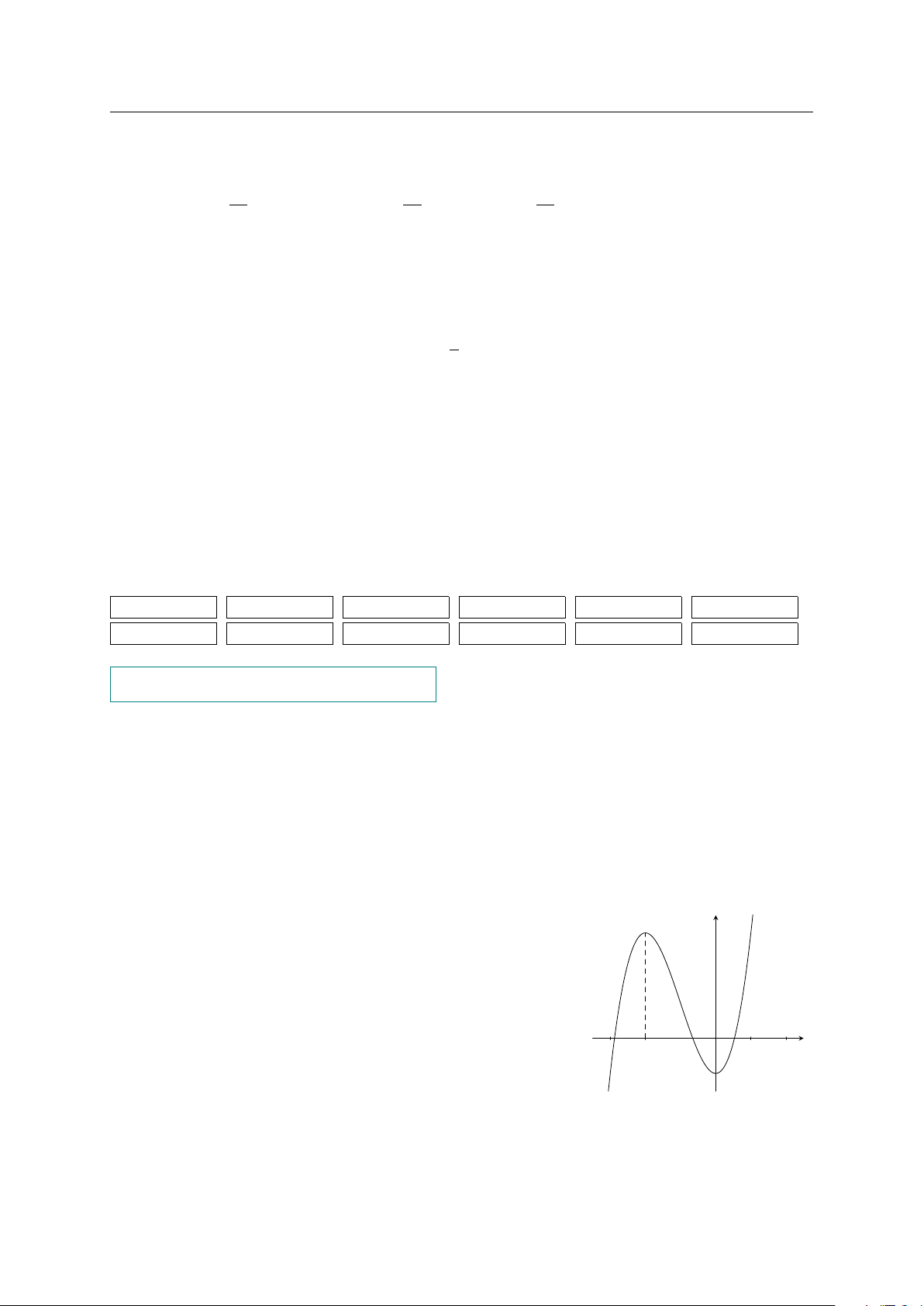
Câu 3. Cho hàm số y = f (x) xác định trên R và có đồ thị của hàm số y = f 0(x) là
đường cong ở hình vẽ dưới.
a) Hàm số f (x) đạt cực đại tại x = 0.
b) Hàm số f (x) nghịch biến trong khoảng (0; 2).
c) Hàm số f (x) có 2 khoảng đồng biến và 2 khoảng nghịch biến.
d) Hàm số f (x) có 3 điểm cực trị. GV: PHẠM LÊ DUY / Trang 17/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 y y = f 0(x) 2 2 x O −2 ï 16 ò
Câu 4. Cho hàm số y = f (x) liên tục trên đoạn 0; thoả mãn 5 Å 1 ã Å 5 ã f 0 = f 0(1) = f 0
= 0 và có đồ thị là đường cong như hình dưới. 3 2 y 3 1 O 5 3 1 2 16 x − 1 5 3 −2
a) x = 1 là điểm cực đại của hàm số. 1 5 b) x = , x =
là điểm cực tiểu của hàm số. 3 2 Å 1 ã Å 5 ã
c) Hàm số đã cho nghịch biến trên ; 1 và ; +∞ . 3 2
d) Giá trị lớn nhất của hàm số là 3.
PHẦN 3. Câu trắc nghiệm trả lời ngắn. 1 1 Câu 1. Hàm số y = x4 −
x3 có bao nhiêu điểm cực trị? KQ: 4 2 mx + 2 Câu 2. Cho hàm số y =
, m là tham số thực. Gọi S là tập hợp tất cả các giá 2x + m
trị nguyên của m để hàm số nghịch biến trên khoảng (0; 1). Tìm số phần tử của S. KQ:
Câu 3. Tìm giá trị của tham số m để hàm số f (x) = (m2 − 3)x − 2m ln x đạt cực tiểu tại điểm x0 = 1. KQ: GV: PHẠM LÊ DUY / Trang 18/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919
Câu 4. Gọi A, B là hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 4. Tính diện tích
S của tam giác OAB với O là gốc tọa độ. KQ: 1
Câu 5. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 −(m−1)x2 −(m− 3
3)x + 2024m đồng biến trên các khoảng (−3; −1) và (0; 3)? KQ: 1
Câu 6. Gọi (P ) là parabol qua 3 điểm cực trị của đồ thị hàm số y = x4 −mx2 +m2. Tìm 4
tất cả các giá trị thực của tham số m để (P ) qua A(2; 24). KQ: 1. 1 2. 2 3. 3 4. 4 5. 4 6. 6 GV: PHẠM LÊ DUY / Trang 19/327
p TOÁN 12 - BỘ ĐỀ ÔN TẬP THEO CẤU TRÚC 2025 Ô 0704.963.919 BÀI 2.
GIÁ TRỊ LỚN NHẤT VÀ NHỎ NHẤT CỦA HÀM SỐ A. ĐỀ 1
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn x + 3
Câu 1. Tìm giá trị nhỏ nhất của hàm số y = trên đoạn [−1; 0]. x − 1 A. min y = −3. B. min y = −2. C. min y = −4. D. min y = 3. [−1;0] [−1;0] [−1;0] [−1;0] Câu 2.
Giá trị nhỏ nhất trên tập xác định của hàm số có đồ thị sau là y −1 A. min y = −1. B. min y = 1. O 1 D D x C. min y = 0. D. min y = −2. D D −1
Câu 3. Tìm giá trị lớn nhất của hàm số f (x) = x3 − 2x2 − 4x + 1 trên đoạn [1; 3]. A. max f (x) = −7. B. max f (x) = −4. [1;3] [1;3] 67 C. max f (x) = −2. D. max f (x) = − . [1;3] [1;3] 27 x + 1
Câu 4. Giá trị lớn nhất của hàm số y = trên [−1; 0] là x − 2 1 2 A. − . B. − . C. 2. D. 0. 2 3
Câu 5. Cho hàm số f (x) = −2x4 + 4x2 + 10. Tìm giá trị lớn nhất M và giá trị nhỏ nhất
m của hàm số trên đoạn [0; 2]. A. M = 10; m = −6. B. M = 12; m = −6. C. M = 10; m = −8. D. M = 12; m = −8. √
Câu 6. Giá trị lớn nhất của hàm số y = x + 2 − x là 5 √ 9 A. − . B. 3 − 1. C. . D. 2. 4 4 √
Câu 7. Tìm giá trị lớn nhất M của hàm số y = −2 4 − x. A. M = −4. B. M = −2. C. M = 1. D. M = 0. x + 1
Câu 8. Tìm giá trị lớn nhất M của hàm số y = √ trên khoảng (−∞; +∞). x2 + 1 √ √ A. M = 2 2. B. M = 1. C. M = 2. D. M = 2. 1
Câu 9. Giá trị lớn nhất của hàm số y = 2x + khi x < 0 là x √ √ A. 2 2. B. −2 2. C. Không tồn tại. D. 4. GV: PHẠM LÊ DUY / Trang 20/327