Bộ đề ôn tập thi HK2 Toán 12 năm học 2016 – 2017 trường THPT Nho Quan A – Ninh Bình

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Lan Tường
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
1
TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 01
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM: 30 câu (6 điểm)
Câu 1. Hàm số
3
ln( 2)
2
yx
x

đồng biến trên khoảng nào ?
A. (;1). B. (1; ). C.
1
;1 .
2



D.
1
;.
2




Câu 2. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số (sin cos )yxm x x đồng biến
trên
.
A.
11
;;.
22
m




B.
11
.
22
m
C.
1
3.
2
m
D.
11
;;.
22
m





Câu 3.
Cho hàm số ( )yfx xác định, liên tục trên
\2 và có bảng biến thiên sau
x

0
2
4

y
- 0 + + 0 -
y
1
15
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số đạt cực đại tại điểm 0x và đạt cực tiểu tại điểm 4x .
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng -15.
Câu 4. Hàm số nào sau đây không có cực trị ?
A.
3
31.yx x B.
2
.
3
x
y
x
C.
43
431.yx x x  D.
2*
2017 .
n
yx xn
Câu 5.
Kí hiệu
M
và m lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số
2
4
1
xx
y
x

trên
đoạn
0;3 . Tính giá trị của tỉ số .
m
A.
4
.
3
B.
5
.
3
C.
2.
D.
2
.
3
Câu 6. Cho hàm số

yfx
có đồ thị như hình vẽ sau. Hỏi với
giá trị thực nào của
m thì đường thẳng 2ym cắt đồ thị
hàm số đã cho tại hai điểm phân biệt.
A.
2.m
B.
02.m
C.
0.m
D.
0 2.mm
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
2
Câu 7. Cho hàm số
32
2725yxxx có đồ thị là (C). Số giao điểm của đồ thị (C) với đường
thẳng
:21dy x là
A. 2 B. 3 C. 4 D. 1
Câu 8.
Cho hàm số
32
yax bx cxd
0a
có đồ thị như hình vẽ
dưới đây. Khẳng định nào sau đây về dấu của , , ,
abcd là đúng
nhất ?
A. , 0.ad B.
0, 0 .ac b
C.
, , , 0.abcd
D.
, 0, 0.ad c
Câu 9.
Tìm tập xác định D của hàm số

1000
3
2
log 8 .yx
A.
\2.D
B.
2; .D 
C.
;2 .D  D.
2; ; 2 .D 
Câu 10.
Tập xác định của hàm số
2
2
43yx x
 là
A.
1, 3.xx C.

1; 3 .
B.
.
D.
(;1)3; . 
Câu 11. Tính đạo hàm của hàm số
3
.
9
x
x
y
A.
2
12 3ln3
.
3
x
x
y

B.

2
12 3ln3
.
3
x
x
y

C.
2
12 3ln3
.
3
x
x
y

D.
2
12 3ln3
.
3
x
x
y

Câu 12. Tính đạo hàm của hàm số

6
1cos3 .yx
A.

5
'6sin31cos3 .yxx B.

5
'6sin3cos3 1.yxx
C.

5
'18sin31cos3 .yxx
D.

5
'18sin3 cos3 1.yxx
Câu 13. Giải bất phương trình
500
1
3
log 9 1000.x 
A. 0.x B.
500
9.x 
C. 0.x D.
1000
30.x
Câu 14. Xét a và b là hai số thực dương tùy ý. Đặt

1000
22
1000
1
ln , 1000ln ln .
xaabb y a
b

Khẳng định nào dưới đây là khẳng định đúng ?
A. .
x
y B. .
x
y C. .
x
y D. .
x
y
Câu 15. Khẳng định nào dưới đây là khẳng định đúng ?
A.
 
22
20
2.
f
xdx f xdx


B.
 
22
20
2.
f
xdx f xdx

C.
 
22
20
.
f
xdx f x f x dx




D.
 
22
20
.
f
xdx f x f x dx




Câu 16. Tìm nguyên hàm

F
x
của hàm số
1000 .
x
fx
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
3
A.

3
10
.
3ln10
x
Fx C B.

3
3.10 ln10.
x
Fx
C.

1
1000
.
1
x
Fx C
x

D.
1000 .
x
Fx C
Câu 17. Tính tích phân

3
1000
1
1.Ixx dx
A.
1002
2003.2
.
1003002
I
B.
1001
1502.2
.
501501
I
C.
1002
3005.2
.
1003002
I
D.
1001
2003.2
.
501501
I
Câu 18. Tính tích phân

1000
2
2
1
ln
.
1
x
Idx
x
A.
1000
1000 1000
ln 2 2
1000ln .
12 12
I 

B.
1000
1000 1000
1000ln 2 2
ln .
12 12
I 

C.
1000
1000 1000
ln 2 2
1000ln .
12 12
I 

D.
1000
1000 1000
1000ln 2 2
ln .
12 12
I 

Câu 19. Tính diện tích hình phẳng giới hạn bởi các đường
2
24yx x và 2.yx
A.
1
.
6
B.
1
.
2
C.
1
.
3
D.
1
.
4
Câu 20. Ký hiệu

H là hình phẳng giới hạn bởi các đường

2
2
1, 0, 2.
xx
yxe yx
 Tính
thể tích
V của khối tròn xoay thu được khi quay hình
H xung quanh trục hoành.
A.
21
.
2
e
V
e
B.

23
.
2
e
V
e
C.
1
.
2
e
V
e
D.

3
.
2
e
V
e
Câu 21. Cho số phức
711
.
2
i
z
i
Tìm phần thực và phần ảo của .z
A. Phần thực bằng 5 và phần ảo bằng 3.i B. Phần thực bằng 5 và phần ảo bằng 3.
C. Phần thực bằng 5 và phần ảo bằng 3. D. Phần thực bằng
5
và phần ảo bằng
3.i
Câu 22. Cho hai số phức
12
13, 42.ziz i Tính môđun của số phức
21
2.zz
A.
217.
B.
2 13.
C.
4.
D.
5.
Câu 23. Cho số phức z thỏa mãn (2 ) 7 .iz i Hỏi điểm biểu
diễn của
z là điểm nào trong các điểm M, N, P, Q ở hình
dưới ?
A. Điểm P. B. Điểm Q.
C. Điểm M. D. Điểm N.
Câu 24.
Cho số phức
23.zi
Tìm số phức (3 2 ) 2 .wizz
A.
57.wi
B.
47.wi
C.
75.wi
D.
74.wi
Câu 25. Kí hiệu
1
z
;
2
z
;
3
z
là ba nghiệm của phương trình phức
32
240.zzz
Tính giá trị của
biểu thức
123
.Tz z z
A. 4.T B. 45.T  C. 45.T D. 5.T
Câu 26. Cho hình chóp tam giác đều cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy
một góc
0
60 . Tính thể tích V của khối chóp.
A.
3
3
.
24
a
V
B.
3
3
.
8
a
V
C.
3
3
.
4
a
V
D.
3
2
.
6
a
V
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
4
Câu 27. Cho lăng trụ tứ giác đều
.
A
BCDABCD

đáy hình có cạnh bằng
,a
đường chéo
A
C
tạo
với mặt bên

B
CC B

một góc
0
045.
 Tính thể tích của lăng trụ tứ giác đều
.
A
BCDABCD

.
A.
32
cot 1.a
B.
32
tan 1.a
C.
3
cos 2 .a
D.
32
cot 1.a
Câu 28. Hình nón có thiết diện qua trục là tam giác đều. Tính độ dài đường cao của hình nón.
A. .
4
a
B.
3
.
4
a
C.

2; 1;1I . D.
3
.
2
a
Câu 29. Một cái cốc hình trụ cao 15cm đựng được 0,5 lít nước. Hỏi bán kính đường tròng đáy của
cái cốc sấp sỉ bằng bao nhiêu (làm tròn đến hàng thập phân thứ hai) ?
A.
3, 26
cm. B.
3, 27
cm. C.
3, 25cm.
D.
3, 28cm.
Câu 30. Cho hình chóp tam giác đều
.S ABC
có đáy
A
BC
là tam giác đều cạnh
,a
cạnh
23
.
3
a
SA Gọi
D là điểm đối xứng của B qua .C Tính bán kính R của mặt cầu ngoại
tiếp hình chóp
..S ABD
A.
39
.
7
a
R
B.
35
.
7
a
R
C.
37
.
6
a
R
D.
39
.
7
a
R
II. PHẦN TỰ LUẬN: 8 câu ( 4 điểm)
Bài 1.
Viết phương trình tham số của của đường thẳng d đi qua điểm
5; 4;1M
và có vectơ chỉ
phương
2; 3;1a 
.
Bài 2. Trong không gian với hệ tọa độ
,Oxyz
cho hai điểm
1;1; 0A
và
3;1; 2 .B
Viết phương
trình mặt phẳng
P
đi qua trung điểm
I
của cạnh
A
B
và vuông góc với đường thẳng .
A
B
Bài 3. Trong không gian với hệ trục tọa độ Oxyz . Cho mặt phẳng
:2 10Px yz
và ba
điểm
1;1; 0 , 1; 0;1 , 0; 2;1AB C
. Viết phương trình mặt cầu có tâm thuộc mặt phẳng
P
và đi qua ba điểm
,,
A
BC
.
Bài 4. Trong không gian ,Oxyz cho đường thẳng có phương trình
412
:.
211
xyz
d

 Xét mặt
phẳng
:32 40,Px y mz với m là tham số thực. Tìm m sao cho đường thẳng d
song song với mặt phẳng
.
P
Bài 5. Tìm tọa độ hình chiếu của điểm
3; 2; 5A lên mặt phẳng
:2 3 5 13 0Pxyz?
Bài 6.
Cho bốn điểm
2;6;3A ,
1; 0; 6B ,
0; 2; 1C ,

1; 4; 0C . Tính chiều cao
A
H
của tứ
diện
A
BCD .
Bài 7. Trong không gian Oxyz , cho đường thẳng
1
:d
11- 2-
34
x
yz
m

và

2
:d
31
113
x
yz

. Tìm tất cả giá trị thức của
m để
12
dd ?
Bài 8.
Trong không gian với hệ tọa độ ,Oxyz cho mặt phẳng
:2 3 4 5 0Pxyz
và điểm
1; 3;1 .A Tính khoảng cách
d
từ điểm
A
đến mặt phẳng
.
P
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
5
TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 01
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Th
ờ
i
g
ian làm bài: 90
p
hút.
I. PHẦN TRẮC NGHIỆM ( 7 điểm ).
Câu 1.
Nguyên hàm F(x) của hàm số

tan
f
xx
là:
A.
ln cosFx x C
B.
ln cosFx x C
.
C.
ln sinFx x C
.
D.
ln sFx inx C
.
Câu 2. Nguyên hàm của hàm số
2
3
()
cos
fx
x
là:
A.
F( ) 3tan 4
x
x
B.
P( ) 3tan 4xx
C.
() 3tan 3Gx x x
D.
() 3 tHx co x
Câu 3. Biết F(x) là một nguyên hàm của hàm số

2
324fxxx và

13F 
. Trong các
khẳng định sau, khẳng định nào
đúng?
A.
32
41Fx x x x B.

62Fx x
C.
32
2
3ln
() ln
32
xx
Fx x x C
D.
22
625Fx x x
Câu 4. Nguyên hàm của hàm số
x
f
xxe
A.
1
xx
x
edx x e C


B.
1
xx
x
edx x e C

C.
1
xx
x
edx x e C

D.
1
xx
x
edx x e C


Câu 5. Tìm nguyên hàm của hàm số

10
x
x
e
fx
e
A.
ln
10
x
x
e
C
e
B.
ln 10
x
e
C
e
C.
ln 10
xx
ee C
D.
ln 10
x
eC
Câu 6. Công thức nguyên hàm nào sau đây không đúng?
A.
1
lndx x C
x

B.
01()
ln
x
x
a
adx C a
a

C.
1
1
1
()
x
xdx C

D.
2
1
tan
cos
dx x C
x

Câu 7. Cho
6
2
6fxdx
()
. Tính tích phân
2
1
2Ifxdx
()
A.
3
B. 6 C. 12 D. 36
Câu 8. Tính tích phân
0
sinIxxdx
A.
I

B.
I
C.
1I

D.
1I

Câu 9. Cho

6
0
1
sin cos
128 1
n
xxdx
n
. Tìm giá trị của n
A.
5n
B. n = 4 C. n = 3 D. n = 6
Câu 10. Cho
2
1
ln
e
Ixxdxaeb
. Khi đó
ab
có giá trị:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
6
A.
2
B. 2 C. 1 D.
1
4
Câu 11. Cho
9
3
0
1Ix xdx
. Đặt
3
1tx, ta có :
A.
1
33
2
3(1 )Ittdt

B.
1
33
2
(1 )Ittdt

C.
2
33
1
3(1 )Ittdt
D.
2
32
1
(1 )2Ittdt

Câu 12. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
6yx()
và đồ thị hàm số
2
6
y
xx
A. 9S B. 477S C. 153S D. 13S
Câu 13. Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số
2
31yx
và
2
3yx
A.
16
3
B.
8
3
C.
16
3
D.
8
3
Câu 14. Cho hình (H) giới hạn bởi (P)
2
yx 4x3
và trục Ox. Tính thể tích vật thể tròn xoay khi
quay hình (H) quanh trục Ox.
A.
16
π
15
B.
15
π
16
C.
15
16
D.
16
15
Câu 15. Hình phẳng S
1
giới hạn bởi
(), 0, , ( )
yf
x
y
xaxbab
quay quanh Ox, tạo ra vật thể
có thể tích V
1
. Hình phẳng S
2
giới hạn bởi
2(), 0, , ( )
yf
x
y
xaxbab
quay
quanh Ox, tạo ra vật thể có thể tích
2
V . Lựa chọn đáp án đúng?
A.
12
4VV B.
21
4VV C.
12
2VV D.
12
2VV
Câu 16. Cho đồ thị hàm số y = f(x). Diện tích S của hình phẳng (phần bôi đen trong hình) được tính
theo công thức:
A.
() ()

bc
ab
Sfxdxfxdx
B.
()
c
a
Sfxdx
C.
()
c
a
S
f
xdx
D.
() ()
cb
ba
S
f
xdx
f
xdx

Câu 17. Cho hai số phức thỏa
12
23, 1zizi
. Tính giá trị của biểu thức
12
3zz .
A. 61 B.
5
C.
6
D. 55
Câu 18. Cho số phức
zabi
thỏa mãn
23zz i
. Tính giá trị của biểu thức
3ab
A.
34ab
B.
33ab
C.
36ab
D.
35ab
Câu 19. Tìm số phức z thỏa mãn phương trình

2
3322zz i i
.
A.
11 19
22
zi
B.
11 19zi
C.
11 19
22
zi
D.
11 19zi
Câu 20. Cho số phức z thỏa
12zi
. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Tập hợp điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
2
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
7
B. Tập hợp điểm biểu diễn số phức z là một đường thẳng.
C. Tập hợp điểm biểu diễn số phức z là một đường Parabol.
D. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng
4
.
Câu 21. Cho các số phức thoả mãn
1zi
. Biết rằng tập hợp các điểm biểu diễn các số phức
2zi

là một đường tròn. Tâm của đường tròn đó là
A.
03I (; )
B.
01I (; )
C.
03I (;)
D.
01I (;)
Câu 22. Gọi
12
,zz
là nghiệm của phương trình
2
450zz
.Khi đó, phần thực của số phức
22
12
zz
 bằng
A. 6 B. 0 C. 8 D. 16
Câu 23. Gọi
12
,
M
M
là hai điểm lần lượt biểu diễn cho các số phức
12
,zz
là nghiệm của phương
trình
2
240zz
. Tính số đo góc
12
M
OM
A.
120
o
B.
60
o
C.
90
o
D.
150
o
Câu 24. Cho bốn véc tơ

1;1; 0 , 1; 1; 0 , 1;1;1 , 2; 0;1abcd

.Chọn mệnh đề đúng?
A.
,,acd

đồng phẳng B.
,,bcd

đồng phẳng C.
,,abc

đồng phẳng D.
,,abd

đồng phẳng
Câu 25. Viết phương trình mặt cầu đường kính AB biết
2;3; 1 , 0; 1;1AB
A.

22
2
11 24xyz
B.

222
1216xy z
C.

22
2
11 6xyz
D.

222
2316xyz
Câu 26. Cho hai điểm
(1; 2;0), (4;1;1)AB
. Độ dài đường cao OH của tam giác OAB là:
A.
86
19
B.
19
86
C.
19
2
D.
1
19
Câu 27. Viết phương trình mặt phẳng (P) đi qua điểm
(1; 1; 2)A
và có véc tơ pháp tuyến

4; 2; 6n 
A.
:2 3 5 0Pxyz
B.
:4 2 6 5 0Pxyz
C.
:2 3 2 0Pxyz  D.
:2 3 5 0Pxyz
Câu 28. Mặt phẳng (P) đi qua
(0; 1;4)A
và có hai vectơ chỉ phương (3;2;1), ( 3;0;1)uv

A.
33150xyz
B.
23140xyz
C.
30xyz
D.
3390xyz
Câu 29. Tìm tọa độ giao điểm của đường thẳng
2
:8
4
x
t
dy t
zt



và mặt phẳng
:30Pxyz
A.
1; 11; 7
B.

2;8; 4
C.
5;5; 1
D.
0;10; 7
Câu 30. Cho
(0;1;2)A
và hai đường thẳng
11
():
21 1
x
yz
d


và
1
12
2
x
t
yt
zt



. Viết phương trình
mặt phẳng (P) đi qua A đồng thời song song với (d) và (d’)
A.
35130xyz
B.
35130xyz
C.
2 6 10 11 0xy z
D.
235130xyz
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
8
Câu 31. Trong không gian vơ
i hê
to
a đô
Oxyz, đươ
ng thă
ng d đi qua hai điê
m
(2;3;4), (3;2;5)MN
co
phương trı
nh chı
nh tắc là:
A.
1
5
1
2
1
3
zyx
B.
1
4
1
3
1
2
zyx
C.
1
5
1
2
1
3
zyx
D.
1
4
1
3
1
2
zyx
Câu 32. Trong không gian với hệ trục tọa độ Oxyz , toạ độ giao điểm của hai đường thẳng



32
23
64
x
t
(d) : y t
z
t
và



5
14
28
x
t'
(d') : y t '
z
t'
là
A.
(;; )3718
B.
(;;)326
C.
(; ; )5120
D.
(; ;)311
Câu 33. Trong không gian với hệ trục tọa độ Oxyz , cho hai đường thẳng
x
yz
d:


112
12 3
và
xt
d' : y t (t
zt


2
14
26
). Mệnh đề nào dưới đây đúng ?
A.
d
và
d'
chéo nhau. B. d và
d'
trùng nhau.
C. d song song
d'
. D.
d
và
d'
cắt nhau.
Câu 34. Trong không gian với hệ tọa độ Oxyz cho
():2 2 9 0,(): 4 0Pxyz Qxyz  
và
đường thẳng
133
:
12 1
xyz
d


. Một phương trình mặt cầu có tâm thuộc d tiếp xúc với
(P) và cắt (Q) theo một đường tròn có chu vi
2
là
A.

222
3574xyz
B.

22
2
144xy z
C.

222
2524xyz
D.

22
2
234xyz
Câu 35. Trong không gian với hệ tọa độ Oxyz, cho các điểm (0;0;2), (1;0;0), (2;2;0),ABC
(0; ;0)Dm . Tìm m để khoảng cách giữa hai đường thẳng AB và CD bằng 2
A.
4
2
m
m
B.
4
2
m
m

C.
4
2
m
m

D.
4
2
m
m


II. PHẦN TỰ LUẬN ( 3 điểm ).
Bài 1. (1 điểm).
Tính tích phân sau
22
3
1
(1 ) ln
e
xxx
Idx
x

Bài 2. (1 điểm)
Cho số phức z thoả mãn điều kiện
2
2
1(1)zzi iz
. Tìm mô đun của số phức
4
1
z
z
Bài 3. (1 điểm).
Trong không gian Oxyz, viết phương trình đường thẳng (d) vuông góc với mp(P):
7430xy z
và cắt cả hai đường thẳng
1
12
();
211
xy z
d


,
2
12
(): 1
3
x
t
dy t
z


ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
9
TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 03
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM (
4 điểm)
Câu 1.
Giá trị của
os
2
2
cx
dx
bằng
A.
sin 2
.
48
xx
C

B.
sin 2
.
48
xx
C

C.
sin 2
.
24
xx
C

D.
sin 2
.
24
xx
C

Câu 2. Hàm số
() .cosfx x x
có nguyên hàm là
A.
inx.cos s .xx C
B.
inx.cos s .xx C
C.
osx.sin .xxc C
D.
osx.sin .xxc C
Câu 3. Hàm số
cos
() 2.sin
x
fx xe
có một nguyên hàm là
A.
cos
2.
x
e
B.
cos
2.
x
e
C.
inxs
2.e
D.
inxs
2.e
Câu 4. Biểu thức
4
1
ln( 2 )
44
x
x



là một nguyên hàm của hàm số
A.
4
() ln2 .fx x x
B.
3
() ln2 .fx x x
C.

4
() ln2 .
f
xx x
D.

3
() ln2 .
f
xx x
Câu 5. Tích phân
4
1
1
dx
x
bằng
A.
ln 4.
B.
0.
C.
1.
D.
ln 4.
Câu 6. Nếu
3
1
() 2fxdx
và
3
1
() 2fxdx
thì
1
1
3() 2fx dx


bằng
A.
7.
B.
5.
C.
5.
D.
7.
Câu 7. Số nào sau đây không phải là số thuần ảo?
A.
02, .ia
B. 0.i C. 00.i D. 0.i
Câu 8. Số nào sau đây có số đối, số liên hợp và số nghịch đảo của nó bằng nhau?
A.
2.i
B.
.i
C.
1
.
2
i
D.
0.
Câu 9. Kết quả của phép tính
32i
i
là
A.
23.i
B.
23.i
C.
23.i
D.
23.i
Câu 10. Số liên hợp ở dạng lượng giác của một số phức
13zi
là
A. os i2sin.
33
c



B. icos2sin .
33



C. os -i2sin.
33
c



D. -icos2sin .
33



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
10
Câu 11. Nếu
1; 0; 1u 
và
1; 1; 1v 
thì một vecto vuông góc với cả
u
và
v
sẽ có tọa độ là
A.
1; 2; 1 .
B.

1; 2; 1 .
C.

1; 1; 2 .
D.
1; 1; 2 .
Câu 12. Cho ba điểm
(1; 1 ;1),
A
(2; 1;0),B (0; 1;1)C
. Diện tích của tam giác
ABC
là
A.
3
.
2
B.
5
.
2
C. 3. D. 5.
Câu 13. Mặt phẳng đi qua hai điểm
(1; 1; 1),
A
(0;2;1)B
và song song với trục 0xcó phương trình là
A.
5230.yz
B.
30.yz
C. 210.xz D.
230.yz
Câu 14. Hai mặt phẳng
240xy z
và
20xyz
A. Cắt nhau. B. Vuông góc nhau.
C. Song song với nhau D. D. Trùng nhau.
Câu 15. Phương trình tham số giao tuyến của hai mặt phẳng
(): 2 4 0xy z

và
(): 20xyz

là
A.
8
3
2
3
xt
yt
z

B.
1
8
3
2
3
xt
yt
z


C.
0
8
3
2
3
x
yt
zt


D.
8
3
2
3
xt
y
zt


Câu 16. Phương trình hình chiếu vuông góc của đường thẳng
2
13
:
231
y
xz
d


trên mặt phẳng
tọa độ
0xy
là
A.
12
23
0
xt
yt
z


B.
12
0
3
xt
y
zt


C.
0
23
3
x
yt
zt



D.
0
23
3
x
yt
zt



II. PHẦN TỰ LUẬN (6 điểm)
Bài 1.
a) (1, 0 điểm) Tính tích phân
1
21
0
2.
x
dx
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
11
b) (1,5 điểm).Trong không gian
0xyz
cho đường thẳng
:14
12
xt
dy t
zt



và mặt
phẳng
:0Pxyz
Bài 2.
a) (1,0 điểm). Viết phương trình mặt phẳng

P
đi qua
d
và vuông góc với mp
().P
b) (1,5 điểm). Viết phương trình hình chiếu vuông góc của
d trên mp
.P
TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 04
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Th
ờ
i
g
ian làm bài: 90
p
hút.
I. PHẦN TRẮC NGHIỆM (
4
điểm)
Câu 1.
Giá trị
2
2sin
dx
x
bằng
A.
anxt.C
B.
cot .xC
C.
anxt
.
2
C
D.
cotx
.
2
C
Câu 2. Hàm số
anx
os
2
t
()fx
cx
có nguyên hàm là
A.
2
tan .xC
B.
2
cot .xC
C.
2
tan
.
2
x
C
D.
2
cot
.
2
x
C
Câu 3. Hàm số
inxs
cos .
()
2
xe
fx
 có một nguyên hàm là
A.
inxs
.
2
e
B.
inxs
.
2
e
C.
inxs
.e
D.
inxs
.e
Câu 4. Biểu thức
4
1
ln( 2 )
24
x
x



là một nguyên hàm của hàm số
A.
4
() 2 ln(2).fx x x
B.
3
() 2 ln(2).fx x x
C.
4
() ln(2).fx x x
D.
3
() ln(2).fx x x
Câu 5. Tích phân
4
1
dx
bằng
A.
3.
B.
0.
C.
1.
D.
3.
Câu 6. Nếu
3
1
() 2fxdx
và
3
1
() 1gxdx
thì
3
1
3() 2() 1
f
xgx dx

bằng
A.
5.
B.
9.
C.
10.
D.
11.
Dùng hình vẽ bên trả lời từ câu
7
đến câu
10
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
12
Câu 7. Vecto BE

biểu diễn số phức nào sau đây?
A.
0.i
B.
1.i
C.
22.i
D.
2.i
Câu 8. Số phức 22i được biểu diễn bởi
A. .CD

B. .DC

C. .DF

D. .FD

Câu 9. Số phức được biểu diễn bởi vecto
OC

códạng lượng giác là
A.
os i2sin.c

B.

icos2sin .

C.
os i2sin.c
D.

icos2sin .

Câu 10. Số liên hợp ở dạng lượng giác của số phức được biểu diễn bởi vecto AC

là
A.

os i3sin.c
B.
icos3sin .
C.

os i3sin.c
D.
icos3sin .
Câu 11. Nếu

0;0;0u
và
1; 1; 1v 
thì một vecto vuông góc với cảu
và v
sẽ có tọa độ là
A.
0;0;0 .
B.
1; 1; 0 .
C.
1; 1; 1 .
D.
0;1;1 .
Câu 12. Cho ba điểm
1; 1; 1 ,A
2;1; 0 ,B

0; 1;1C
. Diện tích của hình bình hành
ABCD
là
A.
3
.
2
B.
5
.
2
C.
5.
D.
25.
Câu 13. Mặt phẳng đi qua hai điểm
1; 2; 1 ,A
0; 2;1B
và song song với mặt phẳng
oxy
có
phương trình là
A.
220.x 
B.
10.y
C.
240.xy
D.
10.z
Câu 14. Hai mặt phẳng
240xy z
và
20xyz
A. cắt nhau. B. vuông góc nhau.
C. song song nhau. D. trùng nhau.
Câu 15. Phương trình tham số giao tuyến của hai mặt phẳng

:240xy z

và

:20xyz

là
A.
8
3
2
.
3
xt
yt
z

B.
1
1
2.
xt
yt
z


C.
1
1
2.
x
yt
zt



D.
1
1
2.
xt
y
zt


ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
13
Câu 16. Phương trình hình chiếu vuông góc của đường thẳng
12
23
3
xt
yt
zt



trên mặt phẳng
Oxz
là
A.
12
23
0.
xt
yt
z


B.
12
0
3.
xt
y
zt


C.
0
23
3.
x
yt
zt



D.
0
23
3.
x
yt
zt



II. PHẦN TỰ LUẬN (6 điểm)
Bài 1.
(2,5 điểm).
a) (1,0 điểm) Tính tích phân
2
0
sin 2 cos 2 .x x xdx
b) (1,5 điểm). Tính diện tích
S
hình phẳng được giới hạn bởi hai parabol:
2
() 3 2;fx x x
2
54gx x x
Bài 2. (1,0điểm). Viết số phức
13
1
i
i
dưới dạng lượng giác
Bài 3. (2,5 điểm). Trong không gian
Oxyz
cho mặt phẳng

:2 3 17 0Pxyz
a) (1,0điểm). Tính khoảng cách từ điểm
0;1; 1M
đến mặt phẳng
.P
b) (1,0điểm).Viết phương trình hình chiếu vuông góc của đường thẳng
d trên mặt phẳng

P
, biết
rẳng phương trình tham số của
d
là
14
12.
xt
yt
zt



TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 05
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM
Câu 1:
Trong không gian với hệ toạ độ Oxyz, cho điê
m A(1; 4; – 4), đươ
ng thă
ng
x1t
d: y 2 t (t )
z2



. Viê
t phương trı
nh cu
a đươ
ng thă
ng ∆ đi qua điê
m A vuông góc với d và đồng
thời că
t d?
A.
x1t
:y 4 t (t ).
z42t



B.
x1t
:y 4 t (t ).
z42t



C.
x1t
:y 4t (t ).
z42t



D.
x1t
:y 4 t (t ).
z42t



Câu 2: Cho số phức
z25i
. Tìm số phức
wizz
.
A.
w73i
. B.
w37i
. C.
w37i
. D.
w77i
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
14
Câu 3: Cho số phức z thỏa mãn:
2(1 2i)
(2 i)z 7 8i (1)
1i

. Môđun của số phức
z1i
là
A. 25. B. 7. C. 7. D. 5.
Câu 4: Cho hình phẳng (H) giới hạn bởi đường cong
2
f(x) 2x x 1 , trục hoành và hai đường
thẳng
x0,x2
. Diện tích của hình phẳng (H) là
A.
7
6
. B.
16
3
. C.
6
7
. D.
3
16
.
Câu 5: Parabol
2
yx chia đường tròn có tâm tại gốc tọa độ O, bán kính
R2
thành hai phần có tỉ
số diện tích bằng
A.
92
32


. B.
32
92


. C.
32
92


. D.
92
32


.
Câu 6: Cho số phức
z23i
. Tìm phần thực, phần ảo của số phức
z
.
A. Phần thực bằng – 2 và phần ảo bằng – 3. B. Phần thực bằng – 2 và phần ảo bằng – 3i.
C. Phần thực bằng – 2 và phần ảo bằng 3. D. Phần thực bằng – 2 và phần ảo bằng 3i.
Câu 7: Cho biết
2
2
1
8x 5
dx aln2 bln3 cln5
6x 7x 2


với a, b, c là các số thực. Tính P = a
2
+ b
3
+ 3c
A. 3. B. 4. C. 1. D. 2.
Câu 8: Cho đường thẳng d có phương trình tham số
x1t
y2t
z12t



và mặt phẳng
:x 3y z 1 0
.
Trong các mệnh đề sau mệnh đề nào đúng.
A.
d()
. B. d cắt
()
. C.
d//( )
. D.
d()
.
Câu 9: Trong không gian với hệ tọa độ
Oxyz,
cho mặt phẳng

P : 2x 3y 4z 5 0
và điểm
A1; 3;1.
Tính khoảng cách
d
từ điểm
A
đến mặt phẳng

P
A.
8
d.
29
B.
3
d.
29
C.
8
d.
9
D.
8
d.
29
Câu 10: Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm I( – 1; 2; 1) và tiếp xúc với mặt
phẳng
(P):x 2y 2z 2 0
có phương trình
A.

222
x1 y2 z1 9.
B.

222
x1 y2 z1 3.
C.

222
x1 y2 z1 3.
D.

222
x1 y2 z1 9.
Câu 11: Họ nguyên hàm của hàm số
2x x
f(x) e elà
A.
xx
e(e x) C
. B.
xx
e(e x) C
. C.
2x x
2e e C
. D.
2x x
1
eeC
2

.
Câu 12: Phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm A(1 ;2 ;-
3) và B(3 ;-1 ;1) ?
A.
x1 y2 z3
234


. B.
x3 y1 z1
12 3


.
C.
x1 y2 z3
311


. D.
x1 y2 z3
234


.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
15
Câu 13: Trong không gian với hệ tọa độ Oxyz cho điểm A(2 ; – 1 ; – 3) và đường thẳng
x2 y1 z1
d:
11 2


. Gọi H(a ; b ; c) là hình chiếu vuông góc của điểm A lên đường thẳng d. Tính S
= a + b – c
A. 7. B. 4. C. 6. D. 5.
Câu 14: Cho
a1;2;3,b2;1;0

. Với
c2ab

, thì tọa độ của
c
là
A.
4;3;3 .
B.
1; 3; 5 .
C.

4;3; 6 .
D.

4;1;3 .
Câu 15: Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2 ; – 1 ; 0), B(1 ; – 3 ; 2) và C( – 2 ; 0 ;
1). Cho biết mặt phẳng (P) : ax + by + cz – 1 = 0 (với a, b, c là số tự nhiên) đi qua ba điểm A, B,
C.
Tính tổng S = a + b + c
A. 19. B. 20. C. 18. D. 21.
Câu 16: Trong không gian Oxyz, cho mặt phẳng
P:x 2y z 4 0
và đường thẳng
x1 y z2
d:
213


. Tìm tọa độ giao điểm A của đường thẳng d và mặt phẳng (P)
A.

A 1;1;1
. B.
A1; 1;5
. C.
A1;0;2
. D.

A 1;1;1
.
Câu 17: Trong không gian với hệ tọa độ Oxyz cho điểm A(4 ; – 3 ; 1) và đường thẳng
x3t
d: y 1 (t )
z1t



. Gọi I(a ; b ; c) là điểm nằm trên đường thẳng d. Cho biết (S) là mặt cầu có tâm là
điểm I, đi qua điểm A và có bán kính bằng 3. Tính tổng a + b + c (với a, b, c là số nguyên khác 0)
A. 4. B. 5. C. 7. D. 6.
Câu 18: Trong không gian với hệ tọa độ
Oxyz,
cho mặt cầu
222
S:x y z 4x 2y 2z 3 0.
Tìm tọa độ tâm
I
và bán kính
R
của
S.
A.

I2; 1;1
và
R3.
B.

I2;1;1
và
R9.
C.
I2;1;1
và
R3.
D.
I2; 1;1
và
R9.
Câu 19: Cho biết
2
0
sin 2x.cos x
dx a ln 2 b
1cosx

với a, b là các số nguyên. Tính P = 2a
2
+ 3b
3
A. 7. B. 5. C. 8. D. 11.
Câu 20: Cho số phức z thỏa mãn
z2i 4
.Biết rằng tập hợp các điểm biểu diễn của số phức
w2iz3
là một đường tròn (C). Tính bán kính của đường tròn (C)
A. 2. B. 4. C. 8. D. 9.
Câu 21: Cho hàm số y = f(x) có đạo hàm liên tục trên [1 ; 3] thỏa mãn
3
1
f'(x)dx 8
và
3
1
f'(x)
dx 2
2f(x)
. Khi đó giá trị của f(3) là
A. 3. B. 4. C. 9. D. 2.
Câu 22: Tìm hàm số
yf(x)
biết
2
f (x) (x x)(x 1)

và
f(0) 3
A.
42
xx
yf(x) 3
42
. B.
42
xx
yf(x) 3
42
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
16
C.
42
xx
yf(x) 3
42
. D.
2
yf(x)3x 1.
Câu 23: Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3 ; – 1 ; 2), B(5 ; – 4 ; 4) và mặt phẳng
(P) : x – 2y + 2z – 3 = 0. Gọi (Q) là mặt phẳng qua điểm A và song song với mặt phẳng (P). Tính
khoảng cách từ điểm B đến mặt phẳng (Q)
A. 7. B. 4. C. 5. D. 6.
Câu 24: Trong chuyến đi tham quan học tập ngoại khóa ở Đà Lạt của Trường THPT Nguyễn Du, xe
số 1 đang chạy với vận tốc v = 30 (m/s) thì đột ngột thay đổi gia tốc a(t) = 4 – t (m/s
2
). Tính quãng
đường xe số 1 đi được kể từ thời điểm thay đổi gia tốc đến thời điểm vận tốc lớn nhất.
A.
424
3
(m). B. 150 (m). C.
848
3
(m). D. 200 (m).
Câu 25: Trong không gian với hệ tọa độ
Oxyz,
cho mặt phẳng

P:x 2z 3 0.
Vectơ nào dưới đây
là một vectơ pháp tuyến của
P
?
A.
n1;2;0.
B.
n1;0;2.
C.
n3;2;1.
D.
n12;3.
Câu 26: Cho
A 2;-1;5 ,B 5;-5;7
và
Mx;y;1
.Với giá trị nào của x, y thì ba điểm A,B,M thẳng
hàng ?
A.
x4,y 7
. B.
x4,y7
. C.
x4,y7
. D.
x4,y7 
.
Câu 27: Trong không gian với hệ tọa độ Oxyz cho điểm A(1 ; – 2 ; 1) và mặt phẳng (P) : 2x + 3y + z –
11 = 0. Gọi H(a ; b ; c) là hình chiếu vuông góc của điểm A lên mặt phẳng (P). Khi đó hãy cho biết
tổng S = a + b + c
A. 7. B. 5. C. 4. D. 6.
Câu 28: Số phức z thỏa mãn :
3iz 12iz 34i
là
A.
z23i
. B.
z25i
. C.
z15i
. D.
z23i
.
Câu 29: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường :
y2cosx,y0,x0,x 
quay quanh trục Ox là
A.
. B.
2
. C.
2
2
. D.
2
.
Câu 30: Trong buổi đối thoại học đường, học sinh có phản ánh trong lớp học có nhiều muỗi. Ban
Giám Hiệu Trường THPT Nguyễn Du đã mời Trung tâm y tế dự phòng về trường để khảo sát. Khi
khảo sát tại phòng học số 39 thì người ta thấy tại ngày thứ x có f(x) con muỗi. Biết rằng
10
f'(x)
x1
và lúc đầu có 100 con muỗi trong phòng học. Hỏi số lượng con muỗi trong phòng học sau
2 ngày gần với số nào sau đây?
A. 111. B. 104. C. 113. D. 115.
II. PHẦN TỰ LUẬN
Bài 1:
Tính các tích phân sau:
a)
7
32
3
Ax.x3dx
.
b)
π
2
0
B(x1).cosxdx
.
Bài 2: Tính thể tích của khối tròn xoay sinh ra khi cho quay quanh trục hoành, hình phẳng giới hạn bởi
các đường: y = x – 2, y = 0, x = 2 và x = 4.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
17
Bài 3: Tìm tập hợp những điểm M biểu diễn bởi số phức z thỏa mãn z2i z1.
TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 06
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM
Câu 1.
Viết phương trình mặt phẳng (P) đi qua ba điểm A(2; 0; 0), B(0; -1; 0), C(0; 0; -3).
A.
-3x - 6y + 2z - 6 = 0
B.
-3x + 6y + 2z + 6 = 0
C.
-3x + 6y - 2z + 6 = 0
D.
-3x - 6y + 2z +
6 = 0
Câu 2.
Phương trình mặt phẳng (P) đi qua M(1; 0; -2) đồng thời vuông góc với hai mặt phẳng (α):
2x + y - z - 2 = 0 và (β): x - y - z - 3 = 0 là.
A.
-2x - y + 3z + 4 = 0
B.
-2x + y + 3z - 4 = 0
C.
-2x + y - 3z + 4 = 0
D.
-2x + y - 3z - 4 = 0
Câu 3.
Gọi
1
z
và
2
z
lần lượt là nghiệm của phươngtrình:
2
z2z100
. Tính
22
12
zz
A.
15
B.
100
C.
50
D.
20
Câu 4.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1; 2; 3), B(1; 0; -5) và mặt phẳng (P):
2x + y - 3z - 4 = 0. Tìm tọa độ điểm M thuộc (P) sao cho 3 điểm A, B, M thẳng hàng.
A.
(3; 1; 1)
B.
(-2; 1; -3)
C.
(0; 1; -1)
D.
(0; 1; 2)
Câu 5.
Thể tích của khối tròn xoay được giới hạn bởi đường
ysinx
, trục hoành và hai đường thẳng
x0,x
là :
A.
2
2
B.
2
4
C.
3
3
D.
2
Câu 6.
Diện tích hình phẳng giới hạn bởi các đường
3
yx 4x
;Ox ; x3
x4
bằng ?
A.
44
B.
201
4
C.
36
D.
119
4
Câu 7.
Góc hợp bởi mặt phẳng
(): 2 1 0xyz

và mặt phẳng
Oxy
là bao nhiêu độ?
A.
0
45 .
B.
0
90 .
C.
0
30 .
D.
0
60 .
Câu 8.
Tính
2017
1i
z
2i
.
A.
13
i
55
B.
31
i
55
C.
31
i
55
D.
13
i
55
Câu 9.
Giả sử M(z) là điểm biểu diễn số phức z. Tập hợp các điểm M(z) thoả mãn điều kiện sau đây:
z1i
=2 là một đường tròn:
A.
Có tâm
1; 1
và bán kính là 2
B.
Có tâm

1; 1
và bán kính là 2
C.
Có tâm

1; 1
và bán kính là
2
D.
Có tâm

1; 1
và bán kính là 2
Câu 10.
Mặt phẳng nào sau đây có vectơ pháp tuyến
(3;1; 7)n
A.
3x + y -7 = 0
B.
3x + z -7 = 0
C.
3x - y -7z +1 = 0
D.
- 6x - 2y +14z -1 = 0
Câu 11.
Nếu
1
0
f(x)dx
=5 và
1
2
f(x)dx
= 2 thì
2
0
f(x)dx
bằng :
A.
3
B.
8
C.
-3
D.
2
Câu 12.
Cho số phức
zm m+1i
. Xác định m để
z13
A.
m2,m 3
B.
m2,m4
C.
m1,m3
D.
m3,m2
Câu 13.
Cho
a
= (2; -1; 2). Tìm y, z sao cho
c
= (-2; y; z) cùng phương với
a
A.
y = 2; z = -1
B.
y = -2; z = 1
C.
y = -1; z = 2
D.
y = 1; z = -2
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
18
Câu 14.
Công thức nguyên hàm nào sau đây
không đúng
?
A.
1
dx ln x C
x

B.
2
1
dx tan x C
cos x

C.
1
x
xdx C( 1)
1



D.
x
x
a
adx C(0 a 1)
ln a

Câu 15.
Xác định m, n, p để cặp mặt phẳng sau song song
( P ) : 2x -3y -5z + p = 0, ( Q ) : ( m+2 ) x + ( n - 1 )y +10z -2 = 0
A.
m = -6, n = 7, p
1
B.
m = 6, n = -4, p
2
C.
m = - 2, n = 3, p
1
D.
m = 2, n = -3, p
5
Câu 16.
Xác định tọa độ tâm và bán kính của mặt cầu (S): x² + y² + z² - 8x + 2y + 1 = 0.
A.
I(4; -1; 0), R = 4
B.
I(-4; 1; 0), R = 4
C.
I(-4; 1; 0), R = 2
D.
I(4; -1; 0), R = 2
Câu 17.
Tìm nguyên hàm
3
2
4
xdx
x



A.
3
5
3
x4lnxC
5

B.
3
5
3
x4lnxC
5

C.
3
5
3
x4lnxC
5

D.
3
5
5
x4lnxC
3

Câu 18.
Tích phân
1
0
2dx
ln a
32x
. Giá trị của a bằng:
A.
3
B.
1
C.
2
D.
4
Câu 19.
Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức
z' = -2 + 5i. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
Hai điểm A và B đối xứng với nhau qua trục hoành
B.
Hai điểm A và B đối xứng với nhau qua trục tung
C.
Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
D.
Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
Câu 20.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 2x - y +2z + 1 =
0. Phương trình mặt cầu (S) tâm A tiếp xúc với mặt phẳng (P) là
A.
(x - 2)² + (y - 1)² + (z - 1)² = 9
B.
(x - 2)² + (y - 1)² + (z - 1)² = 4
C.
(x - 2)² + (y - 1)² + (z - 1)² = 5
D.
(x - 2)² + (y - 1)² + (z - 1)² = 3
Câu 21.
Trong
, phương trình
3
z10
có nghiệm là:
A.
- 1
B.
- 1;
2i3
2
C.
- 1;
1i3
2
D.
- 1;
5i3
4
Câu 22.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 1; 2). Tìm điểm N thuộc mặt phẳng
Oxy sao cho độ dài đoạn thẳng MN là ngắn nhất.
A.
(1; 2; 2)
B.
(2; 1; 0)
C.
(2; 2; 0)
D.
(1; 1; 0)
Câu 23.
Cho
a
= (2; -3; 3),
b
= (0; 2; -1),
c
= (1; 3; 2). Tọa độ của vectơ
u2a3bc

là:
A.
(3; -3; 1)
B.
(0; -3; 4)
C.
(0; -3; 1)
D.
(3; 3; -1)
Câu 24.
Tìm công thức sai?
A.
 
[] ()
bbb
aaa
f
xgxdx fxdx gxdx

B.
  
[.] .()
bbb
aaa
f
xgxdx fxdxgxdx

C.
 
.
bb
aa
kf xdx k f xdx

D.
  
()
bcb
aac
f
xdx f xdx f xdx a c b


Câu 25.
Diện tích hình phẳng được giới hạn bởi đường
2
3yx x
và đường thẳng
21yx
là :
A.

7
dvdt
6
B.

1
dvdt
6
C.
5dvdt
D.

1
dvdt
6
Câu 26.
Gọi
H
là hình phẳng giới hạn bởi (C) của hàm số
3
yx
và đường thẳng
d:y x 2;
trục
Ox. Quay
H
xung quanh trục Ox ta được khối tròn xoay có thể tích là:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
19
A.
4
21
B.
10
21
C.
7
D.
3
Câu 27.
Cho x, y là các số thực. Hai số phức
z3i
và
z' (x 2y) yi
bằng nhau khi:
A.
x3,y0
B.
x1,y1
C.
x2,y 1
D.
x5,y 1
Câu 28.
Số phức
1i
z34i
1i

có số phức liên hợp là:
A.
z33i
B.
z3
C.
z3i
D.
z33i
Câu 29.
Phương trình chính tắc của đường thẳng(d) đi qua điểm A(-1; 0; 2), vuông góc với (P):
2x - 3y + 6z + 4 = 0.
A.
x1 y z2
23 6



B.
x1 y z2
236


C.
x1 y z2
23 6



D.
x1 y z2
23 6


Câu 30.
Nguyên hàm của hàm số f(x) = 2sin3xcos2x
A.
5cos5x cosx C
B.
1
cos5x cos x C
5

C.
1
cos5x cos x C
5

D.
1
cos5x cos x C
5

II. PHẦN TỰ LUẬN
Bài 1:
(1,25 điểm) Tính các tích phân sau:
a)
1
1ln
e
x
dx
x
b) b)
1
0
(1 )
x
exdx
Bài 2: (0,75 điểm)
a) Tính môđun của số phức z biết
(3 2 )(1 )
2
23
ii
zi
i


b) Giải phương trình
2
8410zz
trên tập số phức.
Bài 3: (2 điểm)
Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm A(1;0;0), B(0;2;0) và C(0;0;3)
a) Viết phương trình mặt phẳng (ABC)
b) Tìm tọa độ hình chiếu của điểm D(1,1,-2) lên mặt phằng (ABC)
c) Viết phương trình mặt cầu tâm I(1;-2;2) tiếp xúc với mặt phẳng (ABC)
TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 07
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM (8,0 điểm)
Câu 1.
Đồ thị đã cho có bao nhiêu điểm cực trị?
A.
2. B. 3.
C.
0. D. 1.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
20
Câu 2. Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
41
23
x
y
x
.
A.
3
,2
2
xy
B.
2
;2
3
xy
C.
2
,2
3
xy 
D.
3
,2
2
xy
Câu 3.
H
là hình phẳng giới hạn bởi đồ thị hàm số
21,
x
yxe trục hoành và trục tung. Tính
thể tích tròn xoay thu được khi quay
H
quanh trục hoành
.Ox
A.
42 .Ve
 B.
2
5.Ve
C.
2
5.Ve

D. 42.Ve
Câu 4.
Đồ thị đã cho là đồ thị của hàm số nào?
A.
42
22.yx x
B.
42
22.yx x
C.
42
22.yx x
D.
42
22.yx x
Câu 5.
Viết công thức tính thể tích
V
của phần vật thể giới hạn bởi hai
mặt phẳng vuông góc với trục
Ox
tại các điểm
,,
x
ax ba b
có thiết
diện bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
axb
là
.Sx
A.

.
b
a
VSxdx
B.

.
b
a
VSxdx
C.

.
b
a
VSxdx
D.

2
..
b
a
VSxdx
Câu 6.
Cho hàm số
f
x liên tục trên đoạn
;.ab Hãy chọn mệnh đề sai?
A.
 
.
ba
ab
f
xdx f xdx

B.

.,\0.
b
a
kdx k b a k
C.
  
bcb
aac
f
xdx f xdx f xdx

với
;.cab
D.
 
.
ba
ab
f
xdx f xdx

Câu 7.
Cho
1
13ln
e
x
Idx
x
và 13ln.tx Chọn khẳng định sai trong các khẳng định sau đây.
A.
2
1
2
..
3
Itdt
B.
2
2
1
2
..
3
Itdt
C.
2
3
1
2
9
It
D.
14
.
9
I
Câu 8.
Tìm điểm biểu diễn của số phức 45.zi
A.
4; 5 .
B.
4;5 .
C.
4;5 .
D.
4; 5 .
Câu 9.
Tìm giá trị lớn nhất của hàm số
13
y
xx
.
A.
2
B.
2
C.
3
D.
22
Câu 10.
Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị hàm số

2
2
,
1
y
x
trục hoành và các
đường thẳng
0,x
4.x
A.
4
.
25
S
B.
7
.
5
S
C.
8
.
5
S
D.
2
.
25
S
Câu 11.
Tìm m để phương trình 1
x
xm có ngiệm.
A.
0.m
B.
0.m
C.
01.m
D.
1.m
Câu 12. Cho số phức
,, .zabiab
Tìm điều kiện của
a
và
b
để tập
hợp điểm biểu diễn của số phức
z nằm trong hình tròn tâm
O
(với
O
là gốc
tọa độ), bán kính bằng
3
(như hình vẽ).
A.
22
9.ab
B.
22
9.ab
C.
9.ab
D.
22
9.ab
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
21
Câu 13. Tìm các giá trị của tham số m để hàm số
32
1y x mx mx có hai cực trị.
A.
0m
B.
3m
C.
0; 3mm
D.
03m
Câu 14.
Giả sử
f
x có đạo hàm trên khoảng
;.ab Khẳng định nào sau đây là đúng?
A.
Nếu
f
x đồng biến trên khoảng
;ab thì
0fx
trên khoảng
;.ab
B. Nếu
f
x
đồng biến trên khoảng
;ab
thì
0fx
trên khoảng
;.ab
C. Nếu
f
x
đồng biến trên khoảng
;ab
thì
0fx
trên khoảng
;.ab
D. Nếu
f
x
đồng biến trên khoảng
;ab
thì
0fx
trên khoảng
;.ab
Câu 15.
Cho số phức
,, , 0, 0zabiab a b có điểm biểu diễn là
;.
M
ab Điểm
'
M
là
điểm biểu diễn của số phức
'z sao cho
'OMM
cân tại
.
M
Tìm điểm
'.
M
A.
';0;Ma

'0; .
M
b B.
'2;0;Ma

'0;2 .
M
b
C.
'; .
M
ab
D.
';.
M
ab
Câu 16. Tính diện tích
S
giới hạn bởi đồ thị hàm số
,
x
f
xex
trục hoành, trục tung và đường
thẳng
1.x
A.
1
.
2
Se
B.
1
.
2
Se
C. 1.Se D. 1.Se
Câu 17.
Rút gọn số phức
2
23zi ta được số phức nào sau đây?
A.
743.i B. 743.i C. 14 3.i D. 14 3.i
Câu 18.
Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
A.
23
1
x
y
x

B.
3
3
x
y
x

C.
21
21
x
y
x

D.
21
2
x
y
x
Câu 19.
Gọi
,
A
B
lần lượt là điểm biểu diễn của số phức
13,' 13.ziz i
Hai điểm
A
và
B
đối
xứng với nhau qua trục, đường hay điểm nào sau đây?
A.
Đường thẳng
.
y
x
B. Trục tung.
C.
Trục hoành. D. Gốc tọa độ.
Câu 20.
Kết quả tích phân

1
0
23
x
Ixedx
được viết dưới dạng
Iaeb
với
,.ab
Khẳng định
nào sau đây là đúng?
A.
2.ab
B.
33
28.ab C.
3.ab
D.
21.ab
Câu 21.
Cho số phức
13
.
22
zi
Số phức
2
.zz
bằng số phức nào sau đây?
A.
.z B.
.z
C. .z D. 1.
Câu 22.
Đồ thị đã cho là đồ thị của hàm số nào?
A.
3
2
2
.
33
x
yxx
 B.
32
.yx x x
C.
3
2
2
33
x
yxx
 D.
3
3.yx x
Câu 23.
Cho số phức
25.zi
Tính số phức
2
w..zz
A.
w 58 145 .i
B.
w29.
C.
w14265.i
D.
w58145.i
Câu 24.
Cho hai điểm

0;0;3 , 1;2;0AM
. Viết phương trình mặt phẳng

P
qua A và cắt các trục
,Ox Oy
lần lượt tại
,
B
C
sao cho tam giác ABC có trọng tâm thuộc đường thẳng AM.
A.
:6 4 3 12 0.Pxyz
B.
: 6 3 4 12 0.Pxyz
C.
:6 3 4 12 0.Pxyz
D.

: 6 3 4 12 0.Pxyz
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
22
Câu 25. Trong không gian với hệ tọa độ
Ox
y
z
cho 2 vectơ u
và v
thỏa: 2, 1uv

và
,60.uv

Tính góc giữa 2 vectơ
v
và
?uv

A.
30 .
B.
45 .
C.
60 .
D.
90 .
Câu 26. Viết phương trình mặt phẳng

P
qua
0;0;0O vuông góc với mặt phẳng
:2 0Qx yz và tạo với mặt phẳng
Oyz
một góc
45 .
A.
:2 0Pxy và
:3 0.Pxyz B.
:5 4 3 0Pxyzvà
:2 0.Pxy
C.

:0Pxz và
:5 4 3 0.Px yz D.

:0Pxz và
:2 0.Pxy
Câu 27.
Viết phương trình mặt phẳng (P) đi qua điểm

1; 2; 3M
và nhận
2;1; 5n 
làm vectơ pháp
tuyến.
A.
:2 5 15 0.Pxyz
B.

:2 5 0.Pxyz
C.

:25150.Px y z
D.

:2 5 15 0.Pxyz
Câu 28.
Trong không gian
,Ox
y
z
viết phương trình chính tắc của đường thẳng đi qua điểm
1; 2; 1M
và có vectơ chỉ phương
2; 1;1 .u 
A.
121
.
211
xy z

B.
121
.
211
xy z

C.
121
.
211
xy z

D.
121
.
211
xy z

Câu 29.
Tìm phương trình mặt phẳng đi qua
(
)
0000
;;Mxyz
và nhận
;;nABC
(với
0n
) làm
vectơ pháp tuyến.
A.
000
()()()0.xx A yy B zz C  B.

000
0.Ax x By y Cz z
C.
000
()()()0.xx A yy B zzC  D.

000
0.Ax x By y Cz z
Câu 30. Trong không gian
,Ox
y
z
cho hai điểm
4;3;0 , 0;3; 2AB
và đường thẳng
32
:.
411
x
yz

Tìm tọa độ điểm
M
thuộc
sao cho tam giác
M
AB
có diện tích nhỏ nhất.
A.

2;3; 1 .M
B.

2; 3;1 .M 
C.
1;1;1 .M
D.

1; 1; 1 .M 
Câu 31.
Trong không gian
,Oxyz
viết phương trình tham số của đường thẳng đi qua điểm
1;1; 1M
và song song với giao tuyến của hai mặt phẳng

:10xyz

và
:2 2 0.xy z

A.

13
:14 .
1
xt
ytt
zt



B.

13
:14 .
1
xt
ytt
zt



C.

13
:14 .
1
xt
ytt
zt



D.

13
:14 .
1
xt
ytt
zt



Câu 32.
Phát biểu nào dưới đây là sai?
A.
Trong không gian
,Ox
y
z
mọi đường thẳng đều có vectơ chỉ phương có độ dài bằng
1.
B.
Trong không gian ,Oxyz mọi đường thẳng đều có phương trình tham số.
C.
Trong không gian
,Oxyz
mọi đường thẳng đều có vô số vectơ chỉ phương.
D.
Trong không gian
,Oxyz
mọi đường thẳng đều có phương trình chính tắc.
Câu 33.
Trong không gian
,Ox
y
z
tìm tất cả các giá trị của
a
để đường thẳng

1
:2,
3
xat
ytt
zt



song song với mặt phẳng

:270.ax ay z

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
23
A. 2.a  B.
1; 2 .aa
C. 1.a D.
1; 2.aa
Câu 34.
Trong không gian
,Ox
y
z
cho đường thẳng với

1; 2;3 , 2; 1;1 .MN
Vectơ
u
nào dưới đây
là một vectơ chỉ phương của đường thẳng
?
M
N
A.

1; 3; 2 .u 
B.
1; 3; 2 .u 
C.

1; 3; 2 .u 
D.

1; 3; 2 .u 
Câu 35.
Trong không gian
,Ox
y
z
cho hai đường thẳng
12
, lần lượt có các vectơ chỉ phương là
12
,uu
 
thỏa
12
0uu
 
. Phát biểu nào dưới đây là đúng?
A.
1
và
2
chéo nhau. B.
1
và
2
vuông góc.
C.
1
và
2
song song. D.
1
và
2
cắt nhau.
Câu 36.
Trong không gian Oxyz cho đường thẳng
12
:
21 3
xyz
d


và điểm (3;1;1).A Viết phương
trình mp
()
P
chứa d và khoảng cách từ điểm
A
đến mặt phẳng ()
P
bằng
23.
A.
10;7 5 30.xyz x yz
B.
10; 30.xyz xyz 
C.
10; 110.xyz xyz 
D.
10;7 5 30.xyz xy z 
Câu 37.
Trong không gian với hệ tọa độ
Ox
y
z
cho 2 vec tơ
a
và
b
khác
0.
Phát biểu nào sau đây là
sai?
A.

.
cos ,
.
ab
ab
ab
B.

,
cos ,
.
ab
ab
ab


C.
cos , cos , .ab ba


D.
.ab
là một số.
Câu 38.
Trong không gian với hệ tọa độ
.Ox
y
z
Mặt cầu nào sau đây có tâm nằm trên trục ?Oz
A.

222
:620.Sx y z z
B.

222
:2620Sx y z x z
.
C.

222
:24620Sx y z x y z
. D.
222
:2420Sx y z x y
.
Câu 39.
Trong không gian với hệ tọa độ
,Oxyz
cho 2 mặt phẳng
11 1 1 1
(): 0;Ax By Cz D

22 2 2 2
(): 0.Ax By Cz D
 Khẳng định nào sau đây là sai?
A.
1 2 12 12 12
() () 1AA BB CC
 . B.
111 2 2 2
12
12
(;; ) (; ; )
()//()
A
BC kABC
DkD

.
C.

111 2 2 2
12
12
;; ;;
.
A
BC kA B C
DkD



D.
1
cắt
2111 222
() (;;) (;;).
A
BC kA BC

Câu 40.
Phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm

4; 1;2A và chứa trục
?Ox
A.
20.xz
B.
20.yz
C.
20.yz
D.
20.xz
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1. (1,0 điểm)
a) Cho hai số phức
1
3zi
và
2
43.zi
Tính môđun của số phức
12
.zz
b) Tìm phần thực và phần ảo của số phức

3
43 1 .zii
Bài 2. (1,0 điểm)
a) Trong không gian với hệ tọa độ
,Ox
y
z
cho điểm

1; 2; 3A
và đường thẳng
13
:.
34 1
xy z
d


Viết phương trình mp
đi qua điểm
A
và chứa đường thẳng
.d
b) Trong không gian với hệ tọa độ
.Ox
y
z
Viết phương trình đường thẳng đi qua điểm
3; 2;1M
và vuông góc với mp
:3 2 3 9 0.Pxyz
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
24
TRƯỜNG THPT NHO QUAN A
GV: ĐẶNG VIỆT ĐÔNG
Đề 08
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
Môn: Toán 12
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM (gồm 40 Câu, 8 điểm, thời gian làm 75 phút)
Câu 1:
Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2100zz
. Tính
22
12
A
zz
A. 410. B.
20
. C. 210. D. 220.
Câu 2: Tìm
ln
x
dx
x
ta được:
A.
ln
.
4
x
C
B.
2
ln
.
4
x
C
C.
ln
.
2
x
C
D.
2
ln
.
2
x
C
Câu 3: Trong không gian với hệ tọa độ
Ox
y
z
, cho điểm
3; 2; 0M
và mặt phẳng
: 3 5 3 24 0.xyz

Tọa độ của điểm
M
đối xứng với
M
qua
là:
A.
3; .8; 6
B.
0; .3; 3
C.
6;7; 3 .
D.
5; 0; 3 .
Câu 4: Trong không gian với hệ tọa độ
Ox
y
z
, lập phương trình mặt phẳng
đi qua M(3; 2; 1) và
cắt ba tia
Ox
,
O
y
,
Oz
lần lượt tại
A
,
B
,
C
sao cho thể tích tứ diện
OABC
nhỏ nhất
A.
236180.xyz
B.
236180.xyz
C.
263210.xyz
D.
326190.xyz
Câu 5: Số phức liên hợp của số phức

2
32 23zii
là:
A.
946.zi
B.
946.zi
C.
946.zi
D.
946.zi
Câu 6: Cho hai số phức
12
13; 46zizi . Tìm số phức z sao cho
21
20.zz z
A.
6.z
B.
212.zi
C.
6.z 
D.
6.zi
Câu 7: Trong không gian với hệ tọa độ Oxyz , cho tam giác
A
BC
với

5; 0; 4A
,

3; 1; 2B
,
4; 2; 6.C
Khẳng định nào sau đây đúng khi nói về tam giác
A
BC
?
A. Cân và không vuông. B. Đều.
C. Vuông cân. D. Vuông và không cân.
Câu 8: Tìm mệnh đề sai trong các mệnh đề sau:
A. Điểm
;
M
ab
là điểm biểu diễn của số phức
() , zabiab
trên mặt phẳng
Ox
y
.
B.
.
ac
abi cdi
bd

C. Số phức
() , zabiab
có số phức liên hợp là
.zabi
D. Số phức
() , zabiab
có môđun là
22
.ab
Câu 9: Tích phân

4
0
tan d ln 2xx m

thì m bằng:
A.
12.
B.
22.
C.
0
. D.
21.
Câu 10: Thể tích của vật thể tròn xoay sinh bởi phép quay quanh trục
Ox
của hình phẳng giới hạn
bởi các đường
x
ye
,
2
x
ye
,
1
x
,
2x
bằng:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
25
A.
2
2
1
.
2
e
B.

2
1
.
2
e
C.

2
1
.
2
e
D.
2
2
1
.
2
e
Câu 11: Diện tích hình phẳng giới hạn bởi các đường
2
6yx ,
22
16xy trong miền
0x
bằng:
A.

4
73.
3
B.

4
43.
3
C.
8
.
3
D.

4
83.
3
Câu 12: Trong không gian với hệ tọa độ
Ox
y
z
, cho đường thẳng
2
:1
2
x
t
yt
zt


và mặt phẳng
:3 2 7 0xy z
 . Khẳng định nào sau đây đúng khi nói về quan hệ giữa
và
?
A.

.
 B. Cắt nhau và vuông góc.
C.
// .
D. Cắt nhau và không vuông góc.
Câu 13: Trong không gian với hệ tọa độ
Ox
y
z
, phương trình tham số của đường thẳng đi qua điểm
0; 1;3A
và có vectơ chỉ phương
(1; 2;1)u 
là:
A.
12.
3
xt
yt
zt


B.
12.
3
xt
yt
zt


C.
1
2.
13
x
yt
zt


D.
1.
3
xt
yt
zt



Câu 14: Biết rằng

1
1
2
15
.d
64
xf x x
. Tính tích phân

2
6
sin 2 . sin d .
x
fxx
A.
15
.
64
B.
45
.
32
C.
15
.
128
D.
15
.
32
Câu 15: Trong không gian với hệ tọa độ
Ox
y
z
, tọa độ của điểm đối xứng với điểm

1; 2; 1A
qua
trục
O
y
là:
A.
1; 2; .1
B.

1; .2; 1
C.

1; 2; 1 .
D.

1; 2 1 .;
Câu 16: Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
1; 0; 0A
,
0; 2; 0B
,
0; 0; 3C
.
Phương trình nào sau đây không phải là phương trình mặt phẳng
A
BC
?
A.
1.
23
yz
x 
B.
63260.xyz
C.
12 6 4 12 0.xyz
D.
63260.xyz
Câu 17: Gọi
M
là điểm biểu diễn của số phức 12zi và N là điểm biểu diễn của số phức
12zi

. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm
M
và
N
cùng nằm trên đường thẳng
2.x
B. Hai điểm
M
và
N
đối xứng với nhau qua trục tung.
C. Hai điểm
M
và
N
đối xứng với nhau qua gốc toạ độ
O
.
D. Hai điểm
M
và
N
đối xứng với nhau qua trục hoành.
Câu 18: Diện tích hình phẳng giới hạn bởi các đường
2
2yx,
3
y
x
bằng:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
26
A.
1
.
2
B.
1
.
6
C.
1
.
12
D.
1
.
3
Câu 19: Cho hình phẳng
A
giới hạn bởi các đường
cosyx
,
0y
,
0x
,
4
x
. Khối tròn xoay
được tạo thành khi
A quay quanh trục hoành có thể tích bằng:
A.
2
2
.
6
B.

2
.
8
C.

2
.
8

D.
2
.
4
Câu 20: Trong tập số phức, căn bậc hai của số
4
là:
A. Không tồn tại. B.
2.i
C.
2.
D.
2.i
Câu 21: Cho số phức tùy ý 1z . Xét các số phức

2017
2
2
1
ii
zz
z

và

3
2
1
zz
zz
z

.
Trong các khẳng định sau khẳng định nào đúng?
A.
,
là số thực. B.
,
là số ảo.
C.
là số ảo,
là số thực. D.
là số thực,
là số ảo.
Câu 22: Nguyên hàm của hàm số
3
213
f
xx x
là:
A.
22
13 .
x
xC
B.
2
5
6
.
25
x
x
C
C.
23
.
x
xx C
D.
23
6
1.
5
x
xC




Câu 23: Trong không gian hệ tọa độ
Ox
y
z
, cho ba điểm
0; 2; 3M ,
1; 2; 0N ,
1; 0; 3Q .
Khoảng cách giữa
M
N và
OQ
là:
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 24: Hàm số
1
cosy
x
là một nguyên hàm của hàm số:
A.
1
sin .y
x
B.
1
sin .y
x

C.
2
11
sin .y
x
x
D.
2
11
sin .y
x
x

Câu 25: Trong không gian với hệ tọa độ
Ox
y
z
, phương trình của đường thẳng đi qua điểm
1; 0; 1M và vuông góc với mặt phẳng
:2 9 0xyz
 là:
A.
12
.
1
x
t
yt
zt



B.
11
.
211
xyz

C.
1
4.
13
x
yt
zt


D.
2
1.
1
x
t
y
zt



Câu 26: Diện tích hình phẳng giới hạn bởi các đường
0x
,
1
x
,
0y
.
32
32yx x x bằng:
A.
7
.
2
B.
5
.
2
C.
5
.
4
D.
7
.
4
Câu 27: Trong không gian với hệ tọa độ
Ox
y
z
, khoảng cách giữa hai điểm
4; 1; 1A
,

2; 1; 0B
là:
A. 2 . B. 4 . C.
5
. D.
3
.
Câu 28: Tích phân
2
1
ln d
e
x
xx
bằng:
A.
3
21
.
9
e
B.
2
1
.
4
e
C.
3
32
.
8
e
D.
2
23
.
3
e
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
27
Câu 29: Tích phân
25
1
d
x
x
bằng:
A.
262
.
3
B.
248
.
3
C.
247
.
3
D.
278
.
3
Câu 30: Trong không gian với hệ tọa độ
Ox
y
z
, phương trình mặt phẳng song song với mặt phẳng
22 30xyz
và tiếp xúc với mặt cầu
222
62420xyz xyz là:
A.
22 70
.
22 50
xyz
xyz


B.
442280
.
442200
xyz
xyz


C.
442280
.
442200
xyz
xyz


D.
22 140
.
22 100
xyz
xyz


Câu 31: Tìm một nguyên hàm
Fx
của hàm số

1
1cos2
fx
x
biết
0
6
F



.
A.

1
() 3 cot .
2
F
xx
B.

1
() tan 3.
2
Fx x
C.

1
() 3 cot .
2
Fx x
D.
13
() 2 .
sinx 3
Fx





Câu 32: Trong không gian với hệ tọa độ
Ox
y
z
, xác định giá trị của
m
và
n
để cặp mặt phẳng

: 8 6 1999 0nx y z

và

: 2 3 2017 0xmy z

song song với nhau.
A.
2
.
2
m
n

B.
2
.
2
m
n

C.
4
.
4
m
n

D.
4
.
4
m
n

Câu 33: Trong không gian với hệ tọa độ
Ox
y
z
, cho hai điểm

1; 1; 1M
và
2; 2; 2N
phương
trình nào sau đây không phải phương trình đường thẳng
M
N ?
A.
111
.
111
xy z

B.
1
1.
1
x
t
yt
zt



C.
111
.
111
xyz

D.
111
.
222
xyz

Câu 34: Tích phân
2
1
0
x
x
edx
bằng:
A.

1
1.
3
e
B.
1
1.
2
e
C.
11
.
45
e
D.

1
1.
2
e
Câu 35: Cho phương trình
2
z0(;)zab ab . Nếu phương trình nhận
1zi
làm một
nghiệm thì
a
và
b
bằng:
A.
2, 2.ab
B.
4, 3.ab
C.
1, 3.ab
D.
2, 2.ab
Câu 36: Trong tập số phức, phương trình
2
10zz
có nghiệm là:
A. 13.zi B.
13
.
2
z

C. Vô nghiệm. D.
13
.
2
i
z

Câu 37: Phần ảo của số phức
zi
là:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
28
A. 1. B.
–i
. C. 0 . D.
2
.
Câu 38: Trong không gian với hệ tọa độ
Ox
y
z
, mặt phẳng đi qua
2; 5; 1M ,

1; 4; 2N  và
song song với trục
O
y
là:
A.
10.xy
B. 10.xz C. 30.xz D.
0.yz
Câu 39: Tích phân
6
0
14sincosd
x
xx
bằng:
A.
1
.
6
B.
3
.
6
C.
1
33 1.
6
D.
31
.
23
Câu 40: Trong không gian với hệ tọa độ
Ox
y
z
, cho
1; 3; 4A
và
3; 1; 4 ,B 
mặt cầu
đường kính
AB
có phương trình:
A.

22
2
2 1 20.xyz
B.
222
4 2 10 0.xyz xy
C.
222
4 2 16 0.xyz xy
D.

22
2
2 1 20.xyz
II. PHẦN TỰ LUẬN (gồm 2 Câu, 2 điểm, thời gian làm 15 phút)
Câu 1:
(1.0 điểm) Tính tích phân
23
2
5
d
4
x
I
xx
.
Câu 2: (1.0 điểm) Trong không gian với hệ tọa độ
Ox
y
z
, cho đường thẳng
133
:
12 1
xy
z
d


và mặt phẳng

:2 2 9 0Pxyz
.
.
Gọi
A
là giao điểm của
d
và
P
. Viết phương trình tham số của đường thẳng nằm
trong
P
, đi qua
A
và vuông góc với
d
.
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

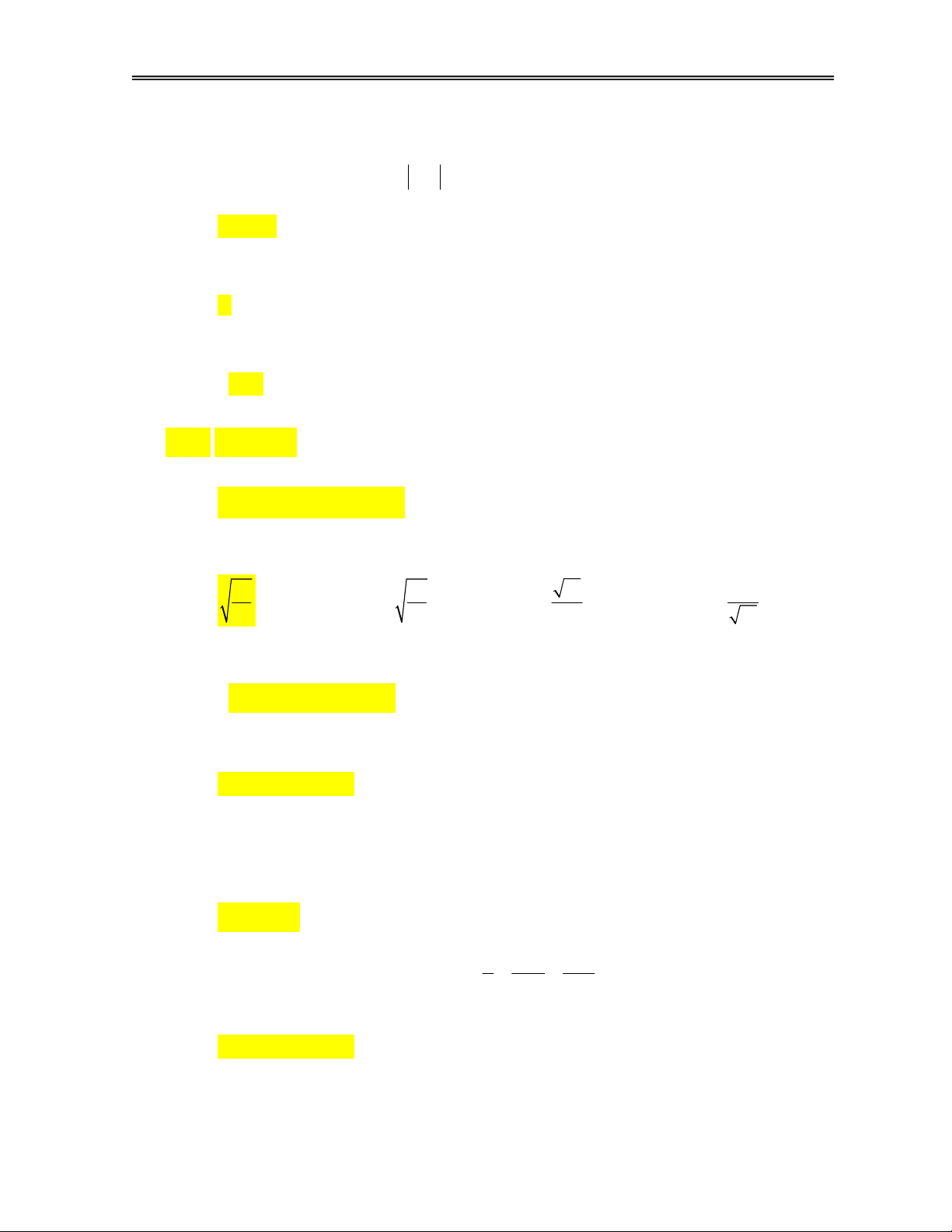
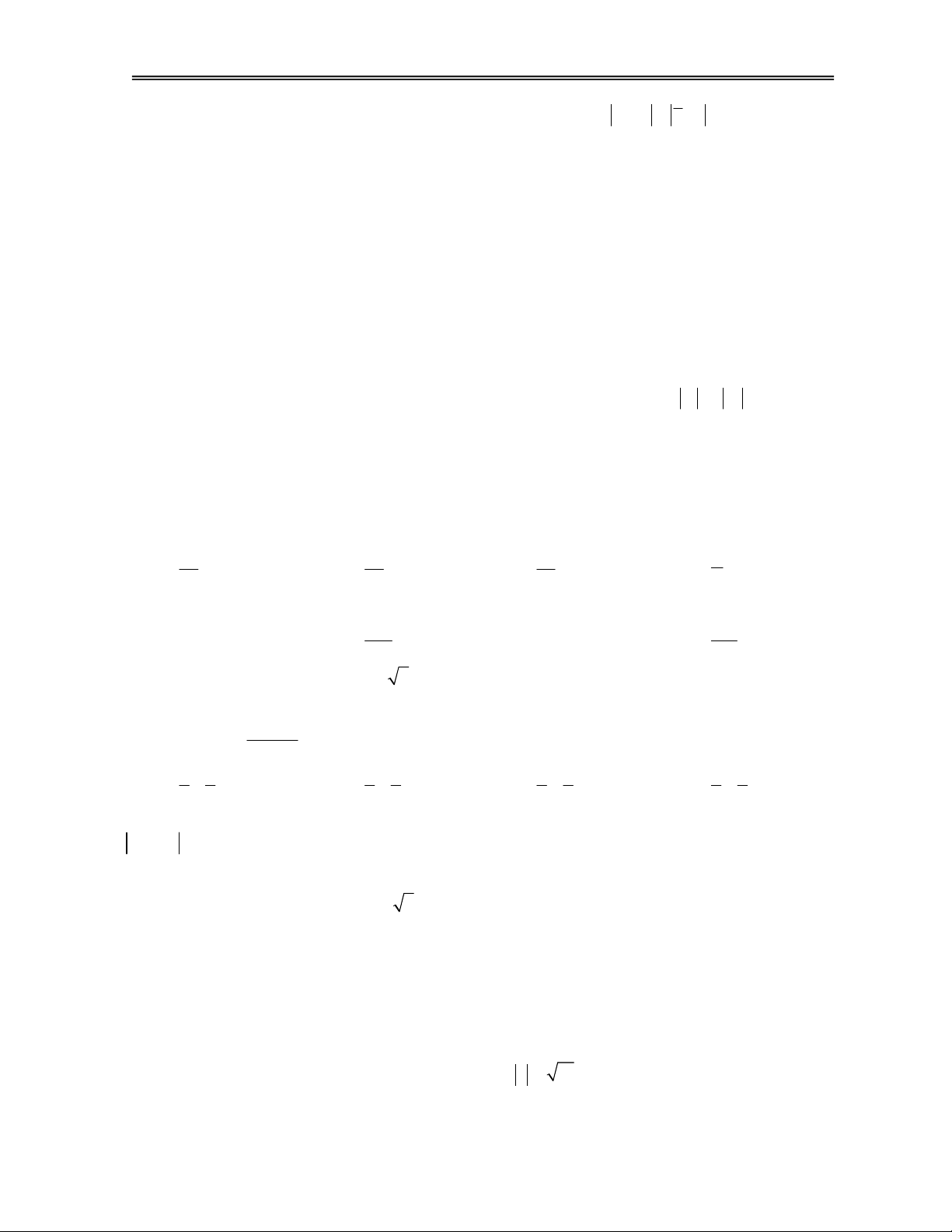
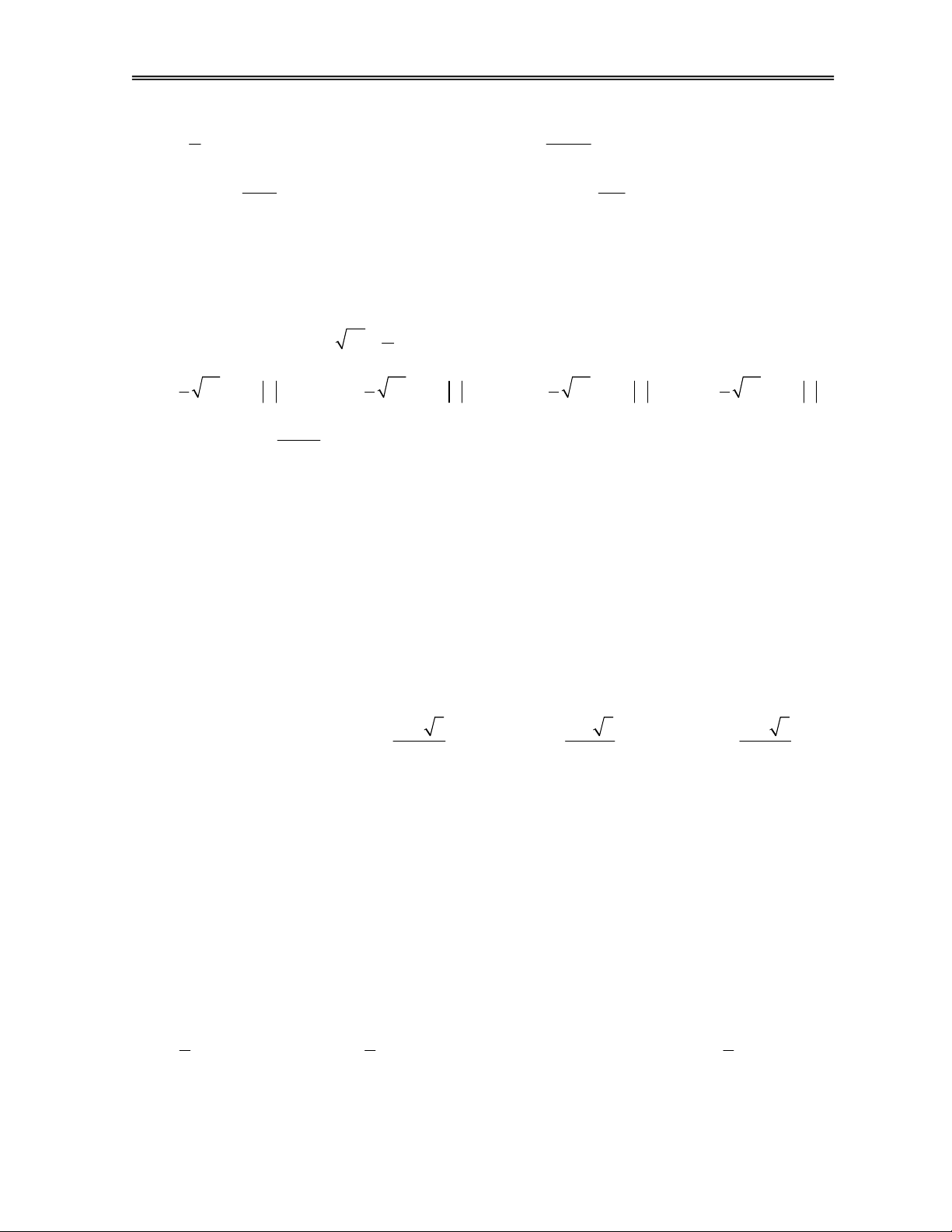
Preview text:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 01
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM: 30 câu (6 điểm) 3
Câu 1. Hàm số y  ln(x  2) 
đồng biến trên khoảng nào ? x  2  1   1  A. ( ;  1). B. (1;). C. ;1 .   D.  ; .    2   2 
Câu 2. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y x m(sin x  cos x) đồng biến trên .   1    1  1 1 A. m   ;   ; .     B.   m  .  2   2  2 2 1  1   1  C. 3   m  . D. m   ;    ; .     2  2   2 
Câu 3. Cho hàm số y f (x) xác định, liên tục trên  \ 
2 và có bảng biến thiên sau x  0 2 4  y - 0 + + 0 - y 1 15
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số đạt cực đại tại điểm x  0 và đạt cực tiểu tại điểm x  4 .
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng -15.
Câu 4. Hàm số nào sau đây không có cực trị ? 2  x A. 3
y x  3x 1. B. y  . x  3 C. 4 3
y x  4x  3x 1. D. 2n y x x  *
2017 n   . 2 x x  4
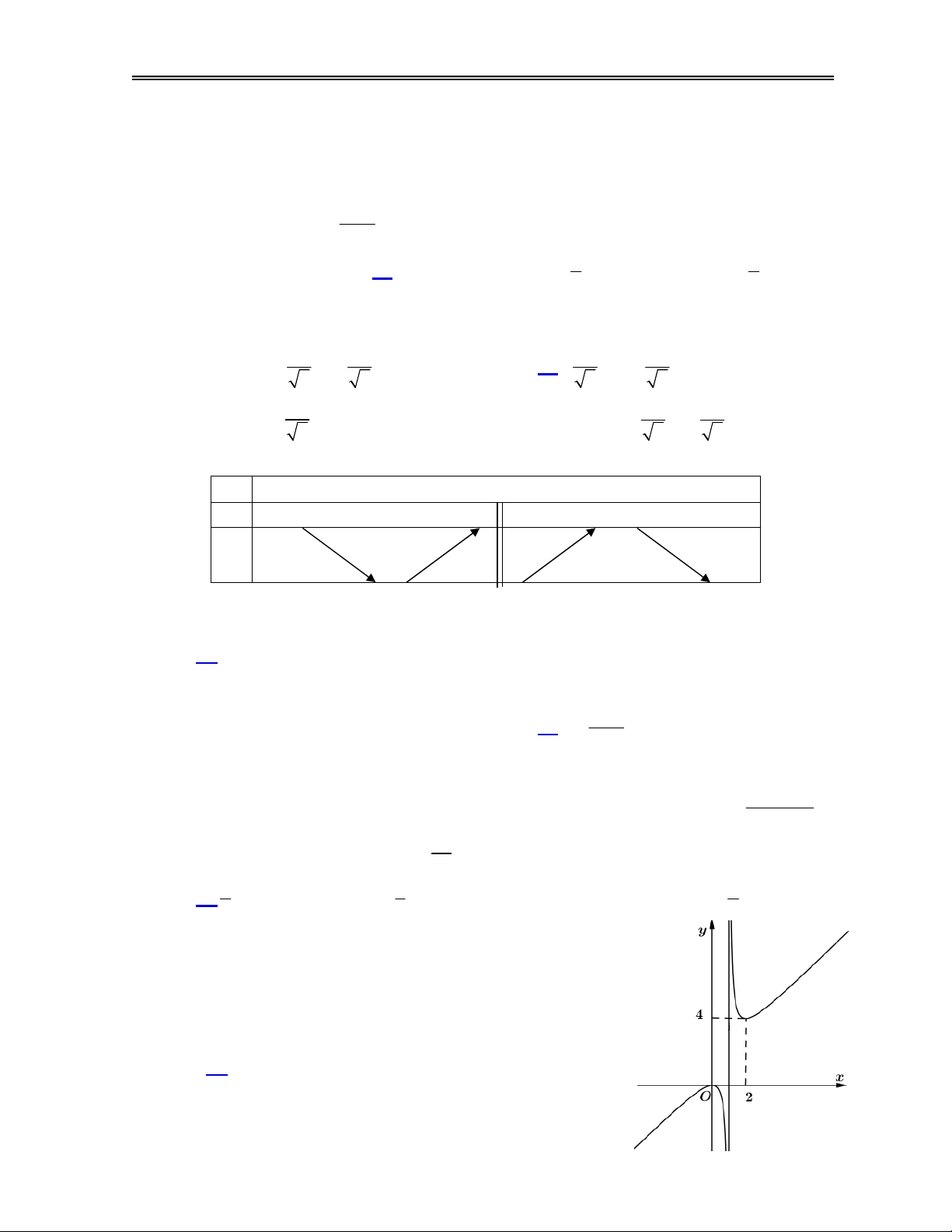
Câu 5. Kí hiệu M và m lần lượt là giá trị lớn nhất giá trị nhỏ nhất của hàm số y  trên x 1 M đoạn 0; 
3 . Tính giá trị của tỉ số . m 4 5 2 A. . B. . C. 2. D. . 3 3 3
Câu 6. Cho hàm số y f x có đồ thị như hình vẽ sau. Hỏi với
giá trị thực nào của m thì đường thẳng y  2m cắt đồ thị
hàm số đã cho tại hai điểm phân biệt.
A. m  2.
B. 0  m  2. C. m  0.
D. m  0  m  2. 1
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
Câu 7. Cho hàm số 3 2 y  2
x  7x  2x  5 có đồ thị là (C). Số giao điểm của đồ thị (C) với đường
thẳng d : y  2x 1 là A. 2 B. 3 C. 4 D. 1 Câu 8. Cho hàm số 3 2
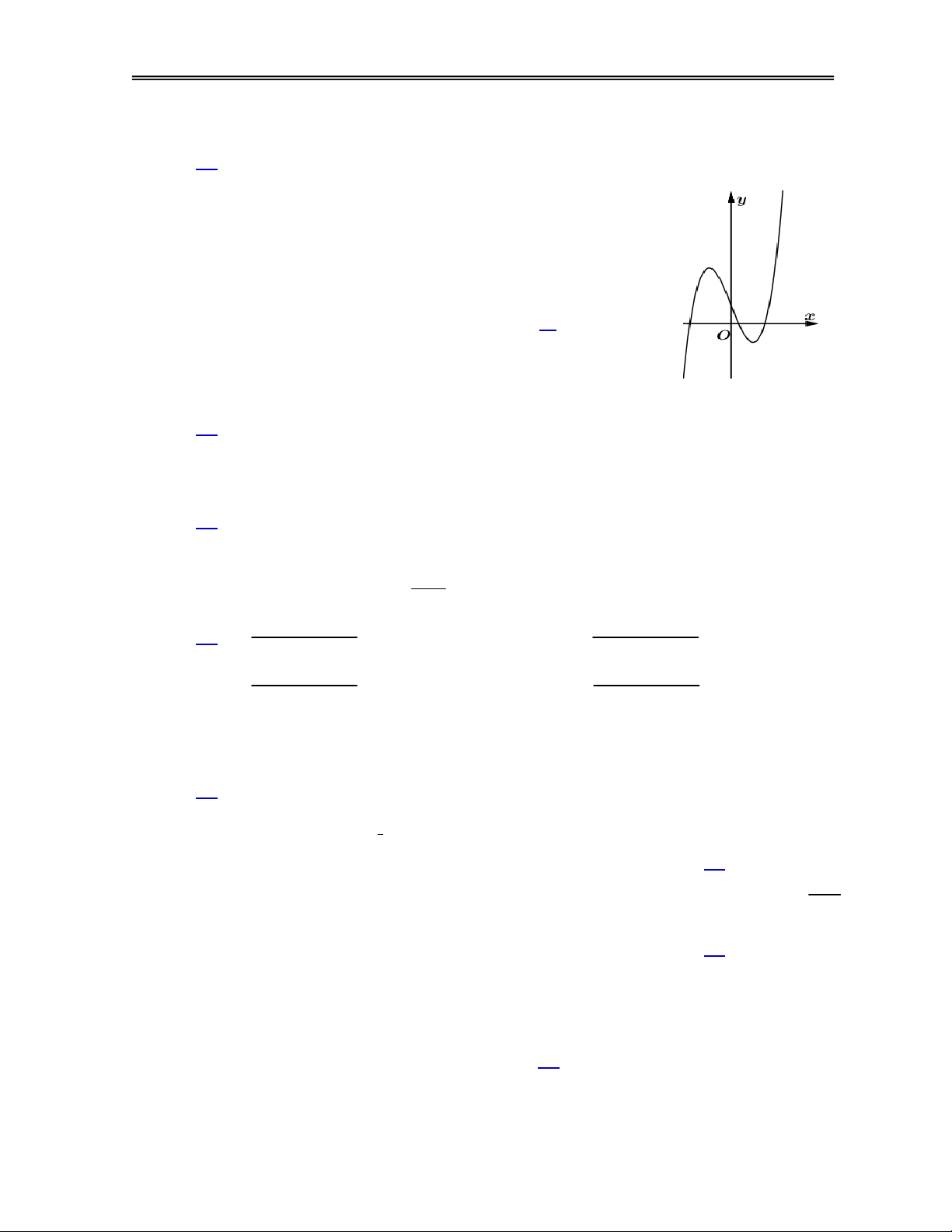
y ax bx cx d a  0 có đồ thị như hình vẽ
dưới đây. Khẳng định nào sau đây về dấu của a, b, c, d là đúng nhất ?
A. a, d  0. B.
a  0, c  0  . b C. a, ,
b c, d  0. D.
a, d  0, c  0.
Câu 9. Tìm tập xác định D của hàm số y  log x 81000 3 . 2
A. D   \  2 .
B. D  2;.
C. D   ;  2. D. D   2;    ;  2.
Câu 10. Tập xác định của hàm số y  x x   2 2 4 3 là
A. x  1, x  3. C. 1;3. B. .  D. ( ;  1)  3;. x  3
Câu 11. Tính đạo hàm của hàm số y  . 9x
1 2 x  3ln 3
1 2 x  3ln 3 A. y  . B. y  . 2 3 x 2 3 x
1 2 x  3ln 3
1 2 x  3ln 3 C. y  . D. y  . 2 3x 2 3x
Câu 12. Tính đạo hàm của hàm số y    x6 1 cos3 . A. y x   x5 ' 6sin 3 1 cos3 . B. y x x  5 ' 6sin 3 cos3 1 . C. y x   x5 ' 18sin 3 1 cos 3 . D. y x x  5 ' 18sin 3 cos3 1 .
Câu 13. Giải bất phương trình log  500 x  9  1  000. 1  3
A. x  0. B. 500 x  9  .
C. x  0. D. 1000 3   x  0. 1
Câu 14. Xét a và b là hai số thực dương tùy ý. Đặt x  ln a ab b 1000 2 2
, y  1000ln a  ln . 1000 b
Khẳng định nào dưới đây là khẳng định đúng ? A. x  . y B. x  . y C. x  . y D. x  . y
Câu 15. Khẳng định nào dưới đây là khẳng định đúng ? 2 2 2 2 A. f
 xdx  2  f
 xd .x B. f
 xdx  2 f
 xd .x 2  0 2  0 2 2 2 2 C. f
 xdx    f
 x f xd .x D. f
 xdx   f
 x f xd .x 2  0 2  0
Câu 16. Tìm nguyên hàm F x của hàm số   1000x f x  . 2
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 3 10 x
A. F x   C. B.   3 3.10 x F x  ln10. 3ln10 x 1 1000 
C. F x   C.
D.   1000x F xC. x 1 3
Câu 17. Tính tích phân I x x   1000 1 d . x 1 1002 2003.2 1001 1502.2 1002 3005.2 1001 2003.2 A. I  . B. I  . C. I  . D. I  . 1003002 501501 1003002 501501 1000 2 ln x
Câu 18. Tính tích phân I d . x  x  2 1 1 1000 ln 2 2 1000 1000ln 2 2 A. I   1000ln . B. I    ln . 1000 1000 1 2 1 2 1000 1000 1 2 1 2 1000 ln 2 2 1000 1000ln 2 2 C. I  1000ln . D. I   ln . 1000 1000 1 2 1 2 1000 1000 1 2 1 2
Câu 19. Tính diện tích hình phẳng giới hạn bởi các đường 2
y x  2x  4 và y x  2. 1 1 1 1 A. . B. . C. . D. . 6 2 3 4
Câu 20. Ký hiệu H  là hình phẳng giới hạn bởi các đường     2x2 1 x y x e
, y  0, x  2. Tính
thể tích V của khối tròn xoay thu được khi quay hình H  xung quanh trục hoành.  2e   1  2e 3  e   1  e 3 A. V  . B. V  . C. V  . D. V  . 2e 2e 2e 2e 7 11i
Câu 21. Cho số phức z
. Tìm phần thực và phần ảo của z. 2  i
A. Phần thực bằng 5  và phần ảo bằng 3  .i
B. Phần thực bằng 5  và phần ảo bằng 3. 
C. Phần thực bằng 5 và phần ảo bằng 3.
D. Phần thực bằng 5 và phần ảo bằng 3 .i
Câu 22. Cho hai số phức z  1 3i, z  4  2 .i Tính môđun của số phức z  2z . 1 2 2 1 A. 2 17. B. 2 13. C. 4. D. 5.
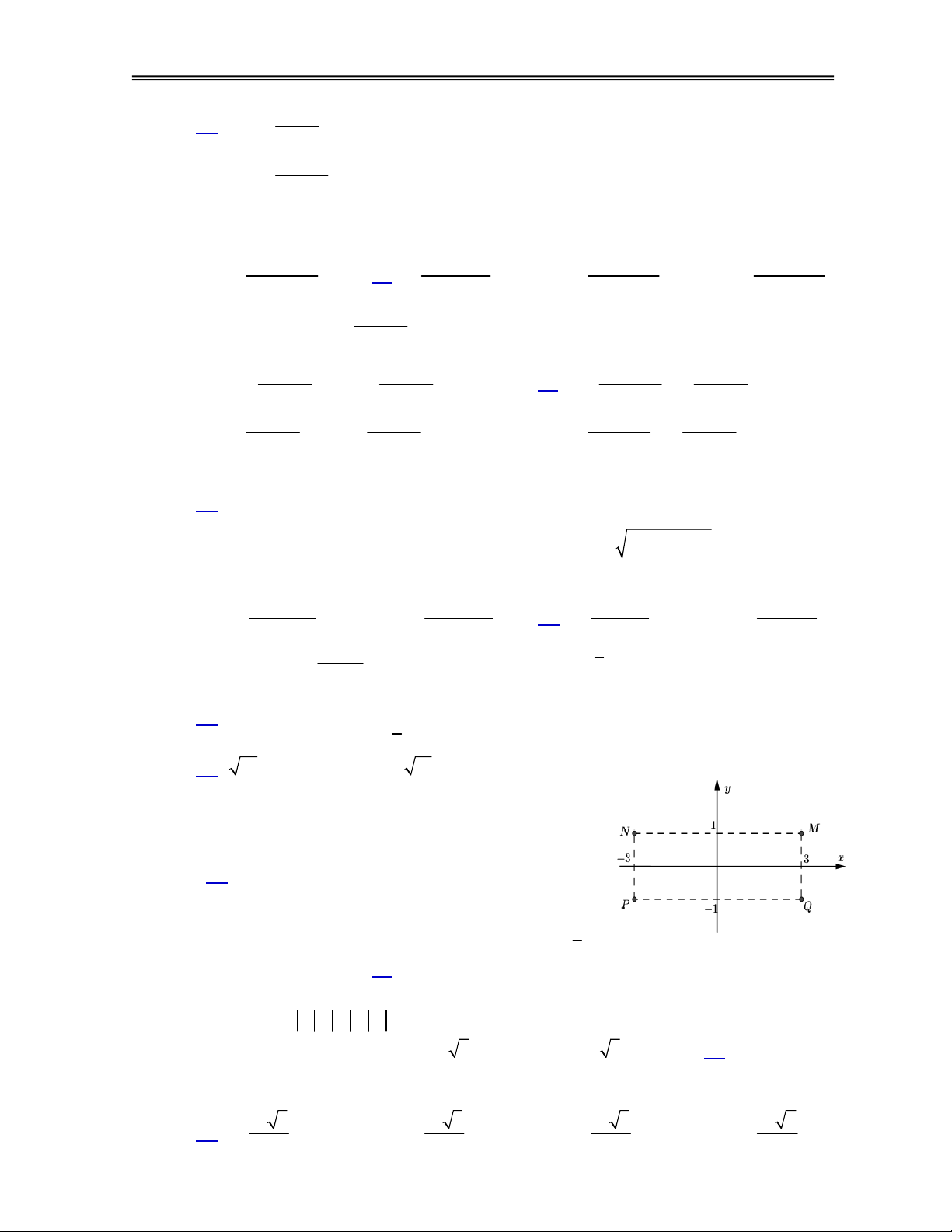
Câu 23. Cho số phức z thỏa mãn (2  i)z  7  .i Hỏi điểm biểu
diễn của z là điểm nào trong các điểm M, N, P, Q ở hình dưới ? A. Điểm P. B. Điểm Q. C. Điểm M. D. Điểm N.
Câu 24. Cho số phức z  2  3 .i Tìm số phức w  (3  2i)z  2z.
A. w  5  7 .i
B. w  4  7 .i
C. w  7  5 .i
D. w  7  4 .i
Câu 25. Kí hiệu z ; z ; z là ba nghiệm của phương trình phức 3 2
z  2z z  4  0. Tính giá trị của 1 2 3
biểu thức T z z z . 1 2 3
A. T  4.
B. T  4  5.
C. T  4 5.
D. T  5.
Câu 26. Cho hình chóp tam giác đều cạnh đáy bằng a và các mặt bên đều tạo với mặt phẳng đáy một góc 0
60 . Tính thể tích V của khối chóp. 3 a 3 3 a 3 3 a 3 3 a 2 A. V  . B. V  . C. V  . D. V  . 24 8 4 6 3
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
Câu 27. Cho lăng trụ tứ giác đều ABC . D AB CD
  đáy hình có cạnh bằng a, đường chéo AC tạo
với mặt bên BCC B   một góc   0
0    45 . Tính thể tích của lăng trụ tứ giác đều ABC . D AB CD   . A. 3 2 a cot  1. B. 3 2 a tan  1. C. 3 a cos 2 . D. 3 2
a cot  1.
Câu 28. Hình nón có thiết diện qua trục là tam giác đều. Tính độ dài đường cao của hình nón. a 3 3 A. . B. . a C. I 2; 1  ;  1 . D. . a 4 4 2
Câu 29. Một cái cốc hình trụ cao 15cm đựng được 0,5 lít nước. Hỏi bán kính đường tròng đáy của
cái cốc sấp sỉ bằng bao nhiêu (làm tròn đến hàng thập phân thứ hai) ? A. 3, 26 cm. B. 3, 27 cm. C. 3, 25cm. D. 3, 28cm.
Câu 30. Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh 2a 3 SA
. Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại 3 tiếp hình chóp S. . ABD a 39 a 35 a 37 a 39 A. R  . B. R  . C. R  . D. R  . 7 7 6 7
II. PHẦN TỰ LUẬN: 8 câu ( 4 điểm) Bài 1.
Viết phương trình tham số của của đường thẳng d đi qua điểm M 5;4;  1 và có vectơ chỉ 
phương a  2; 3;  1 . Bài 2.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1
 ;1;0 và B3;1; 2  . Viết phương
trình mặt phẳng P đi qua trung điểm I của cạnh AB và vuông góc với đường thẳng A . B Bài 3.
Trong không gian với hệ trục tọa độ Oxyz . Cho mặt phẳng P : x  2y z 1  0 và ba
điểm A1;1;0, B 1;  0;  1 ,C 0;2; 
1 . Viết phương trình mặt cầu có tâm thuộc mặt phẳng
P và đi qua ba điểm , A B,C . x  4 y 1 z  2 Bài 4.
Trong không gian Oxyz, cho đường thẳng có phương trình d :   . Xét mặt 2 1 1
phẳng P : x  3y  2mz  4  0, với m là tham số thực. Tìm m sao cho đường thẳng d
song song với mặt phẳng P. Bài 5.
Tìm tọa độ hình chiếu của điểm A 3;
 2;5 lên mặt phẳng P : 2x  3y  5z 13  0 ? Bài 6.
Cho bốn điểm A 2;
 6;3 , B1;0;6, C 0;2; 
1 , C 1;4;0 . Tính chiều cao AH của tứ diện ABCD . x 1 1- y 2 - z Bài 7. Trong không gian Oxyz , cho đường thẳng d :   và 1  3 m 4  x  3 y z 1 d :  
. Tìm tất cả giá trị thức của m để d d ? 1   2 2  1 1 3 Bài 8.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2x  3y  4z  5  0 và điểm A1; 3  ; 
1 . Tính khoảng cách d từ điểm A đến mặt phẳng P. 4
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 01
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM ( 7 điểm ).
Câu 1. Nguyên hàm F(x) của hàm số f x  tan x là:
A. F x  ln cos x C
B. F x  ln cos x C .
C. F x  ln sin x C .
D. F x  ln sinx C . 3
Câu 2. Nguyên hàm của hàm số f (x)  là: 2 cos x
A. F(x)  3 tan x  4 B. P(x)  3
 tan x  4 C. G(x)  3tan x  3x D. H (x)  3co t x
Câu 3. Biết F(x) là một nguyên hàm của hàm số f x 2
 3x  2x  4 và F   1  3. Trong các
khẳng định sau, khẳng định nào đúng?
A. F x 3 2
x x  4x 1
B. F x  6x  2 3 2 x 3ln x C. 2
F(x)  x ln x    C
D. F x 2 2
 6x  2x  5 3 2
Câu 4. Nguyên hàm của hàm số   x f x xe  A. x       1 x xe dx x e C B. x     1 x xe dx x e C C. x      1 x xe dx x e C D. x       1 x xe dx x e C x e
Câu 5. Tìm nguyên hàm của hàm số f x  10 xe x e ln  x e 10 A. ln  C B.
C C. x ln  x e
e 10  C D. ln  x
e 10  C x e 10 e
Câu 6. Công thức nguyên hàm nào sau đây không đúng? 1 x A.
dx  ln x CB. x a a dx   C 0 (  a  1)  x ln a  1   x 1 C. x dx   C (  1  )  D.
dx  tan x C   1 2 cos x 6 2
Câu 7. Cho f x dx  6  ( )
. Tính tích phân I f 2x dx  ( ) 2 1 A. 3 B. 6 C. 12 D. 36 
Câu 8. Tính tích phân I x sin xdx  0 A. I    B. I   C. I    1
D. I   1  6 n 1
Câu 9. Cho sin x cos xdx   . Tìm giá trị của n 128 n 1 0   A. n  5 B. n = 4 C. n = 3 D. n = 6 e Câu 10. Cho 2
I x ln xdx ae b
. Khi đó a b có giá trị: 1 5
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 1 A. 2 B. 2 C. 1 D. 4 9 Câu 11. Cho 3
I x 1 xdx  . Đặt 3
t  1 x , ta có : 0 1 1 2 A. 3 3
I  3 (1 t )t dtB. 3 3
I  (1 t )t dtC. 3 3
I  3 (1 t )t dtD. 2 2 1 2 3 2
I  (1 t )2t dt  1
Câu 12. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  (x  6) và đồ thị hàm số 2
y  6x x A. S  9 B. S  477 C. S  153 D. S  13
Câu 13. Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số 2 y  3  x 1và 2 y x  3 16 8 16 8 A. B. C. D. 3 3 3 3
Câu 14. Cho hình (H) giới hạn bởi (P) 2
y  x  4x  3 và trục Ox. Tính thể tích vật thể tròn xoay khi
quay hình (H) quanh trục Ox. 16 15 15 16 A. π B. π C. D. 15 16 16 15
Câu 15. Hình phẳng S1 giới hạn bởi y f (x), y  0, x a, x b (a b) quay quanh Ox, tạo ra vật thể
có thể tích V1. Hình phẳng S2 giới hạn bởi y  2 f (x), y  0, x a, x b (a b) quay
quanh Ox, tạo ra vật thể có thể tích V . Lựa chọn đáp án đúng? 2
A. V  4V
B. V  4V
C. V  2V
D. 2V V 1 2 2 1 1 2 1 2
Câu 16. Cho đồ thị hàm số y = f(x). Diện tích S của hình phẳng (phần bôi đen trong hình) được tính theo công thức: b c c A. S
f (x)dx f (x)   dx
B. S f (x)dxa b a c c b C. S f (x)dxD. S
f (x)dx f (x)dx   a b a
Câu 17. Cho hai số phức thỏa z  2  3i, z  1 i . Tính giá trị của biểu thức z  3z . 1 2 1 2 A. 61 B. 5 C. 6 D. 55
Câu 18. Cho số phức z a bi thỏa mãn 2z z  3  i . Tính giá trị của biểu thức 3a b
A. 3a b  4
B. 3a b  3 C. 3a b  6
D. 3a b  5
Câu 19. Tìm số phức z thỏa mãn phương trình z z    i2 3 3 2 2  i . 11 19 11 19 A. z   i B. z  1119i z  
i D. z  1119i 2 2 C. 2 2
Câu 20. Cho số phức z thỏa z 1 i  2 . Chọn mệnh đề đúng trong các mệnh đề sau:
A. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 2 . 6
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
B. Tập hợp điểm biểu diễn số phức z là một đường thẳng.
C. Tập hợp điểm biểu diễn số phức z là một đường Parabol.
D. Tập hợp điểm biểu diễn số phức z là một đường tròn có bán kính bằng 4 .
Câu 21. Cho các số phức thoả mãn z i  1. Biết rằng tập hợp các điểm biểu diễn các số phức
  z  2i là một đường tròn. Tâm của đường tròn đó là A. I (0; 3) B. I (0; 1) C. I (0;3) D. I(0;1)
Câu 22. Gọi z , z là nghiệm của phương trình 2
z  4z  5  0 .Khi đó, phần thực của số phức 1 2 2 2
  z z bằng 1 2 A. 6 B. 0 C. 8 D. 16
Câu 23. Gọi M , M là hai điểm lần lượt biểu diễn cho các số phức z , z là nghiệm của phương 1 2 1 2 trình 2
z  2z  4  0 . Tính số đo góc  M OM 1 2 A. 120o B. 60o C. 90o D. 150o    
Câu 24. Cho bốn véc tơ a 1;1;0, b1;1;0, c1;1;  1 , d 2;0; 
1 .Chọn mệnh đề đúng?            
A. a,c, d đồng phẳng B. , b , c d đồng phẳng C. a, , b c đồng phẳng D. a, , b d đồng phẳng
Câu 25. Viết phương trình mặt cầu đường kính AB biết A2;3;  1 , B 0; 1  ;  1
A. x  2   y  2 2 1 1  z  24
B. x  2   y  2   z  2 1 2 1  6
C. x  2   y  2 2 1 1  z  6
D. x  2   y  2   z  2 2 3 1  6
Câu 26. Cho hai điểm ( A 1; 2
 ;0), B(4;1;1) . Độ dài đường cao OH của tam giác OAB là: 86 19 19 1 A. B. C. D. 19 86 2 19
Câu 27. Viết phương trình mặt phẳng (P) đi qua điểm (1
A ;1; 2) và có véc tơ pháp tuyến
n  4;2; 6
A. P : 2x y  3z  5  0
B. P : 4x  2y  6z  5  0
C. P : 2x y  3z  2  0
D. P : 2x y  3z  5  0  
Câu 28. Mặt phẳng (P) đi qua (0 A ; 1
 ;4) và có hai vectơ chỉ phương u  (3;2;1),v  ( 3  ;0;1)
A. x  3y  3z 15  0
B. x  2y  3z 14  0
C. x y z  3  0
D. x  3y  3z  9  0 x  2  t
Câu 29. Tìm tọa độ giao điểm của đường thẳng d : y  8  t và mặt phẳngP : x y z  3  0 z  4   tA.  1  ;11; 7   B. 2;8; 4   C. 5;5;  1  D. 0;10; 7   x 1 t x y 1 z 1  Câu 30. Cho (0
A ;1;2) và hai đường thẳng (d) :   và y  1
  2t . Viết phương trình 2 1 1  z  2t
mặt phẳng (P) đi qua A đồng thời song song với (d) và (d’)
A. x  3y  5z 13  0
B. x  3y  5z 13  0
C. 2x  6y 10z 11  0
D. 2x  3y  5z 13  0 7
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
Câu 31. Trong không gian với hê ̣ to ̣a đô ̣ Oxyz, đường thẳng d đi qua hai điểm M (2;3;4), N(3;2;5)
có phương trı̀nh chı́nh tắc là: x  3 y  2 z  5 x  2 y  3 z  4 A.   B.   1 1 1 1 1 1 x  3 y  2 z  5 x  2 y  3 z  4 C.   D.   1 1 1 1 1 1
Câu 32. Trong không gian với hệ trục tọa độ Oxyz , toạ độ giao điểm của hai đường thẳng
x  3  2t
x  5  t'(d) :
y  2  3t và (d') : y  1 4t' là z  6    4t z  2   8t' A. ( ; 3 ; 7 1 ) 8 B. (; 3 2;6) C. ( ; 5  ; 1 20) D. ( ; 3  ; 1 ) 1
x 1 y 1 z 2
Câu 33. Trong không gian với hệ trục tọa độ Oxyz , cho hai đường thẳng d :      và 1 2 3  x  2t
d' : y 1 4t (t  ). Mệnh đề nào dưới đây đúng ?
z  2  6t
A. d và d' chéo nhau.
B. d và d' trùng nhau.
C. d song song d' .
D. d và d' cắt nhau.
Câu 34. Trong không gian với hệ tọa độ Oxyz cho (P) : 2x y  2z  9  0, (Q) : x y z  4  0 và x 1 y  3 z  3 đường thẳng d :  
. Một phương trình mặt cầu có tâm thuộc d tiếp xúc với 1 2 1
(P) và cắt (Q) theo một đường tròn có chu vi 2 là
A. x  2   y  2   z  2 3 5 7  4
B. x   y  2   z  2 2 1 4  4
C. x  2   y  2   z  2 2 5 2  4
D. x  2   y  2 2 2 3  z  4
Câu 35. Trong không gian với hệ tọa độ Oxyz, cho các điểm (
A 0;0; 2), B(1;0;0),C(2; 2;0), D(0; ;
m 0) . Tìm m để khoảng cách giữa hai đường thẳng AB và CD bằng 2 m  4 m  4 m  4  m  4  A. B. C. D.  m  2 m  2  m  2 m  2 
II. PHẦN TỰ LUẬN ( 3 điểm ). e 2 2
(1 x ) ln x x
Bài 1. (1 điểm). Tính tích phân sau I dx 3 x 1 2
Bài 2. (1 điểm) Cho số phức z thoả mãn điều kiện 2
1 z z i  (iz 1) . Tìm mô đun của số phức 4 z z 1
Bài 3. (1 điểm). Trong không gian Oxyz, viết phương trình đường thẳng (d) vuông góc với mp(P): x  1   2t x y 1 z  2 
7x y  4z  3  0 và cắt cả hai đường thẳng (d );  
, (d ) : y 1 t 1 2 1 1 2 z  3  8
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 03
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM ( 4 điểm)
Câu 1. Giá trị của os2 c x dx  bằng 2
A. x sin 2x   x x C. B. sin 2   C. 4 8 4 8
C. x sin 2x   x x C. D. sin 2   C. 2 4 2 4
Câu 2. Hàm số f (x)  .
x cos x có nguyên hàm là A. .c
x os x  s inx  C. B. .c
x os x  s inx  C. C. .s x in x  os c x  C. D. .s x in x  os c x  C. Câu 3. Hàm số cos ( )  2  .sin x f x xe có một nguyên hàm là A. cos 2 x e . B. cos 2 xe . C. sinx 2e . D. sinx 2  e . 4  
Câu 4. Biểu thức x 1 ln(2x)  
 là một nguyên hàm của hàm số 4  4  A. 4
f (x)  x ln 2x. B. 3
f (x)  x ln 2x. C. 4
f (x)  x ln 2x. D. 3
f (x)  x ln 2x. 4 Câu 5. Tích phân 1 dx  bằng 1 x A.  ln 4. B. 0. C. 1. D. ln 4. 3 3 1 Câu 6. Nếu
f (x)dx  2  và
f (x)dx  2  thì
3 f (x)  2 dx    bằng 1 1 1  A. 7.  B. 5.  C. 5. D. 7.
Câu 7. Số nào sau đây không phải là số thuần ảo?
A. 0  2i,a . B. 0  i. C. 0  0i. D. 0  i.
Câu 8. Số nào sau đây có số đối, số liên hợp và số nghịch đảo của nó bằng nhau? A. 2  .i B. .iC. 1  i. D. 0. 2 
Câu 9. Kết quả của phép tính 3 2i là i A. 2   3 .i B. 2   3 .i C. 2  3 .i D. 2  3i.
Câu 10. Số liên hợp ở dạng lượng giác của một số phức z  1 3i là        
A. 2cos  i sin .
B. 2sin  icos .  3 3   3 3         
C. 2cos -i sin . D. 2sin -icos .  3 3   3 3  9
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017    
Câu 11. Nếu u  1;0;   1 và v  1; 1;
 1thì một vecto vuông góc với cảuvà v sẽ có tọa độ là
A. 1; 2; 1. B. 1; 2;1.
C. 1; 1; 2. D. 1;1; 2.
Câu 12. Cho ba điểm (1 A ; 1;1), (2
B ;1; 0), C(0; 1;1) . Diện tích của tam giác ABC là A. 3 . B. 5 . 2 2 C. 3. D. 5.
Câu 13. Mặt phẳng đi qua hai điểm (1 A ;1; 1), (0
B ; 2;1) và song song với trục 0x có phương trình là
A. 5y  2z  3  0.
B. y z  3  0. C. 2
x z 1  0.
D. 2y z  3  0.
Câu 14. Hai mặt phẳng x y  2z  4  0 và x y z  2  0 A. Cắt nhau. B. Vuông góc nhau.
C. Song song với nhau D. D. Trùng nhau.
Câu 15. Phương trình tham số giao tuyến của hai mặt phẳng
( ) : x y  2z  4  0 và ( )
 : x y z  2  0 là   x tx  1 t   A. 8 8
y    t
B. y    t 3  3   2  2 z   z    3  3   x  0 x t   C. 8
y    t D. 8 y   3  3   2  2 z   tz   t   3  3 x  1 y  2 
Câu 16. Phương trình hình chiếu vuông góc của đường thẳng z 3 d :   trên mặt phẳng 2 3 1
tọa độ 0xy là x  1 2tx  1 2tx  0 x  0    
A. y  2  3t B. y  0
C. y  2  3t
D. y  2  3t     z  0  z  3  tz  3  tz  3  t
II. PHẦN TỰ LUẬN (6 điểm) Bài 1. 1
a) (1,0 điểm) Tính tích phân 2x1 2 . dx  0 10
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 x t
b) (1,5 điểm).Trong không gian 0xyz cho đường thẳng d : y  1 4t và mặt
z  1 2t
phẳng P : x y z  0 Bài 2.
a) (1,0 điểm). Viết phương trình mặt phẳng Pđi qua d và vuông góc với mp(P).
b) (1,5 điểm). Viết phương trình hình chiếu vuông góc của d trên mp P. TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 04
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM ( 4 điểm) Câu 1. Giá trị dx  bằng 2 2 sin x A. t t anx  C.
B.  cot x C. C. anx  C. D. cotx   C. 2 2 Câu 2. Hàm số t anx f (x)  có nguyên hàm là os2 c x 2 2 A. 2 tan x cot x tan x C. B. 2 cot x C. C. C. D.   C. 2 2 sinx Câu 3. Hàm số cos . x e f (x)   có một nguyên hàm là 2 sinx sinx A. ee . B. . 2 2 C. sinx e . D. sinx e . 4  
Câu 4. Biểu thức x 1 ln(2x)  
 là một nguyên hàm của hàm số 2  4  A. 4
f (x)  2x ln(2x). B. 3
f (x)  2x ln(2x). C. 4
f (x)  x ln(2x). D. 3
f (x)  x ln(2x). 4
Câu 5. Tích phân dx  bằng 1 A. 3.  B. 0. C. 1. D. 3. 3 3 3 Câu 6. Nếu
f (x)dx  2  và ( g x)dx  1   thì
3 f (x)  2 ( g x)  1 dx    bằng 1 1 1 A. 5. B. 9. C. 10. D. 11.
Dùng hình vẽ bên trả lời từ câu 7 đến câu10 11
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017  Câu 7.
Vecto BE biểu diễn số phức nào sau đây? A. 0  i. B. 1 .i C. 2  2 .i D. 2  i.
Câu 8. Số phức 2  2i được biểu diễn bởi   A. . CD B. DC.   C. DF. D. . FD 
Câu 9. Số phức được biểu diễn bởi vectoOC códạng lượng giác là
A. 2cos  i sin .
B. 2sin  icos . C. 2 os
c   i sin .
D. 2sin  icos . 
Câu 10. Số liên hợp ở dạng lượng giác của số phức được biểu diễn bởi vecto AC là A. 3 os
c   i sin .
B. 3sin  icos . C. 3 os
c   i sin .
D. 3sin  icos .    
Câu 11. Nếu u  0;0;0 và v  1; 1; 
1thì một vecto vuông góc với cảu vàv sẽ có tọa độ là A. 0;0;0. B. 1; 1;  0. C. 1; 1;1. D. 0;1;1.
Câu 12. Cho ba điểm A1; 1;1 , B2;1;0 , C 0; 1;1 . Diện tích của hình bình hành ABCD là A. 3 . B. 5 . C. 5. D. 2 5. 2 2
Câu 13. Mặt phẳng đi qua hai điểm A1; 2;1 , B0; 2;1và song song với mặt phẳngoxy có phương trình là
A. 2x  2  0.
B. y  1  0.
C. 2x y  4  0.
D. z  1  0.
Câu 14. Hai mặt phẳng x y  2z  4  0 và x y z  2  0 A. cắt nhau. B. vuông góc nhau. C. song song nhau. D. trùng nhau.
Câu 15. Phương trình tham số giao tuyến của hai mặt phẳng
: xy  2z 4  0và: xy z 2  0 là  x t  x  1 tx  1 x  1 t     A. 8
y    t
B. y  1 t
C. y  1 t D. y  1 3      z  2. z  2  t. z  2  t. 2    z  .  3 12
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 x  1 2t
Câu 16. Phương trình hình chiếu vuông góc của đường thẳng y  2  3t trên mặt phẳngOxz là z  3t  x  1 2tx  1 2tx  0 x  0    
A. y  2  3t B. y  0
C. y  2  3t
D. y  2  3t     z  0.  z  3  t.  z  3  t.  z  3  t. 
II. PHẦN TỰ LUẬN (6 điểm)
Bài 1. (2,5 điểm). 
a) (1,0 điểm) Tính tích phân 2 x sin 2x cos 2 . xdx  0
b) (1,5 điểm). Tính diện tíchS hình phẳng được giới hạn bởi hai parabol: 2
f (x)  x  3x  2; g x 2
 x  5x  4
Bài 2. (1,0điểm). Viết số phức 1 i 3    dưới dạng lượng giác 1  i
Bài 3. (2,5 điểm). Trong không gian Oxyz cho mặt phẳng P : 2x  3y z 17  0
a) (1,0điểm). Tính khoảng cách từ điểm M 0;1; 1 đến mặt phẳngP.
b) (1,0điểm).Viết phương trình hình chiếu vuông góc của đường thẳng d trên mặt phẳng P , biết x t
rẳng phương trình tham số của d là y  1 4t
z  1 2t.  TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 05
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM
Câu 1: Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 4; – 4), đường thẳng  x  1 t 
d : y  2  t (t  ) . Viết phương trı̀nh của đường thẳng ∆ đi qua điểm A vuông góc với d và đồng  z  2   thời cắt d? x 1 t x  1 t  
A.  : y  4  t (t  ).
B.  : y  4  t (t  ).  z  4 2t   z  4  2t  x  1 t x 1 t  
C.  :  y  4  t (t  ).
D.  : y  4  t (t  ).  z  4 2t   z  4  2t 
Câu 2: Cho số phức z  2  5i . Tìm số phức w  iz  z . A. w  7  3i . B. w  3  7i . C. w  3  7i . D. w  7  7i . 13
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 2(1 2i)
Câu 3: Cho số phức z thỏa mãn: (2  i)z 
 7  8i (1) . Môđun của số phức   z 1 i là 1 i A. 25. B. 7. C. 7 . D. 5.
Câu 4: Cho hình phẳng (H) giới hạn bởi đường cong 2 f (x)  2
 x  x 1, trục hoành và hai đường
thẳng x  0, x  2 . Diện tích của hình phẳng (H) là 7 16 6 3 A. . B. . C. . D. . 6 3 7 16 Câu 5: Parabol 2
y  x chia đường tròn có tâm tại gốc tọa độ O, bán kính R  2 thành hai phần có tỉ số diện tích bằng 9  2 3  2 3  2 9  2 A. . B. . C. . D. . 3  2 9  2 9  2 3  2
Câu 6: Cho số phức z  2  3i . Tìm phần thực, phần ảo của số phức z .
A. Phần thực bằng – 2 và phần ảo bằng – 3.
B. Phần thực bằng – 2 và phần ảo bằng – 3i.
C. Phần thực bằng – 2 và phần ảo bằng 3.
D. Phần thực bằng – 2 và phần ảo bằng 3i. 2 8x  5 Câu 7: Cho biết
dx  a ln 2  b ln 3  c ln 5 
với a, b, c là các số thực. Tính P = a2 + b3 + 3c 2 6x  7x  2 1 A. 3. B. 4. C. 1. D. 2. x  1 t 
Câu 8: Cho đường thẳng d có phương trình tham số y  2  t và mặt phẳng  : x  3y  z 1  0 . z 1 2t 
Trong các mệnh đề sau mệnh đề nào đúng. A. d  () . B. d cắt ( )  . C. d / /() . D. d  () .
Câu 9: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2x  3y  4z  5  0 và điểm A 1; 3; 
1 . Tính khoảng cách d từ điểm A đến mặt phẳng P 8 3 8 8 A. d  . B. d  . C. d  . D. d  . 29 29 9 29
Câu 10: Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm I( – 1; 2; 1) và tiếp xúc với mặt
phẳng (P) : x  2y  2z  2  0 có phương trình
A.   2    2    2 x 1 y 2 z 1  9.
B.   2    2    2 x 1 y 2 z 1  3.
C.   2    2    2 x 1 y 2 z 1  3.
D.   2    2    2 x 1 y 2 z 1  9.
Câu 11: Họ nguyên hàm của hàm số 2x x f (x)  e  e là 1 A. x x e (e  x)  C . B. x x e (e  x)  C . C. 2x x 2e  e  C . D. 2x x e  e  C . 2
Câu 12: Phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm A(1 ;2 ;- 3) và B(3 ;-1 ;1) ? x 1 y  2 z  3 x  3 y 1 z 1 A.   . B.   . 2 3  4 1 2 3  x 1 y  2 z  3 x 1 y  2 z  3 C.   . D.   . 3 1  1 2 3  4 14
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
Câu 13: Trong không gian với hệ tọa độ Oxyz cho điểm A(2 ; – 1 ; – 3) và đường thẳng x  2 y 1 z 1 d :  
. Gọi H(a ; b ; c) là hình chiếu vuông góc của điểm A lên đường thẳng d. Tính S 1  1 2 = a + b – c A. 7. B. 4. C. 6. D. 5.      
Câu 14: Cho a   1
 ;2;3,b  2;1;0. Với c  2a  b , thì tọa độ của c là A. 4;3;3. B. 1;3;5. C. 4;3;6. D. 4;1;3.
Câu 15: Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2 ; – 1 ; 0), B(1 ; – 3 ; 2) và C( – 2 ; 0 ;
1). Cho biết mặt phẳng (P) : ax + by + cz – 1 = 0 (với a, b, c là số tự nhiên) đi qua ba điểm A, B, C.
Tính tổng S = a + b + c A. 19. B. 20. C. 18. D. 21.
Câu 16: Trong không gian Oxyz, cho mặt phẳng P : x  2y  z  4  0 và đường thẳng x 1 y z  2 d :  
. Tìm tọa độ giao điểm A của đường thẳng d và mặt phẳng (P) 2 1 3 A. A 1;1  ;1 . B. A 1;1;5 .
C. A 1;0;2 . D. A 1;1  ;1 .
Câu 17: Trong không gian với hệ tọa độ Oxyz cho điểm A(4 ; – 3 ; 1) và đường thẳng x  3  t 
d : y  1 (t  ) . Gọi I(a ; b ; c) là điểm nằm trên đường thẳng d. Cho biết (S) là mặt cầu có tâm là z 1 t 
điểm I, đi qua điểm A và có bán kính bằng 3. Tính tổng a + b + c (với a, b, c là số nguyên khác 0) A. 4. B. 5. C. 7. D. 6. Câu 18: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu   2 2 2
S : x  y  z  4x  2y  2z  3  0. Tìm tọa độ tâm I và bán kính R của S. A. I 2;1;  1 và R  3. B. I 2;1;   1 và R  9. C. I 2;1;  1 và R  3. D. I 2;1;  1 và R  9.  2 sin 2x.cos x Câu 19: Cho biết dx  a ln 2  b 
với a, b là các số nguyên. Tính P = 2a2 + 3b3 1 cos x 0 A. 7. B. 5. C. 8. D. 11.
Câu 20: Cho số phức z thỏa mãn z  2i  4 .Biết rằng tập hợp các điểm biểu diễn của số phức
w  2iz  3 là một đường tròn (C). Tính bán kính của đường tròn (C) A. 2. B. 4. C. 8. D. 9. 3
Câu 21: Cho hàm số y = f(x) có đạo hàm liên tục trên [1 ; 3] thỏa mãn f '(x)dx  8  và 1 3 f '(x) dx  2 
. Khi đó giá trị của f(3) là 2 f (x) 1 A. 3. B. 4. C. 9. D. 2.
Câu 22: Tìm hàm số y  f (x) biết 2 f (
 x)  (x  x)(x 1) và f (0)  3 4 2 x x 4 2 x x A. y  f (x)    3. B. y  f (x)    3 . 4 2 4 2 15
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 4 2 x x C. y  f (x)    3. D. 2 y  f (x)  3x 1. 4 2
Câu 23: Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3 ; – 1 ; 2), B(5 ; – 4 ; 4) và mặt phẳng
(P) : x – 2y + 2z – 3 = 0. Gọi (Q) là mặt phẳng qua điểm A và song song với mặt phẳng (P). Tính
khoảng cách từ điểm B đến mặt phẳng (Q) A. 7. B. 4. C. 5. D. 6.
Câu 24: Trong chuyến đi tham quan học tập ngoại khóa ở Đà Lạt của Trường THPT Nguyễn Du, xe
số 1 đang chạy với vận tốc v = 30 (m/s) thì đột ngột thay đổi gia tốc a(t) = 4 – t (m/s2). Tính quãng
đường xe số 1 đi được kể từ thời điểm thay đổi gia tốc đến thời điểm vận tốc lớn nhất. 424 848 A. (m). B. 150 (m). C. (m). D. 200 (m). 3 3
Câu 25: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x  2z  3  0. Vectơ nào dưới đây
là một vectơ pháp tuyến của P ?     A. n  1; 2  ;0. B. n  1;0; 2  . C. n  3; 2  ;  1 .
D. n  1 2;3.
Câu 26: Cho A 2;-1;5,B5;-5;7 và M x; y; 
1 .Với giá trị nào của x, y thì ba điểm A,B,M thẳng hàng ? A. x  4, y  7  . B. x  4  , y  7 . C. x  4, y  7 . D. x  4  , y  7  .
Câu 27: Trong không gian với hệ tọa độ Oxyz cho điểm A(1 ; – 2 ; 1) và mặt phẳng (P) : 2x + 3y + z –
11 = 0. Gọi H(a ; b ; c) là hình chiếu vuông góc của điểm A lên mặt phẳng (P). Khi đó hãy cho biết tổng S = a + b + c A. 7. B. 5. C. 4. D. 6.
Câu 28: Số phức z thỏa mãn : 3  i z  1 2i z  3  4i là A. z  2  3i . B. z  2  5i . C. z  1 5i . D. z  2  3i .
Câu 29: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường : y  2cos x, y  0, x  0, x   quay quanh trục Ox là A.  . B. 2  . C. 2 2 . D. 2 .
Câu 30: Trong buổi đối thoại học đường, học sinh có phản ánh trong lớp học có nhiều muỗi. Ban
Giám Hiệu Trường THPT Nguyễn Du đã mời Trung tâm y tế dự phòng về trường để khảo sát. Khi
khảo sát tại phòng học số 39 thì người ta thấy tại ngày thứ x có f(x) con muỗi. Biết rằng 10 f '(x) 
và lúc đầu có 100 con muỗi trong phòng học. Hỏi số lượng con muỗi trong phòng học sau x 1
2 ngày gần với số nào sau đây? A. 111. B. 104. C. 113. D. 115. II. PHẦN TỰ LUẬN
Bài 1: Tính các tích phân sau: 7 a) 3 2 A  x . x  3dx  . 3 π 2 b) B  (x 1).cos xdx  . 0
Bài 2: Tính thể tích của khối tròn xoay sinh ra khi cho quay quanh trục hoành, hình phẳng giới hạn bởi
các đường: y = x – 2, y = 0, x = 2 và x = 4. 16
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
Bài 3: Tìm tập hợp những điểm M biểu diễn bởi số phức z thỏa mãn z  2i  z 1 . TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 06
Thời gian làm bài: 90 phút. I. PHẦN TRẮC NGHIỆM
Câu 1. Viết phương trình mặt phẳng (P) đi qua ba điểm A(2; 0; 0), B(0; -1; 0), C(0; 0; -3).
A. -3x - 6y + 2z - 6 = 0 B. -3x + 6y + 2z + 6 = 0 C. -3x + 6y - 2z + 6 = 0 D. -3x - 6y + 2z + 6 = 0
Câu 2. Phương trình mặt phẳng (P) đi qua M(1; 0; -2) đồng thời vuông góc với hai mặt phẳng (α):
2x + y - z - 2 = 0 và (β): x - y - z - 3 = 0 là.
A. -2x - y + 3z + 4 = 0
B. -2x + y + 3z - 4 = 0 C. -2x + y - 3z + 4 = 0 D. -2x + y - 3z - 4 = 0 Câu 3. Gọi z z z  z
1 và 2 lần lượt là nghiệm của phươngtrình: 2 z  2z 10  0 . Tính 2 2 1 2 A. 15 B. 100 C. 50 D. 20
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1; 2; 3), B(1; 0; -5) và mặt phẳng (P):
2x + y - 3z - 4 = 0. Tìm tọa độ điểm M thuộc (P) sao cho 3 điểm A, B, M thẳng hàng. A. (3; 1; 1) B. (-2; 1; -3) C. (0; 1; -1) D. (0; 1; 2)
Câu 5. Thể tích của khối tròn xoay được giới hạn bởi đường y  sinx , trục hoành và hai đường thẳng x  0, x   là : 2  2  3   A. B. C. D. 2 4 3 2
Câu 6. Diện tích hình phẳng giới hạn bởi các đường 3 y  x  4x ; Ox ; x  3  x  4 bằng ? 201 119 A. 44 B. C. 36 D. 4 4
Câu 7. Góc hợp bởi mặt phẳng ( ) : 2x y z 1  0 và mặt phẳng Oxy là bao nhiêu độ? A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 . 2017 1 i Câu 8. Tính z  . 2  i 1 3 3 1 3 1 1 3 A.  i B.  i C.  i D.  i 5 5 5 5 5 5 5 5
Câu 9. Giả sử M(z) là điểm biểu diễn số phức z. Tập hợp các điểm M(z) thoả mãn điều kiện sau đây:
z 1 i =2 là một đường tròn: A. Có tâm  1  ;   1 và bán kính là 2 B. Có tâm  1;  1 và bán kính là 2
C. Có tâm 1;   1 và bán kính là 2
D. Có tâm 1;   1 và bán kính là 2 
Câu 10. Mặt phẳng nào sau đây có vectơ pháp tuyến n(3;1; 7) A. 3x + y -7 = 0 B. 3x + z -7 = 0 C. 3x - y -7z +1 = 0
D. - 6x - 2y +14z -1 = 0 1 1 2 Câu 11. Nếu f (x)dx  =5 và f (x)dx  = 2 thì f (x)dx  bằng : 0 2 0 A. 3 B. 8 C. -3 D. 2
Câu 12. Cho số phức z  m  m + 
1 i . Xác định m để z  13 A. m  2, m  3 B. m  2, m  4 C. m  1, m  3 D. m  3, m  2   
Câu 13. Cho a = (2; -1; 2). Tìm y, z sao cho c = (-2; y; z) cùng phương với a A. y = 2; z = -1 B. y = -2; z = 1 C. y = -1; z = 2 D. y = 1; z = -2 17
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
Câu 14. Công thức nguyên hàm nào sau đây không đúng? 1 1 A. dx  ln x  C  B. dx  tan x  C  x 2 cos x 1 x  x a C. x dx   C (  1  )  D. x a dx   C (0  a  1)   1 ln a
Câu 15. Xác định m, n, p để cặp mặt phẳng sau song song
( P ) : 2x -3y -5z + p = 0, ( Q ) : ( m+2 ) x + ( n - 1 )y +10z -2 = 0
A. m = -6, n = 7, p  1
B. m = 6, n = -4, p  2 C. m = - 2, n = 3, p  1 D. m = 2, n = -3, p  5
Câu 16. Xác định tọa độ tâm và bán kính của mặt cầu (S): x² + y² + z² - 8x + 2y + 1 = 0. A. I(4; -1; 0), R = 4 B. I(-4; 1; 0), R = 4 C. I(-4; 1; 0), R = 2 D. I(4; -1; 0), R = 2  4 
Câu 17. Tìm nguyên hàm 3 2 x  dx    x  3 3 3 5 A. 3 5 x  4ln x  C B. 3 5 x  4ln x  C C. 3 5 
x  4ln x  C D. 3 5 x  4ln x  C 5 5 5 3 1 2dx Câu 18. Tích phân  ln a  . Giá trị của a bằng: 3  2x 0 A. 3 B. 1 C. 2 D. 4
Câu 19. Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức
z' = -2 + 5i. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
D. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
Câu 20. Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 2x - y +2z + 1 =
0. Phương trình mặt cầu (S) tâm A tiếp xúc với mặt phẳng (P) là
A. (x - 2)² + (y - 1)² + (z - 1)² = 9
B. (x - 2)² + (y - 1)² + (z - 1)² = 4
C. (x - 2)² + (y - 1)² + (z - 1)² = 5
D. (x - 2)² + (y - 1)² + (z - 1)² = 3
Câu 21. Trong  , phương trình 3
z 1  0 có nghiệm là: 2  i 3 1 i 3 5  i 3 A. - 1 B. - 1; C. - 1; D. - 1; 2 2 4
Câu 22. Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 1; 2). Tìm điểm N thuộc mặt phẳng
Oxy sao cho độ dài đoạn thẳng MN là ngắn nhất. A. (1; 2; 2) B. (2; 1; 0) C. (2; 2; 0) D. (1; 1; 0)    
Câu 23. Cho a = (2; -3; 3),   
b = (0; 2; -1), c = (1; 3; 2). Tọa độ của vectơ u  2a  3b  c là: A. (3; -3; 1) B. (0; -3; 4) C. (0; -3; 1) D. (3; 3; -1)
Câu 24. Tìm công thức sai? b b b b b b A. [f
 x gx]dx f
 xdxg(x)dxB. [f
 x.gx]dx f
 xd .x g(x)dxa a a a a a b b b c b C. k. f
 xdx k f
 xdx D. f
 xdx f
 xdxf
 xdx(a c  )b a a a a c
Câu 25. Diện tích hình phẳng được giới hạn bởi đường 2
y x x  3 và đường thẳng y  2x 1 là : 7 1 1 A. dvdt B. dvdt C. 5 dvdt D.  dvdt 6 6 6
Câu 26. Gọi H là hình phẳng giới hạn bởi (C) của hàm số 3
y  x và đường thẳng d : y  x  2; trục
Ox. Quay H xung quanh trục Ox ta được khối tròn xoay có thể tích là: 18
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 4 10   A. B. C. D. 21 21 7 3
Câu 27. Cho x, y là các số thực. Hai số phức z  3  i và z '  (x  2y)  yi bằng nhau khi: A. x  3, y  0 B. x 1, y 1 C. x  2, y  1  D. x  5, y  1  1 i
Câu 28. Số phức z 
3 4i có số phức liên hợp là: 1 i A. z  3  3i B. z  3 C. z  3i D. z  3  3i
Câu 29. Phương trình chính tắc của đường thẳng(d) đi qua điểm A(-1; 0; 2), vuông góc với (P): 2x - 3y + 6z + 4 = 0. x 1 y z  2 x 1 y z  2 x 1 y z  2 x 1 y z  2 A.   B.   C.   D.   2 3 6 2 3 6 2 3 6 2 3 6
Câu 30. Nguyên hàm của hàm số f(x) = 2sin3xcos2x 1
A. 5cos5x  cos x  C
B. cos5x  cos x  C 5 1 1
C.  cos5x  cos x  C
D. cos5x  cos x  C 5 5 II. PHẦN TỰ LUẬN
Bài 1: (1,25 điểm) Tính các tích phân sau: e 1 ln x 1 a) dx  b) b) (1 xe )xdxx 1 0 Bài 2: (0,75 điểm)
(3  2i)(1 i)
a) Tính môđun của số phức z biết z  2i  2  3i b) Giải phương trình 2
8z  4z 1  0 trên tập số phức. Bài 3: (2 điểm)
Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm A(1;0;0), B(0;2;0) và C(0;0;3)
a) Viết phương trình mặt phẳng (ABC)
b) Tìm tọa độ hình chiếu của điểm D(1,1,-2) lên mặt phằng (ABC)
c) Viết phương trình mặt cầu tâm I(1;-2;2) tiếp xúc với mặt phẳng (ABC) TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 07
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM (8,0 điểm)
Câu 1. Đồ thị đã cho có bao nhiêu điểm cực trị? A. 2. B. 3. C. 0. D. 1. 19
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 4x 1
Câu 2. Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  . 2x  3 3 2 2 3 x  , y  2  x  ; y  2
x   , y  2  x  , y  2 A. 2 B. 3 C. 3 D. 2
Câu 3. H  là hình phẳng giới hạn bởi đồ thị hàm số  2   1 x y x
e , trục hoành và trục tung. Tính
thể tích tròn xoay thu được khi quay H  quanh trục hoành . Ox
A. V  4  2e. B. 2
V e  5. C. V   2 e  5.
D. V  4  2 . e
Câu 4. Đồ thị đã cho là đồ thị của hàm số nào? A. 4 2
y x  2x  2. B. 4 2
y  x  2x  2. C. 4 2
y x  2x  2. D. 4 2
y  x  2x  2.
Câu 5. Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai
mặt phẳng vuông góc với trục Ox tại các điểm x a, x ba b, có thiết
diện bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x a x b là S x. b b b b
A. V   S
 xd .x
B. V   S
 xd .x
C. V S
 xd .x D. 2 V   . S
 xd .x a a a a
Câu 6. Cho hàm số f x liên tục trên đoạn  ;
a b. Hãy chọn mệnh đề sai? b a b A. f
 xdx   f
 xd .x
B. k.dx k
b a, k    \  0 . a b a b c b b a C. f
 xdx f
 xdx f
 xdx với c ;ab. D. f
 xdx f
 xd .x a a c a b e 1 3ln x
Câu 7. Cho I dx
và t  1 3ln x. Chọn khẳng định sai trong các khẳng định sau đây. x 1 2 2 2 2 2 2 14 A. I t.dt.  B. 2 I t .dt.  C. 3 I t D. I  . 3 3 9 9 1 1 1
Câu 8. Tìm điểm biểu diễn của số phức z  4  5 .i A.  4;  5  . B. 4;5. C.  4;  5. D. 4; 5  .
Câu 9. Tìm giá trị lớn nhất của hàm số y x 1  3  x . A. 2 B. 2 C. 3 D. 2 2 2
Câu 10. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y  , trục hoành và các x  2 1
đường thẳng x  0, x  4. 4 7 8 2 A. S  .
B. S  .
C. S  . D. S  . 25 5 5 25
Câu 11. Tìm m để phương trình x x 1  m có ngiệm.
A. m  0.
B. m  0.
C. 0  m 1.
D. m  1.
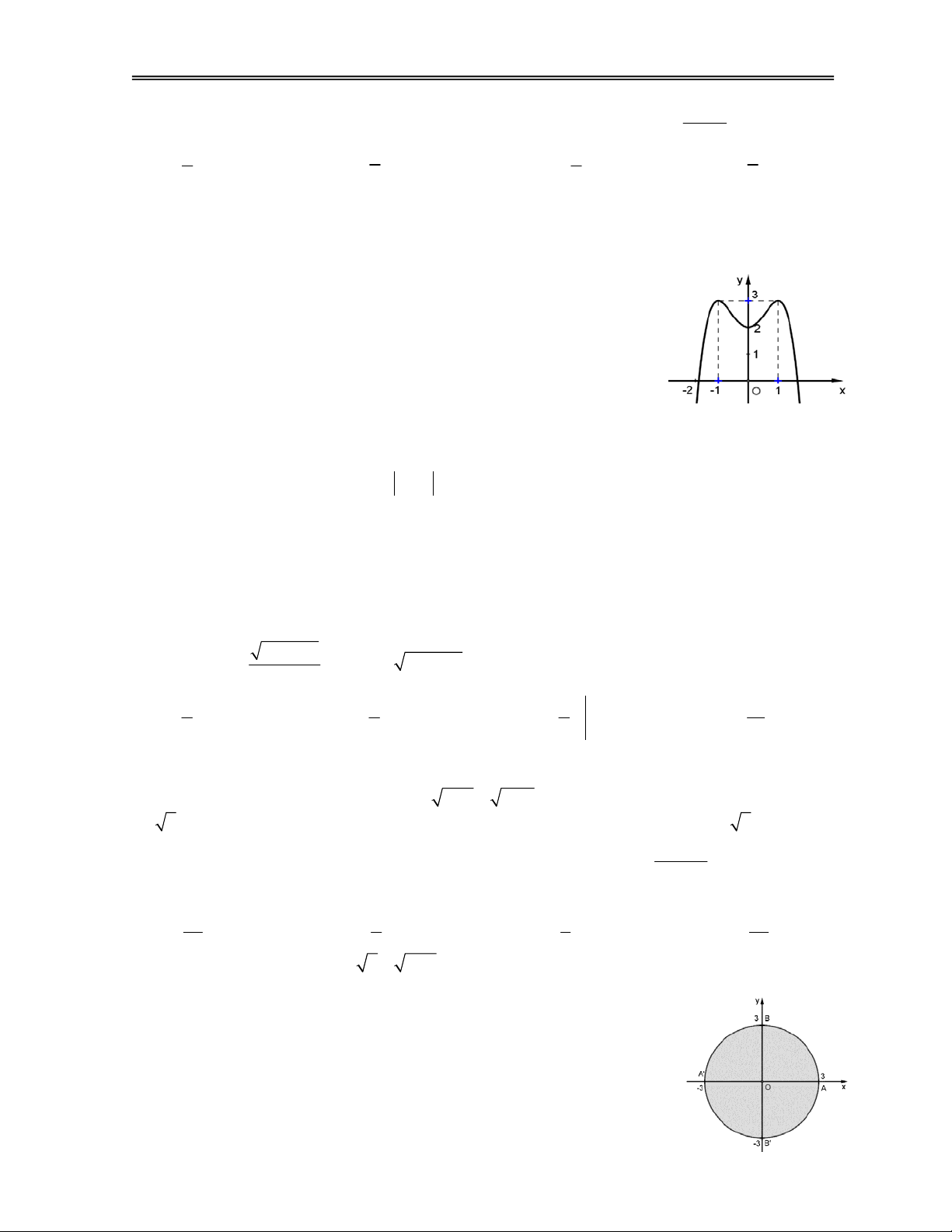
Câu 12. Cho số phức z a bi,a,b. Tìm điều kiện của a và b để tập
hợp điểm biểu diễn của số phức z nằm trong hình tròn tâm O (với O là gốc
tọa độ), bán kính bằng 3 (như hình vẽ). A. 2 2
a b  9. B. 2 2
a b  9.
C. a b  9. D. 2 2
a b  9. 20
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
Câu 13. Tìm các giá trị của tham số m để hàm số 3 2
y x mx mx 1 có hai cực trị.
A. m  0
B. m  3
C. m  0; m  3
D. 0  m  3
Câu 14. Giả sử f x có đạo hàm trên khoảng  ;
a b. Khẳng định nào sau đây là đúng?
A. Nếu f x đồng biến trên khoảng  ;
a b thì f  x  0 trên khoảng  ; a b.
B. Nếu f x đồng biến trên khoảng  ;
a b thì f  x  0 trên khoảng  ; a b.
C. Nếu f x đồng biến trên khoảng  ;
a b thì f  x  0 trên khoảng  ; a b.
D. Nếu f x đồng biến trên khoảng  ;
a b thì f  x  0 trên khoảng  ; a b.
Câu 15. Cho số phức z a bi,a,b,a  0,b  0 có điểm biểu diễn là M  ;
a b. Điểm M ' là
điểm biểu diễn của số phức z ' sao cho OM
M ' cân tại M. Tìm điểm M '. A. M ' ;
a 0; M '0;b. B. M '2 ;
a 0; M '0;2b. C. M ' ; a b  . D. M ' ; a b.
Câu 16. Tính diện tích S giới hạn bởi đồ thị hàm số   x
f x e x, trục hoành, trục tung và đường
thẳng x  1. 1 1
A. S e  .
B. S e  .
C. S e 1.
D. S e 1. 2 2
Câu 17. Rút gọn số phức z    i 2 2
3 ta được số phức nào sau đây?
A. 7  4i 3.
B. 7  4i 3.
C. 1 4i 3.
D. 1 4i 3.
Câu 18. Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó? 2x  3 x  3 2x 1 2x 1 y y y y A. x 1 B. x  3 C. 2x 1 D. x  2 Câu 19. Gọi ,
A B lần lượt là điểm biểu diễn của số phức z  1 3i, z '  1 3 .i Hai điểm A và B đối
xứng với nhau qua trục, đường hay điểm nào sau đây?
A. Đường thẳng y  . x B. Trục tung.
C. Trục hoành.
D. Gốc tọa độ. 1
Câu 20. Kết quả tích phân  2 3 x I x
e dx được viết dưới dạng I ae b với a,b  .  Khẳng định 0 nào sau đây là đúng?
A. a b  2. B. 3 3
a b  28.
C. ab  3.
D. a  2b 1. 1 3
Câu 21. Cho số phức z   i . Số phức 2
z.z bằng số phức nào sau đây? 2 2 A.  . z B. z. C. z. D. 1.
Câu 22. Đồ thị đã cho là đồ thị của hàm số nào? 3 x 2 A. 2 y
x x  . B. 3 2
y x x  . x 3 3 3 x 2 C. 2 y
x x D. 3 y x  3 . x 3 3
Câu 23. Cho số phức z  2  5 .i Tính số phức 2
w  z .z.
A. w  58 145 .i B. w  29.
C. w 142  65 .i D. w  5  8 145 .i
Câu 24. Cho hai điểm A0;0;3, M 1;2;0 . Viết phương trình mặt phẳng P qua A và cắt các trục
Ox,Oy lần lượt tại B,C sao cho tam giác ABC có trọng tâm thuộc đường thẳng AM.
P:6x  4y  3z 12  0.
P:6x 3y  4z 12  0. A. B. P    
P:6x 3y  4z 12  0. C.
: 6x 3y 4z 12 0. D. 21
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017      
Câu 25. Trong không gian với hệ tọa độ Oxyz cho 2 vectơ u và v thỏa: u  2, v  1 và u,v   60 .   
Tính góc giữa 2 vectơ v và u v ? A. 30 . B. 45 . C. 60 . D. 90 .
Câu 26. Viết phương trình mặt phẳng P qua O0;0;0 vuông góc với mặt phẳng
Q: x  2y z  0 và tạo với mặt phẳng Oyz một góc 45 .
A. P :2x y  0 và P :3x y z  0.
B. P : 5x  4y  3z  0 và P :2x y  0.
C. P :x z  0 và P :5x  4y  3z  0.
D. P :x z  0 và P :2x y  0.
Câu 27. Viết phương trình mặt phẳng (P) đi qua điểm M 1;2;3 và nhận n  2;1; 5   làm vectơ pháp tuyến. P     P    A.
: 2x y 5z 15 0. B.
: 2x y 5z 0. P     P     C.
: x 2 y 5z 15 0. D.
: 2x y 5z 15 0.
Câu 28. Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng đi qua điểm  M 1;2; 
1 và có vectơ chỉ phương u  2; 1  ;  1 . x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 2 1 1 2 1 1 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 2 1 1 2 1 1   
Câu 29. Tìm phương trình mặt phẳng đi qua M x ;y ;z và nhận n   ; A ;
B C  (với n  0 ) làm 0 ( 0 0 0 ) vectơ pháp tuyến.
A. x (x  )
A y ( y B)  z (z C)  0.
B. Ax x B y y C z z  0. 0   0   0  0 0 0
C. x (x  )
A y ( y B)  z (z C)  0.
D. Ax x B y y C z z  0. 0   0   0  0 0 0
Câu 30. Trong không gian Oxyz, cho hai điểm A4;3;0, B0;3; 2   và đường thẳng x  3 y  2 z  : 
 . Tìm tọa độ điểm M thuộc  sao cho tam giác MAB có diện tích nhỏ nhất. 4 1 1
A. M 2;3;  1 . B. M  2;  3  ;  1 . C. M 1;1;  1 . D. M  1  ; 1  ;  1 .
Câu 31. Trong không gian Oxyz, viết phương trình tham số của đường thẳng  đi qua điểm M 1;1; 
1 và song song với giao tuyến của hai mặt phẳng   : x y z 1  0 và
 :2x y 2z  0. x 1 3tx 1 3t  
A.  : y 1 4t t .
B.  : y 1 4t t . z  1   t   z  1   t  x 1 3tx 1 3t  
C.  : y 1 4t t .
D.  : y 1 4t t . z  1   t   z  1   t
Câu 32. Phát biểu nào dưới đây là sai?
A. Trong không gian Oxyz, mọi đường thẳng đều có vectơ chỉ phương có độ dài bằng 1.
B. Trong không gian Oxyz, mọi đường thẳng đều có phương trình tham số.
C. Trong không gian Oxyz, mọi đường thẳng đều có vô số vectơ chỉ phương.
D. Trong không gian Oxyz, mọi đường thẳng đều có phương trình chính tắc. x 1 at
Câu 33. Trong không gian Oxyz, tìm tất cả các giá trị của a để đường thẳng  : y  2  t ,t  z  3t
song song với mặt phẳng   : ax ay  2z  7  0. 22
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017
A. a  2. 
B. a  1; a  2.
C. a  1.
D. a  1; a  2.
Câu 34. Trong không gian Oxyz, cho đường thẳng với M 1;2;3, N 2; 1  ; 
1 . Vectơ u nào dưới đây
là một vectơ chỉ phương của đường thẳng MN ?     A. u  1; 3  ; 2  .
B. u  1;3; 2  . C. u   1  ;3; 2  . D. u   1  ; 3  ;2.
Câu 35. Trong không gian Oxyz, cho hai đường thẳng  ,  lần lượt có các vectơ chỉ phương là 1 2    
u , u thỏa u u  0 . Phát biểu nào dưới đây là đúng? 1 2 1 2
A.  và  chéo nhau.
B.  và  vuông góc. 1 2 1 2
C.  và  song song.
D.  và  cắt nhau. 1 2 1 2 x 1 y z  2
Câu 36. Trong không gian Oxyz cho đường thẳng d :   và điểm (3
A ;1;1). Viết phương 2 1 3 
trình mp (P) chứa d và khoảng cách từ điểm A đến mặt phẳng (P) bằng 2 3.
A. x y z 1  0;7x  5y z  3  0.
B. x y z 1  0; x y z  3  0.
C. x y z 1  0; x y z 11  0.
D. x y z 1  0;7x y  5z  3  0.   
Câu 37. Trong không gian với hệ tọa độ Oxyz cho 2 vec tơ a và b khác 0. Phát biểu nào sau đây là sai?       a b  a b   A. a b . cos ,      B. a b , cos ,    a . b a . b      
C. cosa,b   cosb,a. D. .
a b là một số.
Câu 38. Trong không gian với hệ tọa độ Oxyz. Mặt cầu nào sau đây có tâm nằm trên trục Oz ? A. S  2 2 2
: x y z  6z  2  0. B. S  2 2 2
: x y z  2x  6z  2  0 . C. S  2 2 2
: x y z  2x  4y  6z  2  0 . D. S  2 2 2
: x y z  2x  4y  2  0 .
Câu 39. Trong không gian với hệ tọa độ Oxyz, cho 2 mặt phẳng ( ) : A x B y C z D  0; 1 1 1 1 1
( ) : A x B y C z D  0. Khẳng định nào sau đây là sai? 2 2 2 2 2
(A ; B ;C )  k(A ; B ;C )
A. ( )  ( )  A A B B C C  1. B. 1 1 1 2 2 2 ( ) / /( )  . 1 2 1 2 1 2 1 2 1 2  D kD  1 2
 A ; B ;C k A ; B ;C
C.      .
D.  cắt ( )  (A ; B ;C )  k(A ; B ;C ). 1  1   2   1 1 1  2 2 2  D kD 2 1 1 1 2 2 2  1 2
Câu 40. Phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm A4; 1
 ;2 và chứa trục Ox?
A. 2x z  0.
B. 2y z  0.
C. y  2z  0.
D. x  2z  0.
II. PHẦN TỰ LUẬN (2,0 điểm)
Bài 1. (1,0 điểm)
a) Cho hai số phức z  3  i và z  4
  3 .i Tính môđun của số phức z z . 1 2 1 2
b) Tìm phần thực và phần ảo của số phức z   i    i3 4 3 1 .
Bài 2. (1,0 điểm) x y 1 z  3
a) Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2;3 và đường thẳng d :   . 3 4 1
Viết phương trình mp   đi qua điểm A và chứa đường thẳng d.
b) Trong không gian với hệ tọa độ Oxyz. Viết phương trình đường thẳng  đi qua điểm M 3; 2  ;  1
và vuông góc với mp P : 3x  2y  3z  9  0. 23
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 TRƯỜNG THPT NHO QUAN A
ĐỀ KIỂM TRA HỌC KÌ II NĂM 2017
GV: ĐẶNG VIỆT ĐÔNG Môn: Toán 12 Đề 08
Thời gian làm bài: 90 phút.
I. PHẦN TRẮC NGHIỆM (gồm 40 Câu, 8 điểm, thời gian làm 75 phút)
Câu 1: Gọi z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Tính 2 2
A z z 1 2 1 2 A. 4 10. B. 20 . C. 2 10. D. 2 20. ln x Câu 2: Tìm dx  ta được: x ln x 2 ln x ln x 2 ln x A. C. B. C. C. C. D. C. 4 4 2 2
Câu 3: Trong không gian với hệ tọa độ Oxyz , cho điểm M  3;  2;0 và mặt phẳng
 : 3x 5y 3z  24  0. Tọa độ của điểm M đối xứng với M qua   là: A. 3; 8;  6. B. 0; 3;  3. C.  6;  7; 3  . D. 5;0;3.
Câu 4: Trong không gian với hệ tọa độ Oxyz , lập phương trình mặt phẳng   đi qua M(3; 2; 1) và
cắt ba tia Ox , Oy , Oz lần lượt tại A , B , C sao cho thể tích tứ diện OABC nhỏ nhất
A. 2x  3y  6z 18  0.
B. 2x  3y  6z 18  0.
C. 2x  6 y  3z  21  0.
D. 3x  2 y  6z 19  0.
Câu 5: Số phức liên hợp của số phức z    i  i2 3 2 2 3 là: A. z  9   46 .i
B. z  9  46 .i
C. z  9  46 .i D. z  9   46 .i
Câu 6: Cho hai số phức z  1
  3i; z  4  6i . Tìm số phức z sao cho z z  2z  0. 1 2 2 1 A. z  6.
B. z  2 12 .i C. z  6. 
D. z  6  .i
Câu 7: Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với A5; 0;  4 , B3; 1;  2 ,
C 4; 2;  6. Khẳng định nào sau đây đúng khi nói về tam giác ABC ?
A. Cân và không vuông. B. Đều. C. Vuông cân.
D. Vuông và không cân.
Câu 8: Tìm mệnh đề sai trong các mệnh đề sau:
A. Điểm M  ;
a b là điểm biểu diễn của số phức zabi( a,b  ) trên mặt phẳng Oxy . a c
B. a bi c di   . b   d
C. Số phức zabi( a,b  ) có số phức liên hợp là z  a b .i
D. Số phức zabi( a,b  ) có môđun là 2 2 a b .  4
Câu 9: Tích phân tan d x x  ln 
m 2 thì m bằng: 0 A. 1 2. B. 2 2. C. 0 . D. 2 1.
Câu 10: Thể tích của vật thể tròn xoay sinh bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường x y e , 2 x y e  
, x  1, x  2 bằng: 24
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017  e  2 2 1   2e   1   2e   1 e  2 2 1 A. . B. . C. . D. . 2 2 2 2
Câu 11: Diện tích hình phẳng giới hạn bởi các đường 2 y  6x , 2 2
x y  16 trong miền x  0 bằng: 4 4 8 4 A. 7  3. B. 4  3. C. . D. 8  3. 3 3 3 3 x  2  t
Câu 12: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng  : y  1
  t và mặt phẳng z  2t
 :3x y  2z 7  0 . Khẳng định nào sau đây đúng khi nói về quan hệ giữa  và  ? A.    .
B. Cắt nhau và vuông góc. C.  / /  .
D. Cắt nhau và không vuông góc.
Câu 13: Trong không gian với hệ tọa độ Oxyz , phương trình tham số của đường thẳng đi qua điểm  A0; 1
 ;3 và có vectơ chỉ phương u  (1; 2;1) là: x tx tx 1 x t      A. y  1   2t . B. y  1   2t . C. y  2   t. D. y  1   t . z  3t     z  3  tz  1 3tz  3  t   1 15 2 Câu 14: Biết rằng .
x f xdx   . Tính tích phân sin 2 . x f  sin xd .x 64 1  2 6 15 45 15 15 A. . B. . C. . D. . 64 32 128 32
Câu 15: Trong không gian với hệ tọa độ Oxyz , tọa độ của điểm đối xứng với điểm A1; 2;  1 qua trục Oy là: A. 1; 2;  1  . B. 1; 2;   1 . C.  1  ; 2;  1 . D.  1  ; 2  ;  1 .
Câu 16: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1; 0; 0 , B0; 2; 0 , C 0; 0; 3 .
Phương trình nào sau đây không phải là phương trình mặt phẳng  ABC ? y z
A. x    1.
B. 6x  3y  2z  6  0. 2 3
C. 12x  6y  4z 12  0.
D. 6x  3y  2z  6  0.
Câu 17: Gọi M là điểm biểu diễn của số phức z 1 2i và N là điểm biểu diễn của số phức z  1
  2i . Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm M và N cùng nằm trên đường thẳng x  2.
B. Hai điểm M và N đối xứng với nhau qua trục tung.
C. Hai điểm M và N đối xứng với nhau qua gốc toạ độ O .
D. Hai điểm M và N đối xứng với nhau qua trục hoành.
Câu 18: Diện tích hình phẳng giới hạn bởi các đường 2
y x  2 , y  3x bằng: 25
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 1 1 1 1 A. . B. . C. . D. . 2 6 12 3 
Câu 19: Cho hình phẳng A giới hạn bởi các đường y  cos x , y  0 , x  0 , x  . Khối tròn xoay 4
được tạo thành khi A quay quanh trục hoành có thể tích bằng: 2   2   2    2 2   A. . B. . C. . D. . 6 8 8 4
Câu 20: Trong tập số phức, căn bậc hai của số 4 là: A. Không tồn tại. B. 2 .i C. 2.  D.  2 .i 2017 2 i i 3 2 z z
Câu 21: Cho số phức tùy ý z  1. Xét các số phức 2   
z  z và   
 z  z . z 1 z 1
Trong các khẳng định sau khẳng định nào đúng?
A.  ,  là số thực.
B.  ,  là số ảo.
C.  là số ảo,  là số thực.
D.  là số thực,  là số ảo.
Câu 22: Nguyên hàm của hàm số f x  x  3 2 1 3x  là: 2 x 6  6  A. 2 x  2
1 3x   C. B. 5  x C. C. 2 x  3
x x   C. D. 2 3
x 1 x C.   2 5  5 
Câu 23: Trong không gian hệ tọa độ Oxyz , cho ba điểm M 0; 2; 3 , N 1; 2; 0, Q1; 0; 3 .
Khoảng cách giữa MN và OQ là: A. 1. B. 2 . C. 4 . D. 3 . 1
Câu 24: Hàm số y  cos là một nguyên hàm của hàm số: x 1 1 1 1 1 1 A. y  sin .
B. y  sin . C. y  sin . D. y   sin . x x 2 x x 2 x x
Câu 25: Trong không gian với hệ tọa độ Oxyz , phương trình của đường thẳng đi qua điểm M 1; 0; 
1 và vuông góc với mặt phẳng   : 2x y z  9  0 là: x 1 2tx 1 x  2  tx 1 y z 1  
A. y t  . B.   . C. y  4   t . D. y  1  .  2 1 1 z  1   t    z  1 3tz  1 t
Câu 26: Diện tích hình phẳng giới hạn bởi các đường x  0 , x  1, y  0 . 3 2
y x  3x x  2 bằng: 7 5 5 7 A. . B. . C. . D. . 2 2 4 4
Câu 27: Trong không gian với hệ tọa độ Oxyz , khoảng cách giữa hai điểm A4; 1;  1 , B 2; 1; 0 là: A. 2 . B. 4 . C. 5 . D. 3 . e Câu 28: Tích phân 2 x ln d x x  bằng: 1 3 2e 1 2 e 1 3 3e  2 2 2e  3 A. . B. . C. . D. . 9 4 8 3 26
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 25 Câu 29: Tích phân xdx  bằng: 1 262 248 247 278 A. . B. . C. . D. . 3 3 3 3
Câu 30: Trong không gian với hệ tọa độ Oxyz , phương trình mặt phẳng song song với mặt phẳng
2x  2 y z  3  0 và tiếp xúc với mặt cầu 2 2 2
x y z  6x  2 y  4z  2  0 là:
2x  2y z  7  0
4x  4y  2z  28  0 A. .  B. . 
2x  2y z  5  0
4x  4y  2z  20  0
4x  4y  2z  28  0
2x  2y z 14  0 C. .  D. . 
4x  4y  2z  20  0
2x  2y z 10  0   
Câu 31: Tìm một nguyên hàm F x của hàm số f x 1  biết F  0   . 1 cos 2x  6  1 1
A. F(x)   3  cot x.
B. F(x)  tan x  3. 2 2 1  1 3 
C. F(x)   3  cot x.
D. F(x)  2  . 2  sinx 3   
Câu 32: Trong không gian với hệ tọa độ Oxyz , xác định giá trị của m và n để cặp mặt phẳng
 :nx 8y 6z 1999  0 và  :2x my 3z  2017  0 song song với nhau. m  2 m  2 m  4  m  4 A.  . B.  . C.  . D.  . n  2 n  2 n  4 n  4 
Câu 33: Trong không gian với hệ tọa độ Oxyz , cho hai điểm M 1; 1; 
1 và N 2; 2; 2 phương
trình nào sau đây không phải phương trình đường thẳng MN ? x 1 t 1 x y 1 z 1  A.   .
B. y 1 t . 1 1 1 z 1tx 1 y 1 z 1 x 1 y 1 z 1 C.   . D.   . 1 1 1 2 2 2 1 Câu 34: Tích phân 2 x xe dx  bằng: 0 1 1 1 1 1 A. e   1 . B. e 1. C. e  . D. e   1 . 3 2 4 5 2
Câu 35: Cho phương trình 2 z  z a b  0( ;
a b  ) . Nếu phương trình nhận z 1 i làm một
nghiệm thì a và b bằng:
A. a  2, b  2.
B. a  4, b  3.
C. a  1, b  3.
D. a  2, b  2.
Câu 36: Trong tập số phức, phương trình 2
z z 1  0 có nghiệm là: 1   3 1 i 3 A. z  1   i 3. B. z  . C. Vô nghiệm. D. z  . 2 2
Câu 37: Phần ảo của số phức z  i là: 27
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 12 năm 2017 A. 1.  B. –i . C. 0 . D. 2 .
Câu 38: Trong không gian với hệ tọa độ Oxyz , mặt phẳng đi qua M 2;  5;  1 , N  1  ; 4;  2 và
song song với trục Oy là:
A. x y 1  0.
B. x z 1  0.
C. x z  3  0.
D. y z  0.  6 Câu 39: Tích phân 1 4sin x cos d x x  bằng: 0 1 3 1 3 1 A. . B. . C. 3 3   1 . D.  . 6 6 6 2 3
Câu 40: Trong không gian với hệ tọa độ Oxyz , cho A 1
 ; 3; 4 và B 3;
 1;  4, mặt cầu
đường kính AB có phương trình: 2 2 2
A. x  2   y   1  z  20. B. 2 2 2
x y z  4x  2 y 10  0. C. 2 2 2
x y z  4x  2 y 16  0.
D. x  2   y  2 2 2 1  z  20.
II. PHẦN TỰ LUẬN (gồm 2 Câu, 2 điểm, thời gian làm 15 phút) 2 3 dx
Câu 1: (1.0 điểm) Tính tích phân I   . 2  5 x x 4 x 1 y  3 z  3
Câu 2: (1.0 điểm) Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   1 2 1
và mặt phẳng P : 2x y  2z  9  0 . .
Gọi A là giao điểm của d và P . Viết phương trình tham số của đường thẳng  nằm
trong P , đi qua A và vuông góc với d . 28