56 trang 9 lượt tải

Bộ đề ôn thi cuối học kì 2 Toán 10 KNTTVCS định hướng cấu trúc 2025

18

Một nhóm có 5 nhà hoá học nam, 3 nhà hoá học nữ và 4 nhà vật lý nam. Lập một đoàn công tác từ nhóm đó, gồm 3 người cần có cả nam và nữ, có cả nhà hoá học và vật lý thì có tất cả bao nhiêu cách. Tài liệu giúp bạn tham khảo ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Chủ đề: Đề thi THPTQG môn Toán năm 2025 340 tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Thu Hoài

1 tháng trước
Danh sách Quiz
/56
BỘ ĐỀ ÔN THI
CUỐI KÌ 2
TOÁN 10
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
THEO FORM 2025
CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 01_TrNg 2025
¤N TËP CuèI Kú 2
M«n:
To¸n 10 – KNTT
Định hướng cấu trúc 2025+
Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ Trung tâm Km10- Hương Trà – Huế
NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án.
Câu 1. Cho tập hợp
X
gồm
10
phần tử. Số các hoán vị của
10
phần tử của tập hợp
X
là
A.
10!
. B.
2
10
. C.
10
2
. D.
10
10
.
Câu 2. Gieo một đồng xu liên tiếp hai lần. Số phần tử của không gian mẫu
n
là
A.
8
. B.
1
. C.
2
. D.
4
.
Câu 3. Hệ số của số hạng chứa
2
x
trong khai triển
4
23x
là
A.
32
. B.
216
. C.
81
. D.
16
.
Câu 4. Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng?
A.
300
. B.
15
. C.
35
. D.
20
.
Câu 5. Tập xác định của hàm số
2
2 5 2y x x
là
A.
2; D
. B.
1
;
2



D
. C.
1
;2
2



D
. D.
1
; 2;
2



D
.
Câu 6. Gieo một đồng xu cân đối đồng chất liên tiếp hai lần. Tính xác suất để cả hai lần gieo đều
được mặt sấp.
A.
1
4
. B.
1
6
. C.
1
8
. D.
1
2
Câu 7. Trong mặt phẳng
,Oxy
cho đường thẳng
12
: , .
23
xt
dt
yt


Vectơ nào dưới đây là một
vectơ chỉ phương của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Câu 8. Tính tổng các nghiệm của phương trình
22
11 2 13 16x x x x
.
A.
16
3
. B.
14
3
. C.
14
3
. D.
16
3
.
Câu 9. Trong một lớp có
20
học sinh nam và
15
học sinh nữ. Chọn ngẫu nhiên
3
học sinh, tính xác
suất để
3
học sinh được chọn có cùng giới tính.
A.
90
119
. B.
29
119
. C.
80
119
. D.
39
119
.
Câu 10. Với
n
là số nguyên dương bất kỳ,
3n
, công thức nào sau đây đúng?
A.
3
3!
!
n
n
A
n
. B.
3
!
3! 3 !
n
n
A
n
. C.
3
!
3!
n
n
A
n
. D.
3
3! 3 !
!
n
n
A
n
.
Câu 11. Đường thẳng nào dưới đây là đường chuẩn của parabol
2
4y x
?
A.
1.x
B.
2.x
C.
1.x
D.
2.x
Câu 12. Cho
A
và
A
là hai biến cố đối nhau. Khẳng định nào dưới đây đúng?
A.
1P A P A
. B.
P A P A
. C.
1P A P A
. D.
0P A P A
.
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Có 5 bông hồng, 4 bông trắng (mỗi bông đều khác nhau về hình dáng). Một người cần chọn
một bó bông từ số bông này.
Khẳng định
Đúng
Sai
a)
Số cách chọn 4 bông tùy ý là 126.
b)
Số cách chọn 4 bông mà số bông mỗi màu bằng nhau là 50.
c)
Số cách chọn 4 bông, trong đó có 3 bông hồng và 1 bông trắng là 30.
d)
Số cách chọn 4 bông có đủ hai màu là
120
.
Câu 14. Cho các chữ số
0,1,2,3,4,5,6,7,8,9
. Gọi
X
là tập hợp các số tự nhiên có năm chữ số đôi một
khác nhau. Lấy ngẫu nhiên ra một số từ
X
.
Khẳng định
Đúng
Sai
a)
Số phần tử không gian mẫu là:
27216
.
b)
Xác suất để lấy được số lẻ là:
40
71
c)
Xác suất để lấy được số đó chia hết cho 10 là:
1
9
d)
Xác suất để lấy được số đó lớn hơn 59000 là:
47
81
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15. Trong mặt phẳng
,Oxy
gọi
C
là đường tròn có tâm
2; 1I
và cắt đường thẳng
: 3 15 0xy
theo dây cung
6AB
. Tính bán kính đường tròn
.C
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 16. Từ các số
0,1,2,3,5
có thể lập được bao nhiêu số tự nhiên không chia hết cho
5
gồm
4
chữ
số khác nhau?
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 17. Cho
n
là số nguyên dương thỏa mãn:
12
15
nn
CC
. Tìm số hạng không chứa
x
trong khai
triển:
4
2



n
x
x
.
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 18. Tại một quán ăn, lúc đầu có 50 khách trong đó có 2x đàn ông và y phụ nữ. Sau một tiếng,
6y
đàn ông ra về và
25x
khách mới đến là nữ. Chọn ngẫu nhiên một khách. Biết rằng
xác suất để chọn được một khách nữ là
9
13
. Tính
.xy
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
PHẦN IV. (3,0 điểm) Câu hỏi tự luận. Thí sinh trả lời từ câu 19 đến câu 21.
Câu 19. a) Khai triển đa thức
4
2
xy
.
b) Tìm hệ số của
2
x
trong khai triển của
5
32x
.
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 20. Một nhóm có
5
nhà hoá học nam,
3
nhà hoá học nữ và
4
nhà vật lý nam. Lập một đoàn công
tác từ nhóm đó, gồm
3
người cần có cả nam và nữ, có cả nhà hoá học và vật lý thì có tất cả
bao nhiêu cách?
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 21. Có ba hộp đựng thẻ. Hộp
I
chứa các tấm thẻ đánh số
1;2;3
. Hộp
II
chứa các tấm thẻ đánh
số
2;4;6;8
. Hộp
III
chứa các tấm thẻ đánh số
1;3;5;7;9;11
. Từ mỗi hộp rút ngẫu nhiên
một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ.
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
____________________HẾT____________________
Huế, 14h00’ Ngày 4 tháng 4 năm 2025
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 01_TrNg 2025
¤N TËP CuèI Kú 2
M«n:
To¸n 10 – KNTT
Định hướng cấu trúc 2025+
LỜI GIẢI CHI TIẾT
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án.
Câu 1. Cho tập hợp
X
gồm
10
phần tử. Số các hoán vị của
10
phần tử của tập hợp
X
là
A.
10!
. B.
2
10
. C.
10
2
. D.
10
10
.
Lời giải:
Số các hoán vị của
10
phần tử:
10!
.
Câu 2. Gieo một đồng xu liên tiếp hai lần. Số phần tử của không gian mẫu
n
là
A.
8
. B.
1
. C.
2
. D.
4
.
Lời giải:
Số phần tử của không gian mẫu
n
=
2.2 4
.
Câu 3. Hệ số của số hạng chứa
2
x
trong khai triển
4
23x
là
A.
32
. B.
216
. C.
81
. D.
16
.
Lời giải:
Ta có:
4
4
4
23
4 3 2
2 3 16 96 216 216 81.

k
kk
Cx
x x x x x
Câu 4. Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng?
A.
300
. B.
15
. C.
35
. D.
20
.
Lời giải:
Lớp có
20 15 35
học sinh.
Câu 5. Tập xác định của hàm số
2
2 5 2y x x
là
A.
2; D
. B.
1
;
2



D
. C.
1
;2
2



D
. D.
1
; 2;
2



D
.
Lời giải:
Hàm số xác định
2
2 5 2 0xx
1
2
2
x
x
.
Câu 6. Gieo một đồng xu cân đối đồng chất liên tiếp hai lần. Tính xác suất để cả hai lần gieo đều
được mặt sấp.
A.
1
4
. B.
1
6
. C.
1
8
. D.
1
2
Lời giải:
Gọi
Ω
là không gian mẫu. Gieo một đồng xu hai lần liên tiếp nên
2 2 4Ω.n 
Gọi
A
” Cả hai lần gieo đều mặt sấp” nên
1 1 1.nA
Vậy
1
4
Ω
nA
PA
n

.
Câu 7. Trong mặt phẳng
,Oxy
cho đường thẳng
12
: , .
23
xt
dt
yt


Vectơ nào dưới đây là một
vectơ chỉ phương của
?d
A.
1
1;2 .u
B.
2
2;1 .u 
C.
3
3;2 .u 
D.
4
2;3 .u
Lời giải:
Các vectơ chỉ phương của
d
có tọa độ
2 ;3 , 0 .k k k
Câu 8. Tính tổng các nghiệm của phương trình
22
11 2 13 16x x x x
.
A.
16
3
. B.
14
3
. C.
14
3
. D.
16
3
.
Lời giải:
Ta có
22
11 2 13 16 1x x x x
.
Bình phương hai vế của phương trình
1
ta được
22
11 2 13 16 2x x x x
.
Ta có
2
5
2 3 14 5 0 .
1
3
x
xx
x

Thay lần lượt
5x 
và
1
3
x
vào phương trình
1
ta thấy
5x 
và
1
3
x
đều thỏa mãn.
Vậy phương trình
1
có hai nghiệm là
5x 
và
1
3
x
.
Nên tổng các nghiệm của phương trình
1
là
1 14
5
33
.
Câu 9. Trong một lớp có
20
học sinh nam và
15
học sinh nữ. Chọn ngẫu nhiên
3
học sinh, tính xác
suất để
3
học sinh được chọn có cùng giới tính.
A.
90
119
. B.
29
119
. C.
80
119
. D.
39
119
.
Lời giải:
Ta có số phần tử của không gian mẫu là:
3
35
nC
cách chọn
Số phần tử của biến cố
A
“Ba học sinh được chọn có cùng giới tính” là:
33
20 15
n A C C
Xác suất của biến cố
A
là:
29
119
PA
.
Câu 10. Với
n
là số nguyên dương bất kỳ,
3n
, công thức nào sau đây đúng?
A.
3
3!
!
n
n
A
n
. B.
3
!
3! 3 !
n
n
A
n
. C.
3
!
3!
n
n
A
n
. D.
3
3! 3 !
!
n
n
A
n
.
Lời giải:
Với
n
là số nguyên dương bất kỳ,
3n
thì
3
!
3!
n
n
A
n
.
Câu 11. Đường thẳng nào dưới đây là đường chuẩn của parabol
2
4y x
?
A.
1.x
B.
2.x
C.
1.x
D.
2.x
Lời giải:
Phương trình chính tắc của parabol
2
: 2Py px
2p
Phương trình đường chuẩn là
1
2
p
x
.
Câu 12. Cho
A
và
A
là hai biến cố đối nhau. Khẳng định nào dưới đây đúng?
A.
1P A P A
. B.
P A P A
. C.
1P A P A
. D.
0P A P A
.
Lời giải:
Vì
AA
và
AA
. Nên
11P A P A P A P A
.
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Có 5 bông hồng, 4 bông trắng (mỗi bông đều khác nhau về hình dáng). Một người cần chọn
một bó bông từ số bông này.
Khẳng định
Đúng
Sai
a)
Số cách chọn 4 bông tùy ý là 126.
b)
Số cách chọn 4 bông mà số bông mỗi màu bằng nhau là 50.
c)
Số cách chọn 4 bông, trong đó có 3 bông hồng và 1 bông trắng là 30.
d)
Số cách chọn 4 bông có đủ hai màu là
120
.
Lời giải:
a) Đúng
b) Sai
c) Sai
d) Đúng
a) Số cách chọn 4 bông từ 9 bông:
4
9
126C
(cách).
b) Số cách chọn 2 bông hồng từ 5 bông hồng:
2
5
C
(cách).
Số cách chọn 2 bông trắng từ 4 bông trắng:
2
4
C
(cách).
Số cách chọn một bó bông thỏa mãn đề bài:
22
54
60CC
(cách).
c) 3 bông hồng, 1 bông trắng: có
31
54
40CC
(cách).
d) Cách giải 1: Làm trực tiếp.
Trường hợp 1: 3 bông hồng, 1 bông trắng: có
31
54
40CC
(cách).
Trường hợp 2: 2 bông hồng, 2 bông trắng: có
22
54
60CC
(cách).
Trường hợp 3: 1 bông hồng, 3 bông trắng: có
13
54
20CC
(cách).
Theo quy tắc cộng ta có tất cả
40 60 20 120
(cách chọn).
Cách giải 2: Phương pháp loại trừ.
Số cách chọn 4 bông từ 9 bông (tùy ý):
4
9
126C
(cách).
Số cách chọn 4 bông chỉ một màu (hồng hoặc trắng):
44
54
6CC
(cách).
Vậy số cách chọn 4 bông có đủ hai màu:
126 6 120
(cách).
Câu 14. Cho các chữ số
0,1,2,3,4,5,6,7,8,9
. Gọi
X
là tập hợp các số tự nhiên có năm chữ số đôi một
khác nhau. Lấy ngẫu nhiên ra một số từ
X
.
Khẳng định
Đúng
Sai
a)
Số phần tử không gian mẫu là:
27216
.
b)
Xác suất để lấy được số lẻ là:
40
71
c)
Xác suất để lấy được số đó chia hết cho 10 là:
1
9
d)
Xác suất để lấy được số đó lớn hơn 59000 là:
47
81
Lời giải:
a) Đúng
b) Sai
c) Đúng
d) Sai
a) Số phần tử không gian mẫu là:
( ) 9.9 8.7 6 27216 n
.
b)
A
: "Chọn được số tự nhiên lẻ từ tập
X
".
Gọi số tự nhiên năm chữ số là
abcde
. Chọn
{1;3;5;7;9}d
: có 5 cách.
Số cách chọn
, , ,a b c d
lần lượt là
8,8,7,6
nên số các số tự nhiên thỏa mãn là 5.8.8.7.6
13440
hay
( ) 13440nA
.
Do đó:
13440 40
()
27216 81
PA
.
c) Gọi biến cố
B
: "Số được chọn chia hết cho 10 ".
Số tự nhiên được chọn phải có dạng
0abcd
.
Số cách chọn
, , ,a b c d
lần lượt là
9,8,7,6
nên
( ) 9nB
.8.7.6
3024
.
Do vậy
( ) 3024 1
()
( ) 27216 9
nB
PB
n
.
d) Gọi biến cố
C
: "Số có năm chữ số khác nhau lớn hơn 59000 ".
Gọi số có năm chữ số khác nhau lớn hơn 59000 là:
abcde
.
Trường hợp 1:
59 ab
. Chọn
,,c d e
thì lần lượt có
8,7,6
cách.
Suy ra số cách chọn trường hợp này là 8.7.6
336
.
Trường hợp 2:
5 {6;7;8;9} aa
nên có 4 cách chọn
a
.
Số cách chọn
,,b c d
, e lần lượt là
9,8,7,6
. Suy ra có 4.9.8.7.6
12096
cách chọn trong trường
hợp này.
Do vậy
( ) 336 12096 12432 nC
.
Suy ra
( ) 12432 37
()
( ) 27216 81
nC
PC
n
.
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15. Trong mặt phẳng
,Oxy
gọi
C
là đường tròn có tâm
2; 1I
và cắt đường thẳng
: 3 15 0xy
theo dây cung
6AB
. Tính bán kính đường tròn
.C
Kết quả:
7
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
Δ
R
H
B
I
A
Ta có:
2
2
2 3 15
, 2 10
13
h d I


.
Bán kính đường tròn
C
là
2
2
7
2
AB
Rh



.
Câu 16. Từ các số
0,1,2,3,5
có thể lập được bao nhiêu số tự nhiên không chia hết cho
5
gồm
4
chữ
số khác nhau?
Kết quả:
54
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
Gọi số cần tìm có dạng
abcd
.
d
có
3
cách chọn,
0,5d
.
a
có
3
cách chọn,
0,a a d
.
b
có
3
cách chọn,
,b a b d
.
c có
2
cách chọn,
,,c a c d c b
.
có
3.3.3.2 54
số các số tự nhiên có
4
chữ số khác nhau được lập từ các số
0,1,2,3,5
không chia hết cho 5.
Câu 17. Cho
n
là số nguyên dương thỏa mãn:
12
15
nn
CC
. Tìm số hạng không chứa
x
trong khai
triển:
4
2



n
x
x
.
Kết quả:
10
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
Điều kiện:
*
2,nn
.
Ta có:
1 2 2
5
( 1)
15 15 30 0 5
6
2

nn
n
nn
C C n n n n
n
.
Khi đó
5
55
5 5 5
55
44
00
21
22



k
k k k k k k
kk
x C x C x
xx
.
Số hạng không chứa
x
tương ứng
5 5 0 1 kk
.
Suy ra số hạng không chứa
x
là:
11
5
2 10C
.
Câu 18. Tại một quán ăn, lúc đầu có 50 khách trong đó có 2x đàn ông và y phụ nữ. Sau một tiếng,
6y
đàn ông ra về và
25x
khách mới đến là nữ. Chọn ngẫu nhiên một khách. Biết rằng
xác suất để chọn được một khách nữ là
9
13
. Tính
.xy
Kết quả:
34
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
Ta có
2 50 50 2x y y x
.
Sau một tiếng, trong quán có
50 6 2 5 51 2y x x y
người, trong đó có
25xy
là nữ.
Vậy ta có:
2 5 9
8 22 524 4 11 262
51 2 13
xy
x y x y
xy


.
Suy ra
4 11 50 2 262 18 288 16 18x x x x y
.
Vậy
34.xy
PHẦN IV. (3,0 điểm) Câu hỏi tự luận. Thí sinh trả lời từ câu 19 đến câu 21.
Câu 19. a) Khai triển đa thức
4
2
xy
.
b) Tìm hệ số của
2
x
trong khai triển của
5
32x
.
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
a) Ta có:
4
4
1 2 3 4
2 2 0 8 1 6 2 4 3 2 4
4 4 4 4 4


x y x y C x C x y C x y C x y C y
4
2 8 6 4 2 2 3 4
4 6 4x y x x y x y x y y
.
b) Ta có:
5 5 4 3 2
0 1 2 2 3 3 4 4 5 5
5 5 5 5 5 5
3 2 . 3 . 3 .2 3 .2 3 .2 3 .2 .2 x C x C x C x C x C x C
Số hạng chứa
2
x
là
2
3 3 2 2
5
. 3 .2 10.9.8. 720C x x x
nên hệ số của
2
x
trong khai triển là
720.
Câu 20. Một nhóm có
5
nhà hoá học nam,
3
nhà hoá học nữ và
4
nhà vật lý nam. Lập một đoàn công
tác từ nhóm đó, gồm
3
người cần có cả nam và nữ, có cả nhà hoá học và vật lý thì có tất cả
bao nhiêu cách?
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
Ta có các trường hợp sau:
TH 1: Chọn được
1
nhà vật lý nam,
2
nhà hoá học nữ có
12
43
. 12CC
cách chọn.
TH 2: Chọn được
1
nhà vật lý nam,
1
nhà hoá học nữ và
1
nhà hoá học nam có
1 1 1
4 3 5
. . 60C C C
cách chọn.
TH 3: Chọn được
2
nhà vật lý nam,
1
nhà hóa học nữ có
21
43
. 18CC
cách chọn.
Vậy theo quy tắc cộng, có
12 60 18 90
cách chọn thoả yêu cầu bài toán.
Câu 21. Có ba hộp đựng thẻ. Hộp
I
chứa các tấm thẻ đánh số
1;2;3
. Hộp
II
chứa các tấm thẻ đánh
số
2;4;6;8
. Hộp
III
chứa các tấm thẻ đánh số
1;3;5;7;9;11
. Từ mỗi hộp rút ngẫu nhiên
một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ.
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
Gọi
,,a b c
, trong đó
1; 2; 3 , 2; 4; 6; 8 , 1; 3; 5; 7; 9; 11a b c
3.4.6 72n
.
Gọi
, , ,A a b c a b c
lẻ
Vậy
2, ,A b c
, trong đó
2; 4; 6; 8 , 1; 3; 5; 7; 9; 11bc
,
Suy ra:
1.4.6 24nA
.
Vậy
24 1
72 3
PA
.
____________________HẾT____________________
Huế, 14h00’ Ngày 4 tháng 4 năm 2025
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2025
¤N TËP CuèI Kú 2
M«n:
To¸n 10 – KNTT
Định hướng cấu trúc 2025+
Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ Trung tâm Km10- Hương Trà – Huế
NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án.
Câu 1. Cho biến cố
A
với không gian mẫu
.
Xác suất của biến cố
A
là
A.
.
n
PA
nA
B.
1.
nA
PA
n

C.
.
nA
PA
n
D.
.P A n A n
Câu 2. Có bao nhiêu cách sắp xếp
6
học sinh theo một hàng dọc?
A.
46656
. B.
4320
. C.
720
. D.
360
.
Câu 3. Gieo một đng tin (c hai mt
,SN
) cân đối v đng chất hai ln. Không gian mẫu của php
th l:
A.
,,SS NN SN
. B.
,,SS NN NS
. C.
, , ,SS NN SN NS
. D.
,SN
.
Câu 4. Trong khai triển nhị thức:
5
2ab
, hệ số của số hạng thứ ba là
A.
80
. B.
80
. C.
10
. D.
10
.
Câu 5. Trong mt phẳng tọa độ
,Oxy
tâm
I
và bán kính
R
của đường tròn
22
: 1 2 16C x y
là
A. Tâm
1;2 ,I
bán kính
4R
. B. Tâm
1;2 ,I
bán kính
16R
.
C. Tâm
1; 2 ,I
bán kính
4R
. D. Tâm
1; 2 ,I
bán kính
16R
.
Câu 6. Có bao nhiêu số có
5
chữ số khác nhau được lập từ
7
chữ số
1,2,3,4,5,6,7
?
A.
5
7
C
. B.
7!
. C.
5
7
A
. D.
5!
.
Câu 7. C bao nhiêu vctơ khác vctơ – không c điểm đu v điểm cuối l các đỉnh của ngũ giác?
A.
2
5
.A
B.
5
.P
C.
2
5.
D.
2
5
.C
Câu 8. Biết phương trình
22
28 4xx
có hai nghiệm
12
;xx
với
1
0x
. Tính
12
2S x x
.
A.
2S
. B.
8S 
. C.
8S
. D.
4S
.
Câu 9. Cho
*
,kn
và
nk
. Công thức no dưới đây đúng?
A.
!
!
k
n
n
C
k
. B.
!
!
k
n
n
C
nk
. C.
!
!!
k
n
n
C
n k k
. D.
!
k
n
Cn
.
Câu 10. Tam thức bậc hai
2
12 13f x x x
nhận giá trị không âm khi và chỉ khi
A.
1;13x
. B.
\ 1;13x
. C.
1;13x
. D.
; 1 13;x  
.
Câu 11. Gieo ngẫu nhiên
2
con xúc sắc cân đối đng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên
2
con xúc sắc bằng
1
”.
A.
2
9
. B.
1
9
. C.
5
18
. D.
5
6
.
Câu 12. Trong mt phẳng tọa độ
,Oxy
phương trình chính tắc của parabol c tiêu điểm
2;0F
là
A.
2
4y x
. B.
2
8y x
. C.
2
2y x
. D.
2
1
6
yx
.
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Một nhm c 14 người trong đ c hai bạn tên
A
và
B
. Người ta cn chọn một tổ công tác
gm 6 người từ nhm đ.
Khẳng định
Đúng
Sai
a)
Chọn nhóm 6 bạn bất kỳ ta có
3003
cách
b)
Chọn nhóm 6 bạn trong đ c cả
A
và
B
, có
1848
cách
c)
Chọn nhóm 6 bạn trong đ không c hai bạn
A
và
B
, có
924
cách
d)
Có
9504
cách chọn sao cho trong tổ phải có 1 tổ trưởng và 5 tổ viên hơn
nữa
A
hoc
B
phải có mt nhưng không đng thời có mt cả hai người
trong tổ.
Câu 14. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ
đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ c kích thước và khối lượng như
nhau. Ln lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.
Khẳng định
Đúng
Sai
a)
Số các kết quả có thể xảy ra của phép th là
( ) 12n
b)
Xác suất của biến cố "Trong 3 thẻ lấy ra có ít nhất 1 thẻ mu đỏ" là:
5
7
c)
Xác suất của biến cố "Trong 3 thẻ lấy ra có nhiu nhất 1 thẻ màu
xanh" là:
5
7
d)
Xác suất của biến cố "Trong 3 thẻ lấy ra tất cả đu l mu đỏ" là:
1
12
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15. Tính độ dài trục lớn của elip
E
, biết
E
đi qua điểm
0; 4A
và có một tiêu điểm
2
3;0F
.
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 16. Tổ
1
lớp 11A có
6
học sinh nam và
5
học sinh nữ. Giáo viên chủ nhiệm cn chọn ra
4
học
sinh của tổ
1
để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn
4
học sinh từ
Tổ đ, trong đ c ít nhất một học sinh nam?
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 17. Tìm hệ số của số hạng chứa
4
x
trong khai triển
5
2
( ) 3 3 2 P x x x
.
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 18. Một lớp có 15 học sinh nữ và 20 học sinh nam. Chọn ngẫu nhiên bốn học sinh tham gia trực
tun cùng Đon trường. Tính xác suất để trong bốn học sinh được chọn có số học sinh nữ ít
hơn số học sinh nam (làm tròn đến hàng phần trăm).
Kết quả:
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
PHẦN IV. (3,0 điểm) Câu hỏi tự luận. Thí sinh trả lời từ câu 19 đến câu 21.
Câu 19. Giải phương trình sau:
2
3 9 1 2x x x
.
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 20. Trong mt phẳng tọa độ
Oxy
, cho ba điểm
1;0 , 1;2AB
và
3;3C
.
a) Viết phương trình tham số đường thẳng
.AB
b) Tìm tọa độ điểm
D
thuộc đường thẳng
AB
sao cho
5DC
.
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 21. a) Một hộp chứa
15
quả cu gm
6
quả mu đỏ được đánh số từ
1
đến
6
và
9
quả màu
xanh được đánh số từ
1
đến
9
. Lấy ngẫu nhiên hai quả từ hộp đ. Tính xác suất để lấy được
hai quả khác mu đng thời tổng hai số ghi trên chúng là số chẵn.
b) Từ các số
1;2;3;4;5;6;7;8;9
lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác
nhau sao cho số tự nhiên đ không có hai chữ số liên tiếp nào cùng chẵn?
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
____________________HẾT____________________
Huế, 14h00’ Ngày 4 tháng 4 năm 2025
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2025
¤N TËP CuèI Kú 2
M«n:
To¸n 10 – KNTT
Định hướng cấu trúc 2025
LỜI GIẢI CHI TIẾT
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án.
Câu 1. Cho biến cố
A
với không gian mẫu
.
Xác suất của biến cố
A
là
A.
.
n
PA
nA
B.
1.
nA
PA
n

C.
.
nA
PA
n
D.
.P A n A n
Câu 2. Có bao nhiêu cách sắp xếp
6
học sinh theo một hàng dọc?
A.
46656
. B.
4320
. C.
720
. D.
360
.
Lời giải:
Số cách sắp xếp
6
học sinh theo một hàng dọc là số hoán vị của
6
phn t.
Vậy có
6
6!P
720
cách.
Câu 3. Gieo một đng tin (c hai mt
,SN
) cân đối v đng chất hai ln. Không gian mẫu của php
th l:
A.
,,SS NN SN
. B.
,,SS NN NS
. C.
, , ,SS NN SN NS
. D.
,SN
.
Lời giải:
Không gian mẫu của php th l:
, , ,SS NN SN NS
.
Câu 4. Trong khai triển nhị thức:
5
2ab
, hệ số của số hạng thứ ba là
A.
80
. B.
80
. C.
10
. D.
10
.
Lời giải:
Ta có
5
5
(2 )
0 5 1 4 2 3 2
55
5
5
.(2 ) (2 ) ( ) (2 ) ( ) ...2

k k k
C a b
C a C a bb Caa b
0 5 5 1 4 4 2 3 3 2
5 5 5
.2 2 2 ...C a C a b C a b
Hệ số của số hạng thứ ba là:
23
5
.2 80.C
Câu 5. Trong mt phẳng tọa độ
,Oxy
tâm
I
và bán kính
R
của đường tròn
22
: 1 2 16C x y
là
A. Tâm
1;2 ,I
bán kính
4R
. B. Tâm
1;2 ,I
bán kính
16R
.
C. Tâm
1; 2 ,I
bán kính
4R
. D. Tâm
1; 2 ,I
bán kính
16R
.
Câu 6. Có bao nhiêu số có
5
chữ số khác nhau được lập từ
7
chữ số
1,2,3,4,5,6,7
?
A.
5
7
C
. B.
7!
. C.
5
7
A
. D.
5!
.
Lời giải:
Mỗi số có
5
chữ số khác nhau được lập từ
7
chữ số
1,2,3,4,5,6,7
là một chỉnh hợp chập
5
của
7
số. Do đ, số các số tự nhiên cn tìm là
5
7
A
.
Câu 7. C bao nhiêu vctơ khác vctơ – không c điểm đu v điểm cuối l các đỉnh của ngũ giác?
A.
2
5
.A
B.
5
.P
C.
2
5.
D.
2
5
.C
Lời giải:
Số vctơ khác vctơ – không c điểm đu v điểm cuối l các đỉnh của ngũ giác bằng
2
5
A
.
Câu 8. Biết phương trình
22
28 4xx
có hai nghiệm
12
;xx
với
1
0x
. Tính
12
2S x x
.
A.
2S
. B.
8S 
. C.
8S
. D.
4S
.
Lời giải:
Bình phương hai vế của phương trình, ta được
22
4
28 4
4
x
xx
x

Thay ln lượt
4x 
và
4x
vo phương trình đã cho, ta thấy
4x 
và
4x
đu thỏa
mãn; Vì
40
Suy ra nghiệm của phương trình đã cho l
1
2
4
4
x
x

.
Vậy
12
2 2.4 4 4S x x
.
Câu 9. Cho
*
,kn
và
nk
. Công thức no dưới đây đúng?
A.
!
!
k
n
n
C
k
. B.
!
!
k
n
n
C
nk
. C.
!
!!
k
n
n
C
n k k
. D.
!
k
n
Cn
.
Lời giải:
Công thức tính số các tổ hợp chập
k
của
n
phn t là
!
!!
k
n
n
C
k n k
.
Câu 10. Tam thức bậc hai
2
12 13f x x x
nhận giá trị không âm khi và chỉ khi
A.
1;13x
. B.
\ 1;13x
. C.
1;13x
. D.
; 1 13;x  
.
Lời giải:
Ta có:
2
1
0 12 13 0
13
x
f x x x
x

.
Câu 11. Gieo ngẫu nhiên
2
con xúc sắc cân đối đng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên
2
con xúc sắc bằng
1
”.
A.
2
9
. B.
1
9
. C.
5
18
. D.
5
6
.
Lời giải:
Số phn t của không gian mẫu:
6.6 36n
.
Gọi
A
là biến cố thỏa mãn yêu cu bài toán:
1; 2 , 2; 1 , 3; 2 , 2; 3 , 3; 4 , 4; 3 , 4; 5 , 5; 4 , 5; 6 , 6; 5A
nên
10nA
.
Vậy
10 5
36 18
PA
.
Câu 12. Trong mt phẳng tọa độ
,Oxy
phương trình chính tắc của parabol c tiêu điểm
2;0F
là
A.
2
4y x
. B.
2
8y x
. C.
2
2y x
. D.
2
1
6
yx
.
Lời giải:
Phương trình chính tắc của parabol
2
20:Py px p
.
Tiêu điểm
2;0F
4p
.
Vậy phương trình parabol l
2
8.y x
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Một nhm c 14 người trong đ c hai bạn tên
A
và
B
. Người ta cn chọn một tổ công tác
gm 6 người từ nhm đ.
Khẳng định
Đúng
Sai
a)
Chọn nhóm 6 bạn bất kỳ ta có
3003
cách
b)
Chọn nhóm 6 bạn trong đ c cả
A
và
B
, có
1848
cách
c)
Chọn nhóm 6 bạn trong đ không c hai bạn
A
và
B
, có
924
cách
d)
Có
9504
cách chọn sao cho trong tổ phải có 1 tổ trưởng và 5 tổ viên hơn
nữa
A
hoc
B
phải có mt nhưng không đng thời có mt cả hai người
trong tổ.
Lời giải:
a) Đúng
b) Sai
c) Đúng
d) Đúng
Chọn nhóm 6 bạn bất kỳ ta có
6
14
C
cách.
Chọn nhóm 6 bạn trong đ c cả
A
và
B
, có
4
12
C
cách.
Chọn nhóm 6 bạn trong đ không c hai bạn
A
và
B
, có
6
12
C
cách.
Suy ra số cách chọn 6 bạn có mt
,AB
nhưng không đng thời có mt cả hai người trong tổ
là:
6 4 6
14 12 12
1584 CCC
cách.
Chọn 1 tổ trưởng từ nhóm 6 bạn này, có 6 cách.
Vậy có
1584.6 9504
cách chọn thỏa yêu cu đ bài.
Câu 14. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ
đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ c kích thước và khối lượng như
nhau. Ln lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.
Khẳng định
Đúng
Sai
a)
Số các kết quả có thể xảy ra của phép th là
( ) 12n
b)
Xác suất của biến cố "Trong 3 thẻ lấy ra có ít nhất 1 thẻ mu đỏ" là:
5
7
c)
Xác suất của biến cố "Trong 3 thẻ lấy ra có nhiu nhất 1 thẻ màu
xanh" là:
5
7
d)
Xác suất của biến cố "Trong 3 thẻ lấy ra tất cả đu l mu đỏ" là:
1
12
Lời giải:
a) Đúng
b) Sai
c) Sai
d) Đúng
Kí hiệu
X
là thẻ xanh, Đ thẻ l đỏ và
V
là thẻ vàng. Các kết quả có thể xảy ra trong 3 ln lấy
thẻ từ hộp có thể được mô tả bởi sơ đ hình cây ở trên.
a) Số các kết quả có thể xảy ra của phép th là
( ) 12n
b) Biến cố
A
: "Trong 3 thẻ lấy ra có ít nhất 1 thẻ mu đỏ".
( ) 10nA
.
Xác suất của biến cố
( ) 5
: ( )
( ) 6

nA
A P A
n
.
c) Số các kết quả có thể xảy ra
( ) 12n
Biến cố B: "Trong 3 thẻ lấy ra có nhiêu nhất 1 thẻ màu xanh".
( ) 10nB
.
Xác suất của biến cố
( ) 5
: ( )
( ) 6

nB
B P B
n
.
d)
1
( ) .
12
PD
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15. Tính độ dài trục lớn của elip
E
, biết
E
đi qua điểm
0; 4A
và có một tiêu điểm
2
3;0F
.
Kết quả:
10
Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Lời giải:
Phương trình chính tắc của elip
E
có dạng
22
22
1 0
xy
ab
ab
.
Ta có
2
2
2
2 2 2 2
16
1
16
39
25


b
b
cc
a b c a
.
Vậy phương trình của elip
E
là
22
1
25 16

xy
nên c độ dài trục lớn là
2 10.a

Tài liệu khác của Toán

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 10 BỘ ĐỀ ÔN THI CUỐI KÌ 2  THEO FORM 2025
 CẬP NHẬT TỪ ĐỀ THI MỚI NHẤT
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP CuèI Kú 2 M«n: To¸n 10 – KNTT
Định hướng cấu trúc 2025+
ĐỀ ÔN TẬP SỐ 01_TrNg 2025 Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung tâm Km10- Hương Trà – Huế NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án. Câu 1.
Cho tập hợp X gồm 10 phần tử. Số các hoán vị của 10 phần tử của tập hợp X là A. 10! . B. 2 10 . C. 10 2 . D. 10 10 . Câu 2.
Gieo một đồng xu liên tiếp hai lần. Số phần tử của không gian mẫu n  là A. 8 . B. 1 . C. 2 . D. 4 . Câu 3.
Hệ số của số hạng chứa 2
x trong khai triển  x  4 2 3 là A. 32 . B. 216 . C. 81. D. 16 . Câu 4.
Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng? A. 300 . B. 15 . C. 35 . D. 20 . Câu 5.
Tập xác định của hàm số 2 y
2x  5x  2 là  1  1   1 
A. D  2;   . B. D   ;    . C. D  ; 2 . D. D   ;  2;    .     2  2   2  Câu 6.
Gieo một đồng xu cân đối đồng chất liên tiếp hai lần. Tính xác suất để cả hai lần gieo đều được mặt sấp. 1 1 1 1 A. . B. . C. . D. 4 6 8 2 x  1 2t Câu 7.
Trong mặt phẳng Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới đây là một y  2   3t
vectơ chỉ phương của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1   Câu 8.
Tính tổng các nghiệm của phương trình 2 2
x x 11  2
x 13x 16 . 16 14 14 16 A. . B. . C.  . D.  . 3 3 3 3 Câu 9.
Trong một lớp có 20 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 3 học sinh, tính xác
suất để 3 học sinh được chọn có cùng giới tính. A. 90 . B. 29 . C. 80 . D. 39 . 119 119 119 119
Câu 10. Với n là số nguyên dương bất kỳ, n  3 , công thức nào sau đây đúng? n  3 ! 3! n  3 ! 3   3   n! n! A. A  3 A  3 A A n . B. . n! n n 3  ! n  . C. 3! nn  . D. 3! n!
Câu 11. Đường thẳng nào dưới đây là đường chuẩn của parabol 2 y  4x ?
A. x  1.
B. x  2.
C. x  1. D. x  2.
Câu 12. Cho A và A là hai biến cố đối nhau. Khẳng định nào dưới đây đúng?
A. P A  1 P A .
B. P A  P A .
C. P A  1 P A . D. PA  PA  0 .
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Có 5 bông hồng, 4 bông trắng (mỗi bông đều khác nhau về hình dáng). Một người cần chọn
một bó bông từ số bông này. Khẳng định Đúng Sai
a) Số cách chọn 4 bông tùy ý là 126.
b) Số cách chọn 4 bông mà số bông mỗi màu bằng nhau là 50.
c) Số cách chọn 4 bông, trong đó có 3 bông hồng và 1 bông trắng là 30.
d) Số cách chọn 4 bông có đủ hai màu là 120 .
Câu 14. Cho các chữ số 0,1, 2,3, 4,5, 6, 7,8,9 . Gọi X là tập hợp các số tự nhiên có năm chữ số đôi một
khác nhau. Lấy ngẫu nhiên ra một số từ X . Khẳng định Đúng Sai
a) Số phần tử không gian mẫu là: 27216 . b) 40
Xác suất để lấy được số lẻ là: 71 c) 1
Xác suất để lấy được số đó chia hết cho 10 là: 9 d) 47
Xác suất để lấy được số đó lớn hơn 59000 là: 81
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
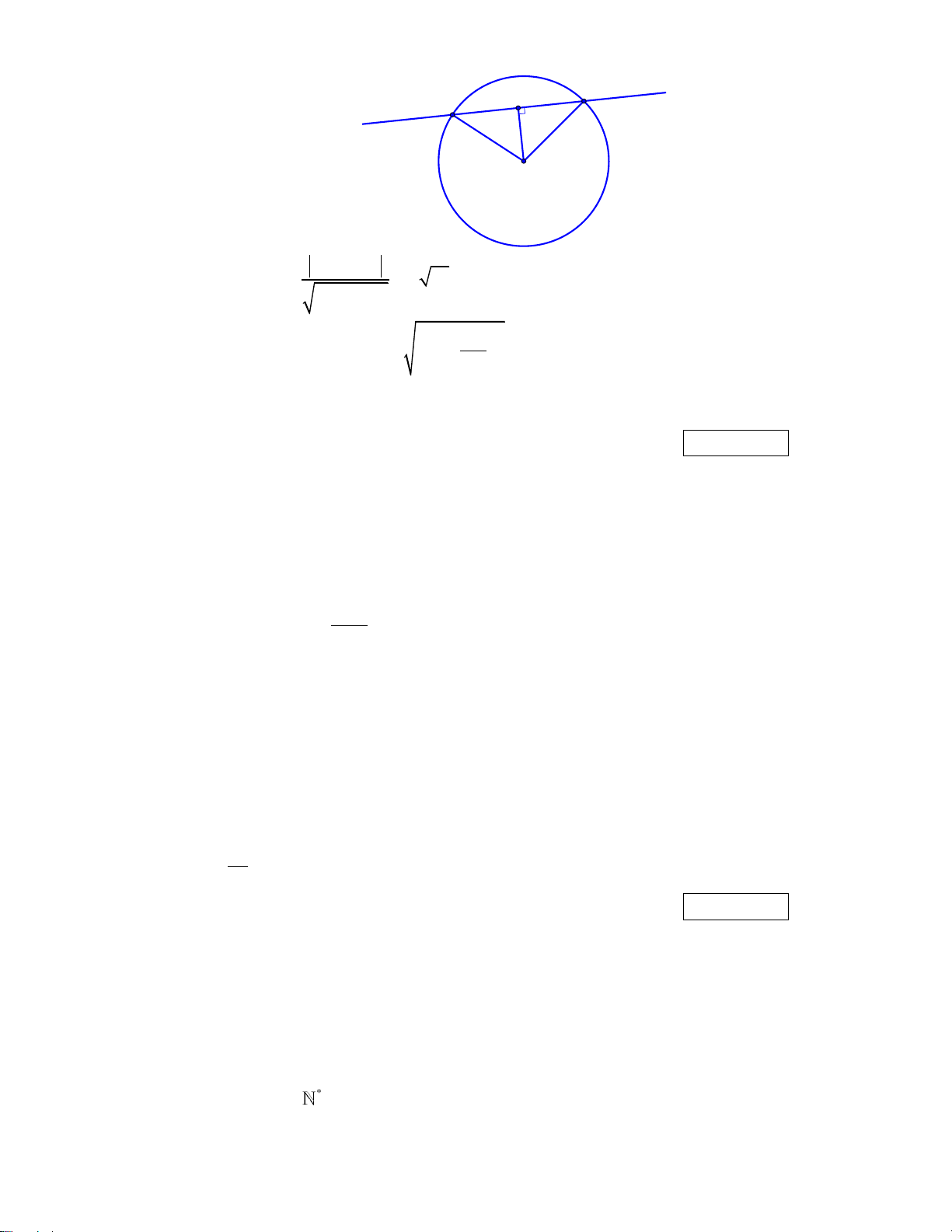
Câu 15. Trong mặt phẳng Oxy, gọi C  là đường tròn có tâm I 2;   1 và cắt đường thẳng
 : x  3y 15  0 theo dây cung AB  6. Tính bán kính đường tròn C. Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 16. Từ các số 0,1, 2,3,5 có thể lập được bao nhiêu số tự nhiên không chia hết cho 5 gồm 4 chữ số khác nhau? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 17. Cho n là số nguyên dương thỏa mãn: 1 2
C C  15 . Tìm số hạng không chứa x trong khai n nn 2  triển: x    . 4  x Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 18. Tại một quán ăn, lúc đầu có 50 khách trong đó có 2x đàn ông và y phụ nữ. Sau một tiếng,
y  6 đàn ông ra về và 2x  5 khách mới đến là nữ. Chọn ngẫu nhiên một khách. Biết rằng 9
xác suất để chọn được một khách nữ là . Tính x  . y 13 Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
PHẦN IV. (3,0 điểm) Câu hỏi tự luận. Thí sinh trả lời từ câu 19 đến câu 21.
Câu 19. a) Khai triển đa thức  x y 4 2  . b) Tìm hệ số của 2
x trong khai triển của  x  5 3 2 . Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 20. Một nhóm có 5 nhà hoá học nam, 3 nhà hoá học nữ và 4 nhà vật lý nam. Lập một đoàn công
tác từ nhóm đó, gồm 3 người cần có cả nam và nữ, có cả nhà hoá học và vật lý thì có tất cả bao nhiêu cách? Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 21. Có ba hộp đựng thẻ. Hộp I chứa các tấm thẻ đánh số 1; 2; 
3 . Hộp II chứa các tấm thẻ đánh số 2; 4;6; 
8 . Hộp III chứa các tấm thẻ đánh số 1;3;5;7;9; 
11 . Từ mỗi hộp rút ngẫu nhiên
một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ. Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
____________________HẾT____________________
Huế, 14h00’ Ngày 4 tháng 4 năm 2025
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP CuèI Kú 2 M«n: To¸n 10 – KNTT
Định hướng cấu trúc 2025+
ĐỀ ÔN TẬP SỐ 01_TrNg 2025
LỜI GIẢI CHI TIẾT
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án. Câu 1.
Cho tập hợp X gồm 10 phần tử. Số các hoán vị của 10 phần tử của tập hợp X là A. 10! . B. 2 10 . C. 10 2 . D. 10 10 . Lời giải:
Số các hoán vị của 10 phần tử: 10! . Câu 2.
Gieo một đồng xu liên tiếp hai lần. Số phần tử của không gian mẫu n  là A. 8 . B. 1 . C. 2 . D. 4 . Lời giải:
Số phần tử của không gian mẫu n  = 2.2  4 . Câu 3.
Hệ số của số hạng chứa 2
x trong khai triển  x  4 2 3 là A. 32 . B. 216 . C. 81. D. 16 . Lời giải: k  4 k k Ta có:  x   C 2 x4 4 3 4 3 2 2 3 
16x  96x  216x  216x  81. Câu 4.
Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng? A. 300 . B. 15 . C. 35 . D. 20 . Lời giải:
Lớp có 20 15  35 học sinh. Câu 5.
Tập xác định của hàm số 2 y
2x  5x  2 là  1  1   1 
A. D  2;   . B. D   ;    . C. D  ; 2 . D. D   ;  2;    .     2  2   2  Lời giải:  1 x  Hàm số xác định 2
 2x  5x  2  0   2  . x  2 Câu 6.
Gieo một đồng xu cân đối đồng chất liên tiếp hai lần. Tính xác suất để cả hai lần gieo đều được mặt sấp. 1 1 1 1 A. . B. . C. . D. 4 6 8 2 Lời giải:
Gọi Ω là không gian mẫu. Gieo một đồng xu hai lần liên tiếp nên nΩ  2.2  4
Gọi A ” Cả hai lần gieo đều mặt sấp” nên nA  1 1 .  1 n A 1 Vậy P A     . nΩ 4 x  1 2t Câu 7.
Trong mặt phẳng Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới đây là một y  2   3t
vectơ chỉ phương của d?
A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 .
D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của d có tọa độ 2k; 3k, k  0. Câu 8.
Tính tổng các nghiệm của phương trình 2 2
x x 11  2
x 13x 16 . 16 14 14 16 A. . B. . C.  . D.  . 3 3 3 3 Lời giải: Ta có 2 2
x x 11  2
x 13x 16   1 .
Bình phương hai vế của phương trình   1 ta được 2 2
x x 11  2
x 13x 16 2 . x  5  Ta có   2 2
 3x 14x  5  0  1 .  x   3 1 1
Thay lần lượt x  5 và x  vào phương trình  
1 ta thấy x  5 và x  đều thỏa mãn. 3 3 1 Vậy phương trình  
1 có hai nghiệm là x  5 và x  . 3 1 14
Nên tổng các nghiệm của phương trình   1 là 5     . 3 3 Câu 9.
Trong một lớp có 20 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 3 học sinh, tính xác
suất để 3 học sinh được chọn có cùng giới tính. A. 90 . B. 29 . C. 80 . D. 39 . 119 119 119 119 Lời giải:
Ta có số phần tử của không gian mẫu là: n  3  C35 cách chọn
Số phần tử của biến cố A “Ba học sinh được chọn có cùng giới tính” là: n A 3 3  C C 20 15
Xác suất của biến cố A là: P A 29  . 119
Câu 10. Với n là số nguyên dương bất kỳ, n  3 , công thức nào sau đây đúng? n  3 ! 3! n  3 ! 3   3   n! n! A. A  3 A  3 A A n . B. . n! n n 3  ! n  . C. 3! nn  . D. 3! n! Lời giải: n!
Với n là số nguyên dương bất kỳ, 3
n  3 thì A nn  . 3!
Câu 11. Đường thẳng nào dưới đây là đường chuẩn của parabol 2 y  4x ?
A. x  1.
B. x  2.
C. x  1. D. x  2. Lời giải:
Phương trình chính tắc của parabol  P 2 : y  2 px   p
p  2  Phương trình đường chuẩn là x   1  . 2
Câu 12. Cho A và A là hai biến cố đối nhau. Khẳng định nào dưới đây đúng?
A. P A  1 P A .
B. P A  P A .
C. P A  1 P A . D. PA  PA  0 . Lời giải:
Vì A A   và A A   . Nên P A  P A 1  PA 1 PA .
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Có 5 bông hồng, 4 bông trắng (mỗi bông đều khác nhau về hình dáng). Một người cần chọn
một bó bông từ số bông này. Khẳng định Đúng Sai
a) Số cách chọn 4 bông tùy ý là 126.
b) Số cách chọn 4 bông mà số bông mỗi màu bằng nhau là 50.
c) Số cách chọn 4 bông, trong đó có 3 bông hồng và 1 bông trắng là 30.
d) Số cách chọn 4 bông có đủ hai màu là 120 . Lời giải: a) Đúng b) Sai c) Sai d) Đúng
a) Số cách chọn 4 bông từ 9 bông: 4 C  126 (cách). 9
b) Số cách chọn 2 bông hồng từ 5 bông hồng: 2 C (cách). 5
Số cách chọn 2 bông trắng từ 4 bông trắng: 2 C (cách). 4
Số cách chọn một bó bông thỏa mãn đề bài: 2 2
C C  60 (cách). 5 4
c) 3 bông hồng, 1 bông trắng: có 3 1
C C  40 (cách). 5 4
d) Cách giải 1: Làm trực tiếp.
Trường hợp 1: 3 bông hồng, 1 bông trắng: có 3 1
C C  40 (cách). 5 4
Trường hợp 2: 2 bông hồng, 2 bông trắng: có 2 2
C C  60 (cách). 5 4
Trường hợp 3: 1 bông hồng, 3 bông trắng: có 1 3
C C  20 (cách). 5 4
Theo quy tắc cộng ta có tất cả 40  60  20  120 (cách chọn).
Cách giải 2: Phương pháp loại trừ.
Số cách chọn 4 bông từ 9 bông (tùy ý): 4 C  126 (cách). 9
Số cách chọn 4 bông chỉ một màu (hồng hoặc trắng): 4 4
C C  6 (cách). 5 4
Vậy số cách chọn 4 bông có đủ hai màu: 126  6  120 (cách).
Câu 14. Cho các chữ số 0,1, 2,3, 4,5, 6, 7,8,9 . Gọi X là tập hợp các số tự nhiên có năm chữ số đôi một
khác nhau. Lấy ngẫu nhiên ra một số từ X . Khẳng định Đúng Sai
a) Số phần tử không gian mẫu là: 27216 . b) 40
Xác suất để lấy được số lẻ là: 71 c) 1
Xác suất để lấy được số đó chia hết cho 10 là: 9 d) 47
Xác suất để lấy được số đó lớn hơn 59000 là: 81 Lời giải: a) Đúng b) Sai c) Đúng d) Sai
a) Số phần tử không gian mẫu là: n()  9.9 8.7  6  27216 .
b) A : "Chọn được số tự nhiên lẻ từ tập X ".
Gọi số tự nhiên năm chữ số là abcde . Chọn d {1;3;5; 7;9} : có 5 cách.
Số cách chọn a, b, c, d lần lượt là 8,8, 7, 6 nên số các số tự nhiên thỏa mãn là 5.8.8.7.6  13440 hay n( ) A  13440 . 13440 40 Do đó: P( ) A   . 27216 81
c) Gọi biến cố B : "Số được chọn chia hết cho 10 ".
Số tự nhiên được chọn phải có dạng abcd 0 .
Số cách chọn a, b, c, d lần lượt là 9,8, 7, 6 nên n(B)  9 .8.7.6  3024 . n(B) 3024 1
Do vậy P(B)    . n() 27216 9
d) Gọi biến cố C : "Số có năm chữ số khác nhau lớn hơn 59000 ".
Gọi số có năm chữ số khác nhau lớn hơn 59000 là: abcde .
Trường hợp 1: a  5  b  9 . Chọn c, d , e thì lần lượt có 8, 7, 6 cách.
Suy ra số cách chọn trường hợp này là 8.7.6  336 .
Trường hợp 2: a  5  a {6;7;8;9} nên có 4 cách chọn a .
Số cách chọn b, c, d , e lần lượt là 9,8, 7, 6 . Suy ra có 4.9.8.7.6  12096 cách chọn trong trường hợp này.
Do vậy n(C)  336  12096  12432. n(C) 12432 37 Suy ra P(C)    . n() 27216 81
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15. Trong mặt phẳng Oxy, gọi C  là đường tròn có tâm I 2;   1 và cắt đường thẳng
 : x  3y 15  0 theo dây cung AB  6. Tính bán kính đường tròn C. Kết quả: 7 Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: Δ H A B R I 2  3 15
Ta có: h d I ,    2 10 . 1  32 2 2  AB
Bán kính đường tròn C  là 2 R h   7   .  2 
Câu 16. Từ các số 0,1, 2,3,5 có thể lập được bao nhiêu số tự nhiên không chia hết cho 5 gồm 4 chữ số khác nhau? Kết quả: 54 Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Gọi số cần tìm có dạng abcd .
d có 3 cách chọn, d 0,  5 .
a có 3 cách chọn, a  0, a d .
b có 3 cách chọn, b a,b d .
c có 2 cách chọn, c a, c d, c b .
 có 3.3.3.2  54 số các số tự nhiên có 4 chữ số khác nhau được lập từ các số 0,1,2,3,5 không chia hết cho 5.
Câu 17. Cho n là số nguyên dương thỏa mãn: 1 2
C C  15 . Tìm số hạng không chứa x trong khai n nn 2  triển: x    . 4  x Kết quả: 10 Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: Điều kiện: * n  2, n  . n(n 1)  n  5 Ta có: 1 2 2
C C  15  n
15  n n  30  0 
n  5 . n n  2 n  6  5 5 k 5  2  k kk  1  Khi đó 5 k k 55 x
 C 2 x   C 2     k x . 4 5 4 5  x x k    0 k 0
Số hạng không chứa x tương ứng 5  5k  0  k  1 .
Suy ra số hạng không chứa x là: 1 1 C  2  10 . 5
Câu 18. Tại một quán ăn, lúc đầu có 50 khách trong đó có 2x đàn ông và y phụ nữ. Sau một tiếng,
y  6 đàn ông ra về và 2x  5 khách mới đến là nữ. Chọn ngẫu nhiên một khách. Biết rằng 9
xác suất để chọn được một khách nữ là . Tính x  . y 13 Kết quả: 34 Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Ta có 2x y  50  y  50  2x .
Sau một tiếng, trong quán có 50   y  6  2x  5  51 2x y người, trong đó có
2x  5  y là nữ. 2x  5  y 9 Vậy ta có: 
 8x  22y  524  4x 11y  262 51 2x  . y 13
Suy ra 4x 1150  2x  262  18x  288  x  16  y  18 .
Vậy x y  34.
PHẦN IV. (3,0 điểm) Câu hỏi tự luận. Thí sinh trả lời từ câu 19 đến câu 21.
Câu 19. a) Khai triển đa thức  x y 4 2  . b) Tìm hệ số của 2
x trong khai triển của  x  5 3 2 . Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: a) Ta có:
x y4  x y 4  C x C x y1 C x y2 C x y3 C y4 2 2 0 8 1 6 2 4 3 2 4   4 4 4 4 4 
x y4 2 8 6 4 2 2 3 4
x  4x y  6x y  4x y y . 5 5 4 3 2
b) Ta có: 3x  2 0  C .3x 1  C .3x 2
.2  C 3x 2 3
.2  C 3x 3 4
.2  C 3x 4 5 5 .2  C .2 5 5 5 5 5 5 Số hạng chứa 2
x là C .3x2 3 3 2 2
.2  10.9.8.x  720x nên hệ số của 2
x trong khai triển là 720. 5
Câu 20. Một nhóm có 5 nhà hoá học nam, 3 nhà hoá học nữ và 4 nhà vật lý nam. Lập một đoàn công
tác từ nhóm đó, gồm 3 người cần có cả nam và nữ, có cả nhà hoá học và vật lý thì có tất cả bao nhiêu cách? Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải:
Ta có các trường hợp sau: 1 2
TH 1: Chọn được 1 nhà vật lý nam, 2 nhà hoá học nữ có C .C  12 4 3 cách chọn. 1 1 1
TH 2: Chọn được 1 nhà vật lý nam, 1 nhà hoá học nữ và 1 nhà hoá học nam có C .C .C  60 4 3 5 cách chọn. 2 1
TH 3: Chọn được 2 nhà vật lý nam, 1 nhà hóa học nữ có C .C  18 4 3 cách chọn.
Vậy theo quy tắc cộng, có 12  60 18  90 cách chọn thoả yêu cầu bài toán.
Câu 21. Có ba hộp đựng thẻ. Hộp I chứa các tấm thẻ đánh số 1; 2; 
3 . Hộp II chứa các tấm thẻ đánh số 2; 4;6; 
8 . Hộp III chứa các tấm thẻ đánh số 1;3;5;7;9; 
11 . Từ mỗi hộp rút ngẫu nhiên
một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ. Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: Gọi   
a, b, c, trong đó a1; 2; 3, b2; 4; 6; 8, c1; 3; 5; 7; 9; 1 1
n  3.4.6  72 . Gọi A  
a, b, c,abc lẻ  A  
 2, b, c, trong đó b2; 4; 6; 8, c1; 3; 5; 7; 9; 1 1, Vậy
Suy ra: nA  1.4.6  24 .
Vậy PA 24 1   . 72 3
____________________HẾT____________________
Huế, 14h00’ Ngày 4 tháng 4 năm 2025
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP CuèI Kú 2 M«n: To¸n 10 – KNTT
Định hướng cấu trúc 2025+
ĐỀ ÔN TẬP SỐ 02_TrNg 2025 Líp To¸n thÇy L£ B¸ B¶O
Trường THPT Đặng Huy Trứ
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung tâm Km10- Hương Trà – Huế NỘI DUNG ĐỀ BÀI
Trong quá trình sưu tầm và biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của
quý thầy cô cùng các em học sinh! Xin chân thành cảm ơn!
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án. Câu 1.
Cho biến cố A với không gian mẫu . Xác suất của biến cố A là n n A n A
A. PA   
B. PA    1
. C. P A   
D. PA  nA  n. nA . n n . Câu 2.
Có bao nhiêu cách sắp xếp 6 học sinh theo một hàng dọc? A. 46656 . B. 4320 . C. 720 . D. 360 . Câu 3.
Gieo một đồng tiền (có hai mặt S, N ) cân đối và đồng chất hai lần. Không gian mẫu của phép thử là:
A. SS, NN , SN .
B. SS, NN , NS .
C. SS, NN, SN, NS . D. S, N . Câu 4.
Trong khai triển nhị thức:   5
2a b , hệ số của số hạng thứ ba là A. 80 . B. 80 . C. 10 . D. 10 . Câu 5.
Trong mặt phẳng tọa độ Oxy, tâm I và bán kính R của đường tròn
C x  2  y  2 : 1 2 16 là
A. Tâm I 1; 2, bán kính R  4 .
B. Tâm I 1; 2, bán kính R  16 .
C. Tâm I 1; 2, bán kính R  4 .
D. Tâm I 1; 2, bán kính R  16 . Câu 6.
Có bao nhiêu số có 5 chữ số khác nhau được lập từ 7 chữ số 1, 2,3, 4,5, 6, 7 ? A. 5 C . B. 7!. C. 5 A . D. 5!. 7 7 Câu 7.
Có bao nhiêu véctơ khác véctơ – không có điểm đầu và điểm cuối là các đỉnh của ngũ giác? A. 2 A . B. P . C. 2 5 . D. 2 C . 5 5 5 Câu 8. Biết phương trình 2 2
x  28  x  4 có hai nghiệm x ; x với x  0 . Tính S  2x x . 1 2 1 1 2 A. S  2 . B. S  8 . C. S  8 . D. S  4 . Câu 9. Cho * k, n
và n k . Công thức nào dưới đây đúng? n n n k ! k ! k ! A. C  . B. C C k C n . n n n k ! n  . C. k ! n . D. ! k !k ! n
Câu 10. Tam thức bậc hai f x 2
x 12x 13 nhận giá trị không âm khi và chỉ khi A. x  1;1  3 . B. x  \  1  ;  13 . C. x  1;1  3 . D. x   ;   
1  13;  .
Câu 11. Gieo ngẫu nhiên 2 con xúc sắc cân đối đồng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên 2 con xúc sắc bằng 1”. 2 1 5 5 A. . B. . C. . D. . 9 9 18 6
Câu 12. Trong mặt phẳng tọa độ Oxy, phương trình chính tắc của parabol có tiêu điểm F 2;0 là 1 A. 2 y  4x . B. 2 y  8x . C. 2 y  2x . D. 2 y x . 6
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Một nhóm có 14 người trong đó có hai bạn tên A và B . Người ta cần chọn một tổ công tác
gồm 6 người từ nhóm đó. Khẳng định Đúng Sai
a) Chọn nhóm 6 bạn bất kỳ ta có 3003 cách
b) Chọn nhóm 6 bạn trong đó có cả A và B , có 1848 cách
c) Chọn nhóm 6 bạn trong đó không có hai bạn A và B , có 924 cách
d) Có 9504 cách chọn sao cho trong tổ phải có 1 tổ trưởng và 5 tổ viên hơn
nữa A hoặc B phải có mặt nhưng không đồng thời có mặt cả hai người trong tổ.
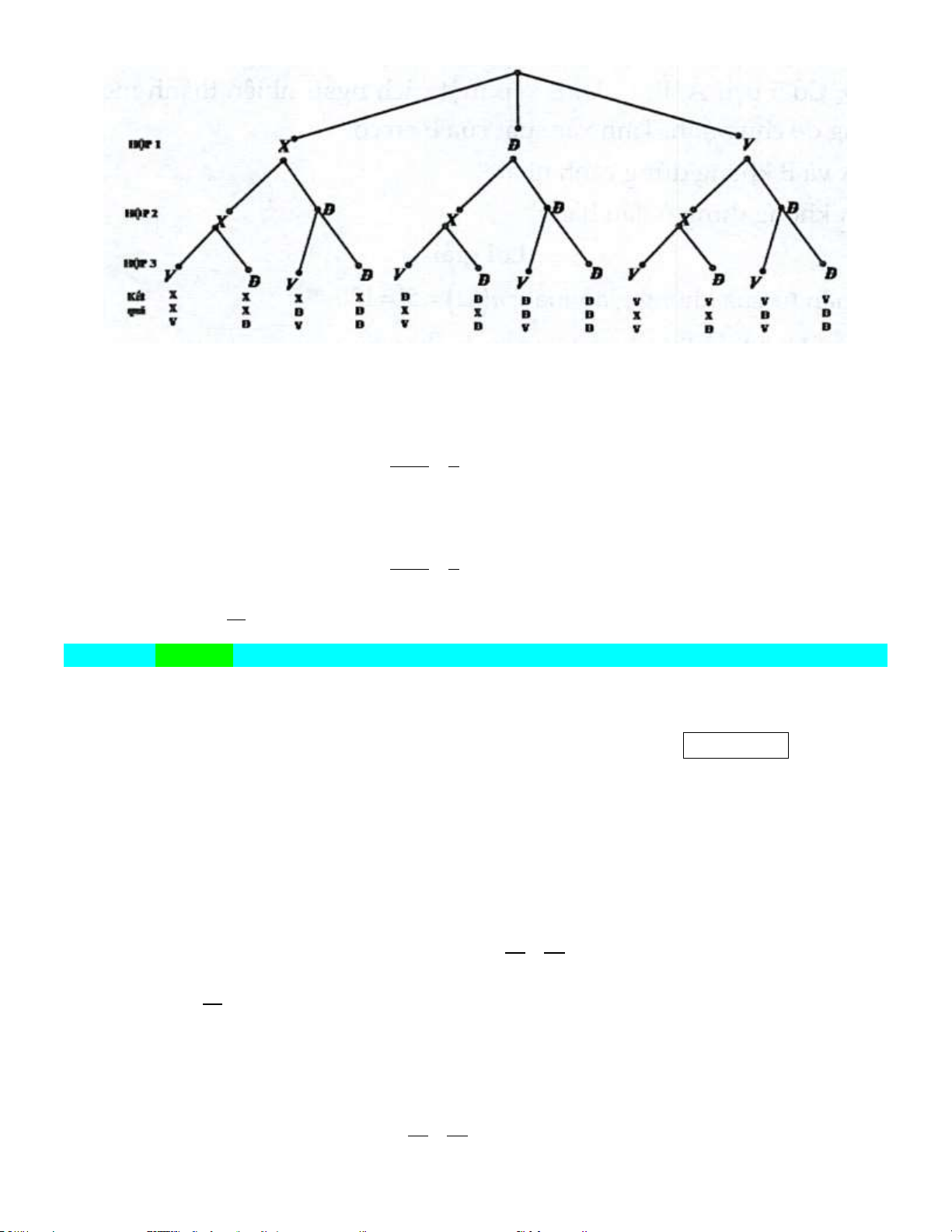
Câu 14. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ
đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như
nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ. Khẳng định Đúng Sai
a) Số các kết quả có thể xảy ra của phép thử là n()  12 b) 5
Xác suất của biến cố "Trong 3 thẻ lấy ra có ít nhất 1 thẻ màu đỏ" là: 7
c) Xác suất của biến cố "Trong 3 thẻ lấy ra có nhiều nhất 1 thẻ màu 5 xanh" là: 7 d) 1
Xác suất của biến cố "Trong 3 thẻ lấy ra tất cả đều là màu đỏ" là: 12
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15. Tính độ dài trục lớn của elip  E  , biết  E  đi qua điểm A0;4 và có một tiêu điểm F 3; 0 . 2   Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 16. Tổ 1 lớp 11A có 6 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm cần chọn ra 4 học
sinh của tổ 1 để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn 4 học sinh từ
Tổ đó, trong đó có ít nhất một học sinh nam? Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 17. Tìm hệ số của số hạng chứa 4
x trong khai triển P x    x   x5 2 ( ) 3 3 2 . Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 18. Một lớp có 15 học sinh nữ và 20 học sinh nam. Chọn ngẫu nhiên bốn học sinh tham gia trực
tuần cùng Đoàn trường. Tính xác suất để trong bốn học sinh được chọn có số học sinh nữ ít
hơn số học sinh nam (làm tròn đến hàng phần trăm). Kết quả: Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
PHẦN IV. (3,0 điểm) Câu hỏi tự luận. Thí sinh trả lời từ câu 19 đến câu 21.
Câu 19. Giải phương trình sau: 2
3x  9x 1  x  2 . Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 20. Trong mặt phẳng tọa độ Oxy , cho ba điểm A 1  ;0,B1;  2 và C 3;3 .
a) Viết phương trình tham số đường thẳng . AB
b) Tìm tọa độ điểm D thuộc đường thẳng AB sao cho DC  5 . Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
Câu 21. a) Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu
xanh được đánh số từ 1 đến 9 . Lấy ngẫu nhiên hai quả từ hộp đó. Tính xác suất để lấy được
hai quả khác màu đồng thời tổng hai số ghi trên chúng là số chẵn.
b) Từ các số 1; 2;3; 4;5;6;7;8; 
9 lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác
nhau sao cho số tự nhiên đó không có hai chữ số liên tiếp nào cùng chẵn? Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
____________________HẾT____________________
Huế, 14h00’ Ngày 4 tháng 4 năm 2025
Page: CLB GIÁO VIÊN TRẺ TP HUẾ ¤N TËP CuèI Kú 2 M«n: To¸n 10 – KNTT
Định hướng cấu trúc 2025
ĐỀ ÔN TẬP SỐ 02_TrNg 2025
LỜI GIẢI CHI TIẾT
PHẦN I. (3,0 điểm) Câu trắc nghiệm với nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi, thí sinh chỉ chọn một phương án. Câu 1.
Cho biến cố A với không gian mẫu . Xác suất của biến cố A là n n A n A
A. PA   
B. PA    1
. C. P A   
D. PA  nA  n. nA . n n . Câu 2.
Có bao nhiêu cách sắp xếp 6 học sinh theo một hàng dọc? A. 46656 . B. 4320 . C. 720 . D. 360 . Lời giải:
Số cách sắp xếp 6 học sinh theo một hàng dọc là số hoán vị của 6 phần tử.
Vậy có P  6!  720 cách. 6 Câu 3.
Gieo một đồng tiền (có hai mặt S, N ) cân đối và đồng chất hai lần. Không gian mẫu của phép thử là:
A. SS, NN , SN .
B. SS, NN , NS .
C. SS, NN, SN, NS . D. S, N . Lời giải:
Không gian mẫu của phép thử là:   SS, NN, SN, NS . Câu 4.
Trong khai triển nhị thức:   5
2a b , hệ số của số hạng thứ ba là A. 80 . B. 80 . C. 10 . D. 10 . Lời giải: 5 kk k
Ta có 2a b 5 C (2a) b 5 0 5 1 4 2 3 2 
C .(2a)  C (2a) (b)  C (2a) (b) ... 5 5 5 0 5 5 1 4 4 2 3 3 2
C .2 a C 2 a b C 2 a b ... 5 5 5
Hệ số của số hạng thứ ba là: 2 3 C .2  80. 5 Câu 5.
Trong mặt phẳng tọa độ Oxy, tâm I và bán kính R của đường tròn
C x  2  y  2 : 1 2 16 là
A. Tâm I 1; 2, bán kính R  4 .
B. Tâm I 1; 2, bán kính R  16 .
C. Tâm I 1; 2, bán kính R  4 .
D. Tâm I 1; 2, bán kính R  16 . Câu 6.
Có bao nhiêu số có 5 chữ số khác nhau được lập từ 7 chữ số 1, 2,3, 4,5, 6, 7 ? A. 5 C . B. 7!. C. 5 A . D. 5!. 7 7 Lời giải:
Mỗi số có 5 chữ số khác nhau được lập từ 7 chữ số 1, 2,3, 4,5, 6, 7 là một chỉnh hợp chập
5 của 7 số. Do đó, số các số tự nhiên cần tìm là 5 A . 7 Câu 7.
Có bao nhiêu véctơ khác véctơ – không có điểm đầu và điểm cuối là các đỉnh của ngũ giác? A. 2 A . B. P . C. 2 5 . D. 2 C . 5 5 5 Lời giải:
Số véctơ khác véctơ – không có điểm đầu và điểm cuối là các đỉnh của ngũ giác bằng 2 A . 5 Câu 8. Biết phương trình 2 2
x  28  x  4 có hai nghiệm x ; x với x  0 . Tính S  2x x . 1 2 1 1 2 A. S  2 . B. S  8 . C. S  8 . D. S  4 . Lời giải: x  4 
Bình phương hai vế của phương trình, ta được 2 2
x  28  x  4   x  4
Thay lần lượt x  4 và x  4 vào phương trình đã cho, ta thấy x  4 và x  4 đều thỏa mãn; Vì 4  0 x  4
Suy ra nghiệm của phương trình đã cho là 1  . x  4   2
Vậy S  2x x  2.4  4   4 . 1 2   Câu 9. Cho * k, n
và n k . Công thức nào dưới đây đúng? n n n k ! k ! k ! A. C  . B. C C k C n . n n n k ! n  . C. k ! n . D. ! k !k ! n Lời giải: n k !
Công thức tính số các tổ hợp chập k của n phần tử là C n k  ! n  . k !
Câu 10. Tam thức bậc hai f x 2
x 12x 13 nhận giá trị không âm khi và chỉ khi A. x  1;1  3 . B. x  \  1  ;  13 . C. x  1;1  3 . D. x   ;   
1  13;  . Lời giải: x  1 
Ta có: f x 2
 0  x 12x 13  0   . x 13
Câu 11. Gieo ngẫu nhiên 2 con xúc sắc cân đối đồng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên 2 con xúc sắc bằng 1”. 2 1 5 5 A. . B. . C. . D. . 9 9 18 6 Lời giải:
Số phần tử của không gian mẫu: n   6.6  36 .
Gọi A là biến cố thỏa mãn yêu cầu bài toán: A    1; 2, 2; 
1 , 3; 2, 2; 3, 3; 4, 4; 3, 4; 5, 5; 4, 5; 6, 6; 5
nên n A  10 .
Vậy P A 10 5   . 36 18
Câu 12. Trong mặt phẳng tọa độ Oxy, phương trình chính tắc của parabol có tiêu điểm F 2;0 là 1 A. 2 y  4x . B. 2 y  8x . C. 2 y  2x . D. 2 y x . 6 Lời giải:
Phương trình chính tắc của parabol  P 2
: y  2 px p  0 .
Tiêu điểm F 2; 0  p  4 .
Vậy phương trình parabol là 2 y  8 . x
PHẦN II. (2,0 điểm) Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c),
d) ở mỗi câu, thí sinh chọn đúng hoặc sai (điền dấu X vào ô chọn)
Câu 13. Một nhóm có 14 người trong đó có hai bạn tên A và B . Người ta cần chọn một tổ công tác
gồm 6 người từ nhóm đó. Khẳng định Đúng Sai
a) Chọn nhóm 6 bạn bất kỳ ta có 3003 cách
b) Chọn nhóm 6 bạn trong đó có cả A và B , có 1848 cách
c) Chọn nhóm 6 bạn trong đó không có hai bạn A và B , có 924 cách
d) Có 9504 cách chọn sao cho trong tổ phải có 1 tổ trưởng và 5 tổ viên hơn
nữa A hoặc B phải có mặt nhưng không đồng thời có mặt cả hai người trong tổ. Lời giải: a) Đúng b) Sai c) Đúng d) Đúng
Chọn nhóm 6 bạn bất kỳ ta có 6 C cách. 14
Chọn nhóm 6 bạn trong đó có cả A và B , có 4 C cách. 12
Chọn nhóm 6 bạn trong đó không có hai bạn A và B , có 6 C cách. 12
Suy ra số cách chọn 6 bạn có mặt ,
A B nhưng không đồng thời có mặt cả hai người trong tổ là: 6 4 6
C C C  1584 cách. 14 12 12
Chọn 1 tổ trưởng từ nhóm 6 bạn này, có 6 cách.
Vậy có 1584.6  9504 cách chọn thỏa yêu cầu đề bài.
Câu 14. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ
đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như
nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ. Khẳng định Đúng Sai
a) Số các kết quả có thể xảy ra của phép thử là n()  12 b) 5
Xác suất của biến cố "Trong 3 thẻ lấy ra có ít nhất 1 thẻ màu đỏ" là: 7
c) Xác suất của biến cố "Trong 3 thẻ lấy ra có nhiều nhất 1 thẻ màu 5 xanh" là: 7 d) 1
Xác suất của biến cố "Trong 3 thẻ lấy ra tất cả đều là màu đỏ" là: 12 Lời giải: a) Đúng b) Sai c) Sai d) Đúng
Kí hiệu X là thẻ xanh, Đ thẻ là đỏ và V là thẻ vàng. Các kết quả có thể xảy ra trong 3 lần lấy
thẻ từ hộp có thể được mô tả bởi sơ đồ hình cây ở trên.
a) Số các kết quả có thể xảy ra của phép thử là n()  12
b) Biến cố A : "Trong 3 thẻ lấy ra có ít nhất 1 thẻ màu đỏ". n( ) A  10 . n( ) A 5
Xác suất của biến cố A : P( ) A   . n() 6
c) Số các kết quả có thể xảy ra n()  12
Biến cố B: "Trong 3 thẻ lấy ra có nhiêu nhất 1 thẻ màu xanh". n(B)  10 . n(B) 5
Xác suất của biến cố B : P(B)   . n() 6 1 d) P(D)  . 12
PHẦN III. (2,0 điểm) Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 15 đến câu 18.
Câu 15. Tính độ dài trục lớn của elip  E  , biết  E  đi qua điểm A0;4 và có một tiêu điểm F 3; 0 . 2   Kết quả: 10 Trình bày:
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….………………………….
………………………………………………………………………………….…………………………. Lời giải: 2 2 x y
Phương trình chính tắc của elip  E  có dạng 
 1 a b  0 . 2 2 a b 16 1 2  2 b  16 b  Ta có 2 c  3  c  9 .   2 2 2 2
a b c a  25    2 2 x y
Vậy phương trình của elip  E  là 
 1 nên có độ dài trục lớn là 2a 10. 25 16

Tài liệu liên quan: