Bộ đề ôn thi học kỳ 2 môn Toán năm học 2016 – 2017 trường THPT Thủ Đức – TP.HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

Chủ đề:

Đề HK2 Toán 12 491 tài liệu

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
16 trang 1 năm trước
Tác giả:
L
Lan Tường
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Bộ đề ôn thi học kỳ 2 môn Toán năm học 2016 – 2017 trường THPT Thủ Đức – TP.HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 2 môn Toán 12 năm học 2016 – 2017 .Mời bạn đọc đón xem.

40 20 lượt tải Tải xuống

Chủ đề: Đề HK2 Toán 12 491 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

16 trang 1 năm trước

Tác giả:

Profile Lan Tường
Trang 1/4 - Mã đề thi 101
THPT THỦ ĐỨC
ĐỀ ÔN TẬP HKII
(Đề gồm 04 trang)
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017
Môn thi. TOA
N
Thời gian làm bài. 90 phút, không kể thời gian phát đề
Mã đề thi 101
Họ, tên thí sinh.......................................................................................
Số báo danh. ..........................................................................................
Câu 1. Nguyên hàm của hàm số
2
3
() 2
fx x x
x
= +−
bằng
A.
3
3
4
3ln
33
x
x xC+−+
B.
3
3
4
3ln
33
x
xx+−
C.
3
3
4
3ln
33
x
x xC+++
D.
3
3
4
3ln
33
x
x xC−−+
Câu 2. Biết F(x) là một nguyên hàm của hàm số
1
()
1
fx
x
=
+
và F(0) = 2. Giá trị của F(1) bằng
A. F(1) = ln2 - 2 B. F(1) = ln2 + 2 C. F(1) =
D. F(1) = 2
Câu 3. Cho f(x) là hàm số liên tục trên [a; b] thỏa mãn
() 7
b
a
f x dx
=
∫
. Giá trị của
()
b
a
I f a b x dx= +−
∫
bằng
A. 7 B. a+b-7 C. 7-a-b D. a+b+7
Câu 4. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
2yx= −
và
yx=
bằng
A. 5 B. 7 C.
9
2
D.
11
2
Câu 5. Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị hàm số
(), ()
y fx y gx= =
và hai đường thẳng
, ( , , )x ax b a b ab==<∈
là
A.
( ) (
)
( )
b
a
S f x g x dx= −
∫
B.
( ) ( )
b
a
S f x g x dx= −
∫
C.
( ) ( )
( )
2
b
a
S f x g x dx= −
∫
D.
( ) ( )
( )
22
b
a
S f x g x dx= −
∫
Câu 6. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
2
2y xx
= −
và y = 0. Tính thể tích vật
thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox
A.
16
15
π
B.
17
15
π
C.
18
15
π
D.
19
15
π
Câu 7. Parabol
2
2
x
y =
chia hình tròn có tâm tại gốc tọa độ, bán kính
22
thành 2 phần, tỉ số diện
tích của chúng thuộc khoảng nào
A.
( )
0,4;0,5
B.
( )
0,5;0,6
C.
( )
0,6;0,7
D.
( )
0,7;0,8
Câu 8. Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc
2
3
() ( / )
1
at m s
t
=
+
. Vận tốc ban đầu
của vật là 6 (m/s). Hỏi vận tốc của vật sau 10s là bao nhiêu?
A. 3ln11 + 6 B. 2ln11 + 6 C. 3ln11 - 6 D. 3ln6 + 6
Câu 9. Nguyên hàm của hàm số
1
()
23
fx
x
=
−
bằng
Trang 2/4 - Mã đề thi 101
A.
ln | 2 3 |xC−+
B.
1
ln | 2 3 |
2
xC
−+
C.
3ln | 2 3 |xC− −+
D.
1
ln | 2 3 |
3
xC
− −+
Câu 10. F(x) là một nguyên hàm của
1
()
x
fx e
−
=
và F(1) = 0. Giá trị F(2) bằng
A.
1
1
e
−
B.
1
1
e
−−
C.
1
1
e
−+
D.
1
1
e
+
Câu 11. Tìm nguyên hàm của hàm số
2
()
x
fx e=
A.
2x
eC+
B.
2
2
x
e
C
+
C.
2
2
x
eC+
D.
2
x
eC+
Câu 12. Biết
3
2
x
I x e dx=
∫
. Đặt
3
ux
=
, khi đó I được viết thành
A.
3
u
I e du=
∫
B.
u
I e du
=
∫
C.
1
3
u
I e du=
∫
D.
u
I ue du
=
∫
Câu 13. Kết quả tích phân
1
2
0
3
()
1
x
e dx
x
+
+
∫
có dạng
2
ln 2
2
e
ab++
với a, b là các số hữu tỷ. Giá trị
của tích
2.ab
bằng
A. 3 B. 1 C. 0 D. -3
Câu 14. Tính mô đun của số phức
z
thoả mãn
. 3( ) 4 3zz z z i+ −=−
A.
2z =
B.
3z =
C.
4z =
D.
1z =
Câu 15. Cho số phức
z
thoả mãn
(2 ) 3zi
−+=
. Biết rằng tập hợp các điểm biểu diễn số phức
z
trong mặt phẳng phức là một đường tròn. Tính diện tích S của đường tròn.
A.
S3= π
B. S = 3π C. S = 6π D. S = 9π
Câu 16. Số phức
23
zi
= −
có điểm biểu diễn là
A. (2; 3) B. (-2; -3) C. (2; -3) D. (-2; 3)
Câu 17. Gọi z
1
, z
2
là hai nghiệm phức của phương trình
2
2 10 0zz++=
. Giá trị của biểu thức
22
12
|| ||Az z= +
bằng
A. 15 B. 17 C. 19 D. 20
Câu 18. Số phức z =
34
4
i
i
−
−
có môđun bằng
A.
5 17
17
B.
17
17
C.
3 17
17
D.
2 17
17
Câu 19. Cho số phức z thỏa mãn
2
(2 3 ) (4 ) (1 3 )iz iz i− + + =−+
. Xác định phần thực và phần ảo của z
A. Phần thực – 2; Phần ảo 5i B. Phần thực – 2; Phần ảo 5
C. Phần thực – 2; Phần ảo 3 D. Phần thực – 3; Phần ảo 5i
Câu 20. Trong mp tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn
( )
1z i iz−= +
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2; –1), bán kính R =
2
.
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0; 1), bán kính R =
3
.
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0; –1), bán kính R =
3
.
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0; –1), bán kính R =
2
.
Câu 21. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức
34
zi= −
; M’ là điểm
biểu diễn cho số phức
1
'
2
i
zz
+
=
. Tính diện tích
'OMM∆
.
A.
OMM'
25
S
4
∆
=
. B.
OMM'
25
S
2
∆
=
C.
OMM'
15
S
4
∆
=
D.
OMM'
15
S
2
∆
=
Trang 3/4 - Mã đề thi 101
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1; –1; 2), B(2; 0; 1) và mặt phẳng (P).
x + 2y – 2z – 5 = 0. Tìm tọa độ giao điểm I của đường thẳng AB và mặt phẳng (P).
A. I(–2; –6; 8) B. I (–1; –3; 4) C. I(3; 1; 0) D. I(0; 2; –1)
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 1; 1) và đường thẳng
64
: 2 ( )
12
xt
dy tt
zt
= −
=−− ∈
=−+
. Tọa độ hình chiếu vuông góc của A lên đường thẳng d là
A. (2; –3; –1) B. (2; 3; 1) C. (2; –3; 1) D. (–2; 3; 1)
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho hình hành ABDC với A(1; 2; 1), B(1; 1; 0),
C(1; 0; 2). Tọa độ đỉnh D là
A. (1; –1; 1) B. (1; 1; 3) C. (1; –1; 3) D. (–1; 1; 1)
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1; 2; 3), B(3; 2; 1). Gọi M là điểm
thuộc mặt phẳng Oxy. Tọa độ của M để P = |
MA MB+
 
| đạt giá trị nhỏ nhất là
A. (1; 2; 1) B. (1; 1; 0) C. (2; 1; 0) D. (2; 2; 0)
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có các điểm A(0; 1; 0), B(0; 1; 1),
C(2; 1; 1), D(1; 2; 1). Thể tích của tứ diện ABCD bằng
A.
1
6
B.
1
3
C.
2
3
D.
4
3
Câu 27. Trong không gian với hệ tọa độ Oxyz, gọi (P) là mặt phẳng đi qua G(1; 2; –1) và cắt Ox, Oy,
Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng (P).
A. (P). x + 2y – z – 4 = 0 B. (P). 2x + y – 2z – 2 = 0
C. (P). x + 2y – z – 2 = 0 D. (P). 2x + y – 2z – 6 = 0
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M(2; 0; -1) và có vectơ
chỉ phương
a (4; 6;2)= −
. Phương trình tham số của đường thẳng ∆ là
A.
24
6 ( )
12
xt
ytt
zt
=−+
=−∈
= +
B.
22
3 ( )
1
xt
yt t
zt
=−+
=−∈
= +
C.
22
3 ( )
1
xt
ytt
zt
= +
=−∈
=−+
D.
42
3 ( )
2
xt
ytt
zt
= +
=−∈
= +
Câu 29. Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm I(-1; 2; 1) và tiếp xúc với mặt
phẳng
( ): 2 2 2 0Px y z− − −=
có phương trình
A.
( )
( )
( )
2 22
1 2 13
xyz+ +− +− =
B.
( ) ( ) ( )
2 22
1 2 19xyz+ +− +− =
C.
( ) ( ) ( )
2 22
1 2 13xyz+ +− ++ =
D.
( ) (
) ( )
2 22
1 2 19xyz+ +− ++ =
Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt phẳng chứa 2 điểm A(1; 0; 1) và B(-1; 2; 2) và
song song với trục Ox có phương trình là
A. x + 2z – 3 = 0 B. y – 2z + 2 = 0 C. 2y – z + 1 = 0 D. x + y – z = 0
Câu 31. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) tâm I bán kính R và có phương trình
2 22
2 10xyzxy+ + −+ +=
. Trong các mệnh đề sau, mệnh đề nào đúng
A.
1
;1; 0
2
I

−


và R=
1
4
B.
1
; 1; 0
2
I

−


và R=
1
2
C.
1
; 1; 0
2
I

−


và R=
1
2
D.
1
;1; 0
2
I

−


và R=
1
2
Trang 4/4 - Mã đề thi 101
Câu 32. Trong không gian với hệ tọa độ Oxyz, giao điểm M của đường thẳng
31
:
1 12
xyz
d
−+
= =
−
và
( )
:2 7 0P xyz−−−=
là
A. M(3; -1; 0) B. M(0; 2; -4) C. M(6; -4; 3) D. M(1; 4; -2)
Câu 33. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
12
:
12 3
xy z
d
++
= =
và mặt phẳng
( )
: 2 2 30Px y z+ − +=
. Tìm tọa độ điểm M có tọa độ âm thuộc d sao cho khoảng cách từ M đến (P)
bằng 2.
A.
(
)
M 2;3;1−−−
B.
( )
M 1;3;5
−−−
C.
( )
M 2;5;8−−−
D.
( )
M 1;5;7−−−
Câu 34. Trong không gian Oxyz cho A(0; 1; 0), B(2; 2; 2), C(-2; 3; 1) và đuờng thẳng
123
:
2 12
xy z
d
−+−
= =
−
. Tìm điểm M thuộc đường thẳng d để thể tích khối tứ diện MABC bằng 3.
A.
3 3 1 15 9 11
M ; ; ;M ; ;
2 42 2 4 2
−

−− −


B.
3 3 1 15 9 11
M ; ; ;M ; ;
5 42 2 4 2

−− −


C.
3 3 1 15 9 11
M ; ; ;M ; ;
2 42 2 4 2

−


D.
3 3 1 15 9 11
M ; ; ;M ; ;
5 42 2 4 2

−


Câu 35. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
2 22
2220xyz xyz++−− − =
và
điểm A(2; 2; 2). Điểm B thay đổi trên mặt cầu (S). Diện tích của tam giác OAB có giá trị lớn nhất là
A. 1(đvdt) B. 2(đvdt) C.
3
(đvdt) D. 3(đvdt)
-----------------------------------------------
----------- HẾT ----------
ĐÁP ÁN
1
A
2
B
3
A
4
C
5
B
6
A
7
A
8
A
9
D
10
A
11
B
12
C
13
D
14
A
15
B
16
C
17
D
18
A
19
B
20
D
21
A
22
C
23
C
24
A
25
D
26
B
27
D
28
C
29
B
30
B
31
B
32
A
33
B
34
A
35
D
Trang 1/4 - Mã đề thi 102
THPT THỦ ĐỨC
ĐỀ ÔN TẬP HKII
(Đề gồm 04 trang)
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017
Môn thi: TOA
N
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi 102
Họ, tên thí sinh.......................................................................................
Số báo danh. ..........................................................................................
Câu 1. Hàm nào trong các hàm sau là nguyên hàm của hàm số
( ) sin 2
fx x
=
A.
cos2x
B.
cos2
2
x
C.
cos2xx
D.
cos2
2
x
−
Câu 2. Cho hàm số F(x) là nguyên hàm của hàm số f(x) trên K. Khẳng định nào sau đây là sai
A. F’(x) = f(x)
B. F(x) + C cũng là nguyên hàm của f(x)
C. Có duy nhất F(x) là nguyên hàm của hàm số f(x)
D. Mọi nguyên hàm của f(x) đều có dạng F(x) + C.
Câu 3. Nguyên hàm của hàm số
23
()
2
x
fx
x
−
=
+
bằng
A.
2 7ln 2
xC
+ ++
B.
2 7ln 2
xC
− ++
C.
2 7ln 2x xC+ ++
D.
2 7ln 2x xC− ++
Câu 4. Nguyên hàm của hàm số
( ) 3sin 2cosfx x x= +
bằng
A. 3cosx + 2sinx B. 3cosx + 2sinx + C C. -3cosx + 2sinx + C D. 3cosx - 2sinx + C
Câu 5. Nguyên hàm của hàm số
3
( ) sin cosfx x x=
bằng
A.
4
1
sin
4
xC−+
B.
4
1
sin
4
xC+
C.
4
sin xC+
D.
4
sin
xC
−+
Câu 6. Nguyên hàm của hàm số
() 2fx x x
= −
bằng
A.
( )
2
2 22x x xC− −+ +
B.
( )
2
2 22
x xC− −−+
C.
(
)
2
2
2 22
5
x x xC− − −+ +
D.
( ) ( )
2
24
2 2 22
53
x x x xC− −− − −+
Câu 7. Cho F(x) là một nguyên hàm của hàm số f(x) liên tục trên đoạn [a;b]. Khẳng định nào sau đây
sai?
A.
() 0
a
a
f x dx =
∫
B.
() ()
ba
ab
f x dx f x dx
= −
∫∫
C.
() () ()
b
a
f x dx F a F b= −
∫
D.
() () ()
b
a
f x dx F b F a= −
∫
Câu 8. Nguyên hàm của hàm số
()
2
x
x
e
fx
e
=
+
là
A.
2ln( 2)
x
eC++
B.
ln( 2)
x
eC++
C.
ln( 2)
xx
ee C++
D.
2x
eC+
Câu 9. Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi
các đường
2
4 4, 0, 0, 3yx x y x x=−+ = = =
bằng
A.
53
5
V
π
=
B.
33
5
V
π
=
C.
3
5
V
π
=
D.
35
3
V
π
=
Câu 10. Biết
2
1
ln ln 2xdx a b= +
∫
với
,ab∈
. Khi đó tổng
ab+
bằng
A. -1 B. 2 C. 1 D. -2
Trang 2/4 - Mã đề thi 102
Câu 11. Cho hàm số f(x) liên tục trên [a; d]. Biết
( ) ( )
5; 2
dd
ab
f x dx f x dx= =
∫∫
với
abd<<
thì
( )
b
a
f x dx
∫
bằng
A. -2 B. 7 C. 0 D. 3
Câu 12. Biết
(
)
x
I f x xe dx= =
∫
và
( )
0 2016f =
, biểu thức I bằng
A.
2017
xx
I xe e
= ++
B.
2017
xx
I xe e= −+
C.
2016
xx
I xe e= ++
D.
2016
xx
I xe e= −+
Câu 13. Biết rằng
2
23
ln 2 1 ln 1
2 13 3
xa b
dx x x C
xx
+
= ++ −+
−−
∫
. Khi đó tích
.ab
bằng
A. 10 B. -10 C.
10
9
D.
10
9
−
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
1
()
2
x
y fx
x
+
= =
−
và các trục tọa độ là
biểu thức có dạng
3
ln
2
mn+
. Khi đó tích
.mn
bằng
A. 3 B.
1
3
C.
2
3
D. -3
Câu 15. Tích phân
( )
2
1
2 1 ln .
e
I x x dx m e n=−=+
∫
. Khi đó tích
.
mn
bằng
A.
1
4
−
B. 0 C.
3
16
−
D.
3
4
−
Câu 16. Cho số phức
z a bi= +
. Tìm mệnh đề đúng trong các mệnh đề sau
A.
2z z bi
+=
B.
2zz a
−=
C.
22
.zz a b= −
D.
2
2
zz=
Câu 17. Cho số phức
23zi= −
. Số phức liên hợp của
z
có điểm biểu diễn là
A. (2; 3) B. (-2; -3) C. (2; -3) D. (-2; 3)
Câu 18. Cho số phức
( )
2
23zi= +
. Tìm phần thực và phần ảo của số phức
z
A. Phần thực bằng
7−
và phần ảo bằng
62i
B. Phần thực bằng
7
và phần ảo bằng
62
C. Phần thực bằng
7−
và phần ảo bằng
62
D. Phần thực bằng
7
và phần ảo bằng
62i
Câu 19. Cho hai số phức
1
4zi= +
và
2
13zi
= −
. Tính
12
zz−
A.
12
17 10zz
−= −
B.
12
13zz−=
C.
12
25zz−=
D.
12
5zz−=
Câu 20. Cho sô
phư
c z = 5 + 2i. Tı
m phâ
n thư
c va
phâ
n a
o cu
a sô
phư
c
z
A. Phâ
n thư
c bă
ng -5 va
phâ
n a
o bă
ng -2 B. Phâ
n thư
c bă
ng 5 va
phâ
n a
o bă
ng 2
C. Phâ
n thư
c bă
ng 5 va
phâ
n a
o bă
ng -2 D. Phâ
n thư
c bă
ng 5 va
phâ
n a
o bă
ng -2i
Câu 21. Xét phương trı
nh
42
3 2 10zz− −=
trên tập số phức, khẳng định nào sau đây đúng?
A. Phương trình có 2 nghiệm thực B. Phương trình có 3 nghiệm phức
C. Phương trình có 1 nghiệm z = 0 D. Phương trình vô nghiệm
Câu 22. Cho sô
phư
c z tho
a ma
n (2 - i)z = (2 + i)(1- 3i). Go
i M la
điê
m biê
u diê
n cu
a z. Khi đo
to
a
đô
điê
m M la
A. M(3; 1 ) B. M(3; -1) C. M(1; 3) D. M(1; -3)
Câu 23. Cho sô
phư
c z co
phâ
n a
o âm, go
i
2w z z zi= +−
. Khi đo
khă
ng đi
nh na
o sau đây vê
số
phức w la
đu
ng ?
A. w la
sô
thư
c B. w co
phâ
n thư
c bă
ng 0
C. w co
phâ
n a
o là số thực âm D. w co
phâ
n a
o là số thực dương
Trang 3/4 - Mã đề thi 102
Câu 24. Cho số phức
13zi
= −
. Số phức
1
z
bằng
A.
11 3
44
i
z
= +
B.
11 3
22
i
z
= +
C.
1
13i
z
= +
D.
1
13i
z
=−+
Câu 25. Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng
1
1 1 12
:
113
xyz
d
−+−
= =
−−
và
2
1
: 2 2 ( )
3
xt
d y tt
zt
= −
=+∈
= +
A.
1
d
và
2
d
cắt nhau B.
1
d
và
2
d
trùng nhau C.
1
d
và
2
d
chéo nhau D.
1
d
và
2
d
song song
Câu 26. Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng qua điểm M(1; 0; 0) và có
vectơ pháp tuyến
( )
1; 2;1n =
có dạng
A.
20
x yz−+ + =
B.
2 20
x yz+ −+=
C.
2 10x yz
+ +−=
D.
2 10x yz− ++=
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho điểm
( ) ( )
3; 5; 7 , 1;1; 1AB−−
. Tọa độ trung điểm I
của đoạn thẳng AB là
A.
( )
1; 2; 3 .I −−
B.
( )
2; 4;6 .I
−−
C.
( )
2;3; 4 .I −
D.
( )
4;6; 8 .I −
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số
2
: 1 2 ( )
5
xt
d y tt
zt
= −
=+∈
= −
. Trong các vectơ sau, vectơ nào là vectơ chỉ phương của đường thẳng d
A.
( 1; 2; 0).b = −
B.
(2;1; 0).v
=
C.
( 1; 2; 5).u =−−
D.
(2;1; 5).a = −
Câu 29. Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) đi qua gốc tọa độ và song song với mặt
phẳng
( )
:5 3 2 3 0Qxyz− + −=
có dạng
A.
( ):5 3 2 0Pxyz+−=
B.
( )
:5 3 2 0Pxyz−−=
C.
( )
:5 3 2 0Pxyz−+=
D.
( )
:5 3 2 0P xyz−+ + =
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hai điểm
( )
2;1; 2M −
và
( )
4; 5;1N −
. Độ dài đoạn
thẳng MN bằng
A.
7
B.
41
C.
7
D.
49
Câu 31. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
( ) ( ) ( )
22
2
:5 4 9Sx y z− ++ +=
. Tìm tọa
độ tâm I và bán kính R của mặt cầu (S)
A.
( )
5; 4;0I
−
và R = 9 B.
( )
5; 4;0I −
và R = 3 C.
(
)
5;4; 0
I
−
và R = 9 D.
( )
5;4; 0I −
và R = 3
Câu 32. Trong không gian Oxyz, cho đường thẳng
21
:
2 11 2
x yz
m
+−
∆==
+−
và mặt phẳng
( ): 2 3 0Pxy z−+ −=
. Giá trị của m để đường thẳng ∆ song song với mp(P) là
A. m = 3 B. m = -1 C. m = 2 D. m = 0
Câu 33. Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình tham số
của đường thẳng ∆ đi qua điểm A(1; 4; 7) và vuông góc với mặt phẳng
( ): 2 2 3 0Px y z+ − −=
A.
12
4 2 ( )
73
xt
y tt
zt
= +
=−∈
= −
B.
12
4 4 ( )
73
xt
y tt
zt
= +
=+∈
= −
C.
1
24( )
27
xt
y tt
zt
= +
=+∈
=−+
D.
1
4 2 ( )
72
xt
y tt
zt
= +
=+∈
= −
Câu 34. Trong không gian với hệ tọa độ Oxyz, cho ba điểm
( ) ( ) ( )
3;2;1 , 1;3;2 , 2; 4; 3AB C−−
. Tính
tích vô hướng
.AB AC
 
A.
.6AB AC = −
 
B.
. 4.AB AC =
 
C.
. 4.AB AC = −
 
D.
. 2.AB AC =
 
Trang 4/4 - Mã đề thi 102
Câu 35. Trong không gian với hệ tọa độ Oxyz, cho điểm I(0; 0; 3) và đường thẳng
12
:
121
x yz
d
+−
= =
. Phương trình mặt cầu (S) có tâm I và cắt d tại hai điểm A, B sao cho ∆IAB
vuông tại I có dạng
A.
( ) ( )
2
22
8
:3
3
Sx y z+ ++ =
B.
( ) (
)
2
22
8
:3
3
Sx y z+ +− =
C.
( ) ( )
2
22
4
:3
3
Sx y z++− =
D.
( ) ( )
2
22
4
:3
3
Sx y z+++ =
-----------------------------------------------
----------- HẾT ----------
ĐÁP ÁN
1
D
2
C
3
D
4
C
5
B
6
D
7
C
8
B
9
B
10
C
11
D
12
B
13
B
14
D
15
D
16
D
17
A
18
C
19
D
20
C
21
A
22
B
23
A
24
A
25
C
26
C
27
C
28
C
29
C
30
A
31
B
32
C
33
D
34
D
35
B
Trang 1/3 - Mã đề thi 103
THPT THỦ ĐỨC
ĐỀ ÔN TẬP HKII
(Đề gồm 03 trang)
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017
Môn thi: TOA
N
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi 103
Họ, tên thí sinh.......................................................................................
Số báo danh. ..........................................................................................
Câu 1. Nguyên hàm của hàm sổ
() 5
x
fx=
là
A.
( ) 5 ln 5
x
f x dx =
∫
B.
() 5
x
f x dx
=
∫
C.
5
()
ln5
x
f x dx
=
∫
D.
1
()
5 ln 5
x
f x dx =
∫
Câu 2. Nguyên hàm F(x) của hàm số
13
()
x
fx e
−
=
là
A.
13
()
x
Fx e C
−
= +
B.
13
() 3
x
Fx e C
−
=−+
C.
13
1
()
3
x
Fx e C
−
=−+
D.
13
()
x
Fx e C
−
=−+
Câu 3. Nguyên hàm F(x) của hàm số
2
()fx x x=
là
A.
3
2
()
7
xx
Fx C= +
B.
5
2
5
()
2
Fx x C= +
C.
3
()
3
x
Fx C
x
= +
D.
7
2
2
()
7
Fx x C= +
Câu 4. Tìm nguyên hàm của hàm số
ln
()
x
fx
x
=
A.
2
1
( ) ln +C
2
f x dx x=
∫
B.
2
1
( ) ln +C
2
f x dx x
= −
∫
C.
1
( ) ln +C
2
f x dx x=
∫
D.
( ) ln +Cf x dx x=
∫
Câu 5. Biết
()Fx
là một nguyên hàm của của hàm số
sin
()
1 3cos
x
fx
x
=
+
và
2
2
F
π

=


. Tính
(0)
F
A.
1
(0) ln 2 2
3
F =−+
B.
2
(0) ln 2 2
3
F =−+
C.
2
(0) ln 2 2
3
F =−−
D.
1
(0) ln 2 2
3
F =−−
Câu 6. Thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số
()y fx=
liên tục, trục Ox và hai đường thẳng x = a, x = b với
ab≤
quanh trục Ox được tính bởi công
thức
A.
2
()
b
a
V f x dx
π
=
∫
B.
22
()
b
a
V f x dx
π
=
∫
C.
2
()
b
a
V f x dx
=
∫
D.
| ( )|
b
a
V f x dx
π
=
∫
Câu 7. Cho hàm số
()fx
có đạo hàm trên đoạn [-1; 3], biết
( 1) 2f −=−
và
(3) 5f =
. Tính giá trị của
3
1
'( )
I f x dx
−
=
∫
A. I = 3 B. I = 7 C. I = -7 D. I = -10
Câu 8. Diện tích hình phẳng giới hạn bởi hàm số
2
3yx x= −
và trục hoành là S, khi đó giá trị của S
A.
3S =
B.
9
2
S = −
C.
9
2
S =
D.
10
3
S =
.
Câu 9. Biết
4
32
1
ln
32
e
ae b
x xdx
+
=
∫
với a, b là những số nguyên. Tính giá trị
b
S
a
=
A.
1
5
S = −
B.
1
32
S = −
C.
5
32
S =
D.
1
5
S =
.
Trang 2/3 - Mã đề thi 103
Câu 10. Diện tích S của hình phẳng giới hạn bởi các đường
5
( 1)yx= +
,
x
ye=
và
1x =
có giá trị bằng
A.
23
2
e+
B.
23
2
e
−
C.
23
3
e−
D.
23
2
2
e−
Câu 11. Cho f(x) là hàm số liên tục trên [1;3] thỏa
3
1
() 7f x dx =
∫
. Tính
3
1
(4 )I f x dx
= −
∫
A.
7I =
B.
3I
=−
C.
3I =
D.
7I = −
Câu 12. Hình phẳng (H) giới hạn bới đồ thị hàm số
24
1
x
y
x
−
=
+
và hai trục tọa độ. Tính thể tích khối
tròn xoay tạo bởi hình phẳng (H) khi quay quanh trục hoành
A.
(32 12ln3).
π
+
B.
(32 11ln3).
π
−
C.
(30 12ln3).
π
−
D.
(32 24ln3).
π
−
Câu 13. Biết
1
2
0
ln 2 ln 3
56
dx
ab
xx
= +
−+
∫
, với a, b là các số nguyên. Tính
S ab= +
A.
3S = −
B.
2S
=−
C.
1S =
D.
0
S =
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
2
x
y
x
+
=
+
, tiệm cận ngang và các đường
thẳng x = 0, x = 3
A.
2
4ln
5
B.
5
4 ln
2
+
C.
5
4ln
2
D.
5
4 ln
2
−
Câu 15. Một vật đang chuyển động chậm dần với vận tốc 10m/s thì tăng tốc với gia tốc
22
() 3 ( / )at t t m s= +
. Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ bắt đầu tăng tốc
bằng
A.
1450
3
m
B.
145
3
m
C.
4300
3
m
D.
430
3
m
Câu 16. Cho số phức z = 5 - 4i. Liên hợp của số phức z có môđun là
A. 1 B.
41
C. 3 D. 9
Câu 17. Cho số phức z = 2 + i. Phần thực và phần ảo của số phức z lần lượt là
A. 1 và 2 B. 2 và -1 C. 1 và -2 D. 2 và 1
Câu 18. Cho số phức z thoả mãn điều kiện.
(
) (
)
2
32 2 4iz i i+ +− =+
. Phần ảo của số phức
( )
w1zz= +
là
A. 0 B. 2 C. -1 D. -2
Câu 19. Trong mặt phẳng phức, cho 3 điểm A,B,C lần lượt là 3 điểm biểu diễn cho 3 số phức
( ) ( )
2
12 3
1, 1 ,z iz i z a ia=+ =+ =−∈
. Để tam giác ABC vuông tại B thì giá trị của a bằng
A. -3 B. -2 C. 3 D. -4
Câu 20. Cho số phức z = 2 + 5i, phần thực của số phức là
A. 2. B. -2. C. -5. D. 5.
Câu 21. Rút gọn biểu thức
(2 )(3 )zi i i=−+
ta được
A. z = 6. B. z = 1+ 7i. C. z = 2+ 5i. D. z = 5i.
Câu 22. Cho số phức
(, )z a bi a b=+∈
thoả
(1 )(2 1) ( 1)(1 ) 2 2 .iz z i i+ −+ + −=−
Tính
Pab= +
A.
0P =
B.
1P
=
C.
1P = −
D.
1
3
P = −
Câu 23. Nghiệm phức của phương trình
2
10zz−+=
là
A.
3
2
i±
B.
3 i±
C.
13i±
D.
13
2
i±
Câu 24. Tìm mô đun của số phức z thỏa
2 24zz i+=−
Trang 3/3 - Mã đề thi 103
A.
2 37
3
B.
37
3
C.
14
3
D.
10
3
−
Câu 25. Cho số phức z thỏa mãn
28zz i
+=−
. Số phức liên hợp của z là
A.
15 8i
−+
B.
15 6i−+
C.
15 2i−+
D.
15 7i
−+
Câu 26. Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm
(1; 2;0), (3; 2;1)
AB−
và
( 2;1;3)
C −
.
Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)?
A.
11 9 14 29 0xy z
− −+ −=
B.
11 9 14 29 0xy z
−+ −=
C.
11 9 14 29 0xy z++ +=
D.
11 9 14 29 0xy z
++ −=
Câu 27. Trong không gian với hệ tọa độ Oxyz, trong các phương trình sau, phương trình nào là
phương trình của một mặt cầu
A.
( ) ( ) ( )
2 22
1 2 11xyz− +− ++ =−
B.
( ) ( ) ( )
2 22
1 22 1 1x yz− + − ++ =−
C.
( )
2
22
1 2 15xy z x+++ − =
D.
( ) ( ) ( )
2 22
21 2 2 21 1xyz−+ − − +=
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
12
:
1 32
xy z
d
−+
= =
−
. Vectơ chỉ
phương của đường thẳng d là
A.
( )
1; 2; 0n = −
B.
( )
1; 3; 2n = −
C.
( )
1; 2; 0n
= −
D.
( )
1; 3; 2n =
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai vec tơ
( )
;3; 4am=
và
( )
4; ; 7bm= −
. Tìm giá
trị của m để
ab⊥

A. 4 B. -2 C. -4 D. 2
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho ∆ABC với
(
)
1; 2; 1A
−
,
( )
2;3; 2B −
,
( )
1; 0;1C
. Tìm
tọa độ đỉnh D sao cho ABCD là hình bình hành
A. D(0; -1; -2) B. D(0; 1; 2) C. D(0; 1; -2) D. D(0; -1; 2)
Câu 31. Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(2; 3; -1), N(-1; 1; 1), P(0; m; 0). Giá trị
của m để tam giác MNP vuông tại M bằng
A. m = 7 B. m = -7 C.
15
m
2
=
D.
13
m
2
=
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(1; 1; 1) và N(-1; 1; 0), P(3; 1; -1). Tìm
tọa độ điểm Q thuộc mặt phẳng (Oxz) và cách đều ba điểm M, N, P.
A.
57
;0;
66
Q

−


B.
37
;0;
22
Q

−−


C.
57
;0;
66
Q

−


D.
57
;0;
66
Q



Câu 33. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
15
:
1 31
x yz
d
+−
= =
−−
và mặt phẳng
( ): 2 11 0Pxy z+− + =
. Mệnh đề nào sau đây đúng ?
A. d cắt và không vuông góc với (P). B. d vuông góc với (P).
C. d song song với (P). D. d nằm trong (P)
Câu 34. Trong không gian với hệ trục tọa độ Oxyz, cho I(3; -1; 2). Phương trình mặt cầu tâm I, bán
kính R = 4 là
A.
16)
2()1()3(
222
=
++−++ zyx
B.
0
426
222
=−+
−++ yxzyx
C.
4)
2()1()3(
222
=++−+
+ zyx
D.
02426
222
=−−+−++ zyx
zyx
Câu 35. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) . 2x – 2y – z – 4 = 0 và mặt
cầu (S).
2 22
2 4 6 11 0yx xyzz −−−−+ =+
. Bán kính đường tròn giao tuyến là
A. 3 B. 5 C. 2 D. 4
-----------------------------------------------
----------- HẾT ----------
Trang 4/3 - Mã đề thi 103
ĐÁP ÁN
1
C
2
C
3
A
4
A
5
B
6
A
7
B
8
C
9
A
10
B
11
A
12
D
13
C
14
C
15
C
16
B
17
D
18
C
19
A
20
A
21
B
22
A
23
D
24
A
25
A
26
D
27
C
28
B
29
A
30
D
31
A
32
A
33
D
34
D
35
D
Trang 1/4 - Mã đề thi 104
THPT THỦ ĐỨC
ĐỀ ÔN TẬP HKII
(Đề gồm 04 trang)
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017
Môn thi: TOA
N
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi 104
Họ, tên thí sinh.......................................................................................
Số báo danh. ..........................................................................................
Câu 1. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
( )
fx
liên tục; trục hoành và hai
đường thẳng
( )
;x ax ba b= = <
bằng
A.
( )
.
b
a
S f x dx
π
=
∫
B.
(
)
.
b
a
S f x dx
=
∫
C.
( )
.
b
a
S f x dx=
∫
D.
( )
.
b
a
S f x dx
π
=
∫
Câu 2. Nguyên hàm của hàm số
(
)
( )
5
21fx x
= +
là
A.
( ) ( )
6
1
21 .
12
f x dx x C
= ++
∫
B.
( ) ( )
6
1
21 .
6
f x dx x C== ++
∫
C.
( ) ( )
4
22 1f x dx x C= ++
∫
. D.
( )
( )
4
1
21 .
2
f x dx x C= ++
∫
Câu 3. Nguyên hàm của hàm số
21
()
x
fx e
+
=
là
A.
21
() .
x
f x dx e C
+
= +
∫
B.
1
() .
2
x
f x dx e C= +
∫
C.
21
1
() .
2
x
f x dx e C
+
= +
∫
D.
1
() .
x
f x dx e C
+
= +
∫
Câu 4. Gọi F(x) là nguyên hàm của hàm số
2
1
()
32
fx
xx
=
−+
và
3
0
2
F

=


. Giá trị F(3) bằng
A. ln2. B. 2ln2 . C. –ln2. D. -2ln2.
Câu 5. Nguyên hàm của hàm số
2
() .
x
f x xe=
là
A.
2
11
() .
22
x
Fx e x C

= −+


B.
2
1
() 2 .
2
x
Fx e x C

= −+


C.
( )
2
() 2 2 .
x
Fx e x C= −+
D.
( )
2
1
() 2 .
2
x
Fx e x C= −+
Câu 6. Giá trị của
2
3
0
sin cosI x xdx
π
=
∫
bằng
A.
1
.
4
I =
B.
4.I =
C.
1
.
4
I
π
=
D.
0.I =
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
31yx x=−+
và đồ thị hàm số
21yx=−+
bằng
A.
1
.
6
B. 6. C. 8. D.
1
.
3
Câu 8. Biểu thức tích phân
2
1
1
.ln
e
a
I x xdx e
mb
= = +
∫
với m là số nguyên khác 0,
a
b
là phân số tối
giản. Giá trị của tổng
Smab= ++
bằng
A. S = 10. B. S = 5. C. S = 9. D. S = 13.
Trang 2/4 - Mã đề thi 104
Câu 9. Ký hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
x
ye=
; trục hoành; đường thẳng
0x =
và đường thẳng
1x =
. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục
Ox?
A.
2
1.e −
B.
2
( 1).e
π
−
C.
( 1).e
π
−
D.
(
)
2
1.
2
e
π
−
Câu 10. Một chiếc lò xo có độ dài tự nhiên 0,15m. Khi lò xo bị kéo giãn thêm x(m) thì xuất hiện lực
đàn hồi
( ) ( )
800f x xN=
. Tính công A của lực đàn hồi thực hiện được khi lò xo từ trạng thái có độ
dài 0,18m về trạng thái tự nhiên?
A.
2
36.10 .AJ
−
=
B.
2
72.10 .AJ
−
=
C.
36 .AJ=
D.
72 .AJ=
Câu 11. Cho hàm số
()fx
có đạo hàm trên đoạn [2; 4],
(2) 12f =
,
'( )
fx
liên tục và
4
2
'( ) 17f x dx =
∫
.
Giá trị
(4)f
bằng
A. 9. B. 5. C. 19. D. 29.
Câu 12. Cho đồ thị hàm số
()y fx
=
. Diện tích hình phẳng (phần tô đậm trong hình) là
A.
14
31
() () .f x dx f x dx
−
+
∫∫
B.
00
34
() () .f x dx f x dx
−
+
∫∫
C.
04
30
() () .f x dx f x dx
−
+
∫∫
D.
4
3
() .f x dx
−
∫
Câu 13. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
2
4
x
y
x
=
−
, trục tung, trục hoành và x
= 1. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A.
14
ln .
23
B.
3
ln .
24
π
C.
4
ln .
3
π
D.
4
ln .
23
π
Câu 14. Biết
2
3
cos 3xdx a b
π
π
= +
∫
, với a, b là các số hữu tỉ. Giá trị biểu thức
4Sa b= −
A.
9
.
2
S =
B.
3.S =
C.
1
.
2
S = −
D.
1
.
2
S =
Câu 15. Cho hai hàm
( ) ( )
,y f x y gx= =
có đạo hàm trên
. Phát biểu nào sau đây đúng ?
A. Nếu
( )
( )
''
f x dx g x dx=
∫∫
thì
( ) ( )
,.fx gx x= ∀∈
B. Nếu
( )
( )
f x dx g x dx=
∫∫
thì
( ) ( )
,.fx gx x≠ ∀∈
C. Nếu
( )
( )
f x dx g x dx=
∫∫
thì
( ) ( )
,.f x gx x= ∀∈
D. Nếu
( ) ( )
2017,f x gx x= + ∀∈
thì
( ) ( )
' '.f x dx g x dx=
∫∫
Câu 16. Cho hai số phức
12
3 3, 2z iz i=+=−
. Môđun của số phức
12
zzz= −
bằng
A.
17.
B. 17. C. 5. D.
5.
Câu 17. Tìm số phức liên hợp của số phức
2 (1 )z ii=−+
?
Trang 3/4 - Mã đề thi 104
A.
2 2.zi= +
B.
2 2.
zi= −
C.
2 2.zi=−+
D.
2 2.zi=−−
Câu 18. Cho số phức z thỏa
(2 )(1 ) 1 3z ii i
= + − ++
. Môdun của số phức z bằng
A.
13.
z
=
B.
2 2.
z
=
C.
2 5.
z
=
D.
4 2.z =
Câu 19. Gọi
12
,zz
là hai nghiệm của phương trình
2
4 50zz− +=
. Tổng
12
Sz z= +
bằng
A.
5.
S =
B.
4.S =
C.
2 5.S =
D.
2.S =
Câu 20. Tọa độ điểm biểu diễn hình học của số phức z thỏa mãn
(2 3 ) 7 4iz i+=+
là
A.
(2;1).
B.
(2;2).
C.
(2; 1).−
D.
( 1; 2).−
Câu 21. Cho số phức
=−+
13
zi
22
. Số phức
( )
2
z
bằng
A.
13
.
22
i−−
B.
13
.
22
i−+
C.
1 3.i+
D.
3.i−
Câu 22. Cho
s
ố phức z thỏa mãn
(1 2 ) 7 4 0zi i+ −− =
. Môđun
s
ố phức
2wz i= +
bằng
A. 4. B.
17.
C.
24.
D. 5.
Câu 23
.
G
ọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 30zz+ +=
. Trên mặt phẳng tọa
độ. Điểm M biểu diễn số phức
1
z
có tọa độ là
A. M(-1; 2). B. M(-1; -2). C.
M( 1; 2 ).−−
D.
M( 1; 2i).−−
Câu 24. Cho
s
ố phức
(, )
z a bi a b=+∈
thỏa mãn.
2
(3 2 ) (2 ) 4iz i i+ +− =+
. Giá trị biểu thức
Pab= −
bằng
A. 1. B. 0. C. 4. D. 6.
Câu 25. Biết rằng nghịch đảo của số phức z bằng số phức liên hợp của nó. Trong các kết luận sau, kết
luận nào đúng?
A.
2.z = −
B.
1.z
=
C.
3.z =
D.
2.z =
Câu 26. Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 1; -1) và đường thẳng
21
:
21
xy
dz
−+
= =
−
. Viết phương trình mặt phẳng qua A và vuông góc với đường thẳng d
A. 2x - y + z = 0. B. 2x + y + z = 0. C. 2x - y - 1 = 0. D. 2x - y + 1 = 0.
Câu 27. Trong không gian với hệ toạ độ Oxyz, cho vectơ
( )
1; 1; 2n −−
. Mặt phẳng nào có phương trình
dưới đây nhâ
n vectơ
n
làm vectơ pháp tuyến?
A.
2 30
xy z−− + + =
B.
2 30
xy z−+ − + =
.
C.
2 30xy z−− +=
. D.
2 30
xy z−+ +=
.
Câu 28. Trong không gian với hệ toạ độ Oxyz, tìm toạ độ tâm I và bán kính R của mặt cầu (S) có
phương trình
22 2
( 3) ( 1) 9x yz− + +− =
A.
( )
3;0; 1 , 9IR−− =
B.
( )
3;0;1 , 9IR=
. C.
( )
3;0; 1 , 3IR
−− =
. D.
( )
3;0;1 , 3IR=
Câu 29. Trong không gian với hệ toạ độ Oxyz, cho mă
t phă
ng
( ):2 2 5 0P x yz− +−=
. Điê
m na
o dươ
i
đây co
khoa
ng ca
ch đê
n mă
t phă
ng (P) bă
ng 3?
A. (1; 1; -4). B. (1; 1; 2). C. (1; -1; 0). D. (-1; 1; 6).
Câu 30. Trong không gian với hệ toạ độ Oxyz, cho 3 điê
m
( ) ( ) ( )
3;0;0 , 0; 2;0 , 0;0;1AB C−
. Phương
trı
nh na
o dươ
i đây la
phương trı
nh mă
t phă
ng (ABC)?
A.
0.
321
xyz
−+=
B.
1.
321
xyz
−+=
C.
1.
32
xy
z− +=−
D.
0.
32
xy
z+ +=
Trang 4/4 - Mã đề thi 104
Câu 31. Trong không gian với hệ toạ độ Oxyz, cho đươ
ng thă
ng
1
: 2( )
1
xt
dy t t
zt
= +
= ∈
= −
va
mă
t phă
ng
( )
: 3 7 50xyz
α
+ + −=
. Mê
nh đê
na
o dươ
i đây đu
ng?
A. d song song vơ
i (α). B. d nă
m trong (α). C. d vuông go
c vơ
i (α). D. d că
t (α).
Câu 32. Trong không gian với hệ toạ độ Oxyz, cho điê
m A(4; -3; 1) va
đươ
ng thă
ng
3
: 1( )
1
xt
dy t
zt
= +
=−∈
= +
. Viê
t phương trı
nh cu
a mă
t câ
u (S) đi qua điểm A có bán kính bằng 3 và tâm của
mă
t câ
u (S) nă
m trên đươ
ng thă
ng d?
A.
( ) ( )
22
2
2 1 9.x yz− +− +=
B.
( ) ( )
22
2
2 1 9.x yz+ ++ +=
C.
( ) ( )
22
2
2 1 9.x yz− ++ +=
D.
( ) ( )
22
2
2 1 3.x yz+ ++ +=
Câu 33. Trong không gian với hệ toạ độ Oxyz, cho điê
m A(1; 4; -4), đươ
ng thă
ng
1
: 2( )
2
xt
d y tt
z
= −
=+∈
= −
. Viê
t phương trı
nh cu
a đươ
ng thă
ng ∆ đi qua điê
m A vuông góc với d và đồng
thời că
t d?
A.
1
: 4 ( ).
42
xt
y tt
zt
= +
∆=+ ∈
=−−
B.
1
: 4 ( ).
42
xt
y tt
zt
= +
∆=+ ∈
=−+
C.
1
: 4 ( ).
42
xt
y tt
zt
= +
∆=− ∈
=−−
D.
1
: 4 ( ).
42
xt
y tt
zt
= +
∆=+ ∈
= −
Câu 34. Trong không gian với hệ toạ độ Oxyz, cho điê
m M(1; 2; 4). Viê
t phương trı
nh mă
t phă
ng (P)
đi qua điê
m M va
că
t ca
c tia Ox, Oy, Oz lâ
n lươ
t ta
i ca
c điê
m A, B, C sao cho thê
tı
ch khô
i cho
p
OABC nho
nhâ
t?
A.
1.
124
xyz
++=
B.
1.
3 6 12
xy z
++ =
C.
2 4 1 0.xyz
+ + −=
D.
1.
124
xyz
++=−
Câu 35. Trong không gian với hệ toạ độ Oxyz, tìm toạ độ tiếp điểm của mặt cầu (S).
2 22
2 4 2 80xyz xyz+ + − + − −=
và mặt phẳng (P). 2x + 3y + z – 11 = 0?
A. (3; 1; 2). B. (-3; 1; 2). C. (0; 0; 11). D. (-1; 2; 15).
-----------------------------------------------
----------- HẾT ----------
ĐÁP ÁN
1
B
2
A
3
C
4
C
5
A
6
A
7
A
8
C
9
D
10
A
11
D
12
B
13
D
14
B
15
D
16
A
17
A
18
C
19
C
20
A
21
B
22
D
23
C
24
B
25
B
26
A
27
C
28
D
29
A
30
B
31
A
32
C
33
A
34
B
35
A
| 1/16

Tài liệu khác của Toán 12

Preview text:

THPT THỦ ĐỨC
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017 Môn thi. TOÁN ĐỀ ÔN TẬP HKII
Thời gian làm bài. 90 phút, không kể thời gian phát đề (Đề gồm 04 trang) Mã đề thi 101
Họ, tên thí sinh.......................................................................................
Số báo danh. .......................................................................................... 3
Câu 1. Nguyên hàm của hàm số 2
f (x) = x + − 2 x bằng x 3 x 4 3 x 4 A. 3 + 3ln x − x + C B. 3 + 3ln x − x 3 3 3 3 3 x 4 3 x 4 C. 3 + 3ln x + x + C D. 3 − 3ln x − x + C 3 3 3 3
Câu 2. Biết F(x) là một nguyên hàm của hàm số 1
f (x) = x + và F(0) = 2. Giá trị của F(1) bằng 1 1 A. F(1) = ln2 - 2 B. F(1) = ln2 + 2 C. F(1) = D. F(1) = 2 2 b b
Câu 3. Cho f(x) là hàm số liên tục trên [a; b] thỏa mãn f (x)dx = 7 ∫ . Giá trị của I =
f (a + b − x)dx ∫ a a bằng A. 7 B. a+b-7 C. 7-a-b D. a+b+7
Câu 4. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = 2 − x và y = x bằng 9 11 A. 5 B. 7 C. D. 2 2
Câu 5. Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị hàm số
y = f (x), y = g(x) và hai đường thẳng x = a, x = b (a < ,
b a, b ∈ ) là b b
A. S = ∫ ( f (x) − g (x))dx B. S = f
∫ (x)− g(x)dx a a b b
C. S = ∫ ( f (x) − g (x))2dx D. S = ∫ ( 2 f ( x) 2
− g (x))dx a a
Câu 6. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số 2
y = 2x − x và y = 0. Tính thể tích vật
thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục Ox 16π 17π 18π 19π A. B. C. D. 15 15 15 15 2 x
Câu 7. Parabol y =
chia hình tròn có tâm tại gốc tọa độ, bán kính 2 2 thành 2 phần, tỉ số diện 2
tích của chúng thuộc khoảng nào A. (0, 4;0,5) B. (0,5;0, 6) C. (0, 6;0, 7) D. (0, 7;0,8) 3
Câu 8. Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc 2 a(t) =
(m / s ) . Vận tốc ban đầu t +1
của vật là 6 (m/s). Hỏi vận tốc của vật sau 10s là bao nhiêu? A. 3ln11 + 6 B. 2ln11 + 6 C. 3ln11 - 6 D. 3ln6 + 6
Câu 9. Nguyên hàm của hàm số 1 f (x) = bằng 2 − 3x
Trang 1/4 - Mã đề thi 101 1 1
A. ln | 2 − 3x | +C B.
ln | 2 − 3x | +C C. 3
− ln | 2 − 3x | +C
D. − ln | 2 − 3x | +C 2 3
Câu 10. F(x) là một nguyên hàm của 1 ( ) x f x e − =
và F(1) = 0. Giá trị F(2) bằng 1 1 1 1 A. 1− B. 1 − − C. 1 − + D. 1+ e e e e
Câu 11. Tìm nguyên hàm của hàm số 2 ( ) x f x = e 2 x e A. 2x e + C B. + C C. 2 2 x e + C D. 2 x e + C 2 Câu 12. Biết 3 2 x I = x e dx ∫ . Đặt 3
u = x , khi đó I được viết thành 1 A. = 3 u I e du ∫ B. u I = e du ∫ C. u I = e du ∫ D. u I = ue du ∫ 3 1 2 e x 3
Câu 13. Kết quả tích phân 2 (e + )dx ∫ có dạng
+ a ln 2 + b với a, b là các số hữu tỷ. Giá trị x +1 2 0 của tích 2 . a b bằng A. 3 B. 1 C. 0 D. -3
Câu 14. Tính mô đun của số phức z thoả mãn z.z + 3(z − z) = 4 − 3i A. z = 2 B. z = 3 C. z = 4 D. z = 1
Câu 15. Cho số phức z thoả mãn z − (2 + i) = 3 . Biết rằng tập hợp các điểm biểu diễn số phức z
trong mặt phẳng phức là một đường tròn. Tính diện tích S của đường tròn. A. S = π 3 B. S = 3π C. S = 6π D. S = 9π
Câu 16. Số phức z = 2 − 3i có điểm biểu diễn là A. (2; 3) B. (-2; -3) C. (2; -3) D. (-2; 3)
Câu 17. Gọi z1, z2 là hai nghiệm phức của phương trình 2
z + 2z +10 = 0 . Giá trị của biểu thức 2 2
A = | z | + | z | bằng 1 2 A. 15 B. 17 C. 19 D. 20 − i
Câu 18. Số phức z = 3 4 có môđun bằng 4 − i 5 17 17 3 17 2 17 A. B. C. D. 17 17 17 17
Câu 19. Cho số phức z thỏa mãn 2
(2 − 3i)z + (4 + i)z = −(1+ 3i) . Xác định phần thực và phần ảo của z
A. Phần thực – 2; Phần ảo 5i
B. Phần thực – 2; Phần ảo 5
C. Phần thực – 2; Phần ảo 3
D. Phần thực – 3; Phần ảo 5i
Câu 20. Trong mp tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn z − i = (1+ i) z
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2; –1), bán kính R = 2 .
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0; 1), bán kính R = 3 .
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0; –1), bán kính R = 3 .
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0; –1), bán kính R = 2 .
Câu 21. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức z = 3 − 4i ; M’ là điểm biểu diễn cho số phức 1+ i z ' =
z . Tính diện tích O ∆ MM ' . 2 25 25 15 15 A. S = . B. S = C. S = D. S = OM ∆ M ' ∆ ∆ ∆ 4 OMM ' 2 OMM ' 4 OMM ' 2
Trang 2/4 - Mã đề thi 101
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1; –1; 2), B(2; 0; 1) và mặt phẳng (P).
x + 2y – 2z – 5 = 0. Tìm tọa độ giao điểm I của đường thẳng AB và mặt phẳng (P). A. I(–2; –6; 8) B. I (–1; –3; 4) C. I(3; 1; 0) D. I(0; 2; –1)
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 1; 1) và đường thẳng x = 6 − 4td :  y = 2
− − t (t ∈ ) . Tọa độ hình chiếu vuông góc của A lên đường thẳng d là z = 1 − + 2tA. (2; –3; –1) B. (2; 3; 1) C. (2; –3; 1) D. (–2; 3; 1)
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho hình hành ABDC với A(1; 2; 1), B(1; 1; 0),
C(1; 0; 2). Tọa độ đỉnh D là A. (1; –1; 1) B. (1; 1; 3) C. (1; –1; 3) D. (–1; 1; 1)
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1; 2; 3), B(3; 2; 1). Gọi M là điểm  
thuộc mặt phẳng Oxy. Tọa độ của M để P = | MA + MB | đạt giá trị nhỏ nhất là A. (1; 2; 1) B. (1; 1; 0) C. (2; 1; 0) D. (2; 2; 0)
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có các điểm A(0; 1; 0), B(0; 1; 1),
C(2; 1; 1), D(1; 2; 1). Thể tích của tứ diện ABCD bằng 1 1 2 4 A. B. C. D. 6 3 3 3
Câu 27. Trong không gian với hệ tọa độ Oxyz, gọi (P) là mặt phẳng đi qua G(1; 2; –1) và cắt Ox, Oy,
Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng (P).
A. (P). x + 2y – z – 4 = 0
B. (P). 2x + y – 2z – 2 = 0
C. (P). x + 2y – z – 2 = 0
D. (P). 2x + y – 2z – 6 = 0
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M(2; 0; -1) và có vectơ  chỉ phương a = (4; 6;
− 2) . Phương trình tham số của đường thẳng ∆ là x = 2 − + 4tx = 2 − + 2t   A. y = 6 − t (t ∈ ) B. y = 3 − t (t ∈ )   z = 1+ 2tz = 1+ t  x = 2 + 2tx = 4 + 2t   C. y = 3 − t (t ∈ ) D. y = 3 − t (t ∈ )   z = 1 − + tz = 2 + t
Câu 29. Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm I(-1; 2; 1) và tiếp xúc với mặt
phẳng (P) : x − 2y − 2z − 2 = 0 có phương trình 2 2 2 2 2 2 A. ( x + )
1 + ( y − 2) + ( z − ) 1 = 3 B. ( x + ) 1
+ ( y − 2) + (z − ) 1 = 9 2 2 2 2 2 2 C. ( x + )
1 + ( y − 2) + ( z + ) 1 = 3 D. ( x + )
1 + ( y − 2) + ( z + ) 1 = 9
Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt phẳng chứa 2 điểm A(1; 0; 1) và B(-1; 2; 2) và
song song với trục Ox có phương trình là A. x + 2z – 3 = 0 B. y – 2z + 2 = 0 C. 2y – z + 1 = 0 D. x + y – z = 0
Câu 31. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) tâm I bán kính R và có phương trình 2 2 2
x + y + z − x + 2 y +1 = 0 . Trong các mệnh đề sau, mệnh đề nào đúng  1  1  1  1 A. I − ;1; 0   và R= B. I ; 1 − ;0   và R=  2  4  2  2  1  1  1  1 C. I ; 1 − ;0   và R= D. I − ;1; 0   và R=  2  2  2  2
Trang 3/4 - Mã đề thi 101 x − y + z
Câu 32. Trong không gian với hệ tọa độ Oxyz, giao điểm M của đường thẳng 3 1 d : = = và 1 1 − 2
(P):2x − y − z −7 = 0 là A. M(3; -1; 0) B. M(0; 2; -4) C. M(6; -4; 3) D. M(1; 4; -2) x y + z +
Câu 33. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 1 2 d : = = và mặt phẳng 1 2 3
(P): x + 2y − 2z +3 = 0. Tìm tọa độ điểm M có tọa độ âm thuộc d sao cho khoảng cách từ M đến (P) bằng 2. A. M ( 2 − ; 3 − ;− ) 1 B. M ( 1 − ; 3 − ; 5 − ) C. M ( 2 − ; 5 − ; 8 − ) D. M ( 1 − ; 5 − ; 7 − )
Câu 34. Trong không gian Oxyz cho A(0; 1; 0), B(2; 2; 2), C(-2; 3; 1) và đuờng thẳng x −1 y + 2 z − 3 d : = =
. Tìm điểm M thuộc đường thẳng d để thể tích khối tứ diện MABC bằng 3. 2 1 − 2  3 3 1   15 9 11 −   3 3 1   15 9 11 A. M − ; − ; ; M − ; ;     B. M − ; − ; ; M − ; ;      2 4 2   2 4 2   5 4 2   2 4 2   3 3 1  15 9 11  3 3 1  15 9 11 C. M ; − ; ; M ; ;     D. M ; − ; ; M ; ;      2 4 2   2 4 2   5 4 2   2 4 2 
Câu 35. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): 2 2 2
x + y + z − 2x − 2 y − 2z = 0 và
điểm A(2; 2; 2). Điểm B thay đổi trên mặt cầu (S). Diện tích của tam giác OAB có giá trị lớn nhất là A. 1(đvdt) B. 2(đvdt) C. 3 (đvdt) D. 3(đvdt)
----------------------------------------------- ----------- HẾT ---------- ĐÁP ÁN 1 A 8 A 15 B 22 C 29 B 2 B 9 D 16 C 23 C 30 B 3 A 10 A 17 D 24 A 31 B 4 C 11 B 18 A 25 D 32 A 5 B 12 C 19 B 26 B 33 B 6 A 13 D 20 D 27 D 34 A 7 A 14 A 21 A 28 C 35 D
Trang 4/4 - Mã đề thi 101 THPT THỦ ĐỨC
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017 Môn thi: TOÁN ĐỀ ÔN TẬP HKII
Thời gian làm bài: 90 phút, không kể thời gian phát đề (Đề gồm 04 trang) Mã đề thi 102
Họ, tên thí sinh.......................................................................................
Số báo danh. ..........................................................................................
Câu 1. Hàm nào trong các hàm sau là nguyên hàm của hàm số f (x) = sin 2x cos 2x cos 2x A. cos 2x B.
C. x cos 2x D. − 2 2
Câu 2. Cho hàm số F(x) là nguyên hàm của hàm số f(x) trên K. Khẳng định nào sau đây là sai A. F’(x) = f(x)
B. F(x) + C cũng là nguyên hàm của f(x)
C. Có duy nhất F(x) là nguyên hàm của hàm số f(x)
D. Mọi nguyên hàm của f(x) đều có dạng F(x) + C. 2x − 3
Câu 3. Nguyên hàm của hàm số f (x) = bằng x + 2
A. 2 + 7 ln x + 2 + C
B. 2 − 7 ln x + 2 + C
C. 2x + 7 ln x + 2 + C
D. 2x − 7 ln x + 2 + C
Câu 4. Nguyên hàm của hàm số f (x) = 3sin x + 2 cos x bằng A. 3cosx + 2sinx B. 3cosx + 2sinx + C C. -3cosx + 2sinx + C D. 3cosx - 2sinx + C
Câu 5. Nguyên hàm của hàm số 3
f (x) = sin x cos x bằng 1 1 A. 4 − sin x + C B. 4 sin x + C C. 4 sin x + C D. 4 −sin x + C 4 4
Câu 6. Nguyên hàm của hàm số f (x) = x 2 − x bằng A. ( − x)2 2
2 − x + 2x + C B. ( − x)2 2
2 − x − 2 + C 2 2 2 4
C. − (2 − x)2 2 − x + 2x + C D. (2 − x) 2 − x −
(2− x) 2− x +C 5 5 3
Câu 7. Cho F(x) là một nguyên hàm của hàm số f(x) liên tục trên đoạn [a;b]. Khẳng định nào sau đây sai? a b a A.
f (x)dx = 0 ∫ B.
f (x)dx = − f (x)dx ∫ ∫ a a b b b C.
f (x)dx = F (a) − F (b) ∫ D.
f (x)dx = F (b) − F (a) ∫ a a x e
Câu 8. Nguyên hàm của hàm số f (x) = là x e + 2 A. 2 ln( x e + 2) + C B. ln( x e + 2) + C
C. x ln( x e e + 2) + C D. 2x e + C
Câu 9. Thể tích V của khối tròn xoay thu được khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường 2
y = x − 4x + 4, y = 0, x = 0, x = 3 bằng 53π 33π 3π 35π A. V = B. V = C. V = D. V = 5 5 5 3 2
Câu 10. Biết ln xdx = a ln 2 + b ∫
với a,b ∈  . Khi đó tổng a + b bằng 1 A. -1 B. 2 C. 1 D. -2
Trang 1/4 - Mã đề thi 102 d d
Câu 11. Cho hàm số f(x) liên tục trên [a; d]. Biết f
∫ (x)dx = 5; f
∫ (x)dx = 2 với a < b < d thì a b b f ( x) dx ∫ bằng a A. -2 B. 7 C. 0 D. 3 Câu 12. Biết = ( ) x I f x = xe dx ∫
và f (0) = 2016 , biểu thức I bằng A. x x
I = xe + e + 2017 B. x x
I = xe − e + 2017 C. x x
I = xe + e + 2016 D. x x
I = xe − e + 2016 2x + 3 a b Câu 13. Biết rằng dx = ln 2x +1 + ln x −1 + C ∫ . Khi đó tích . a b bằng 2 2x − x −1 3 3 A. 10 B. -10 C. 10 D. 10 − 9 9 x +
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số 1
y = f (x) =
và các trục tọa độ là x − 2 biểu thức có dạng 3 m ln + n . Khi đó tích . m n bằng 2 1 2 A. 3 B. C. D. -3 3 3 e
Câu 15. Tích phân I = 2x ∫ (1−ln x) 2 dx = .
m e + n . Khi đó tích . m n bằng 1 1 − 3 − A. − B. 0 C. 3 D. 4 16 4
Câu 16. Cho số phức z = a + bi . Tìm mệnh đề đúng trong các mệnh đề sau 2
A. z + z = 2bi
B. z − z = 2a C. 2 2
z.z = a − b D. 2 z = z
Câu 17. Cho số phức z = 2 − 3i . Số phức liên hợp của z có điểm biểu diễn là A. (2; 3) B. (-2; -3) C. (2; -3) D. (-2; 3)
Câu 18. Cho số phức z = ( + i)2 2 3
. Tìm phần thực và phần ảo của số phức z
A. Phần thực bằng 7
− và phần ảo bằng 6 2i
B. Phần thực bằng 7 và phần ảo bằng 6 2
C. Phần thực bằng 7
− và phần ảo bằng 6 2
D. Phần thực bằng 7 và phần ảo bằng 6 2i
Câu 19. Cho hai số phức z = 4 + i và z = 1− 3i . Tính z − z 1 2 1 2
A. z − z = 17 − 10
B. z − z = 13 1 2 1 2
C. z − z = 25
D. z − z = 5 1 2 1 2
Câu 20. Cho số phức z = 5 + 2i. Tı̀m phần thực và phần ảo của số phức z
A. Phần thực bằng -5 và phần ảo bằng -2
B. Phần thực bằng 5 và phần ảo bằng 2
C. Phần thực bằng 5 và phần ảo bằng -2
D. Phần thực bằng 5 và phần ảo bằng -2i
Câu 21. Xét phương trı̀nh 4 2
3z − 2z −1 = 0 trên tập số phức, khẳng định nào sau đây đúng?
A. Phương trình có 2 nghiệm thực
B. Phương trình có 3 nghiệm phức
C. Phương trình có 1 nghiệm z = 0
D. Phương trình vô nghiệm
Câu 22. Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1- 3i). Go ̣i M là điểm biểu diễn của z. Khi đó to ̣a đô ̣ điểm M là A. M(3; 1 ) B. M(3; -1) C. M(1; 3) D. M(1; -3)
Câu 23. Cho số phức z có phần ảo âm, go ̣i w = 2z + z − z i . Khi đó khẳng đi ̣nh nào sau đây về số
phức w là đúng ?
A. w là số thực
B. w có phần thực bằng 0
C. w có phần ảo là số thực âm
D. w có phần ảo là số thực dương
Trang 2/4 - Mã đề thi 102
Câu 24. Cho số phức z = 1− 3i . Số phức 1 bằng z 1 1 3 1 1 3 1 1 A. = + i B. = + i C. = 1+ 3i D. = 1 − + 3i z 4 4 z 2 2 z z
Câu 25. Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng x =1− t x −1 y +1 z −12  d : = =
d :  y = 2 + 2t (t ∈ ) 1 1 1 − 3 − và 2  z = 3 + t
A. d và d cắt nhau
B. d và d trùng nhau C. d và d chéo nhau D. d và d song song 1 2 1 2 1 2 1 2
Câu 26. Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng qua điểm M(1; 0; 0) và có
vectơ pháp tuyến n = (1;2; ) 1 có dạng
A. −x + 2 y + z = 0
B. x + 2 y − z + 2 = 0
C. x + 2 y + z −1 = 0
D. x − 2 y + z +1 = 0
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho điểm A(3;5; 7 − ),B(1;1;− )
1 . Tọa độ trung điểm I của đoạn thẳng AB là A. I ( 1 − ; 2 − ;3). B. I ( 2; − 4; − 6). C. I (2;3; 4 − ). D. I (4;6; 8 − ).
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 − t
d :  y = 1+ 2t (t ∈ ) . Trong các vectơ sau, vectơ nào là vectơ chỉ phương của đường thẳng d z = 5 − t      A. b = ( 1 − ;2;0).
B. v = (2;1; 0). C. u = ( 1 − ;2; 5 − ). D. a = (2;1; 5 − ).
Câu 29. Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) đi qua gốc tọa độ và song song với mặt
phẳng (Q):5x −3y + 2z −3 = 0 có dạng
A. (P) : 5x + 3y − 2z = 0
B. ( P) : 5x − 3y − 2z = 0
C. ( P) : 5x − 3y + 2z = 0 D. ( P) : 5
− x + 3y + 2z = 0
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hai điểm M (2;1; 2 − ) và N (4; 5; − ) 1 . Độ dài đoạn thẳng MN bằng A. 7 B. 41 C. 7 D. 49 2 2
Câu 31. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ) ( x − ) + ( y + ) 2 : 5 4 + z = 9 . Tìm tọa
độ tâm I và bán kính R của mặt cầu (S) A. I (5; 4
− ;0) và R = 9 B. I (5; 4
− ;0) và R = 3 C. I ( 5;
− 4;0) và R = 9 D. I ( 5; − 4;0) và R = 3 x + 2 y z −1
Câu 32. Trong không gian Oxyz, cho đường thẳng ∆ : = = và mặt phẳng 2m +1 1 2 −
(P) : x − y + 2z − 3 = 0 . Giá trị của m để đường thẳng ∆ song song với mp(P) là A. m = 3 B. m = -1 C. m = 2 D. m = 0
Câu 33. Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình tham số
của đường thẳng ∆ đi qua điểm A(1; 4; 7) và vuông góc với mặt phẳng (P) : x + 2y − 2z − 3 = 0 x =1+ 2tx =1+ 2tx = 1+ tx =1+ t    
A. y = 4 − 2t (t ∈ ) B. y = 4 + 4t (t ∈ ) C. y = 2 + 4t (t ∈ ) D. y = 4 + 2t (t ∈ )     z = 7 − 3tz = 7 − 3tz = 2 − + 7tz = 7 − 2t
Câu 34. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(3; 2; ) 1 , B ( 1 − ;3;2),C (2;4; 3 − ) . Tính   tích vô hướng A . B AC         A. A . B AC = 6 − B. A . B AC = 4. C. A . B AC = 4. − D. A . B AC = 2.
Trang 3/4 - Mã đề thi 102
Câu 35. Trong không gian với hệ tọa độ Oxyz, cho điểm I(0; 0; 3) và đường thẳng x +1 y z − 2 d : = =
. Phương trình mặt cầu (S) có tâm I và cắt d tại hai điểm A, B sao cho ∆IAB 1 2 1 vuông tại I có dạng 8 8
A. (S ) : x + y + ( z + 3)2 2 2 =
B. (S ) : x + y + ( z − 3)2 2 2 = 3 3 4 4
C. (S ) : x + y + ( z − 3)2 2 2 =
D. (S ) : x + y + ( z + 3)2 2 2 = 3 3
----------------------------------------------- ----------- HẾT ---------- ĐÁP ÁN 1 D 8 B 15 D 22 B 29 C 2 C 9 B 16 D 23 A 30 A 3 D 10 C 17 A 24 A 31 B 4 C 11 D 18 C 25 C 32 C 5 B 12 B 19 D 26 C 33 D 6 D 13 B 20 C 27 C 34 D 7 C 14 D 21 A 28 C 35 B
Trang 4/4 - Mã đề thi 102 THPT THỦ ĐỨC
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017 Môn thi: TOÁN ĐỀ ÔN TẬP HKII
Thời gian làm bài: 90 phút, không kể thời gian phát đề (Đề gồm 03 trang) Mã đề thi 103
Họ, tên thí sinh.......................................................................................
Số báo danh. ..........................................................................................
Câu 1. Nguyên hàm của hàm sổ ( ) 5x f x = là 5x 1 A. ( ) 5x f x dx = ln 5 ∫ B. ( ) 5x f x dx = ∫ C. f (x)dx = ∫ D. f (x)dx = ∫ ln 5 5x ln 5
Câu 2. Nguyên hàm F(x) của hàm số 1 3 ( ) x f x e − = là 1 A. 1−3 ( ) x F x = e + C B. 1−3 ( ) = 3 x F x − e + C C. 1−3 − ( ) x F x = − e + C D. 1 3 ( ) x F x = −e + C 3
Câu 3. Nguyên hàm F(x) của hàm số 2 f (x) = x x là 3 2x x 5 5 3 x 7 2
A. F (x) = + C B. 2 F (x) = x + C
C. F (x) = + C D. 2 F (x) = x + C 7 2 3 x 7 x
Câu 4. Tìm nguyên hàm của hàm số ln f (x) = x 1 1 A. 2 f (x)dx = ln x+C ∫ B. 2
f (x)dx = − ln x + C ∫ 2 2 1 C. f (x)dx = ln x+C ∫ D. = 2 f (x)dx ln x + C ∫ x  π 
Câu 5. Biết F (x) là một nguyên hàm của của hàm số sin f (x) = và F = 2   . Tính F (0) 1+ 3cos x  2  1 2 2 1
A. F (0) = − ln 2 + 2
B. F (0) = − ln 2 + 2
C. F (0) = − ln 2 − 2
D. F (0) = − ln 2 − 2 3 3 3 3
Câu 6. Thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số
y = f (x) liên tục, trục Ox và hai đường thẳng x = a, x = b với a ≤ b quanh trục Ox được tính bởi công thức b b b b A. 2 V = π f (x)dx ∫ B. 2 2 V = π f (x)dx ∫ C. 2 V = f (x)dx ∫
D. V = π | f (x) | dx ∫ a a a a
Câu 7. Cho hàm số f (x) có đạo hàm trên đoạn [ − = − = . Tính giá trị của -1; 3], biết f ( 1) 2 và f (3) 5 3 I = f '(x)dx ∫ 1 − A. I = 3 B. I = 7 C. I = -7 D. I = -10
Câu 8. Diện tích hình phẳng giới hạn bởi hàm số 2
y = x − 3x và trục hoành là S, khi đó giá trị của S 9 9 10 A. S = 3 B. S = − C. S = D. S = . 2 2 3 e 4 ae + b Câu 9. Biết 3 2 x ln xdx = ∫
với a, b là những số nguyên. Tính giá trị b S = 32 a 1 1 1 5 1 A. S = − B. S = − C. S = D. S = . 5 32 32 5
Trang 1/3 - Mã đề thi 103
Câu 10. Diện tích S của hình phẳng giới hạn bởi các đường 5 y = (x +1) , x
y = e và x = 1 có giá trị bằng 23 23 23 23 A. + e B. − e C. − e D. − 2e 2 2 3 2 3 3
Câu 11. Cho f(x) là hàm số liên tục trên [1;3] thỏa f (x)dx = 7 ∫ . Tính I =
f (4 − x)dx ∫ 1 1 A. I = 7 B. I = − 3 C. I = 3 D. I = − 7 x −
Câu 12. Hình phẳng (H) giới hạn bới đồ thị hàm số 2 4
y = x + và hai trục tọa độ. Tính thể tích khối 1
tròn xoay tạo bởi hình phẳng (H) khi quay quanh trục hoành A. (32 +12 ln 3).π B. (32 −11ln 3).π C. (30 −12 ln 3).π D. (32 − 24 ln 3).π 1 dx Câu 13. Biết
= a ln 2 + b ln 3 ∫
, với a, b là các số nguyên. Tính S = a + b 2 x − 5x + 6 0 A. S = 3 − B. S = − 2 C. S =1 D. S = 0 x +
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2 y =
, tiệm cận ngang và các đường x + 2 thẳng x = 0, x = 3 2 5 5 5 A. 4 ln B. 4 + ln C. 4 ln D. 4 − ln 5 2 2 2
Câu 15. Một vật đang chuyển động chậm dần với vận tốc 10m/s thì tăng tốc với gia tốc 2 2
a(t) = 3t + t (m / s ) . Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ bắt đầu tăng tốc bằng 1450 145 4300 430 A. m B. m C. m D. m 3 3 3 3
Câu 16. Cho số phức z = 5 - 4i. Liên hợp của số phức z có môđun là A. 1 B. 41 C. 3 D. 9
Câu 17. Cho số phức z = 2 + i. Phần thực và phần ảo của số phức z lần lượt là A. 1 và 2 B. 2 và -1 C. 1 và -2 D. 2 và 1
Câu 18. Cho số phức z thoả mãn điều kiện. ( + i) z + ( − i)2 3 2 2
= 4 + i . Phần ảo của số phức
w = (1+ z) z là A. 0 B. 2 C. -1 D. -2
Câu 19. Trong mặt phẳng phức, cho 3 điểm A,B,C lần lượt là 3 điểm biểu diễn cho 3 số phức
z = 1+ i, z = (1+ i)2 , z = a − i a ∈  . Để tam giác ABC vuông tại B thì giá trị của a bằng 1 2 3 ( ) A. -3 B. -2 C. 3 D. -4
Câu 20. Cho số phức z = 2 + 5i, phần thực của số phức là A. 2. B. -2. C. -5. D. 5.
Câu 21. Rút gọn biểu thức z = i(2 − i)(3 + i) ta được A. z = 6. B. z = 1+ 7i. C. z = 2+ 5i. D. z = 5i.
Câu 22. Cho số phức z = a + bi (a,b ∈ ) thoả (1+ i)(2z −1) + (z +1)(1− i) = 2 − 2 .
i Tính P = a + b 1 A. P = 0 B. P = 1 C. P = 1 − D. P = − 3
Câu 23. Nghiệm phức của phương trình 2
z − z +1 = 0 là 3 ± i 1± i 3 A. B. 3 ± i C. 1± i 3 D. 2 2
Câu 24. Tìm mô đun của số phức z thỏa z + 2z = 2 − 4i
Trang 2/3 - Mã đề thi 103 2 37 37 14 10 A. B. C. D. − 3 3 3 3
Câu 25. Cho số phức z thỏa mãn z + z = 2 − 8i . Số phức liên hợp của z là A. 15 − + 8i B. 15 − + 6i C. 15 − + 2i D. 15 − + 7i
Câu 26. Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm (
A 1; 2; 0), B(3; 2; − 1) và C( 2; − 1;3) .
Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)? A. 11
− x − 9y +14z − 29 = 0
B. 11x − 9 y +14z − 29 = 0
C. 11x + 9 y +14z + 29 = 0
D. 11x + 9 y +14z − 29 = 0
Câu 27. Trong không gian với hệ tọa độ Oxyz, trong các phương trình sau, phương trình nào là
phương trình của một mặt cầu 2 2 2 2 2 2 A. ( x − )
1 + ( y − 2) + ( z + ) 1 = 1 − B. ( x − )
1 + (2 y − 2) + ( z + ) 1 = 1 − 2 2 2
C. x + y + ( z + )2 2 2 1 − 2x = 15 D. (2x − )
1 + (2 y − 2) − (2z + ) 1 =1 x − y + z
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 1 2 d : = = . Vectơ chỉ 1 3 − 2
phương của đường thẳng d là     A. n = (1; 2 − ;0) B. n = (1; 3 − ;2) C. n = ( 1 − ;2;0) D. n = (1;3; 2)  
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai vec tơ a = ( ;
m 3; 4) và b = (4; ; m 7 − ) . Tìm giá  
trị của m để a ⊥ b A. 4 B. -2 C. -4 D. 2
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho ∆ABC với A(1; 2; − ) 1 , B (2;3; 2 − ) , C (1;0; ) 1 . Tìm
tọa độ đỉnh D sao cho ABCD là hình bình hành A. D(0; -1; -2) B. D(0; 1; 2) C. D(0; 1; -2) D. D(0; -1; 2)
Câu 31. Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(2; 3; -1), N(-1; 1; 1), P(0; m; 0). Giá trị
của m để tam giác MNP vuông tại M bằng 15 13 A. m = 7 B. m = -7 C. m = D. m = 2 2
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(1; 1; 1) và N(-1; 1; 0), P(3; 1; -1). Tìm
tọa độ điểm Q thuộc mặt phẳng (Oxz) và cách đều ba điểm M, N, P.  5 7   3 7   5 7   5 7  A. Q ; 0; −  
B. Q − ; 0; −   C. Q − ; 0;   D. Q ; 0;    6 6   2 2   6 6   6 6  x + y z −
Câu 33. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 1 5 d : = = và mặt phẳng 1 3 − 1 −
(P) : x + y − 2z +11 = 0 . Mệnh đề nào sau đây đúng ?
A. d cắt và không vuông góc với (P).
B. d vuông góc với (P).
C. d song song với (P). D. d nằm trong (P)
Câu 34. Trong không gian với hệ trục tọa độ Oxyz, cho I(3; -1; 2). Phương trình mặt cầu tâm I, bán kính R = 4 là A. (x + ) 3 2 + ( y − ) 1 2 + (z + 2)2 = 16 B. 2 2 2
x + y + z − 6x + 2 y − 4 = 0 C. (x + ) 3 2 + ( y − ) 1 2 + (z + 2)2 = 4 D. 2 2 2
x + y + z − 6x + 2 y − 4z − 2 = 0
Câu 35. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) . 2x – 2y – z – 4 = 0 và mặt cầu (S). 2 2 2
x + y + z − 2x − 4 y − 6z −11 = 0 . Bán kính đường tròn giao tuyến là A. 3 B. 5 C. 2 D. 4
----------------------------------------------- ----------- HẾT ----------
Trang 3/3 - Mã đề thi 103 ĐÁP ÁN 1 C 8 C 15 C 22 A 29 A 2 C 9 A 16 B 23 D 30 D 3 A 10 B 17 D 24 A 31 A 4 A 11 A 18 C 25 A 32 A 5 B 12 D 19 A 26 D 33 D 6 A 13 C 20 A 27 C 34 D 7 B 14 C 21 B 28 B 35 D
Trang 4/3 - Mã đề thi 103 THPT THỦ ĐỨC
KỲ KIỂM TRA HỌC KÌ II NĂM HỌC 2016 - 2017 Môn thi: TOÁN ĐỀ ÔN TẬP HKII
Thời gian làm bài: 90 phút, không kể thời gian phát đề (Đề gồm 04 trang) Mã đề thi 104
Họ, tên thí sinh.......................................................................................
Số báo danh. ..........................................................................................
Câu 1. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f ( x) liên tục; trục hoành và hai đường thẳng x = ;
a x = b (a < b) bằng b b b b A. S = π f ∫ (x) . dx B. S = f ∫ (x) . dx C. S = f ∫ (x) . dx D. S = π f ∫ (x) . dx a a a a
Câu 2. Nguyên hàm của hàm số f ( x) = ( x + )5 2 1 là 1 1 A. f
∫ (x)dx = (2x+ )6 1 + C. B. f
∫ (x)dx = = (2x+ )6 1 + C. 12 6 1 C. f
∫ (x)dx = ( x+ )4 2 2 1 + C . D. f
∫ (x)dx = (2x+ )4 1 + C. 2
Câu 3. Nguyên hàm của hàm số 2 1 ( ) x f x e + = là 1 A. 2 x 1 f (x)dx e + = + C. ∫ B. ( ) x f x dx = e + C. ∫ 2 1 C. 2 x 1 f (x)dx e + = + C. ∫ D. x 1 f (x)dx e + = + C. ∫ 2 1  3 
Câu 4. Gọi F(x) là nguyên hàm của hàm số f (x) = và F = 0   . Giá trị F(3) bằng 2 x − 3x + 2  2  A. ln2. B. 2ln2 . C. –ln2. D. -2ln2.
Câu 5. Nguyên hàm của hàm số 2 ( ) = . x f x x e là 1     x 1 x 1 A. 2 F (x) = e x − + C.   B. 2
F (x) = 2e x − + C.   2  2   2  1 C. 2 ( ) = 2 x F x
e ( x − 2) + C. D. 2 ( ) x F x =
e ( x − 2) + C. 2 π 2
Câu 6. Giá trị của 3
I = sin x cos xdx ∫ bằng 0 1 1 A. I = . B. I = 4. C. I = π. D. I = 0. 4 4
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x − 3x +1 và đồ thị hàm số y = 2 − x +1 bằng 1 1 A. . B. 6. C. 8. D. . 6 3 e 1 a
Câu 8. Biểu thức tích phân 2 I = . x ln xdx = e + ∫
với m là số nguyên khác 0, a là phân số tối m b b 1
giản. Giá trị của tổng S = m + a + b bằng A. S = 10. B. S = 5. C. S = 9. D. S = 13.
Trang 1/4 - Mã đề thi 104
Câu 9. Ký hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số x
y = e ; trục hoành; đường thẳng x = 0
và đường thẳng x =1. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox? π A. 2 e −1. B. 2 π (e −1). C. π (e −1). D. ( 2e − )1. 2
Câu 10. Một chiếc lò xo có độ dài tự nhiên 0,15m. Khi lò xo bị kéo giãn thêm x(m) thì xuất hiện lực
đàn hồi f (x) = 800x(N ). Tính công A của lực đàn hồi thực hiện được khi lò xo từ trạng thái có độ
dài 0,18m về trạng thái tự nhiên? A. 2 A 36.10− = J. B. 2 A 72.10− = J.
C. A = 36J.
D. A = 72J. 4
Câu 11. Cho hàm số f (x) có đạo hàm trên đoạn [2; 4], f (2) = 12 , f '(x) liên tục và f '(x)dx = 17 ∫ . 2
Giá trị f (4) bằng A. 9. B. 5. C. 19. D. 29.
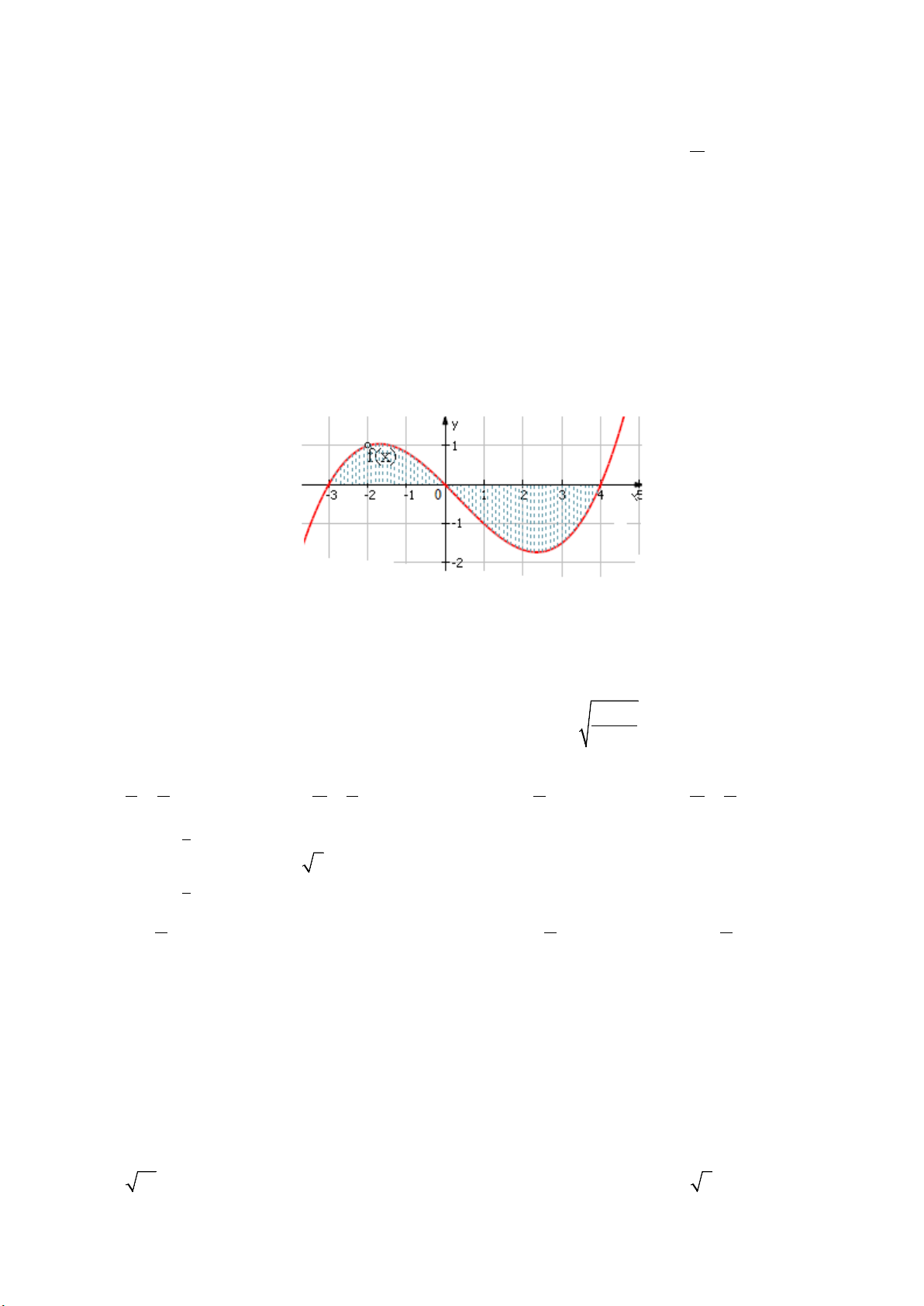
Câu 12. Cho đồ thị hàm số y = f (x) . Diện tích hình phẳng (phần tô đậm trong hình) là 1 4 0 0 A. f (x)dx + f (x) . dx ∫ ∫ B. f (x)dx + f (x) . dx ∫ ∫ 3 − 1 3 − 4 0 4 4 C. f (x)dx + f (x) . dx ∫ ∫ D. f (x) . dx ∫ 3 − 0 3 − x
Câu 13. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y =
, trục tung, trục hoành và x 2 4 − x
= 1. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox. 1 4 π 3 4 π 4 A. ln . B. ln . C. π ln . D. ln . 2 3 2 4 3 2 3 π 2
Câu 14. Biết cos xdx = a + b 3 ∫
, với a, b là các số hữu tỉ. Giá trị biểu thức S = a − 4b π 3 9 1 1 A. S = . B. S = 3. C. S = − . D. S = . 2 2 2
Câu 15. Cho hai hàm y = f ( x), y = g ( x) có đạo hàm trên  . Phát biểu nào sau đây đúng ? A. Nếu f '
∫ (x)dx = g '
∫ (x)dx thì f (x) = g(x), x ∀ ∈ .  B. Nếu f
∫ (x)dx = g
∫ (x)dx thì f (x) ≠ g(x), x ∀ ∈ .  C. Nếu f
∫ (x)dx = g
∫ (x)dx thì f (x) = g(x), x ∀ ∈ . 
D. Nếu f ( x) = g ( x) + 2017, x ∀ ∈  thì f '
∫ (x)dx = g ' ∫ (x) . dx
Câu 16. Cho hai số phức z = 3 + 3i, z = 2 − i . Môđun của số phức z = z − z bằng 1 2 1 2 A. 17. B. 17. C. 5. D. 5.
Câu 17. Tìm số phức liên hợp của số phức z = 2 − i(1+ i) ?
Trang 2/4 - Mã đề thi 104 A. z = 2 + 2 . i B. z = 2 − 2 . i C. z = 2 − + 2 .i D. z = 2 − − 2 .i
Câu 18. Cho số phức z thỏa z = (2 + i)(1− i) +1+ 3i . Môdun của số phức z bằng A. z = 13. B. z = 2 2. C. z = 2 5. D. z = 4 2.
Câu 19. Gọi z , z là hai nghiệm của phương trình 2
z − 4z + 5 = 0 . Tổng S = z + z bằng 1 2 1 2 A. S = 5. B. S = 4. C. S = 2 5. D. S = 2.
Câu 20. Tọa độ điểm biểu diễn hình học của số phức z thỏa mãn (2 + 3i)z = 7 + 4i là A. (2;1). B. (2; 2). C. (2; 1) − . D. ( 1 − ;2). 1 3
Câu 21. Cho số phức z = − + i . Số phức ( )2 z bằng 2 2 1 3 1 3 A. − − . i B. − + . i C. 1+ 3 . i D. 3 − . i 2 2 2 2
Câu 22. Cho số phức z thỏa mãn z (1+ 2i) − 7 − 4i = 0 . Môđun số phức w = z + 2i bằng A. 4. B. 17. C. 24. D. 5.
Câu 23. Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z + 2z + 3 = 0 . Trên mặt phẳng tọa 1
độ. Điểm M biểu diễn số phức z có tọa độ là 1 A. M(-1; 2). B. M(-1; -2). C. M( 1 − ;− 2). D. M( 1 − ;− 2i).
Câu 24. Cho số phức z = a + bi (a,b ∈ ) thỏa mãn. 2
(3 + 2i)z + (2 − i) = 4 + i . Giá trị biểu thức
P = a − b bằng A. 1. B. 0. C. 4. D. 6.
Câu 25. Biết rằng nghịch đảo của số phức z bằng số phức liên hợp của nó. Trong các kết luận sau, kết luận nào đúng? A. z = 2. − B. z = 1. C. z = 3. D. z = 2.
Câu 26. Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 1; -1) và đường thẳng x − 2 y +1 d : =
= z . Viết phương trình mặt phẳng qua A và vuông góc với đường thẳng d 2 1 − A. 2x - y + z = 0. B. 2x + y + z = 0. C. 2x - y - 1 = 0. D. 2x - y + 1 = 0. 
Câu 27. Trong không gian với hệ toạ độ Oxyz, cho vectơ n (1; 1 − ; 2
− ) . Mặt phẳng nào có phương trình 
dưới đây nhâ ̣n vectơ n làm vectơ pháp tuyến?
A. −x − y + 2z + 3 = 0
B. −x + y − 2z + 3 = 0 .
C. x − y − 2z + 3 = 0 .
D. x − y + 2z + 3 = 0 .
Câu 28. Trong không gian với hệ toạ độ Oxyz, tìm toạ độ tâm I và bán kính R của mặt cầu (S) có phương trình 2 2 2
(x − 3) + y + (z −1) = 9 A. I ( 3 − ;0;− ) 1 , R = 9 B. I (3;0; ) 1 , R = 9 . C. I ( 3 − ;0;− ) 1 , R = 3 . D. I (3;0; ) 1 , R = 3
Câu 29. Trong không gian với hệ toạ độ Oxyz, cho mă ̣t phẳng (P) : 2x − 2 y + z − 5 = 0 . Điểm nào dưới
đây có khoảng cách đến mă ̣t phẳng (P) bằng 3? A. (1; 1; -4). B. (1; 1; 2). C. (1; -1; 0). D. (-1; 1; 6).
Câu 30. Trong không gian với hệ toạ độ Oxyz, cho 3 điểm A(3;0;0), B (0; 2; − 0),C (0;0; ) 1 . Phương
trı̀nh nào dưới đây là phương trı̀nh mă ̣t phẳng (ABC)? x y z x y z x y x y A. − + = 0. B. − + = 1. C. − + z = 1. − D. + + z = 0. 3 2 1 3 2 1 3 2 3 2
Trang 3/4 - Mã đề thi 104 x =1+ t
Câu 31. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d :  y = 2t (t ∈ ) và mă ̣t phẳng z =1−t
(α ): x +3y + 7z −5 = 0 . Mê ̣nh đề nào dưới đây đúng?
A. d song song với (α). B. d nằm trong (α).
C. d vuông góc với (α). D. d cắt (α).
Câu 32. Trong không gian với hệ toạ độ Oxyz, cho điểm A(4; -3; 1) và đường thẳng x = 3 + td :  y = 1
− (t ∈ ) . Viết phương trı̀nh của mă ̣t cầu (S) đi qua điểm A có bán kính bằng 3 và tâm của z =1+t
mă ̣t cầu (S) nằm trên đường thẳng d? 2 2 2 2
A. ( x − ) + ( y − ) 2 2 1 + z = 9.
B. ( x + ) + ( y + ) 2 2 1 + z = 9. 2 2 2 2
C. ( x − ) + ( y + ) 2 2 1 + z = 9.
D. ( x + ) + ( y + ) 2 2 1 + z = 3.
Câu 33. Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 4; -4), đường thẳng  x =1− t
d :  y = 2 + t (t ∈ ) . Viết phương trı̀nh của đường thẳng ∆ đi qua điểm A vuông góc với d và đồng  z = 2 −  thời cắt d? x =1+ tx =1+ t  
A. ∆ :  y = 4 + t (t ∈ ).
B. ∆ :  y = 4 + t (t ∈ ).   z = 4 − − 2tz = 4 − + 2t  x =1+ tx =1+ t  
C. ∆ :  y = 4 − t (t ∈ ).
D. ∆ :  y = 4 + t (t ∈ ).   z = 4 − − 2tz = 4 − 2t
Câu 34. Trong không gian với hệ toạ độ Oxyz, cho điểm M(1; 2; 4). Viết phương trı̀nh mă ̣t phẳng (P)
đi qua điểm M và cắt các tia Ox, Oy, Oz lần lượt ta ̣i các điểm A, B, C sao cho thể tı́ch khối chóp OABC nhỏ nhất? x y z x y z x y z A. + + = 1. B. + + = 1.
C. x + 2 y + 4z −1 = 0. D. + + = 1. − 1 2 4 3 6 12 1 2 4
Câu 35. Trong không gian với hệ toạ độ Oxyz, tìm toạ độ tiếp điểm của mặt cầu (S). 2 2 2
x + y + z − 2x + 4 y − 2z − 8 = 0 và mặt phẳng (P). 2x + 3y + z – 11 = 0? A. (3; 1; 2). B. (-3; 1; 2). C. (0; 0; 11). D. (-1; 2; 15).
----------------------------------------------- ----------- HẾT ---------- ĐÁP ÁN 1 B 8 C 15 D 22 D 29 A 2 A 9 D 16 A 23 C 30 B 3 C 10 A 17 A 24 B 31 A 4 C 11 D 18 C 25 B 32 C 5 A 12 B 19 C 26 A 33 A 6 A 13 D 20 A 27 C 34 B 7 A 14 B 21 B 28 D 35 A
Trang 4/4 - Mã đề thi 104
Document Outline

  • De on tap HKII De 101
  • On Tap HKII De 102
  • De on tap HKII De 103
  • De on HKII De 104