Bộ đề ôn thi tốt nghiệp THPT 2023 môn Toán sở GD&ĐT Tiền Giang

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 1

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT CHUYÊN

ÔN THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho cấp số cộng

( )

n

u

với

1

1u =

; công sai

2d =

. Số hạng thứ 3 của cấp số cộng đã cho là

A.

3

4u =

. B.

3

5u =

. C.

3

7u =

. D.

3

3u =

.

Câu 2: Có bao nhiêu cách xếp 7 học sinh thành một hàng dọc?

A.

7

. B.

49

. C.

7!

. D.

1

.

Câu 3: Chọn ngẫu nhiên hai số khác nhau từ

21

số nguyên dương đầu tiên. Xác suất để chọn được hai

số có tích là một số lẻ bằng

A.

11

42

. B.

9

42

. C.

121

210

. D.

1

2

.

Câu 4: Cho hàm số

( )

fx

có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

( )

0;

+∞

. B.

( )

0; 2

. C.

( )

2; 0−

. D.

( )

;2−∞ −

.

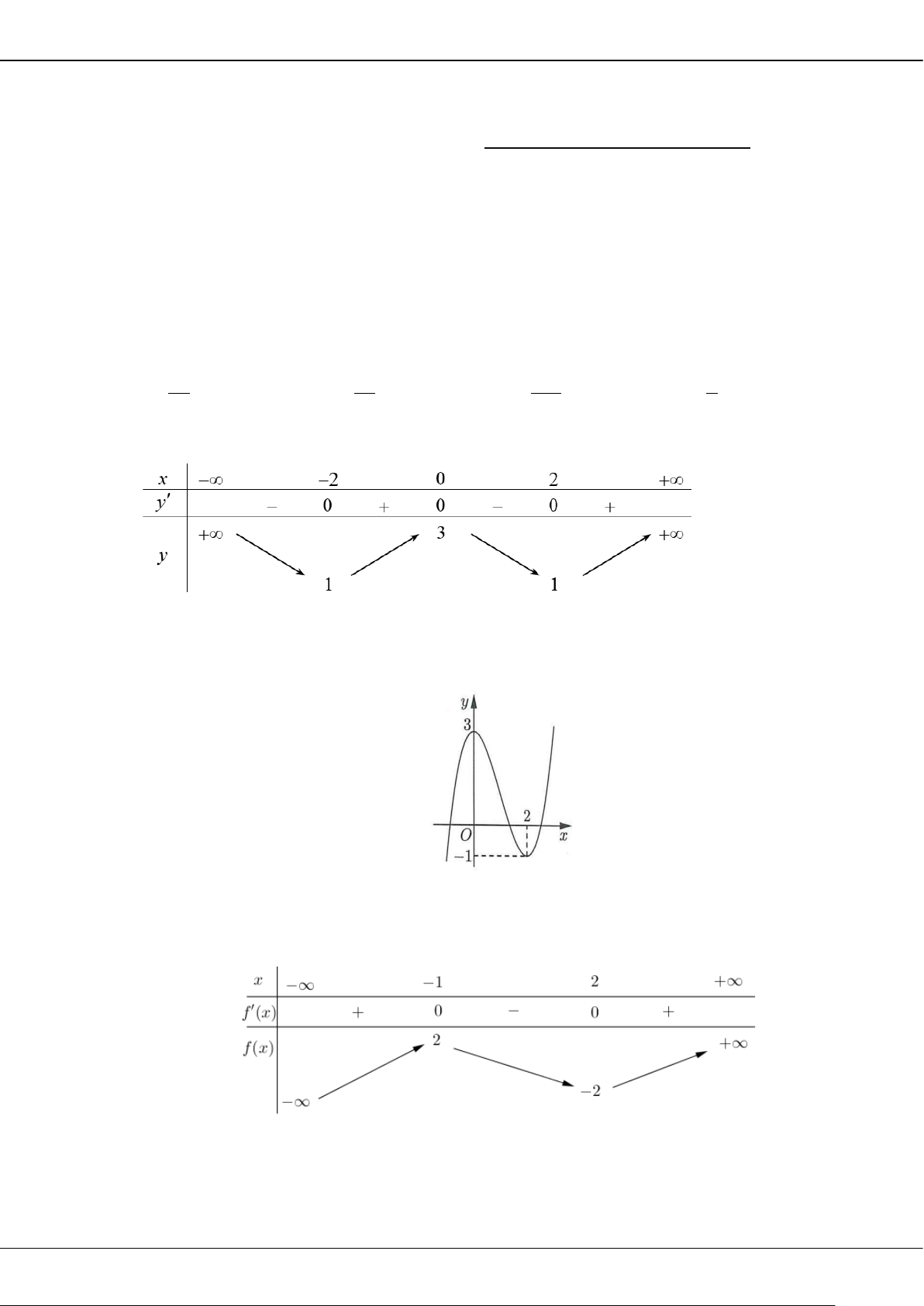
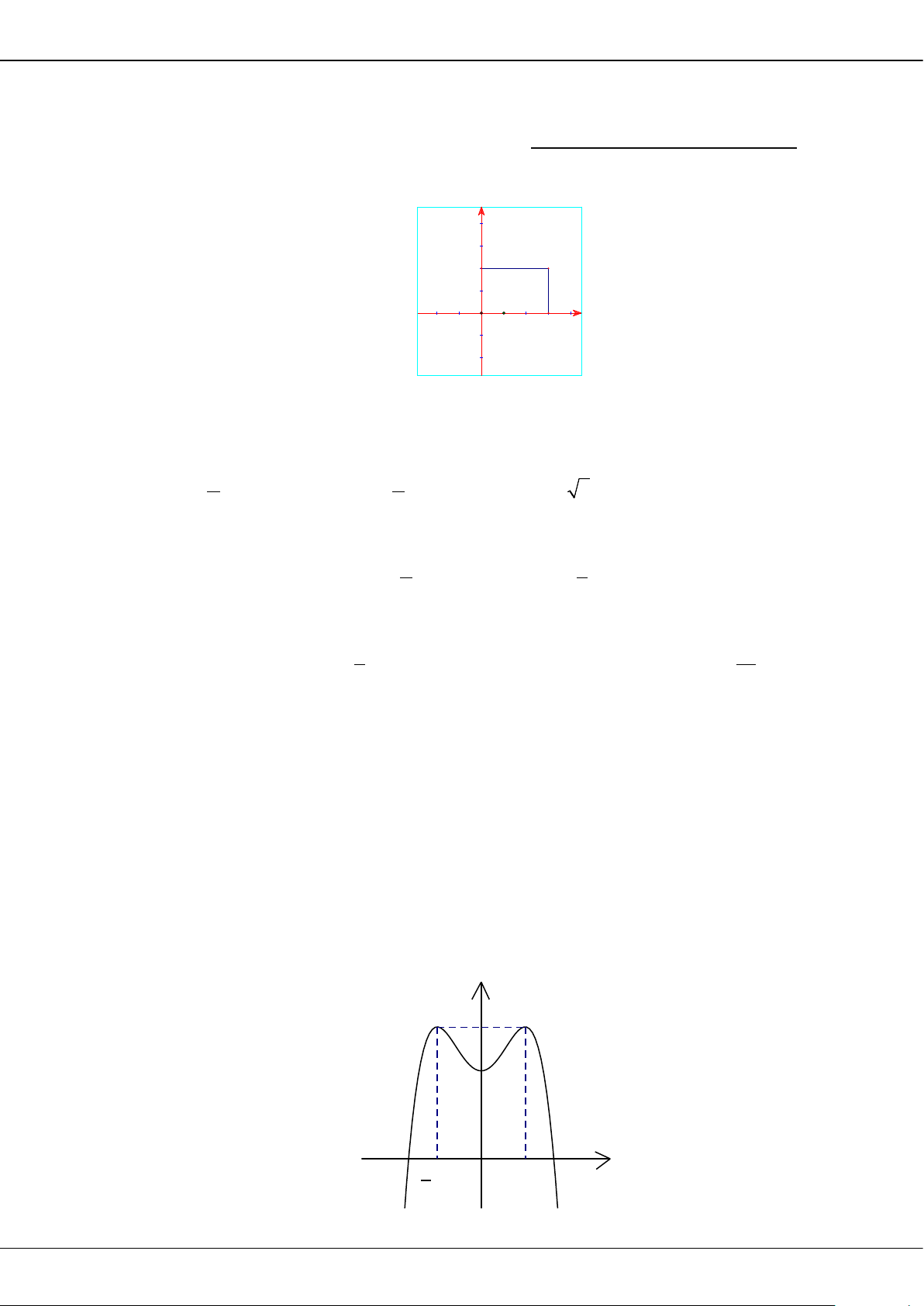
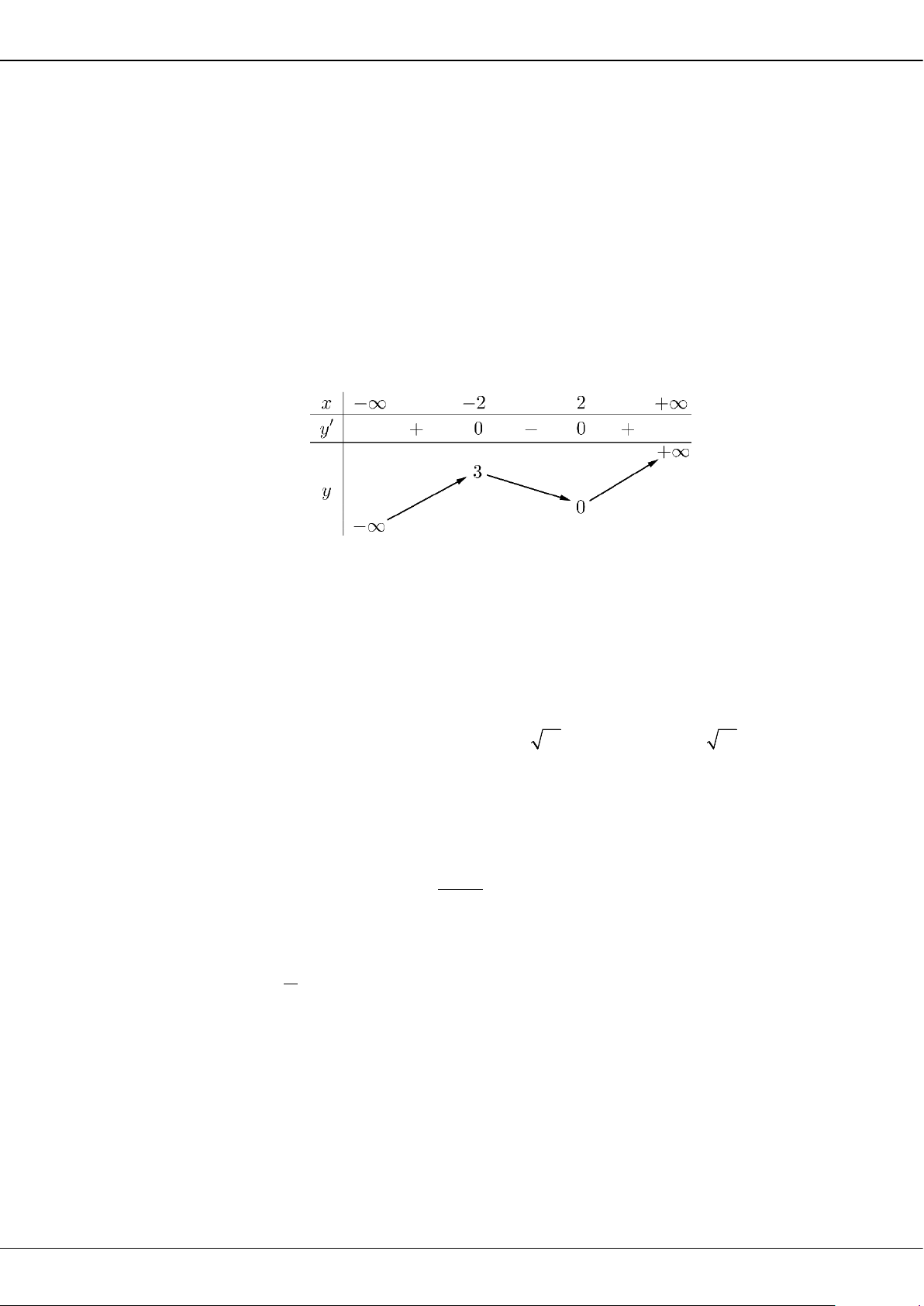
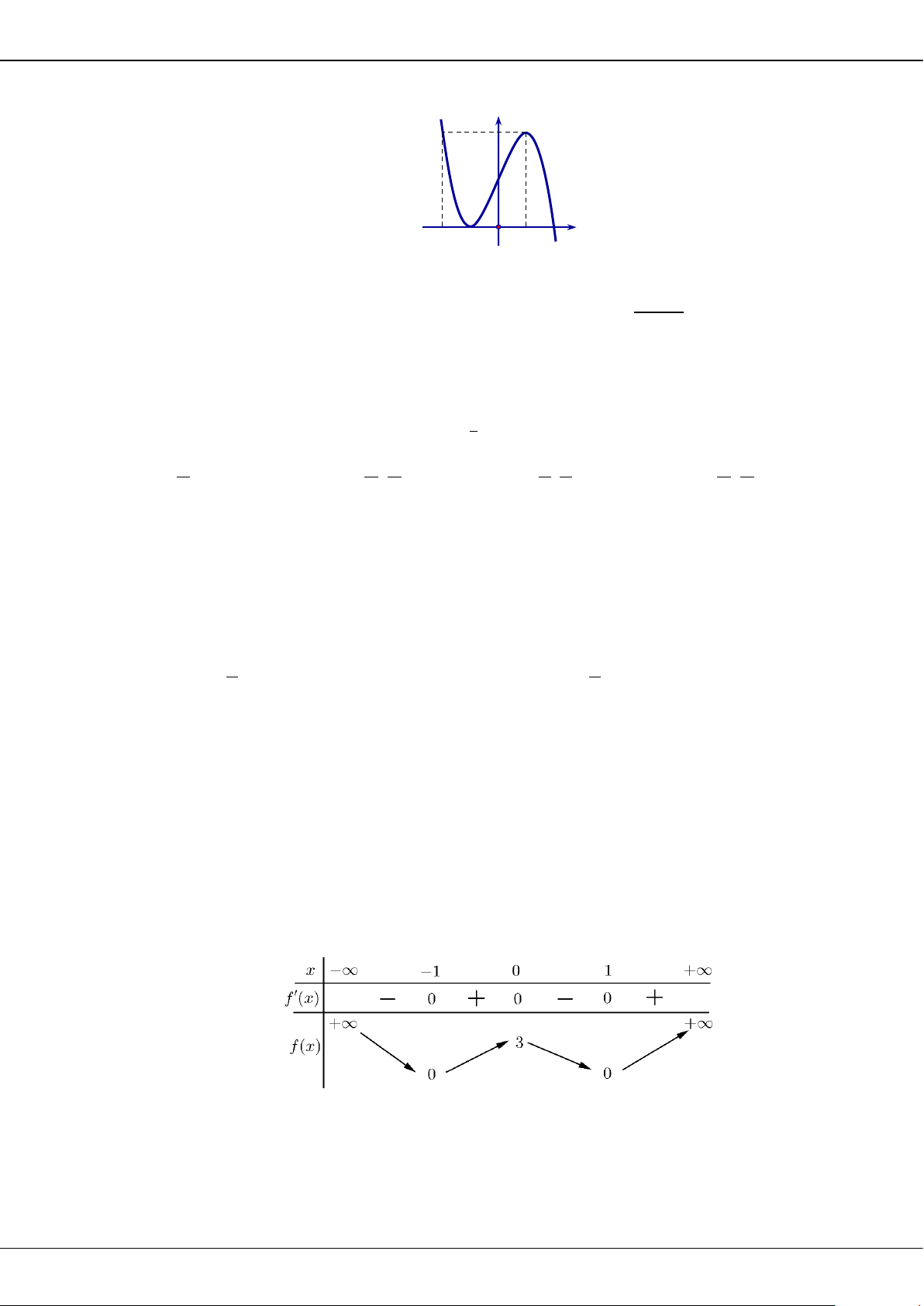
Câu 5: Cho hàm số bậc ba  = () có đồ thị là đường cong trong hình bên.

Giá trị cực tiểu của hàm số đã cho là

A.

1−

. B.

3

. C.

2

. D.

0

.

Câu 6: Cho hàm số

( )

fx

có bảng biến thiên như sau:

Số nghiệm của phương trình

( )

1fx=

là

A.

3

. B.

1.

C.

2

. D.

0

.

Câu 7: Đồ thị hình bên dưới là đồ thị của hàm số nào?

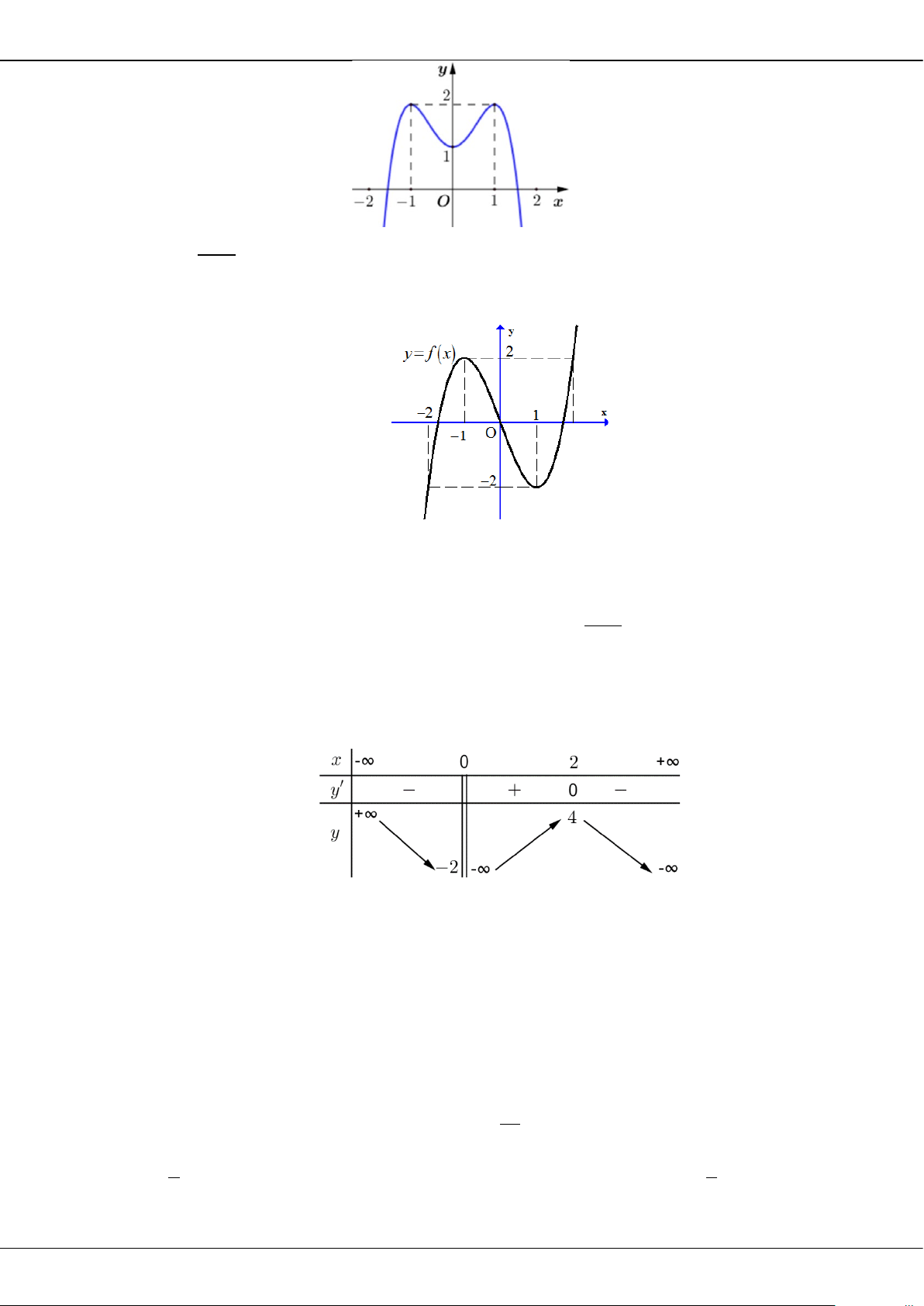
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 2

A.

1

2

x

y

x

+

=

−

. B.

2

21yx x=−+ +

. C.

42

21yx x=−+ +

. D.

3

34yx x

= +−

Câu 8: Cho hàm số

( )

y fx=

có đồ thị như hình vẽ sau:

Điểm cực đại của đồ thị hàm số

(

)

y fx=

là

A.

1

. B.

(

)

1; 2−

. C.

1−

. D.

( )

1; 2−

.

Câu 9: Phương trình đường tiệm cận ngang của đồ thị hàm số

1

2

x

y

x

+

=

−

là

A.

1y

=

. B.

2y = −

. C.

1

y = −

. D.

0

y =

.

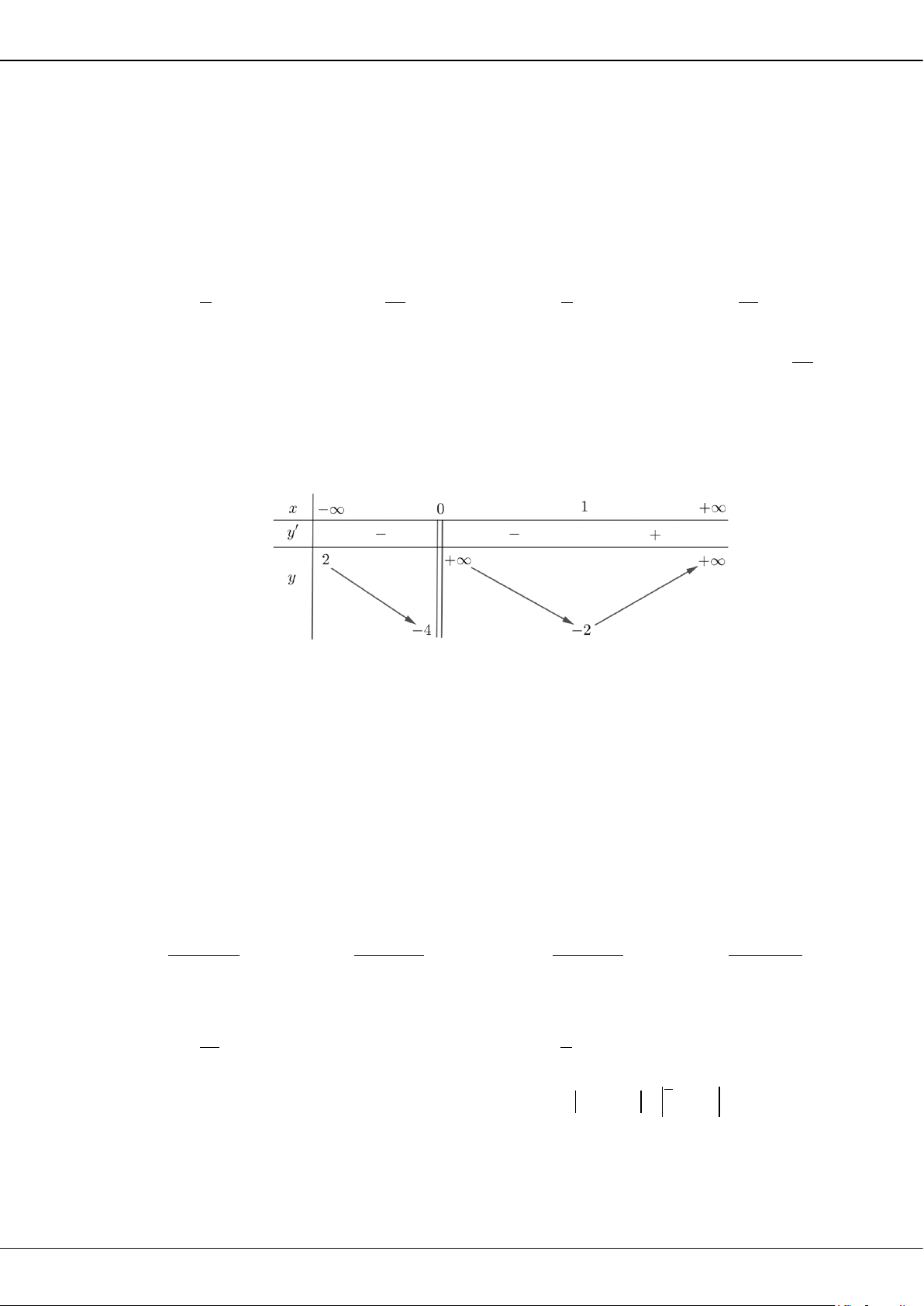
Câu 10: Cho hàm số

( )

y fx=

xác định trên

{ }

\0

, liên tục trên mỗi khoảng xác định và có bảng biến

thiên như sau:

Tập hợp tất cả các giá trị thực của tham số

m

sao cho phương trình

( )

fx m=

có ba nghiệm

thực phân biệt là

A.

( )

2; 4−

. B.

[ ]

2; 4−

. C.

(

]

2; 4−

. D.

(

]

;4−∞

.

Câu 11: Cho hàm số

( )

y fx=

liên tục trên



và có đạo hàm

( ) ( ) ( ) (

)

23

1 13fx x x x

′

=− +−

. Hàm số

( )

y fx=

đồng biến trên khoảng nào dưới đây?

A.

( )

;1−∞

. B.

( )

;1−∞ −

. C.

( )

1; 3

. D.

( )

3; +∞

.

Câu 12: Cho

0a >

và khác

1

, giá trị của biểu thức

3

1

log

a

bằng

A.

2

3

. B.

3−

. C.

3

. D.

1

3

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 3

Câu 13: Tập xác định của hàm số

( )

3

2yx

−

= −

là

A.

( )

2; +∞

. B.

( )

;2−∞

. C.

{ }

\2



. D.



.

Câu 14: Đạo hàm của hàm số

logyx=

là

A.

1

.

x

B.

1

.

ln10x

C.

1

.

10ln x

D.

ln10

.

x

Câu 15: Tổng tất cả các nghiệm của phương trình

( )

2

log 5 2 2

x

x−=−

bằng

A.

3

.

B.

1

.

C.

2

.

D.

0

.

Câu 16: Tập nghiệm bất phương trình

28

x

>

là

A.

( )

;3

−∞

. B.

[

)

3;+∞

. C.

( )

3;

+∞

. D.

(

]

;3−∞

.

Câu 17: Bất phương trình

(

)

2

log 1 2 2

x−<

có bao nhiêu nghiệm nguyên?

A. 2. B.

4

. C.

3

. D.

1

.

Câu 18: Nếu

( )

1

d

fx x C

x

= +

∫

thì

( )

fx

là

A.

( )

2

1

fx

x

=

. B.

( )

lnfx x=

. C.

(

)

fx x

= −

. D.

( )

2

1

fx

x

= −

.

Câu 19: Họ nguyên hàm của hàm số

(

)

2

3fx x x

= +

là

A.

32

xxC

++

. B.

3

1xC++

. C.

32

1

3

2

x xC++

. D.

32

1

2

x xC++

.

Câu 20: Cho

( )

2

0

d1fx x

=

∫

, khi đó

( )

2

0

3 1dfx x−





∫

bằng

A.

2

. B.

1

. C.

5

. D.

4

.

Câu 21: Cho

3

1

( )d 3fx x=

∫

và

3

1

( )d 4gx x=

∫

. Giá trị

[

]

3

1

4 () ()df x gx x+

∫

bằng

A.

16

. B.

11

. C.

19

. D.

7

.

Câu 22: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

2

2yx x= −

và trục hoành là

A.

1

3

. B.

1

. C.

2

3

. D.

4

3

.

Câu 23: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm

M

như hình vẽ bên dưới?

A.

12i−

. B.

2i +

. C.

2 i−+

. D.

12i+

.

Câu 24: Số phức nào dưới đây là số thuần ảo?

A.

2z = −

. B.

3zi= +

. C.

3zi=

. D.

23zi=−+

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 4

Câu 25: Cho hai số phức

1

37zi= −

và

2

23zi

= +

. Số phức

12

zz z= +

là

A.

1 10zi= −

. B.

54zi

= −

. C.

3 10zi= −

. D.

33zi

= +

.

Câu 26: Cho khối lăng trụ đứng có cạnh bên bằng

5

, đáy là hình vuông có cạnh bằng

4

. Thể tích khối

lăng trụ đã cho bằng

A.

100

. B.

80

. C.

64

. D.

20

.

Câu 27: Cho hình chóp

SABCD

có đáy

ABCD

là hình vuông cạnh

a

,

( )

SA ABCD⊥

,

2SB a

=

.

Khi đó, thể tích khối chóp

.S ABCD

bằng

A.

3

a

. B.

3

a

. C.

3

6

a

. D.

3

2

3

a

.

Câu 28: Cho khối chóp

S ABC

có đáy

ABC

là tam giác vuông cân tại

,B AB a=

. Canh bên

( )

SA ABC⊥

, góc tạo bởi hai mặt phẳng

( )

ABC

và

( )

SBC

bằng

0

60

.

Thể tích của khối chóp đã cho bằng

A.

3

6

a

. B.

3

2

a

. C.

3

6

2

a

. D.

3

6

a

.

Câu 29: Diện tích mặt cầu bán kính

2a

bằng

A.

2

16a

. B.

2

16 a

π

. C.

2

4a

. D.

2

4 a

π

.

Câu 30: Một hình trụ có bán kính đáy là

R

và chiều cao bằng

3R

thì diện tích xung quanh của nó bằng

A.

2

23R

π

. B.

2

R

π

. C.

2

2 R

π

. D.

2

3 R

π

.

Câu 31: Trong không gian

Oxyz

, một vectơ pháp tuyến của mặt phẳng

( )

:2 3 1 0xz

α

− +=

là

A.

( )

1

2; 3;1n = −

 

. B.

( )

2

2; 0; 3n = −

 

. C.

(

)

2

0; 2; 3n = −

 

. D.

( )

2

2; 3; 0n = −

 

.

Câu 32: Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 2 4 6 50Sx y z x y z+ + − − − +=

. Bán kính mặt cầu

( )

S

bằng

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 5

A.

3

. B.

6

. C.

1

. D.

19

.

Câu 33: Trong không gian

Oxyz

, cho ba điểm

( )

1;0;0A

,

( )

0; 2; 0B

và

( )

0, 0,3C

. Khoảng cách từ gốc

tọa độ

O

đến

( )

ABC

bằng

A.

3

5

. B.

1

3

. C.

6

11

. D.

6

7

.

Câu 34: Trong không gian

Oxyz

, đường thẳng

123

:

22 1

xy z

d

−−−

= =

−

đi qua điểm nào dưới đây?

A.

( )

1; 2; 3

.

B.

( )

2; 2; 1−

. C.

( )

1;2;3−−−

.

D.

( )

2; 2; 1−−

.

Câu 35: Trong không gian

Oxyz

, đường thẳng

Oy

có phương trình tham số là

A.

( )

xt

y tt

zt

=





= ∈





=





. B.

( )

0

2

0

x

y tt

z

=





=+∈





=





. C.

( )

0

x

yt

zt

=





= ∈





=





. D.

( )

0

xt

yt

z

=





= ∈





=





.

Câu 36: Tập hợp các điểm biểu diễn các số phức

z

thỏa mãn

2z zi+=−

là một đường thẳng có phương

trình là

A.

4 2 30xy+ +=

. B.

2 4 13 0

xy

+ +=

. C.

4 2 30xy− +=

. D.

2 4 13 0xy− +=

.

Câu 37: Trong không gian

Oxyz

, gọi

( )

;;M abc

′

là hình chiếu vuông góc của điểm

( )

3; 0; 4M

trên mặt

phẳng

( )

: 2 3 10Px y z+ − +=

, giá trị của

abc

++

là

A.

7

. B.

8

. C.

4

7

. D.

2

.

Câu 38: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2

a

. Tam giác

SAD

cân tại

S

và nằm trong

mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp bằng

3

4

3

a

. Khoảng cách từ

B

đến

mặt phẳng

( )

SCD

bằng

A.

3

a

. B.

2

a

. C.

3a

. D.

2a

.

Câu 39: Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

(

)

fx

trên



thỏa

mãn

(

) ( )

424 4

FG+=

và

( ) ( )

020 2FG+=−

. Khi đó

( )

2

0

2df xx

∫

bằng

B.

1

3

. B.

2

3

. C.

2

. D.

1

.

Câu 40: Số giá trị nguyên của tham số

m

để hàm số

( )

4 22

3y mx m x m= −− +

không có điểm cực đại là

A. 2. B. vô số. C. 0. D. 4.

Câu 41: Có bao nhiêu cặp số nguyên

(

)

;xy

thỏa mãn

( )

22

log 4 log 2 1xy xy+ +− + ≤

và

20xy−≥

?

A.

5

. B.

3

. C.

4

. D.

2

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 6

Câu 42: Cho hai số phức

1

z

,

2

z

khác

0

thỏa mãn

1

2

z

là số thuần ảo và

12

10

zz−=

. Giá trị lớn nhất của

12

zz+

bằng

A.

10

. B.

10 2

. C.

10 3

. D.

20

.

Câu 43: Cho khối lăng trụ đứng

.ABC A B C

′′′

có



0

60BAC

=

,

3AB a=

và

4AC a=

. Gọi

M

là trung

điểm của

BC

′′

, biết khoảng cách từ

M

đến mặt phẳng

( )

B AC

′

bằng

3 15

10

a

. Thể tích khối lăng

trụ đã cho bằng

A.

3

27a

. B.

3

9a

. C.

3

4a

. D.

3

a

.

Câu 44: Cho hàm số

()fx

có đạo hàm liên tục trên đoạn

[ ]

1; 2

và thỏa mãn

1

(1)

2

f = −

và

( )

3 22

() () 2 (), [1;2].f x xf x x x f x x

′

+ = + ∀∈

Giá trị của tích phân

2

1

()x f x dx

∫

bằng

A.

4

ln

3

. B.

3

ln

4

. C.

ln 3

. D. 0.

Câu 45: Gọi

S

là tập hợp tất cả số thực

m

để phương trình

2

21 0zz m− +− =

có nghiệm phức

z

thỏa

mãn

2z =

. Tổng các phần tử của

S

bằng

A.

7

. B.

5

. C.

4

. D.

6

.

Câu 46: Cho hàm số

( )

32

337 2023f x x mx nx= + ++

với

,mn

là các số thực. Biết rằng hàm số

( ) ( ) ( ) ( )

'"gx fxfxfx=++

có hai giá trị cực trị là

2023

2022e −

và

2022

e −

. Diện tích hình

phẳng giới hạn bởi các đường

(

)

(

)

2022

fx

y

gx

=

+

và

1y =

bằng

A.

2023

. B.

2022

. C.

2024

. D.

2021

.

Câu 47: Cho các số phức

, ,wzv

thay đổi thỏa mãn

2023

34 2i zi

− +⋅ =

, phần thực của

v

bằng phần ảo

của

w

và bằng

1−

. Giá trị nhỏ nhất của biểu thức

22

wT zv z

=− +−

bằng

A.

3

. B.

9

. C.

4

. D.

7

.

Câu 48: Có bao nhiêu bộ

( )

;xy

với

,xy

là các số nguyên và

1 , 2023xy≤≤

, đồng thời thỏa mãn điều

kiện

( )

32

2 21

2 4 8 log 2 3 6 log

23

yx

xy x y x y xy

yx

+

+++ ≤ +−−

+−

?

A.

4046

. B.

4040

. C.

4036

. D.

4030

.

Câu 49: Trong không gian

Oxyz

, cho hai điểm

( )

1; 5; 2A −−

,

( )

3; 3; 2B −

và đường thẳng

d

có phương

trình

334

111

xyz−++

= =

; hai điểm

C

và

D

thay đổi trên

d

thỏa

63CD =

. Biết rằng khi

( ) ( )

;; 2C abc b<

thì tổng diện tích tất cả các mặt của tứ diện

ABCD

đạt giá trị nhỏ nhất. Khi

đó, tổng

abc

++

bằng

A.

2

. B.

1−

. C.

4−

. D.

7−

.

Câu 50: Cho hàm đa thức

()fx

có

( )

( )( ) ( )

2022

1 2023 3fx x x x

′

=+− −

. Hỏi có tất cả bao nhiêu cặp số

nguyên không âm

(;)mn

để hàm số

( )

2

( 1) cos 2y f m xn=+−

đồng biến trên

0;

2

π







?

A.

0

. B.

1

. C.

2

. D.

3

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 7

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT ĐỐC BINH KIỀU

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Điểm

A

trong hình vẽ bên dưới biểu diễn cho số phức

z

. Mệnh đề nào sau đây đúng?

A. Phần thực là

3

, phần ảo là

2

. B. Phần thực là

3

, phần ảo là

2i

.

C. Phần thực là

3−

, phần ảo là

2

i

. D. Phần thực là

3−

, phần ảo là

2

.

Câu 2: Hàm số nào sau đây đồng biến trên



?

A.

e

x

y



=



π



. B.

2

e

x

y



=





. C.

( )

2

x

y =

. D.

( )

0,5

x

y =

.

Câu 3: Đạo hàm của hàm số

3

yx

−

=

là:

A.

4

yx

−

′

= −

. B.

2

1

2

yx

−

′

= −

. C.

3

1

3

yx

−

′

= −

. D.

4

3yx

−

′

= −

.

Câu 4: Giải bất phương trình

( )

2

log 3 1 3

x −>

.

A.

3x >

B.

1

3

x<<

C.

3x <

D.

10

3

x

>

Câu 5: Cho cấp số cộng

( )

n

u

có

1

1u =

và

2

3u

=

. Giá trị của

3

u

bằng

A.

6.

B.

9.

C.

4.

D.

5.

Câu 6: Trong không gian

Oxyz

, cho đường thẳng

2

: 12

13

= +





= −





=−+



xt

dy t

zt

. Vectơ nào dưới đây là một vectơ chỉ

phương của

d

?

A.

( )

4

2;1;1

=

 

u

. B.

(

)

1

2; 1; 1= −



u

. C.

( )

3

1; 2; 3

= −

 

u

. D.

(

)

2

1; 2; 3=

 

u

.

Câu 7: Cho hàm số

( )

42

f x ax bx c=++

có đồ thị là đường cong trong hình vẽ bên. Số nghiệm của

phương trình

( )

1fx=

là

A.

1.

B.

2.

C.

4.

D.

3.

x

y

3

A

O

2

3

2

O

1

x

y

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 8

Câu 8: Nếu

(

)

2

1

d2fx x

−

=

∫

và

( )

5

2

d5fx x= −

∫

thì

(

)

5

1

dfx x

−

∫

bằng

A.

7−

. B.

3−

. C.

4

. D.

7

.

Câu 9: Đồ thị của hàm số nào dưới đây có dang như đường cong trong hình bên?

A.

42

2 1.yx x=−+ −

B.

42

2 1.yx x=−−

C.

32

3 1.yx x=−−

D.

32

3 1.yx x=−+ −

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( ) ( ) ( ) ( )

222

: 2 1 34Sx y z−+++−=

. Tâm của

( )

S

có tọa

độ là

A.

( )

4; 2; 6−−

. B.

(

)

4; 2; 6−

. C.

( )

2; 1; 3

−

. D.

(

)

2; 1; 3−−

.

Câu 11: Trong không gian

,Oxyz

cho điểm

( )

1; 2; 3A −

. Hình chiếu vuông góc của

A

lên mặt phẳng

()Oxy

có tọa độ là

A.

( )

0; 2; 3−

. B.

( )

1; 0; 3−

. C.

( )

1; 2; 0

. D.

( )

1;0;0

.

Câu 12: Phần ảo của số phức

( )( )

21z ii=−+

bằng

A.

3

. B.

1

. C.

1−

. D.

3−

.

Câu 13: Cho khối chóp

.S ABC

có chiều cao bằng

3

, đáy

ABC

có diện tích bằng

10

. Thể tích khối chóp

.S ABC

bằng

A.

2

. B.

15

. C.

10

. D.

30

.

Câu 14: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, cạnh bên

SA

vuông góc

với mặt phẳng đáy và

2SA a=

. Tính thể tích

V

của khối chóp

.

S ABCD

A.

3

2

6

a

V =

B.

3

2

4

a

V

=

C.

3

2Va=

D.

3

2

3

a

V =

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

theo thiết diện là một đường tròn. Gọi

d

là khoảng

cách từ

O

đến

( )

P

. Khẳng định nào dưới đây đúng?

A.

dR=

. B.

dR>

. C.

2dR=

. D.

dR<

.

Câu 16: Số phức liên hợp của số phức

z 2 5i= −

là

A.

z 2 5i= +

. B.

z 2 5i=−+

. C.

z 2 5i= −

. D.

z 2 5i=−−

.

Câu 17: Diện tích xung quanh của hình trụ có bán kính đáy

R

, chiều cao

h

là

A.

xq

2S Rh

π

=

. B.

xq

S Rh

π

=

. C.

xq

4S Rh

π

=

. D.

xq

3S Rh

π

=

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

252

:

34 1

xyz

d

−+−

= =

−

. Vectơ nào dưới đây là một

vectơ chỉ phương của

d

?

A.

( )

2

3; 4; 1u = −

 

. B.

( )

1

2; 5; 2u = −



. C.

( )

3

2; 5; 2u = −

 

. D.

( )

4

3; 4;1u =

 

.

Câu 19: Cho hàm số

( )

y fx=

liên tục trên

{ }

\0

và có bảng xét dấu đạo hàm như hình bên. Số điểm

cực trị của hàm số đã cho là

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 9

A.

4

. B.

3

. C.

1

. D.

2

.

Câu 20: Cho hàm số

2020

2021

y

x

=

+

. Số tiệm cận của đồ thị hàm số bằng

A.

3

. B.

1

. C.

0

. D.

2

.

Câu 21: Tập nghiệm của bất phương trình

2

4

1

27

3

x −



≥





là

A.

[ ]

1;1−

. B.

(

]

;1−∞

. C.

7; 7



−



. D.

[

)

1; +∞

.

Câu 22: Có bao nhiêu cách chọn ra

5

học sinh từ một nhóm

10

học sinh?

A.

5!

. B.

5

10

A

. C.

5

10

C

. D.

5

10

.

Câu 23: Cho

( )

2

d3 23fx x x x C= + −+

∫

. Hỏi

(

)

fx

là hàm số nào?

A.

( )

62fx x= +

. B.

( )

32

3fx x x xC=+−+

.

C.

( )

62

fx x C= ++

. D.

(

)

32

3

fx x x x=+−

.

Câu 24: Biết

( )

cosFx x

=

là một nguyên hàm của hàm số

( )

fx

trên



. Giá trị của

( )

0

3 2d

fx x

π

+





∫

bằng

A.

26

π

−

. B.

4−

. C.

2

π

. D.

2

.

Câu 25: Họ các nguyên hàm của hàm số

( )

3

1= +

x

fx e

là

A.

3

3 +

x

eC

. B.

3

1

3

++

x

e xC

. C.

3

1

3

+

x

eC

. D.

3

3 ++

x

e xC

.

Câu 26: Cho hàm số

()fx

xác định, liên tục trên



và có đồ thị của hàm số

()

fx

′

là đường cong như

hình vẽ bên dưới. Hỏi khẳng định nào đúng?

A. Hàm số

()y fx=

đồng biến trên khoảng

( 2; 0).−

B. Hàm số

()y fx=

nghịch biến trên khoảng

(0; ).+∞

C. Hàm số

()y fx=

đồng biến trên khoảng

( ; 3).−∞ −

D. Hàm số

()y fx=

nghịch biến trên khoảng

( 3; 2).−−

Câu 27: Cho hàm số

( )

y fx=

có bảng biến thiên như sau:

O

x

y

2

3

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 10

Giá trị cực tiểu của hàm số đã cho bằng

A.

3

. B.

2

. C.

0

. D.

5−

.

Câu 28: Cho hai số thực dương

a

,

b

thỏa mãn

22

log 2log 3ab

+=

. Giá trị của

2

ab

bằng

A.

3

log 2

. B.

9

. C.

3

. D.

8

.

Câu 29: Cho hình phẳng

( )

H

giới hạn bởi đồ thị hàm số

2

y xx= −

và trục hoành. Tính thể tích

V

của

vật thể tròn xoay sinh ra khi cho

( )

H

quay quanh trục

Ox

.

A.

4

3

V

π

=

. B.

16

15

V =

. C.

4

3

V =

. D.

16

15

V

π

=

.

Câu 30: Cho hình lăng trụ tam giác đều

.ABC A B C

′′′

có cạnh đáy bằng

a

và cạnh bên bằng

3

2

a

. Góc

giữa hai mặt phẳng

( )

A BC

′

và

(

)

ABC

bằng

A.

30°

. B.

60°

. C.

45°

. D.

90°

.

Câu 31: Cho hàm số

( )

y fx

=

có bảng biến thiên như sau:

Phương trình

( )

fx m=

có ba nghiệm thực phân biệt khi và chỉ khi

A.

42m− < <−

. B.

22m−< <

. C.

22m

−< ≤

. D.

42m−< <

.

Câu 32: Cho hàm số

( )

y fx=

liên tục trên



và có đạo hàm

( )

( ) (

)

( )

2020 2021

' 1 12fx x x x=+−−

. Hỏi

hàm số

( )

y fx=

đồng biến trên khoảng nào dưới đây?

A.

( )

1;1

−

. B.

(

)

2;

+∞

. C.

(

)

1; 2

. D.

( )

;1−∞ −

.

Câu 33: Lớp 11A1 có 21 học sinh nam và 22 học sinh nữ, cần chọn 20 học sinh để tham gia chương trình

mùa hè xanh năm 2021. Xác suất trong 20 học sinh được chọn có cả học sinh nam và học sinh

nữ là

A.

20 20

21 22

20

43

CC

C

+

. B.

20 20

21 22

20

43

AA

A

+

. C.

20 20

21 22

20

43

1

AA

A

+

−

. D.

20 20

21 22

20

43

1

CC

C

+

−

.

Câu 34: Tính tổng

T

tất cả các nghiệm của phương trình

4.9 13.6 9.4 0− +=

x xx

.

A.

13

4

=T

. B.

3=T

. C.

1

4

=T

. D.

2T =

.

Câu 35: Tìm tập hợp các điểm biểu diễn các số phức

z

thỏa mãn

13 1z iz i−+ = +−

.

A.

20xy−+=

. B.

2 20xy− −=

. C.

20xy−−=

. D.

20xy+−=

.

Câu 36: Trong không gian

Oxyz

, cho ba điểm

(1; 2; 3)A

,

(1; 1; 1)B

và

(3; 4; 0)C

. Đường thẳng đi qua

A

và song song

BC

có phương trình là:

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 11

A.

123

451

xy z

+++

= =

. B.

123

451

xy z−−−

= =

.

C.

123

23 1

xy z−−−

= =

−

. D.

123

23 1

xy z+++

= =

−

.

Câu 37: Trong không gian

Oxyz

, cho tam giác

ABC

có trọng tâm

G

với

( )

1; 6; 1A

−−

,

( )

2;2;3B −

,

( )

4; 5; 11C −−

. Gọi

( )

;;I mn p

là điểm đối xứng của

G

qua mặt phẳng

( )

Oxy

. Tính

2021

mn p

T

++

=

.

A.

1

2021

T =

. B.

2021

T =

. C.

1T =

. D.

5

1

2021

T =

.

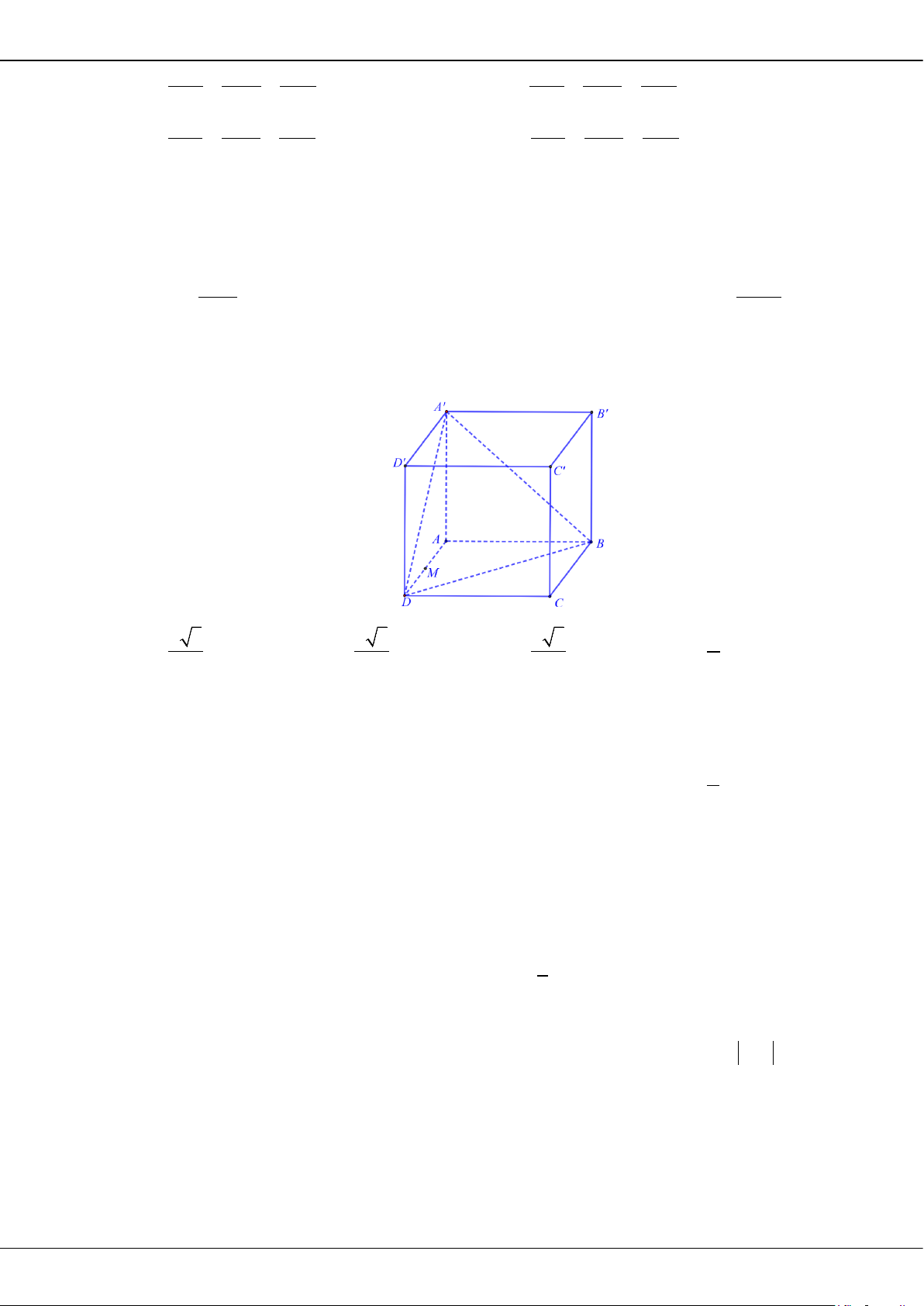
Câu 38: Cho hình lập phương

.ABCD A B C D

′′′′

có cạnh bằng

a

. Gọi

M

là trung điểm của

AD

. Khoảng

cách từ điểm

M

đến mặt phẳng

( )

A BD

′

bằng

A.

3

6

a

. B.

3

12

a

. C.

3

a

. D.

2

a

.

Câu 39: Tập hợp các số thực m để phương trình

( )

2

ln 3 1 ln 4 3

x mx x x− += −+ −

có nghiệm là nửa

khoảng

[

)

;ab

. Giá trị của

2

2ab−

bằng:

A.

1

. B.

10

. C.

7

. D.

7

3

.

Câu 40: Hàm số

( )

y fx=

liên tục và có đạo hàm trên



thỏa

( ) ( ) ( ) ( )

1 1 4 5 41x fx x f x+ −+ − − =

và

( ) ( )

13fx fx+ +=

. Tính

( )

1

2

0

2

′

=

∫

I xf x dx

A.

1I

= −

. B.

1I =

. C.

2

I = −

. D.

2I =

.

Câu 41: Tìm số giá trị nguyên của tham số

m

để hàm số

( )

2 32

1

1 31

3

y m x mx x= − + ++

có cực đại

A.

2

. B.

0

. C.

1

. D.

3

.

Câu 42: Biết số phức

( )

z,a bi a b=+∈

thỏa mãn

( )( )

2 12zi i+−

là một số thực và

1z −

đạt giá trị

nhỏ nhất. Khi đó biểu thức

( )

22

625 2021P ab= ++

bằng

A.

2412

. B.

2421

. C.

12021

. D.

52021

.

Câu 43: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

a

, đường chéo

AC a=

, tam giác

SAB

cân tại

S

và nằm trong mặt phẳng vuông góc với đáy, góc giữa

( )

SCD

và đáy bằng

0

45

. Tính

theo

a

thể tích

V

của khối chóp

.S ABCD

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 12

A.

3

4

a

V =

. B.

3

4

a

V =

. C.

3

2

a

V =

. D.

3

12

a

V =

.

Câu 44: Hàm số

( )

y fx

=

có đạo hàm liên tục trên



và thỏa mãn

( ) ( )

( )

32

. 4 6 24fx xfx fx x x x

′′

+ + = − −+

. Tính diện tích hình phẳng giới hạn bởi đồ thị các

hàm số

( )

y fx=

,

(

)

y fx

′

=

?

A.

8S =

. B.

4S =

. C.

8S

π

=

. D.

4S

π

=

.

Câu 45: Có bao nhiêu số nguyên

a

để phương trình

( )

22

30

z a za a

− − + +=

có hai nghiệm phức

1

z

,

2

z

thỏa mãn

12 12

zz zz

+=−

?

A.

4

. B.

2

. C.

3

. D.

1

.

Câu 46: Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

(

)

: 10Pxyz+ −−=

và đường thẳng

4 21

:

22 1

xyz

d

−++

= =

−

. Gọi đường thẳng

d

′

là hình chiếu vuông góc của

d

trên mặt phẳng

( )

P

. Trong các điểm sau, điểm nào không thuộc

d

′

?

A.

( )

5;9;3H −

. B.

(

)

10;16; 5K

−

. C.

(

)

0; 2;1M

. D.

( )

1; 2; 0N

.

Câu 47: Có bao nhiêu số nguyên

x

sao cho ứng với mỗi

x

có không quá 63 số nguyên

y

thỏa mãn

( )

2

54

log logx y xy+≥ +

A.

16

. B.

5

. C.

6

. D.

15

.

Câu 48: Cắt hình nón đỉnh

S

bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền

bằng

2a

. Gọi

BC

là dây cung của đường tròn đáy hình nón sao cho mặt phẳng

( )

SBC

tạo

với mặt đáy một góc

o

60

. Tính diện tích tam giác

SBC

.

A.

2

SBC

a

S =

. B.

2

3

SBC

a

S =

. C.

2

3

SBC

a

S =

. D.

2

3

SBC

a

S =

.

Câu 49: Cho một hình trụ

( )

T

có hai đường tròn đáy là

(

)

O

và

( )

'O

. Gọi

,MN

nằm trên đường tròn

(

)

O

và

P

nằm trên đườn tròn

( )

'O

. Biết rằng tam giác

MNP

đều có cạnh bằng

12 6

5

và mặt

phẳng

( )

MNP

tạo với đáy trụ một góc

45°

, giao điểm của mặt phẳng

( )

MNP

với trục của hình

trụ

( )

T

nằm trong tam giác

MNP

. Thể tích khối trụ

( )

T

bằng

A.

144

π

. B.

162

5

π

. C.

163

3

π

. D.

82 6

5

π

.

Câu 50: Tổng tất cả các giá trị nguyên thuộc

[ 5; 5]−

của

m

để hàm số

32

12

( ) ( 1) ( 2 3)

33

= +− + − −gx x m x m x

đồng biến trên là:

A. 1. B. -1. C. 0. D. 2.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 13

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho số phức

z

có số phức liên hợp

3 2.zi

Tổng phần thực và phần ảo của số phức

z

bằng

A.

1.



B.

1.

C.

5.



D.

5.

Câu 2: Với

0x 

, đạo hàm của hàm số

ln 2yx

là

A.

1

.

x

B.

1

.

2x

C.

2

.

x

D.

.

2

x

Câu 3: Cho cấp số cộng

 

n

u

có số hạng đầu

1

2u 

và công sai

5.d



Khi đó

4

u

bằng

A.

22.

B.

17.

C.

12.

D.

250.

Câu 4: Gọi

S

là tập hợp tất cả các nghiệm nguyên của bất phương trình

 

1

2

log 2 2.x  

Tổng các

phần tử của

S

bằng

A.

4.

B.

0.

C.

2.

D.

3.

Câu 5: Trong không gian

,Oxyz

cho mặt phẳng

 

: 2 1 0.Px z 

Vectơ nào dưới đây là một vectơ

pháp tuyến của

 

P

?

A.

 

1

1; 2; 1 .n 



B.

 

2

1; 0; 2 .n 



C.

 

3

1; 2; 0 .n





D.

 

4

0; 1; 2 .n





Câu 6: Trong không gian

,Oxyz

cho hai điểm



 



1;1; 0 , 0;1; 2 .AB

Vectơ nào dưới đây là một vectơ chỉ

phương của đường thẳng

AB

?

A.

 

1; 0; 2 .

u 



B.

 

1;2;2 .u 



C.





1; 0; 2 .u





D.

 

1; 0; 2 .u  



Câu 7: Đường cong trong hình bên dưới là đồ thị của hàm số nào dưới đây?

A.

1

.

1

x

y

x







B.

1

.

1

x

y

x







C.

42

.yx x

D.

2

.yx

Câu 8: Thể tích khối chóp tam giác đều có độ dài cạnh đáy là

2,

a

chiều cao là

3a

bằng

A.

3

43 .a

B.

3

33 .

a

C.

3

43

.

3

a

D.

3

3.a

Câu 9: Số tam giác xác định bởi các đỉnh của một đa giác đều

10

cạnh là

A.

35.

B.

120.

C.

240.

D.

720.

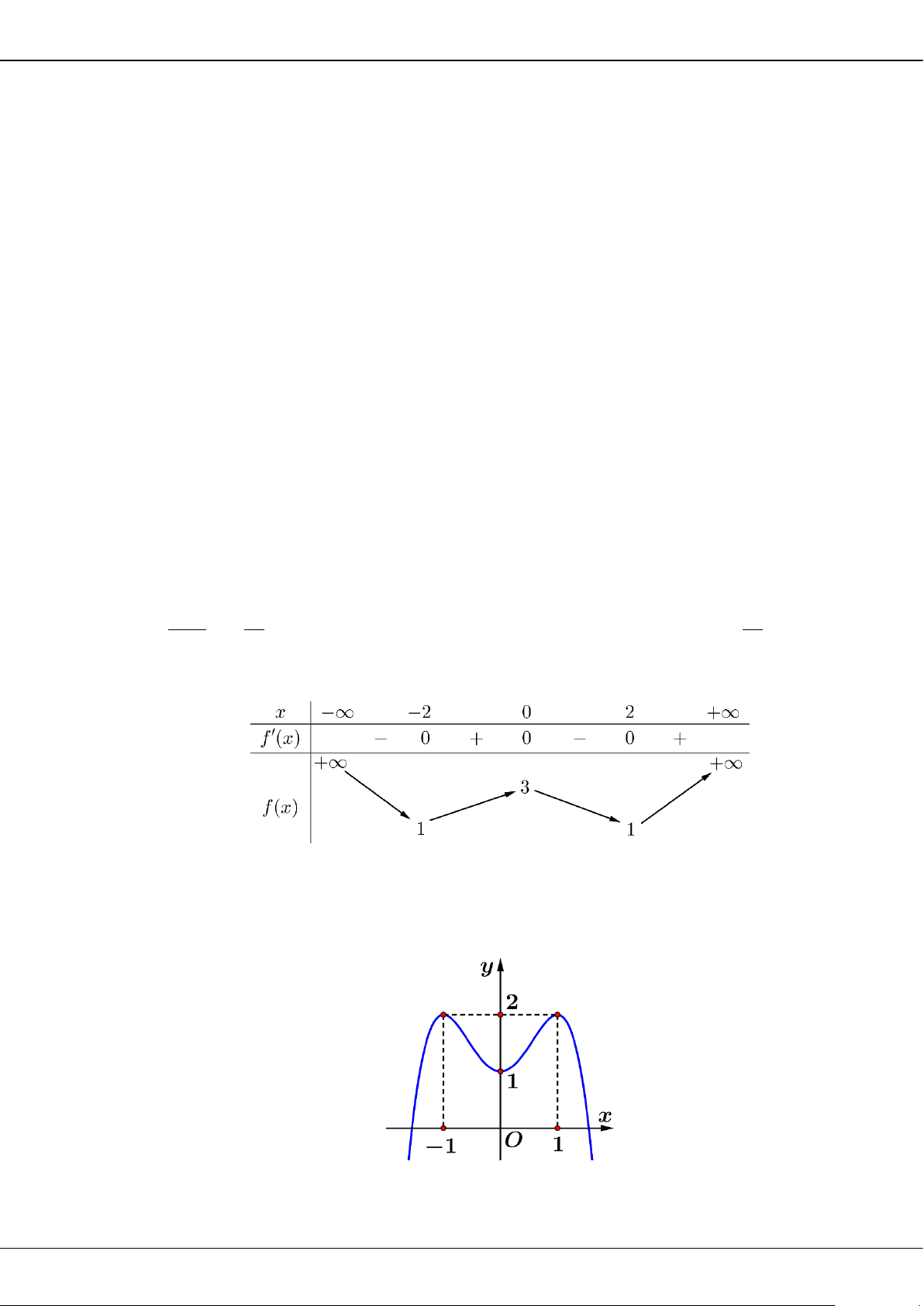
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 14

Câu 10: Trong không gian

,

Oxyz

điểm nào thuộc đường thẳng

12

:3

45

xt

dy t

zt







 











?

A.

 

3;2;1.P 

B.

 

2; 1; 5 .N

C.

 

1; 3; 4 .M 

D.

 

4; 1; 3 .Q

Câu 11: Cho khối nón có bán kính đáy bằng

3

và diện tích xung quanh bằng

15 .



Thể tích của khối nón

đã cho bằng

A.

12 .

B.

60 .



C.

20 .



D.

36 .



Câu 12: Cho số phức

z

thỏa mãn

 

1 3,iz i

 

phần ảo của

z

bằng

A.

2.

i

B.

1.

C.

2.

D.

2.

Câu 13: Cho hàm số





y fx

có bảng biến thiên như sau

Giá trị cực đại

CD

y

và giá trị cực tiểu

CT

y

của hàm số đã cho lần lượt là

A.

3, 2.

CD CT

yy 

B.

2, 0.

CD CT

yy

C.

2, 2.

CD CT

yy 

D.

3, 0.

CD CT

yy

Câu 14: Trong không gian với hệ tọa độ

Oxyz

, cho điểm





1; 3; 4 .M

Khoảng cách từ điểm

M

đến trục

Ox

bằng

A.

5.

B.

25.

C.

10.

D.

17.

Câu 15: Cho

 

1

d2fx x







và

 

3

1

d 5.fx x



Khi đó

 

3

1

2dfx x





bằng

A.

14.

B.

14.

C.

12.

D.

6.

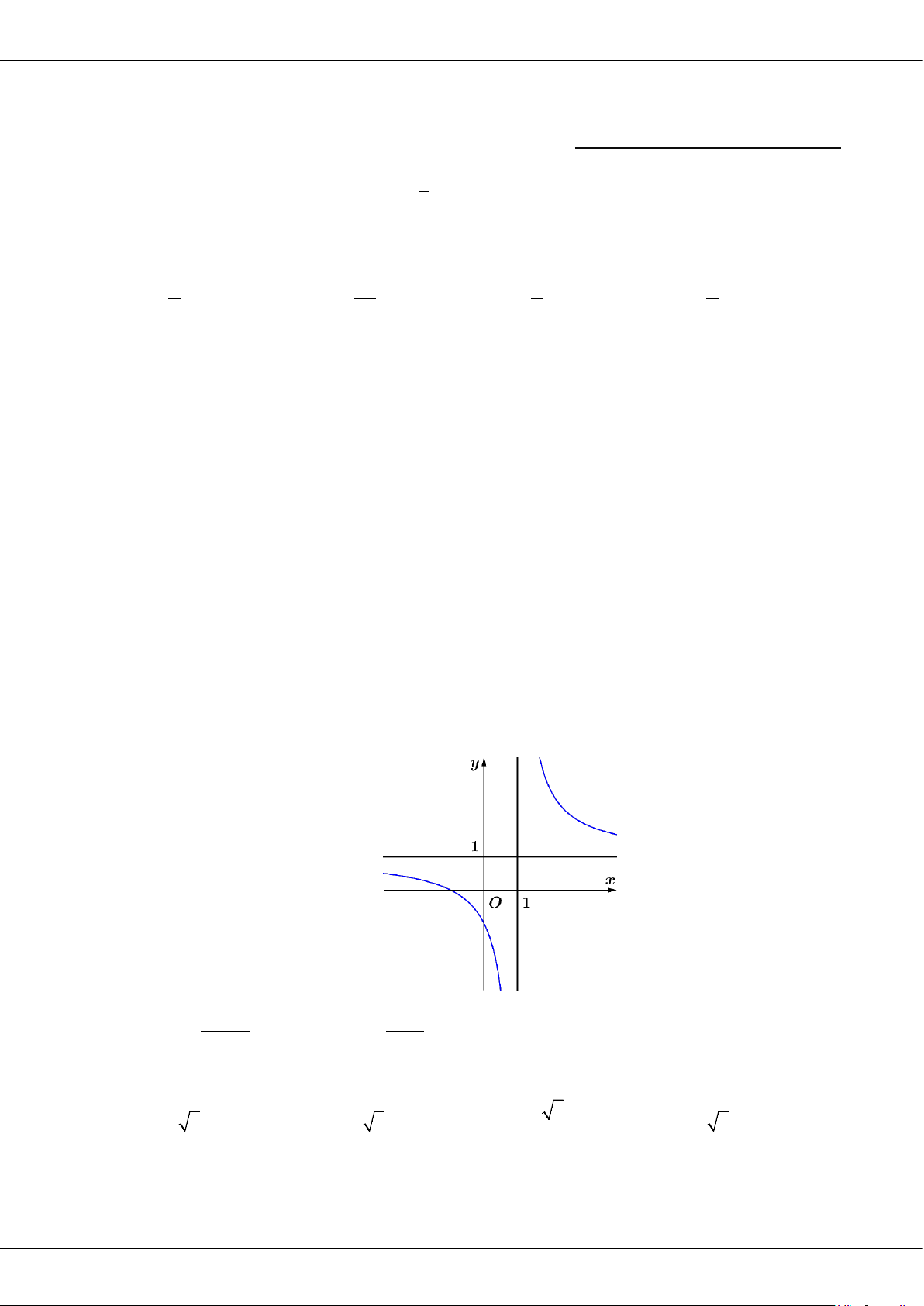
Câu 16: Tiệm cận ngang của đồ thị hàm số

13

1

x

y

x







là

A.

3.y 

B.

1.y 

C.

3.x 

D.

1.x 

Câu 17: Bất phương trình

1

4

x





















có tập nghiệm là

A.





0; .

B.

 

0;1 .

C.

 

1; .

D.





;0 .

Câu 18: Nếu

 

3

1

d2fx x



và

 

3

1

d4gx x



thì

   

3

1

df x gx x









bằng

A.

2.

B.

6.

C.

6.

D.

2.

Câu 19: Cho hình trụ có chiều cao bằng

5

và đường kính đáy bằng

8

. Diện tích xung quanh của hình trụ

đó bằng

A.

20 .

B.

40 .

C.

160 .

D.

80 .

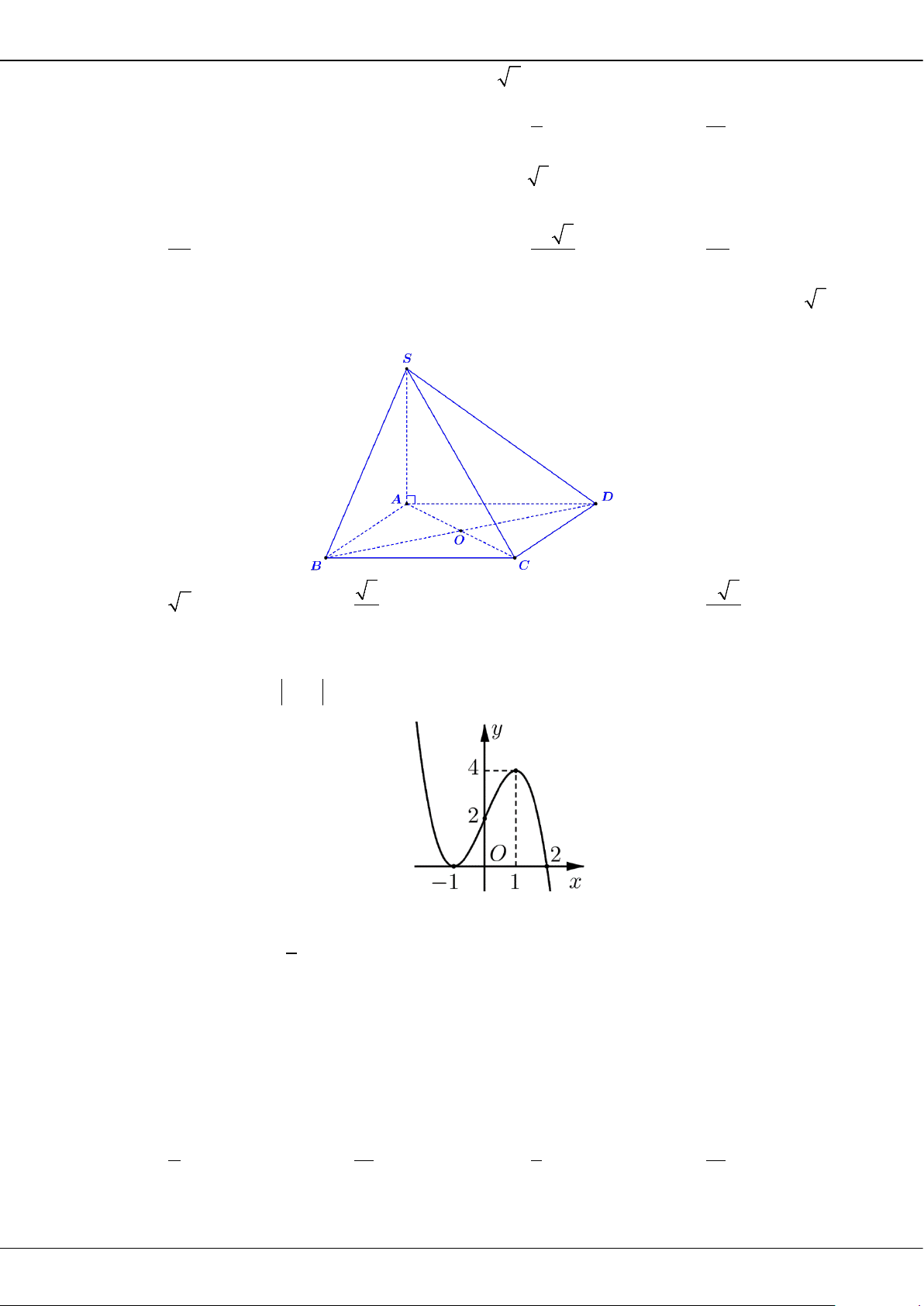
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 15

Câu 20: Trong không gian

Oxyz

, mặt cầu

       

2 22

: 2 4 6 25Sx y z

có tọa độ tâm

I

là

A.

 

2; 4; 6 .I 

B.

 

2; 4; 6 .I 

C.

 

1; 2; 3 .I 

D.

 

1; 2; 3 .I



Câu 21: Thể tích của khối lập phương có độ dài cạnh

3a 

là

A.

27.

B.

9.

C.

6.

D.

16.

Câu 22: Trong không gian

,Oxyz

tích vô hướng của

 

3; 2;1a





và

 

5; 2; 4b  



bằng

A.

15.

B.

10.

C.

7.

D.

15.

Câu 23: Cho các số thực

 

,.

ab a b

Nếu hàm số

 

y Fx

là một nguyên hàm của hàm số

 

y fx



thì

A.

  

 



d.

b

a

Fx x fa fb



B.



 

  

d.

b

a

Fx x fb fa



C.

   





d.

b

a

f x x Fb Fa





D.

     

d.

b

a

f x x Fa Fb



Câu 24: Trong không gian

,Oxyz

tìm tất cả các giá trị thực của tham số

m

để phương trình

2 22

224 0x y z x y zm



là phương trình của một mặt cầu?

A.

6.m 

B.

6.m 

C.

6.m 

D.

6.m 

Câu 25: Họ các nguyên hàm của hàm số

 

x

fx e x

là

A.

2

1

.

12

x

eC

x





B.

2

.

x

exC

C.

1.

x

eC

D.

2

.

2

x

eC

Câu 26: Cho hàm số





y fx



có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.





0; 2 .

B.

 

2; 2 .

C.

 

; 2. 

D.

 

2; .



Câu 27: Cho hàm số bậc bốn

 

y fx

có đồ thị là đường cong trong hình bên dưới.

Cực tiểu của hàm số đã cho là

A.

1.

B.

1.

C.

2.

D.

0.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 16

Câu 28: Với

a

là số thực dương khác

1,

giá trị





3

4

log .

a

aa

bằng

A.

7.

B.

12.

C.

3

.

4

D.

13

.

4

Câu 29: Cho hình phẳng

D

giới hạn bởi đồ thị hàm số

3yx

và các đường thẳng

0, 1, 2.y xx 

Thể tích khối tròn xoay tạo thành khi quay

D

quanh trục hoành bằng

A.

3

.

2



B.

7.

C.

33

.

2



D.

9

.

2



Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

,3AB SA a AD a 

và

 

.SA ABCD

Tan của góc giữa hai mặt phẳng

 

SBD

và

 

ABCD

bằng

A.

2.

B.

3

.

2

C.

1.

D.

23

.

3

Câu 31: Cho hàm số bậc ba

 

y fx

có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

 

20fx m

có

4

nghiệm phân biệt?

A.

3.

B.

4.

C.

7.

D.

8.

Câu 32: Cho hàm số

 

32

1

3 2 2022.

3

y x mx m x    

Tìm tất cả các giá trị của tham số

m

để hàm

số nghịch biến trên khoảng

 

;. 

A.

2.m 

B.

2 1.m  

C.

1

.

2

m











D.

1

.

2

m











Câu 33: Năm đoạn thẳng có độ dài lần lượt là

1 cm,

3 cm,

5 cm,

7 cm,

9 cm.

Lấy ngẫu nhiên ba đoạn

thẳng trong năm đoạn trên. Xác suất ba đoạn ấy tạo thành

3

cạnh của một tam giác bằng

A.

2

.

5

B.

7

.

10

C.

3

.

5

D.

3

.

10

Câu 34: Tổng tất cả các nghiệm thực của phương trình





22

log .log 32 4 0xx

bằng

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 17

A.

7

.

16

B.

9

.

16

C.

1

.

32

D.

1

.

2

Câu 35: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức

z

thỏa mãn

13 2

z iz i

   

là một đường thẳng. Đường thẳng đó có phương trình là

A.

6 8 5 0.xy 

B.

6 8 5 0.xy

 

C.

6 4 5 0.xy 

D.

6 4 5 0.xy 

Câu 36: Trong không gian

Oxyz

, cho hình chóp

.S ABCD

có đáy là hình vuông,

SA

vuông góc với đáy

và



 



2;3; 7 , 4;1; 3 .

BD

Phương trình mặt phẳng





SAC

là

A.

2 9 0.xy z

 

B.

2 9 0.

xy z 

C.

2 9 0.xy z 

D.

2 9 0.

xy z 

Câu 37: Với các số thực

,ab

biết phương trình

2

8 64 0z az b

có nghiệm phức

0

8 16 .zi



Môđun

của số phức

w a bi

bằng

A.

19.

B.

3.

C.

7.

D.

29.

Câu 38: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

,a

2.

SD a

Hai mặt phẳng

 

SAB

và

 

SAC

cùng vuông góc với mặt đáy

 

.ABCD

Gọi

G

là trọng tâm của tam giác

.SDC

Khoảng

cách từ

G

đến mặt phẳng

 

SBD

bằng

A.

2 17

.

17

a

B.

2 21

.

7

a

C.

21

.

21

a

D.

2 21

.

21

a

Câu 39: Có bao nhiêu số nguyên

x

thỏa mãn



  

23

2 3 23

log log log .log 4

x x xx 

?

A.

27.

B.

26.

C.

133.

D.

134.

Câu 40: Cho hàm số

 

fx

liên tục trên



. Biết rằng



  

,xF x G x x

là hai nguyên hàm của

 

fx

trên



thỏa mãn



 



 

1

0

d 21 1 2fx x F G

 



và

   

2 2 9.FG

Khi đó, giá trị của

   

2

0

dxf x F x x



bằng

A.

196

.

9

B.

16.

C.

98

.

9

D.

8.

Câu 41: Có bao nhiêu số nguyên

7a 

để hàm số

   

42

2 2 4 31

yx a x a x    

có ba điểm cực

trị?

A.

4.

B.

3.

C.

5.

D.

2.

Câu 42: Cho hai số phức

z

và

w

thỏa mãn

24zw

và

22

2 8 6 34.z zw w i   

Gọi

M

và

m

lần lượt là GTLN và GTNN của biểu thức

22

2.Pz w

Tính

.Mm

A.

43.

B.

160

.

3

C.

91

.

2

D.

170

.

3

Câu 43: Cho khối lăng trụ đứng

.ABC A B C



có đáy

ABC

là tam giác đều cạnh

.a

Biết thể tích của khối

lăng trụ đã cho bằng

3

.

2

a

Khoảng cách từ điểm

A



đến mặt phẳng





ACB



bằng

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 18

A.

6

.

7

a

B.

2 57

.

19

a

C.

57

19

a

D.

3

.

7

a

Câu 44: Cho hàm số

 

y fx

có đạo hàm cấp hai liên tục trên



và hàm số

 

32

.g x ax x cx d

 

Đồ thị của hai hàm số

 

y fx

và

 

y gx

cắt nhau tại ba điểm có hoành độ lần lượt là

1;1; 2.

Biết rằng

   

2 6 6,f x xf x x x

 

   

và

   

1 3 1 3.ff



 

Diện tích hình

phẳng giới hạn bởi hai đồ thị

 

y fx

và

 

y gx

bằng

A.

91

.

12

B.

37

.

6

C.

37

.

12

D.

91

.

6

Câu 45: Trên tập hợp các số phức, xét phương trình

2

4 40z mz m 

(

m

là tham số thực). Biết rằng

với

0

mm

thì phương trình đã cho có hai nghiệm phân biệt

12

,zz

thỏa mãn

 

2

12 2

4 12 .z mz z  

Khẳng định nào sau đây là đúng?

A.

0

52

;.

12 3

m



















B.

0

3

;1 .

5

m



















C.

0

12

;.

35

m



















D.

0

11

;.

72

m



















Câu 46: Trong không gian

Oxyz

, cho đường thẳng

11

:

1 12

xyz

d





. Gọi

 

P

là mặt phẳng chứa

trục

Oy

sao cho đường thẳng

d

không cắt mặt phẳng

 

.P

Khi đó sin của góc tạo bởi trục

Ox

và mặt phẳng

 

P

bằng

A.

5

.

5

B.

2

.

2

C.

25

.

5

D.

3

.

2

Câu 47: Có bao nhiêu cặp số nguyên

 

;xy

thỏa mãn

 





22

ln

ln 16 2

22

16 2

2023 2023 ln 2023

xy

































?

A.

41.

B.

42.

C.

40.

D.

16.

Câu 48: Cho hình nón có đường sinh bằng

2a

và góc ở đỉnh bằng

90 .



Cắt hình nón bằng mặt phẳng

 

P

đi qua đỉnh sao cho góc giữa

 

P

và mặt đáy hình nón bằng

60 .

Tính diện tích

S

của thiết

diện tạo thành.

A.

2

42

.

3

a

S 

B.

2

.

3

a

S 

C.

2

52

.

3

a

S 

D.

2

82

.

3

a

S 

Câu 49: Trong không gian

,Oxyz

cho điểm

 

   

8;0; 0 , 2;9; 3 3 , 4; 6; 2 3 .AB C

Xét các điểm

M

có

hoành độ dương thay đổi sao cho

AM

luôn tạo với trục

Ox

một góc

30



và tam giác

OAM

vuông. Tìm giá trị nhỏ nhất của biểu thức

22

192

2.P MA MB

MC

 

A.

176.

B.

144.

C.

240.

D.

80.

Câu 50: Có bao nhiêu giá trị nguyên của tham số

 

2023;2023m 

để hàm số





 

3 43 2

1 13

84 82

4 24

y m xx mxx 

đồng biến trên khoảng

 

1; 3

?

A.

4047.

B.

4045.

C.

4044.

D.

2022.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 19

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT CHỢ GẠO

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Điểm

M

trong hình vẽ bên biểu diễn phức nào sau đây?

A.

1

2zi= +

. B.

2

2zi= −

. C.

3

12zi= +

. D.

4

12zi= −

.

Câu 2: Đạo hàm của hàm số





ln 2 1yx

trên khoảng

1

;

2























bằng:

A.





1

21xe

. B.

1

21x

. C.





2

21xe

. D.

2

21x

.

Câu 3: Trên khoảng

( )

0;

+∞

, đạo hàm của hàm số

e

yx

=

là

A.

1

e

y ex

−

′

=

. B.

1e

yx

−

′

=

. C.

1

e

yx

e

−

′

=

. D.

e

y ex

′

=

.

Câu 4: Tìm tập nghiệm

S

của bất phương trình

( ) (

)

11

22

log 1 log 2 1xx+< −

.

A.

( )

2;S = +∞

. B.

( )

1; 2S = −

. C.

( )

;2S = −∞

. D.

1

;2

2

S



=





.

Câu 5: Cho cấp số cộng

( )

n

u

có

1

2u =

và công sai

4d =

. Số hạng thứ 12 của cấp số cộng đã cho bằng

A.

46

. B.

50

. C.

96

. D.

28

.

Câu 6: Trong không gian

Oxyz

, cho mặt phẳng

( ):2 1 0

xyz

α

+ −+=

. Vectơ nào sau đây không là

vectơ pháp tuyến của mặt phẳng

()

α

?

A.

( )

4

4; 2; 2 .= −

 

n

B.

( )

2

2; 1;1 .

−= −

 

n

C.

( )

3

2;1;1 .=

 

n

D.

( )

1

2; 1; 1 .= −



n

Câu 7: Đồ thị hàm của hàm số

3

32yx x=−+ −

cắt trục tung tại điểm có tung độ bằng

A.

0

. B.

1

. C.

2

. D.

2

−

.

Câu 8: Cho hàm số

( )

fx

liên tục và có đạo hàm trên đoạn

[ ]

2;1−

, biết

( ) ( )

15, 21ff= −=

. Tính

( )

2

1

'I f x dx

−

=

∫

.

A.

7I =

. B.

5=I

. C.

6I =

. D.

4I =

.

Câu 9: Hàm số nào dưới đây có đồ thị dạng như đường cong hình vẽ bên?

1

2

O

M

y

x

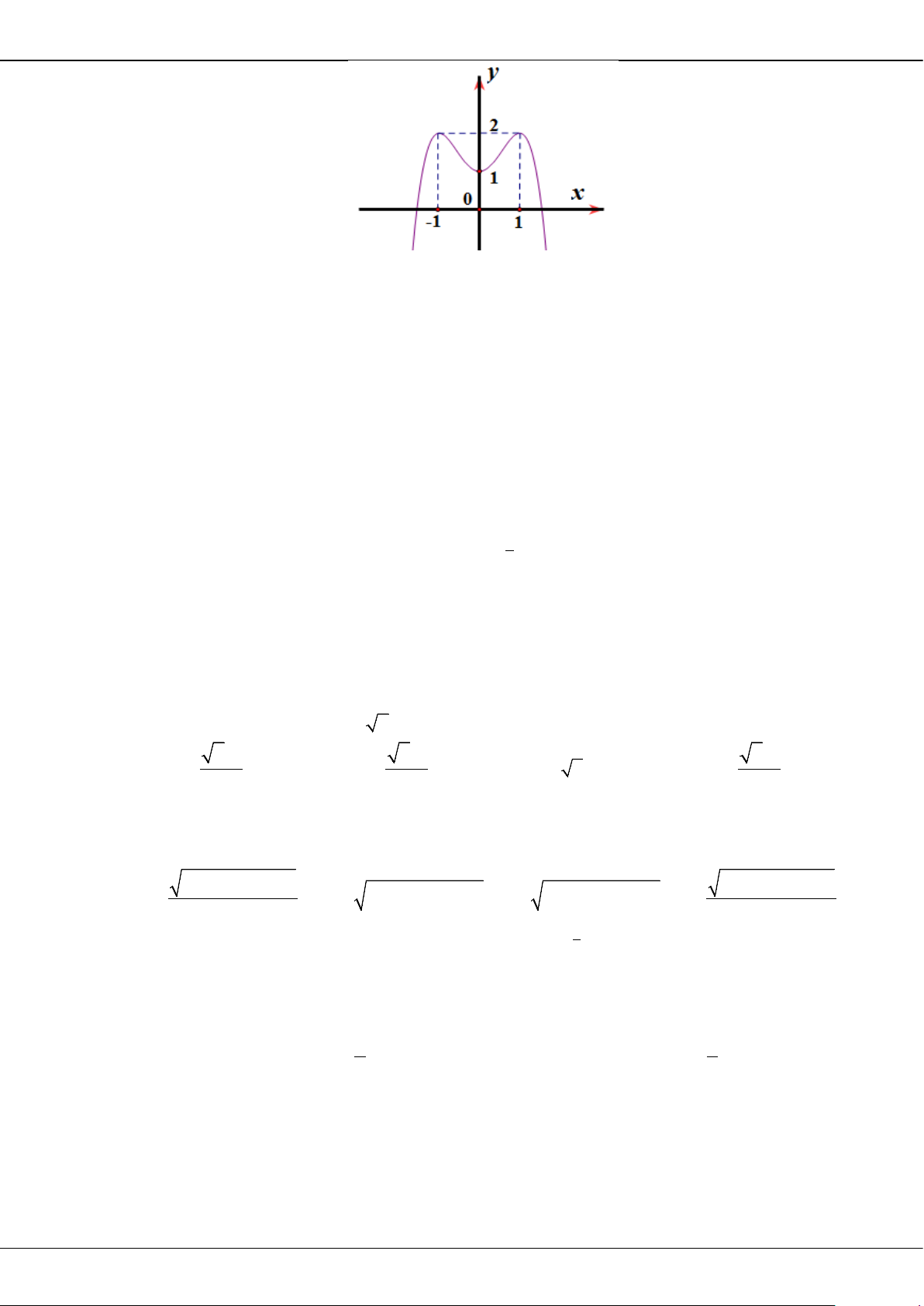
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 20

A.

3

31yx x=−++

. B.

3 2

31yx x+= +

. C.

24

2yx x= − +

. D.

42

1

2yx x

= −

++

.

Câu 10: Trong không gian vơi hệ tọa độ

Oxyz

, cho mặt cầu

( )

2 22

: 8 2 10Sx y z x y+ + − + +=

. Tìm tọa độ

tâm và bán kính mặt cầu

( )

S

:

A.

( )

4; 1; 0 , 2IR−=

. B.

( )

4; 1; 0 , 4

IR−=

. C.

( )

4; 1; 0 , 2IR−=

. D.

(

)

4; 1; 0 , 4IR−=

.

Câu 11: Trong không gian

,Oxyz

cho hai mặt phẳng

( )

P

và

( )

Q

lần lượt có hai vectơ pháp tuyến là

P

n

 

và

Q

n

 

. Biết góc giữa hai vectơ

P

n

 

và

Q

n

 

bằng

120 .°

Góc giữa hai mặt phẳng

( )

P

và

( )

Q

bằng.

A.

30



B.

45



C.

60



D.

90



Câu 12: Cho số phức

( )

2

75zi= −

, phần ảo của số phức

z

bằng

A.

70i

. B.

70

. C.

70−

. D.

70i−

.

Câu 13: Cho khối lập phương có thể tích bằng

216

. Cạnh của khối lập phương đã cho bằng

A.

9.

B.

6

. C.

8

. D.

12

.

Câu 14: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, cạnh bên

SA

vuông góc

với mặt phẳng đáy và

2SA a=

. Thể tích

V

của khối chóp

.S ABCD

bằng

A.

3

2

6

a

V =

. B.

3

2

4

a

V =

. C.

3

2Va

=

. D.

3

2

3

a

V =

.

Câu 15: Một mặt phẳng

( )

P

cắt mặt cầu

( )

;S IR

theo giao tuyến là đường tròn. Khi đó đường tròn giao

tuyến có bán kính bằng:

A.

( )

22

;( )

2

R d IP−

. B.

( )

22

;( )R d IP+

. C.

( )

22

;( )R d IP−

. D.

( )

22

;( )

2

R d IP+

.

Câu 16: Cho số phức

( )( )

12 34z ii=+−

. Phần thực của số phức

iz

tương ứng là

A.

2

. B.

11

. C.

2−

. D.

11

−

.

Câu 17: Cho hình trụ có đường kính đáy

2

r

và độ dài đường cao

h

. Thể tích của khối trụ đã cho bằng

A.

2 rh

π

. B.

2

3

rh

π

. C.

2

rh

π

. D.

2

1

3

hr

π

.

Câu 18: Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

∆

có phương trình tham số

1

2 2, .

3

xt

y tt

zt

= +





=−∈





= +





Hỏi điểm

M

nào sau đây thuộc đường thẳng

∆

?

A.

( )

3; 2; 5M −

. B.

( )

3; 2; 5M

. C.

( )

3;2;5M −−−

. D.

( )

3;2;5M −−

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 21

Câu 19: Cho hàm số

32

y ax bx cx d= + ++

có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ

thị hàm số đã cho có tọa độ là

A.

( 1; 0)−

. B.

(0; 1)−

. C.

(1; 4)

. D.

(0; 2)

.

Câu 20: Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

23

1

x

y

x

−

=

+

tương ứng có phương

trình là

A.

2x =

và

1y

=

. B.

1x = −

và

2

y =

. C.

1x =

và

3y = −

. D.

1

x =

và

2y

=

.

Câu 21: Tìm tập nghiệm T của bất phương trình

1

4

log (4 2) 1x

− ≥−

.

A.

3

;

2



+∞







. B.

13

;

22







. C.

13

;

22







. D.

13

;

22









Câu 22: Số cách xếp

6

bạn học sinh ngồi vào bàn dài

6

chỗ là

A.

270

B.

18

C.

720

D.

36

Câu 23: Tìm nguyên hàm

( ) ( )

sin dFx x x x= +

∫

biết

( )

0 19F =

.

A.

( )

2

cos 20Fx x x=++

. B.

( )

2

cos 20Fx x x=−+

.

C.

( )

2

1

cos 20

2

Fx x x=−+

. D.

( )

2

1

cos 20

2

Fx x x=++

.

Câu 24: Cho

( )

1

0

1f x dx

=

∫

tích phân

(

)

(

)

1

2

0

23f x x dx−

∫

bằng

A.

1

. B.

0

. C.

3

. D.

1−

.

Câu 25: Cho hàm số

( )

2

x

fx e x= −

. Khẳng định nào dưới đây đúng?

A.

( )

2

d 2.

x

fx x e x C=−+

∫

B.

( )

d 2.

x

fx x e xC=−+

∫

C.

( )

2

d 2.

fx x e xC=++

∫

D.

( )

2

d.

x

fx x e x C=−+

∫

Câu 26: Cho hàm số

( )

fx

có bảng biến thiên như hình vẽ bên.

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

( )

1; 0−

. B.

( )

1;− +∞

. C.

( )

;1−∞ −

. D.

( )

0;1

.

Câu 27: Cho hàm số

( )

fx

có bảng biến thiên như sau

O

x

y

2

2−

1

4

1

−

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 22

x

−∞

+∞

+

−

y

′

y

−∞

0

+

+∞

3−

1−

0

4−

Giá trị cực tiểu của hàm số đã cho bằng

A.

1

−

. B.

0

. C.

4−

. D.

3−

.

Câu 28: Với các số thực dương

,

ab

bất kì. Mệnh đề nào dưới đây đúng?

A.

( )

log log .logab a b

=

. B.

log

aa

bb

=

.

C.

( )

log log logab a b= +

. D.

log logb loga

a

b

= −

.

Câu 29: Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số

2

1

yx

= −

và y = 0 quanh trục Ox.

A.

5

.

3

π

B.

4.

π

C.

16

.

15

π

D.

3.

π

Câu 30: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng

a

. Tính côsin của góc giữa mặt bên và

mặt đáy.

A.

1

3

. B.

1

2

. C.

1

2

. D.

1

3

.

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên. Số nghiệm thực của

phương trình

( )

10fx

+=

là:

A.

3

. B.

1

. C.

0

. D.

2

.

Câu 32: Cho hàm số

()y fx=

có đạo hàm

2

( ) ( 2)f x xx

′

= −

,

x∀∈

. Hàm số nghịch biến trên khoảng

A.

( )

0; 2

. B.

( )

1;− +∞

. C.

( )

;0−∞

. D.

( )

;1−∞

.

Câu 33: Từ một đội văn nghệ gồm 5 nam và 8 nữ cần lập một nhóm gồm 4 người hát tốp ca. Xác suất để

trong 4 người được chọn đều là nam bằng

A.

C

4

8

4

13

. B.

A

C

4

5

4

8

. C.

C

4

5

4

13

. D.

C

A

4

8

4

13

.

Câu 34: Tổng tất cả các nghiệm của phương trình

2.4 9.2 4 0

xx

− +=

bằng

A.

9

.

2

B.

2.

C.

1.

D.

4.

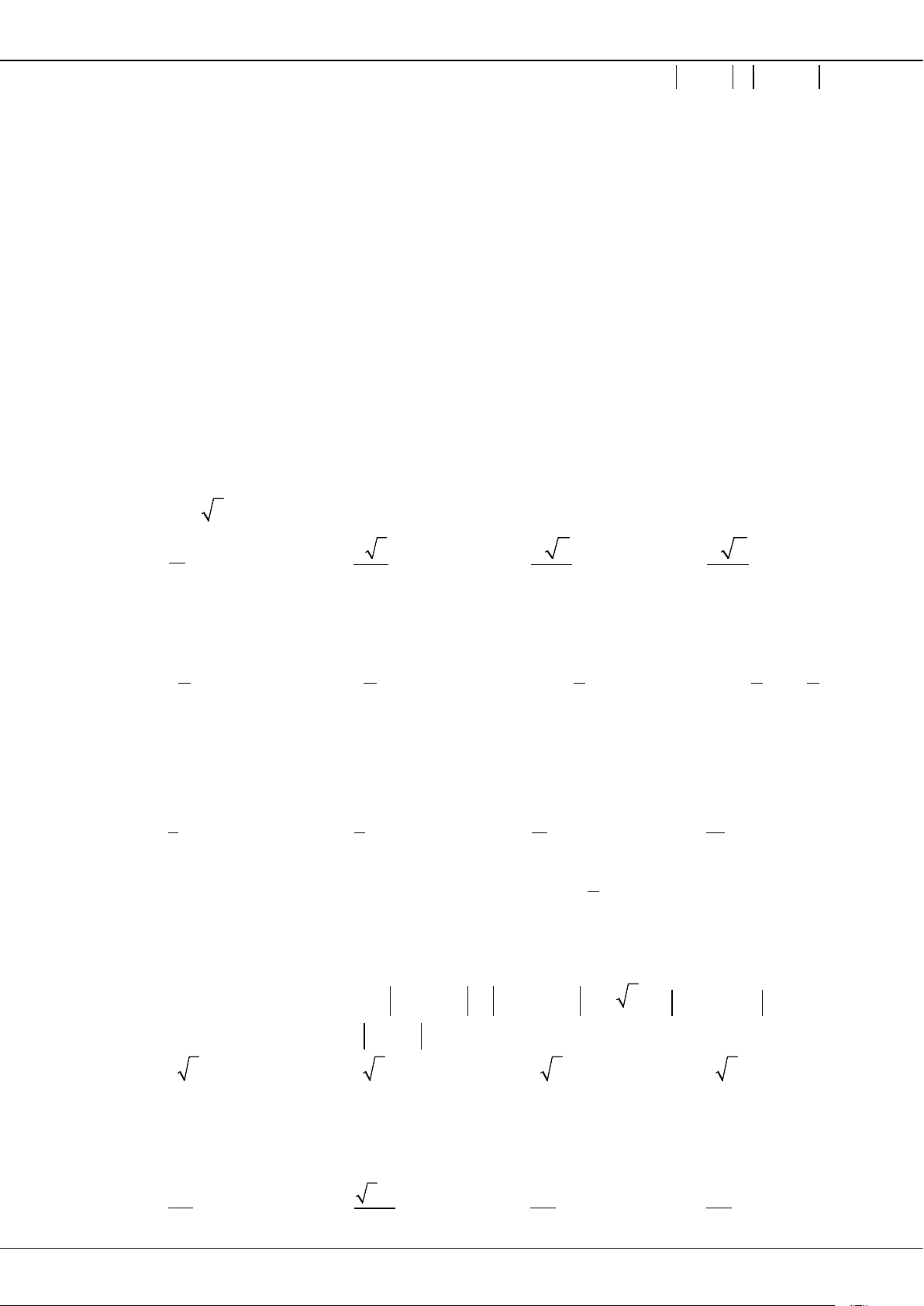
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 23

Câu 35: Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức

z

thỏa mãn

1 12z iz i+− = −+

một

đường thẳng có phương trình

A.

4 6 30

xy

+ −=

. B.

4 6 30xy+ +=

.

C.

4 6 30xy− +=

. D.

4 6 30xy− −=

.

Câu 36: Trong không gian

Oxyz

, cho tam giác

ABC∆

có

( )

1; 0; 2A −

,

(

)

2; 2;1

B

−

và

( )

0; 0; 1C

. Đường

trung tuyến

AM

có phương trình là

A.

1

13

1

xt

yt

zt

= +





=−+





= +



. B.

1

23

xt

yt

zt

= −





= −





=−+



. C.

12

1

13

xt

yt

zt

=−+





= +





=−−



.

D.

1

23

x

yt

zt

=





= −





=−+



.

Câu 37: Trong không gian

Oxyz

, cho mặt phẳng

( )

:2 2 3 0P x yz+ −−=

và điểm

( )

1; 2; 4M −

. Tìm tọa

độ hình chiếu vuông góc của điểm trên mặt phẳng

A.

( )

5;2;2

. B.

( )

0; 0; 3−

. C.

(

)

3; 0; 3

. D.

( )

1;1; 3

.

Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a,

( )

SA ABCD⊥

,

3SA a=

. Tính theo a khoảng cách từ điểm O đến mặt phẳng

( )

SBC

.

A.

2

a

B.

3

4

a

C.

5

6

a

D.

7

8

a

Câu 39: Tập hợp nào sau đây thuộc khoảng nghiệm của bất phương trình

( )

1

22

log 2 1 .log 2 2 2

xx

+

− −<

?

A.

5

;3

4







. B.

5

;3

2







. C.

22

5

log ;log 3

4







. D.

22

57

log ;log

33







.

Câu 40: Cho hàm sô

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa

mãn

( ) ( )

31 31 2FG+=

và

(

) (

)

25 25 0

FG+=

. Tính

( )

11

9

3 2dfx x−

∫

.

A.

1

3

. B.

1

6

. C.

1

2

. D.

11

31

.

Câu 41: Có bao nhiêu giá trị nguyên của tham số

m

để hàm số

32

1

2023

3

y x x mx

  

có hai điểm

cực trị thuộc khoảng





4; 3

?

A.

5

. B.

4

. C.

3

. D.

2

.

Câu 42: Cho hai số phức

12

,zz

thỏa mãn

11

2 4 7 62z iz i  

và

2

1 2 1.

iz i 

Giá trị

nhỏ nhất của biểu thức

12

Pzz

bằng

A.

3 2 2.

B.

2 2 2.



C.

3 2 1.

D.

2 2 1.

Câu 43: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều,

( )

SA ABC⊥

. Mặt phẳng

( )

SBC

cách

A

một khoảng bằng

a

và hợp với mặt phẳng

( )

ABC

góc

0

30

. Thể tích của khối chóp

.S ABC

bằng

A.

3

8

9

a

. B.

3

12

a

. C.

3

4

9

a

. D.

3

8

3

a

.

M

( )

.P

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 24

Câu 44: Cho đường thẳng

3

4

yx=

và parabol

2

1

2

y xa= +

(

a

là tham số thực dương). Gọi

12

,SS

lần

lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.

Khi

12

SS

=

thì

a

thuộc khoảng nào dưới đây?

A.

19

;

4 32







. B.

71

;

32 4







. C.

37

;

16 32







. D.

3

0;

16







.

Câu 45: Trên tập hợp các số phức, xét phương trình

 

22

21 0z m zm 

(

m

là tham số thực).

Có bao nhiêu giá trị của

m

để phương trình đó có nghiệm

0

z

thỏa mãn

0

7?z 

A.

2

. B.

3

. C.

1

. D.

4

.

Câu 46: Trong không gian với hệ tọa độ

,Oxyz

cho hai đường thẳng

1

12

:

21 1

x yz

d

−+

= =

−

và

2

122

:

13 2

xy z

d

−+−

= =

−

. Gọi

∆

là đường thẳng song song với

( )

: 70Pxyz++−=

và cắt

12

, dd

lần lượt tại hai điểm

,AB

sao cho

AB

ngắn nhất. Phương trình của đường thẳng

∆

là.

A.

12

5.

9

xt

y

zt

= −





=





=−+



B.

6

5

.

2

9

2

xt

y

zt





= −



=





=−+





C.

6

5

.

2

9

2

x

yt

zt





=



= −





=−+





D.

62

5

.

2

9

2

xt

yt

zt





= −



= +





=−+





Câu 47: Có bao nhiêu cặp số nguyên

( )

,xy

thỏa mãn

( ) ( )

22

3

log 3 3 .

2

xy

x x y y xy

x y xy

+

= −+ −+

+++

A.

1

. B.

2

. C.

4

. D.

6

.

Câu 48: Cho khối nón

( )

N

có chiều cao bằng

6a

và thể tích bằng

3

90 a

π

. Cắt

( )

N

bởi một mặt phẳng đi

qua đỉnh và cách tâm của đáy một khoảng bằng

3a

ta được thiết diện có diện tích bằng

A.

2

65a

. B.

2

6 11a

. C.

2

12 11a

. D.

2

12 5a

.

Câu 49: Trong không gian

Oxyz

cho

( )

1;1;1A

và hai đường thẳng

1

22

:1

2

xt

dy

zt

= −





=





=−+



,

2

53

:1

3

xs

dy

zs

= +





=





= −



. Gọi

B

,

C

là các điểm lần lượt di động trên

1

d

,

2

d

. Giá trị nhỏ nhất của biểu thức

P AB BC CA=++

là:

A.

2 29

. B.

29

. C.

30

. D.

2 30

.

Câu 50: Có bao nhiêu số nguyên

m

thuộc khoảng

( 10;10)−

để hàm số

3

22 3y x mx=−+

đồng biến

trên

(1; )+∞

?

A. 11. B. 7. C. 12. D. 8.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 25

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT VĨNH BÌNH

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho số phức

67zi= +

. Số phức liên hợp của

z

là

A.

67

zi= +

. B.

67zi=−−

. C.

67zi=−+

. D.

67zi= −

.

Câu 2: Trên khoảng

(

)

0, +∞

, đạo hàm của hàm số

3

log 2023=yx

là

A.

1

ln 3

y

x

′

=

. B.

1

2023

′

=y

x

. C.

1

y

x

′

=

. D.

1

2023 ln3

′

=

y

x

.

Câu 3: Trên khoảng

( )

0; +∞

, đạo hàm của hàm số

3

4

yx=

là :

A.

3

1

3

yx

′

=

. B.

4

3

yx

′

=

. C.

3

4

3

yx

′

=

. D.

1

3

yx

′

=

.

Câu 4: Tập nghiệm của bất phương trình

23

1

5

25

x+

>

là:

A.

5

;

2



− +∞





. B.

5

;

2



−∞ −





. C.

( )

0; +∞

. D.

1

;

2



− +∞





.

Câu 5: Cho cấp số nhân

(

)

n

u

với

2

6u =

và

5

162u =

. Công bội của cấp số nhân đã cho bằng

A. 3. B.

3−

. C.

2

. D.

1

3

.

Câu 6: Trong không gian

Oxyz

, cho hai điểm

( ) ( )

1; 0; 2 , 3; 4; 6AB−

. Một vectơ pháp tuyến của mặt

phẳng vuông góc với đường thẳng

AB

là:

A.

(

)

1; 2; 4−

. B.

(

)

2; 4;8−

. C.

(

)

1;2;4

. D.

( )

2; 4;8−−

.

Câu 7: Cho hàm số

32

y ax bx cx d= + ++

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm

của đồ thị hàm số đã cho và trục tung là điểm nào trong các điểm sau

A.

( )

1; 0

. B.

( )

2;0

. C.

(

)

1; 0

−

. D.

( )

0; 2

.

Câu 8: Nếu

( )

4

1

dx 2fx = −

∫

và

( )

4

1

dx 6gx = −

∫

thì

( ) ( )

4

1

dx

f x gx−





∫

bằng

A.

8−

. B.

4

. C.

4−

. D.

8

.

Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 26

A.

42

21yx x=−+ −

. B.

42

21yx x=−−

. C.

32

31

yx x

=−−

. D.

32

31

yx x=−+ −

.

Câu 10: Trong không gian

Oxyz

, cho hai điểm

( )

1;1; 1I

và

( )

1; 2; 3A

. Phương trình của mặt cầu có tâm

I

và đi qua điểm

A

là

A.

( ) ( ) ( )

2 22

1 1 1 29+++++=xyz

. B.

( ) ( ) ( )

2 22

1 1 15−+−+−=xyz

.

C.

( ) ( ) ( )

2 22

1 1 1 25−+−+−=xyz

. D.

( )

(

)

2 22

1 1 15+++++=xyz

.

Câu 11: Trong không gian với hệ trục tọa độ

,Oxyz

cho hai mặt phẳng

( )

: 2 2 0,Px yz− −+=

( )

: 2 1 0.Q xyz− ++=

Góc giữa

( )

P

và

( )

Q

là

A.

60°

. B.

90°

. C.

30°

. D.

120°

.

Câu 12: Cho hai số phức

1

12

zi= +

và

2

23zi= −

. Phần ảo của số phức

12

32wz z= −

là

A. 12. B. 11. C. 1. D.

12i

.

Câu 13: Cho hình hộp chữ nhật có độ dài ba cạnh là 3; 4; 5. Thể tích khối hộp đã cho bằng

A. 20 B. 60 C. 12 D. 30

Câu 14: Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB= AC= AD =2. Thể tích khối tứ

diện đã cho bằng

A.

1

3

B.

8

3

C.

4

3

D.

1

6

Câu 15: Cho mặt cầu S(O; R) và mặt phẳng (P). Gọi d là khoảng cách từ O đến mặt phẳng (P). Khi (P)

cắt mặt cầu (S) theo thiết diện là đường tròn lớn. Khẳng định nào là đúng?

A. d= 0 B. d < R C. d > R D. d= R

Câu 16: Các số thực

,xy

thỏa mãn:

( ) ( ) ( ) ( )

231 2 32 2 4 3x y x yi x y x y i+ + +−+ = − + + − −

là

A.

( )

94

;;

11 11

xy



=−−





. B.

( )

94

;;

11 11

xy



=





.

C.

( )

94

;;

11 11

xy



= −





. D.

( )

94

;;

11 11

xy



= −





.

Câu 17: Cho hình nón có đường kính đáy bằng 4 và độ dài đường cao hình nón 3. Diện tích xung quanh

của hình nón bằng

A.

20

π

B.

12

π

C.

6

π

D.

10

π

Câu 18: Trong không gian

Oxyz

, điểm nào dưới đây không thuộc đường thẳng

( )

32

:1 ?

xt

dy tt

zt

= −





=+∈





=





A.

( )

3; 1; 0P

. B.

( )

1; 2; 1Q

. C.

( )

1; 3; 1N −

. D.

( )

5; 0; 1M −

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 27

Câu 19: Cho hàm số

( )

42

, ,,y ax bx c a b c

=++ ∈



có đồ thị là đường cong như hình bên. Giá trị cực đại

của hàm số đã cho bằng

A.

0

. B.

1−

. C.

3−

. D.

2

.

Câu 20: Cho hàm số

()y fx=

có

lim ( ) 1

x

fx

→+∞

=

và

lim ( ) 1

x

fx

→−∞

= −

. Khẳng định nào sau đây là khẳng định

đúng?

A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng

1x =

và

1x = −

.

B. Đồ thị hàm số đã cho không có tiệm cận ngang.

C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.

D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng

1y =

và

1y = −

.

Câu 21: Số nghiệm nguyên của bất phương trình

( )

1

2

log 2 0x −≥

là

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 22: Một học sinh muốn chọn

20

trong

30

câu trắc nghiệm. Học sinh đó đã chọn được

5

câu. Tìm

số cách chọn các câu còn lại

A.

5

30

C

B.

15

25

A

C.

15

30

C

D.

15

25

C

Câu 23:

2d

x

∫

bằng

A.

1

2

x

C

+

. B.

1

2

1

x

C

x

+

. C.

2 ln 2

x

C+

. D.

2

ln 2

x

C+

.

Câu 24: Cho

( )

5

2

d 10fxx=

∫

. Khi đó

( )

2

5

24 dfx x−





∫

bằng

A.

46

. B.

32

. C.

42

. D.

34

.

Câu 25: Tìm nguyên hàm của hàm

( )

2

cos

fx x=

A.

sin 2

24

xx

C−+

. B.

cos2

24

xx

C−+

. C.

cos2

24

xx

C++

. D.

sin 2

24

xx

C++

.

Câu 26: Cho hàm số

()y fx

=

có bảng biến thiên như sau :

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

( )

0; +∞

. B.

( )

;2−∞ −

. C.

( )

0; 2

. D.

( )

2;0−

.

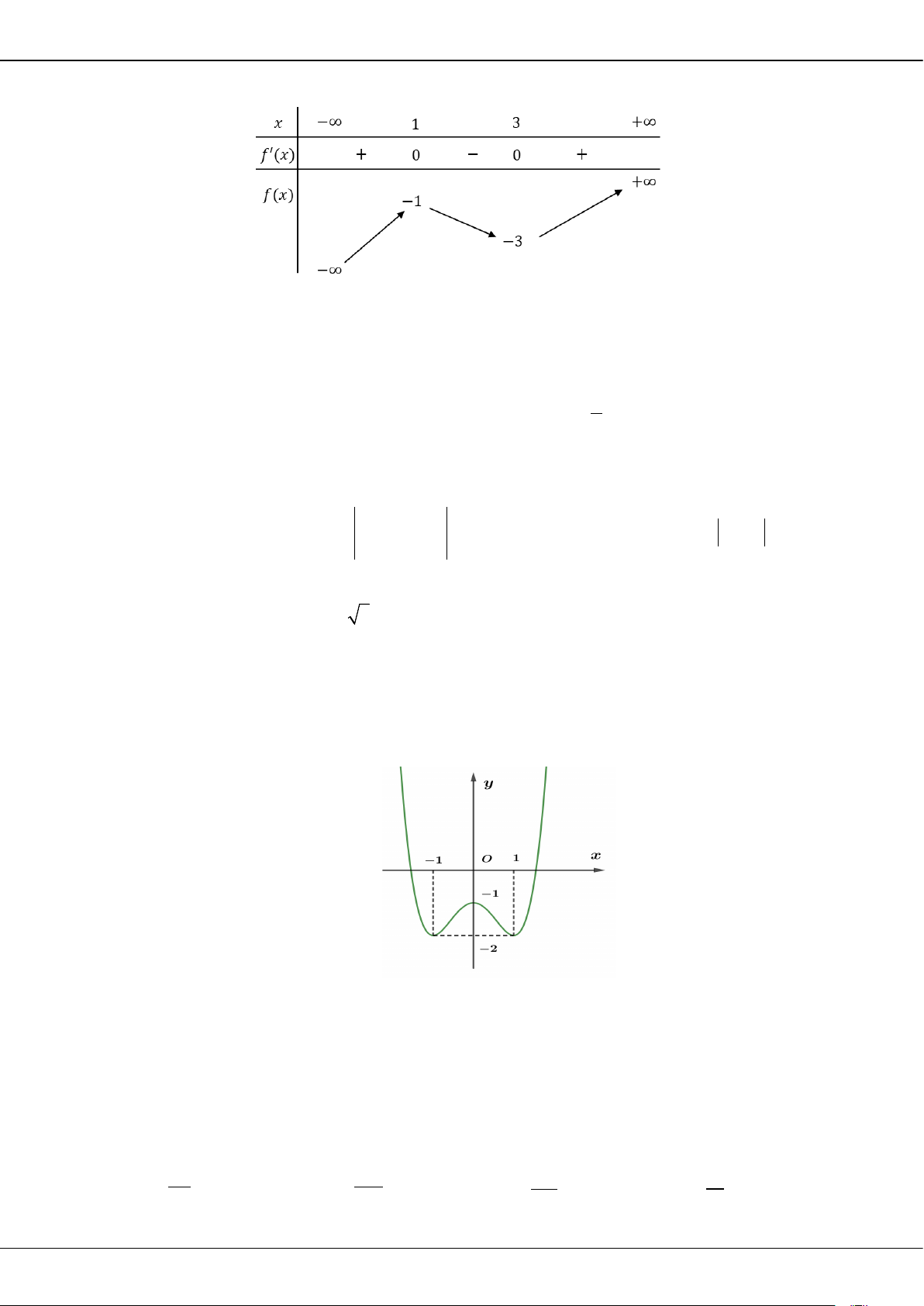
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 28

Câu 27: Cho hàm số

(

)

fx

có bảng biến thiên như hình vẽ.

Điểm cực đại của đồ thị hàm số đã cho là

A.

1

x

=

. B.

3x =

. C.

1x = −

. D.

(

)

1; 1−

.

Câu 28: Với

,ab

là các số thực dương tùy ý,

(

)

2

3

log .ab

bằng

A.

33

log 2logab+

. B.

( )

33

2 log logab+

. C.

33

1

log log

2

ab+

. D.

33

2 log logab⋅⋅

.

Câu 29: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

2

2yx= −

, trục

Ox

và các đường thẳng

1x =

,

2

x =

được tính bằng công thức nào sau đây?

A.

( )

2

1

2dxx

π

−

∫

. B.

( )

2

1

2dxx−

∫

. C.

( )

2

1

2dxx−

∫

. D.

2

1

2dxx−

∫

.

Câu 30: Cho hình lăng trụ đứng tam giác

.' ' '

ABC A B C

có đáy

ABC

là tam giác vuông tại

B

và

4, 5BC AC= =

và

' 33AA =

. Góc giữa mặt phẳng

( )

'C'AB

và

( )

'B'C'

A

bằng

A.

0

90

B.

0

60

. C.

0

45

. D.

0

30

.

Câu 31: Cho hàm số

( )

42

f x ax bx c

=++

có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị

nguyên thuộc đoạn

[ ]

2;5−

của tham số

m

để phương trình

( )

fx m=

có đúng hai nghiệm phân

biệt?

A.

1

. B.

6

. C.

7

. D.

5

.

Câu 32: Cho hàm số

( )

fx

có đạo hàm là

(

) ( ) ( )

2

3

12fx xx x

′

=−+

. Khoảng nghịch biến của hàm số là

A.

( )

;2−∞ −

và

( )

0;1

. B.

( )

2; 0−

và

( )

1; +∞

. C.

( )

;2−∞ −

và

( )

0; +∞

. D.

( )

2; 0−

.

Câu 33: Cho tập hợp

{ }

1; 2; 3; 4; 5; 6; 7;8;9;10;11;12;13A =

. Lấy ngẫu nhiên 3 số trong tập

A

. Tính xác

suất để lấy được ba số có tổng là số lẻ

A.

3

25

. B.

71

143

. C.

70

.

143

D.

5

.

11

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 29

Câu 34: Tích các nghiệm của phương trình

2

33

log log (9 ) 4 0xx

− −=

bằng

A.

6−

. B.

3−

. C.

3

. D.

27

.

Câu 35: Xác định tập hợp các điểm

M

trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện:

| || |zi zi+= −

.

A. Trục Oy. B. Trục Ox. C.

yx=

. D.

yx= −

.

Câu 36: Trong không gian

Oxyz

, phương trình của đường thẳng đi qua điểm

(

)

0; 3; 1A

−

và vuông góc

với mặt phẳng

3 4 20xyz− + −=

là

A.

13

13 4

x yz−−

= =

−−

. B.

31

134

xy z++

= =

−

. C.

31

13 4

xy z−−

= =

−−

. D.

31

134

xy z+−

= =

−

.

Câu 37: Trong không gian với hệ toạ độ

Oxyz

, cho điểm

( )

2;4;6

K

, gọi

K



là hình chiếu vuông góc

của

K

trên trục

Oz

, khi đó trung điểm

OK



có toạ độ là:

A.

( )

1;0;0

. B.

( )

0;0;3

. C.

( )

0;2;0

. D.

( )

1;2;3

.

Câu 38: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

, mặt bên

SAB

là tam giác đều và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ điểm

A

đến mặt phẳng

( )

SBD

bằng

A.

21

14

a

. B.

21

7

a

. C.

2

a

. D.

21

28

a

Câu 39: Có bao nhiêu giá trị nguyên dương của

y

để tập nghiệm của bất phương trình

( )

2

log 2 2 0

x

xy− −<

có ít nhất

1

số nguyên và không quá

6

số nguyên?

A.

2048

. B.

2016

. C.

1012

. D.

2023

.

Câu 40: Cho

,fg

là hai hàm số liên tục trên

[ ]

1; 3

thỏa mãn điều kiện

( ) ( )

3

1

3 dx=10f x gx+





∫

đồng thời

( ) ( )

3

1

2 dx=6f x gx−





∫

. Tính

( ) ( )

3

2

1

3 dxf x gx x



+−



∫

.

A.

9

. B.

20−

. C.

6

. D.

32

.

Câu 41: Có bao nhiêu giá trị nguyên của tham số để hàm số

32

2 ( 2) 1y mx mx m x= − +− +

không có

cực trị

A. vô số. B.

5

. C.

6

. D.

7

.

Câu 42: Trong mặt phẳng phức

Oxy

, các số phức

z

thỏa

21z i zi+ −= +

. Tìm số phức

z

được biểu

diễn bởi điểm

M

sao cho

MA

ngắn nhất với

( )

1, 3A

.

A.

3 i+

. B.

13i+

. C.

23i

−

. D.

23i−+

.

Câu 43: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, diện tích tam giác

A’BC bằng

2

5

4

a

. Thể tích khối lăng trụ đã cho bằng

A.

3

6

24

a

B.

3

6

a

C.

3

36

8

a

D.

3

6

8

a

Câu 44: Cho hàm số

(

)

y fx=

liên tục trên



và có đồ thị hàm số

( )

y fx

′

=

như hình bên

m

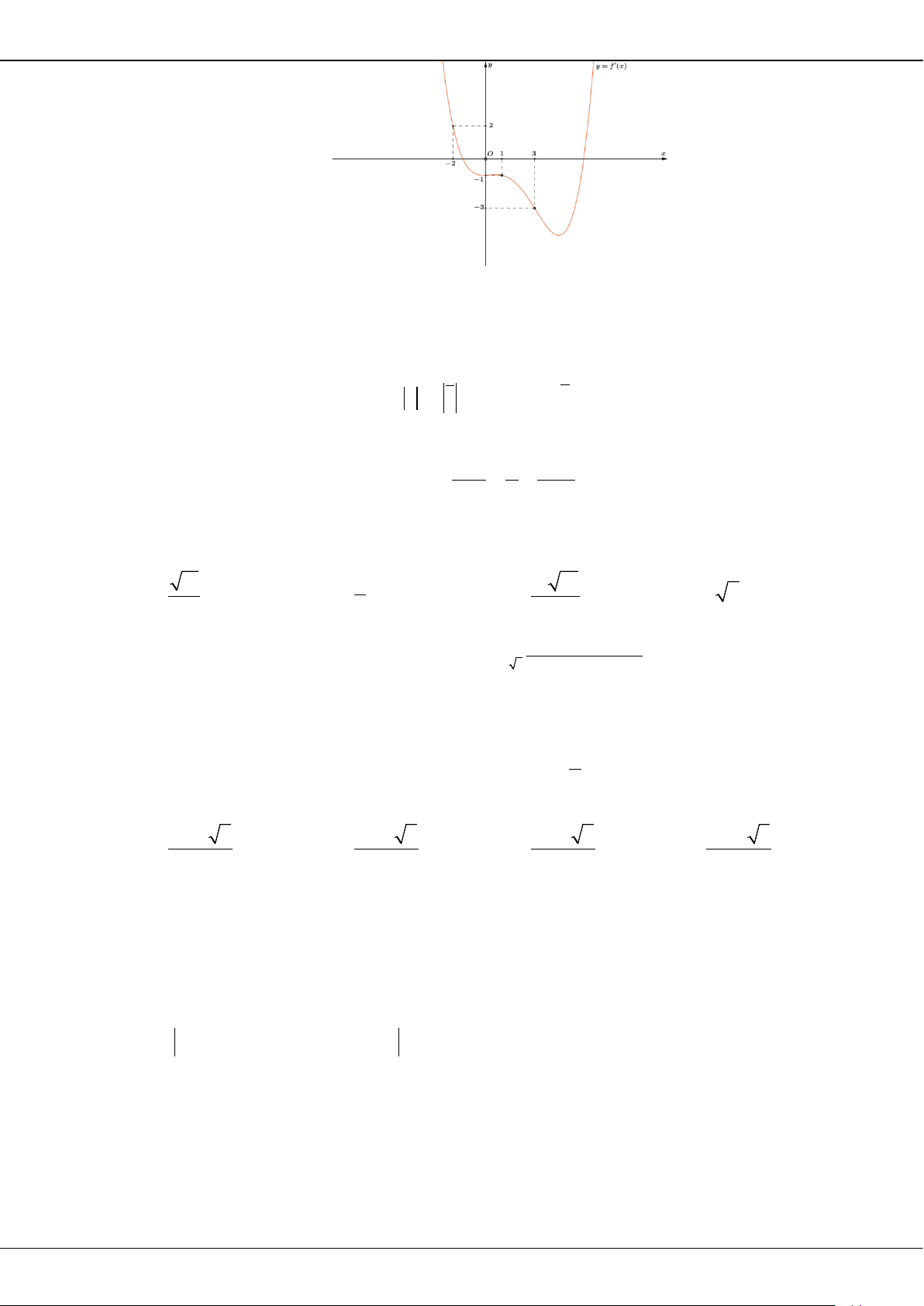
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 30

Xét hàm số

( )

2

2gx f x x

= +

. Hỏi mệnh đề nào sau đây là đúng?

A.

( ) ( ) ( )

1 23gg g< −<

. B.

( ) ( ) ( )

231g gg−> =

.

C.

( ) ( ) (

)

231

g gg

−< <

. D.

( ) ( ) ( )

13 2gg g< <−

.

Câu 45: Có bao nhiêu số phức z thỏa mãn:

2

26zz+=

và

6zz+=

A. 2. B. 3. C. 2. D. 1.

Câu 46: Cho điểm

( )

2;5;3A

và đường thẳng

12

:

212

x yz

d

−−

= =

. Gọi

( )

P

là mặt phẳng chứa đường

thẳng

d

sao cho khoảng cách từ

A

đến

( )

P

lớn nhất. Khoảng cách từ điểm

( )

1; 2; 1M −

đến

( )

P

bằng

A.

11

18

. B.

4

3

. C.

11 18

18

. D.

32

.

Câu 47: Có bao nhiêu cặp số nguyên

( )

,xy

thỏa mãn

( ) ( )

22

3

log 3 3 .

2

xy

x x y y xy

x y xy

+

= −+ −+

+++

A.

1

. B.

2

. C.

4

. D.

6

.

Câu 48: Cho hình nón có trục SO = a. Mặt phẳng (P) đi qua đỉnh của hình nón và cắt hình nón theo thiết

diện là tam giác đều. Biết khoảng cách từ O đến (P) bằng

2

a

. Tính diện tích xung quanh của hình

nón đã cho.

A.

2

87

9

a

π

B.

2

47

9

a

π

C.

2

47

3

a

π

D.

2

25

9

a

π

Câu 49: Trong không gian

Oxyz

, cho hai điểm

( )

1;1; 3A −

và

( )

2; 3;1B −

. Xét hai điểm

,MN

thay đổi

thuộc mặt phẳng

( )

Oxz

sao cho

2MN =

. Giá trị nhỏ nhất của

AM BN+

bằng

A.

5

. B.

6

. C.

4

. D.

7

.

Câu 50: Có bao nhiêu giá trị nguyên thuộc đoạn

− 



2023;2023

của tham số thực

m

để hàm số

( ) ( )

=−+ + +

32

32 3 4yx mxmmx

đồng biến trên khoảng

( )

0;4

?

A.

4041

. B.

9

. C.

2021

. D.

2020

.

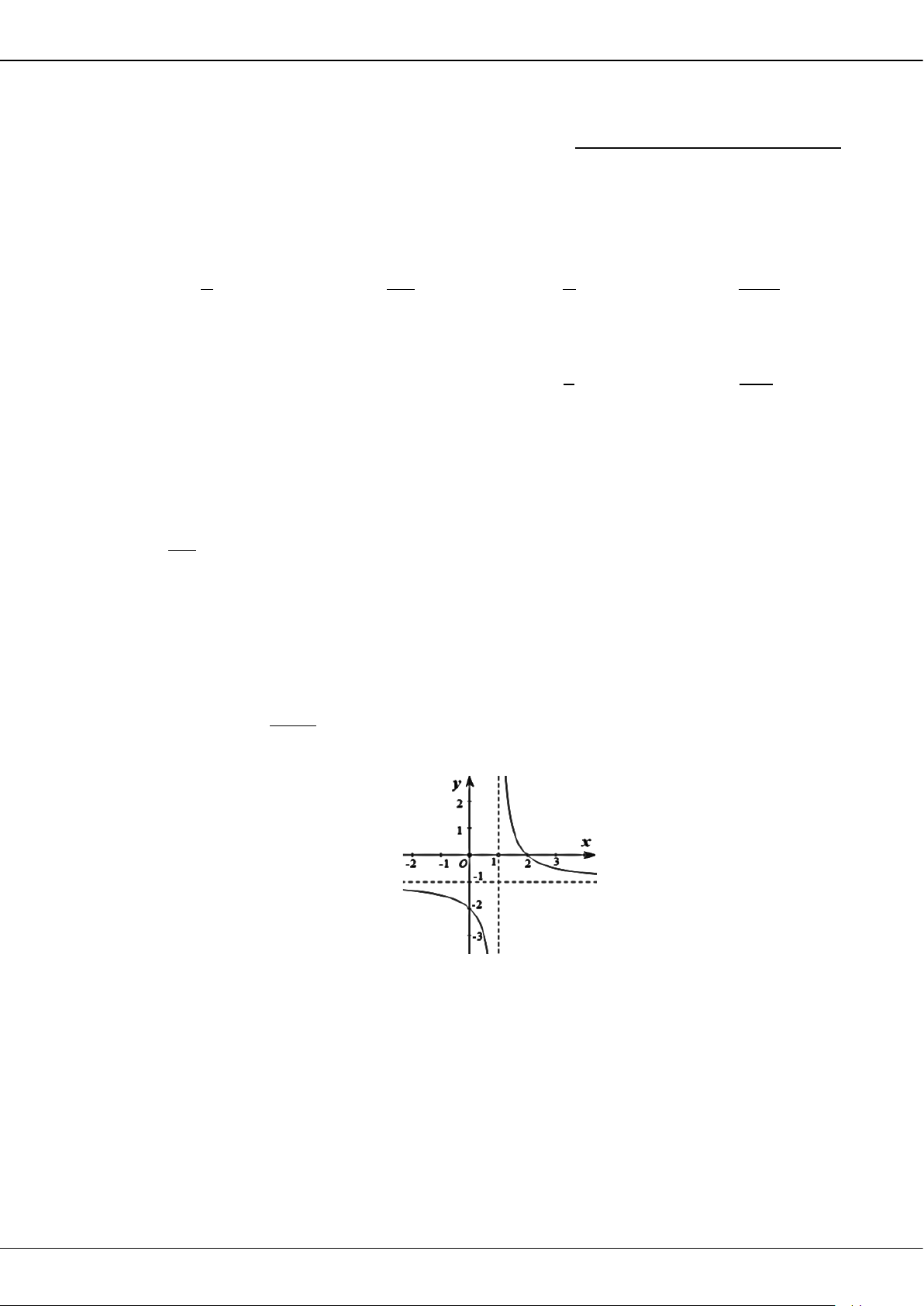
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 31

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT TRƯƠNG ĐỊNH

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Trong mặt phẳng tọa độ

Oxy

, điểm biểu diễn số phức

z 4 3i

= −

có tọa độ là:

A.

( )

3; 4−

. B.

(

)

4;3

. C.

( )

4; 3−

. D.

( )

3; 4

.

Câu 2: Trên khoảng

( )

0; +∞

, đạo hàm của hàm số

5

y log x=

là:

A.

5

y

x

′

=

. B.

ln 5

y

x

′

=

. C.

1

y

x

′

=

. D.

1

y

x ln 5

′

=

.

Câu 3: Đạo hàm của hàm số là

e

yx=

trên khoảng

( )

0; +∞

là:

A.

e1

y ex

+

′

=

. B.

e1

y ex

−

′

=

C.

e1

1

yx

e

−

′

=

D.

e1

1

yx

e1

+

′

=

+

.

Câu 4: Tập nghiệm của bất phương trình

x2

3 27

+

<

là:

A.

(

]

;1−∞

. B.

( )

;7−∞

. C.

( )

;1−∞ −

. D.

( )

;1−∞

.

Câu 5: Cho cấp số nhân

( )

n

u

có

1

u 5, q 2= =

. Số hạng thứ 6 của cấp số nhân đó là:

A.

1

160

. B.

25

C.

32

. D.

160

.

Câu 6: Trong không gian

Oxyz

, cho 3 điểm

(

)

M 2; 1; 3−

;

( )

N 1; 0; 2

;

( )

P 2; 3; 5−

. Tìm một vectơ pháp

tuyến

n



của mặt phẳng

( )

MNP

.

A.

( )

n 12; 4;8=



B.

( )

n 8;12; 4

=



C.

( )

n 3;1; 2=



D.

( )

n 3; 2;1=



Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong như hình vẽ. Tọa độ giao điểm của đồ thị hàm

số đã cho và trục hoành là:

A.

( )

0;2

. B.

( )

2;0

. C.

( )

0; 2−

. D.

( )

1;0

.

Câu 8: Nếu

( )

0

2023

f x dx 2=

∫

và

( )

2023

0

g x dx 5= −

∫

thì

(

) ( )

2023

0

2f x g x dx−





∫

bằng

A.

9

. B.

7

. C.

3−

D.

1−

.

Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình vẽ

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 32

A.

32

y x 3x 1=−+ +

. B.

32

y x 3x 3=−+

.

C.

4

y x 2x 1=−+

. D.

x2

y

2x 1

−

=

+

.

Câu 10: Trong không gian

Oxyz

, mặt cầu

( )

2 22

04S : x y z x 2y 6z 5++− + − +=

có bán kính bằng

A.

3

. B.

11

. C.

9

. D.

11

.

Câu 11: Góc giữa hai mặt phẳng

(P) :x y 2z 1 0+ − −=

và

(Q) :5x 2y 11z 3 0+ + −=

bằng

A.

o

120

. B.

o

45

. C.

o

60

. D.

o

150

.

Câu 12: Cho số phức

z 7 6i= +

, phần ảo của số phức

2

z

bằng

A.

13

. B.

84

. C.

6

. D.

48

.

Câu 13: Thể tích của khối hộp chữ nhật có ba kích thước lần lượt là

4, 7, 9

bằng

A.

252

.

B.

20

. C.

126

. D.

84

.

Câu 14: Cho khối chóp

S.ABC

có đáy là tam giác vuông tại

A

, biết

AB 3, AC 4= =

;

SA

vuông góc với

đáy và

SA 3=

(tham khảo hình vẽ).

Thể tích khối chóp đã cho bằng

A.

18

. B.

12

. C.

6.

D.

36.

Câu 15: Trong không gian

Oxyz

, cho mặt cầu

222

(S):(x1)(y3)(z5)3.

+ +− ++ =

Tâm của mặt cầu

(S)

có tọa độ là:

A.

(1;3;5).

B.

( 1; 3; 5).−−

C.

(1;3;5).−−−

D.

(1; 3; 5) .−

.

Câu 16: Gọi

l,h,r

lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích xung

quanh

xq

S

của hình nón là.

A.

xq

1

S rl

2

π

=

. B.

xq

S rh

π

=

. C.

xq

S rl

π

=

. D.

2

xq

1

S rh

3

π

=

.

Câu 17: Số phức liên hợp của số phức

z 1 2i= −

là:

A.

z 1 2i=−−

. B.

z 1 2i=−+

. C.

z 1 2i= +

. D.

z 2i= −

.

Câu 18: Trong không gian

Oxyz

cho đường thẳng

x1 y2 z

d:

132

+−

= =

−

. Hỏi véc tơ nào trong các véc tơ

dưới đây là một véctơ chỉ phương của

d

?

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 33

A.

( )

u 1; 2; 0

= −



. B.

(

)

u 1; 3; 2

=



. C.

(

)

u 1; 3; 2

=−−



. D.

( )

u 1;3;2= −−



.

Câu 19: Cho hàm số

42

y ax bx c=++

(với

a, b, c

∈



), có đồ thị như hình vẽ.

Số điểm cực trị của hàm số đã cho là:

A. 0. B. 3. C. 2. D. 1.

Câu 20: Phương trình đường tiệm cận đứng của đồ thị hàm số

2x 1

y

x2

−

=

−

là:

A.

1

x

2

=

. B.

x2=

. C.

1

y

2

=

. D.

y2

=

.

Câu 21: Phương trình

2

2x 5x 4

7 49

++

=

có tổng tất cả các nghiệm bằng

A.

1

. B.

5

2

. C.

1−

. D.

5

2

−

.

Câu 22: Một hộp đựng 5 viên bi màu xanh, 7 viên bi màu vàng. Có bao nhiêu cách lấy ra 6 viên bi bất

kỳ?

A. 665280. B. 924. C. 7. D. 942.

Câu 23: Tìm họ nguyên hàm của hàm số

x

f(x) x 3= +

A.

2x

x3

f (x)dx C

2 ln 3

=++

∫

B.

2

x

f (x)dx 3 ln 3 C

2

=++

∫

C.

2

x

f (x)dx 3 C

2

= ++

∫

D.

x

3

f (x)dx 1 C

ln 3

=++

∫

Câu 24: Cho

F(x)

là một nguyên hàm của hàm số

f (x).

Khi đó hiệu số

F(1) F(2)−

bằng

A.

2

1

f (x)dx

∫

B.

2

1

f (x)dx

−

∫

C.

2

1

F(x)dx

∫

D.

2

1

F(x)dx−

∫

Câu 25: Tìm họ nguyên hàm của hàm số

( )

f x 3x sin x= −

.

A.

( )

2

3x

f x dx cos x C

2

=++

∫

. B.

( )

f x dx 3 cos x C=++

∫

.

C.

( )

2

3x

f x dx cos x C

2

=−+

∫

. D.

( )

2

f x dx 3x cos x C=++

∫

.

Câu 26: Cho hàm số

( )

y fx=

có đồ thị như hình vẽ

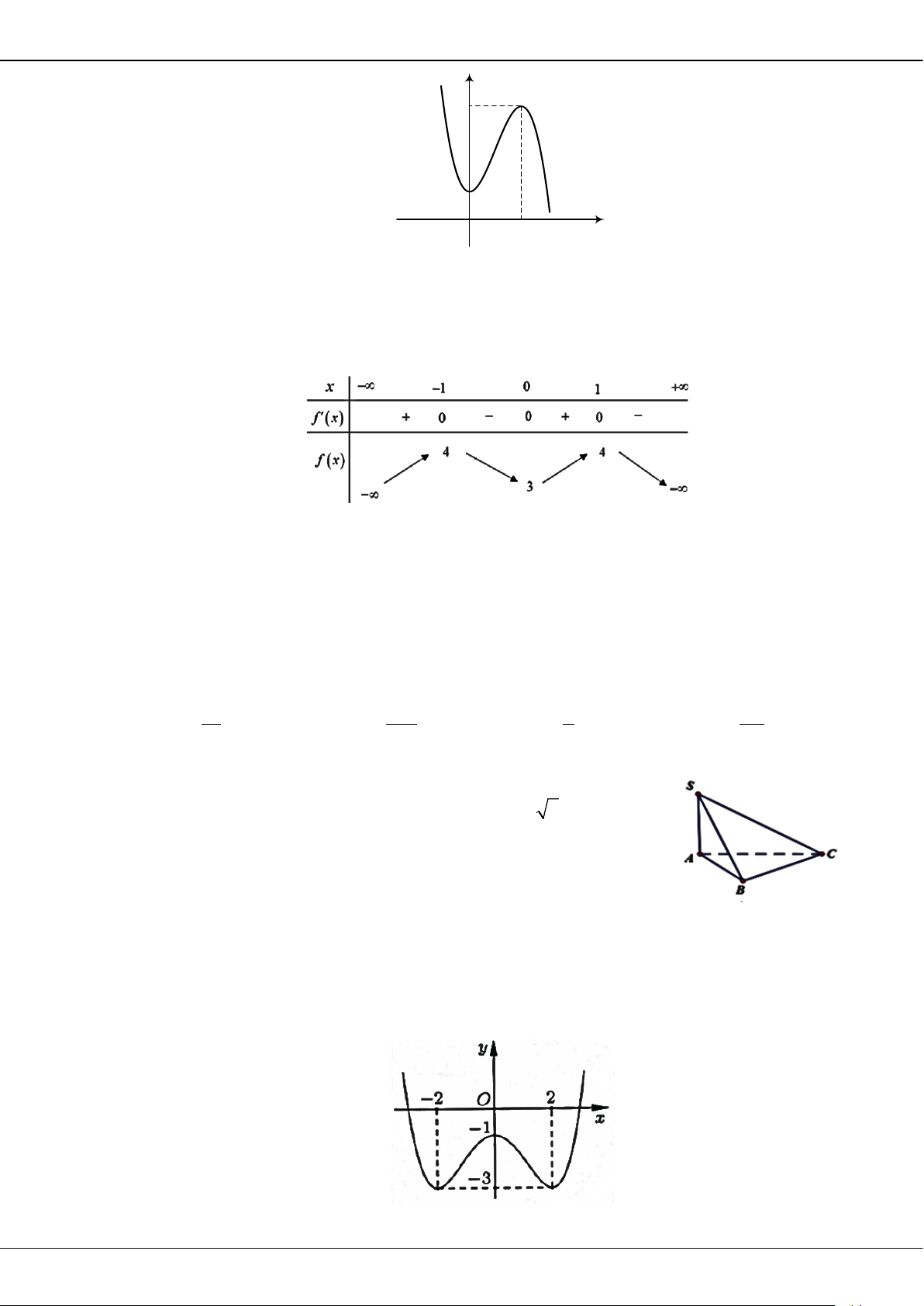
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 34

y

O

2

5

1

x

Hàm số đã cho đồng biến trên khoảng nào dưới đây

A.

( )

;1−∞

. B.

( )

2;+∞

. C.

( )

0;2

. D.

(

)

1;5

.

Câu 27: Cho hàm số

( )

y fx=

có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng

A. 1. B. 4. C. 0. D. 3.

Câu 28: Với

a

là số thực dương tùy ý,

( )

4

log 4a

bằng

A.

4

1 log a+

. B.

4

4 log a−

. C.

4

4 log a+

. D.

4

1 log a−

.

Câu 29: Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường

2

y1x= −

và

y0

=

quanh trục

Ox

?

A.

16

V

15

= ⋅

B.

16

V

15

π

= ⋅

C.

4

V

3

= ⋅

D.

4

V

3

π

= ⋅

Câu 30: Cho hình chóp

S.ABC

có

SA

vuông góc với mặt phẳng

( )

ABC

,

SA 2a=

, tam giác

ABC

vuông cân tại

B

và

AB 2a=

(minh họa

như hình vẽ bên).

Góc giữa đường thẳng

SC

và mặt phẳng

( )

ABC

bằng

A.

60°

. B.

45°

.

C.

30°

. D.

90°

.

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên.

Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

( )

f x 2m 0−=

có bốn nghiệm thực

phân biệt?

A.

2

. B.

1

. C.

3

. D.

4

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 35

Câu 32: Cho hàm số

( )

y fx=

có đạo hàm

( ) ( )( )

2

fx x1x3x

′

=+−

với mọi

x ∈

. Hàm số đã cho đồng

biến trên khoảng nào dưới đây?

A.

( )

1; 3−

. B.

( )

0;

+∞

. C.

( )

1;− +∞

. D.

( )

;3−∞

.

Câu 33: Một hộp chứa 16 quả cầu gồm 7 quả màu đỏ được đánh số từ 1 đến 7 và 9 quả màu xanh được

đánh số từ

1

đến

9

. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu

đồng thời tích hai số ghi trên chúng là số chẵn bằng

A.

9

.

80

B.

43

.

240

C.

43

.

120

D.

9

.

40

Câu 34: Tập nghiệm S của bất phương trình

(

) ( )

33

log x 1 log 2x 1+> −

là:

A.

1

S ;2

2



=





. B.

( )

S 1;2

= −

. C.

( )

S ;2= −∞

. D.

( )

S 2;= +∞

.

Câu 35: Trong mặt phẳng phức, tập hợp các điểm biểu diễn số phức

z

thỏa mãn

z 3 4i 5−− =

là

A. Một đường tròn. B. Một điểm.

C. Một đường elip. D. Một đường thẳng.

Câu 36: Trong không gian

Oxyz

, phương trình đường thẳng

d

đi qua

( )

A 1; 2; 1

và vuông góc với

( )

P:x2yz10

− +−=

là:

A.

x1 y2 z1

1 21

+++

= =

−

. B.

x2 y z2

2 42

+−

= =

−

.

C.

x2 y z2

1 21

++

= =

−

. D.

x1 y2 z1

1 21

−−−

= =

−

.

Câu 37: Trong không gian

Oxyz

, cho ba điểm

( ) ( ) ( )

A 1; 2; 3 , B 1; 0; 2 , C x ; y; 2−− −

thẳng hàng. Khi đó

xy+

bằng

A.

xy1+=

. B.

x y 17

+=

. C.

11

xy

5

+=−

. D.

11

xy

5

+=

.

Câu 38: Cho hình chóp

S.ABC

có đáy

ABC

là tam giác vuông tại A,

AB a, AC a 3= =

. Tam giác

SBC

đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách từ B đến mặt phẳng

( )

SAC

?

A.

a 39

.

13

B.

a.

C.

2a 39

.

13

D.

a3

V.

2

=

Câu 39: Có bao nhiêu số nguyên x thỏa mãn

( )

2

log x 2 x 2x 9−+− <

?

A. 1. B. 2. C. 3. D. 4.

Câu 40: Cho hàm số

( )

fx

có đạo hàm liên tục trên



. Biết

( )

f4 1=

và

( )

1

0

xf 4x dx 1,=

∫

khi đó

( )

4

2

0

dxxxf

′

∫

bằng

A.

31

2

. B.

16−

. C.

8

. D.

14

.

Câu 41: Có bao nhiêu giá trị nguyên của tham số

m

để hàm số

42

13

y x 3x mx

22

= −+

có ba điểm cực trị?

A.

5

. B.

6

. C.

7

. D.

4

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 36

Câu 42: Giả sử

12

z ,z

là hai trong các số phức

z

thỏa mãn

(

)

(

)

z 6 8 iz

−−

là số thực. Biết rằng

12

zz 6−=

. Giá trị nhỏ nhất của

12

z 3z+

bằng

A.

5 73−+

. B.

5 21+

C.

20 2 73−

D.

20 4 21−

Câu 43: Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh a. Tam giác SAD cân tại S và mặt bên

(SAD) vuông góc với mặt đáy. Biết thể tích khối chóp SABCD bằng a

3

. Tính khoảng cách từ B

đến mặt phẳng (SCD)?

A.

6a

37

B.

a

37

C. 3a D.

3a

37

Câu 44: Cho hàm số

( )

4 32

f (x) x bx cx dx e b,c,d,e=+ + ++ ∈

có các giá trị cực trị là 1; 4; 9. Diện tích

hình phẳng giới hạn bởi đồ thị hàm số

'

f (x)

g(x)

f(x)

=

và trục hoành bằng

A. 4 B. 6 C. 2 D. 8

Câu 45: Trên tập hợp các số phức, xét phương trình

( )

2

z 2m 1z m 3 0− + + +=

(

m

là tham số thực). Có

bao nhiêu giá trị của tham số

m

để phương trình có nghiệm phức

0

z

thoả mãn

0

z 26+=

?

A.

2

. B.

1

. C.

4

. D.

3

.

Câu 46: Trong không gian

Oxyz

, cho điểm

( )

M 2;1;3−

. Ba điểm

A

,

B

,

C

tương ứng là hình chiếu

vuông góc của điểm

M

lên các trục

Ox

,

Oy

,

Oz

. Khoảng cách từ điểm O đến

( )

ABC

bằng

A.

5

. B.

1

3

. C.

6

7

. D.

11

3

.

Câu 47: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình

(

) ( )

22

log 7x 7 log mx 4x m+≥ + +

nghiệm đúng với mọi x?

A. 1. B. 2. C. 3. D. 4.

Câu 48: Cắt hình nón đỉnh

S

bởi một mặt phẳng không đi qua trục hình nón ta được một tam giác vuông

cân có cạnh huyền bằng

a2

;

AB

là dây cung của đường tròn đáy hình nón sao cho mặt phẳng

( )

SAB

tạo với mặt phẳng chứa đáy hình nón một góc

60°

. Tính theo

a

khoảng cách từ tâm O

của đường tròn đáy đến mặt phẳng

( )

SAB

.

A.

a6

d

8

=

. B.

a6

d

3

=

. C.

a

d

3

=

. D.

a2

d

6

=

.

Câu 49: Trong không gian Oxyz, cho mặt cầu

2 22

(S) : (x 1) (y 1) (z 1) 6− ++ +− =

tâm I. Gọi

( )

α

là mặt

phẳng vuông góc với đường thẳng

x1 y3 z

d:

1 41

+−

= =

−

và cắt mặt cầu (S) theo đường tròn (C)

sao cho khối nón có đỉnh I, đáy là đường tròn (C) có thể tích lớn nhất. Biết

( )

α

không đi qua gốc

tọa độ, gọi

( )

H HH

H x ;y ;z

là tâm đường tròn (C). Giá trị của biểu thức

H HH

Tx y z

=++

bằng.

A.

1

2

−

B.

4

3

C.

2

3

D.

1

3

Câu 50: Có bao nhiêu giá trị nguyên của tham số

( )

a 10;

∞

∈− +

để hàm số

( )

22

f x ln x 2x a 2ax 1= + −− −

đồng biến trên khoảng

( )

0;10

?

A. 7. B. 11. C. 6. D. 9.

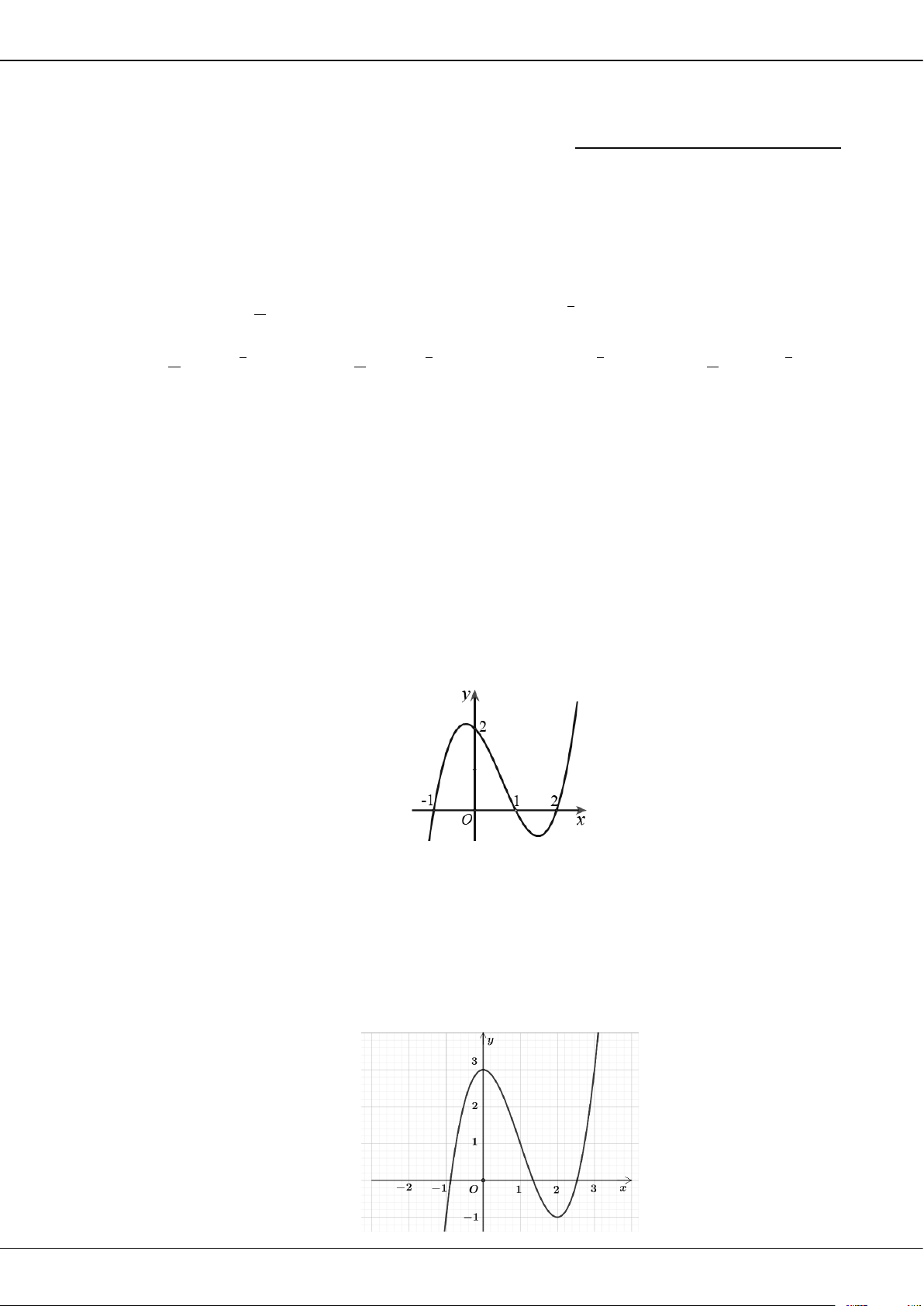
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 37

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT TÂN HIỆP

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức

12zi=−+

là điểm nào dưới đây?

A.

(

)

1; 2Q

. B.

( )

1; 2

P −

. C.

( )

1; 2N −

. D.

( )

1; 2M

−−

.

Câu 2: Tính đạo hàm của hàm số

2023

x

y =

A.

1

.2023

x

yx

−

′

=

. B.

2023

x

y

′

=

. C.

2023 ln

x

yx

′

=

. D.

2023 ln 2023

x

y

′

=

.

Câu 3: Trên khoảng

1

;

2



+∞





, đạo hàm của hàm số

( )

3

2

21yx= −

là

A.

( )

2

5

21

2

x −

. B.

( )

1

2

3

21

2

x −

. C.

( )

1

2

32 1x −

. D.

( )

1

2

3

21

2

x

−

.

Câu 4: Tập nghiệm của bất phương trình

2

7

24

x −

<

là

A.

( 3; 3)−

. B.

(0; 3)

. C.

( ; 3)−∞

. D.

(3; )+∞

.

Câu 5: Cho cấp số cộng

( )

n

u

có số hạng đầu

=

1

3

u

và số hạng thứ hai

= −

2

6u

. Giá trị của

4

u

bằng

A.

12−

. B.

24−

. C.

12

. D.

24

.

Câu 6: Trong không gian

Oxyz

, phương trình mặt phẳng đi qua điểm

( )

5; 2;1M −

và song song với

mặt phẳng

( ): 4 3 0Q x y z+9−+ =

là

A.

4 3 60xyz− + −=

. B.

4 3 16 0xyz− +−=

.

C.

4 3 21 0xy z++ − =

. D.

43 0

x y z+15− −+ =

.

Câu 7: Cho hàm số

32

y ax bx cx d= + ++

có đồ thị là đường cong trong hình vẽ bên dưới.

Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là điểm nào trong các điểm sau:

A.

( )

1; 0

. B.

( )

2;0

. C.

( )

1; 0−

. D.

( )

0; 2

.

Câu 8: Biết

( )

2

1

d3

fx x=

∫

và

( )

2

1

d2gx x= −

∫

. Khi đó

( ) ( )

2

1

df x gx x



−



∫

bằng?

A.

6

. B.

1

. C.

5

. D.

1−

.

Câu 9: Đường cong trong hình vẽ bên dưới là của hàm số nào?

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 38

A.

42

21yx x=−+

. B.

32

31

yx x

=−+ +

. C.

32

33yx x=−+

. D.

32

23yx x=++

.

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

2 22

( ): 2 2 7 0Sx y z x z+ + + − −=

. Bán kính của

mặt cầu đã cho bằng

A.

7

. B.

9

. C.

3

. D.

15

.

Câu 11: Trong không gian

Oxyz

, góc giữa hai mặt phẳng

( )

: 2 10

Px yz− −+=

và

( )

: 2 70Qx y z++ +=

bằng

A.

0

60

. B.

0

45

. C.

0

120

. D.

0

30

.

Câu 12: Cho số phức

z

thỏa mãn

( )

2

1 3 43iz i−=−

. Môđun của

z

bằng:

A.

5

4

B.

5

2

C.

2

5

D.

4

5

Câu 13: Cho khối lăng trụ có đáy là hình vuông cạnh

a

và chiều cao bằng

2a

. Thể tích của khối lăng

trụ đã cho bằng

A.

3

2

3

a

. B.

3

4

3

a

. C.

3

2a

. D.

3

4a

.

Câu 14: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

,a

cạnh bên

SA

vuông góc với

đáy,

3.SA a=

Thể tích khối chóp

.S ABCD

bằng

A.

3

.

3

a

B.

3

.

33

a

C.

3

.

3

a

D.

3

3.a

Câu 15: Trong không gian

Oxyz

, cho mặt cầu

2 22

2 2 4 10 0xyz x yz+++ − +−=

và điểm

( )

1; 0;1A

. Khẳng định nào sau đây là đúng?

A. Điểm A nằm ngoài mặt cầu

( )

S

. B. Điểm A nằm trong mặt cầu

( )

S

.

C. Điểm A nằm trên mặt cầu

(

)

S

. D.

2OA =

.

Câu 16: Phần ảo của số phức z biết

23

zi= −

bằng

A.

3−

. B.

2−

. C. 2. D. 3.

Câu 17: Cho khối trụ

(

)

T

có bán kính đáy

1R =

, thể tích

5V

π

=

. Tính diện tích toàn phần của hình trụ

tương ứng.

A.

12S

π

=

B.

11S

π

=

C.

10S

π

=

D.

7S

π

=

Câu 18: Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

d

:

1

5

23

xt

yt

zt

= −





= +





= +



?

A.

( )

1; 2; 5P

. B.

( )

1; 5; 2N

. C.

( )

1;1; 3Q −

. D.

( )

1;1; 3M

.

Câu 19: Cho hàm số

42

(,, )y ax bx c a b c=++ ∈

có đồ thị là đường cong trong hình bên dưới.

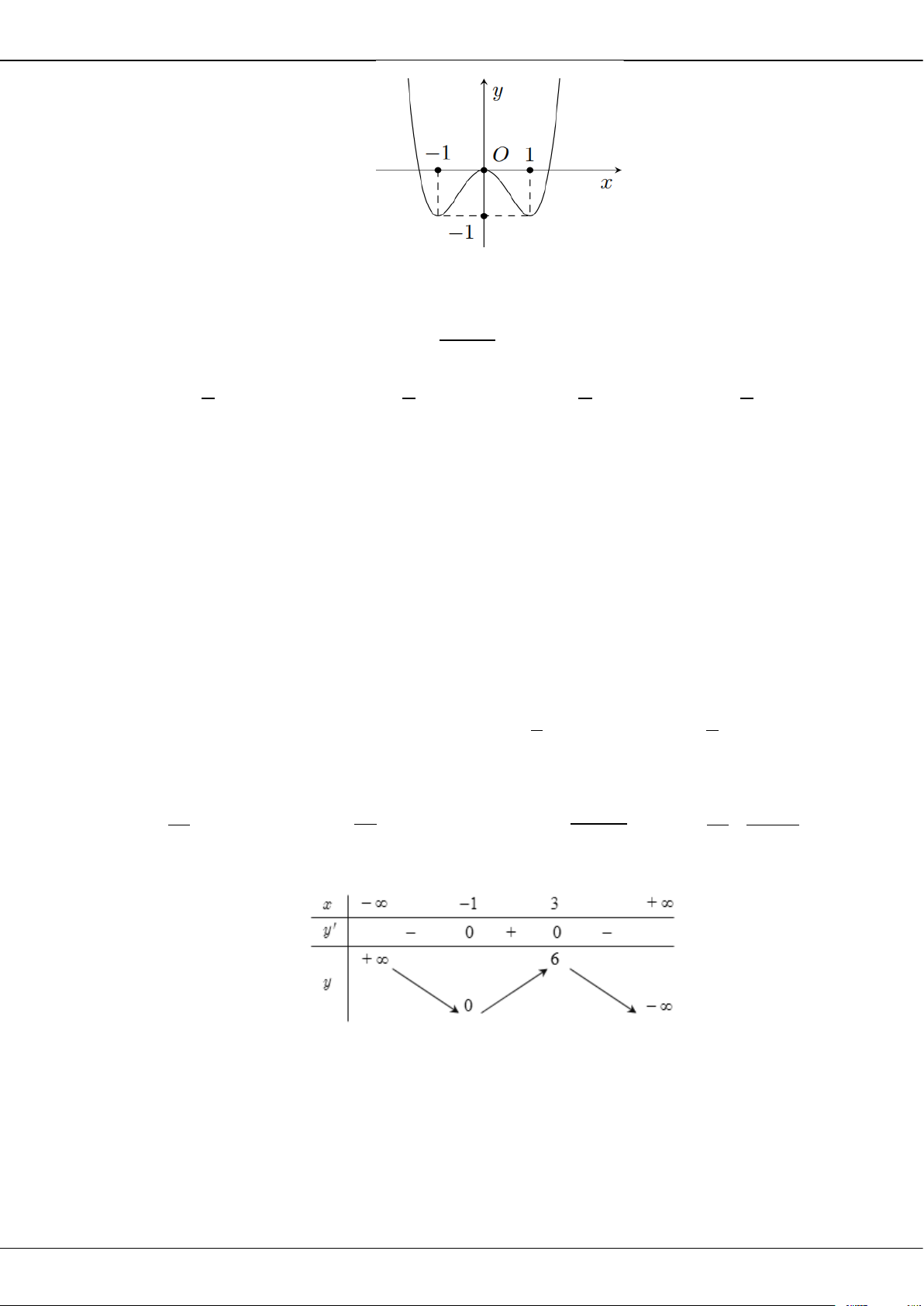
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 39

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

A.

(

)

1; 1

M −−

. B.

( )

1; 0M −

. C.

( )

0; 1M −

. D.

( )

1;1M

.

Câu 20: Tiệm cận ngang của đồ thị hàm số

23

31

x

y

x

−

=

+

là đường thẳng có phương trình:

A.

2

3

y =

. B.

1

3

y = −

. C.

2

3

y = −

. D.

1

3

y =

.

Câu 21: Tập nghiệm của bất phương trình

( )

2

3

log 36 3x−≥

là

A.

(

] [

)

; 3 3;

−∞ − ∪ +∞

. B.

(

]

;3−∞

. C.

[ ]

3; 3−

. D.

(

]

0;3

.

Câu 22: Cho

8

điểm trong đó không có

3

điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh

của nó được chọn từ

8

điểm trên?

A.

336

. B.

56

. C.

168

. D.

84

.

Câu 23: Cho tập hợp

A

có

20

phần tử. Hỏi

A

có bao nhiêu tập con gồm

6

phần tử?

A.

6

20

C

. B. 20. C.

6

P

. D.

6

20

A

.

Câu 24: Nếu

( )

3

1

2 15f x dx



+=



∫

thì

( )

3

1

f x dx

∫

bằng

A.

3.

B.

2.

C.

3

.

4

D.

3

.

2

Câu 25: Tính

( )

sin 2 dx xx−

∫

.

A.

2

sin

2

x

xC++

. B.

2

cos 2

2

x

xC++

. C.

2

cos 2

2

x

xC++

. D.

2

cos 2

22

xx

C++

.

Câu 26: Cho hàm số

( )

y fx=

liên tục trên



và có bảng biến thiên như sau:

Khẳng định nào sau đây là sai về sự biến thiên của hàm số

( )

y fx=

?

A. Nghịch biến trên khoảng

( )

3; +∞

. B. Đồng biến trên khoảng

( )

0;6

.

C. Nghịch biến trên khoảng

( )

;1−∞ −

. D. Đồng biến trên khoảng

( )

1; 3−

.

Câu 27: Cho hàm số

( )

y fx=

có đồ thị như hình vẽ:

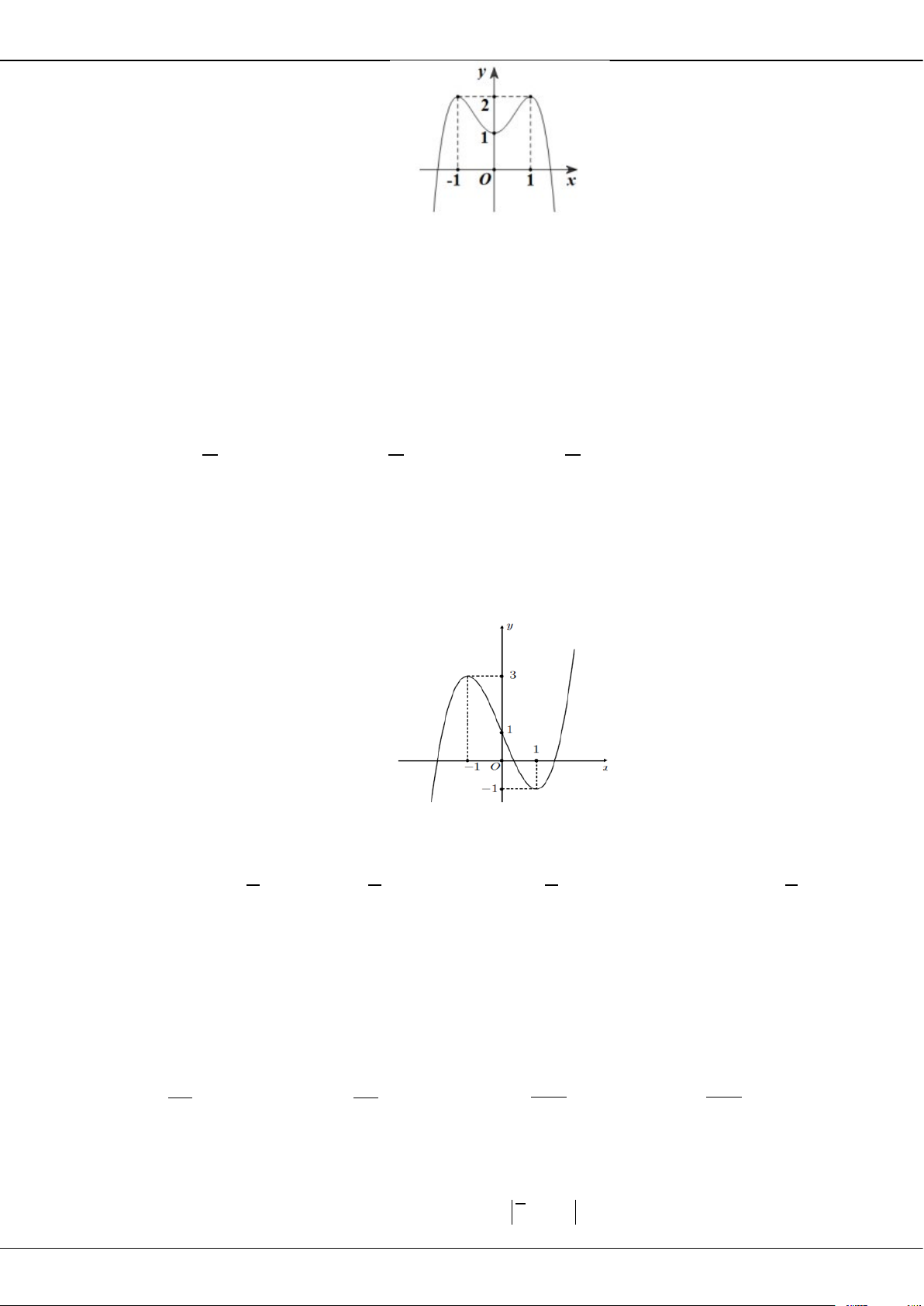
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 40

Giá trị cực đại của hàm số đã cho bằng:

A.

1−

. B.

1

. C.

0

. D.

2

.

Câu 28: Với

,ab

là các số thực dương tùy ý và

a

khác

1

, đặt

2

36

log log

a

Pb b= +

. Mệnh đề nào dưới

đây đúng?

A.

27log

a

Pb

=

. B.

15log

a

Pb=

. C.

9log

a

Pb=

. D.

6log

a

Pb

=

.

Câu 29: Thể tích V của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường

2

2,y xxy x=−=

xung quanh trục Ox là:

A.

.

3

V

π

=

B.

.

4

V

π

=

C.

.

5

V

π

=

D.

.V

π

=

Câu 30: Cho lăng trụ đứng

.'' 'ABC A B C

và

ABC∆

vuông tại

B

. Góc giữa

(' )A BC

và

()ABC

là

góc nào sau đây

?

A.



'

A BA

. B.



'

A AB

. C.



'A CA

. D.



'A AC

Câu 31: Cho hàm số

( )

y fx=

có đồ thị như sau

Tìm tất cả các giá trị của tham số

m

để phương trình

( )

2 3 30

fx m+ −=

có 3 nghiệm phân

biệt.

A.

5

1

3

m−< <

B.

5

1

3

m−< <

C.

5

1

3

m−≤ ≤

D.

5

1

3

m−≤ ≤

Câu 32: Cho hàm số

( )

y fx=

có đạo hàm

( ) ( )( )

( )

2

2 5 1.fx x x x

′

=−++

Hàm số

( )

y fx=

nghịch biến trên khoảng nào dưới đây?

A.

( )

4; 2−−

. B.

( )

;1−∞ −

. C.

( )

;5−∞ −

. D.

(

)

3; 4

.

Câu 33: Từ một hộp chứa 12 quả cầu, trong đó có 8 quả màu đỏ, 3 quả màu xanh và 1 quả màu vàng, lấy

ngẫu nhiên 3 quả. Xác suất để lấy được 3 quả cầu có đúng hai màu bằng

A.

23

44

. B.

21

44

. C.

139

220

. D.

81

220

.

Câu 34: Tổng tất cả các nghiệm của phương trình

2

2023

log ( 2022 ) 1xx+=

bằng

A.

2022−

. B.

2023−

C.

2023

. D.

2022

.

Câu 35: Tập hợp các điểm biểu diễn số phức

z

thỏa mãn

12zi+− =

là đường tròn có phương trình là

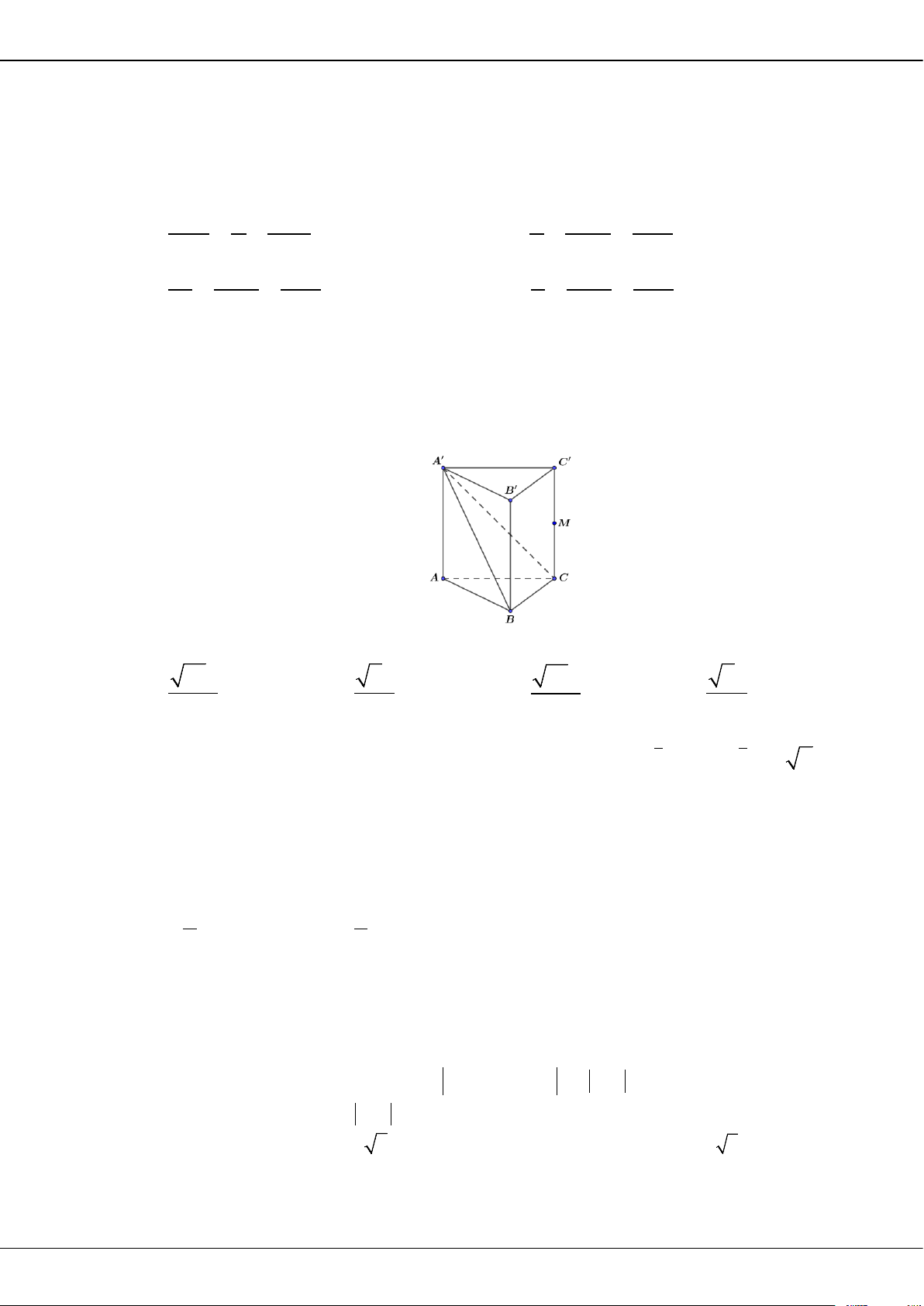
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 41

A.

( ) ( )

22

1 14− ++ =xy

. B.

( ) ( )

22

1 14+ +− =xy

.

C.

( ) ( )

22

1 14+ ++ =xy

. D.

( ) ( )

22

1 14− +− =xy

.

Câu 36: Trong không gian

Oxyz

, đường thẳng đi qua điểm

( )

0; 3; 1A −

và vuông góc với mặt phẳng

3 4 20xyz− + −=

có phương trình là

A.

13

13 4

x yz

−−

= =

−−

. B.

31

134

xy z++

= =

−

.

C.

31

13 4

xy z−−

= =

−−

. D.

31

134

xy z+−

= =

−

.

Câu 37: Trong không gian

Oxyz

, điểm đối xứng với điểm

( )

4; 5;3

M −

qua trục

Oz

có tọa độ là

A.

( )

4;5;3−−

. B.

( )

4;5;3−

. C.

( )

4;5; 3−−

. D.

( )

0;0;3

.

Câu 38: Cho hình lăng trụ đứng

.ABC A B C

′′′

có tất cả các cạnh đều bằng

a

. Gọi

M

là trung điểm

CC

′

.

Khoảng cách từ

M

đến mặt phẳng

( )

A BC

′

bằng

A.

21

14

a

. B.

2

a

. C.

21

7

a

. D.

2

4

a

.

Câu 39: Có bao nhiêu số tự nhiên x ∈[1; 2023] thỏa bất phương trình

44

11

log log

22

334

xx

x





?

A. 2017. B. 2022. C. 2024. D. 2023.

Câu 40: Cho hàm số

( )

fx

liên tục trên



. Gọi

(

) (

)

,

Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa

mãn

( ) ( )

8 88FG+=

và

( ) ( )

0 02FG+=−

. Khi đó

0

2

(4)f x dx

−

∫

bằng

A.

5

4

−

. B.

5

4

. C.

5

. D.

5−

.

Câu 41: Có bao nhiêu giá trị nguyên thuộc

[ ]

20;20−

của tham số

m

để đồ thị hàm số

( )

42 2

91y mx m x=+− +

có ba điểm cực trị?

A. 20. B. 19. C. 18. D. 17.

Câu 42: Xét các số phức

z

thoả mãn điều kiện

2

2 44 2 1zz i z+ ++ = +

. Gọi

M

và

m

lần lượt là giá

trị lớn nhất và nhỏ nhất của

1z +

. Giá trị của

Mm−

bằng

A.

2

. B.

26

. C.

14

. D.

46

.

Câu 43: Cho khối lăng trụ đứng

.ABC A B C

′′′

có đáy là tam giác đều. Mặt phẳng

()A BC

′

tạo với đáy một

góc

30°

và tam giác

A BC

′

có diện tích bằng

32

. Thể tích của khối lăng trụ đã cho bằng

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 42

A.

64 3

B.

64 3

3

. C.

128

. D.

128

3

.

Câu 44: Cho hàm số

(

)

y fx=

có đạo hàm liên tục trên



, thỏa mãn

( ) (

)

2

42 1 ,

f x x fx

′



= +−





x

∀∈

và

( )

12

f =

. Diện tích hình phẳng giới hạn bởi các đường

( ) ( )

,yfxyfx

′

= =

và trục

tung bằng

A.

1

3

. B.

4

3

. C.

3

4

. D.

5

3

.

Câu 45: Trên tập hợp các số phức, xét phương trình

( )

22

30z a za a− − + +=

(

a

là tham số thực). Có

bao nhiêu giá trị nguyên của

a

để phương trình có 2 nghiệm phức

12

, zz

thỏa mãn

12 12

zz zz+=−

?

A.

2

. B.

4

. C.

3

. D.

1

.

Câu 46: Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

( ) ( )

1; 2;1 , 3;4;0AB

, mặt phẳng

( )

: 46 0P ax by cz+++ =

. Biết rằng khoảng cách từ

,AB

đến mặt phẳng

( )

P

lần lượt bằng

6

và

3

. Giá trị của biểu thức

T abc=++

bằng

A.

3−

. B.

6−

. C.

3

. D.

6

.

Câu 47: Có bao nhiêu cặp số tự nhiên

(

)

;

xy

thỏa mãn

4 2 55

5

5(5 4 ) 2028 2024 log ( 2023) (1 )

y

y xx x x



+ + ≤− + + − −



?

A. 2023. B. 4042. C. 4024. D. 4040.

Câu 48: Cho hình trụ tròn xoay có hai đáy là hai hình tròn

( )

;3

O

và

( )

;3O

′

. Biết rằng tồn tại dây cung

AB

thuộc đường tròn

( )

O

sao cho

O AB

′

∆

là tam giác đều và mặt phẳng

( )

O AB

′

hợp với mặt

phẳng chứa đường tròn

( )

O

một góc

60°

. Tính diện tích xung quanh

xq

S

của hình nón có đỉnh

O

′

, đáy là hình tròn

( )

;3

O

.

A.

54 7

7

xq

S

π

=

. B.

81 7

7

xq

S

π

=

. C.

27 7

7

xq

S

π

=

. D.

36 7

7

xq

S

π

=

.

Câu 49: Trong không gian tọa độ

Oxyz

, gọi

( )

P

là mặt phẳng cắt các tia

Ox

,

Oy

,

Oz

lần lượt tại

( )

;0;0Aa

,

( )

0; ;0Bb

,

( )

0;0;Cc

sao cho

222

12abc++=

và diện tích tam giác

ABC

lớn nhất. Mặt phẳng

( )

P

đi qua điểm nào sau đây?

A.

( )

1; 0;1S

. B.

( )

2;0; 2M

. C.

(

)

3; 0;3

N

. D.

( )

2; 2; 0

Q

.

Câu 50: Cho hàm số bậc ba

( )

=y fx

có đồ thị như hình bên dưới:

Số giá trị nguyên của tham số

m

để hàm số

( )

−

=

−

9mf x

y

fx m

nghịch biến trên

( )

−1; 1

là

A.

0.

B.

2.

C.

3.

D. Vô số.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 43

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT PHƯỚC THẠNH

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức

32

zi

= −

?

A.

( )

3; 2

P −

. B.

( )

2; 3Q −

. C.

( )

3; 2N −

. D.

( )

2;3M

−

.

Câu 2: Tìm đạo hàm của hàm số

logyx=

.

A.

ln10

y

x

′

=

B.

1

ln10

y

x

′

=

C.

1

10ln

y

x

′

=

D.

1

y

x

′

=

Câu 3: Tập xác định của hàm số

3

2

yx=

là

A.

( )

0; +∞

. B.

( )

2; +∞

. C.



. D.

{ }

\0

.

Câu 4: Tập nghiệm của bất phương trình

2

2 16

x

−

≥

là

A.

[

)

6;

+∞

. B.

( )

4; +∞

. C.

( )

6; +∞

. D.

[

)

4;

+∞

.

Câu 5: Cho cấp số nhân

( )

n

u

với

4

1=u

;

3q =

. Tìm

1

u

?

A.

1

9

u =

. B.

1

9u =

. C.

1

27u =

. D.

1

27

u

=

.

Câu 6: Trong không gian

Oxyz

, mặt phẳng

( )

:2 3 1 0P xy z+ + −=

có một vectơ pháp tuyến là

A.

( )

3;1; 2n =



. B.

( )

2; 1; 3n

=



. C.

( )

1; 3; 2n =



. D.

( )

1; 3; 2n = −



.

Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị

hàm số đã cho và trục tung là

A.

( )

0; 1−

. B.

( )

1; 0

. C.

(

)

1; 0−

. D.

( )

0;1

Câu 8: Nếu

1

0

() 2f x dx =

∫

,

4

1

() 5f x dx =

∫

thì

4

0

()f x dx

∫

bằng

A.

7

. B.

3

. C.

10

. D.

3−

.

Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

A. B. C. D.

32

3 3.yx x=−+

32

3 3.yx x=−+ +

43

2 3.yx x=−+

43

2 3.yx x=−+ +

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 44

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

(

)

2 22

: 4 2 4 16 0Sx y z x y z++++ −−=

. Tìm tâm và bán

kính của mặt cầu

( )

S

.

A.

( )

2; 1; 2 , 5

IR−=

. B.

( )

2; 1; 2 , 1 3

IR−=

.

C.

( )

2; 1; 2 , 13IR−− =

. D.

( )

2; 1; 2 , 5IR−− =

.

Câu 11: Trong không gian

Oxyz

, góc giữa hai mặt phẳng

()Oyz

và

()Oxz

bằng

A.

30°

. B.

45°

. C.

60°

. D.

90°

.

Câu 12: Điểm

M

trong hình vẽ bên biểu diễn số phức

z

. Chọn kết luận đúng về số phức

z

.

A.

35zi= +

. B.

35zi=−+

. C.

35

zi= −

. D.

35zi=−−

.

Câu 13: Thể tích của khối hình hộp chữ nhật có các cạnh lần lượt là a, 2a, 3a bằng

A. . B. . C. . D. .

Câu 14: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

. Biết

(

)

SA ABC

⊥

và

3SA a=

.

Thể tích khối chóp đã cho bằng

A.

4

a

B.

3

2

a

C.

3

4

a

D.

3

4

a

Câu 15: Trong không gian với hệ tọa độ

,Oxyz

cho mặt cầu

 

S

có phương trình

2 22

2 4 6 0.xyz x yz

Mặt phẳng

 

Oxy

cắt

 

S

theo giao tuyến là một đường tròn. Đường

tròn giao tuyến này có bán kính

r

bằng

A.

2.r 

B.

5.r 

C.

6.r 

D.

4.r 

Câu 16: Cho số thực

,xy

thỏa

2 1 (3 2) 5−+ + = −x yi i

. Khi đó giá trị của

2

6= +M x xy

là

A.

27M =

. B.

3M =

. C.

9M = −

. D.

12M = −

.

Câu 17: Cho hình trụ có bán kính đáy

8R

=

và độ dài đường sinh

3l =

. Diện tích xung quanh của hình

trụ đã cho bằng

A.

24

π

. B.

192

π

. C.

48

π

. D.

64

π

.

3

6a

3

3a

3

a

3

2a

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 45

Câu 18: Trong không gian

Oxyz

, đường thẳng

12

: 22

33

xt

dy t

zt

= +





= −





=−−



đi qua điểm nào dưới đây?

A. Điểm

(

)

2; 2;3Q

. B. Điểm

( )

2; 2; 3N −−

.

C. Điểm

(

)

1; 2; 3M −

. D. Điểm

( )

1; 2; 3P

.

Câu 19: Cho hàm số

( )

y fx=

có đồ thị như sau

Hàm số đạt cực đại tại điểm

A.

1x =

. B.

1

x = −

. C.

2x =

. D.

3x = −

.

Câu 20: Tiệm cận đứng của đồ thị hàm số là

A. . B. . C. . D. .

Câu 21: Tập nghiệm của bất phương trình

5

log 1

x ≥

là

A.

(

]

;5 .−∞

B.

(

]

0;5 .

C.

[

)

1; .+∞

D.

[

)

5; .+∞

Câu 22: Có bao nhiêu cách chọn

3

học sinh từ một nhóm gồm

8

học sinh?

A.

3

8

A

. B.

8

3

. C.

3

8

. D.

3

8

C

.

Câu 23: Biết

( ) ( )

d = +

∫

f u u Fu C

. Khi đó

( )

2 3d

−

∫

fx x

bằng kết quả nào sau đây?

A.

( )

1

23

2

Fx C−+

. B.

( )

23Fx C−+

. C.

( )

223Fx C−+

. D.

(

)

23Fx C

−+

.

Câu 24: Cho hàm số

( )

fx

có đạo hàm trên đoạn

[ 1; 2]−

và

( ) ( )

1 2018, 2 1.−= =−ff

Tích phân

( )

2

1

dfxx

−

′

∫

bằng

A.

2019.

B.

2019.−

C.

1.

D.

2017.

Câu 25: Họ nguyên hàm của hàm số

3

(x) =

x

fe

là hàm số nào sau đây?

A.

3 +

x

eC

. B.

3

1

3

+

x

eC

. C.

1

3

+

x

eC

. D.

3

3 +

x

eC

.

Câu 26: Cho hàm số

( )

fx

có bảng biến thiên như sau

2

3

x

y

x







2

x 

3x 

1y 

3y 

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 46

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A.

( )

;1−∞ −

. B.

( )

0;1

. C.

( )

1; 0−

. D.

( )

;0−∞

.

Câu 27: Cho hàm số

()

fx

liên tục trên



và có bảng xét dấu của

()

fx

′

như sau

Số điểm cực tiểu của hàm số đã cho là

A.

2.

B.

4.

C.

3.

D.

1.

Câu 28: Với

a

là số thực dương tùy ý,

3

log

a







bằng

A.

3

1 log

a−

B.

3

3 log a

−

C.

3

1

log a

D.

3

1 log

a+

Câu 29: Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường

y xx

=

,

0y

=

,

1x =

xung quanh trục

Ox

là

A.

2

5

V

π

=

. B.

2

5

V =

. C.

1

4

V =

. D.

1

4

V

π

=

.

Câu 30: Cho hình chóp

.S ABC

có

SA

vuông góc với mặt phẳng

( )

3

,

2

a

ABC SA =

, tam giác

ABC

đều cạnh bằng a (minh

họa như hình dưới). Góc tạo bởi giữa mặt phẳng

( )

SBC

và

( )

ABC

bằng

A.

0

90

. B.

0

30

.

C.

0

45

. D.

0

60

.

Câu 31: Cho hàm số

( )

42

481fx x x=−+ −

. Có bao nhiêu giá trị nguyên của

m

để phương trình

(

)

fx m=

có bốn nghiệm phân biệt?

A. 0. B. 2. C. 3. D. 1.

Câu 32: Cho hàm số

( )

y fx=

liên tục trên



và có đạo hàm

(

) ( )

( )( )

43

1 12

′

=+ −−

fx x x x

. Hàm số

( )

y fx=

đồng biến trên khoảng nào dưới đây?

A.

( )

1; 2

. B.

( )

;1−∞ −

. C.

( )

1;1

−

. D.

(

)

2; +∞

.

Câu 33: Một hộp chứa 11 quả cầu gồm 5 quả màu xanh và

6

quả cầu màu đỏ. Chọn ngẫu nhiên đồng thời

2 quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng

A.

5

22

B.

6

11

C.

5

11

D.

8

11

Câu 34: Tích hai nghiệm của phương trình

2

33

log 6 log 8 0xx− +=

bằng

A.

729

. B.

8

. C.

90

. D.

6

.

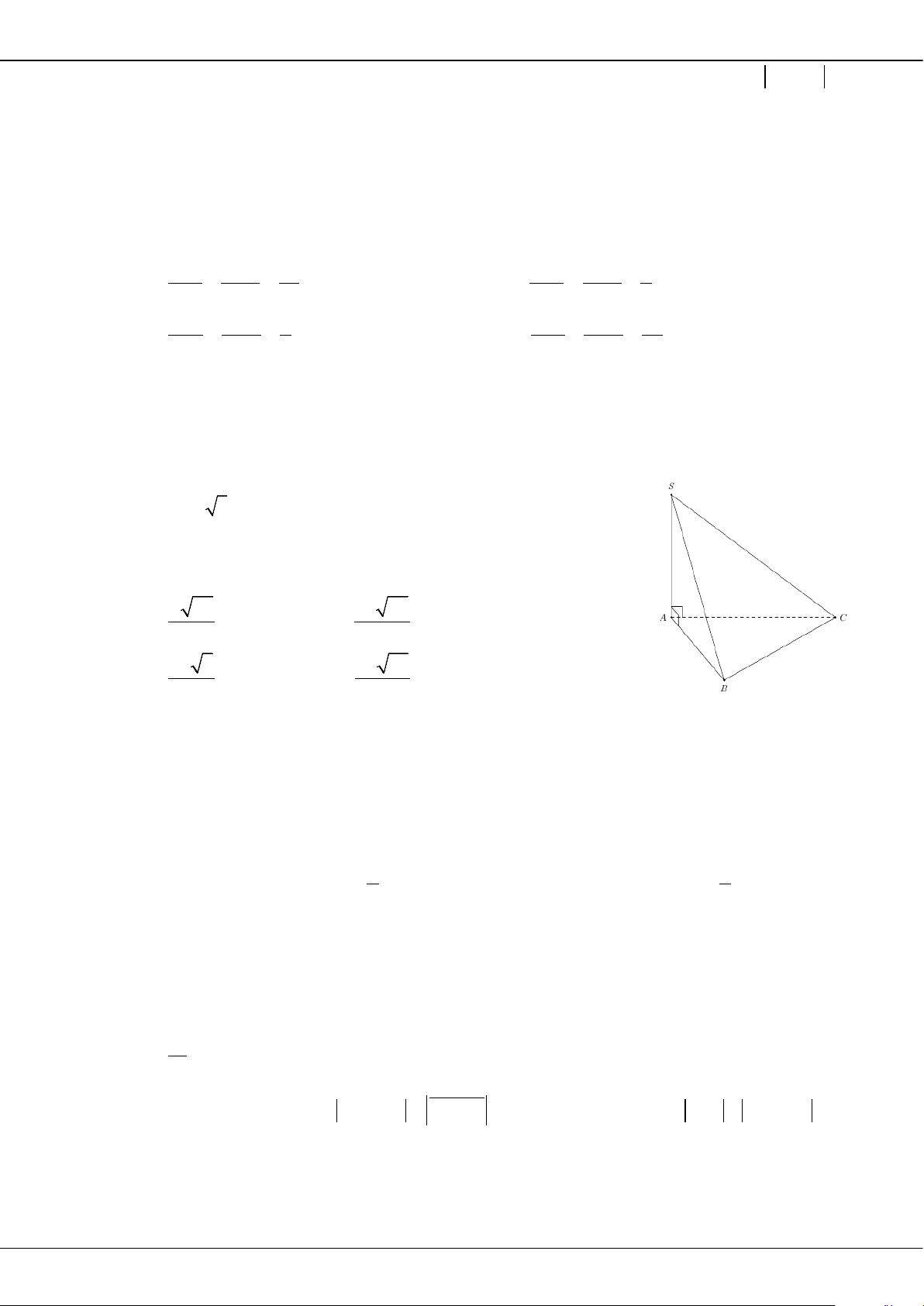
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 47

Câu 35: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức

z

thỏa mãn điều kiện

22zi

−+ =

là

A. Đường thẳng

2 3 10xy− +=

. B. Đường tròn

( ) ( )

22

2 14xy

+ +− =

.

C. Đường thẳng

yx=

. D. Đường tròn

( )

2

22

xy+− =

.

Câu 36: Trong không gian

Oxyz

, cho ba điểm

(1; 2; 0), (1; 1; 2)AB

và

(2; 3;1)

C

. Đường thẳng đi qua

A

và

song song với

BC

có phương trình là

A.

12

.

121

xy z−−

= =

−

B.

12

.

3 43

xy z−−

= =

C.

12

.

3 43

xy z++

= =

D.

12

.

121

xy z++

= =

−

Câu 37: Trong không gian

Oxyz

, cho điểm

(1; 2; 3)−M

. Điểm đối xứng với M qua mặt phẳng

()Oyz

có

tọa độ là

A.

(1; 2; 3)−

. B.

(1; 2; 3)−

. C.

( 1; 2; 3)−−

. D.

( 1; 2; 3)−−

.

Câu 38: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

A

,

=AB a

,

3AC a=

,

SA

vuông góc với mặt phẳng đáy và

2

=SA a

.

Khoảng cách từ điểm

A

đến mặt phẳng

()SBC

bằng

A.

57

19

a

B.

2 57

19

a

C.

23

19

a

D.

2 38

19

a

Câu 39: Có bao nhiêu giá trị nguyên của

x

thoả mãn

( )

(

)

21

22

log 1 log 31 32 2 0

x

xx

−



+− + − ≥



?

A.

27

. B.

25

. C.

26

. D.

28.

Câu 40: Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

(

)

fx

trên



thỏa

mãn

( )

114 114 2FG+=−

và

(

) ( )

44 44 0FG+=

. Tính

( )

21

7

5 9dfx x∫+

.

A. 3. B.

3

4

−

. C. 6. D.

1

5

−

.

Câu 41: Cho hàm số

( ) 10

x

fx x

và hàm số

 

3 22

() 1 2g x x mx m x   

. Gọi

M

là giá trị

lớn nhất của hàm số

( ( ))gx fx

trên đoạn

0;1







. Khi

M

đạt giá trị nhỏ nhất thì giá trị của tham

số

m

bằng

A.

21

2

. B. 6. C. 21. D. 5.

Câu 42: Cho số phức

z

thỏa mãn

52 3z iz i+− = +−

. Giá trị nhỏ nhất của

4 22Pz z i=−+−+

bằng

A.

5

. B.

15

. C.

10

. D.

20

.

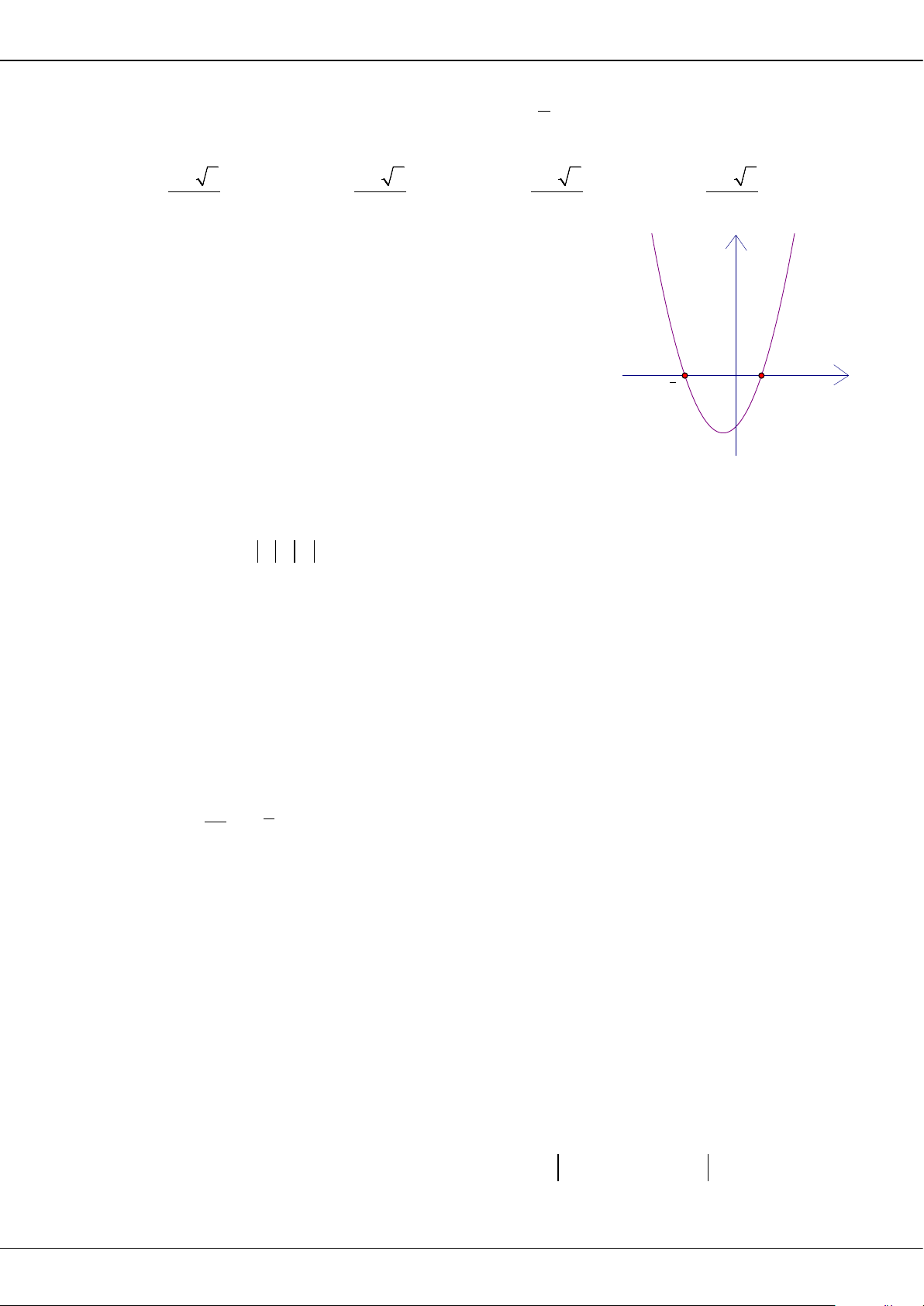
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 48

Câu 43: Cho hình lăng trụ đứng

.ABC A B C

′′′

, biết đáy

ABC

là tam giác đều cạnh

a

. Khoảng cách từ tâm

O

của tam giác

ABC

đến mặt phẳng

(

)

A BC

′

bằng

6

a

. Tính thể tích khối lăng trụ

.ABC A B C

′′′

.

A.

3

32

8

a

. B.

3

32

28

a

. C.

3

32

4

a

. D.

3

32

16

a

.

Câu 44: Cho hàm số

( ) ( )

32

, ,,,= + ++ ∈f x ax bx cx d a b c d

thỏa

mãn

(

)

( )

2130 0

−=ff

. Hàm số

( )

′

fx

có đồ thị như hình bên.

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số

( )

,=y fx

( )

′

=y fx

và các đường

1x =

,

3x =

.

A.

14,31

a

. B.

24a

.

C.

31a

. D.

26a

.

Câu 45: Trong tập hợp các số phức, cho phương trình

( )

2

2 45 2016 80 0zaz a−− + −=

(

a

là tham số

thực). Có tất cả bao nhiêu giá trị nguyên dương của

a

để phương trình có hai nghiệm phân biệt

12

,

zz

sao cho

12

zz=

A.

7

. B.

8

. C.

9

. D.

10

.

Câu 46: Trong không gian

Oxyz

cho hai điểm

( )

0; 8; 2A

,

( )

9; 7; 23

B −

và mặt cầu

( )

S

có phương trình

222

():(5)( 3)(7)72

Sx y z

−+++−=

. Mặt phẳng

( )

:0+ + +=P x by cz d

đi qua điểm

A

và

tiếp xúc với mặt cầu

( )

S

sao cho khoảng cách từ

B

đến mặt phẳng

( )

P

lớn nhất. Giá trị của

bcd

++

khi đó là

A.

2

. B.

4

. C.

3

. D.

1

.

Câu 47: Có bao nhiêu số nguyên

y

trong đoạn

[

]

2021;2021−

sao cho bất phương trình

(

)

11

log

10

10 10

x

y

x

+

≥

đúng với mọi

x

thuộc

( )

1;100

.

A.

2021

. B.

4026

. C.

2013

. D.

4036

.

Câu 48: Cho hình nón tròn xoay có chiều cao

( )

20 cmh =

, bán kính đáy

( )

25 cmr =

. Một thiết diện đi

qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là

( )

12 cm

.

Tính diện tích của thiết diện đó.

A.

(

)

2

400 cm

S =

. B.

(

)

2

500 cm

S =

. C.

( )

2

406

S cm=

. D.

( )

2

300S cm

=

.

Câu 49: Trong không gian

Oxyz

, cho mặt phẳng (P):

2 2 14 0−+ − =xy z

và mặt cầu

( )

2 22

: 2 4 2 30+ + − + + −=Sx y z x y z

. Gọi tọa độ điểm

( )

;;M abc

thuộc mặt cầu (S) sao cho

khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Tính giá trị của biểu thức

=++K abc

.

A.

1=K

. B.

2=K

. C.

5= −K

. D.

2= −K

.

Câu 50: Có tất cả bao nhiêu giá trị nguyên của

m

để hàm số

32

12 2y x mx x m=− ++

luôn đồng biến trên

khoảng

( )

1; +∞

?

A.

18

. B.

19

. C.

21

. D.

20

.

O

x

y

y = f

'(

x

)

1

2

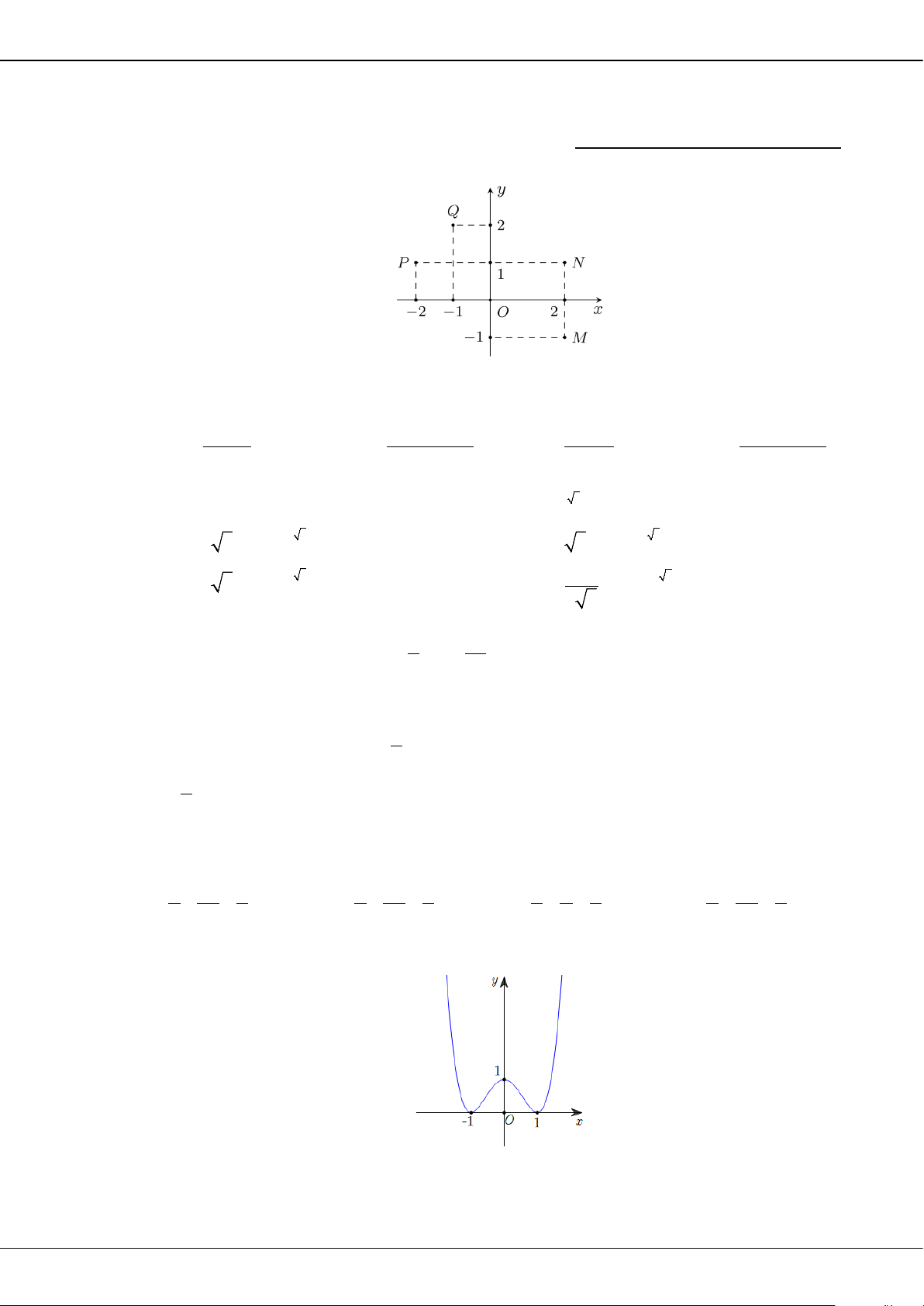
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 49

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT PHAN VIỆT THỐNG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức

12zi=−+

:

A.

N

. B.

P

. C.

M

. D.

Q

.

Câu 2: Đạo hàm của hàm số

(

)

2

3

log 2= +

yx

là:

A.

2

x

y

x

′

=

+

. B.

( )

2

2 ln 3

′

=

+

x

y

x

. C.

2

2 ln 3

2

′

=

+

x

y

x

. D.

( )

2

1

2 ln 3

′

=

+

y

x

.

Câu 3: Trong khoảng

(

)

2;

+∞

đạo hàm của hàm số

( )

3

36yx= −

là:

A.

( )

31

' 333 6yx

−

= −

. B.

( )

31

' 33 6yx

−

= −

.

C.

(

)

31

' 333 6yx

+

= −

. D.

( )

31

1

' 36

33

yx

−

= −

.

Câu 4: Tập nghiệm của bất phương trình

1

11

5 25

x−



≥





là

A.

[

)

1;− +∞

. B.

( )

2;− +∞

. C.

( )

;2−∞

. D.

(

]

;1−∞ −

.

Câu 5: Cho cấp số nhân

( )

n

u

với

17

1

; 32

2

uu=−=−

. Giá trị của

q

bằng

A.

1

2

±

. B.

2±

. C.

4±

. D.

1

±

.

Câu 6: Trong không gian

Oxyz

, vectơ

( )

6; 3; 2n = −



là một vectơ pháp tuyến của mặt phẳng nào dưới

đây?

A.

1

1 23

xyz

− +=

−

. B.

0

1 23

xyz

+ +=

−

. C.

1

123

xyz

++=

. D.

1

1 23

xyz

+ +=

−

.

Câu 7: Cho hàm số

( )

y fx=

có đồ thị là đường cong như hình vẽ sau

Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là:

A.

( )

0; 1−

. B.

( )

1;0

. C.

( )

0;1

. D.

( )

1;0−

và

( )

1;0

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 50

Câu 8: Nếu

( )

2

1

1dfxx= −

∫

và

( ) ( )

2

1

5df x gx x−=−





∫

thì

( )

2

1

dgx x

∫

bằng:

A.

4

. B.

3

. C.

1

. D.

2

.

Câu 9: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên dưới?

A.

2

1.y xx=− +−

B.

3

3 1.

yx x

=−+ +

C.

42

1.yx x=−+

D.

3

3 1.yx x=−+

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

(

)

2 22

: 2 4 8 40Sx y z x y z+ + + − + −=

. Tìm tâm và bán

kính của đường tròn

( )

S

?

A. Tâm

( )

1; 2; 4I −

, bán kính

5R =

. B. Tâm

( )

1;2; 4I −−

, bán kính

5

R =

.

C. Tâm

( )

1; 2; 4I −

, bán kính

17R

=

. D. Tâm

( )

1;2; 4I −−

, bán kính

17

R =

.

Câu 11: Trong không gian

Oxyz

, cho hai mặt phẳng

( )

: 2 10Px yz− −+=

,

(

)

: 2 70Qxy z++ +=

. Tính

góc giữa hai mặt phẳng đó.

A.

0

60

. B.

0

45

. C.

0

120

. D.

0

30

.

Câu 12: Cho hai số phức

1

32zi= +

và

2

14zi= −

. Phần thực của số phức

12

zz+

là:

A.

2

−

. B.

2

. C.

4

. D.

4

−

.

Câu 13: Khối lăng trụ có đáy là hình chữ nhật có hai kích thước lần lượt là

2 ,3aa

, chiều cao của khối

lăng trụ bằng

5a

. Thể tích khối lăng trụ bằng:

A.

3

30a

. B.

3

10a

. C.

2

30a

. D.

2

10a

.

Câu 14: Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

()SA ABCD⊥

và

3SA a=

. Thể tích của khối chóp

.S ABCD

là:

A.

3

a

. B.

3

4

a

. C.

3

3a

. D.

3

12

a

.

Câu 15:

Trong không gian

Oxyz

, cho mặt cầu

( )

S

có tâm

( )

1;1; 2I

−

và tiếp xúc với mặt phẳng

( )

: 2 2 5 0.Px y z+ − +=

Tính bán kính

R

của mặt cầu

( )

.S

A.

3R =

. B.

2R

=

. C.

4R =

. D.

6R =

.

Câu 16: Cho số phức

43zi= −

. Tìm phần thực và phần ảo của số phức

z

.

A. Phần thực bằng

4

, phần ảo bằng

3

. B. Phần thực bằng

4

−

, phần ảo bằng

3−

.

C. Phần thực bằng

4

, phần ảo bằng

3−

. D. Phần thực bằng

4−

, phần ảo bằng

3

.

Câu 17: Cho khối nón

( )

N

có bán kính đáy bằng

3

và diện tích xung quanh bằng

15 .

π

Tính thể tích

V

của khối nón

( )

N

A.

12 .V

π

=

B.

20 .V

π

=

C.

36 .V

π

=

D.

60 .V

π

=

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

3

: 52

2

xt

yt

zt

= −





∆ =−+





= −



. Điểm nào sau đây thuộc

∆

?

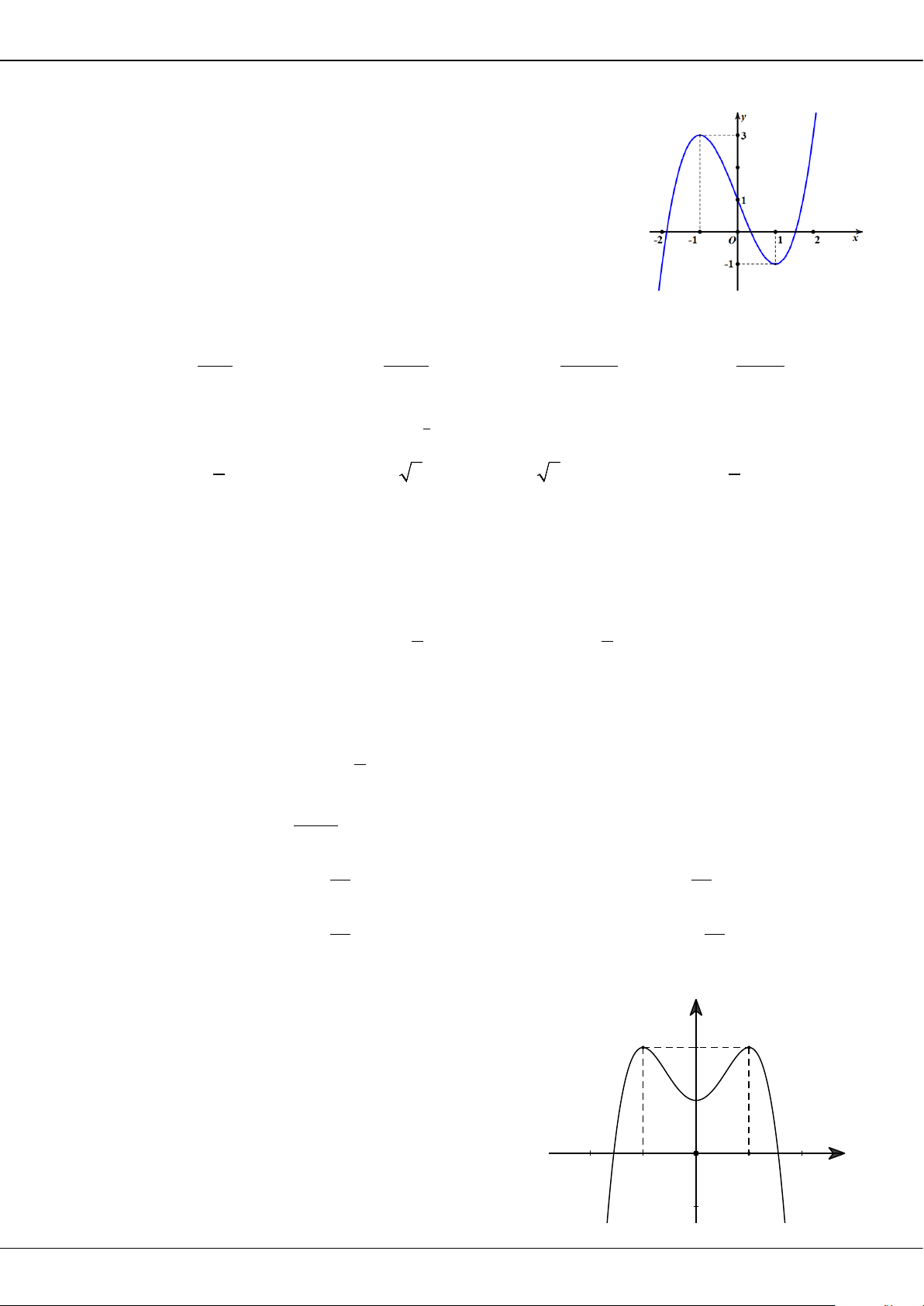
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 51

A.

( )

3; 5; 0M −

. B.

( )

3;5;2

N

−−

. C.

( )

3; 5; 0P −

. D.

(

)

1; 2; 2Q −−

.

Câu 19: Cho hàm số

32

y ax bx cx d= + ++

có đồ thị là đường cong trong

hình bên. Điểm cực đại của đồ thị hàm số đã cho có toạ độ là

A.

( )

1; 1−

. B.

( )

1;1−

.

C.

( )

1; 3−

. D.

( )

3; 1−

.

Câu 20: Đường thẳng

2y

=

là tiệm cận ngang của đồ thị hàm số nào dưới đây?

A.

2

1

y

x

=

+

. B.

1

12

x

y

x

+

=

−

. C.

23

2

x

y

x

−+

=

−

. D.

22

2

x

y

x

−

=

+

.

Câu 21: Tập nghiệm của bất phương trình

2

3

log 2x 

là

A.

4

;

9



















. B.

 

3

;4

. C.

 

3

4;

. D.

4

0;

9

















.

Câu 22: Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được lập từ các số

1; 2;3; 4; 5

.

A.

15

. B.

120

. C.

10

. D.

24

.

Câu 23: Cho

( )

d 3sin 2 Cfx x x= +

∫

. Khẳng định nào dưới đây là đúng?

A.

( )

6 cos 2fx x= −

. B.

( )

3

cos 2

2

fx x=

. C.

( )

3

cos 2

2

fx x= −

. D.

( )

6 cos 2fx x=

.

Câu 24: Cho

( )

ln 2

0

2 ed 5

x

fx x+=

∫

. Tính

( )

ln 2

0

dfx x

∫

.

A.

3

. B.

5

2

. C.

2

. D.

1

.

Câu 25: Cho hàm số

2

co

1

() 1

s

fx x

x

= −+

. Khẳng định nào dưới đây là đúng?

A.

2

( )d tan

2

= −+ +

∫

x

fx x x x C

. B.

2

( )d tan

2

= −− +

∫

x

fx x x x C

.

C.

2

( )d tan

2

= ++ +

∫

x

fx x x x C

. D.

2

( )d tan

2

=− −+ +

∫

x

fx x x x C

.

Câu 26: Cho hàm số

( )

y fx=

có đồ thị sau. Hàm số đã cho

đồng biến trên khoảng nào dưới đây?

A.

( )

;0−∞

. B.

( )

1; +∞

.

C.

( )

;1−∞ −

. D.

( )

2; +∞

.

x

y

1

2

1

-1

O

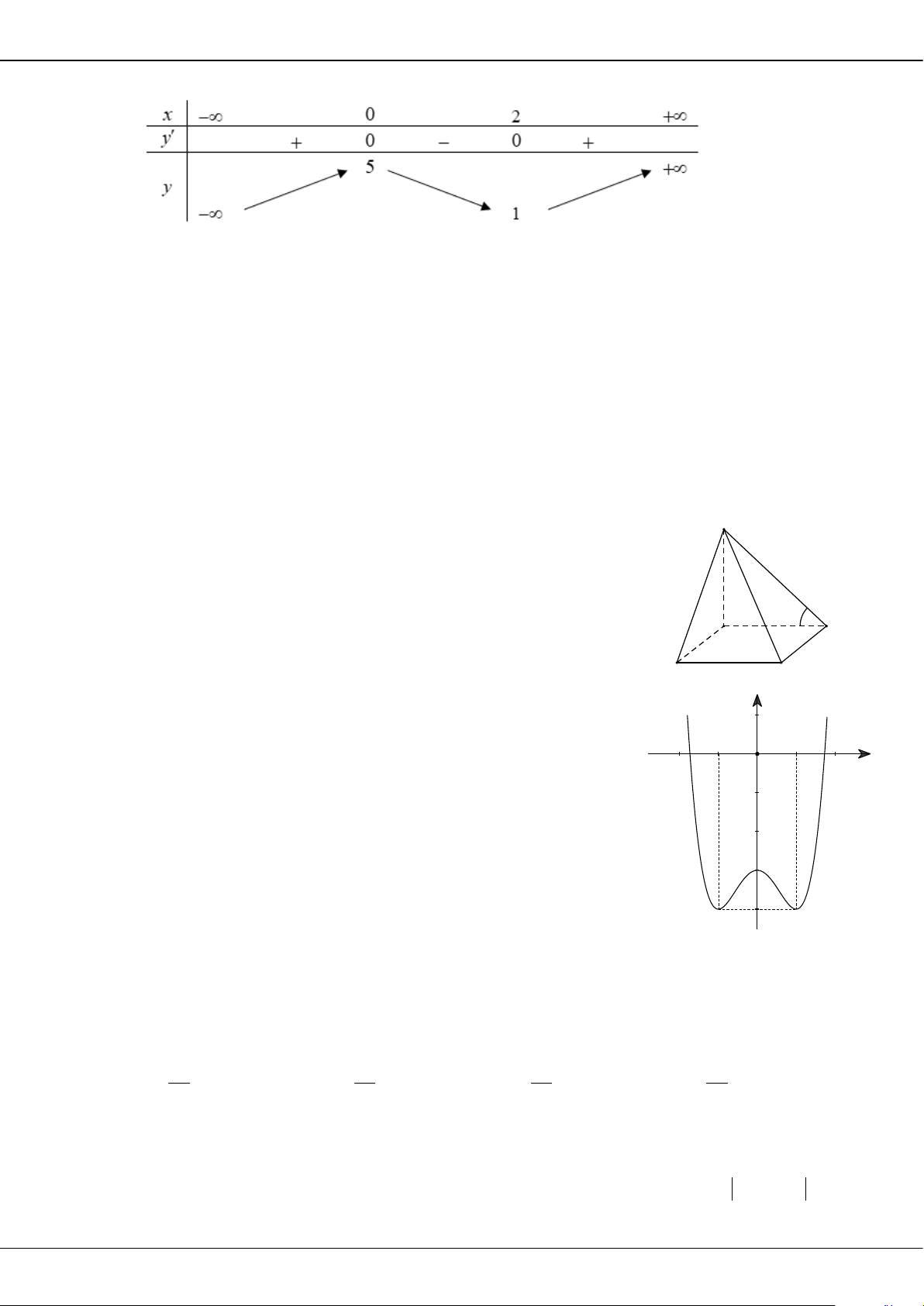
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 52

Câu 27: Cho hàm số

( )

y fx

=

có bảng biến thiên như hình vẽ. Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực đại tại

5x =

. B. Hàm số đạt cực tiểu tại

1x =

.

C. Hàm số đạt cực tiểu tại

0x =

. D. Hàm số đạt cực đại tại

0x =

.

Câu 28: Cho các số thực dương

;ab

thỏa mãn

2

log ax=

,

2

log by

=

. Giá trị biểu thức

( )

23

2

logP ab=

theo

;

xy

bằng:

A.

23xy

−

. B.

3xy+

. C.

32xy+

. D.

23xy+

.

Câu 29: Gọi

D

là hình phẳng giới hạn bởi các đường

4

, 0, 0, 1

x

yey x x 

. Thể tích của khối tròn

xoay tạo thành khi quay

D

quanh trục

Ox

bằng:

A.

1

4

0

d

x

ex



B.

1

8

0

d

x

ex



. C.

1

4

0

d

x

ex



. D.

1

8

0

d

x

ex



.

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật cạnh

AB a=

,

SA

vuông góc với mặt phẳng đáy và

2SB a=

(tham khảo hình

bên). Góc giữa mặt phẳng

()SBC

và mặt phẳng đáy bằng

A.

90°

. B.

60°

.

C.

45°

. D.

30

°

.

Câu 31: Cho hàm số

( )

42

f x ax bx c=++

có đồ thị là đường cong trong

hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn

[

]

2;5−

của

tham số

m

để phương trình

( )

fx m=

có đúng hai nghiệm thực

phân biệt?

A.

6

. B. 7.

C.

8

. D.

9

Câu 32: Cho hàm số

()fx

xác định trên



và có đạo hàm

( ) (

)( ) (

)

25

2 11

fx xx x

′

=−+ −

. Hàm số đã cho nghịch biến trên

khoảng nào dưới đây?

A.

( )

;2−∞

B.

( )

2; +∞

C.

( )

1; 2−

D.

( )

1; +∞

.

Câu 33: Chọn ngẫu nhiên

2

số khác nhau từ

30

số nguyên dương đầu tiên. Tính xác suất để chọn được

2

số có tích là một số lẻ?

A.

7

29

. B.

15

29

. C.

22

29

. D.

8

29

.

Câu 34: Tổng tất cả các nghiệm của phương trình

2

lg 3lg 2 0xx− +=

là

A.

110

. B.

100

. C.

10

. D.

1000

.

Câu 35: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức

z

thỏa mãn

12 3iz i+− =

là

một đường tròn. Tâm của đường tròn đó có tọa độ là

D

C

B

A

S

x

y

-4

-3

1

-1

O

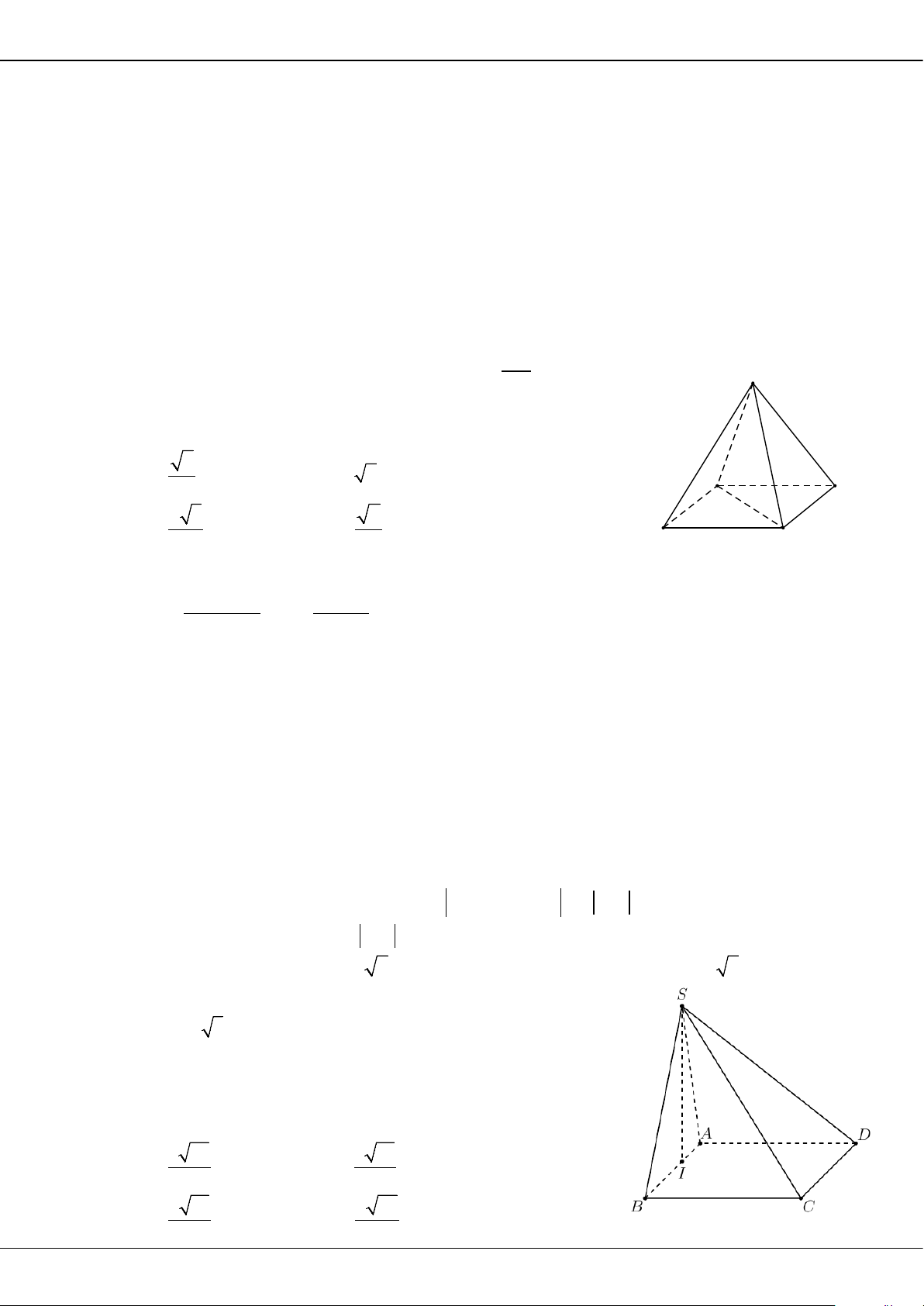
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 53

A.

( )

2; 1I −−

. B.

( )

2;1I −

. C.

( )

2;1I

. D.

( )

2; 1I −

.

Câu 36: Trong không gian

Oxyz

, cho

5 4 2, 3

OE i j k OF j k=+− =−

      

. Đường thẳng đi qua hai điểm

E

và

F

có phương trình là

A.

5

13

3

xt

yt

zt

=





= +





=−+



. B.

5

4

23

x

yt

zt

=





= +





=−−



. C.

5

13

3

xt

yt

zt

=





= +





=−−



. D.

5

13

3

xt

yt

zt

= −





= +





=−+



.

Câu 37: Trong không gian với hệ toạ độ

Oxyz

, cho điểm

( )

2; 5;7

M −

. Điểm

M

′

đối xứng với điểm

M

qua mặt phẳng

Oxy

có tọa độ là:

A.

( )

2;5;7−−

. B.

( )

2;5;7

. C.

( )

2; 5;7−−

. D.

( )

2;5;7−

.

Câu 38: Cho hình chóp đều

.S ABCD

thể tích

3

2

3

SABCD

a

V =

,

2AC a=

(tham khảo hình bên). Tính khoảng cách từ điểm

A

đến mặt

phẳng

( )

SCD

.

A.

3

a

. B.

2a

.

C.

23

3

a

. D.

2

a

.

Câu 39: Có bao nhiêu số nguyên

x

thỏa mãn

22

2

3

409

( 4) 4

log lo

76

g

2

xx xx−−

<

?

A.

78

. B.

80

. C.

76

. D.

82

.

Câu 40: Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa

mãn

( ) ( )

7278FG+=

và

( ) ( )

121 2FG+=

. Khi đó

( )

3

0

2 1dfx x+

∫

bằng

A.

6

. B.

4

. C.

1

. D.

3

.

Câu 41: Số các giá trị thực của tham số

m

để đồ thị hàm số

32

32y x mx=−+

có hai điểm cực trị

A

và

B

sao cho các điểm

A

,

B

và

( )

1; 2M −

thẳng hàng.

A.

4

. B.

3

. C.

1

. D.

2

.

Câu 42: Xét các số phức

z

thoản mãn điều kiện

2

2 44 2 1zz i z+ ++ = +

. Gọi

M

và

m

lần lượt là giá

trị lớn nhất và nhỏ nhất của

1z +

. Giá trị của

Mm−

bằng

A.

2

. B.

26

. C.

14

. D.

46

.

Câu 43: Cho hình chóp

.S ABCD

, đáy

ABCD

là hình vuông có cạnh

bằng

3a

. Hình chiếu vuông góc của

S

lên mặt phẳng đáy là

điểm

I

thuộc đoạn thẳng

AB

sao cho

2BI AI=

. Góc giữa

mặt bên

( )

SCD

với mặt phẳng đáy là

60°

(tham khảo hình vẽ).

Tính khoảng cách giữa hai đường thẳng

AD

và

SC

.

A.

3 93

31

a

. B.

9 31

31

a

.

C.

6 31

31

a

. D.

6 93

31

a

.

S

A

D

C

B

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 54

Câu 44: Cho hàm số

( )

fx

luôn dương với mọi

[ ]

0;1x ∈

và có đạo hàm liên tục trên đoạn

[ ]

0;1

thỏa

mãn

( )

11

f

=

và

(

) (

)

(

)

2

2.

fx

f x xf x

x

′

+=





với mọi

[ ]

0;1x ∈

. Khi đó diện tích hình phẳng

giới hạn bởi các đường

( )

y fx=

và

54yx

= −

gần giá trị nào nhất sau đây?

A.

0,58

. B.

0, 49

. C.

1, 22

. D.

0,97

.

Câu 45: Có bao nhiêu số nguyên

m

để phương trình

(

)

22

30z m zm m− − + +=

có hai nghiệm phức

12

,zz

thỏa mãn

12 12

zz zz+=−

?

A.

3

. B.

4

. C.

1

. D.

8

.

Câu 46: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

1;2; 2A −

; mặt phẳng

( )

: 2 2 80Px y z− − +=

và hai đường thẳng

1

11

1

2

: 12

43

xt

dy t

zt

= +





= +





= −



;

2

22

2

32

:3

5

xt

dy t

zt

= +





= +





=−+



. Đường thẳng

d

đi qua điểm

A

, cắt hai

đường thẳng

1

d

và

2

d

lần lượt tại

B

và

C

. Tính tổng khoảng cách từ

B

và

C

đến mặt phẳng

( )

P

.

A.

9

. B.

10

. C.

7

. D.

8

.

Câu 47: Có bao nhiêu bộ số

(

)

;xy

với

,xy

nguyên và

1 , 2022xy≤≤

thoả mãn

( ) ( )

3 2

2 21

2 4 8 log 2 3 6 log

23

yx

xy x y x y xy

yx

+

+++ ≤ +−−

+−

.

A.

4036.

B.

4038.

C.

4040.

D.

2019.

Câu 48: Cho khối nón đỉnh

S

, chiều cao bằng

6

và thể tích bằng

128

π

. Gọi

A

và

B

là hai điểm thuộc

đường tròn đáy sao cho

10AB =

, khoảng cách từ tâm của đường tròn đáy đến mặt phẳng

( )

SAB

bằng

A.

6 15

5

. B.

6 13

5

. C.

3 15

5

. D.

3 13

5

.

Câu 49: Trong không gian

,Oxyz

cho hai điểm

5

1; 2;

2

A



−





và

5

4; 2; .

2

B







Tìm hoành độ điểm

M

trên

mặt phẳng

()Oxy

sao cho



45ABM = °

và tam giác

MAB

có diện tích nhỏ nhất?

A.

5

2

. B.

1

. C.

3

2

. D.

2

.

Câu 50: Cho các hàm số

( )

2

4fx x x m=−+

và

( )

( )( )

2023

22

1 2.gx x x=++

Số các giá trị nguyên của

tham số

( )

2023; 2023m ∈−

để hàm số

( )

y gfx=

đồng biến trên khoảng

( )

3; +∞

là:

A.

2019

. B.

2021

. C.

2022

. D.

2020

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 55

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT CÁI BÈ

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho số phức

45

zi=−+

. Biểu diễn hình học của

z

là điểm có tọa độ

A.

( )

4;5−

B.

( )

4; 5−−

C.

( )

4; 5−

D.

( )

4;5

Câu 2: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

1

3

log=yx

là

A.

1

3

′

=y

x

. B.

1

ln3

y

x

′

=

. C.

ln3

y

x

′

=

. D.

1

ln3

y

x

′

= −

.

Câu 3: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

3

=yx

là

A.

0,7

3

′

=yx

. B.

31−

′

=yx

. C.

31

1

3

−

′

=yx

. D.

31

3

−

′

=yx

.

Câu 4: Tập nghiệm của bất phương trình

1

11

24

+



>





x

là

A.

(

]

;1−∞

. B.

( )

1; +∞

. C.

[

)

1; +∞

. D.

( )

;1−∞

.

Câu 5: Cho cấp số cộng

( )

n

u

có

1

2u = −

và công sai

3.d =

Tìm số hạng

10

.u

A.

9

10

u 2.3= −

. B.

10

u 25

=

. C.

10

u 28

=

. D.

10

u 29= −

.

Câu 6: Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng (P):

02023

22 =

++

− zy

x

. Vectơ nào dưới

đây là một vectơ pháp tuyến của

( )

P

?

A.

( )

3

2; 2; 1n =−−

 

. B.

( )

4

1; 2; 2n = −

 

. C.

( )

1

1; 1; 4n = −



. D.

( )

2

2; 2;1n =

 

.

Câu 7: Đồ thị hàm số

2

43yx x=−+

cắt trục tung tại điểm có tung độ bằng

A. 3. B. 1. C. 4. D. 0.

Câu 8: Gọi

F(x)

là một nguyên hàm của hàm số

f(x)

trên đoạn [a ; b], k là một hằng số. Trong các

đẳng thức sau, đẳng thức nào đúng?

A.

 

b

a

k.f (x)dx k F b F(a)









B.

 

b

a

f (x)dx F a F(b)



C.

bc c

ab a

f (x)dx f (x)dx f (x)dx



D.

ba

ab

f (x)dx f (x)dx



Câu 9: Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên?

A.

32

3yx x=−+

. B.

42

3yx x= −

. C.

32

3yx x= −

. D.

42

3yx x=−+

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 56

Câu 10: Trong không gian

Oxyz

, tâm mặt cầu (S):

(

) (

)

( )

2 22

–1 2 1 4++ ++ =

xy z

có tọa độ là

A.

( )

1; 2;1

−

. B.

( )

1;2;1−−

. C.

( )

1; 2;1−

. D. (1, 2, 1).

Câu 11: Trong không gian

Oxyz

, cho các điểm

( )

2; 2;1A −

,

( )

1; 1; 3B −

. Tọa độ của vectơ

AB



là

A.

( )

3; 3; 4−−

. B.

(

)

1; 1; 2

−−

. C.

( )

3; 3; 4

−

. D.

( )

1;1; 2−

.

Câu 12: Cho số phức

76zi= +

, phần ảo của số phức

2

z

bằng

A.

13

. B.

84

. C.

6

. D.

48

.

Câu 13: Cho khối lập phương có cạnh bằng

2

. Thể tích của khối lập phương đã cho bằng

A.

3 2.

B.

22

. C.

22

3

. D.

42

.

Câu 14: Cho khối chóp

.S ABC

có đáy là tam giác vuông cân tại

A

, AB = 4;

SA

vuông góc với đáy và

3SA =

(tham khảo hình vẽ).

Thể tích khối chóp đã cho bằng

A. 48. B. 8. C. 12. D. 16.

Câu 15: Trong không gian

Oxyz

, cho mặt cầu (S):

( ) ( ) ( )

2 22

–1 2 1 9++ ++ =xy z

, Gọi d là khoảng cách

từ tâm I của mặt cầu đến mặt phẳng (P), khi đó mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là

đường tròn khi

A.

3>d

B.

3<d

C.

9<d

D.

3

=d

Câu 16: Cho hai số phức 

1

= −1 + 2 và 

2

= 4 − . Khi đó số phức liên hợp của 

1

+ 

2

là

A.

3 i−−

. B.

3 i−+

. C.

3 i+

. D.

3 i−

.

Câu 17: Cho hình nón có đường kính đáy 4 và độ dài đường sinh

l

. Diện tích xung quanh của hình nón

đã cho bằng

A. 4πrl. B.

2

4

3

rl

π

. C. 2πrl. D.

2

1

3

rl

π

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

421

:

2 51

xzz

d

−−+

= =

−

. Điểm nào sau đây thuộc

d

?

A.

(2; 5;1)Q

. B.

(4; 2;1)M

. C.

(4; 2; 1)N −

. D.

(2; 5;1)P −

.

Câu 19: Cho hàm số

42

2022 2023=−+ −yx x

. Số điểm cực trị của đồ thị hàm số là

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 57

A.

3

. B.

0

. C.

1

. D.

2

.

Câu 20: Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số

21

1

x

y

x

−

=

+

.

A.

1

,

2

x =

1y = −

. B.

1,

x

=

2y = −

. C.

1,x = −

2y =

. D.

1,x = −

1

2

y =

.

Câu 21: Tập nghiệm của bất phương trình

( )

2

log 2 0

−>

x

là

A.

( )

;2

−∞

B.

( )

;1

−∞

C.

( )

1;

+∞

D.

( )

2;

+∞

Câu 22: Số cách chọn

3

học sinh từ một nhóm gồm

8

học sinh là:

A.

3

8

A

. B.

8

3

. C.

3

8

. D.

3

8

C

.

Câu 23: Tìm khẳng định đúng trong các khẳng định sau

A.

 

1

x dx x C 1

1

 

  





B.

 

1

x dx x C 1

1

 

  





C.





1

x dx x C 1

1

 

  





D.

 

1

x dx x C 1

1

 

  





Câu 24: Cho

( )

2

0

3

f x dx =

∫

.Khi đó

( )

2

0

43

f x dx

−





∫

bằng:

A. 6 B. 4 C. 2 D. 8

Câu 25: Tìm

1

dx

2x 1





ta được kết quả là:

A.

1

ln 2x 1 C

2



B.

ln 2x 1 C 

C.

1

ln 2x 1 C

2

 

D.

ln 2x 1 C



Câu 26: Cho hàm số

( )

y fx=

có đồ thị như hình sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A.

( )

0; +∞

. B.

( )

;1−∞

. C.

( )

1; +∞

. D.

( )

0;1

.

Câu 27: Cho hàm số

()y fx=

xác định, liên tục trên



và có bảng biến thiên như hình dưới.

Khẳng định nào dưới đây là khẳng định đúng?

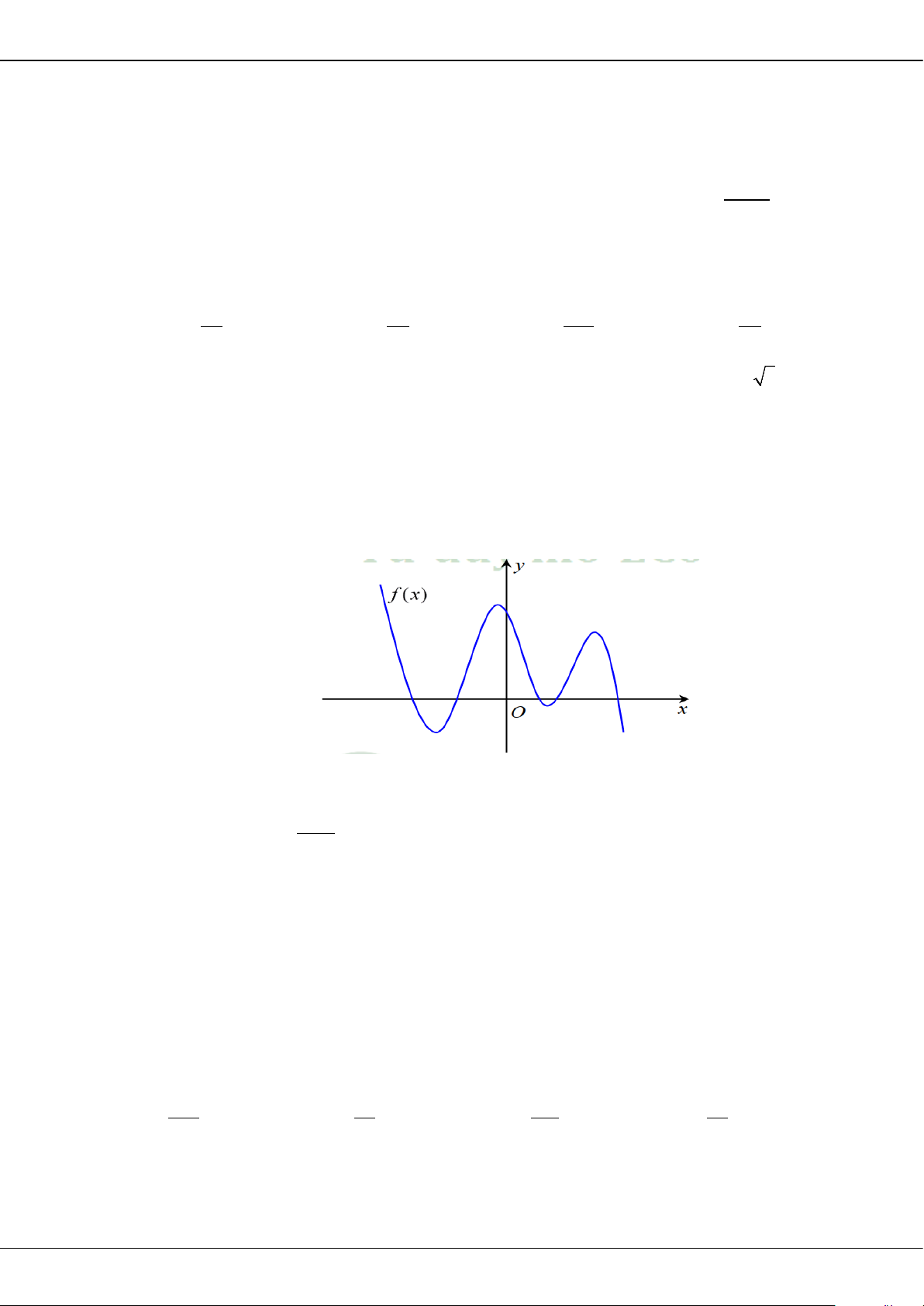
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 58

A. Hàm số đạt cực đại tại

1x

=

. B. Đồ thị hàm số có điểm cực đại

0x =

.

C. Hàm số có giá trị lớn nhất bằng

3−

. D. Hàm số đạt cực đại tại

0x =

.

Câu 28: Với  là số thực tùy ý,

22

ln(3a 3) ln(a 1)+− +

bằng:

A.

(

)

2

ln 1+a

. B.

ln 3

. C.

ln 6

. D.

2

3

ln

1+a

.

Câu 29: Cho hình phẳng (H) giới hạn bởi các đường

2

y x 2x= −

, trục hoành, trục tung, đường thẳng

x1=

. Gọi V là thể tích của khối tròn xoay sinh ra khi quay (H) quanh trục Ox. Giá trị của V là:

A.

8

V

15

π

=

B.

4

V

3

π

=

C.

15

V

8

π

=

D.

7

V

8

π

=

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

. SA ⊥ (ABCD); SA =

a3

. Tính góc

giữa hai mặt phẳng

( )

SAB

và

( )

SCD

.

A.

30

o

. B.

90

o

. C.

60

o

. D.

45

o

.

Câu 31: Cho đồ thị hàm số

( )

y fx=

như hình vẽ. Hỏi phương trình

( )

=fx m

có tối đa bao nhiêu

nghiệm thực

x

?

A.

3

. B.

6

. C.

5

. D.

4

.

Câu 32: Cho hàm số

( )

1

2

x

fx

x

−

=

+

. Mệnh đề nào sau đây sai?

A. Hàm số

( )

fx

nghịch biến trên

( )

;2−∞ −

.

B. Hàm số

( )

fx

nghịch biến trên các khoảng

( )

;2−∞ −

và

( )

2;− +∞

.

C. Hàm số

( )

fx

nghịch biến trên

{ }

\2−

.

D. Hàm số

( )

fx

nghịch biến trên từng khoảng của tập xác định.

Câu 33: Lớp 11A có 25 đoàn viên trong đó 10 nam và 15 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp để

tham dự hội trại. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ.

A.

7

920

. B.

27

92

. C.

3

115

. D.

9

92

.

Câu 34: Tích tất cả các nghiệm của phương trình

2

ln 2ln 3 0− −=xx

bằng

A.

3

.e

B.

2

e

. C.

3.

D.

1.−

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 59

Câu 35: Tập hợp các điểm trong mặt phẳng Oxy biểu diễn số phức z thỏa mãn

z 1 2i z 3−+ = +

là

đường thẳng có phương trình

A. 2x – y + 1 = 0. B. 2x + y + 1 = 0. C. 2x + y – 1 = 0. D. 2x – y – 1 = 0.

Câu 36: Trong không gian tọa độ

Oxyz

, cho điểm

( )

1; 3; 4M −

, đường thẳng

252

:

3 51

xyz

d

+ −−

= =

−−

và

mặt phẳng

( )

:2 2 0

P xz+−=

. Viết phương trình đường thẳng

∆

qua

M

vuông góc với

d

và

song song với

( )

P

.

A.

134

:

1 12

xyz−+−

∆==

−−

. B.

134

:

112

xyz−+−

∆==

−−−

.

C.

134

:

11 2

xyz−+−

∆==

−

. D.

134

:

1 12

xyz−+−

∆==

−

.

Câu 37: Trong không gian với hệ tọa độ

Oxyz

, cho hình bình hành ABCD có A(1, 1, –2); B(–2, –1, 4);

C(3, –2, –5). Tìm tọa độ đỉnh D.

A.

(6; 0; 11)

D −

B.

( 6;1;11)D

−

C.

(5;2;1)D −−

D.

( 3; 6;1)D

−

Câu 38: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông tâm O cạnh

2a

,

5SA SB SC SD a= = = =

. Tính khoảng cách từ điểm

B

đến mặt phẳng

( )

SCD

.

A.

3

2

a

. B.

3a

. C.

a

. D.

5

2

a

.

Câu 39: Có bao nhiêu số nguyên

x

thỏa mãn

3

22

5

44

ll

2

og > g

72

o

1

−−xx

?

A. 58. B. 112. C. 116. D. 117.

Câu 40: Biết rằng

b

0

6dx 6



và

a

x

0

xe dx 1



. Khi đó, biểu thức

23 2

b a 3a 2a 

có giá trị bằng:

A. 7. B. 4. C. 5. D. 3.

Câu 41: Tìm tham số

m

để hàm số

( )

32

1

2 2018

3

y x mx m x= − ++ +

không có cực trị.

A.

1m ≤−

hoặc

2m ≥

. B.

1m ≤−

. C.

2m ≥

. D.

12m−≤ ≤

.

Câu 42: Cho hai số phức

12

,zz

thỏa mãn đồng thời hai điều kiện sau

1 34,−=z

12++ = + +z mi z m i

và sao cho

12

−zz

là lớn nhất. Khi đó giá trị của

12

+zz

bằng

A.

2

. B.

10

. C. 2 D.

130

.

Câu 43: Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình chữ nhật

AB a=

và

2AD a=

, cạnh bên

SA

vuông góc với đáy. Tính thể tích

V

của khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

bằng

0

60

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 60

A.

3

4 15

15

a

V =

. B.

3

15

6

a

V =

. C.

3

15

3

a

V =

. D.

3

15

a

V =

.

Câu 44: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số

() , () 2f x xgx x 

và trục hoành.

Kết quả là giá trị nào sau đây?

A.

10

3

B.

11

3

C.

7

3

D.

8

3

Câu 45: Trên tập hợp các số phức, xét phương trình

( )

2

2 1 30z m zm− + + +=

(

m

là tham số thực). Có

bao nhiêu giá trị của tham số

m

để phương trình có nghiệm phức

0

z

thỏa mãn

0

26z +=

?

A.

3

. B.

1

. C.

4

. D. 2

Câu 46: Cho mặt cầu (S):

(

)

(

) (

)

25

1

11

22

2

=−

+

−+

− z

y

x

và mặt phẳng

( )

0722: =+++ zyx

α

. Mặt

phẳng (P) đi qua hai điểm A(1; -1; 2), B(3; 5; -2) và cắt (S) theo một đường tròn có bán kính nhỏ

nhất. Phương trình (P) là

A.

04

24 =

−−+ zyx

B.

0424 =+−+ zyx

C.

012 =−−+ zyx

D.

04

24 =

−−− zyx

Câu 47: Có bao nhiêu cặp số nguyên

(; )xy

thỏa mãn

( )

( ) (

)

2

2 32

2 22

3

22

log 4 log log log 15 15 48 ?

++ + + ≤ + + +xy x xy x x y x

A. 22. B. 28. C. 15. D. 12.

Câu 48: Cho hình nón đỉnh

S

, đường cao SO,

A

và

B

là hai điểm thuộc đường tròn đáy sao cho khoảng

cách từ

O

đến

( )

SAB

bằng

3

a

và



00

30 , 60SAO SAB= =

. Độ dài đường sinh của hình nón

theo

a

bằng

A.

2

a

B.

3a

C.

23a

D.

5a

Câu 49: Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

(

) ( )

2;5;

3,4;

2;0

−− BA

. Tọa độ điểm M sao

cho

22

2MBMA +

có giá trị nhỏ nhất

A.

( )

2;3;1−M

B.

( )

0

;4

;2

−M

C.

( )

2;7;3 −−M

D.













−1;

2

7

;

7

3

M

Câu 50: Có bao nhiêu số nguyên

m

thuộc khoảng

( )

10;10−

để hàm số

32

8y x x mx= −− +

đồng biến

trên khoảng

( )

1; +∞

?

A.

10

. B.

13

. C.

12

. D.

11

.

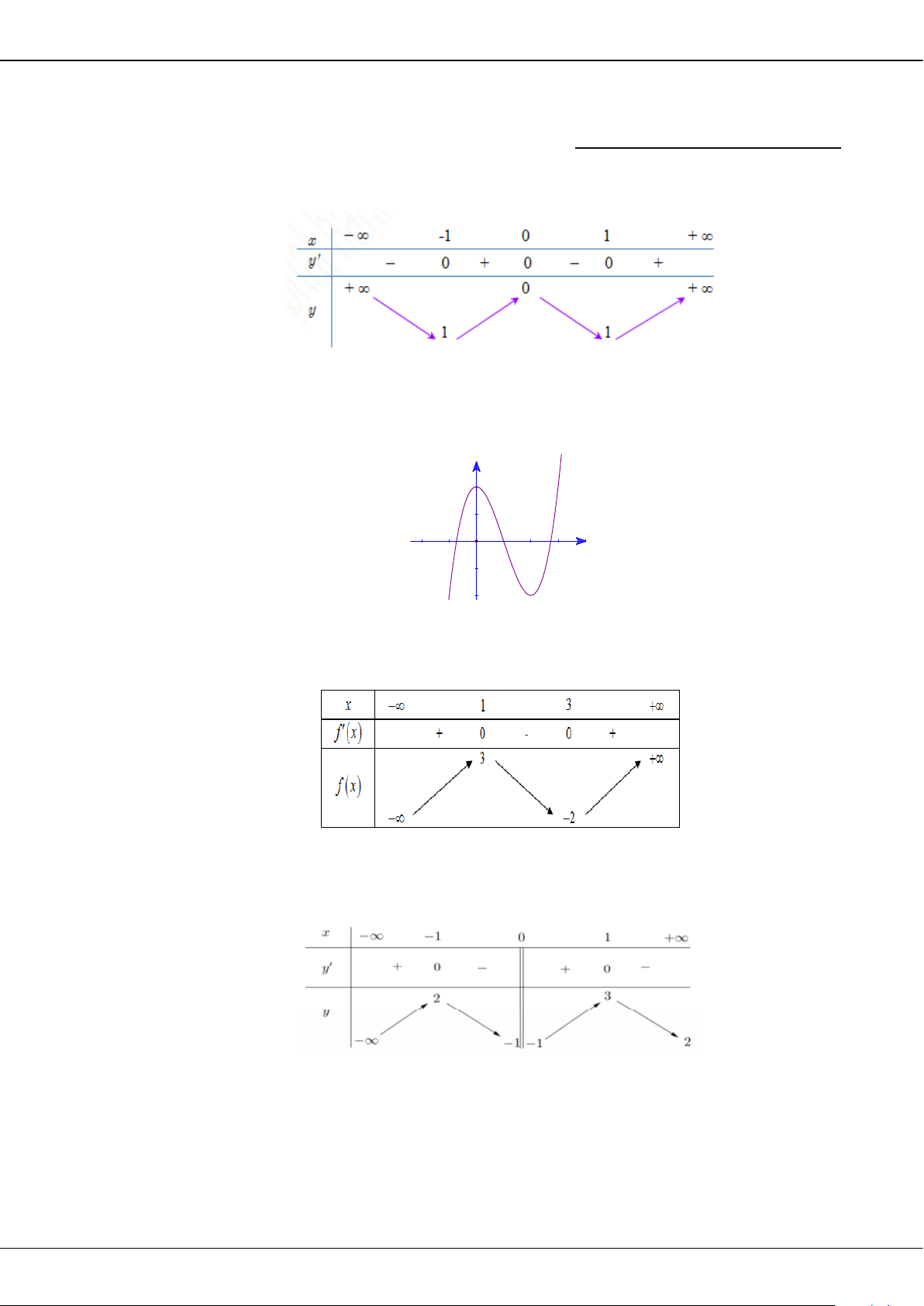
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 61

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT PHẠM THÀNH TRUNG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho hàm số

(

)

y fx

=

có bảng biến thiên như sau

Hàm số

(

)

y fx=

đồng biến trên khoảng nào dưới đây?

A.

( )

1;− +∞

. B.

( )

0;1

. C.

( )

1; 0−

. D.

( )

;1−∞ −

.

Câu 2: Cho hàm số

32

y ax bx cx d= + ++

(,, )abc∈

có đồ thị như hình vẽ bên.

Số điểm cực trị của hàm số đã cho là

A.

2

. B.

0

. C.

3

. D.

1

.

Câu 3: Cho hàm số

(

)

y fx=

có bảng biến thiên như sau:

Hàm số đạt cực đại tại

A.

2x

= −

. B.

2x =

. C.

1x

=

. D.

3x =

.

Câu 4: Cho hàm số có bảng biến thiên

Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?

A.

3

B. C. D.

Câu 5: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

y

x

O

( )

y fx=

4

2

1

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 62

A.

32

31yx x=−+

. B.

32

31yx x

=−+ +

. C.

42

21yx x

=−+ +

. D.

42

21

yx x=−+

.

Câu 6: Biết rằng đường thẳng

y 2x 2=−+

cắt đồ thị hàm số

3

yx x2= ++

tại điểm duy nhất có tọa độ

( )

00

x ;y

. Tìm

0

y.

A.

0

y1= −

. B.

0

y2=

. C.

0

y4=

. D.

0

y0=

.

Câu 7: Cho số dương

a

khác

1

và các số thực

x

,

y

. Đẳng thức nào sau đây đúng?

A.

x y xy

aa a





B.

 

y

x xy

aa

C.

x

y

a



D.

.

x y xy

aa a

Câu 8: Cho

a

là số thực dương khác

1

. Tính

3

log

a

Ia

=

.

A.

6I =

. B.

2

3

I

=

. C.

3

2

I =

. D.

1

6

I =

.

Câu 9: Tập xác định

D

của hàm số

 

ln 1yx

là

A.

( )

1; .D = +∞

B.

.D = 

C.

 

;1 .D  

D.

{

}

\1.

D =



Câu 10: Tìm tập nghiệm

S

của bất phương trình

21 32

11

22

xx+−

 

<

 

 

.

A.

( )

;3S = −∞

. B.

( )

;3S = −∞ −

. C.

( )

3;S = +∞

. D.

1

;3

2

S



= −





.

Câu 11: Tập nghiệm của bất phương trình

(

)

22

log 1 log 3x −>

là

A.

( )

4; +∞

. B.

[

)

4; +∞

. C.

1

;1

2









. D.

( )

;1−∞ −

.

Câu 12: Họ các nguyên hàm của hàm số

( )

5

x

fx x= −

là

A.

5

1

ln 5

x

C−+

B.

5 ln 5 1

x

C−+

C.

2

5 ln 2

2

x

C−+

D.

2

5

ln 5 2

x

C−+

Câu 13: Giả sử

()Fx

là một nguyên hàm của hai hàm số

()fx

trên

[ ]

,ab

,

k

là hằng số khác

0

. Trong

các đẳng thức sau, đẳng thức nào đúng?

A.

() () ()

b

a

f x dx F a F b= −

∫

. B.

() ()

ba

ab

f x dx f x dx=

∫∫

.

C.

[ ]

. () () ()

b

a

k f x dx k F b F a= −

∫

. D.

() () ()

bc c

ab a

f x dx f x dx f x dx−=

∫∫ ∫

.

Câu 14: Cho

( )

2

0

d3fx x=

∫

,

( )

2

0

d7gx x=

∫

, khi đó tính tích phân

( ) ( )

2

0

3df x gx x+





∫

bằng:

A. 24. B. 10. C. 16. D.

18−

.

Câu 15: Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa

mãn

( ) ( )

8 88FG

+=

và

( ) ( )

0 02FG+=−

. Khi đó

( )

8

1

5ln d

e

f xx

x

∫

bằng:

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 63

A.

1

−

. B.

1

. C.

5

. D.

5

−

.

Câu 16: Cho số phức

32

zi= +

. Tìm số phức liên hợp của số phức

z

A.

23zi= −

. B.

23zi

= +

. C.

22

3 ( 2) 13.z = +− =

. D.

32zi= −

.

Câu 17: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức

2zi=−+

?

A. N. B. P. C. Q.

D. M.

Câu 18: Cho số phức z thỏa mãn

( )

1 14 2

iz i+=−

. Tổng phần thực và phần ảo của

z

là?

A.

4

. B.

14

. C.

4

−

. D.

14−

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Cạnh bên

SA

vuông góc với đáy

và có độ dài bằng

a

. Tính thể tích khối tứ diện

.S BCD

.

A.

3

2

a

. B.

3

4

a

. C.

3

6

a

. D.

3

a

.

Câu 20: Khối trụ có bán kính đáy

3r =

và chiều cao

4h =

. Thể tích của khối trụ đã cho bằng

A.

48

π

. B.

12

π

. C.

36

π

. D.

16

π

.

Câu 21: Cho khối nón có bán kính đáy

2,r =

chiều cao

3.h

=

Thể tích của khối nón là

A.

23

.

3

π

B.

4 3.

π

C.

43

.

3

π

D.

4

.

3

π

Câu 22: Trong không gian

Oxyz

với hệ tọa độ

( )

;;;Oi jk





cho

25OA i k=−+

  



. Tìm tọa độ điểm

A

.

A.

( )

2; 5; 0−

. B.

( )

2;5−

. C.

( )

5; 2; 0−

. D.

( )

2; 0; 5−

.

Câu 23: Trong không gian

Oxyz

, cho hai điểm

( )

1; 2; 3 , 3;0;1 .

AB−

Véctơ nào dưới đây là một véctơ

pháp tuyến của mặt phẳng trung trực đoạn

AB

?

A.

( )

4

2;1;1

n = −−

 

. B.

(

)

2

4; 2; 2n = −

 

. C.

( )

3

2; 1;1n = −

 

. D.

( )

1

2; 2; 4

n =



.

Câu 24: Trong không gian với hệ trục tọa độ

,Oxyz

cho điểm

(1; 1;1)I

−

và mặt phẳng

( )

: 2 2 10 0xy z

α

+− + =

. Mặt cầu

( )

S

tâm

I

tiếp xúc với

( )

α

có phương trình là

A.

( )

( ) ( )

2 22

1 1 11xyz+ +− ++ =

. B.

( ) (

) ( )

2 22

1 1 13xyz+ +− ++ =

.

C.

( ) (

) ( )

2 22

1 1 11

xyz− ++ +− =

. D.

( ) (

) ( )

2 22

1 1 19

xyz− ++ +− =

.

Câu 25: Trong không gian

Oxyz

, đường thẳng đi qua điểm

 

3 21

;;M



và nhận véctơ





4 35;;u 



làm véctơ chỉ phương có phương trình tham số là

A.

34

23

15

xt

yt

zt







 











. B.

43

32

5

xt

yt

zt







 











. C.

34

23

15

xt

yt

zt



















. D.

34

23

15

xt

yt

zt







 











.

Câu 26: Phương trình tổng quát của

( )

α

qua

( ) ( )

2; 1; 4 , 3; 2; 1AB−−

và vuông góc với mặt phẳng

( )

: 2 30xy z

β

++ −=

là.

A.

11 7 2 21 0xyz−−−=

. B.

11 7 2 21 0xyz−++=

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 64

C.

11 7 2 21 0xyz+−−=

. D.

11 7 2 21 0xyz+++=

.

Câu 27: Trong một tuần bạn A dự định mỗi ngày đi thăm một người bạn trong

12

người bạn của mình.

Hỏi bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình (thăm một bạn không quá

một lần).

A.

3991680

. B.

12!

. C.

35831808

. D.

7!

.

Câu 28: Cho

(

)

n

u

là cấp số nhân có

34

6; 2uu= =

. Tìm công bội

q

của cấp số nhân.

A.

4q =

. B.

2

q

=

. C.

1

3

q =

. D.

4q = −

.

Câu 29: Cho hàm số

( )

fx

liên tục trên



và có

( )

0fx

′

>

,

( )

0;x∀ ∈ +∞

. Xét các mệnh đề

(I)

( )

(

)

12ff>

.(II)

(

)

( )

31ff

>

.(III)

(

)

( )

11

ff

>−

.(IV)

45

34

ff

 

>

 

 

.

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 3. B. 2. C. 1. D. 4.

Câu 30: Cho hàm số

32

6 9 ()y x x xmC=− ++

, với

m

là tham số, giả sử đồ thị

()C

cắt trục hoành tại

ba điểm phân biệt có hoành độ thỏa mãn

123

xxx<<

. Khẳng định nào sau đây đúng.

A.

12 3

13 4xx x< << <<

. B.

12 3

013 4xx x< << < < <

.

C.

12 3

1 34xx x

< < << <

. D.

1 23

01 3 4x xx< << << <

.

Câu 31: Tổng tất cả các nghiệm của phương trình

21

2 5.2 2 0

xx+

− +=

bằng bao nhiêu?

A.

1

. B.

3

2

. C.

5

2

. D.

0

.

Câu 32: Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số

1yx= −

, trục hoành và đường thẳng

4

x =

.

Thể tích khối tròn xoay thu được khi cho (H) quay quanh trục

Ox

bằng

A.

2

3

V

π

=

. B.

7

6

V

π

=

. C.

5

6

V

π

=

. D.

7

6

V =

.

Câu 33: Cho hai số phức

1

2zai= +

và

2

1

z bi= −

, với

,ab∈

. Phần ảo của số phức

12

zz+

bằng

A.

2 .b−

B.

2.b−−

C.

1.a +

D.

(2 ).bi−−

Câu 34: Cho ba điểm

( ) ( ) ( )

3;1; 0 , 0; 1; 0 , 0; 0; 6AB C−−

. Nếu tam giác

ABC

′′′

thỏa mãn hệ thức

0AA BB CC

′′′

++ =

   

thì có tọa độ trọng tâm là:

A.

(

)

3; 2;1

−

. B.

( )

1; 0; 2−

. C.

( )

3; 2; 0−

. D.

( )

2; 3; 0−

.

Câu 35: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

1; 3; 4

M −

, đường thẳng

252

:

3 51

xyz

d

+ −−

= =

−−

và mặt phẳng

( )

:2 2 0

P xz+−=

. Viết phương trình đường thẳng

∆

qua

M

vuông góc với

d

và song song với

( )

.P

A.

134

:

11 2

xyz−+−

∆==

−

. B.

134

:

112

xyz

−+−

∆==

−−−

.

C.

134

:

1 12

xyz−+−

∆==

−

. D.

134

:

1 12

xyz−+−

∆==

−−

.

Câu 36: Trên giá sách có

4

quyển sách Toán,

3

quyển sách Vật lý,

2

quyển sách Hoá học. Lấy ngẫu

nhiên

3

quyển sách trên giá sách ấy. Tính xác suất để

3

quyển được lấy ra đều là sách Toán.

A.

2

7

. B.

1

21

. C.

37

42

. D.

5

42

.

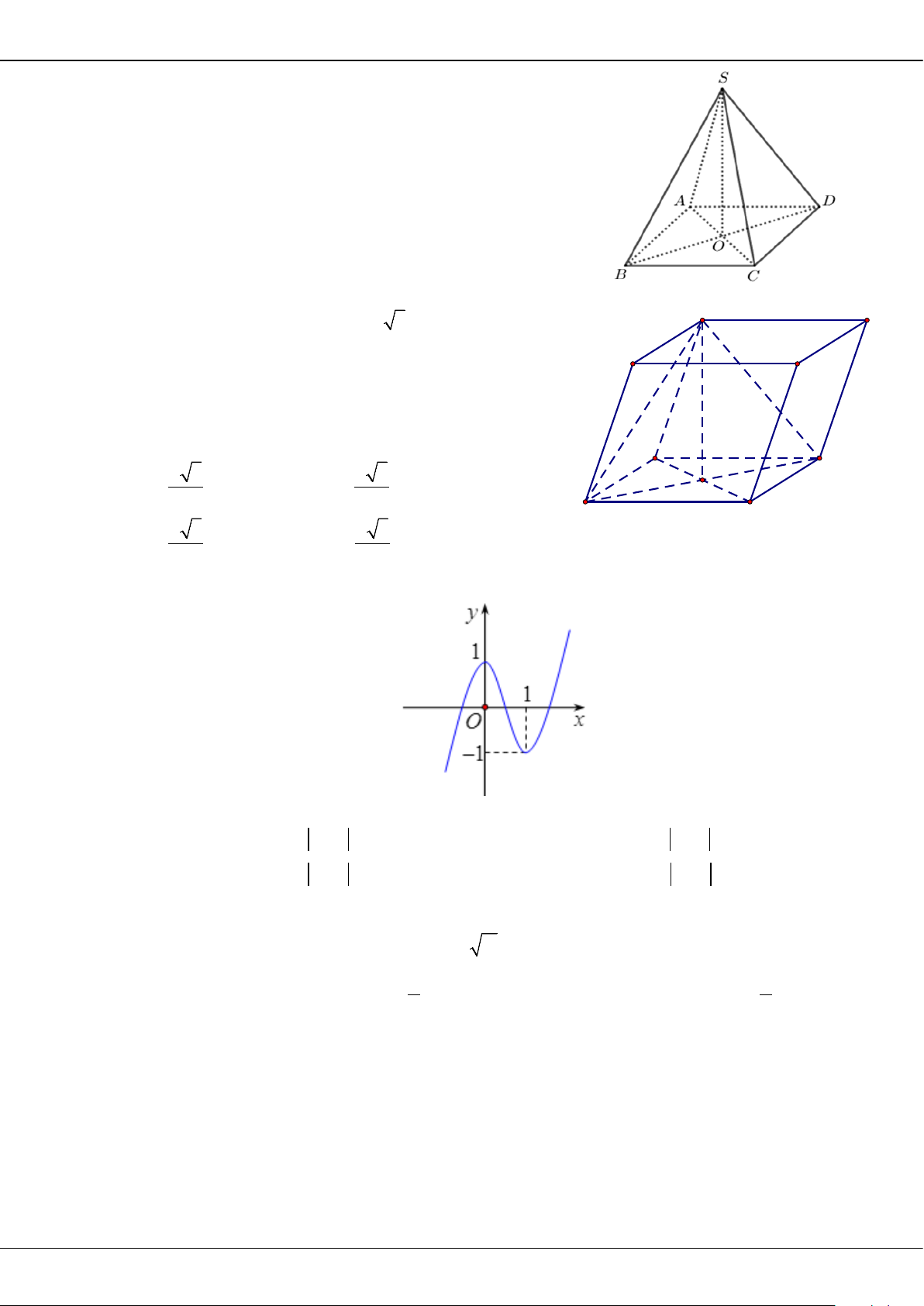
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 65

Câu 37: Cho khối chóp

.S ABCD

có tất cả các cạnh bên và cạnh đáy

đều bằng nhau và

ABCD

là hình vuông. Góc giữa đường

thẳng

SB

và mặt phẳng đáy là góc giữa cặp đường thẳng nào

sau đây?

A.

(

)

,SB BD

. B.

( )

,SB AB

. C.

( )

,SB SC

. D.

( )

,SB AC

.

Câu 38: Cho hình lăng trụ

.ABCD A B C D

′′′′

có đáy

ABCD

là

hình chữ nhật,

AB a=

,

3AD a=

. Hình chiếu vuông

góc của điểm

A

′

trên mặt phẳng

( )

ABCD

trùng với

giao điểm

AC

và

BD

. Tính khoảng cách từ điểm

B

′

đến mặt phẳng

( )

A BD

′

.

A.

3

a

. B.

3

4

a

.

C.

3

2

a

. D.

3

6

a

.

Câu 39: Biết rằng hàm số

()

y fx=

có đồ thị như hình vẽ sau:

Phát biểu nào sau đây là phát biểu đúng?

A. Đồ thị hàm số

()y fx=

có 3 cực trị. B. Đồ thị hàm số

()y fx=

có 1 cực trị.

C. Đồ thị hàm số

()y fx=

có 5 cực trị. D. Đồ thị hàm số

()

y fx=

có 2 cực trị.

Câu 40: Xét bất phương trình

( )

2

22

log 2 2 1 log 2 0xm x− + −<

. Tìm tất cả các giá trị của tham số

m

để

bất phương trình có nghiệm thuộc khoảng

( )

2; +∞

.

A.

( )

0;m ∈ +∞

. B.

3

;0

4

m



∈−





. C.

( )

;0m∈ −∞

. D.

3

;

4

m



∈ − +∞





.

Câu 41: Cho

( )

fx

liên tục trên



và

(

)

4

1

d9fx x=

∫

. Khi đó giá trị của

( )

1

0

4 3 5dfx x−+





∫

là

A.

8

. B.

4

. C.

6

. D.

3

.

Câu 42: Cho hàm số

( )

y fx=

liên tục trên



, thỏa mãn

( ) ( )

2

8 16 4f x fx x x

′

− =−+ −

và

( )

00f =

.

Thể tích khối tròn xoay thu được khi cho hình phẳng giới hạn bởi đồ thị hàm số

( )

y fx=

và

trục hoành quay quanh trục

Ox

bằng

C'

D'

B'

O

D

A

B

C

A'

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 66

A.

256

15

. B.

256

15

π

. C.

16

3

π

. D.

16

3

.

Câu 43: Gọi

12

,zz

là hai nghiệm của phương trình

2

2 3 20zz− +=

trên tập số phức. Tính giá trị biểu thức

22

1 12 2

P z zz z

=++

.

A.

33

4

P =

. B.

5

2

P =

. C.

3

4

P =

. D.

5

2

P =

.

Câu 44: Cho tam giác

ABC

vuông cân tại đỉnh

A

và độ dài cạnh huyền bằng 2. Quay hình tam giác

ABC

quanh trục chứa cạnh

BC

thu được khối tròn xoay có thể tích bằng

A.

2

3

π

. B.

1

3

π

. C.

4

3

π

. D.

22

3

π

.

Câu 45: Cho hình nón có chiều cao

20cmh =

, bán kính đáy

25cm

r =

. Một thiết diện đi qua đỉnh của

hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là

12cm

. Tính diện tích

S

của thiết diện đó.

A.

2

400cmS =

. B.

2

500cmS =

. C.

2

300cmS =

. D.

2

406cmS =

.

Câu 46: Trong không gian

Oxyz

, cho hai đường thẳng chéo nhau

1

262

:

2 21

xyz

d

−−+

= =

−

và

2

412

:

13 2

x yz

d

− ++

= =

−

. Gọi mặt phẳng

( )

P

là chứa

1

d

và

( )

P

song song với đường thẳng

2

d

. Khoảng cách từ điểm

( )

1;1;1M

đến

( )

P

bằng:

A.

10

. B.

1

53

. C.

2

3 10

. D.

3

5

.

Câu 47: Cho hàm số

( )

32 2 3

331y x mx m x m m=− + − −−

, với

m

là tham số. Gọi

A

,

B

là hai điểm cực

trị của đồ thị hàm số và

( )

2; 2I −

. Tổng tất cả các số

m

để ba điểm

I

,

A

,

B

tạo thành tam giác

nội tiếp đường tròn có bán kính bằng

5

là:

A.

2

17

−

. B.

4

17

. C.

14

17

. D.

20

17

.

Câu 48: Cho các số thực dương

,,,

abx y

thỏa mãn

1, 1ab>>

và

1

3

xy

a b ab

−

= =

. Giá trị nhỏ nhất của

biểu thức

34Pxy= +

thuộc tập hợp nào dưới đây?

A.

[

)

5; 7

. B.

(

]

7;9

. C.

( )

11;13

. D.

(

)

1; 2

.

Câu 49: Có bao nhiêu số phức

z

thỏa mãn

(

)

2

2023

11z z zi z z i− +− + + =

?

A. 4 B. 2 C. 1 D. 3

Câu 50: Cho hình chóp

.S ABCD

biết

(

) ( ) (

) (

)

2; 2; 6 , 3;1; 8 , 1; 0; 7 , 1; 2; 3A BC D− −−

. Gọi

H

là trung điểm

của

,CD

( )

SH ABCD⊥

. Để khối chóp

.S ABCD

có thể tích bằng

27

2

(đvtt) thì có hai điểm

12

,SS

thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm

I

của

12

SS

A.

( )

0; 1; 3I

. B.

(

)

1; 0; 3 .−−I

C.

( )

0;1;3−−I

. D.

( )

1; 0; 3I

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 67

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT LÊ VĂN PHẨM

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho cấp số nhân

()

n

u

với

1

2u

=

và

2

10.u =

Công bội của cấp số nhân bằng

A.

18

. B.

12

. C.

5

. D.

1

5

.

Câu 2: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

. Biết cạnh

SA

vuông góc với mặt

phẳng

( )

ABC

và

3SA a=

. Thể tích khối chóp

.S ABC

bằng

A.

3

4

a

B.

3

4

a

C.

3

2

a

D.

3

a

Câu 3: Cho

(

)

sinxd

x Fx C= +

∫

. Khẳng định nào dưới đây đúng?

A.

( )

cos

Fx x

= −

′

. B.

( )

sinFx x

′

=

. C.

( )

sinFx x= −

′

. D.

( )

cosFx x

′

=

.

Câu 4: Cho tập hợp

A

có

10

phần tử. Số tập con gồm ba phần tử của tập

A

bằng

A.

225

B.

120

C.

105

D.

30

Câu 5: Trong không gian với hệ toạ độ

Oxyz

, phương trình đường thẳng

d

đi qua điểm

(

)

3;1; 2

M −

và có một vectơ chỉ phương

( )

2;4; 1u = −



là:

A.

32

14 .

2

xt

yt

zt



=−+



= +





= −



B.

32

14 .

2

xt

yt

zt



=−+



= +





= +



C.

32

1 4.

2

xt

yt

zt



= +



= +





= −



D.

23

4.

12

xt

yt

zt



= −



= +





=−+



Câu 6: Cho hình nón có đường kính đáy bằng

2a

, đường cao là

3a

. Diện tích xung quanh hình nón

bằng

A.

2

10 a

π

. B.

2

5 a

π

. C.

2

13 a

π

. D.

2

2a

π

.

Câu 7: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A.

42

241yx x=−−

. B.

42

241y xx=−+ −

.

C.

4

1yx

=−−

. D.

2

1yx

=−−

.

Câu 8: Nghiệm của phương trình

3

log 2x =

là:

A.

3x =

. B.

4x =

. C.

8x =

. D.

9x =

.

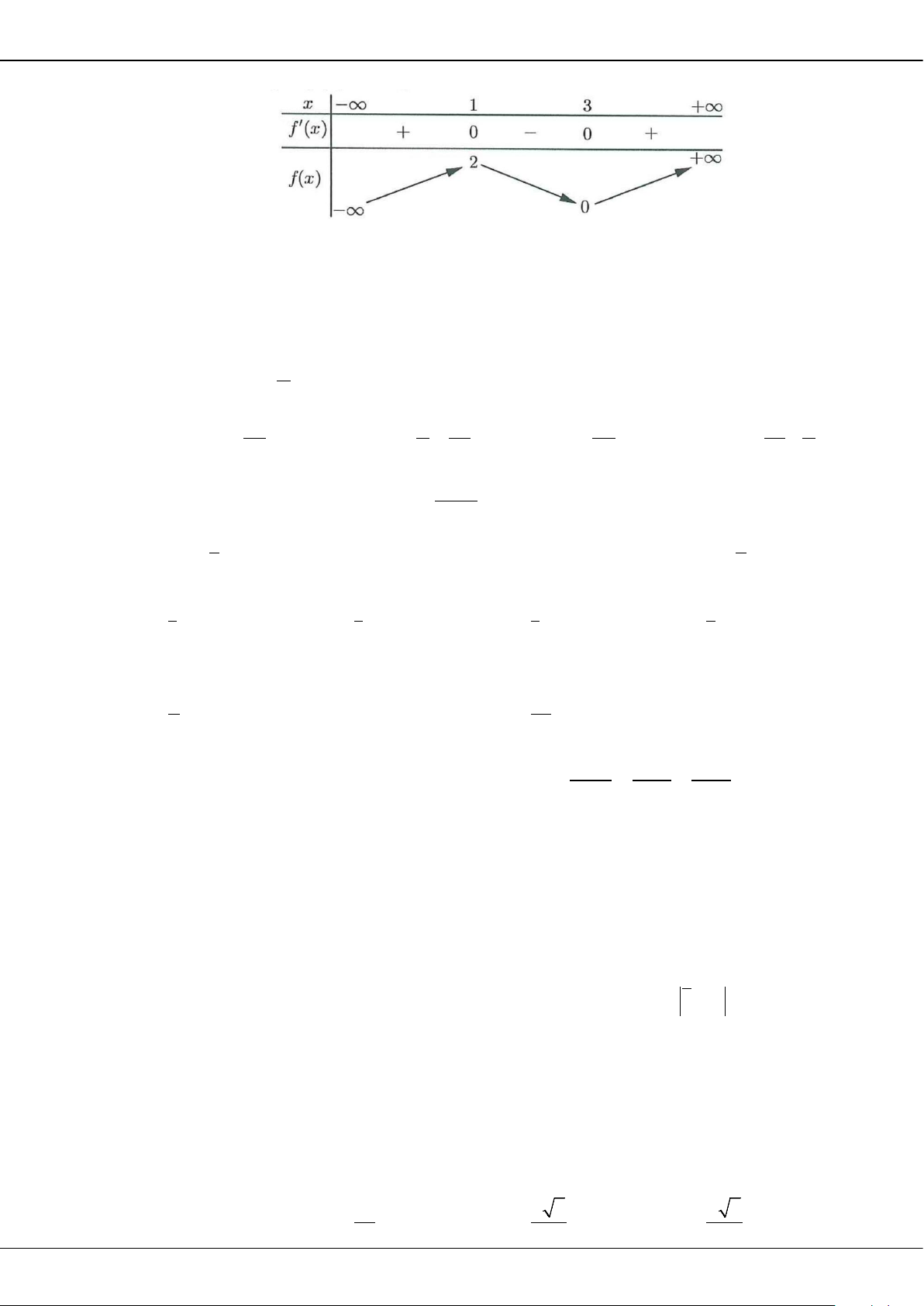
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 68

Câu 9: Cho hàm số

()y fx=

có bảng biến thiên như sau:

Giá trị cực đại của hàm số đã cho là

A.

3

. B.

0

. C.

1−

. D.

2

.

Câu 10: Số giao điểm của đồ thị hàm số

42

43yx x−= −

và đường thẳng

2y =

là

A.

2.

B.

4.

C.

0.

D.

3.

Câu 11: Nếu

( )

1

ln ,( 0)f x dx x C x

x

=++ >

∫

thì

( )

fx

là hàm số nào trong các hàm số sau?

A.

( )

2

1

lnfx x

x

=−+

. B.

( )

2

11

fx

x

= +

C.

( )

1

x

fx e

x

−

= +

. D.

( )

2

11

fx

x

−

= +

.

Câu 12: Tiệm cận ngang của đồ thị hàm số

1

31

−

=

+

x

y

x

là đường thẳng có phương trình:

A.

1

3

y

= −

B.

1= −y

C.

1=y

D.

1

3

y =

Câu 13: Cho số phức

32zi

= −

. Số phức liên hợp của

z

là:

A.

32=−+zi

. B.

32= +zi

. C.

23= +zi

. D.

32=−−zi

.

Câu 14: Tổng tất cả các nghiệm của phương trình

23

22

log log 4 0+ −=xx

bằng

A.

1

.

8

B.

3.−

C.

33

.

16

D.

4−

.

Câu 15: Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

213

:.

12 1

x yz

d

− −+

= =

−

Vectơ nào dưới

đây là một vectơ chỉ phương của

d

?

A.

( )

1

2;1; 3 .u

= −



B.

( )

3

1;2;1.u = −−



C.

(

)

4

1; 2; 1 .u =−−



D.

( )

2

2; 1; 3 .u =−−



Câu 16: Nếu

( )

4

1

2

−

=

∫

f x dx

và

( )

4

1

3

−

=

∫

g x dx

thì

( ) ( )

4

1

12

−



++



∫

f x g x dx

bằng

A.

5

. B.

7

C.

6

. D.

12

.

Câu 17: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức

z

thỏa mãn

21+=

zi

là một đường

tròn. Tâm của đường tròn đó có tọa độ là

A.

( )

0; 2

. B.

( )

2; 0

. C.

( )

0; 2−

. D.

( )

2; 0−

.

Câu 18: Góc giữa hai mặt phẳng

2 50

x yz

− ++=

và

2 10xyz−−+=

bằng

A.

0

30

. B.

0

60

. C.

0

45

. D.

0

90

.

Câu 19: Cho tứ diện đều

ABCD

có cạnh bằng

a

. Khoảng cách từ

A

đến mặt phẳng

( )

BCD

bằng

A.

2a

. B.

3

2

a

. C.

6

2

a

. D.

6

3

a

.

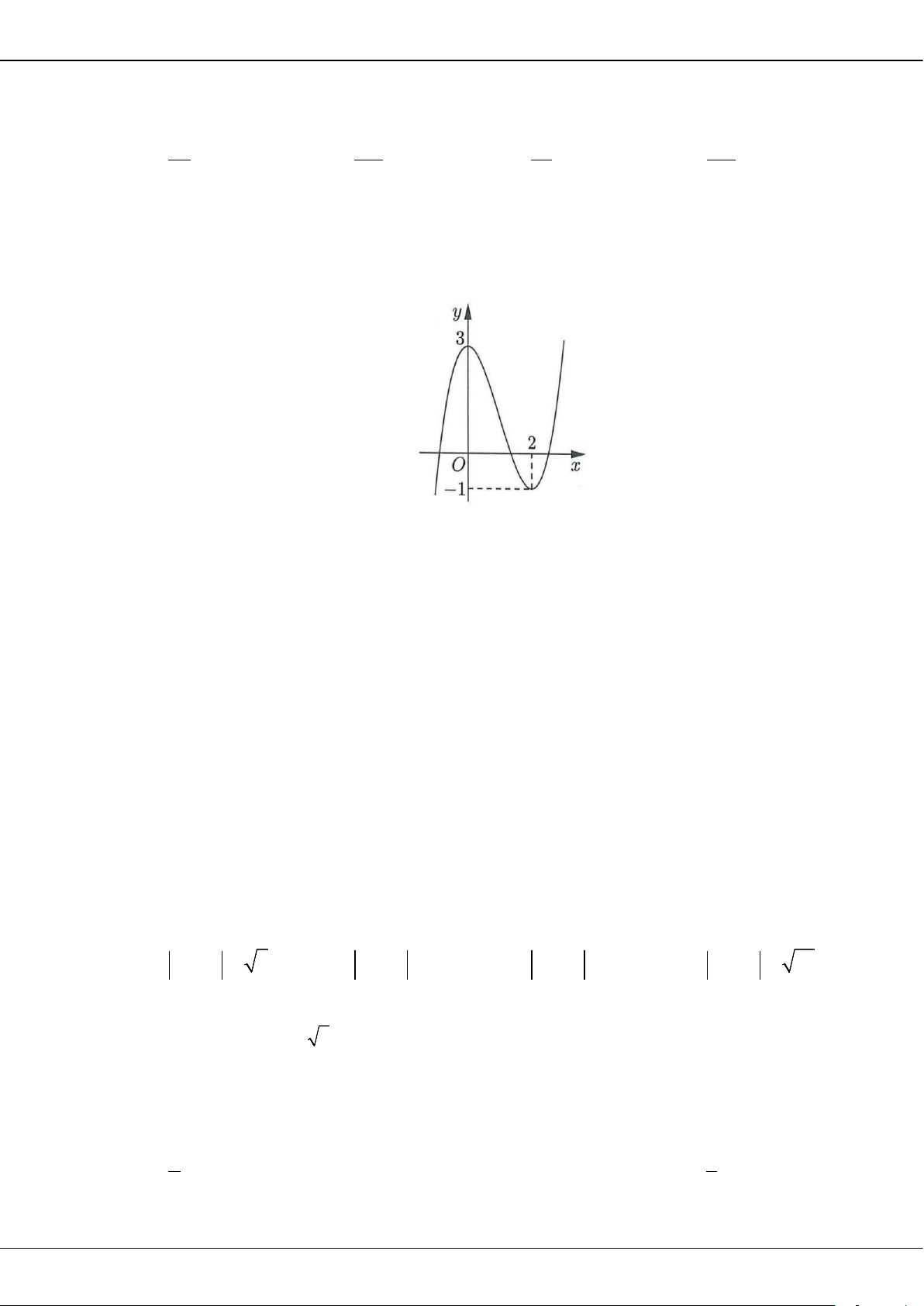
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 69

Câu 20: Xếp ngãu nhiên 3 quả cầu màu đỏ có kích thước khác nhau và 3 quả cầu màu xanh giống nhau

vào một giá chứa đồ nằm ngang có 7 ô trống, mỗi quả cầu được xếp vào một ô. Tính xác suất để

3 quả cầu màu đỏ xếp cạnh nhau và 3 quả cầu màu xanh xếp cạnh nhau.

A.

3

.

70

B.

3

.

160

C.

3

.

80

D.

3

.

140

Câu 21: Với  là số thực dương tùy ý,

ln(3a) ln(2a)+

bằng

A.

2

ln(6 )a

. B.

(

)

2ln 6

a

. C.

ln 5

a

. D.

5ln a

.

Câu 22: Cho hàm số bậc ba  = () có đồ thị là đường cong trong hình bên

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A.

( )

;0−∞

. B.

( )

2; +∞

. C.

( )

0; 2

. D.

( )

1; 3

−

.

Câu 23: Đồ thị của hàm số

32

21=+−yx x

cắt trục tung tại điểm có tung độ bằng

A.

1

. B.

1

−

. C.

0

. D.

3

.

Câu 24: Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

(

)

: 2 2 12 0xyz

α

−−−=

. Phương trình

mặt cầu

( )

S

có tâm

O

là gốc tọa độ và tiếp xúc với mặt phẳng

( )

α

là

A.

2 22

24xyz++=

. B.

2 22

12xyz++=

.

C.

2 22

9

xyz++=

. D.

2 22

16xyz++=

.

Câu 25: Cho hàm số

( )

y fx=

có đạo hàm

( ) ( ) ( )

23

21

′

=−−fx x x

với mọi

x ∈ 

. Hàm số đã cho nghịch

biến trên khoảng nào dưới đây?

A.

(

)

1; 2

. B.

( )

2; +∞

. C.

( )

;1−∞

. D.

( )

1; +∞

.

Câu 26: Cho hai số phức

1

1zi= +

và

2

23zi= +

. Môđun của số phức

12

zz+

là:

A.

12

5zz+=

. B.

12

1zz+=

. C.

12

5zz+=

. D.

12

13zz+=

.

Câu 27: Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại

B

, cạnh

AB a=

. Cạnh bên

SA

vuông

góc với đáy và

6=SA a

. Góc giữa đường thẳng

SC

và

( )

ABC

bằng

A.

60 .°

B.

30°⋅

C.

45°⋅

D.

90°⋅

Câu 28: Cho hình lăng trụ có diện tích đáy

2

3Ba=

và chiều cao

ha=

. Thể tích của khối lăng trụ đã cho

bằng

A.

3

2

a

. B.

3

a

. C.

3

3a

. D.

3

1

3

a

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 70

Câu 29: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

4

3

yx=

là:

A.

1

3

4

3

yx

′

=

. B.

1

3

4

yx

′

=

. C.

1

3

4

3

yx

−

′

=

. D.

7

3

7

yx

′

=

.

Câu 30: Tập xác định của hàm số

ln 1= +yx

là

A.



. B.

(

)

1;

− +∞

. C.

( )

0; +∞

. D.

{ }

\0

.

Câu 31: Tập nghiệm của bất phương trình

3

log 1x <

là

A.

( )

;3 .−∞

B.

(

)

3; .+∞

C.

( )

0;3 .

D.

( )

3;3 .−

Câu 32: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

1;2;3A

. Điểm đối xứng với A qua mặt phẳng

( )

Oxy

có tọa độ là

A.

( )

1;2;3−

. B.

( )

1; 2; 3−− −

. C.

( )

1; 2;3−

. D.

( )

1; 2; 3−

.

Câu 33: Cho hình phẳng D giới hạn bởi đường cong

2

1yx= +

, trục hoành và các đường thẳng

0, 2xx= =

. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao

nhiêu?

A.

5

3

V

π

=

B.

4

3

V

π

=

C.

7

3

V

π

=

D.

14

3

V

π

=

Câu 34: Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu có phương trình

2 22

6 2 2 70

xyz xyz+ + − + − −=

. Bán kính của mặt cầu bằng

A.

23

. B.

32

. C.

16

. D.

4

.

Câu 35: Phần thực của số phức

23

zi

= −

là

A.

3

−

. B. 3. C. 2. D.

2−

.

Câu 36: Diện tích

S

của mặt cầu có chu vi đường tròn lớn bằng

4

π

là:

A.

16S

π

=

B.

32S

π

=

C.

8S

π

=

D.

64S

π

=

Câu 37: Cho hàm số

( )

sin= +fx x x

. Khẳng định nào dưới đây đúng?

A.

( )

2

d cos .

2

=− ++

∫

x

fx x x C

B.

(

)

2

d cos .

=− ++

∫

fx x x x C

C.

( )

d cos 1 .= ++

∫

fx x x C

D.

( )

2

d cos .

2

= ++

∫

x

fx x x C

Câu 38: Cho hàm số

23

= + ++y ax bx cx d

có đồ thị là đường cong trong hình bên.

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

A.

( )

1;1

. B.

( )

1; 3−−

. C.

( )

1;1−

. D.

( )

1; 3−

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 71

Câu 39: Có bao nhiêu giá trị nguyên âm của tham số

a

để hàm số

42

8y x ax x=+−

có đúng ba điểm

cực trị?

A.

10

. B.

5

. C.

6

. D.

11

.

Câu 40: Số các giá trị nguyên của tham số

m

để phương trình

( ) ( )

3

log 1 log 8−= −x mx

có hai nghiệm

thực phân biệt là

A.

5

. B.

4

. C.

4

. D.

3

.

Câu 41: Cho các số thực dương

x

,

y

thỏa mãn

( )

22

2

log 9 10 20 1

x xy y

xy

++

+−=

. Gọi

M

,

m

lần lượt là

giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

y

S

x

=

. Giá trị

Mm+

là:

A.

5

3

Mm+=

. B.

27Mm+=

. C.

52Mm+= +

. D.

7

2

Mm+=

.

Câu 42: Cho hàm số

(

)

fx

biết

( ) ( )

( )

3

22

12 6

′

= − − ++f x x x x mx m

. Số giá trị nguyên của tham số

m

để hàm số đã cho có đúng một điểm cực trị là

A.

6

. B.

7

. C.

4

. D.

5

.

Câu 43: Cho khối nón có đỉnh

S

, chiều cao bằng 4 và thể tích bằng

192

π

. Gọi

A

và

B

là hai điểm

thuộc đường tròn đáy sao cho

8=AB

. Khoảng cách từ tâm của đường tròn đáy đến mặt phẳng

( )

SAB

bằng

A.

32

5

. B.

82

3

. C.

42

3

. D.

23

5

.

Câu 44: Trong không gian với hệ trục tọa độ

Oxyz

, cho ba mặt phẳng

 

: 50Px y z

;

 

: 10

Qx y z 

và

 

: 20Rx y z

. Ứng với mỗi cặp điểm

A

,

B

lần lượt thuộc

hai mặt phẳng

( )

P

,

( )

Q

thì mặt cầu đường kính

AB

luôn cắt mặt phẳng

 

R

theo một đường

tròn. Bán kính nhỏ nhất của đường tròn đó bằng

A.

1

3

. B.

2

3

. C.

1

2

. D.

1

.

Câu 45: Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

( )

Q

song song với mặt phẳng

( )

: 2x 2 17 0P yz

− +− =

. Biết mặt phẳng

( )

Q

cắt mặt cầu

( ) ( ) ( )

22

2

: 2 1 25Sx y z

++ +− =

theo

một đường tròn có chu vi bằng

6

π

. Khi đó mặt phẳng

( )

Q

có phương trình là:

A.

2x 2 17 0yz− +− =

. B.

2x 2 7 0yz− ++=

.

C.

x 2 70yz−+ −=

. D.

2x 2 17 0yz− ++ =

.

Câu 46: Cho

( )

y fx=

là hàm đa thức có các hệ số nguyên. Biết

( )

(

)

2

5 4,fx f x x x x

′

− = + + ∀∈

.

Khi đó

( )

2

0

∫

f x dx

bằng

A.

7

3

. B.

14

3

. C.

20

3

. D.

11

3

.

Câu 47: Xét các số phức

z

thỏa mãn

1 2 25zi−+ =

và số phức

w

thỏa

( ) ( )

5 10 3 4 25iw iz i+ =−−

.

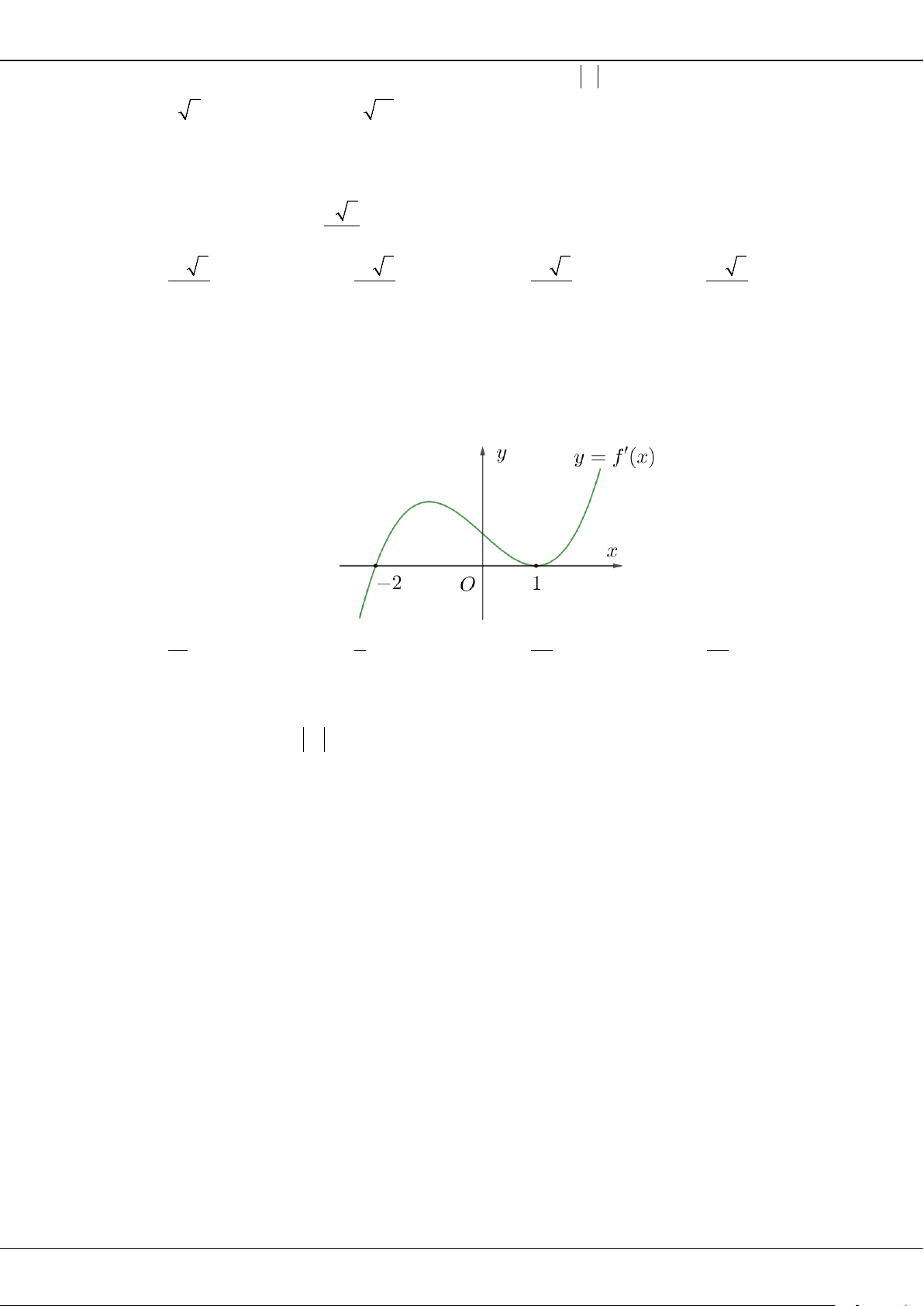
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 72

Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

Pw=

bằng

A.

45

. B.

2 10

. C. 4. D. 6.

Câu 48: Cho lăng trụ

.ABC A B C

′′′

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A

′

lên

mặt phẳng

( )

ABC

trùng với trọng tâm của tam giác

ABC

. Biết khoảng cách giữa hai đường

thẳng

AA

′

và

BC

bằng

3

4

a

. Thể tích của khối lăng trụ đã cho bằng

A.

3

36

a

. B.

3

6

a

. C.

3

12

a

. D.

3

24

a

.

Câu 49: Cho hàm số

( )

y fx=

là hàm đa thức bậc 4. Biết hàm số

( )

y fx

′

=

có đồ thị

( )

C

như hình vẽ

và diện tích của hình phẳng giới hạn bởi đồ thị

( )

C

và trục hoành bằng 9. Gọi

M

và

m

lần lượt

là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

( )

y fx

=

trên đoạn

[

]

3; 2−

. Khi đó giá trị

Mm−

bằng

A.

16

3

. B.

5

3

. C.

27

3

. D.

32

3

.

Câu 50: Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

( )

2

2 1 60mz m z m+ + − +=

có

nghiệm

0

z

thỏa mãn

0

1

z =

?

A.

1

. B.

0

. C.

2

. D.

3

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 73

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT GÒ CÔNG ĐÔNG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức

2022 2023zi= −

có tọa độ là

A.

( )

2022; 2023−

. B.

(

)

2022; 2023−

. C.

( )

2023; 2022

. D.

( )

2023; 2022−

.

Câu 2: Trên khoảng

( )

0;

+∞

, đạo hàm của hàm số

5

logyx=

là

A.

1

y

x

′

=

. B.

1

ln 5

y

x

′

=

. C.

ln 5

y

x

′

=

. D.

1

ln 5

y

x

′

= −

.

Câu 3: Trên khoảng

(

)

0;+∞

, đạo hàm của hàm số

3

yx=

là

A.

31

3yx

−

′

=

. B.

31

yx

−

′

=

. C.

31

1

3

yx

−

′

=

. D.

3

3yx

′

=

.

Câu 4: Tập nghiệm của bất phương trình

2

log 3x >

là

A.

(

]

;8−∞

. B.

( )

8; +∞

. C.

[

)

8; +∞

. D.

( )

;8

−∞

.

Câu 5: Cho cấp số cộng

(

)

n

u

với

1

2u =

và công sai

3d =

. Giá trị của

5

u

bằng

A.

162

. B.

10−

. C.

11

. D.

14

.

Câu 6: Trong không gian

Oxyz

, đường thẳng

3

:2

4

xt

dy t

zt

= +





=−+





= +



có một vectơ chỉ phương là

A.

( )

1;1; 1a = −



. B.

( )

1;1; 1a = −



. C.

( )

1;1; 1a =



. D.

( )

1; 1;1a = −



.

Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình

vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục

tung là

A.

(

)

0; 2−

. B.

(

)

2;0

.

C.

( )

2;0

−

. D.

( )

0; 2

.

Câu 8: Nếu

( )

4

1

d 2023fx x

−

=

∫

và

(

)

4

1

d 2022

gx x

−

=

∫

thì

( ) ( )

4

1

df x gx x

−





∫

bằng

A. 5. B. 6. C. 1. D.

1

−

.

Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A.

42

32yx x=−+

. B.

3

1

x

y

x

−

=

−

.

C.

2

41yx x=−+

. D.

3

35yx x=−−

.

Câu 10: Trong không gian

Oxyz

cho mặt cầu

( )

S

có phương trình

2 22

2460xyz x yz++−+ −=

. Tìm tọa độ tâm

I

và bán kính

R

của mặt

cầu

( )

S

.

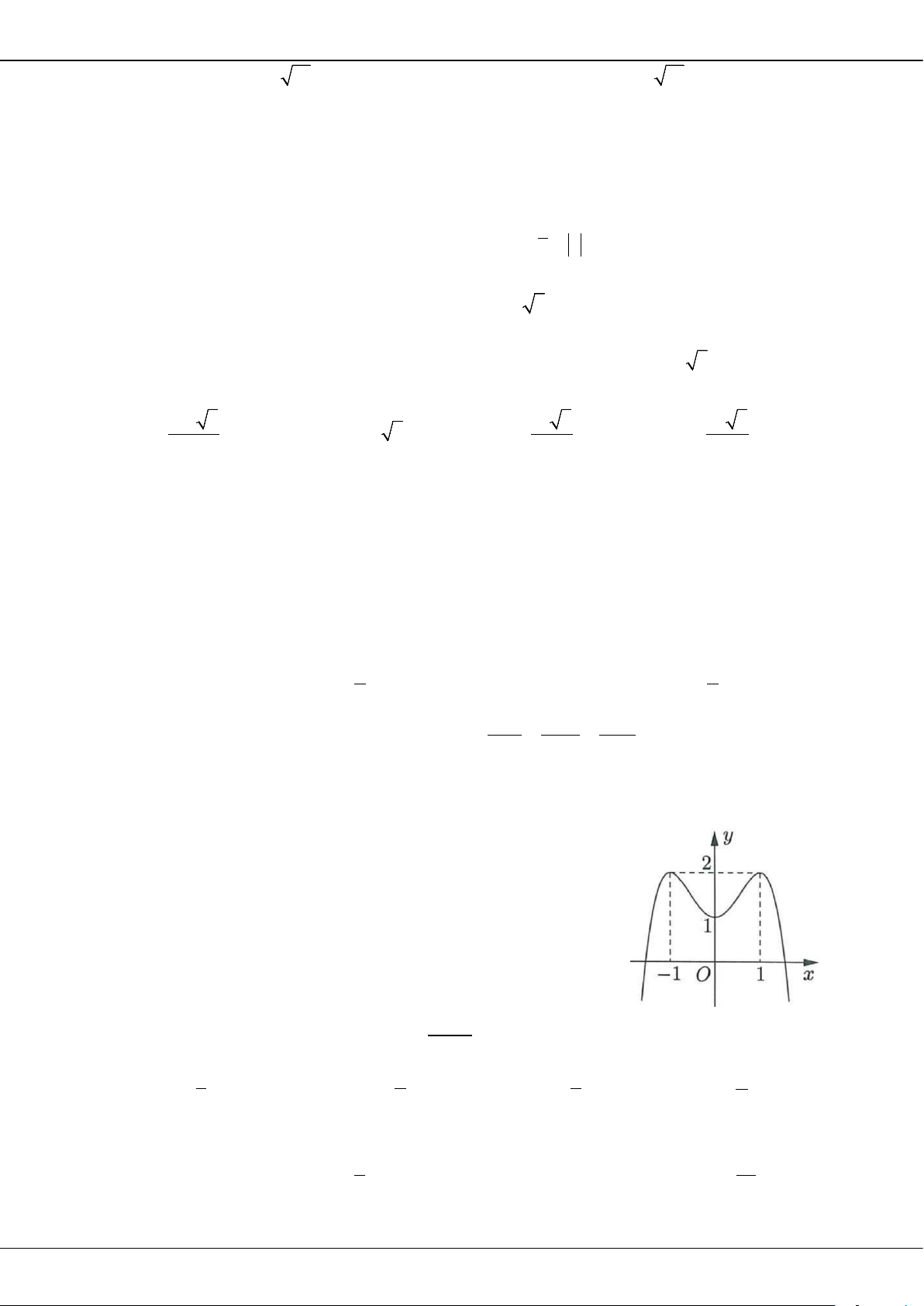
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 74

A.

( )

1; 2; 3 ; 1 4IR−=

. B.

(

)

1; 2; 3 ; 1 4IR−− =

.

C.

(

)

1; 2; 3 ; 1 4IR−− =

. D.

( )

1; 2; 3 ; 1 4IR−=

.

Câu 11: Trong không gian

Oxyz

, góc giữa hai mặt phẳng

( )

: 11 0Pxyz+−− =

và

( )

:2 2 2 7 0Qxyz

+ − +=

bằng

A.

0°

. B.

90

°

. C.

180°

. D.

45°

.

Câu 12: Cho số phức

3 4.

zi

Phần thực của số phức

wz z

là

A.

8

. B.

4

. C.

5

. D.

3

.

Câu 13: Cho khối lập phương có độ dài đường chéo bằng

33

. Thể tích khối lập phương đã cho bằng

A.

9

. B.

12

. C.

27

. D.

18

.

Câu 14: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

,3AB a BC a= =

,

SA

vuông góc với

đáy và

2SA a=

. Thể tích khối chóp đã cho bằng

A.

3

23

3

a

. B.

3

23

a

. C.

3

a

. D.

3

6

a

.

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

theo giao tuyến là đường tròn

( )

;

OR

. Gọi

d

là

khoảng cách từ

O

đến

( )

P

. Khẳng định nào dưới đây đúng?

A.

dR<

. B.

dR>

. C.

dR=

. D.

0d =

.

Câu 16: Phần thực của số phức

23zi= −

là

A.

3−

. B.

2−

. C. 2. D. 3.

Câu 17: Cho hình nón có đường kính đáy bằng độ dài đường sinh

l

. Diện tích xung quanh của

hình nón đã cho bằng:

A.

2 rl

π

. B.

2

1

2

l

π

. C.

2

r

π

. D.

2

3

rl

π

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

123

:

2 12

xy z

d

−−+

= =

−−

. Vectơ nào dưới đây

không là vectơ chỉ phương của

d

?

A.

( )

4; 2; 4a = −−



. B.

( )

1; 2; 3b = −



. C.

( )

2; 1; 2c = −



. D.

( )

2;1;2d

= −−



.

Câu 19: Cho hàm số

42

y ax bx c=++

có đồ thị là đường cong trong hình

bên. Giá trị cực đại của đồ thị hàm số đã cho là:

A.

1, 1xx=−=

. B.

0x =

.

C.

2y =

. D.

1y =

.

Câu 20: Tiệm cận đứng của đồ thị hàm số

21

31

x

y

x

+

=

−

là đường thẳng có phương trình

A.

1

3

x =

. B.

2

3

x = −

. C.

1

3

x = −

. D.

2

3

y =

Câu 21: Giải bất phương trình

( )

2

log 3 1 3x −>

.

A.

3x >

B.

1

3

x<<

C.

3

x <

D.

10

3

x >

Câu 22: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm

34

học sinh?

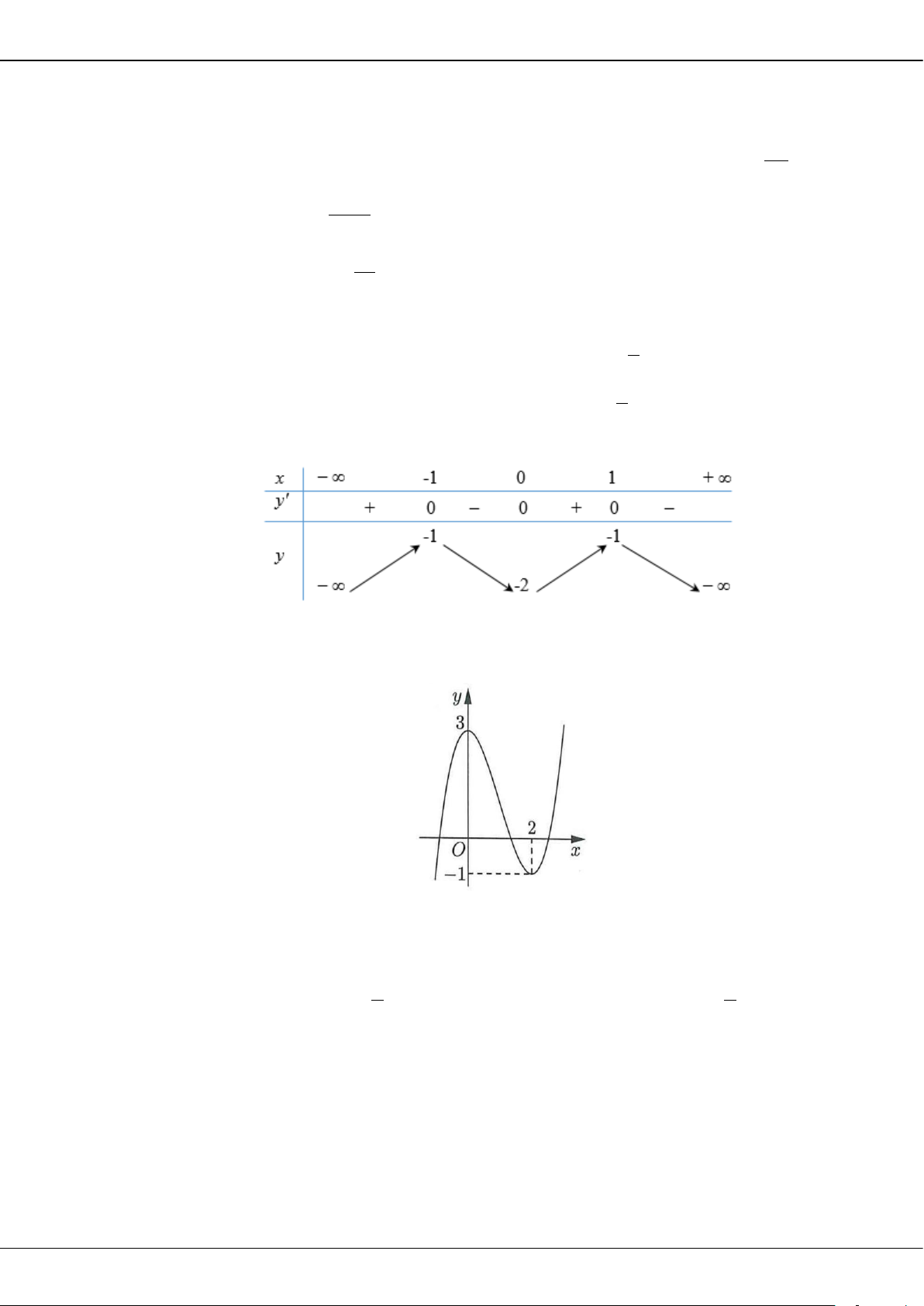
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 75

A.

34

2

. B.

2

34

A

. C.

2

34

. D.

2

34

C

.

Câu 23: Hàm số

( )

2

x

Fx e=

là một nguyên hàm của hàm số

A.

( )

2x

fx e

=

. B.

( )

2

.1

x

f x xe= −

. C.

( )

2

x

f x xe=

. D.

( )

2

x

e

fx

x

=

.

Câu 24: Nếu

( )

5

1

d6fx x

−

=

∫

thì

( )

1

5

d

3

fx

x

−

∫

bằng

A. 18. B.

49

8

. C. 2. D.

2−

.

Câu 25: Tìm họ nguyên hàm của hàm số

( )

sin 2fx x=

.

A.

( )

d cos2fxx xC= +

∫

. B.

( )

1

d cos2

2

fxx xC=−+

∫

.

C.

( )

d cos2

fxx xC=−+

∫

. D.

( )

1

d cos2

2

fxx xC= +

∫

.

Câu 26: Cho hàm số

( )

y fx=

có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

( )

1; 0−

. B.

( )

1; +∞

. C.

( )

;1−∞

. D.

( )

0;1

.

Câu 27: Cho hàm số bậc ba  = () có đồ thị là đường cong trong hình bên.

Hàm số nghịch biến trong khoảng:

A.

(2;3)

. B.

( 1; 3)−

. C.

(0; 2)

. D.

( 1; 2)−

.

Câu 28: Với ,b là hai số thực dương tùy ý,

ln(3ab) ln(2ab)−

bằng:

A.

ln ab

. B.

2

ln

3

. C.

ln(6)

. D.

3

ln

2

.

Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường

2

4

yx x= −

và

0y =

quanh trục

Ox

là:

A.

4

2

0

( 4)x x dx

π

−⋅

∫

B.

4

22

0

(4 )x x dx

π

−⋅

∫

C.

2

22

2

( 4)x x dx

π

−

−⋅

∫

D.

4

22

0

( 4)x x dx−⋅

∫

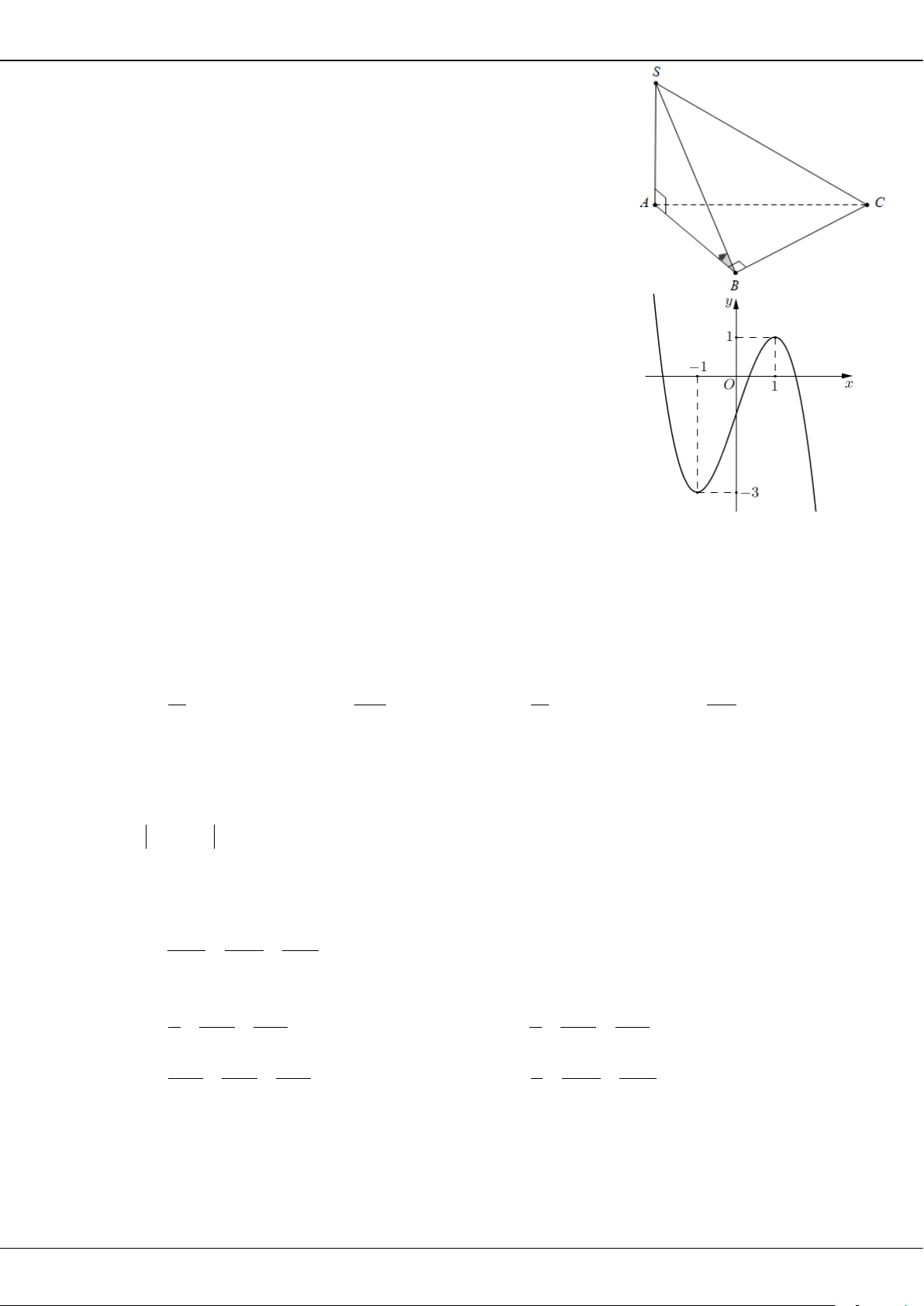
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 76

Câu 30: Cho hình chóp

.

S ABC

có đáy là tam giác vuông tại

B

,

SA

vuông

góc với đáy và

SA AB

=

(tham khảo hình vẽ). Góc giữa đường

thẳng SB và mặt phẳng

( )

ABC

bằng

A.

60 .

°

B.

30°⋅

C.

90°⋅

D.

45°⋅

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình

bên. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

( )

2. fx m=

có ba nghiệm thực phân biệt?

A.

3

. B.

7

.

C.

10

. D.

8

.

Câu 32: Cho hàm số

( )

y fx=

có đạo hàm

( )

(

)

2

29fx x x

′

=−−

với mọi

x ∈ 

. Hàm số đã cho có

bao nhiêu điểm cực đại?

A.

1

. B.

2

. C.

3

. D.

4

.

Câu 33: Bạn Bình có

30

tấm thẻ đánh số từ

1

đến

30

, Bình chọn ngẫu nhiên

10

tấm thẻ. Tính xác suất

để trong

10

tấm thẻ lấy ra có

5

tấm thẻ mang số lẻ,

5

tấm thẻ mang số chẵn và chỉ có một tấm

thẻ mang số chia hết cho

10

.

A.

8

11

. B.

99

667

. C.

3

11

. D.

99

167

.

Câu 34: Tính tổng các nghiệm của phương trình

( )

2

log 3 1 9xx− +=−

bằng

A.

3−

. B.

9

. C.

9

10

−

. D.

3

.

Câu 35: Trên mặt phẳng tọa độ, gọi

M

là điểm biểu diễn của số phức

z

có mô đun lớn nhất thỏa mãn:

43 5zi+− =

. Tọa độ của điểm

M

là

A.

( )

6;8M −

. B.

( )

8; 6M −

. C.

( )

8; 6M

. D.

( )

8; 6M −

.

Câu 36: Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

( )

1;2;3A −−

;

(

)

1; 4;1B −

và đường thẳng

223

:

1 12

xyz

d

+−+

= =

−

. Phương trình nào dưới đây là phương trình của đường thẳng đi qua

trung điểm của đoạn

AB

và song song với

d

?

A.

11

11 2

xy z

−+

= =

. B.

11

112

xy z−+

= =

−

.

C.

111

1 12

xyz−−+

= =

−

. D.

22

112

xy z−+

= =

−

.

Câu 37: Trong không gian

Oxyz

, cho điểm

( 4;1; 3)A −

. Điểm đối xứng với

A

qua mặt phẳng

()Oxy

có

tọa độ là

A.

(4;1; 3)

. B.

(4; 1;3)−

. C.

( 4;1; 3)−−

. D.

( 4; 1; 3)−−−

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 77

Câu 38: Một hình lăng trụ đứng

.ABC A B C

′′′

có đáy

ABC

là tam giác

vuông tại

, , 2.B AB a AA a

′

= =

(tham khảo hình bên). Khoảng

cách từ điểm

A

đến mặt phẳng

( )

A BC

′

là:

A.

25a

. B.

25

5

a

.

C.

5

a

. D.

35

5

a

.

Câu 39: Có bao nhiêu số nguyên

m

để tập nghiệm của bất phương trình

( )

33

log 3 3logxm x+>

chứa đúng

2

số nguyên?

A.

18

. B.

15

. C.

17

. D.

16

.

Câu 40: Hàm số

( )

32

f x ax bx cx d= + ++

có

(

)

02

f

=

và

( ) ( )

3

4 4 2, .f x fx x x x− = + ∀∈

Tích phân

( )

1

0

I f x dx=

∫

bằng

A.

148

63

. B.

146

63

. C.

149

63

. D.

145

63

.

Câu 41: Có bao nhiêu số nguyên

m

để hàm số

( )

652 4

5 18 15 3 2 1y x mx m m x= + + −+ +

chỉ có điểm cực

tiểu mà không có điểm cực đại?

A.

28

. B.

27

. C.

25

. D.

26

.

Câu 42: Trong mặt phẳng tọa độ

Oxy

, tập hợp điểm biểu diễn số phức

1

iz

w

z

+

=

+

là một đường tròn có

bán kính bằng

2

. Môđun của

z

thuộc tập nào dưới đây?

A.

1

;2

2







. B.

1

;2

2







. C.

{ }

2;2

. D.

1

;2

2







.

Câu 43: Cho khối lăng trụ

.ABC A B C

′′′

có đáy là tam giác đều, góc giữa hai mặt phẳng

( )

ABC

′′′

và

(

)

BCC B

′′

bằng

60°

, hình chiếu vuông góc của

B

′

lên mặt phẳng

(

)

ABC

trùng với trọng tâm

tam giác

ABC

. Khoảng cách giữa hai đường thẳng

AA

′

và

BC

′′

bằng

3a

. Thể tích khối lăng

trụ đã cho bằng

A.

3

83a

. B.

3

83

3

a

. C.

3

86

3

a

. D.

3

86a

.

Câu 44: Cho hàm số

( )

fx

thỏa mãn

( )

23

4

6

f =

và

( )

1

1fx x f x

x



′

=+−





,

0x∀>

. Diện tích hình

phẳng giới hạn bởi đồ thị hàm số

( )

()g x xf x=

, trục hoành, đường thẳng

1; 4xx= =

bằng

A.

1283

30

. B.

743

30

. C.

157

30

. D.

563

30

.

Câu 45: Trên tập hợp số phức, xét phương trình

( )

2

2 1 12 8 0z mzm+ + + −=

(

m

là tham số thực). Có

bao nhiêu giá trị nguyên của

m

để phương trình đó có hai nghiệm phân biệt

12

,zz

thỏa mãn

12

11zz+= +

?

A.

7

. B.

12

. C.

8

. D.

9

.

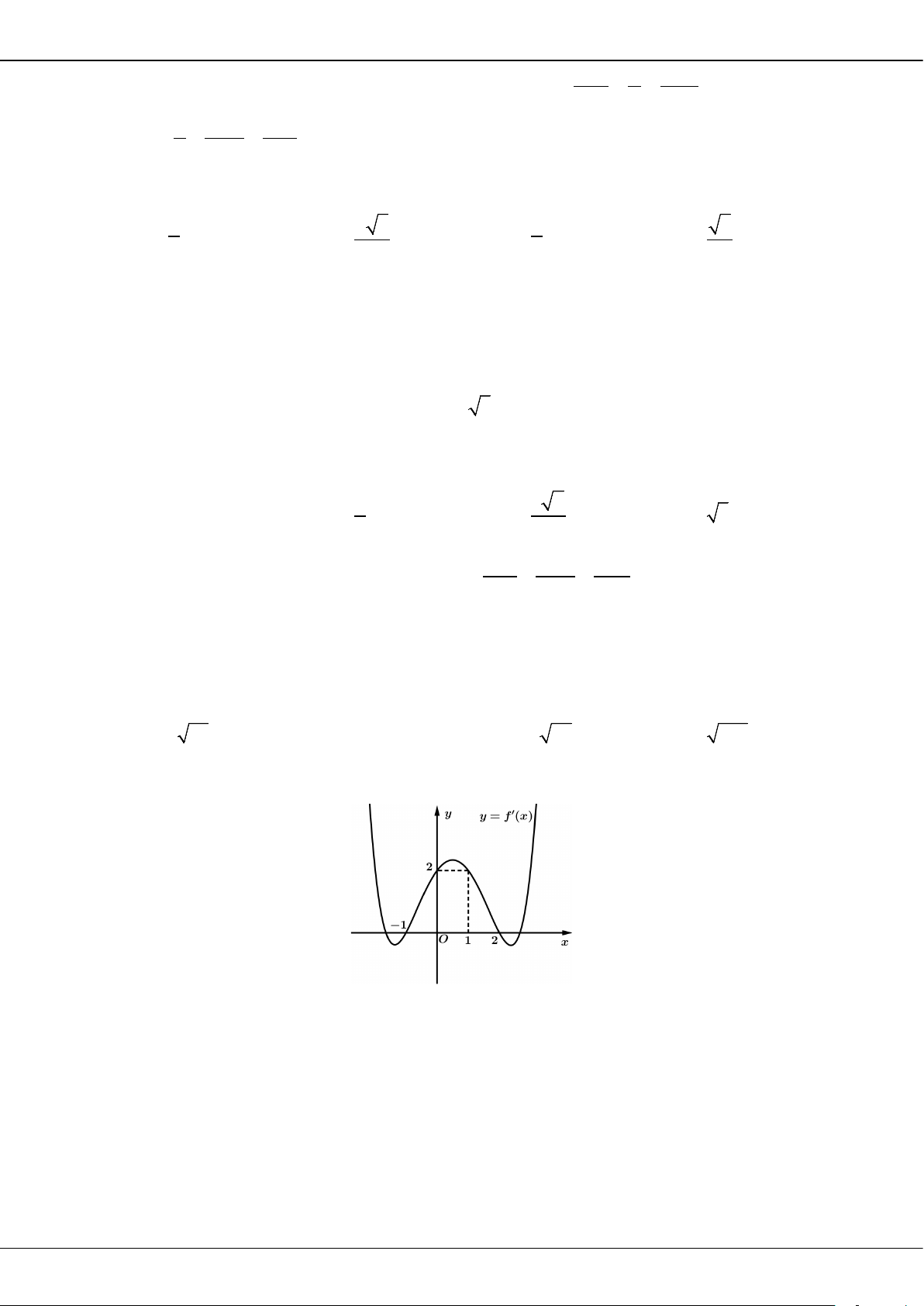
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 78

Câu 46: Trong không gian

Oxyz

, cho đường thẳng

1

12

:

212

x yz

d

−−

= =

và đường thẳng

2

21

:

11 2

xy z

d

−+

= =

. Gọi

( )

P

là mặt phẳng chứa đường thẳng

1

d

và song song với

2

d

. Tính

khoảng cách giữa đường thẳng

2

d

và mặt phẳng

( )

P

.

A.

1

5

. B.

75

5

. C.

7

5

. D.

5

.

Câu 47: Có bao nhiêu cặp số nguyên dương

( )

;xy

thỏa

( )

2 33

3

3 81 4 2026 2024 log ( 2023) (1 )

y

y xx xx



++ + + − −≤



−



?

A.

2021

. B.

2003

. C.

4042

. D.

4024

.

Câu 48: Cho khối nón đỉnh

S

, bán kính đáy bằng

33

và có góc ở đỉnh bằng

120



. Gọi

A

và

B

là hai

điểm thuộc đường tròn đáy sao cho tam giác

SAB

là tam giác vuông, khoảng cách từ tâm đường

tròn đáy đến mặt phẳng

()

SAB

bằng

A.

3

. B.

3

2

. C.

32

2

. D.

3

.

Câu 49: Trong không gian

Oxyz

cho đường thẳng

123

:

234

xy z

d

−−−

= =

và mặt cầu

(

)

S

:

( )

2 22

3 4 5 729xyz

+ ++ ++ =

. Cho biết điểm

( )

2; 2; 7A −−−

, điểm

B

thuộc giao

tuyến của mặt cầu

( )

S

và mặt phẳng

( )

: 2 3 4 107 0Pxyz++− =

. Khi điểm

M

di động trên

đường thẳng

d

, giá trị nhỏ nhất của biểu thức

MA MB+

bằng

A.

5 30

. B.

27

. C.

5 29

. D.

742

.

Câu 50: Cho hàm số

( )

y fx=

có đạo hàm liên tục trên



. Hàm số

( )

y fx

′

=

có đồ thị như hình vẽ.

Xét hàm số

( )

( ) (

) ( )

2

33 3

3 3 3 2 62 6gx f x x m x x m x x m

= −− + + + − − − + −

. Số giá trị nguyên của

tham số

m

thuộc đoạn

[ ]

2023; 2023−

để hàm số

( )

gx

nghịch biến trên khoảng

( )

2; 2−

là

A.

4019

. B.

2023

. C.

2008

. D.

4029

.

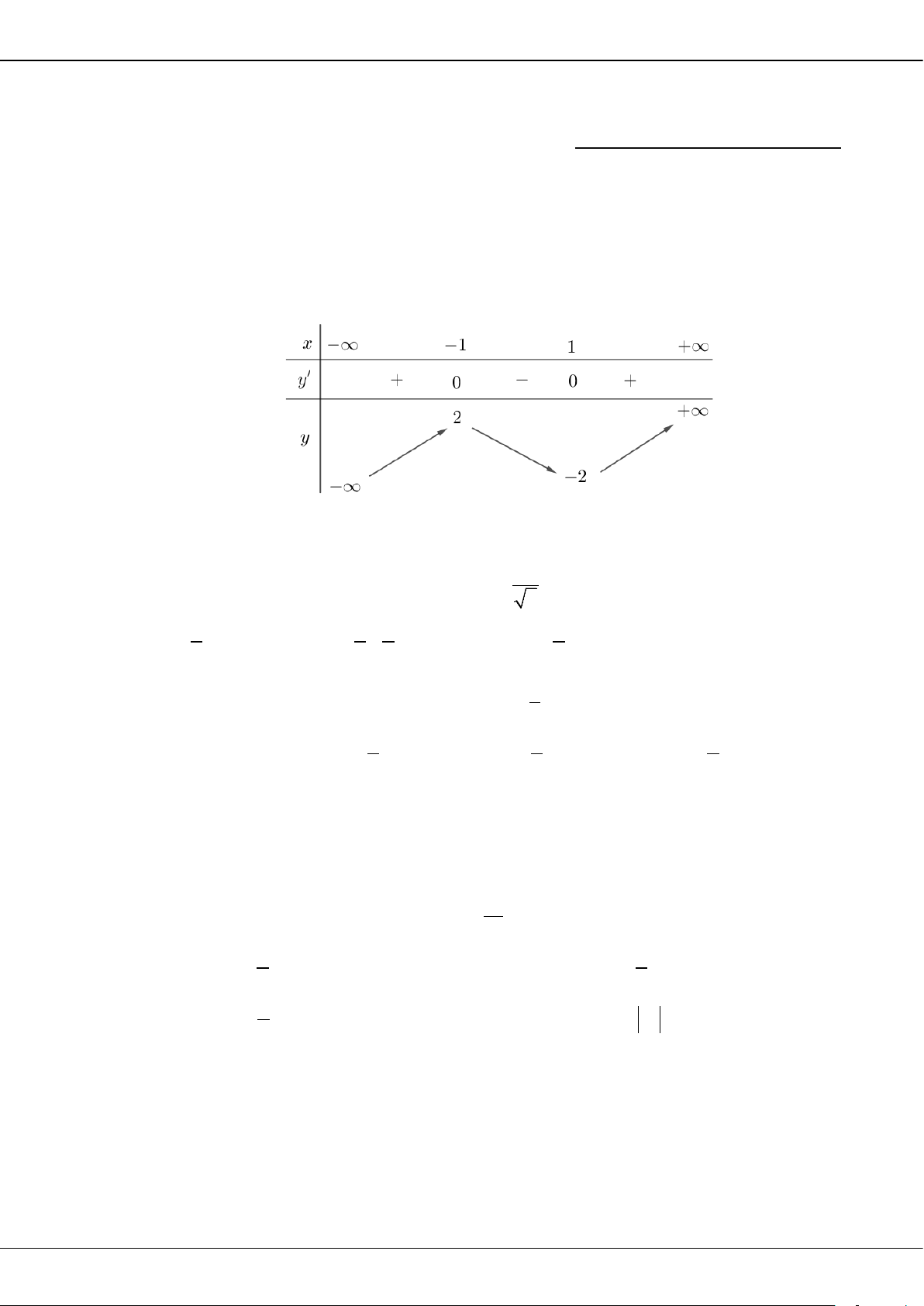
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 79

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT THỦ KHOA HUÂN

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Trong mặt phẳng tọa độ, biết điểm

( 2; 1)M 

là điểm biểu diễn số phức

z

. Phần thực của

z

bằng:

A.

2



. B.

2

. C.

1

. D.

1

.

Câu 2: Phần thực của số phức

( )

213zi i= −

bằng

A.

3

−

. B.

2

. C.

6

−

. D.

6

.

Câu 3: Cho hàm số

(

)

y fx

=

có bảng biến thiên như hình bên.

Hàm số đã cho đạt cực tiểu tại

A.

2

x

=

. B.

2x = −

. C.

1x = −

. D.

1x =

.

Câu 4: Với

a

và

b

là hai số thực dương và

1a ≠

,

log

a

b







bằng

A.

1

1 log

2

a

b+

. B.

11

log

22

a

b

−

. C.

1

1 log

2

a

b−

. D.

1 2log

a

b+

.

Câu 5: Cho cấp số nhân

( )

n

u

với

1

3u =

và công bội

1

3

q = −

. Giá trị của

4

u

bằng

A. 3. B.

1

9

−

. C.

1

9

. D.

7

2

.

Câu 6: Trong không gian

Oxyz

, cho mặt phẳng

( ):2 1 0xyz

α

+ −+=

. Vectơ nào sau đây không là

vectơ pháp tuyến của mặt phẳng

()

α

?

A.

( )

4

4; 2; 2 .= −

 

n

B.

( )

2

2; 1; 1 .−= −

 

n

C.

( )

3

2;1;1 .

=

 

n

D.

( )

1

2; 1; 1 .= −



n

Câu 7: Họ các nguyên hàm của hàm số

3

2

1

() 4fx x

x

= −

là:

A.

4

1

()Fx x C

x

= ++

. B.

2

1

( ) 12Fx x C

x

= ++

.

C.

4

1

()Fx x C

x

= −+

. D.

42

( ) lnFx x x C=++

.

Câu 8: Nếu

( )

3

2

4f x dx =

∫

và

( )

3

2

2g x dx = −

∫

thì

( ) (

)

3

2

f x g x dx−





∫

bằng

A.

2

. B.

6

. C.

8

D.

2−

.

Câu 9: Tích phân

1

0

ed

x

Ix

+

=

∫

bằng

A.

2

e1−

. B.

2

ee−

. C.

2

ee+

. D.

2

ee−

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 80

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 8 2 4 20Sx y z x y z+ + − + + −=

. Tâm của (S) có

tọa độ là

A.

( )

4; 1; 2

−

B.

(

)

8;2;4

−−

C.

( )

8;2;4−

D.

( )

4;1;2

−−

Câu 11: Cho cấp số nhân

( )

n

u

có số hạng đầu

1

2u

=

và công bội

4q =

. Giá trị của

3

u

bằng

A.

32

. B.

16

. C.

8

. D.

6

.

Câu 12: Cho hai số phức:

1

23zi= −

,

2

1zi

=−+

. Phần ảo của số phức

12

w zz=

bằng

A.

5

. B.

7

. C.

5−

. D.

7−

.

Câu 13: Cho khối lập phương có cạnh bằng

3

. Thể tích của khối lập phương đã cho bằng

A.

9.

B.

27

. C.

6

. D.

3

.

Câu 14: Cho khối chóp

.

S ABC

có đáy là tam giác vuông tại

A

,

3

AB =

,

5BC =

,

SA

vuông góc với đáy và

6SA

=

(tham

khảo hình vẽ).

Thể tích khối chóp đã cho bằng

A.

12

. B.

15

.

C.

36.

D.

24.

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;

S OR

. Gọi

d

là khoảng cách từ

O

đến

( )

P

. Khẳng định

nào dưới đây đúng?

A.

dR<

. B.

dR>

. C.

dR

=

. D.

0d

=

.

Câu 16: Đường tiệm cận đứng của đồ thị hàm số

31

1

x

y

x

−+

=

−

có phương trình là

A.

1y =

. B.

1x =

. C.

1x = −

. D.

3y

= −

.

Câu 17: Cho hai số thực

x

,

y

thoả mãn phương trình

2 34x i yi+=+

. Khi đó giá trị của

x

và

y

là:

A.

3x =

,

1

2

y =

. B.

3x =

,

1

2

y = −

. C.

3x =

,

2y =

. D.

3xi=

,

1

2

y =

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

22

:

1 23

xyz

d

−+

= =

. Điểm nào dưới đây thuộc

d

?

A.

( )

2; 2; 0P −

. B.

( )

3; 0; 3Q

. C.

( )

2; 2; 0N

. D.

( )

3; 0; 3M −

.

Câu 19: Cho hàm số

42

yaxbxc=++

có đồ thị là đường cong như hình bên dưới:

Điểm cực đại của đồ thị hàm số đã cho có tọa độ là

x

y

-1

-2

O

1

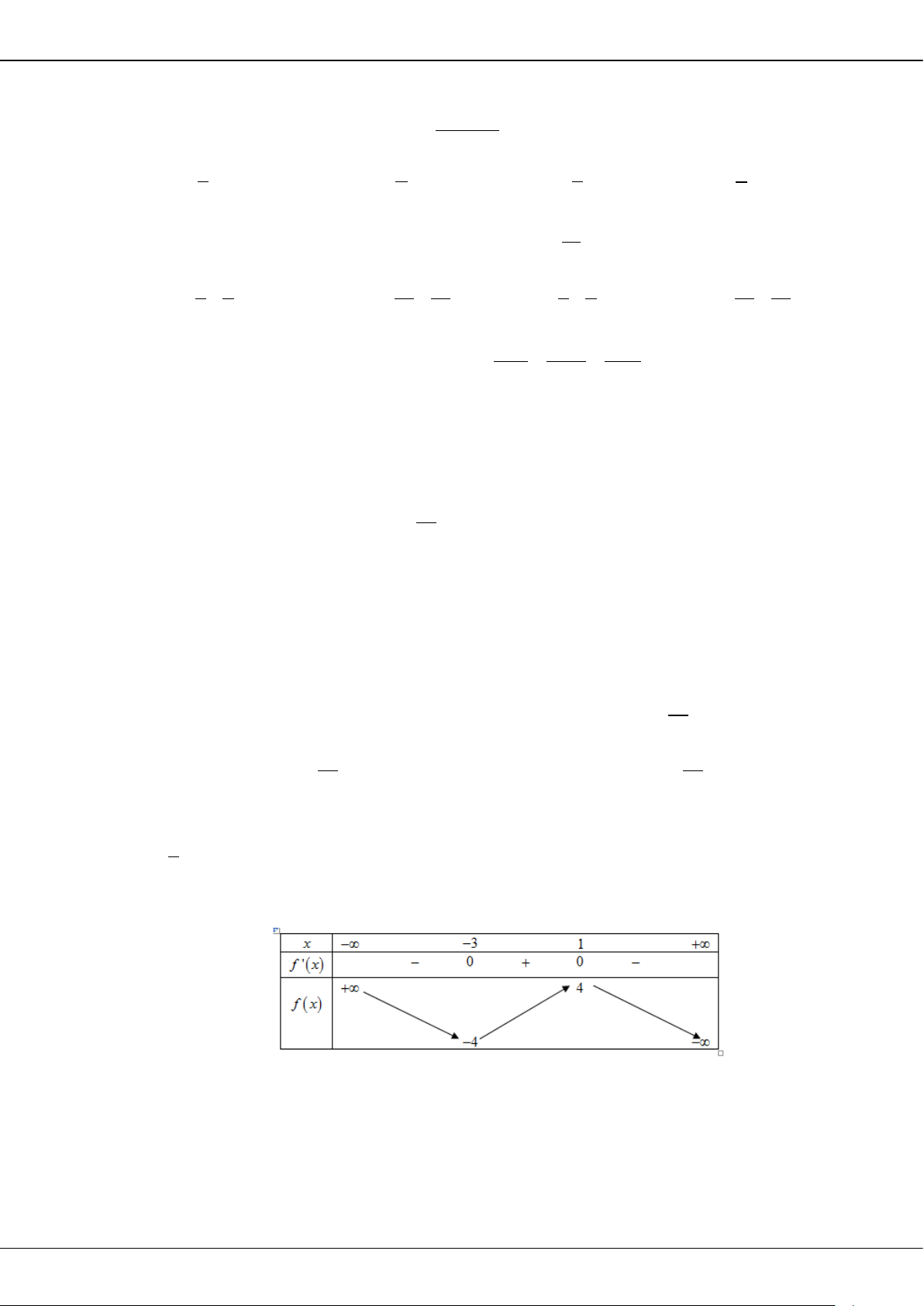
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 81

A.

( )

0; 1 .−

B.

( )

1; 0 .−

C.

( )

1; 2 .−

D.

( )

1; 2 .

−−

Câu 20: Tiệm cận ngang của đồ thị hàm số

2 11

33

x

y

x

−+

=

+

là đường thẳng có phương trình

A.

1

3

y =

B.

2

3

y = −

C.

1

3

y

= −

D.

2

3

y =

Câu 21: Cho hai số phức , . Tìm số phức .

A. . B. . C. . D. .

Câu 22: Trong không gian

Oxyz

, cho đường thẳng

123

:

2 11

xy z−++

∆==

−−

. Vectơ nào dưới đây là một

vectơ chỉ phương của

∆

?

A.

( )

2

1; 2; 3u = −



. B.

(

)

1

2;1;1u =



. C.

( )

4

1;2;3u = −−



. D.

( )

3

2;1;1u = −−



.

Câu 23: Cho

( )

3

dx x Fx C= +

∫

. Khẳng định nào dưới đây đúng?

A.

( )

4

Fx x

′

=

. B.

( )

4

x

Fx

′

=

. C.

( )

3

Fx x

′

=

. D.

( )

2

3Fx x

′

=

.

Câu 24: Nếu

( )

4

1

6f x dx

=

∫

thì

(

)

4

1

23

f x dx

+





∫

bằng

A.

21.

B.

15.

C.

12.

D.

8.

Câu 25: Cho hàm số

( )

sinfx x x= −

. Khẳng định nào dưới đây đúng?

A.

(

)

2

osd.fx x cx x C

= −+

∫

B.

( )

2

osd.

2

x

fx x cx C= −+

∫

C.

( )

2

osd.

2

x

fx x cx C=− ++

∫

D.

( )

2

osdc .

2

x

fx x x C

=− −+

∫

Câu 26: Cho hình nón có đường sinh

l

, bán kính đáy

r

. Diện tích xung quanh của hình nón bằng

A.

1

3

rl

π

. B.

4 l

π

. C.

rl

π

. D.

2

rl

π

.

Câu 27: Cho hàm số

( )

fx

có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số là

A.

3y = −

. B.

1y =

. C.

4y = −

. D.

4y =

.

Câu 28: Tính thể tích khối hộp chữ nhật có ba kích thước là

2

,

3

,

4

.

A.

9

. B.

12

. C.

20

. D.

24

.

Câu 29: Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số

2

3= −y xx

và trục hoành, quanh trục hoành.

1

12zi

= +

2

3zi= −

2

1

z

=

17

55

zi= −

17

10 10

zi=−+

17

55

zi= +

17

10 10

zi

= +

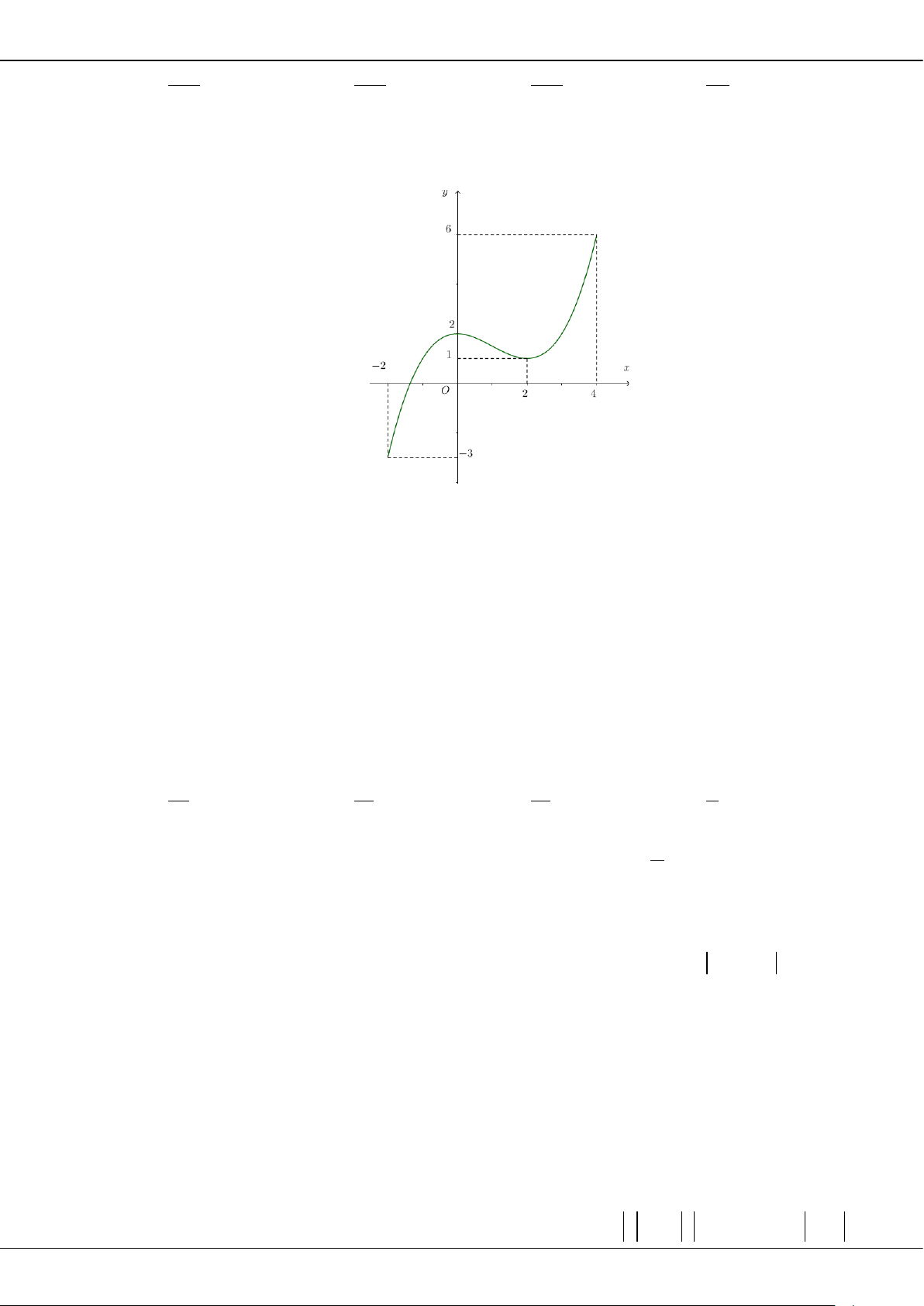
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 82

A.

81

10

π

(đvtt). B.

85

10

π

(đvtt). C.

41

7

π

(đvtt). D.

8

7

π

(đvtt).

Câu 30: Cho hàm số

()y fx=

liên tục trên đoạn

[ ]

2; 4−

và có đồ thị như hình vẽ bên. Số nghiệm thực của

phương trình

3 () 5 0fx

−=

trên đoạn

[ ]

2; 4−

là

A.

1

. B.

0

. C.

3

. D.

2

.

Câu 31: Tập nghiệm của bất phương trình

26

22

xx



là:

A.

 

0; 64

B.

 

6;

C.





0; 6

D.

 

;6

Câu 32: Tìm hai số thực

x

và

y

thỏa mãn điều kiện

(2 3 ) (3 ) 5 4  x yi i x i

với

i

là đơn vị ảo.

A.

1; 1 .

 

xy

B.

1; 1 .

xy

C.

1; 1 . xy

D.

1; 1 . 

xy

Câu 33: Một hộp chứa

17

quả cầu gồm

8

quả màu đỏ được đánh số từ

1

đến

8

và

9

quả màu xanh được

đánh số từ

1

đến

9

. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu

đồng thời tổng hai số ghi trên chúng là số chẵn bằng

A.

9

.

34

B.

9

.

17

C.

2

.

17

D.

1

.

7

Câu 34: Cho hình chóp tứ giác đều có cạnh đáy bằng

a

và chiều cao bằng

2

a

. Số đo của góc giữa mặt

bên và mặt đáy là

A.

60

o

. B.

45

o

. C.

75

o

. D.

30

o

.

Câu 35: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức

z

thỏa mãn

32 4

zi+− =

là một

đường tròn. Tâm của đường tròn đó có tọa độ là.

A.

( )

3; 2−

. B.

(

)

3; 2

. C.

( )

3; 2−

. D.

( )

3; 2−−

.

Câu 36: Trong không gian

Oxyz

, cho hai điểm

( )

1; 2; 3M

−

và

( )

2; 3; 1N −

. Đường thẳng

MN

có

phương trình là:

A.

1

25

34

xt

yt

zt

= +





= −





= +



B.

2

35

14

xt

yt

zt

= +





=−+





= +



C.

1

25

34

xt

yt

zt

= +





= −





=−+



D.

1

25

32

xt

yt

zt

= +





= −





=−−



Câu 37: Trong không gian

Oxyz

, cho

a



,

b



tạo với nhau

1

góc

120°

và

3a =



;

5b =



. Tìm

T ab= −



.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 83

A.

6T =

. B.

7T

=

. C.

4T =

. D.

5T =

.

Câu 38: Cho hình chóp đều

.

S ABCD

có chiều cao

2, 4

a AC a=

(tham khảo hình bên). Tính khoảng cách

từ điểm

B

đến mặt phẳng

( )

SCD

.

A.

23

3

a

. B.

2

a

. C.

43

3

a

. D.

2

a

.

Câu 39: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

sin 1,yx= +

trục hoành và hai đường thẳng

0x =

và

7

6

x

π

=

là.

A.

37

1

23

π

++

. B.

37

1

46

π

+−

. C.

37

1

26

π

+−

. D.

37

1

26

π

++

.

Câu 40: Cho hàm số

( )

fx

liên tục trên



. Biết

( )

fx

có đạo hàm là

( )

5

'2fx x= +

và

( )

12

f =

. Khi

đó

2

0

2

d

x

f







∫

bằng

A.

1

7

. B.

3

7

. C. 6. D.

6

7

.

Câu 41: Có bao nhiêu giá trị nguyên của tham số

( )

10;10m ∈−

để hàm số

( ) ( )

53

3 5 10 15 45 2024yx m x m x=−+ − + +

có hai điểm cực trị?

A.

10

. B.

12

. C.

8

. D.

14

.

Câu 42: Cho số phức

z

thỏa mãn

2 12 2z i zz i

− = −+

. Tìm giá trị nhỏ nhất của

z

.

A.

11

2

. B. 0. C.

22

2

D.

13

2

Câu 43: Gọi

( )

m

C

là đồ thị của hàm số

( )

3 22

1 21

32

m

y x x m mx

+

=− ++

với

m

là tham số. Có bao nhiêu

điểm

M

sao cho tồn tại hai giá trị khác nhau

12

,

mm

mà

M

là điểm cực đại của đồ thị

( )

1

m

C

và

là điểm cực tiểu của đồ thị

(

)

2

m

C

?

A.

2

. B.

0

. C.

1

. D. vô số.

Câu 44: Cho số phức

z

thỏa mãn

2

2 30zz− +=

. Tính

w

biết

2018 2017 2016 2015 2

33 9wz z z z z z= − + + + −+

.

A.

53

. B.

2018 3

. C.

93

. D.

3

.

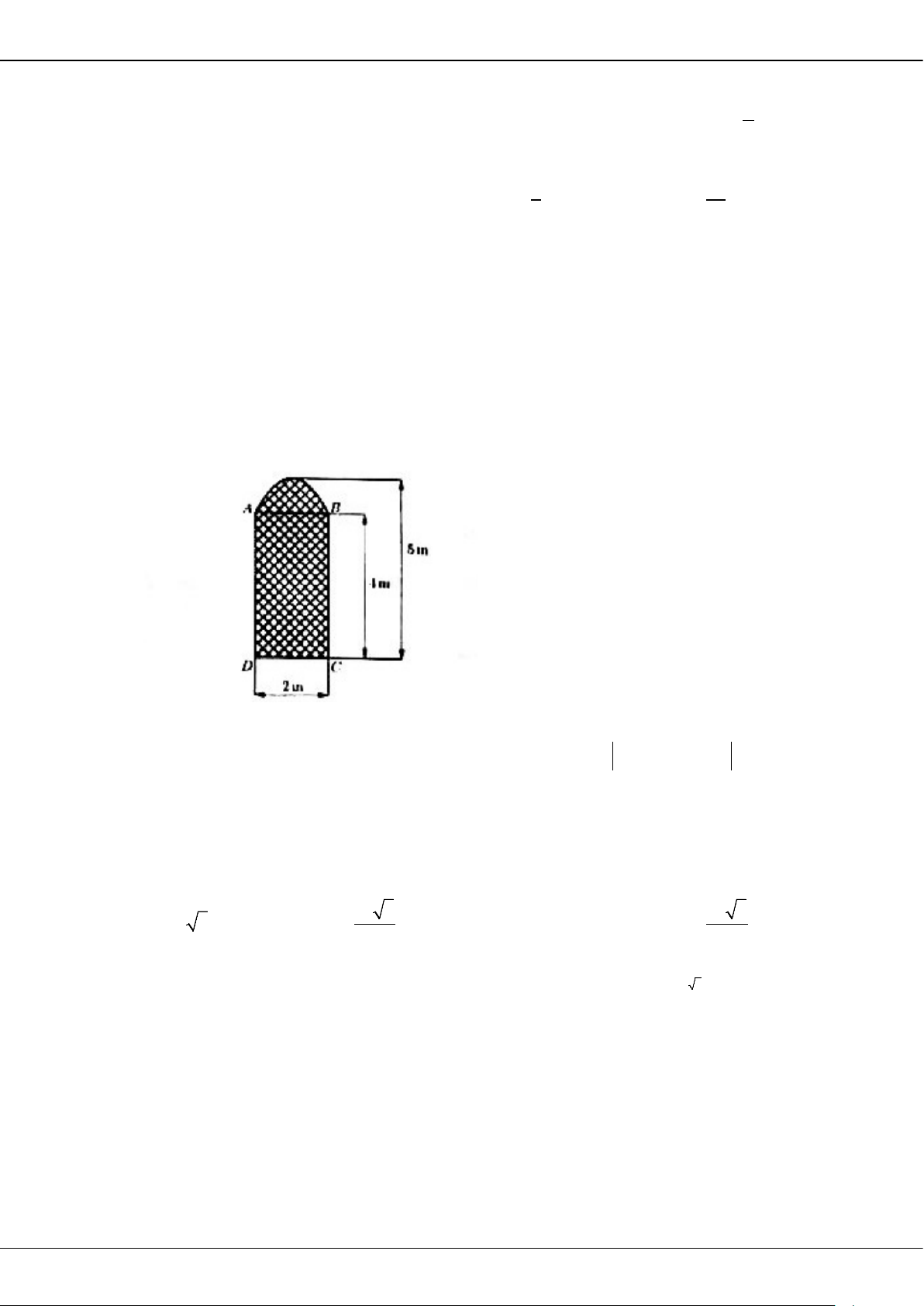
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 84

Câu 45: Trong không gian với hệ tọa độ

Oxy

, cho mặt phẳng

( )

:2 3 0P yz−+=

và điểm

( )

2; 0; 0

A

. Mặt

phẳng

( )

α

đi qua

A

, vuông góc với

( )

P

, cách gốc tọa độ

O

một khoảng bằng

4

3

và cắt các tia

Oy

,

Oz

lần lượt tại các điểm

B

,

C

khác

O

. Thể tích khối tứ diện

OABC

bằng

A.

8

. B.

16

. C.

8

3

. D.

16

3

.

Câu 46: Cho

2

mặt cầu

( )

(

) (

)

2 22

1

:3 2 24

Sx y z

− +− +− =

,

( ) ( ) ( )

22

2

:1 11Sx yz− + +− =

. Gọi

d

là

đường thẳng đồng thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt cầu và cách

gốc tọa độ

O

một khoảng lớn nhất. Nếu

( )

; 1;uab=



là một vectơ chỉ phương của

d

thì tổng

23S ab= +

bằng bao nhiêu?

A.

2S =

. B.

1S =

. C.

0S =

. D.

4S =

.

Câu 47: Ông An muốn làm một cánh cửa bằng sắt có hình dạng và kích thước như hình vẽ. Biết rằng

đường cong phía trên là một parabol, tứ giác

ABCD

là một hình chữ nhật. Giá cánh cửa sau khi

hoàn thành là

900000

đồng/

2

m

. Số tiền ông An phải trả để làm cánh cửa đó bằng

A. 8 160 000 đồng. B. 8 400 000 đồng. C. 9 600 000 đồng. D. 15 600 000 đồng.

Câu 48: Tìm số giá trị nguyên của

[ ]

2020;2020m ∈−

để hàm số

32

65yx x m= − ++

đồng biến trên

khoảng

( )

5; +∞

?

A.

2001

. B.

2018

. C.

2019

. D.

2000

.

Câu 49: Cho hình nón đỉnh S có đường cao

ha=

, đường sinh

2la=

. Một mặt phẳng đi qua đỉnh S và

cắt đường tròn đáy tại hai điểm M, N. Diện tích tam giác SMN lớn nhất bằng

A.

2

3a

. B.

2

3

2

a

. C.

2.

2a

. D.

2

3

4

a

.

Câu 50: Có bao nhiêu

m

nguyên

[ ]

2021;2021m ∈−

để phương trình

( )

3

6

6 2 log 18 1 12

x

m xm− = ++

có

nghiệm?

A.

212

. B.

211

. C.

2020

. D.

2023

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 85

SỞ GD&ĐT TIỀN GIANG

TRUNG TÂM GDNN-GDTX GCĐ

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Hình nào biểu diễn cho số phức

32zi=−+

:

A. . B. .

C. . D. .

Câu 2: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

( )

ln 3

yx=

là

A.

1

3

y

x

′

=

. B.

1

y

x

′

=

. C.

3

y

x

′

=

. D.

1

ln 3

y

x

′

=

.

Câu 3: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

3

yx=

là

A.

31

3yx

−

′

=

. B.

2

3yx

′

=

. C.

31

1

3

yx

−

′

=

. D.

3

3yx

′

=

.

Câu 4: Tập nghiệm của bất phương trình

2

3 27

x+

≥

là

A.

(

]

;1−∞

. B.

( )

1; +∞

. C.

[

)

1; +∞

. D.

( )

;1

−∞

.

Câu 5: Cho cấp số nhân

( )

n

u

với

1

3u =

và

4

1

9

u =

. Công bội

q

của cấp số nhân bằng

A. 3. B.

1

9

. C.

9

. D.

1

3

.

Câu 6: Trong không gian

Oxyz

, mặt phẳng

( )

:2 3 4 0P x yz+ ++=

có một vectơ pháp tuyến là

A.

(

)

1

1; 3; 2n =



. B.

(

)

4

2; 3;1n =

 

. C.

( )

3

1; 2; 3n =

 

. D.

( )

2

2; 1; 3n =

 

.

Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị

hàm số đã cho và trục tung là

x

y

3

_

2

O

M

x

y

3

2

O

M

x

y

3

_

2

O

M

x

y

_

3

_

2

O

M

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 86

A.

( )

0; 2

. B.

( )

2;0

. C.

( )

6; 0

. D.

(

)

0; 6

.

Câu 8: Nếu

( )

2

3

2f x dx

−

=

∫

và

( )

2

3

5

g x dx

−

=

∫

thì

( ) ( )

(

)

2

3

f x g x dx

−

∫

bằng

A.

3

. B.

7

. C.

3−

. D.

7−

.

Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên

A.

42

32yx x=−+

. B.

3

32yx x=−+

. C.

2

32

yx x=−+

. D.

2

1

x

y

x

+

=

+

.

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 4 6 2 50Sx y z x y z+ + − + − +=

. Bán kính của mặt

cầu của (S) bằng

A.

1

R =

B.

4R =

C.

2R =

D.

3R =

Câu 11: Cho hình lập phương ABCD.A’B’C’D’, góc giữa hai mặt phẳng AA’B’B và AA’C’C bằng

A.

30



B.

45



C.

60



D.

Câu 12: Cho số phức

2zi= +

, phần ảo của số phức

3

z

bằng

A.

1

B.

13

C.

11

D.

2

Câu 13: Cho khối tứ diện đều có cạnh bằng

2

. Thể tích của khối tứ diện đã cho bằng

A.

2

. B.

22

. C.

2

3

. D.

22

3

.

Câu 14: Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

3AB =

;

SA

vuông góc với đáy và

2SA

=

(tham khảo hình vẽ).

x

y

1

2

3

6

O

x

y

1

_

4

2

O

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 87

Thể tích khối chóp đã cho bằng

A.

18

. B.

6

. C.

8

. D.

4

.

Câu 15: Cho mặt phẳng

( )

P

đi qua tâm của mặt cầu

( )

;S OR

. Gọi

d

là khoảng cách từ

O

đến

( )

P

.

Khẳng định nào dưới đây đúng?

A.

dR

<

. B.

dR>

. C.

dR=

. D.

0

d

=

.

Câu 16: Phần thực của số phức

43zi= +

là

A.

4

. B.

3

. C.

2

. D.

1

.

Câu 17: Cho hình trụ có đường kính đáy

2r

và độ dải đường sinh

l

. Diện tích xung quanh của hình nón

đã cho bằng

A.

2 rl

π

. B.

2

3

rl

π

. C.

rl

π

. D.

2

1

3

rl

π

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

234

:

1 25

xyz

d

+ −+

= =

−

. Vectơ nào trong các vectơ

sau là vectơ chỉ phương của

d

?

A.

( )

2; 3; 4a =−−



. B.

(

)

1; 2; 5b = −



. C.

( )

1; 2; 5c =



. D.

( )

2; 3; 4d = −



.

Câu 19: Cho hàm số

3 2

y ax bx cx d= + ++

có đồ thị là đường cong trong hình bên. Điểm cực đại của đồ

thị hàm số đã cho có tọa độ là

A.

( )

1; 0

. B.

( )

0; 2

. C.

( )

2; 2

. D.

( )

2; 0−

.

Câu 20: Tiệm cận đứng của đồ thị hàm số

1

52

x

y

x

+

=

−

là đường thẳng có phương trình

3

2

C

S

A

B

D

x

y

2

1

2

_

2

O

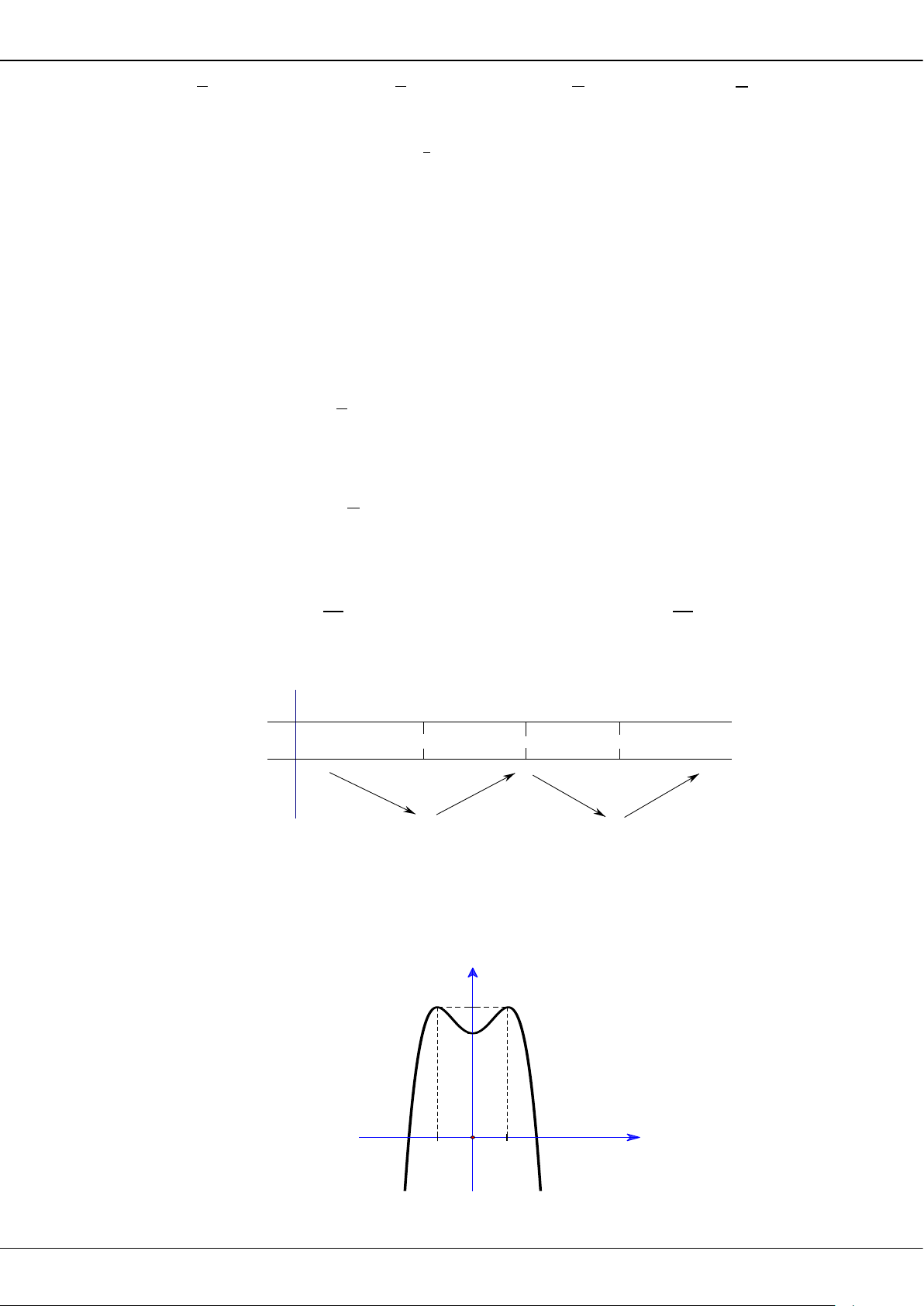
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 88

A.

1

5

y =

B.

1

5

y = −

C.

2

5

y = −

D.

2

5

y =

Câu 21: Tập nghiệm của bất phương trình

( )

1

2

log 3 0x −>

là

A.

[

)

4; +∞

B.

[ ]

3; 4

C.

( )

3; 4

D.

(

)

4;

+∞

Câu 22: Cho tập hợp

A

có

9

phần tử. Số tập con gồm ba phần tử của

A

bằng

A.

9!

B.

6

C.

84

D.

504

Câu 23: Cho

( )

51

ed

x

x Fx C

+

= +

∫

. Khẳng định nào dưới đây đúng?

A.

( )

51

x

Fx e

+

=

′

. B.

( ) ( )

5

51

x

Fx x e= +

′

. C.

( )

5x

Fx e

′

=

. D.

( )

51

5

x

Fx e

+

=

′

.

Câu 24: Nếu

(

)

1

3

d6

fx x

−

=

∫

thì

( )

1

3

1

d

3

fx x x

−



+





∫

bằng

A.

26

. B.

33

. C.

2

. D.

22

.

Câu 25: Cho hàm số

( )

1

sin

fx x

x

= −

. Khẳng định nào dưới đây đúng?

A.

(

)

d cos ln .fx x x xC

= −+

∫

B.

( )

d cos ln .fx x x xC=− −+

∫

C.

( )

2

d cos .fx x x C

x

=− ++

∫

D.

( )

2

d cos .

fx x x C

x

= ++

∫

Câu 26: Cho hàm số

()y fx=

có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

(

)

2; +∞

. B.

( )

0;1

. C.

( )

1; 0−

. D.

( )

2;3

.

Câu 27: Cho hàm số bậc ba  = () có đồ thị là đường cong trong hình bên.

Giá trị cực tiểu của hàm số đã cho là:

0

_

1

x

y

_

∞

+

∞

+

∞

2

3

+

_

y'

0

_

+

1

x

y

5

_

1

4

O

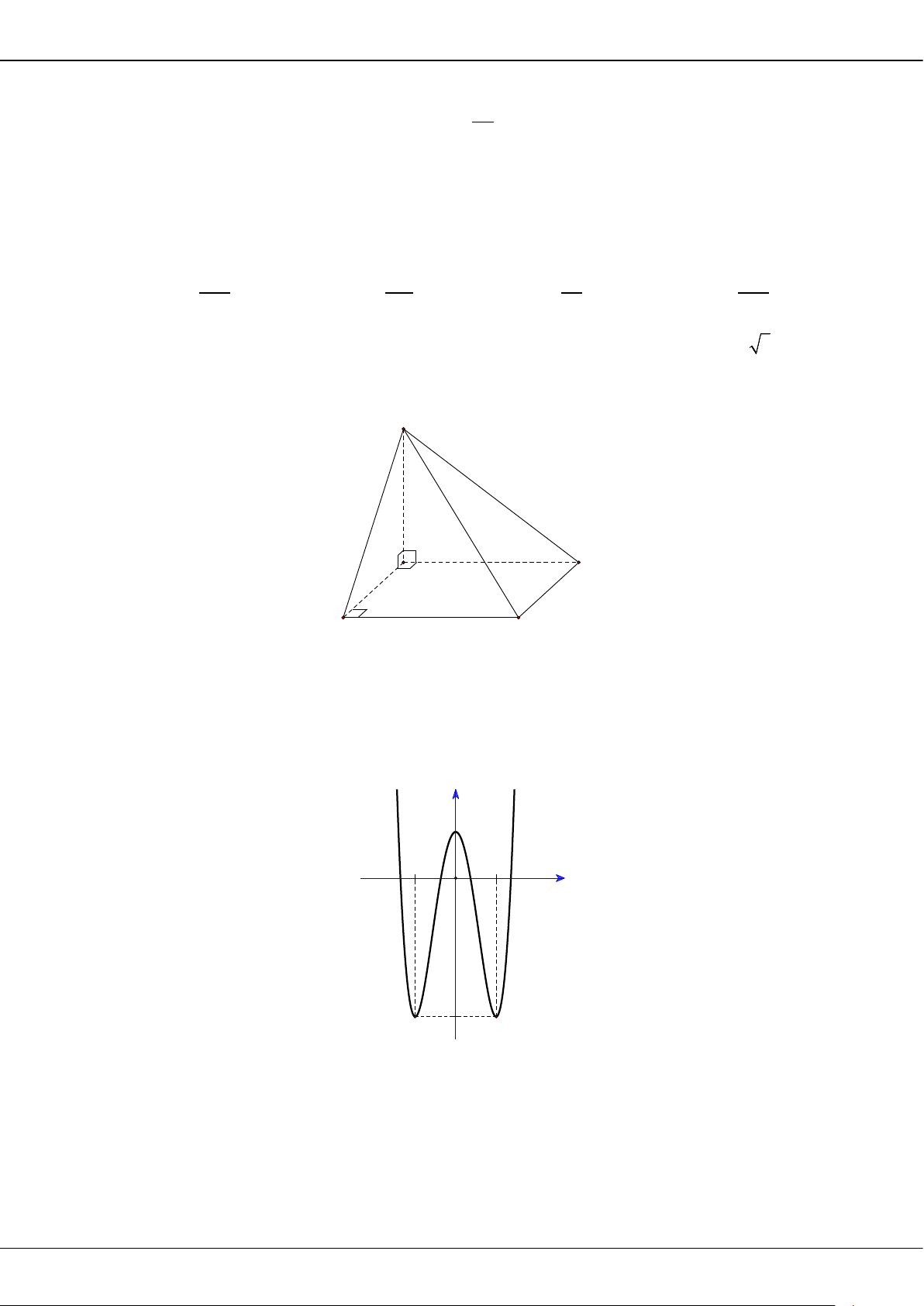
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 89

A.

4

. B.

5

. C.

1

−

. D.

1

.

Câu 28: Với  là số thực dương tùy ý,

1

log(6 ) log( )

2

a

+

bằng:

A.

log( )2

. B.

2

log(3 )

a

. C.

2log 2

. D.

log 3

.

Câu 29: Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường

3

yx x

= −

và

0y =

quanh trục

Ox

bằng

A.

16

105

V

π

=

. B.

8

105

V

π

=

. C.

30

V

π

=

. D.

16

15

V = ⋅

π

.

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình vuông,

SA

vuông góc với đáy và

3SA AB=

(tham khảo

hình vẽ). Góc giữa hai mặt phẳng

(

)

SBC

và

(

)

ABCD

bằng

A.

60 .

°

B.

30°⋅

C.

90

°⋅

D.

45°⋅

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên

của tham số

m

để phương trình

( )

fx m=

có bốn nghiệm thực phân biệt?

A.

2

. B.

5

. C.

3

. D.

4

.

Câu 32: Cho hàm số

( )

y fx=

có đạo hàm

( ) ( ) ( )

3

2

32fx x x x

′

=−−

với mọi

x ∈ 

. Hàm số đã cho

đồng biến trên khoảng nào dưới đây?

A.

( )

0;3

. B.

( )

0; 2

. C.

( )

2; +∞

. D.

( )

2;3

.

Câu 33: Một hộp chứa

11

quả cầu gồm

4

quả màu đỏ được đánh số từ

1

đến

4

và

7

quả màu xanh được

C

S

A

B

D

x

y

2

1

_

1

4

_

O

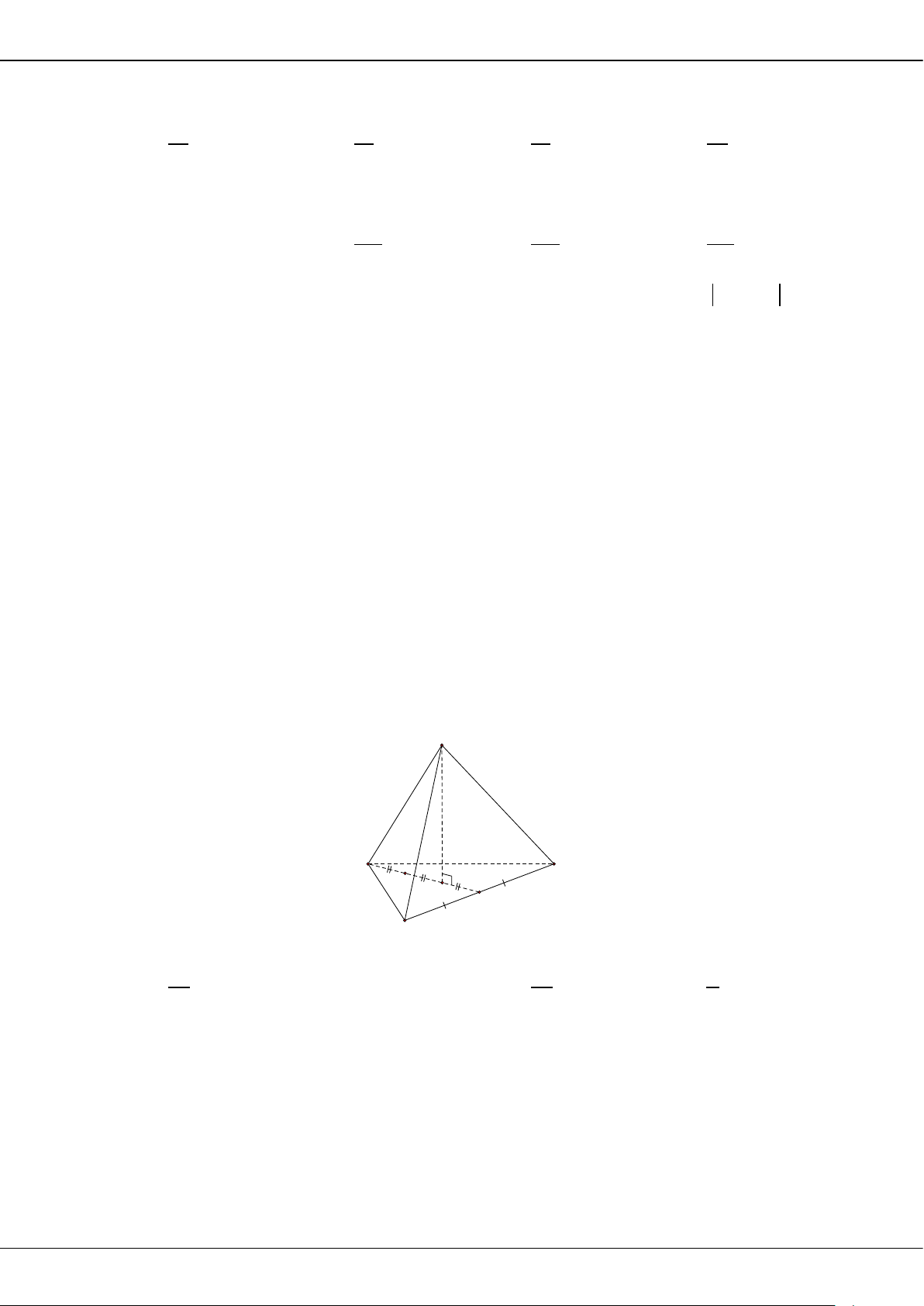
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 90

đánh số từ

1

đến

7

. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu

đồng thời tổng hai số ghi trên chúng là số chẵn bằng

A.

8

55

. B.

14

55

. C.

6

55

. D.

16

55

.

Câu 34: Tích tất cả các nghiệm của phương trình

2

log 4log 5 0xx+ −=

bằng

A.

10

B.

5

1

10

. C.

4

1

10

. D.

3

1

10

.

Câu 35: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức

z

thỏa mãn

12 1zi−− =

là một

đường tròn. Tâm của đường tròn đó có tọa độ là.

A.

( )

1; 2

−

. B.

( )

1; 2−

. C.

( )

1; 2−−

. D.

( )

1; 2

.

Câu 36: Trong không gian

Oxyz

, điểm nào sau đây thuộc đường thẳng

1

: 12

13

xt

dy t

zt

= +





=−+





=−+



?

A.

(

)

1;1; 1−

B.

(

)

1; 2; 3

C.

( )

2; 1; 2

D.

( )

1;1; 2

Câu 37: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

2;3; 5A −

. Điểm đối xứng với A qua trục

Ox

có tọa độ là

A.

( )

2; 3;5−

. B.

( )

2;3;5−−

. C.

( )

2;3;5

. D.

( )

2;3; 5−−

.

Câu 38: Cho hình chóp đều

.S ABC

có chiều cao

,2a AB a

=

(tham khảo hình bên). Tính khoảng cách từ

điểm

A

đến mặt phẳng

( )

SBC

.

A.

3

2

a

. B.

2a

. C.

2

3

a

. D.

2

a

.

H

M

A

B

C

S

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 91

SỞ GD&ĐT TIỀN GIANG

TRUNG TÂM GDTX TỈNH TIỀN GIANG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Trong mặt phẳng tọa độ

Oxy

, điểm biểu diễn số phức

43zi= −

có tọa độ là

A.

( )

3; 4−

. B.

(

)

4;3

. C.

(

)

4; 3−

. D.

( )

3; 4

.

Câu 2: Phần ảo của số phức

( )

2

12zi= −

là

A.

5

. B.

4

. C.

4−

. D.

3−

.

Câu 3: Đạo hàm của hàm số

5

logyx=

trên khoảng

( )

0; +∞

là

A.

ln 5

'y

x

=

. B.

'

ln 5

x

y =

. C.

1

'

ln 5

y

x

=

. D.

1

'y

x

=

.

Câu 4: Trên khoảng

(

)

0;

+∞

, đạo hàm của hàm số

5

3

yx=

là

A.

8

3

8

yx

′

=

. B.

2

3

5

yx

′

=

. C.

2

3

5

3

yx

′

=

. D.

2

3

5

3

yx

−

′

=

.

Câu 5: Tập nghiệm của bất phương trình

2

39

x+

>

là

A.

( )

;0−∞

. B.

( )

;1−∞

. C.

( )

0;

+∞

. D.

( )

1; +∞

.

Câu 6: Cho cấp số nhân

(

)

n

u

với

1

2u =

, công bội

3q =

. Số hạng

4

u

của cấp số nhân bằng

A.

54

. B.

11

. C.

12

. D.

24

.

Câu 7: Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

( )

:3 2 0P xz−+=

. Vectơ nào dưới đây

là một vectơ pháp tuyến của

( )

P

?

A.

( )

4

1; 0; 1n =−−



B.

( )

1

3; 1; 2

n = −



C.

( )

3

3; 1; 0n = −



D.

( )

2

3; 0; 1n = −



Câu 8: hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm

số đã cho và trục tung là

A.

( )

0; 1−

. B.

( )

1; 0

. C.

( )

1; 0−

. D.

( )

0;1

.

Câu 9: Biết tích phân

( )

1

0

3f x dx =

∫

và

( )

1

0

4g x dx = −

∫

. Khi đó

( ) ( )

1

0

f x g x dx+





∫

bằng

A.

7−

. B.

7

. C.

1−

. D.

1

.

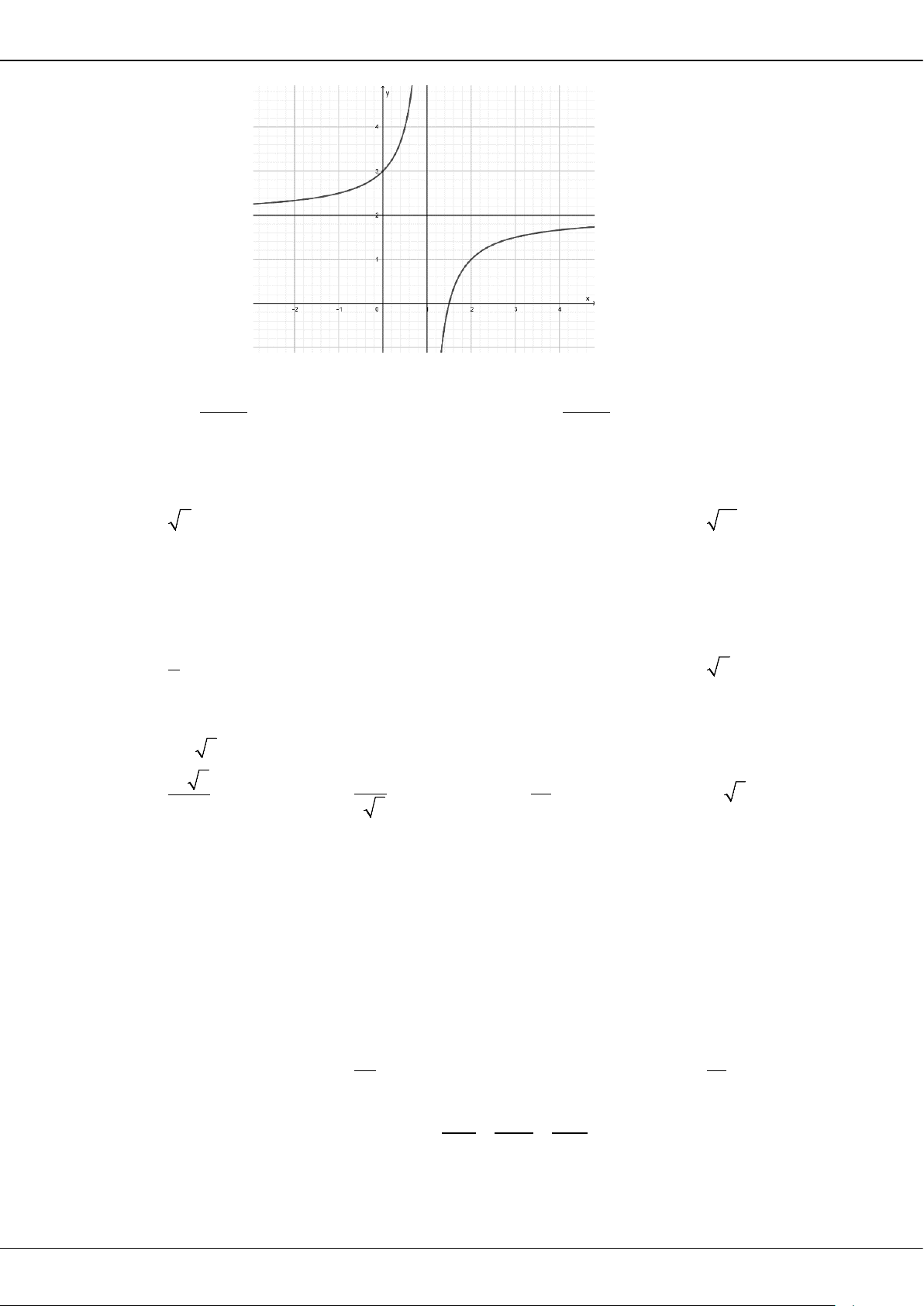
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 92

Câu 10: Đường cong trong hình vẽ là đồ thị của một trong bốn hàm số bên dưới. Đó là hàm số nào?

A.

42

22

yx x 

. B.

3

32yx x

.

C.

23

1

x

y

x







. D.

21

1

x

y

x







.

Câu 11: Trong không gian

Oxyz

, cho mặt cầu

2 22

( ): 2 2 7 0Sx y z x z+ + + − −=

. bán kính của mặt cầu

đã cho bằng

A.

7

. B.

9

. C.

3

. D.

15

.

Câu 12: Trong không gian

Oxyz

, góc giữa hai mặt phẳng

( )

Oxy

và

(

)

Oxz

bằng

A.

30



B.

45



C.

60



D.

90



Câu 13: Thể tích của khối lập phương cạnh bằng 1 là

A.

1

3

. B.

1

. C.

3

. D.

3

.

Câu 14: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

,a

cạnh bên

SA

vuông góc với đáy,

3.SA a=

Thể tích khối chóp

.S ABCD

là

A.

3

.

3

a

B.

3

.

33

a

C.

3

.

3

a

D.

3

3.a

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

theo thiết diện là một đường tròn. Gọi

d

là khoảng

cách từ

O

đến

( )

P

. Khẳng định nào dưới đây đúng?

A.

dR=

. B.

dR>

. C.

2dR=

. D.

dR<

.

Câu 16: Số phức

56i+

có phần thực bằng

A.

5−

. B.

5

. C.

6−

. D.

6

.

Câu 17: Cho hình nón có bán kính đáy

2r =

và độ dài đường sinh

5l

=

. Diện tích xung quanh của hình

nón đã cho bằng

A.

20

π

. B.

20

3

π

. C.

10

π

. D.

10

3

π

Câu 18: Trong không gian

Oxyz

, đường thẳng

123

:

2 12

−−−

= =

−

xy z

d

đi qua điểm nào sau đây?

A.

( )

2; 1; 2−Q

. B.

( )

1;2;3−−−M

. C.

( )

1; 2; 3P

. D.

( )

2; 1; 2−−N

.

Câu 19: Hàm số có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

 

y fx

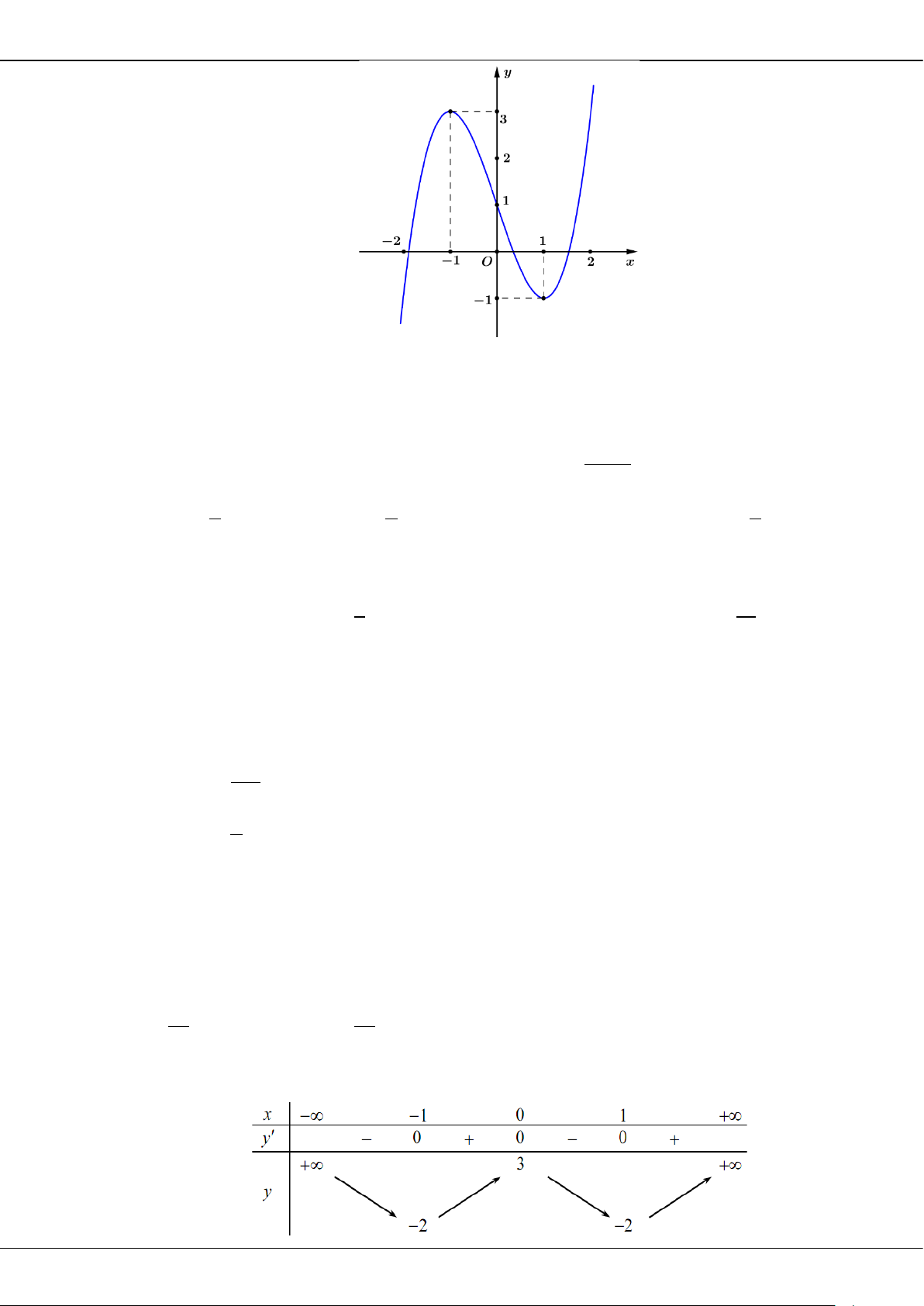
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 93

A. Đồ thị hàm số có điểm cực tiểu là . B. Đồ thị hàm số có điểm cực tiểu là .

C. Đồ thị hàm số có điểm cực đại là

.

D. Đồ thị hàm số có điểm cực tiểu là

Câu 20: Phương trình đường tiệm cận ngang của đồ thị hàm số là

A. . B. . C. . D. .

Câu 21: Giải bất phương trình .

A. B. C. D.

Câu 22: Cho tập hợp có phần tử. Số tập con gồm hai phần từ của là

A. B. C. D.

Câu 23: Hàm số là một nguyên hàm của hàm số trên nếu

A. . B. .

C. . D. .

Câu 24: Cho . Khi đó bằng

A. B. C. D.

Câu 25: Họ nguyên hàm của hàm số là

A. . B. . C. . D. .

Câu 26: Cho hàm số có bảng biến thiên như sau

 

1; 3





1;1

 

1; 1





1; 1

34

21

x

y

x

−

=

+

1

2

x = −

3

2

y =

2y = −

1

2

y = −

( )

2

log 3 1 3x −>

3x >

1

3

x<<

3x <

10

3

x >

M

10

M

8

10

A

2

10

A

2

10

C

2

10

( )

Fx

lnyx

=

(

)

0;+∞

( )

1

, 0;

ln

Fx x

x

′

= ∀ ∈ +∞

( ) (

)

ln , 0;Fx x x

′

= ∀ ∈ +∞

( )

1

, 0;Fx x

x

′

= ∀ ∈ +∞

( ) ( )

, 0;

x

Fx e x

′

= ∀ ∈ +∞

( )

3

1

d 18fx x=

∫

( )

3

1

52 d

fx x

−





∫

46.

26.

16.

31.

( )

4

sinfx x x= +

5

cos

5

x

xC++

5

cos

5

x

xC−+

3

4 cosx xC−+

3

4 cosx xC++

( )

y fx=

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 94

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. . B. . C. . D. .

Câu 27: Cho hàm số liên tục trên và có đồ thị như hình vẽ sau

Khẳng định nào sau đây là đúng?

A. Hàm số đạt cực tiểu tại . B. Hàm số không có điểm cực trị.

C. Hàm số đạt cực đại tại . D. Giá trị cực tiểu của hàm số bằng .

Câu 28: Với là số thực dương tùy ý, bằng

A. . B. . C. . D. .

Câu 29: Diện tích của hình phẳng giới hạn bởi đồ thị hàm số và trục hoành bằng

A. . B. . C. . D. .

Câu 30: Cho hình chóp có đáy là hình vuông cạnh vuông góc với đáy và . Góc

giữa hai mặt phẳng và bằng

A. . B. . C. .

D.

.

Câu 31: Cho hàm số . Đồ thị của hàm số như hình vẽ bên.

Số nghiệm của phương trình là

A. . B. . C. . D. .

Câu 32: Cho hàm số có đạo hàm , với mọi . Hàm số đã cho nghịch biến

trên khoảng nào dưới đây?

( )

0; 1

( )

;0−∞

( )

1; +∞

(

)

1; 0−

( )

fx



1x = −

4x =

1

−

a

( ) ( )

ln 7 ln 3aa

−

( )

ln 7

ln 3

a

ln 7

ln 3

7

ln

3

( )

ln 4a

2

yx x

= +−

9

13

6

9

2

3

2

ABCD

a

SA

SA a=

( )

ABCD

( )

SCD

30°

90°

60°

45°

( )

42

,,f x ax bx c a b c=++ ∈



( )

y fx=

( )

4 30fx−=

4

3

2

0

( )

y fx=

( ) ( )

3

2f x xx

′

= −

x ∈ 

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 95

A. . B. . C. . D. .

Câu 33: Một đoàn đại biểu gồm người được chọn ra từ một tổ gồm nam và nữ để tham dự hội nghị.

Xác suất để chọn được đoàn đại biểu có đúng người nữ là

A. . B. . C. . D. .

Câu 34: Biết phương trình có hai nghiệm . Giá trị của bằng

A. B. C. D.

Câu 35: Trong không gian , tập hợp các điểm biểu diễn số phức thỏa mãn là

A. đường tròn . B. đường tròn .

C. đường tròn . D. đường tròn .

Câu 36: Trong không gian , phương trình chính tắc của đường thẳng với và

là

A. . B. .

C. . D. .

Câu 37: Trong không gian , điểm đối xứng với điểm qua trục có tọa độ là

A. . B. . C. . D. .

Câu 38: Cho hình chóp có đáy là tam giác vuông tại , , vuông góc với mặt phẳng

đáy và . Khoảng cách từ đến mặt phẳng bằng

A. . B. . C. . D. .

( )

1; 3

(

)

1; 0−

( )

0; 1

( )

2; 0−

5

8

7

2

56

143

140

429

1

143

28

715

( )

2

22

log 2log 2 1 0xx− −=

12

,xx

12

.xx

4.

1

.

8

3.−

1

.

2

Oxy

M

z

32zi−+=

(

) ( )

22

3 14xy− ++ =

3 20xy−+=

(

) ( )

22

3 14xy+ +− =

(

) (

)

22

3 12

xy− ++ =

Oxyz

CD

(1; 1; 2)

C

( 4; 3; 2)

D −−

432

1 22

xyz

+ −+

= =

−−

112

1 22

xyz−−−

= =

−−

112

52 4

xyz+++

= =

−−

432

52 4

xyz+ −+

= =

−−

Oxyz

( )

4; 5;3

M −

Oz

( )

4;5;3−−

( )

4;5;3−

( )

4;5; 3−−

( )

0;0;3

.S ABC

B

AB a=

SA

2SA a=

A

( )

SBC

25

5

a

5

3

a

22

3

a

5

a

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 96

SỞ GD&ĐT TIỀN GIANG

TRUNG TÂM GDTX GÒ CÔNG TÂY

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho số phức

45

zi=−+

. Biểu diễn hình học của

z

là điểm có tọa độ

A.

( )

4;5

−

B.

( )

4; 5−−

C.

( )

4; 5−

D.

( )

4;5

Câu 2: Trên khoảng

(

)

0; +∞

, đạo hàm của hàm số

2

logyx=

là:

A.

1

'

ln 2

y

x

=

. B.

ln 2

'y

x

=

. C.

1

'y

x

=

. D.

1

'

2

y

x

=

.

Câu 3: Trên khoảng

( )

0;

+∞

, đạo hàm của hàm số

e

yx

là

A.

1e

y ex

+

′

=

. B.

1e

y ex

−

′

=

.

C.

1

e

yx

e

−

′

=

. D.

1

e

yx

e

+

′

=

+

.

Câu 4: Tập nghiệm của bất phương trình

1

28

x+

>

là

A.

( )

;2−∞

. B.

(

]

;2−∞

. C.

[

)

2; +∞

. D.

( )

2; +∞

.

Câu 5: Cho cấp số cộng

( )

n

u

có

1

3u =

và

2

1u = −

. Công sai của cấp số cộng đó bằng

A.

1

. B.

4−

. C.

4

. D.

2

.

Câu 6: Trong không gian

Oxyz

, cho 3 điểm

(

)

2; 1; 3M

−

,

( )

1; 0; 2N

;

( )

2; 3; 5

P

−

. Tìm một vectơ pháp

tuyến

n



của mặt phẳng

( )

MNP

.

A.

( )

12; 4;8n



. B.

( )

8;12; 4n



. C.

( )

3;1; 2n



. D.

( )

3; 2;1

n



.

Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị

hàm số đã cho và trục hoành là

A.

(

)

0;2

. B.

(

)

2;0

. C.

( )

0; 2−

. D.

( )

1;0

.

Câu 8: Biết

( )

2

1

d6fx x=

∫

,

( )

5

2

d1fx x=

∫

, tính

( )

5

1

dI fx x=

∫

.

A.

5I =

. B.

5I = −

. C.

7

I =

. D.

4I

=

.

Câu 9: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 97

A.

42

2

x

yx

+

= −

. B.

3

xyx

+

= −

. C.

42

2x

yx

−

=

. D.

42

3

x

yx

−

= −

.

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 2 4 20

Sx y z y z

+ + − + −=

. Bán kính mặt cầu bằng

A.

1

. B.

7

. C.

22

. D.

7

.

Câu 11: Trong không gian

Oxy

, góc giữa hai trục

Ox

và

Oz

bằng

A.

30



B.

45



C.

60



D.

90



Câu 12: Cho số phức

35zi

= +

, phần ảo của số phức

2

z

bằng

A.

16

. B.

30

. C.

16−

. D.

30−

.

Câu 13: Cho khối lăng trụ đứng có chiều cao bằng

3

và đáy là tam giác đều có độ dài cạnh bằng

2

. Tính

thể tích khối lăng trụ đã cho

A.

3

. B.

33

. C.

3

. D.

6

.

Câu 14: Cho khối chóp

.

S ABC

có đáy là tam giác vuông tại

.B

Biết

3,BC a AB a= =

,

SA

vuông góc

với đáy,

23

SA a=

. Thể tích khối chóp

.S ABC

bằng

A.

3

3.a

B.

3

.

3

a

C.

3

3.a

D.

3

.a

Câu 15: Trong không gian

Oxyz

, cho hai mặt cầu

( ) ( )

2

22

:3 9S x yz− ++=

và

(

) ( )

2

22

': 2 4

S x yz+ ++=

. Khẳng định nào sau đây là đúng?

A. Hai mặt cầu tiếp xúc ngoài. B. Hai mặt cầu tiếp xúc trong.

C. Hai mặt cầu không có điểm chung. D. Hai mặt cầu có nhiều hơn một điểm chung.

Câu 16: Phần thực của số phức

42zi= −

bằng

A.

2−

. B.

4−

. C. 2. D. 4.

Câu 17: Diện tích xung quanh của hình nón có bán kính đáy

5r cm=

và độ dài đường sinh

7l cm=

bằng

A.

2

60 ( )cm

π

B.

2

175 ( ).cm

π

C.

2

70 ( ).cm

π

D.

2

35 ( ).cm

π

Câu 18: Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

( )

P

có phương trình

2 3 20x yz+ − −=

. Điểm nào sau đây thuộc mặt phẳng

( )

P

?

A.

( )

1; 2; 3−

. B.

( )

1; 2; 3

−

. C.

( )

1; 2;1

. D.

( )

1; 2; 2−

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 98

Câu 19: Cho hàm số

42

y ax bx c=++

có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị

hàm số đã cho có tọa độ là

A.

( 1; 1)−

. B.

(0;1)

. C.

(1; 1)

. D.

(0; 0)

.

Câu 20: Tiệm cận đứng của đồ thị hàm số

1

3

x

y

x

−

=

−

là đường thẳng có phương trình

A.

3x = −

. B.

1

x = −

. C.

1

x =

. D.

3x =

.

Câu 21: Tập nghiệm của bất phương trình

( )

2

log x 1 3+<

là

A.

(

)

;8S

= −∞

. B.

( )

;7S

= −∞

. C.

( )

1; 8S = −

. D.

( )

1; 7S = −

.

Câu 22: Cho tập hợp

{

}

1; 2; 3; 4; 5M =

. Số tập con gồm hai phần tử của tập hợp

M

là:

A. 11. B.

2

5

A

. C.

2

5

C

. D.

2

P

.

Câu 23: Cho

( )

cos 3 .x dx F x C= +

∫

. Khẳng định nào dưới đây đúng?

A.

(

)

sin 3

3

x

Fx

′

=

. B.

( )

cos 3Fx x

′

=

. C.

( )

3sin 3Fx x

′

=

. D.

( )

3sin 3

Fx x

′

= −

.

Câu 24: Cho

( )

4

2

d 10fx x=

∫

. Tính

( )

4

2

3 5dI fx x= −





∫

A.

10

I =

. B.

15I

=

. C.

5

I = −

. D.

20

I =

.

Câu 25: Họ tất cả các nguyên hàm của hàm số

( )

2

3 2 cosfx x x= −

là

A.

( )

3

3 2sinFx x x C=++

. B.

( )

3

2sinFx x x C=−+

.

C.

( )

3

3 2sinFx x x C=−+

. D.

( )

3

sinFx x x C=++

.

Câu 26: Cho hàm số bậc ba

( )

y fx=

có đồ thị như hình sau

Hàm số

( )

y fx=

nghịch biến trên khoảng nào dưới đây?

A.

( )

0;2

. B.

( )

;1−∞ −

. C.

( )

2;4

. D.

( )

1;2−

.

Câu 27: Cho hàm số

()y fx=

có bảng biến thiên như sau

O

x

y

1−

1

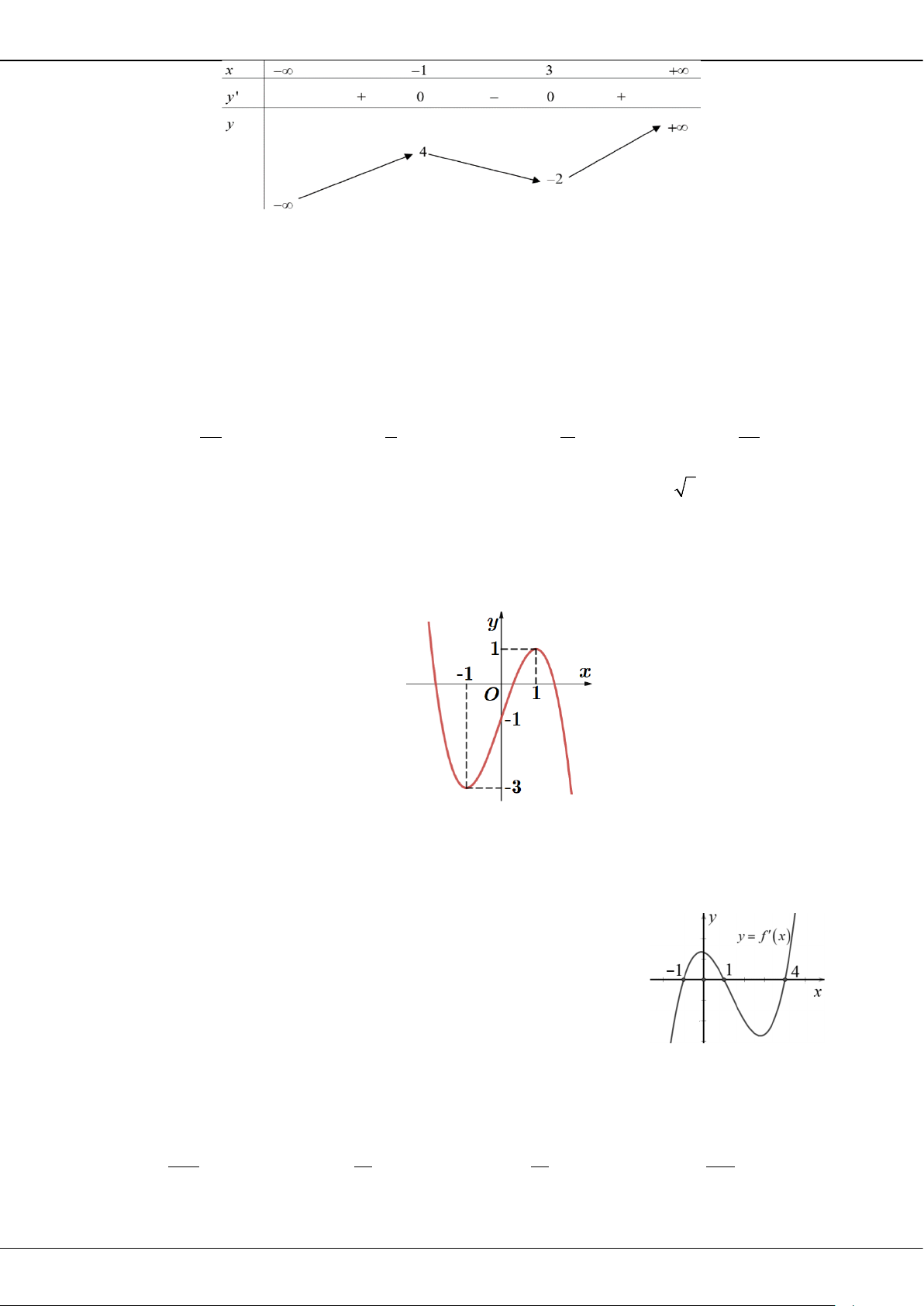
BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 99

Giá trị cực đại của hàm số đã cho là

A.

1.−

B.

4.

C.

3.

D.

2.−

Câu 28: Kết quả thu gọn biểu thức

( ) ( )

ln 4 ln 2Px x= −

là

A.

( )

ln 2Px=

. B.

ln 2P =

. C.

( )

ln 8 .Px=

D.

( )

2

ln 8Px=

Câu 29: Giả sử

D

là hình phẳng giới hạn bởi đường parabol

2

32yx x=−+

và trục hoành. Quay

D

quanh trục hoành ta thu được khối tròn xoay có thể tích bằng

A.

30

V

π

=

. B.

1

6

V =

. C.

6

V

π

=

. D.

1

30

V =

.

Câu 30: Cho hình hộp chữ nhật

.' ' ' 'ABCD A B C D

,

, 2, 3BC a AC a A A a

′

= = =

. Tính góc giữa mặt

phẳng

( )

''BCD A

và mặt phẳng

( )

ABCD

.

A.

30°

. B.

45°

. C.

60°

. D.

90°

.

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên.

Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

( )

1fx m

+=

có hai nghiệm không

âm?

A.

2

B.

1

C.

3

D.

4

Câu 32: Cho hàm số bậc bốn

(

)

y fx=

. Hàm số

( )

y fx

′

=

có đồ thị như

hình vẽ sau. Hàm số

( )

y fx=

nghịch biến trên khoảng nào trong

các khoảng sau?

A.

( )

1;4

. B.

( )

1;1−

.

C.

( )

0;3

. D.

( )

;0−∞

.

Câu 33: Thầy Bình đặt lên bàn

30

tấm thẻ đánh số từ

1

đến

30

. Bạn An chọn ngẫu nhiên

10

tấm thẻ.

Tính xác suất để trong

10

tấm thẻ lấy ra có

5

tấm thẻ mang số lẻ,

5

tấm mang số chẵn trong đó

chỉ có một tấm thẻ mang số chia hết cho

10

.

A.

99

667

. B.

8

11

. C.

3

11

. D.

99

167

.

BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 100

Câu 34: Tích các nghiệm của phương trình

2

22

log 3log 2 0xx− +=

là

A.

3

. B.

6

. C.

8

. D.

2

.

Câu 35: Tập hợp các điểm biểu diễn số phức

z

thỏa mãn

(

)

1z i iz−= +

là một đường tròn, tâm của

đường tròn đó có tọa độ là

A.

( )

1;1

. B.

(

)

0; 1

−

. C.

( )

0;1

. D.

( )

1;0−

.

Câu 36: Trong không gian

Oxyz

, cho ba điểm

( )

3; 1 ;2A −

,

( )

0;1;3B

và

( )

1;1;1C −

. Đường thẳng đi

qua

C

và song song với đường thẳng

AB

có phương trình là:

A.

3 21

11 1

xyz+−−

= =

−

. B.

3 21

11 1

xyz−++

= =

−

.

C.

111

32 1

xyz−++

= =

−

. D.

111

32 1

xyz+−−

= =

−

.

Câu 37: Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

( )

2; 0; 1A −

,

( )

1; 2; 3B −

,

( )

0; 1; 2C

. Tìm tọa

độ điểm

O

′

là điểm đối xứng với gốc tọa độ

O

qua mặt phẳng

( )

ABC

.

A.

11

1; ;

22

O



′





. B.

( )

2;1;1O

′

. C.

( )

10;5;5O

′

− −−

. D.

11

2; ;

22

O



′





.

Câu 38: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

B

,

AB a=

,

3AC a=

và

SA

vuông góc với

mặt phẳng đáy. Khoảng cách từ

C

đến mặt phẳng

( )

SAB

bằng

A.

2a

. B.

2a

. C.

a

. D.

22a

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 1

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT CHUYÊN

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.B

2.C

3.A

4.C

5.A

6.A

7.C

8.D

9.A

10.A

11.C

12.B

13.C

14.B

15.C

16.C

17.A

18.D

19.D

20.B

21.A

22.D

23.A

24.C

25.B

26.B

27.B

28.A

29.B

30.A

31.B

32.A

33.D

34.A

35.B

36.A

37.A

38.B

39.D

40.D

41.B

42.B

43.A

44.B

45.A

46.B

47.B

48.B

49.D

50.B

HƯỚNG DẪN GIẢI

Câu 40: Số giá trị nguyên của tham số

m

để hàm số

( )

4 22

3y mx m x m

= −− +

không có điểm cực đại là

A. 2. B. vô số. C. 0. D. 4.

Lời giải

TH 1:

0

m

=

thì

2

3yx=

. Hàm số không có điểm cực đại. Vậy

0m =

( thỏa mãn).

TH 2:

0m ≠

Hàm số là hàm bậc bốn trùng phương

Ta có

( )

32

4 2 3 22 3y mx m x x mx m

′

= − − = −+

Để hàm số không có điểm cực đại thì

0m >

và

0y

′

=

có một nghiệm.

0y

′

=

có một nghiệm

2

2 30mx m⇔ − +=

vô nghiệm hoặc có nghiệm kép

0x

=

3

00 3

2

m

−

⇔ ≤⇔< ≤

.

Vì

m

nguyên nên

{ }

1; 2; 3m =

. Vậy

m

có 4 giá trị nguyên.

Câu 41: Có bao nhiêu cặp số nguyên

(

)

;

xy

thỏa mãn

( )

22

log 4 log 2 1xy xy+ +− + ≤

và

20

xy−≥

?

A.

5

. B.

3

. C.

4

. D.

2

.

Lời giải

Từ giả thiết ta có

( )

( ) (

)

( )

22

log 4 log 2 1 1

20 2

20 3

xy xy

xy



+ +− + ≤



+>





−≥





.

( )

22

log 4 log 2 1xy xy+ +− + ≤

( )

( ) (

) ( )

22

22 22 2

22

log 4 log 2 4 4 2 4 2 1 4 4 1 1 2

xy xy xy xyxx y y x y⇔ ++≤ + ⇔++≤+⇔−++−+≤⇔−+− ≤

Từ điều kiện trên suy ra cặp số nguyên

( )

;xy

chỉ có thể là tọa độ tâm hoặc những điểm có tọa độ nguyên

năm trên đường tròn tâm

(

)

1; 2I

bán kính 1. Do đó cặp số nguyên

( )

;xy

chỉ có thể là các cặp số sau

( ) ( )

( )

1; 2 , 1; 3 ; 1;1

( ) ( )

0; 2 , 2; 2

.

So điều kiện

( )

2

và

( )

3

ta nhận các cặp số

( ) ( ) ( )

1; 2 , 1; 1 , 2; 2

.

Câu 42: Cho hai số phức

1

z

,

2

z

khác

0

thỏa mãn

1

2

z

là số thuần ảo và

12

10zz−=

. Giá trị lớn nhất của

12

zz+

bằng

A.

10

. B.

10 2

. C.

10 3

. D.

20

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 2

Lời giải

Vì

1

2

z

là số thuần ảo nên

1

2

z

ai

z

=

(với

a

∈

) ⇔

12

z aiz=

.

Ta có

12

10zz−=

⇔

22

10aiz z−=

⇔

2

1 10z ai −=

⇔

2

1 10za

+=

⇔

2

10

1

z

a

=

+

.

Từ

12

z aiz=

⇒

12

2

10

1

a

z aiz

a

= =

+

.

Do đó

12

22

10

11

a

zz

aa

+= +

++

( )

2

10 1

1

a

+

=

+

(

)

(

)

2

10 1 1 1

1

a

++

≤

+

10 2

≤

.

Đẳng thức xảy ra ⇔

1a = ±

⇔

12

z iz= ±

. Vậy

(

)

12

10 2

max z z+=

.

Câu 43: Cho khối lăng trụ đứng

.ABC A B C

′′′

có



0

60BAC =

,

3AB a=

và

4AC a=

. Gọi

M

là trung

điểm của

BC

′′

, biết khoảng cách từ

M

đến mặt phẳng

( )

B AC

′

bằng

3 15

10

a

. Thể tích khối lăng

trụ đã cho bằng

A.

3

27a

. B.

3

9a

. C.

3

4a

. D.

3

a

.

Lời giải

Ta có



02

11

. .sin .3 .4 .sin 60 3 3

22

ABC

S AB AC BAC a a a

∆

= = =

.

Gọi

H

là giao điểm của

MB

và

BC

′

. Khi đó, theo định lý Ta-let ta có

'1

2

HM MB

HB BC

= =

.

Ta có

( )

(

)

( )

(

)

( )

(

)

,

1 3 15

, 2,

25

,

d M B AC

HM a

d B B AC d M B AC

HB

d B B AC

′

′′

==⇒= =

′

.

Từ

B

kẻ

BK

vuông góc với

AC

với

K AC∈

. Kẻ

BI

vuông góc với

BK

′

với

I BK

′

∈

.

Ta có

( ) ( )

( )

3 15

,

5

BI B K

a

BI B AC BI d B B AC

BI AC

′

⊥



′′

⇒⊥ ⇒= =



⊥



.

Lại có

2

2.3 3 3 3

42

ABC

S

aa

BK

AC a

∆

= = =

và

22

2 2 2 22

11 1 .

33

'

BI BK

BB a

BI BK BB BK BI

′

= + ⇒= =

−

.

Vậy

23

.

. 3 3 .3 3 27 .

ABC A B C ABC

V S BB a a a

′′′

∆

′

= = =

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 3

Câu 44: Cho hàm số

()

fx

có đạo hàm liên tục trên đoạn

[ ]

1; 2

và thỏa mãn

1

(1)

2

f = −

và

( )

3 22

() () 2 (), [1;2].

f x xf x x x f x x

′

+ = + ∀∈

Giá trị của tích phân

2

1

()x f x dx

∫

bằng

A.

4

ln

3

. B.

3

ln

4

. C.

ln 3

. D. 0.

Lời giải

 Từ giả thiết, ta có

( )

3 22

2

() ()

() () 2 () 2 1

[ ( )]

f x xf x

f x xf x x x f x x

xf x

′

+

′

+=+ ⇒ =+

2

11 1

21 (21)

() () ()

x x dx x x C

xf x xf x xf x

′



⇒ =−−⇒ =−− ⇒ =−−+





∫

.



11

(1) 0 ( )

2 ( 1)

f C xf x

xx

=−⇒ =⇒ =−

+

2

22 2

11 1

1

1 11 1 3

( ) ln ln

( 1) 1 4

x

x f x dx dx dx

xx x x x

−+



⇒ = = −= =



++



∫∫ ∫

.

Câu 45: Gọi

S

là tập hợp tất cả số thực

m

để phương trình

2

21 0zz m− +− =

có nghiệm phức

z

thỏa

mãn

2z =

. Tổng các phần tử của

S

bằng

A.

7

. B.

5

. C.

4

. D.

6

.

Lời giải

Phương trình

2

21 0zz m− +− =

có

m

′

∆=

+ Trường hợp 1:

0

′

∆=

, tức

0m =

Phương trình đã cho có nghiệm

1z =

(Loại).

+ Trường hợp 2:

0

′

∆>

, tức

0m >

Phương trình có hai nghiệm

1zm= ±

Yêu cầu của bài toán

⇔

|1 | 2

m



+=



−=





⇔

1

9

m

=





=



(Nhận).

+ Trường hợp 3:

0

′

∆<

, tức

0m <

Phương trình có hai nghiệm

1z im=±−

Yêu cầu của bài toán

⇔

|1 | |1 | 2im im

+−=−−=

⇔

12m−=

⇔

3m = −

(Nhận).

⇒

{

}

3;1;9S = −

.

Vậy tổng các phần tử của

S

là

7

.

Câu 46. Cho hàm số

( )

32

337 2023f x x mx nx= + ++

với

,mn

là các số thực. Biết rằng hàm số

( ) (

) ( )

( )

'"gx fxfxfx=++

có hai giá trị cực trị là

2023

2022e −

và

2022e −

. Diện tích hình

phẳng giới hạn bởi các đường

( )

2022

fx

y

gx

=

+

và

1

y =

bằng

A.

2023

. B.

2022

. C.

2024

. D.

2021

.

Lời giải

Ta có

( )

2

' 1011 2f x x mx n= ++

,

( )

" 2022 2fx x m= +

,

( )

'" 2022fx=

. Suy ra,

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 4

( ) ( ) (

) (

)

( )

32

' " 337 1011 2 2022 2 4045

gx fxfxfx x m x nm xnm= + + = ++ +++ +++

.

Ta có

( ) ( ) ( ) ( ) ( )

2

' ' " '" 1011 2 2022 2 2022gxfxfxfx x m xnm= + + = + + ++ +

.

Do

(

)

gx

có hai điểm cực trị nên

( )

'0

gx=

có hai nghiệm phân biệt

ab<

. Suy ra

( ) ( )

2023

2022, 2022ga e gb e=−=−

.

Xét phương trình

( )

(

) (

)

(

) (

)

( )

1 2022 2022 0

2022

' " "'0'0

.

fx

f x gx f x gx

gx

xa

fxfxfx gx

xb

=⇔ =+⇔ −−=

+

=



⇔++ =⇔=⇔



=



Diện tích hình phẳng cần tìm là

( )

(

) (

)

(

)

( )

( ) ( )

( )

2022 '

1

2022 2022 2022

ln 2022 ln 2022 ln 2022 1 2023 2022.

2022

bb b

aa a

b

a

fx fx gx g x

S dx dx dx

gx gx gx

dg x

gx gb ga

gx

−− −

= −= =

+ ++

= = + = + − + =−=

+

∫∫ ∫

∫

Câu 47. Cho các số phức

, ,w

zv

thay đổi thỏa mãn

2023

34 2i zi− +⋅ =

, phần thực của

v

bằng phần ảo của

w

và bằng

1−

. Giá trị nhỏ nhất của biểu thức

22

wT zv z

=− +−

bằng

A.

3

. B.

9

. C

4

. D.

7

.

Lời giải

Ta có

2023

34 2 34 2 43 2 43 2izi izizizi− +⋅ =⇔ − − =⇔ ++ =⇔ +− =

.

Suy ra, tập hợp các điểm

M

biểu diễn số phức

z

là đường tròn tâm

(

)

4;3I −

, bán kính

2R =

.

Theo đề bài, tập hợp các điểm

A

biểu diễn số phức

v

là đường thẳng

1

:1dx= −

, tập hợp các

điểm

B

biểu diễn số phức

w

là đường thẳng

2

:1dy= −

. Gọi

,NP

lần lượt là hình chiếu vuông

góc của điểm

M

lên

1

d

,

2

d

và

( )

1; 1C −−

là giao điểm của

12

,dd

. Khi đó,

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 5

22 22 2

T MA MB MN MP MC=+≥ +=

.

Như vậy,

T

đạt giá trị nhỏ nhất khi và chỉ khi

MC

đạt giá trị nhỏ nhất. Dựa vào hình vẽ ta có

(

)

2

min min 9T MC IC R

= =−=

.

Đẳng thức xảy ra khi và chỉ khi

,,IMC

theo thứ tự thẳng hàng và

,A NB P≡≡

.

Khi đó,

6 14

4

2 14 7

55

;

87

5 55

3

55

MM

xx

IM IC M

yy



+= =−





= ⇔ ⇔ ⇒−





−





−= =





 

,

7 14

1; , ; 1

55

NP

  

− −−

  

  

Vậy

min 9T =

khi

14 7 7 14

, 1 ,w

55 5 5

z iv i i=−+ =−+ =−−

.

Câu 48. Có bao nhiêu bộ

( )

;xy

với

,xy

là các số nguyên và

1 , 2023xy≤≤

, đồng thời thỏa mãn điều kiện

( )

32

2 21

2 4 8 log 2 3 6 log

23

yx

xy x y x y xy

yx

+

+++ ≤ +−−

+−

?

A.

4046

. B.

4040

. C.

4036

. D.

4030

.

Lời giải

Điều kiện

, , , 2023

21 2

0, 0

3, 0.

32

xy xy

xy

+



∈≤



∈≤



⇔



+

>>







−+





Với điều kiện trên, bất phương trình đã cho tương đương với

( )( )

( )

32

2 21

4 2 log 3 2 log *

23

yx

xy x y

yx

+

+ + ≤− −

+−

• Với

1y =

thì

( ) ( )

**

0VT VP

<<

với mọi

3x >

nên (*) luôn đúng, suy ra

{

}

4;5;6; ;2023

x

∈ 

.

• Với

2y =

thì

( ) ( )

**

0

VT VP= =

nên (*) luôn đúng, suy ra

{ }

4;5;6; ;2023x ∈ 

.

• Với

2y >

thì

( ) ( )

**

0VP VT<<

nên (*) vô nghiệm.

Vậy có

4040

bộ

( )

;

xy

thỏa mãn.

Câu 49. Trong không gian

Oxyz

, cho hai điểm

(

)

1; 5; 2A −−

,

( )

3; 3; 2B

−

và đường thẳng

d

có phương

trình

334

111

xyz−++

= =

; hai điểm

C

và

D

thay đổi trên

d

thỏa

63CD =

. Biết rằng khi

( ) ( )

;; 2C abc b<

thì tổng diện tích tất cả các mặt của tứ diện

ABCD

đạt giá trị nhỏ nhất. Khi

đó, tổng

abc++

bằng

A.

2

. B.

1−

. C.

4−

. D.

7−

.

Lời giải

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 6

Gọi

,MN

lần lượt là hình chiếu vuông góc của

,AB

xuống đường thẳng

d

. Do

,,AM BN CD

không đổi nên tổng diện tích toàn phần của tứ diện đạt giá trị nhỏ nhất khi và chỉ khi tổng diện

tích hai tam giác

ABC

và diện tích tam giác

ABD

nhỏ nhất.

Gọi

( )

3 ;3 ;4Cc c c+−+−+

và

(

)

3 ;3 ;4

Dd d d

+−+−+

. Do

63CD =

nên

6

6.

cd

dc

= +



−=⇔



= +



• Với

6dc= +

thì

( )

9; 3; 2Dc c c+++

. Ta có

( )

4; 8; 4AB = −



,

( )

4; 2; 6ACccc=++−



,

( )

10; 8;AD c c c=++



. Khi đó,

( )

, 40 12 ;8 8; 4 24AC AB c c c



=− −+



 

và

( )

, 12 32;8 40;4 48

AD AB c c c



=−− + +



 

.

Suy ra

( )

2

2 14 2 6

ABC

Sc= ⋅−+

và

( )

2

2 14 4 6

ABD

Sc= ⋅++

.

Khi đó, tổng diện tích của hai tam giác này là

( ) ( )

22

2 14 2 6 4 6 2 14 36 24 4 210S cc



= ⋅ − ++ + + ≥ ⋅ + =





.

Đẳng thức xảy ra khi và chỉ khi

2 41cc c−=+⇔=−

. Khi đó,

( ) ( )

2; 4; 5 , 8; 2;1CD−−

(thỏa

mãn

2b

<

).

• Với

6cd= +

thì vai trò của

,CD

thay đổi cho nhau nên loại.

Câu 50. Cho hàm đa thức

()fx

có

2022

( ) ( 1)( 2023) ( 3)

fx x x x

′

=+− −

. Hỏi có tất cả bao nhiêu cặp số

nguyên không âm

(;)mn

để hàm số

(

)

2

( 1) cos 2

y f m xn

=+−

đồng biến trên

0;

2

π







?

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Ta có

( ) 0 1 3 2023fx x x

′

≤ ⇔− ≤ ≤ ∨ =

.

Hàm số

( )

2

( 1) cos 2y f m xn=+−

đồng biến trên

0;

2

π







khi và chỉ khi

( )

(

)

(

)

2

22

2

2 1 sin 2 ( 1) cos 2 0, 0;

2

( 1) cos 2 0, 0; 1 ( 1) cos 2 3, 0;

22

3

cos 2 , 0;

1

2

1

, 0;

1

s

2

1

co 2

1

y m xf m x n x

f m xn x m xn x

n

xx

m

n

x

m

n

x

m

π

ππ

π







⇔ ⇔⇔



′′

=− + + − ≥ ∀∈





 

′

⇔ + − ≤ ∀∈ ⇔−≤ + − ≤ ∀∈

 

 

+



+

≤ ∀∈

≥



+



+

−



≤−

∀∈







≥

+



−





2

13

11

mn









+≤ +

≤−



+

Suy ra

22

22 1 0 1m m mm≤ ⇔ ≤⇒ =∨ =

(do

m ∈

).

• Với

0m =

. ta có

20 0nn−≤ ≤ ⇒ =

(do

n ∈

).

• Với

1m =

ta có

1n = −

, vô lý do

n ∈

.

Vậy

( , ) (0,0)mn =

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 7

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT ĐỐC BINH KIỀU

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

HƯỚNG DẪN GIẢI

Câu 1: Điểm

A

trong hình vẽ bên dưới biểu diễn cho số phức

z

. Mệnh đề nào sau đây đúng?

A. Phần thực là

3

, phần ảo là

2

. B. Phần thực là

3

, phần ảo là

2i

.

C. Phần thực là

3−

, phần ảo là

2

i

. D. Phần thực là

3−

, phần ảo là

2

.

Lời giải

Chọn A

Câu 2: Hàm số nào sau đây đồng biến trên



?

A.

e

x

y



=



π



. B.

2

e

x

y



=





. C.

( )

2

x

y =

. D.

( )

0,5

x

y =

.

Lời giải

Chọn C

Hàm số

x

ya=

đồng biến khi

1

a >

và nghịch biến khi

01a<<

.

Suy ra hàm số

( )

2

x

y =

đồng biến trên



.

Câu 3: Đạo hàm của hàm số

3

yx

−

=

là:

A.

4

yx

−

′

= −

. B.

2

1

2

yx

−

′

= −

. C.

3

1

3

yx

−

′

= −

. D.

4

3yx

−

′

= −

.

Lời giải

Chọn D

Ta có

( )

34

3yx x

−−

′

= = −

.

Câu 4: Giải bất phương trình

( )

2

log 3 1 3x

−>

.

A.

3x >

B.

1

3

x<<

C.

3x <

D.

10

3

x

>

Lời giải

Chọn A

Đkxđ:

1

3 10

3

xx−> ⇔ >

x

y

3

A

O

2

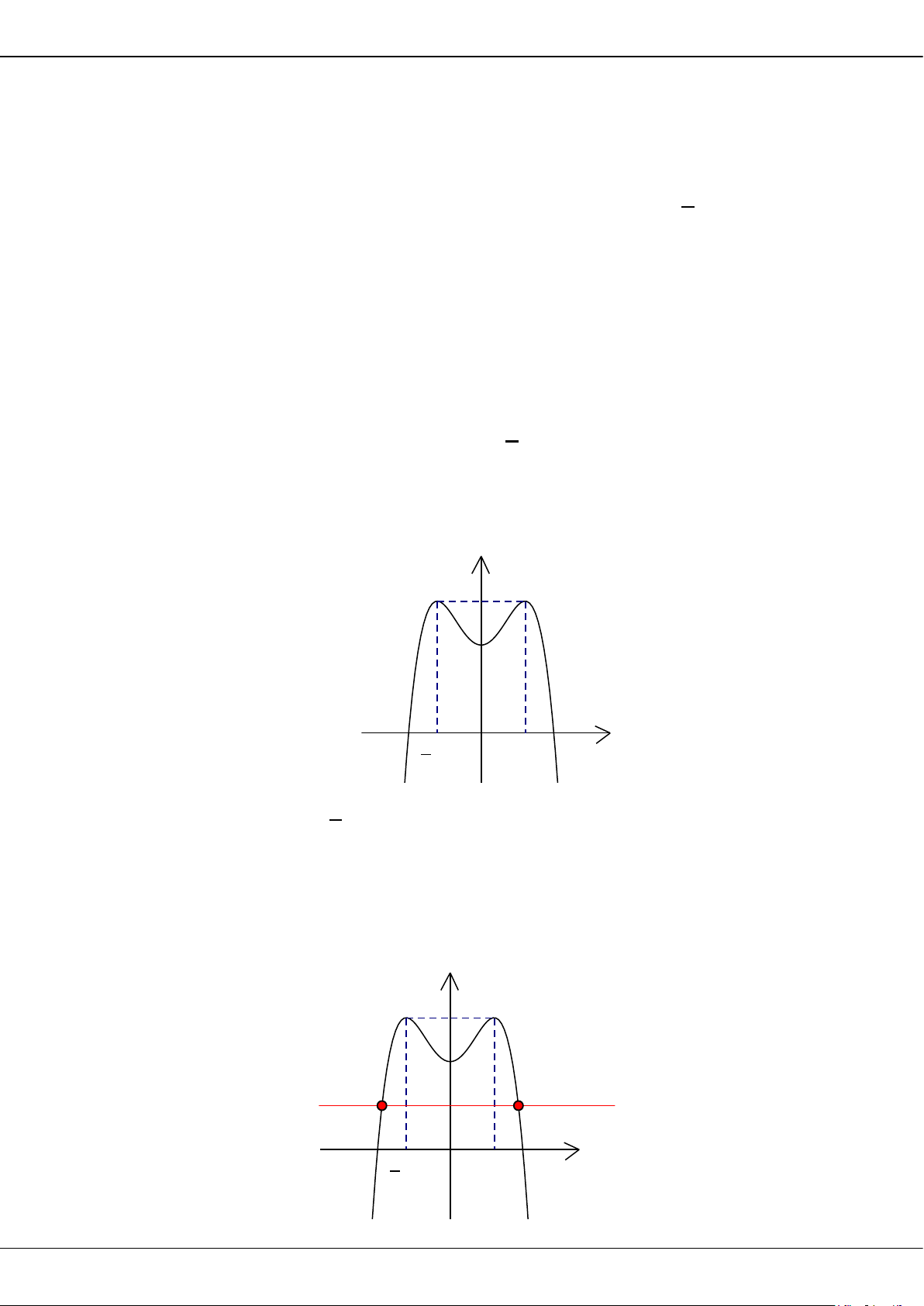
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 8

Bất phương trình

3

3 12 3 9 3x xx

⇔ −> ⇔ > ⇔ >

.

Vậy bpt có nghiệm

3x 

.

Câu 5: Cho cấp số cộng

( )

n

u

có

1

1u

=

và

2

3u =

. Giá trị của

3

u

bằng

A.

6.

B.

9.

C.

4.

D.

5.

Lời giải

Công sai

21

2duu

nên

32

5.uud

 

Câu 6: Trong không gian

Oxyz

, cho đường thẳng

2

: 12

13

= +





= −





=−+



xt

dy t

zt

. Vectơ nào dưới đây là một vectơ

chỉ phương của

d

?

A.

( )

4

2;1;1=

 

u

. B.

( )

1

2; 1; 1= −



u

. C.

( )

3

1; 2; 3= −

 

u

. D.

( )

2

1; 2; 3=

 

u

.

Câu 7: Cho hàm số

( )

42

f x ax bx c=++

có đồ thị là đường cong trong hình vẽ bên. Số nghiệm của

phương trình

( )

1fx=

là

A.

1.

B.

2.

C.

4.

D.

3.

Lời giải

Chọn B

Ta có số nghiệm của phương trình

( )

1fx=

là số giao điểm của đồ thị hàm số

( )

y fx=

và

đường thẳng

1y =

.

3

2

O

1

x

y

y =1

1

3

2

O

1

x

y

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 9

Từ hình vẽ, ta có đồ thị hàm số

( )

y fx=

và đường thẳng

1y =

có hai giao điểm nên phương

trình

( )

1

fx

=

có 2 nghiệm.

Câu 8: Nếu

( )

2

1

2

f x dx

−

=

∫

và

(

)

5

2

5

f x dx

= −

∫

thì

( )

5

1

f x dx

−

∫

bằng

A.

7−

. B.

3−

. C.

4

. D.

7

.

Lời giải

Chọn B

Ta có

( ) ( ) ( ) ( )

5 25

1 12

d d d2 5 3fx x fx x fx x

−−

= + = +− =−

∫∫∫

.

Câu 9: Đồ thị của hàm số nào dưới đây có dang như đường cong trong hình bên?

A.

42

2 1.yx x=−+ −

B.

42

2 1.yx x=−−

C.

32

3 1.

yx x

=−−

D.

32

3 1.yx x=−+ −

Lời giải

Đây chính là dạng của đồ thị hàm trùng phương có hệ số cao nhất dương, có ba điểm cực trị và

cắt trục tung tại điểm có tung độ âm. Khi đó chỉ có

42

21yx x 

là thỏa mãn.

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( ) ( ) ( ) ( )

222

: 2 1 34Sx y z−+++−=

. Tâm của

( )

S

có

tọa độ là

A.

( )

4; 2; 6

−−

. B.

(

)

4; 2; 6−

. C.

( )

2; 1; 3−

. D.

( )

2; 1; 3

−−

.

Lời giải

Chọn C

Tâm mặt cầu

( )

S

có tọa độ là:

( )

2; 1; 3−

.

Câu 11: Trong không gian

,Oxyz

cho điểm

( )

1; 2; 3A −

. Hình chiếu vuông góc của

A

lên mặt phẳng

()Oxy

có tọa độ là

A.

( )

0; 2; 3−

. B.

( )

1; 0; 3−

. C.

( )

1; 2; 0

. D.

( )

1;0;0

.

Lời giải

Chọn C

Hình chiếu vuông góc của

( )

1; 2; 3A −

lên mặt phẳng

()Oxy

có tọa độ là

( )

1; 2; 0 .

Câu 12: Phần ảo của số phức

( )( )

21z ii=−+

bằng

A.

3

. B.

1

. C.

1−

. D.

3−

.

Lời giải

Chọn B

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 10

Ta có:

( )( )

21 3z ii i

= − +=+

.

Vậy phần ảo của số phức

z

bằng

1

.

Câu 13: Cho khối chóp

.S ABC

có chiều cao bằng

3

, đáy

ABC

có diện tích bằng

10

. Thể tích khối chóp

.S ABC

bằng

A.

2

. B.

15

. C.

10

. D.

30

.

Lời giải

Chọn C

Thể tích khối chóp

.

S ABC

là:

.

11

10 3 10.

33

S ABC ABC

V Sh=⋅ ⋅= ⋅ ⋅=

Câu 14: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, cạnh bên

SA

vuông góc

với mặt phẳng đáy và

2

SA a

=

. Tính thể tích

V

của khối chóp

.S ABCD

A.

3

2

6

a

V

=

B.

3

2

4

a

V =

C.

3

2Va=

D.

3

2

3

a

V

=

Lời giải

Chọn D

Ta có

(

)

SA ABCD SA⊥⇒

là đường cao của hình chóp

Thể tích khối chóp

.S ABCD

:

3

2

11 2

. . 2.

33 3

ABCD

a

V SA S a a= = =

.

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

theo thiết diện là một đường tròn. Gọi

d

là khoảng

cách từ

O

đến

( )

P

. Khẳng định nào dưới đây đúng?

A.

dR=

. B.

dR>

. C.

2dR=

. D.

dR<

.

Lời giải

Chọn D

Mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

theo thiết diện là một đường tròn suy ra

dR<

.

Câu 16: Số phức liên hợp của số phức

z 2 5i= −

là

A.

z 2 5i= +

. B.

z 2 5i=−+

. C.

z 2 5i= −

. D.

z 2 5i=−−

.

Lời giải

Chọn A

Ta có:

z 2 5i z 2 5i=−⇒=+

Câu 17: Diện tích xung quanh của mặt trụ có bán kính đáy

R

, chiều cao

h

là

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 11

A.

xq

2S Rh

π

=

. B.

xq

S Rh

π

=

. C.

xq

4S Rh

π

=

. D.

xq

3S Rh

π

=

.

Lời giải

Chọn A

Theo lý thuyết ta có:

xq

2S Rh

π

=

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

252

:

34 1

xyz

d

−+−

= =

−

. Vectơ nào dưới đây là một

vectơ chỉ phương của

d

?

A.

(

)

2

3; 4; 1u = −

 

. B.

( )

1

2; 5; 2u

= −



. C.

( )

3

2; 5; 2

u = −

 

. D.

(

)

4

3; 4;1u =

 

.

Lời giải

Chọn A

Dựa vào phương trình chính tắc của đường thẳng

d

ta có vectơ chỉ phương của

d

là

(

)

2

3; 4; 1

u

= −

 

.

Câu 19: Cho hàm số

( )

y fx=

liên tục trên

{ }

\0

và có bảng xét dấu đạo hàm như hình bên. Số điểm

cực trị của hàm số đã cho là

A.

4

. B.

3

. C.

1

. D.

2

.

Lời giải

Chọn D

Từ bảng xét dấu của đạo hàm ta có hàm số

( )

y fx=

đạt cực đại tại

1

x = −

và

2x =

nên hàm

số

( )

y fx=

có hai điểm cực trị.

Do hàm số

( )

y fx=

liên tục trên

{ }

\0



điểm

0x =

không là điểm cực trị của hàm số.

Câu 20: Cho hàm số

2020

2021

y

x

=

+

. Số tiệm cận của đồ thị hàm số bằng

A.

3

. B.

1

. C.

0

. D.

2

.

Lời giải

Chọn D

Ta có:

2020

lim lim 0

2021

xx

y

x

→±∞ →±∞

= =

+

suy ra tiệm cận ngang

0y =

.

Ta có:

2021 2021

2020

lim lim

2021

xx

y

x

++

→− →−

= = +∞

+

suy ra tiệm cận đứng

2021x = −

.

Vậy đồ thị hàm số có 2 đường tiệm cận.

Câu 21: Tập nghiệm của bất phương trình

2

4

1

27

3

x −



≥





là

A.

[ ]

1;1−

. B.

(

]

;1−∞

. C.

7; 7



−



. D.

[

)

1; +∞

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 12

Lời giải

Chọn A

Ta có

22

4 43

22

1 11

27 4 3 1 1 1

3 33

xx

x xx

− −−

  

≥ ⇔ ≥ ⇔ − ≤− ⇔ ≤ ⇔− ≤ ≤

  

  

.

Câu 22: Có bao nhiêu cách chọn ra

5

học sinh từ một nhóm

10

học sinh?

A.

5!

. B.

5

10

A

. C.

5

10

C

. D.

5

10

.

Lời giải

Chọn A

Số cách chọn ra

5

học sinh từ một nhóm

10

học sinh là tổ hợp chập

5

của

10

phần tử.

Vậy Số cách chọn ra

5

học sinh từ một nhóm

10

học sinh là

5

10

C

.

Câu 23: Cho

(

)

2

d3 23fx x x x C

= + −+

∫

. Hỏi

( )

fx

là hàm số nào?

A.

( )

62fx x= +

. B.

( )

32

3fx x x xC=+−+

.

C.

( )

62fx x C= ++

. D.

( )

32

3

fx x x x=+−

.

Lời giải

Chọn A

Ta có

( )

2

3 23 62fx x x C x

′

= + −+ = +

.

Câu 24: Biết

(

)

cos

Fx x=

là một nguyên hàm của hàm số

( )

fx

trên



. Giá trị của

( )

0

3 2dfx x

π

+





∫

bằng

A.

26

π

−

. B.

4−

. C.

2

π

. D.

2

.

Lời giải

Chọn A

Ta có:

( )

0

3 2dfx x

π

+





∫

( )

00

3 d 2dfx x x

ππ

= +

∫∫

( )

0

32Fx x

π

= +

00

3cos 2xx

ππ

= +

26

π

= −

.

Câu 25: Họ các nguyên hàm của hàm số

(

)

3

1= +

x

fx e

là

A.

3

3 +

x

eC

. B.

3

1

3

++

x

e xC

. C.

3

1

3

+

x

eC

. D.

3

3 ++

x

e xC

.

Lời giải

Chọn B

Ta có

( )

3

1= +

∫∫

dd

x

fx x e x

3

1

3

= ++

x

e xC

.

Câu 26: Cho hàm số

()fx

xác định, liên tục trên



và có đồ thị của hàm số

()fx

′

là đường cong như

hình vẽ bên dưới. Hỏi khẳng định nào đúng?

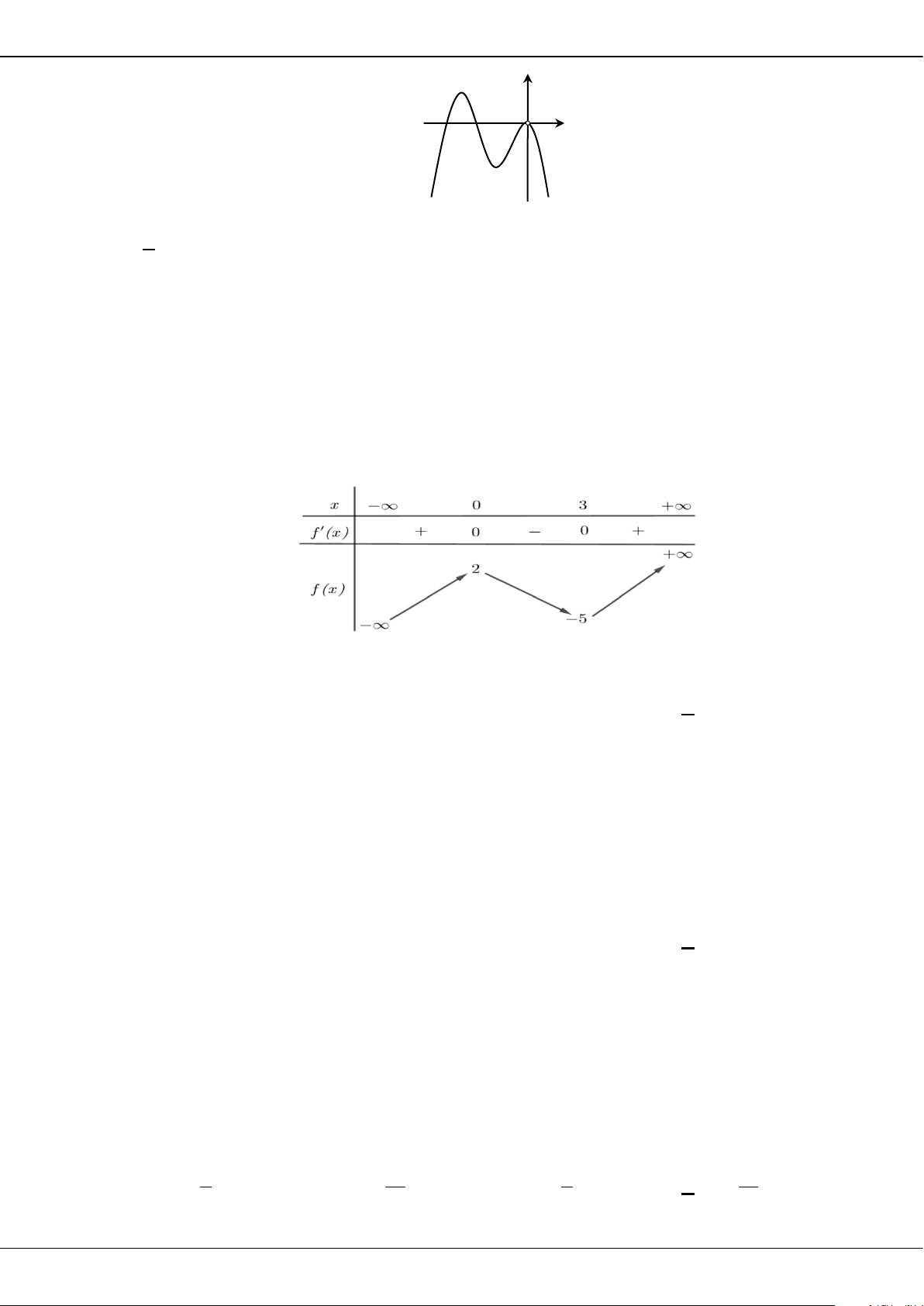
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 13

A. Hàm số

()y fx=

đồng biến trên khoảng

( 2;0).−

B. Hàm số

()y fx=

nghịch biến trên khoảng

(0; ).+∞

C. Hàm số

()y fx=

đồng biến trên khoảng

( ; 3).−∞ −

D. Hàm số

()y fx=

nghịch biến trên khoảng

( 3; 2).−−

Lời giải

Chọn B

Từ đồ thị của hàm số

( )

fx

′

, ta có:

( ) ( ) ( )

0, ; 3 2;fx x

′

≤ ∀ ∈ −∞ − ∪ − +∞

. Vậy hàm số

()y fx=

nghịch biến trên khoảng

(0; ).+∞

Câu 27: Cho hàm số

( )

y fx=

có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng

A.

3

. B.

2

. C.

0

. D.

5−

.

Lời giải

Chọn D

Ta có

( )

fx

′

đổi dấu từ âm sang dương khi qua điểm

3x =

.

Suy ra hàm số đạt cực tiểu tại

3.x =

Giá trị cực tiểu bằng

5.−

Câu 28: Cho hai số thực dương

a

,

b

thỏa mãn

22

log 2log 3ab+=

. Giá trị của

2

ab

bằng

A.

3

log 2

. B.

9

. C.

3

. D.

8

.

Lời giải

Chọn D

( )

2 22

2 2 22 2

log 2 log 3 log log 3 log 3 8ab b baa ab+ =⇔ + =⇔ =⇔=

.

Câu 29: Cho hình phẳng

( )

H

giới hạn bởi đồ thị hàm số

2

2y xx= −

và trục hoành. Tính thể tích

V

của vật thể tròn xoay sinh ra khi cho

( )

H

quay quanh trục

Ox

.

A.

4

3

V

π

=

. B.

16

15

V =

. C.

4

3

V =

. D.

16

15

V

π

=

.

Lời giải

O

x

y

2

3

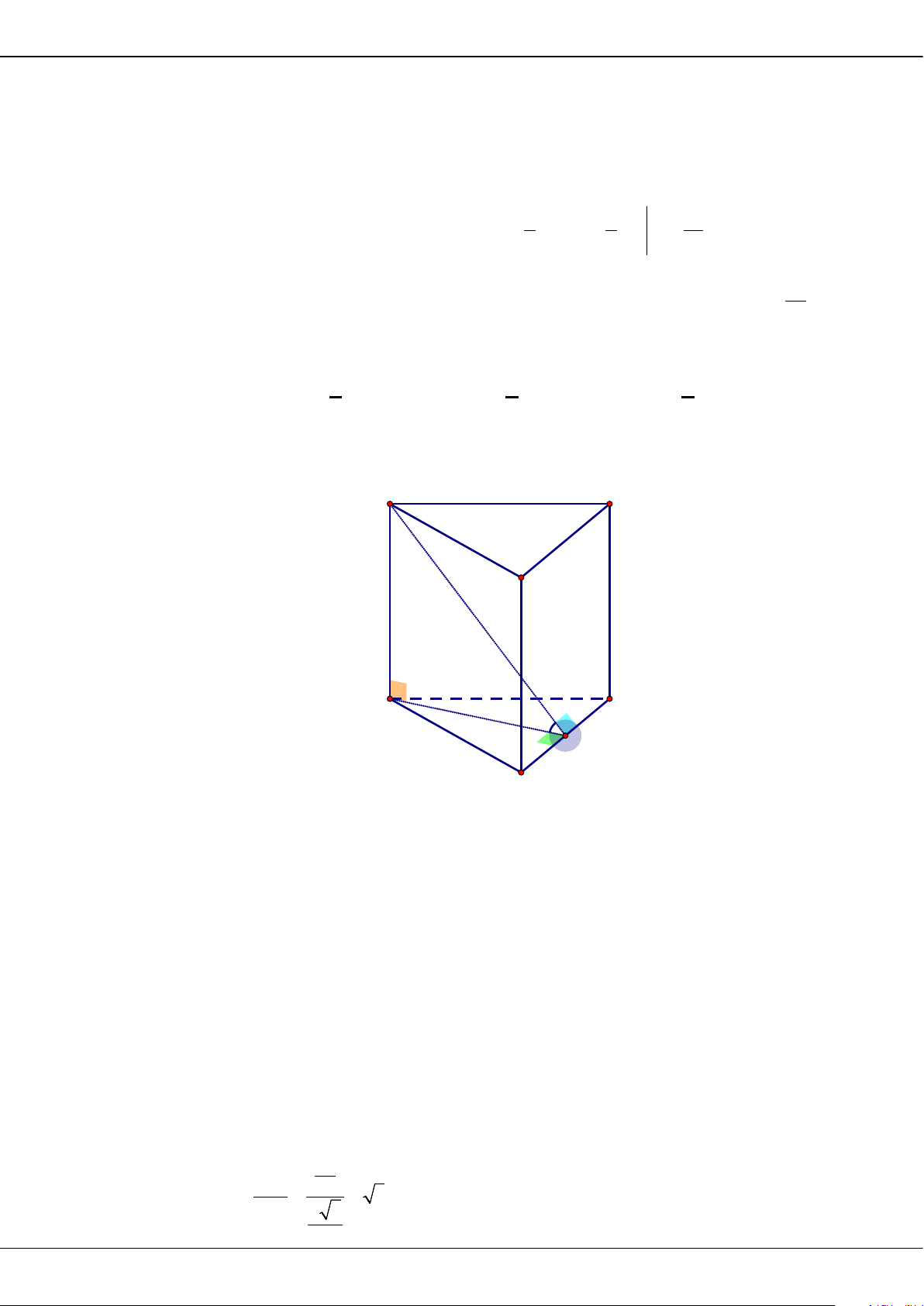
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 14

Chọn D

Phương trình hoành độ giao điểm là

2

0

20

2

x

xx

x

=



−=⇔



=



.

Thể tích cần tìm là

( ) ( )

2

22

2

2 2 34 34 5

00

0

4 1 16

2 44

3 5 15

V x x dx x x x dx x x x

ππ π π





= − = − + = −+ =











∫∫

.

Câu 30: Cho hình lăng trụ tam giác đều

.

ABC A B C

′′′

có cạnh đáy bằng

a

và cạnh bên bằng

3

2

a

. Góc

giữa hai mặt phẳng

( )

A BC

′

và

(

)

ABC

bằng

A.

30°

. B.

60°

. C.

45°

. D.

90°

.

Lời giải

Chọn B

Ta có

( ) ( )

ABC A BC BC

′

∩=

.

Gọi trung điểm của cạnh

BC

là

M

.

Tam giác

ABC

đều nên ta có:

AM BC⊥

.

.ABC A B C

′′′

là lăng trụ đều nên

( )

AA ABC AA BC

′′

⊥ ⇒⊥

.

Từ và ta suy ra

( )

BC AA M BC A M

′′

⊥ ⇒⊥

.

Suy ra: góc

ϕ

giữa hai mặt phẳng

( )

A BC

′

và

( )

ABC

là góc giữa hai đường thẳng

AM

và

AM

′

.

Vì tam giác

A AM

′

vuông tại

A

nên suy ra



A MA

ϕ

′

=

.

Ta có:

3

2

tan 3

3

2

a

AA

AM

a

ϕ

′

= = =

.

M

C'

B'

A

C

B

A'

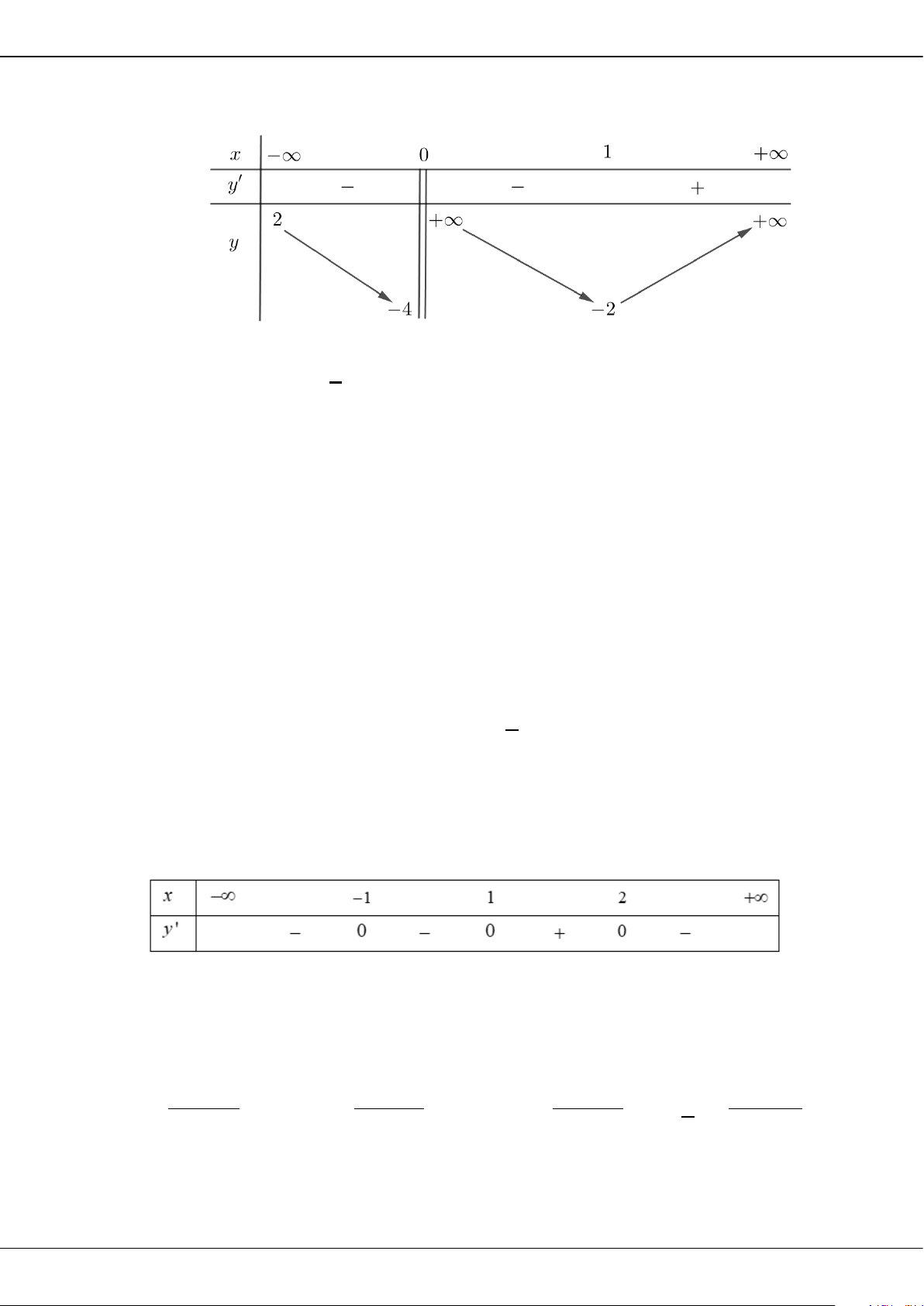
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 15

Suy ra

60

ϕ

= °

.

Câu 31: Cho hàm số

( )

y fx

=

có bảng biến thiên như sau:

Phương trình

(

)

fx m

=

có ba nghiệm thực phân biệt khi và chỉ khi

A.

42

m− < <−

. B.

22m−< <

. C.

22m−< ≤

. D.

42m−< <

.

Lời giải

Chọn B

Số nghiệm của phương trình

( )

fx m=

bằng số giao điểm của đồ thị hàm số

( )

y fx=

và đường

thẳng

ym=

.

Dựa vào bảng biến thiên, ta có phương trình

( )

fx m=

có ba nghiệm thực phân biệt

22m⇔− < <

.

Câu 32: Cho hàm số

( )

y fx=

liên tục trên



và có đạo hàm

( ) (

) ( ) ( )

2020 2021

' 1 12fx x x x=+−−

. Hỏi

hàm số

( )

y fx=

đồng biến trên khoảng nào dưới đây?

A.

( )

1;1−

. B.

( )

2; +∞

. C.

( )

1; 2

. D.

(

)

;1

−∞ −

.

Lời giải

Chọn C

Ta có

( )

1

'0 1

2

x

fx x

x

= −





=⇔=



=



. Ta có bảng xét dấu

Dựa vào bảng biến thiên, hàm số đồng biến trên

( )

1; 2

.

Câu 33: Lớp 11A1 có 21 học sinh nam và 22 học sinh nữ, cần chọn 20 học sinh để tham gia chương

trình mùa hè xanh năm 2021. Xác suất trong 20 học sinh được chọn có cả học sinh nam và học

sinh nữ là

A.

20 20

21 22

20

43

CC

C

+

. B.

20 20

21 22

20

43

AA

A

+

. C.

20 20

21 22

20

43

1

AA

A

+

−

. D.

20 20

21 22

20

43

1

CC

C

+

−

.

Lời giải

Chọn D

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 16

Ta có số phần tử của không gian mẫu:

( )

20

43

nCΩ=

.

Gọi

A

là biến cố chọn được 20 học sinh có cả nam và nữ.

Suy ra

A

là biến cố chọn được 20 học sinh toàn nam hoặc toàn nữ.

Ta có

( )

20 20

21 22

nA C C= +

,

( )

20 20

21 22

20

43

nA

CC

pA

nC

+

= =

Ω

.

Vậy

( )

20 20

21 22

20

43

11

CC

pA pA

C

+

=−=−

.

Câu 34: Tính tổng

T

tất cả các nghiệm của phương trình

4.9 13.6 9.4 0− +=

x xx

.

A.

13

4

=T

. B.

3=T

. C.

1

4

=T

. D.

2T =

.

Lời giải

Chọn A

Ta có:

2

33

4.9 13.6 9.4 0 4 13 9 0

22

xx

x xx

 

− + =⇔⋅ − ⋅ +=

 

 

.

3

1

0

2

39

24

x





=





=







⇔⇔



=







=









. Suy ra:

022T =+=

.

Câu 35: Tìm tập hợp các điểm biểu diễn các số phức

z

thỏa mãn

13 1z iz i−+ = +−

.

A.

20

xy−+=

. B.

2 20xy− −=

. C.

20xy−−=

. D.

20

xy+−=

.

Lời giải

Chọn C

Gọi

( )

;M xy

là điểm biểu diễn cho số phức

z x yi= +

( )

,xy∈

. Khi đó:

( )

( ) ( )

(

) ( )

2 2 22

13 1 1 3 1 1

13 11

20

z iz i x y ix y i

xy xy

xy

−+ = +− ⇔ −+ + = +− +

⇔ − ++ = + ++

⇔−−=

Vậy tập hợp các điểm biểu diễn các số phức

z

thỏa mãn

13 1z iz i−+ = +−

là đường thẳng

20xy−−=

.

Câu 36: Trong không gian

Oxyz

, cho ba điểm

(1; 2;3)A

,

(1;1;1)B

và

(3; 4; 0)C

. Đường thẳng đi qua

A

và song song

BC

có phương trình là:

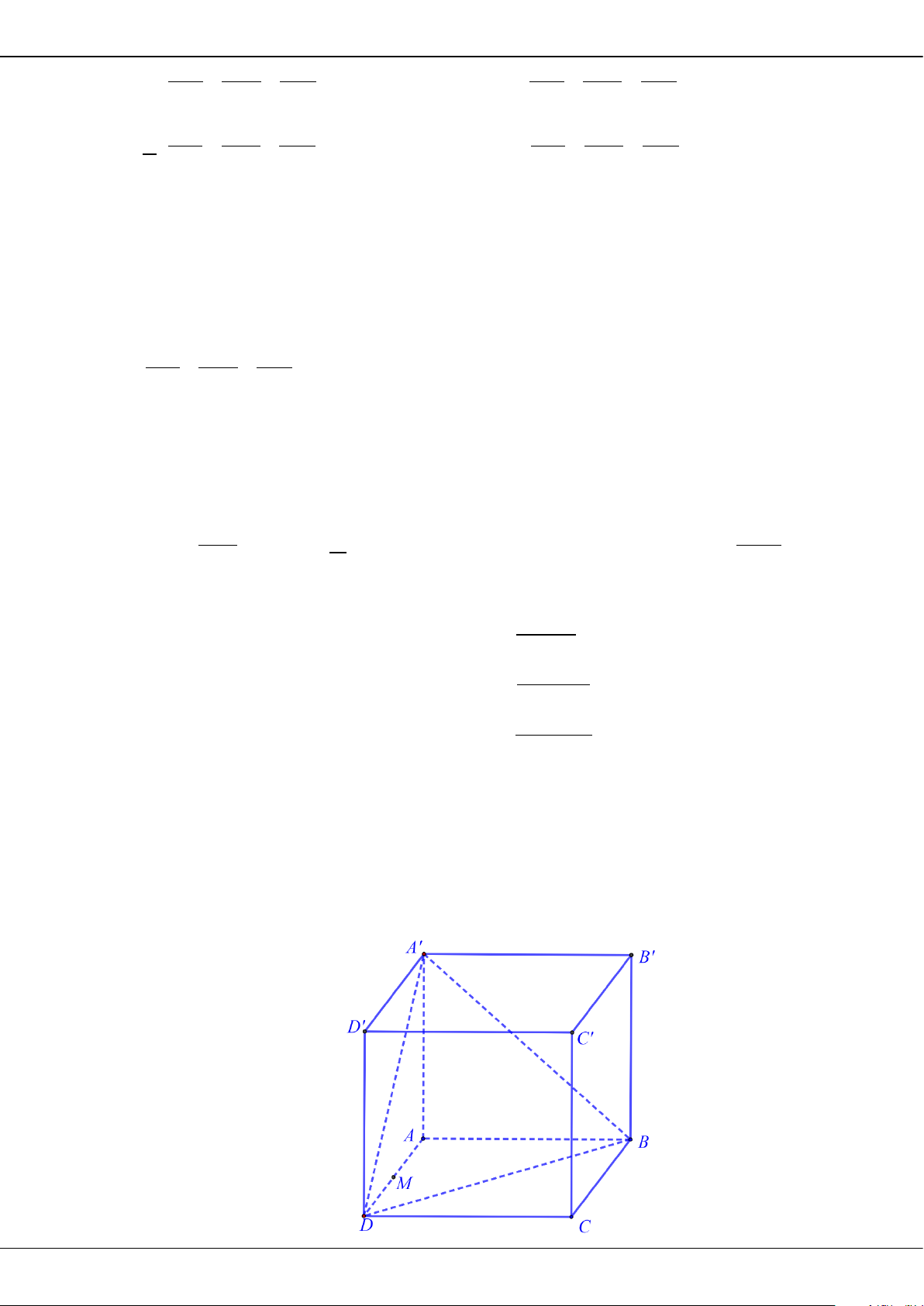
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 17

A.

123

451

xy z+++

= =

. B.

123

451

xy z−−−

= =

.

C.

123

23 1

xy z−−−

= =

−

. D.

123

23 1

xy z+++

= =

−

.

Lời giải

Chọn C

Gọi

∆

là đường thẳng cần tìm ta có

(2; 3; 1)

u BC

∆

= = −

 

Vậy phường trình chính tắc

∆

đi qua

A

và song song

BC

là:

123

23 1

xy z−−−

= =

−

Câu 37: Trong không gian

Oxyz

, cho tam giác

ABC

có trọng tâm

G

với

( )

1; 6; 1A −−

,

( )

2;2;3B −

,

( )

4; 5; 11C −−

. Gọi

( )

;;

I mn p

là điểm đối xứng của

G

qua mặt phẳng

( )

Oxy

. Tính

2021

mn p

T

++

=

.

A.

1

2021

T =

. B.

2021

T =

. C.

1T =

. D.

5

1

2021

T =

.

Lời giải

Tọa độ trọng tâm

G

của tam giác

ABC

là

( )

124

3

625

1;3;3

3

1 3 11

3

G

x

yG

z

−+



=



−+ −



= ⇒ −−





−+ −



=





.

I

là điểm đối xứng của

G

qua mặt phẳng

( )

Oxy

nên

( )

1; 3; 3I −

, suy ra

2021

mn p

T

++

=

133

2021

−+

=

2021

.

Câu 38: Cho hình lập phương

.ABCD A B C D

′′′′

có cạnh bằng

a

. Gọi

M

là trung điểm của

AD

.

Khoảng cách từ điểm

M

đến mặt phẳng

( )

A BD

′

bằng

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 18

A.

3

6

a

. B.

3

12

a

. C.

3

a

. D.

2

a

.

Lời giải

Chọn A

Ta có

M

là trung điểm của

AD

nên

( )

1

,,

2

d M A BD d A A BD

′′

=

.

Gọi

N

là trung điểm của

BD

thì

AN BD

A A BD

⊥





′

⊥



( )

BD A AN

′

⇒⊥

.

Trong mặt phẳng

( )

A AN

′

kẻ

AH A N

′

⊥

thì

( )

AH A BD

′

⊥

( )

,

AH d A A BD

′

⇒=

.

Ta có

AA a

′

=

và

2

22

AC a

AN = =

.

Xét tam giác

A AN

′

vuông tại với đường cao

AH

ta có

22

.AN A A

AH

AN A A

′

=

′

+

2

.

3

2

3

6

2

a

= =

.

Vậy

( )

3

,

6

a

d M A BD

′

=

.

Câu 39: Tập hợp các số thực m để phương trình

( )

2

ln 3 1 ln 4 3x mx x x− += −+ −

có nghiệm là nửa

khoảng

[

)

;ab

. Giá trị của

2

2ab

−

bằng:

A.

1

. B.

10

. C.

7

. D.

7

3

.

Lời giải

Chọn A

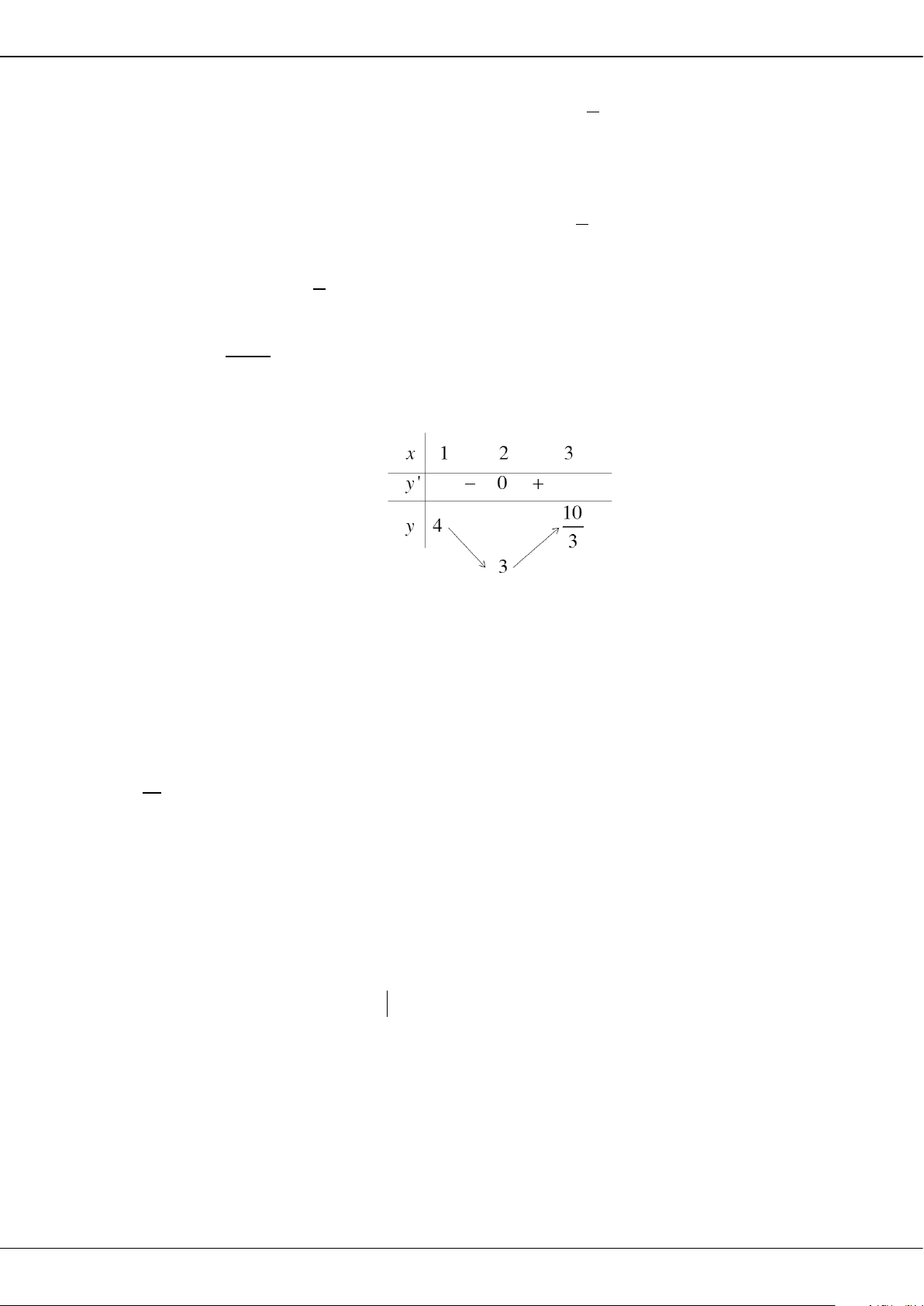
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 19

Phương trình

2

13

4 30

4

1 (*)

3 1 43

x

xx

mx

x mx x x

x

<<



− + −>



⇔⇔



= −+

− +=− + −









.

Để phương trình đã cho có nghiệm thì phương trình phải có nghiệm

( )

1; 3

x ∈

⇔

Đường thẳng

ym=

phải cắt đồ thị hàm số

4

1yx

x

= −+

trên

( )

1; 3

.

Xét hàm số

4

1yx

x

= −+

trên

(

)

1; 3

.

Ta có

2

4

x

y

x

−

′

=

;

02yx

′

=⇔=

Bảng biến thiên:

Từ bảng biến thiên ta có

[

)

3; 4m ∈

.

Vậy

22

2 3 2.4 1

ab

−=− =

.

Câu 40: Hàm số

( )

y fx=

liên tục và có đạo hàm trên



thỏa

( ) ( ) ( ) ( )

1 1 4 541x fx x f x+ −+ − − =

và

( ) ( )

13fx fx+ +=

. Tính

(

)

1

2

0

2

′

=

∫

I xf x dx

A.

1I = −

. B.

1I =

. C.

2I = −

. D.

2

I =

.

Lời giải

Đặt

2

2=⇒=t x dt xdx

Đổi cận

1 1=⇒=xt

0 0=⇒=xt

( ) ( ) ( ) ( ) ( )

11

1

0

00

10= = = = −

′′

∫∫

I f t dt f x dx f x f f

Thế

1 =x

vào

(

) ( ) ( ) ( )

1 1 4 541x fx x f x+ −+ − − =

suy ra

( ) ( )

2 0 311−=ff

(1)

Thế

0 =x

vào

( ) ( )

13fx fx+ +=

suy ra

( ) ( )

0 13+=ff

(2)

Từ (1) và (2) suy ra

( )

0 2 =f

và

( )

11=f

Suy ra

1= −

I

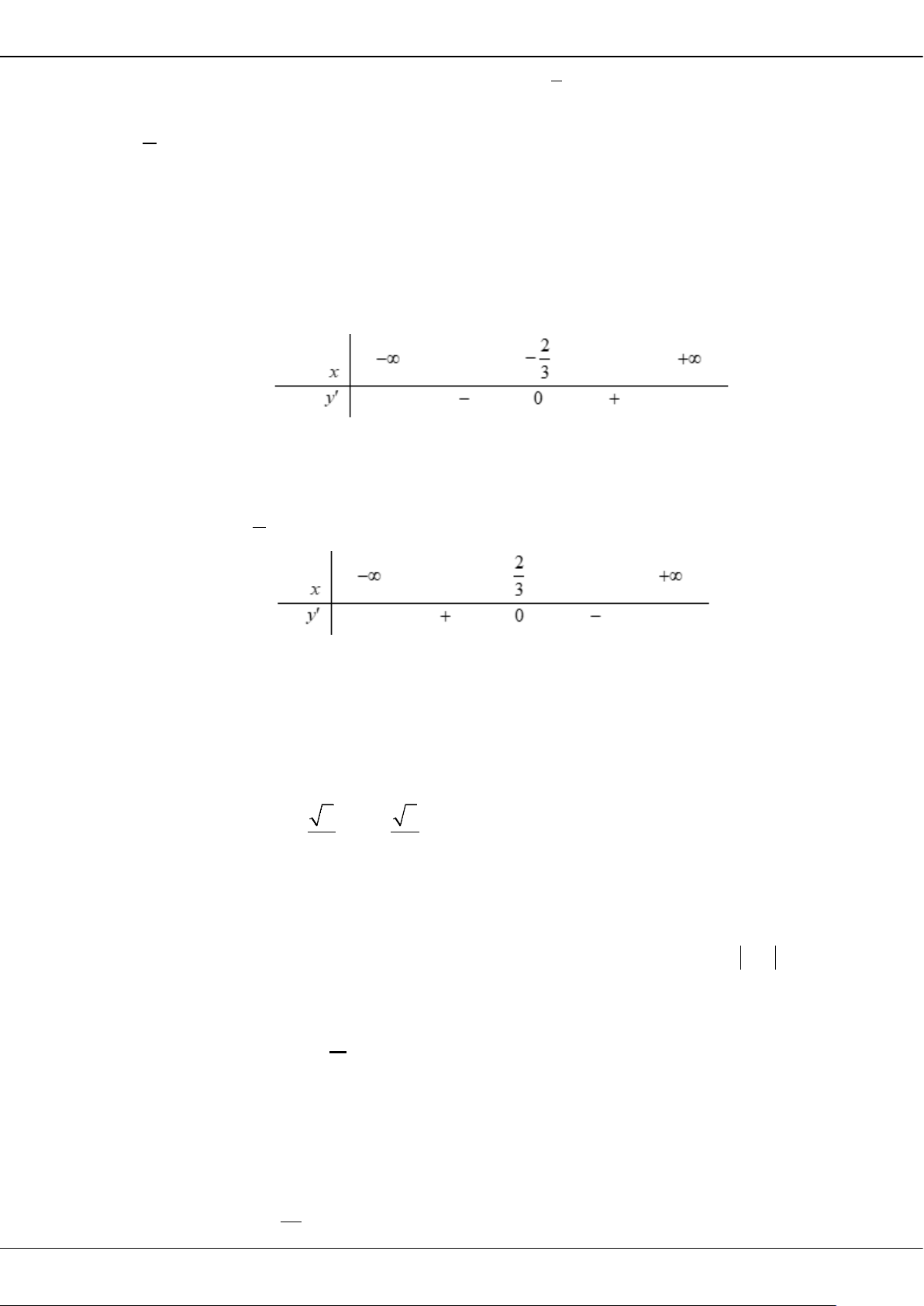
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 20

Câu 41: Tìm số giá trị nguyên của tham số

m

để hàm số

( )

2 32

1

1 31

3

y m x mx x= − + ++

có cực đại

A.

2

. B.

0

. C.

1

. D.

3

.

Lời giải

Chọn A

(

)

22

1 23y m x mx

′

=−++

Trường hợp 1.

1m =

ta có

23yx

′

= +

Xét dấu

y

′

1

m⇒=

loại

Trường hợp 2.

1m = −

ta có

23yx

′

=−+

3

0

2

yx

′

=⇔=

1m⇒=−

thỏa mãn



1m ≠±

Hàm số có cực đại

⇔

phương trình

0y

′

=

có hai nghiệm phân biệt

0

′

⇔∆ >

( )

22

3 10

mm⇔ − −>

2

66

32 0

22

mm

⇔ − > ⇔− < <

Vì

m ∈

nên

{ }

1; 0;1m ∈−

kết hợp với điều kiện ta được

0m =

Vậy có 2 giá trị nguyên của

m

thỏa mãn bài toán.

Câu 42: Biết số phức

( )

z,a bi a b=+∈

thỏa mãn

( )( )

2 12zi i+−

là một số thực và

1z −

đạt giá trị

nhỏ nhất. Khi đó biểu thức

( )

22

625 2021P ab= ++

bằng

A.

2412

. B.

2421

. C.

12021

. D.

52021

.

Lời giải

Chọn B

Ta có

( )( ) ( )( )

( ) ( )

2 1 2 4 3 4a 3 4 3az i i a bi i b b i+ −=+ −= + + −

là số thực nên

3

4 3a 0

4

a

bb− =⇔=

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 21

Mặt khác ta lại có

( )

2

11 1T z a bi a b

= −= − + = − +

( )

2

31

1 25 32 16

44

a

a aa



= −+ = − +





2

1 16 144 1 144 3

5

4 5 25 4 25 5

a



= − +≥ =





.

Vậy

3 16 12

,

5 25 25

MinT a b=⇔= =

. Suy ra

( )

22

625 2021 2421P ab= ++ =

.

Câu 43: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

a

, đường chéo

AC a=

, tam giác

SAB

cân tại

S

và nằm trong mặt phẳng vuông góc với đáy, góc giữa

(

)

SCD

và đáy bằng

45°

.

Tính theo

a

thể tích

V

của khối chóp

.S ABCD

.

A.

3

4

a

V

=

. B.

3

4

a

V =

. C.

3

2

a

V =

. D.

3

12

a

V

=

.

Lời giải

Chọn A

Ta có diện tích đáy

2

3

2

ABCD ACD

a

SS

∆

= =

.

Gọi

H

là trung điểm

AB SH AB⇒⊥

, vì

( ) ( )

( )

SAB ABCD

SH ABCD

SAB ABCD AB

⊥





⇒⊥



∩=





.

Ta có

(

)

()

AB SH

AB SHC

AB CH do AB BC CA

⊥



⇒⊥



⊥==



, vì

( )

//CD AB CD SHC⇒⊥

.

Lại có

( )

,

SCD ABCD CD

SC CD SC SCD

HC CD HC ABCD

∩=





⊥⊂





⊥⊂



suy ra góc giữa

(

)

SCD

và

( )

ABCD

là góc



SCH

.

Suy ra

SHC∆

vuông cân tại

H

3

2

a

SH CH⇒= =

.

Vậy

23

1 1 33

. ..

3 32 2 4

ABCD

aa a

V S SH= = =

.

H

C

A

B

S

D

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 22

Câu 44: Hàm số

( )

y fx=

có đạo hàm liên tục trên



và thỏa mãn

( ) ( ) ( )

32

. 4 6 24fx xfx fx x x x

′′

+ + = − −+

. Tính diện tích hình phẳng giới hạn bởi đồ thị các

hàm số

( )

y fx=

,

(

)

y fx

′

=

?

A.

8S =

. B.

4S =

. C.

8S

π

=

. D.

4S

π

=

.

Lời giải

Chọn A

Ta có

( ) (

) (

)

( )

( ) ( ) ( )

. 11fx xf x f x fx x f x x fx

′

′′ ′

+ + = ++ = +





Nên

(

)

( ) ( )

32

. 4 6 24

fx xfx fx x x x

′′

+ + = − −+

( ) ( )

32

4 6 24 1x x x x fx

′

⇔ − − += +





( ) ( )

4 32

1 24x fx x x x xC

⇒+ =− −++

( )

1

Thay

1x = −

vào

( )

1

ta được

20 2

CC−=⇔ =

. Suy ra

( ) ( )

4 32

1 2 42x fx x x x x+ =− −++

( )

32

3 22fx x x x⇒ =− ++

Khi đó

(

)

2

3 62fx x x

′

= −+

.

Xét phương trình

32 2 32

3 223 62 6 80xx x xx xxx− + += − +⇔ − + =

0

2

4

x

=





⇔=



=



4

32

0

6 8d 8S x x xx⇒= − + =

∫

Câu 45: Có bao nhiêu số nguyên

a

để phương trình

( )

22

30z a za a− − + +=

có hai nghiệm phức

1

z

,

2

z

thỏa mãn

12 12

zz zz

+=−

?

A.

4

. B.

2

. C.

3

. D.

1

.

Lời giải

Chọn A

Trường hợp 1: Hai nghiệm là hai số phức

1

z

và

2

z

có phần ảo khác không

Để phương trình bậc hai với hệ số thực có hai nghiệm phức có phần ảo khác không khi

( )

2

22

3 4 0 3 10 9 0a aa a a∆= − − + < ⇔− − + <

2 13 5 2 13 5

;;

33

a

  

−− −

⇔ ∈ −∞ ∪ +∞

  

  

.

Giả sử

1

2

bi

z

−− ∆

=

;

2

bi

z

−+ ∆

=

Ta có

2

12 12

3 3 10 9

zz zz a a a+ = − ⇔−=− − +

( )

2

9

3 3 10 9 1

0

a

a aa a

a

= −





⇔ − =− − +⇔ =±



=



so với điều kiện ta nhận được

9a = −

;

1a =

.

Trường hợp 2: Hai nghiệm là hai số thực

1

z

và

2

z

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 23

22

12 12

0

40

1

a

zz zz S S P P

a

=



+ =− ⇔ = − ⇔=⇔



= −



. Thử lại thỏa mãn.

Câu 46: Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

( )

: 10Pxyz+ −−=

và đường thẳng

4 21

:

22 1

xyz

d

−++

= =

−

. Gọi đường thẳng

d

′

là hình chiếu vuông góc của

d

trên mặt phẳng

( )

P

. Trong các điểm sau, điểm nào không thuộc

d

′

?

A.

( )

5;9;3H −

. B.

( )

10;16; 5K −

. C.

( )

0; 2;1M

. D.

( )

1; 2; 0N

.

Lời giải

Chọn D

Đường thẳng

d

đi qua điểm

( )

4; 2; 1I −−

và có véc-tơ chỉ phương

( )

2; 2;1

u = −



.

Mặt phẳng

(

)

Q

chứa

d

và vuông góc với

( )

P

là mặt phẳng đi qua

I

và nhận véc-tơ

( )

, 3;1; 4

P

n nu



= =



   

, phương trình

( )

Q

là

( ) ( ) ( )

3 4 2 4 1 0 3 4 60x y z xy z− + + + + =⇔ ++ −=

.

Hình chiếu

d

′

của

d

lên

( )

P

là giao tuyến của

( )

P

và

( )

Q

, do đó tọa độ các điểm thuộc

d

′

thỏa mãn hệ phương trình

10

3 4 60

xyz

xy z

+ −−=





++ −=



.

Thay tọa độ các điểm trong các đáp án, suy ra điểm

(

)

1; 2; 0N

không thuộc

d

′

.

Câu 47: Có bao nhiêu số nguyên

x

sao cho ứng với mỗi

x

có không quá 63 số nguyên

y

thảo mãn

(

)

( )

2

54

log log

x y xy+≥ +

A.

16

. B.

5

. C.

6

. D.

15

.

Lời giải

Chọn A

( )

2

54

log logx y xy+≥ +

Điều kiện

2

0

1

0

,

xy

+>



+≥





+> ⇔



∈





∈





Đặt

( )

,1t x yt t=+∈≥

ta có

( )

2

54

log logx y xy

+≥ +

(

)

( )

2

54

log log 0 1

x xt t⇔ −+ − ≥

Do mỗi

y

tương ứng với một và chỉ một

t

nên ứng với mỗi

x

có không quá 63 số nguyên

y

thỏa mãn

( )

2

54

log logx y xy+≥ +

khi và chỉ khi ứng với mỗi

x

có không quá 63 số

nguyên

1t ≥

thỏa mãn

Xét hàm số

( )

2

54

log logft x x t t= −+ −

có tập xác định

[

)

1;D = +∞

Ta có:

( )

2

11

0 ,ln 5 ln 4

ln 4

ln 5

f t x Dx x t t

t

x xt

′

= − < ∀∈ − + > >

−+

nên hàm số

( )

ft

nghịch biến trên

D

Suy ra

( ) ( ) ( ) ( )

1 2 ... 63 64 .....

ff f f> >> > >

Vì ứng với mỗi số nguyên

x

có không có quá 63số nghiệm

t

thỏa mãn nên

( )

64 0f <

( )

2

54

log 64 log 64 0xx⇔ −+ − <

( )

2 23

5

log 64 3 64 5xx xx⇔ −+ <⇔ −+ <

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 24

2

61 0

xx

⇔ −− <

175 1 75

22

x

−+

⇔ <<

Vì

x ∈



nên

{ }

7; 6;.....;8x ∈− −

, do đó có

( )

8 7 1 16−− + =

số nguyên

x

thỏa mãn bài toán.

Câu 48: Cắt hình nón đỉnh

S

bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh

huyền bằng

2a

. Gọi

BC

là dây cung của đường tròn đáy hình nón sao cho mặt phẳng

( )

SBC

tạo với mặt đáy một góc

o

60

. Tính diện tích tam giác

SBC

.

A.

2

SBC

a

S =

. B.

2

3

SBC

a

S =

. C.

2

3

SBC

a

S =

. D.

2

3

SBC

a

S =

.

Lời giải

Chọn B

Gọi

O

là tâm đường tròn đáy của hình nón.

Ta có

SAD∆

vuông cân tại

S

với

2AD a SA a= ⇒=

và

2

22

AD a

SO = =

.

Gọi

H

là giao điểm của

AD

và

BC

. Suy ra

AD BC⊥

và

H

là trung điểm

BC

.

Khi đó

SH BC

⊥

.

Vậy góc giữa mặt phẳng

( )

SBC

và mặt phẳng đáy là góc



SHO

hay



o

60SHO =

.

Trong

SOH∆

vuông tại

O

ta có



o

26

cotS .cotS .cot 60

26

OH a a

HO OH SO HO

SO

=⇔= = =

.

Suy ra

22 2

22

2 6 24 2 6

4 36 36 6

aaaa

SH SO OH= + = += =

.

Trong

SHB∆

vuông tại

H

ta có

22

222

24 12 2 3 2 3

2

36 36 6 3

aaa a

BH SB SH a BC BH= − = − = = ⇒= =

.

Vậy diện tích tam giác

SBC

là

2

1 126 2 3 2

.. . .

2 26 3 3

SBC

aa a

S SH BC

∆

= = =

.

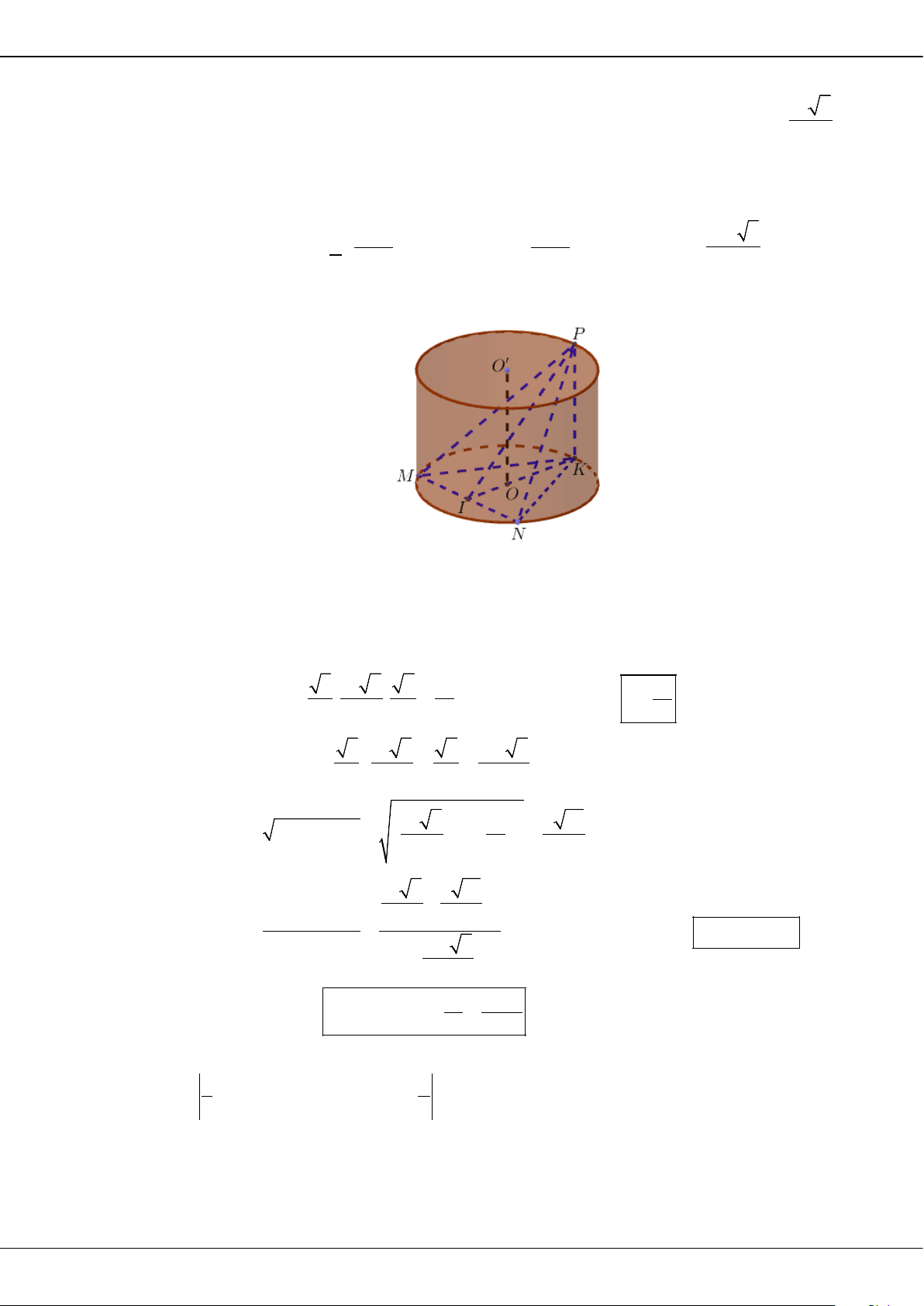
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 25

Câu 49: Cho một hình trụ

( )

T

có hai đường tròn đáy là

( )

O

và

( )

'O

. Gọi

,MN

nằm trên đường

tròn

( )

O

và

P

nằm trên đườn tròn

( )

'O

. Biết rằng tam giác

MNP

đều có cạnh bằng

12 6

5

và mặt phẳng

(

)

MNP

tạo với đáy trụ một góc

45°

, giao điểm của mặt phẳng

(

)

MNP

với trục

của hình trụ

( )

T

nằm trong tam giác

MNP

. Thể tích khối trụ

( )

T

bằng

A.

144

π

. B.

162

5

π

. C.

163

3

π

. D.

82 6

5

π

.

Lời giải

Chọn B

+) Kẻ đường sinh

PK

của hình trụ

K⇒

là hình chiếu của

P

trên mặt đáy chứa đường tròn

(

)

O

. Vì

PM PN=

nên

KM KN=

.

+) Gọi

I

là trung điểm của

MN

.

Ta có

( ) ( )

( )

 

, , , 45PI MN KI MN MNP MNK PI KI PIK PIK⊥ ⊥⇒ = =⇒ =°

.

3 12 6 2 18

.sin 45 . .

2525

PK PI⇒ = °= =

⇒

chiều cao hình trụ

18

5

h =

.

+)

2

3 12 6 2 108 6

.cos45

4 5 2 25

MNK MNP

SS



= °= =





.

+)

2

22

12 6 18 6 15

5 55

MK NK NP PK



== −= − =





.

Suy ra

(

)

2

12 6 6 15

.

55

..

3

4.

108 6

4.

25

MNK

MN MK NK

R

S







= = =

⇒

bán kính hình trụ

( )

3

MNK

rR= =

.

Vậy thể tích hình trụ là

22

18 162

3.

55

V rh

π

ππ

= = =

.

Câu 50: Tổng tất cả các giá trị nguyên thuộc

[ 5;5]−

của

m

để hàm số

32

12

( ) ( 1) (2 3)

33

= +− + − −gx x m x m x

đồng biến trên là:

A. 1 . B. -1 . C. 0 . D. 2 .

Lời giải

Chọn B

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 26

Xét hàm số

32

12

( ) ( 1) (2 3)

33

= +− + − −

fx x m x m x

2

( ) 2( 1) 2 3

′

=+ −+−fx x m x m

1

() 0 .

32

′

= −



= ⇔



= −



x

fx

xm

Hàm số

()gx

đồng biến trên

(1; 5)

khi và chỉ khi xảy ra một trong hai trường hợp sau:

32 1 1

( ) (1; 5)

13

, TH1:

1 13

(1) 0

9

34 0 3

33



−≤ ≥



 

+ ⇔ ⇔ ⇔≥

 

≥

−− ≥ ≥

 



mm

fx

m

f

mm

db tren

Kết hợp điều kiện m nguyên và thuộc

[ 5;5]

−

ta được

{2; 3; 4; 5}

∈m

532 1

( ) ngb trên (1;5)

,TH2 : 1

1 13

(1) 0

34 0 3

33



≤ − ≤−



 

+ ⇔ ⇔ ⇔ ≤−

 

≤

−− ≤ ≤

 



mm

fx

m

f

mm

Kết hợp điều kiện m nguyên và thuộc

[ 5;5]−

ta được

{1;2;3;4;5}

∈−−−−−m

Vậy tổng tất cả các số nguyên của

m

để hàm số đồng biến trên

[ 5;5]

−

là: -1 .

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 27

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT NGUYỄN ĐÌNH CHIỂU

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.D

2.A

3.B

4.C

5.B

6.C

7.B

8.D

9.B

10.C

11.A

12.D

13.D

14.A

15.D

16.A

17.D

18.C

19.B

20.A

21.A

22.A

23.C

24.D

25.D

26.D

27.B

28.D

29.B

30.D

31.C

32.B

33.D

34.B

35.C

36.A

37.D

38.C

39.D

40.D

41.B

42.D

43.B

44.C

45.A

46.C

47.C

48.A

49.A

50.B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Cho số phức

z

có số phức liên hợp

3 2.zi

Tổng phần thực và phần ảo của số phức

z

bằng

A.

1.

B.

1.

C.

5.

D.

5.

Lời giải

Chọn D

3 2 3 2.z iz i 

Tổng phần thực và phần ảo của số phức

z

là

3 2 5.

Câu 2: Với

0

x 

, đạo hàm của hàm số

ln 2yx



là

A.

1

.

x

B.

1

.

2x

C.

2

.

x

D.

.

2

x

Lời giải

Chọn A

Với

0x 

, ta có

 

2

1

.

2

x

y

xx





Câu 3: Cho cấp số cộng

 

n

u

có số hạng đầu

1

2

u 

và công sai

5.d 

Khi đó

4

u

bằng

A.

22.

B.

17.

C.

12.

D.

250.

Lời giải

Chọn B

Ta có

41

3 2 3.5 17.uu d   

Câu 4: Gọi

S

là tập hợp tất cả các giá trị nghiệm nguyên của bất phương trình

 

1

2

log 2 2.x

 

Tổng

các phần tử của

S

bằng

A.

4.

B.

0.

C.

2.

D.

3.

Lời giải

Chọn C

Điều kiện:

2.x 

 

2

1

2

1

log 2 2 2 2.

2

xx x









      











Vì

x  

và kết hợp điều kiện, ta suy ra

 

1; 0;1; 2 .S 

Vậy tổng các phần tử của

S

bằng

2.

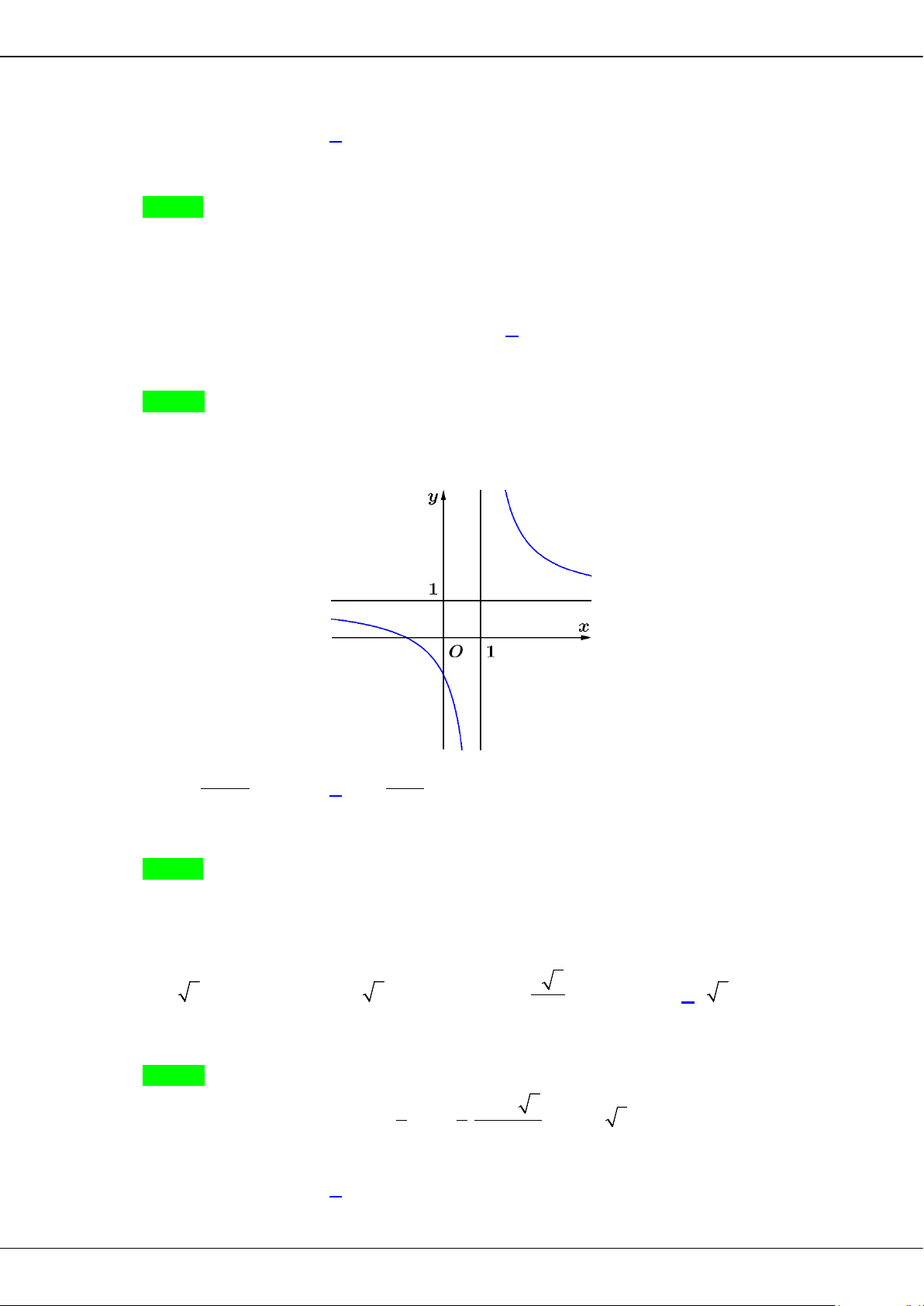
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 28

Câu 5: Trong không gian

,Oxyz

cho mặt phẳng

 

: 2 1 0.Px z 

Vectơ nào dưới đây là một vectơ

pháp tuyến của

 

P

?

A.





1

1; 2; 1 .

n 



B.

 

2

1; 0; 2 .

n





C.

 

3

1; 2; 0 .n 



D.

 

4

0; 1; 2 .n





Lời giải

Chọn B

Mặt phẳng





: 2 10

Px z

 

có VTPT





1; 0; 2 .

n





Câu 6: Trong không gian

,Oxyz

cho hai điểm

   

1;1; 0 , 0;1; 2 .AB

Vectơ nào dưới đây là một vectơ chỉ

phương của đường thẳng

AB

?

A.

 

1; 0; 2 .

u 



B.

 

1;2;2 .u 



C.

 

1; 0; 2 .u





D.

 

1; 0; 2 .

u  



Lời giải

Chọn C

Vectơ chỉ phương của đường thẳng

AB

là

 

1; 0; 2 .AB 

  

Câu 7: Đường cong trong hình bên dưới là đồ thị của hàm số nào dưới đây?

A.

1

.

1

x

y

x







B.

1

.

1

x

y

x







C.

42

.

yx x



D.

2

.

yx

Lời giải

Chọn B

Đồ thị hàm số đã cho là đồ thị của hàm phân thức hữu tỷ bậc nhất có đường tiệm cận ngang

1y 

và đường tiệm cận đứng

1

x 

nên ta chọn đáp án B.

Câu 8: Thể tích khối chóp tam giác đều có độ dài cạnh đáy là

2,a

chiều cao là

3a

bằng

A.

3

43 .a

B.

3

33 .a

C.

3

43

.

3

a

D.

3

3.a

Lời giải

Chọn D

Thể tích khối chóp đã cho là

 

2

3

23

11

. . .3 3

3 34

a

V Bh a a 

(đvtt).

Câu 9: Số tam giác xác định bởi các đỉnh của một đa giác đều

10

cạnh là

A.

35.

B.

120.

C.

240.

D.

720.

Lời giải

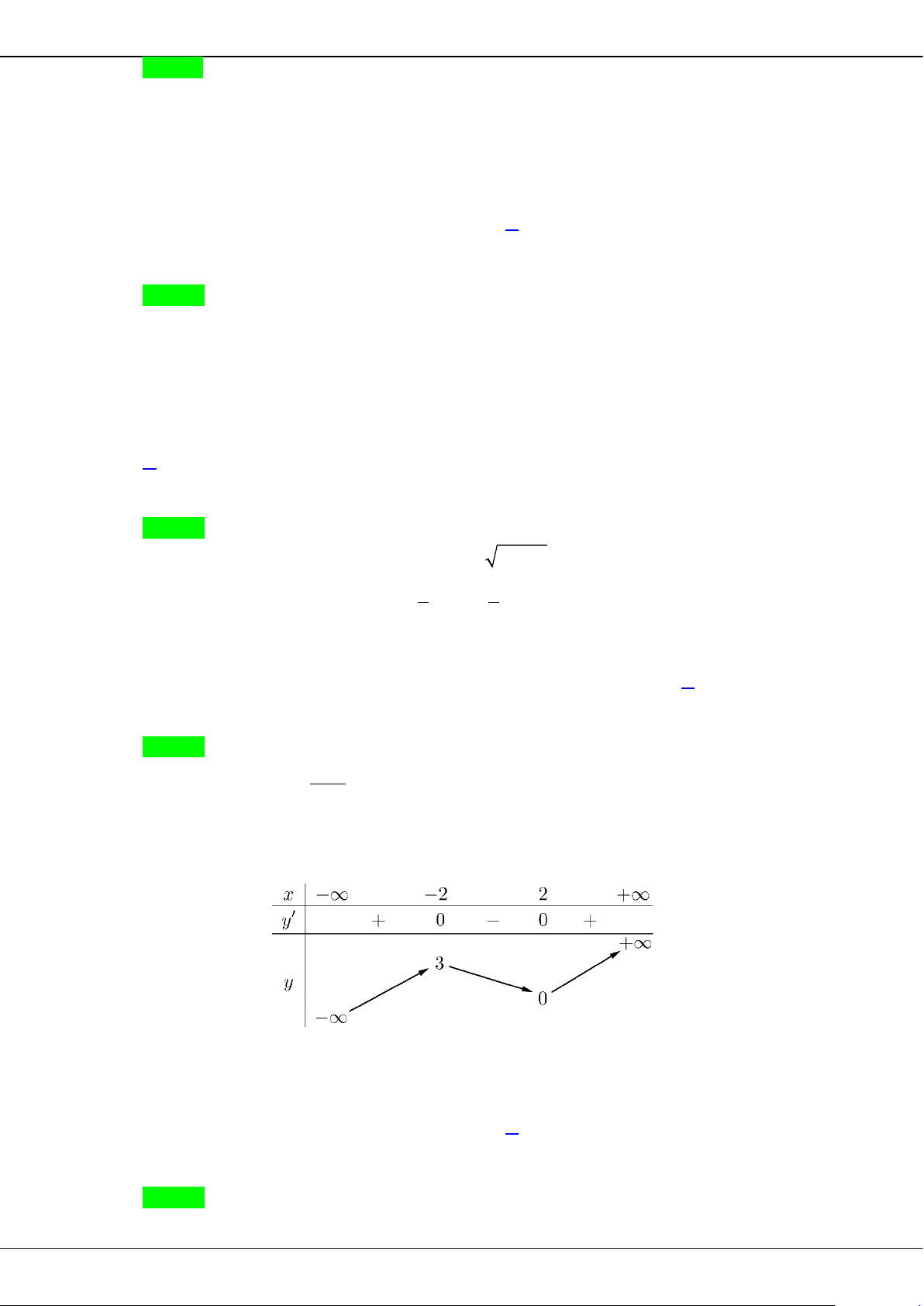
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 29

Chọn B

Số tam giác cần tìm là

3

10

120.C 

Câu 10: Trong không gian

,Oxyz

điểm nào thuộc đường thẳng

12

:3

45

xt

dy t

zt







 











?

A.

 

3;2;1.P 

B.

 

2; 1; 5 .N

C.

 

1; 3; 4 .M 

D.

 

4; 1; 3 .Q

Lời giải

Chọn C

Điểm

 

1; 3; 4

thuộc đường thẳng

12

: 3.

45

xt

dy t

zt







 











Câu 11: Cho khối nón có bán kính đáy bằng

3

và diện tích xung quanh bằng

15 .

Thể tích của khối nón

đã cho bằng

A.

12 .

B.

60 .

C.

20 .

D.

36 .

Lời giải

Chọn A

15 .3. 5.

xq

S rl l l    

Suy ra

22

4.h lr 

Thể tích của khối nón đã cho là

22

11

.3 .4 12

33

V rh  

(đvtt).

Câu 12: Cho số phức

z

thỏa mãn

 

1 3,iz i 

phần ảo của

z

bằng

A.

2.i

B.

1.

C.

2.

D.

2.

Lời giải

Chọn D

 

3

1 3 1

2.

1

i

iz i z i

i



    



Vậy phần ảo của số phức

z

bằng

2.

Câu 13: Cho hàm số

 

y fx

có bảng biến thiên như sau

Giá trị cực đại

CD

y

và giá trị cực tiểu

CT

y

của hàm số đã cho lần lượt là

A.

3, 2.

CD CT

yy 

B.

2, 0.

CD CT

yy

C.

2, 2.

CD CT

yy 

D.

3, 0.

CD CT

yy

Lời giải

Chọn D

Dựa vào BBT, ta thấy

3, 0.

CD CT

yy

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 30

Câu 14: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 3; 4 .M

Khoảng cách từ điểm

M

đến trục

Ox

bằng

A.

5.

B.

25.

C.

10.

D.

17.

Lời giải

Chọn A

Ta có





22

, 5.

MM

d M Ox y z

 

Câu 15: Cho

 

1

d2fx x







và





3

1

d 5.fx x





Khi đó

 

3

1

2d

fx x





bằng

A.

14.

B.

14.

C.

12.

D.

6.

Lời giải

Chọn D

       

3 13

1 11

2 d 2 d d 2. 2 5 6.fx x fx x fx x







    





 

Câu 16: Tiệm cận ngang của đồ thị hàm số

13

1

x

y

x







là

A.

3.y 

B.

1.y 

C.

3.x



D.

1.x 

Lời giải

Chọn A

Tiệm cận ngang của đồ thị hàm số

13

1

x

y

x







có phương trình là

3.

y 

Câu 17: Bất phương trình

1

4

x





















có tập nghiệm là

A.





0; .

B.





0;1 .

C.

 

1; .

D.





;0 .

Lời giải

Chọn D

0

1 0.

4 44

xx

x

 

  

 

 



 

 

 

 

  

Vậy tập nghiệm của bất phương trình là

 

;0 .S  

Câu 18: Nếu

 

3

1

d2fx x



và

 

3

1

d4gx x



thì

   

3

1

df x gx x









bằng

A.

2.

B.

6.

C.

6.



D.

2.



Lời giải

Chọn C

       

3 33

1 11

d d d 2 4 6.f x gx x f x x gx x



     



 

Câu 19: Cho hình trụ có chiều cao bằng

5

và đường kính đáy bằng

8

. Diện tích xung quanh của hình trụ

đó bằng

A.

20 .

B.

40 .

C.

160 .

D.

80 .

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 31

Lời giải

Chọn B

Diện tích xung quanh của hình trụ là

8

2 2 . .5 40

2

xq

S rl  

(đvdt).

Câu 20: Trong không gian

Oxyz

, mặt cầu



 

  

2 22

: 2 4 6 25

Sx y z

có tọa độ tâm

I

là

A.





2; 4; 6 .

I 

B.

 

2; 4; 6 .I 

C.





1; 2; 3 .

I 

D.

 

1; 2; 3 .I



Lời giải

Chọn A

Mặt cầu

       

2 22

: 2 4 6 25Sx y z

có tâm

 

2; 4; 6 .

I 

Câu 21: Thể tích của khối lập phương có độ dài cạnh

3a 

là

A.

27.

B.

9.

C.

6.

D.

16.

Lời giải

Chọn A

Thể tích của khối lập phương là

33

3 27.Va

Câu 22: Trong không gian

,Oxyz

tích vô hướng của





3; 2;1a





và

 

5; 2; 4

b  



bằng

A.

15.

B.

10.

C.

7.

D.

15.

Lời giải

Chọn A



 



. 3. 5 2.2 1. 4 15.ab

     



Câu 23: Cho các số thực

 

,.ab a b

Nếu hàm số

 

y Fx

là một nguyên hàm của hàm số

 

y fx

thì

A.



    

d.

b

a

Fx x fa fb





B.

    



d.

b

a

Fx x fb fa



C.

 

  



d.

b

a

f x x Fb Fa



D.

 

   

d.

b

a

f x x Fa Fb





Lời giải

Chọn C

   

d.

b

a

f x x Fx Fb Fa 



Câu 24: Trong không gian

,

Oxyz

tìm tất cả các giá trị thực của tham số

m

để phương trình

2 22

224 0x y z x y zm

là phương trình của một mặt cầu?

A.

6.m 

B.

6.m 

C.

6.m 

D.

6.m 

Lời giải

Chọn D

Phương trình đã cho là phương trình mặt cầu

222

0abcd   

22 2

1 1 2 0 6.mm   

Câu 25: Họ các nguyên hàm của hàm số

 

x

fx e x

là

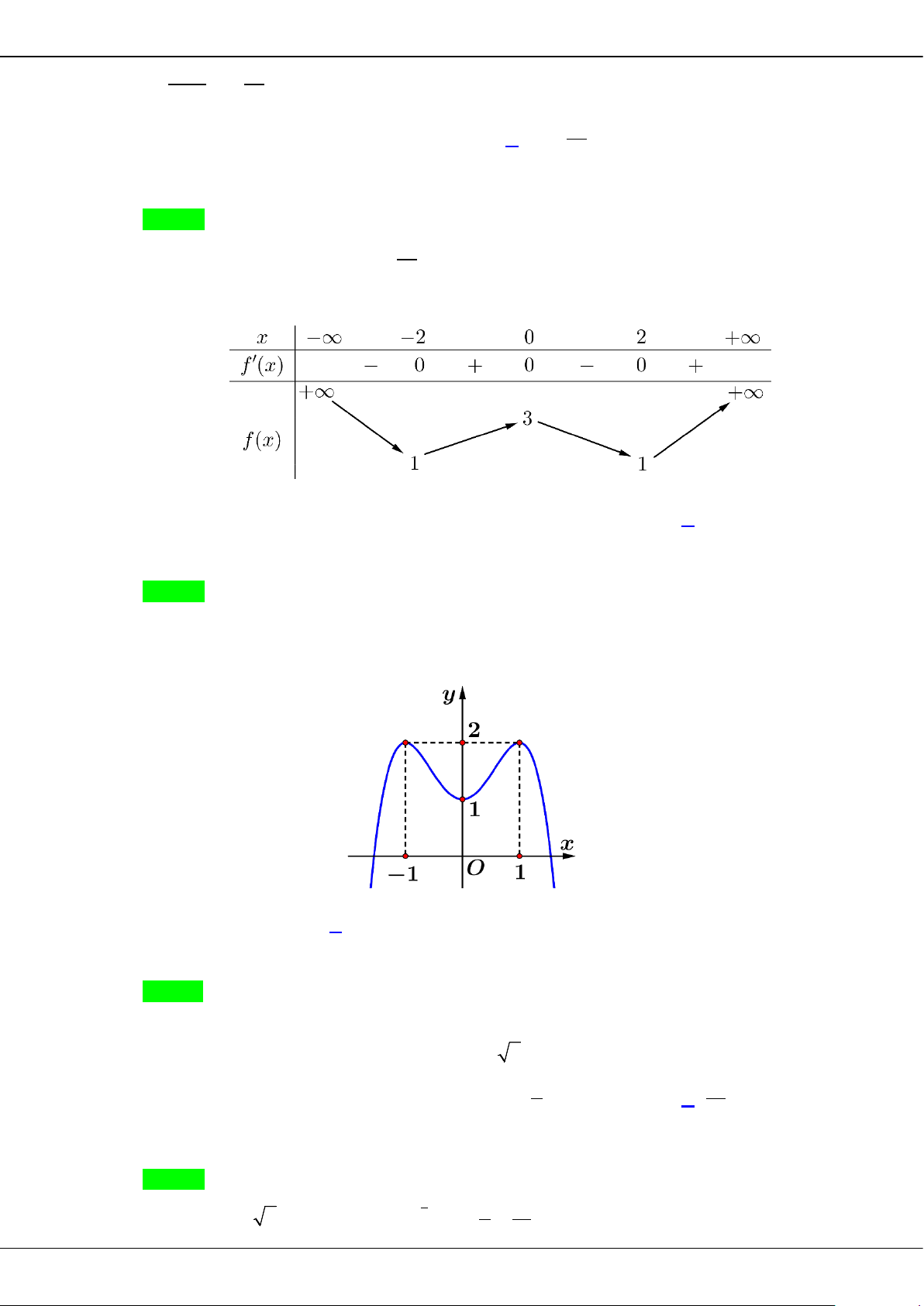
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 32

A.

2

1

.

12

x

eC

x





B.

2

.

x

exC

C.

1.

x

eC

D.

2

.

2

x

eC

Lời giải

Chọn D

 

2

.

2

dd

x x

fxx e xx

x

eC 



Câu 26: Cho hàm số

 

y fx

có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

 

0; 2 .

B.

 

2; 2 .

C.

 

; 2. 

D.

 

2; .

Lời giải

Chọn D

Dựa vào BBT, ta thấy hàm số đồng biến trên các khoảng

 

2; 0

và

 

2; .

Câu 27: Cho hàm số bậc bốn

 

y fx

có đồ thị là đường cong trong hình bên dưới.

Cực tiểu của hàm số đã cho là

A.

1.

B.

1.

C.

2.

D.

0.

Lời giải

Chọn B

Dựa vào đồ thị, cực tiểu của hàm số đã cho bằng

1.

Câu 28: Với

a

là số thực dương khác

1,

giá trị

 

3

4

log .

a

aa

bằng

A.

7.

B.

12.

C.

3

.

4

D.

13

.

4

Lời giải

Chọn D

Ta có

 

1

33

4

1 13

log . log log 3 .

44

a aa

aa a a   

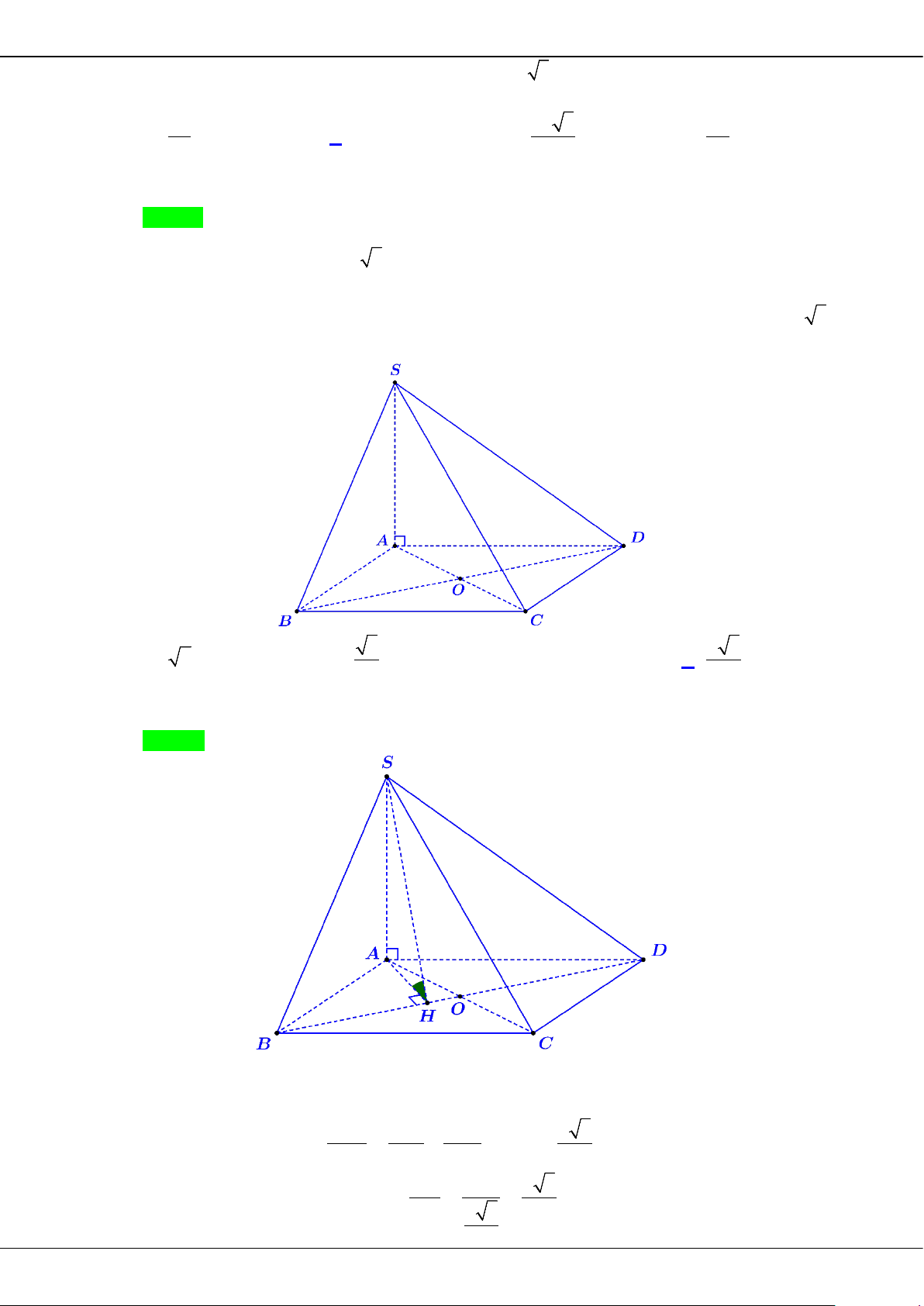
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 33

Câu 29: Cho hình phẳng

D

giới hạn bởi đồ thị hàm số

3yx

và các đường thẳng

0, 1, 2.y xx 

Thể tích khối tròn xoay tạo thành khi quay

D

quanh trục hoành bằng

A.

3

.

2



B.

7.

C.

33

.

2



D.

9

.

2



Lời giải

Chọn B

Thể tích cần tìm là

 

22

2

11

3 d 3d 7V x x xx  



(đvtt).

Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

,3AB SA a AD a 

và

 

.SA ABCD

Tan của góc giữa hai mặt phẳng

 

SBD

và

 

ABCD

bằng

A.

2.

B.

3

.

2

C.

1.

D.

23

.

3

Lời giải

Chọn D

Kẻ

AH BD

tại

.H BD SH

Suy ra góc giữa hai mặt phẳng

 

SBD

và

 

ABCD

bằng



.SHA

ABD

vuông tại

A

có

222

1 11 3

.

2

a

AH

AH AB AD

  

SAH

vuông tại

A

có



23

tan .

3

2

SA a

SHA

AH

a

 

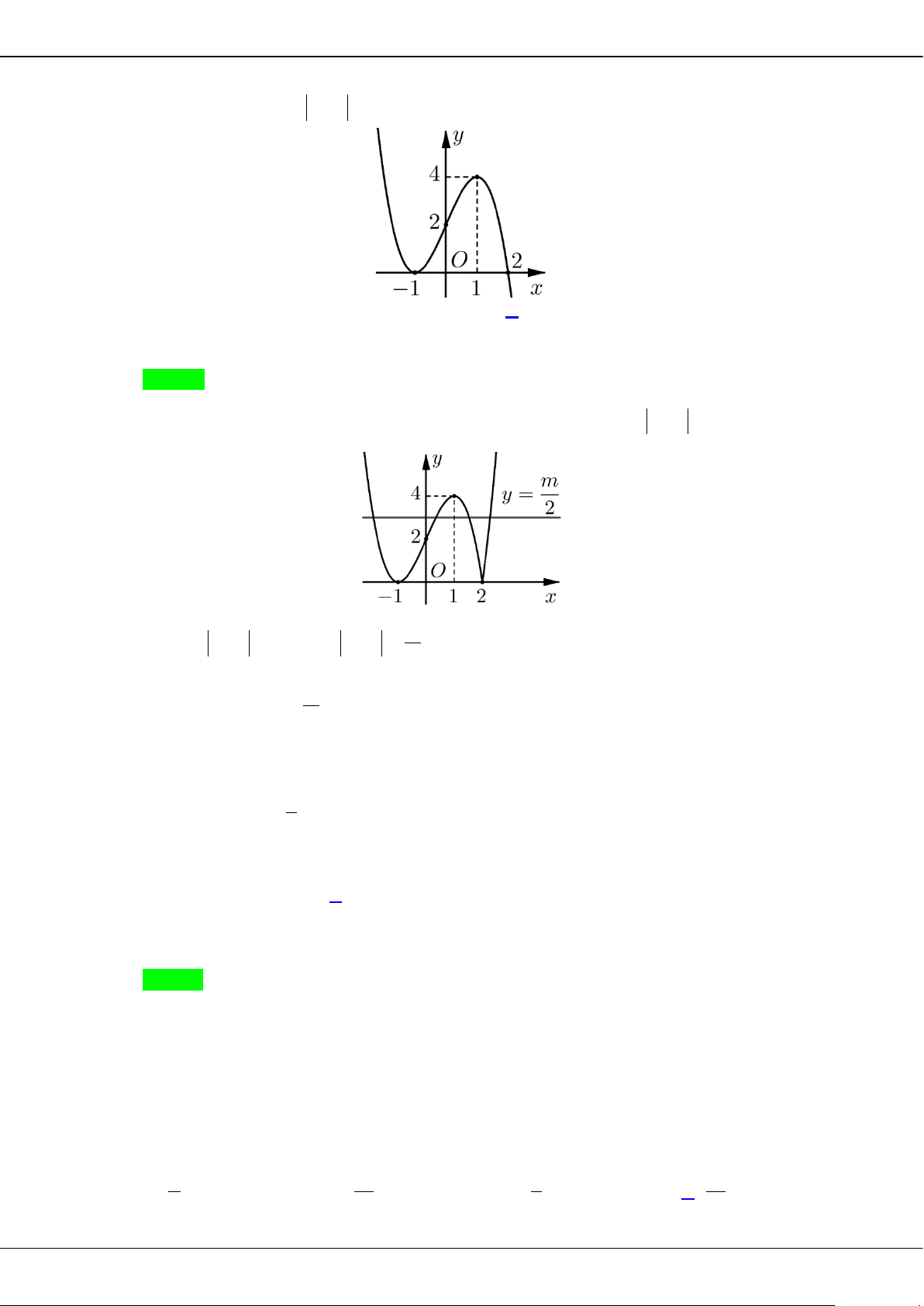
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 34

Câu 31: Cho hàm số bậc ba

 

y fx

có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

 

20fx m

có

4

nghiệm phân biệt?

A.

3.

B.

4.

C.

7.

D.

8.

Lời giải

Chọn C

Trước tiên từ đồ thị hàm số

 

,y fx

ta suy ra đồ thị hàm số

 

y fx

như hình vẽ sau

Ta có

   

20 .

2

m

fx m fx 

Do đó YCBT

0 4 0 8.

2

m

m  

Vì

m  

nên

 

1; 2; ; 7 .m  

Vậy có

7

số nguyên

m

thỏa mãn bài toán.

Câu 32: Cho hàm số

 

32

1

3 2 2022.

3

y x mx m x    

Tìm tất cả các giá trị của tham số

m

để hàm

số nghịch biến trên khoảng

 

;. 

A.

2.m 

B.

2 1.m  

C.

1

.

2

m











D.

1

.

2

m











Lời giải

Chọn B

Ycbt

2

0, 2 3 2 0,y x x mx m x



        

2

10

2 1.

3 20

a

m

mm



 



 

 







   





Câu 33: Năm đoạn thẳng có độ dài lần lượt là

1 cm,

3 cm,

5 cm,

7 cm,

9 cm.

Lấy ngẫu nhiên ba đoạn

thẳng trong năm đoạn trên. Xác suất ba đoạn ấy tạo thành

3

cạnh của một tam giác bằng

A.

2

.

5

B.

7

.

10

C.

3

.

5

D.

3

.

10

Lời giải

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 35

Chọn D

Lấy

3

đoạn thẳng từ

5

đoạn thẳng, ta có

 

3

5

.nC

Gọi

A

là biến cố: “Lấy được ba đoạn thẳng tạo thành ba cạnh của một tam giác”.

Gọi

,,abc

là ba cạnh đó. Ta phải có

abc

acb

bca



















nên bộ ba số thỏa mãn điều kiện là

     

3;5;7 , 3;7;9 , 5;7;9

nên

 

3.nA

Vậy

 





 

3

5

33

.

10

nA

PA

nC

 



Câu 34: Tổng tất cả các nghiệm thực của phương trình

 

22

log .log 32 4 0xx

bằng

A.

7

.

16

B.

9

.

16

C.

1

.

32

D.

1

.

2

Lời giải

Chọn B

Điều kiện:

0.x 

Phương trình





2

22 2 2

log log 5 4 0 log 5log 4 0xx x x    

2

log 1

11

;.

log 4

16 2

x











 















Vật tổng các nghiệm của phương trình bằng

119

.

16 2 16



Câu 35: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức

z

thỏa mãn

13 2z iz i   

là một đường thẳng. Đường thẳng đó có phương trình là

A.

6 8 5 0.xy

 

B.

6 8 5 0.xy 

C.

6 4 5 0.

xy 

D.

6 4 5 0.xy

 

Lời giải

Chọn C

Giả sử

.z x yi

Ta có

   

13 2 1 3 2 1z iz i x y ix yi      

     

 

2 2 22

1 3 2 1 6 4 5 0.x y x y xy         

Vậy điểm biểu diễn số phức

z

thỏa mãn bài toán thuộc đường thẳng

6 4 5 0.xy 

Câu 36: Trong không gian

Oxyz

, cho hình chóp

.S ABCD

có đáy là hình vuông,

SA

vuông góc với đáy

và

   

2;3; 7 , 4;1; 3 .BD

Phương trình mặt phẳng

 

SAC

là

A.

2 9 0.xy z 

B.

2 9 0.xy z 

C.

2 9 0.

xy z 

D.

2 9 0.xy z 

Lời giải

Chọn A

Gọi

I AC BD

suy ra

I

là trung điểm của

BD

nên

 

3; 2; 5 .I

Ta có

 

.

BD AC

BD SAC

BD SA



















Khi đó

 

   

2;2;4 21;1;2

SAC

n BD    

 

và

 

SAC

đi qua điểm

 

3; 2; 5 .I

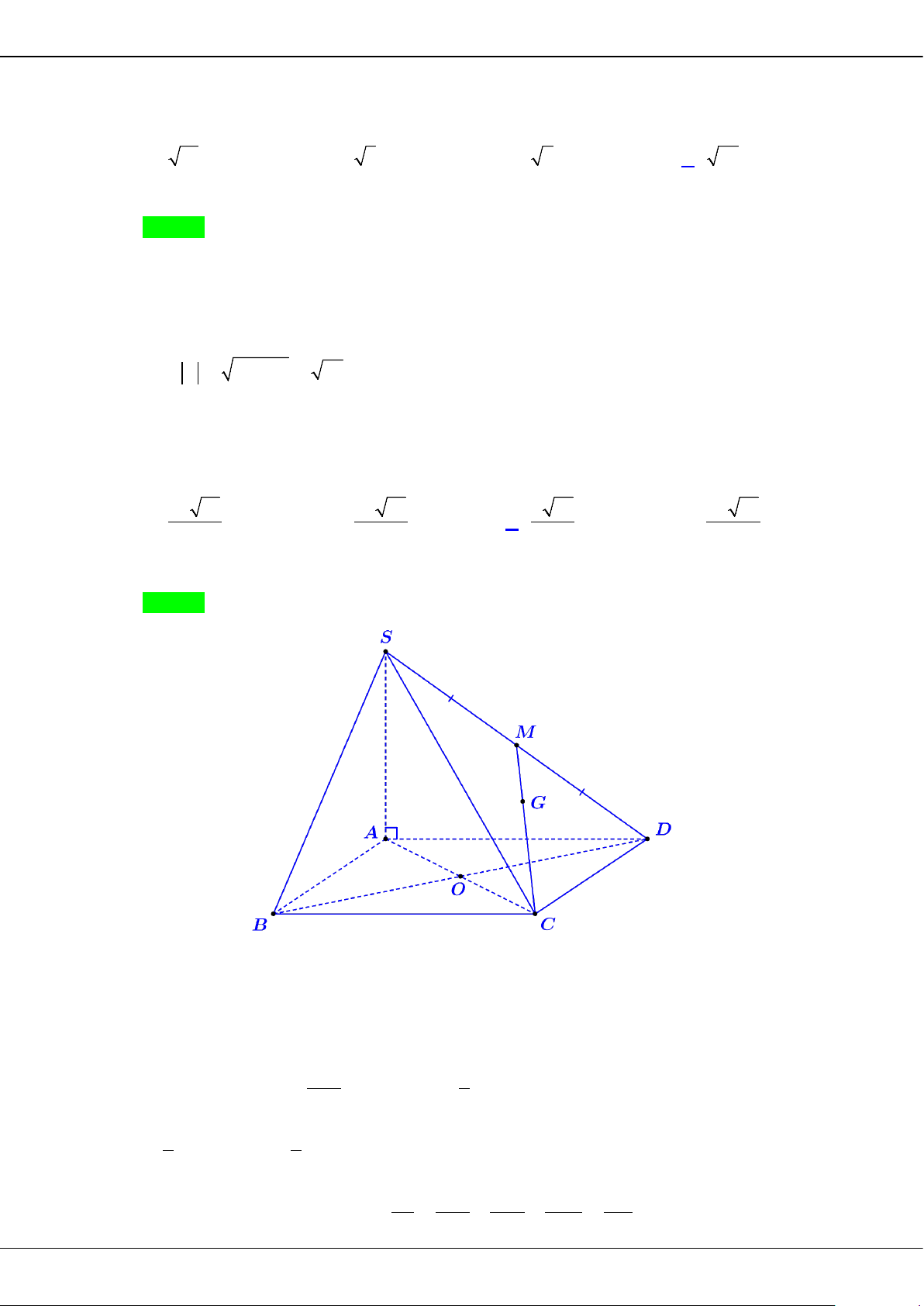
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 36

Vậy phương trình mặt phẳng

 

SAC

là

2 9 0.xy z 

Câu 37: Với các số thực

,ab

biết phương trình

2

8 64 0z az b 

có nghiệm phức

0

8 16 .zi

Môđun

của số phức

w a bi

bằng

A.

19.

B.

3.

C.

7.

D.

29.

Lời giải

Chọn D

Vì

0

8 16zi

là nghiệm phức của phương trình đã cho nên suy ra

1

8 16zi

cũng là

nghiệm của phương trình.

Theo định lý Vi-et, ta có

01

8

2

.

64 5

zz a

a

zz b b



 























Vậy

22

29.w ab 

Câu 38: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

,a

2.SD a

Hai mặt phẳng

 

SAB

và

 

SAC

cùng vuông góc với mặt đáy

 

.ABCD

Gọi

G

là trọng tâm của tam giác

.SDC

Khoảng

cách từ

G

đến mặt phẳng

 

SBD

bằng

A.

2 17

.

17

a

B.

2 21

.

7

a

C.

21

.

21

a

D.

2 21

.

21

a

Lời giải

Chọn C

Vì

   

     

.

SAB ABCD

SAB SAC SA ABCD

SAC ABCD







  











Gọi

O AC BD

và

M

là trung điểm của

.SD

Ta có

 

1

, ,,

3

GM

d G SBD d C SBD d C SBD

CM



 

11

,

33

d A SBD d

(do

AC

cắt

 

SBD

tại trung điểm

O

).

Xét tứ diện vuông

.,S ABD

ta có

2 2 2 22

11 1 1 7

3d AS AB AD a

 

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 37

21

.

7

a

d

Vậy

 

1 21

,.

3 21

a

d G SBD d

Câu 39: Có bao nhiêu số nguyên

x

thỏa mãn

   

23

2 3 23

log log log .log 4x x xx 

?

A.

27.

B.

26.

C.

133.

D.

134.

Lời giải

Chọn D

Điều kiện:

0.x 

BPT

 

2

ln

ln ln 2 ln 3ln 2 3

. 4 ln 4 0

ln 2 ln 3 ln 2 3 ln 2.ln 3 ln 2 ln 3

x

xx x x

x







      











0,621 ln 4,898 0,536 134,087.xx      

Vì

x

 

nên

 

1;2; ;134 .x  

Vậy có

134

số nguyên

x

thỏa mãn bất phương trình.

Câu 40: Cho hàm số

 

fx

liên tục trên



. Biết rằng

   

,xF x G x x

là hai nguyên hàm của

 

fx

trên



thỏa mãn

     

1

0

d 21 1 2fx x F G 



và

   

2 2 9.FG

Khi đó, giá trị của

   

2

0

dxf x F x x



bằng

A.

196

.

9

B.

16.

C.

98

.

9

D.

8.

Lời giải

Chọn D

Vì

   

,xF x G x x

là hai nguyên hàm của

 

fx

nên

   

,xF x G x x C x  

(với

C

là hằng số). Khi đó

   

     



    

01

1 1 1 2.

22 22 3

GC

FG C







 





 





Ta có

   



  

1

0

d 1 01fxxGxx G G



   





      

    

  



2112101211 03*.FG GG FG G



         



Thay

 

1

và





2

vào

 

*

, ta được





2 1 3 1.CC C     

Mặt khác, từ

   

2 29FG

kết hợp với

 

3

và

1,C 

ta suy ra

 

2 2.F 

Ta có

    

      

22 2

22

0

00

11

d d . 2 2 0 8.

22

xf x F x x xF x xF x xF x F

 

   

 



Câu 41: Có bao nhiêu số nguyên

7a 

để hàm số

 

42

2 2 4 31yx a x a x    

có ba điểm cực

trị?

A.

4.

B.

3.

C.

5.

D.

2.

Lời giải

Chọn B

Ta có

   

3

4 4 2 4 3.yx a xa





LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 38

Xét





3

0 2 30y x a xa



    

 

2

1

1 30 .

3 0*

x

x x xa

x xa







   









Hàm số có ba điểm cực trị khi và chỉ khi

 

*

có hai nghiệm phân biệt khác

1

 

2

14 3 0

11

5.

4

1 1 30

a



   



   





  





Vì

7

a



















nên





6; 4; 3 .

a



Vậy có

3

giá trị nguyên của

a

thỏa mãn bài toán.

Câu 42: Cho hai số phức

z

và

w

thỏa mãn

24zw



và

22

2 8 6 34.z zw w i   

Gọi

M

và

m

lần lượt là GTLN và GTNN của biểu thức

22

2.Pz w

Tính

.

Mm

A.

43.

B.

160

.

3

C.

91

.

2

D.

170

.

3

Lời giải

Chọn D

Ta có



 

22

2 86 2 86.z zw w i z w z w i      

Áp dụng BĐT môđun, ta có

        

2 86 2 86 2 86z wz w i z wz w i z wz w i

4 10 34 4 10 6 11.

zw zw zw

        

Mặt khác, ta có

22

22 2 2

4 2.6 2 2 4 2.11z w zw     

22

88

88 3 6 258 88 3 258 86.

3

zw P P     

Suy ra

88

86, .

3

Mm

Vậy

170

.

3

Mm

Câu 43: Cho khối lăng trụ đứng

.ABC A B C



có đáy

ABC

là tam giác đều cạnh

.a

Biết thể tích của khối

lăng trụ đã cho bằng

3

.

2

a

Khoảng cách từ điểm

A



đến mặt phẳng

 

ACB



bằng

A.

6

.

7

a

B.

2 57

.

19

a

C.

57

19

a

D.

3

.

7

a

Lời giải

Chọn B

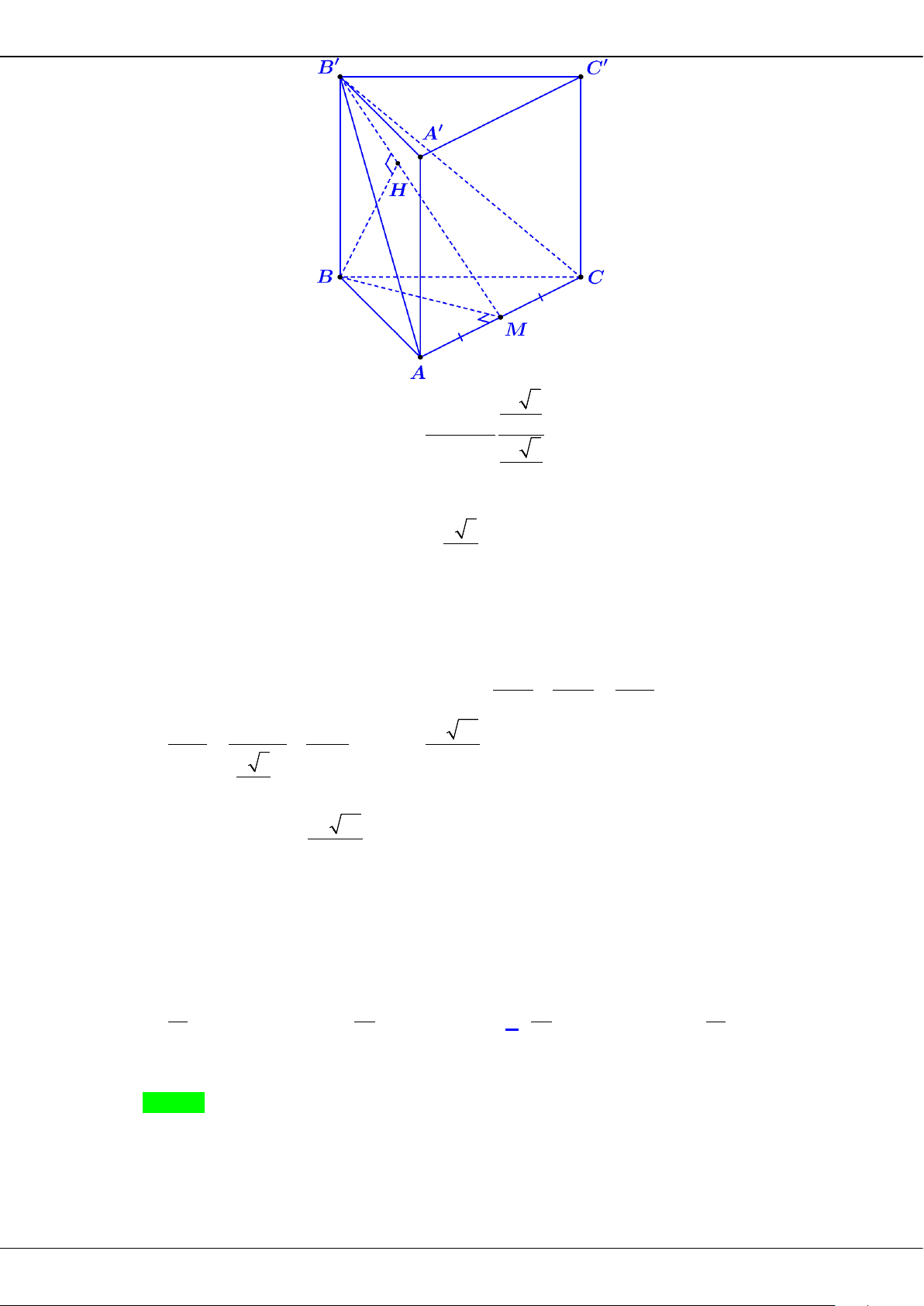
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 39

Ta có

3

.

2

3

2

.2

3

4

ABC A B C

ABC

ABC A B C

ABC

a

V

V BB S BB a

S

a





  

và

 

, ,.d A ACB d B ACB

 



Kẻ

,BM AC M AC

và

,.BH BM H BM





Suy ra

M

là trung điểm

AC

và

3

.

2

a

BM 

Vì

 

.

AC BB

AC BB M

AC BM























Mà

 

BH BB M





suy ra

.AC BH

Ta có

 

,.AC BH B M BH BH ACB



 

Do đó

 

,.d B ACB BH





Xét tam giác vuông

MBB



vuông tại

,B

ta có

222

111

BB BM BH





 

22

2

1 1 1 2 57

.

19

2

3

2

a

BH

a

   





















Vậy

 

2 57

,.

19

a

d A ACB





Câu 44: Cho hàm số

 

y fx

có đạo hàm cấp hai liên tục trên



và hàm số

 

32

.g x ax x cx d 

Đồ thị của hai hàm số

 

y fx

và

 

y gx

cắt nhau tại ba điểm có hoành độ lần lượt là

1;1; 2.

Biết rằng

   

2 6 6,f x xf x x x

 

   

và

   

1 3 1 3.ff



 

Diện tích hình

phẳng giới hạn bởi hai đồ thị

 

y fx

và

 

y gx

bằng

A.

91

.

12

B.

37

.

6

C.

37

.

12

D.

91

.

6

Lời giải

Chọn C

Ta có

       

2 66 66.f x xf x x xf x f x x





  

   



Lấy nguyên hàm hai vế, ta được

   

2

1

36 .xf x f x x x C



  

Vì

   

131 3ff



 

nên suy ra

1

1.C 

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 40

Khi đó

  

 



22

3 61 3 61.

xf x f x x x xf x x x







    



Lấy nguyên hàm hai vế, ta được

 

32

2

3.xf x x x x C  

Vì





13f



nên suy ra

2

0.C



Khi đó

 

32

3

xf x x x x 

hay

 

2

3 1.fx x x



Mặt khác, đồ thị của hai hàm số

 

y fx

và

 

y gx



cắt nhau tại ba điểm có hoành độ lần

lượt là

1;1; 2

suy ra

       

2 1 1,gx f x ax x x  

với

0.a 

Đồng nhất hệ số của

2

x

hai vế, ta được





11 11 2 1.aa

   

Suy ra

       

2 1 1.gx f x x x x   

Phương trình hoành độ giao điểm của

 

y gx

và

 

y fx

là



 



1

0 1.

2

x

gx f x x

x







  







Vậy diện tích hình phẳng cần tìm là

   

 







22

11

37

d 2 1 1d .

12

S gx f x x x x x x



     



Câu 45: Trên tập hợp các số phức, xét phương trình

2

4 40z mz m 

(

m

là tham số thực). Biết rằng

với

0

mm

thì phương trình đã cho có hai nghiệm phân biệt

12

,zz

thỏa mãn

 

2

12 2

4 12 .z mz z  

Khẳng định nào sau đây là đúng?

A.

0

52

;.

12 3

m



















B.

0

3

;1 .

5

m



















C.

0

12

;.

35

m



















D.

0

11

;.

72

m



















Lời giải

Chọn A

2

4 4.mm



 

TH1:

2

1

04 4 0 .

0

m

mm

m









  







Suy ra phương trình có hai nghiệm thực phân biệt

12

,.zz

Khi đó

 

22

22 2 2

4 4 04 1 .z mz m m z z   

Ta có

 

22

2 22 22 2 2

1 2 2 12 2 12 2 1

4 12 2 2 2z mz z zz z zz z z          

(vô lý).

TH2.

2

0 4 4 0 0 1.mm m



   

Suy ra phương trình có hai nghiệm phức liên hợp

12

,.zz

Khi đó

 

22

22 2 2

4 4 04 1 .z mz m m z z   

Theo định lý Vi-et, ta có

12

4

.

4

Szz m

P zz m

















Mà

 

2

2 22 2

1 2 2 1 2 12

4 12 2 2 2z m z z z z zz S P P        

2

1

4 20

2

1

16 8 2 4 .

16 8 4 2

16 12 2 0

2

16 8 2 4

16 4 2 0

m

mm m m

m mm

mm

mm m

mm



















      









 











 









 











LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 41

Vậy

0

1 52

;.

2 12 3

m



















Câu 46: Trong không gian

Oxyz

, cho đường thẳng

11

:

1 12

xyz

d





. Gọi

 

P

là mặt phẳng chứa

trục

Oy

sao cho đường thẳng

d

không cắt mặt phẳng

 

.P

Khi đó sin của góc tạo bởi trục

Ox

và mặt phẳng

 

P

bằng

A.

5

.

5

B.

2

.

2

C.

25

.

5

D.

3

.

2

Lời giải

Chọn C

Vì mặt phẳng

 

P

chứa trục

Oy

nên

 

:0P ax cz

(với

22

0ac

).

Ta có

d

không cắt mặt phẳng





P

nên suy ra





// .

dP

Khi đó

 

. 0 2 0.

d

P

nu a c 

    

Chọn

1c 

ta được

2.a 

Suy ra

 

: 2 0.P xz

Vậy

 





 

2

22222

2

sin , cos , .

5

100.20 1

P

Ox P i n 

 

  



Câu 47: Có bao nhiêu cặp số nguyên

 

;xy

thỏa mãn

 

22

ln

ln 16 2

22

16 2

2023 2023 ln 2023

xy

































?

A.

41.

B.

42.

C.

40.

D.

16.

Lời giải

Chọn C

Điều kiện:

22

0

.

16 2 0



















xy

Bất phương trình đã cho tương đương

 





22

16 2

ln

22

16 2

2023 ln .2023 1 * .

xy

xy x y

xy



















 



































Với





22

ln

2023 0, ,

xy x y

xy

 

 

ta xét các trường hợp sau

• TH1. Nếu

22

16 2

ln 0

xy



























ta suy ra

 

*

1VT 

(thỏa mãn).

• TH2. Nếu

22

16 2

ln 0

xy



























ta suy ra

 

*

1VT 

(thỏa mãn).

• TH3. Nếu

22

16 2

ln 0

xy



























ta suy ra





*

1

VT 

(loại).

Khi đó bất phương trình

 

22 22

16 2 16 2

* ln 0 1

xy xy











  















 

2

22

16 2 16 4.xy xy xy xy   

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 42

Dựa vào hình vẽ và kết hợp với điều kiện đề bài, ta suy ra có

40

cặp số nguyên

 

;xy

thỏa mãn

bài toán.

Câu 48: Cho hình nón có đường sinh bằng

2a

và góc ở đỉnh bằng

90 .

Cắt hình nón bằng mặt phẳng

 

P

đi qua đỉnh sao cho góc giữa

 

P

và mặt đáy hình nón bằng

60 .

Tính diện tích

S

của thiết

diện tạo thành.

A.

2

42

.

3

a

S 

B.

2

.

3

a

S 

C.

2

52

.

3

a

S 

D.

2

82

.

3

a

S 

Lời giải

Chọn A

Vì tam giác

SOC

vuông cân ở

O

suy ra

2.OC SO a

Giả sử mặt phẳng

 

P

cắt đường tròn đáy theo dây cung

.AB

Gọi

H

là trung điểm của

AB

suy ra

,OH AB

kết hợp với

SO

vuông góc với đáy suy ra

 

,AB SOH

từ đó suy ra



60 .SHO 

Trong tam giác vuông

SOH

có

6

tan 30

3

a

OH SO 

và

26

.

sin 60 3

SO a

SH 



Trong tam giác vuông

OHB

có

2 2 22

6 23

2.

93

a

BH OB OH a a   

Vậy diện tích thiết diện tạo thành là

2

1 2 62 3 4 2

.. . .

2 33 3

SAB

aa a

S SH AB SH BH  

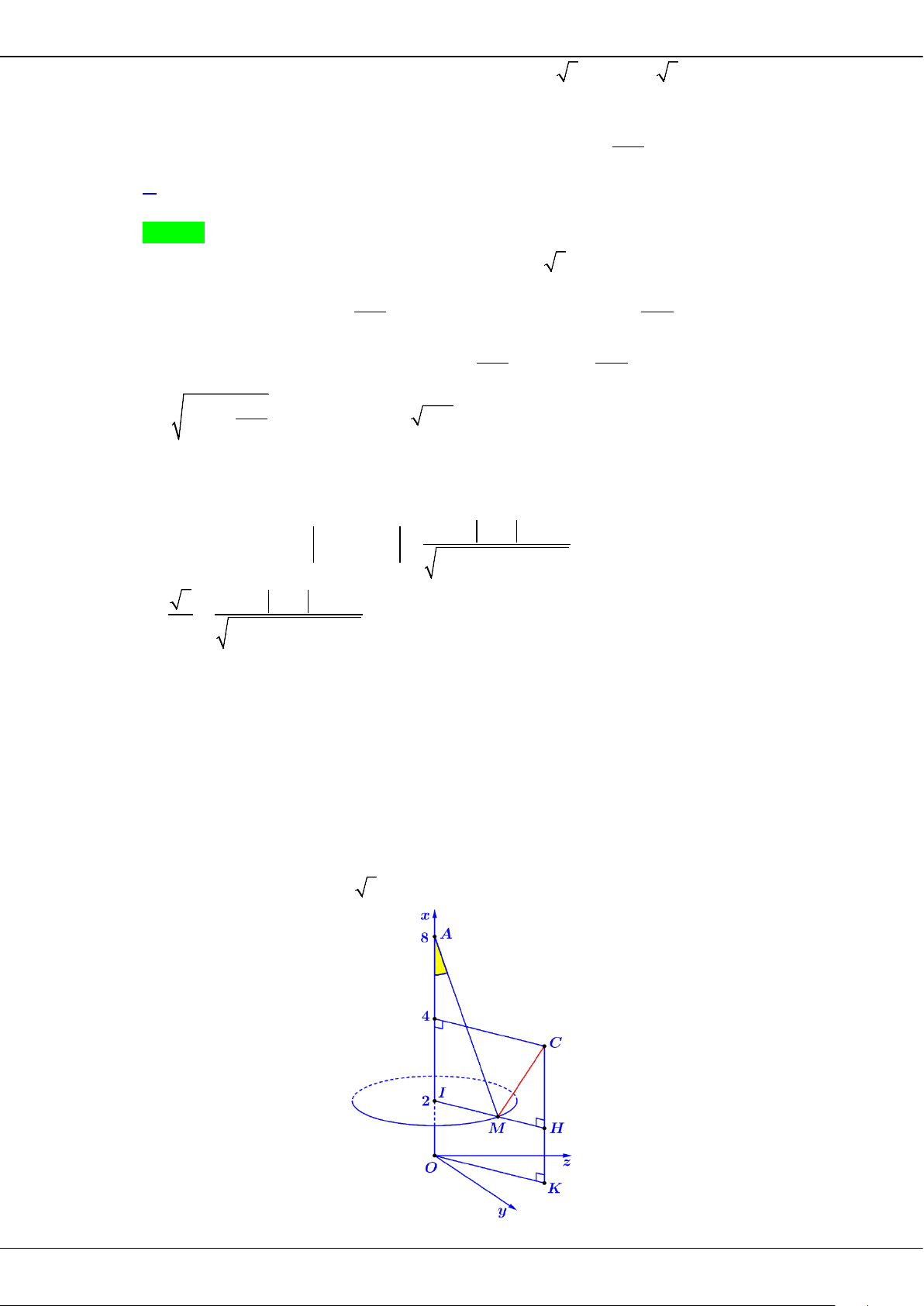
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 43

Câu 49: Trong không gian

,

Oxyz

cho điểm









 

8;0; 0 , 2;9; 3 3 , 4; 6; 2 3 .AB C

Xét các điểm

M

có

hoành độ dương thay đổi sao cho

AM

luôn tạo với trục

Ox

một góc

30

và tam giác

OAM

vuông. Tìm giá trị nhỏ nhất của biểu thức

22

192

2.

P MA MB

MC

 

A.

176.

B.

144.

C.

240.

D.

80.

Lời giải

Chọn A

Xét điểm

E

thỏa mãn

20

EA EB

  

suy ra

 

4; 6; 2 3E

trùng với điểm

.C

Khi đó

   

22

192 192

22P MA MB ME EA ME EB

MC MC

    

   

 

2 22 2 22

192 192

32 2 3ME ME EA EB EA EB MC CA CB

MC MC

    

  

2 22 22

192

2 3 . 48MC CA CB MC CA CB

MC

  

(Theo BĐT Côsi).

Vì

22

CA CB

không đổi nên để

min min

.P MC

Gọi





;;M xyz

với

0,x



suy ra

     

8; ; , ; ; , 8; 0; 0 .AM x y z OM x y z OA  

  

Ta có

 

2

22

8

cos , cos ,

8

x

AM Ox AM i

x yz





 

 

 

2

22

2

22

8

3

8 3 0 *.

2

8

x

x yz



     

 

Mặt khác, vì tam giác

OAM

vuông nên ta có 2 trường hợp sau

TH1. Tam giác

OAM

vuông tại

,O

khi đó

.0 0OM OA x

 

(loại do

0x 

).

TH2. Tam giác

OAM

vuông tại

,M

khi đó

 

22

. 0 8 0.AM OM x x y z   

 

Kết hợp với

 

*

ta suy ra

   

2

8

3 8 80

2

x

xx x

x







  







(loại

8x 

do

MA

).

Thay

2x 

vào

 

*

ta được

22

12.yz



Suy ra điểm

M

thuộc đường tròn đáy của hình nón với trục

,AI

mặt đáy là hình tròn có tâm

 

2; 0; 0I

và bán kính

2 3.R 

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 44

Ta có

22 2

4.MC HC HM HM  

Để

min min

.MC HM



Dựa vào hình vẽ, ta thấy

 

2

min

6 23 23 23.

HM IH IM   

Suy ra

 

2

min

4 2 3 4.MC

 

Vậy

22

min

48 176.P MC CA CB 

Câu 50: Có bao nhiêu giá trị nguyên của tham số

 

2023; 2023

m 

để hàm số

 

3 43 2

1 13

84 82

4 24

y m xx mxx 

đồng biến trên khoảng

 

1; 3

?

A.

4047.

B.

4045.

C.

4044.

D.

2022.

Lời giải

Chọn B

Xét hàm số

 

3 43 2

1 13

84 82

4 24

m xx mxx

fx 

có

 





 

33 2

8 12 8 2.fx m x x m x



    

Để

 

y fx

đồng biến trên khoảng

 

1; 3

ta có hai trường hợp sau

TH1: Nếu

   

 

   

33 2

3

8 12 8 2 0, 1; 3

0, 1; 3

3

10

0

4 24

m x xmx x

fx x

mm

f





      







 











 









   

 

3

33

21 21, 1;3

*.

1

m x mx x x x

m





     















Xét hàm số

 

3

gt t t

có





2

3 1 0, .

gt t t



  



Suy ra hàm số

 

gt

luôn đồng biến trên

.

Khi đó

 

       

2 1 , 1; 3 2 1, 1; 3

*

11

g mx g x x mx x x

mm



     















 

1;3

21

5

max

5

.

3

1

x

m

x

m

































  















TH2: Nếu

   

 

0, 1; 3

10

fx x

f





 













, tương tự ta cũng có

 

1;3

21

min

1.

1

x

m

x

m









































Kết hợp cả hai trường hợp, ta suy ra

 

5

;1 ; .

3

m







   









Vì

 

2023; 2023

m



















nên





2022; 2021; ;2021; 2022 .m   

Vậy có tất cả

4045

số nguyên

m

thỏa mãn yêu cầu bài toán.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 45

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT CHỢ GẠO

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.A

2.D

3.A

4.A

5.A

6.C

7.D

8.D

9.D

10.D

11.C

12.B

13.B

14.D

15.C

16.A

17.C

18.A

19.A

20.B

21.D

22.C

23.C

24.A

25.D

26.A

27.C

28.C

29.C

30.A

31.A

32.C

33.C

34.C

35.D

36.D

37.C

38.B

39.C

40.A

41.C

42.D

43.A

44.C

45.B

46.B

47.D

48.C

49.A

50.C

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Điểm

M

trong hình vẽ bên biểu diễn phức nào sau đây?

A.

1

2zi= +

. B.

2

zi= −

. C.

3

12zi= +

. D.

4

12zi= −

.

Lời giải

Chọn A

( )

2;1M

là điểm biểu diễn của số phức

1

2

zi= +

.

Câu 2. Đạo hàm của hàm số





ln 2 1yx

trên khoảng

1

;

2























bằng:

A.





1

21xe

. B.

1

21x

. C.





2

21xe

. D.

2

21x

.

Lời giải:

Chọn D.

Điều kiện xác định:

1

2 10

2

  xx

.

Do hàm số

ln

yu

có đạo hàm





u

y

u

trên miền xác định của nó với





u ux

.

Vậy hàm số





ln 2 1yx

có đạo hàm





21

2

21 21











x

y

xx

.

Câu 3. Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

e

yx=

là

A.

1e

y ex

−

′

=

. B.

1e

yx

−

′

=

. C.

1

e

yx

e

−

′

=

. D.

e

y ex

′

=

.

Lời giải

Chọn A

Ta có

(

)

1ee

y x ex

−

′

= =

.

Câu 4. Tìm tập nghiệm

S

của bất phương trình

( ) ( )

11

22

log 1 log 2 1xx+< −

.

1

2

O

M

y

x

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 46

A.

( )

2;S = +∞

. B.

( )

1; 2S = −

. C.

( )

;2

S = −∞

. D.

1

;2

2

S



=





.

Lời giải

Chọn A

Ta có

(

) ( )

11

22

log 1 log 2 1xx+< −

12 1

2 10

xx

x

+> −



⇔



−>



1

2

x⇔ <<

.

Câu 5. Cho cấp số cộng

( )

n

u

có

1

2u =

và công sai

4d =

. Số hạng thứ 12 của cấp số cộng đã cho bằng

A.

46

. B.

50

. C.

96

. D.

28

.

Lời giải

Chọn A

Áp dụng công thức số hạng tổng quát của cấp số cộng

( )

1

1 2.

n

uu n d n= + − ∀≥

Ta có:

12 1

11 2 11.4 46uu d=+=+ =

.

Câu 6. Trong không gian

Oxyz

, cho mặt phẳng

( ):2 1 0

xyz

α

+ −+=

. Vectơ nào sau đây không là

vectơ pháp tuyến của mặt phẳng

()

α

?

A.

( )

4

4; 2; 2 .

= −

 

n

B.

( )

2

2; 1;1 .−= −

 

n

C.

( )

3

2;1;1 .=

 

n

D.

( )

1

2; 1; 1 .= −



n

Lời giải

Chọn C

Mặt phẳng

( ):2 1 0

xyz

α

+ −+=

có vectơ pháp tuyến là

( )

1

2; 1; 1= −



n

nên các vectơ

21

= −

   

nn

,

41

2=

   

nn

cũng là các vectơ pháp tuyến của mặt phẳng

()

α

.

Vectơ

( )

3

2;1;1=

 

n

không cùng phương với

( )

1

2; 1; 1=

−



n

nên không phải là vectơ pháp tuyến

của mặt phẳng

()

α

.

Câu 7. Đồ thị hàm của hàm số

3

32yx x=−+ −

cắt trục tung tại điểm có tung độ bằng

A.

0

. B.

1

. C.

2

. D.

2−

.

Lời giải

Chọn D

Gọi

( )

00

;Mx y

là giao điểm của đồ thị hàm số với trục tung.

Ta có

0

x

=

suy ra

0

2y = −

.

Câu 8. Cho hàm số

( )

fx

liên tục và có đạo hàm trên đoạn

[

]

2;1−

, biết

( ) ( )

15, 21ff

= −=

. Tính

( )

2

1

'I f x dx

−

=

∫

.

A.

7I =

. B.

5=I

. C.

6I

=

. D.

4I =

.

Lời giải.

Chọn D

Ta có

(

) ( ) ( )

( )

2

1

' 1 2 51 4

2

I f x dx f x f f

−

= = = − − = −=

−

∫

.

Câu 9. Hàm số nào dưới đây có đồ thị dạng như đường cong hình vẽ bên?

A.

3

31yx x=−++

. B.

3 2

31yx x+= +

. C.

24

2yx x= − +

. D.

42

12yx x= − ++

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 47

Lời giải.

Chọn D

Câu 10. Trong không gian vơi hệ tọa độ

Oxyz

, cho mặt cầu

( )

2 22

: 8 2 10Sx y z x y+ + − + +=

. Tìm tọa độ

tâm và bán kính mặt cầu

( )

S

:

A.

(

)

4; 1; 0 , 2IR−=

. B.

( )

4; 1; 0 , 4IR−=

. C.

( )

4; 1; 0 , 2IR−=

. D.

( )

4; 1; 0 , 4IR

−=

.

Lời giải

Chọn D

( )

2 22

: 8 2 10Sx y z x y+ + − + +=

( )

4; 1; 0I⇒−

4R =

.

Câu 11. Trong không gian

,Oxyz

cho hai mặt phẳng

( )

P

và

( )

Q

lần lượt có hai vectơ pháp tuyến là

P

n

 

và

Q

n

 

. Biết góc giữa hai vectơ

P

n

 

và

Q

n

 

bằng

120 .°

Góc giữa hai mặt phẳng

( )

P

và

( )

Q

bằng.

A.

30



B.

45



C.

60



D.

90



Lời giải

Chọn C

Ta có:

( )



( )

(

)

(

)



; 120 ; 180 120 60 .

PQ

nn P Q= °⇒ = °− °= °

 

Câu 12. Cho số phức

( )

2

75zi= −

, phần ảo của số phức

z

bằng

A.

70i

. B.

70

. C.

70−

. D.

70i−

.

Lời giải

Chọn B

Ta có

( )

2

7 5 24 70 24 70

z i iz i= − = − ⇒= +

Vậy phần ảo của số phức

z

bằng

70

.

Câu 13. Cho khối lập phương có thể tích bằng

216

. Cạnh của khối lập phương đã cho bằng

A.

9.

B.

6

. C.

8

. D.

12

.

Lời giải:

Chọn B

Thể tích của lập phương là: V=a

3

=216

Suy ra a = 6

Câu 14. Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, cạnh bên

SA

vuông góc

với mặt phẳng đáy và

2SA a

=

. Thể tích

V

của khối chóp

.S ABCD

bằng

A.

3

2

6

a

V =

. B.

3

2

4

a

V =

. C.

3

2Va=

. D.

3

2

3

a

V =

.

Lời giải

Chọn D

Ta có

( )

SA ABCD SA⊥⇒

là đường cao của hình chóp

Câu 15. Một mặt phẳng

( )

P

cắt mặt cầu

( )

;S IR

theo giao tuyến là đường tròn. Khi đó đường tròn giao

tuyến có bán kính bằng:

A.

( )

22

;( )

2

R d IP−

. B.

( )

22

;( )R d IP+

. C.

( )

22

;( )R d IP−

. D.

( )

22

;( )

2

R d IP+

.

Lời giải

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 48

Chọn C

Thể tích khối chóp

.S ABCD

:

3

2

11 2

. . 2.

33 3

ABCD

a

V SA S a a= = =

.

Câu 16. Cho số phức

( )( )

12 34z ii=+−

. Phần thực của số phức

iz

tương ứng là

A.

2

. B.

11

. C.

2

−

. D.

11−

.

Lời giải

Chọn A

Ta có:

(

)

( )

12 34

z ii

=+−

11 2i= +

.

iz

( )

11 2 2 11ii i= −=+

.

Vậy phần thực của số phức

iz

là 2.

Câu 17. Cho hình trụ có đường kính đáy

2r

và độ dài đường cao

h

. Thể tích của khối trụ đã cho bằng

A.

2 rh

π

. B.

2

3

rh

π

. C.

2

rh

π

. D.

2

1

3

hr

π

.

Lời giải

Chọn C

Hình trụ có đường kính đáy

2r

nên nó có bán kính đáy bằng

r

. Vậy thể tích của khối trụ đã

cho bằng

2

rh

π

Câu 18. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

∆

có phương trình tham số

1

2 2, .

3

xt

y tt

zt

= +





=−∈





= +





Hỏi điểm

M

nào sau đây thuộc đường thẳng

∆

?

A.

( )

3; 2; 5M −

. B.

( )

3; 2; 5M

. C.

( )

3;2;5M −−−

. D.

( )

3;2;5M −−

.

Lời giải

Chọn A

Ứng với tham số

2t =

ta được điểm

( )

3; 2; 5M −

.

Câu 19. Cho hàm số

32

y ax bx cx d= + ++

có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ

thị hàm số đã cho có tọa độ là

A.

( 1; 0)−

. B.

(0; 1)−

. C.

(1; 4)

. D.

(0; 2)

.

Lời giải

Chọn A

Từ đồ thị, ta có đồ thị hàm số đã cho có điểm cực tiểu là

( 1; 0)−

.

Câu 20. Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

23

1

x

y

x

−

=

+

tương ứng có phương

trình là

A.

2

x =

và

1y =

. B.

1x = −

và

2y =

. C.

1x =

và

3y = −

. D.

1x =

và

2y =

.

Lời giải

Chọn B

Ta có:

lim 2

x

y

→±∞

=

nên đồ thị hàm số có đường tiệm cận ngang là

2y =

.

O

x

y

2

2−

1

4

1−

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 49

( )

1

lim

x

y

+

−

→−

= −∞







= +∞





nên đồ thị hàm số có đường tiệm cận đứng là

1x = −

.

Câu 21. Tìm tập nghiệm T của bất phương trình

1

4

log (4 2) 1

x − ≥−

.

A.

3

;

2



+∞







. B.

13

;

22







. C.

13

;

22







. D.

13

;

22









Lời giải:

Chọn D

Bất phương trình tương đương

1

1 13

04 2

4 22

xx

−



< −≤ ⇔ <≤





Vậy tập nghiệm là

13

;

22

T



=







.

Câu 22. Số cách xếp

6

bạn học sinh ngồi vào bàn dài

6

chỗ là

A.

270

B.

18

C.

720

D.

36

Lời giải

Chọn C

Số cách xếp là:

6! 720=

(cách).

Câu 23. Tìm nguyên hàm

( ) ( )

sin dFx x x x= +

∫

biết

(

)

0 19

F

=

.

A.

(

)

2

cos 20Fx x x=++

. B.

( )

2

cos 20Fx x x=−+

.

C.

(

)

2

1

cos 20

2

Fx x x

=−+

. D.

( )

2

1

cos 20

2

Fx x x=++

.

Lời giải

Chọn C

Ta có:

( )

sin dFx x x x= +

∫

2

cos

2

x

xC=−+

Mà

( )

0 19 1 19

FC= ⇔− + =

20C⇔=

Vậy

( )

2

cos 20

2

x

Fx x=−+

.

Câu 24. Cho

( )

1

0

1f x dx =

∫

tích phân

( )

1

2

0

23f x x dx−

∫

bằng

A.

1

. B.

0

. C.

3

. D.

1−

.

Lời giải

Chọn A

Ta có:

(

)

( )

1 11

22

0 00

2 3 2 3 211f x x dx f x dx x dx− = − = −=

∫ ∫∫

.

Câu 25. Cho hàm số

( )

2

x

fx e x= −

. Khẳng định nào dưới đây đúng?

A.

( )

2

d 2.

x

fx x e x C=−+

∫

B.

( )

d 2.

x

fx x e xC=−+

∫

C.

( )

2

d 2.fx x e xC=++

∫

D.

( )

2

d.

x

fx x e x C=−+

∫

Lời giải

Chọn D

Ta có

( )

2

d 2d .

xx

fx x e x x e x C



= − =−+



∫∫

Câu 26. Cho hàm số

( )

fx

có bảng biến thiên như hình vẽ bên.

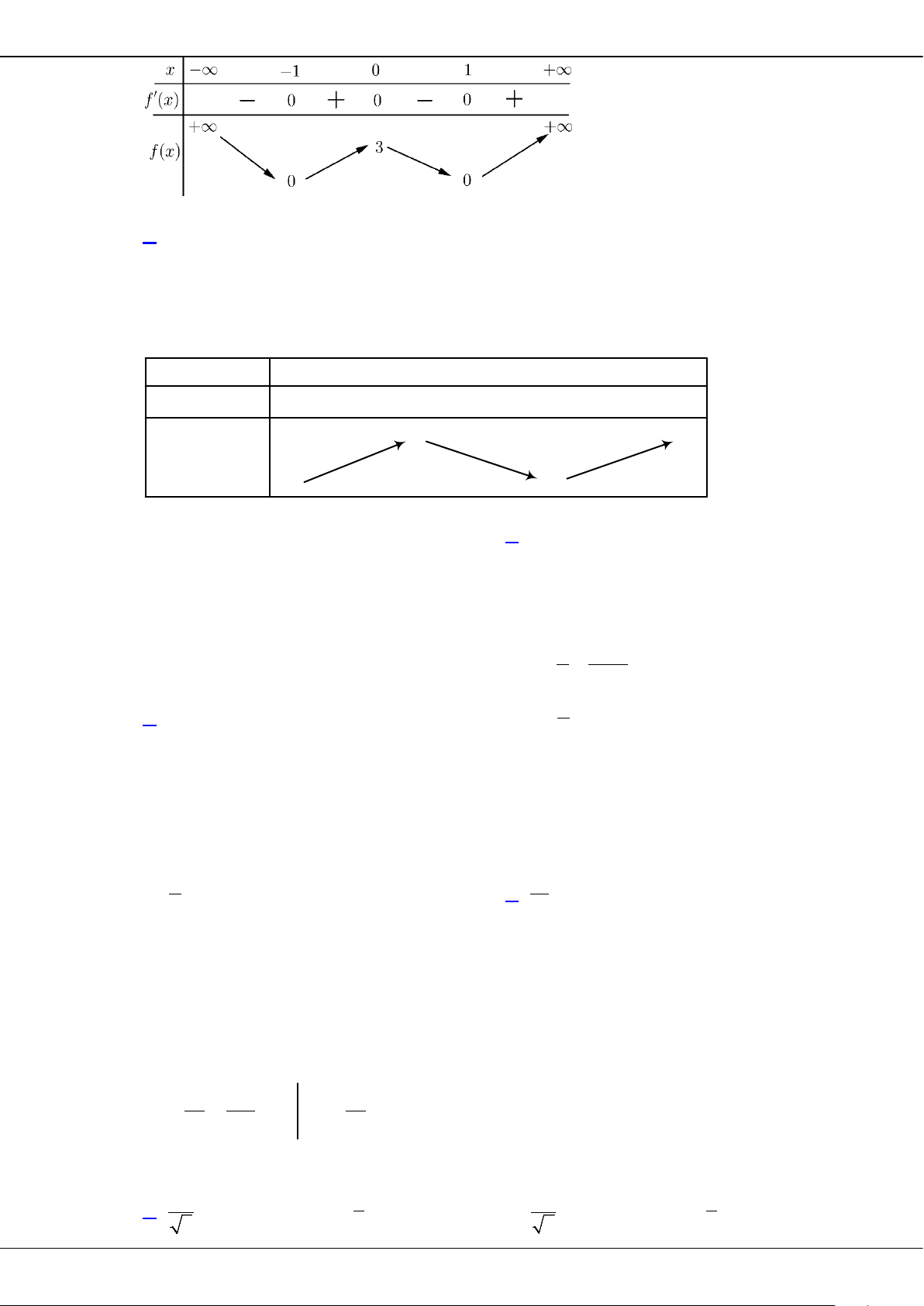
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 50

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

( )

1; 0−

. B.

( )

1;− +∞

. C.

( )

;1−∞ −

. D.

( )

0;1

.

Lời giải

Chọn A

Ta có

( )

1; 0 1;x ∈ − ∪ +∞

thì

'( ) 0

fx

>

nên hàm số đồng biến biến trên khoảng

( )

1; 0 .−

Câu 27. Cho hàm số

(

)

fx

có bảng biến thiên như sau

x

−∞

+∞

+

−

y

′

y

−∞

0

+

+∞

3−

1−

0

4−

Giá trị cực tiểu của hàm số đã cho bằng

A.

1−

. B.

0

. C.

4−

. D.

3−

.

Lời giải

Chọn C

Dựa vào BBT, hàm số có giá trị cực tiểu là

4y = −

.

Câu 28. Với các số thực dương

,ab

bất kì. Mệnh đề nào dưới đây đúng?

A.

( )

log log .logab a b=

. B.

log

aa

bb

=

.

C.

( )

log log logab a b= +

. D.

log logb loga

a

b

= −

.

Lời giải

Chọn C

Ta có

( )

log log logab a b= +

.

Câu 29. Tính thể tích V của khối tròn xoay khi quay hình phẳng (H) giới hạn bởi đồ thị hàm số

2

1yx= −

và trục Ox quanh trục Ox.

A.

5

.

3

π

B.

4.

π

C.

16

.

15

π

D.

3.

π

Lời giải:

Chọn C

Phương trình hoành độ giao điểm

2

1

10 .

1

=



−= ⇔



= −



x

Thể tích:

 

 

 

    

 

11 1

2

2 2 42

11 1

1 21

V y dx x dx x x dx

=

53

1

2 16

1

5 3 15

xx

x









  















.

Câu 30. Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng

a

. Tính côsin của góc giữa mặt bên và

mặt đáy.

A.

1

3

. B.

1

2

. C.

1

2

. D.

1

3

.

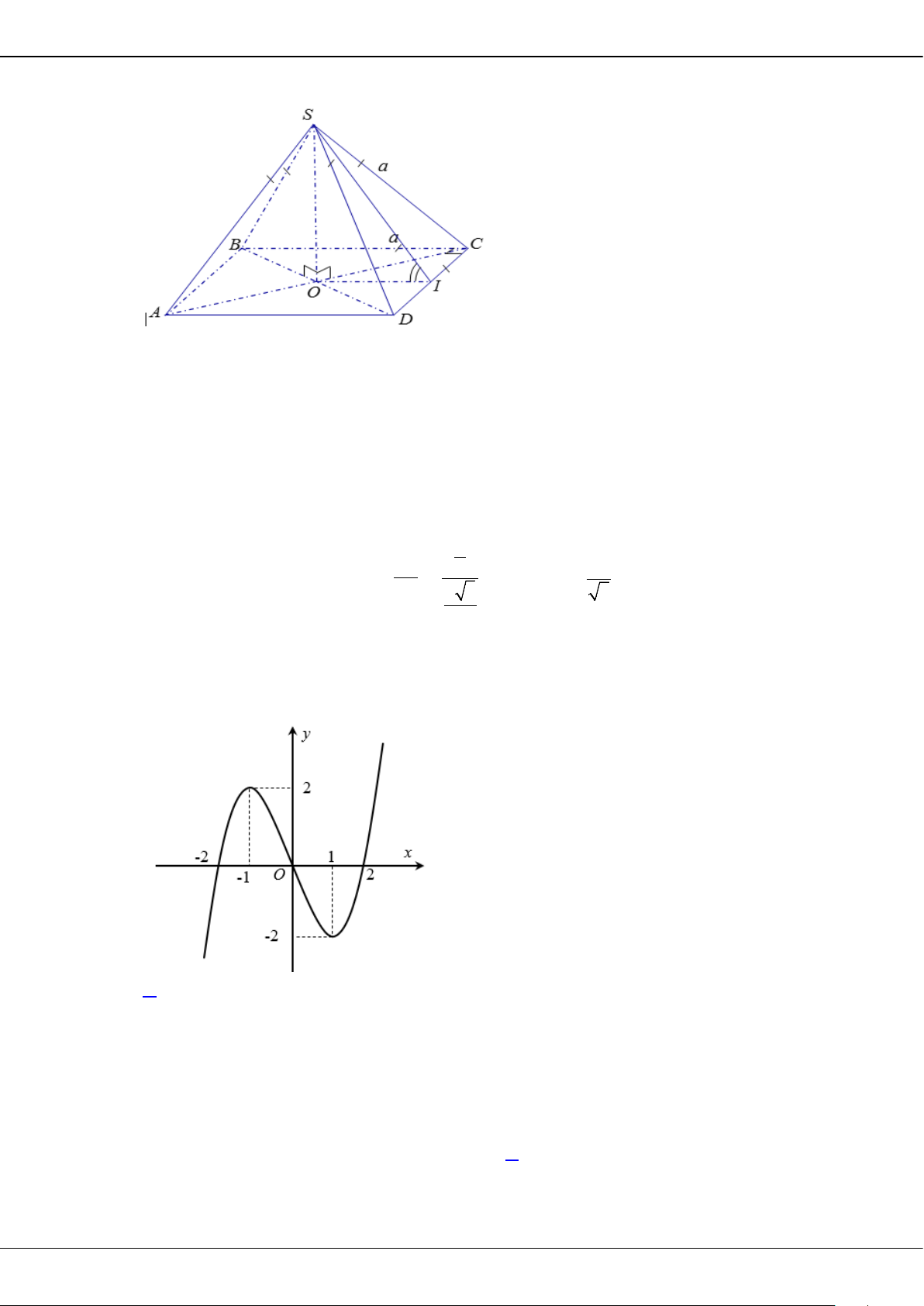
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 51

Lời giải

Chọn A

+ Gọi

O

là tâm của hình chóp tứ giác đều

.S ABCD

. Ta có

( )

SO ABCD⊥

, đáy

ABCD

là hình

vuông cạnh

a

và các mặt bên là các tam giác đều cạnh

a

.

+ Gọi

I

là trung điểm cạnh

CD

.

Theo giả thiết ta có:

(

)

(

)

SCD ABCD CD

OI CD

SI CD

∩=





⊥





⊥



nên góc giữa mặt bên

( )

SCD

và mặt đáy

(

)

ABCD

bằng góc giữa hai đường thẳng

OI

và

SI

bằng góc



SIO

. Khi đó:



cos

OI

SIO

SI

=

2

3

2

a

=



1

cos

3

SIO⇔=

.

Câu 31. Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên. Số nghiệm thực của

phương trình

( )

10

fx+=

là:

A.

3

. B.

1

. C.

0

. D.

2

.

Lời giải

Chọn A

Số nghiệm thực của phương trình

( )

1fx= −

chính là số giao điểm của đồ thị hàm số

( )

y fx=

và đường thẳng

1y = −

.

Câu 32. Cho hàm số

()y fx=

có đạo hàm

2

( ) ( 2)f x xx

′

= −

,

x∀∈

. Hàm số nghịch biến trên khoảng

A.

( )

0; 2

. B.

( )

1;− +∞

. C.

( )

;0−∞

. D.

(

)

;1−∞

.

Lời giải

Chọn C

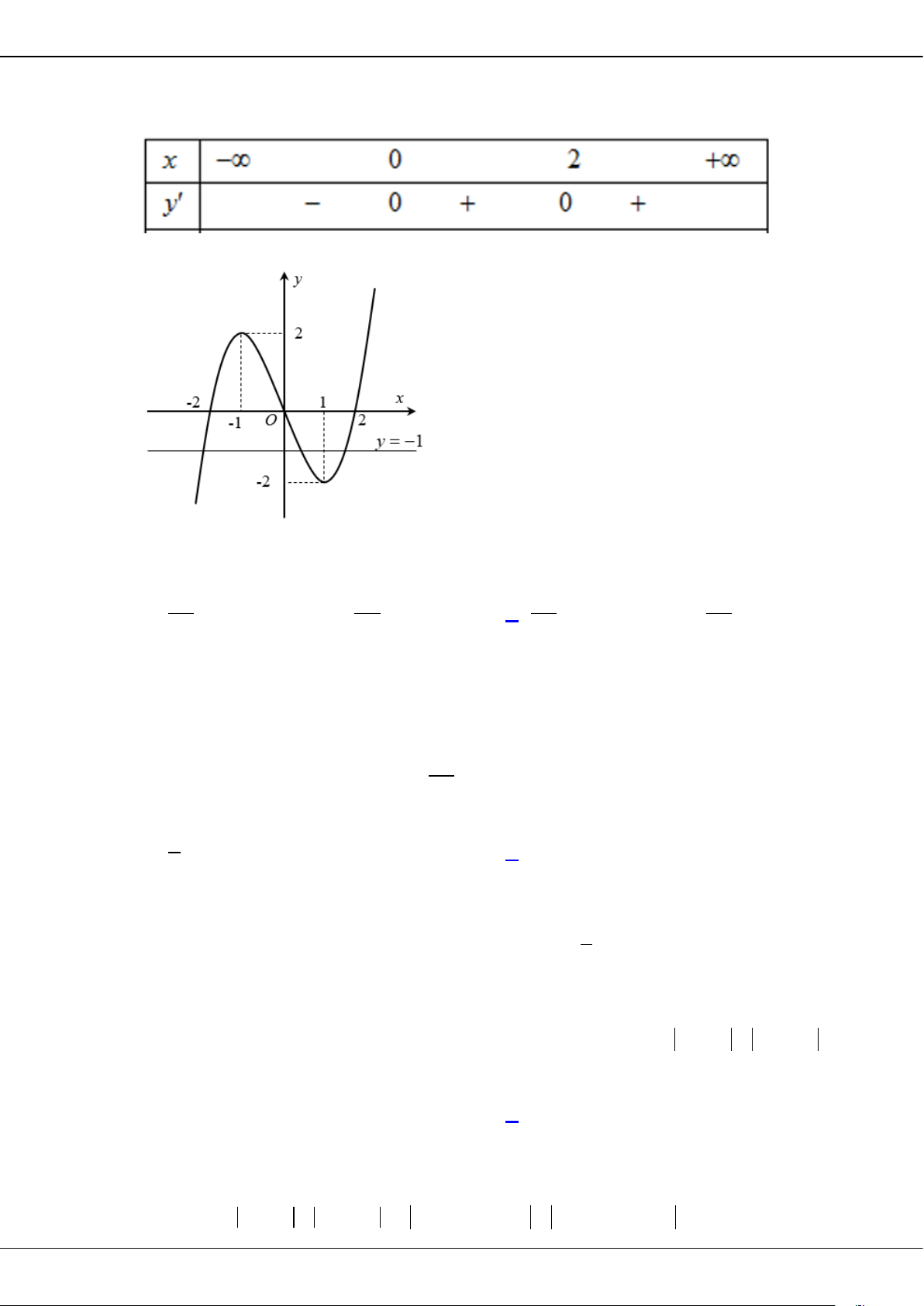
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 52

Ta có:

2

00

( ) 0 ( 2) 0

20 2

xx

f x xx

xx

= =



′

=⇔ −=⇔ ⇔



−= =



Bảng biến thiên:

Vậy hàm số nghịch biến trên khoảng

( )

;0−∞

Từ hình vẽ suy ra

3

nghiệm.

Câu 33. Từ một đội văn nghệ gồm 5 nam và 8 nữ cần lập một nhóm gồm 4 người hát tốp ca. Xác suất để

trong 4 người được chọn đều là nam bằng

A.

C

4

8

4

13

. B.

A

C

4

5

4

8

. C.

C

4

5

4

13

. D.

C

A

4

8

4

13

.

Lời giải

Chọn C

Chọn 4 người trong 13 người hát tốp ca có

C

4

13

. Nên

()nC

4

13

Gọi A là biến cố chọn được 4 người đều là nam và

()nA C

4

5

Nên xác suất của biến cố A là

()

C

PA

C



4

5

4

13

.

Câu 34. Tổng tất cả các nghiệm của phương trình

2.4 9.2 4 0

xx

− +=

bằng

A.

9

.

2

B.

2.

C.

1.

D.

4.

Lời giải

Chọn C

Ta có

( )

2

1

21

2.4 9.2 4 0 2. 2 9.2 4 0

2

24 2

x

xx x

x



=⇒=−



− +=⇔ − +=⇔



=⇒=





Vậy tổng các nghiệm của phương trình là

121−+ =

Câu 35. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức

z

thỏa mãn

1 12z iz i+− = −+

một

đường thẳng có phương trình

A.

4 6 30xy+ −=

. B.

4 6 30xy+ +=

.

C.

4 6 30xy− +=

. D.

4 6 30xy− −=

.

Lời giải

Chọn D

Đặt

z x yi= +

với

,xy∈

. Khi đó điểm

( )

;M xy

là điểm biểu diễn cho số phức

z

.

Từ giả thiết

( ) ( ) ( ) ( )

1 12 1 1 1 2z iz i x y i x y i+−=−+⇔ ++− = −++

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 53

( ) ( ) ( ) ( )

222 2

1112

4 6 3 0.

xyxy

xy

⇔+ +− =−++

⇔ − −=

Vậy tập hợp điểm biểu diễn số phức

z

là đường thẳng có phương trình:

4 6 30xy− −=

.

Câu 36. Trong không gian

Oxyz

, cho tam giác

ABC

∆

có

( )

1; 0; 2A −

,

(

)

2; 2; 1B −

và

( )

0; 0; 1C

. Đường

trung tuyến

AM

có phương trình là

A.

1

13

1

xt

yt

zt

= +





=−+





= +



. B.

1

23

xt

yt

zt

= −





= −





=−+



. C.

12

1

13

xt

yt

zt

=−+





= +





=−−



.

D.

1

23

x

yt

zt

=





= −





=−+



.

Lời giải

Chọn D

Do

M

là trung điểm của

BC

nên

(

)

1; 1; 1

M −

.

Ta có

( )

0; 1; 3AM = −



.

Đường thẳng

AM

đi qua

( )

1; 0; 2A −

, nhận

( )

0; 1; 3AM = −



làm vectơ chỉ phương có phương

trình là

1

23

x

yt

zt

=





= −





=−+



.

Câu 37. Trong không gian

Oxyz

, cho mặt phẳng

( )

:2 2 3 0P x yz+ −−=

và điểm

( )

1; 2; 4M −

. Tìm tọa độ

hình chiếu vuông góc của điểm trên mặt phẳng

A.

( )

5;2;2

. B.

( )

0; 0; 3−

. C.

( )

3; 0; 3

. D.

( )

1;1; 3

.

Lời giải

Chọn C

+ Gọi

∆

là đường thẳng đi qua

(

)

1; 2; 4M

−

và vuông góc với mặt phẳng .

Phương trình tham số của

∆

là:

( )

12

22

4

xt

y tt

zt

= +





=−+ ∈





= −





.

+ Gọi

( )

1 2; 2 2;4H t tt+ −+ −

là hình chiếu vuông góc của

M

trên

( )

P

.

Vì

H

nằm trên

( )

P

nên thay tọa độ của

H

vào phương trình của

( )

P

, ta được:

( ) ( ) ( )

21 2 2 2 2 4 3 0 9 9 0 1t tt t t++−+−−−=⇔−=⇔=

.

Vậy

( )

3; 0; 3H

.

Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a,

( )

SA ABCD⊥

,

3SA a=

. Tính theo a khoảng cách từ điểm O đến mặt phẳng

( )

SBC

.

A.

2

a

B.

3

4

a

C.

5

6

a

D.

7

8

a

Lời giải

Chọn B

M

( )

.P

( )

P

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 54

Ta có:

( )

, 2,d A SBC d O SBC=

Gọi H là hình chiếu của A lên SB.

Ta có

( ) ( )

SA BC

BC SAB BC AH AH SBC

AB BC

⊥



⇒⊥ ⇒⊥⇒ ⊥



⊥



Mà

2 2 2222

1 1 1 114 3

33 2

a

AH

AH SA AB a a a

= + = += ⇒ =

Do đó

( )

1 13

,,

2 24

a

d O SBC d A SBC AH= = =

Câu 39. Tập hợp nào sau đây thuộc khoảng nghiệm của bất phương trình

(

) (

)

1

22

log 2 1 .log 2 2 2

xx+

− −<

?

A.

5

;3

4







. B.

5

;3

2







. C.

22

5

log ;log 3

4







. D.

22

57

log ;log

33







.

Lời giải

Chọn D

Điều kiện:

{

0

1 11

2 10 2 2 0

0

11

2 20 2 2

xx

x

++



−> > >

⇔ ⇔ ⇔>



+>

−> >



.

Ta có:

( ) ( )

( )

222

log 2 1 . log 2 1 log 2 2 1

xx

BPT



⇔ − −+ <



Đặt

(

)

2

log 2 1

x

t

= −

, khi đó:

( ) ( )

2

1 . 1 2 20tt t t⇔ + < ⇔ +− <

Suy ra:

( )

21

2

22

2 1 2log211 2 212

15

1 2 3 log log 3

44

xx

x

t

x

−

−<< ⇔−< − <⇔ < −<

⇔ +< < ⇔ < <

Kết hợp với đk ta có tập nghiệm của bất phương trình là:

22

5

log ;log 3

4

S



=





Kết luận: Chọn C

Câu 40. Cho hàm sô

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa

mãn

( ) (

)

31 31 2FG+=

và

( )

25 25 0FG+=

. Tính

( )

11

9

3 2dfx x−

∫

.

A.

1

3

. B.

1

6

. C.

1

2

. D.

11

31

.

Lời giải.

Chọn A

Đặt

3 2 d 3 dux u x= −⇒ =

, hay

1

d d

3

xu=

.

Khi

9x =

thì

( )

9 25u =

. Khi

11x =

thì

( )

11 31u =

. Khi đó

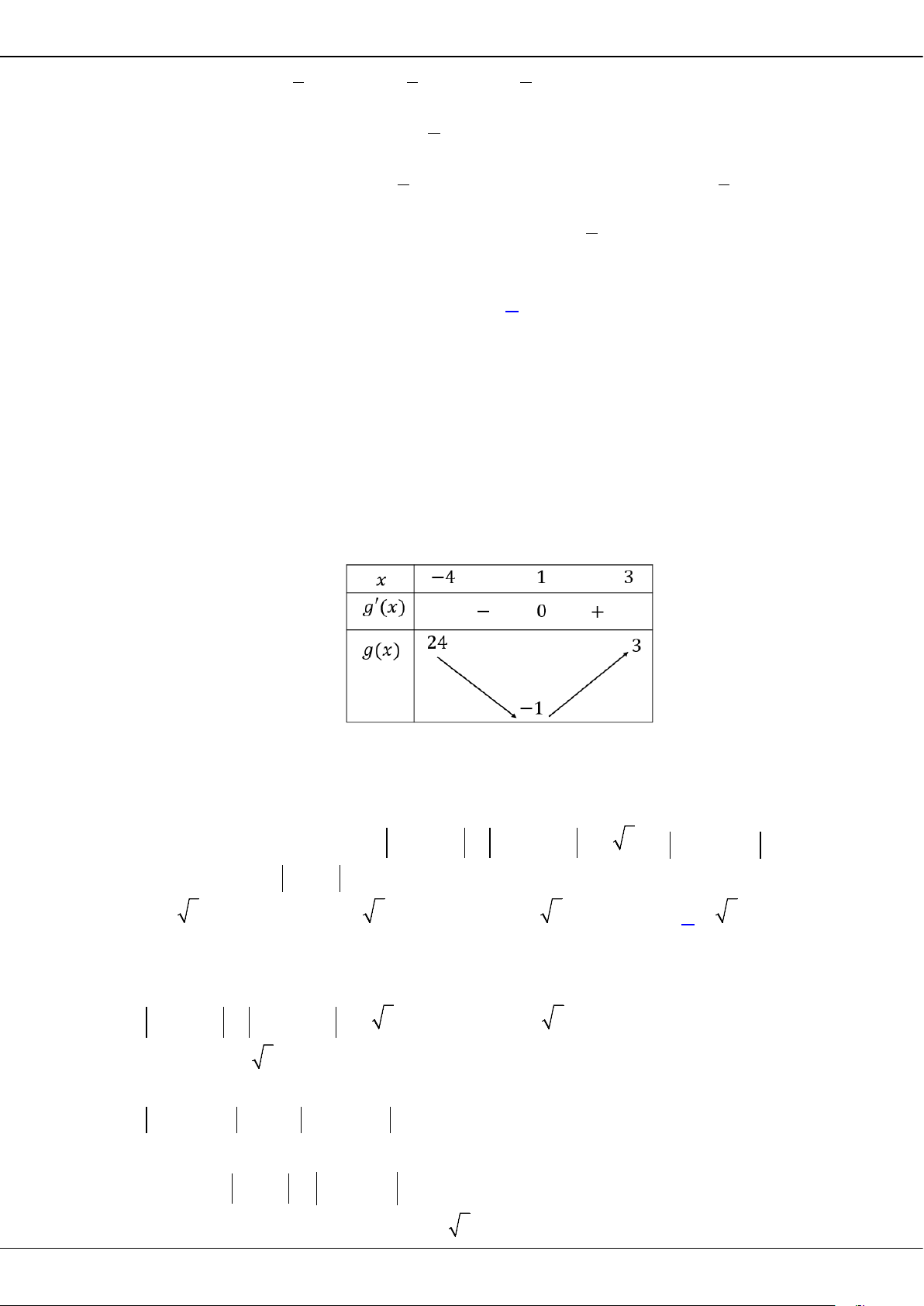
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 55

( )

( ) ( ) ( ) ( )

( ) ( )

( )

( ) ( )

( )

( ) ( )

( )

( ) ( )

( )

11 31 31 31 31

9 25 25 25 25

111

3 2d d d d d

336

1

31 25 31 25

6

11

31 31 25 25

63

f x x fu u fx x fx x fx x

F F GG

FG FG



−= = = +







= −+−





= +−+ =



∫ ∫ ∫ ∫∫

Câu 41. Có bao nhiêu giá trị nguyên của tham số

m

để hàm số

32

1

2023

3

y x x mx

  

có hai điểm

cực trị thuộc khoảng

 

4; 3

?

A.

5

. B.

4

. C.

3

. D.

2

.

Lời giải

Chọn C

Ta có:

2

'2y x xm

. Xét phương trình

 

2

'0 2 01y x xm   

.

Để hàm số có hai điểm cực trị thuộc khoảng

 

4; 3

thì phương trình

 

1

phải có 2 nghiệm

phân biệt thuộc khoảng





4; 3

Ta có:

 

2

12mx x

.

Xét hàm số

 

2

2gx x x

có

 

' 22gx x

. Cho

 

' 0 2 20 1gx x x

 

.

Bảng biến thiên của





gx

Dựa vào bảng biến thiên ta thấy, phương trình

 

1

có 2 nghiệm phân biệt thuộc khoảng

 

4; 3

khi

13m 

.Do

 

0; 1; 2mm 

.

Vậy có 3 giá trị nguyên của tham số

m

thỏa yêu cầu đề bài.

Câu 42. Cho hai số phức

12

,zz

thỏa mãn

11

2 4 7 62z iz i  

và

2

1 2 1.iz i

 

Giá trị

nhỏ nhất của biểu thức

12

Pzz

bằng

A.

3 2 2.



B.

2 2 2.

C.

3 2 1.

D.

2 2 1.

Lời giải

Chọn D

Gọi

M

là điểm biểu diễn số phức

1

z

, khi đó



  

11

2 4 7 62 62; 2;1; 4;7z i z i MA MB A B

      

Ta có

62AB 

, khi đó M thuộc đoạn thẳng

AB

.

Gọi

N

là điểm biểu diễn số phức

2

z

, khi đó

 

22

1 2 1 2 1 1, 2; 1iz i z i NI I  

Khi đó

N

nằm trên đường tròn tâm

 

2;1 ; 1IR

Ta có

 

12 1 2

P z z z z MN    

Ta có

: 30AB x y

;

 

; 22d I AB 

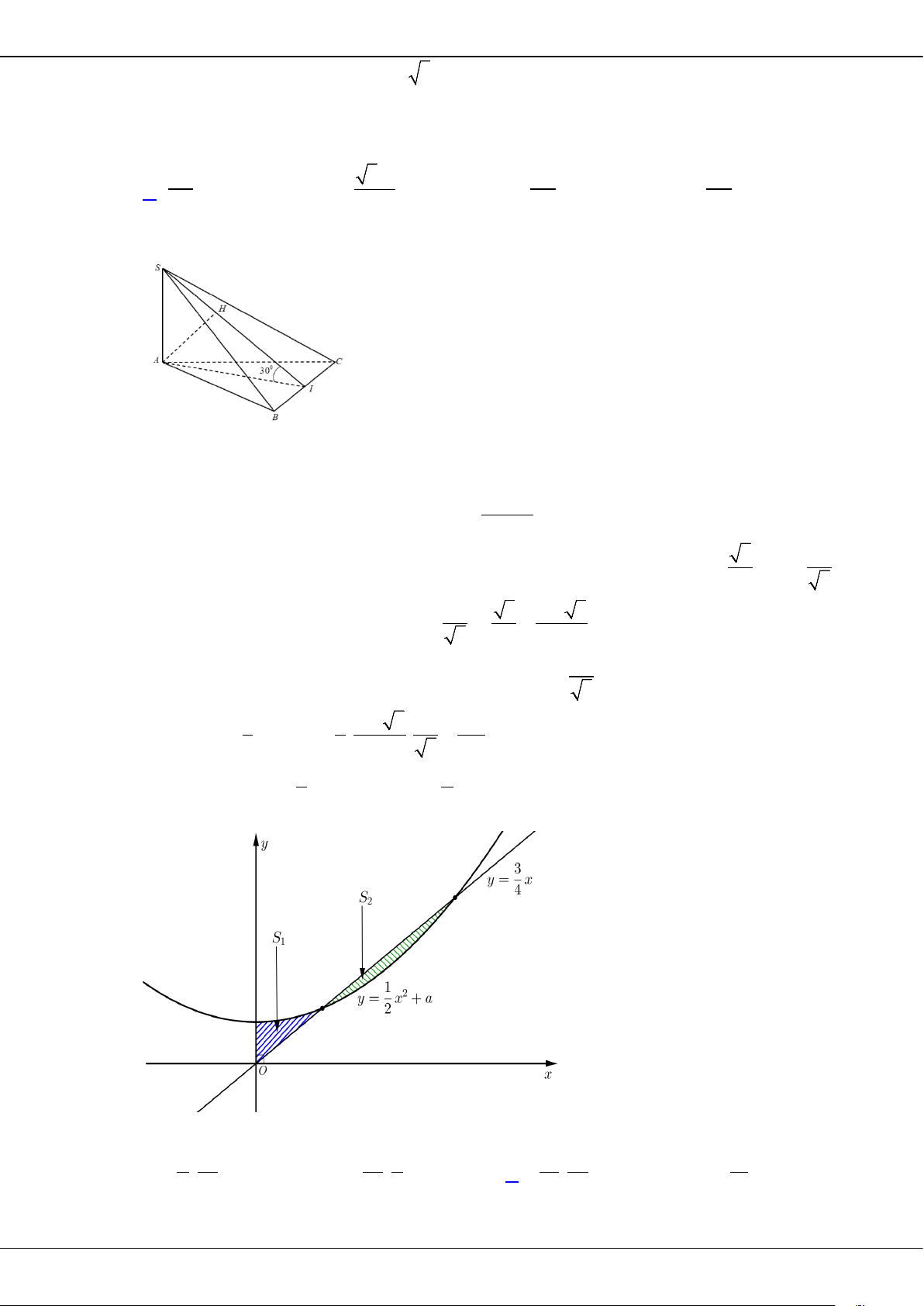
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 56

Khi đó

 

min ; 2 2 1P d I AB R

  

.

Câu 43. Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều,

( )

SA ABC⊥

. Mặt phẳng

( )

SBC

cách

A

một khoảng bằng

a

và hợp với mặt phẳng

( )

ABC

góc

0

30

. Thể tích của khối chóp

.S ABC

bằng

A.

3

8

9

a

. B.

3

12

a

. C.

3

4

9

a

. D.

3

8

3

a

.

Lời giải

Chọn A

Gọi

I

là trung điểm sủa

BC

suy ra góc giữa mp

( )

SBC

và mp

( )

ABC

là



0

30

SIA =

.

H

là hình chiếu vuông góc của

A

trên

SI

suy ra

( )

,d A SBC AH a= =

.

Xét tam giác

AHI

vuông tại

H

suy ra

0

2

sin 30

AH

AI a= =

.

Giả sử tam giác đều

ABC

có cạnh bằng

x

, mà

AI

là đường cao suy ra

34

2

3

a

ax x

= ⇒=

.

Diện tích tam giác đều

ABC

là

2

4 34 3

.

43

3

ABC

aa

S



= =





.

Xét tam giác

SAI

vuông tại

A

suy ra

0

2

.tan 30

3

a

SA AI= =

.

Vậy

23

.

1 14 3 2 8

.. . .

3 33 9

3

S ABC ABC

a aa

V S SA= = =

.

Câu 44. Cho đường thẳng

3

4

yx

=

và parabol

2

1

2

y xa

= +

(

a

là tham số thực dương). Gọi

12

,SS

lần

lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên.

Khi

12

SS=

thì

a

thuộc khoảng nào dưới đây ?

A.

19

;

4 32







. B.

71

;

32 4







. C.

37

;

16 32







. D.

3

0;

16







.

Lời giải

Chọn C

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 57

Xét phương trình hoành độ giao điểm

22

1 313

0

2 4 24

x a x x xa+= ⇔ − +=

(

)

*

.

Do đường thẳng

3

4

yx=

cắt parabol

2

1

2

y xa= +

tại hai điểm phân biệt có hoành độ dương nên

phương trình

(

)

*

có hai nghiệm dương phân biệt

12

0 xx<<

0

9

20

9

00

16

32

20

0

a

Sa

a

P

∆>



−>



⇔ >⇔ ⇔<<





>



.

Ta có:

1

2

1

0

13

24

x

S x a x dx



= +−





∫

;

22

11

22

2

31 1 3

42 2 4

xx

S x x a dx x a x dx

  

= − − =− +−

  

  

∫∫

.

12

1

22

1 2 12

0

13 13

00

24 24

xx

x

S S S S x a x dx x a x dx



= ⇔ − =⇔ +− + +− =





∫∫

2

3

22

0

13 3

00

2 4 68

x

x a x dx ax x



⇔ +− =⇔ + − =





∫

2

3 22

22 2 2

1 3 13

00

6 8 68

x ax x x a x

⇔ + − =⇔ +− =

.

Mà

2

x

là nghiệm phương trình

(

)

*

nên

2

13

0

24

x xa− +=

.

Trừ vế với vế hai phương trình được:

( )

2

0

13

0

9

38

8

xL

xx

x TM

=





−+=⇔



=





.

Với

2

9

8

x

=

27

128

a⇒=

(tm). Vậy

27 3 7

;

128 16 32

a



= ∈





.

Mà trong khoảng

( )

0; 20

và

0

m ∈



nên có 10 giá trị

0

m

thoả mãn.

Câu 45. Trên tập hợp các số phức, xét phương trình

 

22

21 0z m zm 

(

m

là tham số thực). Có

bao nhiêu giá trị của

m

để phương trình đó có nghiệm

0

z

thỏa mãn

0

7?z



A.

2

. B.

3

. C.

1

. D.

4

.

Lời giải

Chọn B

22

( 1) 2 1m mm



    

.

+) Nếu

1

0 2 10

2

mm



  

, phương trình có 2 nghiệm thực. Khi đó

00

77zz  

.

Thế

0

7z 

vào phương trình ta được:

2

14 35 0 7 14mm m   

(nhận).

Thế

0

7z 

vào phương trình ta được:

2

14 63 0mm 

, phương trình này vô nghiệm.

+) Nếu

1

0 2 10

2

mm



  

, phương trình có 2 nghiệm phức

12

,zz 

thỏa

21

zz



. Khi đó

2

22

12 1

.7zz z m 

hay

7m 

(loại) hoặc

7m 

(nhận).

Vậy tổng cộng có 3 giá trị của

m

là

7 14m 

và

7m 

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 58

Câu 46. Trong không gian với hệ tọa độ

,Oxyz

cho hai đường thẳng

1

12

:

21 1

x yz

d

−+

= =

−

và

2

122

:

13 2

xy z

d

−+−

= =

−

. Gọi

∆

là đường thẳng song song với

( )

: 70Pxyz++−=

và cắt

12

, dd

lần

lượt tại hai điểm

,AB

sao cho

AB

ngắn nhất. Phương trình của đường thẳng

∆

là.

A.

12

5.

9

xt

y

zt

= −





=





=−+



B.

6

5

.

2

9

2

xt

y

zt





= −



=





=−+





C.

6

5

.

2

9

2

x

yt

zt





=



= −





=−+





D.

62

5

.

2

9

2

xt

yt

zt





= −



= +





=−+





Lời giải

Chọn B

( )

1

2

1 2;; 2

1 ;23;22

A d A aa a

Bd B b b b

∈ ⇒ + −−

∈ ⇒ + −+ −

∆

có vectơ chỉ phương

( )

2 ; 3 2; 2 4

AB b a b a b a

= − −− − ++



( )

P

có vectơ pháp tuyến

(

)

1; 1; 1

P

n =

 

Vì

( )

// P∆

nên

.0 1

PP

AB n AB n b a⊥ ⇔ =⇔=−

   

.Khi đó

( )

1; 2 5; 6AB a a a=−− − −



( )

(

) ( )

2 22

2

1 25 6

6 30 62

5 49 7 2

6;

222

AB a a a

aa

= −− + − + −

= −+



= − + ≥ ∀∈







Dấu

""=

xảy ra khi

5 59 7 7

6; ; , ; 0;

2 22 2 2

a A AB



=⇒−=−







Đường thẳng

∆

đi qua điểm

59

6; ;

22

A



−





và vec tơ chỉ phương

( )

1; 0;1

d

u = −

 

Vậy phương trình của

∆

là

6

5

2

9

2

xt

y

zt



= −



=





=−+





Câu 47. Có bao nhiêu cặp số nguyên

(

)

,xy

thỏa mãn

( ) ( )

22

3

log 3 3 .

2

xy

x x y y xy

x y xy

+

= −+ −+

+++

A.

1

. B.

2

. C.

4

. D.

6

.

Lời giải

Chọn D

Điều kiện

22

0 0.

2

xy

x y xy

+

>⇔+>

+++

( ) ( )

22

3

log 3 3

2

xy

x x y y xy

x y xy

+

= −+ −+

+++

( )

22 22

33

2log 2log 2 3 3x y x y xy x y xy x y⇔ +− +++=++−−

( )

22 22

33

2log 2 2log 2 2 3 3x y x y xy x y xy x y⇔ + +− + + + = + + +− −

( ) ( )

( )

22 22

33

2log 3 3 3 3 2log 2 2x y x y x y xy x y xy⇔ + + + = +++++++

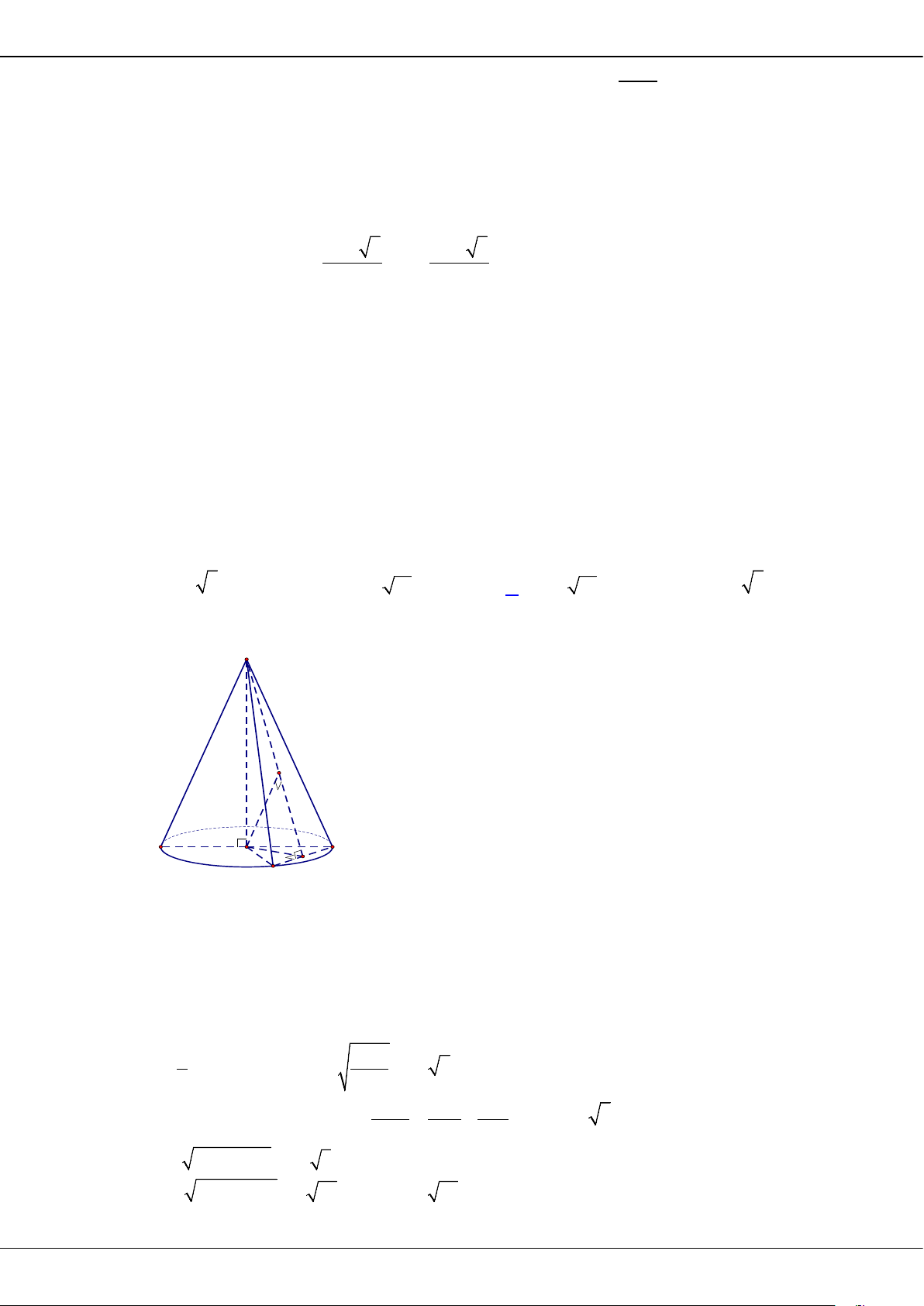
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 59

Xét hàm đặc trưng

( ) ( )

3

2 log , 0; ,f t t tt= + ∈ +∞

ta có

( )

2

1 0, 0; .

.ln 3

ft t

t

′

= + > ∀ ∈ +∞

Suy ra hàm

( )

ft

đồng biến trên khoảng

( )

0; +∞

.

Phương trình

( )

22 22

33 2 233f x y f x y xy x y xy x y⇔ + = +++⇔+++=+

( )

22

3 3 20⇔ + − + − +=x y xy y

.

Điều kiện của

y

để phương trình có nghiệm là

( )

2

3 4 320− − −+≥y yy

2

3 23 3 23

3 6 10

33

−+

⇔− + + ≥ ⇔ ≤ ≤yy y

.

Do

y ∈

nên

{ }

0;1;2∈y

.

+ Với

0y =

, ta được

2

1

3 20

2

x

xx

x

=



− +=⇔



=



.

+ Với

1y =

, ta được

2

0

20

2

=



−=⇔



=



x

xx

x

.

+ Với

2y =

, ta được

2

0

1

x

xx

x

=



−=⇔



=



.

Vậy có

6

cặp số thỏa mãn đề bài.

Câu 48. Cho khối nón

( )

N

có chiều cao bằng

6a

và thể tích bằng

3

90 a

π

. Cắt

( )

N

bởi một mặt phẳng đi

qua đỉnh và cách tâm của đáy một khoảng bằng

3a

ta được thiết diện có diện tích bằng

A.

2

65a

. B.

2

6 11a

. C.

2

12 11a

. D.

2

12 5a

.

Lời giải

Chọn C

Giả sử mặt phẳng

( )

P

đi qua đỉnh của hình nón cắt hình nón theo thiết diện là tam giác

SBC

.

Gọi

I

là trung điểm của

BC

. Ta có

( )

BC OI

BC SOI

BC SO

⊥



⇒⊥



⊥



.

Kẻ

OH SI⊥

( )

H SI∈

, mà

OH BC⊥

(vì

( )

BC SOI⊥

và

( )

OH SOI⊂

)

suy ra

( )

OH SBC⊥

⇒

( )

;3d O SBC OH a= =

.

2

13

π. . 3 5

3

V

V SO OC OC a

SO

π

= ⇒= =

.

Trong

SOI∆

vuông tại

O

có:

2 22

1 11

OH SO OI

= +

23OI a⇒=

22

43SI SO OI a= +=

.

22

33 2 33IC OC OI a BC a= − = ⇒=

.

H

I

C

O

B

A

S

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 60

Vậy

2

1

. 12 11

2

SBC

S SI BC a= =

.

Câu 49. Trong không gian

Oxyz

cho

( )

1;1;1A

và hai đường thẳng

1

22

:1

2

xt

dy

zt

= −





=





=−+



,

2

53

:1

3

xs

dy

zs

= +





=





= −



. Gọi

B

,

C

là các điểm lần lượt di động trên

1

d

,

2

d

. Giá trị nhỏ nhất của biểu thức

P AB BC CA=++

là:

A.

2 29

. B.

29

. C.

30

. D.

2 30

.

Lời giải

Chọn A

+ Từ giả thiết suy ra hai đường thẳng

12

,

dd

cùng nằm trong mặt phẳng

( )

:1y

α

=

và

(

)

A

α

∈

.

+

1

d

có một véc tơ chỉ phương

( )

1

2; 0;1u = −



;

2

d

có một véc tơ chỉ phương

( )

2

3; 0; 1u = −



.

Do

[ ]

( )

12

, 0; 1; 0 0uu = ≠





nên

1

d

cắt

2

d

.

+ Gọi

12

,AA

lần lượt là điểm đối xứng của

A

qua

1

d

và

2

d

.

+ Gọi

( )

β

là mặt phẳng qua

A

và vuông góc với

1

d

( )

:2 1 0xz

β

⇒ − ++=

.

+ Gọi

( )

1

Id

β

= ∩

, thì tọa độ của

I

là nghiệm của hệ

( )

22

1

0; 1; 1

2

2 10

xt

y

I

zt

xz

= −





=



⇒−



=−+



− ++=



( )

1

1;1; 3A⇒ −−

.

+ Gọi

( )

δ

là mặt phẳng qua

A

và vuông góc với

2

d

( )

:3 2 0xz

δ

⇒ −−=

.

+ Gọi

( )

2

Jd

δ

= ∩

, thì tọa độ của

J

là nghiệm của hệ

( )

53

1

2; 1; 4

3

3 20

xs

y

J

zs

xz

= +





=



⇒



= −



−−=



(

)

2

3;1; 7A⇒

.

+ Ta có:

1 2 12

P AB BC CA A B BC CA A A=++= ++ ≥

P⇒

đạt GTNN khi

12

P AA=

min 1 2

2 29

P AA⇒= =

.

Vậy giá trị nhỏ nhất của

P

là

2 29

.

Câu 50. Có bao nhiêu số nguyên

m

thuộc khoảng

( 10;10)−

để hàm số

3

22 3y x mx=−+

đồng biến

trên

(1; )+∞

?

A. 11. B. 7. C. 12. D. 8.

Lời giải

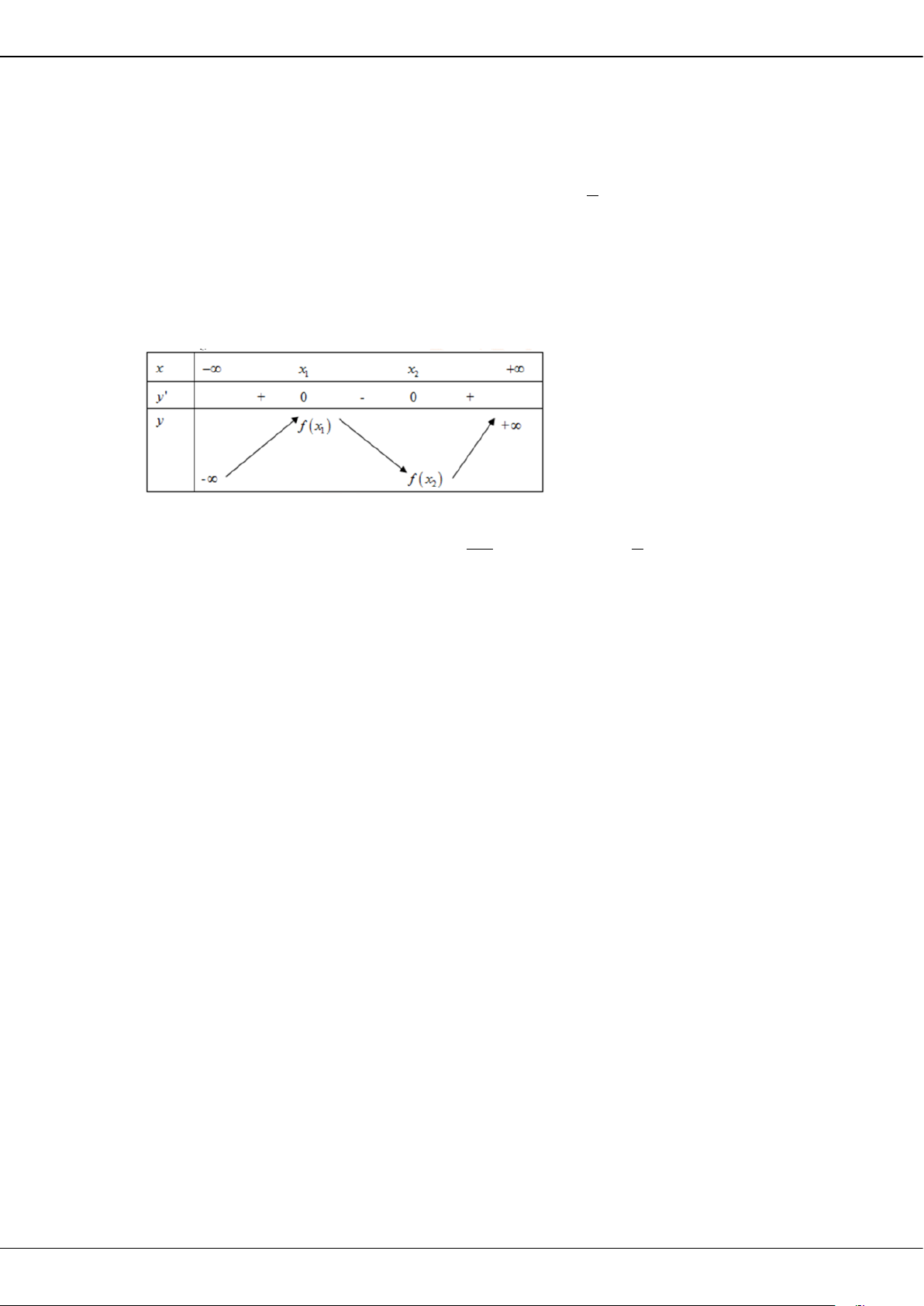
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 61

Chọn C

Xét hàm số:

3

() 2 2 3f x x mx=−+

có:

2

( ) 6 2 ; 12fx x m m

′′

= − ∆=

+ Trường hợp 1:

00m

′

∆≤ ⇔ ≤

. Suy ra

( ) 0, (1; )fx x

′

≥ ∀ ∈ +∞

.

Vậy yêu cầu bài toán

0

00

0

5

(1) 0 5 2 0

2

m

mm

m

fm

m



≤



≤≤

 

⇔ ⇔ ⇔ ⇔≤

 

≥ −≥

≤

 



.

Kết hợp với điều kiện

; ( 10;10)mm∈ ∈−

ta được

m ∈

{9;8;7;6;5;4;3;2;1;0}−−−−−−−−−

Ta có 10 giá trị của

m

thoả mãn yêu cầu bài toán (1)

+ Trường hợp 2:

00m

′

∆> ⇔ >

. Suy ra

() 0fx

′

=

có 2 nghiệm phân biệt

( )

12 1 2

,xx x x<

Ta có bảng biến thiên:

Vậy yêu cầu bài toán

12

0

25

1 10 0

62

(1) 0

52 0

m

xx m

f

m



>



>





⇔ < ≤⇔− +≥ ⇔ < ≤





≥

−≥





.

Kết hợp với điều kiện

; ( 10;10)

mm∈ ∈−

ta được

{1; 2}m ∈

.

Ta có 2 giá trị của

m

thoả mãn yêu cầu bài toán (2).

Từ (1) và (2) suy ra: có tất cả có 12 giá trị của

m

thoả mãn yêu cầu bài toán.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 62

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT VĨNH BÌNH

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

LỜI GIẢI CHI TIẾT

Câu 1. Cho số phức

67zi

= +

. Số phức liên hợp của

z

là

A.

67zi= +

. B.

67zi=−−

. C.

67

zi=−+

. D.

67zi= −

.

Hướng dẫn giải

Chọn D.

67 67z iz i=+ ⇔=−

Câu 2. Trên khoảng

( )

0, +∞

, đạo hàm của hàm số

3

log 2023=yx

là

A.

1

ln 3

y

x

′

=

. B.

1

2023

′

=y

x

. C.

1

y

x

′

=

. D.

1

2023 ln3

′

=

y

x

.

Hướng dẫn giải

Chọn A.

Ta có

( )

2023

1

2023 ln 3 ln 3

′

= =

x

y

xx

.

Câu 3. Trên khoảng

( )

0; +∞

, đạo hàm của hàm số

3

4

yx=

là :

A.

3

1

3

yx

′

=

. B.

4

3

yx

′

=

. C.

3

4

3

yx

′

=

. D.

1

3

yx

′

=

.

Hướng dẫn giải

Chọn C.

Trên khoảng

( )

0; +∞

ta có

4

3

4

3

y xx= =

, do đó ta có:

41

3

33

44

33

yx x x

′



′

= = =





.

Câu 4. Tập nghiệm của bất phương trình

23

1

5

25

x+

>

là:

A.

5

;

2



− +∞





. B.

5

;

2



−∞ −





. C.

( )

0; +∞

. D.

1

;

2



− +∞





.

Hướng dẫn giải

Chọn A.

Ta có:

23 23 2

15

5 5 5 23 2

25 2

xx

+ +−

> ⇔ > ⇔ + >− ⇔ >−

.

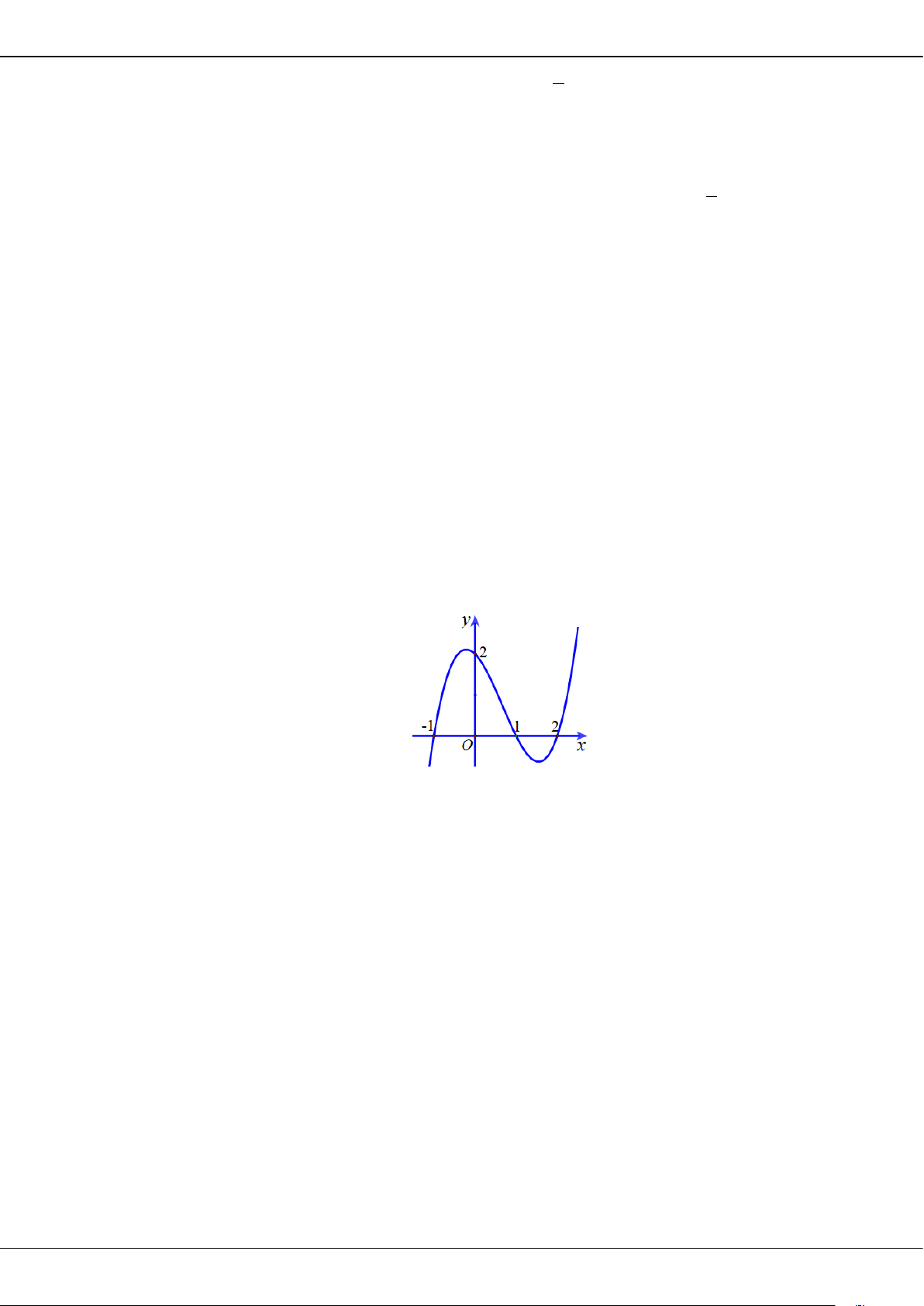
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 63

Vậy tập nghiệm của bất phương trình đã cho là:

5

;

2

S



= − +∞





.

Câu 5: Cho cấp số nhân

( )

n

u

với

2

6u =

và

5

162u =

. Công bội của cấp số nhân đã cho bằng

A. 3. B.

3−

. C.

2

. D.

1

3

.

Hướng dẫn giải

Chọn A.

Câu 6: Trong không gian

Oxyz

, cho hai điểm

( ) ( )

1; 0; 2 , 3; 4; 6AB−

. Một vectơ pháp tuyến của mặt phẳng

vuông góc với đường thẳng

AB

là:

A.

( )

1; 2; 4−

. B.

( )

2; 4;8−

. C.

( )

1;2;4

. D.

( )

2; 4;8

−−

.

Hướng dẫn giải

( )

2; 4;8AB =



.

Một vectơ pháp tuyến của mặt phẳng vuông góc với đường thẳng

AB

là

( )

1;2;4

.

Câu 7: Cho hàm số

32

y ax bx cx d= + ++

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm

của đồ thị hàm số đã cho và trục tung là điểm nào trong các điểm sau

A.

( )

1; 0

. B.

( )

2;0

. C.

(

)

1; 0−

. D.

( )

0; 2

.

Hướng dẫn giải

Chọn D

Từ đồ thị, ta dễ thấy đồ thị hàm số cắt trục tung tại điểm có tọa độ

( )

0; 2

.

Câu 8. Nếu

( )

4

1

dx 2fx = −

∫

và

( )

4

1

dx 6

gx = −

∫

thì

( ) ( )

4

1

dxf x gx−





∫

bằng

A.

8

−

. B.

4

. C.

4−

. D.

8

.

Hướng dẫn giải

Chọn D.

Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

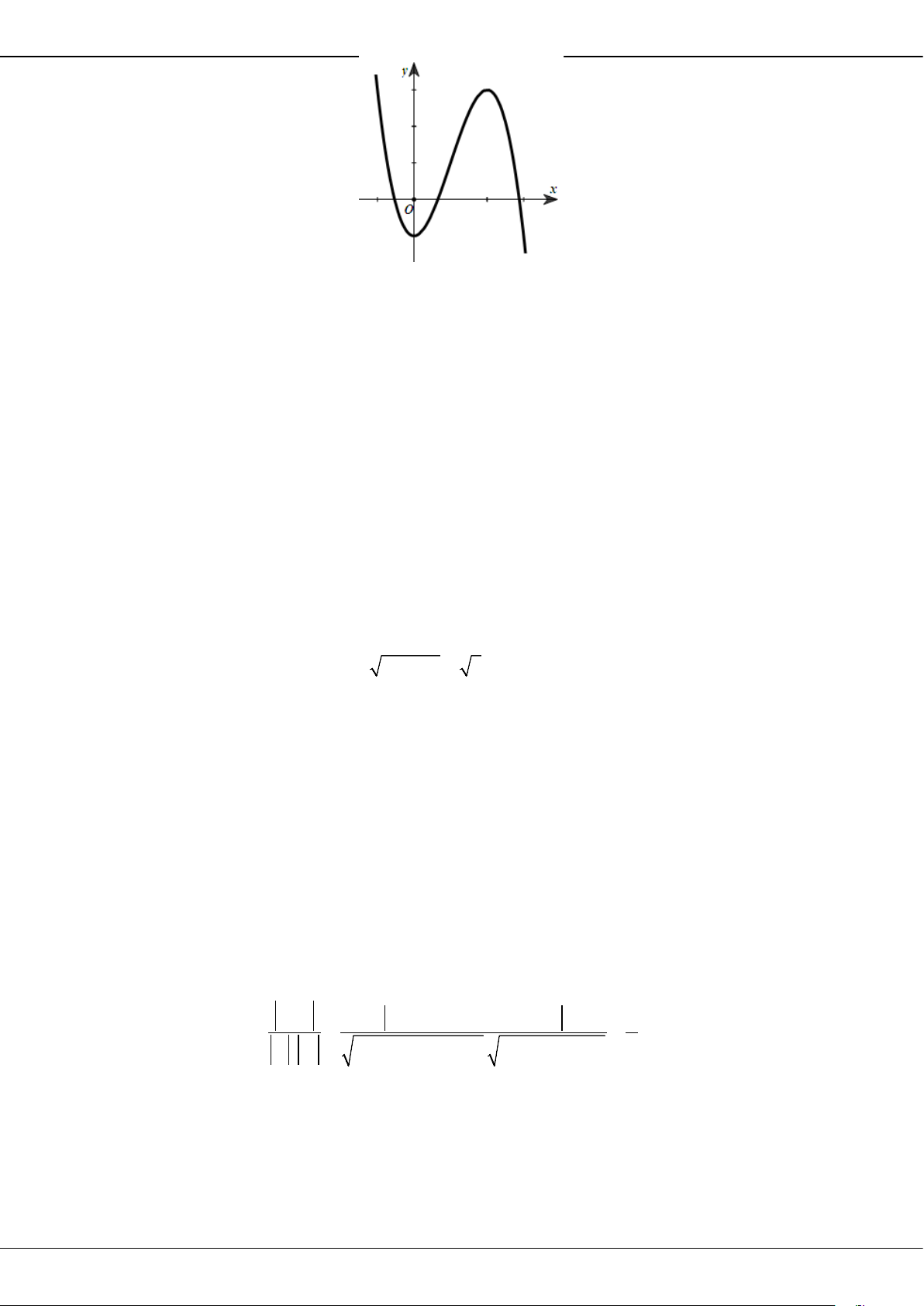
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 64

A.

42

21

yx x

=−+ −

. B.

42

21yx x=−−

. C.

32

31yx x=−−

. D.

32

31

yx x=−+ −

.

Hướng dẫn giải

Chọn D

Dựa vào đồ thị có dạng đồ thị của hàm số bậc 3 có hệ số

0a <

nên đáp án D đúng.

Câu 10: Trong không gian

Oxyz

, cho hai điểm

( )

1;1; 1I

và

( )

1; 2; 3A

. Phương trình của mặt cầu có tâm

I

và đi qua điểm

A

là

A.

(

) ( )

( )

2 22

1 1 1 29+++++=xyz

. B.

( ) ( ) ( )

2 22

1 1 15−+−+−=xyz

.

C.

( ) ( ) ( )

2 22

1 1 1 25−+−+−=xyz

. D.

( ) ( ) ( )

2 22

1 1 15+++++=xyz

.

Hướng dẫn giải

Chọn B

Mặt cầu có bán kính

014 5= = ++ =R IA

.

Suy ra phương trình mặt cầu là

( )

2 22

1 1 15

−+−+−=xyz

.

Câu 11: Trong không gian với hệ trục tọa độ

,Oxyz

cho hai mặt phẳng

( )

: 2 2 0,Px yz− −+=

(

)

: 2 1 0.Q xyz− ++=

Góc giữa

( )

P

và

(

)

Q

là

A.

60

°

. B.

90

°

. C.

30°

. D.

120°

.

Hướng dẫn giải

Chọn A

( )

: 2 20Px yz− −+=

có véc tơ pháp tuyến là

(

)

1

1;2;1n

= −−



.

( )

:2 1 0Q xyz− ++=

có véc tơ pháp tuyến là

( )

2

2; 1; 1n = −

 

.

Áp dụng công thức:

( ) ( )

(

)

( )

( ) ( )

(

) ( ) ( )

12

22 2

2 22

12

.

1.2 2 . 1 1 .1

1

cos ,

2

.

1 2 1.2 1 1

nn

PQ

nn

+− − +−

= = =

+− +− +− +

   

Suy ra góc giữa

( )

P

và

( )

Q

là

60

°

.

Câu 12. Cho hai số phức

1

12zi= +

và

2

23zi= −

. Phần ảo của số phức

12

32

wz z= −

là

A. 12. B. 11. C. 1. D.

12i

.

Hướng dẫn giải

( ) ( )

12

w 3 2 3 1 2 2 2 3 1 12zz i i i= − = + − − =−+

. Vậy phần ảo của số phức

w

là

12

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 65

Vậy chọn đáp án A.

Câu 13. Cho hình hộp chữ nhật có độ dài ba cạnh là 3; 4; 5. Thể tích khối hộp đã cho bằng

A. 20 B. 60 C. 12 D. 30

Hướng dẫn giải

Chọn B

Câu 14. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB= AC= AD =2. Thể tích khối tứ diện

đã cho bằng

A.

1

3

B.

8

3

C.

4

3

D.

1

6

Hướng dẫn giải

Chọn C

Câu 15. Cho mặt cầu S(O; R) và mặt phẳng (P). Gọi d là khoảng cách từ O đến mặt phẳng (P). Khi (P) cắt

mặt cầu (S) theo thiết diện là đường tròn lớn. Khẳng định nào là đúng?

A. d= 0 B. d < R C. d > R D. d= R

Hướng dẫn giải

Chọn A

Câu 16. Các số thực

,xy

thỏa mãn:

( ) ( ) ( ) ( )

231 2 32 2 4 3x y x yi x y x y i+ + +−+ = − + + − −

là

A.

( )

94

;;

11 11

xy



=−−





. B.

( )

94

;;

11 11

xy



=





.

C.

( )

94

;;

11 11

xy



= −





. D.

(

)

94

;;

11 11

xy



= −





.

Hướng dẫn giải

Chọn B

( ) ( ) ( )

( )

231 2 32 2 4 3

9

2 3 13 2 2 5 1

11

2 4 3 53 3 4

11

x y x yi x y x y i

x

xy xy xy

x y xy x y

y

+ + +−+ = − + + − −



=



+ += − + − =−





⇔ ⇔⇔

 

−+ = − − − =





=





Vậy

( )

94

;;

11 11

xy



=





Câu 17. Cho hình nón có đường kính đáy bằng 4 và độ dài đường cao hình nón 3. Diện tích xung quanh

của hình nón bằng

A.

20

π

B.

12

π

C.

6

π

D.

10

π

Hướng dẫn giải

Chọn D

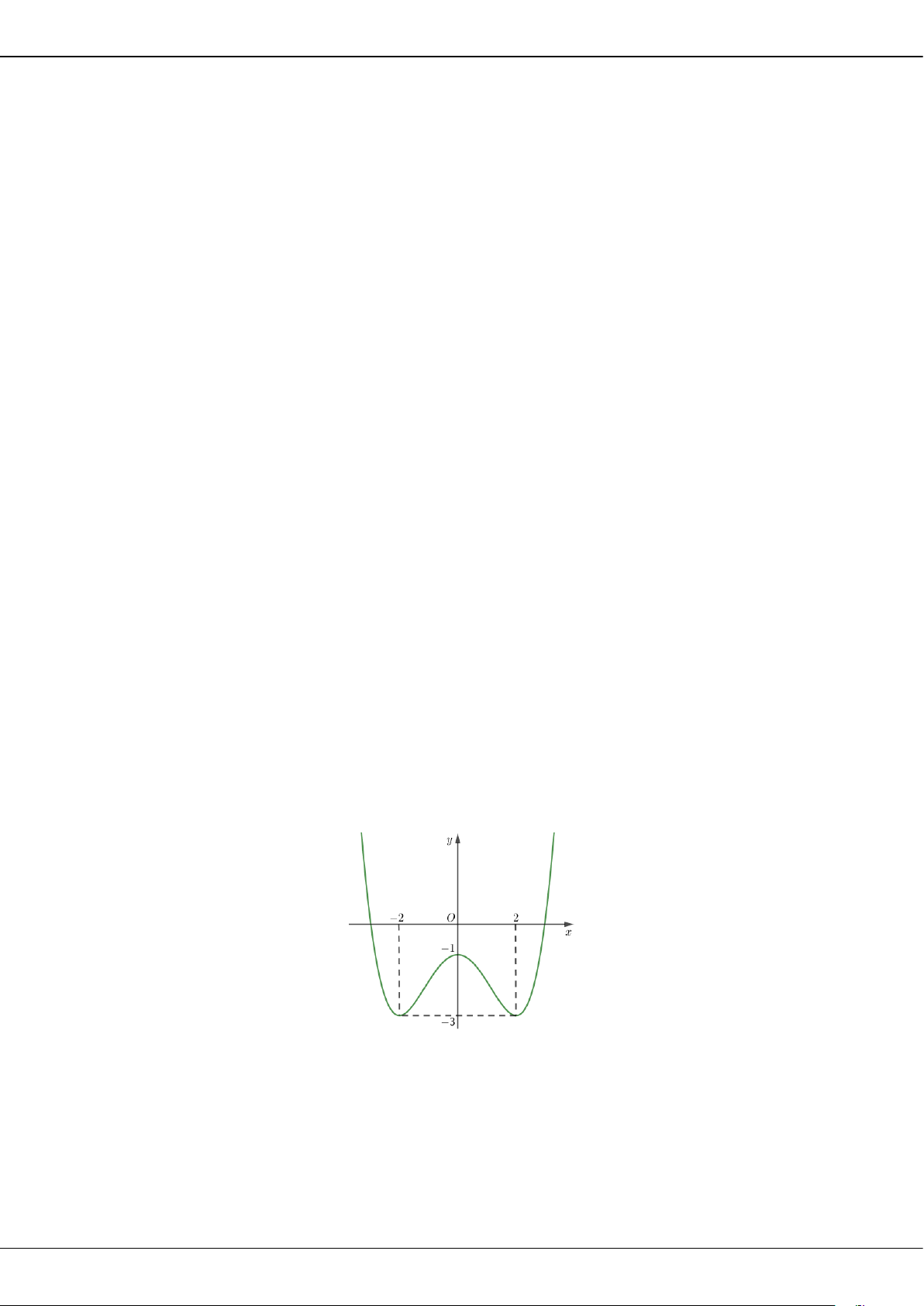
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 66

Câu 18: Trong không gian

Oxyz

, điểm nào dưới đây không thuộc đường thẳng

(

)

32

:1 ?

xt

dy tt

zt

= −





=+∈





=





A.

( )

3; 1; 0

P

. B.

( )

1; 2; 1Q

. C.

( )

1; 3; 1N −

. D.

( )

5; 0; 1M −

.

Hướng dẫn giải

Chọn C

+) Thay tọa độ

( )

3; 1; 0P

vào phương trình đường thẳng ta được:

332

11 0

0

t

tt

t

= −





=+ ⇔=





=



Vậy điểm

(

)

3; 1; 0

P

thuộc đường thẳng

d

.

+) Thay tọa độ

(

)

1; 2; 1Q

vào phương trình đường thẳng ta được:

132

21 1

1

t

tt

t

= −





=+ ⇔=





=



Vậy điểm

( )

1; 2; 1Q

thuộc đường thẳng

d

.

+) Thay tọa độ

( )

1; 3; 1

N −

vào phương trình đường thẳng ta được:

132

31

1

t

tt

t

−= −





=+ ⇔=∅





=



Vậy điểm

( )

1; 3; 1N −

không thuộc đường thẳng

d

.

Câu 19: Cho hàm số

( )

42

, ,,

y ax bx c a b c=++ ∈

có đồ thị là đường cong như hình bên. Giá trị cực đại

của hàm số đã cho bằng

A.

0

. B.

1−

. C.

3−

. D.

2

.

Hướng dẫn giải

Chọn B

Dựa vào đồ thị, ta thấy hàm số có giá trị cực đại

1y = −

.

Câu 20: Cho hàm số

()y fx=

có

lim ( ) 1

x

fx

→+∞

=

và

lim ( ) 1

x

fx

→−∞

= −

. Khẳng định nào sau đây là khẳng định

đúng?

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 67

A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng

1x =

và

1x = −

.

B. Đồ thị hàm số đã cho không có tiệm cận ngang.

C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.

D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng

1y =

và

1y = −

.

Hướng dẫn giải

Chọn D

Dựa vào định nghĩa đường tiệm cận ngang của đồ thị hàm số ta chọn đáp án D.

Câu 21. Số nghiệm nguyên của bất phương trình

( )

1

2

log 2 0x −≥

là

A.

0

. B.

1

. C.

2

. D.

3

.

Hướng dẫn giải

Chọn B.

Ta có:

( )

1

2

log 2 0 0 2 1 2 3x xx− ≥ ⇔ < −≤⇔ < ≤

.

Vì

x

∈



nên

{

}

3x ∈

.

Câu 22: Một học sinh muốn chọn

20

trong

30

câu trắc nghiệm . Học sinh đó đã chọn được

5

câu. Tìm

số cách chọn các câu còn lại

A.

5

30

C

B.

15

25

A

C.

15

30

C

D.

15

25

C

Hướng dẫn giải

Chọn D.

Câu 23.

2d

x

∫

bằng

A.

1

2

x

C

+

. B.

1

2

1

x

C

x

+

. C.

2 ln 2

x

C+

. D.

2

ln 2

x

C+

.

Hướng dẫn giải

Chọn D.

Câu 24. Cho

( )

5

2

d 10fxx=

∫

. Khi đó

( )

2

5

24 dfx x−





∫

bằng

A.

46

. B.

32

. C.

42

. D.

34

.

Hướng dẫn giải

Chọn D.

Câu 25. Tìm nguyên hàm của hàm

( )

2

cosfx x=

A.

sin 2

24

xx

C−+

. B.

cos2

24

xx

C−+

.

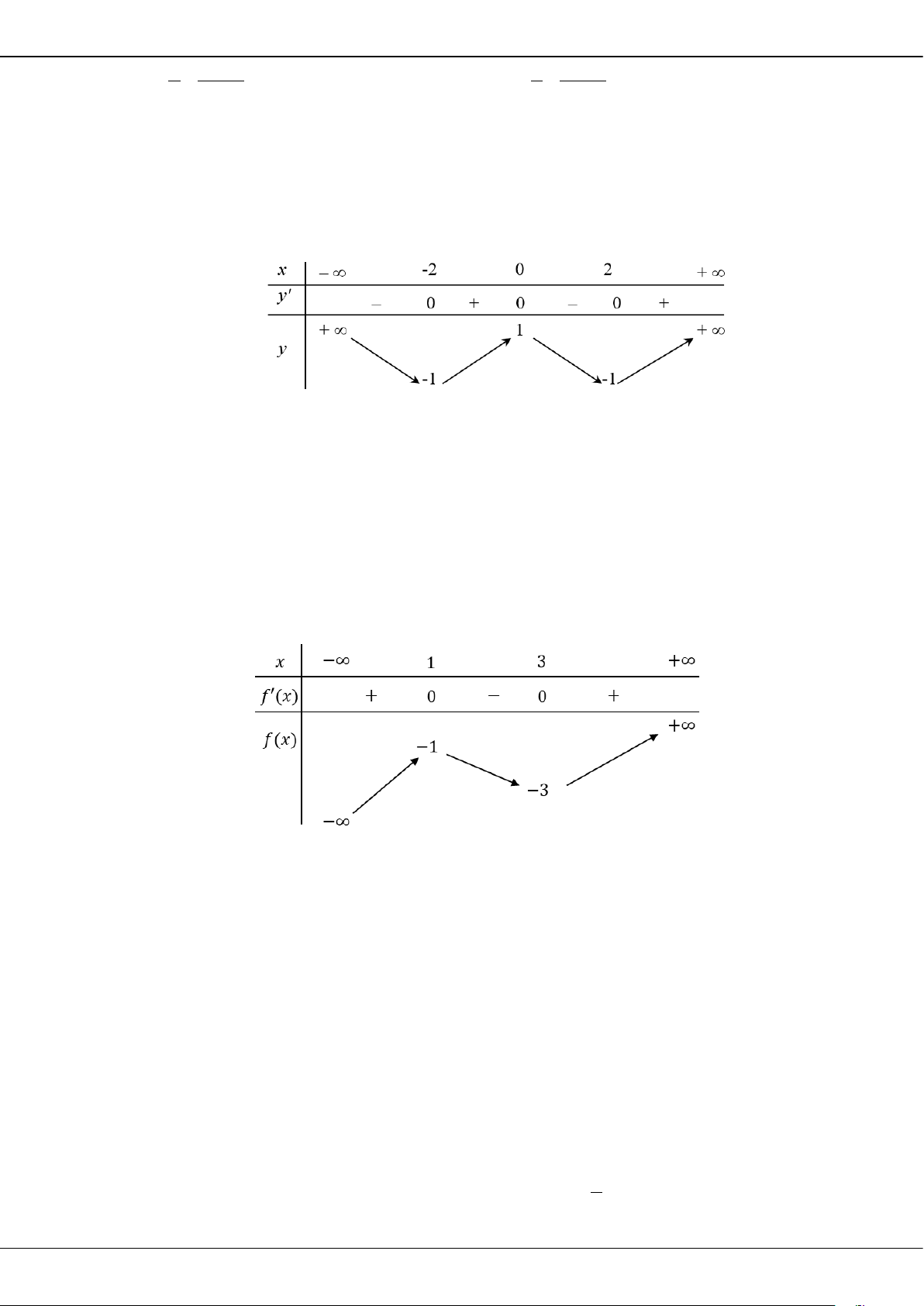
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 68

C.

cos2

24

xx

C

++

. D.

sin 2

24

xx

C

++

.

Hướng dẫn giải

Chọn D.

Câu 26: Cho hàm số

()y fx=

có bảng biến thiên như sau :

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

( )

0; +∞

. B.

( )

;2−∞ −

. C.

( )

0; 2

. D.

( )

2;0−

.

Hướng dẫn giải

Chọn D

Từ bảng biến thiên suy ra hàm số đã cho đồng biến trên

( )

2;0−

.

Câu 27: Cho hàm số

( )

fx

có bảng biến thiên như hình vẽ.

Điểm cực đại của đồ thị hàm số đã cho là

A.

1x =

. B.

3x =

. C.

1

x

= −

. D.

( )

1; 1−

.

Hướng dẫn giải

Chọn D

Hàm số đạt cực đại tại điểm

x

mà

( )

fx

′

đổi dấu từ dương sang âm.

Từ bảng biến thiên ta thấy hàm số đạt cực đại tại

1x =

và

D

1

C

y = −

.

Vậy điểm cực đại của đồ thị hàm số đã cho là

( )

1; 1−

.

Câu 28. Với

,ab

là các số thực dương tùy ý,

( )

2

3

log .ab

bằng

A.

33

log 2logab+

. B.

( )

33

2 log logab+

. C.

33

1

log log

2

ab+

. D.

33

2 log logab⋅⋅

.

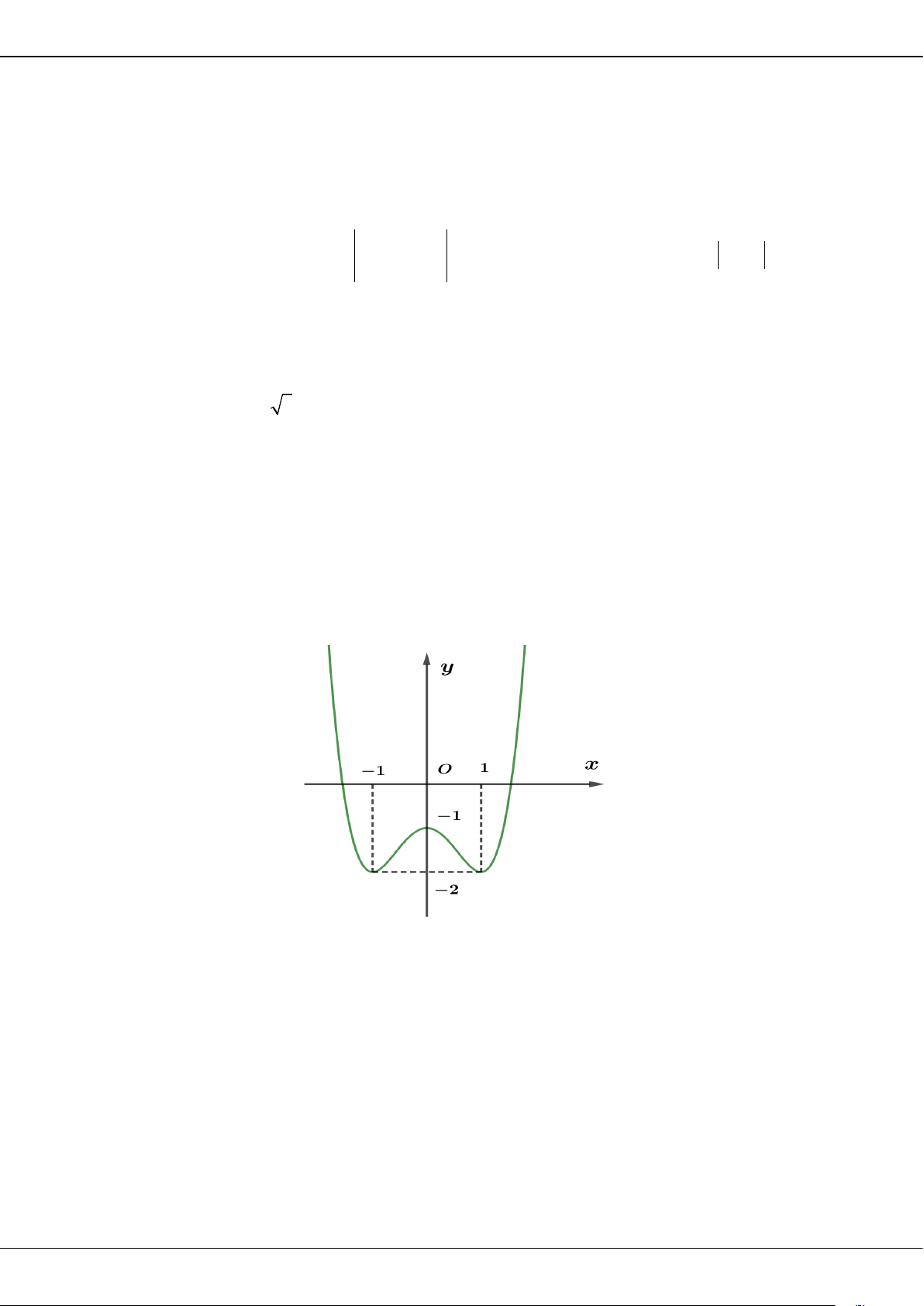
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 69

Hướng dẫn giải

Chọn A.

( )

2

3 33

log . log 2logab a b= +

.

Câu 29. Diện tích hình phẳng giới hạn bởi đồ thị hàm số

2

2yx= −

, trục

Ox

và các đường thẳng

1x =

,

2

x =

được tính bằng công thức nào sau đây?

A.

( )

2

1

2dxx

π

−

∫

. B.

(

)

2

1

2dxx−

∫

. C.

( )

2

1

2dxx−

∫

. D.

2

1

2dxx

−

∫

.

Hướng dẫn giải

Chọn D.

Câu 30: Cho hình lăng trụ đứng tam giác

.' ' 'ABC A B C

có đáy

ABC

là tam giác vuông tại

B

và

4, 5BC AC= =

và

' 33AA =

. Góc giữa mặt phẳng

( )

'C'AB

và

( )

'B'C'A

bằng

A.

0

90

B.

0

60

. C.

0

45

. D.

0

30

.

Hướng dẫn giải

Chọn B.

Câu 31: Cho hàm số

( )

42

f x ax bx c=++

có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị

nguyên thuộc đoạn

[ ]

2;5−

của tham số

m

để phương trình

( )

fx m=

có đúng hai nghiệm phân

biệt?

A.

1

. B.

6

. C.

7

. D.

5

.

Hướng dẫn giải

Chọn C

Số nghiệm của phương trình

( )

fx m=

chính là số giao điểm của đồ thị hàm số

( )

y fx=

và

đường thẳng

:dy m

=

Dựa vào đồ thị ta có phương trình

( )

fx m=

có đúng hai nghiệm phân biệt khi và chỉ khi

2

1.

m

= −





>−



Mặt khác

[ ]

{ }

2;5 2; 0;1; 2; 3; 4; 5mm∈− ⇒ ∈−

.

Suy ra có 7 giá trị thỏa mãn yêu cầu.

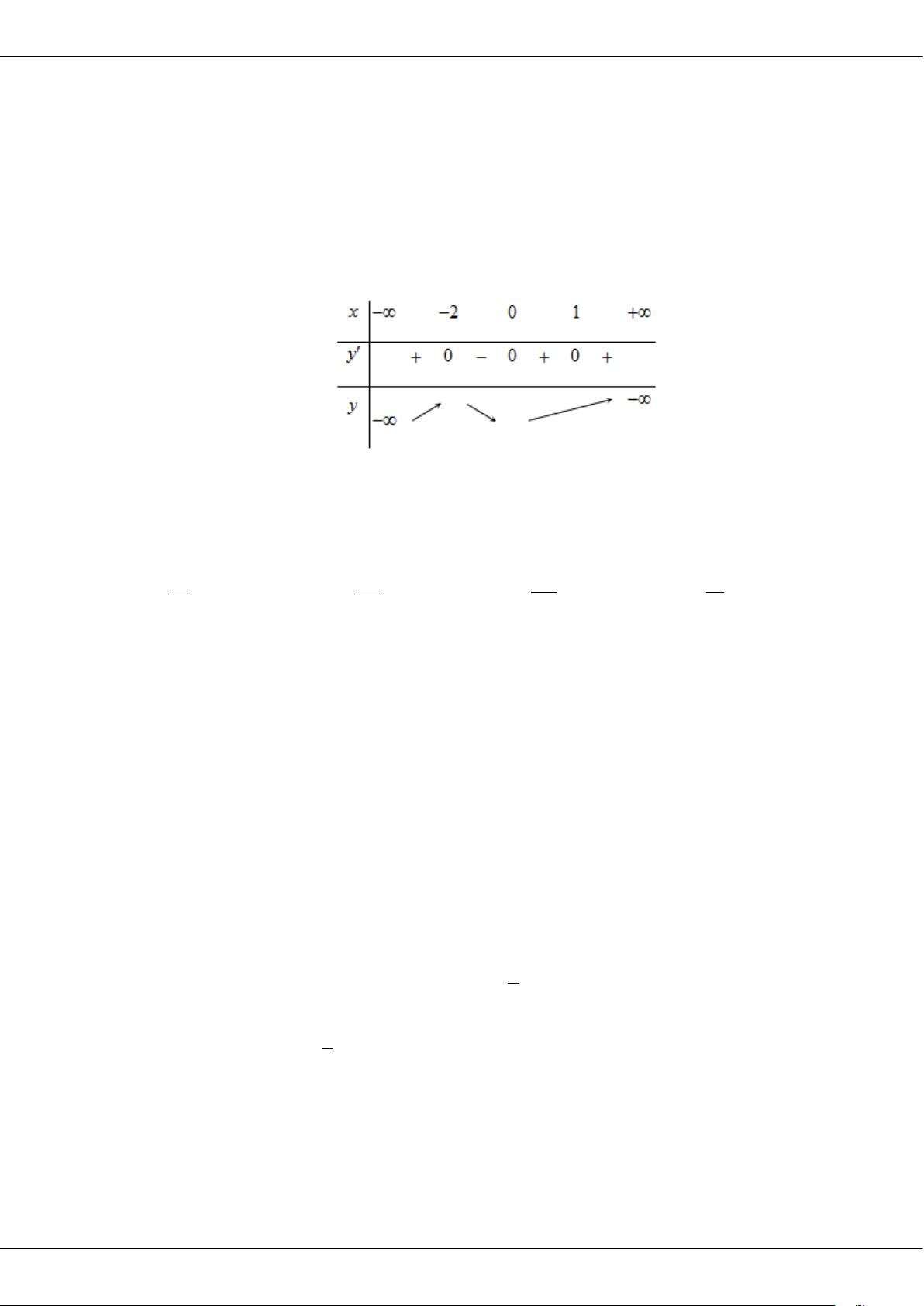
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 70

Câu 32: Cho hàm số

(

)

fx

có đạo hàm là

( ) ( ) ( )

2

3

12fx xx x

′

=−+

. Khoảng nghịch biến của hàm số là

A.

(

)

;2

−∞ −

và

( )

0;1

. B.

( )

2; 0−

và

( )

1; +∞

.

C.

( )

;2−∞ −

và

( )

0; +∞

. D.

( )

2; 0−

.

Hướng dẫn giải

Chọn D

Bảng biến thiên:

Vậy hàm số nghịch biến trên khoảng

( )

2; 0−

.

Câu 33: Cho tập hợp

{ }

1; 2; 3; 4; 5; 6; 7;8;9;10;11;12;13A =

. Lấy ngẫu nhiên 3 số trong tập

A

. Tính xác suất

để lấy được ba số có tổng là số lẻ

A.

3

25

. B.

71

143

. C.

70

.

143

D.

5

.

11

Hướng dẫn giải

Chọn C.

Câu 34. Tích các nghiệm của phương trình

2

33

log log (9 ) 4 0xx− −=

bằng

A.

6−

. B.

3−

. C.

3

. D.

27

.

Hướng dẫn giải

Chọn C.

Điều kiện:

0x >

22

33 333

log log (9 ) 4 0 log log 9 log 4 0xx x x− −=⇔ − − −=

3

2

33

3

27

log 3

log log 6 0

1

log 2

.

9

x

xx

x

=



=





⇔ − −=⇔ ⇔



= −

=



Tích các nghiệm là:

1

27. 3

9

=

Câu 35. Xác định tập hợp các điểm

M

trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện:

| || |zi zi+= −

.

A.Trục Oy. B. Trục Ox. C.

yx=

. D.

yx= −

.

Hướng dẫn giải

Chọn B

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 71

Gọi

( )

,M xy

là điểm biểu diễn của số phức

z x yi= +

trong mặt phẳng phức

( )

,

xy R∈

.

Theo đề bài ta có

| | | | | ( 1) | | ( 1) |zizi xy ixy i+=−⇔++ =+−

2 22 2

( 1) ( 1) 0xy xy y⇔ ++ = +− ⇔=

Vậy tập hợp các điểm

M

là đường thẳng y = 0 hay trục Ox

Câu 36: Trong không gian

Oxyz

, phương trình của đường thẳng đi qua điểm

(

)

0; 3; 1A

−

và vuông góc với

mặt phẳng

3 4 20

xyz

− + −=

là

A.

13

13 4

x yz−−

= =

−−

. B.

31

134

xy z++

= =

−

.

C.

31

13 4

xy z−−

= =

−−

. D.

31

134

xy z+−

= =

−

.

Hướng dẫn giải

Chọn A

Ta có VTPT của mặt phẳng

3 4 20xyz− + −=

là

( ) (

)

1; 3; 4 1; 3; 4

n =− =−−



.

Đường thẳng

d

vuông góc với mặt phẳng

3 4 20xyz− + −=

nhận một vectơ

( )

1; 3; 4

u = −



hay

( )

1; 3; 4u

′

=−−



làm vectơ chỉ phương và đi qua điểm

( )

0; 3; 1A −

nên có phương trình

13

13 4

x yz−−

= =

−−

.

Câu 37: Trong không gian với hệ toạ độ

Oxyz

, cho điểm

( )

2;4;6K

, gọi

K



là hình chiếu vuông góc của

K

trên trục

Oz

, khi đó trung điểm

OK



có toạ độ là:

A.

( )

1;0;0

. B.

( )

0;0;3

. C.

( )

0;2;0

. D.

( )

1;2;3

.

Hướng dẫn giải

Chọn B

Vì

'K

là hình chiếu vuông góc của

( )

2;4;6

K

lên trục

Oz

nên

( )

K

′

0;0;6 .

Gọi

( )

I xyz

;;

là trung điểm

.

OK



Suy ra

( )

I 0;0;3 .

Câu 38: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

, mặt bên

SAB

là tam giác đều và nằm

trong mặt phẳng vuông góc với mặt phẳng đáy . Khoảng cách từ điểm

A

đến mặt phẳng

(

)

SBD

bằng

A.

21

14

a

. B.

21

7

a

. C.

2

a

. D.

21

28

a

Hướng dẫn giải

Chọn B.

Câu 39. Có bao nhiêu giá trị nguyên dương của

y

để tập nghiệm của bất phương trình

( )

2

log 2 2 0

x

xy− −<

có ít nhất

1

số nguyên và không quá

6

số nguyên?

A.

2048

. B.

2016

. C.

1012

. D.

2023

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 72

Hướng dẫn giải

Chọn D

Điều kiện:

0.

x >

Ta có

( )

2

log 2 0

4

log

20

log 2 2 0 .

log 2 0

4

log

20

x

xy

y

xy

x

xy

y

 −<





<









>

−>





− − <⇔ ⇔



−>

>









<



−<









TH1. Nếu

2

4

.

log

x

xy

<





>



Để tập nghiệm bất phương trình có ít nhất

1

số nguyên và không quá

6

số nguyên thì

2

1

3 log 3 8.

8

yy

−≤ < ⇔ ≤ <

Suy ra có

7

giá trị nguyên dương của

y

thỏa mãn (1).

TH2. Nếu

2

4

.

log

x

xy

>





<



Để tập nghiệm bất phương trình có ít nhất

1

số nguyên và không quá

6

số nguyên thì

2

5 log 11 32 2048.

yy

< ≤ ⇔ <≤

Suy ra có

2048 33

1 2016

1

−

+=

giá trị nguyên dương của

y

thỏa mãn (2).

Từ (1), (2) suy ra có

2023

giá trị nguyên dương của

y

thỏa mãn yêu cầu bài toán.

Câu 40. Cho

,

fg

là hai hàm số liên tục trên

[

]

1; 3

thỏa mãn điều kiện

( ) ( )

3

1

3 dx=10f x gx+





∫

đồng thời

( )

3

1

2 dx=6f x gx−





∫

. Tính

( ) ( )

3

2

1

3 dxf x gx x



+−



∫

.

A.

9

. B.

20−

. C.

6

. D.

32

.

Hướng dẫn giải

Chọn B

Ta có:

( )

3

1

3 dx=10f x gx+





∫

( ) ( )

33

11

dx+3 dx=10f x gx⇔

∫∫

.

( ) ( )

3

1

2 dx=6f x gx−





∫

( ) ( )

33

11

2 dx- dx=6f x gx⇔

∫∫

.

( )

3

1

3

1

dx=4

dx=2

fx

gx





⇒







∫

Vậy

( ) ( ) ( ) ( ) ( )

3 33

3

2 23

1

1 11

3 dx= dx- 3 dx= 6- 6 27 1 20f x gx x f x gx x x



+ − + =− −=−





∫ ∫∫

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 73

Câu 41: Có bao nhiêu giá trị nguyên của tham số để hàm số

32

2 ( 2) 1y mx mx m x= − +− +

không có

cực trị

A. vô số. B.

5

. C.

6

. D.

7

.

Hướng dẫn giải

Chọn D

Ta có

2

' 3 4 ( 2)y mx mx m= − +−

.

+ Nếu

0m

=

.

' 2 0 ( )yx⇒ =− < ∀∈

. Nên hàm số không có cực trị.

Do đó

0m =

.

+ Nếu

0m ≠

.

Hàm số không có cực trị

'y⇔

không đổi dấu

22

' 0 4 3 ( 2) 0 6 0 6 0m mm m m m⇔∆≤⇔ − − ≤⇔ + ≤⇒−≤ <

.

Kết hợp và ta được

60m−≤ ≤

Vậy có 7 giá trị nguyên của tham số m.

Câu 42. Trong mặt phẳng phức

Oxy

, các số phức

z

thỏa

21z i zi+ −= +

. Tìm số phức

z

được biểu

diễn bởi điểm

M

sao cho

MA

ngắn nhất với

( )

1, 3A

.

A.

3 i+

. B.

13i+

. C.

23i−

. D.

23

i−+

.

Hướng dẫn giải

Chọn A

Gọi

( )

,M xy

là điểm biểu diễn số phức

( )

,z x yi x y R=+∈

Gọi

( )

1, 2E

−

là điểm biểu diễn số phức

12

i−

Gọi

( )

0, 1F −

là điểm biểu diễn số phức

i−

Ta có :

21z i z i ME MF+ −= +⇔ =

⇒

Tập hợp điểm biểu diễn số phức

z

là đường trung trực

: 20EF x y

−−=

.

Để

MA

ngắn nhất khi

MA EF⊥

tại

M

( )

3,1 3M zi

⇔ ⇒=+

Câu 43. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, diện tích tam giác A’BC

bằng

2

5

4

a

. Thể tích khối lăng trụ đã cho bằng

A.

3

6

24

a

B.

3

6

a

C.

3

36

8

a

D.

3

6

8

a

Hướng dẫn giải

Chọn D

Gọi H là trung điểm BC

'A H BC⇒⊥

2

'

15 5

'. '

24 2

A BC

S AHBC a AH a= = ⇒=

m

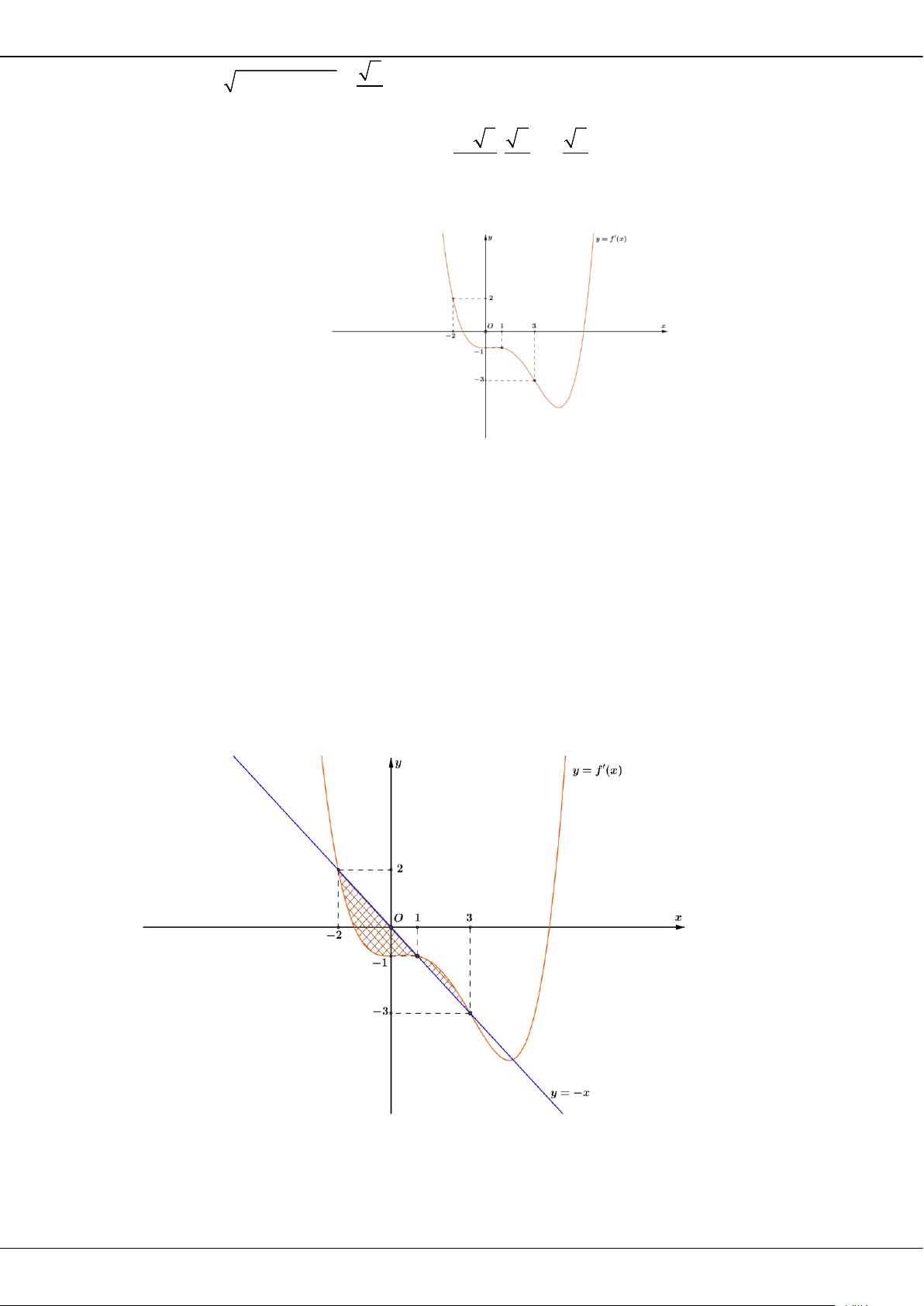
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 74

Do đó

22

2

''

2

AA A H AH a= −=

Do đó thể tích khối lăng trụ

2

3

32 6

.' .

42 8

ABC

a

V S AA a a= = =

Câu 44. Cho hàm số

(

)

y fx

=

liên tục trên



và có đồ thị hàm số

( )

y fx

′

=

như hình bên

Xét hàm số

(

)

( )

2

2gx f x x= +

. Hỏi mệnh đề nào sau đây là đúng?

A.

( )

( ) (

)

1 23

gg g

< −<

. B.

( )

( ) (

)

231

g gg−> =

.

C.

( ) (

) ( )

231

g gg−< <

. D.

( ) ( ) ( )

13 2gg g< <−

.

Hướng dẫn giải

Chọn D

Ta có

( ) ( ) ( ) ( )

2 22gx fx x fx x

′′ ′

= + = −−





.

Vẽ đồ thị hàm số

( )

y fx

′

=

và đường thẳng

yx= −

trên cùng một hệ trục như hình vẽ sau:

Gọi

1

S

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

( )

y fx

′

=

, đường thẳng

yx= −

và

các đường thẳng

2x = −

,

1x =

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 75

Ta có

(

) (

)

( )

( ) ( )

11

1

2

22

1 11

d d 12

2 22

S f x x x g x x gx g g

−

−−

′′

=− −− =− =− =− − −

  

  

∫∫

.

Gọi

2

S

là diện tích hình phẳng giới hạn bởi đồ thị hàm số

(

)

y fx

′

=

, đường thẳng

yx= −

và

các đường thẳng

1x =

,

3x =

.

Ta có

( )

(

)

(

)

( ) ( )

33

3

1

11

1 11

d d 31

2 22

S f x x x g x x gx g g

′′

= −− = = = −

  

  

∫∫

.

(

)

( )

(

) ( )

(

) ( )

( )

( ) (

)

( ) (

)

( )

(

)

( )

1

2

12

1

1 20

2

21

0

1

0 3 10 3 1 1 3 2

2

23

11

1 2 31

22

gg

S

S gg g g gg g

SS

gg

gg g g



− −− >







−>



>







>⇔ − > ⇔ > ⇔ < <−



 



 

>

−>





− −− > −

  

  





.

Câu 45. Có bao nhiêu số phức z thỏa mãn:

2

26zz

+=

và

6zz+=

A. 2. B. 3. C. 2. D. 1.

Hướng dẫn giải

Chọn A

Đặt

(, )z x iy x y=+∈

, ta có

2

22

,

z x yi z z x y=−==+

Ta có:

2

22

26

3

13

2

3

6

zz

x

xy

y

x

zz



+=

=



+=





⇔⇔

 

= ±

=





+=



⇒

có 2 số phức thỏa yêu cầu đề bài.

Câu 46: Cho điểm

( )

2;5;3A

và đường thẳng

12

:

212

x yz

d

−−

= =

. Gọi

( )

P

là mặt phẳng chứa đường thẳng

d

sao cho khoảng cách từ

A

đến

( )

P

lớn nhất. Khoảng cách từ điểm

( )

1; 2; 1M −

đến

( )

P

bằng

A.

11

18

. B.

4

3

. C.

11 18

18

. D.

32

.

Hướng dẫn giải

Chọn C

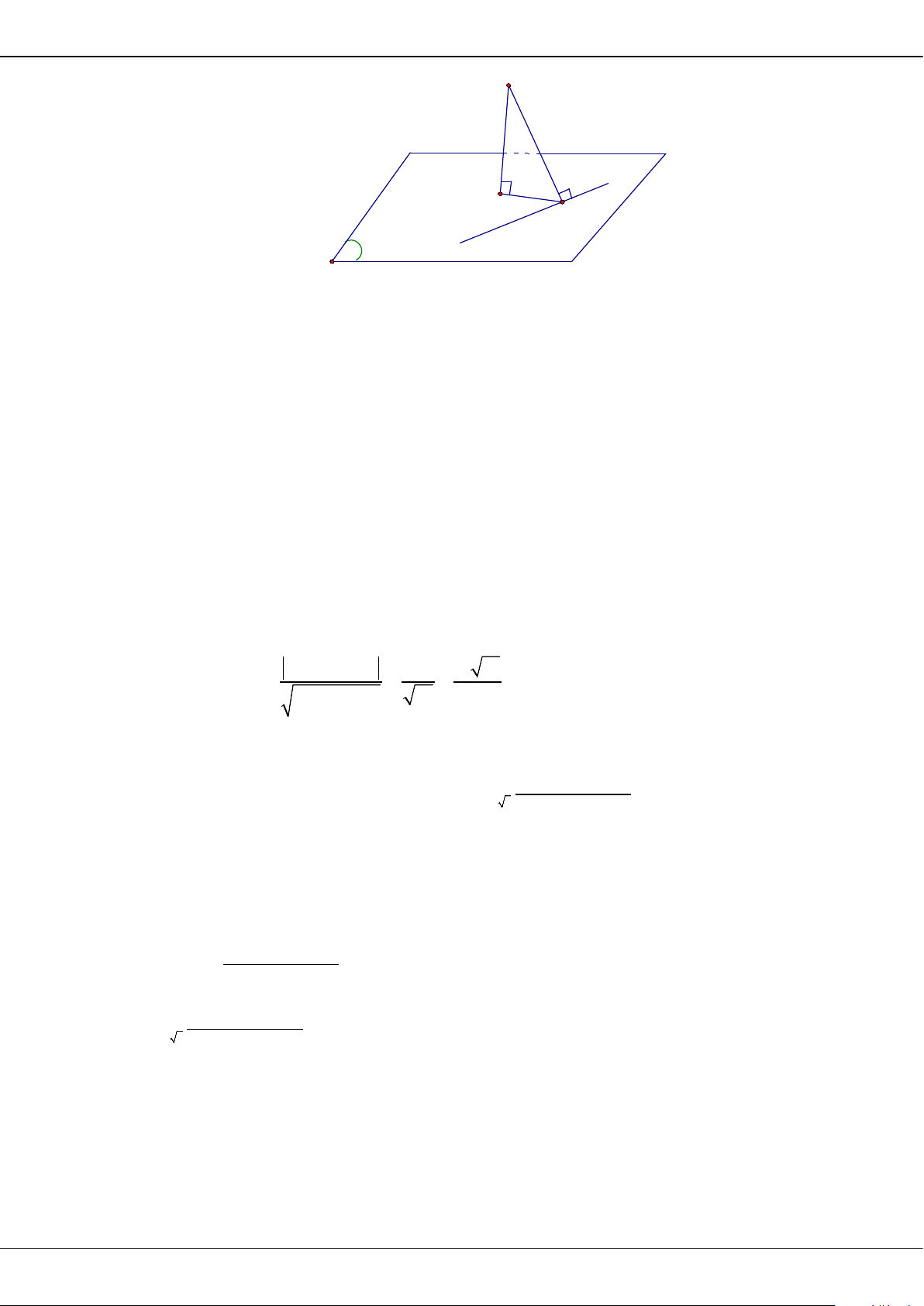
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 76

Gọi

H

là hình chiếu vuông góc của

A

lên đường thẳng

d

.

Ta có

( )

2; 1; 2

d

u =

 

là một vectơ chỉ phương của đường thẳng

d

.

Do

Hd∈

nên

( )

1 2 ; ;2 2H tt t++

;

( )

21; 5;21AH t t t−− −



.

Khi đó

( ) ( ) (

)

. 0 2. 2 1 1. 5 2. 2 1 0

d

u AH t t t

=⇔ −+ − + −=

 

1

t⇔=

. Vậy

( )

3;1;4H

.

Gọi

K

là hình chiếu vuông góc của

A

lên mặt phẳng

( )

P

. Ta có

AK AH≤

.

Suy ra

( )

,d A P AK=

đạt giá trị lớn nhất khi

AK AH=

, hay

HK

≡

.

Khi đó

( )

1; 4; 1AH = −



là một vectơ pháp tuyến của

(

)

P

.

Phương trình mp

( )

P

chứa điểm

H

là:

( ) ( ) ( )

1341140x yz−− −+ − =

4 30x yz⇔− +−=

.

Vậy

( )

2

1 4.2 1 3

11 11 18

,

18

1 41

dM P

− −−

= = =

+− +

.

Câu 47. Có bao nhiêu cặp số nguyên

( )

,xy

thỏa mãn

( ) ( )

22

3

log 3 3 .

2

xy

x x y y xy

x y xy

+

= −+ −+

+++

A.

1

. B.

2

. C.

4

. D.

6

.

Hướng dẫn giải

Chọn D.

Điều kiện

22

0 0.

2

xy

x y xy

+

>⇔+>

+++

( ) ( )

22

3

log 3 3

2

xy

x x y y xy

x y xy

+

= −+ −+

+++

( )

22 22

33

2log 2log 2 3 3x y x y xy x y xy x y⇔ +− +++=++−−

( )

22 22

33

2log 2 2log 2 2 3 3x y x y xy x y xy x y⇔ + +− + + + = + + +− −

( ) ( )

( )

22 22

33

2log 3 3 3 3 2log 2 2x y x y x y xy x y xy⇔ + + + = +++++++

d

P

A

K

H

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 77

Xét hàm đặc trưng

( ) ( )

3

2 log , 0; ,f t t tt= + ∈ +∞

ta có

(

)

(

)

2

1 0, 0; .

.ln 3

ft t

t

′

= + > ∀ ∈ +∞

Suy ra hàm

( )

ft

đồng biến trên khoảng

( )

0; +∞

.

Phương trình

( )

22 22

33 2 233f x y f x y xy x y xy x y+ = +++⇔+++=+

( )

22

3 3 20x yx y y⇔ + − + − +=

.

Điều kiện của

y

để phương trình có nghiệm là

( )

2

3 4 320y yy− − −+≥

2

3 22 3 22

3 6 10

33

yy y

−+

⇔− + + ≥ ⇔ ≤ ≤

.

Do

y ∈

nên

{ }

0; 1; 2y

∈

.

+ Với

0y =

, ta được

2

1

3 20

2

x

xx

x

=



− +=⇔



=



.

+ Với

1y =

, ta được

2

0

20

2

x

xx

x

=



+=⇔



= −



.

+ Với

2

y =

, ta được

2

0

1

x

xx

x

=



+=⇔



= −



.

Vậy có

6

cặp số thỏa mãn đề bài.

Câu 48. Cho hình nón có trục SO = a. Mặt phẳng (P) đi qua đỉnh của hình nón và cắt hình nón theo thiết

diện là tam giác đều. Biết khoảng cách từ O đến (P) bằng

2

a

. Tính diện tích xung quanh của hình nón đã

cho.

A.

2

87

9

a

π

B.

2

47

9

a

π

C.

2

47

3

a

π

D.

2

25

9

a

π

Hướng dẫn giải

Chọn B

Gọi thiết diện là tam giác SAB

Gọi I là trung điểm của đoạn AB.

Dựng

( ) ( )

( )

,

2

a

OH SI OH SAB d O SAB OH⊥⇒ ⊥ ⇒ = =

.

Ta có

2 22

1 11

OH SO OI

= +

2 2 2222

1 1 1 41 3

3

a

OI

OI OH SO a a a

⇒ = − =−=⇒=

.

2

22 2

2

3

aa

SI SO OI a⇒= + = + =

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 78

24

3

SI a

SA⇒= =

2

22 2

16 7

93

aa

OA SA SO a⇒ = − = −=

.

Vậy hình nón đã cho có diện tích xung quanh

2

74 4 7

..

33 9

xq

aaa

S rl

π

ππ

= = =

Câu 49: Trong không gian

Oxyz

, cho hai điểm

( )

1;1; 3A −

và

( )

2; 3;1B −

. Xét hai điểm

,MN

thay đổi

thuộc mặt phẳng

( )

Oxz

sao cho

2MN =

. Giá trị nhỏ nhất của

AM BN

+

bằng

A.

5

. B.

6

. C.

4

. D.

7

.

Hướng dẫn giải

Chọn A

Ta có

(

)

1; 0; 3H

−

,

(

)

2; 0;1K −

lần lượt là hình chiếu vuông góc của

(

)

1;1; 3A −

và

( )

2; 3;1B

−

xuống mặt phẳng

(

)

Oxz

.

Nhận xét:

A

,

B

nằm về cùng một phía với mặt phẳng

( )

Oxz

.

Gọi

A

′

đối xứng với

A

qua

( )

Oxz

, suy ra

H

là trung điểm đoạn

AA

′

nên

AM A M

′

=

.

Mà

1; 3; 5

A H AH BK HK

′

= = = =

.

Do đó

2 2 22

AM BN A M BN HA HM BK KN

′′

+= += + + +

( ) ( )

( )

22 2

16HA BK HM KN HM KN

′

≥ +++ =++

Lại có

523HM MN NK HK HM NK HK MN++≥⇒ +≥−=−=

Dấu “=” xảy ra khi và chỉ khi

, ,,

HMNK

thẳng hàng và theo thứ tự đó.

Suy ra

( )

22

16 16 3 5AM BN HM KN+≥+ + ≥+ =

.

Vậy giá trị nhỏ nhất của

AM BN+

bằng

5

.

(Oxz)

K

B

H

A

A'

M

N

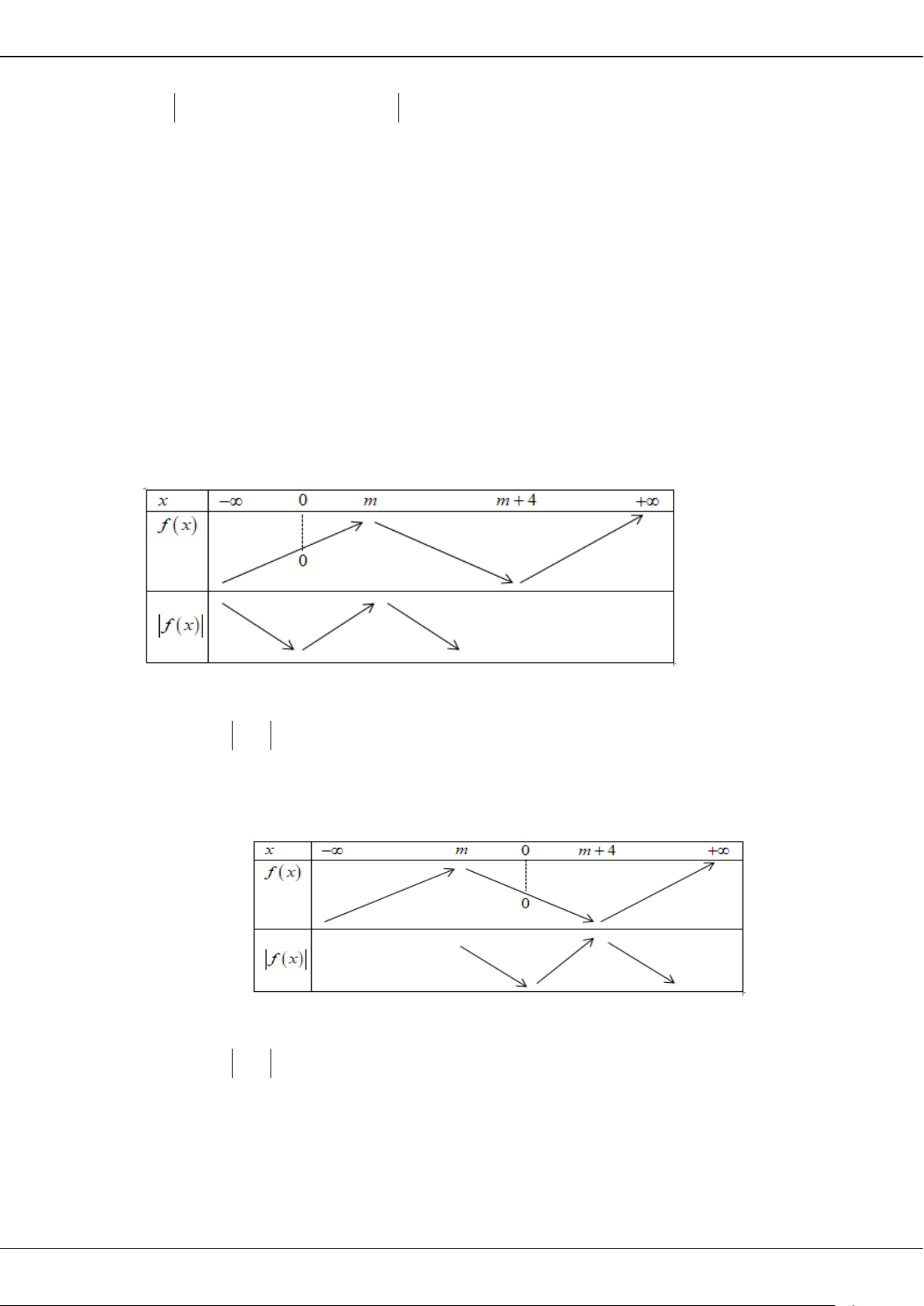
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 79

Câu 50: Có bao nhiêu giá trị nguyên thuộc đoạn

− 



2023; 2023

của tham số thực

m

để hàm số

(

)

(

)

=−+ + +

32

32 3 4yx mxmmx

đồng biến trên khoảng

( )

0;4

?

A.

4041

. B.

9

. C.

2021

. D.

2020

.

Hướng dẫn giải

Chọn A

Xét hàm số

( ) (

) ( )

=−+ + +

32

32 3 4fxx mxmmx

trên khoảng

( )

0;4

( )

( ) ( )

=− ++ +

2

' 36 23 4f x x m x mm

( ) ( )



= − ++ +



2

3 22 4x m x mm

(

)

='0fx

=

⇔



= +



4

xm

(

)

<+

4mm

Nhận xét: Đồ thị hàm số

(

)

=

y fx

luôn đi qua điểm

( )

0;0O

.

Trường hợp 1: Nếu

> 0

m

Từ bảng biến thiên, suy ra

hàm số

( )

=y fx

đồng biến trên khoảng

( )

0;4

( ) ( )

⇔⊂0;4 0;m

⇔≥4m

Kết hợp với

> 0m

, ta có

≥ 4m

.

Trường hợp 2: Nếu

≤< +04mm

⇔− < ≤40m

Từ bảng biến thiên, suy ra

hàm số

( )

=y fx

đồng biến trên khoảng

( )

0;4

( ) ( )

⇔ ⊂+0; 4 0; 4m

⇔ +≥44m

⇔≥0m

Kết hợp với

−< ≤40m

, ta có

= 0m

.

Trường hợp 3: Nếu

+≤40m

⇔ ≤−4m

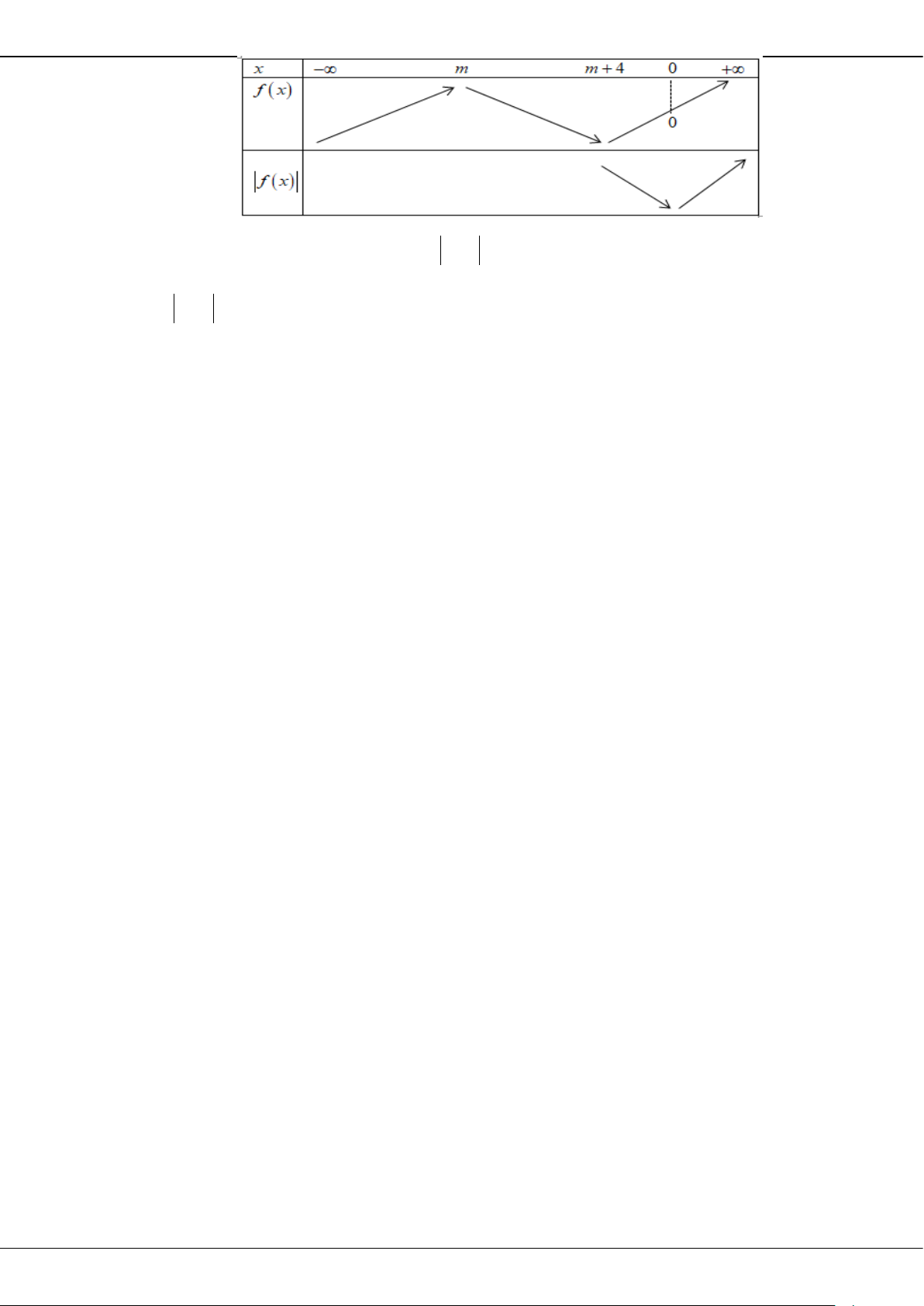
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 80

Từ bảng biến thiên, suy ra hàm số

( )

=y fx

luôn đồng biến trên khoảng

( )

+∞

0;

nên hàm số

(

)

=y fx

đồng biến trên khoảng

( )

0;4

với mọi

≤−4

m

.Vậy

≥



=



≤−



4

0

4

m

Mà

m

nguyên thuộc khoảng

− 



2023; 2023

nên có 4041 giá trị

m

thỏa mãn yêu cầu bài toán.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 81

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT TRƯƠNG ĐỊNH

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1C

2D

3B

4D

5D

6D

7B

8A

9B

10A

11C

12B

13A

14C

15B

16C

17C

18C

19B

20B

21D

22B

23A

24B

25A

26C

27D

28A

29B

30B

31B

32A

33C

34A

35A

36D

37A

38C

39A

40B

41A

42C

43A

44B

45A

46C

47C

48A

49D

50A

HƯỚNG DẪN GIẢI CÁC CÂU VD, VDC

Câu 39. Có bao nhiêu số nguyên x thỏa mãn

( )

2

log x 2 x 2x 9−+− <

A. 1. B. 2. C. 3. D. 4.

Chọn A

+ Điều kiện:

( )

x 2*>

+ Xét hàm số

( )

2

f x log x 2 x 2x= −+−

trên khoảng

(

)

2; +∞

Ta có

( )

( ) ( )

'

1

f x 2 x 1 0 x 2;

x 2 ln 2

= + − > ∀ ∈ +∞ ⇒

−

Hàm số đồng biến trên khoảng

( )

2; +∞

mà

( )

f4 9=

nên BPT

( ) ( )

fx f4 x 4⇔ < ⇔<

+ Kết hợp với điều kiện (*)

2x4⇒<<

. Vì x nguyên nên x = 3

Câu 40. Cho hàm số

( )

fx

có đạo hàm liên tục trên



. Biết

( )

f4 1

=

và

( )

1

0

1

dxxf 4x

=

∫

, khi đó

( )

4

2

0

dxxxf

′

∫

bằng

A.

31

2

. B.

16−

. C.

8

. D.

14

.

Chọn B

+ Đặt

t 4x

=

ddt x4⇒=

. Khi đó.

( )

14

00

t.f t

xf 4x dt 1

16

dx = =

∫∫

( )

4

0

xf x 16dx⇒=

∫

+ Xét

( )

4

2

0

x f x dx

′

∫

Áp dụng công thức tích phân từng phần ta có:

( ) ( )

( )

44 4

4

22

0

00 0

x f x x f x 2x.f x 16.f 4 2 x.f x 16 2.16 16dx dx dx

′

=−=−=−=−

∫∫∫

Câu 41. Có bao nhiêu giá trị nguyên của tham số

m

để hàm số

42

13

y x 3x mx

22

= −+

có ba điểm cực trị?

A.

5

. B.

6

. C.

7

. D.

4

.

Chọn A

+ Ta có

3

y' 2x 6x m

2

= −+

.

( )

3

y' 0 2x 6x m 0 1

2

=⇔ −+ =

.

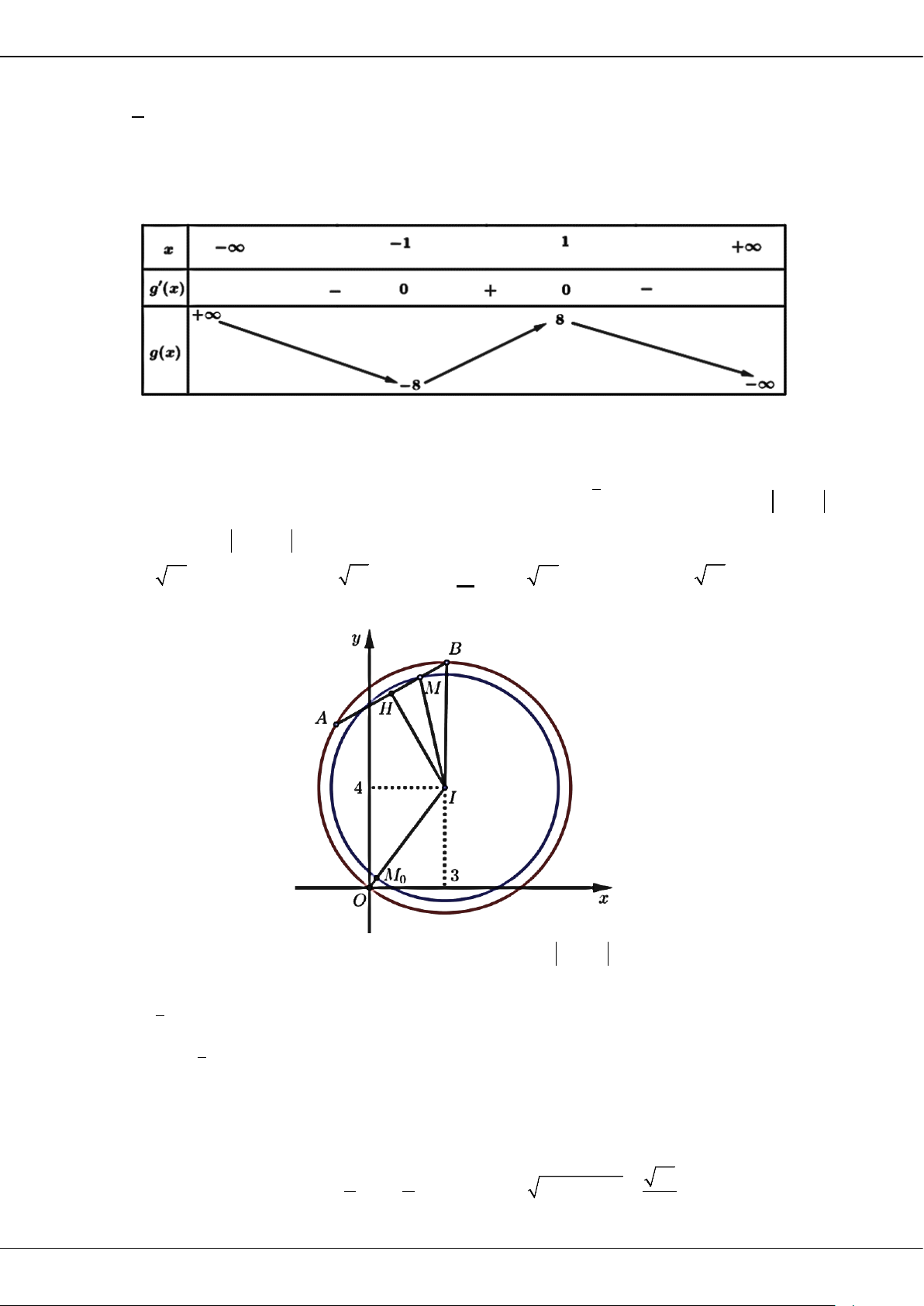
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 82

Để hàm số có ba cực trị thì phương trình

( )

1

phải có

3

nghiệm phân biệt.

+

( )

33

3

1 m 2x 6x 3m 4x 12x

2

⇔ =−+⇔=−+

+ Xét hàm số

( )

3

g x 4x 12x=−+

. Ta có

( )

2

g ' x 12x 12=−+

;

( )

2

g ' x 0 12x 12 0 x 1= ⇔− + = ⇔ =±

Bảng biến thiên của

(

)

gx

Dựa vào bảng biến thiên ta thấy, phương trình

( )

1

có 3 nghiệm phân biệt khi

8 3m 8−< <

Do

{ }

m 2; 1; 0;1; 2m∈ ⇒ ∈− −

. Vậy có 5 giá trị

m

thoả mãn.

Câu 42. Giả sử

12

z ,z

là hai trong các số phức

z

thỏa mãn

( )

z 6 8 iz−−

là số thực. Biết rằng

12

zz 6−=

. Giá trị nhỏ nhất của

12

z 3z+

bằng

A.

5 73−+

. B.

5 21

+

C.

20 2 73−

D.

20 4 21

−

Chọn C

+ Gọi

A,B

lần lượt là điểm biểu diễn cho các số phức

12

z ,z

. Từ

12

z z 6 AB 6−=⇒ =

.

+ Đặt

( )

z x yi, x, y=+∈

.

( )

(

)

( ) ( )

( )

( )(

)

22

z 6 8 iz x yi 6 8 i x yi x yi 6 8 ix y 8x x i xy 8yi xy y i 48 6xi 6y− − = +− − − = +− −− = − − + + − − + +

+ Do

( )

z 6 8 iz−−

là số thực nên ta được

22

x y 6x 8y 0+−−=

. Vậy tập hợp các điểm biểu diễn của

z

là

đường tròn (C) tâm

( )

I 3; 4

bán kính

R 5 A,B (C).=⇒∈

+ Xét điểm

M

thỏa

MA 3MB 0 MA 3MB+ =⇔=− ⇒

    

M nằm trên đoạn AB với MA = 3MB.

Gọi

H

là trung điểm

AB

13

HM AB

42

⇒= =

Từ đó ,

22

73

IM HI HM

2

=+=

suy ra điểm

M

thuộc

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 83

đường tròn

( )

C

′

tâm

( )

I 3; 4

, bán kính

73

r

2

=

.

+ Ta có

12

z 3z OA 3OB 4OM 4OM

+=+ = =

  

, do đó

12

z 3z+

nhỏ nhất khi

OM

nhỏ nhất.

Ta có

min 0

73

OM OM OI r 5

2

= = −=−

. Vậy

12 0

min

z 3z 4OM 20 2 73

+==−

.

Câu 43. Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh a. Tam giác SAD cân tại S và mặt bên

(SAD) vuông góc với mặt đáy. Biết thể tích khối chóp SABCD bằng a

3

. Tính khoảng cách từ B đến mặt

phẳng (SCD).

A.

6a

37

B.

a

37

C. 3a D.

3a

37

Chọn A

+ Gọi M là trung điểm AD

Tam giác SAD cân tại S và mặt bên (SAD) vuông góc (ABCD) nên

SM (ABCD)⊥

+

S.ABCD ABCD

1

V S .SM SM 3a

3

= ⇒=

+ Gọi H là hình chiếu vuông góc của M lên SD. Vì AB//CD nên AB // (SCD)

⇒

( )

d(B, SCD ) d(A;(SCD)) 2d(M;(SCD)) 2 MH= = =

+ Xét tam giác SMD vuông tại M, ta có

22 2

1 1 1 3a

MH

MH SM MD

37

= + ⇒=

Vậy

(

)

6a

d(B, SCD ) 2MH

37

= =

.

Câu 44. Cho hàm số

( )

4 32

f (x) x bx cx dx e b,c,d,e R=+ + ++ ∈

có các giá trị cực trị là 1;4;9. Diện tích

hình phẳng giới hạn bởi đồ thị hàm số

'

f (x)

g(x)

f(x)

=

và trục hoành bằng:

A. 4 B. 6 C. 2 D. 8

Chọn B

+ Gọi

123

xxx<<

là ba điểm cực trị của hàm số y = f(x)

Bảng biến thiên

+PT hoành độ giao điểm:

( )

i

x x (i 1; 2;3)

f '(x) 0

f '(x)

g(x) 0

f(x) 0 f(x ) 0

fx

= =

=



==⇔⇔



>>



H

M

D

C

B

A

S

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 84

+ Từ BBT

⇒

f(x

2

) = 9 , còn f(x

1

), f(x

3

) sẽ chọn 1 trong 2 giá trị 1 hoặc 4

+Diện tích:

( )

( ) ( ) ( )

3

2

23

12

x

xx

213

xx

f '(x) f '(x)

S dx dx 2f(x) 2f(x) 4fx 2fx 2fx

f(x)

fx

4 9 2( 4 1) 6

= − = − = −−

= − +=

∫∫

Câu 45. Trên tập hợp các số phức, xét phương trình

( )

2

z 2m 1z m 3 0− + + +=

(

m

là tham số thực). Có

bao nhiêu giá trị của tham số

m

để phương trình có nghiệm phức

0

z

thoả mãn

0

z 26+=

?

A.

2

. B.

1

. C.

4

. D.

3

.

Chọn A

( )

2

m1 m3 m m2

′

∆= + − − = + −

.

•Nếu

2

0 m m20 m 2;m1

′

∆≥⇔ + −≥⇔ ≤− ≥

. Khi đó phương trình có 2 nghiệm thực

0

11

z4m

7

z 26

83

z 8m

17



=⇒=



+=⇔



=−⇒ =−





(thoả mãn).

•Nếu

2

0 m m20 2m1

′

∆<⇔ + −<⇔−< <

.

Khi đó phương trình có 2 nghiệm.

22

12

z m1 m m2i ; z m1 m m2i= +− − − + = ++ − − +

.

Để phương trình có nghiệm phức

0

z

thoả mãn

0

z 26+=

thì

( )

(

)

2

12

z 2 z 2 m3 m m2 6+= += + +− −+ =

m5⇔=

(không thoả mãn).

Vậy có 2 giá trị của

m

thoả mãn yêu cầu bài toán.

Câu 46. Trong không gian

Oxyz

, cho điểm

( )

M 2;1;3−

. Ba điểm

A

,

B

,

C

tương ứng là hình chiếu vuông

góc của điểm

M

lên các trục

Ox

,

Oy

,

Oz

. Khoảng cách từ điểm O đến

( )

ABC

bằng:

A.

5

. B.

1

3

. C.

6

7

. D.

11

3

.

Chọn C

+ Hình chiếu của

( )

M 2;1;3

−

lần lượt lên các trục Ox, Oy, Oz là

( )

A 2;0;0−

( )

,B 0;1;0

( )

, C 0; 0 ;3

+ Phương trình mặt phẳng (ABC):

x yz

1 3x 6y 2z 6 0

213

+ + = ⇔− + + − =

−

+

( )

2

22

6

d O; ABC

7

3 62

−

= =

− ++

Câu 47. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình

( ) ( )

22

log 7x 7 log mx 4x m+≥ + +

nghiệm đúng với mọi x

A. 1 B. 2. C. 3. D. 4.

Chọn C

+ ĐK:

2

mx 4x m 0

mx 4x m 0 (1)

7x 7 0



+ +>



⇔ + +>



+>





+

22 2

BPT 7x 7 mx 4x m (7 m)x 4x 7 m 0 (2)⇔ +≥ + + ⇔ − − +− ≥

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 85

+ YCBT

⇔

Cả 2 BPT (1) và (2) cùng nghiệm đúng với mọi x.

2

(1)

2

(2)

0

70

2 5 {3; 4; 5} ( )

'4 0

' 4 (7 ) 0

m

mm m

m

>





−>



⇔ ⇔< ≤ ⇒ ∈ ∈



∆=− <



∆ =−− ≤





Câu 48. Cắt hình nón đỉnh

S

bởi một mặt phẳng không đi qua trục hình nón ta được một tam giác vuông

cân có cạnh huyền bằng

a2

;

AB

là dây cung của đường tròn đáy hình nón sao cho mặt phẳng

( )

SAB

tạo với mặt phẳng chứa đáy hình nón một góc

60°

. Tính theo

a

khoảng cách từ tâm O của đường tròn đáy

đến mặt phẳng

( )

SAB

.

A.

a6

d

8

=

. B.

a6

d

3

=

. C.

a

d

3

=

. D.

a2

d

6

=

.

Chọn A

+ Gọi

O

,

R

lần lượt là tâm và bán kính đáy của khối nón,

K

,

H

lần lượt là hình chiếu của

O

lên

AB

,

SK

.

Khi đó khoảng cách từ tâm của đường tròn đáy đến mặt phẳng

(

)

SAB

bằng

OH.

+

SK

trung tuyến trong tam giác vuông cân

AB a 2

SAB SK .

22

⇒= =

+Xét tam giác vuông

SOK

có :

6

SO sin 60 . SK

4

= °=

2

; OK cos 60 . SK

4

= °=

22

SO.OK 6

OH

8

SO OK

⇒= =

+

Câu 49. Trong không gian Oxyz, cho mặt cầu

2 22

(S) : (x 1) (y 1) (z 1) 6− ++ +− =

tâm I. Gọi

( )

α

là mặt

phẳng vuông góc với đường thẳng

x1 y3 z

d:

1 41

+−

= =

−

và cắt mặt cầu (S) theo đường tròn (C) sao cho khối

nón có đỉnh I, đáy là đường tròn (C) có thể tích lớn nhất. Biết

( )

α

không đi qua gốc tọa độ, gọi

( )

H HH

H x ;y ;z

là tâm đường tròn (C). Giá trị của biểu thức

H HH

Tx y z=++

bằng.

A.

1

2

−

B.

4

3

C.

2

3

D.

1

3

Chọn D

+Mặt cầu (S) tâm I(1;-1;1) , bán kính R =

R6=

+Gọi x là khoảng cách từ tâm I đến mặt phẳng

( )

(0 x 6)

α

<<

+ Ta có

( )

23

11

V x 6 x x 2x

33

−

= −= +

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 86

+ Xét

3

1

f (x) x 2x (0 x 6)

3

−

= + <<

. Lập BBT, ta có

( )

0; 6

max f (x) 2 x 2= ⇔=

+

u (1; 4;1)= −



là một véc tơ chỉ phương của d cũng là VTCP của đường thẳng IH

+

(1 ; 1 4 ;1 )H IH H t t t∈ ⇒ + −− +

+

22

11

22

93

IH IH t t

= ⇔ = ⇔ = ⇔=±

+

( )

1 212

t H ; ; :x 4y z 0

3 333

α



=−⇒ ⇒ − +=





(Loại vì O không thuộc mặt phẳng)

(

)

1 4 74

t H ; ; : x 4y z 6 0

3 333

α

−



= ⇒ ⇒ − +−=





( Nhận)

Vậy

H HH

1

Tx y z

3

=++=

Câu 50. Có bao nhiêu giá trị nguyên của tham số

( )

a 10;

∞

∈− +

để hàm số

( )

22

f x ln x 2x a 2ax 1= + −− −

đồng biến trên khoảng

(

)

0;10

?

A. 7. B. 11. C. 6. D. 9.

Chọn A

+ ĐK:

2

x 2x a 0+ −>

+ Xét

( )

22

2

2x 2

f x ln x 2x a 2ax 1 f ' x 4ax

x 2x a

+

= + − − −⇒ = −

+−

+ YCBT

⇔

Một trong hai trường hợp sau xảy ra

1) TH1:

+

( )

(

) (

)

(

)

(

)

( )

2

( 0;10)

2

a Min(x 2x)

x 2x a 0 x 0;10

2x 2

f ' x 0 x 0;10 4ax 0, x 0;10

x 2x a

f0 0

ln a 1 0

a0

2x 2

4ax 0, x 0;10 (*)

x 2x a

ae



<+





+ − > ∀∈



+



≥ ∀∈ ⇔ − ≥ ∀∈



+−



≥





− −≥





≤





+



⇔ − ≥ ∀∈



+−



≤−





Vì với

; (0;10)a ex

≤− ∈

thì (*) luôn luôn đúng nên ta có

ae≤−

.

Kết hợp điều kiện suy ra

{ }

a 9,8,7,6,5,4,3∈−−−−−−−

.

2) TH2:

( )

(

) ( )

( )

2

( 0;10)

2

a Min(x 2x)

x 2x a 0 x 0;10

2x 2

f ' x 0 x 0;10 4ax 0, x 0;10

x 2x a

f0 0

ln a 1 0



<+





+ − > ∀∈



+



≤ ∀∈ ⇔ − ≤ ∀∈



+−



≤





− −≤





( )

2

a0

2x 2

4ax 0, x 0;10 (**)

x 2x a

ae

≤





+



⇔ − ≤ ∀∈



+−



≥−





Với

0 ; (0;10)ea x−≤ ≤ ∈

thì (**) không xảy ra do đó không có a trong trường hợp này.

Vậy:

{ }

a 9,8,7,6,5,4,3∈−−−−−−−

.

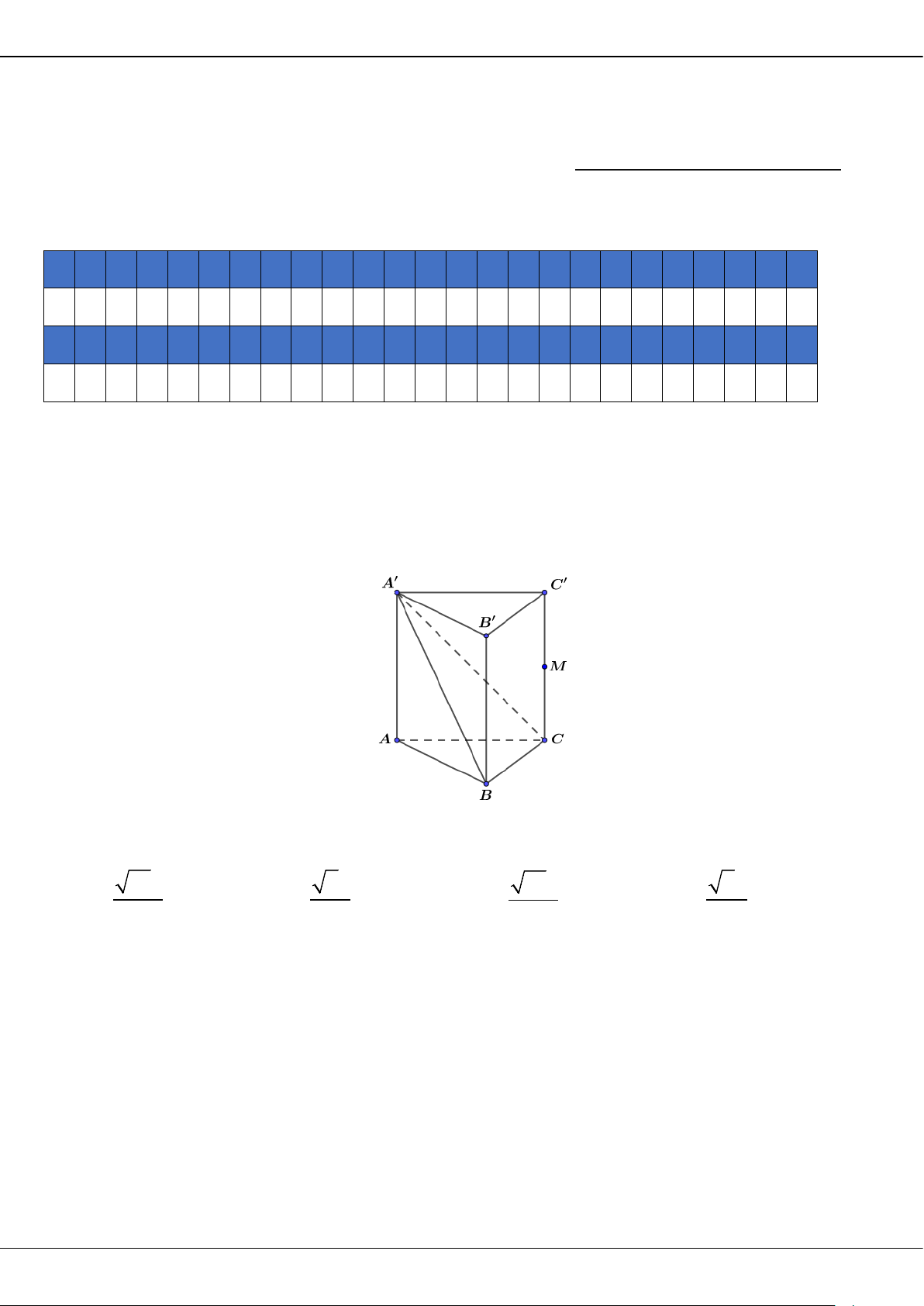
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 87

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT TÂN HIỆP

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

B

D

C

A

B

D

C

A

C

A

B

D

A

B

A

C

B

A

D

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

B

D

C

A

C

A

C

A

B

A

B

A

B

D

A

B

LỜI GIẢI CHI TIẾT

Câu 38. Cho hình lăng trụ đứng

.ABC A B C

′′′

có tất cả các cạnh đều bằng

a

. Gọi

M

là trung điểm

CC

′

.

Khoảng cách từ

M

đến mặt phẳng

( )

A BC

′

bằng

A.

21

14

a

. B.

2

a

. C.

21

7

a

. D.

2

4

a

.

Lời giải

Chọn A

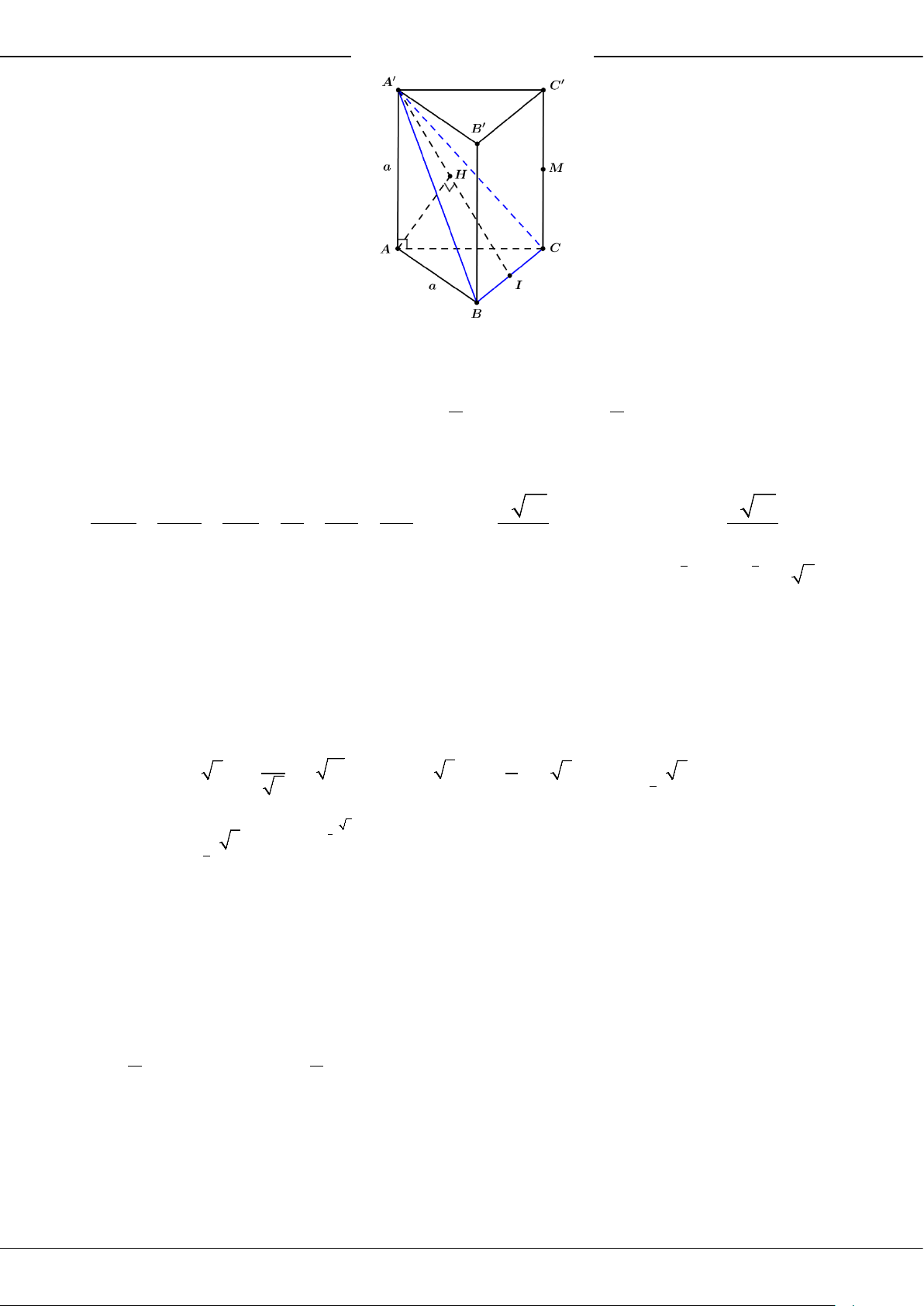
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 88

Gọi

I

là trung điểm

BC

. Kẻ

AH A I

′

⊥

tại

H

.

Ta có

( )

AH A BC

′

⊥

nên

(

)

( )

(

)

( )

11

, ,,

22

d M A BC d C A BC d A A BC

′ ′′ ′

= =

.

Xét

AA I

′

∆

có

( )

2 2 22 2 2

1 1 1 1 4 7 21 21

,

3 3 7 14

aa

AH d M A BC

AH AA AI a a a

′

= + =+=⇒= ⇒ =

′

Câu 39. Có bao nhiêu số tự nhiên x ∈[1; 2023] thỏa bất phương trình

44

11

log log

22

334

xx

x





.

A. 2017. B. 2022. C. 2024. D. 2023.

Lời giải

Chọn A

ĐK: x > 0, đặt t = log

4

x  4

t

= x.

BPT trở thành

3

3.3 4 4

3

t

tt





4.3 4 3.2

tt





3

2

3

3 log ( 3)

2

t







 













3

2

log ( 3)

43

2

log log ( 3) 4 6,54xx  

Vì x ∈[1; 2023] => x ∈ {7, 8, 9,..., 2023}.Vậy có 2017 số tự nhiên thỏa đề bài.

Câu 40. Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa mãn

( ) ( )

8 88FG+=

và

( ) ( )

0 02FG+=−

. Khi đó

0

2

(4)f x dx

−

∫

bằng:

A.

5

4

−

. B.

5

4

. C.

5

. D.

5−

.

Lời giải

Đặt

44t x dt dx=−⇒=−

Đổi cận:

28xt=−⇒=

00xt=⇒=

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 89

( ) ( )

0

8

0

2

8

0

1 11

()( ) () (8) (0)

44

4

d ft dt ftd F Fx tfx

−

− = −= = −

∫∫ ∫

Ta lại có:

( ) ( )

88

00

GFC

Gx Fx C

GFC



= +



= +⇒



= +





Mà

( ) ( )

2 (8) 8

(8) (0) 5.

2 (0) 2

(0) (0) 2

8 88F

FC

FF

FC

F

G



+=





⇔ ⇔−=



+



+=

= −

+=−





Vậy:

( )

8

0

2

11 5

( ) (8) (0) .4

44

d

4

f Fx t dt Fx f

−

= = −=−

∫ ∫

Câu 41. Có bao nhiêu số nguyên

[ ]

20;20m∈−

để đồ thị hàm số

( )

42 2

91y mx m x=+− +

có

ba điểm cực trị?

A. 20. B. 19. C. 18. D. 17.

Lời giải

Ta có

( ) ( )

3 2 22

4 2 9 22 9y mx m x x mx m



′

= + −= +−



.

22

0

2 90

x

y

mx m

=



′

= ⇔



+ −=



(

)

1

.

Hàm số có ba điểm cực trị khi và chỉ khi

0y

′

=

có ba nghiệm phân biệt hay

( )

1

có hai nghiệm phân biệt

khác 0

( )

2

3

2 90

03

m

mm

m

<−



⇔ − <⇔



<<



.

Vậy có 19 giá trị của

m

thỏa mãn đề bài.

Câu 42. Xét các số phức

z

thoản mãn điều kiện

2

2 44 2 1zz i z+ ++ = +

. Gọi

M

và

m

lần lượt là

giá trị lớn nhất và nhỏ nhất của

1

z +

. Giá trị của

Mm−

bằng

A.

2

. B.

26

. C.

14

. D.

46

.

Lời giải

( )

2

24421 1 3421zz iz z iz

+++= +⇔+++= +

(1)

Áp dụng bất đẳng thức tam giác ta có:

( )

(

)

2

22

2 1 1 34 1 34 1 5z z i z iz+= + ++ ≥ + − + = + −

(Vì

( )

2

11zz+=+

)

Dấu “=” xảy ra khi và chỉ khi

( ) ( )

2

1 34z ki+= +

. Với

0k <

.

Suy ra

( )

2

22

4 1 15zz+≥ +−

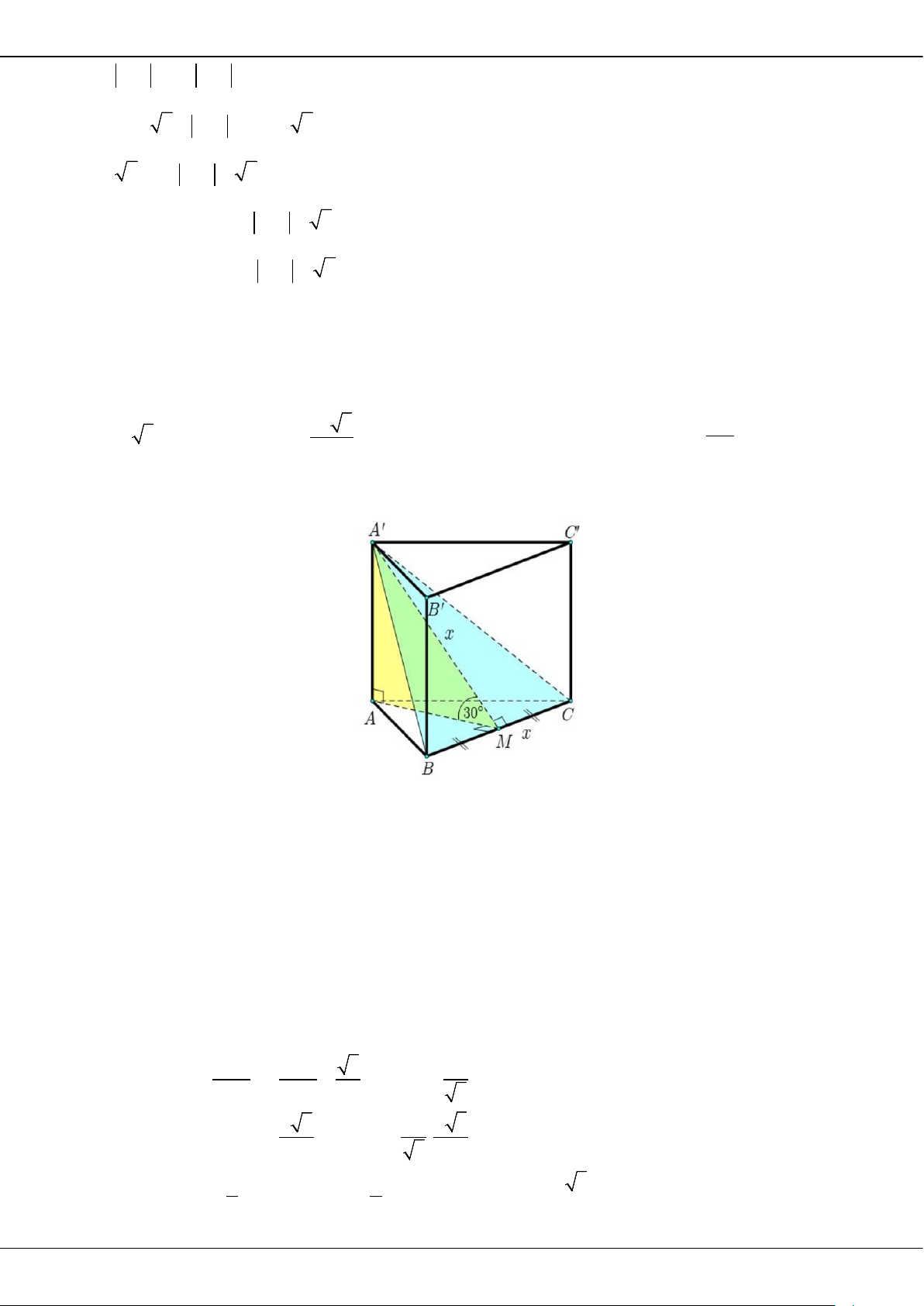
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 90

42

1 14 1 25 0zz⇔+− ++ ≤

2

7 26 1 7 26

z⇔− ≤ + ≤+

61 1 61

z⇔ −≤ + ≤ +

* Giá trị lớn nhất của

1 61

z += +

.

* Giá trị nhỏ nhất của

1 61

z += −

.

Vậy

2

Mm

−=

.

Câu 43. Cho khối lăng trụ đứng

.ABC A B C

′′′

có đáy là tam giác đều. Mặt phẳng

()A BC

′

tạo với đáy

một góc

30°

và tam giác

A BC

′

có diện tích bằng

32

. Thể tích của khối lăng trụ đã cho bằng

A.

64 3

B.

64 3

3

. C.

128

. D.

128

3

.

Lời giải

Gọi

ϕ

là góc giữa mặt phẳng

( )

A BC

′

và

( )

ABC

.

Gọi

M

là trung điểm của

BC

.

Khi đó

AM BC⊥

.

AA BC

′

⊥

.

Suy ra

( )

BC A AM BC A M

′′

⊥ ⇒⊥

.

Ta có:

( ) ( )

A BC ABC BC

AM BC

A M BC

′

∩=





⊥





′

⊥



.

Suy ra góc



30A MA

ϕ

′

= = °

.

Ta có:

32

cos30

2

3

AM AM

A M AM

AM AM

°

′

=⇔ =⇔=

′′

.

Đặt

3

0

2

x

BC x AM

=>⇒ =

và

23

.

2

3

x

AM x

′

= =

.

Ta lại có:

11

43

. 32 . 8 4.

22

8

A BC

AM

S AM BC xx x AA

AM

′

∆



=



′′

= ⇔ = ⇒=⇒ ⇒ =



′

=





LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 91

Suy ra

2

83

.4 64 3.

4

.

ABC A B C ABC

V S AA

′′′

⋅∆

′

= = =

.

Câu 44. Cho hàm số

( )

y fx=

có đạo hàm liên tục trên



, thỏa mãn

( ) ( )

2

42 1 ,f x x fx

′



= +−





x∀∈

và

( )

12f =

. Diện tích hình phẳng giới hạn bởi các đường

( ) ( )

,yfxyfx

′

= =

và trục tung bằng

A.

1

3

. B.

4

3

. C.

3

4

. D.

5

3

.

Lời giải

Đặt

( )

1

0

d

I fx x=

∫

.

Dùng tích phân từng phần, ta có:

( )

dd

u fx

vx

=







=





( )

ddu fxx

vx

′

=





⇒



=





.

( )

11

1

0

00

d2 d

I xf x xf x x xf x x

′′

=−=−





∫∫

.

Ta có

( ) ( )

2

4 84f x fx x

′

+=+





( ) ( )

( )

1 1 11

2

22

0 0 00

d 4 d 4 d 12 4 dfx x xfxx xx x x

′′

⇒ − +=−





∫ ∫ ∫∫

( )

1

2

0

2d0

fx x x

′

⇔ −=





∫

( )

2fx x

′

⇔=

( )

2

fx x C⇒=+

,

C ∈

.

Mà

(

)

12 1fC

=⇒=

( )

2

1

fx x⇒=+

.

Phương trình hoành độ giao điểm:

( ) ( )

01fx f x x

′

− =⇒=

Vậy diện tích hình phẳng

( ) ( )

11

2

00

1

d 2 1d

3

S fx f x x x x x

′

= − = −+ =

∫∫

.

Câu 45. Trên tập hợp các số phức, xét phương trình

( )

22

30z a za a− − + +=

(

a

là tham số thực).

Có bao nhiêu giá trị nguyên của

a

để phương trình có 2 nghiệm phức

12

, zz

thỏa mãn

12 12

zz zz+=−

?

A.

2

. B.

4

. C.

3

. D.

1

.

Lời giải

Ta có

( )

2

22

3 4 3 10 9

a aa a a∆= − − + =− − +

.

+ TH1:

5 2 13 5 2 13

0

33

a

−− −+

∆≥ ⇔ ≤ ≤

. Khi đó

12

, zz

là 2 nghiệm thực.

Theo Viet

( )

2

12

2

1 2 1 2 12

2

12

3

4 . 3 10 9

.

zz a

z z z z zz a a

zz a a

+=−



⇒−= + − =− − +



= +



.

Từ đó ta có

( )

2

22

12 12

3 3 10 9 3 3 10 9zzzza aa a aa+=−⇔−=−− +⇔−=−− +

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 92

(

)

2

0

4 40

1

a

a a TM

a

=



⇔ +=⇔



= −



.

+ TH2:

5 2 13

3

0

5 2 13

3

a



−+

>



∆< ⇔



−−

<





.

Khi đó

2

22

1,2 12 12

3 3 10 9

3 10 9 3 10 9

2

a ia a

z zz ia a zz a a

−± + −

= ⇒−= +−⇒−= +−

.

( )

2

22

12 12

2

3 3 10 9 3 3 10 9

1

8 90

9

zzzza aa a aa

a

a a TM

a

+=−⇔−= +−⇔−=+−

=



⇔ + −=⇔



= −



Vậy có 4 giá trị của

a

thỏa mãn yêu cầu đề bài.

Câu 46. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

( ) ( )

1; 2;1 , 3;4;0AB

, mặt phẳng

( )

: 46 0P ax by cz+++ =

. Biết rằng khoảng cách từ

,AB

đến mặt phẳng

(

)

P

lần lượt bằng

6

và

3

. Giá trị của biểu thức

T abc=++

bằng

A.

3−

. B.

6−

. C.

3

. D.

6

.

Lời giải

Chọn B

Gọi

,HK

lần lượt là hình chiếu của

,AB

trên mặt phẳng

( )

P

.

Khi đó theo giả thiết ta có:

3AB

=

,

6AH =

,

3BK =

.

Do đó

,AB

ở cùng phía với mặt phẳng

( )

P

Lại có:

AB BK AK AH H K

+ ≥ ≥ ⇒≡

.

Suy ra

,,

ABH

là ba điểm thẳng hàng và

B

là trung điểm của

AH

nên tọa độ

( )

5; 6; 1H

−

.

Vậy mặt phẳng

( )

P

đi qua

( )

5; 6; 1H −

và nhận

( )

2; 2; 1AB = −



là VTPT có nên phương trình

( ) (

) ( )

2 5 2 6 1 1 0 2 2 23 0x y z x yz− + − − + =⇔ + −− =

.

Theo bài ra thì

( )

: 4 4 2 46 0P xyz−−++=

, nên

4, 4, 2abc=−=−=

.

Vậy

6T abc=++=−

.

Câu 47. Có bao nhiêu cặp số tự nhiên

( )

;xy

thỏa mãn

4 2 55

5

5(5 4 ) 2028 2024 log ( 2023) (1 )

y

y xx x x



+ + ≤− + + − −



A. 2023. B. 4042. C. 4024. D. 4040.

Lời giải

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 93

Chọn D

ĐK: (x – 2023)

5

(1-x)

5

> 0  (x – 2023)(1-x) > 0  1 < x < 2023. Vì x ∈ N => 2 ≤ x ≤ 2022.

4 2 55

5

5(5 4 ) 2028 2024 log ( 2023) (1 )

y

y xx x x



+ + ≤− + + − −



(1)



42

5

5.5 20 2028 2024 5log ( 2023)(1 )

y

y xx x x+ + ≤− + + − −



41 2 2

5

5 5(4 1) 2024 2023 5log ( 2024 2023)

y

yxx xx

+

+ +≤−+ − + −+ −

Đặt u = log

5

(- x

2

+ 2024x – 2023)  5

u

= (- x

2

+ 2024x – 2023)

(1)Trở thành 5

4y + 1

+ 5(4y +1) ≤ 5

u

+ 5u (2).

Xét hàm số f(t) = 5

t

+ 5t, f’(t) = 5

t

.ln5 + 5 > 0 ∀t => f(t) là hàm số đồng biến trên R

(2) f(4y + 1) ≤ f(u)  4y + 1 ≤ u  4y + 1 ≤ log

5

(- x

2

+ 2024x – 2023)

Xét hàm số g(x) = - x

2

+ 2024x – 2023, với 2 ≤ x ≤ 2022.

g’(x) = - 2x + 2024; g’ = 0  x = 1012

g(2) = g(2022)= 2021, g(1012) = 1022121 => g(x) ≤ 1022121

Do đó: 4y + 1 ≤ log

5

(1022121)∼8,6 => y ≤ 1,9, y ∈ N => y ∈{0; 1}

* Với y = 0, ta có u ≥ 1 5

u

≥ 5 - x

2

+ 2024x – 2023≥ 5 - x

2

+ 2024x – 2028≥ 0

 1,0024 ≤ x ≤ 2022,9975

 x ∈ { 2, 3,..., 2022} có 2021 số tự nhiên.

* Với y = 1, ta có u ≥ 5  5

u

≥ 5

5

 - x

2

+ 2024x – 2023≥ 3125

- x

2

+ 2024x – 5148≥ 0

 2,54 ≤ x ≤ 2021,45

 x ∈ { 3,4,..., 2021} có 2019 số tự nhiên.

Kết luận: có 4040 cặp số tự nhiên (x, y) thỏa đề bài.

Câu 48. Cho hình trụ tròn xoay có hai đáy là hai hình tròn

( )

;3O

và

( )

;3O

′

. Biết rằng tồn tại dây

cung

AB

thuộc đường tròn

( )

O

sao cho

O AB

′

∆

là tam giác đều và mặt phẳng

( )

O AB

′

hợp với mặt phẳng

chứa đường tròn

( )

O

một góc

60°

. Tính diện tích xung quanh

xq

S

của hình nón có đỉnh

O

′

, đáy là hình

tròn

( )

;3O

.

A.

54 7

7

xq

S

π

=

. B.

81 7

7

xq

S

π

=

. C.

27 7

7

xq

S

π

=

. D.

36 7

7

xq

S

π

=

.

Lời giải

Chọn D

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 94

Gọi

H

là trung điểm của

( )

1AB OH AB⇒⊥

.

Lại có:

( ) ( )

2OO OAB OO AB

′′

⊥ ⇒⊥

.

Từ

(

)

1

và

( )

2

suy ra

( )



60AB OOH AB OH OHO

′ ′′

⊥ ⇒⊥ ⇒ =°

Đặt

OH x=

. Khi đó:

03

x<<

và

0

tan 60 3OO x x

′

= =

.

Xét

OAH∆

, ta có:

22

9AH x= −

.

Vì

O AB

′

∆

đều nên:

( )

2

2 29 3O A AB AH x

′

= = = −

.

Mặt khác

AOO

′

∆

vuông tại

O

nên

( )

2 22 2

3 3 9 4AO OO x

′′

= += +

.

Từ

( ) ( )

3,4

ta có:

(

)

22 2

27 3 21

49 3 9

77

xx x x− = +⇔ = ⇔=

97

3

7

h OO x

′

⇒= = =

.

Độ dài đường sinh hình nón là

12 7

7

l OA

′

= =

.

Vậy:

36 7

7

xq

S Rl

π

= =

.

Câu 49. Trong không gian tọa độ

Oxyz

, gọi

( )

P

là mặt phẳng cắt các tia

Ox

,

Oy

,

Oz

lần lượt

tại

( )

;0;0Aa

,

( )

0; ;0Bb

,

( )

0;0;Cc

sao cho

222

12

abc

++=

và diện tích tam giác

ABC

lớn nhất.

Mặt phẳng

(

)

P

đi qua điểm nào sau đây?

A.

( )

1; 0;1S

. B.

( )

2;0; 2M

. C.

(

)

3; 0;3

N

. D.

(

)

2; 2; 0Q

.

Lời giải

Chọn A

Vì mặt phẳng

( )

P

cắt các tia

Ox

,

Oy

,

Oz

lần lượt tại

( )

;0;0Aa

,

( )

0; ;0Bb

,

( )

0;0;Cc

.

Nên ta có

,, 0abc>

.

Áp dụng phương trình mặt phẳng theo đoạn chắn

( )

:1

xyz

P

abc

++=

.

Ta có diện tích tam giác

ABC

là

( )

( ) (

)

222

11

,

22

S AB AC ab bc ca



= = ++



 

( )

2

22 2

1

2

S ab c a b⇔= + +

.

Ta có:

2 22

12 cab

−=+

và

2

12 2c ab−≥

.

( )

2

2 2 24

1 12 1 3

12 36 6

22 2 4

c

S c c cc



−

≤ + −= +−





( )

2

13

48 4 2 3

24

Sc

⇔≤ − − ≤

.

Diện tích tam giác

ABC

lớn nhất khi

2

222

42

23 2

2

12

ca

S ab b

c

abc



= =





= ⇔= ⇔=





=

++=



.

Khi đó mặt phẳng

( )

:1

222

xyz

P ++=

đi qua điểm

( )

1; 0;1S

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 95

Câu 50. Cho hàm số bậc ba

( )

=y fx

có đồ thị như hình bên dưới:

Số giá trị nguyên của tham số

m

để hàm số

( )

−

=

−

9mf x

y

fx m

nghịch biến trên

( )

−1; 1

là:

A.

0.

B.

2.

C.

3.

D. Vô số.

Lời giải

Điều kiện:

( )

≠ .m fx

Ta có:

( ) ( ) ( ) ( ) ( )

′

∀∈− ⇒ ∈− < ∀∈−1; 1 1; 3 ; 0, 1; 1 .x fx f x x

Ta có:

( )

−

′′

=

−

2

9

..

m

y fx

fx m

Yêu cầu bài toán

( )

( ) ( )

( )



−>

−



′′

⇔ < ∀∈− ⇔ < ∀∈− ⇔



∉−



−



2

90

9

0, 1; 1 . 0, 1; 1

1; 3

m

y x fx x

m

fx m

( )

(

∈



∈−



⇔ ⇔ ∈ − −    → = − = −





∈ −∞ −  ∪  +∞









3; 3

3; 1 2; 1.

; 1 3;

m

m mm

m

⇒

Chọn đáp án B.

x

y

3

-1

1

-1

O

1

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 96

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT PHƯỚC THẠNH

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.C

2.B

3.A

4.A

5.D

6.B

7.A

8.A

9.A

10.D

11.D

12.D

13.A

14.C

15.B

16.C

17.C

18.C

19.B

20.B

21.D

22.D

23.B

24.B

25.B

26.C

27.A

28.A

29.D

30.C

31.C

32.A

33.C

34.A

35.B

36.A

37.D

38.B

39.A

40.D

41.A

42.B

43.D

44.C

45.B

46.B

47.A

48.B

49.C

50.D

HƯỚNG DẪN GIẢI

Câu 39. Có bao nhiêu giá trị nguyên của

x

thoả mãn

(

)

(

)

( )

21

22

log 1 log 31 32 2 0

x

xx

−



+− + − ≥



?

A.

27

. B.

25

. C.

26

. D.

28.

Chọn C

Điều kiện xác định

31 0 31xx+ > ⇔ >−

.

Đặt

( )

21

22

log 1 log 31 32 2

x

fx x x

−



= +− + −



Ta có

22

22 2 2

11

log ( 1) log ( 31) 0 log ( 1) log ( 31)

() 0

32 2 0 32 2

xx

xx x x

fx

−−



+− + = += +

=⇔⇔



−= =





5

6

x

=−





⇔

=





=



.

Bảng xét dấu:

Khi đó

( )

0 31 5, 6≥ ⇔− < ≤− =

fx x x

Do

x ∈

nên có 27 giá trị nguyên của

x

thoả mãn yêu cầu bài toán.

Câu 40. Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa

mãn

( ) ( )

114 114 2FG+=−

và

( ) ( )

44 44 0FG+=

. Tính

( )

21

7

5 9dfx x∫+

.

A. 3. B.

3

4

−

. C. 6. D.

1

5

−

.

Chọn D

Đặt

1

5 9 d d

5

ux u x= +⇒ =

, hay

1

d d

5

xu=

.

Khi

7x =

thì

( )

7 44u =

. Khi

21x =

thì

( )

21 114u =

. Khi đó

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 97

(

)

(

) ( )

( ) (

)

( ) ( )

( )

(

) (

)

(

)

( )

(

)

(

) (

)

( )

21 114 114 114 114

7 44 44 44 44

11

5 9d d 5 d d d

5 10

1

114 44 114 44

10

11

114 114 44 44

10 5

f x x fu u fx x fx x fx x

F F GG

F G FG



+= = = +







= −+ −





= + −+ =−



∫ ∫ ∫ ∫∫

Câu 41. Cho hàm số

( ) 10

x

fx x

và hàm số

 

3 22

() 1 2g x x mx m x   

. Gọi

M

là giá trị

lớn nhất của hàm số

( ( ))gx fx



trên đoạn

0;1







. Khi

M

đạt giá trị nhỏ nhất thì giá trị của tham số

m

bằng

A.

21

2

. B. 6. C. 21. D. 5.

Lời giải

Chọn B.

Đặt

()t x fx

,

[0;1] [1;12]xt 

.

Xét

 

322

() 1 2g t t mt m t   

trên

1; 12







22

() 3 2 1

g t t mt m



  

.

( ) 0 [1; 12 ]gt t



 

[1;12 ]

2

max ( ) (12) 12 144 1738

t

M gt g m m



    

.

min

M

khi

6m 

.

Câu 42. Cho số phức

z

thỏa mãn

52 3z iz i+− = +−

. Giá trị nhỏ nhất của

4 22Pz z i=−+−+

bằng:

A.

5

. B.

15

. C.

10

. B.

20

.

 Gọi

( )

;M xy

là điểm biểu diễn của số phức

( )

,,z x yi x y=+∈



.

Ta có

( ) ( )

52 3 5 2 3 1z iz i x y ix y i

+− = +−⇔ ++ − = +− −

.

(

) ( ) (

) ( )

2222

5 2 3 1 4 2 19 0x y x y xy⇔+ +− =+ +− ⇔−+=

là phương trình đường thẳng

∆

.

 Gọi

(

) ( )

4;0 , 2; 2AB−

lần lượt là điểm biểu diễn của số phức

12

4; 2 2

zz i= = −

ta có

P MA MB= +

; với

M ∈∆

.

 Do

,AB

nằm cùng phía với

∆

. Đường thẳng

d

đi qua

( )

2; 2B −

và vuông góc với đường

thẳng

∆

có phương trình

( ) ( )

1 2 2 2 0 2 20x y xy− + + =⇔+ +=

.

Hd= ∩∆⇒

Tọa độ điểm

H

là nghiệm của hệ phương trình:

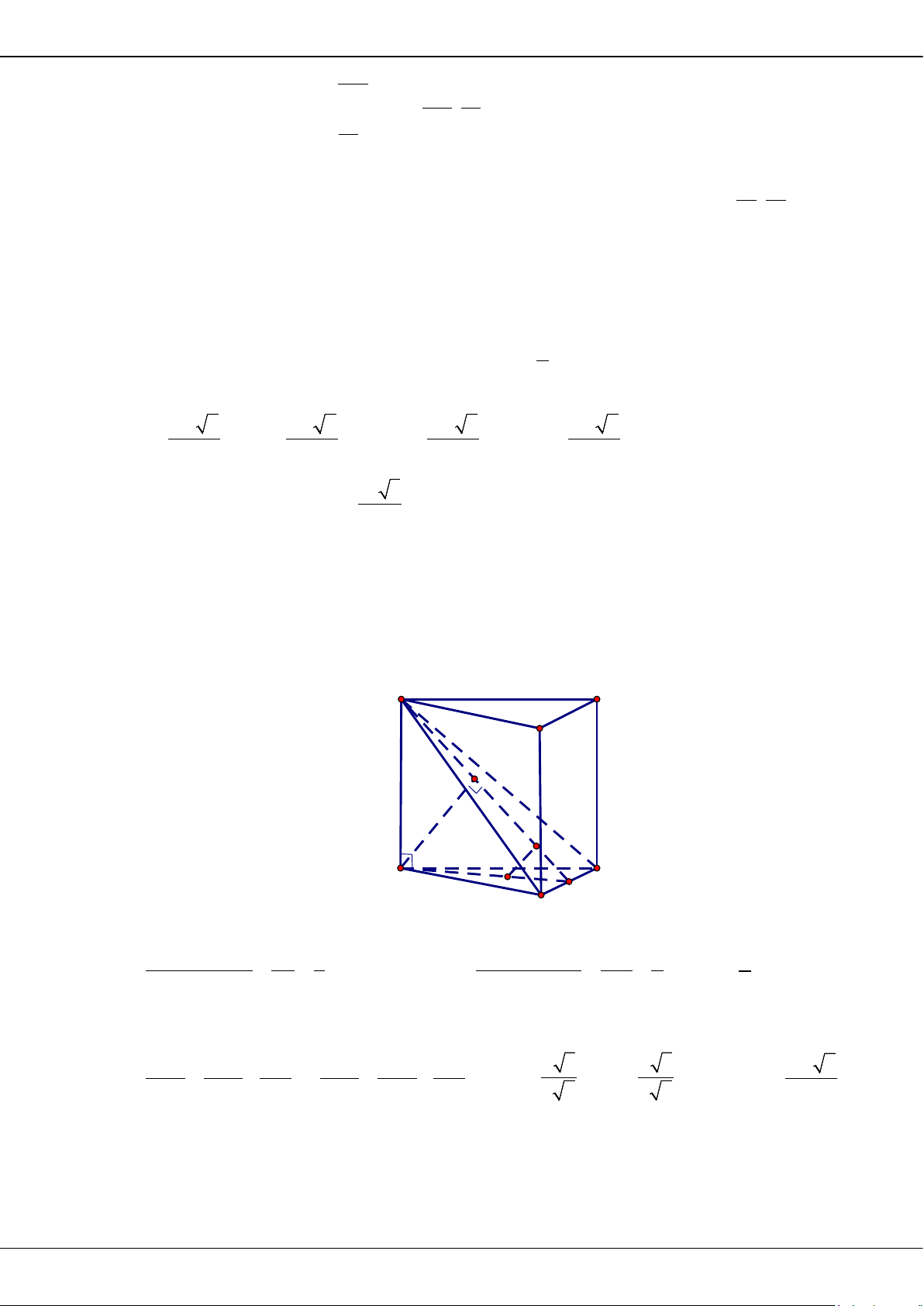
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 98

21

4 2 19 0

21 11

5

;

2 2 0 11

5 10

10

x

xy

H

xy

y

−



=



−+=



−





⇔⇒





+ +=







=





.

Gọi

B

′

đối xứng với

B

qua

∆

ta có

H

là trung điểm của đoạn

BB

′

nên

52 21

;

55

B



′

−





.

Khi đó

15P MA MB MA MB AB

′′

=+=+ ≥=

.

 Vậy giá trị nhỏ nhất của

P

là

15

Câu 43. Cho hình lăng trụ đứng

.ABC A B C

′′′

, biết đáy

ABC

là tam giác đều cạnh

a

. Khoảng cách từ tâm

O

của tam giác

ABC

đến mặt phẳng

( )

A BC

′

bằng

6

a

. Tính thể tích khối lăng trụ

.

ABC A B C

′′′

.

A.

3

32

8

a

. B.

3

32

28

a

. C.

3

32

4

a

. D.

3

32

16

a

.

Diện tích đáy là

2

3

4

ABC

a

BS

∆

= =

.

Chiều cao là

( ) ( )

( )

;h d ABC A B C AA

′′′ ′

= =

.

Do tam giác

ABC

là tam giác đều nên

O

là trọng tâm của tam giác

ABC

. Gọi

I

là trung điểm

của

BC

,

H

là hình chiếu vuông góc của

A

lên

AI

′

ta có

( ) ( )

( )

;AH A BC d A A BC AH

′′

⊥⇒ =

( )

;

1

3

;

d O A BC

IO

IA

d A A BC

′

= =

′

( )

(

)

( )

(

)

;

3 36

d A A BC

AH a

d O A BC

′

⇒===

2

a

AH

⇒=

Xét tam giác

A AI

′

vuông tại

A

ta có:

2 22

1 11

AH AA AI

= +

′

2 22

1 11

AA AH AI

⇒=−

′

3

22

a

AA

′

⇒=

3

22

a

h⇒=

3

.

32

16

ABC A B C

a

V

′′′

⇒=

.

Câu 44. Cho hàm số

( ) ( )

32

, ,,,= + ++ ∈f x ax bx cx d a b c d

thỏa mãn

( ) ( )

2130 0−=ff

. Hàm số

( )

′

fx

có đồ thị như hình bên. Diện tích hình phẳng giời hạn bởi hai đồ thị hàm số

( )

=y fx

;

( )

′

=y fx

và các đường

1x =

,

3x =

.

I

A'

B'

C'

A

B

C

H

O

K

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 99

A.

14,31

a

. B.

24

a

. C.

31a

. D.

26a

.

 Ta có

( )

2

32f x ax bx c

′

= ++

cắt trục hoành tại 2 điểm và bề lõm hướng lên nên ta có

0a >

nên

( ) ( )(

)

(

)

2

3 1 23 2f x ax x ax x

′

= − + = +−

(

)

32

xx

fx a x d



⇒ = +− +







( )

0fd=

;

( )

7

1

2

f ad=−+

ta có

( ) ( )

2130 0 7f f da− =⇒=−

.

 Gọi

S

là diện tích hình phẳng giới hạn bởi các đường:

( ) (

)

; ; 1; 3

yfxyfxx x

′

= = = =

.

Ta có:

( ) ( )

33

32

11

3

d 9 1 d 31

2

S fx f x x ax x x x a

′

= − = − −− =

∫∫

Câu 45. Trong tập hợp các số phức, cho phương trình

( )

2

2 45 2016 80 0zaz a−− + −=

(a là tham số thực).

Có tất cả bao nhiêu giá trị nguyên dương của a để phương trình có hai nghiệm phân biệt

12

,zz

sao cho

12

zz=

A.

7

. B.

8

. C.

9

. D.

10

.

Lời giải

Chọn B

Ta có

( ) ( )

2

' 45 2016 80 10 9a aa a∆= − − − = − +

Th1:

2

1

' 0 10 9 0

9

a

aa

a

<



∆>⇔ − +>⇔



>



Phương trình có 2 nghiệm thực phân biệt, khi đó:

12

()z zl

zz

=



= ⇔



= −



( )

12

0 2 45 0 45

zz a a⇔ + =⇔ − =⇔=

.

Th2:

( )

2

' 0 10 9 0 1; 9aa a∆<⇔ − +<⇔∈

.

Khi đó phương trình có 2 nghiệm phức

12

,zz

là 2 số phức liên hợp của nhau, ta luôn có

12

zz=

O

x

y

y = f

'(

x

)

1

2

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 100

.

Với

{ }

2;3;4;5;6;7;8;45aa

+

∈ ⇒∈



. Vậy có

8

giá trị nguyên dương cần tìm.

Câu 46. Trong không gian

Oxyz

cho hai điểm

( )

0; 8; 2A

,

( )

9; 7; 23

B −

và mặt cầu

( )

S

có phương trình

222

():(5)( 3)(7)72Sx y z

−+++−=

. Mặt phẳng

(

)

:0

+ + +=P x by cz d

đi qua điểm

A

và tiếp xúc với

mặt cầu

( )

S

sao cho khoảng cách từ

B

đến mặt phẳng

( )

P

lớn nhất. Giá trị của

bcd++

khi đó là

A.

2

. B.

4

. C.

3

. D.

1

.

Chọn B

Lời giải

Vì

( )

AP∈

nên

82 0 82 (): (82)0b cd d b c Pxbycz b c+ +=⇔=−− ⇒ + + − + =

Do

( )

P

tiếp xúc mặt cầu

( )

S

nên

22

| 5 11 5 |

( ;( )) 6 2

1

bc

dI P R

bc

−+

=⇔=

++

.

Ta có:

22 22

| 9 7 23 8 2 | | (5 11 5 ) 4(1 4 ) |

( ;( ))

11

b cbc bc bc

dB P

bc bc

− + − − − + + −+

= =

++ ++

22 22 22

|5 11 5 | |1 4 | |1 4 |

( ;( )) 4 ( ;( )) 6 2 4

11 1

bc bc bc

dB P dB P

bc bc bc

− + −+ −+

⇒ ≤ + ⇔ ≤+

++ ++ ++

( )

22

Cosi-Svac

22

(1 1 16) 1

( ;( )) 6 2 4 ( ;( )) 18 2

1

bc

dB P dB P

bc

++ + +

⇔ ≤+ ⇔ ≤

++

Dấu

""=

xảy ra khi và chỉ khi

22

1

4

| 5 11 5 |

62

0

1

c

b

c

bc

d

bc



= −

=−=







⇔=



−+



=





++



Vậy

max

18 2P =

khi

3bcd++ =

Câu 47. Có bao nhiêu số nguyên

y

trong đoạn

[ ]

2021;2021−

sao cho bất phương trình

( )

11

log

10

10 10

x

y

x

+

≥

đúng với mọi

x

thuộc

( )

1;100

A.

2021

. B.

4026

. C.

2013

. D.

4036

.

Lời giải

Chọn A.

( ) ( )

11

log

10

log 11

10 10 log 10 log

10 10

x

y

x

x y xx

+



≥ ⇔+ ≥





( ) ( )

log 11

1 log log 1

10 10

x

y xx



⇔+ + ≥





.

Đặt

log xt=

. Ta có

( ) ( )

1;100 log 0;2xx∈ ⇒∈

( )

0; 2

t ∈

. Bất phương trình trở thành

( ) ( ) ( )

2

11 10

12 1

10 10 10

t tt

y t t yt

−+



+ +≥ ⇔ +≥





( )

2

10

2

10 1

tt

y

t

−+

⇔≤

+

.

Xét hàm số

( )

2

10

10 1

tt

ft

t

−+

=

+

trên khoảng

( )

0; 2

, ta có

( )

2

2 10

10 1

tt

ft

t

−− +

′

=

+

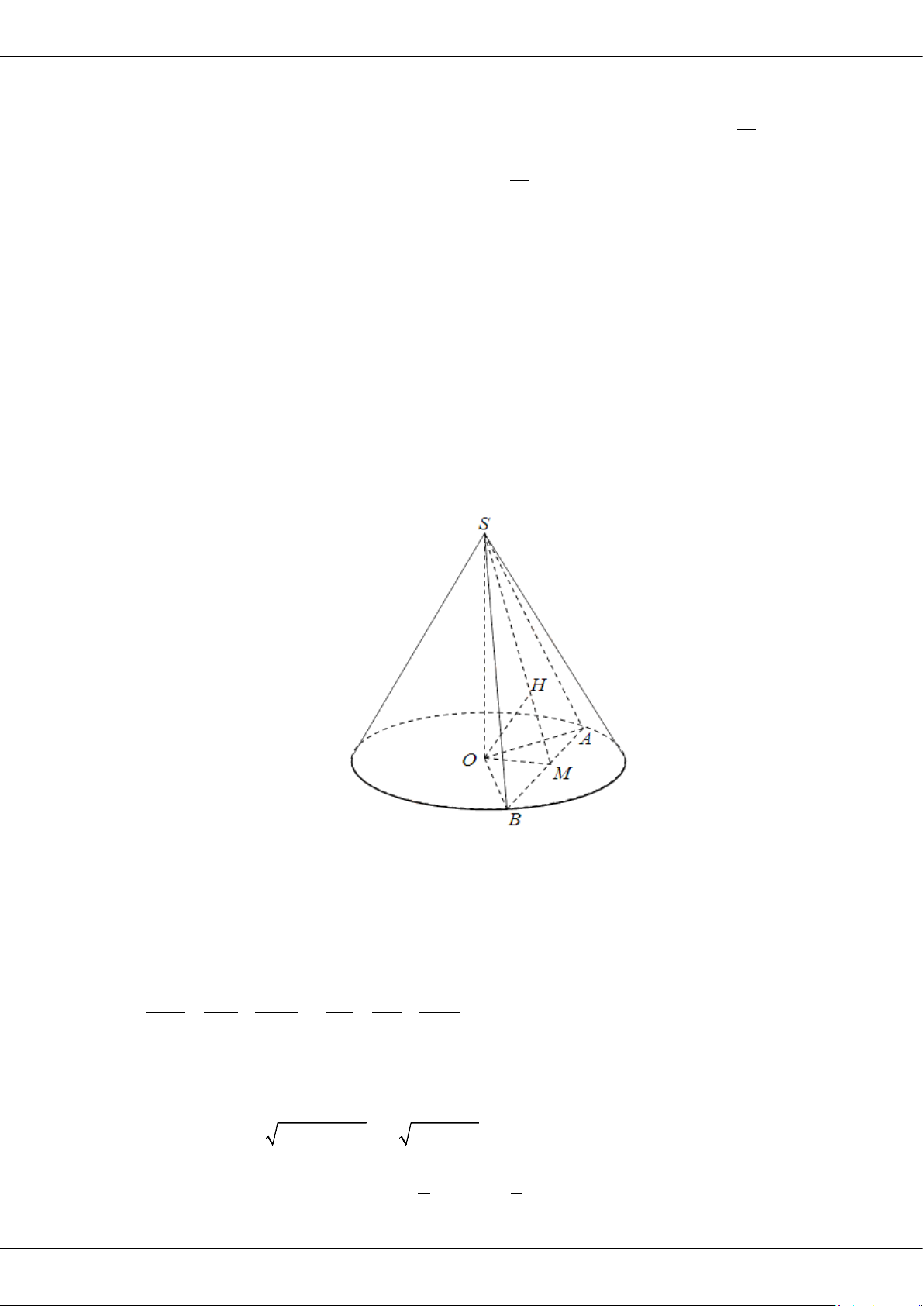
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 101

( ) ( )

0, 0; 2ft t

′

⇒ > ∀∈

( )

( ) ( ) ( )

0 2 , 0; 2f ft f t

⇒ < < ∀∈

( )

8

0 , 0; 2

15

ft t⇔ < < ∀∈

.

Yêu cầu bài toán

( )

2⇔

đúng với mọi

( )

0; 2t ∈

( ) ( )

8

, 0; 2

15

ft y t y⇔ ≤ ∀∈ ⇔ ≥

.

Kết hợp với điều kiện

[ ]

8

2021;2021 ;2021

15

yy



∈− ⇒ ∈





. Vậy có tất cả

2021

giá trị nguyên

của

y

thỏa mãn yêu cầu bài toán.

Câu 48. Cho hình nón tròn xoay có chiều cao

( )

20 cmh =

, bán kính đáy

( )

25 cmr =

. Một thiết diện đi qua

đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là

( )

12 cm

. Tính

diện tích của thiết diện đó.

A.

( )

2

400 cmS =

. B.

( )

2

500 cmS =

.

C.

( )

2

406S cm=

. D.

( )

2

300S cm=

.

Lời giải.

Chọn B

Gọi thiết diện đi qua đỉnh của hình nón là tam giác

SAB

và

O

là tâm của đường tròn đáy;

M

là

trung điểm

AB

. Hạ

OH

là đường cao trong tam giác

SOM

. Khi đó khoảng cách từ tâm đáy đến

mặt phẳng

( )

SAB

chính là đoạn

OH

.

Áp dụng hệ thức lượng ta có:

( )

222222

1 1 1 11 1

15

12 20

OM cm

OH SO OM OM

=+⇔=+⇔=

.

Có:

( )

22 2

2 2 22

25

2. 2. 2. 25 15 40

SM SO OM SM cm

AB AM OA OM cm

=+ ⇒=

= = − = −=

Vậy diện tích của thiết diện

SAB

là:

( )

2

11

. . .25.40 500

22

SM AB cm= =

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 102

Câu 49. Trong không gian

Oxyz

, cho mặt phẳng

( )

P

:

2 2 14 0−+ − =xy z

và mặt cầu

( )

2 22

: 2 4 2 30+ + − + + −=Sx y z x y z

. Gọi tọa độ điểm

( )

;;M abc

thuộc mặt cầu

(

)

S

sao cho khoảng

cách từ M đến mặt phẳng

( )

P

là lớn nhất. Tính giá trị của biểu thức

K abc=++

.

A.

1K =

. B.

2

K

=

. C.

5K = −

. D.

2K = −

.

Lời giải

Chọn C

Mặt cầu

( )

S

có tâm

( )

1;2;1−−I

, bán kính

3=R

.

Ta có:

(

) ( )

( )

2

22

2.1 2 2. 1 14

( ,( ))

2 12

−− + − −

=

+− +

dI P

4 R

= >

. Suy ra mặt phẳng (P) và mặt cầu (S) không có điểm

chung. Từ đó, điểm thuộc mặt cầu có khoảng cách nhỏ nhất hoặc lớn nhất tới mặt phẳng (P) là giao điểm

của mặt cầu với đường thẳng qua I và vuông góc với (P).

Trước hết ta lập phương trình đường thẳng d đi qua I và vuông góc với (P).

+ Mặt phẳng

( )

P

có véctơ pháp tuyến là

( )

2; 1; 2= −



n

.

+ Vì

(

)

⊥dP

nên nhận

( )

2; 1; 2= −



n

làm véctơ chỉ phương.

+ Từ đó

d

có phương trình

12

2

12

= +





=−−





=−+



xt

yt

zt

với

( )

∈



t

.

Ta tìm giao điểm của d và (S). Xét hệ:

2 22

12

2

12

2 4 2 30

= +





=−−





=−+



+ + − + + −=



xt

yt

zt

xyz xyz

( ) ( ) ( ) ( ) ( ) ( )

22 2

12

2

12

12 2 12 212 4 2 2 12 3 0

xt

yt

zt

tt t t t t

= +





=−−



⇔



=−+



+ +−− +−+ − + + −− + −+ − =



2

1

3

12

1

2

12

1

9 90

1

3

=







=









= −

= +









=

=−−





⇔⇔





=−+

= −









−=

= −











= −









= −





t

x

y

xt

z

yt

zt

t

x

y

z

. Suy ra có hai giao điểm là

( )

3; 3;1−A

và

( )

1; 1; 3−−−B

.

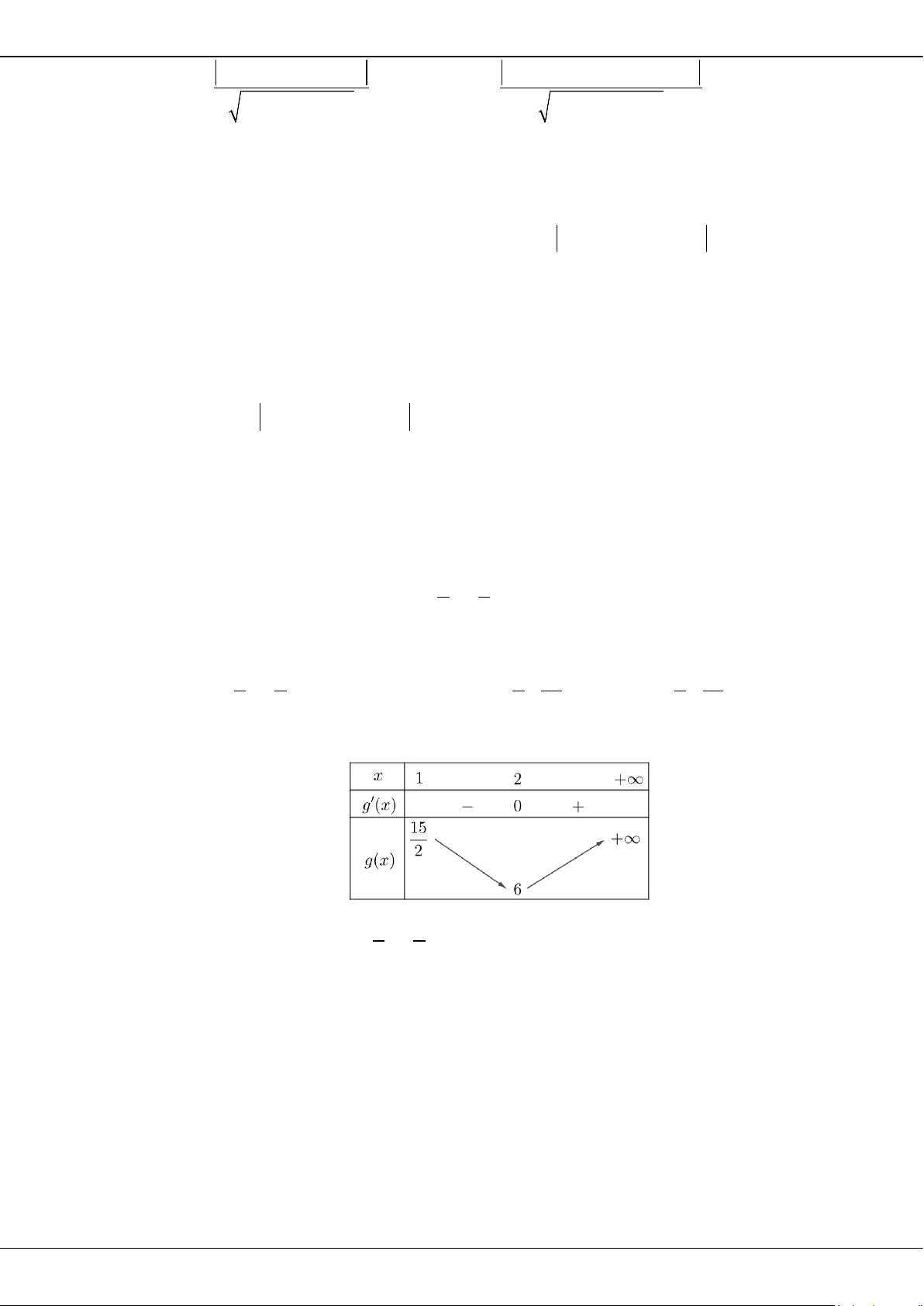
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 103

Ta có:

( )

2

22

2.3 3 2.1 14

,1

2 12

−− + −

= =

+− +

dAP

;

( )

( ) ( ) ( )

( )

2

22

2. 1 1 2 3 14

,7

2 12

−−−+ −−

= =

+− +

dB P

.

Suy ra

(

)

1; 1; 3

≡ −−−

MB

. Từ đó

1= −a

;

1= −b

;

3

= −

c

.

Vậy

5= −K

.

Câu 50. Có tất cả bao nhiêu giá trị nguyên của

m

để hàm số

32

12 2

y x mx x m

=− ++

luôn đồng biến trên

khoảng

( )

1;

+∞

?

A.

18

. B.

19

. C.

21

. D.

20

.

Lời giải

Chọn D

Xét

( )

32

12 2f x x mx x m

=− ++

. Ta có

( )

2

3 2 12f x x mx

′

=−+

và

( )

1 13fm= +

.

Để hàm số

32

12 2y x mx x m=− ++

đồng biến trên khoảng

( )

1;+∞

thì có hai trường hợp sau

Trường hợp 1: Hàm số

( )

fx

nghịch biến trên

( )

1;+∞

và

( )

10f

≤

.

Điều này không xảy ra vì

( )

32

lim 12 2

x

x mx x m

→+∞

− + + = +∞

.

Trường hợp 2: Hàm số

( )

fx

đồng biến trên

(

)

1;+∞

và

( )

10f ≥

.

( )

2

36

,1

3 2 12 0, 1

2

13 0

13 *

mx x

x mx x

x

m



≤ + ∀>



− + ≥ ∀>



⇔⇔



+≥





≥−



.

Xét

( )

36

2

gx x

x

= +

trên khoảng

( )

1; +∞

:

( )

2

36

2

gx

x

′

= −

;

( )

2

36

0 02

2

gx x

x

′

=⇔− =⇒=

.

Bảng biến thiên:

Từ bảng biến thiên suy ra

36

,1

2

mx x

x

≤ + ∀>

6m⇔≤

.

Kết hợp

( )

*

suy ra

13 6m−≤≤

. Vì

m

nguyên nên

{ }

13; 12; 11;...;5;6m ∈− − −

. Vậy có

20

giá

trị nguyên của

m

.

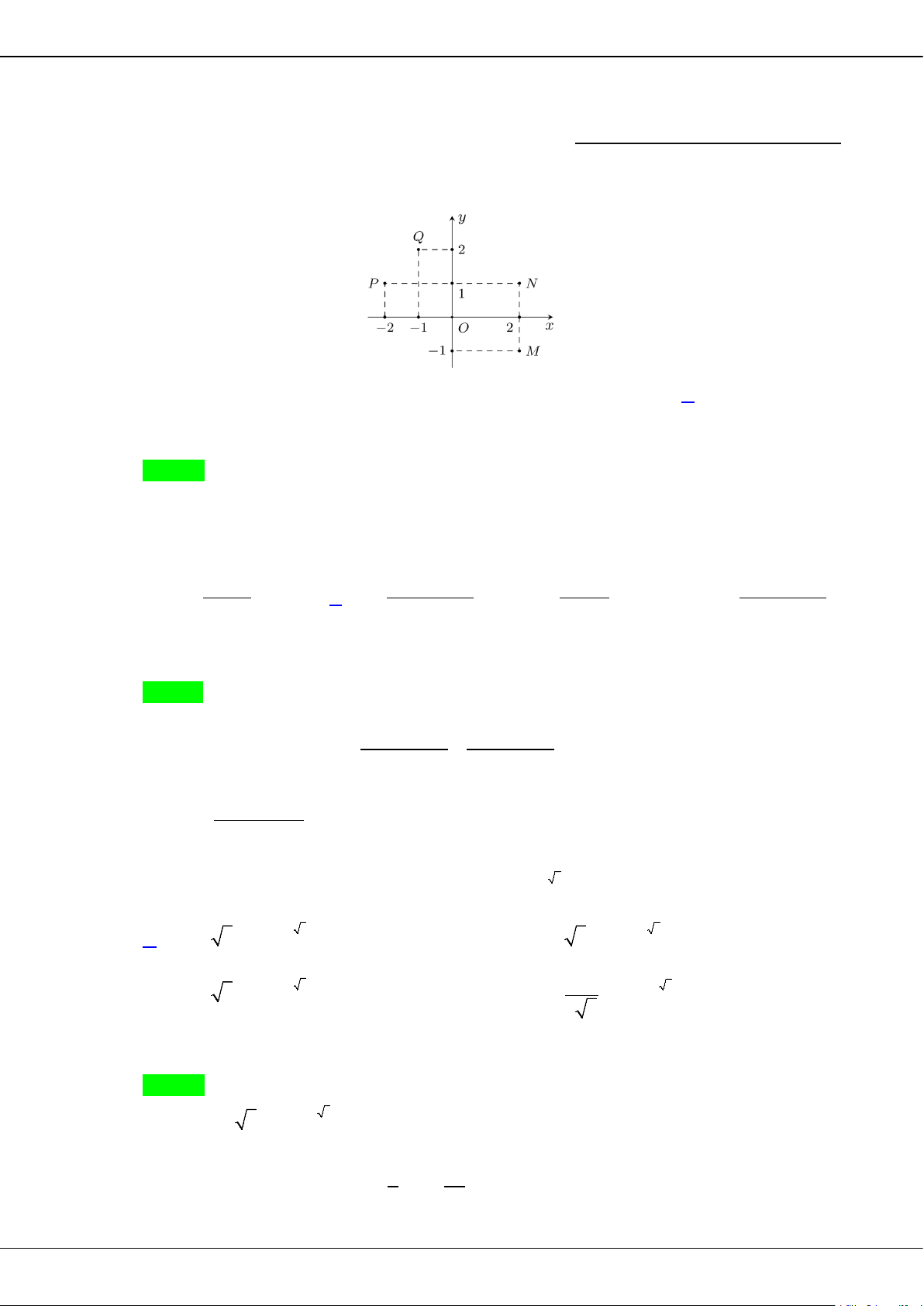
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 1

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT PHAN VIỆT THỐNG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1. Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức

12zi=−+

:

A.

N

. B.

P

. C.

M

. D.

Q

.

Lời giải

Chọn D

Điểm biểu diễn số phức

12

zi

=−+

là

Q

.

Câu 2. Đạo hàm của hàm số

( )

2

3

log 2= +yx

là:

A.

2

x

y

x

′

=

+

. B.

(

)

2

2 ln 3

′

=

+

x

y

x

. C.

2

2 ln 3

2

′

=

+

x

y

x

. D.

( )

2

1

2 ln 3

′

=

+

y

x

.

Lời giải

Chọn B

Ta có:

( )

2

3

22

2

log 2

2 ln 3 2 ln 3

′

+

′



′

= += =



++

x

yx

xx

Vậy

( )

2

2 ln 5

x

y

x

′

=

+

.

Câu 3. Trong khoảng

( )

2; +∞

đạo hàm của hàm số

( )

3

36yx= −

là:

A.

( )

31

' 333 6yx

−

= −

. B.

( )

31

' 33 6yx

−

= −

.

C.

( )

31

' 333 6yx

+

= −

. D.

(

)

31

1

' 36

33

yx

−

= −

.

Lời giải

Chọn A

Ta có

( )

31

' 333 6yx

−

= −

.

Câu 4. Tập nghiệm của bất phương trình

1

11

5 25

x−



≥





là

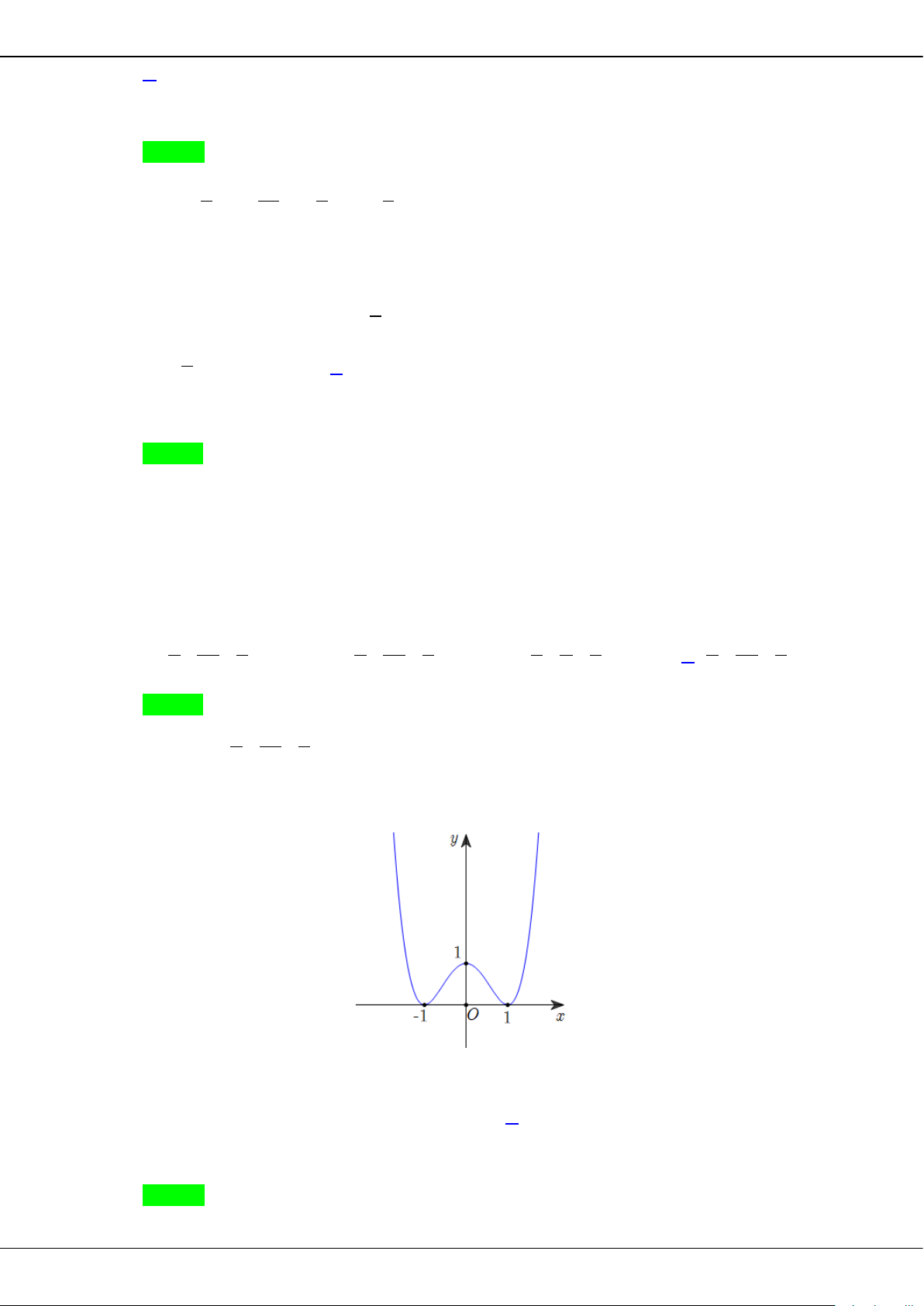
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 2

A.

[

)

1;− +∞

. B.

(

)

2;

− +∞

. C.

( )

;2−∞

. D.

(

]

;1

−∞ −

.

Lời giải

Chọn A

Ta có

1 12

1 11 1

12 1

5 25 5 5

xx

−−

  

≥ ⇔ ≥ ⇔ − ≤ ⇔ ≥−

  

  

.

Vậy tập nghiệm của bpt là

[

)

1;T = − +∞

.

Câu 5. Cho cấp số nhân

( )

n

u

với

17

1

; 32

2

uu=−=−

. Giá trị của

q

bằng

A.

1

2

±

. B.

2±

. C.

4

±

. D.

1

±

.

Lời giải

Chọn B

Áp dụng công thức số hạng tổng quát cấp số nhân ta có:

1 66

1 71

2

. 64

2

n

q

u uq u u q q

q

−

=



= ⇒= ⇒=⇒



= −



Câu 6. Trong không gian

Oxyz

, vectơ

( )

6; 3; 2

n = −



là một vectơ pháp tuyến của mặt phẳng nào dưới

đây?

A.

1

1 23

xyz

− +=

−

. B.

0

1 23

xyz

+ +=

−

. C.

1

123

xyz

++=

. D.

1

1 23

xyz

+ +=

−

.

Chọn B

Mặt phẳng

1 6 3 2 60

1 23

xyz

xyz+ + =⇔ − + −=

−

có một vectơ pháp tuyến

( )

6; 3; 2

n

= −



.

Câu 7. Cho hàm số

( )

y fx=

có đồ thị là đường cong như hình vẽ sau

Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là:

A.

( )

0; 1−

. B.

( )

1;0

. C.

(

)

0;1

. D.

( )

1;0−

và

( )

1;0

.

Lời giải

Chọn C

Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là

( )

0;1

.

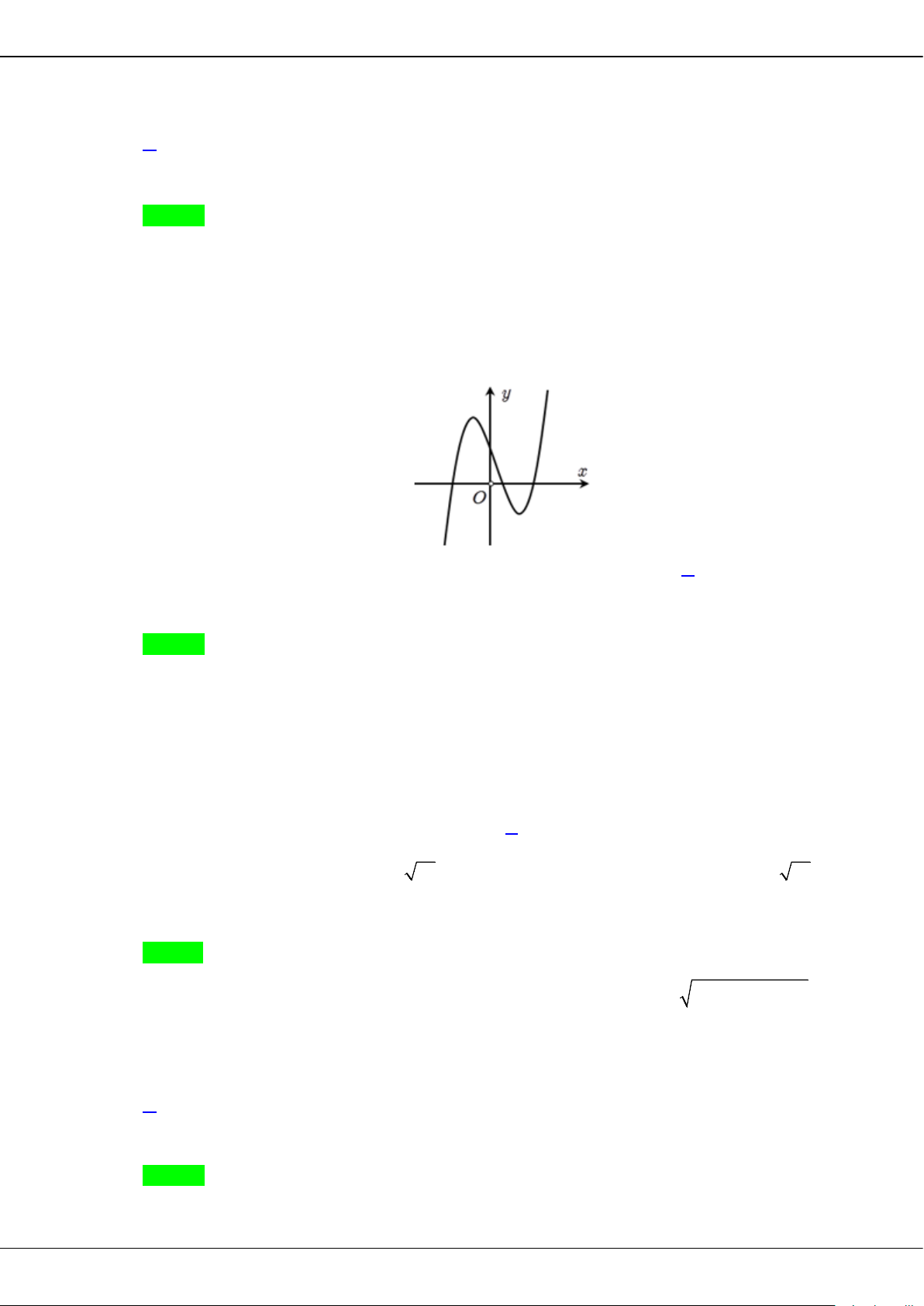
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 3

Câu 8. Nếu

( )

2

1

1d = −

∫

fxx

và

( ) ( )

2

1

5d−=−





∫

f x gx x

thì

( )

2

1

d

∫

gx x

bằng:

A.

4

. B.

3

. C.

1

. D.

2

.

Lời giải

Chọn A

Ta có

( ) ( ) (

) (

)

2 22

1 11

d ddf x gx x f x x gx x

−= −





∫ ∫∫

( )

2

1

1 d5 gx x⇔− =− −

∫

( )

2

1

4dgx x⇔=

∫

.

Câu 9. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên dưới?

A.

2

1.

y xx=− +−

B.

3

3 1.

yx x=−+ +

C.

42

1.yx x=−+

D.

3

3 1.yx x=−+

Lời giải

Chọn D

Dạng đồ thị hàm số đã cho là của hàm số

32

xy ax bx c

d

+= +

+

, loại

,AC

.

Có nhánh đồ thị ngoài cùng bên phải đi lên

0,a⇒>

loại

B

.

Câu 10. Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 2 4 8 40Sx y z x y z+ + + − + −=

. Tìm tâm và bán

kính của đường tròn

( )

S

?

A. Tâm

( )

1; 2; 4

I −

, bán kính

5R =

. B. Tâm

( )

1;2; 4I −−

, bán kính

5R =

.

C. Tâm

(

)

1; 2; 4I −

, bán kính

17R

=

. D. Tâm

( )

1;2; 4I

−−

, bán kính

17R =

.

Lời giải

Chọn B

( )

2 22

: 2480Sx y z x y z+++−+=

có tâm

(

)

1;2; 4

I −−

, bán kính

( )

1 4 16 4 5R = + + −− =

.

Câu 11. Trong không gian

Oxyz

, cho hai mặt phẳng

( )

: 2 10Px yz− −+=

,

( )

: 2 70Qxy z++ +=

. Tính

góc giữa hai mặt phẳng đó.

A.

0

60

. B.

0

45

. C.

0

120

. D.

0

30

.

Lời giải

Chọn A

( )

1; 2; 1

P

n −−

 

là một véctơ pháp tuyến của

( )

P

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 4

( )

1;1; 2

Q

n

 

là một véctơ pháp tuyến của

( )

Q

.

Gọi

α

là góc giữa hai mặt phẳng

( )

P

và

( )

Q

0

.

122

1

cos 60

2

.

6. 6

PQ

nn

αα

−−

⇒ = = =⇒=



.

Câu hỏi nên đổi là: Góc giữa hai mặt phẳng

( )

P

và

( )

Q

là:

Đáp án:

( )

1; 2; 1

P

n

= −−

 

là một vectơ pháp tuyến của

(

)

P

.

( )

1;1; 2

Q

n

=

 

là một vectơ pháp tuyến của

( )

Q

.

Gọi

α

là góc giữa hai mặt phẳng

( )

P

và

( )

Q

0

.

122

1

cos 60

2

.

6. 6

PQ

nn

αα

−−

⇒ = = =⇒=



.

Câu 12. Cho hai số phức

1

32zi= +

và

2

14zi= −

. Phần thực của số phức

12

zz+

là:

A.

2−

. B.

2

. C.

4

. D.

4

−

.

Lời giải

Chọn C

Ta có:

( ) ( )

12

32 14 42zz i i i+ = + +− =−

.

Vậy phần thực của số phức

12

zz+

là

4

.

Câu 13: Khối lăng trụ có đáy là hình chữ nhật có hai kích thước lần lượt là

2 ,3aa

, chiều cao của khối

lăng trụ bằng

5a

. Thể tích khối lăng trụ bằng:

A.

3

30a

. B.

3

10a

. C.

2

30a

. D.

2

10a

.

Lời giải

Chọn A

Ta có thể tích khối lăng trụ là:

3

. 2 .3 .5 30V Sh a a a a

= = =

.

Câu 14: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết

()

SA ABCD⊥

và

3SA a=

.

Thể tích của khối chóp

.

S ABCD

là:

A.

3

a

. B.

3

4

a

. C.

3

a

. D.

3

12

a

.

Lời giải

Chọn A

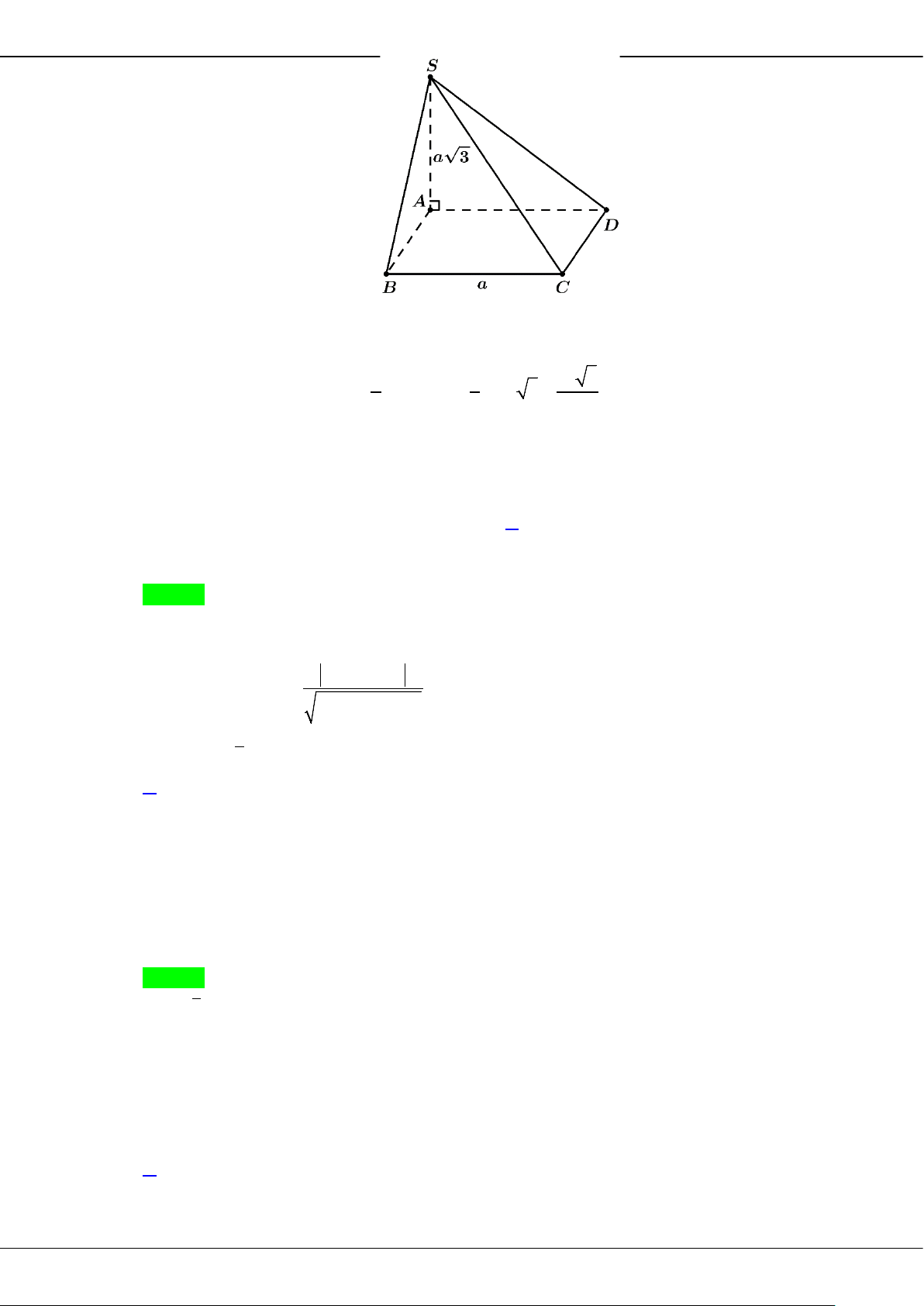
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 5

Ta có diện tích hình vuông là:

2

ABCD

Sa=

.

Vậy thể tích cần tìm là:

3

2

.

11 3

. . .. 3

33 3

S ABCD ABCD

a

V S SA a a= = =

.

Câu 15: Trong không gian

Oxyz

, cho mặt cầu

( )

S

có tâm

(

)

1;1; 2I

−

và tiếp xúc với mặt phẳng

( )

: 2 2 5 0.Px y z+ − +=

Tính bán kính

R

của mặt cầu

(

)

.S

A.

3R =

. B.

2R =

. C.

4R =

. D.

6R =

.

Lời giải

Chọn C

Vì mặt cầu

( )

S

tiếp xúc với mặt phẳng

( )

: 2 2 50Px y z+ − +=

nên

(

)

( )

,R dI P

=

( )

2

22

1245

4

12 2

+++

= =

+ +−

.

Câu 16: Cho số phức

43zi= −

. Tìm phần thực và phần ảo của số phức

z

.

A. Phần thực bằng

4

, phần ảo bằng

3

.

B. Phần thực bằng

4−

, phần ảo bằng

3−

.

C. Phần thực bằng

4

, phần ảo bằng

3−

.

D. Phần thực bằng

4−

, phần ảo bằng

3

.

Lời giải

Chọn A

Ta có

43 43z iz i=− ⇒=+

.

Suy ra

z

có phần thực bằng

4

, phần ảo bằng

3

.

Câu 17: Cho khối nón

( )

N

có bán kính đáy bằng

3

và diện tích xung quanh bằng

15 .

π

Tính thể tích

V

của khối nón

( )

N

A.

12 .

V

π

=

B.

20 .V

π

=

C.

36 .

V

π

=

D.

60 .V

π

=

Lời giải

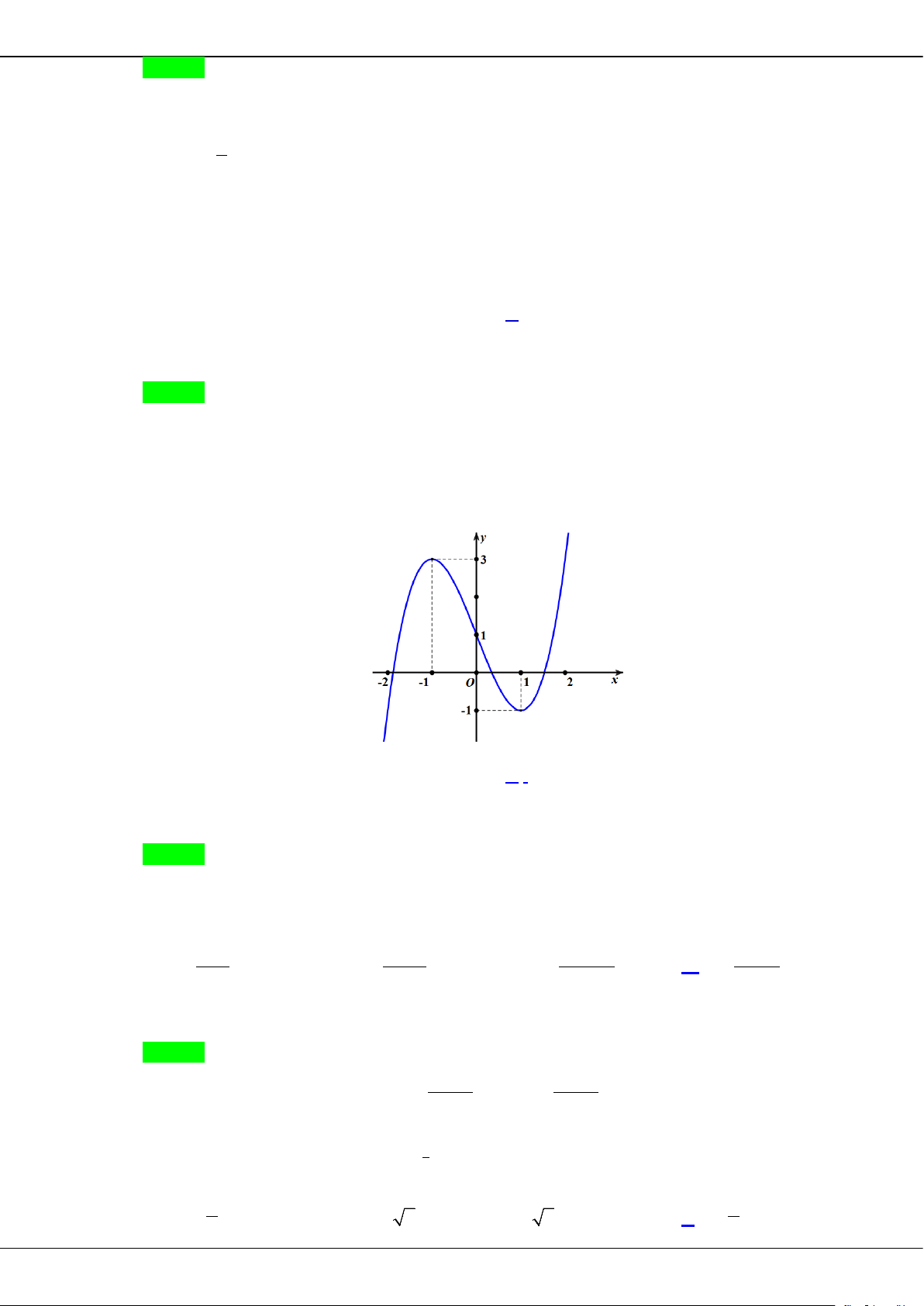
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 6

Chọn A

Ta có

15 15 5 4.

xq

S rl l h

ππ π

= ⇒ = ⇔=⇒ =

Vậy

2

1

12

3

.

V rh

ππ

= =

Câu 18. Trong không gian

Oxyz

, cho đường thẳng

3

: 52

2

xt

yt

zt

= −





∆ =−+





= −



. Điểm nào sau đây thuộc

∆

?

A.

( )

3; 5; 0M −

. B.

( )

3;5;2N −−

. C.

( )

3; 5; 0P −

. D.

( )

1; 2; 2Q

−−

.

Lời giải

Chọn C

Nhận thấy điểm

( )

3; 5; 0P −

thuộc đường thẳng

∆

.

Câu 19. Cho hàm số

32

y ax bx cx d= + ++

có đồ thị là đường cong trong hình bên. Điểm cực đại của

đồ thị hàm số đã cho có toạ độ là

A.

( )

1; 1−

. B.

( )

1;1−

. C.

( )

1; 3

−

. D.

( )

3; 1−

.

Lời giải

Chọn C

Dựa vào đồ thị hàm số ta thấy điểm cực đại của đồ thị hàm số là

( )

1; 3−

.

Câu 20. Đường thẳng

2y =

là tiệm cận ngang của đồ thị hàm số nào dưới đây?

A.

2

1

y

x

=

+

. B.

1

12

x

y

x

+

=

−

. C.

23

2

x

y

x

−+

=

−

. D.

22

2

x

y

x

−

=

+

.

Lời giải

Chọn D

Trong 4 đáp án trên chỉ có đáp án

22

2

x

y

x

−

=

+

thoả

22

lim 2

2

x

→±∞

−

=

+

.

Câu 21. Tập nghiệm của bất phương trình

2

3

log 2x 

là

A.

4

;

9



















. B.

 

3

;4

. C.

 

3

4;

. D.

4

0;

9

















.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 7

Lời giải

Chọn D

Ta có

2

3

24

log 2 0 0

39

xx x







 











. Vậy tập nghiệm của bất phương trình là

4

0;

9

















.

Câu 22. Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được lập từ các số

1; 2;3;4;5

.

A.

15

. B.

120

. C.

10

. D.

24

.

Lời giải

Chọn B

Số các số cần lập là

4

5

120A =

.

Câu 23. Cho

( )

d 3sin 2 Cfx x x= +

∫

. Khẳng định nào dưới đây là đúng?

A.

(

)

6cos 2fx x= −

. B.

( )

3

cos 2

2

fx x

=

. C.

( )

3

cos 2

2

fx x= −

. D.

( )

6cos 2fx x=

.

Lời giải

Chọn D

Ta có:

(

) ( ) (

)

6cd 3sin 2 3sin s22 oCffx x x xxxC

′

+⇔ = =

= +

∫

.

Câu 24. Cho

( )

ln 2

0

2 ed 5

x

fx x+=

∫

. Tính

( )

ln 2

0

dfx x

∫

.

A.

3

. B.

5

2

. C.

2

. D.

1

.

Lời giải

Chọn C

Ta có:

( )

( ) ( )

ln 2 ln 2 ln 2

ln 2 0

00 0

ln 2

2 ed2 de 2 de e

0

xx

fx x fx x fx x+ = + = +−

∫∫ ∫

.

( )

ln 2

0

2 d1fx x= +

∫

.

Theo đề bài ta có:

( )

ln 2 ln 2

00

2 ed 5 2 d 15

x

fx x fx x+ = ⇔ +=

∫∫

.

( )

ln 2

0

d2fx x⇒=

∫

.

Câu 25. Cho hàm số

2

co

1

() 1

s

fx x

x

= −+

. Khẳng định nào dưới đây là đúng?

A.

2

( )d tan

2

= −+ +

∫

x

fx x x x C

. B.

2

( )d tan

2

= −− +

∫

x

fx x x x C

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 8

C.

2

( )d tan

2

= ++ +

∫

x

fx x x x C

. D.

2

( )d tan

2

=− −+ +

∫

x

fx x x x C

.

Lời giải

Chọn A

Ta có:

2

cos

1

( )d 1 d tan

2

x

fx x x x x x C

x



= −+ = − + +





∫∫

.

Câu 26. Cho hàm số

( )

y fx=

có đồ thị sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

( )

;0−∞

. B.

( )

1; +∞

. C.

( )

;1

−∞ −

. D.

( )

2; +∞

.

Lời giải

Chọn C

Hàm số đã cho đồng biến trên khoảng

( )

;1−∞ −

.

Câu 27. Cho hàm số

( )

y fx=

có bảng biến thiên như hình vẽ. Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực đại tại

5x =

. B. Hàm số đạt cực tiểu tại

1x =

.

C. Hàm số đạt cực tiểu tại

0x =

. D. Hàm số đạt cực đại tại

0x =

.

Lời giải

Chọn D

Qua bảng biến thiên ta thấy hàm số có

y

′

đổi dấu từ dương sang âm qua

0x =

nên hàm số đạt

cực đại tại

0x =

.

x

y

1

2

1

-1

O

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 9

Câu 28. Cho các số thực dương

;ab

thỏa mãn

2

log ax=

,

2

log by=

. Giá trị biểu thức

(

)

23

2

logP ab=

theo

;xy

bằng:

A.

23xy−

. B.

3

xy+

. C.

32xy+

. D.

23xy+

.

Lời giải

Chọn B

Theo tính chất Logarit ta có:

( )

23

2

logP ab=

23

22

log logab= +

22

2log 3logab= +

23xy= +

.

Câu 29. Gọi

D

là hình phẳng giới hạn bởi các đường

4

, 0, 0, 1

x

yey x x 

. Thể tích của khối

tròn xoay tạo thành khi quay

D

quanh trục

Ox

bằng:

A.

1

4

0

d

x

ex



B.

1

8

0

d

x

ex



. C.

1

4

0

d

x

ex



. D.

1

8

0

d

x

ex



.

Lời giải

Chọn B

Thể tích của khối tròn xoay tạo thành khi quay

D

quanh trục

Ox

là

 

11

2

48

00

dd

xx

V e x ex







.

Câu 30. Cho hình chóp

.S ABCD

có đáy là hình chữ nhật cạnh

AB a=

,

SA

vuông góc với mặt phẳng

đáy và

2SB a=

(tham khảo hình bên). Góc giữa mặt phẳng

()SBC

và mặt phẳng đáy bằng

A.

90°

. B.

60°

. C.

45°

. D.

30°

.

Lời giải

Chọn B

Vì

()SA ABCD⊥

nên

SA BC⊥

.

Mặt khác, theo giả thiết

AB BC⊥

. Do đó

()BC SAB⊥

nên

SB BC⊥

.

Ta có:

Giao tuyến giữa mặt phẳng

()SBC

và mặt phẳng

()ABCD

là

BC

Trong

()SBC

có

BC SB⊥

Trong

()ABCD

có

BC AB⊥

D

C

B

A

S

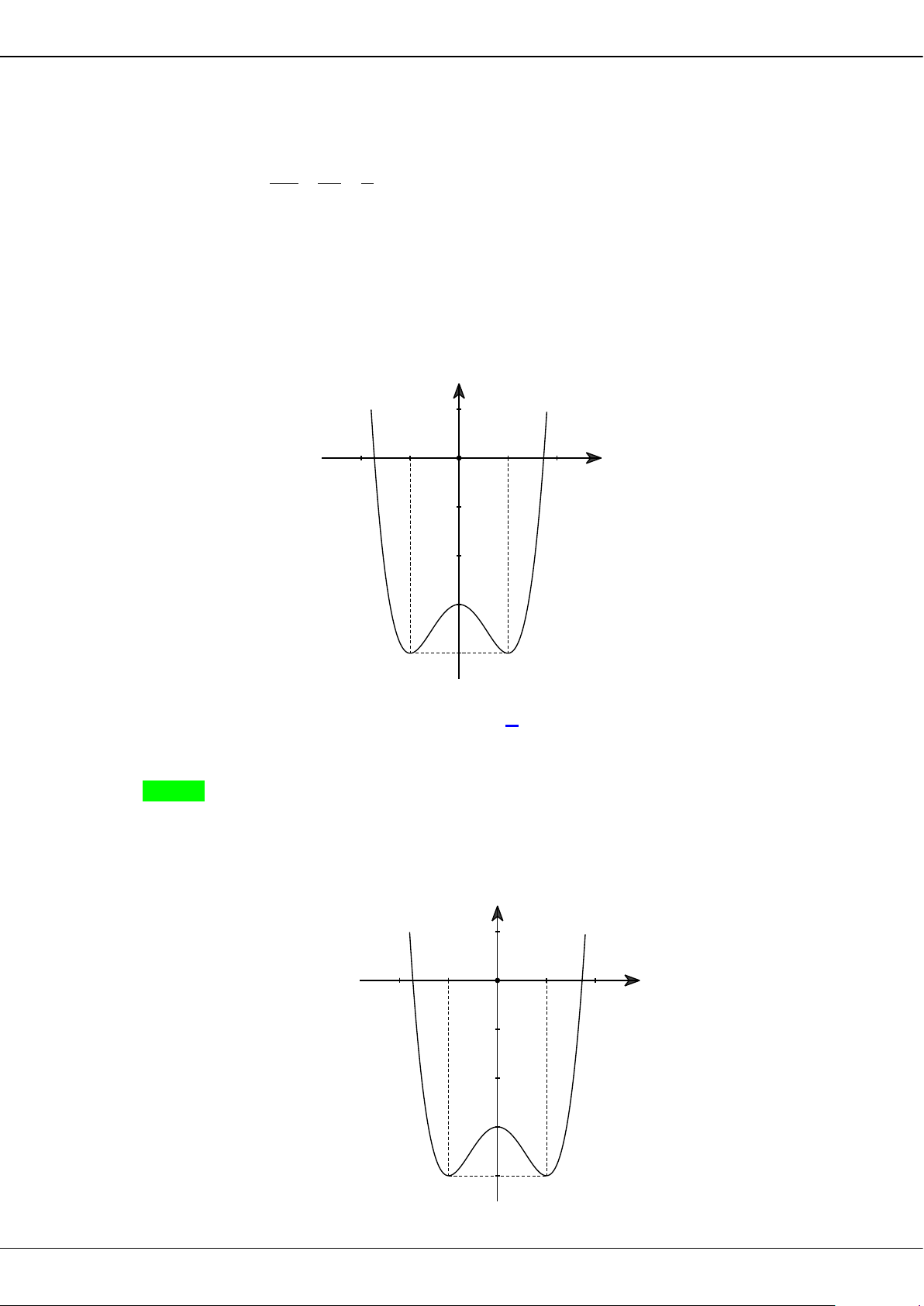
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 10

Góc giữa hai mặt phẳng

()SBC

và

()ABCD

là góc giữa hai đường thẳng

SB

và

AB

là góc



SBA

Xét tam giác

SAB

vuông tại

A

Ta có



1

cos

22

AB a

SBA

SB a

= = =

⇒



60SBA = °

.

Vậy góc giữa hai mặt phẳng

()SBC

và

()ABCD

bằng

60°

.

Câu 31. Cho hàm số

(

)

42

f x ax bx c

=++

có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị

nguyên thuộc đoạn

[ ]

2;5−

của tham số

m

để phương trình

( )

fx m=

có đúng hai nghiệm

thực phân biệt?

A.

6

. B. 7. C.

8

. D.

9

Lời giải

Chọn C

Để phương trình

( )

fx m=

có đúng hai nghiệm thực phân biệt thì ĐTHS

ym=

cắt ĐTHS

()

y fx=

tại hai điểm phân biệt .

x

y

-4

-3

1

-1

O

x

y

-4

-3

1

-1

O

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 11

Dựa vào đồ thị hàm số ta có

3

4

m

>−





= −



Do

m ∈

;

[

]

2;5

m

∈−

nên

{ }

2; 1;....;5m ∈− −

. Có

8

giá trị cuả

m

thỏa mãn yêu cầu bài toán.

Câu 32. Cho hàm số

()fx

xác định trên



và có đạo hàm

(

) (

)

( )

25

2 11

fx xx x

′

=−+ −

. Hàm số đã cho

nghịch biến trên khoảng nào dưới đây?

A.

(

)

;2

−∞

B.

( )

2; +∞

C.

( )

1; 2−

D.

( )

1; +∞

.

Lời giải

Chọn B

( ) ( )

( )

25

2

0 2 1 10 1

1

x

fx xx x x

x

=





′

=⇔− + − =⇔=−



=



Bảng xét dấu

( )

fx

′

Từ bảng xét dấu suy ra hàm số nghịch biến trên các khoảng

(

)

;1−∞

và

( )

2;

+∞

.

Câu 33. Chọn ngẫu nhiên

2

số khác nhau từ

30

số nguyên dương đầu tiên. Tính xác suất để chọn được

2

số có tích là một số lẻ?

A.

7

29

. B.

15

29

. C.

22

29

. D.

8

29

.

Lời giải

Chọn A

Không gian mẫu

2

30

435.C =

Từ số

1

đến số

30

có

15

số lẻ và

15

số chẵn.

Để chọn được

2

số có tích là một số lẻ thì cả

2

số đó phải đều là số lẻ nên có

2

15

105C =

số.

Vậy xác suất cần tìm là:

105 7

435 29

=

.

Câu 34. Tổng tất cả các nghiệm của phương trình

2

lg 3lg 2 0xx− +=

là

A.

110

. B.

100

. C.

10

. D.

1000

.

Lời giải

Chọn A

Phương trình:

2

lg 3lg 2 0xx− +=

lg 1 10

lg 2 100

xx

= =



⇔⇔



= =



.

Suy ra tổng các nghiệm của phương trình đã cho là 110.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 12

Câu 35. Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức

z

thỏa mãn

12 3iz i+− =

là

một đường tròn. Tâm của đường tròn đó có tọa độ là

A.

( )

2; 1I −−

. B.

( )

2;1I −

. C.

( )

2;1I

. D.

( )

2; 1I −

.

Lời giải

Chọn C

Gọi

z x yi

= +

(với

;xy∈ 

).

Ta có:

(

)

23iz i

−− =

. 23iz i⇔ −− =

23zi

⇔ −− =

( ) ( )

2 13x yi⇔ −+− =

( ) ( )

22

2 13xy⇔ − +− =

⇔

( ) ( )

22

2 19xy

− +− =

.

Vậy tập hợp điểm biểu diễn các số phức

z

là đường tròn tâm

( )

2;1I

, bán kính

3R =

.

Câu 36. Trong không gian

Oxyz

, cho

5 4 2, 3OE i j k OF j k=+− =−

      

. Đường thẳng đi qua hai điểm

E

và

F

có phương trình là

A.

5

13

3

xt

yt

zt

=





= +





=−+



. B.

5

4

23

x

yt

zt

=





= +





=−−



. C.

5

13

3

xt

yt

zt

=





= +





=−−



. D.

5

13

3

xt

yt

zt

= −





= +





=−+



.

Lời giải

Chọn A

Ta có:

( )

5 4 2 5; 4; 2OE i j k E=+−⇒ −

   

;

( )

3 0;1; 3OF j k F=−⇒ −

  

.

Đường thẳng đi qua hai điểm

E

và

F

có một vectơ chỉ phương là

( )

5; 3;1FE =



.

Vậy phương trình tham số của đường thẳng đi qua hai điểm

E

và

F

là:

5

13

3

xt

yt

zt

=





= +





=−+



.

Câu 37. Trong không gian với hệ toạ độ

Oxyz

, cho điểm

(

)

2; 5;7M −

. Điểm

M

′

đối xứng với điểm

M

qua mặt phẳng

Oxy

có tọa độ là:

A.

( )

2;5;7−−

. B.

( )

2;5;7

. C.

( )

2; 5;7−−

. D.

( )

2;5;7−

.

Lời giải

Chọn A

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 13

Do điểm

( )

;;M xyz

′′′′

đối xứng điểm

( )

;;M xyz

qua mặt phẳng

Oxy

nên

2

5

7

xx x

yy y

zz z

′′

= =





′′

=⇔=−





′′

=−=−



. Vậy

( )

2;5;7

M

′

−−

.

Câu 38. Cho hình chóp đều

.

S ABCD

thể tích

3

2

3

SABCD

a

V =

,

2AC a=

(tham khảo hình bên). Tính

khoảng cách từ điểm

A

đến mặt phẳng

( )

SCD

.

A.

3

a

. B.

2

a

. C.

23

3

a

. D.

2

a

.

Lời giải

Chọn C

Gọi

O AC BD= ∩

,

H

là trung điểm

CD

. Trong

(

)

SOH

, kẻ

OI SH

⊥

.

Có

( )

CD SO

CD SOH CD OI

CD SH

⊥



⇒⊥ ⇒⊥



⊥



.

Mà

OI SH⊥

nên

( )

OI SCD⊥

( )

,d O SCD OI⇒=

.

Có

( )

2

sin 45 2 2 2

ABCD

AD AC a S a a= °= ⇒ = =

S

A

D

C

B

H

O

A

D

B

C

S

I

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 14

Ta có:

33

2

21 2

. .2

33 3

SABCD

aa

V SO a SO a= ⇔ = ⇔=

.

Vì O là trung điểm AC nên

( )

22

2.

,2,2

SO OH

d A SCD d O SCD OI

SO OH

= = =

+

.

Mà

2

sin 45 2

2

AD AC a OH a

= °= ⇒ =

( )

23

,

3

d A SCD a⇒=

.

Câu 39. Có bao nhiêu số nguyên

x

thỏa mãn

22

2

3

409

( 4) 4

log lo

76

g

2

xx xx−−

<

?

A.

78

. B.

80

. C.

76

. D.

82

.

Lời giải

Chọn A

TXĐ:

( )

(

)

; 0 4; .

D = −∞ ∪ +∞

Ta có:

22

2

3

409

( 4) 4

log lo

76

g

2

xx xx−−

<

2

3

2

23

2

( ) log 409log 4 lo6 ( ) log 2g4 7xx xx

−−−⇔− <

22

233 2

2 log 4 log 64 log 4 log 27() ()xx xx



⇔ −− < −−



2

23

2

33 2

2 log 4 6log 2 log 4 3( ) 3.log ( log 3)xx xx



⇔ −− < −−



[

]

2

32 23

log 4 2 log 3 12log

() 23log 3xx⇔ −− < −

2

3

2

12log 3log 3

log 4

2l

)

3

2

o

(

g

xx

−

⇔ −<

−

2

3

22

3(4 log 3)

log 4

log 3.(2

(

log 3

)

xx

−

⇔ −<

−

2

3

2

3(2 +log

()

3)

log 4

log 3

xx⇔ −<

2

33

log 4 3(2.log() 2 +1)xx⇔ −<

23

33

log 4 g(

2) lo 1xx

⇔ −<

2

4 1728 0xx⇔−− <

2 2 433 2 2 433x⇔− <<+

Kết hợp điều kiện ta có

{ }

39; 38;...; 1;5;...;42;43x ∈− − −

.

Vậy có 78 số nguyên x thỏa mãn.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 15

Câu 40. Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa

mãn

( ) ( )

7278FG

+=

và

(

) ( )

121 2FG+=

. Khi đó

( )

3

0

2 1d

fx x+

∫

bằng

A.

6

. B.

4

. C.

1

. D.

3

.

Lời giải

Chọn C

Vì

( ) ( )

,Fx Gx

là hai nguyên hàm của

( )

fx

trên



nên tồn tại hằng số

C

thỏa mãn điều kiện

( ) ( )

,Gx Fx C x

= + ∀∈

.

Suy ra

( ) ( ) ( ) ( )

71 71GGF F−= −

.

Theo giả thiết ta có:

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

7127163716 712FF GG FF FF−+ − =⇔ − =⇔ −=

  

  

.

Xét

( )

3

0

2 1dfx x+

∫

Đặt

1

21 d d

2

x tx t+=⇒ =

Đổi cận:

01

xt=⇒=

37

xt=⇒=

Khi đó

( ) (

) (

) ( )

37

01

11

2 1d d 7 1 1

22

f x x ft t F F

+= = − =





∫∫

.

Câu 41. Số các giá trị thực của tham số

m

để đồ thị hàm số

32

32y x mx=−+

có hai điểm cực trị

A

và

B

sao cho các điểm

A

,

B

và

( )

1; 2M −

thẳng hàng.

A.

4

. B.

3

. C.

1

. D.

2

.

Lời giải

Chọn D

 Tập xác định:

D = 

.

Ta có:

2

0

36 0

2

x

y x mx y

xm

=



′′

= − ⇒=⇔



=



.

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi phương trình

0y

′

=

có hai nghiệm phân biệt

⇔

20m ≠

⇔

0m ≠

.

 Khi đó hai điểm cực trị là

( )

3

0;2 ; 2 ;2 4A Bm m−

.

Ta có

( )

1; 4MA = −



,

( )

3

2 1; 4 4MB m m= −−



.

,,ABM

thẳng hàng

⇔

MA



,

MB



cùng phương

⇔

3

2 1 44

14

mm−−

=

−

⇔

3

2 11

11

mm−−

=

−

⇔

3

21 1mm

−= −

⇔

3

2mm=

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 16

⇔

2

2m =

⇔

2m

= ±

(do

0m ≠

).

 Vậy có hai giá trị của tham số

m

thỏa mãn bài toán.

Câu 42. Xét các số phức

z

thoản mãn điều kiện

2

2 44 2 1zz i z+ ++ = +

. Gọi

M

và

m

lần lượt là

giá trị lớn nhất và nhỏ nhất của

1z

+

. Giá trị của

Mm−

bằng

A.

2

. B.

26

. C.

14

. D.

46

.

Lời giải

Chọn A

( )

2

24421 1 3421zz iz z iz+++= +⇔+++= +

(1)

Áp dụng bất đẳng thức tam giác ta có:

( ) ( )

2

22

2 1 1 34 1 34 1 5z z i z iz+= + ++ ≥ + − + = + −

(Vì

( )

2

11zz+=+

)

Dấu “=” xảy ra khi và chỉ khi

( )

1 34zk i+= +

.

Suy ra

( )

2

22

4 1 15zz+≥ +−

42

1 14 1 25 0zz⇔+− ++ ≤

2

7 26 1 7 26z⇔− ≤ + ≤+

61 1 61z⇔ −≤ + ≤ +

Suy ra giá trị lớn nhất của

1 61z += +

đạt được khi và chỉ khi

( )

61

1 34

5

zi

+

=−± +

, giá trị

nhỏ nhất của

1 61z

+= −

đạt được khi và chỉ khi

( )

61

1 34

5

zi

−

=−± +

.

Vậy

2Mm−=

.

Câu 43. Cho hình chóp

.S ABCD

, đáy

ABCD

là hình vuông có cạnh bằng

3a

. Hình chiếu vuông góc

của

S

lên mặt phẳng đáy là điểm

I

thuộc đoạn thẳng

AB

sao cho

2BI AI=

. Góc giữa mặt

bên

(

)

SCD

với mặt phẳng đáy là

60°

(tham khảo hình vẽ). Tính khoảng cách giữa hai đường

thẳng

AD

và

SC

.

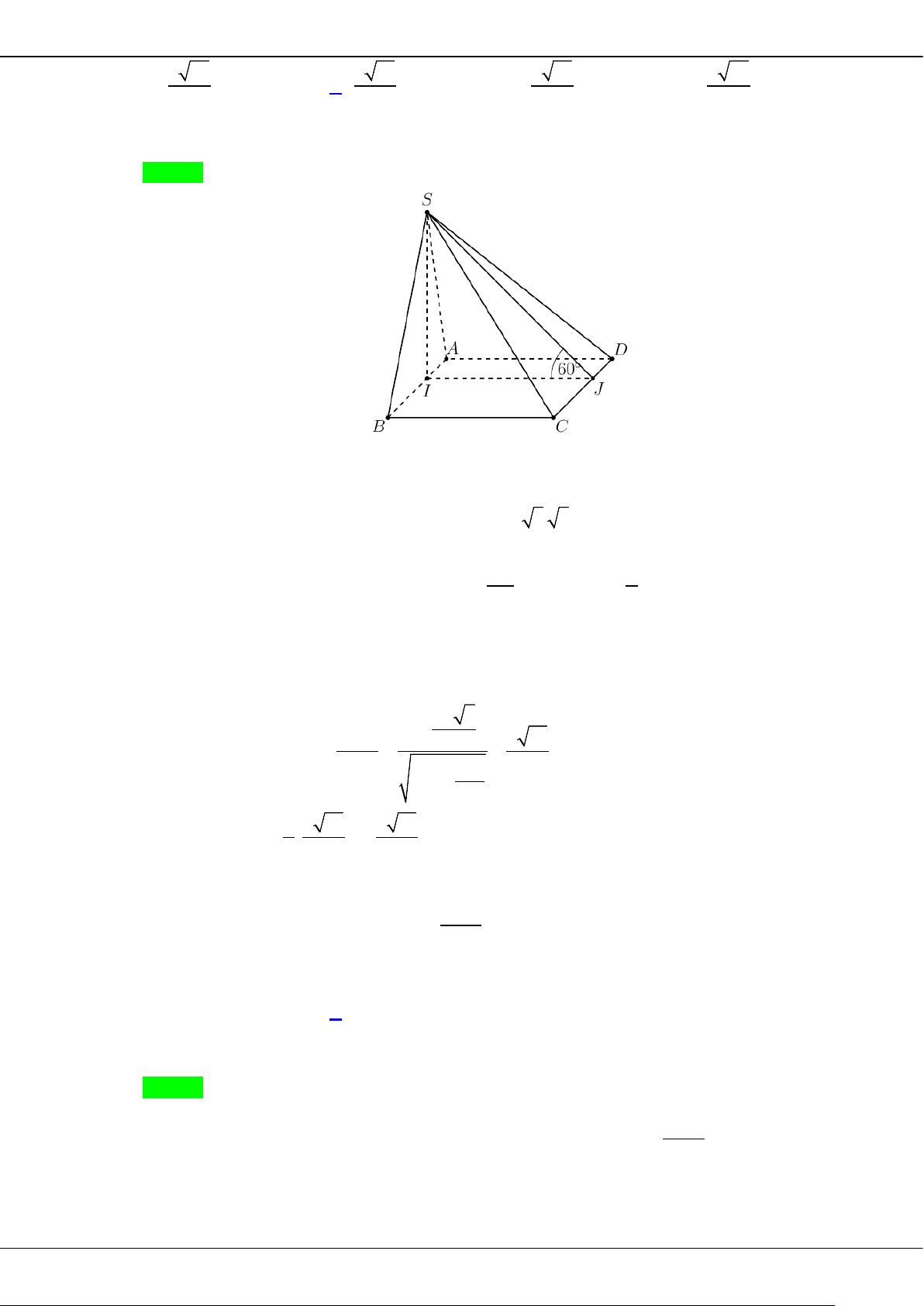
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 17

A.

3 93

31

a

. B.

9 31

31

a

. C.

6 31

31

a

. D.

6 93

31

a

.

Lời giải

Chọn B

Qua

I

kẻ

IJ AD



, ta có

IJ CD⊥

mà

( )

SI ABCD SI CD⊥ ⇒⊥

, do đó góc giữa

( )

SCD

và

mặt phẳng đáy bằng góc



SJI

, do đó



60SJI = °

.

Tam giác

SIJ

vuông tại

I

nên

tan 60 3. 3 3SI IJ a a

= °= =

.

Vì

AD BC

nên ta có

( )

(

)

( )

(

)

( )

3

d , d , d , d, d,

2

AB

AD SC AD SBC A SBC I SBC I SBC

IB

= = = =

.

Ta có

( )

( ) ( ) (

)

SI ABCD

SI BC

BC SAB SAB SBC

BAB

AB C

C

B

⊥



⊥





⇒ ⇒⊥ ⇒ ⊥



⊥





.

Lại vì tam giác

SIB

vuông tại

I

nên suy ra

( )

(

)

( )

2

23

3.

. 6 31

3

d, d,

31

4

9

3

a

IS IB

I SBC I SB a

SB

a

= = = =

+

.

Vậy

( )

3 6 31 9 31

d, .

2 31 31

AD SC a a= =

.

Câu 44. Cho hàm số

( )

fx

luôn dương với mọi

[ ]

0;1x ∈

và có đạo hàm liên tục trên đoạn

[ ]

0;1

thỏa

mãn

( )

11

f =

và

( ) ( )

( )

2

2.

fx

f x xf x

x

′

+=





với mọi

[

]

0;1x ∈

. Khi đó diện tích hình phẳng

giới hạn bởi các đường

( )

y fx=

và

54yx= −

gần giá trị nào nhất sau đây?

A.

0,58

. B.

0, 49

. C.

1, 22

. D.

0,97

.

Lời giải

Chọn B

Vì

(

)

0fx>

với mọi

[ ]

0;1x ∈

nên từ giả thiết

( ) ( )

( )

2

2.

fx

f x xf x

x

′

+=





LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 18

( ) ( )

(

)

2.

fx

f x xf x

x

′

⇔+ =

( )

.

1

2.

xf x

fx

x

fx

′

⇔ +=

( ) ( )

( )

1

2 . 2.

2

fx

x fx x

x

fx

′

⇔ +=

( )

1

2.x fx

x

′

⇔=

( )

1

2.x f x dx

x

⇔=

∫

( )

2. 2x fx x C⇔=+

Vì

( )

1 1 2.1. 1 2 1 0f f CC

=⇒ = +⇒=

.

Do đó

( )

1

2. 2x fx x fx

x

=⇒=

.

Phương trình hoành độ giao điểm của hàm số

( )

y fx=

và đường thẳng

5yx= −

là

2

1

54 4 5 10

4

1

x

x xx

x



=



= − ⇔− + − = ⇔



=



.

Diện tích hình phẳng giới hạn bởi hai đồ thị là

( ) ( )

11

44

1

5 4 0,488S f x g x dx x dx

x

= − = −+ =

∫∫

.

Câu 45. Có bao nhiêu số nguyên

m

để phương trình

( )

22

30z m zm m

− − + +=

có hai nghiệm phức

12

,zz

thỏa mãn

12 12

zz zz+=−

?

A.

3

. B.

4

. C.

1

. D.

8

.

Lời giải

Chọn B

Ta có

 

2

22

( 3) 4( ) 3 10 9m mm m m       

Trường hợp 1:

2

5 2 13 5 2 13

0 3 10 9 0 (*)

33

mm m

 

    

Khi đó phương trình đã cho có hai nghiệm thực

12

,zz

(nghiệm thực cũng là nghiệm phức có

phần ảo bằng

0

), thỏa mãn

12

3

.

zz m

zz











 





Suy ra

12 12

zz zz

2

3 ( 3)mm      

22

( 3) 3 10 9m mm    

2

0

4 40

1

m

mm

m







  







đều thỏa mãn (*)

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 19

Trường hợp 2:

2

5 2 13

3

0 3 10 9 0 (**)

5 2 13

3

m

mm

m











  













Khi đó phương trình có hai nghiệm phức

12

,zz

, thỏa mãn

12

3

.

zz m

zz i











 





Suy ra

12 12

zz zz

2

3 ( 3)mi m       

22

( 3) 3 10 9m mm  

2

1

2 16 18 0

9

m

mm

m







   







đều thỏa mãn (**)

Vậy có 4 số nguyên

m

thỏa mãn yêu cầu bài toán

Câu 46. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

1;2; 2A −

; mặt phẳng

( )

: 2 2 80Px y z− − +=

và hai đường thẳng

1

11

1

2

: 12

43

xt

dy t

zt

= +





= +





= −



;

2

22

2

32

:3

5

xt

dy t

zt

= +





= +





=−+



. Đường thẳng

d

đi qua điểm

A

, cắt hai đường thẳng

1

d

và

2

d

lần lượt tại

B

và

C

. Tính tổng khoảng cách từ

B

và

C

đến mặt phẳng

( )

P

.

A.

9

. B.

10

. C.

7

. D.

8

.

Lời giải

Chọn D

Do

1

Bd∈

nên tọa độ

B

có dạng

( )

11 1

2 ;1 2 ;4 3Bt t t++ −

;

2

Cd∈

nên tọa độ

C

có dạng

( )

22 2

3 2 ;3 ; 5C tt t+ + −+

.

⇒

( )

1 11

1 ; 1 2 ;6 3

AB t t t= + −+ −



;

(

)

22 2

2 2 ;1 ; 3AC t t t

= + + −+



.

Do

A

;

B

;

C

thẳng hàng nên

AB k AC=

 

( )

k ∈ 

⇔

( )

12

1 22

12 1

63 3

tk t

+= +





−+ = +





− = −+



⇔

( )

12

1

12 1

33 0

75 4

tk t

t

tk

−+ = +





−=





−+ =



⇔

1

2

1

2

3

t

k

t

=





= −





= −





⇒

( )

3;3;1B

;

( )

3;0; 8C −−

.

Vậy tổng khoảng cách từ

B

và

C

đến mặt phẳng

( )

P

là

( )

( ) ( )

( )

( ) ( )

22 22

22

3 2.0 2. 8 8

3 2.3 2.1 8

,, 8

12 2 12 2

dB P dC P

−− − − +

−−+

+= + =

+− +− +− +−

.

Câu 47. Có bao nhiêu bộ số

( )

;xy

với

,xy

nguyên và

1 , 2022xy≤≤

thoả mãn

( ) ( )

3 2

2 21

2 4 8 log 2 3 6 log

23

yx

xy x y x y xy

yx

+

+++ ≤ +−−

+−

.

A.

4036.

B.

4038.

C.

4040.

D.

2019.

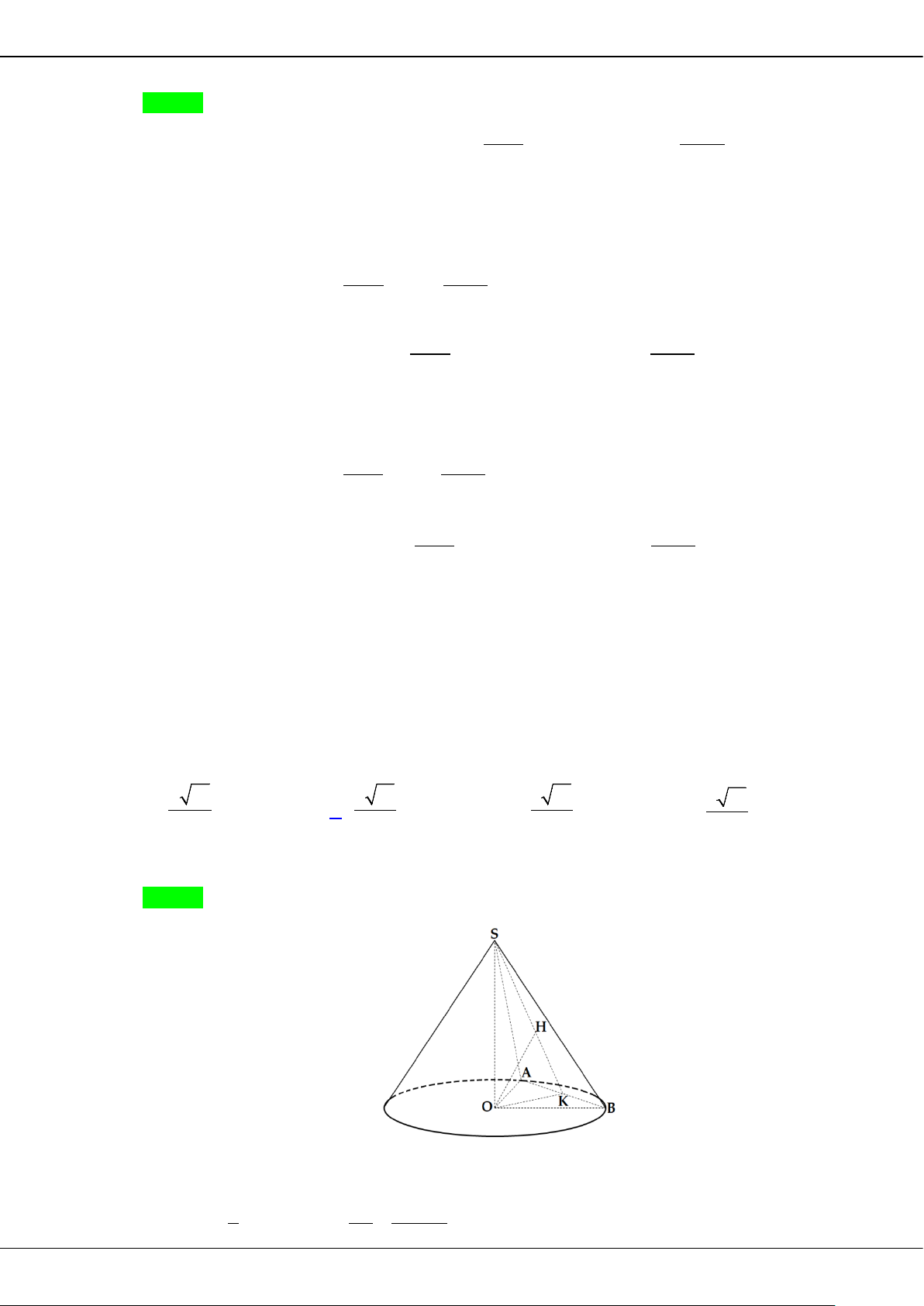
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 20

Lời giải

Chọn B

Giả thiết tương đương với

( )

( )( )

23

2 21

4 2 log 3 2 log

23

yx

xy x y

yx

+

+ + ≤− −

+−

(1).

Với

,xy

nguyên và

1 , 2022xy

≤≤

, bất phương trình có nghĩa khi

4 2022

1 2022

x

y

≤≤





≤≤



(*)

- Với

4 2022

3 2022

x

y

≤≤





≤≤



ta có

2

1

2

y

>

+

và

21

1

3

x

+

>

−

, do đó

( )( )

3

2

4 2 log 0

2

y

xy

y

++ >

+

và

( )( )

2

21

3 2 log 0

3

x

xy

x

+

−− <

−

.

Suy ra

( )

1

vô nghiệm.

- Với

{ }

4 2022

1; 2

x

y

≤≤







∈





ta có

2

1

2

y

≤

+

và

21

1

3

x

+

>

−

, do đó

( )( )

3

2

4 2 log 0

2

y

xy

y

++ ≤

+

và

( )( )

2

21

3 2 log 0

3

x

xy

x

+

−− ≥

−

Suy ra (1) thoả mãn, khi đó bpt có

2 2019 4038× =

bộ

(

)

;

xy

với

,xy

nguyên thoả mãn.

Vậy, có tất cả

4038

bộ số

( )

;xy

với

,xy

nguyên và

1 , 2022xy≤≤

thoả mãn bài toán.

Câu 48. Cho khối nón đỉnh

S

, chiều cao bằng

6

và thể tích bằng

128

π

. Gọi

A

và

B

là hai điểm

thuộc đường tròn đáy sao cho

10AB =

, khoảng cách từ tâm của đường tròn đáy đến mặt phẳng

( )

SAB

bằng

A.

6 15

5

. B.

6 13

5

. C.

3 15

5

. D.

3 13

5

.

Lời giải

Chọn B

Gọi

,OR

lần lượt là tâm và bán kính của đường tròn đáy.

,KH

lần lượt là hình chiếu của

O

lên

AB

và

SK

. Khi đó khoảng cách từ

O

đến mặt phẳng

( )

SAB

bằng

OH

.

Ta có:

2

1

3

V Rh

π

=

2

3 3.128

64

.6

V

R

h

π

ππ

⇒= = =

8R⇒=

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 21

Xét tam giác vuông

OAK

có:

2 2 22

8 5 39OK OA AK= − = −=

.

Xét tam giác vuông

SOK

có:

( )

2

2 2 22

1 1 11 1

6

39

OH SO OK

=+=+

6 13

5

OH⇒=

.

Câu 49: Trong không gian

,Oxyz

cho hai điểm

5

1; 2;

2

A



−





và

5

4; 2; .

2

B







Tìm hoành độ điểm

M

trên

mặt phẳng

()Oxy

sao cho



45ABM = °

và tam giác

MAB

có diện tích nhỏ nhất?

A.

5

2

. B.

1

. C.

3

2

. D.

2

.

Lời giải

Chọn A

Dễ thấy đường thẳng

AB

song song với mặt phẳng

()Oxy

.

Do hai điểm

,AB

cố định nên

MAB∆

có diện tích nhỏ nhất

⇔

khoảng cách từ

M

đến đường

thẳng

AB

nhỏ nhất

⇔

M

thuộc đường thẳng

∆

là hình chiếu của đường thẳng

AB

trên mặt

phẳng

()Oxy

.

Gọi

A

′

là hình chiếu của

A

trên mặt phẳng

( )

( ) 1; 2; 0Oxy A

′

⇒−

Đường thẳng

∆

đi qua điểm

A

′

và song song với đường thẳng

AB

nên có phương trình là:

13

: 24

0

xt

yt

z

= +





∆ =−+





=



M ∈∆

nên gọi

( )

1 3 ; 2 4 ;0

Mt t+ −+

5

3 3; 4 4; ;

2

BM t t



= − −−







( )

3; 4; 0BA =−−

  



( )

( ) (

)

( ) ( )

22

33 3 44 4

1

cos cos ;

25 2

5. 3 3 4 4

4

tt

ABM BM BA

tt

− −− −

= = =

−+−+

 

( )

( ) ( )

2

22

25 1

1

25 2

5. 25 1

4

25

50 1 25 1 ( 1)

4

t

tt t

−−

⇒=

−+

⇔ −= −+ ≤

( )

2

3

(

1

2

1

4

2

)t

t

l

t



=



⇔− =⇔



=





Vậy hoành độ của điểm

M

bằng

5

2

.

Câu 50. Cho các hàm số

( )

2

4fx x x m=−+

và

( )

( )( )

2023

22

1 2.

gx x x=++

Số các giá trị nguyên của

tham số

( )

2023; 2023m ∈−

để hàm số

( )

y gfx=

đồng biến trên khoảng

( )

3; +∞

là:

A.

2019

. B.

2021

. C.

2022

. D.

2020

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 22

Lời giải

Chọn D

(

)

( )

2

4 24fx x x m f x x

′

= − +⇒ = −

.

( )

( )( )

2023

22

12gx x x=++

( )

( ) ( )

2023 2022

22 2

2 . 2 1 .2023.2 . 2gx xx x xx

′

⇒ = + ++ +

( ) ( )

2022

22

2 2 2024 2025

xx x=++

Do đó:

( )

( ) ( )

( )

( ) ( ) ( )

( )

2022

22

. 2 4 .2 . 2 2024 2025gfx f xg fx x fx f x f x

′



′′

==−++



Vì

( )

2022

22

2 2024 2025 0fx fx+ +>

và

( )

2 4 0, 3;xx

− > ∀ ∈ +∞

nên

( ) ( )

( )

(

)

(

)

( )

2022

22

2 2 4 2 2024 2025 0, 3;x fx fx x− + + > ∀ ∈ +∞

.

Hàm số

( )

gfx

đồng biến trên khoảng

( )

3; +∞

( )

0, 3;gfx x

′



⇔ ≥ ∀ ∈ +∞



( ) (

) ( ) ( ) ( )

22

0, 3; 4 0, 3; 4 , 3;f x x x x m x m hx x x x⇔ ≥ ∀ ∈ +∞ ⇔ − + ≥ ∀ ∈ +∞ ⇔ ≥ = − + ∀ ∈ +∞

3m⇒≥

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 23

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT CÁI BÈ

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.A

2.D

3.D

4.D

5.B

6.A

7.A

8.A

9.B

10.B

11.D

12.B

13.B

14.B

15.B

16.D

17.C

18.C

19.A

20.C

21.B

22.D

23.A

24.A

25.A

26.C

27.D

28.B

29.A

30.A

31.C

32.C

33.B

34.B

35.A

36.C

37.A

38.B

39.B

40.A

41.D

42.C

43.A

44.A

45.D

46.D

47.D

48.A

49.B

50.D

Câu 1. Cho số phức

45zi

=−+

. Biểu diễn hình học của

z

là điểm có tọa độ

A.

( )

4;5−

B.

( )

4; 5−−

C.

( )

4; 5−

D.

( )

4;5

Câu 2. Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

1

3

log=yx

là

A.

1

3

′

=y

x

. B.

1

ln3

y

x

′

=

. C.

ln3

y

x

′

=

. D.

1

ln3

y

x

′

= −

.

Câu 3. Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

3

=

yx

là

A.

0,7

3

′

=

yx

. B.

31−

′

=yx

. C.

31

1

3

−

′

=yx

. D.

31

3

−

′

=yx

.

Câu 4. Tập nghiệm của bất phương trình

1

11

24

+



>





x

là

A.

(

]

;1−∞

. B.

( )

1;

+∞

. C.

[

)

1; +∞

. D.

( )

;1−∞

.

Câu 5. Cho cấp số cộng

( )

n

u

có

1

2u = −

và công sai

3.d =

Tìm số hạng

10

.

u

A.

9

10

u 2.3= −

. B.

10

u 25=

. C.

10

u 28=

. D.

10

u 29= −

.

Câu 6. Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng (P):

0

202322 =++− z

yx

. Vectơ nào dưới

đây là một vectơ pháp tuyến của

( )

P

?

A.

( )

3

2; 2; 1n =−−

 

. B.

( )

4

1; 2; 2n = −

 

. C.

( )

1

1; 1; 4n = −



. D.

( )

2

2; 2;1n

=

 

.

Câu 7. Đồ thị hàm số

2

43

yx x=−+

cắt trục tung tại điểm có tung độ bằng

A. 3. B. 1. C. 4. D. 0.

Câu 8. Gọi

F(x)

là một nguyên hàm của hàm số

f(x)

trên đoạn [a ; b], k là một hằng số. Trong các

đẳng thức sau, đẳng thức nào đúng?

A.

 

b

a

k.f (x)dx k F b F(a)









B.

 

b

a

f (x)dx F a F(b)



LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 24

C.

bc c

ab a

f (x)dx f (x)dx f (x)dx



D.

ba

ab

f (x)dx f (x)dx



Câu 9. Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên?

A.

32

3yx x=−+

. B.

42

3yx x= −

. C.

32

3yx x= −

. D.

42

3yx x=−+

.

Câu 10. Trong không gian

Oxyz

, tâm mặt cầu (S):

(

) (

)

2 22

–1 2 1 4

++ ++ =xy z

có tọa độ là

A.

( )

1; 2;1−

. B.

( )

1;2;1

−−

. C.

( )

1; 2;1−

. D. (1, 2, 1).

Câu 11. Trong không gian

Oxyz

, cho các điểm

( )

2; 2;1A −

,

(

)

1; 1; 3B −

. Tọa độ của vectơ

AB



là

A.

( )

3; 3; 4−−

. B.

( )

1; 1; 2−−

. C.

( )

3; 3; 4−

. D.

( )

1;1; 2−

.

Câu 12. Cho số phức

76zi= +

, phần ảo của số phức

2

z

bằng

A.

13

. B.

84

. C.

6

. D.

48

.

Câu 13. Cho khối lập phương có cạnh bằng

2

. Thể tích của khối lập phương đã cho bằng

A.

3 2.

B.

22

. C.

22

3

. D.

42

.

Câu 14. Cho khối chóp

.S ABC

có đáy là tam giác vuông cân tại

A

, AB = 4;

SA

vuông góc với

đáy và

3SA =

(tham khảo hình vẽ).

Thể tích khối chóp đã cho bằng

A. 48. B. 8. C. 12. D. 16.

Câu 15. Trong không gian

Oxyz

, cho mặt cầu (S):

( ) ( ) ( )

2 22

–1 2 1 9++ ++ =xy z

, Gọi d là

khoảng cách từ tâm I của mặt cầu đến mặt phẳng (P), khi đó mặt phẳng (P) cắt mặt cầu (S) theo giao

tuyến là đường tròn khi

A.

3>d

B.

3<d

C.

9<d

D.

3=d

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 25

Câu 16. Cho hai số phức 

1

= −1 + 2 và 

2

= 4 − . Khi đó số phức liên hợp của 

1

+ 

2

là

A.

3

i−−

. B.

3 i−+

. C.

3 i+

. D.

3 i−

.

Câu 17. Cho hình nón có đường kính đáy 4 và độ dài đường sinh

l

. Diện tích xung quanh của

hình nón đã cho bằng

A. 4πrl. B.

2

4

3

rl

π

. C. 2πrl. D.

2

1

3

rl

π

.

Câu 18. Trong không gian

Oxyz

, cho đường thẳng

421

:

2 51

xzz

d

−−+

= =

−

. Điểm nào sau đây

thuộc

d

?

A.

(2; 5;1)Q

. B.

(4; 2;1)M

. C.

(4; 2; 1)N −

. D.

(2; 5;1)

P −

.

Câu 19. Cho hàm số

42

2022 2023=−+ −yx x

. Số điểm cực trị của đồ thị hàm số là

A.

3

. B.

0

. C.

1

. D.

2

.

Câu 20. Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số

21

1

x

y

x

−

=

+

.

A.

1

,

2

x =

1

y = −

. B.

1,x =

2y = −

. C.

1,x = −

2y =

. D.

1,x = −

1

2

y

=

.

Câu 21. Tập nghiệm của bất phương trình

( )

2

log 2 0

−>x

là

A.

( )

;2−∞

B.

( )

;1

−∞

C.

( )

1; +∞

D.

(

)

2; +∞

Câu 22. Số cách chọn

3

học sinh từ một nhóm gồm

8

học sinh là:

A.

3

8

A

. B.

8

3

. C.

3

8

. D.

3

8

C

.

Câu 23. Tìm khẳng định đúng trong các khẳng định sau

A.





1

x dx x C 1

1

 

  





B.

 

1

x dx x C 1

1

 

  





C.

 

1

x dx x C 1

1

 

  





D.

 

1

x dx x C 1

1

 

  





Câu 24. Cho

( )

2

0

3

=

∫

f x dx

.Khi đó

( )

2

0

43−





∫

f x dx

bằng:

A. 6 B. 4 C. 2 D. 8

Câu 25. Tìm

1

dx

2x 1



ta được kết quả là:

A.

1

ln 2x 1 C

2



B.

ln 2x 1 C 

C.

1

ln 2x 1 C

2

 

D.

ln 2x 1 C

Câu 26. Cho hàm số

( )

y fx=

có đồ thị như hình sau:

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 26

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A.

(

)

0; +∞

. B.

( )

;1−∞

. C.

( )

1; +∞

. D.

( )

0;1

.

Câu 27. Cho hàm số

()y fx=

xác định, liên tục trên



và có bảng biến thiên như hình dưới.

Khẳng định nào dưới đây là khẳng định đúng?

A. Hàm số đạt cực đại tại

1x =

. B. Đồ thị hàm số có điểm cực đại

0x =

.

C. Hàm số có giá trị lớn nhất bằng

3−

. D. Hàm số đạt cực đại tại

0x =

.

Câu 28. Với  là số thực tùy ý,

22

ln(3a 3) ln(a 1)+− +

bằng:

A.

( )

2

ln 1

+

a

. B.

ln 3

. C.

ln 6

. D.

2

3

ln

1+a

.

Câu 29. Cho hình phẳng (H) giới hạn bởi các đường

2

y x 2x= −

, trục hoành, trục tung, đường

thẳng

x1=

. Gọi V là thể tích của khối tròn xoay sinh ra khi quay (H) quanh trục Ox. Giá trị của V là:

A.

8

V

15

π

=

B.

4

V

3

π

=

C.

15

V

8

π

=

D.

7

V

8

π

=

Câu 30. Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

. SA ⊥ (ABCD) ; SA =

a3

. Tính

góc giữa hai mặt phẳng

( )

SAB

và

( )

SCD

.

A.

30

o

. B.

90

o

. C.

60

o

. D.

45

o

.

Câu 31. Cho đồ thị hàm số

( )

y fx=

như hình vẽ. Hỏi phương trình

( )

=fx m

có tối đa bao nhiêu

nghiệm thực

x

?

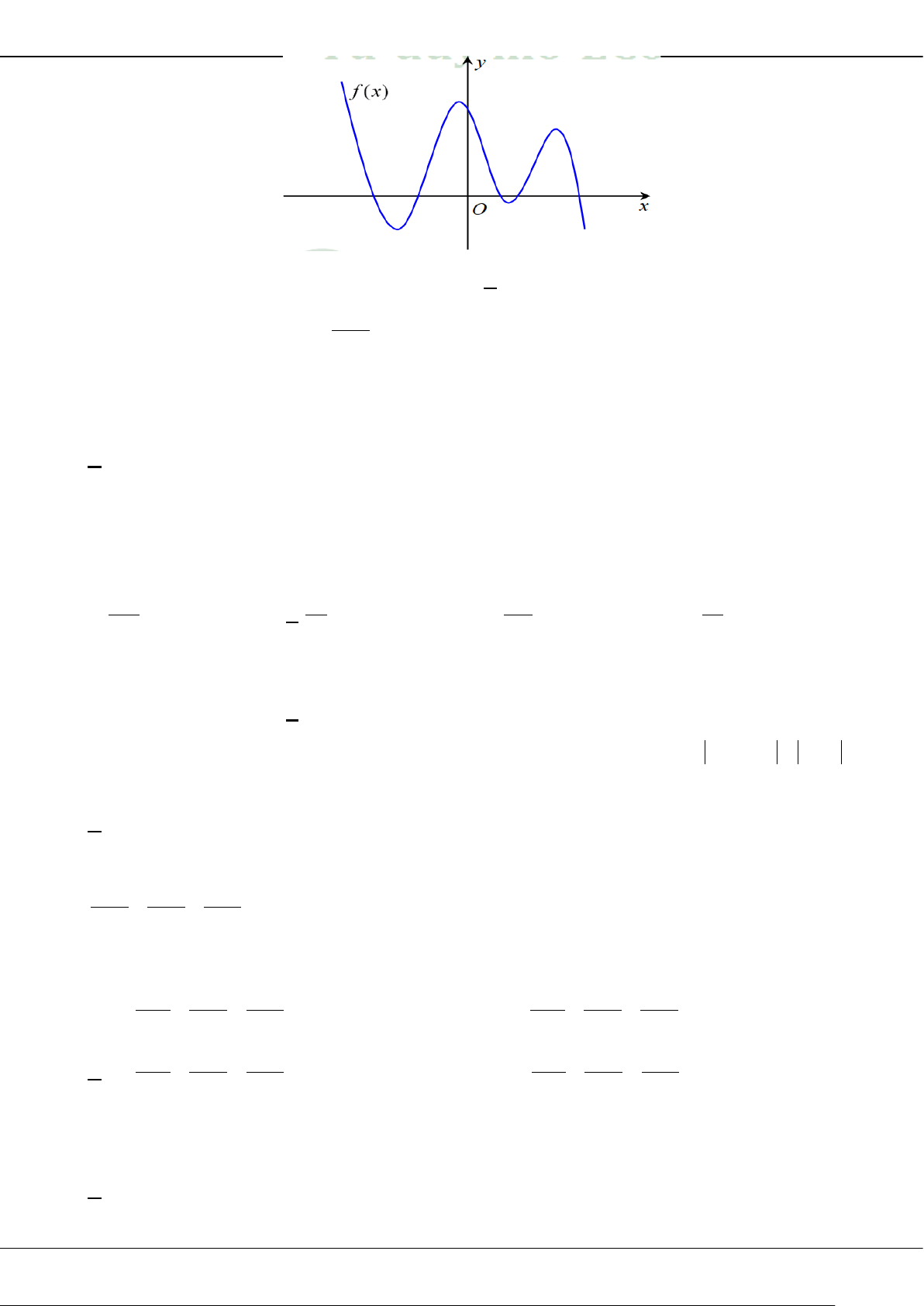
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 27

A.

3

. B.

6

. C.

5

. D.

4

.

Câu 32. Cho hàm số

( )

1

2

x

fx

x

−

=

+

. Mệnh đề nào sau đây sai?

A. Hàm số

( )

fx

nghịch biến trên

( )

;2−∞ −

.

B. Hàm số

( )

fx

nghịch biến trên các khoảng

( )

;2−∞ −

và

(

)

2;

− +∞

.

C. Hàm số

( )

fx

nghịch biến trên

{ }

\2−

.

D. Hàm số

( )

fx

nghịch biến trên từng khoảng của tập xác định.

Câu 33. Lớp 11A có 25 đoàn viên trong đó 10 nam và 15 nữ. Chọn ngẫu nhiên 3 đoàn viên trong

lớp để tham dự hội trại. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ.

A.

7

920

. B.

27

92

. C.

3

115

. D.

9

92

.

Câu 34. Tích tất cả các nghiệm của phương trình

2

ln 2ln 3 0− −=xx

bằng

A.

3

.e

B.

2

e

. C.

3.

D.

1.−

Câu 35. Tập hợp các điểm trong mặt phẳng Oxy biểu diễn số phức z thỏa mãn

z 1 2i z 3−+ = +

là đường thẳng có phương trình

A. 2x – y + 1 = 0. B. 2x + y + 1 = 0. C. 2x + y – 1 = 0. D. 2x – y – 1 = 0.

Câu 36. Trong không gian tọa độ

Oxyz

, cho điểm

( )

1; 3; 4M −

, đường thẳng

252

:

3 51

xyz

d

+ −−

= =

−−

và mặt phẳng

( )

:2 2 0P xz+−=

. Viết phương trình đường thẳng

∆

qua

M

vuông góc với

d

và song song với

( )

P

.

A.

134

:

1 12

xyz−+−

∆==

−−

. B.

134

:

112

xyz−+−

∆==

−−−

.

C.

134

:

11 2

xyz−+−

∆==

−

. D.

134

:

1 12

xyz−+−

∆==

−

.

Câu 37. Trong không gian với hệ tọa độ

Oxyz

, cho hình bình hành ABCD có A(1, 1, –2) ; B(–2, –

1, 4) ; C(3, –2, –5). Tìm tọa độ đỉnh D.

A.

(6; 0; 11)D −

B.

( 6;1;11)D −

C.

(5;2;1)D −−

D.

( 3; 6;1)D −

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 28

Câu 38. Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông tâm O cạnh

2

a

,

5SA SB SC SD a= = = =

. Tính khoảng cách từ điểm

B

đến mặt phẳng

( )

SCD

.

A.

3

2

a

. B.

3a

. C.

a

. D.

5

2

a

.

Câu 39. Có bao nhiêu số nguyên

x

thỏa mãn

3

22

5

44

ll

2

og > g

72

o

1

−−xx

?

A. 58. B. 112. C. 116. D. 117.

Lời giải

TXĐ:

( ) ( )

; 2 2; .= −∞ − ∪ +∞D

Ta có:

( ) ( )

( )

53

22

53 3 3

2

5 3 53

53

2

3

5

2

33

23

33

2

3

2

27 125

3. 43> 43 5

3 1 .l 4 3 3 3 5

33 5

log 4

log 3 1

log 4 3 1 log 5

log 4 log 15

4 15

3379 3379

44

log > log

log log log log

log og log log

log log



⇔ −− −−



⇔ − −> −

−

⇔ −<

−

⇔ −< +

⇔ −<

⇔

−

− <<

−

xx

x

Kết hợp điều kiện ta có

{ }

58; 57;...; 3;3;...;57;58∈− − −x

. Vậy có 112 số nguyên x thỏa mãn.

Câu 40. Biết rằng

b

0

6dx 6



và

a

x

0

xe dx 1



. Khi đó, biểu thức

23 2

b a 3a 2a 

có giá trị

bằng:

A. 7. B. 4. C. 5. D. 3.

Lời giải

•Ta có:

bb

b

0

00

6dx 6 dx 1 x 1 b 1    



•Đặt

xx

u x du dx

dv e dx v e



















LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 29

aa

x x x ax

00

aa

xe dx 1 xe e dx 1 ae e 1

ae e 1 1 a 1

    

   



Vậy

23 2

b a 3a 2a 7  

Câu 41. Tìm tham số

m

để hàm số

( )

32

1

2 2018

3

y x mx m x= − ++ +

không có cực trị.

A.

1m ≤−

hoặc

2m ≥

. B.

1m

≤−

. C.

2

m

≥

. D.

12m−≤ ≤

.

Lời giải

Hàm số xác định trên



.

Ta có

2

22y x mx m

′

= − ++

Hàm số không có cực trị khi và chỉ khi

2

2 20x mx m− + +=

không có hai nghiệm phân biệt

2

' 20 1 2

⇔∆ = − − ≤ ⇔− ≤ ≤

mm m

.

Câu 42. Cho hai số phức

12

,zz

thỏa mãn đồng thời hai điều kiện sau

1 34,

−=z

12++ = + +z mi z m i

và sao cho

12

−zz

là lớn nhất. Khi đó giá trị của

12

+zz

bằng

A.

2

. B.

10

. C. 2 D.

130

.

Lời giải

Gọi

,MN

lần lượt là điểm biểu diễn của số phức

12

,.zz

Gọi số phức  =  +  (,  ∈ ℝ)

Ta có:

1 34−=z

,⇒ MN

thuộc đường tròn

( )

C

có tâm

( )

1; 0I

, bán kính

34.=

R

Mà

12++ = + +z mi z m i

12⇔+++ =+++

x iy mi x iy m i

( ) ( )

2 2 22

12x ym xm y⇔ + ++ = + ++ ⇔

( ) ( )

21 2 2 3 0mx m y−+−−=

,⇒ MN

thuộc đường thẳng

( ) ( )

:2 1 2 2 3 0d mx m y−+−−=

Do đó

,MN

là giao điểm của đường thẳng

d

và đường tròn

( )

C

M

d

y

x

O

I(1;0)

N

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 30

Ta có:

12

−=z z MN

nên

12

−

zz

lớn nhất

⇔ MN

lớn nhất

⇔

MN

là đường kính của đường tròn (C).

Khi đó:

12

2. 2.+= =z z OI

Câu 43. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật

AB a=

và

2

AD a=

, cạnh bên

SA

vuông góc với đáy. Tính thể tích

V

của khối chóp

.S ABCD

biết góc giữa hai mặt phẳng

( )

SBD

và

(

)

ABCD

bằng

0

60

.

A.

3

4 15

15

a

V =

. B.

3

15

6

a

V =

. C.

3

15

3

a

V =

. D.

3

15

a

V =

.

Lời giải

Kẻ

AE BD⊥

( ) ( )



(

)



0

, 60SBD ABCD SEA= =

ABD∆

vuông tại

A

:

2

22

. 2 25

5

AD AB a a

AE

a

AD AB

= = =

+

SAE∆

vuông tại

A

:

0

2 5 2 15

.tan 60 . 3

55

aa

SA AE= = =

3

2

1 1 2 15 4 15

. . .2

3 3 5 15

ABCD

aa

V SA S a= = =

.

Câu 44. Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số

() , () 2f x xgx x

 

và trục

hoành. Kết quả là giá trị nào sau đây?

A.

10

3

B.

11

3

C.

7

3

D.

8

3

Lời giải

Hàm số

()fx x=

cắt trục hoành tại điểm

0x =

Hàm số

() 2gx x= −

cắt trục hoành tại điểm

2x =

Hàm số

() , () 2f x xgx x 

cắt nhau tại điểm

4x =

A

D

B

C

S

E

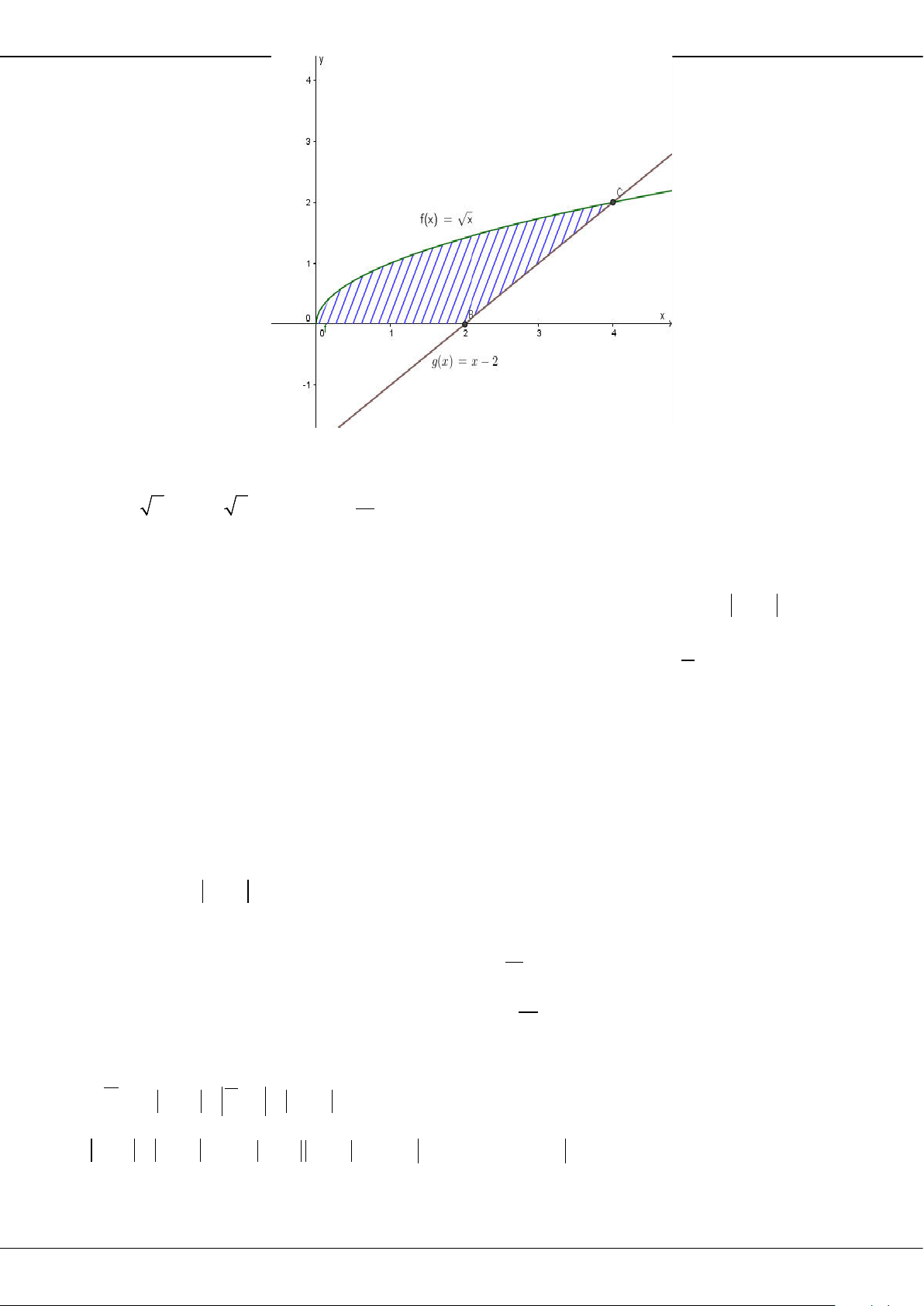
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 31

Vậy diện tích hình phẳng cần tìm là:

 

24

02

10

S xdx x x 2 dx

3

   



Câu 45. Trên tập hợp các số phức, xét phương trình

( )

2

2 1 30z m zm− + + +=

(

m

là tham số

thực). Có bao nhiêu giá trị của tham số

m

để phương trình có nghiệm phức

0

z

thỏa mãn

0

26z +=

?

A.

3

. B.

1

. C.

4

. D. 2

Lời giải

Phương trình

( )

2

2 1 30z m zm− + + +=

(

m

là tham số thực).

Ta có

( ) ( )

2

13 2m m mm

′

∆= + − + = + −

.

Nếu

2

0 20

1

m

mm

m

≤−



′

∆≥⇔ + −≥⇔



≥



thì phương trình có nghiệm thực. Khi đó theo đầu bài, nghiệm

0

z

phải thỏa mãn

00

0

00

26 4

26

26 8

zz

z

zz

+= =



+=⇔ ⇔



+=− =−



Do đó suy ra

( )

( ) ( )( )

2

11

4 2 14 3 0

7

83

8 2 1 8 30

17

m

mm

m



=



− + + +=



⇔



− − + − + +=





= −





.( nhận)

Nếu

2

0 20 2 1mm m

′

∆<⇔ + −<⇔−< <

thì phương trình có hai nghiệm phức phân biệt

12

,zz

với

21

zz=

⇒

112

222

zzz+= += +

. Do đó theo điều kiện đầu bài, ta có

12

2 26zz+= +=

( )

1 2 12 1 2

2 2 36 2 4 36z z zz z z⇒ + += ⇔ + + +=

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 32

( )

3 4 1 4 36mm⇔ ++ + + =

5 11 36m⇔ +=

5 11 36

m

+=



⇔



+=−



5

47

5

m

=





⇔



= −



.( loại)

Vậy với

11

7

m =

hoặc

83

17

m = −

thì phương trình có nghiệm phức thỏa mãn điều kiện đầu bài.

Câu 46. Cho mặt cầu (S):

( ) ( ) ( )

25111

222

=−+−+− zyx

và mặt phẳng

( )

0722: =+++ zyx

α

.

Mặt phẳng (P) đi qua hai điểm A(1; -1; 2), B(3; 5; -2) và cắt (S) theo một đường tròn có bán kính nhỏ

nhất. Phương trình (P) là

A.

0424 =−−+ zyx

B.

0424 =+−+ zyx

C.

012 =−−+ zyx

D.

0424 =−−− zyx

Lời giải

Mặt cầu có tâm I(1, 1, 1), bán kính R = 5 .

Ta có

AB (2;6; 4)= −



nên phương trình đường thẳng

x1t

AB: y 1 3t

z 2 2t

= +





=−+





= −



Vì

IA 5 R 5= <=

nên mặt phẳng (P) luôn cắt mặt cầu (S) theo đường tròn có bán kính

( )

22

r R d I; P= −

.

Do đó r nhỏ nhất

( )

d I; P⇔

lớn nhất.

Gọi K, H lần lượt là hình chiếu của I lên AB và mp(P).

Ta có IH ≤ IK nên suy ra

( )

d I; P

lớn nhất ⇔ H ≡ K

Do H∈ AB nên H(1 + t ; –1 + 3t ; 2 – 2t) ⇒

( )

IH t; 2 3t;1 2t= −+ −

 

Vì IH ⊥ AB nên

IH.AB 0=

 

4

t

7

⇒=

421

IH ; ;

777



⇒ = −−





 

Vậy phương trình (α): 4x – 2y – z – 4 = 0.

Câu 47. Có bao nhiêu cặp số nguyên

(; )xy

thỏa mãn

( ) ( ) ( )

2

2 32

2 22

3

22

log 4 log log log 15 15 48 ?++ + + ≤ + + +xy x xy x x y x

A. 22. B. 28. C. 15. D. 12.

Lời giải

Điều kiện:

0x >

.

Ta có:

( ) ( ) ( )

2

2 32

2 22

3

22

log 4 log log log 15 15 48 ?++ + + ≤ + + +xy x xy x x y x

( ) ( ) ( )

22 2 2 22

2 23 3

log log log 15 15 48 log⇔ ++− ≤ ++− +xyx x x y x xy

()S

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 33

2

23

22 2 2

2

4 15 15 48

log log

  

++ + +

⇔≤

  

+

  

xy x x y x

x xy

2

23

22

2

48

log l g4 15o



+

⇔≤



+





++



xy

x

xy

22

2

23

2

48

log log 04 15



+

⇔− ≤





++





+





xy x

x xy

Đặt:

22

( 0)

xy

tt

x

+

= >

, bất phương trình trở thành:

23

log (4 ) log 1 0

48

5



+− + ≤





t

(1).

Xét hàm số

23

48

( ) log (4 ) log 15



= +− +





ft t

t

có

( )

2

1

( ) 0, 0

(4 )ln 2

15 48

48

ln 3

′

= + > ∀>

+

ft t

t

tt

.

Suy ra hàm số đồng biến trên khoảng

(0; )+∞

.

Ta có

23

48

(4) log (4 4) log 15 0

4



= +− + =





f

Từ đó suy ra:

22

(1) ( ) (4) 4 4 ( 2) 4

+

⇔ ≤ ⇔≤⇔ ≤⇔ − + ≤

xy

ft f t x y

x

.

Đếm các cặp giá trị nguyên của

(; )xy

Ta có:

2

( 2) 4 0 4− ≤⇔≤≤xx

, mà

0x

>

nên

04<≤x

.

Với

1, 3 { 1; 0}

= =⇒=±xx y

nên có 6 cặp.

Với

2 { 2; 1; 0}=⇒ =±±xy

nên có 5 cặp.

Với

40=⇒=xy

nên có 1 cặp.

Vậy có 12 cặp giá trị nguyên

(; )xy

thỏa mãn đề bài.

Câu 48. Cho hình nón đỉnh

S

, đường cao SO,

A

và

B

là hai điểm thuộc đường tròn đáy sao cho

khoảng cách từ

O

đến

( )

SAB

bằng

3

a

và



00

30 , 60SAO SAB= =

. Độ dài đường sinh của hình nón

theo

a

bằng

A.

2a

B.

3a

C.

23a

D.

5a

Lời giải

K

H

B

A

O

S

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 34

Gọi

K

là trung điểm của

AB

ta có

OK AB⊥

Mà

SO AB

⊥

nên

(

)

AB SOK

⊥

(

)

(

)

SOK SAB

⇒⊥

Từ

O

dựng

OH SK

⊥

thì

( ) ( )

( )

,OH SAB OH d O SAB⊥ ⇒=

Tam giác

SAO

có:



sin

2

SO SA

SAO SO

SA

=⇒=

Tam giác

SAB

có:



3

sin

2

SK SA

SAB SK

SA

=⇒=

Tam giác

SOK

ta có:

2 2 2 22 2

1 11 1 1

OH OK OS SK SO SO

= += +

−

2 22

1 1 1 42

3

4 44

SA SA SA

OH SA SA

⇒=+ =+

−

2

22

63

22SA a SA a

SA a

⇒ =⇒= ⇒=

Câu 49. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

( ) ( )

2;5;3,4;2;0 −− BA

. Tọa độ điểm M

sao cho

22

2MBMA +

có giá trị nhỏ nhất

A.

(

)

2;3;1−M

B.

( )

0;4;

2−M

C.

( )

2;7;3 −−M

D.













−1

;

2

7

;

7

3

M

Lời giải

Gọi M(x;y;z)

Khi đó

(

) (

)

22

2

42 +

+−+

= zyx

AM

(

) ( ) (

)

22

2

25

3 −+

−++=

zy

xBM

( ) ( ) ( )

( ) ( )

22

2

22

22523

2422 −+−+++++−+=+ zyx

zyxMBMA

( )

( ) (

)

[ ]

3612

.3124

2332

8

43

2

22

=≥+

+−+

+=+−

+++= z

yxyx

zyx

22

2MBMA +

nhỏ nhất khi

362

22

=+ MBMA

( )

0;4;2−⇒ M

Câu 50. Có bao nhiêu số nguyên

m

thuộc khoảng

( )

10;10−

để hàm số

32

8y x x mx= −− +

đồng

biến trên khoảng

( )

1; +∞

?

A.

10

. B.

13

. C.

12

. D.

11

.

Lời giải

Xét hàm số

( ) ( )

32 2

8; ' 3 2

f x x x mx f x x x m=−− + = −−

.

Hàm số

32

8y x x mx= −− +

đồng biến trên khoảng

( )

1; +∞

có hai trường hợp sau

TH1:

( ) ( )

( )

2

' 0, 1;

1

3 2 , 1;

1

8

10

80

fx x

m

x xmx

m

f

m

≥ ∀ ∈ +∞



≤

− ≥ ∀ ∈ +∞





⇔ ⇔ ⇔≤

 

≤

≥

−≥









.

Kết hợp với Đk ta được

{ }

9;8;7;6;5;4;3;2;1;0;1m ∈−−−−−−−−−

. Có

11

giá trị của

m

.

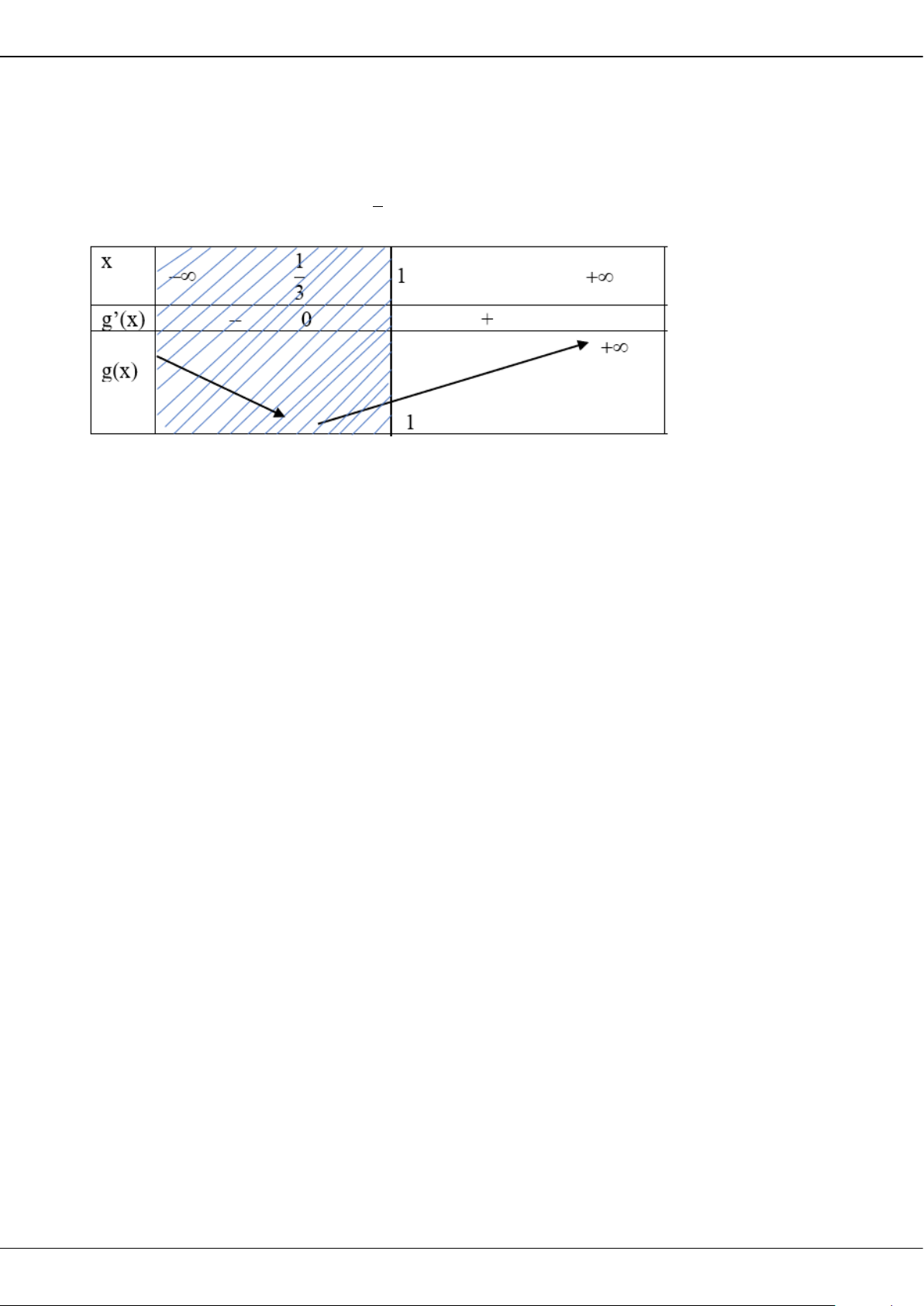
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 35

TH2:

( ) ( )

( )

( )( )

2

' 0, 1;

3 2 , 1; *

10

80

fx x

x xmx

f

m

≤ ∀ ∈ +∞



− ≤ ∀ ∈ +∞



⇔



≤

−≤





.

Xét hàm số

( )

2

32gx x x

= −

với

( )

1;x ∈ +∞

.

Ta có

(

) (

)

1

6 2; 0

3

gx x gx x

′′

= − =⇔=

.

Không có giá trị nào của

m

thỏa mãn

( )

*

.

Vậy có

11

giá trị nguyên của

m

cần tìm.

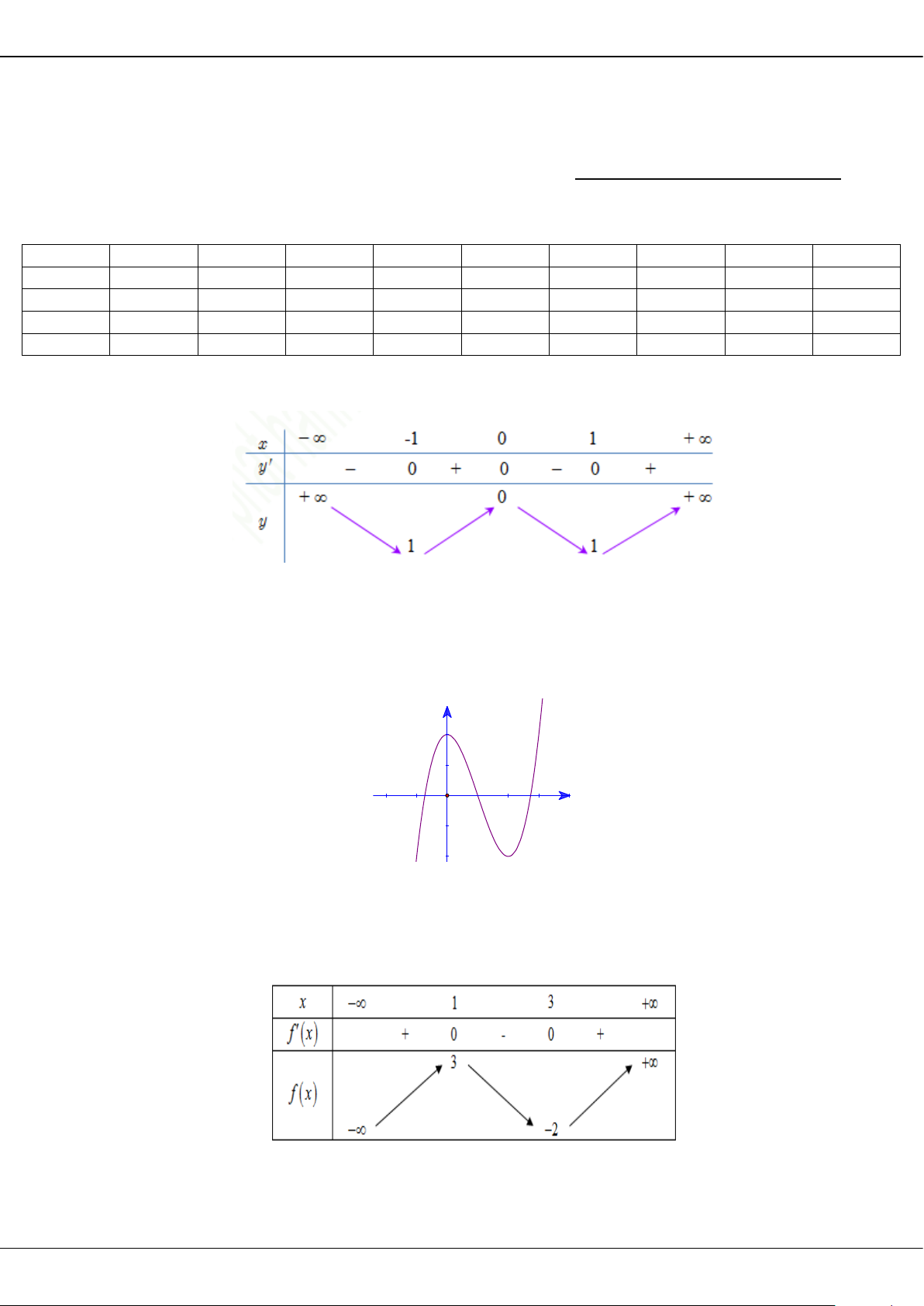
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 36

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT PHẠM THÀNH TRUNG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.C

2.A

3.C

4.D

5.C

6.B

7.B

8.A

9.A

10.A

11.A

12.D

13.C

14.A

15.B

16.D

17.B

18.B

19.C

20.C

21.C

22.D

23.A

24.D

25.A

26.A

27.A

28.C

29.B

30.B

31.D

32.B

33.B

34.B

35.A

36.B

37.A

38.C

39.C

40.D

41.A

42.B

43.D

44.A

45.B

46.C

47.D

48.B

49.D

50.A

Câu 1: Cho hàm số

( )

y fx

=

có bảng biến thiên như sau

Hàm số

( )

y fx=

đồng biến trên khoảng nào dưới đây?

A.

(

)

1;− +∞

. B.

( )

0;1

. C.

( )

1; 0−

. D.

( )

;1−∞ −

.

Câu 2: Cho hàm số

32

y ax bx cx d= + ++

(,, )abc∈



có đồ thị như hình vẽ bên.

Số điểm cực trị của hàm số đã cho là

A.

2

. B.

0

. C.

3

. D.

1

.

Câu 3: Cho hàm số

( )

y fx=

có bảng biến thiên như sau:

Hàm số đạt cực đại tại

A.

2x = −

. B.

2x =

. C.

1x =

. D.

3x =

.

y

x

O

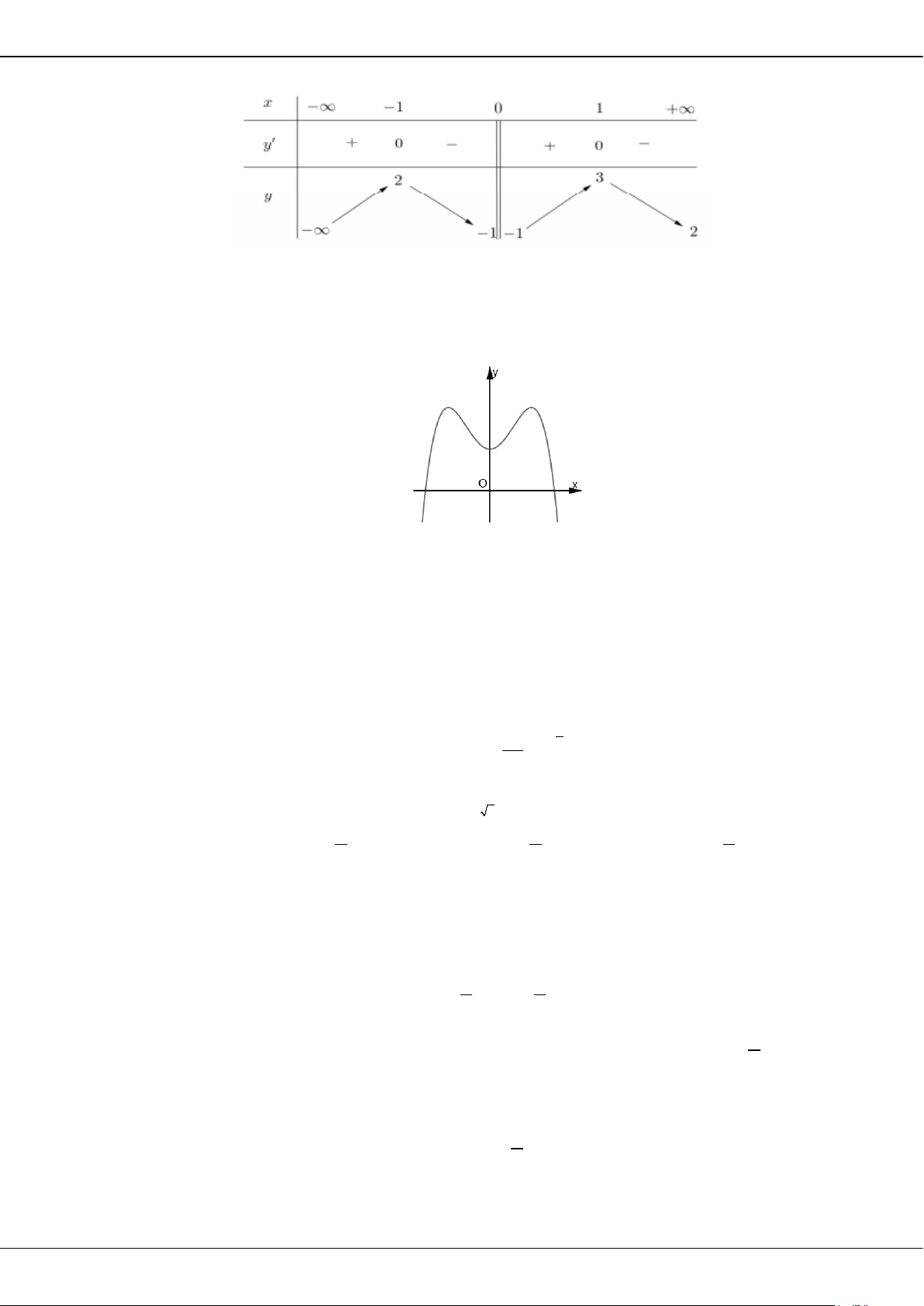
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 37

Câu 4: Cho hàm số có bảng biến thiên

Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?

A.

3

B. C. D.

Câu 5: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

A.

32

31yx x=−+

. B.

32

31yx x=−+ +

. C.

42

21yx x=−+ +

. D.

42

21yx x=−+

.

Câu 6: Biết rằng đường thẳng

y 2x 2=−+

cắt đồ thị hàm số

3

yx x2= ++

tại điểm duy nhất có tọa độ

( )

00

x ;y

. Tìm

0

y.

A.

0

y1= −

. B.

0

y2=

. C.

0

y4=

. D.

0

y0=

.

Câu 7: Cho số dương

a

khác

1

và các số thực

x

,

y

. Đẳng thức nào sau đây đúng?

A.

x y xy

aa a





B.

 

y

x xy

aa

C.

x

y

a



D.

.

x y xy

aa a

Câu 8: Cho

a

là số thực dương khác

1

. Tính

3

log

a

Ia=

.

A.

6I =

. B.

2

3

I =

. C.

3

2

I =

. D.

1

6

I =

.

Câu 9: Tập xác định

D

của hàm số

 

ln 1yx

là

A.

( )

1; .D = +∞

B.

.D = 

C.

 

;1 .D  

D.

{ }

\1.D = 

Câu 10: Tìm tập nghiệm

S

của bất phương trình

21 32

11

22

xx+−

 

<

 

 

.

A.

( )

;3S = −∞

. B.

( )

;3S = −∞ −

. C.

( )

3;S = +∞

. D.

1

;3

2

S



= −





.

Câu 11: Tập nghiệm của bất phương trình

( )

22

log 1 log 3x −>

là

A.

( )

4; +∞

. B.

[

)

4; +∞

. C.

1

;1

2









. D.

( )

;1−∞ −

.

Câu 12: Họ các nguyên hàm của hàm số

( )

5

x

fx x= −

là

( )

y fx=

4

2

1

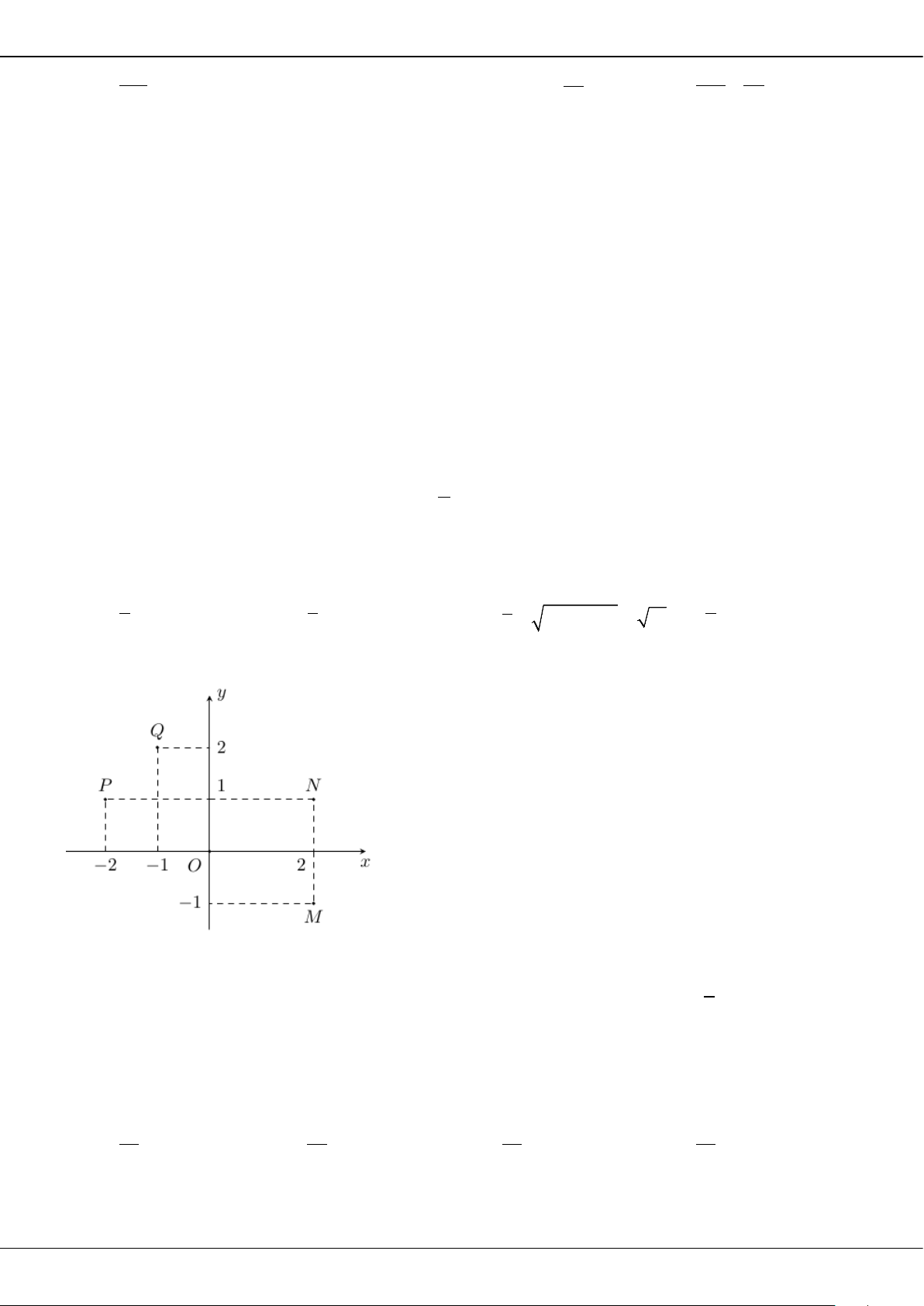
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 38

A.

5

1

ln 5

x

C−+

B.

5 ln 5 1

x

C

−+

C.

2

5 ln 2

2

x

C−+

D.

2

5

ln 5 2

x

C

−+

Câu 13: Giả sử

()

Fx

là một nguyên hàm của hai hàm số

()fx

trên

[ ]

,ab

,

k

là hằng số khác

0

. Trong

các đẳng thức sau, đẳng thức nào đúng?

A.

() () ()

b

a

f x dx F a F b= −

∫

. B.

() ()

ba

ab

f x dx f x dx=

∫∫

.

C.

[ ]

. () () ()

b

a

k f x dx k F b F a= −

∫

. D.

() () ()

bc c

ab a

f x dx f x dx f x dx−=

∫∫ ∫

.

Câu 14: Cho

(

)

2

0

d3fx x=

∫

,

( )

2

0

d7gx x=

∫

, khi đó tính tích phân

( ) ( )

2

0

3df x gx x+





∫

bằng:

A. 24. B. 10. C. 16. D.

18

−

.

Câu 15: Cho hàm số

( )

fx

liên tục trên



. Gọi

( ) ( )

,

Fx Gx

là hai nguyên hàm của

( )

fx

trên



thỏa mãn

( ) ( )

8 88FG+=

và

( )

0 02FG+=−

. Khi đó

(

)

( )

8

1

5ln d

e

f xx

x

∫

bằng:

A.

1−

. B.

1

. C.

5

. D.

5−

.

Câu 16: Cho số phức

32zi= +

. Tìm số phức liên hợp của số phức

z

A.

23zi= −

. B.

23zi= +

. C.

22

3 ( 2) 13.z = +− =

. D.

32zi= −

.

Câu 17: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức

2

zi=−+

?

A. N. B. P. C. Q.

D. M.

Câu 18: Cho số phức z thỏa mãn

( )

1 14 2iz i+=−

. Tổng phần thực và phần ảo của

z

là?

A.

4

. B.

14

. C.

4−

. D.

14−

.

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Cạnh bên

SA

vuông góc với đáy

và có độ dài bằng

a

. Tính thể tích khối tứ diện

.S BCD

.

A.

3

2

a

. B.

3

4

a

. C.

3

6

a

. D.

3

a

.

Câu 20: Khối trụ có bán kính đáy

3r =

và chiều cao

4h =

. Thể tích của khối trụ đã cho bằng

A.

48

π

. B.

12

π

. C.

36

π

. D.

16

π

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 39

Câu 21: Cho khối nón có bán kính đáy

2,

r

=

chiều cao

3.h =

Thể tích của khối nón là

A.

23

.

3

π

B.

4 3.

π

C.

43

.

3

π

D.

4

.

3

π

Câu 22: Trong không gian

Oxyz

với hệ tọa độ

( )

;;;Oi jk





cho

25OA i k

=−+

  



. Tìm tọa độ điểm

A

.

A.

( )

2; 5; 0−

. B.

( )

2;5

−

. C.

( )

5; 2; 0−

. D.

( )

2;0;5−

.

Câu 23: Trong không gian

Oxyz

, cho hai điểm

( ) ( )

1; 2; 3 , 3;0;1 .AB−

Véctơ nào dưới đây là một véctơ

pháp tuyến của mặt phẳng trung trực đoạn

AB

?

A.

( )

4

2;1;1n = −−

 

. B.

( )

2

4; 2; 2n = −

 

. C.

( )

3

2; 1; 1

n = −

 

. D.

( )

1

2; 2; 4n =



.

Câu 24: Trong không gian với hệ trục tọa độ

,Oxyz

cho điểm

(1; 1;1)I −

và mặt phẳng

( )

: 2 2 10 0xy z

α

+− + =

. Mặt cầu

( )

S

tâm

I

tiếp xúc với

( )

α

có phương trình là

A.

( ) ( ) ( )

2 22

1 1 11xyz+ +− ++ =

. B.

( ) ( ) (

)

2 22

1 1 13xyz+ +− ++ =

.

C.

( ) ( ) ( )

2 22

1 1 11xyz− ++ +− =

. D.

( ) (

) (

)

2 22

1 1 19xyz− ++ +− =

.

Câu 25: Trong không gian

Oxyz

, đường thẳng đi qua điểm

 

3 21;;M 

và nhận véctơ





4 35;;

u 



làm véctơ chỉ phương có phương trình tham số là

A.

34

23

15

xt

yt

zt







 











. B.

43

32

5

xt

yt

zt







 











. C.

34

23

15

xt

yt

zt



















. D.

34

23

15

xt

yt

zt







 











.

Câu 26: Phương trình tổng quát của

( )

α

qua

( ) ( )

2; 1; 4 , 3; 2; 1AB−−

và vuông góc với mặt phẳng

( )

: 2 30

xy z

β

++ −=

là.

A.

11 7 2 21 0xyz−−−=

. B.

11 7 2 21 0xyz−++=

.

C.

11 7 2 21 0xyz+−−=

. D.

11 7 2 21 0xyz+++=

.

Câu 27: Trong một tuần bạn A dự định mỗi ngày đi thăm một người bạn trong

12

người bạn của mình.

Hỏi bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình (thăm một bạn không quá

một lần).

A.

3991680

. B.

12!

. C.

35831808

. D.

7!

.

Câu 28: Cho

( )

n

u

là cấp số nhân có

34

6; 2uu= =

. Tìm công bội

q

của cấp số nhân.

A.

4q =

. B.

2q =

. C.

1

3

q =

. D.

4q = −

.

Câu 29: Cho hàm số

( )

fx

liên tục trên



và có

( )

0fx

′

>

,

( )

0;x∀ ∈ +∞

. Xét các mệnh đề

(I)

( ) ( )

12ff>

.(II)

( )

31ff>

.(III)

( ) ( )

11ff

>−

.(IV)

45

34

ff

 

>

 

 

.

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 3. B. 2. C. 1. D. 4.

Câu 30: Cho hàm số

32

6 9 ()y x x xmC=− ++

, với

m

là tham số, giả sử đồ thị

()C

cắt trục hoành tại

ba điểm phân biệt có hoành độ thỏa mãn

123

xxx<<

. Khẳng định nào sau đây đúng.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 40

A.

12 3

13 4xx x< << <<

. B.

12 3

013 4xx x

< << < < <

.

C.

12 3

1 34xx x< < << <

. D.

1 23

01 3 4x xx< << << <

.

Câu 31: Tổng tất cả các nghiệm của phương trình

21

2 5.2 2 0

xx+

− +=

bằng bao nhiêu?

A.

1

. B.

3

2

. C.

5

2

. D.

0

.

Câu 32: Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số

1yx= −

, trục hoành và đường thẳng

4x =

.

Thể tích khối tròn xoay thu được khi cho (H) quay quanh trục

Ox

bằng

A.

2

3

V

π

=

. B.

7

6

V

π

=

. C.

5

6

V

π

=

. D.

7

6

V =

.

Câu 33: Cho hai số phức

1

2zai= +

và

2

1z bi= −

, với

,ab∈

. Phần ảo của số phức

12

zz+

bằng

A.

2 .b−

B.

2.b

−−

C.

1.a +

D.

(2 ).

bi−−

Câu 34: Cho ba điểm

( )

3;1; 0 , 0; 1; 0 , 0; 0; 6

AB C−−

. Nếu tam giác

ABC

′′′

thỏa mãn hệ thức

0

AA BB CC

′′′

++ =

   

thì có tọa độ trọng tâm là:

A.

( )

3; 2;1−

. B.

( )

1; 0; 2−

. C.

( )

3; 2; 0−

. D.

( )

2; 3; 0

−

.

Câu 35: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

1; 3; 4M −

, đường thẳng

252

:

3 51

xyz

d

+ −−

= =

−−

và mặt phẳng

( )

:2 2 0P xz+−=

. Viết phương trình đường thẳng

∆

qua

M

vuông góc với

d

và song song với

( )

.P

A.

134

:

11 2

xyz

−+−

∆==

−

. B.

134

:

112

xyz−+−

∆==

−−−

.

C.

134

:

1 12

xyz−+−

∆==

−

. D.

134

:

1 12

xyz−+−

∆==

−−

.

Câu 36: Trên giá sách có

4

quyển sách Toán,

3

quyển sách Vật lý,

2

quyển sách Hoá học. Lấy ngẫu

nhiên

3

quyển sách trên giá sách ấy. Tính xác suất để

3

quyển được lấy ra đều là sách Toán.

A.

2

7

. B.

1

21

. C.

37

42

. D.

5

42

.

Câu 37: Cho khối chóp

.

S ABCD

có tất cả các cạnh bên và cạnh đáy đều bằng nhau và

ABCD

là hình

vuông. Góc giữa đường thẳng

SB

và mặt phẳng đáy là góc giữa cặp đường thẳng nào sau đây?

A.

( )

,SB BD

. B.

( )

,SB AB

. C.

( )

,SB SC

. D.

( )

,SB AC

.

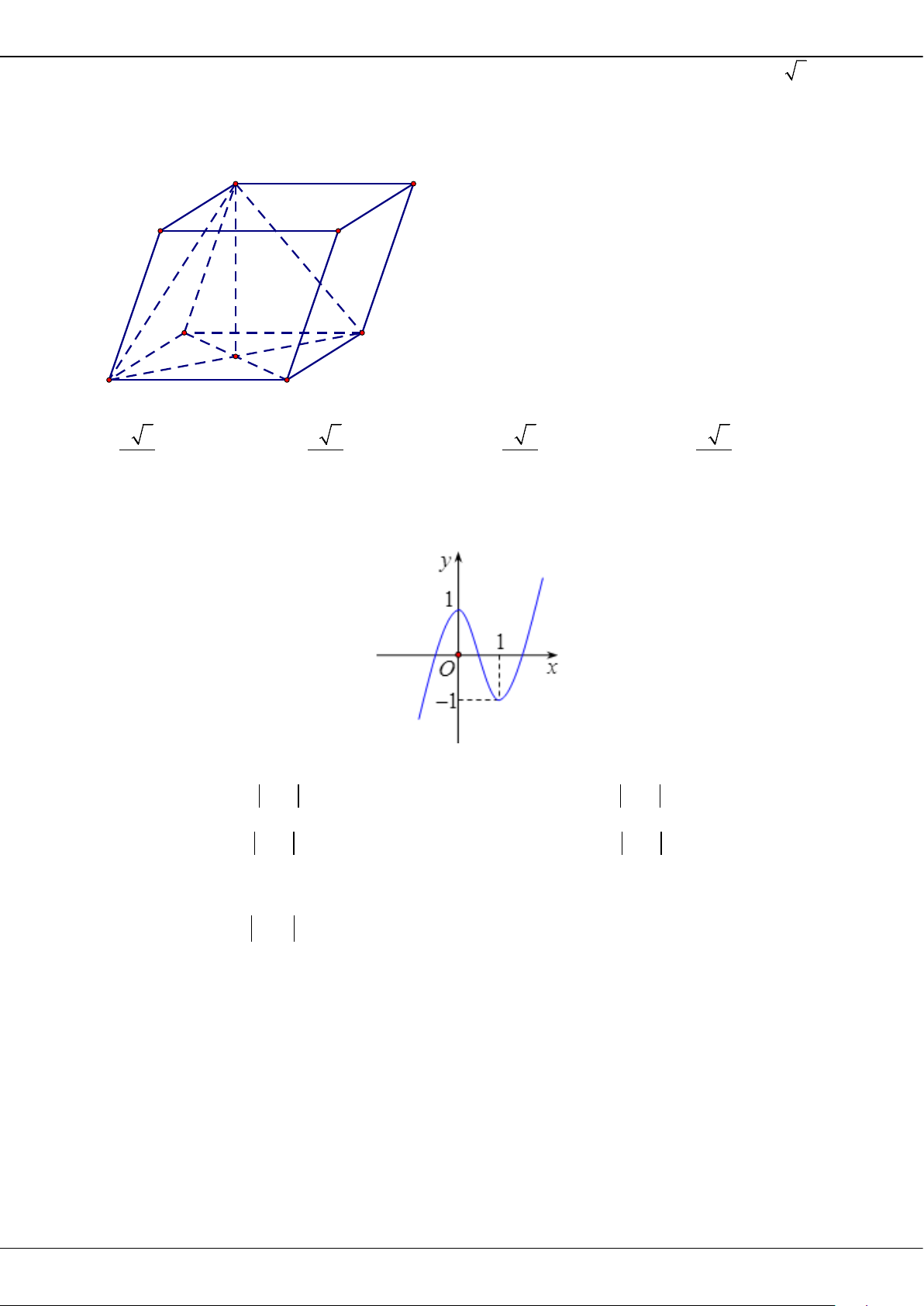
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 41

Câu 38: Cho hình lăng trụ

.ABCD A B C D

′′′′

có đáy

ABCD

là hình chữ nhật,

AB a

=

,

3AD a

=

. Hình

chiếu vuông góc của điểm

A

′

trên mặt phẳng

( )

ABCD

trùng với giao điểm

AC

và

BD

. Tính

khoảng cách từ điểm

B

′

đến mặt phẳng

( )

A BD

′

.

A.

3

a

. B.

3

4

a

. C.

3

2

a

. D.

3

6

a

.

Câu 39: Biết rằng hàm số

()y fx=

có đồ thị như hình vẽ sau:

Phát biểu nào sau đây là phát biểu đúng?

A. Đồ thị hàm số

()y fx=

có 3 cực trị. B. Đồ thị hàm số

()y fx=

có 1 cực trị.

C. Đồ thị hàm số

()y fx=

có 5 cực trị. D. Đồ thị hàm số

()y fx=

có 2 cực trị.

<!>

Ta vẽ đồ thị hàm số

( )

y fx=

như sau:

+) Giữ nguyên đồ thị hàm số

( )

y fx=

phần phía trên trục hoành.

+) Lấy đối xứng qua trục hoành phần đồ thị hàm số

( )

y fx=

phần phía dưới trục hoành.

C'

D'

B'

O

D

A

B

C

A'

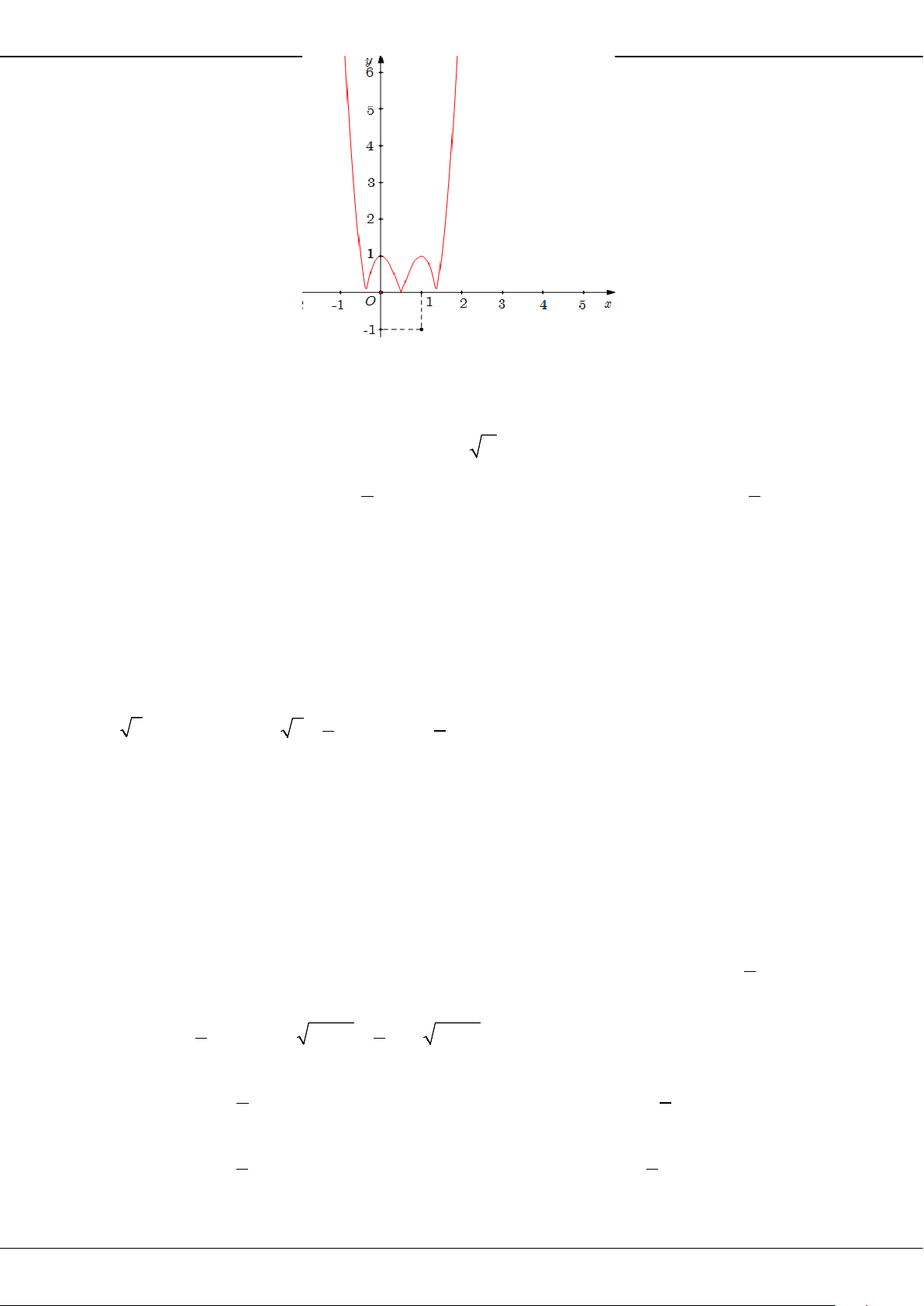
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 42

.

Từ đồ thị hàm số ta thấy hàm số có 5 cực trị.

Câu 40: Xét bất phương trình

( )

2

22

log 2 2 1 log 2 0xm x− + −<

. Tìm tất cả các giá trị của tham số

m

để

bất phương trình có nghiệm thuộc khoảng

( )

2; +∞

.

A.

( )

0;m ∈ +∞

. B.

3

;0

4

m



∈−





. C.

( )

;0m∈ −∞

. D.

3

;

4

m



∈ − +∞





.

<!>

 Điều kiện:

0x >

.

 Ta có

( )

2

22

log 2 2 1 log 2 0xm x− + −<

( ) ( ) ( )

2

22

1 log 2 1 log 2 0 1xm x⇔ + − + −<

.

Đặt

2

logtx=

.

Vì

2x >

nên

22

1

log log 2

2

x >=

. Do đó

1

;

2

t



∈ +∞





.

( )

1

trở thành

( ) ( )

2

1 2 1 20t mt+ − + −<

2

2 10t mt⇔ − −<

( )

2

.

Xét bất phương trình (2) có:

2

' 1 0, mm∆= + > ∀ ∈

.

Do

( )

2

2 10f t t mt= − −=

có

10ac =−<

nên phương trình

( )

0ft=

luôn có 2 nghiệm phân biệt

12

0tt<<

. Tập nghiệm của bất phương trình (2) là

( )

12

;S tt=

.

 Yêu cầu bài toán tương đương tìm

m

để bất phương trình (2) có nghiệm thuộc khoảng

1

;

2



+∞





.

Khi đó ta cần có

22

2

11

1 2 112

22

t mm m m< ⇔ + +> ⇔ +>−

( )

3

Nếu

1

12 0

2

mm− <⇔ >

, do

2

1 0,mm+> ∀∈

nên

( )

3

luôn đúng với

1

;

2

m



∀ ∈ +∞





.

Nếu

1

12 0

2

mm− ≥⇔ ≤

,

( )

2

3 4 1 12mm⇔ +>−

3

4 30

4

mm⇔ + > ⇔ >−

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 43

Kết hợp điều kiện

1

2

m ≤

ta có

31

;

42

m



∈−







.

 Tóm lại kết hợp cả 2 trường hợp ta có

3

;

4

m



∈ − +∞





.

Câu 41: Cho

( )

fx

liên tục trên



và

(

)

4

1

d9fx x=

∫

. Khi đó giá trị của

( )

1

0

4 3 5d

fx x

−+





∫

là

A.

8

. B.

4

. C.

6

. D.

3

.

<!>

Ta có:

( ) (

) ( )

1 1 11

0 0 00

43 5d 43 d 5d 43 d 5fx xfxxxfxx−+=−+=−+





∫ ∫ ∫∫

.

Tính

( )

1

0

43 df xx−

∫

.

Đặt

1

43d3dd d

3

t xt xx t=−⇒=− ⇒=−

.

Đổi cận:

Khi đó:

( )

( ) ( )

1 14

0 41

111

4 3 d d d .9 3

333

f xx fxx fxx−=− = ==

∫ ∫∫

.

Vậy

(

) ( )

11

00

43 5d 43 d 5358

fx xfxx− + = − +=+=





∫∫

.

Câu 42: Cho hàm số

( )

y fx=

liên tục trên



, thỏa mãn

( )

(

)

2

8 16 4

f x fx x x

′

− =−+ −

và

( )

00f =

.

Thể tích khối tròn xoay thu được khi cho hình phẳng giới hạn bởi đồ thị hàm số

( )

y fx=

và

trục hoành quay quanh trục

Ox

bằng

A.

256

15

. B.

256

15

π

. C.

16

3

π

. D.

16

3

.

<!>

Từ giả thiết ta có

( ) ( ) ( ) ( )

( )

( ) ( )

( )

22

2

8 16 4 . . 8 16 4 .

. 8 16 4 . . 8 16 4 .

. 4 8.

xx x

x xx x

xx

f x f x x x f xe f xe x x e

f xe x x e f xe x x edx

f xe x xe C

−− −

− −− −

−−

′′

− =−+ − ⇔ − =−+ −

′

⇔ =−+ − ⇒ = −+ −

⇔ =−+

∫

Vì

( )

00 0fC=⇒=

. Ta có

( )

2

48fx x x= −

Hoành độ giao điểm của đồ thị hàm số

( )

y fx=

và trục hoành thỏa mãn phương trình

( )

0

2

x

fx

x

=



= ⇔



=



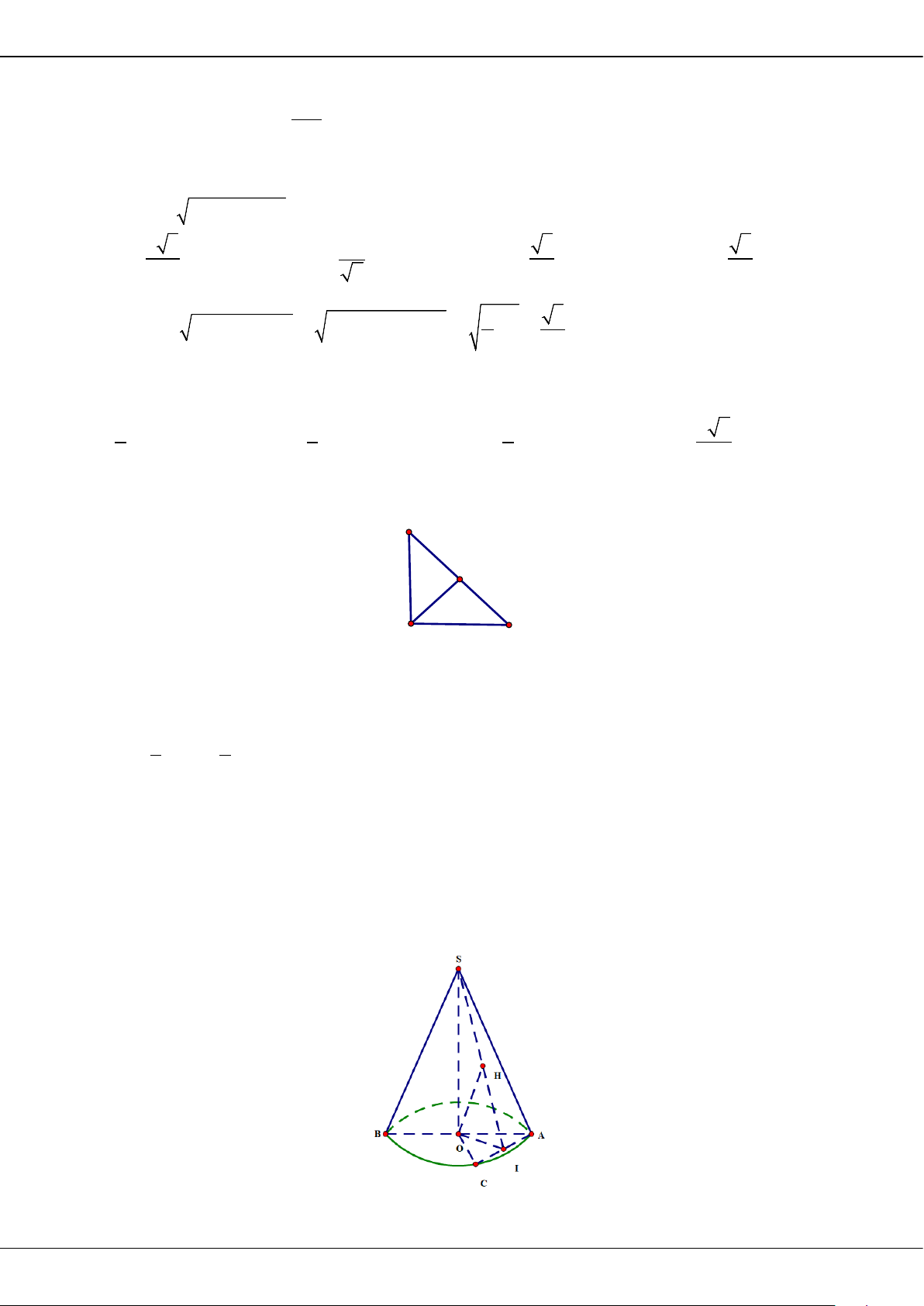
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 44

Vậy thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số

( )

y fx=

và trục

Ox

quay quanh

Ox

là

( )

2

0

256

48

15

V x x dx

ππ

= −=

∫

.

Câu 43: Gọi

12

,

zz

là hai nghiệm của phương trình

2

2 3 20zz− +=

trên tập số phức. Tính giá trị biểu thức

22

1 12 2

P z zz z=++

.

A.

33

4

P

=

. B.

5

2

P =

. C.

3

4

P =

. D.

5

2

P

=

.

<!>

Ta có

22

1 12 2

P z zz z=++

( )

2

1 2 12

z z zz= +−

95

1

42

= −=

.

Câu 44: Cho tam giác

ABC

vuông cân tại đỉnh

A

và độ dài cạnh huyền bằng 2. Quay hình tam giác

ABC

quanh trục chứa cạnh

BC

thu được khối tròn xoay có thể tích bằng

A.

2

3

π

. B.

1

3

π

. C.

4

3

π

. D.

22

3

π

.

<!>

Gọi

H

là trung điểm

BC

. Khi quay hình tam giác

ABC

quanh trục chứa cạnh

BC

thu được khối tròn

xoay gồm 2 khối nón có đường tròn đáy tâm

H

bán kính

1r AH= =

và hai đường cao tương ứng là

1, 1HB HC= =

.

Vậy

2

12

2.

33

V rh

ππ

= =

.

Câu 45: Cho hình nón có chiều cao

20cmh =

, bán kính đáy

25cmr =

. Một thiết diện đi qua đỉnh của

hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là

12cm

. Tính diện tích

S

của thiết diện đó.

A.

2

400cmS =

. B.

2

500cmS =

. C.

2

300cmS =

. D.

2

406cmS =

.

<!>

Theo đề, ta có:

20cmSO =

,

25cmOA =

,

12cmOH =

.

2

A

B

C

H

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 45

Khi đó:

22

2 22

1 11

15cm 2 2 40cmOI AC IA OA OI

OH SO OI

= + ⇒= ⇒ = = − =

.

2 2 22

20 15 25cmSI SO OI= + = +=

.

Suy ra:

2

1

. . 500cm

2

SAC

S SI AC

∆

= =

.

Câu 46: Trong không gian

Oxyz

, cho hai đường thẳng chéo nhau

1

262

:

2 21

xyz

d

−−+

= =

−

và

2

412

:

13 2

x yz

d

− ++

= =

−

. Gọi mặt phẳng

( )

P

là chứa

1

d

và

( )

P

song song với đường thẳng

2

d

. Khoảng cách từ điểm

( )

1;1;1M

đến

( )

P

bằng:

A.

10

. B.

1

53

. C.

2

3 10

. D.

3

5

.

<!>

Đường thẳng

1

d

đi qua

( )

2; 6; 2

A −

và có một véc tơ chỉ phương

( )

1

2; 2;1u = −



.

Đường thẳng

2

d

có một véc tơ chỉ phương

(

)

2

1; 3; 2u

= −

 

.

Gọi

n



là một véc tơ pháp tuyến của mặt phẳng

(

)

P

. Do mặt phẳng

(

)

P

chứa

1

d

và

(

)

P

song

song với đường thẳng

2

d

nên

( )

12

1; 5; 8

nu u=∧=

    

.

Phương trình mặt phẳng

( )

P

đi qua

( )

2; 6; 2A −

và có một véc tơ pháp tuyến

(

)

1; 5; 8

n =



là

5 8 16 0xyz++−=

.

Vậy

( )

222

5 8 16

2

d,

3 10

158

M MM

xyz

MP

++−

= =

++

.

Câu 47: Cho hàm số

( )

32 2 3

331

y x mx m x m m=− + − −−

, với

m

là tham số. Gọi

A

,

B

là hai điểm cực

trị của đồ thị hàm số và

( )

2; 2I −

. Tổng tất cả các số

m

để ba điểm

I

,

A

,

B

tạo thành tam giác

nội tiếp đường tròn có bán kính bằng

5

là:

A.

2

17

−

. B.

4

17

. C.

14

17

. D.

20

17

.

<!>

Ta có

22

36 3 3y x mx m

′

=−+−

( )

2

31xm



= −−



;

0

y

′

=

1

xm

= +



⇔



= −



.

Do đó, hàm số luôn có hai cực trị với mọi

m

.

Giả sử

( )

1; 4 2Am m+− −

;

( )

1; 4 2Bm m−− +

. Ta có

25AB =

,

m

∀∈

.

Mặt khác, vì

IAB∆

có bán kính đường tròn ngoại tiếp là

5R =

nên từ



2

sin

AB

R

AIB

=

suy ra



sin 1

2

AB

AIB

R

= =



o

90AIB⇒=

hay

AIB∆

vuông tại

I

.

Gọi

M

là trung điểm

AB

, ta có

( )

;4Mm m−

và

1

2

IM AB=

2

5

4

AB

IM⇔==

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 46

(

) (

)

22

2 42 5

mm

⇔ − +− + =

2

17 20 3 0mm⇔ − +=

1

3

17

m

=





⇔



=



.

Tổng tất cả các số

m

bằng

3 20

1

17 17

+=

.

Câu 48: Cho các số thực dương

,,,abx y

thỏa mãn

1, 1ab>>

và

1

3

xy

a b ab

−

= =

. Giá trị nhỏ nhất của

biểu thức

34Pxy= +

thuộc tập hợp nào dưới đây?

A.

[

)

5; 7

. B.

(

]

7;9

. C.

( )

11;13

. D.

( )

1; 2

.

<!>

( )

1

3

1

log

1 .log

1 1 41

1

31 31

. 1 log

log

3

31

a

xy

b

a

x

b

x yb

y

xy

a b ab x

yy y

ya

b

y

−



=

−=





−−



= = ⇒ ⇒ ⇒ = ⇔=



−−

= +



=





−



Vì

1, 1ab>>

nên

log 0

a

b >

. Suy ra

1

3

y >

.

2

4 1 12 8 3

3 4 3. 4

31 31

y yy

Pxy y

yy

− +−

=+= +=

−−

Xét hàm số

( )

2

12 8 3 1

;

31 3

yy

fy y

y

+−

= >

−

( )

(

)

2

/

2

36 24 1 2 3

0

6

31

yy

fy y

y

−+ ±

= =⇔=

−

Bảng biến thiên:

Từ bảng biến thiên, suy ra

min

23

7,64

6

Pf



+

= ≈





.

Câu 49: Có bao nhiêu số phức

z

thỏa mãn

( )

2

2023

11z z zi z z i− +− + + =

?

A. 4 B. 2 C. 1 D. 3

<!>

Gọi

z a bi= +

;

( )

,ab∈

z a bi⇒=−

.

Ta có:

( )

22

2

1 11z a bi a b−=+−=− +

,

( )

2

22z z i a bi a bi i b i b i

− = + −+ = =

,

2023

ii= −

,

( )

2023

2z z i i a bi a bi ai+ =− + +− =−

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 47

Suy ra phương trình đã cho tương đương với:

( )

2

1 2 21a b b i ai− ++ − =

( )

2

22

2

0

20

1 1 2 20

1

2 20

1

=







=







=







−+=

−+= − =

=





  



⇔ ⇔ ⇔ ⇔=⇔

   





=



−=

=





 



=







=









= −





a

b

a ab

a b bb

a

b

ab

ba

ab

a

b

Vậy có 3 số phức

z

thỏa mãn.

Câu 50: Cho hình chóp

.S ABCD

biết

( ) ( ) ( ) ( )

2; 2; 6 , 3;1; 8 , 1; 0; 7 , 1; 2; 3A BC D− −−

. Gọi

H

là trung điểm

của

,CD

( )

SH ABCD⊥

. Để khối chóp

.

S ABCD

có thể tích bằng

27

2

(đvtt) thì có hai điểm

12

,SS

thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm

I

của

12

SS

A.

( )

0; 1; 3I

. B.

( )

1; 0; 3 .−−I

C.

(

)

0;1;3−−I

. D.

( )

1; 0; 3I

<!>

Ta có

( ) ( )

1 33

1; 1; 2 , 1; 2; 1 ,

22

ABC

AB AC S AB AC



=−− = − ⇒ = =



   

(

)

( )

2; 2; 4 , 1; 1; 2 2 .

DC AB DC AB=−− =−− ⇒ =

   

ABCD

⇒

là hình thang và

93

3

2

ABCD ABC

SS= =

Vì

.

1

. 33

3

S ABCD ABCD

V SH S SH= ⇒=

Lại có

H

là trung điểm của

( )

0;1; 5

CD H⇒

Gọi

(

) (

)

( )

; ; ;1 ;5 , 3;3;3 3 ;3 ;3S a b c SH a b c SH k AB AC k k k k



⇒=−−−⇒= = =



   

Suy ra

222

33999 1kkk k= + + ⇒=±

+) Với

(

) ( )

1 3; 3; 3 3; 2; 2

k SH S=⇒ = ⇒ −−



+) Với

( ) (

)

1 3; 3; 3 3; 4; 8k SH S=−⇒ =−−− ⇒



Suy ra

( )

0; 1; 3I

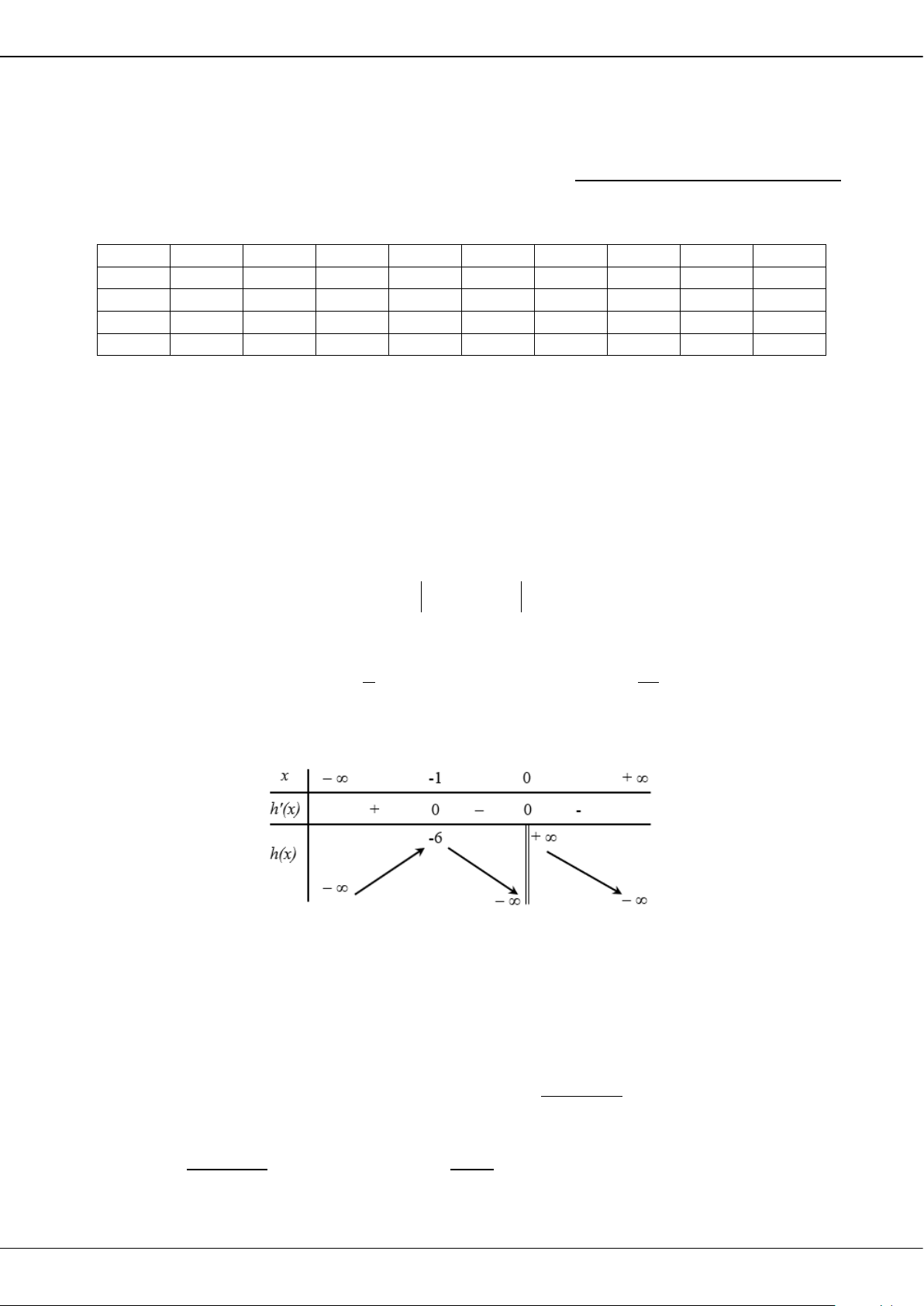
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 48

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT LÊ VĂN PHẨM

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.C

2.C

3.B

4.B

5.A

6.A

7.B

8.A

9.D

10.A

11.D

12.D

13.B

14.C

15.B

16.D

17.A

18.B

19.D

20.A

21.A

22.C

23.B

24.D

25.D

26.C

27.A

28.C

29.A

30.C

31.C

32.D

33.D

34.B

35.C

36.A

37.A

38.B

39.C

40.D

41.A

42.B

43.B

44.D

45.B

46.C

47.B

48.C

49.D

50.C

HƯỚNG DẪN GIẢI CHI TIẾT (CÂU 39 ĐẾN CÂU 50)

Câu 39. Ta đặt

42

() 8g x x ax x=+−

. Ta có

( )

3

428g x x ax

′

=+−

.

Thấy rằng

3

0

() 0

8 0 (*)

x

gx

x ax

=



= ⇔



+ −=



.

Vì phương trình

( )

*

luôn có ít nhất một nghiệm khác

0

nên phương trình

() 0

gx=

có ít nhất hai nghiệm

trong đó

0x =

là nghiệm đơn.

Kết hợp với

lim

x

y

→±∞

= +∞

ta suy ra hàm số

42

8

y x ax x

=+−

có đúng ba điểm cực trị

⇔

()

gx

có đúng

một cực trị

⇔

() 0gx

′

=

có đúng một nghiệm bội lẻ.

( )

32

4

4 2 8 0 2 ( ) **

g x x ax a x h x

x

′

= + −=⇔ =− + =

. Ta có

2

4

() 4 0 1hx x x

x

′

=− − =⇔=−

.

Bảng biến thiên của hàm

()hx

:

Dựa vào bảng biến thiên suy ra

(**)

có một nghiệm bội lẻ khi và chỉ khi

6

a ≥−

.

Do đó có tất cả

6

giá trị nguyên âm của tham số

a

thỏa đề bài.

Câu 40:

( )

2

10

80

18



−>



⇔ −>





−=−





x

pt mx

x mx

( )

2

1

18

x

x mx

>





⇔



−=−





2

1

29

x

xx

m

x

>





⇔



−+

=





Xét hàm số

2

29xx

y

x

−+

=

trên

( )

1; +∞

, ta có:

2

9

'

x

y

x

−

=

;

'0 3yx=⇔=±

Bảng biến thiên

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 49

Để thỏa mãn yêu cầu thì

48m

<<

nên các giá trị nguyên của tham số

m

là

5,6,7

.

Câu 41. Điều kiện:

22

9 10 20 0

21

xy

x xy y

+ −>





++ ≠



. Có

y

S y Sx

x

=⇔=

.

Giả thiết

( )

22

2

log 9 10 20 1 2 9 10 20

x xy y

xy xxyyxy

++

+−=⇔++=+−

(

)

( )

2 2 22 2 2

2 9 10 20 2 1 9 10 20 0x Sx S x x Sx S S x S x⇔ + + = + − ⇔ ++ − + + =

(

)

1

.

Để phương trình

( )

1

có nghiệm thì

( )

(

)

2

22

25 8 10 25 8 10

0 9 10 80 2 1 0 60 100 1 0

30 30

S SS S S S

−+

∆≥⇔ + − ++ ≥⇔− + +≥⇔ ≤≤

Suy ra

1

25 8 10

30

MS

+

= =

dấu “=” xảy ra khi và chỉ khi

( )

1

2

11

1

9 10

0

22 1

0

S

x

SS

y Sx

+



= >



++





= >



2

25 8 10

30

mS

−

= =

dấu “=” xảy ra khi và chỉ khi

(

)

2

22

2

9 10

0

22 1

0.

S

x

SS

y Sx

+



= >



++





= >



Vậy

5

3

Mm+=

.

Câu 42. Cho

(

)

0fx

′

=

2

0

1

2 60

x

x mx m



=



⇒=



− + +=



.

Trong đó

0

x =

là nghiệm bội chẵn,

1x =

là nghiệm bội lẻ.

Để hàm số đã cho có đúng một điểm cực trị thì

( )

0fx

′

=

chỉ đổi dấu 1 lần.

Trường hợp 1:

2

2 60x mx m− + +≥

,

x∀∈

2

60 2 3mm m⇔ − − ≤ ⇔− ≤ ≤

.

Do

m ∈

nên

{ }

2; 1;0;1;2;3m

∈− −

. Suy ra có 6 giá trị nguyên của

m

thỏa mãn.

Trường hợp 2:

( )

2

26g x x mx m= − ++

có hai nghiệm phân biệt trong đó một nghiệm là

1x =

Khi đó

2

1 2 .1 6 0 7mm m− + +=⇒ =

.

Vậy

{ }

2; 1;0;1;2;3;7m ∈− −

.

Câu 43.

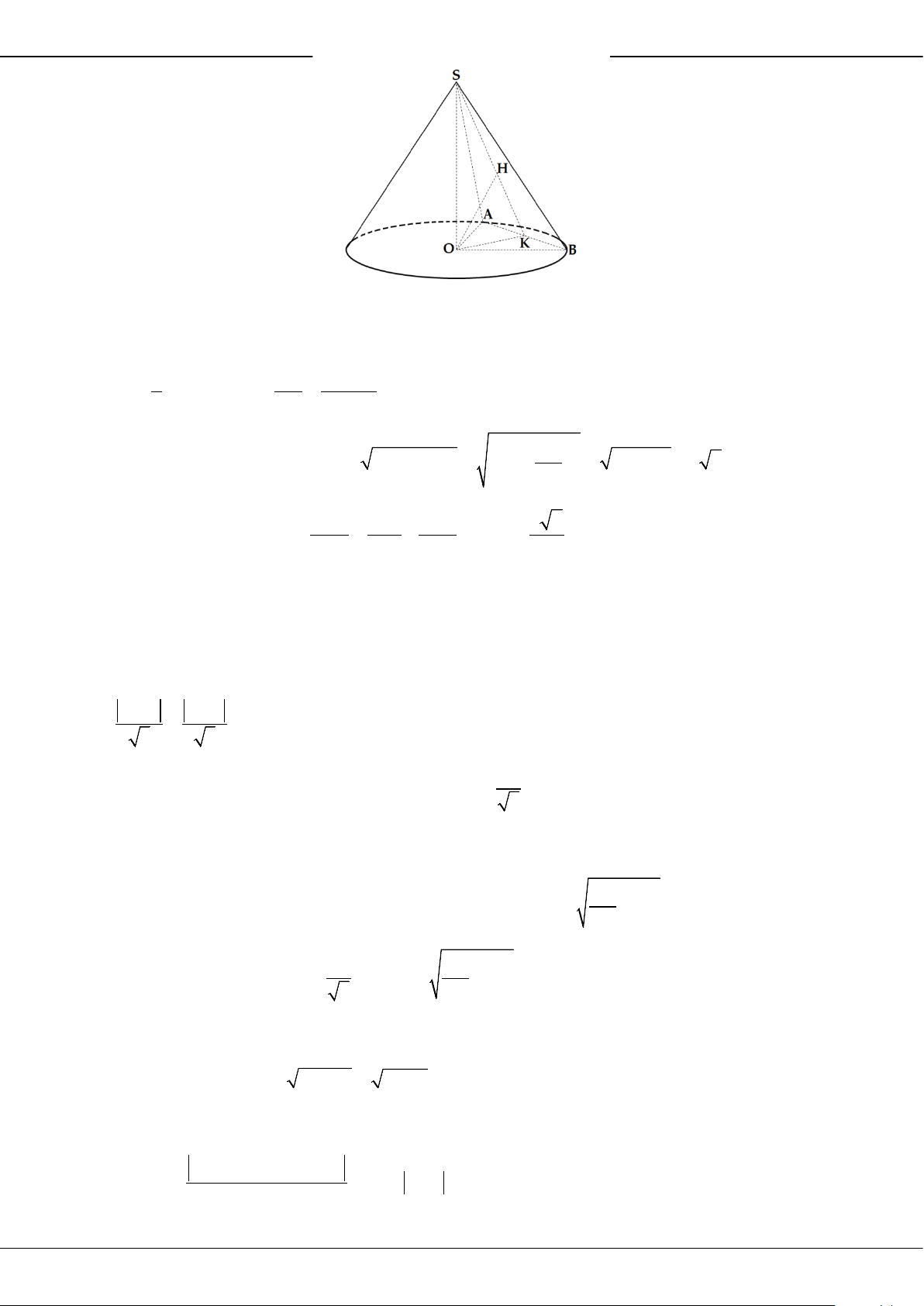
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 50

Gọi

O

,

R

lần lượt là tâm và bán kính đáy của khối nón,

K

,

H

lần lượt là hình chiếu của

O

lên

AB

,

SK

.

Khi đó khoảng cách từ tâm của đường tròn đáy đến mặt phẳng

( )

SAB

bằng

OH

.

Ta có:

22

1 3 3.192

. 144 12

3 . .4

π

ππ

= ⇒ = = = ⇒=

V

V Rh R R

h

Trong tam giác vuông

OBK

có:

2

2 2 2 22

12 4 8 2

2



= − = − = −=





AB

OK OB BK R

.

Trong tam giác vuông

SOK

có:

22 2

1 1 1 82

3

= + ⇒=OH

OH SO OK

.

Câu 44. Ba mặt phẳng

( )

P

,

(

)

Q

,

( )

R

song song với nhau và mặt phẳng

( )

R

nằm giữa hai mặt phẳng

( )

P

,

( )

Q

.

Gọi

(

)

:0xyzD

α

+++ =

là mặt phẳng cách đều hai mặt phẳng

( )

P

,

( )

Q

.

Ta có

( )

51

3 : 30

33

DD

D xyz

α

−−

= ⇔ =⇒ +++=

.

Suy ra khoảng cách giữa hai mặt phẳng

( )

R

,

( )

α

là

1

3

d =

.

Mặt cầu đường kính

AB

có tâm

I

luôn thuộc mặt phẳng

( )

α

cách đều hai mặt phẳng

( )

P

,

( )

Q

.

nên luôn cắt mặt phẳng

 

R

theo một đường tròn có bán kính là

2

4

AB

rd= −

.

Để

min

r

thì

( ) ( )

min

4

,

3

AB d P Q= =





. Vậy

2

1

4

AB

rd= −=

.

Câu 45. Mặt cầu

(

)

S

có tâm

( )

0; 2;1I −

và bán kính

5R =

.

2r 6

S

ππ

= =

3r⇒=

22

25 9 4h Rr⇒= − = −=

.

( )

Q

song song với

( )

P

nên phương trình mặt phẳng

( )

Q

có dạng

( )

: 2x 2 0Q yzd− ++ =

( )

2.0 2. 2 1.1

7

, 4 5 12

17

3

d

h dI Q d

d

− −+ +

=



= = =⇔ += ⇔



= −



LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 51

Với

17d = −

thì

( )

QP

≡

.

Với

7

d =

thì

( )

: 2x 2 7 0Q yz− ++=

.

Câu 46: Gọi

( ) ( )

2

2f x ax bx c f x ax b

′

= + +⇒ = +

Thay vào

( ) ( )

( )

2

5 4,fx f x x x x

′

− = + + ∀∈

ta được

( )

2

22

52 4ax bx c ax b x x+ + − + = ++

( )

22 2 2

54 54 5 4a a x b ab x c b x x⇔ − + − + − = ++

2

54 1

1

54 1

1 13

;

4 16

54



−=

= = =







⇔−=⇔





= = =





−=



aa

abc

b ab

ab c

cb

Giả thiết suy ra

( )

2

11abc fx x x===⇒ = ++

và

( )

22

2

00

20

1

3

= ++ =

∫∫

f x dx x x dx

.

Câu 47. Gọi

w x yi

= +

với

x

,

y ∈



.

Ta có

( ) ( )

5 10 3 4 25iw iz i

+ =−−

( )

12 43z iw i⇔ =−+ − +

.

Lại có

( )

12 25 12 43 12 25z i iw i i−+ = ⇔ −+ − + −+ =

( )

1 2 5 5 25iw i

⇔ −+ − + =

32wi⇔ ++=

Vậy tập hợp các điểm biểu diễn số phức

w

là đường tròn tâm

( )

3;1 ,I −

bán kính

2R

=

.

max 2 10P OM R OI= =+=+

;

min 10 2P ON OI R= = −= −

.

Vậy

max min 2 10PP

+=

.

Câu 48.

Gọi

G

là trọng tâm của

ABC∆

,

M

là trung điểm của

BC

( )

A G ABC

′

⇒⊥

.

Trong

( )

AA M

′

dựng

MN AA

′

⊥

, ta có:

BC AM

BC A G

⊥





′

⊥



( )

BC AA G

′

⇒⊥

BC MN⇒⊥

.

N

H

B'

C'

M

A

C

B

A'

G

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 52

( )

,d AA BC MN

′

⇒=

3

4

a

=

.

Gọi

H

là hình chiếu của

G

lên

AA

′

.

Ta có:

//GH MN

GH AG

MN AM

⇒=

2

3

=

2

3

GH MN⇒=

3

6

a

=

.

Xét tam giác

AA G

′

vuông tại

G

, ta có:

22 2

1 11

GH GA GA

= +

′

2 22

1 11

GA GH GA

⇒=−

′

22

11

33

63

aa

= −







2

9

=

a

.

3

a

GA

′

⇒=

.

Vậy thể tích của khối lăng trụ là:

.

ABC

V S AG

′

=

2

3

.

43

aa

=

3

12

a

=

.

Câu 49. Dựa vào đồ thị ta thấy

( )

2

0

1

x

fx

x

= −



′

= ⇔



=



, trong đó

1x =

là nghiệm kép.

Do vậy

( ) ( )( )

(

)

2

3

2 1 32f x ax x ax x

′

= + − = −+

.

Suy ra

( ) ( )

42

3

d2

42

xx

fx f x x a x C



′

= = −++





∫

.

Diện tích của hình phẳng giới hạn bởi đồ thị

( )

C

và trục hoành bằng 9 nên

( ) ( ) ( ) ( )

1

2

d9 9 1 29f x x fx f f

−

′

=⇔ =⇔ − −=

∫

( )

34

69

43

aa



⇔ −− = ⇔ =





.

Vậy

(

)

4

2

8

2

33

x

fx x xC=− ++

.

Dựa vào đồ thị ta có nhận xét:

( )

0 2, 1

fx x x

′

=⇔=− =

;

( )

02fx x

′

< ∀ <−

và

( )

02fx x

′

≥ ∀ ≥−

.

Do đó ta có bảng biến thiên

Vậy

8

3

MC= +

và

8mC=−+

. Do đó

32

3

Mm−=

.

Câu 50. Xét phương trình

( )

2

2 1 60mz m z m+ + − +=

.

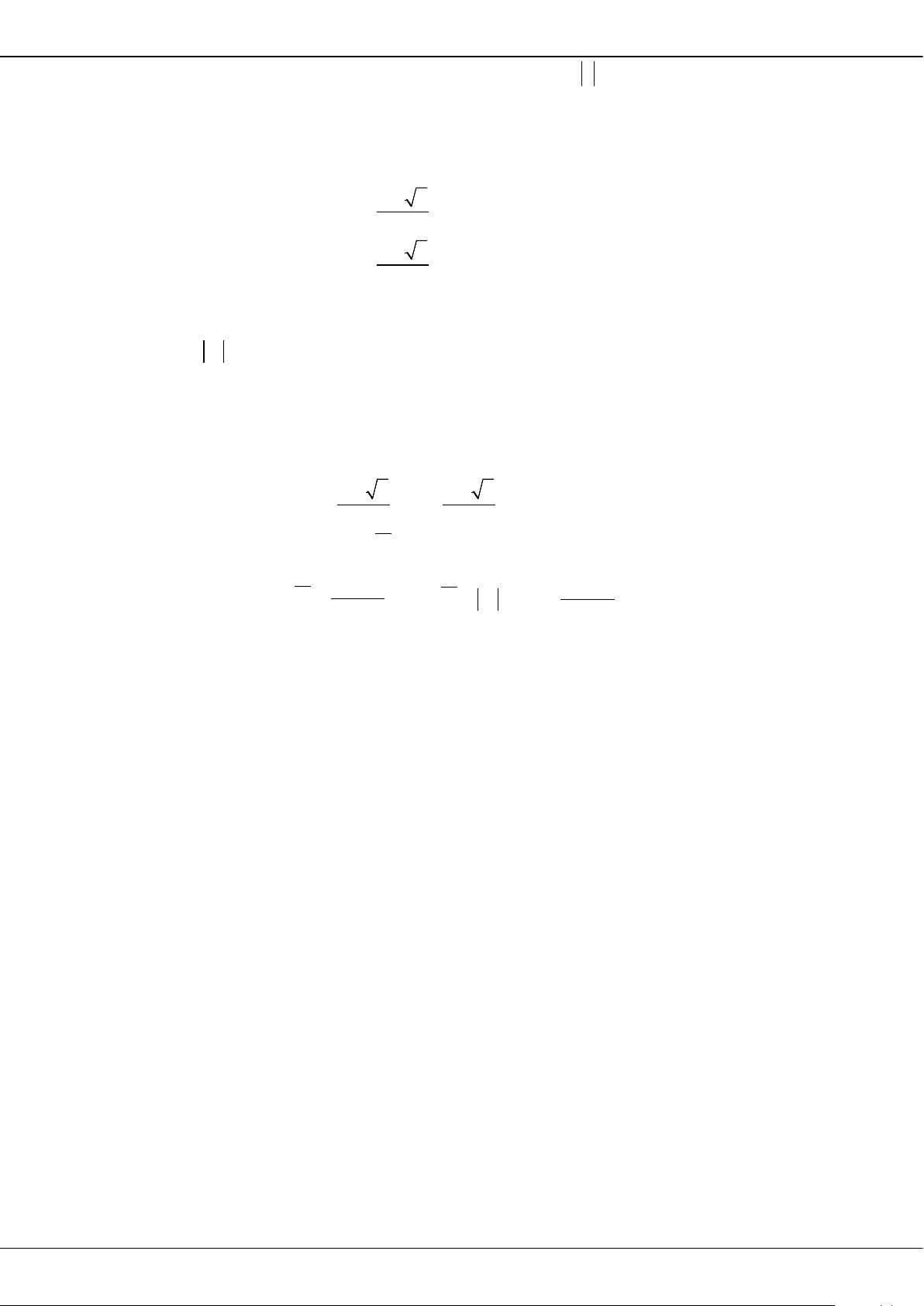
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 53

TH1:

0m = ⇒

Phương trình đã cho có dạng

2 60 3 3z zz+ = ⇔ =−⇒ =

không thõa mãn.

TH2:

0m ≠

Ta có

(

) (

)

2

1 62 4 1

m mm m m

′

∆= + − − + = − +

.

Nếu:

2

22

2

0 2 4 10

22

2

m

mm

m



−

≤



′

∆≥⇔ − +≥⇔



+

≥





thì phương trình đã cho có hai nghiệm thực

⇒

0

z

là số

thực

Theo bài ra, ta có

0

1

z

=



= ⇔



= −



.

Với

0

1z =

, ta có

2 2 60 4mm m m+ +− +=⇔ =−

.

Với

0

1z = −

, ta có

2 2 60 2mm m m− −− +=⇔ =

.

Nếu:

2

22 22

0 2 4 10

22

mm m

−+

′

∆<⇔ − +<⇔ < <

, thì phương trình đã cho có hai nghiệm phức.

0

z

là nghiệm của phương trình đã cho

⇒

0

z

cũng là nghiệm của phương trình đã cho.

Áp dụng hệ thức viét, ta có

00

6

.

m

zz

m

−+

=

mà

2

00 0

6

. 1 13

m

zz z m

m

−+

= =⇒ =⇔=

Vậy

4; 2=−=mm

.

-------------------------------------------------------HẾT---------------------------------------------------------

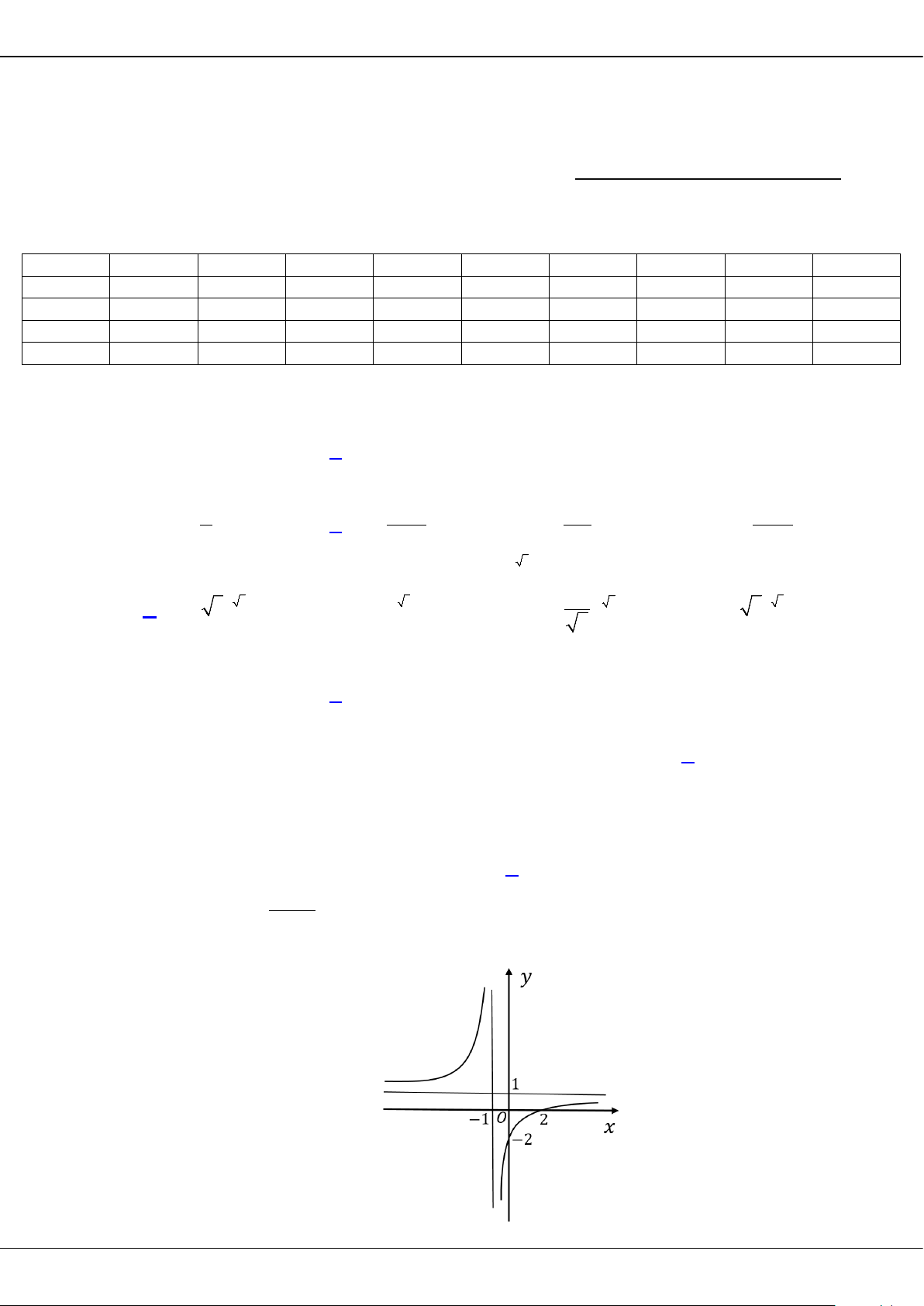
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 54

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT GÒ CÔNG ĐÔNG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1.B

2.B

3.A

4.B

5.D

6.C

7.A

8.C

9.D

10.A

11.A

12.A

13.C

14.A

15.D

16.C

17.B

18.B

19.C

20.A

21.A

22.D

23.C

24.D

25.B

26.D

27.C

28.D

29.B

30.D

31.B

32.A

33.B

34.D

35.D

36.B

37.C

38.B

39.D

40.A

41.B

42.B

43.A

44.B

45.C

46.B

47.D

48.C

49.A

50.A

LỜI GIẢI CHI TIẾT

Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức

2022 2023zi= −

có tọa độ là

A.

( )

2022; 2023−

. B.

( )

2022; 2023−

. C.

(

)

2023; 2022

. D.

( )

2023; 2022−

.

Câu 2: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

5

logyx=

là

A.

1

y

x

′

=

. B.

1

ln 5

y

x

′

=

. C.

ln 5

y

x

′

=

. D.

1

ln 5

y

x

′

= −

.

Câu 3: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

3

yx=

là

A.

31

3yx

−

′

=

. B.

31

yx

−

′

=

. C.

31

1

3

yx

−

′

=

. D.

3

3yx

′

=

.

Câu 4: Tập nghiệm của bất phương trình

2

log 3x >

là

A.

(

]

;8−∞

. B.

( )

8; +∞

. C.

[

)

8; +∞

. D.

( )

;8−∞

.

Câu 5: Cho cấp số cộng

(

)

n

u

với

1

2u =

và công sai

3d =

. Giá trị của

5

u

bằng

A.

162

. B.

10−

. C.

11

. D.

14

.

Câu 6: Trong không gian

Oxyz

, đường thẳng

3

:2

4

xt

dy t

zt

= +





=−+





= +



có một vectơ chỉ phương là

A.

( )

1;1; 1a

= −



. B.

( )

1;1; 1a = −



. C.

( )

1;1; 1a

=



. D.

( )

1; 1;1a

= −



.

Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị

hàm số đã cho và trục tung là

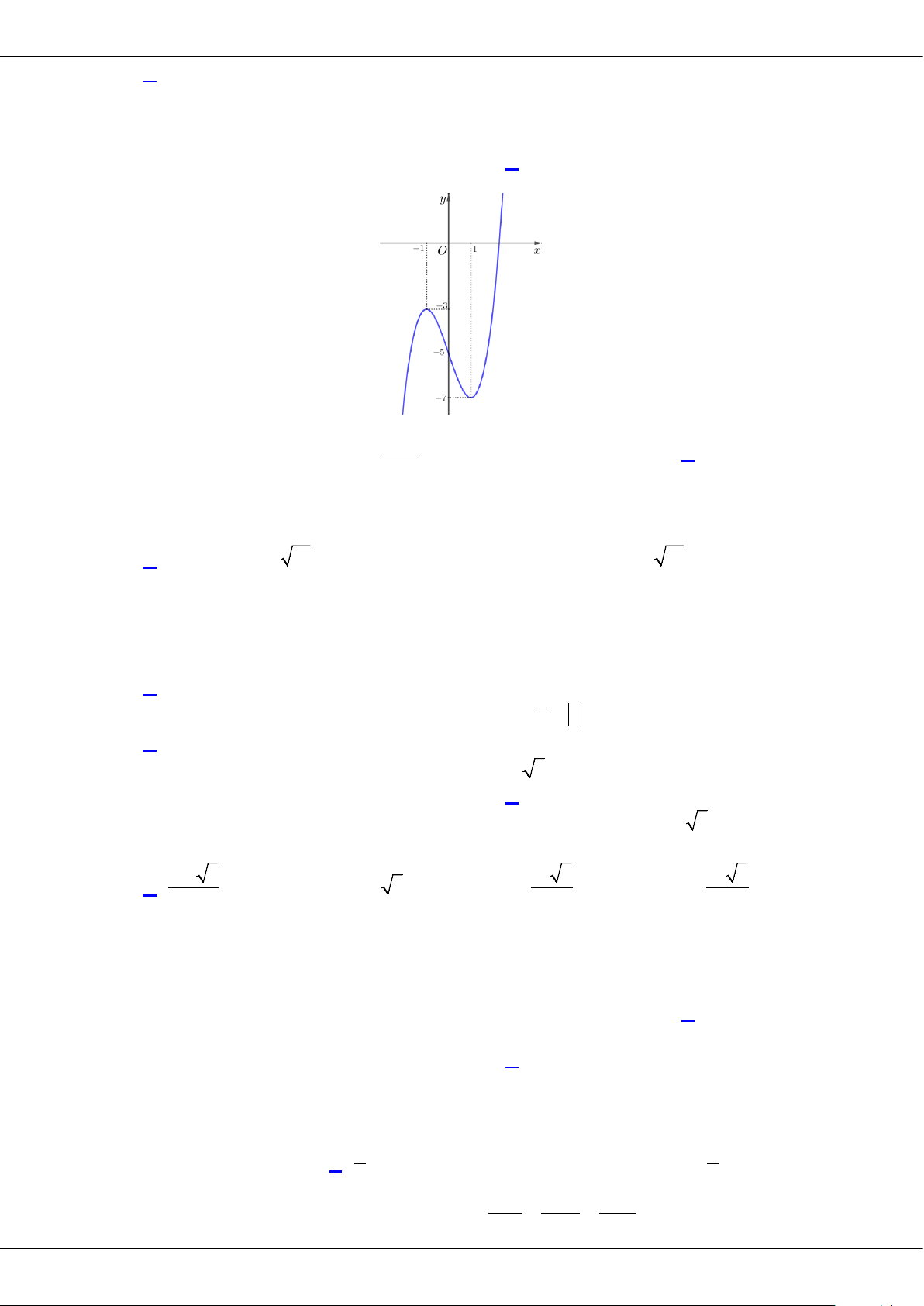
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 55

A.

( )

0; 2−

. B.

( )

2;0

. C.

( )

2;0−

. D.

( )

0; 2

.

Câu 8: Nếu

( )

4

1

d 2023fx x

−

=

∫

và

( )

4

1

d 2022gx x

−

=

∫

thì

( ) ( )

4

1

df x gx x

−



−



∫

bằng

A. 5. B. 6. C. 1. D.

1

−

.

Câu 9: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A.

42

32yx x=−+

. B.

3

1

x

y

x

−

=

−

. C.

2

41yx x=−+

. D.

3

35

yx x

=−−

.

Câu 10: Trong không gian

Oxyz

cho mặt cầu

( )

S

có phương trình

2 22

2460xyz x yz++−+ −=

. Tìm

tọa độ tâm

I

và bán kính

R

của mặt cầu

( )

S

.

A.

(

)

1; 2; 3 ; 1 4

IR−=

. B.

( )

1; 2; 3 ; 1 4IR−− =

.

C.

(

)

1; 2; 3 ; 1 4IR−− =

. D.

( )

1; 2; 3 ; 1 4IR−=

.

Câu 11: Trong không gian

Oxyz

, góc giữa hai mặt phẳng

( )

: 11 0Pxyz+−− =

và

( )

:2 2 2 7 0Qxyz+ − +=

bằng

A.

0°

. B.

90°

. C.

180°

. D.

45°

.

Câu 12: Cho số phức

3 4.zi



Phần thực của số phức

wz z

là

A.

8

. B.

4

. C.

5

. D.

3

.

Câu 13: Cho khối lập phương có độ dài đường chéo bằng

33

. Thể tích khối lập phương đã cho bằng

A.

9

. B.

12

. C.

27

. D.

18

.

Câu 14: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

,3

AB a BC a= =

,

SA

vuông góc với

đáy và

2SA a=

. Thể tích khối chóp đã cho bằng

A.

3

23

3

a

. B.

3

23a

. C.

3

a

. D.

3

6

a

.

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

theo giao tuyến là đường tròn

( )

;OR

. Gọi

d

là

khoảng cách từ

O

đến

( )

P

. Khẳng định nào dưới đây đúng?

A.

dR<

. B.

dR

>

. C.

dR=

. D.

0d =

.

Câu 16: Phần thực của số phức

23zi= −

là

A.

3−

. B.

2−

. C. 2. D. 3.

Câu 17: Cho hình nón có đường kính đáy bằng độ dài đường sinh

l

. Diện tích xung quanh của

hình nón đã cho bằng:

A.

2 rl

π

. B.

2

1

2

l

π

. C.

2

r

π

. D.

2

3

rl

π

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

123

:

2 12

xy z

d

−−+

= =

−−

. Vectơ nào dưới đây

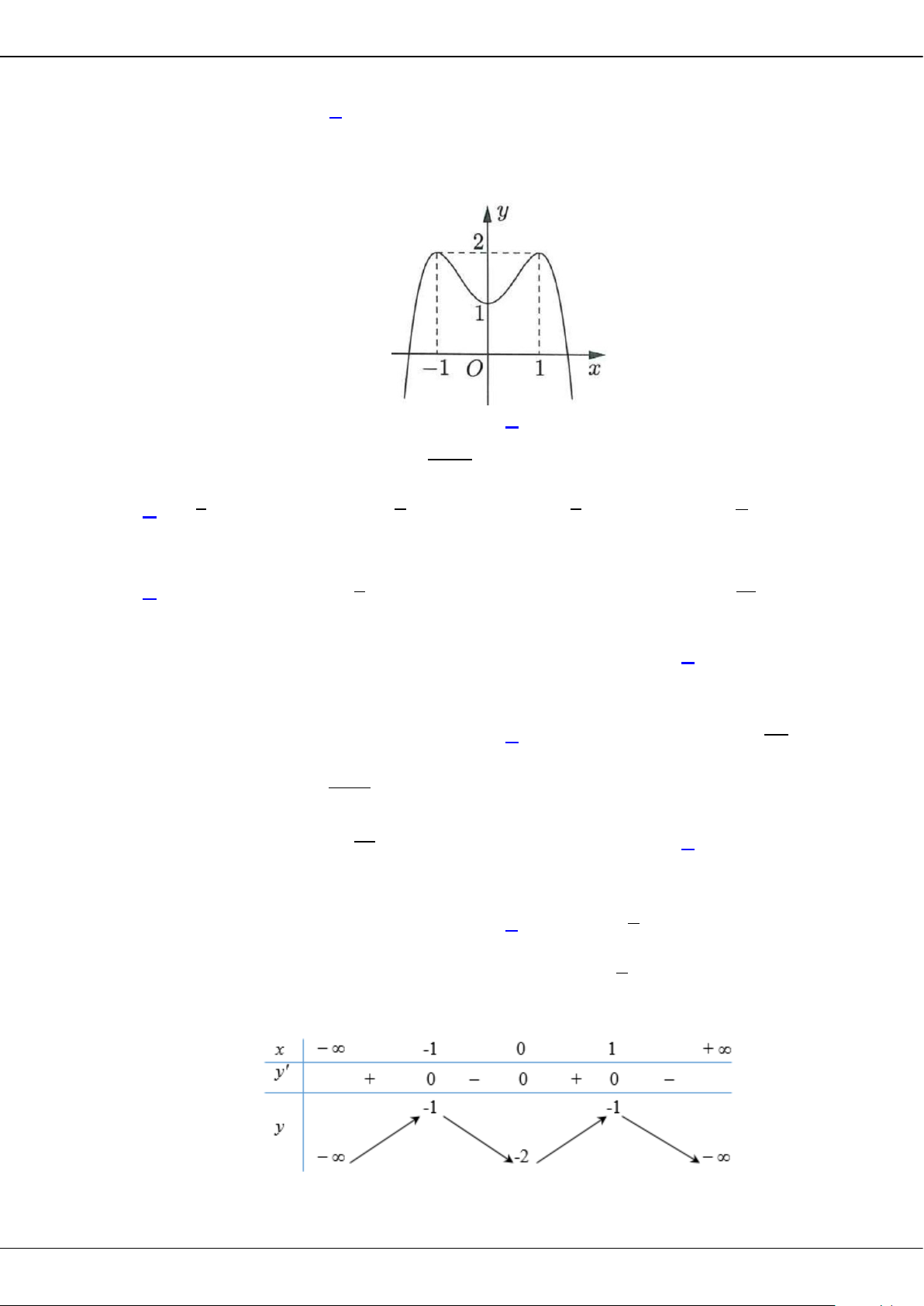
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 56

không là vectơ chỉ phương của

d

?

A.

( )

4; 2; 4a = −−



. B.

( )

1; 2; 3b = −



. C.

( )

2; 1; 2c = −



. D.

( )

2;1;2d = −−



.

Câu 19: Cho hàm số

42

y ax bx c=++

có đồ thị là đường cong trong hình bên. Giá trị cực đại của

đồ thị hàm số đã cho là:

A.

1, 1xx

=−=

. B.

0x =

. C.

2y =

. D.

1y =

.

Câu 20: Tiệm cận đứng của đồ thị hàm số

21

31

x

y

x

+

=

−

là đường thẳng có phương trình

A.

1

3

x =

. B.

2

3

x = −

. C.

1

3

x = −

. D.

2

3

y =

Câu 21: Giải bất phương trình

( )

2

log 3 1 3x

−>

.

A.

3

x >

B.

1

3

x

<<

C.

3x <

D.

10

3

x >

Câu 22: Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm

34

học sinh?

A.

34

2

. B.

2

34

A

. C.

2

34

. D.

2

34

C

.

Câu 23: Hàm số

(

)

2

x

Fx e

=

là một nguyên hàm của hàm số

A.

( )

2x

fx e=

. B.

( )

2

.1

x

f x xe= −

. C.

( )

2

x

f x xe=

. D.

( )

2

x

e

fx

x

=

.

Câu 24: Nếu

( )

5

1

d6fx x

−

=

∫

thì

( )

1

5

d

3

fx

x

−

∫

bằng

A. 18. B.

49

8

. C. 2. D.

2−

.

Câu 25: Tìm họ nguyên hàm của hàm số

(

)

sin 2fx x=

.

A.

( )

d cos2fxx xC= +

∫

. B.

( )

1

d cos2

2

fxx xC=−+

∫

.

C.

( )

d cos2fxx xC=−+

∫

. D.

( )

1

d cos2

2

fxx xC= +

∫

.

Câu 26: Cho hàm số

( )

y fx=

có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

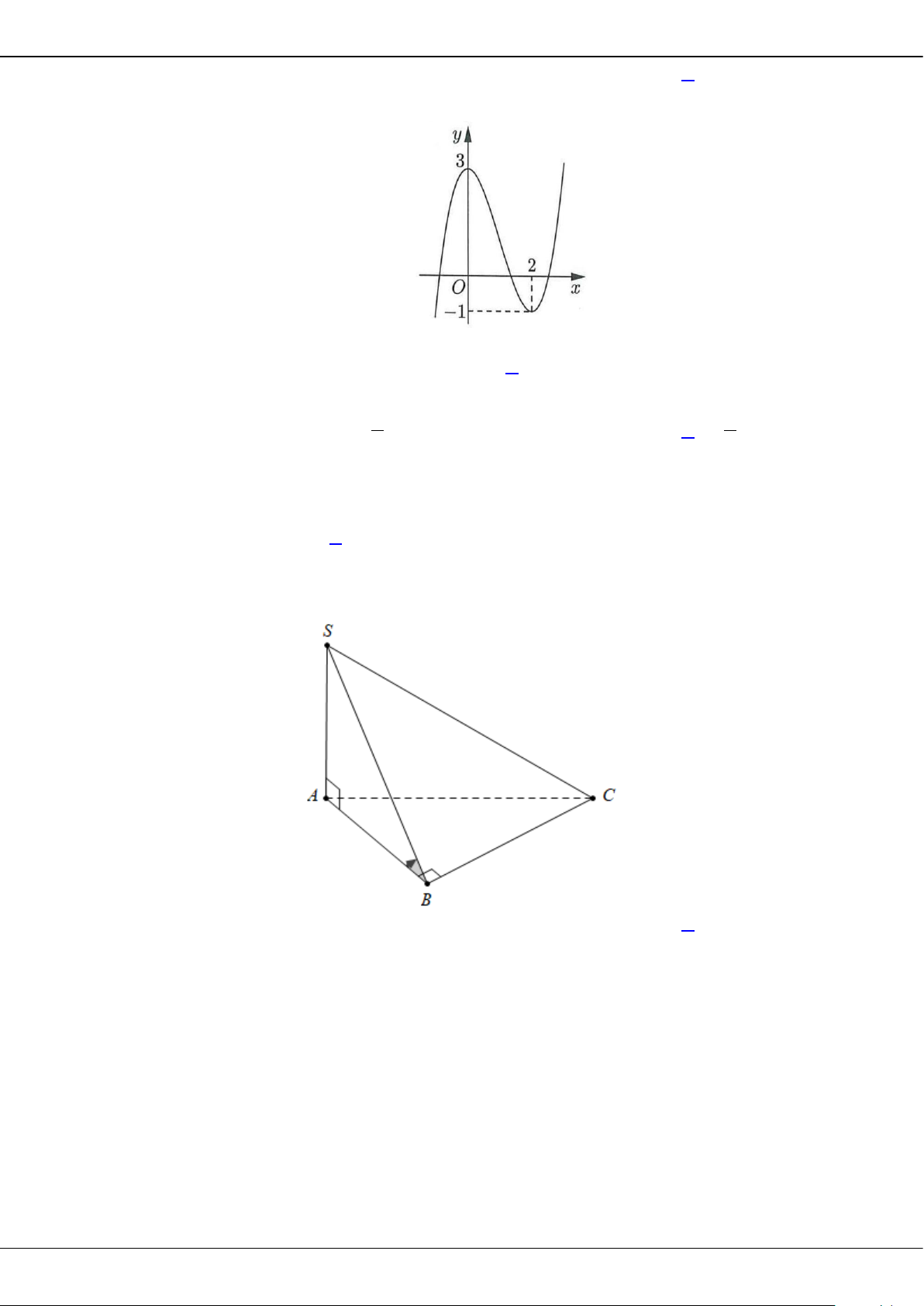
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 57

A.

( )

1; 0

−

. B.

( )

1; +∞

. C.

(

)

;1

−∞

. D.

( )

0;1

.

Câu 27: Cho hàm số bậc ba  = () có đồ thị là đường cong trong hình bên.

Hàm số nghịch biến trong khoảng:

A.

(2;3)

. B.

( 1; 3)−

. C.

(0; 2)

. D.

( 1; 2)−

.

Câu 28: Với ,b là hai số thực dương tùy ý,

ln(3ab) ln(2ab)−

bằng:

A.

ln ab

. B.

2

ln

3

. C.

ln(6)

. D.

3

ln

2

.

Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường

2

4yx x= −

và

0y =

quanh trục

Ox

là:

A.

4

2

0

( 4)x x dx

π

−⋅

∫

B.

4

22

0

(4 )x x dx

π

−⋅

∫

C.

2

22

2

( 4)x x dx

π

−

−⋅

∫

D.

4

22

0

( 4)x x dx−⋅

∫

Câu 30: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

B

,

SA

vuông góc với đáy và

SA AB=

(tham

khảo hình vẽ). Góc giữa đường thẳng SB và mặt phẳng

( )

ABC

bằng

A.

60 .°

B.

30°⋅

C.

90°⋅

D.

45°⋅

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên

của tham số

m

để phương trình

( )

2. fx m=

có ba nghiệm thực phân biệt?

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 58

A.

3

. B.

7

. C.

10

. D.

8

.

Câu 32: Cho hàm số

( )

y fx=

có đạo hàm

( ) ( )

( )

2

29fx x x

′

=−−

với mọi

x ∈ 

. Hàm số đã cho có

bao nhiêu điểm cực đại?

A.

1

. B.

2

. C.

3

. D.

4

.

Câu 33: Bạn Bình có

30

tấm thẻ đánh số từ

1

đến

30

, Bình chọn ngẫu nhiên

10

tấm thẻ. Tính xác suất

để trong

10

tấm thẻ lấy ra có

5

tấm thẻ mang số lẻ,

5

tấm thẻ mang số chẵn và chỉ có một tấm

thẻ mang số chia hết cho

10

.

A.

8

11

. B.

99

667

. C.

3

11

. D.

99

167

.

Câu 34: Tính tổng các nghiệm của phương trình

( )

2

log 3 1 9xx− +=−

bằng

A.

3−

. B.

9

. C.

9

10

−

. D.

3

.

Câu 35: Trên mặt phẳng tọa độ, gọi

M

là điểm biểu diễn của số phức

z

có mô đun lớn nhất thỏa mãn:

43 5zi+− =

. Tọa độ của điểm

M

là

A.

( )

6;8M

−

. B.

(

)

8; 6

M

−

. C.

( )

8; 6M

. D.

( )

8; 6M −

.

Câu 36: Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

( )

1;2;3A −−

;

(

)

1; 4;1B

−

và đường thẳng

223

:

1 12

xyz

d

+−+

= =

−

. Phương trình nào dưới đây là phương trình của đường thẳng đi qua

trung điểm của đoạn

AB

và song song với

d

?

A.

11

11 2

xy z−+

= =

. B.

11

112

xy z

−+

= =

−

.

C.

111

1 12

xyz−−+

= =

−

. D.

22

112

xy z−+

= =

−

.

Câu 37: Trong không gian

Oxyz

, cho điểm

( 4;1; 3)

A −

. Điểm đối xứng với

A

qua mặt phẳng

()Oxy

có

tọa độ là

A.

(4;1; 3)

. B.

(4; 1; 3)−

. C.

( 4;1; 3)−−

. D.

( 4; 1; 3)−−−

.

Câu 38: Một hình lăng trụ đứng

.ABC A B C

′′′

có đáy

ABC

là tam giác vuông tại

, , 2.B AB a AA a

′

= =

(tham khảo hình bên). Khoảng cách từ điểm

A

đến mặt phẳng

( )

A BC

′

là:

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 59

A.

25

a

. B.

25

5

a

. C.

5

a

. D.

35

5

a

.

Câu 39: Có bao nhiêu số nguyên

m

để tập nghiệm của bất phương trình

( )

33

log 3 3logxm x+>

chứa

đúng

2

số nguyên?

A.

18

. B.

15

. C.

17

. D.

16

.

Lời giải

Chọn D

Ta có:

( )

33

log 3 3logxm x

+>

3

0

3

x

xm x

>



⇔



+>



3

0

30

x

x xm

>



⇔



− −<



.

Xét hàm số

( )

3

3y fx x xm= =−−

trên

( )

0;

+∞

Có

( )

2

1

3 30

1

x

fx x

x

= −



′

= −=⇔



=



.

Bảng biến thiên:

Dựa vào bảng biến thiên, tập nghiệm của bất phương trình

( )

33

log 3 3logxm x+>

chứa đúng

2

số nguyên chỉ xảy ra khi tập nghiệm của bất phương trình có dạng

( )

0;a

và

23a

<≤

hay

( )

20

30

f

<







≥





20 2

2 18

18 0 18

mm

m

mm

−< >



⇔ ⇔ ⇔< ≤



−≥ ≤



.

Vậy có

16

giá trị nguyên của

m

thỏa mãn yêu cầu bài toán.

Câu 40: Hàm số

( )

32

f x ax bx cx d= + ++

có

(

)

02f =

và

( ) ( )

3

4 4 2, .f x fx x x x− = + ∀∈

Tích phân

( )

1

0

I f x dx=

∫

bằng

A.

148

63

. B.

146

63

. C.

149

63

. D.

145

63

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 60

Lời giải

Chọn A

Ta có:

(

)

(

)

(

)

3

4 4 2,

02

f x fx x x x

f



− = + ∀∈





=







( )

3

4

64 4

63

16 0 0

42

2

42 2

63 3

3

2

a

aa

bb b

fx x x

cc

c

d



=



−=





−= =



⇔ ⇔ ⇒ = ++



−=



=



=





=



Vậy

(

)

11

3

00

4 2 148

2

63 3 63

I f x dx x x dx



= = ++ =





∫∫

.

Câu 41: Có bao nhiêu số nguyên

m

để hàm số

( )

652 4

5 18 15 3 2 1y x mx m m x

= + + −+ +

chỉ có điểm cực

tiểu mà không có điểm cực đại?

A.

28

. B.

27

. C.

25

. D.

26

.

Lời giải

Chọn B

Ta có:

( ) ( )

( )

5 4 2 3 32 2

30 90 60 3 2 30 3 2 3 2y x mx m m x x x mx m m

′

= + + −+ = + + −+

.

( )

(

)

22

0

() 3 2 3 2 01

x

y

g x x mx m m

=



′

= ⇔



=+ + − +=





.

Xét phương trình

( )

1

:

( )

22 2

9 8 3 2 24 16m mm m m∆= − − + = + −

.

Trường hợp 1:

0 12 4 10 12 4 10m∆≤⇔−− ≤≤−+

. Khi đó

( )

0,gx x≥∀

.

Khi đó

( )

3

30y xg x

′

=

chỉ đổi dấu khi qua

0x =

. Khi đó

y

′

đổi dấu từ âm sang dương khi qua

0x =

. Suy ra hàm số đã cho chỉ có điềm cực tiểu mà không có điểm cực đại (thoả mãn).

Các số nguyên

m

thoả mãn trường hợp này là

{ }

24, ,0m ∈− …

.

Trường hợp 2:

12 4 10

0

12 4 10

m



<− −

∆> ⇔



>− +





Nếu

( )

0gx=

có 2 nghiệm phân biệt

12

,xx

khác 0

( )( )

3

12

30y xxx xx

′

⇒= − −

có 3 nghiệm

phân biệt và đổi dấu qua 3 nghiệm đó nên hàm số đã cho có cả điềm cực tiểu và điểm cực đại

(không thoả mãn).

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 61

Nếu

( )

0gx=

có 2 nghiệm phân biệt

12

,xx

thỏa mãn

12

0xx= ≠

(

)

2

0

(0) 2 3 2 0g mm

∆>





⇔



= − +=





1

2

m

=



⇔



=



(

)

4

2

30y xxx

′

⇒= −

chỉ đổi dấu khi qua

2

xx=

. Khi

đó

y

′

đổi dấu từ âm sang dương khi qua

2

xx

=

(thoả mãn).

Vậy tất cả 27 các số nguyên

m

thoả mãn yêu cầu bài toán.

Câu 42: Trong mặt phẳng tọa độ

Oxy

, tập hợp điểm biểu diễn số phức

1

iz

w

z

+

=

+

là một đường tròn có

bán kính bằng

2

. Môđun của

z

thuộc tập nào dưới đây?

A.

1

;2

2







. B.

1

;2

2







. C.

{

}

2;2

. D.

1

;2

2







.

Lời giải

Chọn B

Điều kiện

1z ≠−

.

Đặt

(

)

,w x yi x y=+∈

, điểm

( )

;M xy

là điểm biểu diễn số phức

w

trên mặt phẳng tọa độ

Oxy

. Đặt

2

.zt=

Ta có

(

)

( )

1

1 1 11

1

iz

w w z iz z w i w

z

+

= ⇔ + =+⇔ −=−

+

.

( ) ( )

( )

1 1 11z w i w z x y i x yi⇒ − =− ⇔ + − =−−

22 22

21 21txy y xy x



⇔ +−+=+−+



( )

22

1 2 2 1 02t x y x yt t⇔ − + + − +−=

.

Do tập hợp điểm biểu diễn số phức

w

là một đường tròn có bán kính bằng

2

nên

1t

≠

.

Khi đó

( )

22

2 10

11

x y x yt

tt

⇔ + + − +=

−−

.

Theo đề bài ta được

22

2

22

1

14 2 5 20

11

2

tz

t

tt

tz



=⇒=

  



− + −= ⇔ − + = ⇔

  



−−

=⇒=

  





.

Câu 43: Cho khối lăng trụ

.ABC A B C

′′′

có đáy là tam giác đều, góc giữa hai mặt phẳng

( )

ABC

′′′

và

(

)

BCC B

′′

bằng

60°

, hình chiếu vuông góc của

B

′

lên mặt phẳng

(

)

ABC

trùng với trọng tâm

tam giác

ABC

. Khoảng cách giữa hai đường thẳng

AA

′

và

BC

′′

bằng

3a

. Thể tích khối lăng

trụ đã cho bằng

A.

3

83a

. B.

3

83

3

a

. C.

3

86

3

a

. D.

3

86

a

.

Lời giải

Chọn A

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 62

Gọi

M

là trung điểm

BC

,

O

là trọng tâm tam giác

ABC

,

H

là hình chiếu vuông góc của

O

lên

BM

′

. Giả sử cạnh đáy bằng

x

.

Ta có

( )

B O ABC

′

⊥

và

( )

(

) ( )

( )



,,

A B C BCC B ABC BCC B B MO

′′′ ′′ ′′ ′

= =

.

( ) ( )

( )

, , ,3,33d AA BC d AA BCCB d A BCCB d O BCCB OH a

′ ′′ ′ ′′ ′′ ′′

= = = = =

OH a⇒=

.

Trong tam giác

B OM

′

có

2 22

111

'OH B O OM

= +

, trong đó

3

6

.tan 60

2

x

OM

x

B O OM



=







′

= °=





.

Suy ra

222

1 4 12

4xa

axx

= + ⇒=

.

Thể tích khối lăng trụ

2

3

. . 83

24

ABC

xx

V BOS a

′

= = =

.

Câu 44: Cho hàm số

( )

fx

thỏa mãn

( )

23

4

6

f =

và

( ) ( )

1

1fx x f x

x



′

=+−





,

0x∀>

. Diện tích hình

phẳng giới hạn bởi đồ thị hàm số

( )

()g x xf x=

, trục hoành, đường thẳng

1; 4

xx

= =

bằng

A.

1283

30

. B.

743

30

. C.

157

30

. D.

563

30

.

Lời giải

Chọn B

Với mọi

0x

>

ta có:

( ) ( )

f x xf x x x

′

+=+

( )

.xf x x x

′

⇔=+

.

Lấy nguyên hàm hai vế ta được:

( )

2

.

23

x

xf x x x C=++

.

Mà

( )

23

42

6

fC= ⇒=

( )

2

23

x

xf x x x⇒=++

.

Vậy

( )

44

2

11

2 743

d 2d .

2 3 30

x

S xf x x x x x= = + +=

∫∫

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 63

Câu 45: Trên tập hợp số phức, xét phương trình

( )

2

2 1 12 8 0z mzm+ + + −=

(

m

là tham số thực). Có

bao nhiêu giá trị nguyên của

m

để phương trình đó có hai nghiệm phân biệt

12

,zz

thỏa mãn

12

11zz+= +

?

A.

7

. B.

12

. C.

8

. D.

9

.

Lời giải

Chọn C

Phương trình

( )

2

2 1 12 8 0z mzm

+ + + −=

(*)

Ta có:

( ) ( )

2

' 1 12 8 10 9m m mm∆= + − − = − +

.

Trường hợp 1:

2

1

' 0 10 9 0

9

m

mm

m

<



∆>⇔ − +>⇔



>



(**).

Khi đó phương trình (*) có hai nghiệm thực phân biệt.

Ta có:

12

11

zz

+= +

12

11

zz

=



⇔



+=− −



.

Do

12

zz≠

nên

12

2

zz+=−

.

Áp dụng định lí Viét, ta có

12

22zz m

+=− −

.

Khi đó

222 0mm

− − =−⇔ =

(thỏa mãn điều kiện (**)).

Trường hợp 2:

2

0 10 9 0 1 9mm m

′

∆<⇔ − +<⇔< <

.

Khi đó phương trình (*) có hai nghiệm phức liên hợp nhau

12

,.zz

Do đó hai số phức

12

1, 1zz++

cũng liên hợp nhau nên

12

1 1.zz

+= +

Trường hợp này luôn đúng với

19m<<

.

Vì

m ∈



nên

{ }

2;3;4;5;6;7;8m

∈

.

Vậy

{ }

0; 2;3;4;5;6;7;8m ∈

, có tất cả có

8

số nguyên của

m

thỏa mãn đề bài.

Câu 46: Trong không gian

Oxyz

, cho đường thẳng

1

12

:

212

x yz

d

−−

= =

và đường thẳng

2

21

:

11 2

xy z

d

−+

= =

. Gọi

( )

P

là mặt phẳng chứa đường thẳng

1

d

và song song với

2

d

. Tính

khoảng cách giữa đường thẳng

2

d

và mặt phẳng

( )

P

.

A.

1

5

. B.

75

5

. C.

7

5

. D.

5

.

Lời giải

Chọn B

Ta có

1

d

đi qua

( )

1

1; 0; 2M

và có vtcp

( )

1

2; 1; 2u =



;

2

d

đi qua

( )

2

0; 2; 1M −

và có vtcp

( )

2

1;1; 2u =



Vì

( )

P

là mặt phẳng chứa đường thẳng

1

d

và song song với

2

d

nên vtpt

( )

(

)

1

2

; 0; 2;1

P

n uu



= = −



   

.

Do

( )

P

chứa

1

d

nên điểm

( )

1

MP∈

. Khi đó phương trình

( )

:2 2 0P yz− +−=

.

Vì

2

d

song song với

( )

P

nên

( )

22

412

75

,,

5

41

dd P dM P

−−−

= = =

+

.

Câu 47: Có bao nhiêu cặp số nguyên dương

( )

;xy

thỏa

( )

2 33

3

3 81 4 2026 2024 log ( 2023) (1 )

y

y xx xx



++ + + − −≤



−



?

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 64

A.

2021

. B.

2003

. C.

4042

. D.

4024

.

Lời giải

Chọn D

Điều kiện:

33

( 2023) (1 ) 0 ( 2023)(1 ) 0 1 2023x xx x x− − >⇔ − − >⇔<<

Mà

2 2022x x

+

∈ ⇒≤≤

( )

[ ]

3

2 33

3

42

3

41

3

log

41

3

0( 2 2 3 ) ( 1 )

3 81 4 2026 2024 log ( 2023) (1 )

3.3 3.4 3 2024 2023 3log ( 2023)(1 )

3 3(4 1) ( 2023)(1 ) 3log ( 2023)(1 )

3 3(4 1) 3log ( 2023)(1 ) (*)3

y

x

y

x

y xx x

y x xx

yx x x

x

y xx

x

−

+

−

+



++ + + − −



⇔ ++ + − + − −

⇔++

+

≤−

≤ −−+ −−

⇔ + +−≤ −

Xét hàm số

() 3 3,

t

ft tt= +

∈

Ta có

( ) 3 ln3 3 0

t

ft t

′

= +> ∀∈



Suy ra

() 3 3,

t

ft tt= +

∈

đồng biến trên



Khi đó:

[

] [ ]

33

(*) (4 1) log ( 2023)(1 ) 4 1 log ( 2023)(1 ) (1)fyfxxyxx

⇔+≤ −−⇔+≤−−

Ta có:

[ ]

33

( 2023)(1 ) 1022121, (1; 2023)

log ( 2023)(1 ) log 1022121 12,6 (2)

xx x

xx

− − ≤ ∀∈

⇒ − −≤ 

Từ (1) và (2) suy ra

}4 1 12, 6 2,9, {1,2y yy y

+

+≤ ⇒ ≤ ∈ ⇒ ∈

Ta có:

41 2 41

(1) ( 2023)(1 ) 3 3 02024 2023

yy

xxx x

++

⇔− +−−

−⇔≥ ≥−

Với

1:y =

2

0 1,12 2022,88 2 2022

2024 2266 xxx x− ≥⇔ ≤≤ ⇒≤+− ≤

: có 2021 giá trị

x

Với

2:y =

2

0 10,78 2013, 22 11 20132024 21706 xxxx− ≥⇔ ≤≤ ⇒ ≤+− ≤

: có 2003 giá trị

x

Vậy có

2021 2003 4024

+=

cặp số nguyên dương

( )

;xy

thỏa yêu cầu bài toán.

Câu 48: Cho khối nón đỉnh

S

, bán kính đáy bằng

33

và có góc ở đỉnh bằng

120



. Gọi

A

và

B

là hai

điểm thuộc đường tròn đáy sao cho tam giác

SAB

là tam giác vuông, khoảng cách từ tâm đường

tròn đáy đến mặt phẳng

()SAB

bằng

A.

3

. B.

3

2

. C.

32

2

. D.

3

.

Lời giải

Chọn C

Gọi

O

là tâm của đường tròn đáy và

CD

là đường kính vuông góc với dây cung

AB

.

Ta có

33OA OB OC OD R= = = = =

.

Do khối nón có góc ở đỉnh bằng

120°

nên



60OSD

= °

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 65

Tam giác vuông

SOD

có:



33 33

tan tan 60 3

tan 60

33 33

sin sin 60 6

sin 60

OD

OSD SO

SO SO

OD

OSD SD

SD SD

°



⇔ °

°



= ⇔ = ⇔= =







= = ⇔= =



⇒

Khối nón có chiều cao

3h =

và đường sinh

6l =

.

Do tam giác

SAB

vuông cân tại

S

, có

6SA SB l= = =

nên

2 62AB SA= =

.

Gọi

M

là giao điểm của

AB

và

CD

ta có

M

là trung điểm của

AB

(tính chất đường kính

vuông góc với dây cung thì đi qua trung điểm của dây cung đó).

Suy ra

62

32

22

AB

MA MB= = = =

.

Tam giác vuông

MOA

có

( )

22

33 32 3OM OA AM

= −= − =

.

Kẻ

OH

vuông góc với

SM

tại

H

ta có:

()

OH SM

OH SAB

AB SO

OH AB do AB SOM AB OH

AB OM

⊥





⇒⊥



⊥





⊥ ⇒⊥ ⇒⊥

 



⊥







.

Suy ra

( )

,( )

d O SAB OH=

. Tam giác

SOM

vuông tại

O

có

OH

là đường cao ứng với cạnh

huyền

SM

nên ta có:

2 2 2 2 22

1 1 1 1 1 1 32

33 2

OH

OH OS OM OH

= + ⇔ =+⇔ =

.

Câu 49: Trong không gian

Oxyz

cho đường thẳng

123

:

234

xy z

d

−−−

= =

và mặt cầu

( )

S

:

( )

( ) ( )

2 22

3 4 5 729xyz+ ++ ++ =

. Cho biết điểm

( )

2; 2; 7A −−−

, điểm

B

thuộc giao

tuyến của mặt cầu

( )

S

và mặt phẳng

( )

: 2 3 4 107 0

Pxyz++− =

. Khi điểm

M

di động trên

đường thẳng

d

, giá trị nhỏ nhất của biểu thức

MA MB+

bằng

A.

5 30

. B.

27

. C.

5 29

. D.

742

.

Lời giải

Chọn A

Mặt cầu

( )

S

có tâm

( )

3;4;5I −−−

và bán kính

27R =

.

Đường thẳng

d

có 1 véc-tơ chỉ phương là

( ) ( )

2; 3; 4u dP= ⇒⊥



.

Gọi

K

là giao điểm của mặt phẳng

( )

P

và đường thẳng

d

. Vì

Id

∈

nên

K

là tâm của đường

tròn giao tuyến và

KB d⊥

.

Ta có

( )

1; 2; 2 3IA IA= −⇒ =

 

và

.0IA u IA d=⇒⊥

  

.

d

M

K

I

B

A

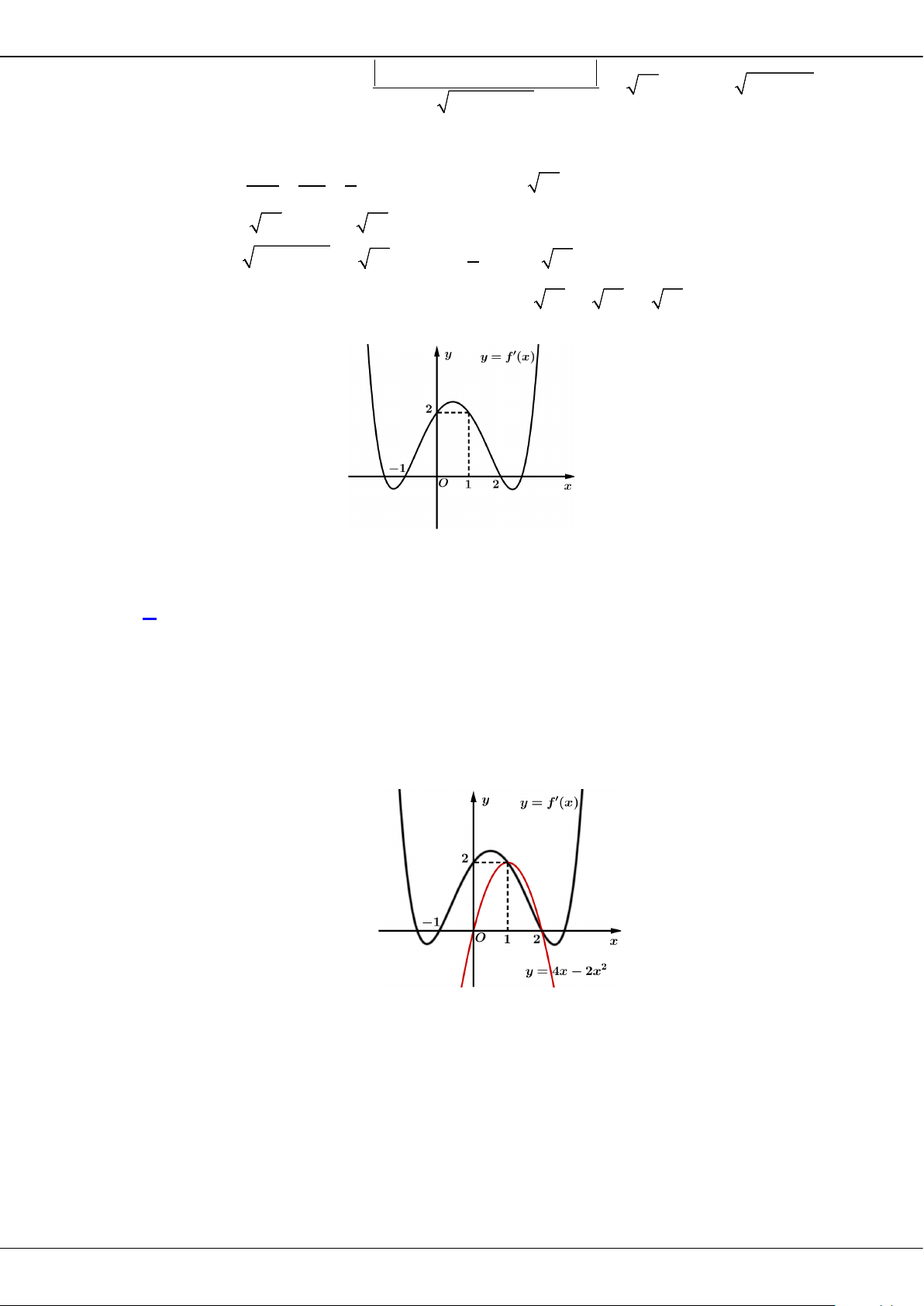
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 66

Ta tính được

( )

(

)

( )

222

2. 3 3. 4 4 5 107

d , 5 29

234

IK I P

−+ −+ −−

= = =

++

và

22

2

KB R IK=−=

.

Do

M

di động trên đường thẳng

d

(trục của đường tròn giao tuyến) và

B

thuộc đường tròn

giao tuyến nên biểu thức

MA MB

+

nhỏ nhất khi và chỉ khi

M AB d= ∩

.

Khi đó, ta có

3

2

MI IA

MK KB

= =

và

5 29MI MK IK+==

.

Suy ra

3 29MI =

,

2 29MK =

.

Ta có

22

3 30AM IA MI= +=

2

2 30

3

BM AM⇒= =

.

Vậy giá trị nhỏ nhất của

MA MB+

là

3 30 2 30 5 30AM BM+= + =

.

Câu 50: Cho hàm số

( )

y fx=

có đạo hàm liên tục trên



. Hàm số

( )

y fx

′

=

có đồ thị như hình vẽ.

Xét hàm số

( )

( ) ( ) ( )

2

33 3

3 3 3 2 62 6gx f x x m x x m x x m= −− + + + − − − + −

. Số giá trị nguyên của

tham số

m

thuộc đoạn

[

]

2023; 2023−

để hàm số

(

)

gx

nghịch biến trên khoảng

(

)

2; 2

−

là

A.

4019

. B.

2023

. C.

2008

. D.

4029

.

Lời giải

Chọn A

Đặt

3

3t x xm=−− +

2

3 3 0,tx x

′

⇒ =− − < ∀∈

⇒

hàm số

3

3t x xm=−− +

luôn nghịch biến

trên



. Vì

( ) ( )

2; 2 14; 14x tm m∈− ⇒∈ − +

.

Khi đó ta được

( )

( ) (

) (

)

2 32

323326gt ft t t ft t t= + −= + −

( ) (

) (

)

( )

22

3 6 12 3 4 2gt ft t t ft t t



′′ ′

⇒ = +−= −−



.

Dựa vào đồ thị hàm số

( )

y ft

′

=

và

2

42ytt= −

ta được

Hàm số

( )

gx

nghịch biến trên khoảng

( )

2; 2−

( )

gt⇔

đồng biến trên

( )

14; 14mm−+

.

Ta có

( ) ( )

( )

2

0 42 0

gt f t t t

′′

≥⇔ − − ≥

( )

2

42ft t t

′

⇔ ≥−

2

1

t

≥



⇔



≤



.

Do đó

( )

gt

đồng biến trên khoảng

( )

14; 14mm−+

14 2 16

14 1 13

mm

−≥ ≥



⇔⇔



+ ≤ ≤−



.

Vì

[ ]

2023; 2023 ,mm∈− ∈

nên

{ }

2023; 2021;...; 13;16;17;....; 2023m ∈− − −

.

Vậy có

4019

giá trị nguyên

m

thoả mãn.

- - - - - HẾT - - - -

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 67

SỞ GD&ĐT TIỀN GIANG

TRƯỜNG THPT THỦ KHOA HUÂN

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

BẢNG ĐÁP ÁN

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

A

D

C

B

C

A

B

D

A

B

A

C

B

A

B

A

B

A

D

C

A

D

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

C

D

A

C

D

B

A

B

C

B

C

D

B

A

C

A

C

A

B

A

C

D

LỜI GIẢI CHI TIẾT

Câu 1: Trong mặt phẳng tọa độ, biết điểm

( 2; 1)M 

là điểm biểu diễn số phức

z

. Phần thực của

z

bằng:

A.

2



. B.

2

. C.

1

. D.

1

.

Lời giải

Chọn A

Điểm

( 2; 1)M 

là điểm biểu diễn số phức

z

2zi  

Vậy phần thực của

z

là

2

.

Câu 2: Phần thực của số phức

( )

213zi i= −

bằng

A.

3−

. B.

2

. C.

6−

. D.

6

.

Lời giải

Chọn D

Ta có

( )

213 6 2zi i i= −=+

.Vậy phần thực của số phức

z

bằng

6.

Câu 3: Cho hàm số

( )

y fx=

có bảng biến thiên như hình bên.

Hàm số đã cho đạt cực tiểu tại

A.

2x =

. B.

2x = −

. C.

1x = −

. D.

1x =

.

Lời giải

Chọn D

Qua điểm

1x =

,

'y

đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại

1x =

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 68

Câu 4: Với

a

và

b

là hai số thực dương và

1

a ≠

,

log

a

b







bằng

A.

1

1 log

2

a

b+

. B.

11

log

22

a

b−

. C.

1

1 log

2

a

b−

. D.

1 2log

a

b+

.

Lời giải

Chọn C

Ta có

( )

1

log log log 1 log

2

a aa a

a

ab b

b



=−=−





.

Câu 5: Cho cấp số nhân

( )

n

u

với

1

3u =

và công bội

1

3

q = −

. Giá trị của

4

u

bằng

A. 3. B.

1

9

−

. C.

1

9

. D.

7

2

.

Lời giải

Chọn B

Ta có

3

41

1 11

. 3. 3.

3 27 9

u uq

  

= =−=− =−

  

  

.

Câu 6: Trong không gian

Oxyz

, cho mặt phẳng

( ):2 1 0xyz

α

+ −+=

. Vectơ nào sau đây không là

vectơ pháp tuyến của mặt phẳng

()

α

?

A.

( )

4

4; 2; 2 .=

−

 

n

B.

( )

2

2; 1; 1 .−= −

 

n

C.

(

)

3

2;1;1 .=

 

n

D.

( )

1

2; 1; 1 .= −



n

Lời giải

Chọn C

Mặt phẳng

( ):2 1 0xyz

α

+ −+=

có vectơ pháp tuyến là

(

)

1

2; 1; 1=

−



n

nên các vectơ

21

= −

   

nn

,

41

2=

   

nn

cũng là các vectơ pháp tuyến của mặt phẳng

()

α

.

Vectơ

( )

3

2;1;1=

 

n

không cùng phương với

(

)

1

2; 1; 1= −



n

nên không phải là vectơ pháp tuyến

của mặt phẳng

()

α

.

Câu 7: Họ các nguyên hàm của hàm số

3

2

1

() 4fx x

x

= −

là:

A.

4

1

()Fx x C

x

= ++

. B.

2

1

( ) 12Fx x C

x

= ++

.

C.

4

1

()Fx x C

x

= −+

. D.

42

( ) lnFx x x C=++

.

Lời giải

Chọn A

Ta có:

34

2

11

(4 )x dx x C

xx

− = ++

∫

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 69

Câu 8: Nếu

(

)

3

2

4f x dx

=

∫

và

(

)

3

2

2g x dx

= −

∫

thì

(

) (

)

3

2

f x g x dx−





∫

bằng

A.

2

. B.

6

. C.

8

D.

2−

.

Lời giải

Chọn B

Ta có:

( ) (

) (

)

( )

3 33

2 22

4 26f x g x dx f x dx g x dx− = − = −− =





∫ ∫∫

.

Câu 9: Tích phân

1

0

ed

x

Ix

+

=

∫

bằng

A.

2

e1

−

. B.

2

ee−

. C.

2

ee+

. D.

2

ee−

.

Lời giải

Chọn B

Ta có

1

0

ed

x

Ix

+

=

∫

1

12

0

e ee

x+

= = −

.

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 8 2 4 20Sx y z x y z+ + − + + −=

. Tâm của (S) có

tọa độ là

A.

(

)

4; 1; 2

−

B.

( )

8;2;4−−

C.

( )

8;2;4

−

D.

( )

4;1;2−−

Lời giải

Chọn D

Điểm

(

)

4;1;2

−−

là tâm của mặt cầu

( )

S

.

Câu 11: Cho cấp số nhân

( )

n

u

có số hạng đầu

1

2u =

và công bội

4q =

. Giá trị của

3

u

bằng

A.

32

. B.

16

. C.

8

. D.

6

.

Lời giải

Chọn A

Số hạng tổng quát của cấp số nhân

( )

n

u

có số hạng đầu

1

u

và công bội

q

là:

1

.

n

u uq

−

=

.

Vậy giá trị của số hạng thứ ba là

22

31

. 2.4 32u uq= = =

.

Câu 12: Cho hai số phức:

1

23zi= −

,

2

1zi=−+

. Phần ảo của số phức

12

w zz=

bằng

A.

5

. B.

7

. C.

5−

. D.

7−

.

Lời giải

Chọn A

12

15w zz i= = +

.

Câu 13: Cho khối lập phương có cạnh bằng

3

. Thể tích của khối lập phương đã cho bằng

A.

9.

B.

27

. C.

6

. D.

3

.

Lời giải

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 70

Chọn B

Ta có:

33

3 27

Va

= = =

.

Câu 14: Cho khối chóp

.S ABC

có đáy là tam giác vuông tại

A

,

3

AB =

,

5BC =

,

SA

vuông góc với

đáy và

6SA =

(tham khảo hình vẽ).

Thể tích khối chóp đã cho bằng

A.

12

. B.

15

. C.

36.

D.

24.

Lời giải

Chọn A

Tam giác

ABC

vuông tại

A

có

2 2 22

53 4AC BC AB

= − = −=

.

Thể tích khối chóp

.S ABC

là

11 1

. . . .6.3.4 12

32 6

V SA AB AC= = =

.

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;

S OR

. Gọi

d

là khoảng cách từ

O

đến

( )

P

. Khẳng định

nào dưới đây đúng?

A.

dR<

. B.

dR>

. C.

dR=

. D.

0d =

.

Lời giải

Chọn A

Mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

khi và chỉ khi

dR<

Câu 16: Đường tiệm cận đứng của đồ thị hàm số

31

1

x

y

x

−+

=

−

có phương trình là

A.

1y =

. B.

1x =

. C.

1x

= −

. D.

3y = −

.

Lời giải

Chọn B

Ta có:

1

31

lim

1

x

−

→

−+

= +∞

−

;

1

31

lim

1

x

+

→

−+

= −∞

−

, suy ra đồ thị hàm số đã cho có đường tiệm cận

đứng là

1x =

.

Câu 17: Cho hai số thực

x

,

y

thoả mãn phương trình

2 34x i yi+=+

. Khi đó giá trị của

x

và

y

là:

A.

3x =

,

1

2

y =

. B.

3

x =

,

1

2

y = −

. C.

3x =

,

2y =

. D.

3xi=

,

1

2

y =

.

Lời giải

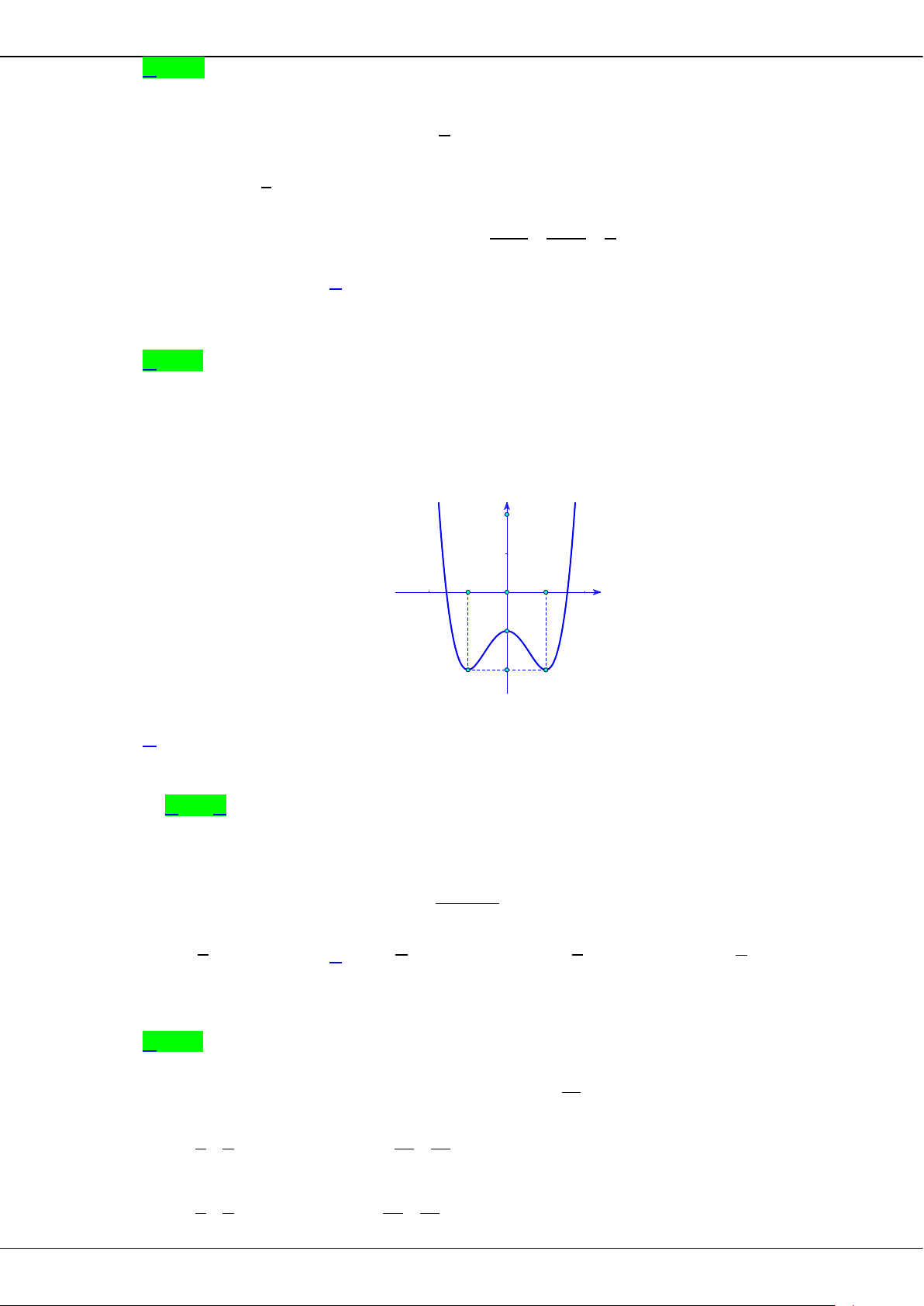
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 71

Chọn A

Từ

2 34x i yi+=+

3

24

x

y

=



⇒



=



3

1

2

x

y

=





⇔



=





.

Vậy

3x =

,

1

3

y =

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

22

:

1 23

xyz

d

−+

= =

. Điểm nào dưới đây thuộc

d

?

A.

( )

2; 2; 0P −

. B.

( )

3; 0; 3Q

. C.

( )

2; 2; 0N

. D.

( )

3; 0; 3M −

.

Lời giải

Chọn B

Lần lượt thay tọa độ của 4 điểm đã cho vào phương trình đường thẳng

d

, ta thấy tọa độ của

điểm

( )

3; 0; 3Q

thỏa mãn. Vậy điểm

( )

3; 0; 3Q

thuộc đường thẳng

.d

Câu 19: Cho hàm số

42

yaxbxc=++

có đồ thị là đường cong như hình bên dưới:

Điểm cực đại của đồ thị hàm số đã cho có tọa độ là

A.

( )

0; 1 .−

B.

( )

1; 0 .−

C.

( )

1; 2 .−

D.

( )

1; 2 .−−

Lời giải

Chọn A

Dựa vào hình dạng đồ thị hàm số có một điểm cực đại là

( )

0; 1 .−

Câu 20: Tiệm cận ngang của đồ thị hàm số

2 11

33

x

y

x

−+

=

+

là đường thẳng có phương trình

A.

1

3

y =

B.

2

3

y = −

C.

1

3

y = −

D.

2

3

y =

Lời giải

Chọn B

Câu 21: Cho hai số phức , . Tìm số phức .

A. . B. .

C. . D. .

x

y

-1

-2

O

1

12zi= +

2

3zi= −

2

1

z

=

17

55

zi= −

17

10 10

zi=−+

17

55

zi= +

17

10 10

zi= +

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 72

Lời giải

Chọn A

Ta có .

Câu 22: Trong không gian

Oxyz

, cho đường thẳng

123

:

2 11

xy z−++

∆==

−−

. Vectơ nào dưới đây là một

vectơ chỉ phương của

∆

?

A.

( )

2

1; 2; 3u = −



. B.

( )

1

2;1;1u =



.

C.

( )

4

1;2;3u = −−



. D.

( )

3

2;1;1u = −−



.

Lời giải

Chọn D

Đường thẳng

∆

nhận

( )

3

2;1;1u = −−



là một vectơ chỉ phương.

Câu 23: Cho

( )

3

dx x Fx C= +

∫

. Khẳng định nào dưới đây đúng?

A.

( )

4

Fx x

′

=

. B.

( )

4

x

Fx

′

=

. C.

( )

3

Fx x

′

=

. D.

( )

2

3Fx x

′

=

.

Lời giải

Chọn C

Ta có

( )

33

dFx x x x

′

= =





∫

.

Câu 24: Nếu

( )

4

1

6f x dx =

∫

thì

( )

4

1

23f x dx+





∫

bằng

A.

21.

B.

15.

C.

12.

D.

8.

Lời giải

Chọn A

Ta có

( ) ( )

4 44

1 11

2 3 2 3 2.6 9 21f x dx f x dx dx+ = + = +=





∫ ∫∫

.

Câu 25: Cho hàm số

( )

sinfx x x= −

. Khẳng định nào dưới đây đúng?

A.

( )

2

osd.fx x cx x C= −+

∫

B.

( )

2

osd.

2

x

fx x cx C= −+

∫

C.

( )

2

osd.

2

x

fx x

cx C=− ++

∫

D.

( )

2

osdc .

2

x

fx x x C=− −+

∫

Lời giải

Chọn D

( )

[ ]

2

d sin s

2

.od

x

fx x x x x cx C= − =− −+

∫∫

2

1

z

=

3

12

i

−

=

+

17

55

i= −

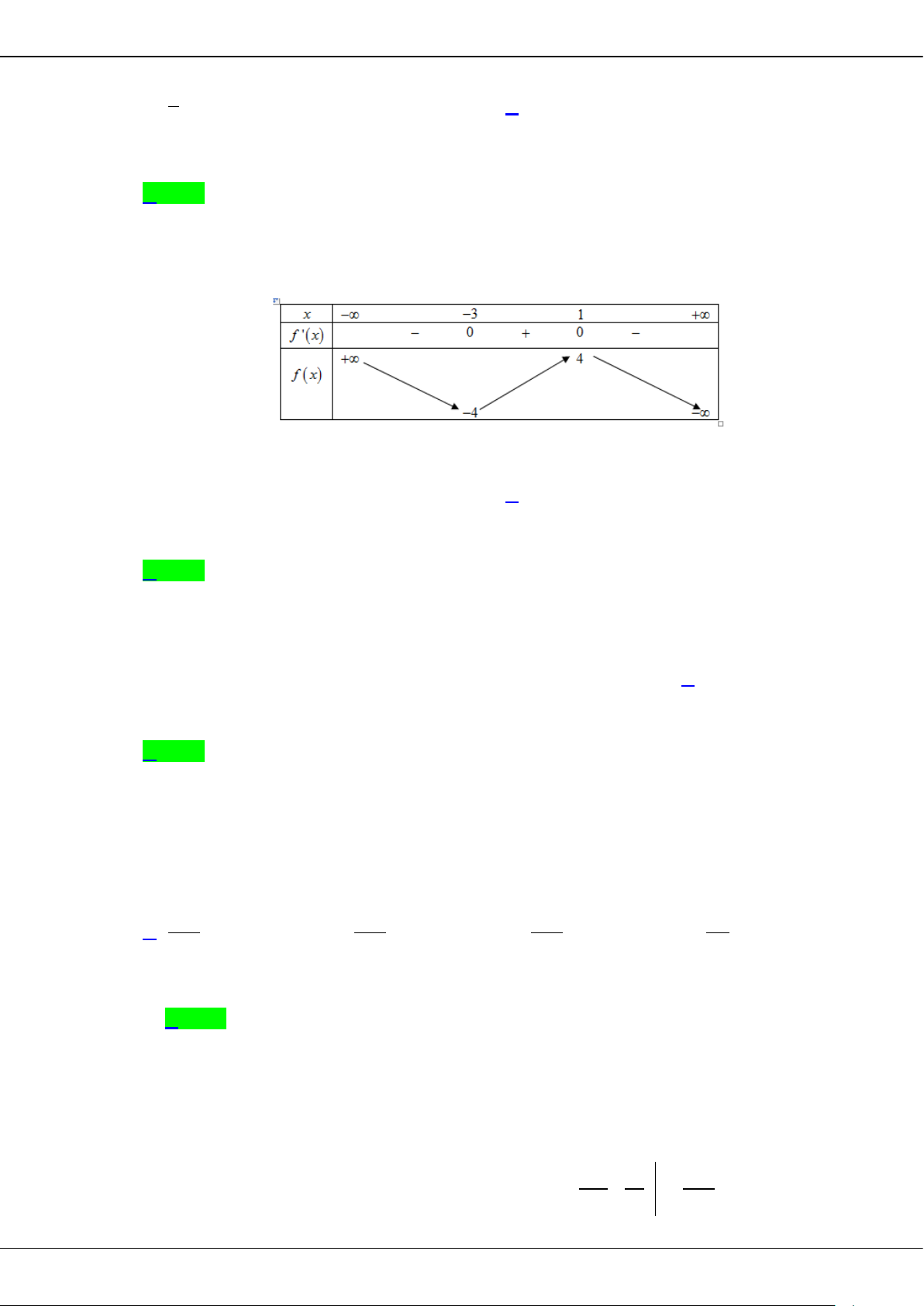
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 73

Câu 26: Cho hình nón có đường sinh

l

, bán kính đáy

r

. Diện tích xung quanh của hình nón bằng

A.

1

3

rl

π

. B.

4 l

π

. C.

rl

π

. D.

2

rl

π

.

Lời giải

Chọn C

Công thức tính diện tích xung quanh của hình nón là

xq

S rl

π

=

.

Câu 27: Cho hàm số

( )

fx

có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số là

A.

3y

= −

. B.

1y =

. C.

4y

= −

. D.

4y =

.

Lời giải

Chọn C

Dựa vào bảng biến thiên giá trị cực tiểu của hàm số là

4y = −

Câu 28: Tính thể tích khối hộp chữ nhật có ba kích thước là

2

,

3

,

4

.

A.

9

. B.

12

. C.

20

. D.

24

.

Lời giải

Chọn D

Áp dụng công thức tính thể tích khối hộp chữ nhật ta có:

V abc

2.3.4

24

Câu 29: Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số

2

3= −y xx

và trục hoành, quanh trục hoành.

A.

81

10

π

(đvtt). B.

85

10

π

(đvtt). C.

41

7

π

(đvtt). D.

8

7

π

(đvtt).

Lời giải

Chọn A

Ta có

2

0

30

3

=



−=⇔



=



x

xx

x

.

Thể tích khối tròn xoay cần tìm là:

( ) ( )

3

33

45

2

2 2 34 3

00

0

3 81

3 96 3

2 5 10

π

ππ π



= − = −+ = − + =





∫∫

xx

V x x dx x x x dx x

(đvtt).

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 74

Câu 30: Cho hàm số

()

y fx=

liên tục trên đoạn

[ ]

2; 4−

và có đồ thị như hình vẽ bên. Số nghiệm thực

của phương trình

3 () 5 0fx−=

trên đoạn

[ ]

2; 4−

là

A.

1

. B.

0

. C.

3

. D.

2

.

Lời giải

Chọn C

Ta có

5

3 () 5 0 ()

3

fx fx−=⇔ =

.

Dựa vào đồ thị ta thấy đường thẳng

5

3

y =

cắt đồ thị hàm số

()y fx=

tại ba điểm phân biệt

thuộc đoạn

[ ]

2; 4−

.

Do đó phương trình

3 () 5 0fx−=

có ba nghiệm thự

Câu 31: Tập nghiệm của bất phương trình

26

22

xx



là:

A.

 

0; 64

B.

 

6;

C.

 

0; 6

D.





;6



Lời giải

Chọn D

Đặt

2

x

t 

,

0t 

Bất phương trình trở thành:

2

64 0tt

0 64t 

0 2 64 6

x

x  

.

Câu 32: Tìm hai số thực

x

và

y

thỏa mãn điều kiện

(2 3 ) (3 ) 5 4

  x yi i x i

với

i

là đơn vị ảo.

A.

1; 1 . xy

B.

1; 1 .xy

C.

1; 1 . xy

D.

1; 1 .

 xy

Lời giải

Chọn B

Ta có:

2 35 1

(2 3 ) (3 ) 5 4

31 4 1



 



    





   





x xx

x yi i x i

yy

.

Câu 33: Một hộp chứa

17

quả cầu gồm

8

quả màu đỏ được đánh số từ

1

đến

8

và

9

quả màu xanh

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 75

được đánh số từ

1

đến

9

. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác

màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng

A.

9

.

34

B.

9

.

17

C.

2

.

17

D.

1

.

7

Lời giải

Chọn A

Số cách lấy ngẫu nhiên

2

quả cầu từ hộp là:

2

17

136C =

cách

Để tổng hai số ghi trên hai quả cầu là số chẵn ta có

2

TH sau:

TH1: Hai quả cầu khác màu cùng đánh số lẻ:

11

45

. 20

CC=

cách

TH2: Hai quả cầu khác màu nhau cùng đánh số chẵn:

11

44

. 16CC=

cách

Vậy xác suất cần tính là:

20 16 9

.

136 34

P

+

= =

Câu 34: Cho hình chóp tứ giác đều có cạnh đáy bằng

a

và chiều cao bằng

2

a

. Số đo của góc giữa mặt

bên và mặt đáy là

A.

60

o

. B.

45

o

. C.

75

o

. D.

30

o

.

Lời giải

Chọn B

Gọi

O

là tâm hình vuông

ABCD

.

M

là trung điểm của

CD

.

Ta có:

[ ]



[ ]



[ ]



[ ]



( ), ( ) ( ),( ) ( ), ( ) ( ), ( )SAB ABCD SBC ABCD SAD ABCD SCD ABCD= = =

.

Ta có:

[ ]



( )( )

( ), ( )

( ), ( ) .

SCD ABCD CD

SM SCD OM ABCD

SM CD M SCD S

OM CD M OM AD AD CD

SCD ABCD SMO

∩=





⊂⊂





⊥∆



⊥⊥



⇒=

t¹i ( v× // mµ )

Ta lại có:

1

22

a

OM AD= =

,

2

a

SO =

.

Trong tam giác

SOM

vuông tại

O

có:



tan 1

SO

SMO

OM

= =

.



45

o

SMO⇒=

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 76

Câu 35: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức

z

thỏa mãn

32 4zi+− =

là một

đường tròn. Tâm của đường tròn đó có tọa độ là.

A.

(

)

3; 2−

. B.

( )

3; 2

. C.

( )

3; 2−

. D.

(

)

3; 2

−−

.

Lời giải

Chọn C

Câu 36: Trong không gian

Oxyz

, cho hai điểm

( )

1; 2; 3M −

và

( )

2; 3; 1N −

. Đường thẳng

MN

có

phương trình là:

A.

1

25

34

xt

yt

zt

= +





= −





= +



B.

2

35

14

xt

yt

zt

= +





=−+





= +



C.

1

25

34

xt

yt

zt

= +





= −





=−+



D.

1

25

32

xt

yt

zt

= +





= −





=−−



Lời giải

Chọn C

Ta có

( )

1; 5; 4MN = −



.

Đường thẳng

MN

qua

( )

1; 2; 3M

−

nhận

( )

1; 5; 4MN = −



làm vectơ chỉ phương có phương trình

1

25

34

xt

yt

zt

= +





= −





=−+



.

Câu 37: Trong không gian

Oxyz

, cho

a



,

b



tạo với nhau

1

góc

120°

và

3a =



;

5b

=



. Tìm

T ab

= −



.

A.

6T =

. B.

7T =

. C.

4

T =

. D.

5T =

.

Lời giải

Chọn B

Cách 1: Ta có

2

22

2

2.T a b a b ab=− =+−

    

( )

22

2

2. . .cos ,T a b a b ab⇔ =+−

    

2 32

3 5 2.3.5.cos120T⇔ =+− °

2

49T

⇔=

7T⇒=

.

Cách 2:

Đặt

a OA=

   

,

b OB=

 

. Khi đó

T a b OA OB BA=−= − =

    

T BA⇔=

.

Theo định lý Côsin trong tam giác

OAB

có:



222

2..cosBA OA OB OA OB AOB=+−

2 22

3 5 2.3.5.cos120 47BA⇔ = + − °=

7T⇔=

.

B

A

O

a



b



120°

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 77

Câu 38: Cho hình chóp đều

.S ABCD

có chiều cao

2, 4a AC a=

(tham khảo hình bên). Tính khoảng

cách từ điểm

B

đến mặt phẳng

( )

SCD

.

A.

23

3

a

. B.

2a

. C.

43

3

a

. D.

2

a

.

Lời giải

Chọn C

- Gọi

O AC BD= ∩

,

H

là trung điểm

CD

. Trong

( )

SOH

, kẻ

OI SH

⊥

.

Có

( )

CD SO

CD SOH CD OI

CD SH

⊥



⇒⊥ ⇒⊥



⊥



.

Mà

OI SH⊥

nên

( )

OI SCD⊥

( )

,d O SCD OI⇒=

.

- Vì O là trung điểm BD nên

( )

22

2.

, ,2

SO OH

d B SCD d O SCD OI

SO OH

= = =

+

.

Có

sin 45 2 2AD AC a= °=

,

2

OH a=

( )

43

,

3

d B SCD a⇒=

.

Câu 39: Diện tích hình phẳng giới hạn bởi đồ thị hàm số

sin 1,yx= +

trục hoành và hai đường thẳng

0x =

và

7

6

x

π

=

là.

A.

37

1

23

π

++

. B.

37

1

46

π

+−

. C.

37

1

26

π

+−

. D.

37

1

26

π

++

.

Lời giải

H

O

A

D

B

C

S

I

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 78

Chọn D

Ta thấy

7

sin 1 0 0;

6

xx

π



+≥ ∀∈





nên diện tích

S

cần tìm bằng:

( )

77

66

00

sin 1 sin 1S x dx x dx

ππ

= += +

∫∫

( )

7 7 37

cos cos0 0 1

66 26

ππ π



= − + −− + = + +





.

Câu 40: Cho hàm số

( )

fx

liên tục trên



. Biết

( )

fx

có đạo hàm là

( )

5

'2

fx x

= +

và

( )

12f

=

. Khi

đó

2

0

2

dx

x

f







∫

bằng

A.

1

7

. B.

3

7

. C. 6. D.

6

7

.

Lời giải

Chọn B

Xét

2

0

2

dx

x

f







∫

, đặt

22

x dx

t dt=⇒=

.

Đổi cận:

0xt=⇒=0

21xt= ⇒=

Suy ra

( )

21 1

00 0

11

22

d

2

f x f td

x

t f t dt



= =





∫∫ ∫

Xét

( )

1

0

f t dt

∫

, đặt

( ) ( )

'

u f t du f t dt

dv dt v t

= ⇒=





= ⇒=



( ) (

) ( )

( )

1 11

1 5 7 21

00

0 00

1

. .' 2 2 2

7

f t dt t f t t f t dt t t dt t t



= − =− +=−+





∫ ∫∫

16

21

77

= − −=

Suy ra,

( )

1

0

1 16 3

.

2 27 7

f t dt = =

∫

.

Câu 41: Có bao nhiêu giá trị nguyên của tham số

( )

10;10m ∈−

để hàm số

( ) ( )

53

3 5 10 15 45 2024yx m x m x=−+ − + +

có hai điểm cực trị?

A.

10

. B.

12

. C.

8

. D.

14

.

Lời giải

Chọn B

Ta có

( )

42

15 3 5 10 15 45

′

= − + −−yx m xm

.

( )

( )( )

( )

4 2 22 2

0 2 3 0 1 3 0 31

′

=⇔ − + −−=⇔ + −− =⇔= −y x m xm x xm mx

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 79

Xét hàm số

( )

2

3= −gx x

( )

20 0

′

= =⇔=gx x x

.

Bảng biến thiên của

( )

gx

Để hàm số có hai điểm cực trị thì phương trình

( )

1

phải có 2 nghiệm phân biệt.

Dựa vào bảng biến thiên ta thấy phương trình

( )

1

có hai nghiệm phân biệt khi

3

>−

m

.

Do

( )

{ }

10;10 2, 1,0,...,7,8,9∈− ⇒ ∈− −mm

.

Vậy có 12 giá trị nguyên của tham số

m

thỏa yêu cầu đề bài.

Câu 42: Cho số phức

z

thỏa mãn

2 12 2z i zz i− = −+

. Tìm giá trị nhỏ nhất của

z

.

A.

11

2

. B. 0. C.

22

2

D.

13

2

Lời giải

Chọn A

Gọi

z x yi= +

với

,xy∈

.

Vì

2 12 2z i zz i− = −+

nên

( )

22

2

2 12 2 2

xy y+− = +

2 22

2

( 12) ( 1)

11

26 2

xy y

x

y

⇔+− =+

⇔= +

Do đó, tập hợp điểm biểu diễn của z là parabol (P):

2

11

26 2

x

y = +

có bề lõm quay lên và đỉnh

11

0;

2

I







.

Vậy giá trị nhỏ nhất của

z

= OI=

11

2

.

Câu 43: Gọi

( )

m

C

là đồ thị của hàm số

( )

3 22

1 21

32

m

y x x m mx

+

=− ++

với

m

là tham số. Có bao

nhiêu điểm

M

sao cho tồn tại hai giá trị khác nhau

12

,

mm

mà

M

là điểm cực đại của đồ thị

( )

1

m

C

và là điểm cực tiểu của đồ thị

( )

2

m

C

?

A.

2

. B.

0

. C.

1

. D. vô số.

Lời giải

Chọn C

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 80

- Tập xác định

D

=



.

- Ta có:

( )

22

' 21f x x m xm m=− + ++

.

(

)

'0

1

xm

fx

xm

=



= ⇔



= +



- Bảng biến thiên:

- Theo BBT, đồ thị hàm số có điểm cực đại

( )

;mf m

và có điểm cực tiểu

( )

1; 1m fm++

- Ta có:

Khi

1

mm=

đồ thị hàm số có điểm cực đại là

( )

11

;Mm fm

.

Khi

2

mm

=

đồ thị hàm số có điểm cực tiểu là

( )

22

1; 1Mm fm++

.

- Khi đó:

( ) (

)

12

1

mm

fm fm

= +







= +





( )

12

3

2

22 2

11 2

1 111 2 222

1

21 2 1

11

32 3 2

mm

m

mm m

m mmm m mmm

= +





⇔



+

++

− ++ = − +++ +





1

2

0

1

m

=



⇔



= −



- Thử lại:

*

32

11

0,

32

m yx x= = −

: đồ thị hàm số có điểm cực đại là

(

)

0; 0M

.

*

32

11

1,

32

m yx x=−= +

: đồ thị hàm số có điểm cực tiểu là

( )

0; 0M

- Vậy có

1

điểm

M

thỏa yêu cầu của bài toán.

Câu 44: Cho số phức

z

thỏa mãn

2

2 30

zz− +=

. Tính

w

biết

2018 2017 2016 2015 2

33 9wz z z z z z= − + + + −+

.

A.

53

. B.

2018 3

. C.

93

. D.

3

.

Lời giải

Chọn A

Ta có

2

2 30zz− +=

⇔

1 2.

zi



= −



= +





LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 81

Theo giả thiết

( )

2018 2017 2016 2015 2 2015 3 2 2

339 339wz z z z zz z zzz zz

= − + + + −+= − ++ + −+

Với

1

12zi= −

⇒

1

5 52wi= −

⇒

1

53w =

.

Với

2

12zi= +

⇒

2

5 52wi= =

⇒

2

53w =

.

Vậy

53

w =

.

Câu 45: Trong không gian với hệ tọa độ

Oxy

, cho mặt phẳng

( )

:2 3 0P yz

−+=

và điểm

( )

2; 0; 0A

.

Mặt phẳng

( )

α

đi qua

A

, vuông góc với

( )

P

, cách gốc tọa độ

O

một khoảng bằng

4

3

và cắt

các tia

Oy

,

Oz

lần lượt tại các điểm

B

,

C

khác

O

. Thể tích khối tứ diện

OABC

bằng

A.

8

. B.

16

. C.

8

3

. D.

16

3

.

Lời giải

Chọn C

Giả sử

( )

0; ; 0Bb

và

( )

0; 0;

Cc

, với

b

,

0

c >

.

Khi đó phương trình mặt phẳng

( )

α

là:

1

2

xyz

bc

++=

.

Vì

(

) (

)

P

α

⊥

nên

21

0

bc

−=

11

2.

cb

⇔=

.

Mặt khác

( )

4

,

3

dO

α

=

222

14

3

111

2 bc

⇔=



++





2

55

16b

⇔=

2

16b⇔=

42

bc⇔=⇒=

.

Vậy

.

18

...

63

O ABC

V OA OB OC= =

.

Câu 46: Cho

2

mặt cầu

( )

( ) ( ) ( )

2 22

1

:3 2 24Sx y z− +− +− =

,

( ) (

) ( )

22

2

:1 11Sx yz

− + +− =

. Gọi

d

là

đường thẳng đồng thời tiếp xúc với hai mặt cầu trên, cắt đoạn thẳng nối tâm hai mặt cầu và

cách gốc tọa độ

O

một khoảng lớn nhất. Nếu

( )

; 1;uab=



là một vectơ chỉ phương của

d

thì

tổng

23S ab= +

bằng bao nhiêu?

A.

2S =

. B.

1S =

. C.

0S =

. D.

4S =

.

Lời giải

Chọn A

( )

1

S

có tâm

( )

1

3;2;2I

, bán kính

1

2R =

.

(

)

2

S

có tâm

( )

2

1; 0; 1I

, bán kính

2

1R =

.

Ta có:

12 1 2

3II R R= = +

, do đó

( )

1

S

và

( )

2

S

tiếp xúc ngoài với nhau tại điểm

524

;;

333

A







.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 82

Vì

d

tiếp xúc với hai mặt cầu, đồng thời cắt đoạn thẳng nối hai tâm

12

II

nên

d

phải tiếp xúc với

hai mặt cầu tại

A

12

d II

⇒⊥

.

Mặt khác

( )

;d d O d OA= ≤

max

d OA⇒=

khi

d OA⊥

.

Khi đó,

d

có một vectơ chỉ phương là

( )

12

, 6; 3; 6I I OA



= −−



 

(

)

2; 1; 2

u

⇒=−



.

Suy ra

2a = −

,

2

b =

.

Vậy

2S

=

.

Câu 47: Ông An muốn làm một cánh cửa bằng sắt có hình dạng và kích thước như hình vẽ. Biết rằng

đường cong phía trên là một parabol, tứ giác

ABCD

là một hình chữ nhật. Giá cánh cửa sau

khi hoàn thành là

900000

đồng/

2

m

. Số tiền ông An phải trả để làm cánh cửa đó bằng

A. 8 160 000 đồng. B. 8 400 000 đồng. C. 9 600 000 đồng. D. 15 600 000 đồng.

Lời giải

Chọn B

Chọn hệ trục tọa độ

Oxy

sao cho cạnh

AB

nằm trên

Ox

và

O

là trung điểm

AB

. Khi đó, ta

có phương trình parabol là:

2

1

yx= −

.

Diện tích cánh cửa là:

( )

2

1

28

2.4 1 d

3

S xx

−

=+− =

∫

( )

2

m

.

Câu 48: Tìm số giá trị nguyên của

[ ]

2020;2020m ∈−

để hàm số

32

65yx x m= − ++

đồng biến trên

khoảng

( )

5; +∞

?

A.

2001

. B.

2018

. C.

2019

. D.

2000

.

Lời giải

Chọn A

Xét hàm số

( ) ( )

32 2

0

6 5 3 12 0

4

x

fx x x m f x x x

x

=



′

= − ++ ⇒ = − =⇔



=



Bảng biến thiên:

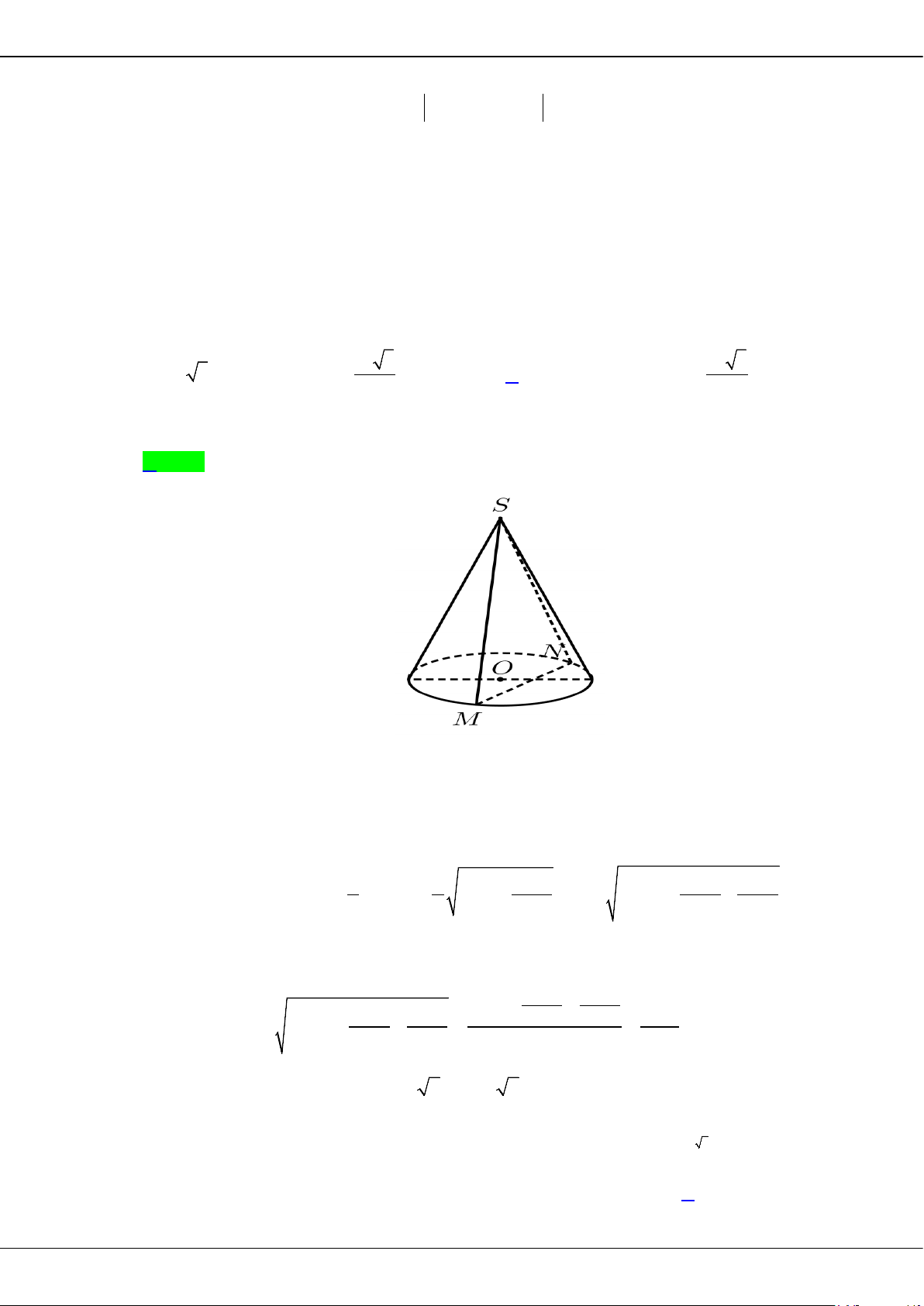
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 83

TH1:

27 0 27

mm

− ≥⇔ ≥

. Khi đó hàm số

( )

32

65

fx x x m= − ++

đồng biến và không âm

trên khoảng

( )

4; +∞

nên hàm số

32

65yx x m

= − ++

đồng biến trên khoảng

( )

5;

+∞

.

TH2:

27 0 27

mm− <⇔ <

.

Yêu cầu bài toán

( )

5 0 20 0 20

fm m⇔ ≥⇔ − ≥⇔ ≥

.

Tóm lại các giá trị của

m

thỏa mãn bài toán là

20

m ≥

, mà

m

là số nguyên thuộc đoạn

[

]

2020;2020

−

nên có tất cả

2001

giá trị

m

.

Câu 49: Cho hình nón đỉnh S có đường cao

ha=

, đường sinh

2la=

. Một mặt phẳng đi qua đỉnh S và

cắt đường tròn đáy tại hai điểm M, N. Diện tích tam giác SMN lớn nhất bằng

A.

2

3a

. B.

2

3

2

a

. C.

2.

2a

. D.

2

3

4

a

.

Lời giải

Chọn C

Gọi O là tâm đáy của hình nón; I là trung điểm của MN.

Ta có

2

= =SM l a

Khi đó

OI MN SI MN⊥ ⇒⊥

Diện tích tam giác

2 22

22

11

.. .

2 2 4 44

∆



==−=−





SMN

MN MN MN

S SI MN SM MN SM

Áp dụng bất đẳng thức Cauchy, ta có:

22

2

22 2

22

44

.2

44 2 2

−+



−≤ ==





MN MN

SM

MN MN SM

SM a

SMN

S

∆

lớn nhất bằng

2.

2a

khi

2 22MN SM a= =

.

Câu 50: Có bao nhiêu

m

nguyên

[ ]

2021;2021m ∈−

để phương trình

( )

3

6

6 2 log 18 1 12

x

m xm− = ++

có nghiệm?

A.

212

. B.

211

. C.

2020

. D.

2023

.

Lời giải

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 84

Chọn D

Phương trình

( )

3

6

6 2 log 18 1 12 6 2 3log 6 3 2 3

xx

m x m m xm− = ++ ⇔ = + + +





( )

( ) ( )

6

6231log323

63log32323,*

x

m xm

xm m

⇔= + + + +





⇔= ++++

Đặt

( ) ( )

6

log32 3 632 3,1

y

y xm xm

= ++⇔=++

Mặt khác, PT trở thành:

( )

6 3 2 3, 2

x

ym=++

Lấy trừ vế với vế cho, ta được

( )

6633 63 63 3

yx x y

xy x y−=−⇔+=+

Xét hàm số

( )

6 3, .

t

f t tt

=+∈

Ta có

( )

' 6 ln 6 3 0, .

t

ft t= + > ∀∈



Suy ra hàm số

(

)

ft

đồng biến trên



Mà PT

(

) ( )

.fx fy x y= ⇔=

Thay

yx=

vào PT, ta được

63236323

xx

xm xm= + +⇔ − = +

.

Xét hàm số

( )

63

x

gx x= −

, với

x

∈

. Ta có

( ) (

)

6

3

' 6 ln 6 3 ' 0 log

ln 6

x

gx gx x



= −⇒ = ⇔ =





BBT:

Từ đó suy ra PT đã cho có nghiệm

6

3

2 3 log 0,81 1,095

ln 6

mg m



⇔ + ≥ ≈ ⇒ ≥−





Vậy có 2023 số nguyên

m

thỏa mãn yêu cầu.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 85

SỞ GD&ĐT TIỀN GIANG

TRUNG TÂM GDNN-GDTX GCĐ

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Hình nào biểu diễn cho số phức

32zi=−+

:

A. . B. .

C. . D. .

Câu 2: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

( )

ln 3yx=

là

A.

1

3

y

x

′

=

. B.

1

y

x

′

=

. C.

3

y

x

′

=

. D.

1

ln 3

y

x

′

=

.

Câu 3: Trên khoảng

( )

0;+∞

, đạo hàm của hàm số

3

yx=

là

A.

31

3yx

−

′

=

. B.

2

3yx

′

=

. C.

31

1

3

yx

−

′

=

. D.

3

3yx

′

=

.

Câu 4: Tập nghiệm của bất phương trình

2

3 27

x+

≥

là

A.

(

]

;1−∞

. B.

( )

1; +∞

. C.

[

)

1; +∞

. D.

( )

;1−∞

.

Câu 5: Cho cấp số nhân

( )

n

u

với

1

3u =

và

4

1

9

u =

. Công bội

q

của cấp số nhân bằng

A. 3. B.

1

9

. C.

9

. D.

1

3

.

Câu 6: Trong không gian

Oxyz

, mặt phẳng

( )

:2 3 4 0P x yz+ ++=

có một vectơ pháp tuyến là

A.

( )

1

1; 3; 2n =



. B.

( )

4

2; 3;1n =

 

. C.

( )

3

1; 2; 3n =

 

. D.

( )

2

2; 1; 3n =

 

.

Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị

hàm số đã cho và trục tung là

x

y

3

_

2

O

M

x

y

3

2

O

M

x

y

3

_

2

O

M

x

y

_

3

_

2

O

M

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 86

A.

( )

0; 2

. B.

( )

2;0

. C.

( )

6; 0

. D.

(

)

0; 6

.

Câu 8: Nếu

( )

2

3

2f x dx

−

=

∫

và

( )

2

3

5

g x dx

−

=

∫

thì

( ) ( )

(

)

2

3

f x g x dx

−

∫

bằng

A.

3

. B.

7

. C.

3−

. D.

7−

.

Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên

A.

42

32

yx x

=−+

. B.

3

32yx x=−+

. C.

2

32

yx x=−+

. D.

2

1

x

y

x

+

=

+

.

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 4 6 2 50Sx y z x y z+ + − + − +=

. Bán kính của mặt

cầu của (S) bằng

A.

1R =

B.

4R =

C.

2R =

D.

3R =

Câu 11: Cho hình lập phương ABCD.A’B’C’D’, góc giữa hai mặt phẳng AA’B’B và AA’C’C bằng

A.

30



B.

45



C.

60



D.

Câu 12: Cho số phức

2zi= +

, phần ảo của số phức

3

z

bằng

A.

1

B.

13

C.

11

D.

2

Câu 13: Cho khối tứ diện đều có cạnh bằng

2

. Thể tích của khối tứ diện đã cho bằng

A.

2

. B.

22

. C.

2

3

. D.

22

3

.

Câu 14: Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

3AB =

;

SA

vuông góc với đáy và

2SA =

(tham khảo hình vẽ).

x

y

1

2

3

6

O

x

y

1

_

4

2

O

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 87

Thể tích khối chóp đã cho bằng

A.

18

. B.

6

. C.

8

. D.

4

.

Câu 15: Cho mặt phẳng

( )

P

đi qua tâm của mặt cầu

( )

;S OR

. Gọi

d

là khoảng cách từ

O

đến

( )

P

.

Khẳng định nào dưới đây đúng?

A.

dR<

. B.

dR>

. C.

dR=

. D.

0d =

.

Câu 16: Phần thực của số phức

43zi= +

là

A.

4

. B.

3

. C.

2

. D.

1

.

Câu 17: Cho hình trụ có đường kính đáy

2r

và độ dải đường sinh

l

. Diện tích xung quanh của hình nón

đã cho bằng

A.

2

rl

π

. B.

2

3

rl

π

. C.

rl

π

. D.

2

1

3

rl

π

.

Câu 18: Trong không gian

Oxyz

, cho đường thẳng

234

:

1 25

xyz

d

+ −+

= =

−

. Vectơ nào trong các vectơ

sau là vectơ chỉ phương của

d

?

A.

( )

2; 3; 4

a =−−



. B.

( )

1; 2; 5b = −



. C.

( )

1; 2; 5c =



. D.

( )

2; 3; 4d = −



.

Câu 19: Cho hàm số

3 2

y ax bx cx d= + ++

có đồ thị là đường cong trong hình bên. Điểm cực đại của đồ

thị hàm số đã cho có tọa độ là

A.

( )

1; 0

. B.

( )

0; 2

. C.

( )

2; 2

. D.

( )

2; 0−

.

Câu 20: Tiệm cận đứng của đồ thị hàm số

1

52

x

y

x

+

=

−

là đường thẳng có phương trình

A.

1

5

y =

B.

1

5

y = −

C.

2

5

y = −

D.

2

5

y =

Câu 21: Tập nghiệm của bất phương trình

( )

1

2

log 3 0x −>

là

3

2

C

S

A

B

D

x

y

2

1

2

_

2

O

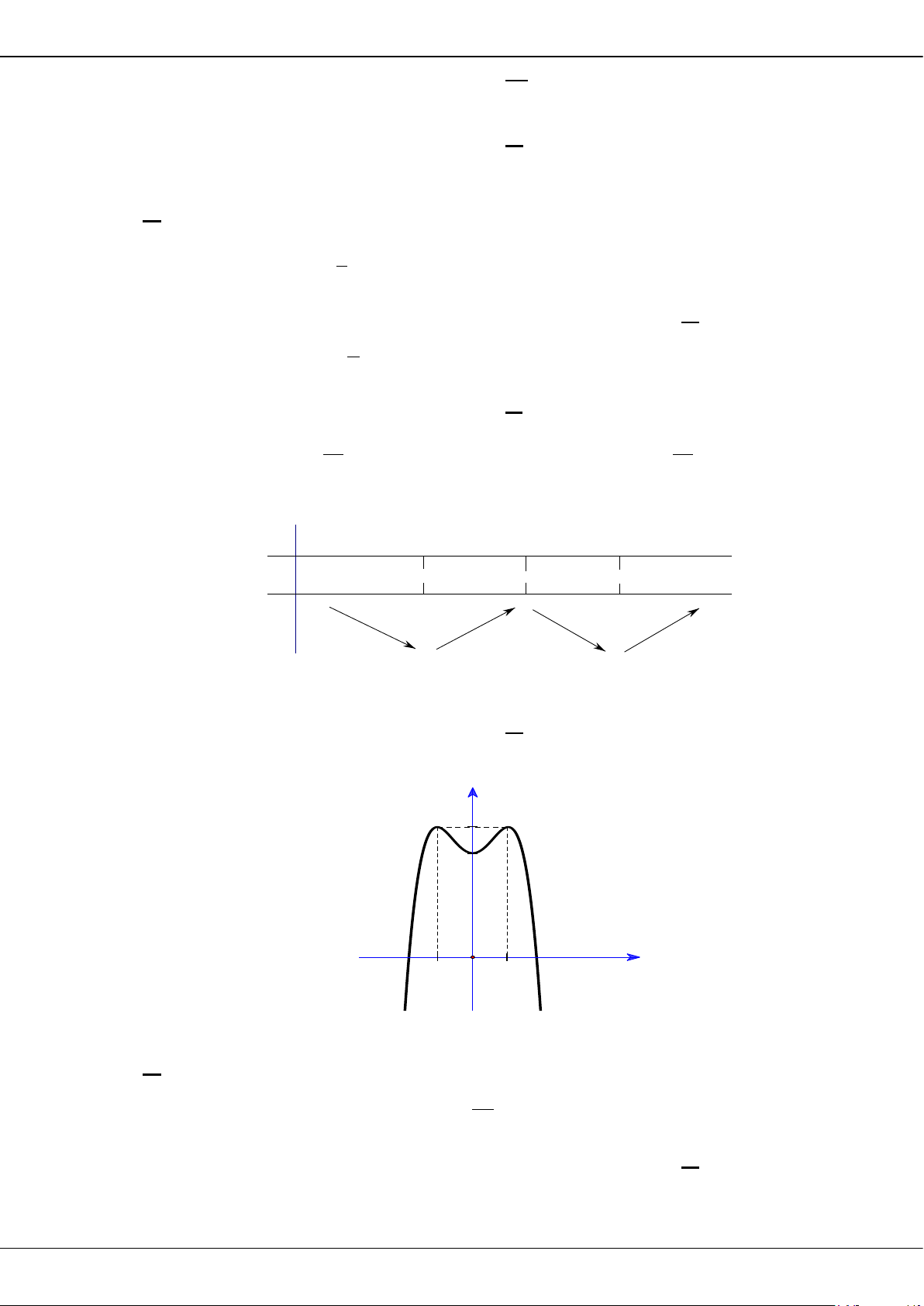
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 88

A.

[

)

4;

+∞

B.

[ ]

3; 4

C.

( )

3; 4

D.

( )

4; +∞

Câu 22: Cho tập hợp

A

có

9

phần tử. Số tập con gồm ba phần tử của

A

bằng

A.

9!

B.

6

C.

84

D.

504

Câu 23: Cho

( )

51

ed

x

x Fx C

+

= +

∫

. Khẳng định nào dưới đây đúng?

A.

( )

51

x

Fx e

+

=

′

. B.

( ) ( )

5

51

x

Fx x e= +

′

. C.

( )

5x

Fx e

′

=

. D.

( )

51

5

x

Fx e

+

=

′

.

Câu 24: Nếu

(

)

1

3

d6fx x

−

=

∫

thì

(

)

1

3

1

d

3

fx x x

−



+





∫

bằng

A.

26

. B.

33

. C.

2

. D.

22

.

Câu 25: Cho hàm số

( )

1

sinfx x

x

= −

. Khẳng định nào dưới đây đúng?

A.

(

)

d cos ln .

fx x x xC

= −+

∫

B.

( )

d cos ln .fx x x xC=− −+

∫

C.

(

)

2

d cos .fx x x C

x

=− ++

∫

D.

( )

2

d cos .fx x x C

x

= ++

∫

Câu 26: Cho hàm số

()y fx=

có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.

(

)

2; +∞

. B.

( )

0;1

. C.

( )

1; 0−

. D.

( )

2;3

.

Câu 27: Cho hàm số bậc ba  = () có đồ thị là đường cong trong hình bên.

Giá trị cực tiểu của hàm số đã cho là:

A.

4

. B.

5

. C.

1−

. D.

1

.

Câu 28: Với  là số thực dương tùy ý,

1

log(6 ) log( )

2

a

+

bằng:

A.

log( )2

. B.

2

log(3 )a

. C.

2log 2

. D.

log 3

.

Câu 29: Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường

3

yx x= −

và

0y =

quanh trục

Ox

bằng

0

_

1

x

y

_

∞

+

∞

+

∞

2

3

+

_

y'

0

_

+

1

x

y

5

_

1

4

O

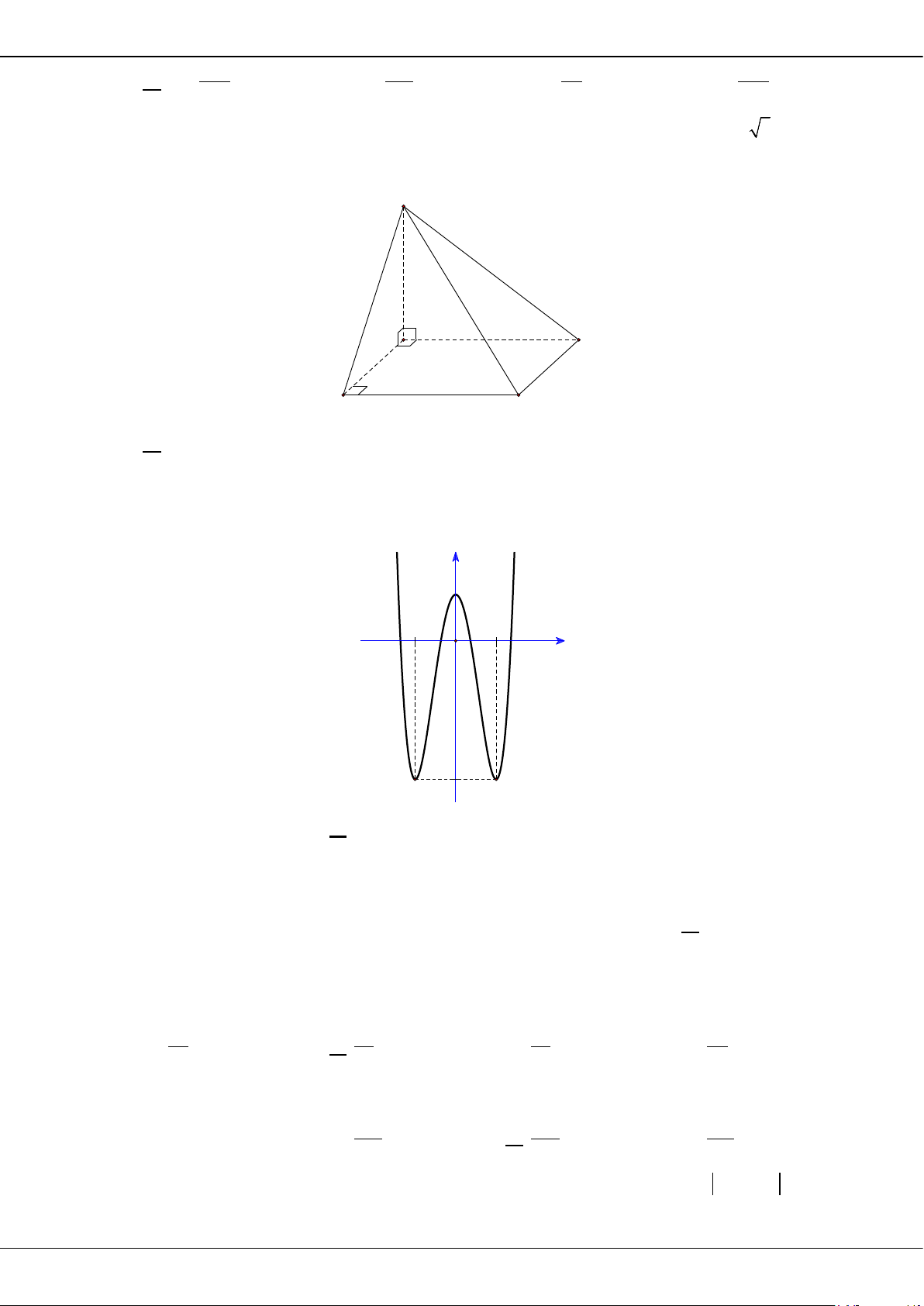
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 89

A.

16

105

V

π

=

. B.

8

105

V

π

=

. C.

30

V

π

=

. D.

16

15

V = ⋅

π

.

Câu 30: Cho hình chóp

.S ABCD

có đáy là hình vuông,

SA

vuông góc với đáy và

3SA AB=

(tham khảo

hình vẽ). Góc giữa hai mặt phẳng

( )

SBC

và

(

)

ABCD

bằng

A.

60 .°

B.

30°⋅

C.

90°⋅

D.

45°⋅

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên

của tham số

m

để phương trình

( )

fx m=

có bốn nghiệm thực phân biệt?

A.

2

. B.

5

. C.

3

. D.

4

.

Câu 32: Cho hàm số

( )

y fx=

có đạo hàm

( )

( ) (

)

3

2

32fx x x x

′

=−−

với mọi

x ∈ 

. Hàm số đã cho

đồng biến trên khoảng nào dưới đây?

A.

( )

0;3

. B.

( )

0; 2

. C.

( )

2; +∞

. D.

( )

2;3

.

Câu 33: Một hộp chứa

11

quả cầu gồm

4

quả màu đỏ được đánh số từ

1

đến

4

và

7

quả màu xanh được

đánh số từ

1

đến

7

. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả khác màu

đồng thời tổng hai số ghi trên chúng là số chẵn bằng

A.

8

55

. B.

14

55

. C.

6

55

. D.

16

55

.

Câu 34: Tích tất cả các nghiệm của phương trình

2

log 4log 5 0

xx+ −=

bằng

A.

10

B.

5

1

10

. C.

4

1

10

. D.

3

1

10

.

Câu 35: Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức

z

thỏa mãn

12 1

zi−− =

là một

đường tròn. Tâm của đường tròn đó có tọa độ là.

C

S

A

B

D

x

y

2

1

_

1

4

_

O

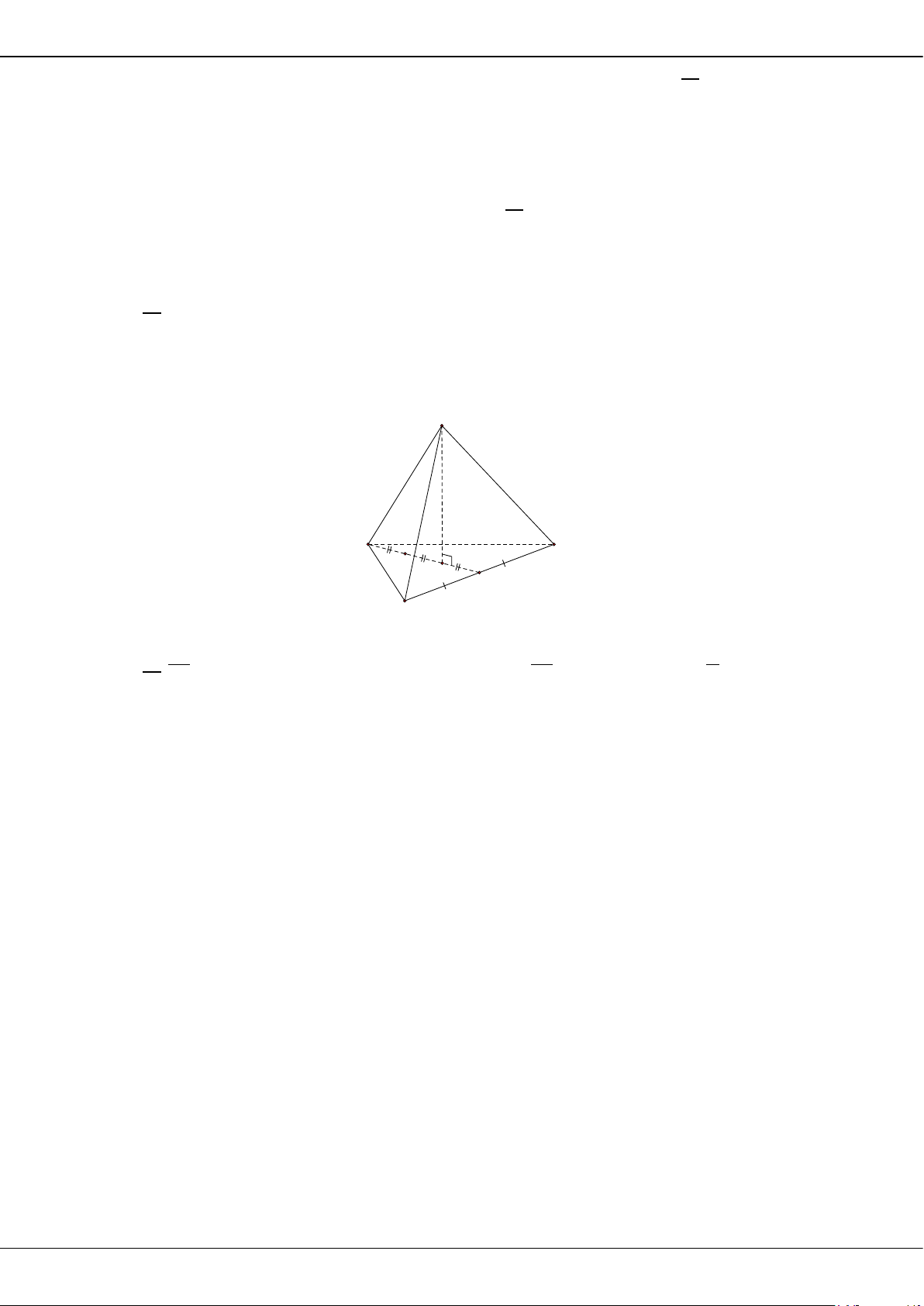
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 90

A.

( )

1; 2−

. B.

( )

1; 2−

. C.

( )

1; 2−−

. D.

( )

1; 2

.

Câu 36: Trong không gian

Oxyz

, điểm nào sau đây thuộc đường thẳng

1

: 12

13

xt

dy t

zt

= +





=−+





=−+



?

A.

( )

1;1; 1

−

B.

( )

1; 2; 3

C.

( )

2; 1; 2

D.

(

)

1;1; 2

Câu 37: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

2;3; 5A −

. Điểm đối xứng với A qua trục

Ox

có tọa độ là

A.

( )

2; 3;5−

. B.

( )

2;3;5−−

. C.

( )

2;3;5

. D.

(

)

2;3; 5−−

.

Câu 38: Cho hình chóp đều

.

S ABC

có chiều cao

,2a AB a=

(tham khảo hình bên). Tính khoảng cách từ

điểm

A

đến mặt phẳng

(

)

SBC

.

A.

3

2

a

. B.

2a

. C.

2

3

a

. D.

2

a

.

H

M

A

B

C

S

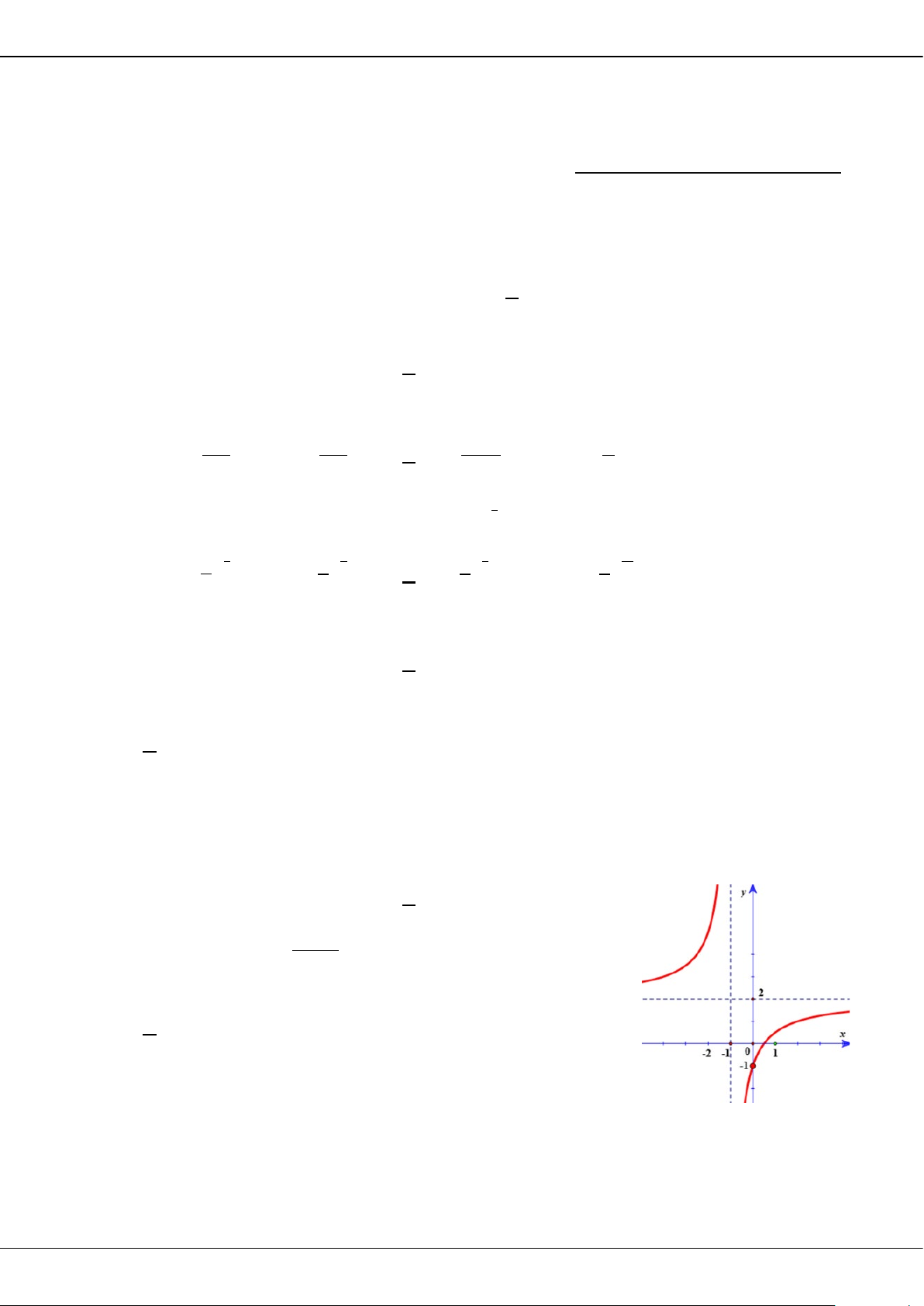
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 91

SỞ GD&ĐT TIỀN GIANG

TRUNG TÂM GDTX TỈNH TIỀN GIANG

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Trong mặt phẳng tọa độ

Oxy

, điểm biểu diễn số phức

43zi= −

có tọa độ là

A.

( )

3; 4−

. B.

(

)

4;3

. C.

( )

4; 3−

. D.

( )

3; 4

.

Câu 2: Phần ảo của số phức

(

)

2

12zi= −

là

A.

5

. B.

4

. C.

4−

. D.

3−

.

Câu 3: Đạo hàm của hàm số

5

logyx=

trên khoảng

( )

0; +∞

là

A.

ln 5

'y

x

=

. B.

'

ln 5

x

y

=

. C.

1

'

ln 5

y

x

=

. D.

1

'y

x

=

.

Câu 4: Trên khoảng

( )

0; +∞

, đạo hàm của hàm số

5

3

yx=

là

A.

8

3

8

yx

′

=

. B.

2

3

5

yx

′

=

. C.

2

3

5

3

yx

′

=

. D.

2

3

5

3

yx

−

′

=

.

Câu 5: Tập nghiệm của bất phương trình

2

39

x+

>

là

A.

( )

;0−∞

. B.

( )

;1−∞

. C.

( )

0; +∞

. D.

( )

1; +∞

.

Câu 6: Cho cấp số nhân

( )

n

u

với

1

2u =

, công bội

3q =

. Số hạng

4

u

của cấp số nhân bằng

A.

54

. B.

11

. C.

12

. D.

24

.

Câu 7: Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

( )

:3 2 0P xz−+=

. Vectơ nào dưới đây là

một vectơ pháp tuyến của

( )

P

?

A.

( )

4

1; 0; 1n =−−



B.

( )

1

3; 1; 2n = −



C.

( )

3

3; 1; 0n = −



D.

( )

2

3; 0; 1n = −



Câu 8: hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ

bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là

A.

( )

0; 1−

. B.

( )

1; 0

.

C.

( )

1; 0−

. D.

( )

0;1

.

Câu 9: Biết tích phân

( )

1

0

3f x dx =

∫

và

( )

1

0

4g x dx = −

∫

. Khi đó

( ) ( )

1

0

f x g x dx+





∫

bằng

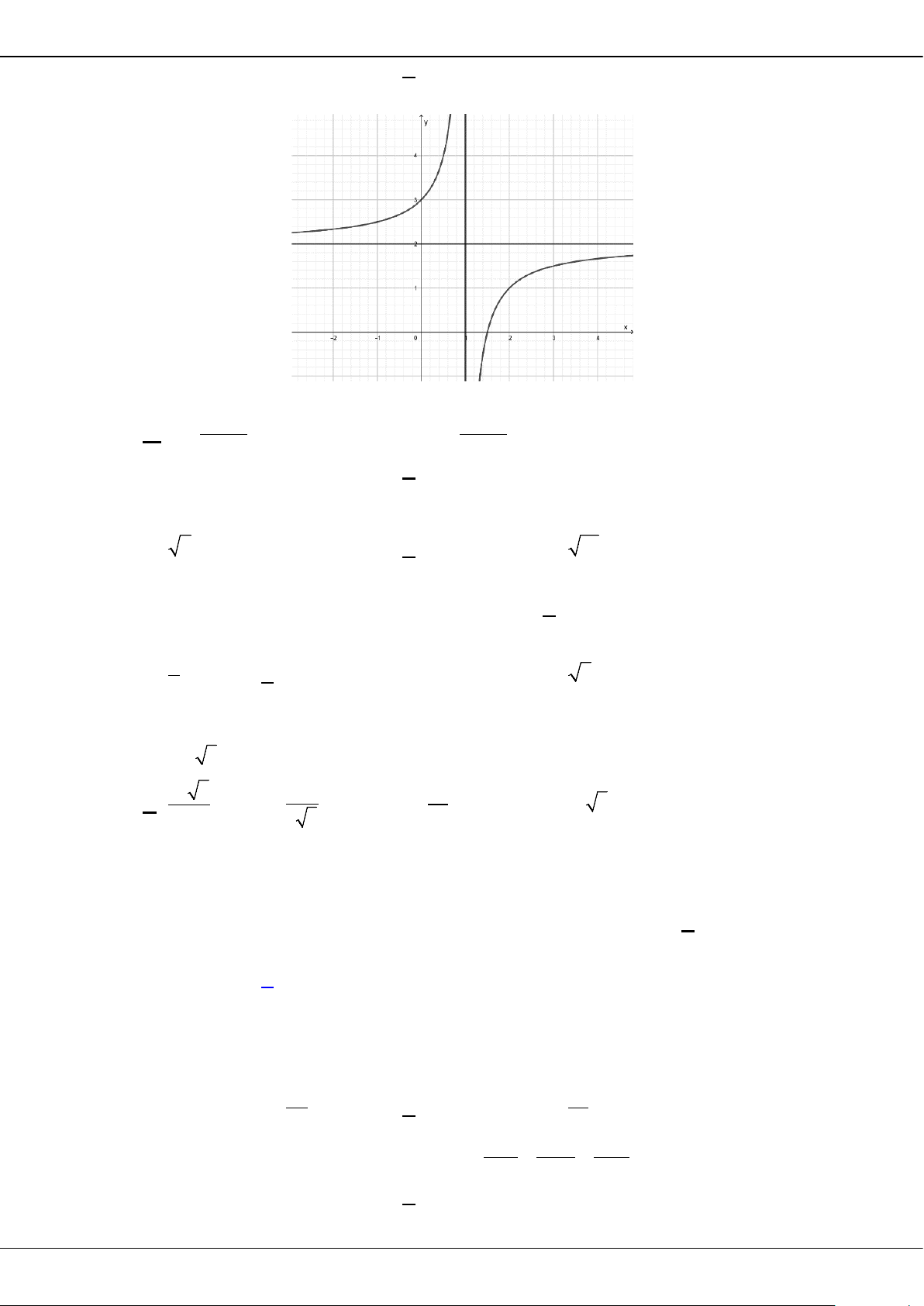
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 92

A.

7

−

. B.

7

. C.

1−

. D.

1

.

Câu 10: Đường cong trong hình vẽ là đồ thị của một trong bốn hàm số bên dưới. Đó là hàm số nào?

A.

42

22yx x

 

. B.

3

32yx x

.

C.

23

1

x

y

x







. D.

21

1

x

y

x







.

A.

7−

. B.

7

. C.

1−

. D.

1

.

Câu 11: Trong không gian

Oxyz

, cho mặt cầu

2 22

( ): 2 2 7 0Sx y z x z+ + + − −=

. bán kính của mặt cầu đã

cho bằng

A.

7

. B.

9

. C.

3

. D.

15

.

Câu 12: Trong không gian

Oxyz

, góc giữa hai mặt phẳng

( )

Oxy

và

( )

Oxz

bằng

A.

30



B.

45



C.

60



D.

90



Câu 13: Thể tích của khối lập phương cạnh bằng 1 là

A.

1

3

. B.

1

. C.

3

. D.

3

.

Câu 14: Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông cạnh

,a

cạnh bên

SA

vuông góc với đáy,

3.SA a=

Thể tích khối chóp

.S ABCD

là

A.

3

.

3

a

B.

3

.

33

a

C.

3

.

3

a

D.

3

3.a

Câu 15: Cho mặt phẳng

( )

P

cắt mặt cầu

( )

;S OR

theo thiết diện là một đường tròn. Gọi

d

là khoảng

cách từ

O

đến

(

)

P

. Khẳng định nào dưới đây đúng?

A.

dR=

. B.

dR>

. C.

2dR=

. D.

dR<

.

Câu 16: Câu 16: Số phức

56i+

có phần thực bằng

A.

5−

. B.

5

. C.

6−

. D.

6

.

Câu 17: Cho hình nón có bán kính đáy

2

r =

và độ dài đường sinh

5l =

. Diện tích xung quanh của

hình nón đã cho bằng

A.

20

π

. B.

20

3

π

. C.

10

π

. D.

10

3

π

Câu 18: Trong không gian

Oxyz

, đường thẳng

123

:

2 12

−−−

= =

−

xy z

d

đi qua điểm nào sau đây?

A.

( )

2; 1; 2−Q

. B.

( )

1;2;3−−−M

. C.

( )

1; 2; 3P

. D.

( )

2; 1; 2−−N

.

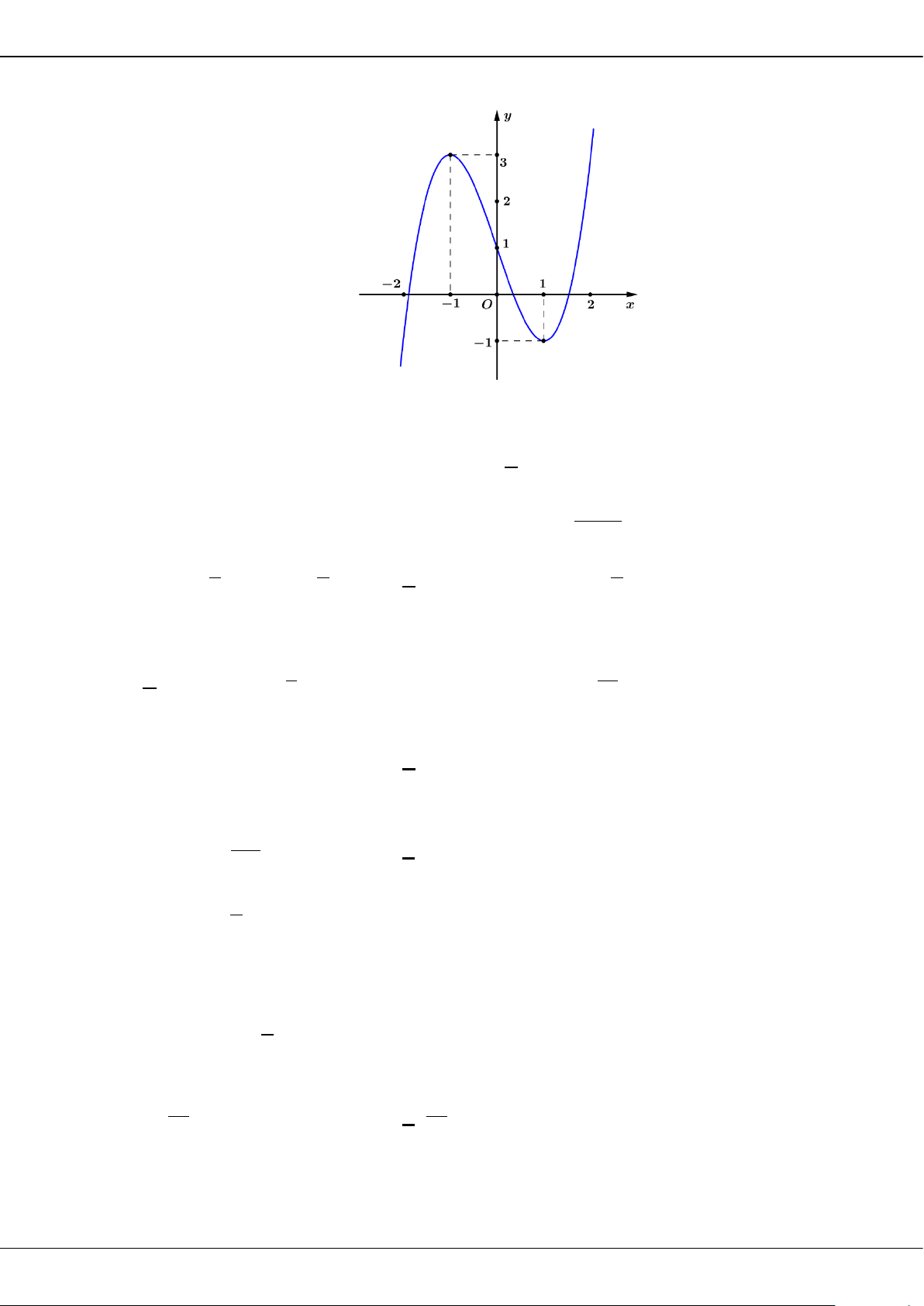
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 93

Câu 19: Hàm số

 

y fx



có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

A. Đồ thị hàm số có điểm cực tiểu là

 

1; 3

. B. Đồ thị hàm số có điểm cực tiểu là

 

1;1

.

C. Đồ thị hàm số có điểm cực đại là

 

1; 1

.

D. Đồ thị hàm số có điểm cực tiểu là

 

1; 1

Câu 20: Phương trình đường tiệm cận ngang của đồ thị hàm số

34

21

x

y

x

−

=

+

là

A.

1

2

x

= −

. B.

3

2

y

=

. C.

2y = −

. D.

1

2

y = −

.

Câu 21: Giải bất phương trình

( )

2

log 3 1 3x −>

.

A.

3x >

B.

1

3

x<<

C.

3x <

D.

10

3

x >

Câu 22: Cho tập hợp

M

có

10

phần tử. Số tập con gồm hai phần từ của

M

là

A.

8

10

A

B.

2

10

A

C.

2

10

C

D.

2

10

Câu 23: Hàm số

( )

Fx

là một nguyên hàm của hàm số

lnyx=

trên

( )

0;+∞

nếu

A.

( )

1

, 0;

ln

Fx x

x

′

= ∀ ∈ +∞

. B.

( ) (

)

ln , 0;Fx x x

′

= ∀ ∈ +∞

.

C.

( ) ( )

1

, 0;Fx x

x

′

= ∀ ∈ +∞

. D.

( ) ( )

, 0;

x

Fx e x

′

= ∀ ∈ +∞

.

Câu 24: Cho

( )

3

1

d 18fx x=

∫

. Khi đó

(

)

3

1

52 dfx x−





∫

bằng

A.

46.

B.

26.

C.

16.

D.

31.

Câu 25: Họ nguyên hàm của hàm số

( )

4

sinfx x x= +

là

A.

5

cos

5

x

xC++

. B.

5

cos

5

x

xC−+

.

C.

3

4 cosx xC−+

. D.

3

4 cosx xC++

.

Câu 26: Cho hàm số

( )

y fx=

có bảng biến thiên như sau

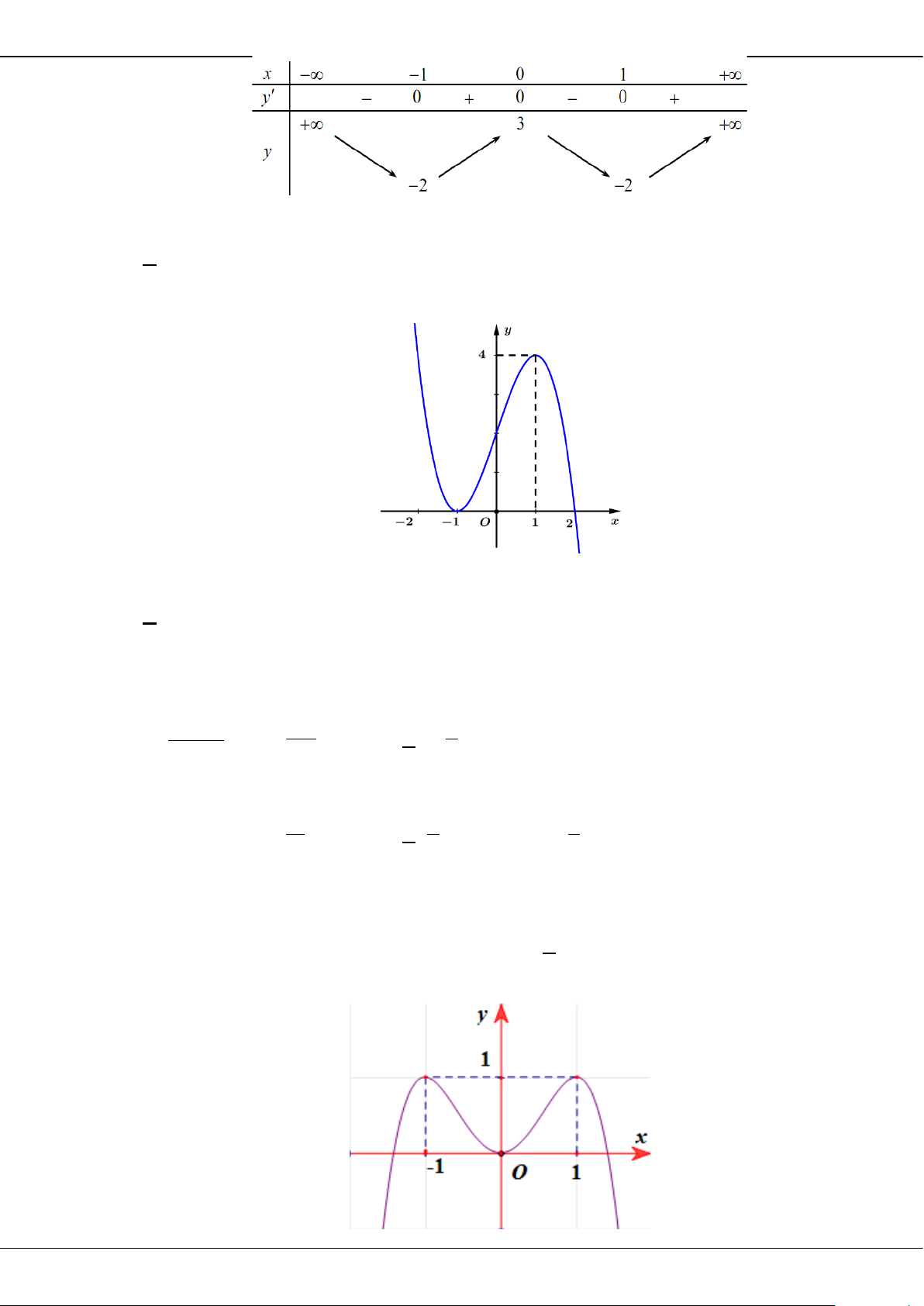
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 94

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A.

( )

0; 1

. B.

(

)

;0−∞

. C.

(

)

1; +∞

. D.

( )

1; 0−

.

Câu 27: Cho hàm số

(

)

fx

liên tục trên



và có đồ thị như hình vẽ sau

Khẳng định nào sau đây là đúng?

A. Hàm số đạt cực tiểu tại

1x = −

. B. Hàm số không có điểm cực trị.

C. Hàm số đạt cực đại tại

4x =

. D. Giá trị cực tiểu của hàm số bằng

1−

.

Câu 28: Với

a

là số thực dương tùy ý,

( )

ln 7 ln 3aa−

bằng

A.

( )

ln 7

ln 3

a

. B.

ln 7

ln 3

. C.

7

ln

3

. D.

(

)

ln 4a

.

Câu 29: Diện tích của hình phẳng giới hạn bởi đồ thị hàm số

2

2yx x= +−

và trục hoành bằng

A.

9

. B.

13

6

. C.

9

2

. D.

3

2

.

Câu 30: Cho hình chóp

ABCD

có đáy là hình vuông cạnh

a

SA

vuông góc với đáy và

SA a=

. Góc giữa

hai mặt phẳng

( )

ABCD

và

( )

SCD

bằng

A.

30°

. B.

90°

. C.

60°

.

D.

45°

.

Câu 31: Cho hàm số

( ) ( )

42

,,f x ax bx c a b c=++ ∈

. Đồ thị của hàm số

( )

y fx=

như hình vẽ bên.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 95

Số nghiệm của phương trình

(

)

4 30

fx

−=

là

A.

4

. B.

3

. C.

2

. D.

0

.

Câu 32: Cho hàm số

( )

y fx

=

có đạo hàm

( ) ( )

3

2f x xx

′

= −

, với mọi

x

∈

. Hàm số đã cho nghịch biến

trên khoảng nào dưới đây?

A.

( )

1; 3

. B.

( )

1; 0−

. C.

( )

0; 1

. D.

( )

2; 0

−

.

Câu 33: Một đoàn đại biểu gồm

5

người được chọn ra từ một tổ gồm

8

nam và

7

nữ để tham dự hội nghị.

Xác suất để chọn được đoàn đại biểu có đúng

2

người nữ là

A.

56

143

. B.

140

429

. C.

1

143

. D.

28

715

.

Câu 34: Biết phương trình

( )

2

22

log 2log 2 1 0xx− −=

có hai nghiệm

12

,xx

. Giá trị của

12

.xx

bằng

A.

4.

B.

1

.

8

C.

3.−

D.

1

.

2

Câu 35: Trong không gian

Oxy

, tập hợp các điểm

M

biểu diễn số phức

z

thỏa mãn

32zi−+=

là

A. đường tròn

( ) ( )

22

3 14xy− ++ =

. B. đường tròn

3 20xy−+=

.

C. đường tròn

( ) ( )

22

3 14xy+ +− =

. D. đường tròn

( ) ( )

22

3 12xy− ++ =

.

Câu 36: Trong không gian

Oxyz

, phương trình chính tắc của đường thẳng

CD

với

(1; 1; 2)C

và

( 4; 3; 2)D −−

là

A.

432

1 22

xyz+ −+

= =

−−

. B.

112

1 22

xyz−−−

= =

−−

.

C.

112

52 4

xyz+++

= =

−−

. D.

432

52 4

xyz+ −+

= =

−−

.

Câu 37: Trong không gian

Oxyz

, điểm đối xứng với điểm

( )

4; 5;3M −

qua trục

Oz

có tọa độ là

A.

( )

4;5;3−−

. B.

( )

4;5;3−

. C.

( )

4;5; 3−−

. D.

( )

0;0;3

.

Câu 38: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

B

,

AB a

=

,

SA

vuông góc với mặt phẳng

đáy và

2SA a=

. Khoảng cách từ

A

đến mặt phẳng

( )

SBC

bằng

A.

25

5

a

. B.

5

3

a

. C.

22

3

a

. D.

5

a

.

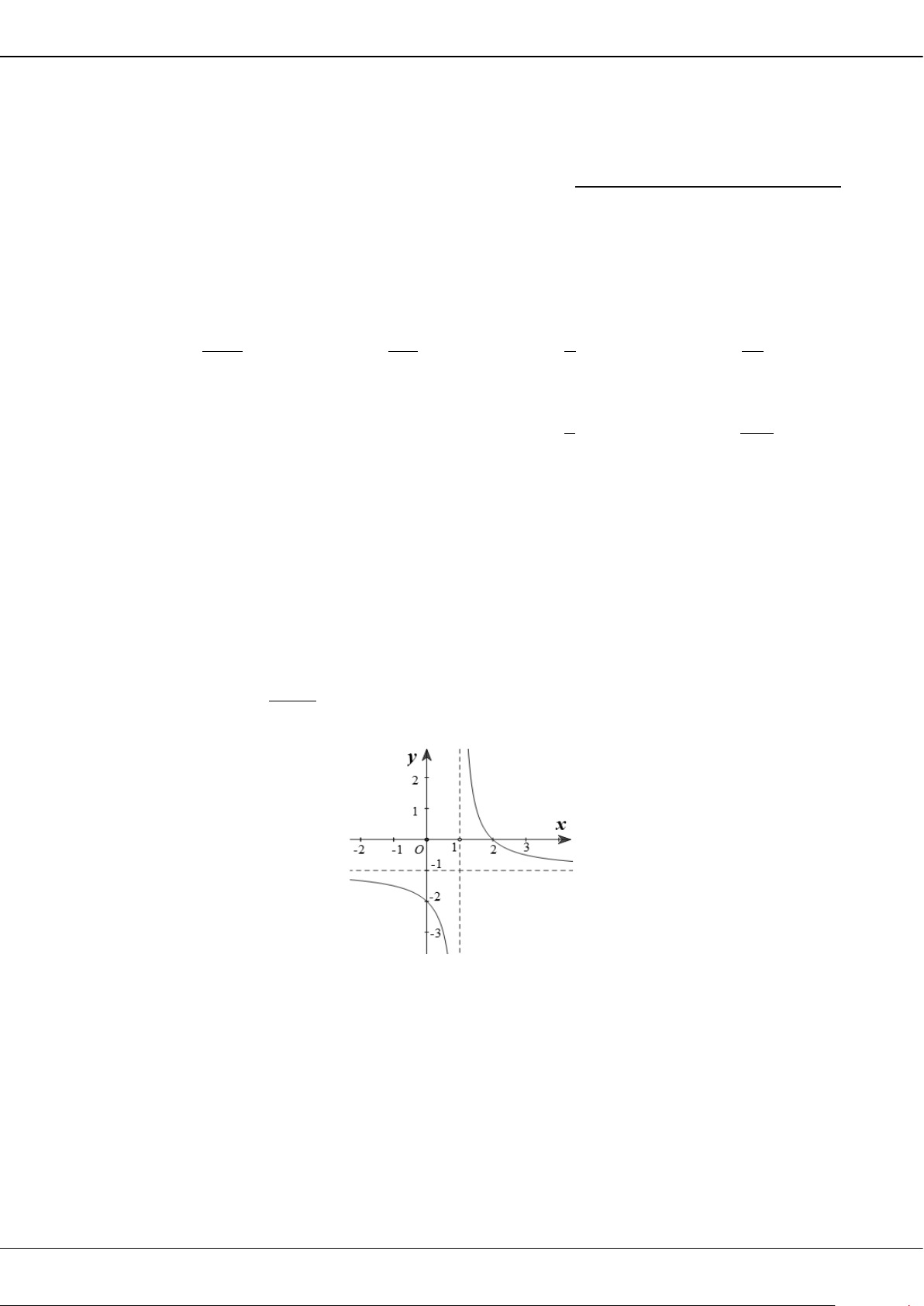
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 96

SỞ GD&ĐT TIỀN GIANG

TRUNG TÂM GDTX GÒ CÔNG TÂY

ĐỀ ÔN THI TỐT NGHIỆP THPT NĂM 2023

MÔN : TOÁN

Thời gian làm bài: 90 phút.

Câu 1: Cho số phức

45zi=−+

. Biểu diễn hình học của

z

là điểm có tọa độ

A.

( )

4;5

−

B.

(

)

4; 5

−−

C.

( )

4; 5−

D.

( )

4;5

Câu 2: Trên khoảng

( )

0; +∞

, đạo hàm của hàm số

2

log

yx=

là:

A.

1

'

ln 2

y

x

=

. B.

ln 2

'

y

x

=

. C.

1

'y

x

=

. D.

1

'

2

y

x

=

.

Câu 3: Trên khoảng

( )

0; +∞

, đạo hàm của hàm số

e

yx

là

A.

1e

y ex

+

′

=

. B.

1

e

y ex

−

′

=

.

C.

1

e

yx

e

−

′

=

. D.

1

e

yx

e

+

′

=

+

.

Câu 4: Tập nghiệm của bất phương trình

1

28

x+

>

là

A.

( )

;2−∞

. B.

(

]

;2−∞

. C.

[

)

2; +∞

. D.

( )

2; +∞

.

Câu 5: Cho cấp số cộng

( )

n

u

có

1

3u =

và

2

1u = −

. Công sai của cấp số cộng đó bằng

A.

1

. B.

4−

. C.

4

. D.

2

.

Câu 6: Trong không gian

Oxyz

, cho 3 điểm

( )

2; 1; 3M −

,

( )

1; 0; 2N

;

( )

2; 3; 5P −

. Tìm một vectơ pháp

tuyến

n



của mặt phẳng

( )

MNP

.

A.

( )

12; 4;8n



. B.

( )

8;12; 4n



. C.

( )

3;1; 2n



. D.

( )

3; 2;1n



.

Câu 7: Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị

hàm số đã cho và trục hoành là

A.

( )

0;2

. B.

( )

2;0

. C.

( )

0; 2−

. D.

( )

1;0

.

Câu 8: Biết

( )

2

1

d6fx x=

∫

,

( )

5

2

d1fx x=

∫

, tính

( )

5

1

dI fx x=

∫

.

A.

5I

=

. B.

5I = −

. C.

7I =

. D.

4I =

.

Câu 9: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 97

A.

42

2

x

yx

+

= −

. B.

3

x

yx+

= −

. C.

42

2x

yx

−

=

. D.

42

3

x

yx

−

= −

.

Câu 10: Trong không gian

Oxyz

, cho mặt cầu

( )

2 22

: 2 4 20Sx y z y z+ + − + −=

. Bán kính mặt cầu bằng

A.

1

. B.

7

. C.

22

. D.

7

.

Câu 11: Trong không gian

Oxy

, góc giữa hai trục

Ox

và

Oz

bằng

A.

30



B.

45



C.

60



D.

90



Câu 12: Cho số phức

35zi= +

, phần ảo của số phức

2

z

bằng

A.

16

. B.

30

. C.

16−

. D.

30−

.

Câu 13: Cho khối lăng trụ đứng có chiều cao bằng

3

và đáy là tam giác đều có độ dài cạnh bằng

2

. Tính

thể tích khối lăng trụ đã cho

A.

3

. B.

33

. C.

3

. D.

6

.

Câu 14: Cho khối chóp

.S ABC

có đáy là tam giác vuông tại

.B

Biết

3,BC a AB a= =

,

SA

vuông góc

với đáy,

23SA a=

. Thể tích khối chóp

.S ABC

bằng

A.

3

3.

a

B.

3

.

3

a

C.

3

3.

a

D.

3

.a

Câu 15: Trong không gian

Oxyz

, cho hai mặt cầu

( ) ( )

2

22

:3 9S x yz− ++=

và

( ) ( )

2

22

': 2 4S x yz+ ++=

. Khẳng định nào sau đây là đúng?

A. Hai mặt cầu tiếp xúc ngoài. B. Hai mặt cầu tiếp xúc trong.

C. Hai mặt cầu không có điểm chung. D. Hai mặt cầu có nhiều hơn một điểm chung.

Câu 16: Phần thực của số phức

42zi= −

bằng

A.

2−

. B.

4−

. C. 2. D. 4.

Câu 17: Diện tích xung quanh của hình nón có bán kính đáy

5r cm=

và độ dài đường sinh

7l cm=

bằng

A.

2

60 ( )

cm

π

B.

2

175 ( ).cm

π

C.

2

70 ( ).cm

π

D.

2

35 ( ).cm

π

Câu 18: Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

( )

P

có phương trình

2 3 20x yz+ − −=

. Điểm nào sau đây thuộc mặt phẳng

( )

P

?

A.

( )

1; 2; 3

−

. B.

( )

1; 2; 3

−

. C.

( )

1; 2;1

. D.

( )

1; 2; 2−

.

Câu 19: Cho hàm số

42

y ax bx c=++

có đồ thị là đường cong trong hình bên. Điểm cực tiểu của đồ thị

hàm số đã cho có tọa độ là

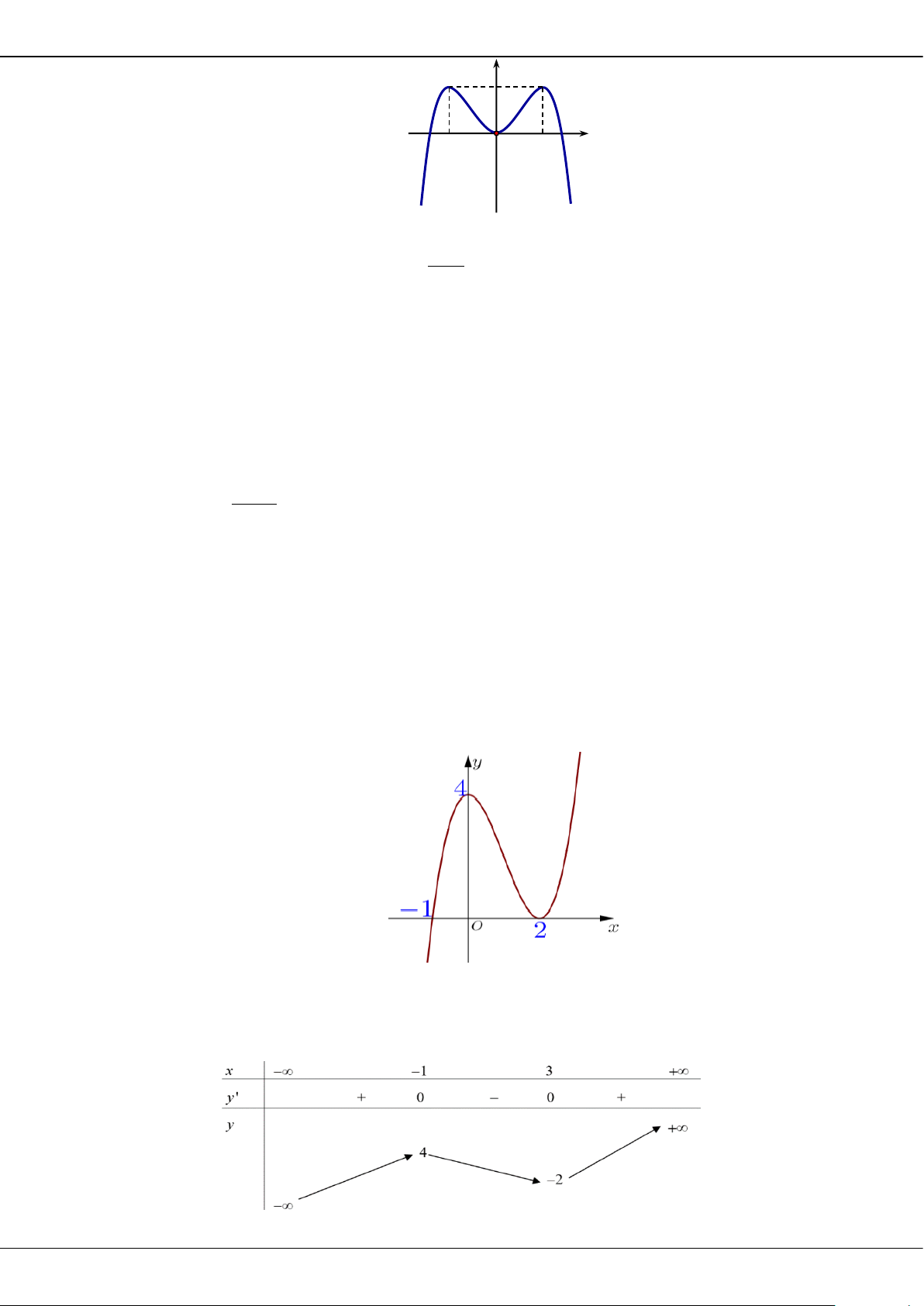
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 98

A.

( 1; 1)−

. B.

(0;1)

. C.

(1; 1)

. D.

(0; 0)

.

Câu 20: Tiệm cận đứng của đồ thị hàm số

1

3

x

y

x

−

=

−

là đường thẳng có phương trình

A.

3x = −

. B.

1x = −

. C.

1

x

=

. D.

3x =

.

Câu 21: Tập nghiệm của bất phương trình

( )

2

log x 1 3+<

là

A.

(

)

;8S

= −∞

. B.

( )

;7S = −∞

. C.

( )

1; 8S = −

. D.

(

)

1; 7

S = −

.

Câu 22: Cho tập hợp

{ }

1; 2;3;4;5

M =

. Số tập con gồm hai phần tử của tập hợp

M

là:

A. 11. B.

2

5

A

. C.

2

5

C

. D.

2

P

.

Câu 23: Cho

( )

cos3 .x dx F x C= +

∫

. Khẳng định nào dưới đây đúng?

A.

( )

sin 3

3

x

Fx

′

=

. B.

( )

cos3Fx x

′

=

. C.

( )

3sin3Fx x

′

=

. D.

(

)

3sin3Fx x

′

= −

.

Câu 24: Cho

( )

4

2

d 10fx x=

∫

. Tính

( )

4

2

3 5dI fx x= −





∫

A.

10I

=

. B.

15I

=

. C.

5

I = −

. D.

20I

=

.

Câu 25: Họ tất cả các nguyên hàm của hàm số

( )

2

3 2cosfx x x= −

là

A.

( )

3

3 2sinFx x x C=++

. B.

( )

3

2sinFx x x C=−+

.

C.

( )

3

3 2sinFx x x C=−+

. D.

( )

3

sinFx x x C

=++

.

Câu 26: Cho hàm số bậc ba

( )

y fx=

có đồ thị như hình sau

Hàm số

( )

y fx=

nghịch biến trên khoảng nào dưới đây?

A.

( )

0;2

. B.

( )

;1

−∞ −

. C.

( )

2;4

. D.

( )

1;2−

.

Câu 27: Cho hàm số

()y fx=

có bảng biến thiên như sau

Giá trị cực đại của hàm số đã cho là

O

x

y

1

−

1

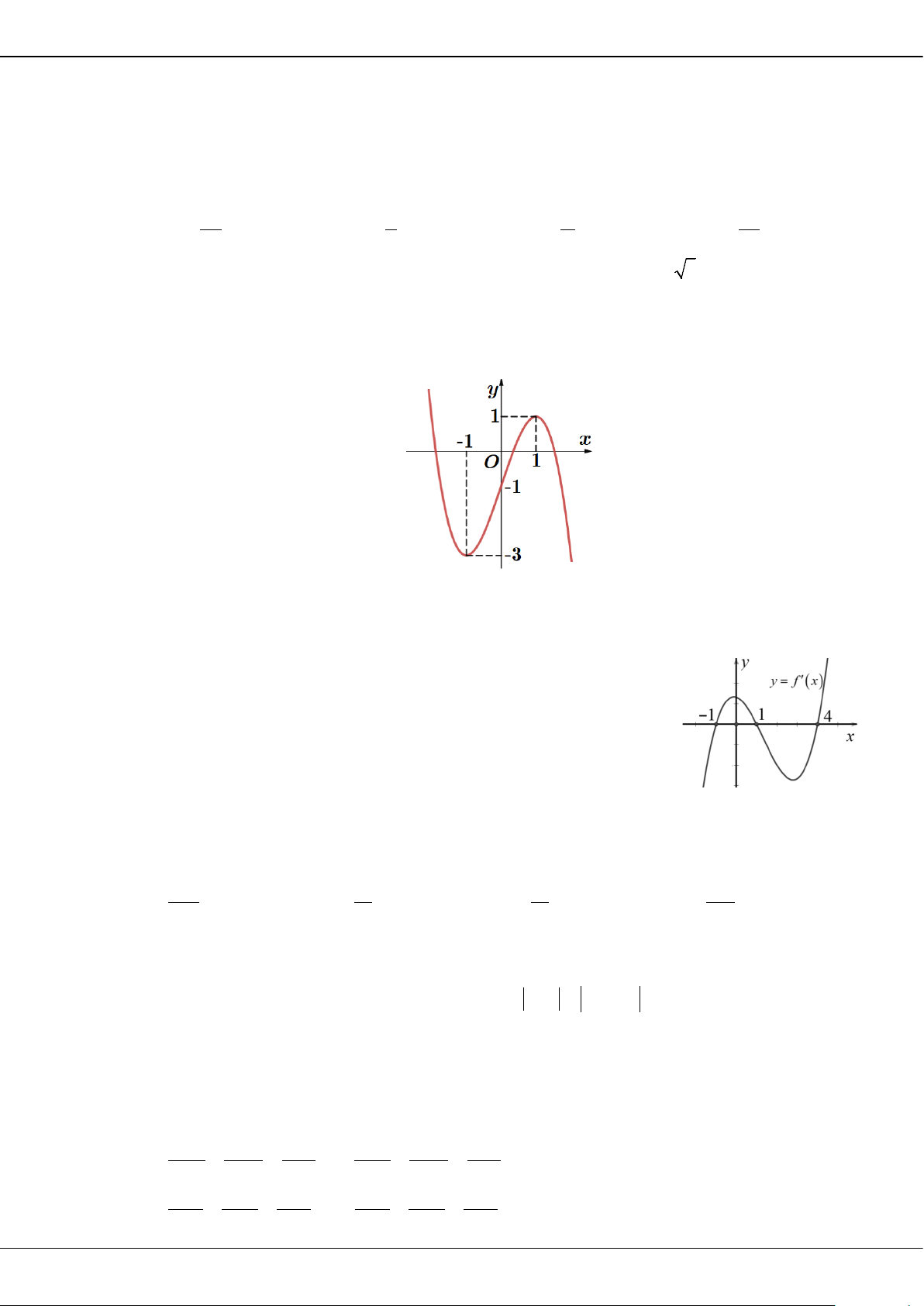
LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 99

A.

1.

−

B.

4.

C.

3.

D.

2.−

Câu 28: Kết quả thu gọn biểu thức

(

)

( )

ln 4 ln 2Px x

= −

là

A.

( )

ln 2Px=

. B.

ln 2

P =

. C.

( )

ln 8 .Px=

D.

( )

2

ln 8Px=

Câu 29: Giả sử

D

là hình phẳng giới hạn bởi đường parabol

2

32

yx x=−+

và trục hoành. Quay

D

quanh trục hoành ta thu được khối tròn xoay có thể tích bằng

A.

30

V

π

=

. B.

1

6

V =

. C.

6

V

π

=

. D.

1

30

V =

.

Câu 30: Cho hình hộp chữ nhật

.' ' ' 'ABCD A B C D

,

, 2, 3BC a AC a A A a

′

= = =

. Tính góc giữa mặt

phẳng

(

)

''BCD A

và mặt phẳng

( )

ABCD

.

A.

30

°

. B.

45°

. C.

60°

. D.

90°

.

Câu 31: Cho hàm số bậc ba

( )

y fx=

có đồ thị là đường cong trong hình bên.

Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

( )

1fx m+=

có hai nghiệm

không âm?

A.

2

B.

1

C.

3

D.

4

Câu 32: Cho hàm số bậc bốn

(

)

y fx

=

. Hàm số

( )

y fx

′

=

có đồ thị như hình

vẽ sau. Hàm số

(

)

y fx

=

nghịch biến trên khoảng nào trong các

khoảng sau?

A.

( )

1;4

. B.

( )

1;1−

.

C.

(

)

0;3

. D.

( )

;0−∞

.

Câu 33: Thầy Bình đặt lên bàn

30

tấm thẻ đánh số từ

1

đến

30

. Bạn An chọn ngẫu nhiên

10

tấm thẻ.

Tính xác suất để trong

10

tấm thẻ lấy ra có

5

tấm thẻ mang số lẻ,

5

tấm mang số chẵn trong đó

chỉ có một tấm thẻ mang số chia hết cho

10

.

A.

99

667

. B.

8

11

. C.

3

11

. D.

99

167

.

Câu 34: Tích các nghiệm của phương trình

2

22

log 3log 2 0xx− +=

là

A.

3

. B.

6

. C.

8

. D.

2

.

Câu 35: Tập hợp các điểm biểu diễn số phức

z

thỏa mãn

( )

1z i iz−= +

là một đường tròn, tâm của

đường tròn đó có tọa độ là

A.

( )

1;1

. B.

( )

0; 1−

. C.

( )

0;1

. D.

( )

1;0−

.

Câu 36: Trong không gian

Oxyz

, cho ba điểm

( )

3; 1 ;2A −

,

( )

0;1;3B

và

( )

1;1;1C −

. Đường thẳng đi

qua

C

và song song với đường thẳng

AB

có phương trình là:

A.

3 21

11 1

xyz+−−

= =

−

. B.

3 21

11 1

xyz−++

= =

−

.

C.

111

32 1

xyz−++

= =

−

. D.

111

32 1

xyz+−−

= =

−

.

LỜI GIẢI BỘ ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN NĂM 2023 – TỈNH TIỀN GIANG

Trang 100

Câu 37: Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

( )

2; 0; 1A −

,

( )

1; 2; 3B −

,

( )

0; 1; 2C

. Tìm tọa

độ điểm

O

′

là điểm đối xứng với gốc tọa độ

O

qua mặt phẳng

(

)

ABC

.

A.

11

1; ;

22

O



′





. B.

( )

2;1;1O

′

. C.

( )

10;5;5O

′

− −−

. D.

11

2; ;

22

O



′





.

Câu 38: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

B

,

AB a=

,

3AC a=

và

SA

vuông góc với

mặt phẳng đáy. Khoảng cách từ

C

đến mặt phẳng

( )

SAB

bằng

A.

2a

. B.

2a

. C.

a

. D.

22a

.

---------- HẾT ----------

BẢNG ĐÁP ÁN

1.A

2.A

3.B

4.D

5.B

6.D

7.B

8.C

9.A

10.B

11.D

12.D

13.B

14.D

15.A

16.D

17.C

18.C

19.D

20.D

21.D

22.C

23.B

24.D

25.B

26.A

27.B

28.B

29.A

30.B

31.A

32.A

33.A

34.B

35.B

36.D

37.B

38.B

Bộ đề ôn thi tốt nghiệp THPT 2023 môn Toán sở GD&ĐT Tiền Giang

Tài liệu liên quan:

Đề cuối kì 2 Toán 11 năm 2024 – 2025 trường THPT Lương Ngọc Quyến – Thái Nguyên

Đề kiểm tra cuối học kì 2 Toán 11 năm 2024 – 2025 sở GD&ĐT Bắc Giang

Đề cuối học kỳ 2 Toán 10 năm 2024 – 2025 trường THPT Nguyễn An Ninh – TP HCM

Đề học kỳ 2 Toán 11 năm 2024 – 2025 trường THPT Nguyễn Tất Thành – TP HCM

Đề cuối học kì 2 Toán 11 năm 2023 – 2024 trường THPT Phạm Thành Trung – Tiền Giang