Bộ đề Toán khối 12 – Nguyễn Văn Huy

Bộ đề Toán khối 12 – Nguyễn Văn Huy được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

73 37 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

113 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
å
TÀI LIỆU TỰ HỌC
Nguyễn Văn Huy
Nội dung
5 đề ôn thi học kỳ 2 có đáp án và giải chi tiết.
15 ôn thi THPT Quốc Gia có đáp án và hướng
dẫn giải câu khó.
TÀI LIỆU CỦA: ..........................................................
Địa chỉ lớp học: 66 Đặng Đức Thuật, Phường Tam Hiệp,
TP. Biên Hòa – Tỉnh Đồng Nai.
LƯU HÀNH NỘI BỘ
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 1 Tài liệu ôn thi HK2 – Khối 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG NAI
Nguyễn Văn Huy
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 01
Câu 1. Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
3
31y x x
.
B.
32
31y x x
.
C.
32
31y x x
.
D.
32
31y x x
.
Câu 2. Cho hàm số
y f x
có


2
lim
x
fx
và
. Chọn mệnh đề đúng?
A. Đồ thị hàm số đã cho không có tiệm cận đứng.
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng
2x
và
2x
.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng
2y
và
2y
.
Câu 3. Đồ thị hàm số
42
2y x x
có dạng
A.
-2 -1 1 2
-2
-1
1
2
x
y
B.
-2 -1 1 2
-2
-1
1
2
x
y
C.
-2 -1 1 2
-2
-1
1
2
x
y
D.
-2 -1 1 2
-2
-1
1
2
x
y
Câu 4. Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên
-1
+
∞
+
∞
+
∞
0
0
-1
-
∞
y'
y
x
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng hai cực trị. B. Hàm số có giá trị nhỏ nhất bằng 1.
C. Hàm số có giá trị cực tiểu bằng 0. D. Hàm số không xác định tại
1x
Câu 5. Hàm số
3
32y x x
có giá trị cực đại
ĐC
y
là
A.
1
CĐ
y
. B.
5
CĐ
y
C.
2
CĐ
y
. D.
0
CĐ
y
.
Câu 6. Khoảng đồng biến của hàm số
3
31y x x
là
A.
 ;1
và
1;
.
B.
0;2 .
C.
1;1 .
D.
0;1 .
Câu 7. Cho
0a
và
1a
. Tìm mệnh đề đúng trong các mệnh đề sau
A.
log
a
x
có nghĩa với
x
. B.
log 1
a
a
và
log 1
a
a
C.
log log .log
a a a
xy x y
. D.
log log
n
aa
x n x
0, 0 .xn
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 2 Tài liệu ôn thi HK2 – Khối 12
Câu 8. Giá trị lớn nhất của hàm số
32
3 9 2y x x x
.
trên đoạn

2;2
là
A.
24.
B.
2.
C.
3.
D.
26.
Câu 9. Đặt

12 12
log 6, log 7ab
. Hãy biểu diễn
2
log 7
theo
a
và
b
A.
.
1
a
b
B.
.
1
b
a
C.
.
1
a
b
D.
.
1
b
a
Câu 10. Khối bát diện đều có các mặt là
A. Hình vuông. B. Tam giác đều. C. Hình chữ nhật. D. Tam giác vuông.
Câu 11. Đặt
2
log 3a
. Hãy biểu diễn
6
log 24
theo
a
.
A.
3
.
1
a
a
B.
1
.
3
a
a
C.
3
.
1
a
a
D.
.
1
a
a
Câu 12. Cho
H
là khối lập phương có độ dài cạnh bằng
3 cm
. Thể tích của
H
bằng
A.
3
27 .cm
B.
2
27 .cm
C.
3
9 .cm
D.
3
3 .cm
Câu 13. Cho
0 1.a
Giá trị của biểu thức
2log 3
a
a
bằng
A.
2 2.
B.
3 2.
C.
2 3.
D.
3.
Câu 14. Cho
H
là khối lăng trụ có chiều cao bằng
3,a
đáy là hình vuông cạnh
.a
Thể tích của
H
bằng
A.
3
.a
B.
3
2 .a
C.
3
3 .a
D.
3
4 .a
Câu 15. Cho
01a
. Giá trị của biểu thức
2
3
M 3log
a
aa
bằng?
A.
5
.
2
B.
5.
C.
7.
D.
3
.
2
Câu 16. Biểu thức
3
22K
viết dưới dạng lũy thừa với số mũ hữu tỉ là
A.
5
3
2.
B.
2
3
2.
C.
4
3
2.
D.
1
3
2.
Câu 17. Tìm tất cả các giá trị thực của
a
để biểu thức
2
log 3aB
có nghĩa.
A.
3.a
B.
3.a
C.
3.a
D.
3.a
Câu 18. Cho
.ABC A B C
là khối lăng trụ đứng có
5, ,A B a AB a
đáy
ABC
có diện tích
bằng
2
3a
. Thể tích của khối lăng trụ
.ABC A B C
bằng
A.
3
.a
B.
3
2.a
C.
3
4.a
D.
3
6.a
Câu 19. Nếu độ dài các cạnh của khối hộp chữ nhật tăng lên
3
lần thì thể tích của khối hộp chữ
nhật sẽ tăng lên
A.
3
lần .B.
9
lần. C.
27
lần. D.
81
lần.
Câu 20. Cho
H
là khối hộp chữ nhật có độ dài cạnh bằng
,2 ,3a a a
. Thể tích của
H
bằng
A.
3
.a
B.
3
2.a
C.
3
4.a
D.
3
6.a
Câu 21. Đường thẳng
3yx
cắt đồ thị hàm số

32
2 2y x x
tại điểm có tọa độ
00
;xy
thì
A.
0
1y
. B.

0
3y
. C.

0
2y
. D.

0
1y
.
Câu 22. Cho khối chóp
H
có thể tích là
3
2a
, đáy là hình vuông cạnh
2a
. Độ dài chiều cao
khối chóp
H
bằng
A.
4.a
B.
3.a
C.
2.a
D.
.a
Câu 23. Cho khối lăng trụ
H
có thể tích là
3
4a
, đáy là tam giác vuông cân có độ dài cạnh
huyền bằng a
2
. Độ dài chiều cao khối lăng trụ
H
bằng
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 3 Tài liệu ôn thi HK2 – Khối 12
A.
2.a
B.
4.a
C.
6.a
D.
8.a
Câu 24. Giá trị lớn nhất của hàm số

2
33
1
xx
y
x
trên đoạn



1
2;
2
bằng.
A.
3.
B.
4.
C.
7
.
2
D.
13
.
3
Câu 25. Nếu độ dài chiều cao của khối chóp tăng lên 5 lần ,diện tích đáy không đổi thì thể tích
của khối chóp sẽ tăng lên
A.
5
lần. B.
10
lần. C.
15
lần. D.
20
lần.
Câu 26. Cho hàm số
32
3 5 1y x x x
có đồ thị
C
. Tiếp tuyến với đồ thị
C
tại điểm có hệ
số góc lớn nhất, có phương trình là
A.
2.yx
B.
2 1.yx
C.
2.yx
D.
2 2.yx
Câu 27. Hàm số
4 2 2
( 3) 2y x m x m
có đúng một cực trị khi và chỉ khi:
A.
3.m
B.
0.m
C.
3.m
D.
3.m
Câu 28. Tìm tất cả các giá trị thực của tham số
m
để của hàm số
22
2 ) 1(y x x m m
có ba
điểm cực trị là ba đỉnh của một tam giác vuông.
A.
2
.
3
m
B.
1.m
C.
3
3.m
D.
1
.
3
m
Câu 29. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số


2
11
1
mx
y
xx
có
đúng một đường tiệm cận ngang.
A. Không có giá trị nào của
m
thỏa mãn. B.
.m
C.
0.m
D.
1.m
Câu 30. Tìm tất cả các giá trị thực của tham số
m
để hàm số
sin
sin
xm
y
xm
đồng biến trên



;0 .
2
A.
1.m
B.
0.m
C.
1 0.m
D.
0.m
Câu 31. Cho một tấm nhôm hình chữ nhật có chiều dài bằng
12 cm
và chiều rộng bằng
10 cm
. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình
vuông có cạnh bằng
,x cm
rồi gập tấm nhôm lại như hình vẽ dưới đây để được một
cái hộp không nắp.
Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
12 3 5
.
2
x
B.
11 31
.
3
x
C.
11 31
.
3
x
D.
10 2 7
.
3
x
Câu 32. Cho hai số thực
vàab
, với
01ba
. Khẳng định nào dưới đây là đúng?
A.
log 0 log .
ab
ba
B.
0 log log .
ab
ba
C.
log log 0.
ba
ab
D.
log log 0.
ab
ba
Câu 33. Hàm số
3 2 2
1
2 3 2 1
3
y x m x m x m
không có cực trị khi và chỉ khi
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 4 Tài liệu ôn thi HK2 – Khối 12
A.
  1.3m m
B.
3 1.m
C.
3.m
D.
1.m
Câu 34. Gọi
I
là giao điểm hai đường tiệm cận của hypebol
1
1
:H
x
y
x
. Tiếp tuyến với đồ thị
H
tại điểm
0; 1M
cắt hai đường tiệm cận của
H
tại hai điểm
A
và
B
. Khi đó
diện tích tam giác
ABI
bằng
A.
8
đvdt. B.
6
đvdt. C.
4
đvdt. D.
2
đvdt.
Câu 35. Tìm các giá trị nguyên của tham số
m
để đồ thị hàm số
42
4 2 4 1y x m x m
cắt trục
hoành tại 4 điểm phân biệt có hoành độ
1 2 3 4 1 2 3 4
, , , ( )x x x x x x x x
lập thành cấp số cộng
A.
3.m
B.
0, 2.mm
C.
2.m
D.
3.m
Câu 36. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
42
2 3 4y x mx m
có các
cực trị đều nằm trên các trục tọa độ.
A.
1;0;4 .m
B.
1;2;3 .m
C.
1;0;1 .m
D.
( ;0) 4 .m
Câu 37. Cho
 0, 0ab
thỏa mãn

22
7a b ab
. Chọn mệnh đề đúng.trong các mệnh đề
A.
3
lg lg lg .
2
a b a b
B.
2 lg lg lg 7 .a b ab
C.
1
3lg lg lg .
2
a b a b
D.

1
lg lg lg .
32
ab
ab
Câu 38. Cho khối lăng trụ
.,ABC A B C
M
thuộc cạnh
AA
sao cho
3MA MA
. Tỉ số thể tích của
khối lăng trụ
.ABC A B C
và thể tích khối chóp
.M A B C
bằng
A.
4.
B.
8.
C.
12.
D.
18.
Câu 39. Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi 1 triệu đồng, với lãi suất kép
1%/
tháng. Gửi được hai năm
6
tháng người đó có công việc nên đã rút toàn bộ gốc và
lãi về. Số tiền người đó rút được là
A.



30
101. 1,01 1
(triệu đồng). B.



29
101. 1,01 1
(triệu đồng).
C.



30
100. 1,01 1
(triệu đồng). D.



30
100. 1,01 1
(triệu đồng).
Câu 40. Cho khối chóp
.S ABC
có
SAB
là tam giác vuông cân tại
S
và nằm trong mặt phẳng vuông
góc với
,ABC
2AB a
và tam giác
ABC
có diện tích bằng
2
3a
. Thể tích khối chóp
.S ABC
bằng
A.
3
.a
B.
3
3 .a
C.
3
6 .a
D.
3
2 3.a
Câu 41. Cho khối chóp
.S ABC
,
M
là trung điểm của cạnh
SA
. Tỉ số thể tích của khối chóp
.S MBC
và thể tích khối chóp
.S ABC
bằng
A.
1
.
6
B.
1
.
4
C.
1
.
2
D.
1.
Câu 42. Cho khối chóp
.S ABC
;
M
và
N
lần lượt là trung điểm của cạnh
,SA
;SB
thể tích khối
chóp
.S MNC
bằng
3
a
. Thể tích của khối chóp
.S ABC
bằng
A.
3
.a
B.
3
4 .a
C.
3
8 .a
D.
3
12 .a
Câu 43. Cho hình lăng trụ đứng
.,ABC A B C
có góc giữa
AB
và
ABC
bằng
o
45
; đáy
ABC
là
tam giác vuông cân tại
A
và
22BC a
. Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
.a
B.
3
2 .a
C.
3
3 .a
D.
3
4.a
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 5 Tài liệu ôn thi HK2 – Khối 12
Câu 44. Cho hình chóp
.S ABC
có
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc của
S
trên
ABC
là điểm
H
thuộc cạnh
AB
sao cho
2HA HB
. Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
o
60
. Thể tích khối chóp
.S ABC
bằng
A.
3
7
.
4
a
B.
3
7
.
8
a
C.
3
7
.
12
a
D.
3
7
.
16
a
Câu 45. Cho khối chóp
.S ABCD
có
,SA ABCD
SB a
và
ABCD
là hình vuông cạnh
.a
Thể
tích khối chóp
.S ABCD
bằng
A.
3
2
.
3
a
B.
3
.a
C.
3
4
.
3
a
D.
3
2.a
Câu 46. Cho khối chóp
.S ABC
,
M
là trung điểm của cạnh
.BC
Thể tích của khối chóp
.S MAB
là
3
2.a
Thể tích khối chóp
.S ABC
bằng
A.
3
4 .a
B.
3
2 .a
C.
3
1
2
.a
D.
3
.
4
a
Câu 47. Cho hình chóp
.S ABCD
có
SA ABCD
,
5SB a
;
ABCD
là hình thoi cạnh
a
và góc
o
30ABC
. Thể tích khối chóp
.S ABCD
bằng
A.
3
1
.
3
a
B.
3
2
.
3
a
C.
3
3
.
3
a
D.
3
3.a
Câu 48. Cho hình chóp
.S ABC
có
,SA ABC
góc giữa
SB
và
ABC
bằng
o
60
; tam giác
ABC
đều cạnh
.a
Thể tích khối chóp
.S ABC
bằng
A.
3
3.a
B.
3
1
.
4
a
C.
3
1
.
2
a
D.
3
.a
Câu 49. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2 2
1
1 2 1
3
y x m x m x m
nghịch biến trên tập xác định của nó.
A.
1
.
2
m
B.
1.m
C.
0.m
D.
1
.
2
m
Câu 50. Cho hình chóp
SABCD
có đáy
ABCD
là hình vuông cạnh
2a
. Gọi
,PQ
lần lượt là trung
điểm của
,AD CD
. Gọi
H
là trung điểm của
AP
. Tam giác
SAP
là tam giác đều và
SH
vuông góc với mp
ABCD
. Khoảng cách của hai đường thẳng chéo nhau
SP
và
BQ
theo
a
.
A.
3
.
4
a
B.
3
.
2
a
C.
3.a
D.
33
.
4
a
ĐÁP ÁN ĐỀ SỐ 01
1
2
3
4
5
6
7
8
9
10
B
C
A
B
D
C
D
C
B
A
11
12
13
14
15
16
17
18
19
20
C
A
D
C
C
B
A
D
C
D
21
22
23
24
25
26
27
28
29
30
B
B
B
A
A
C
D
B
D
A
31
32
33
34
35
36
37
38
39
40
B
C
B
C
C
D
D
C
A
A
41
42
43
44
45
46
47
48
49
50
C
B
D
C
B
A
A
B
A
D
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 6 Tài liệu ôn thi HK2 – Khối 12
HƯỚNG DẪN GIẢI ĐỀ SỐ 01
Câu 1. Chọn B.
Nhìn đồ thị ta thấy:
Đây là đồ thị của hàm bậc
3
với hệ số
a
dương
Điểm cực trị của hàm số là
0x
và
2.x
Cắt trục tung tại
.0;1M
Câu 2. Chọn C.
Từ


2
lim ( )
x
fx
và

2
lim ( )
x
fx
.
Ta có: hàm số
fx
có tiệm cận đứng tại
2x
và
 2.x
Câu 3. Chọn A.
Hàm số
42
2y x x
có hệ số
0a
, hệ số
c =0.
Do đó đồ thì là hình chữ M, cắt trục tung tại gốc tọa độ.
Câu 4. Chọn B.
Nhìn BBT ta thấy
 1y
là giá trị nhỏ nhất của hàm số.
Câu 5. Chọn D.

x
2
' 3 3
1 4( )
'0
1 0( )
CT
CD
y
x y y
y
x y y
Câu 6. Chọn C.


x
2
1
' 3 3; ' 0
1
x
yy
x
Hệ số
0a
Câu 7. Chọn D.
Câu 8. Chọn C.




y' = 0
2
2;2
1 2;2
) ' 3 6 9
3 2;2
) ( 2) 4
) (2) 24
) ( 1) 3
max 3
x
y x x
x
y
y
y
y
Câu 9. Chọn B.

12
2
12 12 12 12
12
log 7
1: log 7
12
log 2 log 2 log 12 log 6 1
log
6
b b b b
C
a
C2 : Dùng máy casio text.

12
2
12
log 7
log 7 0
1 log 6
Câu 10. Chọn A.
Câu 11. Chọn C.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 7 Tài liệu ôn thi HK2 – Khối 12

2 2 2
6
2 2 2
log 24 log 8 log 3
3
log 24
log 6 log 2 log 3 1
a
a
Câu 12. Chọn A.
33
3 ( )V cm
Câu 13. Chọn D.
2log 3 log 3
22
( ) ( 3) 3
aa
aa
Câu 14. Chọn C.
23
. 3 . 3V B h a a a
Câu 15. Chọn C.



7
2
3
3
7
M 3log 3log 3. log 7
3
a a a
a a a a
Câu 16. Chọn B.



1
1 4 4 2
2
3
3 3 3 3
2 2 2.2 2 2 2K
Câu 17. Chọn A.
Câu 18. Chọn D.
AA'=
AA
2 2 2 2
23
' 5 2
'. 2 .3 6
ABC
A B AB a a a
V S a a a
Câu 19. Chọn C.
Câu 20. Chọn D.
3
.2 .3 6V abc a a a a
Câu 21. Chọn B.
3 2 3 2
00
2 3 3 2 0 1 122x x x x x x x y
Câu 22. Chọn A.
3
23
2
1 1 6
. ( 2 ) 2 3
33
2
a
V B h a a h a
a
Câu 23. Chọn B.
3
23
2
14
. ( 2 ) 4 4
2
a
V B h a h a h a
a
Câu 24. Chọn A.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 8 Tài liệu ôn thi HK2 – Khối 12














22
22
2
2
1
2;
2
(2 3)( 1) ( 3 3).1 2
)'
11
1
0 2;
2
2
) ' 0 0
1
1
2 2;
2
) (0) 3
13
) ( 2)
3
17
)
22
max 3
x x x x x x
y
xx
x
xx
y
x
x
y
y
y
y
Câu 25. Chọn A.
Câu 26. Chọn C.
32
2 2 2
00
3 5 1
' 3 6 5 3( 2 1) 2 3( 1) 2 2
max ' 2 1 2
: 2( 1) 2 2
y x x x
y x x x x x
y x y
PTTT y x x
Câu 27. Chọn A.
4 2 2
( 3) 2
0 3 0 3
y x m x m
ab m m
Câu 28. Chọn B.
2 4 2
3
2
2
) 2 ) 1 2 1
) ' 4 4 (
(
4)
y x x m m x mx m
y x mx x x m
Hàm số đã cho có ba cực trị khi và chỉ khi phương trình
’0y
có ba nghiệm phân
biệt.
Khi và chỉ khi phương trình

2
0xm
có hai nghiệm phân biệt khác
0.
00mm
. Đối chiếu với các phương án trong đề ra thì B là đáp án.
Câu 29. Chọn D.
1 0 1mm
Ta có
0y
là tiệm cận ngang duy nhất của đồ thị hàm số đã cho.

10
( 1)
10
m
ym
m
là tiệm cận ngang của đồ thị hàm số.
Câu 30. Chọn A.
)sin ( 1;0) ( )
tm
x t t y t m
tm
Hàm số đồng biến trên
1;0
khi và chỉ khi






2
2
'0
0
1
( 1;0)
( 1;0)
m
y
m
m
tm
m
m
Câu 31. Chọn B.
Chiều dài của cái hộp là :
12 2 0 .10xx
Chiều rộng của cái hộp là
10 2 .x
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 9 Tài liệu ôn thi HK2 – Khối 12
Chiều cao của cái hộp là :
.x
Thể tích cái hộp là :
12 2 10 2 .V x x x
Tìm giá trị lớn nhất của hàm số
( ) (12 2 )(10 2 )f x x x x
trên
0; 10
ta có
11 31
3
x
Câu 32. Chọn C.
Lấy

1
;3ba
c
thử bằng máy
Câu 33. Chọn B.
22
' 2(2 3)y x m x m
Hàm số không có cực trị khi và chỉ khi phương trình
’0y
vô nghiệm hoặc có nghiệm
kép
2
' 0 3 12 9 0 3 1m m m
Câu 34. Chọn C.
Ta có
1 ;1I
.
Tiếp tuyến của (H) tại
0 ; 1M
là :
2 1.yx
Đường thẳng d cát tiệm cận ngang tại
1 ;1 ,A
cắt tiệm cận đứng tại
1 ; 3B

1
.4
2
ABC
S IA IB
Câu 35. Chọn C.
Đặt

2
( 0)t x t
Đồ thị hàm số cắt Ox tại
4
điểm phân biệt khi và chỉ khi phương trình
2
(4 2) 4 1 0t m t m
có
2
nghiệm dương
2
' 0 4 0 0mm
Mặt khác
1 2 3 4
, , ,x x x x
lập thành một cấp số cộng nên
12
3xx
Suy ra
12
9tt
.Theo vi ét lại ta có

12
12
42
. 4 1
t t m
t t m


2
42
9 4 1 2
10
m
mm
Câu 36. Chọn D.
TH1 : Đồ thị chỉ có một cực trị
0 0 0x ab m
Ta có
(0) 3 4 (0;3 4)y m m Oy
TH2: Đò thị có
3
cực trị
0; 0 0x x m ab m
Ta có
22
( ) 3 4 ( ; 3 4)y m m m m m m Ox
2
1( )
3 4 0
4( / )
ml
mm
m t m
Câu 37. Chọn D.
2 2 2
7 ( ) 9 3
3
1
lg lg (lg lg )
32
ab
a b ab a b ab a b ab ab
ab
ab a b
Câu 38. Chọn C.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 10 Tài liệu ôn thi HK2 – Khối 12



. ' ' ' ' ' '
. ' ' ' ' ' '
. ' ' ' . ' ' '
).
1
).
34
12
ABC A B C A B C
M A B C A B C
ABC A B C M A B C
V S h
h
VS
VV
Câu 39. Chọn A.
30 30
1
1 1 (1 ) 1,01 1 (1,01) 101 (1,01) 1
0,01
n
A
P r r
r
Câu 40. Chọn A.
Gọi H là trung điểm của AB.

23
1
()
2
1
3.
3
SH ABC SH HB AB a
V a a a
Câu 41. Chọn C.
Theo công thức tính thể tích tỷ số thể tích

.
.
1
2
S MBC
S ABC
V
SM
V SA
Câu 42. Chọn B.
Theo công thức tính tỷ số thể tích

.
.
.1
.4
S MNC
S ABC
V
SM SN
V SA SB
Câu 43. Chọn D.


0
3
. ' ' '
' 45
2 ' 2
. ' 4
ABC A B C ABC
A BA
AB a A A a
V V A A a
Câu 44. Chọn C.
Gọi
I
là trung điểm của
.AB
CI AB




2
2
22
00
23
.
3 28
)
2 36 6
28 21
) 60 .tan 60 . 3
63
1 3 21 7
) . .
3 4 3 12
S ABC
a a a
CH CI IH
aa
SCH SH CH
a a a
V
Câu 45. Chọn B.
22
23
.
)3
11
. . 3 .
33
S ABC ABCD
SA SB AB a
V SA S a a a
Câu 46. Chọn A

3
.
24
S ABC SMAB
V V a
Câu 47. Chọn A.
M
B
C'
B'
A'
C
A
45
0
2a
2
B
C'
B'
A'
C
A
A
C
H
S
B
2a
A
C
I
S
B
60
0
H
a
10
D
S
a
B
C
A
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 11 Tài liệu ôn thi HK2 – Khối 12

2
00
2
3
)
1
) 30 . .sin 30
24
2
2
)
3
ABC
ABCD ABC
AC BD O
a
ABC S BA BC
a
SS
a
V
Câu 48. Chọn B.
0
23
.
) .tan60 3
1 1 3
) . 3.
3 3 4 4
S ABC ABC
SA AB a
aa
V SA S a
Câu 49. Chọn A.
22
' 2( 1)y x m x m
Hàm số nghịch biến trên tập xác định khi và chỉ khi
22
'0
1
( 1) 0 2 1 0
0
2
m m m m
a
Câu 50. Chọn D.
Gọi K là trung điểm của AB.
I là trung điểm của AK
Ta có
//IP BQ



/ / / /( )
( , ) ( ,( ))
( ,( )) 3 ( ,( ))
6 ( ,( ))
IP BQ BQ SPI
d BQ SP d BQ SPI
d B SPI d A SPI
d H SPI
Kẻ
HE
vuông góc với
.PI
Ta có
.
25
PH AI a
PAI PEH EH
PI
Gọi h là khoảng cách từ H đến mp(SPI), ta có :
2 2 2
1 1 1 3 3 3
( , )
84
aa
h d BQ SP
h SH HE
a
5
D
O
S
a
B
C
A
60
0
S
a
B
C
A
M
E
K
D
P
I
Q
S
F
2a
B
H
C
A
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 12 Tài liệu ôn thi HK2 – Khối 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG NAI
Nguyễn Văn Huy
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 02
Câu 1. Đồ thị hàm số ở hình bên dưới là của đồ thị hàm số nào
dưới đây.
A.
3
32y x x
.
B.

3
3y x x
.
C.
1
1
x
y
x
.
D.
4
yx
.
Câu 2. Hàm số

42
2y x x
nghịch biến trên khoảng nào sau đây?
A.
1;
. B.
0; 1
. C.
1; 0
. D.
1; 1
.
Câu 3. Gọi
I
là giao điểm của hai đường tiệm cận của đồ thị hàm số
1
2
x
y
x
. Tìm tọa độ điểm
I
.
A.
2; 1I
. B.
2; 1I
. C.
1; 2
. D.
1; 2I
.
Câu 4. Tìm giá trị cực đại của hàm số
32
31y x x
.
A.
3
CĐ
y
. B.
1
CĐ
y
. C.
2
CĐ
y
. D.
0
CĐ
y
.
Câu 5. Đường cong
2
2
9
x
y
x
có bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 6. Tìm giá trị lớn nhất của hàm số
2
2
, 0.y x x
x
A.
Max
526
15
y
. B.
Max
142
15
y
. C.
Max
127
15
y
. D.
Max
38
3
y
.
Câu 7. Tìm các giá trị của
m
để đồ thị hàm số
42
21y x mx
có ba điểm cực trị tạo thành một
tam giác có một đường trung bình là
1
2
y
.
A.
1
2
m
. B.
1m
. C.

1
2
m
. D.
1m
.
Câu 8. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
1y x k k x
trên đoạn

1; 2
. Khi
k
thay đổi trên
R
, giá trị nhỏ nhất của
Mm
bằng
A.
33
4
. B.
37
4
. C.
12
. D.
45
4
.
Câu 9. Cho hàm số
32
2 3 5y x x
có hai điểm cực trị
,AB
. Điểm
;M a b
thuộc đường thẳng
: 3 7d x y
sao cho
. . .T MO MA MA MB MB MO
đạt giá trị nhỏ nhất ( với
O
là gốc
tọa độ). Khi đó,
ab
nhận giá trị thuộc
A.
3; 2
. B.
2; 1
. C.
1; 5
. D.
5; 3
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 13 Tài liệu ôn thi HK2 – Khối 12
Câu 10. Cho tam giác
ABC
cân tại
A
,
5,AB AC a
6BC a
. Hình
chữ nhật
MNPQ
có
,MN
lần lượt thuộc cạnh
,AB AC
và
,PQ
thuộc cạnh
BC
. Quay hình chữ nhật
MNPQ
(và miền
trong nó) quanh trục đối xứng của tam giác
ABC
được một
khối tròn xoay. Tính độ dài đoạn
MN
để thể tích khối tròn
xoay lớn nhất.
A.
2MN a
. B.
4MN a
. C.
MN a
. D.
5MN a
.
Câu 11. Cho hàm số

2
2
4
x
y
x x m
. Tìm
m
để đồ thị hàm số có một tiệm cận đứng và một tiệm
cận ngang?
A.
4; 12m
. B.
4; 12m
. C.
4m
. D.
12m
.
Câu 12. Đồ thị hàm số
3
11y x x
có bao nhiêu điểm cực trị?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 13. Giải phương trình

2
log 2 1 3x
.
A.
9
2
x
. B.
5x
. C.
3
2
x
. D.
8x
.
Câu 14. Tính đạo hàm hàm số
2
x
y
.
A
,
2
x
y
. B.
,1
2
x
yx
. C.
,
2 ln2
x
y
. D.
,
2
x
yx
.
Câu 15. Giải bất phương trình
1
39
x
.
A.
1x
. B.
1x
. C.
2x
. D.
0x
.
Câu 16. Tìm tập xác định
D
của hàm số

1
3
(2 1)yx
.
A.


1
;
2
D
. B.
D
. C.



1
\
2
DR
. D.



1
;
2
D
.
Câu 17. Cho
1ab
. Khẳng định nào sau đây là khẳng định sai?
A.
log log
ab
ba
. B.
log 1
2
a
ab
. C.
ba
ab
. D.

a b b a
ab
.
Câu 18. Tính đạo hàm của hàm số
ln 2y x x
.
A.
2y
. B.
. C.
ln 2 2yx
. D.

2
yx
x
.
Câu 19. Tính
4
M log 1250
theo
a
biết
2
log 5a
.
A.

1
2
Ma
. B.

1
2
2
Ma
. C.
2 1 2Ma
. D.
2 1 4Ma
.
Câu 20. Gọi
S
là tập tất cả các số thực dương thỏa mãn
inxsx
xx
. Xác định số phần tử
nS
.
A.
0nS
. B.
2nS
. C.
1nS
. D.
3nS
.
Câu 21. Viết công thức tính diện tích
S
của hình
H
giới hạn bởi đồ thị hàm số
()y f x
, trục
hoành và hai đường thẳng
,x a x b a b
.
A.
d
b
a
S f x x
. B.
. C.
d
2
b
a
S f x x
. D.
d
2
b
a
S f x x
.
Câu 22.
F x
là nguyên hàm của hàm số
21f x x
. Khi đó,
Fx
là hàm số
A.
d
2
2 1 2 1
3
f x x x x C
. B.
d
1
( ) 2 1 2 1
3
f x x x x C
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 14 Tài liệu ôn thi HK2 – Khối 12
C.
d
1
21
3
f x x x C
. D.
d
1
21
2
f x x x C
.
Câu 23. Một ô tô đang chạy đều với vận tốc
/a m s
thì người ta đạp phanh; từ thời điểm đó, ô
tô chuyển động chậm dần đều với vận tốc
5/v t t a m s
, trong đó
t
là thời gian
tính bằng giây, kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn ô tô di
chuyển được
40
mét thì vận tốc ban đầu
a
bằng bao nhiêu?
A.
40a
. B.
80a
. C.
20a
. D.
25a
.
Câu 24. Tính tích phân
d
1
0
lnI x x
.
A.
0I
. B.
1I
. C.
2I
. D.
1I
.
Câu 25. Tính tích phân

d
2
23
0
1I x x x
A.
16
9
I
. B.

16
9
I
. C.
52
9
I
. D.
2
9
I
.
Câu 26. Diện tích
S
hình phẳng giới hạn bởi đồ thị hàm số
2
2
1
y
x
, trục hoành, đường
thẳng
0x
và đường thẳng
4x
là
A.

8
5
S
. B.
8
5
S
. C.
1S
. D.
1
5
S
.
Câu 27. Tìm phần thực, phần ảo của số phức
32zi
.
A. Phần thực bằng
3
, phần ảo bằng
3i
. B. Phần thực băng
3
, phần ảo bằng
2i
.
C. Phần thực bằng
3
, phần ảo bằng
2
. D. Phần thực bằng
3
, phần ảo bằng
2
.
Câu 28. Cho số phức
12
,zz
với
12
1 , 3 2z i z i
. Khi đó

12
M z z
bằng
A.
5M
. B.
5M
. C.
13M
. D.
17M
.
Câu 29. Cho số phức z thỏa mãn
2 15 10i z i
. Hỏi điểm biểu diễn
cho số phức
z
là điểm nào trong các điểm
, , ,M N P Q
cho hình
dưới đây.
A. Điểm
M
.
B. Điểm
N
.
C. Điểm
Q
.
D. Điểm
P
.
Câu 30. Cho số phức
24zi
. Tìm số phức
w iz z
.
A.
22wi
. B.
22wi
. C.
22wi
. D.
22wi
.
Câu 31. Kí hiệu
1 2 3
,,z z z
và
4
z
là nghiệm phức của phương trình
42
60zz
. Tính tổng
1 2 3 4
S z z z z
.
A.
1S
. B.
2 3 2S
. C.
22S
. D.
23S
.
Câu 32. Cho số phức
z
. Biết tập hợp các điểm biểu diễn số phức
34w i z i
là một đường
tròn có bán kính bằng
20
. Tính
z
.
A.
2z
. B.
8z
. C.
10z
. D.
4z
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 15 Tài liệu ôn thi HK2 – Khối 12
Câu 33. Tính thể tích
V
của khối lập phương
1 1 1 1
.ABCD A B C D
, biết diện tích mặt chéo
11
ACC A
bằng
2
42a
.
A.
3
2Va
. B.
3
4Va
. C.
3
8Va
. D.
3
16Va
.
Câu 34. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SAD ABCD
,
SA SD
. Tính thể tích
V
của khối chóp
.S ABCD
biết
21
2
a
SC
.
A.
3
2
3
a
V
. B.
3
7
6
a
V
. C.
3
2Va
. D.
3
7
2
a
V
.
Câu 35. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác cân đỉnh
C
, đường thẳng
BC
tạo với mặt phẳng

ABB A
một góc
60
và
AB AA a
. Gọi
,,M N P
lần lượt là
trung điểm

,,BB CC BC
. Khoảng cách giữa hai đường thẳng
AM
và
NP
bằng
A.
3
5
a
. B.
15
5
a
. C.
5
5
a
. D.
5
15
a
.
Câu 36. Cho tam giác
ABC
vuông tại
A
có
3, 4AB AC
. Quay tam giác
ABC
quanh trục
AC
, ta được một hình nón tròn xoay. Tính thể tích
V
khối nón tròn xoay.
A.
12V
. B.
16V
. C.
V
. D.
3
4
V
.
Câu 37. Cho hình lăng trụ
.ABC A B C
có đáy là tam giác vuông cân tại
A
, cạnh
20BC a a
, cạnh bên
2AA a
và
A
cách đều các đỉnh
,,A B C
. Gọi
,MN
lần
lượt là trung điểm của
AA
và
AC
. Thể tích khối chóp
.C MNB
là
A.
3
14
48
a
V
. B.
3
14
4
a
V
. C.
3
14
16
a
V
. D.
3
7
8
a
V
.
Câu 38. Có ba quả bóng với kích thước bằng nhau. Một miếng tôn hình chữ nhật được cuốn
thành hình trụ sao cho chiều cao của hình trụ gấp
3
lần đường kính quả bóng, đáy của
hình trụ bằng hình tròn lớn trên quả quả bóng. Gọi
1
S
là tổng diện tích của ba quả
bóng,
2
S
là diện tích xung quanh của hình trụ. Tính tỉ số
1
2
S
S
.
A.
1
2
2
S
S
. B.
1
2
1
S
S
. C.
1
2
5
S
S
. D.
1
2
1
2
S
S
.
Câu 39. Một tấm nhôm hình chữ nhật có hai kích thước là
a
và
2a
(
a
là độ dài cho sẵn). Người
ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài
đường sinh bằng
2a
thì bán kính đáy
r
bằng.
A
a
r
. B.
2
a
r
. C.
2
a
r
. D.
2ra
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 16 Tài liệu ôn thi HK2 – Khối 12
Câu 40. Cho hình nón có đường sinh
2la
và hợp với đáy một góc
60
. Diện tích xung quanh
xq
S
của khối nón bằng.
A.
2
xq
Sa
. B.
2
3
2
xq
Sa
. C.
2
2
xq
Sa
. D.
2
2
xq
Sa
.
Câu 41. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
, mặt bên
SAD
là tam giác
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích khối chóp
.S ABCD
bằng
3
4
3
a
. Tính thể tích
V
của khối cầu ngoại tiếp hình chóp
.S ABCD
.
A.
3
113
64
a
V
. B.
3
113 113
48
a
V
. C.
3
113 113
84
a
V
. D.
3
113 113
384
a
V
.
Câu 42. Trong không gian
Oxyz
cho

1
:
1 2 1
y
xz
d
. Khi đó vectơ chỉ phương của đường thẳng
d
là
A.
0; 1; 0u
. B.
1; 2; 1u
. C.
1; 0; 1u
. D.
2; 0; 1u
.
Câu 43. Trong không gian
Oxyz
cho mặt cầu
S
có phương trình
22
2
1 2 9x y z
. Xác
định tọa độ tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 0; 2I
,
9R
. B.
1; 0; 2I
,
3R
. C.
1; 0; 2I
,
3R
. D.
1; 0; 2I
,
3R
.
Câu 44. Trong không gian
Oxyz
cho
: 3 4 2 5 0P x y z
, điểm
2; 1; 3A
. Tính khoảng
cách
d
từ
A
đến
P
.
A.
13
9
d
. B.
13
29
d
. C.
13
29
d
. D.
13
3
d
.
Câu 45. Trong không gian
Oxyz
cho hai mặt phẳng
: 3 2 1 0P x y z
,
: 2 1 1 2 2 4 14 0Q m x m m y m z
. Tìm
m
để
P
và
Q
vuông góc nhau.
A.




3
1;
2
m
. B.



3
1;
2
m
. C.
2m
. D.



3
2
m
.
Câu 46. Trong không gian tọa độ
Oxyz
, cho điểm
1; 1; 2M
và mặt phẳng
: 2 3x y z
.
Viết phương trình mặt cầu
S
có tâm
M
tiếp xúc với mặt phẳng
.
A.
2 2 2
16
: 2 2 4 0
3
S x y z x y z
. B.
2 2 2
35
: 2 2 4 0
6
S x y z x y z
.
C.
2 2 2
35
: 2 2 4 0
6
S x y z x y z
. D.
2 2 2
14
: 2 2 4 0
3
S x y z x y z
.
Câu 47. Trong không gian tọa độ
Oxyz
, cho đường thẳng


1
35
:
2 1 2
y
xz
d
và mặt phẳng
: 1 0P x y z
. Có tất cả bao nhiêu điểm thuộc đường thẳng
d
sao cho khoảng
cách từ điểm đó đến mặt phẳng
P
bằng
3
.
A. Vô số điểm. B. Một. C. Hai. D. Ba.
Câu 48. Trong không gian tọa độ
Oxyz
, cho đường thẳng
1
:
23
y
z
x
và mặt phẳng
: 4 2 1 0P x y z
. Khi đó khẳng định nào sau đây là đúng?
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 17 Tài liệu ôn thi HK2 – Khối 12
A.
P
. B.
P
.
C. Góc tạo bởi
và
P
lớn hơn
30
. D.
// P
.
Câu 49. Trong không gian tọa độ
Oxyz
, cho đường thẳng
1
d
qua điểm
3; 2; 1M
và có VTCP
1; 1; 2u
, gọi
2
d
là giao tuyến của hai mặt phẳng
: 2 0P x y z
và
: 2 3 0Q x y z
. Viết phương trình mặt phẳng
chứa
1
d
và song song với
2
d
.
A.
: 5 13 4 7 0x y z
. B.
: 5 13 4 45 0x y z
.
C.
: 5 13 4 7 0x y z
. D.
: 5 13 4 45 0x y z
.
Câu 50. Trong không gian tọa độ
Oxyz
, cho điểm
1; 3; 4M
, đường thẳng



5
22
:
3 5 1
y
xz
d
và mặt phẳng
: 2 2 0P x z
. Viết phương trình đường thẳng
qua
M
vuông góc với
d
và song song với
P
.
A.


3
14
:
112
y
xz
. B.


3
14
:
1 1 2
y
xz
.
C.

3
14
:
1 1 2
y
xz
. D.

3
14
:
1 1 2
y
xz
.
-------oOo-------
ĐÁP ÁN ĐỀ SỐ 02
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
B
B
A
C
D
D
D
B
B
D
A
C
B
D
C
B
B
C
A
B
C
B
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B
D
D
C
A
B
D
C
A
B
A
C
B
C
C
D
B
C
C
A
B
C
C
A
D
HƯỚNG DẪN GIẢI ĐỀ SỐ 02
Câu 1. Chọn A.
Đồ thị cắt trục tung tại điểm
0; 2A
.
Câu 2. Chọn B.
Hàm số có ba điểm cực trị:


0
1
x
x
và hàm số có hệ số
0a
nên hàm số nghịch biến trên
0; 1
.
Câu 3. Chọn B.
Đồ thị hàm số có tiệm cận đứng:
2x
.
Đồ thị hàm số có tiệm cận ngang:
1y
.
2; 1I
.
Câu 4. Chọn B.
Ta có:

2
0
3 6 0
2
x
y x x
x
Hàm số đạt cực đại tại
2; 3A
nên
3
CD
y
.
Câu 5. Chọn C.
Đồ thị hàm số có hai tiệm cận đứng:
3x
.
Đồ thị hàm số có một tiệm cận ngang:
0y
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 18 Tài liệu ôn thi HK2 – Khối 12
Câu 6. Tìm giá trị lớn nhất của hàm số
2
2
, 0.y x x
x
A.
ax
526
15
My
. B.
ax
142
15
My
. C.
ax
127
15
My
. D.
ax
38
3
My
.
Không tồn tại GTLN. SAI ĐỀ.
Câu 7. Chọn D.
Ta có:
32
4 4 4y x mx x x m
.
Hàm số có 3 cực trị khi
0m
.
Khi đó 3 điểm cực trị của đồ thị hàm số là:
22
0; 1 , ; 1 ; ; 1A B m m C m m
.
Ba điểm cực trị tạo thành một tam giác có một đường trung bình là

2
1 1 1 1
1
2 2 2
m
ym
.
Câu 8. Chọn D.
Ta có:



2
2 2 2
13
3 1 3 0
24
y x k k x k
.
Nên hàm số đồng biến trên
R
.
2
2
2 8 2 1
1 1 1
M y k k
m y k k



2
2
1 45 45
9 3 1 3
2 4 4
M m k k k
.
Câu 9. Chọn D.
Đồ thị hàm số có hai điểm cực trị
0; 5 , 1; 4AB
. Gọi
G
là trọng tâm tam giác
ABO



1
;3
3
G
.
Ta có:
. . .T MO MA MA MB MB MO
2
2
3 2 . . .
3 . .
MG GO MG GA MG GA MG GB MG GB MG GO
MG MG GO GA GB GO GA GA GB GB GO
MG GO GA GA GB GB.GO
Mà
. . .GO GA GA GB GBGO
là hằng số, do đó
T
min khi
MG
min khi
M
là hình chiếu
vuông góc của
G
trên
d
.
Vậy




13 19
;
10 10
M
.
Câu 10. Chọn B.
Ta có:
3 ; 4BH a AH a
.
Đặt
3HQ x BQ a x
03xa
.
Ta có:
43
3
x
MQ BQ
MQ
AH BH
.
Khi đó:




3
22
43
. . 4 0 3
33
T
x
x
V x x x a
Xét hàm số
3
2
03
3
x
f x x x a
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 19 Tài liệu ôn thi HK2 – Khối 12
Hàm số
fx
đạt giá trị lớn nhất tại
24x a MN a
.
Câu 11. Chọn B.
Khi

2
2
4
44
x
my
xx
Đồ thị hàm số có 3 tiệm cận.
Khi



22
22
12
4 12
28
xx
my
xx
x
Đồ thị hàm số có
1
tiệm cận.
Câu 12. Chọn D.
Ta có:
3
3
3
1
1 1 ;
1
11
1 1 ; 1; 1
x
f x x x
x
y x x
g x x x x
Xét hàm số:
3
1
1 1 ;
1
x
f x x x
x
Không có cực trị.
Xét hàm số:
3
1 1 ; 1; 1g x x x x
có một cực trị.
Vậy hàm số
3
11y x x
có một cực trị.
Câu 13. Chọn A.
Ta có:

2
1
9
log 2 1 3
2
2
2 1 8
x
xx
x
.
Câu 14. Chọn C.
Ta có:
,
2 ln2
x
y
.
Câu 15. Chọn B.
Ta có:

1 1 2
3 9 3 3 1
xx
x
.
Câu 16. Chọn D.
Tập xác định của hàm số:

1
3
21yx
là
1
2 1 0
2
xx
.
Câu 17. Chọn C.
Ta có:
2
1
log log log log 1
log
a b b b
b
b a a a
a
do
1ab
A. Đúng.

log 1 0
22
a
a b a b
a a b
B. Đúng.

log 1 log 0
a b b a
aa
a b a b b a b a b b
D. Đúng.
Câu 18. Chọn B.
Ta có:
2
ln 2 . 1 ln 2
2
y x x x
x
.
Câu 19. Chọn B.
Ta có:
4
42
2
1 1 1
M log 1250 log 5 .2 4log 5 1 2
2 2 2
a
.
Câu 20. Chọn C.
Xét các trường hợp:
0x
: Không thỏa.
1x
: Thỏa.
01x
, ta có
inx
inx
s
s
x
x x x
( vô nghiệm).
Vậy số phần tử
( ) 1nS
.
Câu 21. Chọn A.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 20 Tài liệu ôn thi HK2 – Khối 12
Câu 22. Chọn B.
Ta có:
d d d
1
2
1 1 1
2 1 2 1 2 1 2 1 2 1 2 1
2 2 3
f x x x x x x x x C
.
Câu 23. Chọn C.
Khi ôtô dừng hẳn
( ) 0 5 0
5
a
v t t a t
.
Theo đề bài:



dt
5
2
5
0
0
5
40 5 40 20
2
a
a
t a t at a
.
Câu 24. Chọn B.
Bấm máy tính.
Câu 25. Chọn C.
Bấm máy tính.
Câu 26. Chọn B.
Ta có:

d
4
2
0
28
5
1
Sx
x
Bấm máy tính.
Câu 27. Chọn D.
Số phức
32zi
có phần thực bằng
3
, phần ảo bằng
2
.
Câu 28. Chọn D.
Ta có:

1
1zi
.
22
3 2 3 2z i z i
.
1 2 1 2
4 17z z i M z z
.
Câu 29. Chọn C.
Ta có:
15 10
2 15 10 4 7 4 7
2
i
i z i z i z i
i
.
Câu 30. Chọn A.
Ta có:
2 4 2 4 2 2w iz z i i i i
.
Câu 31. Chọn B.
Ta có:


4 2 2 2
3
6 0 3 2 0
2
z
z z z z
zi
.
1 2 3 4
2 3 2S z z z z
.
Câu 32. Chọn D.
Đặt

1
11
3 4 3 4 4 3 4 3
3 4 25 25
x y i
w i z i x yi z x y y x
i
22
2 2 2
2
.25 3 4 4 3 4 3 1 .5z x y y x x y z
2
.5 400 4zz
.
Câu 33. Chọn C.
Gọi
11
22
2 2 4 2 2
ACC A
AB x AC x S x a x a
.

3
3
28V a a
.
Câu 34. Chọn A.
Ta có:
3
2
5 1 2
2 . .2
2 3 3
aa
HC SH a V a a
.
H
A
D
B
C
S
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 21 Tài liệu ôn thi HK2 – Khối 12
Câu 35. Chọn B.
Ta có:
KC AA BB
,
2
5 15 15
2 2 4
A B C
a a a
BK KC S
3
15
4
LT
a
V
.
Câu 36. Chọn A.
Ta có:


2
1
. 12
3
V AB AC
.
Câu 37. Chọn C.
Ta có
H
là tâm đường tròn ngoại tiếp
2 14
22
aa
ABC AH A H

14
4
a
MK
.

23
1 1 14
. . .
2 4 3 48
ABN ABMN ABN
aa
S AN AB V MK S
.
3
.
14
3
16
C BMN ABMN
a
VV
.
Câu 38. Chọn B.
Ta có:


22
1
3.4. 12S R R
.


2
2
2 . . 12 .S R h R
.
Khi đó:
1
2
1
S
S
.
Câu 39. Chọn C.
Ta có:
2
2
a
r a r
.
Câu 40. Chọn C.
Đường sinh
2la
hợp với đáy một góc
60
Ra
.
Ta có:


2
2
xq
S Rl a
.
Câu 41. Chọn D.
Gọi
,HK
lần lượt là trung điểm của
,AB CD
.
O
là tâm hình vuông.
J
là tâm đường tròn ngoại tiếp tam giác
SAD
.
I
là tâm mặt cầu ngoại tiếp hình chóp
.S ABCD
.
Ta có:
2
2
ABCD
Sa
,
3
.
4
2
3
S ABCD
a
V SH a
.
2 3 2
22
aa
AH SA
.
90SA AD ASD J
thuộc đoạn SH.
K
B
A
C
C'
A'
B'
4
3
A
D
B
C
F
E
K
N
M
C'
B'
H
A
C
B
A'
K
I
o
H
D
C
A
B
S
J
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 22 Tài liệu ôn thi HK2 – Khối 12
Ta có:

22
sin
3
SH
SAH
AH
.
Mà
9
2
8
sin
SD a
SJ SJ
SAH
(định lí sin).
7
8
a
OI JH SH SJ
113
28
BD a
OD a R ID
.
Vậy
3
113 113
384
KC
a
V
.
Câu 42. Chọn B.
Câu 43. Chọn C.
Câu 44. Chọn C.
Ta có:





,
6 4 6 5
13
9 16 4 29
AP
d
.
Câu 45. Chọn A.
Mặt phẳng
: 3 2 1 0P x y z
có một VTPT là
1
1; 3; 2n
.
Mặt phẳng
: 2 1 1 2 2 4 14 0Q m x m m y m z
có một VTPT là
2
2
2m 1; 2 ; 2 4n m m m
.


2
12
2
. 0 2m 1 3 2 4 8 0
1
6 3 9 0
3
2
P Q n n m m m
m
mm
m
Câu 46. Chọn B.
Ta có:


M,
1 1 4 3
1
66
dR
.
Phương trình mặt cầu
S
có tâm
M
tiếp xúc với mặt phẳng
là
2 2 2
35
: 2 2 4 0
6
S x y z x y z
.
Câu 47. Chọn C.
Đường thẳng
d
cắt mặt phẳng
P
nên có hai điểm thuộc đường thẳng
d
sao cho khoảng
cách từ điểm đó đến mặt phẳng
P
bằng
3
.
Câu 48. Chọn C.
Đường thẳng
1
:
23
y
z
x
có một VTCP là
1; 2; 3u
.
Mặt phẳng
: 4 2 1 0P x y z
có một VTPT là
4; 2; 1n
.
Ta có:
sin
443
11 6 1
, sin30
42 2
14. 21
un
nên góc tạo bởi
và
P
lớn hơn
30
.
Câu 49. Chọn A.
Mặt phẳng
: 2 0P x y z
vó một VTPT
1
1; 1; 2n
.
Mặt phẳng
: 2 3 0Q x y z
vó một VTPT
2
1; 1; 1n
.
Đường thẳng
2
d
có một VTCP


12
, 5; 1; 3a n n
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 23 Tài liệu ôn thi HK2 – Khối 12
Mặt phẳng
chứa
1
d
và song song với
2
d
có một VTPT


, 5; 13; 4n u a
.
Mặt phẳng
đi qua điểm
3; 2; 1M
và có VTPT
5; 13; 4n
có phương trình
: 5 13 4 7 0x y z
.
Câu 50. Chọn D.
Đường thẳng



5
22
:
3 5 1
y
xz
d
có một VTCP
3; 5; 1u
Mặt phẳng
: 2 2 0P x z
vó một VTPT
2; 0; 1n
Đường thẳng
có một VTCP


, 5 1; 1; 2a u n
.
Đường thẳng
có phương trình

3
14
:
1 1 2
y
xz
.
…………………………Hết……………………
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 24 Tài liệu ôn thi HK2 – Khối 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG NAI
Nguyễn Văn Huy
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 04
Câu 1. Đường cong trong hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A, B,
C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
42
2.y x x
B.
42
2.y x x
C.
42
2.y x x
D.
42
2 1.y x x
Câu 2. Đồ thị hàm số
2
2
32
1
xx
y
x

có bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 3. Hỏi hàm số
32
15
6
32
y x x x
nghịch biến trên khoảng nào?
A.
1;6
. B.
6; 1
. C.
2;3
. D.
3; 2 .
Câu 4. Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định sai?
A. Đồ thị hàm số có
3
điểm cực trị.
B. Hàm số có giá trị nhỏ nhất bằng
16
.
C. Hàm số đồng biến trên mỗi khoảng
2;0
và
2;
.
D. Đồ thị của hàm số có hai tâm đối xứng.
Câu 5. Tìm giá trị thực của tham số
m
để hàm số
3 2 2
3 3 1 2016f x x mx m x
đạt cực tiểu
tại
2x
?
A.
3m
. B.
1m
. C.
3.m 
D.
1m 
.
Câu 6. Tìm các giá trị thực của tham số
m
sao cho giá trị nhỏ nhất của hàm số
2
1
1
mx
fx
x
trên đoạn
2; 1
bằng
4
?
A.
.m
B.
26
.
2
m
C.
3.m 
D.
9.m 
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 25 Tài liệu ôn thi HK2 – Khối 12
Câu 7. Biết đường thẳng
1yx
cắt đồ thị
C
của hàm số
7 17
25
x
y
x
tại
2
điểm phân biệt, gọi
A
là giao điểm thuộc nhánh bên phải đường tiệm cận đứng của
C
, kí hiệu
;
AA
xy
là
tọa độ của điểm
A
. Tìm
AA
xy
?
A.
5
AA
xy
. B.
13
AA
xy
. C.
3
AA
xy
. D.
7
AA
xy
.
Câu 8. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
4 2 2 4
21y x m x m
có
3
điểm cực trị, đồng thời
3
điểm cực trị tạo với gốc tọa độ
O
một tứ giác nội tiếp
trong một đường tròn?
A.
1m
. B.
0m
. C.
2m 
. D.
2m 
.
Câu 9. Đồ thị của hàm số
2
2
3
41
ax x
y
x bx


có một đường tiệm cận ngang là
yc
và chỉ có một
đường tiệm cận đứng. Tính
a
bc
biết rằng
a
là số thực dương và
4ab
?
A.
1
4
a
bc
. B.
2
a
bc
. C.
1
a
bc
. D.
4
a
bc
.
Câu 10. Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng như hình vẽ. Hai mặt
bên
ABB A

và
ACCA

là hai tấm kính hình chữ nhật dài
20 m
và rộng
5 m
. Gọi
x mét
là độ dài của cạnh
BC
. Tìm
x
để khoảng không gian của hành lang (kể cả hai
tấm kính) là lớn nhất?
A.
5.xm
B.
25 .xm
C.
5 17 .xm
D.
5 2 .xm
Câu 11. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
2
sin
cos
mx
y
x
nghịch biến trên
khoảng
0;
6



?
A.
5
.
4
m
B.
0.m
C.
1.m
D.
2m
.
Câu 12. Tính đạo hàm của hàm số
2
2016
log 1yx
?
A.
2
2
.
1 ln2016
x
x
B.
2
1
'
1
y
x
. C.
2 ln2016x
. D.
2
1
1 ln2016x
.
Câu 13. Tìm giá trị thực của tham số m sao cho hàm số
2
ln 1y x mx
có tập xác định là ?
A.
2
2
m
m

.
B.
11m
.
C.
22m
. D.
2 2.m
Câu 14. Giải phương trình
21
3 27
x
A.
2x
. B.
5x
. C.
3
1
log 30
2
x
. D.
1x 
.
Câu 15. Giải bất phương trình
1
2
log 3 4 4x
. Tập nghiệm
T
của bất phương trình là
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 26 Tài liệu ôn thi HK2 – Khối 12
A.
4;T 
. B.
4
;4
3
T




. C.
4
;4
3
T



. D.
;4 .T 
Câu 16. Cho hàm số
2
1
1
1
.
3
x
x
f x e



. Khẳng định nào sau đây là khẳng định sai?
A.
2
1 1 1 ln3 0f x x x
. B.
2
1
1 1 log3 0
ln10
x
f x x
.
C.
2
1
1 1 0
ln3
x
f x x
. D.
2
22
1 1 log 1 log 3 0f x x e x
.
Câu 17. Cho các số thực dương
,ab
thỏa mãn:
22
7a b ab
. Khẳng định nào sau đây là khẳng định
đúng?
A.
1
3ln ln ln
2
a b a b
. B.
3
log log log
2
a b a b
.
C.
2 ln ln 7ln .lna b a b
. D.
1
log log log
32
ab
ab

.
Câu 18. Tính đạo hàm của hàm số
xx
y xe e
.
A.
2
x
e
. B.
2
x
xe
. C.
2
x
xe
. D.
1
x
xe
.
Câu 19. Đặt
log5, log3ab
. Hãy biểu diễn
30
log 8
theo
,ab
.
A.
30
3
log 8 .
1
ab
b
B.
30
31
log 8 .
1
a
b
C.
30
2
log 8 .
ab
ab
D.
30
21
log 8 .
a
ab
Câu 20. Cho hai số thực dương
a
và
b
, với
ab
,
1 1 0ab
. Khẳng định nào dưới đây là
khẳng định sai?
A.
1
log 0
b
a b a
. B.
22
1
log 0
a
ab
b




.
C.
log 0
a
a b b
. D.
22
log 0
b
b a a
.
Câu 21. Một người quan sát một đám bèo phát triển trên mặt hồ thì thấy cứ sau một giờ thì diện
tích của đám bèo lớn gấp
10
lần diện tích đám bèo trước đó, với tốc độ tăng không đổi
thì sau
9
giờ đám bèo ấy phủ kín mặt hồ. Hỏi sau bao nhiêu giờ thì đám bèo ấy phủ kín
một phần ba mặt hồ?
A.
3
. B.
9
10
3
. C.
9 log3
. D.
9
log3
.
Câu 22. Cho hàm số
y f x
liên tục trên thỏa mãn
d 10
d
a
f x x
,
d8
d
b
f x x
và
d7
c
a
f x x
. Tính
d
c
b
f x x
?
A.
d 5.
c
b
f x x 
B.
d 5.
c
b
f x x
C.
d 11.
c
b
f x x
D.
d 11.
c
b
f x x 
Câu 23. Tìm nguyên hàm của hàm số
sin2 cos3 df x x x x
.
A.
11
d cos2 sin3
23
f x x x x C
. B.
d cos2 sin3 .f x x x x C
C.
d cos2 sin3 .f x x x x C
D.
11
d cos2 sin3 .
23
f x x x x C
Câu 24. Tính tích phân
2
2
3
0
d
1
x
Ix
x
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 27 Tài liệu ôn thi HK2 – Khối 12
A.
4
3
I
. B.
ln3.I
C.
26
.
3
I
D.
8
.
3
I
Câu 25. Tính tích phân
1
2
0
1d
x
I x e x
.
A.
2
33
4
e
I
. B.
2
31
4
e
I
. C.
2
Ie
. D.
2
53Ie
.
Câu 26. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
4y x x
, trục hoành, trục tung
và đường thẳng
4x
.
A.
44
. B.
48
. C.
40
. D.
36
.
Câu 27. Kí hiệu
H
là hình phẳng giới hạn bởi đồ thị hàm số
4 2.lny x x
, trục hoành và
đường thẳng
xe
. Tính thể tích
V
của khối tròn xoay thu được khi quay hình
H
xung quanh trục
Ox
.
A.
2
65ee

. B.
2
25ee
. C.
2
65ee
. D.
2
25V e e
.
Câu 28. Trong một phòng thí nghiệm, người ta quan sát một đám vi trùng ban đầu có
250000( )con
, tới ngày thứ
n
thì số lượng vi trùng trong đám ấy là
fn
con, với
4000
1 0,5
fn
n
. Gọi
x
là số lượng vi trùng trong đám ấy sau
10
ngày, giá trị của x gần
với kết quả nào nhất trong các kết quả sau đây?
A.
264334x
. B.
14334x
. C.
264000x
. D.
14000x
.
Câu 29. Tìm phần thực và phần ảo của số phức
z
, biết
25 10zi
.
A. Phần thực bằng
25
và Phần ảo bằng
10i
.
B. Phần thực bằng
25
và Phần ảo bằng
10i
.
C. Phần thực bằng
25
và Phần ảo bằng
10
.
D. Phần thực bằng
25
và Phần ảo bằng
10
.
Câu 30. Cho hai số phức
1
23zi
và
2
17zi
. Tính mô đun của số phức
12
zz
.
A.
101
. B.
5
. C.
17
. D.
8
.
Câu 31. Cho số phức
2
2 0.5 1zi
. Hỏi điểm biểu diễn của
z
là điểm nào trong các điểm
, , ,M N P Q
ở hình bên?
A. Điểm
M
. B. Điểm
N
.
C. Điểm
P
. D. Điểm
Q
.
Câu 32. Cho số phức
32zi
. Tìm số phức
5
2
2
z
wz
i

?
A.
25wi
. B.
25wi
. C.
25wi
. D.
25wi
.
Câu 33. Kí hiệu
1 2 3
,,z z z
và
4
z
là bốn nghiệm phức của phương trình
2
22
1 2 46zz
. Tính
tổng
1 2 3 4
M z z z z
.
A.
6 2 5M 
. B.
25M
. C.
6.M
D.
3 2 5.M 
Câu 34. Trong các số phức
z
thỏa mãn điều kiện
2 3 1 2z i z i
, hãy tìm phần ảo của số
phức có môđun nhỏ nhất ?
A.
2
.
13
B.
10
.
13
C.
2
.
5
D.
2.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 28 Tài liệu ôn thi HK2 – Khối 12
Câu 35. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
2a
, cạnh bên
SA
vuông
góc với mặt phẳng
ABC
. Gọi
M
là trung điểm của
BC
, góc giữa
SM
và mặt phẳng
đáy
ABC
bằng
o
60
. Tính thể tích
V
của khối chóp
.S ABC
?
A.
3
63Va
. B.
3
2 3 .Va
C.
3
3.Va
D.
3
3 3 .Va
Câu 36. Cho lăng trụ đứng
1 1 1
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
với
3AB a
,
5AC a
,
1
4A B a
. Tính thể tích
V
của lăng trụ
1 1 1
.ABC A B C
?
A.
3
12 7Va
. B.
3
2 7 .Va
C.
3
30 .Va
D.
3
6 7 .Va
Câu 37. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
, mặt bên
SAB
là tam
giác vuông cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của khối
chóp
.S OCD
bằng
3
3
a
. Tính khoảng cách
h
từ
A
đến mặt phẳng
SBD
?
A.
2 3 .ha
B.
26
.
3
a
h
C.
3
.
3
a
h
D.
23
.
3
a
h
Câu 38. Cho lăng trụ
1 1 1
.ABC A BC
có đáy
ABC
là tam giác vuông tại
C
, cạnh
5AC a
. Hình
chiếu vuông góc của
1
A
lên mặt phẳng
ABC
là trung điểm của cạnh
AC
, góc giữa mặt
phẳng
11
AAB B
với
11
AAC C
bằng
o
30
, cạnh bên của lăng trụ tạo với đáy một góc
o
60
.
Tính thể tích
V
của lăng trụ
1 1 1
.ABC A BC
?
A.
3
3.
8
a
V
. B.
3
3.
.
24
a
V
C.
3
.
8
a
V
D.
3
.
24
a
V
Câu 39. Trong không gian cho tam giác
ABC
vuông cân tại
A
với đường cao
AH
,
2AB a
.
Tính bán kính
R
của đáy hình nón, nhận được khi quay tam giác
ABC
xoay quanh trục
AH
?
A.
2
.
2
a
R
B.
2.Ra
C.
2.Ra
D.
2 2.Ra
Câu 40. Trong không gian cho hình vuông
ABCD
có cạnh bằng
4
. Quay hình vuông đó xung
quanh trục
AB
, ta nhận được một hình trụ. Tính diện tích toàn phần
tp
S
của hình trụ
đó.
A.
32 .
tp
S
B.
48 .
tp
S
C.
64 .
tp
S
D.
80 .
Câu 41. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy là
2a
, cạnh bên là
6a
. Tính thể tích
V
của khối cầu ngoại tiếp hình chóp đã cho?
A.
3
9
2
a
V
. B.
3
81
.
32
a
V
C.
3
9
.
2
a
V
D.
3
3
.
2
a
V
Câu 42. Một cơ sở sản xuất đồ gia dụng được đặt hàng làm các chiếc cốc hình nón không nắp
bằng nhôm có thể tích là
3
9Va
. Để tiết kiệm sản suất và mang lại lợi nhuận cao nhất
thì cơ sở sẽ sản suất những chiếc cốc hình nón có bán kính miệng cốc là
R
sao cho diện
tích nhôm cần sử dụng là ít nhất. Tính
R
?
A.
3
3
.
2
a
R
B.
6
3
.
2
a
R
C.
3.Ra
D.
3
9.Ra
Câu 43. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
có phương trình:
12
2
3
xt
yt
z

(
t
là tham số thực). Vectơ nào dưới đây là một vectơ chỉ phương của
?
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 29 Tài liệu ôn thi HK2 – Khối 12
A.
1
1; 2;3u 
. B.
3
2;1;3 .u
C.
2
2;1;0 .u
D.
4
2; 1;3 .u
Câu 44. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
1;0; 1 , 2;1;0 , 0;1; 2A B C
.
Vectơ nào dưới đây là một vec tơ pháp tuyến của mặt phẳng
ABC
?
A.
1
1;1;2 .n
B.
2
1; 1; 2 .n
C.
3
1;2;1 .n 
D.
4
1;2;1 .n
Câu 45. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt cầu
2 2 2
: 2 4 6 2 0x y x zS zy
. Tìm tọa độ tâm
I
và bán kính của mặt cầu
S
.
A.
1; 2; 3I 
và
4R
. B.
1;2;3I
và
4.R
C.
1; 2; 3I 
và
23R
. D.
1; 2; 3I 
và
23R
.
Câu 46. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
: 4 0P y z
và mặt
phẳng
: 2 5 0Q x y z
. Gọi
là góc giữa hai mặt phẳng
P
và
Q
. Tính
?
A.
o
150
. B.
o
60 .
C.
o
30 .
D.
o
120 .
Câu 47. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
1;2; 1A
và
3; 2;3B
. Viết
phương trình mặt phẳng trung trực
P
của đoạn thẳng
AB
.
A.
2 2 4 0.x y z
B.
2 2 4 0.x y z
C.
2 2 0.x y z
D.
2 2 4 0x y z
.
Câu 48. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
d
có phương trình:
1 2 3
2 4 1
x y z

.Xét mặt phẳng
: 2 7 0P x y mz
,
m
là tham số thực. Tìm tất cả
các giá trị của
m
để đường thẳng
d
song song với mặt phẳng
P
?
A.
6.m 
B.
10.m
C.
2.m 
D.
1
.
2
m 
Câu 49. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt cầu
S
có tâm
(2; 1;1)I
và mặt
phẳng
: 2 2 4 0P x y z
. Biết mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là
một đường tròn có bán kính bằng
5
. Viết phương trình mặt cầu
S
.
A.
2 2 2
2 1 1 9.x y z
B.
2 2 2
2 1 1 9x y z
.
C.
2 2 2
2 1 1 81.x y z
D.
2 2 2
2 1 1 81.x y z
Câu 50. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
: 2 0P x y z
, đường
thẳng
có phương trình:
3 1 2
2 1 1
x y z

và điểm
1;0; 1M
. Viết phương trình
đường thẳng
d
đi qua
M
cắt đường thẳng
tại điểm
A
và cắt mặt phẳng
P
tại
B
sao cho
M
là trung điểm
AB
?
A.
11
.
6 1 5
x y z

B.
3 3 2
.
2 3 1
x y z

C.
11
.
4 5 3
x y z

D.
13
.
2 3 1
x y z


--------oOo-------
ĐÁP ÁN ĐỀ SỐ 03
1
2
3
4
5
6
7
8
9
10
A
B
C
D
B
C
D
A
C
C
11
12
13
14
15
16
17
18
19
20
A
A
D
A
B
C
D
C
B
A
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 30 Tài liệu ôn thi HK2 – Khối 12
21
22
23
24
25
26
27
28
29
30
C
B
D
A
B
C
D
C
D
B
31
32
33
34
35
36
37
38
39
40
C
A
A
B
C
D
B
B
C
41
42
43
44
45
46
47
48
49
50
A
B
C
D
A
C
B
B
B
A
HƯỚNG DẪN GIẢI
Câu 1. Chọn A.
Ta thấy đây là đồ thị hàm bậc bốn trùng phương
42
0y ax bx c a
, do đồ thị có
các cực trị là :
1;1A
;
0;0O
; ta có hệ:
(0) 0 0 0
(1) 1 1 1
y (1) 0 0 4 2 2
y c c
y a b c a
a b b
Câu 2. Chọn B.
Ta có
2
2
32
lim 1
1
x
xx
x






,
1y 
là tiệm cận ngang.
2
2
11
3 2 2 1
lim lim
1 1 2
xx
x x x
xx








;
2
2
11
3 2 2
lim lim
11
xx
x x x
xx









1x 
là tiệm cận đứng.
Có
2
đường tiệm cận.
Câu 3. Chọn C.
Ta có
2
2
5 6; 0 ; 0 2,3
3
x
y x x y y x
x
hàm số nghịch biến trên khoảng
2;3
.
Câu 4. Chọn D.
Đồ thị của hàm số có hai tâm đối xứng là sai.
Câu 5. Chọn B.
Ta có
22
3 6 3 1 ;f x x mx m
để hàm số đạt cực tiểu tại
2x
thì
2
1
2 0 12 12 3 1 0
3
m
f m m
m
thay m=1 vào ta thấy
fx
chỉ đổi dấu từ
âm sang dương tại
2x
nên
1m
.
Câu 6. Chọn C.
Ta có :
2
2
1
01
1
m
f x x
x

hàm số
fx
liên tục trên đoạn
2; 1
nên giá trị nhỏ
nhất của
2
2
1
4 1 4 4 9 3
11
m
f x f m m


.
Câu 7. Chọn D.
Ta có hoành độ giao điểm là nghiệm của :
2
2
7 17
1 2 10 12 0
3
25
x
x
x x x
x
x
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 31 Tài liệu ôn thi HK2 – Khối 12
Mặt khác tiệm cận đứng của
C
là
5
2
x
,
A
là giao điểm thuộc nhánh bên phải
đường tiệm cận đứng của
C
nên
3 4 7
A A A A
x y x y
Câu 8. Chọn A.
Để hàm số
4 2 2 4
21y x m x m
có
3
điểm cực trị thì
32
3 4 0y x m x
có ba nghiệm
phân biệt nên
0m
. Mặt khác
3
điểm cực trị tạo với gốc tọa độ
O
một tứ giác nội tiếp
trong một đường tròn nên tứ giác đó là hình vuông. Gọi
,,A B C
là ba cực trị và:
4
,1 ;B ,1 ;C 0, 1A m m m
, do
2
22
. 0 1 0
1.
0
.0
OA OB OAOB m
m
OA AC
mm
OA AC


Câu 9. Chọn C.
Do đồ thị của hàm số
2
2
3
41
ax x
y
x bx


có một đường tiệm cận ngang là
yc
nên
4
4
aa
c
bc b
và chỉ có một đường tiệm cận đứng nên:
Th1:
2
4 1 0x bx
có nghiệm kép
4 4( 0, 4)b b a ab
thay vào hàm số thõa
mãn.Nên
1
a
bc
Th2:
2
4 1 0x bx
và
2
30ax x
có nghiệm chung. Thay
a
bc
lần lượt bằng
1
;2;4
4
ta
thấy không thõa mãn.
Câu 10. Chọn C.
Do
. ' ' 'ABC A B C
là hình lăng trụ đứng nên
. ' ' '
'.S '. . .sin BAC 20.5.5.sin BAC
ABC A B C ABC
V A A A A AB AC
Để khoảng không gian của hành lang (kể cả hai tấm kính) là lớn nhất thì
sin BAC
lớn
nhất hay
90
o
ABC
hay
ABC
vuông cân tại
A
hay
52BC m
.
Câu 11. Chọn A.
Đặt
1
inx = t 0,
2
s



ta có
2
2
22
2
sin 2 1
cos 1
1
m x m t t mt
y y y
xt
t
để hàm số nghịch
biến trên khoảng
0;
6



thì
2
11
0 0, 2 1 0 0,
22
y x t mt x
Th1:
2
( ) 0 1 0 1 1
2
b
y y m m m
a




Th2:
1m
để
1
0 0,
2
yx



thì
1 1 5
0 1 0
2 4 4
y m m



hay
5
1
4
m
Th3:
1m
để
1
0 0,
2
yx



thì
0 0 1 0y
hay
1m
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 32 Tài liệu ôn thi HK2 – Khối 12
Vậy
5
.
4
m
Câu 12. Chọn A.
2
2016
2
2
log 1
1 ln2016
x
y x y
x
?
Câu 13. Chọn D.
Ta có tập xác định của
2
ln 1y x mx
là
2
10x mx x
2
4 0 2 2mm
Câu 14. Chọn A.
Ta có
2 1 2 1 3
3 27 3 3 2 1 3 2
xx
xx

.
Câu 15. Chọn B.
4
1
2
3 4 0
4
log 3 4 4
3
1
34
4
2
x
x
x
x
x








.
Câu 16. Chọn C.
2
1
12
11
. log 1 log 1 log
33
x
x
a a a
f x e f x x e x



khi
( 1)a
thì thay
;3;10;2ae
vào
2
1
log 1 log 1 log
3
a a a
f x x e x
thì
2
1 1 log 1 log 3 0
aa
f x x e x
ta thấy C sai
Câu 17. Chọn D.
22
2
22
7 9 log log
33
1
2log log log log log log
3 3 2
cc
a b a b
a b ab a b ab ab ab
a b a b
a b a b


.
Câu 18. Chọn C.
Tính đạo hàm của hàm số
1 1 2
x x x x x x
y xe e x e y e x e x e
.
Câu 19. Chọn B.
Ta có
30 30
22
3 3 3 3
log 8 3log 2
log15 log3 log5
log 30 1 log 15
11
10
log2
log
5
3 1 log5
3 3(1 )
log3 log5
1 log5 log3 log5 1
1
1 log5
a
b

.
Câu 20. Chọn A.
ab
nên
0(1)ab
,
Mặt khác
1
0
1
log log 0(2)
1 1 0
10
b
b
ab
ab
aa
ab
ab


.
Từ
(1);(2)
1
log 0
b
a b a
sai
Câu 21. Chọn C.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 33 Tài liệu ôn thi HK2 – Khối 12
Một người quan sát một đám bèo phát triển trên mặt hồ thì thấy cứ sau một giờ thì
diện tích của đám bèo lớn gấp
10
lần diện tích đám bèo trước đó, với tốc độ tăng
không đổi thì sau
9
giờ đám bèo ấy phủ kín mặt hồ. Hỏi sau bao nhiêu giờ thì đám
bèo ấy phủ kín một phần ba mặt hồ?
Gọi
a
diện tích ban đầu của đám bèo.
Sau một giờ diện tích đám bèo là
1
a 10a
; Sau
n
giờ diện tích đám bèo là
a .10
n
n
a
Sau 9 giờ diện tích đám bèo là
9
9
.10a a S
;
()S
là diện tích của mặt hồ.
Ta có đám bèo ấy phủ kín một phần ba mặt
hồ
9 9 9
.10 10 10
.10 10 log 9 log3
3 3 3 3
nn
Sa
an
Câu 22. Chọn B.
Ta có :
d d d d
d d d 8 10 7 5
c d a c
b b d a
d d c
b a a
f x x f x x f x x f x x
f x x f x x f x x
?
Câu 23. Chọn D.
11
sin 2 cos3 d cos2 sin3
23
f x x x x x x C
.
Câu 24. Chọn A.
22
2
2
33
33
0
00
1 1 2 2 4
d d 1 1 2
3 3 3 3
11
x
I x x x
xx


.
Câu 25. Chọn B.
1
2
0
1d
x
I x e x
đặt
2
2
dd
1
1
dv
2
x
x
ux
ux
ve
e dx


1
1
22
1
2 2 2
0
0
0
1 1 4 1 3 1
. 1 d .
2 2 4 4 4
x x x
e e e
I e x e x e




.
Câu 26. Chọn C.
Ta có
3
4 0 0; 2; 2.x x x x x
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
4y x x
, trục hoành, trục tung và đường thẳng
4x
.là
4 0 2 4
3 3 3 3
2 2 0 2
4 d 4 d 4 d 4 d 40S x x x x x x x x x x x x

Câu 27. Chọn D.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 34 Tài liệu ôn thi HK2 – Khối 12
4 2.ln 0 1x x x
,
2
2
11
4 2.ln d 4 2 .ln .d
ee
V x x x x x x


đặt
2
22
1
2
1
2ln
ln
dd
ln 2 2 4 1 .ln .d
.dv 4 2 d
22
e
e
x
ux
ux
V x x x x x x
x
xx
v x x





đặt
22
1
2
1
1
dd
ln
2 2 ln 2 4 2 4 .d
.dv 1 d
2
e
e
ux
ux
x
V e e x x x x x
xx
x
vx




22
1
2 4 2 5 .
e
V e x x e e
Câu 28. Chọn C.
Ta có
4000 8000
2 8000ln 2 .
1 0,5 2
f n f n dn dn d n n C
nn







0 8000ln2 250000 250000 8000ln2
10 8000ln10 8000ln10 250000 8000ln2 262876.
f C C
fC
Câu 29. Chọn D.
25 10 25 10z i z i
.
Câu 30. Chọn B.
12
2 3 1 7 3 4z z i i i
.
Câu 31. Chọn C.
2
2 0.5 1 2 0,5. 2 2z i i i
.
Câu 32. Chọn A.
5 3 2 5 3 2 2
5
2 2 3 2 2 3 2 2 5 .
2 2 5
i i i
z
w z i i i
ii

Câu 33. Chọn A.
2
2
2 2 4 2
2
3
9
1 2 46 4 45 0
5
5
z
z
z z z z
zi
z



.
Câu 34. Chọn B.
,bz a bi a
2 2 2 2
2 3 1 2 2 3 1 2
2 3 1 2 2 10 8 0
z i z i a bi i a bi i
a b a b a b
2
2
2 2 2 2
8
5 4 26 40 16
13
z a b b b b b
,
z
có môđun nhỏ nhất khi
10
13
b
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 35 Tài liệu ôn thi HK2 – Khối 12
Câu 35. Chọn C.
2
3
ABC
Sa
,
3AM a
,
60 .tan 3. 3 3
o
SMA SA AM SMA a a
,
3
.
1
.SA a 3.
3
S ABC ABC
VS
Câu 36. Chọn D.
2 2 2
1
4 .BC 6a
2
ABC
BC AC AB a S AB
,
22
11
7AA A B AB a
,
1 1 1
3
. 1 ABC
. 6 7.
ABC A B C
V AA S a
Câu 37. Chọn B.
Gọi
x
là độ dài
AB
,kẻ
SF AB
tại
F
, ta có
3
23
.OCD .ABCD
1 1 1
.SF 2 2
2 4 12 24 3
SS
xa
SF V V AB x x a
Do
F
là trung điểm của
AB
nên khoảng cách
h
từ
A
đến mặt phẳng
SBD
gấp
2
lần
khoảng cách
d
từ
F
đến mặt phẳng
SBD
mà
sin45
22
o
FB x
EF a
Tính
d
: kẽ
;FE DB
FH SE
, ta chứng minh được
SH SBD
,
2 2 2 2 2 2
1 1 1 1 1 3 6
2 2 3
a
FH d
FH FE FS a a a
, vậy
26
2.
3
a
hd
Câu 38. Chọn .
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 36 Tài liệu ôn thi HK2 – Khối 12
Gọi
G
là trung điểm của
0
1 1 1
53
( ) A 60 .tan 60 .
2
O
AC AG ABC AG AG AG a
Ta có
11
BC AAC C
Câu 39. Chọn B.
11
2 2 2.
22
R HB BC a a
Câu 40. Chọn C.
2 2 2
2 2 4 4 4 64 .
tp
S R Rh R
Câu 41. Chọn A.
Gọi
2 2 2 2
6 2 2 .H AC BD SH ABCD SH SA AH a a a
2 2 3
3
6 3 4 9
.
2 2.2 2 3 2
SA a a a
R V R
SH a
Câu 42. Chọn B.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 37 Tài liệu ôn thi HK2 – Khối 12
6
6
3
3 2 2 2
24
3
1 27
9.
3
aR
a
V a R h h l h R
RR

66
66
42
6 6 6 6 12
2
44
66
2 2 2 2
3
33
. . .
3 3 3 3 3
9
..
2 2 2 2 4
2
xq
a R a R
S R l R
RR
a a a a a
a
RR
R R R R

Dấu bằng xảy ra khi
6
6
46
2
6
3
3
3 2 .
2
2
a
a
R a R R
R
Câu 43. Chọn C.
Ta có
2
2;1;0 .u
là một vectơ chỉ phương của
.
Câu 44. Chọn D.
( 3,1,1);AC ( 1,1,1) 2, 4, 2 .AB AB AC
Câu 45. Chọn A.
Câu 46. Chọn C.
Ta có
0 2 1
3
cos 30 .
2
2. 6
o


Câu 47. Chọn B.
Ta có
2; 4;4 ; 2,0,1 ,AB M
phương trình mặt phẳng trung trực
P
của đoạn
thẳng
AB
là
2 2 4 0.x y z
Câu 48. Chọn B.
Ta có
2, 4,1 ; 1, 2, / /
. 0 2 8 0 10.
dP
d P d P
v n m d P
v n v n m m
Câu 49. Chọn B.
Ta có khoảng cách từ
I
đến
P
là
2
22
2224
, 2 5 9
1 4 4
h I P R h




.
Câu 50. Chọn A.
Do
3 2 ,1 ,2A A t t t 
,
mà
M
là trung điểm
AB
nên
1 2 , 1 , 4B t t t
: 1 2t 1 t 4 t 2 0 2 5,1, 6 . MB 6,1, 5B P P t B
11
:.
6 1 5
x y z
-------------------------------------- HẾT ------------------------------------
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 38 Tài liệu ôn thi HK2 – Khối 12
x
y
3
2
O
4
2
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG NAI
Nguyễn Văn Huy
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 04
Câu 1. 
43
85 y x x
 :
A.
( 6;0)
. B.
(0; )
. C.
( ; 6)
. D.
( ; ) 
.
Câu 2. 
m

25
mx
y
xm

( ;1)
là:
A.
55 m
. B.
51 m
. C.
55 m
. D.
1m
.
Câu 3. 
3
34 y x x
là:
A.
x
1
. B.
1x
. C.
3x
. D.
3x
.
Câu 4. 
3 2 2
22 y x mx m x

1x
khi
A.
2m
. B.
3m
. C.
1m
. D.
1m
.
Câu 5. Cho hàm s
31
21
x
y
x
đúng ?
A.  th hàm s có tim cn ngang là
3
2
y
.
B.  th hàm s có tim cng là
3
2
y
.
C.  th hàm s có tim cng là
1
2
x
.
D.  th hàm s không có tim cn.
Câu 6. 
2
1
2

xx
y
x

A.
0
. B.
1
. C.
2
. D.
3
.
Câu 7. 
2
2 y x x

A.
0
. B.
1
. C.
2
. D.
3
.
Câu 8. 
M
và giá 
m

42
23 y x x
trên
0;2
là:
A.
11, 2Mm
. B.
3, 2Mm
. C.
5, 2Mm
. D.
11, 3Mm
.
Câu 9.  
và
( ): 1 d y x
là :
A.
1;1 ,( 1;2)
. B.
1;0 ,( 1;2)
. C.
1;0 ,(1;2)
. D.
1; 2
.
Câu 10. 
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 39 Tài liệu ôn thi HK2 – Khối 12
A.
32
3y x x
. B.
32
3 y x x
. C.
32
3y x x
. D.
32
3 y x x
.
Câu 11. 
m

yx

5
x
y
xm

A
và
B
sao cho
42AB
là:
A.
2
. B.
5
. C.
7
. D. 
Câu 12. 
2
2
log 2 1yx
là:
A.
2
2log 2 1
2 1 ln2
x
x
. B.
2
4log 2 1
2 1 ln2
x
x
. C.
2
4log 2 1
21
x
x
. D.
2
2 1 ln2x
.
Câu 13. 
log3 ; a
log2 b

125
log 30
theo
a
và
b
là
A.
125
12
log 30
a
b
. B.
125
2
log 30
1
a
b
. C.
125
1
log 30
1
a
b
. D.
125
1
log 30
3(1 )
a
b
.
Câu 14. Cho
a
,
b

2
11
22
1 2 :







bb
ab
aa

A.
1
a
. B.
ab
. C.
ab
. D.
1
b
.
Câu 15. 
6
5
3
. . ( 0)x x x x
 
A.
7
3
x
. B.
5
2
x
. C.
2
3
x
. D.
5
3
x
.
Câu 16. Cho
9 9 23

xx

5 3 3
1 3 3


xx
xx
P

A.
5
2
. B.
1
2
. C.
3
2
. D.
2
.
Câu 17. 
2
3 .2 1
xx
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 18. 
2
3
3
log ( 1) log (2 1) 2 xx
là:
A. Vô nghim. B.
1
. C.
2
. D.
3
.
Câu 19. 
0,2 0,2
log 1 log 3 xx
là:
A.
1;3S
. B.
1; S
. C.
;1 S
. D.
( 1;1)S
.
Câu 20. 
31
13
10 3 10 3


xx
xx
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 21.   
0,2%

1998
  
125932000
. Và
140000000
?
A. 
2049
. B. 
2050
. C. 
2051
. D. 
2052
.
Câu 22. Cho
0a
và
1a
.
C
đúng ?
A.
.ln
xx
a dx a a C
. B.
2
2
2ln

x
x
a
a dx C
a
.
C.
22

xx
a dx a C
. D.
22
.ln
xx
a dx a a C
.
Câu 23. 

2
1 , 0 y x y
A.
2
31416
0001
. B.
4
3
. C.
2
. D.
3
2
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 40 Tài liệu ôn thi HK2 – Khối 12
Câu 24.  
2
( 2)
()
( 1)
xx
fx
x
?
A.
2
1
()
1

xx
Fx
x
. B.
2
1
()
1

xx
Fx
x
. C.
2
1
()
1

xx
Fx
x
. D.
2
()
1
x
Fx
x
.
Câu 25. 
2
2
0
2
x
e dx
là :
A.
4
e
. B.
4
1e
. C.
4
4e
. D.
4
3e
.
Câu 26. 
ln5
2
ln2
x
1
x
x
e
d
e
là :
A.
22
3
. B.
19
3
. C.
23
3
. D.
20
3
.
Câu 27. 
2
yx

2yx
là:
A.
4
3
. B.
3
2
. C.
5
3
. D.
23
15
.
Câu 28. 
H

2
1yx
và
42yx


H

Ox
là:
A.
4
3
. B.
248
3
. C.
224
15
. D.
1016
15
.
Câu 29. 
12zi
là:
A.
12i
. B.
12i
. C.
2 i
. D.
12 i
.
Câu 30. 
z

2
1 2 8 1 2 i i z i i z
là
A.
2
. B.
3
. C.
2
. D.
3
Câu 31.            
z
   
1 z i i z
là :
A.
1R
. B.
2R
. C.
2R
.
D.
4R
Câu 32. 
1
1zi
và
2
35 zi

1 2 2
.w z z z
A.
130w
B.
130w
C.
112w
D.
112w
Câu 33. 
z

1 14 2 i z i

z


Oxy

A.
6;8
. B.
8;6
. C.
8;6
. D.
6; 8
.
Câu 34. 
12
,zz

2
2 2 5 0 zz


22
12
11 A z z

A.
25
. B.
5
. C.
5
. D.
25
.
Câu 35. 
z

2z
và
2
z

A.
1
B.
2
C.
3
D.
4
Câu 36.  ?
A.
4
. B.
7
. C.
8
. D.
9
.
Câu 37. Cho
H

a

H
:
A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 38. 
13
,
14
,
15
 

0
30

8
:
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 41 Tài liệu ôn thi HK2 – Khối 12
A.
340
. B.
336
. C.
274 3
. D.
124 3
.
Câu 39. Cho hình chóp
.S ABCD

ABCD

O
,
SA ABCD


.S ABCD

V

OSCD
theo
V
?
A.
3
V
. B.
4
V
. C.
2
3
V
. D.
8
V
.
Câu 40. 
2

4


A.
8
. B.
24
. C.
32
. D.
16
.
Câu 41. 
3
:
A.
3
3
. B.
83
3
. C.
43
3
. D.
23
3
.
Câu 42. 
O

'
O


a

O

A

'
O

B
sao cho
2AB a

'
OO AB
theo
a
là:
A.
3
3
8
a
V
. B.
3
3
6
a
V
. C.
3
3
12
a
V
. D.
3
3
4
a
V
.
Câu 43. Cho hình chóp
.S ABC
 
ABC
     
B
,
3AB BC a
,
90
o
SAB SCB

A

()SBC

2a


.S ABC
theo
a
?
A.
2
3
Sa
. B.
2
16
Sa
. C.
2
2
Sa
. D.
2
12
Sa
.
Câu 44. 
Oxyz

( ): 2 2 2017 0 P x z z


()P
?
A.
4
1; 2;2n
. B.
1
1; 1;4n
. C.
3
2;2; 1 n
. D.
2
2;2;1n
.
Câu 45. 
Oxyz
, 
2 2 2
( ): 4 4 6 3 0 S x y z x y z
.

I
và tính bán kính
R

()S
?
A.
2;2; 3I
và
20R
. B.
4; 4;6I
và
71R
.
C.
4;4; 6I
và
71R
. D.
2; 2;3I
và
20R
.
Câu 46. 
Oxyz

d

(1;2;3)A
và vuông

:2 2 2017 0 P x z z
 :
A.
1 2 3
2 2 1

x y z
. B.
1 2 3
2 2 1

x y z
.
C.
2 2 1
1 2 3

x y z
. D.
2 2 1
1 2 3

x y z
.
Câu 47. Trong không g    
Oxyz
  
()P
   
(1;0;0),A
(0;2;0),B
(0;0;3)C

A.
2 3 1 0 x z z
. B.
0
1 2 3
x y z
.
C.
6 3 2 6 0 x z z
. D.
1
3 2 1
x y z
.
Câu 48. 
()S
   
(2;1; 1)I
     
)
  
2 2 3 0 x y z
. Bán 
()S

A.
4
3
. B.
2
9
. C.
2
3
. D.
2
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 42 Tài liệu ôn thi HK2 – Khối 12
Câu 49.       
Oxyz
  
(1;2;3)A
  
13
:
2 1 2


x y z
d
. 

A


d

Ox
?
A.
1 2 3
2 2 3

x y z
. B.
2 2 3
1 2 3

x y z
.
C.
1 2 3
2 2 3

x y z
. D.
2 2 3
1 2 3

x y z
.
Câu 50.       
Oxyz
   
12
:
2 1 2


x y z
d
 
(2;5;3)A

()P

d

A

()P
là
:
A.
4 3 0 x y z
. B.
4 3 0 x y z
.
C.
4 3 0 x y z
. D.
4 3 0 x y z
.
----------- HẾT ----------
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 43 Tài liệu ôn thi HK2 – Khối 12
ĐÁP ÁN: ĐỀ SỐ 04
1
C
11
C
21
C
31
C
41
B
2
B
12
B
22
B
32
A
42
C
3
A
13
D
23
B
33
D
43
D
4
C
14
A
24
A
34
C
44
C
5
A
15
D
25
B
35
D
45
A
6
D
16
A
26
D
36
D
46
B
7
B
17
C
27
A
37
B
47
C
8
A
18
C
28
C
38
B
48
D
9
B
19
D
29
D
39
C
49
A
10
D
20
D
30
A
40
D
50
D
Câu 1. 
43
85 y x x
 :
A.
( 6;0)
. B.
(0; )
. C.
( ; 6)
. D.
( ; ) 
.
Hướng dẫn giải
32
0
' 4 24 ' 0
6

x
y x x y
x

x
60
'y
- 0 + 0 +
y
Đáp án: C.
( ; 6)
Câu 2. 
m

25
mx
y
xm

( ;1)
là:
A.
55 m
. B.
51 m
. C.
55 m
. D.
1m
.
Hướng dẫn giải
2
2
25
'
()
m
y
xm

;1 ' 0 ;1 yx
2
25 0
51
1


m
m
m
Đáp án: B.
51 m
Câu 3. 
3
34 y x x
là:
A.
x
1
. B.
1x
. C.
3x
. D.
3x
.
Hướng dẫn giải
2
1
' 3 3 ' 0
1

x
y x y
x

x
11
'y
0 + 0
y
Đáp án: A.
x
1
Câu 4. 
3 2 2
22 y x mx m x

1x
khi
A.
2m
. B.
3m
. C.
1m
. D.
1m
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 44 Tài liệu ôn thi HK2 – Khối 12
Hướng dẫn giải
22
' 3 4 y x mx m
1
'(1) 0
3

m
y
m

1m

Đáp án: C.
1m
Câu 5. 
31
21
x
y
x

A.  th hàm s có tim cn ngang là
3
2
y
.
B.  th hàm s có tim cng là
3
2
y
.
C.  th hàm s có tim cng là
1
2
x
.
D.  th hàm số không có tim cn.
Hướng dẫn giải
Đáp án: A. 
3
2
y
.
Câu 6. 
2
1
2

xx
y
x

A.
0
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
22
lim 1; lim 1; lim ; lim

 

xx
xx
y y y y

Đáp án: D.
3
.
Câu 7. 
2
2 y x x

A.
0
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
2
1
0;2 . ' ' 0 1
2
(1) 1, (0) (2) 0


x
D y y x
xx
y y y
Đáp án: B. 1
Câu 8. 
M

m

42
23 y x x
trên
0;2
là:
A.
11, 2Mm
. B.
3, 2Mm
. C.
5, 2Mm
. D.
11, 3Mm
.
Hướng dẫn giải
3
0
' 4 4 ' 0 1 (0) 3, (1) 2, (2) 11
1 0;2
x
y x x y x y y y
x
Đáp án: A.
11, 2Mm
Câu 9. 
và
( ): 1 d y x
là :
A.
1;1 ,( 1;2)
. B.
1;0 ,( 1;2)
. C.
1;0 ,(1;2)
. D.
1; 2
.
Hướng dẫn giải
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 45 Tài liệu ôn thi HK2 – Khối 12

2
1 2 1 1
2 2 0
1 ( 1;2)
1
1
1 (1;0)
2
2







x x x
x
x
x
x
x
Đáp án: B.
1;0 ,( 1;2)
Câu 10. 
A.
32
3y x x
. B.
32
3 y x x
. C.
32
3y x x
. D.
32
3 y x x
.
Hướng dẫn giải

0a

2;4
32
3 y x x
Đáp án: D.
32
3 y x x
Câu 11. 
m
sao 
yx

5
x
y
xm

A
và
B
sao cho
42AB
là
A.
2
. B.
5
. C.
7
. D. Đáp án:khác.
Hướng dẫn giải

2
5
1 5 0 ( )




x x m x
x m x f x
xm
xm

A
,
B

2
0
2 19 0
0
5




f
mm
fm
m

1 1 2 2
; , ;A x x B x x

12
;xx

( ) 0fx
2
2
2 1 1 2 1 2
7
4 2 4 4 16 2 35 0
5

m
AB x x x x x x m m
m

7m
Đáp án: C. 7
Câu 12. 
2
2
log 2 1yx
là:
A.
2
2log 2 1
2 1 ln2
x
x
. B.
2
4log 2 1
2 1 ln2
x
x
. C.
2
4log 2 1
21
x
x
. D.
2
2 1 ln2x
.
Hướng dẫn giải
x
y
3
2
O
4
2
1
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 46 Tài liệu ôn thi HK2 – Khối 12
'
22
22
2log (2 1).(2 1)' 4log (2 1)
' 2log (2 1)[log (2 1)]
(2 1)ln2 (2 1)ln2

x x x
y x x
xx
Đáp án: B.
2
4log 2 1
2 1 ln2
x
x
Câu 13. 
log3 ; a
log2 b

125
log 30
theo
a
và
b
là
A.
125
12
log 30
a
b
. B.
125
2
log 30
1
a
b
. C.
125
1
log 30
1
a
b
. D.
125
1
log 30
3(1 )
a
b
.
Hướng dẫn giải
125
log 30
=
log30 1 log3 1
log125 3log5 3(1 )


a
b
Đáp án: D.
125
1
log 30
3(1 )
a
b
Câu 14. Cho
a
,
b

2
11
22
1 2 :







bb
ab
aa
sau k
A.
1
a
. B.
ab
. C.
ab
. D.
1
b
.
Hướng dẫn giải
2
2
2
11
22
1
11
1 2 :
















b
bb
a
ab
a a a
a b a
Đáp án: A.
1
a
Câu 15. 
6
5
3
. . ( 0)x x x x

A.
7
3
x
. B.
5
2
x
. C.
2
3
x
. D.
5
3
x
.
Hướng dẫn giải
1 5 10 5
1
6
5
3
3 6 6 3
2
. . . . x x x x x x x x
Đáp án: D.
5
3
x
Câu 16. Cho
9 9 23

xx

5 3 3
1 3 3


xx
xx
P

A.
5
2
. B.
1
2
. C.
3
2
. D.
2
.
Hướng dẫn giải
Ta có
2
(3 3 ) 9 9 2 23 2 25

x x x x
nên
(3 3 ) 5

xx
Suy ra
5 3 3 5 5 5
1 3 3 1 5 2
xx
xx
P
Đáp án:
A.
5
2
Câu 17. 
2
3 .2 1
xx
là:
A.
0
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
22
2
2 2 2
3 .2 1 log (3 .2 ) 0 log 3 0 log 3
x x x x
x x x x
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 47 Tài liệu ôn thi HK2 – Khối 12
Đáp án: C. 2
Câu 18. 
2
3
3
log ( 1) log (2 1) 2 xx
là:
A. Vô nghim. B.
1
. C.
2
. D.
3
.

1
1
2
x
x
2
3
3
log ( 1) log (2 1) 2 xx
33
2log 1 2log (2 1) 2 xx
33
2log 1 2log (2 1) 2 xx
3
log 1 (2 1) 1 xx
1 (2 1) 3 xx

1x
ta có
2
2
1 (2 1) 3 2 3 2 0
1
()
2

x
x x x x
xl

1
1
2
x
ta có
2
1 (2 1) 3 2 3 2 0 x x x x

Đáp án: C. 2
Câu 19. 
0,2 0,2
log 1 log 3 xx
là:
A.
1;3S
. B.
1; S
. C.
;1 S
. D.
( 1;1)S
.
Hướng dẫn giải

13 x
0,2 0,2
log 1 log 3 1 3 1 x x x x x


( 1;1)S
Đáp án: D.
( 1;1)S
Câu 20. 
31
13
10 3 10 3


xx
xx
là
A.
0
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
3 1 3 1
1 3 1 3
10 3 10 3 10 3 10 3
x x x x
x x x x
3 1 8
0 ( 1)( 3) 0 3 1 2, 1,0
1 3 ( 1)( 3)
xx
x x x x
x x x x
Đáp án: D. 3
Câu 21. 
0,2%

1988

125932000

140000000
?
A. 
2049
. B. 
2050
. C. 
2051
. D. 
2052
.
Hướng dẫn giải
0,2
14000000 125932000. 1 53
100



n
n
Đáp án: C. 
Câu 22. Cho
0a
và
1a
.
C

A.
.ln
xx
a dx a a C
. B.
2
2
2ln

x
x
a
a dx C
a
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 48 Tài liệu ôn thi HK2 – Khối 12
C.
22

xx
a dx a C
. D.
22
.ln
xx
a dx a a C
.
Hướng dẫn giải
Đáp án: B.
2
2
2ln

x
x
a
a dx C
a
Câu 23. 

2
1 , 0 y x y
A.
2
31416
0001
. B.
4
3
. C.
2
. D.
3
2
.
Hướng dẫn giải

2
1 0 1 xx
1
2
1
4
(1 )
3
V x dx
Đáp án: B.
4
3
Câu 24. không 
2
( 2)
()
( 1)
xx
fx
x
?
A.
2
1
()
1

xx
Fx
x
. B.
2
1
()
1

xx
Fx
x
. C.
2
1
()
1

xx
Fx
x
. D.
2
()
1
x
Fx
x
.
Hướng dẫn giải
Vì
'
22
2
1 2 2
'( )
1
1




x x x x
Fx
x
x
Đáp án: A.
2
1
()
1

xx
Fx
x
Câu 25. 
2
2
0
2
x
e dx
là :
A.
4
e
. B.
4
1e
. C.
4
4e
. D.
4
3e
.
Hướng dẫn giải
2
24
0
21
x
e dx e
.
Đáp án: B.
4
1e
Câu 26. 
ln5
2
ln2
x
1
x
x
e
d
e
là
A.
22
3
. B.
19
3
. C.
23
3
. D.
20
3
.
Hướng dẫn giải
ln5
2
ln2
20
3
1
x
x
e
dx
e
.
Đáp án: D.
20
3
Câu 27. 
2
yx

2yx
là:
A.
4
3
. B.
3
2
. C.
5
3
. D.
23
15
.
Hướng dẫn giải
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 49 Tài liệu ôn thi HK2 – Khối 12
2
0
2
2

x
xx
x
2
2
0
4
2
3
S x xdx
Đáp án: A.
4
3
Câu 28. 
H

2
1yx
và
42yx


H
qua
Ox
là:
A.
4
3
. B.
248
3
. C.
224
15
. D.
1016
15
.
Hướng dẫn giải
22
1
1 4 2 4 3 0
3
x
x x x x
x
3
2
2
2
1
224
4 2 1
15
V x x dx
Đáp án: C.
224
15
Câu 29. 
12zi
là
A.
12i
. B.
12i
. C.
2 i
. D.
12 i
.
Hướng dẫn giải

12zi
là
12zi
Đáp án: D.
12 i
Câu 30. 
z

2
1 2 8 1 2 i i z i i z
là
A.
2
. B.
3
. C.
2
. D.
3
Hướng dẫn giải
Ta có:
2
1 2 8 1 2 2 4 1 2 8
8 1 2
8
1 2 8 2 3
1 2 5

i i z i i z i z i z i
ii
i
i z i z i
i

z

2
Đáp án: A.
2
Câu 31.            
z
   
1 z i i z
là 
A.
1R
. B.
2R
. C.
2R
.
D.
4R
Hướng dẫn giải

;M x y

;, z x iy x y

2
2
11 z i x y i x y
22
1 1 1 i z i x iy x y x y i i z x y x y

1 z i i z
nên ta có:
2 2 2
2 2 2
1 2 1 0 (*) x y x y x y x y y

0; 1I
bán kính
2
1 1 2 R
C. R =
2
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 50 Tài liệu ôn thi HK2 – Khối 12
Câu 32. 
1
1zi
và
2
35 zi

1 2 2
.w z z z
A.
130w
B.
130w
C.
112w
D.
112w
Hướng dẫn giải
Ta có:
2 1 2
3 5 . 1 3 5 8 2 z i z z i i i

2
2
11 3 11 3 130 w i w
Đáp án: A.
130w
Câu 33. 
z

1 14 2 i z i

z


Oxy

A.
6;8
. B.
8;6
. C.
8;6
. D.
6; 8
.
Hướng dẫn giải

1 14 2 i z i
suy ra
14 2 1
14 2
68
12

ii
i
zi
i

;M x y

68zi

Oxy
suy ra
6; 8M
.
Đáp án: D.
6; 8
Câu 34. 
12
,zz

2
2 2 5 0 zz


22
12
11 A z z

A.
25
. B.
5
. C.
5
. D.
25
.
Hướng dẫn giải

2
2 2 5 0 zz

12
1 3 1 3
;
2 2 2 2
z i z i
Tính
22
12
55
1 1 5
22
A z z
Đáp án: C.
5
Câu 35. 
z

2z
và
2
z

A.
1
B.
2
C.
3
D.
4
Hướng dẫn giải

,, z a bi a b
Ta có:
2 2 2 2
22 z a b a b
(1)
2 2 2
2 z a b abi

22
0ab
(2)

22
22
22
2
1
0


ab
ab
ab

1 2 3 4
1 ; 1 ; 1 ; 1 z i z i z i z i
Đáp án: D.
4
Câu 36. 
A.
4
. B.
7
. C.
8
. D.
9
.
Hướng dẫn giải
  
. ' ' ' 'ABCD A B C D
            
, , 'AB AD AA

D. 9
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 51 Tài liệu ôn thi HK2 – Khối 12
O
S
B
C
A
D
Câu 37. Cho
H

a

H

A.
3
3
a
. B.
3
2
6
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Hướng dẫn giải

ABCD
:
2
ABCD
Sa

D O AC B SO

SOA

O
cho ta
2
2 2 2
1
22
a
SO SA AO a a

3
2
1 1 2 2
. . .
3 3 2 6
SABCD ABCD
aa
V S SO a
Đáp án: B.
3
2
6
a
Câu 38.    
13
,
14
,
15
 

0
30

8

A.
340
. B.
336
. C.
274 3
. D.
124 3
.
Hướng dẫn giải
Ta có :
S 21(21 13)(21 14)(21 15) 84
ABC

O

'
A
trên
ABC
'A AO
O cho ta :
0
' '.sin30 4A O AA

. ' ' '
84.4 336
ABC A B C
V
Đáp án: B.
336
Câu 39. Cho hình chóp
.S ABCD

ABCD

O
,
SA ABCD


.S ABCD

V

OSCD
theo
V
.
A.
3
V
. B.
4
V
. C.
2
3
V
. D.
8
V
.
Hướng dẫn giải
Ta có
.
.
1
3

S ABCD ABCD
V SA S V
.
Do
1
4
OCD ABCD
SS
và
.
.
1
3

OSCD S BCD BCD
V V SA S
O
D
A
C
B
S
a
a
a
O
H
C'
B'
A'
C
B
A
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 52 Tài liệu ôn thi HK2 – Khối 12
Câu 40. 
2

4


A.
8
. B.
24
. C.
32
. D.
16
.Gii
Hướng dẫn giải
2
.4.4 16
V R h
Đáp án: D.
16
Câu 41. 
3

A.
3
3
. B.
83
3
. C.
43
3
. D.
23
3
.
Hướng dẫn giải
Bán kính hình nón:
0
3
2
sin60
R

0
.tan60 2 3hR
2
83
33


Rh
V
Đáp án: B.
83
3
Câu 42. 
O

'
O


a
y tâm
O

A

'
O


B
sao cho
2AB a

'
OO AB
theo
a
là
A.
3
3
8
a
V
. B.
3
3
6
a
V
. C.
3
3
12
a
V
. D.
3
3
4
a
V
.
Hướng dẫn giải
  
'
AA

D
   
'
A
qua
'
O
và
H
  
B
trên

'
AD
.
Do
' , ' ( ' ') BH A D BH AA BH AOO A
2 2 2 2
' ' 3 ' ' A B AB A A a BD A D A B a
S
A
O
H
B
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 53 Tài liệu ôn thi HK2 – Khối 12
'O BD

3
2
a
BH
2
'
2
AOO
a
S
. Suy ra tOOAB là:
3
3
12
a
V
Đáp án: C.
3
3
12
a
V
Câu 43. Cho hình chóp
.S ABC
 
ABC
     
B
,
3AB BC a
,
90
o
SAB SCB

A

()SBC

2a


.S ABC
theo
a
.
A.
2
3
Sa
. B.
2
16
Sa
. C.
2
2
Sa
. D.
2
12
Sa
.
Hướng dẫn giải

D

S
trên
()ABC
, ( ) AB SA AB SD AB SAD AB AD

() CB SCD BC DC
. Suy ra
ABCD
là hình vuông

H

D
trên
SC
( ) ( ,( ) ( ,( ) 2 DH SBC d A SBC d D SBC DH a
2 2 2
1 1 1
6 SD a
SD SH DC

I

SB
ta có
IA IB IC IS
nên
I

3
2

SC
ra
. D
.S ABC
là:
22
4 12

S r a
Đáp án: D.
2
12
Sa
Câu 44. 
Oxyz

( ): 2 2 2017 0 P x z z


()P
?
A.
4
1; 2;2n
. B.
1
1; 1;4n
. C.
3
2;2; 1 n
. D.
2
2;2;1n
.
Hướng dẫn giải

()P
là
3
2;2; 1 n
.
Đáp án: C.
3
2;2; 1 n
Câu 45. 
Oxyz

2 2 2
( ): 4 4 6 3 0 S x y z x y z
.

I
và tính bán kính
R

()S
.
A.
2;2; 3I
và
20R
. B.
4; 4;6I
và
71R
.
C.
4;4; 6I
và
71R
. D.
2; 2;3I
và
20R
.
Hướng dẫn giải
Tâm
I

S
là
2;2; 3I
, bán kính là
2 2 2
2 2 ( 3) 3 20 R
.
Đáp án: A.
2;2; 3I
và
20R
Câu 46. 
Oxyz

d

(1;2;3)A
và vuông

:2 2 2017 0 P x z z

A.
1 2 3
2 2 1

x y z
. B.
1 2 3
2 2 1

x y z
.
C.
2 2 1
1 2 3

x y z
. D.
2 2 1
1 2 3

x y z
.
Hướng dẫn giải
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 54 Tài liệu ôn thi HK2 – Khối 12
     
d
      
P
nên
(2;2;1)
d
P
un

d

(1;2;3)A

(2;2;1)
d
u
nên có

1 2 3
2 2 1

x y z
.
Đáp án: B.
1 2 3
2 2 1

x y z
Câu 47.       
Oxyz
  
()P
   
(1;0;0),A
(0;2;0),B
(0;0;3)C

A.
2 3 1 0 x z z
. B.
0
1 2 3
x y z
.
C.
6 3 2 6 0 x z z
. D.
1
3 2 1
x y z
.
Hướng dẫn giải
1
1 2 3
x y z
6 3 2 6 0 x z z
Đáp án: C.
6 3 2 6 0 x z z
Câu 48. 
()S
   
(2;1; 1)I
    
)
  
2 2 3 0 x y z

()S

A.
4
3
. B.
2
9
. C.
2
3
. D.
2
.
Hướng dẫn giải
Bán kính
R

()S
chí
I

()S

:
2 2 2
2.2 2.1 ( 1) 3
;2
2 ( 2) ( 1)
R d I
Đáp án: D. 2
Câu 49.       
Oxyz
  
(1;2;3)A
  
13
:
2 1 2


x y z
d
. 

A


d

Ox
A.
1 2 3
2 2 3

x y z
. B.
2 2 3
1 2 3

x y z
.
C.
1 2 3
2 2 3

x y z
. D.
2 2 3
1 2 3

x y z
.
Hướng dẫn giải

B


Ox

;0;0Bb
Vì
d nên
d
AB u

( 1; 2; 3) AB b
,
2;1; 2
d
u
)
Suy ra
. 0 1
d
ABu b

( 2; 2; 3) AB

là
2;2;3
u
.

là
1 2 3
2 2 3

x y z
.
Đáp án: A.
1 2 3
2 2 3

x y z
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 55 Tài liệu ôn thi HK2 – Khối 12
Câu 50. Trong không 
Oxyz

12
:
2 1 2


x y z
d

(2;5;3)A

()P

d

A

()P
là

A.
4 3 0 x y z
. B.
4 3 0 x y z
.
C.
4 3 0 x y z
. D.
4 3 0 x y z
.
Hướng dẫn giải

H
là hình ch
A
trên
d
. 
1 2 ; ;2 2H t t t
.
Ta có
d
AH u

2 1; 5;2 1 AH t t t
,
2;1;2
d
u
) Nên
. 0 1
d
AH u t
Suy ra
1; 4;1AH
,
3;1;4H

()P

d

A

()P

()P

3;1;4H


1; 4;1AH

()P
là
1. 3 4. 1 1. 4 0 4 3 0 x y z x y z
Đáp án: D.
4 3 0 x y z
----------- HẾT ----------
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 56 Tài liệu ôn thi HK2 – Khối 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG NAI
Nguyễn Văn Huy
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017
Môn: TOÁN – Khối 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 05
Câu 1. 
32
32y x x

A. 
0; .
B. 
0;2 .
C. 
;2 .
D. 
;0 ; 2;
.
Câu 2. 
32
3y x x mx m

m

A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Câu 3. 
m

32
3 2 1x x m
t ?
A.
20m
. B.
31m
. C.
24m
. D.
03m
.
Câu 4. 
1
1
x
y
x

tr
A.
2
.
B.
2
.
C.
1
.
D.
1
.
Câu 5. Tìm
M
trên
3
:
1
x
y
x
H

M

: 2017d y x
A.
1; 1M
,
2; 3M
. B.
5;3M
,
2; 3M
.
C.
5;3M
,
1; 1M
. D.
1; 1M
,
4;5M
.
Câu 6. Cho 
2
1
x
y
x


A. 
1x

1y 
.
B. 
1x 

1y 
.
C. 
1y

1x 
.
D. 
1x 

1y
.
Câu 7. 
2
53
21
x
y
x mx


m


A.
1m 
. B.
1m
. C.
1; 1mm
. D.
11m
.
Câu 8. 
4
2
26
4
x
f x x

A.
6
CÐ
f
. B.
2
CÐ
f
. C.
20
CÐ
f
. D.
6
CÐ
f 
.
Câu 9. 
32
2
5
3
y x mx m x



m
1x
A.
2
5
m
. B.
7
3
m
. C.
3
7
m
. D.
0m
.
Câu 10. 
2
4
2
y
x

A.
3
. B.
2
. C.
5
. D.
10
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 57 Tài liệu ôn thi HK2 – Khối 12
Câu 11. 
A.
42
23y x x
. B.
42
2y x x
.
C.
42
2y x x
. D.
42
23y x x
.
Câu 12. 
22
log 36 log 144

A.
4
. B.
2
. C.
2
. D.
4
.
Câu 13. Cho
0,2 0,2
log logxy

A.
0yx
. B.
0xy
. C.
0xy
. D.
0yx
.
Câu 14. 
15


1,65%

20
 ?
A.
15
. B.
18
. C.
17
. D.
16
.
Câu 15. Cho
,ab

1

24
35
74
;log log
53
bb
aa


A.
0 1; 1ab
. B.
1; 1ab
.
C.
0 1;0 1ab
. D.
1;0 1ab
.
Câu 16. 
A.
2 2 2
33
log 2logaa
. B.
2 2 2
33
log 4logaa
.
C.
2 2 2
33
log 4logaa
. D.
2 2 2
33
log 2logaa
.
Câu 17. 
2
1
1
5 5. 26
5
x
x





1
x
và
2
x

12
xx
là
A.
4
. B.
3
. C.
2
D.
1
.
Câu 18. 
42
23
32
xx

A.
2
3
x
. B.
2
3
x 
. C.
2
5
x
. D.
2
5
x
.
Câu 19. 
2
log 975 10x 
là
A.
1998
. B.
2000
. C.
1999
. D.
1997
.
Câu 20. 
2
log 7 12 log 2 8x x x
có bao nhiêu nghi
A.
0
. B.
1
. C.
2
. D.
4
.
Câu 21. 
2
log 3 2 0
x


A.
1 x
. B.
3
log 2 1x
. C.
01x
. D.
3
log 2x
.
Câu 22. 
.S ABC
,
', 'AB

, .SA SB

chóp
. ' 'S A B C
và
.S ABC

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 58 Tài liệu ôn thi HK2 – Khối 12
A.
1
2
. B.
1
4
. C.
1
6
. D.
1
8
.
Câu 23. 
a
là
A.
3
2
3
a
. B.
3
2
4
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Câu 24.   
.S ABC
có
,SA ABC
tam giác
ABC
 
B
,
, 3.AB a AC a
T
.S ABC

5SB a
.
A.
3
2
3
a
. B.
3
6
4
a
. C.
3
6
6
a
. D.
3
15
6
a
.
Câu 25.   
.S ABC
có 
ABC
    
a
   
SAB
và
SAC

3SC a
.
A.
3
26
9
a
. B.
3
6
12
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 26. 
, , l h R

T
.

tp
S

T
là
A.
2
22
tp
S Rl R


. B.
2
tp
S Rl R


. C.
2
2
tp
S Rl R


. D.
2
tp
S Rh R


.
Câu 27. 
4a
, o là
3a
. 

A.
2
36 a
. B.
2
30 a
. C.
2
38 a
. D.
2
32 a
.
Câu 28. 
2
8
3
a

A.
6
3
a
. B.
3
3
a
. C.
6
2
a
. D.
2
3
a
.
Câu 29. 
ABCD

a

ABCD

A.
3
6
8
a
. B.
3
6
6
a
. C.
3
6
4
a
. D.
3
36
8
a
.
Câu 30. 
2
tanf x x
là
A.
tanxC
. B.
tanx x C
. C.
2tan xC
. D.
tanx x C
.
Câu 31. Nguyên hàm
Fx

32
4 3 2 2f x x x x

19F
là
A.
4 3 2
2x x xfx
. B.
4 3 2
10x x xfx
.
C.
4 3 2
2x x x xfx
. D.
4 3 2
2 10x x x xfx
.
Câu 32. Tính tích phân
1
4
2
0
1dI x x x
.
A.
31
10
. B.
30
10
. C.
31
10
. D.
32
10
.
Câu 33. 
sinxu
thì tích phân
2
4
0
sin cos dx x x
thành
A.
1
42
0
1du u u
. B.
2
4
0
duu
. C.
1
4
0
duu
. D.
2
32
0
1du u u
.
Câu 34. 
S
 
1
y f x
,
2
y f x

,x a x b
ab
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 59 Tài liệu ôn thi HK2 – Khối 12
A.
12
d
b
a
S f x f x x
.
B.
21
d
b
a
S f x f x x
.
C.
12
d
b
a
S f x f x x
. D.
12
d
b
a
S f x f x x
.
Câu 35.
         
21yx
    
2
3y x x
A.
1
6
. B.
1
6
. C.
1
7
. D.
1
8
.
Câu 36.       
tanyx
     
0,
4
xx


V

quan
Ox
.
A.
1
4
V



. B.
1
4
V




. C.
1
4
V




. D.
2
4
V




.
Câu 37. Cho
(2;3;0)A
và
(1;2;1)B
 
;;I a b c
là tr  
.AB
    
2bac

A.
3
. B.
2
. C.
0
. D.
1
.
Câu 38.  
0;1;2 ,I

: – 6 0P x y z

A.
22
2
1 2 4x y z
. B.
22
2
1 2 4x y z
.
C.
22
2
1 2 1x y z
. D.
22
2
1 2 3x y z
.
Câu 39. Cho 
–3;2;4 ,M

,,A B C
      M trên
, , .Ox Oy Oz


ABC

A.
4 – 6 – 3 12 0x y z 
. B.
3 – 6 – 4 12 0x y z 
.
C.
6 – 4 – 3 –12 0x y z
. D.
4 – 6 – 3 –12 0x y z
.
Câu 40. 
P

1;2;0A

1
:
11
21
xy
d
z


A.
2 – 4 0x y z
. B.
–2 – 4 0x y z
.
C.
–2 – – 4 0x y z
. D.
2 – 5 0xy
.
Câu 41. Hình 
0;1;2A

:0P x y z

A.
–2;2;0
. B.
–2;0;2
. C.
–1;1;0
. D.
–1;0;1
.
Câu 42. Côsin 
Oy

:4 3 2 7 0P x y z 
là
A.
2
3
. B.
1
3
. C.
2
3
. D.
4
3
.
Câu 43. Cho
1
7 5 9
:
3 1 4
x y z
d


và
2
4 18
:
3 1 4
x y z
d



A.
12
,dd
song song. B.
12
,dd
trùng nhau.
C.
12
,dd
 D.
12
,dd
chéo nhau.
Câu 44. 
2 2 2
: 4 2 6 5 0S x y z x y z
và
:2 2 16 0P x y z

M
di

S
,
N

P

MN
là
A.
5
. B.
4
. C.
3
. D.
2
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 60 Tài liệu ôn thi HK2 – Khối 12
Câu 45. Cho 
2 1 1 3z i i i

z
là
A.
25
. B.
22
. C.
13
. D.
42
.
Câu 46. Cho 
z

2
2 3 4 1 3i z i z i


z
.
A. 
2

5i
. B. 
2

5
.
C. 
2

3
. D. 
3

5i
.
Câu 47. Trong 
Oxy

z

1z i i z
.
A.
z
2; 1I
, bán kính
2R
.
B. 
z
0;1I
, bán kính
3R
.
C. 
z
0; 1I
, bán kính
3R
.
D. 
z
0; 1I
, bán kính
2R
.
Câu 48. 
12
, zz

2
2 10 0zz
. 

22
12
| | | |A z z
.
A.
15
. B.
17
. C.
19
. D.
20
.
Câu 49. S
2 20
1 1 1 ... 1i i i

A.
10
2
. B.
10 10
2 2 1 i
. C.
10 10
2 2 1 i
. D.
10 10
22i
.
Câu 50. 
z

20iz i

A.
1
. B.
2
. C.
3
. D.
4
.
-----------
1
2
3
4
5
6
7
8
9
10
D
D
B
B
C
A
D
A
B
B
11
12
13
14
15
16
17
18
19
20
C
B
D
B
B
D
C
B
C
B
21
22
23
24
25
26
27
28
29
30
B
B
D
A
B
A
A
A
A
B
31
32
33
34
35
36
37
38
39
40
D
C
C
A
B
C
A
D
D
B
41
42
43
44
45
46
47
48
49
50
D
A
A
D
A
A
D
D
B
A
Hướng dẫn giải
Câu 1. Chn D.
Ta có
2
0
' 3 6 . ' 0 .
2
x
y x x y
x
Bng bin thiên
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 61 Tài liệu ôn thi HK2 – Khối 12
Câu 2. Chn D.
Ta có
2
' 3 6y x x m
. Hàm s ng bin
2
' 3 6 0y x x m x
Suy ra
30
3.
' 9 3 0
m
m
Câu 3. Chn B.

3 2 3 2
3 2 1 3 3 0.x x m x x m
t
32
3 3 .f x x x m C
Suy ra
2
' 3 6f x x x
.
2
' 0 .
0
x
fx
x


    m phân bit
 th
C
có hai cc tr tha
D
.0
C CT
f x f x
.
2 0 0 1 3 0 3 1f f m m x
.
Câu 4. Chn B.
Ta có
2
2
'.
1
fx
x
m c th và trc tung là
0; 1 .M
H s góc cn tìm
' 0 2.kf
Câu 5.
Chn C.
Gi s
4
;1
3
M a H
a




.
Ta có
2
4
''
3
y f x
x

. Tip tuyn ca
H
ti
M
có h s góc
2
4
'.
3
k f a
a

Tip tuyn ca
H
ti
M
vuông góc vi
: 2017d y x
suy ra
2
5
4
.1 1 1 .
1
3
a
k
a
a
Vm cn tìm là
12
5;3 , 1; 1 .MM
Câu 6. Chn A.
Câu 7. Chn D.
Hàm s không có tim cng khi
2
21x mx
vô nghim hoc có nghim kép bng
3
5
. Suy ra
2
1 0 1 1.mm
Câu 8. Chn A.
Ta có
3
' 2 . ' 0 0 2 2.f x x x f x x x x
Da vào d th suy ra hàm s t ci ti
0x
.
Vy
D
0 6.
C
ff
Câu 9. Chn B.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 62 Tài liệu ôn thi HK2 – Khối 12
Ta có
2
2
' 3 2 .
3
f x x mx m
Hàm s t cc tiu ti
1x
suy ra
7
' 1 0 .
3
fm
Nu làm t lui th lng hp này thì vì ch ra
mt kt qu
m
nên ta ch
Câu 10. Chn B.
Câu 11. Chn C.
Da vào d th suy ra h s
0a
A và B b lo th c
t
0;0O
. Mà t m
O
không th th ca hàm s D.
Câu 12. Chn B.
Câu 13. Chn D.
Câu 14. Chn B.
S tin nhc sau
x
quý là
15. 1,0165
x
.
Ta có bpt
1,0165
20
15. 1,0165 20 log 17,58.
15
x
xx
i gi ít nht 18 quý.
Câu 15. Chn B.
Câu 16. Chn D.
Câu 17. Chn C.
t
5
x
t
 thành
2
5 130 125 0 25 1.t t t t
Suy ra
12
2 0.xx
Vy tng 2 nghim là 2.
Câu 18. Chn B.
B
4 2 4 2
2 3 2 2 2
4 2 .
3 2 3 3 3
x x x x
x x x

Câu 19. Chn C.

10
2
log 975 10 975 2 1999.x x x
Câu 20. Chn B.

2
2
2 8 0
log 7 12 log 2 8 5.
9 20 0
x
x x x x
xx

Vm
Câu 21. Chn B.
B
23
log 3 2 0 0 3 2 1 2 3 3 log 2 1.
x x x
x
Câu 22. Chn B.
Ta có
. ' '
.
'. ' 1
.
.4
S A B C
S ABC
V
SA SB
V SA SB

Câu 23. Chn D.
Ta có
23
33
. . .
44
V h B a a a
Câu 24. Chn A.
Ta có:
2
22
12
2 . .
22
ABC
a
BC AC AB a S AB BC
23
22
1 1 2 2
2 . .2 . .
3 3 2 3
ABC
aa
SA SB AB a V SA S a
Câu 25. Chn B.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 63 Tài liệu ôn thi HK2 – Khối 12
Ta có
()
.
SAB ABC
SAC ABC SA ABC
SAB SAC SA

Suy ra
SAC
vuông ti A. 
22
2.SA SC AC a
Vy
23
1 1 3 6
. 2. .
3 3 4 12
ABC
aa
V SA S a
Câu 26: A.

2
22
tp
S Rl R


Câu 27: A.

22
5l R h a
2 2 2
.4a.5a 16a 36
tp
S Rl R a
Câu 28: A.
2
2
86
4
33
mc
aa
S R R
Câu 29: A.
I
H
G
F
B
C
D
A
a
2
a
6
3
a
3
3
a
I
H
A
G
B

G

BCD
.
Ta có
I

AB
và
AG
.
Ta có
22
3 2 3 6
;;
2 3 3 3
a a a
BF BG BF AG AB BG
AH AG
AI AB
suy ra
.
.6
2
4
6
3
a
a
AH AB a
AI
AG
a
3
4 6 6
3 4 8
aa
V





Câu 30: B.
22
2
1
tan 1 tan 1 tan
cos
xdx x dx x dx x x C
x



Câu 31: D.
4 3 2
2F x x x x x C
11FC
9 10C
Câu 32: C.

2
12t x dt xdx
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 64 Tài liệu ôn thi HK2 – Khối 12
2
2
5
4
1
1
1 31
2 2 5 10
dt t
It
Câu 33: C.
sinux
cosdu xdx
1
4
0
I u du
Câu 34: A.

Câu 35: CB.
2
2
1
1
3 2 1
6
S x x x dx
Câu 36: C.
4
2
0
tan 1
4
V xdx




Câu 37: A.

351
;;
222
I



23bac
Câu 38: D.
3
;3
3
R d I P
Câu 39: D.
3;0;0 , 0;2;0 , 0;0;4A B C
: 1 4 6 3 12 0
3 2 4
x y z
ABC x y z
Câu 40: B.
P
có vtpt
P
n
2;1; 1
d
u 
PTTQ:
2 1 2 0 0 2 4 0x y z x y z
Câu 41: D.

d

A

P
d
có vtcp
1;1;1
dP
un
PTTS
:1
2
xt
d y t
zt



1
2
0
xt
yt
zt
x y z


Suy ra
1 2 0 1t t t t
. Suy ra
1;0;1H
Câu 42: A.
Oy
có vtcp
0;1;0j
P
có vtpt
4; 3; 2
P
n 
.
33
sin , cos ,
3
33
.
P
P
P
jn
Oy P j n
jn

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 65 Tài liệu ôn thi HK2 – Khối 12
2
6
cos , 1 sin ,
3
Oy P Oy P
Câu 43: A.
12
1
,0
, 9; 53; 20
uu
u MN



Câu 44: D.

2; 1;3I
, bán kính
3r
4 2 3 16
,5
4 4 1
d I P



,,I M N

M

,IN

,2h d I P r
Câu 45: A.
42zi
22
4 2 2 5z
Câu 46: A.

,,z a bi a b R
2
2 3 4 1 3i a bi i a bi i
6 4 2 2 8 6a b a b i i
6 4 8 2
2 2 6 5
a b a
a b b



Câu 47: D.

,,z a bi a b R
2 2 2
2
22
1
1
1
2 1 0
z i i z
a b i a b a b i
a b a b a b
a b b
22
0 1 2ab
m
0; 1I
, bán kính
2
Câu 48: D.
1
2
13
13
zi
zi
2 2 2
2
1 3 1 3 20A
Câu 49: B.
2 3 4
1 2 ; 1 2 2 ; 1 4i i i i i
23
1 1 1 1 1 1 2 2 2 5i i i i i i i
4 2 3
1 1 1 1 1 4 5i i i i i


8 2 3 2
1 1 1 1 1 4 5i i i i i


12 2 3 3
1 1 1 1 1 4 5i i i i i


16 2 3 4
1 1 1 1 1 4 5i i i i i


Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 66 Tài liệu ôn thi HK2 – Khối 12
5
20 4 5
1 1 4ii


2 20
1 (1 ) (1 ) ... (1 )i i i
=
2345
5 4.5 4 5 4 5 4 5 4 1024 1025i i i i i i
Câu 50: A.
2
12
i
zi
i

1
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 67 Tài liệu ôn thi THPT Quốc Gia 2017
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ SỐ 01
Nguyễn Văn Huy
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 01
Câu 1. 
x x mx
y
x
2
1
1

A.
m 0
. B.
mR
. C.
m 1
. D.
m 1
.
Câu 2. 
y f x


A
y f x

1y
.
B
y f x

1y
.
C
y f x

1y

1.x
D
y f x

1y

1.x
Câu 3. 
32
15
3
33
y x x x
là:
A.
;1
. B.
1;3
.
C.
3;
. D.
;1
và
3;
.
Câu 4. 
y f x

0
x


A
B
C
D
Câu 5. 
2
2
yx
x

0x

A. 4. B. 3. C. 1. D. 2.
Câu 6. 
2
21y x x

A. 0. B. 1. C.2. D. 3.
Câu 7. 
2
1y x x mx m
. Tìm
m


x
2
1
0
'y
y
1
1
x
1
x
0
'y
y
2
x
0
x
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 68 Tài liệu ôn thi THPT Quốc Gia 2017
A.
4.m
B.
1
0.
2
m
C.
0 4.m
D.
1
0
.
2
4
m
m
Câu 8. 
32
1y ax ax

2
3
x

a
:
A.
0a
. B.
0a
. C.
2a
. D.
0a
.
Câu 9. Cho 
2
:
2
x
Cy
x

C
?
A.
2;2L
. B.
2;1M
. C.
2; 2N
. D.
2;1K
.
Câu 10. 
, ab


A.
2
ab
. B.
2
ab
. C.
ab
. D.
a
b
.
Câu 11.       
m
  
sin
sin 1
xm
y
x
   
;
2
.
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 12.  
2
24
log 2log 4 4 0xx
     
12
,xx
. Tính tích
12
.xx
.
A.
8
. B.
2
. C.
1
4
. D.
33
4
.
Câu 13. 
.5
x
f x x

25 ' .5 .ln 5 2 0
xx
f x x

A.
0x
. B.
2x
. C.
0
2
x
x
. D.
1
2
x
x
.
Câu 14. 
3
3
log log 1 1xx
là:
A.
1 13
;
2
S
. B.
1 13 1 13
;;
22
S
.
C.
1 13 1 13
;
22
S
. D.
1 13
;
2
S
.
Câu 15. 
2
2
1 log 4y x x
là:
A.
;0
. B.
1;
. C. . D.
2;
.
Câu 16. 
2
2
3
4yx
là:
A.
D 2;2
. B.
D \ 2
. C.
D
. D.
D 2;
.
Câu 17. Cho
,ab

12
2
12
log 7
log 7
1 log 6
a
b

22
ab

A.
2
. B.
5
. C.
8
. D.
5
4
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 69 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 18. 
4 .ln
x
yx
.
A.
2
1
' 4 ln
x
yx
x
. B.
1
' 4 ln
x
yx
x
.
C.
1
' 4 ln .ln 4
x
yx
x
. D.
1
' 4 .ln
x
yx
x
.
Câu 19. 
3
log 2a
và
2
log 5b

10
log 45
theo
a
và
b
.
A.
10
2
2
log 45
1
ab
b
ab
. B.
10
2
log 45
ab
a ab
.
C.
10
2
2
log 45
1
bb
b
ba
. D.
10
2
log 45
ab
b ab
.
Câu 20. 
, , a b c

1a
sai ?
A.
1a
thì
log log
aa
b c b c
. B.
log log log
a a a
bc b c
.
C.
log log log
a a a
b
bc
c
. D.
1a
thì
log 0 1
a
bb
.
Câu 21. 
2001

78685800

là
1,7%

.
Nr
S Ae


100
 ?
A.
14
. B.
15
. C.
16
. D.
20
.
Câu 22.   
D
    
1yx
 
Ox
  
3x

D

Ox
là:
A.
2
. B.
3
. C. . D.
4
.
Câu 23. 
2
sinf x x
là:
A.
1
sin2
24
x
F x x C
. B.
1
sin2
24
x
F x x C
.
C.
1
sin2
22
x
F x x C
. D.
1
cos2
22
x
F x x C
.
Câu 24. Cho
3
2
0
15
1d
8
m
x x x
m là:
A.
2m
. B.
1m
. C.
3m
. D.
2m
.
Câu 25. 
fx
 ,
2016fa
và
2017 ; ;f b a b

d
2016
2014
2017
2015I f x f x x
là
A.
2015 2015
.I b a
B.
2017 2017
.I b a
C.
2015 2015
.I a b
D.
2016 2016
.I a b
Câu 26. Cho tích phân
2
2
0
sin 2 d 1I x x m x

m
là:
A.
5
. B.
3.
C.
4.
D.
6.
Câu 27. 
D

yx

Ox

2x
.

D
là:
A.
3
2
. B.
1
. C.
2
. D.
3
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 70 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 28. 
 

A.
5
27
. B.
27
5
. C.
11
25
. D.
22
5
.
Câu 29. 
23zi

z
là:
A.
23
13 13
i
. B.
23
13 13
i
. C.
32
13 13
i
. D.
32
13 13
i
.
Câu 30. 
13zi

12w z i i
là:
A.
2
. B.
2
. C.
22
. D.
1
.
Câu 31. 



5 cm
2 cm
8 mm
A. 45,96 cm
2
B. 45,97 cm
2
C. 45,99 cm
2
D. 45,98 cm
2
Câu 32. 
3z i z

A.
62
55
zi
. B.
72
55
zi
. C.
12
55
zi
. D.
34
55
zi
.
Câu 33. 
1
z

2
4 20 0zz


2
22
1 1 2
2A z z z

A.
0
. B.
2
. C.
28
. D.
16
.
Câu 34. T
Oxy

z


z

A
B
C 
D
Câu 35. 
H

4


2

H
là:
A.
43
3
. B.
4
. C.
4
3
. D.
42
3
.
Câu 36.   
. ' ' ' 'ABCD A B C D
    

5 : 3 : 1

' 35AC

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 71 Tài liệu ôn thi THPT Quốc Gia 2017
A.
5
. B.
3
. C.
10
. D.
15
.
Câu 37. 
.S ABC

V

,,M N I

,SB
SC
,
BC

IMNA
tính theo
V
là:
A.
4
V
. B.
2
V
. C.
3
V
. D.
2
3
V
.
Câu 38. Cho hình chóp
.S ABCD

a
;
SA

SB

0
45

C

SBD

A.
a
. B.
3a
. C.
3
a
. D.
2
a
.
Câu 39. Cho hình chóp
.S ABC

ABC

A
,
60ABC
, tam giác
SBC

2a


SA

ABC
:
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
90
.
Câu 40. 
S

S

T


1
4

S
là
3.

S
là:
A.
25
. B.
36
. C.
64
. D.
32
.
Câu 41. 
4cm

6cm


A.
10cm.
B.
6cm.
C.
5cm.
D.
8cm.
Câu 42. Trong không gian, cho tam giác
ABC

A
có
3AB a
và
4AC a

 khi quay tam giác
ABC

AB
:
A.
a
. B.
5a
. C.
5a
. D.
3a
.
Câu 43. 
Oxyz

:2 3 0P x y z


P
?
A.
13
2
xt
yt
zt
. B.
4
2
3
xt
yt
zt
.
C.
2
1 1 1
x y z
. D.
31
2 1 1
x y z
.
Câu 44. Trong k     
Oxyz
, c  
2; 1;3A
,
10;5;3B
và
2 1;2; 2M m n

, , A B M

, mn
là:
A.
3
1;
2
mn
. B.
3
;1
2
mn
.
C.
3
1;
2
mn
. D.
23
;
32
mn
.
Câu 45. 
Oxyz
, cho 
2;0;0M
,
0; 3;0N
,
0;0;4P
. 
MNPQ

Q
là:
A.
2; 3;4
. B.
3;4;2
. C.
2;3;4
. D.
2; 3; 4
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 72 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 46. 
Oxyz
, c
1; 2;0A
,
1;0; 1B
,
0; 1;2C
và
0; ;D m p
m
và
p

, , , A B C D
A.
20mp
. B.
1mp
. C.
23mp
. D.
2 3 0mp
.
Câu 47. Tro      
Oxyz
, c  
ABCD
v
1; 2;4A
,
4; 2;0B
,
3; 2;1C
và
1;1;1D

ABCD

D

A.
3
. B.
1
. C.
2
. D.
1
2
.
Câu 48. 
Oxyz
Oz
?
A.
2 2 2
1
: 2 4 2 0S x y z x y
.
B.
2 2 2
2
: 6 2 0S x y z z
.
C.
2 2 2
3
: 2 6 0S x y z x z
.
D.
2 2 2
4
: 2 4 6 2 0S x y z x y z
.
Câu 49.     
,Oxyz
 
: 2 5 15 0Q x y z
và

1;2; 3E

P
qua
E

Q

A.
: 2 3 15 0P x y z
. B.
: 2 3 15 0P x y z
.
C.
: 2 5 15 0P x y z
. D.
: 2 5 15 0P x y z
.
Câu 50. 
Oxyz

3;3;1A
,
0;2;1B

: 7 0P x y z

d

P

d
cách

, AB

A.
73
2
xt
yt
zt
. B.
2
73
xt
yt
zt
. C.
73
2
xt
yt
zt
. D.
73
2
xt
yt
zt
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 73 Tài liệu ôn thi THPT Quốc Gia 2017
BẢNG ĐÁP ÁN
Câu 1
C
Câu 11
C
Câu 21
A
Câu 31
D
Câu 41
A
Câu 2
A
Câu 12
B
Câu 22
A
Câu 32
A
Câu 42
B
Câu 3
B
Câu 13
A
Câu 23
B
Câu 33
C
Câu 43
D
Câu 4
D
Câu 14
A
Câu 24
B
Câu 34
A
Câu 44
B
Câu 5
B
Câu 15
D
Câu 25
C
Câu 35
C
Câu 45
C
Câu 6
B
Câu 16
A
Câu 26
C
Câu 36
D
Câu 46
C
Câu 7
D
Câu 17
A
Câu 27
C
Câu 37
A
Câu 47
C
Câu 8
B
Câu 18
C
Câu 28
B
Câu 38
D
Câu 48
B
Câu 9
D
Câu 19
B
Câu 29
B
Câu 39
C
Câu 49
C
Câu 10
A
Câu 20
D
Câu 30
C
Câu 40
B
Câu 50
B
HƯỚNG DẪN GIẢI CÁC CÂU KHÓ ĐỀ SỐ 01
Câu 10. 
x
.

Cosi
2
1
.
2
S a x b x a b

'' ''

2
ab
a x b x x
. Chọn A.
Câu 11. 
sintx

;
2
x
thì
sint x x

, 0;1
1
tm
y t t
t
.
Ta có
2
1
'
1
m
yt
t
,
0;1t

yt
 
0;1

' 0, 0;1y t t
1 0 1mm
. Chọn C.
Câu 17. 
12 12 12
12
12 12
12
log 7 log 7 log 7
1 log 6
log 12 log 6
log 12.6
aa
b
b
a
b
.
Mà
12
2
12
log 7
log 7
log 2

12 12
12
12
log 7 log 7
log 2
log 12.6
a
b
.

2
2 2 2
7 7 1
1 1 2
1
12.6 2
a
b
a
ab
b
. Chọn A.
Câu 21. Ta có
0,017 0,017
ln100 ln 78,6858
100 78,6858 ln100 ln 78,6858 14
0, 017
NN
N

100
Chọn A.
Câu 28. 
1
V


2
V

V

12
V V V
.

2
1
3
h
V h R

h


22
RR
R h h
.

2
23
1
5
3 2 6 24
h R R
V h R R R
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 74 Tài liệu ôn thi THPT Quốc Gia 2017
Mà
3
4
3
VR
nên
3 3 3
1 2 2 2
4 5 9
3 24 8
V V V R R V V R
.

33
2
1
9 5 27
:
8 24 5
V
RR
V
. Chọn B.
Câu 31. 

2
1
4. .0, 4 .2 1,28V

2
5.5.2 50V

21
45,98VVV
Câu 32.
,z x yi x y
. Suy ra
z x yi
.
Ta có
33z i z x yi i x yi
.
2 2 2 2
( 1) ( 3) ( 1) ( 3) 3 4 0x y i x yi x y x y x y
.

;M x y

z

3 4 0xy
.
Ta có
22
z x y OM
,
z

OM

M


O

3 4 0xy
.

d
qua
O

3 4 0xy

30xy
.

M

6
34
6 2 6 2
5
;
3 0 2
5 5 5 5
5
x
xy
M z i
xy
y
. Chọn A.
Câu 37. Ta có
SABC SAMN IMNA BAMI CANI
V V V V V
.

1 1 1
. . .
2 2 4 4
SAMN
SAMN
SABC
V
SA SM SN V
V
V SA SB SC
.
1 1 1
. . .
2 2 4 4
BMAI
BMAI
BSAC
V
BM BA BI V
V
V BS BA BC
,
1 1 1
. . .
2 2 4 4
CANI
CANI
CASB
V
CA CN CI V
V
V CA CS CB

4 4 4 4
IMNA IMNA
V V V V
V V V
. Chọn A.
Câu 40.

R

R


2
SR

T
là:
2
TT
SR
.

T
:
3
23
2
T T T
C R R

2
1
23
4
TT
T
SR
RR
SR
.

S
là:
3
44
27 36
33
VR
. Chọn B.
Câu 50. 
AB
là
: 3 7 0xy
.

d

, AB
 .

dP
, suy ra
dP
hay
70
:
3 7 0
x y z
d
xy
.

zt
c
2
73
xt
yt
. Chọn B.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 75 Tài liệu ôn thi THPT Quốc Gia 2017
x
y
-2
-1
2
2
O
1
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ SỐ 02
Nguyễn Văn Huy
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 02
Câu 1. 
22
1
x
y
x

A
( ; 1)
và
( 1; )
B .
C
( ; 1)
và
(1; )
.
D
( ; 1)
và
( 1; )
.
Câu 2. 
3
yx

A. 0 B. 1 C. 2 D. 3
Câu 3. 
2
1
x
y
x
là
A.
1y
và
2x
B.
2yx
và
1x
C.
1y
và
1x
D.
2y
và
1x
Câu 4. 
2
( 3)( 4)y x x x

A. 2 B. 3 C. 0 D. 1
Câu 5. 
nào?
A.
2
32y x x
B.
42
2y x x
C.
3
32y x x
D.
32
32y x x
Câu 6. 
3
2
2
23
33
x
y x x


A. (-1; 2) B. (1; 2)
C.
2
(3; )
3
D. (1; -2)
Câu 7. 
32
35y x x

1; 4
là
A. 5 B. 1 C. 3 D. 21
Câu 8. Th
32
3 3 1y x x mx
 là:
A.
1m
B.
1m
C.
1m
D.
1m
Câu 9. 
2
2y x x
là
A. 0 B. 1 C. 2 D.
3
Câu 10. 
m

:d y m

()C

32
32y x x

A.
2m
B.
2m
C.
2m
D.
22m
Câu 11. 
 

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 76 Tài liệu ôn thi THPT Quốc Gia 2017
Mặt đất
4m
5m
1m

A.
41m
B.
37m
C.
29m
D.
35m
Câu 12. 
x

2
log ( 1)x

A.
x
> 0 B.
x
> 1 C.
10x
D.
21x
Câu 13. 
1
2
yx
có t
A. B.
[0; )
C.
(0; )
D.
\0
Câu 14. 
22
x

A. 0 B. 1 C. 2 D. 3
Câu 15. 
1
1
7
5
aa
và
11
log log
64
bb
thì
A.
0 1; 1ab
B.
1; 1ab
C.
1; 0 1ab
D.
0 1; 0 1ab
Câu 16. 
2
log
1
x
y
x

A.
\1
B.
\ 1;2
C.
1;2
D.
;1 2;+
Câu 17. 
1
3
log ( 1) 2 x

A.
1x
B.
1 10x
C.
10x
D.
1 10x
Câu 18. 
(I):
0x
thì
2
ln( 1) ln2xx
(II):
0x
thì
1
2
xx

log log
1 0; 0; 0
aa
yx
a x y x y

A. 0 B. 1 C. 2 D. 3
Câu 19. 
1
y ln
1 x
,
1x
ta có
A.
' 2 1yy
B.
' e 0
y
y
C.
' 2 0yy
D.
' 4e 0
y
y
Câu 20. 
9 3 0
xx
m

A.
1
4
m
B.
0m
C.
1
4
m
D.
0m
Câu 21. 
0
log logAA


0

XX

     


Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 77 Tài liệu ôn thi THPT Quốc Gia 2017
A.
4
3
B.
3
4
C. 20 D. 100
Câu 22. 
2
()x dx f x
và
(0) 0f
thì :
A.
( ) 2f x x
B.
( ) 2f x x
C.
3
1
()
3
f x x
D.
2
1
()
3
f x x
Câu 23. 
( ), ( )u u x v v x
 
;ab

 ?
A.
. . .
bb
b
a
aa
u dv u v v du
B.
. . .
bb
b
a
aa
u dv u v v dv
C.
. . .
bb
b
a
aa
u dv u v u du
D.
. . | .
ba
b
a
ab
u dv u v v du
.
Câu 24. Cho
2 ln
()
x
F x dx
x
và
(1) 1F

A.
2
( ) lnF x x
B.
2
( ) ln ( 1)F x x
C.
2
( ) 1 ln( )F x x
D.
2
( ) 1 lnF x x
Câu 25. Cho
1
0
( ) 2f x d x
,
2
1
( ) 4f x dx

2
0
(2 )f x dx
 :
A. 1 B. 2 C. 3 D. 6
Câu 26.
Ditích hình phng gii hn bi hai thàm s
2
2yx
và
yx
là :
A.
9
12
B.
2
9
C.
9
2
D.
19
2
Câu 27. Cho
()H

2
4
x
y
x

Ox


1x

()H

Ox

A.
4
ln
23
B.
14
ln
23
C.
3
ln
24
D.
4
ln
3
Câu 28. 
/km h


/km h


( ) 30 2v t t
(
/ms

t
 gian tính

72
/km h

A. 100
m
. B. 125
m
. C. 150
m
. D. 175
m
Câu 29. 
12 5zi
là
A. 7 B. 17 C. 169 D.
13
Câu 30. 
25zi

A. -5 B. 5 C. 5
i
D. -2
Câu 31. 
67zi

A.
(6; 7)
B.
(6;7)
C.
( 6;7)
D.
( 6; 7)
Câu 32. 
12
2 3 , 1z i z i

12
3zz
là
A. 10. B. 61. C.
61
D.
10
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 78 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 33. 
1
z

2
2 3 0zz

1
z

1
z
là
A.
12i
B.
12i
. C.
12i
. D.
12i
.
Câu 34. z 
1z i i z
là
A. 
(2; 1)I
, bán kính R=
2
. B. ng tròn tâm
(0;1)I
, R=
3
.
C. 
(0; 1)I
, bán kính R=
3
.D. 
(0; 1)I
, R=
2
.
Câu 35. 
a

A.
3
a
B. 4
3
a
C. 6
3
a
D. 8
3
a
Câu 36.  
.S ABC
      
a
,  
SA
   

3SA a
:
A.
3
3
4
a
B.
3
4
a
C.
3
2
a
D.
3
3
4
a
Câu 37. 
. ' ' 'ABC A B C

ABC

B

BA BC a

'AB

()ABC

0
60
.Th
là:
A.
3
3
2
a
B.
3
3
4
a
C.
3
3
6
a
D.
3
3a
Câu 38. 

m

cm
(hình vẽ

A. 8000 lít .B. 7220 lít. C. 6859 lít. D. 7039,5 lít
dày 5cm
2m
Câu 39. 
A.
3
4
3
R
B.
2
4 R
C.
3
32
3
R
D.
3
24
3
R
Câu 40. 
a
A.
3
12
3a
B.
3
24
3a
C.
3
6
3a
D.
3
3
a
Câu 41. 
ABCD
có
,5AB a AC a


AD
là:
A.
2
4 a
B.
2
5 a
C.
2
6 a
D.
2
2 (1 5)a
.
Câu 42. Cho hình chóp
.S ABCD

2BD a
. Tam giác
SAC
vuông cân

S


Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 79 Tài liệu ôn thi THPT Quốc Gia 2017
A.
3
43a
B.
3
4
3
a
C.
3
a
D.
3
4 a
Câu 43. 
Oxyz
, 
2 2 2
( ) : ( 3) ( 2) ( 1) 4S x y z

I
và bán kính
R

A.
( 3;2;1)I
và
2R
B.
(3; 2; 1)I
và
4R
C.
( 3;2;1)I
và
4R
D.
(3; 2; 1)I
và
2R
Câu 44.   
Oxyz
, 
m
  
( ) : 2 2 0P x y z
và
( ) : 1 0Q x y mz
 :
A.
1
2
m
B.
1
2
m
C.
1m
D.
1
2
m
Câu 45. 
Oxyz

(2; 3; 1)A
(4; 1;2)B


AB
là
A.
2 2 3 1 0x y z
B.
15
4 4 6 0
2
x y z
C.
0x y z
D.
4 4 6 7 0x y z
Câu 46. 
Oxyz
không phải 

Ox
?
A.
0
0
xt
y
z
B.
2
0
1
xt
y
z
C.
1
0
0
xt
y
z
D.
0
0
xt
y
z
Câu 47. 
Oxyz
,cho
(2;0;0); (0;3;1); ( 3;6;4)A B C

M


BC
sao cho
2MC MB

AM
là:
A. 5 B.
29
C.
5
D. 29
Câu 48. 
Oxyz
cho
(1;1;1)I

( ) : 2 2 4 0P x y z

()S
tâm
I

()P

()S
là
A.
2 2 2
( 1) ( 1) ( 1) 16x y z
B.
2 2 2
( 1) ( 1) ( 1) 9x y z
C.
2 2 2
( 1) ( 1) ( 1) 5x y z
D.
2 2 2
( 1) ( 1) ( 1) 25x y z
Câu 49. 
Oxyz
, c
()P
:
2 2z 11 0xy
và
()Q
:
2 2z 2 0xy

()P
và
()P
là
A. 9 B. 3 C. 1 D. 13
Câu 50. 
Oxyz
, c
(1;0;0), (0;1; 0), (0;0;1), (0;0;0)A B C D


( ),( ),( ),( )ABC BCD CDA DAB
?
A. 8 B. 5 C. 1 D. 4
----------- ----------
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 80 Tài liệu ôn thi THPT Quốc Gia 2017
BẢNG ĐÁP ÁN
Câu 1
D
Câu 11
A
Câu 21
D
Câu 31
B
Câu 41
C
Câu 2
A
Câu 12
B
Câu 22
C
Câu 32
C
Câu 42
B
Câu 3
C
Câu 13
C
Câu 23
A
Câu 33
A
Câu 43
A
Câu 4
D
Câu 14
B
Câu 24
D
Câu 34
D
Câu 44
A
Câu 5
D
Câu 15
A
Câu 25
C
Câu 35
D
Câu 45
D
Câu 6
B
Câu 16
C
Câu 26
C
Câu 36
B
Câu 46
B
Câu 7
D
Câu 17
B
Câu 27
A
Câu 37
A
Câu 47
B
Câu 8
C
Câu 18
C
Câu 28
B
Câu 38
D
Câu 48
D
Câu 9
B
Câu 19
B
Câu 29
D
Câu 39
C
Câu 49
B
Câu 10
D
Câu 20
D
Câu 30
B
Câu 40
B
Câu 50
A
HƯỚNG DẪN GIẢI CÁC CÂU VẬN DỤNG CAO
Câu 11: 

 

A.
41m
B.
37m
C.
29m
D.
35m
HD:
x
4m
1m
H
N
M
A
C
B
3m
5m
1m


22
[0;4]
1 (4 ) 16 ( ), [0;4] min ( ) 41AB AC x x f x x f x

Câu 21: 
0
log logAA


0




A.
4
3
B.
3
4
C. 20 D. 100
HD:

1
M
và
1
A
ta có:
2
1 0 1 0
11
2 8 6 lg lg (lg lg ) lg 10 100
AA
M M A A A A
AA
.

Câu 28: k


( ) 30 2v t t

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 81 Tài liệu ôn thi THPT Quốc Gia 2017


A. 100m. B. 125m. C. 150m. D. 175m
HD:
5
0
72 / 20 / , 30 2 20 5 (30 2 ) 125km h m s t t S t dt

Câu 38: 
hình vẽ

A. 8000 lít. B. 7220 lít.
C. 6859 lít. D. 7039,5 lít
dày 5cm
2m
HD:

3

Câu 50: Trong , 

A. 8 B. 5 C. 1 D. 4
HD:

1
3
x y z
x y z

A
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 82 Tài liệu ôn thi THPT Quốc Gia 2017
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ SỐ 03
Nguyễn Văn Huy
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 03
Câu 1.          
m
   
3
2
( ) 7 14 2
3
mx
y f x mx x m
g
[1;+¥)
?
A.
-¥;-
14
15
(
ù
û
. B.
-¥;-
14
15
( )
. C.
-2;-
14
15
é
ë
ù
û
. D.
-
14
15
;+¥
é
ë
)
.
Câu 2. 
()y f x

00
;x h x h
, v
0h
.

A. 
( ) 0
o
fx
và
( ) 0
o
fx

()y f x

.
o
x
B. 
( ) 0
o
fx
và
( ) 0
o
fx

()y f x

.
o
x
C. 
( ) 0
o
fx
và
( ) 0
o
fx

()y f x

.
o
x
D. 
( ) 0
o
fx

()y f x

.
o
x
Câu 3. 
2
32y x x
?
A. 
B. 
C. 
D. 
Câu 4. 
()y f x

;3 ; 3;



A. 
1x

2x
.
B. 
1x
và
3x
C. Hàm 
D
1x
và
3x
Câu 5. 
21
1
x
y
x
là ?
A.
2.
B.
4.
C.
6.
D.
8.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 83 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 6. 
m

32
3 2 0x x m

1
2
A.
9
2
8
m
B.
20m
C.
02m
D.
22m
Câu 7.             
m
    
2
1
2
x
y
x x m
        
ma
    
mb

ab
?
A.
1ab
B.
2ab
C.
3ab
D.
4ab
Câu 8.                
32
1
( 1) 1 3
3
y x m x m

,AB
sao cho
,AB
và
0; 5C

hàng ?
A.
1m
B.
2.m
C.
12m
D.
12m
Câu 9. 
;T a b

2
1
1
x
y
x
trên
1;2
nh nào sau

A.
22
2ab
B.
22
9
5
ab
C.
22
19
5
ab
D.
22
2ab
Câu 10. 
4BD km
 
20km
.Hàng ngày

15 /km h


CD


5
3


A.
5CD km
B.
4CD km
C.
3CD km
D.
2CD km
Câu 11. 
4 2 2
2 3 1y x x m m
?
A. 
B. 
C. 
D. 
Câu 12. 
2
log 2 3 3x
.
A.
7
3
x
B.
4x
C.
2x
D.
2
3
x
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 84 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 13. 
1
3
x
y
.
A.
1
1
'.
3
x
yx
B.
' 3 .ln 3
x
y
C.
1
' 3 .ln
3
x
y
D.
ln 3
'
3
x
y
Câu 14. Cho
01a

2
log log 1 1
aa
x x x
là :
A.
0;a
B.
;a
C.
;a
D.
;1a
Câu 15. 
log2 ,log 7ab
thì
log 35
tính theo
a
và
b

A.
1 ba
B.
1 ba
C.
5b
D.
1ab
Câu 16. 
2
ln 2 1y x x m
 khi
A.
0m
B.
0m
C.
0
1
m
m
D.
03m
Câu 17. 
11
43
aa
và
11
log log
43
bb
thì
A.
0 1, 1ab
B.
0 1, 0 1ab
C.
1, 1ab
D.
1,0 1ab
Câu 18. 
3
( ) log 2 1
x
f x x
là
A.
3
3
2 3 1
'( )
2 1 ln 5 ln2
x
x
x
fx
x
B.
3
3
2 3 1 ln 2
'( )
21
x
x
x
fx
x
C.
2 3 1 3
3
3 2 ln2 2
'( )
2 1 ln 5 ln2
xx
x
x
fx
x
D.
3
3
2 3 ln 2 1
'( )
2 1 ln 5 ln2
x
x
x
fx
x
Câu 19. Cho
01a
ng trình
12
1
5 log 1 log
aa
xx

A.
32
5
1
0
x
a
a x a
xa
B.
23
5
1
0 x
a
a x a
xa
C.
23
5
1
x
a
a x a
xa
D.
32
5
1
x
a
a x a
xa
Câu 20.  
;T a b
              trình
22
13
3
log log 1 1 5 0x x m

22
1; 3
?
Tính
22
ab
A.
22
4ab
B.
22
6ab
C.
22
8ab
D.
22
10ab
Câu 21. 


ng sau :
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 85 Tài liệu ôn thi THPT Quốc Gia 2017
5 cm
6 cm
6 cm
6 cm
1 cm
   
Câu 22. 
y f x

;ab
. 
        
y f x
, 
Ox
   
,x a x b a b
.
A.
b
a
S f x dx
B.
()
b
a
S f x dx
C.
2
b
a
S f x dx
D.
b
a
S f x dx
Câu 23. Cho
1 4 4
0 1 0
( ) 2, ( ) 3, g( ) 4f x dx f x dx x d x
 sai ?
A.
4
0
( ) 5f x dx
B.
44
00
( ) g( )f x d x x d x
C.
4
0
( ) g 1f x x dx
D.
44
00
( ) g( )f x dx x dx
Câu 24. 
Fx

44f x x

Fx
và
fx

A.
2
2 4 4F x x x
B.
2
24F x x x
C.
2
24F x x x C
D.
2
24F x x
Câu 25. Tính tích phân
2
32
1
ln 3
4
e
x x a
dx
b
xe

,ab

a
b


ab
A.
10ab
B.
20ab
C.
20ab
D.
30ab
Câu 26. 

60 , 30AB cm OH cm
     
Linh mua là ?
A.
2
1000( )cm
B.
2
1200( )cm
C.
2
1400( )cm
D.
2
900( )cm
Câu 27. 
2
y x x

0y
.Tính

A.
()
15
dvtt
B.
6
dvtt
C.
30
dvtt
D.
40
dvtt
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 86 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 28.                

 

2 cm
2 cm
2 cm
2 cm
4 cm
12 cm
A.0,67 cm B. 0,75 cm C. 0,25 cm D. 0,33 cm
Câu 29. c
1
3
2
zi
 phc
z
:
A. c bng
1
2
ng
3
B. c bng
1
2
ng
3
C. c bng
1
2
ng
3i
D. c bng
1
2
ng
3i
Câu 30. c
1
12zi

2
56zi
 phc
12
zz
A.
12
10zz
B.
12
10zz
C.
12
42zz
D.
12
100zz
Câu 31. 
,,,A B C D
và
E
 
1 2 ;2 3 ;3 5 ; 2 3i i i i
và
54i

A. 
2;2G

BCD
B. 
2;2G

ABC
C. 
2;2G

ABD
C. 
2;2G

CED
Câu 32. c
34zi
c
2
1w i z z
:
A.
8 31wi
B.
8 31wi
C.
31 8wi
D.
31 8wi
Câu 33.  
1 2 3
;;z z z
      
32
7 31 25 0z z z
 

1 2 3
T z z z
.
A.
11T
B.
11T
C.
121T
D.
22T
Câu 34. c
z

23z
ng tp him biu di
phc
w 1 3 2i z i

r

A.
2r
B.
4r
C.
6r
D.
8r
Câu 35. 
ABCD.A’B’C’D’

.B’C’D’C


ABCD.A’B’C’D’
A.
3
2.a
B.
3
2
a
C.
3
2
.
3
a
D.
3
2
6
a
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 87 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 36. Cho hình chóp
.S ABCD

ABCD

2 2 ,AC BD a
tam giác
SAD

S

( ).A BCD

.S ABCD
theo
?a
A.
3
5
12
a
B.
3
5
6
a
C.
3
5
4
a
D.
3
3
12
a
Câu 37. Cho hình chóp
.S ABCD
     
()SC ABCD
và
2, 5.AC SA

AB
 

SM

SBD
. Tính
sin
.
A.
1
sin
6
B.
1
sin
27
C.
1
sin
7
D.
1
sin
3
Câu 38.     
. ' ' 'ABC A B C
      
3AC BC a
.
 
'AC
    
0
60
  
'AC
    
'2A M MC

' 31A B a
M 
''ABB A
là:
A.
32
4
a
B.
42
3
a
C.
32a
D.
22a
Câu 39. 
AA’ 2 ,a BC a
và
0
120B AC
. 
tích hình tr
A.
3
2
3
a
B.
3
2 a
C.
3
3
a
D.
3
4
3
a
Câu 40. 


    
3
1
128
3
V dm
 
2
V
  

2
1
V
V

t

A.
2
1
1
2
V
V
B.
2
1
1
3
V
V
C.
2
1
1
4
V
V
D.
2
1
1
5
V
V
Câu 41. 
50SO cm

10cm

20OM cm

      

C
 nón

C

A.
2
16 26 cm
B.
2
26 26 cm
C.
2
36 26 cm
D.
2
46 26 cm
Câu 42. Cho hình chóp
.S ABCD


SC

1
V

.S AMPN
 
1
V
V


Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 88 Tài liệu ôn thi THPT Quốc Gia 2017
A.
1
0;
5
B.
11
;
53
C.
11
;
32
D.
1
;1
2
Câu 43. 
Oxyz
ng
: 3 2 0P x z


?P
A.
4
1;0; 1n
B.
1
3; 1;2n
C.
3
3; 1;0n
D.
2
1;0; 3n
Câu 44.        
Oxyz
  
cu:
222
: 1 2 3 9S x y z
âm
I

R

S
:
A.
1; 2; 1I

3R
B.
1;2;3I

3R
C.
1;2;1I

9R
D.
1; 2; 3I

9R
Câu 45.       
Oxyz
   
2 2 2
: 2 2 2 3 0S x y z x y z


A.
2AB
B.
4AB
C.
6AB
D.
8AB
Câu 46. Trong không gian 
Oxyz

2
: 1 2
3
xt
y t t
zt
hai

2;0;3A
và
2; 2; 3B
  
0 0 0
;;M x y z
 thì
44
MA MB

t .Tìm
0
x
A.
0
0x
B.
0
1x
C.
0
2x
D.
0
3x
Câu 47.       
Oxyz
  
1; 1;3A
    
 
2 2 3 0x y z
        

A.
2 2 21 0x y z
B.
2 2 3 0x y z
C.
: 2 2 6 0Q x y z
D.
2 2 7 0x y z
Câu 48. 
Oxyz

1; 1;1A


1; 1;1A

3;0;5N


A.
2
B.
3
C.
5
D.
7
Câu 49.       
Oxyz
  
2;0;0 , 0;2;0 , 0;0;2 , 2;2;2A B C D

A. 3 B.
3
C.
3
2
D.
2
3
Câu 50.   
Oxyz
 
1;4;2 , 1;2;4AB


12
:
1 1 2
x y z

M
và
22
MA MB


A.
0; 1;4
B.
1;0;4
C.
1;0;4
D.
1;0; 4
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 89 Tài liệu ôn thi THPT Quốc Gia 2017
BẢNG ĐÁP ÁN
Câu 1
A
Câu 11
C
Câu 21
B
Câu 31
B
Câu 41
C
Câu 2
A
Câu 12
C
Câu 22
D
Câu 32
B
Câu 42
C
Câu 3
A
Câu 13
D
Câu 23
D
Câu 33
A
Câu 43
D
Câu 4
B
Câu 14
A
Câu 24
A
Câu 34
C
Câu 44
B
Câu 5
B
Câu 15
A
Câu 25
B
Câu 35
B
Câu 45
B
Câu 6
A
Câu 16
B
Câu 26
B
Câu 36
A
Câu 46
C
Câu 7
C
Câu 17
A
Câu 27
C
Câu 37
B
Câu 47
A
Câu 8
B
Câu 18
D
Câu 28
A
Câu 38
B
Câu 48
A
Câu 9
D
Câu 19
A
Câu 29
A
Câu 39
A
Câu 49
B
Câu 10
C
Câu 20
A
Câu 30
B
Câu 40
B
Câu 50
B
HƯỚNG DẪN GIẢI CÁC CÂU KHÓ
Câu 1:

  
2
14 14 0, 1mx mx x

2
14
()
14
g x m
xx

(1)

()gx

"x Î 1;+¥
é
ë
)
suy ra
1
14
min ( ) (1)
15
x
g x g

1
14
min ( )
15
x
g x m m
Câu 10:

CD x
suy ra
2
20 ; 16,0 20AC x CB x x

20
15 15
AC
AC x
t

 
5
15 9 /
3
v v km h

2
16
9
CB
x
t


2
20 16
15 9
AB
xx
t

2
2
20 16 1
'( ) '( ) 0 3
15 9 15
9 16
x x x
f x f x f x x
x
Ta có :
76 16 4 26
3 ; 0 ; 20
45 9 9
f f f

76
45

3CD km

Câu 20:

0x
ta có
2 2 2 2
1 3 1 3
33
log log 1 1 5 0 log log 1 1 5x x m x x m

2 2 2 2
33
log 1 log 1, 1;3 5 2 1 5t x x t t m t t m f t

2
2, 1;3f t t t t
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 90 Tài liệu ôn thi THPT Quốc Gia 2017
Ta có :
' 2 1 0, 1;3f t t t
suy ra
ft

1;3
1;3 max ( ) (3) 10f x f
1;3
,min ( ) (1) 0f x f

22
1;3
khi

1;3
. Hay
0 5 10 0 2 0;2m m T

Câu 21:



viên
Câu 26:

0;0A
,
30;30H
60;0B

2
,0y ax bx c a

2
2
0
0
0
1
.60 60. 0 60. 0
30
30. 1
.30 30. 30
2
c
c
c
a b c a b a
ab
a b c
b

2
1
2
30
y x x
 
60
22
0
1
2 1200
30
S x x dx cm

Câu 28:

.4.12 48V

.4.10 40
nc
V

4 16
4. .
33
bi
V

0
16 8
48 40
33
V

:
8
3
0,67
4
h
Câu 34:

2
2
; ; , , , 2 9z a bi w x yi a b x y a b

3
1 3 2 3 ( 2 3 )
23
x a b
w i z i x yi a b b a i
y b a
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 91 Tài liệu ôn thi THPT Quốc Gia 2017
2 2 2
2
2 2 3
2 2 2 3 2 3 3 2
2 3 2 3 2
x a b
x y a b b a
y b a
22
2 2 2 2
2 2 2 3 3 2( 2) 3 3( 2) 4 2 4.9 36a a b b b a b a a b
2
2
2 2 2 3 36xy
suy ra b
36 6r
. 
Cách 2 : 
1 2 1 2
.z z z z
.Ta có :
22
1 1 1 2 2 2 1 2 1 2 1 2 1 2 2 1 1 2 1 2 1 2 1 2 2 1
,z a b i z a b i z z a a b b a b a b i z z a a b b a b a b
2 2 2 2
1 2 1 2 1 2 2 1
1a a b b a b a b

:
12
2 2 2 2
2 2 2 2
1 2 1 2 1 2 1 2 2 1 1 2
2z z a b a b a a a b a b b b

1 2 1 2
.z z z z

w 1 3 2 w 2 2 1 3 1 3 2i z i i i i z
w 2 2 1 3 1 3 2 1 3 . 2 6i i i z i z
2
2
x-2+ y 2 2 3 6 2 y 2 2 3 36ix
suy ra b
6r
. 
Câu 40: Xét hình nón tròn xoay , ta có :
2 , ,h SO R r OA l SA

R
là bán kính

r

l

nón .

3
4
3
R
V

là
3
128
3
dm
nên ta có
3
1 4 128
.
2 3 3
R
3
64 4RR
suy ra
8h
.
Xét tam giác vuông
SOA

4OH R
ta có :
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 3 3 8
64
OS 4R 4
3
OA dm
OH OA R OA OA R

2
3
1 8 512
. .8
39
3
V dm

3
2
512 128 128
9 3 9
V dm
suy ra
2
1
1
3
V
V
suy ra ch
Câu 41:
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 92 Tài liệu ôn thi THPT Quốc Gia 2017
Ta có :
50; 20 30SO OM SM cm



30.10
/ / 6
50
MB SM
MB OA MB cm
OA SO

2 2 2 2 2
30 6 936 6 26SB SM MB SB cm
.


C
là :
2
36 26S cm

Câu 42:

; ,(0 , 1)
SM SN
x y x y
SD SB

2
SABC SADC SABD SBCD
V
V V V V
Ta có :
1
11
.1
2 2 2 4
SAMPN SAMP SANP SAMP SANP
SADC SABC
V V V V V V
SM SP SN SP
xy
V V V V V SD SC SB SC
 có :
1
1 1 3
2
2 2 2 2 4
SAMPN SAMN SMNP
SABD SBCD
V V V V
xy xy xy
V V V V

13
4 4 3 1
x
x y xy y
x
do
1
0 1 1
3 1 2
x
yx
x

2
1
3 3 3 3 1
. . ( ), 1
4 4 3 1 4 2
4 3 1
V
xx
xy x f x x
Vx
x

1
1
1
2
1 1 3 1 1
( ), 1 m ax ( ) 1 ;
2 2 8 3 2
xx
V
y f x x f x f
V
suy ra

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 93 Tài liệu ôn thi THPT Quốc Gia 2017
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ SỐ 04
Nguyễn Văn Huy
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 04
Câu 1. 
()fx
là
3
3
x
x

( 1)fx
là .
A.
2
22xx
. B.
( 2)xx
. C.
3
1
3
x
x
. D.
2
( 1)x
.
Câu 2. 
m

y =
(m +3)x - 2
x + m


A. Không có
m
. B.
m = -2
. C.
m = 0
. D.
m = -1
.
Câu 3. D 
3
2
2
y
log x
.
A.
0; \ 9D
. B.
9;D
. C.
2; \ 9D
. D.
0;D
.
Câu 4. 
. ' ' ' 'ABCD A B C D

'. ' 'A BDB D
là
3
8
3
dm
.

'DD
.
A.
2cm
. B.
0,2m
. C.
20dm
. D.
20mm
.
Câu 5. 
2
2
(12 )log x log x
.
A.
9x

16x
. B.
09x

16x
.
C.
09x
. D.
0 12x
.
Câu 6.       
Oxyz
  
1;2;3A
   
: 2 0Px
và
: 1 0Q y z

A
và vuông

,PQ
.
A.
50x y z
. B.
0xz
. C.
50yz
. D.
50xy
.
Câu 7.              


 

    

A.  B.  C.  D. 
Câu 8. 
2
2
1
2
x
y
xx

A.
1
.
B.
2
. C.
4
. D.
3
.
Câu 9. 
F( )x

2
12
()
x
fx
x
và
F 1 3
thì
F( )x

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 94 Tài liệu ôn thi THPT Quốc Gia 2017
A.
2
F( ) 2x ln x x
. B.
2
F( ) 2x lnx x
.
C.
2
F( ) 2x ln x x
. D.
2
F( ) 2 1x ln x x
.
Câu 10. 
2
( 5 ) (1 5 )z i i
.
A. 
14

25
.
B. 
14

25i
.
C. 
14

25
.
D. 
14

25i
.
Câu 11.   
z
   
1z
      
1 3 1A z z
.
A.
48
. B.
2 15
. C.
10
. D.
2 10
.
Câu 12. Cho tích phân
2
0
43
sinx
I dx
cosx cosx
    
43t cosx
thì
2
1
I f t dt

ft

A.
41
2
41
ft
tt
. B.
41
41
ft
tt
.
C.
2 1 1
5 4 1
ft
tt
. D.
2 4 1
5 4 1
ft
tt
.
Câu 13. Trong cá
.
A.
42
21y x x
. B.
32
1
21
3
y x x x
.
C.
42
21y x x
. D.
2
2
x
y
x
.
Câu 14. 
Oxyz

M


: 1 0P x y z
và
: 5 0Q x y z
.
A.
6;0;0M
. B.
0;2;0M
. C.
0; 2;0M
. D.
0;1;0M
.
Câu 15. 
A.
2017
2016y x x cosx
. B.
(2016 ) 2017y tan x x
.
C.
(2016 ) 4032 2017y cos x x
. D.
(2016 ) 4032 2017y sin x x
.
Câu 16. 
;;a b c
và
1; . 0a b c

A.
( . )
a a a
log b c log b log c
. B.
( . ) .
a a a
log b c log b log c
.
C.
( . )
a a a
log b c log b log c
. D.
( . ) ( ) ( )
a a a
log b c log b log c
.
Câu 17.  2017 150i phiê







Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 95 Tài liệu ôn thi THPT Quốc Gia 2017
A. 25 tháng. B. 27 tháng. C. 12 tháng. D. 28 tháng.
Câu 18. 
11
23
( 1) ( 1)aa
và
5 2016
6 2017
bb
log log
thì .
A.
1 2;0 1ab
. B.
1 2; 1ab
. C.
2; 1ab
. D.
0 1; 1ab
.
Câu 19. 
42
11
22
y x x
đúng .
A. 
0x

(0) 0y
.
B.  
1x

( 1) 1y
.
C. 
0x

1
(0)
2
y
.
D. 
1x

( 1) 1y
.
Câu 20. 



60.000

2
m


2
m


x
y
A.
2
6250 m
B.
2
1250 m
C.
2
3125 m
D.
2
50 m
Câu 21. Cho hình chóp
.S ABCD

ABCD
là hình vuông,
SA

()ABCD
. Cho
SB a

SB
 . Tính
sin

hóp
.S ABCD

A.
3
3
. B.
3
3
. C.
3
3
. D.
1
.
Câu 22. Cho
4
3
1
e
ae b
x ln xdx
c

,,a b c
và
1 30c
. Tính
a b c
.
A.
16
. B.
20
. C.
1
. D.
19
.
Câu 23.      
.S ABC
  
SB
    
0
30
và
100SB cm
      
150 ,cm
200 ,cm
250 .cm
   
.S ABC
là
A.
250
lít. B.
750
lít. C.
3
150m
. D.
1500
lít.
Câu 24. 
;Mm
              
( ) 3 ln( 2)f x x x

Mm
.
A.
5 18 13ln
. B.
5 18ln
. C.
5 3 2ln
. D.
5 3 18ln
.
Câu 25. 
2y xsin x
,
2yx
,
2
x
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 96 Tài liệu ôn thi THPT Quốc Gia 2017
A.
2
44
. B.
2
4
4
. C.
2
44
. D.
2
.
Câu 26. 

A.
24
1
x
y
x
. B.
21
1
x
y
x
. C.
1
1
x
y
x
. D.
34
1
x
y
x
.
Câu 27. Cho
25
3 ; 3log a log b

54
60log
theo a và b.
A.
54
2
60
a b ab
log
ab b
. B.
54
3
60
2
b ab
log
ab
.
C.
54
2
60
2
ab
log
ab b
. D.
54
2
60
3
a b ab
log
ab b
.
Câu 28. 
1
24zi
và
2
13zi

12
2z iz
.
A.
12
28z iz
. B.
12
2 10z iz
. C.
12
21z iz
. D.
12
2 10z iz
.
Câu 29.  
2
22
11
69
2 1 4
log x
log x log x
  
12
xx
  

A.
12
8 . 1xx
. B.
12
xx
. C.
2
12
8xx
. D.
2
12
80xx
.
Câu 30. 
3mx
y
xm

m


A.
3m

3m
. B.
23m
.
C.
24m
. D.
33m
.
Câu 31. Cho
12
,zz
     
2
2017 2016 2017 0zz
. Tính
2
2
1 2 1 2
1.M z z z z
.
A.
3
.
B.
1
3
. C.
1
. D.
0
.
Câu 32. 
2
1
y log
x

Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 97 Tài liệu ôn thi THPT Quốc Gia 2017
A. B.
C. D.
Câu 33. Cho
1 2 3 4
, , ,z z z z
      
4
1
1
2
z
zi
.Tính
2222
1 2 3 4
1111zzzz
.
A.
85
. B.
1
2
. C.
15
9
. D.
17
9
.
Câu 34. 

5cm

0,5cm

4cm


A.
3
8 cm
. B.
3
25 cm
. C.
3
20,25 cm
. D.
3
16 cm
.
Câu 35. 
32
( 1) 2 3(C)y x m x mx
. Tìm
m

25yx


A.
1m

7m
. B.
71m
.
C.
7 m
. D.
01m
.
Câu 36. 
ABCD
 

H

AD
   
,AB CD
     chi  
ABCD

AB

1
V


CD

2
V

1
2
V
V
.
A.
1
. B.
2
. C.
1
2
. D.
3
.
Câu 37. 
Oxyz

1
1 3 2
:
1 2 1
x y z
d
và
2
2 1 1
:
3 1 2
x y z
d

d
 

: 3 3 4 0P x y z

12
,dd
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 98 Tài liệu ôn thi THPT Quốc Gia 2017
A.
232
:
3 5 4
x y z
d
. B.
2 5 1
:
3 3 4
x y z
d
.
C.
2 5 1
:
3 3 4
x y z
d
. D.
2 1 1
:
1 3 4
x y z
d
.
Câu 38. 
S
và
O


3h cm


A.
2
36
17
cm
. B.
2
36
17
m
. C.
2
18
5
cm
. D.
2
18
5
m
.
Câu 39. 
. ' ' ' 'ABCD A B C D

,ABCD
' ',ABB A
''BCC B



A.
192
5
. B.
193
6
. C.
207
5
. D.
183
6
.
Câu 40. 
12cm

10cm


10cm


2cm
. Và


15%

 chàn ra
ngoài.
A. 4. B. 5.
C. 6. D. 7.
Câu 41. 
4 2 2 4
21y x m x m
có
3

,,A Oy B C


,,,A B C O

1

m

A.
1m
. B.
0m
. C.
1m
. D.
1m
.
Câu 42.       
Ox yz
    
u
khác
0
. Tính
2 2 2
, , ,cos u i cos u j cos u k
.
A.
1
. B.
1
2
. C.
3
. D.
1
.
Câu 43. 
3
1
;
2
x
y
e
0y
,
0;x
3ln2x
.

A.
33
42
V ln
. B.
31
6
46
V ln
. C.
3 3 1
4 2 6
V ln
. D.
33
1
42
V ln
.
Câu 44.       
Oxyz
, cho tam giác
ABC
có
1;4;5 ,A
0;3;1 ,B
2; 1;0C

: 3 3 2 15 0P x y z

M
   
P
         
,,A B C

A.
M
l
,,A B C

P
.
B.
M

ABC


P
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 99 Tài liệu ôn thi THPT Quốc Gia 2017
C.
M

ABC

P
.
D.
M

ABC

P
.
Câu 45. 
Ox yz


A.
2 2 2
( 1) ( 3) (2 ) 16x y z
. B.
2 2 2
2 2 2 5 6 2 0x y z x y z
.
C.
2 2 2
4 3 8 0x y z x y z
. D.
2 2 2
2 4 9 0x y z x y
.
Câu 46. 
Oxyz

:0P x y z m

m

2 2 2
(S) : 6 2 4 0x y z x y z

m

P

(S)

A.
42 42m
. B.
42 42m
. C.
42 m
. D.
0 42m
.
Câu 47.  
Oxyz

2
: 2 9 0P m x y z

m

26
:
1 2 5
x y z m
d

m

d

P
.
A.
3m
. B.
3m
. C.
7
2
m
. D.
3m
.
Câu 48. 
3.
x
y sin lnx
.
A.
3
' 3. .
x
y ln x sin lnx cos lnx
x
. B.
3
'.
x
y x sin lnx cos lnx
x
.
C.
3
'
x
y sin lnx cos lnx
x
. D.
' 3 .
x
y x sin lnx cos lnx
.
Câu 49. 
2
2
2 6 9y x mx
 .
A.
22m
. B.
0 m
. C.
22m
. D.
02m
.
Câu 50.                 
1
5
z
zi

A.  5 = 0.
B.   ; 5).
C. 
22
( 5) 0xy
 ; 5).
D. 
22
( 5) 0xy
.
----------- ----------
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 100 Tài liệu ôn thi THPT Quốc Gia 2017
BẢNG ĐÁP ÁN
Câu 1
B
Câu 11
D
Câu 21
B
Câu 31
D
Câu 41
C
Câu 2
A
Câu 12
D
Câu 22
B
Câu 32
D
Câu 42
D
Câu 3
A
Câu 13
C
Câu 23
A
Câu 33
D
Câu 43
C
Câu 4
B
Câu 14
B
Câu 24
D
Câu 34
D
Câu 44
C
Câu 5
C
Câu 15
C
Câu 25
A
Câu 35
A
Câu 45
B
Câu 6
C
Câu 16
C
Câu 26
B
Câu 36
A
Câu 46
A
Câu 7
A
Câu 17
B
Câu 27
A
Câu 37
B
Câu 47
A
Câu 8
D
Câu 18
B
Câu 28
D
Câu 38
A
Câu 48
A
Câu 9
A
Câu 19
B
Câu 29
D
Câu 39
D
Câu 49
C
Câu 10
C
Câu 20
A
Câu 30
D
Câu 40
C
Câu 50
B
HƯỚNG DẪN GIẢI CÁC CÂU KHÓ
Câu 7.

x


x


200x

600 200x

 

4 x

là:
4 600 200f x x x


4 600 200f x x x
trên
0;
Ta có:
2
1
' 400 200 0
2
f x x x
.

1
2450
2
Maxf x f
.

1
2


Câu 11.

z a bi
thì
22
1,ab
11z a bi
11z a bi
.
Ta có
2 2 2 2
(1 ) 3 (1 ) 2 1 3 1A a b a b a a
.

2 1 3 1f a a a

1;1a
.
1 3 1 4
' 2. 0
5
2 1 . 1
aa
f a a
aa
.
Ta có
12f
,
4
2 10
5
f
.

2 10
.
Câu 17.

0
A

n
A

0
T


n

r


Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 101 Tài liệu ôn thi THPT Quốc Gia 2017
00
11
1.
n
n
n
r
A A r T
r

12
1
1 0,012 1
20000000 1 0, 012 800000. 12818250, 87
0, 012
n
A

0
00
1
00
11
1 . 0 14, 00184553
.
n
n
n
r
r
T
A A r T n log
r T A r

Câu 20. 
xm
 

ym


6
60000 3.50000 15.10 6 15 1500x y x y

2
2
6 15
11
.6 .15 6250
90 90 4
xy
S xy x y m
Câu 34. 
1
2,5r cm
.
 
21
0,5 2r r cm
.

23
16 ( )V r h cm
.
Câu 36.

,,E F G

,,AC BD BC

 
HEGF
.

;
ABC ADC
SS
;
AHE GEC
SS
CDHE ABGE
SS
.
Ta có
11
,( ) .S D,( ) .S
33
ABCD ACD ABC
V d B ACD d ABC
,( ) D,( )d B ACD d ABC
Hay
2 F,( ) 2 F,( ) F,( ) F,( )d ACD d ABC d ACD d ABC
Ta có
1 . .
11
F,( ) . F,( ) .
33
F AEGB F AHE ABGE AHE
V V V d ABC S d ACD S
,
2 . .G
11
F,( ) . F,( ) .
33
F HDCE F CE CDHE GEC
V V V d ABC S d ACD S
.

12
VV
. Chọn A.
Câu 39.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 102 Tài liệu ôn thi THPT Quốc Gia 2017

,ABCD
' ',ABB A
''BCC B

nên ta có.
3
. ' 6
. 4 ' 2 3
'. 8
43
3
AB
AB BB
AB BC BB
BB BC
BC

,O'O

ABCD
,
' ' ' 'A B C D
và
I

O'O
.
 
'ID
.
Xét tam giác
' ' 'A B D
có
22
5 3 5 3
' ' ' ' 'D' 'O'
36
B D A B A D
.
Xét tam giác
O'I 'D
có
183
I'
6
D
. Chọn D.
Câu 40. 
23
1
300 ( )V r h cm
.

3
2
250 ( )V cm
.

3
3
32
()
3
V cm
.

3
4
8
()
5
V cm
.

3
34
136
()
15
V V cm
.

3
12
50 ( )V V cm
.

12
34
136
50 : 5,51
15
VV
VV
.

ngoài. Chọn C.
Câu 41. Ta có
32
' 4 4 0 0y x m x x

2
xm

2
00mm

4 2 2
(0;1 ); ( ;1); ( ;1)A m B m C m
giác

,,,A B C O


I(0; )
I
y
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 103 Tài liệu ôn thi THPT Quốc Gia 2017

4
1
2
I
m
y
Mà
22
IO IB IO IB
2 2 2
(1 )
II
y m y
24
01m m m
. Chọn C.
Câu 44. 
G

ABC
.
Ta có
2 2 2
2.MA MG GA MA MG GA MGGA

2 2 2
2 . ,MB MG GB MGGB
2 2 2
2.MC MG GC MGGC
.

2 2 2 2 2 2 2
3 2 .MA MB MC MG GA GB GC MG GA GB GC
.
Do
G

ABC
nên
0GA GB GC
nên
2 2 2 2 2 2 2
3MA MB MC MG GA GB GC
.

1;2;2G

ABC

P

2 2 2
MA MB MC

MG

M

G
trên
P
. Chọn C.
Câu 50. 
R
)
 5i
0
05
5
x
x yi i
y
2 2 2 2 2 2
1 1 ( 1 )[ ( 5) ] ( 1) ( 5) [5 5]
5 ( 5)
( 5) ( 5) ( 5)
z x yi x yi x y i x x y y x y i
z i x y i
x y x y x y
Vì
1
5
z
zi
 : 5x + y 5 = 0.
ng 5x + y 
(0 ; 5). Chọn B.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 104 Tài liệu ôn thi THPT Quốc Gia 2017
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ SỐ 05
Nguyễn Văn Huy
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 05
Câu 1. 
32
31y x x

A.
-5 5
-5
5
x
y
B.
-5 5
-5
5
x
y
C.
-5 5
-5
5
x
y
D.
-5 5
-5
5
x
y
Câu 2. 
()y f x
có
lim ( ) 3
x
fx
và
lim ( ) 3
x
fx


A. 
B. 
C. 
3y
và
3y
.
D. 
3x
và
3x
.
Câu 3. 
42
41y x x

A.
2;0
và
2;
B.
2; 2
C.
( 2; )
D.
2;0 2; 
Câu 4. 
y f(x)
 
x
0 1

+
0 +
y
2
-3

A. 
B. 
C. -3.
D. 
Câu 5. 
4 3 2
3 4 6 12 1y x x x x

11
( ; )M x y

11
xy

A. 5 B. 6 C. -11 D. 7
Câu 6. 
2
3
1
x
y
x

2;4
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 105 Tài liệu ôn thi THPT Quốc Gia 2017
A.
[2;4]
6miny
B.
[2;4]
miny 2
C.
[2;4]
3miny
D.
[2;4]
19
3
miny
Câu 7. 
42
76y x x
và
3
13y x x
là :
A. 1 B. 2 C. 3 D. 4
Câu 8. 
C

32
34y x x

y mx m


1;0 , ,A B C
sao cho
OBC

A.
m
=3 B.
m
=1 C.
m
=4 D.
m
=2
Câu 9. 
2
1
23
x
y
xx

A.1 B. 2 C. 3 D. 4
Câu 10. 
 






A.
6x
B.
3x
C.
2x
D.
4x
Câu 11. 
2
2
x
x
em
y
em



1
ln ;0
4
:
A.
1;2m
B.
11
;
22
m
C.
1;2m
D.
11
; 1;2
22
m
Câu 12. 
log 1 2x
A.
2
1e
B.
2
1e
C. 101 D.
2
1
Câu 13. 
1
2
x
y
A.
2
1
'
2
x
y
B.
ln 2
'
2
x
y
C.
1
1
'.
2
x
yx
D.
2
ln 2
'
2
x
y
Câu 14. 
1
3
log 1 0x
A. x = 0 B. x < 0 C. x > 0 D. 0 < x < 1
Câu 15. 
2
ln 2 7 3y x x
A.
1
D= ; 3;
2
B.
1
;3
2
D
C.
1
D= ; 3;
2
D.
1
;3
2
D
Câu 16. 
2
3 .4
xx
fx

A.
2
3
9 2 log 2 2f x x x
B.
2
22
9 log 3 2 2log 3f x x x
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 106 Tài liệu ôn thi THPT Quốc Gia 2017
C.
9fx
2 log 3 log 4 log 9xx
D.
90
Câu 17. 
3cos cosf x x x
là
A.
3
3
sin
sin
x
xC
. B.
2 4 2sin sinx x C
.
C.
42
84
sin sinxx
C
. D.
42
84
sin sinxx
C
.
Câu 18. 
2
2
x
ye
A.
2
' 2 2
x
ye
B.
22
' 2.2 . . 1 ln2
xx
ye
C.
22
' 2.2 . ln2
xx
ye
D.
21
' 2 2
x
y x e
Câu 19. n (H
HOy là
A.
b
a
V g y f y x



22
.d
B.
b
a
V f y g y y



22
.d
x
y
O
g(y)
f(y)
b
a
C.
a
b
V g y f y y



22
.d
D.
b
a
V f y g y y



22
.d
Câu 20. Cho
23
log 5 ; log 5ab
. Khi 
6
log 5
Tính theo
a
và
b
A.
1
ab
B.
ab
ab
C.
a
+
b
D.
22
ab
Câu 21.
Tìm nguyên hàm ca hàm s
2
3
2x x dx
x
A.
3
3
4
3 ln
33
x
x x C
B.
3
3
4
3 ln
33
x
xx
C.
3
3
4
3 ln
33
x
x x C
D.
3
3
4
3 ln
33
x
x x C
Câu 22. 
sau 
A. 96; B. 97 C. 98 D. 99
Câu 23. 
, , ,y f x y g x x a x b
(
a
<
b
) .
A.
b
a
S f x g x dx
B.
b
a
S f x g x dx
C.
2
b
a
S f x g x dx
D.
22
b
a
S f x g x dx
Câu 24. 
m

32
3 2 4 3F x mx m x x


2
( ) 3 10 4f x x x
là:
A.
m
= 3 B.
m
= 0 C.
m
= 1 D.
m
= 2
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 107 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 25. Tính tích phân
2
0
.sin .I x xdx
A.
3I
B.
2I
C. I =1 D.
1I
Câu 26. Tính tích phân
4
3
2
6
1 sin
sin
x
dx
x
A.
32
2
; B.
3 2 2
2
; C.
32
2
. D.
3 2 2 2
2
Câu 27. 
C

32
25y x x x


'C

2
5y x x

A. 0 B. 1 C. 2 D. 3
Câu 28. Cho hình
H

2
4
x
y
x

Ox
và

1x

H
xung

Ox

A.
4
ln
23
B.
14
ln
23
C.
3
ln
24
D.
4
ln
3
Câu 29. 
13zi

23w i z

A.-3 và -7 B. 3 và -11 C. 3 và 11 D. 3 và -7
Câu 30. 
12
4 2 ; 2z i z i

12
zz

A.5 B.
5
C.
3
D. 3
Câu 31. S
O 
,AB CD


,AC BD

M SO
1
V


2
V


1
2
4
9
V
V

SI
SO
.
A.
7
.
9
SI
SO
B.
2
.
3
SI
SO
C.
4
.
5
SI
SO
D.
5
.
6
SI
SO
Câu 32. 
32zi
.Tìm 
2 3 2 1w i i z iz
?
A.
85wi
B.
85wi
C.
85wi
D.
85wi
Câu 33. 
1 2 3 4
, , ,z z z z

42
2 3 2 0zz

1 2 3 4
T z z z z

A.5 B.
52
C.
32
D.
2
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 108 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 34. 
2z

3 2 2w i i z

A.20 B.
20
C.
7
D.7
Câu 35. 
. ' ' 'ABC A B C

ABC

B
2 , ' 3AB BC a AA a

. ' ' 'ABC A B C
.
A.
3
23a
B.
3
23
3
a
C.
3
3
3
a
D.
3
3a
Câu 36. Cho hình chop
.S ABCD

ABCD

,2AB a BC a

SA

2SA a

.S ABCD
.
A.
3
23
3
a
B.
3
22
3
a
C.
3
22a
D.
3
2a
Câu 37. 
OABC

,,OA OB OC

, 2 , 3OA a OB a OC a

,MN

,AC BC


OCMN
tính theo
a

A.
3
2
3
a
B.
3
a
C.
3
3
4
a
D.
3
4
a
Câu 38. Cho hình chóp
.S ABCD

ABCD

a
,
SA


3
2
3
a

A
ng
SBD
.
A.
2
3
a
B.
3
a
C.
4
3
a
D.
3
2
a
Câu 39. Trong không gian cho tam giác
ABC

A

3 , 4AC a AB a
.

l

ABC

AC
.
A.
9a
B.
a
C.
7a
D.
5a
Câu 40. Cho hình chóp
.S ABC

,A AB AC a
. 
SAB

a


.S ABC
.
A.
3
54
a
B.
3
21
54
a
C.
3
3
a
D.
3
7 21
54
a
Câu 41.  

a
. 
A.
2
3a
B.
2
27
2
a
C.
2
3
2
a
D.
2
13
6
a
Câu 42. Mng có máy ct và máy tin  sn xut trc st và c. Sn xut 1 tn
trc st thì lt máy ct chy trong 3 gi và máy tin chy trong 1 gi, tin lãi là 2
triu. Sn xut 1 tc thì lt máy ct và máy tin chy trong 1 gi, tin lãi
là 1 triu. Mt máy không th sn xut c 2 loi. Máy ct làm không quá 6gi/ngày,
máy tin làm không quá 4gi/ngày. Mng nên sn xut bao nhiêu tn mi
lo tin lãi cao nht.
 c
 
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 109 Tài liệu ôn thi THPT Quốc Gia 2017
Câu 43. Trong không gian
Ox yz

1;0;2 , 3; 4;1 , 2;5;3M N P


MNP
là
A.
3 16 33 0x y z
B.
3 16 31 0x y z
C.
3 16 33 0x y z
D.
3 16 31 0x y z
Câu 44. Trong không gian
Oxyz

2 2 2
: 2 4 2 3 0S x y z x y z


1
:
22
xy
z

P
 
S
có

A.
2 2 2 0x y z
và
2 2 16 0x y z
B.
2 2 3 8 6 0xy
và
2 2 3 8 6 0xy
C.
2 2 3 8 6 0xy
và
2 2 3 8 6 0xy
D.
2 2 2 0x y z
và
2 2 16 0x y z
Câu 45. Trong không gian
Oxyz
, cho A(4;-2;3),
23
4
1
xt
y
zt

vuông góc 
A.
( 2; 15;6)
B.
( 3; 0; 1)
C.
( 2;15; 6)
D. (3;0;-1)
Câu 46. Trong không gian
Oxyz

: 4 2 0, : 2 2 7 0P x y z Q x z

,PQ
là:
A.
0
60
B.
0
45
C.
0
30
D. 90
0
Câu 47. Trong không gian
Oxyz

( ) : 3 4 0x y z
3x-y+z-4 =0 . mp
()

S
tâm
1; 3;3I

2;0;1H
, bán kính r

S
là:
A.
2 2 2
( 1) ( 3) ( 3) 18x y z
B.
2 2 2
( 1) ( 3) ( 3) 18x y z
C.
2 2 2
( 1) ( 3) ( 3) 4x y z
D.
2 2 2
( 1) ( 3) ( 3) 4x y z
Câu 48. Trong không gian
Oxyz

1;2;0 , 2;3;1AB

12
:
3 2 1
x y z
. 
M
trên sao cho
MA MB
là :
A.
15 19 43
( ; ; )
4 6 12
B.
15 19 43
( ; ; )
4 6 12
C.
(45;38;43)
D.
( 45; 38; 43)
Câu 49. 
d

3; 1;0H

Oxz

A.
3
1
x
y
zt
B.
3
1
0
x
yt
z
C.
3
1
0
xt
y
z
D.
3
1
x
yt
zt
Câu 50. Trong không gian
Oxyz
, cho
5;2;3 ,EF

E

Oy

dài
EF
là:
A.
13
B.
29
C.
14
D.
34
-----------------------Hết -------------------------
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 110 Tài liệu ôn thi THPT Quốc Gia 2017
BẢNG ĐÁP ÁN
Câu 1
A
Câu 11
D
Câu 21
B
Câu 31
b
Câu 41
B
Câu 2
C
Câu 12
C
Câu 22
B
Câu 32
A
Câu 42
A
Câu 3
A
Câu 13
B
Câu 23
B
Câu 33
C
Câu 43
B
Câu 4
D
Câu 14
B
Câu 24
C
Câu 34
B
Câu 44
A
Câu 5
C
Câu 15
D
Câu 25
C
Câu 35
A
Câu 45
C
Câu 6
A
Câu 16
C
Câu 26
B
Câu 36
B
Câu 46
A
Câu 7
C
Câu 17
C
Câu 27
B
Câu 37
D
Câu 47
B
Câu 8
C
Câu 18
B
Câu 28
A
Câu 38
A
Câu 48
A
Câu 9
C
Câu 19
C
Câu 29
C
Câu 39
D
Câu 49
B
Câu 10
B
Câu 20
B
Câu 30
B
Câu 40
D
Câu 50
D
HƯỚNG DẪN GIẢI CÂU VẬN DỤNG CAO
CÂU 10. 
x09
V h B x x f x
2
. .(18 2 ) ( )

Cách khác: -2x; 18-2x
x x x
V x x x x x
3
2
1 1 4 (18 2 ) (18 2 )
.(18 2 ) .4 (12 2 ).(12 2 ) .
4 4 3

x x x4 18 2 3

CÂU 11. 
m
2
\
x
mm
y
em
2
2
2
2
'

1
ln ;0
4
:
yx
m
mm
m m m
mm
m
2
22
2
1
' 0, ln ;0
12
20
4
11
1
1
11
1
;1
22
4
4
mm
11
12
22
CÂU 22.



x1.007

x
2
1.007

n
x1.007

nn
x x n1.007 2 1.007 2 99, 33
B
CÂU 31.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 111 Tài liệu ôn thi THPT Quốc Gia 2017
ID IM MO SM
I SO CD MO IM OI SO SO
OB IO SO SO
2 3 3 3 1 1 1 4
.
3 2 5 5 3 5 5 5

RR
12
,

Ta có
R
SI ID
SID SOA
SO OA R
1
2
R SO SI
V R IO
SI SI SI
V SO SO SO
R SO
R SO
2
32
2
2
1
11
2
2
2
2
2
3
.
42
3 3 0
1 9 3
.
3
CÂU 34. 
w x yi x y,,
w i i z
x yi i i z
x y i
x y x y
zi
i
x y x y
x y x y
xy
22
22
22
3 2 2
3 2 2
32
2 8 2 1
2 5 5
2 8 2 1
2
55
6 4 7 0
3 2 20

r 20
CÂU 40. 





Ta có: IO=GH=
aa
SH
1 1 3 3
.
3 3 2 6
,OB=
a 2
2
R=IB=
a
IO OB
22
21
6
 V=
a
R
3
3
4 7 21
3 54

CÂU 42. Gi
xy;
là s tn trc st và c sn xut trong ngày.
S tin lãi mi ngày:
L x y x y( , ) 2
.
S gi làm vic mi ngày ca máy ct:
xy36
.
S gi làm vic mi ngày ca máy tin:
xy4
.

L x y( , )

xy
xy
xy
36
4 (*)
0, 0
.
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Trang 112 Tài liệu ôn thi THPT Quốc Gia 2017
d
2
d
1
x
y
d
4
d
3
B
C
4
6
A
O
1

(*)

OABC

O A B C(0;0), (2; 0), (1;3), (0; 4)
.
Ta có:
L L L L(0;0) 0, (2;0) 4, (0, 4) 4, (1, 3) 5
.


| 1/113
| | Tải xuống

Có thể bạn quan tâm:

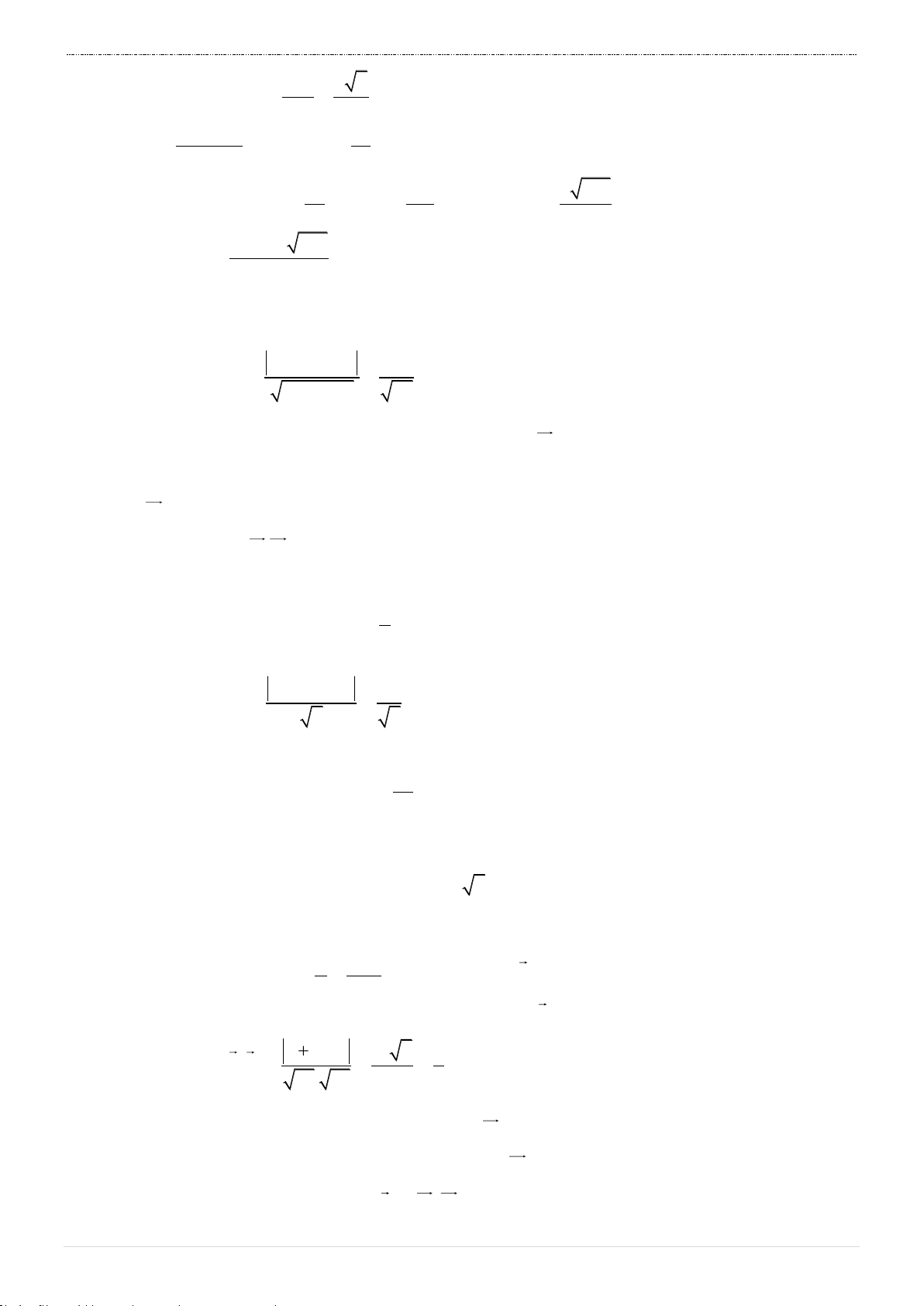
Preview text:

å TÀI LIỆU TỰ HỌC Nguyễn Văn Huy Nội dung
5 đề ôn thi học kỳ 2 có đáp án và giải chi tiết.
15 ôn thi THPT Quốc Gia có đáp án và hướng
dẫn giải câu khó.
TÀI LIỆU CỦA: ..........................................................
Địa chỉ lớp học: 66 Đặng Đức Thuật, Phường Tam Hiệp,
TP. Biên Hòa – Tỉnh Đồng Nai. LƯU HÀNH NỘI BỘ
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017 TỈNH ĐỒNG NAI
Môn: TOÁN – Khối 12 Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97 NỘI DUNG ĐỀ SỐ 01
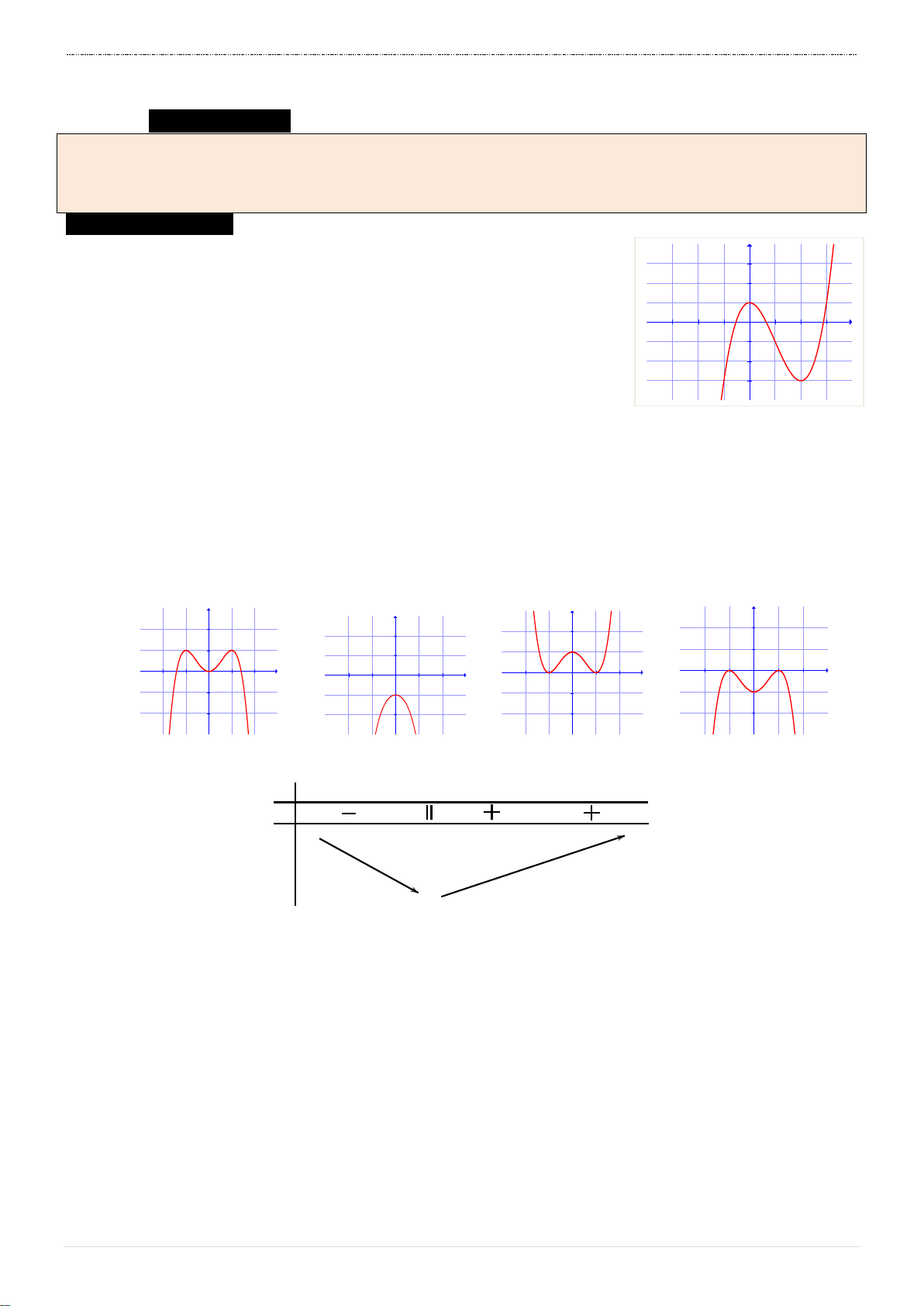
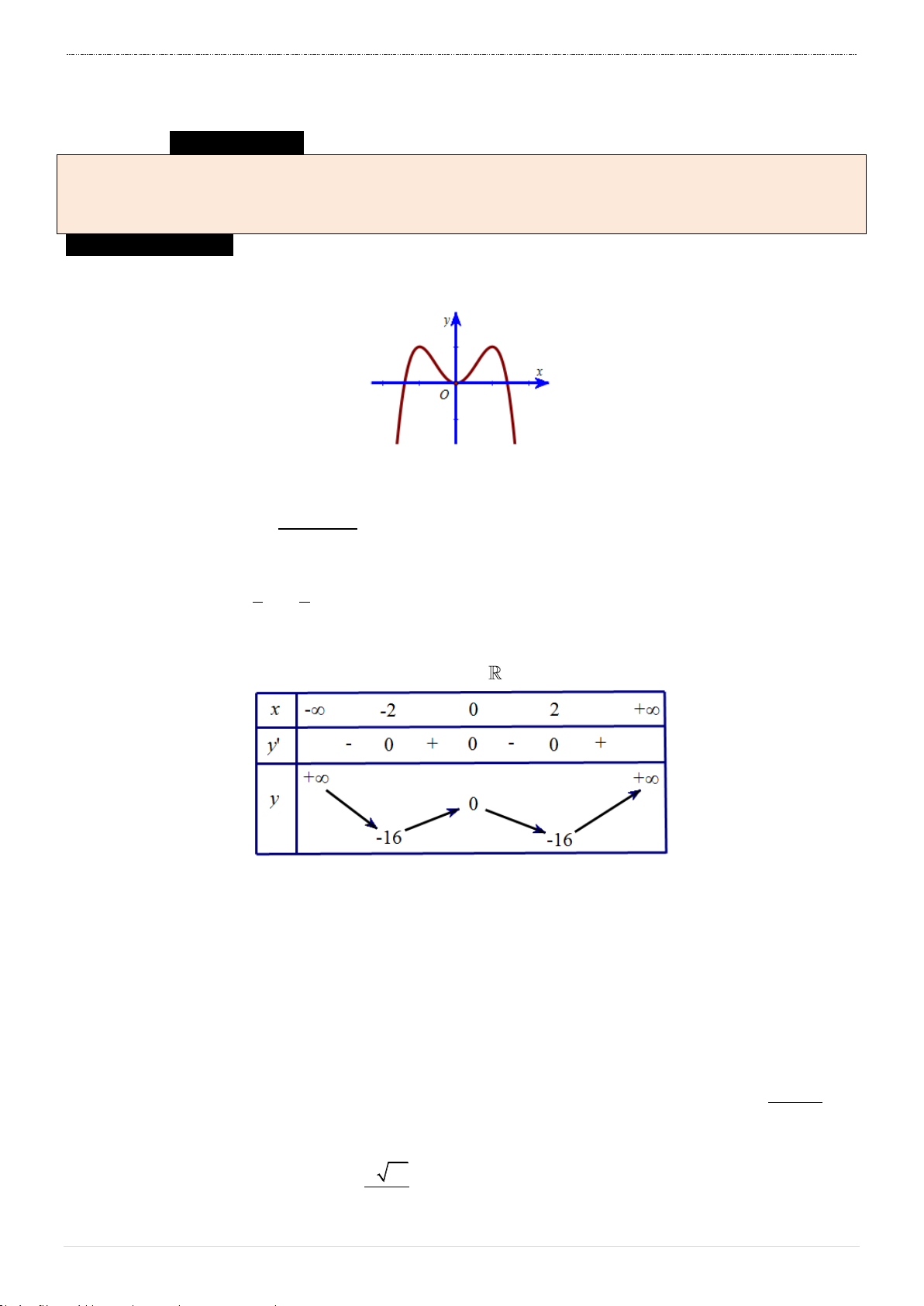
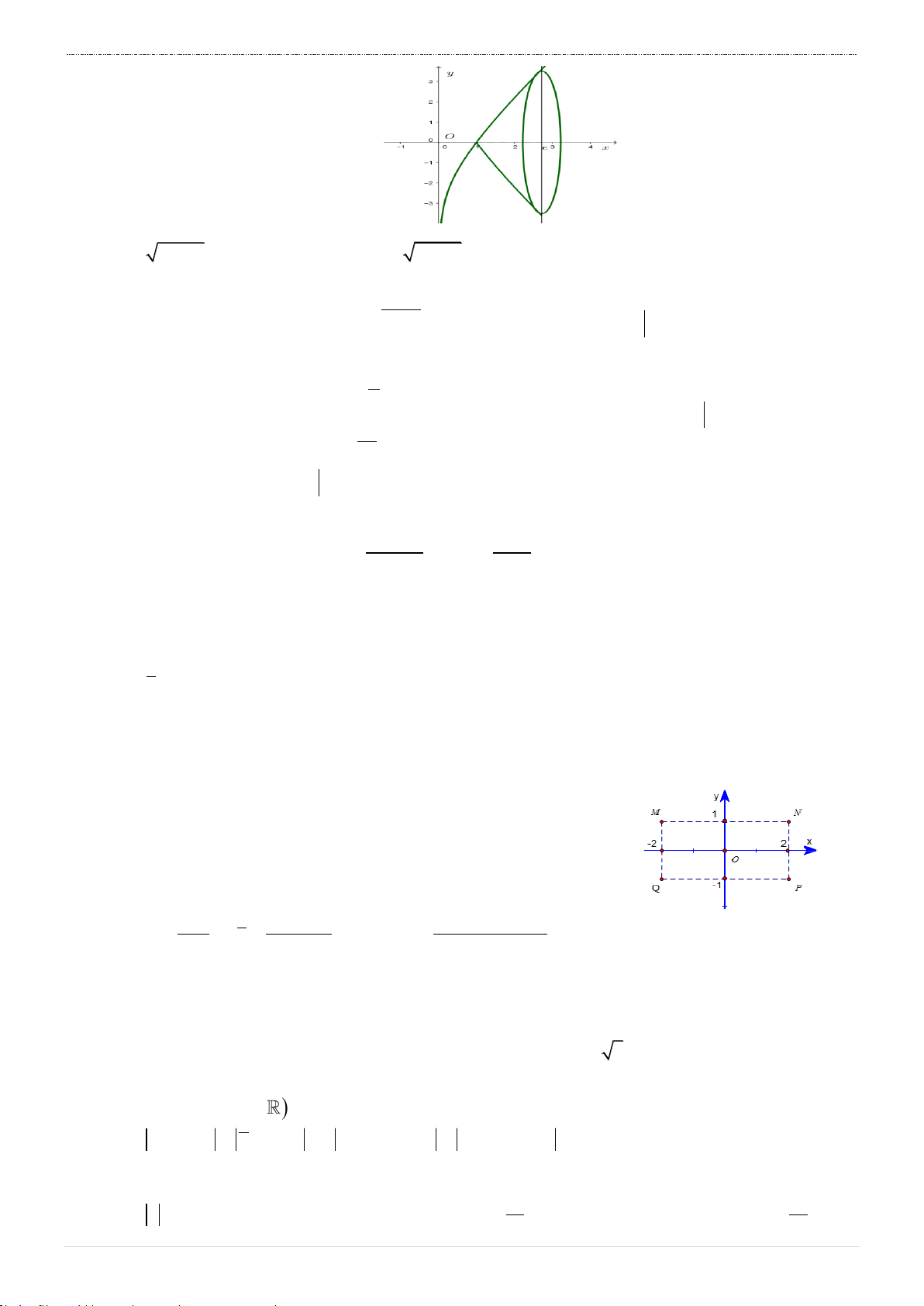
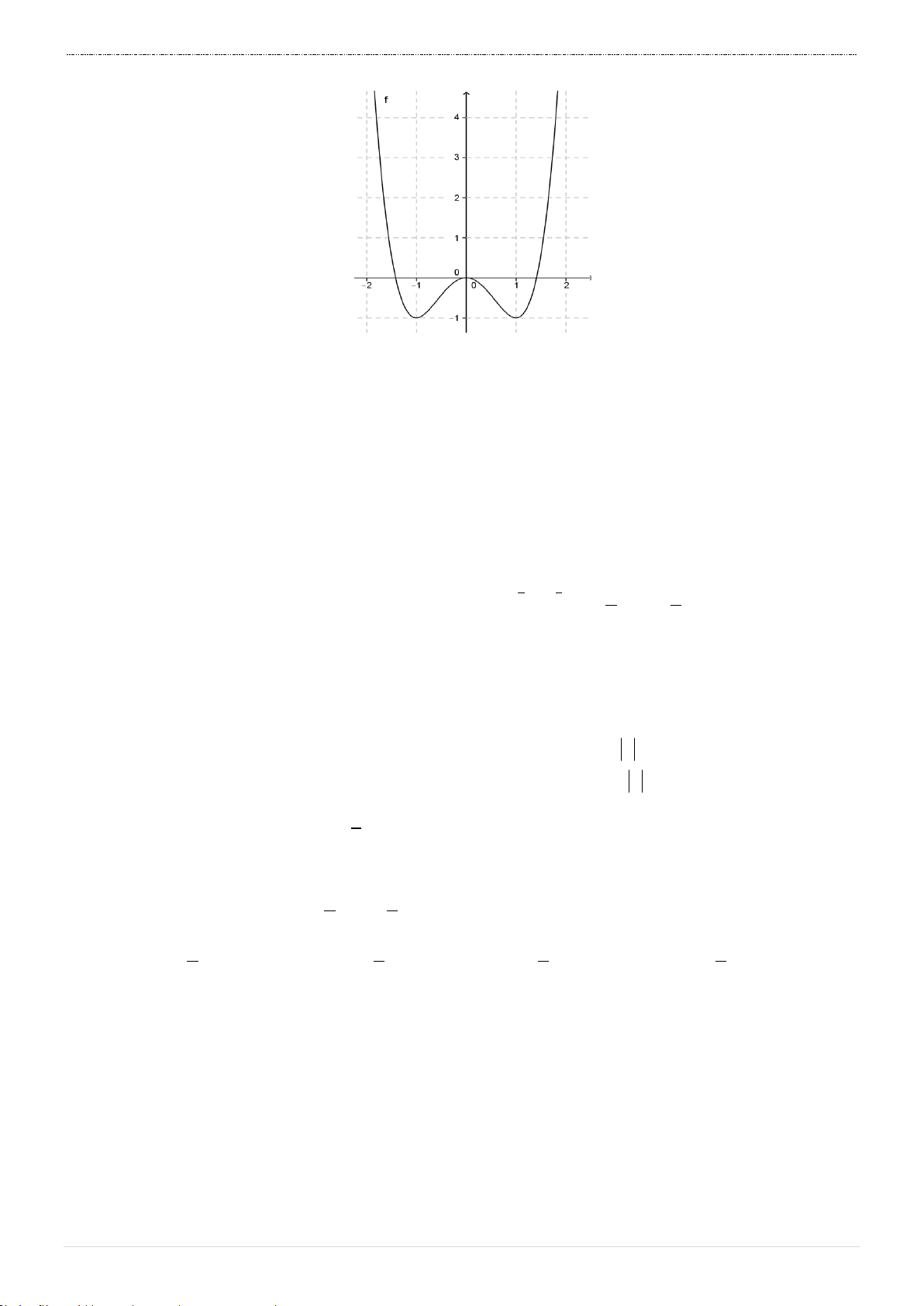
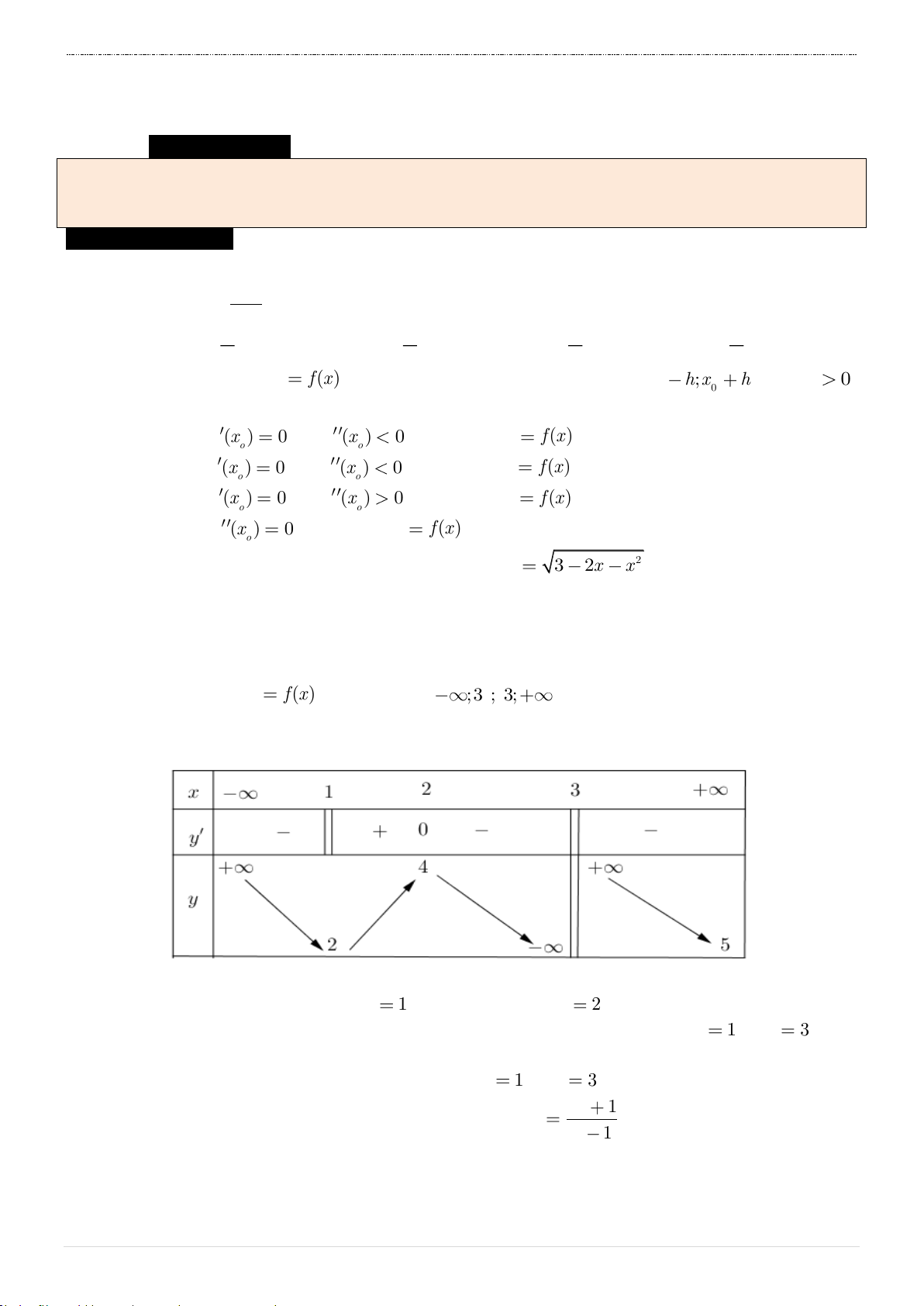
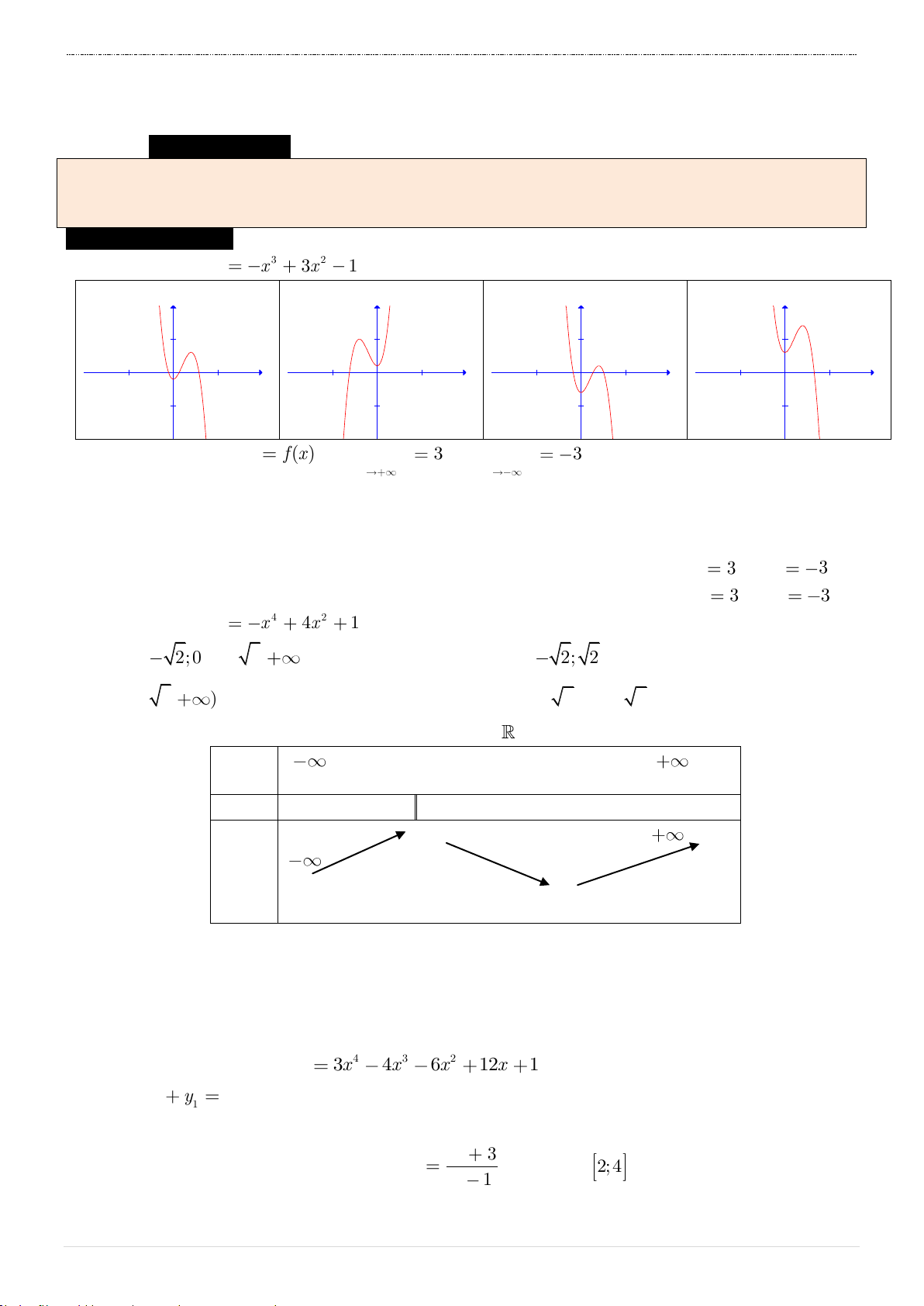
Câu 1. Đường cong trong hình bên là đồ thị của một hàm số trong y 3
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới 2
đây. Hỏi hàm số đó là hàm số nào? 1 x A. y  3
x  3x  1 . -3 -2 -1 1 2 3 -1 B. y  3 x  2 3x  1 . -2 C. y  3 x  2 3x  1 . -3 D. y  3 x  2 3x  1 .
Câu 2. Cho hàm số y f x có lim f x   và lim f x   . Chọn mệnh đề đúng? x2 x2
A. Đồ thị hàm số đã cho không có tiệm cận đứng.
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x  2 và x  2 .
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y  2 và y  2 .
Câu 3. Đồ thị hàm số y   4 x  2 2x có dạng y y y y 2 2 2 2 1 1 1 1 x x x x -2 -1 1 2 -2 -1 1 2 -2 -1 1 2 -2 -1 1 2 -1 -1 -1 -1 -2 -2 -2 -2 A. B. C. D.
Câu 4. Cho hàm số y f x xác định, liên tục trên  và có bảng biến thiên x -∞ -1 0 +∞ y' 0 +∞ +∞ y -1
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng hai cực trị.
B. Hàm số có giá trị nhỏ nhất bằng 1.
C. Hàm số có giá trị cực tiểu bằng 0.
D. Hàm số không xác định tại x  1
Câu 5. Hàm số y   3
x  3x  2 có giá trị cực đại y là CĐ A. y  1. B. y  5 C. y  2 . D. y  0 . CĐ CĐ CĐ CĐ
Câu 6. Khoảng đồng biến của hàm số y   3
x  3x  1 là A. ;  
1 và 1;  . B. 0; 2. C. 1;  1 . D. 0;  1 .
Câu 7. Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau
A. log x có nghĩa với x .
B. log 1  a và log a  1 a a a
C. log xy  log . x log y . D. log n
x nlog x x  0,n  0. a a a a a Trang 1
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 8. Giá trị lớn nhất của hàm số y  3 x  2
3x  9x  2 trên đoạn 2; 2   là . A. 24. B. 2. C. 3. D. 26.
Câu 9. Đặt a  log 6, b  log 7 . Hãy biểu diễn log 7 theo a và b 12 12 2 a b a b A. . B. . C. . D. . b  1 1  a b  1 a  1
Câu 10. Khối bát diện đều có các mặt là A. Hình vuông. B. Tam giác đều. C. Hình chữ nhật. D. Tam giác vuông.
Câu 11. Đặt a  log 3 . Hãy biểu diễn log 24 theo a . 2 6 a  3 a  1 a  3 a A. . B. . C. . D. . a  1 a  3 a  1 a  1
Câu 12. Cho H là khối lập phương có độ dài cạnh bằng 3cm. Thể tích của H bằng A.  3 27 cm . B.  2 27 cm . C.  3 9 cm . D.  3 3 cm .
Câu 13. Cho 0  a  1. Giá trị của biểu thức 2log 3 a a bằng A. 2 2. B. 3 2. C. 2 3. D. 3.
Câu 14. Cho H là khối lăng trụ có chiều cao bằng 3a, đáy là hình vuông cạnh .a Thể tích của H bằng A. 3 a . B. 3 2a . C. 3 3a . D. 3 4a .
Câu 15. Cho 0  a  1. Giá trị của biểu thức   23 M 3 log a a bằng? a  5 3 A. . B. 5. C. 7. D. . 2 2
Câu 16. Biểu thức K  3
2 2 viết dưới dạng lũy thừa với số mũ hữu tỉ là 5 2 4 1 A. 3 2 . B. 3 2 . C. 3 2 . D. 3 2 .
Câu 17. Tìm tất cả các giá trị thực của a để biểu thức B  log a 3 có nghĩa. 2   
A. a  3.
B. a  3.
C. a  3. D. a  3.
Câu 18. Cho AB . C A B
C là khối lăng trụ đứng có AB a 5 , AB a, đáy ABC có diện tích bằng 2
3a . Thể tích của khối lăng trụ AB . C A B C bằng A. 3 a . B. 3 2a . C. 3 4a . D. 3 6a .
Câu 19. Nếu độ dài các cạnh của khối hộp chữ nhật tăng lên 3 lần thì thể tích của khối hộp chữ nhật sẽ tăng lên A. 3 lần .B. 9 lần. C. 27 lần. D. 81 lần.
Câu 20. Cho H là khối hộp chữ nhật có độ dài cạnh bằng a,2a,3a . Thể tích của H bằng A. 3 a . B. 3 2a . C. 3 4a . D. 3 6a .
Câu 21. Đường thẳng y  3x cắt đồ thị hàm số y  3 x  2
2x  2 tại điểm có tọa độ x ; y thì 0 0 
A. y  1 . B. y  3 . C. y  2 . D. y  1. 0 0 0 0
Câu 22. Cho khối chóp H có thể tích là 3
2a , đáy là hình vuông cạnh a 2 . Độ dài chiều cao
khối chóp H bằng A. 4 . a B. 3 . a C. 2 . a D. . a
Câu 23. Cho khối lăng trụ H có thể tích là 3
4a , đáy là tam giác vuông cân có độ dài cạnh
huyền bằng a 2 . Độ dài chiều cao khối lăng trụ H bằng Trang 2
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. 2 . a B. 4 . a C. 6 . a D. 8 . a 2 x  3x   1  Câu 24. 3
Giá trị lớn nhất của hàm số y  trên đoạn   2;  bằng. x  1  2  A. 3. B. 4. C.  7 . D.  13 . 2 3
Câu 25. Nếu độ dài chiều cao của khối chóp tăng lên 5 lần ,diện tích đáy không đổi thì thể tích
của khối chóp sẽ tăng lên A. 5 lần. B. 10 lần. C. 15 lần. D. 20 lần.
Câu 26. Cho hàm số y   3 x  2
3x  5x  1 có đồ thị C . Tiếp tuyến với đồ thị C tại điểm có hệ
số góc lớn nhất, có phương trình là A. y  2 . x
B. y  2x 1. C. y  2 . x
D. y  2x  2.
Câu 27. Hàm số y  4 x m  2 x  2 ( 3)
m  2 có đúng một cực trị khi và chỉ khi: A. m  3. B. m  0. C. m  3. D. m  3.
Câu 28. Tìm tất cả các giá trị thực của tham số m để của hàm số y   2 2 x (x  2 )
m  1 m có ba
điểm cực trị là ba đỉnh của một tam giác vuông. A. m  2 . B. m  1. C. m  3 3. D. m  1 . 3
3 m1x1
Câu 29. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y  có 2 x x  1
đúng một đường tiệm cận ngang.
A. Không có giá trị nào của m thỏa mãn. B.m . C. m  0. D. m  1. sin x     Câu 30. m
Tìm tất cả các giá trị thực của tham số m để hàm số y  đồng biến trên   ; 0 . sin x m  2  A. m  1. B. m  0.
C. 1  m  0. D. m  0.
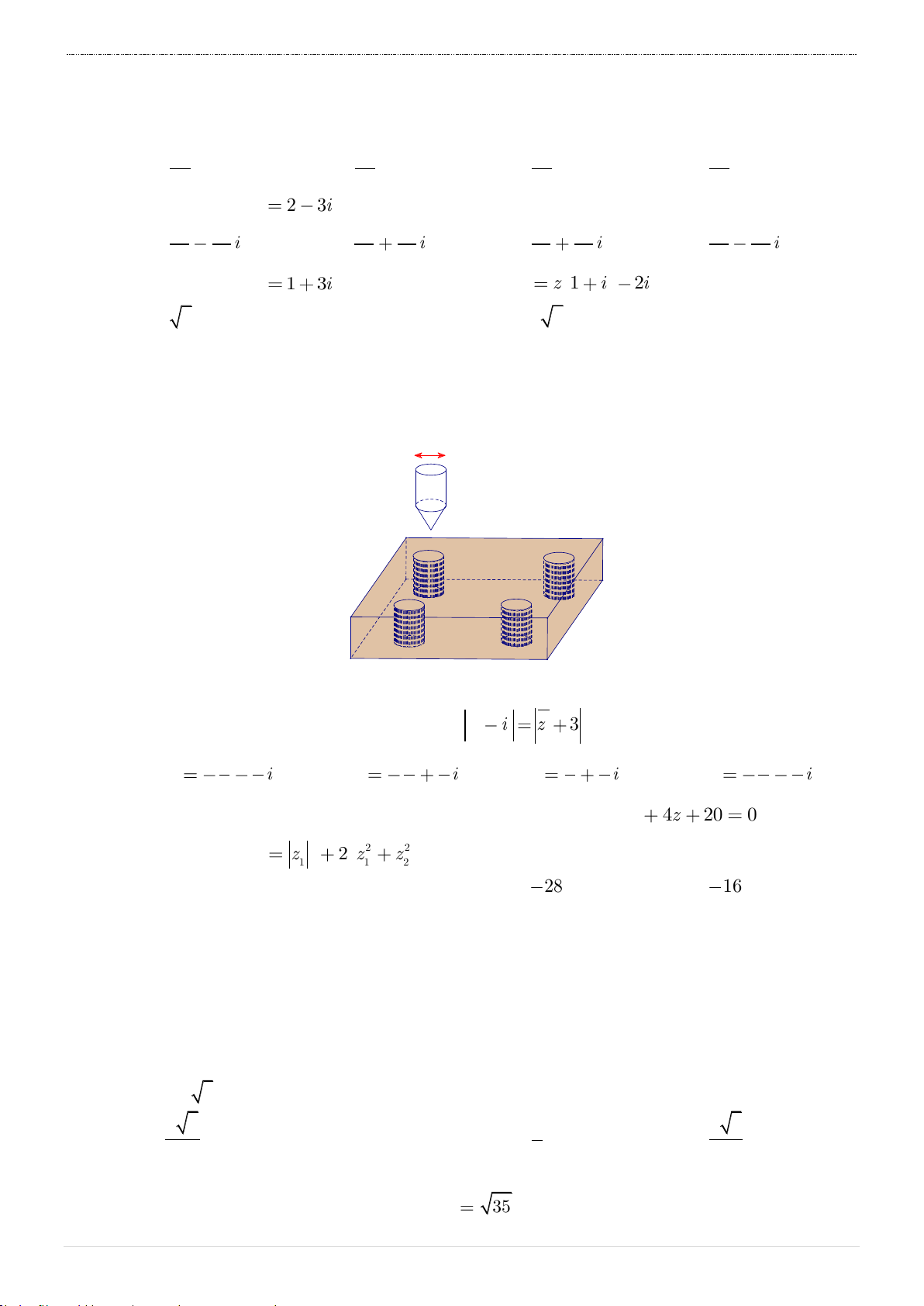
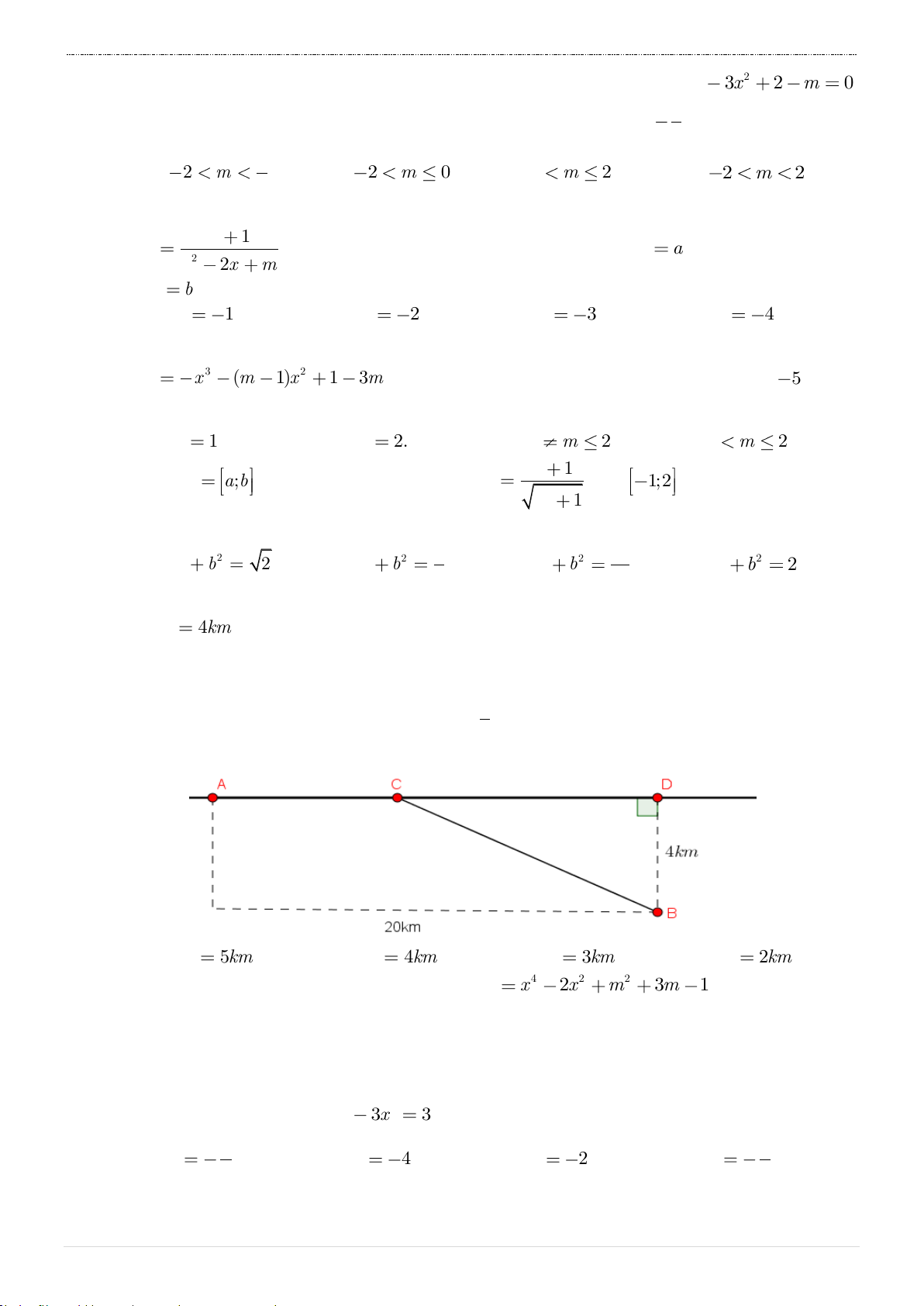
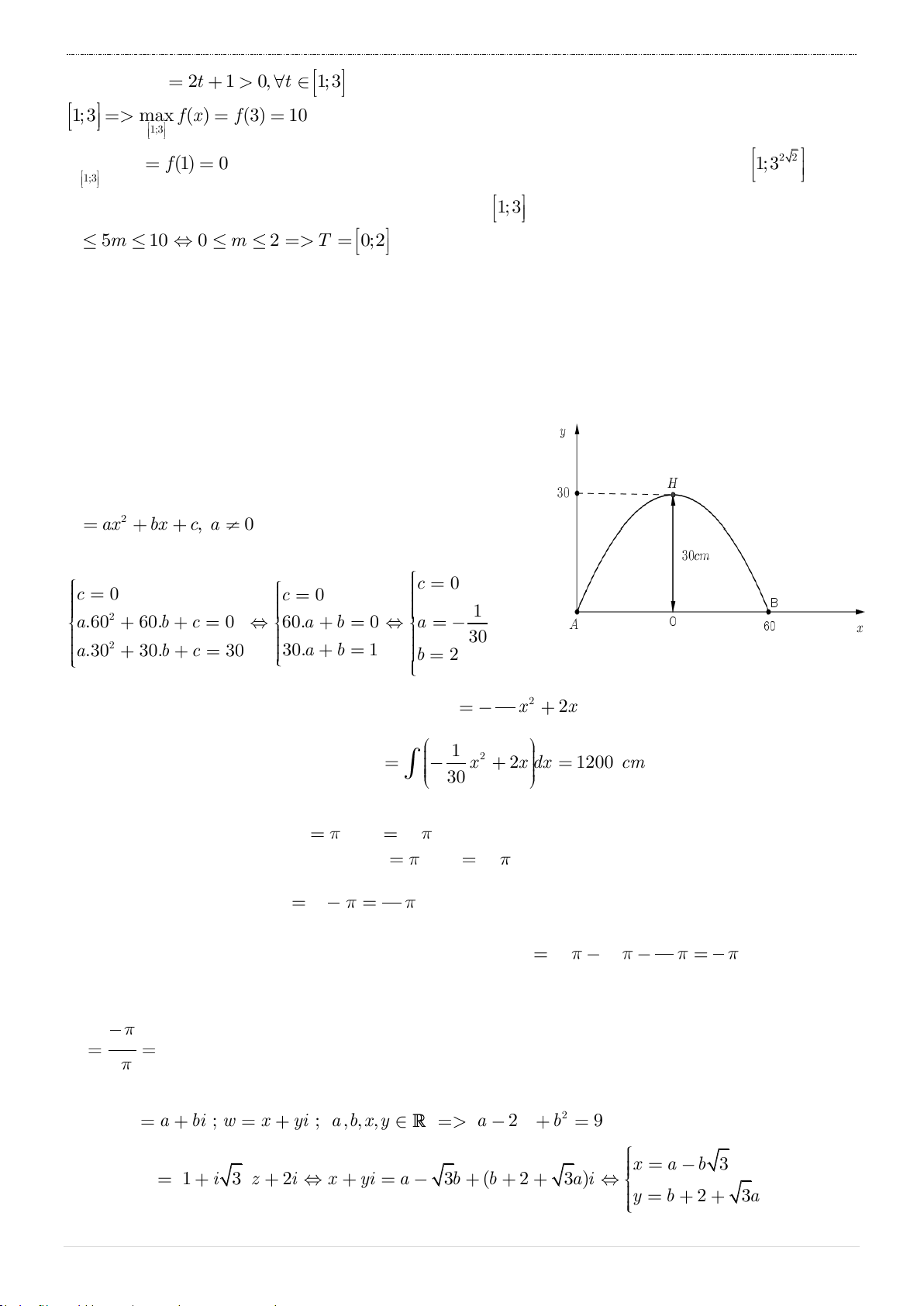
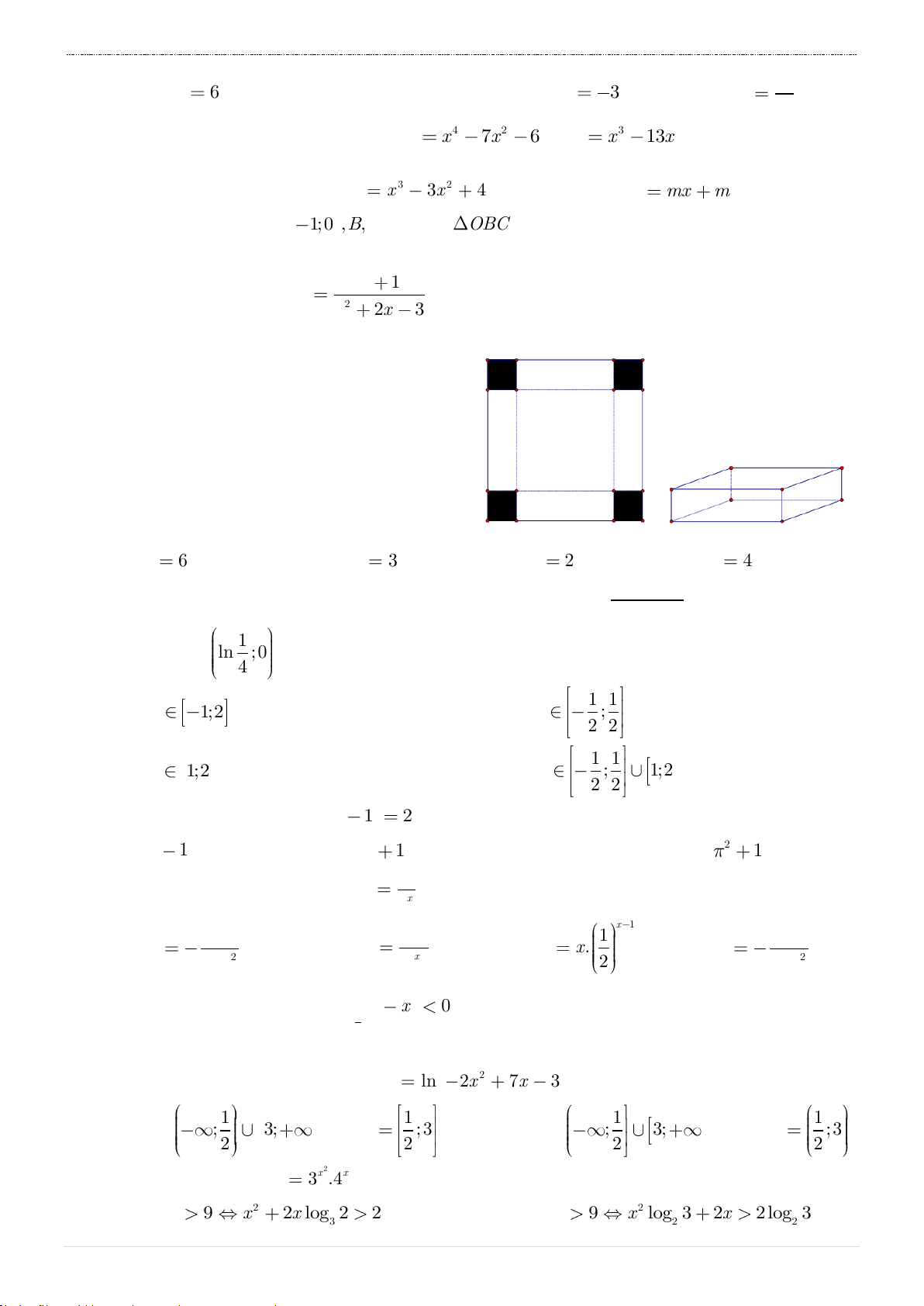
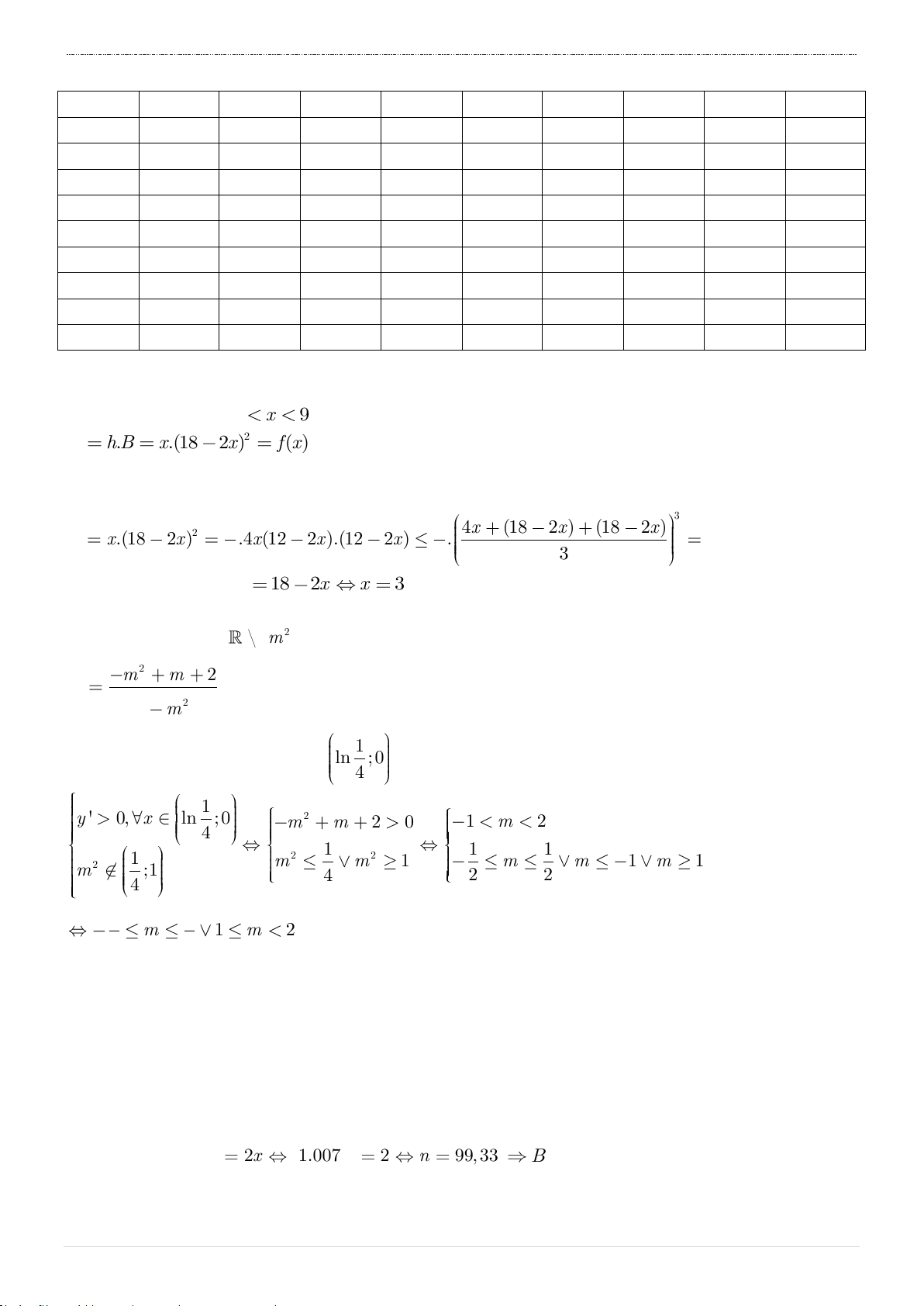
Câu 31. Cho một tấm nhôm hình chữ nhật có chiều dài bằng 12cm và chiều rộng bằng
10cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình
vuông có cạnh bằng xcm , rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp.
Tìm x để hộp nhận được có thể tích lớn nhất.    
A. x  12 3 5 . B. x  11 31 . C. x  11 31 .
D. x  10 2 7 . 2 3 3 3
Câu 32. Cho hai số thực a và b , với 0  b  1 a . Khẳng định nào dưới đây là đúng?
A. log b  0  log . a
B. 0  log b  log . a a b a b
C. log a  log b  0.
D. log b  log a  0. b a a b Câu 33. 1 Hàm số y  3
x  2m  3 2 x  2
m x  2m  1 không có cực trị khi và chỉ khi 3 Trang 3
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. m  3
m  1. B. 3  m  1. C. m  3. D. m  1. Câu 34. x 1
Gọi I là giao điểm hai đường tiệm cận của hypebol H  : y
. Tiếp tuyến với đồ thị x  1
H tại điểm M0; 1cắt hai đường tiệm cận của H tại hai điểm A và B. Khi đó
diện tích tam giác ABI bằng A. 8 đvdt. B. 6 đvdt. C. 4 đvdt. D. 2 đvdt.
Câu 35. Tìm các giá trị nguyên của tham số m để đồ thị hàm số y  4
x   m   2 4
2 x  4m  1 cắt trục
hoành tại 4 điểm phân biệt có hoành độ x , x , x , x (x x x x )lập thành cấp số cộng 1 2 3 4 1 2 3 4 A. m  3.
B. m  0,m  2. C. m  2. D. m  3.
Câu 36. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  4 x  2
2mx  3m  4 có các
cực trị đều nằm trên các trục tọa độ.
A. m  1;0;  4 .
B. m1; 2;  3 .
C. m1;0;  1 .
D. m(; 0)   4 .
Câu 37. Cho a  0, b  0 thỏa mãn 2 a  2
b  7ab . Chọn mệnh đề đúng.trong các mệnh đề 3
A. lg a b  lg a  lg b.
B. 2lg a  lg b  lg7ab. 2 1 a b 1
C. 3lg a b  lg a  lg b. D. lg
 lg a  lgb. 2 3 2
Câu 38. Cho khối lăng trụ AB . C A
B C, M thuộc cạnh AA sao cho MA  3M
A . Tỉ số thể tích của khối lăng trụ AB . C A B
C và thể tích khối chóp . M A B C bằng A. 4. B. 8. C. 12. D. 18.
Câu 39. Một người gửi tiết kiệm ngân hàng, mỗi tháng gửi 1 triệu đồng, với lãi suất kép
1% / tháng. Gửi được hai năm 6 tháng người đó có công việc nên đã rút toàn bộ gốc và
lãi về. Số tiền người đó rút được là 30 29 A.  101. 1,01      101. 1,01    1 (triệu đồng). B.     1 (triệu đồng). 30 30 C.  100. 1,01      100. 1,01    1 (triệu đồng). D.     1 (triệu đồng).
Câu 40. Cho khối chóp .
S ABC có SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông
góc với  ABC , AB  2a và tam giác ABC có diện tích bằng 2
3a . Thể tích khối chóp . S ABC bằng A. 3 a . B. 3 3a . C. 3 6a . D. 3 2a 3.
Câu 41. Cho khối chóp .
S ABC , M là trung điểm của cạnh SA . Tỉ số thể tích của khối chóp .
S MBC và thể tích khối chóp . S ABC bằng 1 1 1 A. . B. . C. . D. 1. 6 4 2
Câu 42. Cho khối chóp .
S ABC ; M và N lần lượt là trung điểm của cạnh SA, ; SB thể tích khối chóp . S MNC bằng 3
a . Thể tích của khối chóp . S ABC bằng A. 3 a . B. 3 4a . C. 3 8a . D. 3 12a .
Câu 43. Cho hình lăng trụ đứng AB . C A
B C, có góc giữa 
A B và  ABC bằng o 45 ; đáy ABC là
tam giác vuông cân tại A và BC  2 2a . Thể tích khối lăng trụ AB . C A B C bằng A. 3 a . B. 3 2a . C. 3 3a . D. 3 4a . Trang 4
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 44. Cho hình chóp .
S ABC có ABC là tam giác đều cạnh a . Hình chiếu vuông góc của
S trên  ABC là điểm H thuộc cạnh AB sao cho HA  2HB. Góc giữa đường thẳng SC
và mặt phẳng  ABC bằng o
60 . Thể tích khối chóp . S ABC bằng 7 7 7 7 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 8 12 16
Câu 45. Cho khối chóp .
S ABCDcó SA   ABCD , SB a và ABCD là hình vuông cạnh . a Thể tích khối chóp . S ABCD bằng 3 2a 4 A. . B. 3 a . C. 3 a . D. 3 2a . 3 3
Câu 46. Cho khối chóp .
S ABC , M là trung điểm của cạnh .
BC Thể tích của khối chóp . S MAB là 3
2a . Thể tích khối chóp . S ABC bằng 1 3 a A. 3 4a . B. 3 2a . C. 3 a . D. . 2 4
Câu 47. Cho hình chóp . S ABCD có SA
ABCD , SB a 5 ; ABCD là hình thoi cạnh a và góc ABC  o
30 . Thể tích khối chóp . S ABCD bằng 1 2 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a 3. 3 3 3
Câu 48. Cho hình chóp .
S ABC có SA  ABC , góc giữa SB và  ABC bằng o 60 ; tam giác ABC đều cạnh .
a Thể tích khối chóp . S ABC bằng 1 1 A. 3 3a . B. 3 a . C. 3 a . D. 3 a . 4 2 Câu 49. 1
Tìm tất cả các giá trị của tham số m để hàm số y   3
x  m   2 1 x  2
m x  2m  1 3
nghịch biến trên tập xác định của nó. A. m  1 . B. m  1. C. m  0. D. m  1 . 2 2
Câu 50. Cho hình chóp SABCDcó đáy ABCD là hình vuông cạnh 2a . Gọi P,Q lần lượt là trung
điểm của AD,CD . Gọi H là trung điểm của AP . Tam giác SAP là tam giác đều và SH
vuông góc với mp  ABCD . Khoảng cách của hai đường thẳng chéo nhau SP và BQ theo a . a 3 a 3 3a 3 A. . B. . C. a 3. D. . 4 2 4
ĐÁP ÁN ĐỀ SỐ 01 1 2 3 4 5 6 7 8 9 10 B C A B D C D C B A 11 12 13 14 15 16 17 18 19 20 C A D C C B A D C D 21 22 23 24 25 26 27 28 29 30 B B B A A C D B D A 31 32 33 34 35 36 37 38 39 40 B C B C C D D C A A 41 42 43 44 45 46 47 48 49 50 C B D C B A A B A D Trang 5
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
HƯỚNG DẪN GIẢI ĐỀ SỐ 01 Câu 1. Chọn B. Nhìn đồ thị ta thấy:
Đây là đồ thị của hàm bậc 3 với hệ số a dương
Điểm cực trị của hàm số là
x  0 và x  2.
Cắt trục tung tại M 0;  1 .
Câu 2. Chọn C.
Từ lim f (x)   và lim f (x)   . x2 x2
Ta có: hàm số f x có tiệm cận đứng tại x  2 và x  2.
Câu 3. Chọn A. Hàm số y   4 x  2
2x có hệ số a  0 , hệ số c =0.
Do đó đồ thì là hình chữ M, cắt trục tung tại gốc tọa độ.
Câu 4. Chọn B.
Nhìn BBT ta thấy y  1 là giá trị nhỏ nhất của hàm số.
Câu 5. Chọn D. y   x2 ' 3  3
x  1  y   y   4(y ) ' 0  CT
x  1  y   0(y ) CD
Câu 6. Chọn C. x  1 y '   x2 3  3; y'  0   x    1 Hệ số a  0
Câu 7. Chọn D.
Câu 8. Chọn C.
x  1 2; 2 2  
)y'  3x  6x  9 y' = 0  x  32;2    ) ( y 2)  4 ) ( y 2)  24 ) ( y 1)  3  max y  3 2;2  
Câu 9. Chọn B. log 7 b b b b C1 : log 7  12     2 log 2 log 2 12 log 12  log 6 1  a 12 12 12 12 log12 6 log 7
C2 : Dùng máy casio text. log 7  12  0 2 1 log 6 12
Câu 10. Chọn A.
Câu 11. Chọn C. Trang 6
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai log 24 log 8  log 3 3  a log 24  2  2 2  6 log 6 log 2  log 3 1 a 2 2 2
Câu 12. Chọn A. V  3 3 3 (cm )
Câu 13. Chọn D. 2log 3 a  log 3 2 a a a  2 ( ) ( 3)  3
Câu 14. Chọn C. V B h  2 a a  3 . 3 . 3a
Câu 15. Chọn C. 7 7 M 3log a a a a a  2 3    
 3loga  3   3. log  7   3 a
Câu 16. Chọn B. 1 1 4  4  2 2 K  3  3  3   3   3 2 2 2.2 2 2 2  
Câu 17. Chọn A.
Câu 18. Chọn D. AA'= 2 A' B  2 AB  2 5a  2 a  2a V  AA'.S  2 2 . a 3a  3 6a ABC
Câu 19. Chọn C.
Câu 20. Chọn D.
V abc a a a  3 .2 .3 6a
Câu 21. Chọn B. 3 x  2
2x  2  3x  3 x  2
2x  3x  2  0  x  1  y  1 0 0
Câu 22. Chọn A. 3 1 1 6a V  . B h  2 ( 2a)  3 2a h   3a 2 3 3 2a
Câu 23. Chọn B. 3 1 4a V  . B h  2 ( 2a) h  3 4a h   4a 2 2 a
Câu 24. Chọn A. Trang 7
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
(2x  3)(x  1)  2 (x  3x  2 3).1 x   y   2x ) ' x12 x12   1  x  0  2; 2    x  2x   2  )y'  0   0  x12   1  x  2    2;    2  ) ( y 0)  3   y   13 ) ( 2) 3  1    y  7 )    2  2 max y  3  1    2;   2 
Câu 25. Chọn A.
Câu 26. Chọn C. y   3 x  2 3x  5x  1 y '   2
3x  6x  5   2
3(x  2x  1)  2  3(x  2 1)  2  2
max y '  2  x  1  y  2 0 0
PTTT : y  2(x  1)  2  2x
Câu 27. Chọn A. y  4 x m  2 x  2 ( 3) m  2
ab  0  m  3  0  m  3
Câu 28. Chọn B. )y   2 2 x (x  2 )
m  1 m   4 x  2 2mx  1 m )y'   3
4x  4mx   2 4 ( x x m)
Hàm số đã cho có ba cực trị khi và chỉ khi phương trình y’  0 có ba nghiệm phân biệt.
Khi và chỉ khi phương trình 2
x m  0 có hai nghiệm phân biệt khác 0.
 m  0  m  0. Đối chiếu với các phương án trong đề ra thì B là đáp án.
Câu 29. Chọn D.
m1  0  m  1 Ta có y  0 là tiệm cận ngang duy nhất của đồ thị hàm số đã cho. m 1  0 
y  (m  là tiệm cận ngang của đồ thị hàm số. m  1  1)  0
Câu 30. Chọn A. t m
)sin x t t (1;0)  y  (t  ) m t m    2m y '   0 2 m  0
Hàm số đồng biến trên 1;0 khi và chỉ khi  t m    m   m ( 1   1; 0) m (  1; 0)
Câu 31. Chọn B.
Chiều dài của cái hộp là : 12  2x  0  x  10 .
Chiều rộng của cái hộp là 10  2 . x Trang 8
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Chiều cao của cái hộp là : x.
Thể tích cái hộp là : V  12  2x10  2x . x
Tìm giá trị lớn nhất của hàm số f ( ) x  ( x 12  2 ) x (10  2 )
x trên 0; 10 ta có x  11 31 3
Câu 32. Chọn C. 1
Lấy b  ; a  3 thử bằng máy c
Câu 33. Chọn B. y  2 x m x  2 ' 2(2 3) m
Hàm số không có cực trị khi và chỉ khi phương trình y’  0 vô nghiệm hoặc có nghiệm kép     2 ' 0
3m  12m  9  0  3  m  1
Câu 34. Chọn C. Ta có I 1 ;  1 .
Tiếp tuyến của (H) tại M 0 ; 1 là : y  2x 1.
Đường thẳng d cát tiệm cận ngang tại A1 ;1, cắt tiệm cận đứng tại B1 ; 3 1 SI . A IB   4 ABC 2
Câu 35. Chọn C. Đặt t  2 x (t  0)
Đồ thị hàm số cắt Ox tại 4 điểm phân biệt khi và chỉ khi phương trình 2
t (4m  2)t  4m 1  0 có 2 nghiệm dương     2 ' 0
4m  0  m  0
Mặt khác x , x , x , x lập thành một cấp số cộng nên x  3x 1 2 3 4 1 2
t t  4m  2
Suy ra t  9t .Theo vi ét lại ta có  1 2 1 2
t .t  4m   1 1 2  m  2 4 2  9
 4m  1  m    2  10 
Câu 36. Chọn D.
TH1 : Đồ thị chỉ có một cực trị x  0  ab  0  m  0 Ta có (
y 0)  3m  4  (0; 3m  4)Oy
TH2: Đò thị có 3 cực trị x  0; x   m ab  0  m  0
Ta có y m   2
m m    m  2 ( ) 3 4 (
; m  3m  4) Ox m  1(l)  2
m  3m  4  0   m   4(t / ) m
Câu 37. Chọn D. a
2  2  ab a  2 b a b 7 (
b)  9ab a b  3 ab   ab 3 a   b ab  1 lg lg (lg a  lg b) 3 2
Câu 38. Chọn C. Trang 9
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai )VS .h A
ABC.A' B'C ' A'B'C' C 1 h )VS .
M.A' B'C ' A'B'C' 3 4 B  V  12V
ABC.A' B'C '
M.A' B'C ' M
Câu 39. Chọn A. A' C' A n 1 P
 1r 1(1r)  30 1,01  1(1,01)  101 30 (1,01)  1 r 0,01 B'
Câu 40. Chọn A.
Gọi H là trung điểm của AB. S
SH ABC SH HB  1 ( ) AB a 2 V  1 2 3a .a  3 a 3
Câu 41. Chọn C. 2a B A H
Theo công thức tính thể tích tỷ số thể tích V SM 1 C S.MBC   V SA 2 S.ABC
Câu 42. Chọn B.
Theo công thức tính tỷ số thể tích A C V SM.SN 1 S.MNC   V S . A SB 4 2a 2 S.ABC 450 B
Câu 43. Chọn D. A' BA  0 45 A' C'
AB  2a A' A  2a VV .A' A  3 4a
ABC.A'B'C ' ABC B'
Câu 44. Chọn C.
Gọi I là trung điểm của .
AB CI AB S  2 2  CH  2 CI  2
IH   a 3   a a 28 )    2  36 6 a 28 a 21   ) SCH  0 60  SH  0 CH.tan 60  . 3  6 3 I H 2 3 A B  V
 1 a 3 a 21  a 7 ) . . 600 S.ABC 3 4 3 12 Câu 45. C Chọn B. )SA  2 SB  2 AB  3a S V  1 .S . A S  1 2 3 . a a  3 a S.ABC 3 ABCD 3 a 10
Câu 46. Chọn A V  2V  3 4a S.ABC SMAB
Câu 47. Chọn A. A B a D C Trang 10
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
)AC BD O S 2   a ) ABC  0 30  S  1 0 . BA BC.sin 30  ABC 2 4 a 5 2   a S 2SABCDABC 2 A B 3  a a )V  O 3 D C
Câu 48. Chọn B. S )SA  0 A . B tan 60  a 3 2 3  V  1 SA S  1 a 3 a ) . a 3.  S.ABC 3 ABC 3 4 4
Câu 49. Chọn A. y   2 x m x  2 ' 2( 1) m A B 600
Hàm số nghịch biến trên tập xác định khi và chỉ khi a '  0 1 C   (m  2 1)  2
m  0  2m  1  0  m a   0 2
Câu 50. Chọn D.
Gọi K là trung điểm của AB. S I là trung điểm của AK
Ta có IP / /BQ
IP / /BQ BQ / /(SPI)  ( d BQ,SP)  ( d BQ,(SPI)) K B A I F  (
d B,(SPI))  3 ( d A,(SPI)) H M  6 ( d H,(SPI)) E 2a P
Kẻ HE vuông góc với PI. Ta có Q C PH.AI a D
PAI PEH EH   PI 2 5
Gọi h là khoảng cách từ H đến mp(SPI), ta có :
1  1  1  h a 3  d BQ SP  3a 3 ( , ) 2 2 2 h SH HE 8 4 Trang 11
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017 TỈNH ĐỒNG NAI
Môn: TOÁN – Khối 12 Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97 NỘI DUNG ĐỀ SỐ 02
Câu 1. Đồ thị hàm số ở hình bên dưới là của đồ thị hàm số nào dưới đây. A. y  3
x  3x  2 . B. y  3 x  3x . x  1 C. y  . x  1 D.  4 y x .
Câu 2. Hàm số y  4 x  2
2x nghịch biến trên khoảng nào sau đây?
A. 1;   . B. 0;  1 . C. 1; 0 . D. 1;  1 . x Câu 3. 1
Gọi I là giao điểm của hai đường tiệm cận của đồ thị hàm số y  . Tìm tọa độ điểm 2  x I . A. I 2;  1 .
B. I 2;   1 . C. 1; 2 .
D. I 1; 2.
Câu 4. Tìm giá trị cực đại của hàm số y   3 x  2 3x  1 . A. y  3 . B. y  1 . C. y  2 . D. y  0 . CĐ CĐ CĐ CĐ x Câu 5. 2
Đường cong y
có bao nhiêu đường tiệm cận? 2 x  9 A. 1 . B. 2 . C. 3 . D. 4 . Câu 6. 2
Tìm giá trị lớn nhất của hàm số y  2
x  , x  0. x 526 142 127 38 A. Max y  . B. Max y  . C. Max y  . D. Max y  . 15 15 15 3
Câu 7. Tìm các giá trị của m để đồ thị hàm số y  4 x  2
2mx  1 có ba điểm cực trị tạo thành một
tam giác có một đường trung bình là y  1 . 2 A. m  1 . B. m  1.
C. m   1 . D. m  1. 2 2
Câu 8. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  3 x   2
k k  1 x trên đoạn 1; 2 
 . Khi k thay đổi trên R , giá trị nhỏ nhất của M m bằng 33 37 45 A. . B. . C. 12 . D. . 4 4 4
Câu 9. Cho hàm số y  3 x  2 2
3x  5 có hai điểm cực trị A, B . Điểm M a;b thuộc đường thẳng
d : x  3y  7 sao cho T M . O MA M . A MB M .
B MO đạt giá trị nhỏ nhất ( với O là gốc
tọa độ). Khi đó, a b nhận giá trị thuộc A. 3;  2 . B. 2;  1 . C. 1; 5 . D. 5;  3 . Trang 12
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
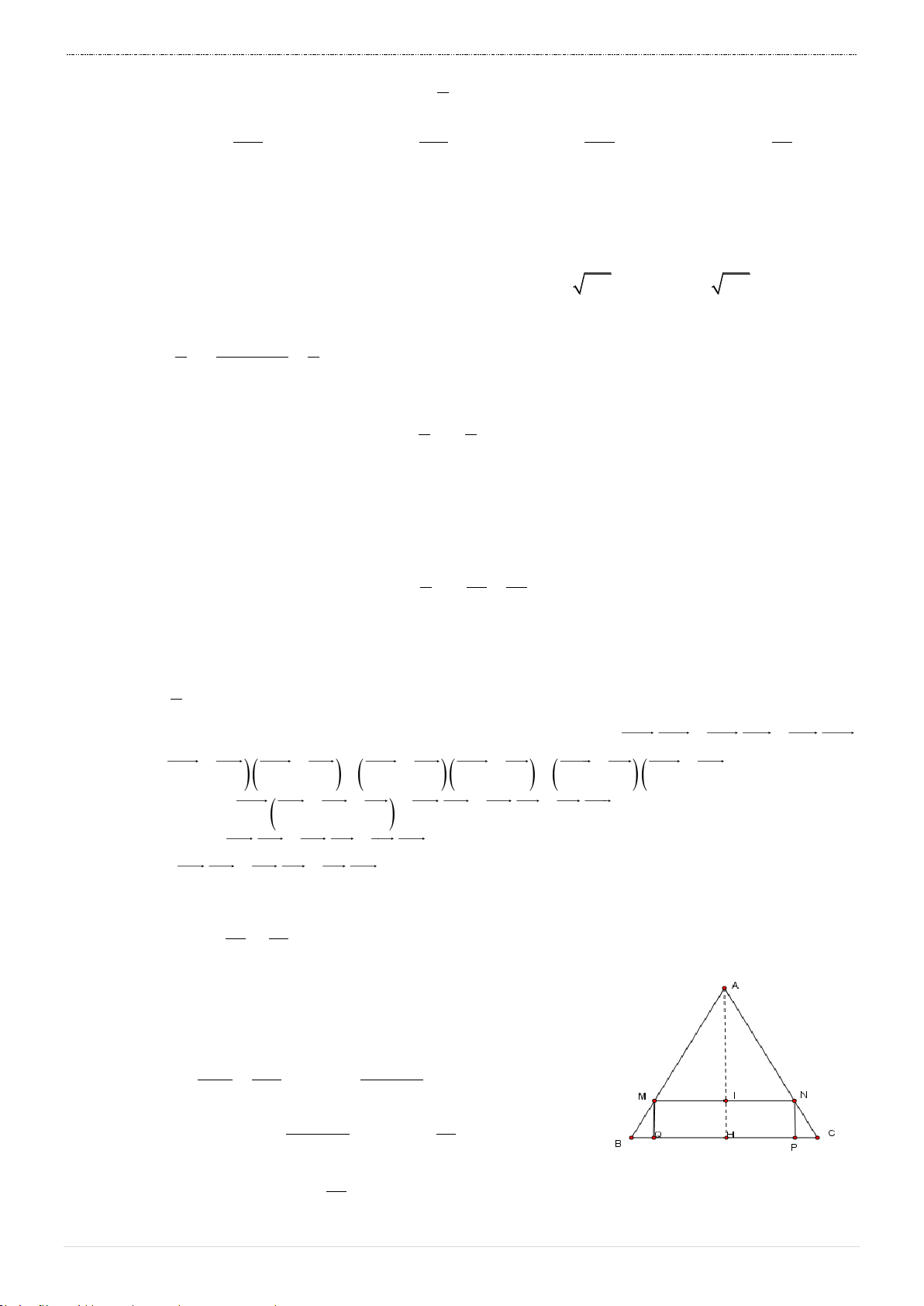
Câu 10. Cho tam giác ABC cân tại A , AB AC  5a, BC  6a. Hình
chữ nhật MNPQ có M, N lần lượt thuộc cạnh AB, AC và
P, Q thuộc cạnh BC . Quay hình chữ nhật MNPQ (và miền
trong nó) quanh trục đối xứng của tam giác ABC được một
khối tròn xoay. Tính độ dài đoạn MN để thể tích khối tròn xoay lớn nhất.
A. MN  2a.
B. MN  4a.
C. MN a .
D. MN  5a . x Câu 11. 2
Cho hàm số y
. Tìm m để đồ thị hàm số có một tiệm cận đứng và một tiệm 2
x  4x m cận ngang?
A. m4; 1  2 .
B. m4; 1  2 . C. m  4 . D. m  12 . Câu 12. 3
Đồ thị hàm số y  x  1 x  1 có bao nhiêu điểm cực trị? A. 2 . B. 4 . C. 3 . D. 1 .
Câu 13. Giải phương trình log 2x   1  3 . 2 A. x  9 . B. x  5 . C. x  3 . D. x  8 . 2 2
Câu 14. Tính đạo hàm hàm số  2x y . A ,  2x y . B. ,   1 2x y x . C. ,  2x y ln 2 . D. ,  2x y x .
Câu 15. Giải bất phương trình x1 3  9 . A. x  1. B. x  1. C. x  2 . D. x  0 . 1
Câu 16. Tìm tập xác định D của hàm số y x  3 (2 1) .  1  1  1  A. D  ;     . B. D  .
C. D R\  . D. D  ;     . 2  2   2 
Câu 17. Cho a b  1. Khẳng định nào sau đây là khẳng định sai? a b
A. log b  log a . B. log  1.
C. b a a b . D. ab b  a a b . a b a 2
Câu 18. Tính đạo hàm của hàm số y xln2x. A. y  2 . B.
y  1 ln2x . C.
y  ln2x  2 . D.    2 y x . x
Câu 19. Tính M  log 1250 theo a biết a  log 5 . 4 2 1 1 A. M   a. B. M   2a .
C. M  21 2a.
D. M  21 4a. 2 2
Câu 20. Gọi S là tập tất cả các số thực dương thỏa mãn x x  sinx x
. Xác định số phần tử nS .
A. nS  0 .
B. nS  2 .
C. nS  1.
D. nS  3 .
Câu 21. Viết công thức tính diện tích S của hình H giới hạn bởi đồ thị hàm số y f (x), trục
hoành và hai đường thẳng x a, x b a b . b b b b
A. S   f xdx .
B. S    f xdx .
C. S    2
f xdx . D. S   2
f xdx . a a a a
Câu 22. F x là nguyên hàm của hàm số f x  2x 1 . Khi đó, Fx là hàm số 2 1
A. f xx  2x   1 2x  1   d C . B. f ( )
x x  2x   1 2x  1   d C . 3 3 Trang 13
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 1 1
C. f xx   2x  1   d C .
D. f xx  2x  1   d C . 3 2
Câu 23. Một ô tô đang chạy đều với vận tốc am / s thì người ta đạp phanh; từ thời điểm đó, ô
tô chuyển động chậm dần đều với vận tốc vt  5t a m / s , trong đó t là thời gian
tính bằng giây, kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc dừng hẳn ô tô di
chuyển được 40 mét thì vận tốc ban đầu a bằng bao nhiêu? A. a  40 . B. a  80 . C. a  20 . D. a  25 . 1
Câu 24. Tính tích phân I  ln d x x . 0 A. I  0 . B. I  1 . C. I  2 . D. I  1 . 2
Câu 25. Tính tích phân I  2 3 x x   d 1 x 0 A. I  16 .
B. I   16 . C. I  52 . D. I  2 . 9 9 9 9 Câu 26. 2
Diện tích S hình phẳng giới hạn bởi đồ thị hàm số y   , trục hoành, đường x  2 1
thẳng x  0 và đường thẳng x  4 là
A. S   8 . B. S  8 . C. S  1. D. S  1 . 5 5 5
Câu 27. Tìm phần thực, phần ảo của số phức z  32i .
A. Phần thực bằng 3 , phần ảo bằng 3i .
B. Phần thực băng 3 , phần ảo bằng 2i .
C. Phần thực bằng 3 , phần ảo bằng 2 .
D. Phần thực bằng 3 , phần ảo bằng 2 .
Câu 28. Cho số phức z , z với z  1 i, z  3 2i . Khi đó M z z bằng 1 2 1 2 1 2 A. M  5. B. M  5 . C. M  13 . D. M  17 .
Câu 29. Cho số phức z thỏa mãn 2 iz  1510i . Hỏi điểm biểu diễn
cho số phức z là điểm nào trong các điểm M, N, P, Q cho hình dưới đây.
A. Điểm M . B. Điểm N .
C. Điểm Q . D. Điểm P .
Câu 30. Cho số phức z  2  4i . Tìm số phức w iz z .
A. w  2  2i .
B. w  2  2i .
C. w  2  2i .
D. w  2  2i .
Câu 31. Kí hiệu z , z , z và z là nghiệm phức của phương trình 4 z  2
z  6  0 . Tính tổng 1 2 3 4
S z z z z . 1 2 3 4 A. S  1.
B. S  2  3  2  . C. S  2 2 . D. S  2 3 .
Câu 32. Cho số phức z . Biết tập hợp các điểm biểu diễn số phức w  3 4iz i là một đường
tròn có bán kính bằng 20 . Tính z . A. z  2 . B. z  8 . C. z  10 . D. z  4 . Trang 14
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 33. Tính thể tích V của khối lập phương ABC .
D A B C D , biết diện tích mặt chéo ACC A 1 1 1 1 1 1 bằng 2 4 2a . A. V  3 2a . B. V  3 4a . C. V  3 8a . D. V  3 16a .
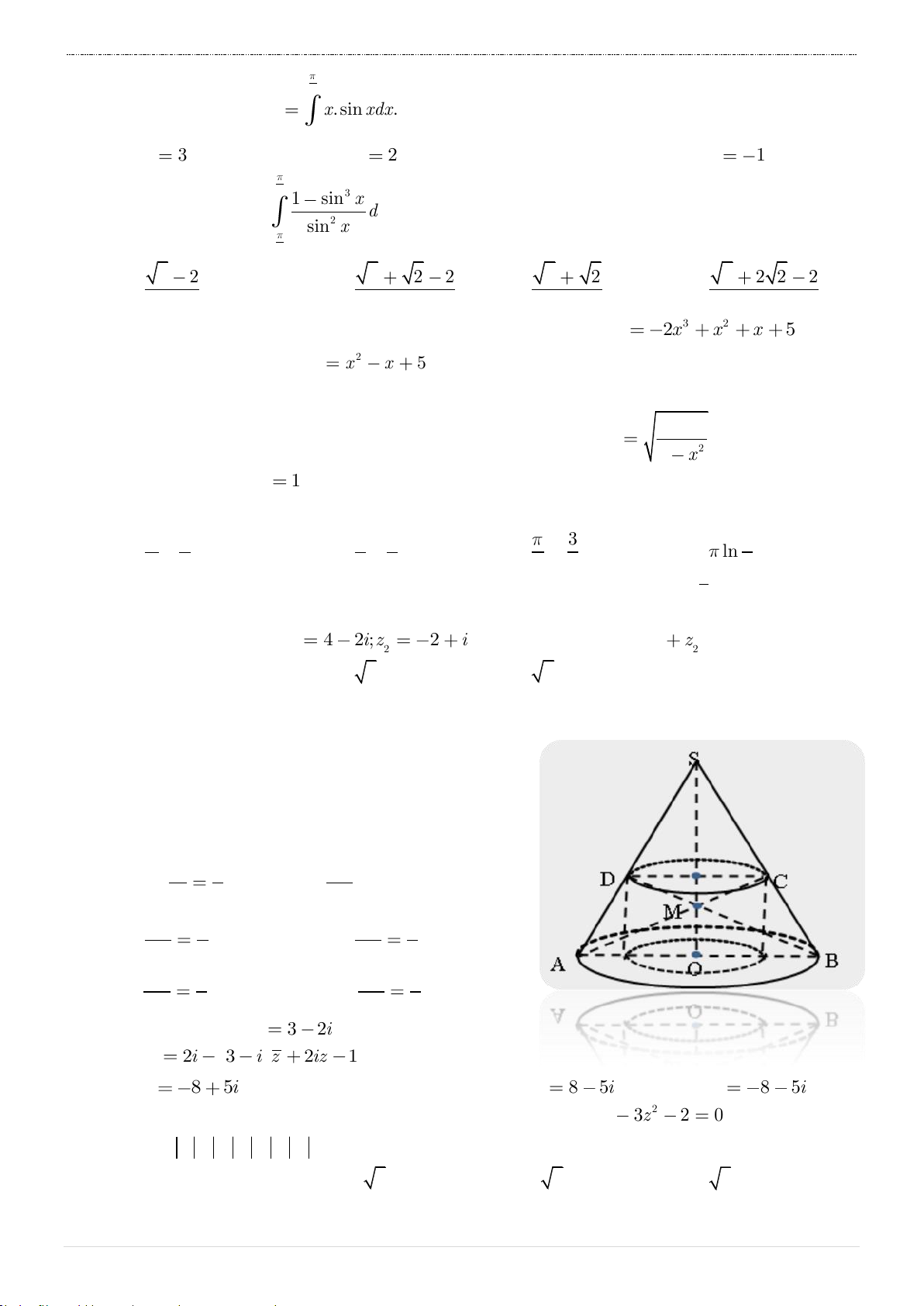
Câu 34. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SAD   ABCD , a
SA SD . Tính thể tích V của khối chóp .
S ABCDbiết SC  21 . 2 3 2a 3 a 7 3 a 7 A. V  . B. V  . C. V  3 2a . D. V  . 3 6 2
Câu 35. Cho hình lăng trụ đứng AB . C A B
C có đáy ABC là tam giác cân đỉnh C , đường thẳng
BC tạo với mặt phẳng  AB B A  một góc 
60 và AB A
A a . Gọi M, N, P lần lượt là trung điểm B
B , CC, BC . Khoảng cách giữa hai đường thẳng AM và NP bằng a 3 a 15 a 5 a 5 A. . B. . C. . D. . 5 5 5 15
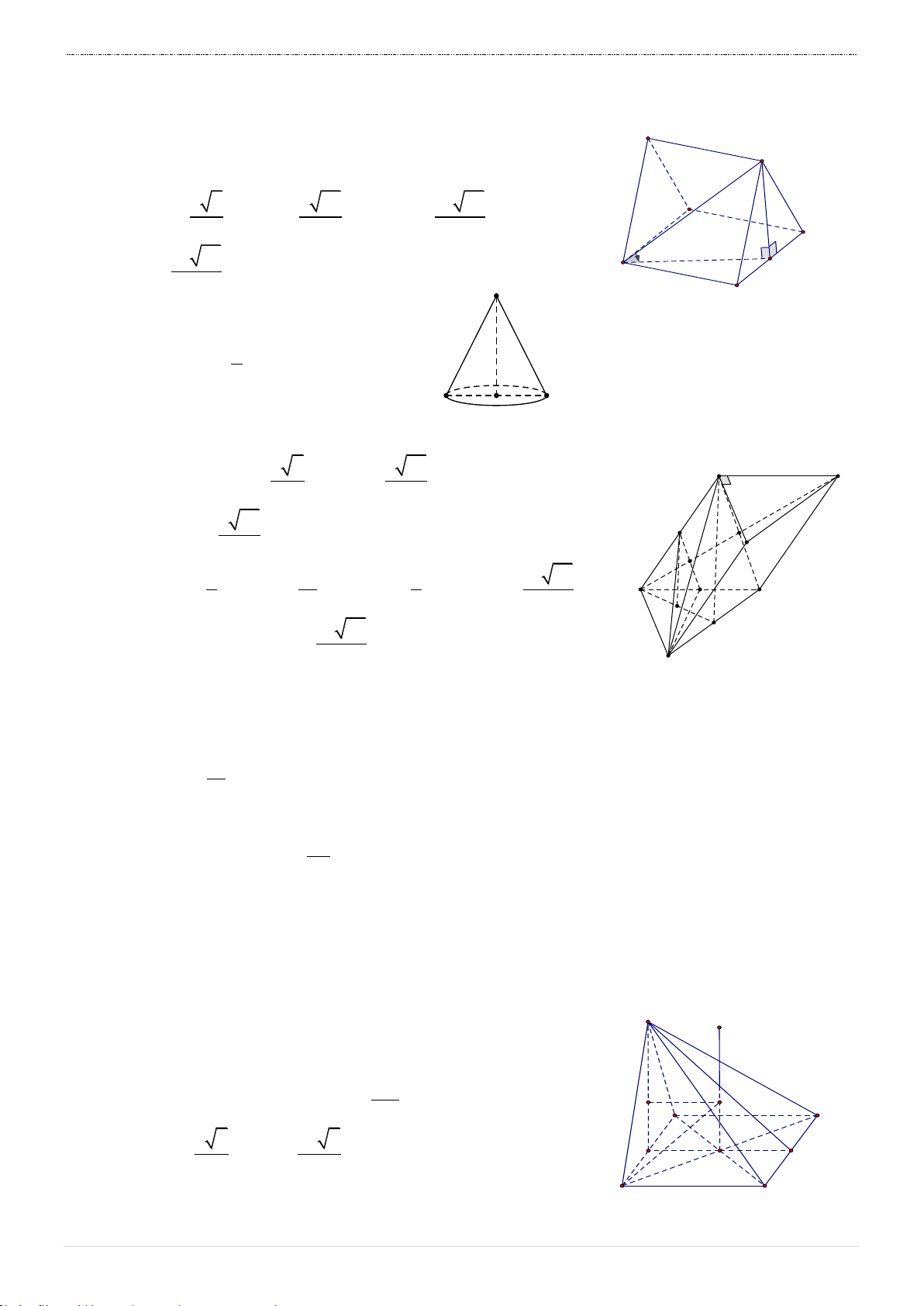
Câu 36. Cho tam giác ABC vuông tại A có AB  3, AC  4 . Quay tam giác ABC quanh trục
AC , ta được một hình nón tròn xoay. Tính thể tích V khối nón tròn xoay. A. V   12 . B. V   16 . C. V   .
D. V  3  . 4
Câu 37. Cho hình lăng trụ AB . C A B
C có đáy là tam giác vuông cân tại A , cạnh
BC a 2 a  0 , cạnh bên A
A  2a và 
A cách đều các đỉnh A, B, C . Gọi M, N lần
lượt là trung điểm của AA và AC . Thể tích khối chóp  C .MNB là 3 a 14 3 a 14 3 a 14 3 7a A. V  . B. V  . C. V  . D. V  . 48 4 16 8
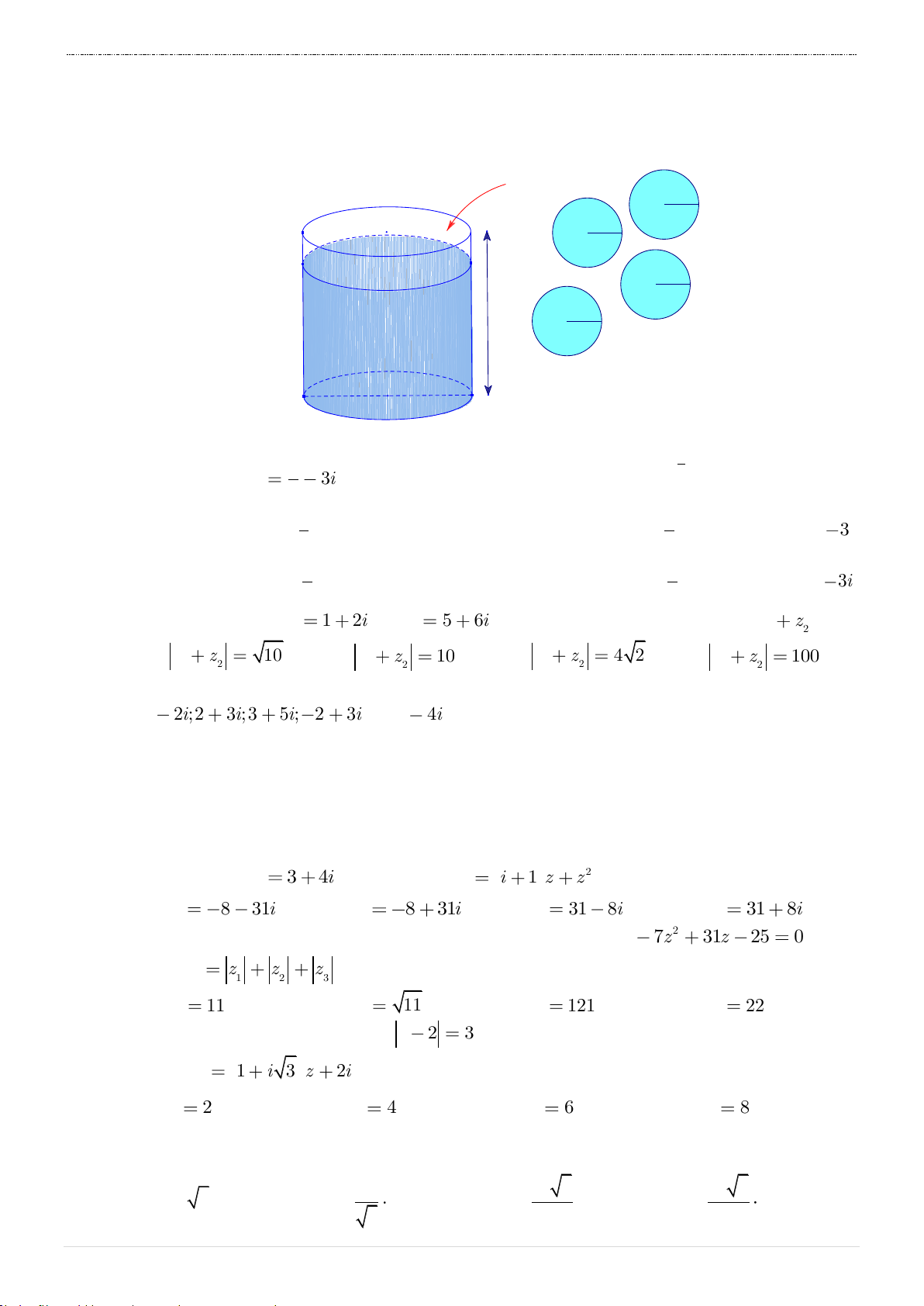
Câu 38. Có ba quả bóng với kích thước bằng nhau. Một miếng tôn hình chữ nhật được cuốn
thành hình trụ sao cho chiều cao của hình trụ gấp 3 lần đường kính quả bóng, đáy của
hình trụ bằng hình tròn lớn trên quả quả bóng. Gọi S là tổng diện tích của ba quả 1 S
bóng, S là diện tích xung quanh của hình trụ. Tính tỉ số 1 . 2 S2 S S S S 1 A. 1  2 . B. 1  1. C. 1  5. D. 1  . S S S S 2 2 2 2 2
Câu 39. Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a ( a là độ dài cho sẵn). Người
ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài
đường sinh bằng 2a thì bán kính đáy r bằng. a a A  a r r r   . B. r  . C. . D.  2 a . 2  2 Trang 15
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 40. Cho hình nón có đường sinh l  2a và hợp với đáy một góc  60 . Diện tích xung quanh
S của khối nón bằng. xq 3 A. S  2 a . B. S  2 a . C. S   2 2 a . D. S  2 2a . xq xq 2 xq xq
Câu 41. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a 2 , mặt bên SAD là tam giác
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích khối chóp . S ABCD 3 4a bằng
. Tính thể tích V của khối cầu ngoại tiếp hình chóp . S ABCD. 3  3 113 a  3 113 a 113  3 113 a 113  3 113 a 113 A. V  . B. V  . C. V  . D. V  . 64 48 84 384 x y Câu 42. 1 z
Trong không gian Oxyz cho d : 
 . Khi đó vectơ chỉ phương của đường thẳng 1 2 1 d là
A. u  0; 1; 0 .
B. u  1; 2;  1 .
C. u  1; 0;  1 .
D. u  2; 0; 1 . Câu 43. 2 2
Trong không gian Oxyz cho mặt cầu S có phương trình x    2 1
y  z  2  9 . Xác
định tọa độ tâm I và bán kính R của mặt cầu S .
A. I 1; 0;  2 , R  9 . B. I 1; 0; 2, R  3 . C. I 1; 0;  2 , R  3 . D. I 1; 0; 2, R  3 .
Câu 44. Trong không gian Oxyz cho P : 3x  4y  2z  5  0 , điểm A2;1; 3 . Tính khoảng
cách d từ A đến P . A. d  13 . B. d  13 . C. d  13 . D. d  13 . 9 29 29 3 Câu 45. Trong không gian Oxyz cho hai mặt phẳng
P: x3y2z1 0,
Q:2m 1xm12my2m4z14  0. Tìm m để P và Q vuông góc nhau.  3   3  3
A. m  1;   .
B. m  1;   . C. m  2 .
D. m    .  2   2  2 
Câu 46. Trong không gian tọa độ Oxyz , cho điểm M1; 1; 2 và mặt phẳng   : x y  2z  3 .
Viết phương trình mặt cầu S có tâm M tiếp xúc với mặt phẳng   . 16 35 A.S 2 : x  2 y  2
z  2x  2y  4z
 0. B.S 2 : x  2 y  2
z  2x  2y  4z   0 . 3 6 35 14 C.S 2 : x  2 y  2
z  2x  2y  4z
 0 . D.S 2 : x  2 y  2
z  2x  2y  4z   0. 6 3 x  3 y 1 z Câu 47. 5
Trong không gian tọa độ Oxyz , cho đường thẳng d  :   và mặt phẳng 2 1 2
P: xyz1 0 . Có tất cả bao nhiêu điểm thuộc đường thẳng d sao cho khoảng
cách từ điểm đó đến mặt phẳng P bằng 3 . A. Vô số điểm. B. Một. C. Hai. D. Ba. Câu 48. y z
Trong không gian tọa độ Oxyz , cho đường thẳng     x   1 : và mặt phẳng 2 3
P:4x2yz1 0 . Khi đó khẳng định nào sau đây là đúng? Trang 16
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
A.   P .
B.   P .
C. Góc tạo bởi  và P lớn hơn  30 .
D.  // P .
Câu 49. Trong không gian tọa độ Oxyz , cho đường thẳng d qua điểm M3;  2;  1 và có VTCP 1
u1;  1; 2 , gọi d là giao tuyến của hai mặt phẳng P : x y  2z  0 và 2
Q: x2yz3  0. Viết phương trình mặt phẳng  chứa d và song song với d . 1 2
A.   : 5x 13y  4z  7  0 .
B.   : 5x 13y  4z  45  0 .
C.   : 5x 13y  4z 7  0.
D.   : 5x 13y  4z  45  0 .
Câu 50. Trong không gian tọa độ Oxyz , cho điểm M1; 3; 4, đường thẳng x  2 y  5 z d   2 :
và mặt phẳng P : 2x z  2  0 . Viết phương trình đường thẳng 3 5 1
 qua M vuông góc với d và song song với P . x  1 y  3 z  4 x  1 y  3 z  4 A.  :   . B.  :   . 1 1 2 1 1 2 x  1 y  3 z  4 x  1 y  3 z  4 C.  :   . D.  :   . 1 1 2 1 1 2 -------oOo-------
ĐÁP ÁN ĐỀ SỐ 02 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 A B B A C
D D D B B D A C B D C B B C A B C B C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B D D C A B D C A B A C B C C D B C C A B C C A D
HƯỚNG DẪN GIẢI ĐỀ SỐ 02 Câu 1. Chọn A.
Đồ thị cắt trục tung tại điểm A0; 2 . Câu 2. Chọn B.x  0
Hàm số có ba điểm cực trị: 
và hàm số có hệ số a  0 nên hàm số nghịch biến trên x    1 0; 1 . Câu 3. Chọn B.
Đồ thị hàm số có tiệm cận đứng: x  2.
Đồ thị hàm số có tiệm cận ngang: y  1.  I 2;  1 . Câu 4. Chọn B.x  0 Ta có: y   2
3x  6x  0   x   2
Hàm số đạt cực đại tại A2; 3 nên y  3 . CD Câu 5. Chọn C.
Đồ thị hàm số có hai tiệm cận đứng: x  3 .
Đồ thị hàm số có một tiệm cận ngang: y  0 . Trang 17
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Câu 6. 2
Tìm giá trị lớn nhất của hàm số y  2
x  , x  0. x 526 142 127 38 A. ax M y  . B. ax M y  . C. ax M y  . D. ax M y  . 15 15 15 3
Không tồn tại GTLN. SAI ĐỀ. Câu 7. Chọn D. Ta có: y  3
x mx x  2 4 4 4 x m .
Hàm số có 3 cực trị khi m  0 .
Khi đó 3 điểm cực trị của đồ thị hàm số là: A
B m  2
m C  m  2 0; 1 , ; 1 ; ; 1 m .
Ba điểm cực trị tạo thành một tam giác có một đường trung bình là 1 1  1  2   m y  1  m  1 . 2 2 2 Câu 8. Chọn D.  1 2 3 Ta có: y  2 3x  2
k k  1  2 3x k      0 .  2  4
Nên hàm số đồng biến trên R .
M y2  8  2 2 k k  1
m y 1  1  2 k k  1 M m 9 3 2 k k 1  1 2        3 k   45  45   .  2  4 4 Câu 9. Chọn D.
Đồ thị hàm số có hai điểm cực trị A0; 5, B1; 4 . Gọi G là trọng tâm tam giác ABO   1  G  ; 3 .  3  Ta có:T M . O MA M . A MB M . B MO
 MG GOMG GAMG GAMG GBMG GBMG GO  2
3MG  2MG GO GA GB G . O GA G . A GB G . B GO  2 3MG G . O GA G .
A GB GB.GO Mà G . O GA G . A GB G .
B GO là hằng số, do đó T min khi MG min khi M là hình chiếu
vuông góc của G trên d .  13 19  Vậy M  ;    .  10 10  Câu 10. Chọn B. Ta có: BH  3 ; a AH  4a .
Đặt HQ x BQ  3a x 0  x  3a . MQ BQ 43  x Ta có:   MQ  . AH BH 3 4 3 x 2     3 x
Khi đó: V   .x .   4 x x a T  2   0   3  3  3  3 x
Xét hàm số f x  2 x
0  x  3a. 3 Trang 18
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Hàm số f x đạt giá trị lớn nhất tại x  2a MN  4a . Câu 11. Chọn B. x  2
Khi m  4  y
Đồ thị hàm số có 3 tiệm cận. 2 x  4x  4 x  2 x  2
Khi m  12  y  
Đồ thị hàm số có 1 tiệm cận. 2 x  4x  12 x22 8 Câu 12. Chọn D.x 1  3 f x x 1 x 1 ; 3              
Ta có: y  x  1 x  1  x    1
gx  x13 x1; x  1; 1 3 x 1
Xét hàm số: f x x
1 x        1 ;  Không có cực trị. x   1 3
Xét hàm số: g x   x  1 x  1 ; x 1; 1 có một cực trị. 3
Vậy hàm số y  x  1 x  1 có một cực trị. Câu 13. Chọn A.  x  1 9 Ta có: log 2x 1 3 x . 2       2    2x  1  2  8 Câu 14. Chọn C. Ta có: ,  2x y ln 2 . Câu 15. Chọn B. Ta có: x1 x   1  2 3 9 3 3  x  1. Câu 16. Chọn D. 1
Tập xác định của hàm số: y   x  3 2
1 là x    x  1 2 1 0 . 2 Câu 17. Chọn C. 1 2
Ta có: log b  log a   log a a
do a b  1 A. Đúng. a b b logb  1 log a b a b a b log  1 
a a b  0 B. Đúng. a 2 2 ab baa b
 a b  balog b a b b D. Đúng. a
  1loga   0 Câu 18. Chọn B. 2
Ta có: y  ln 2x 
.x  1 ln 2x. 2x Câu 19. Chọn B. 1 1 1 Ta có: M  log 1250  log  4 5 .2 4 log 5 1 2a . 4     2    2 2 2 2 Câu 20. Chọn C. Xét các trường hợp:
x  0 : Không thỏa. x  1: Thỏa.
0  x  1, ta có x x  sinx x
x  sinx ( vô nghiệm). Vậy số phần tử ( n S)  1 . Câu 21. Chọn A. Trang 19
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Câu 22. Chọn B. 1 1 1 1 Ta có:
f xdx  2x  d 1 2x   1  2x 2 1 d 2x   1  2x   1 2x  1     C . 2 2 3 Câu 23. Chọn C. a Khi ôtô dừng hẳn (
v t)  0  5t a  0  t  . 5 a 5 5 a
Theo đề bài: 40  5t a      dt  40   2 t  5 ata    20 .  2  0 0 Câu 24. Chọn B. Bấm máy tính. Câu 25. Chọn C. Bấm máy tính. Câu 26. Chọn B. 4 2 8 Ta có: S  dx    Bấm máy tính. x  2 5 0 1 Câu 27. Chọn D.
Số phức z  3  2i có phần thực bằng 3 , phần ảo bằng 2 . Câu 28. Chọn D.
Ta có: z  1  i . 1
z  3  2i z  3  2i . 2 2
z z  4  i M z z  17 . 1 2 1 2 Câu 29. Chọn C. 15 10i Ta có: 2 i 
z  15 10i z
 4  7i z  4 7i . 2  i Câu 30. Chọn A.
Ta có: w iz z i 2  4i  2  4i  2  2i . Câu 31. Chọn B. z 3 Ta có: 4 2 z z 6 0
 2z 3 2z 2           0   . z    2i
S z z z z  2 3  2 . 1 2 3 4  Câu 32. Chọn D.
x y  1 i 1 1
Đặt w  3  4i  
z i x yi z  
3x4y4 3y4x3 3  4i 25 25
z 2  xy 2  yx 2  x y 2 2 .25 3 4 4 3 4 3 1   z .52   z 2 .5  400  z S 4 . Câu 33. Chọn C.
Gọi AB x AC xS  2 x  2 2 2 4a 2  x  2a . ACC A 1 1 A D V  2a3 3 H  8a . Câu 34. Chọn A. B C 3 a 5 1 2a Ta có: HC
SH  2a V  2 .a .2a  . 2 3 3 Trang 20
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Câu 35. C Chọn B. C' Ta có:
KC   A A B B  , 2 A
BK a 5  KC  a 15  Sa 15   A B C 2 2 4 A' 3 Va 15 . K B LT 4 C Câu 36. B' Chọn A. 1 4 Ta có: V   2 AB .AC  1  2 . 3 Câu 37. 3 Chọn C. D B
Ta có H là tâm đường tròn ngoại A tiếp A'C'
ABC AH a 2   A H a 14 2 2 aMK  14 . M E 4 F B' 2 3 1 a 1 a 14 SAN.AB   V  .MK.S   . A ABN ABMN  2 4 3 ABN 48 N C K 3 a 14 HV  3V  . C.BMN ABMN 16 Câu 38. B Chọn B. Ta có: S  3.4  2 . R  1  2 2 R . 1 S   2 . . R h  1  2 2 .R . 2 S Khi đó: 1  1. S2
Câu 39. Chọn C. a Ta có: 
2 r a r   . 2 Câu 40. Chọn C.
Đường sinh l  2a hợp với đáy một góc 
60  R a .
Ta có: S   Rl   2 2 a . xq Câu 41. Chọn D.
Gọi H, K lần lượt là trung điểm của A , B CD .
O là tâm hình vuông. S
J là tâm đường tròn ngoại tiếp tam giác SAD .
I là tâm mặt cầu ngoại tiếp hình chóp . S ABCD. 3 4a Ta có: S  2 2a , V   SH  2a . I ABCD S.ABCD 3 J A B a 2 3a 2 AH   SA  . H K 2 2 o
SA AD ASD  
90  J thuộc đoạn SH. D C Trang 21
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai SH Ta có: SAH   2 2 sin . AH 3 SD a Mà
SJ SJ  9 2 (định lí sin). 8 sin SAH a BD a
OI JH SH SJ  7  OD
a R ID  113 . 8 2 8  3 113 a 113 Vậy V  . KC 384 Câu 42. Chọn B. Câu 43. Chọn C. Câu 44. Chọn C. 6  4  6  5 13 Ta có: d   . A ,P   9  16  4 29 Câu 45. Chọn A.
Mặt phẳng P : x  3y  2z  1  0 có một VTPT là n 1;  3; 2 . 1  Mặt phẳng
Q:2m 1xm12my2m4z14  0 có một VTPT là
n 2 m 1; m 2m ; 2m 4 . 2    2  
P  Q  n .n  0  2m13m 2 2m 4m 8 0 1 2    m  1 2 
 6m  3m  9  0  m   3  2 Câu 46. Chọn B. 1  1  4  3 1 Ta có: d      R . M,     6 6
Phương trình mặt cầu S có tâm M tiếp xúc với mặt phẳng   là
S 2x  2y  2z xyz 35 : 2 2 4  0 . 6 Câu 47. Chọn C.
Đường thẳng d cắt mặt phẳng P nên có hai điểm thuộc đường thẳng d sao cho khoảng
cách từ điểm đó đến mặt phẳng P bằng 3 . Câu 48. Chọn C. y z Đường thẳng     x   1 :
có một VTCP là u1; 2; 3 . 2 3
Mặt phẳng P : 4x  2y z 1  0 có một VTPT là n4; 2; 1 . 4 4 3 11 6 1
Ta có: sin u,n       sin 3 
0 nên góc tạo bởi  và P lớn hơn  30 . 14. 21 42 2 Câu 49. Chọn A.
Mặt phẳng P : x y  2z  0 vó một VTPT n 1;  1; 2 . 1 
Mặt phẳng Q : x  2y z  3  0 vó một VTPT n 1; 1; 1 . 2  
Đường thẳng d có một VTCP a    n ,n  5; 1; 3 . 1 2   2   Trang 22
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Mặt phẳng   chứa d và song song với d có một VTPT n   
u, a  5;  13;  4 . 1 2  
Mặt phẳng   đi qua điểm M3;  2; 
1 và có VTPT n  5;  13;  4 có phương trình
:5x13y4z7  0 . Câu 50. Chọn D. x  2 y  5 z  2 Đường thẳng d :  
có một VTCP u  3;  5;  1 3 5 1
Mặt phẳng P : 2x z  2  0 vó một VTPT n2; 0; 1
Đường thẳng  có một VTCP a   
u,n  51; 1;  2   . x  1 y  3 z  4
Đường thẳng  có phương trình  :   . 1 1 2
…………………………Hết…………………… Trang 23
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017 TỈNH ĐỒNG NAI
Môn: TOÁN – Khối 12 Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97 NỘI DUNG ĐỀ SỐ 04
Câu 1. Đường cong trong hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A, B,
C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 4 2
y  x  2x . B. 4 2
y  x  2x . C. 4 2
y x  2x . D. 4 2    y x 2x 1. 2   Câu 2. x 3x 2
Đồ thị hàm số y  2 1
có bao nhiêu đường tiệm cận? x A. 1. B. 2 . C. 3 . D. 4 . Câu 3. 1 5 Hỏi hàm số 3 2 y x
x  6x nghịch biến trên khoảng nào? 3 2 A. 1;6 . B.  6  ;  1 . C. 2;3 . D.  3  ; 2  .
Câu 4. Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định sai?
A. Đồ thị hàm số có 3 điểm cực trị.
B. Hàm số có giá trị nhỏ nhất bằng 16  .
C. Hàm số đồng biến trên mỗi khoảng  2
 ;0 và 2; .
D. Đồ thị của hàm số có hai tâm đối xứng.
Câu 5. Tìm giá trị thực của tham số m để hàm số f x 3 2
x mx   2 3 3 m  
1 x  2016 đạt cực tiểu tại x  2 ? A. m  3 . B. m 1. C. m  3.  D. m  1  .  Câu 6. m x
Tìm các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số f x 2 1  x 1 trên đoạn  2  ;  1 bằng 4 ?  26 A. m .  B. m  . C. m  3.  D. m  9.  2 Trang 24
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai  Câu 7. 7x 17
Biết đường thẳng y x 1 cắt đồ thị C của hàm số y  2x  tại 2 điểm phân biệt, gọi 5
A là giao điểm thuộc nhánh bên phải đường tiệm cận đứng của C , kí hiệu  x ; y là A A
tọa độ của điểm A . Tìm x y ? A A
A. x y  5 .
B. x y  13 .
C. x y  3 .
D. x y  7 . A A A A A A A A
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số 4 2 2 4
y x  2m x m 1
có 3 điểm cực trị, đồng thời 3 điểm cực trị tạo với gốc tọa độ O một tứ giác nội tiếp trong một đường tròn? A. m  1  . B. m  0. C. m  2  .
D. m   2 . 2   Câu 9. ax x 3
Đồ thị của hàm số y   và chỉ có một 2
4x bx  có một đường tiệm cận ngang là y c 1 a
đường tiệm cận đứng. Tính
biết rằng a là số thực dương và ab  4 ? bc a 1 a a a A.  . B.  2 . C.  1 . D.  4 . bc 4 bc bc bc
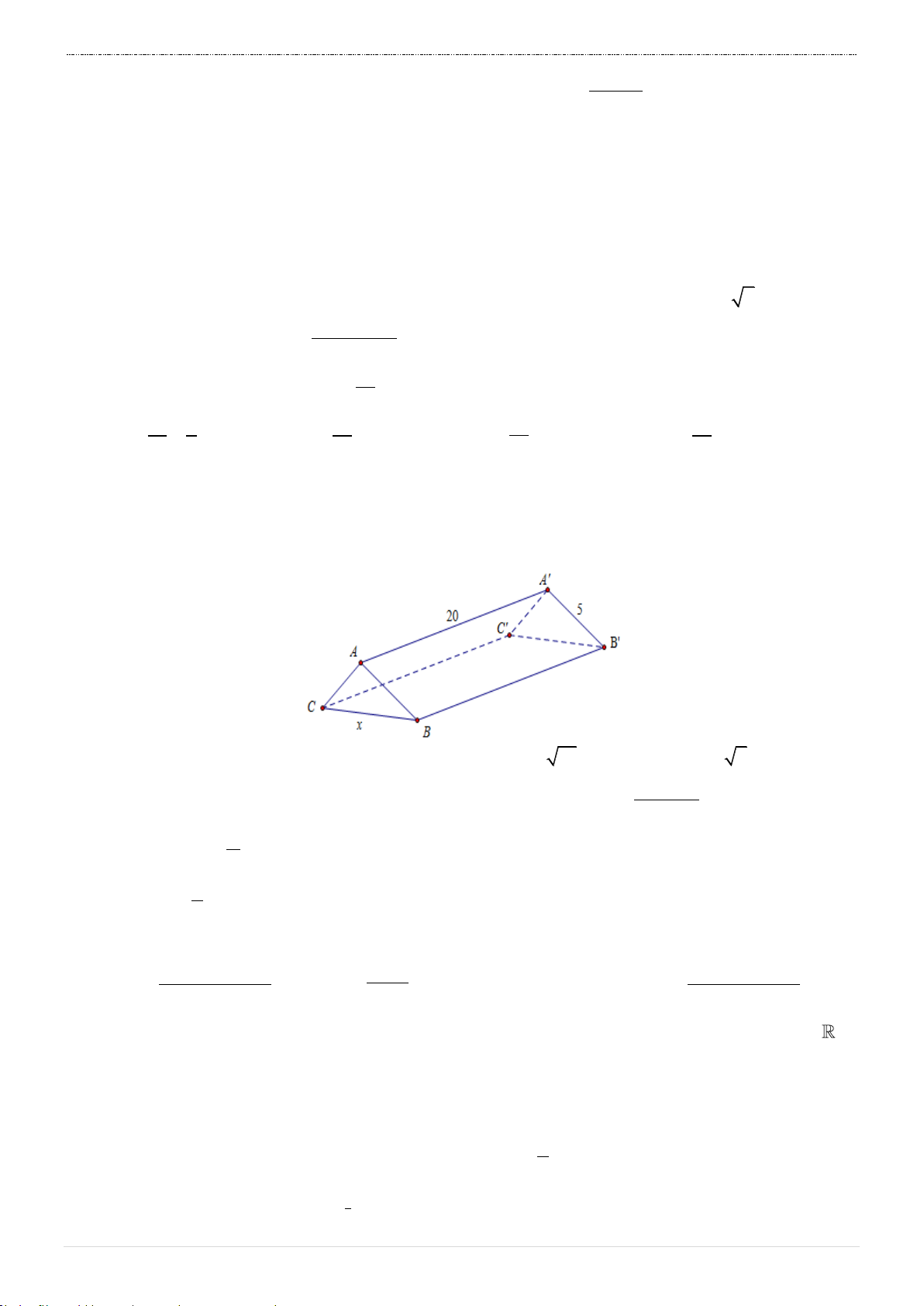
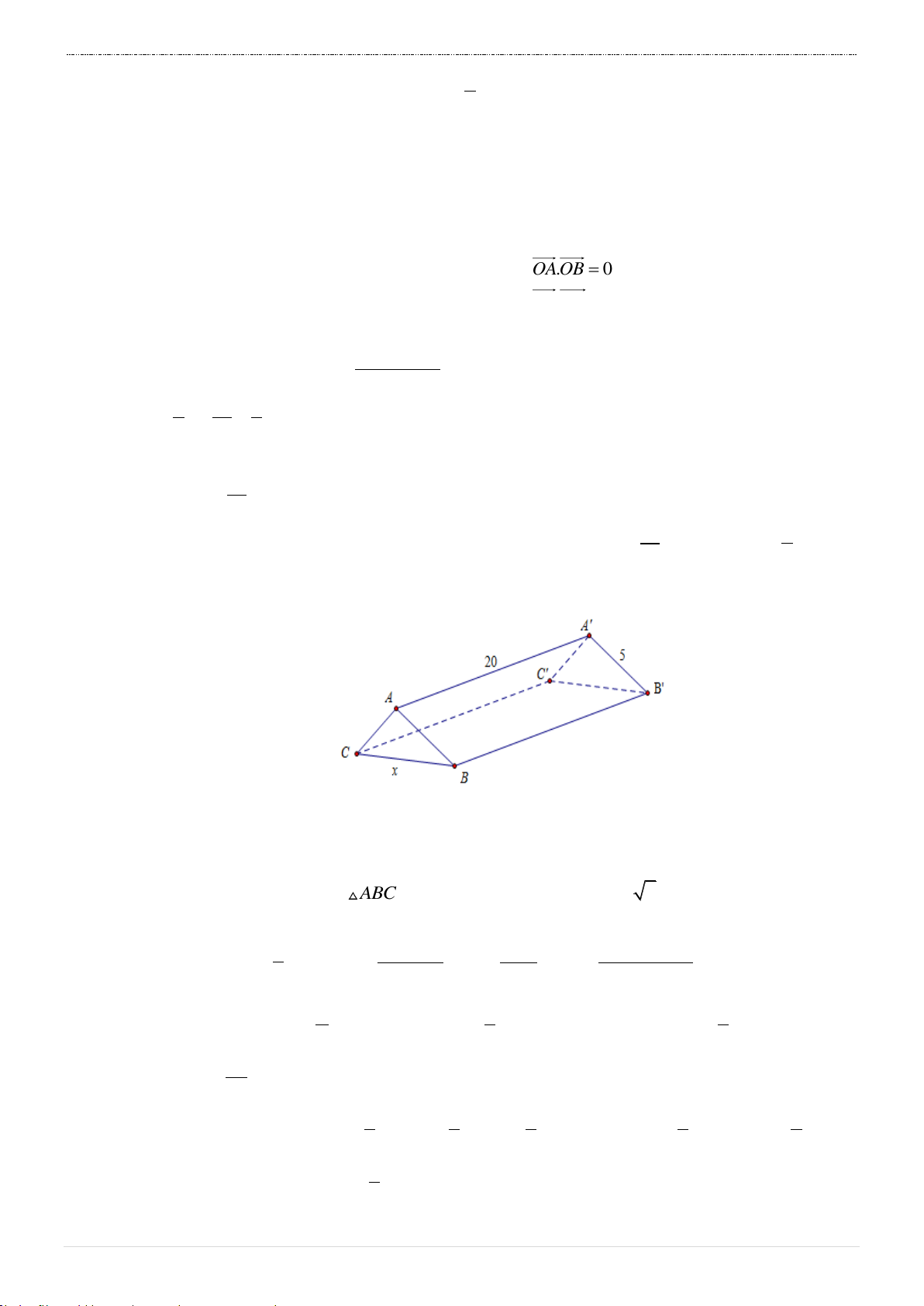
Câu 10. Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng như hình vẽ. Hai mặt bên ABB A   và ACC A
  là hai tấm kính hình chữ nhật dài 20m và rộng 5m . Gọi
x mét  là độ dài của cạnh BC . Tìm x để khoảng không gian của hành lang (kể cả hai
tấm kính) là lớn nhất?
A. x  5m.
B. x  25m.
C. x  5 17 m.
D. x  5 2 m.  Câu 11. m sin x
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  nghịch biến trên 2 cos x    khoảng 0;   ?  6  5 A. m  . B. m  0. C. m 1. D. m  2. 4
Câu 12. Tính đạo hàm của hàm số y  log  2x 1 ? 2016  2x 1 1 A.  . B. y '  x . D. . 2 2 x   1 ln 2016 x  . C. 2 ln 2016 1  2x  1ln2016
Câu 13. Tìm giá trị thực của tham số m sao cho hàm số y   2
ln x mx   1 có tập xác định là ? m  2 A.  . B. 1   m 1. C. 2   m  2 . D. 2   m  2. m  2
Câu 14. Giải phương trình 2x 1 3   27 1 A. x  2 . B. x  5.
C. x  log 30 . D. x  1  . 3 2
Câu 15. Giải bất phương trình log 3x  4  4
 . Tập nghiệm T của bất phương trình là 1   2 Trang 25
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai  4   4 
A. T  4; . B. T   ; 4   . C. T   ; 4   .
D. T   ;  4.  3   3  2 1 x Câu 16.    x 1
Cho hàm số f x 1
e .  . Khẳng định nào sau đây là khẳng định sai?  3  1 x
A. f x    x   2 1 1 x   1 ln 3  0 .
B. f x  1    2 x   1 log 3  0 . ln10 x 1
C. f x 2  1  1 x  0.
D. f x 1  1 xlog e   2 x 1 log 3  0 . 2  ln 3 2
Câu 17. Cho các số thực dương a,b thỏa mãn: 2 2
a b  7ab . Khẳng định nào sau đây là khẳng định đúng? 1 3
A. 3ln a b  ln a  ln b .
B. log a b  log a  log b . 2 2 a b 1
C. 2ln a  ln b  7ln . a ln b . D. log
 log a  logb . 3 2
Câu 18. Tính đạo hàm của hàm số x x
y xe e . A. 2 x e . B. 2 x xe .
C.   2 x x e . D.    1 x x e .
Câu 19. Đặt a  log5, b  log3 . Hãy biểu diễn log 8 theo a,b . 30 3a b 31 a 2a b 2 1 aA. log 8  . log 8  . log 8  . log 8  . 30 1 B. b 30 30 30 1 C. b a D. b a b
Câu 20. Cho hai số thực dương a và b , với a b , a   1 b  
1  0 . Khẳng định nào dưới đây là khẳng định sai?  1 
A.a b log a  0 . B.  2 2 a b log  0   . 1 a b b
C.a blog b  0 . D.  2 2
b a log a  0 . a b
Câu 21. Một người quan sát một đám bèo phát triển trên mặt hồ thì thấy cứ sau một giờ thì diện
tích của đám bèo lớn gấp 10 lần diện tích đám bèo trước đó, với tốc độ tăng không đổi
thì sau 9 giờ đám bèo ấy phủ kín mặt hồ. Hỏi sau bao nhiêu giờ thì đám bèo ấy phủ kín một phần ba mặt hồ? 9 10 9 A. 3 . B. . C. 9  log 3 . D. . 3 log 3 d d
Câu 22. Cho hàm số y f x liên tục trên thỏa mãn f
 xdx 10, f
 xdx 8 và a b c c f
 xdx  7. Tính f xdx  ? a b c c c c A. f
 xdx  5  . B. f
 xdx  5. C. f
 xdx 11. D. f
 xdx  1  1. b b b b
Câu 23. Tìm nguyên hàm của hàm số f x  sin2xcos3xdx . A. f  x 1 1 dx
cos 2x  sin 3x C . B. f
 xdx  cos2xsin3x . C 2 3 C. f
 xdx  cos2xsin3x . C D. f  x 1 1 dx  
cos 2x  sin 3x C. 2 3 2 2 Câu 24. x
Tính tích phân I  dx  . 3  0 x 1 Trang 26
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 4 26 8 A. I  . B. I  ln3. C. I  . D. I  . 3 3 3 1
Câu 25. Tính tích phân      2 1 x I x e dx . 0 2 3e  3 2 3e 1 A. I  . B. I  . C. 2 I e . D. 2
I  5e  3 . 4 4
Câu 26. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y  4x x , trục hoành, trục tung
và đường thẳng x  4 . A. 44 . B. 48 . C. 40 . D. 36 .
Câu 27. Kí hiệu H  là hình phẳng giới hạn bởi đồ thị hàm số y  4x  2.ln x , trục hoành và
đường thẳng x e . Tính thể tích V của khối tròn xoay thu được khi quay hình
H  xung quanh trục Ox . A.  2
e  6e  5 . B. 2
e  2e  5 . C. 2
e  6e  5 . D. V   2
e  2e  5 .
Câu 28. Trong một phòng thí nghiệm, người ta quan sát một đám vi trùng ban đầu có
250000(con) , tới ngày thứ n thì số lượng vi trùng trong đám ấy là f n con, với f n 4000  1
. Gọi x là số lượng vi trùng trong đám ấy sau 10 ngày, giá trị của x gần 0, 5n
với kết quả nào nhất trong các kết quả sau đây?
A. x  264334 . B. x 14334 .
C. x  264000 . D. x 14000 .
Câu 29. Tìm phần thực và phần ảo của số phức z , biết z  2  510i .
A. Phần thực bằng 25  và Phần ảo bằng 10  i .
B. Phần thực bằng 25 và Phần ảo bằng 10  i .
C. Phần thực bằng 25 và Phần ảo bằng 10  .
D. Phần thực bằng 25
 và Phần ảo bằng 10.
Câu 30. Cho hai số phức z  2  3i và z  1
  7i . Tính mô đun của số phức z z . 1 2 1 2 A. 101 . B. 5 . C. 17 . D. 8 .
Câu 31. Cho số phức z    i2 2 0.5 1
. Hỏi điểm biểu diễn của z
là điểm nào trong các điểm M , N, P,Q ở hình bên? A. Điểm M . B. Điểm N . C. Điểm P . D. Điểm Q . Câu 32. 5z
Cho số phức z  3 2i . Tìm số phức w   2z 2  ? i
A. w  2  5i . B. w  2  5i . C. w  2  5i .
D. w  2  5i .
Câu 33. Kí hiệu z , z , z và z là bốn nghiệm phức của phương trình z  2 2 2 1  2z  46 . Tính 1 2 3 4
tổng M z z z z . 1 2 3 4
A. M  6  2 5 . B. M  2 5 . C. M  6.
D. M  3  2 5.
Câu 34. Trong các số phức z thỏa mãn điều kiện z  2 3i z 1 2i , hãy tìm phần ảo của số
phức có môđun nhỏ nhất ? 2 10 2 A.  . B. . C. . D. 2.  13 13 5 Trang 27
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 35. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2a , cạnh bên SA vuông
góc với mặt phẳng  ABC  . Gọi M là trung điểm của BC , góc giữa SM và mặt phẳng
đáy  ABC  bằng o
60 . Tính thể tích V của khối chóp S.ABC ? A. 3 V  6 3a . B. 3 V  2 3a . C. 3 V  3a . D. 3 V  3 3a .
Câu 36. Cho lăng trụ đứng ABC.A B C có đáy ABC là tam giác vuông tại B với AB  3a, 1 1 1
AC  5a , A B  4a . Tính thể tích V của lăng trụ ABC.A B C ? 1 1 1 1 A. 3 V  12 7a . B. 3 V  2 7a . C. 3 V  30a . D. 3 V  6 7a .
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , mặt bên SAB là tam
giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của khối 3 a
chóp S.OCD bằng
. Tính khoảng cách h từ A đến mặt phẳng SBD ? 3 2 6a a 3 2 3a A. h  2 3 . a B. h  . C. h  . D. h  . 3 3 3
Câu 38. Cho lăng trụ ABC.A B C có đáy ABC là tam giác vuông tại C , cạnh AC  5a . Hình 1 1 1
chiếu vuông góc của A lên mặt phẳng ABC là trung điểm của cạnh AC , góc giữa mặt 1
phẳng  AA B B với  AA C C bằng o
30 , cạnh bên của lăng trụ tạo với đáy một góc o 60 . 1 1  1 1 
Tính thể tích V của lăng trụ ABC.A B C ? 1 1 1 3 3.a 3 3.a 3 a 3 a A. V  . B. V  . C. V  . D. V  . 8 24 8 24
Câu 39. Trong không gian cho tam giác ABC vuông cân tại A với đường cao AH , AB  2a .
Tính bán kính R của đáy hình nón, nhận được khi quay tam giác ABC xoay quanh trục AH ? a 2 A. R  .
B. R a 2. C. R  2 . a
D. R  2a 2. 2
Câu 40. Trong không gian cho hình vuông ABCD có cạnh bằng 4 . Quay hình vuông đó xung
quanh trục AB , ta nhận được một hình trụ. Tính diện tích toàn phần S của hình trụ tp đó.
A. S  32 . B. S  48. C. S  64. D. 80. tp tp tp
Câu 41. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là 2a , cạnh bên là a 6 . Tính thể tích
V của khối cầu ngoại tiếp hình chóp đã cho? 3 9a  3 81a  3 9a 3 3a A. V  . B. V  . C. V  . D. V  . 2 32 2 2
Câu 42. Một cơ sở sản xuất đồ gia dụng được đặt hàng làm các chiếc cốc hình nón không nắp
bằng nhôm có thể tích là 3
V  9a  . Để tiết kiệm sản suất và mang lại lợi nhuận cao nhất
thì cơ sở sẽ sản suất những chiếc cốc hình nón có bán kính miệng cốc là R sao cho diện
tích nhôm cần sử dụng là ít nhất. Tính R ? 3a 3a A. R  . B. R  . C. R  3 . a D. 3 R  9 . a 3 2 6 2
Câu 43. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng  có phương trình: x 1 2t  y  2
  t (t là tham số thực). Vectơ nào dưới đây là một vectơ chỉ phương của  ? z  3  Trang 28
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. u  1; 2  ;3 .
B. u  2;1;3 .
C. u  2;1;0 .
D. u  2; 1;3 . 4   2   3   1  
Câu 44. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A1;0;  1 , B  2
 ;1;0, C 0;1; 2  .
Vectơ nào dưới đây là một vec tơ pháp tuyến của mặt phẳng  ABC  ?
A. n  1;1; 2 . B. n  1; 1  ; 2  . C. n  1  ;2;1 .
D. n  1; 2;1 . 4   3   2   1  
Câu 45. Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu S 2 2 2
: x y z  2x  4 y  6z  2  0 . Tìm tọa độ tâm I và bán kính của mặt cầu S  . A. I 1; 2  ; 3   và R  4 . B. I  1
 ;2;3 và R  4. C. I 1; 2  ; 3
  và R  2 3 . D. I 1; 2  ; 3
  và R  2 3 .
Câu 46. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P: y z  4  0 và mặt
phẳng Q : x  2y z  5  0 . Gọi  là góc giữa hai mặt phẳng P và Q . Tính ? A. o   150 . B. o   60 . C. o   30 . D. o   120 .
Câu 47. Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm A1;2;  1 và B 3; 2  ;3. Viết
phương trình mặt phẳng trung trực P của đoạn thẳng AB .
A. x  2 y  2z  4  0.
B. x  2 y  2z  4  0.
C. x  2y  2z  0.
D. x  2 y  2z  4  0 .
Câu 48. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình: x 1 y  2 z  3   P
x y mz
 , m là tham số thực. Tìm tất cả 2 4  .Xét mặt phẳng   : 2 7 0 1
các giá trị của m để đường thẳng d song song với mặt phẳng P ? 1 A. m  6.  B. m 10. C. m  2.  D. m   . 2
Câu 49. Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu S  có tâm I(2; 1  ;1) và mặt
phẳng P : x  2y  2z  4  0 . Biết mặt phẳng P cắt mặt cầu S  theo giao tuyến là
một đường tròn có bán kính bằng 5 . Viết phương trình mặt cầu S  . A.  2 2 2
x  2   y  2   z  2 2 1 1  9.
B.x  2   y   1   z   1  9 . C.  2 2 2
x  2   y  2   z  2 2 1 1  81.
D.x  2   y   1   z   1  81.
Câu 50. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P : x y z  2  0 , đường x  3 y 1 z  2
thẳng  có phương trình:   M 1;0; 1  . Viết phương trình 2 1  và điểm   1
đường thẳng d đi qua M cắt đường thẳng  tại điểm A và cắt mặt phẳng P tại B
sao cho M là trung điểm AB ? x 1 y z 1 x  3 y  3 z  2 A.   .   . 6  B. 1 5 2 3  1 x 1 y z 1 x 1 y  3 z C.   .   . 4 5  D. 3 2 3  1  --------oOo-------
ĐÁP ÁN ĐỀ SỐ 03 1 2 3 4 5 6 7 8 9 10 A B C D B C D A C C 11 12 13 14 15 16 17 18 19 20 A A D A B C D C B A Trang 29
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 21 22 23 24 25 26 27 28 29 30 C B D A B C D C D B 31 32 33 34 35 36 37 38 39 40 C A A B C D B B C 41 42 43 44 45 46 47 48 49 50 A B C D A C B B B A HƯỚNG DẪN GIẢI
Câu 1. Chọn A.
Ta thấy đây là đồ thị hàm bậc bốn trùng phương 4 2
y ax bx c a  0 , do đồ thị có
các cực trị là : A1 
;1 ; O 0;0 ; ta có hệ: y(0)  0 0  cc  0    y(1) 1  1
  a b c  a  1    y (  1)  0 0  4a  2b b  2   
Câu 2. Chọn B. 2
x  3x  2  Ta có lim    1
 , y  1 là tiệm cận ngang. 2 x  1 x  2
x  3x  2   x  2  1 lim    lim    ; 2 x 1  x 1  1 x    1   x  2 2
x  3x  2   x  2  lim    lim     x  1  là tiệm cận đứng.  2  x 1    x 1 1 x    1   x
Có 2 đường tiệm cận.
Câu 3. Chọn C. x  2 Ta có 2
y  x  5x  6; y  0   ; y  0 x
 2,3 hàm số nghịch biến trên khoảng x  3 2;3 .
Câu 4. Chọn D.
Đồ thị của hàm số có hai tâm đối xứng là sai.
Câu 5. Chọn B.
Ta có f  x 2
x mx   2 3 6 3 m  
1 ; để hàm số đạt cực tiểu tại x  2 thì  m f
2  0  12 12m  3 1 2 m   1  0  
thay m=1 vào ta thấy f  x chỉ đổi dấu từ m  3
âm sang dương tại x  2 nên m 1 .
Câu 6. Chọn C. 2 m 1
Ta có : f  x   0 x
  1 hàm số f x liên tục trên đoạn  2  ;  1 nên giá trị nhỏ 2 x   1 m 1
nhất của f x  4  f   2 2 1  4 
 4  m  9  m  3  1   . 1
Câu 7. Chọn D. 7x 17 x  2
Ta có hoành độ giao điểm là nghiệm của : 2 x 1 
 2x 10x 12  0   2x  5 x  3 Trang 30
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 5
Mặt khác tiệm cận đứng của C là x  , A là giao điểm thuộc nhánh bên phải 2
đường tiệm cận đứng của C nên x  3  y  4  x y  7 A A A A
Câu 8. Chọn A. Để hàm số 4 2 2 4
y x  2m x m 1 có 3 điểm cực trị thì 3 2
y  3x  4m x  0 có ba nghiệm
phân biệt nên m  0 . Mặt khác 3 điểm cực trị tạo với gốc tọa độ O một tứ giác nội tiếp
trong một đường tròn nên tứ giác đó là hình vuông. Gọi ,
A B, C là ba cực trị và: 2 OA OB O  . A OB  0 m 1 0 Am  m   4 ,1 ; B ,1 ;C 0, m   1 , do       m  1.  2 2 OA AC O  . A AC  0
m m  0
Câu 9. Chọn C. 2 ax x  3
Do đồ thị của hàm số y   nên 2
4x bx  có một đường tiệm cận ngang là y c 1 a a 4 c  
 và chỉ có một đường tiệm cận đứng nên: 4 bc b Th1: 2
4x bx 1  0 có nghiệm kép  b  4
  b  4(a  0,ab  4) thay vào hàm số thõa a mãn.Nên  1 bc a 1 Th2: 2
4x bx 1  0 và 2
ax x  3  0 có nghiệm chung. Thay
lần lượt bằng ; 2; 4 ta bc 4 thấy không thõa mãn.
Câu 10. Chọn C. Do AB .
C A' B'C ' là hình lăng trụ đứng nên VA A'.S  A A'.A .
B AC.sin BAC  20.5.5.sin BAC
ABC. A' B 'C ' ABC
Để khoảng không gian của hành lang (kể cả hai tấm kính) là lớn nhất thì sin BAC lớn nhất hay 90o ABC
hay ABC vuông cân tại A hay BC  5 2 m .
Câu 11. Chọn A.  1  2 m  sin x m t t   2mt 1 Đặt sinx = t  0,   ta có y   y   y  để hàm số nghịch  2  2 2 cos x 1 t  2t  2 1     1   1  biến trên khoảng 0;   thì 2 y  0 x   0,
 t  2mt 1  0 x   0,      6   2   2   b  Th1: 2 y 
y (m)  0  m 1  0  1  m  1    2a   1   1  1 5 5
Th2: m 1 để y  0 x   0,   thì y
 0   m 1  0  m    hay 1  m   2   2  4 4 4  1 
Th3: m 1 để y  0 x   0, 
 thì y0  0 1 0 hay m  1  .  2  Trang 31
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 5 Vậy m  . 4
Câu 12. Chọn A. x y  log  2 2
x 1  y  ? 2016   2x  1ln2016
Câu 13. Chọn D.
Ta có tập xác định của y   2
ln x mx   1 là 2
x mx 1  0 x   2  m  4  0  2   m  2
Câu 14. Chọn A. Ta có 2x 1  2 x 1  3 3  27  3
 3  2x 1  3  x  2 .
Câu 15. Chọn B. 3  x  4  0  4   x  log 3x  4 4  4      1    3 1 3x  4  . 2        x  4 2
Câu 16. Chọn C. 2 1 x f x    x 1 1 1  e .
 log f x   x e   x  
khi (a  1) thì thay a
  1 loga  2 1 log  3 a  3 1 a  ; e 3;10; 2 vào log f x   x e   x thì a
  1 loga  2 1 loga 3
f x     xe   2 1 1 log x  
1 log 3  0 ta thấy C sai a a
Câu 17. Chọn D. 2 2      
a b ab  a b2 a b a b 2 2 7  9ab   ab  log  log ab      3   3  . a b a b 1  2log
 log a  log b  log  a b c c log log  3 3 2
Câu 18. Chọn C.
Tính đạo hàm của hàm số x x       1 x x       
1 x    2 x y xe e x e y e x e x e .
Câu 19. Chọn B. Ta có 3 3 3 3 log 8  3log 2     30 30 log 30 1 log 15 log15 log 3  log 5 2 2 1 1 log 2 10 log 5 . 3 31 log 5 3(1 a)    log 3  log 5 1 log 5  log 3  log 5 1 b 1 1 log 5
Câu 20. Chọn A.
a b nên a b  0(1) , a b  0  a b 1 Mặt khác  .       a   a   a 1 b   log log 0(2) 1   1  0 1
  a b  0 b b
Từ (1); (2) a blog a  0 sai 1   b
Câu 21. Chọn C. Trang 32
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Một người quan sát một đám bèo phát triển trên mặt hồ thì thấy cứ sau một giờ thì
diện tích của đám bèo lớn gấp 10 lần diện tích đám bèo trước đó, với tốc độ tăng
không đổi thì sau 9 giờ đám bèo ấy phủ kín mặt hồ. Hỏi sau bao nhiêu giờ thì đám
bèo ấy phủ kín một phần ba mặt hồ?
Gọi a diện tích ban đầu của đám bèo.
Sau một giờ diện tích đám bèo là a  10a ; Sau n giờ diện tích đám bèo là a  . a 10n 1 n
Sau 9 giờ diện tích đám bèo là 9 a  .
a 10  S ; (S ) là diện tích của mặt hồ. 9
Ta có đám bèo ấy phủ kín một phần ba mặt 9 9 9 S . a 10 n n 10 10 hồ    . a 10  10   n  log  9  log3 3 3 3 3
Câu 22. Chọn B. Ta có : c d a c f
 xdx f
 xdx f
 xdx f  xdx b b d a ? d d cf
 xdxf
 xdxf
 xdx 8107  5 b a a
Câu 23. Chọn D.
f x   x x 1 1 sin 2 cos 3 dx  
cos 2x  sin 3x C . 2 3
Câu 24. Chọn A. 2 2 2 x 1 1 I  dx  d   x   2 2 2 4 3 3 1  x 1  2   . 3 3  3  3 0 3 3 0 x 1 0 x 1
Câu 25. Chọn B. du  dx 1 u   x 1       2 1 x I x e dx đặt    1 2 x 2 dv xe dx v e 0  2 1 1 1 e e   e x
I e .x   2 2 1 1 x 4 1 x 3 1 2 2 2 1  e dx  . e     . 0 2 2 4  4  4 0 0
Câu 26. Chọn C. Ta có 3
4x x  0  x  0; x  2; x  2
 . Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y  4x x , trục hoành, trục tung và đường thẳng x  4 .là 4 0 S
4x x dx   
 4xx  2
dx  4x x  4 3 3 3 dx   3
4x x dx  40 2  2  0 2
Câu 27. Chọn D. Trang 33
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 2 e e
4x  2.ln x  0  x  1, V    4x  2.ln x dx   4x  2 2 .ln .d x x 1 1  2 ln x 2 u   ln x du  d e x đặt    xV    2 ln x 2
2x  2xe  4 x 1 .ln . x dx  1   .  dv  
4x  2dx  2 1
v  2x  2x  1 du  dx u   ln e x    x đặt   
V   2e  2e  ln x 2x  4 e x
  2x  4 .dx  2  2  2 .dv    x      1   1 dx x  1 v   x  2  
 2   2  4  e V e x x    2
e  2e  5 . 1 
Câu 28. Chọn C.  4000   8000 
Ta có f n  f
 ndn dn d   
 n  2  8000ln n  2  C. 1 0,5n   2  n
f 0  8000ln 2  C  250000  C  250000  8000ln 2
f 10  8000ln10  C  8000ln10  250000  8000ln 2  262876.
Câu 29. Chọn D. z  2
 510i z  2  510i .
Câu 30. Chọn B.
z z  2  3i 1 7i  3  4i . 1 2
Câu 31. Chọn C. z    i2 2 0.5 1
 2 0,5.2i  2 i .
Câu 32. Chọn A. 5z 53  2i  ii w   2z
 23 2i 53 2 2  
 23 2i  2 5 .i 2  i 2  i 5
Câu 33. Chọn A.       z   2 2 z 9 z 3 2 2 4 2 1
 2z  46  z  4z  45  0     . 2 z  5  z   5i
Câu 34. Chọn B.
z a bi a, b  
z  2  3i z 1 2i a bi  2  3i a bi 1 2i
 a  22  b 32  a  2
1  b  22  2a 10b  8  0 2 10
z a b  5b  42 8 2 2 2 2
b  26b  40b 16 
, z có môđun nhỏ nhất khi b  13 13 Trang 34
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 35. Chọn C. 2 S
a 3 , AM a 3 ,  60o SMA
SA AM.tan SMA a 3. 3  3a , ABC 1 3 VS .SA  a 3. S . ABC 3 ABC
Câu 36. Chọn D. 1 2 2 2 BC
AC AB  4a SA . B BC  6 a , 2 2 AA
A B AB a 7 , ABC 2 1 1 3 VAA .S  6a 7. ABC. 1 A 1 B 1 C 1 ABC
Câu 37. Chọn B.
Gọi x là độ dài AB ,kẻ SF AB tại F , ta có 3 x 1 1 1 a 2 3 SF   VVAB .SF  x   x  2 2a S .OCD S .ABCD 2 4 12 24 3
Do F là trung điểm của AB nên khoảng cách h từ A đến mặt phẳng SBD gấp 2 lần FB x
khoảng cách d từ F đến mặt phẳng SBD mà EF    a sin 45o 2 2
Tính d : kẽ FE DB; FH SE , ta chứng minh được SH  SBD , 1 1 1 1 1 3 a 6       2 6a FH
d , vậy h  2d  . 2 2 2 2 2 2 FH FE FS a 2a 2a 3 3
Câu 38. Chọn . Trang 35
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Gọi G là trung điểm của O 5 3 0
AC A G  ( ABC)  A AG  60  A G AG. tan 60  .
a Ta có BC   AA C C 1 1  1 1 1 2
Câu 39. Chọn B. 1 1 R HB BC  2a 2  a 2. 2 2
Câu 40. Chọn C. 2 2 2
S  2 R  2 Rh  4 R  4 4  64. tp
Câu 41. Chọn A.
Gọi H AC BD SH   ABCD 2 2 2 2
SH SA AH  6a  2a  2 . a 2 2 3 SA 6a 3a 4 9 a 3 R   
V   R  . 2SH 2.2a 2 3 2
Câu 42. Chọn B. Trang 36
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 3 1 27a 3aR 3 2 2 2  6 6 V  9a  
R .h h
l h R  2 4 3 R R 3a6  R 3a6 6 6  R S   . R l   . . R   xq 4 2 R R
3a6 3a6
3a6 3a6 3a12 2 9 a 4 4 6 6     R   . .R    2 2 2 2 3 2R 2R 2R 2R 4 2 3a6 6 3a Dấu bằng xảy ra khi 4
R  3a 6  2R R  . 2 6 2R 2
Câu 43. Chọn C.
Ta có u  2;1;0 . là một vectơ chỉ phương của .  2  
Câu 44. Chọn D. AB  ( 3  ,1,1);AC  ( 1
 ,1,1)  AB AC   2  , 4  , 2  .
Câu 45. Chọn A.
Câu 46. Chọn C. 0  2 1 3 Ta có cos     30 .o   2. 6 2
Câu 47. Chọn B. Ta có AB  2; 4  ;4;M 2,0, 
1 , phương trình mặt phẳng trung trực P của đoạn
thẳng AB là x  2 y  2z  4  0.
Câu 48. Chọn B. Ta có v   n   m d P d 2, 4,  1 ; P 1, 2,  / /  
v n v .n  0  2  8  m  0  m 10. d P d P
Câu 49. Chọn B. 2  2  2  4
Ta có khoảng cách từ I đến P là h  I,  P 
 2  R h    52 2 2  9 . 1 4  4
Câu 50. Chọn A.
Do A   A  3 2t,1 t, 2  t  , mà M là trung điểm AB nên B   1   2t, 1   t, 4   t
B   P   P : 1
  2 t1 t 4  t 2  0  t  2  B   5  ,1, 6  . MB   6  ,1, 5     x 1 y z 1 :   . 6 1  5
-------------------------------------- HẾT ------------------------------------ Trang 37
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017 TỈNH ĐỒNG NAI
Môn: TOÁN – Khối 12 Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97 NỘI DUNG ĐỀ SỐ 04 Câu 1. Hàm số 4 3
y x  8x  5 nghịch biến trên khoảng : A. (6;0) . B. (0; ) . C. (; 6) . D. ( ;  ) . mx Câu 2. 25
Các giá trị của tham số m để hàm số y
nghịch biến trên khoảng ( ;  1) là: x m A. 5   m  5. B. 5   m  1  . C. 5   m  5. D. m  1  .
Câu 3. Điểm cực tiểu của hàm số 3
y  x  3x  4 là: A. x  1. B. x 1. C. x  3  . D. x  3. Câu 4. Hàm số 3 2 2
y x  2mx m x  2 đạt cực tiểu tại x 1 khi A. m  2 . B. m  3 . C. m 1. D. m  1  . x Câu 5. 3 1
Cho hàm số y
. Khẳng định nào sau đây đúng ? 2x 1 3
A. Đồ thị hàm số có tiệm cận ngang là y  . 2 3
B. Đồ thị hàm số có tiệm cận đứng là y  . 2 1
C. Đồ thị hàm số có tiệm cận đứng là x   . 2
D. Đồ thị hàm số không có tiệm cận. 2 x x Câu 6. 1
Cho hàm số y
. Số đường tiệm cận của đồ thị hàm số bằng: x  2 A. 0 . B. 1. C. 2 . D. 3 . Câu 7. Cho hàm số 2 y
x  2x . Giá trị lớn nhất của hàm số bằng: A. 0 . B. 1. C. 2 . D. 3 .
Câu 8. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 4 2
y x  2x  3 trên0;2 là:
A. M  11, m  2 .
B. M  3, m  2 .
C. M  5, m  2 .
D. M  11, m  3 . x Câu 9. 1
Tọa độ giao điểm của (C) : y
và (d ) : y  x 1 2x 1 là : A. 1;  1 , ( 1  ;2) . B. 1;0,( 1  ;2) . C.  1  ;0,(1;2) . D. 1; 2   .
Câu 10. Đồ thị sau đây là của hàm số nào ? y 4 2 x O 1 2 3 Trang 38
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. 3 2
y x  3x . B. 3 2
y  x  3x . C. 3 2
y x  3x . D. 3 2
y  x  3x . x Câu 11. 5
Tổng các giá trị của tham số m sao cho đường thẳng y x cắt đồ thị hàm số y x m
tại hai điểm A và B sao cho AB  4 2 là: A. 2 . B. 5 . C. 7 . D. Đáp án khác.
Câu 12. Đạo hàm của hàm số 2 y  log 2x 1 là: 2   2 log 2x 1 4 log 2x 1 4 log 2x 1 2 2   2   2   A.  . B. . C. . D. . 2x   1 ln 2 2x   1 ln 2 2x 1 2x   1 ln 2
Câu 13. Cho biết log 3  a; log 2  b . Biểu diễn log 30 theo a và b là 125 1 2 2a 1 a 1 a A. log 30 
a . B. log 30  . C. log 30  . D. log 30  . 125 b 125 1 b 125 1 b 125 3(1 b) 2 1 1  b b   
Câu 14. Cho a , b là các số dương. Biểu thức 2 2 1 2
  :a b    sau khi rút gọn là:  a a    1 1 A. .
B. a b .
C. a b . D. . a b Câu 15. Biểu thức 3 6 5
x. x. x (x  0) viết dưới dạng luỹ thừa với số mũ hữu tỷ là: 7 5 2 5 A. 3 x . B. 2 x . C. 3 x . D. 3 x . x    x Câu 16. 5 3 3 Cho 9x 9
x  23. Khi đó biểu thức P  có giá trị bằng:
1 3x  3x 5 1 3 A.  . B. . C. . D. 2 . 2 2 2 Câu 17. 2
Số nghiệm của phương trình 3 . x 2x  1 là: A. 0 . B. 1. C. 2 . D. 3 .
Câu 18. Nghiệm của phương trình 2
log (x 1)  log (2x 1)  2 là: 3 3 A. Vô nghiệm. B. 1. C. 2 . D. 3 .
Câu 19. Tập nghiệm của bất phương trình log x 1  log 3  x là: 0,2   0,2  
A. S  1;3 .
B. S  1; .
C. S    ;1 . D. S  ( 1  ;1) . 3 x x 1 
Câu 20. Số nghiệm nguyên của bất phương trình   x 1    x3 10 3 10 3 là: A. 0 . B. 1. C. 2 . D. 3 .
Câu 21. Tỉ lệ tăng dân số hàng năm của nước Nhật là 0, 2% . Năm 1998, dân số của Nhật là
125932 000 . Vào năm nào dân số của Nhật là 140 000 000 ? A. Năm 2049 . B. Năm 2050 . C. Năm 2051. D. Năm 2052 .
Câu 22. Cho a  0 và a 1. C là hằng số. Phát biểu nào sau đây đúng ? 2 x a A.  .ln   x x a dx a a C . B. 2 x a dx    C . 2 ln a C. 2 2    x x a dx a C . D. 2 2  .ln   x x a dx a a C .
Câu 23. Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau quanh trục hoành 2
y  1 x , y  0 31416 4  3 A. . B. . C. . D. . 20001 3 2 2 Trang 39
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai x x Câu 24. ( 2)
Hàm số nào sau đây không là nguyên hàm của hàm số f (x)  ? 2 (x 1) 2 x x 1 2 x x 1 2 x x 1 2 x
A. F (x) 
. B. F(x) 
. C. F (x) 
. D. F (x)  . x 1 x 1 x 1 x 1 2
Câu 25. Giá trị của 2 2  x e dx là : 0 A. 4 e . B. 4 e 1. C. 4 4e . D. 4 3e . ln 5 2 x Câu 26. e Giá trị của x  d là : x e  ln 2 1 22 19 23 20 A. . B. . C. . D. . 3 3 3 3
Câu 27. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y  2x là: 4 3 5 23 A. . B. . C. . D. . 3 2 3 15
Câu 28. Gọi H  là hình phẳng giới hạn bởi các đường 2
y x 1 và y  4x  2 . Khi đó thể tích
khối tròn xoay được sinh ra khi quay hình phẳng  H  quanh trục Ox là: 4 248 224 1016 A. . B. . C.  . D. . 3 3 15 15
Câu 29. Số phức liên hợp của số phức z 1 2i là: A. 1   2i . B. 1   2i . C. 2  i . D. 1 2i . Câu 30. 2
Phần thực của số phức z thỏa mãn: 1 i 2  iz  8  i  1 2iz là A. 2 . B. 3  . C. 2  . D. 3
Câu 31. Tập hợp các điểm trong m t phẳng phức biểu diễn các số z thỏa mãn đi u kiện:
z i  1 iz là đường tròn có bán kính là:
A. R  1 .
B. R  2 . C. R  2 .
D. R  4
Câu 32. Cho hai số phức z 1 i và z  3
  5i . Môđun của số phức w z .z z 1 2 1 2 2 A. w  130 B. w  130 C. w  112 D. w  112
Câu 33. Cho số phức z thỏa 1 iz 14  2i . Điểm biểu diễn của số phức z trong m t phẳng
tọa độ Oxy có tọa độ là: A. 6;8 . B. 8;6 . C.  8  ;6. D. 6; 8  .
Câu 34. Kí hiệu z , z lần lượt là hai nghiệm phức của phương trình 2
2z  2z  5  0 . Giá trị của 1 2 2 2
biểu thức A z 1  z 1 bằng: 1 2 A. 25 . B. 5 . C. 5 . D. 2 5 .
Câu 35. Số các số phức z thỏa mãn: z  2 và 2
z là số thuần ảo là: A. 1 B. 2 C. 3 D. 4
Câu 36. Hình lập phương có bao nhiêu m t phẳng đối xứng ? A. 4 . B. 7 . C. 8 . D. 9 .
Câu 37. Cho H  là khối chóp tứ giác đ u có tất cả các cạnh bằng a . Thể tích của H  bằng: 3 a 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 3 6 4 2
Câu 38. Một khối lăng trụ tam giác có các cạnh đáy bằng 13, 14 , 15, cạnh bên tạo với m t phẳng đáy một góc 0
30 và có chi u dài bằng 8 . Khi đó thể tích khối lăng trụ là: Trang 40
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. 340. B. 336 . C. 274 3 . D. 124 3 .
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O , SA   ABCD . Biết thể
tích của S.ABCD bằng V . Tính thể tích khối OSCD theo V ? V V 2V V A. . B. . C. . D. . 3 4 3 8
Câu 40. Một hình trụ có bán kính đáy bằng 2 và có chi u cao bằng 4 . Thể tích của hình trụ bằng: A. 8 . B. 24 . C. 32 . D. 16 .
Câu 41. Thể tích của khối nón tròn xoay biết khoảng cách từ tâm của đáy đến đường sinh bằng
3 và thiết diện qua trục là một tam giác đ u là:  3 8 3 4 3 2 3 A. . B. . C. . D. . 3 3 3 3
Câu 42. Cho hình trụ có các đáy là 2 hình tròn tâm O và '
O , bán kính đáy bằng chi u cao và
bằng a . Trên đường tròn đáy tâm O lấy điểm A , trên đường tròn đáy tâm ' O lấy điểm
B sao cho AB  2a . Thể tích khối tứ diện '
OO AB theo a là: 3 3 3 3 3 3 3 3 A. a V . B. a V . C. a V . D. a V . 8 6 12 4
Câu 43. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB BC a 3 ,   90o SAB SCB
và khoảng cách từ A đến m t phẳng (SBC) bằng a 2 . Tính diện tích
m t cầu ngoại tiếp hình chóp S.ABC theo a ? A. 2 S  3 a . B. 2 S  16 a . C. 2 S  2 a . D. 2 S  12 a .
Câu 44. Trong không gian với hệ tọa độ Oxyz , m t phẳng (P) : 2x  2z z  2017  0 . Vectơ nào
dưới đây là một vectơ pháp tuyến của (P) ? A. n  1; 2  ;2 . B. n  1; 1  ;4 .
C. n  2; 2; 1 .
D. n  2; 2;1 . 2   3   1   4  
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho m t cầu 2 2 2
(S) : x y z  4x  4 y  6z  3  0 .
Tọa độ tâm I và tính bán kính R của (S ) ? A. I 2;2; 3   và R  20 . B. I  4  ; 4
 ;6 và R  71 . C. I 4;4; 6   và R  71. D. I  2  ; 2
 ;3 và R  20 .
Câu 46. Trong không gian với hệ tọa độ Oxyz , đường thẳng d đi qua điểm ( A 1; 2;3) và vuông
góc với m t phẳng P : 2x  2z z  2017  0 có phương trình là : x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   . 2 2 1 2 2 1 x  2 y  2 z 1 x  2 y  2 z 1 C.   . D.   . 1 2 3 1 2 3
Câu 47. Trong không gian với hệ tọa độ Oxyz , m t phẳng (P) đi qua ba điểm ( A 1; 0; 0),
B(0; 2; 0), C(0;0;3) có phương trình là: x y z
A. x  2z  3z 1 0 . B.    0. 1 2 3 x y z
C. 6x  3z  2z  6  0 . D.    1. 3 2 1
Câu 48. Gọi (S ) là m t cầu tâm I(2;1; 1
 ) và tiếp xúc với m t phẳng () có phương trình:
2x  2 y z  3  0 . Bán kính của (S ) bằng: 4 2 2 A. . B. . C. . D. 2 . 3 9 3 Trang 41
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho điểm (
A 1; 2;3) và đường thẳng x 1 y z  3 d :  
. Viết phương trình đường thẳng  đi qua điểm A , vuông góc với 2 1 2 
đường thẳng d và cắt trục Ox ? x 1 y  2 z  3 x  2 y  2 z  3 A.   . B.   . 2 2 3 1 2 3 x 1 y  2 z  3 x  2 y  2 z  3 C.   . D.   . 2 2 3 1 2 3 x y z Câu 50. 1 2
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1 2 (
A 2;5;3) . Phương trình m t phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là
lớn nhất có phương trình:
A. x  4 y z  3  0 .
B. x  4 y z  3  0 .
C. x  4 y z  3  0 .
D. x  4 y z  3  0 .
----------- HẾT ---------- Trang 42
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
ĐÁP ÁN: ĐỀ SỐ 04 1 C 11 C 21 C 31 C 41 B 2 B 12 B 22 B 32 A 42 C 3 A 13 D 23 B 33 D 43 D 4 C 14 A 24 A 34 C 44 C 5 A 15 D 25 B 35 D 45 A 6 D 16 A 26 D 36 D 46 B 7 B 17 C 27 A 37 B 47 C 8 A 18 C 28 C 38 B 48 D 9 B 19 D 29 D 39 C 49 A 10 D 20 D 30 A 40 D 50 D Câu 1. Hàm số 4 3
y x  8x  5 nghịch biến trên khoảng : A. (6;0) . B. (0; ) . C. (; 6) . D. ( ;  ) . Hướng dẫn giải x  0 3 2
y '  4x  24x y '  0   x  6  Bảng biến thiên: x   6 0   y ' - 0 + 0 + y
Đáp án: C. (; 6) mx Câu 2. 25
Các giá trị của tham số m để hàm số y
nghịch biến trên khoảng ( ;  1) là: x m A. 5   m  5. B. 5   m  1  . C. 5   m  5. D. m  1  . Hướng dẫn giải 2 m  25 y '  2 (x m) 2 m  25  0
Hàm số nghịch biến trên  ;  
1  y '  0 x  ;   1    5   m  1 1   m Đáp án: B. 5   m  1 
Câu 3. Điểm cực tiểu của hàm số 3
y  x  3x  4 là: A. x  1. B. x 1. C. x  3  . D. x  3. Hướng dẫn giải x  1 2 y '  3
x  3  y '  0   x  1  Bảng biến thiên: x  1 1   y '  0 + 0  y
Đáp án: A. x  1 Câu 4. Hàm số 3 2 2
y x  2mx m x  2 đạt cực tiểu tại x 1 khi A. m  2 . B. m  3 . C. m 1. D. m  1  . Trang 43
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Hướng dẫn giải 2 2
y '  3x  4mx m m 1 y '(1)  0   m  3
Thử lại ta thấy m 1 thỏa.
Đáp án: C. m 1 x Câu 5. 3 1 Cho hàm số y
. Khẳng định nào sau đây đúng ? 2x 1 3
A. Đồ thị hàm số có tiệm cận ngang là y  . 2 3
B. Đồ thị hàm số có tiệm cận đứng là y  . 2 1
C. Đồ thị hàm số có tiệm cận đứng là x   . 2
D. Đồ thị hàm số không có tiệm cận. Hướng dẫn giải 3
Đáp án: A. Đồ thị hàm số có tiệm cận ngang là y  . 2 2 x x Câu 6. 1 Cho hàm số y
. Số đường tiệm cận của đồ thị hàm số bằng: x  2 A. 0 . B. 1. C. 2 . D. 3 . Hướng dẫn giải
lim y  1; lim y  1  ; lim y   ;  lim y     x x x2 x2
Đồ thị hàm số có 2 tiệm cận ngang và 1 tiệm cận đứng. Đáp án: D. 3 . Câu 7. Cho hàm số 2 y
x  2x . Giá trị lớn nhất của hàm số bằng: A. 0 . B. 1. C. 2 . D. 3 . Hướng dẫn giải D    x 1 0; 2 . y ' 
y '  0  x  1 2 x  2x
y(1)  1, y(0)  y(2)  0
Đáp án: B. 1
Câu 8. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 4 2
y x  2x  3 trên0;2 là:
A. M  11, m  2 .
B. M  3, m  2 .
C. M  5, m  2 .
D. M  11, m  3 . Hướng dẫn giải x  0  3
y '  4x  4x y '  0  x  1
y(0)  3, y(1)  2, y(2) 11  x  1    0;2
Đáp án: A. M  11, m  2 x Câu 9. 1
Tọa độ giao điểm của (C) : y
và (d ) : y  x 1 2x 1 là : A. 1;  1 , ( 1  ;2) . B. 1;0,( 1  ;2) . C.  1  ;0,(1;2) . D. 1; 2   . Hướng dẫn giải Trang 44
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Phương trình hoành độ giao điểm:
x    x  x   2 1 2 1 1  2  x  2  0  
x  1 (1;2)  1   1   x   x    x  1 (1;0)  2  2
Đáp án: B. 1;0,( 1  ;2)
Câu 10. Đồ thị sau đây là của hàm số nào ? y 4 2 x O 1 2 3 A. 3 2
y x  3x . B. 3 2
y  x  3x . C. 3 2
y x  3x . D. 3 2
y  x  3x . Hướng dẫn giải
Hàm số nghịch biến  a  0 Đồ thị hàm số đi qua 2; 4 3 2
y  x  3x Đáp án: D. 3 2
y  x  3x x Câu 11. 5
Tổng các giá trị của tham số m sao cho đường thẳng y x cắt đồ thị hàm số y x m
tại hai điểm A và B sao cho AB  4 2 là A. 2 . B. 5 . C. 7 . D. Đáp án:khác. Hướng dẫn giải
Phương trình hoành độ giao điểm:
xx m 2  x  5
x  m  
1 x  5  0  f (x)    x  m x  m 2   0  f
m  2m 19  0
Đường thẳng cắt đồ thị tại 2 điểm A, Bkhi và chỉ khi: 
 f m     0 m  5 
Gọi: Ax ; x , B x ; x 1 1   2 2
Với x ; x là 2 nghiệm của phương trình f (x)  0 1 2 m
AB  4 2  x x  4   x x 2 7 2
 4x x  16  m  2m  35  0  2 1 1 2 1 2  m  5 
So với đi u kiện ta nhận m  7 Đáp án: C. 7
Câu 12. Đạo hàm của hàm số 2 y  log 2x 1 là: 2   2 log 2x 1 4 log 2x 1 4 log 2x 1 2 2   2   2   A.  . B. . C. . D. . 2x   1 ln 2 2x   1 ln 2 2x 1 2x   1 ln 2 Hướng dẫn giải Trang 45
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
2 log (2x 1).(2x 1) ' 4 log (2x 1) ' 2 2
y '  2 log (2x 1)[log (2x 1)]   2 2 (2x 1) ln 2 (2x 1) ln 2 4 log 2x 1 2   Đáp án: B.  2x   1 ln 2
Câu 13. Cho biết log 3  a; log 2  b . Biểu diễn log 30 theo a và b là 125 1 2 2a 1 a 1 a A. log 30 
a . B. log 30  . C. log 30  . D. log 30  . 125 b 125 1 b 125 1 b 125 3(1 b) Hướng dẫn giải log 30 1 log 3 1 a log 30   125 = log125 3log 5 3(1 b) 1 a Đáp án: D. log 30  125 3(1 b) 2 1 1  b b   
Câu 14. Cho a , b là các số dương. Biểu thức 2 2 1 2
  :a b    sau khi rút gọn là:  a a    1 1 A. .
B. a b .
C. a b . D. . a b Hướng dẫn giải 2  b  2  1 2 1 1   b b    a  1  1 2 2 1 2
  :a b            a a     a b   a a     1 Đáp án: A. a Câu 15. Biểu thức 3 6 5
x. x. x (x  0) viết dưới dạng luỹ thừa với số mũ hữu tỷ là: 7 5 2 5 A. 3 x . B. 2 x . C. 3 x . D. 3 x . Hướng dẫn giải 1 1 5 10 5 3 6 5 2 3 6 6 3
x. x. x x .x .x xx 5 Đáp án: D. 3 x x    x Câu 16. 5 3 3 Cho 9x 9
x  23. Khi đó biểu thức P  có giá trị bằng:
1 3x  3x 5 1 3 A.  . B. . C. . D. 2 . 2 2 2 Hướng dẫn giải Ta có xx 2 (3 3 ) 9x 9  
x  2  23 2  25 nên (3x 3  x )  5
5  3x  3x 5  5 5 Suy ra P    
1 3x  3x 1 5 2 5
Đáp án: A.  2 Câu 17. 2
Số nghiệm của phương trình 3 . x 2x  1 là: A. 0 . B. 1. C. 2 . D. 3 . Hướng dẫn giải 2 2 x x x x 2 3 .2
1  log (3 .2 )  0  xlog 3  x x  0  x  log 3 2 2 2 Trang 46
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Đáp án: C. 2
Câu 18. Nghiệm của phương trình 2
log (x 1)  log (2x 1)  2 là: 3 3 A. Vô nghiệm. B. 1. C. 2 . D. 3 . x  1   Đi u kiện 1 x    2 2
log (x 1)  log (2x 1)  2  2 log x 1  2 log (2x 1)  2 3 3 3 3
 2log x 1  2log (2x 1)  2 3 3
 log x 1 (2x 1) 1  x 1 (2x 1)  3 3 x  2 Với  x 1 ta có 2
x 1 (2x 1)  3  2x  3x  2  0  1  x   (l)  2 1 Với  x  1 ta có 2
x 1 (2x 1)  3  2x  3x  2  0 pt vô nghiệm 2 Đáp án: C. 2
Câu 19. Tập nghiệm của bất phương trình log x 1  log 3  x là: 0,2   0,2  
A. S  1;3 .
B. S  1; .
C. S    ;1 . D. S  ( 1  ;1) . Hướng dẫn giải Đi u kiện 1   x  3 log x 1  log
3  x x 1  3  x x  1 0,2   0,2   So với đi u kiện ta có
Tập nghiệm của bất phương trình là: S   ( 1;1)
Đáp án: D. S  ( 1  ;1) 3 x x 1 
Câu 20. Số nghiệm nguyên của bất phương trình   x 1    x3 10 3 10 3 là A. 0 . B. 1. C. 2 . D. 3 . Hướng dẫn giảix x x x  3x     1 x     3 x     1 1 3 1 x3 10 3 10 3 10 3 10 3 x  3 x 1 8    
 0  (x 1)(x  3)  0  3
  x 1 x  2  , 1  ,0 x 1 x  3
(x 1)(x  3) Đáp án: D. 3
Câu 21. Tỉ lệ tăng dân số hàng năm của nước Nhật là 0, 2% . Năm 1988 , dân số của Nhật là
125932 000 . Vào năm nào dân số của Nhật là 140 000 000 ? A. Năm 2049 . B. Năm 2050 . C. Năm 2051. D. Năm 2052 . Hướng dẫn giảin 0, 2  14000000  125932000. 1  n  53    100 
Đáp án: C. Năm 2051
Câu 22. Cho a  0 và a 1. C là hằng số. Phát biểu nào sau đây đúng ? 2 x a A.  .ln   x x a dx a a C . B. 2 x a dx    C . 2 ln a Trang 47
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai C. 2 2    x x a dx a C . D. 2 2  .ln   x x a dx a a C . Hướng dẫn giải 2 x a Đáp án: B. 2 x a dx    C 2 ln a
Câu 23. Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau quanh trục hoành 2
y  1 x , y  0 31416 4  3 A. . B. . C. . D. . 20001 3 2 2 Hướng dẫn giải Tìm cận 2
1 x  0  x  1  1 4 2
V   (1 x )dx   3 1  4 Đáp án: B. 3 x x Câu 24. ( 2)
Hàm số nào sau đây không là nguyên hàm của hàm số f (x)  ? 2 (x 1) 2 x x 1 2 x x 1 2 x x 1 2 x
A. F (x)  .
B. F(x) 
. C. F (x) 
. D. F (x)  . x 1 x 1 x 1 x 1 Hướng dẫn giải ' 2 2
x x 1 x  2x  2
Vì F '(x)      x 1  x  2 1 2 x x 1
Đáp án: A. F (x)  x 1 2
Câu 25. Giá trị của 2 2  x e dx là : 0 A. 4 e . B. 4 e 1. C. 4 4e . D. 4 3e . Hướng dẫn giải 2 2 4 2  1  x e dx e . 0 Đáp án: B. 4 e 1 ln 5 2 x Câu 26. e Giá trị của x  d là x e  ln 2 1 22 19 23 20 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải ln 5 2 x e 20 dx   . x e  3 ln 2 1 20 Đáp án: D. 3
Câu 27. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y x và đường thẳng y  2x là: 4 3 5 23 A. . B. . C. . D. . 3 2 3 15 Hướng dẫn giải Trang 48
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai x  0 2 4 2 x  2x   2
S x  2xdx   x  2 3 0 4 Đáp án: A. 3
Câu 28. Gọi H  là hình phẳng giới hạn bởi các đường 2
y x 1 và y  4x  2 . Khi đó thể tích
khối tròn xoay được sinh ra khi quay hình phẳng  H  quanh trục Ox là: 4 248 224 1016 A. . B. . C.  . D. . 3 3 15 15 Hướng dẫn giảix 1 2 2
x 1  4x  2  x  4x  3  0  x  3 3
V   4x  2 x  2 2 224 2 1 dx   15 1 224 Đáp án: C.  15
Câu 29. Số phức liên hợp của số phức z 1 2i là A. 1   2i . B. 1   2i . C. 2  i . D. 1 2i . Hướng dẫn giải
Số phức liên hợp của số phức z 1 2i là z 1 2i
Đáp án: D. 1 2i Câu 30. 2
Phần thực của số phức z thỏa mãn: 1 i 2  iz  8  i  1 2iz là A. 2 . B. 3  . C. 2  . D. 3 Hướng dẫn giải Ta có:  i2 1
2iz  8i 1 2iz  2 4iz 1 2iz  8i    iii 1 2i 8 8 1 2 
z  8  i z    2  3i 1 2i 5
Vậy phần thực của z bằng 2 Đáp án: A. 2
Câu 31. Tập hợp các điểm trong m t phẳng phức biểu diễn các số z thỏa mãn đi u kiện:
z i  1 iz là đường tròn có bán kính là
A. R  1 .
B. R  2 . C. R  2 .
D. R  4 Hướng dẫn giải Gọi M  ;
x y  là điểm biểu diễn của số phức z x i ; y  , x y   trong m t phẳng phức
z i x   y  i x   y  2 2 1 1
 iz   ix iy  x yx yi   iz  x y2  x y2 1 1 1
Theo giả thiết, z i  1 iz nên ta có:
x   y  2   x y2   x y2 2 2 2 1
x y  2y 1  0 (*)
(*) là phương trình đường tròn tâm I 0;  1  bán kính 2 R  1    1  2
Chọn đáp án: C. R = 2 Trang 49
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 32. Cho hai số phức z 1 i và z  3
  5i . Môđun của số phức w z .z z 1 2 1 2 2 A. w  130 B. w  130 C. w  112 D. w  112 Hướng dẫn giải Ta có: z  3
  5i z .z  1i 3   5i  8   2i 2 1 2    Khi đó: w  
i w   2 2 11 3 11  3  130
Đáp án: A. w  130
Câu 33. Cho số phức z thỏa 1 iz 14  2i . Điểm biểu diễn của số phức z trong m t phẳng
tọa độ Oxy có tọa độ là: A. 6;8 . B. 8;6 . C.  8  ;6. D. 6; 8  . Hướng dẫn giải 14  2i
14 2i1i
Từ giả thiết 1 iz 14  2i suy ra z    6 8i 1 i 2 Gọi M  ;
x y  là điểm biểu diễn của z  6 8i trong mp tọa độ Oxy suy ra M 6; 8   . Đáp án: D. 6; 8  
Câu 34. Kí hiệu z , z lần lượt là hai nghiệm phức của phương trình 2
2z  2z  5  0 . Giá trị của 1 2 biểu thức 2 2
A z 1  z 1 bằng: 1 2 A. 25 . B. 5 . C. 5 . D. 2 5 . Hướng dẫn giải 1 3 1 3 Giải phương trình 2
2z  2z  5  0 tính được các nghiệm z
i; z   i 1 2 2 2 2 2 2 2 5 5
Tính A z 1  z 1    5 1 2 2 2 Đáp án: C. 5
Câu 35. Số các số phức z thỏa mãn: z  2 và 2
z là số thuần ảo là: A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải
Giả sử z a bi,a,b   Ta có: 2 2 2 2 z a b
2  a b  2 (1) 2 2 2
z a b  2abi là số thuần ảo nên 2 2
a b  0 (2) 2 2
a b  2
Từ (1) và (2) ta có hệ phương trình 2 2 
a b 1 2 2
a b  0
Vậy có 4 số phức thỏa yêu bài toán: z  1 ; i z  1 ; i z  1   ;i z  1   i 1 2 3 4 Đáp án: D. 4
Câu 36. Hình lập phương có bao nhiêu m t phẳng đối xứng? A. 4 . B. 7 . C. 8 . D. 9 . Hướng dẫn giải
Hình lập phương ABC .
D A' B'C ' D' có 9 m t đối xứng: 3 m t phẳng trung trực của ba cạnh
AB, AD, AA ' và 6 m t phẳng mà mỗi m t phẳng đi qua hai cạnh đối diện. Đáp án: D. 9 Trang 50
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 37. Cho H  là khối chóp tứ giác đ u có tất cả các cạnh bằng a . Thể tích của H  bằng 3 a 3 a 2 3 a 3 3 a 3 A. . B. . C. . D. . 3 6 4 2 S A B O a C Hướng dẫn g a iải D
Tính diện tích ABCD : 2 Sa ABCD
Xác định chi u cao : Gọi O AC  D
B SO là chi u cao của khối chóp 2  a 1
SOA vuông tại O cho ta 2 2 2 SO SA AO a   a 2 2 3 1 1 a 2 a 2 Vậy : 2 VS .SO  . .a SABCD 3 ABCD 3 2 6 3 a 2 Đáp án: B. 6
Câu 38. Một khối lăng trụ tam giác có các cạnh đáy bằng 13, 14 , 15, cạnh bên tạo với m t phẳng đáy một góc 0
30 và có chi u dài bằng 8 . Khi đó thể tích khối lăng trụ là A. 340. B. 336. C. 274 3 . D. 124 3 . Hướng dẫn giải Ta có : S
 21(2113)(2114)(2115)  84  ABC A' C'
Gọi O là hình chiếu của '
A trên  ABC B'
A' AO vuông tại O cho ta : 0
A'O AA'.sin 30  4 Vậy : V  84.4  336
ABC. A' B 'C '
Đáp án: B. 336 C A O a H
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm B
O , SA   ABCD . Biết thể
tích của S.ABCD bằng V . Tính thể tích khối OSCD theo V . V V 2V V A. . B. . C. . D. . 3 4 3 8 Hướng dẫn giải S 1 Ta có VS . A SV . S . ABCD 3 ABCD 1 1 Do SVV   S và . SA S OCD 4 ABCD OSCD S .BCD 3 BCD A D O B C Trang 51
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 40. Một hình trụ có bán kính đáy bằng 2 và có chi u cao bằng 4 . Thể tích của hình trụ bằng: A. 8 . B. 24 . C. 32 . D. 16 .Giải Hướng dẫn giải 2
V   R h   .4.4  16
Đáp án: D. 16
Câu 41. Thể tích của khối nón tròn xoay biết khoảng cách từ tâm của đáy đến đường sinh bằng
3 và thiết diện qua trục là một tam giác đ u là  3 8 3 4 3 2 3 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải S H A O B 3
Bán kính hình nón: R   2 , chi u cao hình nón: 0 h  . R tan 60  2 3 0 sin 60 2  R h 8 3 V   3 3 8 3 Đáp án: B. 3
Câu 42. Cho hình trụ có các đáy là 2 hình tròn tâm O và '
O , bán kính đáy bằng chi u cao và
bằng a . Trên đường tròn đáy tâm O lấy điểm A , trên đường tròn đáy tâm ' O lấy
điểm B sao cho AB  2a . Thể tích khối tứ diện '
OO AB theo a là 3 3 3 3 3 3 3 3 A. a V . B. a V . C. a V . D. a V . 8 6 12 4 Hướng dẫn giải Kẻ đường sinh '
A A Gọi D là điểm đối xứng với ' A qua '
O và H là hình chiếu của B trên đường thẳng ' A D .
Do BH A' D, BH AA'  BH  (AOO ' A') 2 2 2 2 A' B
AB A' A a 3  BD
A' D A' B a Trang 52
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 3 O' BD đ u nên  a BH 2 2 3  a 3 S
. Suy ra thể tích khối tứ diện OO’AB là:  a V AOO ' 2 12 3 3 Đáp án: C. a V 12
Câu 43. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB BC a 3 ,   90o SAB SCB
và khoảng cách từ A đến m t phẳng (SBC) bằng a 2 . Tính diện
tích m t cầu ngoại tiếp hình chóp S.ABC theo a . A. 2 S  3 a . B. 2 S  16 a . C. 2 S  2 a . D. 2 S  12 a . Hướng dẫn giải
Gọi D là hình chiếu vuông góc của S trên (ABC) AB S ,
A AB SD AB  (SAD)  AB AD
Tương tự CB  (SCD)  BC DC . Suy ra ABCD là hình vuông
Gọi H là hình chiếu của D trên SC DH  (SBC)  d( ,
A (SBC)  d( ,
D (SBC)  DH a 2 1 1 1    SD a 6 2 2 2 SD SH DC
Gọi I là trung điểm SB ta có IA IB IC IS nên I là tâm m t cầu. Suy ra bán kính m t cầu  SC r
a 3 . Diện tích m t cầu ngoại tiếp hình chóp S.ABC là: 2 2
S  4 r  12 a 2 Đáp án: D. 2 S  12 a
Câu 44. Trong không gian với hệ tọa độ Oxyz , m t phẳng (P) : 2x  2z z  2017  0 . Vectơ nào
dưới đây là một vectơ pháp tuyến của (P) ? A. n  1; 2  ;2 . B. n  1; 1  ;4 .
C. n  2; 2; 1 .
D. n  2; 2;1 . 2   3   1   4   Hướng dẫn giải
Một vectơ pháp tuyến của m t phẳng (P) là n  2; 2; 1 . 3  
Đáp án: C. n  2; 2; 1 3  
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho m t cầu 2 2 2
(S) : x y z  4x  4 y  6z  3  0 .
Tọa độ tâm I và tính bán kính R của (S ) . A. I 2;2; 3   và R  20 . B. I  4  ; 4
 ;6 và R  71 . C. I 4;4; 6   và R  71. D. I  2  ; 2
 ;3 và R  20 . Hướng dẫn giải
Tâm I của m t cầu  
S là I  2;2; 3   , bán kính là 2 2 2 R  2  2  ( 3  )  3  20 .
Đáp án: A. I 2;2; 3   và R  20
Câu 46. Trong không gian với hệ tọa độ Oxyz , đường thẳng d đi qua điểm ( A 1; 2;3) và vuông
góc với m t phẳng P : 2x  2z z  2017  0 có phương trình là x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   . 2 2 1 2 2 1 x  2 y  2 z 1 x  2 y  2 z 1 C.   . D.   . 1 2 3 1 2 3 Hướng dẫn giải Trang 53
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Vectơ chỉ phương của đường thẳng d là vectơ pháp tuyến của m t phẳng P nên u n
. Đường thẳng d đi qua (
A 1; 2;3) và có vectơ chỉ phương là u  (2; 2;1) nên có dP  (2; 2;1) d x 1 y  2 z  3
phương trình chính tắc là   . 2 2 1 x 1 y  2 z  3 Đáp án: B.   2 2 1
Câu 47. Trong không gian với hệ tọa độ Oxyz , m t phẳng (P) đi qua ba điểm ( A 1; 0; 0),
B(0; 2; 0), C(0;0;3) có phương trình là: x y z
A. x  2z  3z 1 0 . B.    0. 1 2 3 x y z
C. 6x  3z  2z  6  0 . D.    1. 3 2 1 Hướng dẫn giải
x y z 1 6x3z 2z 6  0 1 2 3
Đáp án: C. 6x  3z  2z  6  0
Câu 48. Gọi (S ) là m t cầu tâm I(2;1; 1
 ) và tiếp xúc với m t phẳng () có phương trình:
2x  2 y z  3  0 . Bán kính của (S ) bằng: 4 2 2 A. . B. . C. . D. 2 . 3 9 3 Hướng dẫn giải
Bán kính R của m t cầu (S ) chính là khoảng cách từ tâm I của m t cầu (S ) đến m t phẳng   : R d I         2.2 2.1 ( 1) 3 ;   2 2 2 2 2  ( 2)   ( 1  ) Đáp án: D. 2
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho điểm (
A 1; 2;3) và đường thẳng x 1 y z  3 d :  
. Viết phương trình đường thẳng  đi qua điểm A , vuông góc với 2 1 2 
đường thẳng d và cắt trục Ox x 1 y  2 z  3 x  2 y  2 z  3 A.   . B.   . 2 2 3 1 2 3 x 1 y  2 z  3 x  2 y  2 z  3 C.   . D.   . 2 2 3 1 2 3 Hướng dẫn giải
Gọi B là giao điểm của đường thẳng  và trục Ox . Khi đó B  ; b 0; 0
Vì  vuông góc với đường thẳng d nên AB u ( với AB  (b 1; 2; 3) , u  ) d 2;1;2 d Suy ra A .
B u  0  b  1  d Do đó AB  ( 2
 ;2;3) . Chọn vectơ chỉ phương cho đường thẳng  là u  2;2;3  . x 1 y  2 z  3
Phương trình đường thẳng  là   . 2 2 3 x 1 y  2 z  3 Đáp án: A.   2 2 3 Trang 54
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai x y z Câu 50. 1 2
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và điểm 2 1 2 (
A 2;5;3) . Phương trình m t phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là
lớn nhất có phương trình
A. x  4 y z  3  0 .
B. x  4 y z  3  0 .
C. x  4 y z  3  0 .
D. x  4 y z  3  0 . Hướng dẫn giải
Gọi H là hình chiếu vuông góc của A trên d . Khi đó H 1 2t;t;2  2t  .
Ta có AH u (với AH  2t 1;t  5; 2t   1 , u
) Nên AH.u  0  t 1 d 2;1;2 d d Suy ra AH  1; 4  ;  1 , H 3;1; 4
M t phẳng (P) chứa d và khoảng cách từ A đến (P) lớn nhất khi (P) đi qua H 3;1;4 và nhận vectơ AH  1; 4  ; 
1 làm vectơ pháp tuyến. Phương trình m t phẳng (P) là
1. x  3  4. y  
1 1. z  4  0  x  4y z  3  0
Đáp án: D. x  4 y z  3  0
----------- HẾT ---------- Trang 55
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CHẤT LƯỢNG HK 2 - NĂM 2017 TỈNH ĐỒNG NAI
Môn: TOÁN – Khối 12 Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97 NỘI DUNG ĐỀ SỐ 05 Câu 1. Cho hàm số 3 2
y x  3x  2 . Chọn câu trả lời đúng:
A. Hàm số đồng biến trên tập 0; .
B. Hàm số đồng biến trên khoảng 0; 2.
C. Hàm số đồng biến trên tập  ;  2.
D. Hàm số đồng biến trên các khoảng  ;  0;2;. Câu 2. Cho hàm số 3 2
y x  3x mx m . Tìm tất cả giá trị m để hàm số luôn đồng biến. Kết quả là
A. m  3 .
B. m  3 .
C. m  3 .
D. m  3 .
Câu 3. Tìm m để phương trình 3 2
x  3x  2  m 1 có 3 nghiệm phân biệt ? A. 2   m  0 . B. 3   m 1.
C. 2  m  4 .
D. 0  m  3.Câu 4. x 1
Hệ số góc của tiếp tuyến của đồ thì hàm số y
tại giao điểm của đồ thị hàm số với x 1 trục tung bằng  A. 2  . B. 2 . C. 1 . D. 1 .  Câu 5. x 1
Tìm M trên  H  : y
sao cho tiếp tuyến tại M vuông góc với d : y x  2017 x  3
A. M 1;  1 , M 2; 3  .
B. M 5;3 , M 2; 3  .
C. M 5;3 , M 1;  1 .
D. M 1; 
1 , M 4;5 .   Câu 6. x 2
Cho hàm số y
. Các đường tiệm cận của đồ thị hàm số là x 1
A. Tiệm cận đứng x 1, tiệm cận ngang y  1 .
B. Tiệm cận đứng x  1
 , tiệm cận ngang y  1.
C. Tiệm cận đứng y  1, tiệm cận ngang x  1  .
D. Tiệm cận đứng x  1
 , tiệm cận ngang y 1.  Câu 7. 5x 3
Cho hàm số y
với m là tham số. Đồ thị hàm số đã cho không có tiệm cận 2 x  2mx 1 đứng khi A. m  1  .
B. m 1.
C. m  1; m  1  . D. 1   m 1. Câu 8. x
Cho hàm số f x 4 2 
 2x  6 . Giá trị cực đại của hàm số là 4 A. f  6 . B. f  2 . C. f  20 . D. f  6  . CÐ CÐ CÐ CÐ Câu 9.  2  Cho hàm số 3 2
y x mx m x  5  
. Tìm m để hàm số đạt cực tiểu tại x 1  3  2 7 3 A. m . B. m . C. m .
D. m  0. 5 3 7 Câu 10. 4
Giá lớn nhất của hàm số y  là 2 x  2 A. 3 . B. 2 . C. 5  . D. 10 . Trang 56
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 11. Đồ thị hình bên là đồ thị của hàm số nào ? A. 4 2
y  x  2x  3 . B. 4 2
y  x  2x . C. 4 2
y x  2x . D. 4 2
y x  2x  3 .
Câu 12. Giá trị log 36  log 144 bằng 2 2 A. 4  . B. 2  . C. 2 . D. 4 .
Câu 13. Cho log x  log y . Chọn khẳng định đúng? 0,2 0,2
A. y x  0 .
B. x y  0 .
C. x y  0 .
D. y x  0 .
Câu 14. Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn một quý với
lãi suất 1, 65% một quý. Hỏi sau bao nhiêu quý thì người đó có được ít nhất 20 triệu ? A. 15. B. 18. C. 17 . D. 16 . 2 4 Câu 15. 7 4
Cho a, b là hai số thực dương khác 1 thỏa: 3 5 a a ; log  log . Khi đó khẳng định b 5 b 3 nào sau đây là đúng ?
A. 0  a  1;b  1.
B. a  1;b  1.
C. 0  a  1;0  b  1 .
D. a  1;0  b  1.
Câu 16. Khẳng định nào đúng ? A. 2 2 2
log a  2 log a . B. 2 2 2
log a  4 log a . 3 3 3 3 C. 2 2 2
log a  4 log a . D. 2 2 2
log a  2 log a . 3 3 3 3 x2 Câu 17.x  1 Phương trình sau 1 5  5.  26  
có nghiệm x và x thì tổng x x là  1 2 1 2 5  A. 4 . B. 3 . C. 2 D. 1. 4 x 2x Câu 18.  2   3 
Bất phương trình sau      có nghiệm là  3   2  2 2 2 2 A. x  . B. x   . C. x  . D. x  . 3 3 5 5
Câu 19. Nghiệm của phương trình log x  975 10 là 2   A. 1998. B. 2000 . C. 1999 . D. 1997 .
Câu 20. Phương trình:  2
log x  7x 12  log2x 8 có bao nhiêu nghiệm ? A. 0 . B. 1. C. 2 . D. 4 .
Câu 21. Bất phương trình sau log 3x  2  0có nghiệm là 2   A. 1 x .
B. log 2  x  1.
C. 0  x 1.
D. x  log 2 . 3 3
Câu 22. Cho hình chóp S.ABC , A', B ' lần lượt là trung điểm S , A S .
B Tỉ số thể tích giữa hai khối
chóp S.A' B'C và S.ABC bằng Trang 57
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 1 1 1 1 A. . B. . C. . D. . 2 4 6 8
Câu 23. Thể tích khối lăng trụ tam giác đ u có tất cả các cạnh bằng a là 3 2a 3 2a 3 3a 3 3a A. . B. . C. . D. . 3 4 2 4
Câu 24. Cho khối chóp S.ABC có SA   ABC, tam giác ABC vuông tại B , AB  , a AC a 3.
Tính thể tích khối chóp S.ABC biết rằng SB a 5 . 3 a 2 3 a 6 3 a 6 3 a 15 A. . B. . C. . D. . 3 4 6 6
Câu 25. Cho khối chóp S.ABC có đáy ABC là tam giác đ u cạnh a . Hai m t bên SAB và
SAC cùng vuông góc với đáy. Tính thể tích khối chóp biết SC a 3 . 3 2a 6 3 a 6 3 a 3 3 a 3 A. . B. . C. . D. . 9 12 4 2
Câu 26. Gọi l, ,
h R lần lượt là độ dài đường sinh, chi u cao và bán kính đáy của hình trụ T  .
Diện tích toàn phần S của hình trụ T  là tp A. 2
S  2 Rl  2 R . B. 2
S   Rl   R . C. 2
S   Rl  2 R . D. 2
S   Rh   R . tp tp tp tp
Câu 27. Cho hình nón có bán kính đáy là 4a , chi u cao là 3a . Diện tích toàn phần hình nón bằng A. 2 36 a . B. 2 30 a . C. 2 38 a . D. 2 32 a . 2  Câu 28. 8 a
Cho m t cầu có diện tích bằng
. Khi đó, bán kính m t cầu bằng 3 a 6 a 3 a 6 a 2 A. . B. . C. . D. . 3 3 2 3
Câu 29. Cho tứ diện đ u ABCD cạnh a . Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng 3  a 6 3  a 6 3  a 6 3 3 a 6 A. . B. . C. . D. . 8 6 4 8
Câu 30. Nguyên hàm của hàm số f x 2  tan x là
A. tan x C .
B. tan x x C .
C. 2tan x C .
D. tan x x C .
Câu 31. Nguyên hàm F x của hàm số f x 3 2
 4x 3x  2x  2 thỏa mãn F   1  9 là
A. f x 4 3 2
x x x  2 .
B. f x 4 3 2
x x x 10 .
C. f x 4 3 2
x x x  2x .
D. f x 4 3 2
x x x  2x 10. 1 Câu 32. 4
Tính tích phân I x   2
1 x  dx . 0 31 30 31 32 A. . B. . C. . D. . 10 10 10 10  2
Câu 33. Đổi biến u  sinx thì tích phân 4 sin x cos d x x  thành 0   1 2 1 2 A. 4 2 u 1 u du . B. 4 u du. C. 4 u du. D. 3 2 u 1 u du. 0 0 0 0
Câu 34. Viết công thức tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số y f x , 1   y f
x và các đường thẳng x a, x b a b . 2   Trang 58
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai b b A. S f x f x dx
B. S   f x f x dx . 2   1  1   2   a . a b b
C. S   f x f x dx . D. S f x f x dx 1   2   1   2   a a . Câu 35.  
Tính diện tích hình phẳng giới hạn bởi đường thẳng y
2x 1 và đồ thị hàm số 2
y x x  3 1 1 1 1 A. . B. . C. . D. . 6 6 7 8
Câu 36. Cho hình phẳng giới hạn bởi dường cong y  tan x , trục hoành và hai đường thẳng  x  0, x
. Tính thể tích V khối tròn xoay thu được khi quay hình phẳng này xung 4 quanh trục Ox .       A. V      1   . B. V  1  . C. V     1    . D. V     2    .  4   4   4   4  Câu 37. Cho (
A 2;3; 0) và B(1; 2;1) . Gọi I  ; a ;
b c là trung điểm của .
AB Giá trị của biểu thức
2b a c bằng A. 3 . B. 2  . C. 0 . D. 1.
Câu 38. M t cầu tâm I 0;1;2, tiếp xúc với m t phẳng P : x y z – 6  0 có phương trình là A. 2 2
x   y  2   z  2 2 1 2  4 . B. 2
x   y  
1   z  2  4. C. 2 2
x   y  2   z  2 2 1 2 1. D. 2
x   y  
1   z  2  3 .
Câu 39. Cho điểm M –3;2;4, gọi ,
A B, C lần lượt là hình chiếu của M trên Ox,Oy,O . z M t
phẳng song song với  ABC  có phương trình là
A. 4x – 6 y – 3z 12  0 .
B. 3x – 6 y – 4z 12  0 .
C. 6x – 4 y – 3z –12  0 .
D. 4x – 6 y – 3z –12  0 .   Câu 40. x 1 y z 1
M t phẳng P đi qua điểm A1;2;0 và vuông góc với đường thẳng d :   2 1 1  có phương trình là
A. 2x y – z  4  0 .
B. –2x – y z  4  0 .
C. –2x – yz – 4  0 .
D. x  2 y – 5  0 .
Câu 41. Hình chiếu vuông góc của điểm A0;1;2 trên m t phẳng P : x y z  0 có tọa độ là
A. –2;2;0 .
B. –2;0;2 .
C. –1;1;0 . D. –1;0;  1 .
Câu 42. Côsin của góc giữa Oy và m t phẳng P : 4x  3y  2z  7  0 là 2 1 2 4 A. . B. . C. . D. . 3 3 3 3      Câu 43. x 7 y 5 z 9 x y 4 z 18 Cho d :   và d :  
. Chọn câu trả lời đúng 2  1  3 1  4  3  1 4
A.d , d song song.
B.d , d trùng nhau. 1   2  1   2 
C.d , d cắt nhau .
D.d , d chéo nhau. 1   2  1   2 
Câu 44. Cho m t cầu S  2 2 2
: x y z  4x  2y  6z  5  0 và P : 2x  2y z 16  0 . Điểm M di
động trên S  , N di động trên P . Độ dài ngắn nhất của MN là A. 5 . B. 4 . C. 3 . D. 2 . Trang 59
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 45. Cho số phức z  2  i1i 1 3i . Môđun của z là A. 2 5 . B. 2 2 . C. 13 . D. 4 2 .
Câu 46. Cho số phức z thỏa mãn:   iz  iz    i2 2 3 4 1 3
. Xác định phần thực và phần ảo của z . A. Phần thực 2  ; Phần ảo 5i . B. Phần thực 2  ; Phần ảo 5 . C. Phần thực 2  ; Phần ảo 3 . D. Phần thực 3  ; Phần ảo 5i .
Câu 47. Trong mp tọa độ Oxy , tìm tập hợp điểm biểu diễn các số phức z thỏa mãn z i  1 iz .
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I 2;  
1 , bán kính R  2 .
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I 0 
;1 , bán kính R  3 .
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I 0;  
1 , bán kính R  3 .
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I 0;  
1 , bán kính R  2 .
Câu 48. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Tính giá trị của biểu 1 2 thức 2 2
A  | z |  | z | . 1 2 A. 15. B. 17 . C. 19 . D. 20 . Câu 49. 2 20
Số phức 1 1 i  1 i ... 1 i có giá trị bằng A. 10 2  . B. 10    10 2 2   1 i . C. 10   10 2 2   1 i . D. 10 10 2  2 i .
Câu 50. Số phức z thỏa mãn iz  2i  0 có phần thực bằng A. 1. B. 2 . C. 3 . D. 4 . ----------- 1 2 3 4 5 6 7 8 9 10 D D B B C A D A B B 11 12 13 14 15 16 17 18 19 20 C B D B B D C B C B 21 22 23 24 25 26 27 28 29 30 B B D A B A A A A B 31 32 33 34 35 36 37 38 39 40 D C C A B C A D D B 41 42 43 44 45 46 47 48 49 50 D A A D A A D D B A Hướng dẫn giải Câu 1. Chọn D.x  0 Ta có 2
y '  3x  6 . x y '  0  .  x  2 Bảng biến thiên Trang 60
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Câu 2. Chọn D. Ta có 2
y '  3x  6x m . Hàm số luôn đồng biến 2
y '  3x  6x m  0 x   3   0 Suy ra    m  3.
 '  9  3m  0 Câu 3. Chọn B. Phương trình 3 2 3 2
x  3x  2  m 1  x  3x  m  3  0. Đ t f x 3 2
x  3x m 3 C. x  
Suy ra f x 2 '
 3x  6x . f x 2 '  0   . x  0
Phương trình có 3 nghiệm phân biệt  Đồ thị C có hai cực trị thỏa f x . f x  0 . D C   CT   f  2
  f 0  0  1 m 3
  m  0  3   x 1. Câu 4. Chọn B. 2
Ta có f ' x   
Giao điểm của đồ thị và trục tung là M 0; 1. x   . 2 1
Hệ số góc cần tìm k f '0  2. Câu 5. Chọn C.  4  Giả sử M a;1    H   a  3  . 4  4 
Ta có y '  f ' x    
H tại M có hệ số góc k f 'a . x  . Tiếp tuyến của   32 a  32
Tiếp tuyến của  H  tại M vuông góc với d : y x  2017 suy ra 4 a  5       k.1 1   a  3 1 . 2 a  1 M 5;3 , M 1; 1  . 1   2  
Vậy hai điểm cần tìm là Câu 6. Chọn A. Câu 7. Chọn D.
Hàm số không có tiệm cận đứng khi 2
x  2mx 1vô nghiệm ho c có nghiệm kép bằng 3 . Suy ra 2 m 1  0  1   m  1. 5 Câu 8. Chọn A.
Ta có f x 3 '  x  2 .
x f ' x  0  x  0  x   2  x  2.
Dựa vào dạng đồ thị suy ra hàm số đạt cực đại tại x  0 . Vậy ff 0  6. D C   Câu 9. Chọn B. Trang 61
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 2
Ta có f ' x 2
 3x  2mx m  . Hàm số đ t cực tiểu tại x 1 suy ra f   7 ' 1  0  m  . 3 3
Nếu làm tự luận thì đến đây phải thử lại. Tuy nhiên, trong trường hợp này thì vì chỉ ra
một kết quả m nên ta chọn luôn đáp án,
Câu 10. Chọn B.
Câu 11. Chọn C.
Dựa vào dạng đồ thị suy ra hệ số a  0 . Do đó đáp án A và B bị loại. Đồ thị đi qua gốc
tọa độ O 0;0 . Mà tọa độ điểm O không thỏa đồ thị của hàm số ở đáp án D.
Câu 12. Chọn B.
Câu 13. Chọn D.
Câu 14. Chọn B.
Số ti n nhận được sau x
x quý là 15.1,0165 . x 20
Ta có bpt 15.1,0165  20  x  log  x 17,58. 1,0165 15
Suy ra người đó phải gởi ít nhất 18 quý.
Câu 15. Chọn B.
Câu 16. Chọn D.
Câu 17. Chọn C. Đ t 5x t
. Phương trình trở thành 2
5t 130t 125  0  t  25  t  1.
Suy ra x  2  x  0. Vậy tổng 2 nghiệm là 2. 1 2
Câu 18. Chọn B. 4 x 2x 4 x x2  2   3   2   2  2 Bất phương trình :   
 4x x  2  x   .          3   2   3   3  3 Câu 19. Chọn C.
Phương trình log  x  975 10
10  x 975  2  x 1999. 2
Câu 20. Chọn B. 2x 8  0 Phương trình log  2
x  7x 12  log 2x 8    x  5. 2
x  9x  20  0
Vậy phương trình có 1 nghiệm
Câu 21. Chọn B.
Bất phương trình log 3x  2  0  0  3x  2 1  2  3x  3  log 2  x 1. 2   3
Câu 22. Chọn B. V SA '.SB ' 1
Ta có S.A'B'C   . V S . A SB 4 S . ABC
Câu 23. Chọn D. 3 3 Ta có 2 3 V  . h B  . a aa . 4 4
Câu 24. Chọn A. 2 1 a 2 Ta có: 2 2 BC
AC AB a 2  S  . AB BC  . ABC 2 2 2 3 1 1 a 2 a 2 2 2 SA
SB AB  2a V  . SA S  .2 . a  . 3 ABC 3 2 3
Câu 25. Chọn B. Trang 62
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
(SAB)   ABC  Ta có 
SAC   ABC
SA   ABC.   SAB
SAC  SA Suy ra S
AC vuông tại A. Do đó 2 2
SA SC AC a 2. 2 3 1 1 a 3 a 6 Vậy V S . A Sa 2.  . 3 ABC 3 4 12
Câu 26: Chọn A.
Công thức tính diện tích toàn phần hình trụ: 2
S  2 Rl  2 R tp
Câu 27: Chọn A. Đường sinh 2 2
l R h  5a 2 2 2
S   Rl   R  .4a .5a 16a  36 a tp
Câu 28: Chọn A. 2 8 a a 6 2 S  4 R   R mc 3 3
Câu 29: Chọn A. A A a 2 H H a 6 3 a I I B D G F B G a 3 3 C
Gọi G là trọng tâm BCD.
Ta có I là giao điểm của đường trung trực AB và AG . a 3 2 a 3 a 6 Ta có 2 2 BF  ; BG BF  ; AG AB BG  2 3 3 3 a .a AH AGAH.AB a 6 suy ra 2 AI    AI AB AG a 6 4 3 3 4  a 6  a 6 V        3 4 8  
Câu 30: Chọn B.  1  2 tan xdx    2 1 tan x   1 dx
x dx  tan x x C   2  cos x
Câu 31: Chọn D. F x 4 3 2
x x x  2x C F  
1  C 1  9  C 10
Câu 32: Chọn C. Đ t 2
t  1 x dt  2xdx Trang 63
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 2 2 5 dt 1 t 31 4 I t    2 2 5 10 1 1
Câu 33: Chọn C.
u  sin x du  cos xdx 1 4 I u du  0
Câu 34: Chọn A. Công thức tính
Câu 35: Chọn B. 2 S   1 2
x x  3  2x   1 dx   6 1
Câu 36: Chọn C.  4  2 V  tan xdx      1     4  0
Câu 37: Chọn A.  3 5 1  Trung điểm I ; ;    2 2 2 
2b a c  3
Câu 38: Chọn D.
R d I P 3 ;   3 3
Câu 39: Chọn D. A 3
 ;0;0, B0;2;0,C 0;0;4   x y z ABC :
   1  4x  6y  3z 12  0 3  2 4
Câu 40: Chọn B.
P có vtpt n u   d 2;1;  1 P PTTQ: 2 x  
1   y  2   z  0  0  2x y z  4  0
Câu 41: Chọn D.
Gọi d là đường thẳng qua A và vuông góc với P
d có vtcp u n  1;1  ;1 d Px tx t   y 1 t
PTTS d :  y  1 t . Xét hệ:   z  2  tz  2  t
x y z  0
Suy ra t 1t  2 t  0  t  1  . Suy ra H  1  ;0;  1
Câu 42: Chọn A.
Oy có vtcp j  0;1;0
P có vtpt n  4;3; 2 P    
Oy P   j n  .jn 3 3 sin , cos , P    P j . n 3 3 3 P Trang 64
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
cos Oy, P 6 2
 1 sin Oy,P  3
Câu 43: Chọn A.
u ,u   0 1 2  
u ,MN   9  ; 5  3; 2  0 1    
Câu 44: Chọn D.
M t cầu có tâm I 2; 1
 ;3 , bán kính r  3   
d I P 4 2 3 16 ,   5 4  4 1
ngắn nhất khi I , M , N thẳng hàng và M nằm giữa I , N
Khoảng cách ngắn nhất là h d I,P  r  2
Câu 45: Chọn A. z  4  2i 2 2 z  4  2  2 5
Câu 46: Chọn A.
Gọi z a bi,a,b R
  ia bi ia bi    i2 2 3 4 1 3
6a  4b 2
a  2bi  86i
6a  4b  8 a  2      2
a  2b  6  b   5
Câu 47: Chọn D.
Gọi z a bi,a,b R
z i  1 iz
a  b  
1 i  a b  a bi
a  b  2 1
 a b2  a b2 2 2 2
a b  2b 1  0
 a  2  b  2 0 1
 2 là phương trình đường tròn tâm I 0;  1 , bán kính 2
Câu 48: Chọn D. z  1 3i 1 z  1 3i 2
A   2     2   2 2 1 3 1 3   20
Câu 49: Chọn B.
 i2  i
 i3    i  i4 1 2 ; 1 2 2 ; 1  4 
   i    i2    i3 1 1 1 1
11 i  2i  2  2i  5i 4 2 3 8 2 3 2 1 i 1
  1i 1i  1i   4  5i           
1 i 1 1 i 1 i 1 i   4   5i  
 i12   i i2    i3   3 1 1 1 1 1 4 5i  
 i16   i i2    i3   4 1 1 1 1 1 4 5i   Trang 65
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
 i   i 5 20 4    5 1 1 4   2 20 2 3 4 5
1 (1 i)  (1 i)  ...  (1 i) = 5i  4.5i   4   5i  4   5i  4   5i  4    1  024 1025i
Câu 50: Chọn A. i  2 z
 1 2i phần thực là 1. i Trang 66
Tài liệu ôn thi HK2 – Khối 12
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
ĐỀ THI THỬ SỐ 01 Môn: TOÁN Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 01 x2 x 1 mx Câu 1. Đồ thị h|m số y
có đường tiệm cận đứng khi x 1 A. m 0 . B. m R. C. m 1. D. m 1 . Câu 2. Cho h|m số y
f x có bảng biến thiên: x 1 y ' 0 1 1 y
Kết luận n|o sau đ}y đầy đủ về đường tiệm cận của đồ thị h|m số ? 2
A. Đồ thị h|m số y
f x có đường tiệm cận ngang y 1.
B. Đồ thị h|m số y
f x có đường tiệm cận ngang y 1.
C. Đồ thị h|m số y
f x có đường tiệm cận ngang y
1, tiệm cận đứng x 1.
D. Đồ thị h|m số y
f x có đường tiệm cận ngang y
1, tiệm cận đứng x 1. 1 5 Câu 3.
Khoảng nghịch biến của h|m số 3 2 y x x 3x là: 3 3 A. ; 1 . B. 1;3 . C. 3; . D. ; 1 và 3; . Câu 4. Cho h|m số y
f x liên tục tại x v| có bảng biến thiên: 0 x x x x 0 1 2 y ' 0 y
Khi đó h|m số đã cho có:
A. Hai điểm cực đại, một điểm cực tiểu.
B. Một điểm cực đại, không có điểm cực tiểu.
C. Một điểm cực đại, hai điểm cực tiểu.
D. Một điểm cực đại, một điểm cực tiểu. 2 Câu 5.
Gi{ trị nhỏ nhất của h|m số 2 y x với x 0 bằng: x A. 4. B. 3. C. 1. D. 2. Câu 6. H|m số 2 y x 2x 1 có bao nhiêu cực trị? A. 0. B. 1. C.2. D. 3. Câu 7. Cho h|m số 2 y x 1 x mx
m . Tìm m để đồ thị h|m số cắt trục ho|nh tại ba điểm ph}n biệt. Trang 67
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 1 1 m 0 A. m 4. B. m 0. C. 0 m 4. D. 2 . 2 m 4 2 Câu 8. H|m số 3 2 y ax ax
1 có điểm cực tiểu x
khi điều kiện của a : 3 A. a 0 . B. a 0 . C. a 2 . D. a 0 . x 2 Câu 9.
Cho đường cong C : y
. Điểm n|o dưới đ}y l| giao của hai tiệm cận của C ? x 2 A. L 2;2 . B. M 2;1 . C. N 2; 2 . D. K 2;1 .
Câu 10. Một miếng bìa hình chữ nhật có độ d|i c{c cạnh l| a, b . Hỏi phải tăng cạnh n|y v|
bớt cạnh kia một đoạn bao nhiêu để diện tích hình chữ nhật l| lớn nhất? a b a b a A. . B. . C. ab . D. . 2 2 b sin x m
Câu 11. Tìm tất cả gi{ trị thực của m để h|m số y
nghịch biến trong khoảng sin x 1 ; . 2 A. m 1. B. m 1. C. m 1. D. m 1.
Câu 12. Phương trình 2 log x 2 log 4x 4
0 có hai nghiệm lần lượt l| x , x . Tính tích 2 4 1 2 x .x . 1 2 1 33 A. 8 . B. 2 . C. . D. . 4 4 Câu 13. Cho h|m số .5x f x x . Phương trình 25x ' .5x f x x .ln 5 2 0 có nghiệm: x 0 x 1 A. x 0 . B. x 2 . C. . D. . x 2 x 2
Câu 14. Tập nghiệm của bất phương trình log x log x 1 1 là: 3 3 1 13 1 13 1 13 A. S ; . B. S ; ; . 2 2 2 1 13 1 13 1 13 C. S ; . D. S ; . 2 2 2
Câu 15. Tập x{c định của h|m số 2 y x 1 log x 4 là: 2 A. ;0 . B. 1; . C. . D. 2; . 2
Câu 16. Tập x{c định của h|m số 2 3 y 4 x là: A. D 2;2 . B. D \ 2 . C. D . D. D 2; . a log 7 Câu 17. Cho ,
a b l| hai số thực thỏa mãn điều kiện 12 log 7 . Khi đó 2 2 a b bằng: 2 1 b log 6 12 5 A. 2 . B. 5 . C. 8 . D. . 4 Trang 68
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 18. Tính đạo h|m của h|m số 4x y .ln x . x 1 x 1 A. 2 y ' 4 ln x . B. y ' 4 ln x . x x x 1 x 1 C. y ' 4 ln x.ln 4 . D. y ' 4 .ln x . x x
Câu 19. Đặt a log 2 và b
log 5. Hãy biểu diễn log 45 theo a và b . 3 2 10 2a b 2 ab A. log 45 . B. log 45 . 10 2 a b 1 b 10 a ab 2b b 2 ab C. log 45 . D. log 45 . 10 2 b a 1 b 10 b ab
Câu 20. Cho ba số thực dương a, ,
b c với a
1. Khẳng định n|o sau đ}y l| khẳng định sai ? A. a 1 thì log b log c b c . B. log bc log b log c . a a a a a b C. log log b log c . D. a 1 thì log b 0 b 1 . a a a c a
Câu 21. Năm 2001 d}n số Việt Nam v|o khoảng 78685800 người v| tỉ lệ tăng d}n số năm đó
là 1, 7% v| sự tăng d}n số được ước tính theo công thức . Nr S
Ae . Hỏi cứ tăng d}n số
như vậy thì sau bao nhiêu năm thì d}n số nước ta sẽ l| 100 triệu d}n ? A. 14 . B. 15 . C. 16 . D. 20 .
Câu 22. Cho hình phẳng D giới hạn bởi c{c đường y x
1 ; trục Ox v| đường thẳng x
3 . Thể tích của khối tròn xoay sinh ra khi D xoay quanh trục Ox là:
A. 2 . B. 3 . C. . D. 4 .
Câu 23. Họ nguyên h|m của h|m số 2 f x sin x là: x 1 x 1 A. F x sin 2x C . B. F x sin 2x C . 2 4 2 4 x 1 x 1 C. F x sin 2x C . D. F x cos 2x C . 2 2 2 2 m 3 15 Câu 24. Cho 2 x x 1 dx
. Gi{ trị của tham số m là: 8 0 A. m 2. B. m 1. C. m 3 . D. m 2 .
Câu 25. Cho h|m số f x có đạo h|m trên
, f 2016  a và f 2017  ; b  ; a b  . Gi{ trị 2016 I  2015 f   x 2014 fxdx là 2017 A. 2015 2015 I ba . B. 2017 2017 I ba . C. 2015 2015 I ab . D. 2016 2016 I ab . 2
Câu 26. Cho tích phân 2 I x sin x 2m dx 1
. Gi{ trị của tham số m là: 0 A. 5 . B. 3. C. 4. D. 6.
Câu 27. Cho hình phẳng D giới hạn bởi c{c đường y
x ; trục Ox v| đường thẳng x 2 .
Diện tích hình phẳng D là: 3 A. . B. 1 . C. 2 . D. 3 . 2 Trang 69
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 28. Một ông thợ có một khối gỗ hình cầu, để sử dụng khối gỗ người thợ đã cắt miếng gỗ
bằng một mặt phẳng, sao cho khoảng c{ch từ t}m đến mặt phẳng bằng một nửa b{n
kính. Tỷ số thể tích của hai khối gỗ mới ( khối gỗ lớn chia cho khối gỗ nhỏ ) l|: 5 27 11 22 A. . B. . C. . D. . 27 5 25 5
Câu 29. Cho số phức z 2
3i số phức nghịch đảo của z là: 2 3 2 3 3 2 3 2 A. i . B. i . C. i . D. i . 13 13 13 13 13 13 13 13
Câu 30. Cho số phức z 1
3i , môđun của số phức w z 1 i 2i là: A. 2 . B. 2 . C. 2 2 . D. 1 .
Câu 31. Một tấm kim loại được khoan thủng bốn lỗ như hình (lỗ khoan dạng hình trụ), tấm
kim loại d|y 2 cm, đ{y của nó l| hình vuông có cạnh 5cm. Đường kính của mủi khoan
l| 8mm. Hỏi thể tích phần còn lại của tấm kim loại l| bao nhiêu? (Kết quả l|m tròn 2
chữ số thập ph}n sau dấu phẩy) 8 mm 2 cm 5 cm A. 45,96 cm2 B. 45,97 cm2 C. 45,99 cm2 D. 45,98 cm2
Câu 32. Trong c{c số phức thỏa mãn điều kiện z i z
3 . Số phức có môđun nhỏ nhất l|: 6 2 7 2 1 2 3 4 A. z i . B. z i . C. z i . D. z i . 5 5 5 5 5 5 5 5
Câu 33. Gọi z l| nghiệm phức có phần ảo }m của phương trình 2 z 4z 20 0 . Khi đó gi{ 1 2 trị biểu thức 2 2 A z 2 z z bằng: 1 1 2 A. 0 . B. 2 . C. 28 . D. 16 .
Câu 34. Trong mặt phẳng phức với hệ tọa độ Oxy , tập hợp c{c điểm biểu diễn số phức z thỏa
mãn điều kiện z l| số ảo l|: A. Trục ảo.
B. Trục thực v| trục ảo.
C. Đường ph}n gi{c góc phần tư thứ nhất v| thứ ba.
D. Hai đường ph}n gi{c của c{c gốc tọa độ.
Câu 35. Cho hình chóp tứ gi{c đều H có diện tích đ{y bằng 4 v| diện tích của một mặt bên
bằng 2 . Thể tích của H là: 4 3 4 4 2 A. . B. 4 . C. . D. . 3 3 3
Câu 36. Cho khối hình hộp chữ nhật ABC .
D A'B 'C 'D ' có tỷ lệ giữa chiều d|i, chiều rộng,
chiều cao l| 5 : 3 : 1. Đường chéo AC '
35 . Thể tích của khối chữ nhật l|: Trang 70
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. 5 . B. 3 . C. 10 . D. 15 .
Câu 37. Cho khối chóp S.ABC có thể tích bằng V . Gọi M, N, I lần lượt l| trung điểm của ,
SB SC , BC . Khi đó thể tích của khối đa diện IMNA tính theo V là: V V V 2V A. . B. . C. . D. . 4 2 3 3
Câu 38. Cho hình chóp S.ABCD có đ{y l| hình vuông cạnh a ; SA vuông góc với đ{y; SB hợp với đ{y góc 0
45 . Khoảng c{ch từ điểm C đến mặt phẳng SBD bằng: a a A. a . B. a 3 . C. . D. . 3 2
Câu 39. Cho hình chóp S.ABC có đ{y ABC l| tam gi{c vuông tại A , ABC 60 , tam giác
SBC l| tam gi{c đều có bằng cạnh 2a v| nằm trong mặt phẳng vuông với đ{y. Tính
góc giữa đường thẳng SA v| mặt phẳng đ{y ABC : A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 40. Cho khối cầu S , cắt S bởi một mặt phẳng tạo ra thiết diện T một hình tròn có 1
diện tích bẳng diện tích hình tròn lớn. Biết chu vi của S là 3 . Thể tích của S là: 4 A. 25 . B. 36 . C. 64 . D. 32 .
Câu 41. B{n kính đ{y hình trụ bằng 4cm , chiều cao bằng 6cm . Độ d|i đường chéo của thiết diện qua trục bằng: A. 10cm. B. 6cm. C. 5cm. D. 8cm.
Câu 42. Trong không gian, cho tam giác ABC vuông tại A có AB 3a và AC 4a . Tính độ
d|i đường sinh của hình nón, khi quay tam giác ABC xunh quanh trục AB : A. a . B. 5a . C. a 5 . D. a 3 .
Câu 43. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P :2x y z 3 0 . Đường
thẳng n|o sau đ}y vuông góc với P ? x 1 3t x 4 t A. y 2 t . B. y 2 t . z t z 3t x y z 2 x y 3 z 1 C. . D. . 1 1 1 2 1 1
Câu 44. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A 2; 1; 3 , B 10;5;3 và M 2m 1;2;n 2 . Để , A ,
B M thẳng h|ng thì gi{ trị của ,
m n là: 3 3 A. m 1; n . B.m ; n 1. 2 2 3 2 3 C.m 1; n . D.m ; n . 2 3 2
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho ba điểm M 2;0;0 , N 0; 3;0 , P 0;0;4 . Nếu
MNPQ l| hình bình th|nh thì tọa độ của điểm Q là: A. 2; 3;4 . B. 3; 4;2 . C. 2; 3; 4 . D. 2; 3; 4 . Trang 71
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 46. Trong không gian với hệ tọa độ Oxyz , cho bốn điểm A 1; 2; 0 , B 1; 0; 1 , C 0; 1;2 và D 0; ;
m p . Hệ thức giữa m và p để bốn điểm , A ,
B C, D đồng phẳng l|: A. 2m p 0 . B. m p 1 . C. m 2p 3 . D. 2m 3p 0 .
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD với A 1; 2;4 , B
4; 2;0 , C 3; 2;1 và D 1;1;1 . Độ d|i đường cao của tứ diện ABCD kẻ từ đỉnh D bằng: 1 A. 3 . B. 1 . C. 2 . D. . 2
Câu 48. Trong không gian với hệ tọa độ Oxyz , mặt cầu n|o sau đ}y có t}m nằm trên trục Oz ? A. 2 2 2 S : x y z 2x 4y 2 0 . 1 B. 2 2 2 S : x y z 6z 2 0 . 2 C. 2 2 2 S : x y z 2x 6z 0. 3 D. 2 2 2 S : x y z 2x 4y 6z 2 0 . 4
Câu 49. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng Q : 2x y 5z 15 0 và
điểm E 1;2; 3 . Mặt phẳng P qua E v| song song với Q có phương trình l|: A. P : x 2y 3z 15 0 . B. P : x 2y 3z 15 0. C. P : 2x y 5z 15 0 . D. P : 2x y 5z 15 0 .
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A 3;3;1 , B 0;2;1 v| mặt phẳng P : x y z 7
0 . Đường thẳng d nằm trong P sao cho mọi điểm của d cách đều hai điểm ,
A B có phương trình l|: x t x 2t x t x t A. y 7 3t . B. y 7 3t . C. y 7 3t . D. y 7 3t . z 2t z t z 2t z 2t Trang 72
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai BẢNG ĐÁP ÁN Câu 1 C Câu 11 C Câu 21 A Câu 31 D Câu 41 A Câu 2 A Câu 12 B Câu 22 A Câu 32 A Câu 42 B Câu 3 B Câu 13 A Câu 23 B Câu 33 C Câu 43 D Câu 4 D Câu 14 A Câu 24 B Câu 34 A Câu 44 B Câu 5 B Câu 15 D Câu 25 C Câu 35 C Câu 45 C Câu 6 B Câu 16 A Câu 26 C Câu 36 D Câu 46 C Câu 7 D Câu 17 A Câu 27 C Câu 37 A Câu 47 C Câu 8 B Câu 18 C Câu 28 B Câu 38 D Câu 48 B Câu 9 D Câu 19 B Câu 29 B Câu 39 C Câu 49 C Câu 10 A Câu 20 D Câu 30 C Câu 40 B Câu 50 B
HƯỚNG DẪN GIẢI CÁC CÂU KHÓ ĐỀ SỐ 01
Câu 10. Gọi độ d|i cần điều chỉnh l| x . Cosi 1 2
Diện tích miếng bìa sau khi điều chỉnh l|: S a x b x a b . 2 a b Dấu ' ' xảy ra khi: a x b x x . Chọn A. 2
Câu 11. Đặt t sin x với x ; thì t x
sinx l| h|m ngịch biến v| h|m số 2 t m y t ,t 0;1 . t 1 1 m Ta có y ' t , t
0;1 . Để h|m số y t nghịch biến trong khoảng 0;1 khi v| chỉ khi 2 t 1 y ' t 0, t 0;1 1 m 0 m 1. Chọn C. a log 7 log 7a log 7a
Câu 17. Lời giải. Ta có 12 12 12 . 1 b log 6 log 12 log 6b log 12.6b 12 12 12 12 log 7 log 7 log 7a Mà 12 log 7 , do đó 12 12 . 2 log 2 log 2 log 12.6b 12 12 12 7a 7 a 1 2
Bằng đồng nhất hệ số, ta có được 2 2 2 a b 1 1 2 . Chọn A. 12.6b 2 b 1 N N ln100 ln 78,6858 Câu 21. Ta có 0,017 0,017 100 78,6858 ln100 ln 78,6858 N 14 0, 017
Vậy d}n số Việt Nam sẽ đạt 100 triệu d}n sau 14 năm. Chọn A.
Câu 28. Gọi V l| thể tích của khối gỗ nhỏ, khối gõ n|y còn được gọi l| hình chóp cầu. 1
Gọi V l| thể tích của khối gỗ lớn v| V l| thể tích của khối gỗ hình cầu. Ta có V V V . 2 1 2 h
M| thể tích hình chóp cầu được tính theo công thức 2 V h R
với h l| độ d|i khoảng 1 3 R R
c{ch từ đỉnh khối cầu đến mặt phẳng cắt. Theo giả thiết, ta có R h h . 2 2 2 h R R 5 Do đó 2 3 V h R R R . 1 3 2 6 24 Trang 73
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 4 4 5 9 Mà 3 V R nên 3 3 3 V V V R R V V R . 3 1 2 2 2 3 24 8 V 9 5 27 Vậy 2 3 3 R : R . Chọn B. V 8 24 5 1
Câu 31. C{c lỗ khoan có b{n kính đ{y l| 4mm v| có đường cao bằng với độ d|y của tấm kim
loại nên thể tích của 4 lỗ khoan l| 2 V 4. .0, 4 .2 1,28 1
Thể tích của tấm kim loại l| V 5.5.2 50 2
Suy ra thể tích của phần còn lại của tấm kim loại l| V V V 45,98 2 1 Câu 32. Gọi z x yi x,y . Suy ra z x yi . Ta có z i z 3 x yi i x yi 3 . 2 2 2 2 x (y 1)i (x 3) yi x (y 1) (x 3) y 3x y 4 0 .
Suy ra tập hợp c{c điểm M x;y biểu diễn số phức z thuộc đường thẳng 3x y 4 0 . Ta có 2 2 z x y
OM , z nhỏ nhất khi v| chỉ khi OM nhỏ nhất , suy ra M l| hình chiếu
của O lên đường thẳng 3x y 4 0 .
Đường thẳng d qua O v| vuông góc đường thẳng 3x y 4 0 có phương trình x 3y 0 . 6 3 4 x x y 6 2 6 2
Tọa độ M l| nghiệm của hệ 5 M ; z i . Chọn A. x 3y 0 2 5 5 5 5 y 5
Câu 37. Ta có V V V V V . SABC SAMN IMNA BAMI CANI V SA SM SN 1 1 1 V
Theo công thức tỷ số thể tích, ta được SAMN . . . V . V SA SB SC 2 2 4 SAMN 4 SABC V BM BA BI 1 1 1 V V CA CN CI 1 1 1 V BMAI . . . V , CANI . . . V V BS BA BC 2 2 4 BMAI 4 V CA CS CB 2 2 4 CANI 4 BSAC CASB V V V V Do đó V V V . Chọn A. 4 IMNA 4 4 IMNA 4
Câu 40. Hình tròn lớn nhất l| thiết diện của mặt phẳng đi qua t}m mặt cầu.
Gọi R l| b{n kính mặt cầu thì R c ng l| b{n kính đường tròn lớn nhất.
Diện tích đường tròn lớn nhất: 2 S
R . Điện tích đường tròn T là: 2 S R . T T 2 3 S R 1
Chu vi đường tròn T : C 2 R 3 R . Theo đề T T R 2R 3 . T T T 2 S R 4 T 4 4
Thể tích của khối cầu S là: 3 V R 27 36 . Chọn B. 3 3
Câu 50. Phương trình mặt phẳng trung trực của AB là : 3x y 7 0 .
Đường thẳng cần tìm d c{ch đều hai điểm ,
A B nên sẽ thuộc mặt phẳng . x y z 7 0 Lại có d P , suy ra d P hay d : . 3x y 7 0 x 2t Chọn z t , ta được . Chọn B. y 7 3t Trang 74
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
ĐỀ THI THỬ SỐ 02 Môn: TOÁN Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 02 2x 2 Câu 1. Cho h|m số y Chọn ph{t biểu đúng? x 1
A. H|m số nghịch biến c{c khoảng ( ; 1)và ( 1; )
B. H|m số luôn đồng biến trên .
C. H|m số đồng biến trên c{c khoảng ( ; 1)và (1; ) .
D. H|m số đồng biến trên c{c khoảng ( ; 1)và ( 1; ) . Câu 2. H|m số 3 y
x có bao nhiêu điểm cực trị? A. 0 B. 1 C. 2 D. 3 x 2 Câu 3.
Phương trình c{c đường tiệm cận của đồ thị h|m số y là x 1 A. y 1 vàx 2 B. y x 2 vàx 1 C. y 1 và x 1 D. y 2 và x 1 Câu 4.
Số giao điểm của đồ thị h|m số 2 y (x 3)(x x 4) với trục ho|nh l|: A. 2 B. 3 C. 0 D. 1 Câu 5.
Đường cong hình dưới đ}y l| đồ thị của một trong bốn h|m số đã cho, đó l| h|m số nào? A. 2 y x 3x 2 B. 4 2 y x x 2 C. 3 y x 3x 2 D. 3 2 y x 3x 2 3 x 2 Câu 6. Cho h|m số 2 y 2x 3x
.Tọa độ điểm cực đại của đồ 3 3 y thị h|m số l| A. (-1; 2) B. (1; 2) 2 2 -1 x 1 2 C. (3; ) D. (1; -2) 3 O -2 Câu 7.
Gi{ trị lớn nhất của h|m số 3 2 y x 3x 5 trên đoạn 1; 4 là A. 5 B. 1 C. 3 D. 21 Câu 8.
Tất cả c{c gi{ trị của m để h|m số 3 2 y x 3x 3mx 1 nghịch biến trên là: A. m 1 B. m 1 C. m 1 D. m 1 Câu 9.
Gi{ trị lớn nhất của h|m số 2 y x 2x là A. 0 B. 1 C. 2 D. 3
Câu 10. Tất cả c{c gi{ trị của m m để đường thẳng d : y
m d: y = m cắt đồ thị (C ) của h|m số 3 2 y x 3x
2 tại ba điểm ph}n biệt l|: A. m 2 B. m 2 C. m 2 D. 2 m 2
Câu 11. Có hai c}y cột dựng trên mặt đất lần lượt cao 1mv| 4m, đỉnh của hai c}y cột c{ch nhau
5m .Người ta cần chọn một vị trí trên mặt đất (nằm giữa hai ch}n cột) giăng d}y nối
đến hai đỉnh cột để trang trí mô hình bên dưới . Trang 75
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 5m 4m 1m Mặt đất
Độ d|i d}y ngắn nhất l|: A. 41m B. 37m C. 29m D. 3 5m
Câu 12. Điều kiện của x để biểu thức log (x 1) có nghĩa l| 2 A. x > 0 B. x > 1 C. 1 x 0 D. 2 x 1 1 Câu 13. H|m số 2 y
x có tập x{c định l| A. B. [0; ) C. (0; ) D. \ 0 x
Câu 14. Phương trình 2 2 có bao nhiêu nghiệm ? A. 0 B. 1 C. 2 D. 3 1 1 1 1 Câu 15. Nếu 7 5 a a và log log thì b 6 b 4 A. 0 a 1; b 1 B. a 1; b 1 C. a 1; 0 b 1 D. 0 a 1; 0 b 1 x 2
Câu 16. H|m số y log có tập x{c định l|: 1 x A. \ 1 B. \ 1;2 C. 1;2 D. ;1 2;+
Câu 17. Bất phương trình log (x 1)  2  có nghiệm l|: 1 3 A. x  1
B. 1  x  10 C. x  10
D. 1  x  10
Câu 18. Cho c{c khẳng định: (I): x 0 thì 2 ln(x 1) ln2x 1 (II): x 0 thì 2 x x log y log x (III): Với 1 a 0; x 0; y 0 a a x y
Trong c{c khẳng định trên có bao nhiêu khẳng định đúng? A. 0 B. 1 C. 2 D. 3 1
Câu 19. Xét h|m số y ln , x 1ta có 1 x A. y ' 2y 1 B. ' ey y 0 C. yy ' 2 0 D. ' 4 ey y 0
Câu 20. Tất cả c{c gi{ trị của m để phương trình : 9x 3x m 0 có nghiệm l|: 1 1 A. m B. m 0 C. m D. m 0 4 4
Câu 21. Cường độ một trận động đất M được cho bởi công thức: M = log A log A , với A l| 0
biên độ rung chấn tối đa v| A l| một biên độ chuẩn (hằng số) . Đầu thế kỷ XX , một 0
trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, trận
động đất kh{c ở gần đó đo được 6 độ Richter. Trận động đất ở San Francisco có biên
độ gấp bao nhiêu lần biên độ trận động đất n|y ? Trang 76
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 4 3 A. B. C. 20 D. 100 3 4 Câu 22. Nếu 2 x dx
f (x) và f (0) 0 thì : 1 1 A. f (x) 2x B. f (x) 2x C. 3 f (x) x D. 2 f (x) x 3 3 Câu 23. Nếu u u(x),v
v(x) l| hai h|m số có đạo h|m liên tục trên đoạn a;b . Khẳng định
n|o sau đ}y l| khẳng định đúng ? b b b b b b A. u.dv u.v v.du B. u.dv u.v v.dv a a a a a a b b b a b C. u.dv u.v u.du D. u.dv u.v |b v.du . a a a a a b 2 ln x
Câu 24. Cho F(x) dx và F(1)
1, khẳng định n|o sau đ}y l| đúng? x A. 2 F(x) ln x B. 2 F(x) ln (x 1) C. 2 F(x) 1 ln(x ) D. 2 F(x) 1 ln x 1 2 2 Câu 25. Cho f (x)dx 2 , f (x)dx 4 , khi đó
f (2x)dx bằng : 0 1 0 A. 1 B. 2 C. 3 D. 6
Câu 26. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số 2 y 2 x và y x là : 9 2 9 19 A. B. C. D. 12 9 2 2 x
Câu 27. Cho (H ) l| hình phẳng giới hạn bởi đồ thị h|m số y
,trục Ox v| đường 2 4 x thẳng x
1 .Thể tích của khối tròn xoay thu được khi quay hình (H ) xung quanh trục Ox bằng: 4 1 4 3 4 A. ln B. ln C. ln D. ln 2 3 2 3 2 4 3
Câu 28. Một ô tô đang đi với vận tốc lớn hơn 72km /h , phía trước l| đoạn đường chỉ cho phép
chạy với tốc độ tối đa l| 72 km /h , vì thế người l{i xe đạp phanh để ô tô chuyển động
chậm dần đều với vận tốc v(t) 30
2t (m /s ), trong đó t l| khoảng thời gian tính
bằng gi}y kể từ lúc bắt đầu đạp phanh. Từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ
72 km /h ô tô đã di chuyển quãng đường d|i: A. 100m . B. 125m . C. 150m . D. 175m
Câu 29. Mô đun của số phức z 12 5i là A. 7 B. 17 C. 169 D. 13
Câu 30. Số phức z 2 5i có phần ảo l| A. -5 B. 5 C. 5i D. -2
Câu 31. Số phức z 6
7i có điểm biểu diễn l| A. (6; 7) B. (6;7) C. ( 6;7) D. ( 6; 7)
Câu 32. Cho hai số phức : z 2 3 , i z
1 i . Gi{ trị z 3z là 1 2 1 2 A. 10. B. 61. C. 61 D. 10 . Trang 77
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 33. Gọi z l| nghiệm phức của phương trình 2 z 2z 3
0 . Biết z có phần ảo dương, 1 1 z là 1 A. 1 2i B. 1 2i . C. 1 2i . D. 1 2i .
Câu 34. Tập hợp điểm biểu diễn c{c số phức z thỏa mãn: z i 1 i z là
A. đường tròn t}m I(2; 1) , bán kính R= 2 . B. đường tròn tâm I (0;1) , R= 3 .
C. đường tròn t}m I(0; 1) , bán kính R= 3 .D. đường tròn t}m I(0; 1) , R= 2 .
Câu 35. Thể tích của khối lập phương cạnh 2a bằng: A. 3 a B. 4 3 a C. 6 3 a D. 8 3 a
Câu 36. Khối chóp S.ABC có đ{y l| tam gi{c đều cạnha , cạnh bên SA vuông góc với mặt phẳng đ{y, SA
a 3 có thể tích l|: 3 3a 3 a 3 a 3 a 3 A. B. C. D. 4 4 2 4
Câu 37. Cho lăng trụ đứng tam gi{c ABC.A' B 'C ' có đ{y ABC l| tam gi{c vuông c}n tại B với BA BC
a ,biết A'B hợp với mặt phẳng (ABC ) một góc 0 60 .Thể tích lăng trụ là: 3 a 3 3 a 3 3 a 3 A. B. C. D. 3 a 3 2 4 6
Câu 38. Người ta x}y một c{i bể đựng nước không có nắp l| một hình lập phương với cạnh đo
phía ngo|i bằng 2 m . Bề d|y của đ{y bằng bề d|y c{c mặt bên bằng 5cm (hình vẽ). Bể
chứa được tối đa số lít nước l|: A. 8000 lít .B. 7220 lít. C. 6859 lít. D. 7039,5 lít dày 5cm 2m
Câu 39. Một khối cầu có b{n kính 2R thì có thể tích bằng: 3 4 R 3 32 R 3 24 R A. B. 2 4 R C. D. 3 3 3
Câu 40. Cắt một hình nón bằng một mặt phẳng qua trục của nó được thiết diện l| tam gi{c đều
cạnh bằng a, thể tích của khối nón l|: 3 a 3 3 a 3 3 a 3 3 a A. B. C. D. 12 24 6 3
Câu 41. Trong không gian cho hình chữ nhật ABCD có AB , a AC
a 5 . Diện tích to|n phần
của hình trụ nhận được khi quay hình chữ nhật đó quanh trục AD là: A. 2 4 a B. 2 5 a C. 2 6 a D. 2 2 a (1 5).
Câu 42. Cho hình chóp S.ABCD có đ{y l| hình vuông, BD
2a . Tam giác SAC vuông cân
tại S v| nằm trong mặt phẳng vuông góc với đ{y. Thể tích của khối cầu ngoại tiếp hình chóp đó l|: Trang 78
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 3 4 a A. 3 4 a 3 B. C. 3 a D. 3 4 a 3
Câu 43. Trong hệ tọa độ Oxyz , cho mặt cầu 2 2 2 (S) : (x 3) (y 2) (z 1) 4 . Tọa độ t}m I
và bán kính R của mặt cầu l|:
A. I( 3;2;1)và R 2
B. I(3; 2; 1) và R 4
C. I( 3;2;1)và R 4
D. I(3; 2; 1) và R 2
Câu 44. Trong hệ tọa độ Oxyz ,điều kiện của m để hai mặt phẳng (P) : 2x 2y z 0 và (Q) : x y mz 1 0 cắt nhau l| : 1 1 1 A. m B. m C. m 1 D. m 2 2 2
Câu 45. Trong hệ tọa độ Oxyz , cho hai điểm (
A 2; 3; 1) B(4; 1;2). Phương trình mặt phẳng
trung trực của đoạn thẳng AB là 15 A. 2x 2y 3z 1 0 B. 4x 4y 6z 0 2 C. x y z 0 D. 4x 4y 6z 7 0
Câu 46. Trong hệ tọa độ Oxyz ,phương trình n|o sau đ}y không phải l| phương trình đường
thẳng chứa trục Ox ? x t 2 x t x 1 t x t A. y 0 B. y 0 C. y 0 D. y 0 z 0 z 1 z 0 z 0
Câu 47. Trong hệ tọa độ Oxyz ,cho (
A 2; 0; 0);B(0; 3;1);C( 3;6; 4) . Gọi M l| điểm nằm trên đoạn
thẳng BC sao cho MC
2MB . Độ d|i đoạn AM là: A. 5 B. 29 C. 5 D. 29
Câu 48. Trong hệ tọa độ Oxyz cho I (1;1;1) v| mặt phẳng (P) : 2x y 2z 4 0 . Mặt cầu (S )
tâm I cắt (P) theo một đường tròn b{n kính r = 4. Phương trình của (S ) là A. 2 2 2 (x 1) (y 1) (z 1) 16 B. 2 2 2 (x 1) (y 1) (z 1) 9 C. 2 2 2 (x 1) (y 1) (z 1) 5 D. 2 2 2 (x 1) (y 1) (z 1) 25
Câu 49. Trong hệ tọa độ Oxyz , cho hai mặt phẳng song song (P) : x 2y 2z 11 0 và (Q) :x 2y 2z 2
0. Khoảng c{ch giữa (P) và (P) là A. 9 B. 3 C. 1 D. 13
Câu 50. Trong hệ tọa độ Oxyz , cho c{c điểm (
A 1; 0; 0),B(0;1; 0),C(0; 0;1), (
D 0; 0; 0) . Hỏi có bao
nhiêu điểm c{ch đều 4 mặt phẳng(ABC ),(BCD),(CD ), A (DAB) ? A. 8 B. 5 C. 1 D. 4 ----------- HẾT ---------- Trang 79
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai BẢNG ĐÁP ÁN Câu 1 D Câu 11 A Câu 21 D Câu 31 B Câu 41 C Câu 2 A Câu 12 B Câu 22 C Câu 32 C Câu 42 B Câu 3 C Câu 13 C Câu 23 A Câu 33 A Câu 43 A Câu 4 D Câu 14 B Câu 24 D Câu 34 D Câu 44 A Câu 5 D Câu 15 A Câu 25 C Câu 35 D Câu 45 D Câu 6 B Câu 16 C Câu 26 C Câu 36 B Câu 46 B Câu 7 D Câu 17 B Câu 27 A Câu 37 A Câu 47 B Câu 8 C Câu 18 C Câu 28 B Câu 38 D Câu 48 D Câu 9 B Câu 19 B Câu 29 D Câu 39 C Câu 49 B Câu 10 D Câu 20 D Câu 30 B Câu 40 B Câu 50 A
HƯỚNG DẪN GIẢI CÁC CÂU VẬN DỤNG CAO
Câu 11: Có hai c}y cột dựng trên mặt đất lần lượt cao 1mv| 4m, đỉnh của hai c}y cột c{ch nhau
5m .Người ta cần chọn một vị trí trên mặt đất (nằm giữa hai ch}n cột) giăng d}y nối đến hai
đỉnh cột để trang trí mô hình bên dưới .
Độ d|i d}y ngắn nhất l|: A. 41m B. 37m C. 29m D. 3 5m HD: C 5m 3m B 4m H 1m 1m x M A N
Giả sử đoạn d}y l| đường gấp khúc BAC, gọi MA = x v| c{c yếu tố như hình vẽ Tính được 2 2 AB AC x 1 (4 x) 16 f (x), x [0;4] min f (x) 41 , chọn A [0;4]
Câu 21: Cường độ một trận động đất M được cho bởi công thức: M = log A log A , với A l| 0
biên độ rung chấn tối đa v| A l| một biên độ chuẩn (hằng số) . Đầu thế kỷ XX, một trận động 0
đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, trận động đất kh{c ở gần đó
đo được 6 độ Richter. Trận động đất ở San Francisco có biên độ gấp bao nhiêu lần biên độ trận động đất n|y ? 4 3 A. B. C. 20 D. 100 3 4 HD:
Gọi cường độ v| biên độ trận động đất ở San Francisco l| M v| A, trận động đất còn lại l| A A
M và A ta có: 2 2 8 6 M M lgA lg A (lg A lg A ) lg 10 100 . 1 1 1 0 1 0 A A 1 1 Chọn D.
Câu 28: Một ô tô đang đi với vận tốc lớn hơn 72km/h, phía trước l| đoạn đường chỉ cho phép
chạy với tốc độ tối đa l| 72km/h, vì thế người l{i xe đạp phanh để ô tô chuyển động chậm dần
đều với vận tốc v(t) 30
2t (m/s), trong đó t l| khoảng thời gian tính bằng gi}y kể từ lúc bắt Trang 80
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
đầu đạp phanh. Từ lúc bắt đầu đạp phanh đến lúc đạt tốc độ 72km/h ô tô đã di chuyển quãng đường d|i A. 100m. B. 125m. C. 150m. D. 175m HD: 5 72km / h 20m / , s 30 2t 20 t 5 S (30 2t)dt 125 , chọn B 0
Câu 38: Người ta x}y một c{i bể đựng nước không có nắp l| một hình lập phương với cạnh đo
phía ngo|i bằng 2m. Bề d|y của đ{y bằng bề d|y c{c mặt bên bằng 5cm (hình vẽ). Bể chứa được
tối đa số lít nước l|: A. 8000 lít. B. 7220 lít.
C. 6859 lít. D. 7039,5 lít dày 5cm 2m HD:
Thể tích thực chứa nước l| 190 x 190 x 195 = 7039500 cm3 , chọn D
Câu 50: Trong hệ tọa độ Oxyz, Cho c{c điểm A(1;0;0), B(0;1;0), C(0;0;1), D(0;0;0). Hỏi có bao
nhiêu điểm c{ch đều 4 mặt phẳng (ABC), (BCD), (CDA), (DAB)? A. 8 B. 5 C. 1 D. 4 HD: x y z 1
Gọi I(x;y;z) c{ch đều 4 mặt ta có x y z
, phương trình có 8 nghiệm, chọn 3 A Trang 81
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
ĐỀ THI THỬ SỐ 03 Môn: TOÁN Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97 NỘI DUNG ĐỀ SỐ 03 Câu 1.
Tìm tất cả c{c gi{ trị thực của tham số m sao cho h|m số 3 mx 2
y f (x) 
 7mx 14x m  2 giảm trên nữa khoảng 3 [1;+¥)? A. (-¥;- 14 ù (-¥;-14). C. é-2;- 14 é- 14 ;+¥ 15 û. B. 15 ë ù 15 û . D. ë ). 15 Câu 2. Giả sử h|m số y
f (x) có đạo h|m cấp hai trong khoảng x h;x h , với h 0. 0 0
Khẳng định n|o sau đ}y đúng ?
A. Nếu f (x ) 0 và f (x ) 0 thì h|m số y
f (x) đạt cực đại tại x . o o o
B. Nếu f (x ) 0 và f (x ) 0 thì h|m số y
f (x) đạt cực tiểu tại x . o o o
C. Nếu f (x ) 0 và f (x ) 0 thì h|m số y
f (x) đạt cực đại tại x . o o o
D. Nếu f (x ) 0 thì h|m số y
f (x) đạt cực đại tại x . o o Câu 3.
Khẳng định n|o sau đ}y l| đúng về h|m số 2 y 3 2x x ?
A. Có gi{ trị lớn nhất v| gi{ trị nhỏ nhất
B. Có gi{ trị nhỏ nhất v| không có gi{ trị lớn nhất
C. Có gi{ trị lớn nhất v| không có gi{ trị nhỏ nhất
D. Không có gi{ trị lớn nhất v| gi{ trị nhỏ nhất Câu 4. Cho h|m số y
f (x) liên tục trên ;3 ; 3;
v| có bảng biến thiên như hình bên dưới đ}y.
Khẳng định n|o sau đ}y l| khẳng định sai ?
A. H|m số đạt cực tiểu tại x
1 v| đạt cực đại tại x 2 .
B. Đồ thị h|m số đã cho có hai đường tiệm cận đứng l| c{c đường x 1 và x 3
C. Hàm số đã cho không có gi{ trị lớn nhất v| gi{ trị nhỏ nhất
D. H|m số đã cho không có đạo h|m tại x 1 và x 3 2x 1 Câu 5.
Số điểm có tọa độ nguyên thuộc đồ thị h|m số y là ? x 1 A. 2. B. 4. C. 6. D. 8. Trang 82
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Câu 6.
Tìm tất cả c{c gi{ trị thực của tham số m sao cho phương trình 3 2 x 3x 2 m 0 1
có ba nghiệm ph}n biệt trong đó có đúng hai nghiệm lớn hơn 2 9 A. 2 m B. 2 m 0 C. 0 m 2 D. 2 m 2 8 Câu 7.
Biết rằng chỉ có hai gi{ trị thực kh{c nhau của tham số m thì đồ thị h|m số x 1 y
có đúng hai đường tiệm cận ; kí hiệu m
a l| gi{ trị thứ nhất , 2 x 2x m m
b l| gi{ trị thứ hai . Tính ab ? A. ab 1 B. ab 2 C. ab 3 D. ab 4 Câu 8.
Tìm tất cả c{c gia trị thực của tham số m để đồ thị h|m số 1 3 2 y x (m 1)x 1
3m có hai điểm cực trị , A B sao cho ,
A B và C 0; 5 thẳng 3 hàng ? A. m 1 B. m 2. C. 1 m 2 D. 1 m 2 x 1 Câu 9. Gọi T
a;b l| tập gi{ trị của h|m số y trên 1;2 .Khẳng định nào sau 2 x 1 đ}y l| đúng ? 9 19 A. 2 2 a b 2 B. 2 2 a b C. 2 2 a b D. 2 2 a b 2 5 5
Câu 10. Trường THPT số 3 Bảo Thắng được đặt ở vị trí B có khoảng c{ch đến đường quốc lộ BD
4km . Bạn Linh lớp 12A2 nh| ở vị trí A c{ch D một khoảng 20km .Hàng ngày
Linh đi xe đạp đi học đến vị trí C với vận tốc 15km / h ,rồi đi tiếp từ C đến trường .X{c
định khoảng c{ch CD để bạn Linh đi từ nh| đến trường nhanh nhất .Biết rằng tỉ số 5
vận tốc bạn Linh đi xe từ A đến C gấp lần vận tốc đi xe từ C đến B (Xem hình vẽ 3
minh họa bên dưới đ}y) A. CD 5km B. CD 4km C. CD 3km D. CD 2km
Câu 11. Khẳng định n|o sau đ}y l| sai về h|m số 4 2 2 y x 2x m 3m 1 ?
A. Đồ thị h|m số có ba điểm cực trị
B. Ba điểm cực trị của đồ thị h|m số tạo th|nh một tam gi{c vuông c}n
C. Ba điểm cực trị của đồ thị h|m số tạo th|nh một tam gi{c c}n nhưng không vuông
D. Ba điểm cực trị của đồ thị h|m số tạo th|nh một tam gi{c có diện tích không đổi
Câu 12. Giải phương trình log 2 3x 3 . 2 7 2 A. x B. x 4 C. x 2 D. x 3 3 Trang 83
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai x 1
Câu 13. Tính đạo h|m của h|m số y . 3 x 1 1 ln 3 x 1 A. y ' x. B. ' 3 x y .ln 3 C. y ' 3 .ln D. y ' 3 3 3x Câu 14. Cho 0 a
1. Tập nghiệm của bất phương trình 2 log x x log x 1 1 là : a a A. 0;a B. ;a C. a; D. ;1 a Câu 15. Biết log 2 a, log 7
b thì log 35 tính theo a và b bằng : A. 1 b a B. 1 b a C. 5b D. a b 1 Câu 16. H|m số 2 y ln x 2x m
1 có tập x{c định l| khi m 0 A. m 0 B. m 0 C. D. 0 m 3 m 1 1 1 1 1 Câu 17. Nếu 4 3 a a và log log thì b 4 b 3 A. 0 a 1,b 1 B. 0 a 1, 0 b 1 C. a 1,b 1 D. a 1, 0 b 1
Câu 18. Đạo h|m của h|m số 3 ( ) log 2 x f x x 1 là 3 2 x 3x 1 3 2 x 3x 1 ln 2 A. f '(x) B. f '(x) 3 2 x x 1 ln 5 ln 2 3 2 x x 1 2 3x 1 3 3x 2 ln 2 2 x 3 2 x 3x ln 2 1 C. f '(x) D. f '(x) 3 2 x x 1 ln 5 ln 2 3 2 x x 1 ln 5 ln 2 1 2 Câu 19. Cho 0 a
1.Khi đó bất phương trình 1 có nghiệm l| ? 5 log x 1 log x a a 1 1 1 1 x 0 x x x a a a a A. 3 2 a x a B. 2 3 a x a C. 2 3 a x a D. 3 2 a x a 5 0 x a 5 x a 5 x a 5 x a
Câu 20. Biết rằng T
a;b l| tập tất cả c{c gia trị thực của tham số m để phương trình 2 2 log x log x 1 1 5m
0 có ít nhất một nghiệm thuộc khoảng 2 2 1; 3 ? 1 3 3 Tính 2 2 a b A. 2 2 a b 4 B. 2 2 a b 6 C. 2 2 a b 8 D. 2 2 a b 10
Câu 21. Giả sử viên phấn viết bảng có dạng hình trụ tròn xoay đường kính đ{y bằng 1cm,
chiều d|i 6cm. Người ta l|m những hộp carton đựng phấn dạng hình hộp chữ nhật có
kích thước 6 x 5 x 6 cm. Muốn xếp 350 viên phấn v|o 12 hộp, ta được kết quả n|o trong 4 khả năng sau : Trang 84
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 6 cm 5 cm 6 cm 6 cm 1 cm A.Vừa đủ B.Thiếu 10 viên C.Thừa 10 viên D.Không xếp đươc
Câu 22. H|m số y
f x liên tục trên đoạn a;b . Viết công thức tính diện tích hình phẳng S
được giới hạn bởi đồ thị của h|m số y
f x , trục Ox v| hai đường thẳng x , a x b a b . b b b b A. S f x dx B. S f (x)dx C. 2 S
f x dx D. S f x dx a a a a 1 4 4 Câu 23. Cho f (x)dx 2, f (x)dx 3, g(x)dx
4 khẳng định n|o sau đ}y l| sai ? 0 1 0 4 4 4 A. f (x)dx 5 B. f (x)dx g(x)dx 0 0 0 4 4 4 C. f (x) g x dx 1 D. f (x)dx g(x)dx 0 0 0
Câu 24. Giả sử F x l| nguyên h|m của h|m số f x 4x
4 .Biết rằng đồ thị h|m số F x
và f x cắt nhau tại một điểm trên trục tung .Khẳng định n|o sau đ}y đúng A. 2 F x 2x 4x 4 B. 2 F x 2x 4x C. 2 F x 2x 4x C D. 2 F x 2x 4 e 2 x ln x a 3 a
Câu 25. Tính tích phân dx
,trong đó a,b nguyên dương v| l| ph}n số 3 2 x b 4e b 1
tối giản .Tính ab A. ab 10 B. ab 20 C. ab 20 D. ab 30
Câu 26. Bạn Linh cần mua một chiếc gương có hình dạng đường
Parabol bậc 2 (Xem hình vẽ) .Biết rằng khoảng c{ch đoạn AB 60c , m OH
30cm .Diện tích của chiếc gương bạn Linh mua là ? A. 2 1000(cm ) B. 2 1200(cm ) C. 2 1400(cm ) D. 2 900(cm )
Câu 27. Cho hình phẳng H tạo th|nh bởi hai đường 2 y x
x v| đường thẳng y 0 .Tính
thể tích của khối tròn xoay tạo bởi khi quay H quanh trục Ox A. (dvtt) B. dvtt C. dvtt D. dvtt 15 6 30 40 Trang 85
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 28. Một cốc nước có dạng hình trụ đựng nước chiều cao 12cm, đường kính đ{y 4cm,
lượng nước trong cốc cao 10cm. Thả v|o cốc nước 4 viên bi có cùng đường kính 2cm.
Hỏi nước d}ng cao c{ch mép cốc bao nhiêu cm? (Kết quả l|m tròn sau dấu phẩy 2 chữ số thập ph}n) 2 cm 2 cm 2 cm 12 cm 2 cm 4 cm A.0,67 cm B. 0,75 cm C. 0,25 cm D. 0,33 cm 1
Câu 29. Cho số phức z
3i . Tìm phần thực v| phần ảo của số phức z : 2 1 1
A. Phần thực bằng v| Phần ảo bằng 3
B. Phần thực bằng v| Phần ảo bằng 3 2 2 1 1
C. Phần thực bằng v| Phần ảo bằng 3i D. Phần thực bằng v| Phần ảo bằng 3i 2 2
Câu 30. Cho hai số phức z 1 2i v| z 5
6i . Tính tổng modun của số phức z z 1 2 1 2 A. z z 10 B. z z 10 C. z z 4 2 D. z z 100 1 2 1 2 1 2 1 2 Câu 31. C{c điểm , A ,
B C,D vàE trong mặt phẳng phức biểu diễn theo thứ tự c{c số phức 1 2i;2 3i;3 5 ; i 2
3i và 5 4i . Khẳng định n|o sau đ}y đúng ?
A. Điểm G 2;2 l| trọng t}m của tam gi{c BCD
B. Điểm G 2;2 l| trọng t}m của tam gi{c ABC
C. Điểm G 2;2 l| trọng t}m của tam gi{c ABD
C. Điểm G 2;2 l| trọng t}m của tam gi{c CED
Câu 32. Cho số phức z 3 4i . Tìm số phức 2 w i 1 z z : A. w 8 31i B. w 8 31i C. w 31 8i D. w 31 8i
Câu 33. Kí hiệu z ;z ;z l| ba nghiệm phức của phương trình 3 2 z 7z 31z 25 0. Tính 1 2 3 tổng T z z z . 1 2 3 A. T 11 B. T 11 C. T 121 D. T 22
Câu 34. Cho c{c số phức z thỏa mãn z 2
3 . Biết rằng tập hợp c{c điểm biểu diễn c{c số phức w 1 i 3 z
2i l| một đường tròn . Tính b{n kính r của đường tròn đó? A. r 2 B. r 4 C. r 6 D. r 8
Câu 35. Cho hình hộp ABCD.A’B’C’D’ ,Biết rằng C.B’C’D’ l| một tứ diện đều cạnh a .Tính thể
tích khối hộp ABCD.A’B’C’D’ 3 a 3 a 2 3 a 2 A. 3 a 2. B. C. . D. 2 3 6 Trang 86
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 36. Cho hình chóp S.ABCD có đ{y ABCD l| hình thoi với AC 2BD 2a, tam giác
SAD vuông c}n tại S v| nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD).
Tính thể tích hình chóp S.ABCD theo a ? 3 a 5 3 a 5 3 a 5 3 a 3 A. B. C. D. 12 6 4 12
Câu 37. Cho hình chóp S.ABCD có đ{y l| hình vuông .Cạnh SC (ABCD) và AC 2,SA
5. Bết M l| trung điểm của cạnh AB . Kí hiệu l| góc giữa đường
thẳng SM v| mặt phẳng SBD . Tính sin . 1 1 1 1 A. sin B. sin C. sin D. sin 6 2 7 7 3
Câu 38. Cho hình lăng trụ đứng ABC.A' B 'C ' có đ{y l| tam gi{c c}n có AC BC 3a .
Đường thẳng A'C tạo với đ{y một góc 0
60 . Trên cạnh A'C lấy điểm M sao cho A'M
2MC . Biết rằng A'B
a 31 . Khoảng c{ch từ M đến mặt phẳng ABB 'A' là: 3a 2 4a 2 A. B. C. 3a 2 D. 2a 2 4 3
Câu 39. Cho hình lăng trụ đứng ABC.A’B’C’ có cạnh AA’ 2 , a BC a và 0 BAC 120 . Thể
tích hình trụ ngoại tiếp hình lăng trụ l| 3 2 a 3 a 3 4 a A. B. 3 2 a C. D. 3 3 3
Câu 40. Nh| bạn Linh có một bình đựng nước dạng hình nón (không
có đ{y) ,đựng đầy nước.Bạn Linh thả v|o đó một khối cầu có
đường kính bằng chiều cao của bình nước v| đo được thể tích 128 nước tr|n ra ngo|i l| 3 V
dm .Kí hiệu V l| thể tích 1 3 2 V
của nước còn lại trong bình .Tính tỉ số 2 , biết rằng khối cầu V1
tiếp xúc với tất cả c{c đường sinh của hình nón v| đúng một
nửa khối cầu chìm trong nước V 1 V 1 V 1 V 1 A. 2 B. 2 C. 2 D. 2 V 2 V 3 V 4 V 5 1 1 1 1
Câu 41. Một hình nón có chiều cao SO
50cm v| có b{n kính đ{y bằng
10cm .Lấy điểm M thuộc đoạn SO sao cho OM 20cm . Một
mặt phẳng qua M vuông góc với SO cắt hình nón theo giao
tuyến l| đường tròn C .Tính diện tích xung quanh hình nón
đỉnh S v| đ{y l| hình tròn x{c định bởi C (Xem hình vẽ) A. 2 16 26 cm B. 2 26 26 cm C. 2 36 26 cm D. 2 46 26 cm
Câu 42. Cho hình chóp S.ABCD có đ{y l| hình bình h|nh v| có thể tích l| V . Điểm P l| trung
điểm của SC , một mặt phẳng qua AP cắt hai cạnh SD v| SB lần lượt tại M v| N .Gọi V
V l| thể tích của khối chóp S.AMPN . Gi{ trị lớn nhất của 1 thuộc khoảng n|o sau 1 V đ}y ? Trang 87
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 1 1 1 1 1 1 A. 0; B. ; C. ; D. ;1 5 5 3 3 2 2
Câu 43. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P : x 3z 2 0 . Vector n|o
dưới đ}y l| một vector ph{p tuyến của P ? A. n 1;0; 1 B. n 3; 1;2 C. n 3; 1;0 D. n 1;0; 3 4 1 3 2 Câu 44. Trong không gian với hệ trục tọa độOxyz , cho mặt 2 2 2 cầu: S : x 1 y 2 z 3
9 . Tìm tọa độ tâm I v| tính b{n kính R của S : A. I 1; 2; 1 v| R 3
B. I 1;2; 3 v| R 3 C. I 1;2;1 v| R 9 D. I 1; 2; 3 v| R 9 Câu 45. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu 2 2 2 S : x y z 2x 2y 2z 3
0 . Trục Oz cắt mặt cầu (S) tại hai điểm ph}n biệt
A,B . Tính độ d|i đoạn AB . A. AB 2 B. AB 4 C. AB 6 D. AB 8 x 2 t
Câu 46. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng : y 1 2t t hai z 3t
điểm A 2; 0; 3 và B 2; 2; 3 . Biết điểm M x ;y ;z thuộc thì 4 4 MA MB nhỏ 0 0 0 nhất .Tìm x 0 A. x 0 B. x 1 C. x 2 D. x 3 0 0 0 0
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho điểm A 1; 1; 3 v| mặt phẳng (P) có phương trình x 2y 2z 3
0. Viết phương trình mặt phẳng (Q) song song với
mặt phẳng (P) biết mặt phẳng (Q) c{ch A một đoạn bằng 4 A. x 2y 2z 21 0 B. x 2y 2z 3 0 C. Q : x 2y 2z 6 0 D. 2x y 2z 7 0
Câu 48. Trong không gian với hệ tọa độ Oxyz , cho điểm A 1; 1;1 . Gọi (P) l| mặt phẳng đi
qua điểm A 1; 1;1 v| chứa trục Oy . Khi đó khoảng c{ch từ điểm N 3; 0;5 đến mặt phẳng (P) bằng : A. 2 B. 3 C. 5 D. 7 Câu 49. Trong không gian với hệ tọa độ Oxyz ,cho c{c điểm
A 2;0;0 ,B 0;2;0 ,C 0;0;2 ,D 2;2;2 mặt cầu ngoại tiếp tứ diện ABCD có b{n kính l| : 3 2 A. 3 B. 3 C. D. 2 3
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho c{c điểm A 1; 4;2 ,B 1;2;4 v| đường x 1 y 2 z thẳng :
.Biết rằng điểm M và 2 2 MA
MB có gi{ trị nhỏ nhất 1 1 2
. Tìm tọa độ điểm M ? A. 0; 1;4 B. 1;0;4 C. 1;0;4 D. 1;0; 4 Trang 88
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai BẢNG ĐÁP ÁN Câu 1 A Câu 11 C Câu 21 B Câu 31 B Câu 41 C Câu 2 A Câu 12 C Câu 22 D Câu 32 B Câu 42 C Câu 3 A Câu 13 D Câu 23 D Câu 33 A Câu 43 D Câu 4 B Câu 14 A Câu 24 A Câu 34 C Câu 44 B Câu 5 B Câu 15 A Câu 25 B Câu 35 B Câu 45 B Câu 6 A Câu 16 B Câu 26 B Câu 36 A Câu 46 C Câu 7 C Câu 17 A Câu 27 C Câu 37 B Câu 47 A Câu 8 B Câu 18 D Câu 28 A Câu 38 B Câu 48 A Câu 9 D Câu 19 A Câu 29 A Câu 39 A Câu 49 B Câu 10 C Câu 20 A Câu 30 B Câu 40 B Câu 50 B
HƯỚNG DẪN GIẢI CÁC CÂU KHÓ Câu 1: Hướng dẫn giải +) Tập x{c định
, yêu cầu của b|i to{n đưa đến giải bất phương trình  2 14
mx 14mx 14  0, x
 1, tương đương với g(x)   m (1) 2 x 14x
+) Dễ d|ng có được g(x) l| h|m tăng "x Î 1 é ;+¥ ë ) 14
suy ra min g(x)  g(1)   x 1  15 14
+) Kết luận: (1)  min g(x)  m    m x 1  15 Câu 10: Đặt CD x suy ra 2 AC 20 x;CB x 16, 0 x 20 AC 20 x
Thời thời bạn Linh đi từ A đến C l| t
. Do Linh đi xe từ A đến C gấp ba l}n AC 15 15 5
vận tốc đi từ C đến B nên suy ra vận tốc bạn linh đi xe từ C đến B l| : 15 v v 9km / h 3 2 x 16
suy ra thời gian Linh đi xe từ C đến B l| t
suy ra thời gian bạn linh đi từ nh| đến CB 9 2 20 x x 16 trường l| : t AB 15 9 2 20 x x 16 1 x Xét h|m số f x f '(x) f '(x) 0 x 3 2 15 9 15 9 x 16 76 16 4 26 Ta có : f 3 ; f 0 ; f 20
. Ta thấy thời gian nhỏ để đi từ nh| đến trường 45 9 9
76 (Giờ) . Hay nói c{ch kh{c khoảng c{ch đoạn CD 3km suy ra chọn C 45 Câu 20: ĐK: x 0 ta có 2 2 2 2 log x log x 1 1 5m 0 log x log x 1 1 5m .Đặt 1 3 1 3 3 3 2 2 2 2 t log x 1 log x t 1,t 1; 3 5m t t 2 1 5m f t .Xét h|m số 3 3 2 f t t t 2,t 1;3 Trang 89
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Ta có : f ' t 2t 1 0, t
1;3 suy ra f t đồng biến trên đoạn 1;3 max f (x) f (3) 10 1;3 , min f (x) f (1)
0 suy ra phương trình đã cho có ít nhất một nghiệm thuộc đoạn 2 2 1;3 khi 1;3
phương trình (1) có ít nhất một nghiệm thuộc đoạn 1; 3 . Hay 0 5m 10 0 m 2 T 0;2 suy ra chọn A Câu 21:
Diện tích đ{y của hộp phấn l| S=6.5=30
Mỗi viên phấn có đường kính 1cm nên một hộp ta có thể đựng 30 viên phấn
Suy ra số lượng phấn có thể xếp trong 12 hộp l|: 12.30=360 viên.Do chỉ có 350 viên nên thiếu 10 viên Câu 26:
Chọn hệ trục tọa độ như hình vẽ . Điểm A 0; 0 , H 30;30
B 60;0 .Đường đường Parabol bậc 2 2 y ax bx , c a 0
đi qua c{c điểm A,H,B nên ta có hệ sau : c 0 c 0 c 0 1 2 a.60 60.b c 0 60.a b 0 a 30 2 a.30 30.b c 30 30.a b 1 b 2 1
Suy ra phương trình đường Parabol bậc 2 l| : 2 y x 2x 30 60 1
Do đó diện tích của chiếc gương l| : 2 2 S x 2x dx
1200 cm suy ra chọn B 30 0 Câu 28:
Thể tích của cả cốc nước l| V .4.12 48
Thể tích của phần cốc chứa nước l| V .4.10 40 nc 4 16
Thể tích của 4 viên bi l| V 4. . bi 3 3 16 8
Suy ra thể tích của phần trống khi thả 4 viên bi v|o l| V 48 40 0 3 3
Phần trống đó có diện tích đ{y bằng diện tích đ{y của cốc nước nên độ cao h sẽ l| 8 : 3 h 0, 67 4 Câu 34: 2 Giả sử 2 z a bi ; w x yi ; a , , b x,y a 2 b 9 x a b 3 Theo đề w 1 i 3 z 2i x yi a 3b (b 2 3a)i y b 2 3a Trang 90
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 2 2 2 x 2 a 2 b 3 2 x 2 y 2 2 3 a 2 b 3 b 3 a 2 y 2 3 2 b 3 a 2 2 2 2 2 2 2 a 2 2 a 2 b 3 3b b 2(a 2)b 3 3(a 2) 4 a 2 b 4.9 36 2 2 x 2 y 2 2 3
36 suy ra b{n kính đường tròn l| r 36 6 . Suy ra chọn C
Cách 2 : Dễ chứng minh z .z z z .Ta có : 1 2 1 2 2 2 z a b , i z a b i z z a a b b a b a b i z z a a b b a b a b 1 1 1 2 2 2 1 2 1 2 1 2 1 2 2 1 1 2 1 2 1 2 1 2 2 1 2 2 2 2 a a b b a b a b 1 .Lại có 1 2 1 2 1 2 2 1 2 2 2 2 : 2 2 2 2 z z a b a b a a a b a b b b 2 1 2 1 2 1 2 1 2 1 2 2 1 1 2
Từ (1) v| (2) suy ra z .z
z z . Giờ ta chỉ cần {p dụng công thức trên : 1 2 1 2 w 1 i 3 z 2i w 2i 2 1 i 3 1 i 3 z 2 w 2i 2 1 i 3 1 i 3 z 2 1 i 3 . z 2 6 2 2 x-2+ y 2 2 3 i 6 x 2 y 2 2 3
36 suy ra b{n kính đường tròn l| r 6 . Suy ra chọn C
Câu 40: Xét hình nón tròn xoay , ta có : h SO 2 , R r O , A l
SA .Trong số R là bán kính
khối cầu , r l| b{n kính đ{y hình nón , l l| đường sinh của hình nón . 3 4 R
Thể tích khối cầu l| : V
. Do thể tích nước tr|n ra ngo|i 3 128 là 3 dm 3 3 1 4 R 128 nên ta có . 3 R 64 R 4 suy ra 2 3 3 h 8 .
Xét tam giác vuông SOA đường cao OH R 4 ta có : 1 1 1 1 1 1 1 3 3 8 OA dm 2 2 2 2 2 2 2 2 OH OS OA R 4R OA OA 4R 64 3 2 1 8 512 Thể tích khối nón l| : 3 V . .8 dm 3 3 9 512 128 128 V 1
suy ra thể tích nước còn lại l| : 3 V dm suy ra 2 suy ra chọn B 2 9 3 9 V 3 1 Câu 41: Trang 91
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Ta có : SO 50;OM 20 SM
30 cm .Gọi SA l| một đường
sinh của hình nón đỉnh trục SO v| B l| giao điểm của SA v| (C). Do
M l| t}m của đường tròn (C) suy ra MB SM 30.10 MB / /OA MB 6 cm OA SO 50 Lại có : 2 2 2 2 2 SB SM MB 30 6 936 SB 6 26 cm .
Suy ra diện tích xung quanh hình nón đỉnh S v| đ{y l| hình tròn
x{c định bởi C là : 2 S
36 26 cm do đó chọn C Câu 42: SM SN V Đặt x ;y ,(0 x,y 1) khi đó ta có : V V V V SD SB SABC SADC SABD SBCD 2 V V V V V V 1 SM SP SN SP 1 Ta có : 1 SAMPN SAMP SANP SAMP SANP . x y 1 V V V 2V 2V 2 SD SC SB SC 4 SADC SABC V V V V 1 1 3 Lại có : 1 SAMPN SAMN SMNP xy xy xy 2 V V 2V 2V 2 2 4 SABD SBCD 1 3 x Từ (1) v| (2) suy ra : x y xy y 4 4 3x 1 x 1 do 0 y 1 1 x 3x 1 2 2 V1 3 3 x 3x 3 1 Từ (2) suy ra .xy .x f (x), x 1 V 4 4 3x 1 4 3x 1 4 2 1 1 V 3 1 1 Khảo s{t h|m số 1 y f (x), x 1 m ax f (x) f 1 ; suy ra 1 2 V x x 2 8 3 2 1 2 chọn C Trang 92
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
ĐỀ THI THỬ SỐ 04 Môn: TOÁN Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97
NỘI DUNG ĐỀ SỐ 04 3 x Câu 1.
Nếu một nguyên h|m của h|m số f (x ) là
x thì h|m số f (x 1) là . 3 3 x A. 2 x 2x 2 . B. x(x 2) . C. x 1 . D. 2 (x 1) . 3 Câu 2.
Tìm số nguyên m nhỏ nhất sao cho h|m số y = (m + 3)x - 2 luôn nghịch biến trên c{c x + m
khoảng x{c định của nó? A. Không có m. B. m = -2. C. m = 0. D. m = -1. 2 Câu 3.
Tìm tập x{c định D của h|m số y . log x 2 3 A. D 0; \ 9 . B. D 9; . C. D 2; \ 9 . D. D 0; . 8 Câu 4.
Cho hình lập phương ABC .
D A' B 'C ' D ' ,biết thể tích khối chóp A'.BDB 'D ' là 3 dm . 3
Tính độ d|i cạnh DD ' . A. 2cm . B. 0, 2m . C. 20dm . D. 20mm . Câu 5.
Giải bất phương trình log x log (12 x). 2 2 A. x 9 hoặc x 16 . B. 0 x 9 hoặc x 16 . C. 0 x 9 . D. 0 x 12 . Câu 6.
Trong không gian với hệ tọa độ Oxyz , cho điểm A 1;2;3 v| hai mặt phẳng P : x 2 0 và Q : y z 1
0 . Viết phương trình mặt phẳng đi qua A và vuông
góc với hai mặt phẳng P , Q . A. x y z 5 0 . B. x z 0. C. y z 5 0 . D. x y 5 0 . Câu 7.
Một doanh nghiệp chuyên kinh doanh xe m{y. Hiện nay, doanh nghiệp đang tập
trung chiến lược v|o kinh doanh xe HonDa Future Fi với chi phí mua v|o l| 27 ( triệu
VNĐ) v| b{n ra với gi{ 31 ( triệu VNĐ) mỗi chiếc. Với gi{ b{n n|y thì mỗi năm doanh
nghiệp b{n được 600 chiếc xe Future Fi. Nhằm đẩy mạnh lượng xe tiêu thụ, doanh
nghiệp dự định giảm gi{ b{n v| ước tính rằng nếu giảm 1 ( triệu VNĐ) mỗi xe thì số
xe b{n ra trong một năm tăng 200 chiếc. Vậy doanh nghiệp nên b{n gi{ bao nhiêu
triệu đồng để thu được lợi nhuận cao nhất?
A. 30,5 triệu đồng. B. 30 triệu đồng.
C. 29,5 triệu đồng. D. 29 triệu đồng. 2 x 1 Câu 8. Cho h|m số y
. Số đường tiệm cận của đồ thị h|m số l| . 2 x x 2 A. 1 . B. 2 . C. 4 . D. 3 . 2 1 2x Câu 9.
Nếu F(x) l| nguyên h|m của h|m f (x) và F 1
3 thì F(x) có dạng . x Trang 93
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. 2 F(x) ln x x 2 . B. 2 F(x) lnx x 2 . C. 2 F(x) ln x x 2 . D. 2 F(x) ln x 2x 1.
Câu 10. Tìm phần thực v| phần ảo của số phức z, biết 2 z ( 5 i) (1 5 i) .
A. Phần thực bằng 14 v| phần ảo bằng 2 5 .
B. Phần thực bằng 14 v| phần ảo bằng 2 5i .
C. Phần thực bằng 14 v| phần ảo bằng 2 5 .
D. Phần thực bằng 14 v| phần ảo bằng 2 5i .
Câu 11. Cho số phức z thỏa mãn điều kiện z
1. Tìm gi{ trị lớn nhất của A 1 z 3 1 z . A. 4 8 . B. 2 15 . C. 10 . D. 2 10 . sinx
Câu 12. Cho tích phân 2 I
dx . Nếu đổi biến số t 4 3cosx thì 0 cosx 4 3cosx 2 I
f t dt . Khi đó f t l| h|m số n|o trong c{c h|m số sau? 1 4 1 4 1 A. f t 2 . B. f t . 4 t 1 t 4 t 1 t 2 1 1 2 4 1 C. f t . D. f t . 5 4 t 1 t 5 4 t 1 t
Câu 13. Trong các h|m số dưới đ}y, h|m số n|o chỉ có một điểm cực đại m| không có cực tiểu . 1 A. 4 2 y x 2x 1 . B. 3 2 y x x 2x 1 . 3 x 2 C. 4 2 y x 2x 1. D. y . x 2
Câu 14. Trong không gian với hệ tọa độ Oxyz , x{c định tất cả c{c điểm M trên trục tung c{ch
đều hai mặt phẳng P : x y z 1 0 và Q : x y z 5 0 . A. M 6;0;0 . B. M 0;2;0 . C. M 0; 2; 0 . D. M 0;1; 0 .
Câu 15. H|m số n|o có chiều biến thiên kh{c với chiều biến thiên c{c h|m số còn lại? A. 2017 y x x cosx 2016 . B. y tan(2016x) 2017x . C. y
cos(2016x) 4032x 2017 . D. y sin(2016x) 4032x 2017 .
Câu 16. Cho c{c số thực a; ; b c và a 1; . b c
0 . Khẳng định n|o sau đ}y l| khẳng định đúng. A. log ( . b c) log b log c . B. log ( . b c) log . b log c . a a a a a a C. log ( . b c) log b log c . D. log ( . b c)
log ( b) log ( c) . a a a a a a
Câu 17. Một thầy gi{o gi| muốn mua 1 chiếc xe m{y Honda SH 2017 – 150i phiên bản phanh
ABS có gi{ niêm yết của nh| sản xuất l| 90.000.000đ (chín mươi triệu đồng). Sau nhiều
năm dạy học thầy gi{o tích được số tiền l| 70.000.000đ, thầy gi{o đó quyết định mua
xe m{y trả góp với số tiền còn thiếu l| 20.000.000đ (hai mươi triệu đồng), mức lãi suất
1,2% / th{ng với quy ước 1 th{ng trả 800.000đ cả gốc v| lãi. Sau một năm lãi suất lại
tăng lên l| 1,5% / th{ng v| người đó lại quy ước 1 th{ng trả 1.000.000đ cả gốc v| lãi
(trừ th{ng cuối cùng). Hỏi sau bao nhiêu th{ng thầy gi{o ấy trả hết nợ (th{ng cuối trả không qu{ 500.000đ). Trang 94
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. 25 tháng. B. 27 tháng. C. 12 tháng. D. 28 tháng. 1 1 5 2016 Câu 18. Nếu 2 3 (a 1) (a 1) và log log thì . b 6 b 2017 A. 1 a 2;0 b 1 . B. 1 a 2;b 1 . C. a 2;b 1 . D. 0 a 1;b 1. 1 1 Câu 19. Cho h|m số 4 2 y x x
. Khi đó hãy chọn đ{p {n đúng . 2 2
A. H|m số đạt cực tiểu tại điểm x
0, gi{ trị cực tiểu của h|m số l| y(0) 0 .
B. H|m số đạt cực đại tại c{c điểm x
1 , gi{ trị cực đại của h|m số l| y( 1) 1. 1
C. H|m số đạt cực đại tại điểm x
0, gi{ trị cực đại của h|m số l| y(0) . 2
D. H|m số đạt cực tiểu tại c{c điểm x
1 , gi{ trị cực tiểu của h|m số l| y( 1) 1.
Câu 20. Một người nông d}n có 15 triệu đồng để l|m một c{i h|ng r|o có dạng hình chữ E dọc
theo một con sông với chiều cao h|ng r|o l| 1m (như hình vẽ) để l|m một khu đất có
hai phần chữ nhật để trồng rau. Đối với mặt h|ng r|o song song với bờ sông thì chi
phí nguyên liệu l| 60.000 đồng/ 2
m , còn đối với ba mặt h|ng r|o song song nhau thì
chi phí nguyên vật liệu l| 50.000 đồng/ 2
m . Tính diện tích lớn nhất của đất r|o thu được ? y x A. 2 6250 m B. 2 1250 m C. 2 3125 m D. 2 50 m
Câu 21. Cho hình chóp S.ABCD có đ{y ABCD là hình vuông, SA vuông góc với mặt phẳng (ABCD) . Cho SB
a , góc tạo bởi SB v| mặt đ{y l| . Tính sin sao cho thể tích
khối chóp S.ABCD l| lớn nhất. 3 3 3 A. . B. . C. . D. 1 . 3 3 3 4 e ae b Câu 22. Cho 3 x lnxdx với a, , b c và 1 c 30 . Tính a b c . 1 c A. 16 . B. 20 . C. 1 . D. 19 .
Câu 23. Cho một hình chóp tam gi{c S.ABC , cạnh bên SB tạo với đ{y một góc 0 30 và SB
100cm . C{c cạnh đ{y lần lượt l| 150 , cm 200cm, 250 .
cm Thể tích khối chóp S.ABC là A. 250 lít. B. 750 lít. C. 3 150m . D. 1500 lít.
Câu 24. Gọi M;m lần lượt l| gi{ trị lớn nhất v| gi{ trị nhỏ nhất của h|m số f (x) x 3 ln(x
2) trên đoạn *0; 4+ . Tính M m . A. 5 18 1 ln 3 . B. 5 ln18. C. 5 3ln2 . D. 5 3ln18 .
Câu 25. Tính diện tích hình phẳng giới hạn bởi c{c đường: y
xsin2x , y 2x , x . 2 Trang 95
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 2 2 2 A. . B. 4 . C. . D. 2 . 4 4 4 4 4
Câu 26. Đường cong trong hình bên l| đồ thị của một h|m số trong bốn h|m số được liệt kê ở
bốn phương {n A, B, C, D dưới đ}y. Hỏi h|m số đó l| h|m số n|o? 2x 4 2x 1 x 1 3x 4 A. y . B. y . C. y . D. y . x 1 x 1 x 1 x 1
Câu 27. Cho log 3 a; log 3
b . Hãy biểu diễn log 60 theo a và b. 2 5 54 2a b ab b 3ab A. log 60 . B. log 60 . 54 ab b 54 a 2b 2a b a 2b ab C. log 60 . D. log 60 . 54 2ab b 54 3ab b
Câu 28. Cho hai số phức z 2 4i và z 1
3i . Tính môđun của số phức z 2iz . 1 2 1 2 A. z 2iz 8 . B. z 2iz 10 . C. z 2iz 1. D. z 2iz 10 . 1 2 1 2 1 2 1 2 1 1
Câu 29. Phương trình có hai nghiệm x x . Chọn ph{t 2log x 1 log x 4 6log x 9 1 2 2 2 2 biểu đúng. 2 A. 8x .x 1. B. x x . C. 2 x x 8 . D. 8x x 0 . 1 2 1 2 1 2 1 2 mx 3
Câu 30. Cho h|m số y
. Tìm tất cả c{c gi{ trị của m để h|m số nghịch biến trên từng x m khoảng x{c định. A. m 3 hoặc m 3 . B. 2 m 3 . C. 2 m 4. D. 3 m 3 .
Câu 31. Cho z ,z l| hai nghiệm của phương trình 2 2017z 2016z 2017 0 . Tính 1 2 2 2 M 1 z .z z z . 1 2 1 2 1 A. 3 . B. . C. 1 . D. 0 . 3 1
Câu 32. Cho h|m số y log
. Hãy chọn đồ thị của h|m số trên. 2 x Trang 96
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai A. B. C. D. 4 z 1
Câu 33. Cho z ,z ,z ,z l| c{c nghiệm phức của phương trình 1.Tính 1 2 3 4 2z i 2 2 2 2 z 1 z 1 z 1 z 1 . 1 2 3 4 1 15 17 A. 85 . B. . C. . D. . 2 9 9
Câu 34. Một bạn nữ l|m son Handmade, bạn chuẩn bị một h hình trụ đựng son có đường
kính đo từ bên trong ra mép bên ngo|i l| 5cm . Biết vỏ h l|m bằng thủy tinh d|y
0, 5cm , có chiều cao th}n l| 4cm . Hỏi thể tích son m| bạn nữ có thể đựng trong h
nhiều nhất m| không bị tr|n ra ngo|i l| bao nhiêu. A. 3 8 cm . B. 3 25 cm . C. 3 20,25 cm . D. 3 16 cm . Câu 35. Cho h|m số 3 2 y x (m 1)x 2mx
3(C). Tìm m để đường thẳng y 2x 5 cắt
đồ thi h|m số (C) tại ba điểm ph}n biết . A. m 1 hoặc m 7 . B. 7 m 1. C. 7 m . D. 0 m 1.
Câu 36. Cho tứ diện ABCD có c{c cặp cạnh đối bằng nhau, gọi
l| mặt phẳng đi qua trung
điểm H của AD AB CD v| song song với , . Khi đó mặt phẳng chia tứ diện ABCD V
th|nh hai phần, một phần chứa cạnh AB có thể tích l| v| một phần chứa 1 V
cạnh CD có thể tích l| V . Tính tỉ số 1 . 2 V2 1 A. 1 . B. 2 . C. . D. 3 . 2 x 1 y 3 z 2
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d : 1 1 2 1 x 2 y 1 z 1 và d :
. Viết phương trình đường thẳng d vuông góc với mặt 2 3 1 2 phẳng P : 3x 3y 4z
0 v| cắt hai đường thẳng d ,d . 1 2 Trang 97
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai x 2 y 3 z 2 x 2 y 5 z 1 A. d : . B. d : . 3 5 4 3 3 4 x 2 y 5 z 1 x 2 y 1 z 1 C. d : . D. d : . 3 3 4 1 3 4
Câu 38. Cho hình nón đỉnh S và O l| t}m đ{y.Thiết diện qua trục của hình nón l| một tam
gi{c c}n có đường cao h
3cm , biết hai cạnh bên d|i gấp đôi cạnh đ{y. Tính diện tích xung quanh của hình nón . 36 36 18 18 A. 2 cm . B. 2 m . C. 2 cm . D. 2 m . 17 17 5 5
Câu 39. Cho hình lăng trụ đứng ABC .
D A' B 'C ' D ' ,có diện tích ABC ,
D ABB 'A', BCC 'B ' lần
lượt l| 4, 6, 8. Tính b{n kính mặt cầu ngoại tiếp hình lăng trụ, biết đ{y l| hình chữ nhật. 192 193 207 183 A. . B. . C. . D. . 5 6 5 6
Câu 40. Một chậu nước hình trụ cao 12cm , rộng 10cm . Người ta đổ nước
v|o trong chậu sao cho nước trong chậu cao 10cm . Sau đó người
ta thả c{c viên bi v|o chậu, biết b{n kính mỗi viên bi l| 2cm . Và
sau mỗi lần thả một viên bi v|o chậu nước thì nước bắn ra ngo|i
bằng 15% thể tích mỗi viên bi. Hỏi cần thả ít nhất bao nhiêu viên
bi v|o chậu nước thì nước vừa bắn vừa đầy miệng chậu chàn ra ngoài. A. 4. B. 5. C. 6. D. 7.
Câu 41. Biết rằng h|m số 4 2 2 4 y x 2m x m
1 có 3 điểm cực trị A O , y , B C sao cho bốn điểm ,
A B,C,O cùng nằm trên 1 đường tròn? Tất cả gi{ trị tham số m bằng . A. m 1. B. m 0 . C. m 1. D. m 1.
Câu 42. Trong không gian với hệ tọa độ Oxyz , cho vectơ tùy ý u khác 0 . Tính 2 2 2 cos , u i cos , u j cos , u k . 1 A. 1 . B. . C. 3 . D. 1 . 2 1
Câu 43. Gọi (S) l| hình phẳng giới hạn bởi đồ thi h|m số y ; y 0 , x 0; x 3 ln 2 . 3 x e 2
Tính thể tích V của khối tròn xoay thu được khi quay hình (S) xung quanh trục ho|nh. 3 3 3 1 3 3 1 3 3 A. V ln . B. V ln6 . C. V ln . D. V ln 1 . 4 2 4 6 4 2 6 4 2
Câu 44. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A 1; 4;5 , B 0;3;1 ,
C 2; 1;0 v| mặt phẳng P : 3x 3y 2z 15
0. Hỏi điều kiện cần v| đủ để điểm
M nằm trên mặt phẳng P có tổng c{c bình phương khoảng c{ch đến c{c điểm , A , B C nhỏ nhất.
A. M l| t}m mặt cầu đi qua c{c điểm , A ,
B C v| tiếp xúc mặt phẳng P .
B. M l| hình chiếu vuông góc của t}m đường tròn ngoại tiếp tam gi{c ABC trên mặt phẳng P . Trang 98
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
C. M l| hình chiếu vuông góc của trọng t}m tam gi{c ABC trên mặt phẳng P .
D. M nằm tren giao tuyến của mặt phẳng ABC v| mặt phẳng P .
Câu 45. Trong không gian với hệ tọa độ Oxyz , c{c phương trình dưới đ}y thì phương trình
n|o l| phương trình mặt cầu. A. 2 2 2 (x 1) (y 3) (2 z) 16 . B. 2 2 2 2x 2y 2z 5x 6y z 2 0 . C. 2 2 2 x y z 4x y 3z 8 0 . D. 2 2 2 x y z 2x 4y 9 0 .
Câu 46. Trong không gian với hệ tọa độ Oxyz , Cho mặt phẳng P : x y z m 0 (với m l| tham số) v| mặt cầu 2 2 2 (S) : x y z 6x 2y 4z
0. Tìm tất cả c{c gi{ trị của
m để mặt phẳng P v| mặt cầu (S) có điểm chung. A. 42 m 42 . B. 42 m 42 . C. 42 m . D. 0 m 42 .
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng 2 P : m x 2y z 9 0 (với x 2 y 6 z m
m l| tham số) v| đường thẳng d :
. Tìm tất cả c{c gi{ trị của m 1 2 5
để đường thẳng d song song với mặt phẳng P . 7 A. m 3. B. m 3 . C. m . D. m 3 . 2
Câu 48. Tính đạo h|m của h|m số 3x y .sin lnx . 3x 3x A. y '
ln3.x.sin lnx cos lnx . B. y ' x.sin lnx cos lnx . x x 3x C. y ' sin lnx cos lnx . D. ' 3x y x.sin lnx cos lnx . x
Câu 49. Tìm tất cả c{c gi{ trị của m để h|m số 2 2 y 2x 6mx 9 có tập x{c định l| . A. 2 m 2 . B. 0 m . C. 2 m 2 . D. 0 m 2 .
Câu 50. Tìm tập hợp c{c điểm trong mặt phẳng phức biểu diễn c{c số phức z thỏa mãn z 1 l| số thực. z 5i
A. L| đường thẳng 5x + y – 5 = 0.
B. L| đường thẳng 5x + y – 5 = 0 trừ điểm có tọa độ (0 ; 5). C. L| đường tròn 2 2 x (y 5)
0 trừ điểm có tọa độ (0 ; 5). D. L| đường tròn 2 2 x (y 5) 0 . ----------- HẾT ---------- Trang 99
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai BẢNG ĐÁP ÁN Câu 1 B Câu 11 D Câu 21 B Câu 31 D Câu 41 C Câu 2 A Câu 12 D Câu 22 B Câu 32 D Câu 42 D Câu 3 A Câu 13 C Câu 23 A Câu 33 D Câu 43 C Câu 4 B Câu 14 B Câu 24 D Câu 34 D Câu 44 C Câu 5 C Câu 15 C Câu 25 A Câu 35 A Câu 45 B Câu 6 C Câu 16 C Câu 26 B Câu 36 A Câu 46 A Câu 7 A Câu 17 B Câu 27 A Câu 37 B Câu 47 A Câu 8 D Câu 18 B Câu 28 D Câu 38 A Câu 48 A Câu 9 A Câu 19 B Câu 29 D Câu 39 D Câu 49 C Câu 10 C Câu 20 A Câu 30 D Câu 40 C Câu 50 B
HƯỚNG DẪN GIẢI CÁC CÂU KHÓ Câu 7.
Gọi số tiền cần giảm gi{ mỗi xe l| x ( triệu VNĐ)
Vì cứ giảm 1 ( triệu VNĐ) thì số xe b{n ra tăng 200 chiếc nên giảm x ( triệu VNĐ), số xe b{n ra
tăng 200x chiếc. Do đó tổng số xe b{n ra mỗi năm l|: 600 200x chiếc.
Lúc đầu b{n với gi{ 31 ( triệu VNĐ), mỗi xe có lãi 4 ( Triệu VNĐ). Sau khi giảm gi{, mỗi xe thu được số lãi l|: 4
x ( Triệu VNĐ). Do đó tổng số lợi nhuận một năm thu được sau khi giảm gi{ là: f x 4 x 600 200x ( triệu VNĐ) Xét h|m số f x 4 x 600 200x trên 0; 1 Ta có: 2 f ' x 400x 200 0 x . 2 1 Khi đó Maxf x f 2450 . 2 1
Như vậy, để thu được lợi nhuận cao nhất doanh nghiệp cần giảm gi{ b{n mỗi chiếc xe ( triệu 2
VNĐ), tức l| mỗi xe b{n với gi{ 30,5 ( Triệu VNĐ). Câu 11. Đặt z a bi thì 2 2 a b 1, 1 z 1 a bi 1 z 1 a bi . Ta có 2 2 2 2 A (1 a) b 3 (1 a) b 2 1 a 3 1 a . Xét h|m số f a 2 1 a 3 1 a với a 1;1 . 1 a 3 1 a 4 f ' a 2. 0 a . 5 2 1 a. 1 a 4 Ta có f 1 2 , f 2 10 . 5
Vậy gi{ trị lớn nhất của A l| 2 10 . Câu 17.
Gọi A l| số tiền vay ban đầu; A l| số tiền còn nợ cả vốn lẫn lãi sau n kì hạn; T l| số tiền trả 0 n 0
trong 1 kì hạn; n l| số kì hạn tính lãi; r lãi suất định kì tính theo %.
Công thức tính số tiền còn nợ sau th{ng thứ n l|: Trang 100
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai n n 1 r 1 A A 1 r T . n 0 0 r
Sau 1 năm đầu tiên thì thầy gi{o đó còn nợ l| n 12 1 0, 012 1 A 20000000 1 0, 012 800000. 12818250, 87 1 0, 012
Sau một năm thì lãi tăng lên. Người đó trả hết nợ thì n n 1 r 1 T0 A A 1 r T . 0 n log 14, 00184553 n 0 0 1 r r T A .r 0 0
Vậy l| sau 27 th{ng thì người ấy trả hết nợ.
Câu 20. Gọi x m l| chiều d|i mặt song song bờ song.
Gọi y m l| chiều d|i mỗi mặt còn lại. Tổng tiền: 6 60000x 3.50000y 15.10 6x 15y 1500 2 6x 15 1 1 y Diện tích đất r|o: 2 S xy .6x.15y 6250m 90 90 4
Câu 34. B{n kính h tính cả phần vỏ h l| r 2,5cm . 1
B{n kính phần bên trong h l| r r 0,5 2cm . 2 1 Thể tích son l| 2 3 V r h 16 (cm ). Câu 36.
Gọi E, F,G lần lượt l| trung điểm của AC,BD,BC . Khi đó mặt phẳng
l| mặt phẳng HEGF .
Theo giả thiết thì c{c cặp cạnh đối của tứ diện l| bằng nhau nên S S ; S S ; S S . ABC ADC AHE GEC CDHE ABGE 1 1 Ta có V d , B (ACD) .S d D,(ABC ) .S ABCD 3 ACD 3 ABC d , B (ACD) d D,(ABC) Hay 2d F,(ACD) 2d F,(ABC) d F,(AC ) D d F,(ABC) Ta có 1 1 V V V
d F,(ABC ) .S
d F,(ACD) .S , 1 F .AEGB F .AHE 3 ABGE 3 AHE 1 1 V V V
d F,(ABC ) .S
d F,(ACD) .S . 2 F .HDCE F .GCE 3 CDHE 3 GEC Do đó V V . Chọn A. 1 2 Câu 39. Trang 101
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai Do diện tích ABC ,
D ABB 'A', BCC 'B ' lần lượt l| 4, 6, 8 nên ta có. AB.BB ' 6 AB 3 AB.BC 4 BB ' 2 3 BB '.BC 8 4 3 BC 3
Gọi O, O' lần lượt l| t}m hai đ{y ABCD , A' B 'C ' D ' và I
lần lượt l| trung điểm O O' .
Khi đó mặt cầu goại tiếp lăng trụ có t}m I v| b{n kính l| ID ' . 5 3 5 3
Xét tam giác A' B ' D ' có 2 2 B ' D ' A' B ' A'D' D 'O' . 3 6 183
Xét tam giác O'I D ' có I D ' . Chọn D. 6
Câu 40. Thể tích chậu l| 2 3 V r h 300 (cm ). 1
Thể tích nước trong chậu l| 3 V 250 (cm ) . 2 32 Thể tích một viên bi l| 3 V (cm ). 3 3 8
Thể tích nước bắn ra ngo|i sau một lần thả l| 3 V (cm ) . 4 5 136
Thể tích nước tăng sau một lần thả l| 3 V V (cm ) . 3 4 15
Thể tích còn lại để nước đầy chậu l| 3 V V 50 (cm ) . 1 2 V V 136
Số viên bi ít nhất cần thả l| 1 2 50 : 5, 51. V V 15 3 4
Do đó cần thả ít nhất l| 6 viên bi v|o chậu nước thì nước vừa bắn vừa đầy miệng chậu ch|n ra ngoài. Chọn C. Câu 41. Ta có 3 2 y ' 4x 4m x 0 x 0 hoặc 2 x m
Để h|m số có 3 cực trị thì 2 m 0 m 0
Khi đó gọi 3 điểm cực trị l|: 4 2 2 ( A 0;1
m );B( m ;1);C( m ;1)
Ta có Oy l| một đường trung thực của tam gi{c ABC, nên tam đường tròn ngoại tiếp tam giác
ABC nằm trên trục Oy (đó c ng chính l| đường tròn đi qua 4 điểm ,
A B,C,O ). Gọi t}m đường
tròn ngoại tiếp tam gi{c ABC l| I(0;y ) I Trang 102
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 4 1 m
Khi đó I l| trung điểm OA nên y I 2 Mà 2 2 IO IB IO IB 2 2 2 y m (1 y ) I I 2 4 m m 0 m 1 . Chọn C.
Câu 44. Gọi G l| trọng t}m tam gi{c ABC . Ta có 2 2 2 MA MG GA MA MG GA 2MG.GA Tương tự 2 2 2 MB MG GB 2MG.G , B 2 2 2 MC MG GC 2MG.GC . Khi đó 2 2 2 2 2 2 2 MA MB MC 3MG GA GB GC 2MG. GA GB GC .
Do G l| trọng t}m tam gi{c ABC nên GA GB GC 0 nên 2 2 2 2 2 2 2 MA MB MC 3MG GA GB GC .
Ta có trọng t}m G 1;2;2 của tam gi{c ABC không thuộc mặt phẳng P nên để 2 2 2 MA MB
MC đạt gi{ trị nhỏ nhất thì MG nhỏ nhất. Khi đó M l| hình chiếu của G trên P . Chọn C.
Câu 50. Đặt z = x + yi (x, y R ) x 0 Với z – 5i 0 x yi 5i y 5 z 1 x 1 yi (x 1 yi)[x (y 5)i] x(x 1) y(y 5) [5x y 5]i 2 2 2 2 2 2 z 5i x (y 5)i x (y 5) x (y 5) x (y 5) z 1 Vì
l| số thực nên : 5x + y – 5 = 0. z 5i
V}y t}p hơp c{c điểm biểu diễn c{c số phức z l| đường thẳng 5x + y – 5 = 0 trừ điểm có tọa độ (0 ; 5). Chọn B. Trang 103
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA 2017
ĐỀ THI THỬ SỐ 05 Môn: TOÁN Nguyễn Văn Huy
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Sưu tầm và biên soạn: Thầy Nguyễn Văn Huy – Giáo viên ôn thi THPT môn Toán tại Biên Hòa.
Địa chỉ: 66 Đặng Đức Thuật – Phường Tam Hiệp – Biên Hòa (Cạnh Trường THPT Trấn Biên)
Điện thoại: 0968 64 65 97 NỘI DUNG ĐỀ SỐ 05 Câu 1. H|m số 3 2 y x 3x 1 l| đồ thị n|o sau đ}y A. B. C. D. y y y y 5 5 5 5 x x x x -5 5 -5 5 -5 5 -5 5 -5 -5 -5 -5 Câu 2. Cho h|m số y
f (x) có lim f (x) 3 và lim f (x)
3 . Khẳng định n|o sau đ}y l| x x khẳng định đúng:
A. Đồ thị h|m số đã cho không có tiệm cận ngang.
B. Đồ thị h|m số đã cho có đúng một tiệm cận ngang.
C. Đồ thị h|m số đã cho có hai tiệm cận ngang l| c{c đường thẳng y 3 và y 3 .
D. Đồ thị h|m số đã cho có hai tiệm cận ngang l| c{c đường thẳng x 3 và x 3 . Câu 3. H|m số 4 2 y x 4x
1 nghịch biến trên mỗi khoảng n|o sau đ}y: A. 2; 0 và 2; B. 2; 2 C. ( 2; )
D.  2;0   2; Câu 4.
Cho h|m số y  f (x) x{c định, liên tục trên v| có bảng biến thiên: x 0 1 y’ + – 0 + 2 y -3
Khẳng định n|o sau đ}y l| khẳng định đúng:
A. H|m số có đúng một cực trị.
B. H|m số có gi{ trị cực tiểu bằng 2.
C. H|m số có gi{ trị lớn nhất bằng 2 v| gi{ trị nhỏ nhất bằng -3.
D. H|m số đạt cực đại tại x=0 v| đạt cực tiểu tại x=1. Câu 5. Đồ thị của h|m số 4 3 2 y 3x 4x 6x 12x
1 đạt cực tiểu tại M(x ;y ). Khi đó 1 1 x y bằng 1 1 A. 5 B. 6 C. -11 D. 7 2 x 3 Câu 6.
Tìm gi{ trị nhỏ nhất của h|m số y trên đoạn 2; 4 . x 1 Trang 104
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 19 A. miny 6 B. miny  2  C. miny 3 D. miny [2;4] [2;4] [2;4] [2;4] 3 Câu 7.
Số giao điểm của đồ thị h|m số 4 2 y x 7x 6 và 3 y x 13x là : A. 1 B. 2 C. 3 D. 4 Câu 8.
Tìm m để đồ thị C của 3 2 y x 3x
4 v| đường thẳng y mx m cắt nhau tại 3 điểm ph}n biệt A 1;0 , ,
B C sao cho OBC có diện tích bằng 8. A. m =3 B. m =1 C. m =4 D. m =2 x 1 Câu 9.
Đồ thị của h|m số y có bao nhiêu tiệm cận: 2 x 2x 3 A.1 B. 2 C. 3 D. 4
Câu 10. Cho một tấm nhôm hình vuông cạnh
18 cm. Người ta cắt ở bốn góc của tấm
nhôm đó bốn hình vuông bằng nhau,
mỗi hình vuông có cạnh bằng x (cm),
rồi gập tấm nhôm lại như hình vẽ
dưới đ}y để được một c{i hộp không
nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. x 6 B. x 3 C. x 2 D. x 4 x e m  2
Câu 11. Tìm tất cả gi{ trị thực của tham số m sao cho h|m số y x 2 e  đồng biến trên m 1 khoảng ln ; 0 : 4 1 1 A. m 1;2 B. m ; 2 2 1 1 C. m 1;2 D. m ; 1;2 2 2
Câu 12. Giải phương trình log x 1 2 A. 2 e 1 B. 2 e 1 C. 101 D. 2 1 1
Câu 13. Tính đạo h|m của h|m số y 2x x 1 1 ln 2 1 ln 2 A. y ' B. y ' C. y ' x. D. y ' 2 2 2x 2x 2 2x
Câu 14. Giải bất phương trình log 1 x 0 1 3 A. x = 0 B. x < 0 C. x > 0 D. 0 < x < 1
Câu 15. Tìm tập x{c định của h|m số 2 y ln 2x 7x 3 1 1 1 1 A. D= ; 3; B. D ; 3 C. D= ; 3; D. D ;3 2 2 2 2 2 Câu 16. Cho h|m số 3x .4x f x
. Khẳng định n|o sau đ}y sai : A. 2 f x 9 x 2x log 2 2 B. 2 f x 9 x log 3 2x 2 log 3 3 2 2 Trang 105
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 90 C. f x 9 2x log 3 x log 4 log 9 D.
Câu 17. Họ nguyên h|m của h|m số f x  cos xcos3x là sin 3x A. sin x   C .
B. 2sin 4x  sin 2x C . 3 sin 4x sin 2x sin 4x sin 2x C.   C . D.    C . 8 4 8 4 2x
Câu 18. Tính đạo h|m của h|m số y 2e 2x A. y ' 2 2e B. 2x 2 ' 2.2 . x y e . 1 ln 2  C. 2 x 2 x '  2.2 . x y e ln 2
D. y x e2 1 ' 2 2
Câu 19. Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi
quay hình phẳng (H) quanh trục Oy là b b y
A. V   g  2 2
 y  f y x  d .
B. V    f  2 2
 y  g y y  d . b a a f(y) a b
C. V   g  2 2
 y  f y y  d .
D. V    f  2 2
 y  g y y  d . g(y) b a a x O Câu 20. Cho log 5 ; a log 5
b . Khi đó log 5 Tính theo a và b 2 3 6 1 ab A. B.
C. a +b D. 2 2 a b a b a b 3
Câu 21. Tìm nguyên hàm của hàm số 2 x 2 x dx x 3 x 4 3 x 4 A. 3 3 ln x x C B. 3 3 ln x x 3 3 3 3 3 x 4 3 x 4 C. 3 3 ln x x C D. 3 3 ln x x C 3 3 3 3
Câu 22. Một nguời gửi tiết kiệm với lãi suất 8,4% năm v| lãi h|ng năm đuợc nhập v|o vốn, hỏi
sau bao nhiêu th{ng ngưòi đó thu đuợc gấp đôi số tiền ban đầu (lấy gi{ trị quy tròn) ? A. 96; B. 97 C. 98 D. 99
Câu 23. Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị
y f x, y g x, x a, x b (a < b ) . b b A. S f x g x dx B. S f x g x dx a a b 2 b C. S f x g x dx
D. S    2 f x 2
g xdx a a
Câu 24. Gi{ trị m để h|m số 3 2 F x mx 3m 2 x 4x
3 l| một nguyên h|m của h|m số 2
f (x)  3x  10x  4 là: A. m = 3 B. m = 0 C. m = 1 D. m = 2 Trang 106
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai 2
Câu 25. Tính tích phân I x.sin xdx. 0 A. I 3 B. I 2 C. I =1 D. I 1 4 3 1 sin x
Câu 26. Tính tích phân dx 2 sin x 6 3 2 3 2 2 3 2 3 2 2 2 A. ; B. ; C. . D. 2 2 2 2
Câu 27. Diện tích hình phẳng giới hạn bởi đồ thị C của h|m số 3 2 y 2x x x 5 v| đồ
thị C ' của h|m số 2 y x x 5 bằng: A. 0 B. 1 C. 2 D. 3 x
Câu 28. Cho hình H  l| hình phẳng giới hạn bởi đồ thị h|m số y ,trục Ox và 2 4 x đường thẳng x
1 .Thể tích của khối tròn xoay thu được khi quay hình H xung
quanh trục Ox bằng:  4 1 4 3 4 A. ln B. ln C. ln D. ln 2 3 2 3 2 4 3
Câu 29. Cho số phức z  1
 3i .Phần thực v| phần ảo của số phức w  2i 3z lần lượt l|: A.-3 và -7 B. 3 và -11 C. 3 và 11 D. 3 và -7
Câu 30. Cho hai số phức z 4 2 ; i z 2
i .Môđun của số phức z z bằng: 1 2 1 2 A.5 B. 5 C. 3 D. 3
Câu 31. Xét một hình trụ nội tiếp trong hình nón như hình vẽ minh họa bên dưới, trong đó S
l| đỉnh của hình nón, O l| t}m đường tròn mặt đ{y của hình nón. C{c đoạn A , B CD
lần lượt l| đường kính của đường tròn đ{y
của hình nón v| hình trụ; AC,BD cắt nhau
tại điểm M thuộc SO. Gọi V l| thể tích của 1
khối trụ v| V l| thể tích của khối nón. Biết tỷ 2 V 4 SI số 1 . Tính tỷ số . V 9 SO 2 SI 7 SI 2 A. . B. . SO 9 SO 3 SI 4 SI 5 C. . D. . SO 5 SO 6
Câu 32. Cho số phức z 3 2i .Tìm số phức w 2i 3 i z 2iz 1? A.w 8 5i
B. w  8  5i C. w 8 5i D. w 8 5i
Câu 33. Gọi z ,z ,z ,z l| bốn nghiệm phức của phương trình 4 2 2z 3z 2 0 .Tổng 1 2 3 4
T z z z z bằng: 1 2 3 4 A.5 B. 5 2 C. 3 2 D. 2 Trang 107
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 34. Cho c{c số phức z thỏa mãn z
2 .Biết rằng tập hợp c{c điểm biểu diễn c{c số phức w 3 2i 2
i z l| một đường tròn.Tính b{n kính r của đường tròn đó. A.20 B. 20 C. 7 D.7
Câu 35. Cho khối lăng trụ đứng ABC.A' B 'C ' ,đ{y ABC l| tam gi{c vuông tại B AB BC 2a,AA'
a 3 .Tính thể tích khối lăng trụ ABC.A'B 'C ' . 3 2a 3 3 a 3 A. 3 2a 3 B. C. D. 3 a 3 3 3
Câu 36. Cho hình chop S.ABCD có đ{y ABCD l| hình chữ nhật AB a,BC 2a ,cạnh bên
SA vuông góc với đ{y v| SA a 2 .Tính thể tích khối chop S.ABCD . 3 2a 3 3 2a 2 A. B. C. 3 2a 2 D. 3 a 2 3 3
Câu 37. Cho khối tứ diện OABC với O , A O ,
B OC vuông góc từng đôi một v| OA a,OB 2a,OC
3a . Gọi M,N lần lượt l| trung điểm của hai cạnh AC,BC . Thể
tích của khối tứ diện OCMN tính theo a bằng: 3 2a 3 3a 3 a A. B. 3 a C. D. 3 4 4
Câu 38. Cho hình chóp S.ABCD có đ{y ABCD l| hình vuông cạnh a , SA vuông góc với đ{y 3 2a
,thể tích khối chóp bằng
.Tính khoảng c{ch từ A đến mặt phẳng SBD . 3 2a a 4a 3a A. B. C. D. 3 3 3 2
Câu 39. Trong không gian cho tam giác ABC vuông tại A với AC 3 , a AB
4a .Tính độ d|i
đường sinh l của hình nón nhận được khi quay tam gi{c ABC quanh trục AC . A. 9a B.a C. a 7 D. 5a
Câu 40. Cho hình chóp S.ABC có đ{y l| tam gi{c vuông c}n tại , A AB AC a . Mặt bên
SAB l| tam gi{c đều v| nằm trong mặt phẳng vuông góc với đ{y. Tính theo a thể
tích khối cầu ngoại tiếp hình chóp S.ABC . 3 a 3 a 21 3 a 3 7 a 21 A. B. C. D. 54 54 3 54
Câu 41. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện l| một hình
vuông có cạnh bằng 3a . Diện tích to|n phần của khối trụ l|: 2 27 a 2 a 3 2 13a A. 2 a  3 B. C. D. 2 2 6
Câu 42. Một xưởng có máy cắt và máy tiện dùng để sản xuất trục sắt và đinh ốc. Sản xuất 1 tấn
trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2
triệu. Sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi
là 1 triệu. Một máy không thể sản xuất cả 2 loại. Máy cắt làm không quá 6giờ/ngày,
máy tiện làm không quá 4giờ/ngày. Một ng|y xưởng nên sản xuất bao nhiêu tấn mỗi
loại để tiền lãi cao nhất.
A. 1 tấn trục sắt v| 3 tấn đinh ốc
B. 3 tấn trục sắt v| 1 tấn đinh ốc
C. 2 tấn trục sắt v| 3 tấn đinh ốc
D. 2 tấn trục sắt v| 2 tấn đinh ốc Trang 108
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai
Câu 43. Trong không gian Oxyz , cho 3 điểm M 1;0;2 ,N
3; 4;1 ,P 2;5;3 . Phương trình
mặt phẳng MNP là A. x 3y 16z 33 0 B. x 3y 16z 31 0 C. x 3y 16z 33 0 D. x 3y 16z 31 0
Câu 44. Trong không gian Oxyz , cho mặt cầu 2 2 2 S : x y z 2x 4y 2z 3 0 , đường x y 1 thẳng :
z . Mặt phẳng P vuông góc với v| tiếp xúc với S  có 2 2 phương trình l|: A. 2x 2y z 2 0 và 2x 2y z 16 0 B. 2x 2y 3 8 6 0 và 2x 2y 3 8 6 0 C. 2x 2y 3 8 6 0 và 2x 2y 3 8 6 0 D. 2x 2y z 2 0 và 2x 2y z 16 0 x 2 3t
Câu 45. Trong không gian Oxyz , cho A(4;-2;3), y 4
, đường thẳng d đi qua A cắt v| z 1 t vuông góc có vectơ chỉ phương l| A. ( 2; 15;6) B. ( 3; 0; 1) C. ( 2;15; 6) D. (3;0;-1)
Câu 46. Trong không gian Oxyz , cho 2 mặt phẳng P : x y 4z 2 0, Q : 2x 2z 7
0 . Góc giữa 2 mặt phẳng P , Q là: A. 0 60 B. 0 45 C. 0 30 D. 900
Câu 47. Trong không gian Oxyz , cho mặt phẳng ( ) : 3x y z 4 0 3x-y+z-4 =0 . mp( )
cắt mặt cầu S tâm I 1; 3;3 theo giao tuyến l| đường tròn t}m H 2;0;1 , bán kính r
=2. Phương trình S là: A. 2 2 2 (x 1) (y 3) (z 3) 18 B. 2 2 2 (x 1) (y 3) (z 3) 18 C. 2 2 2 (x 1) (y 3) (z 3) 4 D. 2 2 2 (x 1) (y 3) (z 3) 4
Câu 48. Trong không gian Oxyz , cho 2 điểm A 1;2; 0 ,B 2;3;1 , đường thẳng x 1 y z 2 :
. Tọa độ điểm M trên sao cho MA MB là : 3 2 1 15 19 43 15 19 43 A. ( ; ; ) B. ( ; ; ) C. (45; 38; 43) D. ( 45; 38; 43) 4 6 12 4 6 12
Câu 49. Đường thẳng d đi qua H 3; 1;0 v| vuông góc với (Oxz ) có phương trình l|: x 3 x 3 x 3 t x 3 A. y 1 B. y 1 t C. y 1 D. y 1 t z t z 0 z 0 z t
Câu 50. Trong không gian Oxyz , cho E
5;2;3 ,F l| điểm đối xứng với E qua trục Oy . Độ dài EF là: A. 13 B. 29 C. 14 D. 34
-----------------------Hết ------------------------- Trang 109
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai BẢNG ĐÁP ÁN Câu 1 A Câu 11 D Câu 21 B Câu 31 b Câu 41 B Câu 2 C Câu 12 C Câu 22 B Câu 32 A Câu 42 A Câu 3 A Câu 13 B Câu 23 B Câu 33 C Câu 43 B Câu 4 D Câu 14 B Câu 24 C Câu 34 B Câu 44 A Câu 5 C Câu 15 D Câu 25 C Câu 35 A Câu 45 C Câu 6 A Câu 16 C Câu 26 B Câu 36 B Câu 46 A Câu 7 C Câu 17 C Câu 27 B Câu 37 D Câu 47 B Câu 8 C Câu 18 B Câu 28 A Câu 38 A Câu 48 A Câu 9 C Câu 19 C Câu 29 C Câu 39 D Câu 49 B Câu 10 B Câu 20 B Câu 30 B Câu 40 D Câu 50 D
HƯỚNG DẪN GIẢI CÂU VẬN DỤNG CAO
CÂU 10. Điều kiện: 0 x 9 V h B x x 2 . .(18 2 ) f x ( )
Bấm mod 7 v| tìm được x=3
Cách khác: Áp dụng BĐT Côsi cho 3 số không }m 4x; 18-2x; 18-2x 3 1 1 4 (18 2 ) (18 2 ) 2 x x x V x.(18 x 2 ) x .4 (12 x 2 ).(12 x 2 ) . 4 4 3
Dấu “=” xảy ra khi x 4 18 x 2 x 3
Vậy: x=3 thì thể tích lớn nhất CÂU 11. TXĐ : D = m2 \ m2 m 2 y ' 2 x e m2 1
H|m số đồng biến trên khoảng ln ; 0 : 4 1 y ' 0, x ln ; 0 m2 m 2 0 1 m 2 4 1 1 1 1 m2 m2 2 1 m m 1 m m 1 ;1 4 2 2 4 1 1 m 1 m 2 2 2 CÂU 22.
Gọi x l| số tiền gửi ban đầu (x>0)
Do lãi suất 1 năm la 8,4% nên lãi suất th{ng l| 0,7%
Số tiền sau th{ng đ}u tiên l|: 1.00 x 7 2
Số tiền sau năm thứ 2 l|: 1.007 x n
Số tiền sau năm thứ n l|: 1.007 x n n Giả thiết 1.007 x x 2 1.007 2 n 99, 33 B CÂU 31. Trang 110
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai ID IM 2 3 3 3 1 1 MO 1 SM 4 I SO CD MO IM OI . SO SO OB IO 3 2 5 5 3 5 SO 5 SO 5
Gọi R ,R lần lượt l| b{n kính đ{y khối trụ v| khối nón. 1 2 SI ID R Ta có SID SOA 1 SO OA R2 2 V R IO . R 2 2 3 SO SI 3 2 1 SI SI 4 SI 2 1 1 3 3 0 V 1 R 2 2 S . O SO SO 9 SO 3 2 R SO 2 2 3
CÂU 34. Đặt w x yi, x,y w 3 i 2 2 i z x yi 3 i 2 2 i z x 3 y 2 i x 2 y 8 x y 2 1 z i 2 i 5 5 2 2 x 2 y 8 x y 2 1 2 5 5 x 2 y2 x 6 y 4 7 0 2 2 x 3 y 2 20
B{n kính của đường tròn l| r 20
CÂU 40. Gọi H l| trung điểm của AB,G l| trọng t}m của tam gi{c đều SAB=>G l| t}m đường
tròn ngoại tiếp tam gi{c SAB
Gọi O l| t}m đường tròn ngoại tiếp tam gi{c vuông ABC=>O l| trung điểm của CB
Qua O dựng đường thẳng d vuông góc với mp(ABC)=>d //SH
Qua G dựng đường thẳng vuông góc với mp(SAB) cắt d tại I,ta có :IA=IB=IC=ID=R
=>R l| b{n kính mặt cầu ngoại tiếp hình chóp . 1 1 a 3 a 3 a 2 Ta có: IO=GH= SH . ,OB= 3 3 2 6 2 21 2 2 a R=IB= IO OB 6 4 7 21 3 a3
Vậy thể tích khối cầu ngoại tiếp hình chóp : V= R 3 54 Chọn đ{p {n D
CÂU 42. Gọi x;y là số tấn trục sắt và đinh ốc sản xuất trong ngày.
Số tiền lãi mỗi ngày: L x ( ,y) x 2 y .
Số giờ làm việc mỗi ngày của máy cắt: x 3 y 6 .
Số giờ làm việc mỗi ngày của máy tiện: x y 4 . x 3 y 6
Ta có b|i to{n tìm gi{ trị lớn nhất của L x ( ,y) biết x y 4 (*). x 0,y 0 Trang 111
Tài liệu ôn thi THPT Quốc Gia 2017
Thầy Nguyễn Văn Huy – 0968 64 65 97 Biên Hòa – Đồng Nai y 6 C B d4 O 1 A 4 x d2 d3 d1
Miền nghiệm của (*) l| tứ gi{c OABC như hình vẽ với O(0;0),A(2;0),B(1;3 C ), (0; 4). Ta có: L(0; 0) 0,L(2; 0) 4,L(0, 4) 4,L(1, 3) 5 .
Vậy mỗi ng|y cần sản xuất 1 tấn trục sắt v| 3 tấn đinh ốc thì thu được tiền lãi cao nhấ l| 5 triệu đồng. Trang 112
Tài liệu ôn thi THPT Quốc Gia 2017