20 trang 10 lượt tải

Các bài tập tự luận đa dạng môn Xác suất thống kê| Trường Đại học Ngoại Thương

19

Bạn Thuận có một danh sách gồm 6 bài hát khác nhau, các bài hátđược phát theo thứ tự từ trên xuống. Lần đầu, khi nghe xong bài hát thứ ba trong danh sách, bạn ấy xáo trộn ngẫu nhiên danh sách phát của mình và sau đó nghe 3 bài hát đầu tiên trong danh sách mới. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Môn: Xác suất thống kê (FTU) 355 tài liệu

Trường: Trường Đại học Ngoại Thương 1.1 K tài liệu

Tác giả:

Profile

Lan Anh Trần

3 tuần trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/20
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
BÀI TOÁN V XÁC SU T Ề Ấ
A - XÁC SU P 10, 11 ẤT LỚ
Câu 1: Bạn Thuận có một danh sách gồm 6 bài hát khác nhau, các bài hát được phát theo thứ tự từ trên xuống.
Lần đầu, khi nghe xong bài hát thứ ba trong danh sách, bạn ấy xáo trộn ngẫu nhiên danh sách phát
của mình và sau đó nghe 3 bài hát đầu tiên trong danh sách mới. Tính xác suất để bạn Thuận nghe đủ
6 bài hát khác nhau sau hai lần nghe (kết quả làm tròn đến hàng phần trăm).
Lời gi i ả
Lần đầu nghe được 3 bài 1,2,3 trong danh sách. Xáo 6 bài nên ta có
( )
6!n=
.
A là biến cố “Nghe đủ 6 bài trong danh sách sau 2 lần nghe”.
Suy ra lần 2 phải nghe 3 bài 4,5,6 hay danh sách lần 2 phải là

1;2;3 4;5;6
.
Do đó,
( )
3!.3!n A =
. Vậy
( )
3!.3! 0,05
6!
P A ==
.
Câu 2: Trong tr a v ng viên Nguy i t t huy ận thi đấu bóng bàn đơn nam giữ ận độ ễn Đức Tuân (ngườ ừng đoạ
chương vàng đơn nam môn bóng bàn tạ ận động viên nướ ận đấi Seagames 31) với một v c ngoài, tr u
gồm tối đa 5 set (séc), ngườ ắng trưới nào th c 3 set sẽ giành chi n th ng chung cu c. Xác su v n ế ắ ộ ất để ậ
độ ắ ỗ ế ắng viên Tuân th ng m i set là 0,6. Tính xác su v ng viên Tuân giành chiất để ận độ n th ng trong
trận đấu (làm tròn kế ả đết qu n hàng phần trăm).
Lời gi i: ả
Để ế ắ ầ ủ v ng viên Tuân giành chiận độ n th ng, anh ta c n th i thắng 3 séc trước đố .
Các trường hợp có thể xảy ra là:
+) V ng viên Tuân th u tiên, xác su t là: TH1: ận độ ắng 3 set đầ ấ
=
3
0,6 0,216
.
+) u, v ng viên th ng 2 set, thua 1 set thì có TH2: Trong 3 set đầ ận độ ắ
=
2
33C
cách.
Xác su t v ng viên th ng 2 set, thua 1 set và th ng set th 4 là ấ ận độ ắ ắ ở ứ
=
2
3.0,6 .0,4.0,6 0,2592
.
+) u, v ng viên th ng 2 set, thua 2 set thì có TH3: Trong 4 set đầ ận độ ắ
=
2
46C
cách
Xác su t v ng viên th ng 2 set, thua 1 set và th ng set th 4 là ấ ận độ ắ ắ ở ứ
=
2 2
6.0,6 .0,4 .0,6 0,20736
.
Áp d ng công th c c ng xác su t, ta có xác su v ng viên Tuân giành chi n th ng trong ụ ứ ộ ấ ất để ận độ ế ắ
trận đấu là:
+ + 0,216 0,2592 0,20736 0,68
.
Câu 3: Nhân d p T t Trung thu cô giáo t ng quà cho 3 b ng, Ng c. Trong h p quà có 9 cây bút và ị ế ặ ạn Vũ, Hồ ọ ộ
8 quy n v c s p x p m t cách l n x n. Cô giáo g i 3 b ng x p hàng có th t ng ể ở đượ ắ ế ộ ộ ộ ọ ạn đứ ế ứ ự, Vũ đứ
trước đượ ặng quà trướ ồng đứ ọc đức t c, H ng sau nhận quà sau và Ng ng sau cùng nên nhận quà sau
cùng. Xác su Ng c nh c quà là cây bút b ng bao nhiêu, bi t r ng cô giáo t ng quà b ng ất để ọ ận đượ ằ ế ằ ặ ằ
cách rút ng u nhiên và m i b n ch m t ph n quà trong h ? ẫ ỗ ạ ỉ ộ ầ ộp (k t qu n hàng phế ả làm tròn đế ần trăm)
Lời gi i: ả
Để ọ Ng c nh ng hận được bút, ta xét các trườ ợp:
n bút, H ng nh n bút, Ng c nh n bút: Trường h p 1:ợ Vũ nhậ ồ ậ ọ ậ
Xác su n bút: ất Vũ nhậ
9
17
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Sau khi Vũ nhận bút, còn lại 8 bút và 8 vở, tổng cộng 16 phần quà.
Xác su t H ng nh n bút: ấ ồ ậ =
8 1
16 2
Sau khi H ng nh n bút, còn l i 7 bút và 8 v , t ng c ng 15 ph n quà. ồ ậ ạ ở ổ ộ ầ
Xác su t Ng c nhấ ọ ận bút:
7
15
Xác su t c ng h p này: ấ ủa trườ ợ =
9 1 7 63
. .
17 2 15 510
n bút, H ng nh n v , Ng c nh n bút: Trường h p 2:ợ Vũ nhậ ồ ậ ở ọ ậ
Xác su n bút: ất Vũ nhậ
9
17
Sau khi Vũ nhận bút, còn lại 8 bút và 8 vở, tổng cộng 16 phần quà.
Xác su t H ng nh n v : ấ ồ ậ ở =
8 1
16 2
Sau khi H ng nh n v , còn l i 8 bút và 7 v , t ng c ng 15 ph n quà. ồ ậ ở ạ ở ổ ộ ầ
Xác su t Ng c nhấ ọ ận bút:
8
15
Xác su t c ng h p này ấ ủa trườ ợ =
9 1 8 72
. .
17 2 15 510
:
n v , H ng nh n bút, Ng c nh n bút: Trường h p 3:ợ Vũ nhậ ở ồ ậ ọ ậ
Xác su n v : ất Vũ nhậ ở
8
17
Sau khi Vũ nhận vở, còn lại 9 bút và 7 vở, tổng cộng 16 phần quà.
Xác su t H ng nh n bút: ấ ồ ậ
9
16
.
Sau khi H ng nh n bút, còn l i 8 bút và 7 v , t ng c ng 15 ph n quà. ồ ậ ạ ở ổ ộ ầ
Xác su t Ng c nhấ ọ ận bút:
8
15
Xác su t c ng h p này: ấ ủa trườ ợ
=
8 9 8 72
. .
17 16 15 510
n v , H ng nh n v , Ng c nh n bút: Trường h p 4:ợ Vũ nhậ ở ồ ậ ở ọ ậ
Xác su n v : ất Vũ nhậ ở
8
17
Sau khi Vũ nhận vở, còn lại 9 bút và 7 vở, tổng cộng 16 phần quà.
Xác su t H ng nh n v : ấ ồ ậ ở
7
16
Sau khi H ng nh n v , còn l i 9 bút và 6 v , t ng c ng 15 ph n quà. ồ ậ ở ạ ở ổ ộ ầ
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Xác su t Ng c nhấ ọ ận bút:
9
15
Xác su t c ng h p này: ấ ủa trườ ợ
==
8 7 9 504 63
. .
17 16 15 4080 510
Vậy xác su Ng c nh c quà là cây bút là: ất để ọ ận đượ
+ + + = =
63 72 72 63 270 9 0, 53
510 510 510 510 510 17
.
Câu 4: Trong m t l h i mùa hè, có m i l ng th i b ng ộ ễ ộ ột trò chơi mà mỗ ần chơi, người chơi sẽ tung đồ ờ ốn đồ
xu cân đố ẫu nhiên. Người chơi chỉ ận đượi một cách ng thắng cuộc nếu nh c ít nhất ba mặt ngửa từ
bốn đồng xu đã tung.
Tính xác su trong 5 lất để ần chơi, người chơi thắng được ít nhất ba lần (làm tròn kết quả đến hàng
phần trăm)?
Hướng dẫn gi i ả
Bước 1: Tính xác su ng trong m t l ất thắ ộ ần chơi
Trong một lần chơi, người chơi tung 4 đồng xu cân đối:
• Xác su t nhấ ận được đúng 3 mặt ngửa là
3 1
3
4
1 1 1 1 1 1
4 4
2 2 8 2 16 4
= = =
C .
• Xác su t nhấ ận được cả 4 mặt ngửa là
4
1 1
2 16

=


.
V y ậ xác su t thấ ắng trong một lần chơi là:
1 1 5
4 16 16
+=
; trong m t lxác su t thuaấ ộ ần chơi là
5 11
116 16−=
.
Bước 2: Tính xác su ng ít nhất thắ ất 3 lần trong 5 lần chơi.
Xác su t này bao gấ ồm các trường hợp:
• Thắng đúng 3 lần, thua 2 lần:
3 2
3
5
5 11 125 121 151250
10
16 16 4096 256 1048576
= =
C
.
• Thắng đúng 4 lần, thua 1 lần:
4 1
4
5
5 11 625 11 34375
5
16 16 65536 16 1048576
= =
C
.
• Th n:ắng cả 5 lầ
5
5 3125
16 1048576

=


.
Xác su n tính là: ất cầ
151250 34375 3125 0,02
1048576 1048576 1048576
+ +
.
Câu 5: Ba c u th sút ph n ầ ủ ạt đề
11m
, m t l n v i xác su ng là ỗi người đá mộ ầ ớ ất làm bàn tương ứ
a ; b và
0,7
.
Biết xác su ít nhất ghi bàn để ất một trong ba cầu thủ ghi bàn là
0,982
và xác su ba c u th ghi ất để ầ ủ
bàn là
0,392
. Tính xác suất để có đúng hai cầu th ghi bàn. ủ
Lời gi i ả
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Gọi
i
A
là bi n c i th ế ố “ngườ ứ i i ghi bàn” vớ
1,3i=
.
Ta có các bi n c ế ố
1 2 3
,,A A A là các bi n c c l p và ế ố độ ậ
( ) ( ) ( )
2 31 , , 0,7P A a P A b P A= = =
Gọi
A
là bi n c t m t trong ba c u th ế ố: “Có ít nhấ ộ ầ ủ ghi bàn”
B
là bi n c ba c u th ế ố: “Cả ầ ủ đều ghi bàn”
Clà bi n c u th ế ố: “Có đúng hai cầ ủ ghi bàn”
Ta có
( ) ( ) ( ) ( )
( )( )
12 3 2 31. . . . 0,3. 1 1A A A A P A P A P A P A a b= = = − − .
( ) ( )( )
1 0,3. 1 1P A a b = − − −
.
Lại có
( ) ( ) ( ) ( ) ( )
1 2 31 2 3 1 2 3 . .. 0, .. . 7. bA A A AB A P B P A P A P A P A a= = = =
.
Từ giả thiết ta có hệ phương trình
( ) ( ) ( )
1 0,3. 1 . 1 0,982 1 0,06 1,5 0,8
0,56 0,7
0,7 0,392 0,56
a b ab a b a b a do a b
ab b
ab ab
− − − = + − + = + = =


==
==
 

Mặt khác ta có
1 2 3 1 2 3 1 2 3
. . . . . .A A AC AA A A AA= + + nên
( ) ( ) ( )
1 . .0,7 . 1 .0,7 . .0,3 0, 2.0,7.0,7 0,8.0,3.0,7 0,8.0,7.0,3 0,434P C a b a b a b= − + − + = + + =
.
Câu 6: Có 8 b n cùng ng i xung quanh m t cái bàn tròn, m i b n c m m t c 8 b n ạ ồ ộ ỗ ạ ầ ột đồng xu như nhau. Tấ ả ạ
cùng tung đồ ạn có đồ ửa thì đứng xu của mình, b ng xu ng ng, bạn có đồng xu sấp thì ngồi.
Biết xác su không có hai bất để ạn liền kề cùng đứng bằng
m
n
(trong đó m, là các sn ố tự nhiên và
phân s ố
m
n
t i gi n); tính ố ả
+m n
.
Hướng dẫn gi i ả
Gọi
A
là bi n c ế ố “không có hai người liền k ề cùng đứng”.
Số phần t c a không gian m u là ử ủ ẫ
( )
8
2 256 = =n
.
Nếu có nhiều hơn 4 đồng xu ngửa thì bi n c ế ố
A
không xảy ra. Ta xét các trường hợp sau:
Trường hợp 1: Có nhi u nh ng xu ng a; s k t qu là: ề ấ ồt 1 đ ử ố ế ả 1 8 9+=
.
Trường hợp 2: Có 2 đồng xu ngửa; số k t qu là: ế ả
2
88 20−=C
.
(Loại tr 8 khừ ả năng 2 đồ ửa đó kềng xu ng nhau).
Trường hợp 3: Có 3 đồ ửa trong 8 đồng xu ng ng xu; các kh lo i tr là: ả năng để ạ ừ
• Cả ng xu ng a k nhau: có 8 k t qu . 3 đồ ử ề ế ả
• Có 2 đồng xu ng a k ng xu ng a: có ử ề nhau trong 3 đồ ử 8 4 32= k t qu . ế ả
Suy ra, s k t qu c ng h p này là ố ế ả ủa trườ ợ
3
88 32 16− − =C
.
Trường hợp 4: Có 4 đồng xu ngửa; có 2 kế ảt qu . như thế
(Kết qu cả ủa trường h p này là: ợ S-N-S-N-S-N-S-N N-S-N-S-N-S-N-S và ; với kí hi u i nh n ệ N là ngườ ậ
được đồng xu mặt ngửa và S là người nh n m ng v trí). ậ ặt sấp tương ứ ị
Số kết qu thuả ận lợi là
( )
9 20 16 2 47.= + + + =n A
Xác su không có hai b n li n kấ ểt đ ạ ề ề cùng đứng là:
( ) ( )
( )
47 303
256
= = = + =
n A m
P A m n
n n
.
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Câu 7: Một con châu chấu nh y lên cả ầu thang có 18 bậc. Mỗi lần nh y con châu chả ấu có thể nh y 1 b c ho c ả ậ ặ
2 b c. Tính xác su con châu ch u hoàn thành 18 b c thang v i s l n nh y 2 bậ ất để ấ ậ ớ ố ầ ả ậc không bé hơn
số lần nhảy 1 b c (làm tròn k t qu n hàng phậ ế ả đế ần trăm).
Hướ ẫng d n gi i ả
Gọi là sx ố c nh y 1 b c, là sbướ ả ậ y ố c nh y 2 bbướ ả ậc; suy ra
2 18
,
+=

x y
x y
.
Các c p ( ; ) th a mãn là ặ x y ỏ
( ) ( ) ( ) ( ) ( )
18; 0 , 16; 1 , 14; 2 , 12; 3 , 10; 4
,
( ) ( ) ( ) ( ) ( )
8; 5 , 6; 6 , 4; 7 , 2; 8 , 0; 9
.
• Nếu
( ) ( ) ( )
; 18; 0 , 0; 9x y
thì con châu chấu có 2 cách đi.
• Nếu
( ) ( )
; 16; 1=x y
thì s a châu ch u là ố cách đi củ ấ
1
17
C
.
• Tương tự như vậy các trườ ng hợp còn l i s có s cách là ạ ẽ ố
2 3 4 5 6 7 8
16 15 14 13 12 11 10 4162+ + + + + + =C C C C C (cách).
Vậy tổng số cách nh y c a châu chả ủ ấu để thoàn thành 18 bậc cầu thang là
1
17
2 4162 4181+ + =C
(cách). S ph n t không gian m u là ố ầ ử ẫ ( )
4181=n
.
Số lần nhảy 2 bậc không bé hơn số lần nh y 1 b c nên ả ậ
( ) ( ) ( ) ( ) ( )
; 6; 6 , 4; 7 , 2; 8 , 0; 9x y
.
Gọi A là biến cố thỏa đề bài thì ( )
6 7 8 9
12 11 10 9 1300= + + + =n A C C C C
.
Do v y ậ
( ) ( )
( )
1300 65 0,31
4180 209
= = =
n A
P A n .
Câu 8: Hai b n Hùng ng . Bánh xe s có ạ và Cườ chơi trò quay bánh xe số ố 20 n m là ấc điể
5,10,15,.....,100
với
các v u nhau (gi s r ng kh n t n i các n m còn l i là ạch chia đề ả ử ằ ả năng chuyể ừ ấc điểm đã có tớ ấc điể ạ
như nhau). Trong mỗi lượt chơi, mỗi người được quyền chọn quay 1 ho c ặ 2 lần và điểm số của
người chơi được tính như sau:
(1)
Nếu người chơi chọn quay một lần thì điểm của người chơi là điểm quay được.
(2) N n quay ếu người chơi chọ
2
l n và t c không lầ ổng điểm quay đượ ớn hơn
100
thì điểm của
người chơi là tổng điểm quay được.
(3)
N n quay ếu người chơi chọ 2 l n và t c lầ ổng điểm quay đượ ớn hơn 100 thì điểm người chơi là
tổng điểm quay được trừ đi 100 .
Luật chơi quy đị ỗi lượt chơi người nào có điể cao hơn sẽnh, trong m m số thắng cuộc, hòa nhau sẽ
chơi lại lượt khác. Hùng m s là chơi trước và có điể ố 75. Tính xác su ng th ng cu c ngay ất để Cườ ắ ộ ở
lượt chơi này.( Lấ ần trăm)y kết quả đến hàng ph .
Lời gi i ả
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Ta có:
100 5
( ) 1 20
5
n−
= + =
Để ắ Cường th ng ta có 2 ng h p: trườ ợ
- ng h p Trườ ợ 1 : Cường quay 1 l m s lần ra điể ố ớn hơn 75
, ta có
5 kh c t p h p ả năng thuộ ậ ợ
{80;85;90;95;100}
Do xác su t là ấ
1
5 1
20 4
P==
.
- ng h p Trườ ợ 2 : Cườ ần đầu ra điểng quay l m số là 75a , ta có 15 kh ả năng.
Do đó xác suất
2
15 3
20 4
P==
Khi đó, để ắng Cườ ớn hơn th ng cần phải có tổng hai lần quay l 75, ta có 5 kh c t p h p ả năng thuộ ậ ợ
{80 ;85 ;90 ;95 ;100 }a a a a a− − − − −
.Do đó xác suất là
3
5 1
20 4
P==
.
Vậy xác su ng thất để Cườ ắng ngay trong lượt là
1 2 3
70,44
16
P P P P= + =
.
Đáp án:
0,44
Câu 9: Trong m a c a b ng v trí xu ). Luột trò chơi, con ngự ủ ạn Toàn đang đứ ở ị ất phát (như hình vẽ ật chơi
như sau: Để ặt cân đối, đồ di chuyển con ngựa, bạn Toàn cần gieo một con xúc xắc có sáu m ng chất.
Ở Ở ầ ứ ấ ự ố ứ m n có t n gieo. ỗi lượt chơi, bạ ối đa ba lầ l n gieo th nh t, con ng a di chuy n ô có sển đế th
tự b ng s ng v i s ch c c a con xúc x c. T nh ng l n gieo sau, n u t ng c a ằ ố tương ứ ớ ố ấm gieo đượ ủ ắ ừ ữ ầ ế ổ ủ
số ng v i s ch c c a con xúc x c và s ng ghi ô con ng ng tương ứ ớ ố ấm gieo đượ ủ ắ ố tương ứ ở ựa đang đứ
lớn hơn 6 thì con ngự hơn hoặ ựa đượa sẽ đứng yên, còn nếu tổng này nhỏ c bằng 6 thì con ng c di
chuyển số ô bằng số ch c. Con ngấm gieo đượ ựa này gọi là về c ô sđích nếu nó đến đượ ố 6.
Mệnh đề Đúng Sai
a)
Xác su con ng a l n gieo th nh t b ng ất để ự về đích ở ầ ứ ấ ằ
1
6
b)
Xác su con ng a v l n gieo th hai b ng ất để ự ề đích ở ầ ứ ằ
5
36
c) Xác su con ng a v l n gieo th ba và trong c ba lất để ự ề đích ở ầ ứ ả ần gieo
con ng c di chuy n b ng ựa đều đượ ể ằ
5
108
d)
Xác su con ng a v u nh t ba l n gieo bất để ự ề đích sau nhiề ấ ầ ằng
19
54
Mệnh đề a)
Gieo 1 l n: ầ ( ) 6n= . G i A: "S gieo s 6" ọ ẽ ố
( )
1n A =
1
6
A
P= . ĐÚNG
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Mệnh đề b)
Gieo 2 l n: ầ ( ) 6 6 36n = = . G i B: "T ng 2 l n gieo b ng 6" ọ ổ ầ ằ
Ta có 6x y+ =
( )
; {(1;5),(2; 4),(3;3),(4;2),(5;1)}x y =
( )
1
5.1 5n B C= =
5
36
B
P=
. ĐÚNG
Mệnh đề c)
Gieo 3 l n: ầ ( ) 6 6 6n = . G i C: "T ng 3 l n gieo b ng 6" ọ ổ ầ ằ
Ta có 6x y z+ + =
( )
1
1 6 1
3 1 10
n
k
n C C C
−−
−−
= == (Ch x p vào) ọn 2 trong 5 để ế
Suy ra
10 5
36 108
C
P== . ĐÚNG
Cách 2: Li t kê ệ
Mệnh đề d)
6x y z+ + =
D ch chuy n: ị ể
+ L n 1: 1 ầ
→
5: D ch chuy n ị ể
+ L n 2: ầ ng yên 6: Đứ
+ L n 3: Di chuy n ầ ể
1 1
5 5
6
6 . 25x z y C C
=
+ + =
cách
25 25
6 6 6 216
D
P==

101
216
A B C D
P P P P =+ + + . SAI
Câu 10: Trên m t banner quộ ảng cáo, ngườ ếc bóng đèn vào một khung hình vuông cũng như i ta gắn 17 chi
hai đườ ủa hình vuông đó. Biế ằng các bóng đèn trên mộng chéo c t r t cạnh ho ng chéo thì chia ặc đườ
cạnh ho n b ng nhau (xem hình ặc đường chéo đó làm các đoạ ằ
vẽ). Các bóng đèn sẽ sáng lên theo quy lu t sau: ậ
• Vào phút th nh có ngứ ất sẽ ẫu nhiên 1 bóng đèn sáng lên, đến
cuối phút th nh t nó s t t. ứ ấ ẽ ắ
• Vào phút th 2 s có ngứ ẽ ẫu nhiên 2 bóng đèn sáng lên, đến cuối
phút th hai chúng s t t. ứ ẽ ắ
• Vào phút th 3 s có ngứ ẽ ẫu nhiên 3 bóng đèn sáng lên, đến cuối
phút th ba chúng s t t. ứ ẽ ắ
Quy lu t này c ti p diậ ứ ế ễn cho đến phút thứ 17 và m t chu trình ộ
mới sẽ được lặp lại. Tính xác su t phút th ất để ừ ứ 3 cho đến phút
thứ 17, luôn có ít nhất 3 bóng đèn sáng lên ở 3 đỉ ột tam giác (làm tròn đế ần trăm). nh của m n hàng ph
Hướng dẫn gi i ả
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Gọi
i
A
là bi n c i phút th thì có ít nhế ố: “Tạ ứ i ất 3 bóng đèn sáng lên ở 3 đỉ nh của tam giác”; khi đó
3; 4;...; 17i
.
Phút th 3:ứ
• Số phần t không gian m u là ử ẫ
( )
3
3 17
=n C
.
• Số khả năng để 3 bóng đèn sáng lên là 3 đỉ nh tam giác:
( )
3 3
3 17 7
2 4 10 596= − − − =n A C C
.
(Ta lo i tr ng hạ ừ các trườ ợp 3 điểm thẳng hàng gồm: 2 trường
hợp 3 điể ộc các đường chéo, 4 trườ ợp 3 điểm thu ng h m thuộc các
cạnh, 10 trườ ợp 3 điểng h m thẳng hàng khi v thêm hìnhẽ ).
• Xác suất tương ứng là
( ) ( )
( )
3
33
3 17
598 299
340
= = =
n A
P A n C
.
Phút th 4:ứ Xác su ng là ất tương ứ
( )
4 4
17 7
44
17
233
34
−
==
C C
P A C .
Phút th 5:ứ Xác su ng là ất tương ứ
( )
5 5
17 7
55
17
2439
442
−
==
C C
P A C
.
Phút th 6:ứ Xác su ng là ất tương ứ
( )
6 6
17 7
66
17
2883
884
−
==
C C
P A C
.
Phút th 7:ứ Xác su ng là ất tương ứ
( )
7
17
77
17
29723
9724
−
==
C
P A C
.
Từ phút th 8 tr c ch n luôn có ít nhứ ở đi thì chắ ắ ất 3 bóng sáng lên ở 3 đỉnh của tam giác.
Xác su n tìm là ất cầ
( ) ( ) ( ) ( )
1 2 17
... 0,84= P A P A P A P A .
Câu 11: i tham gia m n theo c nh c a các ô hình ch nhHai ngườ ột trò chơi di chuyể ạ ủ ữ ật như trong hình (hình
có 15 8
ô hình ch nh t nh ) ữ ậ ỏ
Ngườ ứ ứ ế ằ ải th nh i thất đi từ điểm A đến điểm B , ngườ hai đi từ điểm E đến điể m F. Bi t r ng c hai
người cùng đi ngẫu nhiên và theo con đườ ất để hai người cùng đi qua ng ngắn nhất. Tính xác su cả
điể ế ảm I (k t qu n hàng ph làm tròn đế ần trăm).
Lời gi i: ả
Gọi
X
là bi n c "c m ế ố ả hai người cùng đi qua điể
I
"
Xét h tr c t v i ệ ụ ọa độ ớ
( ) ( ) ( ) ( ) ( )
0;0 , 0;8 , 15;0 , 15;8 , 11;5E A B F I
Để đi từ A n đế B ng ng n nh i th nh t c n di chuy c theo đườ ắ ất thì ngườ ứ ấ ầ ển 15 bước ngang và 8 bướ
xuống
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Số cách di chuy n t ể ừ
A
n đế
B
là s cách s p x c xu ng và b ng ố ắ ếp 15 bước ngang và 8 bướ ố ằ
8
23
C
Tương tự có
8
23
C i th hai di chuy n t cách để ngườ ứ ể ừ E n đế F
Như vậy không gian mẫu
( )
2
8
23
Ω=C
Ngườ ứ ấ ừi th nh t di chuyển t
( )
0;8A
n đế
( )
11;5I
c c xu ng ần 11 bước ngang và 3 bướ ố
Ngườ ứ ấ ừi th nh t di chuyển t
( )
11;5I n đế
( )
15;0B c c xu ng ần 4 bước ngang và 5 bướ ố
Như vậ ủa ngườy số cách di chuyển c i thứ nhất từ →→A I B là
8 4
14 9
.C C
Tương tự ủa ngườ số cách di chuyển c i thứ hai từ →→E I F là
5 3
16 7
.C C
Như vậy
8 4 5 3
14 9 16 7
. . .=X C C C C
Vậy xác su cất để ả hai người cùng đi qua
I
là
( )
( )
8 4 5 3
14 9 16 7
2
8
23
0,24
. .
Ω
.
= =
XC C C C
P X
C
B - XÁC SU U KI N ẤT ĐIỀ Ệ
Câu 12: Trong m i ph i tham gia hát hai bài : M t bài theo phong cách âm nh c dân ột đêm thi hát, mỗi ngườ ả ộ ạ
gian, m t bài theo phong cách âm nh c nh c nh . M i có ộ ạ ạ ẹ ột độ 20 người tham gia đêm thi hát đó. Kết
quả là 15 t bài thi theo phong cách âm nh c dân gian, người đạ ạ 17 t bài thi theo phong cách người đạ
âm nh c nh c nh ; ạ ạ ẹ 2 người không đạt c hai bài. Ch n ng u nhiên mả ọ ẫ ột người. Tính xác suất để người
đó đạ ằng người đó đạt bài thi theo phong cách âm nhạc nhạc nhẹ biết r t bài thi theo phong cách âm
nhạc dân gian (Kết quả n hàng phlàm tròn đế ần trăm).
Lời gi i ả
Gọi A là bi n c t bài thi theo phong cách âm nh c nh c nh ế ố: “Người đó đạ ạ ạ ẹ”.
B là bi n c t bài thi theo phong cách âm nh ế ố: “Người đó đạ ạc dân gian”.
Ta có:
( )
17
20
P A = ;
( )
15
20
P B = ;
( )
2
20
P AB = .
Do đó:
( ) ( )
2 18
1 1 20 20
P A B P AB = − = − =
.
( ) ( ) ( ) ( )
17 15 18 14
20 20 20 20
P AB P A P B P A B= + − = + − = .
Vậy
( ) ( )
( )
14
| 0,93
15
P AB
P A B P B= =
.
Câu 13: Một công ty tham gia đấ năng thắu thầu 2 dự án. Khả ng thầu dự án 1 là 60% và dự án 2 là 50%. Khả
năng thắng thầu cả hai dự án là 40%. Gọi A
và
B l t là bi công ty th ng th u d án 1 và ần lượ ến cố ắ ầ ự
dự án 2.
Mệnh đề Đúng Sai
a)
A
và
B
là hai bi n c c l p. ế ố độ ậ
b) Khả ng th án là 30%năng công ty thắ ầu đúng 1 dự
c) Xác su t công ty th ng th u d án 2 bi ng th u d án 1 ấ ắ ầ ự ết công ty đã thắ ầ ự
là
1
2
.
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
d) Xác su t công ty không th ng th u d án 2, biấ ắ ầ ự ết công ty đã không thắng
thầu dự án 1 là
1
4
.
Lời gi i ả
Ta có
( ) ( ) ( ) ( )
0,6 0,4; 0,5 0,5P A P A P B P B= = = = và
( )
0,4P AB =
a) Sai: Vì
( ) ( ) ( )
.P AB P A P B
nên
,A B c l p . không độ ậ
b) Đúng: Do AB và AB là hai bi n c xung kh c nên xác su t công ty th ng th án là: ế ố ắ ấ ắ ầu đúng 1 dự
( )
( ) ( ) ( ) ( ) ( )
0,6 0,4 0,5 0,4 0,3P AB P AB P A P AB P B P AB+ = − + − = − + − =
c) Sai: Xác su t công ty th ng th u d án 2 bi ng th u d án 1 là: ấ ắ ầ ự ết công ty đã thắ ầ ự
( ) ( )
( )
0,4 2
|0,6 3
P BA
P B A P A
= = =
.
d) Sai: Xác su t công ty th ng th u d án 2, bi ng th u d án 1 là: ấ ắ ầ ự ết công ty đã không thắ ầ ự
( ) ( )
( )
( ) ( )
( )
0,5 0,4 1
|0,4 4
P BA P B P AB
P B A P A P A
−−
= = = = .
Vậy xác suất công ty không thắng thầu dự án 2, bi ng thết công ty đã không thắ ầu dự án 1 là
( ) ( )
1 3
1 1 4 4P B A P B A= − = − = .
Câu 14: Kh o sát nh i xem b phim ho t hình v c phát hành cho th y ả ững ngườ ộ ạ ừa đượ ấ 70% người xem là tr ẻ
em và 30% là người lớn. Trong s các trố ẻ em đến xem phim có 50% yêu thích b phim và kh nh ộ ẳng đị
sẽ p ph n 2, đi xem tiế ầ
30%
yêu thích b ộ phim nhưng sẽ không xem ti p ph n 2; ế ầ
20%
còn l i không ạ
thích b phim và không xem ti p ph n 2. Trong s nhộ ế ầ ố ững ngườ ớn đi xem phim có i l 20% yêu thích
bộ phim và kh nh s xem ti p ph n 2, ẳng đị ẽ ế ầ 10% yêu thích b ộ phim nhưng sẽ không xem tiếp ph n 2; ầ
70% còn l i không thích b phim và không xem ti p ph n 2. Ch n ngạ ộ ế ầ ọ ẫu nhiên 1 người đã xem phim.
Mệnh đề Đúng Sai
a) Biết người được ch n là tr em, xác su ọ ẻ ất để người đó yêu thích bộ phim
là 0,56 .
b)
Xác su p ph n 2 là ất để người đó không xem tiế ầ
0,59
.
c) Biết người đó sẽ ất để người đó là xem tiếp phần 2 của bộ phim, xác su
trẻ em lớn hơn
0,85
.
d) Biết người đó yêu thích bộ ất để người đó không xem tiế phim, xác su p
phần 2 là 0,37 n hàng ph(làm tròn đế ần trăm).
Lời gi i ả
a) Sai b) Đúng c) Đúng d) Đúng
Gọi
A
là bi n c ế ố “Người đó là trẻ em”
B
là bi n c ế ố “Người đó thích bộ phim”
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
C là bi n c p ph n 2 b ế ố “Người đó xem tiế ầ ộ phim”
Xét người đi xem là trẻ em có ( )
0,7P A =
.
Suy ra ( )
50% 0,5P BC ==
,
( )
30% 0,3P BC ==
,
( )
20% 0,2P BC ==
,
( )
0P BC =
.
Xét người đi xem là người lớn có
( )
0,3P A =
.
( )
20% 0, 2P BC ==
,
( )
10% 0,1P BC ==
,
( )
70% 0,7P BC ==
,
( )
0P BC =
.
(a) Sai
Ta có
( )
0,5 0,3 0,8P B A =+= .
(b) Đúng
Ta có
C CAB CAB CAB CAB=
.
( ) ( ) ( ) ( ) ( )
P C P CAB P CAB P C AB P C AB= + + +
0,7 0,3 0,7 0,2 0,3 0,1 0,3 0,7 0,59= + + + =
.
(c) Đúng
( )
( )
1 0,41P C P C= − =
.
( )
( )
( )
P AC
P A C P C= .
( )
( )
( )
0,7 0 0,7 0,5 0,35P AC P ACB P ACB= + = + =
.
Suy ra
( )
( )
( )
0,35 0,854 0,85
0,41
P AC
P A C P C= = .
(d) Đúng
( ) ( )
( )
P CB
P C B P B=
( ) ( ) ( )
0,3 0,7 0,1 0,3 0,24P CB P CBA P CB A= + = + =
.
( )
( )
( )
( ) ( )
P B P BAC P BAC P BAC P BAC= + + +
0,7 0,3 0,7 0,5 0,3 0,2 0,3 0,1 0,65= + + + =
.
Suy ra
( )
0, 24 0,37
0,65
P C B =
.
---------------------------------------------------------------------------------------------------------
Câu 15: Có hai đội thi đấ ắn súng. Độ ận động viên, độ ận độ ất đạu môn b i I có 8 v i II có 10 v ng viên. Xác su t
huy chương vàng của m i vỗ ận động viên đội I và đội II tương ứng là 0,6 và 0,55. Ch n ng u nhiên ọ ẫ
một v ng viên. ận độ
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Mệnh đề Đúng Sai
a)
Xác suất để vận động viên chọn ra thuộc đội I là
5
9
b) Xác suất không đạt huy chương vàng của mỗi vận động viên đội II là
0,45
c)
Xác suất để vận động viên này đạt huy chương vàng là
103
180
d) Giả sử vận động viên được chọn đạt huy chương vàng. Xác suất để vận
động viên này thuộc đội I là
48
103
.
Lời giải
a) Sai: Xác suất để vận động viên chọn ra thuộc đội I là
8 4
18 9
=
.
b) Đúng: Xác suất không đạt huy chương vàng của mỗi vận động viên đội II là 1 0,55 0,45−=
c) Đúng: Gọi A là biến cố: “Vận động viên đạt huy chương vàng”, B là biến cố: “Thành viên đội
I” thì biến cố đối của
B
là
B
: “Thành viên đội II đạt huy chương vàng”.
Do đó,
( ) ( )
8 4 5
;
18 9 9
P B P B= = =
;
( )
( )
| 0,6; | 0,55P A B P A B==
Theo công thức xác suất toàn phần ta có
( ) ( ) ( ) ( ) ( )
4 5 103
. | . | .0,6 .0,55
9 9 180
P A P B P A B P B P A B= + = + =
d) Đúng: Ta có
( ) ( ) ( )
( )
4.0,6
. | 48
9
|103 103
180
P B P A B
P B A P A= = =
Câu 16: Trong m t lô s n ph m có 3 h p lo i I và 5 h p lo i II. Bi t r ng trong m i h p lo i I có 97 s n ph m ộ ả ẩ ộ ạ ộ ạ ế ằ ỗ ộ ạ ả ẩ
tốt và 3 ph ph m, trong m i h p lo i II có 95 s n ph m t t và 5 ph ph m. L y ng u nhiên t lô s n ế ẩ ỗ ộ ạ ả ẩ ố ế ẩ ấ ẫ ừ ả
phẩm đó mộ ộp đó lấ ẫu nhiên đồt hộp, rồi từ h y ng ng thời hai sản phẩm.
Mệnh đề Đúng Sai
a)
Xác su h c ch n là h p lo i I b ng ất để ộp đượ ọ ộ ạ ằ
3
8
b) Nếu h c lộp đượ ấy là hộp loại I thì xác su cất để ả hai sản phẩm lấy ra
không có ph ph m b ng ế ẩ ằ
776
825
.
c)
Xác su t c hai s n ph m l y ra không có ph ph m b ng ấ ả ả ẩ ấ ế ẩ ằ
1833
2000
.
d) Biết rằng trong hai sản phẩm l t ph ph m, xác su ấy ra có đúng mộ ế ẩ ất để
hộp lấy ra là hộp loại I bằng
203
2475
.
Lời giải
a) Đúng b) Đúng c) Sai d) Sai
a) Đúng
Xác su h c ch n là h p lo i I b ng ất để ộp đượ ọ ộ ạ ằ
3
8
.
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
b) Đúng
Gọi A là biến cố “hộp l y ra lo ấ ại I”
B là bi n c n ph m l y ra không có phế ố:” 2 sả ẩ ấ ế ph Ta có ẩm “.
( )
2
97
2
100
776
825
C
P B A C==
c) Sai
( ) ( )
( )
( ) ( )
2 2
97 95
2 2
100 100
3 5
. . . . 0,916
8 8
C C
P B P A P B A P A P B A C C= + = +
.
d) Sai
C là bi n c c 1 ph ph m và 1 s n ph m t ế ố: “Lấy ra đượ ế ẩ ả ẩ ốt”
( )
2
100
97.3 97
|1650P C A C==
.
( )
2
100
95.5 19
|198P C A C==
( ) ( )
( )
3 97
.873
8 1650
|3 97 5 19 3248
. .
8 1650 8 198
P AC
P A C P C= = =
+
.
Câu 17: Trong m t giộ ải thi đấu bóng chuy i bóng chuy n cền, độ ề ủa Hà N i s ộ ẽ thi đấu hai tr n. Trậ ậ ứn th nh i ất độ
bóng chuy n c a Hà N i có xác su t th ng là ề ủ ộ ấ ắ 0,6 . Tr n ti p theo, xác su t chi n th ng c a h ph ậ ế ấ ế ắ ủ ọ ụ
thuộc vào k t qu trế ả ận trước đó. Nếu đội bóng chuy n c a Hà N i th ng trề ủ ộ ắ ận trước đó, họ s ẽ hưng phấn
và xác su h th ng là ất để ọ ắ 0,7 . N i bóng chuy n c a Hà N i thua tr c thì h s m t tinh ếu độ ề ủ ộ ận trướ ọ ẽ ấ
thần và xác su hất để ọ thắng là
0,5
. Tính xác su i bóng chuy n c a Hà N i th ng trất để độ ề ủ ộ ắ ận th hai. ứ
Lời gi i ả
Đáp số:0,62
Gọi
A
là bi n c i bóng chuy n c a Hà N i th ng tr n th ế ố : “Độ ề ủ ộ ắ ậ ứ 1”
Gọi
B
là bi n c i bóng chuy n c a Hà N i th ng tr n th ế ố : “Độ ề ủ ộ ắ ậ ứ 2”
Ta có
( )
( )
0,6 0,4P A P A= =
.
Nếu độ ận trước đó, họ hưng phấ ất đểi bóng chuyền của Hà Nội thắng tr sẽ n và xác su họ thắng là
0,7 hay
( )
| 0,7P B A =
.
Nếu độ ận trướ ất đểi bóng chuyền của Hà Nội thua tr c thì họ sẽ mất tinh thần và xác su họ thắng là
0,5
hay
( )
| 0,5P B A = .
Ta có:
( ) ( ) ( )( ) ( )
. | . | 0,7.0,6 0,4.0,5 0,62P B P A P B A P A P B A= + = + =
.
Vậy xác xu ất để đội bóng chuyền Hà Nội thắng trận thứ 2 là
0,62
.
Câu 18: M t h p ch a ộ ộ ứ
10 viên bi xanh và 5
viên bi đỏ. Bạn An lấy ra ngẫu nhiên
1
viên bi t h p, xem màu, ừ ộ
rồi bỏ ra ngoài. Nếu viên bi An lấy ra có màu xanh, bạn Bình sẽ lấy ra ng u nhiên ẫ
2
viên bi t h p; ừ ộ
còn n u viên bi An l , b n Bình s l y ra ng u nhiên ế ấy ra có màu đỏ ạ ẽ ấ ẫ
3
viên bi t h p. Tính xác su t ừ ộ ấ
để ế ằ ấ ả ả An l c viên bi màu xanh, biấy đượ t r ng t t c các viên bi đượ ọn ra đều có đủc hai bạn ch c hai
màu.
Lời gi i ả
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Gọi A là bi n c An l c viên bi màu xanh thì ế ố ấy đượ A là bi n c An l . ế ố ấy được viên bi màu đỏ
Gọi B là bi n c t t c c hai b n ch c hai màu. ế ố ấ ả các viên bi đượ ạ ọn ra đều có đủ ả
Ta có
( )
( )
10 5
,
15 15
P AP A ==
. Ta c n tính ầ
( ) ( )
( )
P AB
P A B P B
=∣
.
Khi A
x y ra thì trong h , Bình c n lả ộp còn 9 viên bi xanh và 5 viên bi đỏ ầ ấy ra 2 viên bi trong đó có
ít nh t m nên ấ ột viên bi đỏ
( )
2 2
14 9
2
14
C C
P B A C
−
=∣
.
Khi A x y ra thì trong hả ộp còn 10 viên bi xanh và 4 viên bi đỏ ấy ra 3 viên bi trong đó có , Bình cần l
ít nh t m t viên bi xanh nên ấ ộ
( )
3 3
14 4
3
14
C C
P B A C
−
=∣
.
Vậy
( ) ( ) ( )
( )
2 2
14 9
2
14
10 110
.15 273
C C
P AB P A P B A C
−
= = =∣
Mặt khác:
( ) ( ) ( )( ) ( )
. .P B P A P B A P B AA P=+∣
( ) ( )
2 2 3 3
14 9 14 4
2 3
14 14
10 5 200
15 15 273
C C C C
C C
−−
= + =
.
Vậy
( )
110
273 0,55
200
273
P A B ==∣
.
Câu 19: Có hai phác đồ ệnh. Phác đồ điều trị A và B cho một loại b A có xác suất chữa khỏi bệnh là 60% và
xác su t gây tác d ng ph nghiêm tr B có xác su t ch a kh i b nh là 70% và ấ ụ ụ ọng là 5%. Phác đồ ấ ữ ỏ ệ
xác su t gây tác d ng ph nghiêm tr ng là 10%. M t b u tr ng u nhiên b ng ấ ụ ụ ọ ộ ệnh nhân được điề ị ẫ ằ
một trong hai phác đồ ỗi phác đồ (xác suất chọn m là 50%).
Mệnh đề Đúng Sai
a) Xác su t b u tr b c ch a kh i b nh là ấ ệnh nhân điề ị ằng phác đồ A và đượ ữ ỏ ệ
0,6.
b) Xác su b nh nhân b tác d ng ph nghiêm tr ng là 0,075. ất để ệ ị ụ ụ ọ
c) Nếu biết bệnh nhân này gặp tác dụng ph nghiêm trụ ọng thì xác suất
bệnh nhân đã được điề ằng phác đồ ớn hơn 0,65.u trị b B l
d)
Biết rằng trong mỗi phác đồ điều tr thì biị ến cố "b c chệnh nhân đượ ữa
khỏi bệnh" và bi n c "b nh nhân không b tác d ng ph nghiêm tr ng" ế ố ệ ị ụ ụ ọ
là độc l p v i nhau. Xác su t b nh nhân kh i b nh và không b tác d ng ậ ớ ấ ệ ỏ ệ ị ụ
phụ nghiêm tr ng là 0,6. ọ
Lời giải
Gọi A là bi n c "b nh nhân ch A". ế ố ệ ọn phác đồ
Gọi
B
là bi n c "b nh nhân kh i b nh". ế ố ệ ỏ ệ
Gọi C là bi n c "b nh nhân b tác d ng ph nghiêm tr ng". ế ố ệ ị ụ ụ ọ
Khi đó:
( ) ( ) 0,5P A P A==
( | ) 0,6P B A =
( | ) 0,7P B A =
( | ) 0,05P C A =
( | ) 0,1P C A =
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
a) Sai. Xác su t b u tr A và kh i b nh là: ấ ệnh nhân điề ị phác đồ ỏ ệ
( ) ( ) ( | ) 0,5 0,6 0,3P AB P A P B A= = = .
b) Đúng. Xác suấ ệ ụ ụ ọt b nh nhân bị tác d ng ph nghiêm tr ng là:
( ) ( ) ( ) ( ) ( | ) ( ) ( | ) 0,5 0,05 0,5 0,1 0,075P C P AC P AC P A P C A P A P C A= + = + = + =
c) Đúng. Nế ế ệ ụ ụ ọ ệu bi t b nh nhân bị tác d ng ph nghiêm tr ng thì xác su bất để nh nhân ch ọn phác đồ
B là:
( ) 0,5 0,1 2
( | ) 0,65
( ) 0,075 3
P AC
P A C P C
= = =
.
d) Đúng. Theo giả ế thi t
/B A
và
/C A
c l p, độ ậ
/B A
và
/C A
c l p. độ ậ
Xác su t b nh nhân kh i b nh và không b tác d ng ph nghiêm tr ng là: ấ ệ ỏ ệ ị ụ ụ ọ
( ) ( )
( )
( )
( )
( )
( ) ( )
( )
( )
( )
| |BC P BC A P BC A P BC A P A P BC A P A + = +
( ) ( | ) ( | ) ( ) ( | ) ( | )P A P B A P C A P A P B A P C A= +
0,5 0,6 (1 0,05) 0,5 0,7 (1 0,1) 0,6= − + − =
---------------------------------------------------------------------------------------------------------
Câu 20: M c th c hi n vi c tinh gi n biên ch thông qua ph ng v n. T l nhân ột cơ quan hành chính nhà nướ ự ệ ệ ả ế ỏ ấ ỷ ệ
viên c i h ng l t là ủa cơ quan thuộc hai nhóm trình độ: Đạ ọc, Cao đẳ ần lượ
65%
và
35%
. Qua ph ng ỏ
vấn thì tỷ lệ nhân viên b tinh giị ản c i hủa nhóm đạ ọc là10%, nhóm cao đẳng là 15%. Ch n m t nhân ọ ộ
viên b t k tinh gi n thì hãy tính xác su i h c ấ ỳ đã bị ả ất để người này có trình độ đạ ọ (kết quả là một s ố
thập phân nhỏ n hàng phhơn 1 đã làm tròn đế ần trăm).
Lời giải
Đáp số:
0,55
.
Gọi
A
là bi n c i h ế ố “ Chọn nhân viên có trình độ đạ ọc” .
Gọi
B
là bi n c n nhân viên b tinh gi n biên ch thông qua ph ng v ế ố “ Chọ ị ả ế ỏ ấn” .
Tỷ lệ nhân viên c i h ng l t là ủa cơ quan thuộc hai nhóm trình độ: Đạ ọc, Cao đẳ ần lượ 65% và 35%
nên
( )
( )
0,65 0,35P A P A= =
.
Qua ph ng v n thì t l nhân viên b tinh gi n c i h c làỏ ấ ỷ ệ ị ả ủa nhóm đạ ọ 10%, nhóm cao đẳng là 15% nên
( )
0,1P B A = và
( )
0,15P B A =
.
Chọn một nhân viên bất kỳ tinh giđã bị ản thì xác su ất để người này có trình độ đại học là ( )
P A B
.
Theo công th c ta có: ứ
( )
( ) ( )
( )
( )
( )
( )
.0,65.0,1 0,55
0,65.0,1 0,35.0,15
. .
P A P B A
P A B
P A P B A P A P B A
= = =
+
+
.
Câu 21: M t chiộ ếc hộp có 50 viên bi, trong đó có 30 viên bi màu xanh và 20 viên bi màu đỏ, các viên bi có kích
thướ ố ấ ốc và kh ng giối lượ ng nhau. Sau khi ki i ta thểm tra, ngườ y có 70% s viên bi màu xanh được
đánh số viên bi màu đỏ được đánh số ại không đánh số và 60% số , những viên bi còn l . Lấy ngẫu
nhiên m t viên bi t h t r ng, viên bi l , xác suộ ừ ộp đó. Biế ằ ấy ra được đánh số ất để viên bi đó có màu
xanh b ng bao nhiêu ( )? ằ kết quả n hàng phlàm tròn đế ần trăm
Lời gi i ả
Trả lời: 0,64
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Gọi
A
là bi n c ế ố: “Viên bi lấy ra có màu xanh”.
Suy ra
A
là bi n c ế ố: “Viên bi lấy ra có màu đỏ”.
B là bi n c ế ố: “Viên bi lấy ra được đánh số”.
( ) ( )
( )
( ) ( )
( )
( )
P B A P A
P A B
P B A P A P B A P A
= +
.
Ta có
( )
30 3
30 20 5
P A ==
+
( )
( )
2
15
P A P A = − =
.
( )
70% 0,7P B A ==
và
( )
60% 0,6P B A ==
.
Vậy
( )
3
0,7 7
50,64
3 2 11
0,7 0,6
5 5
P A B
= =
+
Câu 22: Nhân d p k ni m ị ỷ ệ 50 năm ngày thành lập trường, các h c sinh l a chọ ự ọn tham gia thi đấu thể thao ho c ặ
biểu di . L p ễn văn nghệ ớ 12A có 60% s h u th thao và còn l i ố ọc sinh tham gia thi đấ ể ạ 40% s h c ố ọ
sinh tham gia bi u di . Bi t r ng các b n n u tham gia bi u di . Trong s ể ễn văn nghệ ế ằ ạ ữ đề ể ễn văn nghệ ố
các b n nam có ạ 20% tham gia văn nghệ và 80% tham gia thi đấu thể thao. Chọn ngẫu nhiên 1 h c ọ
sinh trong l p. Bi t r ng h c sinh này tham gia bi u di , xác su h c sinh này là n là ớ ế ằ ọ ể ễn văn nghệ ất để ọ ữ
bao nhiêu ph ần trăm?
Lời gi i ả
Trả lời:
0,625
Gọi
A
: “Bạn đượ ọn là nam” và c ch
B
: “Bạn đượ ễn văn nghệc chọn tham gia biểu di ”.
Khi đó,
A
: “Bạn đượ ữ” và c chọn là n
B
: “Bạn đượ ọn tham gia thi đấc ch u thể thao”.
Lớp 12A có 60% s h u th thao và còn l i ố ọc sinh tham gia thi đấ ể ạ 40% nên ( )
0,4P B =
và
( )
0, 4P B =
.
Các b n n u tham gia bi u di nên ạ ữ đề ể ễn văn nghệ
( )
| 1P B A =
.
Trong s các b n nam có ố ạ 20% và tham gia văn nghệ 80% u th thao nên ta có tham gia thi đấ ể
( )
| 0,2P B A =
và
( )
| 0,8P B A =
.
Ta có:
( ) ( ) ( ) ( ) ( )
| |P B P B A P A P B A P A=+
( )
( )
( ) ( )
0,4 0,2 1 1 0,25P A P A P A = − + =
Khi đó, xác ất để ới điề ễn văn nghệsu chọn ra một học sinh là nữ v u kiện có tham gia biểu di là
( ) ( ) ( )
( )
( )
( )
|0,25
| 0,625
0,4
P B A P A P A
P A B P B P B= = = =
.
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Câu 23: Xác suất để cơ quan Q thuê 1 trong các công ty A và B tư vấ ần lượn l t là 0,4 và 0,6 . Theo kinh
nghiệm khả năng Q phát sinh thêm chi phí khi s d ng d ch v n c a công ty ử ụ ị ụ tư vấ ủ A và B l n ầ
lượt là 0,05
và
0,03 (K t qu n hàng ph ế ả làm tròn đế ần trăm)
Mệnh đề Đúng Sai
a) Xác su ất để Q có phát sinh thêm chi phí khi s d ng d ch v n là ử ụ ị ụ tư vấ
0,038 .
b) Biết Q có phát sinh thêm chi phí khi s d ng d ch v n. Xác su t ử ụ ị ụ tư vấ ấ
để Q thuê công ty A n là tư vấ 0,47
c) Biết Q có phát sinh thêm chi phí khi s d ng d ch v n. Xác su t ử ụ ị ụ tư vấ ấ
để Q thuê công ty B n là tư vấ 0,53
d)
Biết Q không phát sinh thêm chi phí khi s d ng d ch v n. Xác ử ụ ị ụ tư vấ
suất để Q thuê công ty A n là tư vấ 0,4 .
Lời gi i ả
Gọi
1
H
: “cơ quan Q thuê công ty A tư vấn”
2
H
:“cơ quan Q thuê công ty B tư vấn”
a) Đúng: G i ọ A là bi n cế ố “cơ quan Q có phát sinh thêm chi phí khi s d ng d ch v ử ụ ị ụ tư vấn”
Theo đề bài ta có:
( ) ( )
1 2 6 0,4; 0,P H P H==
( )
1
|P A H là xác xu ất để Q có phát sinh thêm chi phí khi s d ng d ch v n v u ki n ử ụ ị ụ tư vấ ới điề ệ Q
thuê công ty
A
( )
1
| 0,05P A H =
( )
2
|P A H
là xác xu ất để Q có phát sinh thêm chi phí khi s d ng d ch v n v u ki n ử ụ ị ụ tư vấ ới điề ệ Q
thuê công ty
B
( )
2
| 0,03P A H =
Theo công th c toàn ph n ta có: ứ ầ
( ) ( ) ( ) ( ) ( )
1 1 2 2
. | . | 0,4.0,05 0,6.0,03 0,038P A P H P A H P H P A H= + = + =
b) Sai: Theo công th c Bayes ta có: ứ
( ) ( ) ( )
( )
1 1
1
. | 0,4.0,05
| 0,53
0,038
P H P A H
P H A P A= =
c) Sai: Theo công th c Bayes ta có: ứ
( ) ( ) ( )
( )
2 2
2
. | 0,6.0,03
| 0,47
0,038
P H P A H
P H A P A= =
d) Đúng: Theo công th c Bayes ta có: ứ
( )
( ) ( )
( )
( ) ( )
( )
( )
1 1 1 1
1
. | . 1 | 0,4. 1 0,05
| 0,4
1 1 0,038
P H P A H P H P A H
P H A P A
P A
−
−

= = =
−−
.
Câu 24: M t kho hàng do hai nhà máy s n xu t. Bi t t l s n ph a nhà máy I b ng ộ ả ấ ế ỉ ệ ả ẩm đóng góp củ ằ
1
3
s n ph m ả ẩ
đóng góp của nhà máy II và t l ph phỉ ệ ế ẩm do nhà máy I, nhà máy II s n xu t l t là ả ấ ần lượ
0,1%
và
0,2%
. Ch n ng u nhiên m t sọ ẫ ộ ản ph m thì th y nó là ph ph m. Bi t xác suẩ ấ ế ẩ ế ất để ph ph II ế ẩm đó do nhà máy
sản xu t là ấ
a
b
. Tính giá tr bi u th c ị ể ứ
2T a b=+
.
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Lời gi i ả
Gọi
A
: “ Sản phẩm được chọn là phế phẩm”.
B : “Sả ẩm đượn ph c chọn thuộc nhà máy I”.
Khi đó
B
: “Sả ẩm đượ ”. n ph c chọn thuộc nhà máy II
Vì t l a nhà máy I b ng ỉ ệ đóng góp củ ằ
1
3
s n ph a nhà máy II nên ta có: ả ẩm đóng góp củ
( )
25% 0,25P B ==
( )
75% 0,75P B ==
; ( )
| 0,1% 0,001P A B ==
;
( )
| 0,2% 0,002P A B ==
.
Áp d ng công th c xác su t toàn ph n ta có xác su t ch c ph ph m là ụ ứ ấ ầ ấ ọn đượ ế ẩ
( ) ( ) ( )
( ) ( )
. | . |P A P B P A B P B P A B=+
( )
7
0, 25.0,001 0,75.0,002 4000
P A = + =
.
Áp d ng công th c Bayes ta có: ụ ứ
( ) ( )
( )
( )
. | 0,75.0,002 6
|77
4000
P B P A B
P B A P A= = =
.
Khi đó xác suất để ẩm đó do nhà máy phế ph II sản xuất là
6
7
66 2.7 20
7
aT
b
=
= + =
=
.
Câu 25: Có hai đồ ột đồng xu cân đối đồ ột đồng xu có hình thức giống nhau, trong có có m ng chất và m ng xu
không cân đối có xác suất khi tung đồng xu xu t hi n m t ng a là ấ ệ ặ ử
2
3
. Một người lấy ngẫu nhiên một
đồng xu trong hai đồng xu đã cho, tung đồng xu đó 3 lần thì đều thấy xuất hiện mặt ngửa, xác suất
người đó lấy được đồng xu cân đối là bao nhiêu? (Kết quả n hàng ph i) làm tròn đế ần mườ
Lời giải
Gọi
A
là bi n c ng chế ố: “Lấy được đồng xu cân đối đồ ất” và
B
là bi n cế ố: “Tung đồng xu ba lần
đề ấ ệ ặu xu t hi n m t ng n tính ửa”. Khi đó ta cầ
( )
|P A B
.
Ta có
( )
1
2
P A =
,
( )
1
2
P A =
và
( )
3
1 1
|2 8
P B A 
==


,
( )
3
2 8
|3 27
P B A 
==


.
Theo công th c Bayes và công th c xác su t toàn ph n ta có ứ ứ ấ ầ
( ) ( ) ( )
( ) ( )
( ) ( )
1 1
|2 8
| 0,3
1 1 1 8
| |
2 8 2 27
P A P B A
P A B
P A P B A P A P B A
= =
+ +
.
Câu 26: Có hai chi c h p, h p I có 5 qu bóng màu tr ng và 7 qu , h p II có 10 qu bóng màu ế ộ ộ ả ắ ả bóng màu đỏ ộ ả
trắng và 15 qu , các quả bóng màu đỏ ả bóng có cùng kích thướ ối lược và kh ng. Lấy ngẫu nhiên
hai qu bóng t h p I b vào h y ra ng u nhiên m t qu bóng t h p II. Xác su t ả ừ ộ ỏ ộp II. Sau đó, lấ ẫ ộ ả ừ ộ ấ
để ả ấ ừ ộ qu bóng được l y ra t h p II là qu c chuy n t h p I sang, bi t r ng quả bóng đượ ể ừ ộ ế ằ ả bóng đó
có màu tr ng là ắ
a
b
(là phân s t i gi n). Tính ố ố ả
+a b
.
Lời giải:
Gọi A là biến cố "Lấy c tđượ ừ hộp II qu bóng màu tr ng" ả ắ
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
B là bi n c "L c t h p II qu c chuy n t h p I sang" ế ố ấy đượ ừ ộ ả bóng đượ ể ừ ộ
Ta có:
( )
( )
( )= = − = − =
2 2 25
1 1
27 27 27
P BBB P P
Lại có:
( ) ( )
( )
( )−+
+
= = =
2 2 2
21 1
12 5 7
52 1
2 1 2 1
12 27 12 27
. . 5
212
27
C C C
CC C
P AB C C C C
P A B P B
∣
( ) ( )
( )
= = =
1
10
1
27
.2
25 5
27
C
P A C
P B
P
B
B
A∣
Suy ra
( ) ( ) ( )
( ) ( )
( ) ( )
= = =
++
2 5
.
.1
27 12
2 5 25 2 13
. | . . .
27 12 27 5
P B P A B
P
B B
B A
P B P A B P P A
∣
∣
∣
Vậy
= = + =1, 13 14a b a b
Câu 27: Có ba đồng xu được đự ộp kín. Đồ ột đồng xu cân đống trong một h ng xu thứ nhất là m i với tỷ lệ mặt
ngửa và mặt sấp b ng xu thằng nhau. Đồ ứ hai là m ng xu b lột đồ ị ỗi có khả năng mặt ngửa xuất hiện
là 70%. Đồ ột đồng xu thứ ba là m ng xu hai mặt ngửa (khi tung luôn ra mặt ngửa). Bạn An lấy ngẫu
nhiên m ng xu t hột đồ ừ ộp và tung nó hai l n. Kầ ết qu c a hai l n tung cho th y xu t hi n m t l n m t ả ủ ầ ấ ấ ệ ộ ầ ặ
sấp và m t l n m t ng a. Tính xác su ng xu b ng xu th ng xu b l i) ộ ầ ặ ử ất để đồ ạn đã chọn là đồ ứ hai (đồ ị ỗ
(Kết quả n hàng ph làm tròn đế ần trăm)
Lời gi iả
Đáp án: 0,46
Gọi
A
là bi n c ch ng xu th ế ố ọn đồ ứ ( )
1;2;3n n =
B
là bi n c tung hai l n thì th y xu t hi n m t l n m t s p và m t l n m t ng a ế ố ầ ấ ấ ệ ộ ầ ặ ấ ộ ầ ặ ử
Vì ch n ng u nhiên nên ọ ẫ
( ) ( ) ( )
1 2 3
1
3
P A P A P A= = =
Lấy ngẫu nhiên m ng xu tung hai l c m t m t s p và m t m t ngột đồ ần đượ ộ ặ ấ ộ ặ ửa thì ta có ba trường hợp
như sau:
Trườ ợng h p 1: Ch ng xu thọn được đồ ứ ấ nh t là S-N và N-S nên
( )
2
1
1 1
| 2. 2 2
P B A 
==


Trườ ợng h p 2: Ch ng xu thọn được đồ ứ hai là S-N và N-S nên ta có:
( )
2
| 0,7.0,3 0,3.0,7 0, 42P B A = + =
Trườ ợng h p 3: Ch ng xu thọn được đồ ứ ba là N-N nên ( )
3
| 0P B A =
Áp d ng công th c xác su t ch ng xu th hai là: ụ ức Bayes ta tính đượ ấ ọn được đồ ứ
( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) ( )
2 2
2
1 1 2 2 3 3
1
0,42.
| . 3
| 0,46
1 1 1 1
. | . | . | . 0,42. 0.
3 2 3 3
P B A P A
P A B P A P B A P A P B A P A P B A= =
++ ++
Vậy xác suất ch ng xu thọn được đồ ứ hai là
0, 46 .
22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu

Tài liệu khác của Trường Đại học Ngoại Thương

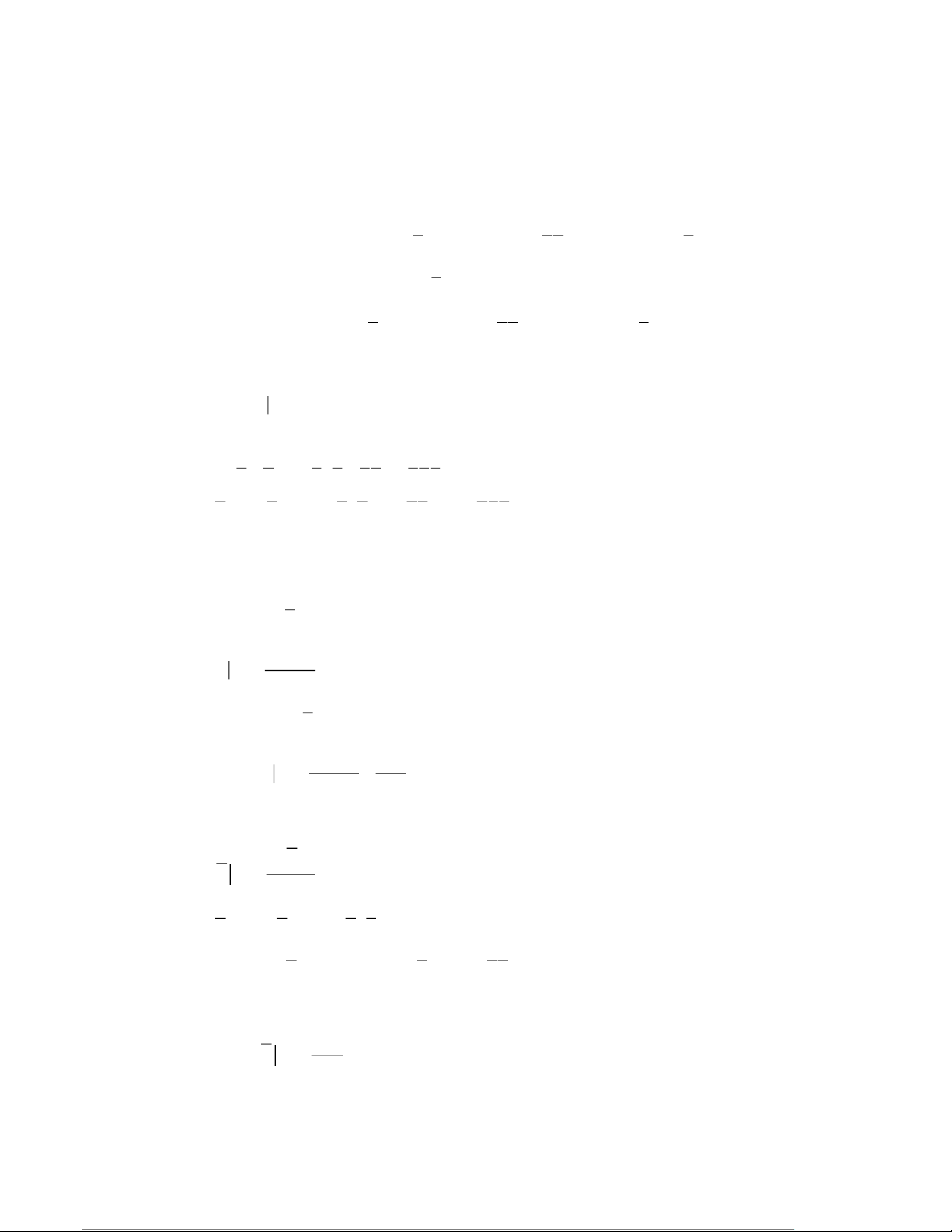
Preview text:

22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
BÀI TOÁN VỀ XÁC SUẤT
A - XÁC SUẤT LỚP 10, 11
Câu 1: Bạn Thuận có một danh sách gồm 6 bài hát khác nhau, các bài hát được phát theo thứ tự từ trên xuống.
Lần đầu, khi nghe xong bài hát thứ ba trong danh sách, bạn ấy xáo trộn ngẫu nhiên danh sách phát
của mình và sau đó nghe 3 bài hát đầu tiên trong danh sách mới. Tính xác suất để bạn Thuận nghe đủ
6 bài hát khác nhau sau hai lần nghe (kết quả làm tròn đến hàng phần trăm). Lời gi i ả ( )
Lần đầu nghe được 3 bài 1,2,3 trong danh sách. Xáo 6 bài nên ta có n= 6!.
A là biến cố “Nghe đủ 6 bài trong danh sách sau 2 lần nghe”.   
Suy ra lần 2 phải nghe 3 bài 4,5,6 hay danh sách lần 2 phải là 1;2;3 4;5;6. ( ) ( ) Do đó, n A = 3!.3!. Vậy 3!.3! 0,05 P A == . 6!
Câu 2: Trong trận thi đấu bóng bàn đơn nam giữa vận ng độ
viên Nguyễn Đức Tuân (người từng đoạt huy
chương vàng đơn nam môn bóng bàn tại Seagames 31) với một vận động viên nước ngoài, trận đấu
gồm tối đa 5 set (séc), người nào thắng trước 3 set sẽ giành chiến thắng chung cu c. Xác su ộ ất để vận
động viên Tuân thắng mỗi set là 0,6. Tính xác suất để vận ng độ
viên Tuân giành chiến thắng trong
trận đấu (làm tròn kết quả đế n hàng phần trăm). Lời gi i: ả
Để vận động viên Tuân giành chiến thắ ầ
ng, anh ta c n thắng 3 séc trước đối thủ.
Các trường hợp có thể xảy ra là:
+) TH1: Vận động viên Tuân thắng 3 set đầu tiên, xác suất là: = . 0,6 0,216 3
+) TH2: Trong 3 set đầu, vận động viên thắng 2 set, thua 1 set thì có C 3 = 3 cách. 2
Xác suất vận động viên thắng 2 set, thua 1 set và thắng ở set thứ 4 là = . 3.0,6 .0,4.0,6 0,2592 2
+) TH3: Trong 4 set đầu, vận động viên thắng 2 set, thua 2 set thì có C 4 = 6 cách 2
Xác suất vận động viên thắng 2 set, thua 1 set và thắng ở set thứ 4 là = . 6.0,6 .0,4 .0,6 0,20736 2 2 Áp d ng công th ụ
ức cộng xác suất, ta có xác suất để vận động viên Tuân giành chiến thắng trong
trận đấu là: 0,216 +0,2592 +0,20736  0,68 .
Câu 3: Nhân dịp Tết Trung thu cô giáo tặng quà cho 3 bạn Vũ, Hồng, Ng c. ọ Trong h p quà có 9 ộ cây bút và
8 quyển vở được sắp xếp một cách lộn x n. ộ Cô giáo g i
ọ 3 bạn đứng xếp hàng có thứ tự, Vũ đứng
trước được tặng quà trước, Hồng đứng sau nhận quà sau và Ngọc đứng sau cùng nên nhận quà sau cùng. Xác suất để Ng c
ọ nhận được quà là cây bút bằng bao nhiêu, biết rằng cô giáo tặng quà bằng
cách rút ngẫu nhiên và mỗi bạn chỉ m t ph ộ
ần quà trong hộp (kết quả làm tròn đến hàng phần trăm)? Lời gi i: ả
Để Ngọc nhận được bút, ta xét các trường hợp:
 Trường hợp 1: Vũ nhận bút, H ng nh ồ
ận bút, Ngọc nhận bút:
Xác suất Vũ nhận bút: 9 17 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Sau khi Vũ nhận bút, còn lại 8 bút và 8 vở, tổng cộng 16 phần quà. Xác suất H ng nh ồ ận bút: 8 = 1 16 2 Sau khi H ng nh ồ
ận bút, còn lại 7 bút và 8 vở, tổng c ng 15 ph ộ ần quà. Xác suất Ng c nh ọ ận bút: 7 15
Xác suất của trường hợp này: 9 1 7 =63 . . 17 2 15 510
 Trường hợp 2: Vũ nhận bút, H ng nh ồ
ận vở, Ngọc nhận bút:
Xác suất Vũ nhận bút: 9 17
Sau khi Vũ nhận bút, còn lại 8 bút và 8 vở, tổng cộng 16 phần quà. Xác suất H ng nh ồ ận vở: 8 = 1 16 2 Sau khi H ng nh ồ
ận vở, còn lại 8 bút và 7 vở, tổng cộng 15 phần quà. Xác suất Ng c nh ọ ận bút: 8 15
Xác suất của trường hợp này 9 1 8 =72 . . : 17 2 15 510
 Trường hợp 3: Vũ nhận vở, H ng nh ồ
ận bút, Ngọc nhận bút:
Xác suất Vũ nhận vở: 8 17
Sau khi Vũ nhận vở, còn lại 9 bút và 7 vở, tổng cộng 16 phần quà. Xác suất H ng nh ồ ận bút: 9 . 16 Sau khi H ng nh ồ
ận bút, còn lại 8 bút và 7 vở, tổng c ng 15 ph ộ ần quà. Xác suất Ng c nh ọ ận bút: 8 15  8  9  8 72  =
Xác suất của trường hợp này:  . .    17  16  15   510
 Trường hợp 4: Vũ nhận vở, H ng nh ồ
ận vở, Ngọc nhận bút:
Xác suất Vũ nhận vở: 8 17
Sau khi Vũ nhận vở, còn lại 9 bút và 7 vở, tổng cộng 16 phần quà. Xác suất H ng nh ồ ận vở: 7 16 Sau khi H ng nh ồ
ận vở, còn lại 9 bút và 6 vở, tổng cộng 15 phần quà. 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu Xác suất Ng c nh ọ ận bút: 9 15
 8   7  9  ==
Xác suất của trường hợp này: 504 63  . .   
17  16  15  4080 510
Vậy xác suất để Ng c nh ọ
ận được quà là cây bút là:   63    72   + + + 7 =2 =63  270 9 0, 53
        .   510 5  10  51  0 5  10  510 17
Câu 4: Trong một lễ hội mùa hè, có một trò chơi mà mỗi lần chơi, người chơi sẽ tung đồng thời bốn đồng
xu cân đối một cách ngẫu nhiên. Người chơi chỉ thắng cuộc nếu nhận được ít nhất ba mặt ngửa từ bốn đồng xu đã tung.
Tính xác suất để trong 5 lần chơi, người chơi thắng được ít nhất ba lần (làm tròn kết quả đến hàng phần trăm)?
Hướng dẫn giải
Bước 1: Tính xác suất thắng trong một lần chơi
Trong một lần chơi, người chơi tung 4 đồng xu cân đối: 3 1 1  1 1 1 1 1 • 3
Xác suất nhận được đúng 3 mặt ngửa là C   = 4 4   =  = 4  . 2  2     8 2 16 4 4  1  1
• Xác suất nhận được cả 4 mặt ngửa là =  2 .  16 1 1 5
Vậy xác suất thắng trong một lần chơi là: +=
; xác suất thua trong một lần chơi là 4 16 16 5 11 116 −=16 .
Bước 2: Tính xác suất thắng ít nhất 3 lần trong 5 lần chơi.
Xác suất này bao gồm các trường hợp: 3 2  5  1  1 125 121 151250
• Thắng đúng 3 lần, thua 2 lần: 3 C   = 10   = 5  . 16   1     6 4 096 256 1048576 4 1  5  1  1 625 11 34375
• Thắng đúng 4 lần, thua 1 lần: 4 C   = 5  = . 5  16  1      6 65536 16 1048576 5  5  3125
• Thắng cả 5 lần: =  . 1   6 1048576 151250 34375 3125 0,02 Xác suất cần tính là: + +  1048576 1048576 1048576 .
Câu 5: Ba cầu th sút ph ủ
ạt đền 11m , mỗi người đá một lần với xác suất làm bàn tương ứng là a ; b và 0,7 .
Biết xác suất ghi bàn để ít nhất một trong ba cầu thủ ghi bàn là 0,982 và xác suất để ba cầu th ghi ủ
bàn là 0,392. Tính xác suất để có đúng hai cầu thủ ghi bàn. Lời gi i ả 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu Gọi A là biến c
ố “người thứ i ghi bàn” với . i i= 1,3 Ta có các biến c
ố A ,A ,A là các biến c ố P A=c l độ ập và a P A ( = )1 b, = P A (2, 0,)7 3 ( ) 1 2 3
Gọi A là biến cố: “Có ít nhất m t trong ba c ộ ầu thủ ghi bàn”
B là biến cố: “Cả ba cầu thủ đều ghi bàn”
Clà biến cố: “Có đúng hai cầu thủ ghi bàn” Ta có A = 1 A .A .2 3 AP A( = )PA 1.P ( A 2 ) P .A (3 =
)0,3.−(1a− ) 1b)( ).
P (A )= 1− 0,3. 1− (a 1− b)(. ) Lại có B = A .A 1 . 2 A  3 = P B ( ) P A= . 1
A (2.A 3 P A ) P . 1 A ( P= . A 2 ) (30a,7 ).b ( . )
Từ giả thiết ta có hệ phương trình 1  −  0,3 
(.1−a .)1 (−b= 0 ),982 1+ ab− +a b= 0, ( 06 a ) b+ = 1,5 0,8 a = do a b         0  ,  7 0 a , b39 a = 2 b = 0,56 ab b   = 0 =,56 0,7 Mặt khác ta có C= A A . A .+ A + A . . A A . A . nên 1 2 3 1 2 3 1 2 3 A
P (C )= (1− a .b ).0,7+ a . 1− b .(0,7+ a ).. b 0,3 = 0, 2 + .0 +,7.
=0,7 0,8.0,3.0,7 0,8.0,7.0,3 0, 434 .
Câu 6: Có 8 bạn cùng ngồi xung quanh một cái bàn tròn, mỗi bạn cầm một đồng xu như nhau. Tất cả 8 bạn
cùng tung đồng xu của mình, bạn có đồng xu ngửa thì đứng, bạn có đồng xu sấp thì ngồi. m
Biết xác suất để không có hai bạn liền kề cùng đứng bằng
(trong đó m, n là các số tự nhiên và n m phân số
tối giản); tính m +n . n
Hướng dẫn giải
Gọi A là biến cố “không có hai người liền kề cùng đứng”.
Số phần tử của không gian mẫu là n  (= ) 8 2 = 256 .
Nếu có nhiều hơn 4 đồng xu ngửa thì biến cố A không xảy ra. Ta xét các trường hợp sau:
Trường hợp 1: Có nhiều nhất 1 đồng xu ngửa; số kết quả là: 1+ 8 = 9 .
Trường hợp 2: Có 2 đồng xu ngửa; số kết q C uả 2 là: −= 88 20 .
(Loại trừ 8 khả năng 2 đồng xu ngửa đó kề nhau).
Trường hợp 3: Có 3 đồng xu ngửa trong 8 đồng xu; các khả năng để loại trừ là:
• Cả 3 đồng xu ngửa kề nhau: có 8 kết quả.
• Có 2 đồng xu ngửa kề nhau trong 3 đồng xu ngửa: có 8 4 = 32 kết quả.
Suy ra, số kết quả của trường hợ 3 p này Clà − 88 − 32= 16 .
Trường hợp 4: Có 4 đồng xu ngửa; có 2 kết quả như thế.
(Kết quả của trường hợp này là: S-N-S-N-S-N-S-N và N-S-N-S-N-S-N-S; với kí hiệu N là người nhận
được đồng xu mặt ngửa và S là người nhận mặt sấp tương ứng vị trí).
Số kết quả thuận lợi là n A ( =)+ 9 20 + 16 + 2= 47 . ( ) n ( A ) 47 303m
Xác suất để không có hai bạn liền kề cùng đứng là: P A = = = m +n = . n( n ) 256 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Câu 7: Một con châu chấu nhảy lên cầu thang có 18 bậc. Mỗi lần nhảy con châu chấu có thể nhảy 1 bậc hoặc
2 bậc. Tính xác suất để con châu chấu hoàn thành 18 bậc thang với số lần nhảy 2 bậc không bé hơn
số lần nhảy 1 bậc (làm tròn kết quả đến hàng phần trăm).
Hướng dẫn giải x +y 2 = 18
Gọi x là số bước nhảy 1 bậc, y là số bước nhảy 2 bậc; suy ra  . x,y
Các cặp (x ; y) thỏa mãn là (18; 0 , )16 (;1 , 14 ) ; 2 (,12; 3 ),1 ( 0; 4 ), ( ) (8; 5 ,)6(;6 , ) 4; ( 7 , 2; )8 , (0; 9 ). ( )
• Nếu (x;y )  1 (  8; 0 , 0 )
; 9 ( thì c )on châu chấu có 2 cách đi.
• Nếu (x;y )= ( 16; 1 t )
hì số cách đi của châu chấ 1 u là 17 C .
• Tương tự như vậy các trường hợp còn lại sẽ có số cách là 2 3 4 5 6 7 8 C C + +
C C+ C+ +16 15 14 + 13 12 11= 10 4162 (cách).
Vậy tổng số cách nhảy của châu chấu để thoàn thành 18 bậc cầu thang là 1 C2 + + 41 = 62 4181 17
(cách). Số phần tử không gian mẫu là n ( ) = 4181 .
Số lần nhảy 2 bậc không bé hơn số lần nhảy 1 bậc nên x (y ;  ) 6; (
6 , 4; )7 ,(2; 8 , )0 (;9 . ) ( )
Gọi A là biến cố thỏa đề bài n th Aì (= C ) 6 7 8 9 C 1 +2C C 1 +1 1 +0 = 9 1300 . ( ) n A ( )1300 65 0,31 Do vậy P A = n = =  () . 4180 209
Câu 8: Hai bạn Hùng và Cường chơi trò quay bánh xe số. Bánh xe số có 20 nấc điểm là 5,10,15,.....,100 với
các vạch chia đều nhau (giả sử rằng khả năng chuyển từ nấc điểm đã có tới các nấc điểm còn lại là
như nhau). Trong mỗi lượt chơi, mỗi người được quyền chọn quay 1 hoặc 2 lần và điểm số của
người chơi được tính như sau:
(1)Nếu người chơi chọn quay một lần thì điểm của người chơi là điểm quay được.
(2) Nếu người chơi chọn quay 2 lần và tổng điểm quay được không lớn hơn 100 thì điểm của
người chơi là tổng điểm quay được.
(3) Nếu người chơi chọn quay 2 lần và tổng điểm quay được lớn hơn 100 thì điểm người chơi là
tổng điểm quay được trừ đi 100 .
Luật chơi quy định, trong mỗi lượt chơi người nào có điểm số cao
hơn sẽ thắng cuộc, hòa nhau sẽ
chơi lại lượt khác. Hùng chơi trước và có điểm số là 75. Tính xác suất để Cường thắng cuộc ngay ở
lượt chơi này.( Lấy kết quả đến hàng phần trăm). Lời gi i ả 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu Ta có: n− 100 5 ( )  = 1 + 2 = 0 5
Để Cường thắng ta có 2 trường hợp:
- Trường hợp 1 : Cường quay 1 lần ra điểm số lớn hơn 75, ta có 5 khả năng thuộc tập hợp 5 1 {80;85;90;95;100} Do xác suất là P== . 1 20 4
- Trường hợp 2 : Cường quay lần đầu ra điểm số là a 75 , ta có 15 khả năng. Do đó xác suất 15 3 P== 2 20 4
Khi đó, để thắng Cường cần phải có tổng hai lần quay lớn hơn 75 , ta có 5 khả năng thuộc tập hợp 5 1 − − a a− − {8 a 0 ;85 − ; a 90 ;95 ; a 100 }
.Do đó xác suất là P== . 3 20 4
Vậy xác suất để Cường thắng ngay trong lượt là 70,44
P = P+ P P=  . 1 2 3 16
Đáp án: 0,44
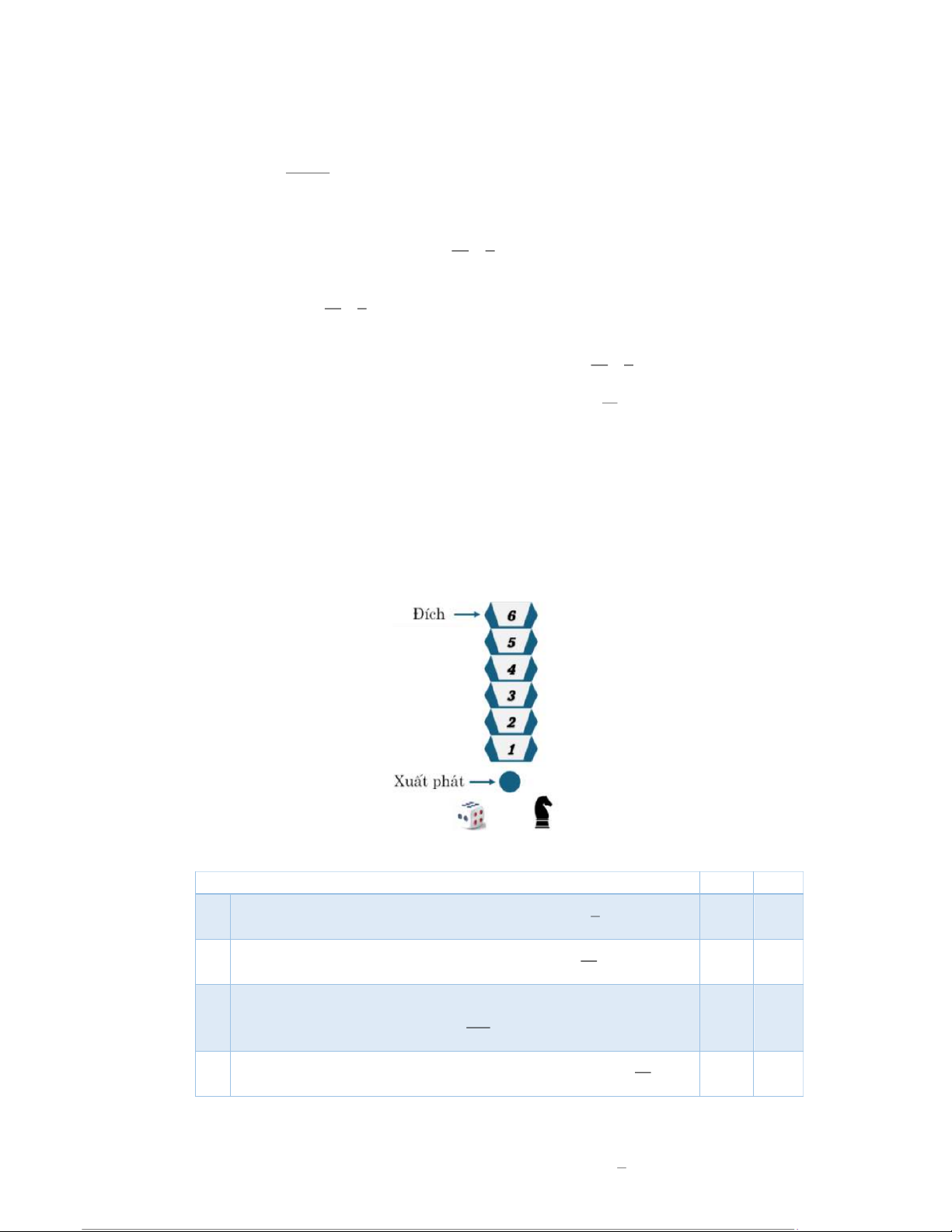
Câu 9: Trong một trò chơi, con ngựa c a b ủ ng ạn Toàn đang đứ
ở vị trí xuất phát (như hình vẽ). Luật chơi
như sau: Để di chuyển con ngựa, bạn Toàn cần gieo một con xúc xắc có sáu mặt cân đối, đồng chất.
Ở mỗi lượt chơi, bạn có tối đa ba lần gieo. Ở lần gieo thứ ấ
nh t, con ngựa di chuyển đến ô có số thứ tự bằng s ố tương ứng với s ch ố
ấm gieo được của con xúc xắc. Từ những lần gieo sau, nếu tổng c a ủ số tương ứng với s ch ố
ấm gieo được c a con xúc x ủ ắc và s ố ng ghi tương ứ
ở ô con ngựa đang đứng
lớn hơn 6 thì con ngựa sẽ đứng yên, còn nếu tổng này nhỏ hơn hoặ
c bằng 6 thì con ngựa được di
chuyển số ô bằng số chấm gieo được. Con ngựa này gọi là về đích nếu nó đến được ô số 6. Mệnh đề Đúng Sai a) 1
Xác suất để con ngựa về đích ở lần gieo thứ nhất bằng 6 b) 5
Xác suất để con ngựa về đích ở lần gieo thứ hai bằng 36
c) Xác suất để con ngựa về đích ở lần gieo thứ ba và trong cả ba lần gieo 5
con ngựa đều được di chuyển bằng 108 d) 19
Xác suất để con ngựa về đích sau nhiều nhất ba lần gieo bằng 54 Mệnh đề a) 1 Gieo 1 lần: n (  )
= 6 . Gọi A: "Sẽ gieo s 6" ố
n(A )= 1 P= . ĐÚNG A 6 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu Mệnh đề b) Gieo 2 lần: n (  ) = 6  6= 36 . Gọi B: "T ng 2 l ổ ần gieo bằng 6" Ta có x+ y = 6  x y(=)
; {(1;5),(2; 4),(3;3),(4; 2),(5;1)} 5 n ( B ) 1 = C 5.1 = 5 ĐÚNG B P= . 36 Mệnh đề c) Gieo 3 lần: n (= )  6 6  6 . Gọi C: "T ng 3 l ổ ần gieo bằng 6"
Ta có x+ y+ z= 6  n (C= ) k 1 C −− = = C 3 1
10 (Chọn 2 trong 5 để xếp vào) n 1 −− 6 1 10 5 Suy ra P== . ĐÚNG C 36 108
Cách 2: Liệt kê Mệnh đề d) x + y+ z= 6 Dịch chuyển:
+ Lần 1: 1 → 5: Dịch chuyển
+ Lần 2:  6: Đứng yên + Lần 3: Di chuyển 1 1 x z y + +  6C C  = 5 5 . 25 cách 25 25 P== D = 6 6 6  6  216 101  + + + = . SAI A P BPCP P D 216
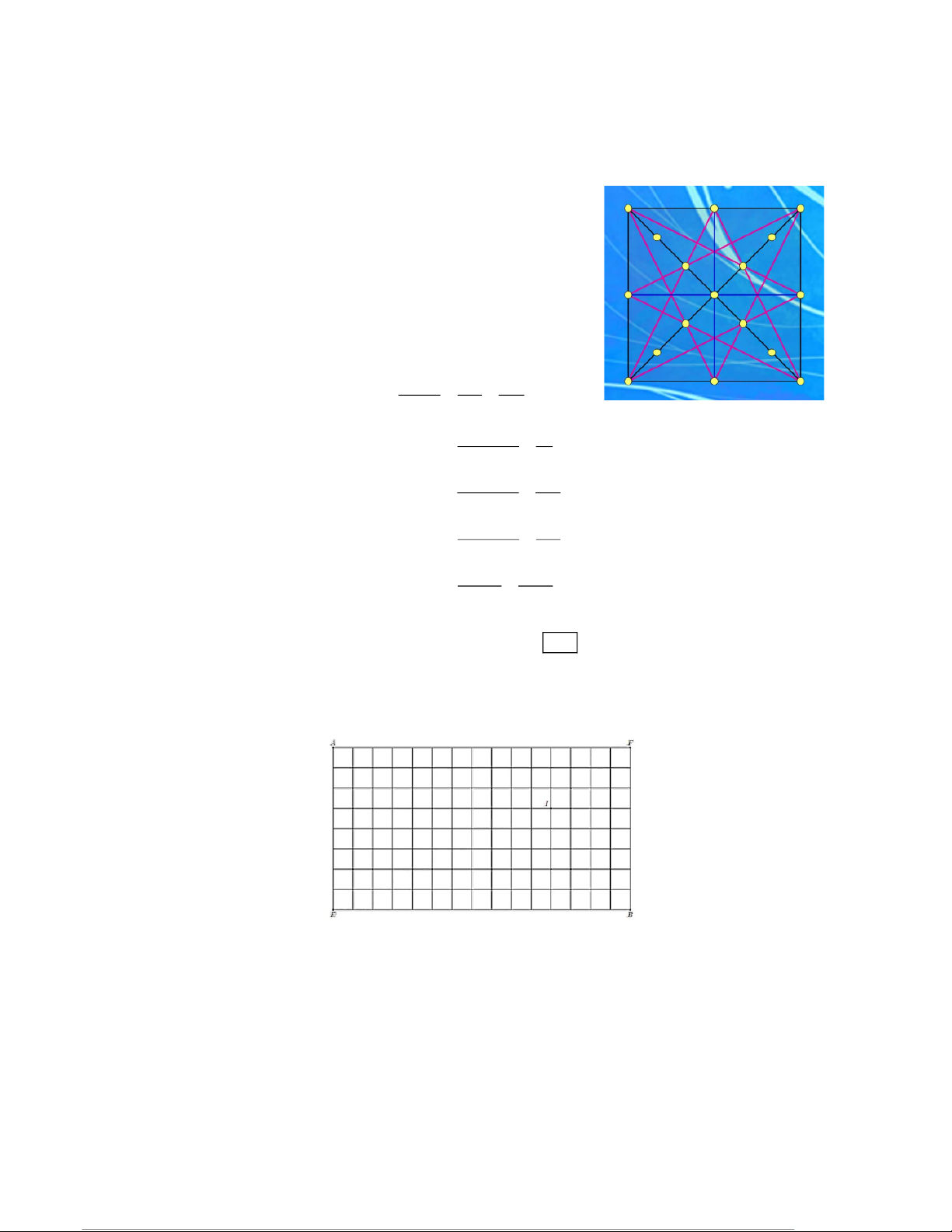
Câu 10: Trên một banner quảng cáo, người ta gắn 17 chiếc bóng đèn vào một khung hình vuông cũng như
hai đường chéo của hình vuông đó. Biết rằng các bóng đèn trên một cạnh hoặc đường chéo thì chia
cạnh hoặc đường chéo đó làm các đoạn bằng nhau (xem hình
vẽ). Các bóng đèn sẽ sáng lên theo quy luật sau:
• Vào phút thứ nhất sẽ có ngẫu nhiên 1 bóng đèn sáng lên, đến
cuối phút thứ nhất nó sẽ tắt.
• Vào phút thứ 2 sẽ có ngẫu nhiên 2 bóng đèn sáng lên, đến cuối
phút thứ hai chúng sẽ tắt.
• Vào phút thứ 3 sẽ có ngẫu nhiên 3 bóng đèn sáng lên, đến cuối
phút thứ ba chúng sẽ tắt.
Quy luật này cứ tiếp diễn cho đến phút thứ 17 và một chu trình
mới sẽ được lặp lại. Tính xác suất để từ phút thứ 3 cho đến phút
thứ 17, luôn có ít nhất 3 bóng đèn sáng lên ở 3 đỉnh của một tam giác (làm tròn đến hàng phần trăm).
Hướng dẫn giải 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Gọi A là biến cố: “Tại phút thứ i thì có ít nhất 3 bóng đèn sáng lên ở 3 đỉnh của tam giác”; khi đó i i   3;4;...; 17 . Phút thứ 3:
• Số phần tử không gian mẫu l n à C ( ) 3 =317 .
• Số khả năng để 3 bóng đèn sáng lên là 3 đỉnh tam giác: n ( A ) 3 3 =C − 2 C − 4 − 10= 596 3 17 7 .
(Ta loại trừ các trường hợp 3 điểm thẳng hàng gồm: 2 trường
hợp 3 điểm thuộc các đường chéo, 4 trường hợp 3 điểm thuộc các
cạnh, 10 trường hợp 3 điểm thẳng hàng khi vẽ thêm hình).
( ) n (A 3) 598 299
• Xác suất tương ứng là P A =n C = = 33 ( )  . 3 17 340 4 4− 233
Phút thứ 4: Xác suất tương ứng là ( ) 17 7 ==C C P A C . 44 34 17 5 5− 2439
Phút thứ 5: Xác suất tương ứng là ( ) 17 7 ==C C P A C 55 . 442 17 6 6− 2883
Phút thứ 6: Xác suất tương ứng là ( ) 17 7 ==C C P A C 66 . 884 17 7 − 29723
Phút thứ 7: Xác suất tương ứng là ( ) 17 ==C P A C 77 . 9724 17
Từ phút thứ 8 trở đi thì chắc chắn luôn có ít nhất 3 bóng sáng lên ở 3 đỉnh của tam giác. Xác suất cần P tì A m là =P A ( ) P A (   P A ..  . 0,84 . 1 2 ) ( 17) ( )
Câu 11: Hai người tham gia một trò chơi di chuyển theo cạnh c a
ủ các ô hình chữ nhật như trong hình (hình
có 158 ô hình chữ nhật nh ) ỏ
Người thứ nhất đi từ điểm A đến điểm B , người thứ hai đi từ điểm
E đến điểm F. Biết rằng cả hai
người cùng đi ngẫu nhiên và theo con đường ngắn nhất. Tính xác suất để cả hai người cùng đi qua
điểm I (kết quả làm tròn đến hàng phần trăm). Lời giải:
Gọi X là biến cố "cả hai người cùng đi qua điểm I " Xét hệ tr c t
ụ ọa độ với E (0;0 ),A 0 B ( ;8 , )15 F ;0 (, 1I5 ) ;8 , (11;5 ) ( )
Để đi từ A đến B theo đường ngắn nhất thì người thứ nhất cần di chuyển 15 bước ngang và 8 bước xuống 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu Số cách di chuyển từ 8
A đến B là s cách s ố
ắp xếp 15 bước ngang và 8 bước xu ng và b ố ằng 2 C 3
Tương tự có 8 cách để ngườ ứ ể ừ đế 2 C i th hai di chuy n t 3 E n F
Như vậy không gian mẫu Ω= ( C )2 8 23
Người thứ nhất di chuyển từ A(0;)8 đến I (1 )
1;5 cần 11 bước ngang và 3 bước xuống
Người thứ nhất di chuyển từ I (1 ) 1;5 đến B (1 )
5;0 cần 4 bước ngang và 5 bước xu ng ố
Như vậy số cách di chuyển của người thứ nhất t AừI →→ B là 8 4 C . 14 9 C
Tương tự số cách di chuyển của người thứ hai t E ừI → F → là 5 3 1 C 6 7. C Như vậy 8 4 5 3 X = C C . . C C . 14 9 16 7 8 4 5 3 XC C . C .C .
Vậy xác suất để cả hai người cùng đi qua I là P (X ) 14 9 16 7 = =  0, 24 Ω (C )2 8 23
B - XÁC SUẤT ĐIỀU KIỆN
Câu 12: Trong một đêm thi hát, mỗi người phải tham gia hát hai bài : M t
ộ bài theo phong cách âm nhạc dân gian, m t bà ộ
i theo phong cách âm nhạc nhạc nhẹ. Một đội có 20 người tham gia đêm thi hát đó. Kết
quả là 15 người đạt bài thi theo phong cách âm nhạc dân gian, 17 người đạt bài thi theo phong cách
âm nhạc nhạc nhẹ; 2 người không đạt cả hai bài. Ch n
ọ ngẫu nhiên một người. Tính xác suất để người
đó đạt bài thi theo phong cách âm nhạc nhạc nhẹ biết rằng người đó đạt bài thi theo phong cách âm
nhạc dân gian (Kết quả làm tròn đến hàng phần trăm). Lời gi i ả
Gọi A là biến cố: “Người đó đạt bài thi theo phong cách âm nhạc nhạc nhẹ”.
B là biến cố: “Người đó đạt bài thi theo phong cách âm nhạc dân gian”.
Ta có: P (A ) 17 = ; P (B ) 15 = ; P (AB ) 2 = . 20 20 20 Do đó: P(A )  B = − P ( AB ) 2 18 1 = 1 − 20 2 = 0 .
P(AB= )P A ( + ) P B − ( P ) A B ( 17 1 = + − =) 5 18 14 . 20 20 20 20 ( ) ( P A ) B 14
Vậy P A |B0,93P = B =  . ( ) 15
Câu 13: Một công ty tham gia đấu thầu 2 dự án. Khả năng
thắng thầu dự án 1 là 60% và dự án 2 là 50%. Khả
năng thắng thầu cả hai dự án là 40%. Gọi A và B lần lượt là biến c công ố
ty thắng thầu dự án 1 và dự án 2. Mệnh đề Đúng Sai a)
A và B là hai biến cố c l độ ập.
b) Khả năng công ty thắng thầu đúng 1 dự án là 30%
c) Xác suất công ty thắng thầu dự án 2 biết công ty đã thắng thầu dự án 1 1 là . 2 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
d) Xác suất công ty không thắng thầu dự án 2, biết công ty đã không thắng 1 thầu dự án 1 là . 4 Lời gi i ả P Ta có A= (  )P = 0, A 6 ( =)P 0 B ,4;  0,=5 ( ) P B 0,5 ( ) và ( P A ) B = 0, 4 a) Sai: Vì ( P AB )  P A ( . P )B ( ) nên , A B c l không độ ập .
b) Đúng: Do AB và AB là hai biến c
ố xung khắc nên xác suất công ty thắng thầu đúng 1 dự án là: P A(B + )P A ( B=
)P A− (P)AB + (P B )− P A (B )= −( 0+,6− )0,4= 0,5 0,4 0,3
c) Sai: Xác suất công ty thắng thầu dự án 2 biết công ty đã thắng thầu dự án 1 là: ( ) ( P B )A 0, 4 2 P B |0, A 6 3 = P = = . (A )
d) Sai: Xác suất công ty thắng thầu dự án 2, biết công ty đã không thắng thầu dự án 1 là: ( )P ( BA ) P ( B )P −− A (B )0,5 0,4 1 P B |0, A 4 4
= P= (A ) P A(= ) = .
Vậy xác suất công ty không thắng thầu dự án 2, biết công ty đã không thắng thầu dự án 1 là P (B ) A = − P B A ( = − )1 3 1 1 4 4 = .
Câu 14: Khảo sát những người xem b
ộ phim hoạt hình vừa được phát hành cho thấy 70% người xem là trẻ
em và 30% là người lớn. Trong số các trẻ em đến xem phim có 50% yêu thích b phim ộ và khẳng định
sẽ đi xem tiếp phần 2, 30% yêu thích b
ộ phim nhưng sẽ không xem tiếp phần 2; 20% còn lại không thích b phim ộ
và không xem tiếp phần 2. Trong s nh ố
ững người lớn đi xem phim có 20% yêu thích
bộ phim và khẳng định sẽ xem tiếp phần 2, 10% yêu thích b
ộ phim nhưng sẽ không xem tiếp phần 2;
70% còn lại không thích b
ộ phim và không xem tiếp phần 2. Ch n
ọ ngẫu nhiên 1 người đã xem phim. Mệnh đề Đúng Sai
a) Biết người được ch n là tr ọ
ẻ em, xác suất để người đó yêu thích bộ phim là 0,56 .
b) Xác suất để người đó không xem tiếp phần 2 là 0,59.
c) Biết người đó sẽ xem tiếp phần 2 của bộ phim, xác suất để người đó là
trẻ em lớn hơn 0,85.
d) Biết người đó yêu thích bộ phim, xác suất để người đó không xem tiếp
phần 2 là 0,37 (làm tròn đến hàng phần trăm). Lời gi i ả a) Sai
b) Đúng c) Đúng d) Đúng
Gọi A là biến cố “Người đó là trẻ em” B là biến c
ố “Người đó thích bộ phim” 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu C là biến c
ố “Người đó xem tiếp phần 2 b ộ phim”
Xét người đi xem là trẻ em có P (A )= 0,7 . Suy ra P B (
C )== 50% 0,5 , P (BC )== 30% 0,3 , P (BC )== 20% 0,2 , (PB ) C = 0 .
Xét người đi xem là người lớn có ( P A)= 0,3 . P B (
C )== 20% 0, 2 , P (BC )== 10% 0,1 , P (BC )== 70% 0,7 , (PB ) C = 0 . (a) Sai Ta có P (B ) A =+ 0 = ,5 0,3 0,8 . (b) Đúng Ta có = C CABCAB CAB CAB . P (C ) P = C + A + ( B+ P CA ) B
(P C AB )P (C AB ) ( ) = 0,7 0,
+3 0,7 0,+2 0,3+ 0,1 0,=3 0,7 0,59 . (c) Đúng P C = − (P ) C 1 = 0, 4(1 ) . ( ) P (A ) C P A C = P . (C )
( )PAC= (PA )CB + P (AC)B = 0,7+0 0,7 0,5 = 0,35 . P AC 0,35 0,854 0,85 Suy ra P(A ) ( ) C = P =   . (C ) 0, 41 (d) Đúng ( ) P C(B )
P C B = P (B )
( P)CB= P(CBA + P)CB(A )=0,3+ 0,7 =0,1 0,3 0,24 .
P (B= )+ P B + (AC
+ ) P BA (C )P BAC ( P BAC ) ( )
= 0,7 0,+3 0,7+ 0,5 0, + 3 0, 2= 0,3 0,1 0,65 . Suy ra P(C ) 0, 24 0,37 B = . 0,65
---------------------------------------------------------------------------------------------------------
Câu 15: Có hai đội thi đấu môn bắn súng. Đội I có 8 vận động viên, đội II có 10 vận động viên. Xác suất đạt
huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,6 và 0,55. Chọn ngẫu nhiên một vận động viên. 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu Mệnh đề Đúng Sai a) 5
Xác suất để vận động viên chọn ra thuộc đội I là 9
b) Xác suất không đạt huy chương vàng của mỗi vận động viên đội II là 0,45
c) Xác suất để vận động viên này đạt huy chương vàng là 103 180
d) Giả sử vận động viên được chọn đạt huy chương vàng. Xác suất để vận
động viên này thuộc đội I là 48 . 103 Lời giải
a) Sai: Xác suất để vận động viên chọn ra thuộc đội I là 8 4= . 18 9
b) Đúng: Xác suất không đạt huy chương vàng của mỗi vận động viên đội II là 1− 0 =,55 0,45
c) Đúng: Gọi A là biến cố: “Vận động viên đạt huy chương vàng”, B là biến cố: “Thành viên đội
I” thì biến cố đối của B là B : “Thành viên đội II đạt huy chương vàng”.
Do đó, P(B ) 8 4 = = P B ( = ) 5 ; ; P A ( B ) = |= 0 P , 6; A |B ( ) 0,55 18 9 9
Theo công thức xác suất toàn phần ta có
P (A= ) P B( ) P A ( B+ P ) B (P ) A B =(+ ) 4 5 103 . | . | .0,6 .0 = ,55 9 9 180 4.0,6 d) Đúng: Ta có ( ) (P ) B . P | (A B ) 48 9 P B |1 A03 1 =03 P = = ( A ) 180
Câu 16: Trong m t lô s ộ
ản phẩm có 3 hộp loại I và 5 hộp loại II. Biết rằng trong m i h
ỗ ộp loại I có 97 sản phẩm
tốt và 3 phế phẩm, trong mỗi hộp loại II có 95 sản phẩm t t
ố và 5 phế phẩm. Lấy ngẫu nhiên từ lô sản
phẩm đó một hộp, rồi từ hộp đó lấ ẫu nhiên đồ y ng ng thời hai sản phẩm. Mệnh đề Đúng Sai
a) Xác suất để hộp được ch n là h ọ p lo ộ ại I bằng 3 8
b) Nếu hộp được lấy là hộp loại I thì xác suất để cả hai sản phẩm lấy ra
không có phế phẩm bằng 776 . 825
c) Xác suất cả hai sản phẩm lấy ra không có phế phẩm bằng 1833 . 2000
d) Biết rằng trong hai sản phẩm lấy ra có đúng một phế phẩm, xác suất để
hộp lấy ra là hộp loại I bằng 203 . 2475
Lời giải a) Đúng b) Đúng c) Sai d) Sai a) Đúng
Xác suất để hộp được ch n là h ọ ộp loại I bằng 3 . 8 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu b) Đúng
Gọi A là biến cố “hộp lấy ra loại I” C 776 B là biến c n ph ố:” 2 sả
ẩm lấy ra không có phế phẩm “. Ta có P(B ) 2 97 A =C = 2 825 100 c) Sai ( )= ( ) C C P B P A .P ( B A) P + ( A ). P B A ( ) 2 2 3 5 97 95 = C. +C . 0,916 . 2 2 8 8 100 100 d) Sai
C là biến cố: “Lấy ra được 1 phế phẩm và 1 sản phẩm tốt” 95.5 19 P (C ) 97.3 97 |16 A 50 = C = . P(C ) |19 A 8= C = 2 2 100 100 3 97 ( ) ( P A) .873 C 8 1650 P A |3 C 97 = P C = 5 19 3248 = . ( ) . . + 8 1650 8 198 Câu 17: Trong m t
ộ giải thi đấu bóng chuyền, đội bóng chuyền của Hà N i s
ộ ẽ thi đấu hai trận. Trận thứ nhất đội bóng chuyền c a
ủ Hà Nội có xác suất thắng là 0,6 . Trận tiếp theo, xác suất chiến thắng của h ọ ph ụ
thuộc vào kết quả trận trước đó. Nếu đội bóng chuyền c a
ủ Hà Nội thắng trận trước đó, họ sẽ hưng phấn và xác suất để h ọ thắng là 0,7 . Nếu i độ bóng chuyền c a ủ Hà N i
ộ thua trận trước thì h ọ sẽ mất tinh
thần và xác suất để họ thắng là 0,5 . Tính xác suất để đội bóng chuyền c a
ủ Hà Nội thắng trận thứ hai. Lời gi i ả Đáp số:0,62 Gọi A là biến c
ố : “Đội bóng chuyền c a Hà N ủ i th ộ ắng trận thứ 1” Gọi B là biến c
ố : “Đội bóng chuyền c a Hà N ủ i th ộ ắng trận thứ 2” P A =  ( ) P A = 0,6 0, 4 ( ) Ta có .
Nếu đội bóng chuyền của Hà Nội thắng trận trước đó, họ sẽ hưng phấ
n và xác suất để họ thắng là 0,7 hay P B ( A =)|0,7 .
Nếu đội bóng chuyền của Hà Nội thua trận trước thì họ sẽ mất tinh thần và xác suất để họ thắng là 0,5 hay P B ( A | = )0,5 . P ( B= )P A ( . P )B (| A + P ) A (P .) B A | ( = + 0,=7.0),6 0,4.0,5 0,62 Ta có: .
Vậy xác xuất để đội bóng chuyền Hà Nội thắng trận thứ 2 là 0,62 . Câu 18: M t h ộ p ch ộ
ứa 10 viên bi xanh và 5 viên bi đỏ. Bạn An lấy ra ngẫu nhiên 1 viên bi từ h p, xem màu, ộ
rồi bỏ ra ngoài. Nếu viên bi An lấy ra có màu xanh, bạn Bình sẽ lấy ra ngẫu nhiên 2 viên bi từ h p; ộ
còn nếu viên bi An lấy ra có màu , b
đỏ ạn Bình sẽ lấy ra ngẫu nhiên 3 viên bi từ h p. ộ Tính xác suất
để An lấy được viên bi màu xanh, biết rằng tất cả các viên bi được hai bạn chọn ra đều có đủ cả hai màu. Lời gi i ả 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Gọi A là biến cố An lấy được viên bi màu xanh thì A là biến c
ố An lấy được viên bi màu . đỏ Gọi B là biến c t
ố ất cả các viên bi được hai bạn chọn ra đều có đủ cả hai màu. 10 5 ( ) (P ) AB Ta có P(A )== , P (A )
. Ta cần tính P A B∣ P = B . 15 15 ( )
Khi A xảy ra thì trong hộp còn 9 viên bi xanh và 5 viên bi đỏ, Bình cần lấy ra 2 viên bi trong đó có 2 2 C C− ít nhất m nên ột viên bi đỏ P(B ) 14 9 A ∣ = C . 2 14
Khi A xảy ra thì trong hộp còn 10 viên bi xanh và 4 viên bi đỏ, Bình cần lấy ra 3 viên bi trong đó có C C−
ít nhất m t viên bi xanh nên ộ P(B ∣) 3 3 14 4 A = C . 3 14 10 ( 110 C ) 2 2 C− 14 9 Vậy P (AB ) =P A (.1 P 5)2 B∣ 73 A( =  ) C = 2 14 10 ( 2 2 5 C C−− )33 C C 14 9 14 2 40 ( 0 ) ∣ P M B = ặ + t khác: P A P ( B A) P A( ) . P . B (A )( ) ( ) =  +  = . 2 3 15 15 C C 273 14 14 110 ∣ Vậy P(A ) 273 0,55 B == . 200 273
Câu 19: Có hai phác đồ điều trị A và B cho một loại ệnh. b
Phác đồ A có xác suất chữa khỏi bệnh là 60% và
xác suất gây tác dụng phụ nghiêm trọng là 5%. Phác đồ B có xác suất chữa kh i b ỏ ệnh là 70% và xác suất gây tác d ng ụ ph ụ nghiêm tr ng ọ là 10%. M t
ộ bệnh nhân được điều trị ngẫu nhiên bằng
một trong hai phác đồ (xác suất chọn mỗi phác đồ là 50%). Mệnh đề Đúng Sai a) Xác suất b u tr ệnh nhân điề
ị bằng phác đồ A và được chữa kh i b ỏ ệnh là 0,6.
b) Xác suất để bệnh nhân bị tác d ng ph ụ nghiêm tr ụ ng là 0,075. ọ
c) Nếu biết bệnh nhân này gặp tác dụng phụ nghiêm trọng thì xác suất
bệnh nhân đã được điều trị bằng phác đồ B lớn hơn 0,65.
d) Biết rằng trong mỗi phác đồ điều trị thì biến cố "bệnh nhân được chữa
khỏi bệnh" và biến cố "bệnh nhân không bị tác d ng ụ ph nghiêm tr ụ ng" ọ
là độc lập với nhau. Xác suất bệnh nhân khỏi bệnh và không bị tác dụng phụ nghiêm tr ng là 0,6. ọ Lời giải
Gọi A là biến c "b ố
ệnh nhân chọn phác đồ A".
Gọi B là biến c "b ố ệnh nhân kh i b ỏ ệnh".
Gọi C là biến c "b ố
ệnh nhân bị tác dụng phụ nghiêm tr ng". ọ Khi đó: P ( A )= P = (A ) 0,5 P B ( |A) = 0, 6 P ( B | A )= 0,7 P C ( |A) = 0,05 P C ( |A) = 0,1 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu a) Sai. Xác suất b u tr ệnh nhân điề ị phác đồ A và kh i b ỏ ệnh là: P ( AB ) = P (
A ) P (B |A )= 0,  5 0, =6 0,3 .
b) Đúng. Xác suất bệnh nhân bị tác dụ ụ ng ph nghiêm trọng là: P C( )
= P (AC )+ P (AC )= P (A )  P ( C |A )
+ P (A ) P (C |A )= 0,5 0,05+ 0,5 0,1 = 0, 075
c) Đúng. Nếu biết bệnh nhân bị tác dụng phụ nghiêm trọng thì xác suất để ệ
b nh nhân chọn phác đồ B là: P(AC ) 0,5 0  ,1 2 P( | A )C = P C = = 0,  65 . ( ) 0,075 3
d) Đúng. Theo giả thiết B /A và C /A độc lập, B /A và C /A c l độ ập.
Xác suất bệnh nhân khỏi bệnh và không bị tác dụng ph nghiêm tr ụ ng là: ọ BC P BC  + (A )P BC  (= () A )P BC  ( A ) P A + P BC ( A) | | P A ( ) ( ) ( ) = PA P B ( ) A (P |C ) + (
A | P)A  (P ) B ( A | ) P (C |A )
= 0,5 0,6 (1− 0,05)+ 0,5 0,7 (1 − 0,1)= 0,6
---------------------------------------------------------------------------------------------------------
Câu 20: Một cơ quan hành chính nhà nước thực hiện việc tinh giản biên chế thông qua phỏng vấn. T l ỷ ệ nhân
viên của cơ quan thuộc hai nhóm trình độ: Đại học, Cao đẳng lần lượt là 65% và 35%. Qua ph ng ỏ
vấn thì tỷ lệ nhân viên bị tinh giản của nhóm đại học là10%, nhóm cao đẳng là 15%. Ch n m ọ t nhân ộ
viên bất kỳ đã bị tinh giản thì hãy tính xác suất để người này có trình độ đại h c
ọ (kết quả là một s ố
thập phân nhỏ hơn 1 đã làm tròn đến hàng phần trăm). Lời giải Đáp số: 0,55. Gọi A là biến c
ố “ Chọn nhân viên có trình độ đại học” . Gọi B là biến c
ố “ Chọn nhân viên bị tinh giản biên chế thông qua ph ng v ỏ ấn” . Tỷ lệ nhân viên c i h
ủa cơ quan thuộc hai nhóm trình độ: Đạ ọc, Cao đẳng lần lượt là 65% và 35% P A nên =  ( )P= 0 A , 65 0,35 ( ) . Qua ph ng v ỏ ấn thì t l
ỷ ệ nhân viên bị tinh giản của nhóm đại h c là ọ
10%, nhóm cao đẳng là 15% nên P (B ) A = 0,1 và P ( B A )= 0,15.
Chọn một nhân viên bất kỳ đã bị tinh giản thì xác suất để
người này có trình độ đại học là P(A )B . P A .0, P 65 B.0, A 1 0,55
Theo công thức ta có: P (A ) ( ) ( ) B = = = .
P (A )P (B ) A P + (A ) P ( B A ) 0,65.0,1 0, + 35.0,15 . . Câu 21: M t chi ộ
ếc hộp có 50 viên bi, trong đó có 30 viên bi màu xanh và 20 viên bi màu đỏ, các viên bi có kích
thước và khối lượng giống nhau. Sau khi kiểm tra, người ta thấy có 70% số viên bi màu xanh được
đánh số và 60% số viên
bi màu đỏ được đánh số, những viên bi còn lại không đánh số. Lấy ngẫu nhiên m t
ộ viên bi từ hộp đó. Biết rằng, viên bi lấy ra được đánh số, xác suất để viên bi đó có màu
xanh bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? Lời gi i ả
Trả lời: 0,64 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Gọi A là biến cố: “Viên bi lấy ra có màu xanh”.
Suy ra A là biến cố: “Viên bi lấy ra có màu đỏ”.
B là biến cố: “Viên bi lấy ra được đánh số”. ( ) P B A  (( P )) A P A B = +  . P (B ) A ( P ) A
(P B)A (P )A Ta có P (A ) 30 3 ==
P (A =)− P A (= ) 2 15 . 30 20 + 5 P (
B A )== 70% 0, 7 và P(B ) A == 60% 0,6 . 3 0,7 7  Vậy P(A ) 50,64 B = 3 2 11 =  0,7 0,6+  5 5
Câu 22: Nhân dịp k ni
ỷ ệm 50 năm ngày thành lập trường, các h c
ọ sinh lựa chọn tham gia thi đấu thể thao hoặc
biểu diễn văn nghệ. Lớp 12 A có 60% s h
ố ọc sinh tham gia thi đấu thể thao và còn lại 40% s h ố c ọ
sinh tham gia biểu diễn văn nghệ. Biết rằng các bạn nữ đều tham gia biểu diễn văn nghệ. Trong s ố
các bạn nam có 20% tham gia văn nghệ và 80% tham gia thi đấu thể thao. Chọn ngẫu nhiên 1 h c ọ
sinh trong lớp. Biết rằng học sinh này tham gia biểu diễn văn nghệ, xác suất để học sinh này là nữ là bao nhiêu phần trăm? Lời gi i ả
Trả lời: 0,625
Gọi A : “Bạn được chọn là nam” và B : “Bạn được chọn tham gia biểu diễn văn nghệ”.
Khi đó, A : “Bạn được chọn là nữ” và B : “Bạn được chọn tham gia thi đấu thể thao”.
Lớp 12 A có 60% số học sinh tham gia thi đấu thể thao và còn lại 40% nên P (B )= 0,4 và ( P B )= 0, 4 .
Các bạn nữ đều tham gia biểu diễn văn nghệ nên P B (A =)|1 . Trong s các b ố
ạn nam có 20% tham gia văn nghệ và 80% tham gia thi đấu thể thao nên ta có P B A (=)|0, 2 và P B (A =)|0,8 . P B=Ta có:
+ P B A (P )A P (B | |A P)A ( ) ( ) ( )  0,4 = 0, ( 2 1 − (
)P A )+  1 (PA ) P A = (0,)2 5
Khi đó, xác suất để chọn ra một học sinh là nữ với điều kiện có tham gia biểu diễn văn nghệ là (
)P B(|0,A25P A )P ( (A ) ) P A |B0,62
=5 P (B ) P= B( ) = = . 0, 4 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu
Câu 23: Xác suất để cơ quan Q thuê 1 trong các công ty A và B tư vấn lần lượt là 0,4 và 0,6 . Theo kinh
nghiệm khả năng Q phát sinh thêm chi phí khi sử d ng d ụ
ịch vụ tư vấn c a công ủ
ty A và B lần
lượt là 0,05 và 0,03 (Kết quả làm tròn đến hàng phần trăm) Mệnh đề Đúng Sai
a) Xác suất để Q có phát sinh thêm chi phí khi sử d ng d ụ ịch v ụ tư vấn là 0,038 .
b) Biết Q có phát sinh thêm chi phí khi sử dụng dịch v ụ tư vấn. Xác suất
để Q thuê công ty A tư vấn là 0,47
c) Biết Q có phát sinh thêm chi phí khi sử dụng dịch v ụ tư vấn. Xác suất
để Q thuê công ty B tư vấn là 0,53 d) Biết
Q không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác
suất để Q thuê công ty A tư vấn là 0,4 . Lời gi i ả
Gọi H : “cơ quan Q thuê công ty A tư vấn” 1 H :“cơ quan tư vấn” 2
Q thuê công ty B
a) Đúng: Gọi A là biến cố “cơ quan Q có phát sinh thêm chi phí khi sử d ng d ụ ịch v ụ tư vấn” Theo đề bài ta có: P H =(= )1 0,4 ;P H (20,6 ) P(A )| H
là xác xuất để Q có phát sinh thêm chi phí khi sử d ng ụ
dịch vụ tư vấn với điều kiện Q 1 thuê công ty A P A H (= )| 0,05 1 P(A )|H
là xác xuất để Q có phát sinh thêm chi phí khi sử d ng ụ
dịch vụ tư vấn với điều kiện Q 2 thuê công ty B P A H (= )| 0,03 2
Theo công thức toàn phần ta có: P A =
P (H )P A ( H + . |P H P A . H | = + 0 =,4.0,05 0,6.0,03 0,038 1 ) ( 12 ) 2 ( ) ( ) ( ) ( P H . | P A H 0,4.0,05 1 1 ) ( )
b) Sai: Theo công thức Bayes ta có: P H = =  1 | 0 A ,53 P (A ) 0,038 (
)P(H . |P A H 0,6.0,03 2 2 ) ( )
c) Sai: Theo công thức Bayes ta có: P H | 0 A ,47 = =  2 P A ( ) 0,038
d) Đúng: Theo công thức Bayes ta có:  − −  P( P H . | P A H P . H 1 P| A H 0,4. 1 0,05 H | 0 A,4= = =  1 ) ( )1 ( ) 111 ( ) ( ) ( ) ( ) P A . P A 1−− ( ) 1 0,038
Câu 24: M t kho hàng d ộ
o hai nhà máy sản xuất. Biết tỉ lệ sản phẩm đóng góp của nhà máy I bằng 1 sản phẩm 3
đóng góp của nhà máy II và tỉ lệ phế phẩm do nhà máy I, nhà máy II sản xuất lần lượt là 0,1% và 0,2% . Ch n ng ọ
ẫu nhiên một sản phẩm thì thấy nó là phế phẩm. Biết xác suất để phế phẩm đó do nhà máy II
sản xuất là a . Tính giá trị biểu thức T= a + 2 b . b 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu Lời gi i ả
Gọi A : “ Sản phẩm được chọn là phế phẩm”. B : “Sả ẩm đượ n ph
c chọn thuộc nhà máy I”.
Khi đó B : “Sản phẩm được chọn thuộc nhà máy II”.
Vì tỉ lệ đóng góp của nhà máy I bằng 1 sản phẩm đóng góp của nhà máy II nên ta có: 3 P B (= )
= 25% 0, 25 P (B ) == 75% 0,75 ; P (
A B)| == 0,1% 0, 001 ; P (A B)|== 0,2% 0,002 . Áp d ng công th ụ
ức xác suất toàn phần ta có xác suất chọn được phế phẩm là P A =+ ( P )
B P A (B ). |P ( B P A). | B ( ) ( ) P (A ) 7 = 0 + , 25.0,001 0,=75.0,002 4000 . (
)P B( .P )|(A )B 0,75.0,002 6 Áp d ng công th ụ
ức Bayes ta có: P B |7 A 7 = P A = = . ( ) 4000 aT= 66 2.7 20
Khi đó xác suất để phế ẩm đó do nhà máy ph II sản xuất là 6  =  = + = . 7 b  7
Câu 25: Có hai đồng xu có hình thức giống nhau, trong có có một đồng xu cân đối đồng chất và một đồng xu
không cân đối có xác suất khi tung đồng xu xuất hiện mặt ngửa là 2 . Một người lấy ngẫu nhiên một 3
đồng xu trong hai đồng xu đã cho, tung đồng xu đó 3 lần thì đều thấy xuất hiện mặt ngửa, xác suất
người đó lấy được đồng xu cân đối là bao nhiêu? (Kết quả làm tròn đến hàng phần mười)
Lời giải
Gọi A là biến cố: “Lấy được đồng xu cân đối đồng chất” và B là biến cố: “Tung đồng xu ba lần đều xuất hiện mặt ng n tính ửa”. Khi đó ta cầ P (A ) |B . 3 3 P B A  1 1 P B A  2 8 Ta có P(A) 1 = , P(A ) 1 = và ( )|2 8 == , ( |)327== . 2 2  
Theo công thức Bayes và công thức xác suất toàn phần ta có 1 1 ( )  P (A ) P ( B |2 A 8 ) P A | B 0,3= =  .
P(A)P (B A )P
+ (A+ P)B A( 1 1 ) 1 8 | | 2 8 2 27
Câu 26: Có hai chiếc h p, ộ h p
ộ I có 5 quả bóng màu trắng và 7 quả bóng màu , đỏ h p
ộ II có 10 quả bóng màu
trắng và 15 quả bóng màu đỏ, các quả bóng có cùng kích thước và ối
kh lượng. Lấy ngẫu nhiên
hai quả bóng từ hộp I bỏ vào hộp II. Sau đó, lấy ra ngẫu nhiên m t qu ộ
ả bóng từ hộp II. Xác suất để ả
qu bóng được lấy ra từ ộ
h p II là quả bóng được chuyển từ hộp I sang, biết rằng quả bóng đó
có màu trắng là a (là phân s t ố i gi ố
ản). Tính a +b . b
Lời giải:
Gọi A là biến cố "Lấy được từ hộp II quả bóng màu trắng" 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu B là biến c "L ố ấy được từ h p II qu ộ
ả bóng được chuyển từ h p I sang" ộ Ta có: P(B ) 2 2 25 = P (B P )=−11 (B )=− = 27 27 27 2 CC C C −( + 2 C )2 21 1 C 12 5 7 52 1 ( )P (AB) . + . 5 2 1 2 1 Lại có: C C C C P A B∣ =P= 12 27 12 27 B ( ) = 212 27 1 ( ) C P A . ( 2B )101 C P BA∣ = P(B )= =27 25 5 27 ( ) P B ( P ) A B ∣ ( ) 2 5. .1 Suy ra P B A ∣ = = = 27 12 (
P B )P A (B ++ P )
(B )BP A ∣ ( 2 5 ) 25 2 13 . | . . . 27 12 27 5 Vậay =1 b , 1 = 3  a b + = 14
Câu 27: Có ba đồng xu được đựng trong một ộp h
kín. Đồng xu thứ nhất là một đồng xu cân đối với tỷ lệ mặt
ngửa và mặt sấp bằng nhau. Đồng xu thứ hai là một ng đồ
xu bị lỗi có khả năng mặt ngửa xuất hiện
là 70%. Đồng xu thứ ba là một đồng xu hai mặt ngửa (khi tung luôn ra mặt ngửa). Bạn An lấy ngẫu
nhiên một đồng xu từ hộp và tung nó hai lần. Kết quả c a hai ủ
lần tung cho thấy xuất hiện một lần mặt sấp và m t
ộ lần mặt ngửa. Tính xác suất để ng x đồ u bạn đã chọn là ng đồ
xu thứ hai (đồng xu bị l i) ỗ
(Kết quả làm tròn đến hàng phần trăm)
Lời gi i ả Đáp án: 0,46
Gọi A là biến cố chọn đồng xu thứ n (n )=1;2;3
B là biến c tung hai l ố
ần thì thấy xuất hiện m t l ộ ần mặt sấp và m t l ộ ần mặt ngửa Vì ch n ng ọ
ẫu nhiên nên P (A ) 1 = P A = P = A 1 2 ( 3 ) ( )3
Lấy ngẫu nhiên một đồng xu tung hai lần được m t m ộ
ặt sấp và một mặt ngửa thì ta có ba trường hợp như sau: 2 P B A  1 1
Trường hợp 1: Chọn được đồng xu thứ nhất là S-N và N-S nên ( )| =2 =. 2 2 1  
Trường hợp 2: Chọn được đồng xu thứ hai là S-N và N-S nên ta có: P ( B )| A = 0 + ,7.0,3 0, =3.0,7 0, 42 2
Trường hợp 3: Chọn được đồng xu thứ ba là N-N nên P B A (= )|03 Áp d ng công th ụ
ức Bayes ta tính được xác suất chọn được đồng xu thứ hai là: 1 ( ) P B ( 0, 42. | . A P A 3 2 2 ) ( ) P A | 0 B , 46P = A P B A P A P B A P A P B A =  2 ( ) . | ++ . | ++ . | . 0, 42. 0. 1 1 1 1 1 ( 1 2) ( 2 ) ( 3 ) 3 ( ) ( ) 3 2 3 3
Vậy xác suất chọn được đồng xu thứ hai là 0, 46 . 22:25, 27/01/2026
12A1 - Xác suất: Các Dạng Bài Tập Đa Dạng - Studocu

Tài liệu liên quan: