Các bài toán về ứng dụng tỉ lệ bản đồ có đáp án chi tiết nhất

Các bài toán về ứng dụng tỉ lệ bản đồ có đáp án chi tiết nhất
1. Lý thuyết về ứng dụng tỉ lệ bản đồ lớp 4
Tỉ lệ bản đồ là tỉ số giữa một khoảng cách đo trên bản đồ và khoảng cách
ngoài thực địa. Trên mỗi bản đồ, tỉ lệ được đặt ở dưới tên bản đồ cho người
đọc biết được mức độ thu nhỏ của đối tượng ngoài thực tế lên bản đồ.
Tỉ lệ bản đồ có thể viết dưới dạng một phân số có tử số là 1.
Ví dụ: 1/1.000;1/500;1/1.000.000
Thước tỉ lệ thường đặt ở dưới góc bản đồ phục vụ cho việc đo đạc các thông
số như khoảng cách và diện tích trên bản đồ
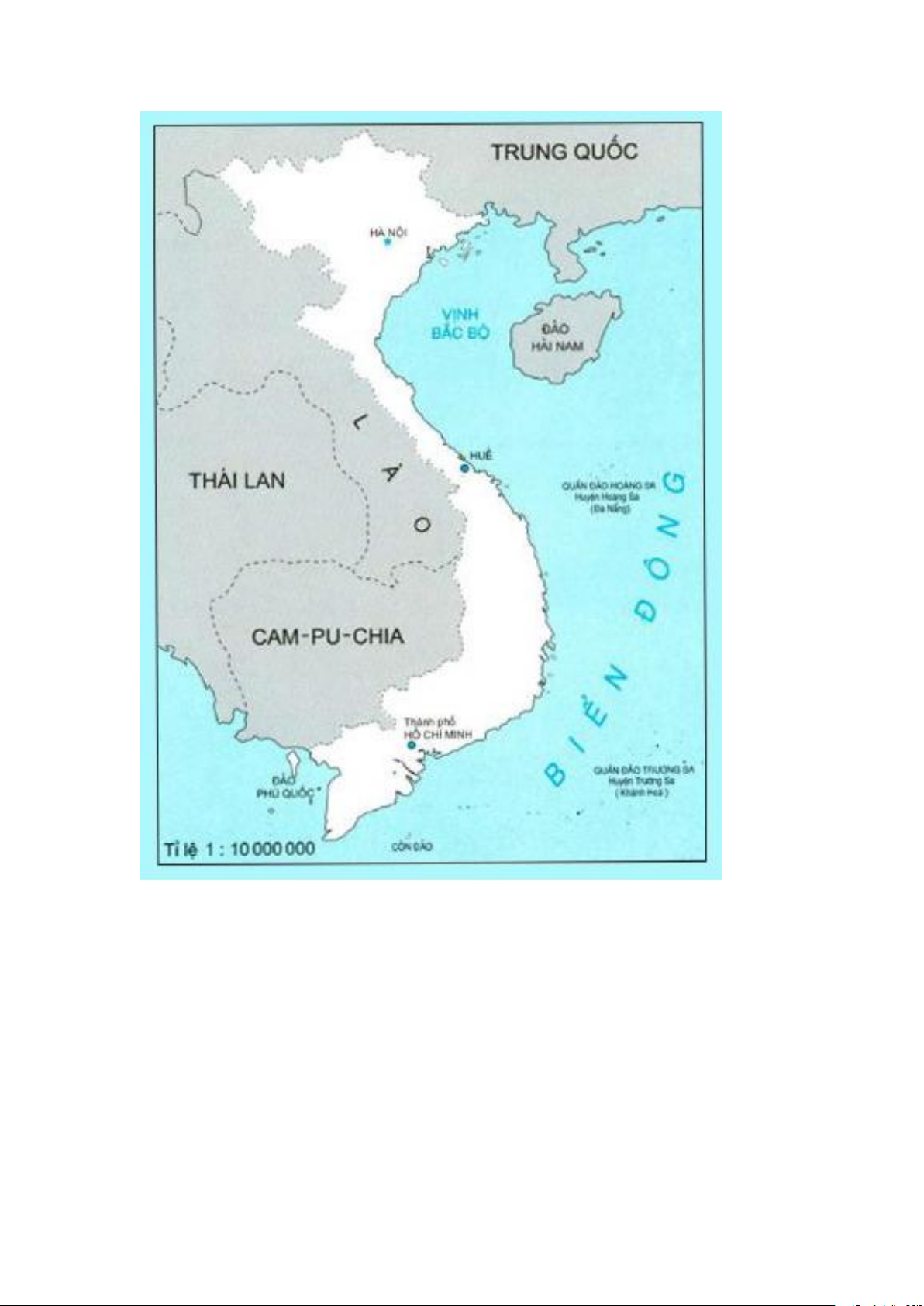
Ở góc phía dưới của bản đồ nước Việt Nam có ghi: Tỉ lệ 1:10.000.000. Tỉ lệ
đó là tỉ lệ bản đồ.
- Tỉ lệ 1:10.000.000 hay 1/10.000.000 cho biết hình nước Việt Nam được
vẽ thu nhỏ lại 10.000.000 lần. Chẳng hạn: độ dài 1cm trên bản đồ ứng với độ
dài thật là 10.000.000cm hay 100km
Ứng dụng của tỉ lệ bản đồ gồm: Tính độ dài thật; Tính độ dài thu nhỏ trên bản đồ Tính độ dài thật
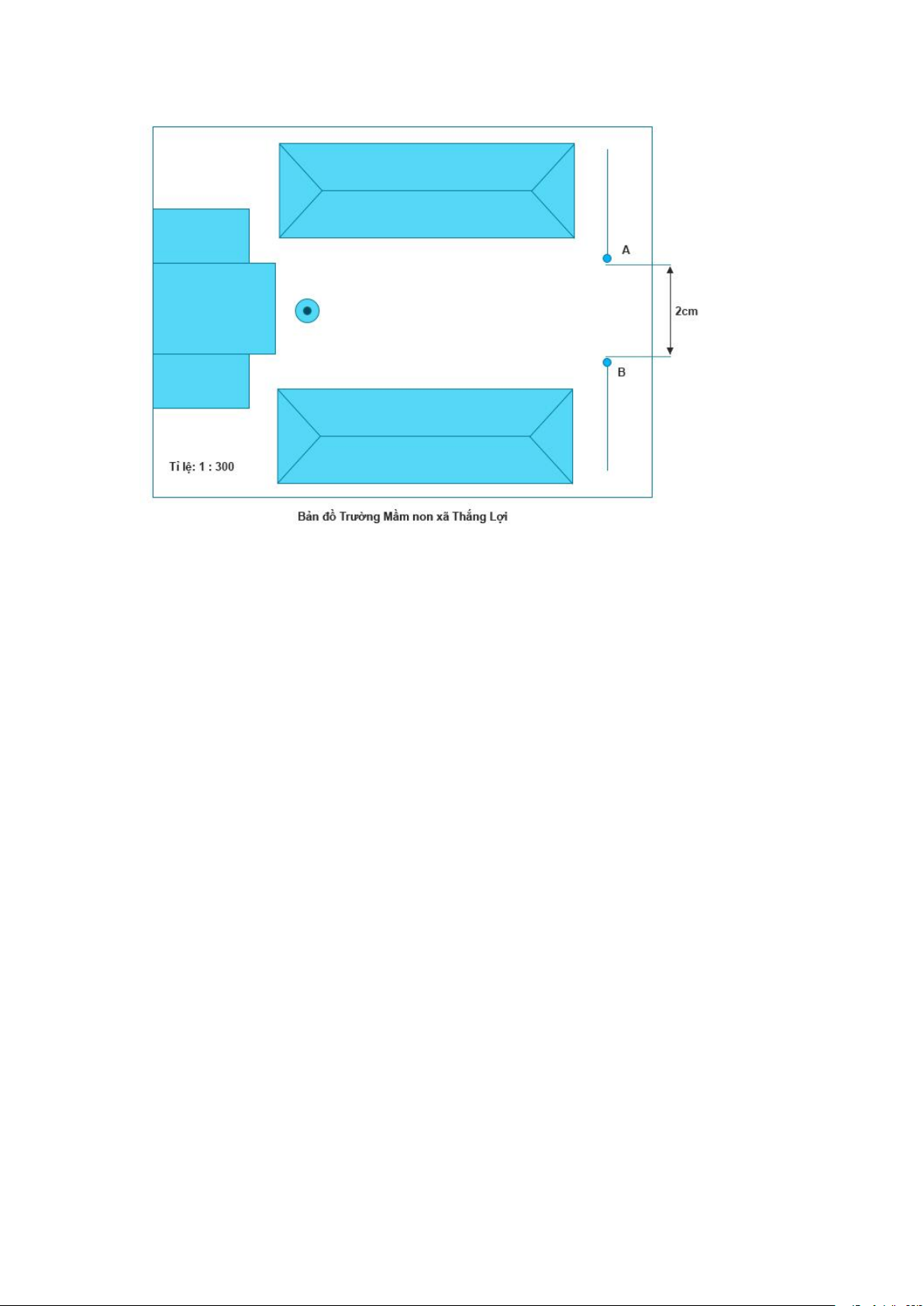
Ví dụ: Bản đồ trường Mầm non xã Thắng Lợi vẽ theo tỉ lệ 1:300.
Trên bản đồ, cổng trường rộng 2cm (khoảng cách từ A đến B). Hỏi chiều rộng
thật của cổng trường là mấy mét? Giải:
Chiều dài thật của cổng trường là: 2×300=600(cm) 600cm=6m Đáp số: 6m
Tính độ dài thu nhỏ trên bản đồ Ví dụ:
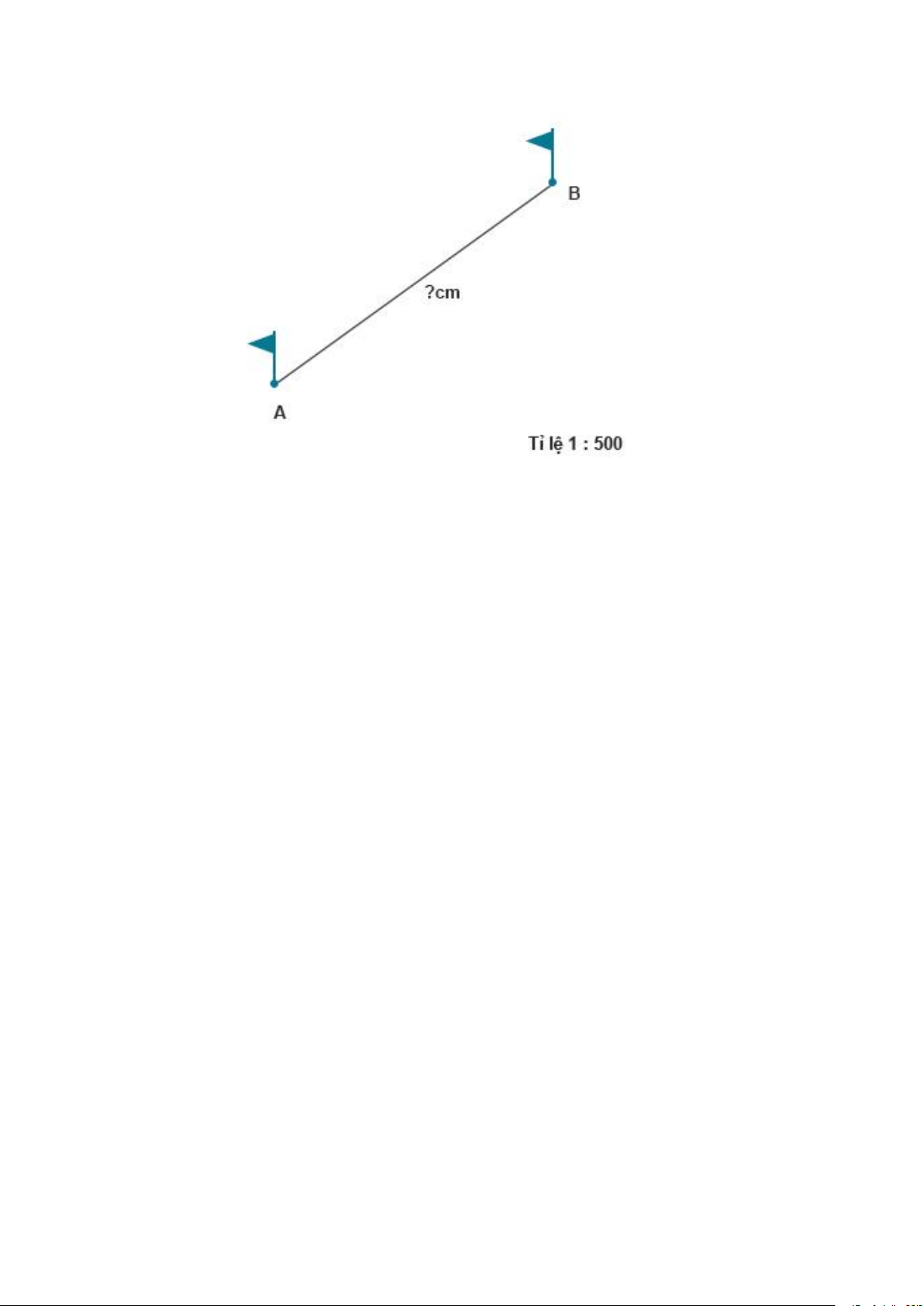
Khoảng cách giữa hai điểm A và B trên sân trường là 20m. Trên bản đồ tỉ
lệ 1:500, khoảng cách giữa hai điểm đó là mấy xăng-ti-mét? Bài giải 20m=2000cm
Khoảng cách giữa hai điểm A và B trên bản đồ là: 2000:500=4(cm) Đáp số: 4cm
2. Các dạng toán và ví dụ về Toán lớp 4 tỉ lệ bản đồ
2.1 Các dạng toán về tỉ lệ bản đồ
Dạng 1: Tìm khoảng cách thực địa khi biết tỉ lệ và khoảng cách bản đồ.
Cách làm: Lấy độ dài thu nhỏ trên bản đồ nhân với mẫu số tí lệ bản đồ
Ví dụ: Trên bản đồ tỉ lệ 1: 2000 khoảng cách giữa hai điểm A và B là 3cm.
Tính khoảng cách hai điểm ngoài thực tế Trả lời:
Khoảng cách giữa 2 điểm A và B ngoài thực tế là: 5 x 2000 = 10.000 (cm) = 100m Đáp số: 100m
Dạng 2: Tìm độ dài trên bản đồ khi biết độ dài thực địa và tỉ lệ
Cách làm: Lấy độ dài thật (sau khi đã đổi về cùng đơn vị đo với chiều dài thu
nhỏ cần tìm) chia cho mẫu số của tỉ lệ bản đồ.
Ví dụ: Khoảng cách giữa 2 tỉnh Vĩnh Phúc và Hà Nội là 60km. Trên bản đồ tỉ
lệ 1 : 100.000 thì khoảng cách giữa hai tỉnh đó là bao nhiêu cm. Trả lời: Đổi 60km = 6.000.000cm
Khoảng cách giữa hai tỉnh trên bản đồ tỉ lệ 1 : 100.000 là: 6000000 : 100000 = 60 (cm) Đáp số 60cm
Dạng 3: Tính tỉ lệ bản đồ khi biết độ dài trên bản đồ và thực tế.
Cách làm: Lấy độ dài thu nhỏ trên bản đồ chia cho độ dài thực tế (sau khi đã
đổi về cùng một đơn vị đo)
Ví dụ: Tính tỉ lệ của bản đồ biết 3cm trên bản đồ tương ứng với 30000cm trên thực địa Trả lời: Tỉ lệ bản đồ là: 3 : 30000 = 1: 10000 Đáp số: 1 : 10000
2.2 Ví dụ về các bài toán ứng dụng tỉ lệ bản đồ
Ví dụ 1: Trên bản đồ tỉ lệ 1 : 2000 khoảng cách giữa hai điểm A và B là 5 cm.
Tính khoảng cách hai điểm đó ngoài thực tế. Hướng dẫn:
Muốn tìm độ dài thật, ta lấy độ dài thu nhỏ trên bản đồ nhân với mẫu số tỉ lệ bản đồ. Lời giải:
Khoảng cách giữa hai điểm A và B ngoài thực tế là: 5 x 2000 = 10 000 (cm) = 100m Đáp số: 100m
Ví dụ 2: Khoảng cách giữa hai tỉnh Bắc Giang và Hà Nội là 60km. Trên bản
đồ tỉ lệ 1 : 100000 thì khoảng cách giữa hai tỉnh đó dài bao nhiêu xăng ti mét. Hướng dẫn:
Muốn tính độ dài trên bản đồ, ta lấy độ dài thật (sau khi đã đổi về cùng đơn vị
đo với chiều dài thu nhỏ cần tìm) chia cho mẫu số của tỉ lệ bản đồ. Lời giải: Đổi 60 km = 6000000 cm
Khoảng cách giữa hai tỉnh trên bản đồ tỉ lệ 1 : 100000 là: 6000000 : 100 000 = 60 (cm) Đáp số: 60cm
Ví dụ 3: Trên bản đồ tỉ lệ 1 : 200 chiều dài hình chữ nhật là 8cm, chiều rộng là
5 cm. Tính diện tích hình chữ nhật đó ngoài thực tế. Hướng dẫn:
+ Muốn tính tỉ lệ bản đồ, ta lấy độ dài thu nhỏ trên bản đồ chia cho độ dài
thực tế (sau khi đã đổi về cùng đơn vị đo) Lời giải:
Chiều dài hình chữ nhật ngoài thực tế là: 8 x 200 = 1600 (cm) = 16 (m)
Chiều rộng hình chữ nhật ngoài thực tế là: 5 x 200 = 1000 (cm )= 10 (m)
Diện tích hình chữ nhật là: 16 x 10 = 160 (m2) Đáp số: 160m2
3. Bài tập vận dụng ứng dụng tỉ lệ bản đồ Toán 4
Bài 1: Trên bản đồ có tỉ lệ: 1 : 1000, mỗi độ dài 1mm, 1cm, 1dm ứng với độ
dài thật nào cho dưới đây? 1000dm; 1000cm; 1000 mm Lời giải:
Trên bản đồ tỉ lệ 1 : 1000 ta có:
Độ dài 1mm ứng với độ dài thật là 1000mm
Độ dài 1cm ứng với độ dài thật là 1000cm
Độ dài 1 dm ứng với độ dài thật là 1000 dm
Bài 2: Viết số thích hợp vào chỗ chấm: Tỉ lệ bản đồ 1: 1000 1: 300 1: 10 000 1: 500 Độ dài thu nhỏ 1cm 1dm 1mm 1m Độ dài thật … cm … dm … mm … m Lời giải: Tỉ lệ bản đồ 1: 1000 1: 300 1: 10 000 1: 500 Độ dài thu nhỏ 1cm 1dm 1mm 1m Độ dài thật 1000cm 300dm 10 000mm 500m
Bài 3: Đúng ghi Đ; sai ghi S:
Trên bản đồ tỉ lệ 1 : 10000, quãng đường từ A đến B đo được 1dm. Như vậy
độ dài thật của quãng đường từ A đến B là: a) 1000m b) 10000dm c) 10000cm d) 1km Lời giải:
Độ dài thật của quãng đường từ A đến B là: 1 x 10 000 = 10 000dm = 1km
Vậy ta điền đúng, sai như sau: a) S b) Đ c) S d) Đ
Bài 4: Một khu công nghiệp hình chữ nhật có chu vi là 56 km. Biết chiều dài
gấp 3 lần chiều rộng. Tính diện tích khu công nghiệp đó trên bản đồ tỉ lệ 1 : 70000. (Đáp số: 21000m2)
Bài 5: Trên bản đồ tỉ lệ 1 : 600 một hình vuông có chu vi là 288 cm. Tính diện
tích hình vuông đó ngoài thực tế. (Đáp số: 3110400cm2)
Bài 6: Trên bản đồ tỉ lệ 1: 2 000 000, quãng đường từ Nha Trang đến Thành
phố Hồ Chí Minh đo được 22 cm. Hỏi quãng đường đó trên thực tế dài bao nhiêu ki- lô- mét? (Đáp số: 440km)
Bài 7: Mảnh đất nhà em hình chữ nhật có chiều dài 20m, chiều rộng 15m. Hỏi
trên bản đồ tỉ lệ 1 : 100, độ dài mỗi cạnh của mảnh đất hình chữ nhật đó là mấy xăng - ti - mét? (Đáp số: 20cm, 15cm)
Bài 8: Bản đồ khu đất trường Tiểu học A vẽ theo tỉ lệ 1 : 500. Trên bản đồ
chiều dài khu đất là 60 cm, chiều rộng 40 cm. Hỏi chiều dài và chiều rộng của
trường Tiểu học A trên thực tế là bao nhiêu mét? (Đáp số: 200m)
Bài 10: Thửa ruộng nhà ông A trên bản đồ địa chính của xã tỉ lệ 1 : 1500 có
ghi: chiều dài 36mm, chiều rộng 20mm. Hỏi trên thực tế, thửa ruộng nhà ông
A có diện tích bao nhiêu mét vuông? Đáp số: 162m2
Bài 11: Trên bản đồ tỉ lệ 1 : 500, một nền nhà hình chữ nhật có chiều dài đo
được 2cm, chiều rộng đo được 14mm. Tính diện tích và chu vi thật của nền nhà đó.
Đáp số: diện tích thật: 70m2; chu vi thật: 34m
Bài 12: Một mảnh đất hình chữ nhật có chu vi 48m, chiều rộng băng 3/5 chiều
dài. Người ta vẽ hình chữ nhật biểu thị mảnh đất đó trên bản đồ tỉ lệ 1 : 300.
Hãy tính chu vi và diện tích hình chữ nhật thu nhỏ trên bản đồ.
Đáp số: chu vi: 16cm, diện tích 4500cm2
Bài 13: Một vườn rau hình chữ nhật có chiều dài 25m, chiều rộng 15m. Đội
khảo sát vẽ sơ đồ vườn rau đó trên giấy theo tỉ lệ 1 : 500. Hỏi trên sơ đồ, phải
vẽ độ dài thu nhỏ của chiều dài, chiều rộng vườn rau bao nhiêu cm?
Đáp số: chiều dài 5cm, chiều rộng 3cm
Bài 14: Bản đồ của xã Nghĩa Phương vẽ theo tỉ lệ 1 : 12000. Con đường từ
trụ sở Uy ban xã đến trường tiểu học A có độ dài 3dm. Hỏi độ dài thực tế của
con đường từ Uy ban xã đến trường tiểu học A là bao nhiêu mét? Đáp số: 3600m
Bài 15: Một mảnh đất hình chữ nhật được vẽ trên bản đồ theo tỉ lệ 1 : 3000 có
chiều dài 15cm, chiều rộng 10cm. Tính chu vi và diện tích thật của mảnh đất đó.
Đáp số: chu vi: 150000cm, diện tích: 450000cm2
Document Outline

• Các bài toán về ứng dụng tỉ lệ bản đồ có đáp án ch
  • 1. Lý thuyết về ứng dụng tỉ lệ bản đồ lớp 4
  • 2. Các dạng toán và ví dụ về Toán lớp 4 tỉ lệ bản
    • 2.1 Các dạng toán về tỉ lệ bản đồ
    • 2.2 Ví dụ về các bài toán ứng dụng tỉ lệ bản đồ
  • 3. Bài tập vận dụng ứng dụng tỉ lệ bản đồ Toán 4