Các dạng bài tập hàm số bậc nhất và bậc hai

Tài liệu gồm 38 trang, được biên soạn bởi quý thầy, cô giáo giảng dạy bộ môn Toán học tại trường THPT Marie Curie, quận 3, thành phố Hồ Chí Minh, phân dạng và tuyển chọn các bài toán trắc nghiệm + tự luận chuyên đề hàm số bậc nhất và bậc hai, giúp học sinh lớp 10 tự học chương trình Đại số 10 chương 2.

62 31 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Bài 1. HÀM SỐ

A.TÓM TẮT LÝ THUYẾT

ĐẠI CƯƠNG VỀ HÀM SỐ

Ở lớp dưới ta đã làm quen với khái niệm hàm số, ví dụ hàm số

( ) 2y f x x x  

 Kí hiệu. Hàm số f còn được ghi y = f(x).

 Tên gọi.  D là tập xác định (hay miền xác định) của hàm số.

 x là biến số (hay đối số) của hàm số f.

 f(x) là giá trị của hàm số f tại x.

Chú ý

 Một hàm số được cho bởi một biểu thức hoặc nhiều biểu thức

Ví dụ. Hàm số

()

y f x







; Hàm số

2 1 1

()

neáu

y g x













 Nếu hàm số

()y f x

không giải thích gì thêm thì tập xác định của nó là tập hợp các số

thực x sao cho giá trị của biểu thức

()fx

được xác định.

 Ứng với x = 1 thì

(1) 1 2.1 3yf   

 Ứng với x = –2 thì

( 2) ( 2) 2.( 2) 0yf      

 Ứng với x = 0 thì

(0) (0) 2.(0) 0yf   

 Ứng với x =

thì

( 2) ( 2) 2.( 2) 2 2 2yf    

Hàm số f xác định trên D là một qui tắc đặt tương ứng mỗi số x

thuộc D với một và chỉ một số

thuộc .

Taäp xaùc ñònh



y =3



x =1



x =–2



y =0

x =0



2x 

2 2 2y 



Bieán soá

(hay ñoái soá)

Giaù trò cuûa haøm soá taïi x=1

Giaù trò cuûa haøm

soá taïi x =–2 vaø x

= 0

Giaù trò cuûa haøm soá

taïi

2x 

( ) 2y f x x x  

Kí hieäu

Trường THPT MARIE CURIE

VẤN ĐỀ 1. Tính giá trị của hàm số tại một điểm

Để tính giá trị của hàm số

()y f x

tại x = a, ta thế x = a vào biểu thức

()fx

và được ghi

()fa

VÍ DỤ

Ví dụ 1. Cho hàm số





















()

x neáu x

y f x

neáu x

Tính

     

(1), (2), 2 , 1 2 , 1 2f f f f f

Lời giải

.......................................................................................................................................................................

Ví dụ 2. Cho hàm số

()

neáu











  





y f x

x x x

Tính f(3), f(2), f(–2),

( 2)f

và

(0)f

Lời giải

.......................................................................................................................................................................

Ví dụ 3. Cho hàm số

 

4 1 khi 2

3 khi 2









  



y f x

a. Tính

 

. b. Tính

 

Lời giải

.......................................................................................................................................................................

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Ví dụ 4. Cho hàm số

2( 1

()

4 1 1

+1) neáu

neáu

y h x

















Tính h(1), h(2),







 

Lời giải

.......................................................................................................................................................................

Ví dụ 5: Cho hàm số







()

y f x

. Giải phương trình









Lời giải

.......................................................................................................................................................................

VẤN ĐỀ 2. Đồ Thị Hàm Số

 Cho hàm số

()y f x

xác định trên tập D. Trong mặt phẳng tọa độ Oxy, tập hợp các điểm

có tọa độ

 

; ( )x f x

với x  D, gọi là đồ thị của hàm số

()y f x

 Để biết điểm

( ; )M a b

có thuộc đồ thị hàm số

()y f x

không, ta thế x = a vào biểu

thức

()fx

- Nếu

()f a b

thì điểm

( ; )M a b

thuộc đồ thị hàm số

()y f x

- Nếu

()f a b

thì điểm

( ; )M a b

không thuộc đồ thị hàm số

()y f x

VÍ DỤ

Ví dụ 1. Cho hàm số

( ) 3y f x x x   

Các điểm

(2;8)A

(4;12)B

và

 

5;25 2C 

điểm nào thuộc đồ thị của hàm số đã cho?

Lời giải

Trường THPT MARIE CURIE

.......................................................................................................................................................................

Ví dụ 2. Cho hàm số

   

2 5 5 y f x x x C   

a. Các điểm

   

1;2 , 1;5 , ;8

A B C









có thuộc đồ thị

 

của hàm số đã cho không ?

b. Tìm các điểm thuộc đồ thị hàm số mà có tung độ là 2.

Lời giải

.......................................................................................................................................................................

Ví dụ 3. Cho hàm số

 

y f x







, gọi đồ thị là

 

và điểm

 

1;1Mm

. Tìm các giá

trị của tham số

để điểm

nằm trên đồ thị

()C

Lời giải

.......................................................................................................................................................................

BÀI TẬP TỰ RÈN LUYỆN

Bài 1 Cho hàm số

()

y g x







. Tìm các điểm thuộc đồ thị hàm số mà có tung độ

là 2.

Bài 2 Cho hàm số

()

neáu

y f x

x x x

















Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

a). Điểm nào trong các điểm sau nằm trên đồ thị hàm số.

 

3;3A

, B(–1; –5),

 

1; 2C 

và D(3; 0)

b). Tìm các điểm thuộc đồ thị hàm số mà có tung độ là –2.

Bài 3 Cho hàm số







()

y f x

. Tìm các điểm trên đồ thị hàm số sao cho điểm

đó cách đều hai trục tọa độ.

Bài 4 Cho hàm số

  



( ) 1

y f x

. Tìm các điểm trên đồ thị sao cho tọa độ là số

nguyên.

VẤN ĐỀ 3. Tập xác định của hàm số

CHÚ Ý 1:

1. Hàm số

()



xác định khi và chỉ khi

( ) 0fx

2. Hàm số

()y k f x

xác định khi và chỉ khi

( ) 0fx

3. Hàm số

()



xác định khi và chỉ khi

( ) 0fx

CHÚ Ý 2:

( ) 0

( ). ( ) 0

( ) 0

P x Q x













CHÚ Ý 3:

 Nếu

a x b

thì

 

;D a b

 Nếu

a x b

thì

 

;D a b

 Nếu

a x b

thì





;D a b

 Nếu

a x b

thì





;D a b

 Nếu

a x b











thì



  

;\D a b x

 Nếu

a x b











thì

 

 

;\D a b x

 Nếu

a x b hay c x d

   









thì



 

  

; ; \D a b c d x

VÍ DỤ

Ví dụ 1. Tìm tập xác định của hàm số

   



( ) 1

y f x x

Lời giải

Trường THPT MARIE CURIE

.......................................................................................................................................................................

Ví dụ 2. Tìm tập xác định của hàm số



   



( ) 5

y f x x

Lời giải

.......................................................................................................................................................................

Ví dụ 3. Tìm tập xác định của hàm số

 

  





()

y f x

Lời giải

.......................................................................................................................................................................

Ví dụ 4. Tìm tập xác định của hàm số

  







()

y f x

Lời giải

.......................................................................................................................................................................

Ví dụ 5. Tìm tập xác định của hàm số

4 2 1 ( 4) 3y x x x    

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Lời giải

.......................................................................................................................................................................

Ví dụ 6. Tìm tập xác định của hàm số

 







()

y f x

x x x

Lời giải

.......................................................................................................................................................................

Ví dụ 7. Tìm tập xác định của hàm số

2 7 3





  

Lời giải

.......................................................................................................................................................................

Ví dụ 8. Tìm tập xác định của hàm số





  

()

y f x

Lời giải

Trường THPT MARIE CURIE

.......................................................................................................................................................................

Ví dụ 9. Tìm m để hàm số

x x m





  

có tập xác định là D = R.

Lời giải

.......................................................................................................................................................................

Ví dụ 10. Tìm m để hàm số

2 3 2 1y x x m   

có tập xác định là

[ 1; )D   

Lời giải

.......................................................................................................................................................................

BÀI TẬP TỰ RÈN LUYỆN

Bài 1 Tìm tập xác định của các hàm số sau.

a).



1

b).





()

y f x

c).

( 9 )( 1)

x x x x





  







()

y f x

()





y f x







Bài 2 Tìm tập xác định của các hàm số sau.

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

a).

2 5 3 2 5

x x x

  





b).

 

3 4 2

(2 5) 1

x x x

  



  

c).







d).

( 2 4) 2 1

x x x





  

e).

( 5 ) 2

x x x







f).



  



g).

2 4 3 4

  





h).







i).

2 5 9 2







j).

2 10







k).

2 7 2

x x x







l).

10 2 11

3 2 4

  





Bài 3 Tìm m để hàm số

x x m





  

có tập xác định là

D

Bài 4 Tìm m để hàm số

3 4 8

mx m







có tập xác định là

 

\2D

Bài 5 Tìm m để hàm số

21    y x mx m m

có tập xác định là

D

VẤN ĐỀ 4. Sự biến thiên của hàm số

1. Hàm số

xác định trên khoảng K và



,x x K

 Hàm số f gọi là đồng biến trên K nếu

  

1 2 1 2

( ) ( )x x f x f x

 Hàm số f gọi là nghịch biến trên K nếu

  

1 2 1 2

( ) ( )x x f x f x

Chú ý 1

Hàm số f xác định trên khoảng K.

Nếu

   



f x f x

với mọi



,x x K

nghĩa là f(x) = c (c là hằng số) thì f gọi là hàm số

hằng (còn gọi là hàm số không đổi) trên K.

Chú ý 2

Khảo sát sự biến thiên của hàm số f nghĩa là xem f đồng biến, hoặc nghịch biến, hoặc không đổi

trên các khoảng nào trong tập xác định của nó.

Trường THPT MARIE CURIE

PHƯƠNG PHÁP GIẢI TOÁN

KHẢO SÁT SỰ BIẾN THIÊN CỦA HÀM SỐ TRÊN KHOẢNG K

Cho hàm số y = f(x) và hai số tùy ý x1, x2  K .

CÁCH 1. Giả sử



 Nếu

   



0f x f x

thì f(x) đồng biến trên K.

 Nếu

   



0f x f x

thì f(x) nghịch biến trên K.

CÁCH 2. Giả sử



 Nếu

( ) ( )

f x f x







thì f(x) đồng biến trên K.

 Nếu

( ) ( )

f x f x







thì f (x) nghịch biến trên K.

VÍ DỤ

Ví dụ 1. Khảo sát sự biến thiên của hàm số



()y f x

trên khoảng

 

0;

và

 

;0

Lời giải

.......................................................................................................................................................................

Ví dụ 2. Khảo sát sự biến thiên của hàm số



( ) 2f x x x

trên

 

1;

Lời giải

.......................................................................................................................................................................

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Ví dụ 3. Khảo sát sự biến thiên của hàm số

( ) 1f x x

trên

 

1;

Lời giải

.......................................................................................................................................................................

BÀI TẬP TỰ RÈN LUYỆN

Bài 1 Khảo sát sự biến thiên của các hàm số sau

a).

  

( ) 1y f x x

trong khoảng

   

 ;0 ; 0;

b).

( ) 2 ( 4)y f x x x   

trên khoảng

(2; )

c).

( ) 1

y f x



  



trên khoảng

(3; )

d).





()

y f x

trên khoảng

 

0;



1yx

trên

 

;0





()

y f x

trên

 

;1 

Bài 2 Khảo sát sự biến thiên của các hàm số sau

a).

  ( ) 1 2y f x x

trong khoảng

( ; ) 

b).





trên khoảng

 

1;

c).

1yx

trên khoảng

 

;1

d).



2y x x

trên khoảng

 

;

1yx

trên

 

1; 

  

2y x x

trên

 

;1 

Bài 3 Cho hàm số

   3y x x

a). Chứng minh hàm số đồng biến trên

 

 3;

b). Cho

 6a

. Chứng minh:

  39aa

Trường THPT MARIE CURIE

VẤN ĐỀ 5. Hàm số chẵn – Hàm số lẻ

A. TÓM TẮT LÝ THUYẾT

1. Tập D là tập con của tập số thực gọi là tập đối xứng nếu thỏa. mọi x thuộc D thì –x

cũng thuộc D.

2. Hàm số chẵn – hàm số lẻ

 Hàm số f xác định trên tập đối xứng D.

3. Đồ thị hàm số chẵn , hàm số lẻ

 Đồ thị hàm số hàm số chẵn nhận trục tung làm trục đối xứng.

 Đồ thị hàm số hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

Đồ thị hàm số chẵn

Đồ thị hàm số lẻ

B. PHƯƠNG PHÁP GIẢI

CÁCH XÉT TÍNH CHẴN – LẺ CỦA HÀM SỐ

Tìm tập xác định D của hàm số y = f(x)

Nếu D không là tập đối xứng

thì hàm số f không chẵn và không lẻ trên D.

Nếu D là tập đối xứng

xD, tính f(–x).

Nếu f(–x) = f(x)

thì f là hàm số chẵn trên D

Nếu f(–x) = – f(x)

thì f là hàm số lẻ trên D

Nếu f(–x) ≠  f(x)

Chọn một giá trị thích hợp x = a  D để có f(–a) ≠  f(a)

Từ đó kết luận hàm số f không chẵn và không lẻ trên D.

 Nếu x  D mà f(–x) = f(x) thì ta nói f là hàm số chẵn trên D.

 Nếu x  D mà f(–x) = –f(x) thì ta nói f là hàm số lẻ trên D.

(

)

–a

–x

D = (–a;a)

;b)

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

C. VÍ DỤ

Ví dụ 1. Xét tính chẵn-lẻ của hàm số



()y f x

Lời giải

.......................................................................................................................................................................

Ví dụ 2. Xét tính chẵn-lẻ của hàm số

  

()y f x x x

Lời giải

.......................................................................................................................................................................

Ví dụ 3. Xét tính chẵn-lẻ của hàm số

()

y f x

  



Lời giải

.......................................................................................................................................................................

Ví dụ 4. Xét tính chẵn-lẻ của hàm số

( ) 1 1y h x x x x x      

Lời giải

.......................................................................................................................................................................

Trường THPT MARIE CURIE

.......................................................................................................................................................................

C. BÀI TẬP RÈN LUYỆN

Bài 1 Chứng minh đồ thị hàm số

()

y f x





nhận gốc tọa độ làm tâm đối xứng.

Bài 2 Chứng minh đồ thị hàm số

( ) 2 2y g x x x    

nhận trục tung làm trục đối

xứng.

Bài 3 Xét tính chẵn-lẻ của các hàm số sau.

a).

()

y f x





b).

( ) 3y h x x x  

c).

( ) 2 2y g x x x    

d).

()

y k x





  

e).

()

y u x

  





f).

()

6 3 6 3

y v x



  

BÀI TẬP TRẮC NGHIỆM

Câu 1: Hàm số nào sau đây có tập xác định là



. B.

()

y f x





. C.

1yx

. D.





Câu 2: Tìm tập xác định

của hàm số





()

y f x

  



0;1D

. B.

( ;1)

 

 \1D

. D.

 

 0;1D

Câu 3: Tìm tập xác định

của hàm số





()

y f x

  



1;1D

. B.

 

 \0D

  



\ 1;1D

. D.

 

\ 1;1D

Câu 4: Tìm tập xác định

của hàm số

22  



 

2;2D 

. B.

   

2;2 \ 0D 

. C.

 

 

2;2 \ 0D 

. D.

D 

Câu 5: Tìm tập xác định

của hàm số



  



 

1;D  

. B.

 

1;6D 

. C.

D 

. D.

 

;6D  

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Câu 6: Tìm tập xác định

của hàm số







x x x



  

2; \ 0;2D   

. B.

D 





2;D   

. D.

   

2; \ 0;2D   

Câu 7: Tìm tập xác định

của hàm số









0;D  

. B.



  

0; \ 9D  

. C.

 

9D 

. D.

D 

Câu 8: Tìm tập xác định

của hàm số

  

  





 

1;4D 

. B.

   

1;4 \ 2;3D 

 

 

1;4 \ 2;3

. D.



 



;1 4;  

Câu 9: Tìm tập xác định

của hàm số

2018

3 2 7



   

x x x

 

\3D 

. B.

D 

   

;1 2;D    

. D.

 

\0D 

Câu 10: Tìm tập xác định

của hàm số



  

x x x

D 

. B.

 

\ 0; 2D 

. C.

 

2;0D 

. D.

 

2;D  

Câu 11: Tìm tập xác định

của hàm số







 

\ 0;4D 

. B.

 

0;D  



  

0; \ 4D  

. D.

   

0; \ 4D  

Câu 12: Tìm tập xác định

của hàm số







 

; \ 1



  





. B.

D 

 

; \ 1



  





. D.

;









Câu 13: Tìm tập xác định

của hàm số

  

2 1 3







 

3;D  

. B.

\ ;3









. C.

;



  





. D.

D 

Câu 14: Tìm tập xác định

của hàm số







 

1; 4D 

. B.

 

\ 1; 4D 

. C.

 

\ 1;4 .D 

. D.

D 

Trường THPT MARIE CURIE

Câu 15: Tìm tập xác định

của hàm số

 

1 3 4





  

x x x

 

\1D 

. B.

 

1D 

. C.

 

\1D 

. D.

D 

Câu 16: Tìm tập xác định

của hàm số







 

\1D 

. B.

 

\ 2;1D 

. C.

 

\2D 

. D.

D 

Câu 17: Tìm tập xác định

của hàm số

23  xx





3;D   

. B.





2;D   

. C.

D 

. D.





2;D  

Câu 18: Tìm tập xác định

của hàm số

6 3 1   y x x

 

1;2D 

. B.

 

1;2D 

. C.

 

1;3D 

. D.

 

1;2D 

Câu 19: Tìm tập xác định

của hàm số

3 2 6







;











. B.

;











. C.

;











. D.

;



 





Câu 20: Tìm tập xác định

của hàm số







   

; 2 2;D     

. B.

D 

   

; 4 4;D     

. D.

 

4;4D 

Câu 21: Tìm tập xác định

của hàm số

2 1 3    y x x x





;3D  

. B.

 

1;3D 

. C.





3;D  

. D.

 

3;D  

Câu 22: Tìm tập xác định

của hàm số







 

3D 

. B.



  

1; \ 3D   

. C.

D 

. D.





1;D   

Câu 23: Tìm tập xác định

của hàm số

 

3 2 1







D 

. B.

 

; \ 3



  





 

; \ 3



 







. D.

 

; \ 3



 





Câu 24: Tìm tập xác định

của hàm số







 

1;D  

. B.

 

1D 

. C.

D 

. D.

 

1;D   

Câu 25: Xét tính đồng biến, nghịch biến của hàm số

 

45  f x x x

trên khoảng

 

;2

và

trên khoảng

 

2;

. Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên

 

;2

, đồng biến trên

 

2;

B. Hàm số đồng biến trên

 

;2

, nghịch biến trên

 

2;

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

C. Hàm số nghịch biến trên các khoảng

 

;2

và

 

2;

D. Hàm số đồng biến trên các khoảng

 

;2

và

 

2;

Câu 26: Xét sự biến thiên của hàm số

 

fx

trên khoảng

 

0;

. Khẳng định nào sau đây

đúng?

A. Hàm số đồng biến trên khoảng

 

0;

B. Hàm số nghịch biến trên khoảng

 

0;

C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng

 

0;

D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng

 

0;

Câu 27: Xét sự biến thiên của hàm số

 

f x x

trên khoảng

 

1; 

. Khẳng định nào sau đây

đúng?

A. Hàm số đồng biến trên khoảng

 

1; 

B. Hàm số nghịch biến trên khoảng

 

1; 

C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng

 

1; 

D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng

 

1; 

Câu 28: Xét tính đồng biến, nghịch biến của hàm số

 







trên khoảng

 

;5 

và trên

khoảng

 

5; 

. Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên

 

;5 

, đồng biến trên

 

5; 

B. Hàm số đồng biến trên

 

;5 

, nghịch biến trên

 

5; 

C. Hàm số nghịch biến trên các khoảng

 

;5 

và

 

5; 

D. Hàm số đồng biến trên các khoảng

 

;5 

và

 

5; 

Câu 29: Cho hàm số

 

2 7.f x x

Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên

;









. B. Hàm số đồng biến trên

;









C. Hàm số đồng biến trên . D. Hàm số nghịch biến trên .

Câu 30: Trong các hàm số

2015 , 2015 2, 3 1, 2 3       y x y x y x y x x

có bao nhiêu hàm số

lẻ?

. B.

. C.

. D.

Câu 31: Cho hai hàm số

 

23  f x x x

và

 

2017

3g x x

. Mệnh đề nào sau đây đúng?

 

là hàm số lẻ;

 

là hàm số lẻ.

 

là hàm số chẵn;

 

là hàm số chẵn.

C. Cả

 

và

 

đều là hàm số không chẵn, không lẻ.

 

là hàm số lẻ;

 

là hàm số không chẵn, không lẻ.

Trường THPT MARIE CURIE

Câu 32: Cho hàm số

 

.f x x x

Khẳng định nào sau đây là đúng.

 

là hàm số lẻ.

 

là hàm số chẵn.

C. Đồ thị của hàm số

 

đối xứng qua gốc tọa độ.

D. Đồ thị của hàm số

 

đối xứng qua trục hoành.

Câu 33: Cho hàm số

 

2.f x x

Khẳng định nào sau đây là đúng.

 

là hàm số lẻ. B.

 

là hàm số chẵn.

 

là hàm số vừa chẵn, vừa lẻ. D.

 

là hàm số không chẵn, không lẻ.

Câu 34: Tìm tập xác định của hàm số



  



 

\4D

. B.

 

\2D

. C.





;2 D

. D.



  

2; \ 4 D

Câu 35: Tập xác định của hàm số







là

D

. B.

 

\ 2;2D

. C.









. D.

 

2;2D

Câu 36: Tập xác định của hàm số

32yx

là

;









. B.

;



 







. C.

;











. D.

;



 







Câu 37: Cho hàm số

 

2 2 1 1

    













x khi x

. Giá trị

 

1f

bằng

6

. B.

. C.

. D.

5

Câu 38: Hàm số nào sau đây đồng biến trên khoảng

 

0;

21  yx

. B.

21  y x x

. C.

yx

. D.

yx

Câu 39: Tập hợp nào sau đây là tập xác định của hàm số.

23yx

;











. B.

;









. C.

;











. D. .

Câu 40: Trong các hàm số sau đây

yx

4y x x

2  y x x

có bao nhiêu hàm số chẵn?

A. 0. B. 1. C. 2. D. 3.

Câu 41: Hàm số nào sau đây là hàm số lẻ?



. B.

  

. C.





. D.

  

Câu 42: Cho hàm số

2 3 1  y x x

. Trong các mệnh đề sau, tìm mệnh đề đúng?

là hàm số chẵn. B.

là hàm số lẻ.

là hàm số không có tính chẵn lẻ. D.

là hàm số vừa chẵn vừa lẻ.

Câu 43: Cho hàm số

3 – 4 3y x x

. Trong các mệnh đề sau, mệnh đề nào đúng?

là hàm số chẵn. B.

là hàm số lẻ.

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

là hàm số không có tính chẵn lẻ. D.

là hàm số vừa chẵn vừa lẻ.

Câu 44: Trong các hàm số sau, hàm số nào không phải là hàm số lẻ?

1yx

. B.

– y x x

. C.

y x x

. D.

y

Câu 45: Trong các hàm số nào sau đây, hàm số nào là hàm số lẻ?

2018

2017yx

. B.

23yx

33   y x x

. D.

33   y x x

Câu 46: Trong các hàm số nào sau đây, hàm số nào là hàm số chẵn?

11   y x x

. B.

32   y x x

23y x x

. D.

23  y x x x

Câu 47: Hàm số







xác định trên





0;1

khi

m

. B.

1m

0m

hoặc

1m

. D.

0m

hoặc

1m

Câu 48: Tìm m để hàm số





  

x x m

có tập xác định là .

1m

. B.

0m

. C.

2m

. D.

3m

Câu 49: Hàm số nào trong các hàm số sau là hàm số lẻ.

11   y x x

. B.

1



. C.





. D.

13  y x x

Câu 50: Trong các hàm số sau, hàm số nào không phải hàm số chẵn.

55   y x x

. B.

12  y x x

. C.

11   y x x

. D.

1  y x x

Câu 51: Trong các hàm số sau, hàm số nào giảm trên khoảng

 

0;1

yx

. B.

yx

. C.

y

. D.

yx

Câu 52: Cho hàm số

 

1y x x

. Khẳng định nào đúng?

A. hàm số chẵn. B. hàm số lẻ.

C. hàm số không chẵn, không lẻ. D. hàm số vừa chẵn, vừa lẻ.

Câu 53: Cho hàm số.

 

y f x







. Phương trình









có nghiệm là

1x 

. B.

x 

. C.





. D.

1x 

Câu 54: Cho hàm số.

 

y f x







. Phương trình

 

  

có nghiệm là

1x 

. B.

0x 

. C.

2x 

. D.

1x 

Câu 55: Tập xác định của hàm số

2 4 2   y x m x

là

 

1;2

khi và chỉ khi.

m

. B.

1m

. C.

m

. D.

m

Trường THPT MARIE CURIE

Câu 56: Tập xác định của hàm số

62   y x m x

là một đoạn trên trục số khi và chỉ khi

3m

. B.

3m

. C.

3m

. D.

m

Câu 57: Điểm nào sau đây thuộc đồ thị hàm số





 

2;1M

. B.

 

1;1M

. C.

 

2;0M

. D.

 

0; 1M

Câu 58: Điểm nào sau đây thuộc đồ thị hàm số

44



 

1; 1A

. B.

 

2;0B

. C.







. D.

 

1; 3D

Câu 59: Cho hàm số

 

 





1 0;2

1 2;5

 





















. Giá trị

 

bằng

 

f

. B.

 

4 15f

. C.

 

45f

. D.

(4) 0f

Câu 60: Cho hàm số

 

2 2 3

2+1





















. Giá trị

   

22  P f f

bằng

P

. B.

4P

. C.

6P

. D.

P

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Bài 2. HÀM SỐ BẬC NHẤT

A. TÓM TẮT LÝ THUYẾT

1. Hàm số bậc nhất:

 

y = ax+b a 0

o Tập xác định:

D

o Sự biến thiên:

 Nếu

 0a

: Hàm số đồng biến (tăng) trên .

 Nếu

 0a

: Hàm số nghịch biến (giảm) trên .

o Đồ thị hàm số là đường thẳng có hệ số góc bằng

, cắt trục hoành tại









, cắt trục tung tại điểm

 

0;Bb

y=ax+b (a>0)

y=ax+b (a<0)

o Vị trí tương đối của hai đường thẳng:

Cho

 

  :0d y ax b a

và

 

   

  :0d y ax b a







































cắt



aa





   .1d d a a



cắt



tại một điểm trên trục tung



aa

và



bb

2. Hàm hằng

yb

Đồ thị hàm số

yb

là một đường thẳng song song hoặc trùng với trục hoành và

cắt trục tung tại điểm

 

0; .b

Đường thẳng này gọi là đường thẳng

 .yb

Trường THPT MARIE CURIE

y=b

3. Hàm số

 

y = ax+b a 0

 

khi



  



  





   





ax b x

y ax b

ax b x

Để vẽ đồ thị hàm số

 

  ,0y ax b a

ta có thể vẽ hai đường thẳng

y ax b

và

  y ax b

rồi xóa đi hai phần đường thẳng nằm phía dưới trục hoành.

B. PHƯƠNG PHÁP GIẢI TOÁN

VẤN ĐỀ 1: Xét tính đồng biến, nghịch biến

Muốn xét tính đơn điệu của hàm số bậc nhất ta cần:

 Đưa hàm số về đúng dạng

 

  ,0y a x b a

 Nếu

 0a

: Hàm số đồng biến (tăng) trên .

 Nếu

 0a

: Hàm số nghịch biến (giảm) trên .

VÍ DỤ

Ví dụ 1. Xét tính đơn điệu của các hàm số sau

21yx

1  yx







..........................................................................................................................................................................

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

..........................................................................................................................................................................

Ví dụ 2. Tìm các giá trị của

để hàm số

 

11  y m x

đồng biến trên b)

1   y mx m

nghịch biến trên

 

11    y m x m

nghịch biến trên d)





đồng biến trên

Lời giải

..................................................................................................................................................................

..........................................................................................................................................................................

VẤN ĐỀ 2: Đồ thị hàm số

y ax b

Đưa hàm số về đúng dạng

 

,0  y a x b a

. Đồ thị hàm số là đường thẳng.

 Nếu

0a 

: Đồ thị “đi lên từ trái sang phải”

 Nếu

0a 

: Đồ thị “đi xuống từ trái sang phải”

 Xác định giao điểm của đường thẳng với hai trục tọa độ rồi nối hai

điểm đó lại ta được đường thẳng là đồ thị của hàm số

VÍ DỤ

Trường THPT MARIE CURIE

Ví dụ 3. Xét tính đơn điệu và vẽ đồ thị các hàm số sau:

21yx

1  yx





  

Lời giải

..................................................................................................................................................................

VẤN ĐỀ 3: Đồ thị hàm số y=|ax+b|



 

khi

ax b x

y ax b

ax b x



  



  





   





 Để vẽ đồ thị hàm số

 

,0y ax b a  

ta có thể vẽ hai đường thẳng

y ax b

và

y ax b  

rồi xóa đi hai phần đường thẳng nằm phía dưới trục hoành.

VÍ DỤ

Ví dụ 4. Xét tính đơn điệu và vẽ đồ thị các hàm số sau:

1yx

11   yx

1  y x x

Lời giải

..................................................................................................................................................................

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

..................................................................................................................................................................

C. BÀI TẬP TRẮC NGHIỆM

Câu 1: Tìm

để hàm số

 

   2 1 3y m x m

đồng biến trên









Câu 2: Tìm

để hàm số

   

   2 2 1y m x x m

nghịch biến trên

2.m



1.m



Câu 3: Có bao nhiêu giá trị nguyên của tham số

thuộc đoạn

 



2017;2017

để hàm số

 

  22y m x m

đồng biến trên

2014.

2016.

C. Vô số

2015.

Câu 4: Đường thẳng nào sau đây song song với đường thẳng

 2.yx

Trường THPT MARIE CURIE

1 2 .yx



2 2.yx



Câu 5: Tìm tất cả các giá trị thực của tham số

để đường thẳng

 

   

3 2 3y m x m

song song với đường thẳng

1yx

 2.m

2.m

2.m

1.m

Câu 6: Tìm tất cả các giá trị thực của tham số

để đường thẳng

31yx

song song với

đường thẳng

 

   

11y m x m

2m

. B.

 2.m

2.m

 0.m

Câu 7: Biết rằng đồ thị hàm số

y ax b

đi qua điểm

 

1;4M

và song song với đường

thẳng

21yx

. Tính tổng

.S a b

 4.S

 2.S

 0.S

4.S

Câu 8: Biết rằng đồ thị hàm số

y ax b

đi qua điểm

 

2; 1E

và song song với đường

thẳng

với

là gốc tọa độ và

 

1;3N

. Tính giá trị biểu thức



.S a b

4.S

40.S

58.S

 58.S

Câu 9: Tìm tất cả các giá trị thực của tham số

để đường thẳng

 

   : 3 2 7 1d y m x m

vuông góc với đường

  : 2 1.yx

 0.m







Câu 10: Biết rằng đồ thị hàm số

y ax b

đi qua điểm

 

4; 1N

và vuông góc với đường

thẳng

  4 1 0xy

. Tính tích

P ab

 0.P







Câu 11: Tìm

và

để đồ thị hàm số

y ax b

đi qua các điểm

   

2;1 , 1; 2AB

2a

và

1.b

 2a

và

 1.b

1a

và

 1.b

1a

và

1.b

Câu 12: Biết rằng đồ thị hàm số

y ax b

đi qua hai điểm

 

1;3M

và

 

1;2N

. Tính tổng

S a b



 3.S

 2.S



Câu 13: Biết rằng đồ thị hàm số

y ax b

đi qua điểm

 

3;1A

và có hệ số góc bằng

2

Tính tích

P ab

10.P

10.P

7.P

5.P

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Câu 14: Tọa độ giao điểm của hai đường thẳng





và



  





là

 

0; 1

. B.

 

2; 3

. C.







. D.

 

3; 2

Câu 15: Tìm tất cả các giá trị thực của

để đường thẳng



2y m x

cắt đường thẳng

43yx

2.m

2.m

 2.m

2.m

Câu 16: Cho hàm số

  21y x m

. Tìm giá trị thực của

để đồ thị hàm số cắt trục hoành

tại điểm có hoành độ bằng 3.

 7.m

 3.m

7.m

7.m

Câu 17: Cho hàm số

  21y x m

. Tìm giá trị thực của

để đồ thị hàm số cắt trục tung

tại điểm có tung độ bằng

2

3.m

 3.m

 0.m

1.m

Câu 18: Tìm giá trị thực của

để hai đường thẳng

:3d y mx

và

  : y x m

cắt nhau

tại một điểm nằm trên trục tung.

3.m

 3.m

3.m

 0.m

Câu 19: Tìm tất cả các giá trị thực của

để hai đường thẳng

:3d y mx

và

  : y x m

cắt nhau tại một điểm nằm trên trục hoành.

 3.m

 3.m

 3.m

 3.m

Câu 20: Cho hàm số bậc nhất

y ax b

. Tìm

và

, biết rằng đồ thị hàm số đi qua điểm

 

1;1M

và cắt trục hoành tại điểm có hoành độ là 5.



   

  

  

Câu 21: Cho hàm số bậc nhất

y ax b

. Tìm

và

, biết rằng đồ thị hàm số cắt đường

thẳng

  

: 2 5yx

tại điểm có hoành độ bằng

2

và cắt đường thẳng

  

: –3 4yx

tại điểm có tung độ bằng

2



  

   

  

Câu 22: Tìm giá trị thực của tham số

để ba đường thẳng

 2yx

   3yx

và

5y mx

phân biệt và đồng qui.

7.m

 5.m

5.m

 7.m

Câu 23: Tìm giá trị thực của tham số

để ba đường thẳng

 

  51yx

3y mx

và

3y x m

phân biệt và đồng qui.

Trường THPT MARIE CURIE

 3.m

13.m

13.m

 3.m

Câu 24: Cho hàm số

1yx

có đồ thị là đường



. Đường thẳng



tạo với hai trục tọa độ

một tam giác có diện tích

bằng bao nhiêu?



1.S

 2.S



Câu 25: Tìm phương trình đường thẳng

:d y ax b

. Biết đường thẳng

đi qua điểm

 

2;3I

và tạo với hai tia

,Ox Oy

một tam giác vuông cân.

5.yx

  5.yx

  5.yx

5.yx

Câu 26: Tìm phương trình đường thẳng

:d y ax b

. Biết đường thẳng

đi qua điểm

 

1;2I

và tạo với hai tia

,Ox Oy

một tam giác có diện tích bằng

  2 4.yx

  2 4.yx

2 4.yx

2 4.yx

Câu 27: Đường thẳng

 

   : 1, 0; 0

d a b

đi qua điểm

 

1;6M

tạo với các tia

,Ox Oy

một tam giác có diện tích bằng

. Tính

2S a b







5 7 7

12.S

 6.S

Câu 28: Tìm phương trình đường thẳng

:d y ax b

. Biết đường thẳng

đi qua điểm

 

1;3I

, cắt hai tia

và cách gốc tọa độ một khoảng bằng

2 5.yx

  2 5.yx

2 5.yx

  2 5.yx

Câu 29: Đồ thị trong hình bên là của hàm hàm nào sau đây?

-2

-1

   





  



2 1 1

()

2 1 1

x khi x

   





   



()

2 2 1

x khi x

   





  



2 2 1

()

2 1 1

x khi x

   





   



()

2 2 1

x khi x

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Bài 3. HÀM SỐ BẬC HAI

A. TÓM TẮT LÝ THUYẾT

ĐỊNH NGHĨA

SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM SỐ BẬC HAI

 Hàm số bậc hai là hàm số có dạng

  

y ax bx c

trong đó a, b, c là hằng số và a ≠ 0.

 Đồ thị hàm số

  

y ax bx c

gọi là một parabol.

Hàm số bậc hai

 0a

 0a

Bảng biến thiên

–∞

+∞







+∞

Bảng biến thiên

–∞

+∞







–∞

 Hàm số nghịch biến trên khoảng



 





;

 Hàm số đồng biến trên khoảng



 





;

 Hàm số đồng biến trên khoảng



 





;

 Hàm số nghịch biến trên khoảng



 





;







Đồ thị







Đồ thị

 Đỉnh

  







;

 Trục đối xứng là đường thẳng



Trường THPT MARIE CURIE

 Đặc biệt:

 Khi

 0a

hàm số đạt giá trị nhỏ nhất là





min

tại





 Khi

 0a

hàm số đạt giá trị nhỏ nhất là





min

tại





CÁC BƯỚC VẼ PARABOL:

   

   

:0P y ax bx c a

Bước 1: Xác định tọa độ đỉnh

  







;

Bước 2: Xác định trục đối xứng

  :

và hướng bề lõm của parabol.

Bước 3: Lập bảng giá trị, xác định các điểm thuộc

 

Bước 4: Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để nối các điểm đó lại.

VÍ DỤ

Ví dụ 1. Cho hàm số

2y x bx   

có đồ thị là parabol (P). Lập bảng biến thiên và vẽ đồ

thị hàm số đã cho, biết rằng (P) có đỉnh nằm trên đường thẳng

2x 

Lời giải

.......................................................................................................................................................................

Ví dụ 2. Cho hàm số

2y x bx c   

có đồ thị là parabol (P). Lập bảng biến thiên và vẽ đồ

thị hàm số đã cho, biết rằng (P) đi qua điểm A(1;–2) và hoành độ của đỉnh là 2.

Lời giải

.......................................................................................................................................................................

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

.......................................................................................................................................................................

Ví dụ 3. Cho hàm số

y x bx c  

có đồ thị là parabol (P). Lập bảng biến thiên và vẽ đồ thị

hàm số đã cho, biết rằng (P) có đỉnh là

( 1; 2)I 

Lời giải

.......................................................................................................................................................................

B. BÀI TẬP TỰ RÈN LUYỆN

Câu 1: Cho parabol

 

  

: 3 2P y x x

a. Khảo sát sự biến thiên và vẽ đồ thị hàm số trên.

b. Biện luận theo

số nghiệm của phương trình

   

3 3 2 0x x m

Câu 2: Cho parabol

 

  

:2P y x x

a. Khảo sát sự biến thiên và vẽ đồ thị hàm số trên.

b. Tìm tham số

để phương trình

  

20x x m

có hai nghiệm phân biệt.

Câu 3: Xác định parabol

 

biết:

 

  

:2P y ax bx

đi qua điểm

 

1;0A

và có trục đối xứng



 

  

:2P y ax bx

đi qua hai điểm

 

1;5B

và

 

2;8C

 

  

:2P y ax bx

đi qua điểm

 

1;6D

và đỉnh có tung độ



Trường THPT MARIE CURIE

 

  

:4P y ax x c

có trục đối xứng là đường thẳng

 2x

và cắt trục hoành

tại điểm có hoành độ bằng 3.

 

  

:2P y x bx c

có trục đối xứng là đường thẳng

 1x

và cắt trục tung tại

điểm có tung độ bằng 4.

 

  

:4P y ax x c

có đỉnh là

 

2; 1I

 

  

:4P y ax x c

có hoành độ đỉnh là

3

và đi qua điểm

 

2;1E

 

  

:P y ax bx c

đi qua điểm

 

0;5F

và có đỉnh

 

3; 4I

 

  

:P y ax bx c

đi qua điểm

 

2; 3G

và có đỉnh

 

1; 4I

 

  

:P y ax bx c

đi qua các điểm

 

1;1H

 

1;3K

và

 

0;0O

 

  

:P y ax bx c

đi qua các điểm

 

1; 1L

 

0;2M

và

 

1; 1N

 

  

:P y ax bx c

có đỉnh

 

3; 1I

và cắt

tại điểm có hoành độ bằng 1.

 

  

:P y ax bx c

có trục đối xứng là đường thẳng

 3x

, qua

 

5;6P

và cắt

trục tung tại điểm có tung độ bằng

2

Câu 4: Tìm tọa độ giao điểm của các cặp đồ thị của các hàm số sau:

  :3d y x

và

 

   

: 4 1P y x x

: 2 5d y x

và

 

  

: 4 4P y x x

 

  

: 2 1P y x x

và

 

  

: 4 4P y x x

 

  

: 3 4 1P y x x

và

 

   

: 3 2 1P y x x

Câu 5: Cho parabol

 

   

: 4 2P y x x

và đường thẳng

  : 2 3d y x m

. Tìm

để:

cắt

 

tại hai điểm phân biệt

,AB

. Tìm tọa độ trung điểm của

và

 

có một điểm chung duy nhất. Tìm tọa độ điểm chung này.

không cắt

 

và

 

có một giao điểm nằm trên đường thẳng

2y

C. BÀI TẬP TRẮC NGHIỆM

Câu 1: Tọa độ đỉnh của parabol

   

43y x x

là

 

2;7I

. B.

 

2; 7I

. C.

 

2;7I

. D.

 

2; 7I

Câu 2: Cho hàm số

  

23y x x

có đồ thị

 

. Trục đối xứng của

 

là

1y

. B.

 1x

. C.

1x

. D.

 1y

Câu 3: Tung độ đỉnh của parabol

  

35y x x

là

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Câu 4: Cho hàm số

 

   

68y f x x x

có đồ thị

 

. Xét các mệnh đề sau đây:

 

cắt Oy tại 2 điểm phân biệt.

II. Tung độ đỉnh của

 

là

1

III.

 

có trục đối xứng

30x

Mệnh đề nào đúng?

A. Chỉ I. B. I và II. C. I và III. D. II và III.

Câu 5: Cho hàm số

   

54y x x

. Khẳng định nào sau đây đúng?

A. Hàm số có giá trị lớn nhất là

. B. Hàm số có giá trị nhỏ nhất là

C. Hàm số có giá trị nhỏ nhất là

. D. Hàm số có giá trị lớn nhất là

Câu 6: Cho hàm số

  

23y x x

. Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên

 

;2

. B. Hàm số nghịch biến trên

 

;1

C. Hàm số đồng biến trên

 

;2

. D. Hàm số đồng biến trên

 

;1

Câu 7: Cho hàm số

   

42y x x

. Khẳng định nào sau đây sai?

A. Hàm số đồng biến trên

 

;3

. B. Hàm số đồng biến trên

 

;2

C. Hàm số nghịch biến trên

 

3;

. D. Hàm số nghịch biến trên

 

2;

Câu 8: Tìm hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây

  

21y x x

. B.

   

43y x x

. C.

  

45y x x

. D.

  

45y x x

Câu 9: Tìm giá trị

lớn nhất của hàm số

   

43y x x

trên





0;4

 3M

. B.

 7M

. C.

29M

. D.

 0M

Câu 10: Gọi

là đỉnh của parabol

  

45y x x

. Tính tổng khoảng cách

từ

đến hai

trục tọa độ.

 1h

. B.

 3h

. C.

 4h

. D.

 5h

Câu 11: Với giá trị của

để parabol

  

3y x x m

cắt trục hoành tại điểm có hoành độ

bằng 2.

2m

. B.

 0m

. C.

1m

. D.

 2m

Câu 12: Xác định parabol

 

  

:4P y ax x c

biết

 

có trục đối xứng

 2x

và cắt trục

hoành tại điểm

 

3;0A

Trường THPT MARIE CURIE

 

  

: 4 3P y x x

. B.

 

  

12 48

P y x x

 

  

: 4 6P y x x

. D.

 

  

: 2 4 6P y x x

Câu 13: Hàm số

  

2 4 1y x x

A. đồng biến trên khoảng

 

 ;2

và nghịch biến trên khoảng

 

 2;

B. nghịch biến trên khoảng

 

 ;2

và đồng biến trên khoảng

 

 2;

C. đồng biến trên khoảng

 

 ;1

và nghịch biến trên khoảng

 

 1;

D. nghịch biến trên khoảng

 

 ;1

và đồng biến trên khoảng

 

 1;

Câu 14: Cho hàm số

 

   

0y ax bx c a

. Khẳng định nào sau đây là sai?

A. Hàm số đồng biến trên khoảng



 





;

B. Hàm số nghịch biến trên khoảng



 





;

C. Đồ thị của hàm số có trục đối xứng là đường thẳng



D. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.

Câu 15: Cho hàm số

 

   

0y ax bx c a

có đồ thị

 

. Tọa độ đỉnh của

 

là

  







  







  







  





Câu 16: Trục đối xứng của parabol

 

  

: 2 6 3P y x x

là



3.x

3.y

Câu 17: Trong các hàm số sau, hàm số nào có đồ thị nhận đường

 1x

làm trục đối xứng?

   

2 4 1y x x

. B.

  

2 4 3y x x

. C.

  

2 2 1y x x

. D.

  

2y x x

Câu 18: Đỉnh của parabol

 

  

: 3 2 1P y x x

là









;

. B.









;

. C.









;

. D.







;

Câu 19: Hàm số nào sau đây có đồ thị là parabol có đỉnh

 

1;3I

  

2 4 3y x x

. B.

  

2 2 1y x x

. C.

  

2 4 5y x x

. D.

  

22y x x

Câu 20: Tọa độ giao điểm của

 



:4P y x x

với đường thẳng

  :2d y x

là

   

  1; 1 , 2;0MN

. B.

   

1; 3 , 2; 4MN

   

0; 2 , 2; 4MN

. D.

   

3;1 , 3; 5MN

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Câu 21: Gọi

 

;A a b

và

 

;B c d

là tọa độ giao điểm của

 



:2P y x x

và

  : 3 6yx

. Giá

trị

bd

bằng :

. B.

7

. C.

. D.

15

Câu 22: Parabol

 

  

: 4 4P y x x

có số điểm chung với trục hoành là

. B.

. C.

. D.

Câu 23: Cho hàm số bậc hai

  

y ax bx c

 

 0a

có đồ thị

 

. Tọa độ đỉnh của

 

là

   





;

. B.

   





;

. C.

   





;

. D.

   





;

Câu 24: Cho hàm số

  

22y x x

. Câu nào sau đây là sai?

tăng trên

 

1;

. B.

giảm trên

 

1;

giảm trên

 

;1

. D.

tăng trên

 

3;

Câu 25: Hàm số nào sau đây nghịch biến trong khoảng

 

  

: 4 3P y x x

:3d y mx

. B.

. C.

 

Câu 26: Hàm số nào

sau đây đồng biến trong khoảng

 

 1;



21yx

. B.

  

21yx

. C.

 



21yx

 

  

21yx

Câu 27: Cho hàm số:

  

23y x x

. Trong các mệnh đề sau, tìm mệnh đề đúng?

tăng trên

 

0;

. B.

giảm trên

 

;1

C. Đồ thị của

có đỉnh

 

1;0I

. D.

tăng trên

 

 1;

Câu 28: Bảng biến thiên của hàm số

   

2 4 1y x x

là bảng nào sau đây?

∞

. B.

∞

. D.

∞

Câu 29: Tìm tập xác định của hàm số

  

21y x x

là

 .D

 

 \1D

. C.

 

 ;1D

. D.

 

 1;D

Câu 30: Cho

 

  

: 2 3P y x x

. Tìm mệnh đề đúng

Trường THPT MARIE CURIE

A. Hàm số đồng biến trên

 

;1

. B. Hàm số nghịch biến trên

 

;1

C. Hàm số đồng biến trên

 

;2

. D. Hàm số nghịch biến trên

 

;2

Câu 31: Cho hàm số

23y x x  

, điểm nào thuộc đồ thị hàm số

 

2;1M

. B.

 

1;1M

. C.

 

2;3M

. D.

 

0;3M

Câu 32: Parabol

  

44y x x

có đỉnh là

 

1;1I

. B.

 

2;0I

. C.

 

1;1I

. D.

 

1;2I

Câu 33: Cho

 

  

: 4 3P y x x

. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên

 

;4

. B. Hàm số nghịch biến trên

 

;4

C. Hàm số đồng biến trên

 

;2

. D. Hàm số nghịch biến trên

 

;2

Câu 34: Trong các hàm số sau, hàm số nào có đồ thị đi qua điểm

 

1;3M

và trục đối xứng

 3x

  

6y x x

. B.

  

31y x x

. C.

  

22y x x

. D.

   

62y x x

Câu 35: Cho hàm số

 

   

0y ax bx c a

có đồ thị

 

. Khi đó, tọa độ đỉnh của

 

là:

  







;

. B.

  







;

. C.

  







;

. D.

  





;

Câu 36: Cho hàm số



2y x x

có đồ thị

 

. Tọa độ đỉnh của

 

là

 

0;0

. B.

 

1; 1

. C.

 

1;3

. D.

 

2;0

Câu 37: Cho hàm số

  

2 6 3y x x

có đồ thị

 

. Trục đối xứng của

 

là



. B.



. C.

3x

. D.

3y

Câu 38: Cho hàm số

  

23y x x

có đồ thị là parabol

()P

. Trục đối xứng của

()P

là

1x

. B.

 1x

. C.

 2x

. D.

2x

Câu 39: Parabol

  

22y x x

có đỉnh là







1 19

;

. B.









1 15

;

. C.







1 15

;

. D.









1 15

;

Câu 40: Giá trị nhỏ nhất của hàm số

   

23y x x

bằng

. B.

. C.

. D.

Câu 41: Đồ thị hàm số

   

23y x x

cắt trục hoành tại mấy điểm

. B.

. C.

. D.

Câu 42: Cho hàm số:

  

47y x x

. Chọn khẳng định đúng?

Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên .

C. Hàm số đồng biến trên khoảng

 

2;

. D. Hàm số đồng biến trên khoảng

 

 ;2

Câu 43: Parabol

  

2 3 1y x x

nhận đường thẳng



làm trục đối xứng. B.



làm trục đối xứng.



làm trục đối xứng. D.



làm trục đối xứng.

Câu 44: Parabol

  

44y x x

có đỉnh là:

 

1;1I

. B.

 

2;0I

. C.

 

1;1I

. D.

 

1;2I

Câu 45: Cho hàm số

  

22y x x

. Câu nào sau đây là sai?

tăng trên

 

1;

. B.

giảm trên

 

1;

giảm trên

 

;1

. D.

tăng trên

 

3;

Câu 46: Hàm số nào sau đây nghịch biến trong khoảng

 

;0



21yx

. B.

  

21yx

. C.

 



21yx

 

  

21yx

Câu 47: Hàm số nào

sau đây đồng biến trong khoảng

 

 1;



21yx

. B.

  

21yx

. C.

 



21yx

 

  

21yx

Câu 48: Cho hàm số:

  

23y x x

. Trong các mệnh đề sau, tìm mệnh đề đúng?

tăng trên

 

0;

. B.

giảm trên

 

;1

C. Đồ thị của

có đỉnh

 

1;0I

. D.

tăng trên

 

 1;

Câu 49: Tìm tập xác định của hàm số

  

21y x x

là

 .D

 

 \1D

. C.

 

 ;1D

. D.

 

 1;D

Câu 50: Cho

 

  

: 2 3P y x x

. Tìm mệnh đề đúng

A. Hàm số đồng biến trên

 

;1

. B. Hàm số nghịch biến trên

 

;1

C. Hàm số đồng biến trên

 

;2

. D. Hàm số nghịch biến trên

 

;2

Câu 51: Cho hàm số

23y x x  

, điểm nào thuộc đồ thị hàm số

 

2;1M

. B.

 

1;1M

. C.

 

2;3M

. D.

 

0;3M

Câu 52: Cho

 

  

: 4 3P y x x

. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên

 

;4

. B. Hàm số nghịch biến trên

 

;4

Trường THPT MARIE CURIE

C. Hàm số đồng biến trên

 

;2

. D. Hàm số nghịch biến trên

 

;2

Câu 53: Parabol

  

32y x x

có đỉnh

và cắt trục hoành tại 2 điểm phân biệt

,MN

Tính diện tích

của tam giác

IMN

 1S

. B.



. C.



. D.



Câu 54: Tính khoảng cách

ngắn nhất từ đỉnh

của parabol

    

3 6 4 2 4y x mx m m

đến trục

 1d

. B.

 2d

. C.

 3d

. D.

 4d

Câu 55: Tính khoảng cách

lớn nhất từ đỉnh

của parabol

    

4 3 4 2y x mx m m

đến trục

 1d

. B.

 2d

. C.

 3d

. D.

 4d

Câu 56: Tìm

để hàm số

    

4 4 9y x mx m

nghịch biến trên khoảng

 

2;

 2m

. B.

1m

. C.

1m

. D.

1m

Câu 57: Tìm giá trị của tham số

để hàm số

    

8 5 24y x x m

có giá trị lớn nhất trên

đoạn





1;6

bằng

1

 1,5m

. B.

 2,5m

. C.

 1,4m

. D.

 5m

Câu 58: Cho hàm số

   

54y x x

. Hàm số có bảng biến thiên nào sau đây?

-9

∞

Câu 59: Gọi

là tập hợp tất cả các giá trị thực của tham số

để giá trị nhỏ nhất của hàm

số

 

 

44 2mx m my f x x

trên đoạn

 



2;0

bằng

Tính tổng

các phần

tử của





Bấm Tải xuống để xem toàn bộ.

| 1/38

| | Tải xuống

Preview text:

Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI Bài 1. HÀM SỐ
A.TÓM TẮT LÝ THUYẾT
ĐẠI CƯƠNG VỀ HÀM SỐ
Ở lớp dưới ta đã làm quen với khái niệm hàm số, ví dụ hàm số 2
y  f (x)  x  2x .
 Ứng với x = 1 thì 2
y  f (1)  1  2.1  3
 Ứng với x = –2 thì 2 y  f ( 2)   ( 2)   2.( 2)   0
 Ứng với x = 0 thì 2
y  f (0)  (0)  2.(0)  0
 Ứng với x = 2 thì 2
y  f ( 2)  ( 2)  2.( 2)  2  2 2 D f R Taäp xaùc ñònh  x =1 f y = 3
Giaù trò cuûa haøm soá taïi x=1  Bieán soá x =–2 x =0 f   y =0 Giaù trò cuûa haøm x  2 (hay ñoái soá) f
soá taïi x =–2 vaø x   y  2  2 2 = 0 Giaù trò cuûa haøm soá Kí hieäu f: D R taïi x  2 x 2
y  f (x)  x  2x
Hàm số f xác định trên D là một qui tắc đặt tương ứng mỗi số x
thuộc D với một và chỉ một số y thuộc .
 Kí hiệu . Hàm số f còn được ghi y = f(x).
 Tên gọi .  D là tập xác định (hay miền xác định) của hàm số.
 x là biến số (hay đối số) của hàm số f.
 f(x) là giá trị của hàm số f tại x. Chú ý
 Một hàm số được cho bởi một biểu thức hoặc nhiều biểu thức 2 x  3x  1
2x 1 neáu x  1
Ví dụ. Hàm số y  f (x) 
y  g(x)   x  ; Hàm số 1 2
x  2 neáu x  1
 Nếu hàm số y  f (x) không giải thích gì thêm thì tập xác định của nó là tập hợp các số
thực x sao cho giá trị của biểu thức f (x) được xác định. 32 Trường THPT MARIE CURIE
VẤN ĐỀ 1. Tính giá trị của hàm số tại một điểm
Để tính giá trị của hàm số y  f (x) tại x = a, ta thế x = a vào biểu thức f (x) và được ghi f (a) . VÍ DỤ  2
x 1 neáu x  2 
Ví dụ 1. Cho hàm số y  f (x)   x 1 .  neáu x  2  x 1
Tính f (1), f (2), f  2 , f 1 2 , f 1 2  Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 8  neáu x  2 
Ví dụ 2. Cho hàm số y  f (x)   . 2
x  2x neáu x  2 
Tính f(3), f(2), f(–2), f ( 2) và f (0) . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
 4x 1 khi x  2
Ví dụ 3. Cho hàm số y  f  x   . 3
x  3 khi x  2
a. Tính f 2 . b. Tính f  2  . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 33
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI 2  2(  x +1) neáu x  1
Ví dụ 4. Cho hàm số y  h(x)   .
4 x 1 neáu x  1  2 
Tính h(1), h(2), h   , h  2 . 2   Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... x  1  1 
Ví dụ 5: Cho hàm số y  f (x) 
. Giải phương trình f  1   2 x  1  x  Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
VẤN ĐỀ 2. Đồ Thị Hàm Số
 Cho hàm số y  f (x) xác định trên tập D. Trong mặt phẳng tọa độ Oxy, tập hợp các điểm
có tọa độ  x; f (x) với x  D, gọi là đồ thị của hàm số y  f (x) .
 Để biết điểm M (a;b) có thuộc đồ thị hàm số y  f (x) không, ta thế x = a vào biểu thức f (x) .
- Nếu f (a)  b thì điểm M (a;b) thuộc đồ thị hàm số y  f (x) .
- Nếu f (a)  b thì điểm M (a;b) không thuộc đồ thị hàm số y  f (x) . VÍ DỤ
Ví dụ 1. Cho hàm số 2
y  f (x)  x  x  3 . Các điểm (
A 2;8) , B(4;12) và C 5;25  2  điểm nào thuộc đồ thị của hàm số đã cho? Lời giải 34 Trường THPT MARIE CURIE
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số y  f  x 2
 2x 5x  5 C   a. Các điểm A  B  1 1; 2 , 1;5 , C  ;8 
 có thuộc đồ thị C của hàm số đã cho không ?  2 
b. Tìm các điểm thuộc đồ thị hàm số mà có tung độ là 2. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... x  2
Ví dụ 3. Cho hàm số y  f  x 
C và điểm Mm 1;  1 . Tìm các giá 2
x  , gọi đồ thị là   1
trị của tham số m để điểm M nằm trên đồ thị (C) . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
BÀI TẬP TỰ RÈN LUYỆN 2  x
Bài 1 Cho hàm số y  g(x)  2
x  2x  . Tìm các điểm thuộc đồ thị hàm số mà có tung độ 3 là 2. 2
x  6 neáu x  1
Bài 2 Cho hàm số y  f (x)   . 2
x  3x neáu x  1 35
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
a). Điểm nào trong các điểm sau nằm trên đồ thị hàm số. A3; 
3 , B(–1; –5), C 1; 2   và D(3; 0)
b). Tìm các điểm thuộc đồ thị hàm số mà có tung độ là –2. 2 x  x
Bài 3 Cho hàm số y  f (x) 
. Tìm các điểm trên đồ thị hàm số sao cho điểm 2 x  x  1
đó cách đều hai trục tọa độ. 2
Bài 4 Cho hàm số y  f (x)  1
. Tìm các điểm trên đồ thị sao cho tọa độ là số x  1 nguyên.
VẤN ĐỀ 3. Tập xác định của hàm số CHÚ Ý 1: k
1. Hàm số y 
xác định khi và chỉ khi f (x)  0 . f (x)
2. Hàm số y  k f (x) xác định khi và chỉ khi f (x)  0 . k 3. Hàm số y 
xác định khi và chỉ khi f (x)  0 . f (x) P(x)  0
CHÚ Ý 2: P(x).Q(x)  0   Q  (x)  0 CHÚ Ý 3:
 Nếu a  x  b thì D  a;b  Nếu a  x  b thì D   ; a b
 Nếu a  x  b thì D  a;b  Nếu a  x  b thì D   ; a b
a  x  b
a  x  b  Nếu 
thì D  a;b \ x  Nếu 
thì D  a;b \ x 0 0 x  x  x  x  0 0
a  x  b hay c  x  d  Nếu 
thì D  a;b  ;
c d  \ x 0 x  x  0 VÍ DỤ 1
Ví dụ 1. Tìm tập xác định của hàm số y  f (x)  1 x  . x  2 Lời giải 36 Trường THPT MARIE CURIE
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... x  2
Ví dụ 2. Tìm tập xác định của hàm số y  f (x)  5  x  . 2 x  1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... x 1
Ví dụ 3. Tìm tập xác định của hàm số y  f (x)   . x  2 xx   1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... x  1
Ví dụ 4. Tìm tập xác định của hàm số y  f (x)   .
x  2x  3 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Tìm tập xác định của hàm số y  4 2x 1  (x  4) 3  x . 37
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 x  2  x
Ví dụ 6. Tìm tập xác định của hàm số y  f (x)   . 2
x  x x  1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 3 x  3
Ví dụ 7. Tìm tập xác định của hàm số y  .
x  2  7  3x Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 x  1
Ví dụ 8. Tìm tập xác định của hàm số y  f (x)  .
x  1  x  1 Lời giải 38 Trường THPT MARIE CURIE
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 3x  5
Ví dụ 9. Tìm m để hàm số y  2
x  3x  m  có tập xác định là D = R. 1 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 10. Tìm m để hàm số 2
y  x  2 3x  2m 1 có tập xác định là D  [1; ) . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
BÀI TẬP TỰ RÈN LUYỆN
Bài 1 Tìm tập xác định của các hàm số sau. x x a). y   x
b). y  f (x)  x  1 2 x  1 2 x  2x  3 x  3 c). y 
d) y  f (x)  2 2
(x  9x)(x  x  1) 2 x  4 x x x 1
e) y  f (x)  f) y   x x 1 x 1 x
Bài 2 Tìm tập xác định của các hàm số sau. 39
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
x 2x  5  3 2  5x 2 3x  4  x  2 a). y  b). y  2 2 4 x  4
(2x  x  5)  x   1 2x  x  2 2 x  4x  3 c). y  d). y  7  2x 2 2
(x  2x  4) 2x  1 2 2x  x  3 2x  3 e). y  f). y   5  x 2
( x  5x) x  2 3  x
2x  4  3 4  x 3x  6  x g). y  y  2 x  3x  h). 2 1  x  4 2 x  2  2 3x
2x  5 9  2x  i). y  j). 2x 10 y  2  x  2 1  3  x 3  4x  x x 2
x  10  2x  11 k). y  y  2x  7  l). 2 3x  2  4 3 x  2
Bài 3 Tìm m để hàm số y  D . 2
x  4x  m  có tập xác định là  5 2 2x  5
Bài 4 Tìm m để hàm số y  D  \ 2 .
3mx  4m  có tập xác định là   8
Bài 5 Tìm m để hàm số 2 2 y 
x  2mx  m  m 1 có tập xác định là D  .
VẤN ĐỀ 4. Sự biến thiên của hàm số
1. Hàm số f xác định trên khoảng K và x , x  K 1 2
 Hàm số f gọi là đồng biến trên K nếu x  x  f (x )  f (x ) 1 2 1 2
 Hàm số f gọi là nghịch biến trên K nếu x  x  f (x )  f (x ) 1 2 1 2 Chú ý 1
Hàm số f xác định trên khoảng K.
Nếu f x   f x với mọi x , x  K nghĩa là f(x) = c (c là hằng số) thì f gọi là hàm số 1  2 1 2
hằng (còn gọi là hàm số không đổi) trên K. Chú ý 2
Khảo sát sự biến thiên của hàm số f nghĩa là xem f đồng biến, hoặc nghịch biến, hoặc không đổi
trên các khoảng nào trong tập xác định của nó. 40 Trường THPT MARIE CURIE
PHƯƠNG PHÁP GIẢI TOÁN
KHẢO SÁT SỰ BIẾN THIÊN CỦA HÀM SỐ TRÊN KHOẢNG K
Cho hàm số y = f(x) và hai số tùy ý x1, x2  K .
CÁCH 1. Giả sử x  x 1 2
 Nếu f x   f x   0 thì f(x) đồng biến trên K. 2 1
 Nếu f x   f x   0thì f(x) nghịch biến trên K. 2 1
CÁCH 2. Giả sử x  x . 1 2   f ( x ) f ( x ) Nếu 1 2  0 x 
thì f(x) đồng biến trên K. x 1 2   f ( x ) f ( x ) Nếu 1 2  0 x 
thì f (x) nghịch biến trên K. x 1 2 VÍ DỤ
Ví dụ 1. Khảo sát sự biến thiên của hàm số y  f x  1 ( )
trên khoảng 0;  và ;0 x Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Khảo sát sự biến thiên của hàm số f x  x  2 ( ) 2
x trên 1;  . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 41
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
Ví dụ 3. Khảo sát sự biến thiên của hàm số f (x)  x  1 trên 1;  . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
BÀI TẬP TỰ RÈN LUYỆN
Bài 1 Khảo sát sự biến thiên của các hàm số sau
a). y  f x  2 ( )
x  1 trong khoảng ;0; 0; 
b). y  f (x)  2  x(x  4) trên khoảng (2; ) x  5
c). y  f (x)  1  
x  trên khoảng (3; ) 3 1
d). y  f (x) 
trên khoảng 0;  2 x  1 e) y  2
x  1 trên ;0 1
f) y  f (x)  trên  ;    1 x  1
Bài 2 Khảo sát sự biến thiên của các hàm số sau a). y  f ( )
x  1 2x trong khoảng ( ;  ) 1 b). y 
trên khoảng 1;  x  1
c). y  1  x trên khoảng   ;1 d). y  2
x  2x trên khoảng ;
e) y  x 1 trên  1  ; f) y   2
x  2x trên  ;    1
Bài 3 Cho hàm số y  x  x  3
a). Chứng minh hàm số đồng biến trên 3;  .
b). Cho a  6 . Chứng minh: a  3  9  a 42 Trường THPT MARIE CURIE
VẤN ĐỀ 5. Hàm số chẵn – Hàm số lẻ
A. TÓM TẮT LÝ THUYẾT
1. Tập D là tập con của tập số thực
gọi là tập đối xứng nếu thỏa. mọi x thuộc D thì –x
cũng thuộc D. –a –x 0 x a ( ) D = (–a;a) ;b)
2. Hàm số chẵn – hàm số lẻ
 Hàm số f xác định trên tập đối xứng D.
 Nếu x  D mà f(–x) = f(x) thì ta nói f là hàm số chẵn trên D.
 Nếu x  D mà f(–x) = –f(x) thì ta nói f là hàm số lẻ trên D.
3. Đồ thị hàm số chẵn , hàm số lẻ
 Đồ thị hàm số hàm số chẵn nhận trục tung làm trục đối xứng.
 Đồ thị hàm số hàm số lẻ nhận gốc tọa độ làm tâm đối xứng. y y O x O x
Đồ thị hàm số lẻ
Đồ thị hàm số chẵn
B. PHƯƠNG PHÁP GIẢI
CÁCH XÉT TÍNH CHẴN – LẺ CỦA HÀM SỐ
Tìm tập xác định D của hàm số y = f(x)
Nếu D không là tập đối xứng
Nếu D là tập đối xứng
thì hàm số f không chẵn và không lẻ trên D.
xD, tính f(–x).
Nếu f(–x) ≠  f(x)
Nếu f(–x) = f(x)
Nếu f(–x) = – f(x)
thì f là hàm số chẵn trên D
thì f là hàm số lẻ trên D
Chọn một giá trị thích hợp
x = a  D để có f(–a) ≠  f(a)
Từ đó kết luận hàm số f không chẵn và không lẻ trên D. 43
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI C. VÍ DỤ
Ví dụ 1. Xét tính chẵn-lẻ của hàm số y  f x  1 ( ) x Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Xét tính chẵn-lẻ của hàm số y  f x  2 ( ) x  x Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
3  x  3  x
Ví dụ 3. Xét tính chẵn-lẻ của hàm số y  f (x)  2 x Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Xét tính chẵn-lẻ của hàm số 3
y  h( x)  x  x  1  x  1  x Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 44 Trường THPT MARIE CURIE
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. BÀI TẬP RÈN LUYỆN 5x
Bài 1 Chứng minh đồ thị hàm số y  f (x)  2
x  nhận gốc tọa độ làm tâm đối xứng. 4
Bài 2 Chứng minh đồ thị hàm số y  g(x)  2  x  2  x nhận trục tung làm trục đối xứng.
Bài 3 Xét tính chẵn-lẻ của các hàm số sau. 4 2x
a). y  f (x) 
y  h x  x  x 2 x  b). 2 ( ) 3 9 3 x  5x
c). y  g(x)  2  x  2  x d). y  k(x) 
x 1  x 1
5  x  5  x 3 2x
e). y  u(x) 
y  v(x)  x  f). 1
6  3x  6  3x
BÀI TẬP TRẮC NGHIỆM Câu 1:
Hàm số nào sau đây có tập xác định là 1 1 1 A. y  .
B. y  f (x)  . C. y  x 1 . D. y  . 2 x x 1 2 x 1 x Câu 2:
Tìm tập xác định D của hàm số y  f (x)  . 1  x
A. D  0;    1 .
B. (;1) . C. D   \  1 .
D. D  0;  1 . 1 Câu 3:
Tìm tập xác định D của hàm số y  f (x)  . 2 x  1
A. D  1;    1 . B. D   \  0 . C. D  \1;    1 . D. D   \ 1;  1 .    Câu 4:
Tìm tập xác định D của hàm số 2 2  x x y . x A. D   2  ;2. B. D   2  ;2 \  0 . C. D   2  ;2\  0 . D. D  . x  Câu 5:
Tìm tập xác định D của hàm số 2 1
y  6  x  . 1 x 1
A. D  1; . B. D  1;6 . C. D  . D. D   ;6  . 45
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI x  2 Câu 6:
Tìm tập xác định D của hàm số y  . 2 x x  4x  4 A. D   2  ; \0;  2 . B. D  . C. D   2;   . D. D   2  ; \0;  2 . x Câu 7:
Tìm tập xác định D của hàm số y  . x  x  6
A. D  0; .
B. D  0; \  9 . C. D    9 . D. D  .
x 1  4  x Câu 8:
Tìm tập xác định D của hàm số y   .
x  2 x  3 A. D  1;4 .
B. D  1;4 \ 2;  3 . C. 1;4 \2;  3 . D.  ;   1 4; . 2018 Câu 9:
Tìm tập xác định D của hàm số y  . 3 2 3 2
x  3x  2  x  7 A. D  \   3 . B. D  . C. D   ;   1  2;. D. D  \   0 . x
Câu 10: Tìm tập xác định D của hàm số y  . 2
x  2  x  2x A. D  . B. D  \ 0;  2 . C. D   2  ;0 .
D. D  2; . x 
Câu 11: Tìm tập xác định D của hàm số 2 1 y  . x x  4 A. D  \ 0;  4 .
B. D  0; .
C. D  0; \   4 .
D. D  0; \   4 . 5  3 x
Câu 12: Tìm tập xác định D của hàm số y  . 2 x  4x  3 5 5 A. D     ; \   1   . B. D  .  3 3 5 5 5 5 C. D     ; \     1 . D. D     ; .    3 3   3 3 2x 1
Câu 13: Tìm tập xác định D của hàm số y   . 2x   1  x  3 1 1
A. D  3; . B. D  
 \  ;3 . C. D     ;   . D. D  .  2   2  2 x 1
Câu 14: Tìm tập xác định D của hàm số y  . 2 x  3x  4 A. D  1;  4 . B. D  \ 1;  4 . C. D  \ 1;  4 . . D. D  . 46 Trường THPT MARIE CURIE x 1
Câu 15: Tìm tập xác định D của hàm số y   x   1  . 2
x  3x  4 A. D  \   1 . B. D    1 . C. D  \   1 . D. D  . 2x 1
Câu 16: Tìm tập xác định D của hàm số y  . 3 x  3x  2 A. D  \   1 . B. D  \  2  ;  1 . C. D  \   2 . D. D  .
Câu 17: Tìm tập xác định D của hàm số x  2  x  3 . A. D   3;   . B. D   2;   . C. D  .
D. D  2; .
Câu 18: Tìm tập xác định D của hàm số y  6  3x  x 1 . A. D  1;2 . B. D  1;2 . C. D  1;  3 . D. D   1  ;2. x   x
Câu 19: Tìm tập xác định D của hàm số 3 2 6 y  . 4  3x 2 4 3 4 2 3 4 A. D    ;   . B. D    ;   . C. D    ;   . D. D    ;   .  3 3   2 3   3 4   3  x  4
Câu 20: Tìm tập xác định D của hàm số y  . 2 x 16 A. D   ;  2  2; . B. D  . C. D   ;  4
 4; . D. D   4  ;4 .
Câu 21: Tìm tập xác định D của hàm số 2 y 
x  2x 1  x  3 . A. D    ;3 . B. D  1;  3 .
C. D  3; .
D. D  3; . x 1
Câu 22: Tìm tập xác định D của hàm số y  . 2 x  x  6 A. D    3 . B. D   1  ; \  3 . C. D  . D. D   1  ;. x 1
Câu 23: Tìm tập xác định D của hàm số y   .
x  3 2x 1 1 A. D  . B. D     ; \     3 .  2  1 1 C. D    ;  \     3 . D. D    ;  \     3 .  2   2  3 x 1
Câu 24: Tìm tập xác định D của hàm số y  . 2 x  x 1
A. D  1; . B. D    1 . C. D  . D. D   1  ; .
Câu 25: Xét tính đồng biến, nghịch biến của hàm số f  x 2
 x  4x  5 trên khoảng  ;2   và
trên khoảng 2; . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên  ;2
 , đồng biến trên 2;.
B. Hàm số đồng biến trên  ;2
 , nghịch biến trên 2;. 47
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
C. Hàm số nghịch biến trên các khoảng  ;2
  và 2;.
D. Hàm số đồng biến trên các khoảng  ;2
  và 2;.
Câu 26: Xét sự biến thiên của hàm số f  x 3
 trên khoảng 0; . Khẳng định nào sau đây x đúng?
A. Hàm số đồng biến trên khoảng 0; .
B. Hàm số nghịch biến trên khoảng 0; .
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng 0; .
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng 0; .
Câu 27: Xét sự biến thiên của hàm số f  x 1
 x  trên khoảng 1; . Khẳng định nào sau đây x đúng?
A. Hàm số đồng biến trên khoảng 1; .
B. Hàm số nghịch biến trên khoảng 1; .
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng 1; .
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng 1; . x 
Câu 28: Xét tính đồng biến, nghịch biến của hàm số f  x 3  trên khoảng  ;  5   và trên x  5 khoảng  5;
  . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên  ;  5
  , đồng biến trên  5;   .
B. Hàm số đồng biến trên  ;  5
  , nghịch biến trên  5;   .
C. Hàm số nghịch biến trên các khoảng  ;  5   và  5;   .
D. Hàm số đồng biến trên các khoảng  ;  5   và  5;   .
Câu 29: Cho hàm số f  x  2x  7. Khẳng định nào sau đây đúng?    
A. Hàm số nghịch biến trên 7 ;    .
B. Hàm số đồng biến trên 7 ;    .  2   2 
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên .
Câu 30: Trong các hàm số 2 3 y  2015 ,
x y  2015x  2, y  3x 1, y  2x  3x có bao nhiêu hàm số lẻ? A. 1. B. 2 . C. 3 . D. 4 .
Câu 31: Cho hai hàm số f  x 3  2
 x  3x và g x 2017  x
 3. Mệnh đề nào sau đây đúng?
A. f  x là hàm số lẻ; g  x là hàm số lẻ.
B. f  x là hàm số chẵn; g  x là hàm số chẵn.
C. Cả f  x và g  x đều là hàm số không chẵn, không lẻ.
D. f  x là hàm số lẻ; g  x là hàm số không chẵn, không lẻ. 48 Trường THPT MARIE CURIE
Câu 32: Cho hàm số f  x 2
 x  x . Khẳng định nào sau đây là đúng.
A. f  x là hàm số lẻ.
B. f  x là hàm số chẵn.
C. Đồ thị của hàm số f  x đối xứng qua gốc tọa độ.
D. Đồ thị của hàm số f  x đối xứng qua trục hoành.
Câu 33: Cho hàm số f  x  x  2 . Khẳng định nào sau đây là đúng.
A. f  x là hàm số lẻ. B. f  x là hàm số chẵn.
C. f  x là hàm số vừa chẵn, vừa lẻ.
D. f  x là hàm số không chẵn, không lẻ. x 
Câu 34: Tìm tập xác định của hàm số 2 5 y  x  2  . x  4 A. D  \   4 . B. D  \   2 .
C. D   ;  2. D.
D  2; \   4 . 2x 1
Câu 35: Tập xác định của hàm số y  là 2 x  4  1  A. D  . B. D  \  2  ;  2 . C. D  \   . D. D   2  ;  2 .  2
Câu 36: Tập xác định của hàm số y  3  2x là  1 3   3   1 3   3  A. D   ;   . B. D  ;    . C.  ;   . D. D  ;  .   2 2   2   2 2   2  2
  x  2 khi 1  x  1
Câu 37: Cho hàm số f  x   . Giá trị f   1  bằng 2
 x 1 khi x 1 A. 6  . B. 6 . C. 5 . D. 5  .
Câu 38: Hàm số nào sau đây đồng biến trên khoảng 0;  . A. y  2  x 1. B. 2
y  x  2x 1.
C. y  x .
D. y  x .
Câu 39: Tập hợp nào sau đây là tập xác định của hàm số. y  2x  3  3   3   3  A. ;    . B.  ;  . C. ;  . D. .   2   2   2 
Câu 40: Trong các hàm số sau đây y  x , 2
y  x  4x , 4 2
y  x  2x có bao nhiêu hàm số chẵn? A. 0. B. 1. C. 2. D. 3.
Câu 41: Hàm số nào sau đây là hàm số lẻ? x 1 x A.   x y . B. y   1. C.   x y . D. y    2 . 2 2 2 2 Câu 42: Cho hàm số 3
y  2x  3x 1. Trong các mệnh đề sau, tìm mệnh đề đúng?
A. y là hàm số chẵn.
B. y là hàm số lẻ.
C. y là hàm số không có tính chẵn lẻ.
D. y là hàm số vừa chẵn vừa lẻ. Câu 43: Cho hàm số 4 2
y  3x – 4x  3 . Trong các mệnh đề sau, mệnh đề nào đúng?
A. y là hàm số chẵn.
B. y là hàm số lẻ. 49
Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI
C. y là hàm số không có tính chẵn lẻ.
D. y là hàm số vừa chẵn vừa lẻ.
Câu 44: Trong các hàm số sau, hàm số nào không phải là hàm số lẻ? 1 A. 3 y  x 1 . B. 3
y  x – x . C. 3
y  x  x . D. y  . x
Câu 45: Trong các hàm số nào sau đây, hàm số nào là hàm số lẻ? A. 2018 y  x  2017 . B. y  2x  3 .
C. y  3 x  3 x .
D. y  x  3  x  3 .
Câu 46: Trong các hàm số nào sau đây, hàm số nào là hàm số chẵn?
A. y  x 1  x 1 .
B. y  x  3  x  2 . C. 3
y  2x  3x . D. 4 2
y  2x  3x  x . x  Câu 47: Hàm số 1 y  xác định trên 0;  1 khi x  m 1 A. m  . B. m 1. 2
C. m  0 hoặc m 1.
D. m  0 hoặc m 1. x 2 1
Câu 48: Tìm m để hàm số y  có tập xác định là . 2
x  2x  m 1 A. m 1. B. m  0 . C. m  2 . D. m  3 .
Câu 49: Hàm số nào trong các hàm số sau là hàm số lẻ. 2 1 1
A. y  x 1  x 1 . B.  x y . C. y  . D. 3
y  1 3x  x . x 4 2 x  2x  3
Câu 50: Trong các hàm số sau, hàm số nào không phải hàm số chẵn.
A. y  x  5  x  5 . B. 4 2
y  x  x 12 .
C. y  1 x  x 1 . D. 2
y  x 1  x .
Câu 51: Trong các hàm số sau, hàm số nào giảm trên khoảng 0;  1 ? 1 A. 2 y  x . B. 3 y  x . C. y  . D. y  x . x
Câu 52: Cho hàm số y  x 1 x  . Khẳng định nào đúng? A. hàm số chẵn. B. hàm số lẻ.
C. hàm số không chẵn, không lẻ.
D. hàm số vừa chẵn, vừa lẻ.  x  1 
Câu 53: Cho hàm số. y  f  x 1  . Phương trình f 
  2 có nghiệm là 1 x  x  1 1 A. x  1  . B. x  . C. x  . D. x 1. 3 3 1 x 1
Câu 54: Cho hàm số. y  f  x 
. Phương trình f  2 x  
1   có nghiệm là 2 x 1 2 A. x  1  . B. x  0 . C. x  2 . D. x 1.
Câu 55: Tập xác định của hàm số y  x  2m  4  2x là 1;2 khi và chỉ khi. 1 1 1 A. m   . B. m 1. C. m  . D. m  . 2 2 2 50 Trường THPT MARIE CURIE
Câu 56: Tập xác định của hàm số y  x  m  6  2x là một đoạn trên trục số khi và chỉ khi 1 A. m  3 . B. m  3 . C. m  3 . D. m  . 3
Câu 57: Điểm nào sau đây thuộc đồ thị hàm số 1 y  . x 1 A. M 2;1 . B. M 1;1 . C. M 2;0 . D. M 0; 1  . 4   3   2   1   2  4  4
Câu 58: Điểm nào sau đây thuộc đồ thị hàm số  x x y . x  1  A. A1;  1  .
B. B 2;0 . C. C 3;   . D. D  1  ; 3   .  3   2 x   ;0    x 1 
Câu 59: Cho hàm số f  x   x 1 x 0;2 . Giá trị f 4 bằng  2 x 1 x  2;5   A. f   2 4  .
B. f 4 15 .
C. f 4  5 .
D. f (4)  0 . 3 2 x  2  3  x  2
Câu 60: Cho hàm số f  x   x 1
. Giá trị P  f 2  f  2   bằng  2 x +1 x  2 8 5 A. P  . B. P  4 . C. P  6 . D. P  . 3 3 51
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
Bài 2. HÀM SỐ BẬC NHẤT
A. TÓM TẮT LÝ THUYẾT
1. Hàm số bậc nhất: y = ax + b a  0 .
o Tập xác định: D  o Sự biến thiên:
 Nếu a  0 : Hàm số đồng biến (tăng) trên .
 Nếu a  0 : Hàm số nghịch biến (giảm) trên .
o Đồ thị hàm số là đường thẳng có hệ số góc bằng a , cắt trục hoành tại  b  A  
; 0  , cắt trục tung tại điểm B0;b .  a  y y B B y=ax+b (a>0) y=ax+b (a<0) A O x A O x
o Vị trí tương đối của hai đường thẳng:
Cho d : y  ax  b a  0 và 
d : y  a  x   b   a  0 a   a  d//  d   b    b a   a  d   d   b    b  d cắt  d  a   a  d   d  . a  a  1  d cắt 
d tại một điểm trên trục tung  a   a và b   b .
2. Hàm hằng y  b
Đồ thị hàm số y  b là một đường thẳng song song hoặc trùng với trục hoành và
cắt trục tung tại điểm 0;b. Đường thẳng này gọi là đường thẳng y  . b 52 Trường THPT MARIE CURIE y y=b O x
3. Hàm số y = ax + b  a  0 .
 axb khi x  b      a y ax b
ax  b khi x   b  a
Để vẽ đồ thị hàm số y  ax  b ,a  0 ta có thể vẽ hai đường thẳng y  ax  b và
y  ax  b rồi xóa đi hai phần đường thẳng nằm phía dưới trục hoành.
B. PHƯƠNG PHÁP GIẢI TOÁN
VẤN ĐỀ 1: Xét tính đồng biến, nghịch biến
Muốn xét tính đơn điệu của hàm số bậc nhất ta cần:
 Đưa hàm số về đúng dạng y  a x  b, a  0 .
 Nếu a  0 : Hàm số đồng biến (tăng) trên .
 Nếu a  0 : Hàm số nghịch biến (giảm) trên . VÍ DỤ
Ví dụ 1. Xét tính đơn điệu của các hàm số sau 1
a) y  2x 1
b) y  x 1 c)  x y d)   x y 2 2
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 53
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Ví dụ 2. Tìm các giá trị của m để hàm số
a) y  m  
1 x 1 đồng biến trên
b) y  mx  m 1 nghịch biến trên 1 c) y   2 m  
1 x  m 1 nghịch biến trên d) y 
x  2 đồng biến trên m 1 Lời giải
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..........................................................................................................................................................................
VẤN ĐỀ 2: Đồ thị hàm số y  ax  b
Đưa hàm số về đúng dạng y  a x  b, a  0 . Đồ thị hàm số là đường thẳng.
 Nếu a  0 : Đồ thị “đi lên từ trái sang phải”
 Nếu a  0 : Đồ thị “đi xuống từ trái sang phải”
 Xác định giao điểm của đường thẳng với hai trục tọa độ rồi nối hai
điểm đó lại ta được đường thẳng là đồ thị của hàm số VÍ DỤ 54 Trường THPT MARIE CURIE
Ví dụ 3. Xét tính đơn điệu và vẽ đồ thị các hàm số sau: 1 x
a) y  2x 1
b) y  x 1 c)  x y d) y    2 2 4 Lời giải
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
VẤN ĐỀ 3: Đồ thị hàm số y=|ax+b|  b
ax  b khi x     a
y  ax  b      b
ax b khi x    a
 Để vẽ đồ thị hàm số y  ax  b ,a  0 ta có thể vẽ hai đường thẳng y  ax  b và
y  ax  b rồi xóa đi hai phần đường thẳng nằm phía dưới trục hoành. VÍ DỤ
Ví dụ 4. Xét tính đơn điệu và vẽ đồ thị các hàm số sau: a) y  x 1
b) y  x 1 1
c) y  x 1  x
d) y  x  x 1 Lời giải
.................................................................................................................................................................. 55
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
C. BÀI TẬP TRẮC NGHIỆM Câu 1:
Tìm m để hàm số y  2m  
1 x  m  3 đồng biến trên . A. m  1 . B. m  1 .
C. m   1 .
D. m   1 . 2 2 2 2 Câu 2:
Tìm m để hàm số y  mx  2  x2m   1 nghịch biến trên . A. m  2.
B. m   1 .
C. m  1.
D. m   1 . 2 2 Câu 3:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 2017; 2017   để hàm số
y  m  2x  2m đồng biến trên . A. 2014. B. 2016. C. Vô số . D. 2015. Câu 4:
Đường thẳng nào sau đây song song với đường thẳng y  2 . x 56 Trường THPT MARIE CURIE 1 2
A. y  1  2 . x B. y  x  3.
C. y  2x  2. D. y  x  5. 2 2 Câu 5:
Tìm tất cả các giá trị thực của tham số m để đường thẳng y   2
m  3 x  2m  3
song song với đường thẳng y  x  1. A. m  2. B. m  2. C. m  2. D. m  1. Câu 6:
Tìm tất cả các giá trị thực của tham số m để đường thẳng y  3x 1 song song với
đường thẳng y   2
m  1 x  m  1 . A. m  2 . B. m  2. C. m  2. D. m  0. Câu 7:
Biết rằng đồ thị hàm số y  ax  b đi qua điểm M 1; 4 và song song với đường
thẳng y  2x 1 . Tính tổng S  a  . b A. S  4. B. S  2. C. S  0. D. S  4. Câu 8:
Biết rằng đồ thị hàm số y  ax  b đi qua điểm E2;  
1 và song song với đường
thẳng ON với O là gốc tọa độ và N 1;3 . Tính giá trị biểu thức S  2 a  2 b . A. S  4. B. S  40. C. S  58. D. S  58. Câu 9:
Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y  3m  2x 7m 1
vuông góc với đường  : y  2x 1. A. m  0.
B. m   5 .
C. m  5 .
D. m   1 . 6 6 2
Câu 10: Biết rằng đồ thị hàm số y  ax  b đi qua điểm N 4;  
1 và vuông góc với đường
thẳng 4x  y  1  0 . Tính tích P  ab. A. P  0.
B. P   1 . C. P  1 .
D. P   1 . 4 4 2
Câu 11: Tìm a và b để đồ thị hàm số y  ax  b đi qua các điểm A2;  1 , B1;2 .
A. a  2 và b  1.
B. a  2 và b  1.
C. a  1 và b  1.
D. a  1 và b  1.
Câu 12: Biết rằng đồ thị hàm số y  ax  b đi qua hai điểm M 1; 3 và N 1;2 . Tính tổng
S  a  b.
A. S   1 .
B. S  3.
C. S  2.
D. S  5 . 2 2
Câu 13: Biết rằng đồ thị hàm số y  ax  b đi qua điểm A3; 
1 và có hệ số góc bằng 2 .
Tính tích P  ab.
A. P  10.
B. P  10.
C. P  7.
D. P  5. 57
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI  x  x 
Câu 14: Tọa độ giao điểm của hai đường thẳng y  1 3 và y     1 là 4  3   1  A. 0;   1 . B. 2;3 . C.  0;  . D. 3;2 .  4 
Câu 15: Tìm tất cả các giá trị thực của m để đường thẳng y  2
m x  2 cắt đường thẳng
y  4x  3 .
A. m  2.
B. m  2.
C. m  2. D. m  2.
Câu 16: Cho hàm số y  2x  m  1 . Tìm giá trị thực của m để đồ thị hàm số cắt trục hoành
tại điểm có hoành độ bằng 3.
A. m  7.
B. m  3.
C. m  7.
D. m  7.
Câu 17: Cho hàm số y  2x  m  1 . Tìm giá trị thực của m để đồ thị hàm số cắt trục tung
tại điểm có tung độ bằng 2 .
A. m  3.
B. m  3.
C. m  0.
D. m  1.
Câu 18: Tìm giá trị thực của m để hai đường thẳng d : y  mx  3 và  : y  x  m cắt nhau
tại một điểm nằm trên trục tung.
A. m  3.
B. m  3.
C. m  3.
D. m  0.
Câu 19: Tìm tất cả các giá trị thực của m để hai đường thẳng d : y  mx  3 và  : y  x  m
cắt nhau tại một điểm nằm trên trục hoành.
A. m  3.
B. m   3.
C. m   3.
D. m  3.
Câu 20: Cho hàm số bậc nhất y  ax  b . Tìm a và b , biết rằng đồ thị hàm số đi qua điểm M1; 
1 và cắt trục hoành tại điểm có hoành độ là 5. 1 5 1 5 1 5 1 5
A. a  ; b  .
B. a   ; b   .
C. a  ; b   .
D. a   ; b  . 6 6 6 6 6 6 6 6
Câu 21: Cho hàm số bậc nhất y  ax  b . Tìm a và b , biết rằng đồ thị hàm số cắt đường
thẳng  : y  2x  5 tại điểm có hoành độ bằng 2 và cắt đường thẳng 1
 : y  –3x  4 tại điểm có tung độ bằng 2 . 2 3 1 3 1 3 1 3 1
A. a  ; b  .
B. a   ; b  .
C. a   ; b   .
D. a  ; b   . 4 2 4 2 4 2 4 2
Câu 22: Tìm giá trị thực của tham số m để ba đường thẳng y  2x , y  x  3 và y  mx  5 phân biệt và đồng qui.
A. m  7.
B. m  5.
C. m  5.
D. m  7.
Câu 23: Tìm giá trị thực của tham số m để ba đường thẳng y  5x  
1 , y  mx  3 và
y  3x  m phân biệt và đồng qui. 58 Trường THPT MARIE CURIE
A. m  3.
B. m  13.
C. m  13.
D. m  3.
Câu 24: Cho hàm số y  x  1 có đồ thị là đường  . Đường thẳng  tạo với hai trục tọa độ
một tam giác có diện tích S bằng bao nhiêu? A. S  1 . B. S  1. C. S  2. D. S  3 . 2 2
Câu 25: Tìm phương trình đường thẳng d : y  ax  b . Biết đường thẳng d đi qua điểm
I 2;3 và tạo với hai tia Ox, Oy một tam giác vuông cân.
A. y  x  5.
B. y  x  5.
C. y  x  5.
D. y  x  5.
Câu 26: Tìm phương trình đường thẳng d : y  ax  b . Biết đường thẳng d đi qua điểm
I 1;2 và tạo với hai tia Ox, Oy một tam giác có diện tích bằng 4 .
A. y  2x  4.
B. y  2x  4.
C. y  2x  4.
D. y  2x  4. x y
Câu 27: Đường thẳng d : 
 1, a  0; b  0 đi qua điểm M1;6 tạo với các tia a b
Ox, Oy một tam giác có diện tích bằng 4 . Tính S  a  2b .  
A. S   38 .
B. S  5 7 7 . C. S  12.
D. S  6. 3 3
Câu 28: Tìm phương trình đường thẳng d : y  ax  b . Biết đường thẳng d đi qua điểm
I 1; 3 , cắt hai tia Ox , Oy và cách gốc tọa độ một khoảng bằng 5 .
A. y  2x  5.
B. y  2x  5.
C. y  2x  5.
D. y  2x  5.
Câu 29: Đồ thị trong hình bên là của hàm hàm nào sau đây? y 1 -1 O x -2
2x  1 khi x  1
x  1 khi x  1
A. f (x)  
B. f (x)  
2x  1 khi x    1
2x  2 khi x    1
2x  2 khi x  1
x  1 khi x  1
C. f (x)  
D. f (x)  
2x  1 khi x    1
2x  2 khi x    1 59
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
Bài 3. HÀM SỐ BẬC HAI
A. TÓM TẮT LÝ THUYẾT ĐỊNH NGHĨA
 Hàm số bậc hai là hàm số có dạng  2 y
ax  bx  c trong đó a, b, c là hằng số và a ≠ 0.
 Đồ thị hàm số  2 y
ax  bx  c gọi là một parabol.
SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM SỐ BẬC HAI Hàm số bậc hai a  0 a  0
Bảng biến thiên
Bảng biến thiên b b x   –∞ +∞ x 2a –∞ +∞ 2a +∞ +∞  y   y 4a  –∞ –∞ 4a
 Hàm số nghịch biến trên khoảng
 Hàm số đồng biến trên khoảng  b    b  ;    ;    2a   2a 
 Hàm số đồng biến trên khoảng
 Hàm số nghịch biến trên khoảng  b    b  ;     ;   2a     2a  Đồ thị Đồ thị y y   4a O x O  b b 2a  x  2a  4a  b    Đỉnh I  ;    .  2a 4a   b
Trục đối xứng là đường thẳng x   . 2a 60 Trường THPT MARIE CURIE  Đặc biệt:  b
 Khi a  0 hàm số đạt giá trị nhỏ nhất là y  tại x  min 4a 2a  b
 Khi a  0 hàm số đạt giá trị nhỏ nhất là y  tại x  min 4a 2a
CÁC BƯỚC VẼ PARABOL: P y  2 :
ax  bx  c a  0  b  
Bước 1: Xác định tọa độ đỉnh I  ;    .  2a 4a  b
Bước 2: Xác định trục đối xứng  : x  
và hướng bề lõm của parabol. 2a
Bước 3: Lập bảng giá trị, xác định các điểm thuộc P .
Bước 4: Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để nối các điểm đó lại. VÍ DỤ
Ví dụ 1. Cho hàm số 2
y  x  bx  2 có đồ thị là parabol (P). Lập bảng biến thiên và vẽ đồ
thị hàm số đã cho, biết rằng (P) có đỉnh nằm trên đường thẳng x  2  . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho hàm số 2 y  2
 x  bx  c có đồ thị là parabol (P). Lập bảng biến thiên và vẽ đồ
thị hàm số đã cho, biết rằng (P) đi qua điểm A(1;–2) và hoành độ của đỉnh là 2. Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 61
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Cho hàm số 2
y  x  bx  c có đồ thị là parabol (P). Lập bảng biến thiên và vẽ đồ thị
hàm số đã cho, biết rằng (P) có đỉnh là I (1; 2) . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
B. BÀI TẬP TỰ RÈN LUYỆN Câu 1:
Cho parabol P y  2 :
x  3x  2 .
a. Khảo sát sự biến thiên và vẽ đồ thị hàm số trên.
b. Biện luận theo m số nghiệm của phương trình 2
x  3x  3  2m  0 Câu 2:
Cho parabol P y  2 : x  x  2 .
a. Khảo sát sự biến thiên và vẽ đồ thị hàm số trên.
b. Tìm tham số m để phương trình 2
x  x  m 2  0 có hai nghiệm phân biệt. Câu 3:
Xác định parabol P biết:
a. P y  2 :
ax  bx  2 đi qua điểm A1;0 và có trục đối xứng x  3 . 2
b. P y  2 :
ax  bx  2 đi qua hai điểm B1; 5 và C2;8 .
c. P y  2 :
ax  bx  2 đi qua điểm D1;6 và đỉnh có tung độ  1 . 4 62 Trường THPT MARIE CURIE
d. P y  2 :
ax  4x  c có trục đối xứng là đường thẳng x  2 và cắt trục hoành
tại điểm có hoành độ bằng 3.
e. P y  2 :
2x  bx  c có trục đối xứng là đường thẳng x  1 và cắt trục tung tại
điểm có tung độ bằng 4.
f. P y  2 :
ax  4x  c có đỉnh là I 2;   1 .
g. P y  2 :
ax  4x  c có hoành độ đỉnh là 3 và đi qua điểm E2;  1 .
h. P y  2 :
ax  bx  c đi qua điểm F 0;5 và có đỉnh I 3;4 .
i. P y  2 :
ax  bx  c đi qua điểm G2;3 và có đỉnh I 1;4 .
j. P y  2 :
ax  bx  c đi qua các điểm H 1; 
1 , K 1; 3 và O0;0 .
k. P y  2 :
ax  bx  c đi qua các điểm L1; 
1 , M0;2 và N1;  1 .
l. P y  2 :
ax  bx  c có đỉnh I 3;  
1 và cắt Ox tại điểm có hoành độ bằng 1.
m. P y  2 :
ax  bx  c có trục đối xứng là đường thẳng x  3 , qua P5;6 và cắt
trục tung tại điểm có tung độ bằng 2 . Câu 4:
Tìm tọa độ giao điểm của các cặp đồ thị của các hàm số sau:
a. d : y  x  3 và P y   2 : x  4x  1.
b. d : y  2x  5 và P y  2 :
x  4x  4 .
c. P : y x
2x 1 và P : y x 4x 4 . 2   2   1   2  
d. P : y 3x
4x 1 và P : y 3x 2x 1 . 2    2   1   2   Câu 5:
Cho parabol P y   2 :
x  4x  2 và đường thẳng d : y  2x  3m . Tìm m để:
a. d cắt P tại hai điểm phân biệt A, B . Tìm tọa độ trung điểm của AB .
b. d và P có một điểm chung duy nhất. Tìm tọa độ điểm chung này.
c. d không cắt P .
d. d và P có một giao điểm nằm trên đường thẳng y  2 .
C. BÀI TẬP TRẮC NGHIỆM Câu 1:
Tọa độ đỉnh của parabol y   2
x  4x  3 là
A. I 2;7 .
B. I 2;7 .
C. I 2;7 .
D. I 2;7 . Câu 2: Cho hàm số y  2
x  2x  3 có đồ thị P . Trục đối xứng của P là A. y  1. B. x  1. C. x  1. D. y  1. Câu 3:
Tung độ đỉnh của parabol y  2
x  3x  5 là 3 11 25 5 A. . B. . C. . D. . 2 4 4 2 63
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI Câu 4:
Cho hàm số y  f x  2
x  6x  8 có đồ thị P . Xét các mệnh đề sau đây:
I. P cắt Oy tại 2 điểm phân biệt.
II. Tung độ đỉnh của P là 1
III. P có trục đối xứng x  3  0 Mệnh đề nào đúng? A. Chỉ I. B. I và II. C. I và III. D. II và III. Câu 5:
Cho hàm số y   2
x  5x  4 . Khẳng định nào sau đây đúng? 5 5
A. Hàm số có giá trị lớn nhất là .
B. Hàm số có giá trị nhỏ nhất là . 2 2 9 9
C. Hàm số có giá trị nhỏ nhất là .
D. Hàm số có giá trị lớn nhất là . 4 4 Câu 6: Cho hàm số y  2
x  2x  3 . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên ; 2 .
B. Hàm số nghịch biến trên   ;1 .
C. Hàm số đồng biến trên ; 2 .
D. Hàm số đồng biến trên   ;1 . Câu 7:
Cho hàm số y   2
x  4x  2 . Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên ; 3 .
B. Hàm số đồng biến trên ; 2 .
C. Hàm số nghịch biến trên 3;  .
D. Hàm số nghịch biến trên 2;  . Câu 8:
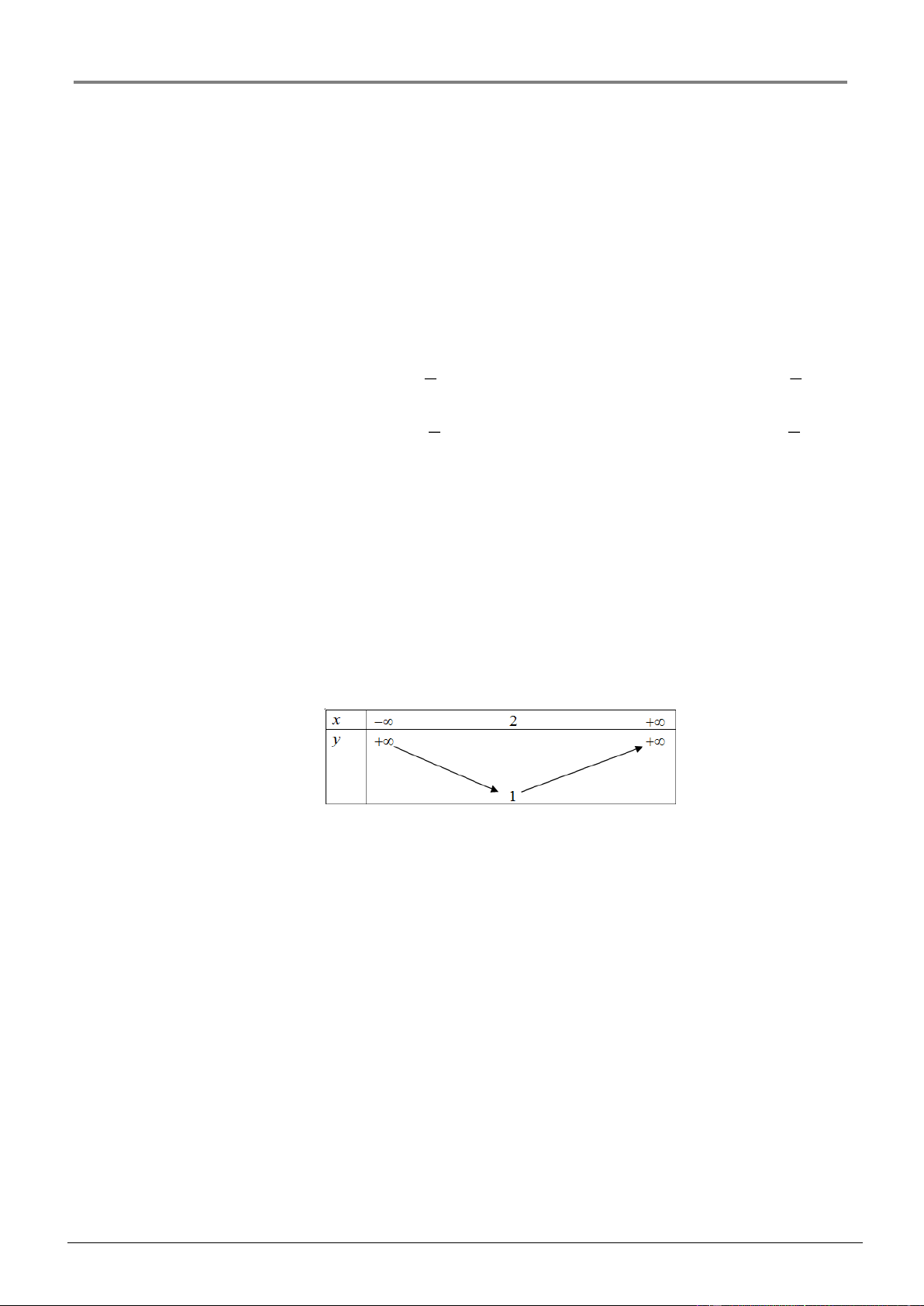
Tìm hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây A. y  2
x  2x  1 . B. y   2
x  4x  3 . C. y  2
x  4x  5 . D. y  2
x  4x  5 . Câu 9:
Tìm giá trị M lớn nhất của hàm số y   2
x  4x  3 trên 0; 4   A. M  3. B. M  7 .
C. M  29 .
D. M  0 .
Câu 10: Gọi I là đỉnh của parabol y  2
x  4x  5 . Tính tổng khoảng cách h từ I đến hai trục tọa độ. A. h  1. B. h  3 . C. h  4 .
D. h  5 .
Câu 11: Với giá trị của m để parabol y  2
x  3x  m cắt trục hoành tại điểm có hoành độ bằng 2. A. m  2 . B. m  0 . C. m  1.
D. m  2 .
Câu 12: Xác định parabol P y  2 :
ax  4x  c biết P có trục đối xứng x  2 và cắt trục
hoành tại điểm A3;0 ? 64 Trường THPT MARIE CURIE 12 48
A. P y  2 :
x  4x  3 .
B. P : y  2 x  4x  . 5 5
C. P y  2 :
x  4x  6 .
D. P y  2 :
2x  4x  6 .
Câu 13: Hàm số y  2
2x  4x  1
A. đồng biến trên khoảng ;2 và nghịch biến trên khoảng 2; .
B. nghịch biến trên khoảng ;2 và đồng biến trên khoảng 2; .
C. đồng biến trên khoảng ; 
1 và nghịch biến trên khoảng 1;  .
D. nghịch biến trên khoảng ; 
1 và đồng biến trên khoảng 1;  .
Câu 14: Cho hàm số y  2
ax  bx  c a  0 . Khẳng định nào sau đây là sai?  b 
A. Hàm số đồng biến trên khoảng  ;    .  2a   b 
B. Hàm số nghịch biến trên khoảng ;    .  2a  b
C. Đồ thị của hàm số có trục đối xứng là đường thẳng x   . 2a
D. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.
Câu 15: Cho hàm số y  2
ax  bx  c a  0 có đồ thị P . Tọa độ đỉnh của P là  b    b    b    b   A. I   ; . B. I  ;   . C. I  ;   . D. I  ; .  2a 4a   a 4a   2a 4a   2a 4a 
Câu 16: Trục đối xứng của parabol P y  2 :
2x  6x  3 là
A. x   3 .
B. y   3 . C. x  3. D. y  3. 2 2
Câu 17: Trong các hàm số sau, hàm số nào có đồ thị nhận đường x  1 làm trục đối xứng? A. y   2
2x  4x  1 . B. y  2
2x  4x  3 . C. y  2
2x  2x  1. D. y  2 x  x  2 .
Câu 18: Đỉnh của parabol P y  2 :
3x  2x  1 là  1 2   1 2   1 2   1 2  A. I   ;  . B. I  ;    . C. I ;    .
D. I  ;  .  3 3   3 3   3 3   3 3 
Câu 19: Hàm số nào sau đây có đồ thị là parabol có đỉnh I 1; 3 ? A. y  2
2x  4x  3 . B. y  2
2x  2x  1. C. y  2
2x  4x  5 . D. y  2
2x  x  2 .
Câu 20: Tọa độ giao điểm của P y  2 :
x  4x với đường thẳng d : y  x  2 là
A. M1;  1 , N 2;0 .
B. M1;3, N2; 4 .
C. M0;2, N2;4 . D. M3;  1 , N 3; 5. 65
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
Câu 21: Gọi Aa;b và Bc;d là tọa độ giao điểm của P y  x  2 : 2
x và  : y  3x  6 . Giá
trị b  d bằng : A. 7 . B. 7 . C. 15 . D. 15.
Câu 22: Parabol P y  2 :
x  4x  4 có số điểm chung với trục hoành là A. 0 . B. 1 . C. 2 . D. 3 .
Câu 23: Cho hàm số bậc hai  2 y
ax  bx  c a  0 có đồ thị P . Tọa độ đỉnh của P là  b    b    c    b   A. I ;   . B. I ;   . C. I ;   . D. I ;   .  a 4a   2a 4a   2a 4a   2a 4a 
Câu 24: Cho hàm số y  2
x  2x  2 . Câu nào sau đây là sai?
A. y tăng trên 1; .
B. y giảm trên 1; .
C. y giảm trên   ;1 .
D. y tăng trên 3;  .
Câu 25: Hàm số nào sau đây nghịch biến trong khoảng P y  2 :
x  4x  3 ?
A. d : y  mx  3 . B. m . C. d D. P . Câu 26: Hàm số nào 1;
sau đây đồng biến trong khoảng  ? 2 2 A. y  2 2x  1. B. y   2 2x  1 .
C. y  2 x  1
D. y   2 x  1 .
Câu 27: Cho hàm số: y  2
x  2x  3 . Trong các mệnh đề sau, tìm mệnh đề đúng?
A. y tăng trên 0;  .
B. y giảm trên   ;1 .
C. Đồ thị của y có đỉnh I 1;0 .
D. y tăng trên 1; .
Câu 28: Bảng biến thiên của hàm số y   2
2x  4x  1 là bảng nào sau đây? x - ∞ 2 + ∞ x - ∞ 2 + ∞ 1 + ∞ + ∞ y y - ∞ A. - ∞ . B. 1 . x - ∞ 1 + ∞ x - ∞ 1 + ∞ 3 y + ∞ + ∞ y - ∞ - ∞ C. . D. 3 .
Câu 29: Tìm tập xác định của hàm số y  2
x  2x  1 là
A. D  . B. D   \  1 .
C. D    ;1 .
D. D  1;.
Câu 30: Cho P y  2 :
x  2x  3 . Tìm mệnh đề đúng 66 Trường THPT MARIE CURIE
A. Hàm số đồng biến trên   ;1 .
B. Hàm số nghịch biến trên   ;1 .
C. Hàm số đồng biến trên ; 2 .
D. Hàm số nghịch biến trên ; 2 . Câu 31: Cho hàm số 2
y  2x  x  3 , điểm nào thuộc đồ thị hàm số A. M 2;  1 . B. M1;  1 . C. M2;3 . D. M0;3 .
Câu 32: Parabol y  2
x  4x  4 có đỉnh là
A. I 1;1 .
B. I 2;0 .
C. I 1;  1 .
D. I 1; 2 .
Câu 33: Cho P y  2 :
x  4x  3 . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên ; 4 .
B. Hàm số nghịch biến trên ; 4 .
C. Hàm số đồng biến trên ; 2 .
D. Hàm số nghịch biến trên ; 2 .
Câu 34: Trong các hàm số sau, hàm số nào có đồ thị đi qua điểm M 1; 3 và trục đối xứng x  3 A. y   2 x  6x . B. y  2
x  3x  1 . C. y  2
x  2x  2 . D. y   2
x  6x  2 .
Câu 35: Cho hàm số y  2
ax  bx  c a  0 có đồ thị P . Khi đó, tọa độ đỉnh của P là:  b    b    b    b   A. I   ;  . B. I  ;    . C. I  ;    . D. I  ;  .  2a 4a   a a   2a 4a   2a 2a 
Câu 36: Cho hàm số y  2
x  2x có đồ thị P . Tọa độ đỉnh của P là A. 0;0. B. 1; 1. C. 1;3 . D. 2;0 .
Câu 37: Cho hàm số y  2
2x  6x  3 có đồ thị P . Trục đối xứng của P là
A. x   3 .
B. y   3 . C. x  3 . D. y  3 . 2 2
Câu 38: Cho hàm số y  2
x  2x  3 có đồ thị là parabol (P) . Trục đối xứng của (P) là
A. x  1.
B. x  1.
C. x  2 . D. x  2 .
Câu 39: Parabol y  2
2x  x  2 có đỉnh là  1 19   1 15   1 15   1 15  A. I  ;  . B. I   ;  . C. I  ;  . D. I  ;    .  4 8   4 8   4 8   4 8 
Câu 40: Giá trị nhỏ nhất của hàm số y   2
x  2x  3 bằng A. 3 . B. 5 . C. 4 . D. 2 .
Câu 41: Đồ thị hàm số y   2
x  2x  3 cắt trục hoành tại mấy điểm A. 0 . B. 1 . C. 3 . D. 2 .
Câu 42: Cho hàm số: y  2
x  4x  7 . Chọn khẳng định đúng? 67
Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên .
C. Hàm số đồng biến trên khoảng 2;  . D. Hàm số đồng biến trên khoảng ;2 .
Câu 43: Parabol y  2
2x  3x  1 nhận đường thẳng
A. x  3 làm trục đối xứng.
B. x   3 làm trục đối xứng. 2 4
C. x   3 làm trục đối xứng.
D. x  3 làm trục đối xứng. 2 4
Câu 44: Parabol y  2
x  4x  4 có đỉnh là:
A. I 1;1 .
B. I 2;0 .
C. I 1;  1 .
D. I 1; 2 .
Câu 45: Cho hàm số y  2
x  2x  2 . Câu nào sau đây là sai?
A. y tăng trên 1; .
B. y giảm trên 1; .
C. y giảm trên   ;1 .
D. y tăng trên 3;  .
Câu 46: Hàm số nào sau đây nghịch biến trong khoảng ;0 ? 2 2 A. y  2 2x  1. B. y   2 2x  1 .
C. y  2 x  1
D. y   2 x  1 . Câu 47: Hàm số nào 1;
sau đây đồng biến trong khoảng  ? 2 2 A. y  2 2x  1. B. y   2 2x  1 .
C. y  2 x  1
D. y   2 x  1 .
Câu 48: Cho hàm số: y  2
x  2x  3 . Trong các mệnh đề sau, tìm mệnh đề đúng?
A. y tăng trên 0;  .
B. y giảm trên   ;1 .
C. Đồ thị của y có đỉnh I 1;0 .
D. y tăng trên 1; .
Câu 49: Tìm tập xác định của hàm số y  2
x  2x  1 là
A. D  . B. D   \  1 .
C. D    ;1 .
D. D  1;
Câu 50: Cho P y  2 :
x  2x  3 . Tìm mệnh đề đúng
A. Hàm số đồng biến trên   ;1 .
B. Hàm số nghịch biến trên   ;1 .
C. Hàm số đồng biến trên ; 2 .
D. Hàm số nghịch biến trên ; 2 . Câu 51: Cho hàm số 2
y  2x  x  3 , điểm nào thuộc đồ thị hàm số A. M 2;  1 . B. M1;  1 . C. M2;3 . D. M0;3 .
Câu 52: Cho P y  2 :
x  4x  3 . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên ; 4 .
B. Hàm số nghịch biến trên ; 4 . 68 Trường THPT MARIE CURIE
C. Hàm số đồng biến trên ; 2 .
D. Hàm số nghịch biến trên ; 2 .
Câu 53: Parabol y  2
x  3x  2 có đỉnh I và cắt trục hoành tại 2 điểm phân biệt M, N .
Tính diện tích S của tam giác IMN ? A. S  1. B. S  1 .
C. S  1 . D. S  1 . 5 8 4
Câu 54: Tính khoảng cách d ngắn nhất từ đỉnh I của parabol y  2 x  mx  2 3 6 4m  2m  4 đến trục Ox . A. d  1.
B. d  2 .
C. d  3 . D. d  4 .
Câu 55: Tính khoảng cách d lớn nhất từ đỉnh I của parabol y  2 x  mx  2 4 3m  4m  2 đến trục Ox . A. d  1.
B. d  2 .
C. d  3 .
D. d  4 .
Câu 56: Tìm m để hàm số y   2
x  4mx  4m  9 nghịch biến trên khoảng 2;  . A. m  2 .
B. m  1.
C. m  1.
D. m  1.
Câu 57: Tìm giá trị của tham số m để hàm số y   2
x  8x  5m  24 có giá trị lớn nhất trên đoạn 1;6   bằng 1 . A. m  1,5 . B. m  2,5 . C. m  1,4 . D. m  5 .
Câu 58: Cho hàm số y   2
x  5x  4 . Hàm số có bảng biến thiên nào sau đây? 5 5 x - ∞ + ∞ x - ∞ + ∞ 2 2 -9 + ∞ 4 + ∞ y y 9 - ∞ - 4 A. - ∞ B. 5 5 x - ∞ + ∞ 2 x - ∞ + ∞ 2 9 + ∞ + ∞ y 4 y 9 4 - ∞ C. D. - ∞
Câu 59: Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm
số y  f x  2 4x  mx  2 4
m  2m trên đoạn 2;0 
 bằng 3. Tính tổng T các phần tử của . S
A. T   3 .
B. T  1 .
C. T  9 . D. T  3 . 2 2 2 2 69
Document Outline

3ham-so_292021113335
- Chương 2. HÀM SỐ BẬC NHẤT VÀ BẬC HAI
  - Bài 1. HÀM SỐ
    - A.TÓM TẮT LÝ THUYẾT
      - VẤN ĐỀ 1. Tính giá trị của hàm số tại một điểm
      - VẤN ĐỀ 2. Đồ Thị Hàm Số
      - VẤN ĐỀ 3. Tập xác định của hàm số
      - VẤN ĐỀ 4. Sự biến thiên của hàm số
    - A. TÓM TẮT LÝ THUYẾT
    - B. PHƯƠNG PHÁP GIẢI
    - C. VÍ DỤ
    - C. BÀI TẬP RÈN LUYỆN
    - BÀI TẬP TRẮC NGHIỆM
4ham-so-bac-nhat_292021113335
- Bài 2. HÀM SỐ BẬC NHẤT
  - A. TÓM TẮT LÝ THUYẾT
    - VẤN ĐỀ 1: Xét tính đồng biến, nghịch biến
    - VẤN ĐỀ 2: Đồ thị hàm số
    - VẤN ĐỀ 3: Đồ thị hàm số y=|ax+b|
  - C. BÀI TẬP TRẮC NGHIỆM
- Word Bookmarks
  - MTBlankEqn
5ham-so-bac-hai_292021113335
- Bài 2. HÀM SỐ BẬC HAI (tiếp theo bài hàm số bậc nhất)
  - A. TÓM TẮT LÝ THUYẾT
- Word Bookmarks
  - MTBlankEqn

Các dạng bài tập hàm số bậc nhất và bậc hai

Thông tin :

Tài liệu liên quan:

Toán 10 Bài 15: Hàm số - Kết Nối Tri Thức

Toán 10 Bài 17: Dấu của tam thức bậc hai Giải SGK Toán 10 trang 24 - Tập 2

Toán 10 Bài 16: Hàm số bậc hai - Kết Nối Tri Thức

Toán 10 Bài tập cuối chương VI - Kết nối tri thức với cuộc sống

Toán 10 Bài 18: Phương trình quy về phương trình bậc hhai - Kết Nối Tri Thức