Các dạng bài tập tích phân Toán 12 Cánh Diều

Tài liệu gồm 120 trang, tổng hợp các dạng bài tập chuyên đề tích phân môn Toán 12 bộ sách Cánh Diều, có đáp án và lời giải chi tiết. Các bài tập trong tài liệu được biên soạn dựa trên định dạng trắc nghiệm mới nhất, với cấu trúc gồm 03 phần: Câu trắc nghiệm nhiều phương án lựa chọn; Câu trắc nghiệm đúng sai; Câu trắc nghiệm trả lời ngắn. Mời bạn đọc đón xem!

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Nguyên hàm. Tích phân (CD)

Môn: Toán 12

Sách: Cánh diều

Thông tin:

120 trang 1 tháng trước

Tác giả:

Profile Lê Phương
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
BÀI 2
TÍCH PHÂN
1. Khái niệm tích phân
a. Diện tích hình thang cong
Nếu hàm số
( )
fx
liên tục và không âm trên đoạn
[
]
;ab
thì diện tích
S
của hình thang cong giới hạn
bởi đồ thị
( )
y fx=
, trục hoành và hai đường thẳng
,x ax b= =
được tính bởi:
(
) ( )
S Fb Fa
= −
trong đó
( )
Fx
là một nguyên hàm của
( )
fx
trên đoạn
[ ]
;ab
.
b. Khái niệm tích phân
Cho hàm số
(
)
fx
liên tục trên đoạn
. Nếu
( )
Fx
là nguyên hàm của hàm số
( )
fx
trên đoạn
[ ]
;ab
thì hiệu số
( ) ( )
Fb Fa−
được gọi là tích phân từ
a
đến
b
của hàm số
( )
fx
, kí hiệu
(
)
b
a
f x dx
∫
Chú ý:
• Hiệu số
( ) ( )
Fb Fa−
còn được kí hiệu là
( )
b
a
Fx
.
Vậy
( )
( ) ( ) ( )
b
b
a
a
f x dx F x F b F a= = −
∫
• Ta gọi
b
a
∫
là dấu tích phân,
a
là cận dưới,
b
là cận trên,
( )
f x dx
là biểu thức dưới dấu tích phân và
( )
fx
là hàm số dưới dấu tích phân.
• Quy ước:
( ) ( ) ( )
;
ab a
aa b
f x dx f x dx f x dx= −
∫∫ ∫
• Tích phân của hàm số
f
từ
a
đến
b
chỉ phụ thuộc vào
f
và các cận
,ab
mà không phụ thuộc vào
biến
x
hay
t
, nghĩa là
( ) ( )
bb
aa
f x dx f t dt=
∫∫
.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
• Ý nghĩa hình học của tích phân
Nếu hàm số
( )
fx
liên tục và không âm trên đoạn
[ ]
;ab
thì
( )
b
a
f x dx
∫
là diện tích
S
của hình thang
cong giới hạn bởi đồ thị
( )
y fx=
, trục hoành và hai đường thẳng
,x ax b= =
.
( )
b
a
S f x dx=
∫
Nhận xét:
• Nếu hàm số
( )
fx
có đạo hàm
( )
'
fx
và
( )
'fx
liên tục trên đoạn
[ ]
;ab
thì
( ) ( ) ( )
'
b
a
f b f a f x dx−=
∫
.
• Cho hàm số
(
)
fx
liên tục trên đoạn
[ ]
;ab
. Khi đó
( )
1
b
a
f x dx
ba−
∫
được gọi là giá trị trung bình của
hàm số
( )
fx
trên đoạn
[ ]
;
ab
.
• Đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mọi
thời điểm:
() '()vt s t=
. Do đó, nếu biết tốc độ
()vt
tại mọi thời điểm
[ ]
;t ab∈
thì tính được quãng đường
di chuyển trong khoảng thời gian từ
a
đến
b
theo công thức:
(
) (
)
()
b
a
s s b s a v t dt=−=
∫
2. Tính chất của tích phân
Cho hai hàm số
( ) ( )
,f x gx
liên tục trên đoạn
[ ]
;ab
. Khi đó:
• Tính chất 1:
( ) ( )
bb
aa
kf x dx k f x dx=
∫∫
, với
k
là hằng số.
• Tính chất 2:
( ) ( ) ( ) ( )
b bb
a aa
f x g x dx f x dx g x dx

+= +

∫ ∫∫
( ) ( ) ( ) (
)
b bb
a aa
f x g x dx f x dx g x dx

−= −

∫ ∫∫
• Tính chất 3:
(
) ( ) ( )
bcb
aac
f x dx f x dx f x dx= +
∫∫∫
với
(
)
;c ab∈
.
CHỦ ĐỀ 1
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
TÍNH TÍCH PHÂN CỦA MỘT SỐ HÀM SỐ
DẠNG 1
TÍNH TÍCH PHÂN SỬ DỤNG BẢNG NGUYÊN HÀM SƠ CẤP
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương
án.
Nguyên hàm của một hàm số sơ cấp
Nguyên hàm của hàm số lũy thừa
0dx C=
∫
Cxdx +=
∫
( )
1
1
1
x
x dx C
α
α
α
α
+
= + ≠−
+
∫
Nguyên hàm của hàm số
1
y
x
=
( )
0ln ≠+=
∫
xCx
x
dx
Nguyên hàm của hàm số lượng giác
Cxxdx +=
∫
sincos
Cxxdx +−=
∫
cossin
Cxdx
x
+=
∫
tan
cos
1
2
Cxdx
x
+−=
∫
cot
sin
1
2
Nguyên hàm của hàm số mũ
Cedxe
xx
+=
∫
( )
10
ln
≠<+=
∫
aC
a
a
dxa
x
x
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Câu 1. Tính tích phân
2
0
(2 1)I x dx= +
∫
A.
5I =
. B.
6
I =
. C.
2I =
. D.
4I =
.
Câu 2. Tích phân
( )( )
1
0
3 1 3dxx x++
∫
bằng
A.
12
. B.
9
. C.
5
. D.
6
.
Câu 3. Tính tích phân
2
1
11
e
I dx
xx

= −


∫
A.
1
I
e
=
B.
1
1I
e
= +
C.
1I =
D.
Ie=
Câu 4. Biết
3
1
2
ln ,
x
dx a b c
x
+
= +
∫
với
, , , 9.abc c∈<
Tính tổng
.S abc=++
A.
7S =
. B.
5S =
. C.
8S =
. D.
6S =
.
Câu 5. Tích phân
1
31
0
d
x
ex
+
∫
bằng
A.
( )
4
1
3
ee+
B.
3
ee−
C.
(
)
4
1
3
ee
−
D.
4
ee−
Câu 6. Biết
1
0
2
x
x
ee
dx b
a
= +
∫
( )
,ab∈
. Khi đó giá trị của
P ab= +
là
A.
3P = −
B.
1P =
C.
1P = −
D.
3P =
Câu 7. Giá trị của
1
2
0
4
2
x
x
e
I dx
e
−
=
+
∫
bằng
A.
( )
23Ie
= +
0. B.
( )
1
3
2
Ie= +
. C.
3Ie
= −
. D.
( )
23Ie= −
.
Câu 8. Biết
2
2
1
1 . ln 2
x
x
e
e dx e a e b
x
−

− =++


∫
( )
,ab∈
. Khi đó giá trị của
.
ab
P
ab
+
=
là
A.
3P = −
B.
1P =
C.
1P = −
D.
2P = −
Câu 9. Biết
1
21 3
0
11
xx
x
ee
I dx b
ea
−−
−+
= = +
∫
( )
,ab∈
. Khi đó giá trị của
.
ab
P
ab
+
=
là
A.
4
1Pe= −
B.
4
2
1e
P
e
−
=
C.
4
4
1e
P
e
−
=
D.
4
4
1 e
P
e
−
=
Câu 10. Giá trị của
2
0
sin xdx
π
∫
bằng
A. 0. B. 1. C. -1. D.
2
π
.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Câu 11. Biết
( )
2
2
3
3
2sin 3cos
2
ab
x x x dx
c
π
π
π
+
+ += +
∫
( )
,,abc∈
. Khi đó giá trị của
23
Pa b c
=++
là
A.
45P =
B.
60P =
C.
65P =
D.
70P =
Câu 12. Biết
3
2
4
3tan 3xdx a b
c
π
π
π
= ++
∫
(
)
,,abc
∈
. Khi đó giá trị của
P abc=++
là
A.
6
P =
B.
4P = −
C.
4P =
D.
6
P = −
Câu 13. Biết
( )
4
2
6
2cot 5 3x dx b c
a
π
π
π
+ =++
∫
(
)
,,abc
∈
. Khi đó giá trị của
P abc=++
là
A.
6P =
B.
4P = −
C.
4P =
D.
6P = −
Câu 14. Biết
2
22
0
sin cos
44
xx a
dx
cb
π
π
= +
∫
với
,ab∈
và
a
b
là phân số tối giản. Khi đó giá trị của
P abc=++
là
A.
17P =
B.
16
P =
C.
32P =
D.
49P =
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý A), B), C), D) ở mỗi câu, thí sinh chọn đúng hoặc
sai.
Câu 15. Cho hàm số
y fx
liên tục trên
;ab


. Các mệnh đề sau đây đúng hay sai?
A.
dd
ba
ab
fx x fx x

B.
dd
ba
ab
fx x fx x

C.
dd
bb
aa
fx x fx x

22
D.
d.
a
a
fx x
2024 0
Câu 16. Cho hàm số
,y f x y gx
liên tục trên
;ab


. Các mệnh đề sau đây đúng hay sai?
A.
ddd
b bb
a aa
f x gx x fx x gx x





. B.
. d d. d
b bb
a aa
fxgxx fxx gxx

.
C.
dd
bb
aa
kfx x k fx x

. D.
d
d
d
b
b
a
b
a
a
fx x
fx
x
gx
gx x
.
Câu 17. Cho hàm số
y fx
liên tục trên
và
,,abc
thỏa mãn
abc
. Các mệnh đề sau đây
đúng hay sai?
A.
d dd
c bc
a ab
fx x fx x fx x

B.
ddd
c bc
a ab
fx x fx x fx x

Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
C.
d dd
c bc
a ab
fx x fx x fx x

D.
ddd
c bb
a ac
fx x fx x fx x


Câu 18. Cho
(
)
fx
,
()gx
là hai hàm số liên tục trên
. Các mệnh đề sau đây đúng hay sai?
A.
( )d ( )d
bb
aa
fx x fy y=
∫∫
B.
( )
() ()d ()d ()d.
b bb
a aa
f x gx x f x x gx x+= +
∫ ∫∫
C.
( )d ( )d
bb
aa
fx x ft x=
∫∫
D.
( )
()()d ()d ()d.
b bb
a aa
f xgx x f x x gx x
=
∫ ∫∫
Câu 19. Các mệnh đề sau đây đúng hay sai?
A.
2024
2024
d 4048x
.
B.
12 1 2
. d d. d
b bb
a aa
fxfxx fxx fxx

.
C. Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
. Khi đó
( )
1
b
a
f x dx
ba−
∫
được gọi là giá trị trung bình
của hàm số
( )
fx
trên đoạn
[ ]
;ab
.
D. Nếu hàm số
( )
fx
có đạo hàm
(
)
'fx
và
( )
'fx
liên tục trên đoạn
[ ]
;ab
thì
( ) ( ) ( )
'
b
a
f b f a f x dx−=
∫
.
Câu 20. Cho hàm
( )
fx
là hàm liên tục trên đoạn
[ ]
;ab
với
ab<
và
( )
Fx
là một nguyên hàm của
hàm
( )
fx
trên
[ ]
;ab
. Các mệnh đề sau đây đúng hay sai?
A.
( ) ( ) ( )
( )
b
a
kf x dx k F b F a= −
∫
B.
(
) ( ) (
)
a
b
f x dx F b F a
= −
∫
C. Diện tích S của hình phẳng giới hạn bởi đường thẳng
;x ax b= =
; đồ thị của hàm số
( )
y fx=
và
trục hoành được tính theo công thức
( )
( )
S Fb Fa= −
D.
( ) (
)
23 23
b
b
a
a
f x dx F x+= +
∫
Câu 21. Các mệnh đề sau đây đúng hay sai
A.
1
2
0
4
3
2
x
x
e
dx e
e
−
= −
+
∫
B.
1
0
1
22
x
x
ee
dx = +
∫
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
C.
2
2
1
1 ln 2
x
x
e
e dx e e
x
−

− = −−


∫
D.
1
21 3
4
0
1
1
xx
x
ee
dx e
e
−−
−+
= −
∫
PHẦN III. Câu trắc nghiệm trả lời ngắn. Mỗi câu hỏi thí sinh chỉ trả lời đáp án.
Câu 22. Với
,ab
là các tham số thực. Tính tích phân
(
)
2
0
3 2 1d
b
I x ax x
= −−
∫
.
Trả lời: ………………..
Câu 23. Cho
(
)
2
0
3 2 1d 6
m
xx x−+ =
∫
. Tính giá trị của tham số m .
A.
( )
1; 2−
. B.
( )
;0−∞
. C.
( )
0; 4
. D.
( )
3;1−
.
Trả lời: ………………..
Câu 24. Tính tích phân
2
1
1
d
x
Ix
x
−
=
∫
.
Trả lời: ………………..
Câu 25. Tính
2
2
3
4
1
xx
I dx
x

−
=



∫
.
Trả lời: ………………..
Câu 26. Tính
( )
( )
2
3
1
11
I x x dx=+−
∫
.
Trả lời: ………………..
Câu 27. Tính
2
23
2
1
( 1)x
I dx
x
+
=
∫
.
Trả lời: ………………..
Câu 28. Tính
1
1 21
0
5 .7
xx
I dx
+−
=
∫
.
Trả lời: ………………..
Câu 29. Tính
( )
1
2
0
x
I x e dx
−−
= +
∫
.
Trả lời: ………………..
Câu 30. Tính
3
2
2
6
sin
1
x
I x dx
x
π
π

= −


∫
.
Trả lời: ………………..
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Câu 31. Tính
2
3
2
6
1
sinI x dx
x
π
π

= −


∫
.
Trả lời: ………………..
Câu 32. Biết
( )
2
1
12
0
2
1
x
x
e
c
dx ae b
e ee
−
−
+
= +++
∫
( )
,,abc∈
. Tính giá trị của
P abc=++
.
Trả lời: ………………..
Câu 33. Biết
3
0
1 cos 2
3
1 cos 2
x
dx a
xb
π
π
−
= +
+
∫
( )
,ab∈
. Tính
ab+
.
Trả lời: ………………..
Câu 34. Tính
( )
2
1
3
0
2024 1
x
x
I dx
e
−
+
=
∫
.
Trả lời: ………………..
Câu 35. Tính
( )
2
1
1
0
2
x
x
e
I dx
e
−
−
+
=
∫
.
Trả lời: ………………..
Câu 36. Tính
2
2
2
3
1
2024
2023
x
x
e
I e dx
x
−

= +


∫
.
Trả lời: ………………..
Câu 37. Tính
2
31
2
1
1
4 2.3
x
I x dx
x
+

= −+


∫
.
Trả lời: ………………..
DẠNG 2
TÍCH PHÂN HÀM TRỊ TUYỆT ĐỐI
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Tính tích phân:
( )
.
b
a
I f x dx=
∫
?
Phương pháp
Bước 1. Xét dấu
( )
fx
trên đoạn
[ ]
;ab
.
Bước 2. Dựa vào bảng xét dấu trên đoạn
[
]
;
ab
để khử
( )
fx
. Sau đó sử dụng các phương pháp tính tích
phân đã học đê tính
( )
.
b
a
I f x dx=
∫
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương
án.
Câu 38. Giá trị của
2
0
1 cos 2I xdx
π
= −
∫
bằng
A.
3
. B.
42
. C.
23
. D.
2
π
.
Câu 39. Tính tích phân
2
0
2I x dx= −
∫
.
A.
2
I = −
. B.
4I =
. C.
2I =
. D.
0I =
.
Câu 40. Tính tích phân
2
3
0
I x x dx= −
∫
.
A.
1
2
I
= −
. B.
5
I =
. C.
1
2
I =
. D.
5
2
I =
.
Câu 41. Tính tích phân
2
2
0
23I x x dx= +−
∫
.
A.
2I = −
. B.
4I =
. C.
5I =
. D.
4I = −
.
Câu 42. Cho tích phân
( )
3
2
3
20 4 16
32 1 3 2
333
I x dx a b
−
= + − = ++ = +
∫
với
,ab∈
. Tính
P ab= +
.
A.
40
3
P =
B.
80
3
P =
C.
17
3
P =
D.
98
3
P =
Câu 43. Tính tích phân
( )
5
2
22I x x dx
−
= +−−
∫
.
A.
38I =
. B.
44I =
. C.
48I =
. D.
40I =
.
Câu 44. Cho tích phân
3
0
24
ln 2
x
b
I dx a
c
=−=+
∫
với
,,abc∈
và
b
c
là phân số tối giản. Tính
222
Pabc=++
.
A.
15P =
B.
10P =
C.
5P =
D.
18P =
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Câu 45. Tính tích phân
1
1
22
xx
I dx
−
−
= −
∫
.
A.
1
ln 2
. B.
ln 2
. C.
2 ln 2
. D.
2
ln 2
.
Câu 46. Tính tích phân
(
)
2
1
1I x x dx
−
= −−
∫
.
A.
0I
=
. B.
2
I =
. C.
2I = −
. D.
3I
= −
.
Câu 47. Cho
a
là số thực dương, tính tích phân
1
d
a
I xx
−
=
∫
theo
a
.
A.
2
1
2
a
I
+
=
. B.
2
2
2
a
I
+
=
. C.
2
21
2
a
I
−+
=
. D.
2
31
2
a
I
−
=
.
Câu 48. Cho số thực
1
m
>
thỏa mãn
1
211
m
mx dx
−=
∫
. Khẳng định nào sau đây đúng?
A.
( )
4; 6m ∈
. B.
( )
2; 4m ∈
. C.
( )
3; 5m∈
. D.
( )
1; 3m ∈
.
Câu 49. Khẳng định nào sau đây là đúng?
A.
11
3
3
11
ddx x xx
−−
=
∫∫
. B.
( )
2018 2018
42 42
11
1d 1 dxx x xx x
−−
−+ = −+
∫∫
.
C.
( )
( )
33
22
1d 1d
xx
ex x ex x
−−
+= +
∫∫
. D.
2
22
22
1 cos d sin dxx xx
ππ
ππ
−−
−=
∫∫
.
Câu 50. Tính tích phân
4
2
1
69I x x dx= −+
∫
.
A.
5
2
I =
. B.
1
2
I = −
. C.
2I = −
. D.
1
2
I
=
.
PHẦN II. Câu trắc nghiệm trả lời ngắn. Mỗi câu hỏi thí sinh chỉ trả lời đáp án.
Câu 51. Tính tích phân
3
2
3
1I x dx
−
= −
∫
.
Trả lời: ………………..
Câu 52. Tính tích phân
2
2
1
23I x x dx
−
=−− +
∫
.
Trả lời: ………………..
Câu 53. Tính tích phân
2
1
1x
I dx
x
+
=
∫
.
Trả lời: ………………..
Câu 54. Tính tích phân
6
2
2
8 16I x x dx= −+
∫
.
Trả lời: ………………..
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Câu 55. Tính tích phân
1
2
2
4 69
I x x dx
−
= ++
∫
.
Trả lời: ………………..
Câu 56. Tính tích phân
1
2
0
9 61I x x dx= −+
∫
.
Trả lời: ………………..
Câu 57. Tính tích phân
2
0
1 cos 2
I xdx
π
= +
∫
.
Trả lời: ………………..
Câu 58. Tính tích phân
2
0
1 cos 2I xdx
π
= −
∫
.
Trả lời: ………………..
Câu 59. Tính tích phân
2
0
1 sin 2
I xdx
π
= −
∫
.
Trả lời: ………………..
Câu 60. Tính tích phân
2
0
1 sin 2I xdx
π
= +
∫
.
Trả lời: ………………..
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
BÀI 2
TÍCH PHÂN
1. Khái niệm tích phân
a. Diện tích hình thang cong
Nếu hàm số
( )
fx
liên tục và không âm trên đoạn
[
]
;ab
thì diện tích
S
của hình thang cong giới hạn
bởi đồ thị
( )
y fx=
, trục hoành và hai đường thẳng
,x ax b= =
được tính bởi:
(
) ( )
S Fb Fa
= −
trong đó
( )
Fx
là một nguyên hàm của
( )
fx
trên đoạn
[ ]
;ab
.
b. Khái niệm tích phân
Cho hàm số
(
)
fx
liên tục trên đoạn
. Nếu
( )
Fx
là nguyên hàm của hàm số
( )
fx
trên đoạn
[ ]
;ab
thì hiệu số
( ) ( )
Fb Fa−
được gọi là tích phân từ
a
đến
b
của hàm số
( )
fx
, kí hiệu
(
)
b
a
f x dx
∫
Chú ý:
• Hiệu số
( ) ( )
Fb Fa−
còn được kí hiệu là
( )
b
a
Fx
.
Vậy
( )
( ) ( ) ( )
b
b
a
a
f x dx F x F b F a= = −
∫
• Ta gọi
b
a
∫
là dấu tích phân,
a
là cận dưới,
b
là cận trên,
( )
f x dx
là biểu thức dưới dấu tích phân và
( )
fx
là hàm số dưới dấu tích phân.
• Quy ước:
( ) ( ) ( )
;
ab a
aa b
f x dx f x dx f x dx= −
∫∫ ∫
• Tích phân của hàm số
f
từ
a
đến
b
chỉ phụ thuộc vào
f
và các cận
,ab
mà không phụ thuộc vào
biến
x
hay
t
, nghĩa là
( ) ( )
bb
aa
f x dx f t dt=
∫∫
.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
• Ý nghĩa hình học của tích phân
Nếu hàm số
( )
fx
liên tục và không âm trên đoạn
[ ]
;ab
thì
( )
b
a
f x dx
∫
là diện tích
S
của hình thang
cong giới hạn bởi đồ thị
( )
y fx=
, trục hoành và hai đường thẳng
,x ax b= =
.
( )
b
a
S f x dx=
∫
Nhận xét:
• Nếu hàm số
( )
fx
có đạo hàm
( )
'
fx
và
( )
'fx
liên tục trên đoạn
[ ]
;ab
thì
( ) ( ) ( )
'
b
a
f b f a f x dx−=
∫
.
• Cho hàm số
(
)
fx
liên tục trên đoạn
[ ]
;ab
. Khi đó
( )
1
b
a
f x dx
ba−
∫
được gọi là giá trị trung bình của
hàm số
( )
fx
trên đoạn
[ ]
;
ab
.
• Đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mọi
thời điểm:
() '()vt s t=
. Do đó, nếu biết tốc độ
()vt
tại mọi thời điểm
[ ]
;t ab∈
thì tính được quãng đường
di chuyển trong khoảng thời gian từ
a
đến
b
theo công thức:
(
) (
)
()
b
a
s s b s a v t dt=−=
∫
2. Tính chất của tích phân
Cho hai hàm số
( ) ( )
,f x gx
liên tục trên đoạn
[ ]
;ab
. Khi đó:
• Tính chất 1:
( ) ( )
bb
aa
kf x dx k f x dx=
∫∫
, với
k
là hằng số.
• Tính chất 2:
( ) ( ) ( ) ( )
b bb
a aa
f x g x dx f x dx g x dx

+= +

∫ ∫∫
( ) ( ) ( ) (
)
b bb
a aa
f x g x dx f x dx g x dx

−= −

∫ ∫∫
• Tính chất 3:
(
) ( ) ( )
bcb
aac
f x dx f x dx f x dx= +
∫∫∫
với
(
)
;c ab∈
.
CHỦ ĐỀ 1
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
TÍNH TÍCH PHÂN CỦA MỘT SỐ HÀM SỐ
DẠNG 1
TÍNH TÍCH PHÂN SỬ DỤNG BẢNG NGUYÊN HÀM SƠ CẤP
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương
án.
Nguyên hàm của một hàm số sơ cấp
Nguyên hàm của hàm số lũy thừa
0dx C=
∫
Cxdx +=
∫
( )
1
1
1
x
x dx C
α
α
α
α
+
= + ≠−
+
∫
Nguyên hàm của hàm số
1
y
x
=
( )
0ln ≠+=
∫
xCx
x
dx
Nguyên hàm của hàm số lượng giác
Cxxdx +=
∫
sincos
Cxxdx +−=
∫
cossin
Cxdx
x
+=
∫
tan
cos
1
2
Cxdx
x
+−=
∫
cot
sin
1
2
Nguyên hàm của hàm số mũ
Cedxe
xx
+=
∫
( )
10
ln
≠<+=
∫
aC
a
a
dxa
x
x
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Câu 1. Tính tích phân
2
0
(2 1)I x dx= +
∫
A.
5I =
. B.
6
I =
. C.
2I =
. D.
4I =
.
Lời giải
Chọn B.
Ta có
(
)
2
2
2
0
0
(2 1) 4 2 6I x dx x x= + = + =+=
∫
.
Câu 2. Tích phân
( )( )
1
0
3 1 3dxx x++
∫
bằng
A.
12
. B.
9
. C.
5
. D.
6
.
Lời giải
Chọn B.
Ta có:
( )( )
( ) ( )
11
1
2 32
0
00
3 1 3 d 3 10 3 d 5 3 9x x x x x xx x x+ + = ++ =++ =
∫∫
.
Vậy :
(
)( )
1
0
3 1 3d 9
xx x++ =
∫
.
Câu 3. Tính tích phân
2
1
11
e
I dx
xx

= −


∫
A.
1
I
e
=
B.
1
1I
e
= +
C.
1I =
D.
Ie=
Lời giải
Chọn A.
2
1
1
11 1 1
ln
e
e
I dx x
xx x e

=− = +=


∫
.
Câu 4. Biết
3
1
2
ln ,
x
dx a b c
x
+
= +
∫
với
, , , 9.abc c∈<
Tính tổng
.
S abc
=++
A.
7S =
. B.
5S =
. C.
8S =
. D.
6S =
.
Lời giải
Chọn A.
Ta có
3 3 33
3
1
1 1 11
22 2
1 2 2ln 2 2 ln 3.
x
dx dx dx dx x
xx x
+

=+=+=+ =+


∫ ∫ ∫∫
Do đó
2, 2, 3 7.abc S= = =⇒=
Câu 5. Tích phân
1
31
0
d
x
ex
+
∫
bằng
A.
( )
4
1
3
ee+
B.
3
ee−
C.
( )
4
1
3
ee−
D.
4
ee−
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
Lời giải
Chọn C.
1
31
0
d
x
ex
+
∫
( )
1
31
0
1
31
3
d
x
ex
+
= +
∫
1
31
0
1
3
x
e
+
=
( )
4
1
3
ee= −
.
Câu 6. Biết
1
0
2
x
x
ee
dx b
a
= +
∫
( )
,ab∈
. Khi đó giá trị của
P ab
= +
là
A.
3P
= −
B.
1P =
C.
1P = −
D.
3P =
Lời giải
Chọn B.
1
11
00
0
1
2 2 22
xx
x
x
e e ee
I dx dx

 
= = = = −

 
 


∫∫
Câu 7. Giá trị của
1
2
0
4
2
x
x
e
I dx
e
−
=
+
∫
bằng
A.
( )
23Ie= +
0. B.
( )
1
3
2
Ie
= +
. C.
3Ie= −
. D.
( )
23Ie= −
.
Lời giải
Chọn C.
(
)( )
( ) ( )
11 1
2
1
0
00 0
22
4
2 23
22
xx
x
xx
xx
ee
e
I dx dx e dx e x e
ee
−+
−
= = =− =−=−
++
∫∫ ∫
Câu 8. Biết
2
2
1
1 . ln 2
x
x
e
e dx e a e b
x
−

− =++


∫
( )
,ab∈
. Khi đó giá trị của
.
ab
P
ab
+
=
là
A.
3P
= −
B.
1P =
C.
1P = −
D.
2P
= −
Lời giải
Chọn D.
( )
22
2
2
1
11
1
1 ln ln 2
x
x xx
e
I e dx e dx e x e e
xx
−


= − = − = − = −−




∫∫
Câu 9. Biết
1
21 3
0
11
xx
x
ee
I dx b
ea
−−
−+
= = +
∫
( )
,ab∈
. Khi đó giá trị của
.
ab
P
ab
+
=
là
A.
4
1Pe= −
B.
4
2
1e
P
e
−
=
C.
4
4
1e
P
e
−
=
D.
4
4
1 e
P
e
−
=
Lời giải
Chọn D.
( )
1
11
21 3 4 4
14 1
44
00
0
1 11
1
41
x x xx
x xx x
x
ee ee e
I dx e e e dx e
e ee
−− − −
−− − −

−+ −
= = −+ = − + = =−

−−

∫∫
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
4
4
1
.
ab e
P
ab e
+−
⇒= =
Câu 10. Giá trị của
2
0
sin xdx
π
∫
bằng
A. 0. B. 1. C. -1. D.
2
π
.
Lời giải
Chọn B.
+ Tính được
2
0
sin cos 1
2
0
xdx x
π
π
=−=
∫
.
Câu 11. Biết
( )
2
2
3
3
2sin 3cos
2
ab
x x x dx
c
π
π
π
+
+ += +
∫
( )
,,abc∈
. Khi đó giá trị của
23
Pa b c
=++
là
A.
45P =
B.
60P =
C.
65P =
D.
70P =
Lời giải
Chọn B.
( )
2
2
2
2
3
3
1 12 3 3
2sin 3cos 2cos 3sin
2 2 18
x x x dx x x x
π
π
π
π
π
−

+ +=− + + = +


∫
2 3 60Pa b c⇒=+ + =
Câu 12. Biết
3
2
4
3tan 3
xdx a b
c
π
π
π
= ++
∫
( )
,,abc∈
. Khi đó giá trị của
P abc=++
là
A.
6P =
B.
4P = −
C.
4P =
D.
6P = −
Lời giải
Chọn B.
( )
33
2
3
2
4
44
1
3tan 3 1 3 tan 3 3 3
cos 4
xdx dx x x
x
ππ
π
π
ππ
π

= − = − = −−


∫∫
334 4
P abc⇒ = ++=−−=−
Câu 13. Biết
( )
4
2
6
2cot 5 3x dx b c
a
π
π
π
+ =++
∫
( )
,,abc∈
. Khi đó giá trị của
P abc=++
là
A.
6P =
B.
4P = −
C.
4P =
D.
6P = −
Lời giải
Chọn C.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
( )
( )
44 4
2
4
22
6
66 6
12
2cot 5 2 1 5 3 3 cot 3 1
sin sin 4
x dx dx dx x x
xx
ππ π
π
π
ππ π
π
−

+ = −+ = − = − =+ −




∫∫ ∫
Câu 14. Biết
2
22
0
sin cos
44
xx a
dx
cb
π
π
= +
∫
với
,ab∈
và
a
b
là phân số tối giản. Khi đó giá trị của
P abc=++
là
A.
17P =
B.
16
P
=
C.
32P =
D.
49P
=
Lời giải
Chọn D.
2 22
2
22 2
0 00
0
1 1 1 cos 1 1 1
sin cos sin sin
4 4 4 2 4 2 8 4 16 32
xx x x
dx dx dx x x
π ππ
π
π
−

= = =−=+


∫ ∫∫
1 32 16 49P abc⇒ =++=+ + =
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý A), B), C), D) ở mỗi câu, thí sinh chọn đúng hoặc
sai.
Câu 15. Cho hàm số
y fx
liên tục trên
;ab


. Các mệnh đề sau đây đúng hay sai?
A.
dd
ba
ab
fx x fx x

B.
dd
ba
ab
fx x fx x

C.
dd
bb
aa
fx x fx x

22
D.
d.
a
a
fx x
2024 0
Lời giải
A.
B.
C.
D.
SAI
SAI
ĐÚNG
ĐÚNG
Lý thuyết
dd
ba
ab
fx x fx x

d.
a
a
fx x
2024 0
Câu 16. Cho hàm số
,y f x y gx
liên tục trên
;ab


. Các mệnh đề sau đây đúng hay sai?
A.
ddd
b bb
a aa
f x gx x fx x gx x





. B.
. d d. d
b bb
a aa
fxgxx fxx gxx

.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
C.
dd
bb
aa
kfx x k fx x

. D.
d
d
d
b
b
a
b
a
a
fx x
fx
x
gx
gx x
.
Lời giải
A.
B.
C.
D.
ĐÚNG
SAI
ĐÚNG
SAI
Lý thuyết
ddd
b bb
a aa
f x gx x fx x gx x





dd
bb
aa
kfx x k fx x

Câu 17. Cho hàm số
y fx
liên tục trên
và
,,abc
thỏa mãn
abc

. Các mệnh đề sau đây
đúng hay sai?
A.
d dd
c bc
a ab
fx x fx x fx x

B.
ddd
c bc
a ab
fx x fx x fx x

C.
d dd
c bc
a ab
fx x fx x fx x

D.
ddd
c bb
a ac
fx x fx x fx x

Lời giải
A.
B.
C.
D.
SAI
ĐÚNG
SAI
SAI
Lý thuyết
ddd
c bc
a ab
fx x fx x fx x


Câu 18. Cho
( )
fx
,
()gx
là hai hàm số liên tục trên
. Các mệnh đề sau đây đúng hay sai?
A.
( )d ( )d
bb
aa
fx x fy y=
∫∫
B.
( )
() ()d ()d ()d.
b bb
a aa
f x gx x f x x gx x+= +
∫ ∫∫
C.
( )d ( )d
bb
aa
fx x ft x=
∫∫
D.
( )
()()d ()d ()d.
b bb
a aa
f xgx x f x x gx x=
∫ ∫∫
Lời giải
A.
B.
C.
D.
ĐÚNG
ĐÚNG
SAI
SAI
Lý thuyết
( )d ( )d
bb
aa
fx x fy y=
∫∫
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
(
)
() ()d ()d ()d.
b bb
a aa
f x gx x f x x gx x+= +
∫ ∫∫
Câu 19. Các mệnh đề sau đây đúng hay sai?
A.
2024
2024
d 4048x
.
B.
12 1 2
. d d. d
b bb
a aa
fxfxx fxx fxx

.
C. Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
;ab
. Khi đó
( )
1
b
a
f x dx
ba−
∫
được gọi là giá trị trung bình
của hàm số
( )
fx
trên đoạn
[ ]
;ab
.
D. Nếu hàm số
( )
fx
có đạo hàm
(
)
'
fx
và
(
)
'
fx
liên tục trên đoạn
[ ]
;
ab
thì
( ) ( ) ( )
'
b
a
f b f a f x dx−=
∫
.
Lời giải
A.
B.
C.
D.
ĐÚNG
SAI
ĐÚNG
ĐÚNG
Câu 20. Cho hàm
( )
fx
là hàm liên tục trên đoạn
[ ]
;ab
với
ab<
và
( )
Fx
là một nguyên hàm của
hàm
( )
fx
trên
[ ]
;ab
. Các mệnh đề sau đây đúng hay sai?
A.
( )
( ) ( )
(
)
b
a
kf x dx k F b F a= −
∫
B.
( ) (
) (
)
a
b
f x dx F b F a
= −
∫
C. Diện tích S của hình phẳng giới hạn bởi đường thẳng
;x ax b
= =
; đồ thị của hàm số
( )
y fx=
và
trục hoành được tính theo công thức
(
) (
)
S Fb Fa
= −
D.
( ) ( )
23 23
b
b
a
a
f x dx F x+= +
∫
Lời giải
A.
B.
C.
D.
ĐÚNG
SAI
SAI
SAI
Câu 21. Các mệnh đề sau đây đúng hay sai
| 1/120
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều BÀI 2 TÍCH PHÂN
1. Khái niệm tích phân
a. Diện tích hình thang cong
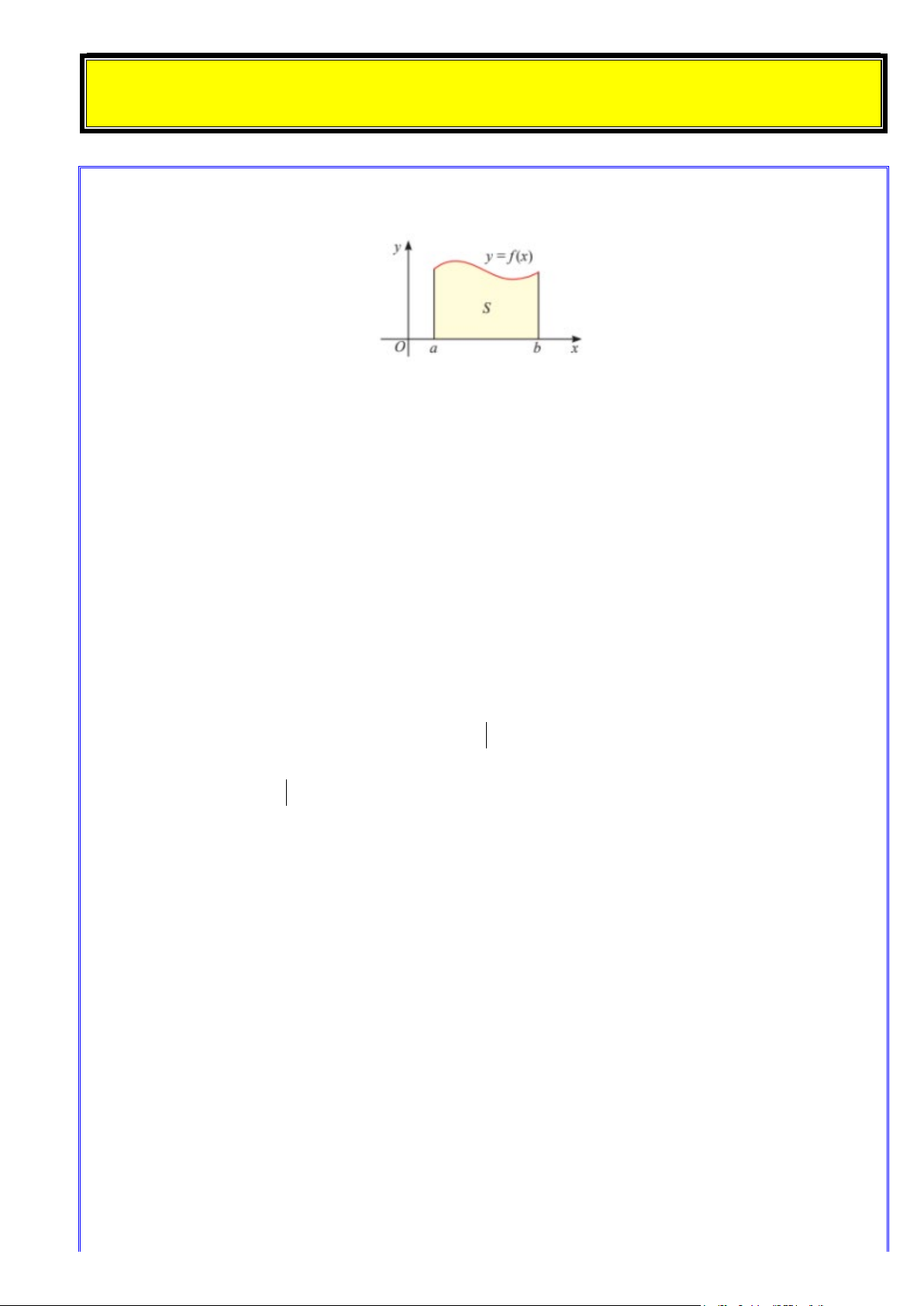
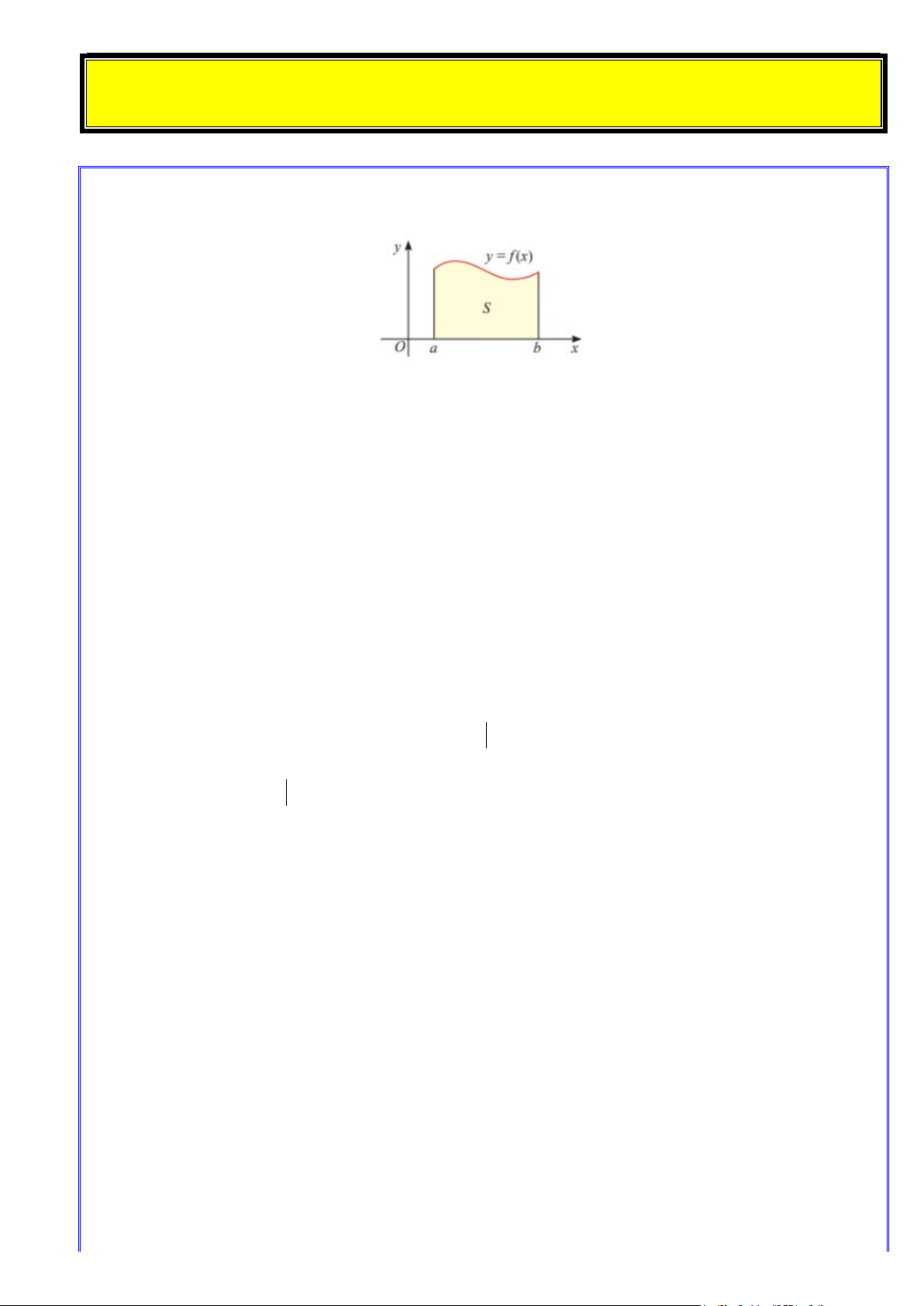
Nếu hàm số f (x) liên tục và không âm trên đoạn [a;b] thì diện tích S của hình thang cong giới hạn
bởi đồ thị y = f (x) , trục hoành và hai đường thẳng x = a, x = b được tính bởi:
S = F (b) − F (a)
trong đó F (x) là một nguyên hàm của f (x) trên đoạn [ ; a b].
b. Khái niệm tích phân
Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Nếu F (x) là nguyên hàm của hàm số f (x) trên đoạn b
[ ;ab] thì hiệu số F (b)− F (a) được gọi là tích phân từ a đến b của hàm số f (x), kí hiệu f (x)dx ∫ a Chú ý:
• Hiệu số F (b) − F (a) còn được kí hiệu là F (x) b . a b Vậy f
∫ (x)dx = F (x)b = F (b)− F (a) a a b
• Ta gọi ∫ là dấu tích phân, a là cận dưới, b là cận trên, f (x)dx là biểu thức dưới dấu tích phân và a
f (x) là hàm số dưới dấu tích phân. a b a • Quy ước: f ∫ (x) ; dx f
∫ (x)dx = − f ∫ (x)dx a a b
• Tích phân của hàm số f từ a đến b chỉ phụ thuộc vào f và các cận a,b mà không phụ thuộc vào b b
biến x hay t , nghĩa là f
∫ (x)dx = f ∫ (t)dt . a a
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
• Ý nghĩa hình học của tích phân b
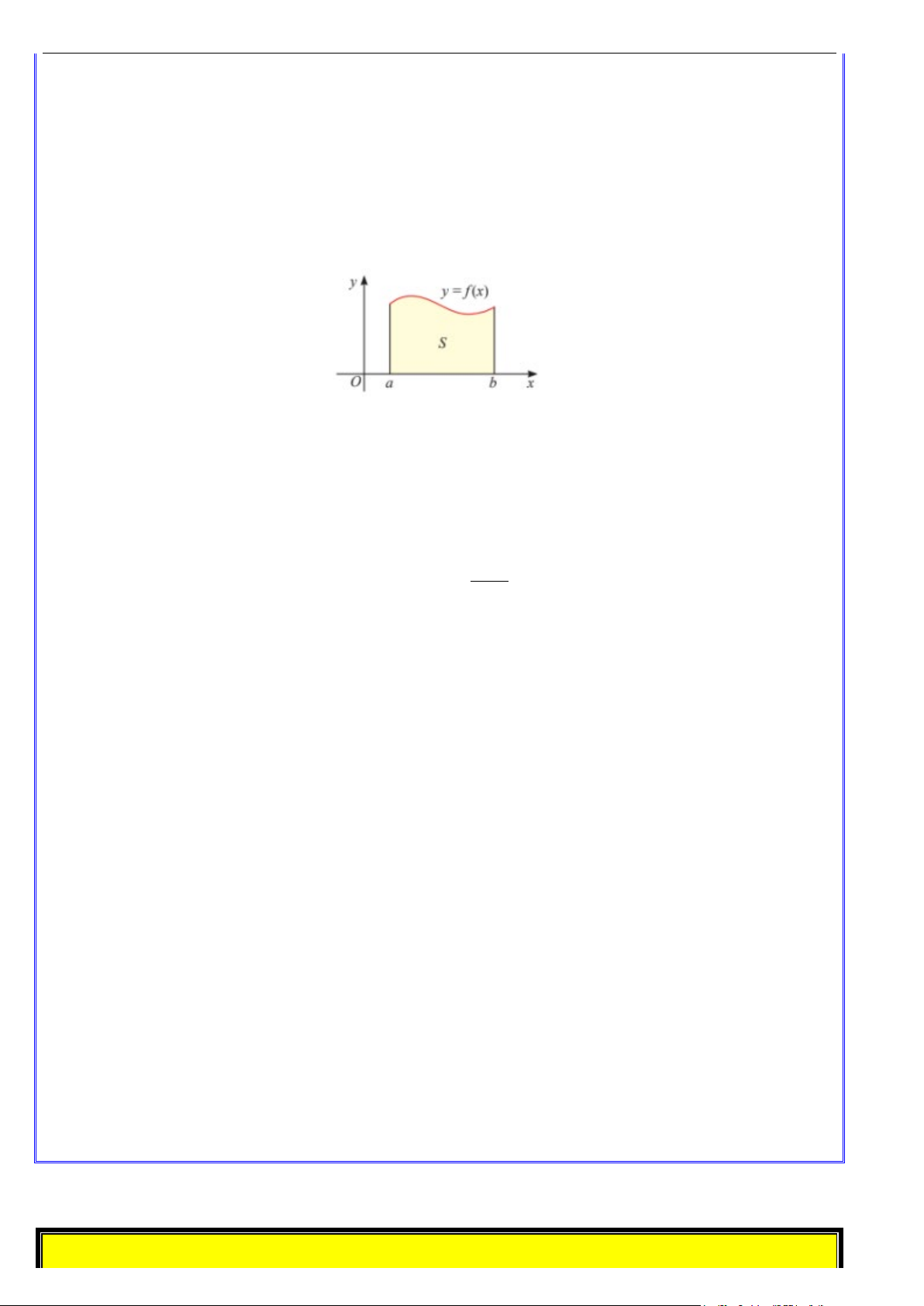
Nếu hàm số f (x) liên tục và không âm trên đoạn [ ;
a b] thì f (x)dx ∫
là diện tích S của hình thang a
cong giới hạn bởi đồ thị y = f (x) , trục hoành và hai đường thẳng x = a, x = b . b S = f ∫ (x)dx a Nhận xét:
• Nếu hàm số f (x) có đạo hàm f '(x) và f '(x) liên tục trên đoạn [ ; a b] thì b
f (b) − f (a) = f ' ∫ (x)dx. a
• Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Khi đó 1 b f
∫ (x)dx được gọi là giá trị trung bình của b − a a
hàm số f (x) trên đoạn [ ; a b].
• Đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mọi
thời điểm: v(t) = s '(t) . Do đó, nếu biết tốc độ v(t) tại mọi thời điểm t ∈[a;b] thì tính được quãng đường b
di chuyển trong khoảng thời gian từ a đến b theo công thức: s = s(b) − s(a) = v(t)dt ∫ a
2. Tính chất của tích phân
Cho hai hàm số f (x), g (x) liên tục trên đoạn [ ; a b]. Khi đó: b b
• Tính chất 1: kf
∫ (x)dx = k f
∫ (x)dx, với k là hằng số. a a b b b
• Tính chất 2:f
∫ (x)+ g(x)dx = f
(x)dx + g(x)dx ∫ ∫ a a a b b bf
∫ (x)− g(x)dx = f
(x)dx − g(x)dx ∫ ∫ a a a b c b
• Tính chất 3: f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ với c∈( ; a b). a a c CHỦ ĐỀ 1
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
TÍNH TÍCH PHÂN CỦA MỘT SỐ HÀM SỐ DẠNG 1
TÍNH TÍCH PHÂN SỬ DỤNG BẢNG NGUYÊN HÀM SƠ CẤP
Nguyên hàm của một hàm số sơ cấp 0dx = C ∫
Nguyên hàm của hàm số lũy thừa
dx = x + C ∫ α 1 + α x x dx = + C ∫ (α ≠ − ) 1 α +1
Nguyên hàm của hàm số 1 y =
dx = ln x + C ( ≠ 0) ∫ x x x cos xdx = x + C ∫ sin sin xdx = − x + C ∫ cos
Nguyên hàm của hàm số lượng giác
1 dx = x + C ∫ tan cos2 x 1 dx = − x + C ∫ cot sin2 x
exdx = ex + C ∫
Nguyên hàm của hàm số mũ x a x = a dx + C (0 < ≠ ) 1 ∫ a ln a
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều 2
Câu 1. Tính tích phân I = (2x +1)dx ∫ 0 A. I = 5 . B. I = 6. C. I = 2 . D. I = 4 . 1
Câu 2. Tích phân ∫(3x + )1(x +3)dx bằng 0 A. 12. B. 9 . C. 5 . D. 6 . e
Câu 3. Tính tích phân  1 1 I dx  = − ∫ 2  x x  1  A. 1 I = B. 1 I = +1 C. I =1
D. I = e e e 3 + Câu 4. x 2 Biết
dx = a + bln c, ∫
với a,b,c ∈,c < 9. Tính tổng S = a + b + .c x 1 A. S = 7 . B. S = 5. C. S = 8. D. S = 6 . 1
Câu 5. Tích phân 3x 1 e + dx ∫ bằng 0 A. 1 ( 4 e + e) B. 3 e − e C. 1 ( 4
e − e) D. 4 e − e 3 3 1 x Câu 6. Biết e e dx = + b ∫
(a,b∈) . Khi đó giá trị của P = a + b là 2x a 0 A. P = 3 − B. P =1 C. P = 1 − D. P = 3 1 2x
Câu 7. Giá trị của e − 4 I = dx ∫ bằng x e + 2 0
A. I = 2(e + 3)0. B. 1 I = (e + 3).
C. I = e − 3 .
D. I = 2(e −3) . 2 2 − x   Câu 8. Biết x e 2 + e ∫ a b 1−  dx = e + .
a e + bln 2 (a,b∈) . Khi đó giá trị của P = là  x . a b 1  A. P = 3 − B. P =1 C. P = 1 − D. P = 2 − 1 2x 1 − 3 − x Câu 9. Biết e − e +1 1 + I = dx = + b ∫ (a,b∈ a b
) . Khi đó giá trị của P = là x e a . a b 0 4 4 4 A. 4 P − − − = e −1 B. e 1 P = C. e 1 P = D. 1 e P = 2 e 4 e 4 e π 2
Câu 10. Giá trị của sin xdx ∫ bằng 0 π A. 0. B. 1. C. -1. D. . 2
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều π 2 2 Câu 11. + π Biết ( x + x + x) a b 3 2sin 3cos dx = + ∫
(a,b,c∈) . Khi đó giá trị của P = a + 2b + 3c là π 2 c 3 A. P = 45 B. P = 60 C. P = 65 D. P = 70 π 3 Câu 12. Biết 2 π
3tan xdx = a 3 + b + ∫
(a,b,c∈) . Khi đó giá trị của P = a + b + c là π c 4 A. P = 6 B. P = 4 − C. P = 4 D. P = 6 − π 4 Câu 13. π Biết ∫( 2
2cot x + 5)dx = + b 3 + c (a,b,c∈) . Khi đó giá trị của P = a + b + c là π a 6 A. P = 6 B. P = 4 − C. P = 4 D. P = 6 − π 2 Câu 14. π Biết 2 x 2 sin cos x a dx = + ∫
với a,b∈ và a 4 4 c b
b là phân số tối giản. Khi đó giá trị của 0
P = a + b + c là A. P =17 B. P =16 C. P = 32 D. P = 49
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý A), B), C), D) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 15. Cho hàm số y f xliên tục trên a;b 
. Các mệnh đề sau đây đúng hay sai? b a b a A. f
 xdx f  xdx B. f
 xdx  f  xdx a b a b b b a C. f
 xdx 2 f
 xd2xD. f
 2024 xdx  .0 a a a
Câu 16. Cho hàm số y f x,y gxliên tục trên a;b 
. Các mệnh đề sau đây đúng hay sai? b b b b b b A. f
  xgx  dx f  
 xdxg  xdx  . B. f
 x.gxdx f
 xd .x g  xdx . a a a a a a b f x x b   d b b f x C. kf
 xdx k f
 xdx. D. a x   . g x a   d b a a g  xdx a
Câu 17. Cho hàm số y f xliên tục trên  và a,b,c   thỏa mãn a b c . Các mệnh đề sau đây đúng hay sai? c b c c b c A. f
 xdx f  xdx f  xdx B. f
 xdx f
 xdxf  xdx a a b a a b
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều c b c c b b C. f
 xdx f
 xdxf  xdx D. f
 xdx f
 xdxf  xdx a a b a a c
Câu 18. Cho f (x) , g(x) là hai hàm số liên tục trên  . Các mệnh đề sau đây đúng hay sai? b b b b b
A. f (x)dx = f (y)dy ∫ ∫
B. ∫( f (x)+ g(x))dx = f (x)dx + g(x)d .x ∫ ∫ a a a a a b b b b b
C. f (x)dx = f (t)dx ∫ ∫
D. ∫( f (x)g(x))dx = f (x)dx g(x)d .x ∫ ∫ a a a a a
Câu 19. Các mệnh đề sau đây đúng hay sai? 2024 A. dx   4048 . 2024 b b b
B. f x . f x dx f x d .x f x d  1  2   1   . 2   x a a a
C. Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Khi đó 1 b f
∫ (x)dx được gọi là giá trị trung bình b − a a
của hàm số f (x) trên đoạn [ ; a b].
D. Nếu hàm số f (x) có đạo hàm f '(x) và f '(x) liên tục trên đoạn [ ; a b] thì b
f (b) − f (a) = f ' ∫ (x)dx. a
Câu 20. Cho hàm f (x) là hàm liên tục trên đoạn [ ;
a b] với a < b và F (x) là một nguyên hàm của
hàm f (x) trên [a;b]. Các mệnh đề sau đây đúng hay sai? b A. kf
∫ (x)dx = k(F (b)− F (a)) a a B. f
∫ (x)dx = F (b)− F (a) b
C. Diện tích S của hình phẳng giới hạn bởi đường thẳng x = ;
a x = b ; đồ thị của hàm số y = f (x) và
trục hoành được tính theo công thức S = F (b) − F (a) b D. f
∫ (2x+3)dx = F (2x+3)ba a
Câu 21. Các mệnh đề sau đây đúng hay sai 1 2x
A. e − 4 dx = e − 3 ∫ x e + 2 0 1 x B. e e dx = +1 ∫ 2x 2 0
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều 2 − x   C. x e 2 e
∫ 1− dx = e −e−ln2  x 1  1 2x 1 − 3 − x D. e − e +1 4 dx = e −1 ∫ x e 0
PHẦN III. Câu trắc nghiệm trả lời ngắn. Mỗi câu hỏi thí sinh chỉ trả lời đáp án. b
Câu 22. Với a,b là các tham số thực. Tính tích phân I = ( 2 3x − 2ax − ∫ )1dx. 0
Trả lời: ……………….. m Câu 23. Cho ∫( 2 3x − 2x + )
1 dx = 6. Tính giá trị của tham số m . 0 A. ( 1; − 2) . B. ( ;0 −∞ ). C. (0;4) . D. ( 3 − ; ) 1 .
Trả lời: ……………….. 2
Câu 24. Tính tích phân x −1 I = dx ∫ . x 1
Trả lời: ……………….. 2 2  4 3  Câu 25. Tính x − x I =   dx ∫ . x  1  
Trả lời: ……………….. 2
Câu 26. Tính I = ( x + )1( 3 x − ∫ )1dx. 1
Trả lời: ……………….. 2 2 3 Câu 27. Tính (x +1) I = dx ∫ . 2 x 1
Trả lời: ……………….. 1 Câu 28. Tính x 1 + 2x 1 I 5 .7 − = dx ∫ . 0
Trả lời: ……………….. 1
Câu 29. Tính I = ∫( − x−2 x + e )dx . 0
Trả lời: ……………….. π 3 Câu 30. Tính 2  sin 1 x I x  = − ∫   dx . 2 π  x  6
Trả lời: ………………..
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều π 2   Câu 31. Tính 1
I = ∫sin x − dx  . 3 2 π  x  6
Trả lời: ……………….. ( −x e + 2)2 1 Câu 32. Biết c 1
dx = ae + b + + ∫
(a,b,c∈) . Tính giá trị của P = a + b + c . x 1 − 2 e e e 0
Trả lời: ……………….. π 3 Câu 33. − π
Biết 1 cos 2x dx = a 3 + ∫
(a,b∈) . Tính a + b . 1+ cos 2x b 0
Trả lời: ……………….. (2024x + )2 1 1
Câu 34. Tính I = dx ∫ . 3x e− 0
Trả lời: ……………….. ( −x e + 2)2 1
Câu 35. Tính I = dx ∫ . x 1 e − 0
Trả lời: ……………….. 2 2 − x   Câu 36. Tính 2x 2024 = ∫ 2023 e I e + dx . 3  x  1 
Trả lời: ……………….. 2 Câu 37. Tính  3 1 + 1 4 2.3x I x dx  = − + ∫ . 2  x  1 
Trả lời: ……………….. DẠNG 2
TÍCH PHÂN HÀM TRỊ TUYỆT ĐỐI
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều b
Tính tích phân: I = f ∫ (x) .dx ? a Phương pháp
Bước 1. Xét dấu f (x) trên đoạn [ ; a b] .
Bước 2. Dựa vào bảng xét dấu trên đoạn [ ;
a b] để khử f (x) . Sau đó sử dụng các phương pháp tính tích b
phân đã học đê tính I = f ∫ (x) .dx a
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. 2π
Câu 38. Giá trị của I = 1− cos 2xdx ∫ bằng 0 π A. 3 . B. 4 2 . C. 2 3 . D. . 2 2
Câu 39. Tính tích phân I = x − 2 dx ∫ . 0 A. I = 2 − . B. I = 4 . C. I = 2 . D. I = 0. 2
Câu 40. Tính tích phân 3
I = x − x dx ∫ . 0 A. 1 I = − . B. I = 5 . C. 1 I = . D. 5 I = . 2 2 2 2
Câu 41. Tính tích phân 2
I = x + 2x − 3dx ∫ . 0 A. I = 2 − . B. I = 4 . C. I = 5 . D. I = 4 − .
Câu 42. Cho tích phân I = ( + ) 3 2 20 4 16 3 2 x −1 dx = + + = a 3 + b 2 ∫
với a,b∈ . Tính − 3 3 3 3
P = a + b . A. 40 P = B. 80 P = C. 17 P = D. 98 P = 3 3 3 3 5
Câu 43. Tính tích phân I = ∫ ( x + 2 − x −2 )dx . 2 − A. I = 38 . B. I = 44 . C. I = 48. D. I = 40 . 3
Câu 44. Cho tích phân = 2x − 4 b I dx = a + ∫
với a,b,c ∈ và b là phân số tối giản. Tính c ln 2 c 0 2 2 2
P = a + b + c . A. P =15 B. P =10 C. P = 5 D. P =18
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều 1
Câu 45. Tính tích phân = 2x − 2−x I dx ∫ . 1 − A. 1 . B. ln 2 . C. 2ln 2. D. 2 . ln 2 ln 2 2
Câu 46. Tính tích phân I = ∫ ( x − x −1)dx. 1 − A. I = 0. B. I = 2 . C. I = 2 − . D. I = 3 − . a
Câu 47. Cho a là số thực dương, tính tích phân I = x dx ∫ theo a . 1 − 2 2 2 2 3a −1 A. a 1 I + = a 2 2a 1 . B. I + = . C. I − + = . D. I = . 2 2 2 2 m
Câu 48. Cho số thực m >1 thỏa mãn 2mx −1 dx =1 ∫
. Khẳng định nào sau đây đúng? 1 A. m∈(4;6). B. m∈(2;4). C. m∈(3;5) . D. m∈(1;3).
Câu 49. Khẳng định nào sau đây là đúng? A. 1 1 3 3 x dx = x dx ∫ ∫ . B. 2018 2018 4 2
x − x +1 dx = ( 4 2 x − x + ∫ ∫ )1dx . 1 − 1 − 1 − 1 − π π C. 3 x ( + ) 3 1 d x e x x = e (x + ∫ ∫ )1dx . D. 2 2 2 − =
∫ π 1 cos xdx ∫ π sin d x x . 2 − 2 − − − 2 2 4
Câu 50. Tính tích phân 2 I =
x − 6x + 9dx ∫ . 1 A. 5 I = . B. 1 I = − . C. I = 2 − . D. 1 I = . 2 2 2
PHẦN II. Câu trắc nghiệm trả lời ngắn. Mỗi câu hỏi thí sinh chỉ trả lời đáp án. 3
Câu 51. Tính tích phân 2
I = x −1 dx ∫ . 3 −
Trả lời: ……………….. 2
Câu 52. Tính tích phân 2
I = −x − 2x + 3 dx ∫ . 1 −
Trả lời: ……………….. 2
Câu 53. Tính tích phân x +1 I = dx ∫ . x 1
Trả lời: ……………….. 6
Câu 54. Tính tích phân 2 I =
x −8x +16dx ∫ . 2
Trả lời: ………………..
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều 1
Câu 55. Tính tích phân 2 I =
4x + 6x + 9dx ∫ . 2 −
Trả lời: ……………….. 1
Câu 56. Tính tích phân 2 I =
9x − 6x +1dx ∫ . 0
Trả lời: ……………….. 2π
Câu 57. Tính tích phân I = 1+ cos 2xdx ∫ . 0
Trả lời: ……………….. 2π
Câu 58. Tính tích phân I = 1− cos 2xdx ∫ . 0
Trả lời: ……………….. 2π
Câu 59. Tính tích phân I = 1− sin 2xdx ∫ . 0
Trả lời: ……………….. 2π
Câu 60. Tính tích phân I = 1+ sin 2xdx ∫ . 0
Trả lời: ………………..
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều BÀI 2 TÍCH PHÂN
1. Khái niệm tích phân
a. Diện tích hình thang cong
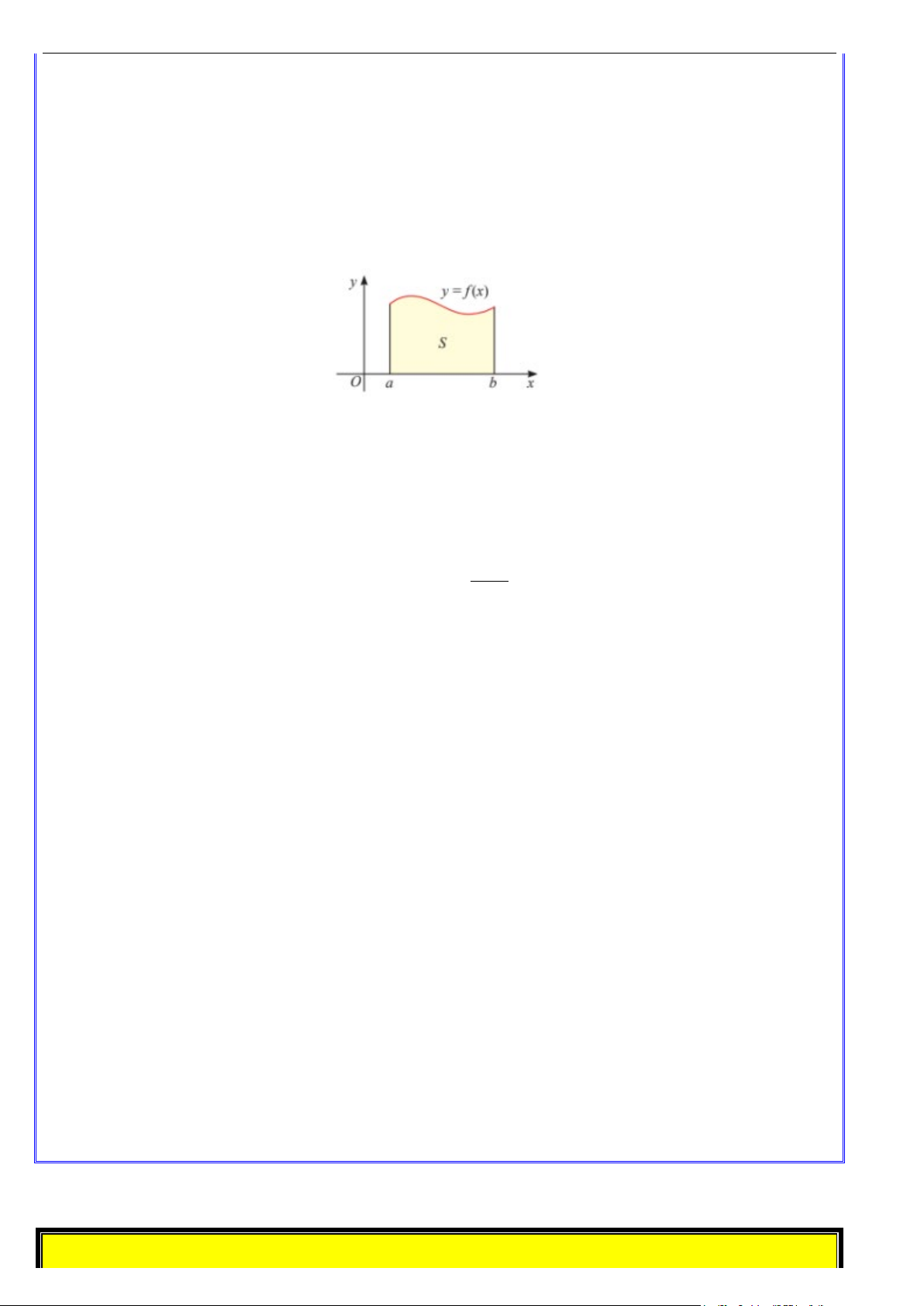
Nếu hàm số f (x) liên tục và không âm trên đoạn [a;b] thì diện tích S của hình thang cong giới hạn
bởi đồ thị y = f (x) , trục hoành và hai đường thẳng x = a, x = b được tính bởi:
S = F (b) − F (a)
trong đó F (x) là một nguyên hàm của f (x) trên đoạn [ ; a b].
b. Khái niệm tích phân
Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Nếu F (x) là nguyên hàm của hàm số f (x) trên đoạn b
[ ;ab] thì hiệu số F (b)− F (a) được gọi là tích phân từ a đến b của hàm số f (x), kí hiệu f (x)dx ∫ a Chú ý:
• Hiệu số F (b) − F (a) còn được kí hiệu là F (x) b . a b Vậy f
∫ (x)dx = F (x)b = F (b)− F (a) a a b
• Ta gọi ∫ là dấu tích phân, a là cận dưới, b là cận trên, f (x)dx là biểu thức dưới dấu tích phân và a
f (x) là hàm số dưới dấu tích phân. a b a • Quy ước: f ∫ (x) ; dx f
∫ (x)dx = − f ∫ (x)dx a a b
• Tích phân của hàm số f từ a đến b chỉ phụ thuộc vào f và các cận a,b mà không phụ thuộc vào b b
biến x hay t , nghĩa là f
∫ (x)dx = f ∫ (t)dt . a a
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
• Ý nghĩa hình học của tích phân b
Nếu hàm số f (x) liên tục và không âm trên đoạn [ ;
a b] thì f (x)dx ∫
là diện tích S của hình thang a
cong giới hạn bởi đồ thị y = f (x) , trục hoành và hai đường thẳng x = a, x = b . b S = f ∫ (x)dx a Nhận xét:
• Nếu hàm số f (x) có đạo hàm f '(x) và f '(x) liên tục trên đoạn [ ; a b] thì b
f (b) − f (a) = f ' ∫ (x)dx. a
• Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Khi đó 1 b f
∫ (x)dx được gọi là giá trị trung bình của b − a a
hàm số f (x) trên đoạn [ ; a b].
• Đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mọi
thời điểm: v(t) = s '(t) . Do đó, nếu biết tốc độ v(t) tại mọi thời điểm t ∈[a;b] thì tính được quãng đường b
di chuyển trong khoảng thời gian từ a đến b theo công thức: s = s(b) − s(a) = v(t)dt ∫ a
2. Tính chất của tích phân
Cho hai hàm số f (x), g (x) liên tục trên đoạn [ ; a b]. Khi đó: b b
• Tính chất 1: kf
∫ (x)dx = k f
∫ (x)dx, với k là hằng số. a a b b b
• Tính chất 2:f
∫ (x)+ g(x)dx = f
(x)dx + g(x)dx ∫ ∫ a a a b b bf
∫ (x)− g(x)dx = f
(x)dx − g(x)dx ∫ ∫ a a a b c b
• Tính chất 3: f (x)dx = f (x)dx + f (x)dx ∫ ∫ ∫ với c∈( ; a b). a a c CHỦ ĐỀ 1
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều
TÍNH TÍCH PHÂN CỦA MỘT SỐ HÀM SỐ DẠNG 1
TÍNH TÍCH PHÂN SỬ DỤNG BẢNG NGUYÊN HÀM SƠ CẤP
Nguyên hàm của một hàm số sơ cấp 0dx = C ∫
Nguyên hàm của hàm số lũy thừa
dx = x + C ∫ α 1 + α x x dx = + C ∫ (α ≠ − ) 1 α +1
Nguyên hàm của hàm số 1 y =
dx = ln x + C ( ≠ 0) ∫ x x x cos xdx = x + C ∫ sin sin xdx = − x + C ∫ cos
Nguyên hàm của hàm số lượng giác
1 dx = x + C ∫ tan cos2 x 1 dx = − x + C ∫ cot sin2 x
exdx = ex + C ∫
Nguyên hàm của hàm số mũ x a x = a dx + C (0 < ≠ ) 1 ∫ a ln a
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều 2
Câu 1. Tính tích phân I = (2x +1)dx ∫ 0 A. I = 5 . B. I = 6. C. I = 2 . D. I = 4 . Lời giải Chọn B. 2 2
Ta có I = (2x +1)dx = ∫
( 2x + x) = 4+ 2 = 6. 0 0 1
Câu 2. Tích phân ∫(3x + )1(x +3)dx bằng 0 A. 12. B. 9 . C. 5 . D. 6 . Lời giải Chọn B. 1 1
Ta có: ∫(3x + )1(x +3)dx = ∫(3x +10x +3)dx = (x +5x +3x)1 2 3 2 = 9 . 0 0 0 1
Vậy : ∫(3x + )1(x +3)dx = 9. 0 e
Câu 3. Tính tích phân  1 1 I dx  = − ∫ 2  x x  1  A. 1 I = B. 1 I = +1 C. I =1
D. I = e e e Lời giải Chọn A.  1 1   1 e e  1 I = − dx = ∫  ln x + =  . 2 x x x      e 1 1 3 + Câu 4. x 2 Biết
dx = a + bln c, ∫
với a,b,c ∈,c < 9. Tính tổng S = a + b + .c x 1 A. S = 7 . B. S = 5. C. S = 8. D. S = 6 . Lời giải Chọn A. 3 3 3 3 x + 2  2  2 Ta có 3 dx = 1+ dx = dx +
dx = 2 + 2ln x = 2 + ∫ ∫  2ln 3. ∫ ∫ 1 xx x 1 1 1 1
Do đó a = 2,b = 2,c = 3 ⇒ S = 7. 1
Câu 5. Tích phân 3x 1 e + dx ∫ bằng 0 A. 1 ( 4 e + e) B. 3 e − e C. 1 ( 4
e − e) D. 4 e − e 3 3
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều Lời giải Chọn C. 1 1 1 3x 1 e + dx ∫ 1 3x 1 e + = d(3x + ) 1 1 3x 1 e + = 1 = ( 4 e − e) . 3 ∫ 3 3 0 0 0 1 x Câu 6. Biết e e dx = + b ∫
(a,b∈) . Khi đó giá trị của P = a + b là 2x a 0 A. P = 3 − B. P =1 C. P = 1 − D. P = 3 Lời giải Chọn B. 1 1 x 1 x x e ee      e I = dx = ∫
∫  dx =    = −1 2x  2   2    2 0 0 0 1 2x
Câu 7. Giá trị của e − 4 I = dx ∫ bằng x e + 2 0
A. I = 2(e + 3)0. B. 1 I = (e + 3).
C. I = e − 3 .
D. I = 2(e −3) . 2 Lời giải Chọn C. 1 2 1 e − 4 ( xe −2)( x x e + 2) 1 I = dx =
dx = e − dx = e − x = e − ∫ x ∫ x ∫( x 2) ( x 2 )1 3 0 e + 2 e + 2 0 0 0 2 − x   Câu 8. Biết x e 2 + e ∫ a b 1−  dx = e + .
a e + bln 2 (a,b∈) . Khi đó giá trị của P = là  x . a b 1  A. P = 3 − B. P =1 C. P = 1 − D. P = 2 − Lời giải Chọn D. 2 − x 2   x ex 1 I e ∫ 1  dx ∫e  = − = − dx = ( x e − ln x )2 2
= e − e − ln 2 1  x   x 1 1  1 2x 1 − 3 − x Câu 9. Biết e − e +1 1 + I = dx = + b ∫ (a,b∈ a b
) . Khi đó giá trị của P = là x e a . a b 0 4 4 4 A. 4 P − − − = e −1 B. e 1 P = C. e 1 P = D. 1 e P = 2 e 4 e 4 e Lời giải Chọn D. 1 1 2x 1 − 3 − x 1 e − e +1  e− e−  − − − − − e I =
dx = e − e + e dx = ∫ ∫ e − +  = = − x ( x x x ) 4x x 4 1 4 x 1 1 1 1 4 4 e  4 − 1 −  e e 0 0 0
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều 4
a + b 1− e ⇒ P = = 4 . a b e π 2
Câu 10. Giá trị của sin xdx ∫ bằng 0 π A. 0. B. 1. C. -1. D. . 2 Lời giải Chọn B. π π 2
+ Tính được sin xdx = −cos x ∫ 2 =1. 0 0 π 2 2 Câu 11. + π Biết ( x + x + x) a b 3 2sin 3cos dx = + ∫
(a,b,c∈) . Khi đó giá trị của P = a + 2b + 3c là π 2 c 3 A. P = 45 B. P = 60 C. P = 65 D. P = 70 Lời giải Chọn B. π π 2 2 ∫(   − π x + x + x) 2 1 2 12 3 3 2sin 3cos dx = 2
− cos x + 3sin x + x = +  2    π π 2 18 3 3
⇒ P = a + 2b + 3c = 60 π 3 Câu 12. π Biết 2
3tan xdx = a 3 + b + ∫
(a,b,c∈) . Khi đó giá trị của P = a + b + c là π c 4 A. P = 6 B. P = 4 − C. P = 4 D. P = 6 − Lời giải Chọn B. π π 3 3 π 2  1  π 3tan xdx = 3 −1 dx = 3 ∫ ∫
(tan x − x) 3 = − −   π 3 3 3 2 π π  cos x  4 4 4 4
⇒ P = a + b + c = 3− 3− 4 = 4 − π 4 Câu 13. π Biết ∫( 2
2cot x + 5)dx = + b 3 + c (a,b,c∈) . Khi đó giá trị của P = a + b + c là π a 6 A. P = 6 B. P = 4 − C. P = 4 D. P = 6 − Lời giải Chọn C.
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều π π π 4∫( π      −  π x + ) 4 4 2 1 2 2cot 5 dx = ∫2 −1 + 5dx = 3− dx = ∫
(3x −cot x) 4 = + −     π 3 1 2 2 π π   sin x   π  sin x  4 6 6 6 6 π 2 Câu 14. π Biết 2 x 2 sin cos x a dx = + ∫
với a,b∈ và a 4 4 c b
b là phân số tối giản. Khi đó giá trị của 0
P = a + b + c là A. P =17 B. P =16 C. P = 32 D. P = 49 Lời giải Chọn D. π π π π 2 2 2 2 2 x 2 x 1 2 x 1 1− cos x  1  1  π 1 sin cos dx = sin dx = ∫ ∫ ∫
dx =  x − sin x = + 4 4 4 2 4 2 8 4      16 32 0 0 0 0
⇒ P = a + b + c =1+ 32 +16 = 49
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý A), B), C), D) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 15. Cho hàm số y f xliên tục trên a;b 
. Các mệnh đề sau đây đúng hay sai? b a b a A. f
 xdx f  xdx B. f
 xdx  f  xdx a b a b b b a C. f
 xdx 2 f
 xd2xD. f
 2024 xdx  .0 a a a Lời giải A. B. C. D. SAI SAI ĐÚNG ĐÚNG Lý thuyết b a f
 xdx  f  xdx a b a f
 2024 xdx  .0 a
Câu 16. Cho hàm số y f x,y gxliên tục trên a;b 
. Các mệnh đề sau đây đúng hay sai? b b b b b b A. f
  xgx  dx f  
 xdxg  xdx  . B. f
 x.gxdx f
 xd .x g  xdx . a a a a a a
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều b f x x b   d b b f x C. kf
 xdx k f
 xdx. D. a x   . g x a   d b a a g  xdx a Lời giải A. B. C. D. ĐÚNG SAI ĐÚNG SAI Lý thuyết b b bf
  xgx  dx f  
 xdxg  xdxa a a b b kf
 xdx k f  xdx a a
Câu 17. Cho hàm số y f xliên tục trên  và a,b,c   thỏa mãn a b c . Các mệnh đề sau đây đúng hay sai? c b c c b c A. f
 xdx f  xdx f  xdx B. f
 xdx f
 xdxf  xdx a a b a a b c b c c b b C. f
 xdx f
 xdxf  xdx D. f
 xdx f
 xdxf  xdx a a b a a c Lời giải A. B. C. D. SAI ĐÚNG SAI SAI Lý thuyết c b c f
 xdx f
 xdxf
 xdx a a b
Câu 18. Cho f (x) , g(x) là hai hàm số liên tục trên  . Các mệnh đề sau đây đúng hay sai? b b b b b
A. f (x)dx = f (y)dy ∫ ∫
B. ∫( f (x)+ g(x))dx = f (x)dx + g(x)d .x ∫ ∫ a a a a a b b b b b
C. f (x)dx = f (t)dx ∫ ∫
D. ∫( f (x)g(x))dx = f (x)dx g(x)d .x ∫ ∫ a a a a a Lời giải A. B. C. D. ĐÚNG ĐÚNG SAI SAI Lý thuyết b b
f (x)dx = f (y)dy ∫ ∫ a a
Đại số 12 - Chương 4 - Nguyên hàm. Tích phân – Bài tập theo chương trình mới 2025 Cánh Diều b b b
∫( f (x)+ g(x))dx = f (x)dx+ g(x)d .x ∫ ∫ a a a
Câu 19. Các mệnh đề sau đây đúng hay sai? 2024 A. dx   4048 . 2024 b b b
B. f x . f x dx f x d .x f x d  1  2   1   . 2   x a a a
C. Cho hàm số f (x) liên tục trên đoạn [ ;
a b]. Khi đó 1 b f
∫ (x)dx được gọi là giá trị trung bình b − a a
của hàm số f (x) trên đoạn [ ; a b].
D. Nếu hàm số f (x) có đạo hàm f '(x) và f '(x) liên tục trên đoạn [ ; a b] thì b
f (b) − f (a) = f ' ∫ (x)dx. a Lời giải A. B. C. D. ĐÚNG SAI ĐÚNG ĐÚNG
Câu 20. Cho hàm f (x) là hàm liên tục trên đoạn [ ;
a b] với a < b và F (x) là một nguyên hàm của
hàm f (x) trên [ ;
a b]. Các mệnh đề sau đây đúng hay sai? b A. kf
∫ (x)dx = k(F (b)− F (a)) a a B. f
∫ (x)dx = F (b)− F (a) b
C. Diện tích S của hình phẳng giới hạn bởi đường thẳng x = ;
a x = b ; đồ thị của hàm số y = f (x) và
trục hoành được tính theo công thức S = F (b) − F (a) b D. f
∫ (2x+3)dx = F (2x+3)ba a Lời giải A. B. C. D. ĐÚNG SAI SAI SAI
Câu 21. Các mệnh đề sau đây đúng hay sai