




Preview text:
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
A. Kiến thức cần nhớ
1. Khái niệm tỉ số lượng giác của góc nhọn
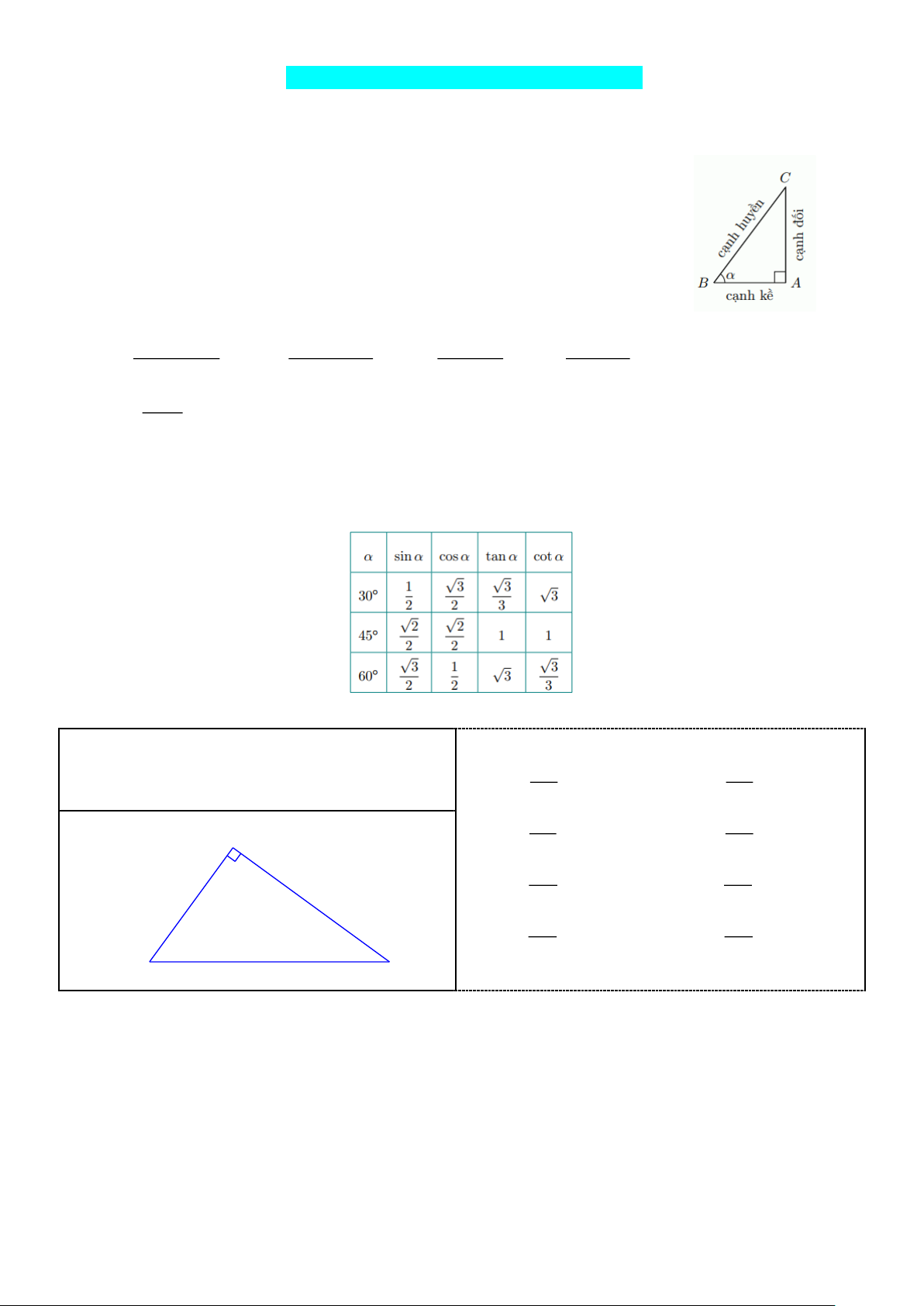
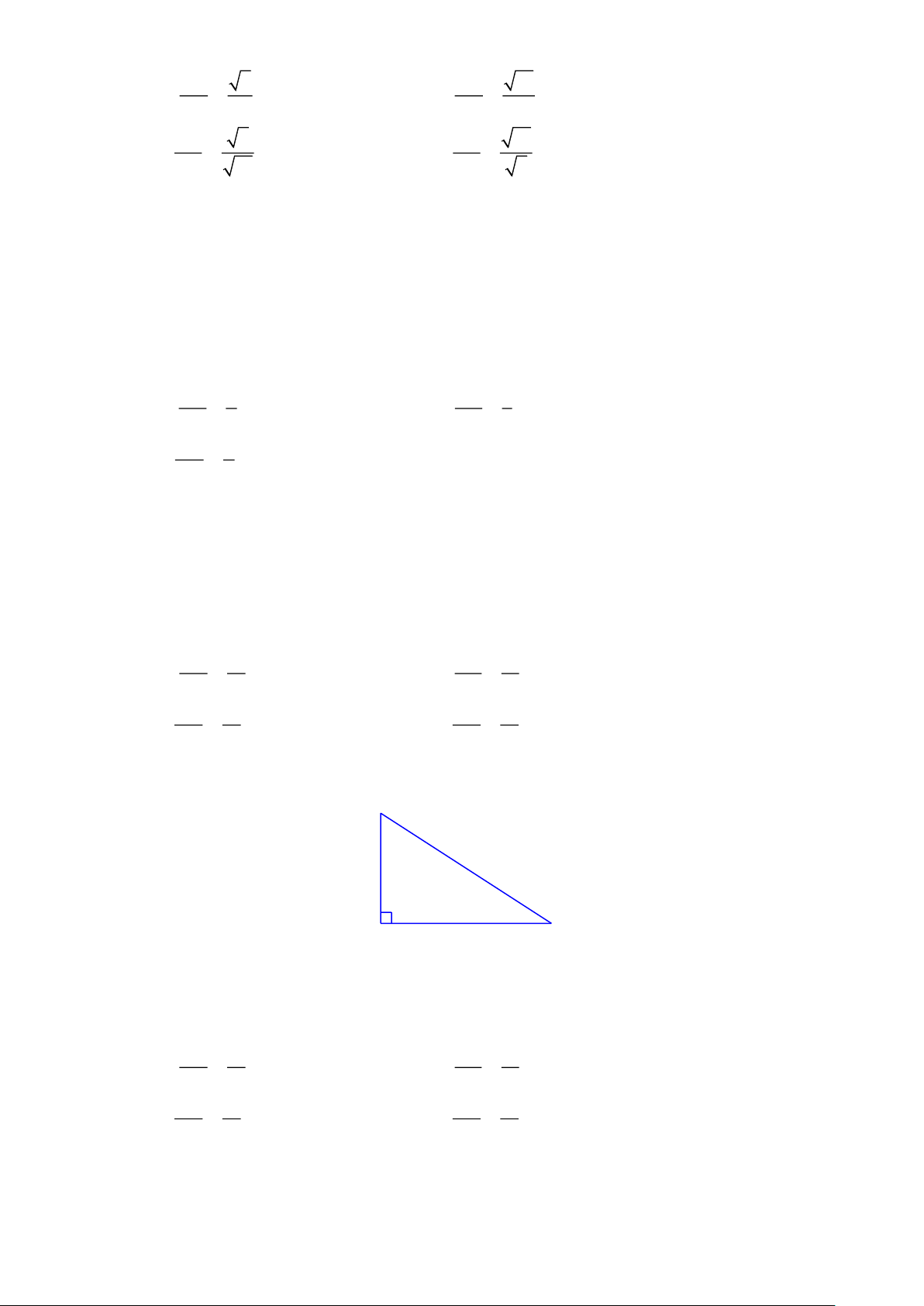
Cho góc nhọn . Xét ABC vuông tại A có góc nhọn B bằng . Ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của , kiế hiệu sin
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là côsin của , kí hiệu là cos
+ Tỉ số giữa cạnh đối và cạnh kề của góc gọi là tang của , kiế hiệu tan
+ Tỉ số giữa cạnh kề và cạnh đối của góc gọi là côtang , kí hiệu cot . * Ta có: + c¹nh ®èi c¹nh ®èi c¹nh kÒ sin= ; c¹nh kÒ cos= ; ta α n = ; cotα= c¹nh huyÒn c¹nhhuyÒn c¹nh kÒ c¹nh®èi + 1 cot = tan
+ sin, cos, tan,cot gọi là các tỉ số lượng giác của góc nhọn
* sin, côsin của góc nhọn luôn dương và bé hơn 1 vì trong tam giác vuông, cạnh huyền dài nhất
Ta có bảng các giá trị lượng giác đặc biệt:
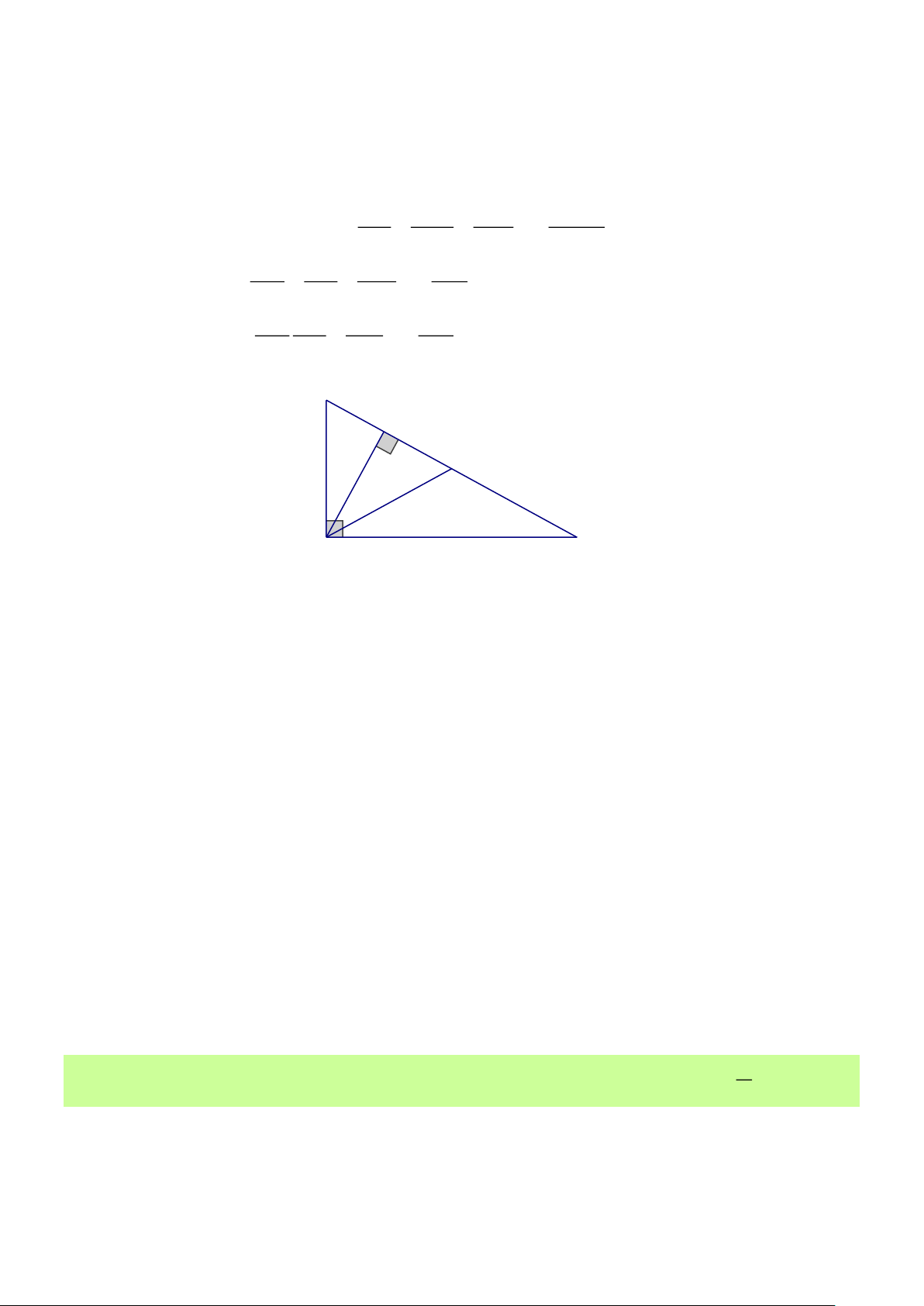
*) Chú ý: Cách tính chính xác cạnh đối và cạnh kề của góc cần viết tỉ số lượng giác Chẳng hạn:
Xét ABC vuông tại A , có:
Viết tỉ số lượng giác của góc nhọn trong tam AC AB sin B = sin C =
giác ABC vuông tại A . BC BC AB AC A cosB = cosC = BC BC AC AB tanB = tanC = AB AC AB AC cotB = cotC = AC AB B C
2. Tỉ số lượng giác của hai góc phụ nhau
* Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
* Cho và là hai góc phụ nhau, khi đó:
sin = cos , sin = cos , tan = cot , cot = tan Trang 1 C α β A B
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của góc nhọn.
* Để tìm góc khi biết cot , ta có thể tìm góc (90 − ) vì tan (90 − ) = cot rồi suy ra . B. Các dạng toán
Dạng 1: Sử dụng MTCT tính tỉ số lượng giác, tính góc
Bài 1: Sử dụng MTCT tính các tỉ số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba. a) sin 27 , cos32 15 ', tan 52 12 ' và cot 35 23 ' b) sin 40 54 ' , cos52 15 ', tan 69 36 ' và cot 25 18 ' Lời giải a)
Làm tròn đến chữ số thập phân thứ ba ta được:
sin 27 0, 454 ; cos32 15 ' 0,846 ; tan 52 12 ' 1, 289 cot 35 23 ' 1, 408 1 Lưu ý: cot 35 2 3 = tan 35 2 3 b)
Làm tròn đến chữ số thập phân thứ ba ta được sin 40 54 ' 0,655 ; cos52 15 ' 0,612 ; tan 69 36 ' 2,689 ; cot 25 18 ' 2,116
Bài 2: Sử dụng MTCT, tìm các góc (làm tròn đến phút) biết:
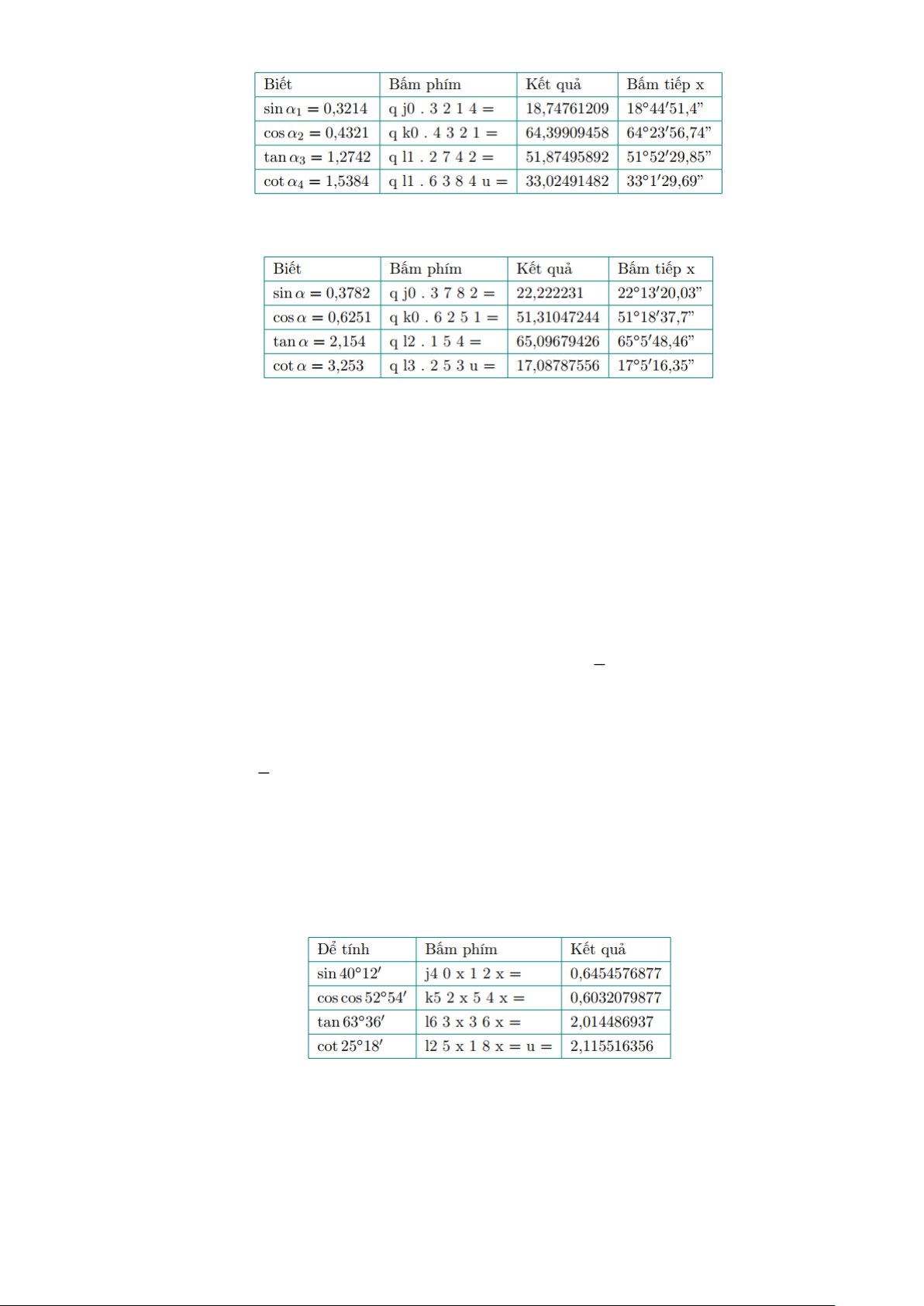
a) sin = 0,3214 , cos = 0, 4321 , tan = 1, 2742 và cot = 1,5384 1 2 3 4
b) sin = 0,3782 , cos = 0,6251, tan = 2,154 và cot = 3, 253 1 1 1 1 Lời giải a) Trang 2
Làm tròn đến phút ta được: 18 45 ; 64 24 ; 51 52 ; 31 1 1 2 3 4 b)
Làm tròn đến phút ta được: 23 13 ; 51 19 ; 65 6 ; 17 5 . 1 2 2 4
Bài 3: Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau: a) 26 b) 72 c) 81 2 7 Lời giải
a) sin 26 0, 44 , cos 26 0,9 , tan 26 0, 49 và cot 26 2,05 .
b) sin 72 0,95 , cos 72 0,31, tan 72 3,08 và cot 72 0,32 . c) sin 81 27 0,99 , cos81 27 0,15 , tan81 27 6,65 và cot 81 27 0,15 .
Bài 4: Sử dụng máy tính cầm tay, tìm góc nhọn trong mỗi trường hợp sau đây a) cos =0,6 b) 3 tan = 4 Lời giải
a) Ta có: cos =0,6 . Từ đo tìm được 53 8 3
b) Ta có: tan = . Từ đó tìm được 36 52 . 4
Bài 5: Dùng MTCT, tính (làm tròn đến chữu số thập phân thứ ba) a) sin 40 12 b) cos52 54 c) tan 63 36 d) cot 25 18 Lời giải
Làm tròn đến chữ số thập phân thứ ba ta được: a) sin 40 12 0,645 b) cos52 54 0,603 c) tan 63 36 2,014 d) cot 25 18 2,116
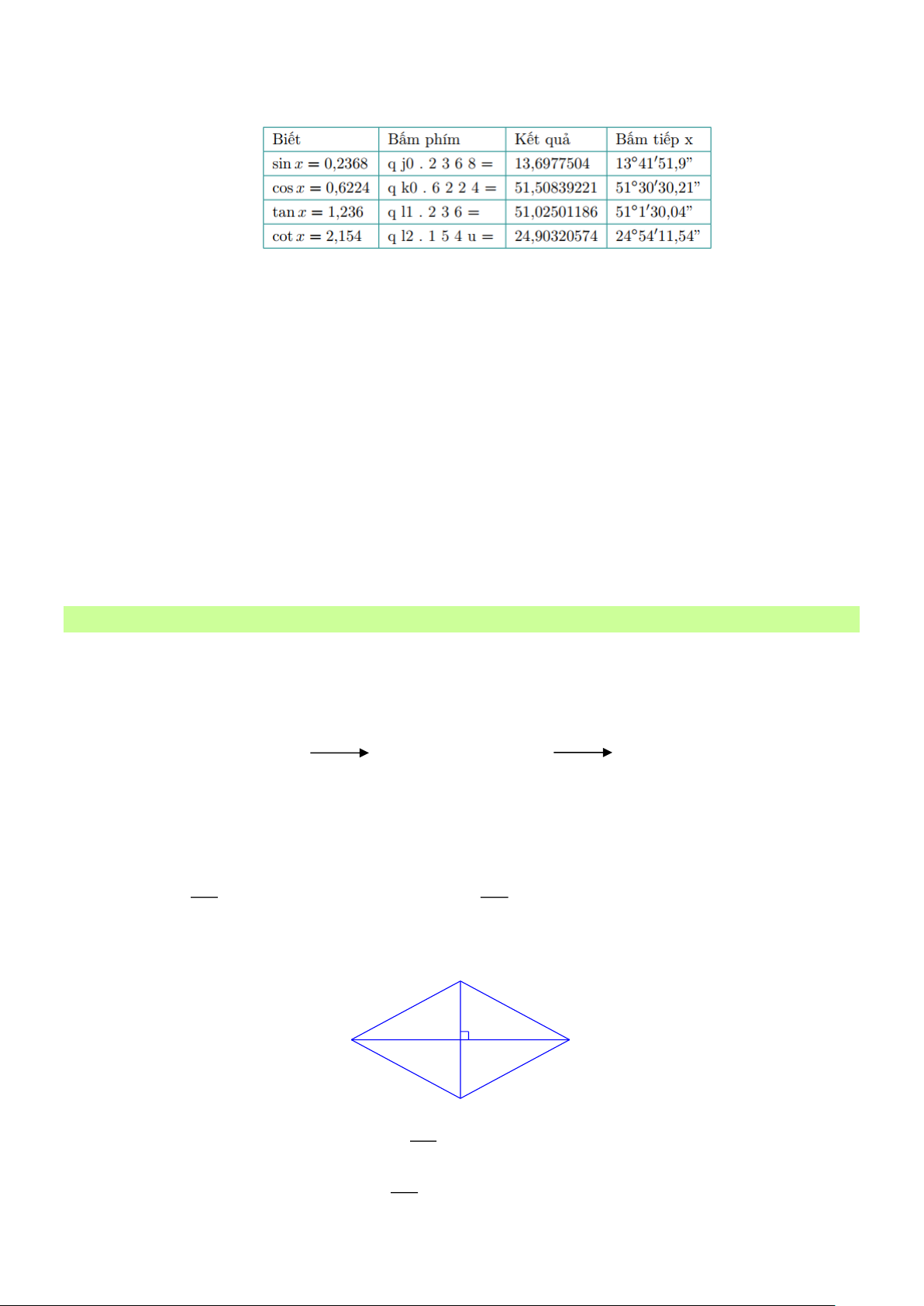
Bài 6: Dùng MTCT. Tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng: a) sin x = 0, 2368 b) cos x = 0,6224 Trang 3 c) tan x = 1, 236 d) cot x = 2,154 Lời giải
Làm tròn đến phút ta được: a) x 13 42 b) x 51 31 c) x 51 2 d) x 24 54
Dạng 2: Tính tỉ số lượng giác của góc nhọn trong một tam giác vuông I. Cách giải:
- Xác định cạnh đối, cạnh kề, cạnh huyền
- Tính đoạn thẳng chưa biết (nhờ định lí Pitago hoặc hệ thức về cạnh, đường cao trong tam giác vuông)
Xác định cạnh đối, kề, huyền Viết tỉ số lượng giác Tính đoạn thẳng chưa biết.
*) Lưu ý: Nếu đề bài yêu cầu tính tỉ số lượng giác của hai góc nhọn trong cùng một tam giác
vuông thi sử dụng tính chất tỉ số lượng giác của hai góc phụ nhau. II. Bài toán
Bài 1: Cho hình thoi ABCD có hai đường chéo cắt nhau tại trung điểm O . OB OB a) Tỉ số
là sin của góc nhọn nào? Tỉ số
là côsin của góc nhọn nào? AB BC
b) Viết tỉ số lượng giác của mỗi góc nhọn sau: tan OCD , cot OAD B A C O Lời giải
Hình thoi ABCD có hai đường chéo cắt nhau t D
ại O nên AC ⊥ BD tại O OA
a) Tam giác OAB vuông tại O nên = sin OAB AB OB
Tam giác OBC vuông tại O nên = cosOAB BC Trang 4
b) Tam giác OCD vuông tại O nên tan = OD OCD OC
Tam giác OAD vuông tại O nên cot = OA OAD OD
Bài 2: Tính các tỉ số lượng giác của góc , trong tam giác ABC ở hình vẽ bên. A 12 9 α B 15 C Lời giải
Xét ABC vuông tại A , B = , ta có: AC 9 AB sin = = = 0,16 ; 12 cos = = = 0,8 BC 15 BC 15 AC 9 AB tan = = = 0,75 ; 12 4 cot = = = AB 12 AC 9 3
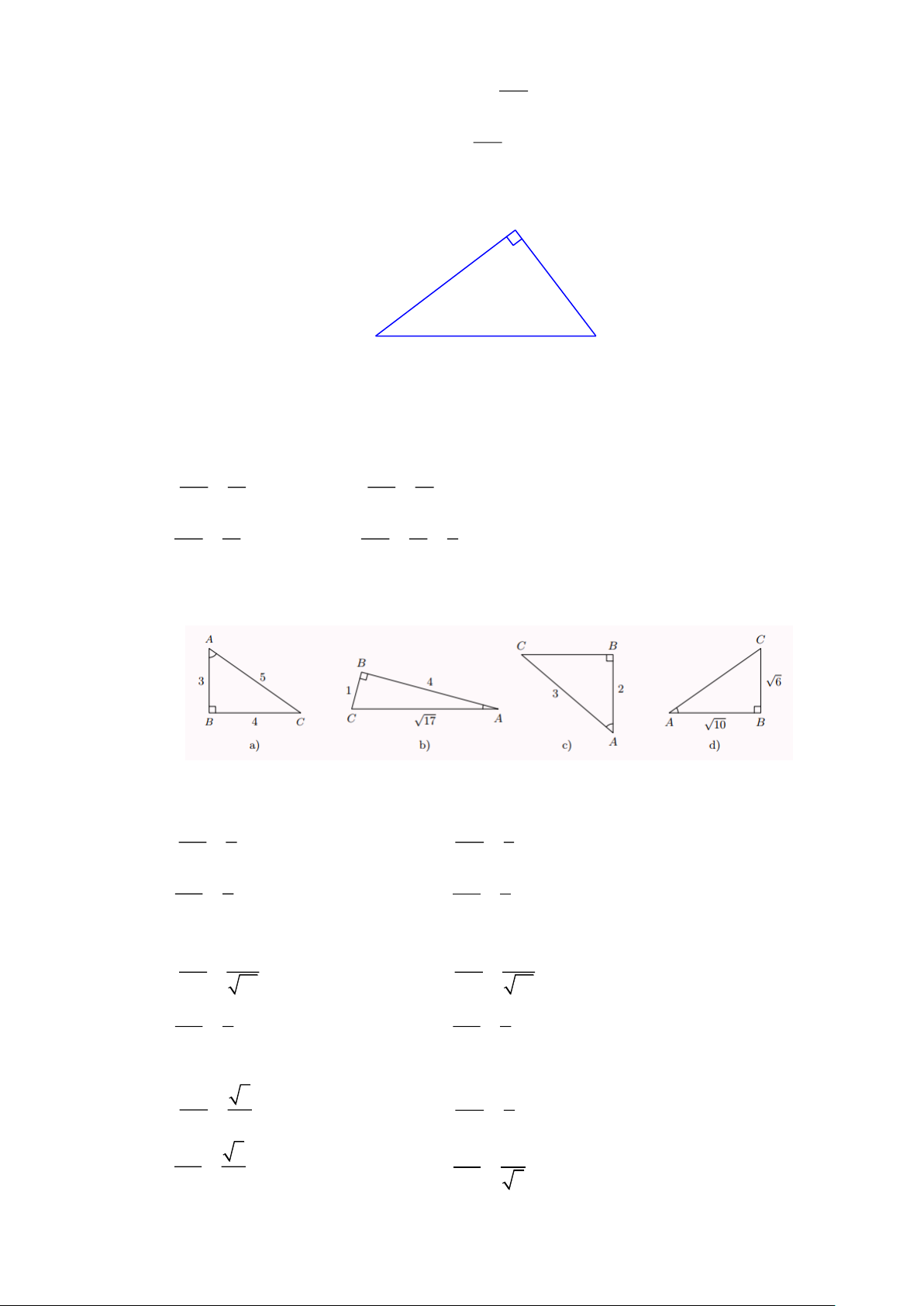
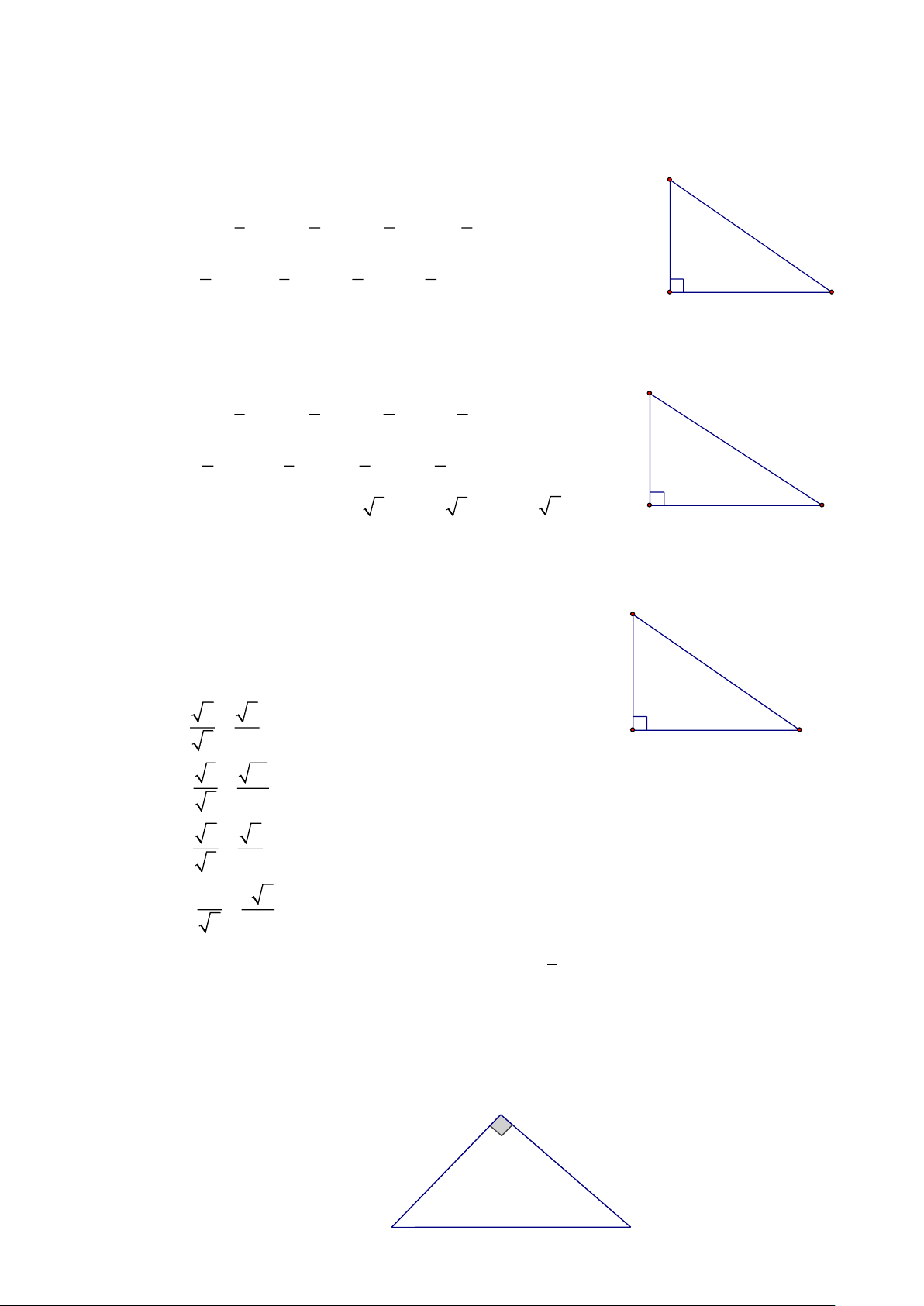
Bài 3: Tính các tỉ số lượng giác của góc nhọn A trong mỗi tam giác vuông ABC có B = 90 ở hình sau. Lời giải
+ Xét ABC vuông tại B (hình a), ta có: BC 4 AB sin A = = ; 3 cosA= = AC 5 AC 5 BC 4 AB 3 tan = = ; cotA= = AB 3 BC 4
+ Xét ABC vuông tại B (hình b), ta có: BC 1 AB sin A = = ; 4 cosA= = AC 17 AC 17 BC 1 AB 4 tan = = ; cotA= = AB 4 BC 1
+ Xét ABC vuông tại B (hình c), ta có: BC 5 AB 2 sin A = = ; cosA= = AC 3 AC 3 BC 5 AB tan = = ; 2 cotA= = AB 2 BC 5
+ Xét ABC vuông tại B (hình d), ta có: Trang 5 BC 6 AB 10 sin A = = ; cosA= = AC 2 AC 2 BC 6 AB 10 tan = = ; cotA= = AB 10 BC 6
Bài 4: Cho tam giác ABC vuông tại A , có AB = 3 cm, AC = 4 cm. Hãy tính các tỉ số lượng giác
sin , cos , tan với = B Lời giải
Xét ABC vuông tại A , B =
Theo định lí pythagore, ta có: 2 2 2 2 2
BC = AC + AB = 4 + 3 = 25 nên BC = 5 cm.
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, ta có: AC 4 AB sin A = = ; 3 cosA= = BC 5 BC 5 AC 4 tan = = ; AB 3
Bài 5: Cho tam giác ABC vuông tại A , có AB = 5 cm, AC = 12cm. Hãy tính các tỉ số lượng giác của góc B Lời giải
Xét ABC vuông tại A
Theo định lí pythagore, ta có: 2 2 2 2 2
BC = AC + AB = 12 + 5 = 169 nên BC = 13 cm.
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, ta có: AC 12 AB sin A = = ; 5 cosA= = BC 13 BC 13 AC 12 AB tan = = ; 5 cotA= = AB 5 AC 12
Bài 6: Tính tỉ số lượng giác của góc B trong hình vẽ bên. B 5 A 12 C Lời giải Ta có: 2 2 2 2 2
BC = AC + AB = 12 + 5 = 169 nên BC = 13 cm. Do đó: AC 12 AB 5 sin A = = ; cosA= = BC 13 BC 13 AC 12 AB 5 tan = = ; cotA= = AB 5 AC 12
Bài 7: Cho tam giác MNP vuông tại M , MN = 3cm, MP = 4 cm. Tính các tỉ số lượng giác của góc Trang 6 P Lời giải
Trong MNP vuông tại M , ta có 2 2 2 2
NP = MN + MP = 3 + 4 = 25 = 5
Xé MNP vuông tại M , ta có: MN 3 MP sin P = = ; 4 cos P = = NP 5 NP 5 MN 3 MP tan = = ; 4 cotA= = MP 4 MN 3
Bài 8: ABC vuông tại A có BC = 2AB . Tính các tỉ số lượng giác của góc C Lời giải
Ta đặt AB = m thì BC = 2 m, suy ra 2 2 2 2 2 2
AC = BC − AB = 4m − m = 3m Suy ra AC = m 3 Ta có: AB m 1 AB m 3 3 sin C = = = ; cosC = = = BC 2m 2 BC 2m 2 AB m 1 AC m 3 tan C = = = ; cot = A = = 3 BC m 3 3 AB m
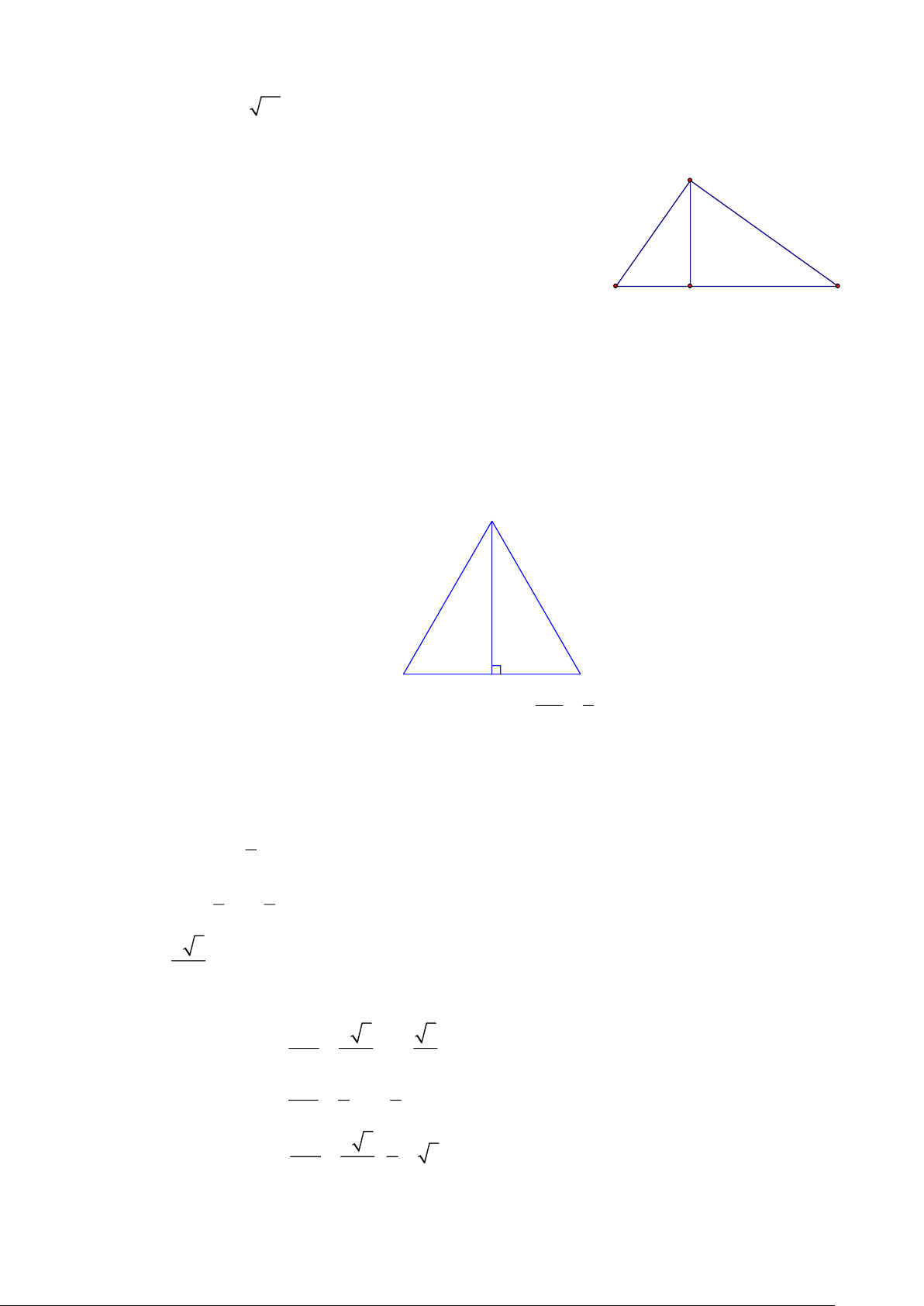
Bài 9: ABC cân tại A , có BC = 6 , đường cao AH = 4 . Tính các tỉ số lượng giác của góc B Lời giải
Ta có: BH = 6 : 2 = 3 ; 2 2 AB = 4 + 3 = 5 Do đó: AH 4 BH 3 sin C = = = 0,8 ; cos B = = = 0,6 AB 5 AB 5 AH 4 BH 3 tan B = = ; cotB= = = 0,75 AB 3 AH 4
Bài 10: Tính tan C trong hình vẽ bên. A 6 B 3 H C Lời giải Ta có: 2 2 2 2 2
AH = AB − BH = 6 − 3 = 27 AH = 3 3 Do đó BH 3 1 tan C = cot B = = = . AH 3 3 3
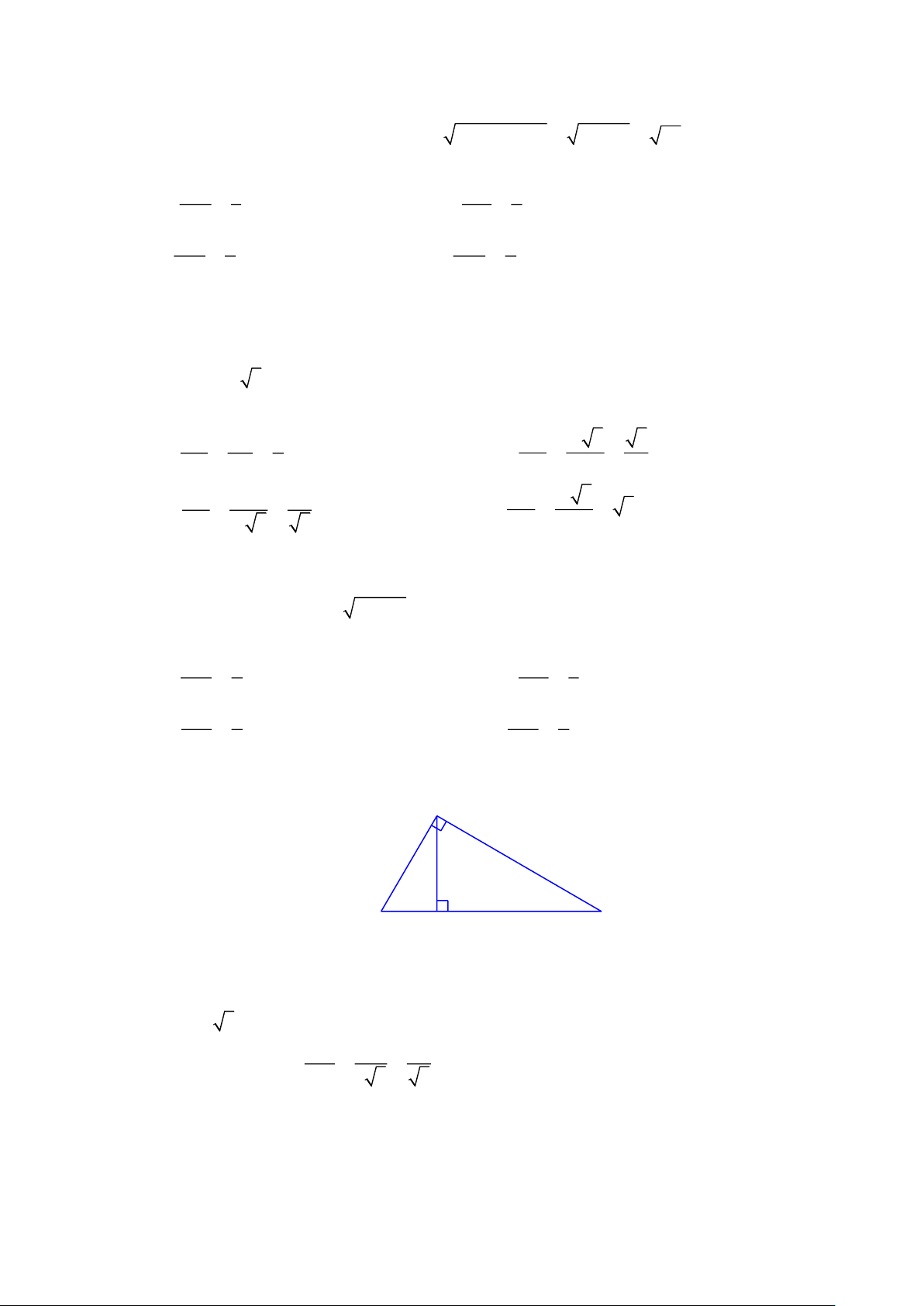
Bài 11: Tính sin M + cos N trong hình vẽ bên. Trang 7 O M 1 H 3 N Lời giải Ta có: 2
OH = HM HN = 13 = 3
OH = 3 ; OM = 1+ = 2 OH 3 Do đó sin M = = OM 2 3
Mặt khác cos N = sin M =
nên cos N + sin M = 3 . 2
Bài 12: Tam giác ABC vuông tại A , AB = 1,5, BC = 3,5 . Tính tỉ số lượng giác của góc C rồi
suy ra các tỉ số lượng giác của góc B Lời giải
Ta có: AC = BC − AB = ( )2 −( )2 2 2 2 3,5
1,5 = 10 , suy ra AC = 10 Do đó AB 1,5 cos B = sin C = = 0,4286 BC 3,5 AC 10 cosC = sin B = = 0,9035 BC 3,5 AB 1,5 cot B = tan C = = 0,4743 AC 10 AC 10 cot C = tan B = = 2,1082. AB 1,5
Bài 13: Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 40 : sin 40 , cos60 , sin 52 30
' , tan 80 , cot 82. Lời giải
sin60 = cos(90 − 60) = cos30
cos75 = sin (90 − 75) = sin15 sin 52 30 = cos(90 − 52 30 ') = cos37 30
cot 82 = tan (90 − 82) = tan 8 .
Bài 14: Tia nắng chiếu qua điểm B của tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB
của tòa nhà một góc y (hình vẽ). Cho biết cosx 0,78 và cot x 1, 25 . Tính sin y và tan y
(kết quả làm tròn đến hàng phần trăm). Trang 8 Lời giải
Do góc x và góc y là hai góc phụ nhau nên sin y = cos x 0,78
Và tan y = cot x 1, 25
Bài 15: Hình bên mô tả một chiếc thang có chiều dài AB = 4 m được đặt dựa vào tường, khoảng
cách từ chân thang đến chân tường là BH =1,5 m. Tính góc tạo bởi cạnh AB và phần
tường nằm ngang trên mặt đất (làm tròn kết quả đến hàng đơn vị) Lời giải
Ta có, góc tạo bởi cạnh AB và phương năm ngang trên mặt đất là ABH Xét tam giác BH
ABH vuông tại H , ta có 1,5 ABH = = = 0,375 AB 4 Vậy ABH 68 .
Bài 16: Treo quả cầu kim loại nhỏ vào giá thí nghiệm bằng sợi dây mảnh nhẹ không dãn. Khi quả
cầu đứng yên tại vị trí cân bằng, dẫy treo có phương thẳng đứng. Kéo quả cầu khỏi vị trí
cân bằng một đoạn nhỏ rồi buông ra thì quả cầu sẽ chueyenr động qua lại quanh vị trí cân
bằng. Khi kéo quả cầu khỏi vị trí cân bằng, giả sử tâm A của quả cầu cách B một
khoảng AB = 60cm và cách vị trí cân bằng một khoảng AH = 20 cm. Tính số đo góc
tạo bởi sợi dây BA và vị trí cân bằng (làm tròn kết quả đến hàng đơn vị của độ). Lời giải AH 20 1
Xét ABH vuông tại H , ta có sin = = = AB 60 3 Do đó 19 Trang 9
Vậy góc tạo bởi sợi dây BA và vị trí cân bằng có số đo khoảng 19 .
BÀI TẬP TƯƠNG TỰ DẠNG TOÁN 2
Bài 1: Cho tam giác ABC vuông tại C có BC = 1, 2c ;
m AC = 0,9cm . Tính các tỉ số lượng giác của
góc B , từ đó suy ra tỉ số lượng giác của góc A A Lời giải Ta có: 3 4 3 4
SinB = ;cosB = ;tanB = ;CotB = 5 5 4 3 0,9 4 3 4 3
SinA = ;CosA = ;tanA = ;cotA = 5 5 3 4 1,2 C B
Bài 2: Cho tam giác ABC vuông tại A có AB = 1,6c ;
m AC = 1, 2cm . Tính các tỉ số lượng giác của
góc B , từ đó suy ra tỉ số lượng giác của góc C . Lời giải C Ta có: 3 4 3 4
SinB = ;cosB = ;tanB = ;cotB = 5 5 4 3 4 3 4 3 1,2
SinC = ;CosC = ;tanC = ;cotC = 5 5 3 4
Bài 3: Cho tam giác ABC có AB = a 5, BC = a 3 , AC = a 2 1,6 B A
a) Chứng minh tam giác ABC vuông
b) Tính các tỉ số lượng giác của góc B , từ đó suy ra các tỉ số lượng giác của góc A Lời giải A
a) Dùng định lý pytago đảo, ta có: 2 2 2
AB = AC + BC ( 2 2 2
5a = 3a + 2a ) ABC vuông tại C b) Tính được: 2 6 - SinB = = 5 5 C B 3 15 - cos B = = 5 5 2 6 - tan B = = 3 3 3 3 6 - CotB = = 6 6 5
Bài 4: Cho tam giác ABC vuông tại A , AB = 5cm , cotB = . Tính độ dài các đoạn thẳng AC và 8 BC
a) Chứng minh tam giác ABC vuông
b) Tính các tỉ số lượng giác của góc B , từ đó suy ra các tỉ số lượng giác của góc A Lời giải A T Brang 10 C
Áp dụng tỉ số cotB trong tam giác vuông ABC và định lý pytago ta tính được AC = 8c , m BC = 89cm
Bài 5: Cho tam giác ABC vuông tại A , đường cao AH (H BC) , hãy tính sinB và sinC làm tròn
kết quả đến chữ số thập phân thứ tư trong các trường hợp sau: A a) AB = 13 , m BH = 0,5dm
b) BH = 3cm,CH = 4cm 13 Lời giải
a) Áp dụng các tỉ số lượng giác cho tam giác vuông ABH để tính 4
sinB , rồ3i từ đó suy ra C H 5 B sinC
b) Áp dụng hệ thức lượng về cạnh góc vuông và hình chiếu lên cạnh huyền trong tam giác
vuông ABC để tính AB . Sau đó làm tương tự câu a
Bài 6: Cho tam giác ABC đều, cạnh a , đường cao AH . Tính tỉ số lượng giác của các góc ABH ,
HAB (không dùng tỉ số lượng giác của các góc đặc biệt) Lời giải A a
Vì tam giác ABC đều (giả thiết) nên đường cao AH đồng thời là đường trung tuyến B H C Suy ra BC
H là trung điểm của BC suy ra 1 BH = HC = = a 2 2
AH ⊥ BC AHB = 90 , suy ra AHB vuông tại H 2 2 2
AB = AH + BH (pitago) 2 1 2 2
a = AH + a 2 1 3 2 2 2 2
AH = a − a = a 4 4 3 = a AH 2
Trong tam giác vuông AHB có ABH , HAB là hai góc phụ nhau nên: AH a 3 3
sin ABH = cosHAB = = : a = AB 2 2 BH a 1
cos ABH = sin HAB = = : a = AB 2 2 AH a 3 a
tan ABH = cot HAB = = : = 3 BH 2 2 Trang 11 BH a a 3 1 3
cot ABH = tan HAB = = : = = AH 2 2 3 3
Bài 7: Cho tam giác ABC vuông tại A , có AB AC , chu vi là 72 cm và trung tuyến AM = 15 cm.
Tính tỉ số lượng giác của các góc B , C Lời giải A 15cm
Vì AM là trung tuyến ứng với cạnh huyền của tam giác vuông ABC nên ta có: B M C
BC = 2AM = 215 = 30 cm
Mà AB + BC + CA = 72 cm nên AB + AC = 42cm
Đặt AC = x cm ( x 0 )
AB = 42 − AC = 42 − x cm Hơn nữa 2 2 2
AB + AC = BC (Pitago) (AB + AC)2 2
− 2AB AC = BC 2 2
42 − 2AB AC = 30 AB AC = 432 ( − x) 2 42
x = 432 x − 42x + 432 = 0
(x − 24)(x −18) = 0
x = 24 hoặc x = 18
Nếu x = 24 thì AC = 24 cm suy ra AB = 42 − 24 = 18 cm (thỏa mãn AB AC )
Nếu x = 18 thì AC = 18cm suy ra AB = 42 −18 = 24 cm (không thỏa mãn AB AC )
Như vậy tam giác ABC vuông tại A và có AB = 18 cm, AC = 24 cm, BC = 30 cm
Hơn nữa B và C là hai góc phụ nhau.
Bài 8: Cho tam giác ABC có AB = 5 cm, AC = 3 cm, B + 2C = 90 . Tính sin C Lời giải Kẻ CH ⊥ AB H K Do M
B + C 90 nên A nằm giữa B và H 1 1 Ta có 2
B + BCH = 90 = B + 2C 1 1 1 1 A
BCH = 2C C = C 1 1 2 2
Kẻ đường thẳng vuông góc với BC tại B và cắt tia 1CA tại K . Ta có: 1 B C
K + C = 90 1 K = A 2 A + C = 90 2 2
Mà A = A (hai góc đối đỉnh) nên K = A 1 2 1
ABK cân tại B (theo dấu hiệu nhận biết)
Kẻ BM ⊥ AK thì BM cũng là đường trung tuyến của ABK
Suy ra M là trung điểm của AK
Đặt AM = MK = x cm, với x 0 Trang 12
Xét BKC vuông tại B có đường cao BM : 2
BK = KM KC (hệ thức về cạnh và đường cao)
( )2 = x( x+ ) 2 5 2
3 2x + 3x − 5 = 0 (x − ) 1 (2x + 5) = 0 x =1 (TM ) 5 x = − (KTM ) 2
Do đó KC = 21+ 3 = 5 KB 5
Trong tam giác BKC có sin C = = . KC 5
Dạng 3: Tính các cạnh trong một tam giác vuông sử dụng tỉ số lượng giác của góc nhọn.
Bài 1: Cho tam giác ABC vuông tại A có C = 30 và BC = a . Tính các cạnh AB , AC theo a Lời giải Ta có: sin = AB C
, suy ra AB = BC sin C = a sin 30 BC Trang 13 Lại có 1 sin 30 = nên = a AB 2 2 3 Tương tự, ta có AC cosC= , suy ra =
cos = cos30 = a AC BC C a BC 2
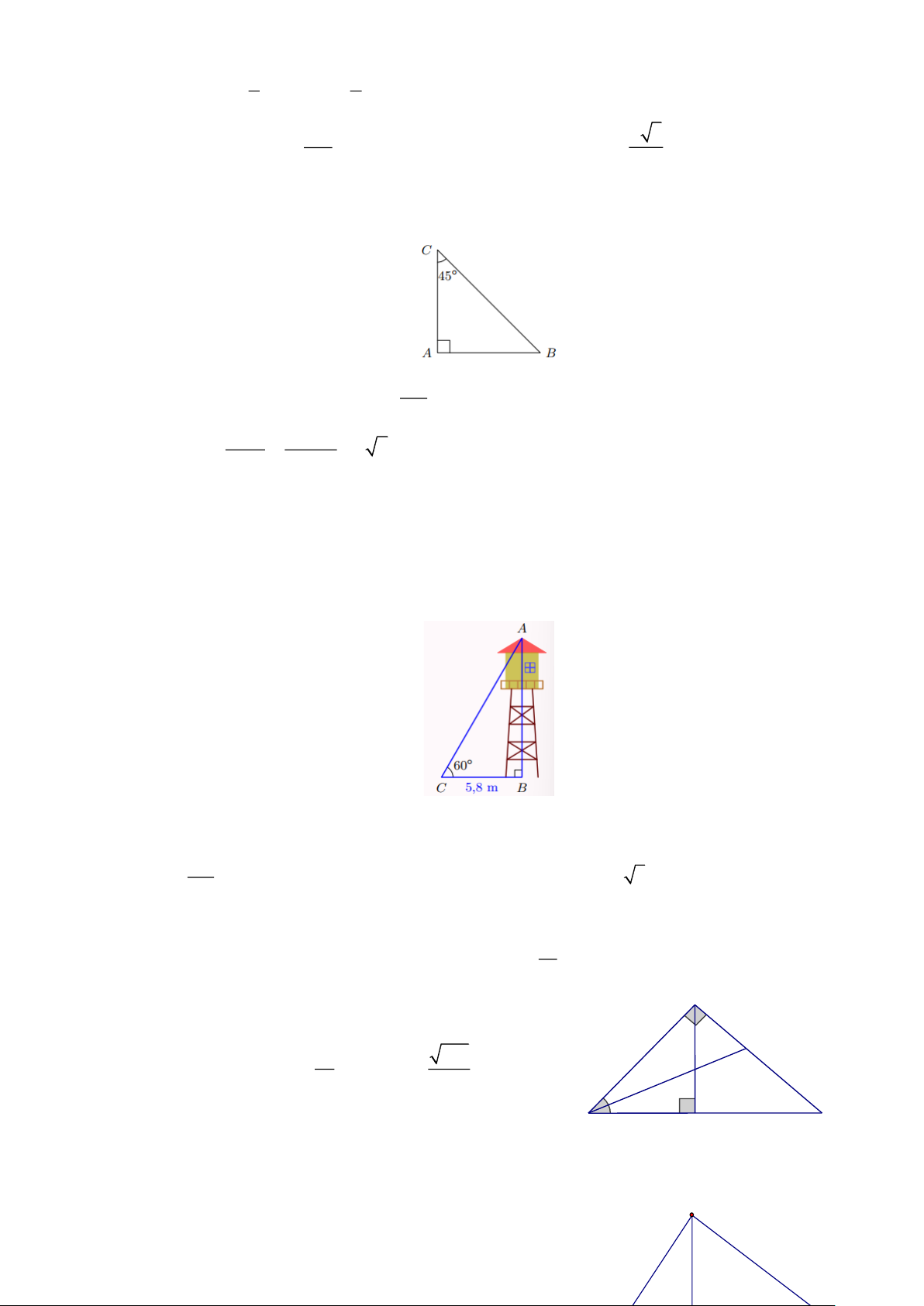
Bài 2: Cho tam giác ABC vuông tại A có C = 45 và AB = c . Tính các cạnh BC , AC theo c Lời giải
Xét ABC vuông tại A có sin = AB C BC Suy ra = AB = c BC = c 2 sin C sin 45
Xét ABC vuông tại A có B + C = 90
Do đó B = C = 45
Suy ra ABC vuông cân tại A
Vậy AB = AC = c .
Bài 3: Tính chiều cao của tháp canh trong hình bên (kết quả làm tròn đén hàng phần trăm). Lời giải
Xét ABC vuông tại B có: tan = AB C
, suy ra AB = BC tan C hay AB = 5,8 tan 60 = 5,8 3 10,5 (m) CB
Vậy chiều cao của tháp canh gần bằng 10,05 mét. 5
Bài 4: Cho tam giác ABC vuông tại A , AB = 6c , m tanB =
. Hãy tính độ dài đường cao AH và 12
trung tuyến BM của tam giác ABC A Lời giải M 6 Xét ABH (H ) 30 601 AH = (cm); BM = (cm) 13 4 B H C
Bài 5: Cho tam giác ABC vuông tại A , đường cao AH (H BC) biết BH = 4cm , CH =1cm .
Hãy tính các cạnh và các góc của tam giác vuông ABC . A Trang 14 1 4 C H B Lời giải
Xét tam giác ABC vuông tại A , áp dụng hệ thức lượng trong tam giác vuông, ta có: +) 2 2
AB = BC.BH AB = 20 AB = 2 5(cm) AC = 5(cm) AC 5 1 AB +) Ta có: 0 0 tanB = =
= B = 45 ;tanC = = 2 C = 45 AB 2 5 2 AC
Bài 6: Cho tam giác ABC vuông tại A , đường cao AH (H BC) , biết BH = 4cm , AC = 3 13cm .
Hãy tính các cạnh và các góc của tam giác vuông ABC . A Lời giải
Đặt HC = x (cm) 3 13
Áp dụng hệ thức lượng trong tam giác vuông ABC , ta có: 4 2 2 C H
AC = BC.CH = (4 + x).x x + 4x = 9.13 B x = 9( ) tm 2
x + 4x + 4 =121 x = 1 − 3(loai)
Ta có: BC = BH + HC = 13(cm) +) 2
AB = BH.BC = 13.4 = 52 AB = 2 13(cm) AC 3 13 3 +) 0 0 SinB = = =
B = 56 C = 34 BC 13 13
Bài 7: Cho tam giác ABC vuông tại A , có AB = 10 cm, AC = 15cm a. Tính góc B
b. Phân giác trong của góc B cắt AC tại I . Tính AI
c. Vẽ AH vuông góc với BI tại H . Tính AH Lời giải A I 15 10 H
a) Xét tam giác ABC vuông tại A , áp dụng hệ thức lượng trong tam giác vuông, ta có: AC 15 3 B 0 tanB = = = B = 56 C AB 10 2 b) Ta có: AI 0 tanABI = AI = A .
B tanABI =10.tan28 = 5,3(cm) AB AH c) 0 SinABH = AH = A .
B Sin28 = 4,7(c ) m AB 2
Bài 8: Cho tam giác ABC vuông tại A , đường cao AH = 6cm(H BC), biết tanC = . Hãy tính 3
độ dài các cạnh: HB, HC, AB, AC Trang 15 Lời giải Theo giả thiết ta có: 2 AH 2 tanC = = 3 CH 3 Lại có: AH HB AB 2 H . A 2 6.2 AH.3 AHB# CH ( A g.g) = = = HB = = = 4;CH = = 9 CH HA AC 3 3 3 2
Xét tam giác ABC vuông tại A, áp dụng hệ thức lượng trong tam giác vuông ta có: 2 2
AB = BH.HC AB = 2 13(cm); AC = CH.CB AC = 3 13(cm)
Bài 9: Cho tam giác ABC vuông tại A , có 0 AC = 15c ,
m B = 50 . Hãy tính độ dài a) AB, AC A b) phân giác CD Lời giải 6
a) Tam giác ABC vuông ở A , theo hệ thức lượng về cạnh và góc trong tam giác vuông, ta B H C có: 0
AB = AC.cotB = 15.cot50 15.0,8391 12,59(cm) AC 15 15
AC = BC.sinB BC = = 19,58 cm 0 ( ) sinB s 5 in 0 0,7660
b) Tam giác ABC vuông ở A nên: 0 0 0
B + C = 90 C = 90 − B = 40 1 1
CD là tia phân giác của C , ta có: 0 0
ACD = C = .40 = 20 2 2
Trong tam giác vuông ACD vuông tại A , theo hệ thức lượng về cạnh và góc ta có: AC 15 0 AC = C . D cos AC . D cos20 CD = = 15,96 cm . 0 ( ) cos20 0,9397
Bài 10: Cho tam giác ABC vuông tại A , góc 0
C = 30 , BC = 10cm
a. Tính AB, AC
b. Kẻ từ A các đường thẳng AM , AN lần lượt vuông góc với các đường phân giác trong và
ngoài của góc B . Chứng minh MN = AB
c. Chứng minh các tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng. Lời giải
b) Chú ý: Hai đường phân giá của hai góc kề bù vuông góc với nhau
c) Ta có: BM là phân giác của góc B . Từ đó tính được số đo các góc của tam giác MAB
*) Chú ý: Tam giác MAB và ABC đều là các tam giác nửa đều, từ đó tính được tỉ số đồng dạng là 0,5. B N M
Bài 11: Cho tam giác ABC vuông tại A( AB AC) , 0
C = 45 , đường trung tuyến AM , đường cao A C
AH , MA = MB = MC = a . Chứng minh rằng: Trang 16
a) sin2 = 2si n . cos b) 2
1+ cos2 = 2cos c) 2
1− cos2 = 2sin Lời giải a) Ta có: AH 2AH 2AH A . = B AC AMH 2; Sin2 = = = = 2. = 2.s in .co s 2 AM 2AM BC BC 2 b) HM HC 2HC AC 2 1+ cos2 =1+ = = = 2. = 2.cos 2 AM AM BC BC 2 c) HM HB 2HB AB 2 1− cos2 = 1− = = 2. = 2.sin . 2 AM AM BC BC B H M A C m
Dạng 4: Dựng góc nhọn biết một tỉ số lượng giác của góc đó bằng n I. Phương pháp giải:
Dựng một tam giác vuông có cạnh là m và n ( m và n tương ứng là cạnh góc vuông và cạnh
huyền nếu tỉ số lượng giác đã co là sin hoặc cos; m và n là hai cạnh góc vuông nếu tỉ số lượng
giác đã cho là tan hoặc cot) rồi vận dụng định nghĩa để nhận ra góc . Trang 17 II. Bài toán
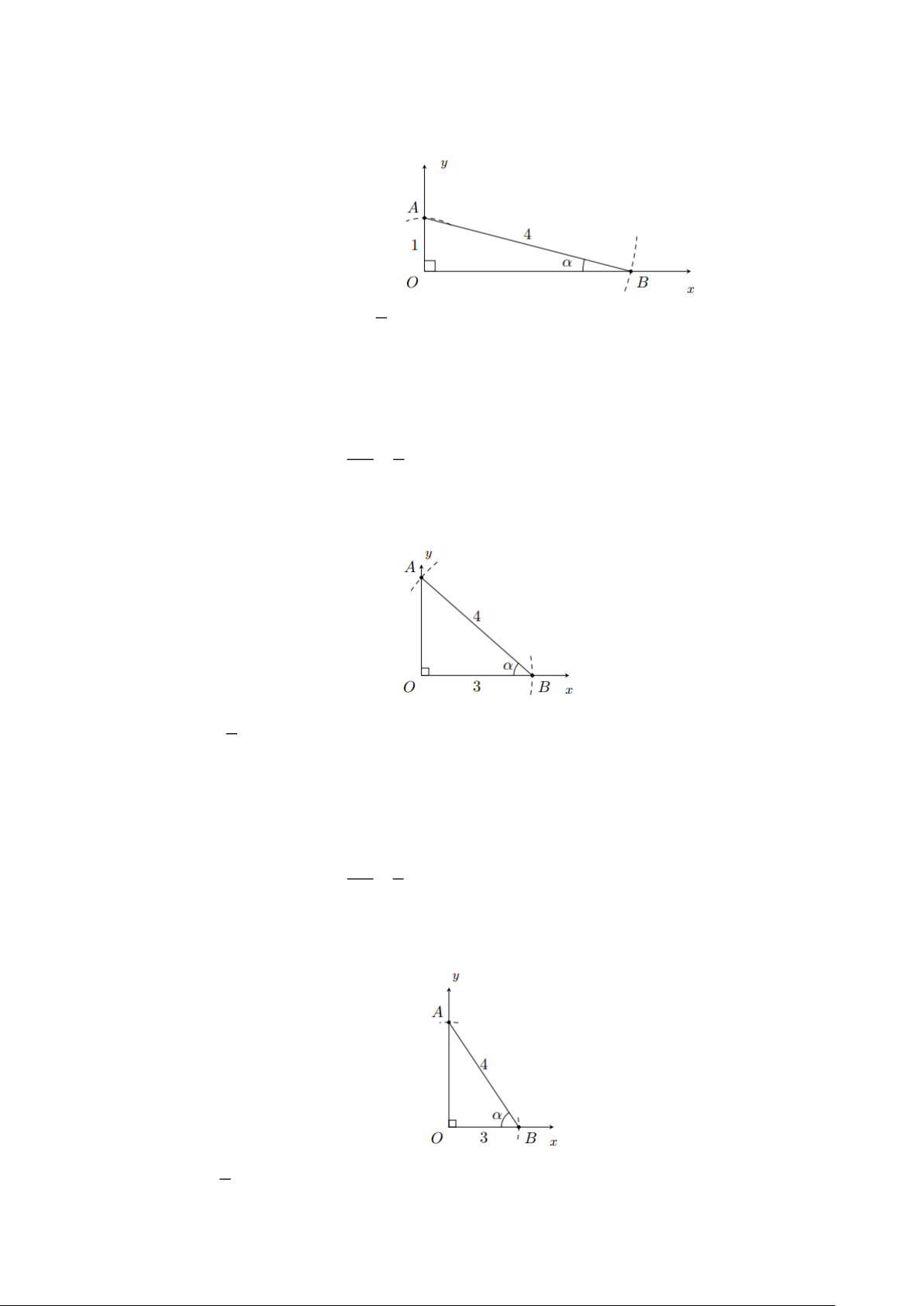
Bài 1: Dựng góc , biết sin = 0, 25 Lời giải Ta có: 1 0, 25 = 4
+ Dựng góc vuông xOy
+ Trên cạnh Ox đặt OA = 1 + Dựng đường tròn ( ;
A 4) căt cạnh Oy tại B Khi đó OA ABO = (vì 1 sin = = ). OB 4
Bài 2: Dựng góc , biết cos =0,75 Lời giải 3 Ta có: 0,75= 4
+ Dựng góc vuông xOy
+ Trên cạnh Oy đặt OB = 3
+ Dựng đường tròn (B;4) cắt cạnh Ox tại A OB 3
Khi đó ABO = (vì cos = = ). BA 4
Bài 3: Dựng góc , biết tan =1,5 Lời giải 3 Ta có: 1,5 = 2 Trang 18
+ Dựng góc vuông xOy
+ Trên cạnh Ox đặt OA = 3
+ Trên cạnh Oy đặt OB = 2 Khi đó OA ABO = (vì 3 tan = = ). OB 2
Bài 4: Dựng góc , biết cot =2 Lời giải
+ Dựng góc vuông xOy
+ Trên cạnh Ox đặt OA = 1
+ Trên cạnh Oy đặt OB = 2 Khi đó OB ABO = (vì cot = = 2 ). OA
Dạng 5: Tính giá trị của biểu thức lượng giác với các góc đặc biệt I. Phương pháp giải
+ Sử dụng bảng giá trị các tỉ số lượng giác của các góc 30 ; 45 ; 60
+ Sử dụng tỉ số lượng giác của hai góc phụ nhau II. Bài toán
Bài 1: Tính giá trị của mỗi biểu thức sau: a) 2 2 sin 45 + cos 45 b) tan 30cot 30 sin 30cos60 c) tan 45 Lời giải a) Ta có: 2 2 sin 45 + cos 45 2 2 2 2 1 1 = + = + = 1 2 2 2 2
b) Ta có: tan 30cot 30 3 = 3 =1 3 Trang 19 c) Ta có: sin 30 cos 60 tan 45 1 1 1 2 2 = = 1 4
Bài 2: Tính giá trị của mỗi biểu thức sau: a) 2cos45 A = + 3 tan 30 b) 2sin 60 B = − cot 45 2 3 Lời giải a) Ta có: 2cos45 A = + 3 tan 30 2 2 2 3 2 = + 3 = 1+1 = 2 2 3 b) Ta có: 2sin 60 B = − cot 45 3 3 2 2 = −1 = 1−1 = 0 3
Bài 3: Tính giá trị của mỗi biểu thức sau: a) 2 3
M = 4cos 45 + 3 cot 30 −16cos 60 − b) 2sin 30 sin 60 N = 2 cos 30 − cos60 Lời giải a) Ta có: 2 3
M = 4cos 45 + 3 cot 30 −16cos 60 2 3 2 1 = 4 + 3 3 −16 2 2 = 2 + 3 − 2 = 3 2sin 30 − sin 60 b) Ta có: N = 2 cos 30 − cos60 1 3 3 2 − 1− 2 2 2 = = = 4 − 2 3 2 3 1 3 1 − − 4 2 2 2 Bài 4: Tính a) sin 61 − cos29 b) cos15 − sin 75 c) tan 28 − cot 62 d) cot 47 − tan 43 Lời giải
a) Ta có: sin 61 − cos29 = sin 61 − sin 61 = 0 .
b) Ta có: cos15 − sin 75 = cos15 − cos15 = 0 .
c) Ta có: tan 28 − cot 62 = tan 28 − tan 28 = 0 .
d) Ta có: cot 47 − tan 43 = cot 47 − cot 47 = 0 . Trang 20
