Các Dạng Toán 9 Kết Nối Tri Thức Bài 12 Một Số Hệ Thức Giữa Cạnh Góc Trong Tam Giác Vuông Và Ứng Dụng
Trong một tam giác vuông, nếu cho biết trước hai cạnh ( hoặc một góc nhọn và một cạnh) thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của tam giác vuông đó. Bài toán này gọi là bài toán Giải tam giác vuông. Trong đo đạc, khi người quan sát có hướng nhìn ngang theo tia Ox. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Chương 4: Hệ thức lượng trong tam giác vuông (KNTT) 2 tài liệu
Môn: Toán 9 2.9 K tài liệu
Sách: Kết nối tri thức
Tác giả:
Preview text:
MỘT SỐ HỆ THỨC GIỮA CẠNH, GÓC TRONG TAM GIÁC VUÔNG VÀ ỨNG DỤNG
A. TRỌNG TÂM KIẾN THỨC
1. Hệ thức giữa cạnh huyền và cạnh góc vuông
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với cô sin góc kề.
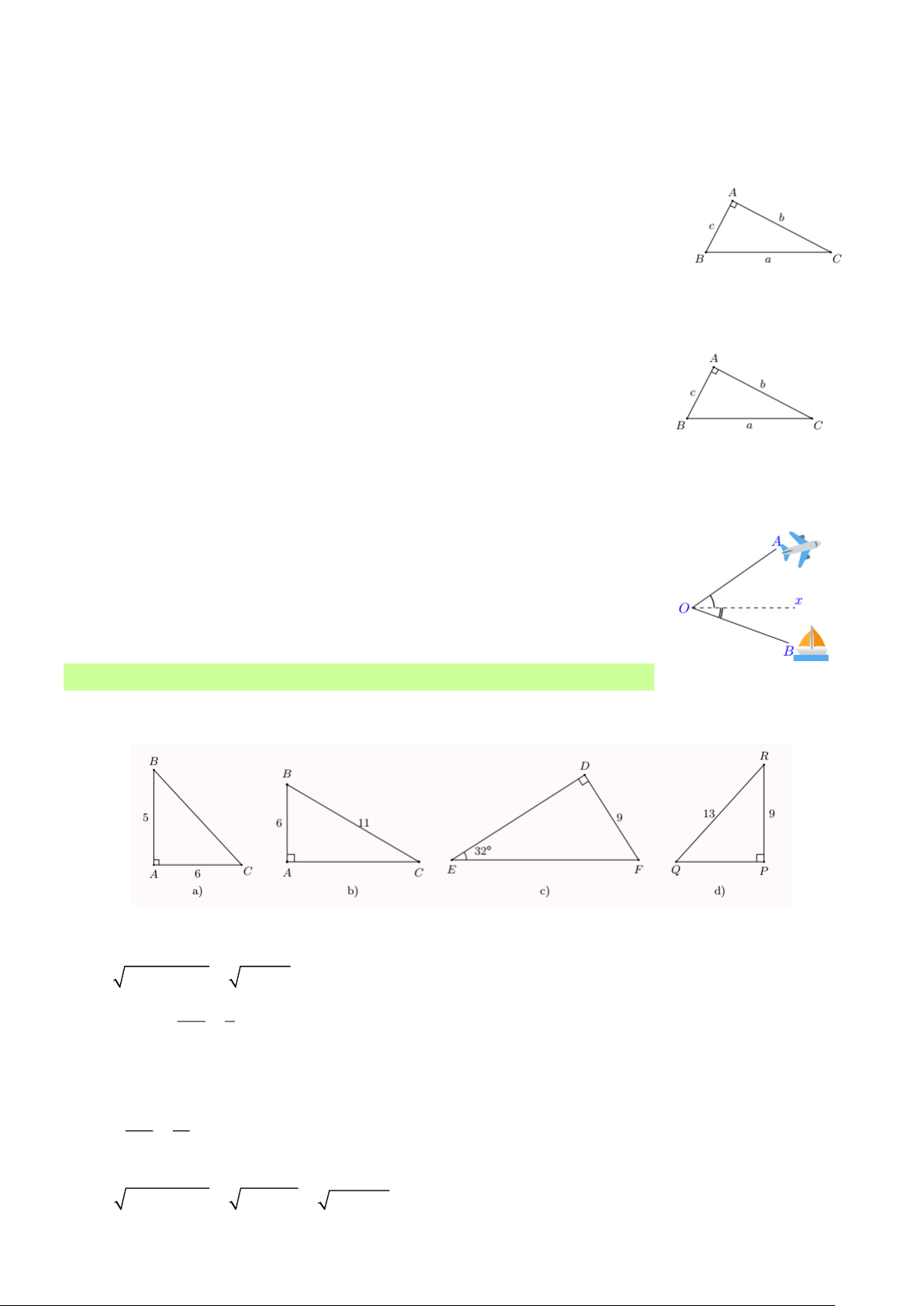
+ Trong tam giác ABC vuông tại A ta có b = . a sin B = . a cosC c = . a sin C = . a cos B
2. Hệ thức giữa hai cạnh góc vuông
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia
nhân với tan góc đối hoặc nhân với cot góc kề.
+ Trong tam giác ABC vuông tại A ta có b = . c tan B = . a cot C c = . b tan C = . b cot B 3. Giải tam giác vuông
Trong một tam giác vuông, nếu cho biết trước hai cạnh ( hoặc một góc
nhọn và một cạnh) thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của tam giác vuông đó.
Bài toán này gọi là bài toán Giải tam giác vuông.
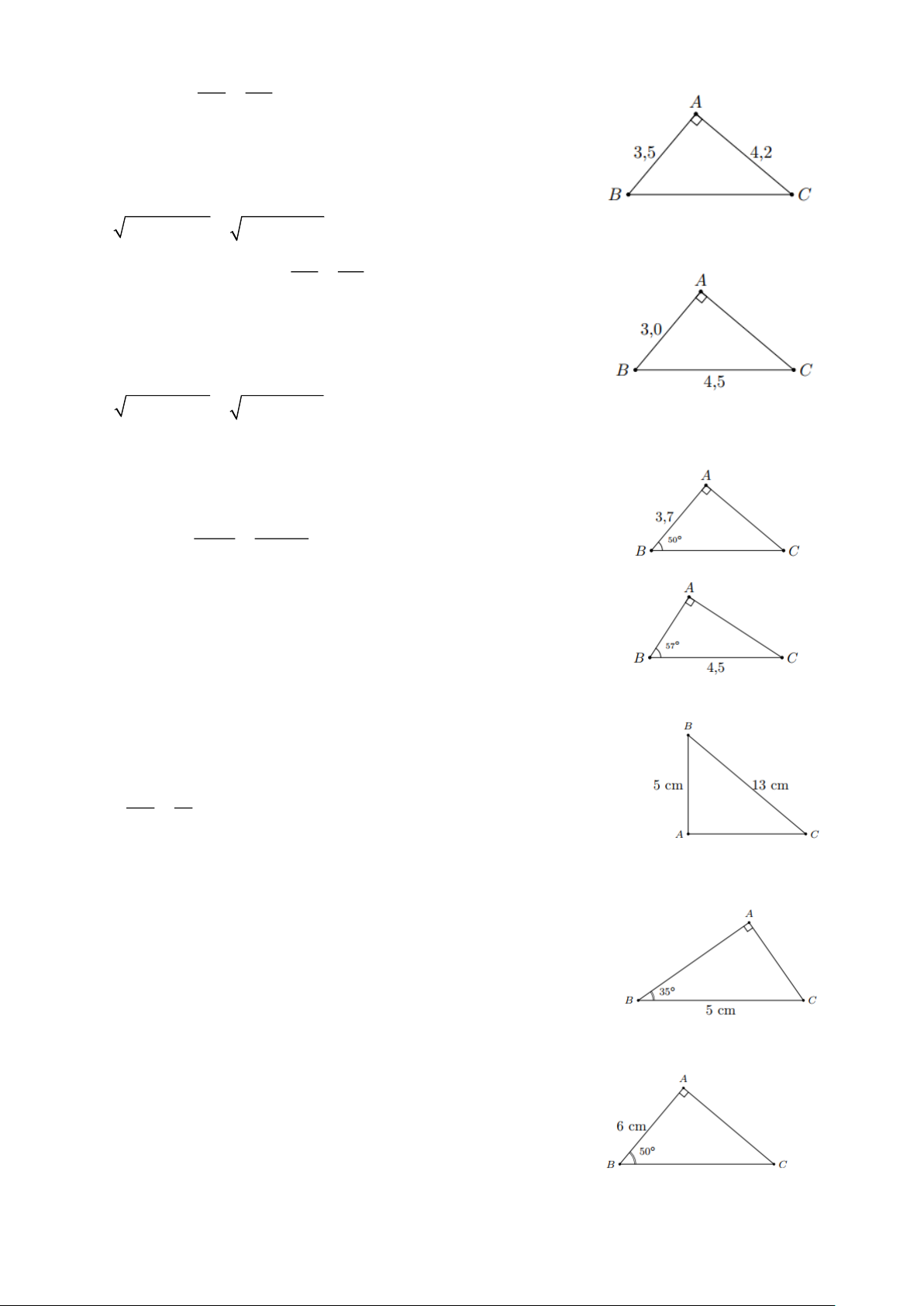
Trong đo đạc, khi người quan sát có hướng nhìn ngang theo tia Ox (hình bên)
+ Góc xOA gọi là góc nghiêng lên hay góc nâng
+ Góc xOB gọi là góc nghiêng xuống hay góc hạ.
B. CÁC DẠNG BÀI TẬP
Dạng 1: Giải tam giác vuông
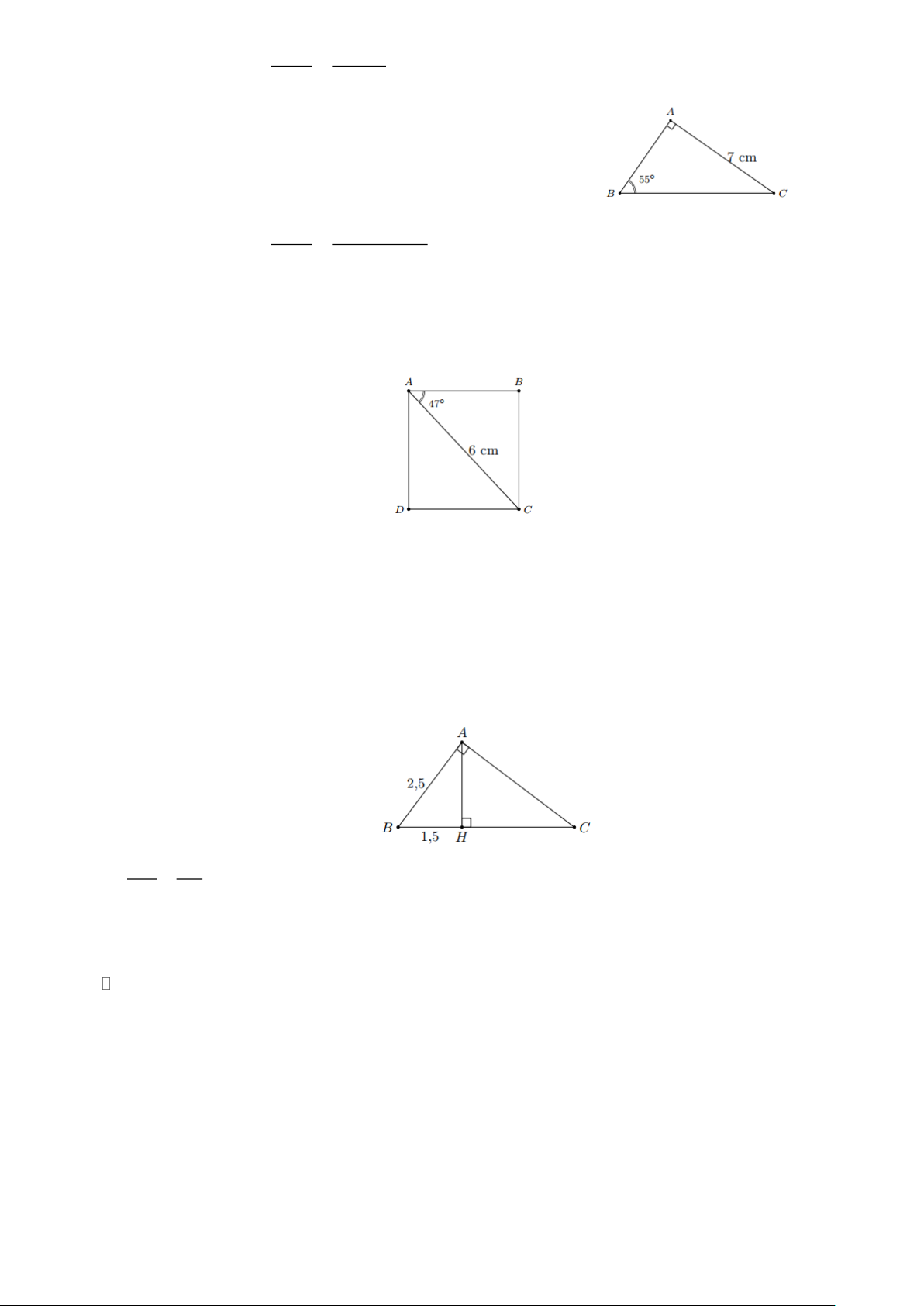
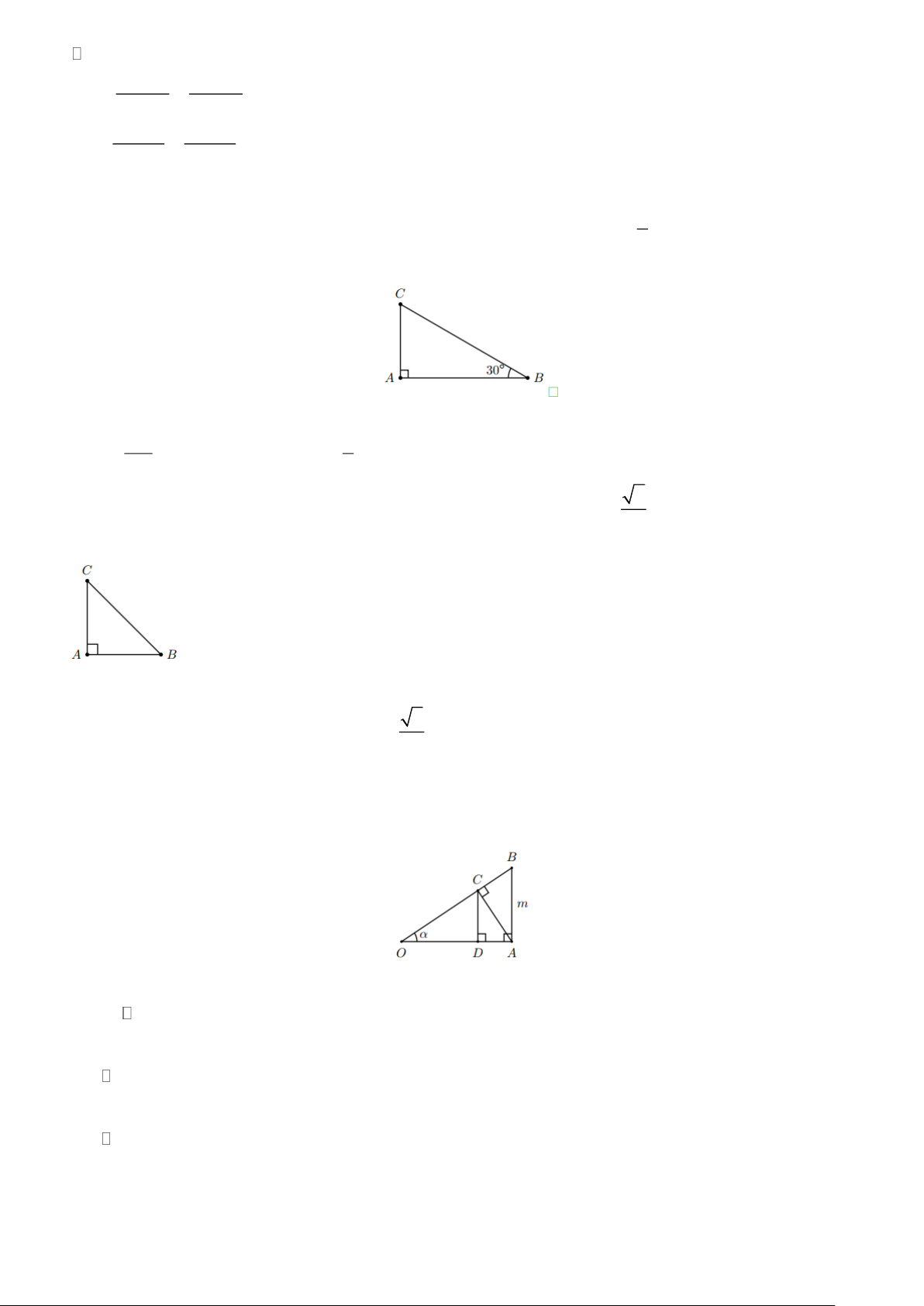
Ví dụ 1. Giải các tam giác vuông ở hình sau. Làm tròn kết quả độ dài đến hàng đơn vị và số đo góc đến độ. Lời giải
a) Xét tam giác ABC vuông tại A , theo định lí Pythagore ta có 2 2 2 2
BC = AB + AC = 5 + 8 9, 4 . Ta có AB 5 tan C = = = 0,625 AC 8
Từ đó tìm được C 32suy ra B = 90 − C 90 − 32 = 58
b) Xét tam giác ABC vuông tại A , ta có AB 6 sin C = = suy ra C 33 ,
B 90 − 33 = 57 BC 11
Theo định lí Pythagore ta có 2 2 2 2
AC = BC − AB = 11 − 6 = 121− 36 9 Trang 1
c) Xét tam giác DEF vuông tại D , ta có
F = 90 − 32 = 58
DE = DF.cot E = 9.cot 32 14 DF sin = DF E nên 9 EF = = 17 EF sin E sin 32
d) Xét tam giác PQR vuông tại P , ta có PR 9 cos R = =
suy ra R 46 ,Q 90 − 46 = 44 QR 13
Theo định lí Pythagore ta có 2 2 2 2
QP = QR − RP = 13 − 9 = 169 − 81 9
Ví dụ 2. Giải tam giác ABC vuông tại A biết
a) AB = 4, AC = 6
b) AB = 4, BC = 8
c) AB = 3; B = 42 d) BC = 9,C = 53 Lời giải
a) Xét tam giác ABC vuông tại A , ta có 2 2 2 2 2
BC = AB + AC = 4 + 6 = 52 hay BC = 52 7, 2 (cm) AC 6 3 tan B = = = suy ra B 56 AB 4 2
B + C = 90 (tổng hai góc nhọn của tam giác vuông)
Suy ra C = 90 − B = 90 − 56 = 34
b) Xét tam giác ABC vuông tại A , ta có 2 2 2 2
AC = BC − AB = 8 − 4 = 4 3 6,928 AB 4 1 cos B = = = BC 8 2 B = 60
C = 90 − 60 = 30
c) Xét tam giác ABC vuông tại A , ta có
C = 90 − B = 90 − 42 = 48 AC = A .
B tan B = 3.tan 42 2.701 Ta có AB cos = AB B suy ra 3 BC = = 4,037 BC cos B cos 42
d) Xét tam giác ABC vuông tại A , ta có AB sin C =
AB = sin C.BC = sin 53 .9 7, 2 BC AC cosC =
AC = BC.cosC = 9.cos53 5, 4 BC
B = 90 − C = 90 − 53 = 37
Ví dụ 3. Giải tam giác ABC vuông tại A biết
a) AB = 3,5 và AC = 4, 2
b) AB = 3,0 và BC = 4,5
c) B = 50 và AB = 3,7
d) B = 57 và BC = 4,5 Trang 2 Lời giải a) Ta có AC 4, 2 tan B = = AB 3,5 suy ra B 50 12
' mà B + C = 90
nên C = 90 − B = 90 − 50 12 ' = 39 48 '
Mặt khác, theo định lí Pythagore ta có 2 2 2 2
BC = AB + AC = 3,5 + 4, 2 5,5 b) Do giả thiết ta có AB 3,0 sin C = = sin 41 4 9' BC 4,5 Suy ra C 41 49 '
Mà B + C = 90 nên B = 90 − C = 90 − 41 49 ' = 48 11 '
Mặt khác, theo định lí Pythagore ta có 2 2 2 2
AC = BC − AB = 4,5 + 3, 0 3, 4 c) Ta có
C = 90 − B = 90 − 50 = 40 Mặt khác AC = .
AB tan B = 3, 7.tan 50 4, 4 Tương tự AB 3,7 BC = = 5,8 cos B cos50
d) Ta có C = 90 − B = 90 − 57 = 33
Mặt khác AB = BC.cos B = 4,5.cos57 2,5
Và AC = BC.sin B = 4,5.sin 57 3,8
Ví dụ 4. Giải tam giác ABC vuông tại A biết
a) Xét tam giác ABC vuông tại A , ta có 2 2 2
BC = AB + AC (theo định lý Pythagorre) suy ra 2 2 2 13 = 5 + AC Suy ra 2
AC = 144 hay AC = 12 (cm) AC 12 tan B = = suy ra B 67 AB 5
B + C = 90 (tổng hai góc nhọn của tam giác vuông)
Suy ra C = 90 − B = 90 − 67 = 23
b) Xét tam giác ABC vuông tại A , ta có
B + C = 90 (tổng hai góc nhọn của tam giác vuông)
Suy ra C = 90 − B = 90 − 35 = 55
AB = BC.cos B = 5.cos35 4,1(cm)
AC = BC.sin B = 5.sin 35 2,9 (cm)
c) Xét tam giác ABC vuông tại A , ta có
B + C = 90 (tổng hai góc nhọn của tam giác vuông)
Suy ra C = 90 − B = 90 − 50 = 40 AC = A .
B tan B = 6.tan 50 7, 2 (cm) Trang 3 AB
AB = BC.cos B hay 6 BC = = 9,3(cm) cos B cos50
d) Xét tam giác ABC vuông tại A , ta có
B + C = 90 (tổng hai góc nhọn của tam giác vuông)
Suy ra C = 90 − B = 90 − 55 = 35
AB = AC.tan C = 7.cos35 4,9 (cm) AB
AB = BC.cos B hay 4,9 BC = = (cm) cos B cos55 8,5
Ví dụ 5. Cho hình chữ nhật ABCD thỏa mãn AC = 6 cm, BAC = 47 . Tính độ dài các đoạn thẳng AB, AD Lời giải
Xét tam giác ABC vuông tại B ta có
AB = AC.cos BAC = 6.cos 47 4,1(cm)
BC = AC.sin BAC = 6.sin 47 4, 4 (cm)
Vì tam giác ABCD là hình chữ nhật nên AD = BC 4,4 (cm)
Ví dụ 6. Cho tam giác ABC vuông tại A , đường cao AH . Biết AB = 2,5; BH =1,5 . Tính ; B C và AC Lời giải
Xét tam giác ABH vuông tại H ta có BH 1,5 cos B = = cos53 8 ' suy ra B 53 8 ' AB 2,5
Mà B + C = 90 (tổng hai góc nhọn của tam giác vuông)
Suy ra C = 90 − B = 90 − 53 8 ' = 36 52 '
Xét ABC vuông tại A , ta có AC = A .
B tan B = 2,5 tan 53 8 ' 3,3
Dạng 2. Giải tam giác nhọn
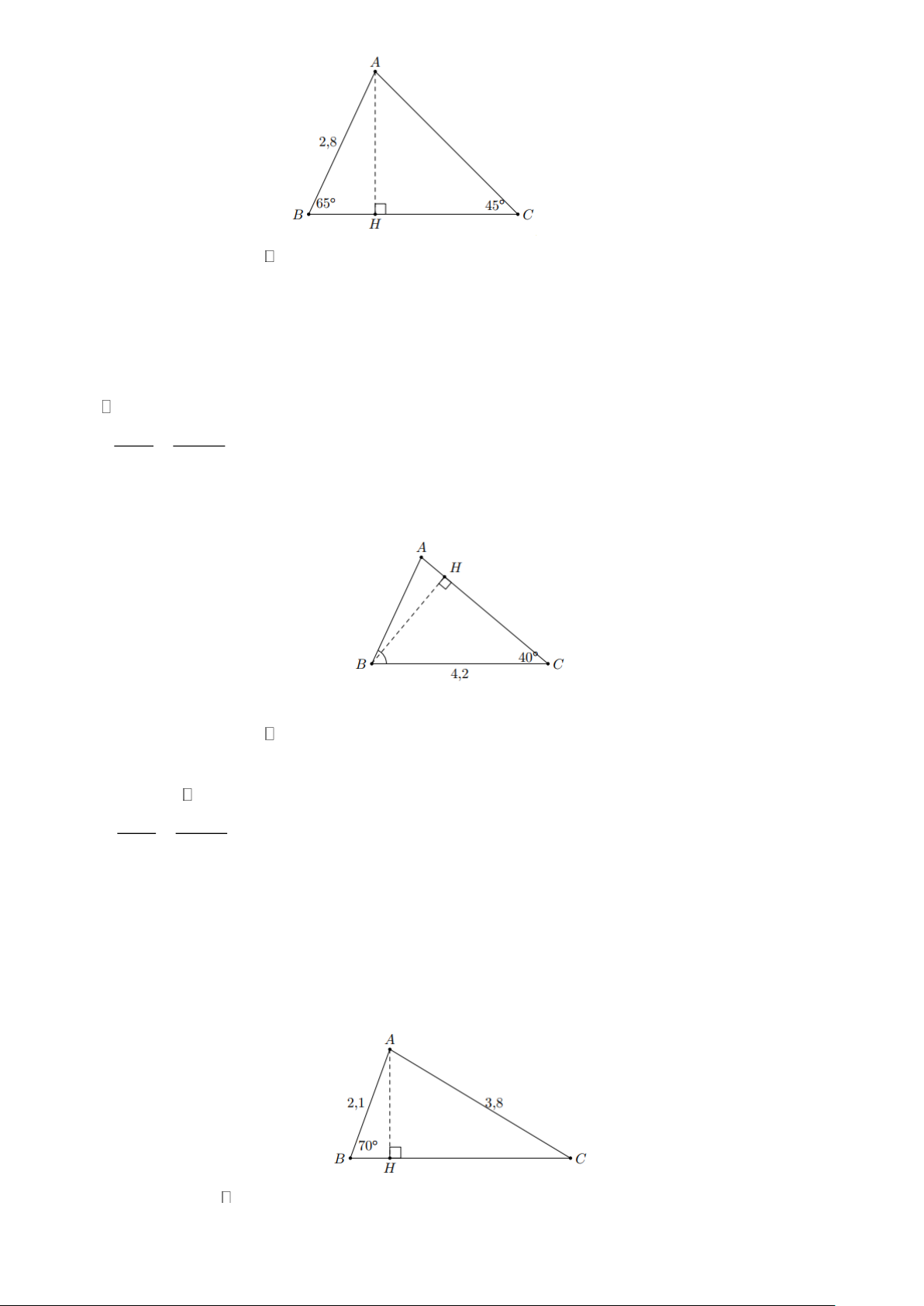
Ví dụ 7. Cho tam giác ABC có B = 65 ,
C = 45 và AB = 2,8 cm. Tính các góc và cạnh còn lại của
tam giác đó (gọi là giải tam giác ABC ). Lời giải Trang 4
Ta có A = 180 − B − C = 70
Kẻ đường cao AH . Xét ABH vuông tại H , ta có AH = A .
B sin B = 2,8.sin 65 2,54 (cm)
Tương tự BH = A .
B cos B = 2,8.cos 65 1,18 (cm)
Mặt khác do giả thiết suy ra tam giác HAC vuông cân tại H nên
HA = HC . Do đó BC 2,54 +1,18 = 3,7 (cm)
Xét AHC vuông tại H , ta có HA 2,54 AC = = 3,6 (cm) sin C sin 45
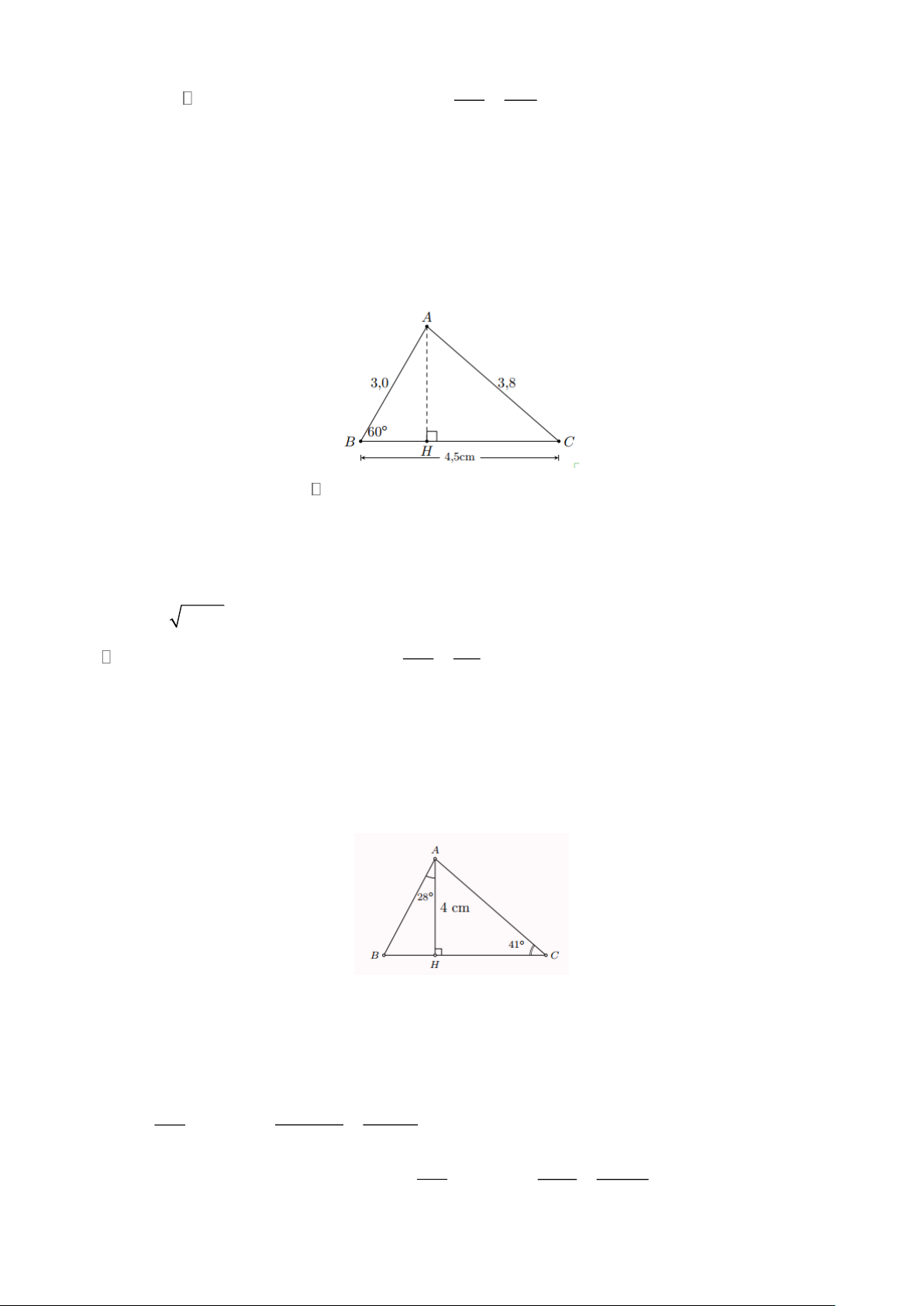
Ví dụ 8. Giải tam giác ABC có B = 65 ,
C = 40 và BC = 4, 2 cm Lời giải
Ta có A = 180 − B − C = 75
Kẻ đường cao BH . Xét BCH vuông tại H , ta có
BH = BC.sin C = 4, 2.sin 40 2,70(cm)
Tương tự, xét ABH vuông tại H , ta có BH 2,70 AB = = 2,8 (cm) sin A sin 75 Mặt khác ta có
AC = AH + CH = BH.(cot A+ cotC)
2,70.(cot 75 + cot 40) 3,9
Ví dụ 9. Giải tam giác ABC có B = 70 và AB = 2,1; AC = 3,8 cm Lời giải
Vẽ AH ⊥ BC . Xét ABH vuông tại H có AH = A .
B sin B = 2,1.sin 70 1,97 Trang 5
Tương tự, xét BH = A .
B cos B = 2,1.cos 70 0,72 Mặt khác, xét AH
AHC vuông tại H ta có 1,97 sin C = sin 31 1
4' do đó C 31 14 ' AC 3,8
Mà A =180 − (70 + 31 1 4') = 78 4 6'
Ta có HC = AC.cosC 3,80.cos31 14 ' 3, 25
Mà BC = BH + HC = 0,72 + 3, 25 = 3,97 .
Ví dụ 10. Giải tam giác ABC biết B = 60 ,
AB = 3,0 và BC = 4,5 . Lời giải
Kẻ đường cao AH ⊥ BC . Xét ABH vuông tại H có AH = A .
B sin B = 3.sin 60 2,6
Tương tự, xét BH = A .
B cos B = 3.cos 60 = 1,5
Mà HC = BC − HB = 4,5 −1,5 = 3,0
Theo định lý Pythagore ta có 2 2 2 2 2
AB = BH + AH = 3 + 2,6 = 15,76
Suy ra AB = 15,76 4,0 Xét AH
AHC vuông tại H ta có 2,6 tan ACH = tan 40 5 5' HC 3,0
Do A =180 − B − C = 180 − (60 + 40 5 5') = 79 5 '
Ví dụ 11. Trong hình bên, tính độ dài của mỗi đoạn thẳng sau: a) HB và HC b) AH và AC Lời giải
a) Xét tam giác ABH vuông tại H , ta có
HB = AH.tan BAH = 4.tan 28 2,1(cm)
Vì tam gaisc AHC vuông tại H nên HC = AH.cot C = 4.cot 41 4,6 (cm)
b) Xét tam giác ABH vuông tại H , ta có AH 4 cos = AH BAH hay AB = = 4,5 (cm) AB cos BAH cos 28 Vì tam giác AH
AHC vuông tại H nên sin = AH C hay 4 AC = = 6,1(cm) AC sin C sin 41
Dạng 3. Tính diện tích tam giác, tứ giác Trang 6
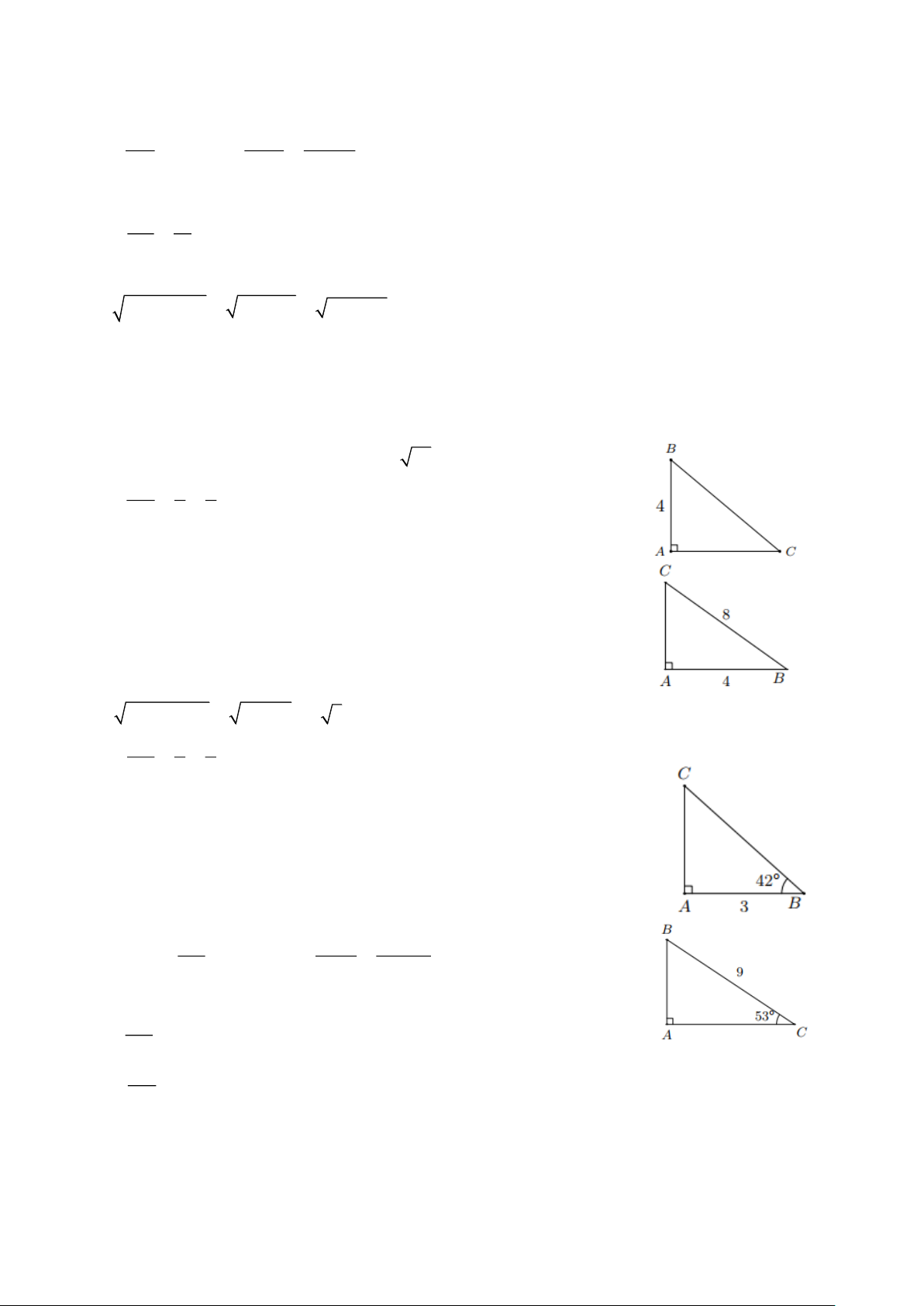
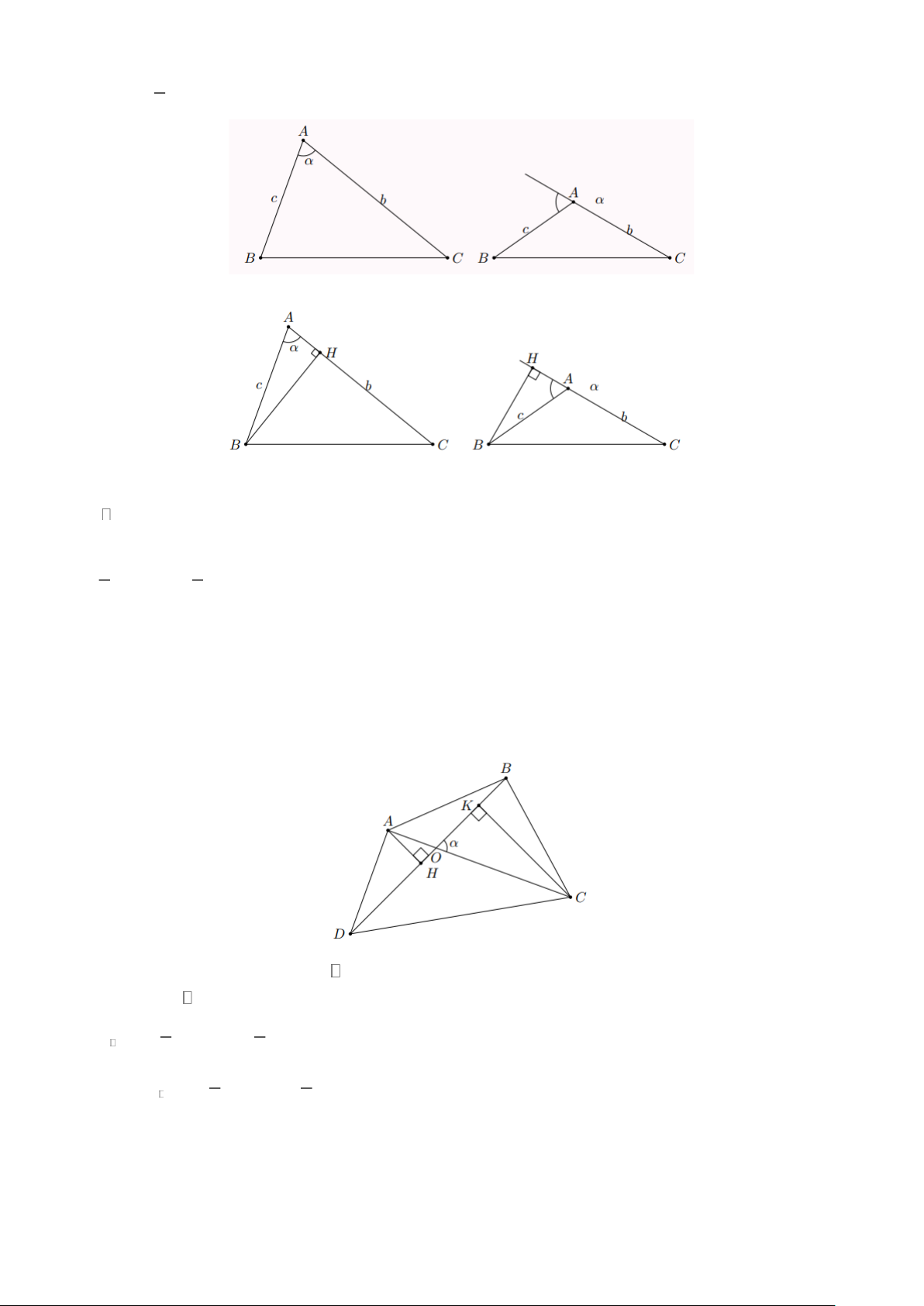
Ví dụ 12. Cho tam giác ABC như hình vẽ bên. Chứng minh rằng diện tích tam giác ABC có diện tích là 1 S = . . b . c sin 2 Lời giải
Vẽ đường cao BH của tam giác ABC .
Xét ABH vuông tại H , ta có BH = A . B sin A = . c sin
Do đó diện tích S của tam giác ABC là 1 1
S = .AC.BH = . . b . c sin 2 2
Nhận xét. Qua ví dụ này ta có thêm một cách tính diện tích tam giác. Diện tích tam giác bằng nửa
tích hai cạnh nhân với sin của góc nhọn xen giữa hai đường thẳng chứa hai cạnh đó.
Ví dụ 13. Tứ giác ABCD như hình vẽ phía dưới. Biết AB = 3,8; BD = 5,0 và = 65 . Tính diện tích của tứ giác đó. Lời giải
Vẽ AH ⊥ BD và CK ⊥ BD . Xét OAH có AH = O . A sin
Tương tự, xét OCK ta có CK = OC.sin Mà 1 1 S = .B . D AH = .B . D O . A sin ABD 2 2 Tương tự 1 1 S = .B . D CK = .B .
D OC.sin . Gọi S là diện tích tứ giác ABCD ta có BCD 2 2 Trang 7 S = S + S ABD BCD 1 1 = . . BD O . A sin + . . BD OC.sin 2 2 1 = . .
BD (OA + OC).sin 2 1 1 = . .
BD AC.sin = .5,0.3,8.sin 65 8,6 2 2
Ví dụ 14. Tam giác ABC có B + C = 60 ;
AB = 3; AC = 6 . Tính độ dài đường phân giác AD . Lời giải
Do B + C = 60 nên BAC = 180 − 60 = 120
Mà AD là đường phân giác nên BAD = CAD = 60 Mà 1 1 18 S = .A .
B AC.sin BAC = .3.6.sin120 = .sin 60 ABC 2 2 2 Mặt khác 1 1 S = .A . B A .
D sin BAD = .A . B A . D sin 60 ABD 2 2 Và 1 1 S = .AC.A .
D sin DAC = .AC.A . D sin 60 ACD 2 2
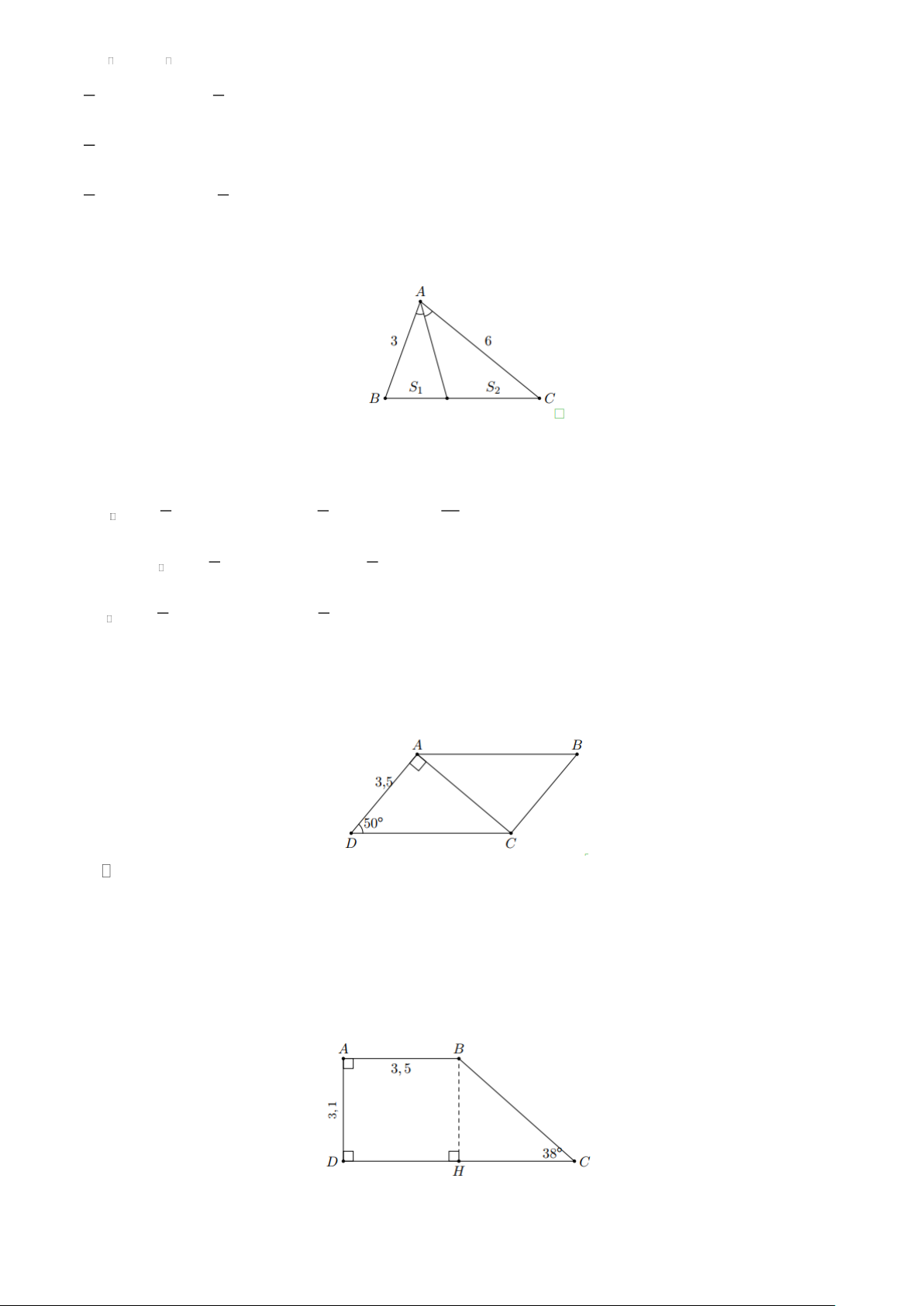
Ví dụ 15. HÌnh bình hành ABCD có AC ⊥ AD và AD = 3,5; D = 50 . Tính diện tích của hình bình hành. Lời giải
Xét ADC vuông tại A , ta có
Khi đó gọi S là diện tích hình bình hành ABCD ta có S = .
AD AC = 3,5.3,5.tan 50 4, 6
Ví dụ 16. Hình thang ABCD( Ab//CD) có D = 90 ;C = 38 , AB = 3,5; AD = 3,1. Tính diện tích hình thang đó. Lời giải
Vẽ BH ⊥ CD , do giả thiết suy ra ABHD là hình chữ nhật. Trang 8
Do đó BH = 3,1; DH = 3,5
Xét BHC vuông tại H , ta có
HC = BH.cot C = 3,1.cot 38 4,0
Mà CD = DH + HC = 3,5 + 4,0 = 7,5
Khi đó gọi S là diện tích hình thang ABCD ta có
(AB +CD).BH (3,5+7,5).3,1 S = = =17,1. 2 2
Dạng 4. Ước lượng chiều cao và khoảng cách Ví dụ 17.
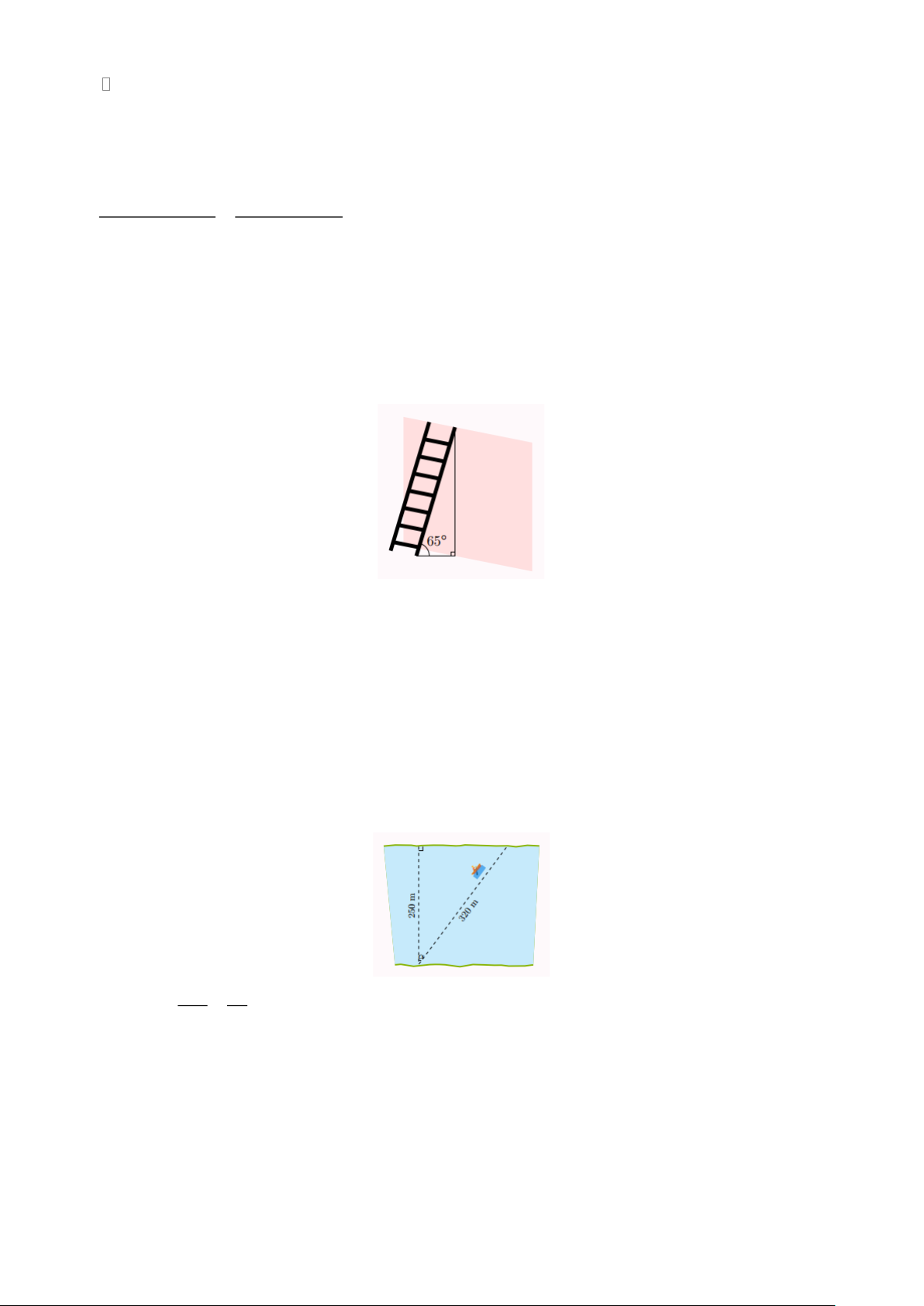
Một chiếc thang dài 3m . Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét
(làm tròn đến số thập phân thứ hai) để nó tạo được với mặt đất một góc an toàn 65 (tức là đảm
bảo thang chắc chắn khi sử dụng) (H.4.14)? Lời giải
Khoảng cách từ thang đến chân tường để nó tạo được với mặt đất một góc an toàn 65 (tức là đảm
bảo thang chắc chắn khi sử dụng) là 3.cos 65 1, 27(m)
Vậy khoảng cách từ thang đến chân tường để nó tạo được với mặt đất một góc an toàn là 1, 27 m Ví dụ 18.
Một khúc sông rộng khoảng 250m . Một con đò chèo qua sông bị dòng nước chảy đẩy xiên nên
phải chèo khaongr 320m mới sang được bờ bên kia. Hỏi dòng nước chảy đã đẩy con đò đi lệch
một góc bằng bao nhiêu độ (làm tròn đến phút)? Lời giải Ta có 250 25 cos = = 38 3 7' 320 32
Vậy dòng nước chảy đã đẩy con đò đi lệch một góc 38 3 7 ' Ví dụ 19.
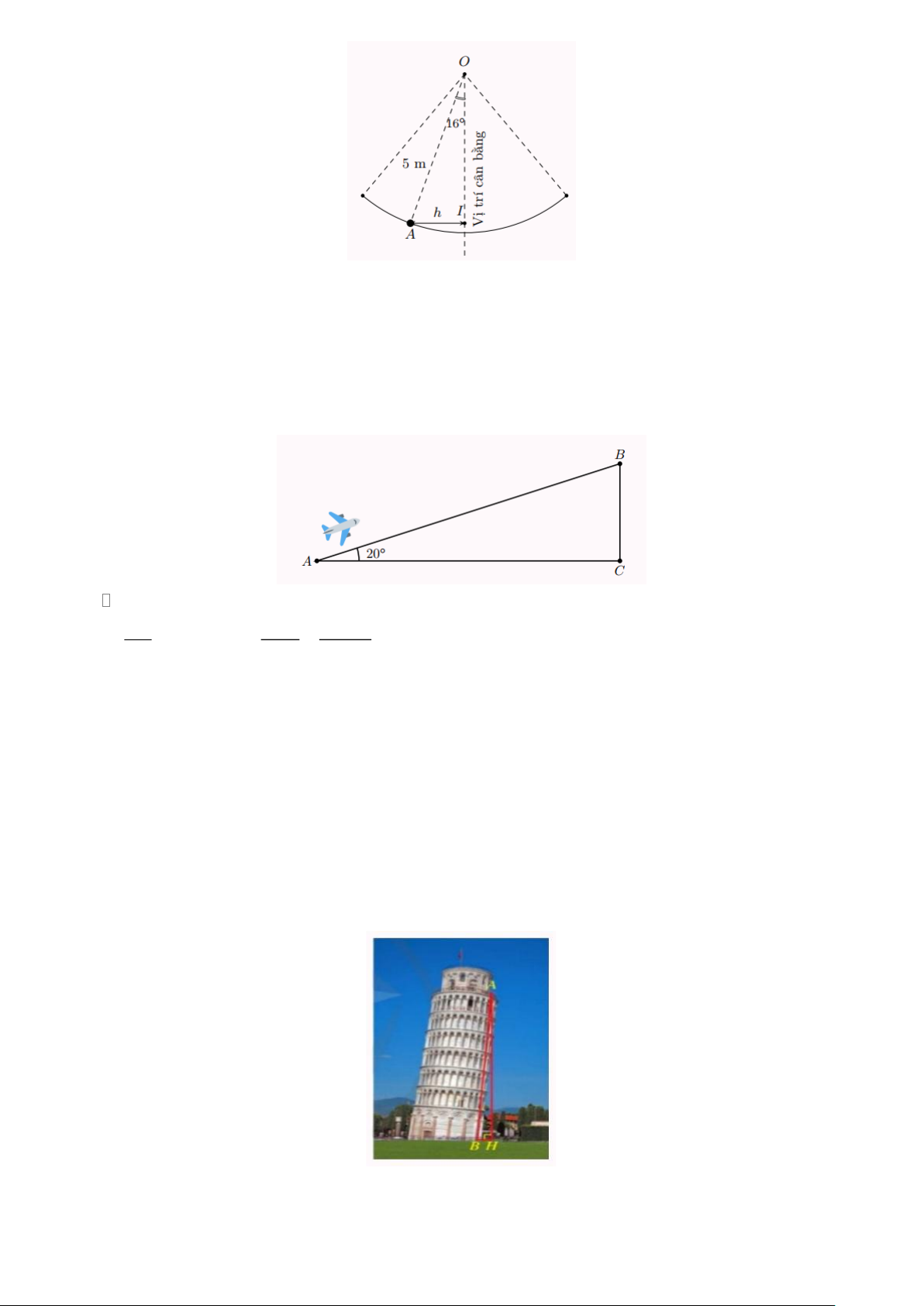
Trong trò chơi đánh đu của một lễ hội vào mùa xuân, khi người chơi nhún đều. Cây đu sẽ
đưa người chơi dạo động quanh vị trí cân bằng. Hình bên minh họa người chơi đang ở vị
trí A với OA = 5m và dây OA tạo với phương thẳng đứng một góc AOI =16 Tính khoảng
cách AI (làm tròn kết quả đến hàng phần trăm của mét)? Lời giải Trang 9
Vì tam giác AOI vuông tại I nên AI = O .
A sin AOI = 5.sin16 1,38(m) Ví dụ 20.
Một máy bay cất cánh từ vị trí A trên đường băng của sân bay và bay theo đường thẳng AB tạo
với phương nằm ngang AC một góc là 20 . Sau 5 giây, máy bay ở độ cao BC = 110m . Em hãy
tính khoảng cách AB (làm tròn kết quả đến hàng trăm của mét). Lời giải
Xét ABC vuông tại C ta có BC 110 sin = BC A suy ra AB = = 361,62(m) AB sin A sin 20
Vậy khoảng cách từ A đến B là 361,62(m) . Ví dụ 21.
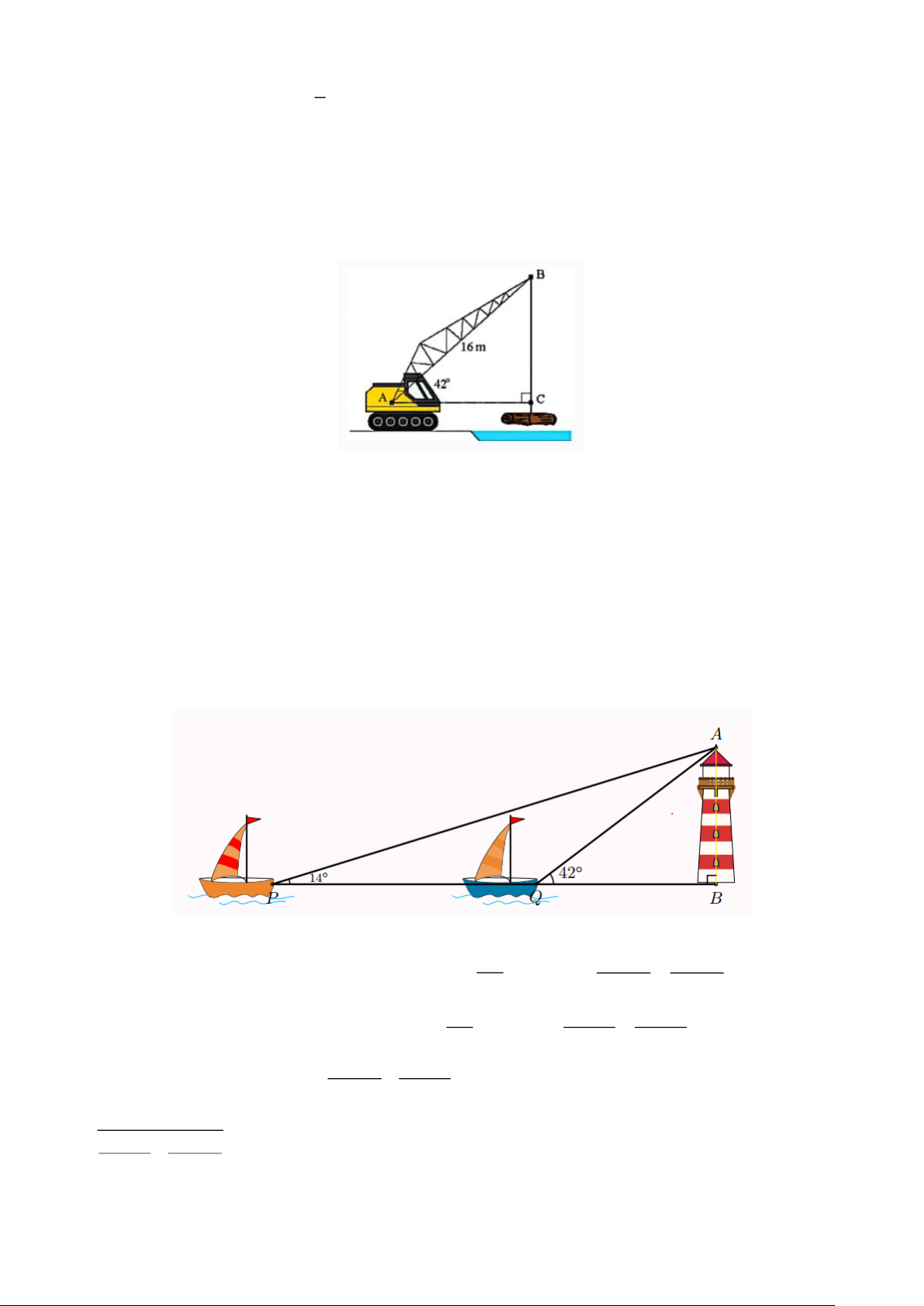
Năm 1990, tháo nghiêng ở thành phố Pisa (Italia) bắt đầu quá trình trùng tu nhằm giảm độ
nghiêng của tháp. Sau 10 năm trùng tu, vào năm 2001, các kĩ sư đã thành công trong việc đưa độ nghiêm của tháp chỉ còn khoảng 4 (Nguồn:
http://en.wikipedia.org/wiki/Leaning_Tower_of_Pisa.). Giả sử một người đứng trên tháp
(tại vị trí A ), cách mặt đất một khoảng là AH = 45m , thả một vật rơi xuống đất (Hình bên).
Tính khoảng cách từ vị trí chạm đất (vị trí H ) đó đến chân tháp (vị trí B ) (làm tròn kết quả
đến hàng trăm của mét). Lời giải Trang 10
Xét tam giác ABH vuông tại H ta có BH = AH.tan A = 45.tan 4 3,15(m)
Vậy khoảng cách từ vị trí chạm đất đến chân tháp là 3,15(m)
Ví dụ 22. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34 và bóng của một tòa
tháp trên mặt đất dài 8,6 m. Tính chiều cao của tòa tháp đó (làm tròn kết quả đến mét). Lời giải
Ta nhận thấy đường cao của tháp đối diện với góc 34 (góc tạo bởi tia nắng mặt trời và bóng của
tháp trên mặt đất). Do đó ta có h = 8,6.tan 34 6(m)
Vậy chiều cao của tháp là khoảng 6 m. Ví dụ 23.
Bóng trên mặt đất của một cái cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm), biết rằng
tia nắng mặt trời tạo với mặt đất góc 40 . Lời giải
Đổi 25m = 250dm
Chiều cao của cây là 250 : cos 40 326dm Ví dụ 24.
Một chiếc máy bay bay lên với vận tốc 500km / h . Đường bay lên tạo với phương nằm ngang một góc 30 .(Hình bên).
Hỏi sau 1,2 phút, máy bao lên cao được bao nhiêu ki-lo-met theo phương thẳng đứng? Lời giải
Trong hình vẽ, AB là đoạn đường máy bay bay lên trong 1, 2 phút và BH chính là độ cao của
máy bay đạt được trong 1, 2 phút đó. Ta có 1, 2 phút 1 = giờ nên 1 AB = 500. =10 (km) 50 50 Trang 11
Tam giác ABH vuông tại H có A = 30 nên theo định lí 1 ta có 1 BH = A .
B sin A = 10.sin 30 = 10. = 5(km) 2
Vậy sau 1, 2 phút máy bay lên cao được 5 km. Ví dụ 25.
Một cần cẩu đang nâng một khối gỗ trên sông, Biết ta cẩu AB có chiều dài bằng 16 m và nghiêng
một góc 42 so với phương nằm ngang. Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần mười). Lời giải
Xét tam giác ABC vuông tại C có AB =16; A = 42 ta có BC = A .
B sin A = 16.sin 42 10,71(m)
Ví dụ 26. Hai con thuyền P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng
ở trên bờ biển. Từ P và Q người ta nhìn thấy tháp hải đăng dưới các góc BPQ = 14 và
BQA = 42 . Đặt h = AB là chiều cao của tháp hải đăng.
a) Tính BQ và BP theo h
b) Tính chiều cao của tháo hải đăng (kết quả làm tròn đến hàng phần mười) Lời giải a) Xét tam giác AB h
BQA vuông tại B , ta có tan = AB Q nên BQ = = QB tan 42 tan 42 Xét tam giác AB h
BPA vuông tại B ta có tan = AB P nên PB = = PB tan14 tan14 b) Ta có h h
BP − BQ = 300 suy ra − = 300 tan 42 tan14 300 h = 103, 4(m) 1 1 − tan14 tan 42
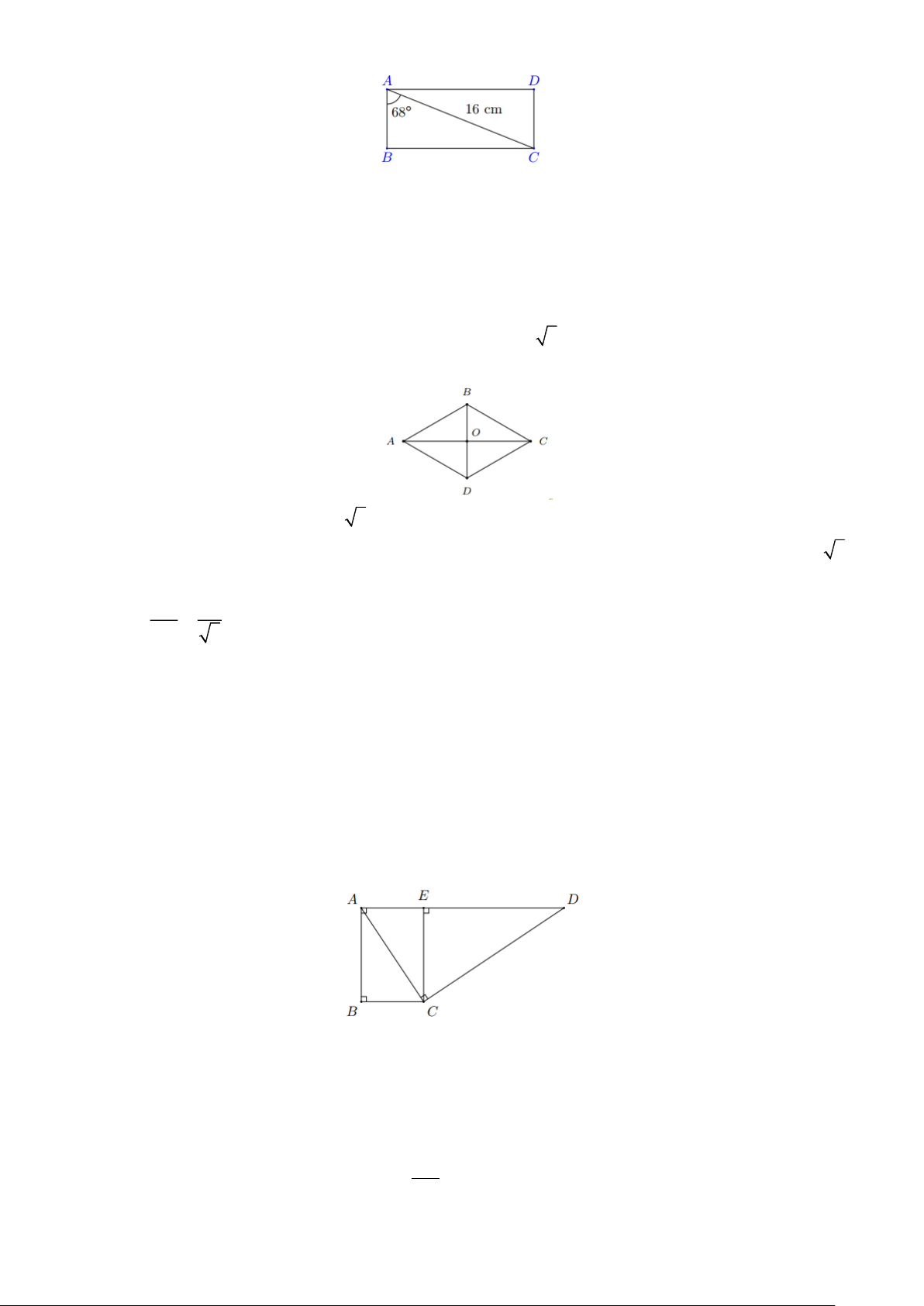
Vậy chiều cao của tháp hải đăng là khoảng 103,4(m) Trang 12 Ví dụ 27.
Trong hình bên cho OH = 4 ; m AOH = 42 ;
HOB = 28 . Tính chiều cao AB của cây Lời giải
Xét tam giác OHA vuông tại H ta có HA = OH.tan HOA = 4.tan 42 3,6(m)
Xét tam giác OHB vuông tại H ta có HB = OH.tan HOB = 4.tan 28 2,1(m)
Vậy chiều dài của cây là AB = HA + HAB = 3,6 + 2,1 = 5,7(m) Ví dụ 28.
Tam giác ABC ở hình bên (có A = 90 ) mô tả cột cờ AB và bóng nắng của cột cờ trên mặt
đất là AC . Người ta đo được độ dài AC =12m và C = 40 . Tính chiều cao AB của cột cờ.
(kết quả làm tròn đến hàng phần trăm của mét). Lời giải
Vì tam giác ABC vuông tại A nên AB = AC.tan C =12.tan 40 10,07(m) Ví dụ 29.
Trong lần tham quan tháp Eiffel (thủ đô Paris, Pháp), bạn Vân muốn ước tính độ cao cảu
tháp. Sau khi quan sát, bạn Vân đã minh họa kết quả đo đạc ở hình bên. Em hãy giúp bạn
Vân tính độ cao h của tháp Eiffiel theo đơn vị mét (làm tròn kết quả đến hàng đơn vị) Lời giải Trang 13
Xét tam giác ADC vuông tại C ta có AC = . h cot DAC = . h cot 60
Xét tam giác BDC vuông tại C ta có BC = . h cot DBC = . h cot 75
Do AC − BC = AB =101 nên . h cot 60 − . h cot 75 = 101 Hay .
h (cot 60 − cot 75) =101 Suy ra 101 h = 326(m) cot 60 − cot 75
Vậy chiều cao của tháp Eiffel khoảng 326m Ví dụ 30.
Để ước lượng chiều cao của một cái tháp mà không cần lên đỉnh tháp, người ta sử dụng
giác kế, máy tính cầm tay. Chẳng hạn, ở hình bên, để đo chiều cao AD của tháp, người ta
đặt giác kế tại một điểm quan sát cách chân tháp một khoảng CD = OB = a , trong dó chiều
cao của điểm đặt giác kế là OC = b . Quay thanh giác kế sao cho khi ngắm thanh này ta
nhìn thấy đỉnh A của tháp, đọc trên giác kế số đo góc của góc AOB . Tính chiều cao của
tháp, biết = 42; b =13,81m ; a = 90 m. (làm tròn kết quả đến hàng phần trăm của mét). Lời giải
Vì tam giác OAB vuông tại B nên AB = O .
B tan AOB = 90.tan 42 81,04(m)
Vậy chiều cao của tháp khoảng
81,04 +13,81 = 94,85(m) C. BÀI TẠP VẬN DỤNG
Bài 1. Giải tam giác ABC vuông tại A có BC = ; a AC = ;
b AB = c trong các trường hợp sau:
a) a = 21;b = 18
b) b = 10;C = 30 c) c = 5;b = 3 Lời giải
a) Tam giac ABC vuông tại A có 2 2 2 2
c = a − b = 21 −18 = 3 13 (Định lí Pythagore) c 3 13 13 cos B = = = B 59 a 21 7
C = 90 − B = 90 − 59 = 31 Trang 14
b) Tam giac ABC vuông tại A có
B = 90 − C = 90 − 30 = 60 B b 10 20 3 cosC = a = = = a cosC cos30 3 2 20 3 10 3 2 2 2
c = a − b = −10 = (Định lí Pythagore) 3 3
c) Tam giac ABC vuông tại A có 2 2 2 2
a = b + c = 3 + 5 = 34 (Định lí Pythagore) c 5 cos B = = B 30,96 a 34
C = 90 − B = 90 − 30,96 = 59,04 Bài 2. Tìm ;
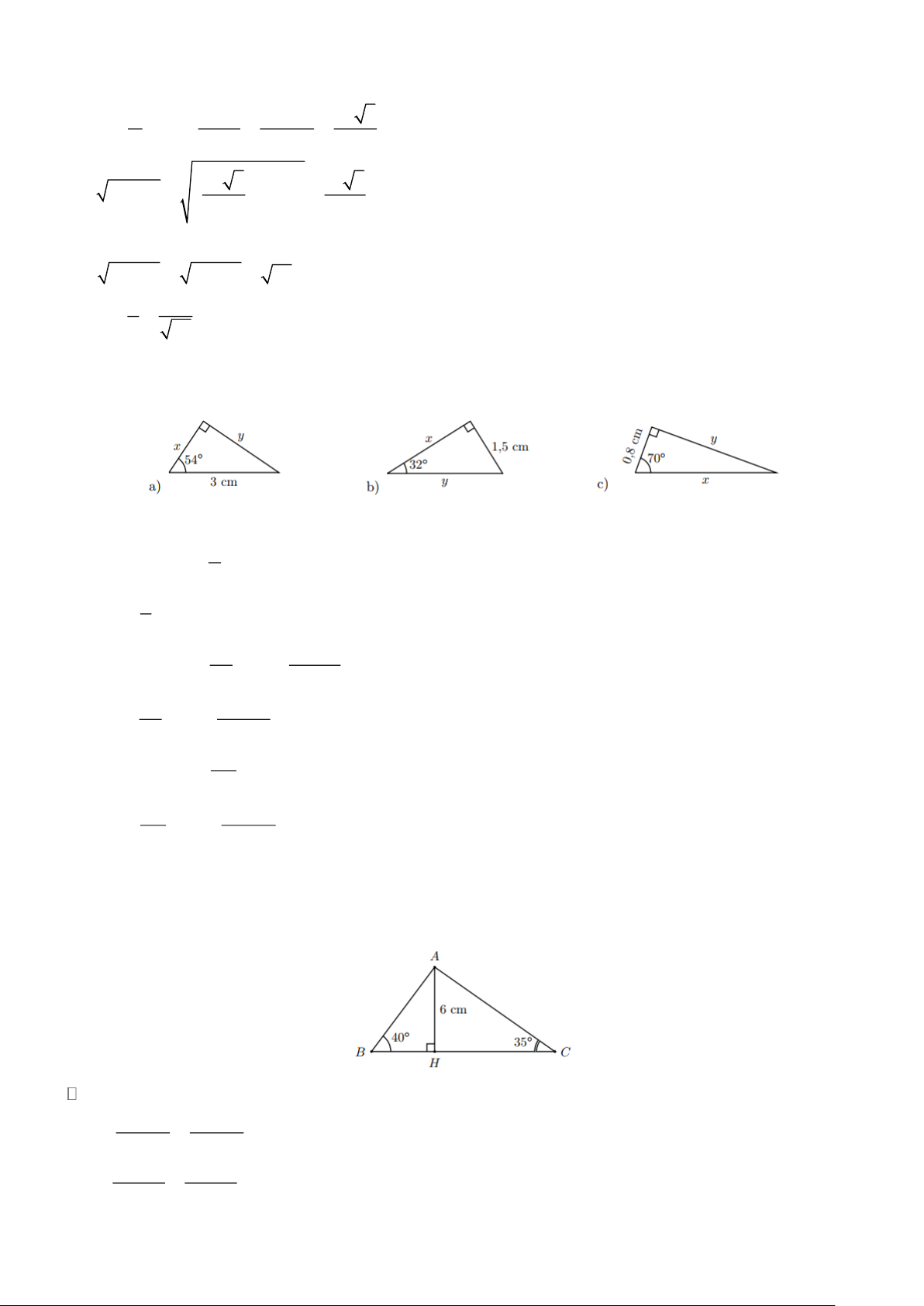
x y trong mỗi hình bên dưới (làm tròn đến hàng phần mười của centimet) Lời giải a) Ta có y sin 54 =
y = 3.sin 54 2,4(cm) 3 x
cos54 = x = 3.cos54 1,8(cm) 3 b) Ta có 1,5 1,5 sin 32 = y = 2,8(cm) y sin 32 1,5 1,5 tan 32 = x = 2,4(cm) x tan 32 y c) Ta có tan 70 =
y = 0,8.tan 70 2,2(cm) 0,8 0,8 0,8 cos 70 = x = 2,3(cm) x cos 70
Bài 3. Cho tam giác ABC có đường cao AH = 6c , m B = 40 ;
C = 35. Tính độ dài các đoạn thẳng
AB, BH , AC, BC (làm tròn kết quả đến hàng phần mười của centimet) Lời giải
ABH vuông tại H có AH 6 BH = = 7,2(cm) tan 40 tan 40 AH 6 AB = = 9,3(cm) sin 40 sin 40 Trang 15
ACH vuông tại H có AH 6 CH = = 8,6(cm) tan 35 tan 35 AH 6 AB = = 10,5(cm) sin 35 sin 35
BC = BH + CH = 7, 2 + 8,6 = 15,8(cm)
Bài 4. Cho tam giác ABC vuông tại A có B = 30 . Chứng minh 1 AC = BC 2 Lời giải
Tam giác ABC vuông tại A nên sin = AC B hay 1
AC = BC.sin 30 = .BC BC 2
Bài 5. Cho tam giác ABC vuông cân tại A . Chứng minh 2 AB = AC = BC 2 Lời giải
Tam giác ABC vuông cân tại A nên B = C = 45 Ta có 2
AC = AB = BC.cos B = BC.cos 45 = BC 2 Bài 6.
Trong hình bên cho O = , AB = m và OAB = OCA = ODC = 90 . Chứng minh a) OA = . m cot b) AC = . m cos c) 2 CD = . m cos Lời giải
a) Xét OAB vuông tại A có OA = . AB cot BOA = . m cot
b) Ta có BAC = 90 − ABC = 90 − ABO =
Xét ABC vuông tại C có AC = . AB cos BAC = . m cos
c) Ta có DCA = 90 − CAD = 90 − CAO =
Xét ACD vuông tại D có CD = AC.cos DCA = AC.cos
Mà theo câu b) ta lại có AC = . m cos nên 2 CD = . m cos Bài 7. Trang 16
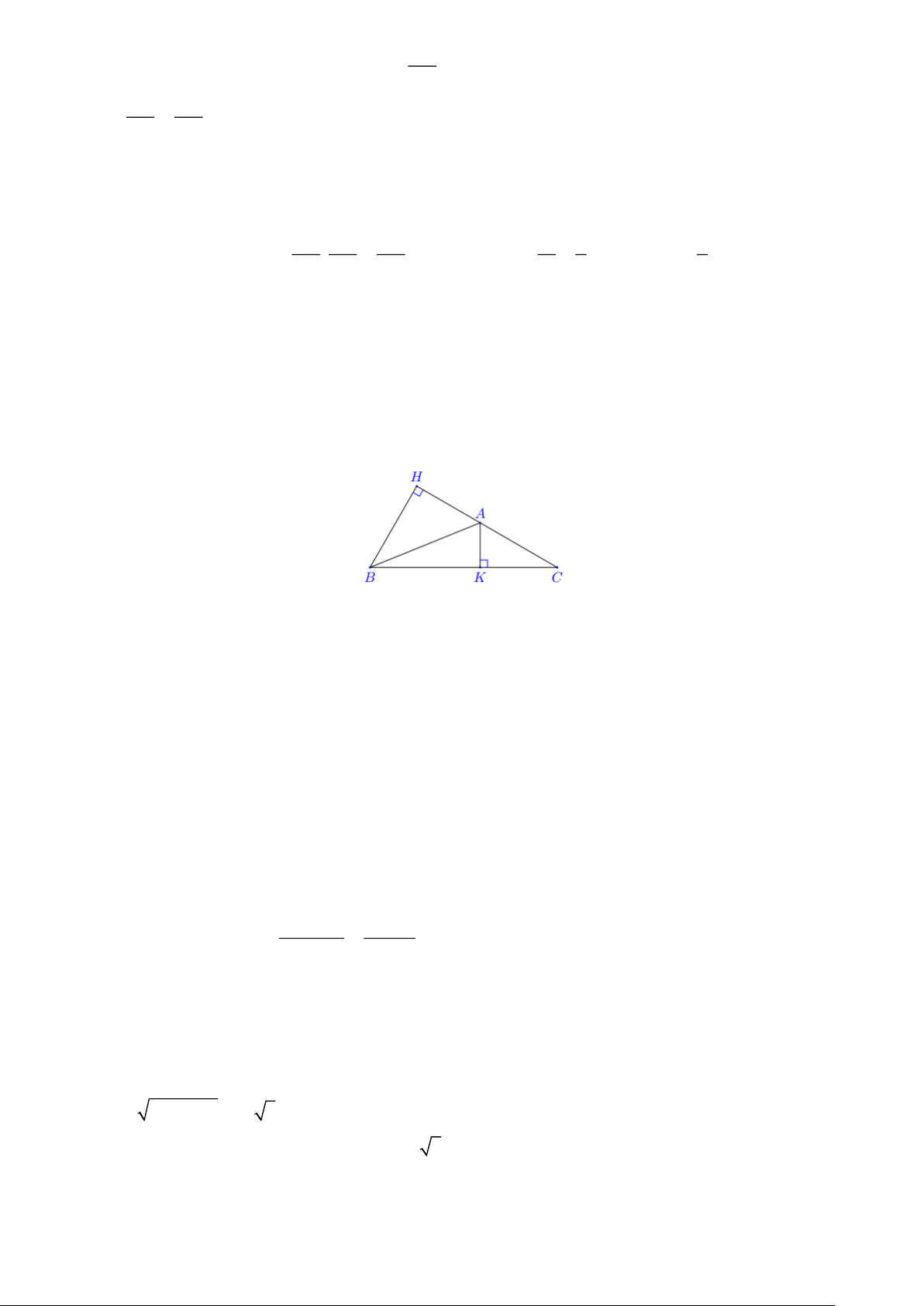
Tính các cạnh của hình chữ nhật ABCD biết AC = 16 cm và BAC = 68 . Lời giải
Xét tam giác ABC vuông tại B ta có
AB = AC.cos BAC = 16.cos 68 6cm
BC = AC.sin BAC =16.sin 68 14,8cm
Vậy AB = CD = 6c ;
m AD = BC = 14,8cm
Bài 8. Tính các góc của hình thoi có hai đường chéo dài 2 3 và 2 Lời giải
Giả sử hình thoi ABCD có AC = 2 3; BD = 2
Gọi O là giảo điểm của AC và BD . Khi đó ta có AC ⊥ BD tại O và BO = DO = 1; AO = OC = 3
Tam giác ABO vuông tại O có BO 1 tan OAB = = OAB = 30 OA 3
ABO = 90 − OAB = 90 − 30 = 60
Suy ra ABC = ACD = 2.ABO = 120 ;
BAD = BCD = 2.BAO = 60
Bài 9. Cho hình thang ABCD( AB//CD) có AD =16c ;
m BC = 4cm và A = B = ACD = 90
a) Kẻ đường cao CE của tam giác ACD . Chứng minh ADC = ACE . Tính sin của các góc
ADC; ACE và suy ra 2
AC = AE.AD . Từ đó tính AC
b) Tính góc D của hình thang. Lời giải a) Ta có
ADC + CAD = 90 (tam giác ACD vuông tại C )
ACE + CAD = 90 (tam giác ACE vuông tại E )
Suy ra ADC = ACE
Tam giác ACD vuông tại C có sin = AC ADC AD Trang 17
Tam giác ACE vuông tại E có sin = AE ADE AC Suy ra AC AD 2 =
AC = AE.AD AE AC
Vì tứ giác AECB có B = BAE = AEC = 90 nên tứ giác AECB là hình chữ nhật.
AE = BC = 4cm và AB = CE Ta có 2
AC = AE.AD = 4.16 = 64 AC = 8cm b) Ta có = AC AE = AE ADC ACE ( ADC)2 4 1 1 sin .sin . sin = = sin ADC = AD AC AD 16 4 2 suy ra D = 30
Bài 10. Cho tam giác ABC có BC = 20c ; m ABC = 22 ; ACB = 30
a) Tính khoảng cách từ điểm B đến đường thắng AC .
b) Tính các cạnh và các góc còn lại của tam giác ABC
c) Tính khoảng cách từ điểm A đến đường thẳng BC . Lời giải
a) Kẻ BH ⊥ AC tại H .
Xét tam giác BHC vuông tại H ta có BH = BC.sin C = 20.sin 30 =10cm
Vậy khoảng cách từ B đến AC là BH =10cm .
b) Xét tam giác ABC ta có
ABC + ACB + BAC = 180
22 + 30 + BAC =180
BAC =180 − 22 − 30 = 128
Ta có BAC + BAH =180 (hai góc kề bù)
BAH = 180 − BAC = 180 −128 = 52
Xét tam giác AHB vuông tại H ta có BH 10 BH = A .
B sin BAH AB = = 12,7(cm) sin BAH sin 52
HA = BH.cot BAH = 10.cot 52 7,8(cm)
Xét tam giác BHC vuông tại H ta có 2 2 2
BC = BH + HC (định lí Pytahgore) 2 2 2 20 = 10 + HC 2 2
HC = 20 −10 = 10 3 (cm)
Lại có HC = HA + AC AC = HC − HA =10 3 − 7,8 9,5(cm)
c) Kẻ AK ⊥ BC
Xét tam giác AKB vuông tại K có BK = AK.cot 22 Trang 18
Xét tam giác AKC vuông tại K có CK = AK.cot 30 Lại có
BC = BK + KC
20 = AK.cot 22 + AK.cot 30 20
AK = cot22+cot30
AK 4,8(cm)
Vậy khoảng cách từ A đến BC là AK 4,8cm Bài 11.
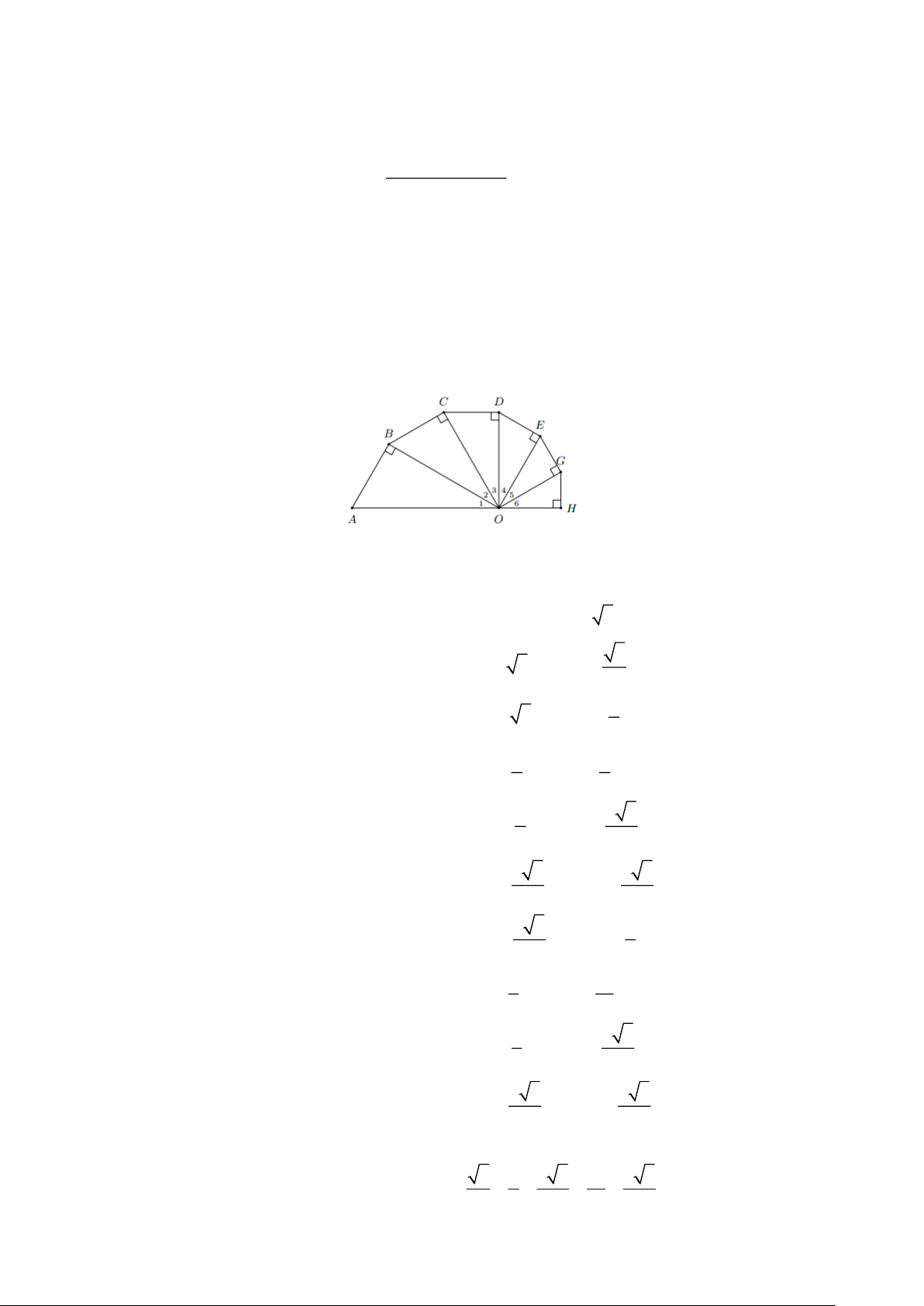
Tính độ dài đường gấp khúc ABCDEGH biết các tam giác ; OAB OBC;OC ;
D ODE;OEG;OGH là
các tam giác vuông tại ác đỉnh lần lượt là B,C, D, E,G, H các góc O ;O ;O ;O ;O ;O đều bằng 1 2 3 4 5 6
30 và OA = 2cm . Lời giải AB = O .
A sin 30 = 2.sin 30 =1
Xét tam giác OAB vuông tại B có OB = O .
A cos30 = 2.cos30 = 3 3 BC = .
OB sin 30 = 3.sin 30 =
Xét tam giác OBC vuông tại C có 2 3 OC = .
OB cos 30 = 3.cos 30 = 2 3 3
CD = OC.sin 30 = .sin 30 = 2 4
Xét tam giác OCD vuông tại D có 3 3 3
OD = OC.cos30 = .cos30 = 2 4 3 3 3 3 DE = . OD sin 30 = .sin 30 =
Xét tam giác ODE vuông tại 4 8 E có 3 3 9 OE = . OD cos 30 = .cos 30 = 4 8 9 9
EG = OE.sin 30 = .sin 30 = 8 16
Xét tam giác OEG vuông tại G có 9 9 3
OG = OE.cos30 = .cos30 = 8 16
Xét tam giác OGH vuông tại H có 9 3 9 3 BH = O . G sin 30 = .sin 30 = 16 32
Vậy độ dài đường gấp khúc ABCDEGH là 3 3 3 3 9 9 3
AB + BC + CD + DE + EG + GH = 1+ + + + + (cm) 2 4 8 16 32 Trang 19
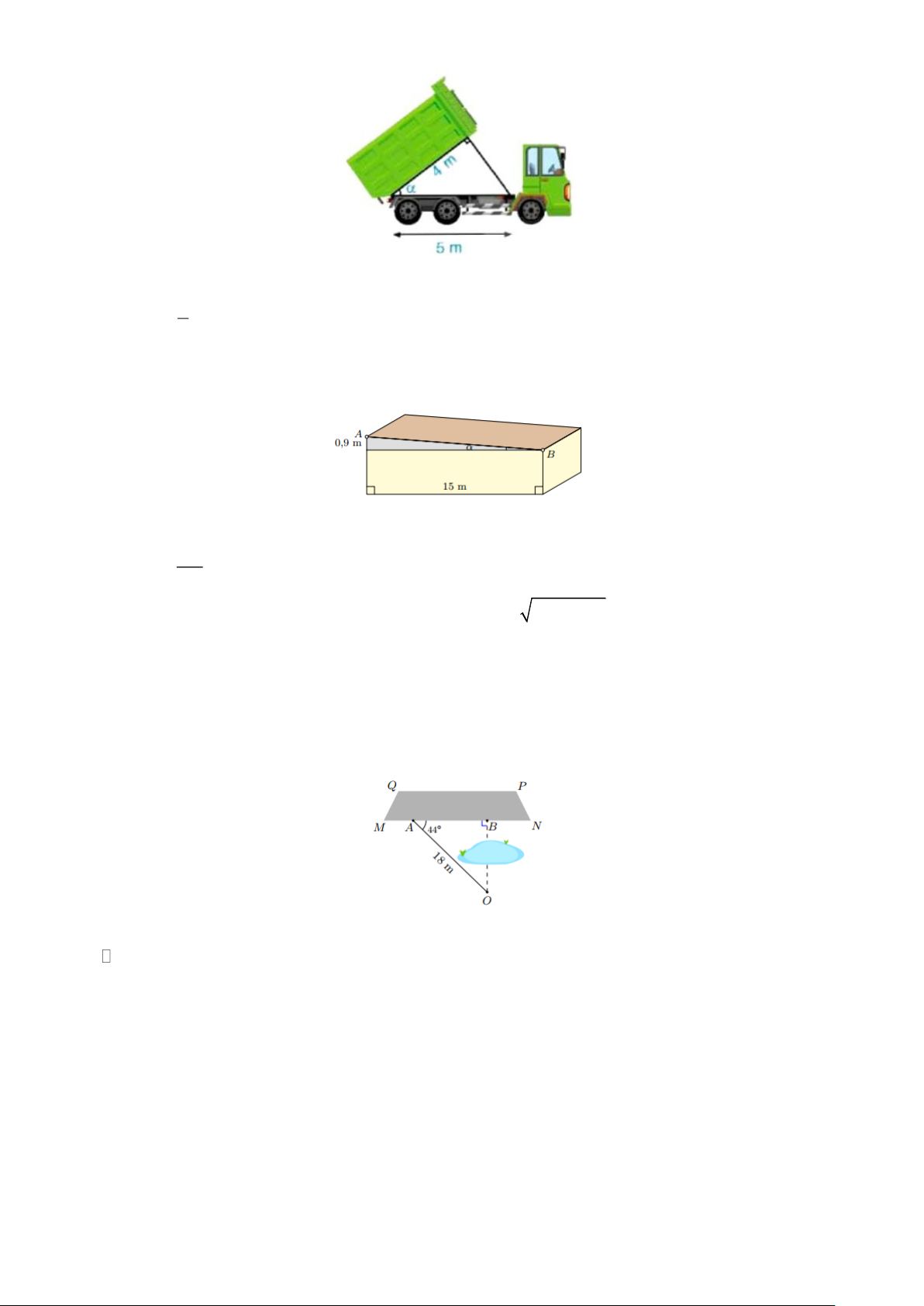
Bài 12. Tính góc nghiêng của thùng xe chở rác trong hình sau: Lời giải Ta có 4 cos = 36,87 5
Vậy góc nghiêng của thùng xe chở rác là khoảng 36,87 .
Bài 13. Tính góc nghiêng và chiều rộng AB của mái nhà kho trong hình sau: Lời giải Ta có 0,9 tan = 3,43 15
Theo định lí Pythagore, chiều rộng của mái nhà là 2 2
AB = 0,9 +15 15,03m Bài 14.
Trong công việc, người ta cần ước lượng khoảng cách từ vị trí O đến khu đất có dạng hình thang
MNPQ nhưng không thể đo được trực tiếp, khoảng cách đó được tính bằng khoảng cách từ O
đến đường thẳng MN . Người ta chọn vị trí A ở đáy MN và đo được OA = 18 m, OAN = 44 . Tính
khoảng cách từ vị trí O đến khu đất (làm tròn kết quả đến hàng phần mười của mét). Lời giải
Xét OAB vuông tại B ta có: OB = O .
A sin A = 18.sin 44 12,5 m
Vậy khoảng cách từ O đến khu đất là 12,5 m. Bài 15.
Hình bên minh họa một phần con sông có bề rộng AB = 100m . Một chiếc thuyền đi thẳng từ vị trí
B bên này sông đến vị trí C bên kia bờ sông. Tính quãng đường BC (làm tròn kết quả đến hàng
phần mười của mét), biết ABC = 35 . Trang 20