Các dạng toán nhị thức Newton và các bài toán liên quan

Tài liệu gồm 215 trang phân dạng và hướng dẫn giải các dạng toán tổ hợp và xác suất trong chương trình Đại số và Giải tích 11 chương 1.

72 36 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 8: Đại số tổ hợp (KNTT)

Môn: Toán 10

Thông tin:

39 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
TOÁN 11
1D2-3
Mục lục
P
hần A. CÂU HỎI .......................................................................................................................................................... 2
Dạng 1. Tiếp cận với khai triển nhị thức newton ............................................................................................................. 2
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton .......................................................................................... 3
Dạng 2.1 Khai triển của 1 biểu thức ............................................................................................................................. 3
Dạng 2.1.1 Bài toán tìm hệ số của số hạng ............................................................................................... 3
Dạng 2.1.2 Bài toán tìm số hạng thứ k ...................................................................................................... 4
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n ............................ 5
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập) ................................................................................ 8
Dạng
2.2 Khai triển của nhiều biểu thức .................................................................................................................... 11
Dạng 2.2.1 Dạng
1
2
...
n
k
a
a a
........................................................................................................... 11
Dạng 2.2.2 Tổng
1
1 2 2
...
n
m h
k
k
a
b a b a b
......................................................................... 12
Dạng 2.2.3 Tích
1
1
..
. ...
m
l
n
n
a
a b b
........................................................................................... 12
Dạng 2.2.4 Dạng kết hợp tích và tổng ..................................................................................................... 13
Dạng
3. Ứng dụng nhị thức newton để giải toán ............................................................................................................ 13
Phần B. LỜI GIẢI THAM KHẢO ................................................................................................................................. 14
Dạng 1. Tiếp cận với khai triển nhị thức newton ........................................................................................................... 14
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton ........................................................................................ 16
Dạng 2.1 Khai triển của 1 biểu thức ........................................................................................................................... 16
Dạng 2.1.1 Bài toán tìm hệ số của số hạng ............................................................................................. 16
Dạng 2.1.2 Bài toán tìm số hạng thứ k .................................................................................................... 18
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n .......................... 20
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập) .............................................................................. 27
Dạng
2.2 Khai triển của nhiều biểu thức .................................................................................................................... 31
Dạng 2.2.1 Dạng
1
2
...
n
k
a
a a
........................................................................................................... 31
Dạng 2.2.2 Tổng
1
1 2 2
...
n
m h
k
k
a
b a b a b
......................................................................... 33
Dạng 2.2.3 Tích
1 1
..
. ...
m
l
n n
a
a b b
........................................................................................... 35
Dạng 2.2.4 Dạng kết hợp tích và tổng ..................................................................................................... 35
Dạng
3. Ứng dụng nhị thức newton để giải toán ............................................................................................................ 36
NHỊ THỨC NEWTON VÀ CÁC BÀI TOÁN LIÊN QUAN
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Phần A. CÂU HỎI
Dạng 1. Tiếp cận với khai triển nhị thức newton
Câu 1. (THPT CHUYÊN HOÀNG VĂN THỤ - HÒA BÌNH - 2018) Số số hạng trong khai triển
5
0
2
x
là
A.
4
9
. B.
5
0
. C.
5
2
. D.
51
.
Câu 2. (HỒNG QUANG - HẢI DƯƠNG - LẦN 1 - 2018) Có bao nhiêu số hạng trong khai triển nhị thức
2018
2 3x
A.
. B.
. C.
. D.
.
Câu 3. (THPT CHU VĂN AN - HKI - 2018) Viết khai triển theo công thức nhị thức Niu-tơn
5
x y
.
A.
5
4 3 2 2 3 4 5
5 10 10 5
x x y x y x y xy y
. B.
5
4 3 2 2 3 4 5
5 10 10 5
x x y x y x y xy y
.
C.
5
4 3 2 2 3 4 5
5 10 10 5
x x y x y x y xy y
. D.
5
4 3 2 2 3 4 5
5 10 10 5
x x y x y x y xy y
.
Câu 4. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Trong khai triển nhị thức Niu-tơn của
2
019
(3 2 )
x
có bao nhiêu số hạng?
A.
2019
. B.
2018
. C.
2020
. D.
2021
.
Câu 5. Từ khai triển biểu thức
1
0
1
x
thành đa thức. Tổng các hệ số của đa
thức là
A.
1
023
. B.
5
12
. C.
1
024
. D.
2
048
.
Câu 6. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Từ khai triển biểu thức
10
1
x
thành đa thức. Tổng các hệ số của đa thức là
A.
1023
. B.
512
. C.
1024
. D.
2048
.
Câu 7. (THPT CHUYÊN HÙNG VƯƠNG - GIA LAI - LẦN 2 - 2018) Tính tổng các hệ số trong khai
triển
2018
1
2x
.
A.
1
. B.
1
. C.
2018
. D.
.
Câu 8. (THPT TRẦN NHÂN TÔNG - QN - LẦN 1 - 2018) Khai triển
124
4
(
5 7)
. Có bao nhiêu số
hạng hữu tỉ trong khai triển trên?
A.
3
0
. B.
31
. C.
3
2
. D.
3
3
.
Câu 9. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trong khai triển nhị thức newton của
201
8
3
(
) ( 2 3)
P
x x
thành đa thức,có tất cả có bao nhiêu số hạng có hệ số nguyên dương?
A. 673. B. 675. C. 674. D. 672.
Câu 10. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Trong khai triển
2
0
2 20
0
1 2 20
1
2 ... .x a a x a x a x
Giá trị của
0
1 2
a a a
bằng
A. 801. B. 800. C. 1. D. 721.
Câu 11. (Chuyên Lê Thánh Tông-Quảng Nam-2018-2019) Có bao nhiêu số hạng là số nguyên trong khai
triển của biểu thức
2
019
3
5
3
5
?
A.
136
. B.
403
. C.
135
. D.
134
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
Câu 12. (Gia Bình I Bắc Ninh - L3 - 2018) Trong khai triển của
2019
1
1 1 1
15 3 3 5
x
y x y
, số hạng mà lũy thừa
của
x
và
y
bằng nhau là số hạng thứ bao nhiêu của khai triển?
A.
13
48
. B.
13
46
. C.
13
45
. D.
1
347
.
Câu 13. (SGD&ĐT BẮC NINH - 2018) Cho khai triển
2
0
2
0
1 2 20 20
1
2
x
a a x a x a x
. Giá trị của
0
1 2 20
a a a a
bằng:
A.
1
. B.
2
0
3
. C.
0
. D.
1
.
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton
Dạng 2.1 Khai triển của 1 biểu thức
Dạng 2.1.1 Bài toán tìm hệ số của số hạng
Câu 14. (Chuyên Thái Bình lần 2 - 2018-2019) Hệ số của số hạng chứa
7
x
trong khai triển nhị thức
12
2
x
x x
(với
0
x
) là:
A.
3
76
. B.
2
64
. C.
2
64
. D.
2
60
.
Câu 15. (HKI CHUYÊN LÊ HỒNG PHONG 2018-2019) Tìm hệ số của số hạng chứa
7
x
trong khai
triển nhị thức
13
1
x
x
, (với
0
x
).
A.
1
716.
B.
6
8.
C.
1
76.
D.
2
86.
Câu 16. (HỌC KỲ I ĐAN PHƯỢNG HÀ NỘI 2017 - 2018) Hệ số của
31
x
trong khai triển
40
2
1
,
0
x
x
x
là.
A.
4
40
C
. B.
2
40
C
. C.
3
40
C
. D.
5
40
C
.
Câu 17. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Hệ số lớn nhất trong khai triển
4
1 3
4 4
x
A.
27
128
. B.
9
3
2
. C.
2
7
32
. D.
2
7
64
.
Câu 18. (HKI-Chu Văn An-2017) Cho biết hệ số của
2
x
trong khai triển
1 2
n
x
bằng
180
.Tìm
n
.
A.
8
n
. B.
12
n
. C.
14
n
. D.
10
n
.
Câu 19. (HKI-Chu Văn An-2017) Tìm hệ số của
7
x
trong khai triển
10
1
x
.
A.
9
0
. B.
72
0
. C.
1
20
. D.
4
5
.
Câu 20. (HKI – TRIỆU QUANG PHỤC 2018-2019) Tìm hệ số
h
của số hạng chứa
5
x
trong khai triển
7
2
2
x
x
.
A.
8
4
h
. B.
6
72
h
. C.
5
60
h
. D.
2
80
h
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
Câu 21. (HKI-Chuyên Hà Nội - Amsterdam 2017-2018) Hệ số của số hạng chứa
6
x
trong khai triển
Newton
15
2
2
x
x
là
A.
3640
. B.
3640
. C. 455. D.
1863680
Câu 22. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Tim hê sô cua
25 10
x y
trong
khai triên
15
3
.x xy
A. 58690. B. 4004. C. 3003. D. 5005.
Câu 23. (CHUYÊN THÁI BÌNH LẦN 1_2018-2019) Cho khai triển
6
2
x
x
với
x
. Tìm hệ số của
số hạng chứa
3
x
trong khai triển trên
A.
80
. B.
160
. C.
240
. D.
60
.
Câu 24. (CHUYÊN THÁI BÌNH LẦN 1_2018-2019) Cho khai triển
6
2
x
x
với
x
. Tìm hệ số của
số hạng chứa
3
x
trong khai triển trên
A.
80
. B.
160
. C.
240
. D.
60
.
Câu 25. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Biết hệ số của
2
x
trong khai
triển của
1 3
n
x
là
90
. Tìm
n
.
A.
7
n
. B.
6
n
. C.
8
n
. D.
5
n
.
Dạng 2.1.2 Bài toán tìm số hạng thứ k
Câu 26. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Số hạng thứ
13
trong khai triển
15
2
x
bằng?
A.
13
3640x
. B.
12
3640x
. C.
12
420x
. D.
3640
.
Câu 27. (DHSP HÀ NỘI HKI 2017-2018) Tìm số hạng chứa trong khai triển
9
1
2
x
x
.
A.
3 3
9
1
8
C x
. B.
3 3
9
1
8
C x
. C.
3 3
9
C x
. D.
3 3
9
C x
.
Câu 28. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Tìm số hạng chứa
7
x
trong khai triển
13
1
x
x
.
A.
3
13
C
. B.
3 7
13
C x
. C.
4 7
13
C x
. D.
4
13
C
.
Câu 29. (TRƯỜNG THPT THANH THỦY 2018 -2019) Tìm số hạng chứa
31
x
trong khai triển
40
2
1
x
x
?
A.
4 31
40
C
x
. B.
37 31
40
C
x
. C.
37 31
40
C
x
. D.
3 31
40
C
x
.
Câu 30. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Số hạng chứa
34
x
trong khai
triển
40
1
x
x
là
3
x
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
A.
37 34
40
C x
. B.
3 34
40
C x
. C.
2 34
40
C x
. D.
4 34
40
C x
.
Câu 31. (HỌC KÌ 1- LỚP 11- KIM LIÊN HÀ NỘI 18-19) Biết hệ số của số hạng chứa
2
x
trong khai
triển
1 4
n
x
là
3040
. Số tự nhiên
n
bằng bao nhiêu?
A.
28
. B.
26
. C.
24
. D.
20
.
Câu 32. (THPT CHUYÊN LƯƠNG VĂN CHÁNH - PHÚ YÊN - 2018) Biết hệ số của
2
x
trong khai
triển của
1 3
n
x
là
90
. Tìm
n
.
A.
5
n
. B.
8
n
. C.
n
. D.
n
.
Câu 33. (THPT CHU VĂN AN - HKI - 2018) Cho biết hệ số của
2
x
trong khai triển
1 2
n
x
bằng
180
. Tìm
n
.
A.
12
n
. B.
14
n
. C.
8
n
. D.
10
n
.
Câu 34. (THPT CHUYÊN NGỮ - HÀ NỘI - 2018) Tìm hệ số của số hạng chứa
10
x
trong khai triển của
biểu thức
5
3
2
2
3x
x
.
A.
. B.
826
. C.
810
. D.
421
.
Câu 35. (THPT HẢI AN - HẢI PHÒNG - LẦN 1 - 2018) Tìm hệ số của số hạng chứa
31
x
trong khai triển
40
2
1
x
x
.
A.
37
40
C
. B.
31
40
C
. C.
4
40
C
. D.
2
40
C
.
Câu 36. (SỞ GD&ĐT LÀO CAI - 2018) Trong khai triển
6
2
x
x
, hệ số của
3
0
x x
là:
A.
80
. B.
160
. C.
240
. D.
60
.
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n
Câu 37. (HKI-Chuyên Hà Nội - Amsterdam 2017-2018) Cho
n
la sô tư nhiên thoa man
0 1 2 2
2. 2 . ... 2 . 59049
n n
n n n n
C C C C
. Biêt sô hang thư
3
trong khai triên Newton cua
2
3
n
x
x
co gia tri băng
81
2
n
. Khi đó giá trị của
x
bằng
A.
1
B.
2
. C.
1
D.
2
.
Câu 38. (HKI-Nguyễn Gia Thiều 2018-2019) Cho nhị thức
2
3
1
2
n
x
x
, trong đó số nguyên dương
n
thỏa mãn
3
72
n
A n
. Tìm số hạng chứa
5
x
trong khai triển.
A.
6 4 5
10
2
C x
. B.
5 5 5
10
2
C x
. C.
7 3 5
10
2
C x
. D.
6 7 5
10
2
C x
.
Câu 39. (HKI – TRIỆU QUANG PHỤC 2018-2019) Tìm số hạng không chứa
x
trong khai triển nhị thức
Newton của
2
3
2
n
x
x
0
x
, biết rằng
1 2 3
1. 2. 3. ... . 256
n
n n n n
C C C n C n
(
k
n
C
là số tổ hợp
chập k của n phần tử).
A.
489888
B.
49888
. C.
48988
. D.
4889888
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
Câu 40. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Cho khai triển
1
0 1
1 3 ...
n
n
n
x a a x a x
trong đó
*
n
và các hệ số thỏa mãn hệ thức
1
0
... 4096
3 3
n
n
a
a
a
. Tìm hệ số
i
a
lớn nhất.
A.
1732104.
B.
3897234.
C.
4330260.
D.
3247695
.
Câu 41. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Tìm hệ số của
6
x
trong khai triển
3 1
3
1
n
x
x
với
0,
x
biết
n
là số nguyên dương thỏa mãn
2 2
1 2
3 4 .
n n
C nP A
A.
6
210 .x
B.
210.
C.
6
120 .x
D.
120.
Câu 42. (TH&TT LẦN 1 – THÁNG 12) Tìm hệ số của số hạng chứa
6
x
trong khai triển
2
3
2
n
x
x
0
x
, biết rằng
2 3
2 14 1
3
n n
C C n
k
n
C
là số tổ hợp chập
k
của
n
phần tử).
A.
326592
. B.
3265922
C.
3265592
D.
32692
.
Câu 43. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Tìm số hạng chứa
26
x
trong khai triển
7
4
1
n
x
x
biết
n
là số nguyên dương thỏa mãn hệ thức
1 2 20
2 1 2 1 2 1
... 2 1
n
n n n
C C C
.
A.
325
. B.
210
. C.
200
. D.
152
.
Câu 44. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Với
n
là số tự nhiên thỏa mãn
6 2
4
454
n
n n
C nA
, hệ số của số hạng chứa
4
x
trong khai triển nhị thức Niu-tơn của
3
2
n
x
x
( với
x
) bằng
A.
1972
. B.
786
. C.
1692
. D.
1792
.
Câu 45. (SGD&ĐT BẮC GIANG - LẦN 1 - 2018) Với
n
là số nguyên dương thỏa mãn
1 3
13
n n
C C n
,
hệ số của số hạng chứa
5
x
trong khai triển của biểu thức
2
3
1
n
x
x
bằng.
A.
120
. B.
252
. C.
45
. D.
210
.
Câu 46. (THPT CHUYÊN LAM SƠN - THANH HÓA - 2018) Cho
n
là số nguyên dương thỏa mãn
2 2 1
4 6
n n n
A C C n
. Hệ số của số hạng chứa
9
x
của khai triển biểu thức
2
3
n
P x x
x
bằng:
A.
18564
. B.
64152
. C.
192456
. D.
194265
.
Câu 47. (HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018) Biết
n
là số nguyên dương thỏa mãn
1 2
78
n n
n n
C C
, số hạng chứa
8
x
trong khai triển
3
2
n
x
x
là
A.
8
101376x
. B.
101376
. C.
112640
. D.
8
101376x
.
Câu 48. (THPT TRẦN PHÚ - ĐÀ NẴNG - 2018) Với
n
là số nguyên dương thỏa mãn
3 2
1
3 3 52 1
n n
C A n
. Trong khai triển biểu thức
3 2
2
n
x y
, gọi
k
T
là số hạng mà tổng số mũ
của
x
và
y
của số hạng đó bằng
34
. Hệ số của
k
T
là
A.
54912
. B.
. C.
. D.
41184
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
Câu 49. (SỞ GD&ĐT QUẢNG NAM - 2018) Cho
n
là số nguyên dương thỏa mãn
1 2
5 5
n n
C C
. Tìm hệ
số
a
của
4
x
trong khai triển của biểu thức
2
1
2
n
x
x
.
A.
11520
a
. B.
256
a
. C.
45
a
. D.
3360
a
.
Câu 50. (THPT QUẢNG YÊN - QUẢNG NINH - 2018) Với
n
là số nguyên dương thỏa mãn
2 3
3 40
n
n n
A C
. Hệ số của
6
x
trong khai triển
2
1
2
n
x
x
là
A.
1024
. B.
1024
. C.
1042
. D.
1042
.
Câu 51. (THPT CHUYÊN NGUYỄN THỊ MINH KHAI - SÓC TRĂNG - 2018) Với
n
là số nguyên
dương thoả mãn
2 1
3 120
n n
A C
, số hạng không chứa
x
trong khai triển của biểu thức
4
3
n
x
x
bằng
A.
295245
. B.
245295
. C.
292545
. D.
259254
.
Câu 52. (THPT PHÚ LƯƠNG - THÁI NGUYÊN - 2018) Tìm hệ số của số hạng chứa
8
x
trong khai triển
nhị thức Niutơn của
2
, 0 ,
2 2
n
n x
x
x
biết số nguyên dương
n
thỏa mãn
3 2
50.
n n
C A
A.
97
12
. B.
29
51
. C.
297
512
. D.
279
215
.
Câu 53. (TOÁN HỌC TUỔI TRẺ SỐ 6) Tìm số hạng không chứa
x
trong khai triển nhị thức Newton
của
2
3
2
n
x
x
0
x
, biết rằng
1 2 3
1. 2. 3. ... 256
n
n n n n
C C C nC n
(
k
n
C
là số tổ hợp chập
k
của
n
phần tử).
A.
489888
. B.
49888
. C.
48988
. D.
4889888
.
Câu 54. (THPT CHUYÊN AN GIANG - 2018) Giả sử có khai triển
2
0 1 2
1 2 ...
n
n
n
x a a x a x a x
. Tìm
5
a
biết
0 1 2
71.
a a a
A.
672
. B.
672
. C.
627
. D.
627
.
Câu 55. (CHUYÊN LONG AN - LẦN 1 - 2018) Với
n
là số nguyên dương thỏa mãn điều kiện
2 3
10
n n
A C
, tìm hệ số
5
a
của số hạng chứa
5
x
trong khai triển
2
3
2
n
x
x
với
x
.
A.
5
10
a
. B.
5
5
10a x
. C.
5
5
10a x
. D.
5
10
a
.
Câu 56. (HỒNG BÀNG - HẢI PHÒNG - LẦN 1 - 2018) Tìm hệ số của
5
x
trong khai triển
2
1 3
n
x
biết
3 2
2 100
n n
A A
A.
61236
. B.
63216
. C.
61326
. D.
66321
.
Câu 57. (CHUYÊN KHTN - LẦN 1 - 2018) Cho
n
là số nguyên dương thỏa mãn
0 1 1 2 2
3 3 3 ..... 1 2048
n
n n n n
n n n n
C C C C
. Hệ số của
10
x
trong khai triển
2
n
x
là:
A.
11264
. B.
22
. C.
220
. D.
24
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
Câu 58. (CHUYÊN VĨNH PHÚC - LẦN 1 - 2018)Trong khai triển
2
1
3
n
x
x
biết hệ số của
3
x
là
4
5
3
n
C
. Giá trị
n
có thể nhận là
A.
9
. B.
1
2
. C.
15
. D.
16
.
Câu 59. (THPT LÊ XOAY - LẦN 3 - 2018) Hệ số của số hạng chứa
8
x
trong khai triển
5
3
1
;
0
n
x
x
x
biết
1
4
3
7
3
n
n
n n
C
C n
là
A.
1303
. B.
313
. C.
495
. D.
13129
.
Câu 60. (CTN - LẦN 1 - 2018) Tìm hệ số của
4
x
trong khai triển nhị thức Newton
5
1
2
n
x
x
với
x
, biết
n
là số tự nhiên lớn nhất thỏa mãn
5
4
2
1
8
n
n
A
A
.
A.
80
64
. B.
3
360
. C.
13
440
. D.
15
360
.
Câu 61. (THTP LÊ QUÝ ĐÔN - HÀ NỘI - LẦN 1 - 2018) Tìm số hạng không chứa
x
trong khai triển
2
1
n
x
x
biết
2
2
105
n
n
A C
.
A.
3003
. B.
5005
. C.
5
005
. D.
3
003
.
Câu 62. (THPT QUỲNH LƯU - NGHỆ AN - 2018) Tìm hệ số của
5
x
trong khai triển thành đa thức của
2
2 3
n
x
, biết n là số nguyên dương thỏa mãn:
0
2 4 2
2 1 2 1 2 1 2 1
..
. 1024
n
n
n n n
C
C C C
.
A.
20
99529
. B.
20
99520
. C.
19
59552
. D.
19
59552
.
Câu 63. [HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018] Biết
n
là số nguyên dương thỏa mãn
1
2
78
n
n
n n
C C
, số hạng chứa
8
x
trong khai triển
3
2
n
x
x
là
A.
8
101376x
. B.
101376
. C.
112640
. D.
8
101376x
.
Câu 64. (ĐỀ THI GIỮA KỲ II YÊN PHONG 1 - 2018) Tìm số hạng chứa
5
x
trong khai triển
2
,
n
x
x
biết
n
là số tự nhiên thỏa mãn
3
2
4
2
3
n
n
C
n C
A.
1
34
B.
1
44
C.
1
15
D.
141
Câu 65. (THPT HOÀNG MAI - NGHỆ AN - 2018) Tìm hệ số không chứa
x
trong khai triển
3
2
n
x
x
, biết
n
là sô nguyên dương thỏa mãn
1
2
7
8
n
n
n n
C
C
.
A.
1
12640
. B.
1
12643
. C.
1
12640
. D.
1
12643
.
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập)
Câu 66. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Trong khai triển
9
2
8
x
x
, số hạng không
chứa
x
là
A. 40096. B. 43008. C. 512. D. 84.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
Câu 67. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Số hạng độc lập với
x
trong
khai triển
8
3
2
x
x
là
A.
1792
. B.
792
. C.
972
. D.
1972
.
Câu 68. (HỌC KÌ 1- LỚP 11- KIM LIÊN HÀ NỘI 18-19) Tìm số hạng không chứa
x
trong khai triển
12
3
1
x
x
.
A.
220
. B.
220
. C.
924
. D.
924
.
Câu 69. (KSCL LẦN 1 CHUYÊN LAM SƠN - THANH HÓA_2018-2019) Cho
x
là số thực dương, số
hạng không chứa
x
trong khai triển nhị thức
30
2
x
x
là
A.
20
2
. B.
20 10
30
2
C
. C.
10 20
30
2
C
. D.
20
30
C
.
Câu 70.
(THPT
NGUYỄN
TRÃI-THANH
HOÁ
-
Lần
1.Năm
2018&2019)
Số hạng không chứa x trong
khai triển
45
2
1
x
x
là
A.
5
45
C
. B.
5
45
C
. C.
15
45
C
. D.
15
45
C
.
Câu 71. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Số hạng không chứa
x
trong khai triển
10
2
x
x
là
A.
5
10
C
. B.
5 5
10
.2
C
. C.
5
10
C
. D.
5 5
10
.2
C
.
Câu 72. (Kim Liên - Hà Nội - L1 - 2018-2019) Số hạng không chứa
x
trong khai triển
7
3
4
1
x
x
là:
A. 5. B. 35. C. 45. D. 7.
Câu 73. (THPT Đoàn Thượng-Hải Dương-HKI 18-19) Tìm số hạng không chứa
x
trong khai triển
6
2
1
2x
x
,
0
x
.
A.
240
. B.
15
. C.
240
. D.
15
.
Câu 74. (Chuyên Lào Cai Lần 3 2017-2018) Số hạng không chứa
x
trong khai triển biểu thức
12
2
1
A x
x
là
A.
. B.
495
. C.
. D.
924
.
Câu 75. (Bình Minh - Ninh Bình - Lần 4 - 2018) Số hạng không chứa
x
trong khai triển
45
2
1
x
x
là
A.
15
45
C
. B.
30
45
C
. C.
5
45
C
. D.
15
45
C
.
Câu 76. (DHSP HÀ NỘI HKI 2017-2018) Tìm số hạng không chứa
x
trong khai triển
5
2
3
1
x
x
.
A.
10
. B.
20
. C.
5
. D.
1
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
Câu 77. (Kim Liên - Hà Nội - Lần 1 - 2019) Số hạng không chứa
x
trong khai triển
7
3
4
1
x
x
là
A. 5. B. 35. C. 45. D. 7.
Câu 78. (Chuyên Lam Sơn-KSCL-lần 2-2018-2019) Cho
x
là số thực dương, số hạng không chứa
x
trong khai triển nhị thức
3
0
2
x
x
là
A.
2
0
2
. B.
2
0 10
30
2 .C
. C.
10
20
30
2 .C
. D.
2
0
30
C
.
Câu 79. (CHUYÊN ĐHSPHN - 2018) Cho biểu thức
10
3 2
3
1
1
1
x x
P
x x
x
x
với
0
x
,
1x
. Tìm
số hạng không chứa
x
trong khai triển Niu-tơn của
P
.
A.
200
. B.
160
. C.
210
. D.
100
.
Câu 80. (THPT CHUYÊN LƯƠNG THẾ VINH - ĐỒNG NAI - 2018) Số hạng không chứa
x
trong khai
triển
9
2
2
,
f
x x
x
x
bằng
A.
5376
. B.
5376
. C.
672
. D.
.
Câu 81. (CHUYÊN TRẦN PHÚ - HẢI PHÒNG - LẦN 1 - 2018) Số hạng không chứa
x
trong khai triển
của
14
3
4
2
x
x
với
0
x
là:
A.
6
8
14
2
C
. B.
6
6
14
2
C
. C.
8
8
14
2
C
. D.
8
8
14
2
C
.
Câu 82. (THPT LƯƠNG ĐẮC BẰNG - THANH HÓA - LẦN 1 - 2018) Tìm số hạng không chứa
x
trong khai triển của
1
1
1
1
5
1
x
x
x
với
0
x
.
A.
4
85
. B.
2
38
. C.
165
. D.
5
25
.
Câu 83. (ĐỀ THAM KHẢO BGD & ĐT 2018) Với
n
là số nguyên dương thỏa mãn
1
2
55
n
n
C
C
, số hạng
không chứa
x
trong khai triển của biểu thức
3
2
2
n
x
x
bằng
A.
1
3440
B.
3
360
C.
8
0640
D.
3
22560
Câu 84. (ĐỀ KT NĂNG LỰC GV THUẬN THÀNH 1 BẮC NINH 2018-2019) Tìm số hạng không chứa
x
trong khai triển của
4
1
n
x x
x
với
0x
, nếu biết rằng
n
là số nguyên dương thỏa mãn
2 1
4
4
n
n
C
C
.
A. 485. B. 525. C. 165. D. 238
Câu 85. (TOÁN HỌC VÀ TUỔI TRẺ SỐ 1 - 2018) Tìm số hạng không chứa
x
trong khai triển của
4
1
n
x
x
x
, với
x
, nếu biết rằng
2
1
4
4
n
n
C
C
.
A.
1
65
. B.
23
8
. C.
48
5
. D.
5
25
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
Câu 86. (THPT PHAN CHU TRINH - ĐẮC LẮC - 2018) Số hạng không chứa
x
trong khai triển
2
3
3
2
n
x
x
với
x
, biết
n
là số nguyên dương thỏa mãn
3
2
1
2
n
n
C n A
là:
A.
12
4 12
16
.2 .3
C
. B.
0
16
16
.2
C
. C.
12
4 12
16
.2 .3
C
. D.
16
0
16
.2
C
.
Câu 87. (SỞ GD&ĐT HÀ TĨNH - 2018) Với số nguyên dương
n
thỏa mãn
2
2
7
n
C
n
, trong khai triển
2
2
n
x
x
số hạng không chứa
x
là
A.
84
. B.
672
. C.
8
. D.
5376
.
Dạng 2.2 Khai triển của nhiều biểu thức
Dạng 2.2.1 Dạng
1
2
...
n
k
a a a
Câu 88. (HKI – TRIỆU QUANG PHỤC 2018-2019) Cho khai triển
2017
2
2 4034
0
1 2 4034
1
3 2 ...
x
x a a x a x a x
. Tìm
2
a
.
A.
9
136578
B.
1
6269122
. C.
8
132544
. D.
18302258
.
Câu 89. (TOÁN HỌC TUỔI TRẺ SỐ 5) Tìm hệ số của
7
x
trong khai triển
10
3
1
3 2
f
x x x
thành
đa thức.
A.
20
4120
. B.
2
62440
. C.
4320
. D.
62
640
.
Câu 90. (CHUYÊN VINH - LẦN 1 - 2018) Cho khai triển
9
2
18 17 16
0 1 2 18
3
2 ... .x x a x a x a x a
Giá trị
1
5
a
bằng
A.
21
8700
. B.
48
9888
. C.
8
04816
. D.
1
74960
.
Câu 91. (THPT CHUYÊN ĐH VINH - LẦN 3 - 2018) Tìm hệ số của
3
x
sau khi khai triển và rút gọn các
đơn thức đồng dạng của
9
2
1
2
x x
x
,
x
.
A.
2940
. B.
3
210
. C.
. D.
3210
.
Câu 92. (THPT CHUYÊN HÙNG VƯƠNG - PHÚ THỌ - LẦN 4 - 2018) Hệ số của số hạng chứa
7
x
trong khai triển
6
2
3 2
x x
bằng
A.
6432
. B.
4032
. C.
1632
.
D.
5418
.
Câu 93. (SGD&ĐT HÀ NỘI - 2018) Tìm hệ số của số hạng chứa
5
x
trong khai triển
1
0
2
3
1
x
x x
.
A.
5
82
. B.
1
902
. C.
. D.
25
2
.
Câu 94. (THPT PHAN ĐÌNH PHÙNG - HÀ TĨNH - LẦN 1 - 2018) Cho
n
là số tự nhiên thỏa mãn
0
1 2
3
4 5 ... ( 3) 3840
n
n
n n n
C
C C n C
.Tổng tất cả các hệ số của các số hạng trong khai triển
2
3
(1 )
n
x x x
là
A.
1
0
4
. B.
9
4
. C.
1
0
2
. D.
9
2
.
Câu 95. (THPT CHUYÊN VĨNH PHÚC - LẦN 4 - 2018) Giả sử
11
2
3 10 2 3 110
0
1 2 3 110
1
... ...
x
x x x a a x a x a x a x
với
0
a
,
1
a
,
2
a
,…,
110
a
là các hệ số.
Giá trị của tổng
0
1 2 3 10 11
11 11 11 10 11 9 11 8 11 1 11 0
..
.
T
C a C a C a C a C a C a
bằng
A.
11T
. B.
11T
. C.
0
T
. D.
1T
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
Dạng 2.2.2 Tổng
1
1 2 2
...
n
m h
k
k
a
b a b a b
Câu 96. (CHUYÊN THÁI BÌNH LẦN 1_2018-2019) Sau khi khai triển và rút gọn thì
1
8
12 2
1
(
) (1 )P x x x
x
có tất cả bao nhiêu số hạng
A.
2
7
. B.
2
8
. C.
3
0
. D.
2
5
Câu 97. (PTNK CƠ SỞ 2-TPHCM-LẦN1- 2018) Cho đa thức
2
017 2018
2
3 2P x x x
2018 2017
2
018 2017 1 0
...
a x a x a x a
. Khi đó
2018 2017 1 0
...
S a a a a
bằng
A.
0
. B.
1
. C.
2
018
. D.
2
017
.
Câu 98. (THPT LÝ THÁI TỔ - BẮC NINH - 2018) Sau khi khai triển và rút gọn biểu thức
1
2 21
2 3
2
3
1
2f x x x
x x
thì
f
x
có bao nhiêu số hạng?
A.
30
. B.
32
. C.
29
. D.
35
.
Câu 99. (THPT NGUYỄN HUỆ - TT HUẾ - 2018) Tìm hệ số của
5
x
trong khai triển
6
7 12
1
1 ... 1
P
x x x x
.
A.
1716
. B.
1715
. C.
1287
. D.
1711
.
Câu 100. (CHUYÊN BẮC NINH - LẦN 2 - 2018) Cho đa thức:
8
9 10 11 12
1 1 1 1 1
P x x x x x x
. Khai triển và rút gọn ta được đa thức:
2
12
0 1 2 12
...
P x a a x a x a x
. Tìm hệ số
8
a
.
A.
72
0
. B.
70
0
. C.
7
15
. D.
73
0
.
Câu 101. (CHUYÊN BẮC NINH - LẦN 2 - 2018) Cho đa thức
8
9 10 11 12
1
1 1 1 1
P
x x x x x x
. Khai triển và rút gọn ta được đa thức
12
0
1 12
...
P x a a x a x
. Tính tổng các hệ số
i
a
,
i
1
;
2
;
.
..;
12
.
A.
5
. B.
. C.
0
. D.
.
Dạng 2.2.3 Tích
1
1
.. . ...
m
l
n
n
a a b b
Câu 102. (THPT CHUYÊN THÁI BÌNH - LẦN 3 - 2018) Tìm hệ số của số hạng chứa
9
x
trong khai triển
nhị thức Newton
11
1 2 3
x x
.
A.
. B.
1380
. C.
9405
. D.
.
Câu 103. (THPT CHUYÊN THĂNG LONG - ĐÀ LẠT - 2018) Cho khai triển
2
1
0
2
2 14
0
1 2 14
1
2 3 4 4
x
x x a x a x a x a x
. Tìm giá trị của
6
a
.
A.
4
82496
. B.
5
29536
. C.
2
78016
. D.
4
53504
.
Câu 104. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Hệ số của
6
x
trong khai triển
4
6
2
1
2
1
4
x
x x
thành đa thức là
A.
6
1
4
1
2
C
. B.
6
1
4
1
4
C
. C.
6
14
C
. D.
8
14
4C
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
Dạng 2.2.4 Dạng kết hợp tích và tổng
Câu 105. (MĐ 103 BGD&ĐT NĂM 2017-2018) Hệ số của
5
x
trong khai triển biểu thức
6 8
2 1 3
x x x
bằng
A.
1752
B.
1272
C.
1272
D.
1752
Câu 106. (Mã đề 102 BGD&ĐT NĂM 2018) Hệ số của
5
x
trong khai triển
6 8
3 1 2 1
x x x
bằng
A.
3007
B.
577
C.
3007
D.
577
Câu 107. (Mã đề 104 BGD&ĐT NĂM 2018) Hệ số của
5
x
trong khai triển biểu thức
6 8
( 2) (3 1)
x x x
bằng
A.
13548
B.
13668
C.
13668
D.
13548
Câu 108. (Mã đề 101 BGD&ĐT NĂM 2018) Hệ số của
5
x
trong khai triển biểu thức
6 8
2 1 3 1
x x x
bằng
A.
13848
B.
13368
C.
13848
D.
13368
Câu 109. (HKI – TRIỆU QUANG PHỤC 2018-2019) Hệ số của
5
x
trong khai triển
6 8
2 3 1
x x x
bằng
A.
13548
. B.
13548
. C.
13668
. D.
13668
.
Câu 110. (TH&TT LẦN 1 – THÁNG 12) Tìm hệ số của
5
x
trong khai triển đa thức
5 10
2
1 1 2 .
f x x x x x
A.
965.
B.
263.
C.
632.
D.
956.
Câu 111. (THPT CHUYÊN THÁI BÌNH - LẦN 4 - 2018) Tìm hệ số của
5
x
trong khai triển
5 10
2
1 2 1 3
P x x x x x
.
A.
3240
. B.
3320
. C.
80
. D.
259200
.
Dạng 3. Ứng dụng nhị thức newton để giải toán
Câu 112. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho biểu thức
19 0 18 1 17 2 20
20 20 20 20
1
3 3 3 ...
3
S C C C C
. Giá trị
3S
là
A.
20
4
. B.
19
4
3
. C.
18
4
3
. D.
21
4
3
.
Câu 113. (HỌC KỲ I ĐAN PHƯỢNG HÀ NỘI 2017 - 2018) Tổng
1 2 3 2017
2017 2017 2017 2017
...C C C C
bằng.
A.
2017
2 1
. B.
2017
2 1
. C.
2017
2
. D.
2017
4
.
Câu 114. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Tổng
1 2 2018
2018 2018 2018
...C C C
bằng
A.
2018
2
. B.
2018
2 1
. C.
2018
2 1
. D.
2016
4
.
Câu 115. (THPT CHUYÊN THÁI BÌNH - LẦN 1 - 2018) Tổng
1 3 5 2017
2017 2017 2017 2017
...T C C C C
bằng:
A.
2017
2 1
. B.
2016
2
. C.
2017
2
. D.
2016
2 1
.
Câu 116. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Tổng
0 1 2 2 5 5
5 5 5 5
2 2 ... 2
S C C C C
bằng:
A.
324
. B.
435
. C.
243
. D.
342
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
Câu 117. (HKI-Chu Văn An-2017) Tính tổng
0
1 2 2 10 10
10 10 10 10
2
2 2
S
C C C C
.
A.
59
050
S
. B.
59
049
S
. C.
1
025
S
. D.
1
024
S
.
Câu 118. (THPT CHU VĂN AN - HKI - 2018) Tính tổng
0 1 2 2 3 3 10 10
10 10 10 10 10
2
2 2 2 .S C C C C C
A.
59
050.
S
B.
10
24.
S
C.
59
049.
S
D.
10
25.
S
Câu 119. (SGD&ĐT ĐỒNG THÁP - 2018) Tổng
1
2 3 2016
2016 2016 2016 2016
...C C C C
bằng
A.
20
16
2
. B.
20
16
4
. C.
20
16
2
1
. D.
2
016
2
1
.
Câu 120. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Cho
n
là số nguyên dương thỏa mãn
0
1 2 2
4
4 ... 4 15625
n
n
n n n n
C
C C C
. Tìm
n
.
A.
3
n
. B.
5
n
. C.
6
n
. D.
4
n
.
Câu 121. (THPT THUẬN THÀNH 1) Tổng
1
2 2018 2019
2019 2019 2019 2019
2
3 ... 2019 2020S C C C C
tương ứng
bằng:
A.
201
9
20
20.2
. B.
201
8
20
19.2
. C.
2
018
2
021.2 1
. D.
2
019
2
020.2 1
.
Câu 122. (HKI-Nguyễn Gia Thiều 2018-2019) Tính tổng
1
2 13 20 21 22
22 22 22 22 22
.
...
S
C C C C C
.
A.
2
1 11
22
2
S
C
. B.
1
1
2
1
2
2
2
2
C
S
. C.
1
1
2
1
2
2
2
2
C
S
. D.
2
1 11
22
2
S
C
.
Câu 123. (THPT CHU VĂN AN -THÁI NGUYÊN - 2018) Kí hiệu
k
n
C
là số tổ hợp chập
k
của
n
phần tử
0
; ,k n k n
tính tổng sau:
0 1 2 2017 2018
2018 2018 2018 2018 2018
2
3 ... 2018 2019S C C C C C
A.
2016
1009
.2
. B.
2
018
1
006.2
. C.
2018
1010.2
. D.
201
8
1
007 2 14
.
.
Câu 124. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Biểu thức
2 10
10
9 8
1 1 1
. . ...
10! 9! 1! 8! 2! 10!
x x x
x x x
bằng
A.
10!
. B.
20!
. C.
1
10!
. D.
1
100!
.
Câu 125. (CỤM 5 TRƯỜNG CHUYÊN - ĐBSH - LẦN 1 - 2018) Có bao nhiêu số dương
n
sao cho
0 0 0 1 1 1 1 1
1 2 1 2 1
2
... ... ...
n n n
n n n n n
S
C C C C C C C C C
là một số có
1
000
chữ số?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 126. (HỌC KÌ 1- LỚP 11- KIM LIÊN HÀ NỘI 18-19) Gọi
n
là số nguyên dương thỏa mãn:
1
1 1 1 1024
.....
1
! 1 ! 3! 3 ! 5! 5 ! 1 !1! !n n n n n
Tìm mệnh đề đúng.
A.
n
là số chia hết cho
10
. B.
n
là số nguyên tố.
C.
n
là số chia hết cho
3
. D.
n
là số chia hết cho
4
.
Phần B. LỜI GIẢI THAM KHẢO
Dạng 1. Tiếp cận với khai triển nhị thức newton
Câu 1. Số số hạng trong khai triển là:
1 50 1 51
n
.
Câu 2. Trong khai triển nhị thức
n
a
b
thì số các số hạng là
1n
nên trong khai triển
2018
2
3x
có
số hạng.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
Câu 3. Ta có:
5
5
1 2 3 4 5
0
5 1 4 2 3 3 2 4 1 5
5 5 5 5 5 5
x
y x y C x C x y C x y C x y C x y C y
Hay
5
5
4 3 2 2 3 4 5
5
10 10 5
x
y x x y x y x y xy y
.
Câu 4. Chọn C
Ta có: Khai triển nhị thức Niu-tơn
( )
n
a b
có
1n
số hạng.
Vậy trong khai triển nhị thức Niu-tơn của
2
019
(3 2 )
x
có
2
020
số hạng.
Câu 5. Chọn C
Xét khai triển
10
10
10
0
(
) 1 .
k
k
k
f
x x C x
.
Gọi
S
là tổng các hệ số trong khai triển thì ta có
1
0
10
(
1) 1 1 2 1024
S
f
.
Câu 6. Chọn C
Xét khai triển
10
10
10
0
(
) 1 .
k
k
k
f
x x C x
.
Gọi
S
là tổng các hệ số trong khai triển thì ta có
10
10
(1) 1 1 2 1024
S f
.
Câu 7. Xét khai triển
201
8 0 1 2 2 3 3 2018 2018
2018 2018 2018 2018 2018
(
1 2x) 2 . ( 2 ) . ( 2 ) . ... ( 2 ) .C x C x C x C x C
Tổng các hệ số trong khai triển là:
0
1 2 2 3 3 2018 2018
2018 2018 2018 2018 2018
2
. ( 2) . ( 2) . ... ( 2) .S C C C C C
Cho
1x
ta có:
201
8 0 1 2 2 3 3 2018 2018
2018 2018 2018 2018 2018
(
1 2.1) 2.1. ( 2.1) . ( 2.1) .C ... ( 2.1) .C
C
C C
2018
1
1
S
S
Câu 8. Ta có
124
124
124
4
2 4
124
0
(
5 7) . 1 .5 .7
k
k
k
k
k
C
Số hạng hữu tỉ trong khai triển tương ứng với
124
2
4
k
k
0
;4;8;12;...;124
k
.
Vậy số các giá trị
k
là:
1
24 0
1
32
4
.
Câu 9. Chọn A
201
8
2018 2018
2018
2018 2018
3 3
3
0 0
(
) ( 2 3) 2 3 2 .3
k
k
k
k k
k
k
P
x x x x
Để hệ số nguyên dương thì
2018 3 2018 3 2018 3k k t k t
,do
0 2018
k
nên ta
có
20
18
0
2018 3 2018 0 672,6
3
t
t
vậy t=0,1,2….672 nên có 673 giá trị
Câu 10. Chọn A
Ta có
20
20
20
0
1
2 2 ,
k
k
k
k
x
C x
k Z
0
0
20
,a
C
1
1
20
2
. ,a C
2
2
2
2 20 20
2
4 .a C C
Vậy
0
1 2
0 1 2 20 20 20
2
4 801.
a
a a C C C
Câu 11. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
Ta có
2019
2019 2019
2019 2019
3 5 3 5
3 5
2019 2019
0 0
3 5 . 3 . 5 .3 .5
k k
k k
k k
k k
C C
.
Để trong khai triển có số hạng là số nguyên thì
0 2019 0 2019
2019
673
3 3
5 5
k k
k k
k k
k k
0 2019
15
k
k
k
.
Ta có
15 15k k m
mà
0 2019 0 15 2019 0 134, 6
k m m
. Suy ra có
135
số
hạng là số nguyên trong khai triển của biểu thức.
Câu 12. Chọn D
Ta có số hạng thứ
1k
là :
2019
1 1 1 1
15 3 3 5
2019
k k
k
C x y x y
2019 4 2019 2
15 15 3 15
2019
k k
k
C x y
Theo đề bài ta có;
2019 4 2019 2
15 15 3 15
k k
1346
k
Vậy số hạng thỏa yêu cầu bài toán là số hạng thứ
1347
.
Câu15. (THPT Yên Dũng 3 - Bắc Giang lần 1- 18-19) Cho khai triển
20 2 20
0 1 2 20
(2 1) ....
x a a x a x a x
. Tìm
1
a
A. 20. B. 40. C. -40. D. -760. Chọn C
Ta có:
1
a
là hệ số của
x
Hạng tử chứa x trong khai triển là:
19
20 1
2 40
C x a
Câu 13.
20
2
0 1 2 20 20
1 2
x a a x a x a x
1
.
Thay
1x
vào
1
ta có:
20
0 1 2 20
1 1
a a a a
.
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton
Dạng 2.1 Khai triển của 1 biểu thức
Dạng 2.1.1 Bài toán tìm hệ số của số hạng
Câu 14. Chọn C
Số hạng tổng quát của khai triển
12
2
x
x x
(với
0
x
) là
12
1 12
2
. .
k
k k
k
T C x
x x
3
12
2
12
2 . . .
k
k
k k
C x x
5
12
2
12
2 . .
k
k
k
C x
.
Số hạng trên chứa
7
x
suy ra
5
12 7 2
2
k
k
.
Vậy hệ số của số hạng chứa
7
x
trong khai triển trên là
2
2
12
2 . 264
C
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
Câu 15. Chọn D
Số hạng tổng quát trong khai triển nhị thức
13
1
x
x
.
13
13 2
1 13 13
1
k
k
k k k
k
T C x C x
x
.
1k
T
chứa
7
1
3 2 7 3
x
k k
.
Vậy hệ số của số hạng chứa
7
x
trong khai triển nhị thức
13
1
x
x
bằng:
3
13
286
C
.
Câu 16. Chọn C
40
40
40
40
2 40 3
40
40
2
0 0
1
.
k
k k k k
k
k
x
C x x C x
x
Theo giả thiết:
40
3 31 3
k
k
.
Vậy hệ số của
3
1
x
là
3
40
9
880
C
.
Câu 17. Chọn D
Ta có
4
4
4
4
0
1 3 1 3
. .
4 4 4 4
k
k
k
k
x C
2
3 4
1
3 27 27 81
256 64 128 64 256
x x x x
Vậy hệ số lớn nhất trong khai triển là
27
64
.
Câu 18. Chọn D
Ta có:
1
.2
.
k
k k
k
n
T
C x
.
Hệ số của
2
x
trong khai triển bằng
1
80
2
2 2 2
1
0
!
.2 180 .2 180 1 90 90 0
9
2
.2
n
n
n
C
n n n n
n l
n
Câu 19. Chọn D
Số hạng tổng quát là:
1
10
.
k
k
k
T
C x
.
Số hạng chứa
7
x
trong khai triển
10
1
x
là:
8
7
8
10
.T C x
nên hệ số là 45.
Câu 20. Chọn D
Ta có:
7
7
7 7
2
2 7 3 7
7
7
0 0
2
2
.2
. .
k
k
k
k k k
k k
x
C x C x
x x
Cần tìm
k
sao cho
3 7 5
k
, suy ra
4.
k
Vậy hệ số
h
của số hạng chứa
5
x
trong khai triển
7
2
2
x
x
là
4
3
7
.2 280.
h C
Câu 21. Chọn A
15
15
15 15
15 15 2 15 3
15
15 15
2 2
0 0 0
2 2
2 2
k
k
k
k
k k k k k k
k k k
x C x C x x C x
x x
Số hạng tổng quát của khái triển
15 3
1
15
2
k
k k
k
T
C x
Số của số hạng chứa
6
x
:
15 3 6 3
k k
. Hệ số của số hạng chứa
6
x
3
3
1
5 15
2
2 3640
k
k
C
C
Câu 22. Chọn C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
Sô hang tông quat cua khai triên đa cho la
15
3 45 2
15 15
. . . . ,
k
k
k k k k
C x xy C x y
vơi
0 15
k
,
k
. Sô hang nay chưa
25 10
x y
khi va chi khi
10
k
(thỏa mãn).
Vây hê sô cua
25 10
x y
trong khai triên
15
3
x xy
la
10
15
3003.
C
Câu 23. Chọn D
Ta có:
6
3
6 6
6
6
2
6 6
0 0
2 2
2
k
k
k k k k
k k
x C x C x
x x
.
Số hạng chứa
3
x
ứng với
3
6 3 2
2
k
k
. Vậy hệ số của số hạng chứa
3
x
bằng
2 2
6
2 . 60
C
.
Câu 24. Chọn D
Ta có:
6
3
6 6
6
6
2
6 6
0 0
2 2
2
k
k
k k k k
k k
x C x C x
x x
.
Số hạng chứa
3
x
ứng với
3
6 3 2
2
k
k
. Vậy hệ số của số hạng chứa
3
x
bằng
2 2
6
2 . 60
C
.
Câu 25. Chọn D
Số hạng thứ
1k
trong khai triển của
1 3
n
x
là:
1
3
k
k k
k n
T C x
.
Số hạng chứa
2
x
ứng với
2
k
.
Ta có:
2
2
3 90
n
C
2
10
n
C
(với
2
n
;
n
)
!
10
2! 2 !
n
n
1 20
n n
5
4
n
n L
. Vậy
5
n
.
Dạng 2.1.2 Bài toán tìm số hạng thứ k
Câu 26. Chọn B
Ta có
15
15
15
15
0
2 .2 .
k
k k
k
x C x
Số hạng thứ
13
trong khai triển tương ứng với
12
k
.
12
12 15 12 12
15
.2 . 3640C x x
.
Câu 27. Chọn A
Số hạng thứ
1k
trong khai triển là:
9 9 2
1 9 9
1 1
2 2
k k
k k k
k
T C x C x
x
.
Số hạng chứa
3
x
có giá trị
k
thỏa mãn:
9 2 3 3
k k
.
Vậy số hạng chứa
3
x
trong khai triển là:
3 3
9
1
8
C x
.
Câu 28. Chọn B
Ta có công thức của số hạng tổng quát:
13 13 13 2
1 13 13 13
1
. 1 . 1
k
k k
k k k k k k k
k
T C x C x x C x
x
Số hạng chứa
7
x
khi và chỉ khi
13 2 7 3
k k
.
Vậy số hạng chứa
7
x
trong khai triển là
3 7
13
C x
.
Câu 29.
Chọn D
Ta có khai triển:
40
40 40
40 2 40 3
40 40
2
0 0
1
k
k k k k
k k
x x x x
x
C C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
Số hạng tổng quát trong khai triển:
40
3
40
k
k
C x
Số hạng chứa
3
1
x
ứng với:
4
0 3 31
3
k k
Vậy số hạng chứa
3
1
x
là:
3 31
4
0
C
x
Câu 30. Chọn B
Số hạng thứ
1k
trong khai triển
40
1
x
x
là:
40 40 40 2
1
40 40 40
1
.
k
k k k k k k k
k
a C x C x x C x
x
.
Số hạng chứa
34
x
trong khai triển
40
1
x
x
tương ứng với:
40
2 34 3
k
k
.
Vậy số hạng chứa
34
x
trong khai triển
40
1
x
x
là:
3
34
4
0
C
x
.
Câu 31. Chọn D
Ta có:
0
0
1
4 4 4
n
n
n k
k k k k
n
n
k k
x
C x C x
.
Hệ số của số hạng chứa
2
x
là:
2
2
4
n
C
.
Giả thiết suy ra
2
2 2 2
20
t/m
1
4 3040 190 190 380 0
2
19
loai
n n
n
n
n
C C n n
n
.
Câu 32. Số hạng tổng quát thứ
1k
là
1
3
3
k k
k
k k
k
n n
T
C x C x
.
Vì hệ số của
2
x
nên cho
k
.
Khi đó ta có
2
2
3
90
n
C
2
5
1
10
10
2
4
n
n
n
n
n
C
n
l
.
Vậy
5
n
.
Câu 33. Ta có
2
0
1 2
1
2 .2 . 2 ... 2
n
n
n
n
n n n
x
C C x C x C x
.
Hệ số của
2
x
bằng
2
1
80 4. 180
n
C
!
4
180
2
! 2 !
n
n
1
90
n
n
2
90 0
n n
9
10
n
l
n
.
Vậy
10
n
.
Câu 34. Ta có
5
5
5
5
3
3 5 15 5
5
5
2 2
0 0
2
2
3 1 . . 3 . 1 . .3 .2
k
k
k
k
k
k k k k
k
k
x
C x C x
x x
.
Số hạng chứa
1
0
x
ứng với
15 5 10 1
k k
.
Hệ số của số hạng chứa
1
0
x
là
1
1
4 1
5
1
.3 .2 810
C
.
Câu 35. Ta có:
40
40
40
40
40 3
40
40
2 2
0 0
1
1
. . .
k
k
k k k
k
k
x
C x C x
x x
.
Số hạng tổng quát của khai triển là:
40 3
1
40
.
k k
k
T
C x
.
Số hạng chứa
3
1
x
trong khai triển tương ứng với
40
3 31 3
k
k
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
Vậy hệ số cần tìm là:
3 37
40 40
C C
(theo tính chất của tổ hợp:
k n k
n n
C C
).
Câu 36. Ta có:
6
6
1
2
2
2x x x
x
1
6
6
2
6
0
2
k
k
k
k
C x x
1
6
6
2
6
0
.2 2
k
k
k k
k
C x x
3
6
6
2
6
0
.2
k
k k
k
C x
Theo đề bài,
3
6
3
2
k
x x
3
6 3
2
k
2
k
Hệ số của
3
0
x x
là:
2 2
6
.2 60
C
.
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n
Câu 37. Chọn C
Ta co:
0 1 2 2 10
2. 2 . ... 2 . 59049 2 1 59049 3 3 10
n
n n n
n n n n
C C C C n
.
Ta được nhị thức
10
2
3
x
x
.
Số hạng thứ ba của khai triển là
2
8
2 2 14
3 10
3
. . 405T C x x
x
.
Theo giả thiết ta có:
14
81
405
2
x n
14
405 405
x
14
1
x
1
x
.
Câu 38. Chọn C
Ta có:
3
!
72 72 1 2 72
3 !
n
n
A n n n n n n
n
10
n
.
Xét khai triển:
10
10 10 10
10
2 2 10 20 2 3 10 20 5
10 10 10
3 3
0 0 0
1 1
2 2 .2 . .2
k
k
k k k k k k k k
k k k
x C x C x x C x
x x
.
Số hạng chứa
5
x
trong khai triển tương đương với:
20 5 5 3
k k
.
Suy ra số hạng chứa
5
x
trong khai triển là:
7 3 5
10
2
C x
.
Câu 39. Chọn A
Tìm
.n
Trước hết ta chứng minh công thức
1
1
k k
n n
k
C C
n
với
1
k n
và
2.
n
Thật vậy,
1
1
! ( 1)!
. .
!( )! ( 1)!( )!
k k
n n
k k n n
C C
n n k n k k n k
(đpcm)
Áp dụng công thức trên ta có
1 2 3 1 2 3
1 2 3
1. 2. 3. ... . . . . ... .
n n
n n n n n n n n
n
C C C n C n C C C C
n n n n
0 1 2 1 1
1 1 1 1
... 2
n n
n n n n
n C C C C n
Theo đề
1 2 3 1 1
1. 2. 3. ... . 256 2 256 2 256 9.
n n n
n n n n
C C C n C n n n n
Chọn A.
Câu 40. Chọn C
Xét khai triển
1
0 1
1 3 ...
n
n
n
x a a x a x
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
Cho
1
3
x
ta được
1
0
1
1
1 3. ... 2 4096 12.
3
3 3
n
n
n
n
a
a
a n
Khi đó
12
12
12
0
1
3 .3 .
k k k
k
x
C x
.
Ta có hệ số
12
12!
3 3 .
!. 12 !
k k k
k
a C
k k
Hệ số
k
a
lớn nhất nên
1
1
1
1
12! 12!
3 . 3 .
!
. 12 ! 1 !. 12 1 !
12
! 12!
3 . 3 .
!
. 12 ! 1 !. 12 1 !
k
k
k k
k k
k k
k
k k k
a a
a a
k k k k
3 1
39
39
3
13
4
1 3 1 36 3 35
12 1 4
k
k k
k k
k k
k
k k
Vì
k
nên nhận
9
.
k
Vậy hệ số lớn nhất
9 9
9 12
3
. 4330260.
a
C
Câu 41. Chọn B
Đk:
2
, .
n
n
2
2
1
2
3 4
n
n
C nP A
1 !
!
3
2! 4
1
!2! 2 !
n
n
n
n n
3
1 2 4 1
2
n n n n n
2
0
5
15
0
2 2
3
n
L
n
n
n
Với
3
n
, nhị thức trở thành
1
0
3
1
.
x
x
Số hạng tổng quát là
1
0
3
4 10
1
0 10
1
.
. .
k
k
k
k k
C x C x
x
Từ yêu cầu bài toán ta cần có:
4 10 6 4.
k k
Vậy hệ số của số hạng chứa
6
x
là
4
1
0
21
0.
C
Câu 42. Chọn A
Xét phương trình
2
3
2
14 1
3
n n
C
C n
1
Điều kiện:
3
, n n
2. 2 !.2! 14 3 !.3!
1 4 28 1
1
!
3. ! 1 1 2
n n
n
n n n n n n n n
2
9
4
28
1 4 2 28 1 2 7 18 0
2
1
1 2
n
n n n n n
n
l
n
n n
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
Với
9
n
ta có:
9
9
9
9
2
2 9 18 3
9
9
0 0
3 3
2 . 2 . .2 . 3 .
k
k
k
k
k k k
k
k
x
C x C x
x x
Số hạng tổng quát của khai triển là
9
18 3
9
.
2 . 3 .
k
k
k k
C
x
Cho
1
8 3 6 4
k
k
hệ số của số hạng chứa
6
x
trong khai triển là
4
4
5
9
.2 . 3 326592
C
.
Câu 43. Chọn B
Từ giả thiết ta suy ra
0
1 2 20
2
1 2 1 2 1 2 1
..
. 2
n
n
n n n
C
C C C
.
Mặt khác:
2
1
2 1 2 1
,
,0 2 1
k
n k
n n
C
C k k n
nên ta có:
2
1
0
1 2 0 1 2 2 1 2
2
1 2 1 2 1 2 1 2 1 2 1 2 1 2 1
1 1
..
. ... 1 1 2
2 2
n
n
n n
n
n n n n n n n
C
C C C C C C C
.
Suy ra:
2 20
2
2 10
n
n
.
Số hạng tổng quát trong khai triển
10
7
4
1
x
x
là:
10
7
11 40
1
10 10
4
1
k
k
k k k
k
T C x C x
x
.
Hệ số của
2
6
x
là
10
k
C
với
k
thỏa mãn:
11
40 26 6
k
k
.
Vậy hệ số của
2
6
x
là
6
1
0
2
10
C
.
Câu 44. Điều kiện
n
và
n
.
6
2
4
454
n
n
n
C
nA
4
!
!
45
4
6
!2! 2 !
n
n
n
n n
2
5
4
1
2
n
n
n n
454
3
2
2
9 888 0
n
n n
8
n
(Vì
n
).
Khi đó ta có khai triển:
8
3
2
x
x
.
Số hạng tổng quát của khai triển là
8
3
8 4 8
8 8
2
1
2
k
k
k
k
k k k
C
x C x
x
.
Hệ số của số hạng chứa
4
x
ứng với
k
thỏa mãn:
4
8 4 3
k
k
.
Vậy hệ số của số hạng chứa
4
x
là:
3
3
5
8
1
2 1792
C
.
Câu 45.
1
3 2
1 2
!
13
13 13 6 3 2 78
3!
3 ! 6
n
n
n n n
n
C C n n n n n n n
n
.
2
7
3 70 0
10
n
n n
n
. Vì
n
là số nguyên dương nên
10
n
.
Ta có khai triển:
10
2
3
1
x
x
.
Số hạng tổng quát của khai triển:
2
10
20
5
1
10 10
3
1
.
k
k
k
k k
k
T
C x C x
x
.
Số hạng chứa
5
x
ứng với
20
5 5 3
k
k
. Vậy hệ số của số hạng chứa
3
10
1
20
C
.
Câu 46.
2
2 1
4
6
n
n n
A
C C n
!
! !
4
6
2 ! 2 !.2! 1 !.1!
n n n
n
n n n
1
1
4 6
2
n
n
n n n n
2
11
12 0
n
n
1
12
n l
n n
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
Khi đó
12
2
3
P x x
x
.
Công thức số hạng tổng quát:
12
2
1 12
3
. .
k
k
k
k
T C x
x
24 3
12
.3 .
k k k
C x
.
Số hạng chứa
9
x
24 3 9 5
k k
.
Vậy hệ số của số hạng chứa
9
x
trong khai triển là
5 5
12
.3 192456
C
.
Câu 47. Ta có:
1 2
78
n n
n n
C C
! !
78
1 !.1! 2 !.2!
n n
n n
1
78
2
n n
n
2
156 0
n n
12
13
n
n
12
n
(vì
n
là số nguyên dương).
Số hạng tổng quát trong khai triển
12
3
2
x
x
là:
12
3
12
2
1
k
k
k
k
C x
x
36 4
12
1 .2 .
k
k k k
C x
.
Cho
36 4 8
k
7
k
.
Vậy số hạng chứa
8
x
trong khai triển
12
3
2
x
x
là
7 7 8
12
.2 .C x
8
101376x
.
Câu 48. Điều kiện:
n
,
*
n
.
Ta có
3 2
1
3 3 52 1
n n
C A n
1 !
!
3. 3 52 1
3! 2 ! 2 !
n
n
n
n n
1 1
3 1 52 1
2
n n n
n n n
2
6 104
n n n
2
5 104 0
n n
13
8
n
n
13
n
.
13
3 2
2x y
13
13
3 2
13
0
2
k k
k
C x y
13
39 3 2
13
0
2
k k k k
C x y
.
Ta có:
39 3 2 34
k k
5
k
. Vậy hệ số
5 5
13
2
C
41184
.
Câu 49. Điều kiện
n
,
n
.
Có
1 2
1
5 5 5 5
2
n n
n n
C C n
2
1
11 10 0
10
n
n n
n
Do
2 10
n n
.
Xét khai triển:
10
10 10
10
10 10 3
10 10
2 2
0 0
1 1
2 2 . 2
k
k
k k k k
k k
x C x C x
x x
Hệ số
a
của
4
x
trong khai triển tương ứng với
10 3 4 2
k k
.
Vậy hệ số cần tìm là
2 8
10
.2 11520
a C
.
Câu 50. Điều kiện
3,n n
.
Ta có
2 3
! ! 3 1
3 40 3 40 ! 40
2! 3! 3 ! 2 6 3 !
n
n n
n n
A C n
n n
.
Vì
3 1
1
2 6 3 !
n
nên
! 40
n
. Lần lượt thử các giá trị
3, 4
n
ta có
n
thỏa mãn.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
Với
n
, số hạng tổng quát trong khai triển
8
1
2x
x
là
8
8 8 2
8 8
1
2 2 1
k
k k
k k k k
C x C x
x
.
Số hạng chứa
6
x
tương ứng với
8 2 6 1k k
. Do đó hệ số cần tìm là
1
1 8 1
8
2 1 1024
C
.
Câu 51. Giải phương trình:
2 1
3 120
n n
A C
, Đk:
2,n n
.
2 1
3 120 1 3 120
n n
A C n n n
10
12
n
n l
Có
4
3
n
x
x
10
40 5
10
0
3
k
k k
k
C x
.
Số hạng không chứa
x
khi
40 5 0 8
k k
.
Vậy số hạng không chứa
x
trong khai triển là
8
8
10
. 3 295245
C
.
Câu 52. điều kiện
, 3.
n N n
3 2
! !
50 50
3! 3 ! 2 !
n n
n n
C A
n n
1 2 6 1 300 0
n n n n n
3 2
3 4 300 0 6
n n n n
.
Ta có nhị thức
12
3
2
x
x
.
Số hạng tổng quát
12
12
2 12
12
12
.33
. .
2 2
k k
k k
k k
k
Cx
C x
x
Cho
2 12 8 10.
k k
Hệ số cần tìm là
10 2
12
10
.3
297
.
2 512
C
Câu 53. Xét khai triển
0 1 2 2 3 3
1 ...
n
n n
n n n n n
x C C x C x C x C x
1
Đạo hàm hai vế của
1
ta được:
1
1 2 3 2 1
1 2 3 ...
n
n n
n n n n
n x C C x C x nC x
2
Trong công thức
2
ta cho
1x
ta được:
1 1 2 3
2 2. 3. ...
n n
n n n n
n C C C nC
1
.2 256
n
n n
1
2 256
n
9
n
.
Khi đó,
2
3
2
n
x
x
9
2
3
2x
x
9
9 18 3
9
0
3 2 .
k
k k k
n
C x
.
Do đó số hạng không chứa
x
trong khai triển
9
2
3
2x
x
nếu
18 3 0
k
hay
k
.
Suy ra số hạng cần tìm là
6
6 3
9
3 2 489888
C
.
Câu 54. Ta có
0
1 2 2
n
n k
k
n
k
x C x
. Vậy
0
1
a
;
1
1
2
n
a C
;
2
2
4
n
a C
.
Theo bài ra
0 1 2
71
a a a
nên ta có:
1 2
1 2 4 71
n n
C C
! !
1 2 4 71
1! 1 ! 2! 2 !
n n
n n
1 2 2 1 71
n n n
2
2 4 70 0
n n
2
2 35 0
n n
7
n
(thỏa mãn) hoặc
5
n
(loại).
Từ đó ta có
5
5
5 7
2 672
a C
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
Câu 55. Ta có
2
3
10
n
n
A C
!
!
10
2
! 3! 3 !
n n
n n
,
, 3
n n
1
1
1 2 10
6
n
n n n n
3
2
2
1
3 4
10
0 6
6
2 3
5
n
n
n n n
n
.
So điều kiện nhận
n
hay
n
.
Khi
n
, ta có
6
6
2
6
2
6
3 3
0
2
2
k
k
k
k
x
C x
x x
6
12 5
6
0
2
k
k k
k
C
x
.
Để có
5
x
thì
7
1
2 5 5
5
k
k
(loại).
Khi
n
, ta có
5
5
2
5
2
5
3 3
0
2
2
k
k
k
k
x
C x
x x
5
10
5
5
0
2
k
k
k
k
C
x
.
Để có
5
x
thì
10
5 5 1
k
k
.
Vậy
1
5
5
2
10
a
C
.
Câu 56. Ta có:
3
2
2
100
n n
A
A
!
!
2 100
3
! 2 !
n n
n n
1
2 2 1 100
n
n n n n
3
2
100 0
n n
5
n
.
Ta có:
2
1
3
n
x
10
1
3
x
1
0
10
0
3
k
k
k
C
x
.
Hệ số
5
x
sẽ là
5
5
10
3
61236
C
.
Câu 57. Ta có
0
1 1 2 2
3 1 3 3 3 ..... 1
n
n
n
n n n
n n n n
C C C C
2
2048
n
1
1
2
2
n
11
n
.
Xét khai triển
11
1
1
11
11
0
2
.2
k
k k
k
x
C x
Tìm hệ số của
1
0
x
tìm
11
k k
thỏa mãn
11
10 1k k
.
Vậy hệ số của
1
0
x
trong khai triển
11
2
x
là
1
11
.2 22
C
.
Câu 58. Ta có
2
2 2 3
0
0
1 1
3 3 3
n
k
n n
n k
k
k n k n k
n
n
k k
x
C x C x
x x
.
Biết hệ số của
3
x
là
4
5
3
n
C
nên
2
3 3
4
5
5
9
0
, ,
n k
n k
k
k
n
k n k n N
.
Vậy
9
n
.
Câu 59. Điều kiện:
n
Ta có
1
4 3
4
! 3 !
7 3 7 3
1 !3! !3!
n n
n n
n
n
C C n n
n n
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
4
3 2 3 2 1
7
3
6 6
n
n n n n n
n
3
36 12
n
n
.
Xét khai triển
12
12
12
5 5
12
3 3
0
1
1
k
k
k
k
x
C x
x x
0
12,k k
60
11
12
2
1
2
0
k
k
k
C
x
.
Để số hạng chứa
8
x
thì
6
0 11
8 4
2
k
k
.
Vậy hệ số chứa
8
x
trong khai triển trên là
4
12
4
95
C
.
Câu 60. Điều kiện:
6
n
n
Khi đó
5
4
2
1
8
n
n
A
A
2
!
!
18
.
5
! 6 !
n
n
n
n
1
2 3 4 18 2 3 4 5
n
n n n n n n n n
1
18 5
n
n n
2
1
9 90 0
n
n
9
10
n
max
1
0
n
n
.
Số hạng tổng quát trong khai triển
10
5
1
2x
x
là
10
1
10
5
1
.
2 .
k
k
k
k
T
C x
x
10
10
5
10
.2 . .
k
k
k k
C x x
50
6
10
5
10
.2 .
k
k
k
C x
.
Tìm
k
sao cho
5
0 6
4
5
k
5
k
.
Vậy hệ số của số hạng chứa
4
x
là
5
10 5
10
.2
8064.
C
Câu 61. Ta có:
2 2
1
05
n
n
A
C
!
!
105
2 ! 2! 2 !
n n
n n
1
1
105
2
n
n
2
2
10 0
n
n
15
14
n
n
L
.
Suy ra số hạng tổng quát trong khai triển:
1
5
2
1 15
1
.
.
k
k
k
k
T
C x
x
30
3
15
.
1 .
k
k
k
C
x
.
Tìm
30
3 0 10
k
k
.
Vậy hệ số của số hạng không chứa
x
trong khai triển là:
10
10
15
.
1 3003
C
.
Câu 62. Ta co
2
1
0
2 1 1 2 2 2 1
2 1 2 1 2 1 2 1
1
. . ... .
n
n
n n n
n n n n
x
C x C x C x C
1
Thay
1x
vao
1
:
2
1 0 1 2 2 1
2 1 2 1 2 1 2 1
2
...
n
n n
n
n n n
C
C C C
2
Thay
1
x
vao
1
:
0
1 2 2 1
2 1 2 1 2 1 2 1
0
...
n
n
n n n n
C
C C C
3
Phương trinh
2
trư
3
theo vê:
2
1 0 2 2
2
1 2 1 2 1
2
2 ...
n
n
n n n
C
C C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
Theo đê ta co
2 1
2 2.1024 5
n
n
Sô hang tông quat cua khai triên
10
2 3
x
:
10 10
1 10 10
.2 . 3 .2 . 3 .
k k
k k k k k
k
T C x C x
Theo gia thiêt ta co
k
.
Vây hê sô cân tim
5
5 5
10
.2 . 3 1959552
C
.
Câu 63. Ta có:
1 2
78
n n
n n
C C
! !
78
1 !.1! 2 !.2!
n n
n n
1
78
2
n n
n
2
156 0
n n
12
13
n
n
12
n
(vì
n
là số nguyên dương).
Số hạng tổng quát trong khai triển
12
3
2
x
x
là:
12
3
12
2
1
k
k
k
k
C x
x
36 4
12
1 .2 .
k
k k k
C x
.
Cho
36 4 8
k
7
k
.
Vậy số hạng chứa
8
x
trong khai triển
12
3
2
x
x
là
7 7 8
12
.2 .C x
8
101376x
.
Câu 64. Điều kiện :
3,n n
.
Ta có
3 2
4 ! 4 !
2 1 2 8 6 1
3 3! 3 ! 3 2 !
n n
n n
C n C n n n n n n n
n n
2 2
0
3 2 8 6 6 9 0
9
n
n n n n n
n
. Đối chiếu điều kiện ta được
n
.
Số hạng tổng quát của khai triển
9
2
,
x
x
là :
9 9 2
9 9
2
. 2
k
k
k k k k
k
C x C x
x
Số hạng này chứa
5
x
ứng với
9 2 5 2
k k
.
Vậy hệ số của số hạng đó là
2
9
4. 144
C
.
Câu 65.
1 2
78
n n
n n
C C
1
78
2
n n
n
12
13
n
n l
.
12
3 3
2 2
n
x x
x x
12
12
3
12
0
1
2
k
k
k
k
k
C x
x
12
36 4
12
0
2
k
k k
k
C x
.
Số hạng không chứa
x
ứng với
36 4 0 9
k k
là
9
9
12
2 112640
C
.
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập)
Câu 66. Chọn B
Số hạng tổng quát
9 3
1 9
.8 . ,0 9
k k k
k
T C x k
.
Số hạng không chứa
x
ứng với
9 3 0 3
k k
.
Vậy số hạng không chứa
x
trong khai triển là
3 3
4 9
.8 43008
T C
.
Câu 67. Chọn A
Ta có số hạng thứ
1k
trong khai triển là
8
3 24 4
1 8 8
2
. . 2
k
k
k
k k k
k
T C x C x
x
.
Do tìm số hạng độc lập với
x
suy ra
24 4 0 6
k k
6
6
7 8
. 2 1792
T C
.
Câu 68. Chọn A
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
Công thức số hạng thứ
1
k
của khai triển
12
3
1
x
x
là:
12
3 36 4
12 12
1
1 . 1 ,0 12,
k
k k
k k k
k
k
T C x C x k k
x
.
Số hạng không chứa
x
ứng với
36 4 0 9
k k
(thỏa mãn).
Suy ra
9
9
7 12
1 220
T C
.
Câu 69. Chọn B
Ta có
30
30
1 1 3
30 30
30
30
2 2 2
30 30
0 0
2
2 2 2
k
k
k k k k
k k
x x x C x x C x
x
Số hạng tổng quát thứ
1k
trong khai triển là
3
30
2
1 30
2
k
k k
k
T C x
.
Số hạng này không chứa
x
tương ứng với trường hợp
3
30 0 20
2
k
k
.
Vậy số hạng không chứa
x
trong khai triển là
20 20 20 10
21 30 30
2 2
T C C
.
Câu 70. Chọn D
Số hạng tổng quát trong khai triển là
45 45 3
1 45 45
2
1
. . . 1
k
k
k k k k
k
T C x C x
x
Số hạng không chứa
x
trong khai triển ứng với
45 3 0 15
k k
.
Vậy số hạng cần tìm là
15
15 15
45 45
. 1
C C
.
Câu 71. Chọn D
Số hạng tổng quát trong khai triển
10
2
x
x
là:
10 10 2
1 10 10
2
. .2
k
k k k k k
k
T C x C x
x
(với
; 10
k k
)
Số hạng không chứa x trong khai triển tương ứng với
10 2 0 5
k k
(thỏa mãn).
Vậy số hạng không chứa x trong khai triển là:
5 5
10
.2
C
.
Câu 72. Chọn B
Ta có:
7
3
4
1
x
x
7
7
3
7
4
0
1
k
k
k
k
C x
x
7 7
7
3 12
7
0
.
k
k
k
C x
Số hạng không chứa
x
trong khai triển ứng với
7 7
0
3 12
0 7,
k
k k
4.
k
Số hạng không chứa
x
trong khai triển
7
3
4
1
x
x
là:
4
7
35.
C
Câu 73. Chọn A
Ta có:
6
6
6 6
6 6 3
6 6
2 2
0 0
1 1
2 . 2 . 1 .2 . 1 .
k
k
k k
k k k k
k k
x C x C x
x x
Số hạng không chứa
x
xảy ra khi:
6 3 0 2
k k
Số hạng đó là
2
2 4
6
.2 . 1 240
C
Vậy số hạng không chứa
x
trong khai triển trên là
240
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
Câu 74. Chọn B
Số hạng tổng quát trong khai triển là
12
2
1 12
1
k
k
k
k
T C x
x
3 12
12
1
k
k k
C x
.
Theo đề bài ta có
3 12 0 4
k k
.
Vậy số hạng không chứa
x
trong khai triển là
4
4
12
1 495
C
.
Câu 75. Chọn D
Có
45
45
45
45
2 2
0
1 1
. .
k
k k
k
x C x
x x
45
45 3
45
0
1 .
k
k k
k
C x
.
Tìm số hạng không chứa
x
thì
45 3 0
k
15
k
.
Vậy số hạng không không chứa
x
là
15
45
C
.
Câu 76.
Chọn A Số hạng tổng quát trong khai trển
5
2
3
1
x
x
là:
5
2 10 5
5 5
3
1
. .
k
k
k k k
k
T C x C x
x
Số hạng cần tìm không chứa
x
nên ta có:
10 5 0 2.
k k
Vậy số hạng không chứa
x
trong khai triển là
2
2 5
10.
T C
Câu 77. Chọn B
Ta có:
7
3
4
1
x
x
7
7
3
7
4
0
1
k
k
k
k
C x
x
7 7
7
3 12
7
0
.
k
k
k
C x
Số hạng không chứa
x
trong khai triển ứng với
7 7
0
3 12
0 7,
k
k k
4.
k
Số hạng không chứa
x
trong khai triển
7
3
4
1
x
x
là:
4
7
35.
C
Câu 78. Chọn B
Ta có
30
30 30
60 3
30
2
30 30
0 0
2 2
2
k
k
k k
k k
k k
x C x C x
x x
.
Số hạng không chứa
x
tương ứng
60 3
0 20
2
k
k
.
Vậy số hạng không chứa
x
là:
20 20 20 10
30 30
2 . 2 .C C
.
Câu 79. Ta có
3 3
3
2
3
1 1 1 1
1
1
x x x
x x
x x x x
x x
.
Nên
10
10
3
3 2
3
1 1 1
1
x x
P x
x x x
x x
.
Số hạng tổng quát của khai triển là:
10 20 5
3 6
10 10
1
. 1
k
k k
k
k k
C x C x
x
.
Khi
k
thì số hạng không chứa
x
là
4
4
10
1 210
C
.
Câu 80. Ta có
9 9
9
2 2 9 2 9
9 9
0 0
2 2 2
k
k
k k k k k
k k
f x x x C x x C x x
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
9 9
2 9 9 3
9 9
0 0
2 2
k k
k k k k k
k k
C x C x
Số hạng không chứa
x
của khai triển
f x
ứng với
9 3 0
k
3
k
Vậy hệ số không chứa
x
là
3
3
9
. 2 672
C
.
Câu 81. Số hạng tổng quát trong khai triển là:
56 7
14
3
12
14 14
4
2
1 . . 1 .2 .
k
k
k
k k
k k k
C x C x
x
Cho
56 7
0 8
12
k
k
.
Vậy số hạng không chứa
x
trong khai triển là:
8 8
14
2
C
.
Câu 82. Ta có
11
11
5
1
x x
x
11
11
11 5
2
11
0
. .
k
k k
k
x C x x
33 11
11
2
11
0
.
k
k
k
C x
.
Số hạng không chứa
x
trong khai triển ứng với
33 11 0 3
k k
.
Số hạng cần tìm là
3
11
165
C
.
Câu 83. Chọn A
Ta có:
1 2
55
n n
C C
2
10
1
! !
55 55 110 0 10
11
1! 1 ! 2! 2 ! 2
n
n n
n n
n n n n
n
n n
Với
10
n
thì ta có:
3
2
2
n
x
x
=
10 10
10 10 10
3 3 3 10 2 20 10 5 20
10 10 10
2 2
0 0 0
2 2
. . . .2 . .2 .
k
k k k k k k k k k
k k k
x C x C x x C x
x x
Để có số hạng không chứa
x
thì
5 20 0 4
k k
.
Do đó hệ số của số hạng không chứa
x
trong khai triển là:
4 6
10
.2 13440
C
.
Câu 84. Chọn C
Điều kiện:
, 2n n
2 1
1
11 ( )
44 44
8
2
n n
n n
n tm
C C n
n
Ta có
11
33 11
11 11
11
2
11 11
4 4
0 0
1 1
k
k
k
k k
k k
x x C x x C x
x x
Số hạng không chứa
x
trong khai triển ứng với
33 11
0 3
2
k
k
Vậy số hạng không chứa
x
trong khai triểnlà
3
11
165
C
.
Câu 85. ĐK:
2
n
n
*
.
Ta có
2 1
1
44 44 11
2
n n
n n
C C n n
hoặc
8
n
(loại).
Với
11
n
, số hạng thứ
1k
trong khai triển nhị thức
11
4
1
x x
x
là
33 11
11
2 2
11 11
4
1
k
k
k
k k
C x x C x
x
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
Theo giả thiết, ta có
33 11
0
2 2
k
hay
3
k
.
Vậy, số hạng không chứa
x
trong khai triển đã cho là
3
11
165
C
.
Câu 86. Với điều kiện
3n ,
n
, ta có
3 2
1
2
n n
C n A
1 2
2 1
3!
n n n
n n n
1 2 12 6 1
n n n
2
1( )
9 8 0
8( )
n
n n
n
loaïi
thoûa
.
Với
8
n
, ta có số hạng thứ
1k
trong khai triển
16
3
3
2x
x
là
16
16
3
3
2
k
k
k
C x
x
4
16
16
3
16
2 3
k
k
k k
C x
.
Theo đề bài ta cần tìm
k
sao cho
4
16 0
3
k
12
k
.
Do đó số hạng không chứa
x
trong khai triển là
12 4 12
16
.2 .3
C
.
Câu 87.
2
1
!
27 27 27
2! 2 ! 2
n
n n
n
C n n n
n
2
9
3 54 0
6
n TM
n n
n L
Xét khai triển
9
2
2
x
x
có số hạng tổng quát
9 9 3
1 9 9
2
2
. .2
k
k k k k k
k
T C x C x
x
Số hạng không chứa
x
nên
9 3 0 3
k k
.
Vậy số hạng không chứa
x
là:
3 3
4 9
.2 672
T C
.
Dạng 2.2 Khai triển của nhiều biểu thức
Dạng 2.2.1 Dạng
1 2
...
n
k
a a a
Câu 88. Chọn D
Ta có
2017
2017
2 2
1 3 2 1 3 2A x x x x
2 2017
2017 2016 2015
0 1 2 2 2 2017 2
2017 2017 2017 2017
1 3 1 3 2 1 3 2 ... 2A C x C x x C x x C x
.
Trong khai triển trên chỉ có hai số hạng
2017
0
2017
1 3C x
,
2016
1 2
2017
1 3 2
C x x
xuất hiện biểu thức
chứa
2
x
2017 2 3 2017
0 0 0 1 2 3 2017
2017 2017 2017 2017 2017 2017 2017
1 3 3 3 3 ... 3C x C C C x C x C x C x
Hệ số chứa
2
x
trong số hạng
2017
0
2017
1 3C x
là:
2
0 2
2017 2017
3
C C
2016 2 2016
1 2 1 2 0 1 2 2016
2017 2017 2016 2016 2016 2016
1 3 2 2 3 3 ... 3C x x C x C C x C x C x
Hệ số chứa
2
x
trong số hạng
2016
1 2
2017
1 3 2
C x x
là:
1 0
2017 2016
2C C
.
Vậy hệ số
2
0 2 1 0
2 2017 2017 2017 2016
3 2 18302258
a C C C C
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
Câu 89.
10 10 10
10
10
3 3 3
10 10 10
0 0 0
1 3 2 1 3 . 2 3 . 2
k
k k
k i
k k i
k
k k i
f x x x C x x C C x x
.
10 10
3
10 10
0 0
3 .2 .
k
i
k i k i k
k
k i
C C x
, ,0 10,0 10
i k k i k
.
Số hạng chứa
7
x
ứng với
3 7
i k
.
Vậy hệ số của
7
x
là:
4 7
2 1 2 1 4 0 7
10 8 10 9 10 10
. . 3 .2 . . 3 .2 . . 3 62640
C C C C C C
.
Câu 90. Ta có:
9 9
9
2 18 2 18 2
9 9
0 0 0
3 2 . . 3 2 . .3 2
k
k i
k k k k i k i
k
k k i
x x C x x C x C x
0 9
i k
Giá trị
15
a
ứng với:
1 3
18 2 3
8 9
i i
k i
k k
.
Vậy:
1 3
8 1 7 9 3 6
15 9 8 9 9
. .3 . 2 . .3 . 2 804816.
a C C C C
Câu 91. Ta có
9 9
2
1 1
2 2 1
x x x x
x x
9
9
9
0
1
. . 2 1
k
k
k k
k
C x x
x
9
2 9
9
0 0
1 2 .
k
k i
i k i k i
k
k i
C C x
.
Theo yêu cầu bài toán ta có
2 9 3
k i
2 12
k i
;
0 9
i k
;
,i k
Ta có các cặp
;i k
thỏa mãn là:
0;6 , 2;5 , 4;4
.
Từ đó hệ số của
3
x
là :
6 0 5 2 4 4
0 6 0 2 5 2 4 4 4
6 9 5 9 4 9
1 .2 1 .2 1 .2
C C C C C C
2940
.
Câu 92.
6
6 6
2
3 2 1 2
x x x x
Số hạng tổng quát trong khai triển
6
1
x
là
6
6
. 1
k
k k
C x
với
0;1;2...;6
k
.
Số hạng tổng quát trong khai triển
6
2
x
là
6
6
. 2
i
i i
C x
với
0;1;2...;6
i
.
Số hạng tổng quát trong khai triển
6
6 6
2
3 2 1 2
x x x x
là
6 6
6 6
1 . 2
k i
k k i i
C x C x
12 6
6 6
1 . 2
i k i
k i i k
C C x
Số hạng chứa
7
x
ứng với
7
i k
. Kết hợp với điều kiện ta được các nghiệm
1 6
i k
hệ số là
5 5
6 1
6 6
1 . 2 192
C C
2 5
i k
hệ số là
5 4
5 2
6 6
1 . 2 1440
C C
3 4
i k
hệ số là
5 3
4 3
6 6
1 . 2 2400
C C
4 3
i k
hệ số là
5 2
3 4
6 6
1 . 2 1200
C C
5 2
i k
hệ số là
5 1
2 5
6 6
1 . 2 180
C C
6 1
i k
hệ số là
5 0
1 6
6 6
1 . 2 6
C C
Vậy hệ số của số hạng chứa
7
x
trong khai triển
6
2
3 2
x x
bằng
5418
Cách 2.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
6 6
2 2
3 2 3 2
x x x x
Số hạng tổng quát trong khai triển trên là
6
2
6
. 3 2
k
k
k
C x x
với
0;1;2...;6
k
.
Số hạng tổng quát trong khai triển
3 2
k
x
là
.2 3
i
i k i
k
C x
với
0
i k
.
Số hạng tổng quát trong khai triển
6
2
3 2
x x
là
6
2
6
. .2 3
k
i
k i k i
k
C x C x
12 2
6
.2 3 .
i
k i k i k i
k
C C x
Số hạng chứa
7
x
ứng với
12 2 7
k i
2 5k i
. Kết hợp với điều kiện ta được các nghiệm
3 1k i
hệ số là
1
3 1 2
6 3
2 3 720
C C
4 3k i
hệ số là
3 1
4 3
6 4
3 . 2 3240
C C
5 5k i
hệ số là
0 5
5 5
6 5
2 . 3 1458
C C
Vậy hệ số của số hạng chứa
7
x
trong khai triển
6
2
3 2
x x
bằng
5418
.
Câu 93. Ta có:
10
2 3
1
x x x
10
10
2
1 1
x x
10 10
2
10 10
0 0
. . .
k k i i
k i
C x C x
10 10
2
10 10
0 0
. .
k i k i
k i
C C x
Hệ số của số hạng chứa
5
x
nên
2 5k i
.
Trường hợp 1:
k
,
5i
nên hệ số chứa
5
x
là
0 5
10 10
.C C
.
Trường hợp 2:
1
k
,
3i
nên hệ số chứa
5
x
là
1 3
10 10
.C C
.
Trường hợp 3:
k
,
1i
nên hệ số chứa
5
x
là
2 1
10 10
.C C
.
Vậy hệ số của số hạng chứa
5
x
là
0 5 1 3 2 1
10 10 10 10 10 10
. . . 1902
C C C C C C
.
Câu 94.
0 1 2
3 4 5 ... ( 3) 3840
n
n n n n
C C C n C
0 1 2
0 3 1 3 2 3 ... 3 3840
n
n n n n
C C C n C
1 2 0 1 2
2 ... 3 ... 3840
n n
n n n n n n n
C C nC C C C C
1
.2 3.2 3840
n n
n
9
n
Cho
1x
9
2 3 9 2 3 9
(1 ) 1 1 1 1 2
x x x
.
Câu 95. Ta có:
11 11
11
2 3 10 11
1 ... 1 1A x x x x x A x
11 110 11
11
11 11
0 0 0
.
m
k
k i m
i
k i m
P Q
C x a x C x
 
.
Hệ số của
11
x
trong
P
là:
0 1 2 3 10 11
11 11 11 10 11 9 11 8 11 1 11 0
...
C a C a C a C a C a C a T
Hệ số của
11
x
trong
Q
là:
1
11
C
Vậy
1
11
11
T C
.
Dạng 2.2.2 Tổng
1 1 2 2
...
n m h
k k
a b a b a b
Câu 96. Chọn A
Đặt
12
1
A x
;
18
2
1
B x
x
Ta có khai triển
12
12
12
1
k k
k
A x C x
có 13 số hạng.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
Và khai triển
18
18
2 36 3
18
0
1
l l
l
B x C x
x
có 19 số hạng.
Ta đi tìm các số hạng có cùng lũy thừa, mà giản ước được trong khai triển
( )P x
, ta phải có :
36 3 3 36 (1)
l k k l
Phương trình (1) cho ta ta 5 cặp nghiệm thỏa mãn
(k;l) {(0;12),(3;11),(6;10),(9;9), (12;8)}
tương
ứng với 5 số hạng.
Vậy sau khi khai triển và rút gọn
( )P x
ta có
13 19 5 27
số hạng.
Câu 97. Ta có
2018 2017
2018 2017 1 0
...
P x a x a x a x a
Cho
1x
1
P
2018 2017 1 0
...
a a a a
2017 2018
1 2 3 2.1 0
.
Câu 98.
12
2
3
x
x
12
12
2
12
0
3
k
k
k
k
C x
x
12
24 3
12
0
3
k k k
k
C x
21
3
2
1
2x
x
21
21
3
21
2
0
1
2
k
k
k
k
C x
x
21
21 63 5
21
0
2
k k k
k
C x
Ta cho
k
chạy từ
0
đến
12
thì các số mũ của
x
không bằng nhau.
Với khai triển
12
2
3
x
x
ta có
13
số hạng; Với khai triển
21
3
2
1
2x
x
ta có
22
số hạng. Vậy tổng
số hạng là:
35
.
Câu 99. Xét nhị thức
1 1
n n
x x
có số hạng tổng quát là
k k
n
C x
. Ta có:
Hệ số của
5
x
trong
6
1
x
là
5
6
C
.
Hệ số của
5
x
trong
7
1
x
là
5
7
C
Hệ số của
5
x
trong
12
1
x
là
5
12
C
.
Vậy hệ số của
5
x
trong khai triển
P x
là
5 5 5
6 7 12
... 1715
C C C
.
Câu 100. Ta có
8
0 1 8 8
8 8 8
1 ...
x C C x C x
suy ra hệ số chứa
8
x
là
8
8
C
.
Lại có
9
0 1 8 8 9 9
9 9 9 9
1 ...
x C C x C x C x
suy ra hệ số của
8
x
là
8
9
C
.
Tương tự trong khai triển
10
1
x
có hệ số của
8
x
là
8
10
C
.
11
1
x
có hệ số của
8
x
là
8
11
C
.
12
1
x
có hệ số của
8
x
là
8
12
C
.
Suy ra hệ số của
8
x
trong
P x
là
8 8 8 8 8
8 8 9 10 11 12
715
a C C C C C
.
Câu 101. Ta có
8 9 10 11 12
1 1 1 1 1
P x x x x x x
.
Áp dụng khai triển
0 1 2 2
1 ...
n
n n
n n n n
x C C x C x C x
.
Cho
1x
, ta có
0 1 2
... 2
n n
n n n n
C C C C
.
Do đó ta có tổng hệ số của
P x
là:
8 9 10 11 12 8 8
2 2 2 2 2 2 1 2 4 8 16 31.2 7936
S
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
Dạng 2.2.3 Tích
1 1
.. . ...
m l
n n
a a b b
Câu 102.
11
1 2 3
x x
11 11
3 2 3
x x x
11 11
11 11
11 11
0 0
.3 . 2 .3 .
k k k k k k
k k
C x x C x
11 11
11 11 1
11 11
0 0
.3 . .2.3 .
k k k k k k
k k
C x C x
Suy ra hệ số của
9
x
khi triển khai nhị thức trên là:
9 2 8 3
11 11
.3 .2.3 9045
C C
.
Câu 103. Ta có:
10
2
10
2 4 3 2
10
0
1 2 3 4 4 .2 . . 16 32 40 24 9
k k k
k
x x x C x x x x x
Do đó
2 2 3 3 4 4 5 5 6 6
6 10 10 10 10 10
.2 .16 .2 .32 .2 .40 .2 .24 .2 .9 482496
a C C C C C
.
Câu 104. Xét khai triển
6 6
6
6 6
0 0
2 1 1 2 1 2 2
n n
k
k k k k k
k k
x x C x C x
8
4 8 8 8
2 8
0
1 1 1 1
4 2 2 2
j
j
j
j
x x x x C x
Vậy
8 8
4 8 8
6
2
6 8 6 8
0 0 0 0
1 1 1
2 1 2 . 2 .
4 2 2
n n
j j
k k k J j k k J j k
k j k j
x x x C x C x C C x
Số hạng của khai triển chứa
6
x
khi
6
j k
Xét bảng:
Vậy hệ số
6
x
trong khai triển
4
6
2
1
2 1
4
x x x
thành đa thức là
6
14
3003 1
4 4
C
.
Dạng 2.2.4 Dạng kết hợp tích và tổng
Câu 105. Chọn B
Hệ số của
5
x
trong khai triển biểu thức
6
2 1
x x
là
2
4 4
6
2 1 240
C
.
Hệ số của
5
x
trong khai triển biểu thức
8
3
x
là
3
5
8
3 1512
C
.
Suy ra hệ số của
5
x
trong khai triển biểu thức
6 8
2 1 3
x x x
là
240 1512 1272
.
Câu 106. Chọn B
6 8
3 1 2 1x x x
6 8
6 8
6 8
0 0
. 3 1 . 2 1
k k m k
k m
k m
x C x C x
6 8
6 8
1
6 8
0 0
.3 1 .2 1
k k
k k k m m m
k m
C x C x
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
Hệ số
5
x
ứng với
4
k
;
5
m
.
Hệ số cần tìm là
2 3
4 4 5 5
6 8
.3 1 .2 1 577
C C
.
Câu 107. Chọn A
Hệ số của
4
x
trong khai triển nhị thức
6
( 2)
x là
4 2
6
2 60
C
.
Hệ số của
5
x
trong khai triển nhị thức
8
(3 1)
x
là
5 5
8
( 3) 13608
C
.
Vậy hệ số của
5
x
trong khai triển biểu thức
6 8
( 2) (3 1)
x x x
bằng
13608 60 13548.
Câu 108. Chọn D
Ta có
6 8
6 8 6 8
6 8
0 0
2 1 3 1 . 2 1 3 1
k k m m
k m
k m
x x x x C x C x
6 8
6 8
7 8
6 8
0 0
2 1 . 3 1 .
k k m m
k k m m
k m
C x C x
Để có số hạng của
5
x
trong khai triển thì
2; 3
k m
Do đó hệ số của
5
x
trong khai triển bằng:
5 3
2 4 3
6 8
.2 . 3 1 13368.
C C
Câu 109. Chọn A
Số hạng tổng quát trong khai triển trên có dạng:
6 8 6 8
1
6 8 6 8
. . 2 . 3 . 1 . 2 .3 . 1 .
k m m k k
k k m k k m m m
x C x C x C x C x
.
Để tìm hệ số của
5
x
ta cần tìm
,k m
sao cho
1 5 4
5 5
k k
m m
.
Hệ số của
5
x
cần tìm bằng:
2 3
4 5 5
6 8
. 2 .3 . 1 13548
C C
.
Câu 110. Chọn A
Hệ số của
5
x
là
4
4 1 3 7 3
5 10
.1 . 1 .1 .2 965.
C C
Câu 111. Khải triển
P x
có số hạng tổng quát
5
2
k
k
xC x
2
10
3
m
m
x C x
1
5
2
k
k k
C x
2
10
3
m m m
C x
(
k
,
5
k
,
m
,
10
m
)
Hệ số của
5
x
ứng với
k
,
m
thỏa hệ
1 5
2 5
k
m
4
3
k
m
.
Vậy hệ số cần tìm là
4
4
5
2 C
3 3
10
3 3320
C
.
Dạng 3. Ứng dụng nhị thức newton để giải toán
Câu 112. Chọn A.
Ta có:
19 0 18 1 17 2 20
20 20 20 20
1
3 3 3 ...
3
S C C C C
20 0 19 1 18 2 20
20 20 20 20
3 3 3 3 ...
S C C C C
Xét khai triển:
20
0 20 0 1 19 1 2 18 2 20 0 20
20 20 20 20
3 1 3 1 3 1 3 1 ... 3 1
C C C C
20
0 20 1 19 2 18 20
20 20 20 20
3 1 3 3 3 ...
C C C C
20
3 4S
Câu 113. Chọn A
Ta có
2017
2017
2017 0 1 2 3 2017
2017 2017 2017 2017 2017 2017
0
1 1 1 1 ...
k k k
k
C C C C C C
.
Vậy
1 2 3 2017 2017
2017 2017 2017 2017
... 2 1
C C C C
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
Câu 114. Chọn C
Ta có
2018
2018
0 1 2 2018
2018 2018 2018 2018 2018
0
1 1 ...
i
i
C C C C C
Suy ra
1 2 2018 2018
2018 2018 2018
... 2 1
C C C
.
Câu 115. Xét hai khai triển:
+
2017
2017 0 1 2 3 2017
2017 2017 2017 2017 2017
2 1 1 ... 1
C C C C C
.
+
2017
0 1 2 3 2017
2017 2017 2017 2017 2017
0 1 1 ... 2
C C C C C
Lấy
1 2
theo vế ta được:
2017 1 3 5 2017 2016
2017 2017 2017 2017
2 2 ... 2
C C C C T
.
Câu 116. Chọn C
Xét tổng
5
0 1 2 2 5 5
5 5 5 5
1 ...
x C xC x C x C
Thay
2
x
ta được:
5
0 1 2 2 5 5 5
5 5 5 5
2 2 ... 2 1 2 3 243
S C C C C
Câu 117. Chọn B
Ta có
10
10
10
0
1 .
k k
k
x C x
Chọn
x
ta có
10
10
10
0
2 1 .2
k k
k
C
10
3 49049
S
.
Câu 118. Xét khai triển
10
0 1 2 2 3 3 10 10
10 10 10 10 10
1 . . . .x C C x C x C x C x
.
Với
x
ta có
10
0 1 2 2 3 3 10 10
10 10 10 10 10
1 2 2 2 2 2 .C C C C C
Vậy
10
3
S
59049
.
Câu 119. Ta có:
2016
0 1 2 2 2016 2016
2016 2016 2016 2016
1 ...
x C C x C x C x
.
Chọn
1x
, ta có:
2016 0 1 2 2016
2016 2016 2016 2016
2 ...C C C C
hay
1 2 2016 2016
2016 2016 2016
... 2 1
C C C
.
Câu 120. Chọn C
Xét khai triển
0 1 2 2
1 ...
n
n n
n n n n
x C C x C x C x
.
Cho
4
x
ta có:
0 1 2 2
5 4 4 ... 4
n n n
n n n n
C C C C
. Suy ra:
15625 5
n
6
5 5 6
n
n
.
Câu 121. Chọn C
Ta có:
2019
2019
0 1 2018 2018 2019 2019
2019 2019 2019 2019 2019
0
. 1 . . ...
k k
k
x x x C x x C C x C x C x
.
0 1 2 2018 2019 2019 2020
2019 2019 2019 2019
...
C x C x C x C x
.
Đạo hàm 2 vế theo biến x ta được.
2019 2018 0 1 2018 2018 2019 2019
2019 2019 2019 2019
(1 ) 2019 (1 ) .2 ... .2019 .2020
x x x C C x C x C x
.
Cho
1x
suy ra
2019 2018 0 1 2018 2019
2019 2019 2019 2019
2 2019.2 2 ... 2019 2020C C C C
.
2018 2018
(2 2019).2 1 2021.2 1
S S
.
Vậy
2018
2021.2 1
S
.
Câu 122. Chọn C
Ta có :
22
22 0 1 2 20 21 22
22 22 22 22 22 22
2 1 1 ....
C C C C C C
.
Áp dụng tính chất :
k n k
n n
C C
, suy ra:
0 22
22 22
C C
,
1 21
22 22
C C
,
2 20
22 22
C C
,……,
10 12
22 22
C C
.
Do đó:
0 1 2 20 21 22 12 13 20 21 22 11
22 22 22 22 22 22 22 22 22 22 22 22
.... 2 ....
C C C C C C C C C C C C
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
0 1 2 20 21 22 11
12 13 20 21 22
22 22 22 22 22 22 22
22 22 22 22 22
....
....
2 2
C C C C C C C
C C C C C
11
22
12 13 20 21 22
22
22 22 22 22 22
2
....
2 2
C
C C C C C
11
12 13 20 21 22 21
22
22 22 22 22 22
.... 2
2
C
C C C C C
.
Vậy
11
21
22
2
2
C
S
.
Câu 123.
2018
1 x
0 1 2 2 3 3 2018 2018
2018 2018 2018 2018 2018
C xC x C x C ... x C
1
Đạo hàm 2 vế của đẳng thức
1
ta được:
2017
2018 1 x
1 2 2 3 2017 2018
2018 2018 2018 2018
2 3 2018C xC x C ... x C
. Cho
1x
ta được:
2017
2018 2.
1 2 3 2018
2018 2018 2018 2018
2 3 2018C C C ... C
.
2
Đồng thời, thay
1x
vào
1
ta cũng có:
2018
2
0 1 2 3 2018
2018 2018 2018 2018 2018
C C C C ... C
.
3
Lấy
2 3
ta được:
S
2017 2018
2018 2 2.
0 1 2 2017 2018
2018 2018 2018 2018 2018
2 3 2018 2019
C C C ... C C .
Vậy
S
2018 2018 2018
1009 2 2 1010 2
. . .
Câu 124. Ta có
10
1
.
! 10 !
k
k
x
x
k k
10
1 10!
. . . 1
10! ! 10 !
k
k
x x
k k
10
10
1
. . . 1
10!
k
k k
C x x
với
0 10
k
.
2 10
10 9 8
1 1 1
. . ...
10! 9! 1! 8! 2! 10!
x x x
x x x
10
10
10
0
1
. . 1
10!
k
k k
k
C x x
10
1
1
10!
x x
1
10!
.
Câu 125.
0 0 0 1 1 1 1 1
1 2 1 2 1
2 ... ... ...
n n n
n n n n n
S C C C C C C C C C
0 1 0 1 2 0 1 1 0 1
1 1 2 2 2 1 1 1
2 ... ... ...
n n
n n n n n n
C C C C C C C C C C C
2 1
2 2 1 1 ... 1 1 1 1
n n
1 2
2 2 2 ... 2
n
2 1
2 2.
2 1
n
1
2
n
S
.
S
là một số có
1000
chữ số
999 1000
10 10
S
999 1 1000
10 2 10
n
2 2
999log 10 1 1000log 10 1
n
Do
n
nên
3318;3319;3320
n
.
Vậy có
3
số nguyên dương
n
thỏa mãn yêu cầu bài toán.
Câu 126. Chọn B
! ! ! !
.... 1024
1! 1 ! 3! 3 ! 5! 5 ! 1 !1!
n n n n
n n n n
1 3 5
..... 1024
n
n n n n
C C C C
(1).
Ta chứng minh đẳng thức
1 3 5 1
..... 2
n n
n n n n
C C C C
(2).
Thật vậy, xét
0 1 2 2
1 ....
n
n n
n n n n
x C C x C x C x
.
Với
n
là số nguyên dương
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
Thay
1x
thì
0 1 2
2 .....
n n
n n n n
C C C C
.
Thay
1
x
thì
0 1 2 3 1
0 ......
n n
n n n n n n
C C C C C C
0 2 4 1 3 1
...... .....
n n
n n n n n n n
A B
C C C C C C C
.
Từ đó ta có:
1
2 2 2
2
n n
n
A B
B B
A B
.
Do đó đẳng thức (2) được chứng minh.
Thay vào
(1)
1 10
2 1024 2
n
nên
11
n
, chọn đáp án B
| 1/39
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 11 1D2-3
NHỊ THỨC NEWTON VÀ CÁC BÀI TOÁN LIÊN QUAN Mục lục
Phần A. CÂU HỎI .......................................................................................................................................................... 2
Dạng 1. Tiếp cận với khai triển nhị thức newton ............................................................................................................. 2
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton .......................................................................................... 3
Dạng 2.1 Khai triển của 1 biểu thức ............................................................................................................................. 3
Dạng 2.1.1 Bài toán tìm hệ số của số hạng ............................................................................................... 3
Dạng 2.1.2 Bài toán tìm số hạng thứ k ...................................................................................................... 4
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n ............................ 5
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập) ................................................................................ 8
Dạng 2.2 Khai triển của nhiều biểu thức .................................................................................................................... 11 n
Dạng 2.2.1 Dạng a a  ...a
........................................................................................................... 11 1 2 k n m h
Dạng 2.2.2 Tổng a ba b
 ...  a b
......................................................................... 12 1 1   2 2   k k m l
Dạng 2.2.3 Tích a  ..  a
. b  ...  b
........................................................................................... 12 1 n   1 n
Dạng 2.2.4 Dạng kết hợp tích và tổng ..................................................................................................... 13
Dạng 3. Ứng dụng nhị thức newton để giải toán ............................................................................................................ 13
Phần B. LỜI GIẢI THAM KHẢO ................................................................................................................................. 14
Dạng 1. Tiếp cận với khai triển nhị thức newton ........................................................................................................... 14
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton ........................................................................................ 16
Dạng 2.1 Khai triển của 1 biểu thức ........................................................................................................................... 16
Dạng 2.1.1 Bài toán tìm hệ số của số hạng ............................................................................................. 16
Dạng 2.1.2 Bài toán tìm số hạng thứ k .................................................................................................... 18
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n .......................... 20
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập) .............................................................................. 27
Dạng 2.2 Khai triển của nhiều biểu thức .................................................................................................................... 31 n
Dạng 2.2.1 Dạng a a  ...a
........................................................................................................... 31 1 2 k n m h
Dạng 2.2.2 Tổng a ba b
 ...  a b
......................................................................... 33 1 1   2 2   k k m l
Dạng 2.2.3 Tích a  ..  a
. b  ...  b
........................................................................................... 35 1 n   1 n
Dạng 2.2.4 Dạng kết hợp tích và tổng ..................................................................................................... 35
Dạng 3. Ứng dụng nhị thức newton để giải toán ............................................................................................................ 36
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Phần A. CÂU HỎI
Dạng 1. Tiếp cận với khai triển nhị thức newton Câu 1.
(THPT CHUYÊN HOÀNG VĂN THỤ - HÒA BÌNH - 2018) Số số hạng trong khai triển  x  50 2 là A. 49 . B. 50 . C. 52 . D. 51. Câu 2.
(HỒNG QUANG - HẢI DƯƠNG - LẦN 1 - 2018) Có bao nhiêu số hạng trong khai triển nhị thức  x  2018 2 3 A. 2019 . B. 2017 . C. 2018 . D. 2020 . Câu 3.
(THPT CHU VĂN AN - HKI - 2018) Viết khai triển theo công thức nhị thức Niu-tơn   5 x y . A. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy y . B. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy y . C. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy y . D. 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy y . Câu 4.
(Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Trong khai triển nhị thức Niu-tơn của 2019 (3  2x) có bao nhiêu số hạng? A. 2019 . B. 2018 . C. 2020 . D. 2021 . Câu 5.
Từ khai triển biểu thức  x  10 1
thành đa thức. Tổng các hệ số của đa thức là A. 1023 . B. 512 . C. 1024 . D. 2048 . Câu 6.
(Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Từ khai triển biểu thức  x  10 1
thành đa thức. Tổng các hệ số của đa thức là A. 1023 . B. 512 . C. 1024 . D. 2048 . Câu 7.
(THPT CHUYÊN HÙNG VƯƠNG - GIA LAI - LẦN 2 - 2018) Tính tổng các hệ số trong khai triển   2018 1 2x . A. 1  . B. 1. C. 2018  . D. 2018 . Câu 8.
(THPT TRẦN NHÂN TÔNG - QN - LẦN 1 - 2018) Khai triển 4 124 ( 5  7) . Có bao nhiêu số
hạng hữu tỉ trong khai triển trên? A. 30 . B. 31. C. 32 . D. 33 . Câu 9.
(LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trong khai triển nhị thức newton của 3 2018
P(x)  ( 2x  3)
thành đa thức,có tất cả có bao nhiêu số hạng có hệ số nguyên dương? A. 673. B. 675. C. 674. D. 672.
Câu 10. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Trong khai triển 1  2x20 2 20
a a x a x  ... a x . 0 1 2 20
Giá trị của a a a bằng 0 1 2 A. 801. B. 800. C. 1. D. 721.
Câu 11. (Chuyên Lê Thánh Tông-Quảng Nam-2018-2019) Có bao nhiêu số hạng là số nguyên trong khai
triển của biểu thức   2019 3 5 3 5 ? A. 136 . B. 403 . C. 135 . D. 134 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2019 1 1 1 1  
Câu 12. (Gia Bình I Bắc Ninh - L3 - 2018) Trong khai triển của 15 3 3 5 x y x y   , số hạng mà lũy thừa  
của x và y bằng nhau là số hạng thứ bao nhiêu của khai triển? A. 1348 . B. 1346 . C. 1345 . D. 1347 .
Câu 13. (SGD&ĐT BẮC NINH - 2018) Cho khai triển 1 2x20 2
a a x a x   a x . Giá trị của 0 1 2 20 20
a a a   a bằng: 0 1 2 20 A. 1. B. 20 3 . C. 0 . D. 1  .
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton
Dạng 2.1 Khai triển của 1 biểu thức
Dạng 2.1.1 Bài toán tìm hệ số của số hạng
Câu 14. (Chuyên Thái Bình lần 2 - 2018-2019) Hệ số của số hạng chứa 7
x trong khai triển nhị thức 12  2  x  
 (với x  0 ) là: x x A. 376 . B. 2  64 . C. 264 . D. 260 .
Câu 15. (HKI CHUYÊN LÊ HỒNG PHONG 2018-2019) Tìm hệ số của số hạng chứa 7 x trong khai 13  1 
triển nhị thức x  
 , (với x  0 ).  x A. 1716. B. 68. C. 1  76. D. 286.
Câu 16. (HỌC KỲ I ĐAN PHƯỢNG HÀ NỘI 2017 - 2018) Hệ số của 31 x trong khai triển 40  1  x  , x  0  là. 2   x A. 4 C . B. 2 C . C. 3 C . D. 5 C . 40 40 40 40 4  1 3 
Câu 17. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Hệ số lớn nhất trong khai triển  x    4 4  27 9 27 27 A. . B. . C. . D. . 128 32 32 64 n
Câu 18. (HKI-Chu Văn An-2017) Cho biết hệ số của 2
x trong khai triển 1 2x bằng 180 .Tìm n . A. n  8 . B. n  12 . C. n  14 . D. n  10 .
Câu 19. (HKI-Chu Văn An-2017) Tìm hệ số của 7
x trong khai triển   10 1 x . A. 90 . B. 720 . C. 120 . D. 45 .
Câu 20. (HKI – TRIỆU QUANG PHỤC 2018-2019) Tìm hệ số h của số hạng chứa 5 x trong khai triển 7  2 2  x    .  x A. h  84 . B. h  672 . C. h  560 . D. h  280 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 21. (HKI-Chuyên Hà Nội - Amsterdam 2017-2018) Hệ số của số hạng chứa 6 x trong khai triển 15  2  Newton x   là 2   x A. 3640  . B. 3640 . C. 455. D. 18  63680
Câu 22. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Tìm hệ số của 25 10 x y trong
khai triển  x xy15 3 . A. 58690. B. 4004. C. 3003. D. 5005. 6  2 
Câu 23. (CHUYÊN THÁI BÌNH LẦN 1_2018-2019) Cho khai triển x  
 với x  0 . Tìm hệ số của  x  số hạng chứa 3
x trong khai triển trên A. 80 . B. 160 . C. 240 . D. 60 . 6  2 
Câu 24. (CHUYÊN THÁI BÌNH LẦN 1_2018-2019) Cho khai triển x  
 với x  0 . Tìm hệ số của  x  số hạng chứa 3
x trong khai triển trên A. 80 . B. 160 . C. 240 . D. 60 .
Câu 25. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Biết hệ số của 2 x trong khai n
triển của 1 3x là 90 . Tìm n . A. n  7 . B. n  6 . C. n  8 . D. n  5 .
Dạng 2.1.2 Bài toán tìm số hạng thứ k
Câu 26. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Số hạng thứ 13 trong khai triển   15 2 x bằng? A. 13 3640x . B. 12 3640x . C. 12 420x . D. 3640 . 9 3  1 
Câu 27. (DHSP HÀ NỘI HKI 2017-2018) Tìm số hạng chứa x trong khai triển x    .  2x  1 1 A. 3 3  C x . B. 3 3
C x . C. 3 3
C x . D. 3 3 C x . 9 8 9 8 9 9
Câu 28. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Tìm số hạng chứa 7 x trong khai triển 13  1  x    .  x A. 3 C . B. 3 7 Cx . C. 4 7 Cx . D. 4 C . 13 13 13 13
Câu 29. (TRƯỜNG THPT THANH THỦY 2018 -2019) Tìm số hạng chứa 31 x trong khai triển 40  1  x   ? 2   x A. 4 31 C x . B. 37 31 Cx . C. 37 31 C x . D. 3 31 C x . 40 40 40 40
Câu 30. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Số hạng chứa 34 x trong khai 40  1  triển x    là  x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 37 34 C x . B. 3 34 C x . C. 2 34 C x . D. 4 34 C x . 40 40 40 40
Câu 31. (HỌC KÌ 1- LỚP 11- KIM LIÊN HÀ NỘI 18-19) Biết hệ số của số hạng chứa 2 x trong khai n
triển 1 4x là 3040 . Số tự nhiên n bằng bao nhiêu? A. 28 . B. 26 . C. 24 . D. 20 .
Câu 32. (THPT CHUYÊN LƯƠNG VĂN CHÁNH - PHÚ YÊN - 2018) Biết hệ số của 2 x trong khai n
triển của 1 3x là 90 . Tìm n . A. n  5 . B. n  8 . C. n  6 . D. n  7 . n
Câu 33. (THPT CHU VĂN AN - HKI - 2018) Cho biết hệ số của 2
x trong khai triển 1 2x bằng 180 . Tìm n . A. n  12 . B. n  14 . C. n  8 . D. n  10 .
Câu 34. (THPT CHUYÊN NGỮ - HÀ NỘI - 2018) Tìm hệ số của số hạng chứa 10
x trong khai triển của 5  2  biểu thức 3 3x   . 2   x A. 81  0 . B. 826 . C. 810 . D. 421 .
Câu 35. (THPT HẢI AN - HẢI PHÒNG - LẦN 1 - 2018) Tìm hệ số của số hạng chứa 31 x trong khai triển 40  1  x   . 2   x A. 37 C . B. 31 C . C. 4 C . D. 2 C . 40 40 40 40 6  2 
Câu 36. (SỞ GD&ĐT LÀO CAI - 2018) Trong khai triển x  3 
 , hệ số của x x  0 là: x A. 80 . B. 160 . C. 240 . D. 60 .
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n
Câu 37. (HKI-Chuyên Hà Nội - Amsterdam 2017-2018) Cho n là số tự nhiên thỏa mãn n 0 1 2 2  3 
C  2.C  2 .C  ...  2 . n n
C  59049 . Biết số hạng thứ 3 trong khai triển Newton của 2 x n n n n    x  81 có giá trị bằng
n . Khi đó giá trị của x bằng 2 A. 1 B. 2 . C. 1  D. 2 . n  1 
Câu 38. (HKI-Nguyễn Gia Thiều 2018-2019) Cho nhị thức 2 2x  
, trong đó số nguyên dương n 3   x  thỏa mãn 3
A  72n . Tìm số hạng chứa 5 x trong khai triển. n A. 6 4 5 2 C x . B. 5 5 5 2 C x . C. 7 3 5 2 C x . D. 6 7 5 2 C x . 10 10 10 10
Câu 39. (HKI – TRIỆU QUANG PHỤC 2018-2019) Tìm số hạng không chứa x trong khai triển nhị thức n  3  Newton của 2 2x n
  x  0 , biết rằng 1 2 3
1.C  2.C  3.C  ...  .
n C  256n ( k C là số tổ hợp n n n n nx
chập k của n phần tử). A. 489888 B. 49888 . C. 48988 . D. 4889888 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n
Câu 40. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Cho khai triển 1 3x 1
a a x  ... na x 0 1 n a a
trong đó n  * và các hệ số thỏa mãn hệ thức 1 a   ... n
 4096 . Tìm hệ số a lớn nhất. 0 3 3n i A. 1732104. B. 3897234. C. 4330260. D. 3247695 . 3n 1   1 
Câu 41. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Tìm hệ số của 6 x trong khai triển 3  x    x
với x  0, biết n là số nguyên dương thỏa mãn 2 2 3C
nP  4 A . n 1  2 n A. 6 210x . B. 210. C. 6 120x . D. 120. n  3 
Câu 42. (TH&TT LẦN 1 – THÁNG 12) Tìm hệ số của số hạng chứa 6 x trong khai triển 2 2x     x   2 14 1
x  0 , biết rằng    k
C là số tổ hợp chập k của n phần tử). 2 3 C 3C n n n n A. 326592 . B. 3265922 C. 3265592 D. 32692 .
Câu 43. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Tìm số hạng chứa 26 x trong khai triển n  1 7   nx
biết n là số nguyên dương thỏa mãn hệ thức 1 2 20 CC  ...  C  2 1 . 4  2n 1  2n 1  2n 1   xA. 325 . B. 210 . C. 200 . D. 152 .
Câu 44. (THPT CHUYÊN HẠ LONG - LẦN 2 - 2018) Với n là số tự nhiên thỏa mãn n6 2 CnA  454 n4 n n  2 
, hệ số của số hạng chứa 4
x trong khai triển nhị thức Niu-tơn của 3  x    x
( với x  0 ) bằng A. 1972 . B. 786 . C. 1692 . D. 1792  .
Câu 45. (SGD&ĐT BẮC GIANG - LẦN 1 - 2018) Với n là số nguyên dương thỏa mãn 1 3
C C  13n , n n n  1 
hệ số của số hạng chứa 5
x trong khai triển của biểu thức 2 x   bằng. 3   x A. 120 . B. 252 . C. 45 . D. 210 .
Câu 46. (THPT CHUYÊN LAM SƠN - THANH HÓA - 2018) Cho n là số nguyên dương thỏa mãn n  3 2 2 1 
A C C  4n  6 . Hệ số của số hạng chứa 9
x của khai triển biểu thức P x 2  x  bằng: n n n    x A. 18564 . B. 64152 . C. 192456 . D. 194265 .
Câu 47. (HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018) Biết n là số nguyên dương thỏa mãn n 1  n2 CC  78 n n n  2  , số hạng chứa 8 x trong khai triển 3 x    là  x A. 8 101376x . B. 101376 . C. 112640 . D. 8 101376x .
Câu 48. (THPT TRẦN PHÚ - ĐÀ NẴNG - 2018) Với n là số nguyên dương thỏa mãn 3 2 n 3C
 3A  52 n  1 . Trong khai triển biểu thức  3 2
x  2 y  , gọi T là số hạng mà tổng số mũ n1 n   k
của x và y của số hạng đó bằng 34 . Hệ số của T là k A. 54912 . B. 1287 . C. 2574 . D. 41184 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 49. (SỞ GD&ĐT QUẢNG NAM - 2018) Cho n là số nguyên dương thỏa mãn 1 2
5C C  5 . Tìm hệ n n n  1  số a của 4
x trong khai triển của biểu thức 2x   . 2   x
A. a  11520 . B. a  256 .
C. a  45 .
D. a  3360 .
Câu 50. (THPT QUẢNG YÊN - QUẢNG NINH - 2018) Với n là số nguyên dương thỏa mãn 2n  1 n2 3  3A
C  40 . Hệ số của 6
x trong khai triển 2x  là n n    x A. 1024 . B. 1024  . C. 1042  . D. 1042 .
Câu 51. (THPT CHUYÊN NGUYỄN THỊ MINH KHAI - SÓC TRĂNG - 2018) Với n là số nguyên n  3  dương thoả mãn 2 1
A  3C  120 , số hạng không chứa x trong khai triển của biểu thức 4 x n n    x  bằng A. 295245 . B. 245295 . C. 292545 . D. 259254 .
Câu 52. (THPT PHÚ LƯƠNG - THÁI NGUYÊN - 2018) Tìm hệ số của số hạng chứa 8 x trong khai triển 2nn x  nhị thức Niutơn của  ,  
x  0, biết số nguyên dương n thỏa mãn 3 2 C A  50. n n  2x 2  97 29 297 279 A. . B. . C. . D. . 12 51 512 215
Câu 53. (TOÁN HỌC TUỔI TRẺ SỐ 6) Tìm số hạng không chứa x trong khai triển nhị thức Newton n  3  của 2 2x n
  x  0 , biết rằng 1 2 3
1.C  2.C  3.C  ...  nC  256n ( k
C là số tổ hợp chập k n n n n nx  của n phần tử). A. 489888 . B. 49888 . C. 48988 . D. 4889888 . n
Câu 54. (THPT CHUYÊN AN GIANG - 2018) Giả sử có khai triển 1 2x 2
a a x a x  ... na x 0 1 2 n
. Tìm a biết a a a  71. 5 0 1 2 A. 6  72 . B. 672 . C. 627 . D. 6  27 .
Câu 55. (CHUYÊN LONG AN - LẦN 1 - 2018) Với n là số nguyên dương thỏa mãn điều kiện n  2 2 3 
A C  10 , tìm hệ số a của số hạng chứa 5 x trong khai triển 2 x  với x  0 . n n 5  3   x A. a  10 . B. 5 a  10  x . C. 5 a  10x .
D. a  10 . 5 5 5 5 n
Câu 56. (HỒNG BÀNG - HẢI PHÒNG - LẦN 1 - 2018) Tìm hệ số của 5
x trong khai triển   x2 1 3 biết 3 2
A  2A  100 n n A. 61236 . B. 63216 . C. 61326 . D. 66321 .
Câu 57. (CHUYÊN KHTN - LẦN 1 - 2018) Cho n là số nguyên dương thỏa mãn n 0 n 1  1 n2 2 n n 3 C  3 C  3 C  .....   C  . Hệ số của 10
x trong khai triển  x  2 là: n n n   1 n 2048 n A. 11264 . B. 22 . C. 220 . D. 24 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n  1 
Câu 58. (CHUYÊN VĨNH PHÚC - LẦN 1 - 2018)Trong khai triển 2 3x    biết hệ số của 3 x là 4 5 3 Cnx
. Giá trị n có thể nhận là A. 9 . B. 12. C. 15 . D. 16 .
Câu 59. (THPT LÊ XOAY - LẦN 3 - 2018) Hệ số của số hạng chứa 8 x trong khai triển n  1 5   x ; x  0 n 1  n  biết CC  7 n  3 là n4 n3   3     xA. 1303 . B. 313 . C. 495 . D. 13129 . n  1 
Câu 60. (CTN - LẦN 1 - 2018) Tìm hệ số của 4
x trong khai triển nhị thức Newton 2x   với x  0 5   x
, biết n là số tự nhiên lớn nhất thỏa mãn 5 4 A  18A . n n2 A. 8064 . B. 3360 . C. 13440 . D. 15360 .
Câu 61. (THTP LÊ QUÝ ĐÔN - HÀ NỘI - LẦN 1 - 2018) Tìm số hạng không chứa x trong khai triển n  1 2  x    biết 2 2
A C  105 . n nx A. 3003  . B. 5005  . C. 5005 . D. 3003 .
Câu 62. (THPT QUỲNH LƯU - NGHỆ AN - 2018) Tìm hệ số của 5
x trong khai triển thành đa thức của   x2n 2 3
, biết n là số nguyên dương thỏa mãn: 0 2 4 2 CCC  ... nC  1024 . 2n 1  2n 1  2n 1  2n 1  A. 2099529 . B. 20  99520 . C. 19  59552 . D. 1959552 .
Câu 63. [HỒNG LĨNH - HÀ TĨNH - LẦN 1 - 2018] Biết n là số nguyên dương thỏa mãn n 1  n2 CC  78 n n n  2  , số hạng chứa 8 x trong khai triển 3 x    là  x A. 8 101376x . B. 101376 . C. 112640 . D. 8 101376x . n  2 
Câu 64. (ĐỀ THI GIỮA KỲ II YÊN PHONG 1 - 2018) Tìm số hạng chứa 5
x trong khai triển x  ,    x  4
biết n là số tự nhiên thỏa mãn 3 2 C n  2C n 3 n A. 134 B. 144 C. 115 D. 141 n  2 
Câu 65. (THPT HOÀNG MAI - NGHỆ AN - 2018) Tìm hệ số không chứa x trong khai triển 3 x     x
, biết n là sô nguyên dương thỏa mãn n 1  n2 CC  78 . n n A. 112640 . B. 112643 . C. 112640 . D. 112643 .
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập) 9  8 
Câu 66. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Trong khai triển x   , số hạng không 2   x  chứa x là A. 40096. B. 43008. C. 512. D. 84.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 67. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Số hạng độc lập với x trong 8  2  khai triển 3 x    là  x A. 1792 . B. 792 . C. 972 . D. 1972 .
Câu 68. (HỌC KÌ 1- LỚP 11- KIM LIÊN HÀ NỘI 18-19) Tìm số hạng không chứa x trong khai triển 12  3 1  x    .  x A.  220 . B. 220 . C. 924 . D.  924 .
Câu 69. (KSCL LẦN 1 CHUYÊN LAM SƠN - THANH HÓA_2018-2019) Cho x là số thực dương, số 30  2 
hạng không chứa x trong khai triển nhị thức x    là  x A. 20 2 . B. 20 10 2 C . C. 10 20 2 C . D. 20 C . 30 30 30
Câu 70. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Số hạng không chứa x trong 45 khai triển  1  x  là  2   x A. 5 C . B. 5 C . C. 15 C . D. 15 C . 45 45 45 45 10  2 
Câu 71. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Số hạng không chứa x trong khai triển x     x  là A. 5 C . B. 5 5 C .2 . C. 5 C . D. 5 5 C .2 . 10 10 10 10 7  1 
Câu 72. (Kim Liên - Hà Nội - L1 - 2018-2019) Số hạng không chứa x 3 trong khai triển x   là: 4   x A. 5. B. 35. C. 45. D. 7.
Câu 73. (THPT Đoàn Thượng-Hải Dương-HKI 18-19) Tìm số hạng không chứa x trong khai triển 6  1  2x   , x  0 . 2   x A. 240 . B. 15 . C. 2  40 . D. 1  5 .
Câu 74. (Chuyên Lào Cai Lần 3 2017-2018) Số hạng không chứa x trong khai triển biểu thức 12  1 2  A   x   là  xA. 92  4 . B. 495 . C. 49  5 . D. 924 . 45  1 
Câu 75. (Bình Minh - Ninh Bình - Lần 4 - 2018) Số hạng không chứa x trong khai triển x   là 2   x A. 15 C . B. 30 C . C. 5 C  . D. 15 C  . 45 45 45 45 5  1 
Câu 76. (DHSP HÀ NỘI HKI 2017-2018) Tìm số hạng không chứa x trong khai triển 2 x   . 3   x A. 10 . B. 20 . C. 5 . D. 1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 7  1 
Câu 77. (Kim Liên - Hà Nội - Lần 1 - 2019) Số hạng không chứa x 3 trong khai triển x   là 4   x A. 5. B. 35. C. 45. D. 7.
Câu 78. (Chuyên Lam Sơn-KSCL-lần 2-2018-2019) Cho x là số thực dương, số hạng không chứa x 30  2   
trong khai triển nhị thức x     là  x  A. 20 2 . B. 20 10 2 .C . C. 10 20 2 .C . D. 20 C . 30 30 30 10  x 1 x 1 
Câu 79. (CHUYÊN ĐHSPHN - 2018) Cho biểu thức P   
 với x  0 , x  1. Tìm 3 2 3  x x 1 x x
số hạng không chứa x trong khai triển Niu-tơn của P . A. 200 . B. 160 . C. 210 . D. 100 .
Câu 80. (THPT CHUYÊN LƯƠNG THẾ VINH - ĐỒNG NAI - 2018) Số hạng không chứa x trong khai 9  2 
triển f x  x  ,  x  0 bằng 2   x A. 5376 . B. 5376  . C. 672 . D. 67  2 .
Câu 81. (CHUYÊN TRẦN PHÚ - HẢI PHÒNG - LẦN 1 - 2018) Số hạng không chứa x trong khai triển 14  2  của 3 x   với x  0 là: 4   x A. 6 8 2 C . B. 6 6 2 C . C. 8 8 2 C . D. 8 8 2 C . 14 14 14 14
Câu 82. (THPT LƯƠNG ĐẮC BẰNG - THANH HÓA - LẦN 1 - 2018) Tìm số hạng không chứa x 11  1  trong khai triển của 11 x x   với x  0 . 5   x A. 485 . B. 238 . C. 165 . D. 525 .
Câu 83. (ĐỀ THAM KHẢO BGD & ĐT 2018) Với n là số nguyên dương thỏa mãn 1 2
C C  55 , số hạng n n n  2 
không chứa x trong khai triển của biểu thức 3 x   bằng 2   x A. 13440 B. 3360 C. 80640 D. 322560
Câu 84. (ĐỀ KT NĂNG LỰC GV THUẬN THÀNH 1 BẮC NINH 2018-2019) Tìm số hạng không chứa n  1  x  
trong khai triển của xx   
với x  0 , nếu biết rằngn là số nguyên dương thỏa mãn 4   x  2 1 C C  44 . n n A. 485. B. 525. C. 165. D. 238
Câu 85. (TOÁN HỌC VÀ TUỔI TRẺ SỐ 1 - 2018) Tìm số hạng không chứa x trong khai triển của n  1  x x  
, với x  0 , nếu biết rằng 2 1
C C  44 . 4  n nx A. 165 . B. 238 . C. 485 . D. 525 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 86. (THPT PHAN CHU TRINH - ĐẮC LẮC - 2018) Số hạng không chứa x trong khai triển 2n  3  2x  
với x  0 , biết n là số nguyên dương thỏa mãn 3 2
C  2n A là: 3  n n 1   x A. 12 4 12 C  .2 .3 . B. 0 16 C .2 . C. 12 4 12 C .2 .3 . D. 16 0 C .2 . 16 16 16 16
Câu 87. (SỞ GD&ĐT HÀ TĨNH - 2018) Với số nguyên dương n thỏa mãn 2
C n  27 , trong khai triển n n  2  x  
số hạng không chứa x là 2   x A. 84 . B. 672 . C. 8 . D. 5376 .
Dạng 2.2 Khai triển của nhiều biểu thức n
Dạng 2.2.1 Dạng a a  ...a 1 2 k Câu 88. (HKI – TRIỆU QUANG PHỤC 2018-2019) Cho khai triển
1 3x  2x 2017 2 2 4034
a a x a x  ...  a x . Tìm a . 0 1 2 4034 2 A. 9136578 B. 16269122 . C. 8132544 . D. 18302258 .
Câu 89. (TOÁN HỌC TUỔI TRẺ SỐ 5) Tìm hệ số của 7
x trong khai triển f x    x x 10 3 1 3 2 thành đa thức. A. 204120 . B. 262440 . C. 4320  . D. 62640 .
Câu 90. (CHUYÊN VINH - LẦN 1 - 2018) Cho khai triển 3  2x x 9 2 18 17 16
a x a x a x  ...  a . 0 1 2 18
Giá trị a bằng 15 A. 218700 . B. 489888 . C. 804816 . D. 174960 .
Câu 91. (THPT CHUYÊN ĐH VINH - LẦN 3 - 2018) Tìm hệ số của 3
x sau khi khai triển và rút gọn các 9  1 
đơn thức đồng dạng của 2  x  2x   , x  0 .  xA. 2940  . B. 3210 . C. 2940 . D. 3210  .
Câu 92. (THPT CHUYÊN HÙNG VƯƠNG - PHÚ THỌ - LẦN 4 - 2018) Hệ số của số hạng chứa 7 x
trong khai triển  x x  6 2 3 2 bằng A. 6432  . B. 4032  . C. 1632  . D. 5418  .
Câu 93. (SGD&ĐT HÀ NỘI - 2018) Tìm hệ số của số hạng chứa 5
x trong khai triển     10 2 3 1 x x x . A. 582 . B. 1902 . C. 7752 . D. 252 .
Câu 94. (THPT PHAN ĐÌNH PHÙNG - HÀ TĨNH - LẦN 1 - 2018) Cho n là số tự nhiên thỏa mãn 0 1 2
3C  4C  5C ... (n  3) n
C  3840 .Tổng tất cả các hệ số của các số hạng trong khai triển n n n n 2 3 (1   )n x x x là A. 10 4 . B. 9 4 . C. 10 2 . D. 9 2 . Câu 95. (THPT CHUYÊN VĨNH PHÚC - LẦN 4 - 2018) Giả sử
1 x x x ... x 11 2 3 10 2 3 110
a a x a x a x  ...  a x
với a , a , a ,…, a là các hệ số. 0 1 2 3 110 0 1 2 110 Giá trị của tổng 0 1 2 3 10 11
T C a C a C a C a  ...  C a C a bằng 11 11 11 10 11 9 11 8 11 1 11 0 A. T  1  1. B. T  11. C. T  0 . D. T  1.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n m h
Dạng 2.2.2 Tổng a ba b
 ...  a b 1 1   2 2   k k
Câu 96. (CHUYÊN THÁI BÌNH LẦN 1_2018-2019) Sau khi khai triển và rút gọn thì 18  1 12 2 
P(x)  (1 x)  x  
 có tất cả bao nhiêu số hạng x A. 27 . B. 28 . C. 30 . D. 25 2017 2018
Câu 97. (PTNK CƠ SỞ 2-TPHCM-LẦN1- 2018) Cho đa thức P x   x  2  3  2x 2018 2017  a xa x
 ...  a x a . Khi đó S aa
 ...  a a bằng 2018 2017 1 0 2018 2017 1 0 A. 0 . B. 1. C. 2018 . D. 2017 .
Câu 98. (THPT LÝ THÁI TỔ - BẮC NINH - 2018) Sau khi khai triển và rút gọn biểu thức 12 21  3   1  f x 2 3  x   2x    
thì f x có bao nhiêu số hạng? 2   x   x A. 30 . B. 32 . C. 29 . D. 35 .
Câu 99. (THPT NGUYỄN HUỆ - TT HUẾ - 2018) Tìm hệ số của 5 x trong khai triển
P x   x  6   x  7    x  12 1 1 ... 1 . A. 1716 . B. 1715 . C. 1287 . D. 1711. Câu 100. (CHUYÊN BẮC NINH - LẦN 2 - 2018) Cho đa thức:
P x    x8    x9    x10    x11    x12 1 1 1 1 1
. Khai triển và rút gọn ta được đa thức: P x 2 12
a a x a x  ...  a x . Tìm hệ số a . 0 1 2 12 8 A. 720 . B. 700 . C. 715 . D. 730 .
Câu 101. (CHUYÊN BẮC NINH - LẦN 2 - 2018) Cho đa thức
P x    x8    x9    x10    x11    x12 1 1 1 1 1
. Khai triển và rút gọn ta được đa thức P x 12
a a x  ...  a x . Tính tổng các hệ số a , i  0; 1; 2; ...; 12 . 0 1 12 i A. 5 . B. 7936 . C. 0 . D. 7920 . m l
Dạng 2.2.3 Tích a  ..  a
. b  ...  b 1 n   1 n
Câu 102. (THPT CHUYÊN THÁI BÌNH - LẦN 3 - 2018) Tìm hệ số của số hạng chứa 9 x trong khai triển
nhị thức Newton   x  x11 1 2 3 . A. 4620 . B. 1380 . C. 9405 . D. 2890 . Câu 103. (THPT CHUYÊN THĂNG LONG - ĐÀ LẠT - 2018) Cho khai triển
1 2x 3 4x  4x 2 10 2 2 14
a x a x a x   a x . Tìm giá trị của a . 0 1 2 14 6 A. 482496 . B. 529536 . C. 278016 . D. 453504 .
Câu 104. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Hệ số của 6 x trong khai triển 4    x  6 2 1 2 1 x x    thành đa thức là  4  1 1 A. 6 C . B. 6 C . C. 6 C . D. 8 4C . 14 2 14 4 14 14
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Dạng 2.2.4 Dạng kết hợp tích và tổng
Câu 105. (MĐ 103 BGD&ĐT NĂM 2017-2018) Hệ số của 5
x trong khai triển biểu thức
x x  6   x  8 2 1 3 bằng A. 1752 B. 1  272 C. 1272 D. 1  752 6 8
Câu 106. (Mã đề 102 BGD&ĐT NĂM 2018) Hệ số của 5
x trong khai triển x 3x   1  2x   1 bằng A. 3  007 B. 5  77 C. 3007 D. 577
Câu 107. (Mã đề 104 BGD&ĐT NĂM 2018) Hệ số của 5
x trong khai triển biểu thức 6 8
x(x  2)  (3x 1) bằng A. 1  3548 B. 13668 C. 1  3668 D. 13548 6 8
Câu 108. (Mã đề 101 BGD&ĐT NĂM 2018) Hệ số của 5
x trong khai triển biểu thức x 2x   1  3x   1 bằng A. 13848 B. 13368 C. 1  3848 D. 1  3368 6 8
Câu 109. (HKI – TRIỆU QUANG PHỤC 2018-2019) Hệ số của 5
x trong khai triển x x  2  3x   1 bằng A. 1  3548 . B. 13548 . C. 1  3668 . D. 13668 .
Câu 110. (TH&TT LẦN 1 – THÁNG 12) Tìm hệ số của 5
x trong khai triển đa thức f x 5 10
x   x  2 1
x 1  2x . A. 965. B. 263. C. 632. D. 956.
Câu 111. (THPT CHUYÊN THÁI BÌNH - LẦN 4 - 2018) Tìm hệ số của 5 x trong khai triển
P x  x   x5  x   x10 2 1 2 1 3 . A. 3240 . B. 3320 . C. 80 . D. 259200 .
Dạng 3. Ứng dụng nhị thức newton để giải toán
Câu 112. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho biểu thức 19 0 18 1 17 2 1 20
S  3 C  3 C  3 C  ...  C . Giá trị 3S là 20 20 20 20 3 19 4 18 4 21 4 A. 20 4 . B. . C. . D. . 3 3 3
Câu 113. (HỌC KỲ I ĐAN PHƯỢNG HÀ NỘI 2017 - 2018) Tổng 1 2 3 2017 CCC  ...  C bằng. 2017 2017 2017 2017 A. 2017 2 1 . B. 2017 2  1 . C. 2017 2 . D. 2017 4 .
Câu 114. (Lương Thế Vinh - Kiểm tra giữa HK1 lớp 11 năm 2018 - 2019) Tổng 1 2 2018 CC  ...  C 2018 2018 2018 bằng A. 2018 2 . B. 2018 2  1 . C. 2018 2 1. D. 2016 4 .
Câu 115. (THPT CHUYÊN THÁI BÌNH - LẦN 1 - 2018) Tổng 1 3 5 2017 T CCC  ...  C bằng: 2017 2017 2017 2017 A. 2017 2 1 . B. 2016 2 . C. 2017 2 . D. 2016 2 1.
Câu 116. (HKI_L11-NGUYỄN GIA THIỀU - HÀ NỘI 1718) Tổng 0 1 2 2 5 5
S C  2C  2 C  ...  2 C bằng: 5 5 5 5 A. 324 . B. 435 . C. 243 . D. 342 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 117. (HKI-Chu Văn An-2017) Tính tổng 0 1 2 2 10 10
S C  2C  2 C   2 C . 10 10 10 10 A. S  59050 . B. S  59049 . C. S  1025 . D. S  1024 .
Câu 118. (THPT CHU VĂN AN - HKI - 2018) Tính tổng 0 1 2 2 3 3 10 10
S C  2C  2 C  2 C   2 C . 10 10 10 10 10 A. S  59050. B. S  1024. C. S  59049. D. S  1025.
Câu 119. (SGD&ĐT ĐỒNG THÁP - 2018) Tổng 1 2 3 2016 CCC  ...  C bằng 2016 2016 2016 2016 A. 2016 2 . B. 2016 4 . C. 2016 2  1 . D. 2016 2 1.
Câu 120. (Chuyên Nguyễn Huệ - Hà Nội -HK1 2018 - 2019) Cho n là số nguyên dương thỏa mãn 0 1 2 2
C  4C  4 C  ...  4n n
C  15625 . Tìm n . n n n n A. n  3 . B. n  5 . C. n  6 . D. n  4 .
Câu 121. (THPT THUẬN THÀNH 1) Tổng 1 2 2018 2019 S  2C  3C  ...  2019C  2020C tương ứng 2019 2019 2019 2019 bằng: A. 2019 2020.2 . B. 2018 2019.2 . C. 2018 2021.2 1. D. 2019 2020.2 1.
Câu 122. (HKI-Nguyễn Gia Thiều 2018-2019) Tính tổng 12 13 20 21 22
S C C  ....  CCC . 22 22 22 22 22 11 C 11 C A. 21 11 S  2  C . B. 21 22 S  2  . C. 21 22 S  2  . D. 21 11 S  2  C . 22 2 2 22
Câu 123. (THPT CHU VĂN AN -THÁI NGUYÊN - 2018) Kí hiệu k
C là số tổ hợp chập k của n phần tử n 0  k  ;
n k, n   tính tổng sau: 0 1 2 2017 2018 S C  2C  3C  ...  2018C  2019C 2018 2018 2018 2018 2018 A. 2016 1009.2 . B. 2018 1006.2 . C. 2018 1010.2 . D. 2018 1007 2 . 14 . Câu 124. (TOÁN HỌC TUỔI TRẺ - THÁNG 4 - 2018) Biểu thức x x
  xx   x2   x10 10 9 8 1 1 1  .  .  ...  bằng 10! 9! 1! 8! 2! 10! 1 1 A. 10! . B. 20!. C. . D. . 10! 100!
Câu 125. (CỤM 5 TRƯỜNG CHUYÊN - ĐBSH - LẦN 1 - 2018) Có bao nhiêu số dương n sao cho S  2   0 0 0
C C  ...  CC C   C
C   C   C là một số có 1000 chữ số? n   1 1 1 ... n  ...  n 1 n 1 n 1 2 1 2 n 1  nn A. 2 . B. 3 . C. 0 . D. 1.
Câu 126. (HỌC KÌ 1- LỚP 11- KIM LIÊN HÀ NỘI 18-19) Gọi n là số nguyên dương thỏa mãn: 1 1 1 1 1024    .....   1!n   1 ! 3!n  3! 5  ! n  5! n   1 !1! n! Tìm mệnh đề đúng.
A. n là số chia hết cho 10 .
B. n là số nguyên tố.
C. n là số chia hết cho 3 .
D. n là số chia hết cho 4 .
Phần B. LỜI GIẢI THAM KHẢO
Dạng 1. Tiếp cận với khai triển nhị thức newton Câu 1.
Số số hạng trong khai triển là: n 1  50 1  51. Câu 2.
Trong khai triển nhị thức   n
a b thì số các số hạng là n 1 nên trong khai triển  x  2018 2 3 có 2019 số hạng.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 3. Ta có:
x y5  x   y 5
  C x C x  y1  C x  y2  C x  y3  C x  y4  C  y5 0 5 1 4 2 3 3 2 4 1 5   5 5 5 5 5 5
Hay  x y5 5 4 3 2 2 3 4 5
x  5x y 10x y 10x y  5xy y . Câu 4. Chọn C
Ta có: Khai triển nhị thức Niu-tơn (  )n
a b có n 1 số hạng.
Vậy trong khai triển nhị thức Niu-tơn của 2019 (3  2x) có 2020 số hạng. Câu 5. Chọn C 10 10
Xét khai triển f (x)   x   1 kC . k x  . 10 k 0
Gọi S là tổng các hệ số trong khai triển thì ta có S f    10 10 (1) 1 1  2  1024 . Câu 6. Chọn C 10 10
Xét khai triển f (x)   x   1 kC . k x  . 10 k 0
Gọi S là tổng các hệ số trong khai triển thì ta có S f    10 10 (1) 1 1  2  1024 . Câu 7. Xét khai triển 2018 0 1 2 2 3 3 2018 2018 (1 2x)  C  2 . x C  ( 2  x) .C  ( 2  x) .C  ...  ( 2  x) .C 2018 2018 2018 2018 2018
Tổng các hệ số trong khai triển là: 0 1 2 2 3 3 2018 2018 S C  2.C  ( 2  ) .C  ( 2  ) .C  ...  ( 2  ) .C 2018 2018 2018 2018 2018 Cho x  1 ta có: 2018 0 1 2 2 3 3 2018 2018 (1 2.1)  C  2.1.C  ( 2  .1) .C  ( 2  .1) .C  ...  ( 2  .1) .C 2018 2018 2018 2018 2018   2018 1
S S  1 124 124k k k Câu 8. Ta có 4 124 ( 5  7 ) kC .   2 4 1 .5 .7 124 k 0 124   k    2
Số hạng hữu tỉ trong khai triển tương ứng với 
k 0; 4;8;12;...;12  4 . k     4 124  0
Vậy số các giá trị k là: 1  32 . 4 Câu 9. Chọn A 2018 2018 2018kk 3
P(x)  ( 2x  3)    3 2x2018 2018 k k 2018 3 3  2 .3 k xk 0 k 0
Để hệ số nguyên dương thì 2018  k 3  2018  k  3t k  2018  3t ,do 0  k  2018 nên ta 2018
có 0  2018  3t  2018  0  t
 672, 6 vậy t=0,1,2….672 nên có 673 giá trị 3
Câu 10. Chọn A 20 20 k Ta có 1  2xkC 2 k x ,  k Z  0  a C , 1 a  2  .C , a  2  C  4C . 2  2 2 2 20   0 20 1 20 20 20 k 0 Vậy 0 1 2
a a a C  2C  4C  801. 0 1 2 20 20 20
Câu 11. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
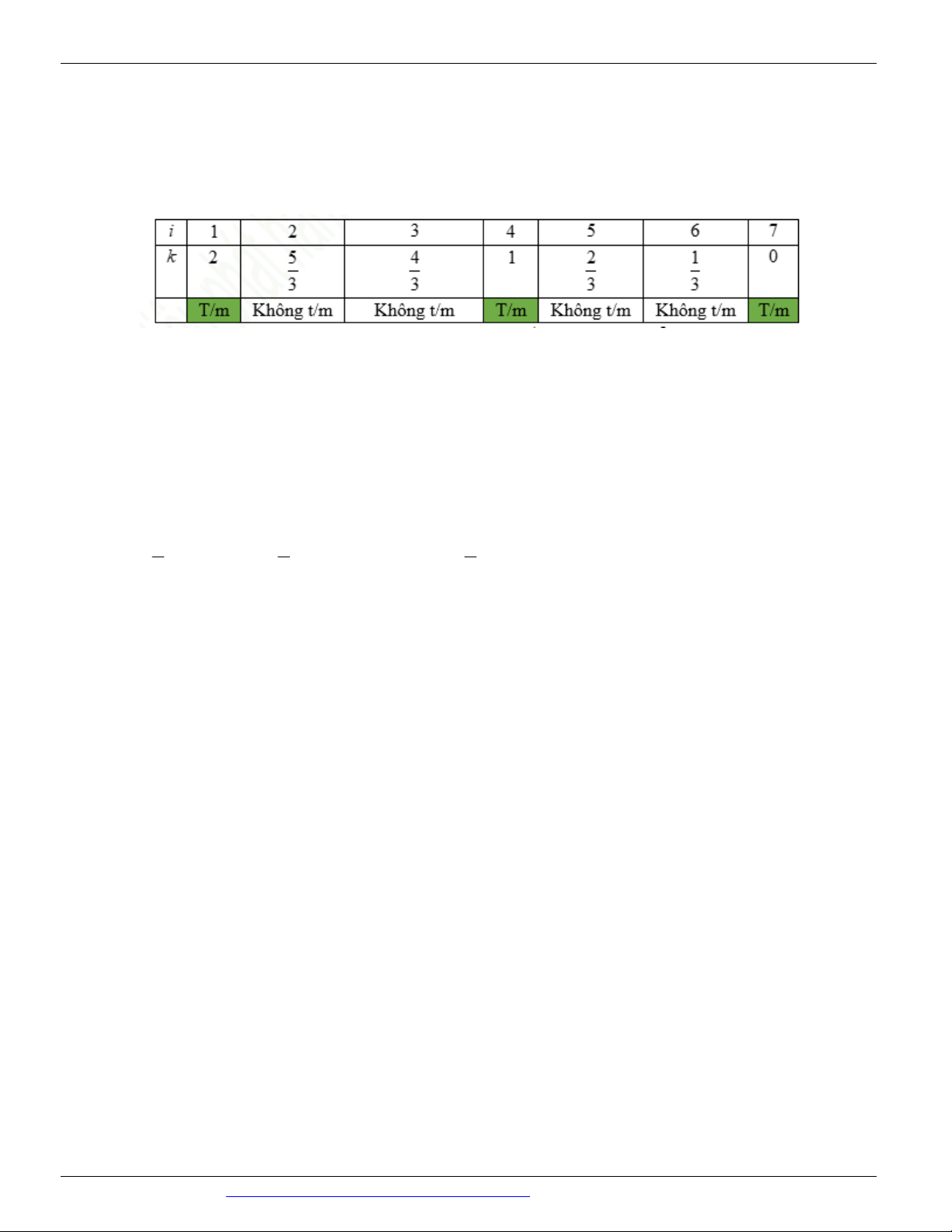
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2019 2019 2019 k k 2019 2019k k Ta có  3 5 3  5  kC .   3 3 . 5 5 k 3 5  C .3 .5 2019  . 2019 k 0 k 0 k   k     0  k  2019 0  k  2019     
Để trong khai triển có số hạng là số nguyên thì 2019 k k     673     3  3  kk        5  5 k   
 0  k  2019 . k 15   Ta có k 1
 5  k  15m mà 0  k  2019  0  15m  2019  0  m  134, 6 . Suy ra có 135 số
hạng là số nguyên trong khai triển của biểu thức.
Câu 12. Chọn D 2019k k 1 1 1 1     2019 4 2019 2  kk
Ta có số hạng thứ k 1 là : k 15 3 3 5 C x y x y k 15 15 3 15  C x y 2019     2019     2019 4 2019 2 Theo đề bài ta có;  k  
k k  1346 15 15 3 15
Vậy số hạng thỏa yêu cầu bài toán là số hạng thứ 1347 .
Câu15. (THPT Yên Dũng 3 - Bắc Giang lần 1- 18-19) Cho khai triển 20 2 20 (2x 1)
a a x a x  ....  a x . Tìm a 0 1 2 20 1 A. 20. B. 40.
C. -40. D. -760. Chọn C
Ta có: a là hệ số của x 1
Hạng tử chứa x trong khai triển là: 19 C  2x a  4  0 20 1
Câu 13. 1 2x20 2
a a x a x   a x   1 . 0 1 2 20 20
Thay x  1 vào  
1 ta có: a a a   a   20 1  1. 0 1 2 20
Dạng 2. Tìm hệ số, số hạng trong khai triển nhị thức newton
Dạng 2.1 Khai triển của 1 biểu thức
Dạng 2.1.1 Bài toán tìm hệ số của số hạng
Câu 14. Chọn C 12  2 
Số hạng tổng quát của khai triển x  
 (với x  0 ) là  x x k 3k 5k  12 kk  2 12  TC .x .  k   k 2 k 12k 2 .C .x .x  2 k 2 .C .x . k 1  12   12 12  x x  5k Số hạng trên chứa 7 x suy ra 12   7  k  2 . 2
Vậy hệ số của số hạng chứa 7
x trong khai triển trên là  22 2 .C  264 . 12
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 15. Chọn D 13  1 
Số hạng tổng quát trong khai triển nhị thức x    .  x k kk  1 13  k 132k TC xC x . k 1  13   13  x T chứa 7
x  13  2k  7  k  3 . k 1  13  1 
Vậy hệ số của số hạng chứa 7
x trong khai triển nhị thức x    bằng: 3 C  286 . 13  x
Câu 16. Chọn C 40 40 40  1  k 40k 2  k k 403 x   C x . k xC x    2  40 40  x k 0 k 0
Theo giả thiết: 40  3k  31  k  3 . Vậy hệ số của 31 x là 3 C  9880 . 40
Câu 17. Chọn D 4 4 4 k k  1 3  k  1   3  Ta có  xC . .    4      4 4  k   4   4 0  1 3 27 27 81 2 3 4   x x x x 256 64 128 64 256 27
Vậy hệ số lớn nhất trong khai triển là . 64
Câu 18. Chọn D Ta có: k TC .2k k x . . k 1  n Hệ số của 2
x trong khai triển bằng 180 n  10 n! 2 2 2 C .2  180  .2  180  n n    n n    n   2 1 90 90 0   n  2.2 n  9  l  
Câu 19. Chọn D Số hạng tổng quát là: k TC . k x . k 1  10 Số hạng chứa 7
x trong khai triển   10 1 x là: 8 7
T C .x nên hệ số là 45. 8 10
Câu 20. Chọn D 7 7 7 k 7  2 kk  2  Ta có: 2 x   C     2 x k 7k 3k 7  C .2 .x . 7    7  x    x k 0  k 0
Cần tìm k sao cho 3k  7  5, suy ra k  4. 7  2 
Vậy hệ số h của số hạng chứa 5 x trong khai triển 2 x    là 4 3
h C .2  280. 7  x
Câu 21. Chọn A 15 15 k 15 15  2    2 k 15  15 x   C x   C x         k k k k k k 2    k xC 2  k x  2 2  2    15 3 15 15 15  x    x k 0  k 0 k 0 k
Số hạng tổng quát của khái triển k TC    2 15 3k x k 1 15
Số của số hạng chứa 6
x : 15  3k  6  k  3 . Hệ số của số hạng chứa 6 xk k C
2  C 23 3  3640 15 15
Câu 22. Chọn C
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 15k k
Số hạng tổng quát của khai triển đã cho là k . 3  .  k 452  . k . k C x xy C x y , 15 15
với 0  k  15 , k   . Số hạng này chứa 25 10
x y khi và chỉ khi k  10 (thỏa mãn). Vậy hệ số của 25 10
x y trong khai triển   15 3 x xy là 10 C  3003. 15
Câu 23. Chọn D 6 k 3 6 6 k 6  2   kk  2  Ta có: 6 k k 2 x   C x  2 C x    6    . 6  x k 0  x k 0 3k Số hạng chứa 3 x ứng với 6 
 3  k  2 . Vậy hệ số của số hạng chứa 3 x bằng 2 2 2 .C  60 . 2 6
Câu 24. Chọn D 6 k 3 6 6 k 6  2   kk  2  Ta có: 6 k k 2 x   C x  2 C x    6    . 6  x k 0  x k 0 3k Số hạng chứa 3 x ứng với 6 
 3  k  2 . Vậy hệ số của số hạng chứa 3 x bằng 2 2 2 .C  60 . 2 6
Câu 25. Chọn D n k
Số hạng thứ k 1 trong khai triển của 1 3x là: k TC 3 k x . k 1  n   Số hạng chứa 2
x ứng với k  2 . Ta có: C  2 2 3  90 2
C  10 (với n  2 ; n   ) n n n! n  5 
 10  n n   1  20   . Vậy n  5 . 2  ! n  2!
n  4  L 
Dạng 2.1.2 Bài toán tìm số hạng thứ k
Câu 26. Chọn B 15 15 k Ta có 2  xk 15 
C .2 k.  x  15   k 0
Số hạng thứ 13 trong khai triển tương ứng với k  12 . C .2   .x12 12 15 12 12  3640x . 15
Câu 27. Chọn A k k kk  1  k  1 
Số hạng thứ k 1 trong khai triển là: 9 92 TC x    C   x . k 1  9   9    2x   2  Số hạng chứa 3
x có giá trị k thỏa mãn: 9  2k  3  k  3. 1 Vậy số hạng chứa 3
x trong khai triển là: 3 3  C x . 9 8
Câu 28. Chọn B
Ta có công thức của số hạng tổng quát: k   1 13  k 13 k k k k TC x . k   C x         1 k k x C .  132 1 k x k 1 13 13 13  x  Số hạng chứa 7
x khi và chỉ khi 13  2k  7  k  3 . Vậy số hạng chứa 7
x trong khai triển là 3 7 Cx . 13
Câu 29. Chọn D 40 40 40  1  k Ta có khai triển: k 40kkx   C x xk   C x 2   2  40 3 40 40  x k 0 k 0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Số hạng tổng quát trong khai triển: k 403k C x 40 Số hạng chứa 31
x ứng với: 40  3k  31  k  3 Vậy số hạng chứa 31 x là: 3 31 C x 40
Câu 30. Chọn B 40  1 
Số hạng thứ k 1 trong khai triển x    là:  x k kk  1 40  k 40kk k 402 aC x . kC x xC x . k 1  40   40 40  x  40  1  Số hạng chứa 34
x trong khai triển x  
 tương ứng với: 40  2k  34  k  3 .  x  40  1  Vậy số hạng chứa 34
x trong khai triển x    là: 3 34 C x . 40  x
Câu 31. Chọn D n n n k Ta có: 1 4xkC  4xkC 4k k x n  . n k 0 k 0
Hệ số của số hạng chứa 2 x là: 2 2 C 4 . n n n 1 n  20 t/m 2 2 2     Giả thiết suy ra 2
C 4  3040  C  190 
 190  n n  380  0  . n n  2
n  19 loai  k k
Câu 32. Số hạng tổng quát thứ k 1 là k TC 3 kxC 3 kx . k 1  n   n   Vì hệ số của 2
x nên cho k  2 . n n 1 n  5 n 2    
Khi đó ta có C  2 2 3  90  C  10   10  . n n  2
n  4 l   Vậy n  5 . n 2 n
Câu 33. Ta có   x 0 1 2 1 2
C C .2x C .2x  ... nC x . n n n n  2  n! Hệ số của 2 x bằng 2
180  4.C  180  4
 180  n n   1  90 n 2  ! n  2!
n  9l  2
n n  90  0   . n  10  Vậy n  10 . 5 5 k 5  2 5kk k  2  k Câu 34. Ta có 3 3x   1  .C . 3x .  1  . k
C .3 k.2kk x    . 2     3   2    5 15 5 5 5  x    x k 0  k 0 Số hạng chứa 10
x ứng với 15  5k  10  k  1 .
Hệ số của số hạng chứa 10
x là  1 1 4 1 1 C .3 .2  810  . 5 40 40 k 40  1  kk  1  Câu 35. Ta có: 40 k 403 x   C .x .  C . k x    . 2  40  2  40  x    x k 0  k 0
Số hạng tổng quát của khai triển là: k 40 3 TC . k x  . k 1  40 Số hạng chứa 31
x trong khai triển tương ứng với 40  3k  31  k  3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Vậy hệ số cần tìm là: 3 37
C C (theo tính chất của tổ hợp: k n k C C   ). 40 40 n n 6 6 k k 1  2   6 1 6 1   6 k     6 k     Câu 36. Ta có: 2 x   x  2x k 2 k k 2      C x 2x   C .2 x 2x  6   6        x    k 0   k 0   6 3 6 k k k 2  C .2 x  6 k 0 3 6 k 3 Theo đề bài, 3 2 xx  6 
k  3  k  2 2 Hệ số của 3
x x  0 là: 2 2 C .2  60 . 6
Dạng 2.1.3 Bài toán tìm hệ số, số hạng trong khai triển nhị thức có thêm điều kiện n
Câu 37. Chọn C n Ta có: 0 1 2 2 n n C C C   C        n  . n n n n   n 10 2. 2 . ... 2 . 59049 2 1 59049 3 3 10 10  3  Ta được nhị thức 2 x    .  x  2 8  3 
Số hạng thứ ba của khai triển là 2 T C . 2 x  14 .   405x . 3 10    x  81 Theo giả thiết ta có: 14 405xn  14 405x  405  14
x  1  x  1  . 2
Câu 38. Chọn C n! Ta có: 3 A  72n
 72n n n n  
n n 10 . n   1  2 72 n  3! Xét khai triển: 10 10 k 10 10  1 kk  1  2x   C 2 k xC .2 kk x .  k k xC .2 kk x     . 3   10 2 2 10 20 2 3 10 20 5 10  3  10 10  x    x k 0  k 0 k 0 Số hạng chứa 5
x trong khai triển tương đương với: 20  5k  5  k  3. Suy ra số hạng chứa 5
x trong khai triển là: 7 3 5 2 C x . 10
Câu 39. Chọn A Tìm . n k
Trước hết ta chứng minh công thức k k 1
C C  với 1  k n và n  2. n n 1 nk k n n k ! ( 1)! Thật vậy, k 1 C  .   C  . (đpcm) n n 1 n
n k !(n k )!
(k 1)!(n k )! 
Áp dụng công thức trên ta có  n n 1 2 3 1 2 3 1 2 3 
1.C  2.C  3.C  ...  . n C n .C  .C  .C  ...  . n C n n n nn n n n   n n n n   n  0 1 2 n 1 CCC  ...  C   nnnnn  n 1 2 1 1 1 1 Theo đề 1 2 3 n n 1  n 1 1.C 2.C 3.C ... . n C 256n n2 256n 2           256  n  9. n n n n Chọn A.
Câu 40. Chọn C n
Xét khai triển 1 3x 1
a a x  ... na x . 0 1 n
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 n 1  1  a a Cho x  ta được 1 1 3.  a   ... n
 2n  4096  n  12.   3 0 1  3  3 3n 12 12 Khi đó 1 3xkC .3k. k x  . 12 k 0 k k k 12!
Ta có hệ số a  3 C  3 . k 12
k !.12  k !  k 12! k  12! 1 3 .  3 . a ak !. 12  k !
k 1 !. 12  k 1 ! k k 1        
Hệ số a lớn nhất nên   ka ak k k 12! k  12! 1 1 3  .  3 . 
k !.12  k ! k   1 !.12  k   1 !   3 1  39  k    39    3 13 k k k k   4       1 3
k 1  36  3k 35     k  12    k k 1   4
Vì k   nên nhận k  9. Vậy hệ số lớn nhất 9 9
a  3 .C  4330260. 9 12
Câu 41. Chọn B
Đk: n  2, n  .  2 2 3CnP  4 A n 1  2 nn   1 ! n!  3  2!n  4 n   1 !2! n  2! 3  n n  
1  2n  4n n   1 2 5 15 n  0 L 2    n n  0   2 2 n  3  10  1 
Với n  3 , nhị thức trở thành 3  x .    x  10k k  1 k
Số hạng tổng quát là C . .    3 x k 4k 1  0  C .x 10 10  x
Từ yêu cầu bài toán ta cần có: 4k 10  6  k  4.
Vậy hệ số của số hạng chứa 6 x là 4 C  210. 10
Câu 42. Chọn A 2 14 1 Xét phương trình     1 2 3 C 3C n n n
Điều kiện: n  3, n  
2.n  2!.2! 14n  3!.3! 1 4 28 1   1       n! 3.n! n n n   1 n n   1 n  2 nn  9 4 28  
 1  4n  2  28  n   1 n  2 2
n  7n 18  0   n 1 n   1 n  2 n  2  l  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 9 9 k 9  3 9kk  3  k Với n  9 ta có: 2 2x   C .   2 2x k 9 .   C .2 k.   3       183 . k x 9 9  x    x k 0  k 0 k
Số hạng tổng quát của khai triển là k 9 .2 k.3 183 . k C x 9
Cho 18  3k  6  k  4  hệ số của số hạng chứa 6
x trong khai triển là C .2 .34 4 5  326592 . 9
Câu 43. Chọn B Từ giả thiết ta suy ra 0 1 2 n 20 CCC  ...  C  2 . 2n 1  2n 1  2n 1  2n 1  Mặt khác: k 2n 1   Ck C
, k  , 0  k  2n 1 nên ta có: 2n 1  2n 1  n 1 n CCC   CC C C C . n n nn        n n    nnnn  1  ... ... 1 2 1 0 1 2 0 1 2 2 1 2 1 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 Suy ra: 2n 20 2  2  n  10 . 10 10k  1  k  1  k
Số hạng tổng quát trong khai triển 7  7 k 11k 40  x là: TC xC x . k 1  10  4    4  10  x   x  Hệ số của 26 x là k
C với k thỏa mãn: 11k  40  26  k  6 . 10 Vậy hệ số của 26 x là 6 C  210 . 10
Câu 44. Điều kiện n  6 và n   . n  4! n!
n  5n  4 n6 2 CnA  454   n   454 2 
n n   1  454 n4 nn  6!2! n  2! 2 3 2
 2n n  9n  888  0  n  8 (Vì n   ). 8  2 
Khi đó ta có khai triển: 3  x   .  x  8k k  2 kk
Số hạng tổng quát của khai triển là C  3 x kC     8k 4k8 1 2 x . 8 8  x
Hệ số của số hạng chứa 4
x ứng với k thỏa mãn: 4k  8  4  k  3 .
Vậy hệ số của số hạng chứa 4
x là: C  3 3 5 1 2  1  792 . 8 n! n n 1 n  2 1 3    Câu 45. 2
C C  13n n
 13n n
 13n  6  n  3n  2  78 . n n  3! n  3! 6 n  7 2
n  3n  70  0  
. Vì n là số nguyên dương nên n  10 . n  10  10  1  Ta có khai triển: 2 x   . 3   x k kk  1 
Số hạng tổng quát của khai triển: 210  k 205 TC x . kC x . k 1  10  3  10  x  Số hạng chứa 5
x ứng với 20  5k  5  k  3 . Vậy hệ số của số hạng chứa 3 C  120 . 10 n! n! n! Câu 46. 2 2 1
A C C  4n  6     4n  6 n n n
n  2! n  2!.2! n   1 !.1! n n   1
n  1 l
n n   1 
n  4n  6 2
n 11n 12  0   . 2
n  12 n 
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 12  3 
Khi đó P x 2  x    .  x kk k  3 
Công thức số hạng tổng quát: TC . x k k 24 3 .3 . k C x   . k   12 2 . 1 12   12  x  Số hạng chứa 9
x  24  3k  9  k  5 .
Vậy hệ số của số hạng chứa 9
x trong khai triển là 5 5 C .3  192456 . 12 n! n! n   1 n
Câu 47. Ta có: n 1  n2 CC  78    78  n   78 n nn   1 !.1! n  2!.2! 2 n  12 2
n n 156  0  
n  12 (vì n là số nguyên dương). n  13  12 k  2  k k k  2  k
Số hạng tổng quát trong khai triển 3 x k k k   là:   1 C x 12 3   36 4 1 C .2 .x    . 12   12  x   x
Cho 36  4k  8  k  7 . 12  2  Vậy số hạng chứa 8 x trong khai triển 3 x  8   là 7 7 8 C
.2 .x  101376x . 12  x
Câu 48. Điều kiện: n  2 , * n   . n  1! n! Ta có 3 2 3C
 3A  52 n  1  3.  3  52 n  1 n1 n   3! n  2! n  2!
n  1 nn  1 
 3n n  1  52 n  1 2
n n  6 n  104 2 n  13 2
n  5n  104  0    n  13 . n  8  13 13  13k k x y 13 3 2 2  k C   3 x   2 2 y k k 393k 2  2 k C x y 13   . 13 0 0
Ta có: 39  3k  2k  34  k  5 . Vậy hệ số 5 5 C 2  41184 . 13
Câu 49. Điều kiện n   , n  2 . n n 1 n  1 1 2  
Có 5C C  5  5n   5 2
n 11n 10  0  n n  2 n  10 
Do n  2  n  10 . 10 10 k 10  1  10k k  1 
Xét khai triển: 2x   C 2x . kC 2 kk x    2    10 10 3 10  2  10  x    x k 0  k 0 Hệ số a của 4
x trong khai triển tương ứng với 10  3k  4  k  2 .
Vậy hệ số cần tìm là 2 8
a C .2  11520 . 10
Câu 50. Điều kiện n  3, n   .    n n n ! ! 3 1 Ta có 2 3 3AC  40  3   40  n!    40 . n n 2! 3!n 3!  2 6n 3!     3 1 Vì 
 1 nên n!  40 . Lần lượt thử các giá trị n  3, 4 ta có n  4 thỏa mãn. 2 6 n  3!
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 8 k  1  8k k  1  k
Với n  4 , số hạng tổng quát trong khai triển 2x k 8k 82k   là C 2x   C 2 1 x . 8     8    x   x  Số hạng chứa 6
x tương ứng với 8  2k  6  k  1. Do đó hệ số cần tìm là C 2   1 1 8 1 1  102  4 . 8
Câu 51. Giải phương trình: 2 1
A  3C  120 , Đk: n  2, n   . n nn  10 2 1
A  3C  120  n n   1  3n  120  n n
n  12l  n  3  10 k Có 4 x k 40 5k    C 3 x   . 10    x k 0
Số hạng không chứa x khi 40  5k  0  k  8 .
Vậy số hạng không chứa x trong khai triển là C . 3  8 8  295245 . 10
Câu 52. điều kiện n N , n  3. n! n! 3 2
C A  50    50 n n 3 
! n  3! n  2!
n n  
1 n  2  6nn   1  300  0 3 2
n  3n  4n  300  0  n  6 . 12  3 x  Ta có nhị thức    .  x 2  12k k k 12    x Ck 3 .3 k Số hạng tổng quát 12 2k 12 C .  .x  12      x   2  2k
Cho 2k 12  8  k  10. 10 2 C .3 297 Hệ số cần tìm là 12  . 10 2 512 n
Câu 53. Xét khai triển   x 0 1 2 2 3 3 1
C C x C x C x  ... n nC x   1 n n n n n n
Đạo hàm hai vế của   1 ta được: n x 1 1 2 3 2 n n 1 1 C 2C x 3C x ... nC x        2 n n n n
Trong công thức 2 ta cho x  1 ta được: n 1  1 2 3 n2
C  2.C  3.C  ... nnC n 1 .2 n    256n n 1 2    256  n  9 . n n n n n 9  3   3  9 k Khi đó, 2 2x  2 k 9k 183k    2x     C 3 2 .x  . 9    x   x n0 9  3 
Do đó số hạng không chứa x trong khai triển 2 2x  
 nếu 18  3k  0 hay k  6 .  x
Suy ra số hạng cần tìm là C  3  6 6 3 2  489888 . 9 n n k
Câu 54. Ta có 1 2xkCx  . Vậy a  1; 1 a  2  C ; 2 a  4C . n  2  0 1 n 2 n k 0
Theo bài ra a a a  71 nên ta có: 0 1 2 n! n! 1 2
1 2C  4C  71  1 2  4
 71  1 2n  2nn   1  71 n n 1  ! n   1 ! 2  ! n  2! 2
 2n  4n  70  0 2
n  2n  35  0  n  7 (thỏa mãn) hoặc n  5  (loại).
Từ đó ta có a C  2  5 5  6  72 . 5 7
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 55. Ta có n! n! 2 3
A C  10    10 , n  ,  n  3 n nn  2!  3! n  3! n  2  1 1 3 4 
n n   1  n n   1 n  2  10 3 2   n n
n 10  0  n  6 . 6 6 2 3  n  5 
So điều kiện nhận n  6 hay n  5 . 6 6 k  2    6 kk 2  k Khi n  6 , ta có 2  2 6  x   C x k 12 5k    C 2 x   . 6   3  6  3   x k 0  x k 0 7 Để có 5
x thì 12  5k  5  k  (loại). 5 5 5 k  2    5 kk 2  k Khi n  5 , ta có 2 25  x   C x k 10 5k    C 2 x   . 5   3  5  3   x k 0  x k 0 Để có 5
x thì 10  5k  5  k  1 . Vậy 1 a C 2   1  0 . 5 5   n! n! Câu 56. Ta có: 3 2
A  2A  100   2
 100  n n  
1 n  2  2nn   1  100 n nn  3! n  2! 3 2
n n 100  0  n  5 . 10 n k Ta có:   x2 1 3    10 1 3x kC 3x  . 10   k 0 Hệ số 5 x sẽ là 5 5 C 3  61236 . 10 n n
Câu 57. Ta có    n 0 n 1  1 n2 2 3 1  3 C  3 C  3
C  .....    1 n C n n n n 2n   2048 n 11
 2  2  n  11. 11 11
Xét khai triển  x  2 k 11 kC x  .2k  11 k 0 Tìm hệ số của 10 x
 tìm k   k  1 
1 thỏa mãn 11 k  10  k  1. Vậy hệ số của 10
x trong khai triển  x  11 2 là 1 C .2  22 . 11 n k  1 n   k  1 n n kCâu 58. Ta có 2 3x   C     2 3x k nk 2n3  C 3 k x n    . nx    x k 0  k 0
2n  3k  3 n k  4  k  5 Biết hệ số của 3 x là 4 5 3 C nên   . nk  5 n  9  
0  k n,k, n N   Vậy n  9 .
Câu 59. Điều kiện: n   Ta có n  4 ! n  3 ! n 1  n     CC  7 n  3    7 n  3 n4 n3     n   1 !3! n!3!
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
n  4n  3n  2 n  3n  2n   1    7 n  3 6 6
 3n  36  n  12 . Xét khai triển 12 12 k  1   1 k k   xC x  
0  k  12, k   3   3   12 5 5 12  x    x k 0  12 60 11  k k 2  C x  . 12 k 0 60 11k Để số hạng chứa 8 x thì  8  k  4 . 2 Vậy hệ số chứa 8
x trong khai triển trên là 4 C  495 . 12 n  6
Câu 60. Điều kiện: n   n! n  2! Khi đó 5 4 A  18A   18. n n2 n  5! n  6!
n n  
1 n  2n  3n  4  18n  2n  3n  4n  5
n n   1  18n  5 2
n 19n  90  0  9  n  10 nmax  n  10 . 10 k  1  k k  1 
Số hạng tổng quát trong khai triển 2x   là TC . 2x . k 1  10  10 5     x  5  x k 506kk 10k 10k 5  C .2 .x .x k 10k 5  C .2 .x . 10 10 50  6k Tìm k sao cho  4  k  5 . 5
Vậy hệ số của số hạng chứa 4 x là 5 105 C .2  8064. 10 n! n! 1 Câu 61. Ta có: 2 2
A C  105    105  n n   1  105 2
n n  210  0 n nn  2! 2  ! n  2! 2 n  15   . n  14   L  kk k  1  k
Suy ra số hạng tổng quát trong khai triển: TC . xk . 1 . k C x    . 15   30 3 k   15 2 . 1 15    x
Tìm 30  3k  0  k  10 .
Vậy hệ số của số hạng không chứa x trong khai triển là: C . 10 10 1  3003 . 15 n
Câu 62. Ta có  x  2 1 0 2n 1  1 2n 2n 2n 1 1  C .xC .x  ...  C
.x C    1 2n 1  2n 1  2n 1  2n 1 
Thay x  1 vào   1 : 2n 1  0 1 2n 2n 1 2  CC  ...  CC  2 2n 1  2n 1  2n 1  2n 1 
Thay x  1 vào   1 : 0 1 2 2 1 0  C   C  ... n nCC  3 2n 1  2n 1  2n 1  2n 1 
Phương trình 2 trừ 3 theo vế: 2n 1 2   2 0 2 2 CC  ... nC 2n 1  2n 1  2n 1  
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Theo đề ta có 2n 1
2   2.1024  n  5
Số hạng tổng quát của khai triển   10 2 3x : 10 k k k T
C .2 k.      3xk 10 C .2 k. 3 . k x k 1 10 10  
Theo giả thiết ta có k  5 .
Vậy hệ số cần tìm C .2 . 3  5 5 5  195  9552 . 10 n! n! n   1 n
Câu 63. Ta có: n 1  n2 CC  78    78  n   78 n nn   1 !.1! n  2!.2! 2 n  12 2
n n 156  0  
n  12 (vì n là số nguyên dương). n  13  12 k  2  k k k  2  k
Số hạng tổng quát trong khai triển 3 x k k k   là:   1 C x 12 3   36 4 1 C .2 .x    . 12   12  x   x
Cho 36  4k  8  k  7 . 12  2  Vậy số hạng chứa 8 x trong khai triển 3 x  8   là 7 7 8 C
.2 .x  101376x . 12  x
Câu 64. Điều kiện : n  3, n   . 4 n! 4 n! Ta có 3 2 C n  2C   n   n n n
n n n n n   1  2 8 6   1 3 3  ! n  3! 3 n  2! n  0 2 2
n  3n  2  8  6n  6  n  9n  0  
. Đối chiếu điều kiện ta được n  9 . n  9  9 k  2  2 k 9k   k
Số hạng tổng quát của khai triển x  , k 92k   là : C x .  2  C x 9 k   9  x x Số hạng này chứa 5
x ứng với 9  2k  5  k  2 .
Vậy hệ số của số hạng đó là 2 4.C  144 . 9 n n   1 n  12 Câu 65. n 1  n2 CC  78  n   78  . n n  2
n  13l   n 12 k  2   2 12 12k 12 k k  1 3 3   k x   x  3 k 36 4k      C x 2    C 2 x   . 12   12        x   x    x k 0  k 0
Số hạng không chứa x ứng với 36  4k  0  k  9 là C  2  9 9  11  2640 . 12
Dạng 2.1.4 Số hạng không chứa x (số hạng độc lập)
Câu 66. Chọn B Số hạng tổng quát k k 93 TC .8 . k x , 0  k  9 . k 1  9
Số hạng không chứa x ứng với 9  3k  0  k  3.
Vậy số hạng không chứa x trong khai triển là 3 3
T C .8  43008 . 4 9
Câu 67. Chọn A k 8k k  2  k
Ta có số hạng thứ k 1 trong khai triển là TC x   C x   . k   3  k 24 4 . k . 2 1 8   8    x
Do tìm số hạng độc lập với x suy ra 24  4k  0  k  6  T C .26 6  1792 . 7 8
Câu 68. Chọn A
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 12  
Công thức số hạng thứ k   1 của khai triển 3 1 x    là:  x  12k k 1 T C x C x       k k   . k   k k 1  3  . k k   36 4 1 k , 0 12, 12 12 x
Số hạng không chứa x ứng với 36  4k  0  k  9 (thỏa mãn).
Suy ra T C  9 9 1  220 . 7 12
Câu 69. Chọn B 30 30 k 1 30 1 30 3        30 2  k Ta có k 30 2 k 2 k k 2 x   x  2xC x 2xC 2 x      30    30  x k 0 k 0     3 30 k
Số hạng tổng quát thứ k 1 trong khai triển là k k 2 TC 2 x . k 1  30 3k
Số hạng này không chứa x tương ứng với trường hợp 30   0  k  20 . 2
Vậy số hạng không chứa x trong khai triển là 20 20 20 10 T C 2  2 C . 21 30 30
Câu 70. Chọn D k kk  1  k
Số hạng tổng quát trong khai triển là 45 TC .x . k   C .       453 1 k x k 1 45 2 45  x
Số hạng không chứa x trong khai triển ứng với 45  3k  0  k  15 .
Vậy số hạng cần tìm là C . 15 15 15 1  C . 45 45
Câu 71. Chọn D 10  2 
Số hạng tổng quát trong khai triển x    là:  x k kk  2 10  k k 102 TC x .  C .2 k x (với k  ;  k  10 ) k 1  10   10  x
Số hạng không chứa x trong khai triển tương ứng với 10  2k  0  k  5 (thỏa mãn).
Vậy số hạng không chứa x trong khai triển là: 5 5 C .2 . 10
Câu 72. Chọn B 7 k  1  7 7 7 7 7kk k  1  Ta có: 3 x  3 k 3 12    C xC x .  7   4    7  x  4 k 0  x k 0  7 7   k  0
Số hạng không chứa x trong khai triển ứng với 3 12  k  4.
0  k  7, k    7  1 
Số hạng không chứa x trong khai triển 3 x   là: 4 C  35. 4  7  x
Câu 73. Chọn A 6 6 6 k k 6  1  k k  1  k Ta có: 2x   C . 2x . 1 k  
C .2 k. 1 .  k x    2      6  2    6 3 6 6  x    x k 0  k 0
Số hạng không chứa x xảy ra khi: 6  3k  0  k  2
Số hạng đó là C .2 . 2 2 4 1  240 6
Vậy số hạng không chứa x trong khai triển trên là 240
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 74. Chọn B 12k k  1 kk
Số hạng tổng quát trong khai triển là TCx k 1 k C x    . 12   3 12 k     2 1 12   x
Theo đề bài ta có 3k 12  0  k  4 .
Vậy số hạng không chứa x trong khai triển là C  4 4 1  495 . 12
Câu 75. Chọn D 45 45 k  1  45 kk  1  k Có 45 x   C . x .  k 45 3k      1 C . x   . 2  45  2  45  x    x k 0  k 0
Tìm số hạng không chứa x thì 45  3k  0  k  15 .
Vậy số hạng không không chứa x là 15 C . 45 Câu 76. 5 k  1  k k  1 
Chọn A Số hạng tổng quát trong khai trển 2 x kk  là: T C x .  C x . k 5  5 2 10 5 3   3  5  x   x
Số hạng cần tìm không chứa x nên ta có: 10  5k  0  k  2.
Vậy số hạng không chứa x trong khai triển là 2 T C  10. 2 5
Câu 77. Chọn B 7 k  1  7 7 7 7 7kk k  1  Ta có: 3 x  3 k 3 12    C xC x .  7   4    7  x  4 k 0  x k 0  7 7   k  0
Số hạng không chứa x trong khai triển ứng với 3 12  k  4.
0  k  7, k    7  1 
Số hạng không chứa x trong khai triển 3 x   là: 4 C  35. 4  7  x
Câu 78. Chọn B 30 30 k 30 60 3  2  k    30 k   k  2 k   Ta có x
  C xk    C   2 x 2 . 30 30       x   k0 x k0 603k
Số hạng không chứa x tương ứng  0  k  20 . 2
Vậy số hạng không chứa x là: 20 20 20 10 2 .C  2 .C . 30 30 x 1 x 1 x 1 1 Câu 79. Ta có 3 3   x 1  x  . 3 2 3 x x 1 x x x x 10 10  x 1 x 1   1  Nên 3 P      x    . 3 2 3  x x 1 x x   x  10 kk 205   k 1 kk
Số hạng tổng quát của khai triển là: 3 C x .      k 6 1 C x . 10 10  x
Khi k  4 thì số hạng không chứa x là  4 4 1 C  210 . 10 9 9 9 k k
Câu 80. Ta có f x   2 x  2x  kC  2 2x  9k k xC  2     2  k 9k x x 9 9 k 0 k 0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 9 9  C   k k k 2 2  k 9k k xC  2 93k x 9 9 k 0 k 0
Số hạng không chứa x của khai triển f x ứng với 9  3k  0  k  3
Vậy hệ số không chứa x là C . 2  3 3  672  . 9 k 567k 14k k k  2  k
Câu 81. Số hạng tổng quát trong khai triển là:   1 C . 3 x  .      k k 12 1 C .2 .x 14 14 4  x  56  7k Cho  0  k  8 . 12
Vậy số hạng không chứa x trong khai triển là: 8 8 2 C . 14 11  1  11 11k 11 33 11  k Câu 82. Ta có 11 x x  11 k 5 2  k k 2   x C .x .x   C .x  . 5  11 11  x k 0 k 0
Số hạng không chứa x trong khai triển ứng với 33 11k  0  k  3. Số hạng cần tìm là 3 C  165 . 11
Câu 83. Chọn A Ta có: 1 2 C C  55 n n n! n! n n   1 n  10 2    55  n
 55  n n 110  0   n  10  1!n   1 ! 2!n  2! 2 n  11 
Với n  10 thì ta có: n 10 10k  2 10 10 10  2  k k  2 3   x  3 3 k 3k 10k 2k 20 k 10k 5k  20  = x   C .x .  C .x .2 .xC .2 .x    2   2  10  2  10 10  x   x    x k 0  k 0 k 0
Để có số hạng không chứa x thì 5k  20  0  k  4 .
Do đó hệ số của số hạng không chứa x trong khai triển là: 4 6 C .2  13440 . 10
Câu 84. Chọn C Điều kiện: n  ,  n  2 n n  1 n   11 (tm) 2 1   C C 44 n 44        n n 2 n   8  11 k 11   11 11 33 11 1       k 1 k k   Ta có k xx    C x x    C x  4      2 11  4  11  x    k0 x k0 33  11k
Số hạng không chứa x trong khai triển ứng với  0  k  3 2
Vậy số hạng không chứa x trong khai triểnlà 3 C  165 . 11 n  2 Câu 85. ĐK:  * . n    n n 1 2 1  
Ta có C C  44 
n  44  n  11 hoặc n  8 (loại). n n 2 11  1 
Với n  11 , số hạng thứ k 1 trong khai triển nhị thức x x   là 4   x k 33 11    
C x x 11 k 1 k k k 2 2  C x . 11  4  11  x
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 33 11k Theo giả thiết, ta có   0 hay k  3 . 2 2
Vậy, số hạng không chứa x trong khai triển đã cho là 3 C  165 . 11
Câu 86. Với điều kiện n  3, n   , ta có n n   1 n  2 3 2
C  2n A
 2n  n  
1 n  n  
1 n  2 12  6n   1 n n 1  3! n  1(loaïi) 2
n  9n  8  0   . n  8(tho )  û a 16  3 
Với n  8 , ta có số hạng thứ k 1 trong khai triển 2x   là 3   x k 4 k 16 k k  3  k C 2x16  k 16  2 k C 3  x . 16   3 16  3   x  4
Theo đề bài ta cần tìm k sao cho 16 
k  0  k  12 . 3
Do đó số hạng không chứa x trong khai triển là 12 4 12 C .2 .3 . 16 n! n n 1 2  
Câu 87. C n  27   n  27   n  27 n 2!n  2! 2
n  9 TM  2
n  3n  54  0   n  6   L  9  2  Xét khai triển x   có số hạng tổng quát 2   x k kk  2 9  k k 93 TC x .  C .2 k x k 1  9  2  9  x
Số hạng không chứa x nên 9  3k  0  k  3 .
Vậy số hạng không chứa x là: 3 3
T C .2  672 4 9 .
Dạng 2.2 Khai triển của nhiều biểu thức n
Dạng 2.2.1 Dạng a a  ...a 1 2 k
Câu 88. Chọn D 2017 2017 Ta có A   2  x x     x 2 1 3 2 1 3  2x    2 2017  A C
1 3x2017  C
1 3x2016 2x   C 1 3x2015 0 1 2 2  2 2x  2017  ...  C  2 2x . 2017 2017 2017 2017  2016
Trong khai triển trên chỉ có hai số hạng C 1 3x2017 0 , 1 C 1 3x  2 2x xuất hiện biểu thức 2017  2017 chứa 2 x C 1 3x2017 C CC 3xC 3x2 C 3x3 ... C 3x2017 0 0 0 1 2 3 2017         2017 2017 2017 2017 2017 2017 2017   Hệ số chứa 2
x trong số hạng C 1 3x2017 0 là: C C 3 2017 2017  2 0 2 2017  C
1 3x2016 2x C 2x C C 3xC 3x2 ... C 3x2016 1 2 1 2 0 1 2 2016        2017 2017 2016 2016 2016 2016   2016 Hệ số chứa 2 x trong số hạng 1 C 1 3x  2 2x là: 1 0 2C C . 2017  2017 2016
Vậy hệ số a C C 32 0 2 1 0  2C C  18302258 2 2017 2017 2017 2016
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 10 10 10k 10 10 k kk i
Câu 89. f x   3
1 3x  2x kC  1 3x . 3 2x k iC Cx x   . k  3  . 3 2 10 10 10  k 0 k 0 i0 10 10kC Cx   
i, k  , 0  k  10, 0  i  10  k  . k i k i 3 k i 3 .2 . k 10 10 k 0 i0 Số hạng chứa 7
x ứng với i  3k  7 . 4 7 Vậy hệ số của 7 x là: 2 1 C .C . 3   2 1 4
.2  C .C . 3   0 7 .2  C .C . 3   626  40 . 10 8 10 9 10 10   9 9 k 9 k i Câu 90. Ta có:  2
3  2x x k 182  C . k x .  3  2xk 182  C . k i x
C .3ki 2x
0  i k  9 9  9    k   k 0 k 0 i0 i   1 i   3
Giá trị a ứng với: 18  2k i  3    . 15  k  8 k  9   1 3 Vậy: 8 1 7
a C .C .3 . 2   9 3 6  C .C .3 . 2   80  4816. 15 9 8 9 9   Câu 91. Ta có 9 9 9k  1   1 9 9 k k  1 2   k k ix  2x   x 2x k i k i 2k i9    1  C .x . 2x 1   C C 1 2 .x   . k 9   9     xx        x k 0  k 0 i0
Theo yêu cầu bài toán ta có 2k i  9  3  2k i  12 ; 0  i k  9 ; i, k   Ta có các cặp  ;
i k  thỏa mãn là: 0;6,2;5,4; 4 . 60 52 44 Từ đó hệ số của 3 x là : 0 6 C C   0 2 5 1 .2  C C   2 4 4 1 .2  C C   4 1 .2  2  940 . 6 9 5 9 4 9 6 6 6 Câu 92.  2
x  3x  2   x   1  x  2 k
Số hạng tổng quát trong khai triển  x  6 1 là k . k C x  6 1
với k  0;1; 2...; 6 . 6 i
Số hạng tổng quát trong khai triển  x  6 2 là i . i C x  2
 6 với i  0;1; 2...; 6 . 6 6 6 6 6k 6i
Số hạng tổng quát trong khai triển  2
x  3x  2   x  
1  x  2 là k k 1  . i i C x C x 2  6   6    
 12iki k i i k C C x 1 .26 6 6 Số hạng chứa 7
x ứng với i k  7 . Kết hợp với điều kiện ta được các nghiệm 5 5
i  1  k  6  hệ số là 6 1  C C 1  . 2  192  6 6     5 4
i  2  k  5  hệ số là 5 2  C C 1  . 2  144  0 6 6     5 3
i  3  k  4  hệ số là 4 3  C C 1  . 2  2  400 6 6     5 2
i  4  k  3  hệ số là 3 4  C C 1  . 2  1  200 6 6     5 1
i  5  k  2  hệ số là 2 5  C C 1  . 2  180  6 6     5 0
i  6  k  1  hệ số là 1 6  C C 1  . 2  6  6 6    
Vậy hệ số của số hạng chứa 7
x trong khai triển  x x  6 2 3 2 bằng 5418  Cách 2.
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
x x  6   6 2 2 3 2
x  3x  2 6k k
Số hạng tổng quát trong khai triển trên là k C . 2 x 3  x  2
với k  0;1; 2...; 6 . 6    k i
Số hạng tổng quát trong khai triển  3
x  2 là i
C .2ki x với 0  i k . k  3  6k i
Số hạng tổng quát trong khai triển  x x  6 2 3 2 là k C . 2 i x
C .2ki 3x 6  k   i k i
C C .2ki x     k  3 . 12 2k i 6  Số hạng chứa 7
x ứng với 12  2k i  7  2k i  5 . Kết hợp với điều kiện ta được các nghiệm
k  3  i  1  hệ số là  C C 2  3  1 3 1 2  720  6 3 3 1
k  4  i  3  hệ số là 4 3  C C 3  . 2  324  0 6 4     0 5
k  5  i  5  hệ số là 5 5  C C 2 . 3   145  8 6 5    
Vậy hệ số của số hạng chứa 7
x trong khai triển  x x  6 2 3 2 bằng 5418  . 10 10 10 10 10 10
Câu 93. Ta có:     10 2 3 1 x x x   2
1 x  1 xk 2  C . k x . i C . i xk i 2 
C .C . k i x  10  10   10 10 k 0 i0 k 0 i0
Hệ số của số hạng chứa 5
x nên 2k i  5 .
Trường hợp 1: k  0 , i  5 nên hệ số chứa 5 x là 0 5 C .C . 10 10
Trường hợp 2: k  1 , i  3 nên hệ số chứa 5 x là 1 3 C .C . 10 10
Trường hợp 3: k  2 , i  1 nên hệ số chứa 5 x là 2 1 C .C . 10 10
Vậy hệ số của số hạng chứa 5 x là 0 5 1 3 2 1
C .C C .C C .C  1902 . 10 10 10 10 10 10 Câu 94. 0 1 2
3C  4C  5C ... (n  3) n C  3840 n n n n     0 C   C   C   n C n   1n   2 0 3 1 3 2 3 ... n  3 n 3840 n   1 2 n C C   nC    0 1 2 2 ...
3 C C C  ... nCn n n n n n n  3840 n 1 .2 3.2n n     3840  n  9 Cho x  1 
x x x      9 2 3 9 2 3 9 (1 ) 1 1 1 1  2 . 11 11 11
Câu 95. Ta có: A   2 3 10
x x x
x     xA   11 1 ... 1 1 x  11 110 11 mC  xk k . i m a x Cx  . i   11 11 11  k 0 i0 m0
   P Q Hệ số của 11
x trong P là: 0 1 2 3 10 11
C a C a C a C a  ...  C a C a T 11 11 11 10 11 9 11 8 11 1 11 0 Hệ số của 11
x trong Q là: 1 C  11 Vậy 1 T C   11  . 11 n m h
Dạng 2.2.2 Tổng a ba b
 ...  a b 1 1   2 2   k k Câu 96. Chọn A 18  1 
Đặt A    x12 1 ; 2 B x     x  12 12
Ta có khai triển A  1 xk kC x  có 13 số hạng. 12 k
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 18 18  1  Và khai triển 2 l 363l B x   C x    có 19 số hạng. 18  x l 0
Ta đi tìm các số hạng có cùng lũy thừa, mà giản ước được trong khai triển P( x) , ta phải có :
36  3l k k  3l  36 (1)
Phương trình (1) cho ta ta 5 cặp nghiệm thỏa mãn (k; l)  {(0;12), (3;11), (6;10), (9;9), (12;8)} tương ứng với 5 số hạng.
Vậy sau khi khai triển và rút gọn P( x) ta có 13 19  5  27 số hạng.
Câu 97. Ta có P x 2018 2017  a xa x
 ... a x a 2018 2017 1 0 2017 2018
Cho x  1  P   1  aa
 ...  a a  1  2  3  2.1  0 . 2018 2017 1 0 12 k  3  12 12k 12 k  3  Câu 98. 2 2 k k 24 3k x     C x   C 3 x  12      12  x    x k 0  k 0 21 k  1 21 21k 21 k  1 3   2x  3 k 21k 635k   C 2x   C 2 x 21    2   2  21  x    x k 0  k 0
Ta cho k chạy từ 0 đến 12 thì các số mũ của x không bằng nhau. 12 21  3   1  Với khai triển 2 x  3 
 ta có 13 số hạng; Với khai triển 2x  
ta có 22 số hạng. Vậy tổng 2   x   x  số hạng là: 35 . n n
Câu 99. Xét nhị thức  x   1
 1 x có số hạng tổng quát là k k C x . Ta có: n Hệ số của 5 x trong   6 1 x là 5 C . 6 Hệ số của 5 x trong   7 1 x là 5 C 7 Hệ số của 5 x trong   12 1 x là 5 C . 12 Vậy hệ số của 5
x trong khai triển P x là 5 5 5
C C  ...  C  1715 . 6 7 12
Câu 100. Ta có 1 x8 0 1 8 8
C C x  ...  C x suy ra hệ số chứa 8 x là 8 C . 8 8 8 8 Lại có 1 x9 0 1 8 8 9 9
C C x  ...  C x C x suy ra hệ số của 8 x là 8 C . 9 9 9 9 9
Tương tự trong khai triển   10 1 x có hệ số của 8 x là 8 C . 10   11 1 x có hệ số của 8 x là 8 C . 11   12 1 x có hệ số của 8 x là 8 C . 12 Suy ra hệ số của 8
x trong P x là 8 8 8 8 8
a C C C C C  715 . 8 8 9 10 11 12 Câu 101. Ta có
P x    x8    x9    x10    x11    x12 1 1 1 1 1 . Áp dụng khai triển   xn 0 1 2 2 1
C C x C x  ... n nC x . n n n n Cho x  1 , ta có 0 1 2
C C C  ... nC  2n . n n n n
Do đó ta có tổng hệ số của P x là: 8 9 10 11 12 8 S             8 2 2 2 2 2
2 1 2 4 8 16  31.2  7936 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 m l
Dạng 2.2.3 Tích a  ..  a
. b  ...  b 1 n   1 n  11 11
Câu 102.   x  x11 1 2 3
 3  x  2x 3  x 11 11 k 11k k k 11  C .3 .x  2x
C .3 k. k x  11  11 k 0 k 0 11 11 k 11k k k 11k k 1  C .3 .x C .2.3 .x   11  11 k 0 k 0 Suy ra hệ số của 9
x khi triển khai nhị thức trên là: 9 2 8 3
C .3  C .2.3  9045 . 11 11 10 2 10  
Câu 103. Ta có: 1 2x  2
3  4x  4x kC .2k. k x .     4 3 2
16x  32x  40x  24x  9 10   k0  Do đó 2 2 3 3 4 4 5 5 6 6
a C .2 .16  C .2 .32  C .2 .40  C .2 .24  C .2 .9  482496 . 6 10 10 10 10 10 n n 6 6 kk k
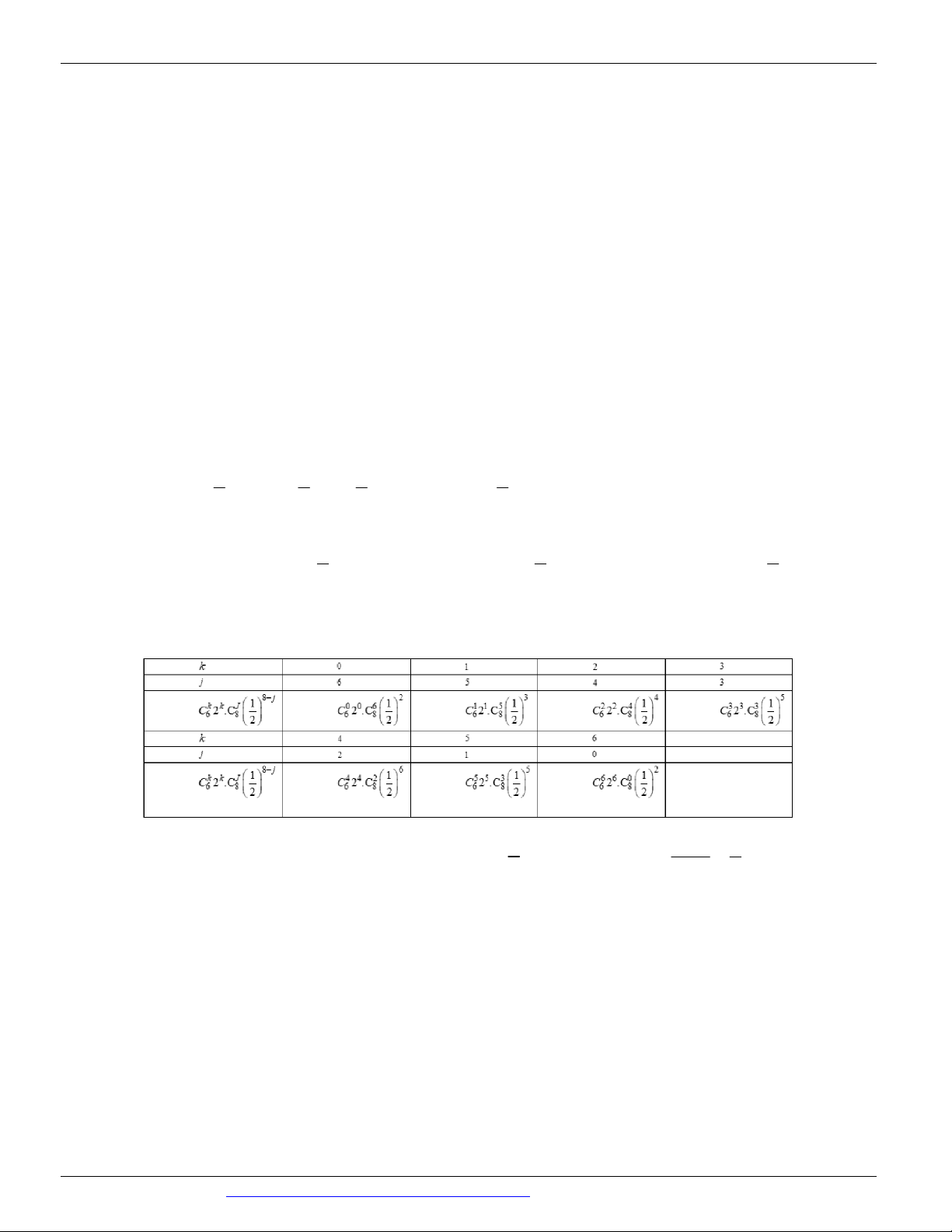
Câu 104. Xét khai triển 2x   1  1 2x 6 k k k  6 C 1 2x  6 C 2 x   k 0 k 0 8 4 8 8 8 j  2 1   1   1  8  1  j x x   x    xC       j x     4   2   2   2  j0 n 8 n 8 4 8 j 8 j 6  1  k k k J  1  j k k J  1  Vậy 2x   2 1 jk x x   6 C 2 x . 8 C x      6 C 2 . 8 C x        4   2   2  k 0 j0 k 0 j0
Số hạng của khai triển chứa 6
x khi j k  6 Xét bảng: 4 6   3003 1 Vậy hệ số 6
x trong khai triển  x   2 1 2 1 x x    thành đa thức là 6  1 C 4 .  4  4 4
Dạng 2.2.4 Dạng kết hợp tích và tổng
Câu 105. Chọn B Hệ số của 5
x trong khai triển biểu thức x x  6 2 1 là C 2  2 4 4 1  240 . 6 Hệ số của 5
x trong khai triển biểu thức  x  8 3 là C 33 5  1512 . 8 6 8 Suy ra hệ số của 5
x trong khai triển biểu thức x 2x   1
  x  3 là 240 1512  1  272 .
Câu 106. Chọn B 6 8 k 6k m 8k
x x  6   x  8 3 1 2 1  k x C . 3x 1 mC . 2x 1  6      8     k 0 m0 6 8 kk k
C .3k  6 1 k m xC .2m    8 1 1 m x . 6 8 k 0 m0
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Hệ số 5
x ứng với k  4 ; m  5 . 2 3 Hệ số cần tìm là 4 4 C .3   5 5 1  C .2 1  577 . 6 8  
Câu 107. Chọn A Hệ số của 4
x trong khai triển nhị thức 6 (x  2) là 4 2 C 2  60 . 6 Hệ số của 5
x trong khai triển nhị thức 8 (3x 1) là 5 5
C (3)  13608 . 8 Vậy hệ số của 5
x trong khai triển biểu thức 6 8
x(x  2)  (3x 1) bằng 1  3608  60  1  3548.
Câu 108. Chọn D 6 8 Ta có   x k k m m 2x  6 1  3x  8 1  . k x C  2x6   1 mC  3x8 1 6 8   k 0 m0 6 8    C k k m m k 26   1 . k m xC 38 7     8 1 . m x 6 8 k 0 m0 Để có số hạng của 5
x trong khai triển thì k  2; m  3 5 3 Do đó hệ số của 5
x trong khai triển bằng: 2 4 3 C .2  C . 3 1  13368. 6 8    
Câu 109. Chọn A
Số hạng tổng quát trong khai triển trên có dạng: k mmkk
. k . k  26 m .3  . 8 1 k . k     26 m  .3 . m  8 1 1 . m x C x C x C x C x . 6 8 6 8 k 1  5 k  4 Để tìm hệ số của 5
x ta cần tìm k , m sao cho    . m  5 m  5   2 3 Hệ số của 5 x cần tìm bằng: 4 C .2 5 5  C .3 . 1  13548 . 6 8  
Câu 110. Chọn A Hệ số của 5 x là C .1 . 1 C .1 .2 965. 5  4 4 1    3 7 3  10 k m k
Câu 111. Khải triển P x có số hạng tổng quát k xC 2  x 2 mx C 3x  2 k k 1 C x    2 3m m m C x   ( 10   5   5 10
k   , k  5 , m   , m  10 ) k 1  5 k  4 Hệ số của 5
x ứng với k , m thỏa hệ    . m  2  5  m  3 
Vậy hệ số cần tìm là  2  4 4 C  3 3 3 C  3320 . 5 10
Dạng 3. Ứng dụng nhị thức newton để giải toán
Câu 112. Chọn A. 1 Ta có: 19 0 18 1 17 2 20
S  3 C  3 C  3 C  ...  C 20 20 20 20 3 20 0 19 1 18 2 20
3S  3 C  3 C  3 C  ...  C 20 20 20 20
Xét khai triển: 3  120 0 20 0 1 19 1 2 18 2 20 0 20
C 3 1  C 3 1  C 3 1  ...  C 3 1 20 20 20 20  3  120 0 20 1 19 2 18 20
C 3  C 3  C 3  ...  C 20  3S  4 20 20 20 20
Câu 113. Chọn A 2017 2017 Ta có 1  k k 2017k 0 1 2 3 2017 1  C 1 1  C C   CC  ...  C  . 2017 2017 2017 2017 2017 2017 k 0 Vậy 1 2 3 2017 2017 CCC  ...  C  2 1. 2017 2017 2017 2017
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 114. Chọn C 2018 2018 Ta có 1  i 0 1 2 2018 1  CCCC  ...  C  2018 2018 2018 2018 2018 i0 Suy ra 1 2 2018 2018 CC  ...  C  2 1 . 2018 2018 2018
Câu 115. Xét hai khai triển: 2017 + 2017 2  1  0 1 2 3 2017 1  CCCC  ...  C 1 . 2017 2017 2017 2017 2017   2017 + 0  1  0 1 2 3 2017 1  CCCC  ...  C 2 2017 2017 2017 2017 2017   Lấy  
1  2 theo vế ta được: 2017 2  2  1 3 5 2017 CCC  ...  C  2016  T  2 . 2017 2017 2017 2017
Câu 116. Chọn C
Xét tổng 1 x5 0 1 2 2 5 5
C xC x C  ...  x C 5 5 5 5
Thay x  2 ta được: S C  2C  2 C  ...  2 C  1 25 0 1 2 2 5 5 5  3  243 5 5 5 5
Câu 117. Chọn B 10 10 Ta có  x   1 kC . k x  10 k 0 10 10
Chọn x  2 ta có 2   1 kC .2k  10
S  3  49049 . 10 k 0
Câu 118. Xét khai triển 1 x10 0 1 2 2 3 3 10 10
C C .x C .x C .x   C .x . 10 10 10 10 10
Với x  2 ta có 1 210 0 1 2 2 3 3 10 10
C  2C  2 C  2 C   2 C . 10 10 10 10 10 Vậy 10 S  3  59049 .
Câu 119. Ta có: 1 x2016 0 1 2 2 2016 2016  CC x C x  ...  C x . 2016 2016 2016 2016
Chọn x  1 , ta có: 2016 0 1 2 2016 2  CCC  ...  C hay 1 2 2016 2016 CC  ...  C  2 1 . 2016 2016 2016 2016 2016 2016 2016
Câu 120. Chọn C n
Xét khai triển   x 0 1 2 2 1
C C x C x  ... n nC x . n n n n
Cho x  4 ta có: n 0 1 2 2
5  C  4C  4 C  ...  4n n C . Suy ra: 15625 5n  6
 5  5n n  6 . n n n n
Câu 121. Chọn C 2019 2019 Ta có: . x 1 x  . x C x  . x  0 1 2018 2018 2019 2019 CC x  ...  C x   k k C x . 2019 2019 2019 2019 2019  k 0 0 1 2 2018 2019 2019 2020  C x C x  ...  C xC x . 2019 2019 2019 2019
Đạo hàm 2 vế theo biến x ta được. 2019 2018 0 1 2018 2018 2019 2019 (1 x)
 2019x(1  x)  CC
.2x  ...  C .2019xC .2020x . 2019 2019 2019 2019 Cho x  1 suy ra 2019 2018 0 1 2018 2019 2  2019.2  C  2C  ...  2019C  2020C . 2019 2019 2019 2019 2018 2018  (2  2019).2
 1 S S  2021.2 1. Vậy 2018 S  2021.2 1 .
Câu 122. Chọn C Ta có : 2  1  22 22 0 1 2 20 21 22 1  CCC  ....  CCC . 22 22 22 22 22 22
Áp dụng tính chất : k n k C C   , suy ra: n n 0 22 CC , 1 21 CC , 2 20 CC ,……, 10 12 CC . 22 22 22 22 22 22 22 22 Do đó: 0 1 2 20 21 22
C C C  ....  CCC  2  12 13 20 21 22 C
C  ....  CCC  11  C . 22 22 22 22 22 22 22 22 22 22 22 22
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 0 1 2 20 21 22 11
C C C  ....  CCC C 12 13 20 21 22 22 22 22 22 22 22 22
C C  ....  CC C   22 22 22 22 22 2 2 22 11 2 C 12 13 20 21 22 22
C C  ....  CCC   22 22 22 22 22 2 2 11 C 12 13 20 21 22 21 22  CC  ....  CCC  2  . 22 22 22 22 22 2 11 C Vậy 21 22 S  2  . 2
Câu 123.   2018 1 x  0 1 2 2 3 3 2018 2018 C  xC  x C  x C  ... x C   1 2018 2018 2018 2018 2018
Đạo hàm 2 vế của đẳng thức   1 ta được:   2017 2018 1 x  1 2 2 3 2017 2018 C  2xC  3x C  ... 2018x C . Cho x  1 ta được: 2018 2018 2018 2018 2017 2018 2 .  1 2 3 2018 C  2C  3C  ...  2018C . 2 2018 2018 2018 2018
Đồng thời, thay x  1 vào   1 ta cũng có: 2018 2  0 1 2 3 2018 C  C  C  C  ...  C . 3 2018 2018 2018 2018 2018
Lấy 2  3 ta được: S  2017 2018 2018 2 .  2  0 1 2 2017 2018 C  2C  3C  ...  2018C  2019C . 2018 2018 2018 2018 2018 Vậy S  2018 2018 2018 1009 2 .  2  1010 2 . .  x   x10 k k 1 1 10! k 1 k Câu 124. Ta có .  . . k
x .1 x10  . k . k C x . 1 x
với 0  k  10 . 10  10
k ! 10  k ! 10! k  ! 10  k ! 10! x x
  xx   x2   x10 10 9 8 1 1 1 10 1 1 1  .  .  ...  k kC . k x . 1 x  
x 1 x10  . 10  10 10! 9! 1! 8! 2! 10! 10! 10! 10! k 0
Câu 125. S  2   0 0 0
C C  ...  CC C   C
C   C   C n   1 1 1 ... n  ...  n 1 n 1 n 1 2 1 2 n 1  nn  2   0 1
C C    0 1 2
C C C   ...  0 1 n 1 CC
 ...  C   C C   C nnn   0 1 ... n 1 1 2 2 2 1 1 1 n n n
     2     n 1  n 2 2 1 1 ... 1 1  1  1 2n 1 1 2 2 2 2 ... 2n       2  2. 1 2n S    . 2 1
S là một số có 1000 chữ số 999 1000  10  S  10 999 n 1  1000  10  2  10
 999 log 10 1  n  1000 log 10 1 2 2
Do n   nên n 3318;3319;33  20 .
Vậy có 3 số nguyên dương n thỏa mãn yêu cầu bài toán.
Câu 126. Chọn B n! n! n! n!     ....   1024 1  ! n   1 ! 3  ! n  3!  5! n  5! n   1 !1! 1 3 5
C C C  ..... nC  1024 (1). n n n n
Ta chứng minh đẳng thức 1 3 5 n n 1 C C C ..... C 2       (2). n n n n n
Thật vậy, xét   x 0 1 2 2 1
C C x C x  .... n nC x . n n n n
Với n là số nguyên dương
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Thay x  1 thì n 0 1 2
2  C C C  ..... nC . n n n n Thay x  1 thì 0 1 2 3 1
0  C C C C  ...... nnCC n n n n n n 0 2 4 n 1 3 n 1 C C C ...... C C C ..... C           n n n n n n n     . A BA B Từ đó ta có: n n 1 
 2B  2  B  2  .
A B  2n
Do đó đẳng thức (2) được chứng minh. n Thay vào (1) 1 10 2
 1024  2 nên n  11 , chọn đáp án B
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39