Thông tin
Hỏi đáp

Các dạng toán trắc nghiệm phương pháp tọa độ trong mặt phẳng

Tài liệu gồm 112 trang được biên soạn bởi thầy Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm có đáp án và lời giải chi tiết các chủ đề: phương trình đường thẳng, phương trình đường tròn, phương trình Elip … trong chương trình Hình học 10 chương 3: phương pháp tọa độ trong mặt phẳng Oxy.

Chủ đề:

Chương 7: Phương pháp tọa độ trong mặt phẳng (KNTT) 78 tài liệu

Môn:

Toán 10 2.8 K tài liệu

Thông tin:

112 trang 9 tháng trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Các dạng toán trắc nghiệm phương pháp tọa độ trong mặt phẳng

84 42 lượt tải Tải xuống

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng h

ợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 1

TOÁN 10

0H3-1

Conte

nts

A.CÂU

HỎI .................................................................................................................................................................... 2

DẠNG1.XÁCĐỊNHVÉCTƠCHỈPHƯƠNG,VÉCTƠPHÁPTUYẾNCỦAĐƯỜNGTHẲNG,HỆSỐGÓC

CỦAĐƯỜNGTHẲNG ................................................................................................................................................... 2

DẠNG2.VIẾTPHƯƠNGTRÌNHĐƯỜNGTHẲNGVÀCÁCBÀITOÁNLIÊNQUAN ........................................ 5

Dạng2.1ViếtphươngtrìnhđườngthẳngkhibiếtVTPThoặcVTCP,HỆSỐGÓCvà1điểmđiqua ...................... 5

Dạng2.2Viếtphươngtrìnhđườngthẳngđiquamộtđiểmvuônggóchoặcvớiđườngthẳngchotrước .................... 6

Dạng2.3Viếtphươngtrìnhcạnh,đườngcao,trungtuyến,phângiáccủatamgiác .................................................... 9

Dạng2.3.1Phươngtrìnhđườngcaocủatamgiác ................................................................................................... 9

Dạng2.3.2Phươngtrìnhđườngtrungtuyếncủatamgiác ..................................................................................... 10

Dạng2.3.3Phươngtrìnhcạnhcủatamgiác ........................................................................................................... 10

Dạng2.3.4Phươngtrìnhđườngphângiáccủatamgiác........................................................................................ 10

DẠNG3.VỊTRÍTƯƠNGĐỐICỦAHAIĐƯỜNGTHẲNG .................................................................................... 12

DẠNG4.GÓCCỦAHAIĐƯỜNGTHẲNG ............................................................................................................... 15

Dạng4.1Tínhgóccủahaiđườngthẳngchotrước .................................................................................................... 15

Dạng4.2Viếtphươngtrìnhđườngthẳngliênquanđếngóc ..................................................................................... 17

DẠNG5.KHOẢNGCÁCH .......................................................................................................................................... 18

Dạng5.1Tínhkhoảngcáchtừ1điểmđếnđườngthẳngchotrước ........................................................................... 18

Dạng5.2Phươngtrìnhđườngthẳngliênquanđếnkhoảngcách ............................................................................... 20

DẠNG6.XÁCĐỊNHĐIỂM ......................................................................................................................................... 22

Dạng6.1Xácđịnhtọahìnhchiếu,điểmđốixứng ..................................................................................................... 22

Dạng6.2Xácđịnhđiểmliênquanđếnyếutốkhoảngcách,góc ............................................................................... 22

Dạng6.3Xácđịnhđiểmliênquanđếnyếutốcựctrị ................................................................................................ 24

Dạng6.4Mộtsốbàitoántổnghợp ............................................................................................................................ 25

DẠNG7.MỘTSỐBÀITOÁNLIÊNQUANĐẾNDIỆNTÍCH ................................................................................ 28

B.LỜIGIẢI ................................................................................................................................................................... 29

DẠNG1.XÁCĐỊNHVÉCTƠCHỈPHƯƠNG,VÉCTƠPHÁPTUYẾNCỦAĐƯỜNGTHẲNG,HỆSỐGÓC

CỦAĐƯỜNGTHẲNG ................................................................................................................................................. 29

DẠNG2.VIẾTPHƯƠNGTRÌNHĐƯỜNGTHẲNGVÀCÁCBÀITOÁNLIÊNQUAN ...................................... 31

Dạng2.1ViếtphươngtrìnhđườngthẳngkhibiếtVTPThoặcVTCP,HỆSỐGÓCvà1điểmđiqua .................... 31

Dạng2.2Viếtphươngtrìnhđườngthẳngđiquamộtđiểmvuônggóchoặcvớiđườngthẳngchotrước .................. 32

Dạng2.3Viếtphươngtrìnhcạnh,đườngcao,trungtuyến,phângiáccủatamgiác .................................................. 35

Dạng2.3.1Phươngtrìnhđườngcaocủatamgiác ................................................................................................. 35

Dạng2.3.2Phươngtrìnhđườngtrungtuyếncủatamgiác ..................................................................................... 36

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 2

Dạng2.3.3Phươngtrìnhcạnhcủatamgiác ........................................................................................................... 36

Dạng2.3.4Phươngtrìnhđườngphângiáccủatamgiác........................................................................................ 37

DẠNG3.VỊTRÍTƯƠNGĐỐICỦAHAIĐƯỜNGTHẲNG .................................................................................... 39

DẠNG4.GÓCCỦAHAIĐƯỜNGTHẲNG ............................................................................................................... 44

Dạng4.1Tínhgóccủahaiđườngthẳngchotrước .................................................................................................... 44

Dạng4.2Viếtphươngtrìnhđườngthẳngliênquanđếngóc ..................................................................................... 46

DẠNG5.KHOẢNGCÁCH .......................................................................................................................................... 49

Dạng5.1Tínhkhoảngcáchtừ1điểmđếnđườngthẳngchotrước ........................................................................... 49

Dạng5.2Phươngtrìnhđườngthẳngliênquanđếnkhoảngcách ............................................................................... 51

DẠNG6.XÁCĐỊNHĐIỂM ......................................................................................................................................... 53

Dạng6.1Xácđịnhtọahìnhchiếu,điểmđốixứng ..................................................................................................... 53

Dạng6.2Xácđịnhđiểmliênquanđếnyếutốkhoảngcách,góc ............................................................................... 55

Dạng6.3Xácđịnhđiểmliênquanđếnyếutốcựctrị ................................................................................................ 57

Dạng6.4Mộtsốbàitoántổnghợp ............................................................................................................................ 59

DẠNG7.MỘTSỐBÀITOÁNLIÊNQUANĐẾNDIỆNTÍCH ................................................................................ 70



A.CÂUHỎI

DẠNG1.XÁCĐỊNHVÉCTƠCHỈPHƯƠNG,VÉCTƠPHÁPTUYẾNCỦAĐƯỜNG

THẲNG,HỆSỐGÓCCỦAĐƯỜNGTHẲNG

Câu 1. Trongmặtphẳng

Oxy

,đườngthẳng

 

2 2

: 0, 0

d ax by c a b

    

.Vectơnàosauđâylàmột

vectơpháptuyếncủađườngthẳng

 

?

 

;

n a b 



. B.

 

;n b a





. C.

 

;

n b a 



. D.

 

;n a b





.

Câu 2. (ChuyênLêHồngPhong-NamĐịnh)Chođườngthẳng

cómộtvectơpháptuyếnlà

 

;n a b





,

,a b



.Xétcáckhẳngđịnhsau:

1.Nếu



thìđườngthẳng

khôngcóhệsốgóc.

2.Nếu



thìhệsốgóccủađườngthẳng

là

.

3.Đườngthẳng

cómộtvectơchỉphươnglà

 

;

u b a 



.

4.Vectơ



,



làvectơpháptuyếncủa

.

Cóbaonhiêukhẳngđịnhsai?

. B.

. C.

. D.

.

Câu 3. (THPT Cộng Hiền - Lần 1 - 2018-2019) Trong mặt phẳng tọa độ Oxy, cho đường thẳng

: 2 3 0

d x y

  

.Vectơpháptuyếncủađườngthẳng

là

 

1; 2

 



 

2;1

n 



 

2;3

n  



 

1;3

n 



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 3

Câu 4. Chođườngthẳng

 

:3 2 10 0

d x y

  

.Véctơnàosauđâylàvéctơchỉphươngcủa

 

3;2

u 



. B.

 

3; 2

 



. C.

 

2; 3

 



. D.

 

2; 3

  



Câu 5. (THPTQuỳnhLưu-NghệAn-2019)Chođườngthẳng

3 3

x t

y t



 









  



mộtvectơpháptuyến

củađườngthẳng



cótọađộ

 

5; 3

. B.

 

6;1

. C.

 

 

 

. D.

 

5;3



.

Câu 6. Tronghêtructoađô

Oxy

,Vectơnaolamôtvectơphaptuyêncuađươngthăng

1 2

x t

y t

  





  



?

 

2; 1

 



. B.

 

2; 1





. C.

 

1;2

n 



. D.

 

1;2



.

Câu 7. Vectơchỉphươngcủađườngthẳng

:

1 4

2 3

x t

y t

 





  



là:

 

4;3

u  



. B.

 

4;3

u 



. C.

 

3;4

u 



. D.

 

1; 2

 



.

Câu 8. Vectornàodướiđâylà1vectorchỉphươngcủađườngthẳngsongsongvớitrục

:

 

1;0

u 



. B.

(1; 1)

 



. C.

(1;1)

u 



. D.

(0;1)

u 



.

Câu 9. Chođườngthẳng

: 7 3 1 0

d x y

  

.VectơnàosauđâylàVectơchỉphươngcủad?

 

7;3

u 



. B.

 

3;7

u 



. C.

 

3;7

u  



. D.

 

2;3

u 



.

Câu 10. Chođườngthẳng



: 2 3 4 0

d x y

  

.Véctơnàosauđâylàvéctơpháptuyếncủađườngthẳng

 

3;2

n 



. B.

 

4; 6

  



. C.

 

2; 3

 



. D.

 

2;3

n  



.

Câu 11. Chođườngthẳng

: 5 3 7 0.

d x y

  

Vectơnàosauđâylàmộtvectơchỉphươngcủađườngthẳng

 

3;5

n 



. B.

 

3; 5

 



. C.

 

5;3

n 



. D.

 

5; 3

  



.

Câu 12. Chođườngthẳng

: 2 3 0

x y

   

.Véctơnàosauđâykhônglàvéctơchỉphươngcủa



?

 

4; 2

 



. B.

 

2; 1

  



. C.

 

2;1

m 



. D.

 

4;2

q 



.

Câu 13. Chohaiđiểm

 

1;2

A 

và

 

5;4

B 

.Vectơpháptuyếncủađườngthẳng

là

 

1; 2 

. B.

 

1;2

. C.

 

2;1



. D.

 

1;2



.

Câu 14. Chođườngthẳng

: 7 3 1 0

d x y

  

.VectơnàosauđâylàVectơchỉphươngcủađườngthẳngd?

 

7;3

u 



. B.

 

3;7

u 



. C.

 

3;7

u  



. D.

 

2;3

u 



.

Câu 15. (THIHK1LỚP11THPTVIỆTTRÌ2018-2019)Vectơnàodướiđâylàmộtvectơpháptuyến

của

: 2 2018 0

d x y

  

?

 

0; 2





. B.

 

2;0

n 



. C.

 

2;1



. D.

 

1; 2





.

Câu 16. Vectơnàotrongcácvectơdướiđâylàvectơpháptuyếncủađườngthẳng

2 1 0

y x

  

?

 

2; 1

. B.

 

1;2

. C.

 

2;1



. D.

 

2; 1 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 4

Câu 17. Trongmặtphẳng

Oxy

,chođườngthẳng

: 2 1 0

d x y

  

,mộtvéctơpháptuyếncủa

là

 

2; 1 

. B.

 

2; 1

. C.

 

1; 2 

. D.

 

1; 2

.

Câu 18. Trongmặtphẳngvớihệtọađộ

Oxy

chođườngthẳng

:2 3 4 0

d x y

  

.Vectơnàosauđâylàmột

vectơchỉphươngcủad.

 

3; 2

 



. B.

 

2;3

u 



.

 

2; 3

 



. D.

 

3;2

u 





Câu 19. (LƯƠNGTÀI2BẮCNINHLẦN1-2018-2019)VectơnàosauđâylàmộtVectơchỉphương

củađườngthẳng

: 6 2 3 0

x y

   

?

 

1;3



u . B.

 

6;2



u . C.

 

1;3





u . D.

 

3; 1



u .

Câu 20. (THPTYênMỹHưngYênlần1-2019)Chohaiđiểm

 

2;3

và

 

2;5

N 

.Đườngthẳng



cómộtvectơchỉphươnglà:

 

4;2

u 



. B.

 

4; 2

 



. C.

 

4; 2

  



. D.

 

2;4

u  



.

Câu 21. Trongmặtphẳngvớihệtọađộ

,Oxy

chođườngthẳng

: 2 1 0.

d x y

  

Mộtvectơchỉphươngcủa

đườngthẳng

là

 

1; 2

 



. B.

 

2; 1

u 



. C.

 

2; 1

 



. D.

 

1; 2

u 



.

Câu 22. Đườngthẳng

cómộtvectơchỉphươnglà

 

2; 1

 



.Trongcácvectơsau,vectơnàolàmột

vectơpháptuyếncủa

?

 

.1;2

n  



 B.

 

1; 2 .







 C.

 

.3;6

n 



 D.

 

3;6 .

n 





Câu 23. Đườngthẳng

cómộtvectơpháptuyếnlà

 

4; 2

 



.Trongcácvectơsau,vectơnàolàmột

vectơchỉphươngcủa

?

 

.2; 4

u 





 B.

 

2;4 .

u 



 C.

 

.1;2

u 



 D.

 

2;1 .

u 





Câu 24. Đườngthẳng

cómộtvectơchỉphươnglà

 

3; 4

 



.Đườngthẳng



vuônggócvới

cómột

vectơpháptuyếnlà:

 

.4;3

n 



 B.

 

4; 3 .

n 

 



 C.

 

.3;4

n 



 D.

 

3; 4 .









Câu 25. Đườngthẳng

cómộtvectơpháptuyếnlà

 

2; 5

  



.Đườngthẳng



vuônggócvới

cómột

vectơchỉphươnglà:

 

.5; 2

u 





 B.

 

5;2 .

u 



 C.

 

.2;5

u 



 D.

 

2; 5 .









Câu 26. Đườngthẳng

cómộtvectơchỉphươnglà

 

3; 4

 



.Đườngthẳng



songsongvới

cómột

vectơpháptuyếnlà:

 

.4;3

n 



 B.

 

4;3 .

n 



 C.

 

.3;4

n 



 D.

 

3; 4 .









Câu 27. Đườngthẳng

cómộtvectơpháptuyếnlà

 

2; 5

  



.Đườngthẳng



songsongvới

cómột

vectơchỉphươnglà:

 

.5; 2

u 





 B.

 

5; 2 .

u 

 



 C.

 

.2;5

u 



 D.

 

2; 5 .









Câu 28. Chođườngthẳng

:3 5 2018 0.

d x y

  

Tìmmệnhđềsaitrongcácmệnhđềsau:

cóvectơpháptuyến

 

3;5 .

n 



 B.

cóvectơchỉphương

 

5; 3 .

 





CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 5

cóhệsốgóc



 D.

songsongvớiđườngthẳng

:3 5 0.

x y

  



Câu 29. Chođườngthẳng

 

: 7 15 0

d x y

  

.Mệnhđềnàosauđâyđúng?

 

cóhệsốgóc



 B.

 

điquahaiđiểm

 



 

 

và

 

5;0



 

7;1

u  



làvectochỉphươngcủa

 

 D.

 

điquagốctọađộ

Câu 30. Trênmặtphẳngtọađộ

Oxy

,chohaiđiểm

 

2;3

A 

và

 

4; 1



.Phươngtrìnhnàosauđâylà

phươngtrìnhđườngthẳng

3 0

x y

  

. B.

2 1y x 

. C.

4 1

6 4

x y 





. D.

1 3

1 2

x t

y t

 





 



.

DẠNG2.VIẾTPHƯƠNGTRÌNHĐƯỜNGTHẲNGVÀCÁCBÀITOÁNLIÊNQUAN

Dạng2.1ViếtphươngtrìnhđườngthẳngkhibiếtVTPThoặcVTCP,HỆSỐGÓCvà1điểmđi

qua



Câu 31. (THIHK1LỚP11THPTVIỆTTRÌ2018-2019)Phươngtrìnhthamsốcủađườngthẳngđiqua

haiđiểm

 

2; 1



và

 

2;5

là

x t

y t







 



. B.

5 6

x t

y t

 





 



. C.

2 6

y t







 



. D.

1 6

y t







  



.

Câu 32. ChuyênLêHồngPhong-NamĐịnhTrongmặtphẳngtoạđộ

Oxy

,chohaiđiểm

 

3; 1



và

 

6;2

B 

.Phươngtrìnhnàodướiđâykhôngphảilàphươngtrìnhthamsốcủađườngthẳng

?

3 3

x t

y t

 





  



. B.

3 3

x t

y t

 





  



. C.

3x t

y t

 









. D.

6 3

x t

y t

  





 



.

Câu 33. Phươngtrìnhthamsốcủađườngthẳngqua

 

1; 2



,

 

4;3

là

3 2

x t

y t

 





 



. B.

1 5

2 3

x t

y t

 





  



. C.

3 3

4 5

x t

y t

 





 



. D.

1 3

2 5

x t

y t

 





  



.

Câu 34. Phươngtrìnhthamsốcủađườngthẳngđiquahaiđiểm

   

3; 1 , 6;2

A B 

là

1 3

x t

y t

  









. B.

3 3

x t

y t

 





  



. C.

3 3

x t

y t

 





  



. D.

3 3

x t

y t

 





  



.

Câu 35. Trongmặtphẳngtọađộ,chohaiđiểm

   

3;0 , 0;2

A B

vàđườngthẳng

: 0

d x y

 

.Lậpphương

trìnhthamsốcủađườngthẳng



qua

vàsongsongvới

.

x t

y t







 



. B.

x t

y t







 



. C.

x t

y t

 





 



. D.

x t

y t

 





 



.

Câu 36. Chođườngthẳng

cóphươngtrìnhthamsố

9 2

x t

y t

 





  





Phươngtrìnhtổngquátcủađường

thẳng

là

2 1 0

x y

  

. B.

2 1 0

x y

   

. C.

2 1 0

x y

  

. D.

2 3 1 0

x y

  

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 6

Câu 37. Trongmặtphẳng

Oxy

chođiểm

(1;2)

.Gọi

,A B

làhìnhchiếucủa

lên

,Ox Oy

.Viếtphương

trìnhđườngthẳng

.

2 1 0

x y

  

. B.

2 2 0

x y

  

. C.

2 2 0

x y

  

. D.

3 0

x y

  

.

Câu 38. TrongmặtphẳngtọađộOxy,chođườngthẳng

3 5

: ( )

1 4

x t

d t

y t

 







 





.Phươngtrìnhtổngquátcủa

đườngthẳngdlà

4 5 7 0.

x y

  

. B.

4 5 17 0.

x y

  

. C.

4 5 17 0.

x y

  

. D.

4 5 17 0.

x y

  



Câu 39. Trongmặtphẳngvớihệtrụctọađộ

Oxy

,chođườngthẳngdcắthaitrục

và

lầnlượttại

haiđiểm

 

;0A a

và

 

0;B b



 

0; 0

a b

 

.Viếtphươngtrìnhđườngthẳngd.

: 0

x y

a b

 

. B.

: 1.

x y

a b

 

 C.

: 1.

x y

a b

 

: 1.

x y

b a

 

.

Câu 40. Phươngtrìnhđườngthẳngđiquahaiđiểm

   

0;4 , 6;0

A B 



là:

6 4

x y

 

. B.

4 6

x y

 



. C.

4 6

x y



 



. D.

6 4

x y



 

.

Dạng2.2Viếtphươngtrìnhđườngthẳngđiquamộtđiểmvuônggóchoặcvớiđườngthẳngcho

trước



Câu 41. Phươngtrìnhđườngthẳng

điqua

 

1; 2



vàvuônggócvớiđườngthẳng

:3 2 1 0

x y

   

là:

3 2 7 0

x y

  

. B.

2 3 4 0

x y

  

. C.

3 5 0

x y

  

. D.

2 3 3 0

x y

  

.



Câu 42. Chođườngthẳng

:8 6 7 0

d x y

  

.Nếuđườngthẳng



điquagốctọađộvàvuônggócvớiđường

thẳngdthì



cóphươngtrìnhlà

4 3 0

x y

 

. B.

4 3 0

x y

 

. C.

3 4 0

x y

 

. D.

3 4 0

x y

 

.

Câu 43. Đườngthẳngđiquađiểm

 

1;11

vàsongsongvớiđườngthẳng

3 5y x 

cóphươngtrìnhlà

3 11

y x

 

. B.

 

3 14

y x  

. C.

3 8y x 

. D.

y x

 

.

Câu 44.

(HKIXUÂNPHƯƠNG-HN)Lậpphươngtrìnhđườngđiqua

 

2;5

vàsongsongvớiđường

thẳng

 

: 3 4?

d y x

 



 

: 3 2

y x

  

. B.

 

: 3 1y x  

. C.

 

: 1

y x   

. D.

 

: 3 1y x   

Câu 45. Tronghệtrục

Oxy

,đườngthẳng

qua

 

1;1

vàsongsongvớiđườngthẳng

': 1 0

d x y

  

có

phươngtrìnhlà

1 0

x y

  

. B.

x y

 

. C.

1 0

x y

   

. D.

2 0

x y

  

.

Câu 46. Viếtphươngtrìnhtổngquátcủađườngthẳngđiquađiểm

 

1;2

I 

vàvuônggócvớiđườngthẳng

cóphươngtrình

2 4 0

x y

  

.

2 0

x y

 

. B.

2 3 0

x y

  

. C.

2 3 0

x y

  

. D.

2 5 0

x y

  

.

Câu 47. TronghệtrụctọađộTronghệtrụctọađộ

Oxy

chohaiđiểm

 

1;0

và

 

0;2

.Đườngthẳngđi

qua

 

 

 

vàsongsongvớiđườngthẳng

cóphươngtrìnhlà

A. Khôngtồntạiđườngthẳngnhưđềbàiyêucầu.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 7

2 2 0

x y

  

.

4 3 0

x y

  

.

2 4 3 0

x y

  

.

Câu 48. Trongmặtphẳngvớihệtọađộ

Oxy

,chobađiểm

 

2;0

¸

 

0;3

và

 

3; 1

 

.Đườngthẳngđi

quađiểm

vàsongsongvới

cóphươngtrìnhthamsốlà:

x t

y t







 



 B.

1 3

y t







 



 C.

3 5

x t

y t







 



 D.

3 5

x t

y t

 











Câu 49. Trongmặtphẳngvớihệtọađộ

Oxy

,chobađiểm

 

3;2

¸

 

4;0

và

 

0; 2



.Đườngthẳngđi

quađiểm

vàsongsongvới

cóphươngtrìnhthamsốlà:

3 4

2 2

x t

y t

 





 



 B.

3 2

x t

y t

 





 



 C.

1 2

x t

y t

  









 D.

1 2

x t

y t

  





  





Câu 50. Trongmặtphẳngvớihệtọađộ

Oxy

,chohìnhbìnhhành

ABCD

cóđỉnh

 

–2;1

vàphươngtrình

đườngthẳngchứacạnh

là

1 4

x t

y t

 









.Viếtphươngtrìnhthamsốcủađườngthẳngchứacạnh

.

2 3

2 2

x t

y t

  





  



. B.

2 4

1 3

x t

y t

  





 



. C.

2 3

1 4

x t

y t

  





 



. D.

2 3

1 4

x t

y t

  





 



.

Câu 51. Viếtphươngtrìnhthamsốcủađườngthẳng

điquađiểm

 

3;5

M 

vàsongsongvớiđườngphân

giáccủagócphầntưthứnhất.

x t

y t

  





 



. B.

x t

y t

  





 



. C.

x t

y t

 





  



. D.

x t

y t

 





  



.

Câu 52. Viếtphươngtrìnhthamsốcủađườngthẳng

điquađiểm

 

4; 7



vàsongsongvớitrục

.

1 4

x t

y t

 





 



. B.

y t







  



. C.

x t

  









. D.

x t







 



.

Câu 53. Đườngthẳng

điquađiểm

 

1;2

vàsongsongvớiđườngthẳng

: 2 3 12 0

x y

   

cóphương

trìnhtổngquátlà:

2 3 8 0

x y

  

. B.

2 3 8 0

x y

  

. C.

4 6 1 0

x y

  

. D.

4 3 8 0

x y

  

.

Câu 54. Phương trình tổng quát của đường thẳng

 đi qua

 và song song với đường thẳng

: 6 4 1 0

x x

   

là:

3 2 0.

x y

 

4 6 0.

x y

 

 C.

3 12 1 0.

x y

  

6 4 1 0.

x y

  



Câu 55. Đườngthẳng

điquađiểm

 

1;2

M 

vàvuônggócvớiđườngthẳng

: 2 3 0

x y

   

cóphươngtrìnhtổngquátlà:

2 0

x y

 

. B.

2 3 0

x y

  

. C.

1 0

x y

  

. D.

2 5 0

x y

  

.

Câu 56. Viết phương trình đường thẳng



 đi qua điểm

 

4; 3



 và song song với đường thẳng

3 2

1 3

x t

y t

 





 



.

3 2 6 0

x y

  

. B.

2 3 17 0

x y

   

.

3 2 6 0

x y

  

. D.

3 2 6 0

x y

  

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 8

Câu 57. Chotamgiác

ABC

có

     

2;0 , 0;3 ,  –3;1

A B C

.Đườngthẳng

điqua

vàsongsongvới

cóphươngtrìnhtổngquátlà:

5 – 3 0

x y

 

. B.

5 – 3 0

x y

 

. C.

5 –15 0

x y

 

. D.

–15 15 0

x y

 

.

Câu 58. Viếtphươngtrìnhtổngquátcủađườngthẳng

điquađiểm

 

1;0

M 

vàvuônggócvớiđường

thẳng

: .

x t

y t









 





2 2 0

x y

  

. B.

2 2 0

x y

  

. C.

2 1 0

x y

  

. D.

2 1 0

x y

  

.

Câu 59. Đườngthẳng

điquađiểm

 

2;1

M 

vàvuônggócvớiđườngthẳng

1 3

2 5

x t

y t

 







  



cóphương

trìnhthamsốlà:

2 3

1 5

x t

y t

  





 



 B.

2 5

1 3

x t

y t

  





 



 C.

1 3

2 5

x t

y t

 





 



 D.

1 5

2 3

x t

y t

 





 





Câu 60. Viếtphươngtrìnhthamsốcủađườngthẳng

điquađiểm

 

1;2

A 

vàsongsongvớiđườngthẳng

:3 13 1 0

x y

   

.

1 13

2 3

x t

y t

  





 



. B.

1 13

2 3

x t

y t

 





  



. C.

1 13

2 3

x t

y t

  





 



. D.

1 3

2 13

x t

y t

 





 



.

Câu 61. Viếtphươngtrìnhthamsốcủađườngthẳng

quađiểm

 

1;2

A 

vàvuônggócvớiđườngthẳng

: 2 4 0

x y

   

.

1 2

x t

y t

  





 



. B.

4 2

x t

y t







 



. C.

1 2

x t

y t

  





 



. D.

1 2

x t

y t

 





 



.

Câu 62. Viếtphươngtrìnhtổngquátcủađườngthẳng

điquađiểm

 

2; 5

 

vàsongsongvớiđường

phângiácgócphầntưthứnhất.

3 0

x y

  

. B.

3 0

x y

  

. C.

3 0

x y

  

. D.

2 1 0

x y

  

.

Câu 63. Viếtphươngtrìnhtổngquátcủađườngthẳng

điquađiểm

 

3; 1



vàvuônggócvớiđường

phângiácgócphầntưthứhai.

4 0

x y

  

. B.

4 0

x y

  

. C.

4 0

x y

  

. D.

4 0

x y

  

.

Câu 64. Viếtphươngtrìnhthamsốcủađườngthẳng

điquađiểm

 

4;0

M 

vàvuônggócvớiđường

phângiácgócphầntưthứhai.

x t

y t







  



. B.

4x t

y t

  





 



. C.

x t

y t







 



. D.

x t

y t







 



.

Câu 65. Viếtphươngtrìnhtổngquátcủađườngthẳng

điquađiểm

 

1;2

M 

vàsongsongvớitrục

.

2 0

 

. B.

1 0

 

. C.

1 0

 

. D.

2 0

 

.

Câu 66. Viếtphươngtrìnhthamsốcủađườngthẳng

điquađiểm

 

6; 10

M 

vàvuônggócvớitrục

.

x t

 









. B.

x t

 





 



. C.

y t







  



. D.

y t







  



.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 9

Dạng2.3Viếtphươngtrìnhcạnh,đườngcao,trungtuyến,phângiáccủatamgiác

Dạng2.3.1Phươngtrìnhđườngcaocủatamgiác



Câu 67. (ĐỘICẤNVĨNHPHÚCLẦN12018-2019)Trênmătphăngtoađô

Oxy

,chotamgiac

ABC

co

     

1;2 , 3;1 , 5;4

A B C

.Phươngtrinhnaosauđâylaphươngtrinhđươngcaoketư

cuatamgiac

ABC

2 3 8 0

x y

  

. B.

2 3 8 0

x y

  

. C.

3 2 1 0

x y

  

. D.

2 3 2 0

x y

  

.

Câu 68. Cho

ABC



có

     

2; 1 , 4;5 , 3;2

A B C 

.Đườngcao



của

ABC



cóphươngtrìnhlà

7 3 11 0

x y

  

. B.

3 7 13 0

x y

   

. C.

3 7 17 0

x y

  

. D.

7 3 10 0

x y

  

.

Câu 69. (ĐộCấn Vĩnh Phúc-lần 1-2018-2019) Trên mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

 có

     

1;2 , 3;1 , 5;4

A B C

.Phươngtrìnhnàosauđâylàphươngtrìnhđườngcaokẻtừ

củatam

giác

ABC

2 3 8 0

x y

  

. B.

2 3 8 0

x y

  

.

3 2 1 0

x y

  

. D.

2 3 2 0

x y

  

Câu 70. Trongmặtphẳngchotamgiác

ABC

cântại

có

 

2; 1



,

 

4;3

.Phươngtrìnhđườngcao

là

2 1 0

x y

  

. B.

2 1 0

x y

  

. C.

2 2 0

x y

  

. D.

2 5 0

x y

  

.

Câu 71. Cho

ABC

co

     

2; 1 , 4;5 , 3;2

A B C 

.Phươngtrinhtôngquatcuađươngcao

la

3 5 37 0

x y

  

. B.

5 3 5 0

x y

  

. C.

3 5 13 0

x y

  

. D.

3 5 20 0

x y

  

.

Câu 72. Đườngtrungtrựccủađoạnthẳng

với

 

3;2

A  

,

 

3;3

B  

cómộtvectơpháptuyếnlà:

 

6;5

n 



. B.

 

0;1

n 



. C.

 

3;5

n  



. D.

 

1;0

n  



.

Câu 73. Chotamgiác

ABC

có

   

1;1 ,  0; 2 , 4 .

( )

A B C

Lậpphươngtrìnhđườngtrungtuyếncủatam

giác

ABC

kẻtừ



2 0.

x y

  

2 3 0.

x y

  

 C.

2 3 0.

x y

  

x y

 

Câu 74. Đườngtrungtrựccủađoạn

với

 

1; 4



và

 

5;2

cóphươngtrìnhlà:

2 3 3 0.

x y

  

3 2 1 0.

x y

  

 C.

3 4 0.

x y

  

1 0.

x y

  



Câu 75. Đườngtrungtrựccủađoạn

với

 

4; 1



và

 

1; 4



cóphươngtrìnhlà:

x y

 

x y

 

 C.

y x

 

x y

 



Câu 76. Đườngtrungtrựccủađoạn

với

 

1; 4



và

 

1;2

cóphươngtrìnhlà:

1 0.

 

1 0.

 

 C.

1 0.

 

4 0.

x y

 



Câu 77. Đườngtrungtrựccủađoạn

với

 

1; 4



và

 

3; 4



cóphươngtrìnhlà:

4 0.

 

2 0.

x y

  

 C.

2 0.

 

4 0.

 



Câu 78. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

   

2; 1 ,  4;5

A B

và

 

3;2

C 

.Lập

phươngtrìnhđườngcaocủatamgiác

ABC

kẻtừ



7 3 11 0.

x y

  

 B.

3 7 13 0.

x y

   

3 7 1 0.

x y

  

 D.

7 3 13 0.

x y

  



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 10

Câu 79. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

   

2; 1 ,  4;5

A B

và

 

3;2 .

C 

Lập

phươngtrìnhđườngcaocủatamgiác

ABC

kẻtừ



3 5 13 0.

x y

  

 B.

3 5 20 0.

x y

  

3 5 37 0.

x y

  

5 3 5 0.

x y

  

Câu 80. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

   

2; 1 ,  4;5

A B

và

 

3;2 .

C 

Lập

phươngtrìnhđườngcaocủatamgiác

ABC

kẻtừ



1 0.

x y

  

 B.

3 3 0.

x y

  

3 11 0.

x y

  

3 11 0.

x y

  



Dạng2.3.2Phươngtrìnhđườngtrungtuyếncủatamgiác

Câu 81. Chotamgiác

ABC

với

 

1;1

,

 

0; 2



,

 

4;2

.Phươngtrìnhtổngquátcủađườngtrungtuyến

điquađiểm

củatamgiác

ABC

là

7 7 14 0  

x y

. B.

5 3 1 0

x y

  

. C.

3 2 0

x y

  

. D.

7 5 10 0

x y

   

.

Câu 82. (THPTYênDũng3-BắcGianglần1-18-19)Tronghệtọađộ

Oxy

,chotamgiác

ABC

có

     

2;3 , 1;0 , 1; 2

A B C

 

.Phươngtrìnhđườngtrungtuyếnkẻtừđỉnh

củatamgiác

ABC

là:

2 1 0

x y

  

. B.

2 4 0

x y

  

. C.

2 8 0

x y

  

. D.

2 7 0

x y

  

.

Câu 83. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

 

1;4

,

 

3;2

và

 

7;3 .

Viết

phươngtrìnhthamsốcủađườngtrungtuyến

củatamgiác.

3 5

y t







 



 B.

3 5

x t

 





 



 C.

x t

 









 D.

y t







 





Câu 84. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

 

2;4

,

 

5;0

và

 

.2;1

Trung

tuyến

củatamgiácđiquađiểm

cóhoànhđộbằng

thìtungđộbằng:

12.

 B.



 C.

13.

 D.





Dạng2.3.3Phươngtrìnhcạnhcủatamgiác



Câu 85. (THPTNGUYỄNTRÃI-THANHHOÁ-Lần1.Năm2018&2019)Trongmặtphẳngvớihệtọa

độ

Oxy

,chotamgiác

ABC

có

 

2;0

làtrungđiểmcủacạnh

. Đườngtrungtuyếnvàđường

caoquađỉnhAlầnlượtcóphươngtrìnhlà

7 2 3 0

x y

  

và

6 4 0

x y

  

.Phươngtrìnhđường

thẳng

là

3 4 5 0

x y

  

. B.

3 4 5 0

x y

  

. C.

3 4 5 0

x y

  

. D.

3 4 5 0

x y

  

.

Câu 86. (NôngCống-ThanhHóa-Lần1-1819)Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

cóphươngtrìnhcạnh

là

2 0,

x y

  

phươngtrìnhcạnh

là

2 5 0

x y

  

.Biết

trọngtâmcủatamgiáclàđiểm

 

3;2

vàphươngtrìnhđườngthẳng

códạng

x my n

  



Tìm

.m n



.

Dạng2.3.4Phươngtrìnhđườngphângiáccủatamgiác



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 11

Câu 87. Trongmặtphẳngvớihệtọađộ

Oxy

,chođườngthẳng

: 0

ax by c

   

vàhaiđiểm

 

;

m m

M x y

,

 

;

n n

N x y

khôngthuộc



.Chọnkhẳngđịnhđúngtrongcáckhẳngđịnhsau:

,M N

khácphíasovới



khi

   

. 0.

m m n n

ax by c ax by c

    



,M N

cùngphíasovới



khi

   

. 0.

m m n n

ax by c ax by c

    



,M N

khácphíasovới



khi

   

. 0.

m m n n

ax by c ax by c

    



,M N

cùngphíasovới



khi

   

. 0.

m m n n

ax by c ax by c

    



Câu 88. Trongmặtphẳngvớihệtọađộ

Oxy

,chođườngthẳng

:3 4 5 0

d x y

  

vàhaiđiểm

 

1;3

,

 

2;B m

.Tìmtấtcảcácgiátrịcủathamsố

để

và

nằmcùngphíađốivới

.



. B.

 

. C.

 

. D.

 

.

Câu 89. Trongmặtphẳngvớihệtọađộ

Oxy

,chođườngthẳng

1 3

x t

y t

 





 



vàhaiđiểm

 

1;2

,

 

2;B m



.Tìmtấtcảcácgiátrịcủathamsố

để

và

nằmcùngphíađốivới

.

13.



 B.



. C.

 13.



 D.

 13



.

Câu 90. Cặpđườngthẳngnàodướiđâylàphângiáccủacácgóchợpbởihaiđườngthẳng

: 2 3 0

x y

   



và

: 2 3 0

x y

   

.

3 0

x y

 

và

3 0

x y

 

. B.

3 0

x y

 

và

3 6 0

x y

  

.

3 0

x y

 

và

3 6 0

x y

   

. D.

3 6 0

x y

  

và

3 6 0

x y

  

.

Câu 91. Cặpđườngthẳngnàodướiđâylàphângiáccủacácgóchợpbởiđườngthẳng

: 0

x y

  

vàtrục

hoành.

 

1 2 0

x y

  

;

 

1 2 0

x y

  

. B.

 

1 2 0

x y

  

;

 

1 2 0

x y

  

.

 

1 2 0

x y

  

;

 

1 2 0

x y

  

. D.

 

1 2 0

x y

  

;

 

1 2 0

x y

  

.

Câu 92. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

 

 

 

,

 

1;2

và

 

4;3

C 

.Phương

trìnhđườngphângiáctrongcủagóc

là:

4 2 13 0.

x y

  

 B.

4 8 17 0.

x y

  



4 2 1 0.

x y

  

 D.

4 8 31 0.

x y

  



Câu 93. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

 

1;5

,

 

4; 5

 

và

 

4; 1



.

Phươngtrìnhđườngphângiácngoàicủagóc

là:

5 0.

 

 B.

5 0.

 

 C.

1 0.

 

 D.

1 0.

 



Câu 94. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng

:3 4 3 0

d x y

  

 và

:12 5 12 0

d x y

  

.Phươngtrìnhđườngphângiácgócnhọntạobởihaiđườngthẳng

và



là:

3 11 3 0.

x y

  

 B.

11 3 11 0.

x y

  



3 11 3 0.

x y

  

 D.

11 3 11 0.

x y

  



Câu 95. Cho tam giác ABC có phương trình cạnh

: 3 4 9 0  

AB x y

, cạnh

:8 6 1 0  

AC x y

, cạnh

: 5 0  

BC x y

.Phươngtrìnhđườngphângiáctrongcủagóc

là:

14 14 17 0  

x y

. B.

2 2 19 0  

x y

. C.

2 2 19 0  

x y

. D.

14 14 17 0  

x y

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 12

Câu 96. (THPTNgôQuyền-BaVì-HảiPhòng,lần1)Trongmặtphẳngtọađộ

Oxy

,chotamgiác

ABC



với

 

1; 2 ,





 

2; 3 ,



 

3;0

.Phươngtrìnhđườngphângiácngoàigóc

củatamgiác

ABC



là

1x 

. B.

 

. C.

2 0

x y

 

. D.

4 2 0

x y

  

.

DẠNG3.VỊTRÍTƯƠNGĐỐICỦAHAIĐƯỜNGTHẲNG



Câu 97. (HKIXUÂNPHƯƠNG-HN)Cóbaonhiêucặpđườngthẳngsongsongtrongcácđườngthẳng

sau?

 

: 2;

d y x

 



 

: 3;

d y x

  



 

: 3;

d y x

 



 

: 2

d y x

 



. B.

. C.

. D.

.

Câu 98. Phương trình nào sau đây là phương trình đường thẳng không song song với đường thẳng

: 3 2

d y x

 

3 0

x y

  

. B.

3 6 0

x y

  

3 6 0

x y

  

. D.

3 6 0

x y

  

.

Câu 99. Trongmặtphẳng

Oxy

,đườngthẳng

: 2 1 0

d x y

  

songsongvớiđườngthẳngcóphươngtrình

nàosauđây?

2 1 0

x y

  

. B.

2 0

x y

 

. C.

2 1 0

x y

   

. D.

2 4 1 0

x y

   

.

Câu 100. Chocácđườngthẳngsau.

: 2

d y x

 



: 1

d y x 



: 1 2

d y x

 

   

 

 



: 1

d y x 



Khẳngđịnhnàođúngtrongcáckhẳngđịnhsau?

2 3 4

, ,d d d

songsongvớinhau. B.

và

songsongvớinhau.

và

vuônggócvớinhau. D.

và

songsongvớinhau.

Câu 101. Tìmcácgiátrịthựccủathamsố

đểđườngthẳng

 

3 3 1

y m x m

   

songsongvớiđường

thẳng

5y x 

 

. B.

m  

. C.

 

. D.



.

Câu 102. Tọađộgiaođiểmcủahaiđườngthẳng

3 6 0

x y

  

và

3 4 1 0

x y

  

là

27 17

;

13 13

 



 

 

. B.

 

27;17



. C.

27 17

;

13 13

 



 

 

. D.

 

27; 17



.

Câu 103. Chođườngthẳng

: 2 3 15 0

d x y

  

và

: 2 3 0

d x y

  

.Khẳngđịnhnàosauđâyđúng?



và

cắtnhauvàkhôngvuônggócvớinhau. B.



và

songsongvới

nhau.



và

trùngnhau. D.



và

vuônggócvớinhau.

Câu 104. Haiđườngthẳng

1 2

: 5, : 9

d mx y m d x my

    

cắtnhaukhivàchỉkhi

 

. B.



. C.

 

. D.



.

Câu 105. Vớigiátrịnàocủa

thìhaiđườngthẳng

:3 4 10 0

d x y

  

và

 

: 2 1 10 0

d m x m y

   

trùngnhau?



. B.

 

. C.



. D.

 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 13

Câu 106. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai đường thẳng có phương trình

 

: 1 2 0

d mx m y m

   

và

: 2 1 0

d x y

  

.Nếu

songsong

thì:



 B.

 

 C.

 

 D.





Câu 107. Tìm

đểhaiđườngthẳng

: 2 3 4 0

d x y

  

và

2 3

1 4

x t

y mt

 





 



cắtnhau.

 

 B.



 C.



 D.





Câu 108. Vớigiátrịnàocủa

thìhaiđườngthẳng

: 2 – 4 1 0

d x y

 

và

 

3 1

x at

y a t

  







  





vuônggócvớinhau?

 

 B.



 C.

 

 D.



.

Câu 109. Vớigiátrịnàocủa

thìhaiđườngthẳng

2 2

x t

y t

  





 



và

 

6 1 2

x mt

y m t

 







   





trùngnhau?



. B.

 

. C.



. D.

 

.

Câu 110. Tìmtấtcảcácgiátrịcủa

đểhaiđườngthẳng

2 2

x t

y mt

 





 



và

: 4 3 0

d x y m

  

trùngnhau.

 

. B.



. C.



. D.



.

Câu 111. Vớigiátrịnàocủa

thìhaiđườngthẳng

: 2 4 0

d x y m

   

và

 

: 3 2 1 0

d m x y m

    

songsong?



 B.

 

 C.



 D.





Câu 112. Tìmtấtcảcácgiátrịcủa

đểhaiđườngthẳng

: 2 3 10 0

x my

   

và

: 4 1 0

mx y

   

cắtnhau.

1 10

 

. B.



. C. Khôngcó

. D. Vớimọi

.

Câu 113. Vớigiátrịnàocủa

thìhaiđườngthẳng

: 19 0

mx y

   



và

   

: 1 1 20 0

m x m y

     

vuônggóc?

A. Vớimọi

. B.



. C. Khôngcó

. D.

 

.

Câu 114. Vớigiátrịnàocủa

thìhaiđườngthẳng

:3 2 6 0

d mx y

  

và

 

: 2 2 6 0

d m x my

   

cắtnhau?

 

. B.



. C.



. D.

1 và 1

m m

  

.

Câu 115. Vớigiátrịnàocủa

thìhaiđườngthẳng

: 2 3 10 0

d x y

  

và

2 3

1 4

x t

y mt

 





 



vuônggóc?



. B.



. C.

 

. D.

 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 14

Câu 116. Vớigiátrịnàocủa

thìhaiđườngthẳng

: 4 3 3 0

d x y m

  

và

1 2

x t

y mt

 





 



trùngnhau?

 

. B.



. C.

 

. D.



.

Câu 117. Vớigiátrịnàocủa

thìhaiđườngthẳng

:3 2 6 0

d mx y

  

và

 

: 2 2 3 0

d m x my

   

songsong?

1; 1.

m m

  

 B.



. C.



. D.

 

.

Câu 118. Vớigiátrịnàocủa

thìhaiđườngthẳng

 

8 1

x m t

y t

  







 





và

: 2 14 0

d mx y

  

songsong?







 



. B.



. C.

 

. D.



.

Câu 119. Vớigiátrịnàocủa

thìhaiđườngthẳng

 

: 3 2 1 0

d m x y m

    

và

: 2 1 0

d x my m m

     

cắtnhau?



. B.











. C.



. D.











.

Câu 120. Vớigiátrịnàocủa

thìhaiđườngthẳng

 

1 1

x m t

y m t

 









  





và

x mt

y m t

 







 



trùngnhau?

A. Khôngcó

. B.



. C.



. D.

 

.

Câu 121. Tìmtọađộgiaođiểmcủahaiđườngthẳng

7 3 16 0

x y

  

và

10 0

 

.

 

10; 18

 

. B.

 

10;18

. C.

 

10;18



. D.

 

10; 18



.

Câu 122. Tìmtoạđộgiaođiểmcủahaiđườngthẳng

3 4

2 5

x t

y t

  





 



và

1 4

: .

7 5

x t

y t



 







 





 

1;7 .

 B.

 

3;2 .



 C.

 

2; 3 .

 D.

 

5;1 .



Câu 123. Chohaiđườngthẳng

 : 2 3 19 0

d x y

  

và

22 2

 :

55 5

x t

y t

 





 



.Tìmtoạđộgiaođiểmcủahaiđường

thẳngđãcho.

 

2;5 .

 B.

 

10;25 .

 C.

 

1;7 .



 D.

 

5;2 .



Câu 124. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđiểm

   

–2;0 ,  1;4

A B

vàđườngthẳng :

x t

y t

 





 



.Tìmtọađộgiaođiểmcủađườngthẳng

và

.

 

2;0

. B.

 

–2;0

. C.

 

0;2

. D.

 

0; – 2

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 15

Câu 125. Xácđịnh

đểhaiđườngthẳng

: 3 – 4 0

d ax y

 

và

3 3

x t

y t

  





 



cắtnhautạimộtđiểmnằm

trêntrụchoành.



 B.

 

 C.



 D.

 



Câu 126. Tìmtấtcảcácgiátrịcủathamsố

đểhaiđườngthẳng

: 4 3 – 0

d x my m

 

và

6 2

x t

y t

 





 



cắt

nhautạimộtđiểmthuộctrụctung.



hoặc

 

. B.



hoặc



.



hoặc

 

. D.



hoặc



.

Câu 127. Chobađườngthẳng

:3 – 2 5 0

d x y

 

,

: 2 4 – 7 0

d x y

 

,

:3 4 –1 0

d x y

 

.Phươngtrìnhđường

thẳng

điquagiaođiểmcủa

và

,vàsongsongvới

là:

24 32 – 53 0

x y

 

. B.

24 32 53 0

x y

  

.

24 – 32 53 0

x y

 

. D.

24 – 32 – 53 0

x y



.

Câu 128. Lập phương trình của đường thẳng



 đi qua giao điểm của hai đường thẳng

: 3 1 0

d x y

  

,

: 3 5 0

d x y

  

vàvuônggócvớiđườngthẳng

: 2 7 0

d x y

  

.

3 6 5 0

x y

  

. B.

6 12 5 0

x y

  

.

6 12 10 0

x y

  

. D.

2 10 0

x y

  

.

Câu 129. Trongmặtphẳngvớihệtọađộ

Oxy

,chobađườngthẳnglầnlượtcóphươngtrình

:3 4 15 0

d x y

  

,

:5 2 1 0

d x y

  

và

 

: 2 1 9 13 0

d mx m y m

    

.Tìmtấtcảcácgiátrịcủathamsố

đểba

đườngthẳngđãchocùngđiquamộtđiểm.



 B.

 

 C.

 

 D.





Câu 130. Nếubađườngthẳng

 : 2 – 4 0

d x y

 

,

:5 – 2 3 0

d x y

 

và

: 3 – 2 0

d mx y

 



đồngquythì

nhậngiátrịnàosauđây?

 B.



 C.

12.

 D.

12.



Câu 131. Với giá trị nào của

 thì ba đường thẳng

:3 – 4 15 0

d x y

 

,

:5 2 –1 0

d x y

 

 và

: – 4 15 0

d mx y

 

đồngquy?

 

. B.



. C.



. D.

 

.

Câu 132. Vớigiátrịnàocủa

thìbađườngthẳng

: 2 –1 0

d x y

 

,

: 2 1 0

d x y

  

và

: – – 7 0

d mx y





đồngquy?

 

. B.



. C.

 

. D.



.

Câu 133. Đườngthẳng

:51 30 11 0

d x y

  

điquađiểmnàosauđây?

1; .

 

 

 

 

 B.

1; .

 



 

 

 C.

1; .

 

 

 

 D.

1; .

 

 

 

 



DẠNG4.GÓCCỦAHAIĐƯỜNGTHẲNG

Dạng4.1Tínhgóccủahaiđườngthẳngchotrước



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 16

Câu 134. (NGÔ GIA TỰ LẦN 1_2018-2019) Tính góc giữa hai đường thẳng

: 3 2 0

x y

   

 và

: 3 1 0

x y



   

.



. B.

120



. C.



. D.



Câu 135. Gócgiữahaiđườngthẳng

: 3 7 0

a x y

  

và

: 3 1 0

b x y

  

là:

30

. B.

90

. C.

60

. D.

45

.

Câu 136. Chohaiđườngthẳng

: 2 5 2 0

d x y

  

và

:3 7 3 0

d x y

  

.Góctạobởiđườngthẳng

và



bằng

. B.

135

. C.

. D.

.

Câu 137. Tìmcôsingócgiữahaiđườngthẳng

: 2 1 0

x y

   

và

x t

y t

 







 



. B.

. C.

. D.

3 10

.

Câu 138. Tìmgócgiữahaiđườngthẳng

: 2 15 0

x y

   

và

 

: .

4 2

 



 



 



x t

y t





. B.



. C.



. D.



.

Câu 139. Tìmcosingócgiữa

đườngthẳng

1 2

: 2 7 0, : 2 4 9 0

d x y d x y

     

.

. B.

. C.

. D.

.

Câu 140. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Tính góc giữa hai đường thẳng

: 3 2 0  ': 3 1 0

x y và x y

       

?

A. 90

. B. 120

. C. 60

. D. 30

.

Câu 141. Tínhgóctạobởigiữahaiđườngthẳng

: 2 10 0

d x y

  

và

: 3 9 0.

d x y

  



30 .

 B.

45 .

60 .

135 .



Câu 142. Tínhgóctạobởigiữahaiđườngthẳng

: 7 3 6 0

d x y

  

và

: 2 5 4 0.

d x y

  





. B.



. C.



. D.



.

Câu 143. Tínhgóctạobởigiữahaiđườngthẳng

: 2 2 3 5 0

d x y

  

và

: 6 0.

d y

 



30 .

 B.

45 .

60 .

90 .



Câu 144. Tínhgóctạobởigiữahaiđườngthẳng

: 3 0

d x y

 

và

.10 0

: xd

 



30 .

 B.

45 .

60 .

90 .



Câu 145. Tínhgóctạobởigiữahaiđườngthẳng

: 6 5 15 0

d x y

  

và

10 6

: .

1 5

x t

y t

 





 





30 .

 B.

45 .

60 .

90 .



Câu 146. Chođườngthẳng

: 2 7 0

d x y

  

và

: 2 4 9 0

d x y

  

.Tínhcosincủagóctạobởigiữahai

đườngthẳngđãcho.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 17



. B.

. C.

. D.

.

Câu 147. Chođườngthẳng

2 2 0

: x yd

  

và

:d x y

 

.Tínhcosincủagóctạobởigiữahaiđường

thẳngđãcho.

. B.

. C.

. D.

.

Câu 148. Chođườngthẳng

:10 5 1d x y

  

và

x t

y t

 





 



.Tínhcosincủagóctạobởigiữahaiđường

thẳngđãcho.

3 10

. B.

. C.

. D.

.

Câu 149. Chođườngthẳng

:3 4 1 0

d x y

  

và

15 12

1 5

x t

y t

 





 



.

Tínhcosincủagóctạobởigiữahaiđườngthẳngđãcho.

. B.



. C.

. D.

.

Dạng4.2Viếtphươngtrìnhđườngthẳngliênquanđếngóc



Câu 150. Xácđịnhtấtcảcácgiátrịcủa

đểgóctạobởiđườngthẳng

7 2

x at

y t

 





 





 

t 



vàđườngthẳng

3 4 2 0

x y

  

bằng

45



,

 

. B.



,

 

. C.

 

,

 

. D.



,



.

Câu 151. Đườngthẳng



điquagiaođiểmcủahaiđườngthẳng

: 2 3 0

d x y

  

và

: 2 1 0

d x y

  

đồng

thờitạovớiđườngthẳng

: 1 0

d y

 

mộtgóc

cóphươngtrình:

(1 2) 0

x y

  

hoặc

: 1 0

x y

   

. B.

: 2 0

x y

  

hoặc

: 4 0

x y

  

.

: 0

x y

  

hoặc

: 2 0

x y

   

. D.

: 2 1 0

  

hoặc

5 0.

 

.

Câu 152. Trongmặtphẳngvớihệtọađộ

Oxy

,cóbaonhiêuđườngthẳngđiquađiểm

 

2;0

vàtạovới

trụchoànhmộtgóc

45 ?



A. Códuynhất. B.

.

C. Vôsố. D. Khôngtồntại.

Câu 153. Đườngthẳng



tạovớiđườngthẳng

: 2 6 0

d x y

  

mộtgóc

.Tìmhệsốgóc

củađường

thẳng



.



hoặc

 

 B.



hoặc





 

hoặc

 

D.

 

hoặc





Câu 154. Biếtrằngcóđúnghaigiátrịcủathamsố

đểđườngthẳng

d y kx

tạovớiđườngthẳng

y x 



mộtgóc

.Tổnghaigiátrịcủa

bằng:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 18

8.

 B.

4.

 C.

1.

 D.

1.



Câu 155. Trong mặt phẳng tọa độ

Oxy

, cho điểm

 

1; 1



 và hai đường thẳng có phương trình

   

1 2

: 1 0, : 2 5 0

d x y d x y

     

.Gọi

làgiaođiểmcủahaiđườngthẳngtrên.Biếtrằngcó

haiđườngthẳng

 

điqua

cắthaiđườngthẳngtrênlầnlượttạihaiđiểm

,B C

saocho

ABC



làtamgiáccó

BC AB

códạng:

ax y b

  

và

cx y d

  

,giátrịcủa

T a b c d   

là



. B.



. C.

2T 

. D.



.

Câu 156. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiáccân

ABC

cócạnhđáy

: 3 1 0BC x y  

,cạnh

bên

: 5 0AB x y  

. Đường thẳng

 đi qua

( 4;1)M 

. Giả sử toạ độ đỉnh

 

,C m n

.Tính

T m n 

.



. B.

 

. C.



. D.

 

.

Câu 157. (Cụm liên trường Hải Phòng-L1-2019) Trong mặt phẳng Oxy, cho hai đường thẳng

 

:2 5 0

d x y

  

 và

 

: 3 0

d x y

  

 cắt nhau tại

. Phương trình đường thẳng đi qua

 

2;0



 cắt

   

1 2

d d

 tại

 và

 sao cho tam giác

IAB

 cân tại

 có phươngtrình dạng

2 0

ax by

  

.Tính

5T a b 

1T  

. B.



. C.



. D.

11T 

.

DẠNG5.KHOẢNGCÁCH

Dạng5.1Tínhkhoảngcáchtừ1điểmđếnđườngthẳngchotrước

Câu 158. Khoảngcáchtừđiểm

 

1;1

đếnđườngthẳng

5 12 6 0

x y

  

là

. B.

13

. C.

1

. D.

Câu 159. Khoảngcáchtừđiểm

 

5; 1



đếnđườngthẳng

3 2 13 0

x y

  

là:

2 13

. B.

. C.

. D.

.

Câu 160. (THPTĐoànThượng-HảiDương-HKI18-19)Khoảngcáchtừđiểm

(

1; )



đếnđườngthẳng

: 3 4 0

x y

   

là

. B.

3 10

. C.

. D.

2 10

.

Câu 161.

Trongmặtphẳng

Oxy

,khoảngcáchtừđiểm

 

3; 4



đếnđườngthẳng

: 3 4 1 0

x y

   



. B.

. C.

. D.



.

Câu 162. Khoảngcáchtừđiểm

( 3; 2)A 

đếnđườngthẳng

: 3 1 0x y   

bằng:

10.

 B.

11 5

 C.

10 5

 D.



Câu 163. Trongmặtphẳng

Oxy

,khoảngcáchtừgốctọađộ

đếnđườngthẳng

: 4 3 1 0

d x y

  

bằng

. B.

. C.

. D.

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 19

Câu 164. Mộtđườngtròncótâm

 

3; 2



tiếpxúcvớiđườngthẳng

: 5 1 0.

x y

   

Hỏibánkínhđường

trònbằngbaonhiêu?

 B.

 C.

26.

 D.



Câu 165. Trong mặt phẳng

Oxy

, khoảng cách từđiểm

 

0;4

 đến đường thẳng

 

: 4 2 0

x cos y sin sin

  

    

bằng

. B.

sin

. C.

cos sin  

. D.

.

Câu 166. Khoảngcáchtừ

(1; 2)



đếnđườngthẳng

: 3 4 26 0

x y

   

bằng

. B.

. C.

. D.

.

Câu 167. Khoảngcáchtừgiaođiểmcủahaiđườngthẳng

3 4 0

x y

  

và

2 3 1 0

x y

  

đếnđườngthẳng

:3 4 0

x y

   

bằng:

2 10

. B.

3 10

. C.

. D.

.

Câu 168. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

 

,1;2



 

0;3

và

 

4;0

.Chiều

caocủatamgiáckẻtừđỉnh

bằng:

. B.

. C.

. D.

.

Câu 169. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

có

 

3; 4 ,





 

1;5

và

 

3;1

.Tính

diệntíchtamgiác

ABC

.

10.

 B.

 C.

26.

 D.

2 5.



Câu 170. Khoảngcáchtừđiểm

 

0;3

đếnđườngthẳng

 

: cos sin 3 2 sin 0

x y

  

    

bằng:

 B. 6. C.

3sin .



 D.

cos sin

 





Câu 171. Khoảngcáchtừđiểm

 

2;0

M đếnđườngthẳng

1 3

2 4

x t

y t

 







 



bằng:

 B.

 C.

 D.



Câu 172. Khoảngcáchnhỏnhấttừđiểm

 

15;1

đếnmộtđiểmbấtkìthuộcđườngthẳng

2 3

x t

y t

 













bằng:

10.

 B.

 C.

 D.



Câu 173. Tìm tất cả các giá trị của tham số

 để khoảng cách từ điểm

 

1;2

A 

 đến đường thẳng

: 4 0

mx y m

    

bằng

2 5

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 20



 B.

 









. C.

 

. D. Khôngtồntại

.

Câu 174. Tìmtấtcảcácgiátrịcủathamsố

đểkhoảngcáchtừgiaođiểmcủahaiđườngthẳng

x t

y t







 





và

: 2 0

d x y m

  

đếngốctoạđộbằng

.

 









 B.

 





 



 C.











 D.







 





Câu 175. Đườngtròn

 

cótâmlàgốctọađộ

 

0;0

vàtiếpxúcvớiđườngthẳng

:8 6 100 0

x y

   

.

Bánkính

củađườngtròn

 

bằng:

4R 

. B.



. C.



. D.



.

Câu 176. Đườngtròn

 

cótâm

 

2; 2

 

vàtiếpxúcvớiđườngthẳng

:5 12 10 0

x y

   

.Bánkính



củađườngtròn

 

bằng:

R 

. B.

R 

. C.

44R 

. D.



.

Câu 177. Cho đường thẳng

: 21 11 10 0.

d x y

  

 Trong các điểm

 

21; 3



,

 

0;4

,

 

19;5

P 

 và

 

1;5

điểmnàogầnđườngthẳng

nhất?

. B.

. C.

. D.

.

Câu 178. Chođườngthẳng

: 7 10 15 0.

d x y

  

Trongcácđiểm

 

1; 3



,

 

0;4

,

 

19;5

P 

và

 

1;5



điểmnàocáchxađườngthẳng

nhất?

. B.

. C.

. D.

.

Câu 179. Khoảngcáchgiữahaiđườngthẳngsongsong

: 6 – 8 3 0

x y

  

và

:3 – 4 – 6 0

x y

 

bằng:

. B.

. C.

. D.

.

Câu 180. Tínhkhoảngcáchgiữahaiđườngthẳng

: 7 3 0

d x y

  

và

:

2 7

x t

y t

  







 



.

3 2

. B.

. C.

. D.

.

Câu 181. Khoảngcáchgiữahaiđườngthẳngsongsong

: 6 – 8 101 0

d x y

 

và

:3 – 4  0

d x y



bằng:

10,1

. B.

1,01

. C.

101

. D.

101

.

Dạng5.2Phươngtrìnhđườngthẳngliênquanđếnkhoảngcách



Câu 182. Chohaiđiểm

   

3;1 , 4;0

A B

.Đườngthẳngnàosauđâycáchđều

và

2 2 3 0.

x y

   

2 2 3 0.

x y

  

2 3 0.

x y

  

 D.

2 2 3 0.

x y

  



Câu 183. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđiểm

 

2;3

và

 

1;4

.Đườngthẳngnàosauđây

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 21

cáchđềuhaiđiểm

và

?

2 0.

x y

  

 B.

2 0.

x y

 

 C.

2 2 10 0.

x y

  

 D.

100 0.

x y

  



Câu 184. Trongmặtphẳngvớihệtọađộ

Oxy

,chobađiểm

 

,0;1



 

12;5

và

 

3;0 .

C 

Đườngthẳng

nàosauđâycáchđềubađiểm



và

.

3 4 0

x y

  

. B.

10 0

x y

   

. C.

x y

 

. D.

5 1 0

x y

  

.

Câu 185. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm

 

,1;1



 

2;4

B 

 và đường thẳng

: 3 0

mx y

   

.Tìmtấtcảcácgiátrịcủathamsố

để



cáchđềuhaiđiểm

,A B

.







 



 B.

 









 C.

 









 D.







 





Câu 186. Đườngthẳng



songsongvớiđườngthẳng

:3 4 1 0

d x y

  

vàcách

mộtkhoảngbằng

có

phươngtrình:

3 4 6 0

x y

  

hoặc

3 4 4 0

x y

  

.

3 4 6 0

x y

  

hoặc

3 4 4 0

x y

  

.

3 4 6 0

x y

  

hoặc

3 4 4 0

x y

  

.

3 4 6 0

x y

  

hoặc

3 4 4 0

x y

  

.

Câu 187. Tậphợpcácđiểmcáchđườngthẳng

:3 4 2 0

x y

   

mộtkhoảngbằng

làhaiđườngthẳngcó

phươngtrìnhnàosauđây?

3 4 8 0

x y

  

hoặc

3 4 12 0

x y

  

.

3 4 8 0

x y

  

hoặc

3 4 12 0

x y

  

.

3 4 8 0

x y

  

hoặc

3 4 12 0

x y

  

.

3 4 8 0

x y

  

hoặc

3 4 12 0

x y

  

.

Câu 188. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđườngthẳng

:5 3 3 0

d x y

  

và

:5 3 7 0

d x y

  



songsongnhau.Đườngthẳngvừasongsongvàcáchđềuvới

1 2

, d d

là:

5 3 2 0.

x y

  

 B.

5 3 4 0.

x y

  



5 3 2 0.

x y

  

 D.

5 3 4 0.

x y

  



Câu 189. Trênhệtrụctọađộ

Oxy

,chohìnhvuông

ABCD

.Điểm

thuộccạnh

saocho 

 

MC DM

,

 

0; 2019

làtrungđiểmcủacạnh

,

làgiaođiểmcủahaiđườngthẳng

và

.Biết

đườngthẳng

cóphươngtrình

  10 2018 0

x y

.Khoảngcáchtừgốctọađộ

đếnđường

thẳng

bằng

2019

. B.

2019 101

. C.

2018

. D.

2019 101

101

.

Câu 190.

Trongmặtphẳngtọađộ

Oxy

,gọi

làđườngthảngđiqua

(4;2)

vàcáchđiểm

(1;0)

khoảng

cách

3 10

.Biếtrằngphươngtrìnhđườngthẳng

códạng

x by c

  

với

,b c

làhaisốnguyên.

Tính

.b c



. B.

. C.

1.

 D.

5

.

Câu 191. (TH&TT LẦN 1 – THÁNG 12) Trong mặt phẳng với hệ tọa độ

,Oxy

 cho đường thẳng

 

: 1 0

x m y m

    

(

làthamsốbấtkì)vàđiểm

 

5;1

.Khoảngcáchlớnnhấttừđiểm



đến



bằng

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 22

2 10

. B.

. C.

4 10

. D.

3 10

.

Câu 192. ChuyênLêHồngPhong-NamĐịnhĐườngthẳng

12 5 60

x y

 

tạovớihaitrụctoạđộmộttam

giác.Tổngđộdàicácđườngcaocủatamgiácđólà

. B.

281

. C.

360

. D.

.

Câu 193. Trênmặtphẳngtọađộ

Oxy

,chocácđiểm

 

1; 1



và

 

3;4

.Gọi

 

làmộtđườngthẳngbấtkì

luônđiquaB. KhikhoảngcáchtừAđếnđườngthẳng

 

đạtgiátrịlớnnhất,đườngthẳng

 



cóphươngtrìnhnàodướiđây?

1 0

x y

  

. B.

3 4 25

x y

 

. C.

5 2 7 0

x y

  

. D.

2 5 26 0

x y

  

.

DẠNG6.XÁCĐỊNHĐIỂM

Dạng6.1Xácđịnhtọahìnhchiếu,điểmđốixứng



Câu 194. Chođườngthẳng

:3 5 15 0

d x y

  

.Trongcácđiểmsauđây,điểmnàokhôngthuộcđườngthẳng

 

5;0

. B.

 

5;6

M 

. C.

 

0;3

. D.

 

5;3

.

Câu 195. Trongmặtphẳngvớihệtrụctọađộ

Oxy

,chotamgiác

ABC

có

 

4;3

,

 

2;7

,

 

3; 8

 

.Tọa

độchânđườngcaokẻtừđỉnh

xuốngcạnh

là:

 

1;4



. B.

 

1; 4

. C.

 

1;4

. D.

 

4;1

.

Câu 196. Chođườngthẳng

: 3 5 0

d x y

   

vàđiểm

 

2;1

M 

.Tọađộhìnhchiếuvuônggóccủa

trên



là

7 4

;

5 5

 



 

 

. B.

7 4

;

5 5

 



 

 

. C.

7 4

;

5 5

 

 

 

 

. D.

5 4

;

7 5

 



 

 

.

Câu 197. Toađôhinhchiêuvuônggoccuađiêm

 

1;2

lênđươngthăng

: 0

x y

  

la

3 3

;

2 2

 

 

 

. B.

 

1;1

. C.

 

2;2

. D.

3 3

;

2 2

 

 

 

 

.

Câu 198. Trongmặtphẳngtọađộ

Oxy

,chotamgiác

ABC

vớiđỉnh

 

2;4

,trọngtâm

 













 

.Biếtrằng

đỉnh

nằmtrênđườngthẳng

 

cóphươngtrình

2 0

x y

  

vàđỉnh

cóhìnhchiếuvuông

góctrên

 

làđiểm

 

2; 4



.Giảsử

 

;B a b

,khiđó

3T a b 

bằng

4T 

. B.

2T  

. C.

2T 

. D.



Câu 199. Trong mặt phẳng tọa độ

Oxy

, cho hình chữ nhật

ABCD

 có điểm

 thuộc đường thẳng d:

2 5 0

x y

  

vàđiểm

( 4;8)



.Gọi

đốixứngvới

qua

,điểm

(5; 4)



làhìnhchiếu

vuônggóccủa

lênđườngthẳng

.Biếttọađộ

( ; )C m n

,giátrịcủa

m n

là

. B.

6

. C.

. D.

Dạng6.2Xácđịnhđiểmliênquanđếnyếutốkhoảngcách,góc

Câu 200. Chohaiđiểm

   

3; 1 , 0;3

A B

.Tìmtọađộđiểm

thuộc

saokhoảngcáchtừ

đếnđường

thẳng

bằng

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 23

 

 

 

và

 

1;0

. B.

 

13;0

 

4;0

. D.

 

2;0

.

Câu 201. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm

 

1;1

,

 

4; 3



 và đường thẳng

: 2 1 0

d x y

  

.Tìmđiểm

thuộc

cótọađộnguyênvàthỏamãnkhoảngcáchtừ

đến

đườngthẳng

bằng

.

 

3;7 .

 B.

 

7;3 .

 C.

 

43; 27 .

M  

 D.

3;M

 

 

 





Câu 202. Trongmặtphẳngvớihệtọađộ

Oxy

,chođiểm

 

0;1

vàđườngthẳng

x t

 





 



.Tìmđiểm

thuộc

vàcách

mộtkhoảngbằng

,biết

cóhoànhđộâm.

 

4;4 .

 B.

 

4;4

24 2

;

5 5





 



 

 



 



 C.

24 2

; .

5 5

 

 

 

 

 D.

 

4;4 .

M 



Câu 203. Biếtrằngcóđúnghaiđiểmthuộctrụchoànhvàcáchđườngthẳng

: 2 5 0

x y

   

mộtkhoảng

bằng

2 5

.Tíchhoànhđộcủahaiđiểmđóbằng:



 B.



 C.

225



 D. Đápsốkhác.

Câu 204. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđiểm

 

3; 1



và

 

0;3

.Tìmđiểm

thuộctrục

hoànhsaochokhoảngcáchtừ

đếnđườngthẳng

bằng

.

 

1;0



 

 



 





 B.



 

 



 



 



 

 



 C.

 

1;0



 



 



 







 D.



 



 



 



 





 

 





Câu 205. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđiểm

 

3;0

và

 

0; 4



.Tìmđiểm

thuộctrục

tungsaochodiệntíchtamgiác

MAB

bằng



 

0;0

0; 8











 B.

 

0; 8 .



 C.

 

6;0 .

 D.

 

0;0

0;6









Câu 206. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđườngthẳng

:3 2 6 0

x y

   

và

:3 2 3 0

x y

   

.Tìmđiểm

thuộctrụchoànhsaocho

cáchđềuhaiđườngthẳngđãcho.

0; .

 

 

 

 B.

;0 .

 

 

 

 C.

;0 .

 



 

 

 D.

 

2;0 .

M 

Câu 207. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđiểm

 

2;2 ,

A 



 

4; 6



vàđườngthẳng :

1 2

x t

y t







 



.Tìmđiểm

thuộc

saocho

cáchđềuhaiđiểm

, .A B



 

3;7 .

 B.

 

3; 5 .

 

 C.

 

2;5 .

 D.

 

2; 3

 



Câu 208. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm

 

1;2 ,

A 



 

3;2

B 

 và đường thẳng

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 24

: 2 3 0

d x y

  

.Tìmđiểm

thuộc

saochotamgiác

ABC

cântại



 

2; 1 .

 

 B.

;0 .

 



 

 

 C.

 

1;1 .

C 

 D.

 

0;3



Câu 209. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđiểm

 

1;2 ,



 

0;3

vàđườngthẳng

: 2

d y



.Tìm

điểm

thuộc

saochotamgiác

ABC

cântại



 

1;2 .

 B.

 

4;2 .

 C.

 

1;2











 D.

 

1;2 .

C 



Câu 210. Trongmặtphẳngvớihệtọađộ

Oxy,

giảsửđiểm

( ; )A a b

thuộcđườngthẳng

: 3 0

d x y

  

vàcách

: 2 1 0

x y

   

mộtkhoảngbằng

Tính

P ab

biết





 B.

2

 C.

 D.

4.



Câu 211. Trongmặtphẳng

Oxy

,chobiếtđiểm

 

;M a b



 



thuộcđườngthẳng

x t

y t

 





 



vàcách

đườngthẳng

:2 3 0

x y

   

mộtkhoảng

2 5

.Khiđó

a b

là.

. B.

. C.

.

Câu 212. Điểm

 

;A a b

thuộcđườngthẳng

x t

y t

 





 



vàcáchđườngthẳng

: 2 3 0

x y

   

mộtkhoảng

bằng

2 5

và



.Tính

.P a b

 

. B.



. C.

132



. D.

132

 

.

Câu 213. (ChuyênLamSơn-KSCL-lần2-2018-2019)Trongmặtphẳngtọađộ

O xy

,chođiểm

 

1;2

và

đườngthẳng

 

:2 5 0

d x y

  

.Biếtrằngcóhaiđiểm

1 2

,M M

thuộc(d)saocho

1 2

IM IM 

.Tổngcáchoànhđộcủa

và

là

 B.

. C.

 D.



Câu 214. Tronghệtọađộ

Oxy

cho

 

1;1

,

 

4; 3



.Gọi

 

;C a b

thuộcđườngthẳng

: 2 1 0

d x y

  

sao

chokhoảngcáchtừ

đếnđườngthẳng

bằng6.Biếtrằng

cóhoànhđộnguyên,tính

a b

a b

 

. B.

a b

 

. C.

a b

 

. D.

a b

  

Dạng6.3Xácđịnhđiểmliênquanđếnyếutốcựctrị



Câu 215. Trongmặtphẳngtọađộ

Oxy

cho

: 1 0

x y

   

vàhaiđiểm

   

2; 1 , 9; 6 .

A B

Điểm

 

;M a b



nằmtrênđường



saocho

MA MB

nhỏnhất.Tính

.a b

7.

 B.

9.

 C.

 D.



Câu 216. Trongmặtphẳngvớihệtọađộ

Oxy

,chođườngthẳng

: 4 15 0d x y  

vàđiểm

 

2; 0

.Tìm

tọađộđiểm

thuộc

đểđoạn

cóđộdàinhỏnhất.

 

15; 0

M 

. B.

 

5; 5

. C.

 

0; 3

. D.

 

1; 4

.

Câu 217. (YênĐịnh1-ThanhHóa-2018-2019)Cho3điểm

( 6;3); (0; 1); (3;2)

A B C

 

.Tìm

trên

đườngthẳng

: 2 3 0

d x y

  

mà

MA MB MC

 

  

nhỏnhấtlà

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 25

13 71

;

15 15

 

 

 

13 19

;

15 15

 

 

 

26 97

;

15 15

 

 

 

13 19

;

15 15



 

 

 

Câu 218. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

cóđỉnh

 

2;2

,

 

1; 3



,

 

2;2

C 

.

Điểm

thuộctrụctungsaocho

MA MB MC

 

  

nhỏnhấtcótungđộlà?

. B.

. C.



. D.

.

Câu 219. TrongmặtphẳngtọađộOxycho

: x y 1 0   

vàhaiđiểm

(2;1)

,

(9;6)

.Điểm

( ; )M a b

nằm

trênđường



saocho

MA MB

nhỏnhất.Tính

a b

tađượckếtquảlà:

A. -9

.

B. 9. C. -7. D. 7

Dạng 6.4 Một số bài toán tổng hợp

Câu 220. Trongmặtphẳngvớihệtrụctọađộ

Oxy

,chohìnhvuông

ABCD

.Gọi

làtrungđiểmcủacạnh

,

làđiểmtrêncạnh

saocho

CN ND

.Giảsử

11 1

;

2 2

 

 

 

vàđườngthẳng

có

phươngtrình

2 3 0

x y

  

.Tìmtọađộđiểm

 

1; 1



hoặc

 

4; 5



. B.

 

1; 1



hoặc

 

4; 5

 

 

1; 1



hoặc

 

4;5

. D.

 

1;1

hoặc

 

4;5

Câu 221. Trong mặt phẳng với hệ tọa độ

Oxy

, cho điểm

 

1; 1



 và hai đường thẳng

1 2

: 3 0, : 2 6 0

d x y d x y

     

.Haiđiểm

,A B

lầnlượtthuộchaiđườngthẳng

1 2

,d d

saocho

làtrungđiểmcủađoạnthẳng

.Đườngthẳng

cómộtvéctơchỉphươnglà

 

1;2

u 



. B.

 

2;1

u 



. C.

 

1; 2

 



. D.

 

2; 1

 



.

Câu 222. (TH&TTLẦN1–THÁNG12)Trongmặt phẳngtọađộ

Oxy

,chođiểmhaiđiểm

 

4;2

A 

,

 

2;6

vàđiểmCnằmtrênđườngthẳng

5 1

3 2

x y

 





saocho

CA CB

.Khiđótọađộđiểm

Clà

2 8

;

5 5

 

 

 

. B.

1 12

;

5 5

 



 

 

. C.

1 11

;

5 5

 

 

 

. D.

2 9

;

5 5

 

 

 

Câu 223. Trongmặtphẳngvớihệtọađộ

Oxy

,cho

   

3;5 , 1;3

A B

vàđườngthẳng

:2 1 0

d x y

  

,đường

thẳng

cắt

tại

.Tínhtỉsố

.

A. 6. B. 2. C. 4. D. 1.

Câu 224. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

cóđỉnh

 

2;1

,

 

2; 3



 

2; 1

 

.

Trựctâm

củatamgiác

ABC

cótọađộ

 

;a b

.Biểuthức

3 2S a b 

bằngbaonhiêu?

. B.

. C.

. D.

1

.

Câu 225. Trongmặtphẳngvớihệtọađộ

Oxy

,chohaiđiểm

 

2;3

B 

và

 

3; 2



.Điểm

 

;I a b

thuộc



sao cho với mọi điểm

 không nằm trên đường thẳng

 thì

2 3

5 5

MI MB MC

 

  

. Tính

2 2

S a b 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 26

. B.

. C.

. D.

.

Câu 226. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

cóđỉnh

 

2;2

vàtrungđiểmcủa

là

 

1; 2

 

.Điểm

 

;M a b

thỏamãn

2 0

MA MB MC

  

   

.Tính

S a b 

.

. B.

. C.



. D.

.

Câu 227. (ĐỀTHITHỬĐỒNGĐẬU-VĨNHPHÚCLẦN01-2018–2019)TrongmặtphẳngtọađộOxy,

chotamgiácABCcó

 

2;1

,đườngcao

cóphươngtrình

3 7 0x y  

vàtrungtuyến



cóphươngtrình

1 0x y  

.Tìmtọađộđỉnh

?

 

1;0

. B.

 

4; 5

. C.

 

1; 2

. D.

 

1; 4

.

Câu 228. Trongmặtphẳngtọađộ

Oxy

,chohìnhvuông

ABCD

;cácđiểm

,

lầnlượtlàtrungđiểm

của

,

;

cắt

tạiđiểm

 

5;2

.Biết

11 11

;

2 2

 

 

 

vàđiểm

cóhoànhđộâm.

Tọađộđiểm

và

là:

 

2;3

A 

và

 

3;8

. B.

 

2;3

A 

và

 

3;8

D 

 

2;3

A 

và

 

3; 8



. D.

 

2; 3

 

và

 

3;8

.

Câu 229. Tronghệtrụctọađộ

Oxy

,chotamgiác

ABC

có

 

4;1

B 

,trọngtâm

 

1;1

vàđườngthẳngphân

giáctronggóc

cóphươngtrình

: 1 0

d x y

  

.Biếtđiểm

 

;A m n

.Tínhtích

.m n

.

. 20

m n



. B.

. 12

m n



. C.

. 12

m n

 

. D.

. 6

m n



.

Câu 230. Trênmặtphẳng

Oxy

,chohìnhvuông

ABCD

.Gọi

làtrungđiểmcủacạnh

,

làđiểm

trên cạnh

 sao cho

CN ND

. Giả sử

11 1

;

2 2

 

 

 

 và đường thẳng

 có phương trình

2 3 0

x y

  

.Gọi

 

;P a b

làgiaođiểmcủa

và

.Giátrị

a b

bằng

Câu 231. Cho

ABC

vuôngtạiA,điểmMthuộccạnhAC,saocho

AB AM

,đườngtròntâmIđường

kínhCMcắtBMtạiD,đườngthẳngCDcóphươngtrình

3 6 0

x y

  

.BiếtđiểmI(1;-1),điểm

 

 

 

thuộcđườngthẳngBC,

 

.GọiBlàđiểmcótọađộ(a, b).Khiđó:

1a b 

. B.

a b

 

. C.

a b

  

. D.

a b

 

.

Câu 232. (THUẬNTHÀNHSỐ2LẦN1_2018-2019)Trênmặtphẳng

Oxy

,chohìnhvuông

ABCD

.Gọi

làtrungđiểmcủacạnh

,

làđiểmtrêncạnh

saocho

CN ND

.Giảsử

11 1

;

2 2

 

 

 



vàđườngthẳng

cóphươngtrình

2 3 0

x y

  

.Gọi

 

;P a b

làgiaođiểmcủa

và

.

Giátrị

a b

bằng:

. B.

. C.

. D.

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 27

Câu 233. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

cóđỉnh

( 12;1)



,đườngphângiáctrong

củagóc

cóphươngtrình

: 2 5 0

d x y

  

.

1 2

;

3 3

 













 

làtrọngtâmtamgiác

ABC

.Đườngthẳng

quađiểmnàosauđây?

 

1;0

. B.

 

2; 3

. C.

 

4; 4

. D.

 

4;3

.

Câu 234. Tronghệtọađộ

,Oxy

chotamgiác

ABC

cóphươngtrìnhđườngthẳng

: 7 13 0.

BC x y

  

Các

chânđườngcaokẻtừ

,B C

lầnlượtlà

   

2;5 , 0;4 .

E F

BiếttọađộđỉnhAlà

 

; .A a b

Khiđó:

a b

 

. B.

2 6

a b

 

. C.

2 6

a b

 

. D.

b a

 



Câu 235. (THPTĐôngSơn1-ThanhHóa-Lần2-Nămhọc2018-2019)Trongmặtphẳngtọađộvới

hệtọađộ

Oxy

,chohìnhchữnhật

ABCD

cóđiểm

 

1;2

làhìnhchiếuvuônggóccủa

lên

.Điểm

 

 

 

làtrungđiểmcạnh

.Phươngtrìnhđườngtrungtuyếnkẻtừđỉnh

củatam

giác

ADH

là

4 4 0

x y

  

.Biếtđiểm

cótọađộlà

 

;

D D

x y

tínhgiátrịbiểuthức

2 2

D D

S x y 

.



. B.



. C.



. D.



.

Câu 236. Chotamgiác

ABC

.Tìmtọađộcácđỉnhcủatamgiácbiếtphươngtrìnhcạnh

: 2 0

BC x y

  

;

haiđườngcao

': 3 0

BB x

 

và

': 2 3 6 0

CC x y

  

?

(1; 2); (0;2); (3; 1)

A B C



. B.

(1; 2); (3; 1); (0;2)

A B C



.

(1; 2); (3; 1); (0;2)

A B C

 

. D.

(2;1); (3; 1); (0;2)

A B C



.

Câu 237. Trongmặtphẳngtọađộ

Oxy

,chotamgiác

ABC

có

     

3 0 3 0 2 6A ; ,B ; ,C ;



.Gọi

 

H a;b

là

trựctâmcủatamgiác

ABC

.Tính

6ab



A. 10. B.

. C. 60. D. 6.

Câu 238. Trong mặt phẳng tọa độ (Oxy), cho hình chữ nhật ABCD có điểm C thuộc đường thẳng

: 2 5 0

d x y

  

vàđiểm

 

4;8

A 

.GọiMlàđiểmđốixứngvớiBquaC,điểm

 

5; 4



làhình

chiếuvuônggóccủaBlênđườngthẳngMD. Biếttọađộ

 

;C m n

,giátrịcủa

m n

là:

. B.

6

. C.

. D.

.

Câu 239. Trongmặtphẳngtọađộ

Oxy

,chotứgiác

ABCD

nộitiếpđườngtrònđườngkính

.Gọi

,

lầnlượtlàhìnhchiếuvuônggóccủa

lên

và

;gọi

làgiaođiểmcủa

và

.

Biếtđườngthẳng

cóphươngtrình

1 0

x y

  

 

0;4

 

2;2

vàhoànhđộđiểm

nhỏ

hơn

.Tìmtọađộcácđiểm

.

5 3

;

2 2

 

 

 

 

0; 1



,

 

4;1

.

5 3

;

2 2

 

 

 

 

0; 1



,

 

1;4

B 

.

5 3

;

3 2

 

 

 

 

0; 1



,

 

1;4

B 

.

5 3

;

2 2

 

 

 

 

1;0

A 

,

 

4;1

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 28

Câu 240. (KSNLGV-THUẬNTHÀNH2-BẮCNINHNĂM2018-2019)Trongmặtphẳngvớihệtrục

tọa độ

Oxy

, cho tam giác

ABC

 cân tại

, phương trình đường thẳng

AB,AC

 lần lượt là

5 2 0 5 14 0

x y ,x y

     

.Gọi

làtrungđiểmcủa

,

làtrungđiểmcủa

,

9 8

5 5

M ;

 

 

 



làhìnhchiếuvuônggóccủa

trên

.Tính

.

OC 

.

OC 

.



.

OC 

.

Câu 241. Trongmặtphẳngvớihệtọađộ

Oxy

,chotamgiác

ABC

cóchânđườngcaohạtừđỉnh

là

17 1

;

5 5

 



 

 

,chânđườngphângiáctronggóc

là

 

5;3

vàtrungđiểmcủacạnh

là

 

0;1

.Tìmtọađộđỉnh

.

 

2;9

C 

. B.

 

9;11

. C.

 

9; 11

 

. D.

 

2; 10

C 

.

DẠNG7.MỘTSỐBÀITOÁNLIÊNQUANĐẾNDIỆNTÍCH



Câu 242. (THPTQuỳnhLưu-NghệAn-2019)Đườngthẳng

:5 3 15

x y

  

tạovớicáctrụctọađộmột

tamgiáccódiệntíchbằngbaonhiêu?

7,5

. B.

. C.

. D.

.

Câu 243. Chohaiđườngthẳng

1 2

: 4; : 4

d y mx d mx

   

.Gọi

làtậphợpcácgiátrịnguyêndươngcủa

đểtamgiáctạothànhbởi

1 2

,d d

vàtrụchoànhcódiệntíchlớnhơn

.Sốphầntửcủatập

là

. B.

. C.

. D.

.

Câu 244. Tìmphươngtrìnhđườngthẳng

: .d y ax b 

Biếtđườngthẳng

điquađiểm

 

1;3

vàtạovới

haitia

,Ox Oy

mộttamgiáccódiệntíchbằng

 

9 72 72 6

y x

   

. B.

 

9 72 72 6

y x

   

.

3 6

y x

 

. D.

3 6.

y x

  



Câu 245. ChuyênLêHồngPhong-NamĐịnhChotamgiác

ABC

có

 

1; 3



,

 

0;2

,

 

2;4

C 

.Đường

thẳng



điqua

vàchiatamgiác

ABC

thànhhaiphầncódiệntíchbằngnhau.Phươngtrìnhcủa



là

2 7 0

x y

  

. B.

2 0

x y

  

. C.

3 10 0

x y

  

. D.

3 0

x y

 

.

Câu 246. Trongmặtphẳng

Oxy

,chođiểm

 

2;1

.Đườngthẳng

điqua

,cắtcáctia

,

lầnlượttại

và

(

,A B

khác

)saochotamgiác

OAB

códiệntíchnhỏnhất.Phươngtrìnhđườngthẳng

là.

2 3 0  

x y

. B.

2 0 

x y

. C.

2 4 0  

x y

. D.

1 0  

x y

.

Câu 247. (THIHK1LỚP11THPTVIỆTTRÌ2018-2019)Đườngthẳng

 

:  1, 0; 0

x y

d a b

a b

   



điqua

 

1;6

M 

tạovớitia

,Ox Oy

mộttamgiáccódiệntíchbằng4.Tính

2 .S a b 

  

5 7 5

 



. B.

 

. C.



. D.



.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 29

B.LỜIGIẢI

DẠNG1.XÁCĐỊNHVÉCTƠCHỈPHƯƠNG,VÉCTƠPHÁPTUYẾNCỦAĐƯỜNG

THẲNG,HỆSỐGÓCCỦAĐƯỜNGTHẲNG

Câu 1. ChọnD

Tacómộtvectơpháptuyếncủađườngthẳng

 

là

 

;n a b





.

Dođóchọnđápán D.

 

; .

a b

 





Câu 2. Chọn B.

cómộtvectơpháptuyếnlà

 

;n a b







phươngtrình

: 0

d ax by c

  

.

Nếu



thìđườngthẳng

: 0

d ax c

 

khôngcóhệsốgóc



khẳngđịnh1đúng.

Nếu



thìđườngthẳng

a c

d y x

b b

  

cóhệsốgóclà





khẳngđịnh2sai.

Với

 

; . 0

u b a u n u n     

    

u



làmộtvectơchỉphươngcủa



khẳngđịnh3đúng.

Chọn

 

0 0;0

k kn   



 khôngphảilàvectơpháptuyếncủa



khẳngđịnh4sai.

Vậycó2mệnhđềsai.

Câu 3. Chọn A.

Câu 4. ChọnC

Đườngthẳng

 

cómộtvéctơpháptuyếnlà

 

3;2

n 



nên

 

cómộtvéctơchỉphươnglà

 

2; 3

 



.

Câu 5. ChọnB

3 3

x t

y t



 









  



cómộtvectơchỉphươnglà

 

 

 

 



suyracómộtvectơpháptuyếnlà

 



 

 



.Dođóđườngthẳng



cũngcómộtvectơpháptuyếncótọađộ

 

6;1

.

Câu 6. ChọnA

MôtVTCPcuađươngthăng

la

 

1;2

u 







môtVTPTcua

la

 

2; 1

 



.

Câu 7. Chọn A.

Đườngthẳng

:

1 4

2 3

x t

y t

 





  



cóvectơchỉphươnglà

 

4;3

u  



Câu 8. ChọnA

Vector

(1;0)

i 



làmộtvectorchỉphươngcủatrục



Cácđườngthẳngsongsongvớitrục

có1vectorchỉphươnglà

(1;0)

u i 

 



Câu 9. ChọnC

Đườngthẳngd có1VTPTlà

 

7;3

n 



nêndcó1VTCPlà

 

3;7

u  



.

Câu 10. ChọnB

Véctơpháptuyếncủađườngthẳng

:

 

4; 6

  



.

Câu 11. ChọnD

Đườngthẳng

: 5 3 7 0

d x y

  

cóvectơpháptuyếnlà:

 

5;3 .

n 





Tacó:

. 0.

n n



 



d

cómộtvectơchỉphươnglà

 

3; 5 .

 





CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 30

Câu 12. ChọnA

Nếu





làmộtvéctơchỉphươngcủađườngthẳng





thì

. , 0

k u k

 



cũnglàvéctơchỉphương

củađườngthẳng



.

Từphươngtrìnhđườngthẳng





tathấyđườngthẳng





cómộtvéctơchỉphươngcótoạđộlà

 

2;1

.Dođóvéctơ

 

4; 2

 



khôngphảilàvéctơchỉphươngcủa



.

Câu 13. ChọnD

Tacó

   

4;2 2 2;1

AB  



suyravectơpháptuyếncủađườngthẳng

là

 

1;2

n  



.

Câu 14. ChọnC

Đườngthẳngd có1VTPTlà

 

7;3

n 



nêndcó1VTCPlà

 

3;7

u  



Câu 15. ChọnD

Đườngthẳng

: 2 2018 0

d x y

  

cóvectơpháptuyếnlà

 

1; 2





.

Câu 16. Chọn D.

 

: 2 1 0

d y x

  

2 1 0

x y

   

;

 

cóVTPTlà

 

2;1

n 



hay

 

2; 1

  



Câu 17. ChọnB

Mộtvéctơpháptuyếncủađườngthẳng

là

 

2; 1

 



.

Câu 18. ChọnD

Tathấyđườngthẳng

cómộtvectơpháptuyếnlà

 

2; 3

.Dođó

 

3;2

u 



làmộtvectơchỉ

phươngcủad.

Câu 19. ChọnA

+)Môtvectơphaptuyêncuađươngthăng



la

 

6; 2





nênvectơchiphươngcuađươngthăng



la

 

1;3



u .

Câu 20. ChọnB

 

4;2

MN  



.Dođóvectơchỉphươngcủa

là

 

4; 2

 



.

Câu 21. 

ChọnB

Đườngthẳng

: 2 1 0.

d x y

  

cóvectơpháptuyếnlà

(1; 2)

  



Vectơchỉphươngcủa

là

(2;1)

u 



.

Câu 22. ĐườngthẳngdcóVTCP:

 

2; 1u

 



VTPT

 

1;2



hoặc

 

3;6 .

n 



Chọn D.

Câu 23. ĐườngthẳngdcóVTPT:

 

4; 2n

 



VTCP

 

2;4



hoặc

 

1u 



Chọn C.

Câu 24. 

 

3; 4

3; 4 .

n u















 









 

Chọn D.

Câu 25. 

 

2; 5

u n













  

   

 





 

haychọn

 

2;5 .



 



Chọn C.

Câu 26. 

 

   

3; 4

3; 4 4;3 .

u u n

 











 

   





 



  

Chọn A.

Câu 27. 

 

   

2; 5

2; 5 5; 2 .

n u u

 







  

      













  

Chọn A.

Câu 28. ChọnC

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 31

Tacó

3 2018

:3 5 2018 0 :

5 5

d x y d y x      

,nên

cóhệsốgóc

 



Câu 29. ChọnA

Tacó

 

: 7 15 0

d x y

  

hay

1 15

7 7

y x

 



Suyrahệsốgóccủađườngthẳnglà



(đúng)

DẠNG2.VIẾTPHƯƠNGTRÌNHĐƯỜNGTHẲNGVÀCÁCBÀITOÁNLIÊNQUAN

Dạng2.1ViếtphươngtrìnhđườngthẳngkhibiếtVTPThoặcVTCP,HỆSỐGÓCvà1điểmđi

qua

Câu 30. ChọnD

Bốnphươngtrìnhđãchotrongbốnphươngánđềulàphươngtrìnhcủađườngthẳng.

Thaylầnlượttọađộcủa

,

vàotừngphươngántathấytọađộcủacà

và

đềuthỏa

phươngán

.

Câu 31. ChọnD

Vectơchỉphương

 

0;6

AB 



.

Phươngtrìnhđườngthẳng

điqua

vàcóvectochỉphương

 

0;6

AB 



là

1 6

y t







  



Câu 32. Chọn B.

Cách1:Thaytọađộcácđiểm

,

lầnlượtvàocácphươngtrìnhtrongcácphươngántrênthì

thấyphươngánBkhôngthỏamãn.

Cách2:NhậnthấyrằngcácphươngtrìnhởcácphươngánA,C,Dthìvectơchỉphươngcủacác

đườngthẳngđócùngphương,riêngchỉcóphươngánBthìkhông.Dođólựachọn B.

Câu 33. ChọnD

Đườngthẳngcóvéctơchỉphươnglà

 

3;5

MN 



vàđiqua

 

1; 2



nêncóphươngtrìnhthamsố

là

1 3

2 5

x t

y t

 





  



.

Câu 34. ChọnB

Tacó

   

9;3 3; 1 .

AB u

    

 



Suyraphươngtrìnhthamsốcủađườngthẳng

là

3 3

x t

y t

 





  



.

Câu 35. ChọnA

Tacó



songsongvới

nên

 

: 0 0

x y C C

    



qua

 

3;0

,suyra

3 0 0 3

C C

     

(nhận)

Nhưvậy

: 3 0

x y

   



Vậy



cóphươngtrìnhthamsố:

x t

y t







 



.

Câu 36. ChọnA

Đườngthẳng

 

9 2

x t

y t

 





  



9 2

t x

y t

 







  



 

9 2 5

y x

    

2 1 0

x y

   

.

Câu 37. Chọn C.

Tacóhìnhchiếucủađiểm

(1; 2)

lên

,Ox Oy

lầnlượtlàA(1;0)vàB(0;2).Dođóphương

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 32

trìnhđườngthẳngABlà

1 2 2 0

1 2

x y

     

.

Câu 38. Chọn.B.

3 5

3 1

: ( ) 4 5 17 0

1 4 1

5 4

x t

x y

d t x y

y t y









 



 



       

 

  











 

Đápán B.

Câu 39. Phươngtrìnhđoạnchắncủađườngthẳng

: 1.

x y

a b

 

Câu 40. ChọnD

Phươngtrìnhđườngthẳngđiquahaiđiểm

   

;0 , 0;M a N b



với



, 0

a b





là

x y

a b

 

Ápdụngphươngtrìnhtrêntachọnphươngán

.

Dạng2.2Viếtphươngtrìnhđườngthẳngđiquamộtđiểmvuônggóchoặcvớiđườngthẳngcho

trước

Câu 41. ChọnB

Do

 

2;3

d n  





Màđườngthẳng

điqua

 

1; 2



nêntacóphươngtrình:

   

2 1 3 2 0 2 3 4 0

x y x y

       

.

Vậyphươngtrìnhđườngthẳng

: 2 3 4 0

d x y

  

.

Câu 42. ChọnC

Vì



vuônggócvớiđườngthẳng

:8 6 7 0

d x y

  

nênphươngtrình

: 6 8 0

x y C

   



Mà



điquagốctọađộnêntacó:

6.0 8.0 0 0

C C

    

.

Vậyphươngtrình

: 6 8 0

x y

  

hay

: 3 4 0

x y

  



Câu 43. ChọnC

Gọi

 

làđườngthẳngcầntìm.Vì

 

songsongvớiđườngthẳng

3 5y x 

nên

 

có

phươngtrình

y x a 

,



.

Vì

 

điquađiểm

 

1;11

nêntacó

11 3 1 8

a a

    

.

Vậyphươngtrìnhđườngthẳng

 

cầntìmlà

3 8y x 

.

Câu 44.

ChọnB

Gọi

 



làđườngthẳngcầntìm.

+)

   

// : 3 4

d y x

  

.Suyraphươngtrình

 



códạng

y x b 

,



.

Có

 

2;5 5 6

A b   

  

(thoả



)

Vậy

 

: 3 1y x  

.

Câu 45. ChọnD

Dođườngthẳng

songsongvớiđườngthẳng

': 1 0

d x y

  

nênđườngthẳng

nhậnvéctơ

 

1;1

n 



làmvéctơpháptuyến.

Khiđóđườngthẳng

qua

 

1;1

vànhậnvéctơ

 

1;1

n 



làmvéctơpháptuyếncóphương

trìnhlà

2 0

x y

  

.

Câu 46. ChọnB

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 33

Tacóđườngthẳngvuônggócvới

2 4 0

x y

  

cóphươngtrình

2 0

x y m

  

,màđườngthẳng

nàyđiquađiểm

 

1;2

I 

,suyra

1 2.2 0 3

m m

      

.

Vậyđườngthẳngcầntìmcóphươngtrình

2 3 0

x y

  

.

Câu 47. ChọnA

Có

 

1;2

 



MN .

Đườngthẳng

 

điqua

 

 

 

nhận

 

1;2

 



MN làmvectơchỉphương:

 

: 2 1 0

 

   

 

 

d x y

 

2 2 0 1

   x y

.

Thửlại:thaytọađộcủa

vào

 

thìnghiệmđúng

 

.Suyraloại

 

.

Vậykhôngtồntạiđườngthẳngnhưđềbàiyêucầu.

Câu 48. GọidlàđườngthẳngquaBvàsongsongvớiAC. Tacó

 

   

 

5; 1 1. 5;1

0;3

x t

y t









 





 

 





    









Chọn A.

Câu 49. GọidlàđườngthẳngquaAvàsongsongvớiPQ.

Tacó:

 

   

4; 2 2 2;

3;2

3 2

A d

u P

x t

y t



 







 

 













   







   

1 2

: .

1;0

x t

d d t



 







   





 





Chọn C.

Câu 50. 

   

 

, 4;3

|| 4; 3

2;1

2 4

: .

1 3

AB CD

A AB u

AB CD u

x t

B t

y t







 



   

 







 

 













 

Chọn B.

Câu 51. Gócphầntư(I):

   

1;1 : .

x t

u u d t

y t

y VTCP





 



  



 







 





Chọn B.

Câu 52. 

     

: .

1;0 1;0 0; 7

Ox d

x t

u u dd

x t



 



     



 













 



 

Chọn D.

Câu 53. 

 

1;2

: 2 3 0

: 2 3 12 0

x y c c

x y



 



 

  







  













2.1 3.2 0 8.

c c

      

Vậy

: 2 3 8 0.

d x y

  

Chọn A.

Câu 54. 

 

0;0

6.0 4.0 0 0.

: 6 4 0 1

|| :6 4 1 0

d x

c c

x c



 

      

 





   

  







Vậy

:6 4 0 :3 2 0.

d x y d x y

    

Chọn A.

Câu 55. 

   

1;2 1;2

1 2.2 0 5.

: 2 3 0 : 2 0

d dM M

c c

x y d x y cd

 

 

 

      

 

      

 



 







Vậy

: 2 5 0.

d x y

  

Chọn D.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 34

Câu 56. Tacó:

 

   

2;3

2;3 3;2

:3 4 2 3 0 :3 2 6 0.

4; 3

A d

u n

x y x y

 



 

  







    

















     



 



Câu 57. 

 

   

0;3

:1 0 .

5;1

5 3 0

: 5 1

1;5

d d

u AC

x y x y

d AC



 







 



 









        











Câu 58. 

 

   

1; 2

1;0

:1 1

; 2

2 0 0 : 2 1 0

d x x

d y











         





 



















Chọn C.

Câu 59. 

 

   

 

3;5

5 5;

2;1

2 5

d d

y t





  







 

  

 









  

   











 

Chọn B.

Câu 60. 

 

   

 

3; 13

3; 1

3 13;3

1;2

1 13

d d

x t

n u





  







 

  

 













  

  







 

Chọn A.

Câu 61. 

 

2; 1

1;2

1 2





  







 

  

 









  

 













Chọn A.

Câu 62. 

 

2; 5

2; 5 0

2 5 0 3.

(I) 0

c c

d x y c c



  



 

  



         

 















Vậy

: 3 0.

d x y

  

Chọn B.

Câu 63. 

 

   

 

3; 1

: 0

3 1 0 4 .

II : 0

: 4 0

d x y c

d x y



 











 

  









     



   











Câu 64. 

 

     

 

II : 0 1;1

4;0 0;4

1;1

d d

x y n

x t

d t

y t





 



  



















 

   

  





 



 









CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 35

Câu 65. 

 

|| : 0

1;2

: 2

M d

d Ox y

d y







 











Chọn D.

Câu 66. 

 

6; 10

: 2

; 10

: 0 1;0

d Oy x u

x t





 





 





   



 

 

















 







Dạng2.3Viếtphươngtrìnhcạnh,đườngcao,trungtuyến,phângiáccủatamgiác

Dạng2.3.1Phươngtrìnhđườngcaocủatamgiác

Câu 67. ChọnA

Goi

lađươngcaoketư

cua

ABC

.Taco:

AH BC vtpt AH 

la

 

2;3

BC 



.

Phươngtrinh

   

:2 1 3 2 0 2 3 8 0.

AH x y x y

       

.

Câu 68. Đườngcao



điquađiểm

 

2; 1





vàcóVTPTlà

 

7; 3

  



.

Vậyphươngtrình



là

   

7 2 3 1 0 7 3 11 0

x y x y

        

.

Câu 69. Chọn A.

Tacó:

 

2;3

BC 





Đườngcaokẻtừ



củatamgiác

ABC

nhận

 

2;3

BC 



làmvectơpháptuyếnvàđiquađiểm



nêncóphươngtrình:

   

2 1 3 2 0 2 3 8 0

x y x y

       

.

Câu 70. ChọnD

Tamgiác

ABC

cântại

nên

làtrungđiểmcủa

và

CH AB

.

Có

 

3;1

và

   

2; 4 2 1;2

AB     



.

Vậyphươngtrìnhđườngcao

là

   

1 3 2 1 0

x y

   

2 5 0

x y

   

.

Câu 71. ChọnB

Do

BH AC

 

ChọnVTPTcủa

la

 

5; 3 .

n CA

  

 



Phươngtrinhtôngquatcua

   

: 5 4 3 5 0 5 3 5 0.

BH x y x y

       



Câu 72. Gọi

làtrungtrựcđoạnAB,tacó:

 

0;1

0;1 .

n AB

d AB





 















Chọn B.

Câu 73. GọiMlàtrungđiểmcủaBC. TacầnviếtphươngtrìnhđườngthẳngAM.

Tacó:

 

     

1; 1 1;1 : 2 0.

0; 2

2;0

4;2

AMAM

u AM n AM x yM





  





      







 

Chọn A.

Câu 74. GọiIlàtrungđiểmcủaABvà

làtrungtrựcđoạnAB. Tacó

     

   

1; 4 , 5;2 3; 1

: 2 3 3 0.

4;6 2 2;3

AB n

B I

d y

d AB

   



   









  









Chọn A.

Câu 75. GọiIlàtrungđiểmcủaAB và

làtrungtrựcđoạnAB. Tacó

   

5 5

4; 1 , 1; 4 ;

2 2

: 0.

13; 3 3 ;1

x y

d AB A





 

   

 



 





      

  











Chọn B.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 36

Câu 76. GọiIlàtrungđiểmcủaABvà

làtrungtrựcđoạnAB. Tacó

     

   

1; 4 , 1;2 1; 1

: 1 0.

10;6 6 0;

dB I

d y

AB n AB

   



  









    





Chọn A.

Câu 77. GọiIlàtrungđiểmcủaABvà

làtrungtrựcđoạnAB. Tacó

     

   

1; 4 , 3; 4 2; 4

: 2 0.

2;0 2 1;0

AB n AB

A B I

d x

    



  













  





Chọn C.

Câu 78. Gọi

làđườngcaokẻtừAcủatamgiácABC. Tacó

 

   

2; 1

: 7 3 11

3 7;

A h

h BC n BC

x y



     

 



   







 





Chọn A.

Câu 79. Gọi

làđườngcaokẻtừBcủatamgiácABC. Tacó

 

   

5;3

4;5

;

5 3 5 0

B h

AC n C

h x





   











      





Chọn D.

Câu 80. Gọi

làđườngcaokẻtừCcủatamgiácABC. Tacó

 

   

2 1

3 3 0

C h

h AB

x y

n AB

 





   





 











Chọn B.

Dạng2.3.2Phươngtrìnhđườngtrungtuyếncủatamgiác

Câu 81. ChọnD

Gọi



làtrungđiểmcủacạnh



5 3 5 7

; ;

2 2 2 2

AC M BM

   

  

   

   



.

Đườngtrungtuyến



nhận

 

7;5

n  



làmmộtvéctơpháptuyến.Vậyphươngtrìnhtổngquát

củađườngtrungtuyếnquađiểm

củatamgiác

ABC

là:

7 5( 2) 0 7 5 10 0

x y x y

        

.

Câu 82. ChọnA

Gọi

làtrungđiểmcủa

 

0; 1

BC I

 



Tacó

   

2; 4 2; 1

AI n

     

 

làvectơpháptuyếncủađườngthẳng

.

Phươngtrìnhđườngthẳng

là:

   

2 2 3 0 2 1 0

x y x y

       



Câu 83. 

 

       

1;4

5;0 5 1;0 : .

2;3

M C







 



   

















Chọn C.

Câu 84. 

 

5 6

5 1

3; 6; 5 : .

2;4

2;1

x t

MB MB





 

 



 

 

 



 

   



 

 















Tacó:

 

20 5 6

20;

y t







 





   

 

 





 





Chọn B.



Dạng2.3.3Phươngtrìnhcạnhcủatamgiác

Câu 85. ChọnC

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 37



+)Gọi

và

lầnlượtlàcácđườngcaovàtrungtuyếnkẻtừ

củatamgiác

ABC

.

+)Tọađộ

lànghiệmcủahệ

 

7 2 3 0 1

1;2

6 4 0 2

x y x

x y y

   

 

 

 

   

 

.

+)

làtrungđiểmcủa

nên

 

2 3

3; 2

2 2

B M A

x x x

y y y

  



 



   



.

+)Đườngthẳng

điqua

 

3; 2



vàvuônggócvớiđườngthẳng

6 4 0

x y

  

nêncó

phươngtrình

 

– 3 6 2 0 6 9 0

x y x y

      

.

+)

làgiaođiểmcủa

và

nêntọađộ

lànghiệmcủahệ

7 2 3 0

6 9 0

x y





  





 

  

 

 

  

 

 







màDlàtrungđiểmcủaBCsuyra

 

3; 1

 



+)Đườngthẳng

điqua

 

1;2

và

 

3; 1

 



cóphươngtrìnhlà

3 4 5 0

x y

  

.

Câu 86. ChọnA

Tọađộđiểm

lànghiệmcủahệ

2 0 3

2 5 0 1

x y x

x y y

   

 



 

   

 

nên

 

3;1



Gọi

 

; 2

B b b



và

 

5 2 ;C c c



,

làtrọngtâmtamgiác

ABC

nên

,b c

lànghiệmcủahệ

5 2 3 9 5

2 1 6 2

c b b

c b c

    

 



 

    

 

.

Vậy

(5;3); (1;2)

B C

 

4; 1

   



chọnmộtvéctơpháptuyếncủađườngthẳng

là

 

1; 4

 



suyraphươngtrìnhđườngthẳng

   

:1 1 4 2 0 : 4 7 0.

BC x y BC x y

       



Dạng2.3.4Phươngtrìnhđườngphângiáccủatamgiác

Câu 87. Chọn D.

Câu 88. 

 

1;3

,

 

2;B m

nằmcùngphíavới

:3 4 5 0

d x y

  

khivàchỉkhi

    

3 4 5 3 4 5 0 10 1 4 0 .

A A B B

x y x y m m

          

Chọn B.

Câu 89. 

: : 3 7 0.

1 3

x t

d d x y

y t

 



   



 



Khiđóđiềukiệnbàitoántrởthành

    

3 7 3 7 0 2 13 0 13.

A A B B

x y x y m m          

Chọn C.

Câu 90. Điểm

 

;M x y

thuộcđườngphângiáccủacácgóctạobởi

1 2

; 

khivàchỉkhi

   

1 2

3 0

2 3 2 3

; ; .

3 6 0

5 5

x y

x y x y

d M d M

x y

 

   



   

 









Chọn C.

Câu 91. Điểm

 

;M x y

thuộcđườngphângiáccủacácgóctạobởi

; : 0

Ox y

 

khivàchỉkhi

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 38

   

 

1 2 0

; ; .

2 1

1 2 0

x y

x y y

d M d M Ox

x y



  





   



  







Chọn D.

Câu 92. 

 

;3 , 1;2 : 4 3 2 0

;3 , 4;3 : 3 0

A B AB x y

A C AC y



 

   

 



  



 



   

 



 





Suyracácđườngphângiácgóc

là:

 

4 2 13 0 ; 4 2 13

4 3 2 3

5 1

4 8 17 0

1;2 5 0

4;3 23 0

x y f x y x y

x y y

x y

f B

f C

      



  

 



  





  







   







suyrađườngphângiáctronggóc

là

4 8 17 0.

x y

  

Chọn B.

Câu 93. 

   

1;5 , 4; 5 : 2 3 0

1;5 , 4; 1 : 2 7 0

A B AB x y

A C AC x y

     







    







Suyracácđườngphângiácgóc

là:

 

4; 5 5 0

1 0 ; 1

2 3 2 7

5 05 5

4; 1 3 0

f B

x f x y x

x y x y

f C



    

    

   



  





 

  









suyrađườngphângiáctronggóc

là

5 0.

 

Chọn B.

Câu 94. Cácđườngphângiáccủacácgóctạobởi

:3 4 3 0

d x y

  

và

:12 5 12 0

d x y

  

là:

3 11 3 0

3 4 3 12 5 12

11 3 11 0

5 13

x y

x y x y

x y

  

   



 



  





Gọi

   

1 2

3 11 3

1;0 ; : ,

0 10;3I d x y M

d I d d

   







Gọi

làhìnhchiếucủa

lên



Tacó:

30 12 3

130, 9,

IM MH

  

  

suyra

  

sin 52 2 90 .

130

MIH MIH MIH

     

 



Suy ra

:3 11 3 0

d x y

  

 là đường phân giác góc tù, suyra đường phân giác góc nhọn là

11 3 11 0

x y

  

.Chọn B.

Câu 95. Chọn D.

: 3 4 9 0  

AB x y



:8 6 1 0  

AC x y



Phươngtrìnhcácđườngphângiáccủagóc

của

ABC

là:

3 4 9 8 6 1

5 10

   

 

x y x y

   

2 3 4 9 8 6 1      

x y x y

 

2 2 19 0

14 14 17 0

   





   





x y



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 39

Có

 

 B AB BC

.Suyra

29 6

;

7 7

 

 

 

.

Có

 

 C AC BC

.Suyra

29 41

;

14 14

 

 

 

.

Xét

 

: 2 2 19 0   x y

có

29 6 29 41

. 2. 2 19 2. 2 19 0

7 7 14 14

  

     

  

  

B c

t t

.

Suyra

,B C

nằmvềcùngmộtphíađốivới

 



,nên

 



làđườngphângiácngoàicủagóc

.

Vậyđườngphângiáctrongcủagóc

là

 

:14 14 17 0   x y

.

Câu 96. ChọnA

Bàitoántổngquát:

Gọi

làphângiácngoàigóc

củatamgiác

ABC

.

Đặt

.AE AB



 

,

.AF AC



 

và

AD AE AF 

  

.

Khiđótứgiác

AEDF

làhìnhthoi(vì

1AE AF 

).

(Hình bình hành có 2 cạnh kề bằng nhau).

Suyratia

làtiaphângiáctronggóc

EAF

.

Dođó:

AD d

.Nên



làvectơpháptuyếncủa

đườngthẳng

.

Ápdụng:

 

1; 1 , 2

2;2 , 2 2

AB AB

AC AC



  





 









 

2;0 2 1;0AD  



.

XemđápánchỉcóđápánAcóvectơpháptuyếnlà

 

1;0

.

DẠNG3.VỊTRÍTƯƠNGĐỐICỦAHAIĐƯỜNGTHẲNG

Câu 97. ChọnD

Haiđườngthẳng

1 1

y a x b  và

2 2

y a x b  songsongvớinhaukhivàchỉkhi

1 2

a a

b b













Trongcácđườngthẳngtrênkhôngcóđườngnàothỏamãn.Vậykhôngcócặpđườngthẳngnào

songsong.

Câu 98. ChọnD

: 3 2 3 2 0d y x x y     

.

 

cóVTPT

 

3; 1n  



.

Đườngthẳng

3 6 0x y  

cóVTPT

 

3;1n kn 

 

nên



và



khôngcùngphương.Dođó

đườngthẳng

3 6 0x y  

khôngsongsongvớiđườngthẳng

 

.

Câu 99. ChọnD

Takiểmtralầnlượtcácđườngthẳng

.+)Với

: 2 1 0d x y   có

1 2

d 



cắt

d .

.+)Với

: 2 0d x y  có

2 1

1 2



 



cắt

d .

.+)Với

: 2 1 0d x y    có

1 2 1



  

 

trùng

d .

.+)Với

: 2 4 1 0d x y    có

1 2 1

2 4 1

 

  

 

songsong

d .

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 40

Câu 100. ChọnB

Vì

3 3 2

3 1

: 1 2 1

d y x x d d

 

       

 

 

.Đườngthẳng

và

cóhệsốgócbằng

nhau;hệsốtựdokhácnhaunênchúngsongsong.

Câu 101. ChọnD

Đểđườngthẳng

 

3 3 1

y m x m

   

songsongvớiđườngthẳng

5y x 

thìđiềukiệnlà

3 1

3 1 5

 



 



  

 

 

  



.

Câu 102. ChọnA

Tacótọađộgiaođiểmcủahaiđườngthẳng

3 6 0

x y

  

và

3 4 1 0

x y

  

lànghiệmcủahệ

phươngtrình

3 6 0

3 4 1 0

x y

  





  

















 







Câu 103. ChọnA

Đường thẳng

: 2 3 15 0

d x y

  

 có một vectơ pháp tuyến là

 

2;3

n 



 và đường thẳng

: 2 3 0

d x y

  



cómộtvectơpháptuyếnlà

 

1; 2

 



.

Tathấy

2 3

1 2





và

1 2

. 2.1 3.( 2) 4 0

n n

     

 

.

Vậy



và

cắtnhauvàkhôngvuônggócvớinhau.

Câu 104. ChọnC

CÁCH1

-Xét

0m 

thì

1 2

5  9

d : y , d :x

  

.Rõrànghaiđườngthẳngnàycắtnhaunên

0m 

thỏa

mãn(1).

-Xét

0m 

thì

: 5

d y mx m

   

và

: 9

d y

  



Haiđườngthẳng

và

cắtnhaut

(2)





    



 



.

Từ(1)và(2)tacó

 

.

CÁCH2

và

theothứtựnhậncácvectơ

1 2

1  1

n ( m; ), n ( ;m ) 

 

làmvectơpháptuyến.

và

cắtnhau

n



và



khôngcùngphương



1 1 1m.m . m .   



(Ápdụngtínhchất:

 

n a;b



và

 

n c;d



cùngphương



a.d b.c

)

Câu 105. 

 

1 2

: 2 1 10 0

2 1 10

3 4 10

:3 4 10 0

2 1 3

d d

d m x m y

m m

d x y





   





  



  





 



  









Câu 106. 

 

1 2

: 1 2

2 1

: 2 1 0

d d

d m

mx y m

m m

d x

    





 



 



 





 

 

 

















CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 41

Câu 107. 

 

: 2 3 4 0

2 3

4 ;

1 4

3 2

dd M

d x y

x t

n m

y mt

 

  



 

 

 

 



 

 





  

 









 





Chọn C.

Câu 108. 

 

1 2

: 2 – 4 1 0

1; 2

0 1 2 0 1.

3 1

d d

d x y

n n a a a

n a a

x at

y a t



 



 



  



      

 

 

  









 







 





Chọn D.

Câu 109. 

 

   

1 2

2 2

1 1

2 2

: 2;

;

1 2

: 2 6

; 2

d d

x t

y t

x mt

d A

y m

A d

m m

d u m















  



  



 



 









   



  

 





 

  















Chọn C.

Câu 110. 

   

 

1 2

11 1

2 2

5 0

: 2;1

: 4 3 0 3

;

, 2;

3 4

4 3

d d

x t

d A

u m

ux y m



  



 









 

 

  



  



  

    



















Chọn D.

Câu 111. Với

: 2 0

: 7 7 0

d x y

m d

d x y

 



  





    







 



loại





Với





thì

 

1 2

: 2 4 0

3 1

: 3 2 1 0

2 1

42 1

d d

d x y m

d m y

x m

   





 





 



    



 

    













 





Chọn B.

Câu 112. 

1 2

: 5 0

0 0 (

: 2 3 10 0

: 4 1 0

)

2 3

0 0

4 1

m m

x my

mx y

  

  



   









 



    



  



 







    







 

thoaû maõn

Chọn D.

Câu 113. Tacó:

 

     

   

1 1

2 2

: 19 0 ;1

: 1 20 0 1; 1

1 1 1 0

mx y m

m x m y m m

m m m m

 

     





         





      





Câu 114. 

Tacó:

 

   

1 1

2 2

:3 2 6 0 3 ;2

: 2 2 6 0 2;2

d mx y m

d m x my m m

    





      









 

1 2

: 3 0

0 0

: 3 0

2 2

0 1

3 2

d d M

d y

m m

d x y

m m

 



 







 



  



    







  









thoaû maõn

Chọn D.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 42

Câu 115. 

 

1 1

2 2

: 2 3 10 0 2; 3

2 3

: 4 ; 3

1 4

d x y

x t

nd m

y m

     





 





  





 







   

2.4 3 . 3 0 .

d d

m m



       

Chọn C.

Câu 116. 

 

   

1 1

2 2

: 4 3 3 0 4; 3

1 2

: 1;4

, 2

;

d x y m

x t

d A

d n m

n     





 













  









1 2

3 8 0

d d



 



 

   

 



 











Chọn B.

Câu 117. Tacó

 

   

 

1 2

2 2

:3 2 6 0 3 ;2

: 2 2 3 0 2;2

: 3 0

2 3

0 1

: 2 2

d d

mx y m

d m x y m m

d y

m m

d x

m m

 

     

    





      





  



   





  











 







Choïn A.

khoâng thoaû maõn



Câu 118. Tacó:

 

   

 

1 1 1

2 2

8 1

: 8;10 , 1; 1

: 2 14 0 ;2

x m t

dA m

y t

d mx mn



  



  





 









    









 

1 2

1;1

0;2

1 1

8 6

d d





 

 



  





























 

  

 



 



 





















 







khoâng thoaû maõn

Chọn A.

Câu 119. 

 

: 3 2 1 0

: 2 1 0

d m x y m

d x my m m



    





     







: 3 2 1 0

: 1 0

3 2

d d M

d x

 



 



   





    



  





  





















thoaû maõn

Chọn B.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 43

Câu 120. 

 

1 2

2 2

1 1

: ;1

1 1

2 1

: ;1

1 1

1 0

1 1.

1 0

1 2 0

, 2; 1

d d

d u m

x m t

A m

y m t

x mt

y m t

m mt

m m m

m t m

m m m



  





 





  







 



 

 







  





 





 

  



 

 

      

  

 

   



 



 







 





.Chọn C.

Câu 121. 

: 7 3 16 0

: 10 0 18

d x y

  

 





 

   



Chọn A.

Câu 122. 

3 4

2 5

3 4 1 4 1

2 5 7 5 1

1 4

7 5

x t

y t

t t t t

x t

y t



   



 

 



 

 

 

     

 

   

  



   



 

    



 



 

 













 



Chọn A.

Câu 123. 

   

1 2

 : 2 3 19 0

2 22 2 3 55 5 19 0 10 .

22 2

 :

55 5

d d

d x y

t t t

x t

d y

y t



  









         

 



 









 





Chọn A.

Câu 124. 

   

–2;0 ,  1;4 : 4 3 8 0

4 3 8 0 2

2 0 0

: : 2 0

AB d

A B AB x y

x y x

x t

x y y

d d x y

y t



   



   

 



 

 

  



   

   

 





 





Chọn B.

Câu 125. 

 

2 1

1 2

3 0

2;0

3 0

x t x

x d Ox

y t

    

 

  

 

   



   



 

2 4 0 2.

a a

      

Chọn D.

Câu 126. 

 

2 2

2 0 0

0;2

2 2

x t x

dOy d Oy

t y

   

 

  

 

















 

6 0 .

m m





   







Chọn D.

Câu 127. 

3 31

; .

:3 – 2 5 0

: 2 4 – 7 0 31

d x y

d x



 



 





 

 

 







 

  









 

Tacó

 

9 31 53

0 .

4:3 4 –1

|| :3 00

8 4

d d x y c

c c

d x y c





        

 

 







    







Vậy

:3 4 – 0 : 24 32 53 0.

d x y d x y

     

Chọn A.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 44

Câu 128. 

: 3 1 0

: 3 5 0

3; .

d x y

d A





  





 

 

  

 



 

 





 

 

Tacó

2 5

3 2. 0 .

: 2

7 0

3 3

d x y c

c c

d x y



 

        

 

 







  

 

 





Vậy

: 2 0 :3 6 5 0.

d x y d x y

      

Chọn A.

Câu 129. Tacó:

 

2 3

:3 4 15 0

:5 2 1

d x y

d x y y

d A d

  

 



 

 

   



   





6 3 9 13 0 5.

m m m m

        

Chọn D.

Câu 130. 

2 3

 : 2 – 4 0

:5 – 2 3 0 26

;

5 26

9 9

d x y

d x

d A







 





 









  

 



 





 







5 26

2 0 12.

9 3

      

Chọn D.

Câu 131. 

 

1 2

:3 – 4 15 0

1;3

:5 2 –1 0 3

d x y

d d A d

d x y y

 

 



     

 

  





12 15 0 3.

m m

      

Chọn C.

Câu 132. 

 

1 2 3

: 2 –1 0

1; 1 1 7 0 6.

: 2 1 0 1

d x y

d d A d m m

d x y y

 





           

 

    





Chọn B.

Câu 133. Đặt

 

1; 0

1; 80 0

; 51 30 11 .

f M f M d

f N f N d

f x y x y

f P

f Q



 

     

 



 



 



      



   

 



 



















Chọn A.



DẠNG4.GÓCCỦAHAIĐƯỜNGTHẲNG

Dạng4.1Tínhgóccủahaiđườngthẳngchotrước

Câu 134. ChọnC

Đườngthẳng



cóvectơpháptuyến

 

1; 3

n  



,đườngthẳng





cóvectơpháptuyến

 

1; 3







.

Gọi



làgócgiữahaiđườngthẳng

, .



 

 

1 3

cos cos , 60

1 3. 1 3

n n

 





    

 



 

.

Câu 135. Chọn A.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 45

Đườngthẳng

cóvectơpháptuyếnlà:

 

3; 1

 



;

Đườngthẳng

cóvectơpháptuyếnlà:

 

1; 3

n  



.

Ápdụngcôngthứctínhgócgiữahaiđườngthẳngcó:

 

1 2

1. 3 1 3

cos ,

2.2 2

n n

a b

n n

  

  

 

.Suyragócgiữahaiđườngthẳngbằng

30

.

Câu 136. ChọnC

Đườngthẳng

: 2 5 2 0

d x y

  

cóvectơpháptuyến

 

2;5

n 



.

Đườngthẳng

:3 7 3 0

d x y

  

cóvectơpháptuyến

 

3; 7

 



.

Gócgiữahaiđườngthẳngđượctínhbằngcôngthức

 

1 2

2 2 2

2.3 5.( 7)

29 1

cos , cos ,

29 2 2

2 5 . 3 7

n n

d d n n

n n

 

    

  

 



 

1 2

; 45

d d 



Vậygóctạobởiđườngthẳng

và

bằng

.

Câu 137. ChọnD

Véctơpháptuyếncủađườngthẳng



là

 

2;1

n 



nênvéctơchỉphương

 

1; 2

 





Véctơchỉphươngcủađườngthẳng



là

 

1; 1



 





Khiđó

 

1 2

3 3 10

cos ; cos ;

5. 2

u u



     



 



Câu 138. ChọnD

Đườngthẳng



cóVTPTlà

   

1; 2 1 2;1

 n VTCP





Đườngthẳng



có

 

1 1;2

VTCP

.

Nhậnxét:

 

1 2 1 2 1 2 1 2

. 0 , 90



          u u u u

   

.

Câu 139. ChọnD

Tacó

   

1 2

1;2 ; 2; 4

d d

vtptn vtptn

  

 



 

1 2

1.2 2.4

; .

5.2 5

d d

n n

cos d d

n n





  

 

Câu 140. ChọnC



cóvectơpháptuyếnlà

 

1; 3

n  



.

'

cóvectơpháptuyếnlà

 

1; 3

n 



.

Khiđó:

 

   

1 2

2 2

1 2

1.1 3 3

cos ; cos( ; )

4. 4

| |.

1 3 . 1 3

n n

 



      

  

 





.

Vậygócgiữahaiđườngthẳng

, ' 

là

.

Câu 141. Tacó

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 46

 

   

1 2

;

2 2

2.1 1 . 3

: 2 10 0 2; 1

cos

: 3 9 1;

. 1 3

d d

x y

d y









     







    



 

 

 



 





45 .



 



Chọn B.

Câu 142. Tacó

 

1 2

1 1

;

2 2

14 15

49 9.

: 7 6 0 7; 3

cos

: 2 5 4 0 2; 5

4 25 2

d d

d nx y





 



     











 

    

 

 









Chọn A.

Câu 143. Tacó

 

1 2

;

2 2

;

30 .

1 3. 0

: 2 2 3 5 0 1 3

cos

: 0 0;1

d d

x y



 







    



  

   





 

 







Chọn A.

Câu 144. 

 

1 2

;

: 3 0 1; 3

cos

1 0

1 3. 1

10 1;

d d

x y











   











 

 

  





60 .



 



Chọn C.

Câu 145. 

 

1 2

;

: 6 5 15 0 6; 5

10 6

0 90 .

5;6

d d

d n

n n

x y

x t

y t





  



     





 

 









 









 



Chọn D.

Câu 146. 

 

1 2

1 1

;

: 2 7 0 1;2

cos

;

: 2 4 9

1 2

1 4. 1 4

d d

x y

d y





    













 

 

 









Chọn C.

Câu 147. 

 

1 2

1 1

;

: 1;2

2 2 0

1 2

0 1;

1 4. 1 1 10

d d

x y n





  



 







 





  

 











Chọn A.

Câu 148. 

 

1 2

1 1

;

: 2;

cos

10 5 1 0

2 1

1;1

4 1

. 1

1 1 0

d d

x y n

y t





  



 

 







 





















Chọn A.

Câu 149. 

 

1 2

1 1

;

:3 4 1 0 3;4

cos

5 12

1 5

15 48

5; 1

9 16. 25 144

d d

x y

x t





    









 









 

 

















Chọn D.



Dạng4.2Viếtphươngtrìnhđườngthẳngliênquanđếngóc

Câu 150. ChọnB

Gọi



làgócgiữahaiđườngthẳngđãcho.

Đườngthẳng

7 2

x at

y t

 





 





 

t 



cóvectơchỉphươnglà

 

; 2

u a

 



.

Đườngthẳng

3 4 2 0

x y

  

cóvectơchỉphươnglà

 

4; 3

 



.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 47

Tacó

 

cos cos ,u v





 



cos 45

u v

  

 



4 6

5 4



 





5 4 2 4 6

a a

   

2 2

25 100 32 96 72

a a a

    



7 96 28 0

a a

   











 



.

Câu 151. 

 

: 2 3 0

: 2 1 1

1;1 .

d x y

d x y y

d A

  





 

 

   



   





Tacó

 

3 3

: 1 0 0;1 ,

d ny    



gọi

   

; ,

;





  



.Khiđó

2 2 2

2 2

1 : 2 0

1, 1 : 0

c s

a b a b x y

a b b

a b a b x y

a b



        



    



         

 



 

Chọn C.

Câu 152. Chọn B.

Chođườngthẳng

vàmộtđiểm

Khiđó.

(i)Códuynhấtmộtđườngthẳngđiqua

songsonghoặctrùnghoặcvuônggócvới



(ii)Cóđúnghaiđườngthẳngđiqua

vàtạovới

mộtgóc



 

 



Câu 153. 

 

: 2 6 0 1;2 ,

d x y n    



gọi

 

; .

a b kn

 

   



Tacó

 

2 2 2 2

2 2

cos45 5 2 8 8

. 5

a b

a b a ab b

a b



      







2 2

1 1

3 8 3 0 .

3 3

a b k

a ab b

a b k





   



    



   



Chọn A.

Câu 154. 

 

1 2

sol

: ,

2 2

1 2

: ; 1

cos60 1 2 4 2

: 1; 1

1. 2

4 1 0 4.

k k k

d y kx k

k k k

y x

k k k k



 

   





       



    







       







Chọn B.



Câu 155. ChọnC



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 48

Tọađộ

 

2;1A



Gọi



làgócgiữahaiđườngthẳng

 

và

 

,

cos



 

sin



  

Xéttamgiác

ABC

tacó:

sin

sin sin

AB BC

C A

   

Gọi



làgócgiữahaiđườngthẳng

 

và

 

,suyra:

1 3

sin cos

10 10

 

   

 



Giảsử

 

cóvectơpháptuyếnlà

 

;n a b





Từ

 

tacó:

2 2

3 3

cos 8 0

10 10

a b

a ab b

a b





      



a b















Với

a b

mộtvectơpháptuyến

 

1;1 : 0n d x y   





Với

7a b

mộtvectơpháptuyến

 

7;1 : 7 6 0n d x y   





Vậy:

1 0 7 6 2T     



Câu 156. ChọnC

Gọi

( ; )n a b



với

2 2

( 0)a b 

làvéctơpháptuyếncủa

,

véctơ

(1; 3)n 



làvéctơpháptuyếncủađườngthẳng

,

(1; 1)n 





là

véctơpháptuyếncủađườngthẳng

.

Tacó:

1 2 1

cos cos |cos( , )||cos( , )|B C n n n n  

   



1 2 1

2 2

1 2 1

| , | | , |

| 3 | |1 3|

10. 2

. .

10.

n n n n

a b

n n n n

a b

 

   



   



 

2 2 2 2

2 2 7 0

63b ab b

a b

a a b a

a b

 



    



 







+Với

a b 

chọn

1, 1 (1; 1)a b n    



loạivì

/ /AC AB

+Với

a 

chọn

1; 7 : 7 3 0a b AC x y     

.Điểm

8 1

;

5 5

C AC BC C

 

  

 

 



Câu 157. ChọnD



Đườngthẳng

   

1 2

,d d

cóvéctơpháptuyếnlầnlượtlà

   

1 2

2; 1 , 1;1n n  

 

.

Gọi

 



làđườngthẳngcầntìmcóvéctơpháptuyếnlà

 

;n a b



.

Gócgiữa2đườngthẳng

   

1 2

,d d

và

   

, d

xácđịnhbởi:

 

1 2

2 2 2

1 2

2.1 1.1

2 1 . 1 1

n n

cos d d

n n



  

  

 

.

 

2 2 2 2 2 2

. 1 1 2.

n n

a b a b

cos d

n n

a b a b

 

   

  

 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 49

Vì

 



cắt

   

1 2

d d

tại

và

tạothànhtamgiác

IAB

cântại

nên

   

2 2

1 2 2

2 2

, , 5

a b

cos d d cos d a b a b

a b



       





 

2 2 2 2

5 2 5 0

a b

a b a b a ab b

a b



 



         



 





.

+

2a b 

:chọn

2 1

a b

  

:phươngtrìnhđườngthẳnglà:

   

2 2 0 2 4 0

x y x y L      

.

+

a b



:chọn

1 2

a b

   

:phươngtrìnhđườngthẳnglà:

   

2 2 0 2 2 0 /x y x y T m      

.Dođó

 

5 1 5 2 11

T a b

     

.

DẠNG5.KHOẢNGCÁCH

Dạng5.1Tínhkhoảngcáchtừ1điểmđếnđườngthẳngchotrước

Câu 158. ChọnD

Khoảngcáchtừđiểm

 

1;1

đếnđườngthẳng

:5 12 6 0

x y

   

là

 

5.1 12.1 6

, 1

5 12

d A

 

  

 

.

Câu 159. ChọnA

Khoảngcách

 

2 2

3.5 2. 1 13

2 13

3 2

  

  



.

Câu 160. ChọnB

Khoảngcáchtừđiểm

(

1; )



đếnđườngthẳng

: 3 4 0

x y

   

là

 

2 2

3.1 1 4

6 3 10

; .

3 1

d M

 

   





Câu 161.

ChọnB

Tacó:

 

3.3 4. 4 1

3 4

d M

  

  

 

.

Câu 162. ChọnA

Tacó

 

3. 3 2 1

; 10.

3 1

d A

  

   

 



Câu 163. ChọnD

Tacó

 

2 2

4.0 3.0 1

4 3

d O d

 

 



.

Câu 164. ChọnA

Gọibánkínhcủađườngtrònlà

Khiđó:

 

3 5. 2 1

, .

1 5

R d I

  

   

 



Câu 165. ChọnD

Tacó:

 

2 2

0. 4. 4 2

, 8

cos sin sin

d M

cos sin

     

  

  

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 50

Câu 166. ChọnA

Khoảngcáchtừđiểm

0 0

( ; )M x y

đếnđườngthẳng

:  0

ax by c

   

là:

0 0

2 2

( , )

ax by c

d M

a b

 

 





Vậykhoảngcáchtừ

(1; 2)



đếnđườngthẳng

: 3 4 26 0

x y

   

bằng

2 2

3.1 4.( 2) 26

( , ) 3

3 ( 4)

d I

  

  

 



Câu 167. 

   

3 4 0 1

3 1 4

1;1 ; .

2 3 1 0 1

9 1 10

x y x

A d A

x y y

    

  

 

     

 

   



 

 Chọn C.

Câu 168. 

 

   

 

3 8 12

; .

, : 3 4 12 0

9 1

;

1;2

0 3 4;0

h d A BC

BCB C x y



 



   



   









Chọn A.

Câu 169. Cách 1:

 

   

 

3; 4

1;5 3;1

3; 4

2 5

; 5

: 2 7 0

h d A BC

BC y











  

  

  

 











 





.2 5. 5 5.

ABC

  

Chọn B.

Cách 2:

 

2 2

. .

ABC

S AB AAB AC



  

 

Câu 170. 

 

2 2

3 2 sin3sin

; 6

cos sin

d M

 













Chọn B.

Câu 171. 

 

8 0 2

: 4 3 2 0 ; 2.

1 3

x t

y t

x y d M

 

    

 







 



  



Chọn A.

Câu 172. 

 

min

15 3 2

: 3 2 0 ; 10.

1 9

2 3

x y MN d M

x t

y t

 

 



 

 

     















Chọn A.

Câu 173. 

 

2 2

2 4

; 2 5 3 5. 1 4 6 4 0

m m

d A m m m m

   

      

  



 













Chọn B.

Câu 174. 

1 1

: 2 0

: 2 0 2

: 2 0

x t

d x y

x m

y t

d x y m y m

d x y m







  

 







  

  



    





  



 

4 ; 2M m m

d   

Khiđó:

   

2 2

2 4 2 4 6 8 0 .

OM m m m m





          







Chọn C.

Câu 175. 

 

100

; 10.

64 36

R d O



  

Chọn D.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 51

Câu 176. 

 

10 24 10

; .

25 144

R d I

  

  



Chọn A.

Câu 177. 

 

21; 3 464

0;4 54

; 21 11 10 .

19;5 464

1;5 44

f M

f N

f x y x y

f P

f Q



 







   



 









Chọn D.

Câu 178. 

 

1; 3 38

0;4 25

; 7 10 15 .

19;5 98

1;5 42

f M

f N

f x y x y

f P

f Q



 







   



 









Chọn C.

Câu 179. 

 

   

2 1

|| : 6

2;0

12 3

; ; .

8 3 0

100

d d A





  

    







   





Chọn B.

Câu 180. 

   

 

2;2 , 7;1

: 7 3 0 7;1

A n

d x y n



  





    









   

14 2 3

; ; .

50 2

d d d d A d

  

       

Chọn A.

Câu 181. 

 

1 2

2 1

4;3

24 24 101

101

; 10,1.

|| : 6 – 8 101 0

100

A d

d d d

d d x y

 

 



   



 





Chọn A.

Dạng5.2Phươngtrìnhđườngthẳngliênquanđếnkhoảngcách

Câu 182. ChọnD

Gọi

làđườngthẳngđượcchotrongcácphươngán.Khiđó:

+)Phươngán A.

 

   

2 2

2.3 2.1 3 2.4 2.0 3

7 11

, ; , , ,

2 2 2 2

d A d d B d d A d d B d

     

     

   

.

Loạiphươngán A.

+)Phươngán B.

 

   

2 2

2.3 2.1 3 2.4 2.0 3

1 5

, ; , , ,

2 2 2 2

d A d d B d d A d d B d

   

     

   

.

Loạiphươngán B.

+)Phươngán C.

       

2 2 2 2

3 2.1 3 4 2.0 3

2 1

, ; , , ,

5 5

1 2 1 2

d A d d B d d A d d B d

   

     

 

.

Loạiphươngán C.

+)Phươngán D.

   

 

   

2 2 2

2.3 2.1 3 2.4 2.0 3

5 5

, ; , , ,

2 2 2 2

2 2

d A d d B d d A d d B d

   

     



 



Chọnphươngán D.

Câu 183. Đườngthẳngcáchđềuhaiđiểm

,A B

thìđườngthẳngđóhoặcsongsong(hoặctrùng)với

,

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 52

hoặcđiquatrungđiểm

củađoạn

.

Tacó:

 

   

3 7

;

2 2

|| : 2 0.

1 1

2;3

1;4

;1 1;

AB d x y



 



 

 

 

    

 





  









Chọn A.

Câu 184. Dễthấybađiểm

, ,A B C

thẳnghàngnênđườngthẳngcáchđiều

, ,A B C

khivàchỉkhichúng

songsonghoặctrùngvới

.

Tacó:

   

12;4 1; 3 || 3:

4 0

AAB n x yB d   

  







Chọn A.

Câu 185. Gọi

làtrungđiểmđoạn

   

1 5

;

2 2

3;3 1;1

AB n



 



 



 







   









Khiđó:

 

: 3 0 ; 1

nmx y m



     



cáchđều

,A B



3 0

I m

 



   



 





 



 











 

Chọn C.

Câu 186. 

 

   

:3 4 1 0 1;1

1 ; ; .

|| :3 4 0

d x y M d

d d d M

d x y c

    



 







      







     









Chọn A.

Câu 187. 

 

3 4 12 0

3 4 2

; ; 2 2 .

3 4 8 0

x y

d M x y

x y

  

 



    



  



Chọn B.

Câu 188. 

 

1 2

5 3 3 5 3 7

; ; ; ; 5 3 2 0.

34 34

x y x y

d M x y d d M x y d x y

   

      

Chọn C.

Câu 189. ChọnD

Gọicạnhhìnhvuôngbằng

.Do

      



1 1

3 4

MD DK DK

ABK MDK

AB KB DB

.

Tacó    

    

AM AD DM AD DC

(1)

 

        

         

3 1 3 1 3 1

4 2 4 2 4 4

NK BK BN BD BC BA BC BC BA BC

(2)

Từ(1)và(2)suyra

    

     

1 1

. . . 0

4 4

AM NK AD BC BA DC AM NK

.

Vì

AM NK

nênNKcóphươngtrìnhtổngquát:

  10 2019 0

x y

.

KhoảngcáchtừOđếnNKlà

 



 



2 2

2019

2019 101

101

10 1

d O NK

.

Câu 190.

Chọn C.

Tacó:

(4;2) 4 2 0 4 2 .M d b c c b        



(1)



2 2

3 10

( , ) 10(1 ) 9(1 ).

d A d c b



     





(2)



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 53

Thay

4 2c b  

vàoPT

(2)

tađượcPT:

3( )

31 120 81 0

( )

b tmdk

b b

b ktmdk

 





   



 





3, 2 1.

b c b c

       

.

Câu 191. ChọnA

   

: 1 0 1 0

x m y m y m x y m

 



           



 



.

Suyra



luônđiquađiểmcốđịnh

 

1; 1

 

.

Khiđó,vớimọi

M  

,tacó

 

;

d A AM AH

  

.

Giátrịlớnnhấtcủa

 

;

d A AH

 

khi

 

max , 2 10

M H d A AH    

.

Câu 192. Chọn B.

Gọi

,

lầnlượtlàgiaođiểmcủađườngthẳngđãchovới

,

.

Tacó

12 5 60

x y

 

5 12

x y

  

.Dođó

 

5;0

,

 

0;12

.

Gọi

làhìnhchiếucủa

lên

.Khiđó:

 

2 2

12.0 5.0 60

;

12 5

OH d O AB

 

  



.

Tamgiác

OAB

làtamgiácvuôngtại

nêntổngđộdàicácđườngcaolà

OA OB OH 

5 12

  

281



.

Câu 193. ChọnD

Gọi

làhìnhchiếucủađiểm

lênđườngthẳng

 

.Khiđótacó:

 

   

2 2

, 3 1 4 1 29

d A d AH AB       .Dođókhoảngcáchtừ

đếnđườngthẳng

 



đạtgiátrịlớnnhấtbằng

khi

H B

hay

 

d AB



tại

.

Vìvậy

 

điqua

vànhận

 

2;5

AB 



làmVTPT.

Dođóphươngtrìnhcủađườngthẳng

 

là

   

2 3 5 4 0 2 5 26 0

x y x y

       

.

DẠNG6.XÁCĐỊNHĐIỂM

Dạng6.1Xácđịnhtọahìnhchiếu,điểmđốixứng

Câu 194. ChọnD

Thaytọađộcácđiểmvàophươngtrìnhđườngthẳng

,tacó

1 4 2

, ,

M M M d

và

M d

.

Câu 195. ChọnC

Phươngtrìnhđườngthẳngđiquahaiđiểm

và

códạng:

3 8

2 3 7 8

x y

 



 

3 1 0

x y

   

.

Đườngthẳngđiqua

vàvuônggócvới

cóphươngtrình:

   

1 4 3 3 0

x y

   

3 13 0

x y

   



Tọađộchânđườngcaokẻtừđỉnh

xuốngcạnh

lànghiệmcủahệphươngtrình:

3 1 0

3 13 0

x y

  





  















.

Câu 196. ChọnB

Gọi





làđườngthẳngđiqua

vàvuônggócvới

.

Tacóphươngtrìnhcủa



là:



3 1 0

x y

  



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 54

Tọa độ hình chiếu vuông góc của



trên



là nghiệm của hệ phương trình:

3 5 0

3 1 0 4

x y



 



   







 

  











.

Câu 197. ChọnA

Đườngthẳng



có1VTPTlà

 

1; 1

 



nên



có1VTCPlà

 

1;1

u 



GoiHlahinhchiêuvuônggoccua

 

1;2

lênđươngthăng



,toađô

 

;H t t



Vi

. 0 1 2 0

MH MH u MH u t t t

             

   



3 3

;

2 2

 

 

 

Câu 198. ChọnC



Gọi

làtrungđiểmcủacạnh

.Tacó

 

2 2 2

3 2

4 4

2 3

AM AG





  



 



 









  













 





 

,suyra

 

2; 1



.

 

0;3





suyra

khôngvuônggócvới

 

nên

khôngtrùngvới



   

; 2

B a b d b a

    

.

Tamgiác

BHC

vuôngtại

và

làtrungtuyếnnêntacó

   

 

2 2

2 1 9 2 0

MB MH a a a a

a l



 



          









Suyra

 

1; 1

 

và

3 2

T a b

  

Câu 199. ChọnC

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 55

Gọi

( ; 2 5) ( )C t t d  

.

Dễthấyhaitứgiác

BCND

và

ADNB

nộitiếp.

Suyra



BNC BDC

BNA BDA

















ANC CN AN

    .

Dođó

. 0 9(5 ) 12(2 1) 0

CN AN t t

     

 

1t 

 

1; 7

 

.

Vậy

1 7 8

m n

   



Dạng6.2Xácđịnhđiểmliênquanđếnyếutốkhoảngcách,góc

Câu 200. ChọnA

Gọi

 

;0M x

.

Tacó

 

3;4

AB  





Phươngtrìnhđườngthẳng

 

: 4 3 3 0

AB x y

  

4 3 9 0

x y

   

.

 

4 9

; 5 4 9

d M AB x



   

















Vậy

 

;0 ; 1;0

M M

 

 

 

.

Câu 201. 

 

: 2 1 0 2 1; ,

: 4 3 7 0

M d x y M m m m

AB x y

      







  







Khiđó

 

8 4 3 7

6 ; 11 3 30 7;3 .

m m

d M AB m M





  



      







Chọn B.

Câu 202. 

 

2 2

2 2 3: ;

x t

M t t

y t

M d

 







 





 

với

2 2 0 1.

t t

    

Khiđó

   

 

2 2

24 2

5 2 2 2 25 5 12 17 0 ;; .

5 5

t l

AM t t t t M





 



             

 



 

 







Chọn C.

Câu 203. Gọi

 

;0M x



thìhoànhđộcủahaiđiểmđólànghiệmcủaphươngtrình:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 56

 

2 5

; 2 5 2 5

x x

d x xM

x x



 





    









 





 

Chọn A.

Câu 204. 

 

7 7

4 9

2 2

1 ; .

: 4 3 9 0

1 1;0

x M

M x

d M AB

AB x y

x M



 

 







 



   

 





  







 



Chọn A.

Câu 205. Tacó

   

 

: 4 3 12 0

0 0;0

3 12

5 6 .5. .

2 5

8 0; 8

3 12

0; ;

MAB

AB x y

y M

AB S

y M

M y h d M AB



  



 







    







   









  







Chọn A.

Câu 206. 

 

   

1 2

3 6 3 3

1 1

;0 .

2 2

; ;

13 13

M x

x x

x M

d M d M



 



 

    



 



 









Chọn B.

Câu 207. 

 

       

2 2 2 2

: ;1 2

2 2 1 4 2 7

1 2

x t

M d M t t

t t t t

y t

MA MB

 



 

 

       

 















 

20 60 0 3 3; 5 .

t t M

        

Chọn B.

Câu 208. 

 

       

2 2 2 2

: 2 3 0 ;2 3

1 2 1 3 2 1

M d x y M m m

m m m m

MA MB

    





       













 

2 2; 1 .

m M

     

Chọn A.

Câu 209. 

 

: 2 ;2

C d y C c

c c

BA BC

 







 







   













Chọn C.

Câu 210. ChọnB

Do

( ; )A a b

thuộcđườngthẳng

: 3 0

d x y

  

nên

3 0 3a b b a     

 

; 3

A a a

 

.

Khoảngcáchtừđiểm

 

; 3

A a a



đếnđườngthẳng

: 2 1 0

x y

   

là

 

2 2

2 3 1

2 1

a a

d a

  



  



.

Theođềbài

 

, 5

d a  

a 

 

4 5

  

4 5 1

4 5 9

a a

  

 

 

 

    

 

.

Theođềbàiđiểm

( ; )A a b

cóhoànhđộdươngnên

 

1 1; 2

a A

  

.Vậy

 

1 2 2

P ab

    

.

Câu 211. ChọnB

Vì

 

; (3 ;2 )M a b d M t t   

.

Lạicó

cáchđườngthẳng

:2 3 0

x y

   

mộtkhoảng

2 5

suyra

9 (12;11)

2(3 ) (2 ) 3

2 5 1 10

11 ( 8; 9)

t M

t t

t M



   

 

     

 

   

 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 57

Vì



nênđiểm

( 8; 9)

 

khôngthỏamãn.

Vậy:

(12;11) 23

M a b

  

.

Câu 212. ChọnB

 

;

a t

A a b d

b t

 



 



 



.

Giảthiết:

0 3 0 3a t t     

.

Tacó

 

   

 

2 3 2 3

; 2 5 2 5 1 10

2 1

t t

d A d t

   





      



 



 

.

Vì

3t 

nênchọn



.Khiđó

 





 



 

.Dođóchọnđápán B.

Câu 213. ChọnB

     

1 1 1

: 2 5 0 ;5 2 1;3 2M d x y M m m IM m m

        



.

   

2 2

10 1 3 2 10 5 14 10 10 .

IM m m m m







          











có2điểmthỏamãnyêucầubàitoánlà

 

1 2

14 3

0;5 ; ;

5 5

M M

 



 

 

.

Tổngcáchoànhđộcủa

và

là:

14 14

0 .

5 5

 



Câu 214. ChọnA

Tacó

 

3; 4

 



.



phươngtrìnhtổngquátcủađườngthẳng

códạng

4 3 0

x y m

  

.

Vì

 

1;1

A AB



nên

4.1 3.1 0 7 : 4 3 7 0

m m AB x y

         

.

Vì

 

; : 2 1 0 2 1 0 2 1C a b d x y a b a b          

.

Theođềra

 

2 2

4 3 7

; 6 6 4 3 7 30

4 3

a b

d C AB a b

 

      



.

Thay

2 1a b 

vàotađược:

 

11 3 30

4 2 1 3 7 30 11 3 30

11 3 30

b b b





 





        



  

 



.

Do

cótọađộnguyênnên

3; 7 10

b a a b

    

.

Dạng6.3Xácđịnhđiểmliênquanđếnyếutốcựctrị

Câu 215. 

ChọnC

Gọi



đốixứng

qua

tacó

'(0;3)

khiđóđiểm

M A B d



 



Tìmđược

(3; 4)

.

Câu 216. ChọnD

Điểm

 

4 15;M d M t t

  



Tacó:

 

2 2

4 17 17 8 17 17 4 1 17

AM t t t t t

 

         

 

 

,

t  

.

 min AM

,đạtđượctại

4t 

.Khiđó

 

1; 4

.

Câu 217. ChọnD

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 58

Cách 1:

Tìmtọađộđiểm

 

;I x y

saocho

0IA IB IC  

   

.Suyra

 



 

 



Tacó:

3MA MB MC MI IA IB IC     

      



3MA MB MC MI  

   

.Vậy MA MB MC 

  

nhỏnhấtkhí MI



nhỏnhất.



nhỏnhấtkhi

làhìnhchiếuvuônggóccủa

xuốngđườngthẳng

.

Đườngthẳng



điqua

vàvuônggócvới

cóphươngtrình:

x y 



làgiaođiểmcủa

và



nên

lànghiệmcủahệ:

2 3

13 19

;

15 15

x y

 







 





 

 

 







Cách 2:

thuộc

suyra

 

;2 3M t t 



( 3 3 ; 6 5)MA MB MC t t      

  



   

2 2

3 3 6 5MA MB MC t t



       

  



13 1

45 78 34 45

15 5

MA MB MC t t t

 

       

 

 

  



MA MB MC 

  

nhỏnhấtkhi

t  

.Suyra

13 19

;

15 15



 

 

 

Câu 218. ChọnB

Gọi

 

;G a b

làtrọngtâmtamgiác

ABC

.Suyra

2 1 2 1

1 1

3 3 3

;

2 3 2 1

3 3

A B C

x x x

a a a

y y y

b b

 

 



 

  



 

  

 

  

  

 

   

 

  

 



 



 



.

Tacó: 3 3MA MB MC MG GA MG GB MG GC MG MG         

         

.

Suyra MA MB MC 

  

nhỏnhấtkhi

nhỏnhất.

Mặtkhác

thuộctrụctungnên

nhỏnhấtkhi

làhìnhchiếucủa

lêntrụctung.

Vậy

 

 

 

.

Câu 219. ChọnD

GọiA’làđiểmđốixứngcủaAquađườngthẳng



 

Tacó:

' '   MA MB MA MB A B



Đẳngthứcxảyra  MtrùngvớiM

(M

làgiaođiểmcủa



vàA’B)

Tacó:

AA '  

nên

 

AA '

n a 1;1



 

 



 

AA ' : x y 3 0  



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 59

Gọi

 

H=AA '

H 1;2

 



VìA’đốixứngvớiAqua



nênHlàtrungđiểmAA’

 

A ' 0;3





ĐườngthẳngA’BquaBcóVTCP

     

A 'B

A 'B 9;3 3 3;1 n 1; 3    

 



A 'B : x 3y 9 0   



TọađộM

thỏahệ:

 

x y 1 0

M 3;4

x 3y 9 0

  







  



 

M 3;4



.Vậy

7 

a b



Dạng6.4Mộtsốbàitoántổnghợp

Câu 220. ChọnC

Gọi



làđộdàicạnhcủahình

ABCD

.

Trêntiađốicủatia

lấyđiểm

saocho

DP a



.

Tamgiác

MCN

có

2 2

MN MC CN a

  

.

Tamgiác

ANP

có

NP ND DP a

  

.

Vậy

AMN APN  

(c.c.c)suyra



MAN

 

.

Suyravới

lầhìnhchiếuvuônggóccủa

trênđườngthẳng thìtamgiác

AHM

vuôngcân

tại

.

Tính được

 

 

 

,

3 5

HM 

 suy ra tọa độ

 là nghiệm của hệ phương trình

 

5 45

2 4

2 3 0

x y











 



   

 



 





 











  





 







Câu 221. ChọnA

Vì

A d

,giảsử

 

A a a

;Vì

B d

,giảsử

 

2 6;B b b





CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 60

làtrungđiểmcủađoạnthẳng

khivàchỉkhi

2 6

a b

 









 



 







     

2 4 2

2;1 ; 0; 3 2;4 2.

5 3

a b a

A B BA BA u

a b b

   

 

       

 

   

 

  

.

Vậyđườngthẳng

cómộtvéctơchỉphươnglà

 

1;2

u 



.

Câu 222. ChọnC

dcóphươngtrìnhthamsốlà

x 5 3t

y 1 2t



 



  





Gọi

 

5 3 ; 1 2

C t t d   

,tacó:

   

9 3 ;3 2 , 3 3 ;7 2CA t t CB t t

       

 



       

2 2 2 2

2 2

9 3 3 2 3 3 7 2

20 32

CA CB CA CB t t t t

t t

          



    



Suyra:

1 11

C ;

5 5

 

 

 



Câu 223. ChọnA

VéctơchỉphươngcủaABlà:

 

4; 2

 







véctơpháptuyếncủaABlà:

 

1;2

n 





Phươngtrìnhđườngthẳng

là:

   

3 2 5 0 2 7 0

x y x y

       



TọađộđiểmIlànghiệmcủahệphươngtrình:

2 1 0

2 7 0 13

x y







  







 

  













9 13

;

5 5

 



 

 

.

Vậytỉsố

   

2 2

2 2 2 2

9 13

3 5

5 5

9 13

1 3

5 5

I A I A

I B I B

x x y y

   

  

   

  

   

  

  

   

  

   

   

.

Câu 224. ChọnB

Tacó

 

4;2

BC  



,

 

4; 2

  



,

 

2; 1

AH a b

  



,

 

2; 3

BH a b

  



.

Vì

làtrựctâmcủatamgiác

ABC

nêntacó

   

4 2 2 1 0

2 3 1

2 1 1

4 2 2 3 0

a b

AH BC a b a

a b b

a b

BH AC



    

   

 

 

  

   

   

    



 





 

.

Vậy

 

3 2 3 1 2 1 1

S a b

       

.

Câu 225. ChọnA

Gọi

 

;M x y

.Khiđó:

2 3

5 5

MI MB MC

 

  

   

2 3

5 5

2 3

3 2

5 5

a x x x

b y y y



     









     



















.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 61

Nên

 

1;0I

.Vậy

2 2

1S a b  

.

Câu 226. ChọnA

Gọi

trungđiểm

AI K

 



 

 

.

Tacó

2 0 2 2 0 4 0         

        

MA MB MC MA MI MK M K



1 1

2 2

a b    

.ChọnA

Câu 227. ChọnB

Điêm

thuôcđươngtrungtuyên

nêngoitoađôđiêm

 

; 1C x x 

.

Toađô

 

2; 2AC x x   



,toađôvectơchiphươngcuađươngthăng

la

 

3;1u 



.

Vi

AC BH

nên

 

. 0 2 .3 2 0 4AC BH x x x       

 

.

Vây

 

4; 5C 

.

Câu 228. ChọnA



Gọi

làgiaođiểmcủa

,ND AP



Tacó:

 

MBC NCD c g c    

nên



MCB NDC .

Mà



90 90 90MCB MCD NDC MCD DIC         

ND MC  ID AP 



 



Do

AMCP

làhìnhbìnhhànhnên

/ /AP MC

 

/ /HP IC

suyra



làtrungđiểmcủa



 



Từ

   

1 , 2 AP

 là đoạn trung trực của

ADP AIP   



AI IP

,

5 2

2 2. 5 2

AI IP  

.

Phươngtrìnhđườngthẳng

5 7

x t

y t

 





 



.

,A ,x 0

A AI I   

 

5 7 ;2 , 5 7 t 0.A t t   



5 2AI  

50 50

 



 







(nhaän)

(loaïi)



 

1 2;3t A   

.

: 3 11 0AP x y  

,

:3 17 0DN x y  

.

H AP DN  

Tọađộcủa

lànghiệmcủahệ

3 11 0 4

3 17 0 5

x y x

x y y

   

 



 

   

 



   

4;5 ,  5;2H I 

 

3;8D

.

Vậy

 

2;3 , A 

 

3;8 .D



Câu 229. ChọnB

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 62



Gọi

làtrungđiểmcạnh

,suyra

2 ;1

BG GM M

 

 

 

 

 

.

Gọiđiểm

làđiểmđốixứngvới

quađườngphângiáctrongcủagóc

.Suyrađiểm

nằm

trên

.

Đườngthẳng

'BB

qua

vàvuônggócvớiđườngthẳng

: 1 0d x y  

nêncóphươngtrình

': 3 0BB x y  



Gọi

'I BB d 

,suyratọađộđiểm

 

1; 2I  

làtrungđiểmcủa

'BB

nêntọađộ

 

' 2; 5B 



Đườngthẳng

điqua

 

' 2; 5B 

vàcóvéctơchỉphương

' ;6

B M

 



 

 



,suyravéctơpháp

tuyếncủa

cótọađộ

 

4; 1

.Đườngthẳng

cóphươngtrìnhlà:

4 13 0x y  



Điểm

(4;3)A d AC A  

.

Vậytích

. 12m n 

.

Câu 230. ChọnD



Tachứngminhđược

MP AN

,nên

làhìnhchiếucủa

trên

.

(Thậtvậygắnhệtrụctoạđộ

Dxy

,

       

0;0 , 1;0 , 1;1 , 0;1D C B A

.Khiđó

1 1

1; ; ;0

2 3

M N

   

   

   

.

Phươngtrìnhđườngthẳng

:BD y x

.Phươngtrìnhđườngthẳng

: 3 1AN x y 

.

Điểm

1 1

;

4 4

 

 

 

.Khiđó

3 1 1

; ; ; 1 . 0

4 4 3

MP AN MP AN MP AN

 

   

      

   

   

   

(đpcm).

Phươngtrìnhđườngthẳng

qua

vàvuônggócvới

là

2 0

x y  

.

làgiaođiểm

và

nêntoạđộ

lànghiệmhệ

2 3 5

x y

 

 



 



 

 

 



 

.

Từđó:

a 

,

2 2 7b a b   

.

Câu 231. ChọnB

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 63



GọiHlàhìnhchiếucủaIlêncạnhCD. 

DotứgiácABCDnộitiếpđườngtrònnên



tan tan tan

ABM MCD ICH ABM MCD ICH

      

.



sin

ICH

   .

Có

 

, 2 4.

IH d I CD IC IC      

 

: 3 6 0 3 6;C CD x y C t t     



Mà

4IC 

và

 

3; 1

x Z C  



ĐườngthẳngBCqua

 

3; 1C 

và

 

 

 

cóphươngtrìnhlà

:3 5 4 0BC x y  

.

IlàtrungđiểmcủaMCnên

 

1; 1M  

.

ĐườngthẳngBDqua

 

1; 1M  

vàvuônggócvớiCDcóphươngtrìnhlà

:3 4 0BD x y  

.

Có

 

2;2B BC BD B   



Câu 232. ChọnD



Tachứngminhđược

MP AN

,nên

làhìnhchiếucủa

trên

.

(Thậtvậygắnhệtrụctoạđộ

Dxy

,

       

0;0 , 1;0 , 1;1 , 0;1D C B A

.Khiđó

1 1

1; ; ;0

2 3

M N

   

   

   

.

Phươngtrìnhđườngthẳng

:BD y x

.Phươngtrìnhđườngthẳng

: 3 1AN x y 

.

Điểm

1 1

;

4 4

 

 

 

.Khiđó

3 1 1

; ; ; 1 . 0

4 4 3

MP AN MP AN MP AN

 

   

      

   

   

   

(đpcm).

Phươngtrìnhđườngthẳng

qua

vàvuônggócvới

là

2 0

x y  

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 64

làgiaođiểm

và

nêntoạđộ

lànghiệmhệ

2 3 5

x y

 

 



 



 

 

 



 

.

Từđó:



,

2 2 7

b a b

   

.

Câu 233. ChọnD

Gọi

làđiểmđốixứngvới

quađườngthẳng

: 2 5 0

d x y

  

suyra

D AC

.

Phươngtrìnhcủađườngthẳng

: 2 25 0

BD x y

   

.

Gọi

làgiaođiểmcủa

và

suyratọađộđiểm

lànghiệmcủahệphươngtrình

 

2 5 0 9

9;7

2 25 0 7

x y x

x y y

 

    

 

  

 

 

    

 

 

.

Mà

làtrungđiểmcủa

suyra

( 6;13)



.

Gọi

(5 2 ; )

A a a d 

.

Tacó

1 2

;

3 3

 













 

làtrọngtâmtamgiác

ABC

nên

3 5 2 12 1 2 8

(2 8;1 )

3 1 2 1

A B C G C C

x x x x a x x a

C a a

y y y y a y y a

  

        

  

    

  

  

       

  

  



Tacó

   

11 2 ; 13 ; 2 14; 12

DA a a DC a a      

 



Mà3điểm

, ,D A C

thẳnghàngnên

DA DC

 

cùngphương

11 2 13

2 14 12

a a

 

    

  



Suyrađiểm

(4;3)

nênđườngthẳng

điquađiểm

(4;3)

.

Câu 234. ChọnD

Gọi

 

13 7 ;



I n n

làtrungđiểmcủaBC,khiđótacó:

IE IF



mà

2 2

50 164 146; 50 190 185

     IE n n IF n n



2 2

50 164 146 50 190 185

       

n n n n n



5 3

;

2 2

 



 

 



Gọi

 

13 7 ;



B m m

.VìIlàtrungđiểmcủaBCnên

 

7 8;3

 C m m

.

   

7 11;5 ; 10 7 ;2      

 

BE m m CE m m

.Vì

BE AC



nên

. 0 3 2 0    

 

BE CE m m

















CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 65

+Với

   

2 11

1 6;1 , 1;2 ;

3 3

 

   

 

 

m B C A

.Trườnghợpnàykhôngthỏamãncácđápán.

+Với

     

2 1;2 ; 6;1 1;6

   m B C A

SuyraChọnD

Câu 235. ChọnB

Gọi

,I K

lầnlượtlàtrungđiểmcủa

và

IK AD IK BM

    

 

tứgiác

IBMK



làhìnhbìnhhành

BI MK 

.(1)

Do

IK AD

và

AD AB IK AB  

I

làtrựctâmtamgiác

ABK

BI AK 

.(2)

Từ(1),(2)suyra

MK AK

.

Phươngtrình

: 4 4 0

AK x y

  

,suyraphươngtrình

:2 8 15 0

MK x y

  

.

Tọađộđiểm

lànghiệmcủahệphươngtrình

4 4 0

2 8 15 0

x y



  







 

 

 

 

  

 









.

Dođó

 

2 0

0;2 4.

2 2

D K H

x x x

D P

y y y

  



  



  



.

Câu 236. 

ChọnB

'B BC BB 

nêncótọađộlànghiệmcủahệ

3 0 3

(3; 1)

2 0 1

x x

x y y

  

 

  

 

    

 

.

'C BC CC 

nêncótọađộlànghiệmcủahệ

2 0 0

(0;2)

2 3 6 0 2

x y x

x y y

   

 

 

 

   

 

.

qua

vàvuôngvới

'CC

cóphươngtrình:

3 2 7 0

x y

  

.

qua

vàvuôngvới

'BB

cóphươngtrình:



.

A AB AC 

nêncótọađộlànghiệmcủahệ

3 2 7 0 1

(1;2)

2 2

x y x

y y

   

 

 

 

 

 

.

Câu 237. ChọnA

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 66



Đườngthẳng

điqua

 

3 0A ;



vànhận

 

1 6BC ;

 



làmvéctơpháptuyến.Suyraphương

trìnhđườngthẳng

là:

6 3 0

x y

  

.

Đườngthẳng

điqua

 

3 0B ;

vànhận

 

5 6AC ;





làmvéctơpháptuyến.Suyraphương

trìnhđườngthẳng

là:

5 6 15 0

x y

  

.

Tacó

H AH BH

  

Tọađộ

lànghiệmcủahệ .

Dođó

2 6 10

a ;b ab

   

.

Câu 238. 

ChọnC

Gọi

 

;I a b

làtrungđiểm



Có



  90

BAD BND

.Suyra

BAND

nộitiếpđườngtrònđườngkính

,tâm



Có

IA IN



       

2 2 2 2

4 8 5 4

a b a b       

6 8 13 0

a b

   



Có

làtrungđiểm

.Nên

 

2 4; 2 8

C a b

 



Có

C d

.Suyra

   

2 2 4 2 8 5 0

a b

    



4 2 5 0

a b

   



Giảihệ:

6 8 13 0

4 2 5 0

a b



  



  







 















.

Có

   

2 4 2 8 8

m n a b

     

.

Câu 239. ChọnB

6 3

5 6 15 0

x y

H ;

  

  



 





 

 



5;-4( )

C c;-2c-5( )

A -4;8( )

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 67



*Tachứngminh

làtrungđiểmcủa

.

Thậtvậy:docáctứgiác

ABMN

ABCD

làcáctứgiácnộitiếpnên



AMP ABN ACD

  

Lạido:

//AM CD

(cùngvuônggócvới

)nên



 



ACD CAM PAM PMA

   

PAM 

cântại

PA PM 

.Đồngthời

PCM

cântại

nên

PC PM



PA PC 

hay

làtrungđiểmcủa

.

-Tacó:

 

2; 2MN

  



đườngthẳng

cóphươngtrình:

4 0

x y

  



Điểm

cótọađộlànghiệmcủahệ

1 0

5 3

;

4 0 3

2 2

x y







  





 

  

 

 

  

 













-Do

 

: 1 0 ; 1

A AC x y A a a

      

(với



)

-Do

2 2 2

5 5 25 5 25

2 2 2 2 4

PA PM a a a

     

        

     

     



   

5 5

2 2

0 0; 1 5;4

5 5 0

2 2

a A C



 







        









  







-Do

điqua

 

0;4

và

 

5;4

nên

cóphươngtrình:

4 0

 

.

-Lạicó:

 

2;3

AN 



làvectơpháptuyếncủa

nênphươngtrình

là:

2 3 10 0

x y

  

.

Tọađộđiểm

lànghiệmcủahệphươngtrình:

 

4 0 1

1;4

2 3 10 0 4

y x

x y y

   

 

   

 

   

 

.

Vậy

   

5 3

; , 0; 1 , 1;4

2 2

P A B

 

 

 

 

.

Câu 240. ChọnD

Cách 1:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 68



Tacó

 

5 2 0 1

1 3

5 14 0 3

x y x

A AB AC A ;

x y y

   

 

    

 

   

 



Dễchứngminhđược

AM MC

 

PhươngtrìnhMC:

4 7 4 0

x y

  



 

4 7 4 0 6

6 4

5 14 0 4

x y x

C MC AC C ;

x y y

   

 

    

 

   

 



Vậy

OC 

Chứngminh

AM MC

PP1:Dùngphươngphápvéctơ.

*

    

. . . 2 . .

MA MC MD DA MB BC MD BC DA MB MD DC DE MB

      

             



*

. . . .MD DC DE MB MD BD DE MB

  

       



*

 



cos , =cos

MD BD MDB

 

MD BD DM

DM DB DB

 

 

MD BD MD

 

 



*

 



cos , cos

DE MB MED

 

 



DE MB ME

DE MB DE

  

 

. .

DE MB ME MB MD

    

 



Dođó

.MA MC

 

=0nên

MA MC

.

PP2:



Vẽhìnhchữnhật

ADCF

(1)

Dễthấytứgiác

AHDB

làhìnhbìnhhành

 

 / / ;

vì AH BD AH BD





Nên

quatrungđiểm

của





HMD  (2)

Từ(1)và(2)tacó5điểm

,  ,  ,  , A M D C F

cùngthuộcđườngtrònđườngkính

.AC



Nên



AMC AM MC

  

.

Cách 2:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 69



Tacó:

A AB AC 



 

1;3

A

.

Giảsử

 

DB kDE k

 



MB DB

  

MB k MC

  

  



2 2

1 1

DM DB DE

k k

  

 

  



Tacó:

MA DA DM 

  

2DE DM 

 

2 2

1 2

1 1

DB DE

k k



  

 

 

.

MC DC DM

 

  

DB DM  

 

2 2

1 1

k k

DB DE

k k



  

 

 

.

 

2 2

. 0

1 1

k k

MA MC DB ED

k k



   

 

 

MA MC 

.

Lạicó:

4 7

;

5 5

 

 

 

 



: 4 7 4 0

MC x y

   

.

Vậy

C MC AC 



 

6;4

C

OC 

.

Câu 241. ChọnB



Đườngthẳngchứacạnh

cóphươngtrình:

5 3

2 7 0

17 1

5 3

5 5

x y

 

    

  



Đường thẳng chứa đường cao

 của tam giác đi qua

17 1

;

5 5

 



 

 

 có véc tơ pháp tuyên

8 16

;

5 5

 

 

 



cóphươngtrình:

8 17 16 1

0 2 3 0

5 5 5 5

x y x y

   

       

   

   

.

Gọi

 

0 0

;B x y

,vì

làtrungđiểmcủa

nên

 

0 0

A x y

 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 70

Tacó:

 

0 0

2 7 0 1

B BC x y    



   

0 0 0 0

2 2 3 0 2 1 0 2

A AH x y x y          



Từ

 

và

 

tacóhệ:

 

0 0 0

2 7 0 3

3;3

2 1 0 1

x y x

x y y

   

 

  

 

    

 



Gọi

 

2 2

; 0

u a b a b

 



làvéctơchỉphươngcủađườngthẳng



+)

   

3; 2 , 8;0

AM AD

 



Đườngthẳng

làphângiáctronggóc

nên:

   

   

cos cos cos ; cos ;BAD CAD BAD CAD AM AD AD u

    

   



2 2

24 8

3 13

13.8

a b a

a b

    





2 2

4 9

a b







  



 







Với

a b

 

.Chọn

 

2 3 3;2

b a u     



(loạivìcùngphươngvới



)

Với

a b



.Chọn

 

2 3 3;2

b a u   



.Đườngthẳng

cóphươngtrình:

3 3

3 2

x t

y t

  





 





Điểm

làgiaođiểmcủa

và

nêncótọađộlànghiệmcủahệ:

 

2 7 0 6 6 3 2 7 0 4

3 3 3 3 9 9;11

3 2 3 2 11

x y t t t

x t x t x C

y t y t y

         

  

  

         

  

  

    

  

.

DẠNG7.MỘTSỐBÀITOÁNLIÊNQUANĐẾNDIỆNTÍCH

Câu 242. ChọnA

Đườngthẳng

:5 3 15

x y

  

cắtcáctrụctọađộtạicácđiểm

 

3;0

,

 

0;5

.

Tacó



,



.Khiđó

1 15

. 7,5

2 2

OAB

S OAOB  

.

Câu 243. ChọnA

: 4

y mx

 

,

: 4

d y mx

  

.

,

cắtnhaucùngcắttrụchoànhkhi



.

Gọi

 

 

 

,

 



 

 

lầnlượtlàgiaođiểmcủa

,

vàtrụchoành.

Phươngtrìnhhoànhđộgiaođiểmcủa

,

:

4 4mx mx   

 

.

Gọi

làgiaođiểmcủa

và

thì

 

0; 4



.

 

, .

ABC

S d C Ox AB



,có

 

, 4

d C Ox y

 

,

A B

AB x x

  

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 71

1 8 16

.4.

ABC

m m

  

.

Có

ABC



 

 

,

m



 

.Vậy

 

S 

.

Câu 244. 

Hướngdẫngiải.

ChọnD

Vìđườngthẳng

điquađiểm

 

1;3

nêntacó:

 

3 1 .

a b 



Đườngthẳng

d y ax b 

cắttrục

,Ox Oy

lầnlượtlà

   

;0 , 0; , 0 .

A B b a

 

 

 

 



Theogiảthiết

 

1 1 1

. . 6 2 .

2 2 2

OAB

b b

S OAOB b

a a



   



Từphươngtrình

 

1 3

a b  

thayvàophươngtrình

 

2 :

   

12 3 , 3

12 12 3

12 3 , 3

b b b

b b

b b b



  

    





   







 

6 6 2

12 36 0, 3 3

6 6 2

12 36 0, 3

6 3

b b b b

b b b

b b



  



    



 



  





   





 







Với



tađược

 



Vậyphươngtrình

: 3 6.

d y x

  



Ghi chú:Với

6 6 2



  



  





thìnhìnvào

đápánkhôngcónêntakhôngcầntìmnữa.

Câu 245. Chọn D.



Gọi

làgiaođiểmcủa



và

.

Gọi

làhìnhchiếucủa

trên

.

Theođềbàitacó:

AIB AIC

S S



1 1

. . . .

2 2

AH IB AH IC

 

IB IC 

.

I

làtrungđiểmcủa

 

1;3

I 

.

 

2;6

AI  



.

Đườngthẳng



điqua

vànhậnvectơ

 

3;1

n 



làmvectơpháptuyến.

Phươngtrìnhđườngthẳng



là

   

3 1 3 0

x y

   

3 0

x y

  

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 72

Câu 246. ChọnC

Gọiđườngthẳngdcắttia

,

lầnlượttại

 

;0A a

và

 

0; ; , 0

B b a b



 

: 1  

x y

a b



Vì

 

qua

 

2 1

2;1 1  

a b



1 2 8   



Tacódiệntíchtamgiácvuông

OAB

tại

là

1 1

. . . . 4

2 2

  

S OAOB a b



Diệntíchtamgiácvuông

OAB

đạtgiátrịnhỏnhất

2 1

4 2    S a b

a b



2 1

1 2, 4

     

b a

b b



 

: 1 2 4 0

4 2

      

x y

d x y

.

Câu 247. ChọnC

điqua

 

1;6M

 



1 6

1(1).

a b



 



Đườngthẳngcắttia

tại

( ;0), 0 .A a a OA a  



Đườngthẳngcắttia

tại

(0; ),  0 .B b b OB b  



OAB

vuôngtạiOnêncódiệntíchlà

1 1

. .

2 2

OAOB ab





Theođề

4 8(2).

ab ab  



Từ

   

1 , 2

suyra:

2; 4 2 10

a b S a b

     

.



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợ

p: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 1

TOÁN 10

0H3-2

Content

PHẦNA.CÂUH

ỎI ......................................................................................................................................................... 1

DẠNG1.NHẬNDẠNGPHƯƠNGTRÌNHĐƯỜNGTRÒN ....................................................................................... 1

DẠNG2.TÌMTỌAĐỘTÂM,BÁNKÍNHĐƯỜNGTRÒN ....................................................................................... 2

DẠNG3.VIẾTPHƯƠNGTRÌNHĐƯỜNGTRÒN ...................................................................................................... 2

Dạng3.1Khibiếttâmvàbánkính ............................................................................................................................... 2

Dạng3.2Khibiếtcácđiểmđiqua ............................................................................................................................... 3

Dạng3.3Sửdụngđiềukiệntiếpxúc ........................................................................................................................... 4

DẠNG4.TƯƠNGGIAOCỦAĐƯỜNGTHẲNGVÀĐƯỜNGTRÒN ...................................................................... 5

Dạng4.1.Phươngtrìnhtiếptuyến ............................................................................................................................... 5

Dạng4.2Bàitoántươnggiao .......................................................................................................................................... 6

DẠNG5.CÂUHỎIMIN-MAX ..................................................................................................................................... 8

PHẦNB.LỜIGIẢITHAMKHẢO ................................................................................................................................ 9

DẠNG1.NHẬNDẠNGPHƯƠNGTRÌNHĐƯỜNGTRÒN ....................................................................................... 9

DẠNG2.TÌMTỌAĐỘTÂM,BÁNKÍNHĐƯỜNGTRÒN ..................................................................................... 10

DẠNG3.VIẾTPHƯƠNGTRÌNHĐƯỜNGTRÒN .................................................................................................... 11

Dạng3.1Khibiếttâmvàbánkính ............................................................................................................................. 11

Dạng3.2Khibiếtcácđiểmđiqua ............................................................................................................................. 11

Dạng3.3Sửdụngđiềukiệntiếpxúc ......................................................................................................................... 13

DẠNG4.TƯƠNGGIAOCỦAĐƯỜNGTHẲNGVÀĐƯỜNGTRÒN .................................................................... 15

Dạng4.1.Phươngtrìnhtiếptuyến ............................................................................................................................. 15

Dạng4.2Bàitoántươnggiao ........................................................................................................................................ 18

DẠNG5.CÂUHỎIMIN-MAX ................................................................................................................................... 24

PHẦNA.CÂUHỎI

DẠNG1.NHẬNDẠNGPHƯƠNGTRÌNHĐƯỜNGTRÒN

Câu 1. Tìmtấtcảcácgiátrịcủathamsố

đểphươngtrình

 

2 2

2 2 4

19 6 0

x y m

x my m

  

   

là

phươngtrìnhđườngtròn.

1 2.

 

 

hoặc

 

 

hoặc



. D.



hoặc



Câu 2. Trongmặtphẳng

Oxy

,phươngtrìnhnàosauđâylàphươngtrìnhcủađườngtròn?

PHƯƠNG TRÌNH ĐƯỜNG TRÒN

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 2

2 2

2 4 8 1 0

x y x y

    

. B.

2 2

4 6 12 0

x y x y

    

2 2

2 8 20 0

x y x y

    

. D.

2 2

4 10 6 2 0

x y x y

    

.

Câu 3. Phươngtrìnhnàosauđâylàphươngtrìnhcủađườngtròn?

2 2

2 6 6 8 0

x y x y

    

. B.

2 2

2 4 8 12 0

x y x y

    

2 2

2 8 18 0

x y x y

    

. D.

2 2

2 2 4 6 12 0

x y x y

    

.

Câu 4. (CụmliêntrườngHảiPhòng-L1-2019)Phươngtrìnhnàosauđâylàphươngtrìnhcủamộtđường

tròn?

2 2

4 2 8 3 0

x y xy x y

     

. B.

2 2

2 4 5 1 0

x y x y

    

2 2

14 2 2018 0

x y x y

    

. D.

2 2

4 5 2 0

x y x y

    

Câu 5. (THPTQuỳnhLưu-NghệAn-2019)Chophươngtrình

 

2 2

2 4 2 6 0(1)

x y mx m y m      

.Điềukiệncủa

để

(1)

làphươngtrìnhcủađườngtròn.



. B.











. C.

1 2

 

. D.











.

DẠNG2.TÌMTỌAĐỘTÂM,BÁNKÍNHĐƯỜNGTRÒN

Câu 6. Trongmặtphẳng

Oxy

,đườngtròn

 

2 2

: 4 6 12 0

C x y x y

    

cótâmlà.

 

2; 3

 

. B.

 

2;3

. C.

 

4;6

. D.

 

4; 6

 

.

Câu 7. Đườngtròn

2 2

10 24 0

x y y

   

cóbánkínhbằngbaonhiêu?

. B.

. C.

. D.

.

Câu 8. Xácđịnhtâmvàbánkínhcủađườngtròn

     

2 2

: 1 2 9.

C x y

   



A. Tâm

 

1;2 ,

I 

bánkính



. B. Tâm

 

1;2 ,

I 

bánkính



C. Tâm

 

1; 2 ,



bánkính



. D. Tâm

 

1; 2 ,



bánkính



.

Câu 9. (ĐỀTHITHỬĐỒNGĐẬU-VĨNHPHÚCLẦN01-2018–2019)Tìmtọađộtâm

vàbán

kính

củađườngtròn

 

:

2 2

2 4 1 0

x y x y

    

.

 

1;2 ; 4

I R

 

. B.

 

1; 2 ; 2

I R

 

. C.

 

1; 2 ; 5

I R  . D.

 

1; 2 ; 4

I R

 

.

Câu 10. Trongmặtphẳng

Oxy

,chođườngtròn

     

2 2

: 2 3 9

C x y

   

.Đườngtròncótâmvàbánkính

là

 

2;3 , 9

I R



. B.

 

2; 3 , 3

I R

 

. C.

 

3;2 , 3

I R

 

. D.

 

2;3 , 3

I R

 

.

Câu 11. Tìmtọađộtâm

vàtínhbánkính

củađườngtròn

   

2 2

( ) : 2 5 9

C x y

   

.

( 2;5), 81.

I R

 

. B.

(2; 5), 9.

I R

 

. C.

(2; 5), 3.

I R

 

. D.

( 2;5), 3.

I R

 



Câu 12. Đườngtròn

 

2 2

: 2 4 3 0

C x y x y

    

cótâm

,bánkính

là

 

1;2 , 2

I R  . B.

 

1;2 , 2 2

I R  . C.

 

1; 2 , 2

I R  . D.

 

1; 2 , 2 2

I R  .

DẠNG3.VIẾTPHƯƠNGTRÌNHĐƯỜNGTRÒN

Dạng3.1Khibiếttâmvàbánkính



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 3

Câu 13. Phươngtrìnhđườngtròncótâm

 

1;2

vàbánkính



là

2 2

2 4 20 0

x y x y

    

. B.

2 2

2 4 20 0

x y x y

    

.

2 2

2 4 20 0

x y x y

    

. D.

2 2

2 4 20 0

x y x y

    

.

Câu 14. Đườngtròntâm

 

1;2

I 

,bánkính



cóphươngtrìnhlà

2 2

2 4 4 0

x y x y

    

2 2

2 4 4 0

x y x y

    

2 2

2 4 4 0

x y x y

    

2 2

2 4 4 0

x y x y

    

.

Câu 15. (THPTNGUYỄNTRÃI-THANHHOÁ-Lần1.Năm2018&2019)Phươngtrìnhnàosauđâylà

phươngtrìnhcủađườngtròntâm

 

1;2

I 

,bánkínhbằng

?

   

2 2

1 2 9

x y

   

. B.

   

2 2

1 2 9

x y

   

.

   

2 2

1 2 9

x y

   

. D.

   

2 2

1 2 9

x y

   

.

Dạng3.2Khibiếtcácđiểmđiqua



Câu 16. Đườngtròn

 

điquahaiđiểm

 

1;1

,

 

5;3

vàcótâm

thuộctrụchoànhcóphươngtrìnhlà

 

4 10

x y

  

. B.

 

4 10

x y

  

.

 

4 10

x y  

. D.

 

4 10

x y  

.

Câu 17. (KSNLGV-THUẬNTHÀNH2-BẮCNINHNĂM2018-2019)Trongmặtphẳngvớihệtọa

độ

Oxy

,tìmtọađộtâm

củađườngtrònđiquabađiểm

 

0;4

,

 

2;4

,

 

2;0

.

 

1;1

. B.

 

0;0

. C.

 

1;2

. D.

 

1;0

.

Câu 18. Chotamgiác

ABC

có

     

1; 1 , 3;2 , 5; 5

A B C

 

.Toạđộtâmđườngtrònngoạitiếptamgiác

ABC

là

47 13

;

10 10

 



 

 

. B.

47 13

;

10 10

 

 

 

. C.

47 13

;

10 10

 

 

 

 

. D.

47 13

;

10 10

 



 

 

.

Câu 19. Trongmặtphẳng

Oxy

,đườngtrònđiquabađiểm

 

1;2

,

 

5; 2

,

 

1; 3



cóphươngtrìnhlà.

2 2

25 19 49 0

x y x y

    

. B.

2 2

2 6 3 0

x y x y

    

2 2

6 1 0

x y x y

    

. D.

2 2

6 1 0

x y x xy

    

Câu 20. Lập phương trình đường tròn đi qua hai điểm

   

3;0 , 0;2

A B

 và có tâm thuộc đường thẳng

: 0

d x y

 

.

2 2

1 1 13

2 2 2

x y

   

   

   

   

. B.

2 2

1 1 13

2 2 2

x y

   

   

   

   

.

2 2

1 1 13

2 2 2

x y

   

   

   

   

. D.

2 2

1 1 13

2 2 2

x y

   

   

   

   

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 4

Câu 21. Chotamgiác

ABC

biết

 

3;2

,

5 8

;

3 3

 

 

 

lầnlượtlàtrựctâmvàtrọngtâmcủatamgiác,đường

thẳng

cóphươngtrình

2 2 0

x y

  

.Tìmphươngtrìnhđườngtrònngoạitiếptamgiác

ABC

   

2 2

1 1 20

x y

   

   

2 2

2 4 20

x y

   

   

2 2

1 3 1

x y

   

   

2 2

1 3 25

x y

   

.

Câu 22. (NôngCống-ThanhHóa-Lần1-1819)Trongmặtphẳngtọađộ

Oxy

,chotamgiác

ABC

có

trựctâm

, trọng tâm

 

1;3

G 

. Gọi

, ,K M N

 lần lượt làtrungđiểm của

, ,AH AB AC

. Tìm

phươngtrìnhđườngtrònngoạitiếptamgiác

ABC

biếtđườngtrònngoạitiếptamgiác

KMN

là

 

2 2

: 4 4 17 0

C x y x y

    

.

   

2 2

1 5 100

x y   

.

   

2 2

1 5 100

x y   

.

   

2 2

1 5 100

x y   

.

   

2 2

1 5 100

x y   

.

Câu 23. (THPTTRIỆUTHỊTRINH-LẦN1-2018)Trongmặtphẳngtọađộ

Oxy

,chotamgiác

ABC



cótrựctâm

.Gọi

làtrungđiểmcủa

;

,

lầnlượtlàchânđườngcaokẻtừ

và

.

Đườngtrònđiquabađiểm

,

cóphươngtrìnhlà

   

1 25

: 1

2 4

T x y

 

   

 

 

.Phương

trìnhđườngtrònngoạitiếptamgiác

ABC

là:

   

2 2

1 2 25

x y

   

. B.

 

1 25

x y

  

.

 

1 50

x y

  

. D.

   

2 2

2 1 25

x y

   

.

Dạng3.3Sửdụngđiềukiệntiếpxúc



Câu 24. (THPTCộngHiền-Lần1-2018-2019)Trongmặtphẳngtọađộ

Oxy

,phươngtrìnhcủađường

tròncótâmlàgốctọađộ

vàtiếpxúcvớiđườngthẳng



:

2 0

x y

  

là

2 2

x y

 

. B.

2 2

x y

 

.

   

2 2

1 1 2

x y   

. D.

   

2 2

1 1 2

x y

   

.

Câu 25. (TrườngTHPTChuyênLamSơn_2018-2019)Trongmặtphẳngtọađộ

 

Oxy

,chođườngtròn

 

cótâm

nằmtrênđườngthẳng

y x 

,bánkính



vàtiếpxúcvớicáctrụctọađộ.Lập

phươngtrìnhcủa

 

,biếthoànhđộtâm

làsốdương.

   

2 2

3 3 9

x y

   

. B.

   

2 2

3 3 9

x y

   

.

   

2 2

3 3 9

x y

   

. D.

   

2 2

3 3 9

x y

   

.

Câu 26. Mộtđườngtròncótâm

 

3;4

tiếpxúcvớiđườngthẳng

:3 4 10 0

x y

   

.Hỏibánkínhđường

trònbằngbaonhiêu?

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 5

. B.

. C.

. D.

.

Câu 27. Tronghệtrụctọađộ

Oxy

,chođiểm

 

1;1

vàđườngthẳng

 

:3 4 2 0

d x y

  

.Đườngtròntâm

vàtiếpxúcvớiđườngthẳng

 

cóphươngtrình

   

2 2

1 1 5

x y

   

.B.

   

2 2

1 1 25

x y

   

.

   

2 2

1 1 1

x y

   

.D.

   

2 2

1 1

x y

   

.

Câu 28. (LƯƠNGTÀI2BẮCNINHLẦN1-2018-2019)Trênhệtrụctọađộ

Oxy

,chođườngtròn

( )C



cótâm

 

3;2

I 

vàmộttiếptuyếncủanócóphươngtrìnhlà

3 4 9 0

x y

  

.Viếtphươngtrìnhcủa

đườngtròn

( )C

.

   

2 2

3 2 2

x y

   

. B.

   

2 2

3 2 2

x y

   

.

   

2 2

3 2 4

x y

   

 D.

   

2 2

3 2 4

x y

   

.

Câu 29. Trênmặtphẳngtoạđộ

Oxy

,chocácđiểm

 

3;0

và

 

0;4

.Đườngtrònnộitiếptamgiác

OAB



cóphươngtrình

2 2

x y

 

. B.

2 2

4 4 0

x y x

   

2 2

x y

 

. D.

   

2 2

1 1 1

x y

   

.

Câu 30. (LẦN01_VĨNHYÊN_VĨNHPHÚC_2019)Chohaiđiểm

 

3;0

,

 

0;4

.Đườngtrònnộitiếp

tamgiác

OAB

cóphươngtrìnhlà

2 2

x y

 

. B.

2 2

2 2 1 0

x y x y

    

.

2 2

6 8 25 0

x y x y

    

. D.

2 2

x y

 

.

DẠNG4.TƯƠNGGIAOCỦAĐƯỜNGTHẲNGVÀĐƯỜNGTRÒN

Dạng4.1.Phươngtrìnhtiếptuyến



Câu 31. Đườngtròn

2 2

1 0

x y

  

tiếpxúcvớiđườngthẳngnàotrongcácđườngthẳngdướiđây?

3 4 5 0

x y

  

x y

 

3 4 1 0

x y

  

1 0

x y

  



Câu 32. ĐườngtrònnàosauđâytiếpxúcvớitrụcOx:

2 2

10 0

x y x

  

. B.

2 2

5 0

x y

  

2 2

10 2 1 0

x y x y

    

. D.

2 2

6 5 9 0

x y x y

    

.

Câu 33. Trongmặtphẳngvớihệtọađộ

Oxy

,chođườngtròn

 

2 2

: 2 4 3 0

C x y x y

    

.Viếtphương

trình tiếp tuyến

 của đường tròn

( )C

 biết tiếp tuyến đó song song với đường thẳng

: 3 4 1 0

x y

   

.

3 4 5 2 11 0

x y

   

;

3 4 5 2 11 0

x y

   

.

3 4 5 2 11 0

x y

   

,

3 4 5 2 11 0

x y

   

3 4 5 2 11 0

x y

   

,

3 4 5 2 11 0

x y

   

3 4 5 2 11 0

x y

   

,

3 4 5 2 11 0

x y

   

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 6

Câu 34. Chođườngtròn

 

2 2

: 2 4 4 0

C x y x y

    

vàđiểm

 

1;5

.Đườngthẳngnàotrongcácđường

thẳngdướiđâylàtiếptuyếncủađườngtròn

 

tạiđiểm

.

5 0

 

. B.

5 0

 

. C.

5 0

x y

  

. D.

5 0

x y

  

.

Câu 35. Chođườngtròn

 

2 2

: 4 0

C x y

  

vàđiểm

 

1;2

A 

.Đườngthẳngnàotrongcácđườngthẳng

dướiđâyđiqua

vàlàtiếptuyếncủađườngtròn

 

?

4 3 10 0

x y

  

. B.

6 4 0

x y

  

. C.

3 4 10 0

x y

  

. D.

3 4 11 0

x y

  

Câu 36. Trongmặtphẳng

Oxy

,chođườngtròn

     

2 2

: 1 4 4

C x y

   

.Phươngtrìnhtiếptuyếnvới

đườngtròn

 

songsongvớiđườngthẳng

: 4 3 2 0

x y

   

là

4 3 18 0

x y

  

. B.

4 3 18 0

x y

  

.

4 3 18 0;4 3 2 0

x y x y

     

. D.

4 3 18 0;4 3 2 0

x y x y

     

.

Câu 37. Số tiếp tuyến chung của 2 đường tròn

 

2 2

: 2 4 1 0

C x y x y

    

 và

 

2 2

' : 6 8 20 0

C x y x y

    

là

. B.

. C.

. D.

.

Câu 38. (THIHK1LỚP11THPTVIỆTTRÌ2018-2019)Viếtphươngtrìnhtiếptuyếncủađườngtròn

2 2

( ) : ( 2) ( 4) 25

C x y

   

,biếttiếptuyếnvuônggócvớiđườngthẳng

: 3 4 5 0

d x y

  

.

4 3 29 0

x y

  

. B.

4 3 29 0

x y

  

hoặc

4 3 21 0

x y

  

.

4 3 5 0

x y

  

hoặc

4 3 45 0

x y

  

 D.

4 3 5 0

x y

  

hoặc

4 3 3 0

x y

  

.

Câu 39. (ĐỀKTNĂNGLỰCGVTHUẬNTHÀNH1BẮCNINH2018-2019)Trongmặtphẳngtọađộ

Oxy,chođườngtròn

 

cóphươngtrình

2 2

2 2 3 0

x y x y

    

.Từđiểm

 

1;1

kẻđượcbao

nhiêutiếptuyếnđếnđườngtròn

 

A. 1. B. 2. C. vôsố. D. 0.

Câu 40. Trongmặtphẳng

Oxy

,chođườngtròn

     

2 2

: 1 4 4

C x y

   

.Phươngtrìnhtiếptuyếnvới

đườngtròn

 

,biếttiếptuyếnđósongsongvớiđườngthẳng

: 4 3 2 0

x y

   

là

4 3 18 0

x y

  

và

4 3 2 0

x y

   

. B.

4 3 18 0

x y

  

và

4 3 2 0

x y

  

4 3 18 0

x y

   

và

4 3 2 0

x y

  

. D.

4 3 18 0

x y

   

và

4 3 2 0

x y

   

.

Câu 41. Trênmặtphẳngtoạđộ

Oxy

,chođiểm

 

3; 2

 

vàđườngtròn

     

2 2

: 3 4 36

C x y

   

.Từ

điểm

kẻcáctiếptuyến

và

tớiđườngtròn

 

,với

làcáctiếpđiểm.Phương

trìnhđườngthẳng

MN

là

1 0

x y

  

. B.

1 0

x y

  

. C.

1 0

x y

  

. D.

1 0

x y

  

.

Câu 42. Trongmặtphẳngvớihệtọađộ

Oxy

,chođiểm

( 3;1)



vàđườngtròn

 

2 2

: 2 6 6 0

C x y x y

    

.Gọi

,

làcáctiếpđiểmcủacáctiếptuyếnkẻtừ

đến(C).Tínhkhoảngcáchtừ

đếnđường

thẳng

1 2

.TT



. B.

. C.

. D.

2 2

.

Dạng4.2Bàitoántươnggiao



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 7

Câu 43. Trongmặtphẳngvớihệtrụctọađộ

Oxy

,chohaiđườngtròn

   

1 2

C C

cóphươngtrìnhlầnlượt

là

2 2 2 2

( 1) ( 2) 9và( 2) ( 2) 4

x y x y

       

.Khẳngđịnhnàodướiđâylàsai?

A. Đườngtròn

 

cótâm

 

1; 2

 

vàbánkính



B. Đườngtròn

 

cótâm

 

2;2

vàbánkính



.

C. Haiđườngtròn

   

1 2

C C



khôngcóđiểmchung.

D. Haiđườngtròn

   

1 2

C C



tiếpxúcvớinhau.

Câu 44. Tìmgiaođiểm

đườngtròn

2 2

( ) : x 4 0

C y

  

và

2 2

( ): x 4 4 4 0.

C y x y

    

 

2;2

và

 

2; 2 

. B.

 

0;2

và

 

0; 2

. C.

 

2;0

và

 

2;0



. D.

 

2;0

và

 

0;2 .



Câu 45. Trong mặt phẳng với hệ trục

Oxy

, cho hai đường tròn

   

: 1 4

C x y

  

 và

     

2 2

: 4 3 16

C x y



   

cắtnhautạihaiđiểmphânbiệt

và

.Lậpphươngtrìnhđường

thẳng



2 0

x y

  

. B.

2. 0

x y

  

2 0

x y

  

. D.

2 0

x y

  

.

Câu 46. Chođườngthẳng

:3 4 19 0

x y

   

vàđườngtròn

     

2 2

: 1 1 25

C x y

   

.Biếtđườngthẳng



cắt

 

tạihaiđiểmphânbiệt

và

,khiđóđộdàiđọanthẳng

là

A. 6. B. 3. C. 4. D. 8.

Câu 47. Trongmặtphẳngtọađộ

Oxy

chođườngtròn

 

cótâm

 

1; 1I 

bánkính

5R 

.Biếtrằngđường

thẳng

 

:3 4 8 0d x y  

cắtđườngtròn

 

tạihaiđiểmphânbiệt

,A B

.Tínhđộdàiđoạnthẳng

.

8AB 

. B.

4AB 

. C.

3.AB 

. D.

6AB 

.

Câu 48. Trong mặt phẳng với hệ trục tọa độ

,Oxy

 cho đường tròn

 

 có phương trình

   

2 2

2 2 4

x y

   

vàđườngthẳng

:3 4 7 0

d x y

  

.Gọi

,A B

làcácgiaođiểmcủađường

thẳng

vớiđườngtròn

 

.Tínhđộdàidâycung

AB  . B.

2 5

AB  . C.

2 3

AB  . D.

4AB 

.

Câu 49. Trongmặtphẳngvớihệtọađộ

Oxy

,chođiểm

 

3;1

,đườngtròn

 

2 2

: 2 4 3 0

C x y x y

    

.

Viếtphươngtrìnhtổngquátcủađườngthẳng

điqua

vàcắtđườngtròn

 

tạihaiđiểm

,

saocho

2 2

BC 

.

: 2 5 0

d x y

  

. B.

: 2 5 0

d x y

  

. C.

: 2 5 0

d x y

  

. D.

: 2 5 0

d x y

  

.

Câu 50. Trongmặtphẳngvớihệtrụctọađộ

Oxy

,chohaiđườngtròn

   

1 2

C C

cóphươngtrìnhlầnlượt

là

2 2 2 2

( 1) ( 2) 9và( 2) ( 2) 4

x y x y

       

.Viếtphươngtrìnhđườngthẳng



điquagốctọa

độvàtạovớiđườngthẳngnốitâmcủahaiđườngtrònmộtgócbằng

45

.

: 7 0

d x y



 



hoặc

: 7 0

d x y



 

. B.

: 7 0

d x y



 



hoặc

: 7 0

d x y



 

: 7 0

d x y



 



hoặc

: 7 0

d x y



 

. D.

: 7 0

d x y



 



hoặc

: 7 0

d x y



 

Câu 51.

(KSCLLẦN1CHUYÊNLAMSƠN-THANHHÓA_2018-2019)Trongmặtphẳngtọađộ

Oxy



chođiểm

 

1;2



vàđườngthẳng

 

: 2 5 0.

d x y

  

Biếtrằngcóhaiđiểm

1 2

,M M



thuộc

 



sao

cho

1 2

10.

IM IM 

Tổngcáchoànhđộcủa



và



là



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 8

 B.

 C.

 D.



Câu 52. (NGÔGIATỰLẦN1_2018-2019)Tronghệtọađộ

Ox ,y

chođườngtròn

 

cóphươngtrình:

2 2

4 2 15 0.x y x y I

     làtâm

 

,đườngthẳng

điqua

 

1; 3



cắt

 

tại

, .A B

Biết

tamgiác

IAB

códiệntíchlà

Phươngtrìnhđườngthẳng

là:

x by c

  

Tính

b c



 B.

 C.

 D.



Câu 53. (KSCLLẦN1CHUYÊNLAMSƠN-THANHHÓA_2018-2019)Trongmặtphẳng

Oxy

cho

tamgiác

ABC

cóđỉnh

 

5;5

,trựctâm

 

1;13

H 

,đườngtrònngoàitiếptamgiáccóphương

trình

2 2

x y

 

.Biếttọađộđỉnh

 

;C a b

,với



.Tổng

a b

bằng

8

. B.

. C.

. D.

6

.

Câu 54. (NôngCống-ThanhHóa-Lần1-1819)Trongmặtphẳng

Oxy

,cho

ABC

nộitiếpđườngtròn

tâm

 

2; 2

,điểm

làchânđườngphângiácngoàicủagóc



BAC

.Đườngthẳng

cắtđường

trònngoạitiếp

ABC

tạiđiểmthứhailàM(khácA).Biếtđiểm

 

2; 2

J 

làtâmđườngtrònngoại

tiếp

ACD

vàphươngtrìnhđườngthẳngCMlà:

2 0.

x y

  

Tìmtổnghoànhđộcủacácđỉnh

,  ,A B C

củatamgiác

ABC

.

. B.

. C.

. D.

.

Câu 55. Trongmặtphẳngtọađộ

Oxy

,chohaiđườngthẳng

 

: 3 8 0

x y

   

;

 

:3 4 10 0

x y



   



vàđiểm

 

2;1



.Đườngtròncótâm

 

;I a b

thuộcđườngthẳng

 



,điqua

vàtiếpxúcvới

đườngthẳng

 





.Tính

a b

.

4

. B.

. C.

. D.

2

.

Câu 56. Trongmặtphẳngvớihệtọađộ

Oxy

,chođườngthẳng

: 3 4 1 0

d x y

  

vàđiểm

 

1; 2



.Gọi

 

làđườngtròncótâmIvàcắtđườngthẳngdtạihaiđiểmAvàBsaochotamgiácIABcódiện

tíchbằng4.Phươngtrìnhđườngtròn

 

là

   

2 2

1 2 8

x y

   

.B.

   

2 2

1 2 20

x y

   

.

   

2 2

1 2 5

x y

   

.D.

   

2 2

1 2 16

x y

   

.

DẠNG5.CÂUHỎIMIN-MAX



Câu 57. Chođươngtron

 

2 2

: 2 4 4 0

C x y x y

    

vađiêm

 

2;1

.Dâycungcua

 

điquađiêmM

cođôdaingănnhâtla

. B.

. C.

3 7

. D.

2 7

.

Câu 58. TrongmặtphẳngtọađộOxy,chohaiđiểm

(0; 3), (4;1)

A B



vàđiểmMthayđổithuộcđườngtròn

2 2

( ) : ( 1) 4

C x y

  

.Gọi

min

làgiátrịnhỏnhấtcủabiểuthức

2P MA MB 

.Khiđótacó

min



thuộckhoảngnàodướiđây?

 

7,7;8,1 .

. B.

 

7,3;7,7 .

. C.

 

8,3;8,5 .

. D.

 

8,1;8,3 .



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 9

Câu 59. Trongmặtphẳngvớihệtọađộ

Oxy

,chođườngtròn

 

2 2

: 2 4 3 0

C x y x y

    

.Tìmtọađộ

điểm

 

0 0

;M x y

nằmtrênđườngtròn

 

saocho

0 0

T x y 

đạtgiátrịlớnnhất.

 

2;3

. B.

 

0;1

. C.

 

2;1

. D.

 

0;3

.

Câu 60. Trongmặtphẳng

Oxy

,chođiểm

nằmtrênđườngtròn

 

2 2

: 8 6 16 0

C x y x y

    

.Tínhđộ

dàinhỏnhấtcủa

. B.

. C.

. D.

Câu 61. Gọi



làtâmcủađườngtròn

 

   

2 2

1 1 4

x y

   

.Sốcácgiátrịnguyêncủa

đểđường

thẳng

x y m

  

cắtđườngtròn

 

tạihaiđiểmphânbiệt

,A B

saochotamgiác

IAB

códiện

tíchlớnnhấtlà

. B.

. C.

. D.

.

Câu 62. Điểmnằm trên đườngtròn

 

2 2

: 2 4 1 0

C x y x y

    

cókhoảngcáchngắnnhất đến đường

thẳng

: 3 0

d x y

  

cótoạđộ

 

;M a b

.Khẳngđịnhnàosauđâyđúng?

a b 

. B.

a b 

. C.

a b

. D.

a b

.

Câu 63. Chotamgiác

ABC

cótrungđiểmcủa

là

 

3;2

,trọngtâmvàtâmđườngtrònngoạitiếptam

giáclầnlượtlà

 

2 2

; , 1; 2

3 3

G I

 



 

 

.Tìmtọađộđỉnh

,biết

cóhoànhđộlớnhơn

.

 

9;1

. B.

 

5;1

. C.

 

4;2

. D.

 

3; 2



.

Câu 64. (THPT Yên Mỹ Hưng Yên lần 1 - 2019) Trong mặt phẳng tọa độ

Oxy

, cho đường tròn

 

2 2

: 2 4 25 0

C x y x y

    

vàđiểm

 

2;1

.Dâycungcủa

 

điqua

cóđộdàingắnnhất

là:

2 7

. B.

16 2

. C.

8 2

. D.

4 7

.

Câu 65. (TrườngTHPTChuyênLamSơn_2018-2019)Chocácsốthực

, , ,a b c d

thayđổi,luônthỏamãn

   

2 2

1 2 1

a b

   

và

4 3d 23 0

  

.Giátrịnhỏnhấtcủabiểuthức

   

2 2

P a c b d

   

là:

min



. B.

min



. C.

min



. D.

min



.

Câu 66. Trongmặtphẳngtọađộ

,Oxy

chođườngtròn

     

2 2

: 1 2 4   

C x y

vàcácđườngthẳng

: 1 0,   

d mx y m 

: 1 0.   

d x my m Tìmcácgiátrịcủathamsốm đểmỗiđườngthẳng

1 2

,d d

cắt

 

tại2điểmphânbiệtsaocho4điểmđólậpthành1tứgiáccódiệntíchlớnnhất.Khi

đótổngcủatấtcảcácgiátrịthamsố mlà:

A. 0. B. 1. C. 3. D. 2.



PHẦNB.LỜIGIẢITHAMKHẢO

DẠNG1.NHẬNDẠNGPHƯƠNGTRÌNHĐƯỜNGTRÒN

Câu 1. ChọnD

Tacó

   

2 2

2 2 4 19 6 0 1

x y m x my m      



2; 2 ; 19 6.

a m b m c m

      



Phươngtrình

 

làphươngtrìnhđườngtròn

2 2

a b c

   



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 10

5 15 10 0 1

m m m

     



hoặc



.

Câu 2. ChọnB

Đểlàphươngtrìnhđườngtrònthìđiềukiệncầnlàhệsốcủa

và

phảibằngnhaunênloại

đượcđápánAvà D.

Tacó:

   

2 2

2 8 20 0 1 4 3 0

x y x y x y

          



vôlý.

Tacó:

   

2 2

4 6 12 0 2 3 25

x y x y x y

         

làphươngtrìnhđườngtròntâm

 

2; 3



,bánkính



.

Câu 3. ChọnD

Biếtrằng

2 2

2 2 0

x y ax by c

    

làphươngtrìnhcủamộtđườngtrònkhivàchỉkhi

2 2

a b c

  

.

Tathấyphươngtrìnhtrongphươngán

và

cóhệsốcủa

,

khôngbằngnhaunênđây

khôngphảilàphươngtrìnhđườngtròn.

Vớiphươngán

có

2 2

1 16 18 0

a b c

     

nênđâykhôngphảilàphươngtrìnhđườngtròn.

Vậytachọnđápán

.

Câu 4. ChọnD

PhươngánA:cótích

nênkhôngphảilàphươngtrìnhđườngtròn.

PhươngánB:cóhệsốbậchaikhôngbằngnhaunênkhôngphảilàphươngtrìnhđườngtròn.

PhươngánC:tacó

   

2 2

14 2 2018 0 7 1 1968 0

x y x y x y

          

khôngtồntại

,x y

nêncũngkhôngphảiphươngtrìnhđườngtròn.

Cònlại,chọn D.

Câu 5. ChọnB

 

2 2

2 4 2 6 0(1)

x y mx m y m      

làphươngtrìnhcủađườngtrònkhivàchỉkhi

     

2 2 6 0 5 15 10 0

m m m m m





          



 





.

DẠNG2.TÌMTỌAĐỘTÂM,BÁNKÍNHĐƯỜNGTRÒN

Câu 6. ChọnA

Tacóphươngtrìnhđườngtrònlà:

   

2 2

2 3 25

x y

   

.

Vậytâmđườngtrònlà:

 

2; 3

 

.

Câu 7. ChọnB

Đườngtròn

2 2

10 24 0

x y y

   

cótâm

 

0;5

,bánkính

 

2 2

0 5 24 7

    

.

Câu 8. ChọnA

Câu 9. ChọnB

 

cótâm

 

1; 2



,bánkính

 

1 2 1 2

    

.

Câu 10. ChọnB

Đườngtròn

 

cótâm

 

2; 3



vàbánkính



.

Câu 11. ChọnD

Theobàiratacótọađộtâm

( 2;5)



vàbánkính



.

Câu 12. ChọnD

Tâm

 

1; 2



,bánkính

   

1 2 3 8 2 2

R       

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 11

DẠNG3.VIẾTPHƯƠNGTRÌNHĐƯỜNGTRÒN

Dạng3.1Khibiếttâmvàbánkính

Câu 13. ChọnA

Phươngtrìnhđườngtròncótâm

 

1;2

vàbánkính



là

   

2 2

1 2 5

x y

   



2 2

2 1 4 4 25

x x y y

      

2 2

2 4 20 0

x y x y

     

.

Câu 14. ChọnC

Đường tròn tâm

 

1;2

I 

, bán kính



 có phương trình là

   

2 2

1 2 9 2 4 4 0

x y x y x y

         

.

Câu 15. ChọnD

Phươngtrìnhđườngtròntâm

 

1;2

I 

vàbánkính



là:

   

2 2

1 2 9

x y

   

.

Dạng3.2Khibiếtcácđiểmđiqua

Câu 16. ChọnB

Gọi

 

I x Ox



;

2 2

IA IB



   

2 2

1 1 5 3

x x

     



2 2

2 1 1 10 25 9

x x x x

       



 

.Vâytâmđươngtronla

 

4;0

vabankinh

 

1 4 1 10

R IA    

.

Phươngtrinhđươngtron

 

codang

 

4 10

x y

  

.

Câu 17. ChọnC

Giảsửphươngtrìnhđườngtrònđiqua3điểm

, ,A B C

códạng

 

2 2

: 2 2 0

C x y ax by c

    



Thaytọađộ3điểm

 

0;4

,

 

2;4

,

 

2;0

tađược:

 

2 2

8 16 1

4 8 20 2 : 2 4 0

4 4 0

b c a

a b c b C x y x y

a c c

    

 

 

           

 

 

   

 

.

Vậy

 

cótâm

 

1;2

vàbánkính

R 

.

Câu 18. ChọnA

Gọi

 

;I x y

làtâmđườngtrònngoạitiếptamgiác

ABC

.

Tacó:

       

2 2 2 2

2 2

2 2 2 2 2 2

1 1 3 2

4 6 11

8 8 48 13

1 1 5 5

x y x y

AI BI x y

x y

AI CI

x y x y









      



  



  

  

   

 







      



 



 





.

47 13

;

10 10

 



 

 



.

Câu 19. ChọnC

Phươngtrìnhđườngtròncódạng

2 2

2 2 0

x y ax by c

    

.Đườngtrònnàyqua

, ,A B C

nên

1 4 2 4 0

25 4 10 4 0

1 9 2 6 0

a b c

a b c b

a b c





    





 

       

 

 

    



 





.

Vậyphươngtrìnhđườngtròncầntìmlà

2 2

6 1 0

x y x y

    

.

Câu 20. ChọnA

 

3;0

,

 

0;2

,

: 0

d x y

 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 12

Gọi

làtâmđườngtrònvậy

 

;I x x

vì

I d

.

2 2

IA IB 

   

2 2

3 2x x x x     



6 9 4 4x x    



x 

.Vậy

1 1

;

2 2

 



 

 

.

2 2

1 1 26

2 2 2

   

   

   

   

làbánkínhđườngtròn.

Phươngtrìnhđườngtròncầnlậplà:

2 2

1 1 13

2 2 2

x y

   

   

   

   

.

Câu 21. ChọnD



*)Gọi

làtâmđườngtrònngoạitiếptamgiác

ABC

.

HI HG 

 

3 5

3 3

2 3

3 8

2 2

2 3



 

  

 



  





 



  

 



 

















.

(DođótacóthểchọnđápánDluônmàkhôngcầntínhbánkính).

*)Gọi

làtrungđiểmcủa



IM BC 



:2 1 0IM x y   

.

M IM BC 



2 1

2 2

x y

  







 















 

0;1M

.

Lạicó:

3MA MG

 



1 3. 1











 



  

 



 

















.

Suyra:bánkínhđườngtrònngoạitiếptamgiác

ABC

là

5R IA 

.

Vậyphươngtrìnhđườngtrònngoạitiếptamgiác

ABC

là

   

2 2

1 3 25x y   

.

Câu 22. ChọnA

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 13

Gọi

làtrungđiểm

,

làtâmđườngtrònngoạitiếp

ABC

.

Tacó

MK BH

ME AC

BH AC

















MK ME 



 

,

KN CH

NE AB

CH AB

















 

2KN NE 



Từ

   

1 , 2



KMEN

làtứgiácnộitiếpđườngtrònđườngkính

.

Đườngtròn

 

2 2

: 4 4 17 0C x y x y    

cótâm

 

2;2I 

bánkính

5r  I

làtrungđiểm

.

KHEJ

làhìnhbìnhhành

I

làtrungđiểm



Tacó:

3IJ IG

 



 

2 3 1 2

2 3 3 2



   







  





















 

1;5J

.

Bánkínhđườngtrònngoạitiếp

ABC

là

2 2 10R JA IK r   

.

Phươngtrìnhđườngtrònngoạitiếp

ABC

là:

   

2 2

1 5 100x y   

.

Câu 23.  

Tacó

làtrungđiểmcủa

;

,

lầnlượtlàchânđườngcaokẻtừ

và

.Đườngtrònđi

quabađiểm

,

làđườngtrònEuler.Dođóđườngtrònngoạitiếptamgiác

ABC

chínhlà

ảnhcủađườngtrònEulerquaphépvịtựtâmlà

,tỷsố

2k 

.

Gọi

và



lầnlượtlàtâmđườngtrònngoạitiếptamgiác

MNP

vàtamgiác

ABC

.

Gọi

và



lầnlượtlàbánkínhđườngtrònngoạitiếptamgiác

MNP

vàtamgiác

ABC

.

Tacó

 



 

 

vàdođó

 

2 2; 1OI OI I

 

  

 

.

Mặtkhác

R R



  

.

Vậyphươngtrìnhđườngtrònngoạitiếptamgiác

ABC

là:

   

2 2

2 1 25x y   

.

Nhậnxét:ĐềbàinàyrấtkhóđốivớihọcsinhnếukhôngbiếtđếnđườngtrònEuler.

Dạng3.3Sửdụngđiềukiệntiếpxúc

Câu 24. ChọnA

Đườngtròn

 

cótâm

,bánkính

tiếpxúcvới



nêncó:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 14

 

; 2

R d O



   

.

Phươngtrìnhđườngtròn

 

:

2 2

2x y 

.

Câu 25. ChọnB

Dotâm

nằmtrênđườngthẳng

 

;y x I a a   

,điềukiện

0a 

.

Đườngtròn

 

cóbánkính

3R 

vàtiếpxúcvớicáctrụctọađộnên:

         

; ; 3 3 3 3 3; 3d I Ox d I Oy a a n a l I          

.

Vậyphươngtrình

     

2 2

: 3 3 9S x y   

.

Câu 26. ChọnC

Đườngtròntâm

 

3;4I

tiếpxúcvớiđườngthẳng

:3 4 10 0x y   

nênbánkínhđườngtròn

chínhlàkhoảngcáchtừtâm

 

3;4I

tớiđườngthẳng

:3 4 10 0x y   

.

Tacó:

 

3 2

3.3 4.4 10

, 3

3 4

R d I

 

    



.

Câu 27. ChọnC

Đườngtròntâm

vàtiếpxúcvớiđườngthẳng

 

cóbánkính

 

2 2

3.1 4.1 2

, 1

3 4

R d I d

 

  





Vậyđườngtròncóphươngtrìnhlà:

   

2 2

1 1 1x y   

.

Câu 28. ChọnD

Vìđườngtròn

( )C

cótâm

 

3;2I 

vàmộttiếptuyếncủanólàđườngthẳng



cóphươngtrình

là

3 4 9 0x y  

nênbánkínhcủađườngtrònlà

2 2

3.( 3) 4.2 9

( , ) 2

3 4

R d I

  

   





Vậyphươngtrìnhđườngtrònlà:

   

2 2

3 2 4x y   



Câu 29. ChọnD

Vìcácđiểm

 

3;0

và

 

0;4

nằmtronggócphầntưthứnhấtnêntamgiác

OAB

cũngnằmtrong

gócphầntưthứnhất.Dovậygọitâmđườngtrònnộitiếplà

 

,I a b

thì

0, 0a b 

.

Theođềratacó:

     

; ; ;d I Ox d I Oy d I AB 

.

PhươngtrìnhtheođoạnchắncủaABlà:

3 4

x y

 

hay

4 3 12 0x y  

.

Dovậytacó:

 

7 12 5

4 3 12 5

7 12 5

a b

a l

a a

a b a

a a

 

  

 



  

 

  



  





 







  





.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 15

Vậyphươngtrìnhđườngtròncầntìmlà:

   

2 2

1 1 1

x y

   

.

Câu 30. ChọnB

Tacó

3, 4, 5.

OA OB AB

  



Gọi

( ; )

I I

I x y

làtâmđườngtrònnộitiếptamgiác

OAB

.

Từhệthức

. . . 0

AB IO OB IA OA IB

  

   

(Chứngminh)tađược

. . . 4.3

5 4 3

(1;1)

.y .y .y 3.4

5 4 3

O A B

AB x OB x OA x

AB OB OA

 



  



   





 



  



   





Mặtkháctamgiác

OAB

vuôngtạiOvới

làbánkínhđườngtrònnộitiếptamgiácthì

3.4

3 4 5

OA OB

OA OB AB

   

 

(

,S p

lầnlượtlàdiệntíchvànửachuvitamgiác).

Vậyphươngtrìnhđườngtrònnộitiếptamgiác

OAB

là

2 2

( 1) ( 1) 1

x y

   



hay

2 2

2 2 1 0.

x y x y

    



DẠNG4.TƯƠNGGIAOCỦAĐƯỜNGTHẲNGVÀĐƯỜNGTRÒN

Dạng4.1.Phươngtrìnhtiếptuyến

Câu 31. ChọnA

2 2

1 0

x y

  

cótâm

 

0;0 , 1

O R



.

Điều kiện để đường thẳng tiếp xúc với đường tròn là khoảng cách từ tâm tới đường thẳng bằng

bán kính.

XétđápánA:

 

2 2

| 3.0 4.0 5 |

: 3 4 5 0 , 1

3 4

x y d O R

 

          



tiếpxúcvớiđườngtròn.



Câu 32. ChọnD

Đườngtròn

 

tiếpxúcvớitrụcOxkhi

 

,Ox

d I R

với

và

lầnlượtlàtâmvàbánkính

củađườngtròn

 

.

Đườngtròn:

2 2

10 0

x y x

  

2 2

( 5) 25

x y

   



cótâm

 

5;0

,bánkính



,

 

I,Ox 0



.Suyra:

 

,Ox

d I R

.Vậy

 

khôngtiếpxúcvớitrụcOx.



khôngphảilàphươngtrìnhđườngtròn.

.Xétphươngtrìnhđườngtròn:

2 2

5 0

x y

  

có

 

0;0

và

R  ,

 

I,Ox 0



.

Suyra:

 

,Ox

d I R

.Vậy

 

khôngtiếpxúcvớitrụcOx.

Xétphươngtrìnhđườngtròn:

2 2

10 2 1 0

x y x y

    

có

 

5;1

và



 

I,Ox 1



.

Suyra:

 

,Ox

d I R

.Vậy

 

khôngtiếpxúcvớitrụcOx.

Xétphươngtrìnhđườngtròn:

2 2

6 5 9 0

x y x y

    

có

 

 

 

 

và



 

I,Ox



.

Suyra:

 

,Ox

d I R

.Vậy

 

tiếpxúcvớitrụcOx



Câu 33. ChọnB

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 16

 

2 2

: 2 4 3 0

C x y x y

    

   

2 2

1 2 2.

x y

    



Dođóđườngtròncótâm

 

1;2

I 

vàbánkính

R 

.

Do

songsongvớiđườngthẳng



nên

cóphươngtrìnhlà

3 4 0

x y k

  

,

 



.

Tacó

 

2 2

11 5 2 5 2 11

; 2 11 5 2

3 4

11 5 2 5 2 11

k k

d I d R k

k k

 

   



       

 



     

 

 

.

Vậycóhaiphươngtrìnhtiếptuyếncầntìmlà

3 4 5 2 11 0

x y

   

,

3 4 5 2 11 0

x y

   

Câu 34. ChọnA

Đườngtròn

 

cótâm

 

1;2

 

0;3

IA 



.

Gọi

làtiếptuyếncủa

 

tạiđiểm

,khiđó

điqua

vànhậnvectơ



làmộtVTPT.

ChọnmộtVTPTcủa

là

 

0;1

n 



.

Vậyphươngtrìnhđườngthẳng

là

5 0

 

.

Câu 35. ChọnA

Đườngtròn

 

cótâmlàgốctọađộ

 

0;0

vàcóbánkính

2R 

.

Họđườngthẳng



qua

     

1;2 : 1 2 0

A a x b y

    

,với

2 2

a b

 

.

Điềukiệntiếpxúc

 

;

d O R 

hay

2 2

a b







 

2 2

2 4

a b a b

   

3 4 0

3 4

a ab

a b





   



 



.

Với



,chọn

1b 

tacó

: 2 0

  

.

Với

3 4a b 

,chọn



và

 

tacó

   

: 4 1 3 2 0 4 3 10 0

x y x y

        

.

Nhậnxét:Thựcrabàinàykhithaytọađộđiểm

 

1;2

A 

vàocácđườngthẳngởcácphươngán

thìtaloại

và

Tínhkhoảngcáchtừtâmcủađườngtrònđếnđườngthẳngthìchỉcóphương

án

thỏa.

Câu 36. ChọnC

Đườngtròn

     

2 2

: 1 4 4

C x y

   

cótâm

 

1;4

vàbánkính

2R 

.

Gọi

làtiếptuyếncủa

 

.

Vì

/ /



nênđườngthẳng

 

: 4 3 0 2

d x y m m

   

.

làtiếptuyếncủa

 



 

4.1 3.4

; 2

4 3

d I d R

 

   

 



8 10





   



 



(thỏamãnđiềukiện)

Vậycó2tiếptuyếncầntìm:

4 3 18 0;4 3 2 0

x y x y

     

.

Câu 37. ChọnC

Đườngtròn

 

2 2

: 2 4 1 0

C x y x y

    

cótâm

 

1; 2



bánkính

2R 

.

Đườngtròn

 

2 2

' : 6 8 20 0

C x y x y

    

cótâm

 

' 3;4

I 

bánkính

' 5

R  .

' 2 13

II  .

Vậy

' 'II R R 

nên2đườngtrònkhôngcóđiểmchungsuyra2đườngtròncó4tiếptuyến

chung.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 17

Câu 38. ChọnB

Đườngtròn

2 2

( ) : ( 2) ( 4) 25

C x y

   

cótâm

(2; 4)



,bánkính



.

Đường thẳng



 vuông góc với đường thẳng

: 3 4 5 0

d x y

  

 có phương trình dạng:

4 3 0

x y c

  





 là tiếp tuyến của đường tròn

( )C

 khi và chỉ khi:

( ; )

d I R 



2 2

4.2 3.( 4)

4 3

c  





4 25 29

4 25

4 25 21

c c

  

 

    

 

    

 

.Vậycóhaitiếptuyếncầntìmlà:

4 3 29 0

x y

  

và

4 3 21 0

x y

  

.

Câu 39. ChọnD

 

cótâm

 

1; 1



bánkínhR=

2 2

1 ( 1) ( 3) 5

    



Vì

2IA R 

nênAnằmbêntrong

 

.Vìvậykhôngkẻđượctiếptuyếnnàotớiđườngtròn

 

.

Câu 40. ChọnB

Đườngtròn

     

2 2

: 1 4 4

C x y

   

cótâm

 

1;4

vàbánkính

2R 

.

Gọi

làtiếptuyếncủa

 

.

Vì

/ /



nênđườngthẳng

 

: 4 3 0 2

d x y m m

   

.

làtiếptuyếncủa

 



 

4.1 3.4

; 2

4 3

d I d R

 

   

 



8 10





   



 



(thỏamãnđiềukiện)

Vậycó2tiếptuyếncầntìm:

4 3 18 0;4 3 2 0

x y x y

     

.

Câu 41. ChọnD



Gọi

làtâmcủađườngtròn,tacótọađộtâm

 

3;4

.

Theođềratacótứgiác

IMPN

làhìnhvuông,nênđườngthẳng

nhận

 

6; 6

  



làm

VTPT,đồngthờiđườngthẳng

điquatrungđiểm

 

0;1

của

.Vậyphươngtrìnhđường

thẳngMN:

   

1. 0 1. 1 0

x y

   

hay

1 0

x y

  

.

Câu 42. ChọnC

     

2 2

: 2 6 6 0 1 3 4

C x y x y x y

         

suyra(C)cótâmI(1;3)vàR=2

+Phươngtrinhđươngthăng

điqua

( 3;1)



cophươngtrinh:

   

3 1 0

A x B y

   

.

-2

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 18

latiêptuyênvơiđươngtronkhivachikhi

 

;

d I d R

.



tacophươngtrinh:

2 2

3 3

2 3 4 0

3 4

A B A B

A AB

A B



  



    



 







+Vơi



,chon

1B 

,phươngtrinhtiêptuyênthưnhâtla

 

: 1d y 

.

Thê

1y 

vao

 

2 2

: 2 6 6 0

C x y x y

    

,tađươctiêpđiêmla

 

1;1

.

+Vơi

3 4A B 

,chon

4; 3

A B

  

,phươngtrinhtiêptuyênthưhaila

 

: 4 3 15 0

d x y

   



Tiêpđiêm

 

; 5

T x C

 

 

 

 

nên

 

4 3

1 5 3 4

3 5

x x

 

        

 

 

3 21

;

5 5

 



 

 

.

+Phươngtrinhđươngthăng

   

1 2

: 2 1 1 1 0 2 3 0

TT x y x y

       

.

+Khoảngcáchtừ

đếnđườngthẳng

1 2

la:

 

1 2

2 2

2 1

d TT



 



.

Dạng4.2Bàitoántươnggiao

Câu 43. ChọnD

Tathấyđườngtròn

 

cótâm

 

I 1; 2 

vàbánkính



.Đườngtròn

 

cótâm

 

2;2

vàbánkính



.

Khiđó:

 

2 2

1 2 1 2 1

5 (2 1) (2 2) 5

R R I I C

        

và

 



tiếpxúcnhau.

Câu 44. ChọnD

Giaođiểm

đườngtrònlànghiệmcủahệphươngtrìnhsau:

2 2 2 2 2 2

2 2

4 0 4 4

4 4 4 0 4 4 8 2

x y x y x y

x y x y x y x y

  

      

 

  

        

  



 

2 2 2

4 2 4 0

2 4

2 2

x y y y

y y

x y x y

x y

 











 

   

  

 



   

  



   



 





 

















Vậygiaođiểm2đườngtrònlà:

 

2;0

và

 

0;2 .



Câu 45. ChọnA



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 19

Cách1:Xéthệ

 

   

2 2

1 4

2 3 0

8 6 9 0

4 3 16

x y

x y x

x y x y

x y



  



   





 

    

   









 

3 7 1 7

2 2

2 6 1 0

2 2 3 0

3 7 1 7

2 2

x y

y x

x x

x x x

x y



 

 



 



 



 

  

  

  

    

 







 







Suyra

3 7 1 7

2 2

 

 

 

 

,

3 7 1 7

2 2

 

 

 

 

.

 

cótâm

 

1;0

,

 



cótâm

 

4;3





 

3;3



 





Nênđườngthẳng

qua

vànhận

 

1;1



làvéctopháptuyến.

Phươngtrình:

3 7 1 7

1 1 0 2 0

2 2

x y x y

   

 

       

   

   

.Chọn

.

Cách2:Giảsửhaiđườngtròn

   

: 1 4

C x y

  

và

     

2 2

: 4 3 16

C x y



   

cắtnhautại

haiđiểmphânbiệt

và



khiđótọađộcủa

vàthỏamãnhệphươngtrình:

 

   

2 2

1 4

2 3 0 (1)

8 6 9 0 (2)

4 3 16

x y

x y x

x y x y

x y



  



   





 

    

   









Lấy

(1)

trừ

(2)

tađược:

6 6 12 0 2 0

x y x y

      

làphươngtrìnhđườngthẳngđiqua2

điểm

và



Câu 46. ChọnA

Từ

 

3 19

:3 4 19 0 1

4 4

x y y x      

.

Thế

 

vào

 

tađược

 

3 23

1 25

4 4

x x

 

   

 

 



25 85 145

0 .

16 8 16

x x







    









+)

 

1 4 1; 4 .

A A

x y A

     



+)

29 2 29 2

; .

5 5 5 5

B B

x y B

 

     

 

 



Độdàiđoạnthẳng

2 2

29 2

1 4 6

5 5

   

     

   

   

.

Câu 47. ChọnA

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 20

Gọi

làtrungđiểmcủađoạnthẳng

.Tacó

IH AB

và

 

3.1 4. 1 8

; 3

3 4

IH d I AB

  

  

 

.

Xéttamgiácvuông

AHI

tacó:

2 2 2 2 2

5 3 16HA IA IH    



4 2 8HA AB HA    



Câu 48. ChọnC

Đườngtròn

 

cótâm

 

2; 2



bánkính

2R 

.

 

2 2

3.2 4. 2 7

, 1 2

3 4

d I d R

  

   



nên

cắt

 

tạihaiđiểmphânbiệt.

Gọi

,A B

làcácgiaođiểmcủađườngthẳng

vớiđườngtròn

 

.

 

2 2

2 , 2 3

AB R d I d  

.

Câu 49. ChọnA

Đườngtròn

 

cótâm

 

1;2

vàbánkính

2 2

1 2 3 2

R    

.

Theo giả thiết đường thẳng

 đi qua

 và cắt đườngtròn

 

 tại hai điểm

,

 sao cho

2 2

BC 

.

Vì

2 2 2BC R

 



nên

làđườngkínhcủađườngtròn

 

suyrađườngthẳng

điquatâm

 

1;2



Tachọn:

 

2; 1

u IA

  

 

 

1;2

n 



.

Vậyđườngthẳng

điqua

 

3;1

vàcóVTPT

 

1;2

n 



nênphươngtrìnhtổngquátcủa

đườngthẳng



là:

   

1 3 2 1 0

x y

   



2 5 0

x y

   

.

Câu 50. ChọnA

Tọađộtâm

củađườngtròn

 

là:

 

1; 2

 

.

Tọađộtâm

củađườngtròn

 

là:

 

2;2

.

Tacó:

 

1 2

3;4

I I



.Gọi

,d d



lầnlượtlàđườngthẳngnốitâmcủahaiđườngtrònđãchovàđường

thẳngcầnlập.Chọnmộtvectơpháptuyếncủađườngthẳng

là:

 

4; 3





.Gọi

 

;

n a b





,

2 2

a b

 

làmộtvectơpháptuyếncủađườngthẳng



.

Theođề

 

2 2 2 2

4 3

2 2 2

cos , ' cos ,

2 2 2

3 4 .

d d

a b

d d n n

a b





    

 

 

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 21

2 2

7 0

7 48 7 0

a b

a ab b

a b

 





    



  



.

Với

a b

  

,chọn

7 1b a   

.Phươngtrìnhđườngthẳng

: 7 0

d x y



 

.

Với

7 0

a b

 

,chọn

1 7

b a

  

.Phươngtrìnhđườngthẳng

: 7 0

d x y



 

.

Câu 51.

ChọnB

 

     

2 2

1 2

, : 1 2 10.

1;2

IM IM

M M C x y



 



     









Mặtkhác,

,



thuộc

 

: 2 5 0

d x y

  



nêntacótọađộ

,



lànghiệmcủahệ

     

 

2 2

1 2 10 1

2 5 0 2

x y



   





  







 

2 2 5,

y x

   



thayvào

 



tacó

5 14 0 .

x x







  









Gọi

1 2

,x x

lầnlượtlàhoànhđộcủa

và

2 1 2

14 14

0 .

5 5

M x x    



Câu 52. ChọnB

 

cótâm

 

2; 1 ,



bánkính

2 5.

R  

Đặt

 

h d I AB



.Tacó:

. 8 . 16.

IAB

S h AB h AB   



Mặtkhác:

2 2

R h

  



Suyra: 

4 2

;

4 8

h h

AB AB

 

 

 

 

 



Vì

điqua

 

1; 3



nên

1 3 0 3 1 3 1b c b c c b        



Với

2 2 2

2 2 3 1 1 2

1 1 1

b c b b b

h b

b b b

     

     

  



Với

2 2 2

2 2 3 1 1 2

3 5

2 2.

4 4

1 1 1

b c b b b

h b c b c

b b b

     

          

  



Câu 53. ChọnD

(C)

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 22



Gọi

làchânđườngcaohạtừ

củatamgiác

ABC

,gọi



làđiểmđốixứngvới

qua

suy

ra

thuộcđườngtrònngoạitiếptamgiác

ABC

(Tínhchấtnàyđãhọcởcấp2).

Tacó

 

6;8AH  



,chọn

 

3; 4

u  



.

Phươngtrìnhđườngthẳng

qua

ởdạngthamsố

5 3

5 4

x t

y t

 





 





K AH

suyratọađộđiểm

códạng

 

5 3 ;5 4K t t 



và

đốixứngnhauqua

suyratọađộ

theot là

 

11 6 ; 3 8E t t  



   

2 2

( ) 11 6 3 8 50

5 9 4 0

E C t t

t t

      

   

 

















Với

1t  

,

 

5;5E

(loạivì

E A

)

Với





,

31 17

;

5 5

 

 

 

,

13 41

;

5 5

 

 

 



Phươngtrìnhđườngthẳng

có

 

4;3

BC AH

u n 

 

vàquađiểm

cóphươngtrìnhthamsố

13 41

4 ; 3

5 5

x t

C BC C t t

y t



 



 

    



 

 



 





.

 

   

 

2 2

13 41

4 3 50

5 5

25 70 24 0

1;7

7;1

C C t t

t t

t C KTM

t C

   

     

   

   

   



   











  







Vậy

   

; 7;1 6C a b C a b     

.

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 23

Câu 54. ChọnA



Tacó:



BCM BAM

 (cùngchắncung

)

 





BAM MAT DAC

  (do

làđườngphângiácngoài

)

 



Từ

   

1 , 2

suyra



DAC BCM

 ,mà



BCM CDA AMC DAC ACM AMC

   

từđósuyra



CDA ACM

 ,dođó

làtiếptuyếncủađườngtrònngoạitiếptamgiác

ACD

cótâm

nên

JC MC

.Hay

làhìnhchiếucủa

lênđườngthẳng

.

Đườngthẳngqua

vàvuônggócvới

cóphươngtrình:

   

2 2 0 4 0

x y x y

       



Tọađộđiểm

lànghiệmcủahệ:

 

2 1

1; 3

4 3

x y x

x y y

   

 

  

 

   

 

.

làđườngthẳngqua

vàvuônggócvới

 

4; 0

IJ 



nêncóphươngtrình:

1 0

 

.

Dođótọađộđiểm

códạng

 

1;A a



.Tacó

 

2 2

9 2 9 1

IA IC a





      







.

Vì

A C

nên

 

1; 1

A 

.

Tọađộđiểm

códạng

 

; 2

M m m

.Tacó

 

2 2 2 2

2 10 2 3 0

IM IC m m m m

 



         







.

Vì

M C

nên

 

3; 1



.

làđườngthẳngqua

vàvuônggócvới

 

1; 3

MI 



nêncóphươngtrình:

   

1 3 3 0 3 10 0

x y x y

        

.

Tọađộđiểm

códạng

 

3 10;B b b



.Tacó

   

2 2

3 12 2 10

IB IC b b







      







.

Vì

B C

nên

19 23

;

5 5

 

 

 

.

Vậytổnghoànhđộcủacácđỉnh

, ,A B C

là

19 9

1 1

5 5

   

.

Câu 55. ChọnD

4 2 2 4

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 24

Vì

 

 

nên

3 8 0 8 3a b a b      

Vìđườngtrònđiqua

vàtiếpxúcvớiđườngthẳng

 





nên:

 

;

d I IA



 



     

2 2

3 4 10

2 1 1

a b

 

      .

Thay

8 3a b  

vào

 

tacó:

 

   

2 2

3 8 3 4 10

2 8 3 1

b b

   

     

14 13 5 10 34 37

b b b     

 

14 13 25 10 34 37

b b b     

81 486 729 0

b b

   

  

Với

3 1

b a

   

.

a b

  

Câu 56. ChọnA



Tacó:

 

; 2

IH d I d

 

.

21 2.4

. 4 2

2 2

IAB

S IH AB AB AH



      

.

2 2 2 2

R IA AH IH      

.

     

2 2

: 1 2 8

C x y

    

.

DẠNG5.CÂUHỎIMIN-MAX

Câu 57. ChọnD

I(1;-2)

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 25

Taco

       

2 2

: 2 4 4 0 : 1 2 9C x y x y C x y         

nêncotâm

 

1;2 , 3I R 



Vi

2 3IM R  

.

Goid lađươngthăngđiquaMcătđươngtron

 

taicacđiêmA, B. Gọi

 là trung điểm

của

.Tacó:

Taco:

2 2 2 2

2 2 2 2 9 2 2 7AB AJ R IJ R IM       

.



Câu 58. Chọn. D.



Đườngtròn

2 2

( ) : ( 1) 4C x y   cótâm

I(0;1)

bánkính

2R 

.

IA IB 4 R  

nên

,A B

nằmngoàiđườngtròn.

Gọi

làgiaođiểmcủa

vàđườngtròn

 



Trênđoạn

lấyđiểm

saocho

1 1

2 4

IP IN IP IA P   

 

trùngvớigốctọađộ.

Tacó

2 2

MA IM IN

IAM IMP MA MP

MP IP IP

       

.

Dođó

 

min min

2 2 2 2 2 2 17 8,1;8,3P MA MB MP MB PB P PB P          .

Chọn. D.

Câu 59. ChọnA

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 26

 

2 2

: 2 4 3 0

C x y x y

    

,

 

cótâm

 

1;2

,

R 

.

Suyra

     

2 2

: 1 2 2 0

C x y

    

.

Có

0 0

T x y 

   

0 0

1 2 3

x y

    

.

Ápdụngbấtđẳngthức B. C. Scho

bộsố

     

 

0 0

1;1 , 1 ; 2

x y  .

       

2 2

0 0 0 0

1 2 2 1 2x y x y

 

      

 

 



2

,do

   

2 2

0 0

1 2 2

x y

   

.

   

0 0

2 1 2 2

x y

      

   

0 0

1 1 2 3 5 1 5

x y T

         

.

Dấuđẳngthứcxảyrakhi

   

0 0

2 2

0 0

1 2

1 2 2

x y



  





   





.

 

1 1

  

1 1



 





  





0 0

2, 3, 5

0, 1, 1

x y T



  





  





.

Vậy

max T 5

khi

0 0

2, 3

x y

 

.

Câu 60. ChọnD

Đườngtròn

 

cótâm

 

4;3

I 

,bánkính



.

Tacó

 

4;3

OI  



suyraphươngtrìnhđườngthẳng

là

x t

y t

 









.

   

OI C M

 

Tọađộ

 

;x y

của

lànghiệmhệ

2 2 2

8 2

5 5

8 6 16 0 25 50 16 0

32 8

4 4

5 5

3 3

24 6

5 5

t t

x y x y t t

x t x t x x

y t y t

y y

 

 

 

 

       

 

 

 

        

   

   

 

 

 

 

 

 



Suyra

1 2

32 24 8 6

; , ;

5 5 5 5

M M

   

 

   

   



Tacó

2 2 2 2

1 2 min 2

32 24 8 6

8, 2 2

5 5 5 5

OM OM OM OM

       

          

       

       

.

Cách2

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 27

Đườngtròn

 

cótâm

 

4;3

I 

,bánkính

2 2

4 3 16 3

   

.

Phươngtrìnhđườngthẳng

điqua

 

0;0

cóvtpt

 

3;4



là:

3 4 0

x y

 

.

Tọađộ

 

M OI C

 

lànghiệmcủahệ:

2 2

3 4 0

8 6 16 0

x y

x y x y

 





    



32 8

5 5

24 6

5 5

x x

y y

 

   

 

 

 

 

 

 

 



Tacó

2 2

32 24

5 5

   

 

   

   

8

;

2 2

8 6

5 5

   

  

   

   

.Vậy

min



.

Câu 61. ChọnC



Gọi:

: 0;

d x y m

  

tâmcủa

 

là

 

1;1

,để

 

d C



tại

phânbiệtkhiđó:

   

0 ; 2 0 2 2 2 2 2 2 2 *

d I d m



         



Xét

IAB

có:

 

2 2

1 1 1

. . .sin . .sin .

2 2 2

AIB

S IA IB AIB R AIB R



  



Dấu“=”xảyrakhi:

 

sin 1 90 2 2

AIB AIB AB    

 

0 ( )

; 2 2

4 ( )

m TM

d I d

m TM







    







.

Câu 62. ChọnC

Đườngtròn

 

cótâm

 

1; 2



,bánkính

2R 

.

Gọi



làđườngthẳngqua

vàvuônggócvới

Khiđó,điểm

cầntìmlàmộttronghaigiao

điểmcủa



và

 

.



Tacóphươngtrình

: 1 0

x y

   

.

Xéthệ:

   

2 2

1 0

2 4 1 0

1 2 4

y x

x y

x y x y

x y

  



  







 

    

   







CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 28

 

1 2

2 2

2 1 4

1 2

2 2

y x





 







  

   



  





  

  



 

 

 





 











  











Với

 

1 2; 2 2 , 2 3 2

B d B d      

Với

 

   

1 2; 2 2 , 2 3 2 ,C d C d d B d

        

Suyra

   

1 2; 2 2 1 2; 2 2 2 1 2 2M a b a

            .

Câu 63. ChọnB

Vì

GA GM

 

 

nên

làảnhcủađiểm

quaphépvịtự

tâm

,tỉsố

2

,suyra

 

4; 2

 

.

Đườngtrònngoạitiếp

ABC

cótâm

,bánkính

R IA

 



cóphươngtrình

   

2 2

3 2 25

x y

   

.

Tacó

 

2;4

IM 



.

Đườngthẳng

điqua

vànhậnvectơ



làmvectơ

pháp tuyến, phương trình

 là:

   

1 3 2 2 0 2 7 0

x y x y

       

.

Điểm

làgiaođiểmcủađườngthẳng

vàđườngtròn

 

;I R

nêntọađộđiểm

lànghiệmcủahệphươngtrình:

   

2 2

1, 3

3 2 25

5, 1

2 7 0

x y



 



   









 

  









Đốichiếuđiềukiệnđềbàitacótọađộđiểm

 

5;1

.

Câu 64. ChọnD



+)

 

cótâm

 

1;2

,bánkính

R  

+)

làdâycungcủa

 

điqua



+)Tacó

min

AB AB IM 

.

Thậtvậy,giảsử

làdâycungqua

vàkhôngvuônggócvới

.

Gọi

làhìnhchiếucủa

lên

tacó:

2 2 2 2

2 2 2

AB AM IA IM R IM

    



2 2 2 2

2 2 2

CD KD ID KD R IK

    



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 29

Dotamgiác

IMK

vuôngtại

nên

IM IK

.

Vậy

CD AB

.

+)Tacó:

   

2 2

2 1 1 2 2

IM     



2 2

30 2 28 2 7

MA R IM     



2 4 7

AB MA   .

Câu 65. ChọnD

Xéttậphợpđiểm

( ; )M a b

thỏamãn

   

2 2

1 2 1

a b

   

thìMthuộcđườngtròntâm

(1; 2); 1

I R





Xétđiểm

( ; )N c d

thỏamãn

4 3d 23 0

  

thìNthuộcđườngthẳngcóphươngtrình

4 3 23 0

x y

  

.

Tathấy

4 6 23

( ; ) 5 1

d I d R

 

   

.Dođóđườngthẳngkhôngcắtđườngtròn.



Đườngthẳngqua

vuônggócvới

tại

vàcắtđườngtrònở

,T K

(

ởgiữa

và

)

Vẽtiếptuyếntại

cắt

tại

.

Có

KL PN MN 

,mà

 

KL d I d R 



Dođó

ngắnnhấtkhi

MN KL



Từđâytasuyra

   

2 2

P a c b d MN

    

bénhấtkhivàchỉkhi

( ; ) 5 1 4

MN d I d R

    

.Vậygiátrịnhỏnhất

min





Câu 66. ChọnA

Tacó

(1;2)

( )











Tadễthấyđườngthẳng

và

cắtnhautạiđiểm

 

1;1

cốđịnhnằmtrongđườngtròn

 

và

1 2

d d

.Gọi

,A B

làgiaođiểmcủa

và

 

,

,C D

làgiaođiểmcủa

và

 

.

,H K

lầnlượt

làhìnhchiếucủa

trên

và



Khiđó

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương:https://www.facebook.com/phong.baovuong 30

   

  

2 2

1 2

2 2

2 2 2

2 2 2 2

. 2 . 2 , . ,

4 3 3 4

1 4 3 3 4

 2 4 4 =2 7

1 1 1 1

       

   

 

  

    

   

ABCD

S AB CD AH CK R d I d R d I d

m m

m m m

m m m m



Dođó

max 7

ABCD

S khi

1 

.Khiđótổngcácgiátrịcủa

bằng



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng

hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1

TOÁN 10

0H3-3

Con

tents

PHẦN A

. CÂU HỎI ......................................................................................................................................................... 1

DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP....................................................................................................................... 1

DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP ........................................................................................................................ 2

DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC .......................................................................................................... 3

PHẦN B. LỜI GIẢI ......................................................................................................................................................... 4

DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP....................................................................................................................... 4

DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP ........................................................................................................................ 6

DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC .......................................................................................................... 8

PHẦN A. CÂU HỎI

DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP

Câu 1. Đường Elip

16 7

x y

 

có tiêu cự bằng

. B.

. C.

. D.

 

;



 

Câu 2. Cho elip

 

có phương trình

16 25 400

x y 

. Khẳng định nào sai trong các khẳng định sau?

 

có trục nhỏ bằng 8.

 

có tiêu cự bằng 3.

 

có trục nhỏ bằng 10.

 

có các tiêu điểm

 

F 

và

 

Câu 3. Trong mặt phẳng với hệ tọa độ Oxy, cho elip

 

2 2

: 1

25 9

x y

 

. Tiêu cự của (E) bằng

A. 10. B. 16. C. 4. D. 8.

Câu 4. Một elip có diện tích hình chữ nhật cơ sở là

, độ dài tiêu cự là

. Tâm sai của elip đó là



. B.



. C.



. D.



Câu 5. Cho elip

 

4 5 20

x y





. Diện tích hình chữ nhật cơ sở của

 

là

2 5

. B.

. C.

8 5

. D.

Câu 6. (Yên Định 1 - Thanh Hóa - 2018-2019) Đường elip

16 7

x y

 

có tiêu cự bằng

. B.

. C.

. D.

PHƯƠNG TRÌNH ELIP

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2

Câu 7. Cho elip có phương trình chính tắc

2 2

4 1

x y

 

. Tính tâm sai của elip.

. B.

. C.

. D.

Câu 8. (TH&TT LẦN 1 – THÁNG 12) Trong mặt phẳng với hệ tọa độ

Oxy

, cho elip

 

2 2

: 1

x y

a b

 

(với

a b

 

) có

1 2

,F F

là các tiêu điểm và M là một điểm di động trên

 

. Khẳng định nào dưới

đây là đúng?

1 2

2MF MF b 

. B.

 

2 2

1 2

4 .

MF MF b OM  

2 2 2

1 2

OM MF MF a b  

. D.

2 2 2

1 2

MF MF OM a b  

Câu 9. Trong hệ trục

,Oxy

cho Elip

 

có các tiêu điểm

   

1 2

4;0 , 4;0

F F

và một điểm

nằm trên

 

. Biết rằng chu vi của tam giác

1 2

MF F

bằng 18. Xác định tâm sai e của

 



. B.



. C.

 

. D.



Câu 10. Cho Elip

 

đi qua điểm

 

3;0

A 

và có tâm sai



. Tiêu cự của

 

là

. B.

. C.

. D.

DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP

Câu 11. Trong mặt phẳng

Oxy

, phương trình nào sau đây là phương trình chính tắc của một elip?

2 2

2 3

x y

 

. B.

2 2

9 8

x y

 

. C.

9 8

x y

 

. D.

2 2

9 1

x y

 

Câu 12. Phương trình chính tắc của đường elip với



là

2 2

16 9

x y

 

. B.

2 2

9 16

x y

 

. C.

2 2

16 9

x y

 

. D.

2 2

9 16

x y

 

Câu 13. Trong mặt phẳng tọa độ

Oxy

, viết phương trình chính tắc của elip biết một đỉnh là

 

5;0

A 

và

một tiêu điểm là

 

2;0

2 2

25 21

x y

 

. B.

2 2

25 4

x y

 

. C.

2 2

29 25

x y

 

. D.

2 2

25 29

x y

 

Câu 14. Tìm phương trình chính tắc của Elip có độ dài trục lớn bằng

4 10

và đi qua điểm

 

0;6

2 2

40 12

x y

 

. B.

2 2

160 36

x y

 

. C.

2 2

160 32

x y

 

. D.

2 2

40 36

x y

 

Câu 15. Lập phương trình chính tắc của Elip đi qua điểm

và có tâm sai

e 

2 2

9 4

x y

 

. B.

2 2

3 2

x y

 

. C.

2 2

9 2

x y

 

. D.

2 2

9 3

x y

 

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3

Câu 16. Phương trình chính tắc của Elip có đỉnh

 

3;0



và một tiêu điểm là

 

1;0

là

2 2

8 9

x y

 

. B.

2 2

9 8

x y

 

. C.

2 2

1 9

x y

 

. D.

2 2

9 1

x y

 

Câu 17. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Tìm phương trình chính tắc của elip có tiêu cự

bằng

và trục lớn bằng

2 2

25 9

x y

 

2 2

16 25

x y

 

2 2

100 81

x y

 

2 2

25 16

x y

 

Câu 18. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Cho elip

 

có độ dài trục lớn gấp hai lần độ

dài trục nhỏ và tiêu cự bằng

. Viết phương

trình của

 

2 2

12 3

 

x y

. B.

2 2

12 3

 

x y

. C.

2 2

3 12

 

x y

. D.

2 2

48 12

 

x y

Câu 19. Phương trình chính tắc của Elip có độ dài trục lớn bằng

, độ dài trục nhỏ bằng

là:

2 2

9 16

x y

 

. B.

2 2

64 36

x y

 

. C.

2 2

8 6

x y

 

. D.

2 2

16 9

x y

 

Câu 20. Elip có một tiêu điểm

 

2;0



và tích độ dài trục lớn với trục bé bằng

12 5

. Phương trình

chính tắc của elip là:

2 2

9 5

x y

 

2 2

45 16

x y

 

2 2

144 5

x y

 

2 2

36 20

x y

 

Câu 21. Trong mặt phẳng

Oxy

, viết phương trình chính tắc của elip

 

biết

 

đi qua

3 4

;

5 5

 

 

 

và

nhìn hai tiêu điểm

1 2

,F F

dưới một góc vuông.

 

2 2

: 1

4 9

x y

 

. B.

 

2 2

: 1

9 4

x y

 

. C.

 

2 2

: 1

2 3

x y

 

. D.

 

2 2

: 1

3 2

x y

 

DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC

Câu 22. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho Elip

2 2

( ) : 1

16 12

x y

 

và điểm

nằm trên

( ).E

Nếu điểm

có hoành độ bằng 1 thì các

khoảng cách từ M đến hai tiêu điểm của (E) bằng:

3,5

và

4,5

. B.

4 2



. C.

và 5. D.



Câu 23. Trong mặt phẳng với hệ tọa độ

Oxy

, cho elip

 

2 2

: 1

25 9

x y

 

. Điểm

 

M E



sao cho



1 2

90 .

F MF  Tìm bán kính đường tròn nội tiếp tam giác

1 2

.MF F

. C.

. D.

Câu 24. Ông Hoàng có một mảnh vườn hình Elip có chiều dài trục lớn và trục nhỏ lần lượt là

60m

và

30m

. Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với Elip để làm mục đích

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4

sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài

đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích

trồng hoa màu. Biết diện tích hình Elip được tính theo công thức

S ab





, với a, b lần lượt là nửa

độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể.



. B.



. C.



. D.

1T 

Câu 25. Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai đường tròn

   

1 2

C C

có phương trình lần lượt

là

2 2 2 2

( 1) ( 2) 9,( 2) ( 2) 4

x y x y

       

và Elip

 

có phương trình

2 2

16 49 1

x y

 

. Có

bao nhiêu đường tròn

 

có bán kính gấp đôi độ dài trục lớn của elip

 

và

 

tiếp xúc với hai

đường tròn

 

. B.

. C.

. D.

Câu 26. Trong mặt phẳng

Oxy

, cho điểm

(3;0)

và elip

2 2

(E) : 1

9 1

x y

 

,A B

là

điểm thuộc

( )E

sao

cho

ABC

đều, biết tọa độ của

;

2 2

a c

 

 

 

và

có tung độ âm. Khi đó

a c

bằng:

. B.

. C.

2

. D.

4

PHẦN B. LỜI GIẢI

DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP

Câu 1. Chọn A

Elip

2 2

16 7

x y

 

có



suy ra

2 2 2

16 7 9

c a b

    

 

Vậy tiêu cự

2 2.3 6

 

Câu 2. Chọn B

 

2 2

16 25 400

x y 

2 2

25 16

x y

  

Elip

 

có



2 2 2 2

5 4 3

c a b

    

Tiêu cự của elip

 

là

2 6



nên khẳng định “

 

có tiêu cự bằng 3” là khẳng định sai.

Câu 3. Chọn D

Phương trình chính tắc của elip có dạng:

 

2 2

1 0, 0

x y

a b

   

Do đó elip (E) có

2 2

c a b





   







Tiêu cự của elip (E) bằng

2 8



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5

Câu 4. Chọn C

Diện tích hình chữ nhật cơ sở là

2 .2 80

a b



, suy ra

 

. 20 1

a b 

Lại có

 

2 2 2

2 6 3 9 2

c c a b c      

Từ

 

1 b

 

, thay vào

 

ta được:

2 4 2

400

9 9 400 0

a a a

     

25 5

a a

   

Do đó tâm sai



Câu 5. Chọn C

 

2 2

: 4 5 20 1

5 4

x y

E x y

    

Độ dài trục lớn:

2 2 5

a  .

Độ dài trục bé:

2 2.2 4

 

Diện tích hình chữ nhật cơ sở của

 

là:

2 5.4 8 5

 .

Câu 6. Chọn C

□ Ta có:



nên

2 2 2

c a b

  

 

□ Tiêu cự của elip là

2 6



Câu 7. Chọn D

Ta có

2 2 2 2 2

4 2; 1 1; 3 3

a a b b c a b c          

Tâm sai của elip là

 

Câu 8. Chọn D

Ta có:

2 2

1 2 1 2

; .

cx cx c x

MF a MF a MF MF a

a a a

       .

   

2 2

2 2 2 2

2 2 2 2 2 2 2 2 2

2 2 2

; 1

1 1

x y

M x y E

a b

x x b x

y b OM x y x b x b

a a a

   

   

           

   

   

 

2 2 2 2 2 2 2 2

2 2 2 2 2 2 2

1 2

2 2 2 2

2 2 2

c x b x c x b x

MF MF OM a x b a b x

a a a a

b c x

a b x

 

          

 

 



   

Vì

2 2 2

a b c 

nên

 

2 2 2

2 2

2 2 2 2 2 2 2 2 2

1 2

2 2

b c x

a x

MF MF OM a b x a b x a b

a a



          

Câu 9. Chọn A

Ta có

 

4;0 4

F c

  

1 2

1 2 1 2

18 2 2 18 2 8 5.

MF F

P MF MF F F

a c a a



  

       



CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6

Tâm sai

 

Câu 10. Chọn C

Gọi phương trình chính tắc của

 

là

2 2

x y

a b

 

với

a b

 

Vì

 

đi qua điểm

 

3;0

A 

nên

1 9 3

a a

    

Lại có

5 5 5

2 5

6 6 2

c a

e c c

      

DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP

Câu 11. Chọn D

Phương trình chính tắc của elip có dạng

 

2 2

1, 0

x y

a b

   

nên chọn phương án

Câu 12. Chọn C

Phương trình chính tắc

 

2 2

: 1

16 9

x y

 

Câu 13. Chọn A

Ta có

5; 2 25 4 21

a c b

     

Vậy

2 2

25 21

x y

 

Câu 14. Chọn D

Ta có phương trình chính tắc Elip (E) có dạng

2) 2

2 2

1( 0)

x y

a b

   

Theo giả thiết ta có

2 4 10

a 

2 10

a  .

Mặt khác (E) đi qua

 

0;6

nên ta có



 

Vậy phương trình chính tắc của (E) là:

2 2

40 36

x y

 

Câu 15. Chọn A

Phương trình chính tắc của Elip có dạng:

 

2 2

1, 0

x y

a b

   

Elip đi qua điểm

nên

2 2

0 2

1 4

a b

   

Tâm sai

5 5 5

3 3 3

e c a

    

2 2 2 2 2

4 9

a b c a a a

 

      

 

 

Vậy phương trình chính tắc của Elip cần tìm là

2 2

9 4

x y

 

Câu 16. Chọn B

Elip có đỉnh

 

3;0



 

và một tiêu điểm

 

1;0

1c 

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7

Ta có

2 2 2

c a b 

2 2 2

9 1 8

b a c

     

Vậy phương trình

 

2 2

: 1

9 8

x y

 

Câu 17.

Lời giai

Chọn D

Phương trình chính tắc của elip:

2 2

x y

a b

 

Độ dài trục lớn

2 10 5

a a

  

Tiêu cự

2 6 3

c c

  

Ta có:

2 2 2 2 2 2

a b c b a c

     

Vậy phương trình chính tắc của elip là

2 2

25 16

x y

 

Câu 18. Chọn B

Ta có:

2 , 2 6 3.   

a b c c

Mà

2 2 2 2 2

4 9







     









a b c b b

Vậy phương trình

 

2 2

12 3

 

x y

Câu 19. Chọn D.

+ Phương trình Elip dạng:

2 2

1, 0.

x y

a b

   

+ Do có độ dài trục lớn bằng

8 2 4

a a

  

+ Do có độ dài trục nhỏ bằng

6 2 3

b a

  

+ Suy ra phương trình là

2 2

16 9

x y

 

Vậy chọn D

Câu 20.

Chọn A

Gọi (E) có dạng

2 2

x y

1 ( a > b >0 )

a b

 

Theo giả thiết ta có:

2 2

a 9

ab 3 5

b 5

a b 4







 



 

 



 

 



Vậy (E) cần tìm là

2 2

9 5

x y

 

Câu 21. Chọn B

Gọi

 

2 2

: 1

x y

a b

 

Ta có:

 

đi qua

3 4

;

5 5

 

 

 

nên:

2 2

9 16

5 5a b

 

2 2 2 2

16 9 5

a b a b

   .

 

Vì

nhìn hai tiêu điểm

1 2

,F F

dưới một góc vuông nên:

1 2

F F

OM c 

2 2

OM c 

9 16

5 5

c  

2 2 2

a b c

   

2 2

a b  

thế vào

 

ta được:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8

   

2 2 2 2

16 5 9 5 5

b b b b

   

 

 

nên



Vậy:

 

2 2

: 1

9 4

x y

 

DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC

Câu 22. Chọn A

Giả sử phương trình

2 2

( ) : 1 ( 0)

x y

E a b

a b

   

Ta có :

2 2 2

c a b













 

  



















Gọi

1 2

,F F

lần lượt là hai tiêu điểm của Elip

( )E

 

1; ( )

M y E



, ta có :

4 .1 4,5

4 .1 3,5

MF a x



    







    





Chọn A.

Câu 23.

Lờigiải

Gọi

 

;M x y

vì



1 2

F MF 

2 2 2 2 2 2

1 2 1 2

MF MF F F x y c

      

(1)

 

2 2

25 9

x y

M E

   

(2)

Giải hệ gồm hai phuơng trình (1) và (2) ta đuợc

2 2

175 81 5 7 9

; ;

16 16 4 4

x y x y

     

Ta có: nửa chu vi

1 2 1 2

2 2

MF MF F F a c

p a c

  

    

Khoảng các từ M đến trục Ox:

 

;O x

d M y

 

 

1 2

; . 9

MF F

S d M Ox F F



 

Bán kính đuờng tròn nội tiếp:

 

Câu 24.

Hướng dẫn giải

Chọn D

Theo đề ta có: Diện tích

 

là:

 

. . 30.15. 450 ,

S a b m

  

  

Vì đường tròn tiếp xúc trong, nên sẽ tiếp xúc tại đỉnh của trục nhỏ, suy ra bán kính đường tròn:

15R m

. Diện tích hình tròn

 

phần trồng cây lâu năm là:

 

2 2 2

. 15 . 225 ,

S R m

  

  

Suy ra diện tích phần trồng hoa màu là:

   

 

225 , 1

E C

S S S m T



    

Câu 25. Chọn A

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9

Ta có

2 2

16 49 1 1

1 1

4 7

x y

    

   

   

   

 



có độ dài trục lớn

1 1

2 2.

4 2

 

Khi đó đường tròn

 

có bán kính là

1R 

. Gọi

 

;I a b

là tâm của đường tròn

 

Xét

1 2

II I

 có

1 1

2 2

1 2 1 2

1 3 4

1 2 3

II R R

I I R R

    





    





  



1 2

II I

  vuông tại

Ta có

 

1 ; 2

II a b    



 

2 ;2

II a b  



. Khi đó điểm

thỏa mãn:

1 2

. 0

II II















 



     

   

2 2

1 2 2 2 0

2 2 9

a a b b

a b

       









   





2 2

6 0

4 4 1 0

a b a

a b a b



   







    





2 2

5 4 5 4

6 0

3 3

5 4

6 4 4 1 0

5 4

b b

a b a

a a b



 

 



  

   



 



  

 

 

  

  



    







 









25 28 44 0

5 4 25

5 4

b b

  



 

 













  







 



  

 















 

















 











Vậy có hai phương trình đường tròn

 

thỏa mãn yêu cầu bài toán là

     

2 2

: 1 2 1

C x y

   

hoặc

 

2 2

71 22

: 1

25 25

C x y

   

   

   

   

Câu 26. Chọn A

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489

Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10

Nhận xét: Điểm

(3;0)

là đỉnh của elip

( )



điều kiện cần để

ABC

đều đó là

,A B

đối xứng

Nhau qua

.Suy ra

,A B

là giao điểm của đường thẳng

x x 

và elip

( )E

+) Ta có elip

2 2

(E) : 1

9 1

x y

 

y x



  







 





+) Theo giả thiết

có tung độ âm nên tọa độ của

0 0

; 9

A x x

 

 

 

 

(điều kiện



A C

)

+) Ta có

2 2

0 0

(3 ) (9 )

AC x x

   

và

( ; ) 0

| 3 |

d x



 

ABC

đều

( ; )

d AC



 

 

2 2

0 0 0

3 1

| 3 | (3 ) 9

2 9

x x x

     

2 2 2

0 0 0

3 1

(3 ) (3 ) (9 )

4 9

x x x

 

     

 

 

0 0

( / )

1 3 3

3 2 2

3( )

x t m

x x

x L







    







3 3

; 2

2 2

A a c

 





     

 



 

 



 

Bấm Tải xuống để xem toàn bộ.

| 1/112

| | Tải xuống

Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 10
PHƯƠNG TRÌNH ĐƯỜNG THẲNG 0H3-1 Contents
A. CÂU HỎI .................................................................................................................................................................... 2
DẠNG 1. XÁC ĐỊNH VÉCTƠ CHỈ PHƯƠNG, VÉC TƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG, HỆ SỐ GÓC
CỦA ĐƯỜNG THẲNG ................................................................................................................................................... 2
DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN ........................................ 5
Dạng 2.1 Viết phương trình đường thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua ...................... 5
Dạng 2.2 Viết phương trình đường thẳng đi qua một điểm vuông góc hoặc với đường thẳng cho trước .................... 6
Dạng 2.3 Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác .................................................... 9
Dạng 2.3.1 Phương trình đường cao của tam giác ................................................................................................... 9
Dạng 2.3.2 Phương trình đường trung tuyến của tam giác ..................................................................................... 10
Dạng 2.3.3 Phương trình cạnh của tam giác ........................................................................................................... 10
Dạng 2.3.4 Phương trình đường phân giác của tam giác........................................................................................ 10
DẠNG 3. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG .................................................................................... 12
DẠNG 4. GÓC CỦA HAI ĐƯỜNG THẲNG ............................................................................................................... 15
Dạng 4.1 Tính góc của hai đường thẳng cho trước .................................................................................................... 15
Dạng 4.2 Viết phương trình đường thẳng liên quan đến góc ..................................................................................... 17
DẠNG 5. KHOẢNG CÁCH .......................................................................................................................................... 18
Dạng 5.1 Tính khoảng cách từ 1 điểm đến đường thẳng cho trước ........................................................................... 18
Dạng 5.2 Phương trình đường thẳng liên quan đến khoảng cách ............................................................................... 20
DẠNG 6. XÁC ĐỊNH ĐIỂM ......................................................................................................................................... 22
Dạng 6.1 Xác định tọa hình chiếu, điểm đối xứng ..................................................................................................... 22
Dạng 6.2 Xác định điểm liên quan đến yếu tố khoảng cách, góc ............................................................................... 22
Dạng 6.3 Xác định điểm liên quan đến yếu tố cực trị ................................................................................................ 24
Dạng 6.4 Một số bài toán tổng hợp ............................................................................................................................ 25
DẠNG 7. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN DIỆN TÍCH ................................................................................ 28
B. LỜI GIẢI ................................................................................................................................................................... 29
DẠNG 1. XÁC ĐỊNH VÉCTƠ CHỈ PHƯƠNG, VÉC TƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG, HỆ SỐ GÓC
CỦA ĐƯỜNG THẲNG ................................................................................................................................................. 29
DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN ...................................... 31
Dạng 2.1 Viết phương trình đường thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua .................... 31
Dạng 2.2 Viết phương trình đường thẳng đi qua một điểm vuông góc hoặc với đường thẳng cho trước .................. 32
Dạng 2.3 Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác .................................................. 35
Dạng 2.3.1 Phương trình đường cao của tam giác ................................................................................................. 35
Dạng 2.3.2 Phương trình đường trung tuyến của tam giác ..................................................................................... 36
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Dạng 2.3.3 Phương trình cạnh của tam giác ........................................................................................................... 36
Dạng 2.3.4 Phương trình đường phân giác của tam giác........................................................................................ 37
DẠNG 3. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG .................................................................................... 39
DẠNG 4. GÓC CỦA HAI ĐƯỜNG THẲNG ............................................................................................................... 44
Dạng 4.1 Tính góc của hai đường thẳng cho trước .................................................................................................... 44
Dạng 4.2 Viết phương trình đường thẳng liên quan đến góc ..................................................................................... 46
DẠNG 5. KHOẢNG CÁCH .......................................................................................................................................... 49
Dạng 5.1 Tính khoảng cách từ 1 điểm đến đường thẳng cho trước ........................................................................... 49
Dạng 5.2 Phương trình đường thẳng liên quan đến khoảng cách ............................................................................... 51
DẠNG 6. XÁC ĐỊNH ĐIỂM ......................................................................................................................................... 53
Dạng 6.1 Xác định tọa hình chiếu, điểm đối xứng ..................................................................................................... 53
Dạng 6.2 Xác định điểm liên quan đến yếu tố khoảng cách, góc ............................................................................... 55
Dạng 6.3 Xác định điểm liên quan đến yếu tố cực trị ................................................................................................ 57
Dạng 6.4 Một số bài toán tổng hợp ............................................................................................................................ 59
DẠNG 7. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN DIỆN TÍCH ................................................................................ 70 A. CÂU HỎI
DẠNG 1. XÁC ĐỊNH VÉCTƠ CHỈ PHƯƠNG, VÉC TƠ PHÁP TUYẾN CỦA ĐƯỜNG
THẲNG, HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG Câu 1.
Trong mặt phẳng Oxy , đường thẳng d  ax  by  c   2 2 :
0, a  b  0 . Vectơ nào sau đây là một
vectơ pháp tuyến của đường thẳng d  ?    
A. n  a; b . B. n   ; b a . C. n   ;
b a .
D. n  a;b .  Câu 2.
(Chuyên Lê Hồng Phong-Nam Định) Cho đường thẳng d có một vectơ pháp tuyến là n   ; a b
, a,b   . Xét các khẳng định sau:
1. Nếu b  0 thì đường thẳng d không có hệ số góc. a
2. Nếu b  0 thì hệ số góc của đường thẳng d là . b 
3. Đường thẳng d có một vectơ chỉ phương là u   ; b a . 
4. Vectơ k n , k   là vectơ pháp tuyến của d .
Có bao nhiêu khẳng định sai? A. 3 . B. 2 . C. 1. D. 4 . Câu 3.
(THPT Cộng Hiền - Lần 1 - 2018-2019) Trong mặt phẳng tọa độ Oxy, cho đường thẳng
d : x  2 y  3  0 . Vectơ pháp tuyến của đường thẳng d là     A. n  1; 2  
B. n  2  ;1
C. n  2;3
D. n  1;3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 4.
Cho đường thẳng d  : 3x  2y 10  0 . Véc tơ nào sau đây là véctơ chỉ phương của d  ?    
A. u  3; 2 .
B. u  3;  2 .
C. u  2 ;  3 .
D. u  2 ;  3 .  1 x  5  t Câu 5.
(THPT Quỳnh Lưu- Nghệ An- 2019) Cho đường thẳng  : 2 một vectơ pháp tuyến  y  3   3t 
của đường thẳng  có tọa độ  1  A. 5; 3 . B. 6  ;1 . C. ;3   . D.  5  ;3 .  2  x  2   t Câu 6.
Trong hệ trục tọa độ Oxy , Véctơ nào là một véctơ pháp tuyến của đường thẳng d :  ? y  1   2t      A. n  2  ;   1 .
B. n 2;   1 . C. n  1  ; 2 .
D. n 1; 2 . x  1 4t Câu 7.
Vectơ chỉ phương của đường thẳng d :  là:
y  2  3t     
A. u  4;3 .
B. u  4;3 .
C. u  3; 4 .
D. u  1; 2 . Câu 8.
Vector nào dưới đây là 1 vector chỉ phương của đường thẳng song song với trục Ox :    
A. u  1;0 . B. u  (1; 1  ) .
C. u  (1;1) .
D. u  (0;1) . Câu 9.
Cho đường thẳng d : 7x  3y 1  0 . Vectơ nào sau đây là Vectơ chỉ phương của d?    
A. u  7;3 .
B. u  3;7 .
C. u  3;7 .
D. u  2;3 .
Câu 10. Cho đường thẳng d : 2x  3y  4  0 . Véctơ nào sau đây là véctơ pháp tuyến của đường thẳng d ?     A. n  3; 2 .
B. n  4 ;  6 .
C. n  2;  3 . D. n  2  ;3 . 1   1   1   1  
Câu 11. Cho đường thẳng d : 5x  3y  7  0. Vectơ nào sau đây là một vec tơ chỉ phương của đường thẳng d ?     A. n  3;5 .
B. n  3; 5 .
C. n  5;3 .
D. n  5; 3 . 4   3   2   1  
Câu 12. Cho đường thẳng  : x  2 y  3  0 . Véc tơ nào sau đây không là véc tơ chỉ phương của  ?    
A. u  4;  2 . B. v   2  ;   1 .
C. m  2;  1 .
D. q  4; 2 .
Câu 13. Cho hai điểm A  1; 2 và B  5; 4 . Vectơ pháp tuyến của đường thẳng AB là A.  1  ; 2   . B. 1; 2 . C.  2   ;1 . D.  1  ; 2 .
Câu 14. Cho đường thẳng d : 7x  3y 1  0 . Vectơ nào sau đây là Vectơ chỉ phương của đường thẳng d?    
A. u  7;3 .
B. u  3;7 . C. u   3  ;7 .
D. u  2;3 .
Câu 15. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Vectơ nào dưới đây là một vectơ pháp tuyến
của d : x  2 y  2018  0 ?     A. n 0; 2   . B. n  2  ;0 . C. n 2  ;1 . D. n 1; 2   . 1 3 4 2
Câu 16. Vectơ nào trong các vectơ dưới đây là vectơ pháp tuyến của đường thẳng y  2x 1  0 ? A. 2;   1 . B. 1;2 . C.  2  ;  1 . D.  2  ;   1 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 17. Trong mặt phẳng Oxy , cho đường thẳng d : 2x  y 1  0 , một véctơ pháp tuyến của d là A.  2  ;   1 . B. 2;  1  . C.  1  ; 2 . D. 1; 2 .
Câu 18. Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d : 2x  3y  4  0 . Vectơ nào sau đây là một
vectơ chỉ phương của d.   A. u  3; 2  . B. u  2;3 . 2   4     C. u  2; 3  . D. u  3; 2 3   1  
Câu 19. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Vectơ nào sau đây là một Vectơ chỉ phương
của đường thẳng  : 6x  2y  3  0 ?    
A. u 1;3 .
B. u 6; 2 .
C. u 1;3 .
D. u 3;   1 .
Câu 20. (THPT Yên Mỹ Hưng Yên lần 1 - 2019) Cho hai điểm M 2;3 và N  2
 ;5 . Đường thẳng M N
có một vectơ chỉ phương là:    
A. u  4; 2 . B. u  4; 2   . C. u   4  ; 2   . D. u   2  ; 4 .
Câu 21. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x  2 y 1  0. Một vectơ chỉ phương của
đường thẳng d là    
A. u  1;  2 .
B. u  2;  1 .
C. u  2;   1 .
D. u  1; 2 . 
Câu 22. Đường thẳng d có một vectơ chỉ phương là u  2;  
1 . Trong các vectơ sau, vectơ nào là một
vectơ pháp tuyến của d ?    
A. n  1; 2 .
B. n  1; 2 .
C. n  3; 6 . D. n  3; 6 . 4   3   2   1   
Câu 23. Đường thẳng d có một vectơ pháp tuyến là n  4; 2 . Trong các vectơ sau, vectơ nào là một
vectơ chỉ phương của d ?    
A. u  2; 4 .
B. u  2; 4 . C. u  1; 2 . D. u  2;1 . 4   3   2   1   
Câu 24. Đường thẳng d có một vectơ chỉ phương là u  3; 4
  . Đường thẳng  vuông góc với d có một vectơ pháp tuyến là:     A. n  4;3 . B. n  4; 3  . C. n  3; 4 .
D. n  3; 4 . 4   3   2   1   
Câu 25. Đường thẳng d có một vectơ pháp tuyến là n  2; 5
  . Đường thẳng  vuông góc với d có một vectơ chỉ phương là:    
A. u  5; 2 . B. u  5  ; 2 . C. u  2;5 .
D. u  2; 5 . 4   3   2   1   
Câu 26. Đường thẳng d có một vectơ chỉ phương là u  3; 4 . Đường thẳng  song song với d có một vectơ pháp tuyến là:     A. n  4;3 . B. n  4  ;3 . C. n  3; 4 .
D. n  3; 4 . 4   3   2   1   
Câu 27. Đường thẳng d có một vectơ pháp tuyến là n  2; 5
  . Đường thẳng  song song với d có một vectơ chỉ phương là:    
A. u  5; 2 .
B. u  5; 2 . C. u  2;5 .
D. u  2; 5 . 4   3   2   1  
Câu 28. Cho đường thẳng d : 3x  5y  2018  0. Tìm mệnh đề sai trong các mệnh đề sau:  
A. d có vectơ pháp tuyến n  3;5.
B. d có vectơ chỉ phương u  5; 3  .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 5
C. d có hệ số góc k  .
D. d song song với đường thẳng  : 3x  5y  0. 3
Câu 29. Cho đường thẳng d  : x  7 y 15  0 . Mệnh đề nào sau đây đúng? 1  1 
A. d  có hệ số góc k 
B. d  đi qua hai điểm M  ;2   và M 5;0 7  3  
C. u  7; 
1 là vecto chỉ phương của d 
D. d  đi qua gốc tọa độ
Câu 30. Trên mặt phẳng tọa độ Oxy , cho hai điểm A 2
 ;3 và B 4;  
1 . Phương trình nào sau đây là
phương trình đường thẳng AB ? x  4 y 1 x  1 3t
A. x  y  3  0 .
B. y  2x 1. C.  . D.  . 6 4  y  1 2t 
DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
Dạng 2.1 Viết phương trình đường thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua
Câu 31. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Phương trình tham số của đường thẳng đi qua
hai điểm A2;  1 và B 2;5 là x  2t x  2  t x  1 x  2 A.  . B.  . C.  . D.  . y  6  t  y  5  6t  y  2  6t 
y  1  6t 
Câu 32. Chuyên Lê Hồng Phong-Nam Định Trong mặt phẳng toạ độ Oxy , cho hai điểm A3;   1 và B  6
 ; 2 . Phương trình nào dưới đây không phải là phương trình tham số của đường thẳng AB ?
x  3  3t
x  3  3t x  3t x  6   3t A.  . B.  . C.  . D.  . y  1 t  y  1 t  y  t  y  2  t 
Câu 33. Phương trình tham số của đường thẳng qua M 1; 2
  , N 4;3 là x  4  t x  1 5t
x  3  3t x  1 3t A.  . B.  . C.  . D.  . y  3  2t  y  2   3t  y  4  5t 
y  2  5t 
Câu 34. Phương trình tham số của đường thẳng đi qua hai điểm A3;   1 , B  6  ; 2 là x  1   3t
x  3  3t
x  3  3t
x  3  3t A.  . B.  . C.  . D.  . y  2t  y  1   t  y  6   t  y  1   t 
Câu 35. Trong mặt phẳng tọa độ, cho hai điểm A3;0, B 0; 2 và đường thẳng d : x  y  0 . Lập phương
trình tham số của đường thẳng  qua A và song song với d . x  t x  t x  t  x  t  A.  . B.  . C.  . D.  . y  3  t  y  3  t  y  3  t  y  3  t  x  5  t
Câu 36. Cho đường thẳng d có phương trình tham số 
. Phương trình tổng quát của đường
y  9  2t  thẳng d là
A. 2x  y 1  0 .
B. 2x  y 1  0 .
C. x  2 y 1  0 .
D. 2x  3y 1  0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 37. Trong mặt phẳng Oxy cho điểm M (1; 2) . Gọi ,
A B là hình chiếu của M lên Ox, Oy . Viết phương
trình đường thẳng AB .
A. x  2 y 1  0 .
B. 2x  y  2  0 .
C. 2x  y  2  0 .
D. x  y  3  0 .
x  3  5t
Câu 38. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : 
(t  ) . Phương trình tổng quát của y  1 4t 
đường thẳng d là
A. 4x  5 y  7  0. .
B. 4x  5 y 17  0. .
C. 4x  5 y 17  0. .
D. 4x  5 y 17  0.
Câu 39. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng d cắt hai trục Ox và Oy lần lượt tại hai điểm A ;
a 0 và B 0;b a  0;b  0 . Viết phương trình đường thẳng d. x y x y x y x y A. d :   0 . B. d :   1. C. d :   1. D. d :   1. . a b a b a b b a
Câu 40. Phương trình đường thẳng đi qua hai điểm A0;4, B  6  ;0 là: x y x y x y x y A.   1. B.   1 . C.   1 . D.   1. 6 4 4 6  4 6  6 4
Dạng 2.2 Viết phương trình đường thẳng đi qua một điểm vuông góc hoặc với đường thẳng cho trước
Câu 41. Phương trình đường thẳng d đi qua A1; 2
  và vuông góc với đường thẳng  : 3x  2 y 1  0 là:
A. 3x  2 y  7  0 .
B. 2x  3y  4  0 .
C. x  3y  5  0 .
D. 2x  3y  3  0 .
Câu 42. Cho đường thẳng d : 8x  6 y  7  0 . Nếu đường thẳng  đi qua gốc tọa độ và vuông góc với đường
thẳng d thì  có phương trình là
A. 4x  3y  0 .
B. 4x  3y  0 .
C. 3x  4 y  0 .
D. 3x  4 y  0 .
Câu 43. Đường thẳng đi qua điểm A1;1 
1 và song song với đường thẳng y  3x  5 có phương trình là
A. y  3x 11 .
B. y  3x 14 .
C. y  3x  8 .
D. y  x 10 .
(HKI XUÂN PHƯƠNG - HN) Lập phương trình đường đi qua A2;5 và song song với đường Câu 44.
thẳng d  : y  3x  4? 1
A.  : y  3x  2 .
B.  : y  3x 1.
C.  : y   x 1. D.  : y  3  x 1. 3
Câu 45. Trong hệ trục Oxy , đường thẳng d qua M 1 
;1 và song song với đường thẳng d ' : x  y 1  0 có phương trình là
A. x  y 1  0 .
B. x  y  0 .
C.  x  y 1  0 .
D. x  y  2  0 .
Câu 46. Viết phương trình tổng quát của đường thẳng đi qua điểm I  1
 ; 2 và vuông góc với đường thẳng
có phương trình 2x  y  4  0 .
A. x  2 y  0 .
B. x  2 y  3  0 .
C. x  2 y  3  0 .
D. x  2y  5  0 .
Câu 47. Trong hệ trục tọa độ Trong hệ trục tọa độ Oxy cho hai điểm M 1;0 và N 0;2 . Đường thẳng đi  1  qua A ;1 
 và song song với đường thẳng MN có phương trình là  2 
A. Không tồn tại đường thẳng như đề bài yêu cầu.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
B. 2 x  y  2  0 .
C. 4x  y  3  0 .
D. 2x  4 y  3  0 .
Câu 48. Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A2;0 ¸ B 0;3 và C 3;   1 . Đường thẳng đi
qua điểm B và song song với AC có phương trình tham số là: x  5t x  5 x  t
x  3  5t A.  . B.  . C.  . D.  . y  3  t  y  1 3t  y  3  5t  y  t 
Câu 49. Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A3; 2 ¸ P 4;0 và Q 0; 2 . Đường thẳng đi
qua điểm A và song song với PQ có phương trình tham số là:
x  3  4t
x  3  2t x  1   2t x  1   2t A.  . B.  . C.  . D.  . y  2  2t  y  2  t  y  t  y  2  t 
Câu 50. Trong mặt phẳng với hệ tọa độ Oxy , cho hình bình hành ABCD có đỉnh A –2  ;1 và phương trình x  1 4t
đường thẳng chứa cạnh CD là 
. Viết phương trình tham số của đường thẳng chứa cạnh y  3t  AB .
x  2  3t x  2   4t x  2   3t x  2   3t A.  . B.  . C.  . D.  .
y  2  2t  y  1 3t  y  1 4t  y  1 4t 
Câu 51. Viết phương trình tham số của đường thẳng d đi qua điểm M 3;5 và song song với đường phân
giác của góc phần tư thứ nhất. x  3   t x  3   t x  3  t x  5  t A.  . B.  . C.  . D.  . y  5  t  y  5  t  y  5  t  y  3  t 
Câu 52. Viết phương trình tham số của đường thẳng d đi qua điểm M 4; 7 và song song với trục Ox . x  1 4t x  4 x  7   t x  t A.  . B.  . C.  . D.  . y  7t  y  7  t  y  4  y  7 
Câu 53. Đường thẳng d đi qua điểm M 1; 2 và song song với đường thẳng  : 2x  3y 12  0 có phương trình tổng quát là:
A. 2x  3y  8  0 .
B. 2x  3y  8  0 .
C. 4x  6 y 1  0 .
D. 4x  3y  8  0 .
Câu 54. Phương trình tổng quát của đường thẳng d đi qua O và song song với đường thẳng
 : 6x  4x 1  0 là:
A. 3x  2 y  0.
B. 4x  6 y  0.
C. 3x 12 y 1  0.
D. 6x  4 y 1  0.
Câu 55. Đường thẳng d đi qua điểm M 1; 2 và vuông góc với đường thẳng
 : 2x  y  3  0 có phương trình tổng quát là:
A. 2x  y  0 .
B. x  2 y  3  0 .
C. x  y 1  0 .
D. x  2 y  5  0 .
Câu 56. Viết phương trình đường thẳng  đi qua điểm A4; 3
  và song song với đường thẳng
x  3  2t d :  . y  1 3t 
A. 3x  2 y  6  0 .
B. 2x  3y 17  0 .
C. 3x  2 y  6  0 .
D. 3x  2 y  6  0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 57. Cho tam giác ABC có A2;0, B 0;3, C  –3 
;1 . Đường thẳng d đi qua B và song song với
AC có phương trình tổng quát là:
A. 5x – y  3  0 .
B. 5x  y – 3  0 .
C. x  5 y – 15  0 .
D. x – 15 y 15  0 .
Câu 58. Viết phương trình tổng quát của đường thẳng d đi qua điểm M  1
 ; 0 và vuông góc với đường x  t thẳng  :  . y  2t 
A. 2x  y  2  0 .
B. 2x  y  2  0 .
C. x  2 y 1  0 .
D. x  2 y 1  0 . x  1 3t
Câu 59. Đường thẳng d đi qua điểm M  2  
;1 và vuông góc với đường thẳng  :  có phương y  2   5t  trình tham số là: x  2   3t x  2   5t x  1 3t x  1 5t A.  . B.  . C.  . D.  . y  1 5t  y  1 3t  y  2  5t  y  2  3t 
Câu 60. Viết phương trình tham số của đường thẳng d đi qua điểm A 1
 ; 2 và song song với đường thẳng
 : 3x 13y 1  0 .
x  113t x  113t
x  113t x  1 3t A.  . B.  . C.  . D.  . y  2  3t 
y  2  3t  y  2  3t  y  2 13t 
Câu 61. Viết phương trình tham số của đường thẳng d qua điểm A1; 2 và vuông góc với đường thẳng
 : 2x  y  4  0 . x  1   2t x  t x  1   2t x  1 2t A.  . B.  . C.  . D.  . y  2  t  y  4  2t  y  2  t  y  2  t 
Câu 62. Viết phương trình tổng quát của đường thẳng d đi qua điểm M  2  ; 5
  và song song với đường
phân giác góc phần tư thứ nhất.
A. x  y  3  0 .
B. x  y  3  0 .
C. x  y  3  0 .
D. 2x  y 1  0 .
Câu 63. Viết phương trình tổng quát của đường thẳng d đi qua điểm M 3;  
1 và vuông góc với đường
phân giác góc phần tư thứ hai.
A. x  y  4  0 .
B. x  y  4  0 .
C. x  y  4  0 .
D. x  y  4  0 .
Câu 64. Viết phương trình tham số của đường thẳng d đi qua điểm M  4
 ; 0 và vuông góc với đường
phân giác góc phần tư thứ hai. x  t x  4   t x  t x  t A.  . B.  . C.  . D.  . y  4  t  y  t  y  4  t  y  4  t 
Câu 65. Viết phương trình tổng quát của đường thẳng d đi qua điểm M 1; 2 và song song với trục Ox .
A. y  2  0 .
B. x 1  0 .
C. x 1  0 .
D. y  2  0 .
Câu 66. Viết phương trình tham số của đường thẳng d đi qua điểm M 6; 10 
 và vuông góc với trục Oy .
x  10  t x  2  t x  6 x  6 A.  . B. d :  . C. d :  . D. d :  . y  6  y  10   y  10   t  y  10   t 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Dạng 2.3 Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác
Dạng 2.3.1 Phương trình đường cao của tam giác
Câu 67. (ĐỘI CẤN VĨNH PHÚC LẦN 1 2018-2019) Trên mặt phẳng tọa độ Oxy , cho tam giác ABC có
A1; 2, B 3 
;1 , C 5; 4 . Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC ?
A. 2x  3y  8  0 .
B. 2x  3y  8  0 .
C. 3x  2 y  1  0 .
D. 2x  3y  2  0 . Câu 68. Cho AB 
C có A2; 
1 , B 4;5,C  3
 ; 2 . Đường cao AH 
của ABC có phương trình là
A. 7x  3y 11  0 . B. 3
 x  7 y 13  0 . C. 3x  7y 17  0 .
D. 7x  3y 10  0 .
Câu 69. (Độ Cấn Vĩnh Phúc-lần 1-2018-2019) Trên mặt phẳng tọa độ Oxy , cho tam giác ABC có
A1;2, B3; 
1 ,C 5;4 . Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC ?
A. 2x  3y  8  0 .
B. 2x  3y  8  0 .
C. 3x  2 y 1  0 .
D. 2x  3y  2  0 .
Câu 70. Trong mặt phẳng cho tam giác ABC cân tại C có B 2;  
1 , A4;3 . Phương trình đường cao CH là
A. x  2 y 1  0 .
B. x  2 y 1  0 .
C. 2x  y  2  0 .
D. x  2 y  5  0 . Câu 71. Cho A
 BC có A2;  
1 , B 4;5,C  3
 ; 2 . Phương trình tổng quát của đường cao BH là
A. 3x  5 y  37  0 .
B. 5x  3y  5  0 .
C. 3x  5 y 13  0 .
D. 3x  5 y  20  0 .
Câu 72. Đường trung trực của đoạn thẳng AB với A  3; 2 , B   3
 ;3 có một vectơ pháp tuyến là:     A. n  6;5 . B. n  0;1 .
C. n  3;5 . D. n  1  ; 0 . 4   3   2   1  
Câu 73. Cho tam giác ABC có A1  ;1 , B(0; 2  ,
) C 4; 2. Lập phương trình đường trung tuyến của tam giác ABC kẻ từ . A
A. x  y  2  0.
B. 2x  y  3  0.
C. x  2 y  3  0.
D. x  y  0.
Câu 74. Đường trung trực của đoạn AB với A1; 4 và B 5; 2 có phương trình là:
A. 2x  3y  3  0.
B. 3x  2 y 1  0.
C. 3x  y  4  0.
D. x  y 1  0.
Câu 75. Đường trung trực của đoạn AB với A4;   1 và B 1; 4
  có phương trình là:
A. x  y  1.
B. x  y  0.
C. y  x  0.
D. x  y  1.
Câu 76. Đường trung trực của đoạn AB với A1; 4 và B 1; 2 có phương trình là:
A. y 1  0.
B. x 1  0.
C. y 1  0.
D. x  4 y  0.
Câu 77. Đường trung trực của đoạn AB với A1; 4 và B 3; 4
  có phương trình là :
A. y  4  0.
B. x  y  2  0.
C. x  2  0.
D. y  4  0.
Câu 78. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A2;  
1 , B 4;5 và C 3; 2 . Lập
phương trình đường cao của tam giác ABC kẻ từ . A
A. 7x  3y 11  0. B. 3
 x  7 y 13  0.
C. 3x  7 y 1  0.
D. 7x  3y 13  0.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 79. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A2;  
1 , B 4;5 và C 3; 2. Lập
phương trình đường cao của tam giác ABC kẻ từ . B
A. 3x  5y 13  0.
B. 3x  5y  20  0.
C. 3x  5y  37  0.
D. 5x  3y  5  0.
Câu 80. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A2;  
1 , B 4;5 và C 3; 2. Lập
phương trình đường cao của tam giác ABC kẻ từ C.
A. x  y 1  0.
B. x  3y  3  0.
C. 3x  y 11  0.
D. 3x  y 11  0.
Dạng 2.3.2 Phương trình đường trung tuyến của tam giác
Câu 81. Cho tam giác ABC với A1; 
1 , B 0;  2 , C 4;2 . Phương trình tổng quát của đường trung tuyến
đi qua điểm B của tam giác ABC là
A. 7x  7 y  14  0 .
B. 5x  3 y  1  0 .
C. 3x  y  2  0. D. 7
 x  5y 10  0.
Câu 82. (THPT Yên Dũng 3 - Bắc Giang lần 1- 18-19) Trong hệ tọa độ Oxy , cho tam giác ABC có A2; 
3 , B 1;0, C  1  ; 2
  . Phương trình đường trung tuyến kẻ từ đỉnh A của tam giác ABC là:
A. 2x  y 1  0 .
B. x  2y  4  0 .
C. x  2y  8  0 .
D. 2x  y  7  0 .
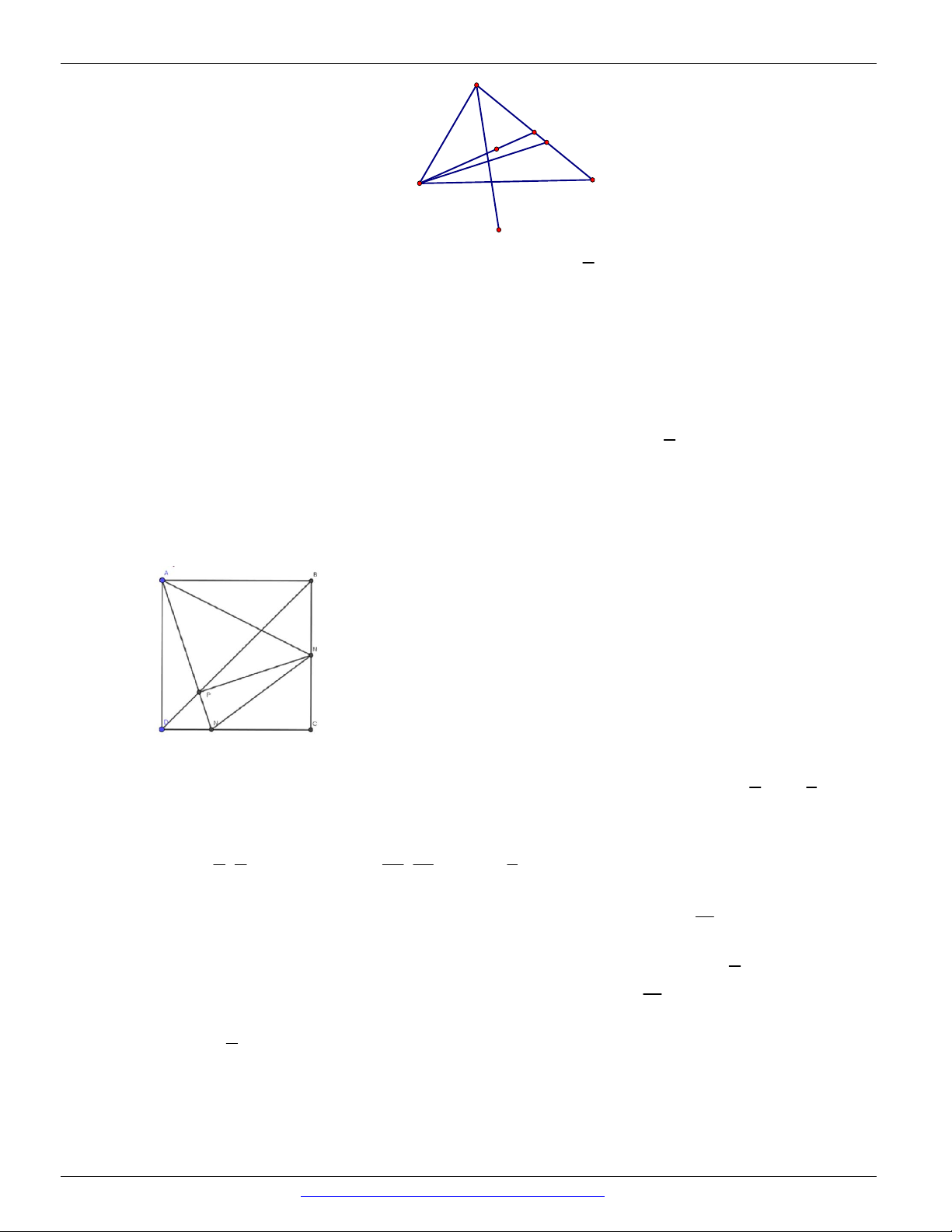
Câu 83. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A1; 4 , B 3; 2 và C 7;3. Viết
phương trình tham số của đường trung tuyến CM của tam giác. x  7
x  3  5t x  7  t x  2 A.  . B.  . C.  . D.  . y  3  5t  y  7  y  3  y  3  t 
Câu 84. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A2; 4 , B 5; 0 và C 2  ;1 . Trung
tuyến BM của tam giác đi qua điểm N có hoành độ bằng 20 thì tung độ bằng: 25 27 A. 12. B.  . C. 13. D.  . 2 2
Dạng 2.3.3 Phương trình cạnh của tam giác
Câu 85. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Trong mặt phẳng với hệ tọa
độ Oxy , cho tam giác ABC có M 2;0 là trung điểm của cạnh AB . Đường trung tuyến và đường
cao qua đỉnh A lần lượt có phương trình là 7 x  2 y  3  0 và 6x  y  4  0 . Phương trình đường thẳng AC là
A. 3x  4 y  5  0 .
B. 3x  4 y  5  0 .
C. 3x  4 y  5  0 .
D. 3x  4 y  5  0 .
Câu 86. (Nông Cống - Thanh Hóa - Lần 1 - 1819) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác
ABC có phương trình cạnh AB là x  y  2  0, phương trình cạnh AC là x  2 y  5  0 . Biết
trọng tâm của tam giác là điểm G 3; 2 và phương trình đường thẳng BC có dạng x  my  n  0. Tìm m  . n A. 3 . B. 2 . C. 5 . D. 4 .
Dạng 2.3.4 Phương trình đường phân giác của tam giác
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 87. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng  : ax  by  c  0 và hai điểm M  x ; y , m m 
N  x ; y không thuộc  . Chọn khẳng định đúng trong các khẳng định sau: n n 
A. M , N khác phía so với  khi ax  by  c.ax  by  c  0. m m n n
B. M , N cùng phía so với  khi ax  by  c.ax  by  c  0. m m n n
C. M , N khác phía so với  khi ax  by  c.ax  by  c  0. m m n n
D. M , N cùng phía so với  khi ax  by  c.ax  by  c  0. m m n n
Câu 88. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : 3x  4 y  5  0 và hai điểm A1;3 ,
B 2; m . Tìm tất cả các giá trị của tham số m để A và B nằm cùng phía đối với d . 1 1 A. m  0 . B. m   . C. m  1  . D. m   . 4 4 x  2  t
Câu 89. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : 
và hai điểm A1; 2 , B 2; m y  1 3t 
. Tìm tất cả các giá trị của tham số m để A và B nằm cùng phía đối với d . A. m  13. B. m  13 . C. m  13. D. m  13 .
Câu 90. Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi hai đường thẳng  : x  2 y  3  0 1
và  : 2x  y  3  0 . 2
A. 3x  y  0 và x  3y  0 .
B. 3x  y  0 và x  3y  6  0 .
C. 3x  y  0 và x  3y  6  0 .
D. 3x  y  6  0 và x  3y  6  0 .
Câu 91. Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi đường thẳng  : x  y  0 và trục hoành.
A. 1 2  x  y  0; x  1 2  y  0 .
B. 1 2  x  y  0; x  1 2  y  0 .
C. 1 2  x  y  0 ; x  1 2  y  0 .
D. x  1 2  y  0; x  1 2  y  0 .  7 
Câu 92. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A ;3 
 , B 1; 2 và C 4;3 . Phương  4 
trình đường phân giác trong của góc A là:
A. 4x  2 y 13  0.
B. 4x  8y 17  0.
C. 4x  2 y 1  0.
D. 4x  8y  31  0.
Câu 93. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A1;5 , B 4; 5 và C 4;   1 .
Phương trình đường phân giác ngoài của góc A là:
A. y  5  0.
B. y  5  0.
C. x 1  0.
D. x 1  0.
Câu 94. Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng d : 3x  4 y  3  0 và 1
d :12x  5y 12  0 . Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng d và d 2 1 2 là:
A. 3x 11y  3  0.
B. 11x  3y 11  0.
C. 3x 11y  3  0.
D. 11x  3y 11  0.
Câu 95. Cho tam giác ABC có phương trình cạnh AB : 3x  4 y  9  0 , cạnh AC : 8x  6 y 1  0 , cạnh
BC : x  y  5  0 . Phương trình đường phân giác trong của góc A là:
A. 14x 14 y 17  0 .
B. 2x  2 y 19  0 .
C. 2x  2 y 19  0 .
D. 14x 14 y 17  0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 96. (THPT Ngô Quyền - Ba Vì - Hải Phòng, lần 1) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC với A1; 2
 , B 2;3, C 3;0 . Phương trình đường phân giác ngoài góc A của tam giác ABC là A. x  1. B. y  2  .
C. 2x  y  0 .
D. 4x  y  2  0 .
DẠNG 3. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
Câu 97. (HKI XUÂN PHƯƠNG - HN) Có bao nhiêu cặp đường thẳng song song trong các đường thẳng sau? 1 1 1 2 d : y  
x  2; d : y   x  3; d : y  x  3; d : y   x  2 4  3  2  1  2 2 2 2 A. 3 . B. 2 . C. 1. D. 0 .
Câu 98. Phương trình nào sau đây là phương trình đường thẳng không song song với đường thẳng
d : y  3x  2 A. 3
 x  y  0 .
B. 3x  y  6  0.
C. 3x  y  6  0.
D. 3x  y  6  0.
Câu 99. Trong mặt phẳng Oxy , đường thẳng d : x  2 y 1  0 song song với đường thẳng có phương trình nào sau đây?
A. x  2y 1  0 .
B. 2x  y  0 .
C. x  2y 1  0 . D. 2
 x  4y 1  0 .
Câu 100. Cho các đường thẳng sau. 3 1  3  3 d : y 
x  2 d : y 
x 1 d : y   1
 x  2 d : y  x 1 1 2 3 4 3 3  3    3
Khẳng định nào đúng trong các khẳng định sau?
A. d , d , d song song với nhau.
B. d và d song song với nhau. 2 3 4 2 4
C. d và d vuông góc với nhau.
D. d và d song song với nhau. 1 4 2 3
Câu 101. Tìm các giá trị thực của tham số m để đường thẳng y   2
m  3 x  3m 1 song song với đường
thẳng y  x  5 . A. m  2  .
B. m   2 . C. m  2  . D. m  2 .
Câu 102. Tọa độ giao điểm của hai đường thẳng x  3y  6  0 và 3x  4 y 1  0 là  27 17   27 17  A. ;    . B.  2  7;17 . C.  ;   . D. 27; 1  7 .  13 13   13 13 
Câu 103. Cho đường thẳng d : 2x  3y 15  0 và d : x  2 y  3  0 . Khẳng định nào sau đây đúng? 1 2
A. d và d cắt nhau và không vuông góc với nhau.
B. d và d song song với 1 2 1 2 nhau.
C. d và d trùng nhau. D. d và d vuông góc với nhau. 1 2 1 2
Câu 104. Hai đường thẳng d :mx  y  m  5, d : x  my  9 cắt nhau khi và chỉ khi 1 2 A. m  1  . B. m  1. C. m  1  . D. m  2 .
Câu 105. Với giá trị nào của m thì hai đường thẳng
d : 3x  4 y 10  0 và d : 2m 1 x  m y 10  0 trùng nhau? 2   2 1 A. m  2 . B. m  1  . C. m  2 . D. m  2 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 106. Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng có phương trình
d : mx  m 1 y  2m  0 và d : 2x  y 1  0 . Nếu d song song d thì: 1   2 1 2 A. m  2. B. m  1  . C. m  2  . D. m  1.
x  2  3t
Câu 107. Tìm m để hai đường thẳng d : 2x  3y  4  0 và d : cắt nhau. 1 2
 y 1 4mt  1 1 1 A. m   . B. m  2. C. m  . D. m  . 2 2 2
Câu 108. Với giá trị nào của a thì hai đường thẳng x  1   at 
d : 2x – 4 y 1  0 và d : vuông góc với nhau? 1 2
 y  3a    1 t  A. a  2. B. a  2. C. a  1. D. a  1 .
Câu 109. Với giá trị nào của m thì hai đường thẳng
x  2  2t
x  2  mt  d : và d : trùng nhau? 1   y  3  t 2  y  6    1 2mt  1 A. m  . B. m  2 . C. m  2 . D. m  2 . 2
Câu 110. Tìm tất cả các giá trị của m để hai đường thẳng
 x  2  2t d :
và d : 4x  3y  m  0 trùng nhau. 1  y 1 mt 2  4 A. m  3 . B. m  1. C. m  . D. m   . 3
Câu 111. Với giá trị nào của m thì hai đường thẳng
d : 2x  y  4  m  0 và d : m  3 x  y  2m 1  0 song song? 2   1 A. m  1. B. m  1  . C. m  2. D. m  3.
Câu 112. Tìm tất cả các giá trị của m để hai đường thẳng
 : 2x  3my 10  0 và  : mx  4 y 1  0 cắt nhau. 1 2
A. 1  m  10 . B. m  1.
C. Không có m .
D. Với mọi m .
Câu 113. Với giá trị nào của m thì hai đường thẳng
 : mx  y 19  0 và  : m 1 x  m 1 y  20  0 vuông góc? 2     1
A. Với mọi m . B. m  2 .
C. Không có m . D. m  1  .
Câu 114. Với giá trị nào của m thì hai đường thẳng
d : 3mx  2 y  6  0 và d :  2
m  2 x  2my  6  0 cắt nhau? 2  1 A. m  1. B. m  1. C. m   .
D. m  1 và m  1  .
Câu 115. Với giá trị nào của m thì hai đường thẳng
 x  2  3t
d : 2x  3y 10  0 và d : vuông góc? 1 2
 y 1 4mt  1 9 9 5 A. m  . B. m  . C. m   . D. m   . 2 8 8 4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 116. Với giá trị nào của m thì hai đường thẳng
 x  1 2t
d : 4x  3y  3m  0 và d : trùng nhau? 1 2
 y  4  mt  8 8 4 4 A. m   . B. m  . C. m   . D. m  . 3 3 3 3
Câu 117. Với giá trị nào của m thì hai đường thẳng
d : 3mx  2 y  6  0 và d :  2
m  2 x  2my  3  0 song song? 2  1
A. m  1; m  1  . B. m   . C. m  2 . D. m  1  .
Câu 118. Với giá trị nào của m thì hai đường thẳng 
x  8  m   1 t d :
và d : mx  2 y 14  0 song song? 1  2
 y  10  t  m  1 A.  . B. m  1. C. m  2 . D. m   . m  2 
Câu 119. Với giá trị nào của m thì hai đường thẳng
d : m  3 2
x  2 y  m 1  0 và 2
d : x  my  m  2m 1  0 cắt nhau? 1 2 m  1 m  1 A. m  1. B.  . C. m  2 . D.  . m  2  m  2 
Câu 120. Với giá trị nào của m thì hai đường thẳng
x  m  2t  x  1 mt  : và  : trùng nhau? 1   y  1  2 m  2   1 t 
y  m  t  4
A. Không có m . B. m  . C. m  1. D. m  3 . 3
Câu 121. Tìm tọa độ giao điểm của hai đường thẳng 7x  3y 16  0 và x 10  0 .
A. 10; 18 . B. 10;18 . C. 10;18 . D. 10; 18 .
Câu 122. Tìm toạ độ giao điểm của hai đường thẳng
x  3  4t
 x  1 4t d : và d :  . 1
 y  2 5t 2 
y  7  5t  A. 1;7. B. 3; 2. C. 2; 3. D. 5  ;1 .
x  22  2t
Câu 123. Cho hai đường thẳng d : 2x  3y 19  0 và d :
. Tìm toạ độ giao điểm của hai đường 1 2
 y  55 5t  thẳng đã cho. A. 2;5. B. 10; 25. C. 1; 7. D. 5; 2. x  t 
Câu 124. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A –2; 0, B 1; 4 và đường thẳng d :  y  2t 
. Tìm tọa độ giao điểm của đường thẳng AB và d . A. 2; 0 . B.  –2; 0 . C. 0; 2 . D. 0; – 2 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
x  1 t
Câu 125. Xác định a để hai đường thẳng d : ax  3y – 4  0 và d :
cắt nhau tại một điểm nằm 1 2
 y  3 3t  trên trục hoành. A. a  1. B. a  1. C. a  2. D. a  2. x  2  t
Câu 126. Tìm tất cả các giá trị của tham số m để hai đường thẳng 2
d : 4x  3my – m  0 và d : cắt 1 2
 y  6 2t 
nhau tại một điểm thuộc trục tung.
A. m  0 hoặc m  6 . B. m  0 hoặc m  2 .
C. m  0 hoặc m  2 . D. m  0 hoặc m  6 .
Câu 127. Cho ba đường thẳng d : 3x – 2 y  5  0 , d : 2x  4 y – 7  0 , d : 3x  4 y – 1  0 . Phương trình đường 1 2 3
thẳng d đi qua giao điểm của d và d , và song song với d là: 1 2 3
A. 24x  32 y – 53  0 . B. 24x  32 y  53  0 .
C. 24x – 32 y  53  0 . D. 24x – 32 y – 53  0 .
Câu 128. Lập phương trình của đường thẳng  đi qua giao điểm của hai đường thẳng d : x  3y 1  0 , 1
d : x  3y  5  0 và vuông góc với đường thẳng d : 2x  y  7  0 . 2 3
A. 3x  6 y  5  0 .
B. 6x 12 y  5  0 .
C. 6x 12 y 10  0 .
D. x  2 y 10  0 .
Câu 129. Trong mặt phẳng với hệ tọa độ Oxy , cho ba đường thẳng lần lượt có phương trình d : 3x  4 y 15  0 , 1
d : 5x  2 y 1  0 và d : mx  2m 1 y  9m 13  0 . Tìm tất cả các giá trị của tham số m để ba 3   2
đường thẳng đã cho cùng đi qua một điểm. 1 1 A. m  . B. m  5  . C. m   . D. m  5. 5 5
Câu 130. Nếu ba đường thẳng
d : 2x  y – 4  0 , d : 5x – 2 y  3  0 và d : mx  3y – 2  0 1 2 3
đồng quy thì m nhận giá trị nào sau đây? 12 12 A. . B.  . C. 12. D. 12. 5 5
Câu 131. Với giá trị nào của m thì ba đường thẳng d : 3x – 4 y 15  0 , d : 5x  2 y – 1  0 và 1 2
d : mx – 4 y 15  0 đồng quy? 3 A. m  5 . B. m  5 . C. m  3 . D. m  3 .
Câu 132. Với giá trị nào của m thì ba đường thẳng d : 2x  y – 1  0 , d : x  2 y 1  0 và d : mx – y – 7  0 1 2 3 đồng quy? A. m  6 . B. m  6 . C. m  5 . D. m  5 .
Câu 133. Đường thẳng d : 51x  30 y 11  0 đi qua điểm nào sau đây?  4   4   3   3  A. M 1  ;  .   B. N 1  ; .   C. P 1; .   D. Q 1  ;  .    3   3   4   4 
DẠNG 4. GÓC CỦA HAI ĐƯỜNG THẲNG
Dạng 4.1 Tính góc của hai đường thẳng cho trước
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 134. (NGÔ GIA TỰ LẦN 1_2018-2019) Tính góc giữa hai đường thẳng  : x  3y  2  0 và
 : x  3 y 1  0 . A. 90 . B. 120 . C. 60 . D. 30 .
Câu 135. Góc giữa hai đường thẳng a : 3x  y  7  0 và b : x  3y 1  0 là: A. 30 . B. 90 . C. 60 . D. 45 .
d : 2x  5y  2  0
d : 3x  7 y  3  0 d d
Câu 136. Cho hai đường thẳng 1 và 2
. Góc tạo bởi đường thẳng 1 và 2 bằng A. 0 30 . B. 0 135 . C. 0 45 . D. 0 60 . x  2  t
Câu 137. Tìm côsin góc giữa hai đường thẳng  : 2x  y 1  0 và  : 1 2  y 1t  10 3 3 3 10 A. . B. . C. . D. . 10 10 5 10 x  2  t
Câu 138. Tìm góc giữa hai đường thẳng  : x  2 y 15  0 và  : t   . 2   1 y  4  2  t A. 5 . B. 60 . C. 0 . D. 90 .
Câu 139. Tìm cosin góc giữa 2 đường thẳng d : x  2 y  7  0, d : 2x  4 y  9  0 . 1 2 3 2 1 3 A. . B. . C. . D. . 5 5 5 5
Câu 140. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Tính góc giữa hai đường thẳng
 : x  3y  2  0 và  ' : x  3y 1  0 ? A. 90o. B. 120o. C. 60o. D. 30o.
Câu 141. Tính góc tạo bởi giữa hai đường thẳng
d : 2x  y 10  0 và d : x  3y  9  0. 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 135 .
Câu 142. Tính góc tạo bởi giữa hai đường thẳng
d : 7x  3y  6  0 và d : 2x  5y  4  0. 1 2   2 3 A. . B. . C. . D. . 4 3 3 4
Câu 143. Tính góc tạo bởi giữa hai đường thẳng d : 2x  2 3y  5  0 và d : y  6  0. 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 90 .
Câu 144. Tính góc tạo bởi giữa hai đường thẳng d : x  3y  0 và d : x 10  0. 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 90 .
Câu 145. Tính góc tạo bởi giữa hai đường thẳng
x  10  6t
d : 6x  5y 15  0 và d :  . 1 2 y  1 5t  A. o 30 . B. o 45 . C. o 60 . D. o 90 .
Câu 146. Cho đường thẳng d : x  2 y  7  0 và d : 2x  4 y  9  0 . Tính cosin của góc tạo bởi giữa hai 1 2 đường thẳng đã cho.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3 2 3 3 A.  . B. . C. . D. . 5 5 5 5
Câu 147. Cho đường thẳng d : x  2 y  2  0 và d : x  y  0 . Tính cosin của góc tạo bởi giữa hai đường 1 2 thẳng đã cho. 10 2 3 A. . B. . C. . D. 3 . 10 3 3 x  2  t
Câu 148. Cho đường thẳng d :10x  5 y 1  0 và d :
. Tính cosin của góc tạo bởi giữa hai đường 1 2  y 1t  thẳng đã cho. 3 10 3 10 3 A. . B. . C. . D. . 10 5 10 10
x  15 12t
Câu 149. Cho đường thẳng d : 3x  4 y 1  0 và d : . 1 2  y 1 5t 
Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho. 56 33 6 33 A. . B.  . C. . D. . 65 65 65 65
Dạng 4.2 Viết phương trình đường thẳng liên quan đến góc
x  9  at
Câu 150. Xác định tất cả các giá trị của a để góc tạo bởi đường thẳng 
t  và đường thẳng y  7  2t 
3x  4 y  2  0 bằng 45 . 2 2
A. a  1, a  1  4 . B. a  , a  1  4 . C. a  2  , a  1  4 . D. a  , a  14 . 7 7
Câu 151. Đường thẳng  đi qua giao điểm của hai đường thẳng d : 2x  y  3  0 và d : x  2 y 1  0 đồng 1 2
thời tạo với đường thẳng d : y 1  0 một góc 0 45 có phương trình: 3
A. x  (1 2) y  0 hoặc  : x  y 1  0 .
B.  : x  2 y  0 hoặc  : x  4 y  0 .
C.  : x  y  0 hoặc  : x  y  2  0 .
D.  : 2x 1  0 hoặc y  5  0. .
Câu 152. Trong mặt phẳng với hệ tọa độ Oxy , có bao nhiêu đường thẳng đi qua điểm A2; 0 và tạo với
trục hoành một góc 45 ? A. Có duy nhất. B. 2 . C. Vô số. D. Không tồn tại.
Câu 153. Đường thẳng  tạo với đường thẳng d : x  2 y  6  0 một góc 0
45 . Tìm hệ số góc k của đường thẳng  . 1 1 A. k 
hoặc k  3. B. k  hoặc k  3. 3 3 1 1
C. k   hoặc k  3. D. k   hoặc k  3. 3 3
Câu 154. Biết rằng có đúng hai giá trị của tham số k để đường thẳng d : y  kx tạo với đường thẳng  : y  x một góc 0
60 . Tổng hai giá trị của k bằng:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 8. B. 4. C. 1. D. 1.
Câu 155. Trong mặt phẳng tọa độ Oxy , cho điểm M 1;  
1 và hai đường thẳng có phương trình
d : x  y 1  0, d : 2x  y  5  0 . Gọi A là giao điểm của hai đường thẳng trên. Biết rằng có 1   2 
hai đường thẳng d  đi qua M cắt hai đường thẳng trên lần lượt tại hai điểm B,C sao cho ABC
là tam giác có BC  3AB có dạng: ax  y  b  0 và cx  y  d  0 , giá trị của T  a  b  c  d là A. T  5 . B. T  6 . C. T  2 . D. T  0 .
Câu 156. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác cân ABC có cạnh đáy BC : x  3 y  1  0 , cạnh
bên AB : x  y  5  0 . Đường thẳng AC đi qua M(4;1) . Giả sử toạ độ đỉnh C m,n.Tính
T  m  n . 5 9 9 A. T  . B. T  3  . C. T  . D. T   . 9 5 5
Câu 157. (Cụm liên trường Hải Phòng-L1-2019) Trong mặt phẳng Oxy, cho hai đường thẳng
d :2x y 5  0 và d :x y3 0 cắt nhau tại I . Phương trình đường thẳng đi qua 2  1  M  2  ; 
0 cắt d , d tại A và B sao cho tam giác IAB cân tại A có phương trình dạng 1   2 
ax  by  2  0 . Tính T  a 5b .
A. T  1 .
B. T  9 . C. T  9  . D. T  11 . DẠNG 5. KHOẢNG CÁCH
Dạng 5.1 Tính khoảng cách từ 1 điểm đến đường thẳng cho trước
Câu 158. Khoảng cách từ điểm A1 
;1 đến đường thẳng 5x 12y  6  0 là A. 13 . B. 1  3 . C. 1  . D. 1.
Câu 159. Khoảng cách từ điểm M 5; 
1 đến đường thẳng 3x  2 y 13  0 là: 28 13 A. 2 13 . B. . C. 26 . D. . 13 2
Câu 160. (THPT Đoàn Thượng-Hải Dương-HKI 18-19) Khoảng cách từ điểm M (1; 1) đến đường thẳng
 : 3x  y  4  0 là 3 10 5 A. 1. B. . C. . D. 2 10 . 5 2
Câu 161. Trong mặt phẳng Oxy , khoảng cách từ điểm M 3;  4 đến đường thẳng  : 3x  4 y 1  0 . 8 24 12 24 A. . B. . C. . D.  . 5 5 5 5
Câu 162. Khoảng cách từ điểm ( A 3
 ; 2) đến đường thẳng  : 3x  y  1  0 bằng: 11 5 10 5 11 A. 10. B. . C. . D. . 5 5 10
Câu 163. Trong mặt phẳng Oxy , khoảng cách từ gốc tọa độ O đến đường thẳng d : 4x  3y 1  0 bằng 1 A. 3 . B. 4 . C. 1. D. . 5
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 164. Một đường tròn có tâm I 3;  2 tiếp xúc với đường thẳng  :x  5y 1  0. Hỏi bán kính đường tròn bằng bao nhiêu? 14 7 A. . B. . C. 26. D. 6. 26 13 Câu 165. Trong mặt phẳng Oxy , khoảng cách
từđiểm M 0; 4 đến đường thẳng
 : x cos  y sin  4 2  sin   0 bằng 4 A. 8 .
B. 4sin . C. . D. 8 .
cos  sin
Câu 166. Khoảng cách từ I (1;2) đến đường thẳng  : 3x  4 y  26  0 bằng 5 A. 3 . B. 12 . C. 5 . D. . 3
Câu 167. Khoảng cách từ giao điểm của hai đường thẳng x  3y  4  0 và 2x  3y 1  0 đến đường thẳng
 : 3x  y  4  0 bằng: 3 10 10 A. 2 10 . B. . C. . D. 2 . 5 5
Câu 168. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A1; 2, B 0;3 và C 4; 0 . Chiều
cao của tam giác kẻ từ đỉnh A bằng: 1 1 3 A. . B. 3 . C. . D. . 5 25 5
Câu 169. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A3; 4, B 1;5 và C 3  ;1 . Tính
diện tích tam giác ABC . A. 10. B. 5. C. 26. D. 2 5.
Câu 170. Khoảng cách từ điểm M 0;3 đến đường thẳng
 : x cos  y sin   32  sin    0 bằng: 3 A. 6. B. 6. C. 3sin . D. . cos  sin
 x  1 3t
Câu 171. Khoảng cách từ điểm M 2; 0 đến đường thẳng  :  bằng: y  2  4t  2 10 5 A. 2. B. . C. . D. . 5 5 2
x  2  3t
Câu 172. Khoảng cách nhỏ nhất từ điểm M 15 
;1 đến một điểm bất kì thuộc đường thẳng  :  y  t  bằng: 1 16 A. 10. B. . C. . D. 5. 10 5
Câu 173. Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A1; 2 đến đường thẳng
 : mx  y  m  4  0 bằng 2 5 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 m  2 1 A. m  2. B.  1 . C. m   .
D. Không tồn tại m . m  2  2 x  t
Câu 174. Tìm tất cả các giá trị của tham số m để khoảng cách từ giao điểm của hai đường thẳng d : 1  y  2t 
và d : x  2 y  m  0 đến gốc toạ độ bằng 2 . 2 m  4 m  4 m  4 m  4 A. .  B. .  C. .  D. .  m  2  m  2  m  2  m  2 
Câu 175. Đường tròn C  có tâm là gốc tọa độ O 0; 0 và tiếp xúc với đường thẳng  : 8x  6y 100  0 .
Bán kính R của đường tròn C  bằng: A. R  4 . B. R  6 . C. R  8 . D. R  10 .
Câu 176. Đường tròn C  có tâm I  2  ; 2
  và tiếp xúc với đường thẳng  : 5x 12y 10  0 . Bán kính R
của đường tròn C  bằng: 44 24 7 A. R  . B. R  . C. R  44 . D. R  . 13 13 13
Câu 177. Cho đường thẳng d : 21x 11y 10  0. Trong các điểm M 21; 3
  , N 0; 4 , P 19;5 và
Q 1;5 điểm nào gần đường thẳng d nhất? A. M . B. N . C. P . D. Q .
Câu 178. Cho đường thẳng d : 7x 10 y 15  0. Trong các điểm M 1; 3
  , N 0; 4 , P 19;5 và Q 1;5
điểm nào cách xa đường thẳng d nhất? A. M . B. N . C. P . D. Q .
Câu 179. Khoảng cách giữa hai đường thẳng song song
 : 6x – 8 y  3  0 và  : 3x – 4 y – 6  0 bằng: 1 2 1 3 5 A. . B. . C. 2 . D. . 2 2 2
x  2  t
Câu 180. Tính khoảng cách giữa hai đường thẳng d : 7x  y  3  0 và  :  . y  2  7t  3 2 9 A. . B. 15 . C. 9 . D. . 2 50
Câu 181. Khoảng cách giữa hai đường thẳng song song
d : 6x – 8 y 101  0 và d : 3x – 4 y  0 bằng: 1 2 A. 10,1. B. 1, 01 . C. 101. D. 101 .
Dạng 5.2 Phương trình đường thẳng liên quan đến khoảng cách
Câu 182. Cho hai điểm A 3;1, B 4; 0 . Đường thẳng nào sau đây cách đều A và B ?
A. 2x  2 y  3  0.
B. 2x  2 y  3  0.
C. x  2 y  3  0.
D. 2x  2 y  3  0.
Câu 183. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A2;3 và B 1; 4 . Đường thẳng nào sau đây
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
cách đều hai điểm A và B ?
A. x  y  2  0.
B. x  2 y  0.
C. 2x  2 y 10  0.
D. x  y 100  0.
Câu 184. Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm A0; 
1 , B 12;5 và C 3;0. Đường thẳng
nào sau đây cách đều ba điểm ,
A B và C .
A. x  3y  4  0 .
B. x  y 10  0 .
C. x  y  0 .
D. 5x  y 1  0 .
Câu 185. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1 
;1 , B 2; 4 và đường thẳng
 : mx  y  3  0 . Tìm tất cả các giá trị của tham số m để  cách đều hai điểm , A B . m  1 m  1 m  1 m  2 A. .  B. .  C. .  D. .  m  2  m  2  m  1  m  2 
Câu 186. Đường thẳng  song song với đường thẳng d : 3x  4 y 1  0 và cách d một khoảng bằng 1 có phương trình:
A. 3x  4 y  6  0 hoặc 3x  4 y  4  0 .
B. 3x  4 y  6  0 hoặc 3x  4 y  4  0 .
C. 3x  4 y  6  0 hoặc 3x  4 y  4  0 .
D. 3x  4 y  6  0 hoặc 3x  4 y  4  0 .
Câu 187. Tập hợp các điểm cách đường thẳng  : 3x  4 y  2  0 một khoảng bằng 2 là hai đường thẳng có
phương trình nào sau đây?
A. 3x  4 y  8  0 hoặc 3x  4 y 12  0 .
B. 3x  4 y  8  0 hoặc 3x  4 y 12  0 .
C. 3x  4 y  8  0 hoặc 3x  4 y 12  0 .
D. 3x  4 y  8  0 hoặc 3x  4 y 12  0 .
Câu 188. Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng d : 5x  3y  3  0 và d : 5x  3y  7  0 1 2
song song nhau. Đường thẳng vừa song song và cách đều với d , d là: 1 2
A. 5x  3y  2  0.
B. 5x  3y  4  0.
C. 5x  3y  2  0.
D. 5x  3y  4  0.  
Câu 189. Trên hệ trục tọa độ Oxy , cho hình vuông ABCD . Điểm M thuộc cạnh CD sao cho MC  2DM
, N 0;2019 là trung điểm của cạnh BC , K là giao điểm của hai đường thẳng AM và BD . Biết
đường thẳng AM có phương trình x 10y  2018  0. Khoảng cách từ gốc tọa độ O đến đường thẳng NK bằng 2018 2019 101 A. 2019 . B. 2019 101 . C. . D. . 11 101
Câu 190. Trong mặt phẳng tọa độ Oxy , gọi d là đường thảng đi qua M (4; 2) và cách điểm ( A 1; 0) khoảng 3 10 cách
. Biết rằng phương trình đường thẳng d có dạng x  by  c  0 với b, c là hai số nguyên. 10 Tính b  . c A. 4 . B. 5 . C. 1  . D. 5  .
Câu 191. (TH&TT LẦN 1 – THÁNG 12) Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng
 : x  m  
1 y  m  0 ( m là tham số bất kì) và điểm A5; 
1 . Khoảng cách lớn nhất từ điểm A đến  bằng
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 2 10 . B. 10 . C. 4 10 . D. 3 10 .
Câu 192. Chuyên Lê Hồng Phong-Nam Định Đường thẳng 12x  5y  60 tạo với hai trục toạ độ một tam
giác. Tổng độ dài các đường cao của tam giác đó là 60 281 360 A. . B. . C. . D. 20 . 13 13 17
Câu 193. Trên mặt phẳng tọa độ Oxy , cho các điểm A1; 
1 và B 3;4 . Gọi d  là một đường thẳng bất kì
luôn đi qua B. Khi khoảng cách từ A đến đường thẳng d  đạt giá trị lớn nhất, đường thẳng d 
có phương trình nào dưới đây?
A. x  y 1  0 .
B. 3x  4y  25 .
C. 5x  2 y  7  0 .
D. 2x  5y  26  0 .
DẠNG 6. XÁC ĐỊNH ĐIỂM
Dạng 6.1 Xác định tọa hình chiếu, điểm đối xứng
Câu 194. Cho đường thẳng d : 3x  5 y 15  0 . Trong các điểm sau đây, điểm nào không thuộc đường thẳng d A. M 5; 0 . B. M 5; 6 . C. M 0; 3 . D. M 5;3 . 3   2   4   1  
Câu 195. Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có A4;3 , B2;7 , C  3  ; 8   . Tọa
độ chân đường cao kẻ từ đỉnh A xuống cạnh BC là: A.  1  ; 4 . B. 1; 4 . C. 1; 4 . D. 4  ;1 .
Câu 196. Cho đường thẳng d : 3x  y  5  0 và điểm M  2  
;1 . Tọa độ hình chiếu vuông góc của M trên d là  7 4   7 4   7 4   5 4  A. ;    . B.  ;   . C.  ;    . D.  ;   .  5 5   5 5   5 5   7 5 
Câu 197. Tọa độ hình chiếu vuông góc của điểm M 1; 2 lên đường thẳng  : x  y  0 là  3 3   3 3  A. ;   . B. 1  ;1 . C. 2;2 . D.  ;    .  2 2   2 2   2
Câu 198. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC với đỉnh A2; 4 , trọng tâm G 2;   . Biết rằng  3
đỉnh B nằm trên đường thẳng d  có phương trình x  y  2  0 và đỉnh C có hình chiếu vuông
góc trên d  là điểm H 2; 
4 . Giả sử Ba ;b, khi đó T  a 3b bằng
A. T  4 .
B. T  2 .
C. T  2 .
D. T  0 .
Câu 199. Trong mặt phẳng tọa độ Oxy , cho hình chữ nhật ABCD có điểm C thuộc đường thẳng d:
2x  y  5  0 và điểm ( A 4
 ;8) . Gọi M đối xứng với B qua C , điểm N (5;  4) là hình chiếu
vuông góc của B lên đường thẳng MD . Biết tọa độ C( ;
m n) , giá trị của m  n là A. 6 . B. 6 . C. 8 . D. 7
Dạng 6.2 Xác định điểm liên quan đến yếu tố khoảng cách, góc
Câu 200. Cho hai điểm A3;  1 , B 0; 
3 . Tìm tọa độ điểm M thuộc Ox sao khoảng cách từ M đến đường thẳng AB bằng 1.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  7  A. M ; 0 
 và M 1;0 .
B. M  13;0 .  2 
C. M 4;0 .
D. M 2;0 .
Câu 201. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1 
;1 , B 4; 3 và đường thẳng
d : x  2 y 1  0 . Tìm điểm M thuộc d có tọa độ nguyên và thỏa mãn khoảng cách từ M đến
đường thẳng AB bằng 6 .  27 
A. M 3; 7. B. M 7;3.
C. M 43; 27. D. M 3;  .    11 
x  2  2t
Câu 202. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm A0; 
1 và đường thẳng d :  . Tìm điểm y  3  t 
M thuộc d và cách A một khoảng bằng 5 , biết M có hoành độ âm. M 4; 4   24 2 
A. M 4; 4. B. . M  ;  .   24 2  C.   D. M  4  ; 4. M  ;     5 5    5 5 
Câu 203. Biết rằng có đúng hai điểm thuộc trục hoành và cách đường thẳng  : 2x  y  5  0 một khoảng
bằng 2 5 . Tích hoành độ của hai điểm đó bằng: 75 25 225 A.  . B.  . C.  . D. Đáp số khác. 4 4 4
Câu 204. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A3;  
1 và B 0;3 . Tìm điểm M thuộc trục
hoành sao cho khoảng cách từ M đến đường thẳng AB bằng 1.   14    14    7  M ; 0   7  M  ; 0 M ; 0           3  M  ; 0     3  A.  2 .   2   B. . C. . D. .    4    4  M 1;0  M ; 0    M 1;0  M  ; 0      3    3 
Câu 205. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A3;0 và B 0; 4 . Tìm điểm M thuộc trục
tung sao cho diện tích tam giác MAB bằng 6. M 0;0 M 0;0 A.  .
B. M 0; 8. C. M 6;0. D.  . M 0; 8  M 0; 6 
Câu 206. Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng  : 3x  2 y  6  0 và  : 3x  2 y  3  0 1 2
. Tìm điểm M thuộc trục hoành sao cho M cách đều hai đường thẳng đã cho.  1   1   1  A. M 0; .   B. M ;0 .   C. M  ; 0 .  
D. M  2;0.  2   2   2  x  t
Câu 207. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A2; 2, B 4; 6 và đường thẳng d :  y 1 2t 
. Tìm điểm M thuộc d sao cho M cách đều hai điểm , A . B
A. M 3; 7. B. M  3  ; 5  . C. M 2;5. D. M  2  ; 3  
Câu 208. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1; 2, B 3; 2 và đường thẳng
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
d : 2x  y  3  0 . Tìm điểm C thuộc d sao cho tam giác ABC cân tại C.  3 
A. C 2;   1 . B. C  ; 0 .   C. C 1  ;1 . D. C 0;3  2 
Câu 209. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1; 2 , B 0;3 và đường thẳng d : y  2 . Tìm
điểm C thuộc d sao cho tam giác ABC cân tại . B C 1; 2
A. C 1; 2.
B. C 4; 2. C.  .
D. C 1; 2. C  1  ; 2 
Câu 210. Trong mặt phẳng với hệ tọa độ Oxy,giả sử điểm (
A a; b) thuộc đường thẳng d : x  y  3  0 và cách
 : 2x  y  1  0 một khoảng bằng 5. Tính P  ab biết a  0. A. 4. B. 2  C. 2. D. 4  . x  3  t
Câu 211. Trong mặt phẳng Oxy , cho biết điểm M  ;
a b a  0 thuộc đường thẳng d :  và cách y  2  t 
đường thẳng  : 2x  y  3  0 một khoảng 2 5 . Khi đó a  b là. A. 21 . B. 23. C. 22 D. 20 . x  3  t
Câu 212. Điểm A ;
a b thuộc đường thẳng d : 
và cách đường thẳng  : 2x  y  3  0 một khoảng y  2  t 
bằng 2 5 và a  0 . Tính P  . a b .
A. P  72 .
B. P  72 .
C. P  132 . D. P  132  .
Câu 213. (Chuyên Lam Sơn-KSCL-lần 2-2018-2019) Trong mặt phẳng tọa độ O xy , cho điểm I 1;2 và
đường thẳng d  : 2x  y 5  0 . Biết rằng có hai điểm M , M thuộc (d) sao cho IM  IM  10 1 2 1 2
. Tổng các hoành độ của M và M là 1 2 7 14 A. . B. . C. 2. D. 5. 5 5
Câu 214. Trong hệ tọa độ Oxy cho A1  ;1 , B 4; 3   . Gọi C  ;
a b thuộc đường thẳng d : x  2 y 1  0 sao
cho khoảng cách từ C đến đường thẳng AB bằng 6. Biết rằng C có hoành độ nguyên, tính a  b ?
A. a  b  10 .
B. a  b  7 .
C. a  b  4 .
D. a  b  4 
Dạng 6.3 Xác định điểm liên quan đến yếu tố cực trị
Câu 215. Trong mặt phẳng tọa độ Oxy cho  : x  y  1  0 và hai điểm A2; 
1 , B 9; 6. Điểm M  ; a b
nằm trên đường  sao cho MA  MB nhỏ nhất. Tính a  . b A. 7. B. 9. C. 7. D. 9.
Câu 216. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : x  4y  15  0 và điểm A 2; 0 . Tìm
tọa độ điểm M thuộc d để đoạn AM có độ dài nhỏ nhất.
A. M 15; 0 .
B. M 5; 5 .
C. M 0; 3 .
D. M 1; 4 .
Câu 217. (Yên Định 1 - Thanh Hóa - 2018-2019) Cho 3 điểm (
A 6; 3) ; B(0; 1); C(3; 2) . Tìm M trên
  
đường thẳng d : 2x  y  3  0 mà MA  MB  MC nhỏ nhất là
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  13 71   13 19   26 97   1  3 19  A. M ;   B. M ;   C. M ;   D. M ;    15 15   15 15   15 15   15 15 
Câu 218. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh A2; 2 , B 1; 3 , C  2  ; 2 .
  
Điểm M thuộc trục tung sao cho MA  MB  MC nhỏ nhất có tung độ là? 1 1 1 A. 1. B. . C.  . D. . 3 3 2
Câu 219. Trong mặt phẳng tọa độ Oxy cho  : x  y  1  0 và hai điểm (
A 2;1) , B(9; 6) . Điểm M ( ; a b) nằm
trên đường  sao cho MA  MB nhỏ nhất. Tính a  b ta được kết quả là: A. -9. B. 9. C. -7. D. 7
Dạng 6.4 Một số bài toán tổng hợp
Câu 220. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hình vuông ABCD . Gọi M là trung điểm của cạnh  11 1 
BC , N là điểm trên cạnh CD sao cho CN  2ND . Giả sử M ; 
 và đường thẳng AN có  2 2 
phương trình 2x  y  3  0 . Tìm tọa độ điểm A . A. A1;  1 hoặc A4; 5   .
B. A1;   1 hoặc A 4  ;  5 . C. A1; 
1 hoặc A4;5 . D. A1; 
1 hoặc A4;5 .
Câu 221. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm I 1;   1 và hai đường thẳng
d : x  y  3  0, d : x  2 y  6  0 . Hai điểm ,
A B lần lượt thuộc hai đường thẳng d , d sao cho 1 2 1 2
I là trung điểm của đoạn thẳng AB . Đường thẳng AB có một véctơ chỉ phương là     A. u  1; 2 . B. u  2;1 .
C. u  1; 2 . D. u  2; 1  . 4   3   2   1  
Câu 222. (TH&TT LẦN 1 – THÁNG 12) Trong mặt phẳng tọa độ Oxy , cho điểm hai điểm A4; 2 , x  5 y 1
B 2;6 và điểm C nằm trên đường thẳng d : 
sao cho CA  CB . Khi đó tọa độ điểm 3 2 C là  2 8   1 12   1 11  2 9  A. ;   . B. ;   . C. ;   . D. ;   .  5 5  5 5   5 5   5 5  
Câu 223. Trong mặt phẳng với hệ tọa độ Oxy , cho A 3
 ;5, B 1;3 và đường thẳng d :2x  y 1  0 , đường IA
thẳng AB cắt d tại I . Tính tỉ số . IB A. 6. B. 2. C. 4. D. 1.
Câu 224. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh A2;  1 , B 2; 3   , C  2  ;   1 .
Trực tâm H của tam giác ABC có tọa độ  ;
a b . Biểu thức S  3a  2b bằng bao nhiêu? A. 0 . B. 1 . C. 5 . D. 1.
Câu 225. Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm B  2  ;3 và C 3; 2
  . Điểm I  ;
a b thuộc BC  2  3 
sao cho với mọi điểm M không nằm trên đường thẳng BC thì MI  MB  MC . Tính 5 5 2 2
S  a  b .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 1. B. 0 . C. 5 . D. 4 .
Câu 226. Trong mặt phẳng với hệ tọa độ Oxy ,cho tam giác ABC có đỉnh A2; 2 và trung điểm của BC là
    I  1  ; 2
  . Điểm M  ;
a b thỏa mãn 2MA  MB  MC  0 . Tính S  a  b . 1 3 1 A. . B. . C.  . D. 1. 2 2 2
Câu 227. (ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Trong mặt phẳng tọa độ Oxy,
cho tam giác ABC có A2; 
1 , đường cao BH có phương trình x  3y  7  0 và trung tuyến CM
có phương trình x  y  1  0 . Tìm tọa độ đỉnh C ? A. 1; 0 . B. 4; 5 . C. 1; 2 . D. 1; 4  .
Câu 228. Trong mặt phẳng tọa độ Oxy , cho hình vuông ABCD ; các điểm M , N , P lần lượt là trung điểm  11 11 
của AB , BC , CD ; CM cắt DN tại điểm I 5; 2 . Biết P ; 
 và điểm A có hoành độ âm.  2 2 
Tọa độ điểm A và D là:
A. A2;3 và D 3;8 . B. A2;3 và D  3  ;8 .
C. A2;3 và D 3;  8 . D. A 2  ; 3
  và D 3;8 .
Câu 229. Trong hệ trục tọa độ Oxy , cho tam giác ABC có B  4  
;1 , trọng tâm G 1;  1 và đường thẳng phân
giác trong góc A có phương trình d : x  y 1  0 . Biết điểm A ; m n . Tính tích . m n . A. . m n  20 . B. . m n  12 . C. . m n  1  2 . D. . m n  6 .
Câu 230. Trên mặt phẳng Oxy , cho hình vuông ABCD . Gọi M là trung điểm của cạnh BC , N là điểm  11 1 
trên cạnh CD sao cho CN  2ND . Giả sử M ; 
 và đường thẳng AN có phương trình  2 2 
2x  y  3  0 . Gọi P a;b là giao điểm của AN và BD. Giá trị 2a  b bằng A. 6 B. 5 . C. 8 . D. 7 . Câu 231. Cho AB 
C vuông tại A, điểm M thuộc cạnh AC, sao cho AB  3AM , đường tròn tâm I đường
kính CM cắtBM tại D, đường thẳng CD có phương trình x  3 y  6  0 . Biết điểm I(1;-1), điểm  4  E ; 0 
 thuộc đường thẳng BC, x   . Gọi B là điểm có tọa độ (a, b). Khi đó: C  3 
A. a  b  1.
B. a  b  0 .
C. a  b  1.
D. a  b  2 .
Câu 232. (THUẬN THÀNH SỐ 2 LẦN 1_2018-2019) Trên mặt phẳng Oxy , cho hình vuông ABCD . Gọi  11 1 
M là trung điểm của cạnh BC , N là điểm trên cạnh CD sao cho CN  2ND . Giả sử M ;    2 2 
và đường thẳng AN có phương trình 2x  y  3  0 . Gọi P  ;
a b là giao điểm của AN và BD .
Giá trị 2a  b bằng: A. 6 . B. 5 . C. 8 . D. 7 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 233. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh B(12;1) , đường phân giác trong 1 2
của góc A có phương trình d : x  2 y  5  0 . G ;  
là trọng tâm tam giác ABC . Đường thẳng 3 3
BC qua điểm nào sau đây? A. 1;  0 . B. 2;  3  . C. 4;  4  . D. 4;  3 .
Câu 234. Trong hệ tọa độ Oxy, cho tam giác ABC có phương trình đường thẳng BC : x  7 y 13  0. Các
chân đường cao kẻ từ B, C lần lượt là E 2;5, F 0; 4. Biết tọa độ đỉnh A là A ; a b. Khi đó:
A. a  b  5 .
B. 2a  b  6 .
C. a  2b  6 .
D. b  a  5
Câu 235. (THPT Đông Sơn 1 - Thanh Hóa - Lần 2 - Năm học 2018 - 2019) Trong mặt phẳng tọa độ với
hệ tọa độ Oxy , cho hình chữ nhật ABCD có điểm H 1;2 là hình chiếu vuông góc của A lên BD  9  . Điểm M ;3 
 là trung điểm cạnh BC . Phương trình đường trung tuyến kẻ từ đỉnh A của tam  2 
giác ADH là 4x  y  4  0 . Biết điểm D có tọa độ là  x ; y
tính giá trị biểu thức 2 2
S  4x  y D D  D D . A. S  3 . B. S  4 . C. S  6 . D. S  5 .
Câu 236. Cho tam giác ABC . Tìm tọa độ các đỉnh của tam giác biết phương trình cạnh BC : x  y  2  0 ;
hai đường cao BB ' : x 3  0 và CC ' : 2x 3 y  6  0 ?
A. A(1; 2); B(0; 2);C(3;1) .
B. A(1; 2); B(3;1);C (0; 2) .
C. A(1;2); B(3;1);C(0; 2) .
D. A(2;1); B(3;1);C (0; 2) .
Câu 237. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A 3
 ;0 ,B 3;0 ,C 2;6 . Gọi H a;b là
trực tâm của tam giác ABC . Tính 6ab 5 A. 10. B. . C. 60. D. 6. 3
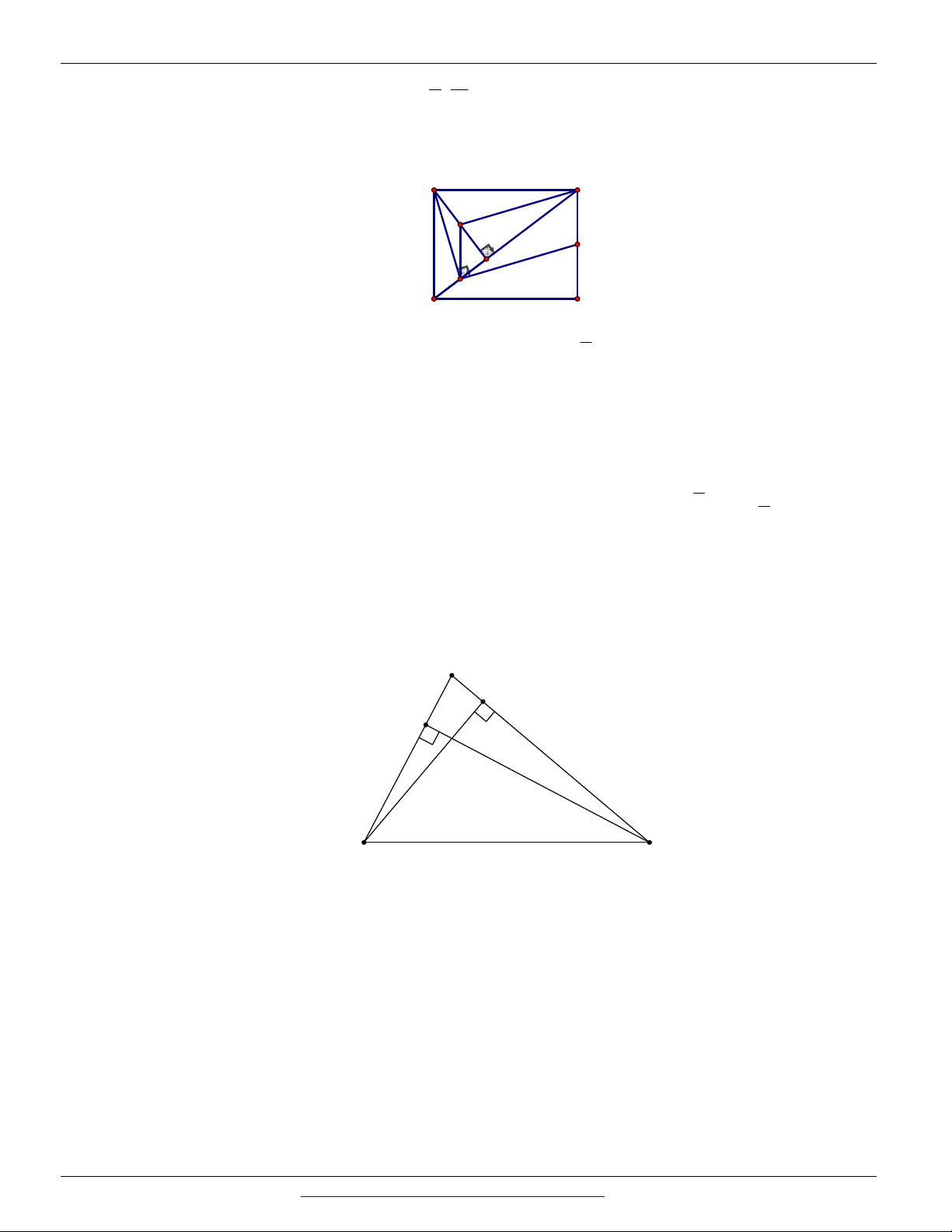
Câu 238. Trong mặt phẳng tọa độ (Oxy), cho hình chữ nhật ABCD có điểm C thuộc đường thẳng
d : 2x  y  5  0 và điểm A4; 
8 . Gọi M là điểm đối xứng với B qua C, điểm N 5; 4   là hình
chiếu vuông góc của B lên đường thẳng MD. Biết tọa độ C  ;
m n , giá trị của m n là: A. 6 . B. 6  . C. 8 . D. 7 .
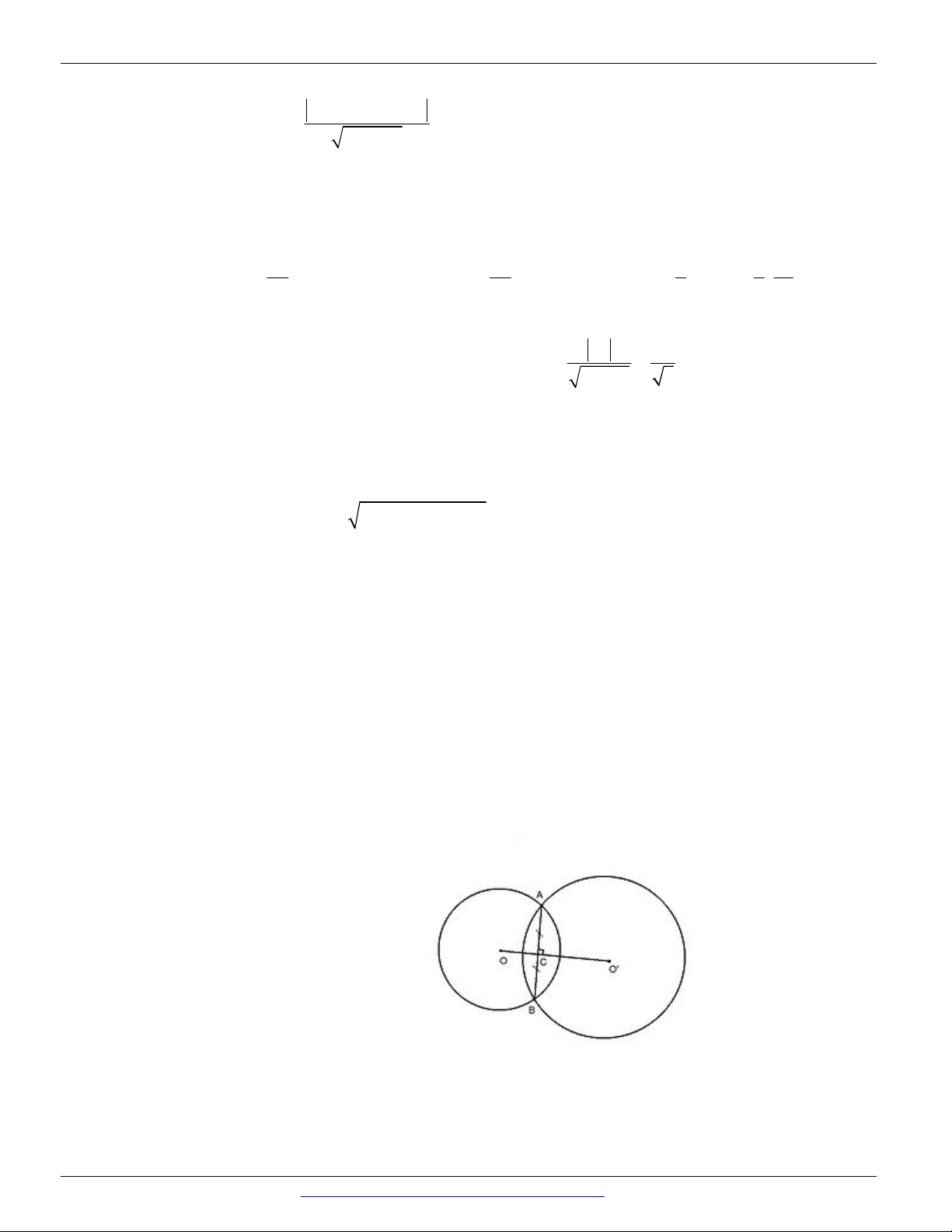
Câu 239. Trong mặt phẳng tọa độ Oxy , cho tứ giác ABCD nội tiếp đường tròn đường kính BD . Gọi M ,
N lần lượt là hình chiếu vuông góc của A lên BC và BD ; gọi P là giao điểm của MN và AC .
Biết đường thẳng AC có phương trình x  y 1  0 , M 0; 4 , N 2; 2 và hoành độ điểm A nhỏ
hơn 2 . Tìm tọa độ các điểm P , A , B .  5 3  A. P ;   , A0;   1 , B 4;  1 .  2 2   5 3  B. P ;   , A0;   1 , B  1  ; 4 .  2 2   5 3  C. P ;   , A0;   1 , B  1  ; 4 .  3 2   5 3  D. P ;   , A 1
 ; 0 , B 4;  1 .  2 2 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 240. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Trong mặt phẳng với hệ trục
tọa độ Oxy , cho tam giác ABC cân tại A , phương trình đường thẳng AB, AC lần lượt là  9 8 
5x  y  2  0, x  5 y  14  0 . Gọi D là trung điểm của BC , E là trung điểm của AD , M ;    5 5 
là hình chiếu vuông góc của D trên BE . Tính OC . A. OC  26 . B. OC  10 . C. OC  5 . D. OC  52 .
Câu 241. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có chân đường cao hạ từ đỉnh A là  17 1  H ;  
 , chân đường phân giác trong góc A là D 5;3 và trung điểm của cạnh AB là M 0  ;1  5 5 
. Tìm tọa độ đỉnh C . A. C  2  ;9 . B. C 9;1  1 . C. C  9  ; 1   1 . D. C 2; 1  0 .
DẠNG 7. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN DIỆN TÍCH
Câu 242. (THPT Quỳnh Lưu- Nghệ An- 2019) Đường thẳng  :5x  3 y  15 tạo với các trục tọa độ một
tam giác có diện tích bằng bao nhiêu? A. 7, 5 . B. 5 . C. 15 . D. 3 .
Câu 243. Cho hai đường thẳng d : y  mx  4; d : mx  4 . Gọi S là tập hợp các giá trị nguyên dương của 1 2
m để tam giác tạo thành bởi d , d và trục hoành có diện tích lớn hơn 8 . Số phần tử của tập S là 1 2 A. 1. B. 3 . C. 2 . D. 4 .
Câu 244. Tìm phương trình đường thẳng d : y  ax  .
b Biết đường thẳng d đi qua điểm I 1;3 và tạo với
hai tia Ox, Oy một tam giác có diện tích bằng 6?
A. y  9  72 x  72  6 .
B. y  9  72  x  72  6 .
C. y  3x  6 .
D. y  3x  6.
Câu 245. Chuyên Lê Hồng Phong-Nam Định Cho tam giác ABC có A1; 3 , B 0; 2 , C 2; 4 . Đường
thẳng  đi qua A và chia tam giác ABC thành hai phần có diện tích bằng nhau. Phương trình của  là
A. 2x  y  7  0 .
B. x  y  2  0 .
C. x  3y 10  0 .
D. 3x  y  0 .
Câu 246. Trong mặt phẳng Oxy , cho điểm M 2 
;1 . Đường thẳng d đi qua M , cắt các tia Ox , Oy lần lượt tại A và B ( ,
A B khác O ) sao cho tam giác OAB có diện tích nhỏ nhất. Phương trình đường thẳng d là.
A. 2x  y  3  0 .
B. x  2y  0 .
C. x  2y  4  0 .
D. x  y 1  0 . x y
Câu 247. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Đường thẳng d : 
 1 , a  0;b  0 a b đi qua M  1
 ; 6 tạo với tia Ox,Oy một tam giác có diện tích bằng 4. Tính S  a  2 . b 5   7 5 38 A. S  . B. S   . C. S  10 . D. S  6 . 3 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 B. LỜI GIẢI
DẠNG 1. XÁC ĐỊNH VÉCTƠ CHỈ PHƯƠNG, VÉC TƠ PHÁP TUYẾN CỦA ĐƯỜNG
THẲNG, HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG Câu 1. Chọn D 
Ta có một vectơ pháp tuyến của đường thẳng d  là n  a;b .  Do đó chọn đáp án D. n   ; a b . 1   Câu 2. Chọn B. 
d có một vectơ pháp tuyến là n   ;
a b  phương trình d : ax  by  c  0 .
Nếu b  0 thì đường thẳng d : ax  c  0 không có hệ số góc  khẳng định 1 đúng. a c a
Nếu b  0 thì đường thẳng d : y   x  có hệ số góc là   khẳng định 2 sai. b b b       Với u   ; b a  .
u n  0  u  n  u là một vectơ chỉ phương của d  khẳng định 3 đúng. 
Chọn k  0    k n  0;0 không phải là vectơ pháp tuyến của d  khẳng định 4 sai. Vậy có 2 mệnh đề sai. Câu 3. Chọn A. Câu 4. Chọn C 
Đường thẳng d  có một véctơ pháp tuyến là n  3; 2 nên d  có một véctơ chỉ phương là 
u  2 ;  3 . Câu 5. Chọn B  1 x  5  t   1   : 2
có một vectơ chỉ phương là u   ;3 
 suy ra có một vectơ pháp tuyến là   2 y  3   3t     1  n  3; 
 . Do đó đường thẳng  cũng có một vectơ pháp tuyến có tọa độ 6  ;1 .  2  Câu 6. Chọn A  
Một VTCP của đường thẳng d là u 1; 2  một VTPT của d là n 2;   1 . Câu 7. Chọn A. x  1 4t 
Đường thẳng d : 
có vectơ chỉ phương là u  4;3 .
y  2  3t  Câu 8. Chọn A 
Vector i  (1;0) là một vector chỉ phương của trục Ox  
Các đường thẳng song song với trục Ox có 1 vector chỉ phương là u  i  (1;0) Câu 9. Chọn C  
Đường thẳng d có 1 VTPT là n  7;3 nên d có 1 VTCP là u  3;7 .
Câu 10. Chọn B 
Véctơ pháp tuyến của đường thẳng d : n  4;  6 . 1  
Câu 11. Chọn D 
Đường thẳng d : 5x  3y  7  0 có vec tơ pháp tuyến là: n  5;3.   Ta có: . n n  0. 2 
 d có một vec tơ chỉ phương là n  3; 5 . 2  
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 12. Chọn A  
Nếu u là một véc tơ chỉ phương của đường thẳng  thì k.u, k
  0 cũng là véc tơ chỉ phương của đường thẳng  .
Từ phương trình đường thẳng  ta thấy đường thẳng  có một véc tơ chỉ phương có toạ độ là  2; 
1 . Do đó véc tơ u  4; 2 không phải là véc tơ chỉ phương của  .
Câu 13. Chọn D  
Ta có AB  4; 2  22 
;1 suy ra vectơ pháp tuyến của đường thẳng AB là n  1; 2 . AB 
Câu 14. Chọn C  
Đường thẳng d có 1 VTPT là n  7; 
3 nên d có 1 VTCP là u   3  ; 7
Câu 15. Chọn D 
Đường thẳng d : x  2 y  2018  0 có vectơ pháp tuyến là n 1; 2   . 2
Câu 16. Chọn D.  
d : y 2x1 0  2x  y1 0 ;d có VTPT là n  2  ;1 hay / n   2  ;   1
Câu 17. Chọn B 
Một véctơ pháp tuyến của đường thẳng d là n  2;   1 .
Câu 18. Chọn D 
Ta thấy đường thẳng d có một vectơ pháp tuyến là 2; 3
  . Do đó u  3;2 là một vectơ chỉ 3   phương của d.
Câu 19. Chọn A 
+) Một véctơ pháp tuyến của đường thẳng  là n 6; 2 nên véctơ chỉ phương của đường thẳng   là u 1;3 .
Câu 20. Chọn B   MN   4
 ; 2 . Do đó vectơ chỉ phương của M N là u  4; 2   .
Câu 21. Chọn B 
Đường thẳng d : x  2 y 1  0. có vectơ pháp tuyến là n  (1; 2)  Vectơ chỉ phương của d là u  (2;1).   
Câu 22. Đường thẳng d có VTCP: u 2;   1 
 VTPT n 1; 2 hoặc 3n  3; 6. Chọn D.   1 
Câu 23. Đường thẳng d có VTPT: n 4; 2 
 VTCP u 2; 4 hoặc u   ; 1 2. Chọn C. 2 u       d 3; 4 Câu 24.    n  u   Chọn D.  d 3; 4.  d     n       d  2; 5 Câu 25.  
u  n    hay chọn n  Chọn C.  2;5.  d  2; 5   d  u      d 3; 4 Câu 26.   u  u     n  Chọn A.  d 3; 4  4;3.  || d    n       d  2; 5 Câu 27.  
 n  u     u   Chọn A.  d  2; 5  5; 2.  || d 
Câu 28. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 3 2018 3
Ta có d : 3x  5y  2018  0  d : y   x 
, nên d có hệ số góc k   . 5 5 5
Câu 29. Chọn A 1 15
Ta có d  : x  7 y 15  0 hay y  x  7 7 1
Suy ra hệ số góc của đường thẳng là k  (đúng) 7
DẠNG 2. VIẾT PHƯƠNG TRÌNH ĐƯỜNG THẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN
Dạng 2.1 Viết phương trình đường thẳng khi biết VTPT hoặc VTCP, HỆ SỐ GÓC và 1 điểm đi qua
Câu 30. Chọn D
Bốn phương trình đã cho trong bốn phương án đều là phương trình của đường thẳng.
Thay lần lượt tọa độ của A , B vào từng phương án ta thấy tọa độ của cà A và B đều thỏa
phương án D .
Câu 31. Chọn D 
Vectơ chỉ phương AB  0;6 . 
Phương trình đường thẳng AB đi qua A và có vecto chỉ phương AB  0;6 là x  2 
y  1  6t 
Câu 32. Chọn B.
 Cách 1: Thay tọa độ các điểm A , B lần lượt vào các phương trình trong các phương án trên thì
thấy phương án B không thỏa mãn.
 Cách 2: Nhận thấy rằng các phương trình ở các phương án A, C, D thì vectơ chỉ phương của các
đường thẳng đó cùng phương, riêng chỉ có phương án B thì không. Do đó lựa chọn B.
Câu 33. Chọn D 
Đường thẳng có véctơ chỉ phương là MN  3;5 và đi qua M 1; 2
  nên có phương trình tham số x  1 3t là  .
y  2  5t 
Câu 34. Chọn B  
Ta có AB  9;3  u  3;   1 . AB
x  3  3t
Suy ra phương trình tham số của đường thẳng AB là  . y  1   t 
Câu 35. Chọn A
Ta có  song song với d nên  : x  y  C  0C  0 .
 qua A3;0 , suy ra 3  0  C  0  C  3  ( nhận)
Như vậy  : x  y  3  0 x  t
Vậy  có phương trình tham số:  . y  3  t 
Câu 36. Chọn A x  5  t t   x  5
Đường thẳng d  :     y  9
  2  x  5  2x  y 1  0 .
y  9  2t  y  9   2t 
Câu 37. Chọn C.
Ta có hình chiếu của điểm M (1; 2) lên Ox, Oy lần lượt là A(1;0) và B(0;2). Do đó phương
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 31
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x y
trình đường thẳng AB là 
 1  2x  y  2  0 . 1 2
Câu 38. Chọn.B.  3  x t 
x  3  5t   5 3  x y 1 d :  (t  )    
 4x  5y 17  0 y  1 4t y 1 5 4  t     4 Đáp án B. x y
Câu 39. Phương trình đoạn chắn của đường thẳng d :   1. a b
Câu 40. Chọn D x y
Phương trình đường thẳng đi qua hai điểm M  ;
a 0, N 0;b với a,b  0 là   1. a b
Áp dụng phương trình trên ta chọn phương án D .
Dạng 2.2 Viết phương trình đường thẳng đi qua một điểm vuông góc hoặc với đường thẳng cho trước
Câu 41. Chọn B 
Do d    n 2;3 d 
Mà đường thẳng d đi qua A1; 2 nên ta có phương trình: 2  x  
1  3 y  2  0  2x  3y  4  0 .
Vậy phương trình đường thẳng d : 2x  3y  4  0 .
Câu 42. Chọn C
Vì  vuông góc với đường thẳng d : 8x  6 y  7  0 nên phương trình  : 6x  8 y  C  0
Mà  đi qua gốc tọa độ nên ta có: 6.0  8.0  C  0  C  0 .
Vậy phương trình  : 6x  8 y  0 hay  : 3x  4 y  0
Câu 43. Chọn C
Gọi d  là đường thẳng cần tìm. Vì d  song song với đường thẳng y  3x  5 nên d  có
phương trình y  3x  a , a  5 .
Vì d  đi qua điểm A1;1 
1 nên ta có 11  31 a  a  8 .
Vậy phương trình đường thẳng d  cần tìm là y  3x  8 . Chọn B Câu 44.
Gọi  là đường thẳng cần tìm.
+)  // d  : y  3x  4 . Suy ra phương trình  có dạng y  3x  b , b  4 .
Có A2;5   5  6  b  b  1  (thoả b  4 )
Vậy  : y  3x 1.
Câu 45. Chọn D
Do đường thẳng d song song với đường thẳng d ' : x  y 1  0 nên đường thẳng d nhận véc tơ n 1 
;1 làm véc tơ pháp tuyến. 
Khi đó đường thẳng d qua M 1 
;1 và nhận véc tơ n  1 
;1 làm véc tơ pháp tuyến có phương
trình là x  y  2  0 .
Câu 46. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 32
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ta có đường thẳng vuông góc với 2x  y  4  0 có phương trình x  2y  m  0 , mà đường thẳng
này đi qua điểm I  1
 ; 2 , suy ra 1 2.2  m  0  m  3 .
Vậy đường thẳng cần tìm có phương trình x  2y  3  0 .
Câu 47. Chọn A 
Có MN  1; 2 .   1 
Đường thẳng d  đi qua A ;1 
 nhận MN  1; 2 làm vec tơ chỉ phương:  2   1 d   : 2 x   y 1  0  
 2x  y  2  0  1 .  2 
Thử lại: thay tọa độ của M vào   1 thì nghiệm đúng   1 . Suy ra loại   1 .
Vậy không tồn tại đường thẳng như đề bài yêu cầu.
Câu 48. Gọi d là đường thẳng qua B và song song với AC. Ta có
B 0;3  d  x  5t     d :   t     Chọn A. u  C A   5;  1  1.5  ;1 y  3  t   d
Câu 49. Gọi d là đường thẳng qua A và song song với PQ.
 A3; 2  d 
x  3  2t Ta có:    d :   u  PQ   4; 2    2  2;  1 y  2  t   d
x  1 2t t 2  
 M 1;0  d  d : 
t  . Chọn C. y  t    A  2  ;1  AB, u  CD 4;3
x  2  4t Câu 50.    AB :  t     . Chọn B.
AB || CD  u  u    y   t   AB CD  4; 3 1 3   
x  3  t
Câu 51. Góc phần tư (I) : x  y  0 
VTCP : u 1  ;1  u   d :  t   d  . y  5  t  Chọn B.   x  4  t x  t Câu 52. u    u    d     A   d  d Ox 1;0 d 1;0 t 4 : 0; 7 :  . y  7 y  7    Chọn D. 
M 1; 2  d M  1;2 d Câu 53.   
d ||  : 2x  3y 12  0
d : 2x  3y  c  0   c  12    
 2.1  3.2  c  0  c  8. Vậy d : 2x  3y  8  0. Chọn A. O   0; 0  d O   0; 0  d Câu 54.    
 6.0  4.0  c  0  c  0.
d ||  : 6x  4x 1  0
d : 6x  4x  c  0   c   1 
Vậy d : 6x  4 y  0  d : 3x  2 y  0. Chọn A.  M  1  ; 2  d  M  1  ; 2  d Câu 55.       1
  2.2  c  0  c  5.
d   : 2x  y  3  0 
d : x  2 y  c  0 
Vậy d : x  2 y  5  0. Chọn D.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 33
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  A4; 3    d    A  4; 3    d
Câu 56. Ta có: u     d  2;3    u          2;3 n 3;2  || d 
  : 3 x  4  2 y  3  0   : 3x  2 y  6  0.
B 0;3  d    B   0;3  d Câu 57. u   AC    AC  5  ;1   n     d 1;5 d || AC  
 d :1 x  0  5 y  3  0  d : x  5y 15  0.
M 1;0  d   M  1;0 d Câu 58. u                 1; 2 d :1 x  1 2  y 0 0
d : x 2 y 1 0. n      d 1; 2 d    Chọn C. M 2;  1  d   M  2  ;1  d
x  2  5t Câu 59. u           Chọn B.   3;5 d :  t . n  
 3;5  u  5;3 y  1 3t  d d  d   
 A1; 2  d    A  1; 2  d x  1  13t
Câu 60. n          Chọn A.  3; 13 d :  t . n   u  y   t     d 3; 13 d 13;3 2 3  d ||  
 A1; 2  d    A  1; 2  d x  1   2t
Câu 61. n         Chọn A.  2;  1 d :  t . u   y   t    d 2;  1 2  d    M  2  ; 5  d  M  2;5  0
Câu 62. (I) : x  y  0     2
  5  c  0  c  3.
d : x  y  c  0   c  0 d ||    
Vậy d : x  y  3  0. Chọn B. M 3;   1  d   M 3;   1 Câu 63. 
 II : x  y  0    
d : x  y  c  0  d     3   
1  c  0  c  4  d : x  y  4  . 0 x  4   t M 4;0 t 4  d  
 A0; 4  d y  t    
 II : x  y  0   n   1  ;1 Câu 64.  
d    u   d 1  ;1 x  t  d :  t  . y  4  t 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 34
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  M  1  ; 2  d Câu 65.    d : y  . 2 Chọn D.
d || Ox : y  0  M  6; 10   d x  6  t Câu 66. t  4     d :   
 A2; 10  d
d  Oy : x  0  u  y     d 1;0 10  x  2  t  d :  . y  10  
Dạng 2.3 Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác
Dạng 2.3.1 Phương trình đường cao của tam giác
Câu 67. Chọn A 
Gọi AH là đường cao kẻ từ A của A
 BC . Ta có: AH  BC  vtpt AH là BC  2;3 .
Phương trình AH :2 x  
1  3 y  2  0  2x  3y  8  0.. 
Câu 68. Đường cao AH đi qua điểm A2; 
1 và có VTPT là BC   7  ; 3   .
Vậy phương trình AH là 7
  x  2  3 y  
1  0  7x  3y 11  0 . Câu 69. Chọn A. 
Ta có: BC  2;3 
Đường cao kẻ từ A của tam giác ABC nhận BC  2;3 làm vectơ pháp tuyến và đi qua điểm
A nên có phương trình: 2 x  
1  3 y  2  0  2x  3y  8  0 .
Câu 70. Chọn D
Tam giác ABC cân tại C nên H là trung điểm của AB và CH  AB .  Có H 3  ;1 và AB   2  ;  4  2  1; 2 .
Vậy phương trình đường cao CH là 1 x  3  2 y  
1  0  x  2 y  5  0 .
Câu 71. Chọn B  
Do BH  AC  Chọn VTPT của BH là n
 CA  5;  3. BH
Phương trình tổng quát của BH : 5 x  4  3 y  5  0  5x  3y  5  0.    AB  0  ;1  
Câu 72. Gọi d là trung trực đoạn AB, ta có:  
 n  AB  0  ;1 . Chọn B. d d  AB 
Câu 73. Gọi M là trung điểm của BC. Ta cần viết phương trình đường thẳng AM. Ta có : B  0; 2    
 M 2;0  u  AM    n 
 AM x  y   Chọn A. AM 1;  1 AM 1  ;1 : 2 0. C  4; 2 
Câu 74. Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có
 A1; 4, B 5; 2  I 3;   1  d    
 d : 2x  3y  3  0.  Chọn A.
d  AB  n AB   4;6  22;3   d 
Câu 75. Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có   5 5  A4;   1 , B 1; 4    I ;   d      2 2  
 d : x  y  0.  Chọn B.  
d  AB  n  B A   3  ; 3    3  1  ;1  d
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 35
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 76. Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có  A1; 4
 , B 1; 2  I 1;   1  d    
 d : y 1  0.  Chọn A.
d  AB  n  AB   0;6  60;  d  1
Câu 77. Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có
 A1; 4, B 3; 4  I 2; 4    d    
 d : x  2  0.  Chọn C. d  AB n  AB    2;0  21;0  d 
Câu 78. Gọi h là đường cao kẻ từ A của tam giác ABC. Ta có A  A2;   1  hA   
 h : 7x  3y 11  0.  Chọn A. A
h  BC  n  BC     A h  7; 3 7;3    A
Câu 79. Gọi h là đường cao kẻ từ B của tam giác ABC. Ta có B
B 4;5  hB   
 h : 5x  3y  5  0.  Chọn D. B
h  AC  n  AC      B h  5;3  ; 5 3   B
Câu 80. Gọi h là đường cao kẻ từ C của tam giác ABC. Ta có C C
 3; 2  hC   
 h : x  3y  3  0.  Chọn B. h AB  n  AB     C h  C 2; 6 21;3  C
Dạng 2.3.2 Phương trình đường trung tuyến của tam giác
Câu 81. Chọn D  5 3    5 7 
Gọi M là trung điểm của cạnh AC  M ;  BM  ;     .  2 2   2 2  
Đường trung tuyến BM nhận n  7;5 làm một véctơ pháp tuyến. Vậy phương trình tổng quát
của đường trung tuyến qua điểm B của tam giác ABC là:
7 x  5( y  2)  0  7 x  5 y  10  0 .
Câu 82. Chọn A
Gọi I là trung điểm của BC  I 0;  1  
Ta có AI  2; 4  n  2;  
1 là vectơ pháp tuyến của đường thẳng AI .
Phương trình đường thẳng AI là: 2 x  2   y  
3  0  2x  y 1  0  A  1; 4  x  7  t Câu 83.   M 2;3  C M
 5;0  51;0  CM : 
t  . Chọn C. B  3; 2 y  3    A  2; 4  5    5  1
x  5  6t Câu 84.    M 2;  MB  3;       6;5   MB :  . C  2  ;1  2   2 2 y  5t     5 t  20  5  6t   2
Ta có: N 20; y  BM        Chọn B. N  y  5t 25  N  y   N   2
Dạng 2.3.3 Phương trình cạnh của tam giác
Câu 85. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 36
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A M B C E D
+) Gọi AH và AD lần lượt là các đường cao và trung tuyến kẻ từ A của tam giác ABC .
7x  2 y  3  0 x  1
+) Tọa độ A là nghiệm của hệ     A1; 2 .
6x  y  4  0 y  2  
x  2x  x  3
+) M là trung điểm của AB nên B M A   B 3; 2   .
y  2 y  y  2   B M A
+) Đường thẳng BC đi qua B 3; 2
  và vuông góc với đường thẳng AH : 6x  y  4  0 nên có
phương trình x – 3  6 y  2  0  x  6y  9  0 .
+) D là giao điểm của BC và AN nên tọa độ D là nghiệm của hệ x  0
7x  2 y  3  0   3     3  D 0;  
 mà D là trung điểm của BC suy ra C  3  ;   1
x  6 y  9  0 y     2    2
+) Đường thẳng AC đi qua A1; 2 và C  3  ;  
1 có phương trình là 3x  4 y  5  0 .
Câu 86. Chọn A
 x  y  2  0 x  3
Tọa độ điểm A là nghiệm của hệ    nên A3;  1
x  2 y  5  0 y  1   Gọi B  ;
b b  2 và C 5  2 ;
c c , G là trọng tâm tam giác ABC nên b, c là nghiệm của hệ 5
  2c  b  3  9 b   5    .
c  b  2 1  6 c  2  
Vậy B(5;3);C(1; 2)  BC  4;  
1 chọn một véctơ pháp tuyến của đường thẳng BC là  n
 1; 4 suy ra phương trình đường thẳng BC :1 x  
1  4 y  2  0  BC : x  4y  7  0. BC 
Dạng 2.3.4 Phương trình đường phân giác của tam giác
Câu 87. Chọn D.
Câu 88. A1;3 , B 2; m nằm cùng phía với d : 3x  4y  5  0 khi và chỉ khi 1
3x  4y  5 x  y     m   m   Chọn B. A A 3 4 5 B B  0 10 1 4  0 . 4 x  2  t
Câu 89. d :  
 d : 3x  y  7  0. Khi đó điều kiện bài toán trở thành y  1 3t 
3x  y  73x  y  7  0  2m 13  0  m  13. Chọn C. A A B B
Câu 90. Điểm M  x; y thuộc đường phân giác của các góc tạo bởi  ;  khi và chỉ khi 1 2 x  2 y  3 2x  y  3
3x  y  0
d M ;   d M ;     . Chọn C. 1   2   5 5
x  3y  6  0 
Câu 91. Điểm M  x; y thuộc đường phân giác của các góc tạo bởi ;
 Ox : y  0 khi và chỉ khi
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 37
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  x x  y y
 1 2  y  0
d M ;  d M ;Ox      . Chọn D. 2 1  x   1 2 y  0    7  A ;3 , B   
1;2  AB : 4x  3y  2  0   4  Câu 92.  .  7   A ;3 , C  
4;3  AC : y  3  0    4 
Suy ra các đường phân giác góc A là: 4x  3y  2 y  3
4x  2 y 13  0  f  ;
x y  4x  2 y 13    5 1
4x  8 y 17  0   f
  B 1; 2  5   0   f
 C 4;3  23   0 
suy ra đường phân giác trong góc A là 4x  8y 17  0. Chọn B.  A
 1;5 , B 4; 5  AB : 2x  y  3  0 Câu 93.  . A
 1;5 ,C 4;  
1  AC : 2x  y  7  0 
Suy ra các đường phân giác góc A là: 2x  y  3 2x  y  7
x 1  0  f  ;
x y   x 1  f
  B 4; 5  5   0      5 5 y  5  0  f  C  4;   1   3  0 
suy ra đường phân giác trong góc A là y  5  0. Chọn B.
Câu 94. Các đường phân giác của các góc tạo bởi
d : 3x  4 y  3  0 và d :12x  5y 12  0 là: 1 2 3x  4 y  3
12x  5 y 12
3x 11y  3  0   .  5 13
11x  3y 11  0 
Gọi I  d  d  I 1; 0 ; d : 3x 11y  3  0  M 10;3  d , 1 2    
Gọi H là hình chiếu của M lên d . 1 30  12  3
Ta có: IM  130, MH   9, suy ra 5  MH 9    sin MIH  
 MIH  52  2MIH  90 .  IM 130
Suy ra d : 3x 11y  3  0 là đường phân giác góc tù, suy ra đường phân giác góc nhọn là
11x  3y 11  0 . Chọn B.
Câu 95. Chọn D.
AB : 3x  4 y  9  0
AC : 8x  6 y 1  0
Phương trình các đường phân giác của góc A của ABC là: 3x  4 y  9 8x  6 y 1
2x  2 y 19  01   
 2 3x  4 y  9   8x  6 y   1   5 10 1
 4x 14 y 17  0   2 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 38
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  29 6  Có  
B  AB  BC . Suy ra B ;   .  7 7   29 41 
Có C  AC  BC . Suy ra C ;   .  14 14   29 6   29 41 
Xét  : 2x  2 y 19  0 có t .t  2.  2 19 2.  2 19  0 . 1  B c      7 7   14 14 
Suy ra B,C nằm về cùng một phía đối với  , nên  là đường phân giác ngoài của góc A . 1  1 
Vậy đường phân giác trong của góc A là  :14x 14 y 17  0 . 2 
Câu 96. Chọn A
Bài toán tổng quát:
Gọi d là phân giác ngoài góc A của tam giác ABC .  1   1 
   Đặt AE  .AB , AF 
.AC và AD  AE  AF . AB AC
Khi đó tứ giác AEDF là hình thoi (vì AE  AF  1 ).
(Hình bình hành có 2 cạnh kề bằng nhau).
Suy ra tia AD là tia phân giác trong góc EAF . 
Do đó: AD  d . Nên AD là vectơ pháp tuyến của đường thẳng d .   AB   1;  1 , AB  2  Áp dụng: 
 AD   2;0  2 1;0 .
 AC  2; 2, AC  2 2 
Xem đáp án chỉ có đáp án A có vectơ pháp tuyến là 1;0 .
DẠNG 3. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
Câu 97. Chọn D a  a
Hai đường thẳng y  a x  b và y  a x  b song song với nhau khi và chỉ khi 1 2  . 1 1 2 2 b  b  1 2
Trong các đường thẳng trên không có đường nào thỏa mãn. Vậy không có cặp đường thẳng nào song song.
Câu 98. Chọn D 
d : y  3x  2  3x  y  2  0 . d có VTPT n  3;  1 .    
Đường thẳng 3x  y  6  0 có VTPT n  3;1  kn nên n và n không cùng phương. Do đó 1   1
đường thẳng 3x  y  6  0 không song song với đường thẳng d .
Câu 99. Chọn D
Ta kiểm tra lần lượt các đường thẳng 1 2
.+) Với d : x  2 y  1  0 có 
 d cắt d . 1 1 2  1 2 1 
.+) Với d : 2x  y  0 có   d cắt d . 2 1 2  2 1  2 1
.+) Với d : x  2 y  1  0 có  
 d trùng d . 3 1 2  1  3 1 2  1  .+) Với d : 2
 x  4 y  1  0 có  
 d song song d . 4 2  4 1  4
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 39
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 100. Chọn B  3  1
Vì d : y   1  x  2 
x 1  d  d . Đường thẳng d và d có hệ số góc bằng 3 3 2  3  2 4 3  
nhau;hệ số tự do khác nhau nên chúng song song.
Câu 101. Chọn D
Để đường thẳng y   2
m  3 x  3m 1 song song với đường thẳng y  x  5 thì điều kiện là 2 m  3  1 m  2      m  2 . 3m 1  5  m  2   
Câu 102. Chọn A
Ta có tọa độ giao điểm của hai đường thẳng x  3y  6  0 và 3x  4 y 1  0 là nghiệm của hệ  27 x 
x  3y  6  0   13 phương trình   
3x  4 y 1  0  17 .  y     3
Câu 103. Chọn A 
Đường thẳng d : 2x  3y 15  0 có một vectơ pháp tuyến là n  2;3 và đường thẳng 1   1 
d : x  2 y  3  0 có một vectơ pháp tuyến là n  1; 2 . 2   2 2 3   Ta thấy 
và n .n  2.1 3.( 2  )  4   0 . 1 2 1 2
Vậy d và d cắt nhau và không vuông góc với nhau. 1 2
Câu 104. Chọn C CÁCH 1
-Xét m  0 thì 1 d : y  5
 , d2 : x  9 . Rõ ràng hai đường thẳng này cắt nhau nên m  0 thỏa mãn (1). x
-Xét m  0 thì d : y  mx  m  5 và d : y    9 1 2 m 1 m  0
Hai đường thẳng d và d cắt nhaut  m     (2) . 1 2 m m  1 
Từ (1) và (2) ta có m  1  . CÁCH 2   1
d và d2 theo thứ tự nhận các vectơ 1 n  ( m 1 ; ), 2
n  (1;m ) làm vec tơ pháp tuyến.   1
d và d2 cắt nhau  1 n và 2
n không cùng phương  m.m  1 1 .  m  1  .   (Áp dụng tính chất: 1
n  a;b và 2
n  c;d  cùng phương  a.d  b.c ) 
d : 2m 1 x  m y 10  0 2   2 2   m m d d 2 1 10 Câu 105. 1 2     
d : 3x  4 y 10  0 3 4 10  1 2m 1  3    m  2. 2 m  4  
d : mx  m 1 y  2m  0 1   d d m m 1 2m Câu 106. 1|| 2     
d : 2x  y 1  0 2 1 1   2 1  2    m  2. m  2m  2 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 40
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
d : 2x  3y  4  0  1 n  2; 3    1      m d d M 4 3 1 Câu 107. 1 2 
x  2  3t       
 m  . Chọn C. d :  n  4 ; m 3  2 3  2 2    2   y  1 4mt  
d : 2x – 4 y 1  0  1 n  1; 2    1     Câu 108. 1 d d2
x  1 at       
 n  n  0  a 1 2a  0  a  1. 1 2 d : 
n  a 1; a 2    2  
y  3  a    1 t   Chọn D.
x  2  2t   d :   u  2; 3 1 1     A d1 y  3  t    Câu 109. 1 d d2  
 m 1 2m  m  2.
x  2  mt    d :     A ; 2 6   d , u  ; m 1 2m  2 3 2   2 2   y  6   1 2mt    Chọn C.
 x  2  2t    A d 5   m  0 d : 
 A 2;1  d ,u  2; m 1   1   2 1    Câu 110. 1 d d2 y  1 mt     2 m   8  m  .    m  d : 4x 3y m 0 u 3; 4          3 4  3 2 2    Chọn D.
d : 2x  y  0 Câu 111. Với 1 m  4    
 d  d   
 loại m  4. 1 2
d : 7x  y  7  0  2 Với m  4 thì
d : 2x  y  4  m  0  1 m   m  m   d d 3 1 2 1 1 1|| 2         m  1  .
d : m  3 x  y  2m 1  0  2 1 4  m m    5  2   Chọn B.   : x  5  0 1 m  0   
 m  0 (thoaû maõn)
 : 2x  3my 10  0  : 4 y 1  0 Câu 112. 1   2   .Chọn D.
 : mx  4 y 1  0   2     m M 2 3 1 2
m  0    m   0  m 4 
 : mx  y 19  0  n  ;1 m  1 1   Câu 113. Ta có :  
 : m 1 x  m 1 y  20  0  n  m 1; m 1   2     2   1   1  
 m m   1 1m   1  0  m  .  Câu 114. 
d : 3mx  2 y  6  0  n  3 ; m 2 1 1    Ta có:   d :   2
m  2 x  2my  6  0  n   2 m  2; 2m 2 2   
d : y  3  0 1 m  0   
 m  0 thoaû maõn
d : x  y  3  0   2  . Chọn D.  2
d d M m  2 2m 1 2
m  0     m  1  3m 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 41
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 
d : 2x  3y 10  0  n  2; 3  1 1    Câu 115. 
 x  2  3t  d :    n  4 ; m 3  2 2   y  1 4 t m   d d 9 1 2   2.4m   3  . 3
   0  m   . Chọn C. 8 
d : 4x  3y  3m  0  n  4; 3  1 1    Câu 116. 
 x  1 2t  d :  
 A 1; 4  d , n  ; m 2  2   2 2   y  4  mt    A d 3  m  8  0 1 d d   8 1 2   m 2    8
 m  . Chọn B.  m  3    4 3   3 
d : 3mx  2 y  6  0  n  3 ; m 2 1 1    Câu 117. Ta có   d :   2
m  2 x  2my  3  0  n   2 m  2; 2m 2 2   
d : y  3  0 1 m  0   
 m  0 khoâng thoaû maõn 
d : 2x  2 y  3  0   2  . Choïn A.  2 d ||d m  2 2m 3 1 2 m  0      m  1  3m 2 6  
x  8   m   1 t  d : 
 A 8;10  d , n  1; m 1 1   1 1   Câu 118. Ta có: 
 y  10  t   
d : mx  2 y 14  0  n  ; m 2  2 2    A  d2    n  1;1 8  m  6  0   1   m    
 khoâng thoaû maõn  m  d d 0 1 1|| 2     m     0 n 0; 2  .   Chọn A.  2   m  2      m  1 1 m 1  m  0      m 2
d : m  3 x  2 y  m 1  0  1   2 Câu 119.  2
d : x  my  m  2m 1  0  2 
d : 3x  2 y 1  0 1 m  0     thoaû maõn
d : x 1  0
d d M   2 1 2   . Chọn B.  m  3 2 m  1 m  0      1 m m  2  
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 42
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 
x  m  2t   2  :   A ;1 m
 d , u  2; m 1 1 2   1 1    A d y  1  m    2 1 t d d   1 2    m 1  x 1 mt       2 m 1  :    u  ;1 m 2 2   2 Câu 120.
y  m  t   . Chọn C. m  1 mt
m  1 m 1 m 2   m 1  0  1   m  t      m  1. 2
m 1 m  m  2  0 m 1  0  3      m m 2  0    
d : 7x  3y 16  0 x  10 Câu 121. 1    . Chọn A.
d : x 10  0 y  18  2   x  3   4t d :  1   x  1 d1 y  2  5t    3
  4t  1 4t t   t  1 t   1    Câu 122.        y  7.  Chọn A.
 x  1 4t
2  5t  7  5t t  t  1    d :   t  0 2  
y  7  5t  
 d : 2x  3y 19  0 1  x  2 Câu 123. 1 d d2 
x  22  2t 
 2 22  2t   355  5t  19  0  t  10    . d :  y  5 2   y  55  5t   Chọn A.
 A –2;0, B 1; 4  AB : 4x  3y  8  0 
4x  3y  8  0 x  2 Câu 124. ABd  x  t       . d :  
 d : x  y  2  0
x  y  2  0 y  0   y  2  t   Chọn B.
x  1 t x  2
Câu 125. Ox  d    
 Ox  d  A 2; 0  d 2 2   1
y  3  3t  0 y  0  
 2a  4  0  a  2. Chọn D.
x  2  t  0 x  0
Câu 126. Oy  d    
 Oy  d  A 0; 2  d 2 2   1 y  6  2t y  2   m  0 2
 6m  m  0  .  Chọn D. m  6   3 x  
d : 3x – 2 y  5  0   8  3 31  Câu 127. 1   
 d  d  A  ; . Ta có 1 2  
d : 2x  4 y – 7  0 31  8 16  2   y    16  A d  A  d  9 31 53      
 c  0  c   .
d || d : 3x  4 y –1  0
d : 3x  4 y  c  0 c  1    8 4 8 3    53
Vậy d : 3x  4 y –
 0  d : 24x  32 y  53  0. Chọn A. 3 8
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 43
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x  3
d : x  3y 1  0   2  Câu 128. 1   
2  d  d  A 3;  . Ta có 1 2  
d : x  3y  5  0 y    3  2    3  A  d  A  d  2  5     3  2. 
 c  0  c   .  
d  d : 2x  y  7  0
d : x  2 y  c  0    3  3 3 5
Vậy d : x  2 y 
 0  d : 3x  6 y  5  0.Chọn A. 3
d : 3x  4 y 15  0 x  1 Câu 129. Ta có: 1   
 d  d  A 1;3  d 1 2   3
d : 5x  2 y 1  0 y  3  2 
 m  6m  3  9m 13  0  m  5. Chọn D.  5 x 
 d : 2x  y – 4  0   9  5 26  Câu 130. 1   
 d  d  A ;  d 1 2   3
d : 5x – 2 y  3  0 26   9 9 2   y    9 5m 26  
 2  0  m  12  . Chọn D. 9 3
d : 3x – 4 y 15  0 x  1 Câu 131. 1   
 d  d  A 1;3  d 1 2  
d : 5x  2 y – 1  0 y  3  2 
 m 12 15  0  m  3. Chọn C.
d : 2x  y – 1  0 x  1 Câu 132. 1   
 d  d  A 1; 1 
 d  m 1 7  0  m  6. 1 2   3
d : x  2 y 1  0 y  1   2  Chọn B.   4 
f M   f 1; 
 0  M  d     3     4   Câu 133. Đặt   f       N   f 1  ;  80   0 ; 51 30 11  N      d f x y x y .  3  
 f  P  0  f  Q  0  Chọn A.
DẠNG 4. GÓC CỦA HAI ĐƯỜNG THẲNG
Dạng 4.1 Tính góc của hai đường thẳng cho trước
Câu 134. Chọn C 
Đường thẳng  có vectơ pháp tuyến n  1; 3 , đường thẳng  có vectơ pháp tuyến  n  1; 3 .   
Gọi  là góc giữa hai đường thẳng ,  .   n n 1 3 1 cos cos ,      60 . 1 3. 1 3 2
Câu 135. Chọn A.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 44
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 
Đường thẳng a có vectơ pháp tuyến là: n  3; 1 ; 1   
Đường thẳng b có vectơ pháp tuyến là: n  1;  3 . 2  
Áp dụng công thức tính góc giữa hai đường thẳng có:   1. 3 n n    1  3 .  3 cos a,b 1 2     
. Suy ra góc giữa hai đường thẳng bằng 30 . n . n 2.2 2 1 2
Câu 136. Chọn C 
Đường thẳng d : 2x  5y  2  0 có vectơ pháp tuyến 1 n  2;5 . 1 
Đường thẳng d : 3x  7 y  3  0 có vectơ pháp tuyến n2  3; 7 . 2
Góc giữa hai đường thẳng được tính bằng công thức     n .n 2.3  5.(7) 29 1 cos d , d  cos n , n       1 2    1 2 1 2 2 2 2 2 n . n 29 2 2 1 2 2  5 . 3   7    d ; d  0  45 1 2
Vậy góc tạo bởi đường thẳng d và d bằng 0 45 . 1 2
Câu 137. Chọn D  
Véctơ pháp tuyến của đường thẳng  là n  2; 
1 nên véctơ chỉ phương u  1;  2 1 
Véctơ chỉ phương của đường thẳng  là u  1;   1 2     u.u 3 3 10
Khi đó cos  ;   cos u;u      1 2  
 u .u 5. 2 10
Câu 138. Chọn D 
Đường thẳng  có VTPT là n 1; 2   1VTCP 2;1 1     1
Đường thẳng  có 1VTCP 1; 2  . 2    
Nhận xét: u .u 0 u u , 90            . 1 2 1 2 1 2  1 2 
Câu 139. Chọn D  
Ta có vtptnd  1; 2 ;vtptnd  2; 4 1   2     nd .nd 1.2  2.4 3
cos d;d  1 2      . nd . nd 5.2 5 5 1 2
Câu 140. Chọn C  
 có vectơ pháp tuyến là n  1;  3 .  ' có vectơ pháp tuyến là n  1; 3 . 2   1   Khi đó:     n .n 1.1  3 3 1 2    cos  2 1 ' ;
    cos(n ;n )      . 1 2   | n | . n
1   32 . 1   32 2 2 4. 4 2 1 2
Vậy góc giữa hai đường thẳng ,   ' là 0 60 . Câu 141. Ta có
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 45
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 
d : 2x  y 10  0  n  2; 1  2.1 1 . 3   1 1    d ;d      1 1 2      cos  
d : x  3y  9  0  n  1; 3  2  2 2   2   2 2 1 . 1  32 2    45 .  Chọn B. Câu 142. Ta có 
d : 7x  3y  6  0  n  7; 3  1 1      14 15 d d 1  1 ; 2      cos      .
d : 2x  5y  4  0  n  2; 5  49  9. 4  25 2 4  2 2   Chọn A. Câu 143. Ta có 
d : 2x  2 3y  5  0  n  ; 1 3 3  1 1 
 d ;d 3  1 2     cos      30 .  d : y  6 1 3. 0  2  . 1 0  n  0;1 2 2    Chọn A. 
d : x  3y  0  n  1; 3  1 1   1 0   d d 1 Câu 144.  ; 1 2     cos   
d : x 10  0  n  1; 0 1 3. 1 0 2 2 2       60 .  Chọn C. 
d : 6x  5y 15  0  n  6; 5  1 1      Câu 145.   1 d ;d2   
x  10  6t 
 n  n  0    90 . Chọn D. 1 2 d :    n  5; 6 2 2   y  1 5t   
d : x  2 y  7  0  n  1; 2  1 1   1 4   d d 3 Câu 146.  1; 2      cos   . Chọn C.
d : 2x  4 y  9  0  n  ; 1 2  1 4. 1 4 5  2 2   
d : x  2 y  2  0  n  1; 2  1 1   1 2   d d 1 Câu 147.  1; 2      cos   . Chọn A.
d : x  y  0  n  1; 1  1 4. 11 10  2 2   
d :10x  5 y 1  0  n  2;1 1 1    2 1   d d 3 Câu 148.  1; 2   x  2  t    cos   . Chọn A. d :    n  1;1 4  . 1 11 10 2 2   y  1 t   
d : 3x  4 y 1  0  n  3; 4 1 1    15  48   d d 33 Câu 149.  1; 2  
x  15 12t    cos   . d :    n  5;  2 1 9 16. 25 144 65 2 2   y  1 5t   Chọn D.
Dạng 4.2 Viết phương trình đường thẳng liên quan đến góc
Câu 150. Chọn B
Gọi  là góc giữa hai đường thẳng đã cho.
x  9  at  Đường thẳng 
t  có vectơ chỉ phương là u  a; 2   . y  7  2t  
Đường thẳng 3x  4 y  2  0 có vectơ chỉ phương là v  4; 3   .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 46
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489     u.v 1 4a  6
Ta có cos  cos u, v   cos 45      u . v 2 2 5 a  4 2
 5 a  4  2 4a  6 2 2
 25a 100  32a  96a  72  2 a  2
 7a  96a  28  0   7 . a  14 
d : 2x  y  3  0 x  1 Câu 151. 1   
 d  d  A 1;1  .  1 2  
d : x  2 y 1  0 y  1  2   
Ta có d : y 1  0  n  0;1 , gọi n  a;b,    . Khi đó   ;d3  3 3   1 b
a  b  a  b  1   : x  y  2  0 2 2 2  o c s 
 a  b  2b  .  2 2 2
a  b  a  1,b  1
   : x  y  0 a  b . 0 1  Chọn C.
Câu 152. Chọn B.
Cho đường thẳng d và một điểm . A Khi đó.
(i) Có duy nhất một đường thẳng đi qua A song song hoặc trùng hoặc vuông góc với d.
(ii) Có đúng hai đường thẳng đi qua A và tạo với d một góc 0    90 .    a
Câu 153. d : x  2 y  6  0  n  1; 2, gọi n     Ta có   ; a b k . d  b 1 a  2b  cos 45   5 2 2 a  b  2 2
 2a  8ab  8b 2 2 2 a  b . 5  1 1
a   b  k  2 2 3a 8ab 3b 0       3  3 . Chọn A.
a  3b  k  3    
d : y  kx  n  k   d  ;  1 1 k 1 Câu 154.  2 2      cos 60 
 k 1  2k  4k  2
 : y  x  n      1;  2 1 2 k 1. 2 2 sol:k  1
k , k k2
 k  4k 1  0 
 k  k  4. 1 2 Chọn B.
Câu 155. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 47
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Tọa độ A2  ;1 1 3
Gọi  là góc giữa hai đường thẳng d và d , cos   sin  2  1  10 10 AB BC 1
Xét tam giác ABC ta có:   sin C  sin C sin A 10 1 3
Gọi  là góc giữa hai đường thẳng d  và d , suy ra: sin    cos     1 1  10 10 
Giả sử d  có vec tơ pháp tuyến là n ; a b 3 2a  b 3 a  b Từ   1 ta có: 2 2 cos    
 a  8ab  b  0   2 2 10 a  b 5 10 a  7b  
Với a  b một vec tơ pháp tuyến n  1; 
1  d : x  y  0 
Với a  7b một vec tơ pháp tuyến n 7 
;1  d : 7x  y  6  0
Vậy: T  1 0  7  6  2
Câu 156. Chọn C  Gọi ( n ; a ) b với 2 2
(a  b  0) là véc tơ pháp tuyến của AC , véctơ   n (1; 3
 ) là véc tơ pháp tuyến của đường thẳng BC , n (1; 1)  là 1 2
véc tơ pháp tuyến của đường thẳng AB .    
Ta có: cos B  cos C |  cos( , n n )| |  cos(n ,n )| 1 2 1     | ,
n n | |n , n | |a  3 | b |1  3| 1 2 1
        2 2 n . n n . n 10. a  b 10. 2 1 2 1  a  b 2 2 a  b  2 2 2 2
 a  3b  7a  6ab  b  0   7a  b   + Với a  b
 chọn a  1,b  1   ( n 1; 1
 ) loại vì AC / / AB b  8 1  + Với a 
chọn a  1;b  7  AC : x  7 y  3  0 . Điểm C  AC  BC  C ;   7  5 5 
Câu 157. Chọn D  
Đường thẳng d , d có véc tơ pháp tuyến lần lượt là n  2; 1  , n  1;1 . 1   2   1   2   Gọi  
 là đường thẳng cần tìm có véc tơ pháp tuyến là n  ; a b.
Góc giữa 2 đường thẳng d , d và  
 , d xác định bởi: 2  1   2    n .n  cosd d  1 2 2.1 1.1 1 ,      . 1 2 n . n 2  2 2 2 2 10  1 2 1 . 1 1   . n n    a b a b cos ,  d  2      . 2 2 2 2 2 2 2 n . n a  b . 1 1 2. a  b 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 48
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Vì  
 cắt d , d tại A và B tạo thành tam giác IAB cân tại A nên 1   2    a b
cos d , d   cos ,  d  1 2 2  
 5 a  b  a  b 1 2 2 2 2 2. a  b 10 a  2b 
 5a b2 2 2 2 2
 a  b  2a 5ab b  0   1 . a   b  2 + a  2
 b : chọn a  2  b  1
 : phương trình đường thẳng là: 2x  
2  y  0  2x  y  4  0 L. 1
+ a   b : chọn a 1 b  2
 : phương trình đường thẳng là: 2 x 
2  2y  0  x  2y  2  0
T / m. Do đó T  a5b 15 2  11. DẠNG 5. KHOẢNG CÁCH
Dạng 5.1 Tính khoảng cách từ 1 điểm đến đường thẳng cho trước
Câu 158. Chọn D
Khoảng cách từ điểm A1 
;1 đến đường thẳng  : 5x 12y  6  0 là 5.112.1 6 d  , A    1 . 5   12  2 2
Câu 159. Chọn A 3.5   2.   1 13 26 Khoảng cách d    2 13 . 2 2 3  2 13
Câu 160. Chọn B
Khoảng cách từ điểm M (1; 1) đến đường thẳng  : 3x  y  4  0 là 3.11 4 6 3 10
d M ;     . 2 2 3 1 10 5
Câu 161. Chọn B 3.3 4. 4   1 24
Ta có: d  M,    .   2 2 5 3 4
Câu 162. Chọn A 3. 3    2  1 10 Ta có d  ; A     10.   2 2 10 3 1
Câu 163. Chọn D 4.0  3.0 1 1
Ta có d O, d    . 2 2 5 4  3
Câu 164. Chọn A 3  5.2 1 14
Gọi bán kính của đường tròn là .
R Khi đó: R  d  I ,    .   2 2 26 1 5
Câu 165. Chọn D
0. cos  4. sin  42  sin
Ta có: d M ,    8 . 2 2
cos   sin 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 49
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 166. Chọn A
ax  by  c
Khoảng cách từ điểm M (x ; y ) đến đường thẳng  : ax  by  c  0 là: 0 0 d (M , )  0 0 2 2 a  b
Vậy khoảng cách từ I (1;2) đến đường thẳng  : 3x  4 y  26  0 bằng 3.1 4.(2)  26 d (I , )    3 2 2 3  (4)
x  3y  4  0 x  1 3  1 4 2 Câu 167.     A 1   ;1  d  ; A    . Chọn C.
2x  3y 1  0 y  1   9 1 10  A  1; 2 3  8 12 1 Câu 168. 
 h  d A BC   A  ;  . B   ;
0 3, C 4;0  BC : 3x  4 y 12  0 9 16 5  Chọn A.  A3; 4    A  3; 4    BC  2 5  
Câu 169. Cách 1:   BC  2 5   B
 1;5 ,C 3  ;1 h  d     ; A BC   5
BC : 2  y  7  0  A x   1  S  .2 5. 5  5. Chọn B. ABC 2 1   Cách 2: S 
AB .AC  AB  AC ABC   2 2 2 . 2
3sin   32  sin 
Câu 170. d M ;    6.Chọn B. 2 2 cos   sin 
 x  1 3t 8  0  2 Câu 171.  : 
  : 4x  3y  2  0  d M ;    2. Chọn A. y  2  4t  6 1  9
x  2  3t 15  3  2 Câu 172.  :    :  3  2  0 N x y     MN  d M ;    10. min   y  t  1 9 Chọn A.
m  2  m  4
Câu 173. d  ; A  2 2 
 2 5  m  3  5. m 1  4m  6m  4  0 2 m 1 m  2   1 . Chọn B. m   2  x  t d :  
d : x  y  2  0 x  4  m Câu 174. 1 1  y  2  t     
d : x  2 y  m  0 y  m  2   2 
d : x  2 y  m  0  2  M 4  ;
m m  2  d  d . 1 2 2 2 m  2
Khi đó: OM  2  4  m  m  2 2
 4  m  6m  8  0  .  Chọn C. m  4  100
Câu 175. R  d O;    10. Chọn D. 64  36
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 50
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 10  24 10 44
Câu 176. R  d  I;    . Chọn A. 25 144 13
 f M 21; 3    464   f
  N 0; 4  54
Câu 177. f  ;
x y  21x 11y 10   . Chọn D. f   P  19  ;5  464  f
 Q 1;5  44 
 f M 1; 3    38   f
  N 0; 4  25
Câu 178. f  ;
x y   7x 10 y 15   . Chọn C. f   P  19  ;5  98  f
 Q 1;5  42   A  2; 0   12  3 3 Câu 179. 2   d  ;   d ; A    . Chọn B. 1 2   1 
 ||  : 6x  8 y  3  0 100 2  2 1   A
 2; 2  , n   7  ;1 Câu 180.  
d : 7x  y  3  0  n   7;  1  d 14  2  3 3
   d  d d;   d  ; A d    . Chọn A. 50 2  A  4;3  d 24  24 101 101 Câu 181. 2 
 d d ; d    10,1. Chọn A. 1 2 
d || d : 6x – 8y 101  0 100 10  2 1
Dạng 5.2 Phương trình đường thẳng liên quan đến khoảng cách
Câu 182. Chọn D
Gọi d là đường thẳng được cho trong các phương án. Khi đó: +) Phương án A. 2.3  2.1 3 7 2.4   2.0  3 11 d  , A d   
; d  B, d     d  ,
A d   d  B, d  .  2 2 2   2 2 2 2 2 2 2 2  2 Loại phương án A. +) Phương án B. 2.3  2.1 3 1 2.4  2.0  3 5 d  , A d   
; d  B, d     d  ,
A d   d  B, d  .   2 2 2   2 2 2 2 2 2 2 2 2 Loại phương án B. +) Phương án C. 3  2.1 3 2 4  2.0  3 1 d  , A d    ; d  , B d     d  ,
A d   d  , B d  . 2 2 2 2 1  2 5 1  2 5 Loại phương án C. +) Phương án D. 2.3  2.1 3 5 2.4  2.0  3 5 d  , A d   
; d  B, d     d  ,
A d   d  B, d  2 2 2  2 2 2 2  22 2 2 2 Chọn phương án D.
Câu 183. Đường thẳng cách đều hai điểm ,
A B thì đường thẳng đó hoặc song song (hoặc trùng) với AB ,
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 51
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
hoặc đi qua trung điểm I của đoạn AB .   3 7   A  2;3 I ;    Ta có:     2 2 
 AB || d : x  y  2  0. Chọn A. B   1; 4    AB  1   ;1  n  1;   AB  1
Câu 184. Dễ thấy ba điểm ,
A B, C thẳng hàng nên đường thẳng cách điều ,
A B, C khi và chỉ khi chúng
song song hoặc trùng với AB .  
Ta có: AB  12; 4  n
 1; 3  AB || d : x  3y  4  . 0 Chọn A. AB   1 5  I  ;   
Câu 185. Gọi I là trung điểm đoạn AB    2 2  .    AB   3  ;3  n  1  ;1  AB 
Khi đó:  : mx  y  3  0 n   ; m  cách đều , A B   1  I    m 5    3  0 m  1    m 1  2 2  .  Chọn C.    m  1  1 m  1 1    
d : 3x  4 y 1  0  M 1  ;1  d c 1 c  4  Câu 186. 
 1  d d;   d M ;    . 
 || d   : 3x  4 y  c  0 5 c  6   Chọn A. 3x  4 y  2
3x  4 y 12  0
Câu 187. d M  ;
x y;   2   2  .  Chọn B. 5
3x  4 y  8  0  5x  3y  3 5x  3y  7
Câu 188. d M  ;
x y; d  d M ; x y ; d  
 5x  3y  2  0. 1     2  34 34 Chọn C.
Câu 189. Chọn D MD DK DK
Gọi cạnh hình vuông bằng a. Do ABK  1 1 MDK      . AB KB 3 DB 4
     1
Ta có AM  AD  DM  AD  DC (1) a A B 3
          3 1 3 1 3 1
NK  BK  BN  BD  BC 
BA BC BC  BA BC (2) 4 2 4 2 4 4 N       1 1 K
Từ (1) và (2) suy ra AM.NK  A . D BC  B .
A DC  0  AM  NK . 4 4 D M C
Vì AM  NK nên NK có phương trình tổng quát: 10x  y  2019  0 . 2019 2019 101
Khoảng cách từ O đến NK là d  , O NK    . 2  2 101 10 1
Câu 190. Chọn C.
Ta có: M (4; 2)  d  4  2b  c  0  c  4  2 . b (1) 1 c 3 10 2 2 d ( , A d )  
 10(1 c)  9(1 b ). (2) 2 10 1 b
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 52
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
b  3(tmdk ) Thay c  4
  2b vào PT (2) ta được PT: 2 31b 120b 81 0      27 b   (ktmdk )  31
 b  3, c  2  b  c  1. .
Câu 191. Chọn A x  1 
 : x  m  
1 y  m  0   y  
1 m  x  y  0 m    . y  1  
Suy ra  luôn đi qua điểm cố định H  1  ;   1 .
Khi đó, với mọi M   , ta có d  ;
A   AM  AH .
Giá trị lớn nhất của d  ;
A   AH khi M  H  max d  ,
A   AH  2 10 .
Câu 192. Chọn B.
Gọi A , B lần lượt là giao điểm của đường thẳng đã cho với Ox , Oy . x y
Ta có 12x  5y  60  
 0 . Do đó A5;0 , B 0;12 . 5 12 12.0  5.0  60 60
Gọi H là hình chiếu của O lên AB . Khi đó: OH  d O ; AB   . 2 2 13 12  5
Tam giác OAB là tam giác vuông tại O nên tổng độ dài các đường cao là 60 281
OA  OB  OH  5 12   . 13 13
Câu 193. Chọn D
Gọi H là hình chiếu của điểm A lên đường thẳng d  . Khi đó ta có:
d  A d   AH  AB    2    2 , 3 1 4 1
 29 . Do đó khoảng cách từ A đến đường thẳng d 
đạt giá trị lớn nhất bằng 29 khi H  B hay d   AB tại B . 
Vì vậy d  đi qua B và nhận AB  2;5 làm VTPT.
Do đó phương trình của đường thẳng d  là 2 x  3  5 y  4  0  2x  5y  26  0 .
DẠNG 6. XÁC ĐỊNH ĐIỂM
Dạng 6.1 Xác định tọa hình chiếu, điểm đối xứng
Câu 194. Chọn D
Thay tọa độ các điểm vào phương trình đường thẳng d , ta có M , M , M  d và M  d . 1 4 2 3
Câu 195. Chọn C x  3 y  8
Phương trình đường thẳng đi qua hai điểm B và C có dạng: 
 3x  y 1  0 . 2  3 7  8
Đường thẳng đi qua A và vuông góc với BC có phương trình: 
1 x  4  3 y  
3  0  x  3y 13  0
Tọa độ chân đường cao kẻ từ đỉnh A xuống cạnh BC là nghiệm của hệ phương trình: 3
 x  y 1  0 x  1    .
x  3y 13  0  y  4 
Câu 196. Chọn B
Gọi  là đường thẳng đi qua M và vuông góc với d . Ta
có phương trình của  là: x  3y 1  0
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 53
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Tọa độ hình chiếu vuông góc của M trên d
là nghiệm của hệ phương trình:  7 x  
3x  y  5  0   5    .
x  3y 1  0 4   y    5
Câu 197. Chọn A  
Đường thẳng  có 1 VTPT là n  1;  
1 nên  có 1 VTCP là u  1  ;1
Gọi H là hình chiếu vuông góc của M 1; 2 lên đường thẳng , tọa độ H t;t      3  3 3 
Vì MH    MH  u  MH .u  0  t 1 t  2  0  t   H ;   2  2 2 
Câu 198. Chọn C A G B C M H
Gọi M là trung điểm của cạnh BC . Ta có  3
x 2  22    3 M  2  AM  AG   , suy ra M 2;  1 . 2  3  2 
y 4   4 M  2  3    HM  0; 
3 suy ra HM không vuông góc với d  nên B không trùng với H.
Ba ;b d   b  a  2 .
Tam giác BHC vuông tại H và CM là trung tuyến nên ta có       a MB MH a  2 1 2 a  2 2
1  9  a  a  2  0   a  2 l  Suy ra B 1  ; 
1 và T  a 3b  2 .
Câu 199. Chọn C
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 54
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A B D C N M Gọi C(t; 2
 t  5)  (d ) .
Dễ thấy hai tứ giác BCND và ADNB nội tiếp.   BNC  BDC Suy ra  o 
 ANC  90  CN  AN . BNA  BDA   
Do đó CN.AN  0  9(5  t) 12(2t 1)  0  t  1  C 1; 7 .
Vậy m  n  1 7  8
Dạng 6.2 Xác định điểm liên quan đến yếu tố khoảng cách, góc
Câu 200. Chọn A Gọi M  ; x 0 . 
Ta có AB  3; 4
Phương trình đường thẳng AB : 4x  3 y  
3  0  4x  3y  9  0 .  7 4x  9 x 
d M ; AB   5  4x  9   2 5  x 1   7  Vậy M ; 0 ; M   1;0 .  2  
M  d : x  2 y 1  0  M 2m 1; m , m   Câu 201.  . Khi đó
 AB : 4x  3y  7  0  m  3
8m  4  3m  7 6
d M ; AB 11m 3 30        27
 M 7;3. Chọn B. 5 m  l  11 Câu 202.
x  2  2t M  d : 
 M 2  2t;3  t  với 2  2t  0  t  1. Khi đó y  3  t 
t  1 l    24 2 
5  AM  2t  22  t  22 2
 25  5t 12t 17  0   M  ;;  . 17   t    5 5   5 Chọn C.
Câu 203. Gọi M  ;
x 0 Ox thì hoành độ của hai điểm đó là nghiệm của phương trình:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 55
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  5 x   x1 2x  5  75 d M  2 ;  2 5   2 5   
 x  x   . Chọn A. 1 2 5 15 4 x    x2  2  7  7   M  ; x 0 4x  9 x   M ; 0    Câu 204. 
 1  d M ; AB   2  2 . Chọn A.
 AB : 4x 3y 9 0 5     
x  1  M 1;0  Câu 205. Ta có
 AB : 4x  3y 12  0  1 3y 12
 y  0  M 0;0  AB  5  6  S  .5.   . MAB   2 5  y  8   M 0; 8 3y 12  
M 0; y  h  d M AB  M  ;    5 Chọn A. M   ; x 0 3x  6 3x  3 1  1  Câu 206.     x   M ; 0 .   Chọn B. d   M ;  d M ;  13 13 2  2   1   2   x  t M  d : 
 M t;1 2t  2 2 2 2 Câu 207.  y  1 2t  
t  2  2t   1
 t  4  2t  7 MA  MB 
 20t  60  0  t  3  M 3; 5. Chọn B. 
M  d : 2x  y  3  0  M  ; m 2m  3 2 2 2 2 Câu 208.   m   1  2m   1
 m  3  2m   1 MA  MB 
 m  2  M 2;   1 . Chọn A. C 
  d : y  2  C  ; c 2 C 1; 2 Câu 209. 2 
 2  c 1  c  1   . Chọn C. BA  BC C   1; 2 
Câu 210. Chọn B Do (
A a; b) thuộc đường thẳng d : x  y  3  0 nên a  b  3  0  b  a  3  A ; a a  3 .
Khoảng cách từ điểm A ;
a a  3 đến đường thẳng  : 2x  y 1  0 là
2a  a  3 1 a  4
d a,    . 2 2 2 1 5 a  4 a  4  5 a  1
Theo đề bài d a,   5 
 5  a  4  5     . 5 a  4  5 a  9   Theo đề bài điểm (
A a; b) có hoành độ dương nên a  1  A1; 2
  . Vậy P  ab   1 2    2  .
Câu 211. Chọn B
Vì M a;b d  M (3  t; 2  t) .
Lại có M cách đường thẳng  : 2x  y  3  0 một khoảng 2 5 suy ra
2(3  t)  (2  t)  3 t  9 M (12;11)
 2 5  t 1  10     . 5 t  11 M (8; 9)  
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 56
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Vì a  0 nên điểm M ( 8  ; 9  ) không thỏa mãn.
Vậy: M (12;11)  a  b  23.
Câu 212. Chọn B a  3  t
Aa;b  d   . b  2  t 
Giả thiết: a  0  3  t  0  t  3 .
2 3  t   2  t   3 t  11 Ta có d  ; A d   2 5 
 2 5  1 t  10   .   2 2 t  9 2 1  a  8
Vì t  3 nên chọn t  11. Khi đó 
 P  72 . Do đó chọn đáp án B. b  9 
Câu 213. Chọn B 
M  d : 2x  y  5  0  M ;
m 5  2m  IM m 1;3  2m . 1   1   1   m  0 IM 10 m 2 1 3 2m2 2 10 5m 14m 10 10             14 . 1 m   5  14 3 
 có 2 điểm thỏa mãn yêu cầu bài toán là M 0;5 ; M ;  . 1   2    5 5  14 14
Tổng các hoành độ của M và M là: 0   . 1 2 5 5
Câu 214. Chọn A 
Ta có AB  3; 4 .
 phương trình tổng quát của đường thẳng AB có dạng 4x  3 y  m  0 . Vì A1 
;1  AB nên 4.1 3.1 m  0  m  7  AB : 4x  3y  7  0 .
Vì C a;b  d : x  2y 1  0  a  2b 1  0  a  2b 1. 4a  3b  7
Theo đề ra d C; AB  6 
 6  4a  3b  7  30 . 2 2 4  3
Thay a  2b 1 vào ta được: b  3 11  b  3  30 4 2b  1 3b 7 30 11b 3 30            27 . 11b  3  30  b     11
Do C có tọa độ nguyên nên b  3; a  7  a  b  10 .
Dạng 6.3 Xác định điểm liên quan đến yếu tố cực trị
Câu 215. Chọn C
Gọi A đối xứng A qua d ta có A '(0;3) khi đó điểm M  A B   d
Tìm được M (3; 4) .
Câu 216. Chọn D
Điểm M  d  M 4t  15; t 2 2 Ta có: AM  t  2 t  2 4 17 17 t 8t 17 17 t 4 1         
 17 , t   .  
 min AM  17 , đạt được tại t  4 . Khi đó M 1; 4 .
Câu 217. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 57
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Cách 1:
     4 
Tìm tọa độ điểm I  ;
x y sao cho IA  IB  IC  0 . Suy ra I 1;    3 
  
   
Ta có: MA  MB  MC  3MI  IA  IB  IC
   
   
MA  MB  MC  3 MI . Vậy MA  MB  MC nhỏ nhất khí MI nhỏ nhất. 
MI nhỏ nhất khi M là hình chiếu vuông góc của I xuống đường thẳng d . 5
Đường thẳng d  đi qua I và vuông góc với d có phương trình: x  2 y  3
2x  y  3   13 19 
M là giao điểm của d và d  nên M là nghiệm của hệ:  5  M ;   x  2 y   15 15    3 Cách 2:
M thuộc d suy ra M t; 2t  3
  
MA  MB  MC  (3  3t; 6t  5)
   
MA  MB  MC    t 2    t 2 3 3 6 5 2
    13  1 2
MA  MB  MC 
45t  78t  34  45 t      15  5
   13  13  19 
MA  MB  MC nhỏ nhất khi t   . Suy ra M ;   . 15  15 15 
Câu 218. Chọn B
Gọi G a;b là trọng tâm tam giác ABC . Suy ra 
x  x  x  2 1 2  1 A B C a  a  a   3  3     3  1 1        G ;   .
y  y  y 2  3  2 1  3 3 A B C  b   b  b      3   3   3
  
      
Ta có: MA  MB  MC  MG  GA  MG  GB  MG  GC  3MG  3MG .
  
Suy ra MA  MB  MC nhỏ nhất khi MG nhỏ nhất.
Mặt khác M thuộc trục tung nên MG nhỏ nhất khi M là hình chiếu của G lên trục tung.  1  Vậy M 0;   .  3 
Câu 219. Chọn D
Gọi A’ là điểm đối xứng của A qua đường thẳng 
Ta có: MA  MB  MA' MB  A' B
Đẳng thức xảy ra  M trùng với M0 (M0 là giao điểm của  và A’B)   Ta có: AA '   nên n  a  1;1 AA '   
AA ' : x  y  3  0
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 58
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Gọi H=AA '   H 1; 2
Vì A’ đối xứng với A qua  nên H là trung điểm AA’  A '0;3  
Đường thẳng A’B qua B có VTCP A ' B  9;3  3 3;1  n  1; 3 A 'B  
 A ' B : x  3y  9  0 x  y  1  0
Tọa độ M0 thỏa hệ:   M 3; 4 0   x  3y  9  0 
 M 3; 4 . Vậy a  b  7
Dạng 6.4 Một số bài toán tổng hợp
Câu 220. Chọn C M B C N H A D P
Gọi a  0 là độ dài cạnh của hình ABCD . 1
Trên tia đối của tia DC lấy điểm P sao cho DP  a . 2 5 Tam giác MCN có 2 2 MN  MC  CN  a . 6 5
Tam giác ANP có NP  ND  DP  a . 6  Vậy A  MN  A
 PN (c.c.c) suy ra MAN  45 .
Suy ra với H lầ hình chiếu vuông góc của M trên đường thẳng thì tam giác AHM vuông cân tại H .  5  3 5 Tính được H ; 2   , HM 
suy ra tọa độ A là nghiệm của hệ phương trình  2  2 x  4 2  5  45   x      y  22  y  5   2  4  . x 1
2x  y 3  0     y  1  
Câu 221. Chọn A
Vì A d , giả sử A ;
a 3  a ; Vì B  d , giả sử B 2b  6;b 1 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 59
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
 a  2b  6 1   I 2
là trung điểm của đoạn thẳng AB khi và chỉ khi  3  a  b   1   2
a  2b  4  a  2         A2  ;1 ; B 0; 3
   BA  2; 4  BA  2.u . 1 a  b  5 b  3    
Vậy đường thẳng AB có một véctơ chỉ phương là u  1; 2 . 1  
Câu 222. Chọn C x  5 3t
d có phương trình tham số là y  1   2t   
Gọi C 5  3t; 1
  2t   d , ta có: CA  9  3t;3  2t ,CB   3
  3t; 7  2t 
CA  CB  CA  CB    t 2    t 2    t 2    t 2 2 2 9 3 3 2 3 3 7 2 8  20t  32   t  5  1 11 Suy ra: C ;   5 5  
Câu 223. Chọn A  
Véc tơ chỉ phương của AB là: AB  4; 2
   véc tơ pháp tuyến của AB là: n  1; 2
Phương trình đường thẳng AB là:  x  3  2 y  5  0  x  2y  7  0  9 x 
2x  y 1  0   5
Tọa độ điểm I là nghiệm của hệ phương trình:   
x  2 y  7  0 13   y    5  9 13   I ;   .  5 5  2 2  9   13   3   5     IA  x  x  y  y I A 2  I A 2  5   5  Vậy tỉ số    6 . IB  x  x  y  y     I B 2  I B 2 2 2 9 13 1   3      5   5 
Câu 224. Chọn B     Ta có BC   4
 ; 2 , AC  4; 2 , AH  a  2;b  
1 , BH  a  2;b  3 .
Vì H là trực tâm của tam giác ABC nên ta có     AH  BC  4  
a  2  2b   1  0
2a  b  3 a  1         . BH  AC 4   
a  2  2b  3  0 2a  b  1 b  1   
Vậy S  3a  2b  31 2   1  1 .
Câu 225. Chọn A  2 3  a  x  2  x  3  x 2  3        5 5 a  1 Gọi M  ;
x y . Khi đó: MI  MB  MC     . 5 5 2 3 b  0 b
  y  3 y  2  y    5 5
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 60
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nên I 1;0 . Vậy 2 2
S  a  b  1 .
Câu 226. Chọn A  1 
Gọi K trung điểm AI  K ; 0   .  2 
        
Ta có 2MA  MB  MC  0  2MA  2MI  0  4MK  0  M  K 1 1  a  b   0  . Chọn A 2 2
Câu 227. Chọn B
Điểm C thuộc đường trung tuyến CM nên gọi tọa độ điểm C  ; x x   1 .  
Tọa độ AC   x  2;  x  2 , tọa độ vectơ chỉ phương của đường thẳng BH là u  3;1 .  
Vì AC  BH nên AC.BH  0   x  2.3  x  2  0  x  4 . Vậy C 4; 5   .
Câu 228. Chọn A
Gọi H là giao điểm của N , D AP
Ta có: MBC  NCD c  g  c nên   MCB  NDC . Mà     
MCB  MCD  90  NDC  MCD  90  DIC  90  ND  MC  ID  AP   1
Do AMCP là hình bình hành nên AP / /MC  HP / /IC suy ra H là trung điểm của ID 2 Từ   1 , 2  AP là đoạn trung trực của ID  A  DP  A
 IP  AI  IP , 5 2
AI  2IP  2.  5 2 . 2
x  5  7t
Phương trình đường thẳng AI :  . y  2  t 
A AI , A  I , x  0  A5  7t; 2  t , 5  7 t  0. A t   1  (nhaä n) AI  5 2  2 50t  50   t  1  (loaïi)
t  1  A2;3 .
AP : x  3y 11  0 , DN : 3x  y 17  0.
 x  3y 11  0 x  4
H  AP  DN  Tọa độ của H là nghiệm của hệ    .
3x  y 17  0 y  5  
H 4;5 , I 5; 2  D 3;8 .
Vậy A2;3, D 3;8.
Câu 229. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 61
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A M B' G I C B d    7 
Gọi M là trung điểm cạnh AC , suy ra BG  2GM  M ;1   .  2 
Gọi điểm B ' là điểm đối xứng với B qua đường phân giác trong của góc A . Suy ra điểm B ' nằm trên AC .
Đường thẳng BB ' qua B và vuông góc với đường thẳng d : x  y 1  0 nên có phương trình
BB ' : x  y  3  0
Gọi I  BB ' d , suy ra tọa độ điểm I  1  ; 2
  là trung điểm của BB ' nên tọa độ B '2; 5     3 
Đường thẳng AC đi qua B '2; 5
  và có véc tơ chỉ phương B ' M  ; 6   , suy ra véc tơ pháp  2 
tuyến của AC có tọa độ 4;  1 
. Đường thẳng AC có phương trình là: 4x  y 13  0
Điểm A  d  AC  ( A 4;3) . Vậy tích . m n  12 .
Câu 230. Chọn D
Ta chứng minh được MP  AN , nên P là hình chiếu của M trên AN .  1   1 
(Thật vậy gắn hệ trục toạ độ Dxy , D 0;0,C 1;0, B 1  ;1 , A0  ;1 . Khi đó M 1; ; N ; 0     .  2   3 
Phương trình đường thẳng BD : y  x . Phương trình đường thẳng AN : 3x  y  1.  1 1 
  3 1   1    Điểm P ;   . Khi đó MP  ; ; AN  ; 1  .
MP AN  0  MP  AN     (đpcm).  4 4   4 4   3  13
Phương trình đường thẳng MP qua M và vuông góc với AN là x  2 y   0 . 2
2x  y  3  5  x 
P là giao điểm MP và AN nên toạ độ P là nghiệm hệ  13   2 . x  2 y    y  2  2  5 Từ đó: a 
, b  2  2a  b  7 . 2
Câu 231. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 62
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A D M H I B C
Gọi H là hình chiếu của I lên cạnh CD.
Do tứ giác ABCD nội tiếp đường tròn nên       AM 1
ABM  MCD  ICH  tan ABM  tan MCD  tan ICH   . AB 3  IH 1  sin ICH   . IC 10 2
Có IH  d  I ,CD 2 
 IC  2  IC  4. 10
C  CD : x  3y  6  0  C 3t  6;t  Mà 2
IC  4 và x  Z  C 3;   1 C  4 
Đường thẳng BC qua C 3;   1 và E ; 0 
 có phương trình là BC : 3x  5 y  4  0 .  3 
I là trung điểm của MC nên M 1;   1 .
Đường thẳng BD qua M 1;  
1 và vuông góc với CD có phương trình là BD : 3x  y  4  0 .
Có B  BC  BD  B 2; 2
Câu 232. Chọn D
Ta chứng minh được MP  AN , nên P là hình chiếu của M trên AN .  1   1 
(Thật vậy gắn hệ trục toạ độ Dxy , D 0;0,C 1;0, B 1  ;1 , A0  ;1 . Khi đó M 1; ; N ; 0     .  2   3 
Phương trình đường thẳng BD : y  x . Phương trình đường thẳng AN : 3x  y  1.  1 1 
  3 1   1    Điểm P ;   . Khi đó MP  ; ; AN  ; 1  .
MP AN  0  MP  AN     (đpcm).  4 4   4 4   3  13
Phương trình đường thẳng MP qua M và vuông góc với AN là x  2 y   0 . 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 63
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
2x  y  3  5  x 
P là giao điểm MP và AN nên toạ độ P là nghiệm hệ  13   2 . x  2 y    y  2  2  5 Từ đó: a 
, b  2  2a  b  7 . 2
Câu 233. Chọn D
Gọi D là điểm đối xứng với B qua đường thẳng d : x  2 y  5  0 suy ra D  AC .
Phương trình của đường thẳng BD : 2x  y  25  0 .
Gọi H là giao điểm của d và BD suy ra tọa độ điểm H là nghiệm của hệ phương trình
x  2y 5  0 x  9       H 9;7  .
2x  y  25  0 y  7  
Mà H là trung điểm của BD suy ra D(6;13) .
Gọi A(5  2a; a)  d . 1 2 Ta có G ;  
là trọng tâm tam giác ABC nên 3 3
x  x  x  3x 5  2a 1  2  x 1
x  2a 8  A B C G  C  C     
 C(2a 8;1a) 
y  y  y  3y a  1 y  2 y 1a  A B C G  C  C  
Ta có DA  11 2a; a 1 
3 ; DC  2a 14;12  a   11 2a a 1  3 Mà 3 điểm D, ,
A C thẳng hàng nên D ,
A DC cùng phương    a  2  2a 14 1  2a
Suy ra điểm C(4;3) nên đường thẳng BC đi qua điểm C(4;3) .
Câu 234. Chọn D A E F C B I Gọi I 13 7 ;
n n là trung điểm của BC,khi đó ta có: IE  IF mà 2 2
IE  50n 164n 146; IF  50n 190n 185 3 2 2
 50n 164n 146  50n 190n 185  n  2  5 3   I ;    2 2  Gọi B 13  7 ;
m m .Vì I là trung điểm của BC nên C 7m 8;3 m .  
 BE  7m 11;5  m;CE  10  7 ;
m 2  m .Vì BE  AC   nên 2
BE.CE  0  m  3m  2  0  m  1   m  2 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 64
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  2 11 
+ Với m  1  B 6; 
1 , C 1; 2  A ; 
 .Trường hợp này không thỏa mãn các đáp án.  3 3 
+ Với m  2  B  1  ; 2;C 6; 
1  A1;6 Suy ra Chọn D
Câu 235. Chọn B A B I M H K C D 1
Gọi I , K lần lượt là trung điểm của AH và DH  IK  
AD  IK  BM  tứ giác IBMK 2
là hình bình hành  BI  MK . (1)
Do IK  AD và AD  AB  IK  AB  I là trực tâm tam giác ABK  BI  AK . (2)
Từ (1), (2) suy ra MK  AK .
Phương trình AK : 4x  y  4  0 , suy ra phương trình MK :2x  8y 15  0 .  1
4x  y  4  0 x   1 
Tọa độ điểm K là nghiệm của hệ phương trình    2  K ; 2   .
2x  8y 15  0   2   y  2 
x  2x  x  0 Do đó D K H 
 D 0; 2  P  4. .
y  2 y  y  2  D K H
Câu 236. Chọn B A B' C' B C x  3  0 x  3
B  BC  BB ' nên có tọa độ là nghiệm của hệ     B(3; 1  ) .
x  y  2  0 y  1   
x  y  2  0 x  0
C  BC  CC ' nên có tọa độ là nghiệm của hệ     C(0; 2) .
2x  3y  6  0 y  2  
AB qua B và vuông với CC ' có phương trình: 3x  2 y  7  0 .
AC qua C và vuông với BB ' có phương trình: y  2 . 3
 x  2 y  7  0 x  1
A  AB  AC nên có tọa độ là nghiệm của hệ     ( A 1; 2) . y  2 y  2  
Câu 237. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 65
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A H B C 
Đường thẳng AH đi qua A 3
 ;0 và nhận BC   1
 ;6 làm véctơ pháp tuyến. Suy ra phương
trình đường thẳng AH là: x  6y  3  0 . 
Đường thẳng BH đi qua B 3;0 và nhận AC  5;6 làm véctơ pháp tuyến. Suy ra phương
trình đường thẳng BH là: 5x  6y 15  0 .
x  6 y  3  0  5 
Ta có H  AH  BH  Tọa độ H là nghiệm của hệ   H 2; .  
5x  6 y 15  0   6  5
Do đó a  2;b   6ab  10 . 6 N 5;- ( 4) A -4; ( 8) D I B C c;-2c ( -5) M Câu 238. Chọn C Gọi I  ;
a b là trung điểm BD  
Có BAD  BND  9 
0 . Suy ra BAND nội tiếp đường tròn đường kính BD , tâm I 2 2 2 2
Có IA  IN  a  4  b  8  a  5  b 
4  6a 8b13  0
Có I là trung điểm AC . Nên C 2a  4;2b   8
Có C  d . Suy ra 22a  4  2b  
8  5  0  4a  2b  5  0  3 a  
6a  8b 13  0   2 Giải hệ:    .
4a  2b  5  0  1 b    2
Có m n  2a  4  2b   8  8.
Câu 239. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 66
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A P B D N M C
* Ta chứng minh P là trung điểm của AC .
Thật vậy: do các tứ giác ABMN , ABCD là các tứ giác nội tiếp nên   
AMP  ABN  ACD
Lại do : AM // CD (cùng vuông góc với BC ) nên    
ACD  CAM  PAM  PMA  P
 AM cân tại P  PA  PM . Đồng thời PC 
M cân tại P nên PC  PM
 PA  PC hay P là trung điểm của AC . 
- Ta có : MN  2;  2  đường thẳng MN có phương trình: x  y  4  0  5 x 
x  y 1  0   2  5 3 
Điểm P có tọa độ là nghiệm của hệ     P  ;  
x  y  4  0 3   2 2   y    2
- Do A AC : x  y 1  0  A  a; a   1 (với a  2 ) 2 2 2  5   5  25  5  25
- Do PA  PM  a   a    a          2   2  2  2  4  5 5 a    a  5 2 2   
 a  0  A   0;  1  C  5; 4 5 5 a  0 a      2 2
- Do BC đi qua M 0; 4 và C 5; 4 nên BC có phương trình: y  4  0 . 
- Lại có: AN  2;3 là vectơ pháp tuyến của BD nên phương trình BD là: 2x  3y 10  0 .  y  4  0 x  1
Tọa độ điểm B là nghiệm của hệ phương trình:     B   1  ; 4 .
2x  3y 10  0 y  4    5 3  Vậy P ; , A   0;  1 , B  1  ; 4 .  2 2 
Câu 240. Chọn D Cách 1:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 67
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A E M B D C 5
 x  y  2  0 x  1
Ta có A  AB  AC      A1;3
x  5 y 14  0 y  3  
Dễ chứng minh được AM  MC  Phương trình MC: 4x  7 y  4  0
4x  7 y  4  0 x  6
C  MC  AC      C 6;4
x  5y 14  0 y  4   Vậy OC  52
Chứng minh AM  MC
PP1: Dùng phương pháp véc tơ.  
   
   
    * M .
A MC  MD  DAMB  BC  M . D BC  . DA MB  2 .
MD DC  DE.MB
   
   
* MD.DC  DE.MB  MD.BD  DE.MB     M . D BD DM   * MD BD  cos , =cosMDB   2
 MD.BD  MD DM .DB DB     DE.MB ME   * DE MB  cos ,  cosMED    2
 DE.MB   ME.MB   MD DE.MB DE   Do đó M .
A MC = 0 nên MA  MC . PP2: A H E M I B D C
Vẽ hình chữ nhật ADCF (1)
Dễ thấy tứ giác AHDB là hình bình hành vì AH / /B ;
D AH  BD
Nên BH qua trung điểm E của AD    90o HMD (2)
Từ (1) và (2) ta có 5 điểm ,
A M , D, C, F cùng thuộc đường tròn đường kính AC.  Nên  90o AMC  AM  MC . Cách 2:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 68
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ta có: A  AB  AC  A1;3 . 2 MB DB   
Giả sử DB  kDE k  0 2    k 2
 MB  k MC  0 2 ME DE 2  1  k   DM  DB  DE 2 2 k 1 k 1
     2 1
 k  2 
Ta có: MA  DA  DM  2DE  DM   DB  DE . 2 2 k 1 k 1
     2 2 k  2  k 
MC  DC  DM  DB  DM   DB  DE . 2 2 k 1 k 1 2   k k   2 2 k  2 2 2  2  . MA MC  DB 
ED  0  MA  MC . 2 2 k 1 k 1   4 7  Lại có: AM  ;  
  MC : 4x  7 y  4  0 .  5 5 
Vậy C  MC  AC  C 6; 4  OC  52 .
Câu 241. Chọn B A N M I B H D C
Đường thẳng chứa cạnh BC có phương trình: x  5 y  3 
 2x  y  7  0 17 1  5   3 5 5  17 1 
Đường thẳng chứa đường cao AH của tam giác đi qua H ;    có véc tơ pháp tuyên  5 5    8 16  8  17  16  1  HD ;   có phương trình: x   y 
 0  x  2 y  3  0     .  5 5  5  5  5  5 
Gọi B  x ; y , vì M là trung điểm của AB nên Ax ; 2  y . 0 0  0 0 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 69
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Ta có: B  BC  2x  y  7  0 1 0 0  
A AH  x  2 2  y
 3  0  x  2 y 1  0 2 0  0  0 0   Từ   1 và 2 ta có hệ:
2x  y  7  0 x  3 0 0 0     A 3  ;3
x  2 y 1  0 y  1   0 0  0 
Gọi u a b  2 2 ;
a  b  0 là véc tơ chỉ phương của đường thẳng AC  
+) AM 3; 2, AD 8;0
Đường thẳng AD là phân giác trong góc A nên:        
BAD  CAD  cos BAD  cos CAD  cos  AM; AD  cos A ; D u 24 8a 2 2  
 3 a  b  a 13 2 2 13.8 8 a  b  3 a  b  2 2 2
 4a  9b   3 a   b  2 3  
Với a   b . Chọn b  2  a  3  u 3; 2 (loại vì cùng phương với AM ) 2 3  x  3   3t Với a 
b . Chọn b  2  a  3  u 3; 2 . Đường thẳng AC có phương trình:  2 y  3  2t 
Điểm C là giao điểm của AC và BC nên có tọa độ là nghiệm của hệ:
2x  y  7  0  6
  6t  3  2t  7  0 t   4    x  3   3t  x  3   3t
 x  9  C 9;1  1 .  y 3 2t  y 3 2t      y  11   
DẠNG 7. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN DIỆN TÍCH
Câu 242. Chọn A
Đường thẳng  :5x  3 y  15 cắt các trục tọa độ tại các điểm A 3;0 , B 0;5 . 1 15
Ta có OA  3 , OB  5 . Khi đó S  O . A OB   7, 5 . OAB 2 2
Câu 243. Chọn A
d : y  mx  4 , d : y  mx  4 . 1 2
d , d cắt nhau cùng cắt trục hoành khi m  0 . 1 2  4   4  Gọi A ; 0   , B  ; 0 
 lần lượt là giao điểm của d , d và trục hoành. 1 2  m   m 
Phương trình hoành độ giao điểm của d , d : mx  4  mx  4  x  0 . 1 2
Gọi C là giao điểm của d và d thì C 0; 4   . 1 2 1 8 S 
d C,Ox.AB , có d C,Ox  y  4 , AB  x  x  . ABC 2 C A B m
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 70
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 8 16  S  .4.  . ABC 2 m m 16 Có S  8   8  m  2 , *
m   m  1 . Vậy S    1 . ABC m Câu 244.
Hướng dẫn giải. Chọn D
Vì đường thẳng d đi qua điểm I 1;3 nên ta có: 3  a  b   1 .  b 
Đường thẳng d : y  ax  b cắt trục Ox, Oy lần lượt là A  ; 0 , B  
0;b,a  0.  a  2 1 1 b 1 b Theo giả thiết S  O . A OB  . b   6 OAB 2. 2 2 a 2 a Từ phương trình  
1  a  3  b thay vào phương trình 2 : 2 2 b  12 b
3  b, b  3 2
 12  b  12 3  b   2 3  b
b  12 3  b , b  3 
b  6  6 2 2
b 12b  36  0, b  3  b  3  
 b  6  6 2 2 
b 12b  36  0, b  3   b  6 b  3 
Với b  6 ta được a  3  .
Vậy phương trình d : y  3x  6. b  6  6 2
Ghi chú: Với 
thì nhìn vào 4 đáp án không có nên ta không cần tìm nữa. b  6  6 2 
Câu 245. Chọn D.
Gọi I là giao điểm của  và BC .
Gọi H là hình chiếu của A trên BC . 1 1
Theo đề bài ta có: S  S  .AH.IB 
.AH.IC  IB  IC . AIB AIC 2 2
 I là trung điểm của BC  I 1;3 . 
 AI  2;6 . 
Đường thẳng  đi qua A và nhận vectơ n  3  ;1 làm vectơ pháp tuyến.
Phương trình đường thẳng  là 3 x  
1   y  3  0  3x  y  0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 71
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 246. Chọn C
Gọi đường thẳng d cắt tia Ox , Oy lần lượt tại Aa;0 và B 0;b;a,b  0 x y  d  :   1 a b 2 1
Vì d  qua M 2;  1    1 a b 2  1  2  ab  8 ab 1 1
Ta có diện tích tam giác vuông OAB tại O là S  .O . A OB  . . a b  4 2 2 2 1
Diện tích tam giác vuông OAB đạt giá trị nhỏ nhất S  4    a  2b a b 2 1  
 1  b  2,a  4 2b b x y  d  : 
 1  x  2 y  4  0 . 4 2
Câu 247. Chọn C 1 6
d đi qua M  1  ; 6    1 (1). a b
Đường thẳng cắt tia Ox tại (
A a; 0), a  0  OA  a.
Đường thẳng cắt tia Oy tại B(0;b), b  0  OB  . b 1 1 O
 AB vuông tại O nên có diện tích là . OA OB  a . b 2 2 1 Theo đề
ab  4  ab  8 (2). 2 Từ  
1 ,2 suy ra: a  2;b  4  S  a  2b  10 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 72
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 10
PHƯƠNG TRÌNH ĐƯỜNG TRÒN 0H3-2 Contents
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN ....................................................................................... 1
DẠNG 2. TÌM TỌA ĐỘ TÂM, BÁN KÍNH ĐƯỜNG TRÒN ....................................................................................... 2
DẠNG 3. VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN ...................................................................................................... 2
Dạng 3.1 Khi biết tâm và bán kính ............................................................................................................................... 2
Dạng 3.2 Khi biết các điểm đi qua ............................................................................................................................... 3
Dạng 3.3 Sử dụng điều kiện tiếp xúc ........................................................................................................................... 4
DẠNG 4. TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN ...................................................................... 5
Dạng 4.1. Phương trình tiếp tuyến ............................................................................................................................... 5
Dạng 4.2 Bài toán tương giao .......................................................................................................................................... 6
DẠNG 5. CÂU HỎI MIN-MAX ..................................................................................................................................... 8
PHẦN B. LỜI GIẢI THAM KHẢO ................................................................................................................................ 9
DẠNG 1. NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN ....................................................................................... 9
DẠNG 2. TÌM TỌA ĐỘ TÂM, BÁN KÍNH ĐƯỜNG TRÒN ..................................................................................... 10
DẠNG 3. VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN .................................................................................................... 11
Dạng 3.1 Khi biết tâm và bán kính ............................................................................................................................. 11
Dạng 3.2 Khi biết các điểm đi qua ............................................................................................................................. 11
Dạng 3.3 Sử dụng điều kiện tiếp xúc ......................................................................................................................... 13
DẠNG 4. TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN .................................................................... 15
Dạng 4.1. Phương trình tiếp tuyến ............................................................................................................................. 15
Dạng 4.2 Bài toán tương giao ........................................................................................................................................ 18
DẠNG 5. CÂU HỎI MIN-MAX ................................................................................................................................... 24 PHẦN A. CÂU HỎI
DẠNG 1. NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN Câu 1.
Tìm tất cả các giá trị của tham số m để phương trình 2 2
x  y  2m  2 x  4my 19m  6  0 là
phương trình đường tròn. A. 1  m  2. B. m  2  hoặc m  1  . C. m  2
 hoặc m  1. D. m  1 hoặc m  2 . Câu 2.
Trong mặt phẳng Oxy , phương trình nào sau đây là phương trình của đường tròn?
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. 2 2
x  2 y  4x  8 y 1  0 . B. 2 2
x  y  4x  6 y 12  0 . C. 2 2
x  y  2x  8y  20  0 . D. 2 2
4x  y 10x  6 y  2  0 . Câu 3.
Phương trình nào sau đây là phương trình của đường tròn? A. 2 2
2x  y  6x  6 y  8  0 . B. 2 2
x  2 y  4x  8 y 12  0 . C. 2 2
x  y  2x  8y 18  0 . D. 2 2
2x  2 y  4x  6 y 12  0 . Câu 4.
(Cụm liên trường Hải Phòng-L1-2019) Phương trình nào sau đây là phương trình của một đường tròn? A. 2 2
x  y 4xy  2x 8y 3  0 . B. 2 2
x  2y 4x 5y 1   0. C. 2 2 x  y 1
 4x 2y 2018  0 . D. 2 2
x  y 4x 5y  2  0 . Câu 5.
(THPT Quỳnh Lưu- Nghệ An- 2019) Cho phương trình 2 2
x  y  2mx  4 m  2 y  6  m  0 (1)
. Điều kiện của m để (1) là phương trình của đường tròn. m  1 m  1 A. m  2 . B.  .
C. 1  m  2 . D.  . m  2  m  2 
DẠNG 2. TÌM TỌA ĐỘ TÂM, BÁN KÍNH ĐƯỜNG TRÒN Câu 6.
Trong mặt phẳng Oxy , đường tròn C 2 2
: x  y  4x  6y 12  0 có tâm là. A. I  2  ; 3   . B. I 2;  3 .
C. I 4;6 . D. I  4  ; 6   . Câu 7. Đường tròn 2 2
x  y  10 y  24  0 có bán kính bằng bao nhiêu? A. 49 . B. 7 . C. 1. D. 29 . 2 2 Câu 8.
Xác định tâm và bán kính của đường tròn C  :  x   1
  y  2  9. A. Tâm I  1
 ; 2, bán kính R  3 . B. Tâm I  1
 ; 2, bán kính R  9 .
C. Tâm I 1; 2
 , bán kính R  3 .
D. Tâm I 1; 2
 , bán kính R  9 . Câu 9.
(ĐỀ THI THỬ ĐỒNG ĐẬU-VĨNH PHÚC LẦN 01 - 2018 – 2019) Tìm tọa độ tâm I và bán
kính R của đường tròn C  : 2 2
x  y  2x  4 y  1  0 . A. I  1  ; 2 ; R  4 . B. I 1; 2   ; R  2 .
C. I 1; 2 ; R  5 . D. I 1; 2 ; R  4 . 2 2
Câu 10. Trong mặt phẳng Oxy , cho đường tròn C  :  x  2   y  3  9 . Đường tròn có tâm và bán kính là
A. I 2;3, R  9 .
B. I 2; 3, R  3 . C. I  3  ; 2, R  3 . D. I  2  ;3, R  3 . 2 2
Câu 11. Tìm tọa độ tâm I và tính bán kính R của đường tròn (C) :  x  2   y  5  9 .
A. I (2;5), R  81. .
B. I (2; 5), R  9..
C. I (2; 5), R  3..
D. I (2;5), R  3.
Câu 12. Đường tròn C  2 2
: x  y  2x  4 y  3  0 có tâm I , bán kính R là
A. I 1; 2, R  2 .
B. I 1; 2, R  2 2 . C. I 1;  2, R  2 . D. I 1;  2, R  2 2 .
DẠNG 3. VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN
Dạng 3.1 Khi biết tâm và bán kính
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 13. Phương trình đường tròn có tâm I 1; 2 và bán kính R  5 là A. 2 2
x  y  2x  4 y  20  0 . B. 2 2
x  y  2x  4 y  20  0 . C. 2 2
x  y  2x  4 y  20  0 . D. 2 2
x  y  2x  4 y  20  0 .
Câu 14. Đường tròn tâm I  1
 ; 2 , bán kính R  3 có phương trình là A. 2 2
x  y  2x  4y  4  0 . B. 2 2
x  y  2x  4 y  4  0 . C. 2 2
x  y  2x  4y  4  0 . D. 2 2
x  y  2x  4y  4  0 .
Câu 15. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Phương trình nào sau đây là
phương trình của đường tròn tâm I  1
 ; 2 , bán kính bằng 3 ? 2 2 2 2 A.  x  
1   y  2  9 . B.  x   1
  y  2  9 . 2 2 2 2 C.  x   1
  y  2  9 . D.  x   1
  y  2  9 .
Dạng 3.2 Khi biết các điểm đi qua
Câu 16. Đường tròn C  đi qua hai điểm A1  ;1 , B 5; 
3 và có tâm I thuộc trục hoành có phương trình là
A.  x  2 2 4  y  10 .
B.  x  2 2 4  y  10 .
C.  x  2 2 4
 y  10 . D.  x  2 2 4  y  10 .
Câu 17. (KSNLGV - THUẬN THÀNH 2 - BẮC NINH NĂM 2018 - 2019) Trong mặt phẳng với hệ tọa
độ Oxy , tìm tọa độ tâm I của đường tròn đi qua ba điểm A0; 4 , B 2; 4 , C 2;0 . A. I 1  ;1 .
B. I 0;0 .
C. I 1; 2 .
D. I 1;0 .
Câu 18. Cho tam giác ABC có A1;  
1 , B 3; 2, C 5; 5
  . Toạ độ tâm đường tròn ngoại tiếp tam giác ABC là  47 13   47 13   47 13   47 13  A. ;    . B. ;   . C.  ;    . D.  ;   .  10 10   10 10   10 10   10 10 
Câu 19. Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A1; 2 , B 5; 2 , C 1; 3
  có phương trình là. A. 2 2
x  y  25x 19 y  49  0 . B. 2 2
2x  y  6x  y  3  0 . C. 2 2
x  y  6x  y 1  0 . D. 2 2
x  y  6x  xy 1  0 .
Câu 20. Lập phương trình đường tròn đi qua hai điểm A3;0, B 0; 2 và có tâm thuộc đường thẳng
d : x  y  0 . 2 2 2 2  1   1  13  1   1  13 A. x   y       . B. x   y       .  2   2  2  2   2  2 2 2 2 2  1   1  13  1   1  13 C. x   y       . D. x   y       .  2   2  2  2   2  2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  5 8 
Câu 21. Cho tam giác ABC biết H 3; 2 , G ; 
 lần lượt là trực tâm và trọng tâm của tam giác, đường  3 3 
thẳng BC có phương trình x  2y  2  0 . Tìm phương trình đường tròn ngoại tiếp tam giác ABC ? 2 2 A.  x   1   y   1  20 . 2 2
B.  x  2   y  4  20 . 2 2 C.  x  
1   y  3  1. 2 2 D.  x   1
  y  3  25 .
Câu 22. (Nông Cống - Thanh Hóa - Lần 1 - 1819) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có
trực tâm H , trọng tâm G  1
 ;3 . Gọi K , M , N lần lượt là trung điểm của AH , AB, AC . Tìm
phương trình đường tròn ngoại tiếp tam giác ABC biết đường tròn ngoại tiếp tam giác KMN là C 2 2
: x  y  4x  4 y 17  0 . 2 2 A.  x  
1   y  5  100 . 2 2 B.  x  
1   y  5  100 . 2 2 C.  x  
1   y  5  100 . 2 2 D.  x  
1   y  5  100 .
Câu 23. (THPT TRIỆU THỊ TRINH - LẦN 1 - 2018) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC
có trực tâm O . Gọi M là trung điểm của BC ; N , P lần lượt là chân đường cao kẻ từ B và C . 2 2  1  25
Đường tròn đi qua ba điểm M , N , P có phương trình là T  :  x   1  y     . Phương  2  4
trình đường tròn ngoại tiếp tam giác ABC là: 2 2 A.  x  
1   y  2  25 .
B. x   y  2 2 1  25 . 2 2
C. x   y  2 2 1  50 .
D.  x  2   y   1  25 .
Dạng 3.3 Sử dụng điều kiện tiếp xúc
Câu 24. (THPT Cộng Hiền - Lần 1 - 2018-2019) Trong mặt phẳng tọa độ Oxy , phương trình của đường
tròn có tâm là gốc tọa độ O và tiếp xúc với đường thẳng  : x  y  2  0 là A. 2 2 x  y  2 . B. 2 2 x  y  2 . 2 2 2 2 C. x   1  y   1  2 . D. x   1  y   1  2 .
Câu 25. (Trường THPT Chuyên Lam Sơn_2018-2019) Trong mặt phẳng tọa độ Oxy , cho đường tròn
S  có tâm I nằm trên đường thẳng y  x , bán kính R  3 và tiếp xúc với các trục tọa độ. Lập
phương trình của  S  , biết hoành độ tâm I là số dương. 2 2 2 2
A.  x  3   y  3  9 .
B.  x  3   y  3  9 . 2 2 2 2
C.  x  3   y  3  9 .
D.  x  3   y  3  9 .
Câu 26. Một đường tròn có tâm I 3; 4 tiếp xúc với đường thẳng  :3x  4 y 10  0 . Hỏi bán kính đường
tròn bằng bao nhiêu?
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 5 3 A. . B. 5 . C. 3 . D. . 3 5
Câu 27. Trong hệ trục tọa độ Oxy , cho điểm I 1 
;1 và đường thẳng d  :3x  4y  2  0 . Đường tròn tâm
I và tiếp xúc với đường thẳng d  có phương trình 2 2 2 2 A.  x   1   y   1
 5 . B.  x   1   y   1  25 . 2 2 2 2 1 C.  x   1   y   1
 1. D.  x   1   y   1  . 5
Câu 28. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Trên hệ trục tọa độ Oxy , cho đường tròn (C ) có tâm I  3
 ;2 và một tiếp tuyến của nó có phương trình là 3x  4 y  9  0 . Viết phương trình của đường tròn (C ) . 2 2 2 2
A.  x  3   y  2  2 .
B.  x  3   y  2  2 . 2 2 2 2
C.  x  3   y  2  4
D.  x  3   y  2  4 .
Câu 29. Trên mặt phẳng toạ độ Oxy , cho các điểm A3;0 và B 0; 4 . Đường tròn nội tiếp tam giác OAB có phương trình A. 2 2
x  y  1. B. 2 2
x  y  4x  4  0 . 2 2 C. 2 2 x  y  2 . D.  x   1   y   1  1 .
Câu 30. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho hai điểm A3;0 , B 0;4 . Đường tròn nội tiếp
tam giác OAB có phương trình là A. 2 2 x  y  1 . B. 2 2
x  y  2x  2 y  1  0 . C. 2 2
x  y  6x  8 y  25  0 . D. 2 2 x  y  2 .
DẠNG 4. TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Dạng 4.1. Phương trình tiếp tuyến
Câu 31. Đường tròn 2 2
x  y 1  0 tiếp xúc với đường thẳng nào trong các đường thẳng dưới đây?
A. 3x  4 y  5  0
B. x  y  0
C. 3x  4 y  1  0
D. x  y  1  0
Câu 32. Đường tròn nào sau đây tiếp xúc với trục Ox: A. 2 2
x  y 10x  0 . B. 2 2
x  y  5  0 . C. 2 2
x  y 10x  2 y 1  0 . D. 2 2
x  y  6x  5y  9  0 .
Câu 33. Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn C  2 2
: x  y  2x  4 y  3  0 . Viết phương
trình tiếp tuyến d của đường tròn (C ) biết tiếp tuyến đó song song với đường thẳng
 : 3x  4 y  1  0 .
A. 3x  4 y  5 2 11  0 ; 3x  4 y  5 2  11  0 .
B. 3x  4 y  5 2 11  0 , 3x  4 y  5 2 11  0 .
C. 3x  4 y  5 2 11  0 , 3x  4 y  5 2  11  0 .
D. 3x  4 y  5 2 11  0 , 3x  4 y  5 2 11  0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 34. Cho đường tròn C  2 2
: x  y  2x  4 y  4  0 và điểm A1;5 . Đường thẳng nào trong các đường
thẳng dưới đây là tiếp tuyến của đường tròn C  tại điểm A .
A. y  5  0 .
B. y  5  0 .
C. x  y  5  0 .
D. x  y  5  0 .
Câu 35. Cho đường tròn C 2 2
: x  y  4  0 và điểm A 1
 ; 2 . Đường thẳng nào trong các đường thẳng
dưới đây đi qua A và là tiếp tuyến của đường tròn C ?
A. 4x  3y 10  0 .
B. 6x  y  4  0 .
C. 3x  4 y  10  0 .
D. 3x  4 y  11  0 . 2 2
Câu 36. Trong mặt phẳng Oxy , cho đường tròn C  :  x   1
  y  4  4 . Phương trình tiếp tuyến với
đường tròn C  song song với đường thẳng  : 4x  3y  2  0 là
A. 4x  3 y  18  0 .
B. 4x  3y 18  0 .
C. 4x  3 y  18  0; 4x  3 y  2  0 .
D. 4x  3y 18  0; 4x  3y  2  0 . Câu 37. Số tiếp tuyến chung của 2 đường tròn C 2 2
: x  y  2x  4 y 1  0 và C  2 2
' : x  y  6x  8y  20  0 là A. 1. B. 2 . C. 4 . D. 3 .
Câu 38. (THI HK1 LỚP 11 THPT VIỆT TRÌ 2018 - 2019) Viết phương trình tiếp tuyến của đường tròn 2 2
(C) : (x  2)  ( y  4)  25 , biết tiếp tuyến vuông góc với đường thẳng d : 3x  4 y  5  0 .
A. 4x  3 y  29  0 .
B. 4x  3 y  29  0 hoặc 4x  3 y  21  0 .
C. 4x  3y  5  0 hoặc 4x  3y  45  0
D. 4x  3 y  5  0 hoặc 4x  3 y  3  0 .
Câu 39. (ĐỀ KT NĂNG LỰC GV THUẬN THÀNH 1 BẮC NINH 2018-2019) Trong mặt phẳng tọa độ
Oxy, cho đường tròn C có phương trình 2 2
x  y  2x  2 y  3  0 . Từ điểm A1  ;1 kẻ được bao
nhiêu tiếp tuyến đến đường tròn C A. 1. B. 2. C. vô số. D. 0. 2 2
Câu 40. Trong mặt phẳng Oxy , cho đường tròn C  :  x 1   y  4  4 . Phương trình tiếp tuyến với
đường tròn C  , biết tiếp tuyến đó song song với đường thẳng  : 4x  3y  2  0 là
A. 4x  3y 18  0 và 4x  3 y  2  0 .
B. 4x  3y 18  0 và 4x  3y  2  0 . C. 4
 x  3y 18  0 và 4x  3y  2  0 . D. 4
 x  3y 18  0 và 4x  3y  2  0 . 2 2
Câu 41. Trên mặt phẳng toạ độ Oxy , cho điểm P  3  ; 2
  và đường tròn C  :  x  3   y  4  36 . Từ
điểm P kẻ các tiếp tuyến PM và PN tới đường tròn C  , với M , N là các tiếp điểm. Phương
trình đường thẳng MN là
A. x  y  1  0 .
B. x  y 1  0 .
C. x  y 1  0 .
D. x  y 1  0 .
Câu 42. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M (3;1) và đường tròn C  2 2
: x  y  2x  6 y  6  0
. Gọi T , T là các tiếp điểm của các tiếp tuyến kẻ từ M đến (C). Tính khoảng cách từ O đến đường 1 2 thẳng T T . 1 2 3 A. 5 . B. 5 . C. . D. 2 2 . 5
Dạng 4.2 Bài toán tương giao
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 43. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai đường tròn C , C có phương trình lần lượt 1   2  là 2 2 2 2
(x 1)  ( y  2)  9 và (x  2)  ( y  2)  4 . Khẳng định nào dưới đây là sai?
A. Đường tròn C có tâm I 1  ; 2 
và bán kính R  3 . 1   1  1
B. Đường tròn C có tâm I 2; 2 và bán kính R  2 . 2   2  2
C. Hai đường tròn C , C không có điểm chung. 1   2 
D. Hai đường tròn C , C tiếp xúc với nhau. 1   2 
Câu 44. Tìm giao điểm 2 đường tròn 2 2
(C ) : x  y  4  0 và 2 2
(C ) : x  y  4x  4 y  4  0. 1 2 A. 2; 2 và  2  ; 2
  . B. 0; 2 và 0; 2
  . C. 2;0 và  2
 ; 0 . D. 2;0 và 0; 2.
Câu 45. Trong mặt phẳng với hệ trục Oxy , cho hai đường tròn C  x  2 2 : 1  y  4 và
C  x  2   y  2 : 4 3
 16 cắt nhau tại hai điểm phân biệt A và B . Lập phương trình đường thẳng AB
A. x  y  2  0 .
B. x  y  2.  0
C. x  y  2  0 .
D. x  y  2  0 . 2 2
Câu 46. Cho đường thẳng  :3x  4 y 19  0 và đường tròn C : x   1   y  
1  25 . Biết đường thẳng
 cắt C  tại hai điểm phân biệt A và B , khi đó độ dài đọan thẳng AB là A. 6. B. 3. C. 4. D. 8.
Câu 47. Trong mặt phẳng tọa độ Oxy cho đường tròn C  có tâm I 1; 
1 bán kính R  5 . Biết rằng đường
thẳng d  : 3x  4y  8  0 cắt đường tròn C  tại hai điểm phân biệt ,
A B . Tính độ dài đoạn thẳng AB . A. AB  8 . B. AB  4 . C. AB  3. . D. AB  6 .
Câu 48. Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường tròn C  có phương trình
 x  2   y  2 2 2
 4 và đường thẳng d :3x  4 y  7  0 . Gọi ,
A B là các giao điểm của đường
thẳng d với đường tròn C  . Tính độ dài dây cung AB . A. AB  3 . B. AB  2 5 .
C. AB  2 3 . D. AB  4 .
Câu 49. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm A3 
;1 , đường tròn C  2 2
: x  y  2x  4 y  3  0 .
Viết phương trình tổng quát của đường thẳng d đi qua A và cắt đường tròn C  tại hai điểm B ,
C sao cho BC  2 2 .
A. d : x  2 y  5  0 .
B. d : x  2 y  5  0 . C. d : x  2 y  5  0 . D. d : x  2 y  5  0 .
Câu 50. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai đường tròn C , C có phương trình lần lượt 1   2  là 2 2 2 2
(x 1)  ( y  2)  9 và (x  2)  ( y  2)  4 . Viết phương trình đường thẳng d  đi qua gốc tọa
độ và tạo với đường thẳng nối tâm của hai đường tròn một góc bằng 45 .
A. d  : x  7 y  0 hoặc d : 7x  y  0 .
B. d  : x  7 y  0 hoặc d : 7x  y  0 .
C. d  : x  7 y  0   
hoặc d : 7x  y  0 .
D. d : x  7 y  0 hoặc d : 7x  y  0 .
Câu 51. (KSCL LẦN 1 CHUYÊN LAM SƠN - THANH HÓA_2018-2019) Trong mặt phẳng tọa độ Oxy
cho điểm I 1;2 và đường thẳng d  : 2x  y  5  0. Biết rằng có hai điểm M , M d 1 2 thuộc   sao
cho IM  IM  10. Tổng các hoành độ của M M 1 2 1 và 2 là
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 7 14 A. . B. . C. 2. D. 5. 5 5
Câu 52. (NGÔ GIA TỰ LẦN 1_2018-2019) Trong hệ tọa độ Oxy, cho đường tròn C  có phương trình: 2 2
x  y  4x  2 y 15  0. I là tâm C  , đường thẳng d đi qua M 1; 3
  cắt C  tại , A B. Biết
tam giác IAB có diện tích là 8. Phương trình đường thẳng d là: x  by  c  0. Tính b  c A. 8. B. 2. C. 6. D. 1.
Câu 53. (KSCL LẦN 1 CHUYÊN LAM SƠN - THANH HÓA_2018-2019) Trong mặt phẳng Oxy cho
tam giác ABC có đỉnh A5;5 , trực tâm H  1
 ;13 , đường tròn ngoài tiếp tam giác có phương trình 2 2
x  y  50 . Biết tọa độ đỉnh C  ;
a b , với a  0 . Tổng a  b bằng A. 8  . B. 8 . C. 6 . D. 6  .
Câu 54. (Nông Cống - Thanh Hóa - Lần 1 - 1819) Trong mặt phẳng Oxy , cho A
 BC nội tiếp đường tròn
tâm I 2; 2 , điểm D là chân đường phân giác ngoài của góc 
BAC . Đường thẳng AD cắt đường
tròn ngoại tiếp  ABC tại điểm thứ hai là M (khác A). Biết điểm J  2
 ; 2 là tâm đường tròn ngoại
tiếp  ACD và phương trình đường thẳng CM là: x  y  2  0. Tìm tổng hoành độ của các đỉnh ,
A B, C của tam giác ABC . 9 12 3 6 A. . B. . C. . D. . 5 5 5 5
Câu 55. Trong mặt phẳng tọa độ Oxy , cho hai đường thẳng : x  3y  8  0 ;  : 3x  4 y 10  0
và điểm A2 
;1 . Đường tròn có tâm I a;b thuộc đường thẳng ,đi qua A và tiếp xúc với
đường thẳng  . Tính a  b . A. 4  . B. 4 . C. 2 . D. 2  .
Câu 56. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : 3x  4 y 1  0 và điểm I 1;  2 . Gọi
C là đường tròn có tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện
tích bằng 4. Phương trình đường tròn C  là 2 2 2 2 A.  x  
1   y  2  8. B.  x  
1   y  2  20 . 2 2 2 2 C.  x  
1   y  2  5. D.  x  
1   y  2 16 . DẠNG 5. CÂU HỎI MIN-MAX
Câu 57. Cho đường tròn C  2 2
: x  y  2x  4 y  4  0 và điểm M 2; 
1 . Dây cung của C  đi qua điểm M
có độ dài ngắn nhất là A. 6 . B. 7 . C. 3 7 . D. 2 7 .
Câu 58. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(0; 3), B(4;1) và điểm M thay đổi thuộc đường tròn 2 2
(C) : x  ( y 1)  4 . Gọi P
là giá trị nhỏ nhất của biểu thức P  MA  2MB . Khi đó ta có P min min
thuộc khoảng nào dưới đây? A. 7, 7;8  ,1 . . B. 7,3;7, 7.. C. 8,3;8,5.. D. 8,1;8,  3 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 59. Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn C  2 2
: x  y  2x  4 y  3  0 . Tìm tọa độ
điểm M  x ; y nằm trên đường tròn C sao cho T  x  y đạt giá trị lớn nhất. 0 0  0 0
A. M 2;3 . B. M 0  ;1 . C. M 2;  1 .
D. M 0;3 .
Câu 60. Trong mặt phẳng Oxy , cho điểm M nằm trên đường tròn C  2 2
: x  y  8x  6 y 16  0 . Tính độ
dài nhỏ nhất của OM ? A. 3 . B. 1. C. 5 . D. 2 . 2 2
Câu 61. Gọi I là tâm của đường tròn C :  x   1   y   1
 4 . Số các giá trị nguyên của m để đường
thẳng x  y  m  0 cắt đường tròn C tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích lớn nhất là A. 1. B. 3 . C. 2 . D. 0 .
Câu 62. Điểm nằm trên đường tròn C  2 2
: x  y  2x  4 y 1  0 có khoảng cách ngắn nhất đến đường
thẳng d : x  y  3  0 có toạ độ M  ;
a b . Khẳng định nào sau đây đúng?
A. 2a  b .
B. a  b .
C. 2a  b .
D. a  b .
Câu 63. Cho tam giác ABC có trung điểm của BC là M 3; 2 , trọng tâm và tâm đường tròn ngoại tiếp tam  2 2 
giác lần lượt là G ; , I  
1;2 . Tìm tọa độ đỉnh C , biết C có hoành độ lớn hơn 2 .  3 3  A. C 9;  1 . B. C 5  ;1 .
C. C 4;2 . D. C 3; 2   .
Câu 64. (THPT Yên Mỹ Hưng Yên lần 1 - 2019) Trong mặt phẳng tọa độ Oxy , cho đường tròn C 2 2
: x  y  2x  4 y  25  0 và điểm M 2; 
1 . Dây cung của C  đi qua M có độ dài ngắn nhất là: A. 2 7 . B. 16 2 . C. 8 2 . D. 4 7 .
Câu 65. (Trường THPT Chuyên Lam Sơn_2018-2019) Cho các số thực a, b, c, d thay đổi, luôn thỏa mãn  2 2
a  2  b  2 1 2
 1 và 4c  3d  23  0 . Giá trị nhỏ nhất của biểu thức P  a  c  b  d  là: A. P  28 . B. P  3. C. P  4 . D. P  16 . min min min min 2 2
Câu 66. Trong mặt phẳng tọa độ Oxy, cho đường tròn C  :  x  
1   y  2  4 và các đường thẳng
d : mx  y  m 1  0, d : x  my  m 1  0. Tìm các giá trị của tham số m để mỗi đường thẳng 1 2
d , d cắt C  tại 2 điểm phân biệt sao cho 4 điểm đó lập thành 1 tứ giác có diện tích lớn nhất. Khi 1 2
đó tổng của tất cả các giá trị tham số m là: A. 0. B. 1. C. 3. D. 2.
PHẦN B. LỜI GIẢI THAM KHẢO
DẠNG 1. NHẬN DẠNG PHƯƠNG TRÌNH ĐƯỜNG TRÒN Câu 1. Chọn D Ta có 2 2
x  y  2m  2 x  4my 19m  6  0   1
 a  m  2; b  2 ;
m c  19m  6. Phương trình  
1 là phương trình đường tròn 2 2
 a  b  c  0
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2
 5m 15m 10  0  m  1 hoặc m  2 . Câu 2. Chọn B
Để là phương trình đường tròn thì điều kiện cần là hệ số của 2 x và 2
y phải bằng nhau nên loại
được đáp án A và D. 2 2 Ta có: 2 2
x  y  2x  8 y  20  0   x  
1   y  4  3  0 vô lý. 2 2 Ta có: 2 2
x  y  4x  6 y 12  0   x  2   y  3  25 là phương trình đường tròn tâm I 2; 
3 , bán kính R  5 . Câu 3. Chọn D Biết rằng 2 2
x  y  2ax  2by  c  0 là phương trình của một đường tròn khi và chỉ khi 2 2
a  b  c  0 .
Ta thấy phương trình trong phương án A và B có hệ số của 2 x , 2
y không bằng nhau nên đây
không phải là phương trình đường tròn.
Với phương án C có 2 2
a  b  c 116 18  0 nên đây không phải là phương trình đường tròn.
Vậy ta chọn đáp án D . Câu 4. Chọn D
Phương án A: có tích xy nên không phải là phương trình đường tròn.
Phương án B: có hệ số bậc hai không bằng nhau nên không phải là phương trình đường tròn. 2 2 Phương án C: ta có 2 2
x  y 14x  2 y  2018  0  x  7  y  
1 1968  0 không tồn tại
x, y nên cũng không phải phương trình đường tròn. Còn lại, chọn D. Câu 5. Chọn B 2 2
x  y  2mx  4 m  2 y  6  m  0 (1) là phương trình của đường tròn khi và chỉ khi m  1
m2  2m  2 2   6  m 2
 0  5m 15m 10  0     . m  2 
DẠNG 2. TÌM TỌA ĐỘ TÂM, BÁN KÍNH ĐƯỜNG TRÒN Câu 6. Chọn A 2 2
Ta có phương trình đường tròn là:  x  2   y  3  25 .
Vậy tâm đường tròn là: I  2  ; 3   . Câu 7. Chọn B Đường tròn 2 2
x  y  10 y  24  0 có tâm I 0; 5 , bán kính 2 2 R 
0  5  24  7 . Câu 8. Chọn A Câu 9. Chọn B
C có tâm I 1; 2
  , bán kính R    2 2 1 2 1  2 .
Câu 10. Chọn B
Đường tròn C  có tâm I 2; 3 và bán kính R  3 .
Câu 11. Chọn D
Theo bài ra ta có tọa độ tâm I (2;5) và bán kính R  3 .
Câu 12. Chọn D 2
Tâm I 1;  2 , bán kính 2 R  1   2     3    8  2 2 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
DẠNG 3. VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN
Dạng 3.1 Khi biết tâm và bán kính
Câu 13. Chọn A 2 2
Phương trình đường tròn có tâm I 1; 2 và bán kính R  5 là  x     y   2 1 2  5 2 2
 x  2x 1 y  4 y  4  25 2 2
 x  y  2x  4 y  20  0 .
Câu 14. Chọn C Đường tròn tâm I  1  ; 2 , bán kính R  3 có phương trình là
 x  2   y  2 2 2 1 2
 9  x  y  2x  4 y  4  0 .
Câu 15. Chọn D 2 2
Phương trình đường tròn tâm I  1
 ; 2 và bán kính R  3 là:  x   1
  y  2  9 .
Dạng 3.2 Khi biết các điểm đi qua
Câu 16. Chọn B 2 2 Gọi I  ; x 0 Ox ; 2 2
IA  IB    x 2     x 2 1 1 5  3 2 2
 x  2x 11  x 10x  25  9
 x  4 . Vậy tâm đường tròn là I 4;0 và bán kính R  IA    2 2 1 4 1  10 .
Phương trình đường tròn C  có dạng  x  2 2 4  y  10 .
Câu 17. Chọn C
Giả sử phương trình đường tròn đi qua 3 điểm ,
A B,C có dạng C  2 2
: x  y  2ax  2by  c  0
Thay tọa độ 3 điểm A0; 4 , B 2; 4 , C 2;0 ta được: 8
 b  c  16  a  1   
4a  8b  c  20   b   2   C  2 2
: x  y  2x  4 y  0 . 4a c 4     c  0  
Vậy C  có tâm I 1; 2 và bán kính R  5 .
Câu 18. Chọn A Gọi I  ;
x y là tâm đường tròn ngoại tiếp tam giác ABC .  47    AI  BI     2 x
x 1   y  2 1
  x  32   y  22 2 2
4x  6 y  11   10 Ta có:        . 2 2  AI  CI  
 x  2   y  2   x  2   y  2
8x  8 y  48 13 1 1 5 5    y     10  47 13   I ;    .  10 10 
Câu 19. Chọn C
Phương trình đường tròn có dạng 2 2
x  y  2ax  2by  c  0 . Đường tròn này qua , A , B C nên a  3 1
  4  2a  4b  c  0    1
25  4 10a  4b  c  0  b    . 2 1  9 2a 6b c 0        c  1  
Vậy phương trình đường tròn cần tìm là 2 2
x  y  6x  y 1  0 .
Câu 20. Chọn A
A3;0 , B 0;2 , d : x  y  0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 11
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Gọi I là tâm đường tròn vậy I  ;
x x vì I  d . 1  1 1 2 2 2 2 
IA  IB    x 2 2 3
 x  x  2  x  6x  9  4x  4  x  . Vậy I ;    . 2  2 2  2 2  1   1  26 IA  3       
là bán kính đường tròn.  2   2  2 2 2  1   1  13
Phương trình đường tròn cần lập là: x   y       .  2   2  2
Câu 21. Chọn D
*) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC .  3  5   x  3   3    3  I  2  3   x  1  HI  HG  I    . 2 3  8   y  3 y  2   2  I I    2   3 
(Do đó ta có thể chọn đáp án D luôn mà không cần tính bán kính).
*) Gọi M là trung điểm của BC  IM  BC  IM : 2x  y 1  0 .
2x  y  1  x  0
M  IM  BC      M 0;  1 . x  2 y  2  y  1   5   x  3. A   3  x  5
Lại có: MA  3MG  A    .  8   y  6 y 1  3. 1  A A      3 
Suy ra: bán kính đường tròn ngoại tiếp tam giác ABC là R  IA  5 . 2 2
Vậy phương trình đường tròn ngoại tiếp tam giác ABC là  x   1
  y  3  25 .
Câu 22. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 12
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Gọi E là trung điểm BC , J là tâm đường tròn ngoại tiếp A  BC . MK  BH KN  CH  
Ta có ME  AC  MK  ME  
1 , NE  AB  KN  NE 2 BH  AC   CH  AB  Từ  
1 ,2  KMEN là tứ giác nội tiếp đường tròn đường kính KE .
Đường tròn C  2 2
: x  y  4x  4 y 17  0 có tâm I  2
 ; 2 bán kính r  5  I là trung điểm KE .
KHEJ là hình bình hành  I là trung điểm JH  
x  2  3    x  1 J  1 2
Ta có: IJ  3IG  J     J 1;5 . y  2  3   y  5 J 3 2   J
Bán kính đường tròn ngoại tiếp A
 BC là R  JA  2IK  2r  10 . 2 2
Phương trình đường tròn ngoại tiếp A
 BC là:  x  
1   y  5  100 . Câu 23.
Ta có M là trung điểm của BC ; N , P lần lượt là chân đường cao kẻ từ B và C . Đường tròn đi
qua ba điểm M , N , P là đường tròn Euler. Do đó đường tròn ngoại tiếp tam giác ABC chính là
ảnh của đường tròn Euler qua phép vị tự tâm là O , tỷ số k  2 .
Gọi I và I  lần lượt là tâm đường tròn ngoại tiếp tam giác MNP và tam giác ABC .
Gọi R và R lần lượt là bán kính đường tròn ngoại tiếp tam giác MNP và tam giác ABC .  1    Ta có I 1;  
 và do đó OI   2OI  I  2;   1 .  2  5 Mặt khác R   R  5 . 2 2 2
Vậy phương trình đường tròn ngoại tiếp tam giác ABC là:  x  2   y   1  25 .
Nhận xét: Đề bài này rất khó đối với học sinh nếu không biết đến đường tròn Euler.
Dạng 3.3 Sử dụng điều kiện tiếp xúc
Câu 24. Chọn A
Đường tròn C  có tâm O , bán kính R tiếp xúc với  nên có:
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 13
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 
R  d O;   2 . 2
Phương trình đường tròn C  : 2 2 x  y  2 .
Câu 25. Chọn B
Do tâm I nằm trên đường thẳng y  x  I  ;
a  a , điều kiện a  0 .
Đường tròn  S  có bán kính R  3 và tiếp xúc với các trục tọa độ nên:
d  I;Ox  d  I;Oy  3  a  3  a  3n  a  3
 l   I 3; 3 .
S  x  2  y  2 : 3 3  9 Vậy phương trình .
Câu 26. Chọn C
Đường tròn tâm I 3; 4 tiếp xúc với đường thẳng  :3x  4 y 10  0 nên bán kính đường tròn
chính là khoảng cách từ tâm I 3; 4 tới đường thẳng  :3x  4 y 10  0 . 3.3  4.4 10 15
Ta có: R  d  I,     3 . 3 2 5 3  4
Câu 27. Chọn C 3.1 4.1 2
Đường tròn tâm I và tiếp xúc với đường thẳng d  có bán kính R  d  I , d    1 2 2 3  4 2 2
Vậy đường tròn có phương trình là:  x   1   y   1  1.
Câu 28. Chọn D
Vì đường tròn (C ) có tâm I  3
 ;2 và một tiếp tuyến của nó là đường thẳng  có phương trình 3.( 3  )  4.2  9
là 3x  4 y  9  0 nên bán kính của đường tròn là R  d (I , )   2 2 2 3  4 2 2
Vậy phương trình đường tròn là:  x  3   y  2  4
Câu 29. Chọn D
Vì các điểm A3;0 và B0;4 nằm trong góc phần tư thứ nhất nên tam giác OAB cũng nằm trong
góc phần tư thứ nhất. Do vậy gọi tâm đường tròn nội tiếp là I a,b thì a  0,b  0 .
Theo đề ra ta có: d  I;Ox  d  I;Oy  d  I; AB . x y
Phương trình theo đoạn chắn của AB là: 
 1 hay 4x  3 y 12  0 . 3 4  a  b a  b  0  a  b    Do vậy ta có: 
 7a 12  5a  a  6 l  .
4a  3b 12  5 a    
7a 12  5a a  1  
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 14
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2
Vậy phương trình đường tròn cần tìm là:  x   1   y   1  1 .
Câu 30. Chọn B
Ta có OA  3, OB  4, AB  5.
Gọi I (x ; y ) là tâm đường tròn nội tiếp tam giác OAB . I I    
Từ hệ thức AB.IO  OB.IA  O .
A IB  0 (Chứng minh) ta được  . AB x  . OB x  . OA x 4.3 O A B x    1 I  
AB  OB  OA 5  4  3   I (1;1) A . B y  . OB y  . OA y 3.4 O A B  y    1 I  
AB  OB  OA 5  4  3
Mặt khác tam giác OAB vuông tại O với r là bán kính đường tròn nội tiếp tam giác thì 1 O . A OB S 3.4 2 r   
 1 ( S, p lần lượt là diện tích và nửa chu vi tam giác). p
OA  OB  AB 3  4  5 2
Vậy phương trình đường tròn nội tiếp tam giác OAB là 2 2
( x  1)  ( y  1)  1 hay 2 2
x  y  2x  2 y  1  0.
DẠNG 4. TƯƠNG GIAO CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Dạng 4.1. Phương trình tiếp tuyến
Câu 31. Chọn A 2 2
x  y 1  0 có tâm O0;0, R 1.
Điều kiện để đường thẳng tiếp xúc với đường tròn là khoảng cách từ tâm tới đường thẳng bằng bán kính. Xét đáp án A: | 3.0  4.0  5 |
 : 3x  4y  5  0  d  , O  
 1  R   tiếp xúc với đường tròn. 2 2 3  4
Câu 32. Chọn D
Đường tròn C  tiếp xúc với trục Ox khi d  I,Ox  R với I và R lần lượt là tâm và bán kính
của đường tròn C  . Đường tròn: 2 2
x  y  10 x  0 2 2
 (x  5)  y  25 có tâm I 5;0 , bán kính R  5 ,
d I,Ox  0 . Suy ra: d  I,Ox  R . Vậy C  không tiếp xúc với trục Ox.
 không phải là phương trình đường tròn.
.Xét phương trình đường tròn: 2 2
x  y  5  0 có I 0;0 và R  5 , d I,Ox  0 .
Suy ra: d  I,Ox  R . Vậy C  không tiếp xúc với trục Ox.
Xét phương trình đường tròn: 2 2
x  y 10x  2 y 1  0 có I 5; 
1 và R  5 , d I,Ox  1.
Suy ra: d  I,Ox  R . Vậy C  không tiếp xúc với trục Ox.  5  5 5
Xét phương trình đường tròn: 2 2
x  y  6x  5y  9  0 có I 3  ;    và R  , d I,Ox  .  2  2 2
Suy ra: d  I,Ox  R . Vậy C  tiếp xúc với trục Ox
Câu 33. Chọn B
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 15
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 C  2 2
: x  y  2x  4 y  3  0   x  2   y  2 1 2  2.
Do đó đường tròn có tâm I  1;2 và bán kính R  2 .
Do d song song với đường thẳng  nên d có phương trình là 3x  4 y  k  0 , k   1 . 11 k 11   k  5 2 k  5 2 11
Ta có d  I; d   R  
2  11 k  5 2     . 2 2 3  4 11   k  5 2  k  5 2 11 
Vậy có hai phương trình tiếp tuyến cần tìm là 3x  4 y  5 2 11  0 , 3x  4 y  5 2 11  0 .
Câu 34. Chọn A 
Đường tròn C  có tâm I 1;2  IA  0;3 . 
Gọi d là tiếp tuyến của C  tại điểm A , khi đó d đi qua A và nhận vectơ IA là một VTPT. 
Chọn một VTPT của d là n  0  ;1 . d
Vậy phương trình đường thẳng d là y  5  0 .
Câu 35. Chọn A
Đường tròn C có tâm là gốc tọa độ O0;0 và có bán kính R  2 .
Họ đường thẳng  qua A 1
 ; 2 : a  x  
1  b  y  2  0 , với 2 2 a  b  0 . a  2b 2
Điều kiện tiếp xúc d  ;
O   R hay
 2  a  b   2 2 2 4 a  b  2 2 a  b a  0 2
 3a  4ab  0   . 3a  4  b 
Với a  0 , chọn b 1 ta có  : y  2  0 . 1 Với 3a  4
 b , chọn a  4 và b  3
 ta có  : 4 x 1  3 y  2  0  4x  3y 10  0 . 2    
Nhận xét: Thực ra bài này khi thay tọa độ điểm A 1
 ; 2 vào các đường thẳng ở các phương án
thì ta loại C. và D. Tính khoảng cách từ tâm của đường tròn đến đường thẳng thì chỉ có phương án A. thỏa.
Câu 36. Chọn C 2 2
Đường tròn C  :  x   1
  y  4  4 có tâm I 1;4 và bán kính R  2 .
Gọi d là tiếp tuyến của C  .
Vì d / / nên đường thẳng d : 4x  3y  m  0m  2 . 4.1 3.4  m
d là tiếp tuyến của C   d I;d   R   2 4   3  2 2 m  18
 m  8  10   (thỏa mãn điều kiện) m  2  
Vậy có 2 tiếp tuyến cần tìm : 4x  3y 18  0; 4x  3y  2  0 .
Câu 37. Chọn C
Đường tròn C  2 2
: x  y  2x  4 y 1  0 có tâm I 1; 2
  bán kính R  2 .
Đường tròn C  2 2
' : x  y  6x  8y  20  0 có tâm I ' 3
 ; 4 bán kính R '  5 . II '  2 13 .
Vậy II '  R  R ' nên 2 đường tròn không có điểm chung suy ra 2 đường tròn có 4 tiếp tuyến chung.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 16
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 38. Chọn B Đường tròn 2 2
(C) : (x  2)  ( y  4)  25 có tâm I (2; 4) , bán kính R  5 .
Đường thẳng  vuông góc với đường thẳng d : 3x  4 y  5  0 có phương trình dạng:
4x  3 y  c  0 4.2  3.(4)  c
 là tiếp tuyến của đường tròn (C ) khi và chỉ khi: d (I ; )  R   5 2 2 4  3 c  4  25 c  29  c  4  25    
. Vậy có hai tiếp tuyến cần tìm là: 4x  3 y  29  0 và c  4  25 c  21  
4x  3 y  21  0 .
Câu 39. Chọn D
C có tâm I 1;  1 bán kính R= 2 2 1  ( 1  )  ( 3  )  5
Vì IA  2  R nên A nằm bên trong C .Vì vậy không kẻ được tiếp tuyến nào tới đường tròn C .
Câu 40. Chọn B
Đường tròn C   x  2   y  2 : 1 4
 4 có tâm I 1; 4 và bán kính R  2 .
Gọi d là tiếp tuyến của C  .
Vì d / / nên đường thẳng d : 4x  3y  m  0 m  2 . 4.1 3.4  m
d là tiếp tuyến của C   d I;d   R   2 4   3  2 2 m  18
 m  8  10   (thỏa mãn điều kiện) m  2  
Vậy có 2 tiếp tuyến cần tìm : 4x  3y 18  0; 4x  3y  2  0 .
Câu 41. Chọn D y 4 I M K D1 O 3 x P -2 N
Gọi I là tâm của đường tròn, ta có tọa độ tâm I 3; 4 . 
Theo đề ra ta có tứ giác IMPN là hình vuông, nên đường thẳng MN nhận IP   6  ; 6 làm
VTPT, đồng thời đường thẳng MN đi qua trung điểm K 0 
;1 của IP . Vậy phương trình đường
thẳng MN: 1. x  0 1. y  
1  0 hay x  y 1  0 .
Câu 42. Chọn C 2 2 + C  2 2
: x  y  2x  6 y  6  0   x   1
  y  3  4 suy ra (C ) có tâm I( 1;3) và R = 2
+ Phương trình đường thẳng d đi qua M (3;1) có phương trình: A x  3  B  y   1  0 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 17
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
d là tiếp tuyến với đường tròn khi và chỉ khi d  I; d   R .
A  3B  3A  B  A  0  ta có phương trình: 2
 2  3A  4 AB  0   2 2 3A  4B A  B 
+ Với A  0 , chọn B  1 , phương trình tiếp tuyến thứ nhất là d : y  1 . 1 
Thế y  1 vào C  2 2
: x  y  2x  6 y  6  0 , ta được tiếp điểm là T 1;1 . 1   + Với 3A  4
 B , chọn A  4; B  3 , phương trình tiếp tuyến thứ hai là d : 4
 x  3y 15  0 2  2  4x  2  4x  3  3 21  Tiếp điểm T x;
 5  C nên  x   1   5  3  4  x    T  ; . 2       2    3   3  5  5 5 
+ Phương trình đường thẳng T T : 2 x 1 1 y 1  0  2x  y  3  0 . 1 2     3  3
+ Khoảng cách từ O đến đường thẳng T T là: d 0;T T   . 1 2  1 2 2 2 2 1 5
Dạng 4.2 Bài toán tương giao
Câu 43. Chọn D
Ta thấy đường tròn C có tâm I 1  ; 2
  và bán kính R  3 . Đường tròn C có tâm I 2;2 2   2  1  1
và bán kính R  2 . 2 Khi đó: 2 2
5  R  R  I I  (2 1)  (2  2)  5  C và C tiếp xúc nhau. 2  1 2 1 2  1
Câu 44. Chọn D
Giao điểm 2 đường tròn là nghiệm của hệ phương trình sau: 2 2 2 2 2 2 
x  y  4  0
 x  y  4 x  y  4      2 2
x  y  4x  4 y  4  0 4x  4 y  8 x  y  2     y  0  2 2 x  y  4    2  y2 2 2  y  4
2 y  4 y  0 x  2          x 2 y   x  2  y x 2 y         y  2   x  0 
Vậy giao điểm 2 đường tròn là: 2;0 và 0; 2.
Câu 45. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 18
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489   x   2 2 2 2 1  y  4 
x  y  2x  3  0
Cách 1: Xét hệ    
 x  2   y  2 2 2
x  y  8x  6 y  9  0 4 3  16    3  7 1 7 x  ,   2 y y  x    y  2  x   2 2       2 x   2  x2 2  2x  3  0
2x  6x 1  0    3  7 1 7 x  , y    2 2  3  7 1 7   3  7 1 7  Suy ra A ,  , B  , .   2 2      2 2  
C có tâm O 1;0 , C có tâm O4;3  OO  3;3 
Nên đường thẳng AB qua A và nhận n 1;  1 là vécto pháp tuyến.  3  7   1 7 
Phương trình: 1 x   1 y 
  0  x  y  2  0 . Chọn A .  2   2      2 2
Cách 2: Giả sử hai đường tròn C  x  2 2 :
1  y  4 và C :  x  4   y  3  16 cắt nhau tại
hai điểm phân biệt A và B khi đó tọa độ của A và thỏa mãn hệ phương trình:   x   2 2 2 2 1  y  4
 x  y  2x  3  0 (1)    
 x  2   y  2 2 2
x  y  8x  6 y  9  0 (2) 4 3  16  
Lấy (1) trừ (2) ta được: 6x  6 y 12  0  x  y  2  0 là phương trình đường thẳng đi qua 2
điểm A và B
Câu 46. Chọn A 3 19
Từ  :3x  4 y 19  0  y  x    1 . 4 4 Thế  
1 vào C  ta được 2    x  2 3 23 1  x   25    4 4  x  1 25 85 145 2 x x 0       29 . 16 8 16 x   5
+) x  1  y  4   A1; 4  . A A 29 2  29 2  +) x   y    B ;  . B   5 B 5  5 5  2 2  29   2 
Độ dài đoạn thẳng AB  1    4  6     .  5   5 
Câu 47. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 19
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A H B I
Gọi H là trung điểm của đoạn thẳng AB . Ta có IH  AB và 3.1 4.  1  8
IH  d I;AB   3 . 3   4  2 2
Xét tam giác vuông AHI ta có: 2 2 2 2 2
HA  IA  IH  5  3  16  HA  4  AB  2HA  8
Câu 48. Chọn C
Đường tròn C  có tâm I 2; 2
  bán kính R  2 . 3.2  4.2  7
d  I , d  
 1  R  2 nên d cắt C tại hai điểm phân biệt. 2 2 3  4
Gọi A, B là các giao điểm của đường thẳng d với đường tròn C . 2 2
AB  2 R  d  I,d   2 3 .
Câu 49. Chọn A
Đường tròn C  có tâm I 1;2 và bán kính 2 2 R  1  2  3  2 .
Theo giả thiết đường thẳng d đi qua A và cắt đường tròn C  tại hai điểm B , C sao cho BC  2 2 .
Vì BC  2 2  2R nên BC là đường kính của đường tròn C suy ra đường thẳng d đi qua tâm
I 1;2   
Ta chọn: u  IA  2;   1  n  1; 2 . d  d 
Vậy đường thẳng d đi qua A3 
;1 và có VTPT n  1; 2 nên phương trình tổng quát của d 
đường thẳng d là: 1 x  3  2 y  
1  0  x  2 y  5  0 .
Câu 50. Chọn A
Tọa độ tâm I của đường tròn C là: I 1  ; 2  . 1   1  1
Tọa độ tâm I của đường tròn C là: I 2; 2 . 2   1  2  Ta có: I I
3; 4 . Gọi d , d  lần lượt là đường thẳng nối tâm của hai đường tròn đã cho và đường 1 2    
thẳng cần lập. Chọn một vectơ pháp tuyến của đường thẳng d là: n 4; 3 . Gọi n ,   a; b d  d  2 2
a  b  0 là một vectơ pháp tuyến của đường thẳng d  . 2   2 4a  3b 2
Theo đề cos d, d '   cos n ,n    . d d   2 2 2 2 2 2 2
3  4 . a  b
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 20
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
a  7b  0 2 2 7a 48ab 7b 0       1 .
a   b  0  7 1
Với a   b  0 , chọn b  7
  a  1. Phương trình đường thẳng d  : x  7 y  0 . 7
Với a  7b  0 , chọn b  1 a  7 . Phương trình đường thẳng d  : 7x  y  0 .
Câu 51. Chọn B 
IM  IM  10 
 M , M  C : x 1  y  2  10. 1 2    2  2 1 2 I  1; 2 
Mặt khác, M , M d x  y   M , M 1 2 thuộc   : 2 5 0 nên ta có tọa độ 1 2 là nghiệm của hệ  
 x  2   y  2 1 2  10   1  .
2x  y  5  0  2   x  0 2  y  2  x  5,  thay vào   1 ta có 2
5x 14x  0  14 .  x   5 14 14
Gọi x , x lần lượt là hoành độ của M và M  x  x  0   . 1 2 1 2 1 2 5 5
Câu 52. Chọn B (C) d I R B h H M A
C có tâm I 2; 
1 , bán kính R  2 5. 1
Đặt h  d  I, AB . Ta có: S  . h AB  8  . h AB  16. IAB 2 2 AB Mặt khác: 2 2 R  h   20 4 h  4 h  2 Suy ra:  ;  AB  4 AB  8  
Vì d đi qua M 1; 3
  nên 1 3b  c  0  3b  c 1 c  3b 1 2  b  c
2  b  3b 1 1 2b Với h  4     b   2 2 2 1 b 1 b 1 b 2  b  c
2  b  3b 1 1 2b 3 5 Với h  2     b   c 
 b  c  2. 2 2 2 4 4 1 b 1 b 1 b
Câu 53. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 21
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Gọi K là chân đường cao hạ từ A của tam giác ABC , gọi E là điểm đối xứng với H qua K suy
ra E thuộc đường tròn ngoại tiếp tam giác ABC (Tính chất này đã học ở cấp 2).   Ta có AH   6  ;8 , chọn u  3; 4  . AH 
 x  5  3t
Phương trình đường thẳng AH qua A ở dạng tham số  y  5  4t 
K  AH suy ra tọa độ điểm K có dạng K 5  3t;5  4t 
H và E đối xứng nhau qua K suy ra tọa độ E theo t là E 11 6t; 3   8t  E  (C) 
11 6t 2   3   8t 2  50 2  5t  9t  4  0  t  1    4  t   5 Với t  1
 , E 5;5 (loại vì E  A ) 4   31 17   13 41  Với t  , E ;   , K ;   5  5 5   5 5   
Phương trình đường thẳng BC có u  n
 4;3 và qua điểm K có phương trình tham số BC AH   13 x   4t   5  13 41  
 C  BC  C  4t;  3t   . 41  5 5   y   3t   5 2 2  13   41 
C  C    4t   3t  50      5   5  2 
25t  70t  24  0  2 t  
 C 1;7   KTM   5   12   t   C  7  ;  1  5 Vậy C  ;
a b  C  7  
;1  a  b  6  .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 22
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 54. Chọn A 5 B 4 C 3 D 2 J I A 1 4 2 2 4 1 M T Ta có:  
BCM  BAM (cùng chắn cung BM )   1   
BAM  MAT  DAC (do AD là đường phân giác ngoài A ) 2       Từ   1 , 2 suy ra  
DAC  BCM , mà BCM  CDA  AMC, DAC  ACM  AMC từ đó suy ra  
CDA  ACM , do đó MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ACD có tâm J nên
JC  MC . Hay C là hình chiếu của J lên đường thẳng CM .
Đường thẳng qua J và vuông góc với CM có phương trình:
 x  2   y  2  0  x  y  4  0 x  y  2 x  1
Tọa độ điểm C là nghiệm của hệ:     C  1  ; 3 . x  y  4 y  3   
AC là đường thẳng qua C và vuông góc với IJ 4; 0 nên có phương trình: x 1  0 . a  1
Do đó tọa độ điểm A có dạng A 1
 ; a . Ta có IA  IC  9  a  22 2 2  9 1   . a  3 
Vì A  C nên A 1  ;  1 .
Tọa độ điểm M có dạng M  ;
m 2  m . Ta có m  1
IM  IC  m  22 2 2 2 2
 m  10  m  2m  3  0   . m  3 
Vì M  C nên M 3;   1 . 
BC là đường thẳng qua C và vuông góc với MI 1; 3 nên có phương trình:   x  
1  3 y  3  0  x  3y 10  0 . b  3 2 2
Tọa độ điểm B có dạng B 3b 10; b . Ta có 2 2 IB IC 3b 12 b 2 10         23 . b   5  19 23 
Vì B  C nên B ;   .  5 5  19 9
Vậy tổng hoành độ của các đỉnh , A B, C là 1  1  . 5 5
Câu 55. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 23
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 .
Vì I   nên a  3b  8  0  a  83b .
Vì đường tròn đi qua A và tiếp xúc với đường thẳng  nên: 3a  4b 10 R 2 2 I
d I;  IA 
 2a 1b   1 . 5 R
Thay a  8 3b vào   1 ta có: ' A
383b 4b 10  283b2 1b2 5 2
 1413b  5 10b  34b  37
   b2   2 14 13
25 10b  34b  37 2
 81b  486b  729  0  b  3.
Với b  3  a  1 .
a  b  2 .
Câu 56. Chọn A B H A d I(1;-2) Ta có:
IH  d  I; d   2 . 1 2S 2.4 S  IH . IAB AB  AB    4  AH  2 . IAB 2 IH 2 2 2 2 2  R  IA  AH  IH  2  2  2 2 .
 C   x  2   y  2 : 1 2  8 . DẠNG 5. CÂU HỎI MIN-MAX
Câu 57. Chọn D
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 24
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 Ta có C  2 2
: x  y  2x  4 y  4  0  C  :  x   1
  y  2  9 nên có tâm I 1; 2, R  3
Vì IM  2  3  R .
Gọi d là đường thẳng đi qua M cắt đường tròn C  tại các điểm A,
B. Gọi J là trung điểm của AB . Ta có: Ta có: 2 2 2 2
AB  2AJ  2 R  IJ  2 R  IM  2 9  2  2 7 .
Câu 58. Chọn. D. I P M N B A Đường tròn 2 2
(C) : x  ( y 1)  4 có tâm I(0;1) bán kính R  2 .
IA  IB  4  R nên ,
A B nằm ngoài đường tròn.
Gọi N là giao điểm của IA và đường tròn C  1  1 
Trên đoạn IN lấy điểm P sao cho IP  IN  IP 
IA  P trùng với gốc tọa độ. 2 4 MA IM IN
Ta có IAM  IMP   
 2  MA  2MP . MP IP IP
Do đó P  MA  2MB  2MP  2MB  2PB  P
 2PB  2 17  P  8,1;8,3 . min min   Chọn. D.
Câu 59. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 25
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 4 M 3 I 2 1 O 1 2 C 2 2
: x  y  2x  4y  3  0 , C có tâm I 1;2 , R  2 . 2 2
Suy ra C : x  
1  y  2  2  0 .
Có T  x  y   x 1  y  2  3. 0   0  0 0
Áp dụng bất đẳng thức B. C. S cho 2 bộ số 1; 
1 ,x 1 ; y  2 . 0   0   2 2 x  1 y 2 2  x 2 1 y 22       
 2 , do  x 1  y  2  2 . 0   0  0 0 0 0  
 2   x 1  y  2  2 1  x 1  y  2  3  51 T  5. 0   0  0   0  
 x 1  y  2 0   0  
Dấu đẳng thức xảy ra khi  .   x  2
1  y  22  2 0 0   x 1  1
 x  2, y  3,T  5   x  2 1  1 0  0 0  . 0    x 1  1 
 x  0, y  1,T  1 0  0 0
Vậy max T  5 khi x  2, y  3. 0 0
Câu 60. Chọn D
Đường tròn C  có tâm I  4
 ;3 , bán kính R  3 .  x  4  t Ta có OI   4
 ;3 suy ra phương trình đường thẳng OI là  . y  3t 
OI  C   M Tọa độ  ;
x y của M là nghiệm hệ  8  2 t  t    2 2 2 5 5
x  y  8x  6 y 16  0
25t  50t 16  0      32   8  x  4  t  x  4  t  x   x  5 5  y 3t  y 3t        24  6 y  y   5    5  32 24   8 6  Suy ra M  ; , M  ; 1   2    5 5   5 5  2 2 2 2  32   24   8   6  Ta có OM     8, OM     2  OM  OM  2 . 1     2     min 2  5   5   5   5  Cách 2
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 26
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Đường tròn C  có tâm I  4  ;3 , bán kính 2 2
R  4  3 16  3. 
Phương trình đường thẳng OI đi qua O 0;0 có vtpt n3;4 là:
3x  4y  0 .
Tọa độ M  OI  C  là nghiệm của hệ:  32  8 x   x   3
 x  4 y  0  5    5      2 2
x  y  8x  6 y 16  0  24 6  y   y    5   5 2 2 2 2  32   24   8   6  Ta có OM    8 ; OM    2 . Vậy OM  2 . 1     2     min  5   5   5   5 
Câu 61. Chọn C
Gọi: d : x  y  m  0; tâm của C là I 1 
;1 , để d C tại 2 phân biệt khi đó: 2  m
0  d  I; d   2  0 
 2  2  2 2  m  2  2 2 * 2 1  1 1 2  Xét IAB có: 2 S  .I . A I . B sin AIB  .R .sin AIB  .R A  IB 2 2 2   Dấu “=” xảy ra khi: 0
sin AIB  1  AIB  90  AB  2 2 2  m m  0 (TM )
 d  I; d   2   2   . 2 m  4 (TM ) 
Câu 62. Chọn C
Đường tròn C  có tâm I 1; 2 , bán kính R  2 .
Gọi  là đường thẳng qua I và vuông góc với d. Khi đó, điểm M cần tìm là một trong hai giao
điểm của  và C  .
Ta có phương trình  : x  y  1  0 .
x  y 1  0
 y  x 1  Xét hệ:   
x  y  2x  4 y 1  0   x   2 1   y  22 2 2  4 
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 27
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 x 1 2 
 y  x 1 
 y  x 1    y  2  2        2   x  2 1  4 x  1 2    x  1 2   y  2  2 
Với B 1 2; 2  2   d B,d   2  3 2
Với C 1 2; 2  2   d C, d   2  3 2  d B,d 
Suy ra M 1 2; 2  2   a 1 2;b  2
  2  2 1 2   2a .
Câu 63. Chọn B   Vì GA  2
 GM nên A là ảnh của điểm M qua phép vị tự B M tâm G , tỉ số 2  , suy ra A 4  ; 2   . G C
Đường tròn ngoại tiếp ABC có tâm I , bán kính R  IA  5 2 2
có phương trình  x  3   y  2  25 . 
Ta có IM  2; 4 . I  A
Đường thẳng BC đi qua M và nhận vectơ IM làm vectơ pháp tuyến, phương trình BC là:
1 x  3  2 y  2  0  x  2y  7  0 .
Điểm C là giao điểm của đường thẳng BC và đường tròn
 I; R nên tọa độ điểm C là nghiệm của hệ phương trình:  
 x  32   y  22  25
x  1, y  3    x  5, y  1
x  2 y  7  0  
Đối chiếu điều kiện đề bài ta có tọa độ điểm C 5  ;1 .
Câu 64. Chọn D D R I R K A M B C
+) C  có tâm I 1;2 , bán kính R  30
+) AB là dây cung của C  đi qua M
+) Ta có AB min  AB  IM .
Thật vậy, giả sử CD là dây cung qua M và không vuông góc với IM .
Gọi K là hình chiếu của I lên CD ta có: 2 2 2 2
AB  2AM  2 IA  IM  2 R  IM 2 2 2 2
CD  2KD  2 ID  KD  2 R  IK
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 28
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Do tam giác IMK vuông tại K nên IM  IK .
Vậy CD  AB . 2 2
+) Ta có: IM  2   1  1 2  2 2 2
MA  R  IM  30  2  28  2 7
 AB  2MA  4 7 .
Câu 65. Chọn D 2 2
Xét tập hợp điểm M ( ; a )
b thỏa mãn a  
1  b  2 1 thì M thuộc đường tròn tâm
I (1; 2); R  1 Xét điểm N( ;
c d) thỏa mãn 4c  3d  23  0 thì N thuộc đường thẳng có phương trình
4x  3y  23  0 . 4  6  23
Ta thấy d (I ; d ) 
 5  R  1. Do đó đường thẳng không cắt đường tròn. 5
Đường thẳng qua I vuông góc với d tại L và cắt đường tròn ở T , K ( K ở giữa T và L )
Vẽ tiếp tuyến tại K cắt MN tại P .
Có KL  PN  MN , mà KL  d  I, d   R
Do đó MN ngắn nhất khi MN  KL 2 2 Từ đây ta suy ra
        2 P a c b d
 MN bé nhất khi và chỉ khi
MN  d(I; d)  R  5 1  4 . Vậy giá trị nhỏ nhất P  16 min
Câu 66. Chọn A I (1; 2) Ta có (C)  R  2 
Ta dễ thấy đường thẳng d và d cắt nhau tại điểm M 1 
;1 cố định nằm trong đường tròn C  và 1 2
d  d . Gọi ,
A B là giao điểm của d và C  , C, D là giao điểm của d và C  . H , K lần lượt 1 2 1 2
là hình chiếu của I trên d và d 1 2 Khi đó
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 29
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 1 S  A .
B CD  2 AH.CK  2 R  d I d R d I d ABCD  ,  2  .    ,  2 2 2   1   2 2  m  2 4m  3 2 2 3m  4 1  2 2
4m  3  3m  4  2 4  4  =2   7 2 2 2 2 m 1 m 1 m 1 m 1 Do đó max S  7 khi m  1
 . Khi đó tổng các giá trị của m bằng 0. ABCD
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 30
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 10 PHƯƠNG TRÌNH ELIP 0H3-3 Contents
PHẦN A. CÂU HỎI ......................................................................................................................................................... 1
DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP....................................................................................................................... 1
DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP ........................................................................................................................ 2
DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC .......................................................................................................... 3
PHẦN B. LỜI GIẢI ......................................................................................................................................................... 4
DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP....................................................................................................................... 4
DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP ........................................................................................................................ 6
DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC .......................................................................................................... 8 PHẦN A. CÂU HỎI
DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP 2 2 x y Câu 1. Đường Elip   1 có tiêu cự bằng 16 7 A. 6 . B. 8 . C. 9 . D.  2  ;   . Câu 2.
Cho elip  E  có phương trình 2 2
16x  25y  400 . Khẳng định nào sai trong các khẳng định sau?
A.  E  có trục nhỏ bằng 8.
B.  E  có tiêu cự bằng 3.
C.  E  có trục nhỏ bằng 10.
D.  E  có các tiêu điểm F 3  ; 0 và F 3;0 . 2   1   2 2 x y Câu 3.
Trong mặt phẳng với hệ tọa độ Oxy, cho elip  E  : 
 1. Tiêu cự của (E) bằng 25 9 A. 10. B. 16. C. 4. D. 8. Câu 4.
Một elip có diện tích hình chữ nhật cơ sở là 80 , độ dài tiêu cự là 6 . Tâm sai của elip đó là 4 3 3 4 A. e  . B. e  . C. e  . D. e  . 5 4 5 3 Câu 5.
Cho elip E 2 2
: 4x  5y  20 . Diện tích hình chữ nhật cơ sở của E là A. 2 5 . B. 80 . C. 8 5 . D. 40 . 2 2 x y Câu 6.
(Yên Định 1 - Thanh Hóa - 2018-2019) Đường elip   1 có tiêu cự bằng 16 7 A. 3 . B. 9 . C. 6 . D. 18 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 x y Câu 7.
Cho elip có phương trình chính tắc 
 1. Tính tâm sai của elip. 4 1 2 1 1 3 A. . B. . C. . D. . 3 2 4 2 2 2 x y Câu 8.
(TH&TT LẦN 1 – THÁNG 12) Trong mặt phẳng với hệ tọa độ Oxy , cho elip  E  :   1 2 2 a b
(với a  b  0 ) có F , F là các tiêu điểm và M là một điểm di động trên  E  . Khẳng định nào dưới 1 2 đây là đúng? 2
A. MF  MF  2b .
B.  MF  MF   4  2 2 b  OM . 1 2  1 2 C. 2 2 2
OM  MF .MF  a b . D. 2 2 2
MF .MF  OM  a  b . 1 2 1 2 Câu 9.
Trong hệ trục Oxy, cho Elip  E có các tiêu điểm F 4
 ;0 , F 4;0 và một điểm M nằm trên 1   2  
 E . Biết rằng chu vi của tam giác MF F bằng 18. Xác định tâm sai e của E. 1 2 4 4 4 4 A. e  . B. e  . C. e   . D. e  . 5 18 5 9 5
Câu 10. Cho Elip  E đi qua điểm A 3
 ;0 và có tâm sai e 
. Tiêu cự của  E là 6 5 10 A. 10 . B. . C. 5 . D. . 3 3
DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP
Câu 11. Trong mặt phẳng Oxy , phương trình nào sau đây là phương trình chính tắc của một elip? 2 2 x y 2 2 x y x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 2 3 9 8 9 8 9 1
Câu 12. Phương trình chính tắc của đường elip với a  4 , b  3 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 16 9 9 16 16 9 9 16
Câu 13. Trong mặt phẳng tọa độ Oxy , viết phương trình chính tắc của elip biết một đỉnh là A 5; 0 và 1  
một tiêu điểm là F 2; 0 . 2   2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1 . B.  1 . C.  1. D.  1 . 25 21 25 4 29 25 25 29
Câu 14. Tìm phương trình chính tắc của Elip có độ dài trục lớn bằng 4 10 và đi qua điểm A0;6 : 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1 . C.   1 . D.   1. 40 12 160 36 160 32 40 36 5
Câu 15. Lập phương trình chính tắc của Elip đi qua điểm B và có tâm sai e  . 3 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1 9 4 3 2 9 2 9 3
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 16. Phương trình chính tắc của Elip có đỉnh  3
 ; 0 và một tiêu điểm là 1;0 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1 . B.   1 . C.   1 . D.   1 . 8 9 9 8 1 9 9 1
Câu 17. (KSCL lần 1 lớp 11 Yên Lạc-Vĩnh Phúc-1819) Tìm phương trình chính tắc của elip có tiêu cự
bằng 6 và trục lớn bằng 10 . 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1. C.   1. D.   1. 25 9 16 25 100 81 25 16
Câu 18. (LƯƠNG TÀI 2 BẮC NINH LẦN 1-2018-2019) Cho elip  E có độ dài trục lớn gấp hai lần độ
dài trục nhỏ và tiêu cự bằng 6 . Viết phương
trình của  E ? 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1 . C.   1 . D.   1. 12 3 12 3 3 12 48 12
Câu 19. Phương trình chính tắc của Elip có độ dài trục lớn bằng 8 , độ dài trục nhỏ bằng 6 là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.   1. B.   1 . C.   1. D.   1 9 16 64 36 8 6 16 9
Câu 20. Elip có một tiêu điểm F 2;0 và tích độ dài trục lớn với trục bé bằng 12 5 . Phương trình
chính tắc của elip là: 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 9 5 45 16 144 5 36 20  3 4 
Câu 21. Trong mặt phẳng Oxy , viết phương trình chính tắc của elip  E  biết  E  đi qua M ;    5 5 
và M nhìn hai tiêu điểm F , F dưới một góc vuông. 1 2 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  E  :   1. B.  E  : 
 1. C.  E  : 
 1. D.  E  :   1. 4 9 9 4 2 3 3 2
DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC 2 2 x y
Câu 22. (LẦN 01_VĨNH YÊN_VĨNH PHÚC_2019) Cho Elip (E) : 
 1 và điểm M nằm trên 16 12
(E). Nếu điểm M có hoành độ bằng 1 thì các
khoảng cách từ M đến hai tiêu điểm của (E) bằng: 2 A. 3, 5 và 4, 5 . B. 4  2 . C. 3 và 5. D. 4  . 2 2 2 x y
Câu 23. Trong mặt phẳng với hệ tọa độ Oxy , cho elip  E : 
 1. Điểm M   E  sao cho 25 9  0
F MF  90 . Tìm bán kính đường tròn nội tiếp tam giác MF F . 1 2 1 2 1 A. 2 B. 4 . C. 1. D. . 2
Câu 24. Ông Hoàng có một mảnh vườn hình Elip có chiều dài trục lớn và trục nhỏ lần lượt là 60m và 30m
. Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với Elip để làm mục đích
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài
đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích
trồng hoa màu. Biết diện tích hình Elip được tính theo công thức S   ab , với a, b lần lượt là nửa
độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể. 2 3 1 A. T  . B. T  . C. T  .
D. T  1 . 3 2 2
Câu 25. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai đường tròn C , C có phương trình lần lượt 1   2  là 2 2 2 2
(x 1)  ( y  2)  9, (x  2)  ( y  2)  4 và Elip E có phương trình 2 2
16x  49 y  1 . Có
bao nhiêu đường tròn C có bán kính gấp đôi độ dài trục lớn của elip  E và C tiếp xúc với hai
đường tròn C , C ? 2  1  A. 2 . B. 1. C. 3 . D. 4 . 2 2 x y
Câu 26. Trong mặt phẳng Oxy , cho điểm C(3; 0) và elip (E) :   1. ,
A B là 2 điểm thuộc (E) sao 9 1  a c 3 
cho  ABC đều, biết tọa độ của A ;
 và A có tung độ âm. Khi đó a  c bằng:  2 2    A. 2 . B. 0 . C. 2  . D. 4  . PHẦN B. LỜI GIẢI
DẠNG 1. TÌM CÁC YẾU TỐ CỦA ELIP Câu 1. Chọn A 2 2 x y Elip   1 có 2 a  16 , 2 b  7 suy ra 2 2 2
c  a  b  16  7  9  c  3 . 16 7
Vậy tiêu cự 2c  2.3  6 . Câu 2. Chọn B 2 2 x y  E  : 2 2
16x  25y  400    1. 25 16
Elip  E  có a  5 , b  4 , 2 2 2 2
c  a  b  5  4  3 .
Tiêu cự của elip  E  là 2c  6 nên khẳng định “  E  có tiêu cự bằng 3” là khẳng định sai. Câu 3. Chọn D 2 2 x y
Phương trình chính tắc của elip có dạng: 
 1 a  0, b  0 . 2 2   a b a  5 Do đó elip (E) có 2 2 
 c  a  b  4 . b  3 
Tiêu cự của elip (E) bằng 2c  8 .
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Câu 4. Chọn C
Diện tích hình chữ nhật cơ sở là 2 .
a 2b  80 , suy ra . a b  20   1 . Lại có 2 2 2
2c  6  c  3  a  b  c  9 2 . 20 Từ   1  b 
, thay vào 2 ta được: a 2 400 4 2 a 
 9  a  9a  400  0 2
 a  25  a  5 . 2 a 3 Do đó tâm sai e  . 5 Câu 5. Chọn C 2 2 x y E 2 2
: 4x  5y  20    1 5 4
Độ dài trục lớn: 2a  2 5 .
Độ dài trục bé: 2b  2.2  4 .
Diện tích hình chữ nhật cơ sở của E là: 2 5.4  8 5 . Câu 6. Chọn C □ Ta có: 2 a  16 , 2 b  7 nên 2 2 2
c  a  b  9  c  3 .
□ Tiêu cự của elip là 2c  6 . Câu 7. Chọn D Ta có 2 2 2 2 2
a  4  a  2;b  1  b  1; c  a  b  3  c  3 c 3
Tâm sai của elip là e   a 2 Câu 8. Chọn D Ta có: 2 2 cx cx c x 2 MF  a  ; MF  a 
 MF .MF  a  . 1 2 1 2 2 a a a 2 2 x y M  ;
x y   E     1 2 2 a b 2 2 2 2  x   x  b x 2 2 2 2 2 2 2 2 2  y  b 1
 OM  x  y  x  b 1  x  b   2   2  2 a a a     2 2 2 2 2 2 2 2 c x b x  c x b x  2 2 2 2 2 2 2
MF .MF  OM  a   x  b 
 a  b  x   1 2 2 2  2 2  a a a a    2 2 b  c  2 x 2 2 2
 a  b  x  2 a b  c x a x 2 2 2 2  2 2  2 2 2 Vì 2 2 2
a  b  c nên 2 2 2 2 2
MF .MF  OM  a  b  x 
 a  b  x 
 a  b 1 2 2 2 a a Câu 9. Chọn A Ta có F 4  ;0  c  4 . 1   P
 MF  MF  F F M  1 F 2 F 1 2 1 2  2a
 18  2a  2c  18  2a  8  a  5.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 c 4 Tâm sai e   . a 5
Câu 10. Chọn C 2 2 x y
Gọi phương trình chính tắc của  E là 
 1 với a  b  0 . 2 2 a b 9
Vì  E đi qua điểm A 3  ;0 nên 2
 1  a  9  a  3 . 2 a c 5 5a 5 Lại có e    c    2c  5 . a 6 6 2
DẠNG 2. VIẾT PHƯƠNG TRÌNH ELIP
Câu 11. Chọn D 2 2 x y
Phương trình chính tắc của elip có dạng 
 1, a  b  0 nên chọn phương án D . 2 2   a b
Câu 12. Chọn C 2 2 x y
Phương trình chính tắc  E  :   1 . 16 9
Câu 13. Chọn A Ta có 2
a  5; c  2  b  25  4  21 2 2 x y Vậy  1 . 25 21
Câu 14. Chọn D 2) 2 x y
Ta có phương trình chính tắc Elip (E) có dạng 
 1(a  b  0) . 2 2 a b
Theo giả thiết ta có 2a  4 10  a  2 10 . 2 6
Mặt khác (E) đi qua A0;6 nên ta có  1  b  6 . 2 b 2 2 x y
Vậy phương trình chính tắc của (E) là:   1 40 36
Câu 15. Chọn A 2 2 x y
Phương trình chính tắc của Elip có dạng: 
 1, a  b  0 . 2 2   a b 2 2 0 2
Elip đi qua điểm B nên 2   1  b  4 . 2 2 a b 5 c 5 5 Tâm sai e     c  a . 3 a 3 3 2  5  2 2 2 2 2
a  b  c  a  4  
a   a  9 .  3    2 2 x y
Vậy phương trình chính tắc của Elip cần tìm là   1. 9 4
Câu 16. Chọn B Elip có đỉnh  3
 ; 0  a  3 và một tiêu điểm 1;0  c  1.
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 Ta có 2 2 2
c  a  b 2 2 2
 b  a  c  9 1  8 . 2 2 x y
Vậy phương trình  E  :   1 . 9 8 Câu 17. Lời giải Chọn D 2 2 x y
Phương trình chính tắc của elip:   1. 2 2 a b
Độ dài trục lớn 2a  10  a  5
Tiêu cự 2c  6  c  3 Ta có: 2 2 2 2 2 2
a  b  c  b  a  c 16 2 2 x y
Vậy phương trình chính tắc của elip là   1. 25 16 Câu 18. Chọn B
Ta có: a  2b, 2c  6  c  3. 2  b  3 Mà 2 2 2 2 2
a  b  c  4b  b  9   2 a  12  2 2 x y
Vậy phương trình  E :   1 . 12 3
Câu 19. Chọn D. 2 2 x y
+ Phương trình Elip dạng: 
 1, a  b  0. 2 2 a b
+ Do có độ dài trục lớn bằng 8  2a  a  4
+ Do có độ dài trục nhỏ bằng 6  2b  a  3 2 2 x y + Suy ra phương trình là   1 16 9 Vậy chọn D Câu 20. Chọn A 2 2 x y Gọi (E) có dạng   1 ( a > b >0 ) 2 2 a b 2  ab  3 5  a  9   Theo giả thiết ta có:    2 2 2  a   b  4  b    5  2 2 x y Vậy (E) cần tìm là  1. . 9 5
Câu 21. Chọn B 2 2 x y Gọi  E  :   1. 2 2 a b  3 4  9 16
Ta có:  E  đi qua M ;   nên:   1 2 2 2 2
 16a  9b  5a b .   1 2 2  5 5  5a 5b F F
Vì M nhìn hai tiêu điểm F , F dưới một góc vuông nên: 1 2 OM   c . 1 2 2 9 16 2 2  OM  c 2    c 2 2 2
 a  b  c  5 2 2
 a  5  b thế vào   1 ta được: 5 5
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  2  b  2  b   2  b  2 16 5 9 5 5 b 4  b  16 2  b  4 nên 2 a  9 . 2 2 x y Vậy:  E  :   1. 9 4
DẠNG 3. CÁC BÀI TOÁN LIÊN QUAN KHÁC
Câu 22. Chọn A 2 2 2 x y  a  16 a  4
Giả sử phương trình (E) : 
 1 (a  b  0) Ta có :    2 2 a b 2 2 2 2 b   12
c  a  b  4   a  4   c  2 
Gọi F , F lần lượt là hai tiêu điểm của Elip (E) , M 1; y  E , ta có : M  ( ) 1 2  c 1 MF  a  x  4  .1  4,5 1 M   a 2  c 1
MF  a  x  4  .1  3,5 2 M   a 2 Chọn A. Câu 23. Lờigiải  Gọi M  ; x y vì 0 F MF  90 2 2 2 2 2 2
 MF  MF  F F  x  y  c  16 (1) 1 2 1 2 1 2 2 2 x y
Do M   E     1 (2) 25 9 175 81 5 7 9
Giải hệ gồm hai phuơng trình (1) và (2) ta đuợc 2 2 x  ; y   x   ; y  16 16 4 4
MF  MF  F F 2a  2c Ta có: nửa chu vi 1 2 1 2 p  
 a  c  9 2 2 9
Khoảng các từ M đến trục Ox: d M ;O x   y  M 4 1 S  d M Ox F F  MF  F  ; . 9 1 2 1 2 2 S
Bán kính đuờng tròn nội tiếp: r   1 p Câu 24. Hướng dẫn giải Chọn D
Theo đề ta có: Diện tích  E  là: S   a b      2 . . 30.15. 450 , m E   
Vì đường tròn tiếp xúc trong, nên sẽ tiếp xúc tại đỉnh của trục nhỏ, suy ra bán kính đường tròn:
R  15m . Diện tích hình tròn C  phần trồng cây lâu năm là: 2 2 S   R      2 . 15 . 225 , m C   
Suy ra diện tích phần trồng hoa màu là: S  S  S   m  T  . E C  2 225 ,  1    
Câu 25. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 2 2 x y 1 1 Ta có 2 2
16x  49 y  1  
 1   E  có độ dài trục lớn 2a  2.  . 2 2  1   1  4 2      4   7 
Khi đó đường tròn C có bán kính là R  1 . Gọi I a;b là tâm của đường tròn C .
II  R  R  1 3  4 1 1  Xét I
 I I có II  R  R  1 2  3  II 
I vuông tại I . 1 2 2 2 1 2
I I  R  R  5  1 2 1 2  
Ta có II  1 a; 2  b , II  2  a; 2  b . Khi đó điểm I thỏa mãn: 2   1      2 2 II .II  0   1
  a2  a   2
  b2  b  0 
a  b  a  6  0 1 2      2 2  2 2 II  3  2  a 
  2  b  9
a  b  4a  4b 1  0 2   2  5  4b  5  4b 2 2 2  2 2
a  b  6  a   b  6   0 a b 6 a         3  3     5  4b  
6  a  4a  4b 1  0 a     5  4b  3 a    3 a  1 b  2 b  2 2  
25b  28b  44  0 22  b    71   5  4b   25   a  . a      25  3 5 4b    a   22  3 b      25
Vậy có hai phương trình đường tròn C thỏa mãn yêu cầu bài toán là 2 2  71   22  
C   x  2   y  2 : 1 2
 1 hoặc C : x   y   1.      25   25 
Câu 26. Chọn A
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 y B C x O A
Nhận xét: Điểm C(3; 0) là đỉnh của elip (E)  điều kiện cần để  ABC đều đó là , A B đối xứng Nhau qua Ox .Suy ra ,
A B là giao điểm của đường thẳng  : x  x và elip (E) . 0  1 2 y   9  x 2 2 x y  3 +) Ta có elip (E) :   1   . 9 1 1  2 y  9  x  3  1 
+) Theo giả thiết A có tung độ âm nên tọa độ của 2 A x ;  9  x 
(điều kiện x  3 0 0  0  3  do A  C ) 1 +) Ta có 2 2
AC  (3  x )  (9  x ) và d |  3  x | 0 0 9 (C ; ) 0 3 3 1
+)  ABC đều  d  AC 2 |  3  x | (3  x )   2 9  x 0 0 0  (C;) 2 2 9 3  1 2 2 2   (3  x ) 
(3  x )  (9  x ) 0 0 0 4  9     3 1 3 3 x  (t / m) 2 0 x x 0       2 0 0 3 2 2  x  3(L)  0  3 3  a  3  A ;    
 a  c  2 .  2 2  c  1   
Tổng hợp: Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10
Document Outline

1576144858_0H3-1 PHƯƠNG TRÌNH ĐƯỜNG THẲNG
1577006517_0H3-2 PHƯƠNG TRÌNH ĐƯỜNG TRÒN
1577006557_0H3-3 PHƯƠNG TRÌNH ELIP