Các Dạng Toán Về Rút Gọn Biểu Thức Ôn Thi Vào 10 Giải Chi Tiết
Tính giá trị của biểu thức A khi x= 25. Rút gọn biểu thức B. Tìm tất cả các giá trị nguyên của x để B A. Cho P =AB . Tìm các giá trị nguyên của x. Tìm giá trị lớn nhất của biểu thức. Tìm m để có x thỏa mãn. Tìm giá trị nguyên của x để biểu thức. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Chuyên đề Toán 9 100 tài liệu
Môn: Toán 9 2.6 K tài liệu
Tác giả:
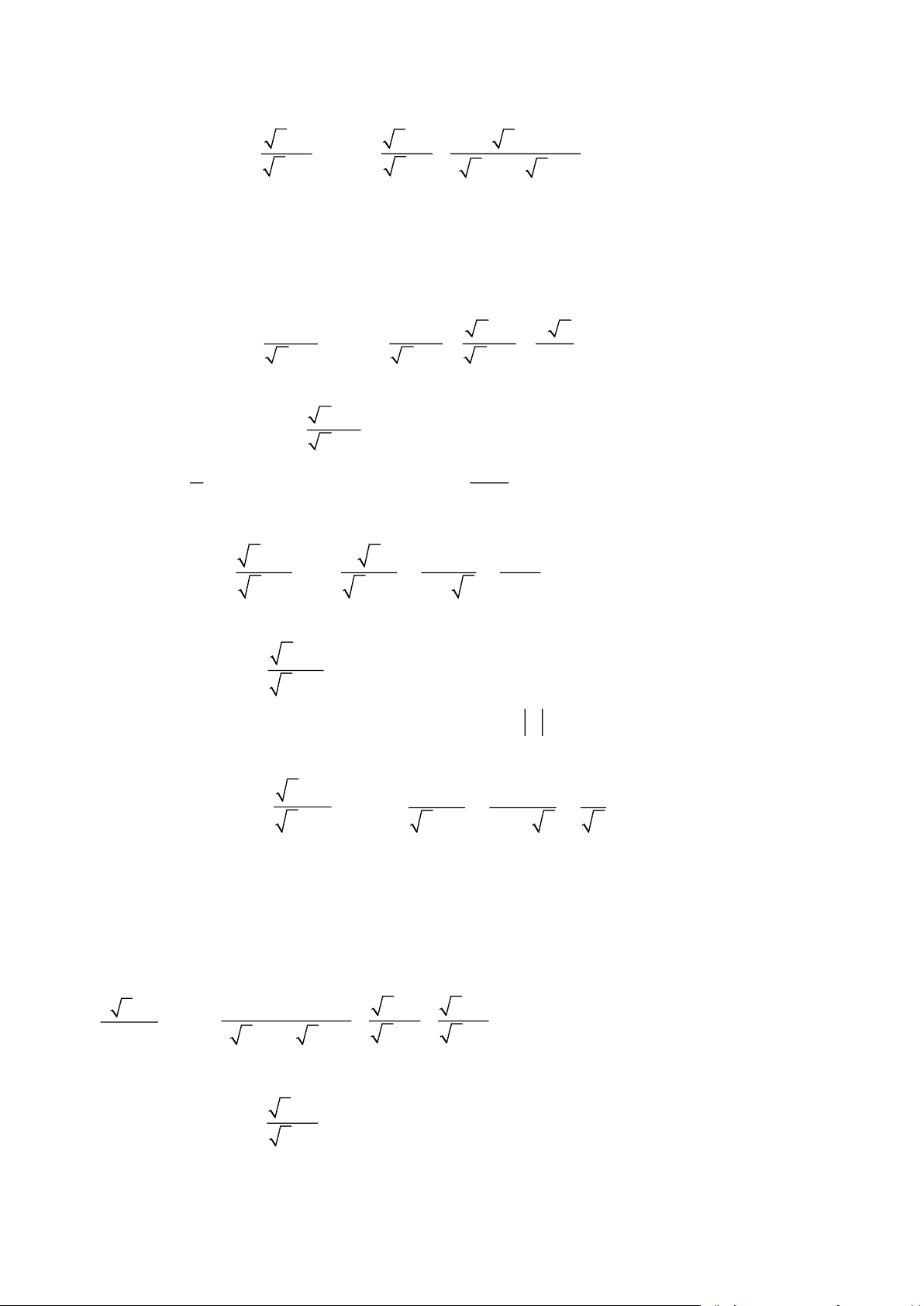
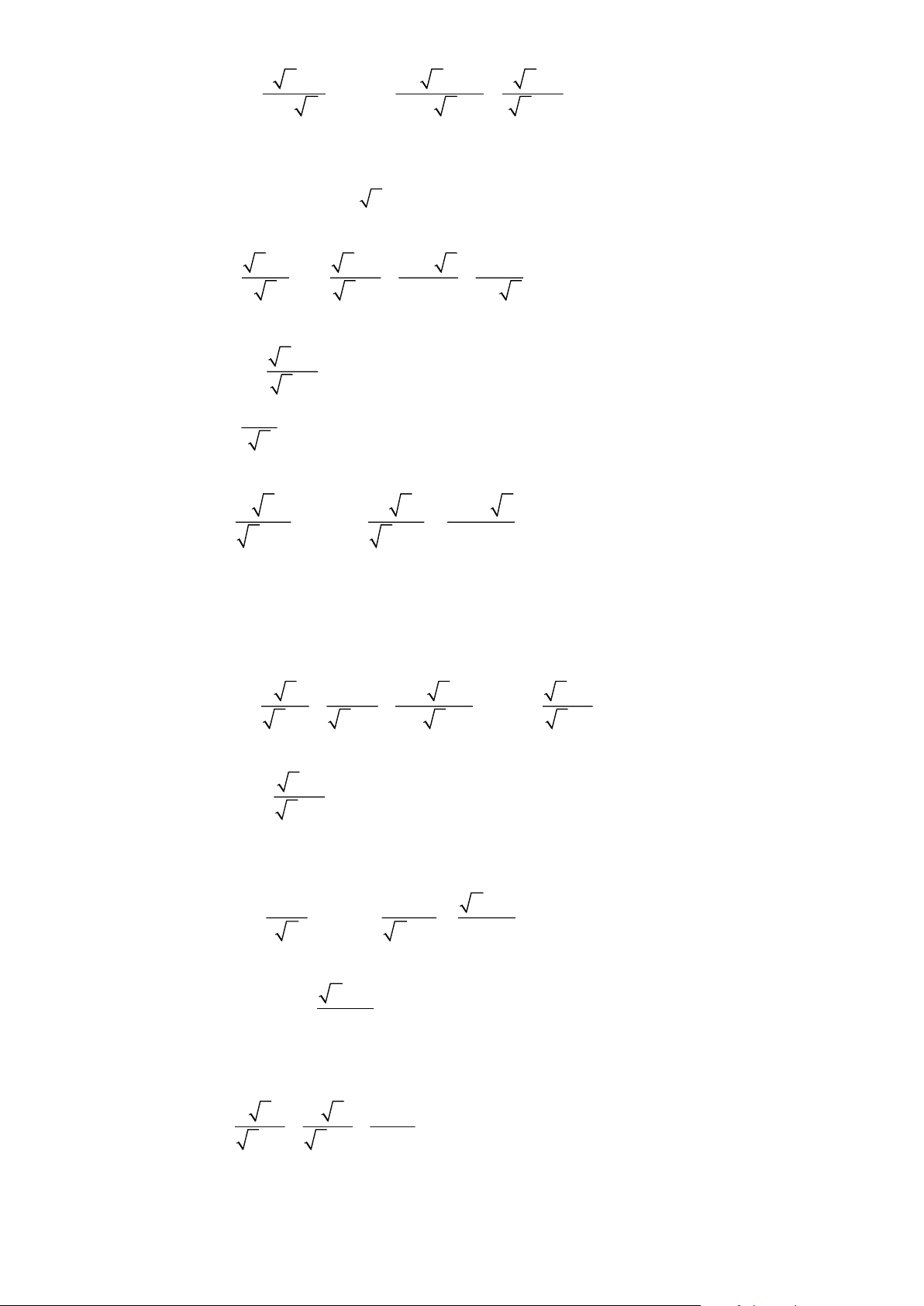
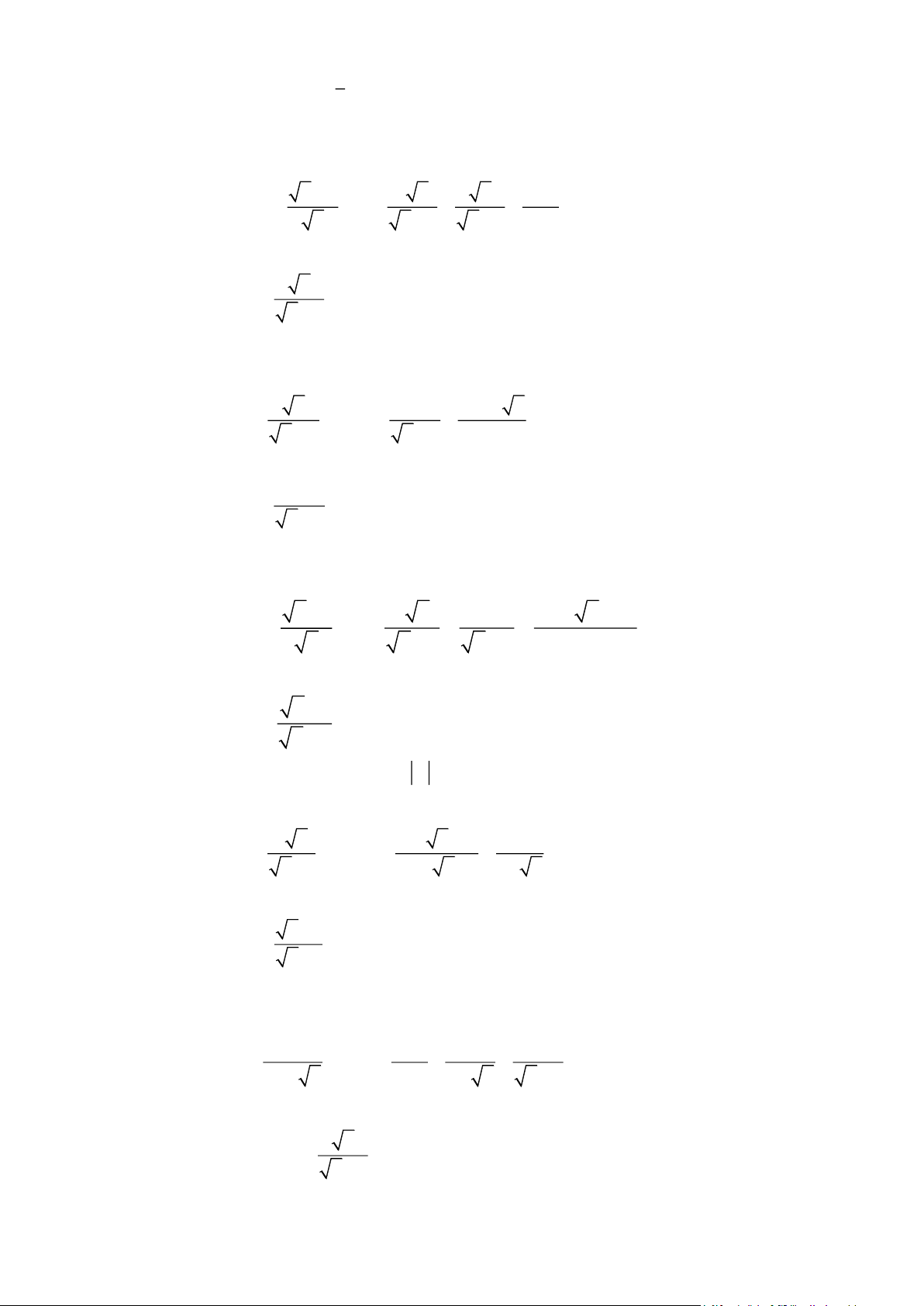
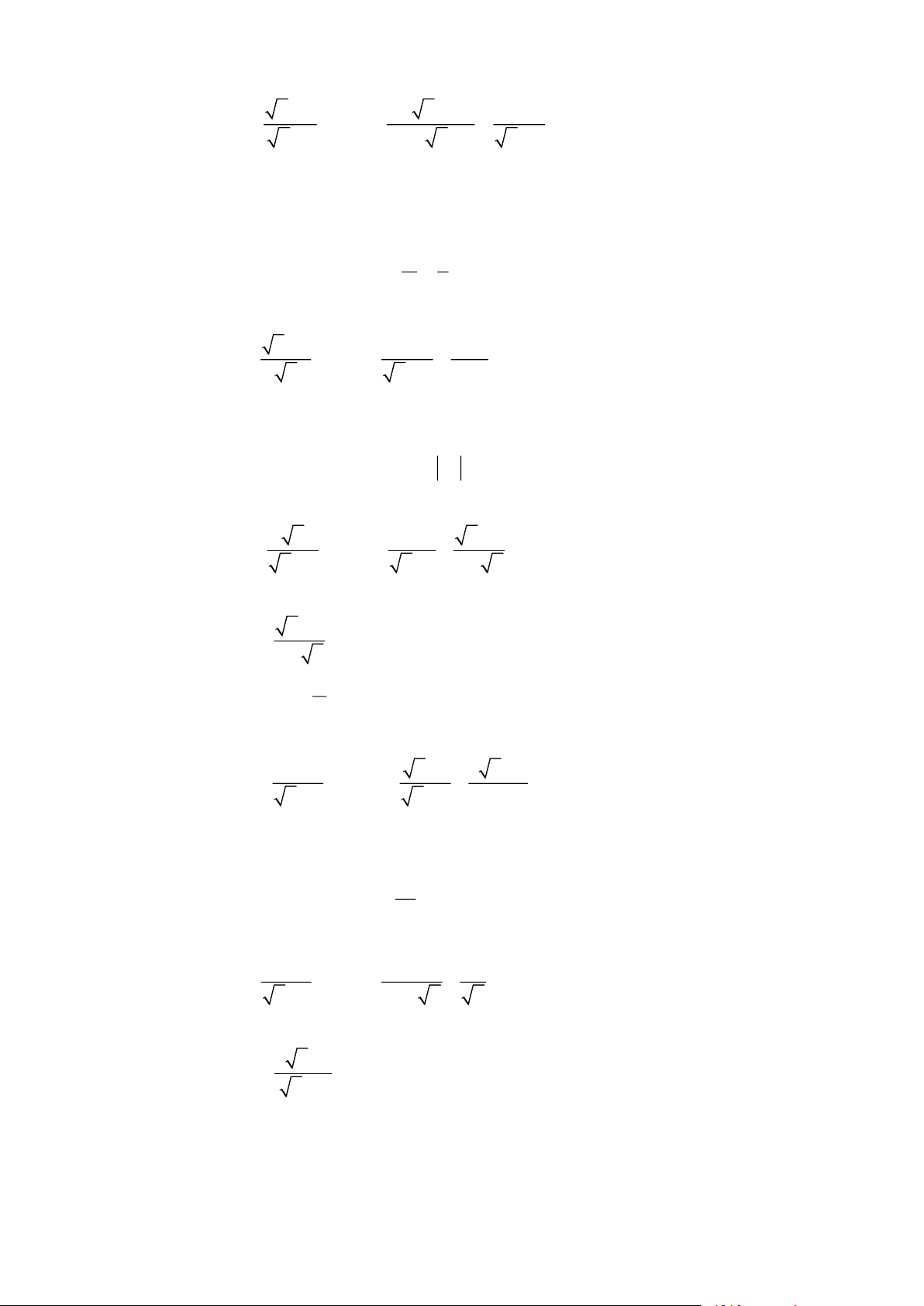
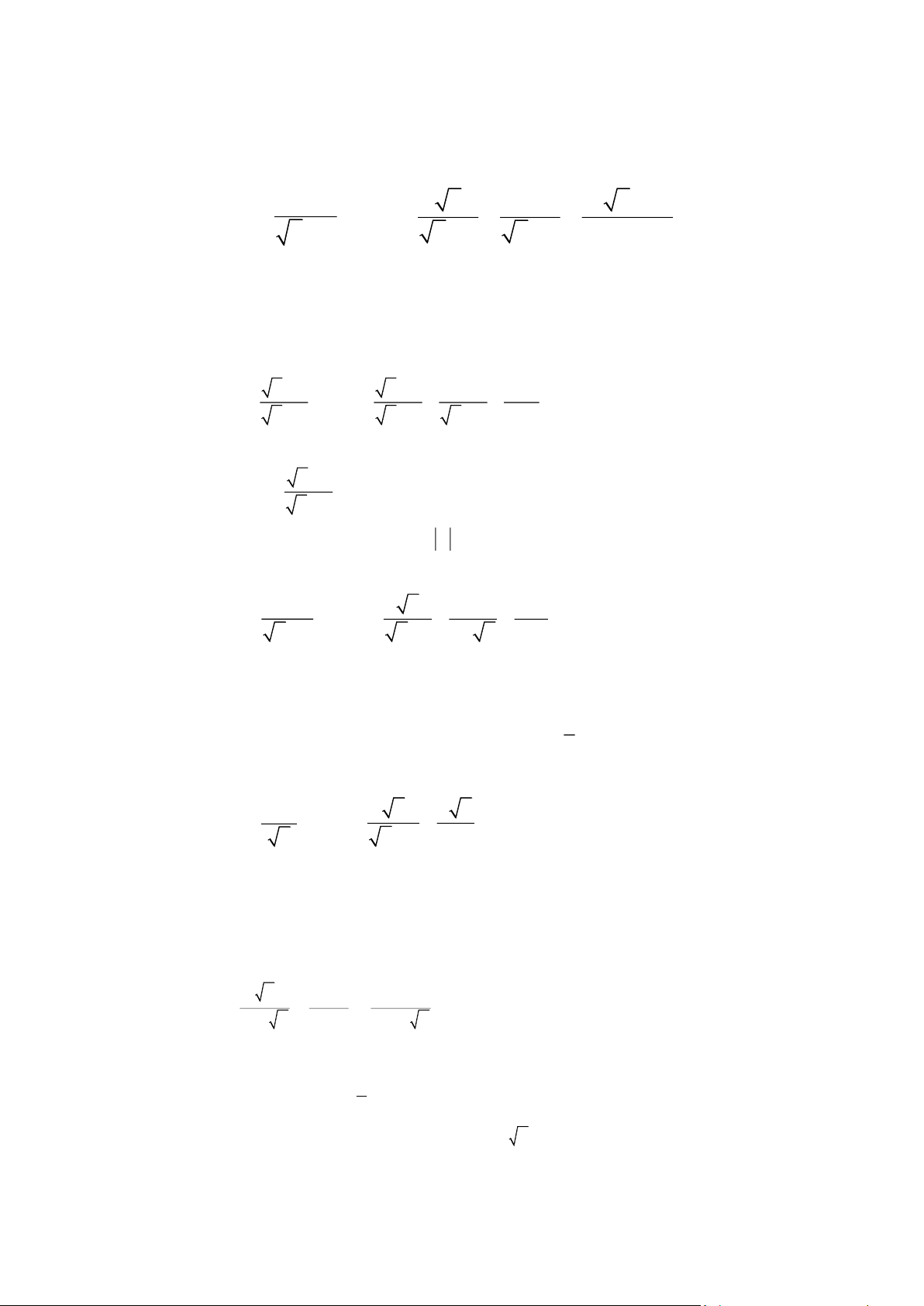
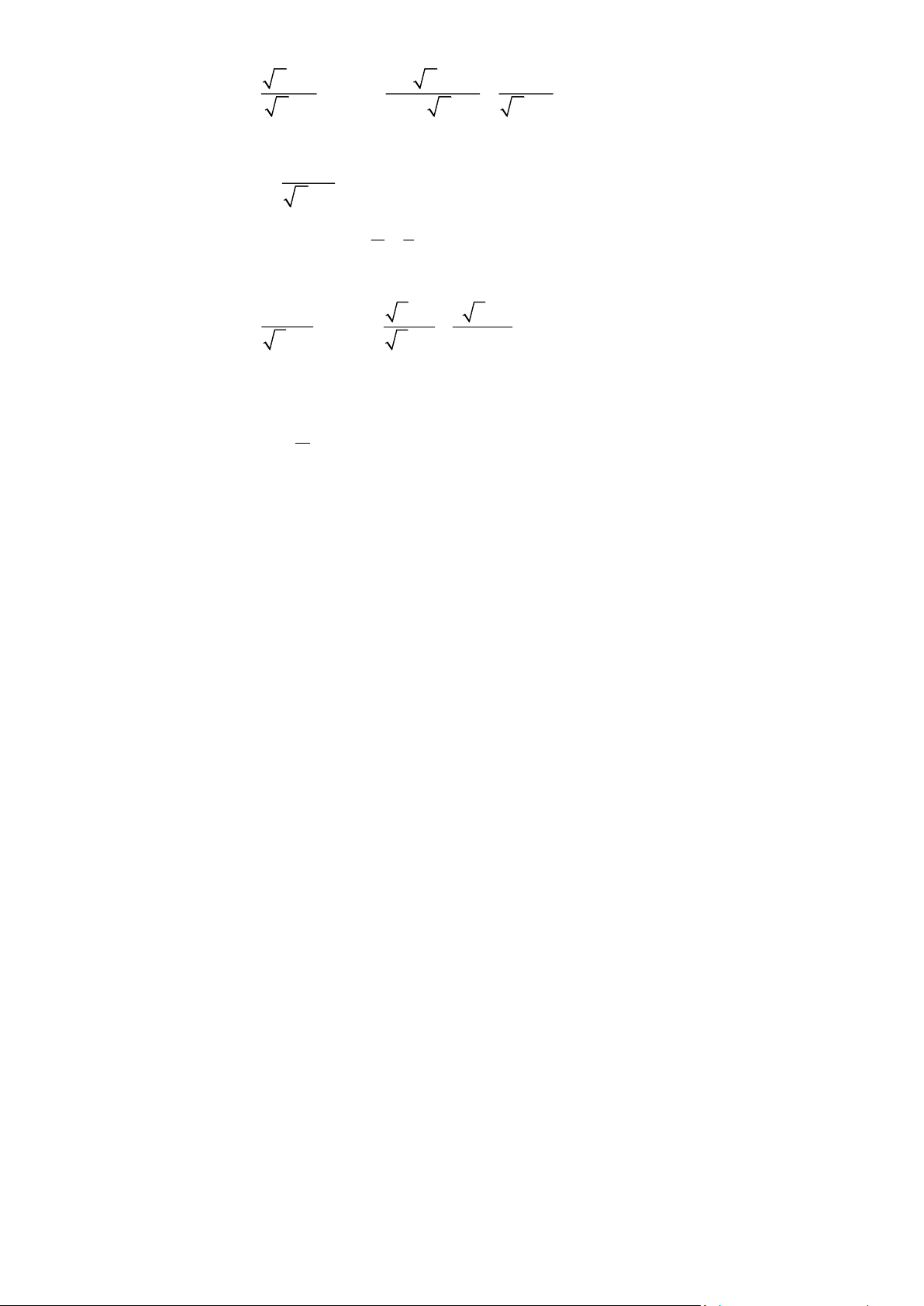
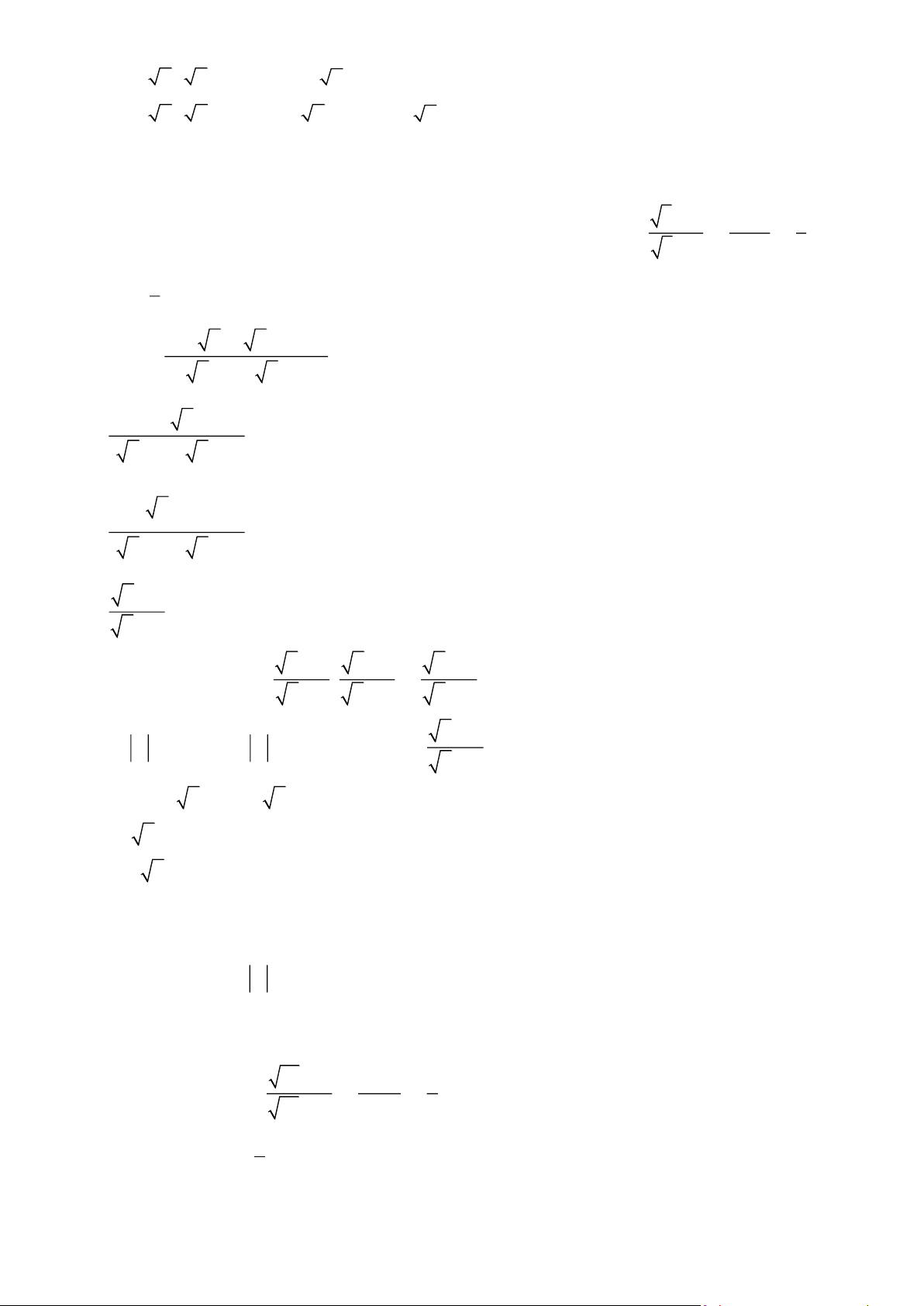
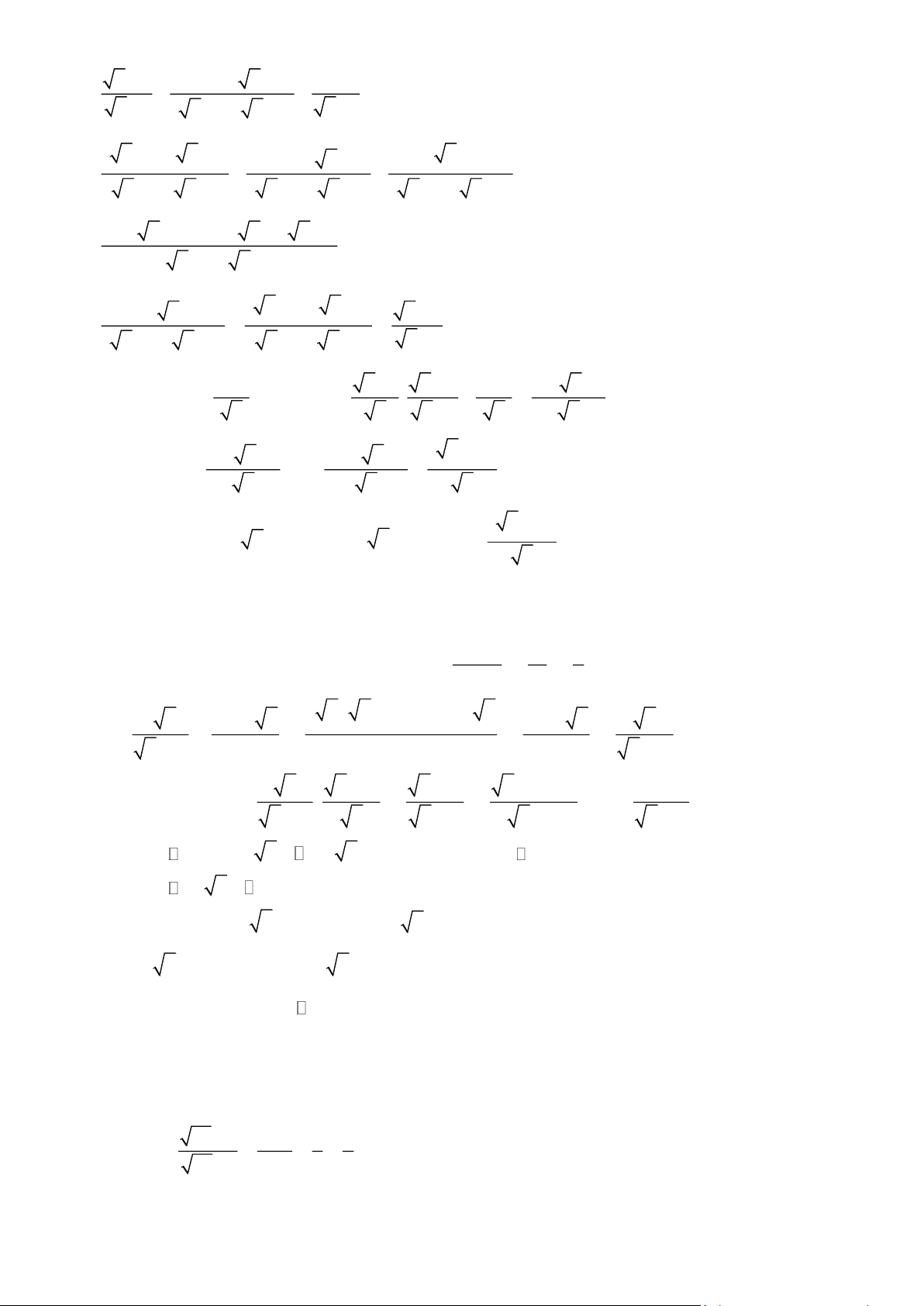
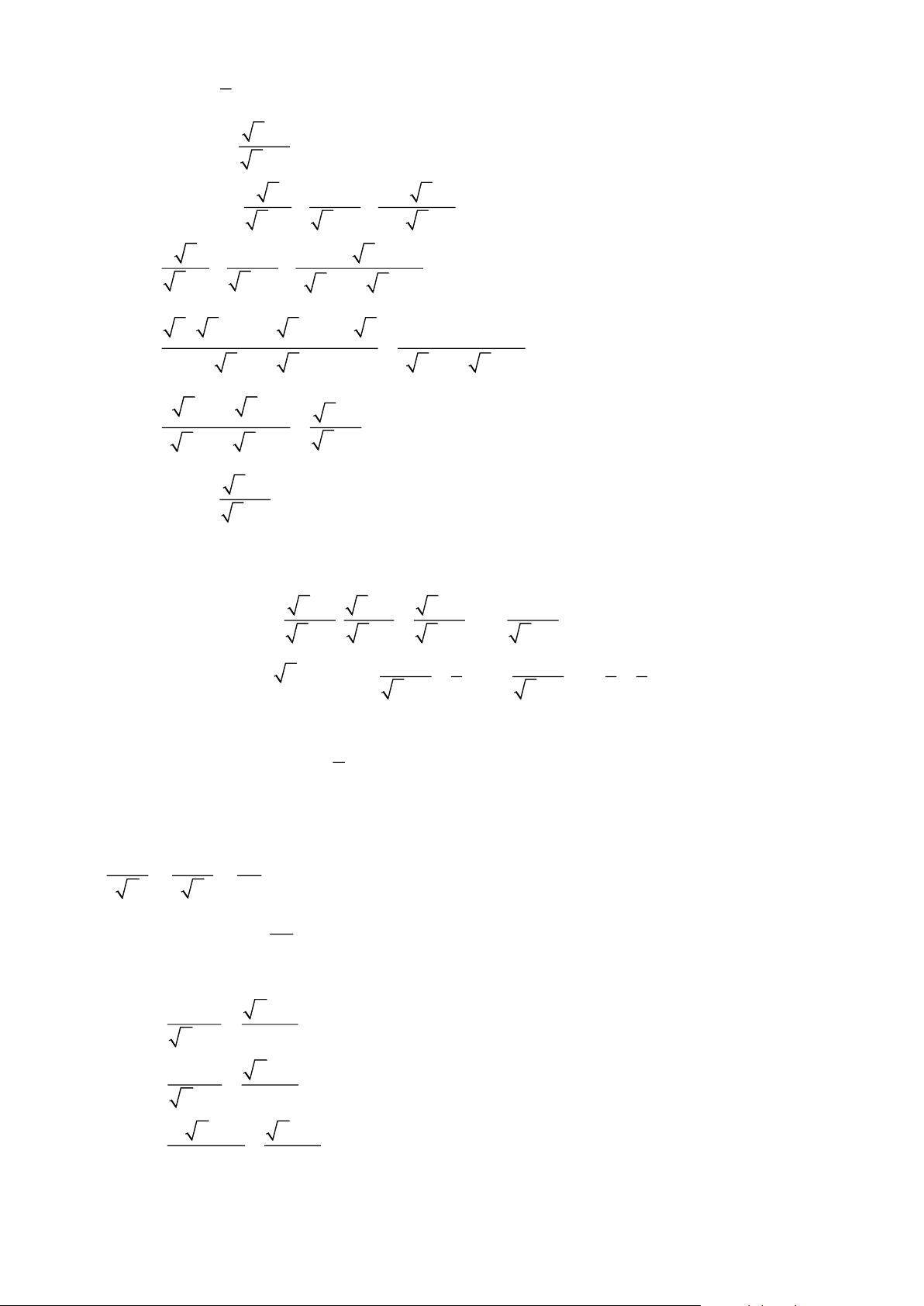
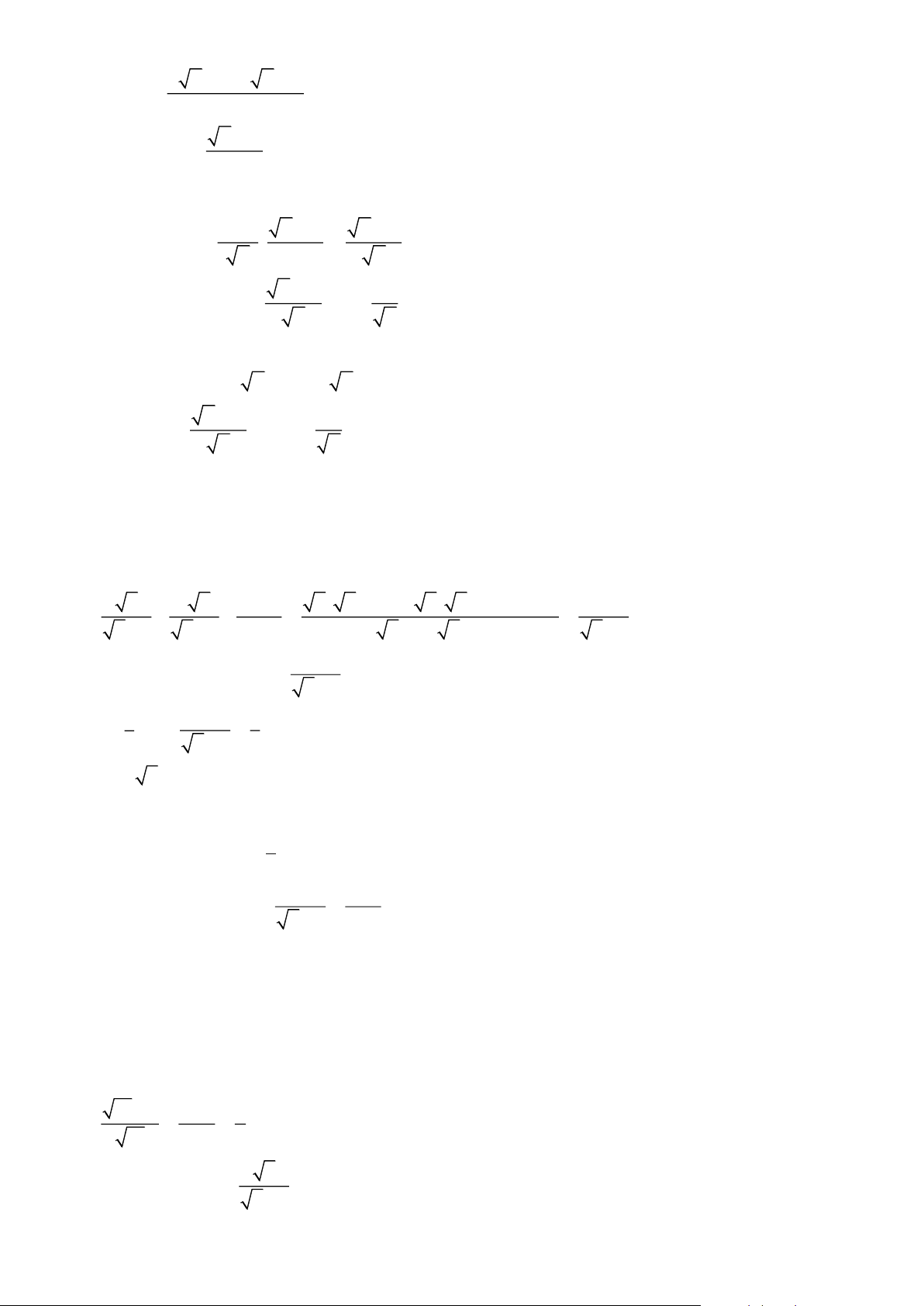
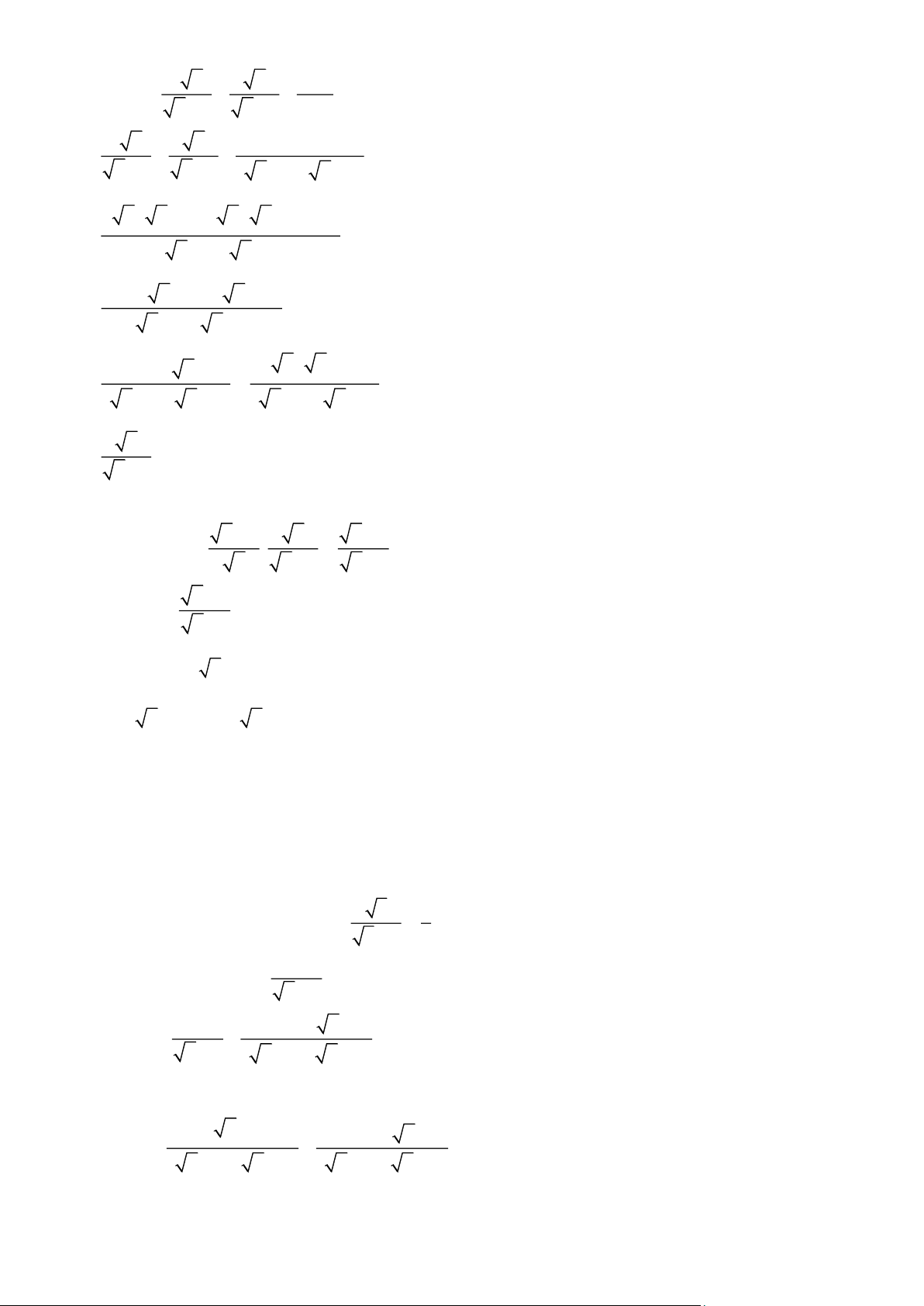
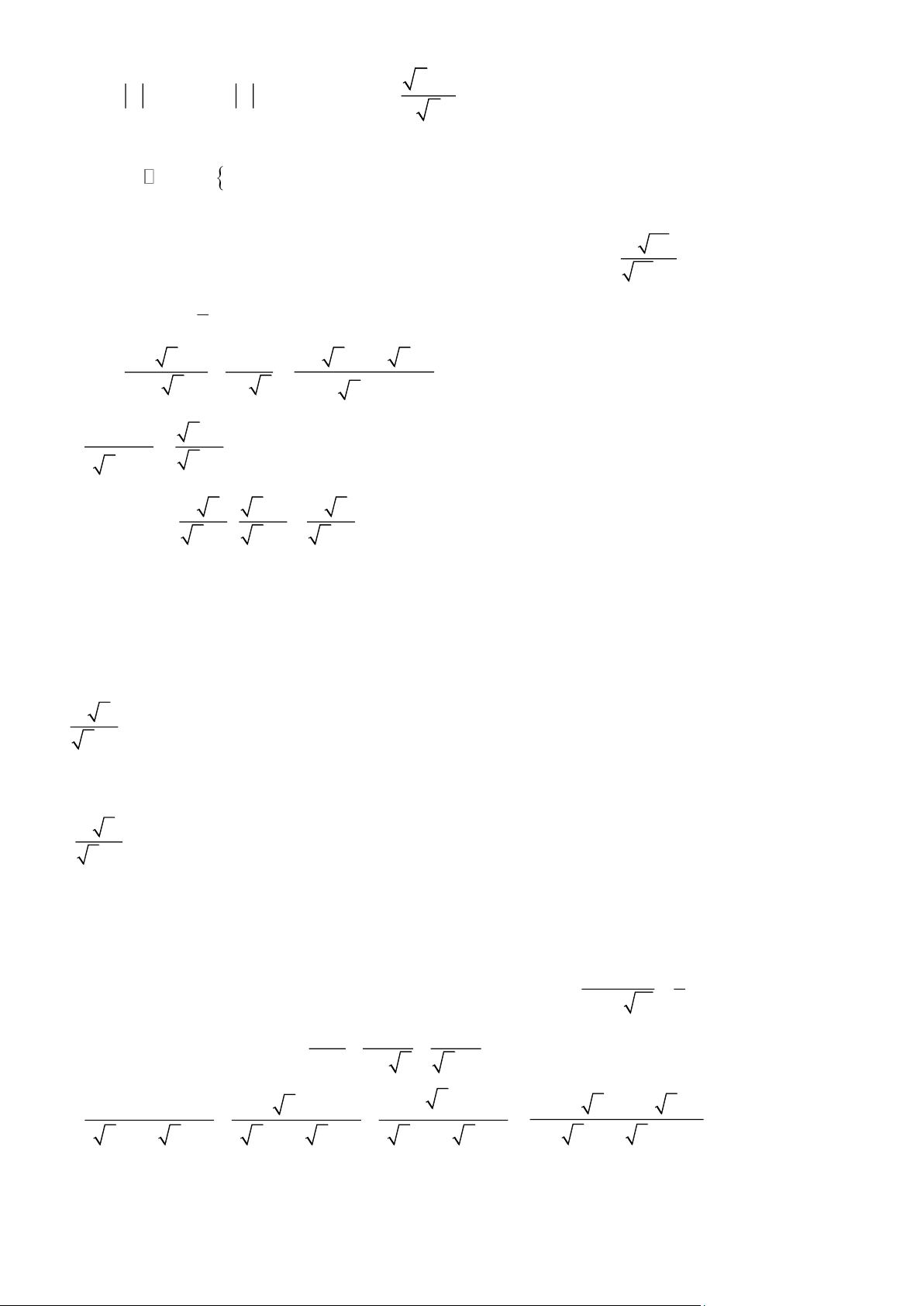
Preview text:
CHỦ ĐỀ 3: CÁC BÀI TOÁN VỀ RÚT GỌN BIỂU THỨC Bài 1. Cho hai biểu thức x +1 x + 2 x − 8 A = và B = +
với x 0; x 4; x 9 . x − 2
x − 3 ( x − 2)( x −3)
1) Tính giá trị của biểu thức A khi x = 25 .
2) Rút gọn biểu thức B
3) Tìm tất cả các giá trị nguyên của x để B A Bài 2. Cho hai biểu thức 2 x + x A = và 3 1 2 B = + −
với x 0, x 4 x − 2 x − 2 x + 2 4 − x
1) Tính giá trị của biểu thức A khi x = 64 2) Chứng minh rằng x + 2 B = x − 2 3) Cho A P =
. Tìm các giá trị của x để 2 P B x + 2 Bài 3. Cho biểu thức x - 2 x 1 2 A = ;B = + +
với x ³ 0;x ¹ 1 . x - 1 x + 1 1 - x x - 1
1) Tính giá trị biểu thức A tại x = 9 2) Chứng minh x - 1 B = . x + 1
3) Cho P = A.B . Tìm các giá trị nguyên của x để P + P = 0 . Bài 4. Cho hai biểu thức: x - 3 x - 3 9 3 A = và B = + +
với x > 0;x ¹ 9. x + 3 x - 3 x - 3 x x
1) Tính giá trị của biểu thức A khi x = 25 .
2) Rút gọn biểu thức B .
3) Xét biểu thức P = A B
× . Chứng minh P > 0 . Bài 5. Cho hai biểu thức 3 x − 9 x +1 x + 3 x − 2 A = và B = + −
( x 0; x 4; x 9 ) x − 4
( x +2)( x −3) x +2 x −3
1) Tính giá trị của biểu thức A khi x = 1 − 2) Chứng minh x 2 B = x − 3
3) Tìm giá trị lớn nhất của biểu thức P = . A B Bài 6. Trang 1 Cho hai biểu thức 3 x − 2 x − x + A = và 15 11 2 3 B = −
với x 0, x 1 1− x x + 2 x − 3 x + 3
1) Tính giá trị của biểu thức A khi x = 16
2) Đặt P = A + B . Rút gọn biểu thức P
3) Tìm m để có x thỏa mãn P( x + 3) = m Bài 7. Cho biểu thức: x −1 x − 2 2 + 8 x 2 M = ; P = + − với x > 0; x ≠ 1. x x +1 x −1 1− x
1) Tính M khi x = 0,49 2) Chứng minh x + 6 P = x −1 3) Đặt x − 5 Q = M.P + . So sánh Q với 3. x Bài 8. Cho biểu thức x x x + x A = và 2 9 B = -
với x > 0;x ¹ 4;x ¹ 9 x - 2 x - 3 x - 9
1) Tính giá trị của biểu thức A khi x = 100
2) Rút gọn biểu thức B
3) Tìm giá trị nguyên của x để biểu thức M = A : B có giá trị nguyên Bài 9. Cho hai biểu thức x 1 3 x x + A = + − và 3 B =
với x 0 ; x 1. x −1
x + 2 x + x − 2 x +1
1) Tính giá trị của biểu thức B với x = 25 . 2) Chứng minh x +1 A = . x + 2
3) Tìm x để biểu thức S = .
A B đạt giá trị lớn nhất. Bài 10. Cho hai biểu thức x - 9 x + A = và 2 4 B = + . x x - 3 9 - x
1) Tính giá trị của biểu thức A khi x = 4 2) Chứng minh rằn: x + 2 B = x - 9
3) Xét biểu thức P = AB . So sánh 2 P với P Bài 11. + Cho biểu thức x 2 x 3x 9 A = + −
(x 0; x 9) x + 3 x − 3 x − 9
1) Rút gọn biểu thức A . Trang 2
2) Tìm giá trị của x để 1 A = 3
3) Tìm giá trị lớn nhất của A Bài 12. − Cho hai biểu thức và x 2 x x x A = ; 2 2 B = + −
với x 0; x 9 . x x + 3 x − 3 x − 9
1) Tính giá trị của biều thức A khi x = 16 . 2) Chứng minh x B = . x + 3
3) Tìm các giá trị nguyên của x để P 0 với P = . A B . Bài 13. Cho hai biểu thức: x + x A = và 5 16 2 B = −
với x 0, x 4 x + 2 x − 2 x − 4
1) Tính giá trị của biểu thức A khi x = 9 . 2) Chứng minh 3 B = . x + 2
3) Tìm giá trị nguyên lớn nhất của x để 5A + B 3. Bài 14. x −1 2 x 4 x − 4 x +15
Cho hai biểu thức: A = ; B = + +
với x 0; x 9 x x + 3 x − 3 9 − x
1) Tính giá trị của biểu thức A khi x = 25. x −1 2) Chứng minh B = . x − 3
3) Cho P = A: B. Tìm x nguyên để P + P = 0 . Bài 15. Cho hai biểu thức: 2 x x + x − A = và 2 1 B = + với 𝑥 ≥ 0; 𝑥 ≠ 1 x −1
x − 2 x +1 1− x
1) Tính giá trị của biểu thức A khi x = 25 2) Chứng minh x +1 B = x −1
3) Đặt P = A: B . Tìm tất cả các giá trị của x để 4 P = P . Bài 16. x − 9 x + 3 1 2
Cho hai biểu thức: A = và B = − +
với x 0; x 9 . x − 3 x x − 9 3− x x + 3
1) Tính giá trị của A khi x = 16 . 2) Chứng minh rằng x B = x − 3 3) Đặt P = .
A B . Tìm các giá trị nguyên của x để P 1 Trang 3 Bài 17. + + Cho hai biểu thức x 4 x A = và 3 1 2 B = − với x 0,x 1. x −1 x + 2 x − 3 x + 3
1) Tính giá trị của biểu thức 𝐴 tại x = 9 .
2) Rút gọn biểu thức 𝐵.
3) Tìm tất cả các giá trị của x A x để = + 5 . B 4 Bài 18. Cho hai biểu thức x + 4 x + A = và 2 4 B = +
với x 0, x 4. x x + 2 x − 4
1) Tính giá trị của biểu thức A khi x = 9.
2) Rút gọn biểu thức B. 3) Cho P = .
A B . Tìm giá trị của x khi P = . P Bài 19. Cho hai biểu thức: x x − A = và 2 2 B = −
với x 0; x 1. x + 2
x −1 x − x
1) Tính giá trị của biểu thức A khi x = 4 . 2) Chứng minh x + 2 B = . x − x 3) Xét biểu thức 1 P = A +
. Tìm x để P 1. B Bài 20.
Cho hai biểu thức M = x + 3 và N = x −1 5 x − 2 +
với x 0, x 4 x − 2 x + 2 x − 4
1) Tính giá trị biểu thức của M khi x = 9.
2) Rút gọn biểu thức N.
3) Tìm giá trị của x để biểu thức M đạt giá trị nhỏ nhất. N Bài 21. Cho hai biểu thức x x − A = và 2 3 1 B = −
với x 0, x 9 . x − 3 x − 3 x x
1) Tính giá trị của biểu thức A khi x = 16 . − 2) Chứng minh 2 x 1 B = . x − 3
3) Tìm tất cả giá trị của x để A − B 0 . Bài 22. Trang 4 Cho hai biểu thức: x −1 x x + x − A = và 2 2 6 8 B = − + x − 3 x − 2 x − 3 x − 5 x + 6
với x 0 , x 4 , x 9
1) Tính giá trị của A khi x = 16 . 2) Chứng minh x + 2 B = . x − 3
3) Cho P = A : B . Tìm x để 1 P 2 Bài 23. Cho hai biểu thức: 3 x x 8 x P = + + và 1 Q =
(với x 0; x 4 ) x + 2 2 − x x − 4 x + 2
1) Tính giá trị của biểu thức Q khi x = 9.
2) Rút gọn biểu thức P . 3) Biết P M =
; Tìm các giá trị của x để M = 18. Q Bài 24. x x − 2 1 1
Cho hai biểu thức A = và B = − + với x 0 . x +1 x + 2 x x x + 2
1) Tính giá trị của A khi x = 9 . x − 2 B = 2) Chứng minh x
3)Tìm giá trị của x để 4 P = 2AB +
đạt giá trị lớn nhất. x +1 Bài 25. + Cho hai biểu thức x 1 + A = và x 1 2 B = −
với x 0; x 1 x −1 x − x x −1
1) Tính giá trị của biểu thức A tại x = 25. 2) Rút gọn B.
3) Cho P = A.B. So sánh giá trị của P với 1. Bài 26. x + 1) Cho biểu thức 4 A =
. Tính giá trị của biểu thức A với x = 36 . x + 2 x x + 2) Rút gọn biểu thức 4 16 B = + :
(với x 0 , x 16 ). x 4 x 4 + − x + 2
3) Với các biểu thức A và B , hãy tìm các giá trị nguyên của x để giá trị của biểu thức B ( A − )
1 là nhận giá trị nguyên. Bài 27. Trang 5 x +1 2 x x + 2 2 x + 4
Cho hai biểu thức: A = và B = − +
(Với x 0; x 1) x + 3 x +1 x −1 x −1
1) Tính giá trị của A khi x = 4 2) Rút gọn B 1 3) Tìm x để . A B 2 Bài 28. + 2 Với x − x +
x 0 , cho hai biểu thức = x x A và 1 2 1 B = + . x x x + x
1) Tính giá trị của biểu thức A khi x = 4 . 2) Chứng minh x + 2 B = . x +1
3) Tìm số nguyên x nhỏ nhất để A 7 . B 4 Bài 29. + − Cho x 2 x 2 x + M = − và 1 N =
Với x 0; x 1. x + 2 x +1 x −1 x
1) Tính giá trị của N khi x = 25
2) Rút gọn S = M.N
3) Tìm x để S −1 Bài 30. − + Cho hai biểu thức: x 3 x 6 x 2 x A = và B = +
với x 0, x 4, x 9 . x − 9 x − 2 x + 2
1) Tính giá trị của biểu thức A khi x = 16 .
2) Rút gọn biểu thức B .
3) Xét biểu thức P = .
A B . Tìm x để P 1. Bài 31. − − Cho hai biểu thức: x 2 x x A = và 3 9 10 B = − +
, với x 0 , x 4 . x + 9 x + 2 2 − x 4 − x −
1) Tính giá trị của biểu thức 3 8 A khi 3 x = − . 2 27
2) Rút gọn biểu thức B .
3) Cho P = B : A . Tìm các giá trị x là số thực để P nhận là một số chính phương. Bài 32. + Cho hai biểu thức: x 3 x x A = và 1 3 B = + −
với x 0; x 1. x +1 x −1 x + 2 x + x − 2
1) Tính giá trị của biểu thức A khi x = 25
2) Rút gọn biểu thức B Trang 6 3) Cho P = .
A B . Hãy so sánh và P và P . Bài 33. + x +1 2 x 7 x + 3 Cho biểu thức x 8 P = và Q = + + 3 x x − 3 x + 3 9 − x
với x 0 và x 9
1) Tính giá trị của biểu thức P khi x = 4 2) Chứng minh: 3 x Q = x + 3
3) Tìm x để A 2 với A = . P Q Bài 34. a 1 Cho biểu thức A = 1 2 − : + a −1 a −
a a +1 a−1 1) Rút gọn biểu thức A
2) Tính giá trị của biểu thức A, biết a = 4 +2 3 3) Tìm a sao cho A < 0 Bài 35. Cho hai biểu thức 1 x 1 3 A = 1− và B = − +
với x 0, x 1 x x + 3 x −1 ( x − ) 1 ( x + 3)
1) Tính giá trị của A khi x = 4 .
2) Rút gọn biểu thức P = B . A
3) Tìm các giá trị của x để P nhận giá trị nguyên. Bài 36. Cho Cho hai biểu thức x + 7 x x A = B = + −
(với x 0; x 9 ) x − và 6 3 3 x − 3 9 − x x + 3
1) Tính giá trị của biểu thức A khi x = 49 . 2) Rút gọn B .
3) Cho M = A B . Tìm x để M đạt giá trị nhỏ nhất. Bài 37. Cho biểu thức 3x +12 x + x x + A = và 1 2 7 3 B = + −
(với x 0; x 9 ) x + 3 x − 3 x + 3 x − 9
1) Tính giá trị của biểu thức A khi x = 4 2) Chứng minh 3 x B = x + 3
3) Tìm giá trị nhỏ nhất của biểu thức A P = B Bài 38. Trang 7 Cho biểu thức 3x +12 x + x x + A = và 1 2 7 3 B = + −
(với x 0; x 9 ) x + 3 x − 3 x + 3 x − 9
1) Tính giá trị của biểu thức A khi x = 4 2) Chứng minh 3 x B = x + 3
3) Tìm giá trị nhỏ nhất của biểu thức A P = B Bài 39. 3 x -6 1 x -3 − A = - + và x 2 B =
với x 0; x 4
x - 2 x 2- x x x +1
1) Tính giá trị của B khi x = 25 − 2) Chứng minh x Q = . A B = 1 x +1
3) Tìm các số nguyên x để 4 Q 3 Bài 40. Cho hai biểu thức: 3 x +10 + A = − và x 2 B = với x 0;x 4 x − 2 x − 4 x − 2
1) Tính giá trị của B tại x = 9 2) Rút gọn A
3) Đặt P = A.B . Tìm số nguyên tố x để P −1 Bài 41. Cho hai biểu thức x − 5 x + x x A = và 2 2 B = −
vói x 0, x 1 . x x −1 x −1
1) Tính giá trị của biểu thức A khi x = 36
2) Rút gọn biểu thức B .
3) Tìm tất cả giá trị nguyên của x để biểu thức P = AB có giá trị nguyên. Bài 42. Cho hai biểu thức x + 3 x x + x − x + A = và 2 3 5 B = − −
với x 0 ; x 4 ; x 9 x +1 x − 2 3 − x x − 5 x + 6
1) Tính giá trị của A khi x = 25 . 2) Rút gọn B .
3) Cho P = A: B . Tìm x để 2P = 2 x − 9 . Bài 43. Cho hai biểu thức x − 7 − + A = và 1 x 2x x 2 B = + + với x 0, x 4 x x + 2 2 − x x − 4 Trang 8
1) Tính giá trị của biểu thức A khi x = 9
2) Rút gọn biểu thức B .
3) Tìm tất cả các giá trị nguyên của x để biểu thức P = A.B có giá trị nguyên Bài 44. 24 x 1 17 x + 30
Cho hai biểu thức N = và M = + +
với x 0, x 36. x + 6 x + 6 x − 6 x − 36
1) Tính giá trị của biểu thức N khi x = 9
2) Rút gọn biểu thức M .
3) Tìm số nguyên x để biểu thức L = N .M có giá trị nguyên lớn nhất. Bài 45. Cho hai biểu thức x − 2 x + A = và 2 3 12 B = − −
với x 0 , x 4 . x + 2 x − 2 x + 2 x − 4
1) Tính giá trị của biểu thức A khi x = 25 . 2) Chứng minh x − 1 B = . x − 2
3) Với P = A.B . Tìm giá trị của x để P P . Bài 46. Cho hai biểu thức x − 2 x A = và 2 4 B = − −
(với x 0 ; x 1). x + 2 x +1 1− x x −1
1) Tính giá trị của A khi x = 16 .
2) Rút gọn biểu thức B . 3) Đặt P = .
A B . Tìm các giá trị nguyên của x để 7 P = . 4 Bài 47. Cho hai biểu thức − 3 x x = x A và 4 B = −
với x 0, x 4 x x + 2 4 − x
1) Tính giá trị của biểu thức A biết x = 16 .
2) Rút gọn biểu thức B . 3) Cho P = .
A B . Tìm các giá trị nguyên của x để P 6. Bài 48. + Cho biểu thức x x 4 x B = + :
(với x 0, x 4).
2 + x 4 − x x − 2 x
1) Rút gọn biểu thức B .
2) Tính giá trị của B với 1 x = . 4
3) Tìm tất cả các giá trị nguyên của x để B − x . Bài 49. Trang 9 + + Cho hai biểu thức x 4 x A = và 3 1 2 B = −
với x 0 , x 1. x −1 x + 2 x −3 x + 3
1) Tính giá trị của biểu thức A khi x = 9 1 2) Chứng minh B = x −1
3) Tìm tất cả giá trị của x để A x + 5 . B 4 Bài 50. Cho hai biểu thức x + 3 x + x + A = và 3 3 6 B = −
với x 0, x 4 x − 2 x − 2 x − 4
1) Tính giá trị của biểu thức A khi x = 16 .
2) Rút gọn biểu thức B .
3) So sánh biểu thức A với 3 . B HƯỚNG DẪN GIẢI Trang 10 Bài 1. 1) Với +
x = 25 (thỏa mãn điều kiện) suy ra 25 1 6 A = = = 2 . 25 − 2 3
Vậy x = 25 thì A = 2 2) Thu gọn biểu thức
( x +2)( x −2)+ x −8 B = (
x − 2)( x −3)
x − 4 + x − 8 = (
x − 2)( x −3)
x + 4 x − 3 x −12 = (
x − 2)( x − 3)
( x +4)( x −3) x +4 = ( =
x − 2)( x −3) x − 2 Vậy x +
x 0; x 4; x 9 thì 4 B = x − 2 3) Ta có: x + 4 x +1 B A x − 2 x − 2 x + 4 x +1 − 0 x − 2 x − 2 3
0 x 2 x 4 x − 2
Kết hợp điều kiện suy ra 0 x 4. Mà x x 0;1;2; 3 .
Vậy x 0;1;2; 3 thì B A Bài 2.
1) . Thay x = 64 (thỏa mãn điều kiện) vào biểu thức A ta được 2 1 A = = . 64 − 2 3
3( x + 2 ) + ( x − 2 )( x +1) + 2 x + + + 2) . Ta có x 4 x 4 x 2 B = ( = = .
x − 2 )( x + 2 )
( x − 2)( x + 2) x − 2
3) . Với x 0, x 4 thì A 2 x + 2 2 P = = : = B x − 2 x − 2 x + 2 . Để 2 2 2 P x + 2 x + 2 x + 2 .
Do 2 0 và x + 2 0, x + 2 0 x + 2 x + 2 x ( x −1) 0 Trang 11
TH1: x ( x −1) = 0 nên x = 0 x = 0 (
TH2: x ( x −1) 0 x −1 0 vì x 0 nên x 1.
Kết hợp với điều kiện x 0, x 4 ta được x = 0 hoặc x 1, x 4 . Bài 3. 1) Thay - -
x = 9 ( thỏa mãn điều kiện) vào biểu thức A ta có 9 2 3 2 1 A = = = . 9 - 1 3 - 1 2 Vậy 1 A = khi x = 9 . 2 2) x - x - x - 1 + 2 B = (
(với x ³ 0,x ¹ 1 ) x + ) 1 ( x - ) 1 x - 2 x + 1 B = ( x + ) 1 ( x - ) 1 ( x - )2 1 B = ( x + )1( x - )1 x - 1 B = ( đpcm) x + 1 3) Ta có x - 2 x - 1 x - 2 P = A.B = . = x - 1 x + 1 x + 1 Ta có: x - 2
P + P = 0 Þ P = - P Þ P £ 0 Þ £ 0 x + 1 Mà x ³ 0 Þ x ³ 0 Þ
x + 1 > 0 , với mọi x thoả mãn ĐKXĐ Suy ra x - 2 £ 0 x £ 2 x £ 4 .
Vì x Î ¢ , x ³ 0,x ¹ 1 Þ x Î {0;2;3;4}.
Vậy x Î {0;2;3;4}thì P + P = 0 . Bài 4. 1)
Khi x = 25 ( ĐKXĐ thoả mãn) Ta có 25 - 3 5 - 3 1 A = = = . 25 + 3 5 + 3 4 Vậy 1 A = 4
2) Rút gọn biểu thức B. Trang 12 Ta có x - 3 9 3 B = + + x - 3 x - 3 x x (x - 3) x 9 3( x - 3) = + + x ( x - 3) x ( x - 3) x ( x - 3)
x x - 3 x + 9 + 3 x - 9 = x ( x - 3) x x = x ( x - 3) x = x - 3 Vậy x B = x - 3
-------------------------------------------
3). Xét biểu thức P = A B
× . Chứng minh P > 0 . Ta có x - 3 x x P = A B × = . = x + 3 x - 3 x + 3 Với x
x > 0;x ¹ 9 , ta có x + 3 > 0 nên P = > 0 x + 3 Bài 5.
1). Thay x = 1 (TMĐK) vào biểu thức A 3 x − 9 3. 1 − 9 6 − A = = = = 3 x − 4 1− 4 2 − x +1 x + x + x + −
( x +3)( x −3)−( x −2)( x +2 1 3 2 ) 2). B = ( + − = x + 2)( x −3) x + 2 x − 3 ( x +2)( x −3)
x +1+ x − 9 − x + 4
B = ( x+2)( x−3) x − 4
B = ( x+2)( x−3) ( x +2)( x −2)
B = ( x +2)( x −3) x − 2 B = x −3 Trang 13 − Vậy x 2 B =
với x 0; x 4; x 9 . x − 3 3 x − x −
( x −3)( x −2 3 9 2 ) 3 3). P = . A B = . = = x − 4
x − 3 ( x − 2)( x + 2)( x −3) x + 2
Vì x 0 nên x + 2 2 0. Suy ra 3 3 P = x + 2 2
Dấu “=” xảy ra khi x = 0 (tmđk)
Vậy giá trị lớn nhất của 3
P = khi x = 0 . 2 Bài 6. 1) Thay x − − − −
x = 16 (tmđk) vào biểu thức 3 2 A = ta được 3 16 2 3.4 2 12 2 10 A = = = = − 1− x 1− 16 1− 4 3 − 3 Vậy khi x = 16 thì 10 A = − 3
1) Với x ≥ 0 , x ≠ 1 . Ta có: 3 x − 2 15 x −11 2 x + 3
P = A + B = + − 1− x x + 2 x − 3 x + 3
( 3− x +2)( x +3) (2 x +3)( x x − − )1 15 11 P = ( + − x − ) 1 ( x + 3)
( x − )1( x +3) ( x − )1( x +3) − x + x − −
( x − )1(5 x −2 5 7 2 ) 3
− x − 7 x + 6 +15 x −11− 2x − x + 3 P = ( = = x − ) 1 ( x + 3)
( x − )1( x +3) ( x − )1( x +3) 5 − x + 2 − x + P =
. Vậy với x 0; x 1 thì 5 2 P = x + 3 x + 3
2) Với x 0; x 1 ta có: − +
m = P ( x + ) 5 x 2 3 = .( x +3) = 5 − x + 2 x + 3 Với x 0 5 − x 0 5 −
x + 2 2 m 2 ( ) 1
Mặt khác x 1 x 1 5 − x 5 − 5 − x + 2 3 − m 3 − (2)
Từ (1) và (2) m 2;m − 3
Vậy với m 2;m − 3 thì có x thỏa mãn P( x +3) = m Bài 7. − −
1) Thay x = 0,49 (thỏa mãn) vào M , ta có: 0, 49 1 3 M = = . 0, 49 7 Vậy 3 − M = khi x = 0,49 7 2) x − 2 2 + 8 x 2 P = + − x +1 x −1 1− x Trang 14 x − 2 2 + 8 x 2 P = + + x +1 ( x − ) 1 ( x + ) 1 x −1
( x −2)( x − )1 2( x x + + )1 2 8 P = ( + + x − ) 1 ( x + ) 1
( x − )1( x + )1 ( x − )1( x + )1
x − 3 x + 2 + 2 + 8 x + 2 x + 2 P = ( x − ) 1 ( x + ) 1 ( x +6)( x x x + + + )1 7 6 x + 6 P = ( = =
(điểu phải chứng minh) x − ) 1 ( x + ) 1
( x − )1( x + )1 x −1 3) Xét x − 5 x − x + x − x + x + Q = M.P + suy ra 1 6 5 1 Q = . + = x x x −1 x x 1 2 1 ( x x x x x − + + − + )2 1 Xét hiệu Q − 3 = − 3 = = x x x ( x − )2 1
Với x 0; x 1 thì ( x − )2
1 0 và x 0 suy ra 0 hay Q 3 x Bài 8.
1) Điều kiện x > 0;x ¹ 4;x ¹ 9
Khi x = 100 (thỏa mãn điều kiện) thì 10 10 5 A = = = 10 - 2 8 4 2 2 x x + 9 x x
( x + 3)- x - 9 x 2) x - 3 x x B = - = = = x - 3 x - 9 x - 9 x - 9 x + 3 3) Ta có x x + 3 x + 3 x - 2 + 5 5
M = A : B = . = = = 1 + x - 2 x x - 2 x - 2 x - 2
TH1: x nhưng x x là số vô tỷ M
TH2: x , x
Để M nguyên thì x - 2 Î U (5) và x - 2 > - 2
Suy ra x - 2 Î {- 1;1; } 5 Û
x Î {1;3;7}Û x Î {1;9;4 } 9 (thỏa mãn đkxđ) Vậy x Î {1;9; } 49 thì M . Bài 9.
1) Tính giá trị của biểu thức B với x = 25 .
Với x = 25 (thỏa mãn điều kiện) thay vào biểu thức B ta có: 25 + 3 5 + 3 8 4 B = = = = . 25 +1 5 +1 6 3 Trang 15 Vậy 4
B = khi x = 25 . 3 2) Chứng minh x +1 A = . x + 2 Ta có: x 1 3 x A = + − x −1
x + 2 x + x − 2 x 1 3 x = + − x −1 x + 2 ( x − ) 1 ( x + 2)
x ( x + 2) + ( x − ) 1 − 3 x x −1 = ( = x − ) 1 ( x + 2)
( x − )1( x +2)
( x − )1( x + )1 x +1 = ( = x − ) 1 ( x + 2) x + 2 Vậy x +1 A =
với x 0 ; x 1. x + 2
3) Tìm x để biểu thức S = .
A B đạt giá trị lớn nhất.
Với x 0 ; x 1. Ta có: x +1 x + 3 x + 3 1 S = . A B = . = =1+ x + 2 x +1 x + 2 x + 2 Ta có: 1 1 3
x 0 x + 2 1 1 2 1+ 1+ = x + 2 2 x + 2 2 2
Dấu " = " xảy ra khi x = 0 (thỏa mãn điều kiện).
Vậy GTLN của S là 3 khi x = 0 . 2 Bài 10.
1) Thay x = 4 (TMĐK) vào biểu thức A ta được: x - 9 4 - 9 - 5 A = = = x 4 2 Vậy, khi 5 x = 4 thì - A = 2
2) ÐKXÐ: x > 0, x ¹ 9 . 2 x + 4 B = + x - 3 9- x 2 x + 4 B = - x - 3 x - 9 2( x + 3) x + 4 B = - x - 9 x - 9 Trang 16 2 x + 6- x - 4 B = x - 9 vậy x + 2 B =
với x > 0, x ¹ 9 . x - 9
3) ÐKXÐ: x > 0, x ¹ 9 x - 9 x + 2 x + 2 P = AB = . = x x - 9 x Xét hiệu x + 2 2 P - 1 = - 1 = x x Ta có: 2
P - P = P (P - 1)
Vì x > 0 nên x > 0 và x + 2 > 0
Khi đó x + 2 > 0 và 2 > 0 hay P > 0 và P - 1> 0 . x x
Suy ra P(P - 1) > 0 hay 2
P - P > 0 Vậy 2
P > P với x > 0, x ¹ 9 Bài 11.
1) Rút gọn biểu thức A . x 2 x 3x + 9
x( x − 3) + 2 x( x + 3) − 3x − 9 3 A = + − = =
Với x 0; x 9 x + 3 x − 3 x − 9
( x + 3)( x − 3) x + 3
Vậy với x 0; x 9 thì 3 A = x + 3 2) 1 A = khi 3 1 = 3 x + 3 3 Suy ra x + 3 = 9 x = 36 (thỏa mãn)
Vậy với x = 36 thì 1 A = 3
3) Với x 0; x 9 có 3 3 A = =1 x + 3 0 + 3
Dấu “=” xảy ra khi x =0 (t/m)
MaxA =1 khi x = 0 Bài 12. 1)
Tính giá trị của biểu thức A khi x = 16 .
Thay x = 16 vào biểu thức A , ta được: 16 − 2 4 − 2 1 A = = = . 16 4 2 2) Chứng minh x B = . x + 3 Trang 17 Ta có: 2 x x 2x B = + − x + 3 x − 3 x − 9 2 x x 2x B = + − x + 3
x − 3 ( x −3)( x + 3)
2 x ( x −3) + x ( x + 3) − 2x B = ( x − 3)( x + 3)
2x − 6 x + x + 3 x − 2x B = ( x −3)( x +3) x x − x ( x −3 3 ) B = ( =
x − 3)( x + 3) ( x −3)( x + 3) x B = x + 3
3) Tìm các giá trị nguyên của x để P 0 với P = . A B . − − Ta có: x 2 x x 2 P = . A B = . = . x x + 3 x + 3 − Để x P 0 thì 2 0 x + 3 x 0 Vì Nên x + 3 0 x 9
Do đó: x − 2 0 x 2 x 4 .
Kết hợp với điều kiện x 0 , ta có: 0 x 4.
Vì x nhận giá trị nguyên nên x 1;2; 3 . Bài 13.
1) Tính giá trị của biểu thức A khi x = 9 .
Thay x = 9 (tmđk) vào biểu thức A ta được 9 3 A = = 9 + 2 5 2) Chứng minh 3 B =
. với x 0, x 4 ta có: x + 2 + 5 16 2 x B = −
x − 2 ( x − 2)( x + 2) 5( x + 2) 16 + 2 x B = ( −
x − 2)( x + 2) ( x − 2)( x + 2) Trang 18 − 3 x 6 B = ( x − 2)( x + 2) 3 B = x + 2
3) Tìm giá trị nguyên lớn nhất của x để 5A + B 3. 5 x + 3
Với x 0, x 4 ta có: 5A+ B = x + 2 5 x + 3
Để 5A + B 3 khi 3 x + 2 5 x + 3 − 3 0 x + 2 3 x + ( x +2 5 3 ) − 0 x + 2 x + 2
5 x + 3 − 3 x − 6 0 x + 2 2 x − 3 0 x + 2 9 0 x 4
Vậy giá trị nguyên lớn nhất của x thỏa mãn yêu cầu là x = 2 . Bài 14. 25 −1 4
1) Thay x = 25 (tmđk) vào A ta được A = = 25 5
Vậy với x = 25 thì 4 A = 5 2 x 4 x − 4 x +15 2)B = + − x + 3 x − 3 x − 9 2 x ( x − 3) 4( x + 3) x − 4 x +15 = ( + −
x − 3)( x + 3) ( x − 3)( x + 3) ( x − 3)( x + 3)
2x − 6 x + (4 x +12) − (x − 4 x +15) + − = x 2 x 3 ( = x − 3)( x + 3) ( x −3)( x +3)
( x +3)( x − )1 x −1 = ( = x − 3)( x + 3) x − 3 x −1 x −1 x − 3
3) P = A: B = : = (đkbs: x 1) x x − 3 x Trang 19 x − 3
P + P = 0 P = −P P 0 0 x 9 x
KHĐK 0 x 9; x 1
Mà x x 2;3;4;5;6;7; 8 Bài 15.
1) Thay x = 25 (thỏa mãn điều kiện) vào biểu thức ta được: 2 25 A = 25 −1 Tính được 5 A = và kết luận 2 2) x + x − 2 1
x + x − 2 − x +1 B = + =
x − 2 x +1 1− x ( x − )2 1 x −1 + = x 1 ( = (đpcm) x − )2 1 x −1 3) 2 x x +1 2 x
P = A : B = : = Có x −1 x −1 x +1 4 P = P 4 P − P = 0 3 P(1− P ) = 0 P = 0; P = 1 P = 0 2 x = 0 x +1 x = 0 (TMĐK) P = 1 2 x =1 x +1 x = 1 (KTM)
Vậy x = 0 là giá trị cần tìm. Bài 16. 16 − 9 7
1) Thay x = 16 (thoả mãn đk) vào biểu thức A ta được: A = = . 16 − 3 16 4 x + 3 1 2
2) Với x 0; x 9 ta có: B = − + x − 9 3− x x + 3 2 x + x + ( x −3 3 3 )
x + 3 + x + 3 + 2 x − 6 = ( + + =
x + 3)( x −3) ( x + 3)( x −3) ( x + 3)( x −3) ( x +3)( x −3) Trang 20