Các giải thuật tìm kiếm - Cấu trúc dữ liệu và giải thuật | Trường Đại học CNTT Thành Phố Hồ Chí Minh
Các giải thuật tìm kiếm - Cấu trúc dữ liệu và giải thuật | Trường Đại học CNTT Thành Phố Hồ Chí Minh được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Cấu trúc dữ liệu và giải thuật (IT003)
Trường: Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Cấu trúc dữ liệu và giải thuật (IT003)
Trường:
Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
CÁC GIẢI THUẬT TÌM KIẾM -
Tìm kiếm tuyến tính là gì?
+ Tìm kiếm tuyến tính (Linear Search) hay còn được gọi là Tìm
kiếm tuần tự (Sequential Search) là phương pháp tìm kiếm vị trí
một phần tử cho trước trong một danh sách nào đó. Phương pháp
này hoạt động bằng cách duyệt qua từng phần tử trong danh sách
để tìm ra giá trị mong muốn. VD:
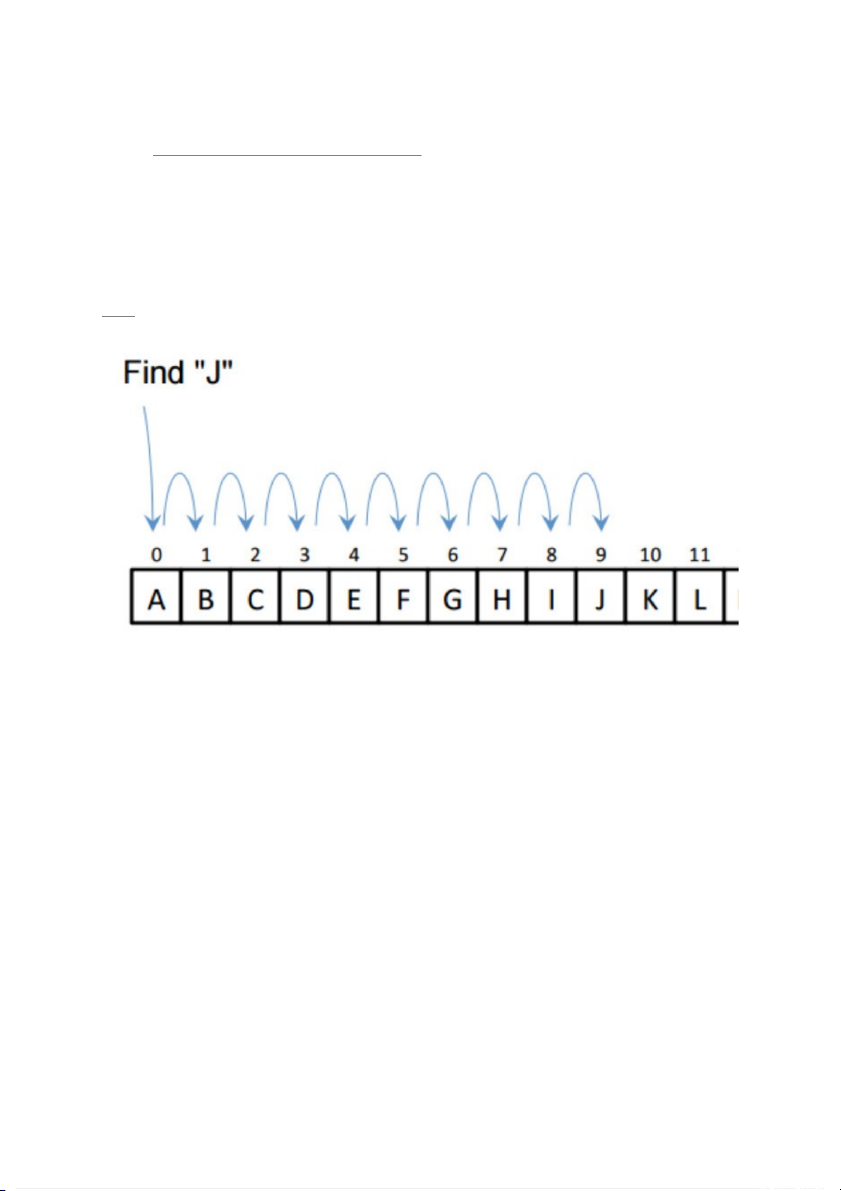
Như trong hình, để tìm được J, cần phải duyệt qua từng phần tử
trước đó để tìm. Nếu danh sách của chúng ta có 1000 phần tử và
phần tử cần tìm nằm ở gần cuối thì việc tìm kiếm sẽ mất rất nhiều thời gian.
Vậy nên, tìm kiếm tuyến tính chỉ nên áp dụng cho những chương
trình đơn giản, phù hợp khi cần tìm kiếm trên một danh sách đủ nhỏ
và chưa được sắp xếp.
+ Thuật toán tìm kiếm tuyến tính: Trong đó:
arr[] là mảng bao gồm các phần tử
n là số lượng phần tử trong mảng
x là giá trị cần tìm VD: -
Tìm kiếm tuyến tính cải tiến là gì?
+ Tìm kiếm tuyến tính cải tiến là một phiên bản cải tiến của tìm
kiếm tuyến tính thông thường. Các cải tiến này được thực hiện để tối
ưu hóa hiệu suất của thuật toán và giảm thiểu số lượng phép so
sánh cần thiết để tìm kiếm một phần tử trong một tập hợp dữ liệu. + Một số cải tiến:
o Tìm kiếm gần nhất (Closest Linear Search):
Trong các tình huống mà phần tử cần tìm không có trong
danh sách, nhưng chúng ta vẫn muốn tìm phần tử gần
nhất với giá trị cần tìm, cải tiến này rất hữu ích
Thuật toán này không chỉ tìm kiếm được các phần tử
chính xác mà còn xem xét phần tử gần nhất với giá trị cần tìm
o Tối ưu hóa bằng cách di chuyển phần tử tìm kiếm lên đầu danh sách:
Khi phần tử cần tìm được tìm thấy, cải tiến này di chuyển nó lên đầu danh sách
Giảm thiểu thời gian tìm kiếm trong các lần truy cập tiếp
theo, đặc biệt là với các dữ liệu có tính chất phân phối không đều
o Thêm phần tử “lính canh” vào cuối danh sách:
Gán phần tử a[n] = x, mảng a sẽ có thêm phần tử cuối
cùng là x. Do đó, khi tìm x trong mảng a thì chắc chắn sẽ
tìm thấy, nhưng nếu tìm thấy x ở vị trí cuối cùng n thì coi
như không tìm thấy x. Nếu tìm thấy x ở vị trí khác n (từ 0
đến n-1) thì có nghĩa là tìm thấy x
Thuật toán tìm kiếm tuyến tính cải tiến chỉ sử dụng một
phép so sánh a[i] != x. Trường hợp xấu nhất, số phép so
sánh của thuật toán là n, tức là giảm được phân nửa
phép so sánh của thuật toán tìm kiếm thông thường -
Ưu điểm của tìm kiếm tuyến tính cải tiến?
Ưu điểm chính của các cải tiến này là cải thiện hiệu suất của
thuật toán tìm kiếm tuyến tính, giảm thời gian tìm kiếm và tăng
cường khả năng xử lý của thuật toán trong nhiều tình huống khác
nhau. Đặc biệt, chúng giúp giảm bớt tải cho bộ nhớ và tăng cường
khả năng tìm kiếm các phần tử gần nhất trong các tập dữ liệu. -
Tìm kiếm nhị phân là gì?
+ Tìm kiếm nhị phân (Binary Search) là phương pháp tìm
kiếm vị trí một phần tử x trên một mảng đã được sắp xếp. Phương
pháp này còn được gọi với cái tên khác là Tìm kiếm một nửa,
thay vì phải duyệt tất cả các phần tử như tìm kiếm tuyến tính thì
nó liên tục chia các khoảng tìm kiếm thành một nửa. VD:
Đầu tiên, thuật toán sẽ bắt đầu tìm kiếm từ đầu mảng đến cuối
mảng. Nếu giá trị cần tìm nhỏ hơn giá trị ở giữa mảng, thì khi đó
thu hẹp phạm vi tìm kiếm từ đầu mảng đến giữa mảng. Ngược lại
nếu giá trị cần tìm lớn hơn giá trị giữa mảng thì thực hiện tìm
kiếm ở phần cuối mảng. Cứ thế tiếp tục chia phạm vi thành các
nửa cho đến khi tìm thấy hoặc đã duyệt hết.
+ Thuật toán tìm kiếm nhị phân: Trong đó:
arr[] là mảng bao gồm tất cả các phần tử đã được sắp xếp
n là số lượng phần tử của mảng
left là vị trí đầu tiên của mảng (= 0)
right là vị trí cuối cùng của mảng (= n – 1)
x là giá trị cần tìm Giải thích thuật toán:
1. Duyệt các phần tử trong khoảng từ left => right, lúc này giá trị
của left là 0 và của right là n – 1
2. So sánh x với giá trị middle (giữa mảng), nếu x = middle thì trả
về vị trí và thoát vòng lặp
3. Nếu x < middle thì nghĩa là x nằm bên trái mảng, tức là từ left => middle – 1
4. Nếu x > middle thì nghĩa là x nằm bên phải mảng, tức là từ middle + 1 => right
5. Cứ tiếp tục vòng lặp cho đến khi tìm thấy giá trị x VD: -
Ưu điểm của tìm kiếm nhị phân? 1. Hiệu suất tối ưu:
Tìm kiếm nhị phân có lợi thế lớn về độ phức tạp thời gian khi
so sánh với các thuật toán tìm kiếm khác (Độ phức tạp thời
gian của thuật toán tìm kiếm nhị phân là O(log n), trong đó n
là số lượng phần tử trong tập dữ liệu)
Với tập dữ liệu lớn, thuật toán tìm kiếm nhị phân hoạt động
nhanh chóng hơn đáng kể so với tìm kiếm tuyến tính (O(n))
2. Sử dụng ít bộ nhớ: Thuật toán tìm kiếm nhị phân chỉ cần lưu
các chỉ số và trạng thái hiện tại của tìm kiếm, không cần lưu
toàn bộ dữ liệu trong bộ nhớ. Điều này giúp giảm tải trọng về
bộ nhớ so một số thuật toán tìm kiếm khác, như tìm kiếm tuyến tính 3. Tính chính xác cao
4. Đơn giản và dễ triển khai
*Lưu ý:wĐối với phương pháp tìm kiếm nhị phân thì yêu cầu mảng phải được sắp xếp.