Các phương pháp giải Toán hình học không gian lớp 11, 12 hay nhất

Các phương pháp giải Toán hình học không
gian lớp 11, 12 hay nhất
1. Dạng 1: Tìm giao tuyến của hai mặt phẳng
Muốn tìm giao tuyến của hai mặt phẳng: ta tìm hai điểm chung thuộc cả hai
mặt phẳng. Nối hai điểm chung đó được giao tuyến cần tìm.
Về dạng này điểm chung thứ nhất thường dễ tìm. Điểm chung còn lại các bạn
phải tìm hai đường thẳng lần lượt thuộc hai mặt phẳng, đồng thời chúng lại
thuộc mặt phẳng thứ ba và chúng không song song. Giao điểm của hai
đường thẳng đó là điểm chung thứ hai.
Chú ý: Giao tuyến là đường thẳng chung của hai mặt phẳng, có nghĩa là giao
tuyến là đường thẳng vừa thuộc mặt phẳng này vừa thuộc mặt phẳng kia.
Câu 1: Cho tứ giác ABCD sao cho các cạnh đối không song song với nhau.
Lấy một điểm S không thuộc mặt phẳng (ABCD). Xác định giao tuyến của mặt
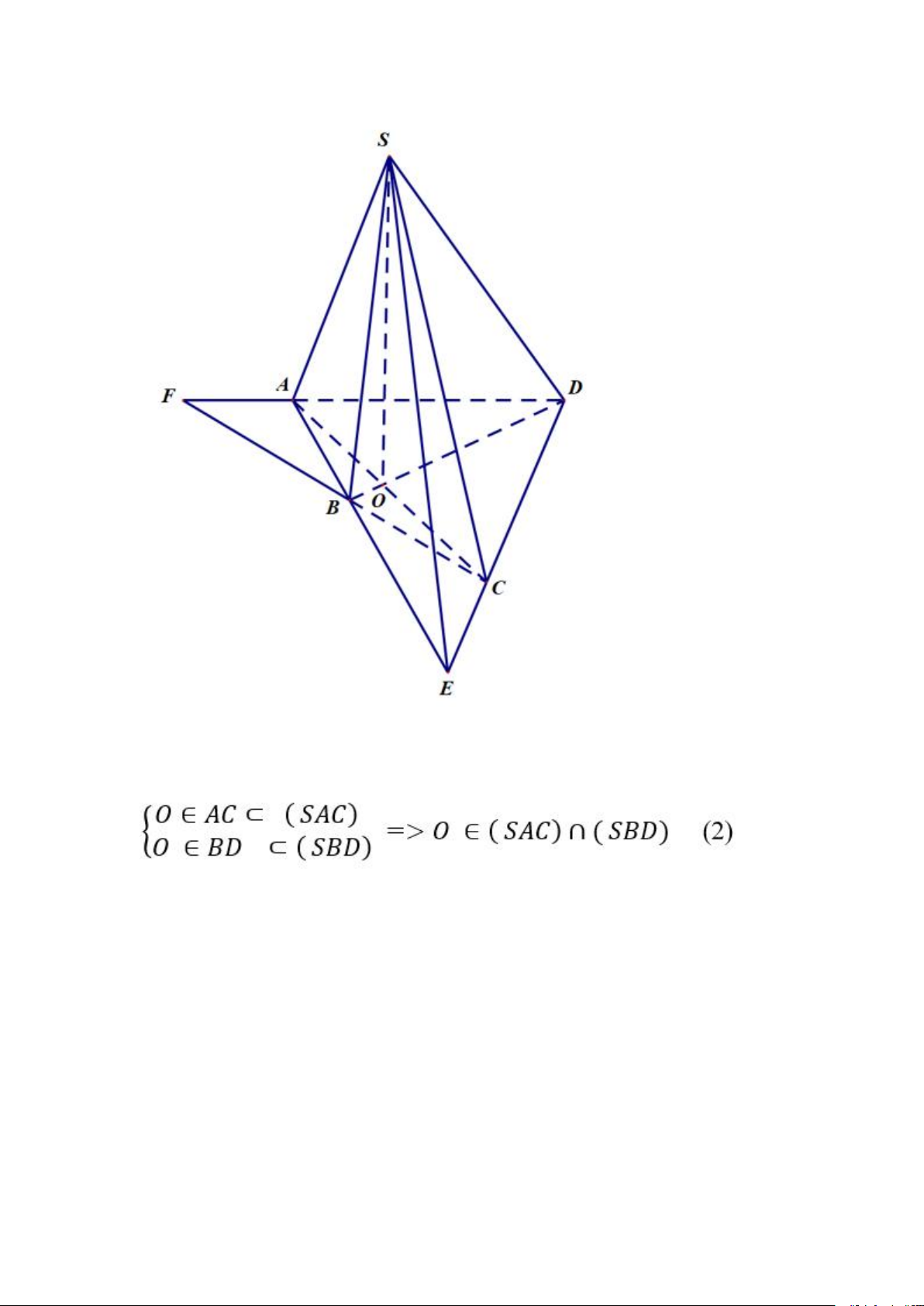
phẳng (SAC) và mặt phẳng (SBD).
A. SO trong đó O là giao điểm của AC và BD.
B. SI trong đó I là giao điểm của AB và CD.
C. SE trong đó E là giao điểm của AD và BC. D. Đáp án khác Lời giải
+ Ta có : S ∈ (SAC) ∩ (SBD) (1)
+ Trong mp(ABCD) gọi giao điểm của AC và BD là O. ( bạn đọc tự vẽ hình) - Vì:
+ Từ (1) và (2) suy ra SO = (SAC) ∩ (SBD) Chọn A
Câu 2: Cho tứ giác ABCD sao cho các cạnh đối không song song với nhau.
Lấy một điểm S không thuộc mặt phẳng (ABCD). Xác định giao tuyến của mặt
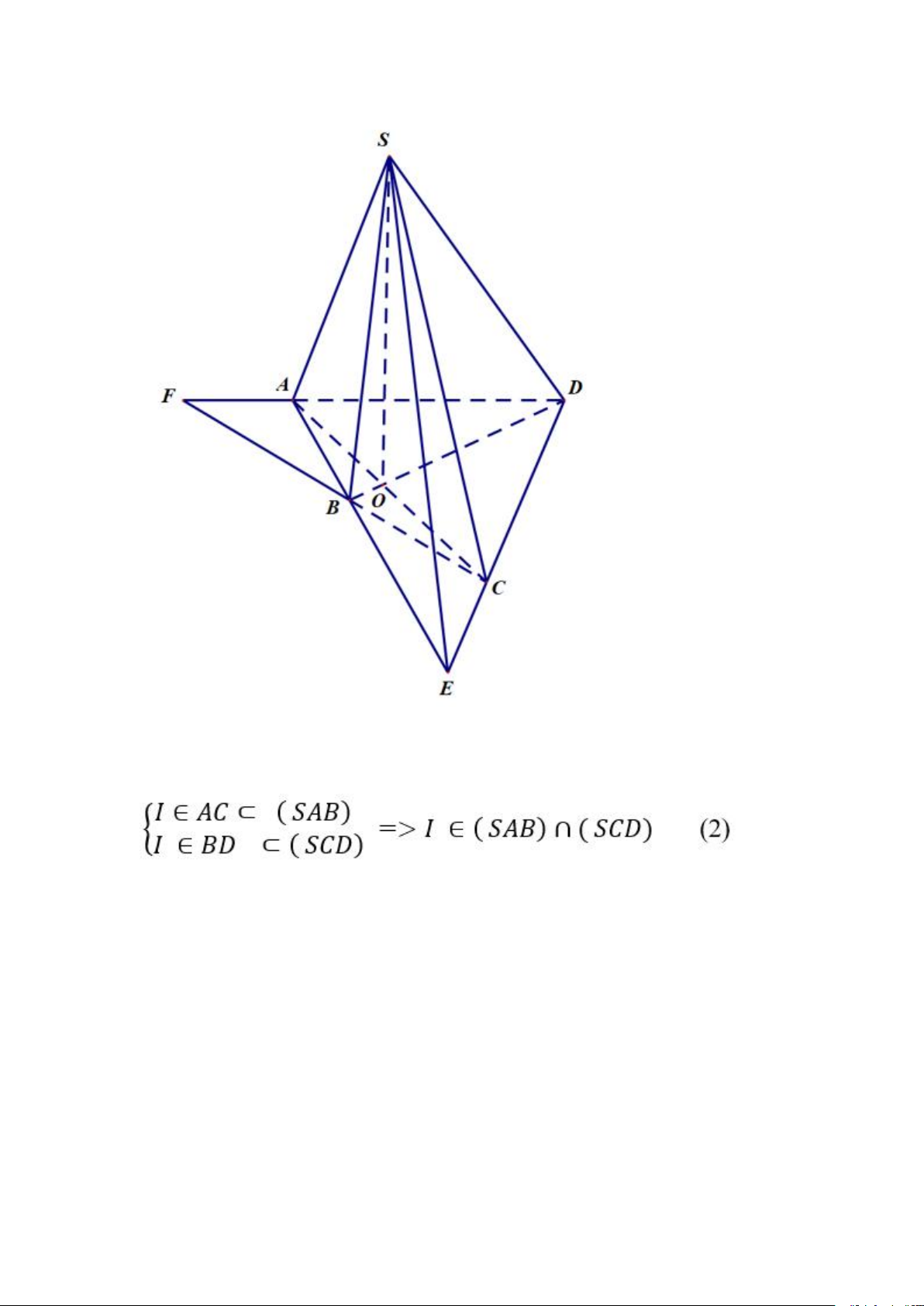
phẳng (SAB) và mặt phẳng (SCD)
A. SO trong đó O là giao điểm của AC và BD
B. SI trong đó I là giao điểm của AB và CD
C. SE trong đó E là giao điểm của AD và BC D. Đáp án khác Lời giải:
+ Ta có: S ∈ (SAB) ∩ (SCD) (1)
+ Trong mp(ABCD) gọi giao điểm của AB và CD là I. (bạn đọc tự vẽ hình) Vì
+ Từ (1) và (2) suy ra SI = (SAB) ∩ (SCD) Chọn B
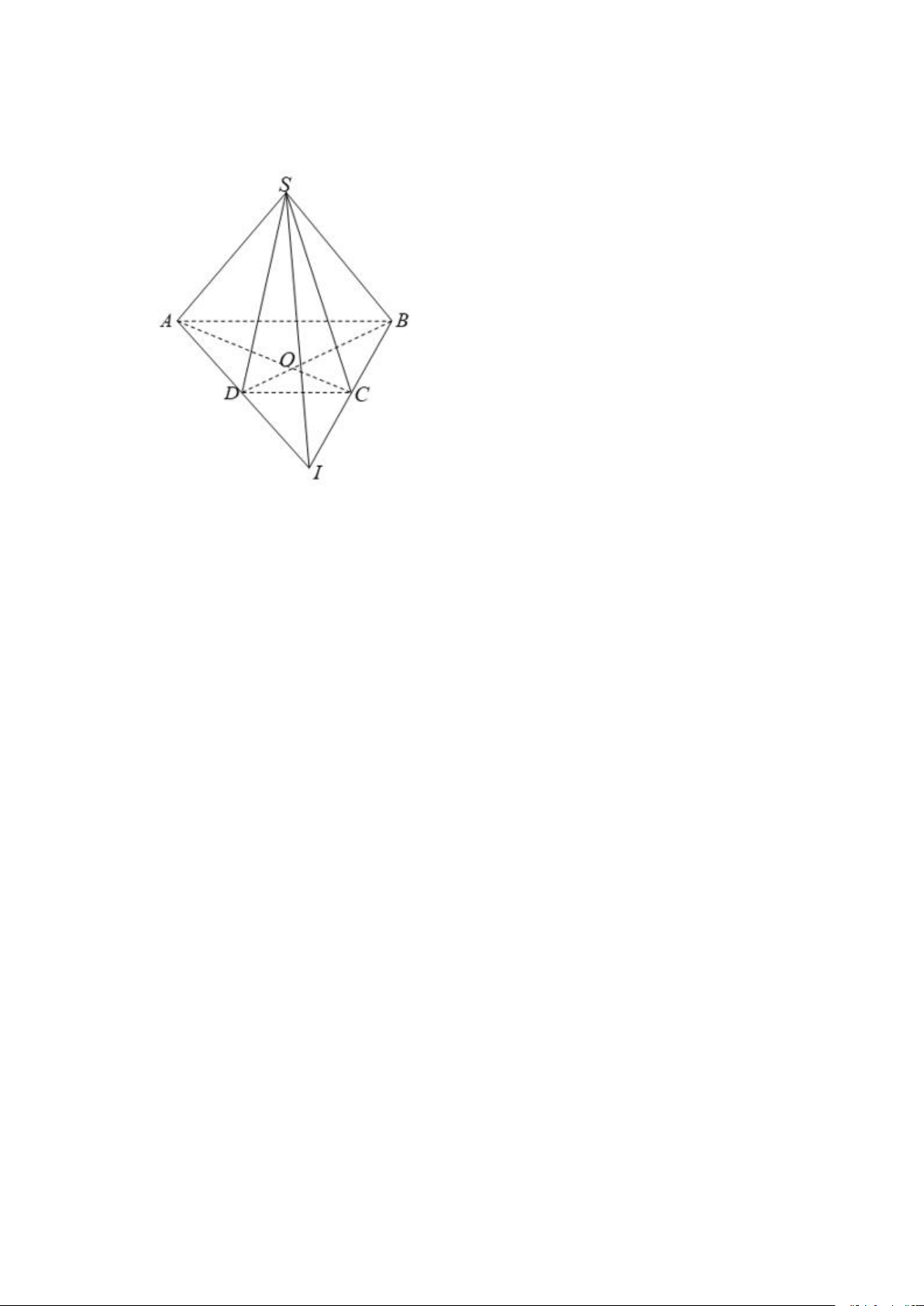
Câu 3: Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB// CD). Khẳng định nào sau đây sai?
A. Hình chóp S.ABCD có mặt bên
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO (O là giao điểm của AC và BD)
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI (I là giao điểm của AD và BC)
D. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABCD Lời giải Chọn D
+ Hình chóp S.ABCD có mặt bên (SAB), (SBC); (SCD) và (SAD) nên A đúng.
+ S và O là hai điểm chung của (SAC) và (SBD) nên B đúng.
+ S và I là hai điểm chung của (SAD) và (SBC) nên C đúng.
+ Giao tuyến của (SAB) và (SAD) là SA, rõ ràng SA không thể là đường
trung bình của hình thang ABCD.
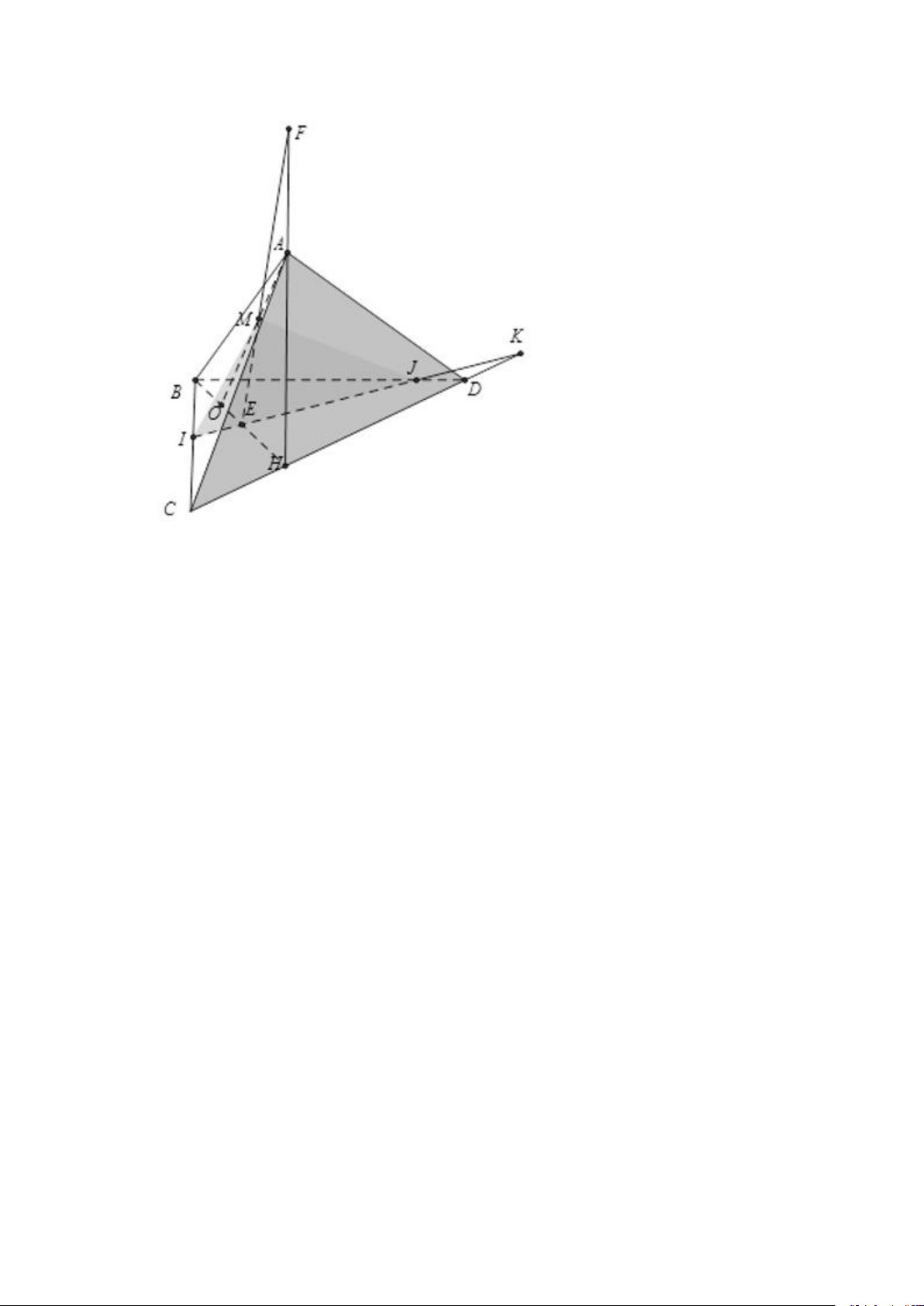
Câu 4: Cho tứ diện ABCD. Gọi O là một điểm bên trong tam giác BCD và M là
một điểm trên đoạn AO. Gọi I và J là hai điểm trên cạnh BC; BD. Giả sử IJ cắt
CD tại K, BO cắt IJ tại E và cắt CD tại H, ME cắt AH tại F. Giao tuyến của hai
mặt phẳng (MIJ) và (ACD) là đường thẳng: A. KM B. AK C. MF D. KF Lời giải Chọn D.
+ Do K là giao điểm của IJ và CD nên: K ∈ (MIJ) ∩ (ACD) (1)
+ Ta có F là giao điểm của ME và AH
Mà AH ⊂ (ACD), ME ⊂ (MIJ) nên F ∈ (MIJ) ∩ (ACD) (2)
Từ (1) và (2) có (MIJ) ∩ (ACD) = KF
Câu 5: Cho hình chóp S.ABCD. Gọi I là trung điểm của SD, J là điểm trên SC
và không trùng trung điểm SC. Giao tuyến của hai mặt phẳng (ABCD) và (AIJ) là:
A. AK với K là giao điểm IJ và BC
B. AH với H là giao điểm IJ và AB
C. AG với G là giao điểm IJ và AD
D. AF với F là giao điểm IJ và CD Lời giải Chọn D.
+ A là điểm chung thứ nhất của (ABCD) và (AIJ)
+ IJ và CD cắt nhau tại F, còn IJ không cắt BC; AD; AB
Nên F là điểm chung thứ hai của (ABCD) và (AIJ)
Vậy giao tuyến của (ABCD) và (AIJ) là AF
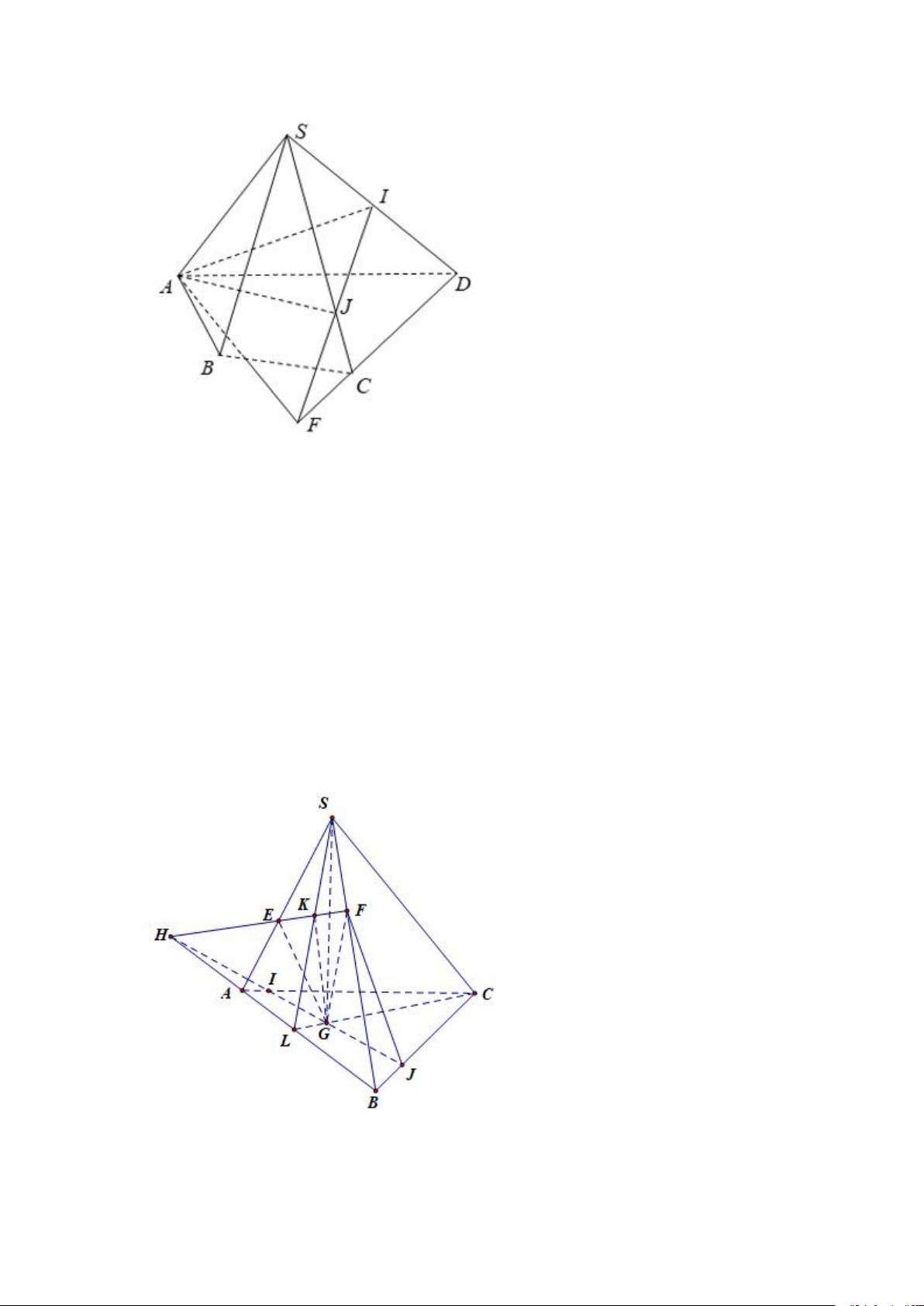
Câu 6: Cho tứ diện S.ABC. Lấy điểm E; F lần lượt trên đoạn SA; SB và điểm
G trọng tâm tam giác ABC . Tìm giao tuyến của mp(EFG) và mp(SBC)
A. FM trong đó M là giao điểm của AB và EG.
B. FN trong đó N là giao điểm của AB và EF.
C. FT trong đó T là giao điểm của EG và SB. D. Đáp án khác Lời giải:
+ Trong mp(SAB); gọi H là giao điểm của EF và AB.
+ Trong mp(ABC); gọi HG cắt AC; BC lần lượt tại I và J. + Ta có:
Từ (1) và (2) suy ra: JF = (EFG) (SBC) Chọn D
2. Dạng 2: Tìm giao điểm của đường thẳng và mặt phẳng
Muốn tìm giao điểm của đường thẳng d và mặt phẳng (P), có hai cách làm như sau: * Cách 1:
+ Những bài đơn giản, có sẵn một mặt phẳng (Q) chứa đường thẳng d và
một đường thẳng a nào đó thuộc mặt phẳng (P)
+ Trong mp( Q), 2 đường thẳng a và d cắt nhau tai điểm A. Khi đó điểm A
chính là giao điểm của đường thẳng d và mp(P)
* Cách 2: Chọn mặt phẳng phụ:
+ Tìm một mặt phẳng (Q) chứa đường thẳng d, sao cho dễ dàng tìm giao
tuyến của mp (Q) với mp (P)
+ Tìm giao tuyến của mp(P) và (Q) - gọi là đường thẳng d.
+ Tìm giao điểm của đường thẳng a và đường thẳng d - gọi là điểm A
Khi đó: điểm A chính là giao điểm của đường thẳng d và mp (P)
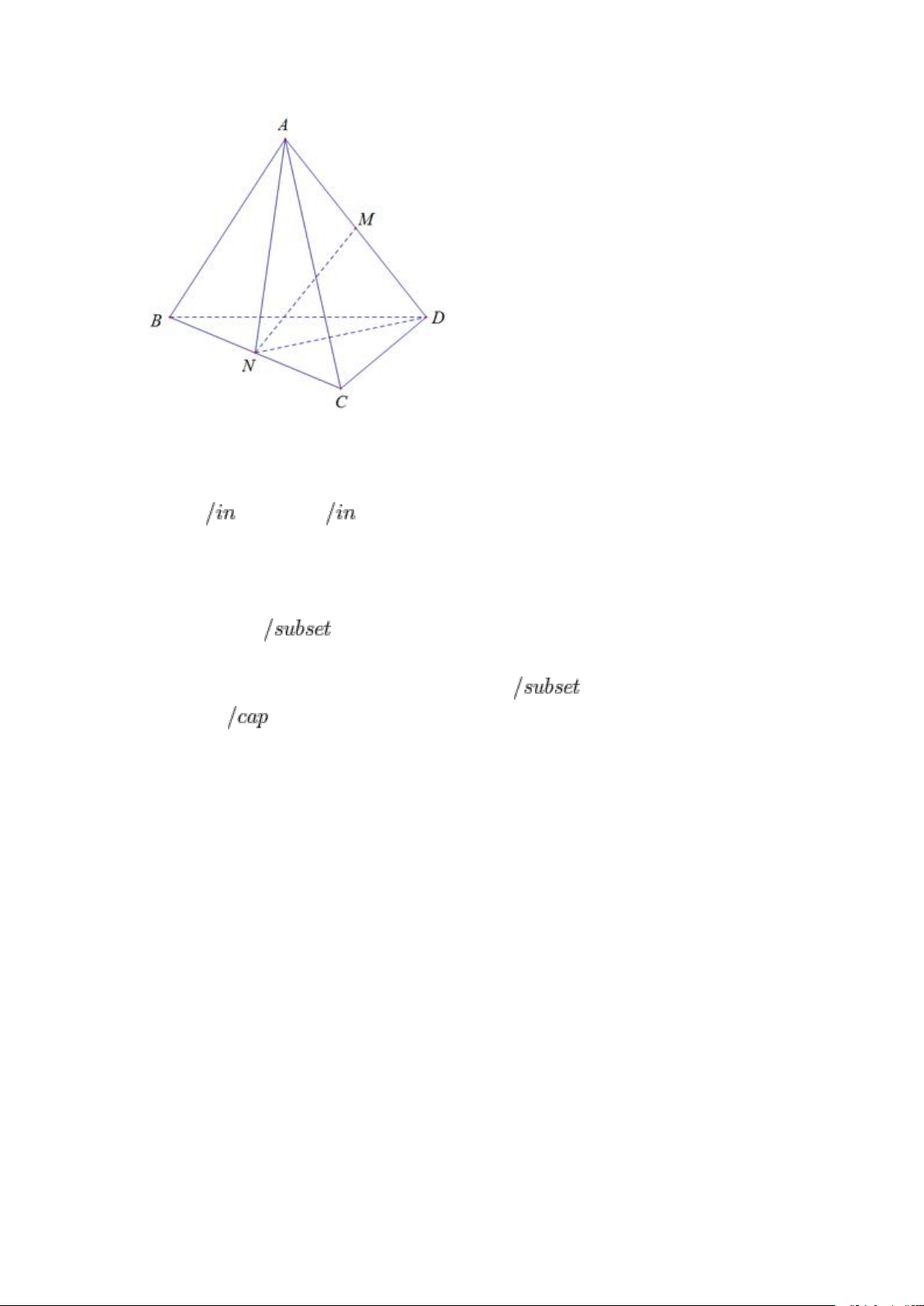
Câu 1: Cho 4 điểm A, B, C, D không đồng phẳng và không có 3 điểm nào
thẳng hàng. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy
điểm P sao cho BP = 2PD. Giao điểm của đường thẳng CD và mp(MNP) là giao điểm của
A. CD và NP B. CD và MN C. CD và MP D. CD và AP Lời giải Cách 1.
+ Chọn mặt phẳng phụ chứa CD là mp(BCD)
+ Do NP không song song CD nên NP cắt CD tại E Điểm E NP nên E (MNP)
⇒ giao điểm của CD và mp(MNP) là điểm E. Chọn A. Cách 2 + Ta có : NP (BCD) ⇒ NP và CD đồng phẳng
+ Gọi E là giao điểm của NP và CD mà NP ( MNP) suy ra CD (MNP) = E
Vậy giao điểm của CD và mp (MNP) là giao điểm E của NP và CD.
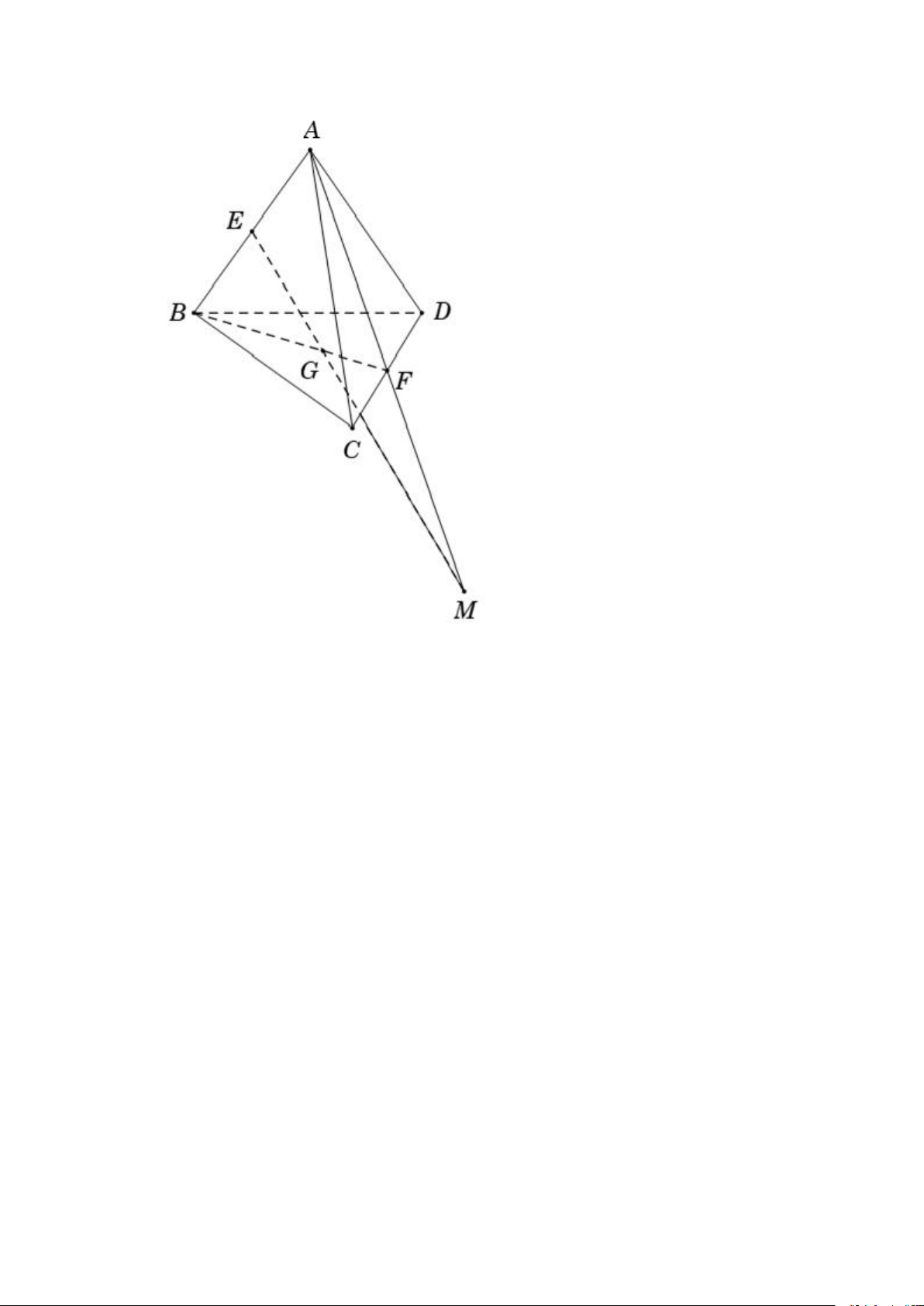
Câu 2: Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G
là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là:
A. Giao điểm của đường thẳng EG và AF.
B. Giao điểm của đường thẳng EG và AC.
C. Giao điểm của đường thẳng EG và CD. Lời giải:
+ Vì G là trọng tâm tam giác BCD; F là trung điểm của CD nên G ∈ BF ⊂ (ABF)
+ Ta có E là trung điểm của A B nên E ∈ (ABF).
+ chọn mp phụ chứa EG là (ABF).
Dễ dàng tìm được giao tuyến của (ACD) và (ABF) là AF.
+ Trong mp(ABF); gọi M là giao điểm của EG và AF .
Vậy giao điểm của EG và mp(ACD) là giao điểm M của EG và AF Chọn B
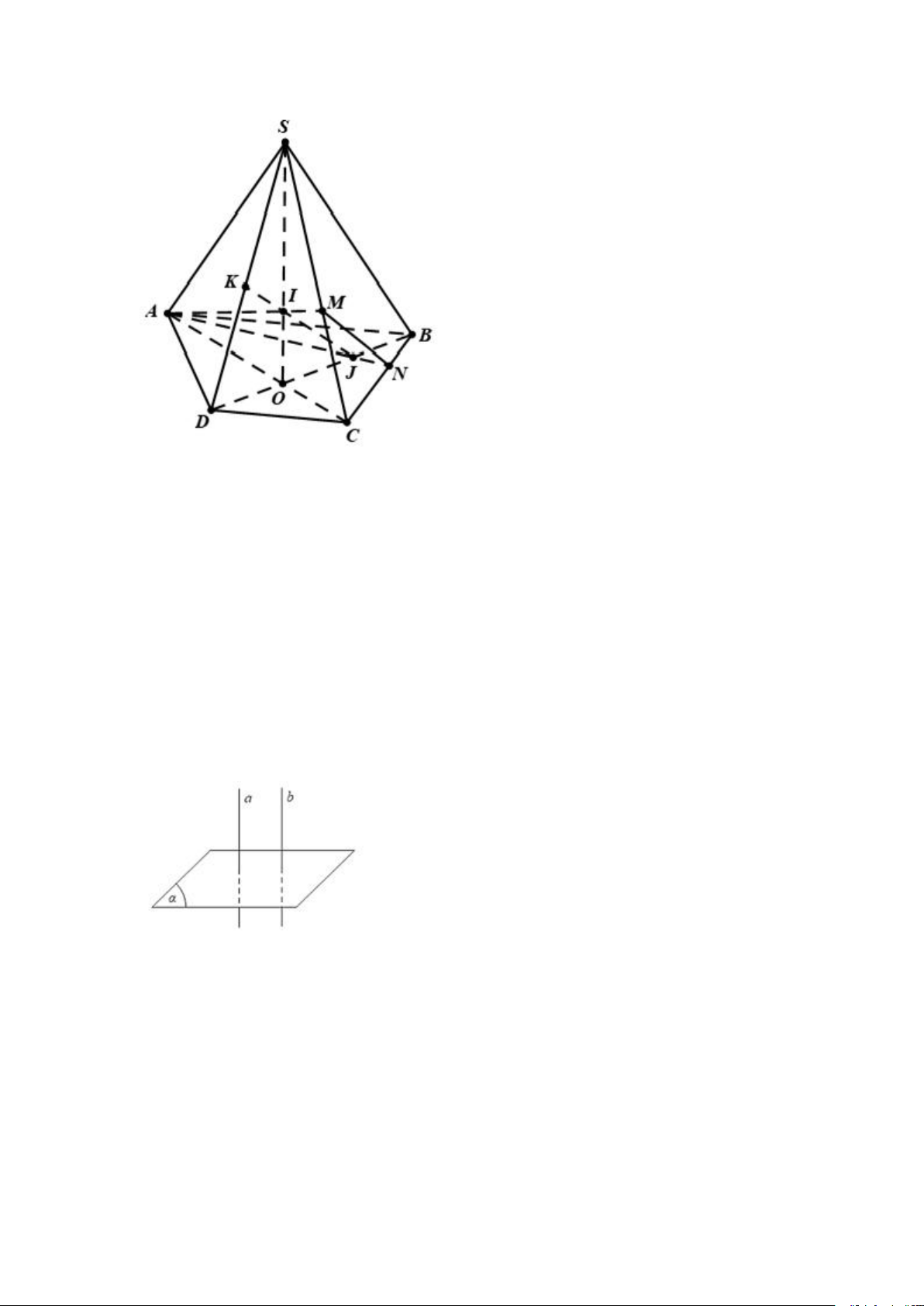
Câu 3: Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SC, N là trên
cạnh BC. Gọi O = AC ∩ BD, J = AN ∩ BD và gọi I = SO ∩ AM. Tìm giao điểm
của đường thẳng SD với mặt phẳng (AMN)
A. là giao điểm của SD và SI
B. là giao điểm của SD và BJ
C. Là giao điểm của SD và MI
D. là giao điểm của SD và IJ Lời giải
Trong mp (SBD), gọi K = IJ ∩ SD
Ta có I ∈ AM ⊂ (AMN), J ∈ AN ⊂ (AMN) ⇒ IJ ⊂ (AMN)
Do đó K ∈ IJ ⊂ (AMN) ⇒ K ∈ (AMN) Vậy K = SD ∩ (AMN) Chọn D
3. Dạng 3: Chứng minh quan hệ vuông góc, song song trong không gian
Áp dụng các tính chất: - Tính chất 1:
+ Cho hai đường thẳng song song. Nếu có một mặt phẳng vuông góc với một
trong hai đường thẳng thì mặt phẳng này thì cũng vuông góc với đường thẳng còn lại.
+ Ngược lại, nếu hai đường thẳng phân biệt cùng vuông góc với một mặt
phẳng nào đó thì hai đường thẳng này song song với nhau. - Tính chất 2:
+ Cho hai mặt phẳng song song với nhau, nếu có một đường thẳng vuông
góc với một trong hai mặt phẳng thì đường thẳng đó vuông góc với mặt phẳng còn lại.
+ Ngược lại, nếu có hai mặt phẳng phân biệt cùng vuông góc với một đường
thẳng bất kì thì hai mặt phẳng đó song song với nhau. - Tính chất 3:
+ Cho đường thẳng a song song với mặt phẳng (α) cho trước. Nếu có một
đường thẳng b nào đó vuông góc với mặt phẳng (α) thì đường thẳng b cũng vuông góc với a.
+ Ngược lại, nếu có một đường thẳng và một mặt phẳng (đường thẳng không
thuộc mặt phẳng) và cùng vuông góc với một đường thẳng khác thì chúng sẽ song song với nhau.
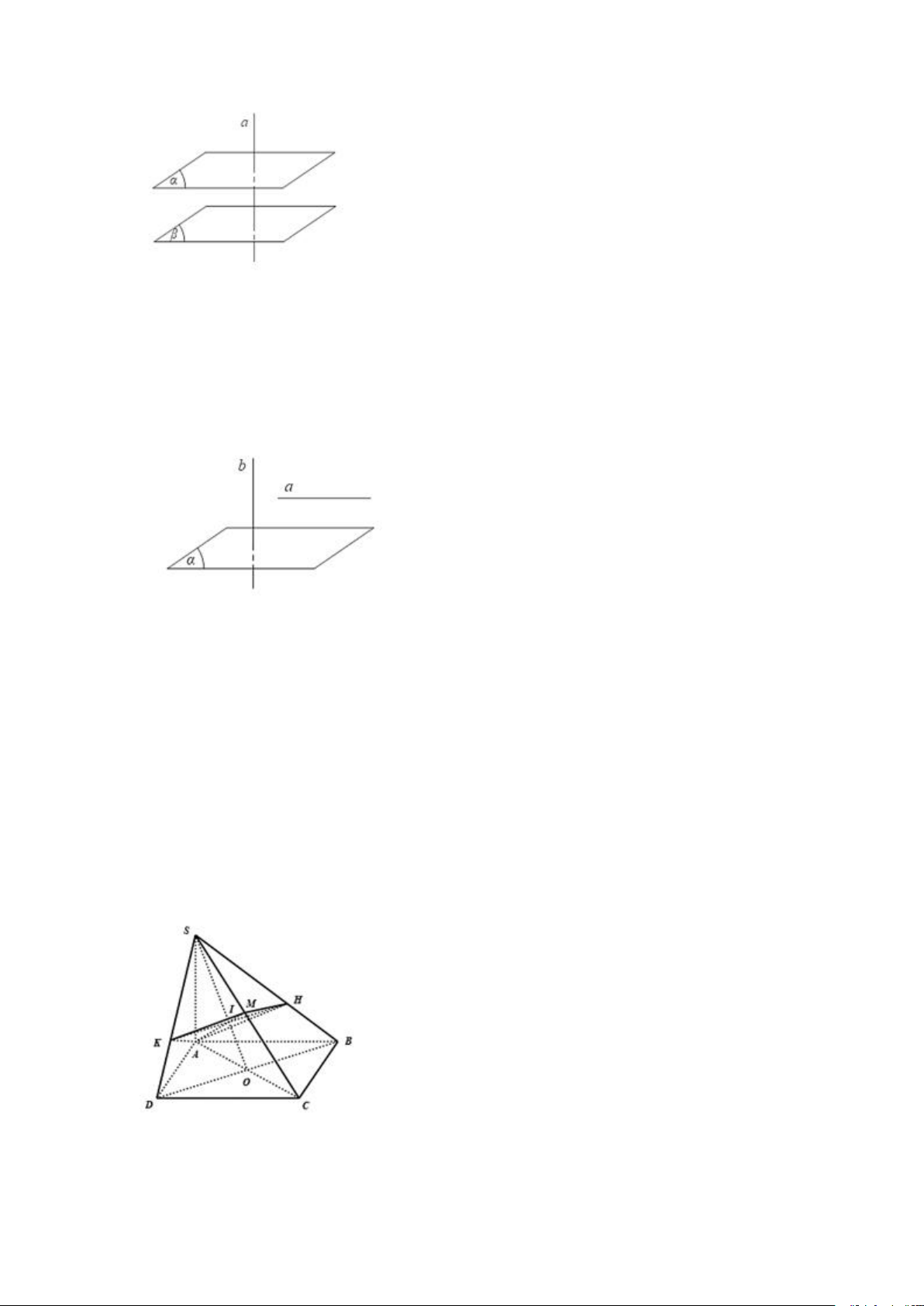
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD).
Mặt phẳng qua A và vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M, K.
Chứng minh rằng AK không vuông góc với HK. Hướng dẫn giải Ta có:
Gọi O là giao điểm của AC và BD, I là giao điểm của SO và HK.
(P) là mặt phẳng qua A và vuông góc với SC
Qua I kẻ ∆ // BC, do đó, ∆ vuông góc với AM. Do đó, ∆ thuộc (P).
Khi đó, K là giao điểm của ∆ với SD, H là giao điểm của ∆ với SB Ta có:
AK vuông góc với (SCD) nên AK vuông góc với mọi đường thẳng nằm trong mp(SCD).
Mà HK giao (SCD) tại K nên HK không nằm trong mp(SCD).
Do đó, AK không vuông góc với HK. Câu 2:
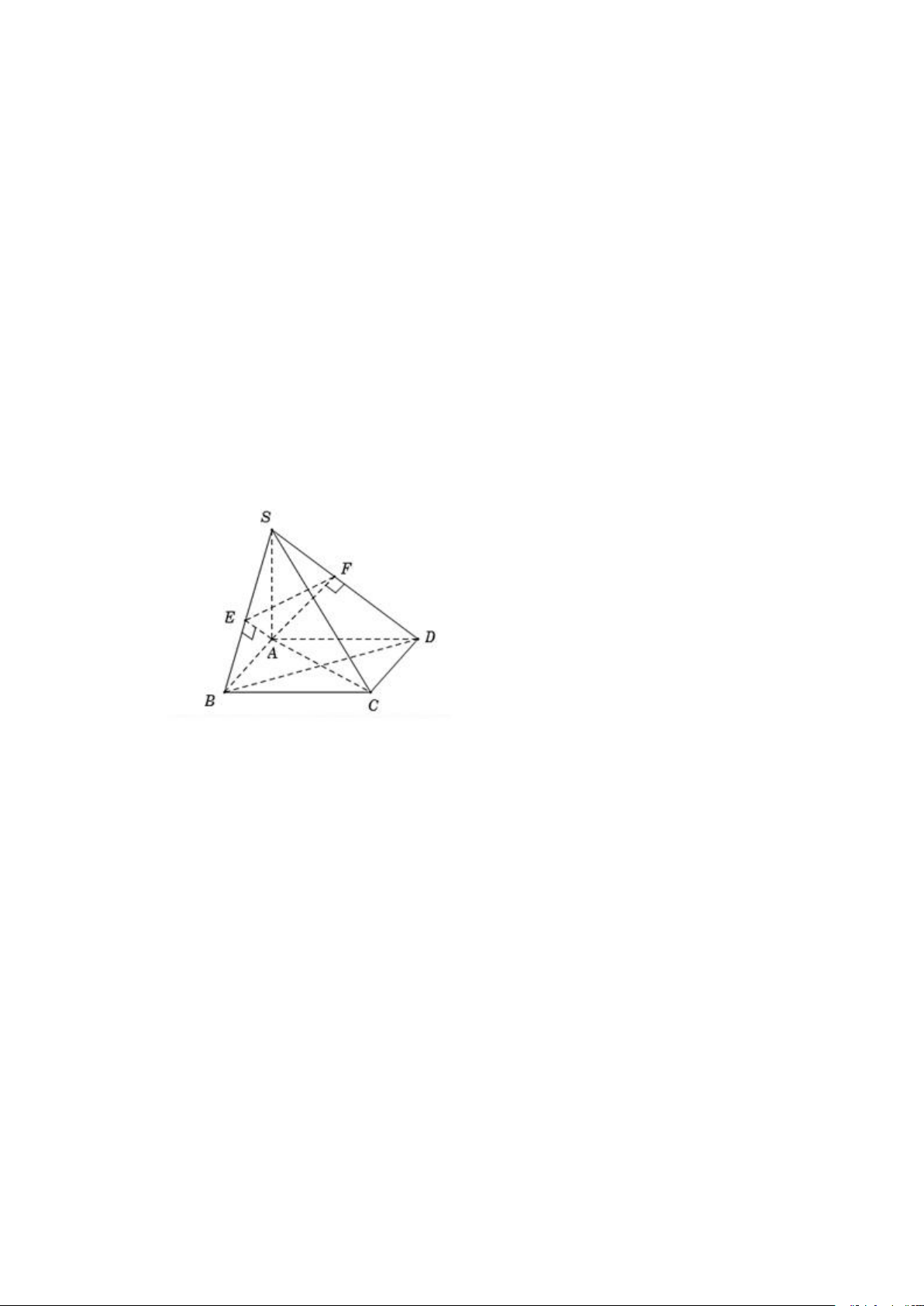
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông
góc với mặt phẳng đáy. Gọi AE, AF lần lượt là đường cao của tam giác SAB
và tam giác SAD. Chứng minh SC ⊥ (AEF). Hướng dẫn giải
Vì SA vuông góc với mặt phẳng (ABCD) nên SA ⊥ BC
Mà AB ⊥ BC nên suy ra: BC ⊥ (SAB)
⇒ BC vuông góc với AE, AE thuộc (SAB)
Tam giác SAB có đường cao AE ⇒ AE ⊥ SB Mà AE ⊥ BC
Nên AE ⊥ (SBC) ⇒ AE ⊥ SC
Tương tự, ta chứng minh được AF ⊥ SC. Do đó, SC ⊥ (AEF).
Document Outline

• Các phương pháp giải Toán hình học không gian lớp
  • 1. Dạng 1: Tìm giao tuyến của hai mặt phẳng
  • 2. Dạng 2: Tìm giao điểm của đường thẳng và mặt ph
  • 3. Dạng 3: Chứng minh quan hệ vuông góc, song song