Cách chứng minh tứ giác nội tiếp đơn giản, dễ hiểu nhất

Cách chứng minh tứ giác nội tiếp đơn giản, dễ hiểu nhất
1. Một số kiến thức về tứ giác nội tiếp
Tứ giác là một đa giác hình gồm 4 cạnh và 4 định trong đó không có bất kỳ hai đoạn
thẳng nào cùng nằm trên một đường thẳng. Tứ giác có tổng các góc đối với tứ giác đơn bằng 360 độ.
Tứ giác nội tiếp là một tứ giác có bốn đỉnh cùng nằm trên một đường tròn. Tứ giác này
còn được gọi với tên gọi là tứ giác nội tiếp đường tròn hay tứ giác nội tiếp, đường tròn
tiếp giáp gọi là đường tròn ngoại tiếp, các định của tứ giác được gọi là đồng viên. Tứ
giác nội tiếp tuân theo định lý là tổng số đo hai góc đối diện bằng 180 độ và ngược lại
nếu một tứ giác có tổng số đo hai góc đối diện bằng 180 độ thì tứ giác đó là tứ giác nội tiếp.
Ngoài ra, tứ giác nội tiếp còn có các hệ quả như hai góc nội tiếp cùng chắn một cung thì
bằng nhau; góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung; góc tạo bởi tiếp tuyến
và dây cung bằng góc nội tiếp cùng chắn một cung.
2. Cách chứng minh tứ giác nội tiếp đơn giản, dễ hiểu nhất
Dưới đây chúng tôi sẽ cung cấp một số cách chứng minh tứ giác nội tiếp phổ biến, thông
dụng, đơn giản, dễ hiểu nhất mà ai cũng làm được.
- Cách 1: Chứng minh tổng hai góc đối diện trong một tứ giác bằng 180 độ.
Cách này là một trong các cách thông dụng nó đi từ định nghĩa của tứ giác nội tiếp "Tứ
giác có bốn định nằm trên cùng một đường tròn gọi là tứ giác nội tiếp". Do đó nếu một tứ
giác có 4 đỉnh phân biệt ABCD bất kỳ mà có tổng hai góc đối diện bằng 180 độ thì tứ giác đó nội tiếp.
Công thức chung: Tứ giác ABCD là tứ giác nội tiếp khi và chỉ khi góc A + góc C = góc B + góc D.
Ví dụ: Cho tứ giác ABCD bất kỳ, chứng minh tứ giác ABCD là tứ giác nội tiếp?
+ Nếu BAD = BCD = 90 độ thì tứ giác ABCD nội tiếp đường tròn tâm O, đường kính BD.
Hoặc ACD = ABC = 90 độ thì tứ giác ABCD nối tiếp đường tròn tâm O, đường kính AC.
+ Nếu tổng hai góc kề bù BAD = BCD thì tứ giác ABCD nối tiếp đường tròn.
Từ đó suy ra tứ giác ABCD có tổng hai góc đối diện bằng 180 độ thì tứ giác ABCD là tứ giác nội tiếp.
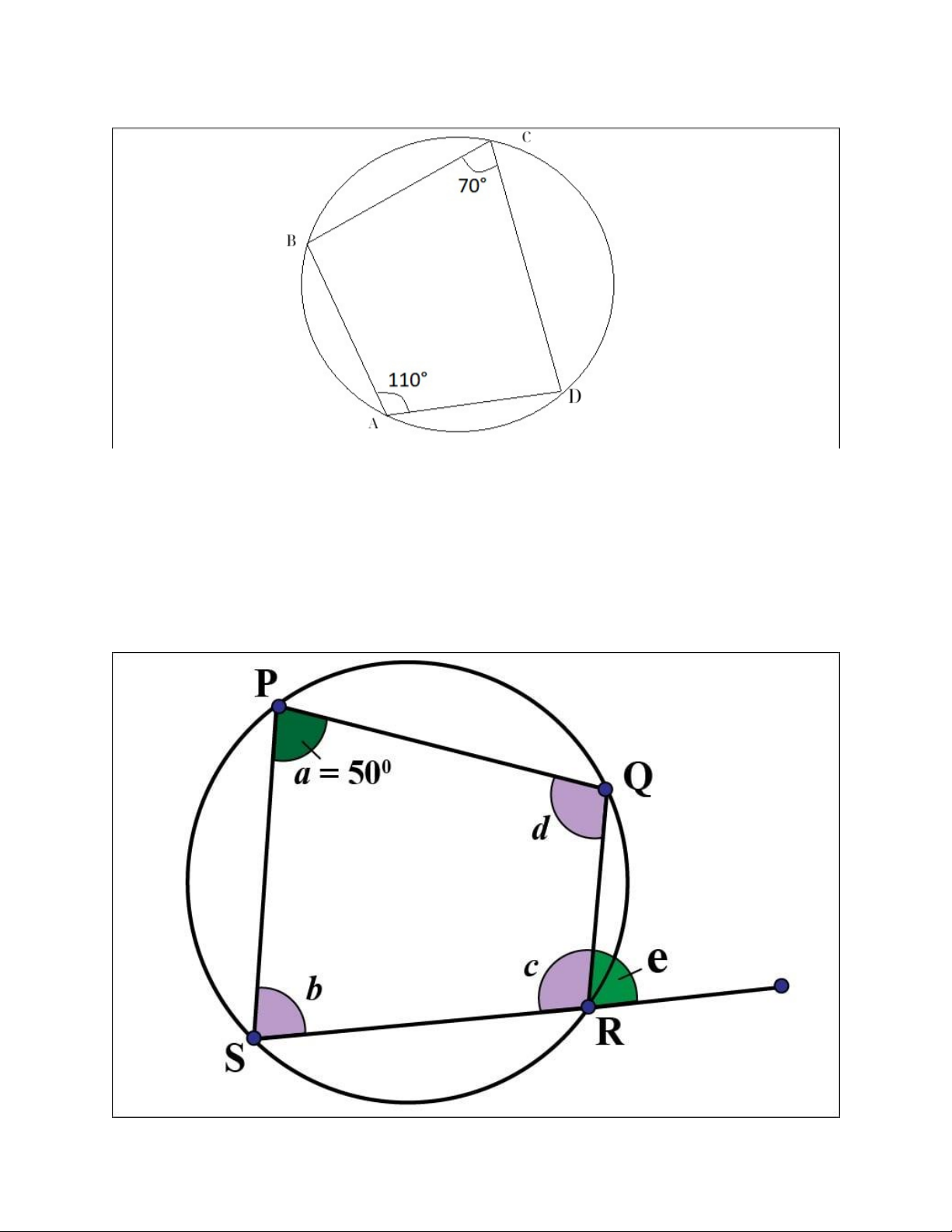
Hình 1: Hình ảnh minh hoạ chứng minh tứ giác nội tiếp bằng cách chứng minh tổng hai góc đối.
- Cách 2: Chứng minh góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
Ví dụ: Cho tứ giác PQRS chứng minh tứ giác PQRS là tứ giác nội tiếp. Với phương pháp
này chúng ta sẽ đi chứng minh góc ngoài tại đỉnh P bằng góc R của tứ giác (góc P và
góc R đối nhau) tương tự đối với góc còn lại (góc ngoài định Q bằng góc S) thì có thể kết
luận tứ giác PQRS là tứ giác nội tiếp.
Hình 2: Hình ảnh minh họa chứng minh tứ giác nội tiếp qua góc ngoài của tứ giác.
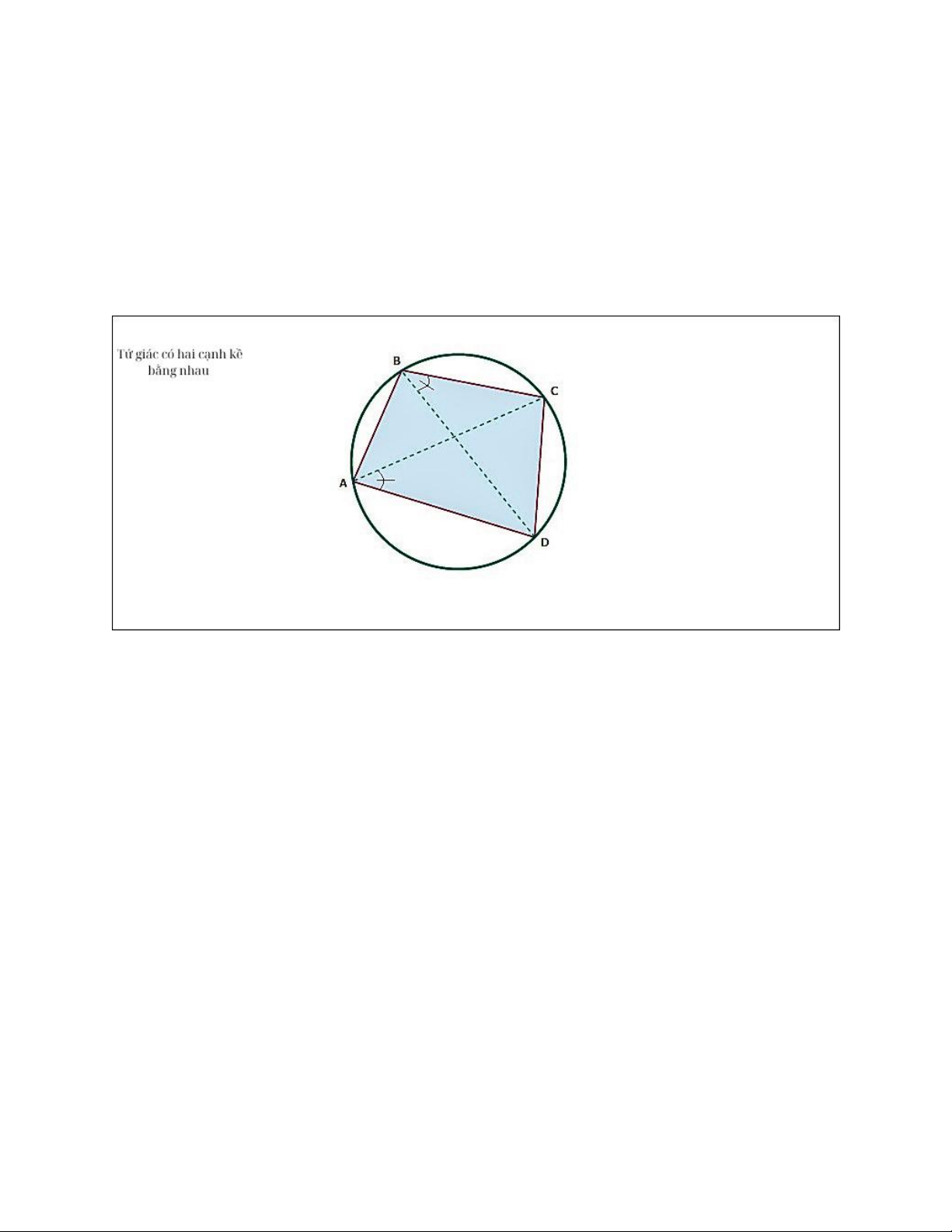
- Cách 3: Chứng minh hai đỉnh cùng kề chung một cạnh, cùng nhìn một cạnh dưới hai
góc bằng nhau và bằng 90 độ.
Tứ giác ABCD là tứ giác nội tiếp khi và chỉ khi góc DAC = góc DBC cùng chắn cung DC.
Ví dụ: Cho tứ giác ABCD chứng minh tứ giác ABCD là tứ giác nội tiếp. Với cách này
chúng ta sẽ phải chứng minh góc DAC = DBC = 90 độ, từ đó có thể suy ra tứ giác ABCD
là tứ giác nội tiếp trong một đường tròn.
Hình 3: Hình ảnh minh họa chứng minh tứ giác nội tiếp bằng cách chứng minh hai đỉnh
cùng kề một cạnh, cùng nhìn cạnh đó dưới hai góc bằng nhau và bằng 90 độ.
- Cách 4: Chứng minh 4 đỉnh của một tứ giác cách đều một điểm cho trước.
Ví dụ: Cho một tứ giác ABCD bất kỳ có đường tròn tâm O, bán kính R. Xác định tứ giác
ABCD là tứ giác nội tiếp.
Vì tứ giác ABCD có đường tròn tâm O, bán kính R nên bất cứ điểm nào nằm trên đường
tròn này đều cách tâm O một khoảng cách đúng bằng bán kính R. Chúng ta sẽ lần lượt
chứng minh điểm O cách đều 4 điểm cho trước ABCD với khoảng cách bằng R.
Từ đó suy ra: OA = OB = OC = R khi đó điểm O được xác định chính là tâm đường tròn
đi qua bốn điểm A, B, C và D. Theo xác định này cũng có thể suy ra tứ giác ABCD là tứ
giác nội tiếp đường tròn với tâm O và bán kính R.
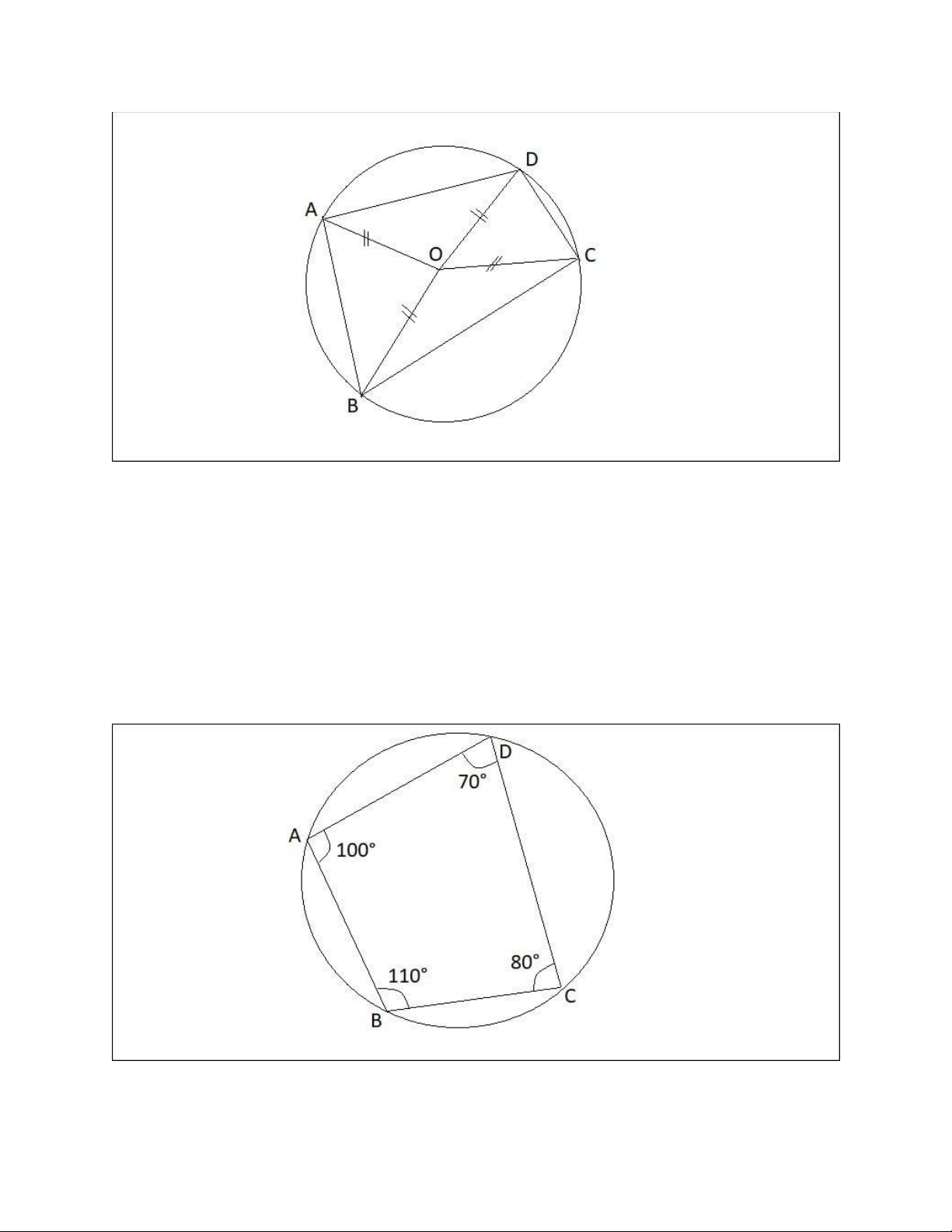
Hình 4: Hình ảnh minh họa tứ giác nội tiếp bằng cách chứng minh cho bốn đỉnh của tứ
giác cùng cách đều một điểm nào đó.
- Cách 5: Tứ giác có tổng số đo hai cặp góc đối diện bằng nhau thì tứ giác đó nội tiếp đường tròn.
Công thức A + C = B + D từ đó suy ra tứ giác ABCD là tứ giác nội tiếp đường tròn.
Ví dụ: Cho một tứ giác ABCD bất kỳ, chứng minh tứ giác ABCD là tứ giác nội tiếp đường tròn.
Với cách này chúng ta sẽ đi chứng minh góc A + góc C = góc B + góc D. Nếu tổng các
góc đối diện này bằng 180 độ thfi tứ giác ABCD là tứ giác nội tiếp đường tròn.
Hình 5: Hình ảnh minh họa chứng minh tứ giác nội tiếp qua tổng số đo hai góc đối bằng nhau
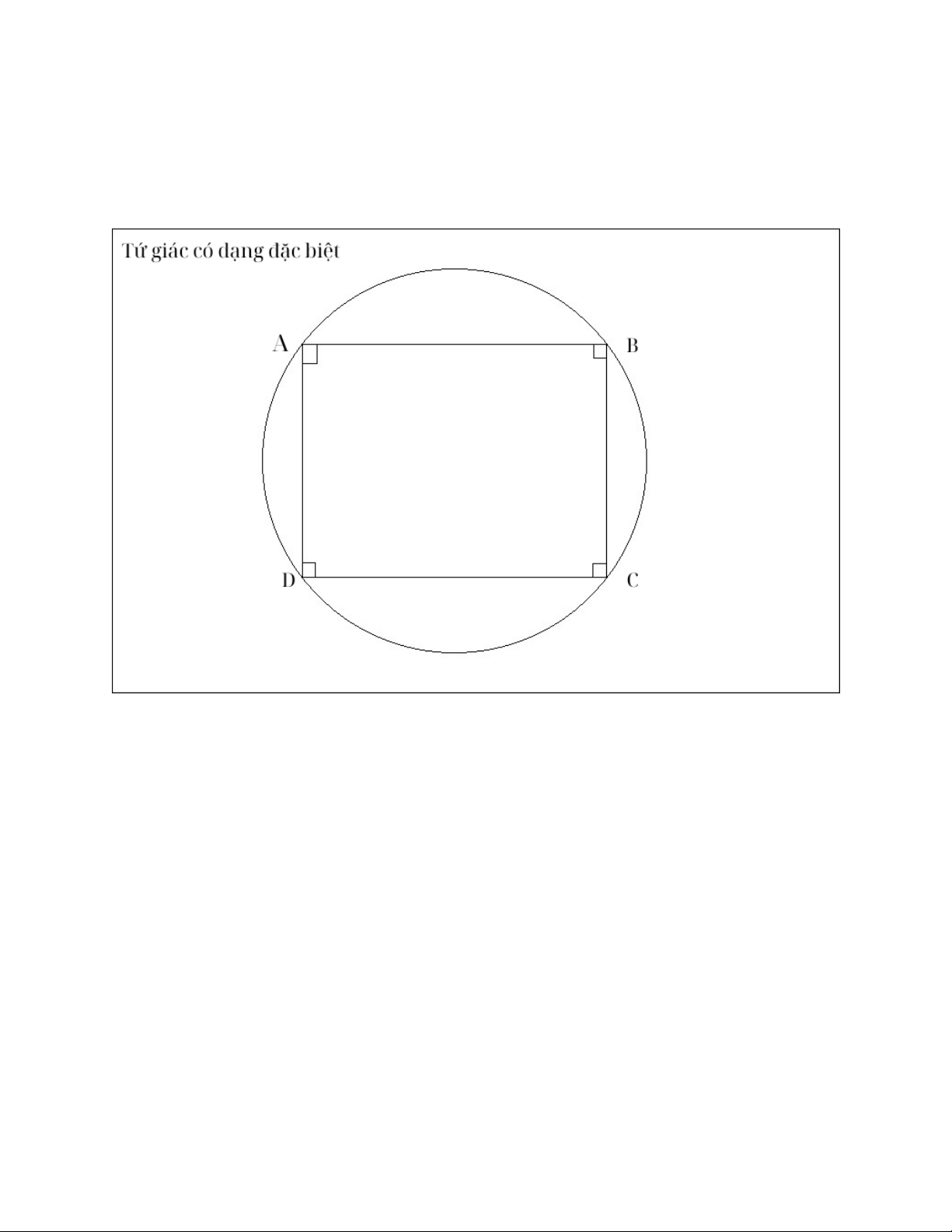
- Cách 6: Chứng minh một tứ giác nội tiếp là tứ giác đặc biệt.
Với cách này chúng ta sẽ chứng minh tứ giác cho trước là một tứ giác đặc biệt. Các tứ
giác đặc biệt này có thể có dạng hình vuông, hình chữ nhật, hình thoi, hình bình hành,
hình thang cân, ... sau đó sẽ đưa ra kết luận tứ giác đó là tứ giác nội tiếp.
Hình 6: Hình ảnh minh họa chứng minh tứ giác nội tiếp bằng cách chứng minh tứ giác
đó có dạng đặc biệt.
3. Một số lưu ý khi làm bài tập dạng chứng minh tứ giác nội tiếp.
Khi làm những dạng bài tập chứng minh hình học, đặc biệt là dạng bài tập chứng minh
tứ giác nội tiếp chúng ta cần phải lưu ý một số vấn đề sau:
- Thứ nhất: Vẽ hình nên rõ ràng, dễ nhìn, tránh vẽ hình tứ giác giống các hình dễ nhận
dạng, trừ trường hợp đặc biệt.
- Thứ hai: Các ký hiệu được sử dụng trong bài làm, như các ký hiệu cho các góc hoặc
đường thẳng mà bằng nhau phải được đánh dấu rõ ràng.
- Thứ ba: Nên căn cứ vào các dữ liệu đề bài và các kiến thức đã học để làm bài hiệu quả hơn.
- Thứ tư: Cần chú ý yêu cầu của bài toán vì có thể là gợi ý hoặc cách thức giải bài tập dạng này.
- Thứ năm: Không dùng điều cần phải chứng minh để chứng minh ngược lại chúng.
4. Một số câu hỏi liên quan về chứng minh tứ giác nội tiếp
Câu 1: Các hình nào sau đây nội tiếp đường tròn?
A. Hình thang, hình chữ nhật.
B. Hình thang cân, hình bình hành. C. Hình thoi, hình vuông.
D. Hình thang cân, hình chữ nhật, hình vuông.
Đáp án là D. Hình thang cân, hình chữ nhật, hình vuông.
Câu 2: Cho tam giác nhọn ABC, đường tròn có đường kính BC cắt AB và AC theo thứ tự
tại D và E. Gọi H là giao điểm của BE và CD, tia AH cắt BC tại F. Hỏi số tứ giác nội tiếp
có trong hình vẽ là bao nhiêu? A. 4 B. 6 C. 7 D. 8
Đáp án là B. 6 vì lần lượt chứng minh ta sẽ có kết quả các tứ giác nội tiếp lần lượt là
ADHE, BDHF, FHEC, BDEC, AEFB và cuối cùng là ADFC. Do đó sẽ có 6 tứ giác nội tiếp trong câu hỏi trên.
Câu 3: Cho tam giác ABC vuông tại A, đường cao AH nội tiếp đường tròn (O;R) gọi I và
K theo thứ tự là điểm đối xứng của H qua hai cạnh AB và AC. Khẳng định nào sau đây là đúng?
A. Tứ giác AHBI nội tiếp đường tròn đường kính AB.
B. Tứ giác AHCK nội tiếp đường tròn đường kính AC.
C. Ba điểm I, A, K thẳng hàng.
D. Cả 3 đáp án A, B và C đều đúng.
Đáp án là D. Cả 3 đáp án A, B và C đều đúng.
Câu 4: Hình nào sau đây không nội tiếp đường tròn? A. Hình vuông B. Hình chữ nhật C. Hình thoi D. Hình thang cân
Đáp án là C. Hình thoi, vì hình vuông, hình chữ nhật và hình thang cân là các hình nội
tiếp đường tròn nhưng hình thoi là hình không nội tiếp đường tròn.