Câu Hỏi Lý Thuyết Chương 2, 3 | Nhiệt động học và vật lý phân tử | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Phát biểu và viết biểu thức nguyên lý thứ nhất của nhiệt động lực học. Giải thích tại sao không thể chế tạo được động cơ nhiệt vĩnh cửu loại I. Áp dụng nguyên lý thứ nhất của nhiệt động lực học để giải thích hiện tượng nhiệt độ của hệ khí giảm trong quá trình giãn nở đoạn nhiệt. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Nhiệt động học và vật lý phân tử 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 0.9 K tài liệu
Tác giả:
Preview text:
NHIỆT ĐỘNG HỌC VÀ VẬT LÝ PHÂN TỬ CÂU HỎI LÝ THUYẾT
1. Phép đo nhiệt độ dựa trên nguyên lý nào của nhiệt động lực học. Phát biểu nguyên lý đó. Phép o đ nhiệt độ d a ự trên nguyên lý s ố không c a ủ nhi t ệ n độ g l c ự h c, ọ c ụ th ể là tính ch t ấ nhiệt độ cân bằng c a ủ các h ệ th n ố g nhi t ệ n độ g. Nguyên lý s ố không có nhi u ề cách phát bi u, ể m t ộ cách ph ổ bi n ế là:
● "Nếu 2 vật A và B cân bằng nhiệt với vật thứ ba thì chúng cân bằng nhiệt với nhau
2. Phân biệt nội năng, nhiệt lượng và công trong một hệ nhiệt động. ● N i ộ năng (U): Là t n ổ g t t ấ c ả các d n ạ g n n ă g l n ượ g ch a ứ trong 1 h ệ cô l p ậ , bao g m ồ n n ă g l n ượ g chuy n ể n độ g nhi t ệ c a ủ các phân t ử ( n độ g n n ă g), th ế n n ă g t n ươ g tác gi a ữ các phân t , ử n n ă g l n ượ g c a ủ các nguyên t ử h t ạ nhân.
● Nhiệt lượng (Q): Là n n ă g l n ượ g trao i đổ gi a ữ h ệ nhiệt n độ g và môi tr n ườ g khi có s ự chênh l ch ệ nhi t ệ . độ ● Công (W): Là s ự chuy n ể d i ờ ho c ặ d ch ị chuyển c a ủ h ệ d i ướ tác d n ụ g c a ủ nhi t ệ l n ượ g và n i ộ n n ă g
3. Phát biểu và viết biểu thức nguyên lý thứ nhất của nhiệt động lực học. Giải thích tại
sao không thể chế tạo được động cơ nhiệt vĩnh cửu loại I. Áp dụng nguyên lý thứ nhất
của nhiệt động lực học để giải thích hiện tượng nhiệt độ của hệ khí giảm trong quá trình giãn nở đoạn nhiệt. ● Nguyên lý th ứ nh t ấ c a ủ nhi t ệ n độ g l c ự h c: ọ ● Phát bi u ể 1: nhi t ệ l n ượ g cung c p ấ cho 1 h ệ dùng
để sinh công và thay i đổ n i ộ n n ă g c a ủ h ệ (Q là nhi t ệ l n ượ g mà h ệ nh n ậ c đượ làm thay i đổ n i ộ n n ă g ΔE và
sinh công A. Q=ΔE+A, ΔE=E2-E1, dQ=dE+dA) ● Phát bi u ể 2: nội n n ă g c a ủ 1 hệ nhi t ệ n độ g là 1 hàm n đơ giá c a ủ tr n ạ g thái, nó chỉ thay i đổ khi b ị n ả h h n ưở g b i ở môi tr n ườ g xung quanh
● Phát biểu 3: Xét 1 chu trình: E2=E1 => ΔE=0. Theo nguyên lí I, Q=A. Nếu
Q=0 thì A=0, hệ không thể sinh công. ● Đ n ộ g c ơ nhi t ệ v n ĩ h c u ử lo i ạ I là n độ g c ơ không c n ầ nhi t ệ l n ượ g mà v n ẫ sinh
công. Mà theo nguyên lí I, h ệ không th ể sinh công n u ế không nh n ậ c đượ nhi t ệ l n ượ g t ừ bên ngoài. Do ó đ không th ể ch ế t o ạ cv đ c lo i ạ I ● Gi i
ả thích quá trình giãn n ở o đ n ạ nhi t
ệ : Trong quá trình giãn n ở o đ n ạ nhi t ệ (Q=0), công th c ự hiện b i ở h ệ l y ấ t ừ nội năng c a ủ h , ệ dẫn n đế gi m ả nhi t ệ độ c a ủ hệ (ΔE + A=0 => A=-ΔE.
4. Biểu diễn trên giản đồ P-V các quá trình: đẳng tích, đẳng áp, đoạn nhiệt, đẳng nhiệt. ● Đ n ẳ g tích: Đ n ườ g th n ẳ g đứng (P thay i đổ , V không i đổ ). ● Đ n ẳ g áp: Đ n ườ g th n ẳ g ngang (P không i đổ , V thay i đổ ). ● Đo n ạ nhi t
ệ : Đường cong d c ố h n ơ n đườ g n đẳ g nhiệt. ● Đ n ẳ g nhi t ệ : Đ n
ườ g hyperbol (P và V thay i đổ sao cho PV = h n ằ g s ) ố .
5. Sự truyền nhiệt lượng: dẫn nhiệt, đối lưu và bức xạ (định nghĩa, cho ví dụ minh họa và
giải thích cơ chế truyền nhiệt của từng ví dụ).
● Dẫn nhiệt: Truy n ề nhiệt qua v t ậ li u ệ rắn do s ự chuy n ể n độ g c a ủ các phân t . ử Ví d : ụ S i ưở m ấ m t ộ đầu thanh kim lo i ạ .
● Cơ chế: Các phân t ử va ch m ạ và truy n ề n n ă g l n ượ g cho nhau. ● Đ i ố l u
ư : Truyền nhiệt qua ch t ấ l n ỏ g ho c ặ khí do s ự chuy n ể n độ g c a ủ dòng ch t ấ l n ỏ g ho c ặ khí. Ví dụ: N c ướ nóng trong n i ồ chuyển n độ g lên trên. ● Cơ chế: S ự chênh l ch ệ nhi t ệ độ t o ạ ra các dòng ch y ả c a ủ ch t ấ l n ỏ g/khí. ● Bức xạ: Truy n
ề nhiệt qua không gian tr n ố g do sóng i đ n ệ t . ừ Ví d : ụ Nhi t ệ t ừ m t ặ trời. ● Cơ chế: Sóng i đ n ệ t ừ mang n n ă g l n ượ g từ ngu n ồ nhi t ệ n đế v t ậ th . ể
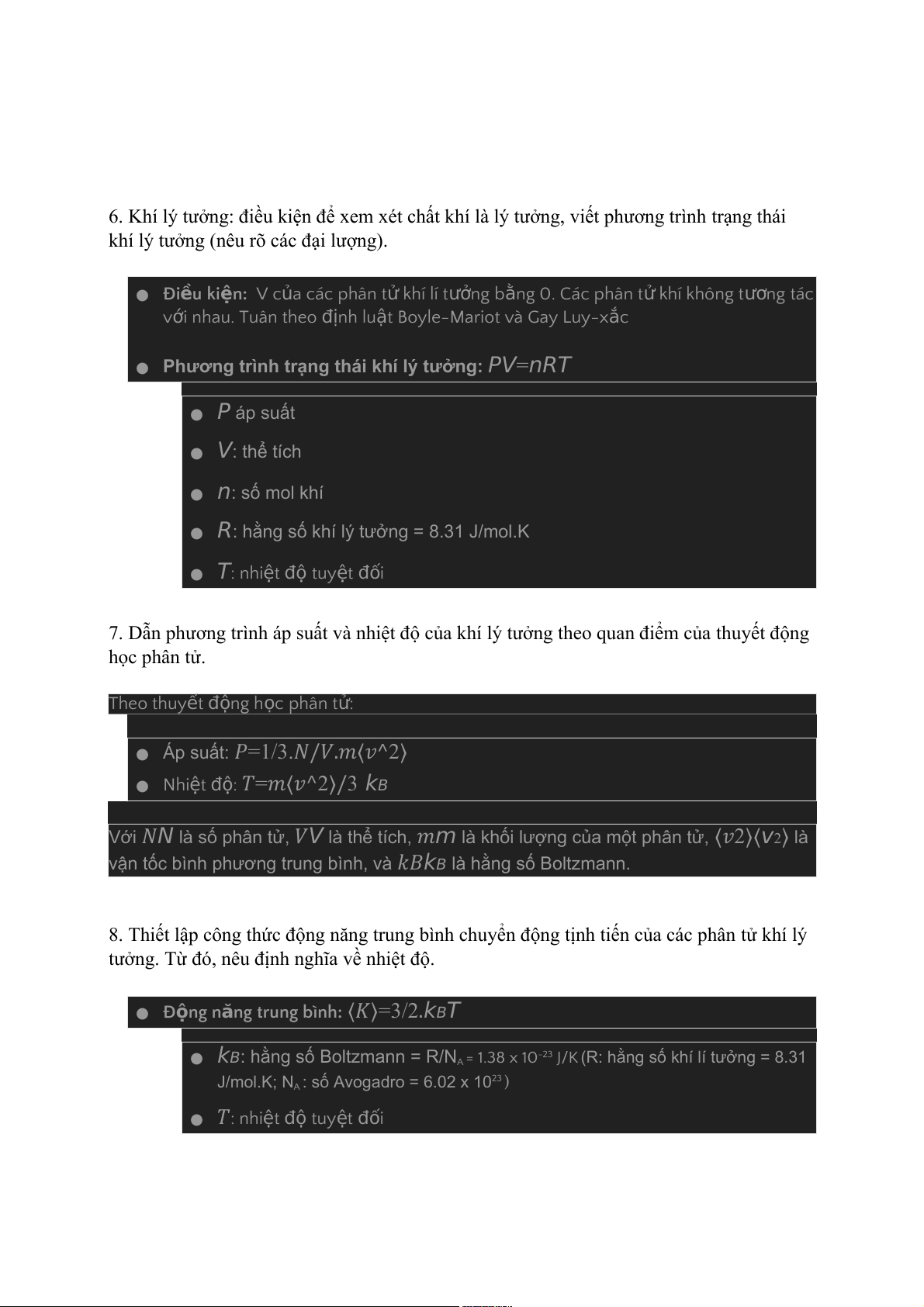
6. Khí lý tưởng: điều kiện để xem xét chất khí là lý tưởng, viết phương trình trạng thái
khí lý tưởng (nêu rõ các đại lượng). ● Đi u ề ki n ệ : V c a ủ các phân t ử khí lí t n ưở g b n ằ g 0. Các phân t ử khí không t n ươ g tác v i ớ nhau. Tuân theo n đị h lu t
ậ Boyle-Mariot và Gay Luy-x c ắ
● Phương trình trạng thái khí lý tưởng: PV=nRT ● P áp suất ● V: thể tích ● n: số mol khí
● R: hằng số khí lý tưởng = 8.31 J/mol.K
● T: nhiệt độ tuy t ệ i đố
7. Dẫn phương trình áp suất và nhiệt độ của khí lý tưởng theo quan điểm của thuyết động học phân tử. Theo thuy t ế n độ g h c ọ phân t : ử
● Áp suất: 𝑃=1/3.𝑁/𝑉.𝑚⟨𝑣^2⟩ ● Nhiệt : độ 𝑇=𝑚⟨𝑣^ ⟩/ 2 3 kB
Với 𝑁N là số phân tử, 𝑉V là thể tích, 𝑚m là khối lượng của một phân tử, ⟨𝑣2⟩⟨v ⟩ 2 là
vận tốc bình phương trung bình, và 𝑘𝐵kB là hằng số Boltzmann.
8. Thiết lập công thức động năng trung bình chuyển động tịnh tiến của các phân tử khí lý
tưởng. Từ đó, nêu định nghĩa về nhiệt độ. ● Đ n ộ g n n
ă g trung bình: ⟨𝐾⟩=3/2.kBT
● kB: hằng số Boltzmann = R/N -23
(R: hằng số khí lí tưởng = 8.31 A = 1.38 x 10 J/K J/mol.K; N 23 A : số Avogadro = 6.02 x 10 ) ● 𝑇: nhiệt độ tuy t ệ i đố ● Đ n ị h nghĩa v ề nhi t ệ :
độ Nhiệt độ là th c ướ o đ động n n ă g trung bình chuy n ể n độ g tịnh tiến c a ủ các phân t ử hay là th c ướ o đ m c ứ độ chuy n ể n độ g h n ỗ lo n ạ c a ủ phân tử
9. Nêu định nghĩa bậc tự do của các phân tử khí. Phát biểu và viết công thức định luật
phân bố đều năng lượng theo bậc tự do. ● Bậc tự do: S ố t a ọ độ c độ l p ậ c n ầ thi t ế để xác n đị h v ịtrí c a ủ 1 v t ậ trong không gian ● Đ n ị h lu t ậ phân bố u đề năng l n ượ g: n độ g năng trung bình c a ủ các phân t ử c đượ phân b ố đều theo các bậc t ự do f và năng l n ượ g n ứ g v i ớ m i ỗ b c ậ t ự do là ½.KB.T ● Đ n ộ g n n
ă g trung bình: ⟨𝐸đ⟩=𝑓/2.kBT ● f: s ố b c ậ t ự do ( n đơ nguyên t : ử 3, nh ịnguyên t : ử 5, a đ nguyên t : ử 6)
10. Nhiệt dung là gì? Dẫn phương trình mối quan hệ của nhiệt dung mol đẳng tích và
nhiệt dung mol đẳng áp của các chất khí. ● Nhiệt dung: L n ượ g nhiệt c n ầ thi t ế để t n ă g nhi t ệ độ của m t ộ đơn vị kh i ố l n ượ g ch t ấ lên 1 . độ
● Đẳng tích: 𝐶𝑉=(f/2).R ● Đẳng áp: 𝐶𝑃=CV+R Q=A+ΔE Q=n.C ΔT P.
A=p. ΔV=n.R. ΔT ΔE = n.CV. ΔT
11. Cho phương trình 𝐴 = 𝑛𝑅𝑇𝑙𝑛 𝑉2/𝑉1, với A là công hoàn thành của một quá trình nhiệt
động biến đổi từ V1 đến V . Hãy cho biết, đây là quá trình nhiệt động nào? Vì sao? Vẽ đồ 2
thị của quá trình trong giản đồ P-V. ● Đây là quá trình n đẳ g nhi t ệ (T không i đổ ). (2 ) ● A=∫ P.dV (1)
● Mà PV=nRT (PT trạng thái) => P=nRT/v (v 2) (2 ) (2 )
● Công: A= ∫ P . dV =∫(nRT /v). dV =nRT.∫dV /v =nRT.ln(v2/v1) (v 1) (1) (1) ●
12. Viết phương trình đoạn nhiệt, nêu rõ từng đại lượng. Tính công trong quá
trình đoạn nhiệt của khí lý tưởng. ●
● Phương trình đoạn nhiệt: 𝑃𝑉𝛾=const ● 𝛾=𝐶𝑃/𝐶V (v 2) (t 2)
● Công trong quá trình đoạn nhiệt: A=∫ P.dV =∫ −n. CV .dT = -n.Cv(T2-T1) = (v 1) (t 1) n.Cv.(T1-T2)
13. Trình bày về cấu tạo, nguyên tắc hoạt động và hiệu suất của động cơ nhiệt.
Phát biểu nguyên lý thứ hai của nhiệt động lực học theo cách của Thomson. ● C u ấ t o ạ và nguyên t c ắ hoạt n độ g: G m ồ ngu n ồ nóng có nhi t ệ đ ộ T1, ngu n ồ lạnh có nhiệt độ T2 và n độ g c . ơ Đ n ộ g c ơ nhi t ệ nh n ậ nhi t ệ l n ượ g từ ngu n ồ nóng có nhiệt độ T1, tỏa nhiệt l n ượ g ra ngu n ồ lạnh có nhi t ệ độ T2, và sinh công A
● Hiệu suất: e=|A|/|Q1| = (|Q1|-|Q2|)/|Q1| = 1- (|Q2|/|Q1|), e nhỏ hơn hoặc bằng 1
Q1: nhiệt lượng nhận từ nguồn nóng
Q2: nhiệt lượng tỏa ra ở nguồn lạnh A: công sinh ra ● Nguyên lý th ứ hai c a ủ nhi t ệ n độ g l c ự h c
ọ (Thomson): Không th ể t n ồ t i ạ trong t ự nhiên 1 quá trình mà h u ậ quả duy nh t ấ là bi n ế hoàn toàn nhi t ệ l n ượ g thành công mà không để l i
ạ dấu vết gì cho môi tr n ườ g xung quanh. Không th ể ch ế t o ạ c đượ n độ g c ơ vĩnh c u ử lo i ạ 2
● Trường hợp lí tưởng: e=1 => |A|=|Q1| => |Q2|=0. Không x y ả ra trong th c ự t . ế Đ n ộ g c ơ vĩnh cửu lo i ạ 2 là n độ g c ơ bi n ế hoàn toàn nhi t ệ lượng thành công
14. Trình bày về cấu tạo, nguyên tắc hoạt động và hệ số làm lạnh của máy lạnh. Phát biểu
nguyên lý thứ hai của nhiệt động lực học theo cách của Claudius. ● C u ấ t o ạ và nguyên t c ắ hoạt n độ g: G m ồ ngu n ồ nóng có nhi t ệ đ ộ T1, ngu n ồ lạnh có nhi t ệ độ T2 và máy l n ạ h. Máy l n ạ h s ử d n ụ g công A để v n ậ chuy n ể nhi t ệ t ừ ngu n ồ l n ạ h sang ngu n ồ nóng h n ơ
● Hệ số làm lạnh: K=|Q2|/A=|Q2|/(|Q1|-|Q2|), K>1
Q1: nhiệt lượng vận chuyển vào nguồn nóng
Q2: nhiệt lượng lấy i đ từ ngu n ồ l n ạ h
Trong trường hợp lý tưởng, K vô tận, A=0, không cần công A, nhiệt lượng vẫn
vận chuyển từ nguồn lạnh sang nguồn nóng hơn. Đi u ề này không x y ả ra trong th c ự tế Nguyên lý th ứ hai c a ủ nhi t ệ n độ g l c ự h c
ọ (Claudius): Không th ể t n ồ t i ạ trong t ự nhiên 1 quá trình mà h u ậ quả duy nh t ấ là nhi t ệ l n ượ g truy n ề t ừ ngu n ồ l n ạ h sang ngu n ồ nóng h n ơ mà không để l i ạ dấu v t ế gì cho môi tr n
ườ g xung quanh. Hay không th ể ch ế t o ạ được máy l n ạ h vĩnh c u. ử T ừ ó đ , nhi t ệ l n ượ g không th ể t ự n độ g truy n ề từ ngu n ồ l n ạ h sang ngu n ồ nóng h n ơ
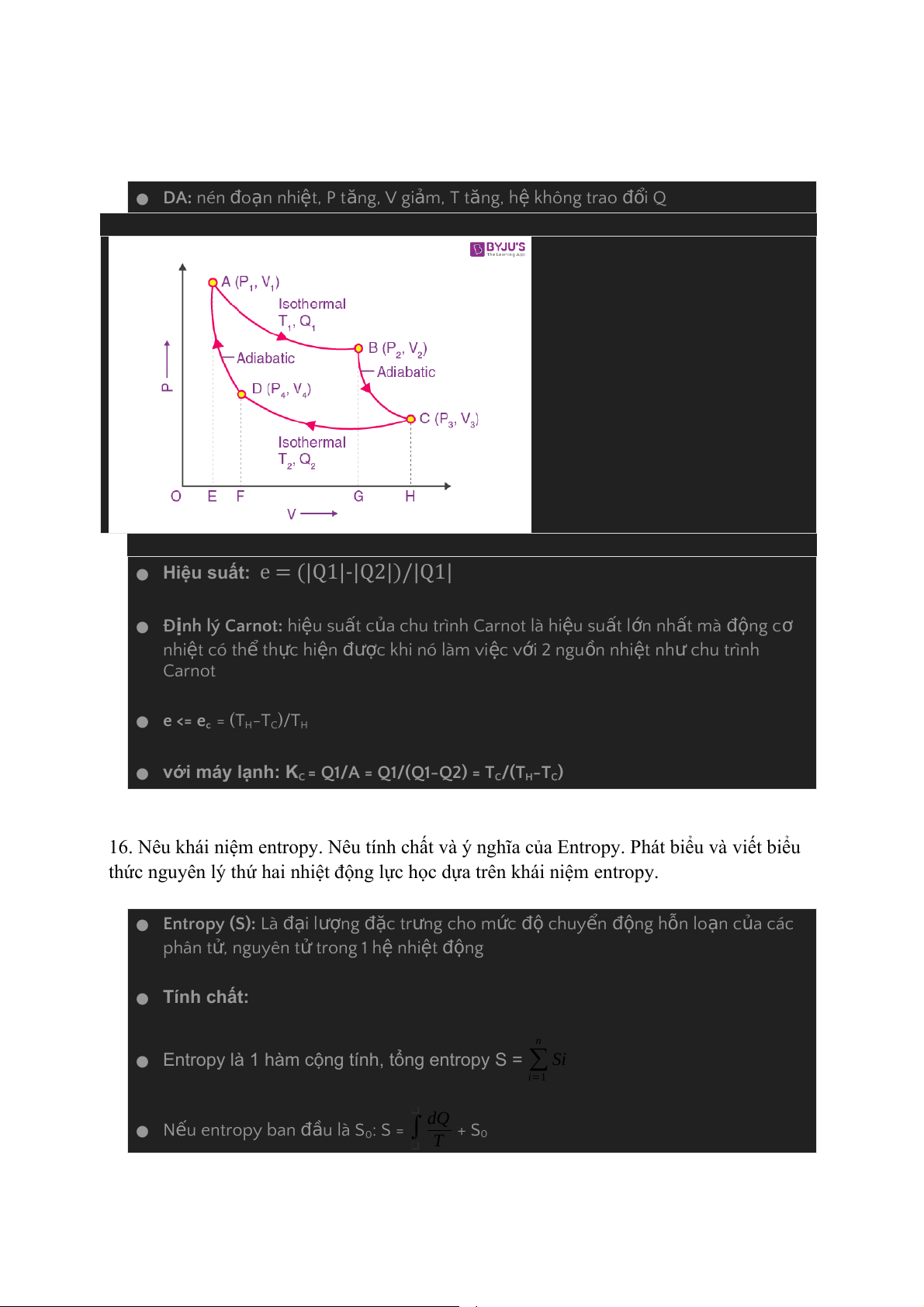
15. Chu trình Carnot: vẽ chu trình trên giản đồ P-V, trình bày vắn tắt về chu trình. Tính
hiệu suất của chu trình Carnot. Phát biểu và viết biểu thức của định lý Carnot.
● Chu trình Carnot: Bao g m ồ 2 quá trình n đẳ g nhi t ệ thu n ậ ngh ch ị và 2 quá trình o đ n ạ nhiệt thu n ậ nghịch xen k ẽ nhau ● AB: giãn n ở n đẳ g nhiệt, P gi m ả , V t n ă g, T const, h ệ nh n ậ Q ● BC: giãn n ở o đ n ạ nhi t ệ , P gi m ả , V t n ă g, T gi m ả t ừ T ệ đổ ớ H -> TC, h không trao i Q v i môi tr n ườ g bên ngoài ● CD: nén n đẳ g nhi t ệ , P tăng, V gi m ả , T const, h ệ t a ỏ nhi t ệ Q2 ● DA: nén o đ n ạ nhiệt, P t n ă g, V gi m ả , T t n ă g, h ệ không trao i đổ Q
● Hiệu suất: e = (|Q1|-|Q2|)/|Q1| ● Đ n
ị h lý Carnot: hiệu su t
ấ của chu trình Carnot là hi u ệ su t ấ l n ớ nh t ấ mà n độ g c ơ nhiệt có th ể th c ự hi n ệ c đượ khi nó làm vi c ệ v i ớ 2 ngu n ồ nhi t ệ nh ư chu trình Carnot
● e <= ec = (TH-TC)/TH
● với máy lạnh: KC = Q1/A = Q1/(Q1-Q2) = TC/(TH-TC)
16. Nêu khái niệm entropy. Nêu tính chất và ý nghĩa của Entropy. Phát biểu và viết biểu
thức nguyên lý thứ hai nhiệt động lực học dựa trên khái niệm entropy. ● Entropy (S): Là i đạ l n ượ g c đặ tr n ư g cho m c ứ độ chuy n ể n độ g hỗn lo n ạ c a ủ các phân t , ử nguyên t ử trong 1 h ệ nhiệt n độ g ● Tính chất: n
● Entropy là 1 hàm cộng tính, tổng entropy S = ∑ Si i=1 ❑ dQ ● N u ế entropy ban u đầ là S0: S = ∫ + S0 ❑ T