












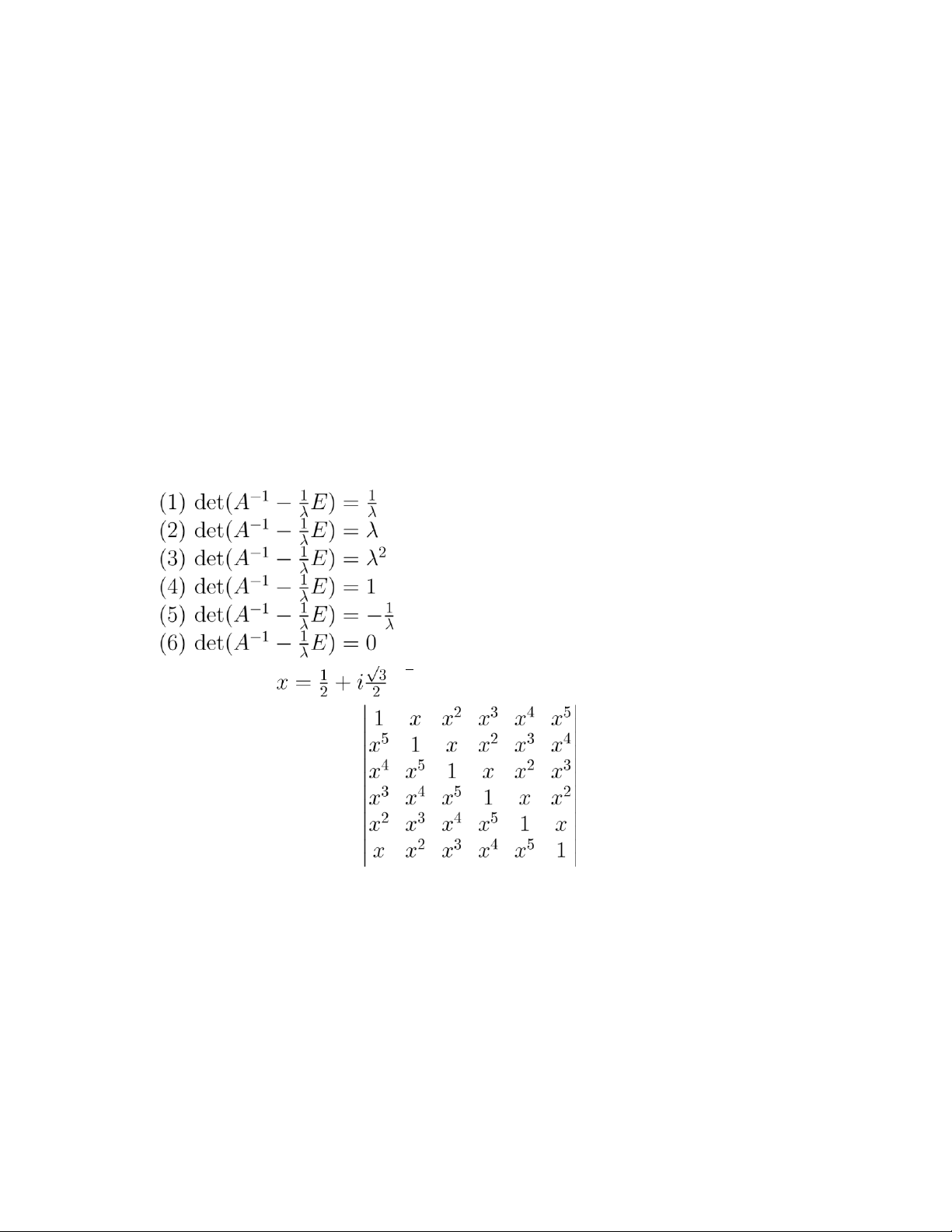
Preview text:
MỘT SỐ CÂU HỎI TRẮC NGHIỆM ÔN TẬP
Câu 1. Cho p,q là hai mệnh đề. Mệnh đề p → q tương đương logic với mệnh đề nào.
Câu 2. Ánh xạ f : R → R nào sau đây là đơn ánh. Câu 3. Cho số phức . Khi đó, (5) Một đáp án khác
Câu 4. Cho ánh xạ f :√C → C xác định bởi f(z) = 2z3 − 1. Khi đó,
tập nghịch ảnh của f−1({ 3i}) là: . Câu 5. Cho
với n ∈ N. Khi đó n > 0 nhỏ nhất để Re(zn) = 0 là: (1) n = 5 1 (2) n = 6 (3) n = 2 (4) n = 3 (5) Một đáp án khác
Câu 6. Cho ánh xạ f : R2 → C xác định bởi f(x,y) = (x + 2y) + i(2x + my). Ánh xạ này toàn ánh khi (1) ∀m ∈ R (2) m ̸= 2 (3) m ̸= −4 (4) m ̸= 4 (5) Một đáp án khác
Câu 7. Cho hai tập hợp A,B khác rỗng. Khẳng định nào sau đây luôn đúng.
Câu 8. Trên trường số phức C số nghiệm của phương trình z2−2z+ 1 = 0 là (1) 1 (2) 3 (3) 0 (4) 5 (5) 2 (6) Đáp án khác.
Câu 9. Cho ánh xạ f : R2 → R2 xác định bởi f(x,y) = (x+2y,2x+
4y). Xét tập hợp B = {(0;0)}. Khi đó (6) Một đáp án khác.
Câu 10. Ký hiệu M2 là tập hợp các ma trận vuông cấp 2 hệ số thực.
Ánh xạ f : M2 → M2 xác định bởi là đơn ánh khi (1) m = 0 (2) m ̸= 0
(3) Không đơn ánh ∀m ∈ R
(4) Đơn ánh ∀m ∈ R
Câu 11. Cho ánh xạ f : R3 → R3 xác định bởi f(x,y,z) = (2x−y + z,x + 2y −
2z,x + z) và B = (2,1,2). Khi đó
(1) f−1(B) = {(0,0,0)}.
(2) f−1(B) = {(−1,1,1)}.
(3) f−1(B) = {(1,1,1)}.
(4) f−1(B) = {(1,0,−1)}.
(5) f−1(B) = {(x,y,z) | x,y,z ∈ R}.
Câu 12. Biết G = R\{1} lập thành nhóm giao hoán với phép toán 2 ngôi *
xác định bởi x ∗ y = x + y − xy. Khi đó, phần tử đối của x ∈ G là: (5) Một đáp án khác
Câu 13. Ký hiệu Mn là tập tất cả các ma trận vuông cấp n hệ số thực và G
= {X ∈ Mn | det(X) = λ}. Khi đó G lập thành một nhóm với phép nhân ma trận nếu: (1) λ = 0 (2) λ = 1 (3) λ ̸= 0. (4) ∀λ ∈ R (5) Một đáp án khác.
Câu 14. Gọi ζk với 1 ≤ k ≤ 5 là nghiệm của phương trình z5 + z4 + 5
z3 + z2 + z + 1 = 0. Khi đó S = P ζk bằng. k=1 (1) 0 (2) 1 (3) -1 (4) Một đáp án khác.
Câu 15. Cho X = {x = (x1,x2) | x1,x2 ∈ R,x1 = 0̸} lập thành nhóm với phép
toán hai ngôi * xác định bởi (x1,x2)∗(y1,y2) = (x1y1,x1y2+x2). Phần tử đối
hay phần tử nghịch đảo của x = (a,b) là: (5) Một đáp án khác.
Câu 16. Cho ánh xạ f : R2 → R3 xác định f(x,y) = (2x − y,x +
3y,4x + 5y) và B = {(m,n,p)} ∈ R3. Khi đó f−1(B) ̸= ∅ nếu
(1) p = m + n
(2) p = 2m + n
(3) p = m + 2n (4) ∀m,n,p ∈ R
(5) f−1(B) = ∅,∀m,n,p ∈ R.
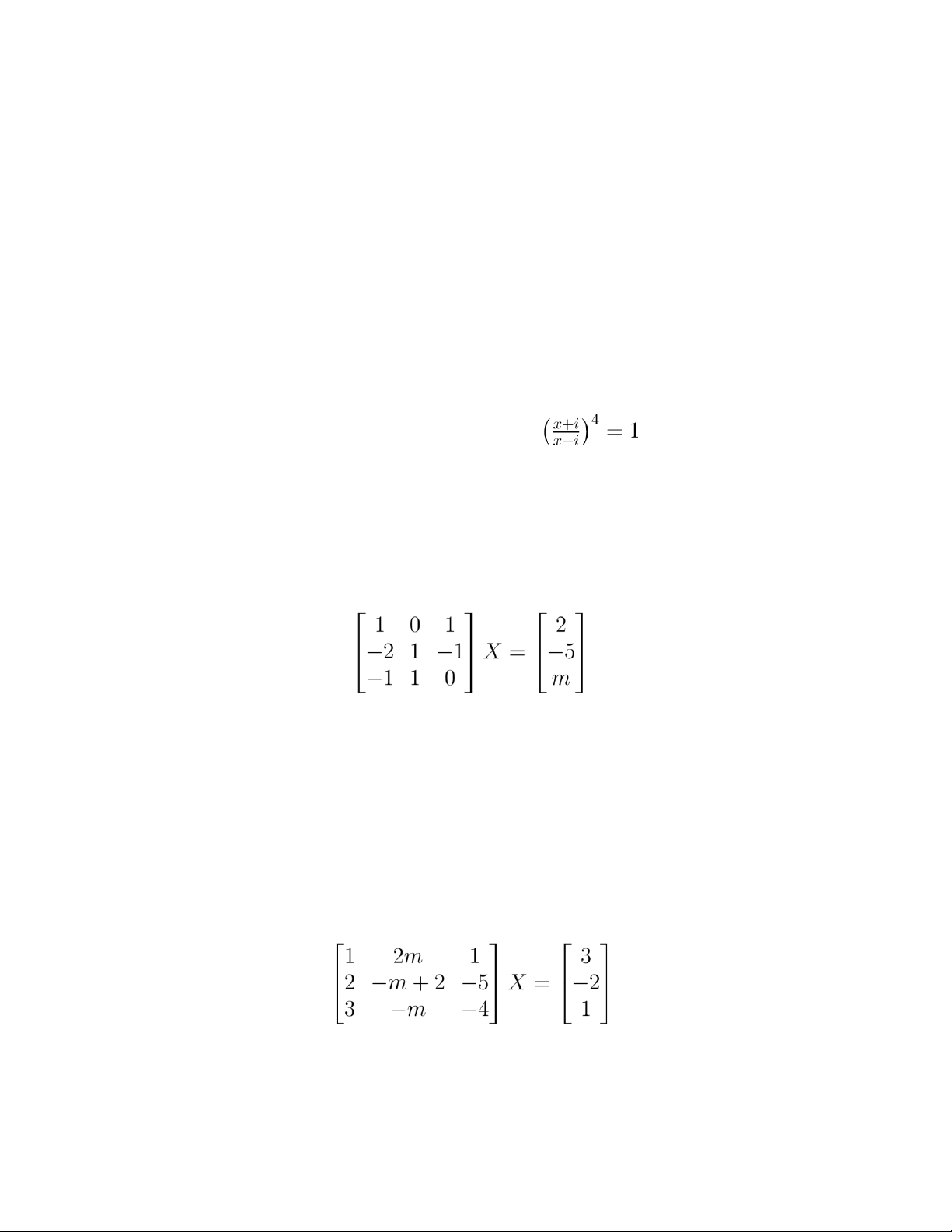
Câu 17. Tập các nghiệm của phương trình là:
(1) {1,1 + i,1 − i,0} (2) {1,−1,0}
(3) {1,i,−i,0} (4) {−1,1 + i,−1 − i,0} (5) Một đáp án khác.
Câu 18. Phương trình ma trận có nghiệm khi (1) m = 1 (2) m = 5 (3) m = 3 (4) m = −3 (5) m = 2 (6) Một đáp án khác.
Câu 19. Phương trình ma trận
có vô số nghiệm khi và chỉ khi (1) m = −1 (2) m = −2
(3) m = 0 (4) m = 3 (5) m = 2 (6) Một đáp án khác. Câu 20. Cho
Khi đó r(A) = 3 (hạng của
ma trận A bằng 3) nếu
(1) x2y + xy2 = 0
(2) x2y + xy2 ̸= 0 (3) ∀x,y ∈ R
(4) Không tồn tại x,y thỏa điều kiện r(A) = 3. Câu 21. Hệ phương trình
với a ∈ R có nghiệm duy nhất khi. (1) a = 0
(2) a = ±1 (3) ∀a ∈ R.
(4) a ̸= 0,a ̸= ±1
(5) Không tồn tại a ∈ R để hệ có nghiệm duy nhất.
Câu 22. Phương trình ma trận
(1) Vô nghiệm khi λ = 6
(2) Vô số nghiệm khi λ = 0
(3) Có nghiệm duy nhất khi λ = −3
(4) Vô số nghiệm với mọi λ
(5) Vô nghiệm với mọi λ
(6) Có nghiệm với mọi λ
Câu 23. Ký hiệu M3 là tập tất cả các ma trận vuông cấp 3 hệ số thực trên
R. Ánh xạ f : M3 → M3 xác định bởi là song ánh khi (1) ∀m
(2) Không tồn tại m (3) m ̸= 1 (4) m = 1 (5) Một đáp án khác.
Câu 24. Ký hiệu M2 là tập các ma trận vuông cấp 2 hệ số thực. Cho
ánh xạ f : M2 → M2 xác định bởi .
Khi đó f−1T bằng (5) Một đáp án khác. Câu 25. Cho biết
. Biết det(A) = 0. Khi đó,
(1) r(A) = 2 (2) r(A) = 3 (3) r(A) = 1
(4) r(A) = 0 (5) Một đáp án khác. Câu 26. Cho biết
với aij ∈ {−1,1} với 1 ≤
i,j ≤ 3 Khi đó giá trị lớn nhất của det(A) bằng: (1) 0 (2) 2 (3) 1 (4) 4 (5) 5 (6) Một đáp án khác.
Câu 27. Cho p,q,r là ba mệnh đề trong đó r là mệnh đề đúng. Khẳng định nào sau đây là đúng.
(1) (p ∨ r) → q luôn có giá trị chân lý bằng 1. (2) (p
∧ q) → r luôn có giá trị chân lý bằng 0.
(3) (p ∨ q) → r luôn có giá trị chân lý bằng 1. (4) (p
∨ r) → q luôn có giá trị chân lý bằng 0.
(5) (p ∧ q) → r luôn có giá trị chân lý bằng 1.
Câu 28. Ánh xạ f : R → R nào sau đây là đơn ánh.
Câu 29. Cho A,B là hai ma trận vuông cùng cấp. Khẳng định nào sau đây là sai.
(1) det(AB) = det(BT)det(A)
(2) r(AB) = r(BTAT)
(3) det(AB)3 = (det(A))3(det(B))3
(4) r(AB) = r(ATBT)
Câu 30. Ánh xạ f : C → C xác định bởi f(z) = 2z4 + m là toàn ánh khi nào. (1) m < 0 (2) m ≥ 0 (3) ∀m ∈ R (4) ∀m ∈ C
(5) Không tồn tại m để f là toàn ánh (6) Một đáp án khác.
Câu 31. Dạng lượng giác của số phức là (5) Một đáp án khác. Câu 32. Hệ phương trình
x1 − x2 + x3 = 0 2x1 + x2 = 8 2x2 + 5x3 = 16 −x1 + x2 − x3 = 0 (1) Hệ vô nghiệm
(2) Có vô số nghiệm phụ thuộc 1 tham số
(3) Có vô số nghiệm phụ thuộc 2 tham số (4) Có nghiệm duy nhất (5) Một đáp án khác. Câu 33. Cho ma trận
có ma trận nghịch đảo là: Khi đó . (6) Một đáp án khác. Câu 34. Hệ phương trình
Hệ phương trình có vô số nghiệm khi
(1) a ̸= 14,b ̸= 7
(2) a = 14,b ̸= 7
(3) a = −14,b = 7
(4) a = 14,b = 7
(5) a = −14,b = −7 (6) Một đáp án khác.
Câu 35. Cho các hàm số thực f,g,h xác định trên R và ba tập hợp A = {x ∈
R | f(x) = 0},B = {x ∈ R | g(x) = 0},C = {x ∈ R | h(x) = 0}. Khi đó A\(B ∩ C)
là tập nghiệm của phương trình nào.
Câu 36. Trên trường số phức các nghiệm của phương trình z4−i = 0 là: (6) Một đáp án khác.
Câu 37. Với A,B là các ma trận vuông cấp 4 tùy ý và khả nghịch, khắng
định nào sau đây là SAI.
Câu 38. Hạng của ma trận 15 14 13 12 9 8 5 1 4 0 bằng (1) 0 (2) 3 (3) 4 (4) 2 (5) 1
Câu 39. Cho A,B,C là ba tập hợp bất kỳ. Khẳng định nào sau đây luôn Đúng.
(1) Nếu A ∩ B = A ∩ C thì B = C
(2) Nếu A ∪ B = A ∪ C thì B = C
(3) Nếu A\B = A\C thì B = C (4) Nếu A × B = A × C thì B = C.
Câu 40. Trong trường số phức C thì số nghiệm của phương trình là: (1) 1 (2) 2 (3) 3 (4) 4 (5) 5 (6) 6 Câu 41. Cho ma trận
. Tồn tại ma trận X =
khác ma trận không thỏa mãn AX = λX. (1) λ ∈ {1;3} (2) λ ∈ {1;−3} (3) λ ∈ {−1;3} (4) λ ∈ {−1;−3}
(5) Không tồn tại λ. (6) Một đáp án khác.
Câu 42. Cho m ∈ R. Khi đó tập hợp
lập thành nhóm đối với phép cộng hai ma trận nếu (1) m = 2 (2) m = 0
(3) Không tồn tại m (4) m = 1 (5) ∀m
Câu 43. Cho ma trận A thỏa mãn và B = . Khi đó B2 bằng (6) Một đáp án khác.
Câu 44. Cho ánh xạ f : C → C xác định bởi f(z) = z2−(i+1)z−m với m ∈ C.
Khi đó f−1({3}) = {−2 − i,3 + 2i} nếu
(1) m = −1 + 7i (2) m = 1 − 7i
(3) m = −1 − 7i
(4) m = 1 + 7i (5) Một đáp án khác. Câu 45. Cho
với z ∈ C. det(A) = 0 khi (5) Một đáp án khác. Câu 46. Ma trận có hạng nhỏ nhất khi (1) λ = 1 (2) λ = −2 (3) λ = 3
(4) λ = {−1,2} (5) Một đáp án khác.
Câu 47. Với a ̸= b,a,b ∈ R, phương trình
với x là ẩn có nghiệm thực duy nhất nếu (1) a = −b (2) a = 2b (3) a = −2b
(4) ∀a,b(a ̸= b) thì phương trình có nghiệm duy nhất.
(5) ∀a,b(a ̸= b) thì phương trình có nhiều hơn một nghiệm. (6) Một đáp án khác.
Câu 48. Cho f : X → X là ánh xạ tùy ý. Khẳng định nào sau đây là SAI.
(1) f(A ∪ B) = f(A) ∪ f(B) với mọi A,B ⊂ X
(2) f(A\B) = f(A)\f(B) với mọi A,B ⊂ X (3) f−1(A ∪ B) =
f−1(A) ∪ f−1(B) với mọi A,B ⊂ Y .
(4) f−1(A\B) = f−1(A)\f−1(B) với mọi A,B ⊂ Y
Câu 49. Cho A là ma trận vuông cấp 6 hệ số thực thỏa mãn A2+E = 0 với
E là ma trận đơn vị cấp 6. Khi đó phương trình det(A−λE) = 0:
(1) Có nghiệm thực là λ = 0
(2) Có nghiệm thực là λ = −1
(3) Có nghiệm thực là λ = 1
(4) Có nghiệm thực là ∀λ ∈ R
(5) Không có nghiệm thực.
(6) Có nghiệm thực là λ = 2
Câu 50. Cho ma trận vuông hệ số thực khả nghịch A và số thực λ ̸= 0,
thỏa mãn det(A−λE) = 0 với E là ma trận đơn vị có cùng cấp với A. Khi đó . Câu 51. Cho . Khi đó định thức bằng (1) -1 (2) 1 (3) 0
(4) 1 + i (5) 1 − i (6) Một đáp án khác.




