Cấu trúc dữ liệu Trie: Tổng Quan & Ứng Dụng | Môn Cấu trúc dữ liệu - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58675420
CẤU TRÚC DỮ LIỆU TRIE: TỔNG QUAN VÀ ỨNG DỤNG
1. ĐỊNH NGHĨA VÀ Ý TƯỞNG
Trie, còn gọi là Prefix Tree hoặc Digital Tree, là một cấu trúc dữ liệu dạng cây được thiết
kế để lưu trữ và tìm kiếm các chuỗi ký tự hiệu quả. Mỗi nút trong Trie đại diện cho một
ký tự, và đường dẫn từ gốc đến một nút lá tạo thành một chuỗi hoàn chỉnh. Trie thường
được sử dụng trong các bài toán xử lý từ điển, tìm kiếm từ, và tự động hoàn thành. Cấu trúc cơ bản:
- Gốc (Root): Nút ban đầu của Trie, không chứa ký tự nào.
- Nút con (Children): Mỗi nút có thể có tối đa 26 nút con (đối với bảng chữ cái tiếng
Anh) hoặc nhiều hơn, tùy thuộc vào tập ký tự.
- Đánh dấu kết thúc từ: Một số nút được đánh dấu để chỉ rằng đường dẫn đến nút này tạo
thành một từ đầy đủ. 2. ỨNG DỤNG
Sắp xếp một danh sách các xâu
Sau khi xây dựng trie gồm các xâu trong danh sách, ta dfs một lượt qua trie đó, đi lần lượt
các cạnh theo thứ tự chữ cái tăng dần. Duyệt tới một đỉnh tới bất kì, ta sẽ in ra các xâu
được thể hiện bởi đỉnh đó nếu có. Dễ thấy ta sẽ lần lượt thu được các xâu trong danh sách
theo thứ tự từ điển tăng dần.
Xử lí truy vấn tiền tố chung dài nhất của hai xâu
Đầu tiên, ta dựng một trie của danh s ách các xâu đã cho.
Với hai xâu bất kì trong danh sách, ta có thể thấy tiền tố chung dài nhất của chúng cũng
có thể được thể hiện bằng một đỉnh trong trie. Nhìn hình vẽ ta có dễ dàng nhận ra đỉnh
cần tìm này cũng chính là tổ tiên chung thấp nhất của hai đỉnh thể hiện cho hai xâu đã cho.
Xử lí truy vấn tìm xâu có thứ tự từ điển thứ k Xử lí truy vấn tìm XOR lớn nhất với
giá trị được cho 3. ƯU ĐIỂM -
Hiệu quả về thời gian: Việc thêm, xóa hoặc tìm kiếm từ có độ phức tạp O(L),
nhanh hơnso với các cấu trúc dữ liệu khác như cây nhị phân hoặc bảng băm khi làm việc với chuỗi. lOMoAR cPSD| 58675420 -
Tiết kiệm không gian cho các từ có tiền tố chung: Chỉ lưu trữ một lần các ký tự
chung, giảm sự lặp lại. 4. KHUYẾT ĐIỂM
- Tốn bộ nhớ: Trie có thể chiếm nhiều không gian hơn các cấu trúc khác nếu không có
nhiều tiền tố chung. Mỗi nút phải lưu trữ nhiều con trỏ đến các nút con.
- Phức tạp trong cài đặt: Trie đòi hỏi cấu trúc phức tạp và khó mở rộng khi tập ký tự lớn.
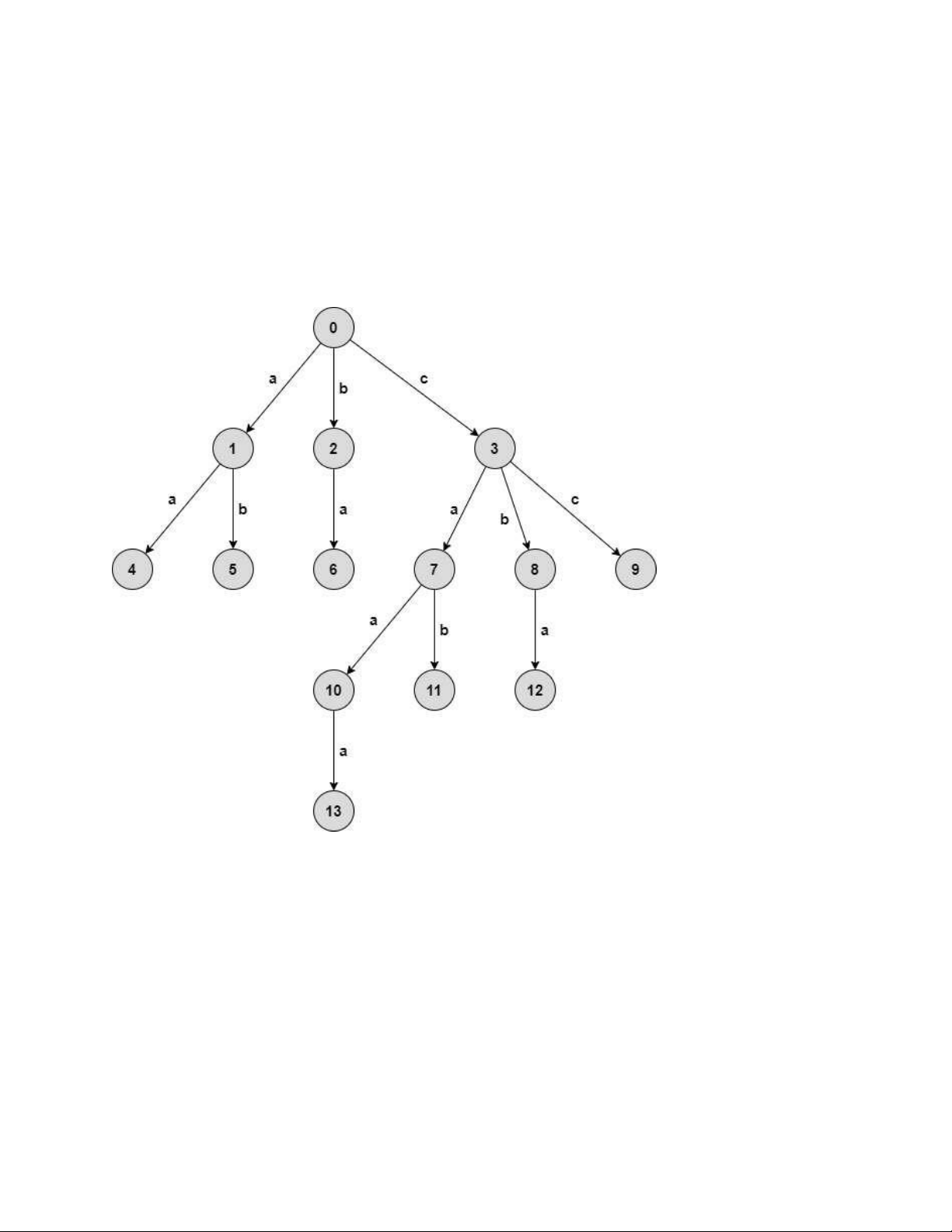
Trong một trie, mỗi cạnh được biểu diễn bằng một kí tự, mỗi đỉnh và đường đi từ gốc đến
đỉnh đó biểu diễn một xâu gồm các kí tự thuộc các cạnh trên đường đi đó. Ví dụ, đỉnh 5
biểu diễn xâu ab, đỉnh 10 biểu diễn xâu caa.
Cấu trúc của trie rất dễ hiểu và cài đặt. Gọi child(u, c) là đỉnh con của đỉnh được nối bởi
cạnh được biểu diễn bằng kí tự , hoặc bằng nếu đỉnh con đó không tồn tại. Xâu được thể
hiện bởi đỉnh con này sẽ chính là xâu được thể hiện bởi đỉnh , thêm kí tự vào cuối. Do
vậy, ta chỉ cần mảng child này với mỗi đỉnh để duy trì cấu trúc của trie. Ví dụ, trong ảnh
trên, child(1, 'b') = 5, child(3, 'c') = 9, child(11, 'b') = -1.