




Preview text:
Cấu trúc dữ liệu và giải thuật
Chương 1: Danh sách liên kết đơn và đôi I. Danh sách liên kết đơn
// Khai báo cấu trúc Node và List typedef struct Node { int data; struct Node *pNext; } Node; typedef struct { Node *pHead; Node *pTail; } List;
// Khởi tạo danh sách rỗng void init(List *l) {
l->pHead = l->pTail = NULL; }
// Kiểm tra danh sách rỗng int Empty(List l) {
return ((l.pHead == NULL) && (l.pTail == NULL)) ? 1 : 0; }
// Thêm một phần tử vào đầu danh sách
void addHead(List *l, Node *pNew) { if (Empty(*l)) {
l->pHead = l->pTail = pNew; } else { pNew->pNext = l->pHead; l->pHead = pNew; } }
// Thêm một phần tử vào cuối danh sách
void addTail(List *l, Node *pNew) { if (Empty(*l)) {
l->pHead = l->pTail = pNew; } else {
l->pTail->pNext = pNew; l->pTail = pNew; } } // Tạo một nút mới Node* createNode(int x) { Node *p;
p = (Node *)malloc(sizeof(Node)); if (p == NULL) {
printf("Không đủ bộ nhớ để cấp phát.\n"); } else { p->data = x; p->pNext = NULL; } return p; }
// Nhập danh sách từ người dùng void input(List *l) { init(l); int x; Node *pNew; do {
printf("Nhập phần tử (0 để dừng): "); scanf("%d", &x); if (x == 0) break; pNew = createNode(x); if (pNew != NULL) addHead(l, pNew); } while (1); } // Xuất danh sách void output(List l) { if (Empty(l)) {
printf("Danh sách rỗng.\n"); } else { Node *p = l.pHead; while (p != NULL) { printf("%d\t", p->data); p = p->pNext; } printf("\n"); } }
// Đếm số lượng phần tử trong danh sách int DemSL(List l) { if (Empty(l)) { return 0; } else { int dem = 0; Node *p = l.pHead; while (p) { dem++; p = p->pNext; } return dem; } }
// Xóa một nút trong danh sách
void deleteNode(List *l, int x) { if (Empty(*l)) {
printf("Danh sách rỗng, không thể xóa.\n"); return; } Node *pDel = findNode(*l, x); if (pDel == NULL) {
printf("Không tim thấy phần tử %d trong danh sách.\n", x); return; } if (pDel == l->pHead) {
// Xóa phần tử đầu tiên
l->pHead = l->pHead->pNext; if (l->pHead == NULL) {
l->pTail = NULL; // Nếu danh sách chỉ có 1 phần tử } } else {
// Xóa phần tử ở giữa hoặc cuối
Node *pPre = findNodePre(*l, pDel);
pPre->pNext = pDel->pNext; if (pDel == l->pTail) {
l->pTail = pPre; // Nếu xóa phần tử cuối } }
free(pDel); // Giải phóng bộ nhớ }
// Tìm một phần tử trong danh sách
Node* findNode(List l, int x) { Node *p = l.pHead; while (p) { if (p->data == x) break; p = p->pNext; } return p; }
// Tìm phần tử đứng trước một nút
Node* findNodePre(List l, Node *p) { if (p == l.pHead) return NULL; else { Node *pPre = l.pHead; while (pPre->pNext != p) { pPre = pPre->pNext; } return pPre; } }
// Sắp xếp danh sách theo thứ tự tăng dần void sortList(List *l) { if (Empty(*l)) {
printf("Danh sách rỗng, không thể sắp xếp.\n"); return; } Node *p, *q; int temp;
for (p = l->pHead; p != NULL; p = p->pNext) {
for (q = p->pNext; q != NULL; q = q->pNext) {
if (p->data > q->data) {
// Hoán đổi giá trị của 2 nút temp = p->data; p->data = q->data; q->data = temp; } } } } II. Danh sách liên kết đôi #include #include
// Cấu trúc Node cho DSLK đôi typedef struct Node { int data;
struct Node *prev; // Con trỏ đến nút trước
struct Node *next; // Con trỏ đến nút sau } Node; // Cấu trúc List typedef struct {
Node *pHead; // Con trỏ tới nút đầu tiên
Node *pTail; // Con trỏ tới nút cuối cùng } List;
// Khởi tạo danh sách rỗng void init(List *l) {
l->pHead = l->pTail = NULL; }
// Kiểm tra danh sách rỗng int Empty(List l) {
return ((l.pHead == NULL) && (l.pTail == NULL)) ? 1 : 0; } // Tạo một nút mới Node* createNode(int x) {
Node *p = (Node *)malloc(sizeof(Node)); if (p == NULL) {
printf("Không đủ bộ nhớ để cấp phát.\n"); } else { p->data = x; p->prev = NULL; p->next = NULL; } return p; }
// Thêm một phần tử vào đầu danh sách
void addHead(List *l, Node *pNew) { if (Empty(*l)) {
l->pHead = l->pTail = pNew; } else { pNew->next = l->pHead; l->pHead->prev = pNew; l->pHead = pNew; } }
// Thêm một phần tử vào cuối danh sách
void addTail(List *l, Node *pNew) { if (Empty(*l)) {
l->pHead = l->pTail = pNew; } else { pNew->prev = l->pTail; l->pTail->next = pNew; l->pTail = pNew; } }
// Nhập danh sách từ người dùng void input(List *l) { init(l); int x; Node *pNew; do {
printf("Nhập phần tử (0 để dừng): "); scanf("%d", &x); if (x == 0) break; pNew = createNode(x); if (pNew != NULL)
addHead(l, pNew); // Thêm vào đầu danh sách } while (1); }
// Xuất danh sách từ đầu đến cuối void output(List l) { if (Empty(l)) {
printf("Danh sách rỗng.\n"); } else { Node *p = l.pHead; while (p != NULL) { printf("%d\t", p->data); p = p->next; } printf("\n"); } }
// Xóa một nút trong danh sách
void deleteNode(List *l, int x) { if (Empty(*l)) {
printf("Danh sách rỗng, không thể xóa.\n"); return; } Node *pDel = l->pHead;
while (pDel != NULL && pDel->data != x) { pDel = pDel->next; } if (pDel == NULL) {
printf("Không tim thấy phần tử %d trong danh sách.\n", x); return; } if (pDel == l->pHead) {
l->pHead = l->pHead->next; if (l->pHead != NULL) { l->pHead->prev = NULL; } else {
l->pTail = NULL; // Danh sách chỉ có 1 phần tử }
} else if (pDel == l->pTail) {
l->pTail = l->pTail->prev; l->pTail->next = NULL; } else {
pDel->prev->next = pDel->next;
pDel->next->prev = pDel->prev; }
free(pDel); // Giải phóng bộ nhớ }
// Tìm một phần tử trong danh sách
Node* findNode(List l, int x) { Node *p = l.pHead; while (p) { if (p->data == x) return p; p = p->next; } return NULL; }
// Sắp xếp danh sách tăng dần void sortList(List *l) { if (Empty(*l)) {
printf("Danh sách rỗng, không thể sắp xếp.\n"); return; } Node *p, *q; int temp;
for (p = l->pHead; p != NULL; p = p->next) {
for (q = p->next; q != NULL; q = q->next) {
if (p->data > q->data) {
// Hoán đổi giá trị của 2 nút temp = p->data; p->data = q->data; q->data = temp; } } } }
Chương 2: Ngăn xếp - hàng đợi ( Stack – Queue )
1. Quy tắc chuyển đổi Infix sang Postfix
Để chuyển biểu thức từ Infix (trung tố) sang Postfix (hậu tố), ta thực hiện theo các bước sau:
1. Duyệt từng ký tự trong biểu thức Infix từ trái sang phải:
o Nếu là toán hạng (chữ cái hoặc số), đưa trực tiếp vào kết quả Postfix.
o Nếu là dấu ngoặc mở (, đẩy vào Stack.
o Nếu là dấu ngoặc đóng ), lấy các toán tử từ Stack ra cho đến khi gặp dấu ngoặc mở (.
o Nếu là toán tử (+, -, *, /, ^):
▪ Lấy các toán tử trong Stack có độ ưu tiên cao hơn hoặc bằng toán tử
hiện tại ra và đưa vào Postfix.
▪ Sau đó, đẩy toán tử hiện tại vào Stack.
2. Sau khi duyệt hết biểu thức Infix, lấy toàn bộ các toán tử còn lại trong Stack ra và thêm vào Postfix.
2. Độ ưu tiên của toán tử
• ^: Cao nhất (lũy thừa).
• *, /: Cao hơn cộng/trừ. • +, -: Thấp nhất.
• Dấu ngoặc:
o (: Không có độ ưu tiên, chỉ dùng để đánh dấu.
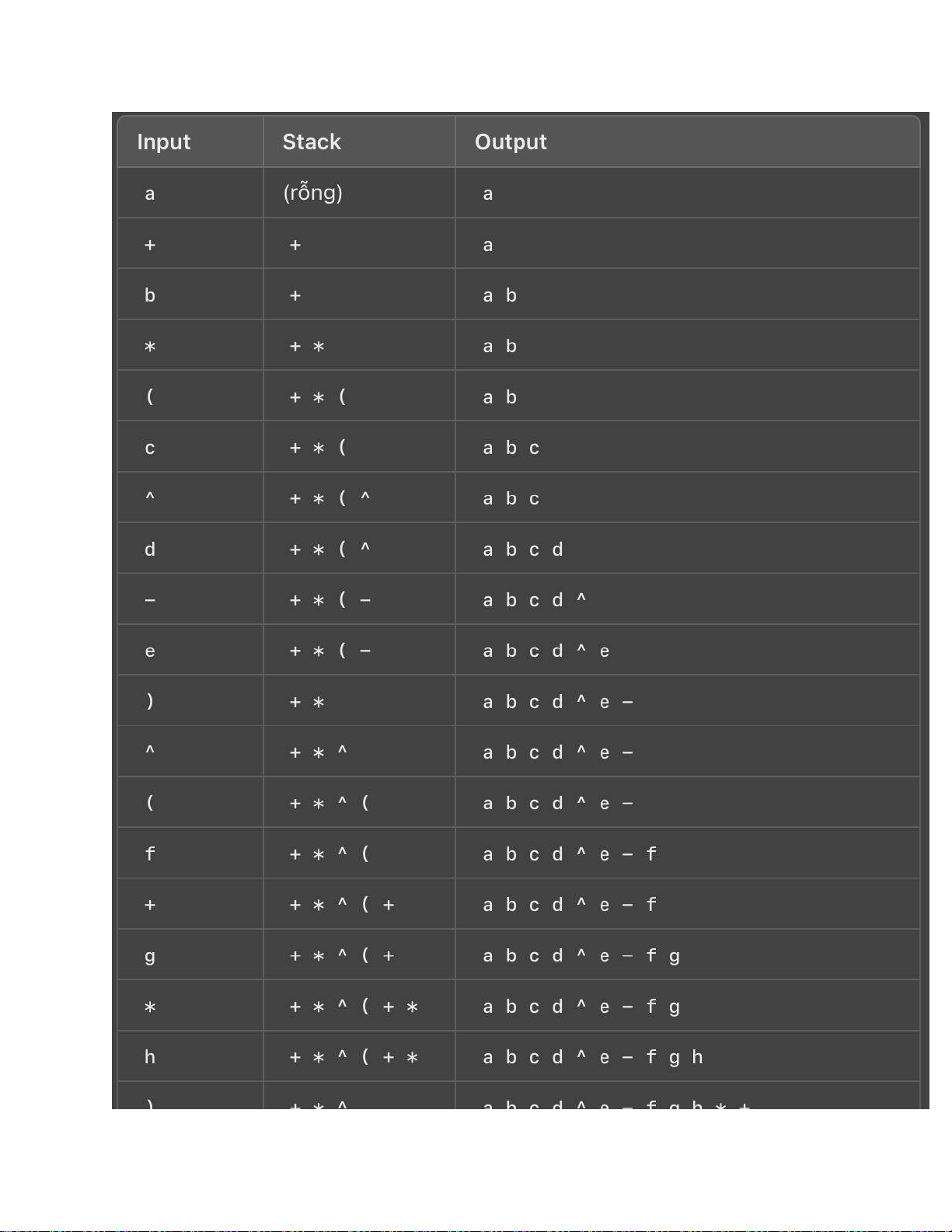
3. Ví dụ minh họa
Ví dụ: a + b * (c ^ d - e) ^ (f + g * h) – i
2. Quy tắc chuyển đổi Infix sang Prefix
Quy trình thực hiện:
1. Đảo ngược biểu thức Infix:
o Đổi toàn bộ biểu thức từ trái sang phải thành từ phải sang trái.
o Đổi dấu ngoặc mở ( thành đóng ) và ngược lại.
2. Áp dụng quy tắc chuyển đổi từ Infix sang Postfix:
o Sau khi đảo ngược biểu thức, áp dụng y nguyên các bước chuyển đổi Infix → Postfix:
▪ Nếu là toán hạng, thêm vào kết quả Prefix.
▪ Nếu là toán tử, xử lý độ ưu tiên giống như trong Postfix.
▪ Sử dụng Stack để quản lý các toán tử và dấu ngoặc.
3. Đảo ngược kết quả Postfix thu được để trở thành Prefix.
2. So sánh giữa Postfix và Prefix Quy tắc
Infix → Postfix
Infix → Prefix
Duyệt từ phải sang trái sau khi đảo Biểu thức
Duyệt từ trái sang phải ngược Toán hạng
Thêm trực tiếp vào kết quả
Thêm trực tiếp vào kết quả Toán tử
Xử lý độ ưu tiên trong Stack
Xử lý độ ưu tiên trong Stack Kết quả
Không cần đảo ngược sau khi duyệt Đảo ngược kết quả sau khi duyệt
3. Độ ưu tiên của toán tử
Toán tử Độ ưu tiên ^ Cao nhất *, /
Cao hơn cộng/trừ +, - Thấp nhất (, )
Chỉ để đánh dấu và không có độ ưu tiên
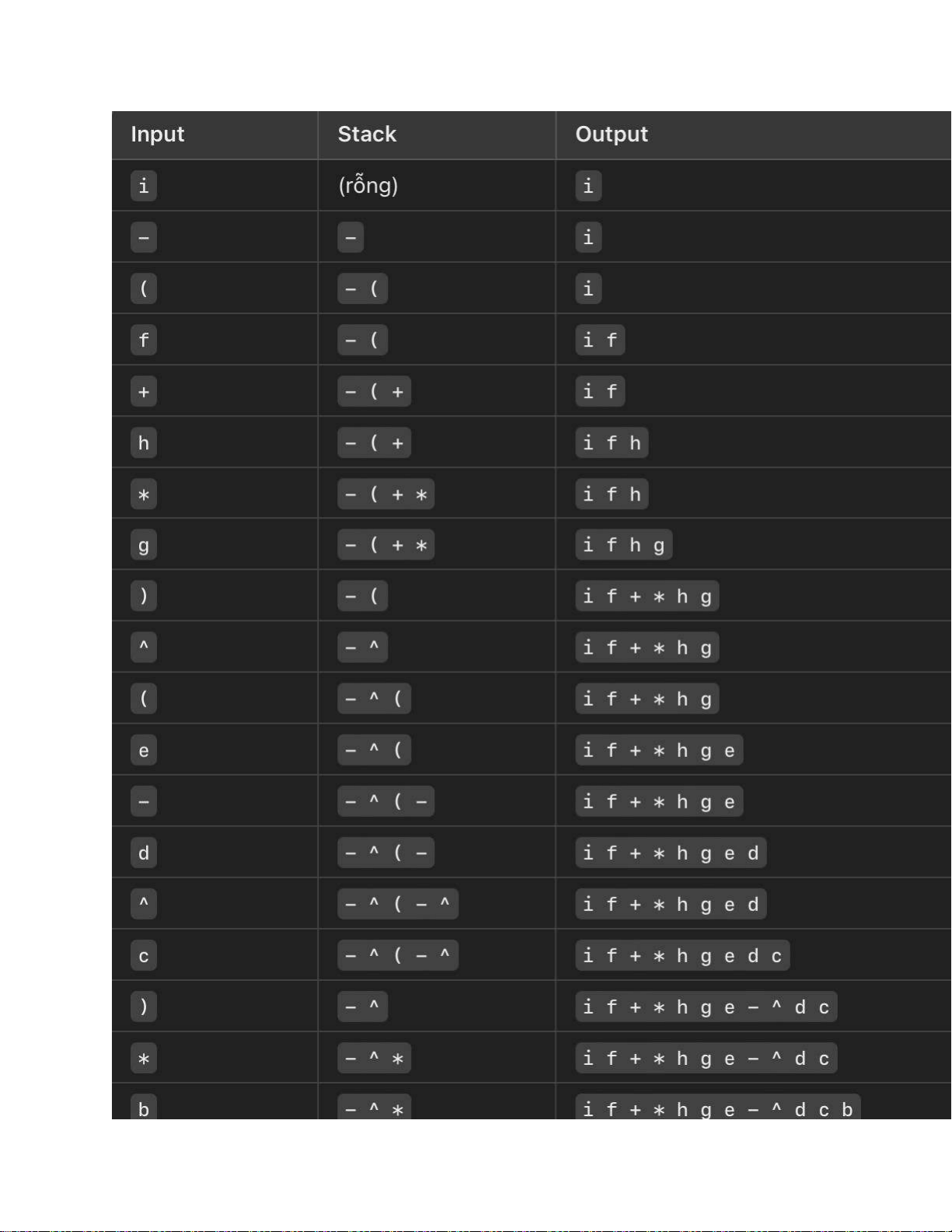
4. Ví dụ minh họa
Ví dụ: i - (f + h * g) ^ (e - d ^ c) * b + a Chương 3: Cây
Kiến thức cơ bản về cây
• Định nghĩa cây:
Một cây là tập hợp các nút trong đó có: o Một nút gốc.
o Các nút con được tổ chức theo quan hệ phân cấp.
• Các khái niệm cơ bản:
o Nút gốc (Root): Là nút cao nhất, không có nút cha.
o Nút lá (Leaf): Là nút không có con.
o Nút nhánh (Internal Node): Là nút không phải lá và không phải gốc.
o Mức của nút (Level): Độ sâu tính từ gốc đến nút đó.
o Độ cao của cây (Height): Là mức lớn nhất trong cây.
o Đường đi (Path): Chuỗi các cạnh nối giữa 2 nút.
o Độ dài đường đi tổng (Path Length): Tổng các đường đi từ gốc đến tất cả các nút. I.
Cây nhị phân (Binary Tree)
• Định nghĩa:
Là cây mà mỗi nút có tối đa 2 cây con (trái và phải).
• Các kiểu cây nhị phân:
o Cây nhị phân đầy đủ: Tất cả các nút đều có 2 con hoặc không có con.
o Cây nhị phân hoàn chỉnh: Tất cả các mức đều đầy đủ ngoại trừ mức cuối, và các
nút ở mức cuối nằm về phía trái.
• Duyệt cây nhị phân:
o Duyệt trước (Preorder - NLR): Gốc → Trái → Phải.
o Duyệt giữa (Inorder - LNR): Trái → Gốc → Phải.
o Duyệt sau (Postorder - LRN): Trái → Phải → Gốc. II.
Cây nhị phân tim kiếm (Binary Search Tree - BST)
• Định nghĩa:
Là cây nhị phân có thêm ràng buộc:
o Khóa tại mỗi nút lớn hơn tất cả các nút trong cây con trái.
o Khóa tại mỗi nút nhỏ hơn tất cả các nút trong cây con phải.
• Tính chất:
o Duyệt giữa (LNR) cho kết quả dãy số theo thứ tự tăng dần.
o Chi phí tim kiếm, thêm, xóa trung bình O(logn)O(logn), nhưng trong trường hợp
xấu nhất (cây suy biến) là O(n)O(n).
• Thao tác trên BST:
o Tìm kiếm: Dựa trên tính chất so sánh trái/phải của khóa.
o Thêm: Chèn vào vị trí phù hợp để giữ nguyên tính chất BST. o Xóa:
▪ Nút lá: Xóa trực tiếp.
▪ Nút có 1 con: Nối cha của nút cần xóa với con của nó.
▪ Nút có 2 con: Thay thế bằng nút thế mạng (lớn nhất bên trái hoặc nhỏ
nhất bên phải), sau đó xóa nút thế mạng. III.
Cây nhị phân tim kiếm cân bằng (AVL Tree)
• Định nghĩa:
Là cây nhị phân tim kiếm với điều kiện cân bằng:
o Hiệu chiều cao giữa cây con trái và cây con phải của mỗi nút không vượt quá 1.
• Chỉ số cân bằng (Balance Factor):
o Balance Factor = hR − hL , trong đó hR, hL là chiều cao của cây con phải và cây con trái.
o Balance Factor có thể là -1, 0, hoặc 1.
• Thao tác trên cây AVL:
o Thêm: Giống BST, nhưng cần kiểm tra và cân bằng lại khi cây bị mất cân bằng.
o Xóa: Giống BST, nhưng cần cân bằng lại sau khi xóa.
o Cân bằng lại cây:
▪ Quay đơn (Single Rotation):
▪ Left-Left (LL): Xảy ra khi cây con trái lệch trái.
▪ Right-Right (RR): Xảy ra khi cây con phải lệch phải.
▪ Quay kép (Double Rotation):
▪ Left-Right (LR): Xảy ra khi cây con trái lệch phải.
▪ Right-Left (RL): Xảy ra khi cây con phải lệch trái. • Lợi ích:
o Đảm bảo chiều cao cây luôn O(logn).
o Các thao tác tim kiếm, thêm, xóa đều có chi phí O(logn).
Các bài tập quan trọng
1. Cây nhị phân:
o Xây dựng cây từ cấu trúc cho trước.
o Duyệt cây theo các thứ tự (NLR, LNR, LRN).
2. Cây nhị phân tim kiếm:
o Tạo cây từ danh sách khóa.
o Thực hiện thêm, xóa, tim kiếm, và duyệt cây. 3. Cây AVL:
o Xây dựng cây từ danh sách khóa.
o Thêm và xóa với các trường hợp phải cân bằng lại cây.




