








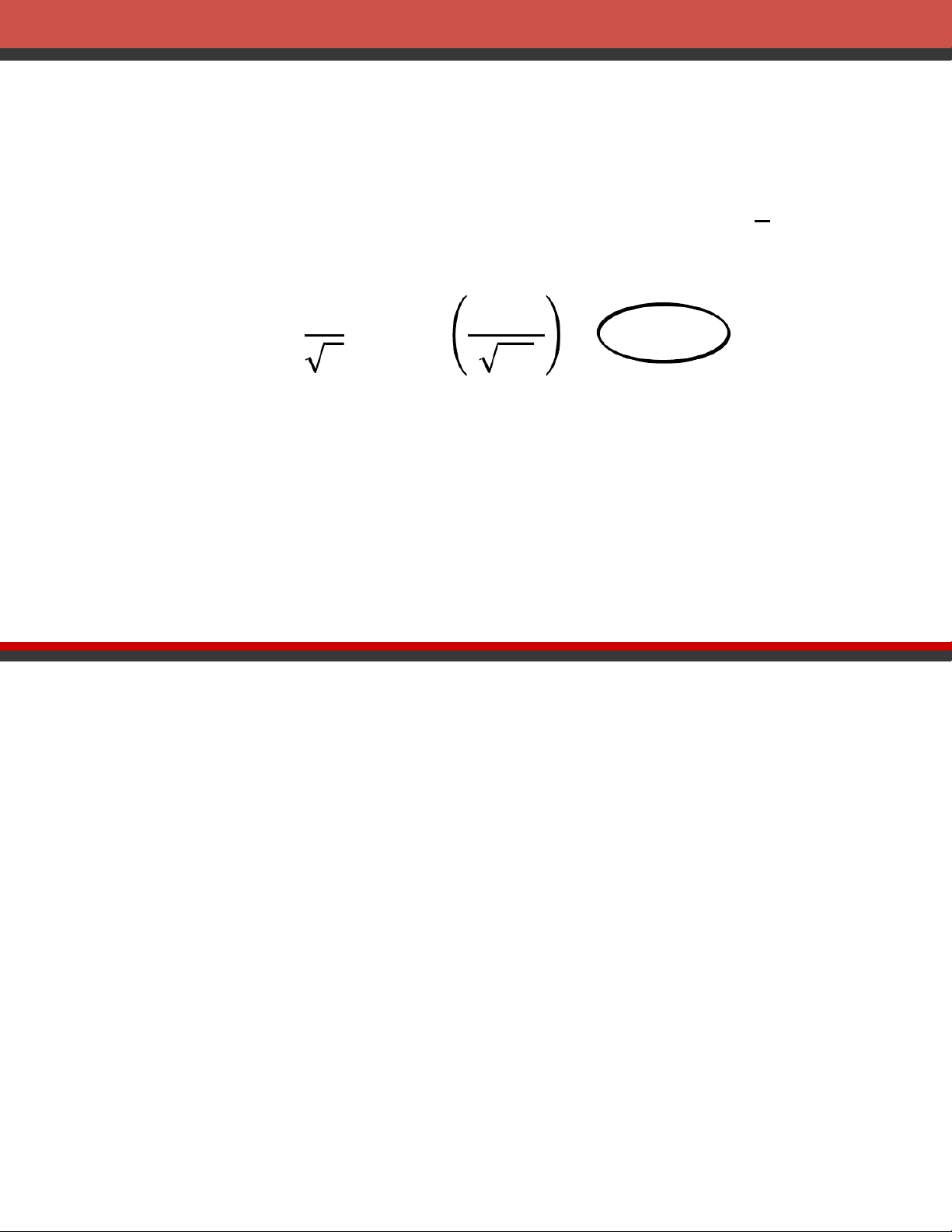








Preview text:
tistics for i Sl
neidsess b yand Economics (13e) John Loucks
on, Sweeney, Williams, Camm, Cochran St. Edward’s 7 Cengage Learning University by John Loucks wards University
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics apter 8 erval Estimation opulation Mean: s Known opulation Mean: s Unknown etermining the Sample Size opulation Proportion
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
rgin of error and the Interval Estimate
point estimator cannot be expected to provide the exact value of the population parameter.
interval estimate can be computed by adding and subtracting a margin of error to the point estimate.
Point estimate ± Margin of error
e purpose of an interval estimate is to provide information about how
lose the point estimate, is to the value of the parameter.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
rgin of Error and the Interval Estimate
e general form of an interval estimate of a population mean is ҧ𝑥 + Margin of error
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known
order to develop an interval estimate of a population mean, the margin of
error must be computed using either:
•the population standard deviation s , or
•the sample standard deviation s
s is rarely known exactly. But often a good estimate can be obtained based
historical data or other information.
e refer to such cases as the s known case.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known
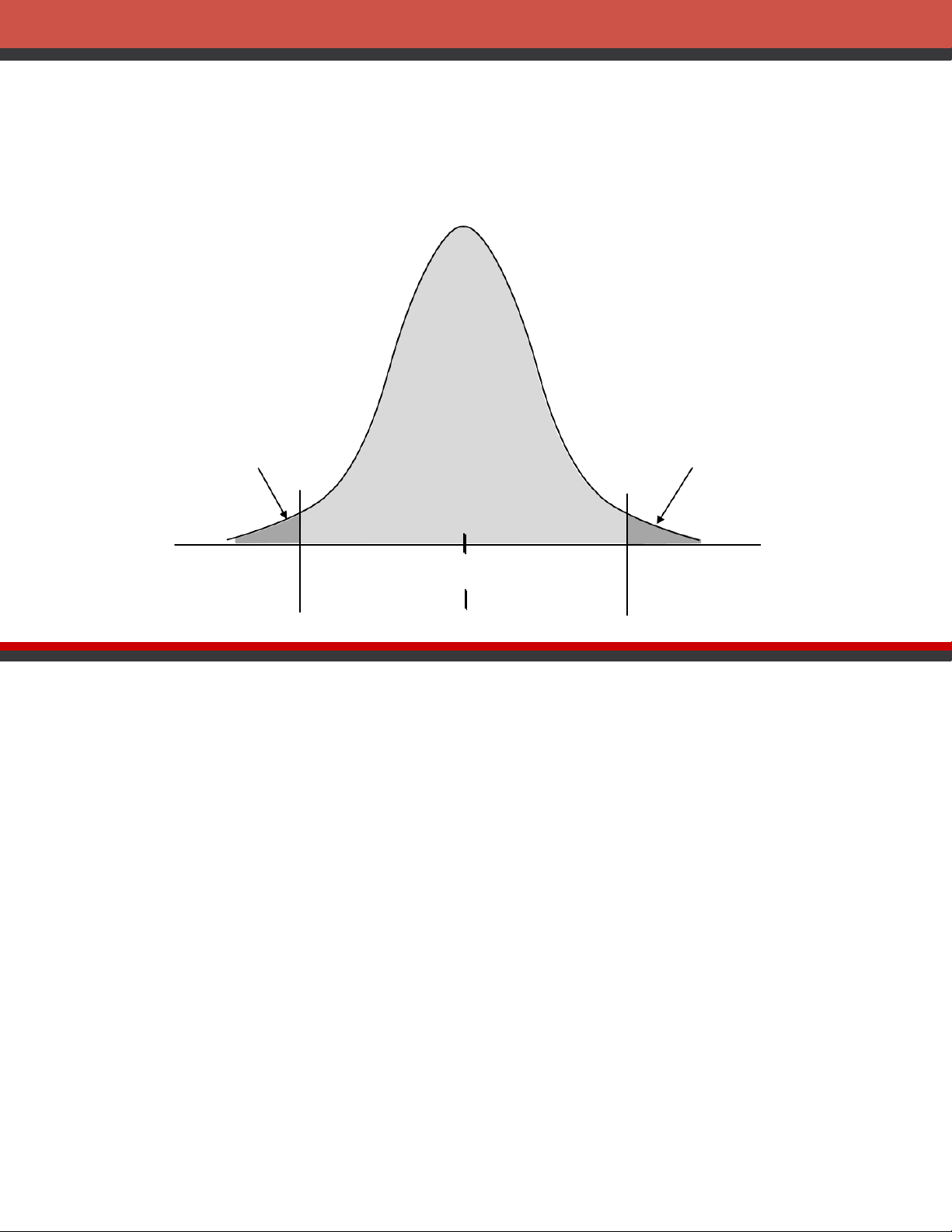
There is a 1 - probability that the value of a sample
mean will provide a margin of error of 𝑧𝛼/2𝜎ҧ𝑥 or less. Sampling distribution of ҧ𝑥 1 - of all /2 /2 ҧ𝑥 values ҧ𝑥
՚ 𝑧𝛼/2𝜎ҧ𝑥 ՜՚ 𝑧𝛼/2𝜎ҧ 𝑥 ՜
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
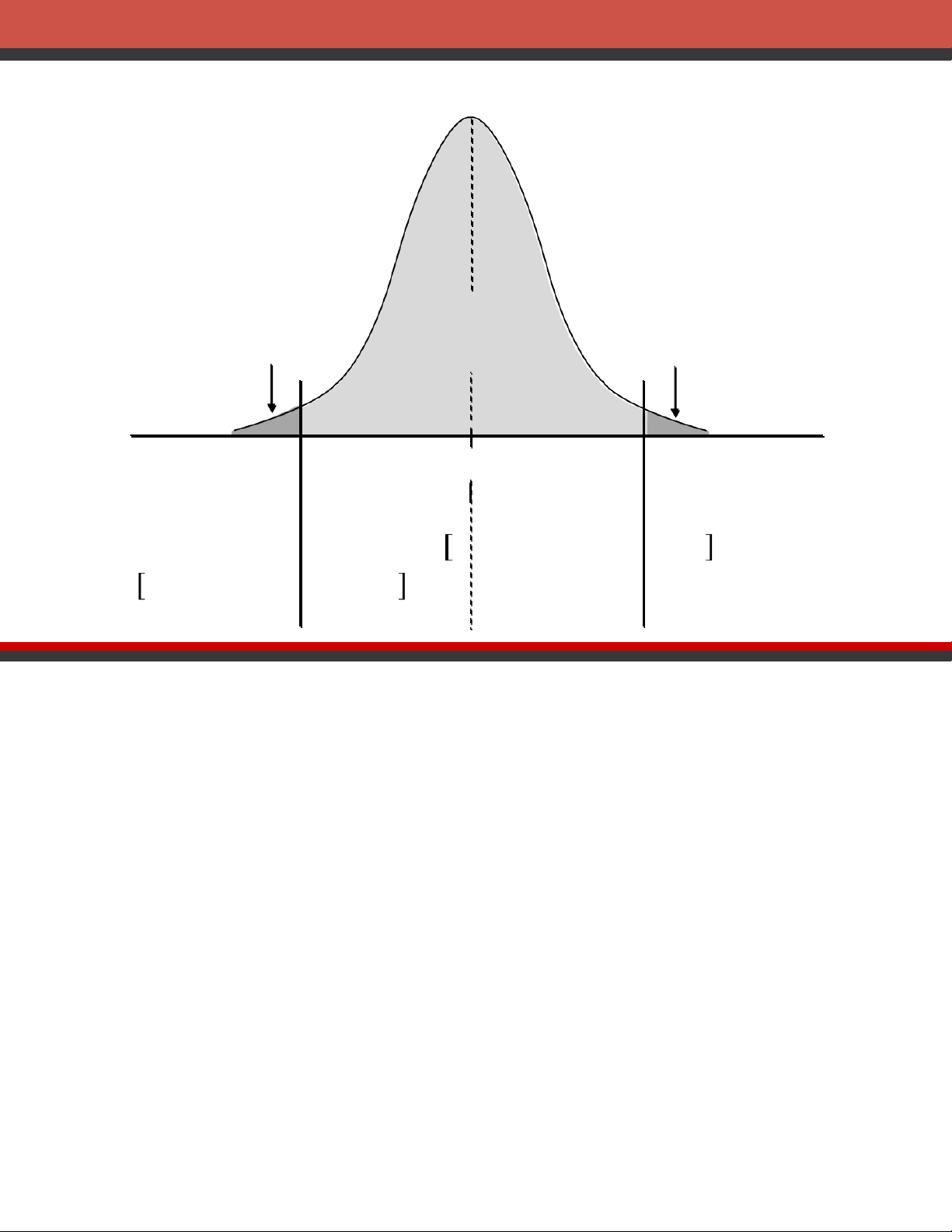
erval Estimate of a Population Mean: s Known Sampling distribution of ҧ𝑥 1 - of all /2 /2 ҧ𝑥 values ҧ𝑥
՚ 𝑧𝛼/2𝜎ҧ𝑥 ՜ ՚ 𝑧𝛼/2𝜎ҧ 𝑥 ՜ nterval interval oes not
−−−− − ҧ𝑥 −−−− − includes nclude
−−−− − ҧ𝑥 −−−− −
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known erval Estimate of 𝜎 ҧ𝑥 ± 𝑧𝛼/2 𝑛
where: ҧ𝑥 is the sample mean
1 - is the confidence coefficient z z
/2 is the value providing an area of
/2 in the upper tail of the standard
normal probability distribution
s is the population standard deviation n is the sample size
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known
ues of z /2 for the Most Commonly Used Confidence Levels Confidence Table
Level /2 Look-up Area z/2 90% .10 .05 .9500 1.645 95% .05 .025 .9750 1.960 99% .01 .005 .9950 2.576
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics aning of Confidence
cause 90% of all the intervals constructed using ഥ
𝑥 + 1.645𝜎 ҧ 𝑥 will contain
he population mean, we say we are 90% confident that the interval ഥ
𝑥 + 1.645𝜎 ҧ𝑥 includes the population mean .
e say that this interval has been established at the 90% confidence level.
e value .90 is referred to as the confidence coefficient.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known ample: Discount Sounds
Discount Sounds has 260 retail outlets throughout the United States. T
firm is evaluating a potential location for a new outlet, based in part, on th
mean annual income of the individuals in the marketing area of the new location.
A sample of size n = 36 was taken; the sample mean income is $41,100.
The population is not believed to be highly skewed. The population standa
deviation is estimated to be $4,500, and the confidence coefficient to be u
in the interval estimate is .95.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known ample: Discount Sounds
95% of the sample means that can be observed are within + 1.96 𝜎ҧ𝑥 of the
population mean . The margin of error is: 𝜎𝑛= 1.96 4,500 𝑧𝛼/2 36 = 1,470
Thus at 95% confidence, the margin of error is $1,470.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known ample: Discount Sounds Interval estimate of is: $41,100 + $1,470 or $39,630 to $42,570
We are 95% confident that the interval contains the population mean.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known ample: Discount Sounds Confidence Margin
level of error Interval estimate 90% 1,234 39,866 to 42,334 95% 1,470 39,630 to 42,570 99% 1,932 39,168 to 43,032
In order to have a higher degree of confidence, the margin of error
and thus the width of the confidence interval must be larger.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known dequate Sample Size
•In most applications, a sample size of n≥ 30 is adequate.
•If the population distribution is highly skewed or contains outliers, a
sample size of 50 or more is recommended.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Known
dequate Sample Size (continued)
•If the population is not normally distributed but is roughly symmetric, a
sample size as small as 15 will suffice.
•If the population is believed to be at least approximately normal, a
sample size of less than 15 can be used.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics
erval Estimate of a Population Mean: s Unknown
n estimate of the population standard deviation s cannot be developed
prior to sampling, we use the sample standard deviation s to estimate s . s is the s unknown case.
this case, the interval estimate for is based on the t distribution.
e’ll assume for now that the population is normally distributed.)
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics Distribution
lliam Gosset, writing under the name “Student”, is the founder of the t distribution.
sset was an Oxford graduate in mathematics and worked for the Guinness Brewery in Dublin.
developed the t distribution while working on small-scale materials nd temperature experiments.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics Distribution
e t distribution is a family of similar probability distributions.
pecific t distribution depends on a parameter known as the degrees of reedom.
grees of freedom refer to the number of independent pieces of
nformation that go into the computation of s.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.
Statistics for Business and Economics Distribution
distribution with more degrees of freedom has less dispersion.
the degrees of freedom increases, the difference between the t
distribution and the standard normal probability distribution becomes maller and smaller.
ge Learning. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part, except for use as permitted in a license distributed with a certain product or service or
a password-protected website or school-approved learning management system for classroom use.




