Chapter 2 Kinematics Analysis | Tài liệu Tiếng Anh

Ho Chi Minh City University of Technology (HCMUT), VNU-HCM CHAPTER 2 KINEMATICS ANALYSIS
Assoc.Prof.Dr. Le Thanh Long ltlong@hcmut.edu.vn 1
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM Outline 2.1. Fundamentals
2.2. Kinematics analysis using vector polygon method
2.3. Kinematics analysis using the instantaneous center method –
Four bar linkage mechanism’s kinematic characteristics
2.4. Kinematics analysis using analytical method
2.5. Kinematics analysis using graph method and complex algebra 2
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic 2. Kinematics analysis 3. Signification 4. Method 3
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic
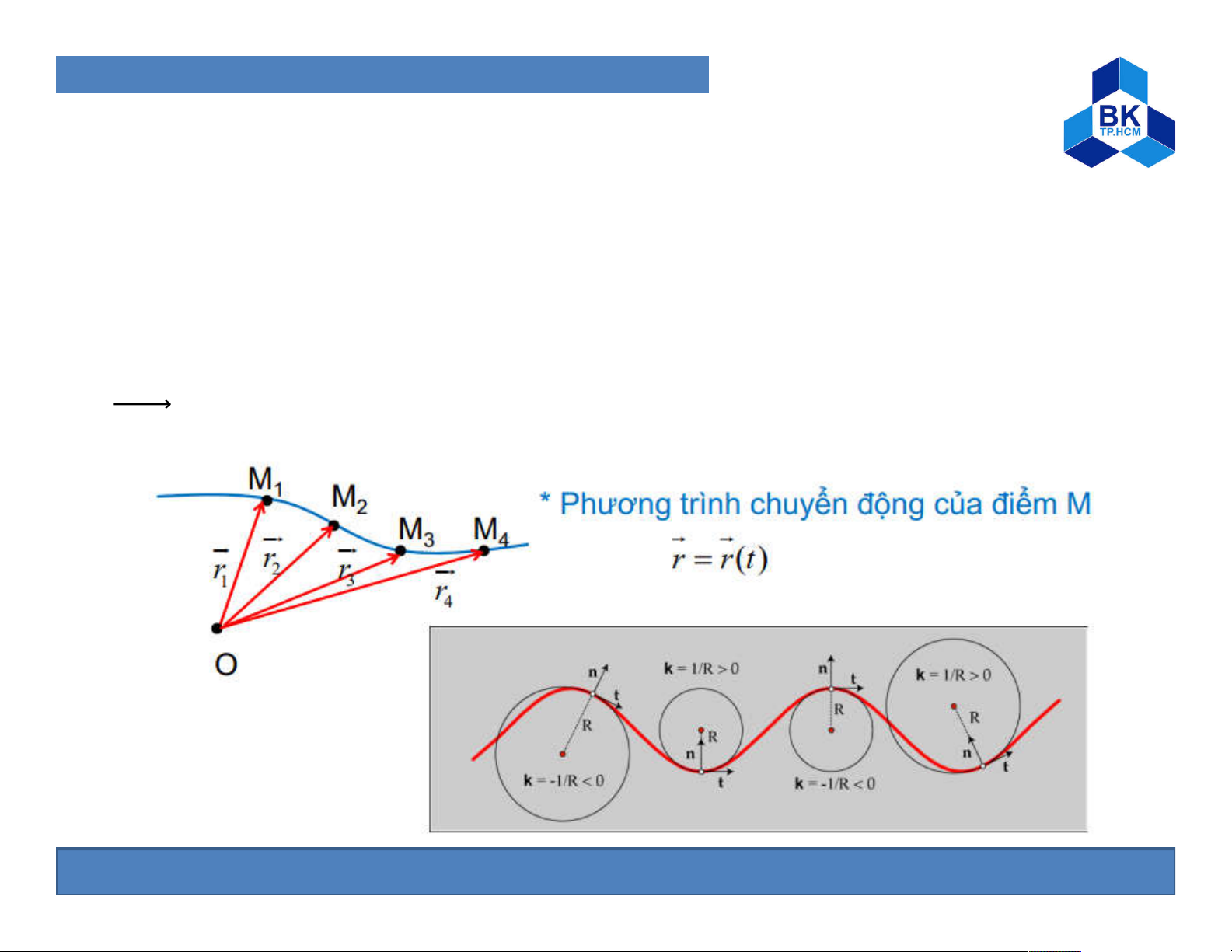
Consider the point M moving in space. If point M moves at a fixed
distance from O, then the position M is determined by vector = ⃗ 4
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic ⃗ ⃗ ∆ ( )  Velocity of M: = = lim ∆ → ∆
 The instantaneous velocity vector at a point is always tangent to the orbit at that point 5
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic
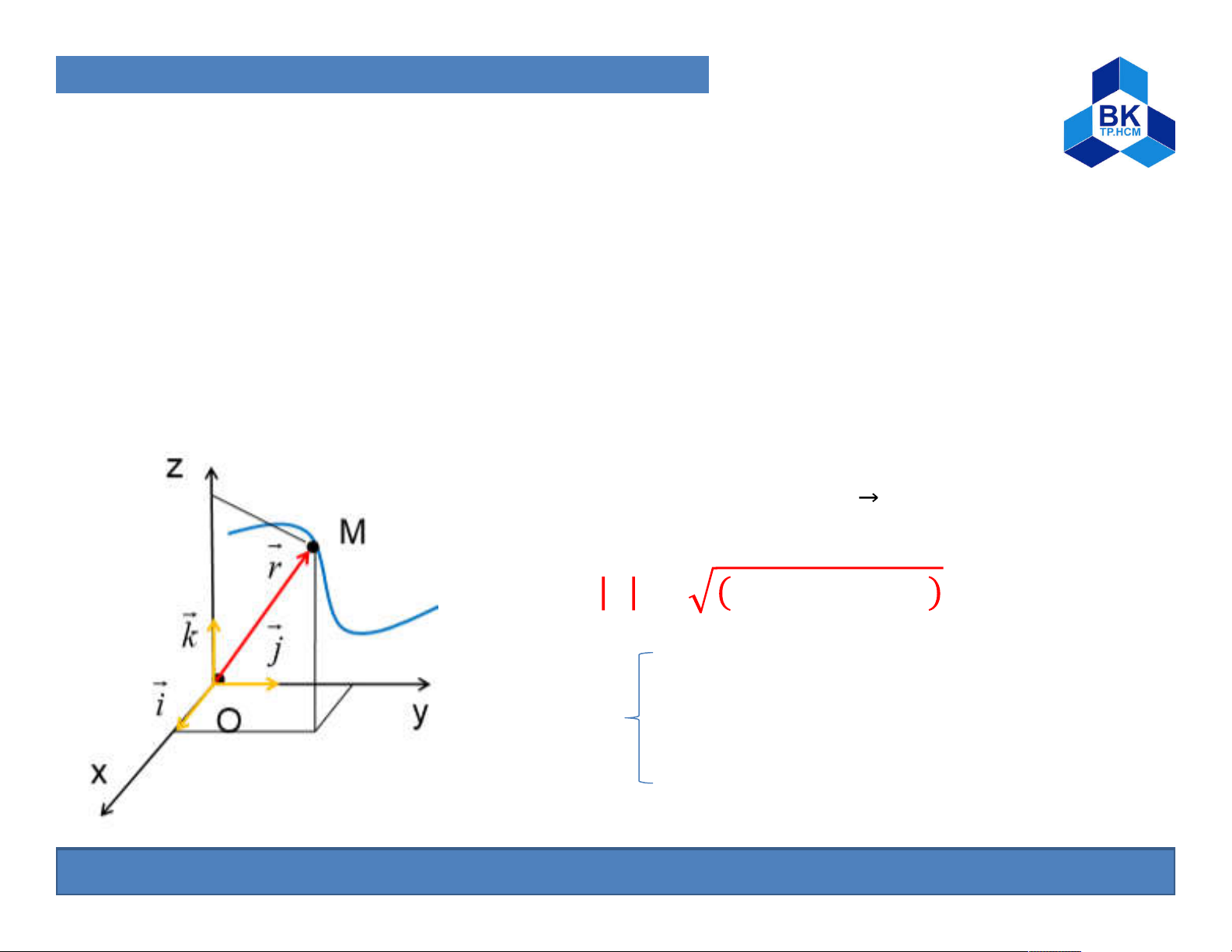
 If we put in O the Cartesian coordinate system Oxyz, the position
of the point M is determined by the vector r Motion equation of M(x,y,z) ⃗ = ⃗ + ⃗ + → ⃗ = + + x = x(t) With y = y(t) z = z(t) 6
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
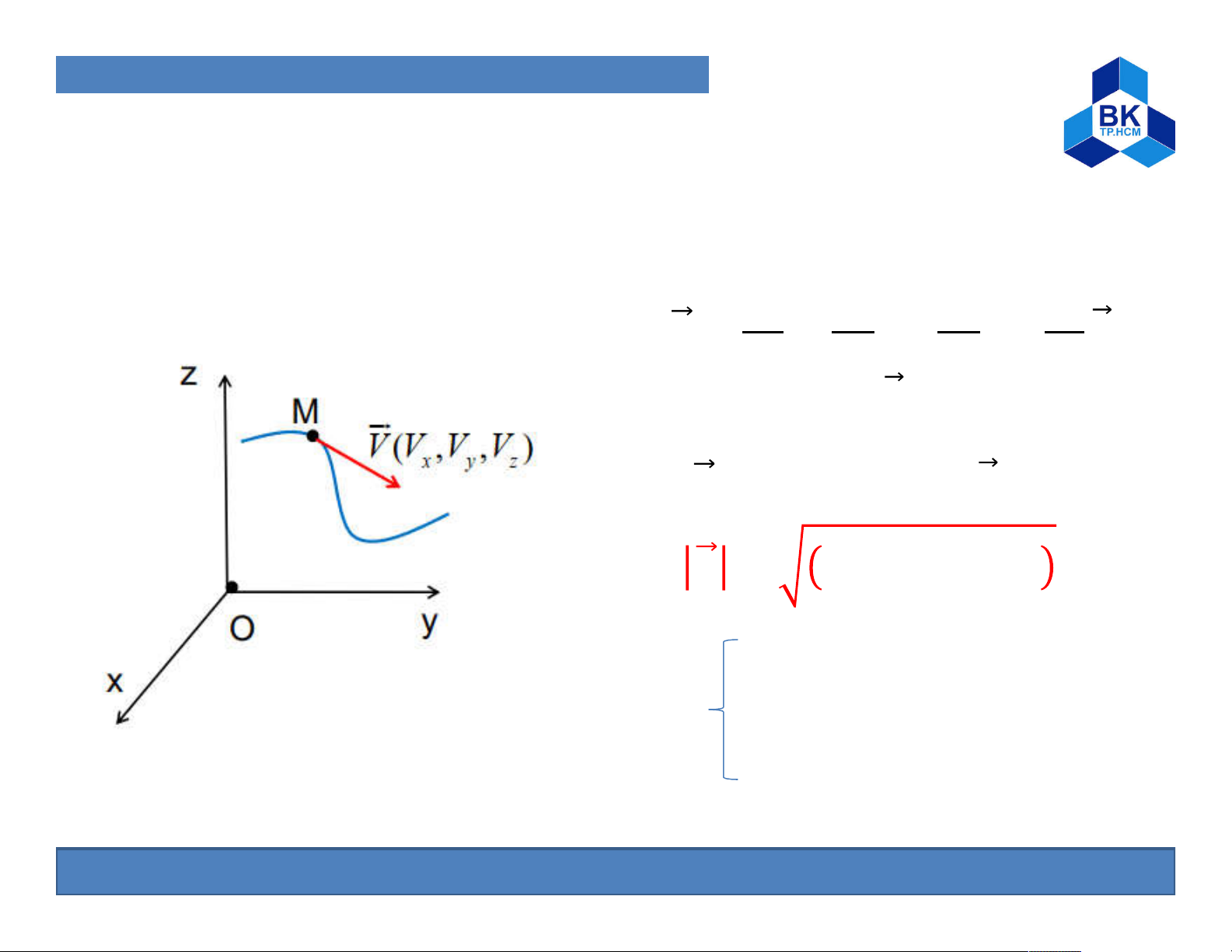
1. Particle and Solid Kinematic A. Particle Kinematic ⃗  Velocity of M = = ⃗ + ⃗ + = ̇ ⃗ + ̇ ⃗ + ̇ → = ⃗ + ⃗ + → = + + = ̇ With = ̇ = ̇
(Velocity components of M in three directions ) 7
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
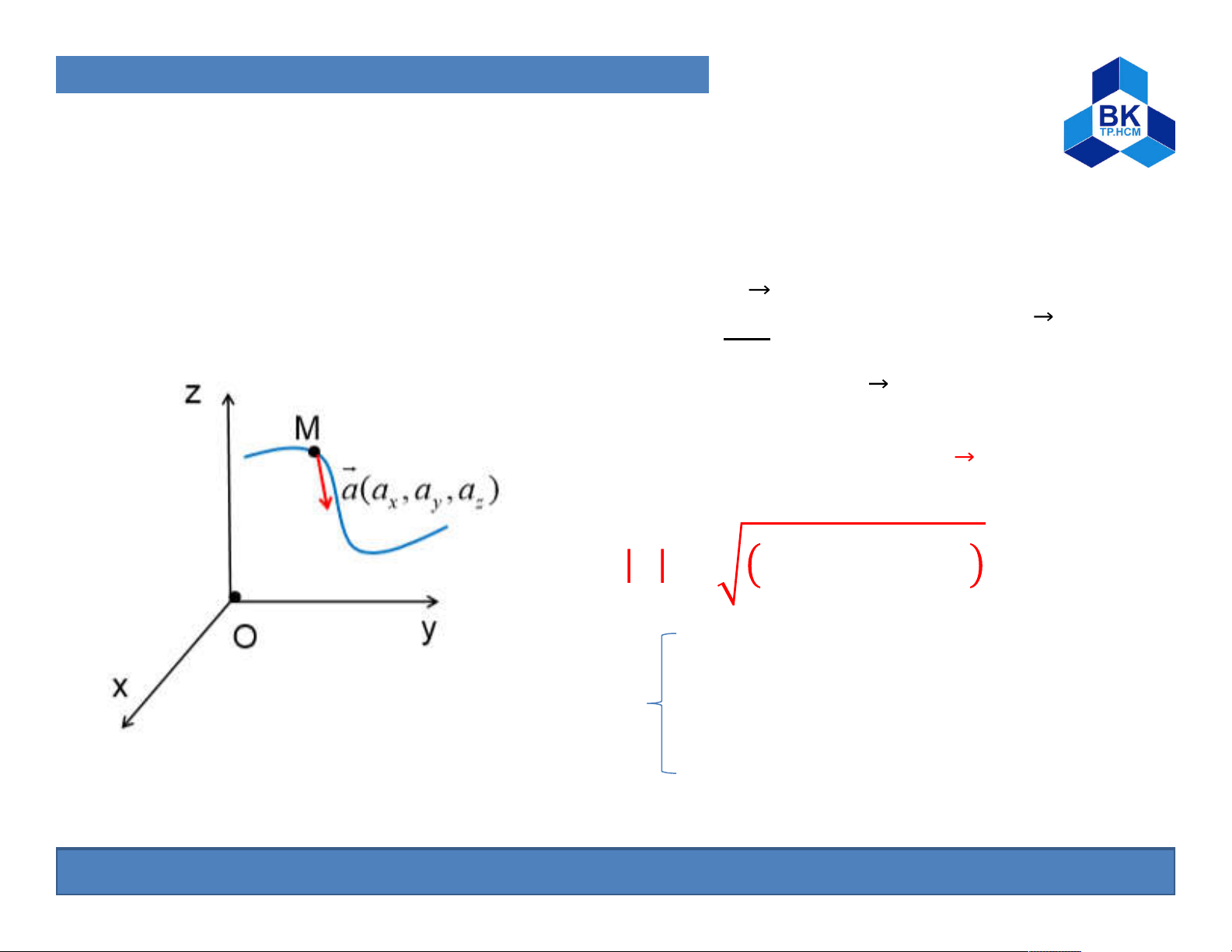
1. Particle and Solid Kinematic A. Particle Kinematic  Acceleration of M ⃗ = = ̇ ⃗ + ̇ ⃗ + ̇ = ̈ ⃗ + ̈ ⃗ + ̈ → ⃗ = ⃗ + ⃗ + → ⃗ = + + = ̇ = ̈ With = ̇ = ̈ = ̇ = ̈
(Acceleration components of M in three directions) 8
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic  Motion properties of M × ⃗ = 0
V and W are collinear: M moves in a straight line × ⃗ ≠ 0
V and W are non-collinear: M moves in a curved line . ⃗ > 0
V increases by time: M moves with increasing speed . ⃗ < 0
V decreases by time: M moves with decreasing speed . ⃗ = 0
V is constant: M moves with constant speed 9
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic
Acceleration is constant = = const
Velocity is a function of time = +
Position is a function of time 1 2 s  s  V t  a t 0 o 2 c
Velocity is a function of position = + 2 ( − ) 10
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic
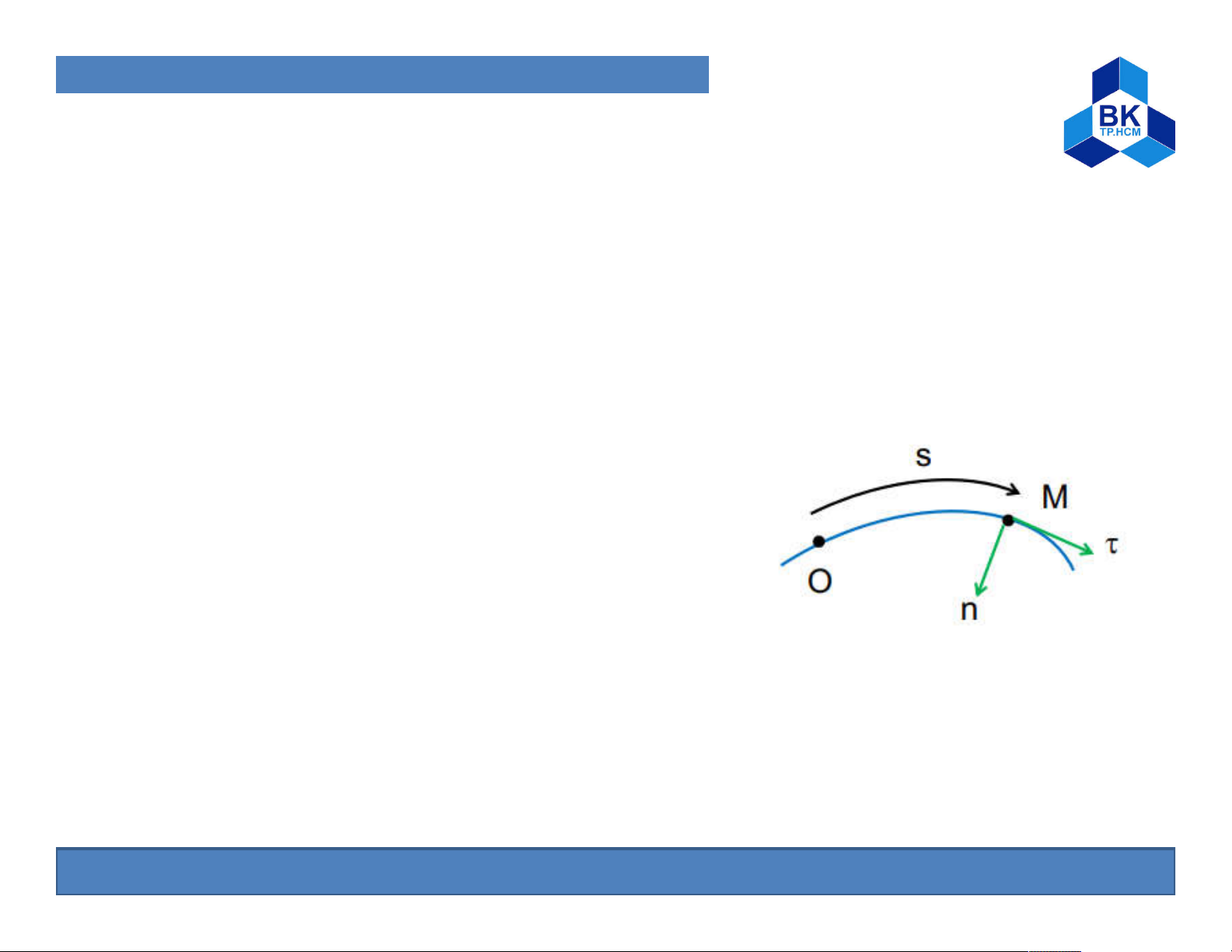
 Consider a point M moving in the space on a known trajectory. If
we take a fixed point O on a known trajectory as the origin and
select a positive convention, the position of point M is completely
determined through the length s = OM  Motion equation of M: s = s(t)
 Construct the coordinate system M attached to the point M such that: -
is the unit vector tangent to the M’s orbit in the positive direction
- n is the unit vector perdendicular to 11
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
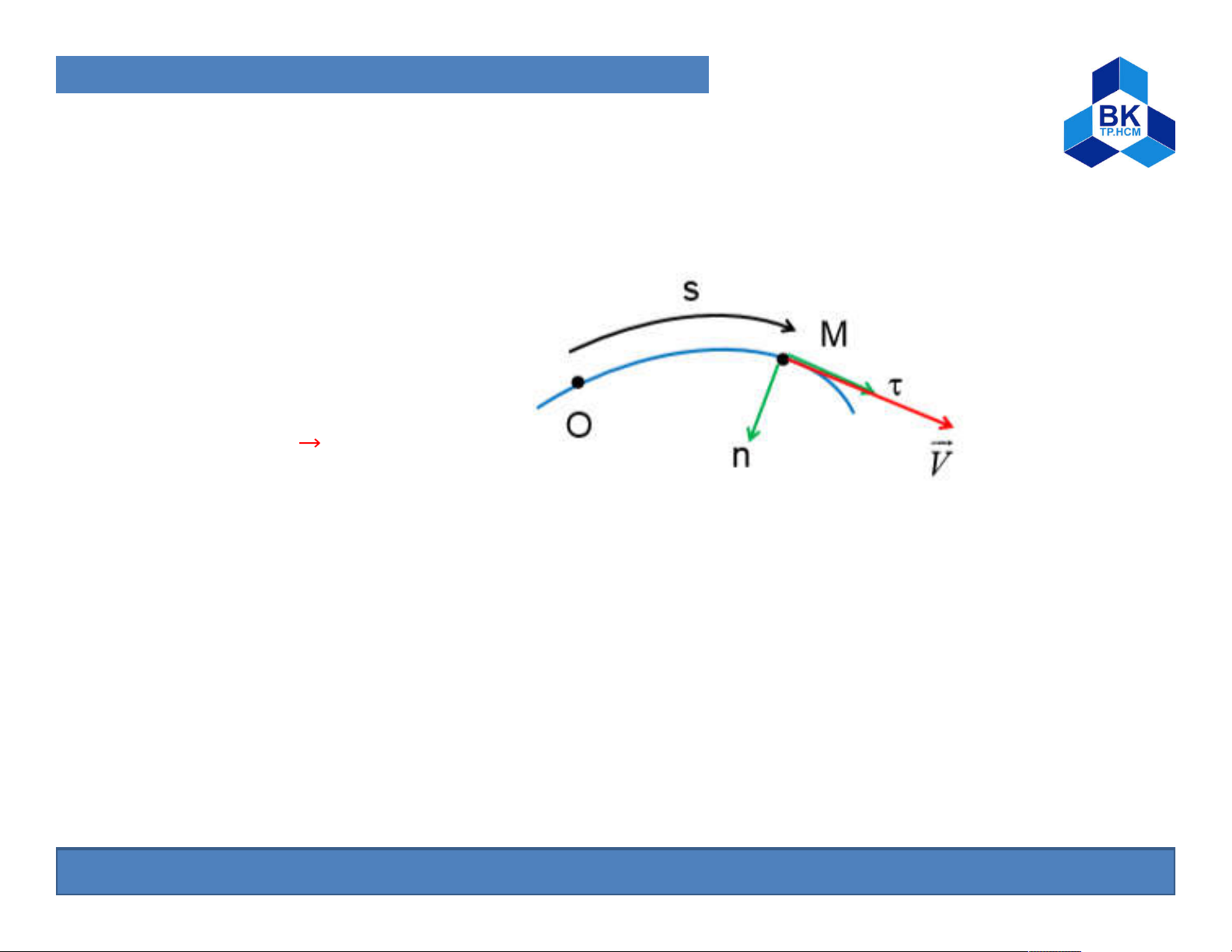
1. Particle and Solid Kinematic A. Particle Kinematic  Velocity of M: = ̇ ⃗
- Velocity vector is always tangent to the trajectory
- The sign depends on the selected positive direction, if following
the positive direction V > 0, and if following in the negative direction V < 0 12
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
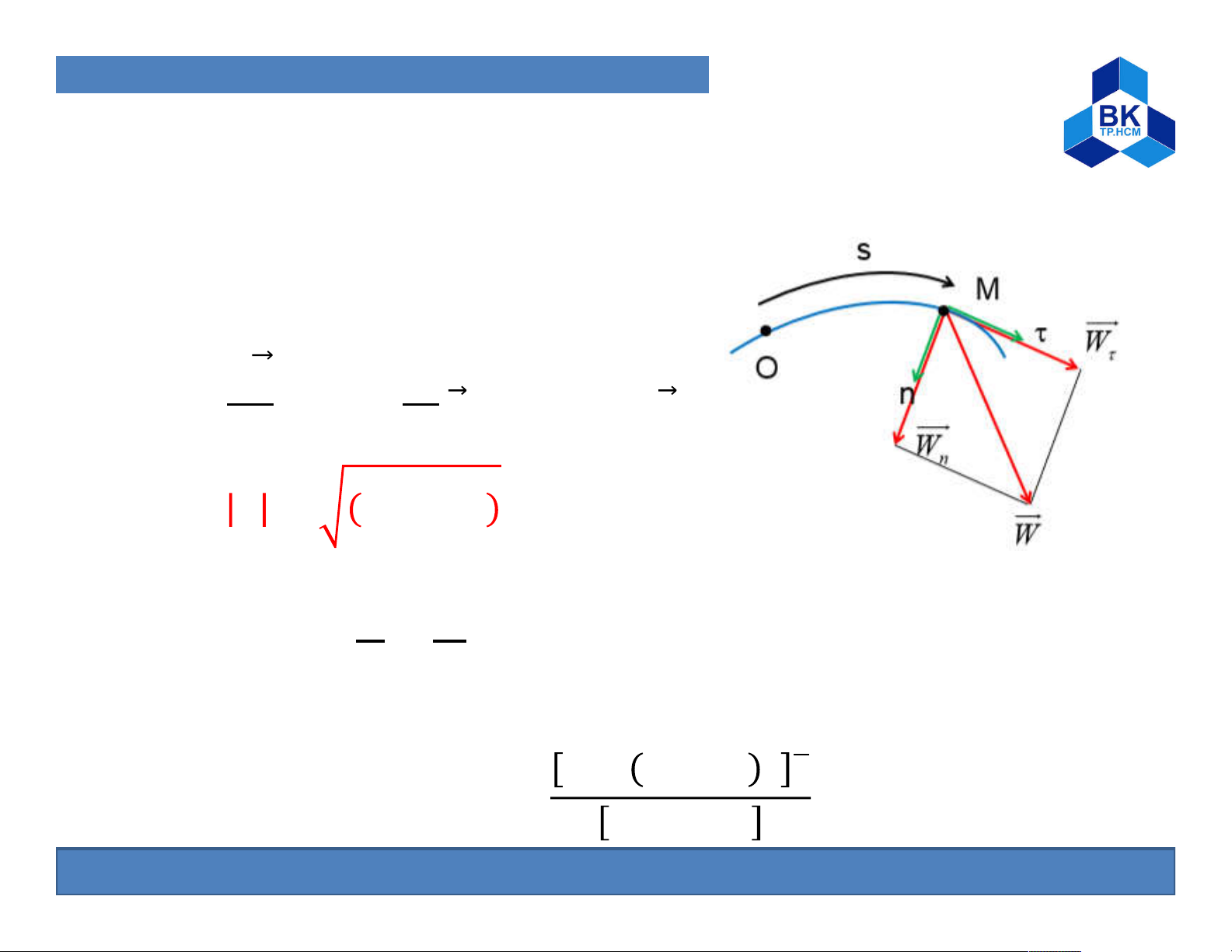
1. Particle and Solid Kinematic A. Particle Kinematic  Acceleration of M: ̇ ⃗ = = ̈ ⃗ + = ⃗ + → ⃗ = + With
= ̇ = ̈ : tangential acceleration ̇ = = : normal acceleration
is the orbit’s radius of curvature. If we have y = f(x) 1 + / = / 13
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic
 Example 2.1: Calculate the radius of curvature of the trajectory
at position x = 1 of the curve equation =  Solution:
Calculate the first and second derivatives of the function: = 3 = 6
Apply the formula to calculate the orbit’s radius of curvature: ( ) = = → 1 = ≈ 5,27 ( ) 14
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic A. Particle Kinematic
 Example 2.2: We have the positional vector of the box sliding on a
curved path. Calculate the velocity and acceleration of the box at t = 2s ⃗ = 2 sin 2 ⃗ + 2 cos ⃗ − 2
Coordinates of the box in Oxyz system x(t) = 2sin(2t) = ̇ = 4 cos 2 y(t) = 2cos(t) = ̇ = −2sin ( ) z(t) = -2 = ̇ = −4 = ̈ = −8sin (2 ) 2 2 2
 V (t  2)  V  V  V  8, 61m / s = ̈ = −2c ( ) x y z = ̈ = −4 2 2 2 2  a(t  2) 
a  a  a  7, 3 m / s x y z 15
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic B. Solid Kinematic
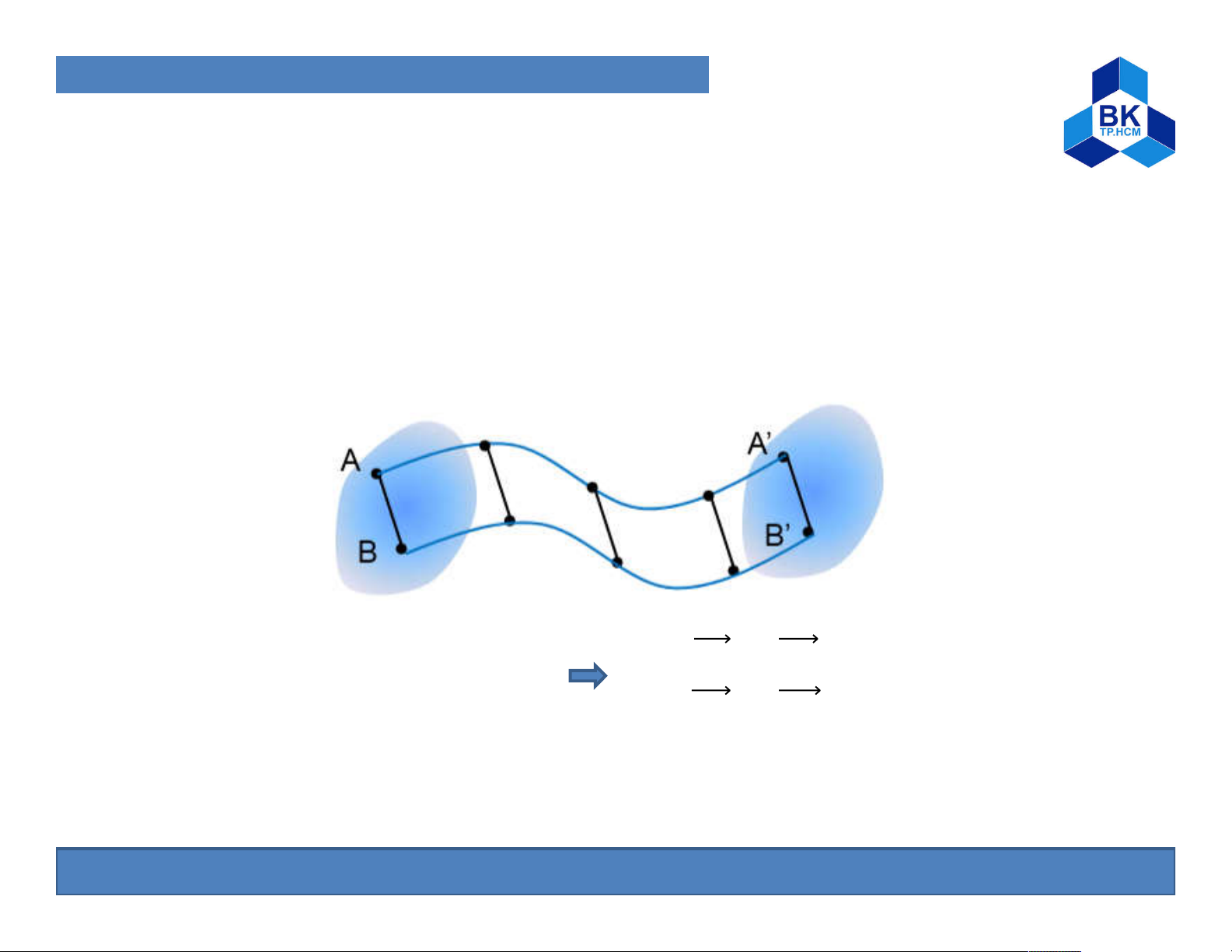
 Translational motion is a motion in which each line of an object
has a constant equation during its motion  Equal speed  Equal acceleration =  Same orbit =
Comment: To survey the motion of an object, it is only necessary
to examine the motion of a point on the object 16
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic B. Solid Kinematic
 Rotational motion around a fixed axis is the motion in which a
rigid body has two fixed points and the rigid body rotates around those two fixed points. = ( ): motion equation = ̇ : angular velocity
= ̇ = ̈ : angular acceleration
> 0 the object rotates counterclockwise from the top view
> 0 the object rotates in the positive direction
= 0 the object rotates uniformly
, in the same direction : rotates faster and faster
, in opposite direction: rotates slower and slower 17
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic B. Solid Kinematic
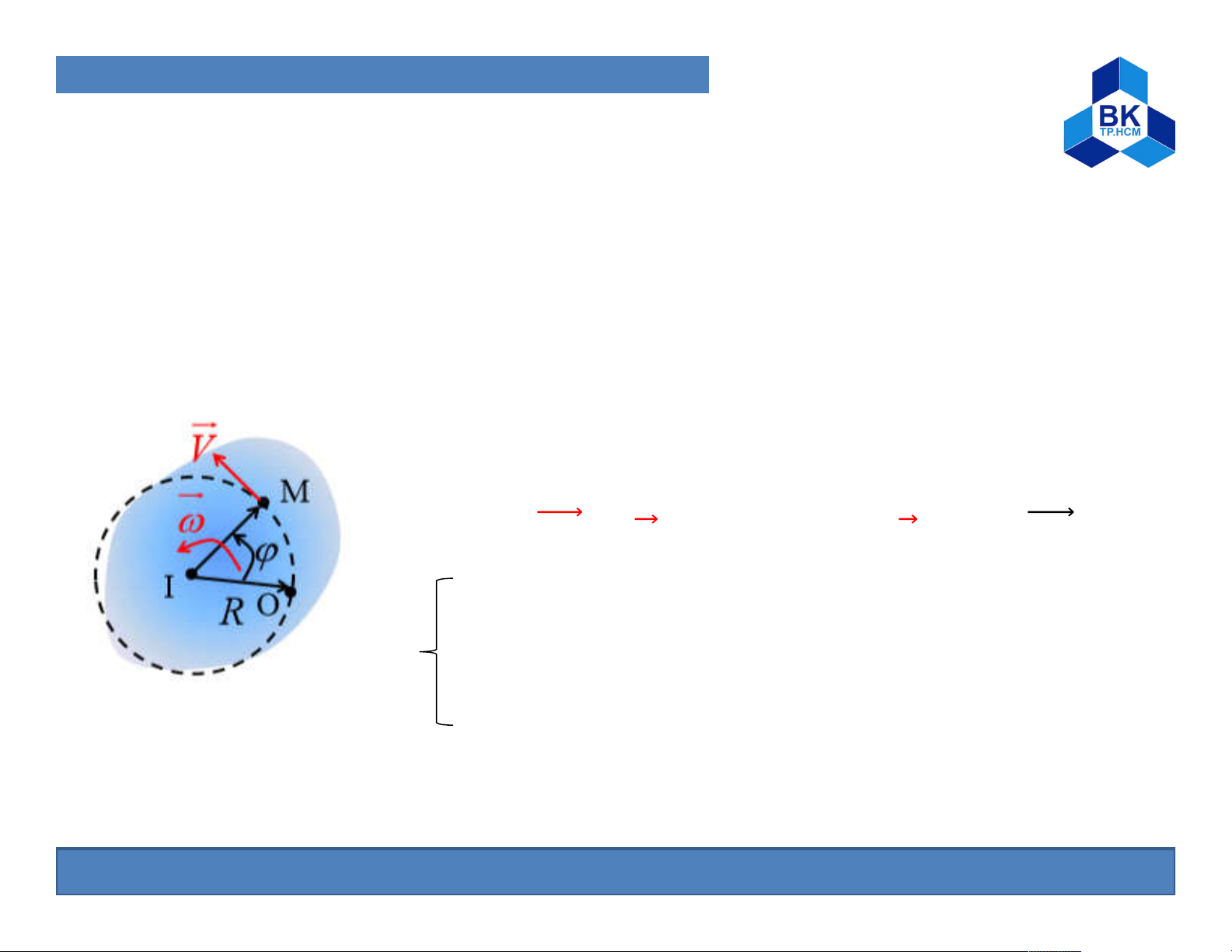
Consider a section perpendicular to the rotational axis and
intersecting it at I. The orbit of the point M is a circle with center I and radius R.
Choose O as the landmark in the M’s orbit
Motion equation: s = OM = R ( ) Velocity: = × ⃗ = = ⃗
Direction: tangent to the orbit
Direction: determined by direction of Magnitude: =R With is the angle between and r
Vector n is the unit vector perpendicular to and r 18
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
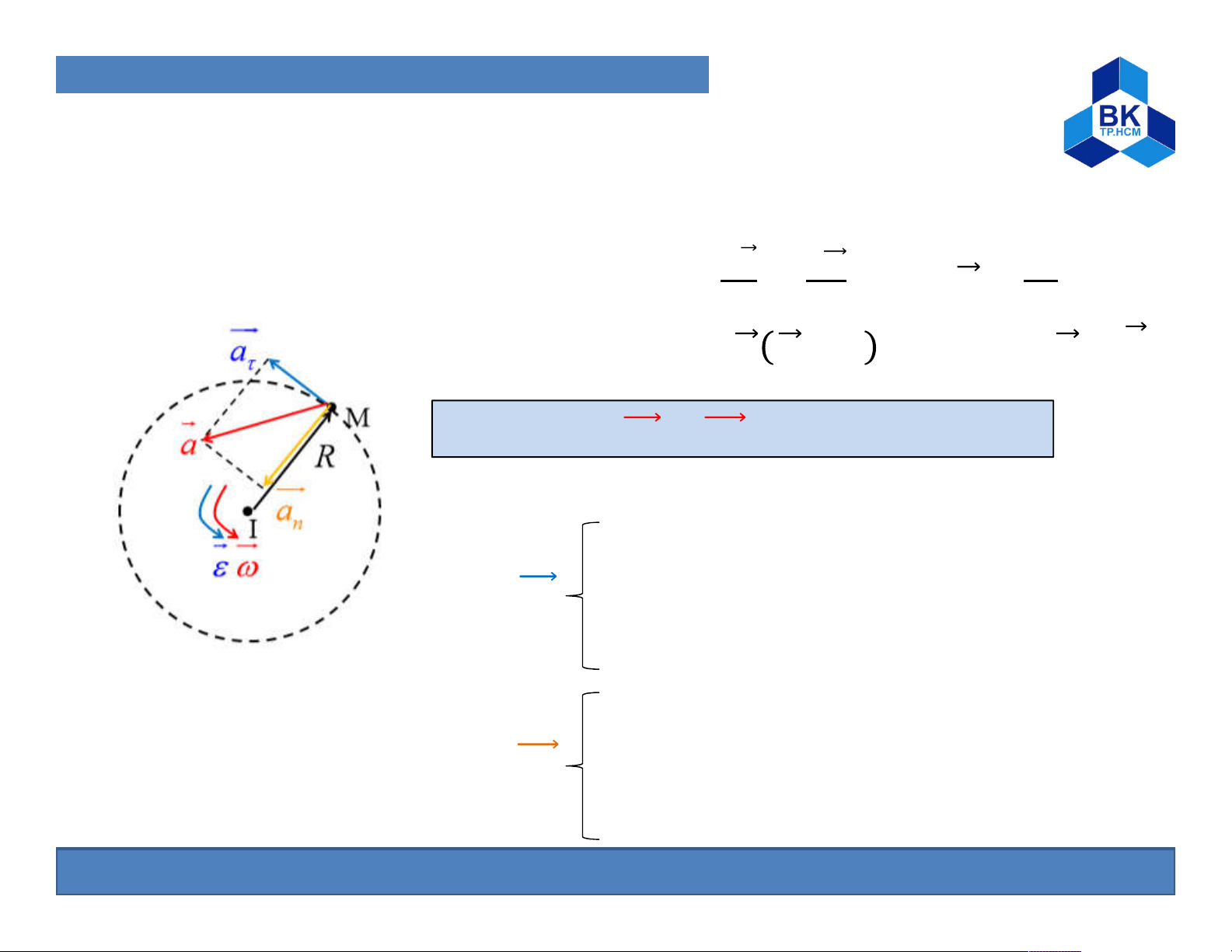
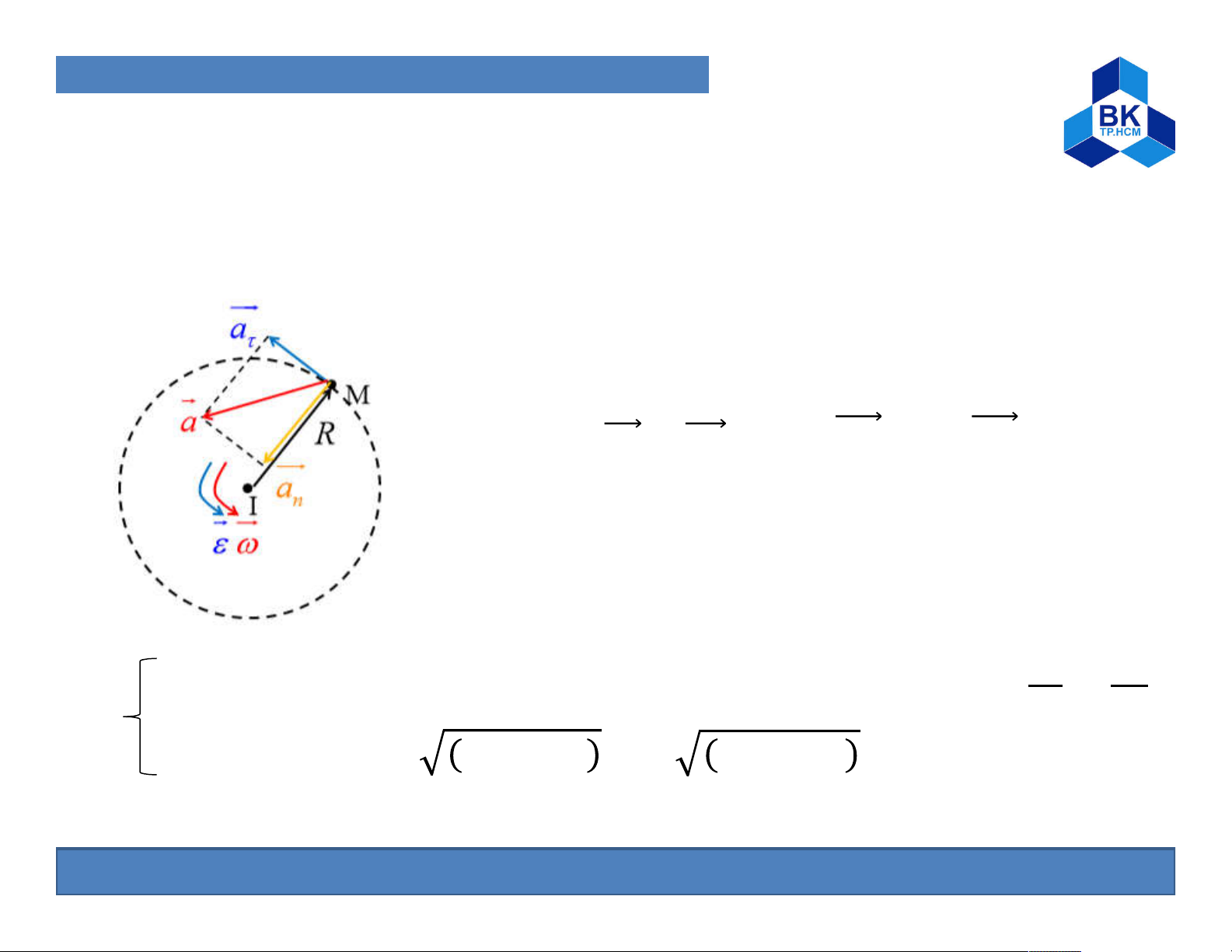
1. Particle and Solid Kinematic B. Solid Kinematic ⃗ Acceleration: ⃗ = = × ⃗ + × = ⃗ × ⃗ + × ⃗ = ⃗ × ⃗ + × → ⃗ = + = ⃗ × ⃗ − ⃗
Tangential acceleration vector:
Direction: tangent to the orbit Direction: determined by the direction of Magnitude: =R Normal acceleration vector:
Direction: collinear with radius
Direction: directed to the center Magnitude: =R 19
Department of Machine Design - Faculty of Mechanical Engineering
Ho Chi Minh City University of Technology (HCMUT), VNU-HCM 2.1. Fundamentals
1. Particle and Solid Kinematic B. Solid Kinematic ⃗ = + = ⃗ × −
Direction: math with radius an angle such that tan = = Magnitude: = + = + 20
Department of Machine Design - Faculty of Mechanical Engineering