Chapter V: Sorting Algorithms | Bài giảng cấu trúc dữ liệu và giải thuật

DATA STRUCTURES AND ALGORITHMS ET2100E/ET2105E 1 Chapter V: Sorting Algorithms
Lecturer: PhD. DO Thi Ngoc Diep
SCHOOL OF ELECTRICAL AND ELECTRONIC ENGINEERING
HANOI UNIVERSITY OF SCIENCE AND TECHNOLOGY Outline 1. Outline 2. Basic sorting algorithms •
Selection sort (Sắp xếp chọn) •
Bubble/Exchange sort (Sắp xếp nổi bọt) •
Insertion sort (Sắp xếp chèn) 3. Advanced sorting algorithms •
Quick sort (Sắp xếp nhanh/phân đoạn) •
Heap sort (Sắp xếp vun đống) •
Merge sort (Sắp xếp trộn) 3 1. Introduction
• General problem: Given a sequence of N elements a1, a2, …, aN.
Need to find an algorithm to sort the elements of the above sequence in a certain order. • Applications in practice: • Words in a dictionary • Files in a folder • Book indexing • Newspaper event calendar • List of courses • Library catalog • etc. 4 1. Introduction
• Problem: Without reducing the generality of the sorting
algorithms, and to simplify the presentation  il ustrate the
algorithms by arranging a series of N numbers in ascending order.
• For each algorithm, it is necessary to provide: • Algorithm idea
• Basic implementation (including 1 or several functions) • Algorithm evaluation 5 1. Introduction • Classification: • Basic sorting algorithm:
• At each step, put each element of the sequence to be sorted into its correct position
• No need to care about the position of other elements
• Advanced sorting algorithm:
• At each step, put each element into its correct position in the result sequence,
• at the same time, arrange the remaining elements, to minimize
the number of operations in the fol owing steps
• Advanced sorting algorithms are often faster than Basic sorting
algorithms, but are also often more complex in algorithm ideas and implementation. 6 1. Introduction • Classification:
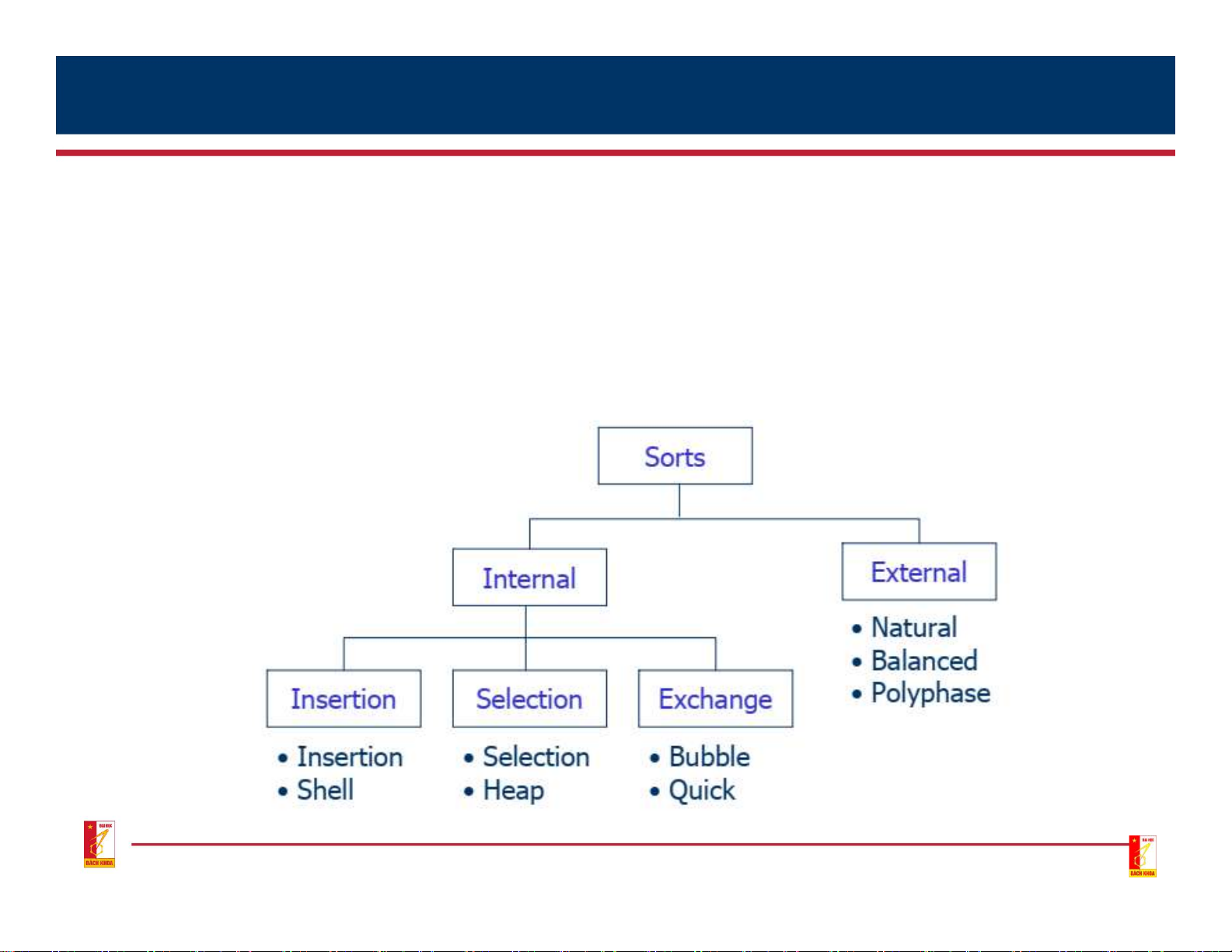
• Internal sorting: Sorting data stored in computer memory
• External sorting: Sorting data stored in files, when the amount of
data is large, it cannot be stored in internal memory 7 1. Introduction • Classification:
• Multi-key sorting: need to use information from multiple keys
• It is possible to sort based on primary key, then sub-key 1, 2, etc.
• Telephone directories: sorted by location, category, and then in an alphabetical order
• Books: sorted based on titles and then by authors’ names
• Customers’ addresses: sorted based on the name of the city and then the street • etc. 8 2. Basic sorting algorithms • Selection Sort • Bubble Sort • Insertion Sort 9 2.1 Selection Sort • Algorithm idea
• Input: Sequence of N numbers a1,a2,…,aN
• Output: Sequence of inputs in ascending order • Algorithm:
• The algorithm is implemented in N-1 steps, numbering the steps i=1,2,…,N-1
• At the ith step, find the ith smal est number and put it in the ith position in the sequence by swapping
• After the ith turn, the sequence to be sorted is considered to be divided into 2 parts:
• Sorted part: from position 1 to i
• Unsorted part: from position i +1 to n
• The next step wil select the smal est element among the unsorted
part, put it in the sorted part at correct position 10 2.1 Selection Sort
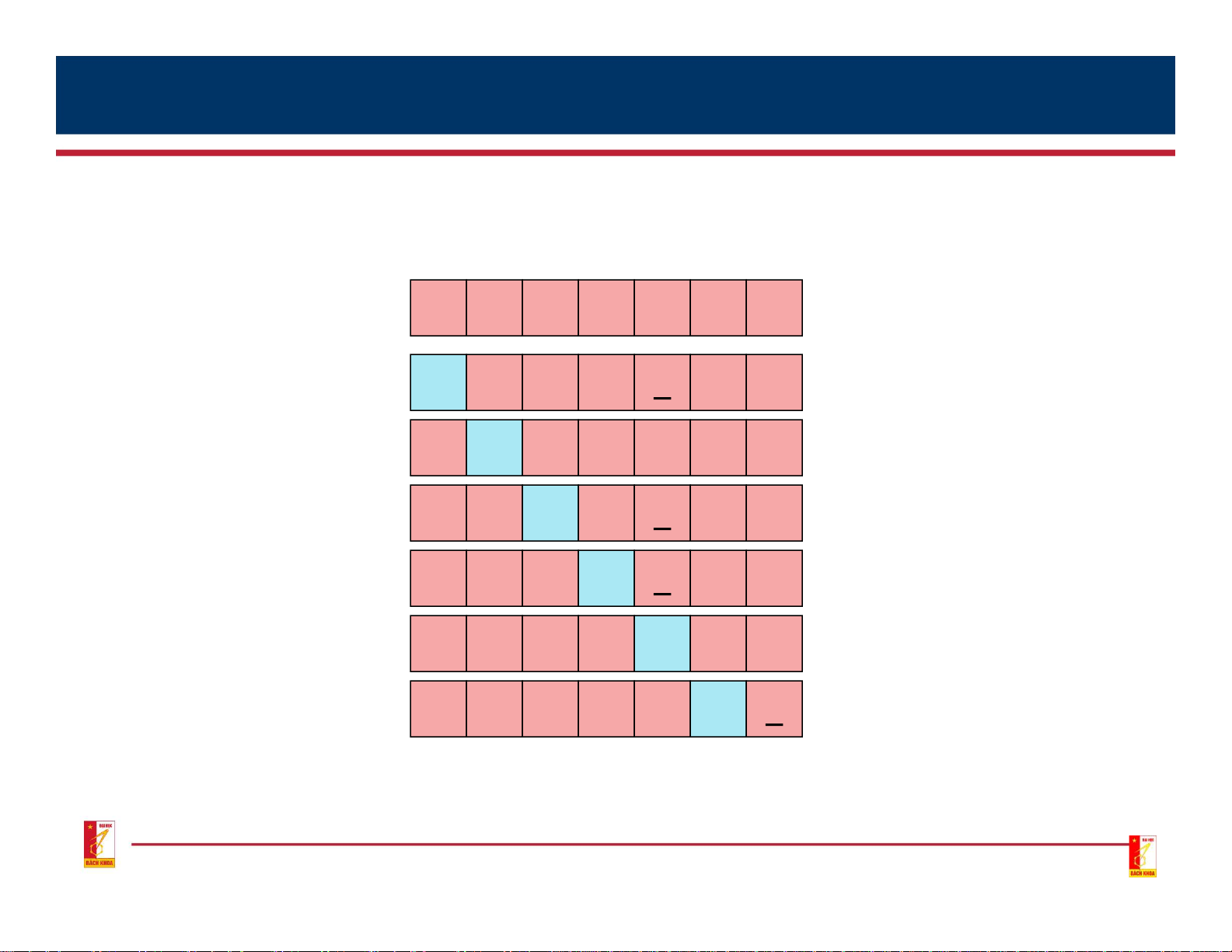
• Il ustration: Given a sequence of numbers with N = 7 3 2 4 5 1 7 6 i = 1 1 2 4 5 3 7 6 i = 2 1 2 4 5 3 7 6 i = 3 1 2 3 5 4 7 6 i = 4 1 2 3 4 5 7 6 i = 5 1 2 3 4 5 7 6 i = 6 1 2 3 4 5 6 7 11 2.1 Selection Sort
• Algorithm for (i=1;i<=N-1;i++) {
Find m so that am = Min(ai,ai+1,…, aN); Swap ai and am; } • Settings:
• Setting up a sequence: Array, List
• Element data type: simple type, structured type
• Structured type: need to build a data type comparison rule
• Depending on the problem, choose the appropriate settings 12 2.1 Selection Sort • Basic settings typedef int Sequence[N];
void SelectionSort (Sequence a) { int i, j, m; for (i=0;im = i; for(j=i+1; j//Find m: // a if (a[j] < a[m]) m = j; m=Min(ai,ai+1,…,aN-1)
if (m != i) Swap(a[i], a[m]); //Move am } } 13 2.1 Selection Sort • Algorithm Evaluation • Computational Time: • Best case: O(n2)
• Original is sorted Sequence
• 0 swap, n(n-1)/2 comparisons • Worst Case: O(n2)
• n-1 swaps, n(n-1)/2 comparisons
• Average Time Complexity O(n2) • Comments: • Simple, easy to implement • Used with smal data
• Inefficient when used with large data 14 2.2. Bubble (Exchange sort) • Algorithm idea:
• Input: Sequence of N numbers a1,a2,…,aN
• Output: Sequence of inputs in ascending order • Idea:
• The Sequence to be sorted is divided into 2 parts: sorted part, unsorted part
• Through the exchange, at each turn the smal est element in the
unsorted part wil be “pushed” gradual y forward and final y entered into the sorted part. unsorted part 15 2.2. Bubble sort • Algorithm idea: • Algorithm:
• performed in N-1 steps, numbering the steps i=1,2,3,…
• At step i, compare N-i pairs of numbers (ak and ak+1), with k=N-1,N-
2,…,i; if ak > ak+1 then Swap ak and ak+1
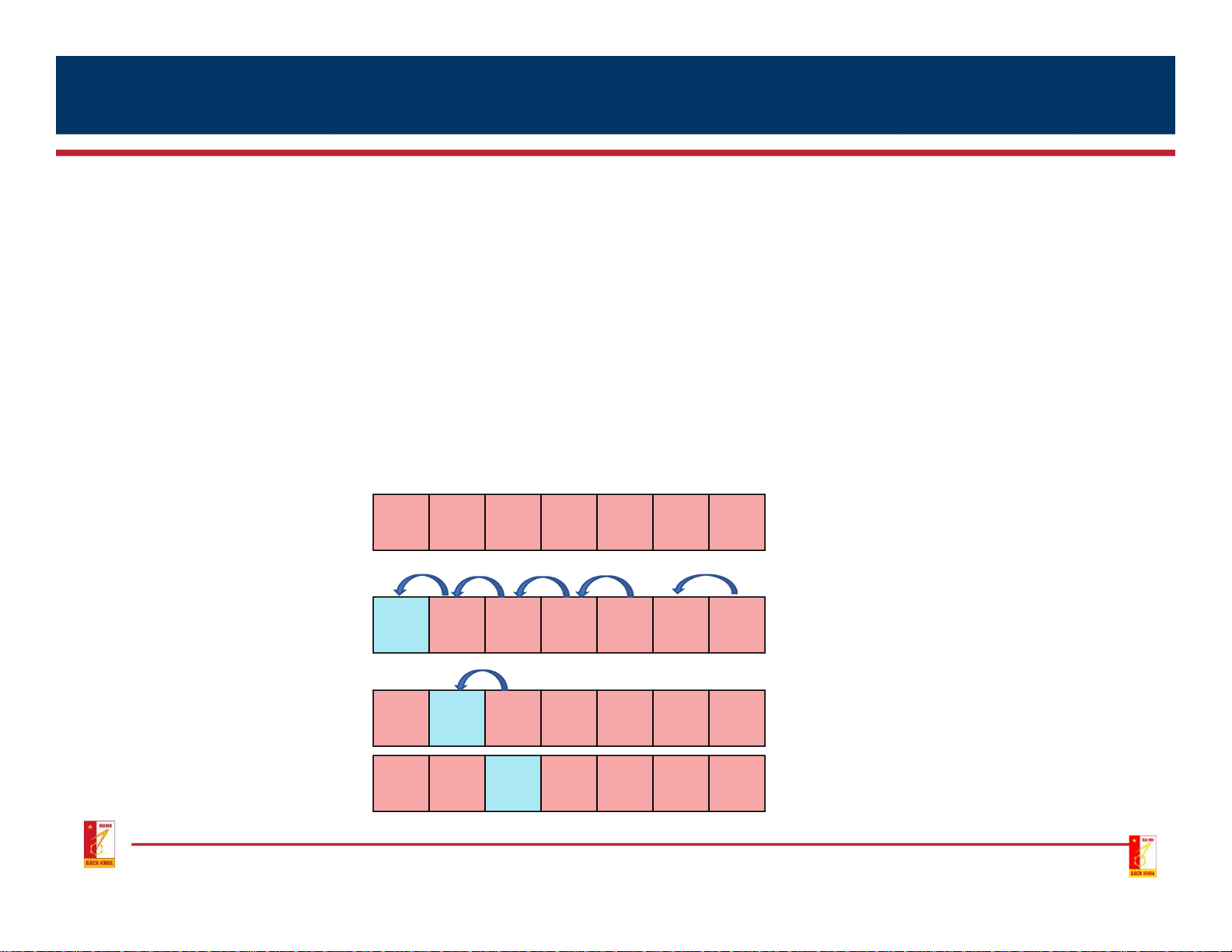
• If at any step i we do not have to swap any pair, it proves that the Sequence is sorted, so stop. 3 2 4 5 1 7 6 1 1 1 1 6 i = 1 1 3 2 4 5 6 7 2 i = 2 1 2 3 4 5 6 7 i = 3 1 2 3 4 5 6 7 Stop ! 16 2.2. Bubble sort • Raw algorithm
• No stopping condition checking void Bubblesort(Sequence a) { for (i = 1; i < N; i++){ for (k=N-1;k>=i;k--) if (ak > ak+1) { swap(ak, ak+1); } } } 17 2.2. Bubble sort • Improved Algorithm
• With Stopping Condition Check void Bubblesort(Sequence a) { i = 1; sorted = False;
while (!sorted && isorted = True; for (k=N-1;k>=i;k--) if (ak > ak+1) { swap(ak, ak+1); sorted = False; } i++; } } 18 2.2. Bubble sort • Algorithm Evaluation • Computational Time: • Best case: O(n)
• The initial Sequence is sorted, the algorithm only needs 1 step.
• 0 swap, (n-1) comparisons (+ assignments) • Worst Case: O(n2) • Must perform n-1 steps
• At step i, perform n-i comparisons and swaps (+ assignments)
• Average Time Complexity O(n2) • Comments: • Simple, easy to implement
• Used with smal , almost sorted data
• Not better than selection sort, although in the best case it is much faster. 19 2.3 Insertion sort • Algorithm idea:
• Build a sorted Sequence with increasing number of elements: from
1, 2, … and final y enough N elements to be sorted.
• At each step, insert an element from the unsorted Sequence into the
sorted Sequence of elements, so that after insertion, the new Sequence is also sorted.
• Input: Sequence of N numbers a1,a2,…,aN
• Output: Sequence of inputs in ascending order • Algorithm:
• The algorithm is performed in N-1 steps,
numbering the steps i=1,2,…,N-1
• At step i, insert element ai+1 into the previously
sorted Sequence (a1,a2,…,ai) so that after
insertion we get a new Sequence that is also sorted. 20