Chapter VI: Searching Algorithms | Bài giảng cấu trúc dữ liệu và giải thuật

DATA STRUCTURES AND ALGORITHMS ET2100E/ET2105E 1
Chapter VI: Searching Algorithms
Lecturer: PhD. DO Thi Ngoc Diep
SCHOOL OF ELECTRICAL AND ELECTRONIC ENGINEERING
HANOI UNIVERSITY OF SCIENCE AND TECHNOLOGY Outline 1. Searching Problem
2. Algorithms for searching elements using comparison • Sequential searching algorithm • Binary searching algorithm 3. Substring searching 4. Direct searching Algorithms • Hash functions • Col ision resolution 3 1. Introduction
• Search Problems: 2 basic search problems::
• Finding an element in a given sequence of elements: • Searching by comparison
• Searching directly from key values
• Finding the occurrence of a substring in a given string
• Simple search algorithms (also cal ed raw search)
• Complex algorithms: Knuth-Morris-Pratt, Boyer-Moore, etc. 4 Finding an element • Basic Problem:
• Given a sequence of N numbers: A = (a0, a1,…, aN-1) and a value K (search key).
• find the position of the element with value equal to K. • Search by Comparison
• Compare K with each element in the sequence until a result is obtained (either found or not found)
• Two types of search algorithms : • Sequential Search • Binary Search • Direct Searching
• Using a hash function: helps to directly calculate the address of the
element to be searched from its value 5 2. Search by Comparison (1) Sequential Searching • Algorithm idea:
• To find an element equal to K in a sequence of N numbers: A = (a0, a1,…, aN-1),
compare K with each element in the sequence in turn, until:
• Either find the element ai = K, then return the position i to be found.
• Or compare with al elements in the sequence but stil not find it, then return the result "not found”. typedef int Sequence[N];
int SeqSearch(Sequence a, int K) { int i=0; while (iif (ireturn -1; //Not Found } 6 2. Search by Comparison (1) Sequential Searching • Algorithm Evaluation • Best case: O(1) • Worst case: O(n) • Average case: O(n) 7 2. Search by Comparison (2) Binary Search
• Algorithm Idea: Recursive Algorithm
• To find an element equal to K in a sequence of N numbers A = (a0, a1,…, aN-1),
provided that the sequence A is sorted (assuming in ascending order):
• Compare K with the element am (m= ).
• If K = am  found at position m
• If K < am  Find K in the sequence (a0,a1,…,am-1)
• If K > am  Find K in the sequence (am+1,am+2,…,aN-1)
• Stopping point: when found or when no element remains in the sequence, return the result "not found". 8 2. Search by Comparison (2) Binary Search
• Algorithm Idea: Recursive Algorithm
int BSearch (Sequence a, int K, int b, int e) { if (b>e) return -1; int m = (b+e)/2; if (K==a[m]) return m; else
if (Kreturn BSearch(a, K, b, m-1); else return BSearch(a, K, m+1,e); }
int BinarySearch(Sequence a, int K){
return BSearch(a,K,0,a.length-1); } 9 2. Search by Comparison (2) Binary Search • Algorithm Evaluation • Best case: O(1) • Worst case: O(log2n) • Average case: O(log2n) 10 3. Substring searching • Problem:
• Given a text V of n characters (v0, v1,…, vn-1) and a substring P (cal ed the
pattern) of m characters (p0, p1,…, pm-1).
• The requirement is to find the first occurrence [of al ] of P in V. • Example
• V: “the rain in spain stays mainly on the plain” • P: “ain” • Applications: • In information retrieval • Text editing
• Biological data processing (DNA)
• Substring search algorithms :
• Brute-Force search algorithm
• Knuth-Morris-Pratt (KMP) algorithm 11 3. Substring searching
• Brute-Force search algorithm (raw search) • Algorithm Idea:
• Match the pattern to the text character by character from left to right
• When a mismatch is identified, shift the entire pattern one position to
the right and continue matching with the text in the same manner.
int BFSearch(char v[], int N, char p[], int M) { P: p0 p1 … pi … pm-1 = = ≠ if (M>N) return -1; int i=0,j=0; V: v
while (j0 … vj vj+1 … vj+i … … vn-1 while (ii++; if (i==M) return j; i=0; j++; } return -1; }
• Algorithm evaluation: Worst-case scenario: number of comparison operations: M*N O(n2) 12 3. Substring searching
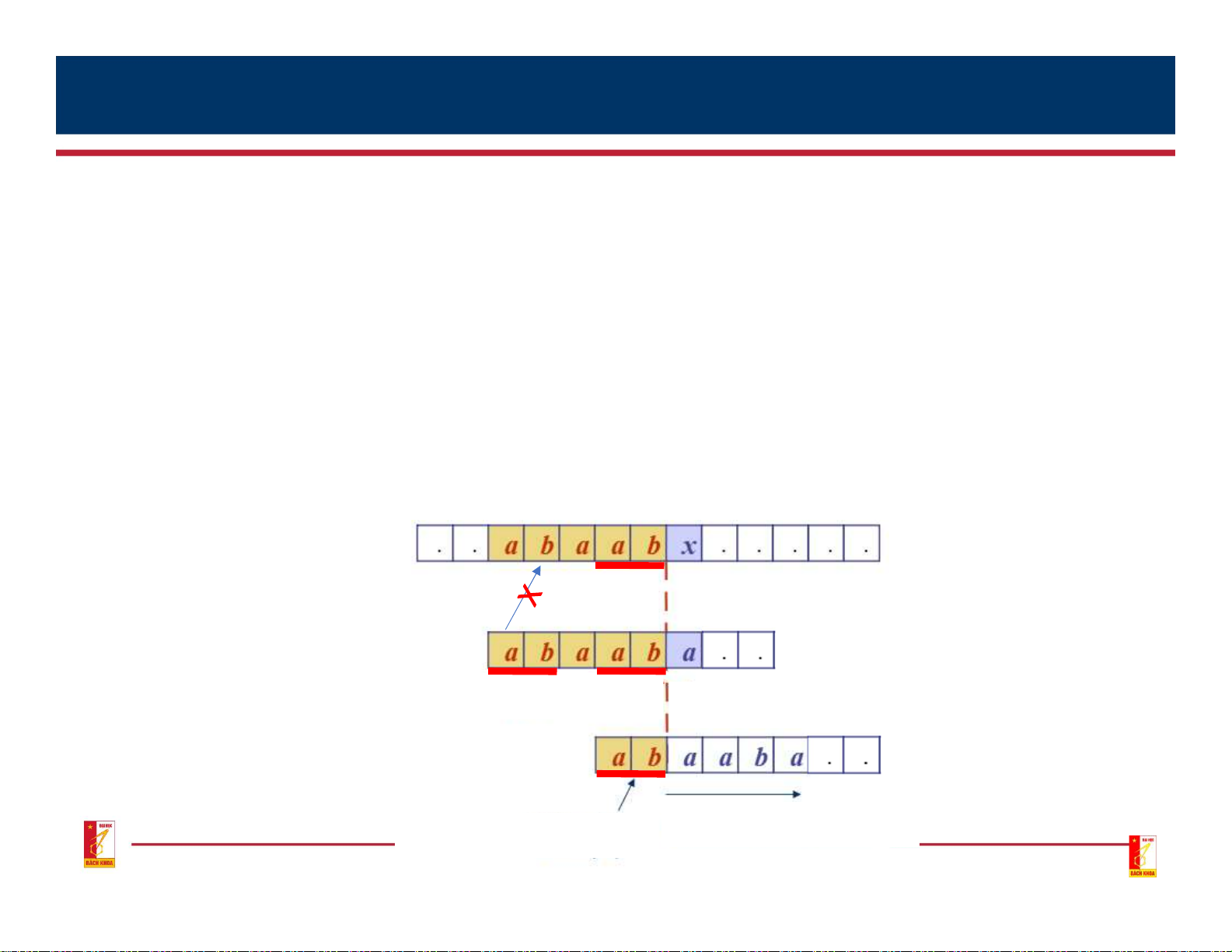
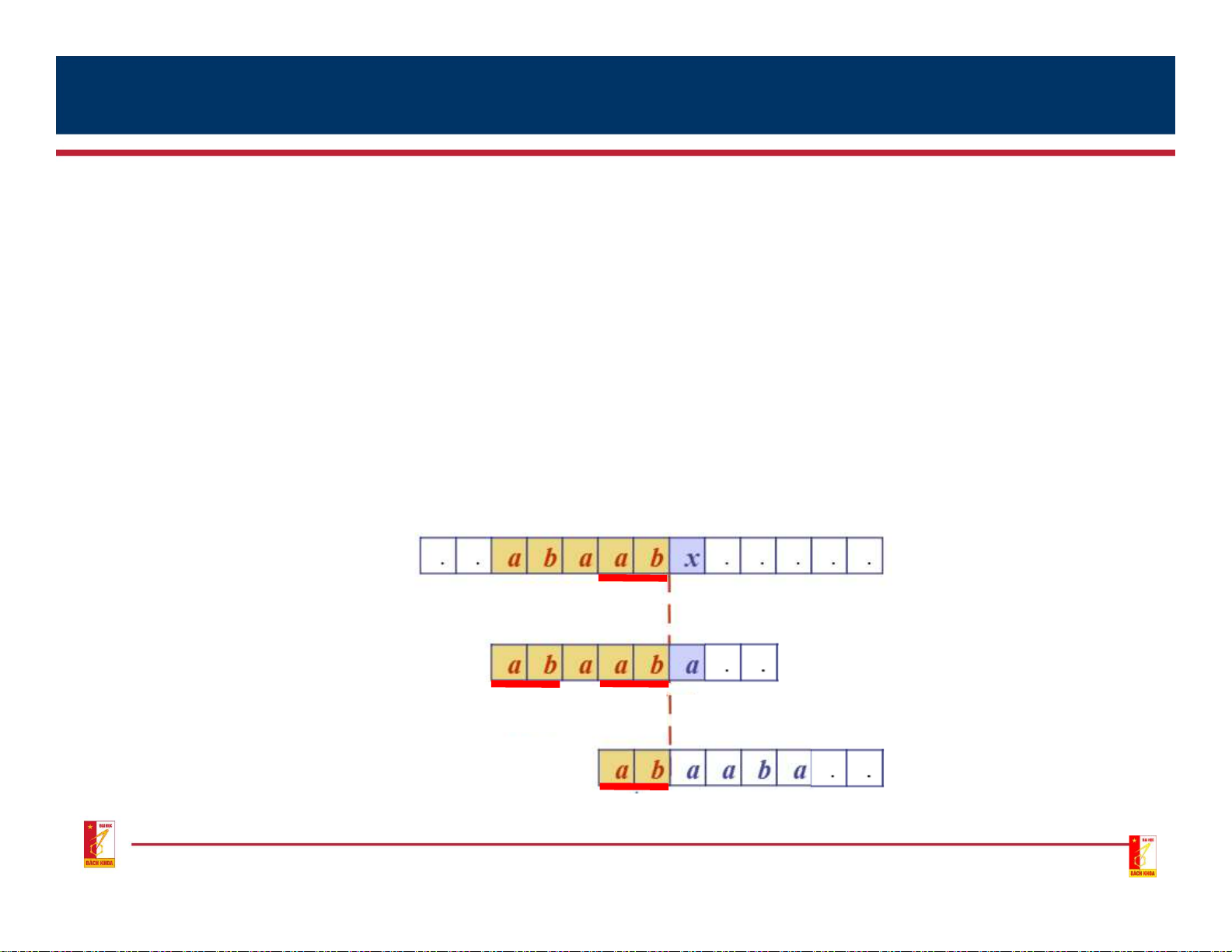
• Knuth-Morris-Pratt Algorithm • Algorithm Idea:
• Improvements from the raw search algorithm
• When comparing to the first pair of characters (vi,pj) where vi ≠ pj (j previous pairs have matched)
• Instead of going back to compare p0 of the pattern with the character vi-j+1
 continue comparing from a character pk in the pattern with the character vi
that currently does not match in the text vi-j vi-j+1 vi V p0 pk-1 pj-kpj-1 pj P p0 p p k-1 k continue comparing No need to go back 13 3. Substring searching
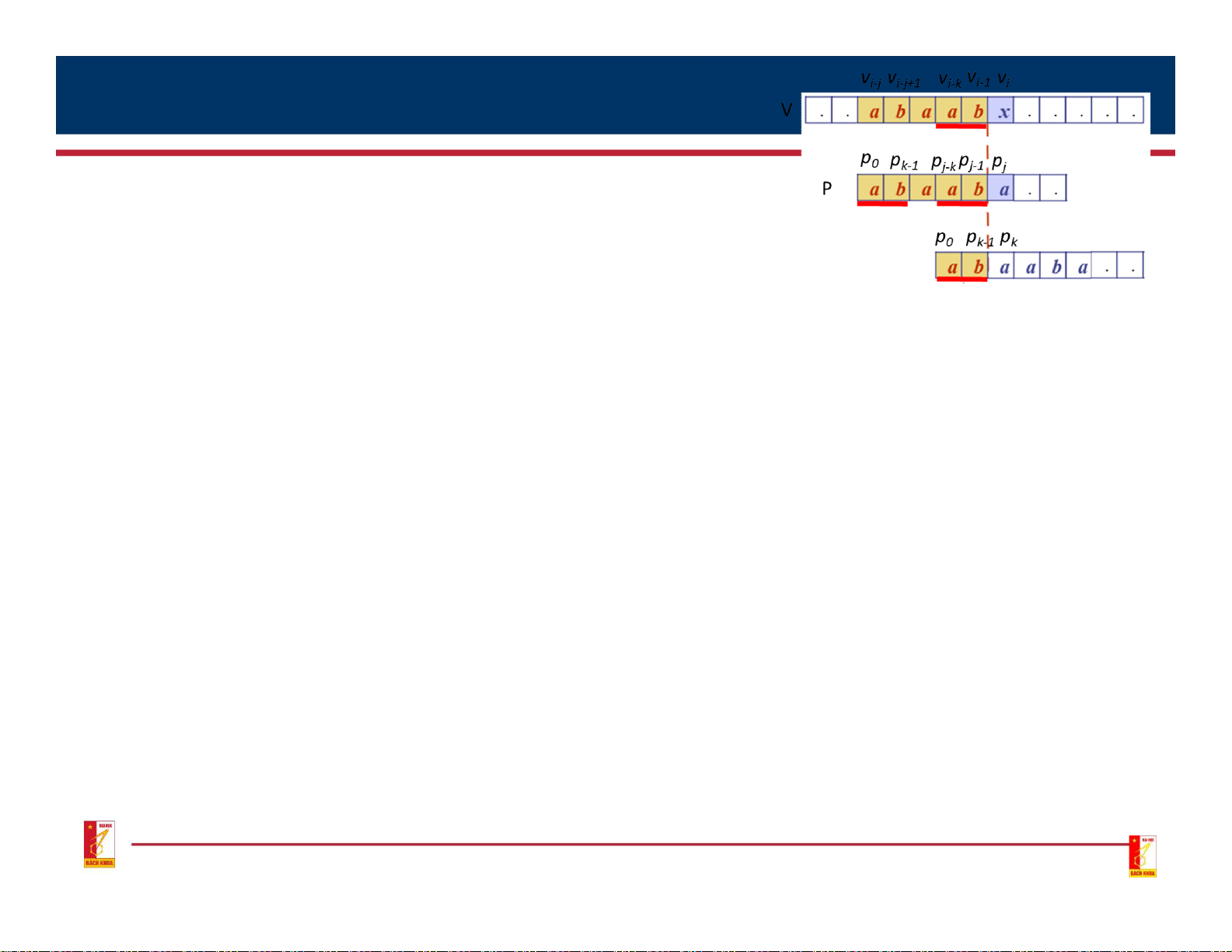
• Knuth-Morris-Pratt Algorithm
• The position k to be found in sample P satisfies the fol owing conditions:
• Maximum possible: k < j, pk≠ pj; • p0p1..pk-1 = vi-k…vi-1; • Properties of k:
• k depends on position j and sample content, not on the text
• [p0p1...pk-1] = [pj-kpj-k+1...pj-1] vi-j vi-j+1 v vi-1 v i-k i V p0 pk-1 pj-kpj-1 pj P p0 p p k-1 k 14 3. Substring searching
• Knuth-Morris-Pratt Algorithm
• k can be calculated before performing the search (even before the text content is available) • Example • Pattern: 10110111 • 0j 0 1 2 3 4 5 6 7 p 1 10 101 1011---- 10110--- 101101-- 1011011- 0..pj-1 k 1 1, 2 1, 2, 3 1, 2, 3,4 1,2, 3,4,5 1,2,3, 4, 5,6 k=1: p0 ≠p1 k=1: p0=p2 k=2: p0p1≠p1p2 Matching ∅ ∅ ∅ 1 1 10 1 or 101 1 or 1011 sequence 1xx----- 1xxx---- 10xxx--- 101xxx-- 1011xxx- xx1----- xxx1---- xxx10--- xxx101-- xxx1011- 15 3. Substring searching • Comment: • Choose k max • Choose pk≠pj Pattern 10110111 j 0 1 2 3 4 5 6 7 p0..pj-1 1 10 101 1011---- 10110--- 101101-- 1011011- 1 1, 2 k k=1: p0 ≠p1 k=1: p0=p2 1, 2, 3 1, 2, 3,4 1,2, 3,4,5 1,2,3, 4, 5,6 k=2: p0p1≠p1p2 Matching ∅ ∅ ∅ 1 1 10 1 or 101 1 or 1011 1xx----- 1xxx---- 10xxx--- 101xxx-- 1011xxx- sequence xx1----- xxx1---- xxx10--- xxx101-- xxx1011- pj 1 0 1 1 0 1 1 1 pk 0 0 1 0, 1 0, 0 pk≠pj
Not satisfied Not satisfied k=1 => pk≠pj pk≠pj New ∅ ∅ ∅ 1 ∅ ∅ 1 1011 matching seq New k 0 0 0 1 0 0 1 4 (max) 16 3. Substring searching
• Knuth-Morris-Pratt Algorithm • Finding k algorithm:
• Returns array next[]: next[j]=k
• j: position in the pattern (0≤ j ≤ M-1)
• k: next matching position (0 ≤kk) step 1: k = j-1;
Step 2: Find the largest k such that p[k] ≠ p[j];
Step 3: Compare the two strings
(p[0] p[1] .. p[k-1]) and (p[j-k] p[1] .. p[j-1]) If they are equal then next[j] = k; End of algorithm; Otherwise, k = k – 1;
Repeat from step 2 of the algorithm; 17 3. Substring searching
• Knuth-Morris-Pratt Algorithm • Finding k algorithm: • Setup:
void initNext(char p[], int next[], int M ){ int j,k; for (j=0; jfor (j=2; jk = j-1; do {
while (k>0 && p[k]==p[j]) k--; if (k>0){ int i = 1; 1: k = j-1;
2: Find the largest k such that p[k] ≠ p[j];
while (i<=k && p[k-i]==p[j-i]) i++; 3: Compare the two strings if (i>k){
(p[0] p[1] .. p[k-1]) and (p[j-k] p[1] .. p[j-1]) If they are equal then next[j] = k; next[j] = k; break; End of algorithm; Otherwise, } k = k – 1;
Repeat from step 2 of the algorithm; } k--; } while (k>0); } } 18 3. Substring searching
• Knuth-Morris-Pratt Algorithm • Setup:
int KMPSearch(char V[], int N, char P[], int M ){ if (Nint next[M]; initNext(P, next, M); int i,j; i=j=0; do {
while (jif (i<=N-M && jif (j==0) i++; else j = next[j]; }
} while (i<=N-M && jif (j==M) return (i-M); else return -1; } • Algorithm evaluation:
• In the worst-case scenario, the algorithm only performs M+N character comparison operations => O(N) 19 4. Direct searching
• Problem: Find the element equal to K in the sequence of N
numbers: A = (a0, a1,…, aN-1)
• Storage and search principles: • No comparison
• Through memory addresses, directly calculated on key values (Search based on/from key values)
• Hash function: a formula to directly calculate the position of the
element to be found through its value • y = h(k): k → y
• k D: the Domain values of key
• y P: the Domain values of the addresses
• Search problem  Calculate h(K) 20