30 trang 58 lượt tải

Chủ đề dấu tam thức bậc hai Toán 10 KNTTVCS – Lê Bá Bảo

115

Tài liệu gồm 30 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, bao gồm tóm tắt lý thuyết, bài tập tự luận và bài tập trắc nghiệm (có đáp án và lời giải chi tiết) chủ đề dấu tam thức bậc hai trong chương trình Toán 10 Kết Nối Tri Thức Với Cuộc Sống (KNTTVCS).

Chủ đề: Chương 6: Hàm số, đồ thị và ứng dụng (KNTT) 58 tài liệu

Môn: Toán 10 2.9 K tài liệu

Tác giả:

Profile

Mai Nguyệt

1 năm trước
Danh sách Quiz
/30
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề: DẤU TAM THỨC BẬC HAI
I. TÓM TẮT LÝ THUYẾT
1. Tam thức bậc hai
Tam thức bậc hai (đối với
x
) là biểu thức có dạng
2
ax bx c
trong đó
,,a b c
là những số
thực cho trước (với
0a
), được gọi là các hệ số của tam thức bậc hai.
Chú ý:
+) Nghiệm của phương trình bậc hai
2
0ax bx c
cũng được gọi là nghiệm của tam thức bậc hai
2
ax bx c
.
+)
2
4b ac
và
2
b ac

, với
tương ứng được gọi là biệt thức và biệt thức thu gọn
của tam thức bậc hai
2
ax bx c
.
2. Định lý về dấu tam thức bậc hai
Cho tam thức bậc hai
2
f x ax bx c
(với
0a
).
+) Nếu
0
thì
fx
cùng dấu với hệ số
a
với mọi
.x
+) Nếu
0
thì
fx
cùng dấu với hệ số
a
với mọi
2
b
x
a

và
0.
2
b
f
a




+) Nếu
0
thì tam thức
fx
có hai nghiệm phân biệt
1
x
và
2
x
12
xx
. Khi đó ,
fx
cùng dấu với hệ số
a
với mọi
12
;;x x x  
;
fx
trái dấu với hệ số
a
với mọi
12
;.x x x
Chú ý. Trong định lí về dấu tam thức bậc hai có thể thay
bởi
.
3. Bất phương trình bậc hai
+) Bất phương trình bậc hai ẩn
x
là bất phương trình có dạng
2
0ax bx c
(hoặc
2
0ax bx c
,
2
0ax bx c
,
2
0ax bx c
), trong đó
,,abc
là những số thực đã cho và
0a
.
+) Số thực
0
x
gọi là một nghiệm của bất phương trình bậc hai
2
0ax bx c
, nếu
2
00
0ax bx c
. Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai
2
0ax bx c
gọi là tập nghiệm của bất phương trình này.
+) Giải bất phương trình bậc hai
2
( ) 0f x ax bx c
là tìm tập nghiệm của nó, tức là tìm
các khoảng mà trong đó
()fx
cùng dấu với hệ số
a
(nếu
0a
) hay trái dấu với hệ số
a
(nếu
0a
).
Để giải bất phương trình bậc hai
2
0a x bx c
(hoặc
2
0ax bx c
,
2
0ax bx c
,
2
0ax bx c
) ta cần xét dấu tam thức
2
ax bx c
, từ đó suy ra tập nghiệm.
II. BÀI TẬP TỰ LUẬN
Câu 1: Xét dấu các tam thức bậc hai sau:
a)
2
1;xx
b)
2
3
9 27;
2
xx
c)
2
2 6 8xx
.
Câu 2: Xét dấu các tam thức bậc hai sau:
a)
2
3 2; xx
b)
2
8 16;xx
c)
2
2 7 3. xx
Câu 3: Xét dấu biểu thức
2
2
21
.
4

xx
fx
x
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 4: Tìm tất cả các giá trị của
x
để biểu thức
22
3 6 9f x x x x x
nhận giá trị dương
Câu 5: Xét dấu biểu thức
2
2
6
.
34
xx
P x x
xx


Câu 6: Giải các bất phương trình sau:
a)
2
3 5 0; xx
b)
2
3 2 3 1 0; xx
c)
2
2 1 0. xx
Câu 7: Giải các bất phương trình bậc hai sau:
a)
2
1 0;x
b)
2
2 1 0; xx
c)
2
3 12 1 0; xx
d)
2
5 1 0. xx
Câu 8: Tìm tập xác định của hàm số
2
2 5.y x x
Câu 9: Giải bất phương trình
2
22
3 2 0.x x x x
Câu 10: Giải bất phương trình :
23
22
1 1 2
2
32
x x x x
x
x x x x

.
Câu 11: Giải bất phương trình:
2 2 2
4 2 3 4 4 .x x x x x
Câu 12: Giải hệ bất phương trình
2
2
4 3 0
.
6 8 0
xx
xx
Câu 13: Tìm tập xác định của hàm số
2
1
3 2 .
3
y x x
x
Câu 14: Giải hệ bất phương trình
2
2
2
4 3 0
2 10 0.
2 5 3 0
xx
xx
xx
Câu 15: Tìm các giá trị của tham số
m
để tam thức bậc hai
2
1 2 3x m x m
dương với mọi
.x
Câu 16: Tìm các giá trị của tham số
m
để bất phương trình
2
2( 2) 2 1 0x m x m
nghiệm đúng
với mọi
.x
Câu 17: Tìm tất cả các giá trị của
m
để biểu thức
2
2 f x x x m
luôn âm.
Câu 18: Tìm tất cả các giá trị của tham số
m
để bất phương trình
22
3 2 1 2 3 2 0 x m x m m
nghiệm đúng
.x
Câu 19: Tìm tất cả các giá trị của
m
để hàm số
2
1
( 1) 2( 2) 2
fx
m x m x m
xác định với mọi
x
.
Câu 20: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2( 2) 2 1 0x m x m
vô nghiệm.
Câu 21: Tìm
m
để mọi
1;1x



đều là nghiệm của bất phương trình
22
3 2 5 2 8 0.x m x m m
Câu 22: Tìm giá trị của tham số
m
để phương trình
2
( 3) ( 3) ( 1) 0m x m x m
có hai nghiệm
phân biệt.
Câu 23: Tìm tham số
m
để phương trình
2
2 3 2 3 0m x x m
có hai nghiệm trái dấu.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 24: Tìm m để phương trình
2
1 2 2 1 0m x m x m
có
2
nghiệm phân biệt khác
0
sao
cho
12
11
2
xx

.
Câu 25: Tìm
m
để phương trình
2
1 2 2 3 0m x m x m
có hai nghiệm phân biệt
12
,xx
thỏa
mãn
1 2 1 2
1.x x x x
Câu 26: Cho hàm số
2
2 3 2 3y m x mx m
(m là tham số). Tìm các giá trị của tham số m để đồ thị
hàm số cắt trục hoành tại hai điểm phân biệt
,AB
sao cho gốc tọa độ
O
nằm giữa
A
và
B
.
Câu 27: Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao
320m
với vận tốc ban đầu
0
20 /v m s
. Hỏi sau ít nhất bao nhiêu giây, vật đó cách mặt đất không quá
100m
? Giả thiết
rằng sức cản của không khí là không đáng kể.
Câu 28: Một công ty đồ gia đụng sản xuất bình đựng nước thấy rằng khi đơn giá của binh đựng nước
là
x
nghìn đồng thì doanh thu
R
(tính theo đơn vị nghìn đồng) sẽ là
2
( ) 560 50000R x x x
.
a) Theo mô hình doanh thu này, thì đơn giá nào là quá cao dẫn đến doanh thu từ việc bán
bình đựng nước bằng 0 (tức là sē không có người mua)?
b) Với khoảng đơn giá nào của bình đựng nước thì doanh thu từ việc bán bình đựng nước
vượt mức 1 tỉ đồng?
Câu 29: Xét đường tròn đường kính
4AB
và một điểm
M
di chuyển trên đoạn
AB
, đặt
AM x
(Hình vẽ). Xét hai đường tròn đường kính
AM
và
MB
.
Kí hiệu
Sx
là diện tích phần hình phẳng nằm trong hình tròn lớn và
nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của
x
để diện tích
Sx
không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
III. BÀI TẬP TRẮC NGHIỆM
Câu 1: Biểu thức nào dưới đây là tam thức bậc hai?
A.
1.y
B.
.yx
C.
2
.yx
D.
3
.yx
Câu 2: Với
m
là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai?
A.
.ym
B.
.y mx
C.
2
.y mx
D.
2
.y x m
Câu 3: Với
m
là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai?
A.
.ym
B.
.y mx
C.
22
1.y m x
D.
2
.y mx m
Câu 4: Tìm tất cả các giá trị của tham số
m
để biểu thức
2
2 5 9 f x m x x
là tam thức bậc hai.
A.
m
. B.
2m
. C.
2m
. D.
0m
.
Câu 5: Cho hàm số bậc hai
y f x
có đồ thị như hình bên dưới:
x
y
2
-1
O
1
Khẳng đinh nào dưới đây đúng?
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
0, 0;2 .f x x
B.
0, 0;2 .f x x
C.
0, 1; .f x x
D.
0, 0;2 .f x x


Câu 6: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
4

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Câu 7: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
2

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Câu 8: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây đúng?
A.
0, 1;2 .f x x
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x  
D.
0, 1;2 .f x x


Câu 9: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây sai?
A.
0, ;1 2; .f x x  
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x

 

D.
0, 1;2 .f x x


Câu 10: Tập hợp tất cả các giá trị của
x
để tam thức
2
2y x x
luôn âm là
A.
0;2 .
B.
;0 2; . 
C.
0;2 .


D.
;0 2; .

 

Câu 11: Tập hợp tất cả các giá trị của
x
để tam thức
2
2f x x x
luôn dương là
A.
0;2 .
B.
;0 2; . 
C.
0;2 .


D.
;0 2; .

 

Câu 12: Tam thức nào dưới đây luôn âm với mọi
?x
A.
2
1.y x x
B.
2
1.y x x
C.
2
1.y x x
D.
2
4.y x x
Câu 13: Tam thức nào dưới đây luôn dương với mọi
?x
A.
2
1.y x x
B.
2
2 1.y x x
C.
2
1.y x x
D.
2
4.y x x
Câu 14: Một nghiệm của bất phương trình
2
2 3 0xx
là
A.
5.x
B.
0.x
C.
2.x 
D.
4.x
Câu 15: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Câu 16: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Câu 17: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Câu 18: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
.
B. C.
1;3 .
D.
; 1 3; .

 

Câu 19: Tập nghiệm của bất phương trình
2
30xx
là
A.
.
B. C.
1;3 .
D.
; 1 3; .

 

Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 20: Tập nghiệm của bất phương trình
2
30xx
là
A.
.
B. C.
1;3 .
D.
; 1 3; .

 

Câu 21: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1;3 .
D.
\ 1 .
Câu 22: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Câu 23: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Câu 24: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Câu 25: Bất phương trình
2
3 4 0xx
có tất cả bao nhiêu nghiệm nguyên dương?
A.
6
. B.
5
. C.
4
. D.
2
.
Câu 26: Bất phương trình nào dưới đây có nghiệm?
A.
2
2 1 0.xx
B.
2
2 3 0.xx
C.
2
3 4 0.xx
D.
2
2 0.xx
Câu 27: Bất phương trình nào dưới đây có nghiệm?
A.
2
2 1 0.xx
B.
2
2 3 0.xx
C.
2
3 4 0.xx
D.
2
2 1 0.xx
Câu 28: Bất phương trình nào dưới đây vô nghiệm?
A.
2
2 0.xx
B.
2
2 3 0.xx
C.
2
4 0.x 
D.
2
0.x
Câu 29: Bất phương trình nào sau đây vô nghiệm?
A.
2
0x
. B.
2
0x
. C.
2
0x
. D.
2
0x
.
Câu 30: Tập xác định của hàm số
2
4yx
là
A.
2; 2 .
B.
; 2 2; . 
C.
2; 2 .


D.
; 2 2; .

 

Câu 31: Tập xác định của hàm số
2
27
4
x
y
x
là
A.
2; 2 .
B.
; 2 2; . 
C.
2; 2 .


D.
; 2 2; .

 

Câu 32: Tập xác định của hàm số
2
1 2 9y x x
là
A.
1;3 .


B.
1; .

C.
3;3 .


D.
3; .

Câu 33: Tập xác định của hàm số
2
9
1 4 10
x
y
xx
là
A.
1;2 .


B.
2; .

C.
1;9 .


D.
1;2 .
Câu 34: Tập nghiệm của bất phương trình
22
3 4 0x x x
là
A.
2; 2 .


B.
; 2 2; .

 

C.
2; 2 .
D.
; 2 2; . 
Câu 35: Tập nghiệm của bất phương trình
22
2 4 2 0x x x x
là
A.
0;2 .


B.
;0 2; .

 

C.
0;2 .
D.
;0 2; . 
Câu 36: Số nghiệm nguyên của bất phương trình
22
2 9 0x x x
là
A. Vô số. B.
0.
C.
5.
D.
7.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 37: Số nghiệm nguyên của bất phương trình
2
2
43
0
16
xx
x

là
A. Vô số. B.
0.
C.
6.
D.
8.
Câu 38: Cho biểu thức
2
6
.
12
xx
fx
x

Khoảng nào dưới đây của
x
thì
0fx
?
A.
3
;2
4



. B.
1
2;
2



. C.
3;
. D.
2;3
.
Câu 39: Với
x
thuộc tập hợp nào sau đây thì
12
21
xx
fx
xx



không âm?
A.
1
2;
2



. B.
2; 
. C.
1
2; 2;
2




.D.
1
; 2 ;1
2



.
Câu 40: Có bao nhiêu số nguyên thỏa mãn bất phương trình
2
1
2
x
x
x

?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 41: Biết tập nghiệm của bất phương trình
2
34
1
21
xx
x
x


là
;;S a b c 
, giá trị của
2a b c
là
A.
1
. B.
3
. C.
2
. D.
3
.
Câu 42: Tìm tập nghiệm của hệ bất phương trình
2
2
2 6 0
3 10 3 0
xx
xx
.
A.
3
; 2 ;
2




. B.
; 2 3;
. C.
1
; 3;
3




. D.
2;3
.
Câu 43: Cho tam thức bậc hai
2
f x ax bx c
0a
có
2
40 b ac
. Mệnh đề nào sau đây
đúng?
A.
fx
luôn cùng dấu với hệ số
b
với mọi
x
.
B.
fx
luôn cùng dấu với hệ số
a
với mọi
x
.
C.
fx
luôn cùng dấu với hệ số
a
với mọi
2
b
x
a
.
D.
fx
luôn trái dấu với hệ số
a
với mọi
x
.
Câu 44: Cho
2
,0f x ax bx c a
và
2
4b ac
. Tìm điều kiện
để
fx
cùng dấu với hệ
số
a
với mọi
x
.
A.
0
. B.
0
. C.
0
. D.
0
.
Câu 45: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Mệnh đề nào dưới
đây đúng?
A.
0
0, .
0
a
f x x

B.
0
0, .
0
a
f x x

C.
0
0, .
0
a
f x x

D.
0
0, .
0
a
f x x

Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 46: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Mệnh đề nào dưới
đây đúng?
A.
0
0, .
0
a
f x x

B.
0
0, .
0
a
f x x

C.
0
0, .
0
a
f x x

D.
0
0, .
0
a
f x x

Câu 47: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Điều kiện cần và đủ
để
0,f x x
là
A.
0
.
0
a

B.
0
.
0
a

C.
0
.
0
a

D.
0
.
0
a

Câu 48: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Điều kiện cần và đủ
để
0,f x x
là
A.
0
.
0
a

B.
0
.
0
a

C.
0
.
0
a

D.
0
.
0
a

Câu 49: Tập hợp tất cả các giá trị của tham số
m
để phương trình
2
0x mx m
có hai nghiệm phân
biệt là
A.
;0 4; . 
B.
0;4 .
C.
;0 4; .

 

D.
0;4 .


Câu 50: Điều kiện cần và đủ của tham số
m
để tam thức
2
2 4 1 f x x m x m
đổi dấu hai lần
là
A.
0 12m
. B.
0m
hoặc
12m
C.
0m
hoặc
12m
D.
0m
.
Câu 51: Với giá trị nào của tham số
m
thì phương trình
2
2 4 0mx mx
vô nghiệm?
A.
04m
. B.
0
4
m
m
. C.
04m
. D.
04m
.
Câu 52: Tập hợp tất cả các giá trị của tham số
m
để phương trình
22
10x mx m
có hai nghiệm
trái dấu là
A.
; 1 1; . 
B.
1;1 .
C.
; 1 1; .

 

D.
1;1 .


Câu 53: Cho tam thức bậc hai
2
2.f x x mx m
Tập hợp tất cả các giá trị của tham số
m
để
0,f x x
là
A.
;0 1; .
B.
0;1 .
C.
;0 1; .

 

D.
0;1 .


Câu 54: Cho tam thức bậc hai
22
2 2 .f x x mx m m
Tập hợp tất cả các giá trị của tham số
m
để
0,f x x
là
A.
;0 1; .
B.
0;1 .
C.
;0 1; .

 

D.
0;1 .


Câu 55: Cho
2
2 4.f x mx mx
Tập hợp tất cả các giá trị của tham số
m
để
0,f x x
là
A.
;0 4; . 
B.
0;4 .
C.
;0 4; .

 

D.
0;4 .
Câu 56: Tập hợp tất cả các giá trị của tham số
m
để hàm số
22
45y x x m m
xác định trên là
A.
;1 4; . 
B.
1;4 .
C.
1;4 .


D.
1;1 .


Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 57: Tập hợp tất cả các giá trị của tham số
m
để hàm số
22
47
45
x
y
x x m m
xác định trên là
A.
;1 4; . 
B.
1;4 .
C.
1;4 .


D.
1;1 .


Câu 58: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2 8 1 0x m x m
vô
nghiệm.
A.
0;28m
. B.
0;28m
.
C.
;0 28;m  
. D.
;0 28;m  
.
Câu 59: Tìm số giá trị nguyên của m để bất phương trình
2
2 3 2 0 x mx m
vô nghiệm.
A.
0
. B.
1
. C.
2
. D. Vô số.
Câu 60: Tìm tất cả các giá trị của tham số
m
để hệ bất phương trình
2
5 4 0
0
xx
xm

có nghiệm.
A.
1m
. B.
14m
. C.
4m
. D.
4m
.
Câu 61: Giá trị của tham số
m
để hệ bất phương trình
2
40
42


x
mx
vô nghiệm là
A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Câu 62: Cho biểu thức
2
2 1 2 3f x x m x m
. Tìm điều kiện của tham số
m
để
0fx
thỏa
mãn với mọi
1;2x
.
A.
2m
. B.
m
. C.
1m
. D.
2m
.
Câu 63: Có tất cả bao nhiêu giá trị nguyên của tham số
0;2022m
để
2;4x
đều là nghiệm bất
phương trình
2
1 0? x m x m
A. 2022. B. 2021. C. 2020. D. 2019.
Câu 64: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2
2
11
0
25
x m x
xx

nghiệm đúng với mọi
x
?
A. 3. B. 5. C. 2. D. 1.
LỜI GIẢI CHI TIẾT
II. BÀI TẬP TỰ LUẬN
Câu 1: Xét dấu các tam thức bậc hai sau:
a)
2
1;xx
b)
2
3
9 27;
2
xx
c)
2
2 6 8xx
.
Lời giải:
a)
2
1f x x x
có
30
và
10a 
nên
0fx
với mọi
.x
b)
2
3 27
9
22
g x x x
có
0
và
3
0
2
a
nên
gx
có nghiệm kép
3x
và
0gx
với mọi
3.x
c) Dễ thấy
2
2 6 8h x x x
có
25 0, 2 0a
và có hai nghiệm phân biệt
12
4; 1xx
.
Do đó ta có bảng xét dấu
hx
:
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Suy ra
0hx
với mọi
; 4 1;x  
và
0hx
với mọi
4;1 .x
Câu 2: Xét dấu các tam thức bậc hai sau:
a)
2
3 2; xx
b)
2
8 16;xx
c)
2
2 7 3. xx
Lời giải:
a)
2
32f x x x
có
1 12 2 0
và
10a
nên
0,f x x
.
b)
2
86g x x x
có
' 0, 1 0a
nên
0gx
có nghiệm kép
4x 
và
0, 4g x x
.
c)
2
2 7 3h x x x
có
25 0, 2 0a
nên
1
0
2
3
x
hx
x

Ta có bảng xét dấu:
Suy ra
1
0, ;3
2
h x x



và
1
0, ; 3; .
2

 


h x x
Câu 3: Xét dấu biểu thức
2
2
21
.
4

xx
fx
x
Lời giải:
Ta có:
2
1
2 1 0
2
1
x
xx
x

;
2
4 0 2. xx
Bảng xét dấu
:fx
Suy ra
1
0, ; 2 ;1 2;
2

 


f x x
và
1
0, 2; 1;2 .
2



h x x
Câu 4: Tìm tất cả các giá trị của
x
để biểu thức
22
3 6 9f x x x x x
nhận giá trị dương
Lời giải:
Ta có
2
0
30
3
x
xx
x
;
2
6 9 0 3. x x x
Lập bảng xét dấu ( Hoặc sử dụng phương pháp khoảng) ta có
0; 3 .x
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 5: Xét dấu biểu thức
2
2
6
.
34
xx
P x x
xx


Lời giải:
Ta có:
2
2 3 2
2 2 2
16
6 2 5 6
3 4 3 4 3 4
x x x
x x x x x
P x x
x x x x x x
Ta có:
22
21
6 0 , 3 4 0
34
xx
x x x x
xx




Bảng xét dấu
Suy ra
0Px
2; 1 1;3 4;x 
,
0Px
; 2 1;1 3;4x 
.
Câu 6: Giải các bất phương trình sau:
a)
2
3 5 0; xx
b)
2
3 2 3 1 0; xx
c)
2
2 1 0. xx
Lời giải:
a) Tam thức
2
( ) 3 5f x x x
có
59 0
hệ số
30a 
nên
()fx
luôn dương (cùng dấu
với
a
với mọi
x
. Suy ra bất phương trình vô nghiệm.
b) Tam thức
2
( ) 3 2 3 1f x x x
có
0
hệ số
30a
nên
()fx
luôn âm (cùng dấu
với
a
với mọi
3
3
x
, tức là
2
3 2 3 1 0xx
với mọi
3
3
x
.
Suy ra bất phương trình có nghiệm duy nhất
3
3
x
c) Tam thức
2
( ) 2 1f x x x
có
20
nên
()fx
có hai nghiệm
1
12x 
và
2
12x 
.
Mặt khác
10a
, do đó ta có bảng xét dấu sau:
Tập nghiệm của bất phương trình là
1 2;1 2S
.
Câu 7: Giải các bất phương trình bậc hai sau:
a)
2
1 0;x
b)
2
2 1 0; xx
c)
2
3 12 1 0; xx
d)
2
5 1 0. xx
Lời giải:
a) Dễ thấy
2
1f x x
có
1 0, 1 0a
và có hai nghiệm phân biệt
12
1; 1xx
.
Do đó ta có bảng xét dấu
fx
:
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Nên bất phương trình
2
10x 
có tập nghiệm là
; 1 1;S  
.
b) Dễ thấy
2
21g x x x
có
2 0, 1 0a
và có hai nghiệm phân biệt
1
1 2;x 
2
12x 
.
Do đó ta có bảng xét dấu
gx
:
Nên bất phương trình
2
2 1 0xx
có tập nghiệm là
1 2;1 2S
.
c) Dễ thấy
2
3 12 1h x x x
có
39 0, 3 0a
và có hai nghiệm phân biệt
1
6 39
;
3
x
2
6 39
3
x
.
Do đó ta có bảng xét dấu
hx
:
Nên bất phương trình
2
3 12 1 0xx
có tập nghiệm là
6 39 6 39
;;
33
S


.
d)
2
51k x x x
có
19 0
và
50a 
nên
0kx
với mọi
.x
Từ đó suy ra bất phương trình
2
5 1 0xx
có tập nghiệm là .
Câu 8: Tìm tập xác định của hàm số
2
2 5.y x x
Lời giải:
Điều kiện:
2
2 5 0xx
Xét tam thức vế trái có
40
và
10a 
nên
2
2 5 0,x x x
.
Vậy tập xác định của hàm số là
D
.
Câu 9: Giải bất phương trình
2
22
3 2 0.x x x x
Lời giải:
Ta có
2 2 2
( ) 3( ) 2 0x x x x
2
2
2
1
xx
xx
2
2
20
10
xx
xx

đúng
.x
Vậy tập nghiệm của bất phương trình
T
.
Câu 10: Giải bất phương trình :
23
22
1 1 2
2
32
x x x x
x
x x x x

.
Lời giải:
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
BPT
2 2 3
2
1 2 2
0
32
x x x x x x x
x x x


2
2
2
0 3 2 0
32
x x x
x x x

01x
2x
.
Câu 11: Giải bất phương trình:
2 2 2
4 2 3 4 4 .x x x x x
Lời giải:
BPT
22
2
2 2 3 2x x x x
2
2
2 2 3 0x x x
2
2
2 3 0
x
xx

2 1 3xx
.
Câu 12: Giải hệ bất phương trình
2
2
4 3 0
.
6 8 0
xx
xx
Lời giải:
Ta có:
2
2
;1 3;
4 3 0
;1 4;
6 8 0
;2 4;
x
xx
x
xx
x
 
 

 
.
Câu 13: Tìm tập xác định của hàm số
2
1
3 2 .
3
y x x
x
Lời giải:
Hàm số xác định khi
2
1
31
3 2 0
2
2
30
3
x
x
xx
x
x
x
x




.
Câu 14: Giải hệ bất phương trình
2
2
2
4 3 0
2 10 0.
2 5 3 0
xx
xx
xx
Lời giải:
Ta có:
2
2
2
4 3 0
2 10 0
2 5 3 0
xx
xx
xx
3
1
5
2
2
1
3
2
x
x
x
x
x

11
35
22
x
x

.
Câu 15: Tìm các giá trị của tham số
m
để tam thức bậc hai
2
1 2 3x m x m
dương với mọi
.x
Lời giải:
Đặt
2
1 2 3f x x m x m
có hệ số
1 0.a
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Ta có
2
2
1 4 2 3 6 11. m m m m
Yêu cầu bài toán
0
0

a
2
6 11 0 3 2 5 3 2 5. m m m
Câu 16: Tìm các giá trị của tham số
m
để bất phương trình
2
2( 2) 2 1 0x m x m
nghiệm đúng
với mọi
.x
Lời giải:
Vì hệ số
10a 
, nên bất phương trình nghiệm đúng với mọi
x
khi và chi khi
2
( 2) (2 1) 0
mm
2
6 5 0 1 5. m m m
Câu 17: Tìm tất cả các giá trị của
m
để biểu thức
2
2 f x x x m
luôn âm.
Lời giải:
Ta có:
10
0, 1.
' 1 0
a
f x x m
m
Câu 18: Tìm tất cả các giá trị của tham số
m
để bất phương trình
22
3 2 1 2 3 2 0 x m x m m
nghiệm đúng
.x
Lời giải:
22
3x 2( 1) 2 3 2 0 m x m m x R
22
' ( 1) 3(2 3 2) 0m m m
2
7 7 7 0mm
bpt vô nghiệm.
Vậy không có m thỏa mãn yêu cầu bài toán.
Câu 19: Tìm tất cả các giá trị của
m
để hàm số
2
1
( 1) 2( 2) 2
fx
m x m x m
xác định với mọi
x
.
Lời giải:
2
( 1) 2( 2) 2 0, 1 m x m x m x
.
TH
1
:
1 0 1mm
2 1 0, xx
(Sai).
TH
2
:
1 0 1mm
.
Khi đó
2
2
1
10
1
3
1 2.
3
2
2 7 6 0
2
2 1 2 0
2
m
m
m
m
mm
m
m m m



Vậy
3
2
2
m
.
Câu 20: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2( 2) 2 1 0x m x m
vô nghiệm.
Lời giải:
BPT có vô nghiệm
2
2 2 2 1 0,x m x m x
2
2 2 1 0mm
2
6 5 0mm
<15m
.
Câu 21: Tìm
m
để mọi
1;1x



đều là nghiệm của bất phương trình
22
3 2 5 2 8 0.x m x m m
Lời giải:
Ta có
22
3 2 5 2 8 0 1 2x m x m m x m
hoặc
4
3
m
x
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
TH 1:
41
2 3 6 4
32
m
m m m m
Ta có, bất phương trình (1)
4
2.
3
m
xm
Vậy tập nghiệm của bất phương trình (1) là
4
;2
3
m
m



Suy ra mọi
1;1x



đều là nghiệm của bất phương trình (1)
khi và chỉ khi
4
1
4
1;1 ; 2
3
3
12
m
m
m
m







7
7
1
m
m
m

Kết hợp với điều kiện
1
2
m 
ta có
7m
thỏa mãn yêu cầu bài toán
TH 2:
41
2
32
m
mm
ta có
Bất phương trình (1)
4
2
3
m
mx
Vậy tập nghiệm của bất phương trình (1) là
4
2;
3
m
m



Suy ra mọi
1;1x



đều là nghiệm của bất phương trình (1)
khi và chỉ khi
12
4
1;1 2;
4
3
1
3
m
m
m
m





3
3
1
m
m
m

Kết hợp với điều kiện
1
2
m 
ta có
3m 
thỏa mãn yêu cầu bài toán
TH 3:
1
2
m 
ta có bất phương trình (1)
3
2
x
nên
1
2
m 
không thỏa mãn yêu cầu bài
toán.
Vậy
[( ; 3] 7; )m  
là giá trị cần tìm.
Câu 22: Tìm giá trị của tham số
m
để phương trình
2
( 3) ( 3) ( 1) 0m x m x m
có hai nghiệm
phân biệt.
Lời giải:
Phương trình có hai nghiệm phân biệt
2
30
( 3) 4( 3)( 1) 0

m
m m m
3
3 3 7 0
m
mm
7
3
3
m
.
Câu 23: Tìm tham số
m
để phương trình
2
2 3 2 3 0m x x m
có hai nghiệm trái dấu.
Lời giải:
Yêu cầu bài toán
2 2 3 0 mm
3
2
2
m
.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 24: Tìm m để phương trình
2
1 2 2 1 0m x m x m
có
2
nghiệm phân biệt khác
0
sao
cho
12
11
2
xx

.
Lời giải:
Phương trình có hai nghiệm phân biệt khác
0
khi
2
1
10
1
2 1 1 0 4 5 0
4
1
10
1
m
m
m
m m m m m
m
m
m





1
.
Theo định lí Viet:
12
12
22
1
.
1
1

m
xx
m
m
xx
m
Khi đó:
1 2 2 2
1 2 1 2
2
11
20
x x x x
x x x x

22
1
2
6
11
0 0 1
1
1
1

m
m
mm
m
m
m
m
2
.
Từ
1 ; 2 1m
.
Câu 25: Tìm
m
để phương trình
2
1 2 2 3 0m x m x m
có hai nghiệm phân biệt
12
,xx
thỏa
mãn
1 2 1 2
1.x x x x
Lời giải:
Phương trình có hai nghiệm phân biệt
12
,xx
khi
0 1 0
1
0 1 0,
am
m
m



(*)
Khi đó, theo định lý Vi-ét ta có:
12
12
22
1
3
1
m
xx
m
m
xx
m

1 2 1 2
22
3
11
11
m
m
x x x x
mm

22
3 1 2 6
0 0 1 3
1 1 1 1
m
m m m
m
m m m m
(thỏa (*)).
Vậy
13m
.
Câu 26: Cho hàm số
2
2 3 2 3y m x mx m
(m là tham số). Tìm các giá trị của tham số m để đồ thị
hàm số cắt trục hoành tại hai điểm phân biệt
,AB
sao cho gốc tọa độ
O
nằm giữa
A
và
B
.
Lời giải:
Phương trình hoành độ giao điểm là
2
2 3 2 3 0m x mx m
Điều kiện để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt
,AB
sao cho gốc tọa độ
O
nằm giữa
A
và
B
là
3
. 0 2 3 2 0 2
2
AB
x x m m m
.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 27: Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao
320m
với vận tốc ban đầu
0
20 /v m s
. Hỏi sau ít nhất bao nhiêu giây, vật đó cách mặt đất không quá
100m
? Giả thiết
rằng sức cản của không khí là không đáng kể.
Lời giải:
Với
2
10 /g m s
ta có phương trình chuyển động
2
5 20 320h t t t
. Vật cách mặt đất
không quá
100m
, tức là
2
100 5 20 320 0h t t t
.
Sử dụng MTCT ta được
2 4 3 2 2 17t
.
Câu 28: Một công ty đồ gia đụng sản xuất bình đựng nước thấy rằng khi đơn giá của binh đựng nước
là
x
nghìn đồng thì doanh thu
R
(tính theo đơn vị nghìn đồng) sẽ là
2
( ) 560 50000R x x x
.
a) Theo mô hình doanh thu này, thì đơn giá nào là quá cao dẫn đến doanh thu từ việc bán
bình đựng nước bằng 0 (tức là sē không có người mua)?
b) Với khoảng đơn giá nào của bình đựng nước thì doanh thu từ việc bán bình đựng nước
vượt mức 1 tỉ đồng?
Lời giải:
a) Theo mô hình doanh thu này, thì đơn giá quá cao dẫn đến doanh thu từ việc bán bình
đựng nước bằng 0 (tức là sē không có người mua) là giá trị
x
thỏa mãn
0Rx
2
0
560 50000 0
625
89,29 nghìn
7
x loai
xx
x


b) Với khoảng đơn giá của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt
mức 1 tỉ đồng là giá trị
x
thỏa mãn
1000000Rx
2
560 50.000 1.000.000 30,25 59,04. x x x
Câu 29: Xét đường tròn đường kính
4AB
và một điểm
M
di chuyển trên
đoạn
AB
, đặt
AM x
(Hình vẽ). Xét hai đường tròn đường kính
AM
và
MB
. Kí hiệu
Sx
là diện tích phần hình phẳng nằm trong
hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị
của
x
để diện tích
Sx
không vượt quá một nửa tổng diện tích hai
hình tròn nhỏ.
Lời giải:
Ta có
2
;
4
O AB
S AB
;
1
2
;
4
O AM
Sx
;
2
2
;
4
4
O MB
Sx

;
12
2
2 2 2
; ; ;
4 2 8
44

x
O AB O AM O MB
S S S S AB x x x x
12
2 2 2
;;
2
11
2 8 . 4
2 4 2 4
6 2 3
0
3
3 12 8 0 .
6 2 3
4
3



x
O AM O MB
S S S x x x x
x
xx
x
III. BÀI TẬP TRẮC NGHIỆM
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 1: Biểu thức nào dưới đây là tam thức bậc hai?
A.
1.y
B.
.yx
C.
2
.yx
D.
3
.yx
Câu 2: Với
m
là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai?
A.
.ym
B.
.y mx
C.
2
.y mx
D.
2
.y x m
Câu 3: Với
m
là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai?
A.
.ym
B.
.y mx
C.
22
1.y m x
D.
2
.y mx m
Câu 4: Tìm tất cả các giá trị của tham số
m
để biểu thức
2
2 5 9 f x m x x
là tam thức bậc hai.
A.
m
. B.
2m
. C.
2m
. D.
0m
.
Lời giải:
Biểu thức
2
2 5 9 f x m x x
là tam thức bậc hai khi:
20m
.
Suy ra
2m
.
Chọn đáp án C.
Câu 5: Cho hàm số bậc hai
y f x
có đồ thị như hình bên dưới:
x
y
2
-1
O
1
Khẳng đinh nào dưới đây đúng?
A.
0, 0;2 .f x x
B.
0, 0;2 .f x x
C.
0, 1; .f x x 
D.
0, 0;2 .f x x


Câu 6: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
4

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Lời giải:
Kiểm tra các sự kiện:
0a
và tam thức có hai nghiệm
0, 4.xx
Chọn đáp án C.
Câu 7: Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ?
x

0
2

fx
0
0
A.
2
2.y x x
B.
2
2.y x x
C.
2
4.y x x
D.
2
4.y x x
Lời giải:
Kiểm tra các sự kiện:
0a
và tam thức có hai nghiệm
0, 2.xx
Chọn đáp án B.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 8: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây đúng?
A.
0, 1;2 .f x x
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x  
D.
0, 1;2 .f x x


Lời giải:
Bảng xét dấu:
x

1
2

fx
0
0
Chọn đáp án B.
Câu 9: Cho tam thức
2
3 2.f x x x
Khẳng định nào dưới đây sai?
A.
0, ;1 2; .f x x  
B.
0, 1;2 .f x x
C.
0, ;1 2; .f x x

 

D.
0, 1;2 .f x x


Lời giải:
Bảng xét dấu:
x

1
2

fx
0
0
Chọn đáp án B.
Câu 10: Tập hợp tất cả các giá trị của
x
để tam thức
2
2y x x
luôn âm là
A.
0;2 .
B.
;0 2; . 
C.
0;2 .


D.
;0 2; .

 

Lời giải:
Bảng xét dấu:
x

0
2

y
0
0
Chọn đáp án B.
Câu 11: Tập hợp tất cả các giá trị của
x
để tam thức
2
2f x x x
luôn dương là
A.
0;2 .
B.
;0 2; . 
C.
0;2 .


D.
;0 2; .

 

Lời giải:
Bảng xét dấu:
x

0
2

fx
0
0
Chọn đáp án B.
Câu 12: Tam thức nào dưới đây luôn âm với mọi
?x
A.
2
1.y x x
B.
2
1.y x x
C.
2
1.y x x
D.
2
4.y x x
Lời giải:
Bảng xét dấu
2
1:y x x
x


y
Chọn đáp án C.
Câu 13: Tam thức nào dưới đây luôn dương với mọi
?x
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
2
1.y x x
B.
2
2 1.y x x
C.
2
1.y x x
D.
2
4.y x x
Lời giải:
Bảng xét dấu
2
1:y x x
x


y
Chọn đáp án A.
Câu 14: Một nghiệm của bất phương trình
2
2 3 0xx
là
A.
5.x
B.
0.x
C.
2.x 
D.
4.x
Câu 15: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Lời giải:
Bảng xét dấu
2
2 3 :f x x x
x

1
3

fx
0
0
Chọn đáp án B.
Câu 16: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Lời giải:
Bảng xét dấu
2
2 3 :f x x x
x

1
3

fx
0
0
Chọn đáp án D.
Câu 17: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
1;3 .


B.
; 1 3; . 
C.
1;3 .
D.
; 1 3; .

 

Lời giải:
Bảng xét dấu
2
2 3 :f x x x
x

1
3

fx
0
0
Chọn đáp án A.
Câu 18: Tập nghiệm của bất phương trình
2
2 3 0xx
là
A.
.
B. C.
1;3 .
D.
; 1 3; .

 

Lời giải:
Bảng xét dấu
2
2 3 :f x x x
x


fx
Chọn đáp án B.
Câu 19: Tập nghiệm của bất phương trình
2
30xx
là
A.
.
B. C.
1;3 .
D.
; 1 3; .

 

Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Lời giải:
Bảng xét dấu
2
3:f x x x
x


fx
Chọn đáp án B.
Câu 20: Tập nghiệm của bất phương trình
2
30xx
là
A.
.
B. C.
1;3 .
D.
; 1 3; .

 

Lời giải:
Bảng xét dấu
2
3:f x x x
x


fx
Chọn đáp án A.
Câu 21: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1;3 .
D.
\ 1 .
Lời giải:
Bảng xét dấu
2
2 1:f x x x
x

1

y
0
Chọn đáp án B.
Câu 22: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Lời giải:
Bảng xét dấu
2
2 1:f x x x
x

1

y
0
Chọn đáp án D.
Câu 23: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Lời giải:
Bảng xét dấu
2
2 1:f x x x
x

1

y
0
Chọn đáp án A.
Câu 24: Tập nghiệm của bất phương trình
2
2 1 0xx
là
A.
.
B. C.
1.
D.
\ 1 .
Lời giải:
Bảng xét dấu
2
2 1:f x x x
x

1

Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
y
0
Chọn đáp án C.
Câu 25: Bất phương trình
2
3 4 0xx
có tất cả bao nhiêu nghiệm nguyên dương?
A.
6
. B.
5
. C.
4
. D.
2
.
Lời giải:
Đặt
2
34f x x x
. Xét
4
0
1
x
fx
x


Bảng xét dấu:
Từ bảng xét dấu,
0 1;4 . f x x
Vậy bất phương trình
2
3 4 0xx
có
4
nghiệm nguyên dương.
Chọn đáp án C.
Câu 26: Bất phương trình nào dưới đây có nghiệm?
A.
2
2 1 0.xx
B.
2
2 3 0.xx
C.
2
3 4 0.xx
D.
2
2 0.xx
Lời giải:
Ta có:
2
2 0 0;2 .x x x


Chọn đáp án D.
Câu 27: Bất phương trình nào dưới đây có nghiệm?
A.
2
2 1 0.xx
B.
2
2 3 0.xx
C.
2
3 4 0.xx
D.
2
2 1 0.xx
Lời giải:
Ta có:
2
2 1 0 1.x x x
Chọn đáp án D.
Câu 28: Bất phương trình nào dưới đây vô nghiệm?
A.
2
2 0.xx
B.
2
2 3 0.xx
C.
2
4 0.x 
D.
2
0.x
Lời giải:
Ta có:
2
2 3 0,x x x
nên bất phương trình
2
2 3 0xx
vô nghiệm.
Chọn đáp án B.
Câu 29: Bất phương trình nào sau đây vô nghiệm?
A.
2
0x
. B.
2
0x
. C.
2
0x
. D.
2
0x
.
Câu 30: Tập xác định của hàm số
2
4yx
là
A.
2; 2 .
B.
; 2 2; . 
C.
2; 2 .


D.
; 2 2; .

 

Lời giải:
Hàm số xác định
2
4 0 ; 2 2; .xx

 

Vậy tập xác định của hàm số là
; 2 2; .D

 

Chọn đáp án D.
Câu 31: Tập xác định của hàm số
2
27
4
x
y
x
là
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
2; 2 .
B.
; 2 2; . 
C.
2; 2 .


D.
; 2 2; .

 

Lời giải:
Hàm số xác định
2
4 0 ; 2 2; .xx  
Vậy tập xác định của hàm số là
; 2 2; .D  
Chọn đáp án B.
Câu 32: Tập xác định của hàm số
2
1 2 9y x x
là
A.
1;3 .


B.
1; .

C.
3;3 .


D.
3; .

Lời giải:
Hàm số xác định
2
3;3
90
1;3 .
10
1
x
x
x
x
x









Vậy tập xác định của hàm số là
1;3 .D


Chọn đáp án A.
Câu 33: Tập xác định của hàm số
2
9
1 4 10
x
y
xx
là
A.
1;2 .


B.
2; .

C.
1;9 .


D.
1;2 .
Lời giải:
Hàm số xác định
2
9 0 9
1 0 1 1;2 .
2;2
40
xx
x x x
x
x








Vậy tập xác định của hàm số là
1;2 .D


Chọn đáp án A.
Câu 34: Tập nghiệm của bất phương trình
22
3 4 0x x x
là
A.
2; 2 .


B.
; 2 2; .

 

C.
2; 2 .
D.
; 2 2; . 
Lời giải:
Đặt
22
3 4 .M x x x
Ta có:
+)
2
30xx
(vô nghiệm)
+)
2
2
4 0 .
2
x
x
x

Bảng xét dấu biểu thức
:M
x

2
2

2
3xx
2
4x
0
0
M
0
0
Chọn đáp án D.
Câu 35: Tập nghiệm của bất phương trình
22
2 4 2 0x x x x
là
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
0;2 .


B.
;0 2; .

 

C.
0;2 .
D.
;0 2; . 
Lời giải:
Đặt
22
2 4 2 .M x x x x
Ta có:
+)
2
2 4 0xx
(vô nghiệm)
+)
2
0
2 0 .
2
x
xx
x
Bảng xét dấu biểu thức
:M
x

0
2

2
24xx
2
2xx
0
0
M
0
0
Chọn đáp án B.
Câu 36: Số nghiệm nguyên của bất phương trình
22
2 9 0x x x
là
A. Vô số. B.
0.
C.
5.
D.
7.
Lời giải:
Đặt
22
2 9 .M x x x
Ta có:
+)
2
0
2 0 .
2
x
xx
x
+)
2
3
9 0 .
3
x
x
x

Bảng xét dấu biểu thức
:M
x

3
0
2
3

2
2xx
0
0
0
2
9x
0
0
M
0
0
0
0
Vậy tập nghiệm của bất phương trình đã cho là
3;0 2;3 3; 2; 1;0;2;3 .
x
Sx

Chọn đáp án D.
Câu 37: Số nghiệm nguyên của bất phương trình
2
2
43
0
16
xx
x

là
A. Vô số. B.
0.
C.
6.
D.
8.
Lời giải:
Đặt
2
2
43
.
16
xx
M
x

Ta có:
+)
2
1
4 3 0 .
3
x
xx
x
+)
2
4
16 0 .
4
x
x
x

Bảng xét dấu biểu thức
:M
x

4
1
3
4

2
2xx
0
0
0
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
2
9x
0
0
M
0
0
Vậy tập nghiệm của bất phương trình đã cho là
4;1 3;4 3; 2; 1;0;1;3 .
x
Sx



Chọn đáp án C.
Câu 38: Cho biểu thức
2
6
.
12
xx
fx
x

Khoảng nào dưới đây của
x
thì
0fx
?
A.
3
;2
4



. B.
1
2;
2



. C.
3;
. D.
2;3
.
Lời giải:
Xét
2
3
60
2
x
xx
x

Xét
1
1 2 0
2
xx
.
Bảng xét dấu:
Từ bảng xét dấu,
1
0 ; 2 ;3
2
f x x




Chọn đáp án A.
Câu 39: Với
x
thuộc tập hợp nào sau đây thì
12
21
xx
fx
xx



không âm?
A.
1
2;
2



. B.
2; 
. C.
1
2; 2;
2




.D.
1
; 2 ;1
2



.
Lời giải:
12
21
xx
fx
xx



22
2 1 4 4
21
x x x x
xx

63
21
x
xx


.
Suy ra
1
;
2
0 ; 2 1f x x

 
.
Chọn đáp án D.
Câu 40: Có bao nhiêu số nguyên thỏa mãn bất phương trình
2
1
2
x
x
x

?
A.
4
. B.
5
. C.
3
. D.
2
.
Lời giải:
Điều kiện:
2x
.
Ta có
2
2
21
2
1 0 0 2 2
2 2 2
x x x
xx
xx
x x x
.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Vậy có 4 số nguyên thỏa mãn bất phương trình đã cho.
Chọn đáp án A.
Câu 41: Biết tập nghiệm của bất phương trình
2
34
1
21
xx
x
x


là
;;S a b c 
, giá trị của
2a b c
là
A.
1
. B.
3
. C.
2
. D.
3
.
Lời giải:
Điều kiện:
1
2 1 0 .
2
xx
Ta có:
22
3 4 3 4
1 1 0
2 1 2 1
x x x x
xx
xx

2
2
3 4 1 2 1
45
0 0 1
2 1 2 1
x x x x
xx
xx

Xét dấu:
Từ bảng xét dấu, suy ra tập nghiệm
1
; 5 ;1
2
S



1
5; ; 1 2 3
2
a b c a b c
.
Chọn đáp án D.
Câu 42: Tìm tập nghiệm của hệ bất phương trình
2
2
2 6 0
3 10 3 0
xx
xx
.
A.
3
; 2 ;
2




. B.
; 2 3;
. C.
1
; 3;
3




. D.
2;3
.
Lời giải:
Ta có
2
2
3
2
2 6 0 2
2
1
3
3 10 3 0
3
3
xx
x x x
x
xx
xx



.
Chọn đáp án B.
Câu 43: Cho tam thức bậc hai
2
f x ax bx c
0a
có
2
40 b ac
. Mệnh đề nào sau đây
đúng?
A.
fx
luôn cùng dấu với hệ số
b
với mọi
x
.
B.
fx
luôn cùng dấu với hệ số
a
với mọi
x
.
C.
fx
luôn cùng dấu với hệ số
a
với mọi
2
b
x
a
.
D.
fx
luôn trái dấu với hệ số
a
với mọi
x
.
Câu 44: Cho
2
,0f x ax bx c a
và
2
4b ac
. Tìm điều kiện
để
fx
cùng dấu với hệ
số
a
với mọi
x
.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
0
. B.
0
. C.
0
. D.
0
.
Câu 45: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Mệnh đề nào dưới
đây đúng?
A.
0
0, .
0
a
f x x

B.
0
0, .
0
a
f x x

C.
0
0, .
0
a
f x x

D.
0
0, .
0
a
f x x

Câu 46: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Mệnh đề nào dưới
đây đúng?
A.
0
0, .
0
a
f x x

B.
0
0, .
0
a
f x x

C.
0
0, .
0
a
f x x

D.
0
0, .
0
a
f x x

Câu 47: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Điều kiện cần và đủ
để
0,f x x
là
A.
0
.
0
a

B.
0
.
0
a

C.
0
.
0
a

D.
0
.
0
a

Câu 48: Cho tam thức bậc hai
2
, ; ; , 0f x ax bx c a b c a
với
2
4.b ac
Điều kiện cần và đủ
để
0,f x x
là
A.
0
.
0
a

B.
0
.
0
a

C.
0
.
0
a

D.
0
.
0
a

Câu 49: Tập hợp tất cả các giá trị của tham số
m
để phương trình
2
0x mx m
có hai nghiệm phân
biệt là
A.
;0 4; . 
B.
0;4 .
C.
;0 4; .

 

D.
0;4 .


Lời giải:
Yêu cầu bài toán
2
4 0 ;0 4; .m m m  
Chọn đáp án A.
Câu 50: Điều kiện cần và đủ của tham số
m
để tam thức
2
2 4 1 f x x m x m
đổi dấu hai lần
là
A.
0 12m
. B.
0m
hoặc
12m
C.
0m
hoặc
12m
D.
0m
.
Lời giải:
Để tam thức
2
2 4 1 f x x m x m
đổi dấu hai lần thì
0
2
2
0
2 4 4 1 0 12 0
12
m
m m m m
m
.
Chọn đáp án B.
Câu 51: Với giá trị nào của tham số
m
thì phương trình
2
2 4 0mx mx
vô nghiệm?
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
A.
04m
. B.
0
4
m
m
. C.
04m
. D.
04m
.
Lời giải:
TH:
0m
Phương trình cho trở thành
2
0 0 4 0xx
(vô nghiệm). Nhận
0m
.
TH:
0m
Để phương trình cho vô nghiệm thì
2
4 0 0 4m m m
.
Hợp 2 trường hợp, ta được
04m
.
Chọn đáp án D.
Câu 52: Tập hợp tất cả các giá trị của tham số
m
để phương trình
22
10x mx m
có hai nghiệm
trái dấu là
A.
; 1 1; . 
B.
1;1 .
C.
; 1 1; .

 

D.
1;1 .


Lời giải:
Yêu cầu bài toán
2
1 1 0 1;1 .mm
Chọn đáp án B.
Câu 53: Cho tam thức bậc hai
2
2.f x x mx m
Tập hợp tất cả các giá trị của tham số
m
để
0,f x x
là
A.
;0 1; . 
B.
0;1 .
C.
;0 1; .

 

D.
0;1 .


Lời giải:
Yêu cầu bài toán
2
0
0 0;1 .
0
a
m m m

Chọn đáp án B.
Câu 54: Cho tam thức bậc hai
22
2 2 .f x x mx m m
Tập hợp tất cả các giá trị của tham số
m
để
0,f x x
là
A.
;0 1; . 
B.
0;1 .
C.
;0 1; .

 

D.
0;1 .


Lời giải:
Yêu cầu bài toán
2
0
0 ;0 1; .
0
a
m m m

 


Chọn đáp án C.
Câu 55: Cho
2
2 4.f x mx mx
Tập hợp tất cả các giá trị của tham số
m
để
0,f x x
là
A.
;0 4; . 
B.
0;4 .
C.
;0 4; .

 

D.
0;4 .
Lời giải:
TH 1:
0 : 4 0,m f x x
(đúng)
0m
thỏa mãn.
TH 2: Yêu cầu bài toán
2
0
0
0;4 .
0
40
m
a
m
mm



Vậy
0;4 .m
Chọn đáp án D.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 56: Tập hợp tất cả các giá trị của tham số
m
để hàm số
22
45y x x m m
xác định trên là
A.
;1 4; . 
B.
1;4 .
C.
1;4 .


D.
1;1 .


Lời giải:
Yêu cầu bài toán
22
4 5 0,x x m m x
22
0
4 5 0 5 4 0 1;4 .
0
a
m m m m m



Chọn đáp án C.
Câu 57: Tập hợp tất cả các giá trị của tham số
m
để hàm số
22
47
45
x
y
x x m m
xác định trên là
A.
;1 4; . 
B.
1;4 .
C.
1;4 .


D.
1;1 .


Lời giải:
Yêu cầu bài toán
22
4 5 0,x x m m x
22
0
4 5 0 5 4 0 1;4 .
0
a
m m m m m

Chọn đáp án B.
Câu 58: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2 8 1 0x m x m
vô
nghiệm.
A.
0;28m
. B.
0;28m
.
C.
;0 28;m  
. D.
;0 28;m  
.
Lời giải:
Bất phương trình
2
2 8 1 0x m x m
vô nghiệm
2
2 8 1 0,x m x m x
.
Điều kiện:
2
2
0
0 2 4 8 1 0 28 0
28
m
m m m m
m
.
Chọn đáp án C.
Câu 59: Tìm số giá trị nguyên của m để bất phương trình
2
2 3 2 0 x mx m
vô nghiệm.
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải:
Yêu cầu bài toán
2
2
10
2mx 3 2 0, 1 2.
' 3 2 0

a
x m x m
mm
Do đó không có giá trị nguyên nào của m thỏa mãn điều kiện bài ra.
Chọn đáp án A.
Câu 60: Tìm tất cả các giá trị của tham số
m
để hệ bất phương trình
2
5 4 0
0
xx
xm

có nghiệm.
A.
1m
. B.
14m
. C.
4m
. D.
4m
.
Lời giải:
2
1;4
5 4 0
0
;
x
xx
xm
xm



.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Hệ đã cho có nghiệm khi
1;4 ; 4mm 
.
Chọn đáp án D.
Câu 61: Giá trị của tham số
m
để hệ bất phương trình
2
40
42


x
mx
vô nghiệm là
A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Lời giải:
+ Xét bất phương trình
1
:
2
40x
.
Ta có:
2
40x
2x
22 x
.
Vậy bất phương trình
1
có tập nghiệm là
1
2;2S
.
+) Xét bất phương trình
2
:
42mx
.
Ta có
42mx
4
2

m
x
.
Vậy bất phương trình
2
có tập nghiệm là
2
4
;
2


m
S
.
+) Hệ bất phương trình
2
40
42


x
mx
vô nghiệm khi và chỉ khi:
12
SS
4
2
2

m
0m
.
Chọn đáp án B.
Câu 62: Cho biểu thức
2
2 1 2 3f x x m x m
. Tìm điều kiện của tham số
m
để
0fx
thỏa
mãn với mọi
1;2x
.
A.
2m
. B.
m
. C.
1m
. D.
2m
.
Lời giải:
Xét biểu thức
2
2 1 2 3f x x m x m
là tam thức bậc hai
22
1 2 3 2 0,m m m m
Nếu
0 2 0m f x
với mọi
x
2m
không thỏa mãn bài toán.
Nếu
20m
tam thức bậc hai có hai nghiệm phân biệt
1 2 1 2
,x x x x
.
Khi đó:
12
12
22
. 2 3
x x m
x x m

và
12
0, 1;2 1;2 ;f x x x x
12
12
12
1 1 0
12
2 2 0
xx
xx
xx
1 2 1 2
1 2 1 2
10
2 4 0
x x x x
x x x x
1
2 3 2 2 1 0
5
2 3 2 2 2 4 0
2
m
mm
m
m
mm


Vậy không có giá trị tham số
m
thỏa mãn bài toán.
Chọn đáp án B.
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Câu 63: Có tất cả bao nhiêu giá trị nguyên của tham số
0;2022m
để
2;4x
đều là nghiệm bất
phương trình
2
1 0? x m x m
A. 2022. B. 2021. C. 2020. D. 2019.
Lời giải:
2
1 0 1 0 x m x m x x m
(*)
Trường hợp 1:
1m
. Khi đó (*) trở thành:
1 1 0 xx
2
10 x
1x
Do đó
1m
không thỏa mãn
Trường hợp 2:
1m
. Khi đó (*)
1 xm
Yêu cầu bài toán thỏa mãn khi
4m
. Kết hợp với điều kiện
1m
ta có
4m
Trường hợp 3:
1m
. Khi đó (*)
1 mx
Không có giá trị
m
thỏa mãn bởi vì
2;4 ;1 m
Vậy
4m
là điều kiện cần tìm. Mặt khác
0;2022
m
m
nên
4;5;6;...;2022m
.
Do đó có
2019
giá trị nguyên của
m
.
Chọn đáp án D.
Câu 64: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2
2
11
0
25
x m x
xx

nghiệm đúng với mọi
x
?
A. 3. B. 5. C. 2. D. 1.
Lời giải:
Ta có:
2
2
2 5 1 4 0,x x x x
Do đó:
2
2
11
0,
25
x m x
x
xx

2
1 1 0,x m x x
2
10
1 4.1.1 0m
2
2 3 0mm
31m
.
Vậy có 5 giá trị nguyên thỏa mãn bài toán là
3; 2; 1;0;1m
.
Chọn đáp án B.
_____________________HẾT_____________________
Huế, 15h30’ Ngày 28 tháng 01 năm 2023

Tài liệu khác của Toán 10

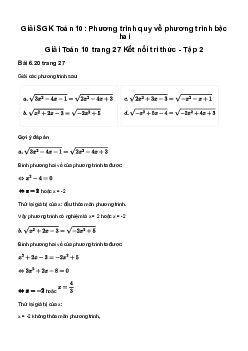
Preview text:

Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Chủ đề:
DẤU TAM THỨC BẬC HAI I. TÓM TẮT LÝ THUYẾT 1. Tam thức bậc hai
Tam thức bậc hai (đối với x ) là biểu thức có dạng 2
ax bx c trong đó a, b, c là những số
thực cho trước (với a  0 ), được gọi là các hệ số của tam thức bậc hai. Chú ý:
+) Nghiệm của phương trình bậc hai 2
ax bx c  0 cũng được gọi là nghiệm của tam thức bậc hai 2
ax bx c . +) 2
  b  4ac và 2
  b  ac , với b  2b tương ứng được gọi là biệt thức và biệt thức thu gọn
của tam thức bậc hai 2
ax bx c .
2. Định lý về dấu tam thức bậc hai
Cho tam thức bậc hai   2
f x ax bx c (với a  0 ).
+) Nếu   0 thì f x cùng dấu với hệ số a với mọi x  . bb
+) Nếu   0 thì f x cùng dấu với hệ số a với mọi x   và f   0.   2a  2a
+) Nếu   0 thì tam thức f x có hai nghiệm phân biệt x và x x x . Khi đó , f x 1 2  1 2
cùng dấu với hệ số a với mọi x   ;
 x x ; ; f x trái dấu với hệ số a với mọi 1   2 
x   x ; x . 1 2 
Chú ý. Trong định lí về dấu tam thức bậc hai có thể thay bởi  .
3. Bất phương trình bậc hai
+) Bất phương trình bậc hai ẩn x là bất phương trình có dạng 2
ax bx c  0 (hoặc 2
ax bx c  0 , 2
ax bx c  0 , 2
ax bx c  0 ), trong đó a, b, c là những số thực đã cho và a  0 .
+) Số thực x gọi là một nghiệm của bất phương trình bậc hai 2
ax bx c  0 , nếu 0 2
ax bx c  0 . Tập hợp gồm tất cả các nghiệm của bất phương trình bậc hai 2
ax bx c  0 0 0
gọi là tập nghiệm của bất phương trình này.
+) Giải bất phương trình bậc hai 2
f (x)  ax bx c  0 là tìm tập nghiệm của nó, tức là tìm
các khoảng mà trong đó f (x) cùng dấu với hệ số a (nếu a  0 ) hay trái dấu với hệ số a (nếu a  0 ).
Để giải bất phương trình bậc hai 2
ax bx c  0 (hoặc 2
ax bx c  0 , 2
ax bx c  0 , 2
ax bx c  0 ) ta cần xét dấu tam thức 2
ax bx c , từ đó suy ra tập nghiệm. II. BÀI TẬP TỰ LUẬN Câu 1:
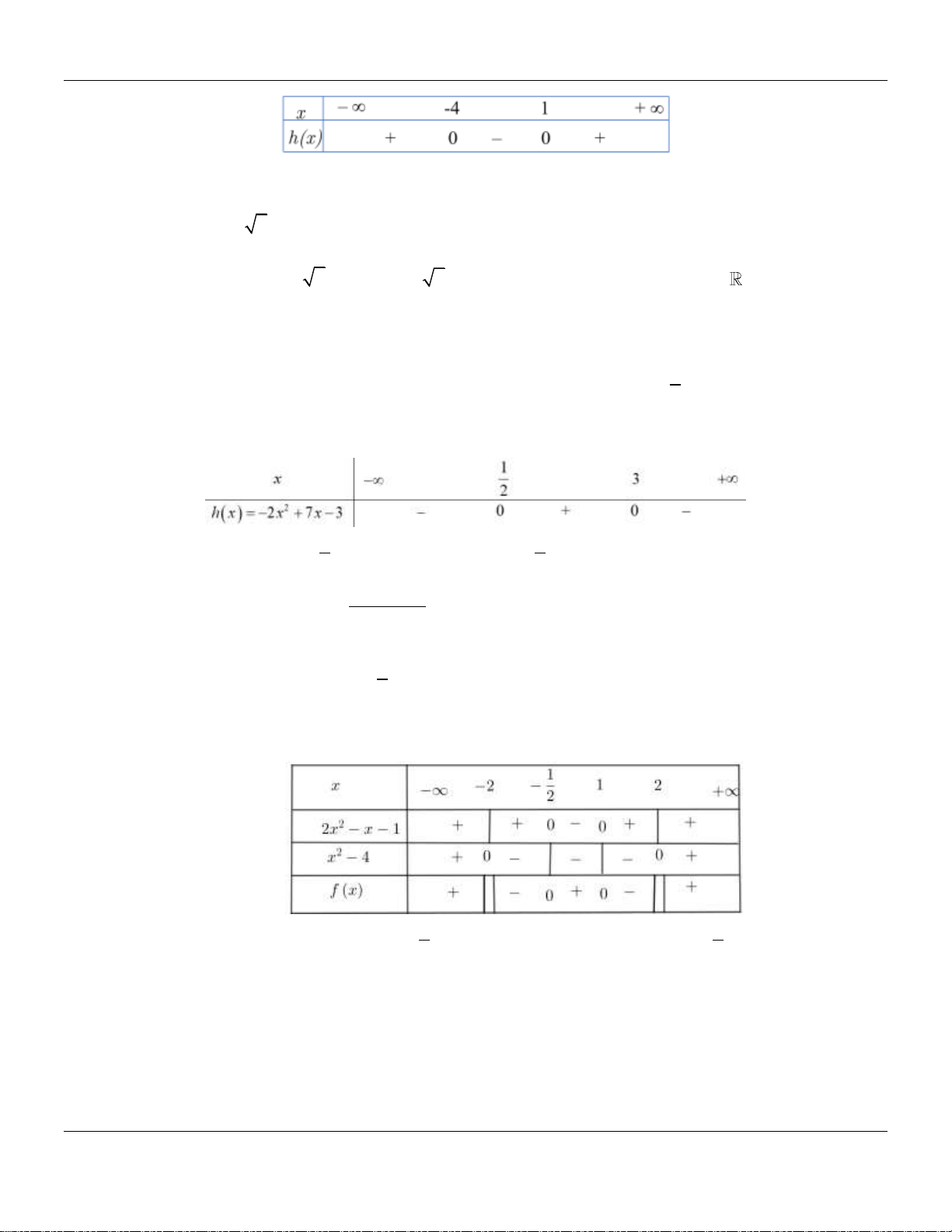
Xét dấu các tam thức bậc hai sau: 3 a) 2 x x 1; b) 2 x 9x 27; c) 2 2x 6x 8 . 2 Câu 2:
Xét dấu các tam thức bậc hai sau: a) 2 3
x x  2; b) 2 x  8x 16; c) 2
2x  7x  3. 2x x 1 Câu 3:
Xét dấu biểu thức f x 2  . 2 x  4
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT Câu 4:
Tìm tất cả các giá trị của x để biểu thức f x   2 x x  2 3
x  6x  9 nhận giá trị dương x x  6 Câu 5:
Xét dấu biểu thức Px 2  x  . 2
x  3x  4 Câu 6:
Giải các bất phương trình sau: a) 2
3x x  5  0; b) 2 3
x  2 3x 1  0; c) 2
x  2x 1  0. Câu 7:
Giải các bất phương trình bậc hai sau: a) 2 x 1  0; b) 2
x  2x 1  0; c) 2 3
x 12x 1  0; d) 2
5x x 1  0. Câu 8:
Tìm tập xác định của hàm số 2
y x  2x  5. 2 Câu 9:
Giải bất phương trình  2
x x   2
3 x x  2  0. 2 3 x x  1 1 x  2x
Câu 10: Giải bất phương trình :   . 2 2 x  2 x x x  3x  2
Câu 11: Giải bất phương trình:  2 x   2
x x   2 4 2
3 x  4x  4. 2
x  4x  3  0
Câu 12: Giải hệ bất phương trình  . 2
x  6x  8  0
Câu 13: Tìm tập xác định của hàm số 2 1
y x  3x  2  . x  3 2
x  4x  3  0 
Câu 14: Giải hệ bất phương trình 2
2x x 10  0.  2
2x  5x  3  0
Câu 15: Tìm các giá trị của tham số m để tam thức bậc hai 2
x  m  
1 x  2m  3 dương với mọi x  .
Câu 16: Tìm các giá trị của tham số m để bất phương trình 2
x  2(m  2)x  2m 1  0 nghiệm đúng với mọi x  .
Câu 17: Tìm tất cả các giá trị của m để biểu thức f x 2
 x  2x m luôn âm.
Câu 18: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  m   2 3 2
1 x  2m  3m  2  0
nghiệm đúng x  . 1
Câu 19: Tìm tất cả các giá trị của m để hàm số f x  xác định với mọi 2
(m  1)x  2(m  2)x  2  m x  .
Câu 20: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  2(m  2)x  2m  1  0 vô nghiệm.
Câu 21: Tìm m để mọi x   1  ;1 
 đều là nghiệm của bất phương trình 2
x  m   2 3 2
5 x m  2m  8  0.
Câu 22: Tìm giá trị của tham số m để phương trình 2
(m  3)x  (m  3)x  (m 1)  0 có hai nghiệm phân biệt.
Câu 23: Tìm tham số m để phương trình m   2
2 x  3x  2m  3  0 có hai nghiệm trái dấu.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Câu 24: Tìm m để phương trình m   2
1 x  2m  2 x m  1  0 có 2 nghiệm phân biệt khác 0 sao 1 1 cho   2 . x x 1 2
Câu 25: Tìm m để phương trình m   2
1 x  2m  2 x m  3  0 có hai nghiệm phân biệt x ,x thỏa 1 2
mãn x x x x  1. 1 2 1 2
Câu 26: Cho hàm số y  m   2
2 x  3mx  2m  3 (m là tham số). Tìm các giá trị của tham số m để đồ thị
hàm số cắt trục hoành tại hai điểm phân biệt A, B sao cho gốc tọa độ O nằm giữa A và B .
Câu 27: Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m với vận tốc ban đầu
v  20 m / s . Hỏi sau ít nhất bao nhiêu giây, vật đó cách mặt đất không quá 100 m ? Giả thiết 0
rằng sức cản của không khí là không đáng kể.
Câu 28: Một công ty đồ gia đụng sản xuất bình đựng nước thấy rằng khi đơn giá của binh đựng nước
là x nghìn đồng thì doanh thu R (tính theo đơn vị nghìn đồng) sẽ là 2 R(x)  560  x  50000x .
a) Theo mô hình doanh thu này, thì đơn giá nào là quá cao dẫn đến doanh thu từ việc bán
bình đựng nước bằng 0 (tức là sē không có người mua)?
b) Với khoảng đơn giá nào của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt mức 1 tỉ đồng?
Câu 29: Xét đường tròn đường kính AB  4 và một điểm M di chuyển trên đoạn
AB , đặt AM x (Hình vẽ). Xét hai đường tròn đường kính AM và MB .
Kí hiệu S x là diện tích phần hình phẳng nằm trong hình tròn lớn và
nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S x
không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
III. BÀI TẬP TRẮC NGHIỆM Câu 1:
Biểu thức nào dưới đây là tam thức bậc hai? A. y  1. B. y  . x C. 2 y x . D. 3 y x . Câu 2:
Với m là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai? A. y  . m
B. y m . x C. 2 y mx . D. 2 y x  . m Câu 3:
Với m là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai? A. y  . m
B. y m . x C. y   2 m   2 1 x . D. 2 y mx  . m Câu 4:
Tìm tất cả các giá trị của tham số m để biểu thức f x  m   2
2 x  5x  9 là tam thức bậc hai. A. m  .
B. m  2 .
C. m  2 . D. m  0 . Câu 5:
Cho hàm số bậc hai y f x có đồ thị như hình bên dưới: y 1 2 x O -1
Khẳng đinh nào dưới đây đúng?
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
A. f x  0, x  0;2.
B. f x  0, x  0;2.
C. f x  0, x  1;.
D. f x  0, x   0;2.   Câu 6:
Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 4  f x  0  0  A. 2 y x  2 . x B. 2 y x  2 . x C. 2 y x  4 . x D. 2
y  x  4 . x Câu 7:
Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 2  f x  0  0  A. 2 y x  2 . x B. 2
y  x  2 . x C. 2 y x  4 . x D. 2 y x  4 . x Câu 8:
Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây đúng?
A. f x  0, x  1;2.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;.
D. f x  0, x   1  ;2.   Câu 9:
Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây sai?
A. f x  0, x
 ;1 2;.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;   .
D. f x  0, x   1  ;2.  
Câu 10: Tập hợp tất cả các giá trị của x để tam thức 2
y  x  2x luôn âm là A. 0; 2.
B. ;0  2; . C. 0; 2.  
D. ;0  2;    .
Câu 11: Tập hợp tất cả các giá trị của x để tam thức f x 2
x  2x luôn dương là A. 0; 2.
B. ;0  2; . C. 0; 2.  
D. ;0  2;    .
Câu 12: Tam thức nào dưới đây luôn âm với mọi x  ? A. 2
y x x  1. B. 2
y  x x  1. C. 2
y  x x  1. D. 2
y  x  4 . x
Câu 13: Tam thức nào dưới đây luôn dương với mọi x  ? A. 2
y x x  1. B. 2
y x  2x  1. C. 2
y  x x  1. D. 2
y  x  4 . x
Câu 14: Một nghiệm của bất phương trình 2
x  2x  3  0 là A. x  5. B. x  0. C. x  2. D. x  4.
Câu 15: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   .
Câu 16: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   .
Câu 17: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   .
Câu 18: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. .  B. C. 1; 3. D. ; 1    3;   .
Câu 19: Tập nghiệm của bất phương trình 2
x x  3  0 là A. .  B. C. 1; 3. D. ; 1    3;   .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Câu 20: Tập nghiệm của bất phương trình 2
x x  3  0 là A. .  B. C. 1; 3. D. ; 1    3;   .
Câu 21: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C. 1; 3. D.  \  1 .
Câu 22: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 .
Câu 23: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 .
Câu 24: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 .
Câu 25: Bất phương trình 2
x  3x  4  0 có tất cả bao nhiêu nghiệm nguyên dương? A. 6 . B. 5 . C. 4 . D. 2 .
Câu 26: Bất phương trình nào dưới đây có nghiệm? A. 2
x  2x  1  0. B. 2
x  2x  3  0. C. 2
x  3x  4  0. D. 2 x  2x  0.
Câu 27: Bất phương trình nào dưới đây có nghiệm? A. 2
x  2x  1  0. B. 2
x  2x  3  0. C. 2
x  3x  4  0. D. 2
x  2x  1  0.
Câu 28: Bất phương trình nào dưới đây vô nghiệm? A. 2 x  2x  0. B. 2
x  2x  3  0. C. 2 x  4  0. D. 2 x  0.
Câu 29: Bất phương trình nào sau đây vô nghiệm? A. 2 x  0 . B. 2 x  0 . C. 2 x  0 . D. 2 x  0 .
Câu 30: Tập xác định của hàm số 2
y x  4 là A. 2; 2. B. ; 2
  2;. C. 2;2.   D. ; 2    2;   . 2x  7
Câu 31: Tập xác định của hàm số y  là 2 4  x A. 2; 2. B. ; 2
  2;. C. 2;2.   D. ; 2    2;   .
Câu 32: Tập xác định của hàm số 2
y x  1  2 9  x là A. 1  ;3.   B. 1;   . C. 3; 3.   D. 3;   . 9  x
Câu 33: Tập xác định của hàm số y  là 2
x  1  4  x  10 A. 1  ;2.   B. 2;   . C. 1  ;9.   D. 1  ;2  .
Câu 34: Tập nghiệm của bất phương trình  2
x x   2 3 x  4  0 là A. 2; 2.   B. ; 2    2;   . C. 2;2. D. ; 2   2;.
Câu 35: Tập nghiệm của bất phương trình  2
x x   2 2
4 x  2x  0 là A. 0; 2.  
B. ;0  2;    . C. 0;2.
D. ;0  2; .
Câu 36: Số nghiệm nguyên của bất phương trình  2 x x 2 2 x  9  0 là A. Vô số. B. 0. C. 5. D. 7.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT 2 x  4x  3
Câu 37: Số nghiệm nguyên của bất phương trình  0 là 2 x  16 A. Vô số. B. 0. C. 6. D. 8. x x
Câu 38: Cho biểu thức f x 2 6 
. Khoảng nào dưới đây của x thì f x  0 ? 1  2x  3   1  A.  ;2 . B. 2   ;  .
C. 3;   . D.  2  ;3.  4   2  x x
Câu 39: Với x thuộc tập hợp nào sau đây thì f x 1 2   không âm? x  2 x  1  1   1    A. 2;     .
B. 2;  . C. 2  ;   2  ;  
 .D.    1 ; 2   ;1   .  2   2   2  2 x
Câu 40: Có bao nhiêu số nguyên thỏa mãn bất phương trình  x 1? x  2 A. 4 . B. 5 . C. 3 . D. 2 . 2 x  3x  4
Câu 41: Biết tập nghiệm của bất phương trình
x 1 là S   ;  a ;
b c , giá trị của 2x 1
a  2b c là A. 1. B. 3 . C. 2  . D. 3  . 2
2x x  6  0
Câu 42: Tìm tập nghiệm của hệ bất phương trình  . 2
3x 10x  3  0    1  A.    3 ; 2  ;   
 . B. ; 2  3;   . C. ;  3;    . D.  2  ;3.  2   3 
Câu 43: Cho tam thức bậc hai f x 2
ax bx c a  0 có 2
  b  4ac  0. Mệnh đề nào sau đây đúng?
A. f x luôn cùng dấu với hệ số b với mọi x  .
B. f x luôn cùng dấu với hệ số a với mọi x  . 
C. f x luôn cùng dấu với hệ số a với mọi  b x . 2a
D. f x luôn trái dấu với hệ số a với mọi x  .
Câu 44: Cho f x 2
ax bx c,a  0 và 2
  b  4ac . Tìm điều kiện  để f x cùng dấu với hệ
số a với mọi x  . A.   0 . B.   0 . C.   0 . D.   0 .
Câu 45: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Mệnh đề nào dưới đây đúng? a  a
A. f x 0  0, x     .
B. f x 0       0, x  .  0    0 a  a
C. f x 0  0, x     .
D. f x 0       0, x  .  0    0
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Câu 46: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Mệnh đề nào dưới đây đúng? a  a
A. f x 0  0, x     .
B. f x 0       0, x  .  0    0 a  a
C. f x 0  0, x     .
D. f x 0       0, x  .  0    0
Câu 47: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Điều kiện cần và đủ
để f x  0, x   là a  0 a  0 a  0 a  0 A.  . B. C. D.    .  .  .  0    0    0    0
Câu 48: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Điều kiện cần và đủ
để f x  0, x   là a  0 a  0 a  0 a  0 A.  . B. C. D.    .  .  .  0    0    0    0
Câu 49: Tập hợp tất cả các giá trị của tham số m để phương trình 2
x mx m  0 có hai nghiệm phân biệt là
A. ;0  4; . B. 0; 4.
C. ;0  4;    . D. 0;4.  
Câu 50: Điều kiện cần và đủ của tham số m để tam thức f x 2
x  m  2 x  4m 1 đổi dấu hai lần là
A. 0  m  12 .
B. m  0 hoặc m  12 C. m  0 hoặc m  12 D. m  0 .
Câu 51: Với giá trị nào của tham số m thì phương trình 2
mx  2mx  4  0 vô nghiệm? m  0
A. 0  m  4 . B.  .
C. 0  m  4 .
D. 0  m  4 . m  4
Câu 52: Tập hợp tất cả các giá trị của tham số m để phương trình 2 2
x mx m  1  0 có hai nghiệm trái dấu là A. ; 1
  1;. B. 1;1. C. ; 1    1  ;   . D. 1;1.  
Câu 53: Cho tam thức bậc hai f x 2
x  2mx  .
m Tập hợp tất cả các giá trị của tham số m để
f x  0, x   là
A. ;0  1; . B. 0;1. C. ;0  1  ;   . D. 0;1.  
Câu 54: Cho tam thức bậc hai f x 2 2
x  2mx  2m  .
m Tập hợp tất cả các giá trị của tham số m để
f x  0, x   là
A. ;0  1; . B. 0;1. C. ;0  1  ;   . D. 0;1.  
Câu 55: Cho f x 2
mx  2mx  4. Tập hợp tất cả các giá trị của tham số m để f x  0, x   là
A. ;0  4; . B. 0; 4.
C. ;0  4;    . D. 0;4  .
Câu 56: Tập hợp tất cả các giá trị của tham số m để hàm số 2 2
y x  4x m  5m xác định trên là
A. ;1  4; . B. 1; 4. C. 1  ;4.   D. 1;1.  
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT 4x  7
Câu 57: Tập hợp tất cả các giá trị của tham số m để hàm số y  xác định trên là 2 2
x  4x m  5m
A. ;1  4; . B. 1; 4. C. 1  ;4.   D. 1;1.  
Câu 58: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  m  2 x  8m 1  0 vô nghiệm.
A. m 0; 28 .
B. m 0; 28 .
C. m   ;
 0 28;. D. m  ;  028; .
Câu 59: Tìm số giá trị nguyên của m để bất phương trình 2
x  2mx  3m  2  0 vô nghiệm. A. 0 . B. 1. C. 2 . D. Vô số. 2
x 5x  4  0
Câu 60: Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm. x m  0
A. m  1.
B. 1  m  4 .
C. m  4 . D. m  4 . 2 x  4  0
Câu 61: Giá trị của tham số m để hệ bất phương trình  vô nghiệm là
m  4  2x A. m  0 . B. m  0 . C. m  0 . D. m  0 .
Câu 62: Cho biểu thức f x 2
x  2m  
1 x  2m  3 . Tìm điều kiện của tham số m để f x  0 thỏa
mãn với mọi x  1  ;2 .
A. m  2 .
B. m  .
C. m  1. D. m  2 .
Câu 63: Có tất cả bao nhiêu giá trị nguyên của tham số m 0; 2022 để x 2; 4 đều là nghiệm bất phương trình 2
x  m  
1 x m  0 ? A. 2022. B. 2021. C. 2020. D. 2019. 2
x  m   1 x 1
Câu 64: Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình  0 2 x  2x  5
nghiệm đúng với mọi x  ? A. 3. B. 5. C. 2. D. 1.
LỜI GIẢI CHI TIẾT II. BÀI TẬP TỰ LUẬN Câu 1:
Xét dấu các tam thức bậc hai sau: 3 a) 2 x x 1; b) 2 x 9x 27; c) 2 2x 6x 8 . 2 Lời giải:
a) f x 2
x x 1 có   3  0 và a  1  0 nên f x  0 với mọi x  . 3 27 3 b) g x 2
  x  9x
có   0 và a  
 0 nên g x có nghiệm kép x  3 và g x  0 2 2 2 với mọi x  3.
c) Dễ thấy h x 2
 2x  6x 8 có   25  0,a  2  0 và có hai nghiệm phân biệt
x  4; x  1. 1 2
Do đó ta có bảng xét dấu h x :
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Suy ra h x  0 với mọi x  ;  4
  1; và hx  0 với mọi x 4   ;1 . Câu 2:
Xét dấu các tam thức bậc hai sau: a) 2 3
x x  2; b) 2 x  8x 16; c) 2
2x  7x  3. Lời giải:
a) f x 2  3
x x  2 có  112 2  0 và a  1 0 nên f x  0, x   . b) g x 2
x  8x  6 có  '  0, a 1  0 nên g x  0 có nghiệm kép x  4 và
g x  0, x   4  .  1 x  c) h x 2  2
x  7x  3 có   
25  0, a  2  0 nên h x  0  2  x  3 Ta có bảng xét dấu:    1 
Suy ra h x 1  0, x   ;3 
 và hx  0,x   ;  3;   .  2   2  2x x 1 Câu 3:
Xét dấu biểu thức f x 2  . 2 x  4 Lời giải:  1 x    Ta có: 2
2x x 1  0  2 x    x    ; 2 4 0 2. x  1
Bảng xét dấu f x :  1   1 
Suy ra f x  0,x  ;  2
   ;1 2;  
và hx  0,x 2  ;    1;2.  2   2  Câu 4:
Tìm tất cả các giá trị của x để biểu thức f x   2 x x  2 3
x  6x  9 nhận giá trị dương Lời giải: x  0 Ta có 2
3x x  0   ; 2
x  6x  9  0  x  3. x  3
Lập bảng xét dấu ( Hoặc sử dụng phương pháp khoảng) ta có x 0; 3.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT x x  6 Câu 5:
Xét dấu biểu thức Px 2  x  . 2
x  3x  4 Lời giải: x x x x xx  1 2 2 3 2 x x        6 6 2 5 6 
Ta có: Px  x    2 2 2
x  3x  4
x  3x  4
x  3x  4 x  2  x  1  Ta có: 2 2
x x  6  0  
,  x  3x  4  0   x  3 x    4 Bảng xét dấu
Suy ra P x  0  x 2  ; 1
   1;3  4; , Px  0  x; 2     1  ;1  3;4 . Câu 6:
Giải các bất phương trình sau: a) 2
3x x  5  0; b) 2 3
x  2 3x 1  0; c) 2
x  2x 1  0. Lời giải: a) Tam thức 2
f (x)  3x x  5 có   59  0 hệ số a  3  0 nên f (x) luôn dương (cùng dấu
với a với mọi x
. Suy ra bất phương trình vô nghiệm. b) Tam thức 2 f (x)  3
x  2 3x 1 có   0 hệ số a  3  0 nên f (x) luôn âm (cùng dấu 3 3
với a với mọi x  , tức là 2 3
x  2 3x 1  0 với mọi x  . 3 3 3
Suy ra bất phương trình có nghiệm duy nhất x  3 c) Tam thức 2
f (x)  x  2x 1 có   2  0 nên f (x) có hai nghiệm x  1 2 và 1 x  1 2 . 2
Mặt khác a  1  0 , do đó ta có bảng xét dấu sau:
Tập nghiệm của bất phương trình là S  1 2;1 2  . Câu 7:
Giải các bất phương trình bậc hai sau: a) 2 x 1  0; b) 2
x  2x 1  0; c) 2 3
x 12x 1  0; d) 2
5x x 1  0. Lời giải:
a) Dễ thấy f x 2
x 1 có  1  0,a 1  0 và có hai nghiệm phân biệt x  1; x 1. 1 2
Do đó ta có bảng xét dấu f x :
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT Nên bất phương trình 2
x 1  0 có tập nghiệm là S   ;    1  1;  .
b) Dễ thấy g x 2
x  2x 1 có   2  0,a 1  0 và có hai nghiệm phân biệt x 1 2; 1 x  1 2 . 2
Do đó ta có bảng xét dấu g x : Nên bất phương trình 2 x 2x 1
0 có tập nghiệm là S 1 2;1 2 .
c) Dễ thấy h x 2
 3x 12x 1 có   39  0, a  3
  0 và có hai nghiệm phân biệt 6  39 6  39 x  ; x  . 1 3 2 3
Do đó ta có bảng xét dấu h x :  6  39   6  39  Nên bất phương trình 2 3
x 12x 1  0 có tập nghiệm là S   ;    ;       . 3 3     d) k x 2
 5x x 1 có   19  0 và a  5  0 nên k x  0 với mọi x  .
Từ đó suy ra bất phương trình 2
5x x 1  0 có tập nghiệm là . Câu 8:
Tìm tập xác định của hàm số 2
y x  2x  5. Lời giải: Điều kiện: 2
x  2x  5  0
Xét tam thức vế trái có   4  0 và a  1  0 nên 2
x  2x  5  0, x   .
Vậy tập xác định của hàm số là D  . 2 Câu 9:
Giải bất phương trình  2
x x   2
3 x x  2  0. Lời giải: 2 x x  2  2
x x  2  0 Ta có 2 2 2
(x x)  3(x x)  2  0      đúng x . 2
x x  1  2
x x  1 0
Vậy tập nghiệm của bất phương trình T  . 2 3 x x  1 1 x  2x
Câu 10: Giải bất phương trình :   . 2 2 x  2 x x x  3x  2 Lời giải:
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
 2x x1 2x xx2 x 3x 2 BPT   x 0 2
x  3x  2 2  
  x x x
  0  x  1  x  2 .
x x  3x  2 0  2 3 2 0 2 
Câu 11: Giải bất phương trình:  2 x   2
x x   2 4 2
3 x  4x  4. Lời giải: 2 2 2
BPT  x    2 2
x  2x  3x  2  x    2 2
x  2x  3  0 x  2   
x  2   1  x  3 2 .
x  2x  3   0 2
x  4x  3  0
Câu 12: Giải hệ bất phương trình  . 2
x  6x  8  0 Lời giải: 2
x  4x  3  0 x    ;   1  3;  Ta có:     x  ;   1  4;  . 2
x  6x  8  0 x    ;  2 4;
Câu 13: Tìm tập xác định của hàm số 2 1
y x  3x  2  . x  3 Lời giải: x  1 2
x  3x  2  0   3   x  1 Hàm số xác định khi 
 x  2   . x  3  0  x  2 x  3   2
x  4x  3  0 
Câu 14: Giải hệ bất phương trình 2
2x x 10  0.  2
2x  5x  3  0 Lời giải:  x  3   x  1 2
x  4x  3  0  1   x  1   5  Ta có: 2
2x x 10  0  2  x   3 5 .  2    x  2
2x  5x  3  0    2 2 x  1  3 x   2
Câu 15: Tìm các giá trị của tham số m để tam thức bậc hai 2
x  m  
1 x  2m  3 dương với mọi x  . Lời giải:
Đặt f x 2
x  m  
1 x  2m  3 có hệ số a  1  0.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT 2
Ta có   m     m   2 1 4 2
3  m  6m 11. a  0 Yêu cầu bài toán   2
m  6m 11 0  3 2 5  m  3 2 5.   0
Câu 16: Tìm các giá trị của tham số m để bất phương trình 2
x  2(m  2)x  2m 1  0 nghiệm đúng với mọi x  . Lời giải:
Vì hệ số a  1  0 , nên bất phương trình nghiệm đúng với mọi x  khi và chi khi 2
  (m  2)  (2m 1)  0  2
m  6m  5  0  1  m  5.
Câu 17: Tìm tất cả các giá trị của m để biểu thức f x 2
 x  2x m luôn âm. Lời giải: a   
Ta có: f x 1 0  0, x     m 1.
 ' 1 m  0
Câu 18: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  m   2 3 2
1 x  2m  3m  2  0
nghiệm đúng x  . Lời giải: 2 2
3x  2(m 1)x  2m  3m  2  0 x   R 2 2
  '  (m 1)  3(2m  3m  2)  0 2
 7m  7m  7  0 bpt vô nghiệm.
Vậy không có m thỏa mãn yêu cầu bài toán. 1
Câu 19: Tìm tất cả các giá trị của m để hàm số f x  xác định với mọi 2
(m  1)x  2(m  2)x  2  m x  . Lời giải: 2
(m 1)x  2(m  2)x  2  m  0, x    1 .
TH 1: m 1  0  m  1  2x 1  0,x  (Sai).
TH 2 : m 1  0  m  1 . m  1 m  1  0  m  1  3 Khi đó 1             m
m  22  m  12  m 2. 2 3  0
2m  7m  6  0   m  2 2 2 3 Vậy  m  2 . 2
Câu 20: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  2(m  2)x  2m  1  0 vô nghiệm. Lời giải: BPT có vô nghiệm 2
x  2m  2x  2m 1  0, x
     m  2 2  2m  1  0 2
m  6m  5  0  < 1 m  5 .
Câu 21: Tìm m để mọi x   1  ;1 
 đều là nghiệm của bất phương trình 2
x  m   2 3 2
5 x m  2m  8  0. Lời giải: 4  m Ta có 2
x  m   2 3 2
5 x m  2m  8  01  x m  2 hoặc x  3
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT 4  m 1 TH 1: m  2 
 3m  6  4  m m   3 2 4  m
Ta có, bất phương trình (1) 
x m  2. 3 4  m
Vậy tập nghiệm của bất phương trình (1) là ; m  2    3 
Suy ra mọi x   1  ;1 
 đều là nghiệm của bất phương trình (1)  4  m  4  m   1    m  7 khi và chỉ khi  1  ;1  ; m  2       3    m  7  3   m  1  1  m   2 1
Kết hợp với điều kiện m   ta có m  7 thỏa mãn yêu cầu bài toán 2 4  m 1 TH 2: m  2   m   ta có 3 2 4  m
Bất phương trình (1)  m  2  x  3  4  m
Vậy tập nghiệm của bất phương trình (1) là m  2;    3 
Suy ra mọi x   1  ;1 
 đều là nghiệm của bất phương trình (1)  1   m  2  4  m   khi và chỉ khi  1  ;1  m  2;       4  m  3   1   3 m  3     m  3  m   1 1
Kết hợp với điều kiện m   ta có m  3 thỏa mãn yêu cầu bài toán 2 1 3 1
TH 3: m   ta có bất phương trình (1)  x  nên m   không thỏa mãn yêu cầu bài 2 2 2 toán.
Vậy m (; 3]  [7; ) là giá trị cần tìm.
Câu 22: Tìm giá trị của tham số m để phương trình 2
(m  3)x  (m  3)x  (m 1)  0 có hai nghiệm phân biệt. Lời giải:
Phương trình có hai nghiệm phân biệt  m  3  0  m  3  7       m  3. 2
(m  3)  4(m  3)(m 1)  0 m3  3m7  0 3
Câu 23: Tìm tham số m để phương trình m   2
2 x  3x  2m  3  0 có hai nghiệm trái dấu. Lời giải: 3
Yêu cầu bài toán  m  22m  3  0  2   m  . 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Câu 24: Tìm m để phương trình m   2
1 x  2m  2 x m  1  0 có 2 nghiệm phân biệt khác 0 sao 1 1 cho   2 . x x 1 2 Lời giải:
Phương trình có hai nghiệm phân biệt khác 0 khi m  1 m 1  0 m  1       
m  22  m   1 m  
1  0  4m  5  0  m     1 . 4    m 1  0 m  1   m  1   2 m  2 x x   1 2  m  Theo định lí Viet: 1  . m 1 x x  1 2  m 1 2 m  2 m 1  2 1 1
x x  2x x m m  6 Khi đó: 1 2 2 2   2   0 1 1   0 
 0  m  1 2 . x x x x m 1 m 1 1 2 1 2 m 1 Từ  
1 ;2  m  1.
Câu 25: Tìm m để phương trình m   2
1 x  2m  2 x m  3  0 có hai nghiệm phân biệt x ,x thỏa 1 2
mãn x x x x  1. 1 2 1 2 Lời giải: a  0 m  1  0
Phương trình có hai nghiệm phân biệt x , x khi     m  1 (*) 1 2   0 1  0, m    
Khi đó, theo định lý Vi-ét ta có:  2m  2 x x  2m  2 1 2  m  1 m  3 
x x x x  1    1  1 2 1 2 m  3 m  1 m  1 x x  1 2  m  1
2m  2 m  3 m  1 2m  6     0 
 0  1  m  3 (thỏa (*)). m  1 m  1 m  1 m  1 Vậy 1  m  3 .
Câu 26: Cho hàm số y  m   2
2 x  3mx  2m  3 (m là tham số). Tìm các giá trị của tham số m để đồ thị
hàm số cắt trục hoành tại hai điểm phân biệt A, B sao cho gốc tọa độ O nằm giữa A và B . Lời giải:
Phương trình hoành độ giao điểm là m   2
2 x  3mx  2m  3  0
Điều kiện để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt A, B sao cho gốc tọa độ O
nằm giữa A và B là x x   m m     m  . A B    3 . 0 2 3 2 0 2 2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Câu 27: Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m với vận tốc ban đầu
v  20 m / s . Hỏi sau ít nhất bao nhiêu giây, vật đó cách mặt đất không quá 100 m ? Giả thiết 0
rằng sức cản của không khí là không đáng kể. Lời giải: Với 2
g  10m / s ta có phương trình chuyển động h t  2
 5t  20t  320 . Vật cách mặt đất
không quá 100 m , tức là   ht 2 100
 5t  20t  320  0 . Sử dụng MTCT ta được 2
  4 3  t  2  2 17 .
Câu 28: Một công ty đồ gia đụng sản xuất bình đựng nước thấy rằng khi đơn giá của binh đựng nước
là x nghìn đồng thì doanh thu R (tính theo đơn vị nghìn đồng) sẽ là 2 R(x)  560  x  50000x .
a) Theo mô hình doanh thu này, thì đơn giá nào là quá cao dẫn đến doanh thu từ việc bán
bình đựng nước bằng 0 (tức là sē không có người mua)?
b) Với khoảng đơn giá nào của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt mức 1 tỉ đồng? Lời giải:
a) Theo mô hình doanh thu này, thì đơn giá quá cao dẫn đến doanh thu từ việc bán bình
đựng nước bằng 0 (tức là sē không có người mua) là giá trị x thỏa mãn 
x  0loai  R x  0 2  560 
x  50000x  0  625  x   89,29nghìn  7
b) Với khoảng đơn giá của bình đựng nước thì doanh thu từ việc bán bình đựng nước vượt
mức 1 tỉ đồng là giá trị x thỏa mãn
R x  1000000 2  560 
x  50.000x  1.000.000  30, 25  x  59, 04.
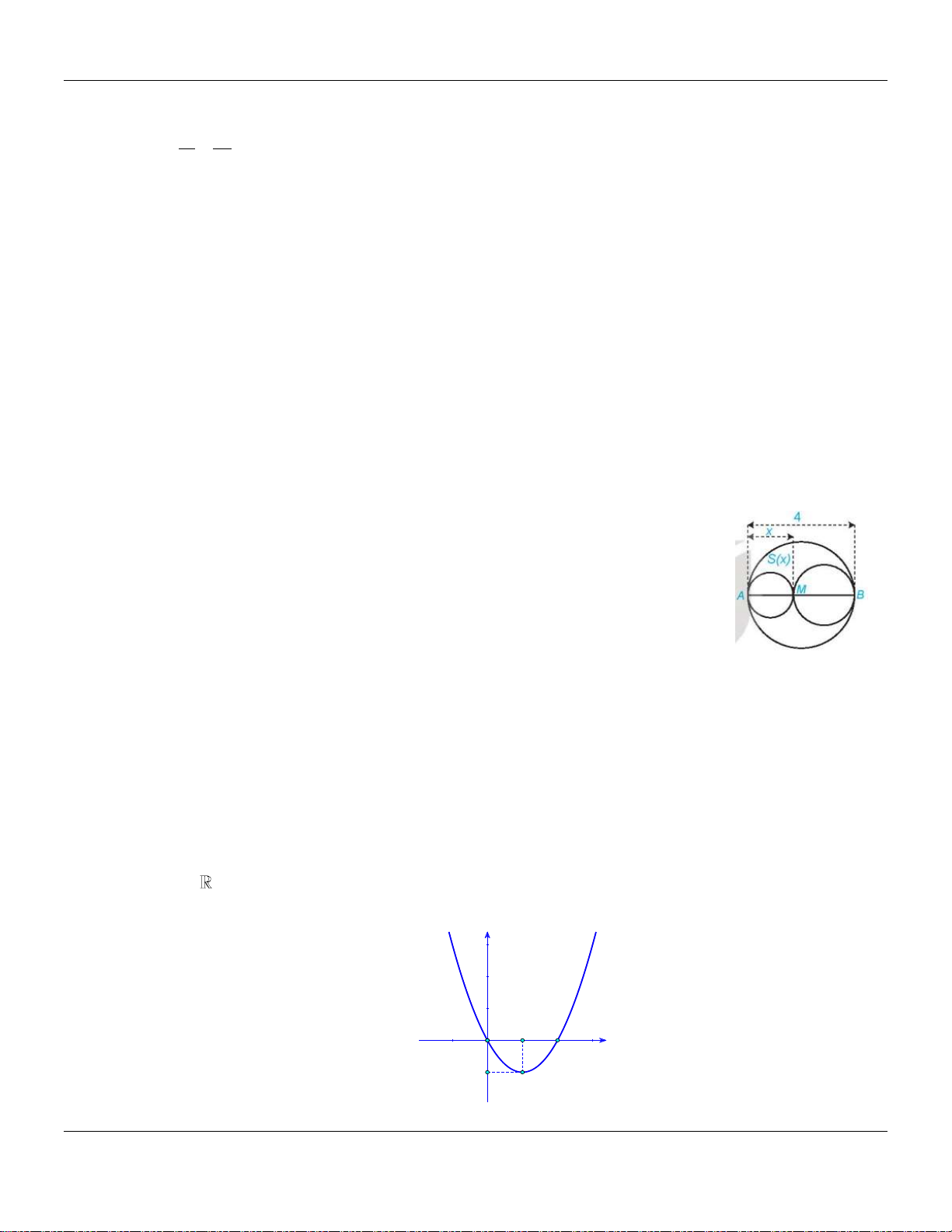
Câu 29: Xét đường tròn đường kính AB  4 và một điểm M di chuyển trên
đoạn AB , đặt AM x (Hình vẽ). Xét hai đường tròn đường kính
AM và MB . Kí hiệu S x là diện tích phần hình phẳng nằm trong
hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị
của x để diện tích S x không vượt quá một nửa tổng diện tích hai hình tròn nhỏ. Lời giải:    2 Ta có 2 S 2 S  4  x ; O ;MB     AB ; Sx ; O; AB   2  1 O ; AM  4 4 4   2 2 2 2 S SSS
AB x  4  x  2  x  8x x O; AB 1 O ; AM 2 O ;MB             4 4 1 S S S x x x x x   1  2 2 2   2  8  .  4  O ; AM O ;MB 1 2           2 4 2 4  6  2 3 0  x  2 3
 3x 12x  8  0   . 6  2 3   x  4  3
III. BÀI TẬP TRẮC NGHIỆM
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT Câu 1:
Biểu thức nào dưới đây là tam thức bậc hai? A. y  1. B. y  . x C. 2 y x . D. 3 y x . Câu 2:
Với m là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai? A. y  . m
B. y m . x C. 2 y mx . D. 2 y x  . m Câu 3:
Với m là tham số bất kì, biểu thức nào dưới đây là tam thức bậc hai? A. y  . m
B. y m . x C. y   2 m   2 1 x . D. 2 y mx  . m Câu 4:
Tìm tất cả các giá trị của tham số m để biểu thức f x  m   2
2 x  5x  9 là tam thức bậc hai. A. m  .
B. m  2 .
C. m  2 . D. m  0 . Lời giải:
Biểu thức f x  m   2
2 x  5x  9 là tam thức bậc hai khi: m  2  0 . Suy ra m  2 .
Chọn đáp án C. Câu 5:
Cho hàm số bậc hai y f x có đồ thị như hình bên dưới: y 1 2 x O -1
Khẳng đinh nào dưới đây đúng?
A. f x  0, x  0;2.
B. f x  0, x  0;2.
C. f x  0, x  1;.
D. f x  0, x   0;2.   Câu 6:
Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 4  f x  0  0  A. 2 y x  2 . x B. 2 y x  2 . x C. 2 y x  4 . x D. 2
y  x  4 . x Lời giải:
Kiểm tra các sự kiện: a  0 và tam thức có hai nghiệm x  0, x  4.
Chọn đáp án C. Câu 7:
Tam thức bậc hai nào dưới đây có bảng xét dấu như hình vẽ? x  0 2  f x  0  0  A. 2 y x  2 . x B. 2
y  x  2 . x C. 2 y x  4 . x D. 2 y x  4 . x Lời giải:
Kiểm tra các sự kiện: a  0 và tam thức có hai nghiệm x  0, x  2.
Chọn đáp án B.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT Câu 8:
Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây đúng?
A. f x  0, x  1;2.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;.
D. f x  0, x   1  ;2.   Lời giải:
Bảng xét dấu: x  1 2  f x  0  0 
Chọn đáp án B. Câu 9:
Cho tam thức f x 2
x  3x  2. Khẳng định nào dưới đây sai?
A. f x  0, x
 ;1 2;.
B. f x  0, x  1;2.
C. f x  0, x
 ;1  2;   .
D. f x  0, x   1  ;2.   Lời giải:
Bảng xét dấu: x  1 2  f x  0  0 
Chọn đáp án B.
Câu 10: Tập hợp tất cả các giá trị của x để tam thức 2
y  x  2x luôn âm là A. 0; 2.
B. ;0  2; . C. 0; 2.  
D. ;0  2;    . Lời giải:
Bảng xét dấu: x  0 2  y  0  0 
Chọn đáp án B.
Câu 11: Tập hợp tất cả các giá trị của x để tam thức f x 2
x  2x luôn dương là A. 0; 2.
B. ;0  2; . C. 0; 2.  
D. ;0  2;    . Lời giải:
Bảng xét dấu: x  0 2  f x  0  0 
Chọn đáp án B.
Câu 12: Tam thức nào dưới đây luôn âm với mọi x  ? A. 2
y x x  1. B. 2
y  x x  1. C. 2
y  x x  1. D. 2
y  x  4 . x Lời giải: Bảng xét dấu 2
y  x x  1 : x   y
Chọn đáp án C.
Câu 13: Tam thức nào dưới đây luôn dương với mọi x  ?
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT A. 2
y x x  1. B. 2
y x  2x  1. C. 2
y  x x  1. D. 2
y  x  4 . x Lời giải: Bảng xét dấu 2
y x x  1 : x   y
Chọn đáp án A.
Câu 14: Một nghiệm của bất phương trình 2
x  2x  3  0 là A. x  5. B. x  0. C. x  2. D. x  4.
Câu 15: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   . Lời giải:
Bảng xét dấu f x 2
x  2x  3 : x  1  3  f x  0  0 
Chọn đáp án B.
Câu 16: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   . Lời giải:
Bảng xét dấu f x 2
x  2x  3 : x  1  3  f x  0  0 
Chọn đáp án D.
Câu 17: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. 1; 3.   B. ; 1
  3;. C. 1;3. D. ; 1    3;   . Lời giải:
Bảng xét dấu f x 2
x  2x  3 : x  1  3  f x  0  0 
Chọn đáp án A.
Câu 18: Tập nghiệm của bất phương trình 2
x  2x  3  0 là A. .  B. C. 1; 3. D. ; 1    3;   . Lời giải:
Bảng xét dấu f x 2
x  2x  3 : x   f x 
Chọn đáp án B.
Câu 19: Tập nghiệm của bất phương trình 2
x x  3  0 là A. .  B. C. 1; 3. D. ; 1    3;   .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT Lời giải:
Bảng xét dấu f x 2
x x  3 : x   f x 
Chọn đáp án B.
Câu 20: Tập nghiệm của bất phương trình 2
x x  3  0 là A. .  B. C. 1; 3. D. ; 1    3;   . Lời giải:
Bảng xét dấu f x 2
x x  3 : x   f x 
Chọn đáp án A.
Câu 21: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C. 1; 3. D.  \  1 . Lời giải:
Bảng xét dấu f x 2
x  2x  1: x  1  y  0 
Chọn đáp án B.
Câu 22: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 . Lời giải:
Bảng xét dấu f x 2
x  2x  1: x  1  y  0 
Chọn đáp án D.
Câu 23: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 . Lời giải:
Bảng xét dấu f x 2
x  2x  1: x  1  y  0 
Chọn đáp án A.
Câu 24: Tập nghiệm của bất phương trình 2
x  2x  1  0 là A. .  B. C.   1 . D.  \  1 . Lời giải:
Bảng xét dấu f x 2
x  2x  1: x  1 
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT y  0 
Chọn đáp án C.
Câu 25: Bất phương trình 2
x  3x  4  0 có tất cả bao nhiêu nghiệm nguyên dương? A. 6 . B. 5 . C. 4 . D. 2 . Lời giải: x
Đặt f x 2
x  3x  4 . Xét f x 4  0   x  1  Bảng xét dấu:
Từ bảng xét dấu, f x  0  x  1;  4. Vậy bất phương trình 2
x  3x  4  0 có 4 nghiệm nguyên dương.
Chọn đáp án C.
Câu 26: Bất phương trình nào dưới đây có nghiệm? A. 2
x  2x  1  0. B. 2
x  2x  3  0. C. 2
x  3x  4  0. D. 2 x  2x  0. Lời giải: Ta có: 2
x  2x  0  x  0; 2.  
Chọn đáp án D.
Câu 27: Bất phương trình nào dưới đây có nghiệm? A. 2
x  2x  1  0. B. 2
x  2x  3  0. C. 2
x  3x  4  0. D. 2
x  2x  1  0. Lời giải: Ta có: 2
x  2x  1  0  x  1.
Chọn đáp án D.
Câu 28: Bất phương trình nào dưới đây vô nghiệm? A. 2 x  2x  0. B. 2
x  2x  3  0. C. 2 x  4  0. D. 2 x  0. Lời giải: Ta có: 2
x  2x  3  0, x
  nên bất phương trình 2
x  2x  3  0 vô nghiệm.
Chọn đáp án B.
Câu 29: Bất phương trình nào sau đây vô nghiệm? A. 2 x  0 . B. 2 x  0 . C. 2 x  0 . D. 2 x  0 .
Câu 30: Tập xác định của hàm số 2
y x  4 là A. 2; 2. B. ; 2
  2;. C. 2;2.   D. ; 2    2;   . Lời giải: Hàm số xác định 2
x  4  0  x;2  2;   .
Vậy tập xác định của hàm số là D  ; 2    2;   .
Chọn đáp án D. 2x  7
Câu 31: Tập xác định của hàm số y  là 2 4  x
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT A. 2; 2. B. ; 2
  2;. C. 2;2.   D. ; 2    2;   . Lời giải: Hàm số xác định 2
 4  x  0  x;2  2;.
Vậy tập xác định của hàm số là D  ; 2    2;.
Chọn đáp án B.
Câu 32: Tập xác định của hàm số 2
y x  1  2 9  x là A. 1  ;3.   B. 1;   . C. 3; 3.   D. 3;   . Lời giải: 2 9  x  0 x 3  ;3   Hàm số xác định      x 1  ;3.   x 1  0 x  1
Vậy tập xác định của hàm số là D  1  ;3.  
Chọn đáp án A. 9  x
Câu 33: Tập xác định của hàm số y  là 2
x  1  4  x  10 A. 1  ;2.   B. 2;   . C. 1  ;9.   D. 1  ;2  . Lời giải: 9  x  0 x  9  
Hàm số xác định  x  1  0  x  1  x 1  ;2.    2  4  x   0 x   2  ;2   
Vậy tập xác định của hàm số là D  1  ;2.  
Chọn đáp án A.
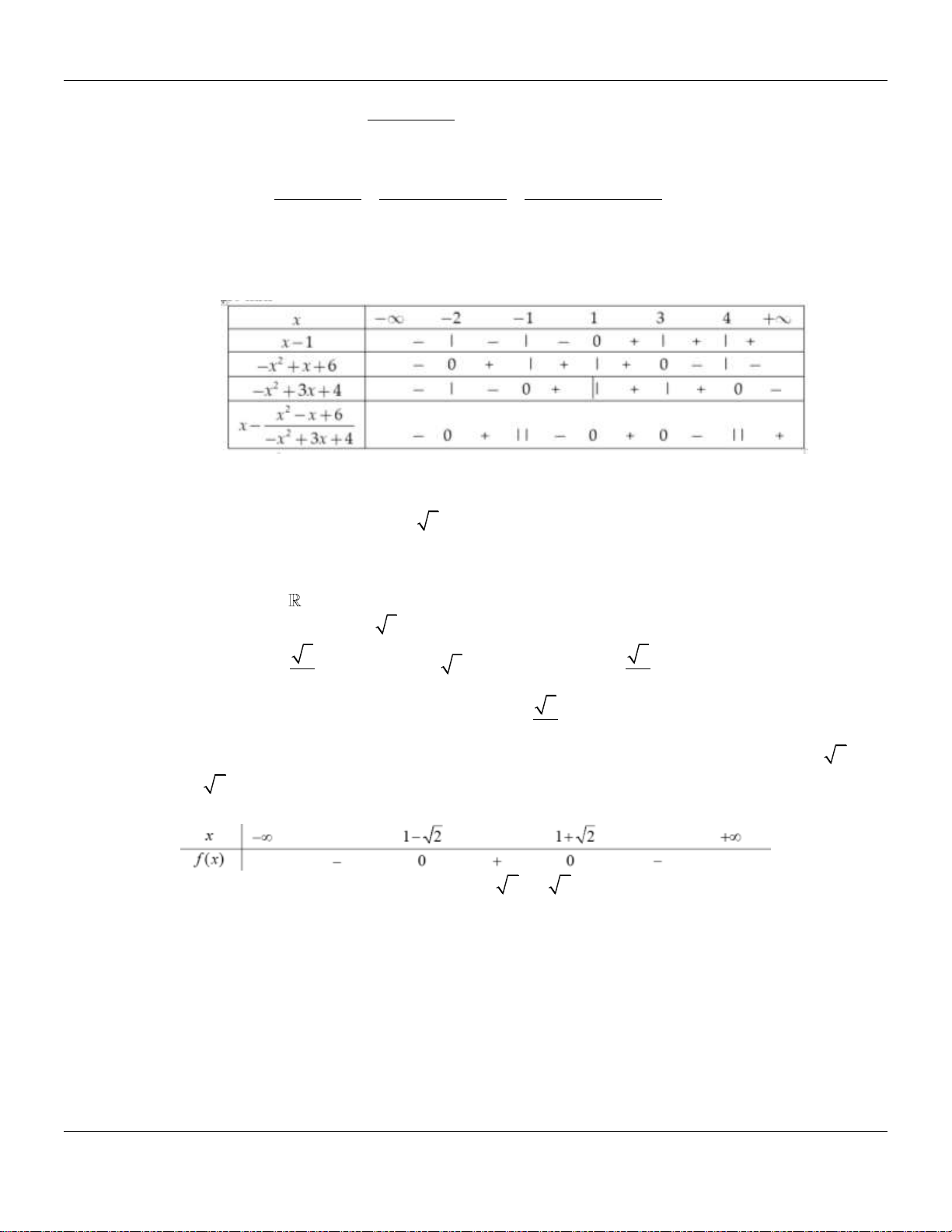
Câu 34: Tập nghiệm của bất phương trình  2
x x   2 3 x  4  0 là A. 2; 2.   B. ; 2    2;   . C. 2;2. D. ; 2   2;. Lời giải:
Đặt M   2
x x   2 3 x  4. Ta có: +) 2
x x  3  0 (vô nghiệm) x  2 +) 2 x  4  0   . x  2  
Bảng xét dấu biểu thức M : x  2  2  2 x x  3    2 x  4  0  0  M  0  0 
Chọn đáp án D.
Câu 35: Tập nghiệm của bất phương trình  2
x x   2 2
4 x  2x  0 là
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT A. 0; 2.  
B. ;0  2;    . C. 0;2.
D. ;0  2; . Lời giải:
Đặt M   2
x x   2 2 4 x  2x. Ta có: +) 2
x  2x  4  0 (vô nghiệm) x  0 +) 2
x  2x  0   . x   2
Bảng xét dấu biểu thức M : x  0 2  2 x  2x  4    2 x  2x  0  0  M  0  0 
Chọn đáp án B.
Câu 36: Số nghiệm nguyên của bất phương trình  2 x x 2 2 x  9  0 là A. Vô số. B. 0. C. 5. D. 7. Lời giải:
Đặt M   2 x x 2 2 x  9. Ta có: x  0 x  3 +) 2
x  2x  0   . +) 2 x  9  0   . x   2 x  3  
Bảng xét dấu biểu thức M : x  3  0 2 3  2 x  2x   0  0  0  2 x  9  0    0  M  0  0  0  0 
Vậy tập nghiệm của bất phương trình đã cho là  3  ;0  2;3 x S       x      3  ; 2  ; 1  ;0;2;  3 .
Chọn đáp án D. 2 x  4x  3
Câu 37: Số nghiệm nguyên của bất phương trình  0 là 2 x  16 A. Vô số. B. 0. C. 6. D. 8. Lời giải: 2 x  4x  3 Đặt M  . 2 x  16 Ta có: x  1 x  4 +) 2
x  4x  3  0   . +) 2 x  16  0   . x   3 x  4  
Bảng xét dấu biểu thức M : x  4  1 3 4  2 x  2x   0  0  0 
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT 2 x  9  0    0  M   0  0  
Vậy tập nghiệm của bất phương trình đã cho là   4  ;1  3;4    x S     x 3  ; 2  ; 1  ;0;1;  3 .
Chọn đáp án C. x x
Câu 38: Cho biểu thức f x 2 6 
. Khoảng nào dưới đây của x thì f x  0 ? 1  2x  3   1  A.  ;2 . B. 2   ;  .
C. 3;   . D.  2  ;3.  4   2  Lời giải: x  3 Xét 2
x x  6  0   x  2   1
Xét 1  2x  0  x  . 2 Bảng xét dấu:  
Từ bảng xét dấu, f x   x   1 0 ; 2   ;3  2 
Chọn đáp án A. x x
Câu 39: Với x thuộc tập hợp nào sau đây thì f x 1 2   không âm? x  2 x  1  1   1    A. 2;     .
B. 2;  . C. 2  ;   2  ;  
 .D.    1 ; 2   ;1   .  2   2   2  Lời giải:   2 2
x  2x  1  x  4x  4 6  x  3
f xx 1 x 2     . x  2 x  1
x  2x  1
x  2x  1  
Suy ra f x  0  x; 2   1   ;1   .  2 
Chọn đáp án D. 2 x
Câu 40: Có bao nhiêu số nguyên thỏa mãn bất phương trình  x 1? x  2 A. 4 . B. 5 . C. 3 . D. 2 . Lời giải:
Điều kiện: x  2 . 2 2 x
x   x  2 x   1 x  2 Ta có  x 1   0   0  2   x  2 . x  2 x  2 x  2
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Vậy có 4 số nguyên thỏa mãn bất phương trình đã cho.
Chọn đáp án A. 2 x  3x  4
Câu 41: Biết tập nghiệm của bất phương trình
x 1 là S   ;  a ;
b c , giá trị của 2x 1
a  2b c là A. 1. B. 3 . C. 2  . D. 3  . Lời giải: 1
Điều kiện: 2x  1  0  x  . 2 2 2 x  3x  4 x  3x  4 Ta có:  x 1   x   1  0 2x 1 2x 1 2
x x    x   x   2 3 4 1 2 1
x  4x  5   0   0   1 2x 1 2x 1 Xét dấu:  
Từ bảng xét dấu, suy ra tập nghiệm S     1 ; 5  ;1    2  1  a  5
 ;b  ;c 1 a  2b c  3  . 2
Chọn đáp án D. 2
2x x  6  0
Câu 42: Tìm tập nghiệm của hệ bất phương trình  . 2
3x 10x  3  0    1  A.    3 ; 2  ;   
 . B. ; 2  3;   . C. ;  3;    . D.  2  ;3.  2   3  Lời giải:  3     2 x 2 2   6  0 x x x  x  2  Ta có 2      . 2
3x 10x  3  0 1  x  3 x   x  3  3
Chọn đáp án B.
Câu 43: Cho tam thức bậc hai f x 2
ax bx c a  0 có 2
  b  4ac  0. Mệnh đề nào sau đây đúng?
A. f x luôn cùng dấu với hệ số b với mọi x  .
B. f x luôn cùng dấu với hệ số a với mọi x  . 
C. f x luôn cùng dấu với hệ số a với mọi  b x . 2a
D. f x luôn trái dấu với hệ số a với mọi x  .
Câu 44: Cho f x 2
ax bx c,a  0 và 2
  b  4ac . Tìm điều kiện  để f x cùng dấu với hệ
số a với mọi x  .
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT A.   0 . B.   0 . C.   0 . D.   0 .
Câu 45: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Mệnh đề nào dưới đây đúng? a  a
A. f x 0  0, x     .
B. f x 0       0, x  .  0    0 a  a
C. f x 0  0, x     .
D. f x 0       0, x  .  0    0
Câu 46: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Mệnh đề nào dưới đây đúng? a  a
A. f x 0  0, x     .
B. f x 0       0, x  .  0    0 a  a
C. f x 0  0, x     .
D. f x 0       0, x  .  0    0
Câu 47: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Điều kiện cần và đủ
để f x  0, x   là a  0 a  0 a  0 a  0 A.  . B. C. D.    .  .  .  0    0    0    0
Câu 48: Cho tam thức bậc hai f x 2
ax bx c,a;b;c ,a  0 với 2
  b  4ac. Điều kiện cần và đủ
để f x  0, x   là a  0 a  0 a  0 a  0 A.  . B. C. D.    .  .  .  0    0    0    0
Câu 49: Tập hợp tất cả các giá trị của tham số m để phương trình 2
x mx m  0 có hai nghiệm phân biệt là
A. ;0  4; . B. 0; 4.
C. ;0  4;    . D. 0;4.   Lời giải: Yêu cầu bài toán 2
m  4m  0  m;0 4;.
Chọn đáp án A.
Câu 50: Điều kiện cần và đủ của tham số m để tam thức f x 2
x  m  2 x  4m 1 đổi dấu hai lần là
A. 0  m  12 .
B. m  0 hoặc m  12 C. m  0 hoặc m  12 D. m  0 . Lời giải:
Để tam thức f x 2
x  m  2 x  4m 1 đổi dấu hai lần thì   0   m
m  22  44m   0 2
1  0  m 12m  0   . m 12
Chọn đáp án B.
Câu 51: Với giá trị nào của tham số m thì phương trình 2
mx  2mx  4  0 vô nghiệm?
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTTm  0
A. 0  m  4 . B.  .
C. 0  m  4 .
D. 0  m  4 . m  4 Lời giải: TH: m  0
Phương trình cho trở thành 2
0x  0x  4  0 (vô nghiệm). Nhận m  0 . TH: m  0
Để phương trình cho vô nghiệm thì 2
  m  4m  0  0  m  4 .
Hợp 2 trường hợp, ta được 0  m  4 .
Chọn đáp án D.
Câu 52: Tập hợp tất cả các giá trị của tham số m để phương trình 2 2
x mx m  1  0 có hai nghiệm trái dấu là A. ; 1
  1;. B. 1;1. C. ; 1    1  ;   . D. 1;1.   Lời giải:
Yêu cầu bài toán   2
1 m  1  0  m 1  ;1.
Chọn đáp án B.
Câu 53: Cho tam thức bậc hai f x 2
x  2mx  .
m Tập hợp tất cả các giá trị của tham số m để
f x  0, x   là
A. ;0  1; . B. 0;1. C. ;0  1  ;   . D. 0;1.   Lời giải: a  0 Yêu cầu bài toán 2  
m m  0  m0;1.    0
Chọn đáp án B.
Câu 54: Cho tam thức bậc hai f x 2 2
x  2mx  2m  .
m Tập hợp tất cả các giá trị của tham số m để
f x  0, x   là
A. ;0  1; . B. 0;1. C. ;0  1  ;   . D. 0;1.   Lời giải: a  0 Yêu cầu bài toán 2  
m m  0  m;0  1  ;   .    0
Chọn đáp án C.
Câu 55: Cho f x 2
mx  2mx  4. Tập hợp tất cả các giá trị của tham số m để f x  0, x   là
A. ;0  4; . B. 0; 4.
C. ;0  4;    . D. 0;4  . Lời giải:
TH 1: m  0 : f x  4  0, x
  (đúng) m  0 thỏa mãn. a  0 m  0
TH 2: Yêu cầu bài toán      m 0;4 . 2      0
m  4m  0 Vậy m 0; 4  .
Chọn đáp án D.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Câu 56: Tập hợp tất cả các giá trị của tham số m để hàm số 2 2
y x  4x m  5m xác định trên là
A. ;1  4; . B. 1; 4. C. 1  ;4.   D. 1;1.   Lời giải: Yêu cầu bài toán 2 2
x  4x m  5m  0, x   a  0    4   2 m  5m 2
 0  m  5m  4  0  m 1  ;4.      0
Chọn đáp án C. 4x  7
Câu 57: Tập hợp tất cả các giá trị của tham số m để hàm số y  xác định trên là 2 2
x  4x m  5m
A. ;1  4; . B. 1; 4. C. 1  ;4.   D. 1;1.   Lời giải: Yêu cầu bài toán 2 2
x  4x m  5m  0, x   a  0    4   2 m  5m 2
 0  m  5m  4  0  m1;4.    0
Chọn đáp án B.
Câu 58: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  m  2 x  8m 1  0 vô nghiệm.
A. m 0; 28 .
B. m 0; 28 .
C. m   ;
 0 28;. D. m  ;  028; . Lời giải:
Bất phương trình 2
x  m  2 x  8m 1  0 vô nghiệm 2
x  m  2 x 8m 1  0, x   .   2 m 0
Điều kiện:   0  m  2  48m   2
1  0  m  28m  0   . m  28
Chọn đáp án C.
Câu 59: Tìm số giá trị nguyên của m để bất phương trình 2
x  2mx  3m  2  0 vô nghiệm. A. 0 . B. 1. C. 2 . D. Vô số. Lời giải: a  1  0 Yêu cầu bài toán 2
x  2mx 3m  2  0,x    1 m  2. 2
 '  m  3m  2  0
Do đó không có giá trị nguyên nào của m thỏa mãn điều kiện bài ra.
Chọn đáp án A. 2
x 5x  4  0
Câu 60: Tìm tất cả các giá trị của tham số m để hệ bất phương trình  có nghiệm. x m  0
A. m  1.
B. 1  m  4 .
C. m  4 . D. m  4 . Lời giải: 2
x  5x  4  0 x   1;4    . x m  0 x    ; m 
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Hệ đã cho có nghiệm khi 1; 4  ;
m     m  4 .
Chọn đáp án D. 2 x  4  0
Câu 61: Giá trị của tham số m để hệ bất phương trình  vô nghiệm là
m  4  2x A. m  0 . B. m  0 . C. m  0 . D. m  0 . Lời giải:
+ Xét bất phương trình   1 : 2 x  4  0 . Ta có: 2
x  4  0  x  2  2  x  2 .
Vậy bất phương trình  
1 có tập nghiệm là S  2  ;2 . 1  
+) Xét bất phương trình 2 : m  4  2x .  4
Ta có m  4  2x   m x . 2 m  4 
Vậy bất phương trình 2 có tập nghiệm là S  ;   . 2    2  2 x  4  0
+) Hệ bất phương trình 
vô nghiệm khi và chỉ khi:
m  4  2x m  4
S S     2  m  0 . 1 2 2
Chọn đáp án B.
Câu 62: Cho biểu thức f x 2
x  2m  
1 x  2m  3 . Tìm điều kiện của tham số m để f x  0 thỏa
mãn với mọi x  1  ;2 .
A. m  2 .
B. m  .
C. m  1. D. m  2 . Lời giải:
Xét biểu thức f x 2
x  2m  
1 x  2m  3 là tam thức bậc hai
  m  2   m    m  2 1 2 3 2  0, m  
Nếu   0  m  2  f x  0 với mọi x
m  2 không thỏa mãn bài toán.
Nếu m  2    0  tam thức bậc hai có hai nghiệm phân biệt x , x x x . 1 2  1 2 
x x  2m  2 1 2 Khi đó: 
và f x  0, x   1  ;2   1
 ;2  x ; x 1 2 
x .x  2m  3  1 2 
x 1 x 1  0 
x x x x 1  0  1 2  1 2  1  2 
x  1  2  x     1 2 
x  2 x  2  0 
x x  2 x x  4  0  1 2  1 2  1  2     m     m   m 1 2 3 2 2 1  0         m     m   5 m 2 3 2 2 2  4  0 m   2
Vậy không có giá trị tham số m thỏa mãn bài toán.
Chọn đáp án B.
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115
Chủ đề DẤU TAM THỨC BẬC HAI Đại số 10 KNTT
Câu 63: Có tất cả bao nhiêu giá trị nguyên của tham số m 0; 2022 để x 2; 4 đều là nghiệm bất phương trình 2
x  m  
1 x m  0 ? A. 2022. B. 2021. C. 2020. D. 2019. Lời giải: 2
x  m  
1 x m  0   x  
1  x m  0 (*)
Trường hợp 1: m  1. Khi đó (*) trở thành:  x   1  x  
1  0   x  2 1  0  x  1
Do đó m  1 không thỏa mãn
Trường hợp 2: m  1. Khi đó (*)  1  x m
Yêu cầu bài toán thỏa mãn khi m  4 . Kết hợp với điều kiện m  1 ta có m  4
Trường hợp 3: m  1. Khi đó (*)  m x  1
Không có giá trị m thỏa mãn bởi vì 2; 4  m;  1 m 
Vậy m  4 là điều kiện cần tìm. Mặt khác 
nên m 4;5;6;...;  2022 . m  0;2022
Do đó có 2019 giá trị nguyên của m .
Chọn đáp án D. 2
x  m   1 x 1
Câu 64: Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình  0 2 x  2x  5
nghiệm đúng với mọi x  ? A. 3. B. 5. C. 2. D. 1. Lời giải:
Ta có: x x    x  2 2 2 5 1  4  0, x   2
x  m   1 x 1 Do đó:  0, x   2
x  m   1 x 1  0, x   2 x  2x  5 1   0   2           m 2m 3 0 3 m 1 .  m   2 1  4.1.1  0
Vậy có 5 giá trị nguyên thỏa mãn bài toán là m  3  ; 2  ; 1  ;0  ;1 .
Chọn đáp án B.
_____________________HẾT_____________________
Huế, 15h30’ Ngày 28 tháng 01 năm 2023
Lớp Toán Thầy Lê Bá Bảo TP Huế 0935.785.115

Tài liệu liên quan: