Thông tin
Hỏi đáp

Chủ đề phương trình đường thẳng trong mặt phẳng Toán 10 KNTTVCS

Tài liệu gồm 44 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, hướng dẫn giải các dạng toán thường gặp thuộc chủ đề phương trình đường thẳng trong mặt phẳng Toán 10 Kết Nối Tri Thức Với Cuộc Sống.

Chủ đề:

Chương 8: Đại số tổ hợp (KNTT) 44 tài liệu

Môn:

Toán 10 2.8 K tài liệu

Thông tin:

44 trang 9 tháng trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chủ đề phương trình đường thẳng trong mặt phẳng Toán 10 KNTTVCS

115 58 lượt tải Tải xuống

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 1

Chủ đề:

PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG MẶT PHẲNG

DẠNG TOÁN 1: Xác định vectơ chỉ phương, vectơ pháp tuyến của đường thẳng

I. PHƯƠNG PHÁP

Đường thẳng

 

: 0 0d ax by c a b    

có một vectơ pháp tuyến là

 

n a b

Đường thẳng

 

: , 0

x x u t

d t u u

y y u t







  









có một vectơ chỉ phương là

 

u u u

Đường thẳng

 

x x y y

d u u





có một vectơ chỉ phương là

 

u u u

Chú ý:

a) Đường thẳng

có một vectơ chỉ phương là

   

1 2 1

; , 0

u u u u

thì

có hệ số góc là



b) (Đọc thêm) Phương trình đoạn chắn:

Đường thẳng

cắt

,Ox Oy

lần lượt tại

     

;0 , 0; , 0A a B b ab 

có phương trình:



c) Đường thẳng

có một vectơ chỉ phương là

 

;

u u u

và có một vectơ pháp tuyến là

 

n a b

Lúc đó:

u n au bu   

Suy ra: Đường thẳng

có một vectơ chỉ phương là

 

;

u u u

thì có một vectơ pháp là

 

n u u

II. BÀI TẬP TRẮC NGHIỆM MINH HỌA

Câu 1: Trong mặt phẳng với hệ tọa độ

,Oxy

vectơ nào dưới đây là một vectơ chỉ phương của

?Ox

 

1;0 .u 

 

1;1 .u 

 

1;4 .u 

 

0;2 .u 

Câu 2: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;3 , 2;7 .AB

Một vectơ chỉ phương của

đường thẳng

là

 

4;1 .u 

 

2;1 .u 

 

3;2 .u 

 

1;4 .u 

Câu 3: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Vectơ nào dưới

đây là một vectơ chỉ phương của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Câu 4: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng





Vectơ nào dưới đây là

một vectơ chỉ phương của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Câu 5: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 3 0.d x y  

Vectơ nào dưới đây là

một vectơ pháp tuyến của

 

1;2 .n 

 

2;1 .n 

 

2;1 .n 

 

2;3 .n 

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 2

Câu 6: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 3 3 0.d x y  

Vectơ nào dưới đây là

một vectơ pháp tuyến của

 

2;3 .n 

 

2;3 .n 

 

4; 6 .n 

 

2; 3 .n 

Câu 7: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 5 0.d x y  

Vectơ nào dưới đây là

một vectơ chỉ phương của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Câu 8: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Vectơ nào dưới

đây là một vectơ pháp tuyến của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Câu 9: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng





Vectơ nào dưới đây

không là một vectơ chỉ phương của

 

1;2 .u 

 

2;4 .u 

 

1; 2 .u   

 

2; 4 .u 

Câu 10: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;3 , 3;7 .AB

Gọi



là đường trung trực

của đoạn thẳng

.AB

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

4;3 .n 

 

4;2 .n 

 

2; 1 .n 

Câu 11: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 1 0.d x y  

Gọi



là đường thẳng

song song với

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

4;3 .n 

 

4; 2 .n 

 

2;1 .n 

Câu 12: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 1 0.d x y  

Gọi



là đường thẳng

vuông góc với

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

1; 2 .n 

 

4;2 .n 

 

2;1 .n 

Câu 13: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Gọi



là đường

thẳng song song với

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

4;3 .n 

 

1; 2 .n 

 

2;1 .n 

Câu 14: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng





Gọi



là đường thẳng

vuông góc với

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

1; 2 .n 

 

4;2 .n 

 

2; 1 .n 

DẠNG TOÁN 2: Viết phương trình đường thẳng

I. PHƯƠNG PHÁP

Để viết phương trình đường thẳng

,

ta cần xác định 2 yếu tố: 1 điểm

 

0 0 0

;M x y

mà đường thẳng



đi qua và một vectơ đặc trưng (hoặc là vectơ pháp tuyến, hoặc là vectơ chỉ phương).

Phương trình tổng quát

Phương trình tham số

Phương trình chính tắc

Đường thẳng



đi qua

 

;M x y

và có một vectơ pháp tuyến

Đường thẳng



đi qua

 

;M x y

và có một vectơ chỉ

Đường thẳng



đi qua

 

;M x y

và có một vectơ chỉ

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 3

 

; , 0n a b a b  

có phương

trình:

   

0a x x b y y   

phương

 

1 2 1 2

; , 0u u u u u  

có phương trình:

 

x x u t

y y u t

















phương

   

1 2 1 2

; , . 0u u u u u

có phương trình:

x x y y





Chú ý:

a) Cho đường thẳng

 

: 0 0 .d ax by c a b    

+) Đường thẳng

//d

thì



có dạng

 

: 0, 0 .ax by m m    

+) Đường thẳng

d

thì



có dạng

: 0.bx ay m   

b) Phương trình đoạn chắn:

Đường thẳng

cắt

,Ox Oy

lần lượt tại

     

;0 , 0; , 0A a B b ab 

có phương trình:



c) Đường thẳng

có một vectơ chỉ phương là

 

;

u u u

và có một vectơ pháp tuyến là

 

n a b

Lúc đó:

u n au bu   

II. BÀI TẬP TỰ LUẬN MINH HỌA

Câu 15: Trong mặt phẳng tọa độ

,Oxy

viết phương trình tham số của đường thẳng đi qua hai điểm

   

3; 1 , 6;2 .AB

Câu 16: Trong mặt phẳng tọa độ

,Oxy

viết phương trình đường thẳng



đi qua gốc tọa độ và vuông

góc với đường thẳng

:8 6 7 0.  d x y

Câu 17: Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

   

3;0 ; 0;2AB

và đường thẳng

:0d x y

. Viết

phương trình tham số của đường thẳng



qua

và song song với

Câu 18: Trong mặt phẳng tọa độ

,Oxy

viết phương trình đường thẳng

qua

 

1;1M

và song song với

đường thẳng

': 1 0.  d x y

Câu 19: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

với

     

2;3 ; 4;5 ; 6; 5A B C

. Gọi

,MN

lần

lượt là trung điểm của

và

. Viết phương trình tham số của đường thẳng

.MN

Câu 20: Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

 

1;0A

và

 

0;4 .B

Viết phương trình đường thẳng

.AB

Câu 21: Trong mặt phẳng tọa độ

,Oxy

cho điểm

 

1;2M

. Gọi

,AB

là hình chiếu của

lên

,Ox Oy

Viết phương trình đường thẳng

Câu 22: Trong mặt phẳng tọa độ

,Oxy

viết phương trình đường thẳng đi qua điểm

 

5; 3M

và cắt hai

trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB.

Câu 23: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

với

 

1;1A

 

0; 2B 

 

4;2C

. Viết phương

trình tổng quát của đường trung tuyến đi qua đỉnh

của tam giác

.ABC

Câu 24: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

cân tại

và

 

2; 1B 

 

4;3A

. Viết phương

trình đường cao

của tam giác

.ABC

Câu 25: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có

     

2; 1 , 4;5 , 3;2A B C

. Viết phương

trình đường cao

của tam giác

.ABC

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 4

Câu 26: Trong mặt phẳng tọa độ

,Oxy

gọi

là trực tâm tam giác

ABC

và

:7 4 0; :2 4 0; : 2 0.AB x y BH x y AH x y        

Viết phương trình đường cao

của

tam giác

.ABC

Câu 27: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có

 

2;0M

là trung điểm của cạnh

.AB

Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là

7 2 3 0xy  

và

6 4 0xy  

. Viết phương trình đường thẳng

.AC

Câu 28: Trong mặt phẳng tọa độ

,Oxy

biết đường thẳng

 

: 1 , 0; 0   

d a b

đi qua

 

1;6M 

tạo với tia

,Ox Oy

một tam giác có diện tích bằng 4. Viết phương trình đường thẳng

Câu 29: Trong mặt phẳng tọa độ

,Oxy

cho điểm

 

2;1M

. Viết phương trình đường thẳng

đi qua

cắt các tia

lần lượt tại

và

(

,AB

khác

) sao cho tam giác

OAB

có diện tích nhỏ

nhất.

Câu 30: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

: 1 0,xy   

:2 1 0xy   

và điểm

 

2;1P

. Viết phương trình đường thẳng đi qua điểm

và cắt hai đường thẳng



lần

lượt tại hai điểm

sao cho

là trung điểm

Câu 31: Trong mặt phẳng tọa độ

,Oxy

cho các điểm

 

1; 1A 

và

 

3;4B

. Gọi

là một đường thẳng bất

kì luôn đi qua B. Viết phương trình đường thẳng

khi khoảng cách từ A đến đường thẳng

đạt giá trị lớn nhất.

III. BÀI TẬP TRẮC NGHIỆM MINH HỌA

Câu 32: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 3 0.d x y  

Điểm nào dưới đây nằm trên

đường thẳng

 

1;4 .M

 

1;0 .N

 

2;3 .P

 

2;0 .Q

Câu 33: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 3 0.d x y  

Điểm nào dưới đây

không nằm trên đường thẳng

 

1;4 .M

 

3;0 .N 

 

0;3 .P

 

2;1 .Q

Câu 34: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng







Biết điểm

 

;M a b

nằm

trên đường thẳng

đẳng thức nào sau đây đúng?

3 2 5.ab

3 2 5.ab

3 5.ab

3 5.ab

Câu 35: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Điểm nào dưới đây

nằm trên đường thẳng

 

1;3 .M

 

1;2 .N

 

1;5 .P

 

2;0 .Q

Câu 36: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Điểm nào dưới đây

nằm trên đường thẳng

 

1;3 .M

 

5;2 .N

 

2;5 .P

 

2;0 .Q

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 5

Câu 37: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Điểm nào dưới đây

không nằm trên đường thẳng

 

0;1 .M

 

1;3 .N

 

2;5 .P

 

1;1 .Q

Câu 38: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;0 , 0;5 .AB

Phương trình đường thẳng

là



  



Câu 39: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;1 , 2;5 .AB

Phương trình đường thẳng

là

4 5 0.xy  

4 3 0.xy  

4 1 0.xy  

4 1 0.xy  

Câu 40: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;1 , 2;5 .AB

Phương trình đường thẳng

là

 













 













 













 



  





  



Câu 41: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;1 , 2;4 .MN

Phương trình đường thẳng

là

 













 













 













 









  



Câu 42: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;0 , 3;6 .AB

Phương trình đường thẳng

trung trực của đoạn thẳng

là

3 11 0xy  

3 11 0.xy  

3 9 0.xy  

3 7 0.xy  

Câu 43: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2A

và đường thẳng

: 2 3 0.d x y  

Phương trình đường thẳng



qua

và song song với

là

2 0.xy

2 5 0.xy  

2 5 0.xy  

2 1 0.xy  

Câu 44: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2A

và đường thẳng

: 2 3 0.d x y  

Phương trình đường thẳng



qua

và vuông góc với

là

2 0.xy

2 5 0.xy  

2 1 0.xy  

2 1 0.xy  

Câu 45: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2;3A

và đường thẳng

 

: , .













Phương trình đường thẳng



qua

và song song với

là

2 7 0.xy  

2 0.xy

2 1 0.xy  

2 4 0.xy  

Câu 46: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2;3A

và đường thẳng

 

: , .













Phương trình đường thẳng



qua

và vuông góc với

là

2 7 0.xy  

2 0.xy

2 1 0.xy  

2 4 0.xy  

Câu 47: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 2;3 , 4;4 .A B C 

Phương

trình đường thẳng chứa cạnh

là

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 6

2 3 0.xy  

2 1 0.xy   

2 1 0.xy  

2 4 0.xy  

Câu 48: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 2;3 , 4;1 .A B C 

Đường

trung tuyến

của tam giác

ABC

có phương trình là

2 3 0.xy  

2 1 0.xy   

2 1 0.xy  

2 4 0.xy  

Câu 49: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 2;3 , 4;1 .A B C 

Đường

trung cao

của tam giác

ABC

có phương trình là

2 0.x 

2 1 0.xy  

2 8 0.xy  

Câu 50: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 0;2 , 1; 2M N P 

lần lượt

là trung điểm

, , .AB BC AC

Phương trình đường thẳng chứa cạnh

là

4 5 0.xy  

4 3 0.xy  

4 3 0.xy  

Câu 51: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1; 1 , 1;9 , 9;1M N P

lần lượt

là trung điểm

, , .BC CA AB

Phương trình đường cao

của tam giác

ABC

là

11 0.xy  

2 11 0.xy  

2 11 0.xy  

0.xy

Câu 52: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

2;1 , 2;3 , 1; 5 .A B C

Đường

phân giác trong của góc

có phương trình là

2 0.xy

1 0.xy  

2 4 0.xy  

3 1 0.xy  

Câu 53: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hình bình hành

ABCD

có tâm

 

1;1 .I

Biết

   

2;0 , 1;4 .AB

Phương trình đường thẳng chứa cạnh

là

4 8 0.xy  

4 2 0.xy  

4 1 0.xy  

4 5 0.xy  

Câu 54: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hình bình hành

ABCD

có tâm

 

3;5I

và hai cạnh

,AB AD

lần lượt nằm trên hai đường thẳng

3 6 0, 2 5 1 0.x y x y     

Viết phương trình hai

cạnh còn lại của hình bình hành

.ABCD

2 5 29 0; 3 40 0.x y x y     

2 5 39 0; 3 30 0.x y x y     

2 5 19 0; 3 20 0.x y x y     

2 5 39 0; 3 30 0.x y x y     

Câu 55: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;1M

và hai đường thẳng

: 3 5 0, : 4 0.d x y d x y     

Gọi



là đường thẳng đi qua

và cắt

,dd

lần lượt tại

,AB

sao cho

2 3 0.MA MB

Các đường thẳng cần tìm là

2 0; 1 0.x y x    

0; 1 0.x y y   

2 1 0; 1 0.x y x    

0; 1 0.x y x   

Câu 56: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Lập phương trình đường thẳng



đi

qua

và cắt các trục tọa độ lần lượt tại

,AB

(khác

) sao cho

là trung điểm

.AB

3 0.xy  

2 2 0.xy  

2 5 0.xy  

2 4 0.xy  

Câu 57: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Lập phương trình đường thẳng



đi

qua

và cắt các tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

2.OA OB

3 0.xy  

2 2 0.xy  

2 5 0.xy  

2 4 0.xy  

Câu 58: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Có bao nhiêu đường thẳng đi qua

và cắt các tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

6?OA OB

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 7

C. Vô số. D.

Câu 59: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2;1 .M

Gọi



là đường thẳng qua

, cắt các

tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

OA OB

nhỏ nhất. Hỏi đường thẳng



đi qua

điểm nào dưới đây?

 

2; 2 .M

 

2; 2 .N 

 

2; 2 .P 

 

2; 2 .Q 

Câu 60: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Gọi



là đường thẳng qua

, cắt các

tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

OA OB



nhỏ nhất. Hỏi đường thẳng



đi qua

điểm nào dưới đây?

 

3;1 .M

 

2; 1 .N 

 

0; 3 .P

 

3;3 .Q

Câu 61: Trong mặt phẳng tọa độ

,Oxy

cho điểm

(3;2)M

. Gọi

là đường thẳng đi qua

và lần lượt

cắt tia

,Ox

tại

( ;0), B(0; )A a b

với

0, 0ab

và diện tích tam giác

OAB

nhỏ nhất. Hỏi

điểm nào dưới đây thuộc

 

3;6 .N

 

2; 1 .S 

 

1;3 .P

 

3;3 .Q

DẠNG TOÁN 3: Khoảng cách. Góc

I. PHƯƠNG PHÁP

1. Khoảng cách

a. Cho đường thẳng

 

: 0 0ax by c a b     

và điểm

 

;.M x y

Khoảng cách từ

đến



là

 

;

ax by c







Đặc biệt:

 

;

d M Ox y

d M Oy x















b. Cho hai đường thẳng

 

: 0 0ax by c a b     

và

 

2 2 1 2

: 0 .ax by c c c    

Khoảng cách giữa



và



là

 

;



  



2. Góc giữa hai đường thẳng

Cho hai đường thẳng

 

1 1 1 1 1 1

: 0 0a x b y c a b     

và

 

2 2 2 2 2 2

: 0 0a x b y c a b     

Đường thẳng



có một vectơ pháp tuyến là

 

1 1 1

;.n a b

Đường thẳng



có một vectơ pháp tuyến là

 

2 2 2

;.n a b

Gọi



là góc giữa hai đường thẳng



và

 

, 0 90 .



    

1 2 1 2 1 2

2 2 2 2

1 1 2 2

cos

n n a a b b

a b a b









Đặc biệt:

1 2 1 2 1 2 1 2

. 0 0n n a a b b       

II. BÀI TẬP TỰ LUẬN MINH HỌA

Câu 62: Trong mặt phẳng tọa độ

,Oxy

tính côsin góc giữa hai đường thẳng

:2 1 0xy   

và













Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 8

Câu 63: Trong mặt phẳng tọa độ

,Oxy

tính góc giữa hai đường thẳng

: 2 15 0xy   

và

 













Câu 64: Trong mặt phẳng tọa độ

,Oxy

tính góc giữa hai đường thẳng

: 3 2 0    xy

và

: 3 1 0 .   xy

Câu 65: Trong mặt phẳng tọa độ

,Oxy

tìm tất cả các giá trị của

để góc tạo bởi đường thẳng











x at

 

t 

và đường thẳng

:3 4 2 0  d x y

bằng

45

Câu 66: Trong mặt phẳng tọa độ

,Oxy

tính khoảng cách từ điểm

 

1; 1M 

đến đường thẳng

:3 4 0.   xy

Câu 67: Trong mặt phẳng tọa độ

,Oxy

tính khoảng cách từ điểm

 

3; 4M 

đến đường thẳng



  





  



Câu 68: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

: 3 0d x y  

và

: 5 0.d x y  

Tính

khoảng cách giữa hai đường thẳng

và

Câu 69: Trong mặt phẳng tọa độ

,Oxy

tính khoảng cách từ điểm

 

0;4A

đến đường thẳng

 

.sin .cos 4 1 cos 0, .

   

    xy

Câu 70: Trong mặt phẳng tọa độ

,Oxy

biết đường tròn

 

có tâm

 

3; 2I 

tiếp xúc với đường thẳng

: 5 1 0,   xy

tính bán kính

của đường tròn

 

Câu 71: Trong mặt phẳng tọa độ

,Oxy

cho điểm

 

0;1A

và đường thẳng











. Tìm điểm

thuộc

và cách

một khoảng bằng

Câu 72: Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

   

3; 1 , 0;3AB

. Tìm tọa độ điểm

thuộc

sao khoảng cách từ

đến đường thẳng

bằng

Câu 73: Trong mặt phẳng tọa độ

,Oxy

tìm điểm

thuộc đường thẳng











và cách đường

thẳng

:2 3 0xy   

một khoảng

Câu 74: Trong mặt phẳng tọa độ

,Oxy

tìm tọa độ hình chiếu vuông góc của điểm

 

1;2M

lên đường

thẳng

: 0.  xy

Câu 75: Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

 

: 1 0x m y m    

(

là tham số bất kì)

và điểm

 

5;1A

. Tính khoảng cách lớn nhất từ điểm

đến

.

III. BÀI TẬP TRẮC NGHIỆM MINH HỌA

Câu 76: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2A

và đường thẳng

: 2 1 0.xy   

Tính

khoảng cách từ điểm

đến đường thẳng

.

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 9

Câu 77: Trong mặt phẳng với hệ tọa độ

,Oxy

tìm giá trị tham số

để khoảng cách từ điểm

 

2; 3I

đến

đường thẳng

: 1 2 0x ny n    

bằng

0.n 

1.n 

1.n 

2.n 

Câu 78: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;3M

và đường thẳng

 

: , .













Tính

khoảng cách từ điểm

đến đường thẳng

.

Câu 79: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 2 3 0d x y  

và

: 2 4 5 0.d x y  

Tính khoảng cách giữa hai đường thẳng

và

Câu 80: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 3 4 3 0.xy   

Viết phương trình các

đường thẳng song song với



và cách



một khoảng bằng

3 4 1 0; 3 4 7 0.x y x y     

3 4 2 0; 3 4 8 0.x y x y     

3 4 2 0; 3 4 6 0.x y x y     

3 4 4 0; 3 4 6 0.x y x y     

Câu 81: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

 

1;4M

và

 

6;2 .N

Viết phương trình các

đường thẳng



qua

sao cho khoảng cách từ

đến



bằng

1 0; 3 4 19 0.x x y    

1 0; 21 20 59 0.x x y    

1 0; 3 4 19 0.y x y    

1 0; 21 20 59 0.y x y    

Câu 82: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

 

1;1P

và

 

4;2 .Q

Viết phương trình các

đường thẳng



sao cho khoảng cách từ

và

đến



lần lượt bằng

và

1 0; 3 4 11 0.y x y    

1 0; 3 4 11 0.x x y    

1 0; 3 4 11 0.y x y    

1 0; 3 4 11 0.x x y    

Câu 83: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 2 10 0d x y  

và

: 3 2 0.d x y  

Tính góc giữa hai đường thẳng

và

30 .

45 .

60 .

90 .

Câu 84: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 1 0d mx y  

và

: 2 10 0.d x y  

Tìm tập hợp tất cả các giá trị của tham số

để hai đường thẳng

và

vuông góc với nhau.







 

2.

 

2.

.

Câu 85: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 7 9 0d mx y m   

và

: 2 10 0.d x y  

Gọi

là tập hợp tất cả các giá trị của tham số

để góc giữa hai đường thẳng

và

bằng

45

. Tính tổng tất cả các phần tử của



DẠNG TOÁN 4: Vị trí tương đối giữa hai đường thẳng

I. PHƯƠNG PHÁP

Cho hai đường thẳng

 

1 1 1 1 1 1

: 0 0a x b y c a b     

và

 

2 2 2 2 2 2

: 0 0a x b y c a b     

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 10

Nếu

2 2 2

, , 0a b c 

thì ta có:



cắt

  



song song với



1 1 1

2 2 2

a b c

  



và



trùng nhau

1 1 1

2 2 2

a b c

  

II. BÀI TẬP TỰ LUẬN MINH HỌA

Câu 86: Trong mặt phẳng tọa độ

,Oxy

tìm

để hai đường thẳng

: 5, : 9d mx y m d x my    

cắt

nhau.

Câu 87: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

 

: 1 2 0d mx m y m   

và

: 2 1 0d x y  

. Tìm

để

và

song song.

Câu 88: Trong mặt phẳng tọa độ

,Oxy

cho ba đường thẳng

 

: 1 2 0, : 4 3 26 0d mx m y m d x y      

và

: 3 4 7 0.d x y  

Tìm

để ba đường thẳng trên đồng quy.

Câu 89: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

:5 7 4 0d x y  

và

:5 7 6 0.d x y  

Viết phương trình đường thẳng

song song và cách đều

và

Câu 90: Trong mặt phẳng tọa độ

,Oxy

tìm tọa độ giao điểm của hai đường thẳng

4 3 26 0xy  

và

3 4 7 0xy  

Câu 91: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có

 

2;1A

, đường cao

:BH

3 7 0xy  

và

trung tuyến

:CM

10xy  

. Tìm tọa độ đỉnh

Câu 92: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

: 1, : 3 3 0d x y d x y    

. Viết

phương trình đường thẳng

đối xứng với

qua đường thẳng

III. BÀI TẬP TRẮC NGHIỆM MINH HỌA

Câu 93: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 3 0d x y  

và

: 2 3 0.d x y  

Khẳng định nào sau đây đúng?

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

Câu 94: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 4 2 1 0d x y  

và

: 2 3 0.d x y  

Khẳng định nào sau đây đúng?

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

Câu 95: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

 













và

: 2 3 0.d x y  

Khẳng định nào sau đây đúng?

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

Câu 96: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

 













và

 

: , .













Khẳng định nào sau đây đúng?

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 11

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

DẠNG TOÁN 5: Các bài toán liên quan đến điểm.

I. PHƯƠNG PHÁP

Một số lưu ý khi xử lí các bài toán liên quan đến điểm:

a. Điểm

 

;0 .M Ox M t 

b. Điểm

 

0; .M Oy M t 

c. Điểm

 

: 2 0 .

M t t

M x y

M t t





    









d. Điểm

 

: 2 2 0 ;2 2 .M x y M t t     

e. Điểm

 

: 2 3 0 2 3; .M x y M t t     

Chú ý: Bài toán hình chiếu vuông góc và điểm đối xứng qua đường thẳng.

Cho điểm

và đường thẳng



(không qua

+) Điểm

là hình chiếu vuông góc của

trên

AH u













  











+) Điểm



là điểm đối xứng của

qua

H

là trung điểm

.AA



II. BÀI TẬP TRẮC NGHIỆM MINH HỌA

Câu 97: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2; 1A 

và đường thẳng

: 2 5 0.xy   

Gọi

 

;H a b

là hình chiếu vuông góc của

trên

,

tính

.ab

3.

Câu 98: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

vuông cân tại

Gọi

 

1; 1M 

là

trung điểm của cạnh

và







là trọng tâm của tam giác

.ABC

Biết

   

; , 0 ,B a b a 

tính

.ab

MỘT SỐ BÀI TOÁN KHÁC

Câu 99: Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 4 15 0d x y  

và điểm

 

2;0A

. Tìm tọa

độ điểm

thuộc

để đoạn

có độ dài nhỏ nhất.

Câu 100: Trong mặt phẳng tọa độ

,Oxy

cho điểm hai điểm

 

4;2A 

 

2;6B

và điểm C nằm trên đường

thẳng







sao cho

CA CB

. Tìm tọa độ điểm C.

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 12

Câu 101: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

. Tìm tọa độ các đỉnh của tam giác biết

phương trình cạnh

: 2 0BC x y  

; hai đường cao

' : 3 0BB x 

và

' : 2 3 6 0.CC x y  

Câu 102: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có

     

3 0 3 0 2 6A ; ,B ; ,C ;

. Tìm tọa độ trực

tâm

là của tam giác

ABC

Câu 103: Trong mặt phẳng tọa độ

,Oxy

cho ba điểm

     

1;1 ; 2;0 ; 3;4A B C

. Viết phương trình đường

thẳng đi qua

và cách đều hai điểm

,BC

Câu 104: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có phương trình đường thẳng

: 7 13 0.BC x y  

Các chân đường cao kẻ từ

,BC

của tam giác

ABC

lần lượt là

   

2;5 , 0;4 .EF

Tìm tọa độ đỉnh A.

Câu 105: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có đỉnh

( 12;1)B 

, đường phân giác trong của

góc

có phương trình

: 2 5 0;d x y  

;







là trọng tâm tam giác

ABC

. Tìm tọa độ đỉnh

Câu 106: Trong mặt phẳng tọa độ

,Oxy

cho 3 điểm

     

6;3 ; 0; 1 ; 3;2A B C

. Tìm

trên đường thẳng

  : 2 3 0d x y

mà

MA MB MC

nhỏ nhất.

Câu 107: Trong mặt phẳng tọa độ

,Oxy

cho hình chữ nhật ABCD có điểm C thuộc đường thẳng

: 2 5 0d x y  

và điểm

 

4;8A 

. Gọi M là điểm đối xứng với B qua C, điểm

 

5; 4N 

là hình

chiếu vuông góc của B lên đường thẳng MD. Tìm tọa độ điểm

Câu 108: Trong mặt phẳng tọa độ

,Oxy

cho hình vuông

ABCD

. Gọi

là trung điểm của cạnh

là điểm trên cạnh

sao cho

2CN ND

. Giả sử

11 1

;







và đường thẳng

có phương

trình

2 3 0xy  

. Tìm tọa độ điểm

là giao điểm của

và

Câu 109: Trong mặt phẳng tọa độ

,Oxy

cho hình thoi

MN PQ

có tâm

 

3;1I

, đỉnh

thuộc đường

thẳng

4 1 0xy  

, đỉnh

thuộc đường thẳng

80xy  

. Xác định tọa độ đỉnh

Câu 110: Trong mặt phẳng tọa độ

,Oxy

cho hình chữ nhật

ABCD

có điểm

thuộc đường thẳng

 

:2 5 0d x y  

và điểm

( 4;8)A 

. Gọi

đối xứng với

qua

, điểm

(5; 4)N 

là hình

chiếu vuông góc của

lên đường thẳng

. Tìm tọa độ đỉnh

_____________________HẾT_____________________

Huế, 15h00’ Ngày 16 tháng 02 năm 2023

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 13

LỜI GIẢI CHI TIẾT

Câu 1: Trong mặt phẳng với hệ tọa độ

,Oxy

vectơ nào dưới đây là một vectơ chỉ phương của

?Ox

 

1;0 .u 

 

1;1 .u 

 

1;4 .u 

 

0;2 .u 

Lời giải:

Các vectơ chỉ phương của

có tọa độ

   

;0 , 0 .kk



Chọn đáp án A.

Câu 2: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;3 , 2;7 .AB

Một vectơ chỉ phương của

đường thẳng

là

 

4;1 .u 

 

2;1 .u 

 

3;2 .u 

 

1;4 .u 

Lời giải:

Ta có:

 

1;4 .AB 

Các vectơ chỉ phương của đường thẳng

có tọa độ

   

;4 , 0 .k k k 



Chọn đáp án D.

Câu 3: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Vectơ nào dưới

đây là một vectơ chỉ phương của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Lời giải:

Các vectơ chỉ phương của

có tọa độ

   

2 ;3 , 0 .k k k 



Chọn đáp án D.

Câu 4: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng





Vectơ nào dưới đây là

một vectơ chỉ phương của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Lời giải:

Các vectơ chỉ phương của

có tọa độ

   

;2 , 0 .k k k 



Chọn đáp án A.

Câu 5: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 3 0.d x y  

Vectơ nào dưới đây là

một vectơ pháp tuyến của

 

1;2 .n 

 

2;1 .n 

 

2;1 .n 

 

2;3 .n 

Lời giải:

Các vectơ pháp tuyến của

có tọa độ

   

2 ; , 0 .k k k 



Chọn đáp án C.

Câu 6: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 3 3 0.d x y  

Vectơ nào dưới đây là

một vectơ pháp tuyến của

 

2;3 .n 

 

2;3 .n 

 

4; 6 .n 

 

2; 3 .n 

Lời giải:

Các vectơ pháp tuyến của

có tọa độ

   

2 ;3 , 0 .k k k 

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 14



Chọn đáp án A.

Câu 7: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 5 0.d x y  

Vectơ nào dưới đây là

một vectơ chỉ phương của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Lời giải:

Các vectơ chỉ phương của

có tọa độ

   

2 ; , 0 .k k k



Chọn đáp án B.

Câu 8: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Vectơ nào dưới

đây là một vectơ pháp tuyến của

 

1;2 .u 

 

2;1 .u 

 

3;2 .u 

 

2;3 .u 

Lời giải:

Các vectơ pháp tuyến của

có tọa độ

   

3 ;2 , 0 .k k k



Chọn đáp án C.

Câu 9: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng





Vectơ nào dưới đây

không là một vectơ chỉ phương của

 

1;2 .u 

 

2;4 .u 

 

1; 2 .u   

 

2; 4 .u 

Lời giải:

Các vectơ chỉ phương của

có tọa độ

   

;2 , 0 .k k k 



Chọn đáp án D.

Câu 10: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;3 , 3;7 .AB

Gọi



là đường trung trực

của đoạn thẳng

.AB

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

4;3 .n 

 

4;2 .n 

 

2; 1 .n 

Lời giải:

Ta có:

 

2;4 .AB 



là đường trung trực của đoạn thẳng

nên

.AB

Vậy các vectơ pháp tuyến của



có tọa độ

   

2 ;4 , 0 .k k k 



Chọn đáp án A.

Câu 11: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 1 0.d x y  

Gọi



là đường thẳng

song song với

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

4;3 .n 

 

4; 2 .n 

 

2;1 .n 

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

2;1 .

n 



song song với

nên các vectơ pháp tuyến của



có tọa độ

   

2 ; , 0 .k k k 



Chọn đáp án D.

Câu 12: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 2 1 0.d x y  

Gọi



là đường thẳng

vuông góc với

Một vectơ pháp tuyến của đường thẳng



là

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 15

 

1;2 .n 

 

1; 2 .n 

 

4;2 .n 

 

2;1 .n 

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

2;1 .

n 



vuông góc với

nên các vectơ pháp tuyến của



có tọa độ

   

; 2 , 0 .k k k



Chọn đáp án B.

Câu 13: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Gọi



là đường

thẳng song song với

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

4;3 .n 

 

1; 2 .n 

 

2;1 .n 

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

1; 2 .

n 



song song với

nên các vectơ pháp tuyến của



có tọa độ

   

; 2 , 0 .k k k



Chọn đáp án C.

Câu 14: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng





Gọi



là đường thẳng

vuông góc với

Một vectơ pháp tuyến của đường thẳng



là

 

1;2 .n 

 

1; 2 .n 

 

4;2 .n 

 

2; 1 .n 

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

1; 2 .

n 



vuông góc với

nên các vectơ pháp tuyến của



có tọa độ

   

2 ; , 0 .k k k 



Chọn đáp án C.

Câu 15: Trong mặt phẳng tọa độ

,Oxy

viết phương trình tham số của đường thẳng đi qua hai điểm

   

3; 1 , 6;2 .AB

Lời giải:

Đường thẳng

qua điểm

 

3; 1A

và có 1 vectơ chỉ phương là

 

9;3AB

nên có phương

trình:

 









  



Câu 16: Trong mặt phẳng tọa độ

,Oxy

viết phương trình đường thẳng



đi qua gốc tọa độ và vuông

góc với đường thẳng

:8 6 7 0.  d x y

Lời giải:

Vì

d

nên



có dạng:

6 8 0.  x y C

 

0;0 O

nên

6.0 8.0 0 0CC    

Vậy phương trình

:6 8 0 3 4 0.     x y x y

Câu 17: Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

   

3;0 ; 0;2AB

và đường thẳng

:0d x y

. Viết

phương trình tham số của đường thẳng



qua

và song song với

Lời giải:

 d

nên

 

: 0 0 .    x y C C



qua

 

3;0A

, suy ra

3 0 0 3CC     

( nhận)

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 16

Như vậy

: 3 0xy   

Vậy



có phương trình tham số:

 













Câu 18: Trong mặt phẳng tọa độ

,Oxy

viết phương trình đường thẳng

qua

 

1;1M

và song song với

đường thẳng

': 1 0.  d x y

Lời giải:

Do đường thẳng

song song với đường thẳng

': 1 0d x y  

nên đường thẳng

nhận

vectơ

 

1;1n 

làm một vectơ pháp tuyến.

Khi đó đường thẳng

qua

 

1;1M

và nhận vectơ

 

1;1n 

làm vectơ pháp tuyến có phương

trình là

20xy  

Câu 19: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

với

     

2;3 ; 4;5 ; 6; 5A B C

. Gọi

,MN

lần

lượt là trung điểm của

và

. Viết phương trình tham số của đường thẳng

.MN

Lời giải:

,MN

lần lượt là trung điểm của

và

nên suy ra

   

1;4 ; 4; 1MN

Đường thẳng

đi qua

 

1;4M 

và nhận

 

5; 5MN 

làm một vectơ chỉ phương

  











Câu 20: Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

 

1;0A

và

 

0;4 .B

Viết phương trình đường thẳng

.AB

Lời giải:

Áp dụng công thức phương trình đoạn chắn

: 1 4 4 0.

AB x y      

Câu 21: Trong mặt phẳng tọa độ

,Oxy

cho điểm

 

1;2M

. Gọi

,AB

là hình chiếu của

lên

,Ox Oy

Viết phương trình đường thẳng

Lời giải:

Ta có, hình chiếu của điểm

(1;2)M

lên

,Ox Oy

lần lượt là A(1;0) và B(0;2).

Do đó phương trình đường thẳng AB là:

1 2 2 0

xy     

Câu 22: Trong mặt phẳng tọa độ

,Oxy

viết phương trình đường thẳng đi qua điểm

 

5; 3M

và cắt hai

trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB.

Lời giải:

Gọi

   

;0 ; 0;

A Ox A x B Oy B y   

Ta có

là trung điểm

2 10

A B M A

A B M B

x x x x

y y y y

  







   



Suy ra

: 1 3 5 30 0

10 6

     



AB x y

Câu 23: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

với

 

1;1A

 

0; 2B 

 

4;2C

. Viết phương

trình tổng quát của đường trung tuyến đi qua đỉnh

của tam giác

.ABC

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 17

Lời giải:

Gọi

là trung điểm của cạnh

5 3 5 7

;;

2 2 2 2

AC M BM

   

  

   

   

Đường thẳng

nhận

 

7;5n 

làm một vectơ pháp tuyến.

Suy ra

: 7 5( 2) 0 7 5 10 0.        BM x y x y

Câu 24: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

cân tại

và

 

2; 1B 

 

4;3A

. Viết phương

trình đường cao

của tam giác

.ABC

Lời giải:

Tam giác

ABC

cân tại

nên

là trung điểm của

và

CH AB

Ta có:

 

3;1H

và

   

2; 4 2 1;2AB     

Vậy phương trình đường cao

:CH

   

1 3 2 1 0xy   

2 5 0xy   

Câu 25: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có

     

2; 1 , 4;5 , 3;2A B C

. Viết phương

trình đường cao

của tam giác

.ABC

Lời giải:

Đường cao

đi qua điểm

 

2; 1A 

và có một vectơ pháp tuyến là

 

7; 3BC   

Vậy phương trình

là

   

7 2 3 1 0 7 3 11 0x y x y        

Câu 26: Trong mặt phẳng tọa độ

,Oxy

gọi

là trực tâm tam giác

ABC

và

:7 4 0; :2 4 0; : 2 0.AB x y BH x y AH x y        

Viết phương trình đường cao

của

tam giác

.ABC

Lời giải:

Ta có:

CH AB

nên

có phương trình

   

1 7 0

x x y y   

   

1 7 0

x x y y   

trong đó

là nghiệm của hệ:

2 4 0 2

2 0 0

x y x

x y y

   







   



Từ đó

 

2;0 .H

Vậy

   

1 2 7 0 0 7 2 0.x y x y       

Câu 27: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có

 

2;0M

là trung điểm của cạnh

.AB

Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là

7 2 3 0xy  

và

6 4 0xy  

. Viết phương trình đường thẳng

.AC

Lời giải:

+) Gọi

và

lần lượt là các đường cao và trung tuyến kẻ từ

của tam giác

ABC

+) Tọa độ

là nghiệm của hệ

 

7 2 3 0 1

1;2

6 4 0 2

x y x

x y y

   







   



Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 18

là trung điểm của

nên

 

3; 2

B M A

x x x

y y y

  







   



+) Đường thẳng

đi qua

 

3; 2B 

và vuông góc với đường thẳng

6 4 0xy  

nên có

phương trình

 

– 3 6 2 0 6 9 0x y x y      

là giao điểm của

và

nên tọa độ

là nghiệm của hệ:

7 2 3 0

6 9 0

  





  











  













Do D là trung điểm của BC nên suy ra

 

3; 1 .C

+) Đường thẳng

đi qua

 

1;2A

và

 

3; 1C 

có phương trình là

3 4 5 0xy  

Câu 28: Trong mặt phẳng tọa độ

,Oxy

biết đường thẳng

 

: 1 , 0; 0   

d a b

đi qua

 

1;6M 

tạo với tia

,Ox Oy

một tam giác có diện tích bằng 4. Viết phương trình đường thẳng

Lời giải:

đi qua

 

1;6M 

1 (1).





Đường thẳng cắt tia

tại

( ;0), 0 .A a a OA a  

Đường thẳng cắt tia

tại

(0; ), 0 .B b b OB b  

OAB

vuông tại O nên có diện tích là



OAB

S OAOB ab

Theo đề

4 4 8 (2).

    

OAB

S ab ab

Từ

   

1 , 2

suy ra:

2; 4 : 1 2 4 0.

        

a b d x y

Câu 29: Trong mặt phẳng tọa độ

,Oxy

cho điểm

 

2;1M

. Viết phương trình đường thẳng

đi qua

cắt các tia

lần lượt tại

và

(

,AB

khác

) sao cho tam giác

OAB

có diện tích nhỏ

nhất.

Lời giải:

Gọi đường thẳng d cắt tia

lần lượt tại

 

;0Aa

và

 

0; ; , 0B b a b

 

:1  

Vì

 

qua

 

2;1 1  M

2 1 2

1 2 8     

Cauchy

a b ab

Ta có diện tích tam giác vuông

OAB

tại

là

. . . . 4

  S OAOB a b

Diện tích tam giác

OAB

đạt giá trị nhỏ nhất

min

42    S a b

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 19

1 2, 4

     ba

 

: 1 2 4 0

      

d x y

Câu 30: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

: 1 0,xy   

:2 1 0xy   

và điểm

 

2;1P

. Viết phương trình đường thẳng đi qua điểm

và cắt hai đường thẳng



lần

lượt tại hai điểm

sao cho

là trung điểm

Lời giải:

Vì

 

;1A A a a  

. Vì

 

2;1P

là trung điểm của đoạn

 

4 ;1B a a  

Mặt khác

8 8 11

;

3 3 3

B a A



   





;











Đường thẳng

có phương trình là:

4 7 0xy  

Câu 31: Trong mặt phẳng tọa độ

,Oxy

cho các điểm

 

1; 1A 

và

 

3;4B

. Gọi

là một đường thẳng bất

kì luôn đi qua B. Viết phương trình đường thẳng

khi khoảng cách từ A đến đường thẳng

đạt giá trị lớn nhất.

Lời giải:

Ta có:

 

2;5 .AB 

Gọi

là hình chiếu của điểm

lên đường thẳng

Khi đó, ta có:

 

   

, 3 1 4 1 29d A d AH AB      

Do đó khoảng cách từ

đến đường thẳng

đạt giá trị lớn nhất bằng

khi

.AB d

Vì vậy

đi qua

 

1; 1A 

và nhận

 

2;5AB 

làm một vectơ pháp tuyến.

Do đó phương trình của đường thẳng

là

   

:2 1 5 1 0 :2 5 3 0d x y d x y       

Câu 32: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 3 0.d x y  

Điểm nào dưới đây nằm trên

đường thẳng

 

1;4 .M

 

1;0 .N

 

2;3 .P

 

2;0 .Q

Lời giải:

Thay tọa độ điểm

vào phương trình

thấy thỏa mãn.



Chọn đáp án A.

Câu 33: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 3 0.d x y  

Điểm nào dưới đây

không nằm trên đường thẳng

 

1;4 .M

 

3;0 .N 

 

0;3 .P

 

2;1 .Q

Lời giải:

Thay tọa độ điểm

vào phương trình

thấy không thỏa mãn.



Chọn đáp án D.

Câu 34: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng







Biết điểm

 

;M a b

nằm

trên đường thẳng

đẳng thức nào sau đây đúng?

3 2 5.ab

3 2 5.ab

3 5.ab

3 5.ab

Lời giải:

     

; 3 1 2 1 3 2 5.

M a b d a b a b



         



Chọn đáp án A.

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 20

Câu 35: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Điểm nào dưới đây

nằm trên đường thẳng

 

1;3 .M

 

1;2 .N

 

1;5 .P

 

2;0 .Q

Lời giải:



Chọn đáp án B.

Câu 36: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Điểm nào dưới đây

nằm trên đường thẳng

 

1;3 .M

 

5;2 .N

 

2;5 .P

 

2;0 .Q

Lời giải:

Thay tọa độ điểm

vào phương trình

ta được:

5 2 3















Chọn đáp án C.

Câu 37: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

 

: , .













Điểm nào dưới đây

không nằm trên đường thẳng

 

0;1 .M

 

1;3 .N

 

2;5 .P

 

1;1 .Q

Lời giải:

Thay tọa độ điểm

vào phương trình

1 1 2











(vô nghiệm).



Chọn đáp án D.

Câu 38: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;0 , 0;5 .AB

Phương trình đường thẳng

là



  



Lời giải:



Chọn đáp án D.

Câu 39: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;1 , 2;5 .AB

Phương trình đường thẳng

là

4 5 0.xy  

4 3 0.xy  

4 1 0.xy  

4 1 0.xy  

Lời giải:

Ta có:

 

1;4 .AB 

Đường thẳng

qua

 

1;1A

và nhận

 

1;4AB 

làm một vectơ chỉ phương nên chọn

 

4; 1n 

làm một vec tơ pháp tuyến của

.AB

Vậy

   

: 4 1 1 0 4 3 0.AB x y x y       



Chọn đáp án B.

Câu 40: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;1 , 2;5 .AB

Phương trình đường thẳng

là

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 21

 













 













 













 



  





  



Lời giải:

Ta có:

 

1;4 .AB 

Đường thẳng

qua

 

1;1A

và nhận

 

1;4AB 

làm một vectơ chỉ phương.

Vậy

 

: , .

AB t















Chọn đáp án A.

Câu 41: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;1 , 2;4 .MN

Phương trình đường thẳng

là

 













 













 













 









  



Lời giải:

Ta có:

 

1;3 .MN 

Đường thẳng

qua

 

1;1M

và nhận

 

1;3MN 

làm một vectơ chỉ phương.

Vậy

 

: , .

MN t













Test phương án D, thấy thỏa mãn.



Chọn đáp án D.

Câu 42: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

   

1;0 , 3;6 .AB

Phương trình đường thẳng

trung trực của đoạn thẳng

là

3 11 0xy  

3 11 0.xy  

3 9 0.xy  

3 7 0.xy  

Lời giải:

Ta có:

 

2;6 .AB 

Gọi

là trung điểm

 

2;3 .AB I

Đường thẳng



qua

 

2;3I

và nhận

 

2;6AB 

làm một vectơ pháp tuyến.

Vậy

   

: 2 2 6 3 0 2 6 22 0 3 11 0.x y x y x y            



Chọn đáp án B.

Câu 43: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2A

và đường thẳng

: 2 3 0.d x y  

Phương trình đường thẳng



qua

và song song với

là

2 0.xy

2 5 0.xy  

2 5 0.xy  

2 1 0.xy  

Lời giải:



song song với

nên



có dạng

 

: 2 0, 3 .x y m m     

 

1;2 1 4 0 5.A m m       

Vậy

: 2 5 0.xy   



Chọn đáp án B.

Câu 44: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2A

và đường thẳng

: 2 3 0.d x y  

Phương trình đường thẳng



qua

và vuông góc với

là

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 22

2 0.xy

2 5 0.xy  

2 1 0.xy  

2 1 0.xy  

Lời giải:



vuông góc với

nên



có dạng

: 2 0.x y m   

 

1;2 2 2 0 0.A m m      

Vậy

: 2 0.xy  



Chọn đáp án A.

Câu 45: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2;3A

và đường thẳng

 

: , .













Phương trình đường thẳng



qua

và song song với

là

2 7 0.xy  

2 0.xy

2 1 0.xy  

2 4 0.xy  

Lời giải:

Đường thẳng

có một vectơ chỉ phương là

 

2;1

u 

nên

có một vectơ pháp tuyến là

 

1; 2 .

n 



song song với

nên



nhận

 

1; 2

n 

làm một vectơ pháp tuyến.

Vậy

   

: 1 2 2 3 0 2 4 0.x y x y        



Chọn đáp án D.

Câu 46: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2;3A

và đường thẳng

 

: , .













Phương trình đường thẳng



qua

và vuông góc với

là

2 7 0.xy  

2 0.xy

2 1 0.xy  

2 4 0.xy  

Lời giải:

Đường thẳng

có một vectơ chỉ phương là

 

2;1 .

u 



vuông góc với

nên



nhận

 

1; 2

n 

làm một vectơ pháp tuyến.

Vậy

   

: 1 2 2 3 0 2 4 0.x y x y        



Chọn đáp án D.

Câu 47: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 2;3 , 4;4 .A B C 

Phương

trình đường thẳng chứa cạnh

là

2 3 0.xy  

2 1 0.xy   

2 1 0.xy  

2 4 0.xy  

Lời giải:

Đường thẳng

có một vectơ chỉ phương là

   

1;2 2;1AB n   

là một vectơ pháp tuyến

của

.AB

Vậy

   

: 2 1 1 1 0 2 1 0.AB x y x y         



Chọn đáp án B.

Câu 48: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 2;3 , 4;1 .A B C 

Đường

trung tuyến

của tam giác

ABC

có phương trình là

2 3 0.xy  

2 1 0.xy   

2 1 0.xy  

2 4 0.xy  

Lời giải:

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 23

Gọi

là trung điểm

 

1;2 .BC M

Đường thẳng

có một vectơ chỉ phương là

   

2;1 1;2AM n   

là một vectơ pháp tuyến

của

.AM

Vậy

   

: 1 1 2 1 0 2 3 0.AM x y x y       



Chọn đáp án A.

Câu 49: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 2;3 , 4;1 .A B C 

Đường

trung cao

của tam giác

ABC

có phương trình là

2 0.x 

2 1 0.xy  

2 8 0.xy  

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

5;0 .AC 

Vậy

   

: 5 2 0 3 0 2 0.BK x y x       



Chọn đáp án A.

Câu 50: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1;1 , 0;2 , 1; 2M N P 

lần lượt

là trung điểm

, , .AB BC AC

Phương trình đường thẳng chứa cạnh

là

4 5 0.xy  

4 3 0.xy  

4 3 0.xy  

Lời giải:

Đường thẳng

qua

 

1;1M

và có một vectơ chỉ phương là

   

1; 4 4; 1NP n     

là vectơ

pháp tuyến của

.AB

Vậy

   

: 4 1 1 1 0 4 3 0.AB x y x y       



Chọn đáp án D.

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 24

Câu 51: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

1; 1 , 1;9 , 9;1M N P

lần lượt

là trung điểm

, , .BC CA AB

Phương trình đường cao

của tam giác

ABC

là

11 0.xy  

2 11 0.xy  

2 11 0.xy  

0.xy

Lời giải:

Ta có:

   

2; 10 , 9 ;1 .

NM AP x y     

Tứ giác

APMN

là hình bình hành nên

 

9 2 11

11;11 .

1 10 11

NM AP A



   



   



   





Đường cao

qua

 

11;11A

và nhận

 

8; 8NP 

hay

 

1; 1n 

làm một vectơ pháp tuyến

nên có phương trình là

   

1 11 11 0 0.x y x y      



Chọn đáp án D.

Câu 52: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

với

     

2;1 , 2;3 , 1; 5 .A B C

Đường

phân giác trong của góc

có phương trình là

2 0.xy

1 0.xy  

2 4 0.xy  

3 1 0.xy  

Lời giải:

Ta có:

   

4;2 2 5, 3; 6 3 5.AB AB AC AC      

Gọi

 

;D x y

là chân đường phân giác trong của góc

ta có:

2 8 1

. . ; .

3 5 5

DB DC DB DC D



      





Đường phân giác

qua

 

2;1A 

và nhận

18 6

;









làm một vectơ chỉ phương nên có

một vectơ pháp tuyến là

Vây

Chọn đáp án D.

Câu 53: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hình bình hành

ABCD

có tâm

 

1;1 .I

Biết

   

2;0 , 1;4 .AB

Phương trình đường thẳng chứa cạnh

là

4 8 0.xy  

4 2 0.xy  

4 1 0.xy  

4 5 0.xy  

Lời giải:

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 25

là trung điểm

 

0;2 .AC C

Đường thẳng

qua

 

0;2C

và có một vectơ chỉ phương là

   

1;4 4;1AB n   

là vectơ

pháp tuyến của

.CD

Vậy

   

: 4 0 1 2 0 4 2 0.CD x y x y       



Chọn đáp án B.

Câu 54: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hình bình hành

ABCD

có tâm

 

3;5I

và hai cạnh

,AB AD

lần lượt nằm trên hai đường thẳng

3 6 0, 2 5 1 0.x y x y     

Viết phương trình hai

cạnh còn lại của hình bình hành

.ABCD

2 5 29 0; 3 40 0.x y x y     

2 5 39 0; 3 30 0.x y x y     

2 5 19 0; 3 20 0.x y x y     

2 5 39 0; 3 30 0.x y x y     

Lời giải:

Tọa độ điểm

là nghiệm của hệ phương trình:

 

3 6 0 3

3;1 .

2 5 1 0 1

x y x

x y y



   





   



là trung điểm

nên

 

3;9 .C

Đường thẳng

đi qua

 

3;9C

và song song với

: 2 5 1 0AD x y  

nên có phương trình

   

2 3 5 9 0 2 5 39 0.x y x y       

Đường thẳng

đi qua

 

3;9C

và song song với

: 3 6 0AB x y  

nên có phương trình

   

3 3 9 0 3 30 0.x y x y       



Chọn đáp án B.

Câu 55: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;1M

và hai đường thẳng

: 3 5 0, : 4 0.d x y d x y     

Gọi



là đường thẳng đi qua

và cắt

,dd

lần lượt tại

,AB

sao cho

2 3 0.MA MB

Các đường thẳng cần tìm là

2 0; 1 0.x y x    

0; 1 0.x y y   

2 1 0; 1 0.x y x    

0; 1 0.x y x   

Lời giải:

   

1 1 1 2 2 2

;3 5 , ;4 .A d A x x B d B x x     

Vì

,,A M B

thẳng hàng và

 

2 3 1

2 3 .

2 3 2

MA MB















Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 26

Ta có:

   

1 1 2 2

1;3 6 , 1;3 .MA x x MB x x     

Từ (1) giải được















Suy ra

 

; , 2;2 : 0.

A B d x y



  





Từ (2) giải được















Suy ra

   

1; 2 , 1;3 : 1 0.A B d x   



Chọn đáp án D.

Câu 56: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Lập phương trình đường thẳng



đi

qua

và cắt các trục tọa độ lần lượt tại

,AB

(khác

) sao cho

là trung điểm

.AB

3 0.xy  

2 2 0.xy  

2 5 0.xy  

2 4 0.xy  

Lời giải:

Giả sử

     

;0 , 0; , . 0 .Ox A a Oy B b a b      

Suy ra

: 1.

  

là trung điểm

nên

   

2;0 , 0; 4 .AB

Vậy

: 1 2 4 0.

xy      



Chọn đáp án D.

Câu 57: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Lập phương trình đường thẳng



đi

qua

và cắt các tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

2.OA OB

3 0.xy  

2 2 0.xy  

2 5 0.xy  

2 4 0.xy  

Lời giải:

Gọi

     

;0 , 0; , 0, 0 .Ox A a Oy B b a b       

Suy ra

: 1.

  

 

1;2 1M

   

(*).

Ta có:

2 2 .OA OB a b  

Thay vào (*) ta được:

1 2 5

1 5.

     

Vậy

: 1 2 5 0.

xy      



Chọn đáp án D.

Câu 58: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Có bao nhiêu đường thẳng đi qua

và cắt các tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

6?OA OB

C. Vô số. D.

Lời giải:

Gọi

     

;0 , 0; , 0, 0 .Ox A a Oy B b a b       

Suy ra

: 1.

  

 

1;2 1M

   

(1).

Ta có:

66OA OB a b    

(2).

Từ (1) và (2), giải hệ ta được:

2; 4ab

hoặc

3.ab

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 27

Vậy có hai đường thẳng thỏa mãn yêu cầu bài toán là

2 4 0xy  

và

3 0.xy  



Chọn đáp án D.

Câu 59: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2;1 .M

Gọi



là đường thẳng qua

, cắt các

tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

OA OB

nhỏ nhất. Hỏi đường thẳng



đi qua

điểm nào dưới đây?

 

2; 2 .M

 

2; 2 .N 

 

2; 2 .P 

 

2; 2 .Q 

Lời giải:

Gọi

     

;0 , 0; , 0, 0 .Ox A a Oy B b a b       

Suy ra

: 1.

  

 

2;1 1M

   

Ta có:

   

2 1 2

.1 . 3 3 2 2.

OA OB a b a b a b

a b b a



            





Vậy

 

min

3 2 2OA OB  

khi

































Vậy phương trình đường thẳng



là

1 2 2 2 0.

2 2 2 1

xy      



Rõ ràng

 

2; 2 .M 



Chọn đáp án A.

Câu 60: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2 .M

Gọi



là đường thẳng qua

, cắt các

tia

,Ox Oy

lần lượt tại

,AB

(khác

) sao cho

OA OB



nhỏ nhất. Hỏi đường thẳng



đi qua

điểm nào dưới đây?

 

3;1 .M

 

2; 1 .N 

 

0; 3 .P

 

3;3 .Q

Lời giải:

Kẻ

.OH AB

Khi đó:

2 2 2

1 1 1

OH OA OB



Ta có:

OA OB



nhỏ nhất



nhỏ nhất

OH

lớn nhất.

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 28

Ta có:

 

max

.OH OM OH OM  

Điều này xảy ra

OH OM

hay đường thẳng



nhận

 

1;2OM 

làm một vectơ pháp tuyến.

Vậy phương trình



là

   

1 1 2 2 0 2 5 0.x y x y       

Rõ ràng

 

3;1 .M 



Chọn đáp án A.

Câu 61: Trong mặt phẳng tọa độ

,Oxy

cho điểm

(3;2)M

. Gọi

là đường thẳng đi qua

và lần lượt

cắt tia

,Ox

tại

( ;0), B(0; )A a b

với

0, 0ab

và diện tích tam giác

OAB

nhỏ nhất. Hỏi

điểm nào dưới đây thuộc

 

3;6 .N

 

2; 1 .S 

 

1;3 .P

 

3;3 .Q

Lời giải:

Phương trình theo đoạn chắn của đường thẳng



là đường thẳng đi qua

(2;3)M

nên



(*)

Tam giác

OAB

vuông tại O nên có diện tích là

. ( , )

S OAOB OA a OB b   

nhỏ nhất



nhỏ nhất

.ab

nhỏ nhất.

Mà theo bất đẳng thức Cô si, ta có

3 2 6 24

1 2 1 24ab

a b ab ab

      

Do đó

.ab

nhỏ nhất

3 2 2

4, 6

b b a

     

(Từ(*))

Lúc đó phương trình của

: 1 2 3 12 0.

     

d x y

Dễ thấy

 

3;6 .Nd

Câu 62: Trong mặt phẳng tọa độ

,Oxy

tính côsin góc giữa hai đường thẳng

:2 1 0xy   

và













Lời giải:

Véctơ pháp tuyến của đường thẳng



là

 

2;1n 

nên vectơ chỉ phương

 

1; 2u 

Véctơ chỉ phương của đường thẳng



là

 

1; 1u





Khi đó

 

3 3 10

cos ; cos ; .

5. 2



     



Câu 63: Trong mặt phẳng tọa độ

,Oxy

tính góc giữa hai đường thẳng

: 2 15 0xy   

và

 













Lời giải:

Đường thẳng



có VTPT là

 

1; 2 .n

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 29

Đường thẳng



có 1 vectơ chỉ phương là

   

1;2 2;1 .   un

Nhận xét :

 

1 2 1 212

. 0 , 90         nn

Câu 64: Trong mặt phẳng tọa độ

,Oxy

tính góc giữa hai đường thẳng

: 3 2 0    xy

và

: 3 1 0 .   xy

Lời giải:



có vectơ pháp tuyến là

 

1; 3n 

;



có vectơ pháp tuyến là

 

1; 3n 

Khi đó:

 

   

1.1 3 3

cos ;

4. 4

| |.

1 3 . 1 3





     

  

Vậy góc giữa hai đường thẳng

;

là

60 .

Câu 65: Trong mặt phẳng tọa độ

,Oxy

tìm tất cả các giá trị của

để góc tạo bởi đường thẳng











x at

 

t 

và đường thẳng

:3 4 2 0  d x y

bằng

45

Lời giải:

Gọi



là góc giữa hai đường thẳng đã cho.

Đường thẳng

có vectơ chỉ phương là

 

;2ua

Đường thẳng

có vectơ chỉ phương là

 

4; 3v 

Ta có

 

cos cos ,uv





cos45

  







5 4 2 4 6aa   

25 100 32 96 72a a a    

7 96 28 0aa   















Câu 66: Trong mặt phẳng tọa độ

,Oxy

tính khoảng cách từ điểm

 

1; 1M 

đến đường thẳng

:3 4 0.   xy

Lời giải:

Khoảng cách từ điểm

 

1; 1M 

đến đường thẳng

:3 4 0xy   

là

 

3.1 1 4

6 3 10



   



Câu 67: Trong mặt phẳng tọa độ

,Oxy

tính khoảng cách từ điểm

 

3; 4M 

đến đường thẳng



  





  



Lời giải:

Ta có

: 3 4 1 0.xy   

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 30

Suy ra

 

3.3 4. 4 1

  

  



Câu 68: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

: 3 0d x y  

và

: 5 0.d x y  

Tính

khoảng cách giữa hai đường thẳng

và

Lời giải:

Ta có:

và

song song.

Cách 1: Chọn

     

1 1 2 2

035

0;3 ; ; 2.

A d d d d d A d



    



Cách 2: Giải nhanh

 

; 2.

d d d







Câu 69: Trong mặt phẳng tọa độ

,Oxy

tính khoảng cách từ điểm

 

0;4A

đến đường thẳng

 

.sin .cos 4 1 cos 0, .

   

    xy

Lời giải:

Khoảng cách từ

 

0;4A

đến đường thẳng

 

: .sin .cos 4 1 cos 0xy

  

    

là

 

0.sin 4.cos 4 1 cos

sin cos

  



  

  



Câu 70: Trong mặt phẳng tọa độ

,Oxy

biết đường tròn

 

có tâm

 

3; 2I 

tiếp xúc với đường thẳng

: 5 1 0,   xy

tính bán kính

của đường tròn

 

Lời giải:

Ta có:

 

3 5. 2 1

R d I

  

   



Câu 71: Trong mặt phẳng tọa độ

,Oxy

cho điểm

 

0;1A

và đường thẳng











. Tìm điểm

thuộc

và cách

một khoảng bằng

Lời giải:

Gọi

 

2 2 ;3 .  M a a d

Ta có:

   

 

1 4;4

5 2 2 2 5 5 12 17 0

17 24 2

;

5 5 5

AM a a a a







          





    









Câu 72: Trong mặt phẳng tọa độ

,Oxy

cho hai điểm

   

3; 1 , 0;3AB

. Tìm tọa độ điểm

thuộc

sao khoảng cách từ

đến đường thẳng

bằng

Lời giải:

Gọi

 

;0 M x Ox

. Ta có

 

3;4AB 

Phương trình đường thẳng

 

:4 3 3 0AB x y  

4 3 9 0xy   

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 31

Ta có:

 

; 5 4 9

d M AB x



   















Vậy

 

;0 ; 1;0







là các điểm cần tìm.

Câu 73: Trong mặt phẳng tọa độ

,Oxy

tìm điểm

thuộc đường thẳng











và cách đường

thẳng

:2 3 0xy   

một khoảng

Lời giải:

Vì

 

3 ;2 .M t t d  

Theo giả thiết:

 

2(3 ) (2 ) 3

; 2 5 2 5

   

   

 

12;11

1 10 .

8; 9





    











Câu 74: Trong mặt phẳng tọa độ

,Oxy

tìm tọa độ hình chiếu vuông góc của điểm

 

1;2M

lên đường

thẳng

: 0.  xy

Lời giải:

Đường thẳng



có 1 VTPT là

 

1; 1n 

nên



có 1 VTCP là

 

1;1u 

Gọi H là hình chiếu vuông góc của

 

1;2M

lên đường thẳng

.

Gọi

 

;.H t t

Vì

. 0 1 2 0

MH MH u MH u t t t             







Câu 75: Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

 

: 1 0x m y m    

(

là tham số bất kì)

và điểm

 

5;1A

. Tính khoảng cách lớn nhất từ điểm

đến

.

Lời giải:

   

1 0 1

: 1 0 1 0,

   



             



   



x m y m y m x y m

x y y

Suy ra



luôn đi qua điểm cố định

 

1; 1H 

Khi đó, với mọi

M 

, ta có

 

;d A AM AH  

Giá trị lớn nhất của

 

;d A AH

khi

 

max , 2 10M H d A AH    

Câu 76: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;2A

và đường thẳng

: 2 1 0.xy   

Tính

khoảng cách từ điểm

đến đường thẳng

.

Lời giải:

Ta có:

 

2.1 2 1

; 5.



  



Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 32



Chọn đáp án A.

Câu 77: Trong mặt phẳng với hệ tọa độ

,Oxy

tìm giá trị tham số

để khoảng cách từ điểm

 

2; 3I

đến

đường thẳng

: 1 2 0x ny n    

bằng

0.n 

1.n 

1.n 

2.n 

Lời giải:

Ta có:

 

2 3 1 2

; 1 1 1 0.

d I n n n

  

        





Chọn đáp án A.

Câu 78: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

1;3M

và đường thẳng

 

: , .













Tính

khoảng cách từ điểm

đến đường thẳng

.

Lời giải:

Ta có

 

: 2 1 2 2 0.

x t t x

y x x y



    

       







Lúc đó:

 

2.1 3 2



  





Chọn đáp án B.

Câu 79: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 2 3 0d x y  

và

: 2 4 5 0.d x y  

Tính khoảng cách giữa hai đường thẳng

và

Lời giải:

Dễ chứng minh được

/ / .dd

Cách 1: Chọn

 

1;1 .Ad

Lúc đó:

   

1 2 2

2.1 4.1 5

; ; .

4 16

d d d d A d



  



Cách 2:

: 2 4 5 0 2 0.

d x y x y      

Lúc đó:

 

d d d









Chọn đáp án B.

Câu 80: Trong mặt phẳng với hệ tọa độ

,Oxy

cho đường thẳng

: 3 4 3 0.xy   

Viết phương trình các

đường thẳng song song với



và cách



một khoảng bằng

3 4 1 0; 3 4 7 0.x y x y     

3 4 2 0; 3 4 8 0.x y x y     

3 4 2 0; 3 4 6 0.x y x y     

3 4 4 0; 3 4 6 0.x y x y     

Lời giải:

//d 

nên

có dạng

3 4 0, 3.x y m m    

Theo giả thiết:

 

; 1 1 3 5 .

9 16

d d m







       









Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 33

Vậy hai đường thẳng cần tìm là

3 4 2 0; 3 4 8 0.x y x y     



Chọn đáp án B.

Câu 81: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

 

1;4M

và

 

6;2 .N

Viết phương trình các

đường thẳng



qua

sao cho khoảng cách từ

đến



bằng

1 0; 3 4 19 0.x x y    

1 0; 21 20 59 0.x x y    

1 0; 3 4 19 0.y x y    

1 0; 21 20 59 0.y x y    

Lời giải:

Gọi

 

; , 0n a b a b  

là một vectơ pháp tuyến của đường thẳng

.

Khi đó

   

: 1 4 0 4 0.a x b y ax by a b         

Theo giả thiết:

 

6 2 4

; 5 5 5 2 5

a b a b

d N a b a b

  

       



 

5 2 25 21 20 0

21 20 0

a b a b b b a





       







TH 1:

0,b 

chọn

1,a 

ta có phương trình

1 0.x 

TH 2:

21 20 0,ba

chọn

21,b 20a   

ta có phương trình

21 20 59 0.xy  



Chọn đáp án B.

Câu 82: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai điểm

 

1;1P

và

 

4;2 .Q

Viết phương trình các

đường thẳng



sao cho khoảng cách từ

và

đến



lần lượt bằng

và

1 0; 3 4 11 0.y x y    

1 0; 3 4 11 0.x x y    

1 0; 3 4 11 0.y x y    

1 0; 3 4 11 0.x x y    

Lời giải:

Giả sử phương trình

 

: 0, 0 .ax by c a b     

Theo giả thiết:

 

(1)

; 3 4 2

3 4 (2)

a b c

d Q a b c

a b c a b





















  







  

   

  



    









Từ (1)

   

5 (1 )

3 2 4 2

11 7

(1 )

3 2 4 2

c a b a

a b c a b c







    













     









Từ (1a) và (2) ta có:

 

8 6 0

4 3 4

c a b

a ab

a b a b























  



  















+) Từ

00ab  

và

.cb

Ta chọn

1bc

ta có

: 1 0.y  

+) Từ

4 3 .ab

Ta chọn

3, 4 11a b c   

ta có

:3 4 11 0.xy   



Chọn đáp án C.

Câu 83: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 2 10 0d x y  

và

: 3 2 0.d x y  

Tính góc giữa hai đường thẳng

và

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 34

30 .

45 .

60 .

90 .

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

2;1 .n 

Đường thẳng

có một vectơ pháp tuyến là

 

1;3 .n 

Lúc đó:

   

1 2 1 2

cos ; ; 45 .

d d d d

    



Chọn đáp án B.

Câu 84: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 1 0d mx y  

và

: 2 10 0.d x y  

Tìm tập hợp tất cả các giá trị của tham số

để hai đường thẳng

và

vuông góc với nhau.







 

2.

 

2.

.

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

;1 .nm

Đường thẳng

có một vectơ pháp tuyến là

 

1;2 .n 

Theo giả thiết:

1 2 1 2

. 0 2 0 2.d d n n m m        



Chọn đáp án B.

Câu 85: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 7 9 0d mx y m   

và

: 2 10 0.d x y  

Gọi

là tập hợp tất cả các giá trị của tham số

để góc giữa hai đường thẳng

và

bằng

45

. Tính tổng tất cả các phần tử của



Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

;1 .nm

Đường thẳng

có một vectơ pháp tuyến là

 

2;1 .n 

Theo giả thiết:

 

. 2 1

2 2 2

cos ; 3 8 3 0

2 2 2

4 1. 1

n n m

d d m m



        



3; .









   















Chọn đáp án D.

Câu 86: Trong mặt phẳng tọa độ

,Oxy

tìm

để hai đường thẳng

: 5, : 9d mx y m d x my    

cắt

nhau.

Lời giải:

+) Xét

0m 

thì

5 9d : y , d :x  

. Rõ ràng hai đường thẳng này cắt nhau nên

0m 

thỏa mãn. (1)

+) Xét

0m 

thì

:5d y mx m   

và

  

Hai đường thẳng

và

cắt nhau

(2)





    







Từ (1) và (2) ta có

1m 

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 35

Câu 87: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

 

: 1 2 0d mx m y m   

và

: 2 1 0d x y  

. Tìm

để

và

song song.

Lời giải:

Ta có

2 1 1

m m m

  



2m

Câu 88: Trong mặt phẳng tọa độ

,Oxy

cho ba đường thẳng

 

: 1 2 0, : 4 3 26 0d mx m y m d x y      

và

: 3 4 7 0.d x y  

Tìm

để ba đường thẳng trên đồng quy.

Lời giải:

Giao điểm

của

và

là nghiệm hệ phương trình:

4 3 26 0 5

3 4 7 0 2

x y x

x y y



   





    



 

5; 2I 

Yêu cầu bài toán

 

5; 2Id  

  

.5 1 2 2 0 .

m m m m        

Câu 89: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

:5 7 4 0d x y  

và

:5 7 6 0.d x y  

Viết phương trình đường thẳng

song song và cách đều

và

Lời giải:

Gọi là

đường thẳng song song và cách đều

và

Suy ra phương trình

có dạng:

 

5 7 0 4, 6x y c c c    

Mặt khác:

   

;;d d d d d d

   

5 7 5 7

cc



   

  







   



5c

Suy ra

: 5 7 0 5 7 5 0.



      d x y x y

Câu 90: Trong mặt phẳng tọa độ

,Oxy

tìm tọa độ giao điểm của hai đường thẳng

4 3 26 0xy  

và

3 4 7 0xy  

Lời giải:

Toạ độ giao điểm

của hai đường thẳng là nghiệm hệ phương trình:

4 3 26 0 5

3 4 7 0 2

x y x

x y y



   





    



Vậy

 

5; 2M 

Câu 91: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có

 

2;1A

, đường cao

:BH

3 7 0xy  

và

trung tuyến

:CM

10xy  

. Tìm tọa độ đỉnh

Lời giải:

Gọi

 

; 1 .C t t CM  

Ta có:

 

2; 2AC t t   

, vectơ chỉ phương của đường thẳng

là

 

3;1u 

Vì

AC BH

nên

 

       . 0 2 .3 2 0 4AC u t t t

Vậy

 

4; 5C 

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 36

Câu 92: Trong mặt phẳng tọa độ

,Oxy

cho hai đường thẳng

: 1, : 3 3 0d x y d x y    

. Viết

phương trình đường thẳng

đối xứng với

qua đường thẳng

Lời giải:

Gọi

 

;I x y d d

. Khi đó, tọa độ điểm

là nghiệm của hệ phương trình

 

0;1 .

3 3 0 1

x y x

x y y

  







   



Chọn

 

3;0Md

. Gọi



đi qua

và vuông góc với

Suy ra



có dạng

0x y c  

Vì

 

3;0 3Mc   

: 3 0xy    

Gọi

 

;H x y d  

. Khi đó tọa độ điểm

là nghiệm của hệ phương trình

  





















 

1;2 .H

Gọi

là điểm đối xứng của

qua

. Khi đó

là trung điểm của

.MN

N H M

x x x

y y y

  







  



 

1;4 .N

Vậy đường thẳng

chính là đường thẳng

, ta có

3 1 0



    

Câu 93: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 3 0d x y  

và

: 2 3 0.d x y  

Khẳng định nào sau đây đúng?

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

Lời giải:

Đường thẳng

có một vectơ pháp tuyến là

 

1;1 .n 

Đường thẳng

có một vectơ pháp tuyến là

 

2;1 .n 

Ta có:

















cắt nhau và không vuông góc.



Chọn đáp án C.

Câu 94: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

: 4 2 1 0d x y  

và

: 2 3 0.d x y  

Khẳng định nào sau đây đúng?

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

Lời giải:

Ta có:

4 2 1

2 1 3



  



và

song song.



Chọn đáp án A.

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 37

Câu 95: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

 













và

: 2 3 0.d x y  

Khẳng định nào sau đây đúng?

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

Lời giải:

Cách 1:

 

: 1 2 1 2 3 0.

x t t x

d y x x y



    

       







Vậy

.dd

Cách 2:

Xét hệ phương trình:

   

1 1 1

1 2 1 2 1 2

2 3 0 0 0

2 1 1 2 3 0

x t x t x t

y t y t y t





     





       

  

  

   

    





(vô số nghiệm)

Vậy

.dd



Chọn đáp án B.

Câu 96: Trong mặt phẳng với hệ tọa độ

,Oxy

cho hai đường thẳng

 













và

 

: , .













Khẳng định nào sau đây đúng?

/ / .dd

.dd

cắt nhau và không vuông góc. D.

.dd

Lời giải:

: : 0.

d d x y





  







 

: 2 2 0.

x k k x

d y x x y



    

       







Đường thẳng

có một vectơ pháp tuyến là

 

1; 1 .n 

Đường thẳng

có một vectơ pháp tuyến là

 

1;1 .n 

.0nn

nên

.dd

Cách khác: Đánh giá mối quan hệ giữa hai vectơ chỉ phương.

.0uu

nên

.dd



Chọn đáp án D.

Câu 97: Trong mặt phẳng với hệ tọa độ

,Oxy

cho điểm

 

2; 1A 

và đường thẳng

: 2 5 0.xy   

Gọi

 

;H a b

là hình chiếu vuông góc của

trên

,

tính

.ab

3.

Lời giải:

Cách 1:

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 38

Đường thẳng

qua

 

2; 1A 

và vuông góc với

: 2 5 0xy   

có phương trình là:

   

       : 2 2 1 1 0 2 5 0.d x y x y

Điểm

là giao điểm của

và

.

Tọa độ điểm

là nghiệm của hệ:

 

2 5 0 3

3;1 3; 1.

2 5 0 1

x y x

H a b

x y y



   

    



   



Vậy

4.ab

Cách 2:

Gọi

 

2 5; .H H t t   

Ta có:

 

2 3; 1 .AH t t   

Đường thẳng



có một vectơ chỉ phương là

 

2; 1 .u





là hình chiếu vuông góc của

trên

   

. 0 2 2 3 1 0AH u t t



        

 

5 5 0 1 3;1 3; 1.t t H a b         

Vậy

4.ab



Chọn đáp án A.

Câu 98: Trong mặt phẳng với hệ tọa độ

,Oxy

cho tam giác

ABC

vuông cân tại

Gọi

 

1; 1M 

là

trung điểm của cạnh

và







là trọng tâm của tam giác

.ABC

Biết

   

; , 0 ,B a b a 

tính

.ab

Lời giải:

Vì

là trọng tâm của tam giác

ABC

và

là trung điểm

nên

 

  3 1;3MA MG

 

 0;2 .A

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 39

Đường thẳng

qua

 

1; 1M 

và vuông góc với

có phương trình:

   

1 3 1 0 3 4 0.x y x y         

Ta thấy

10.MA MB MC  

Tọa độ

,BC

thỏa mãn hệ phương trình

   

3 4 0

4;0 , 2; 2

2; 2 , 4;0

1 1 10



   















   









Từ đề bài, chọn

 

4;0 4; 0.B a b  

Vậy

4.ab



Chọn đáp án A.

MỘT SỐ BÀI TOÁN KHÁC

Câu 99: Trong mặt phẳng tọa độ

,Oxy

cho đường thẳng

: 4 15 0d x y  

và điểm

 

2;0A

. Tìm tọa

độ điểm

thuộc

để đoạn

có độ dài nhỏ nhất.

Lời giải:

Điểm

 

4 15;M d M t t  

Ta có:

 

4 17 17 8 17 17 4 1 17AM t t t t t



         





t

min AM

, đạt được tại

4t 

. Khi đó

 

1;4M

Câu 100: Trong mặt phẳng tọa độ

,Oxy

cho điểm hai điểm

 

4;2A 

 

2;6B

và điểm C nằm trên đường

thẳng







sao cho

CA CB

. Tìm tọa độ điểm C.

Lời giải:

d có phương trình tham số là







  



Gọi

 

5 3 ; 1 2C t t d   

, ta có:

   

9 3 ;3 2 , 3 3 ;7 2CA t t CB t t       

       

2 2 2 2

9 3 3 2 3 3 7 2 20 32 .

CA CB CA CB t t t t t t



               

Suy ra:

1 11

;







Câu 101: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

. Tìm tọa độ các đỉnh của tam giác biết

phương trình cạnh

: 2 0BC x y  

; hai đường cao

' : 3 0BB x 

và

' : 2 3 6 0.CC x y  

Lời giải:

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 40

'B BC BB

nên có tọa độ là nghiệm của hệ

3 0 3

(3; 1)

2 0 1

x y y



  

  



    



'C BC CC

nên có tọa độ là nghiệm của hệ

2 0 0

(0;2)

2 3 6 0 2

x y x

x y y



   





   



qua

và vuông với

'CC

có phương trình:

3 2 7 0xy  

qua

và vuông với

'BB

có phương trình:

2y 

A AB AC

nên có tọa độ là nghiệm của hệ

3 2 7 0 1

(1;2)

x y x



   









Câu 102: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có

     

3 0 3 0 2 6A ; ,B ; ,C ;

. Tìm tọa độ trực

tâm

là của tam giác

ABC

Lời giải:

Đường thẳng

đi qua

 

30A;

và nhận

 

16BC ;

làm vectơ pháp tuyến. Suy ra

phương trình đường thẳng

là:

6 3 0xy  

Đường thẳng

đi qua

 

30B;

và nhận

 

56AC ;

làm véctơ pháp tuyến. Suy ra phương

trình đường thẳng

là:

5 6 15 0xy  

Ta có

H AH BH  

Tọa độ

là nghiệm của hệ

5 6 15 0

  

  















Câu 103: Trong mặt phẳng tọa độ

,Oxy

cho ba điểm

     

1;1 ; 2;0 ; 3;4A B C

. Viết phương trình đường

thẳng đi qua

và cách đều hai điểm

,BC

Lời giải:

Gọi

 

là đường thẳng đi qua

và cách đều

,BC

. Khi đó, ta có các trường hợp sau:

TH1:

đi qua trung điểm của

. Ta có







là trung điểm của

và









là

VTCP của đường thẳng

. Khi đó

     

: 2 1 3 1 0d x y    

2 3 1 0xy    

TH2:

song song với

, khi đó

nhận

 

1;4BC 

làm VTCP, phương trình đường thẳng

   

: 4 1 1 0d x y    

4 3 0xy    

Câu 104: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có phương trình đường thẳng

: 7 13 0.BC x y  

Các chân đường cao kẻ từ

,BC

của tam giác

ABC

lần lượt là

   

2;5 , 0;4 .EF

Tìm tọa độ đỉnh A.

Lời giải:

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 41

Gọi

 

13 7 ;I n n

là trung điểm của BC, khi đó ta có:

I E IF

mà

2 2 2 2

50 164 146; 50 190 185IE n n IF n n     

50 164 146 50 190 185

       n n n n n

;









Gọi

 

13 7 ;B m m

. Vì I là trung điểm của BC nên

 

7 8;3C m m

Ta có

   

7 11;5 ; 10 7 ;2BE m m CE m m     

Vì

BE AC

nên

. 0 3 2 0    BE CE m m













+) Với

   

2 11

1 6;1 , 1;2 : 2 8 0, : 3 0 ;

m B C BF x y CE x y A



          





+) Với

     

2 1;2 ; 6;1 :2 4 0, : 7 0 1;6 .m B C BF x y CE x y A          

Câu 105: Trong mặt phẳng tọa độ

,Oxy

cho tam giác

ABC

có đỉnh

( 12;1)B 

, đường phân giác trong của

góc

có phương trình

: 2 5 0;d x y  

;







là trọng tâm tam giác

ABC

. Tìm tọa độ đỉnh

Lời giải:

Gọi

là điểm đối xứng với

qua đường thẳng

: 2 5 0d x y  

suy ra

D AC

Phương trình của đường thẳng

: 2 25 0BD x y   

Gọi

là giao điểm của

và

suy ra tọa độ điểm

là nghiệm của hệ phương trình

 

2 5 0 9

9;7

2 25 0 7

x y x

x y y



    

  



    



Mà

là trung điểm của

suy ra

( 6;13)D 

Gọi

(5 2 ; )A a a d

Ta có

;







là trọng tâm tam giác

ABC

nên

3 5 2 12 1 2 8

(2 8;1 )

3 1 2 1

A B C G C C

x x x x a x x a

C a a

y y y y a y y a

  

        

  

    

  

       

  

  

Ta có

   

      11 2 ; 13 ; 2 14; 12DA a a DC a a

Mà 3 điểm

,,D A C

thẳng hàng nên

,DA DC

cùng phương

11 2 13

2 14 12



    

  

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 42

Suy ra điểm

(4;3).C

Câu 106: Trong mặt phẳng tọa độ

,Oxy

cho 3 điểm

     

6;3 ; 0; 1 ; 3;2A B C

. Tìm

trên đường thẳng

  : 2 3 0d x y

mà

MA MB MC

nhỏ nhất.

Lời giải:

Gọi

(2 8;1 ) : 2 3 0.C a a d x y

Cách 1:

Tìm tọa độ điểm

 

;I x y

sao cho

0IA IB IC  

. Suy ra









Ta có:

3MA MB MC MI IA IB IC     

3MA MB MC MI  

. Vậy

MA MB MC

nhỏ nhất khí

nhỏ nhất.

nhỏ nhất khi

là hình chiếu vuông góc của

xuống đường thẳng

Đường thẳng



đi qua

và vuông góc với

có phương trình:

xy

là giao điểm của

và



nên

là nghiệm của hệ:

2 3 0

13 19

;

15 15

  























Cách 2:

thuộc

suy ra

 

;2 3M t t 

( 3 3 ; 6 5)MA MB MC t t      

   

3 3 6 5MA MB MC t t



       

13 1

45 78 34 45

15 5

MA MB MC t t t



       





MA MB MC

nhỏ nhất khi

t 

. Suy ra

13 19

;

15 15









Câu 107: Trong mặt phẳng tọa độ

,Oxy

cho hình chữ nhật ABCD có điểm C thuộc đường thẳng

: 2 5 0d x y  

và điểm

 

4;8A 

. Gọi M là điểm đối xứng với B qua C, điểm

 

5; 4N 

là hình

chiếu vuông góc của B lên đường thẳng MD. Tìm tọa độ điểm

Lời giải:

5;-4

( )

c;-2c-5

( )

-4;8

( )

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 43

Gọi

 

;I a b

là trung điểm

Ta có:

  90BAD BND

. Suy ra

BAND

nội tiếp đường tròn đường kính

, tâm

Ta có:

IA IN

       

2 2 2 2

4 8 5 4a b a b       

6 8 13 0ab   

là trung điểm

nên

 

2 4;2 8C a b

Cd

. Suy ra

   

2 2 4 2 8 5 0ab    

4 2 5 0ab   

Giải hệ:

6 8 13 0

4 2 5 0







  





















 

1; 7 .C

Câu 108: Trong mặt phẳng tọa độ

,Oxy

cho hình vuông

ABCD

. Gọi

là trung điểm của cạnh

là điểm trên cạnh

sao cho

2CN ND

. Giả sử

11 1

;







và đường thẳng

có phương

trình

2 3 0xy  

. Tìm tọa độ điểm

là giao điểm của

và

Lời giải:

Ta chứng minh được

MP AN

, nên

là hình chiếu của

trên

(Thật vậy gắn hệ trục toạ độ

Dxy

       

0;0 , 1;0 , 1;1 , 0;1D C B A

. Khi đó

1; ; ;0

   

   

   

Phương trình đường thẳng

:BD y x

. Phương trình đường thẳng

:3 1AN x y

, suy ra giao điểm

của

và

là

;







Khi đó

3 1 1

; ; ; 1 . 0

4 4 3

MP AN MP AN MP AN



   

      

   

   

(đpcm).)

Phương trình đường thẳng

qua

và vuông góc với

là

xy  

là giao điểm

và

nên toạ độ

là nghiệm hệ

2 3 5

;2 .



























Câu 109: Trong mặt phẳng tọa độ

,Oxy

cho hình thoi

MN PQ

có tâm

 

3;1I

, đỉnh

thuộc đường

thẳng

4 1 0xy  

, đỉnh

thuộc đường thẳng

80xy  

. Xác định tọa độ đỉnh

Lời giải:

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT

Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 44

Đặt

: 4 1 0d x y  

;

: 8 0xy   

Nhận thấy:

 

3;1I

thuộc đường thẳng

4 1 0xy  

, theo giả thiết:

.Md

QN IM QN d  

và

đi qua

 

3;1 :4 13 0I QN x y   

,N QN N  

Tọa độ điểm

là nghiệm của hệ:

 

4 13 1

1;9

x y x

x y y

  







   



Vì

là trung điểm của

 

2 6 1 5

5; 7

2 2 9 7

Q I N

x x x

QN Q

y y y

    





  



     





Câu 110: Trong mặt phẳng tọa độ

,Oxy

cho hình chữ nhật

ABCD

có điểm

thuộc đường thẳng

 

:2 5 0d x y  

và điểm

( 4;8)A 

. Gọi

đối xứng với

qua

, điểm

(5; 4)N 

là hình

chiếu vuông góc của

lên đường thẳng

. Tìm tọa độ đỉnh

Lời giải:

Gọi I là giao điểm của

,AC BD

Gọi

( ; 2 5) ( )C t t d  

Dễ thấy hai tứ giác

BCND

và

ADNB

nội tiếp đường tròn

 

;IR

, với

AC BD

R 

Suy ra đa giác

AB CND

nội tiếp đường tròn

 

;IR

BNC BDC

BNA BDA

















90ANC BDC BDA CN AN      

Do đó

.0CN AN 

, với

   

5 ; 2 1 , 9; 12CN t t AN    

Suy ra:

9(5 ) 12(2 1) 0tt   

1t

 

1; 7C

_____________________HẾT_____________________

Huế, 15h00’ Ngày 16 tháng 02 năm 2023

Bấm Tải xuống để xem toàn bộ.

| 1/44

| | Tải xuống

Preview text:

Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT Chủ đề:
PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG MẶT PHẲNG
DẠNG TOÁN 1: Xác định vectơ chỉ phương, vectơ pháp tuyến của đường thẳng I. PHƯƠNG PHÁP
Đường thẳng d ax  by  c   2 2 :
0 a  b  0 có một vectơ pháp tuyến là n  a;b. d
x  x  u t Đường thẳng 0 1 d :   2 2
t  , u  u  0 có một vectơ chỉ phương là u  u ;u . d 1 2  1 2 
y  y  u t  0 2 x  x y  y Đường thẳng 0 0 d : 
 u u  0 có một vectơ chỉ phương là u  u ;u . d 1 2  1 2  u u 1 2 Chú ý: u
a) Đường thẳng d có một vectơ chỉ phương là u  u ;u , u  0 thì d có hệ số góc là 2 k  . d 1 2   1  u1
b) (Đọc thêm) Phương trình đoạn chắn: x y
Đường thẳng d cắt Ox, Oy lần lượt tại Aa;0 , B0;b, ab  0 có phương trình:   1 a b
c) Đường thẳng d có một vectơ chỉ phương là u  u ;u và có một vectơ pháp tuyến là d 1 2 
n  a;b. d
Lúc đó: u  n  au  bu  0 d d 1 2
Suy ra: Đường thẳng d có một vectơ chỉ phương là u  u ;u thì có một vectơ pháp là d 1 2 
n  u ; u  . d 2 1 
II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 1: Trong mặt phẳng với hệ tọa độ Oxy, vectơ nào dưới đây là một vectơ chỉ phương của Ox? A. u  1;0 . B. u  1;1 . C. u  1; 4 . D. u  0; 2 . 4   3   2   1  
Câu 2: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1; 3 , B2;7. Một vectơ chỉ phương của
đường thẳng AB là A. u  4  ;1 . B. u  2  ;1 . C. u  3;  2 . D. u  1; 4 . 4   3   2   1   x  1 2t
Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới y  2   3t
đây là một vectơ chỉ phương của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1   x  2 y  3
Câu 4: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
. Vectơ nào dưới đây là 1 2
một vectơ chỉ phương của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1  
Câu 5: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  y  3  0. Vectơ nào dưới đây là
một vectơ pháp tuyến của d? A. n  1; 2 . B. n  2  ;1 . C. n  2;1 . D. n  2; 3 . 4   3   2   1  
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 1
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 6: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  3y  3  0. Vectơ nào dưới đây là
một vectơ pháp tuyến của d? A. n  2; 3 . B. n  2  ;3 . C. n  4; 6  . D. n  2; 3  . 4   3   2   1  
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x  2y  5  0. Vectơ nào dưới đây là
một vectơ chỉ phương của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1   x  1 2t
Câu 8: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới y  2   3t
đây là một vectơ pháp tuyến của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1   x  2 y  3
Câu 9: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d :  . Vectơ nào dưới đây 1 2
không là một vectơ chỉ phương của d? A. u  1; 2 . B. u  2; 4 . C. u  1  ; 2  . D. u  2; 4  . 4   3   2   1  
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1; 3 , B3;7. Gọi  là đường trung trực của đoạn thẳng .
AB Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  4; 3 . C. n  4; 2 . D. n  2; 1  . 4   3   2   1  
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  y  1  0. Gọi  là đường thẳng
song song với d. Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  4; 3 . C. n  4; 2  . D. n  2;1 . 4   3   2   1  
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  y  1  0. Gọi  là đường thẳng
vuông góc với d. Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  1; 2  . C. n  4; 2 . D. n  2;1 . 4   3   2   1   x  1 2t
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d :
,t  . Gọi  là đường y   t
thẳng song song với d. Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  4; 3 . C. n  1; 2  . D. n  2;1 . 4   3   2   1   x  1 y  2
Câu 14: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
. Gọi  là đường thẳng 2 1
vuông góc với d. Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  1; 2  . C. n  4; 2 . D. n  2; 1  . 4   3   2   1   DẠNG TOÁN 2:
Viết phương trình đường thẳng I. PHƯƠNG PHÁP
Để viết phương trình đường thẳng , ta cần xác định 2 yếu tố: 1 điểm M x ; y mà đường thẳng  0  0 0 
đi qua và một vectơ đặc trưng (hoặc là vectơ pháp tuyến, hoặc là vectơ chỉ phương).
Phương trình tổng quát
Phương trình tham số
Phương trình chính tắc
Đường thẳng  đi qua M x ; y Đường thẳng  đi qua Đường thẳng  đi qua 0 0 
và có một vectơ pháp tuyến M x ; y và có một vectơ chỉ M x ; y và có một vectơ chỉ 0 0  0 0 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 2
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
n  a b  2 2 ;
, a  b  0 có phương phương u  u ;u  ,  2 2
u  u  0 phương
u  u ;u , u .u  0 1 2   1 2  1 2 1 2  trình: có phương trình: có phương trình:
ax  x  b y  y  0
x  x  u t x  x y  y 0   0  0 1 0 0 
t  
y  y  u t  u u 1 2 0 2 Chú ý:
a) Cho đường thẳng d ax  by  c   2 2 :
0 a  b  0.
+) Đường thẳng  / /d thì  có dạng  : ax  by  m  0, m  0.
+) Đường thẳng   d thì  có dạng  : bx  ay  m  0.
b) Phương trình đoạn chắn: x y
Đường thẳng d cắt Ox, Oy lần lượt tại Aa;0 , B0;b, ab  0 có phương trình:   1 a b
c) Đường thẳng d có một vectơ chỉ phương là u  u ;u và có một vectơ pháp tuyến là d 1 2 
n  a;b. d
Lúc đó: u  n  au  bu  0 d d 1 2
II. BÀI TẬP TỰ LUẬN MINH HỌA
Câu 15: Trong mặt phẳng tọa độ Oxy, viết phương trình tham số của đường thẳng đi qua hai điểm A3;   1 , B  6  ;2.
Câu 16: Trong mặt phẳng tọa độ Oxy, viết phương trình đường thẳng  đi qua gốc tọa độ và vuông
góc với đường thẳng d : 8x  6 y  7  0.
Câu 17: Trong mặt phẳng tọa độ Oxy, cho hai điểm A3;0; B 0;2 và đường thẳng d : x  y  0 . Viết
phương trình tham số của đường thẳng  qua A và song song với d .
Câu 18: Trong mặt phẳng tọa độ Oxy, viết phương trình đường thẳng d qua M 1;  1 và song song với
đường thẳng d ' : x  y 1  0.
Câu 19: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A2; 3; B 4  ;5;C6; 5
  . Gọi M , N lần
lượt là trung điểm của AB và AC . Viết phương trình tham số của đường thẳng MN.
Câu 20: Trong mặt phẳng tọa độ Oxy, cho hai điểm A1;0 và B0; 4. Viết phương trình đường thẳng . AB
Câu 21: Trong mặt phẳng tọa độ Oxy, cho điểm M 1; 2 . Gọi ,
A B là hình chiếu của M lên Ox, Oy .
Viết phương trình đường thẳng AB .
Câu 22: Trong mặt phẳng tọa độ Oxy, viết phương trình đường thẳng đi qua điểm M 5; 3   và cắt hai
trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB.
Câu 23: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A1; 
1 , B 0;  2 , C 4; 2 . Viết phương
trình tổng quát của đường trung tuyến đi qua đỉnh B của tam giác ABC.
Câu 24: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại C và B 2;  
1 , A4;3 . Viết phương
trình đường cao CH của tam giác ABC.
Câu 25: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A2; 1
 ,B4;5,C 3  ;2 . Viết phương
trình đường cao AH của tam giác ABC.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 3
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 26: Trong mặt phẳng tọa độ Oxy, gọi
H là trực tâm tam giác ABC và
AB : 7x  y  4  0; BH : 2x  y  4  0; AH : x  y  2  0. Viết phương trình đường cao CH của tam giác ABC.
Câu 27: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có M 2;0 là trung điểm của cạnh . AB
Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x  2 y  3  0 và
6x  y  4  0 . Viết phương trình đường thẳng AC. x y
Câu 28: Trong mặt phẳng tọa độ Oxy, biết đường thẳng d :
 1 , a  0;b  0 đi qua M  1  ;6 a b
tạo với tia Ox, Oy một tam giác có diện tích bằng 4. Viết phương trình đường thẳng d.
Câu 29: Trong mặt phẳng tọa độ Oxy, cho điểm M 2;1 . Viết phương trình đường thẳng d đi qua M ,
cắt các tia Ox , Oy lần lượt tại A và B ( ,
A B khác O ) sao cho tam giác OAB có diện tích nhỏ nhất.
Câu 30: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng  : x  y 1  0,  : 2x  y 1  0 và điểm 1 2 P 2; 
1 . Viết phương trình đường thẳng đi qua điểm P và cắt hai đường thẳng  ,  lần 1 2
lượt tại hai điểm A , B sao cho P là trung điểm AB .
Câu 31: Trong mặt phẳng tọa độ Oxy, cho các điểm A1; 1 và B3; 4 . Gọi d là một đường thẳng bất
kì luôn đi qua B. Viết phương trình đường thẳng d khi khoảng cách từ A đến đường thẳng d
đạt giá trị lớn nhất.
III. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 32: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x  y  3  0. Điểm nào dưới đây nằm trên đường thẳng d ? A. M 1; 4. B. N 1;0. C. P 2; 3. D. Q2;0.
Câu 33: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x  y  3  0. Điểm nào dưới đây
không nằm trên đường thẳng d ? A. M 1; 4. B. N  3  ;0. C. P 0; 3. D. Q2;1. x  1 y  1
Câu 34: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
. Biết điểm M a; b nằm 2 3
trên đường thẳng d, đẳng thức nào sau đây đúng?
A. 3a  2b  5.
B. 3a  2b  5.
C. 3a  b  5.
D. 3a  b  5. x  1 t
Câu 35: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Điểm nào dưới đây y  2   3t
nằm trên đường thẳng d ? A. M 1; 3. B. N 1; 2. C. P 1; 5. D. Q2;0. x  1 t
Câu 36: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Điểm nào dưới đây y  2   3t
nằm trên đường thẳng d ? A. M 1; 3. B. N 5; 2. C. P 2; 5. D. Q2;0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 4
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT x  t
Câu 37: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d :
, t  . Điểm nào dưới đây y  1   2t
không nằm trên đường thẳng d ? A. M 0;1. B. N 1; 3. C. P 2; 5. D. Q1;1.
Câu 38: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;0 , B0; 5. Phương trình đường thẳng AB là x y x y x y x y A.   0. B.   1. C.   1.  D.   1. 1 5 5 1 1 5 1 5
Câu 39: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;1 , B2; 5. Phương trình đường thẳng AB là
A. x  4y  5  0.
B. 4x  y  3  0.
C. x  4y  1  0.
D. 4x  y  1  0.
Câu 40: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;1 , B2; 5. Phương trình đường thẳng AB là x  1 t x  1 4t x  1 t x  1   t A.  , t  . B.  , t  . C.  , t  . D.  , t  . y  1   4t y  1   t y  4   t y  1    4t
Câu 41: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm M 1; 
1 , N 2; 4. Phương trình đường thẳng MN là x  1 t x  1 3t x  1 t x  t A.  , t  . B.  , t  . C.  , t  . D.  , t  . y   3t y  1   t y  3   t y  2    3t
Câu 42: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;0 , B3;6. Phương trình đường thẳng
trung trực của đoạn thẳng AB là
A. x  3y  11  0
B. x  3y  11  0.
C. 3x  y  9  0.
D. 3x  y  7  0.
Câu 43: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2 và đường thẳng d : x  2y  3  0.
Phương trình đường thẳng  qua A và song song với d là
A. 2x  y  0.
B. x  2y  5  0.
C. 2x  y  5  0.
D. x  2y  1  0.
Câu 44: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2 và đường thẳng d : x  2y  3  0.
Phương trình đường thẳng  qua A và vuông góc với d là
A. 2x  y  0.
B. x  2y  5  0.
C. 2x  y  1  0.
D. x  2y  1  0. x  1 2t
Câu 45: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A2; 3 và đường thẳng d :  , t  . y  3   t
Phương trình đường thẳng  qua A và song song với d là
A. 2x  y  7  0.
B. 2x  y  0.
C. x  2y  1  0.
D. x  2y  4  0. x  1 2t
Câu 46: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A2; 3 và đường thẳng d :  , t  . y  3   t
Phương trình đường thẳng  qua A và vuông góc với d là
A. 2x  y  7  0.
B. 2x  y  0.
C. x  2y  1  0.
D. x  2y  4  0.
Câu 47: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A1;1 , B2; 3 , C  4  ;4. Phương
trình đường thẳng chứa cạnh AB là
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 5
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
A. x  2y  3  0.
B. 2x  y  1  0.
C. x  2y  1  0.
D. x  2y  4  0.
Câu 48: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A1;1 , B2; 3 , C  4  ;1. Đường
trung tuyến AM của tam giác ABC có phương trình là
A. x  2y  3  0.
B. 2x  y  1  0.
C. x  2y  1  0.
D. x  2y  4  0.
Câu 49: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A1;1 , B2; 3 , C  4  ;1. Đường
trung cao BK của tam giác ABC có phương trình là A. x  2  0.
B. 2x  y  1  0.
C. x  2y  1  0.
D. x  2y  8  0.
Câu 50: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với M 1;1 , N 0; 2, P 1  ; 2   lần lượt
là trung điểm AB, BC, AC. Phương trình đường thẳng chứa cạnh AB là
A. x  4y  5  0.
B. 4x  y  5  0.
C. x  4y  3  0.
D. 4x  y  3  0.
Câu 51: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với M  1  ; 1
 , N1;9, P9;1 lần lượt
là trung điểm BC, CA, .
AB Phương trình đường cao AH của tam giác ABC là
A. x  y  11  0.
B. 2x  y  11  0.
C. 2x  y  11  0.
D. x  y  0.
Câu 52: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A 2
 ;1, B2;3, C1; 5  . Đường
phân giác trong của góc A có phương trình là
A. 2x  y  0.
B. x  y  1  0.
C. x  2y  4  0.
D. x  3y  1  0.
Câu 53: Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có tâm I 1;1. Biết
A2;0, B1; 4. Phương trình đường thẳng chứa cạnh CD là
A. x  4y  8  0.
B. 4x  y  2  0.
C. x  4y  1  0.
D. 4x  y  5  0.
Câu 54: Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có tâm I 3; 5 và hai cạnh
AB, AD lần lượt nằm trên hai đường thẳng x  3y  6  0, 2x  5y  1  0. Viết phương trình hai
cạnh còn lại của hình bình hành ABCD.
A. 2x  5y  29  0; x  3y  40  0.
B. 2x  5y  39  0; x  3y  30  0.
C. 2x  5y  19  0; x  3y  20  0.
D. 2x  5y  39  0; x  3y  30  0.
Câu 55: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1;1 và hai đường thẳng
d : 3x  y  5  0, d : x  y  4  0. Gọi  là đường thẳng đi qua M và cắt d , d lần lượt tại A, B 1 2 1 2
sao cho 2MA  3MB  0. Các đường thẳng cần tìm là
A. x  y  2  0; x  1  0.
B. x  y  0; y  1  0.
C. 2x  y  1  0; x  1  0.
D. x  y  0; x  1  0.
Câu 56: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Lập phương trình đường thẳng  đi
qua M và cắt các trục tọa độ lần lượt tại A, B (khác O ) sao cho M là trung điểm . AB
A. x  y  3  0.
B. 2x  y  2  0.
C. x  2y  5  0.
D. 2x  y  4  0.
Câu 57: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Lập phương trình đường thẳng  đi
qua M và cắt các tia Ox, Oy lần lượt tại A, B (khác O ) sao cho OA  2O . B
A. x  y  3  0.
B. 2x  y  2  0.
C. x  2y  5  0.
D. 2x  y  4  0.
Câu 58: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Có bao nhiêu đường thẳng đi qua M
và cắt các tia Ox, Oy lần lượt tại A, B (khác O ) sao cho OA  OB  6?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 6
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A. 1. B. 0. C. Vô số. D. 2.
Câu 59: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 2;1. Gọi  là đường thẳng qua M , cắt các
tia Ox, Oy lần lượt tại A, B (khác O ) sao cho OA  OB nhỏ nhất. Hỏi đường thẳng  đi qua điểm nào dưới đây? A. M  2; 2. B. N  2; 2. C. P  2; 2. D. Q 2; 2.
Câu 60: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Gọi  là đường thẳng qua M , cắt các 1 1
tia Ox, Oy lần lượt tại A, B (khác O ) sao cho 
nhỏ nhất. Hỏi đường thẳng  đi qua 2 2 OA OB điểm nào dưới đây? A. M 3;1. B. N 2; 1. C. P 0; 3. D. Q 3; 3.
Câu 61: Trong mặt phẳng tọa độ Oxy, cho điểm M (3; 2) . Gọi d là đường thẳng đi qua M và lần lượt
cắt tia Ox, Oy tại (
A a;0), B(0;b) với a  0, b  0 và diện tích tam giác OAB nhỏ nhất. Hỏi
điểm nào dưới đây thuộc d? A. N  3  ;6. B. S2; 1  . C. P 1; 3. D. Q 3; 3. DẠNG TOÁN 3: Khoảng cách. Góc I. PHƯƠNG PHÁP 1. Khoảng cách
a. Cho đường thẳng  ax  by  c   2 2 :
0 a  b  0 và điểm M x ; y . 0 0 
ax  by  c
Khoảng cách từ M đến  là dM;  0 0  2 2 a  b
dM;Ox   y Đặc biệt: 0  d
 M;Oy   x0
b. Cho hai đường thẳng  : ax  by  c  0 2 2
a  b  0 và  : ax  by  c  0 c  c . 2 2  1 2 1 1  c  c
Khoảng cách giữa  và  là d  ;   1 2  1 2 1 2 2 2 a  b
2. Góc giữa hai đường thẳng
Cho hai đường thẳng  : a x  b y  c  0  2 2
a  b  0 và  : a x  b y  c  0  2 2 a  b  0 2 2 2 2 2 2  1 1 1 1 1 1 
Đường thẳng  có một vectơ pháp tuyến là n  a ; b . 1  1 1 1
Đường thẳng  có một vectơ pháp tuyến là n  a ; b . 2  2 2  2
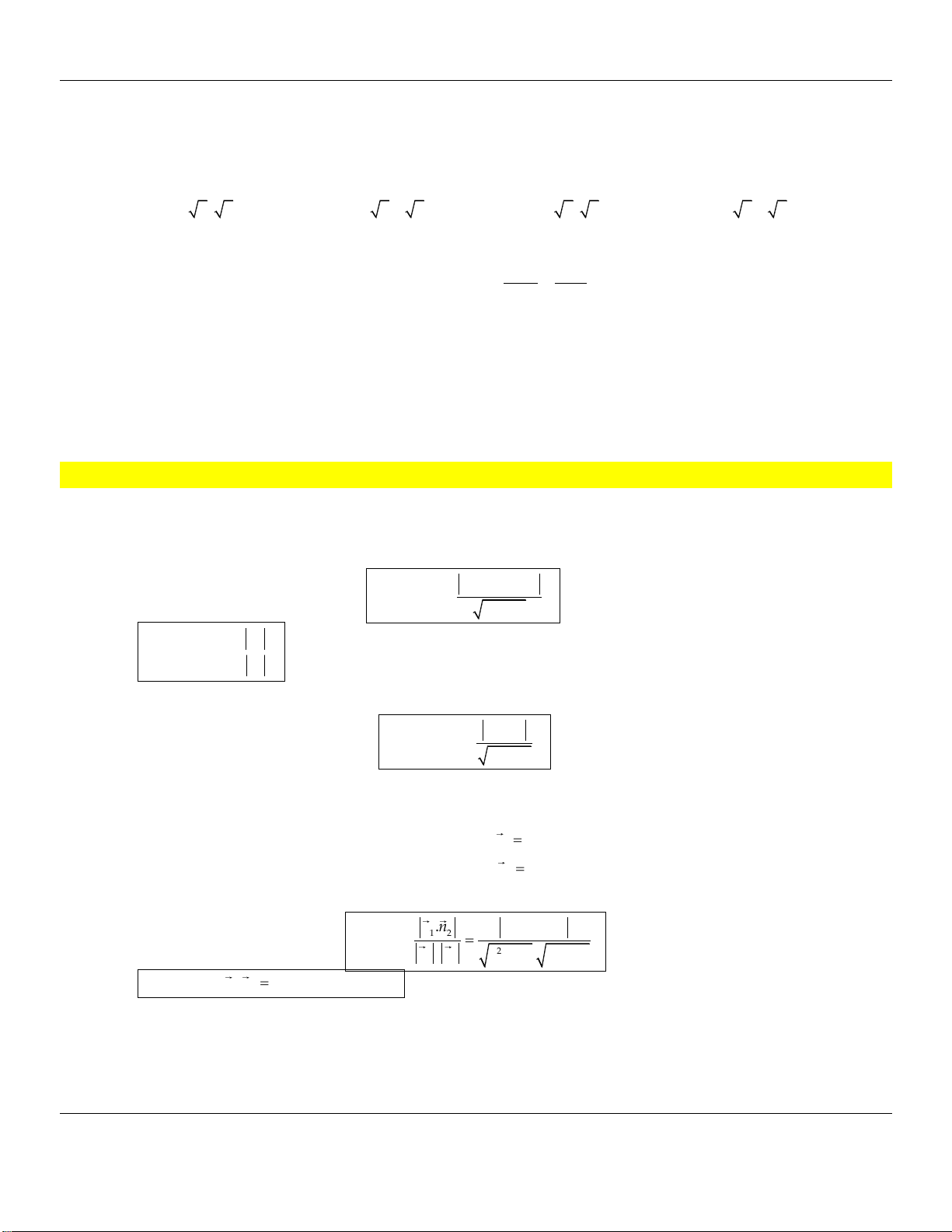
Gọi  là góc giữa hai đường thẳng  và  , 0    90 . 2   1 n .n a a  b b 1 2 1 2 1 2 cos   2 2 2 2 n . n   1 1 a b . a b 1 1 2 2
Đặc biệt:     n .n  0  a a  b b  0 1 2 1 2 1 2 1 2
II. BÀI TẬP TỰ LUẬN MINH HỌA
Câu 62: Trong mặt phẳng tọa độ Oxy, tính côsin góc giữa hai đường thẳng  : 2x  y 1  0 và 1 x  2   t :  . 2 y 1 t
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 7
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 63: Trong mặt phẳng tọa độ Oxy, tính góc giữa hai đường thẳng  :x  2y  15  0 và 1 x  2  t  : t  . 2   y  4   2t
Câu 64: Trong mặt phẳng tọa độ Oxy, tính góc giữa hai đường thẳng  : x  3y  2  0 và 1
 : x  3y 1  0 . 2
Câu 65: Trong mặt phẳng tọa độ Oxy, tìm tất cả các giá trị của a để góc tạo bởi đường thẳng
x  9  at d : 
t   và đường thẳng d :3x  4 y  2  0 bằng 45 . 1
y  7  2t 2
Câu 66: Trong mặt phẳng tọa độ Oxy, tính khoảng cách từ điểm M 1; 1 đến đường thẳng
 : 3x  y  4  0.
Câu 67: Trong mặt phẳng tọa độ Oxy, tính khoảng cách từ điểm M 3; 4 đến đường thẳng x  1   4t  :  . . y  1    3t
Câu 68: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d :x  y  3  0 và d :x  y  5  0. Tính 1 2
khoảng cách giữa hai đường thẳng d và d . 1 2
Câu 69: Trong mặt phẳng tọa độ Oxy, tính khoảng cách từ điểm A0; 4 đến đường thẳng . x sin   .
y cos  4 1 cos   0,  .
Câu 70: Trong mặt phẳng tọa độ Oxy, biết đường tròn C có tâm I 3;  2 tiếp xúc với đường thẳng
 :x  5y 1  0, tính bán kính R của đường tròn C.
x  2  2t
Câu 71: Trong mặt phẳng tọa độ Oxy, cho điểm A0; 
1 và đường thẳng d :  . Tìm điểm M y  3 t
thuộc d và cách A một khoảng bằng 5 .
Câu 72: Trong mặt phẳng tọa độ Oxy, cho hai điểm A3; 1
 ,B0;3 . Tìm tọa độ điểm M thuộc Ox
sao khoảng cách từ M đến đường thẳng AB bằng 1. x  3 t
Câu 73: Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc đường thẳng d :  và cách đường y  2  t
thẳng  : 2x  y  3  0 một khoảng 2 5 .
Câu 74: Trong mặt phẳng tọa độ Oxy, tìm tọa độ hình chiếu vuông góc của điểm M 1; 2 lên đường
thẳng  : x  y  0.
Câu 75: Trong mặt phẳng tọa độ Oxy, cho đường thẳng  : x  m  
1 y  m  0 ( m là tham số bất kì) và điểm A5; 
1 . Tính khoảng cách lớn nhất từ điểm A đến .
III. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 76: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2 và đường thẳng  : 2x  y  1  0. Tính
khoảng cách từ điểm A đến đường thẳng . 5 A. 5. B. 5. C. 2 5 D. . 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 8
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 77: Trong mặt phẳng với hệ tọa độ Oxy, tìm giá trị tham số n để khoảng cách từ điểm I 2; 3 đến
đường thẳng  : x  ny  1 2n  0 bằng 1. A. n  0. B. n  1. C. n  1. D. n  2. x  1 t
Câu 78: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 3 và đường thẳng  :  , t  . Tính y   2t
khoảng cách từ điểm M đến đường thẳng . 3 5 5 A. 5. B. . C. 2 5 D. . 5 5
Câu 79: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : x  2y  3  0 và d : 2x  4y  5  0. 1 2
Tính khoảng cách giữa hai đường thẳng d và d . 1 2 5 5 A. 5. B. . C. 2 5 D. . 10 5
Câu 80: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng  : 3x  4y  3  0. Viết phương trình các
đường thẳng song song với  và cách  một khoảng bằng 1.
A. 3x  4y  1  0; 3x  4y  7  0.
B. 3x  4y  2  0; 3x  4y  8  0.
C. 3x  4y  2  0; 3x  4y  6  0.
D. 3x  4y  4  0; 3x  4y  6  0.
Câu 81: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm M 1; 4 và N 6; 2. Viết phương trình các
đường thẳng  qua M sao cho khoảng cách từ N đến  bằng 5.
A. x  1  0; 3x  4y  19  0.
B. x  1  0; 21x  20y  59  0.
C. y  1  0; 3x  4y  19  0.
D. y  1  0; 21x  20y  59  0.
Câu 82: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm P 1;1 và Q4; 2. Viết phương trình các
đường thẳng  sao cho khoảng cách từ P và Q đến  lần lượt bằng 2 và 3.
A. y  1  0; 3x  4y  11  0.
B. x  1  0; 3x  4y  11  0.
C. y  1  0; 3x  4y  11  0.
D. x  1  0; 3x  4y  11  0.
Câu 83: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : 2x  y  10  0 và d : x  3y  2  0. 1 2
Tính góc giữa hai đường thẳng d và d . 1 2 A. 30 .  B. 45 .  C. 60 .  D. 90 . 
Câu 84: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : mx  y  1  0 và d : x  2y  10  0. 1 2
Tìm tập hợp tất cả các giá trị của tham số m để hai đường thẳng d và d vuông góc với nhau. 1 2 1 A.  . B.   2 . C.   2 . D. . 2 
Câu 85: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : mx  y  7m  9  0 và 1
d : 2x  y  10  0. Gọi S là tập hợp tất cả các giá trị của tham số m để góc giữa hai đường thẳng 2
d và d bằng 45 . Tính tổng tất cả các phần tử của S. 1 2 4 8 8 A. 0. B. . C. . D.  . 3 3 3 DẠNG TOÁN 4:
Vị trí tương đối giữa hai đường thẳng I. PHƯƠNG PHÁP
Cho hai đường thẳng  : a x  b y  c  0  2 2
a  b  0 và  : a x  b y  c  0  2 2 a  b  0 2 2 2 2 2 2  1 1 1 1 1 1 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 9
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Nếu a ,b ,c  0 thì ta có: 2 2 2      a b song song với và trùng nhau cắt 1 1    . 1 2 1 2 1 2 a b 2 2 a b c a b c 1 1 1    1 1 1    . a b c a b c 2 2 2 2 2 2
II. BÀI TẬP TỰ LUẬN MINH HỌA
Câu 86: Trong mặt phẳng tọa độ Oxy, tìm m để hai đường thẳng d :mx  y  m  5, d : x  my  9 cắt 1 2 nhau.
Câu 87: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d : mx  m  1 y  2m  0 và 1  
d : 2x  y  1  0 . Tìm m để d và d song song. 2 1 2
Câu 88: Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng d : mx  m  1 y  2m  0,d : 4x  3y  26  0 1   2
và d : 3x  4y  7  0. Tìm m để ba đường thẳng trên đồng quy. 3
Câu 89: Trong mặt phẳng tọa độ
Oxy, cho hai đường thẳng
d : 5x  7 y  4  0 và 1
d : 5x  7 y  6  0. Viết phương trình đường thẳng d song song và cách đều d và d . 2 1 2
Câu 90: Trong mặt phẳng tọa độ Oxy, tìm tọa độ giao điểm của hai đường thẳng 4x  3y  26  0 và
3x  4y  7  0 .
Câu 91: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A2;1 , đường cao BH : x  3y  7  0 và
trung tuyến CM : x  y  1  0 . Tìm tọa độ đỉnh C .
Câu 92: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d : x  y  1, d : x  3y  3  0 . Viết 1 2
phương trình đường thẳng d đối xứng với d qua đường thẳng d . 2 1
III. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 93: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : x  y  3  0 và d : 2x  y  3  0. 1 2
Khẳng định nào sau đây đúng? A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2
Câu 94: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : 4x  2y  1  0 và 1
d : 2x  y  3  0. Khẳng định nào sau đây đúng? 2 A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2 x  1 t
Câu 95: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d :  , t  và 1   y  1   2t
d : 2x  y  3  0. Khẳng định nào sau đây đúng? 2 A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2 x  1 t
Câu 96: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d :  , t  và 1   y  1   t x  2  k d :  , k 
. Khẳng định nào sau đây đúng? 2   y    k
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 10
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2 DẠNG TOÁN 5:
Các bài toán liên quan đến điểm. I. PHƯƠNG PHÁP
Một số lưu ý khi xử lí các bài toán liên quan đến điểm:
a. Điểm M Ox   Mt;0.
b. Điểm M Oy   M0;t.
Mt;t  2
c. Điểm M  : x  y  2  0   M
 t  t. 2;
d. Điểm M   : 2x  y  2  0 
Mt;2t  2.
e. Điểm M   : x  2y  3  0 
M2t  3;t.
Chú ý: Bài toán hình chiếu vuông góc và điểm đối xứng qua đường thẳng.
Cho điểm A và đường thẳng  (không qua A ). H  H 
+) Điểm H là hình chiếu vuông góc của A trên      . AH   AH.u  0 
+) Điểm A là điểm đối xứng của A qua   H là trung điểm AA . A H Δ A'
II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 97: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A2; 1 và đường thẳng  : x  2y  5  0. Gọi
H a;b là hình chiếu vuông góc của A trên , tính a  . b 11 A. 4. B. 0. C. . D. 3. 4
Câu 98: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông cân tại A. Gọi M 1; 1 là  2 
trung điểm của cạnh BC và G ;0 là trọng tâm của tam giác ABC. Biết Ba;b, a  0, tính  3  a  . b A. 4. B. 6. C. 5. D. 2.
MỘT SỐ BÀI TOÁN KHÁC
Câu 99: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : x  4y  15  0 và điểm A 2; 0 . Tìm tọa
độ điểm M thuộc d để đoạn AM có độ dài nhỏ nhất.
Câu 100: Trong mặt phẳng tọa độ Oxy, cho điểm hai điểm A4; 2 , B 2;6 và điểm C nằm trên đường x  5 y 1 thẳng d : 
sao cho CA  CB . Tìm tọa độ điểm C. 3 2 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 11
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 101: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC . Tìm tọa độ các đỉnh của tam giác biết
phương trình cạnh BC : x  y  2  0 ; hai đường cao BB' : x  3  0 và CC ' : 2x  3y  6  0.
Câu 102: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A 3
 ;0 ,B3;0,C 2;6 . Tìm tọa độ trực
tâm H là của tam giác ABC .
Câu 103: Trong mặt phẳng tọa độ Oxy, cho ba điểm A1; 
1 ; B 2;0;C 3;4 . Viết phương trình đường
thẳng đi qua A và cách đều hai điểm B,C .
Câu 104: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có phương trình đường thẳng
BC : x  7 y 13  0. Các chân đường cao kẻ từ B, C của tam giác ABC lần lượt là
E 2;5, F 0; 4. Tìm tọa độ đỉnh A.
Câu 105: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh (
B 12;1) , đường phân giác trong của  
góc A có phương trình d : x  2y  5  1 2
0; G  ;  là trọng tâm tam giác ABC . Tìm tọa độ đỉnh  3 3  C.
Câu 106: Trong mặt phẳng tọa độ Oxy, cho 3 điểm A 6  ;3;B0; 
1 ;C 3; 2 . Tìm M trên đường thẳng
d : 2x  y  3  0 mà MA  MB  MC nhỏ nhất.
Câu 107: Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộc đường thẳng
d : 2x  y  5  0 và điểm A4;8 . Gọi M là điểm đối xứng với B qua C, điểm N 5;4 là hình
chiếu vuông góc của B lên đường thẳng MD. Tìm tọa độ điểm C.
Câu 108: Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD . Gọi M là trung điểm của cạnh BC , N 11 1 
là điểm trên cạnh CD sao cho CN  2ND . Giả sử M ; 
 và đường thẳng AN có phương  2 2 
trình 2x  y  3  0 . Tìm tọa độ điểm P là giao điểm của AN và BD .
Câu 109: Trong mặt phẳng tọa độ Oxy, cho hình thoi MNPQ có tâm I 3; 
1 , đỉnh M thuộc đường
thẳng x  4 y 1  0 , đỉnh N thuộc đường thẳng x  y  8  0 . Xác định tọa độ đỉnh Q .
Câu 110: Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộc đường thẳng
d:2x  y 5  0 và điểm ( A 4
 ;8) . Gọi M đối xứng với B qua C , điểm N(5; 4) là hình
chiếu vuông góc của B lên đường thẳng MD . Tìm tọa độ đỉnh C.
_____________________HẾT_____________________
Huế, 15h00’ Ngày 16 tháng 02 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 12
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
LỜI GIẢI CHI TIẾT
Câu 1: Trong mặt phẳng với hệ tọa độ Oxy, vectơ nào dưới đây là một vectơ chỉ phương của Ox? A. u  1;0 . B. u  1;1 . C. u  1; 4 . D. u  0; 2 . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của Ox có tọa độ k;0 , k  0.
Chọn đáp án A.
Câu 2: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1; 3 , B2;7. Một vectơ chỉ phương của
đường thẳng AB là A. u  4  ;1 . B. u  2  ;1 . C. u  3;  2 . D. u  1; 4 . 4   3   2   1   Lời giải:
Ta có: AB  1; 4.
Các vectơ chỉ phương của đường thẳng AB có tọa độ k; 4k , k  0.
Chọn đáp án D. x  1 2t
Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới y  2   3t
đây là một vectơ chỉ phương của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của d có tọa độ 2k; 3k, k  0.
Chọn đáp án D. x  2 y  3
Câu 4: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
. Vectơ nào dưới đây là 1 2
một vectơ chỉ phương của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của d có tọa độ k; 2k , k  0.
Chọn đáp án A.
Câu 5: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  y  3  0. Vectơ nào dưới đây là
một vectơ pháp tuyến của d? A. n  1; 2 . B. n  2  ;1 . C. n  2;1 . D. n  2; 3 . 4   3   2   1   Lời giải:
Các vectơ pháp tuyến của d có tọa độ 2k; k , k  0.
Chọn đáp án C.
Câu 6: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  3y  3  0. Vectơ nào dưới đây là
một vectơ pháp tuyến của d? A. n  2; 3 . B. n  2  ;3 . C. n  4; 6  . D. n  2; 3  . 4   3   2   1   Lời giải:
Các vectơ pháp tuyến của d có tọa độ 2k; 3k, k  0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 13
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Chọn đáp án A.
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x  2y  5  0. Vectơ nào dưới đây là
một vectơ chỉ phương của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của d có tọa độ  2
 k; k, k  0.
Chọn đáp án B. x  1 2t
Câu 8: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Vectơ nào dưới y  2   3t
đây là một vectơ pháp tuyến của d? A. u  1; 2 . B. u  2  ;1 . C. u  3;  2 . D. u  2; 3 . 4   3   2   1   Lời giải:
Các vectơ pháp tuyến của d có tọa độ  3
 k;2k, k  0.
Chọn đáp án C. x  2 y  3
Câu 9: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d :  . Vectơ nào dưới đây 1 2
không là một vectơ chỉ phương của d? A. u  1; 2 . B. u  2; 4 . C. u  1  ; 2  . D. u  2; 4  . 4   3   2   1   Lời giải:
Các vectơ chỉ phương của d có tọa độ k; 2k , k  0.
Chọn đáp án D.
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1; 3 , B3;7. Gọi  là đường trung trực của đoạn thẳng .
AB Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  4; 3 . C. n  4; 2 . D. n  2; 1  . 4   3   2   1   Lời giải:
Ta có: AB  2; 4.
 là đường trung trực của đoạn thẳng AB nên   . AB
Vậy các vectơ pháp tuyến của  có tọa độ 2k; 4k, k  0.
Chọn đáp án A.
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  y  1  0. Gọi  là đường thẳng
song song với d. Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  4; 3 . C. n  4; 2  . D. n  2;1 . 4   3   2   1   Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  2;1. d
Do  song song với d nên các vectơ pháp tuyến của  có tọa độ 2k; k , k  0.
Chọn đáp án D.
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x  y  1  0. Gọi  là đường thẳng
vuông góc với d. Một vectơ pháp tuyến của đường thẳng  là
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 14
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A. n  1; 2 . B. n  1; 2  . C. n  4; 2 . D. n  2;1 . 4   3   2   1   Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  2;1. d
Do  vuông góc với d nên các vectơ pháp tuyến của  có tọa độ k; 2
 k, k  0.
Chọn đáp án B. x  1 2t
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d :
,t  . Gọi  là đường y   t
thẳng song song với d. Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  4; 3 . C. n  1; 2  . D. n  2;1 . 4   3   2   1   Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  1; 2  . d
Do  song song với d nên các vectơ pháp tuyến của  có tọa độ k; 2
 k, k  0.
Chọn đáp án C. x  1 y  2
Câu 14: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
. Gọi  là đường thẳng 2 1
vuông góc với d. Một vectơ pháp tuyến của đường thẳng  là A. n  1; 2 . B. n  1; 2  . C. n  4; 2 . D. n  2; 1  . 4   3   2   1   Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  1; 2  . d
Do  vuông góc với d nên các vectơ pháp tuyến của  có tọa độ 2k; k , k  0.
Chọn đáp án C.
Câu 15: Trong mặt phẳng tọa độ Oxy, viết phương trình tham số của đường thẳng đi qua hai điểm A3;   1 , B  6  ;2. Lời giải:
Đường thẳng AB qua điểm A3;  1
 và có 1 vectơ chỉ phương là AB   9  ;3 nên có phương x  3 9t trình:  , t   . y  1   3t
Câu 16: Trong mặt phẳng tọa độ Oxy, viết phương trình đường thẳng  đi qua gốc tọa độ và vuông
góc với đường thẳng d : 8x  6 y  7  0. Lời giải:
Vì   d nên  có dạng: 6x  8y  C  0.
Do O 0;0   nên 6.0  8.0  C  0  C  0 .
Vậy phương trình  : 6x  8y  0  3x  4 y  0.
Câu 17: Trong mặt phẳng tọa độ Oxy, cho hai điểm A3;0; B 0;2 và đường thẳng d : x  y  0 . Viết
phương trình tham số của đường thẳng  qua A và song song với d . Lời giải:
Do  d nên  : x  y  C  0C  0.
 qua A3;0 , suy ra 3 0  C  0  C  3  ( nhận)
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 15
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Như vậy  : x  y  3  0 x  t
Vậy  có phương trình tham số:  ,t   . y  3 t
Câu 18: Trong mặt phẳng tọa độ Oxy, viết phương trình đường thẳng d qua M 1;  1 và song song với
đường thẳng d ' : x  y 1  0. Lời giải:
Do đường thẳng d song song với đường thẳng d ' : x  y 1  0 nên đường thẳng d nhận vectơ n  1; 
1 làm một vectơ pháp tuyến.
Khi đó đường thẳng d qua M 1; 
1 và nhận vectơ n  1; 
1 làm vectơ pháp tuyến có phương
trình là x  y  2  0 .
Câu 19: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A2; 3; B 4  ;5;C6; 5
  . Gọi M , N lần
lượt là trung điểm của AB và AC . Viết phương trình tham số của đường thẳng MN. Lời giải:
Do M , N lần lượt là trung điểm của AB và AC nên suy ra M  1
 ;4; N 4;  1 .
Đường thẳng MN đi qua M  1
 ;4 và nhận MN  5; 5
  làm một vectơ chỉ phương x  1   5  t MN :  .
y  4  5t
Câu 20: Trong mặt phẳng tọa độ Oxy, cho hai điểm A1;0 và B0; 4. Viết phương trình đường thẳng . AB Lời giải: x y
Áp dụng công thức phương trình đoạn chắn  AB : 
 1  4x  y  4  0. 1 4
Câu 21: Trong mặt phẳng tọa độ Oxy, cho điểm M 1; 2 . Gọi ,
A B là hình chiếu của M lên Ox, Oy .
Viết phương trình đường thẳng AB . Lời giải:
Ta có, hình chiếu của điểm M (1; 2) lên Ox,Oy lần lượt là A(1;0) và B(0;2). x y
Do đó phương trình đường thẳng AB là: 
1  2x  y  2  0 . 1 2
Câu 22: Trong mặt phẳng tọa độ Oxy, viết phương trình đường thẳng đi qua điểm M 5; 3   và cắt hai
trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB. Lời giải:
Gọi AOx  A x ;0; B Oy  B 0; y A B 
x  x  2x x 10 Ta có A B M A
M là trung điểm AB    
y  y  2 y y  6   A B M  B x y Suy ra AB : 
1  3x  5y  30  0 . 10 6 
Câu 23: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A1; 
1 , B 0;  2 , C 4; 2 . Viết phương
trình tổng quát của đường trung tuyến đi qua đỉnh B của tam giác ABC.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 16
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT Lời giải:  5 3   5 7 
Gọi M là trung điểm của cạnh AC  M ;  BM  ;      2 2   2 2 .
Đường thẳng BM nhận n   7
 ;5 làm một vectơ pháp tuyến.
Suy ra BM :  7x  5( y  2)  0  7
 x  5y 10  0.
Câu 24: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại C và B 2;  
1 , A4;3 . Viết phương
trình đường cao CH của tam giác ABC. Lời giải:
Tam giác ABC cân tại C nên H là trung điểm của AB và CH  AB . Ta có: H 3;  1 và AB   2  ; 4  2  1;2 .
Vậy phương trình đường cao CH : 1 x  3  2 y  
1  0  x  2 y  5  0 .
Câu 25: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A2; 1
 ,B4;5,C 3  ;2 . Viết phương
trình đường cao AH của tam giác ABC. Lời giải:
Đường cao AH đi qua điểm A2; 
1 và có một vectơ pháp tuyến là BC   7  ; 3   .
Vậy phương trình AH là 7
 x  2 3 y  
1  0  7x  3y 11  0 .
Câu 26: Trong mặt phẳng tọa độ Oxy, gọi
H là trực tâm tam giác ABC và
AB : 7x  y  4  0; BH : 2x  y  4  0; AH : x  y  2  0. Viết phương trình đường cao CH của tam giác ABC. Lời giải:
Ta có: CH  AB nên CH có phương trình 1 x  x   7  y  y   0 1 x  x  y  y  H  7  H  0 H H
2x  y  4  0 x  2
trong đó x , y là nghiệm của hệ:   
. Từ đó H 2;0. H H
x  y  2  0 y  0
Vậy 1 x  2  7  y  0  0  x  7 y  2  0.
Câu 27: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có M 2;0 là trung điểm của cạnh . AB
Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x  2 y  3  0 và
6x  y  4  0 . Viết phương trình đường thẳng AC. Lời giải: A M B C E D
+) Gọi AH và AD lần lượt là các đường cao và trung tuyến kẻ từ A của tam giác ABC .
7x  2y  3  0 x 1
+) Tọa độ A là nghiệm của hệ     A1;2.
6x  y  4  0 y  2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 17
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
x  2x  x  3
+) M là trung điểm của AB nên B M A   B3; 2   .
y  2 y  y  2   B M A
+) Đường thẳng BC đi qua B 3; 2 và vuông góc với đường thẳng AH : 6x  y  4  0 nên có
phương trình x – 3  6 y  2  0  x  6 y  9  0 .
7x  2y  3  0
+) D là giao điểm của BC và AN nên tọa độ D là nghiệm của hệ: 
x  6y  9  0 x  0   3    3  D 0;    y     2   2
Do D là trung điểm của BC nên suy ra C  3  ;  1 .
+) Đường thẳng AC đi qua A1; 2 và C  3  ; 
1 có phương trình là 3x  4 y  5  0 . x y
Câu 28: Trong mặt phẳng tọa độ Oxy, biết đường thẳng d :
 1 , a  0;b  0 đi qua M  1  ;6 a b
tạo với tia Ox, Oy một tam giác có diện tích bằng 4. Viết phương trình đường thẳng d. Lời giải: 1  6
Do d đi qua M  1  ;6   1 (1). a b
Đường thẳng cắt tia Ox tại ( A ;
a 0), a  0  OA  . a
Đường thẳng cắt tia Oy tại B(0; )
b , b  0  OB  . b  1 1
OAB vuông tại O nên có diện tích là S  O . A OB  a . b OAB 2 2 1 Theo đề S
 4  ab  4  ab  8 (2). OAB 2 x y Từ  
1 , 2 suy ra: a  2;b  4  d : 
1  2x  y  4  0. 2 4
Câu 29: Trong mặt phẳng tọa độ Oxy, cho điểm M 2;1 . Viết phương trình đường thẳng d đi qua M ,
cắt các tia Ox , Oy lần lượt tại A và B ( ,
A B khác O ) sao cho tam giác OAB có diện tích nhỏ nhất. Lời giải:
Gọi đường thẳng d cắt tia Ox , Oy lần lượt tại Aa;0 và B 0;b;a,b  0    x y d :   1 a b Cauchy 2 1 2
Vì d  qua M   2 1 2;1    1  1     2  ab  8 a b a b ab 1 1
Ta có diện tích tam giác vuông OAB tại O là S  .O . A OB  . . a b  4 2 2 2 1
Diện tích tam giác OAB đạt giá trị nhỏ nhất S
 4    a  2b min a b
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 18
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT 2 1    x y
1  b  2,a  4  d  : 
 1  x  2y  4  0 . 2b b 4 2
Câu 30: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng  : x  y 1  0,  : 2x  y 1  0 và điểm 1 2 P 2; 
1 . Viết phương trình đường thẳng đi qua điểm P và cắt hai đường thẳng  ,  lần 1 2
lượt tại hai điểm A , B sao cho P là trung điểm AB . Lời giải:
Vì A   A a; a 1 . Vì P 2; 
1 là trung điểm của đoạn AB  B 4  ;1 a  a . 1   8  8 11  2 8 
Mặt khác B    a   A ; ; AP  ; 2     3  3 3   3 3 
Đường thẳng AP có phương trình là: 4x  y  7  0 .
Câu 31: Trong mặt phẳng tọa độ Oxy, cho các điểm A1; 1 và B3; 4 . Gọi d là một đường thẳng bất
kì luôn đi qua B. Viết phương trình đường thẳng d khi khoảng cách từ A đến đường thẳng d
đạt giá trị lớn nhất. Lời giải:
Ta có: AB  2; 5.
Gọi H là hình chiếu của điểm A lên đường thẳng d . 2 2
Khi đó, ta có: dA,d  AH  AB  3  1  4  1  29 .
Do đó khoảng cách từ A đến đường thẳng d đạt giá trị lớn nhất bằng AB khi AB  . d
Vì vậy d đi qua A1; 1 và nhận AB  2; 5 làm một vectơ pháp tuyến.
Do đó phương trình của đường thẳng d là d :2x  1  5y  1  0  d :2x  5y  3  0 .
Câu 32: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x  y  3  0. Điểm nào dưới đây nằm trên đường thẳng d ? A. M 1; 4. B. N 1;0. C. P 2; 3. D. Q2;0. Lời giải:
Thay tọa độ điểm M vào phương trình d thấy thỏa mãn.
Chọn đáp án A.
Câu 33: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x  y  3  0. Điểm nào dưới đây
không nằm trên đường thẳng d ? A. M 1; 4. B. N  3  ;0. C. P 0; 3. D. Q2;1. Lời giải:
Thay tọa độ điểm Q vào phương trình d thấy không thỏa mãn.
Chọn đáp án D. x  1 y  1
Câu 34: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
. Biết điểm M a; b nằm 2 3
trên đường thẳng d, đẳng thức nào sau đây đúng?
A. 3a  2b  5.
B. 3a  2b  5.
C. 3a  b  5.
D. 3a  b  5. Lời giải: a  1 b  1
Do M a;bd  
 3a 1  2b 1  3a  2b  5. 2 3
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 19
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT x  1 t
Câu 35: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Điểm nào dưới đây y  2   3t
nằm trên đường thẳng d ? A. M 1; 3. B. N 1; 2. C. P 1; 5. D. Q2;0. Lời giải:
Chọn đáp án B. x  1 t
Câu 36: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 
,t  . Điểm nào dưới đây y  2   3t
nằm trên đường thẳng d ? A. M 1; 3. B. N 5; 2. C. P 2; 5. D. Q2;0. Lời giải: 2  1 t
Thay tọa độ điểm P vào phương trình d ta được:   t  1. 5  2   3t
Chọn đáp án C. x  t
Câu 37: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d :
, t  . Điểm nào dưới đây y  1   2t
không nằm trên đường thẳng d ? A. M 0;1. B. N 1; 3. C. P 2; 5. D. Q1;1. Lời giải: 1   t
Thay tọa độ điểm Q vào phương trình d :  (vô nghiệm). 1  1   2t
Chọn đáp án D.
Câu 38: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;0 , B0; 5. Phương trình đường thẳng AB là x y x y x y x y A.   0. B.   1. C.   1.  D.   1. 1 5 5 1 1 5 1 5 Lời giải:
Chọn đáp án D.
Câu 39: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;1 , B2; 5. Phương trình đường thẳng AB là
A. x  4y  5  0.
B. 4x  y  3  0.
C. x  4y  1  0.
D. 4x  y  1  0. Lời giải:
Ta có: AB  1; 4.
Đường thẳng AB qua A1;1 và nhận AB  1; 4 làm một vectơ chỉ phương nên chọn n  4; 1
  làm một vec tơ pháp tuyến của . AB
Vậy AB : 4x  1  y  1  0  4x  y  3  0.
Chọn đáp án B.
Câu 40: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;1 , B2; 5. Phương trình đường thẳng AB là
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 20
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT x  1 t x  1 4t x  1 t x  1   t A.  , t  . B.  , t  . C.  , t  . D.  , t  . y  1   4t y  1   t y  4   t y  1    4t Lời giải:
Ta có: AB  1; 4.
Đường thẳng AB qua A1;1 và nhận AB  1; 4 làm một vectơ chỉ phương. x  1 t Vậy AB :  , t  . y  1   4t
Chọn đáp án A.
Câu 41: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm M 1; 
1 , N 2; 4. Phương trình đường thẳng MN là x  1 t x  1 3t x  1 t x  t A.  , t  . B.  , t  . C.  , t  . D.  , t  . y   3t y  1   t y  3   t y  2    3t Lời giải:
Ta có: MN  1; 3.
Đường thẳng MN qua M 1;1 và nhận MN  1; 3 làm một vectơ chỉ phương. x  1 t Vậy MN :  , t  . y  1   3t
Test phương án D, thấy thỏa mãn.
Chọn đáp án D.
Câu 42: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;0 , B3;6. Phương trình đường thẳng
trung trực của đoạn thẳng AB là
A. x  3y  11  0
B. x  3y  11  0.
C. 3x  y  9  0.
D. 3x  y  7  0. Lời giải:
Ta có: AB  2;6.
Gọi I là trung điểm AB  I 2; 3.
Đường thẳng  qua I 2; 3 và nhận AB  2;6 làm một vectơ pháp tuyến.
Vậy  : 2x  2  6y  3  0  2x  6y  22  0  x  3y  11  0.
Chọn đáp án B.
Câu 43: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2 và đường thẳng d : x  2y  3  0.
Phương trình đường thẳng  qua A và song song với d là
A. 2x  y  0.
B. x  2y  5  0.
C. 2x  y  5  0.
D. x  2y  1  0. Lời giải:
Do  song song với d nên  có dạng  : x  2y  m  0, m  3  .
Do A1; 2   1  4  m  0  m  5.
 Vậy  : x  2y  5  0.
Chọn đáp án B.
Câu 44: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2 và đường thẳng d : x  2y  3  0.
Phương trình đường thẳng  qua A và vuông góc với d là
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 21
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
A. 2x  y  0.
B. x  2y  5  0.
C. 2x  y  1  0.
D. x  2y  1  0. Lời giải:
Do  vuông góc với d nên  có dạng  : 2x  y  m  0.
Do A1; 2   2  2  m  0  m  0. Vậy  : 2x  y  0.
Chọn đáp án A. x  1 2t
Câu 45: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A2; 3 và đường thẳng d :  , t  . y  3   t
Phương trình đường thẳng  qua A và song song với d là
A. 2x  y  7  0.
B. 2x  y  0.
C. x  2y  1  0.
D. x  2y  4  0. Lời giải:
Đường thẳng d có một vectơ chỉ phương là u  2;1 nên d có một vectơ pháp tuyến là d  n  1; 2  . d
Do  song song với d nên  nhận n  1; 2
 làm một vectơ pháp tuyến. d 
Vậy  : 1x  2  2y  3  0  x  2y  4  0.
Chọn đáp án D. x  1 2t
Câu 46: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A2; 3 và đường thẳng d :  , t  . y  3   t
Phương trình đường thẳng  qua A và vuông góc với d là
A. 2x  y  7  0.
B. 2x  y  0.
C. x  2y  1  0.
D. x  2y  4  0. Lời giải:
Đường thẳng d có một vectơ chỉ phương là u  2;1. d
Do  vuông góc với d nên  nhận n  1; 2
 làm một vectơ pháp tuyến. d 
Vậy  : 1x  2  2y  3  0  x  2y  4  0.
Chọn đáp án D.
Câu 47: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A1;1 , B2; 3 , C  4  ;4. Phương
trình đường thẳng chứa cạnh AB là
A. x  2y  3  0.
B. 2x  y  1  0.
C. x  2y  1  0.
D. x  2y  4  0. Lời giải:
Đường thẳng AB có một vectơ chỉ phương là AB  1; 2  n   2
 ;1 là một vectơ pháp tuyến của . AB
Vậy AB :  2x  1  1y  1  0  2
 x  y  1  0.
Chọn đáp án B.
Câu 48: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A1;1 , B2; 3 , C  4  ;1. Đường
trung tuyến AM của tam giác ABC có phương trình là
A. x  2y  3  0.
B. 2x  y  1  0.
C. x  2y  1  0.
D. x  2y  4  0. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 22
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A C B M
Gọi M là trung điểm BC  M  1  ;2.
Đường thẳng AM có một vectơ chỉ phương là AM   2
 ;1  n  1;2 là một vectơ pháp tuyến của AM.
Vậy AM : 1x  1  2y  1  0  x  2y  3  0.
Chọn đáp án A.
Câu 49: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A1;1 , B2; 3 , C  4  ;1. Đường
trung cao BK của tam giác ABC có phương trình là A. x  2  0.
B. 2x  y  1  0.
C. x  2y  1  0.
D. x  2y  8  0. Lời giải: A K C B
Đường thẳng BK có một vectơ pháp tuyến là AC   5;  0.
Vậy BK :  5x  2  0y  3  0  x  2  0.
Chọn đáp án A.
Câu 50: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với M 1;1 , N 0; 2 , P 1  ; 2   lần lượt
là trung điểm AB, BC, AC. Phương trình đường thẳng chứa cạnh AB là
A. x  4y  5  0.
B. 4x  y  5  0.
C. x  4y  3  0.
D. 4x  y  3  0. Lời giải: A M P C B N
Đường thẳng AB qua M 1;1 và có một vectơ chỉ phương là NP   1  ; 4
   n  4; 1   là vectơ pháp tuyến của . AB
Vậy AB : 4x  1  1y  1  0  4x  y  3  0.
Chọn đáp án D.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 23
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 51: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với M  1  ; 1
 , N1;9, P9;1 lần lượt
là trung điểm BC, CA, .
AB Phương trình đường cao AH của tam giác ABC là
A. x  y  11  0.
B. 2x  y  11  0.
C. 2x  y  11  0.
D. x  y  0. Lời giải: A P N C B H M Ta có: NM   2  ; 1
 0, AP  9  x ;1 y . A A 9  x  2  x  11
Tứ giác APMN là hình bình hành nên A A
NM  AP      A11;1  1 . 1    y  1  0 y  11 A A
Đường cao AH qua A11;11 và nhận NP  8; 8
  hay n  1; 
1 làm một vectơ pháp tuyến
nên có phương trình là 1x  11  y  11  0  x  y  0.
Chọn đáp án D.
Câu 52: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với A 2
 ;1, B2;3, C1; 5  . Đường
phân giác trong của góc A có phương trình là
A. 2x  y  0.
B. x  y  1  0.
C. x  2y  4  0.
D. x  3y  1  0. Lời giải: A C B D
Ta có: AB  4; 2  AB  2 5, AC  3; 6
   AC  3 5.
Gọi Dx; y là chân đường phân giác trong của góc A, ta có: AB 2  8 1  DB  
.DC  DB   .DC  D ;   . AC 3  5 5   18 6 
Đường phân giác AD qua A2;1 và nhận AD  ;  
 làm một vectơ chỉ phương nên có  5 5 
một vectơ pháp tuyến là Vây
Chọn đáp án D.
Câu 53: Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có tâm I 1;1. Biết
A2;0, B1; 4. Phương trình đường thẳng chứa cạnh CD là
A. x  4y  8  0.
B. 4x  y  2  0.
C. x  4y  1  0.
D. 4x  y  5  0. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 24
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A B I D C
Do I là trung điểm AC  C 0; 2.
Đường thẳng CD qua C 0; 2 và có một vectơ chỉ phương là AB   1
 ;4  n  4;1 là vectơ pháp tuyến của . CD
Vậy CD : 4x  0  1y  2  0  4x  y  2  0.
Chọn đáp án B.
Câu 54: Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có tâm I 3; 5 và hai cạnh
AB, AD lần lượt nằm trên hai đường thẳng x  3y  6  0, 2x  5y  1  0. Viết phương trình hai
cạnh còn lại của hình bình hành ABCD.
A. 2x  5y  29  0; x  3y  40  0.
B. 2x  5y  39  0; x  3y  30  0.
C. 2x  5y  19  0; x  3y  20  0.
D. 2x  5y  39  0; x  3y  30  0. Lời giải: A B I D C
x  3y  6  0 x  3
Tọa độ điểm A là nghiệm của hệ phương trình:     A3;1.
2x  5y  1  0 y    1
Do I là trung điểm AC nên C 3;9.
Đường thẳng BC đi qua C 3;9 và song song với AD : 2x  5y  1  0 nên có phương trình
2x  3  5y  9  0  2x  5y  39  0.
Đường thẳng CD đi qua C 3;9 và song song với AB : x  3y  6  0 nên có phương trình
x  3 3y 9  0  x  3y  30  0.
Chọn đáp án B.
Câu 55: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1;1 và hai đường thẳng
d : 3x  y  5  0, d : x  y  4  0. Gọi  là đường thẳng đi qua M và cắt d , d lần lượt tại A, B 1 2 1 2
sao cho 2MA  3MB  0. Các đường thẳng cần tìm là
A. x  y  2  0; x  1  0.
B. x  y  0; y  1  0.
C. 2x  y  1  0; x  1  0.
D. x  y  0; x  1  0. Lời giải:
A d  A x ; 3x  5 , Bd  B x ; 4  x . 1  1 1  2  2 2 
2MA  3MB 1
Vì A, M, B thẳng hàng và 2MA  3MB  
 MA   MB   . 2 3 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 25
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Ta có: MA  x  1; 3x  6 , MB  x  1; 3  x . 1 1   2 2   5 x   5 5  Từ (1) giải được 1  2 . Suy ra A ;
, B2; 2  d : x  y    0.   2 2 x    2 2 x  1 Từ (2) giải được 1  . Suy ra A1; 2
 , B1;3  d : x 1  0. x  1 2
Chọn đáp án D.
Câu 56: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Lập phương trình đường thẳng  đi
qua M và cắt các trục tọa độ lần lượt tại A, B (khác O ) sao cho M là trung điểm . AB
A. x  y  3  0.
B. 2x  y  2  0.
C. x  2y  5  0.
D. 2x  y  4  0. Lời giải:
Giả sử  Ox  Aa;0 ,  Oy  B0;b ,  . a b  0. x y Suy ra  :   1. a b x y
Do M là trung điểm AB nên A2;0 , B0; 4. Vậy  :   1  2x  y  4  0. 2 4
Chọn đáp án D.
Câu 57: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Lập phương trình đường thẳng  đi
qua M và cắt các tia Ox, Oy lần lượt tại A, B (khác O ) sao cho OA  2O . B
A. x  y  3  0.
B. 2x  y  2  0.
C. x  2y  5  0.
D. 2x  y  4  0. Lời giải:
Gọi  Ox  Aa;0 ,  Oy  B0; b , a  0, b  0. x y Suy ra  :   1. a b Do M   1 2 1; 2      1 (*). a b 1 2 5
Ta có: OA  2OB  a  2 .
b Thay vào (*) ta được:
  1  b   a  5. 2b b 2 x 2y Vậy  : 
 1  x  2y  5  0. 5 5
Chọn đáp án D.
Câu 58: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Có bao nhiêu đường thẳng đi qua M
và cắt các tia Ox, Oy lần lượt tại A, B (khác O ) sao cho OA  OB  6? A. 1. B. 0. C. Vô số. D. 2. Lời giải:
Gọi  Ox  Aa;0 ,  Oy  B0; b , a  0, b  0. x y Suy ra  :   1. a b Do M   1 2 1; 2      1 (1). a b
Ta có: OA  OB  6  a  b  6 (2).
Từ (1) và (2), giải hệ ta được: a  2; b  4 hoặc a  b  3.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 26
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Vậy có hai đường thẳng thỏa mãn yêu cầu bài toán là 2x  y  4  0 và x  y  3  0.
Chọn đáp án D.
Câu 59: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 2;1. Gọi  là đường thẳng qua M , cắt các
tia Ox, Oy lần lượt tại A, B (khác O ) sao cho OA  OB nhỏ nhất. Hỏi đường thẳng  đi qua điểm nào dưới đây? A. M  2; 2. B. N  2; 2. C. P  2; 2 . D. Q 2; 2. Lời giải:
Gọi  Ox  Aa;0 ,  Oy  B0; b , a  0, b  0. x y Suy ra  :   1. a b Do M   2 1 2;1      1 a b   a b
Ta có: OA  OB  a  b  a  b  a  b 2 1 2 .1 .   3    3    2 2.  a b  b a a 2b    a  b 2    a  2  2
Vậy OA  OB  3  2 2 khi b a      . min 2 1 2 1     1    b  2  1 1  a b  a b x y
Vậy phương trình đường thẳng  là 
 1  x  2y  2  2  0. 2  2 2  1
Rõ ràng M  2; 2 . 
Chọn đáp án A.
Câu 60: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 2. Gọi  là đường thẳng qua M , cắt các 1 1
tia Ox, Oy lần lượt tại A, B (khác O ) sao cho 
nhỏ nhất. Hỏi đường thẳng  đi qua 2 2 OA OB điểm nào dưới đây? A. M 3;1. B. N 2; 1. C. P 0; 3. D. Q 3; 3. Lời giải: y B M 2 H A O 1 x 1 1 1 Kẻ OH  . AB Khi đó:   . 2 2 2 OH OA OB 1 1 1 Ta có:  nhỏ nhất 
nhỏ nhất  OH lớn nhất. 2 2 OA OB 2 OH
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 27
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Ta có: OH  OM  OH  OM. max
Điều này xảy ra  OH  OM hay đường thẳng  nhận OM  1; 2 làm một vectơ pháp tuyến.
Vậy phương trình  là 1x  1  2y  2  0  x  2y  5  0.
Rõ ràng M 3;1  . 
Chọn đáp án A.
Câu 61: Trong mặt phẳng tọa độ Oxy, cho điểm M (3; 2) . Gọi d là đường thẳng đi qua M và lần lượt
cắt tia Ox, Oy tại (
A a;0), B(0;b) với a  0, b  0 và diện tích tam giác OAB nhỏ nhất. Hỏi
điểm nào dưới đây thuộc d? A. N  3  ;6. B. S2; 1  . C. P 1; 3. D. Q 3; 3. Lời giải: x y
Phương trình theo đoạn chắn của đường thẳng d :  1 a b 3 2
d là đường thẳng đi qua M (2;3) nên   1 (*) a b 1 . a b
Tam giác OAB vuông tại O nên có diện tích là S  O . A OB 
(OA  a,OB  b) nhỏ nhất 2 2 . a b  nhỏ nhất  . a b nhỏ nhất. 2 3 2 6 24
Mà theo bất đẳng thức Cô si, ta có  1 2  1  ab  24 a b ab ab 3 2 2a Do đó . a b nhỏ nhất   b 
 b  4,a  6 (Từ(*)) a b 3 x y
Lúc đó phương trình của d :
 1  2x  3y 12  0. 6 4 Dễ thấy N  3
 ;6d.
Câu 62: Trong mặt phẳng tọa độ Oxy, tính côsin góc giữa hai đường thẳng  : 2x  y 1  0 và 1 x  2   t :  . 2 y 1 t Lời giải:
Véctơ pháp tuyến của đường thẳng  là n  2; 
1 nên vectơ chỉ phương u  1;  2 1
Véctơ chỉ phương của đường thẳng  là u  1;   1 2 u.u 3 3 10 Khi đó cos  ; 
 cos u;u    . 1 2 
  u.u 5. 2 10
Câu 63: Trong mặt phẳng tọa độ Oxy, tính góc giữa hai đường thẳng  :x  2y  15  0 và 1 x  2  t  : t  . 2   y  4   2t Lời giải:
Đường thẳng  có VTPT là n  1; 2  . 1   1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 28
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Đường thẳng  có 1 vectơ chỉ phương là u  1; 2  n  2;1 . 2   2   2
Nhận xét : n .n  0       ,   90 . 1 2 1 2  1 2 
Câu 64: Trong mặt phẳng tọa độ Oxy, tính góc giữa hai đường thẳng  : x  3y  2  0 và 1
 : x  3y 1  0 . 2 Lời giải:
 có vectơ pháp tuyến là n  1; 3 ; 1   1
 có vectơ pháp tuyến là n  1; 3 . 2   2 n .n 1.1  3 3  1 2   2 1 Khi đó: cos  ;      . 1 2  | n | . n
1   32 . 1   32 2 2 4. 4 2 1 2
Vậy góc giữa hai đường thẳng  ;  là 60 .  1 2
Câu 65: Trong mặt phẳng tọa độ Oxy, tìm tất cả các giá trị của a để góc tạo bởi đường thẳng
x  9  at d : 
t   và đường thẳng d :3x  4 y  2  0 bằng 45 . 1
y  7  2t 2 Lời giải:
Gọi  là góc giữa hai đường thẳng đã cho.
Đường thẳng d có vectơ chỉ phương là u  a ; 2   . 1
Đường thẳng d có vectơ chỉ phương là v  4; 3   . 2 u.v 1 4a  6
Ta có cos  cos u, v   cos 45    u . v 2 2 5 a  4 2
 5 a  4  2 4a  6 2 2
 25a 100  32a  96a  72  2 a  2  
7a  96a  28  0  7  . a  14 
Câu 66: Trong mặt phẳng tọa độ Oxy, tính khoảng cách từ điểm M 1; 1 đến đường thẳng
 : 3x  y  4  0. Lời giải:
Khoảng cách từ điểm M 1; 1 đến đường thẳng  : 3x  y  4  0 là  
dM  3.1 1 4 6 3 10 ;    . 2 2 3  1 10 5
Câu 67: Trong mặt phẳng tọa độ Oxy, tính khoảng cách từ điểm M 3;  4 đến đường thẳng x  1   4t  :  . . y  1    3t Lời giải:
Ta có  : 3x  4y  1  0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 29
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT 3.3  4. 4   1 24
Suy ra dM,     .   2 2 5 3 4
Câu 68: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d :x  y  3  0 và d :x  y  5  0. Tính 1 2
khoảng cách giữa hai đường thẳng d và d . 1 2 Lời giải:
Ta có: d và d song song. 1 2 0  3  5
Cách 1: Chọn A0;3d  d d ;d  d A;d   2. 1  1 2  2 1  1 3  5
Cách 2: Giải nhanh dd ;d   2. 1 2  1  1
Câu 69: Trong mặt phẳng tọa độ Oxy, tính khoảng cách từ điểm A0; 4 đến đường thẳng . x sin   .
y cos  4 1 cos   0,  . Lời giải:
Khoảng cách từ A0; 4 đến đường thẳng  : . x sin   .
y cos  4 1 cos   0 là       d  , A  0.sin 4.cos 41 cos    4. 2 2 sin   cos 
Câu 70: Trong mặt phẳng tọa độ Oxy, biết đường tròn C có tâm I 3;  2 tiếp xúc với đường thẳng
 :x  5y 1  0, tính bán kính R của đường tròn C. Lời giải: 3  5. 2 1 14
Ta có: R  d  I ,      .   2 2 26 1 5
x  2  2t
Câu 71: Trong mặt phẳng tọa độ Oxy, cho điểm A0; 
1 và đường thẳng d :  . Tìm điểm M y  3 t
thuộc d và cách A một khoảng bằng 5 . Lời giải: Gọi M 2  2 ;
a 3  a d.
a  1 M4;4 2 2 
Ta có: AM  5  2  2a  2  a 2
 5  5a  12a  17  0   17  24 2  a    M  ;      5  5 5 
Câu 72: Trong mặt phẳng tọa độ Oxy, cho hai điểm A3; 1
 ,B0;3 . Tìm tọa độ điểm M thuộc Ox
sao khoảng cách từ M đến đường thẳng AB bằng 1. Lời giải: Gọi M  ;
x 0 Ox . Ta có AB   3  ;4
Phương trình đường thẳng AB : 4x  3 y  3  0  4x  3y  9  0 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 30
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT  7 x  x 
Ta có: d M AB 4 9 ;   5  4x  9   2 . 5   x  1  7  Vậy M ;0 ; M  
1;0 là các điểm cần tìm.  2  x  3 t
Câu 73: Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc đường thẳng d :  và cách đường y  2  t
thẳng  : 2x  y  3  0 một khoảng 2 5 . Lời giải:
Vì M 3  t; 2  t . d
 t   t 
Theo giả thiết: dM  2(3 ) (2 ) 3 ;  2 5   2 5 5 t  9 M12;1  1
 t  1  10     t   M    . 11 8; 9
Câu 74: Trong mặt phẳng tọa độ Oxy, tìm tọa độ hình chiếu vuông góc của điểm M 1; 2 lên đường
thẳng  : x  y  0. Lời giải:
Đường thẳng  có 1 VTPT là n  1;  
1 nên  có 1 VTCP là u  1;  1
Gọi H là hình chiếu vuông góc của M 1; 2 lên đường thẳng .
Gọi H t;t   .  3  
Vì MH    MH  u  MH.u  0  t 1 t  2  0  t   3 3 H ; .   2  2 2 
Câu 75: Trong mặt phẳng tọa độ Oxy, cho đường thẳng  : x  m  
1 y  m  0 ( m là tham số bất kì) và điểm A5; 
1 . Tính khoảng cách lớn nhất từ điểm A đến . Lời giải:
 x  m   y  m    y   y 1  0 x  1  : 1 0
1 m  x  y  0, m      . x  y  0 y  1 
Suy ra  luôn đi qua điểm cố định H  1  ;  1 .
Khi đó, với mọi M   , ta có d  ;
A   AM  AH .
Giá trị lớn nhất của d  ;
A   AH khi M  H  max d  ,
A   AH  2 10 .
Câu 76: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A1; 2 và đường thẳng  : 2x  y  1  0. Tính
khoảng cách từ điểm A đến đường thẳng . 5 A. 5. B. 5. C. 2 5 D. . 5 Lời giải:  
Ta có: dA  2.1 2 1 ;   5. 4  1
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 31
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Chọn đáp án A.
Câu 77: Trong mặt phẳng với hệ tọa độ Oxy, tìm giá trị tham số n để khoảng cách từ điểm I 2; 3 đến
đường thẳng  : x  ny  1 2n  0 bằng 1. A. n  0. B. n  1. C. n  1. D. n  2. Lời giải:
2  3n  1  2n
Ta có: dI;  2 
 1  1 n  1 n  n  0. 2 1  n
Chọn đáp án A. x  1 t
Câu 78: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M 1; 3 và đường thẳng  :  , t  . Tính y   2t
khoảng cách từ điểm M đến đường thẳng . 3 5 5 A. 5. B. . C. 2 5 D. . 5 5 Lời giải:
x  1 t  t  x 1 Ta có  : 
 y  2x 1  2x  y  2  0. y   2t  
Lúc đó: dM  2.1 3 2 3 5 ;   . 4  1 5
Chọn đáp án B.
Câu 79: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : x  2y  3  0 và d : 2x  4y  5  0. 1 2
Tính khoảng cách giữa hai đường thẳng d và d . 1 2 5 5 A. 5. B. . C. 2 5 D. . 10 5 Lời giải:
Dễ chứng minh được d / /d . 1 2 2.1  4.1  5 5
Cách 1: Chọn A1;1  d . Lúc đó: dd ;d  d A;d   . 1 2   2  1 4  16 10 5
Cách 2: d : 2x  4y  5  0  x  2y   0. 2 2 5 3  2 5
Lúc đó: dd ;d   . 1 2  4  1 10
Chọn đáp án B.
Câu 80: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng  : 3x  4y  3  0. Viết phương trình các
đường thẳng song song với  và cách  một khoảng bằng 1.
A. 3x  4y  1  0; 3x  4y  7  0.
B. 3x  4y  2  0; 3x  4y  8  0.
C. 3x  4y  2  0; 3x  4y  6  0.
D. 3x  4y  4  0; 3x  4y  6  0. Lời giải:
Do d / / nên d có dạng 3x  4y  m  0, m  3  . m  m 
Theo giả thiết: dd  3 2 ;  1 
 1  m  3  5   . 9  16 m  8 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 32
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Vậy hai đường thẳng cần tìm là 3x  4y  2  0; 3x  4y  8  0.
Chọn đáp án B.
Câu 81: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm M 1; 4 và N 6; 2. Viết phương trình các
đường thẳng  qua M sao cho khoảng cách từ N đến  bằng 5.
A. x  1  0; 3x  4y  19  0.
B. x  1  0; 21x  20y  59  0.
C. y  1  0; 3x  4y  19  0.
D. y  1  0; 21x  20y  59  0. Lời giải:
Gọi n  a b  2 2 ;
, a  b  0 là một vectơ pháp tuyến của đường thẳng .
Khi đó  : ax  1  by  4  0  ax  by  a  4b  0.
6a  2b  a  4b
Theo giả thiết: dN; 2 2  5 
 5  5a  2b  5 a  b 2 2 a  b  b 
 5a  2b2  25 0 2 2
a  b   b21b  20a  0   21b  20a   0
TH 1: b  0, chọn a  1, ta có phương trình x  1  0.
TH 2: 21b  20a  0, chọn a  21, b  20 ta có phương trình 21x  20y  59  0.
Chọn đáp án B.
Câu 82: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm P 1;1 và Q4; 2. Viết phương trình các
đường thẳng  sao cho khoảng cách từ P và Q đến  lần lượt bằng 2 và 3.
A. y  1  0; 3x  4y  11  0.
B. x  1  0; 3x  4y  11  0.
C. y  1  0; 3x  4y  11  0.
D. x  1  0; 3x  4y  11  0. Lời giải:
Giả sử phương trình  ax  by  c   2 2 :
0, a  b  0.
 a  b  c     
a  b  c d P;  2 2  2 2 2   (1)    Theo giả thiết: a b         a b c  d Q;  4 2 3  3 4a  2b    c   3 
a  b  c  4   2 2 a  b  (2) 2 2  a  b    
 a  b  c   a  b  c c 5a b (1a) 3 2 4 2 Từ (1)      a  b 3
 a  b  c  2
 4a  2b  c 11 7 c  (1b)  5
c  5a  b
c  5a  b 
c  5a  b  Từ (1a) và (2) ta có:     a 
43a  b2  4   0 . 2 2 a  b  2
8a  6ab  0 4a  3   b
+) Từ a  0  b  0 và c  .
b Ta chọn b  c  1 ta có  : y  1  0. +) Từ 4a  3 .
b Ta chọn a  3, b  4  c  11 ta có  :3x  4y  11  0.
Chọn đáp án C.
Câu 83: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : 2x  y  10  0 và d : x  3y  2  0. 1 2
Tính góc giữa hai đường thẳng d và d . 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 33
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A. 30 .  B. 45 .  C. 60 .  D. 90 .  Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  2;1 . 1   1
Đường thẳng d có một vectơ pháp tuyến là n  1; 3 . 2   2 n .n 2
Lúc đó: cosd ;d  1 2  
 d ;d  45 .  1 2  1 2  n . n 2 1 1
Chọn đáp án B.
Câu 84: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : mx  y  1  0 và d : x  2y  10  0. 1 2
Tìm tập hợp tất cả các giá trị của tham số m để hai đường thẳng d và d vuông góc với nhau. 1 2 1 A.  . B.   2 . C.   2 . D. . 2  Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  ; m 1 . 1   1
Đường thẳng d có một vectơ pháp tuyến là n  1; 2 . 2   2
Theo giả thiết: d  d  n .n  0  m  2  0  m  2.  1 2 1 2
Chọn đáp án B.
Câu 85: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : mx  y  7m  9  0 và 1
d : 2x  y  10  0. Gọi S là tập hợp tất cả các giá trị của tham số m để góc giữa hai đường thẳng 2
d và d bằng 45 . Tính tổng tất cả các phần tử của S. 1 2 4 8 8 A. 0. B. . C. . D.  . 3 3 3 Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  ; m 1 . 1   1
Đường thẳng d có một vectơ pháp tuyến là n  2;1 . 2   2 2 n .n 2 2m  1 2
Theo giả thiết: cosd ;d  1 2 2     
 3m  8m  3  0 1 2 2 2 n . n 2   2 1 1 4 1. m 1 m  3   1     S   3;  . 1  m   3   3
Chọn đáp án D.
Câu 86: Trong mặt phẳng tọa độ Oxy, tìm m để hai đường thẳng d :mx  y  m  5, d : x  my  9 cắt 1 2 nhau. Lời giải:
+) Xét m  0 thì    1 d : y
5, d2 : x 9 . Rõ ràng hai đường thẳng này cắt nhau nên m  0 thỏa mãn. (1) x 9
+) Xét m  0 thì d : y  mx  m  5 và d : y    1 2 m m 1 m  0
Hai đường thẳng d và d cắt nhau  m     (2) . 1 2 m m  1 
Từ (1) và (2) ta có m  1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 34
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 87: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d : mx  m  1 y  2m  0 và 1  
d : 2x  y  1  0 . Tìm m để d và d song song. 2 1 2 Lời giải: m m  1 2m
Ta có d // d     m  2 . 1 2 2 1 1 
Câu 88: Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng d : mx  m  1 y  2m  0,d : 4x  3y  26  0 1   2
và d : 3x  4y  7  0. Tìm m để ba đường thẳng trên đồng quy. 3 Lời giải:
Giao điểm I của d và d là nghiệm hệ phương trình: 2 3
4x  3y  26  0 x  5     I 5; 2  .
3x  4y  7  0 y  2   
Yêu cầu bài toán  I 5; 2
 d  m  m    2 .5 1
2  2m  0  m   . 1 5
Câu 89: Trong mặt phẳng tọa độ
Oxy, cho hai đường thẳng
d : 5x  7 y  4  0 và 1
d : 5x  7 y  6  0. Viết phương trình đường thẳng d song song và cách đều d và d . 2 1 2 Lời giải:
Gọi là d đường thẳng song song và cách đều d và d . 1 2
Suy ra phương trình d có dạng: 5x  7 y  c  0 c  4, c  6 c  4 c  6
c  4  c  6
Mặt khác: d d; d  d d;d    .  c  5 1   2  
c   c  5  72 5  72 2 2 4 6 6  4
Suy ra d : 5x  7 y 
 0  5x  7y  5  0. 2
Câu 90: Trong mặt phẳng tọa độ Oxy, tìm tọa độ giao điểm của hai đường thẳng 4x  3y  26  0 và
3x  4y  7  0 . Lời giải:
Toạ độ giao điểm M của hai đường thẳng là nghiệm hệ phương trình:
4x  3y  26  0 x  5    .
3x  4y  7  0 y  2    Vậy M 5; 2   .
Câu 91: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A2;1 , đường cao BH : x  3y  7  0 và
trung tuyến CM : x  y  1  0 . Tìm tọa độ đỉnh C . Lời giải:
Gọi C t; t   1CM.
Ta có: AC  t  2; t
  2 , vectơ chỉ phương của đường thẳng BH là u  3;1 .
Vì AC  BH nên AC.u  0  t  2.3  t  2  0  t  4 .
Vậy C 4; 5 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 35
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Câu 92: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d : x  y  1, d : x  3y  3  0 . Viết 1 2
phương trình đường thẳng d đối xứng với d qua đường thẳng d . 2 1 Lời giải: Gọi I  ;
x y  d  d . Khi đó, tọa độ điểm I là nghiệm của hệ phương trình 1 2 x  y 1 x  0     I 0  ;1 .
x  3y  3  0 y 1 Chọn M  3
 ;0d . Gọi  đi qua M và vuông góc với d . 2 1
Suy ra  có dạng x  y  c  0 . Vì M  3
 ;0  c  3   : x  y  3  0 Gọi H  ;
x y   d   . Khi đó tọa độ điểm H là nghiệm của hệ phương trình 1
x  y  3  0 x  1      H  1  ;2. x  y 1 y  2
Gọi N là điểm đối xứng của M qua d . Khi đó H là trung điểm của MN. 1
x  2x  x 1 N H M    N 1;4.
y  2 y  y  4  N H M
Vậy đường thẳng d chính là đường thẳng IN , ta có x  0 y 1 
 3x  y 1  0 . 1 3
Câu 93: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : x  y  3  0 và d : 2x  y  3  0. 1 2
Khẳng định nào sau đây đúng? A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2 Lời giải:
Đường thẳng d có một vectơ pháp tuyến là n  1;1 . 1   1
Đường thẳng d có một vectơ pháp tuyến là n  2;1 . 2   2 n .n  0 1 2  Ta có: 1 2
 d , d cắt nhau và không vuông góc.   1 2 1 1
Chọn đáp án C.
Câu 94: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : 4x  2y  1  0 và 1
d : 2x  y  3  0. Khẳng định nào sau đây đúng? 2 A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2 Lời giải: 4 2 1  Ta có:  
 d và d song song. 2 1 3  1 2
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 36
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT x  1 t
Câu 95: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d :  , t  và 1   y  1   2t
d : 2x  y  3  0. Khẳng định nào sau đây đúng? 2 A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2 Lời giải:
x  1 t  t  x  1 Cách 1: d : 
 y  1 2 x 1  2x  y  3  0. 1   y  1   2t Vậy d  d . 1 2 Cách 2: x  1 t x  1 t x  1 t   
Xét hệ phương trình: y  1  2t
 y  1 2t
 y  1 2t (vô số nghiệm)   
2x  y  3  0 2
 1  t  1  2t  3   0 0  0  Vậy d  d . 1 2
Chọn đáp án B. x  1 t
Câu 96: Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d :  , t  và 1   y  1   t x  2  k d :  , k 
. Khẳng định nào sau đây đúng? 2   y    k A. d / /d . B. d  d . 1 2 1 2
C. d , d cắt nhau và không vuông góc. D. d  d . 1 2 1 2 Lời giải: x  1 t d : 
 d : x  y  0. 1 1 y  1   t
x  2  k  k  x  2 d : 
 y   x  2  x  y  2  0. 2   y    k
Đường thẳng d có một vectơ pháp tuyến là n  1; 1  . 1   1
Đường thẳng d có một vectơ pháp tuyến là n  1;1 . 2   2
Do n .n  0 nên d  d . 1 2 1 2
Cách khác: Đánh giá mối quan hệ giữa hai vectơ chỉ phương.
Do u .u  0 nên d  d . 1 2 1 2
Chọn đáp án D.
Câu 97: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A2; 1 và đường thẳng  : x  2y  5  0. Gọi
H a;b là hình chiếu vuông góc của A trên , tính a  . b 11 A. 4. B. 0. C. . D. 3. 4 Lời giải: Cách 1:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 37
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A H Δ d
Đường thẳng d qua A2; 1
  và vuông góc với  : x  2y  5  0 có phương trình là:
d : 2x  2  1y  1  0  2x  y  5  0.
Điểm H là giao điểm của d và .
x  2y  5  0 x  3
Tọa độ điểm H là nghiệm của hệ:     H3; 
1  a  3; b  1.
2x  y  5  0 y    1
Vậy a  b  4. Cách 2: A Δ H
Gọi H    H  2
 t  5;t. Ta có: AH   2
 t  3;t  1.
Đường thẳng  có một vectơ chỉ phương là u    2; 1.
H là hình chiếu vuông góc của A trên   AH.u  0  2      
 2t 3 t 1 0  5
 t  5  0  t  1 H 3;1  a  3; b  1.
Vậy a  b  4.
Chọn đáp án A.
Câu 98: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông cân tại A. Gọi M 1; 1 là  2 
trung điểm của cạnh BC và G ;0 là trọng tâm của tam giác ABC. Biết Ba;b, a  0, tính  3  a  . b A. 4. B. 6. C. 5. D. 2. Lời giải: A G M C B
Vì G là trọng tâm của tam giác ABC và M là trung điểm BC nên MA  3MG  1; 3  A0;2.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 38
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Đường thẳng BC qua M 1; 1 và vuông góc với MA có phương trình:
x 1  3y  1  0  x  3y  4  0.
Ta thấy MA  MB  MC  10.
x  3y  4  0
B4;0, C 2  ; 2   
Tọa độ B, C thỏa mãn hệ phương trình     x  1 
2 y 12 10 B
    C  . 2; 2 , 4; 0
Từ đề bài, chọn B4;0  a  4; b  0. Vậy a  b  4.
Chọn đáp án A.
MỘT SỐ BÀI TOÁN KHÁC
Câu 99: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : x  4y  15  0 và điểm A 2; 0 . Tìm tọa
độ điểm M thuộc d để đoạn AM có độ dài nhỏ nhất. Lời giải:
Điểm M  d  M 4t  15;t 2 2  
Ta có: AM   t   2  t   2 4 17
17 t  8t  17  17 t  4 1  17      , t .
 min AM  17 , đạt được tại t  4 . Khi đó M 1; 4 .
Câu 100: Trong mặt phẳng tọa độ Oxy, cho điểm hai điểm A4; 2 , B 2;6 và điểm C nằm trên đường x  5 y 1 thẳng d : 
sao cho CA  CB . Tìm tọa độ điểm C. 3 2  Lời giải:
x  5  3t
d có phương trình tham số là  . y  1    2t
Gọi C 5  3t; 1
  2td , ta có: CA   9
  3t;3  2t,CB   3
  3t;7  2t 
CA  CB  CA  CB    t2    t2    t2    t2 2 2 8 9 3 3 2 3 3 7 2  20t  3  2  t  . 5  1 11  Suy ra: C  ;  .  5 5 
Câu 101: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC . Tìm tọa độ các đỉnh của tam giác biết
phương trình cạnh BC : x  y  2  0 ; hai đường cao BB' : x  3  0 và CC ' : 2x  3y  6  0. Lời giải: A B' C' B C
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 39
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT x  3  0 x  3
B  BC  BB' nên có tọa độ là nghiệm của hệ     ( B 3; 1  ) .
x  y  2  0 y  1   
x  y  2  0 x  0
C  BC  CC ' nên có tọa độ là nghiệm của hệ     C(0;2) .
2x  3y  6  0 y    2
AB qua B và vuông với CC ' có phương trình: 3x  2y  7  0 .
AC qua C và vuông với BB' có phương trình: y  2 .
3x  2y  7  0 x  1
A  AB  AC nên có tọa độ là nghiệm của hệ     ( A 1; 2) . y  2 y    2
Câu 102: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A 3
 ;0 ,B3;0,C 2;6 . Tìm tọa độ trực
tâm H là của tam giác ABC . Lời giải: A H B C
Đường thẳng AH đi qua A3;0 và nhận BC   1
 ;6 làm vectơ pháp tuyến. Suy ra
phương trình đường thẳng AH là: x  6 y  3  0 .
Đường thẳng BH đi qua B 3;0 và nhận AC  5;6 làm véctơ pháp tuyến. Suy ra phương
trình đường thẳng BH là: 5x  6 y 15  0 .
x  6y  3  0  5 
Ta có H  AH  BH  Tọa độ H là nghiệm của hệ   H 2;   . 5
 x  6y 15  0  6 
Câu 103: Trong mặt phẳng tọa độ Oxy, cho ba điểm A1; 
1 ; B 2;0;C 3;4 . Viết phương trình đường
thẳng đi qua A và cách đều hai điểm B,C . Lời giải:
Gọi d  là đường thẳng đi qua A và cách đều B,C . Khi đó, ta có các trường hợp sau:  5   3 
TH1: d đi qua trung điểm của BC . Ta có I ; 2 
 là trung điểm của BC và AI  ;1   là  2   2 
VTCP của đường thẳng d . Khi đó d  : 2  x   1  3 y   1  0  2
 x  3y 1  0 .
TH2: d song song với BC , khi đó d nhận BC  1; 4 làm VTCP, phương trình đường thẳng d: 4  x  
1  y 1  0  4
 x  y  3  0 .
Câu 104: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có phương trình đường thẳng
BC : x  7 y 13  0. Các chân đường cao kẻ từ B, C của tam giác ABC lần lượt là
E 2;5, F 0; 4. Tìm tọa độ đỉnh A. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 40
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT A E F C B I Gọi I 13  7 ;
n n là trung điểm của BC, khi đó ta có: IE  IF mà 2 2 2 2
IE  50n 164n 146; IF  50n 190n 185 3  5 3  2 2
 50n 164n 146  50n 190n 185  n   I ;   2  2 2  Gọi B 13  7 ;
m m . Vì I là trung điểm của BC nên C 7m  8;3  m .
Ta có BE  7m 11;5  m;CE  10  7 ; m 2  m .  m 1
Vì BE  AC nên 2
BE.CE  0  m  3m  2  0   m  2  
+) Với m   B   C  2 11 1 6;1 ,
1; 2  BF : x  2 y  8  0, CE : x  y  3  0  A ;   .  3 3 
+) Với m  2  B  1  ;2;C 6 
;1  BF : 2x  y  4  0, CE : x  y  7  0  A1;6.
Câu 105: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh (
B 12;1) , đường phân giác trong của  
góc A có phương trình d : x  2y  5  1 2
0; G  ;  là trọng tâm tam giác ABC . Tìm tọa độ đỉnh  3 3  C. Lời giải:
Gọi D là điểm đối xứng với B qua đường thẳng d : x  2y  5  0 suy ra D  AC .
Phương trình của đường thẳng BD : 2
 x  y  25  0 .
Gọi H là giao điểm của d và BD suy ra tọa độ điểm H là nghiệm của hệ phương trình
x  2y  5  0 x  9      H  9  ;7. 2
 x  y  25  0 y    7
Mà H là trung điểm của BD suy ra D(6;13) . Gọi (
A 5  2a; a)  d .  1 2 
Ta có G ;  là trọng tâm tam giác ABC nên  3 3 
x  x  x  3x
5  2a 12  x  1
x  2a  8 A B C G C C     
 C(2a  8;1 a)
y  y  y  3y 
a  1 y  2  y  1 a A B C G C  C
Ta có DA  11  2a; a  13; DC  2a  14; 12  a 11  2a a  13
Mà 3 điểm D, A,C thẳng hàng nên DA, DC cùng phương    a  2  2a  14 1  2  a
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 41
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT
Suy ra điểm C(4; 3).
Câu 106: Trong mặt phẳng tọa độ Oxy, cho 3 điểm A 6  ;3;B0; 
1 ;C 3; 2 . Tìm M trên đường thẳng
d : 2x  y  3  0 mà MA  MB  MC nhỏ nhất. Lời giải:
Gọi C(2a 8;1 a) d : 2x y 3 0. Cách 1:  4 
Tìm tọa độ điểm I  ;
x y  sao cho IA  IB  IC  0 . Suy ra I 1  ;    3 
Ta có: MA  MB  MC  3MI  IA  IB  IC
MA  MB  MC  3 MI . Vậy MA  MB  MC nhỏ nhất khí MI nhỏ nhất.
MI nhỏ nhất khi M là hình chiếu vuông góc của I xuống đường thẳng d . 5
Đường thẳng d  đi qua I và vuông góc với d có phương trình: x  2 y  3
2x  y  3  0   13  19 
M là giao điểm của d và d  nên M là nghiệm của hệ:  5  M ;   x  2 y    15 15   3 Cách 2:
M thuộc d suy ra M t; 2t  3
MA  MB  MC  ( 3   3t; 6  t  5) 
MA  MB  MC    t 2    t 2 3 3 6 5 2  13  1 2
MA  MB  MC 
45t  78t  34  45 t      15  5 13  1  3 19 
MA  MB  MC nhỏ nhất khi t   . Suy ra M ;   . 15  15 15 
Câu 107: Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộc đường thẳng
d : 2x  y  5  0 và điểm A4;8 . Gọi M là điểm đối xứng với B qua C, điểm N 5;4 là hình
chiếu vuông góc của B lên đường thẳng MD. Tìm tọa độ điểm C. Lời giải: N 5;-4 ( ) A -4;8 ( ) D I B C c ( ;-2c-5) M
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 42
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT Gọi I  ;
a b là trung điểm BD
Ta có: BAD  BND  90 . Suy ra BAND nội tiếp đường tròn đường kính BD , tâm I 2 2 2 2
Ta có: IA  IN  a  4  b  8  a  5  b  4  6a  8b 13  0
Do I là trung điểm AC nên C 2a  4;2b  8
Do C  d . Suy ra 22a  4  2b  8  5  0  4a  2b  5  0  3
6a 8b 13  0 a    2 Giải hệ:     C 1; 7  .
4a  2b  5  0 1 b    2
Câu 108: Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD . Gọi M là trung điểm của cạnh BC , N 11 1 
là điểm trên cạnh CD sao cho CN  2ND . Giả sử M ; 
 và đường thẳng AN có phương  2 2 
trình 2x  y  3  0 . Tìm tọa độ điểm P là giao điểm của AN và BD . Lời giải:
Ta chứng minh được MP  AN , nên P là hình chiếu của M trên AN .  1   1 
(Thật vậy gắn hệ trục toạ độ Dxy , D 0;0,C 1;0, B 1  ;1 , A0  ;1 . Khi đó M 1; ; N ; 0     .  2   3 
Phương trình đường thẳng BD : y  x . Phương trình đường thẳng AN : 3x  y  1, suy ra giao điểm  1 1  của AN và BD là P ;  .  4 4   3  1    1  Khi đó MP  ; ; AN  ; 1   M .
P AN  0  MP  AN     (đpcm).)  4 4   3  13
Phương trình đường thẳng MP qua M và vuông góc với AN là x  2 y   0. 2
2x  y  3  5  x   5 
P là giao điểm MP và AN nên toạ độ P là nghiệm hệ  13   2  P ; 2 .   x  2 y     2   y  2 2
Câu 109: Trong mặt phẳng tọa độ Oxy, cho hình thoi MNPQ có tâm I 3; 
1 , đỉnh M thuộc đường
thẳng x  4 y 1  0 , đỉnh N thuộc đường thẳng x  y  8  0 . Xác định tọa độ đỉnh Q . Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 43
Chủ đề PHƯƠNG TRÌNH ĐƯỜNG THẲNG OXY Toán 10 KNTT N M I Q P d
Đặt d : x  4 y 1  0 ;  : x  y  8  0
Nhận thấy: I 3; 
1 thuộc đường thẳng d : x  4 y 1  0 , theo giả thiết: M  d.
QN  IM  QN  d và QN đi qua I 3; 
1  QN : 4x  y 13  0 .
4x  y 13 x 1
N  QN , N    Tọa độ điểm N là nghiệm của hệ:     N 1;9 x  y  8  y  9
x  2x  x  6 1  5  Q I N
Vì I là trung điểm của QN    Q5; 7   .
y  2y  y  2  9  7   Q I N
Câu 110: Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộc đường thẳng
d:2x  y 5  0 và điểm ( A 4
 ;8) . Gọi M đối xứng với B qua C , điểm N(5; 4) là hình
chiếu vuông góc của B lên đường thẳng MD . Tìm tọa độ đỉnh C. Lời giải: A B D C N M
Gọi I là giao điểm của AC, BD . Gọi C(t; 2
 t  5)(d) . AC BD
Dễ thấy hai tứ giác BCND và ADNB nội tiếp đường tròn  I; R , với R   . 2 2
Suy ra đa giác ABCND nội tiếp đường tròn  I; R
BNC  BDC  
 ANC  BDC  BDA  90  CN  AN .
BNA  BDA
Do đó CN.AN  0 , với CN  5  t; 2t   1 , AN  9; 1  2.
Suy ra: 9(5  t) 12(2t 1)  0  t  1  C 1; 7   .
_____________________HẾT_____________________
Huế, 15h00’ Ngày 16 tháng 02 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115 Trang 44